Ngày 11.6.2022 Ôn tập khối tròn xoay Vấn đề: +) Mặt cầu ngoại tiếp
+) Mặt tròn xoay (Trụ, nón) → Thiết diện, lồng ghép các bài toán không gian (góc, khoảng cách), ng ứ dụng,…
Vấn đề 1. Mặt cầu ngoại tiếp
1. Mặt cầu ngoại tiếp đa diện
+) Mặt cầu ngoại tiếp đa diện là mặt cầu đi qua tất cả các đỉnh của đa diện. Khi đó ta cũng nói đa diện nội tiếp mặt cầu.
+) Ta có các nhận xét sau:
- Các mặt của đa diện đều là các đa giác nội tiếp.
- Nếu O là tâm của mặt cầu ngoại tiếp đa diện thì O cách đều tất cả các đỉnh của đa diện. Vì vậy, O nằm
trên các trục đường tròn ngoại tiếp các mặt của đa diện.
- Hiển nhiên nếu O là tâm của mặt cầu ngoại tiếp đa diện thì O nằm trên các mặt phẳng trung trực của các cạnh của đa diện.
2. Mặt cầu ngoại tiếp hình chóp và lăng trụ.
- Hình chóp có một mặt cầu ngoại tiếp khi và chỉ khi đáy của hình chóp là đa giác nội tiếp.
- Hình lăng trụ có một mặt cầu ngoại tiếp khi và chỉ khi lăng trụ đó là lăng trụ đứng có đáy là đa giác nội tiếp.
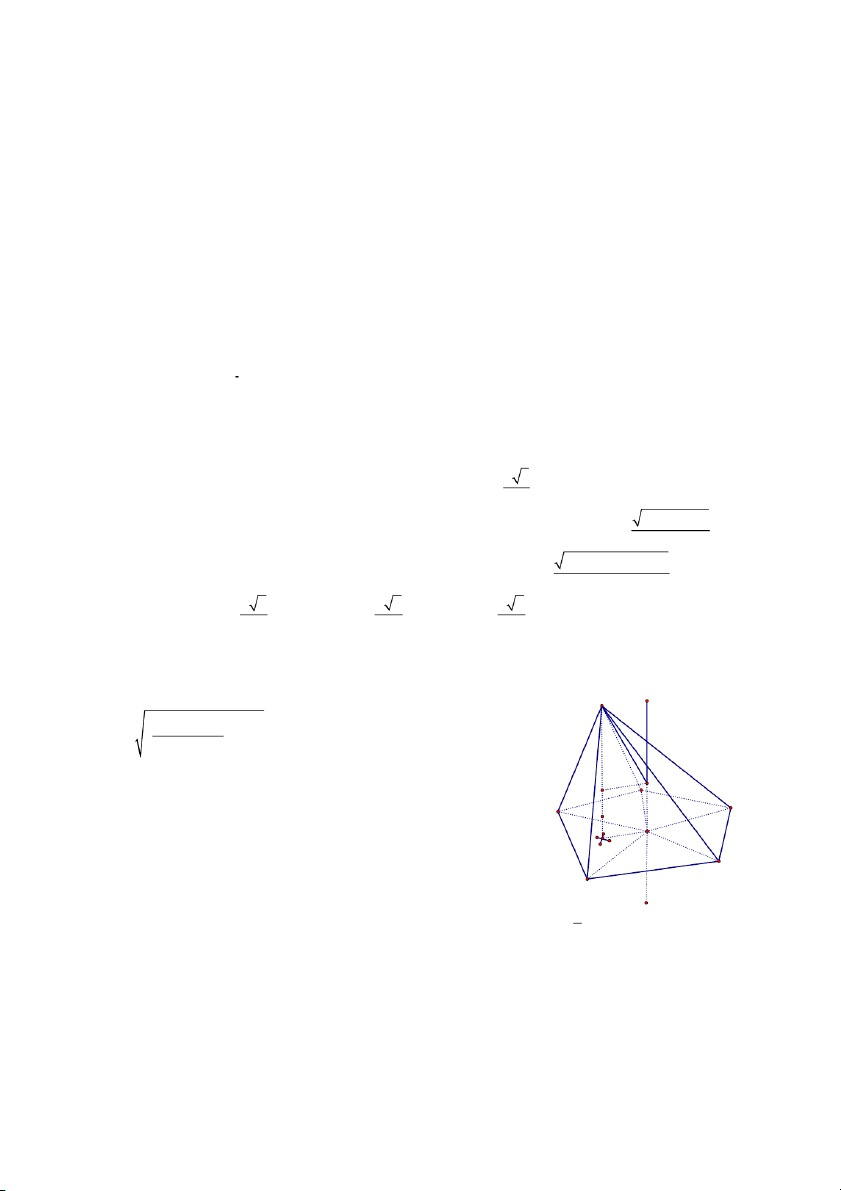
3. Mặt cầu ngoại tiếp các khối đa diện đặc biệt. a 3
- Hình lập phương cạnh a có bán kính mặt cầu ngoại tiếp là R = 2 2 2 2 a +b + c
- Hình hộp chữ nhật ba cạnh chung đỉnh a, b, c có bán kính mặt cầu ngoại tiếp là R = 2 2 2 2
OA + OB + OC
- Hình tam diện vuông OABC thì bán kính mặt cầu ngoại tiếp là R = 2 x 6 x 2 x 2 - Lưu ý: R = ; R = ; R = tudiendeucanhx 4 choptugiacdeucanhx 2 batdiendeucanhx 2
4. Công thức xác định bán kính mặt cầu ngoại tiếp khối đa diện.
Cho hình chóp S.A1A2A3…An. Có đáy A1A2A3…An là đa giác nội tiếp có tâm là O. Đường cao SH
vuông góc với mặt phẳng đáy. Khi đó đặt SH = ; h OH = ; m
OA = OA = ... = OA = . r 1 2 n
Thì bán kính mặt cầu ngoại tiếp khối chóp S.A1A2A3…An. là S 2 2 2 2
m + h − r  2 R = + r   với 2h  
m = OH Khoảng cách t
ừ tâm đáy đến chân đường cao hạ t ừ đỉnh. h
h = SH Chiều cao c a hình chóp; ủ A5 I J
r = OA = ... = OA bán kính đáy A1 x A4 1 n Chú ý H m
+) Với mỗi bài toán cụ thể các tham số: m, h, r có thể suy biến. ví d n ụ ếu O r
H trùng O thì m = 0, Nếu H là một trong các đỉnh của đáy thì m = r . A3
+) Với các hình lăng trụ đứng A1A2…AnB1B2…Bn nếu có mặt cầu ngoại tiếp A2
thì đó cũng là mặt cầu ngoại tiếp của hình chóp A1B1B2…Bn . 4
+) Cho mặt cầu (O; R). Diện tích mặt cầu 2
S = 4 R và thể tích khối cầu 3 V =  R 3
5. Phương pháp chúng xác định bán kính mặt cầu ngoại tiếp đa di hình ện
Hình đa diện đặc biệt (6 hình: HLP, HHCN, tam diện vuông) → T êm b h
ớt đỉnh hoặc xoay hình để
đưa về hình đa diện đặc biệt → Bài toán tổng quát (xác định m, h, r) → Bài toán dị biệt Minh h ọa: 47
Câu 30. Một hình hộp hình chữ nhật nội tiếp mặt cầu và có ba kích thước là a , b , c . Tính bán kính của mặt cầu. 2 2 2 a + b + c 1 A. 2 2 2
a + b + c . B. ( 2 2 2
2 a + b + c ) . C. . D. 2 2 2
a + b + c . 3 2 1 HĐ. 2 2 2 R =
a + b + c 2
Câu 31. Hình chóp đều S.ABCD tất cả các cạnh bằng a . Diện tích mặt cầu ngoại tiếp hình chóp là: A. 2 4 a . B. 2 a . C. 2 2 a  . D. 2 2 a . 1 HD. R = a 2 nên 2 2 S
= 4R = 2a mc 2
Câu 32. Cho khối tứ diện OABC với OA , OB , OC từng đôi một vuông góc và OA = OB = OC = 6 . Tính
bán kính R của mặt cầu ngoại tiếp tứ diện OABC .
A. R = 4 2 .
B. R = 2 .
C. R = 3. D. R = 3 3. 1 HD. Ta có 2 2 2 R =
OA + OB + OC = 3 3 2
Câu 33. Thể tích của khối cầu ngoại tiếp bát diện đều có cạnh bằng a là 3 3 a 3 2 a 3 2 a 3 8 2a A. . B. . C. . D. . 3 6 3 3 1 4 2 HD. R = a 2 nên 3 3 V = R = a mc 2 3 3
Câu 34. Tính bán kính mặt cầu ngoại tiếp tứ diện ABCD biết rằng AB = CD = a , BC = AD = b ,
AC = BD = c . 1 1 A. 2 2 2
a + b + c . B. ( 2 2 2
2 a + b + c ) . C. 2 2 2
a + b + c . D. 2 2 2
a + b + c . 2 2 2 1 1 HD. T
ứ diện đều cạnh a (a =b =c) thì R = a 6 nên 2 2 2 R =
a + b + c 4 2 2
Câu 35. Cho hình chóp S.ABCD có đáy ABCD là hình ch
ữ nhật với AB = 3a , BC = 4a ,SA =12a và SA
vuông góc với đáy. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD . a a a A. 13 R = . B. 5 R = . C. 17 R = .
D. R = 6a . 2 2 2 tam dien vuong 1 , , 2 2 2 13 a HD. R = R ⎯⎯⎯⎯⎯→
AS + AB + AD = S. ABCD S. ABD 2 2
Câu 36. Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = a 3 và AD = a . Đường thẳng SA vuông
góc với đáy và SA = a . Thể tích của khối cầu ngoại tiếp hình chóp S.BCD bằng 3 5a 5 3 5a 5 3 3a 5 3 3 a 5 A. . B. . C. . D. . 6 24 25 8 1 ta , m die , n vuong 2 2 2 a 5 4 5 5 HD. R = R = R ⎯⎯⎯⎯⎯→
AS + AB + AD  =  =  S = 3 3 .BDC S.ABCD S.ABD V R a 2 2 mc 3 6
Câu 37. Cho hình lăng trụ đứng ABC.AB C
  có đáy là tam giác vuông cân tại A , AB = AC = a , AA = 2a
. Thể tích khối cầu ngoại tiếp hình t ứ diện AB A  C  là 3 4 a 3  a A. 3 a . B. . C. . D. 3 4 a . 3 3 tam dien vuong 1 , , 2 2 2 4 4 HD. R = R = R ⎯⎯⎯⎯⎯→
AA ' + AB + AC = a 3 3  =  =  AB 'A 'C
A 'B 'C '.ABC A '.ABC V R a 2 mc 3 3
Câu 38. Cho tứ diện ABCD có AD vuông góc với mặt phẳng ( ABC) , tam giác ABC vuông cân tại A ,
AD = 2a , AB = a . Bán kính mặt cầu ngoại tiếp t
ứ diện ABCD bằng. 48 a 6 a 6 a 6 a 2 A. . B. . C. . D. . 3 2 4 2 1 a 6
tam ,dien,vuong 2 2 2 HD. R = R ⎯⎯⎯⎯⎯→
AD + AB + AC = ABCD D .ABC 2 2
Câu 39. Hình chóp S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với mặt phẳng ( ABCD) và
SA = 2a . Diện tích mặt cầu ngoại tiếp hình chóp S.ABCD bằng: A. 2 2a . B. 2 a . C. 2 3a . D. 2 6 a . 1 a 6 ta , m die , n vuong 2 2 2 HD. R = R ⎯⎯⎯⎯⎯→
AS + AB + AD = 2 2  =  =  S S 4 R 6 a . ABCD S. ABD 2 2 mc
Câu 40. Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với đáy, SA = a, AD = 5 , a AB = 2 .
a Điểm E thuộc BC và CE = a . Tính theo a bán kính mặt cầu ngoại tiếp tứ diện SAED 26a 26a 26a 2 26a A. . B. . C. . D. . 4 3 2 3
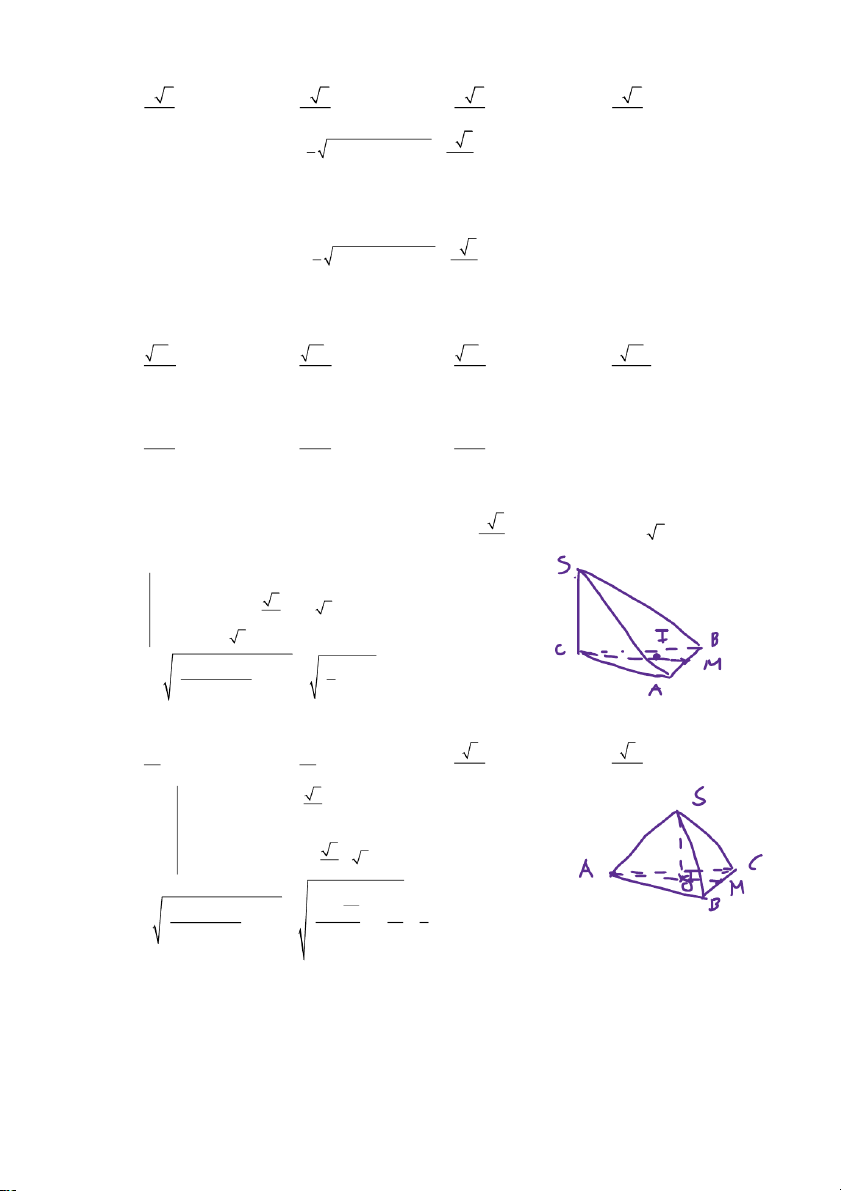
Câu 41. Cho hình chóp S.ABC có S , A S ,
B SC đôi một vuông góc và SA = SB = SC = a . Hình cầu có bánh
kính nhỏ nhất chứa được hình chóp S.ABC có diện tích là 2 2a 2 8a 2 4a A. . B. . C. . D. 2 3a . 3 3 3
Câu 42. Cho hình chóp S.ABC có SC = 2a, SC vuông góc với mặt phẳng ( ABC) , tam giác ABC đều
cạnh 3a . Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC. 2 3
A. R = a .
B. R = 2a . C. R = a .
D. R = a 3 . 3 HD.
h = SC = 2a Ta có 3
r = IC = IA = IB = .3a = 3a 3
m = IC = r = 3a 2 2 2 2  2
m + h − r   h  Vậy 2 R = + r   2 = +   r = 2a 2h    2 
Câu 43. Cho hình chóp tam giác đều có cạnh đáy bằng a , góc giữa cạnh bên và mặt đáy bằng 60 . Tính
bán kính mặt cầu ngoại tiếp hình chóp đã cho. a 4 a 2 3a 4 3a A. 2 . B. . C. . D. . 3 3 3 3 3
r = OC = OA= OB = a 3 HD. Ta có m = II = 0 3
h = SO = OA tan.SAO = . a 3 = a 3 2 2   2 a 2 2 2 2  a −
m + h − r  2   a 2 2  R = + r 3   =   + = a 2h   2a 3 3      
Câu 44. Cho hình chóp S.ABC có tam giác ABC vuông tại ,
B SA vuông góc với mặt phẳng ( ABC) .
SA = 5, AB = 3 , BC = 4 . Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.AB . C 49 5 2 5 2 5 3 5 3 A. R = . B. R = . C. R = . D. R = . 2 3 3 2 h = SA = 5 2 2 2 2  2
m +h −r   h  5 2 HD. Ta có AC 5 Vậy 2 R = + r 2 = + r =   r = IA = =   2h  2  2 2 2   5
m = IA = r = 2
Câu 45. Cho hình chóp S.ABCD có đáy là hình thang vuông tại A , B . Biết SA ⊥ (ABCD ), AB = BC = a
, AD = 2a, SA = a 2 . Gọi E là trung điểm của AD . Tính bán kính mặt cầu đi qua các điểm S , A , B , C , E . a 30 a 6 a 3 A. . B. . C. . D. a . 6 3 2
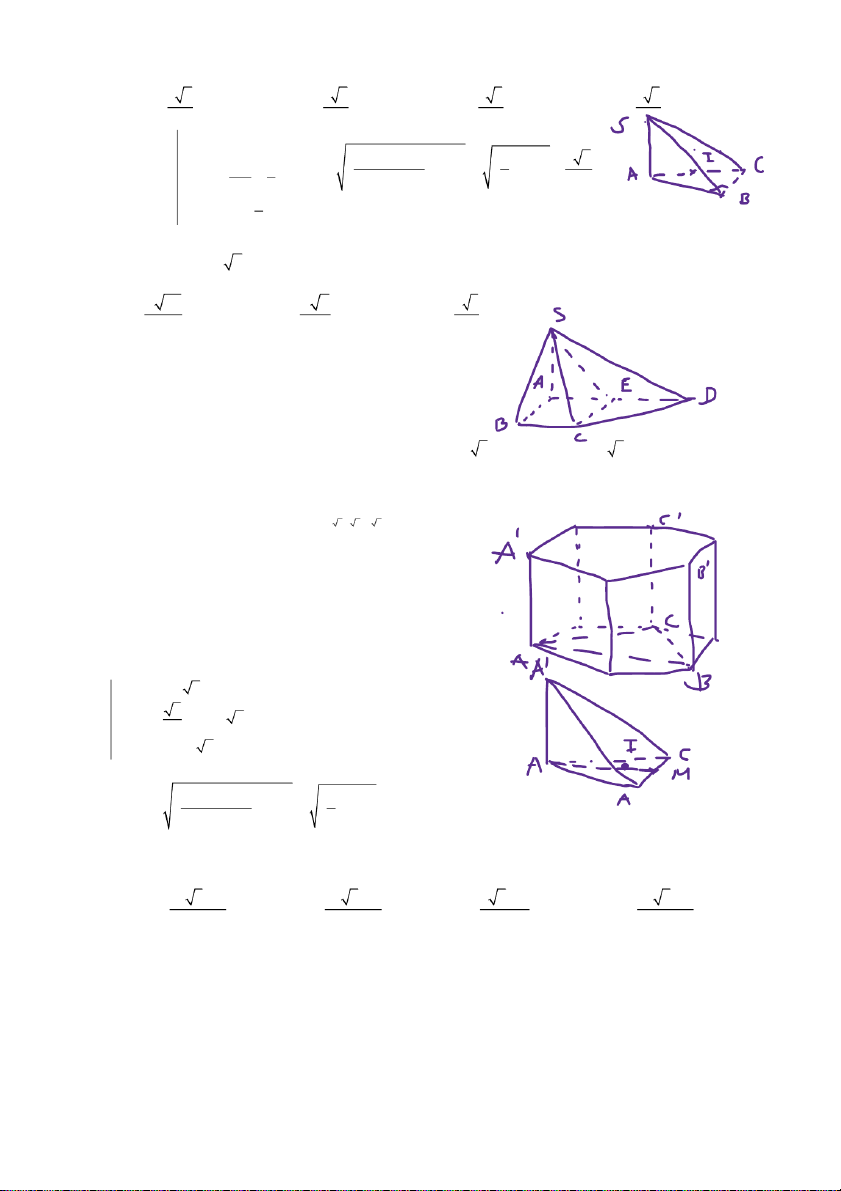
Câu 46. Cho hình lăng trụ ục
l giác đều có cạnh đáy bằng a 2 , cạnh bên bằng 2a 2 . Tính diện tích mặt
cầu ngoại tiếp hình lăng trụ đã cho. A. 2 16a . B. 2 8a . C. 2 4a . D. 2 2 a . HD.
nhu,hinh ,ve AB 3.a 2 a 6 R R = = ⎯⎯⎯⎯→ ⎯⎯⎯⎯⎯⎯⎯⎯⎯ →
luc ,giac ,deu A '.ABC
AB ,canh ,tam ,giac ,can ,goc ,120
h = A' A = 2 2a 3 r = IA = AB = a 2 3
m = IA = r = a 2 2 2 2 2  2
m + h − r   h  Vậy 2 R = + r   2 = + r = 2a   2 2
 S = 4R =16a mc 2h    2 
Câu 47. Cho hình lăng trụ tam giác đều ABC.A B  C
 có độ dài cạnh đáy bằng a và chiều cao bằng 2a .
Tính thể tích V của khối cầu ngoại tiếp hình lăng trụAB . C A B  C  . 3 3 3 3 32 3 a 32 3 a 8 3 a 32 3a A. V = . B. V = . C. V = . D. V = . 27 9 27 81
Câu 48. Cho hình lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông tại A . Biết AB = AA = a ,
AC = 2a. Gọi M là trung điểm của AC . Diện tích mặt cầu ngoại tiếp t ứ diện MA B  C   bằng A. 2 4a . B. 2 2a . C. 2 5a . D. 2 3a . 50
Câu 49. Cho hình chóp S.ABC có cạnh bên SA vuông góc với đáy, AB = a 2 , BC = a , SC = 2a và
SCA = 30 . Tính bán kính R của mặt cầu ngoại tiếp t
ứ diện S.ABC . a
A. R = a 3 . B. 2a .
C. R = a . D. R = . 2
Câu 50. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SAD là tam giác đều và nằm trong mặt
phẳng vuông góc với đáy. Gọi M và N lần lượt là trung đ m iể
của BC và CD (tham khảo hình vẽ bên).
Tính bán kính R của khối cầu ngoại tiếp hình chóp S.CMN . a 93 a 37 a 29 5a 3 A. R = . B. R = . C. R = . D. R = . 12 6 8 12 Câu 51.
Cho hình lăng trụ đứng ABC.A B  C
  có đáy ABC là tam giác vuông tại A , AB = a 3 ,
BC = 2a , đường thẳng AC tạo với( BCC B
 ) một góc 30 . Diện tích c a
ủ mặt cầu ngoại tiếp hình lăng trụ đã cho bằng A. 2 24 a  . B. 2 6a . C. 2 4a . D. 2 3a . Câu 52.
Cho hình chóp đều S.ABCD có cạnh đáy bằng a 2 , góc giữa cạnh bên và mặt đáy bằng o
45 . Diện tích mặt cầu ngoại tiếp hình chóp bằng 2 4πa 2 16πa A. . B. . C. 2 6πa . D. 2 4πa . 3 3 Câu 53.
Cho hình chóp S.ABCD có ABC = ADC = 90 , cạnh bên SA vuông góc với ( ABCD) , góc 2 a 3
tạo bởi SC và đáy ABCD bằng 60 , CD = a và tam giác ADC có diện tích bằng . Diện tích mặt 2
cầu S ngoại tiếp hình chóp S.ABCD là mc A. 2 S = 16a . B. 2 S = 4 a . C. 2 S = 32 a . D. 2 S = 8 a . mc mc mc mc Câu 54.
Cho hình chóp S.ABCD có đáy là hình chữ nhật AB = 3, AD = 2 . Mặt bên ( SA ) B là tam
giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp.     A. 32 V = . B. 20 V = . C. 16 V = . D. 10 V = . 3 3 3 3 Câu 55.
Cho hình lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông tại A . Biết
AB = AA = a , AC = 2a . Gọi M là trung điểm của AC . Thể tích khối cầu ngoại tiếp tứ diện MA B  C   bằng 3 5 5 a 3 2 a 3 4 a 3 3 a A. . B. . C. . D. . 6 3 3 3 Câu 56.
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thang vuông tại A và B ,
AB = BC = a , AD = 2a , SA ⊥ (ABCD ) và SA = a 2 . Gọi E là trung điểm của AD . Kẻ EK ⊥ SD tại K .
Bán kính mặt cầu đi qua sáu điểm S , A , B , C , E, K là: 3 6 A. 1 R = a . B. R = a .
C. R = a . D. R = a . 2 2 2
Câu 57. Cho hình chóp S.ABC có SA vuông góc với ( 
ABC) , AB = a , AC = a 2 , BAC = 45 . Gọi B , C 1 1
lần lượt là hình chiếu vuông góc của A lên SB , SC . Tính thể tích mặt cầu ngoại tiếp hình chóp . A BCC B 1 1 3 a 2 3 4 a A. V = . B. 3 V = a 2 . C. 3 V = a . D. V = . 3 3 2
Câu 58. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh SA vuông góc với mặt đáy
( ABCD) và SA = a . Gọi E là trung điểm của CD. Mặt cầu đi qua bốn điểm S , A , B, E có bán kính là a 41 a 41 a 41 a 2 A. . B. . C. . D. . 8 24 16 16 51
Câu 59. Trong tất cả các hình chóp t ứ u n giác đề
ội tiếp hình cầu có bán kính bằng 9 . Tính thể tích V của
khối chóp có thể tích lớn nhất. A. 576 2 . B. 576 .
C .144 2 . D .144 .
Câu 60. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và BC = a. Cạnh bên SA vuông
góc với đáy ( ABC). Gọi H, K lần lượt là hình chiếu vuông góc của A lên cạnh bên SB và SC . Thể tích
của khối cầu tạo bởi mặt cầu ngoại tiếp hình chóp . A HKB là: 3  a 3 3 2 a  a A. . B. . C. 3 2 a . D. . 2 3 6
Câu 61. Cho tứ diện ABCD có AB = BC = CD = 2, AC = BD =1, AD = 3 . Tính bán kính của mặt cầu
ngoại tiếp tứ diện đã cho. 7 39 2 3 A. 1. B. . C. . D. . 3 6 3 52