ME4201 ÔN TẬP CUỐI KỲ MÔN NHẬP MÔN THỊ GIÁC MÁY TÍNH

ĐẠI HỌC QUỐC GIA TP. HỒ CHÍ MINH
TRƯỜNG ĐẠI HỌC BÁCH KHOA
KHOA CƠ KHÍ – BỘ MÔN CƠ ĐIỆN TỬ
  
NGÔ HUỲNH ANH – PHẠM MẠNH HUY – LÂM HIỆP HƯNG – HỒNG ĐỨC LINH ÔN THI CUỐI KỲ NHẬP MÔN THỊ GIÁC MÁY TÍNH
Thành phố Hồ Chí Minh, tháng 12/2022
Downloaded by Nguyen Linh (vjt58@gmail.com)
NHẬP MÔN THỊ GIÁC MÁY TÍNH – ÔN THI CUỐI KỲ LỜI NÓI ĐẦU
Với mục đích ôn lại những kiến thức cần thiết môn học Nhập môn thị giác máy tính
(ME4201) để bước vào kỳ thi cuối kỳ học kỳ HK221, nhóm tác giả quyết định tổng hợp lại
những kiến thức được cho là có khả năng xuất hiện trong đề thi học kỳ của môn học.
Trong quá trình biên soạn mặc dù đã cố gắng chỉnh sửa và hoàn thiện song những sai
sót là không thể tránh khỏi, mong Quý bạn đọc hãy thông cảm và bỏ qua cho nhóm tác giả. Cảm ơn Tác giả Trang 1
NHẬP MÔN THỊ GIÁC MÁY TÍNH – ÔN THI CUỐI KỲ MỤC LỤC
PHẦN 1: KIẾN THỨC CẦN NẮM. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
CHƯƠNG 1: THỊ GIÁC MÁY TÍNH VÀ ỨNG DỤNG. . . . . . . . . . . . . . . . . . . . . . 4
CHƯƠNG 2: THAO TÁC ĐIỂM ẢNH. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
CHƯƠNG 3: TÌM CẠNH VÀ GÓC. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
CHƯƠNG 4: TÍNH TOÁN KHỐI. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
CHƯƠNG 5: GIẢI THUẬT HOUGH. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
PHẦN 2: BÀI TẬP VẬN DỤNG. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
DẠNG BÀI 1: TÌM THÔNG SỐ CAMERA. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
DẠNG BÀI 2: VẼ HISTOGRAM VÀ PHÂN NGƯỠNG. . . . . . . . . . . . . . . . . . . . 28
DẠNG BÀI 3: CÂN BẰNG HISTOGRAM. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
DẠNG BÀI 4: TÌM CẠNH SỬ DỤNG GIẢI THUẬT CANNY. . . . . . . . . . . . . . . 33
DẠNG BÀI 5: TÌM INTEREST POINT BẰNG GIẢI THUẬT HARRIS CORNER
VÀ SHITOMASHI. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
DẠNG BÀI 6: TÌM VỊ TRÍ GÓC CẠNH SỬ DỤNG GIẢI THUẬT HITMISS. . . 52
DẠNG BÀI 7: ĐIỀN ĐẦY HÌNH SỬ DỤNG GIẢI THUẬT FILL IN HOLE. . . . 55
DẠNG BÀI 8: TÌM CÁC ĐẶC TRƯNG CỦA BLOB. . . . . . . . . . . . . . . . . . . . . . . 59
DẠNG BÀI 9: THINING. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
DẠNG BÀI 10: SKELETON. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
DẠNG BÀI 11: TÌM SỐ ĐƯỜNG THẲNG QUA SỐ ĐIỂM CHO TRƯỚC BẰNG
GIẢI THUẬT HOUGH LINE. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
DẠNG BÀI 12: TÌM CÁC HÌNH TRÒN CÓ BÁN KÍNH CHO TRƯỚC QUA SỐ
ĐIỂM YÊU CẦU BẰNG GIẢI THUẬT HOUGH CIRCLE. . . . . . . . . . . . . . . . . . 77
DẠNG BÀI 13: TÌM VỊ TRÍ TEMPLATE BẰNG GIẢI THUẬT GENERAL
HOUGH LINE. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78 Trang 2
NHẬP MÔN THỊ GIÁC MÁY TÍNH – ÔN THI CUỐI KỲ Phần 1
KIẾN THỨC CẦN NẮM Trang 3
NHẬP MÔN THỊ GIÁC MÁY TÍNH – ÔN THI CUỐI KỲ CHƯƠNG 1
THỊ GIÁC MÁY TÍNH VÀ ỨNG DỤNG
1.1. CÁC THÔNG SỐ CẦN BIẾT CỦA CAMERA
Hình 1. 1: Tính toán thông số camera
Độ phân giải ảnh là số điểm ảnh (pixel) có trên một đơn vị chiều dài của hình ảnh
đó. Độ phân giải ảnh được tính bằng đơn vị ppi (pixels per inch) hoặc dpi (dots per inch).
Những pixel trên một ϴđơn vị chiều dài của màn hình máy tính được gọi là độ phân giải
màn hình. Thường được tính bằng những dấu chấm trên một inch (dpi). = ( )
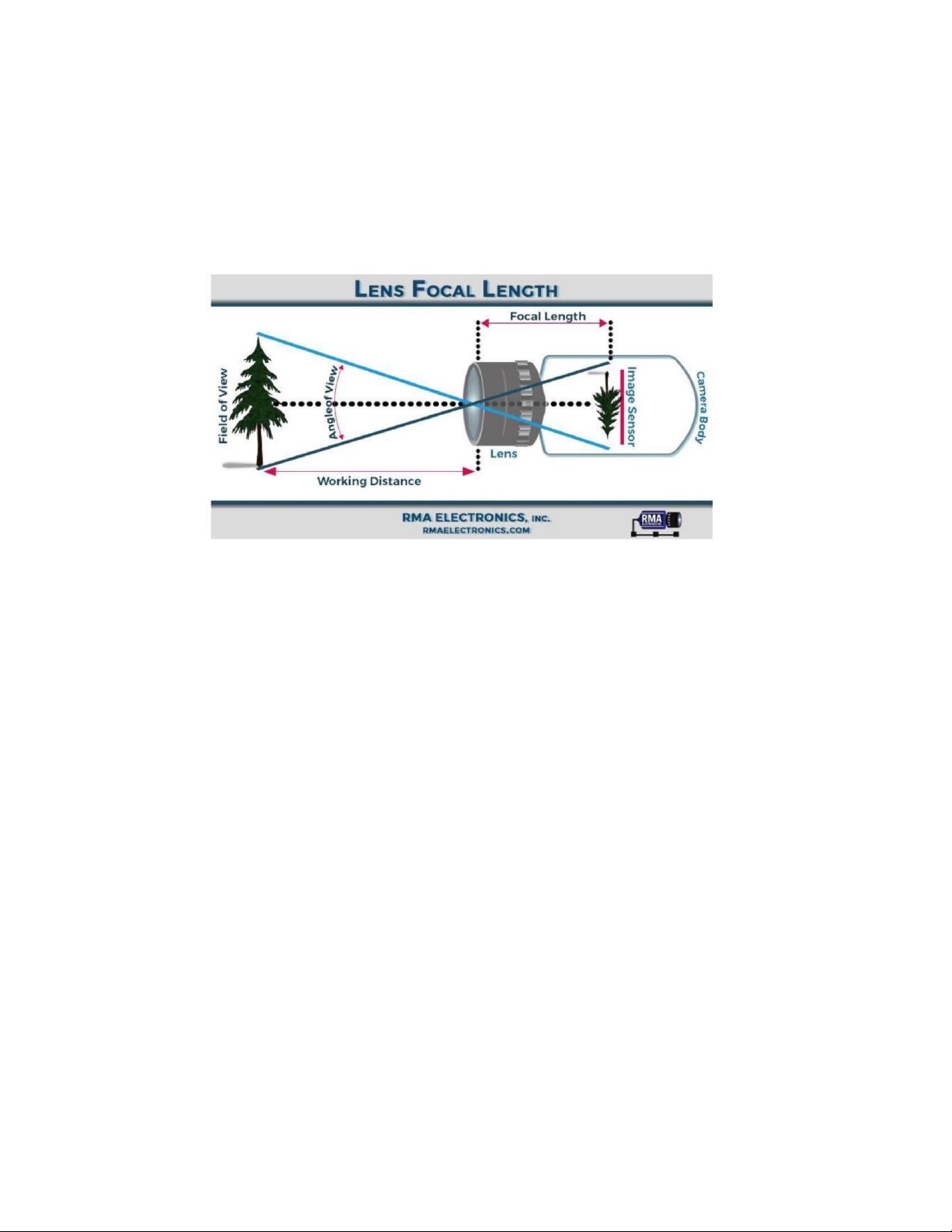
Tiêu cự (Focus length) ống kính là khoảng cách từ ống kính đến cảm biến hình ảnh
Tiêu cự ống kính càng lớn thì tầm nhìn càng xa nhưng góc nhìn (FOV) càng hẹp lại. Trang 4
NHẬP MÔN THỊ GIÁC MÁY TÍNH – ÔN THI CUỐI KỲ CHƯƠNG 2 THAO TÁC ĐIỂM ẢNH
2.1. PHÂN NGƯỠNG HÌNH ẢNH XÁM 2.1.1. Định nghĩa
Phân ngưỡng là giai đoạn quan trọng nhất trong xử lý ảnh giúp tách rời các thông tin
mong muốn có được trong hình ảnh thông qua các giá trị mức xám của hình ảnh. Kỹ thuật
thông dụng là sử dụng biểu đồ histogram. 2.1.2. Histogram
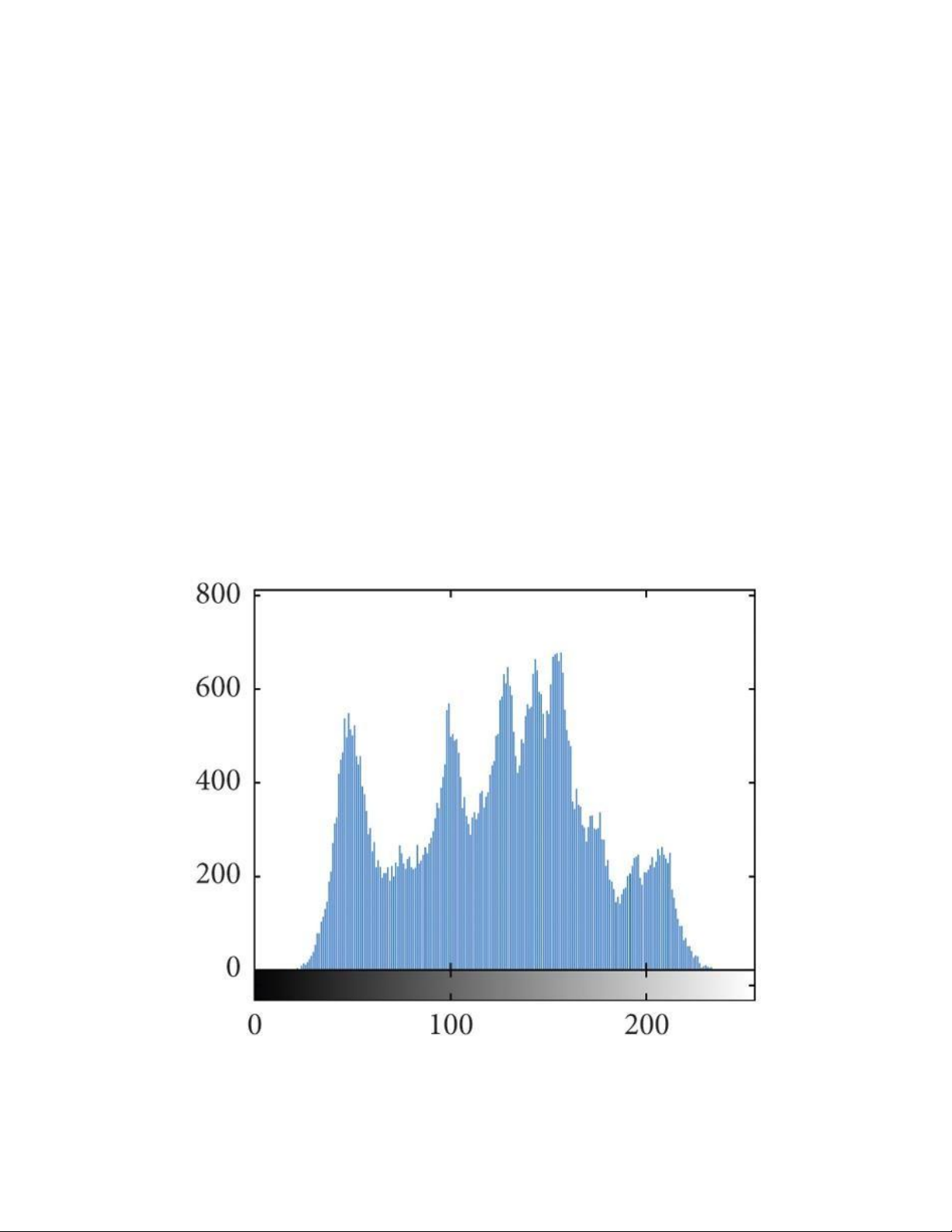
Biểu đồ histogram của một bức ảnh là biểu đồ biểu diễn sự phân bố của các mức
cường độ xám của một bức ảnh. Biểu đồ có hai chiều với trục X là các giá trị màu của ảnh,
trục Y là tổng số pixel. Với ảnh có 8 bit màu mỗi kênh thì trục X có 256 cột giá trị từ 0 -
255. Từ trái qua phải là bit có cường độ sáng thấp nhất là màu đen đến số lượng pixel có
cường độ sáng nhất là màu trắng.
Hình 2. 1: Phân bố histogram của một ảnh Trang 5
NHẬP MÔN THỊ GIÁC MÁY TÍNH – ÔN THI CUỐI KỲ
2.1.3. Các giải thuật phân ngưỡng
Phân ngưỡng đơn giản:
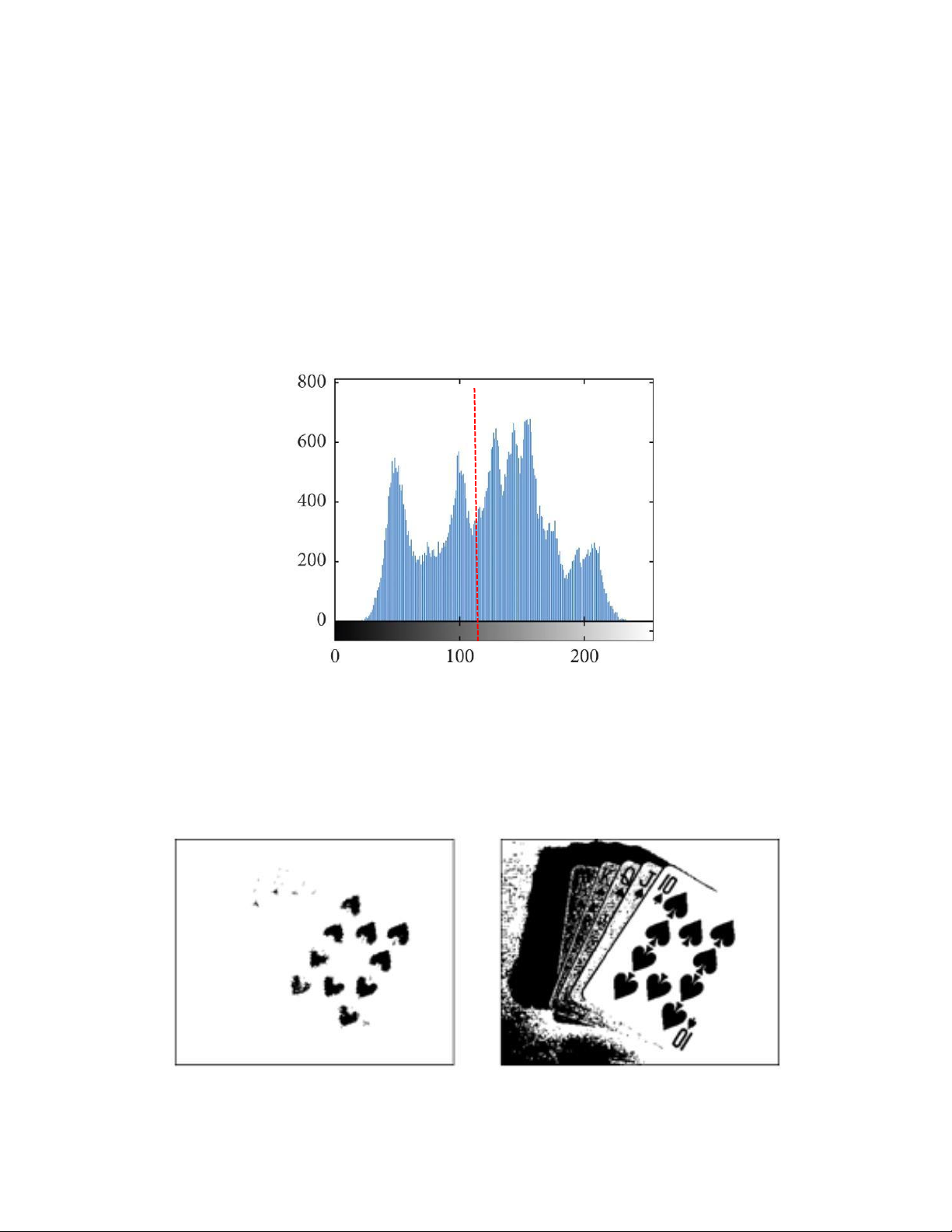
Giả sử ta có histogram của một hình như Hình 2.1. Để có thể nhận biết được vật và
nền ta sử dụng giải thuật đơn giản sau: nếu pixel có giá trị lớn hơn giá trị ngưỡng T thì nó
được gán 1 giá trị thường là mức 1 (255), ngược lại nhỏ hơn giá trị ngưỡng thì nó được gán
1 giá trị khác thường là mức 0 (0). ( , ) = {1 ( , ) > 0 �� �(�, �) ≤ � Object Background T
Hình 2. 2: Giá trị ngưỡng T giữa vật và nền
Phân ngưỡng thích nghi theo giá trị vùng:
Phương pháp đơn giản không phù hợp cho nhiều trường hợp như ánh sáng không đều đều.
Hình 2. 3: Kết quả phân ngưỡng với giá trị không thích hợp Trang 6
NHẬP MÔN THỊ GIÁC MÁY TÍNH – ÔN THI CUỐI KỲ
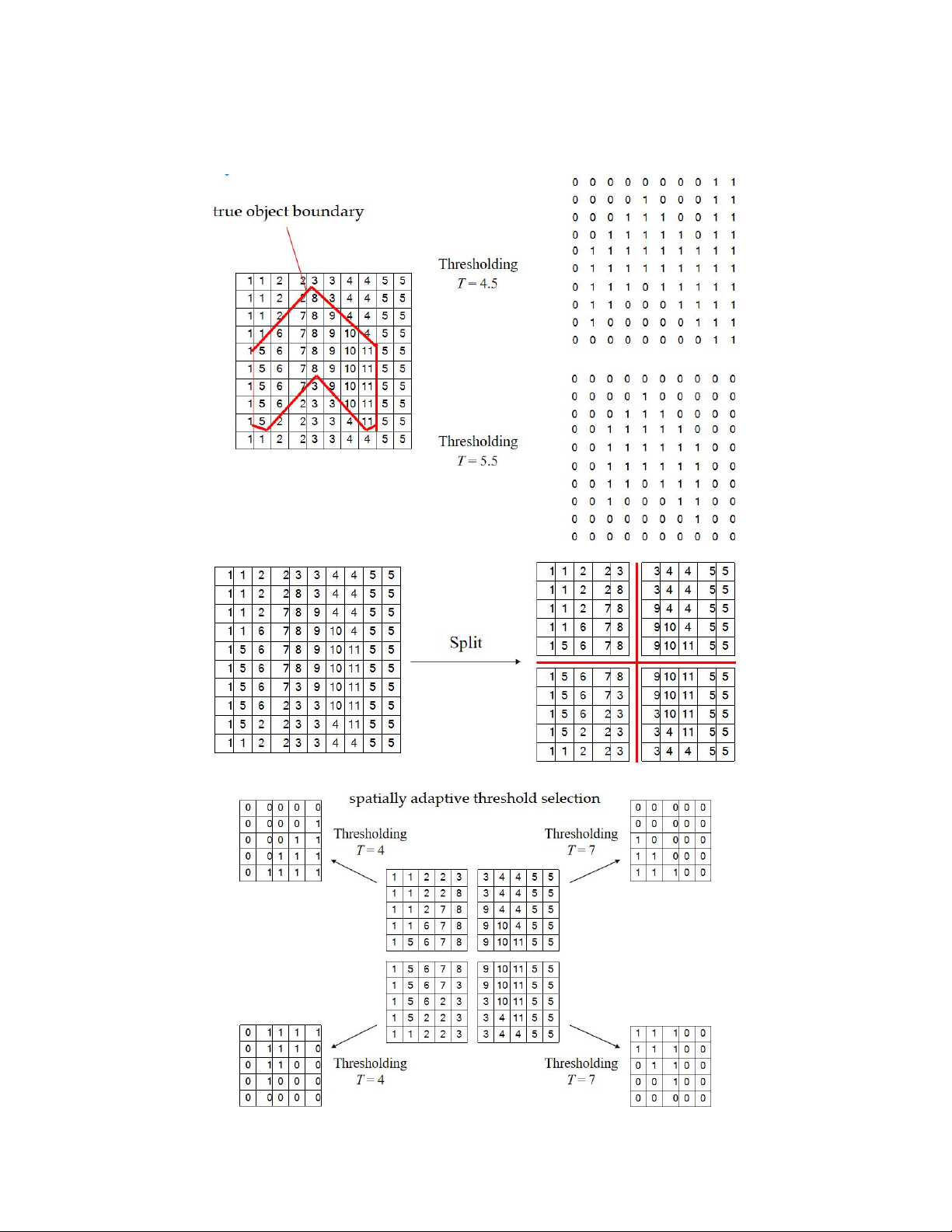
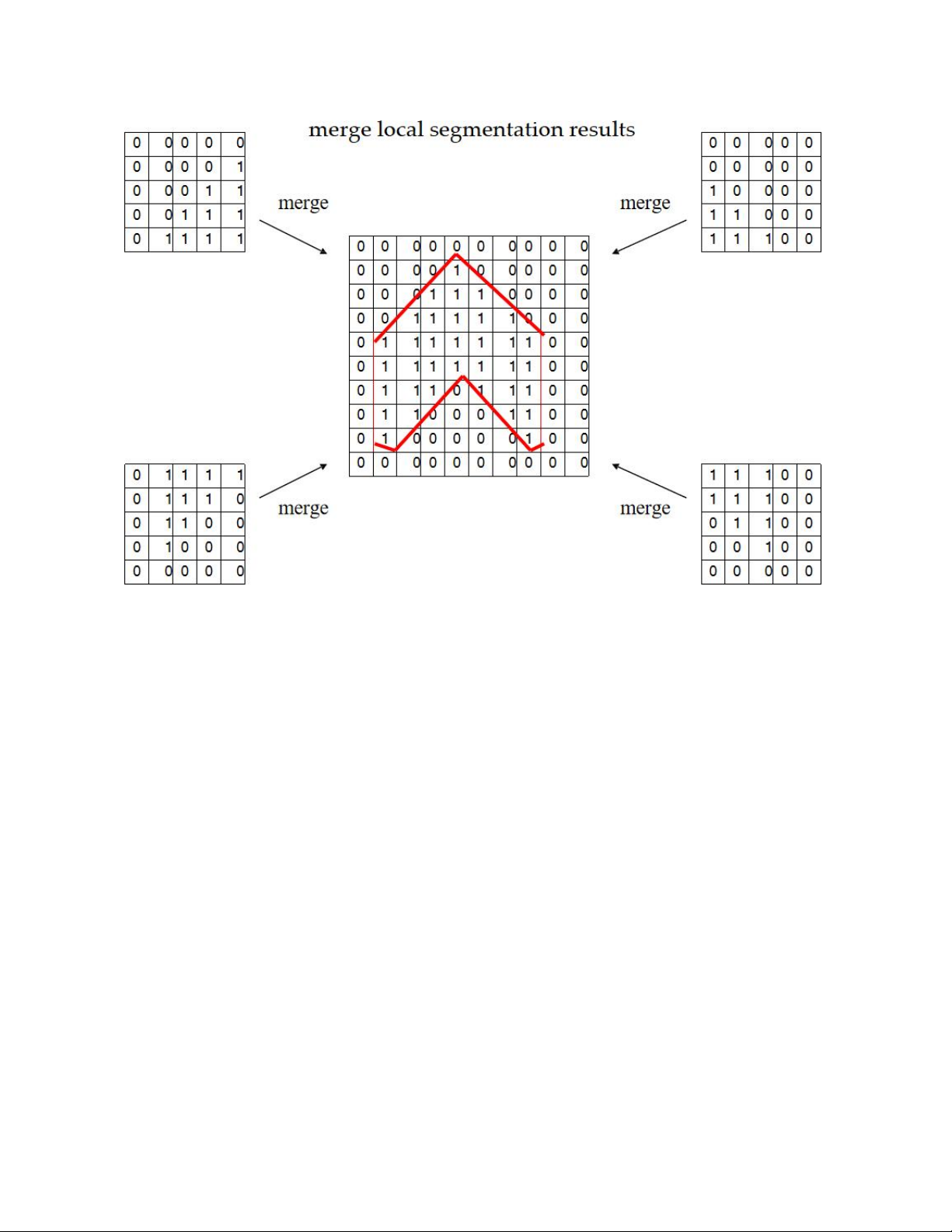
Khắc phục nhược điểm trên bằng cách chia thành nhiều vùng khác nhau và lấy
ngưỡng threshold cho từng vùng sau đó gộp lại toàn bộ hình như sau. Trang 7
NHẬP MÔN THỊ GIÁC MÁY TÍNH – ÔN THI CUỐI KỲ
Hình 2. 4: Quá trình và kết quả phân ngưỡng chia vùng
Phân ngưỡng theo phương pháp Otsu:
Phương pháp này cho kết quả là mỗi ảnh khác nhau có một ngưỡng tương ứng khác
nhau bằng các bước xử lý sau:
- Chọn một giá trị khởi tạo cho T (ví dụ � = (��� + ���)/2, � = ����,…).
- Phân hoạch sử dụng T, kết quả bước này tạo 2 nhóm điểm ảnh �1 > � và �2 ≤ �.
- Tính trung bình (average hay mean) �1 và �2 của các điểm ảnh thuộc �1 và �2.
- Tính lại T dựa vào �1 và �2: = ( 1 + 2)/2.
- Lặp lại bước 2 đến 4 đến khi giá trị chênh lệch giữa T cũ và T mới là không đáng
kể, T được tính ở bước 4 sẽ có phép sai số so với T cũ là:
∆� = 0.5 × (��á ��ị đơ� �ị �ủ� đ�ể� ả�ℎ) Trang 8
NHẬP MÔN THỊ GIÁC MÁY TÍNH – ÔN THI CUỐI KỲ
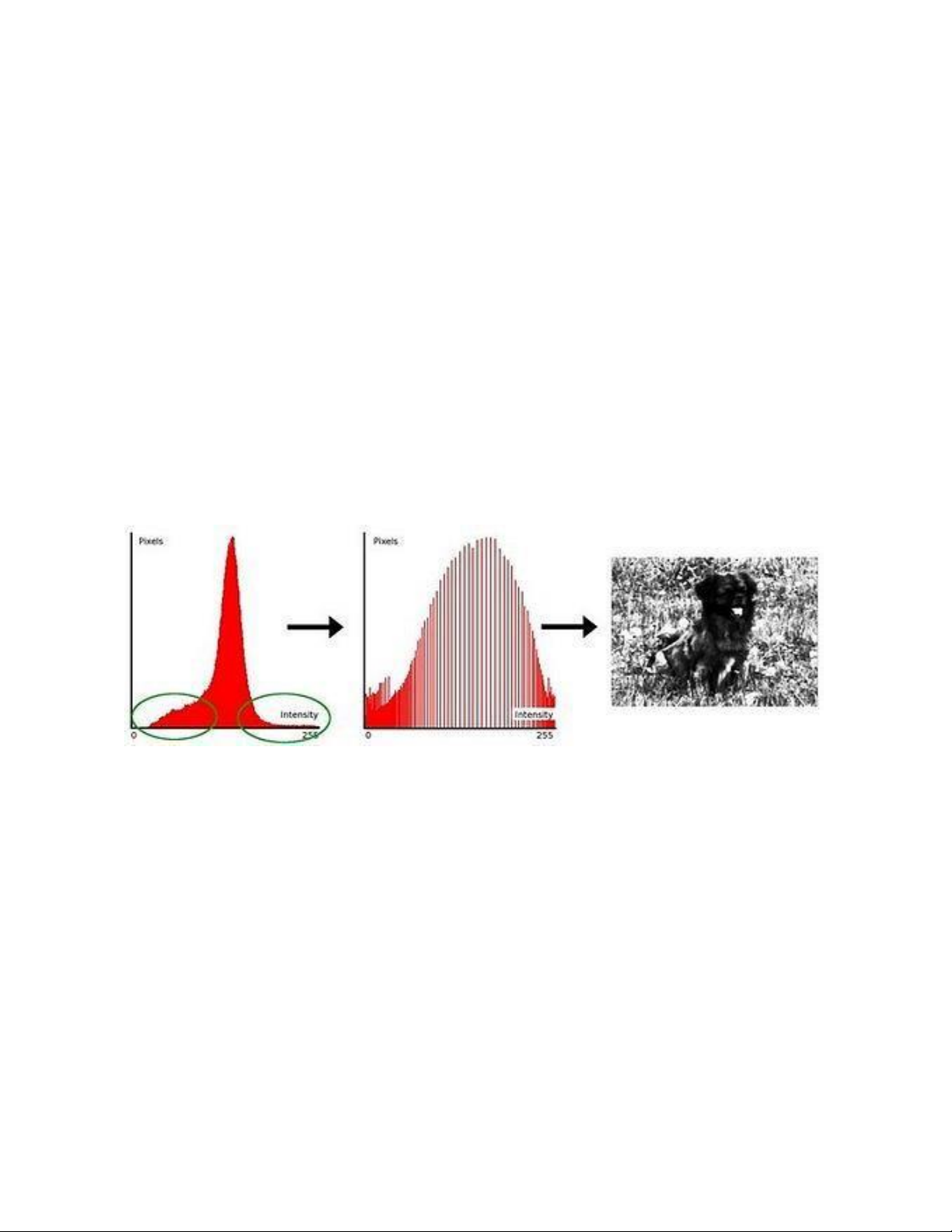
2.2. CÂN BẰNG HISTOGRAM
Phương pháp này được sử dụng nhằm làm tăng cường độ tương phản toàn cục (global
contrast) của bức ảnh, nó đặc biệt có ý nghĩa trong tình huống dữ liệu đầu vào có giá trị
điểm ảnh co cụm, độ tách bạch hình ảnh thấp (close contrast value). Điều này có thể nhận
thấy rõ qua thông qua biểu hiện của biểu đồ histogram. Khi bạn nhận được một histogram
của một hình đa mức xám với dãy giá trị điểm ảnh không phân tán đều và chỉ tập trung
trong một phân đoạn ngắn điều đó có nghĩa là nhiều khả năng bạn đang có trong tay một
ảnh có độ tương phản thấp. Mục tiêu của cân bằng histogram là giúp bạn biến đổi bức ảnh
có độ tương phản thấp thành bức ảnh có độ tương phản cao hơn bằng cách rải đều giá trị
của pixel làm chúng phân tán trên các vùng có giá trị rộng hơn, thay vì co cụm mà vẫn giữ
được nội dung bức ảnh.
Phương pháp này có ưu điểm của sự đơn giản, tính toán không nặng nề, cho phép
phục hồi lại trạng thái ban đầu của ảnh trong tình huống cần thiết. Tuy nhiên, phương pháp
này là có một khuyết điểm rất quan trọng đó là nó dễ dàng làm tăng độ tương phản của
nhiễu trong nền của ảnh và giảm các chi tiết của hữu ích trong ảnh.
Hình 2. 5: Cân bằng histogram Các bước cân bằng:
- Đếm số lượng pixel tương ứng của các mức xám.
- Tính toán khả năng phân bố của các pixel trong hình.
- Tính tổng tích lũy các khả năng này.
- Trải đều số lượng pixel trong hình. Trang 9
NHẬP MÔN THỊ GIÁC MÁY TÍNH – ÔN THI CUỐI KỲ CHƯƠNG 3 TÌM CẠNH VÀ GÓC 3.1. LỌC CANNY Xem ví dụ Phần 2.
3.2. GIẢI THUẬT HARRIS CORNER
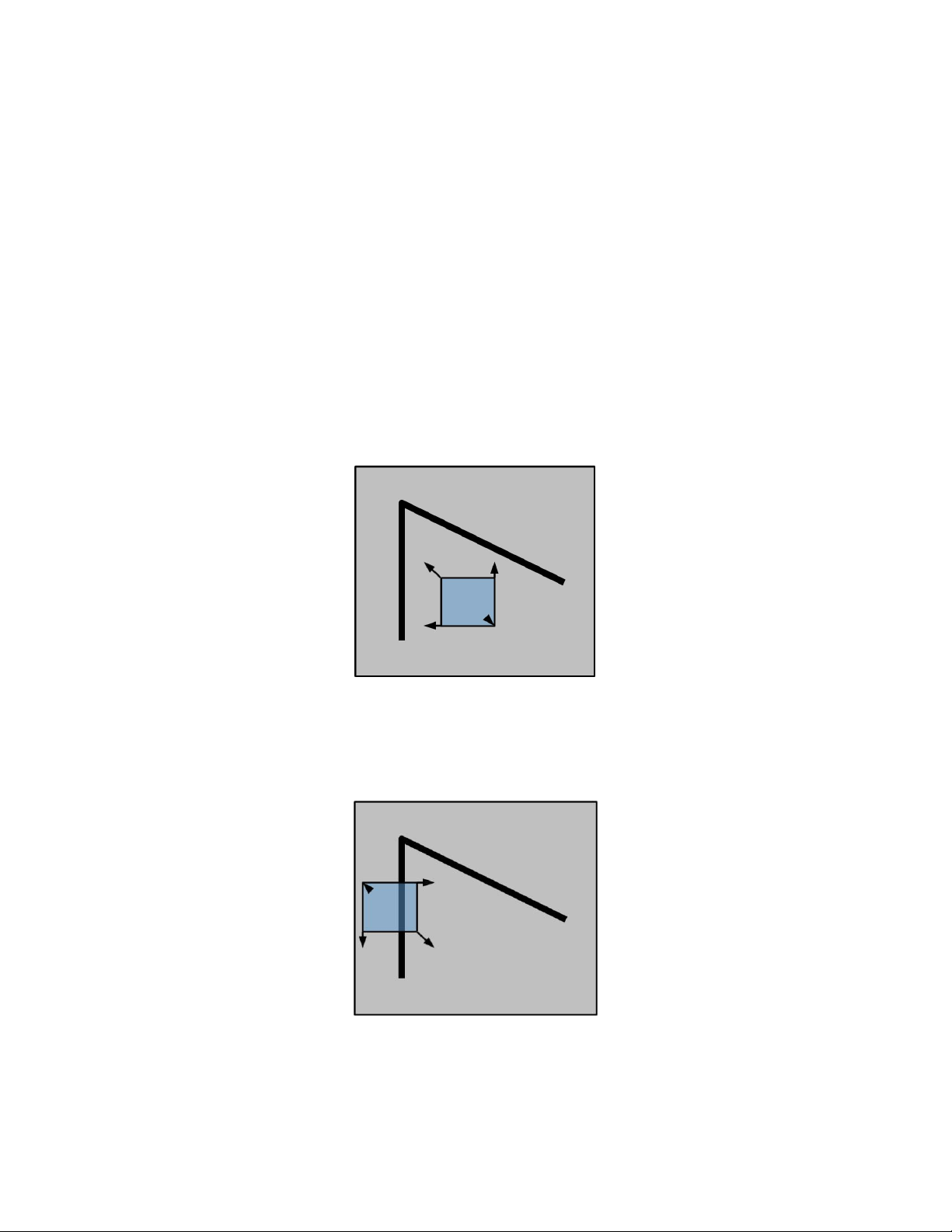
Giả sử để tìm góc của hình ta di chuyển một ô cửa sổ nhỏ trên màn hình. Có 3 trường hợp xảy ra:
Trường hợp 1: Không có gì thay đổi khi ta di chuyển khung hình theo mọi hướng thì
ta đang di chuyển trên vùng phẳng có cường độ ánh sáng hay màu sáng đều nhau.
Hình 3. 1: Trường hợp di chuyển trên mặt phẳng
Trường hợp 2: Không có gì thay đổi khi ta di chuyển khung hình dọc theo đường
thẳng thì ta đang di chuyển trên đường biên hay cạnh.
Hình 3. 2: Trường hợp di chuyển trên cạnh Trang 10
NHẬP MÔN THỊ GIÁC MÁY TÍNH – ÔN THI CUỐI KỲ
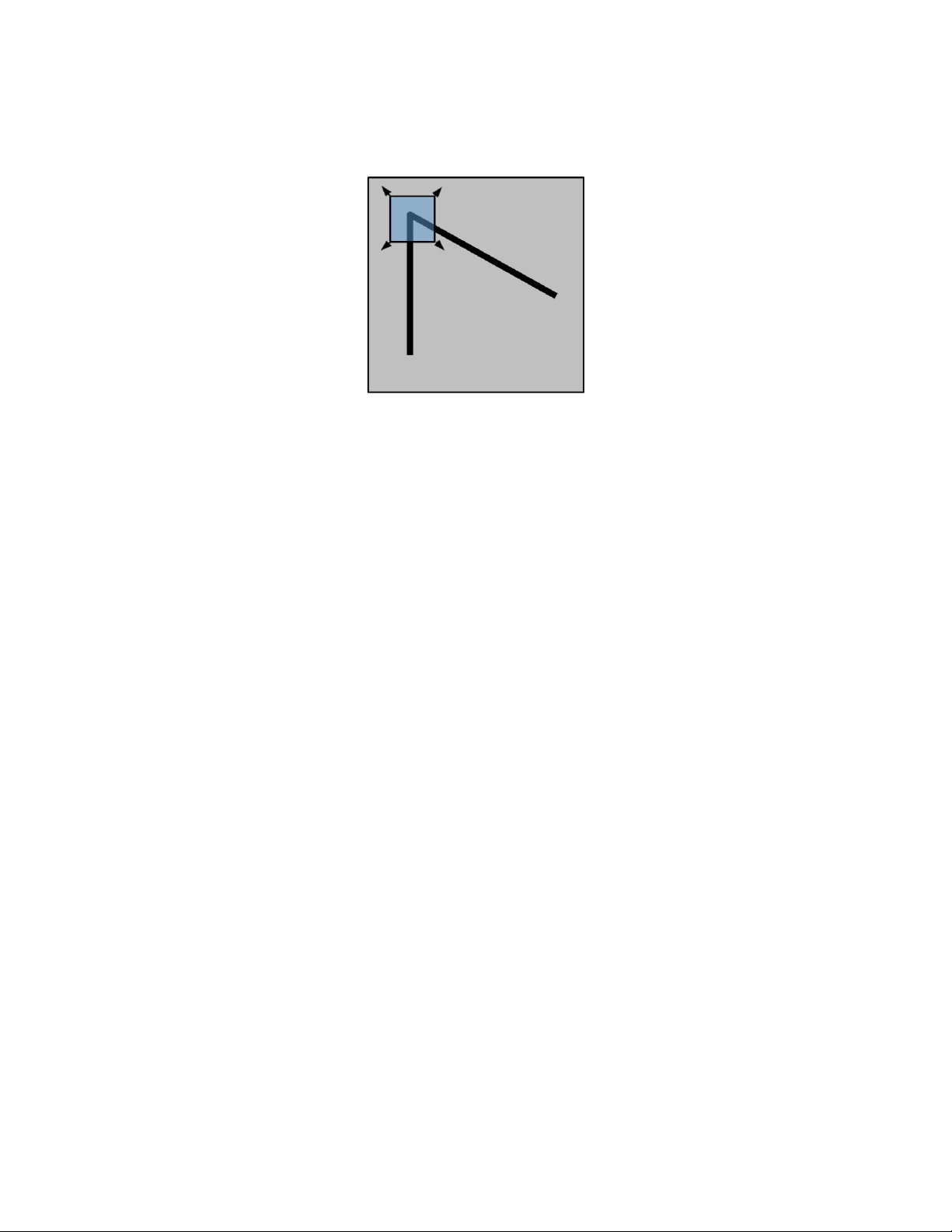
Trường hợp 3: Thay đổi lớn khi ta di chuyển khung hình theo mọi hướng thì ta đang di chuyển ở góc.
Hình 3. 3: Trường hợp di chuyển tại góc
Khi ta di chuyển khung hình, độ sai lệch về cường độ được tính theo công thức
Summing up the Squared Differences (SSD).
�(�, �) = ∑ �(�, �)[�(� + �, � + �) − �(�, �)]2 ,
Trong đó, E(u, v) là tổng số bình phương giá trị độ lệch, w(x, y) là cửa sổ tại (x, y),
I(x, y) và I(x+u, y+v) là giá trị cường độ sáng của pixel tại các vị trí (x, y) và (u+x, v+y).
Khi di chuyển một đoạn (u, v) nhỏ ta có hàm tương đương.
�(�, �) = [� �] × � × [�]
Trong đó, M là một ma trận: 2 � = ∑ �(�, �) [ � ] 2 ,
Gọi �1 và �2 là các trị riêng của M. Khi đó, biểu thức thể hiện đáp ứng góc sẽ quyết
định xem cửa sổ w có chứa góc hay không.
� = det � − �(������)2 Với: det = 1 2 = 1 + 2
Tổng quát, để xác định được góc (corner), ta sử dụng giải thuật Harris Corner Detection: Trang 11
NHẬP MÔN THỊ GIÁC MÁY TÍNH – ÔN THI CUỐI KỲ
- Tính Gradient của vùng pixel ��, ��. 2
- Xây dựng ma trận � = ∑ �(�, �) [ � ]. , 2
- Tính giá trị � = det � − �(������)2.
Với k là Harris detector free parameter và thường có giá trị 0.04 – 0.06. Khi đã có
được các giá trị R, chúng ta sẽ xác định xem vùng pixel này có phải corner không. Bằng cách:
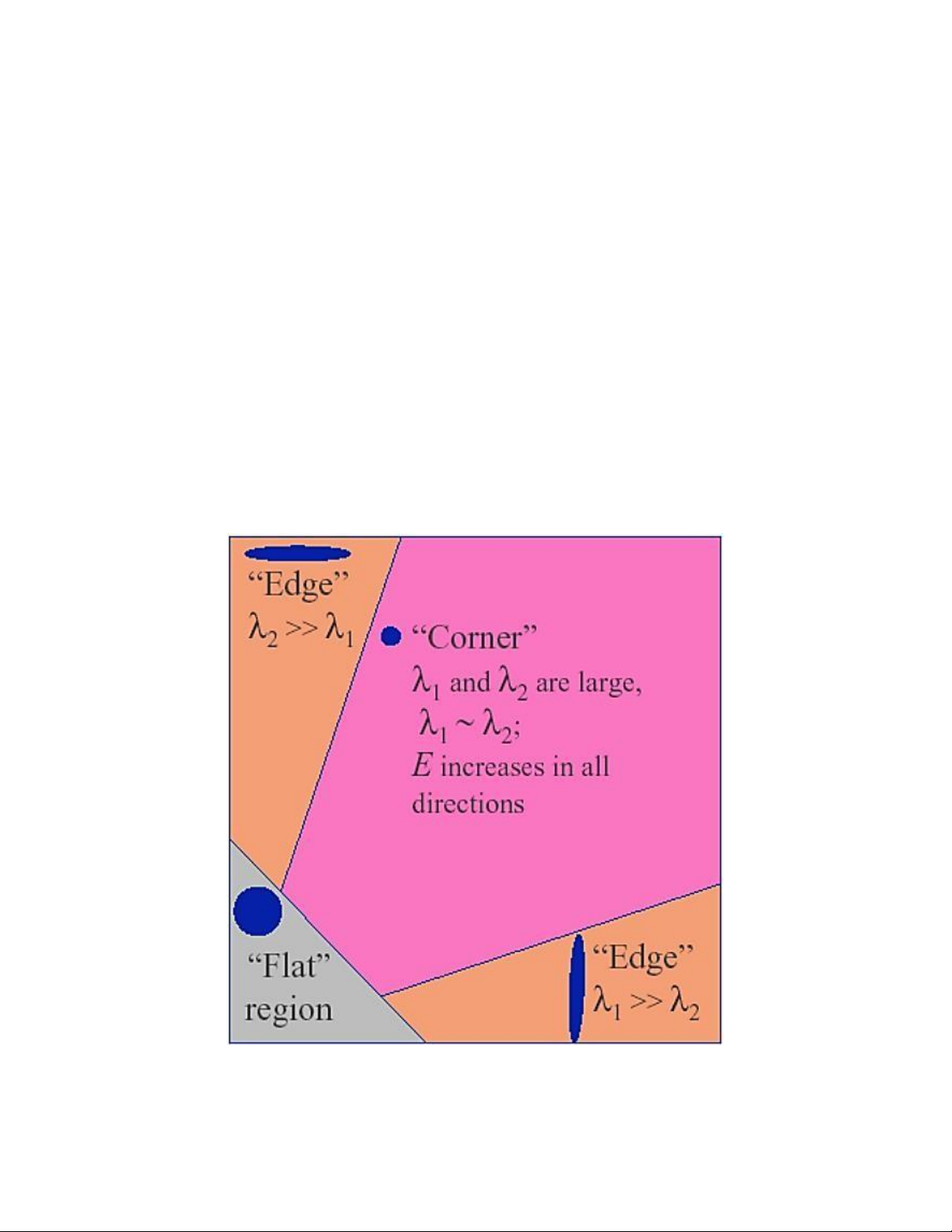
- Nếu giá trị |�| nhỏ thì vùng pixel đó không chứa thông tin có giá trị, còn gọi là “flat” region.
- Nếu � < 0, tức là khi �1 ≫ �2 hoặc �2 ≫ �1, thì vùng pixel đó chỉ chứa cạnh “edge”.
- Nếu giá trị |�| lớn thì, tức là khi �1 ≫ 1, �2 ≫ 1 và �1 ≈ �2, thì vùng pixel này chứa góc “corner”.
Hình 3. 4: Các trường hợp là cạnh, góc và mặt phẳng Trang 12
NHẬP MÔN THỊ GIÁC MÁY TÍNH – ÔN THI CUỐI KỲ
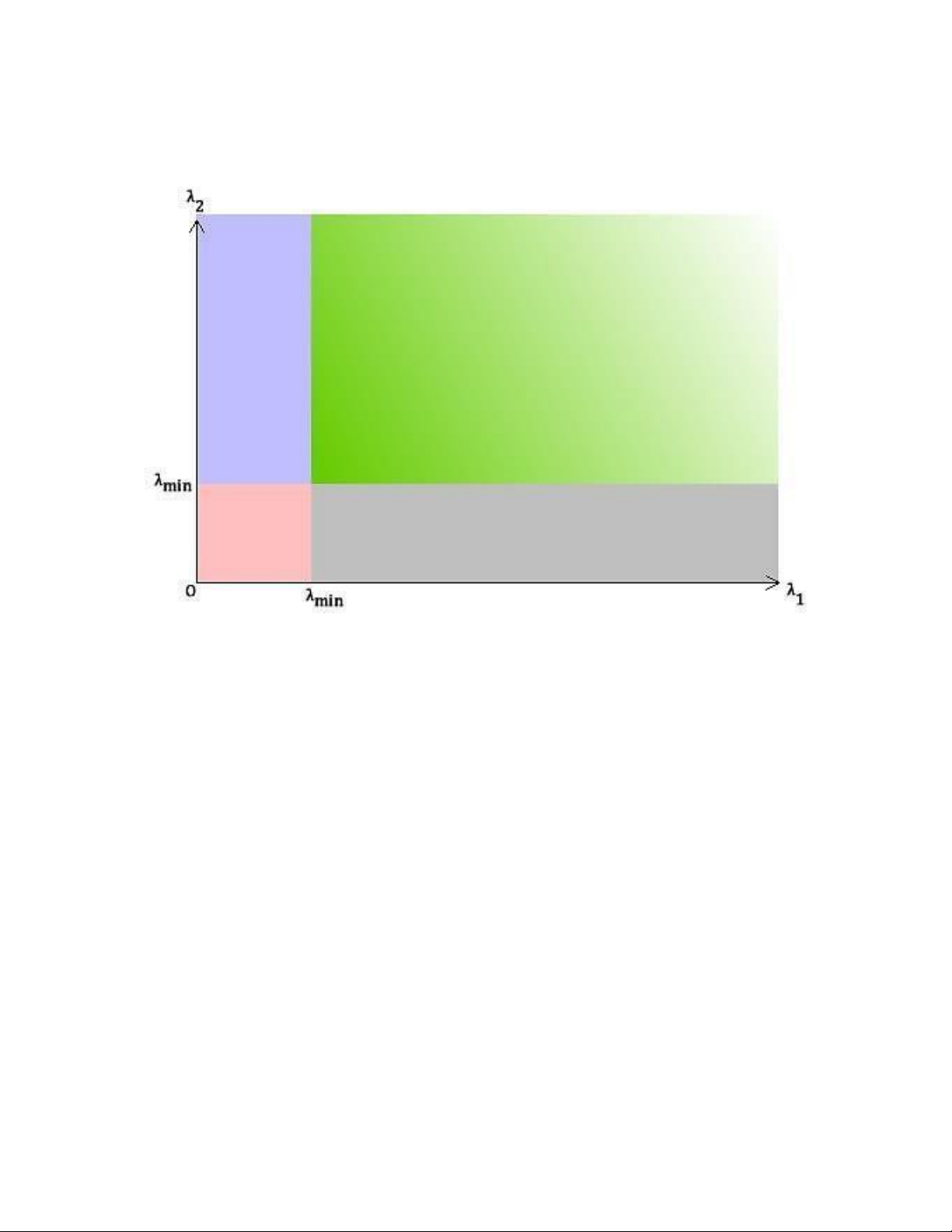
3.3. GIẢI THUẬT SHITOMASHI
Với giải thuật Shitomashi, để tìm góc thì � = min(�1, �2).
Hình 3. 5: Giải thuật tìm cạnh Shitomashi
Khi �1, �2 lớn hơn một giá trị minimum, vùng đó sẽ xuất hiện góc.
3.4. GIẢI THUẬT HITMISS
Phép toán này dùng để xác định một hình ảnh mẫu có trong hình ảnh thật. Đây là
phép tính đơn giản để thực hiện nhận dạng vật.
Phép toán sẽ tìm những pixel mà những điểm lân cận giống với kernel1 B1 đồng
thời không giống với kernel B2.
� ∗ � = (� � �) ∩ (�� � �) Trình tự:
Bước 1: Erode với kernel B1
Bước 2: Lây A bù và erode với kernel B2
Erode là lần lượt so sánh tại các vị trí có giá trị bằng 1 của structuring element B1,
nếu giống nhau hoàn toàn giá trị trả về là 1, ngược lại là 0.
Bước 3: Hợp AND 2 hình lại Trang 13
NHẬP MÔN THỊ GIÁC MÁY TÍNH – ÔN THI CUỐI KỲ
Cấu trúc của một kernel để so sánh tương quan bao gồm pixel -1, 1, 0
Kernel B1 và kernel B2 có thể kết hợp lại với nhau thành kernel kết hợp
Chỉ có một kernel B1 thì B2 là bù của B1
Với kernel chưa kết hợp ta có thể kết luận như sau: 0 lá giá trị nào cũng được, ma
trận bù B2 thì chỉ bù những giá trị nào cần chính xác
Với kerernel kết hợp ta có thế kết luận như sau: -1 là mức thấp, 1 là mức cao, 0 là giá trị nào cũng được Trang 14
NHẬP MÔN THỊ GIÁC MÁY TÍNH – ÔN THI CUỐI KỲ CHƯƠNG 4 TÍNH TOÁN KHỐI
4.1. GIẢI THUẬT FILL IN HOLE
Đầu tiên đề cho hình ma trận ảnh A. Ta sẽ tính ma trận ảnh nghịch đảo ��.
Tiếp ta sẽ sử dụng Kernel B sau: 0 1 0 1 1 1 0 1 0
Ta sẽ chọn một ma trận ảnh �0 mà trong ma trận này chỉ có 1 phần tử có giá trị là 1
trùng với lỗ cần điền đầy của ma trận ảnh A (hay trùng với giá trị ��). Ta gọi đây là điểm mồi.
Tiếp đó, ta lấy �0 dilate với Kernel B để cái hình nó giãn nở ra, sau đó lại giao với
Để thu được �1, nói chung là tổng quát: Xk = (Xk−1 ⊕ B) ∩ �C
Ý nghĩa là cứ mỗi lần cái điểm mồi nó nở ra ( vì Kernel) thì phép giao giúp nó cắt đi
những cái thường, ép thành cái lỗ cần làm đầy.
Cứ tiếp tục lặp lại quá trình trên tạo ra các �2, �3, … , �� tới khi �� là một ma trận ảnh
mà nếu lặp lại thì cũng không còn thay đổi được nữa, thì quá trình được xem là hoàn tất.
Khi này, ta giao �� đó ( ma trận ảnh điền đầy cuối cùng ) với ma trận ảnh � ban đầu
để thu được ma trận ảnh A được điền đầy”
����� = �� ∩ � 4.2. TÌM BLOB
Xem ví dụ minh họa ở Phần 2.
4.3. GIẢI THUẬT THINING Sử dụng 8 Kernel sau: 1: 2: 3: 4: -1 -1 -1 -1 -1 1 -1 1 1 Trang 15
NHẬP MÔN THỊ GIÁC MÁY TÍNH – ÔN THI CUỐI KỲ 1 1 1 -1 1 1 -1 1 1 -1 1 1 1 1 1 1 -1 -1 -1 5: 6: 7: 8: 1 1 1 1 1 -1 1 -1 -1 1 -1 1 1 -1 1 1 -1 1 1 -1 -1 -1 -1 -1 -1 1 1 1
Trượt Kernel theo thứ tự từ trái qua phải, những hình nào giống với kernel ( ví dụ B1 là hình sau: 1 1 1 1
Và các số -1 tương ứng là số 0, còn các ô trống thì số 0 hay 1 đều được) thì ma trận
� ⊛ �1 là ô chứa giá trị chính giữa của Kernel. -1 -1 -1 1 1 1 1
4.4. GIẢI THUẬT SKELETON
Đầu tiên ta có ma trận ảnh gốc (đề cho), Ta padding ma trận ảnh gốc đó.
Tiếp theo, ta sử dụng kernel sau để tiến hành skeleton 0 1 0 1 1 1 0 1 0 Các bước thực hiện:
- Erode ma trận Src0 được ma trận Erode0.
- Tiến hành Dilate ma trận eroded ta được ma trận Dilate0.
- Sau đó lấy ma trạn Src0 trừ cho ma trận Dilate0 vừa tìm được ta được ma trận Temp0.
- Cộng dồn các ma trận Temp mới này với nhau để được kết quả Skeleton. Trang 16
NHẬP MÔN THỊ GIÁC MÁY TÍNH – ÔN THI CUỐI KỲ
- Gán ma trận Eroded0 cho Src1 và tiếp tục lại các bước như trên cho đến khi ma
trận Src thứ i là ma trận 0 thì ta thu được kết quả skeleton cuối cùng bằng cách tiến hành
cộng dồn các ma trận Temp. Trang 17
NHẬP MÔN THỊ GIÁC MÁY TÍNH – ÔN THI CUỐI KỲ CHƯƠNG 5 GIẢI THUẬT HOUGH
5.1. GIẢI THUẬT HOUGH LINE
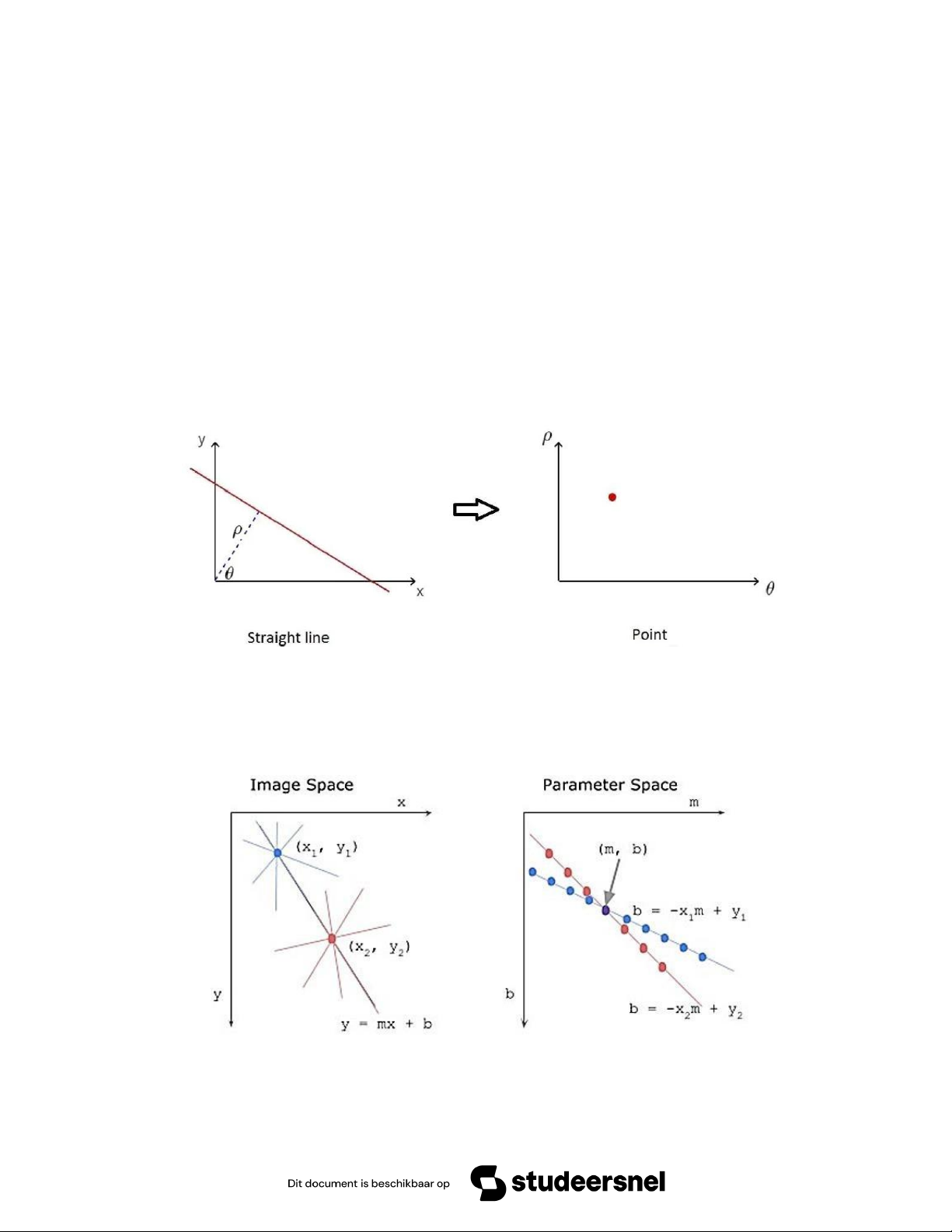
Một đường thẳng trong tọa độ 2D có dạng � = �� + �. Nếu một điểm (�0, �0) thuộc
đường thẳng sẽ thỏa �0 = ��0 + � trong tọa độ ảnh.
Ta có �0 = ��0 + � → � = −��0 + �0. Tọa độ mà có 2 trục m (trục hoành) và b
(trục tung) gọi là tọa độ hough space. Như vậy 1 đường thẳng bên tọa độ ảnh sẽ tương ứng
với 1 điểm trên tọa độ hough space như Hình 5.1.
Hình 5. 1: Chuyển đổi từ image space sang hough space 1 điểm
Giả sử có hai điểm thuộc đường thẳng này. Nếu biểu diễn trong mặt phẳng (m, b) như
Hình 5.2 ta sẽ thấy hai đường thẳng này sẽ cắt nhau tại một điểm như Hình 5.2.
Hình 5. 2: Chuyển đổi từ image space sang hough space 2 điểm Trang 18
NHẬP MÔN THỊ GIÁC MÁY TÍNH – ÔN THI CUỐI KỲ
Và nếu như có ba hay nhiều điểm hơn thuộc đường thẳng, các đường này cũng sẽ cắt
nhau tại một điểm như Hình 5.3.
Hình 5. 3: Chuyển từ image space sang hough space nhiều điểm
Do đó, dựa vào các đặc tính này ta có thể tìm ra được phương trình đường thẳng qua các điểm cho trước.
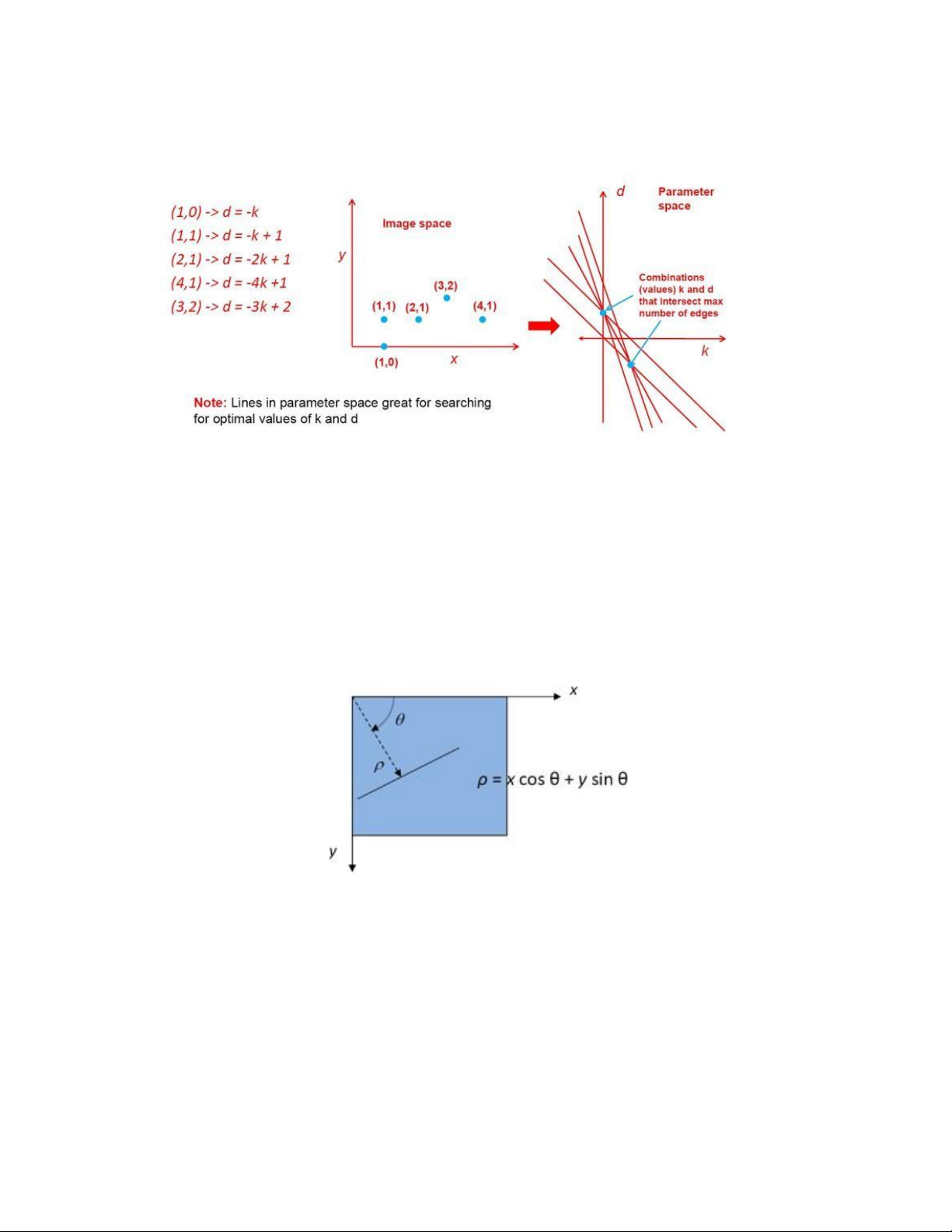
Tuy nhiên, nấu chỉ sử dụng hai biến m và b, giải thuật chỉ đúng cho trường hợp, đường
thẳng, đường tròn và ellipse sẽ không thể thực thi được. Để giải quyết vấn đề này người ta
dùng tọa độ cực để biểu diễn đường thẳng. Ngoài ra, chuyển sang tọa độ cực việc lập trình
và thực thi dễ dàng hơn (Hình 5.4).
Hình 5. 4: Chuyển đồi từ image space sang tọa độ cực hough space
Với � = −90° → 89°, � = −� ��� → +� ��� với d max là độ dài đường chéo của
hình. Ví dụ ở điểm (x, y) = (50, 100), ta có: Trang 19