
















Preview text:
lOMoAR cPSD| 45254322 14 B. MỘT SỐ BÀI TẬP I. XÁC SUẤT Bài 1.
Gieo 1 viên xúc xắc đồng chất, cân đối. Xác suất để gieo được 5 lần đều cho ra mặt có giá trị chắn là: Giải:
Xác suất gieo được mặt chắn sẽ là . Vậy xác suất gieo ra 5 lần đều là mặt chẵn P là: P = Bài 2.
Một đề thi hết môn có 8 câu hỏi trắc nghiệm, mỗi câu hỏi có 5 đáp án, tỉ lệ đúng cho mỗi đáp là như nhau
và bằng 0,2. Một sinh viên vì không học bài lên anh ta làm bài bằng cách đánh lụi tất cả 16 câu hỏi.
Cho biết xác suất anh ta chỉ làm được 2 câu đúng là: Giải:
Gọi p là xác suất anh ta lụi đúng (p=0,2), xác suất anh ta lụi sai là q=0,8. Áp dụng công thức Bernoulli, xác
suất anh ta chỉ làm đúng được 2 câu là T2 là: T Bài 3.
Ném 10 lần độc lập 1 quả bóng vào rổ, xác suất để ném trúng rổ mỗi lần ném là 0,8. Tìm xác suất: a. Có 2 lần trúng rổ
b. Có ít nhất 2 lần trúng rổ Giải: a.
Gọi p là xác suất ném trúng rổ mỗi lần ném (p=0,8). A là xác suất ném trúng rổ 2 lần.Áp dụng
công thức Bernoulli, xác suất 2 lần trúng A là: A = Ckn . b.
Gọi B là biến cố có ít nhất 2 lần trúng rổ, tức biến cố đối của nó B là có không quá 2 lần trúng
hay chỉ có 1 và 0 lần trúng. Ta dễ dàng tính được B : B = C
Lúc này, dễ dàng ta tính được biến cố B:
B = 1 − B = 1 − 4,1983.10−6 = 0,9999958017 Bài 4.
Một xạ thủ bắn 3 phát súng vào 3 tấm bia ở các khoảng cách khác nhau. Xác suất trúng vào tấm bia I, II, III
lần lượt là 0,9; 0,8 và 0,7. Biết rằng 1 viên đạn không thể trứng cùng lúc 2 bia. a. Tính xác suất có đúng một phát trứng bia.
b. Biết rằng có đúng một phát trúng, tính xác suất để phát thứ nhất không trứng bia. Giải: a.
Xác suất chỉ trúng bia I: A1 = 0,9.0,2.0,3 = 0,054
Xác suất chỉ trúng bia II: B1 = 0,1.0,8.0,3 = 0,024 Xác suất
chỉ trúng bia III: C1 = 0,1.0,2.0,7 = 0014
Xác suất chỉ trúng 1 bia, sẽ có 3 th là chỉ trúng bia I, hoặc chỉ trúng bia II hoặc chỉ trúng bia III. Vậy khi đó
xác suất chỉ trúng 1 bia T1 = A1 + B1 + C1 = 0,054 + 0,024 + 0,014 = 0,092. lOMoAR cPSD| 45254322 15
b. Khi chỉ trúng đúng 1 phát, nhưng phát thứ nhất không trúng bia, tức là sẽ rơi vào 2 trường hợp là: B1 và C1.
Do đó, ta dễ dàng tính được xác suất phát thứ 1 không trúng bia A 1 là:
A1 = B1 + C1 = 0,024 + 0,014 = 19 T1 0,092 46 Bài 5.
Một người say mê mua xổ số cào, người đó mua liên tiếp từng tờ vé số và cào đến khi nào được trúng
thưởng thì dừng. Tìm xác suất sao cho người đó mua đến vé thứ 5 thì dừng biết xác suất mỗi lần trúng
thưởng là như nhau và bằng 0,01. Giải:
Xác suất mỗi lần trúng thưởng là 0,01. Vậy xác suất mỗi lần không trúng là 0,99.
Vì mỗi lần mua vé số thì xác suất trúng đều độc lập, không bị ảnh hưởng bới lần mua khác và đều bằng
0,01 nên xác suất người đó mua tới lần thứ 5 thì dừng A sẽ là: A = 0,994.0,01 = 9,60596.10−3. Bài 6.
Hai cửa hàng hàng tạp hóa kinh doanh độc lập. Xác suất để các cửa hàng phá sản lần lượt là 0,01 và 0,02. Tìm xác suất để:
a. Có một cửa hàng nào đó bị phá sản.
b. Ít nhất 1 cửa hàng bị phá sản.
c. Có nhiều nhất 1 cửa hàng bị phá sản.Giải: a.
Gọi xác suất của hàng thứ I bị phá sản là A, A=0,01; biến cố đối của A là cửa hàng thứ I khôngbị phá
sản là A. Xác suất cửa hàng thứ II bị phá sản là B, B = 0,02.
Có 1 cửa hàng nào đó bị phá sản tức chỉ 1 trong 2 cửa hàng bị phá sản, cửa hàng kia vẫn còn. Vây xác xuất
có 1 cửa hàng nào đó bị phá sản là: Pa = AB + AB = 0, . b.
Ít nhất 1 cửa hàng phá sản. Ở đây ta có 2 cửa hàng, tức là xác suất 1 trong 2 cửa hàng bị phásản
hoặc cả 2 cửa hàng bị phá sản. Xác suất cả 2 cửa hàng bị phá sản AB là: AB = 0,
Xác suất cả 2 cửa hàng bị phá sản Pb là: Pb = AB + AB + AB = + = c.
Xác xuất có nhiều nhất 1 cửa hàng bị phá sản. Tức là chỉ có 1 trong 2 cửa hàng hoặc không cửahàng
nào phá sản, không có trường hợp cả 2 cửa hàng phá sản. Do đó, có thể tính nhanh ta lấy 1 xác xuất cả 2 cửa hàng bị phá sản. Pc = 1 − AB = 1 . Bài 7.
Một Ivan kêu gọi vốn để phát triển công ty du lịch mới mở của mình tại Pháp. Anh ta đi gặp 3 nhà đầu tư,
sau buổi gặp mặt, xác xuất anh kêu gọi vốn được từ 3 nhà đầu tư lần lượt là 0,1; 0,2 và 0,5. a. Tính xác
suất anh ta kêu gọi được vốn đầu tư. lOMoAR cPSD| 45254322 16 b.
Để có đủ vốn mở công ty, anh ta cần có được sự đầu tư từ ít nhất 2 trong số 4 nhà đầu tư. Tínhxác
xuất anh ta đủ khả năng mở công ty. c.
Biết rằng dịch vụ du lịch cửa anh mỗi quý (3 tháng, 1 năm có 4 quý) sẽ thu hút các lượt khách(mỗi
lượt sẽ gồm 10 tốp, mỗi tốp có 5 khách) có phân phối theo quá trình Poisson với λ = 4 , tính xác xuất mỗi
mùa Ivan kiếm được 2 và 5 lượt. d.
Biết rằng công ty của Ivan đang cần 17500 e tiền vốn để phát triển. Theo báo cáo tài chính hiện tại
thì mỗi lượt khách ta sẽ kiếm được 500 e. Ivan thấy rằng nếu tự tiền túi bỏ ra, nếu đủ khả năng từ các lượt
khách trên thu hồi vốn trong 2.5 năm tới thì anh ta sẽ không cần kêu gọi đầu tư, khi đó sẽ tránh được việc
phải chia cổ phần. Và một báo cáo khác cho thấy tình hình kinh doanh của Ivan sẽ ổn định như thế này
trong 2 năm tới và các nguồn thu khác (các đoàn khách nhỏ lẻ không theo đợt, việc bán quà lưu niệm, tiền
hoa hồng khi chuyển tiếp khách cho các công ty du lịch lớn hơn ...) của công ty vừa đủ để vận hành và chi
trả cho các công việc khác, tức là Ivan chỉ có thể lấy lại vốn thông qua các đợt khách "Poisson". Hãy cho
biết Ivan có cần phải đi gọi vốn không Giải: a.
Gọi xác suất Ivan gọi được vốn đầu tư từ 3 nhà đầu tư lần lượt là A = 0,1; B = 0,2 và C=0,5. Khi đó biến cố
đối Ivan bị 3 nhà đầu tư từ chối lần lượt là A = 0 ,9;B = 0 ,8 và C = 0 ,5.
Ivan kêu gọi được vốn đầu tư tức chỉ cần 1 trong 3 nhà đầu tư đồng ý. Biến cố đối của biến cố này là Ivan
không kêu gọi được vốn đầu tư, cả 3 đều từ chồi. Để tính toán cho gọn, ta sẽ tính xác suất Ivan gọi được
vốn đầu tư thông qua biến cố đối. Pa = 1 − ABC = 1 . b.
Xác suất Ivan chỉ gọi được vốn đầu tư từ 2 nhà đầu tư A và B là:
ABC = 0,1.0,2.0,5 = 0,01
Xác suất Ivan chỉ gọi được vốn đầu tư từ 2 nhà đầu tư A và C là: ABC = 0,1.
Xác suất Ivan chỉ gọi được vốn đầu tư từ 2 nhà đầu tư B và C là: ABC = 0,9.
Xác suất Ivan gọi được vốn đầu tư từ cả 3 nhà đầu tư A,B và C là:
ABC = 0,1.0,2.0,5 = 0,01 Xác
suất Ivan kêu gọi được vốn đầu tư là:
Pb = ABC + ABC + ABC + ABC = 0,01 + 0,04 + 0,09 + 0,01 = 0,15 c.
Xác suất mỗi quý Ivan kiếm được 2 lượt khách là:
Xác suất mỗi quý Ivan kiếm được 5 lượt khách là: lOMoAR cPSD| 45254322 17 d.
Vì số lượt khách phân phối theo quá trình Poisson với λ = 4 do đó, trung bình mỗi quý Ivan sẽ có được 4
lượt khách. Mỗi lượt khách đem về 500 e.
Tức mỗi quý Ivan thu về: 500.4=2000e. Ta dễ dàng tính được trong 2.5 năm tới Ivan kiếm được:
2000.4.2.5=20000 e>17500 e.
Vậy Ivan không cần phải kêu gọi vốn đầu tư. XIN CHÚC MỪNG IVAN :V !. Bài 8.
Tại một phòng khám chuyên khoa, tỉ lệ người đến khám có bệnh là 0,8. Người ta áp dụng phương pháp
chẩn đoán mới thì thấy nếu khẳng định có bệnh thì đúng 9 trên 10 trường hợp; còn nếu khẳng định không
bệnh thì đúng 5 trên 10 trường hợp. Hãy tìm các xác suất: a. Chẩn đoán có bệnh.
b. Chẩn đoán đoán đúng. Giải:
Tỉ lệ người đến khám bị bệnh là A = 0,8. Tỉ lệ người đến khám không bị bênh A = 0 ,2 a.
Xác suất chẩn đoán có bệnh là tổng của 2 trường hợp là trường hợp có bệnh và được chẩn đoán
cóbệnh và trường hợp không bệnh nhưng được chẩn đoán là có bệnh. Vậy xác suất chẩn đoán có bệnh là:
Pchẩn đoán có bệnh = B = 0,8.0,9 + 0,2.0,5 = 0,82. b.
Xác xuất chẩn đoán có bệnh B= 0,82, xác suất chẩn đoán không bệnh là B = 0.18. Xác suất chẩn
đoán đúng là tổng trường hợp:
Th1 bị bệnh thật được chẩn đoán có bệnh
Th2 không bệnh và được chẩn đoán không bệnh.Vậy xác xuất chẩn đoán đúng là:
Pchẩn đoán đúng = A.B + A.B = 0,8.0,82 + 0,2.0,18 = 0,692
Bài 9. Một loại chứng chỉ trình độ ngoại ngữ rất khó, chỉ số người tham gia là vượt qua. Giả sử có 2048
người tham sát thi lấy chứng chỉ. Cho rằng khả năng lấy chứng chỉ mỗi người đều bằng nhau và là .
a. Có bao nhiêu người chỉ mất 1 lần thi là có được chứng chỉ ? Bao nhiêu người phải mất ít nhất 5lần mới có được chứng chỉ?
b. Về mặt trung bình, một người thi bao nhiêu lần sẽ có được chứng chỉ? Giải: a.
Số người chỉ mất 1 lần thi là có chứng chỉ S1 là: S người.
Số người mất 5 lần thi mới có được chứng chỉ S5 là: S người. b.
Đây là dạng bài toán phân phối hình học. Với dạng toán như thế này thì đáp án sẽ là 1. lOMoAR cPSD| 45254322 18 p 1 1 =4 4 k(x − 1) nếunếu
10 ⩽< xx <⩽ 12
trong các trường hợp còn lại
Tìm EX,DX, f(x), mod(x) và med(x). Giải:
Đầu tiên ta cần tìm được hàm f(x)
- Trong khoản 0 < x < 1f(x) = 2x. - Trong
khoảng 1 ≤ x ≤ 2f(x) = kx − k. Ta có:
Để F(x)=1 trong khoảng từ −∞ → ∞ thì k sẽ = 0. Vậy: 2x nếu 0 < x < 1 f(x) = (
0 trong các trường hợp còn lại
Dễ thấy f(x) là hàm đồng biến, luôn tăng trong khoảng (0,1). Vậy Mod(x) sẽ là giá trị của x khi x tiến tới 1,
không lấy giá trị x = 1 vì tại x = 1 thì f(x) = 0. Tức x chỉ tiến tới 1 chứ không bằng 1. EX = DX = Bài 11.
Một công ty sử dụng 2 hình thức quảng cáo là quảng cáo trên đài phát thanh và quảng cáo trên tivi. Giả sử
có 40% khách hàng biết được thông tin quảng cáo qua tivi, 36% khách hàng biết được thông tin quảng
cáo qua poster và 16% khách hàng biết được thông tin quảng cáo qua cả 2 hình thức quảng cáo. Tính xác
suất để chọn ngẫu nhiên một khách hàng thì người đó biết được thông tin quảng cáo của công ty. Giải: lOMoAR cPSD| 45254322 19 Gọi:
Tỉ lệ số người được thông qua ti vi là A, A= 40%.
Tỉ lệ số người được thông qua poster là B, B= 36%.
Xác xuất 1 người biết được thông tin quảng cáo của công ty P là:
P = A + B − AB = 0,40 + 0,36 − 0,16 = 0,6 Bài 12:
Có 8 xạ thủ loại I và 12 xạ thủ loại II. Xác xuất bắn trúng mục tiêu của 2 loại xả thủ này lần lượt là 0,8 và
0,7. Chọn ngẫu nhiên 1 xạ thủ, xác suất để xạ thủ này bắn trúng mục tiêu là: Giải:
Xác suất để chọn ngẫu nhiên 1 xạ thủ và anh ta bắn mục tiêu P bằng xác suất chọn được xạ thủ loại I và
anh ta bắn trúng mục tiêu cộng với xác suất chọn xạ thủ loại II và anh ta bắn trúng mục tiêu.
Xác xuất chọn được xạ thủ loại I là AI
. Xác suất anh ta bắn trúng mục tiêu là TI = 0,8.
Xác xuất chọn được xạ thủ loại II là AII
. Xác suất anh ta bắn trúng mục tiêu là TII = 0,7.
Xác suất chọn ngẫu nhiên 1 xạ thủ và anh ta bắn mục tiêu P là:
P = AI.TI + AII.TII = 0,4.0,8 + 0,6.0,7 = 0,74
Bài 13. Trong một thành phố có 80 % dân cư thích xem bóng đá và 70% thích xem bóng rổ. a. Chọn
ngẫu nhiên 1 người. Tính xác suất người này thích xem cả bóng đá và bóng rổ.
b.Chọn ngẫu nhiên 12 người, tính xác suất chỉ có đúng 7 người thích xem bóng đá,
c. Chọn ngẫu nhiên 10 người, tính xác suất chỉ có đúng 8 người thích xem bóng rổ. Giải: a. Gọi:
Xác suất 1 người thích xem bóng đá là A, A = 0,8. Biến cố đối A = 1 − A là xác suất người không thích xem bóng đá.
Xác suất 1 người thích xem bóng rổ là B,B = 0,7. Biến cố đối B = 1 − B = 0,3 là xác suất 1 người không thích xem bóng rổ.
Xác suất 1 người thích xem cả bóng đá và bóng rổ Pa là: Pa = A.B = 0,8.0,7 = 0,56.
b. Xác suất trong 12 người được chọn ngẫu nhiên chỉ có đúng 7 người thích xem bóng đá Pb là: PbA)n .
c. Xác suất trong 10 người được chọn ngẫu nhiên chỉ có đúng 8 người thích xem bóng rổ là Pc : PcB)n . Bài 14.
Ở một cửa hàng tạp hóa các khách hàng đến là ngẫu nhiên và độc lập với trung bình là 6 khách hàng/1 giờ.
Biết rằng số khách hàng đến tuân theo quy luật Poisson. a. Xác suất có đúng 7 khách hàng đến trong 1 giờ là?
b. Xác suất có đúng 5 khách hàng đến trong 2 giờ là?
c. Biết cửa hàng mở cửa 12 giờ/ngày và cứ mỗi 10 khách thì có 1 khách đến nhưng không mua hàngdo
cửa hàng không có đồ mình cần. Hỏi trung bình 1 ngày cửa hàng sẽ có bao nhiêu khách mua đồ với điều
kiện chỉ lấy phần nguyên của só tính ra? Trung bình mỗi khách mua đồ đem về cho cửa hàng
20k VN đồng tiền lời (đã trừ đi các chi phí nhập hàng, điện, nhân viên...) với số khách. Giải:
a. Xác suất có đúng 7 khách hàng đến trong 1 giờ là Pa : Pa . lOMoAR cPSD| 45254322 20
b. Trong 1 giờ có trung bình 6 khách vậy trong 2 giờ sẽ có trung bình 12 khách.Xác suất có đúng 5 vị khách đến trong 2 giờ Pb là: Pb .
c. Ta có kỳ vọng về số khách vào cửa hàng mỗi giờ là λ = 6. Vậy 1 ngày cửa hàng mở cửa 12h sẽ có số khách
mua hàng là 12.6 = 72 người. Cứ 10 khách có 1 khách không mua hàng tức xác suất khách mua hàng là
M = 0,9. Vậy 1 ngày cửa hàng có số khác mua hàng K là K = M.72 = 0,9.72 = 64. Vì chỉ lấy phần nguyên
tức số khách mua hàng 1 ngày là 64 người. Thu nhập trong 1 tuần của cửa hàng là: 64.20.103.7 =
8,96.106 đồng.
Vậy trong 1 tuần cửa hàng thu về 8,96 triệu VN đồng tiền lời. Bài 15.
Một cỗ máy có 3 bộ phận là A, B, C có xác suất bị hỏng sau 1 tháng làm việc lần lượt là 0,2; 0,1 và 0,5.
a. Tính xác suất chỉ có 2 bộ phận bị hỏng sau 1 tháng?
b. Cuối tháng có 2 bộ phận bị hỏng, tính xác suất bị hỏng đó là B và C? Giải: a. Gọi:
- Xác suất bộ phận A bị hỏng là A = 0,2; xác suất bộ phận A không bị hỏng là A = 0,8. - Xác suất bộ
phận B bị hỏng là B = 0,1; xác suất bộ phận B không bị hỏng là B = 0,9.
- Xác suất bộ phận C bị hỏng là C = 0,5; xác suất bộ phận C không bị hỏng là C = 0,5.
Xác suất chỉ có 2 bộ phận bị hỏng là xác suất 2 trong 3 bộ phận bị hỏng (A và B hỏng ; A và C hỏng ; B và C hỏng):
Pa = ABC + ABC + ABC =0,2.0,1.0,5 + 0,2.0,9.0,5 + 0,8.0,1.0,5 = 0,14. b.
Xác suất để bộ phận B và C hỏng là: A .B.C = 0,04.
Xác suất để có 2 bộ phận bị hỏng và bộ phận đó là B và C Pb = là: A.B.C 0.04 2 Pb = = = . Pa 0,14 7 Bài 16.
Chiều dài của một loài cây là ĐLNN có phân bố chuẩn với kỳ vọng là 320cm với độ lệch chuẩn là 20cm.
Tìm xác suất 1 cây có chiều cao: a. Thấp hơn 270cm. b. Cao hơn 360 cm.
c. Cao từ 270 - 360cm.Giải: Theo giả thuyết ta có chiều cao của cây là đại lượng ngẫu nhiên có phân phối
chuẩn X ∼ N(320;202). a. Xác suất 1 cây có chiều cao thấp hơn 270 cm là: P(X .
(Tra các giá trị của Φ(Z) ở bảng cuối tài liệu) b.
Xác suất 1 cây có chiều cao hơn 360cm: P(X
c. Xác suất 1 cây có chiều cao từ 270 - 360cm: lOMoAR cPSD| 45254322 21
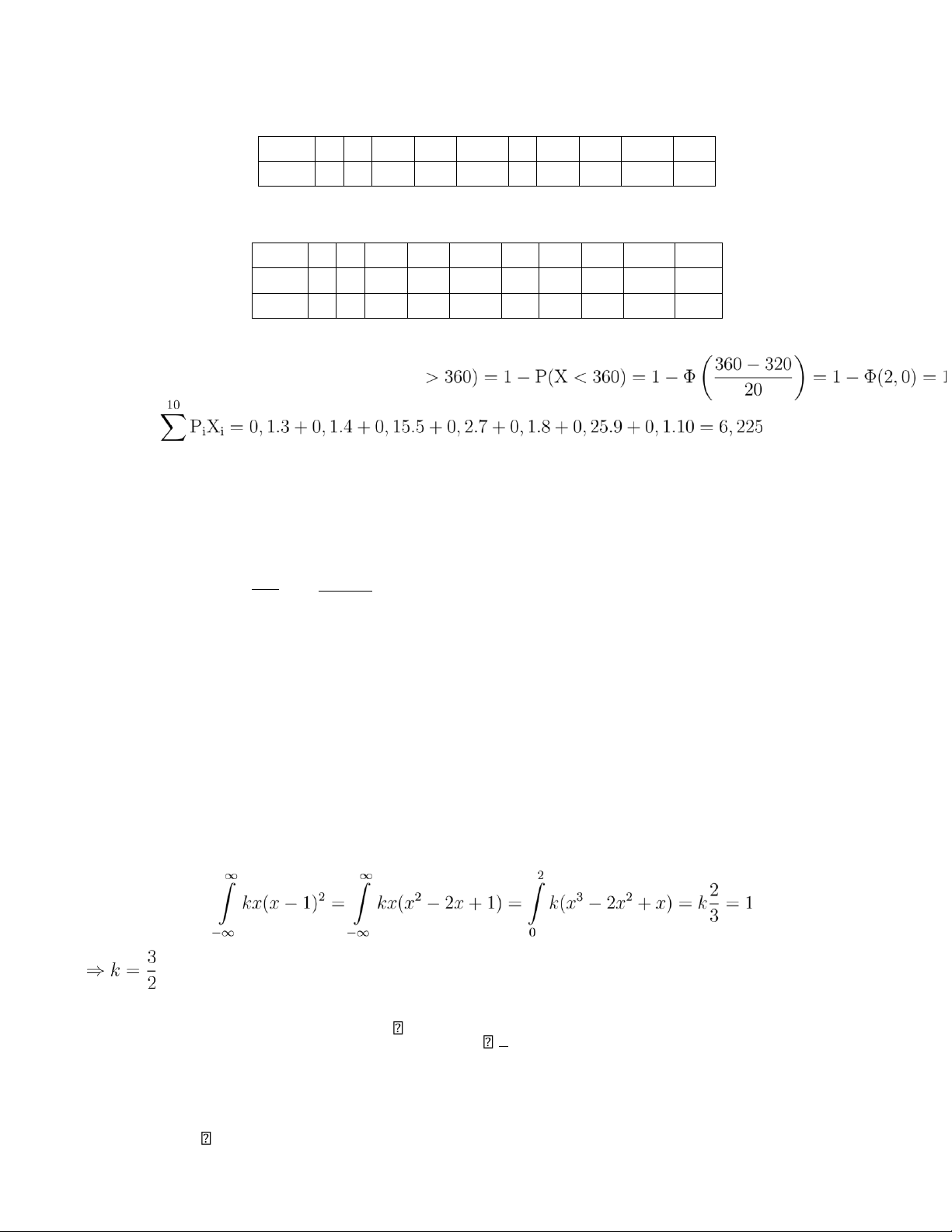
Một ứng dụng livestream cho phép người dùng đánh giá chủ kênh qua số sao ⋆ nguyên (tức không có
trường hợp 2,5 ⋆). Một kênh có tỉ lệ đánh giá như sau: ⋆ 1 2 3 4 5 6 7 8 9 10 Tỉ lệ
0 0 0,1 0,1 0,15 0 0,2 0,1 0,25 0,1
Hãy cho biết kỳ vọng, phương sai, độ lệch chuẩn và mode của điểm thi. Giải:
Từ đề bài ta có bảng sau: Tỉ lệ 0 0 0,1 0,1 0,15 0 0,2 0,1 0,25 0,1 X 1 2 3 4 5 6 7 8 9 10 X2 1 4 9 16 25 36 49 64 81 100 Kỳ vọng EX: EX = i=1 Phương sai:
DX = EX2 − (EX)2 = 0,1.9 + 0,1.16 + 0,15.25 + 0,2.49 + 0,1.64 + 0,25.81 + 0,1.100 − 6,225 = 46,475. Độ
lệch chuẩn σ = √DX =
√46,475 =6,817.
Mode là 9 vì 9 có tần số lớn nhất (0,25). Bài 18.
Cho x là đại lượng ngẫu nhiên liên tục có hàm mật độ xác suất: kx(x f(x) = (
− 1)02nếunếu trái lại0 ⩽ x ⩽ 2 a. Tìm hằng số k.
b. Cho biết kỳ vọng và phương sai.Giải: a. Ta có:
. Vậy hàm mật độc xác suất là:
3x(x − 1)2 nếu 0 ⩽ x
⩽ 2 f(x) =2 0 nếu trái lại b. Kỳ vọng: lOMoAR cPSD| 45254322 22 EX = −∞ Phương sai: DX = −∞
Vậy kỳ vọng EX = 1,6 và phương sai DX = 0,24. Bài 19.
Trọng lượng 1 con bò là 1 đại lượng ngẫu nhiên có phân bố chuẩn. Biết tỉ lệ con bò có cân nặng hơn 300kg
là 10,56% tỉ lệ bò có khối lượng nhỏ hơn 175kg là 3,03%. a. Cho biết khối lượng trung bình của 1 con bò?
b. Cho biết tỉ lệ bò có khối lượng hơn 260kg?
c. Tính tỉ lệ bò có khối lượng nhỏ hơn 220kg?Giải:
a. Khối lượng bò có dạng X ∼ N(µ;σ2)
Ta có P(X>300) = 1 - P(x<300) = .
Từ (1) và (2) ta có hệ phương trình: (
1,25σ + µ = 300
−1,875σ + µ = 175
Giải hệ phương trình ta được : ( σ = 40 µ = 250
Khối lượng trung bình của 1 con bò là kỳ vọng EX = µ = 250 kg.
b. Tỉ lệ bò có khối lượng hơn 260kg là :
P(X>260) = 1 - P(X<260kg) = 1 − Φ(26040− 250) = Φ(25040− 260) = Φ(−0,25) = 0,4013
c. Tỉ lệ bò có khối lượng nhỏ hơn 230kg là:
P(X<230) = Φ(23040− 250) = Φ(−0,75) = 0,2266. lOMoAR cPSD| 45254322 23 Bài 20.
Một công ty bảo hiểm phân loại khách hàng của họ thành 3 nhóm: nhóm ít rủi ro, nhóm có rủi ro
trung bình và nhóm rủi ro cao. Theo nghiên cứu của họ chỉ ra rằng tỉ lệ tai nạn trong 1 năm của 3
nhóm tương ứng là 5%;10%; 20%. Tính tỉ lệ một người không bị tai nạn trong nhóm ít rủi ro biết
rằng trong toàn bộ dân số thì nhóm ít rủi ro chiếm 25%; nhóm rủi ro trung bình chiếm 60 % còn
lại là nhóm rủi ro cao. Giải:
Gọi A1;A2;A3 lần lượt tỉ lệ nhóm ít rủi ro, nhóm rủi ro trung bình và nhóm rủi ro cao trong dân số
A1 = 0,25;A2 = 0,6 ⇒ A3 = 1 −
(A1 + A2) = 1 − 0 85 = 0,15.
H là tỉ lệ bị tai nạn. Vậy P(H| 1 ,
1;P(H|A3) = 0,2 Tỉ lệ 1 người không bị tai nạn là:
H = 1 − H = 1 − [P(H|A1).A1 + P(H|A2).A2 + P(H|A3)A3] = 1 − (0,05.0,25 + 0,1.0,6 + 0,2.0,15) = 0,1025 Tỉ
lệ 1 người không bị tai nạn nằm trong nhóm ít rủi ro là :
P(A1|H) = A1.P(HH|A1) = A1.(1 −HP(H|A1) = 0,025,8975.0,95 = 0,2646 Bài 21.
Trong 10 ngày đầu tiên của tháng 10 tại 1 thành phố có 10 vụ tai nạn xảy ra. Tính xác suất để mỗi
ngày xảy ra 1 vụ. Giải:
Mỗi vụ tai nạn có khả năng xảy ra vào 1 trong 10 ngày. Có 10 vụ tai nạn tất cả. Vậy không gian mẫu là Ω = 1010.
Mỗi ngày xảy ra 1 vụ; vậy vụ thứ nhất có thể xảy ra 1 trong 10 ngày; vụ thứ 2 là 1 trong 9 ngày còn
lại; vụ thứ 3 là 1 trong 8 ngày còn lại ... Vậy cuối cùng có 10! trường hợp có thể xảy ra. Vậy xác suất
mỗi ngày xảy ra 1 vụ A là: A = Bài 22. II. THỐNG KÊ Bài 1.
Trong một cuộc khảo sát ở 121 khách hàng ở 1 nhà hàng, thời gian dùng bữa trung bình là 25 phút
với độ lệch chuẩn là 4 phút. Tìm khoảng tin cậy 99 % cho thời gian dùng bữa trung bình của khách hàng tại nhà hàng này Giải:
Từ đề bài ta có các dữ kiện:
Thời gian dùng bữa trung bình X = 25 phút.
Độ lệch chuẩn σ = 4 phút.
Độ tin cậy β = 99%. Mức ý nghĩa
Khoảng tin cậy 99 % cho khoảng thời gian dùng bữa là: lOMoAR cPSD| 45254322 24 ;X + z .
Vậy với độ tin cậy 99% thì thời gian dùng bữa của khách hàng tại nhà hàng này nằm trong khoảng
(24,063;25,936). Bài 2.
Một cuộc nghiên cứu cho thấy một người Mỹ trưởng thành một năm đọc trung bình 10 cuốn sách. Một
mẫu ngẫu nhiên gồm 136 người được phỏng vấn cho thấy trung bình học đọc 12 cuốn sách trong 1 năm
với độ lệch tiêu chuẩn là 9 cuốn. Nhận định xem có phải thực ra 1 người Mỹ trung bình đọc nhiều hơn 10
cuốn sách trong 1 năm hay không với mức ý nghĩ α = 95%. Giải:
Đây là bài toán kiểm định về giá trị trung bình. Dạng bài toán thứ 2: H0 : µ = µ0;H1 : µ > µ0
Ta có µ0 = 10;X = 12;n = 136,σ = 9. Đặt giả thuyết:
H0: Người Mỹ đọc trung bình 10 cuốn sách 1 năm.
H1: Người mỹ đọc trung bình nhiều hơn 10 cuốn sách 1 năm. Ta có Test TK T: T =
Vùng bác bỏ: Φ(C) = 1 −10, 645)05 = 0,tức,95T ⇒∈ Sc = 1. Vậy ta bác bỏ,645 H0; chấp nhận H1.
Ta thấy T > C (2,592 >
Kết luận: Người Mỹ đọc trung bình nhiều hơn 10 cuốn sách 1 năm. Bài 3.
Một tỉnh báo cáo rằng tỉ lệ học sinh đỗ tốt nghiệp THPT của họ là 93 %. Một mẫu ngẫu nhiên gồm 200 học
sinh được chọn cho thấy trong đó chỉ có 182 em đỗ, Với mức ý nghĩa α = 5%, kiểm định xem báo cáo về tỉ
lệ đỗ tốt nghiệp 93% là cao hơn thực tế? Giải:
Đây là bài toán thứ 3 của dạng toán kiểm định về tỉ lệ.
Gọi tỉ lệ tốt nghiệp giả thuyết đưa ra là p0, tỉ lệ tốt nghiệp thực tế là p. Ta đặt 2 giả thuyết:
H0 : p = p0 Tỉ lệ tốt nghiệp 93% bằng với thực tế; H1 : p
< p0 Tỉ lệ tốt nghiệp 93% cao hơn thực tế. Xét điều kiện:
( n.p0 = 200.0,93 = 186 ⩾ 5 n(1 − p0) = 14 ⩾ 5
Thảo mãn điều kiện, ta chuyển tới bước tính Test TK và vùng bác bỏ:
Tỉ lệ học sinh đỗ tốt nghiệp của mẫu: . Test TK:
T = p(fp−0(p10−)√pn0) = (0,91√−0,930,93).0,07.√200 = −1,109.
Vùng bác bỏ: Φ(C) = 0,95 ⇒ C = 1,645T. ∈/ S. Vậy ta bác bỏ giả thuyết H1 chấp nhận H0. Ta thấy
T > -C (-1,109 > - 1,645), tức lOMoAR cPSD| 45254322 25
Kết luận: Với mẫu 200 em học sinh thu được, ta thấy tỉ lệ học sinh đỗ tốt nghiệp THPT của tỉnh không cao
hơn so với thực tế. Bài 4.
Các nhà khoa học đang xem xét 1 phương pháp canh tác dâu tây mới.
Một mẫu gồm 170 cây dâu tây được canh tác theo phương pháp cũ cho ra sản lượng trung bình là 50,7
quả/cây trong 1 mùa với độ lệch chuẩn là 5,8. Một mẫu khác gồm 200 cây dâu tây được canh tác theo
phương pháp mới cho ra sản lượng là 55,3 quả/cây trong 1 mùa với độ lệch chuẩn là 4,7. Với mức ý nghĩa
α = 1%, hãy cho biết liệu phương pháp canh tác mới có hiệu quả hơn phương pháp cũ không? Giải: Đây là
dạng bài toán thứ 3 của bài toán so sánh 2 giá trị trung bình.
Gọi µ1 là trung bình năng suất dâu tây theo phương án ban đầu và µ2 là trung bình năng suất dâu tây theo
phương án mới. Ta đặt giả thuyết :
H0 : µ1 = µ2 Phương pháp mới hiệu quả giống phương pháp cũ. H1 :
µ1 < µ2 Phương pháp mới hiệu quả hơn phương pháp cũ. Ta có:
X = 50,7 là trung bình năng suất theo phương pháp cũ. Y = 55
,3 là trung bình năng suất theo phương pháp mới.
n = 170 kích cỡ mẫu khảo sát theo phương pháp cũ, m = 200 là kích cỡ mẫu khảo sát theo phương pháp
mới. s1 = 5,8 là độ lệch chuẩn mẫu của phương pháp cũ ; s2 = 4,7 là độ lệch chuẩn mẫu của phương án mới. Test Tk: T =
Vùng bác bỏ: S = {= 1T <%−ta có:C}
Với mức ý nghĩa α Φ(C) = 0,99 ⇒ C = 2,325. S. Vậy ta bác bỏ giả thuyêt H0 chấp nhận H1.
Ta thấy T < - C (-8,28 < -2,325); tức T ∈
Kết luận: Với mức ý nghĩa α = 1%, ta thấy phương pháp canh tác dâu tây mới cho hiệu quả hơn phương pháp cũ. Bài 5.
Một khảo sát với 500 em học sinh 1 tỉnh cho thấy có 320 em chọn bài thi tổ hợp KHTN trong kỳ thi THPTQG.
Với mức ý nghĩa α = 5%; tìm khoảng tin cậy cho tỉ lệ học sinh chọn bài thi tổ hợp KHTN ở tỉnh này. Giải:
Đây là bài toán tìm khoảng tin cậy cho tỉ lệ.
Ta có cỡ mẫu n = 500; tỉ lệ đo được ở mẫu f = . Xét điều kiện: n.p (
0 = 500.0,64 = 320 ⩾
10 n(1 − p0) = 400.0,36 = 180 ⩾
10 Khoảng tin cậy cho tỉ lệ P là: P .
Vậy khoảng tin cậy cho tỉ lệ học sinh chọn bài thi tổ hợp KHTN ở tỉnh này là (0,605;0,675). Bài 6. lOMoAR cPSD| 45254322 26
Một công ty sản xuất báo cáo rằng số công nhân tay nghề cao của họ là 20 %. Kiểm tra ngẫu nhiên 2000
công nhân của công ty này thấy có 460 công nhân có tay nghề cao. Với mức ý nghĩa 2% hãy cho biết liệu
công ty có nói đúng không? Giải:
Đây là bài toán thử nhất của dạng kiểm định tỉ lệ: Xét
( n.p0 = 1600.0,2 = 400 ⩾ 5 n(1 − p0) =
2000.0,8 = 1600 ⩾ 5
Điều kiện thỏa mãn. Đặt giả thuyết:
H0 : p = p0 Tỉ lệ thợ lành nghề = 20% bằng với thực tế; H1 : p ̸=
p0 Tỉ lệ thợ lành nghề khác 20% Tỉ lệ ở mẫu là f = Test thống kê: T = .
Vùng bác bỏ: S = {|T| > C}; Φ(C) = 1 − 0,02/2 = 0,99 ⇒ C = 2,325.
Ta thấy |T| > C (3,188 > 2,325), tức T ∈ S. Vậy ta bác bỏ giả thuyêt H0 chấp nhận đối thuyết H1. Kết luận: Tỉ
lệ thợ lành nghề của công ti khác với 20%.
Lưu ý: Bài toán chỉ hỏi là tỉ lệ có khác hay không. Ta cũng chỉ biết tỉ lệ kiểm định khác 20% chứ không biết
là tỉ lệ thực tế cao hơn hay thấp hơn 20 %. Bài 7:
Các nhà CNSH đang thử nghiên cứu ứng dụng dòng vi sinh vật mới trong sản suất bia. Qua kiểm tra thấy
rằng cả 2 dòng vi sinh vật mới và cũ đều cho ra sản phẩm như nhau chỉ khác về thời gian. Qua mẫu kiểm
tra với 100 mẻ bia của chủng cũ các nhà CNSH thấy mất trung bình 19,3 ngày với độ lệch chuẩn σ1 = 2,9 để
ra đời một mẻ bia đạt chuẩn còn chủng mới với 110 mẻ bia cho thấy sẽ mất 17,9 ngày với độ lệch chuẩn
σ2 = 2,5 để ra đời một mẻ bia đạt chuẩn. Cho biết với mức ý nghĩa α = 0,5% liệu chủng mới có giúp sản
xuất nhanh chủng cũ hơn không? Giải:
Đây là bài toán so sánh 2 giá trị trung bình.
Ta thấy thời gian nhanh hơn nghĩa là mất ít thời gian hơn. Gọi µ1 là thời gian cho ra mẻ bia của chủng cũ và
µ2 là thời gian cho ra mẻ bia ở chủng mới. Ta đặt giả thuyết:
H0 : µ1 = µ2 : thời gian sản xuất của 2 chủng bẳng nhau.
H1 : µ1 > µ2 : thời gian sản xuất của chủng mới nhỏ hơn chủng cũ (hay thời gian chủng cũ nhiều hơn). Ta có Test TK: 19,1 17,8 T =
Vùng bác bỏ S = {T > C = zα = z0,005 = 2,575}
Ta thấy T > C (3,73 > 2,575) tức T ∈ S. Vậy ta bác bỏ giả thuyết H0; chấp nhận giả thuyết H1. lOMoAR cPSD| 45254322 27
Kết luận: Với mức ý nghĩa α = 0,5% thì chủng vi sinh vật mới giúp sản xuất nhanh bia hơn chủng cũ.
Lưu ý: Thời gian sản xuất nhanh hơn hay năng suất cao hơn tức là sẽ mất thời gian ít hơn.
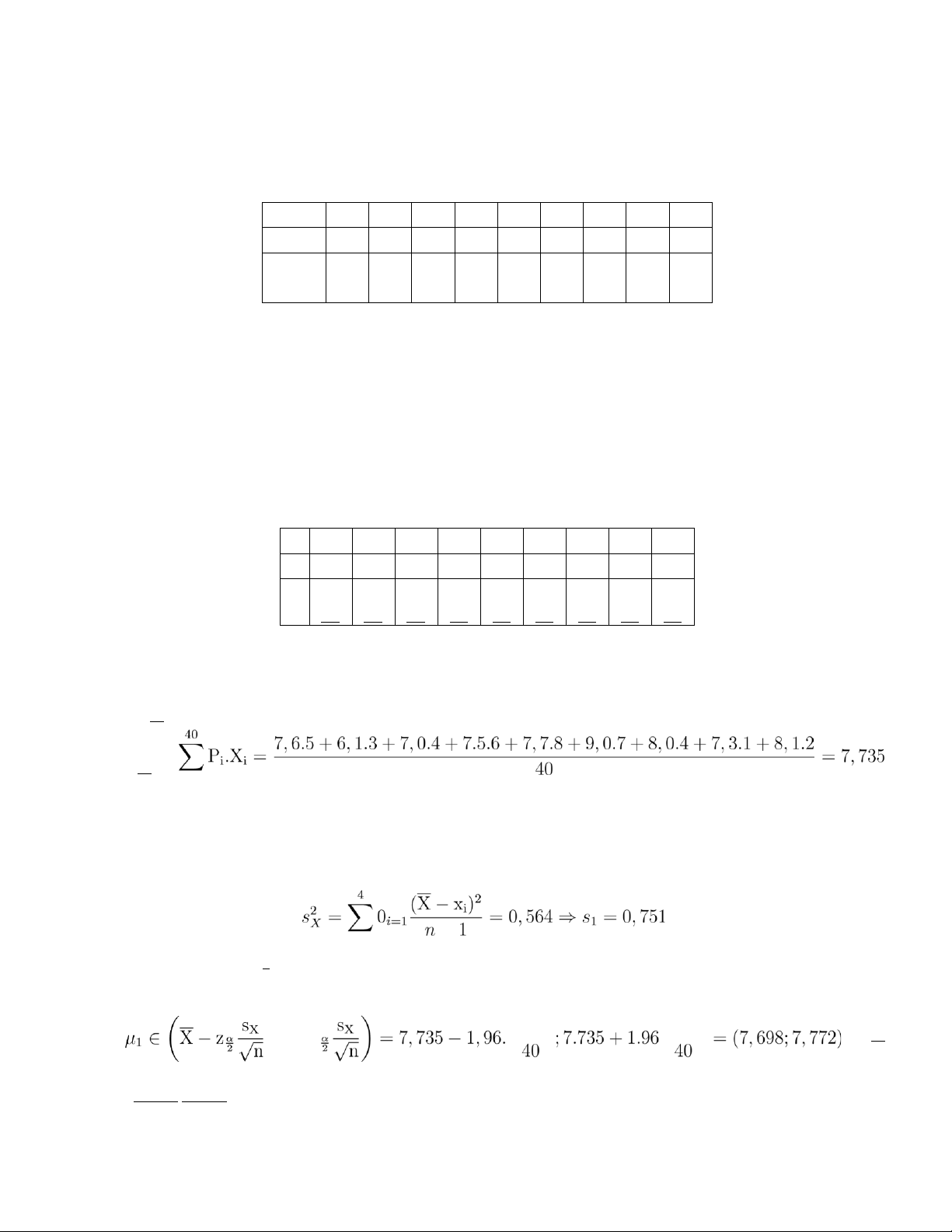
Bài 8. Để tìm hiểu mối liên hệ ở bậc phổ thông trung học (PTTH) và kết quả năm nhất đại học; người
ta thống kê kết quả học tập trung bình bậc PTTH và năm nhất đại học của 40 học sinh; kết quả thu
được như sau: (X: Điểm trung bình của bậc PTTH; Y: Điểm trung bình năm nhất đại học) X
7,6 6,1 7,0 7,5 7,7 9,0 8,0 7,3 8,1 Y
6,3 5,1 6,0 6,2 7,3 8,2 6,3 6,3 8,0 Số 5 3 4 6 8 7 4 1 2 em
a/ Tìm khoảng tin cậy của điểm trung bình ở bậc PTTH với độ tin cậy 95%. Muốn sai số khoảng trên là 0,2
thì với độ tin cậy như trên phải điều tra kết quả học tập của bao nhiêu em?
b/ Có ý kiến cho rằng điểm thi năm nhất đại học thấp hơn điểm trung bình bậc PTTH. Hãy kiểm tra ý kiến này với α = 5%.
c/ Tìm đường hồi quy tuyến tính thực nghiệm của điểm trung bình năm nhất theo điểm trung bình ở
bậc PTTH. Đường hồi quy này dùng để làm gì? Cho ví dụ. Giải: Ta có bảng:
X 7,6 6,1 7,0 7,5 7,7 9,0 8,0 7,3 8,1
Y 6,3 5,1 6,0 6,2 7,3 8,2 6,3 6,3 8,0 P 5 3 4 6 8 7 4 1 2 40 40 40 40 40 40 40 40 40 Ta có cỡ mẫu n = 40
a. Gọi X là điểm trung bình bậc PTTH. X = Phương i sai s2X là: −
Với độ tin cậy 95% thì zα 2 = z0,025 = 1,96 Khoảng
tin cậy 95% của điểm TB bậc PTTH là: 0,751 0,751 ;X + z Kích cỡ mẫu cần là: sx.zα 2 2
0.751.1,962 lOMoAR cPSD| 45254322 28
n ⩾ = = 54,1 ε 0,2
Vậy kích cỡ mẫu cần là 55 em học sinh.
b. Gọi Y là điểm trung bình năm nhất đại học. 4 Y =
Phương sai của Y s2Y = 0,861. Kích cỡ mẫu của Y là m =40. Đây là bài toán so sánh 2 giá trị trung bình. Đặt giả thuyết:
H0 X = Y: Điểm trung bình năm nhất đại học = điểm trung bình bậc PTTH.
H1 X > Y: Điểm trung bình năm nhất đại học thấp hơn điểm trung bình bậc PTTH. Test thống kê: T =
X − Y 7,735 − 6,7825
Vùng bác bỏ : S = T > C = zα = 1,645
Ta thấy T > C ) 5,045 > 1,645). Vậy ta bác bỏ H0 chấp nhận H1.
Kết luận: Với mức ý nghĩa 5% điểm trung bình năm nhất đại học thấp hơn bậc PTTH. c. Ta có: .
Phương trình hồi quy cần tìm có dạng Y = a+bX.
b = n.PXi.Yi − PXi.PYi = 40.2123,2 − 309,4.271,3 = 1,095 n a =
Vậy đường hồi quy có dạng Y = -1,687 + 1,095X.
Đường hồi quy được dùng để dự đoán điểm trung bình năm nhất đại học khi biết điểm trung bình bậc PTTH.
Ví dụ: Điểm trung bình bậc PTTH là 9,2 thì điểm trung bình năm nhất đại học là Y = -1,687 + 1,085.9,2 = 8,295. PHỤ LỤC
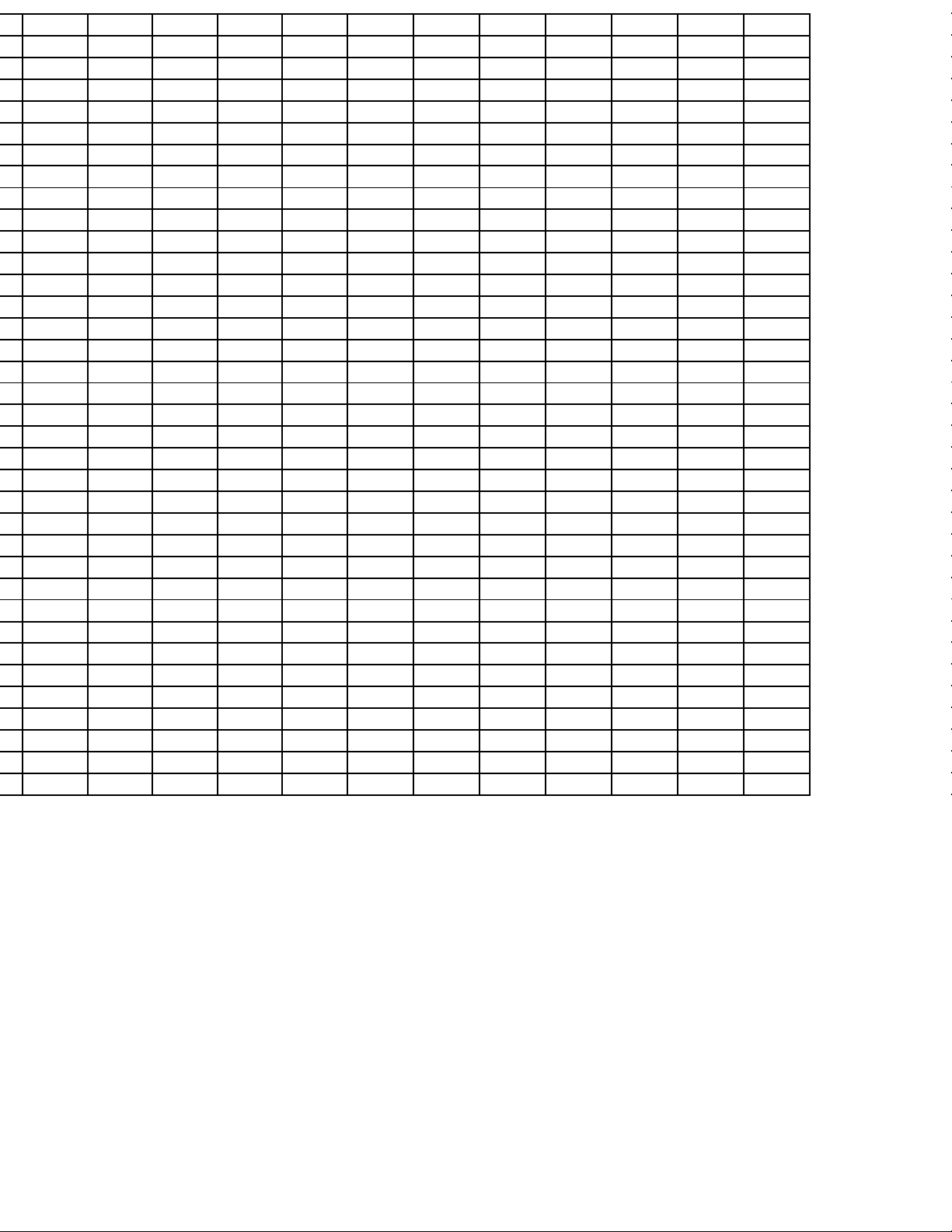
Hướng dẫn tra các bảng số trong XSTK Các bảng phân phối thường dùng: lOMoAR cPSD| 45254322
LÝ THUYẾT XÁC SUẤT VÀ THỐNG KÊ TOÁN – BẢNG SỐ VÀ CÔNG THỨC CƠ BẢN - 2019
Giá trị hàm: 𝚽(𝒛) = 𝑷(𝒁 < 𝒛); 𝒁~𝑵(𝟎, 𝟏) Với 𝒛 > 𝟎 z 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09
0.0 0.5000 0.5040 0.5080 0.5120 0.5160 0.5199 0.5239 0.5279 0.5319 0.5359
0.1 0.5398 0.5438 0.5478 0.5517 0.5557 0.5596 0.5636 0.5675 0.5714 0.5753
0.2 0.5793 0.5832 0.5871 0.5910 0.5948 0.5987 0.6026 0.6064 0.6103 0.6141
0.3 0.6179 0.6217 0.6255 0.6293 0.6331 0.6368 0.6406 0.6443 0.6480 0.6517
0.4 0.6554 0.6591 0.6628 0.6664 0.6700 0.6736 0.6772 0.6808 0.6844 0.6879
0.5 0.6915 0.6950 0.6985 0.7019 0.7054 0.7088 0.7123 0.7157 0.7190 0.7224
0.6 0.7257 0.7291 0.7324 0.7357 0.7389 0.7422 0.7454 0.7486 0.7517 0.7549
0.7 0.7580 0.7611 0.7642 0.7673 0.7704 0.7734 0.7764 0.7794 0.7823 0.7852
0.8 0.7881 0.7910 0.7939 0.7967 0.7995 0.8023 0.8051 0.8078 0.8106 0.8133
0.9 0.8159 0.8186 0.8212 0.8238 0.8264 0.8289 0.8315 0.8340 0.8365 0.8389
1.0 0.8413 0.8438 0.8461 0.8485 0.8508 0.8531 0.8554 0.8577 0.8599 0.8621
1.1 0.8643 0.8665 0.8686 0.8708 0.8729 0.8749 0.8770 0.8790 0.8810 0.8830
1.2 0.8849 0.8869 0.8888 0.8907 0.8925 0.8944 0.8962 0.8980 0.8997 0.9015
1.3 0.9032 0.9049 0.9066 0.9082 0.9099 0.9115 0.9131 0.9147 0.9162 0.9177
1.4 0.9192 0.9207 0.9222 0.9236 0.9251 0.9265 0.9279 0.9292 0.9306 0.9319
1.5 0.9332 0.9345 0.9357 0.9370 0.9382 0.9394 0.9406 0.9418 0.9429 0.9441
1.6 0.9452 0.9463 0.9474 0.9484 0.9495 0.9505 0.9515 0.9525 0.9535 0.9545
1.7 0.9554 0.9564 0.9573 0.9582 0.9591 0.9599 0.9608 0.9616 0.9625 0.9633
1.8 0.9641 0.9649 0.9656 0.9664 0.9671 0.9678 0.9686 0.9693 0.9699 0.9706
1.9 0.9713 0.9719 0.9726 0.9732 0.9738 0.9744 0.9750 0.9756 0.9761 0.9767
2.0 0.9772 0.9778 0.9783 0.9788 0.9793 0.9798 0.9803 0.9808 0.9812 0.9817
2.1 0.9821 0.9826 0.9830 0.9834 0.9838 0.9842 0.9846 0.9850 0.9854 0.9857
2.2 0.9861 0.9864 0.9868 0.9871 0.9875 0.9878 0.9881 0.9884 0.9887 0.9890
2.3 0.9893 0.9896 0.9898 0.9901 0.9904 0.9906 0.9909 0.9911 0.9913 0.9916
2.4 0.9918 0.9920 0.9922 0.9925 0.9927 0.9929 0.9931 0.9932 0.9934 0.9936
2.5 0.9938 0.9940 0.9941 0.9943 0.9945 0.9946 0.9948 0.9949 0.9951 0.9952
2.6 0.9953 0.9955 0.9956 0.9957 0.9959 0.9960 0.9961 0.9962 0.9963 0.9964
2.7 0.9965 0.9966 0.9967 0.9968 0.9969 0.9970 0.9971 0.9972 0.9973 0.9974
2.8 0.9974 0.9975 0.9976 0.9977 0.9977 0.9978 0.9979 0.9979 0.9980 0.9981
2.9 0.9981 0.9982 0.9982 0.9983 0.9984 0.9984 0.9985 0.9985 0.9986 0.9986
3.0 0.9987 0.9987 0.9987 0.9988 0.9988 0.9989 0.9989 0.9989 0.9990 0.9990
3.1 0.9990 0.9991 0.9991 0.9991 0.9992 0.9992 0.9992 0.9992 0.9993 0.9993 lOMoAR cPSD| 45254322
3.2 0.9993 0.9993 0.9994 0.9994 0.9994 0.9994 0.9994 0.9995 0.9995 0.9995
3.3 0.9995 0.9995 0.9995 0.9996 0.9996 0.9996 0.9996 0.9996 0.9996 0.9997
3.4 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9998
3.5 0.9998 0.9998 0.9998 0.9998 0.9998 0.9998 0.9998 0.9998 0.9998 0.9998
3.6 0.9998 0.9998 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999
3.7 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999
3.8 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999 0.9999
Bộ môn Toán kinh tế - Khoa Toán kinh tế - ĐH KTQD - www.mfe.edu.vn hoặc www.mfe.neu.edu.vn
LÝ THUYẾT XÁC SUẤT VÀ THỐNG KÊ TOÁN – BẢNG SỐ VÀ CÔNG THỨC CƠ BẢN - 2019
Giá trị hàm: 𝚽(𝒛) = 𝑷(𝒁 < 𝒛); 𝒁~𝑵(𝟎, 𝟏) Với 𝒛 < 𝟎 z 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09
0.0 0.5000 0.4960 0.4920 0.4880 0.4840 0.4801 0.4761 0.4721 0.4681 0.4641
-0.1 0.4602 0.4562 0.4522 0.4483 0.4443 0.4404 0.4364 0.4325 0.4286 0.4247
-0.2 0.4207 0.4168 0.4129 0.4090 0.4052 0.4013 0.3974 0.3936 0.3897 0.3859
-0.3 0.3821 0.3783 0.3745 0.3707 0.3669 0.3632 0.3594 0.3557 0.3520 0.3483
-0.4 0.3446 0.3409 0.3372 0.3336 0.3300 0.3264 0.3228 0.3192 0.3156 0.3121
-0.5 0.3085 0.3050 0.3015 0.2981 0.2946 0.2912 0.2877 0.2843 0.2810 0.2776
-0.6 0.2743 0.2709 0.2676 0.2643 0.2611 0.2578 0.2546 0.2514 0.2483 0.2451
-0.7 0.2420 0.2389 0.2358 0.2327 0.2296 0.2266 0.2236 0.2206 0.2177 0.2148
-0.8 0.2119 0.2090 0.2061 0.2033 0.2005 0.1977 0.1949 0.1922 0.1894 0.1867
-0.9 0.1841 0.1814 0.1788 0.1762 0.1736 0.1711 0.1685 0.1660 0.1635 0.1611
-1.0 0.1587 0.1562 0.1539 0.1515 0.1492 0.1469 0.1446 0.1423 0.1401 0.1379
-1.1 0.1357 0.1335 0.1314 0.1292 0.1271 0.1251 0.1230 0.1210 0.1190 0.1170
-1.2 0.1151 0.1131 0.1112 0.1093 0.1075 0.1056 0.1038 0.1020 0.1003 0.0985
-1.3 0.0968 0.0951 0.0934 0.0918 0.0901 0.0885 0.0869 0.0853 0.0838 0.0823
-1.4 0.0808 0.0793 0.0778 0.0764 0.0749 0.0735 0.0721 0.0708 0.0694 0.0681
-1.5 0.0668 0.0655 0.0643 0.0630 0.0618 0.0606 0.0594 0.0582 0.0571 0.0559
-1.6 0.0548 0.0537 0.0526 0.0516 0.0505 0.0495 0.0485 0.0475 0.0465 0.0455
-1.7 0.0446 0.0436 0.0427 0.0418 0.0409 0.0401 0.0392 0.0384 0.0375 0.0367
-1.8 0.0359 0.0351 0.0344 0.0336 0.0329 0.0322 0.0314 0.0307 0.0301 0.0294
-1.9 0.0287 0.0281 0.0274 0.0268 0.0262 0.0256 0.0250 0.0244 0.0239 0.0233
-2.0 0.0228 0.0222 0.0217 0.0212 0.0207 0.0202 0.0197 0.0192 0.0188 0.0183 lOMoAR cPSD| 45254322
-2.1 0.0179 0.0174 0.0170 0.0166 0.0162 0.0158 0.0154 0.0150 0.0146 0.0143
-2.2 0.0139 0.0136 0.0132 0.0129 0.0125 0.0122 0.0119 0.0116 0.0113 0.0110
-2.3 0.0107 0.0104 0.0102 0.0099 0.0096 0.0094 0.0091 0.0089 0.0087 0.0084
-2.4 0.0082 0.0080 0.0078 0.0075 0.0073 0.0071 0.0069 0.0068 0.0066 0.0064
-2.5 0.0062 0.0060 0.0059 0.0057 0.0055 0.0054 0.0052 0.0051 0.0049 0.0048
-2.6 0.0047 0.0045 0.0044 0.0043 0.0041 0.0040 0.0039 0.0038 0.0037 0.0036
-2.7 0.0035 0.0034 0.0033 0.0032 0.0031 0.0030 0.0029 0.0028 0.0027 0.0026
-2.8 0.0026 0.0025 0.0024 0.0023 0.0023 0.0022 0.0021 0.0021 0.0020 0.0019
-2.9 0.0019 0.0018 0.0018 0.0017 0.0016 0.0016 0.0015 0.0015 0.0014 0.0014
-3.0 0.0013 0.0013 0.0013 0.0012 0.0012 0.0011 0.0011 0.0011 0.0010 0.0010
-3.1 0.0010 0.0009 0.0009 0.0009 0.0008 0.0008 0.0008 0.0008 0.0007 0.0007
-3.2 0.0007 0.0007 0.0006 0.0006 0.0006 0.0006 0.0006 0.0005 0.0005 0.0005
-3.3 0.0005 0.0005 0.0005 0.0004 0.0004 0.0004 0.0004 0.0004 0.0004 0.0003
-3.4 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0002
-3.5 0.0002 0.0002 0.0002 0.0002 0.0002 0.0002 0.0002 0.0002 0.0002 0.0002
-3.6 0.0002 0.0002 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001
-3.7 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001
-3.8 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001
BẢNG SỐ - X`C SUẤT THỐNG K˚ Bảng 7.
GI` TRỊ TỚI HẠN PH´N PHỐI KHI-B NH PHƯƠNG χ 2(n) α α 0.995 0.99 0.975 0.95 0.9 0.1 0.05 0.025 0.01 0.005 n 1 0.000 0.000 0.001 0.004 0.016
2.706 3.841 5.024 6.635 7.879 2 0.010 0.020
0.051 0.103 0.211 4.605 5.991 7.378 9.210 10.60 3 0.072 0.115 0.216 0.352 0.584
6.251 7.815 9.348 11.34 12.84 4 0.207 0.297 0.484 0.711 1.064 7.779 9.488
11.14 13.28 14.86 5 0.412 0.554 0.831 1.145 1.610 9.236 11.07 12.83 15.09
16.75 6 0.676 0.872 1.237 1.635 2.204 10.64 12.59 14.45 16.81 18.55 7 0.989 1.239 1.690 2.167 2.833 12.02 14.07 16.01 18.48 20.28 8 1.344 1.646 2.180 2.733 3.490 13.36 15.51 17.53 20.09 21.95 9 1.735 2.088 2.700 3.325 4.168 14.68 16.92 19.02 21.67 23.59 10 2.156 2.558 3.247 3.940 4.865 15.99 18.31 20.48 23.21 25.19 11 2.603 3.053 3.816 4.575 5.578 17.28 19.68 21.92 24.72 26.76 12 3.074 3.571 4.404 5.226 6.304 18.55 21.03 23.34 26.22 28.30 13 3.565 4.107 5.009 5.892 7.042 19.81 22.36 24.74 27.69 29.82 14 4.075 4.660 5.629 6.571 7.790 21.06 23.68 26.12 29.14 31.32 15 4.601 5.229 6.262 7.261 8.547 22.31 25.00 27.49 30.58 32.80 lOMoAR cPSD| 45254322 16 5.142 5.812 6.908 7.962 9.312
23.54 26.30 28.85 32.00 34.27 17 5.697 6.408 7.564 8.672 10.09 24.77 27.59 30.19 33.41 35.72 18 6.265 7.015 8.231 9.390 10.86
25.99 28.87 31.53 34.81 37.16 19 6.844 7.633 8.907 10.12 11.65 27.20 30.14 32.85 36.19 38.58 20 7.434 8.260 9.591 10.85 12.44
28.41 31.41 34.17 37.57 40.00 21 8.034 8.897 10.28 11.59 13.24 29.62 32.67 35.48 38.93 41.40 22 8.643 9.542 10.98 12.34 14.04
30.81 33.92 36.78 40.29 42.80 23 9.260 10.20 11.69 13.09 14.85 32.01 35.17 38.08 41.64 44.18 24 9.886 10.86 12.40 13.85 15.66
33.20 36.42 39.36 42.98 45.56 25 10.52 11.52 13.12 14.61 16.47 34.38 37.65 40.65 44.31 46.93 26 11.16 12.20 13.84 15.38 17.29 35.56 38.89 41.92 45.64 48.29 27 11.81 12.88 14.57 16.15 18.11 36.74 40.11 43.19 46.96 49.64 28 12.46 13.56 15.31 16.93 18.94 37.92 41.34 44.46 48.28 50.99 29 13.12 14.26 16.05 17.71 19.77 39.09 42.56 45.72 49.59 52.34 30 13.79 14.95 16.79 18.49 20.60 40.26 43.77 46.98 50.89 53.67 40
20.71 22.16 24.43 26.51 29.05 51.81 55.76 59.34 63.69 66.77 50
27.99 29.71 32.36 34.76 37.69 63.17 67.50 71.42 76.15 79.49 60 35.53 37.48 40.48 43.19 46.46
74.40 79.08 83.30 88.38 91.95 70 43.28 45.44 48.76 51.74 55.33
85.53 90.53 95.02 100.4 104.2 80 51.17 53.54 57.15 60.39 64.28
96.58 101.9 106.6 112.3 116.3 90 59.20 61.75 65.65 69.13 73.29
107.6 113.1 118.1 124.1 128.3 100 67.33 70.06 74.22 77.93 82.36
118.5 124.3 129.6 135.8 140.2 120 83.85 86.92 91.57 95.70 100.6
140.2 146.6 152.2 159.0 163.6 150 109.1 112.7 118.0 122.7 128.3 172.6 179.6 185.8 193.2 198.4
200 152.2 156.4 162.7 168.3 174.8 226.0 234.0 241.1 249.4 255.3
8 Bøi Dương Hải NEU www.mfe.edu.vn/buiduonghai
TABLE of CRITICAL VALUES for STUDENT’S t DISTRIBUTIONS
Column headings denote probabilities (α) above tabulated values. d.f. 0.40 0.25 0.10 0.05 0.04 0.025 0.02 0.01 0.005 0.0025 0.001 0.0005 1 0.325 1.000 3.078 6.314
7.916 12.706 15.894 31.821 63.656 127.321 318.289 636.578 2 0.289 0.816 1.886 2.920 3.320 4.303 4.849 6.965 9.925 14.089 22.328 31.600 3 0.277 0.765 1.638 2.353 2.605 3.182 3.482 4.541 5.841 7.453 10.214 12.924 4 0.271 0.741 1.533 2.132 2.333 2.776 2.999 3.747 4.604 5.598 7.173 8.610 5 0.267 0.727 1.476 2.015 2.191 2.571 2.757 3.365 4.032 4.773 5.894 6.869 6 0.265 0.718 1.440 1.943 2.104 2.447 2.612 3.143 3.707 4.317 5.208 5.959 7 0.263 0.711 1.415 1.895 2.046 2.365 2.517 2.998 3.499 4.029 4.785 5.408 8 0.262 0.706 1.397 1.860 2.004 2.306 2.449 2.896 3.355 3.833 4.501 5.041 9 0.261 0.703 1.383 1.833 1.973 2.262 2.398 2.821 3.250 3.690 4.297 4.781 10 0.260 0.700 1.372 1.812 1.948 2.228 2.359 2.764 3.169 3.581 4.144 4.587 11 0.260 0.697 1.363 1.796 1.928 2.201 2.328 2.718 3.106 3.497 4.025 4.437 12 0.259 0.695 1.356 1.782 1.912 2.179 2.303 2.681 3.055 3.428 3.930 4.318 13 0.259 0.694 1.350 1.771 1.899 2.160 2.282 2.650 3.012 3.372 3.852 4.221 14 0.258 0.692 1.345 1.761 1.887 2.145 2.264 2.624 2.977 3.326 3.787 4.140 lOMoAR cPSD| 45254322 15 0.258 0.691 1.341 1.753 1.878 2.131 2.249 2.602 2.947 3.286 3.733 4.073 16 0.258 0.690 1.337 1.746 1.869 2.120 2.235 2.583 2.921 3.252 3.686 4.015 17 0.257 0.689 1.333 1.740 1.862 2.110 2.224 2.567 2.898 3.222 3.646 3.965 18 0.257 0.688 1.330 1.734 1.855 2.101 2.214 2.552 2.878 3.197 3.610 3.922 19 0.257 0.688 1.328 1.729 1.850 2.093 2.205 2.539 2.861 3.174 3.579 3.883 20 0.257 0.687 1.325 1.725 1.844 2.086 2.197 2.528 2.845 3.153 3.552 3.850 21 0.257 0.686 1.323 1.721 1.840 2.080 2.189 2.518 2.831 3.135 3.527 3.819 22 0.256 0.686 1.321 1.717 1.835 2.074 2.183 2.508 2.819 3.119 3.505 3.792 23 0.256 0.685 1.319 1.714 1.832 2.069 2.177 2.500 2.807 3.104 3.485 3.768 24 0.256 0.685 1.318 1.711 1.828 2.064 2.172 2.492 2.797 3.091 3.467 3.745 25 0.256 0.684 1.316 1.708 1.825 2.060 2.167 2.485 2.787 3.078 3.450 3.725 26 0.256 0.684 1.315 1.706 1.822 2.056 2.162 2.479 2.779 3.067 3.435 3.707 27 0.256 0.684 1.314 1.703 1.819 2.052 2.158 2.473 2.771 3.057 3.421 3.689 28 0.256 0.683 1.313 1.701 1.817 2.048 2.154 2.467 2.763 3.047 3.408 3.674 29 0.256 0.683 1.311 1.699 1.814 2.045 2.150 2.462 2.756 3.038 3.396 3.660 30 0.256 0.683 1.310 1.697 1.812 2.042 2.147 2.457 2.750 3.030 3.385 3.646 31 0.256 0.682 1.309 1.696 1.810 2.040 2.144 2.453 2.744 3.022 3.375 3.633 32 0.255 0.682 1.309 1.694 1.808 2.037 2.141 2.449 2.738 3.015 3.365 3.622 33 0.255 0.682 1.308 1.692 1.806 2.035 2.138 2.445 2.733 3.008 3.356 3.611 34 0.255 0.682 1.307 1.691 1.805 2.032 2.136 2.441 2.728 3.002 3.348 3.601 35 0.255 0.682 1.306 1.690 1.803 2.030 2.133 2.438 2.724 2.996 3.340 3.591 36 0.255 0.681 1.306 1.688 1.802 2.028 2.131 2.434 2.719 2.990 3.333 3.582 37 0.255 0.681 1.305 1.687 1.800 2.026 2.129 2.431 2.715 2.985 3.326 3.574 38 0.255 0.681 1.304 1.686 1.799 2.024 2.127 2.429 2.712 2.980 3.319 3.566 39 0.255 0.681 1.304 1.685 1.798 2.023 2.125 2.426 2.708 2.976 3.313 3.558 40 0.255 0.681 1.303 1.684 1.796 2.021 2.123 2.423 2.704 2.971 3.307 3.551 60 0.254 0.679 1.296 1.671 1.781 2.000 2.099 2.390 2.660 2.915 3.232 3.460 80 0.254 0.678 1.292 1.664 1.773 1.990 2.088 2.374 2.639 2.887 3.195 3.416 100 0.254 0.677 1.290 1.660 1.769 1.984 2.081 2.364 2.626 2.871 3.174 3.390 120 0.254 0.677 1.289 1.658 1.766 1.980 2.076 2.358 2.617 2.860 3.160 3.373 140 0.254 0.676 1.288 1.656 1.763 1.977 2.073 2.353 2.611 2.852 3.149 3.361 160 0.254 0.676 1.287 1.654 1.762 1.975 2.071 2.350 2.607 2.847 3.142 3.352 180 0.254 0.676 1.286 1.653 1.761 1.973 2.069 2.347 2.603 2.842 3.136 3.345 200 0.254 0.676 1.286 1.653 1.760 1.972 2.067 2.345 2.601 2.838 3.131 3.340 250 0.254 0.675 1.285 1.651 1.758 1.969 2.065 2.341 2.596 2.832 3.123 3.330 inf 0.253 0.674 1.282 1.645 1.751 1.960 2.054 2.326 2.576 2.807 3.090 3.290 33 Nguồn tham khảo
1. Xác suất thống kê của Eureka! Uni
2. Bảng số và công thức XSTK Eureka! Uni
3. Sách Thống kê và ứng dụng - Đặng Hùng Thắng 4. Bảng t-Student Math.uni
Bạn có thể tự học thêm về XSTK tại: XSTK Eureka! Uni Ngoài ra bạn có thể tham
gia nhóm Xác suất Thống kê - Eureka! Uni để cùng học XSTK nha!
Một vài bản nhạc để bạn nghe khi học hành áp lực nè :V : 1. Late night
2. Nếu một mai tôi bay lên trời 3. Proud of you 4. If we hold on together
