Một số định hướng giải phương trình vô tỉ

Tài liệu gồm có 81 trang được biên soạn bởi thầy giáo Nguyễn Xuân Chung, hướng dẫn một số phương pháp tiếp cận và giải phương trình vô tỉ (phương trình chứa căn thức), giúp học sinh khối 10 học chuyên sâu chương trình Đại số 10 chương 3: phương trình và hệ phương trình.

200 100 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 10

Môn: Toán 10

Thông tin:

81 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
MỘT SỐ ĐỊNH HƯỚNG GIẢI PT VÔ TỈ - PHẦN 1
UI. Giải phương trình đa thức bậc 4
U1. Sơ lược cách giảiU:
Phương trình bâc 4 dạng:
432
0ax bx cx dx e+ + + +=
(1), (a, b, c, d, e nguyên).
Nhìn chung phương trình có hai nghiệm (trường hợp vô nghiệm ta nói sau), do đó mục
tiêu và thường hay làm là đưa về phương trình tích của hai tam thức bậc hai:
( )
( )( )
22
1 ' ' '0mx nxpmx nxp⇔ ++ + + =
(2).
Trong đó ta chú ý
','mm a pp e= =
và các số m, m’, p, p’ nguyên và thường là nhẩm để thử
tính, kết hợp máy tính cầm tay Casio fx 570 ES, VN.
Đặc biệt nếu hạn chế sử dụng máy tính Casio thì ta chỉ phân tích tự luận. Nếu a khác 1 thì
ta chia cả hai vế cho a để đưa về a = 1. Phương trình (2) là mục tiêu cuối và để giải, bước
trung gian là dựa vào hằng đẳng thức
( )( )
22
00M N MNMN−=⇔ + −=
.
Cụ thể hơn ta xét dạng sau:
( )
( )
2
2
2
0x Bx C Dx E++ − + =
. Xét ví dụ
Ví dụ 1: Giải phương trình
42
10 20 0x xx− −+ =
(1).
Hướng phân tích:
Đầu tiên ta định hướng đưa về dạng:
(
)
( )
2
2
2
0x Bx C Dx E++ − + =
.
Nhưng vì hệ số bậc 3 bằng 0 nên B = 0, còn lại là:
( )
( )
2
2
2
0x C Dx E+−+=
(*).
Để ý số e = 20 ta có
, và ta có thể chọn C để E hữu tỉ.
20 4.47≈
nên chọn C hữu tỉ chẳng hạn
9 11
; 5; ;...
22
± ±±
và
91
22
CE=±⇒ =±
(đẹp)
Hay như
64CE=±⇒ =±
. Bây giờ ta thử trừ và nhẩm trực tiếp:
( )
( )
( ) ( )
2
2 42
2
2
2 42
9
10 20
2
6 10 20
x x xx
Dx E
x x xx

± − − −+


+=
± − − −+
Ta được
( )
2
2
1
2
Dx E x

+=+


ứng với
9
2
C = −
.
Hướng dẫn giải:
( )
( )( )
22
2 22
91
1 0 4 50
22
x x xx xx

⇔ − − − =⇔ +− −− =


…
Ví dụ 2: Giải phương trình
432
2 10 11 1 0
x x xx
− + + −=
(2).
Hướng phân tích:
Đầu tiên ta chia hai vế cho 2 đưa về a = 1, ta có:
43 2
11 1 1
50
2 22
xx x x− + + −=
.
Tiếp theo định hướng đưa về phương trình sau:
.
Để ý
22 2
11 1
22 2
e CE E C=−⇒ − =−⇒ =± +
. Cho C hữu tỉ chạy để tìm E hữu tỉ, chẳng
hạn
13
44
CE
=±⇒ =±
. Ta trừ thử trực tiếp xem sao:
22
2 43 2
3 5 1 11 1 1
5
4 24 2 22
Dx x x x x x x

± = −± − −+ +−


.
Ứng với
( )
2
2
1 13
4 24
C Dx E x

=−⇒ + = +


.
Hướng dẫn giải:
PT
( )
22
2
51 13
20
24 24
xx x

⇔ −− − + =


( )
22
1
2 310
2
xx xx

⇔ − + − −=


…
Ví dụ 3: Giải phương trình
324
61
0612x xx
x++++=
(3).
Hướng phân tích:
Ở đây là
( )
( )
2
2
2
3
x x C Dx E
++ − +
và ta thử chọn C = 2 và tiếp theo là
22 2
42 2CEe E E−=⇔−=⇔=±
.
Nói cách khác
( )
2
Dx E+
hoặc là bình phương đúng hay hằng số và ta thử trừ trực tiếp :
( )
( ) ( )
2
2 4
3
2
2
3 2 6 6 11 2xDx E x
xx xx+= −+ +++++
=
( )
2
2
2 42 22x x
x
− += −
Hướng dẫn giải:
( )
( )
2
2
2
4 32
206 6 11 22
03 2xxxx
xxx+++ + −
++=⇔ − =
( )
( )
22
3222 322 02x xx x++ +− +− +

+
⇔=

…
UNhận xétU :
Cách làm cũng không quá khó khăn khi mà hạn chế hay cấm Casio trong phòng thi!
U2. Bài luyện tậpU:
Bài 1: Giải phương trình
42
10 20 0x xx− −+ =
.
Bài 2: Giải phương trình
42
– 25 60 – 36 0xxx+=
.
Bài 3: Giải phương trình
3
42
8 7 – 26 + 7 0xx x x+ +=
.
U3. Xét trường hợp vô nghiệmU:
Từ cách giải phương trình có nghiệm thì ta cũng có hướng khái quát trong trường hợp
phương trình vô nghiệm là:
( )
2
22
' ' '0Ax Bx C A x B x C++ + + +=
Trong đó
2
' ''
Ax Bx C++
là tam thức luôn dương hoặc cả hai không đồng thời bằng 0.
Ví dụ 4: Giải phương trình
34 2
6 15 10
70xx
x x+++=+
(4).
Hướng phân tích:
Cũng như trên ta nhẩm và trừ trực tiếp:
(
) (
)
2 32 2 2
2
4
' ' ' 6 15 10 3 2 2 3
72Ax Bx C x x x x x
x xx+ += + + +
=++ −− ++
.
Ta thấy số 3 = 7 – 2
P
2
P = C’ là cố định, vậy thì để khỏi bình phương và trừ lâu ta làm như
sau :
( )
( ) ( )
324
2
2
' ' 6 15 0 3127 3Ax B xx xx
xx x+ + + + ++= +− −
Ta cho x = 1 hai vế ta được
' '0AB+=
, cho x = 2 ta có
( )
22' ' 4 2' ' 2AB AB+ =⇔ +=
Và dễ dàng tìm được
' 2; ' 2AB
= = −
.
Hướng dẫn giải:
( )
32 22
2
4
6 15 10 3 270 2 2 30x xx x xxxx+=⇔++ + + + − +=+
…
UNhận xétU :
Các phương trình bậc 4 vô nghiệm thì ít khi gặp. Phương trình bậc 4 cũng đa dạng nên ta
không thể khái quát và nói hết được. Trên đây chỉ là mẹo nhỏ để các bạn tham khảo.
UII. Giải một số phương trình vô tỉ chứa căn bậc hai
U1. Dạng 1U:
Ta để ý đến một số phương trình có thể áp dụng phép khai căn mở rộng:
(
) (
)
2
ux ux
=


Ví dụ 1: Giải phương trình
2
4 12 9 4x xx+ − +=
.
Hướng dẫn giải:
PT
⇔
x +
23x −
= 4
⇔
23x
−
= 4 –x
⇔
40
2 34
23 4
x
xx
xx
−≥
−=−
−=−
⇔
7
3
1
x
x
=
= −
.
Vậy phương trình có hai nghiệm là
7
,1
3
xx= = −
.
Ví dụ 2: Giải phương trình
( )
56
81
16 8
xx
x
+
+ −=
Hướng dẫn giải:
PT
(
)
1 ⇔
56 16 8
2
x
xx
+ + −=
⇔
2
88
88
2
x
x
−+
−+=
(2).
Đặt
80xt−=≥
khi đó (2)
( )( )
2
2 80 4 2 0 4tt t t t⇒ − −= ⇔ − + = ⇒=
(vì
0t ≥
)
Thay trở về
2
8xt= +
suy ra phương trình (1) có một nghiệm
24x =
.
UNhận xétU:
Có thể đặt điều kiện
8x
≥
rồi bình phương hai vế để khử căn theo phương pháp thông
thường, cùng lắm là đưa về bậc 4.
U1.1. Luyện tậpU:
Bài 4: Giải phương trình .
Bài 5: Giải phương trình .
Bài 6: Giải phương trình
11
24
xx x a++++=
(với a > 0).
U2. Dạng 2U:
Do trong căn không có hướng như dạng 1 nên ta biến đổi ngoài căn theo trong căn. Nghĩa
là phương trình có một căn thức
( )
ux
thì ta biến đổi các biểu thức ngoài căn theo
hướng: (
u
)P
2
P , (
u
)P
3
P, (
u
)P
4
P, …đưa về “dạng đa thức”.
1
2611246 =+−+++−+ xxxx
11610145 =+−+++−+ xxxx
Ví dụ 3: Giải phương trình
22
7 5 32
x xx x x
− + += − −
.
Hướng dẫn giải:
Điều kiện:
[ ]
2
3 2 0 1; 3xx x D− − ≥ ⇔ ∈− =
.
Bình phương hai vế ta được phương trình
(
)
(
)
22
7 532 55 52 5 60x xx x x x x x
− + +=− − ⇔ +− ++ + −=
(*).
Đặt
5 , 2 22x tx D t+ = ∈ ⇒ ≤≤
thì từ (*) ta có phương trình:
( )
( )
32 2
5 2 60 2 4 3 0 2
t tt t t t t− + −= ⇔ − + + = ⇒=
(Vì
2t ≥
)
Thay trở về
2
5
xt
= −
suy ra phương trình có 1 nghiệm x = - 1.
Ví dụ 4: Giải phương trình
2
1 1xx+ +=
.
Hướng dẫn giải:
Ở đây ta biến đổi trước rồi đặt ẩn phụ sau.
( )
( )
22
1 1 2 1 2 1 1 1 1xx xx x x
+ += ⇔ + + − + ++ +=
(*).
Đặt
10xt+=≥
thì từ (*) ta có phương trình:
( )
(
)
(
)
42 3 2
2 1 10 210 1 10
t t t tt t tt t t
− ++−= ⇔ − + = ⇔ − +− =
51
0, 1,
2
t tt
−
⇒= = =
(loại một nghiệm t < 0 ).
Thay trở về
2
1xt= −
suy ra phương trình có 3 nghiệm x = - 1, x = 0, x =
15
2
−
.
Ví dụ 5: Giải phương trình
2
2 22 1xx x−= −
.
Hướng dẫn giải:
Ở đây ta thấy trong căn có hệ số 2 nên nhân cả hai vế với 4 và biến đổi.
(
)
( )
22
2 221 4 412213821xx x xx x x− = −⇔ − + − − −= −
(*).
Đặt
21 0xt
−=≥
thì từ (*) ta có phương trình:
( )( )
42 42 2 2
2 38 2 8 30 2 1 2 3 0tt tttt tt tt− −= ⇔ − − −=⇔ − − + + =
(Với
0t ≥
)
2
2 10 1 2tt t⇔ − −= ⇒=+
(loại t < 0).
Thay trở về
2
1
2
t
x
+
=
suy ra phương trình có một nghiệm x =
22+
.
Ví dụ 6: Giải phương trình
2
45
33
12
x
xx
+
+=
.
Hướng dẫn giải:
Nhân cả hai vế của phương trình với 6 ta có:
2
18 18 12 15xx x+= +
tiếp tục nhân cả hai
vế với 8 thì
2
144 144 8 12 15xx x+= +
. Đặt
2
12 15 0 12 15x t xt+ =≥⇒ = −
ta có
phương trình:
( ) ( )
2
2 2 42
15 12 15 8 18 8 45 0t t tt t t− + − =⇔− −+ =
.
( )( )
22
25 290 61, 101tt tt t t⇔ + − − − = ⇒= − = +
(loại các nghiệm âm).
Thay trở về
2
15
12
t
x
−
=
suy ra phương trình có 2 nghiệm
4 6 2 10
,
66
xx
+ −+
=−=
.
UNhận xétU:
Việc giải phương trình bậc 4 góp phần quan trọng khi giải phương trình vô tỉ.
Các ví dụ trên đều có dạng chung khái quát là: ax
P
2
P + bx + c = d
px q+
.
Nếu không có hướng giải theo cách trên thì bình phương để giải phương trình bậc 4 như
phần I.
U2.2. Luyện tậpU:
Bài 7: Giải phương trình
2
5 5
xx+ +=
.
Bài 8: Giải phương trình
2
4 13 5 3 1 0xx x
− ++ +=
.
Bài 9: Giải phương trình
2
3
24
2
x
xx
+
+=
.
U3. Dạng 3U:
Trong căn có chứa tam thức bậc hai nhưng không phải bình phương đúng như dạng 1.
Ngoài căn cũng là tam thức bậc hai, ta gọi là đặt ẩn phụ không hoàn toàn.
Nhìn chung ta đều đưa phương trình về
( )( )
0u ax b u cx d−− −−=
.
Tuy nhiên ở đây ta giải hơi khác, xét ví dụ sau
Ví dụ 7: Giải phương trình
( )
22
6121 23xx x xx+ += + + +
.
Hướng dẫn giải:
Dễ thấy PT xác định với mọi x.
PT
( )
(
)
22
612(21)21 232xx x x xx⇔ + +− + = + + + −
( )
2
2
2
2
2
2 1 0 (a)
21
2121
2 32
2 3 2 1 (b)
xx
xx
xx x
xx
xx x
+ −=
+−
⇔ + −= + ⇔
+ ++
+ += −
+ Giải (a) ta được các nghiệm:
1 2, 1 2xx=−− =−+
+ Với
1
2
x ≥
, PT (b)
2
3 6 20
xx⇒ − −=
giải ra lấy nghiệm
3 15
3
x
+
=
Kết luận: phương trình có 3 nghiệm
1 2, 1 2xx=−− =−+
,
3 15
3
x
+
=
.
UNhận xétU: Phương trình có dạng
( )
22
ax px q mx n ax bx c+ += + + +
.
Ta có PP khái quát: Trừ thêm vào hai vế biểu thức trước căn là
( )
mx n
α
+
nhằm trục căn
vế phải: PT
( )
(
)
22
ax px q mx n mx n ax bx c
αα

⇔ + +− + = + + +−

Số
α
làm nháp thỏa điều kiện sau:
2
2
,0
p mb
pb
nqc
q nc
m
α
α αα
αα
−=
−
⇔ = − +−=
−=−
.
Ở Ví dụ 7 có
62
2
2
α
−
= =
.
Ví dụ 8: Giải phương trình
( )
2
2
2 214
11 xxx x
+ += +−
.
Hướng phân tích:
Làm nháp ta có
20 1
42
pb
m
α
−−
= = =
và ta thử:
PT
( )
( )
22
1
2 21 41 41
2
2
1
1
x
xx x x⇔ + +− − =

+−


−
quy đồng số 2 cho đẹp ta có
PT
( ) ( )
(
)
2
2
4 4 241 4 4 41
1xx x x x⇔ + +− − +
= −−
( )
2
222
2
43
4 41 12 14 34
41
11
4
4xxx x
x
x
xx⇔ + += += −
++
+
⇔ += − −⇔
…
Lạy trời sự may mắn đã đến.
UNhận xétU:
Bình phương hai vế ta cũng đưa về phương trình bậc 4, tuy nhiên đó chỉ là biện pháp cuối
cùng. Để củng cố ta xét thêm ví dụ
Ví dụ 9: Giải phương trình
22
4 20 ( 2) 2 4
xx x xx
+−=+ −+
.
Hướng phân tích:
Làm nháp ta có
( )
42
6
1
pb
m
α
−−
−
= = =
và ta thử:
PT
(
)
(
)
22
4 20 6 2 ( 2) 2 4 6xx x x xx
⇔ + − − + = + − +−
2
2
2
2
2
2 32 0
2 32
2 32 ( 2)
2 46
2 46 2
xx
xx
xx x
xx
xx x
−−=
−−
⇔−−=+ ⇔
− ++
− ++=+
…
Ồ, sự may mắn lại đến lần nữa!.
U3.2. Luyện tậpU:
Bài 10: Giải phương trình
( )
22
2 3 7 52 1xx x x
+ += + +
.
Bài 11: Giải phương trình
22
3 1 ( 2) 2xx x x
+ −= + +
.
Bài 12: Giải phương trình
(
)
22
1 1 23x x xx
+= + − +
.
Bài 13: Giải phương trình
( )
2 2
2 4141 1xxx xx++ +− +=
.
Bài 14: Giải phương trình
( )
22
5421 2x x x xx+ −= + +−
.
Bài 15: Giải phương trình
22
12 2x xx x−= −
.
UNhận xét:
Qua các ví dụ 7, ví dụ 8, ví dụ 9 ta lại thấy: sau khi biến đổi thì xuất hiện một phương
trình liên hệ căn thức và biểu thức trước căn, dạng ban đầu là:
( )
2
mx n ax bx c+ ++
Sau biến đổi thì
2
'ax bx c mx n
+ += +
Hay là
2
'n ax bx c mx= + +−
là số hữu tỉ.
Kết hợp máy tính cho ta thêm một hướng nhẩm nghiệm để phân tích thành nhân tử !
+ Xét phương trình
22
4 20 ( 2) 2 4
xx x xx+−=+ −+
Dùng máy tính tìm được hai nghiệm của phương trình:
2
2 46
xx− +=
.
Như thế ta thử phương trình
22
246 2 24 4xx x xx x−++=+⇔ −+=−
(VN)
Nếu x là nghiệm thì phép trừ
2
24xx x− +−
phải cho ta kết quả
4−
.
+ Xét phương trình
( )
22
6121 23xx x xx+ += + + +
Bằng máy tính ta tìm được các nghiệm: x = 2,29 ; x = -2,414 ; x = 0,414.
Không cần gán, ta tính xấp sĩ xem sao:
2
2 3 2 0.9989 1xx x+ + − ≈− ≈−
và như thế ta
có
(
)
22
2 32 1 2 32 1 0xx x xx x+ +− =−⇔ + +− + =
là một nhân tử ứng với
x =
2.29.
ULưu ý:
Nếu Hội đồng thi cấm sử dụng máy tính thì cách “tính bo” vẫn tốt hơn cả.
Phương trình vô tỉ cực kì đa dạng và phong phú không kém gì bất đẳng thức. Ngoài ra
phương trình vô tỉ sẽ là khâu quan trọng thứ hai trong giải hệ phương trình. Vì vậy
việc giải PT vô tỉ hết sức cần thiết trước khi giải hệ PT (nâng cao).
MỘT SỐ ĐỊNH HƯỚNG GIẢI PT VÔ TỈ - PHẦN 2
UII. Giải một số phương trình vô tỉ chứa căn bậc ba
U1. Cơ sở và định hướng giải:
Đối với học sinh lớp 10, 11 và học sinh THCS thì chúng ta không sử dụng đạo hàm, nên
có một kiến thức quan trọng và hay thường sử dụng là "Bình phương thiếu":
( )
( )
33 2 2
A B A B A AB B−=− + +
Như thế biểu thức
22
A AB B++
là không âm và nếu cộng thêm số dương thì luôn dương.
Mở rộng hơn khi giải một số phương trình vô tỉ thì ta sẽ định hướng đưa về dạng hàm số
bậc ba lẻ như:
( ) ( )
3
,, 0f t at bt a b=+>
. Nếu dùng đạo hàm thì đây là hàm đồng biến trên
R. Như trên đã nói, chúng ta đưa về phương trình
( ) ( )
fu fv=
và sau đó là chuyển vế đưa
về bình phương thiếu:
( )
( )
22
0u v au auv av b u v− + + + =⇔=
.
Chúng ta cũng lưu ý là: không phải bài nào cũng đưa về hàm số kiểu trên!
U2. Các ví dụ giải toán:
UVí dụ 1:U Giải phương trình
3
3
1 22 1xx+= −
(1).
Hướng phân tích:
Ta thấy hệ số trước căn là 2, hay nói như trên ta đoán b = 2 và
3
21vx= −
như thế còn
thiếu
3
av
, mà hệ số vế trái của xP
3
P là 1 nên khả năng a = 1, như vậy ta thêm bớt để tạo ra
3
21vx= −
. Ta có (1)
3
3
2 (2 x 1) 2 2 1xx x⇔ + = −+ −
Hướn
g dẫn giải:
Ta có (1)
3
3
2 (2 x 1) 2 2 1xx x⇔ + = −+ −
. Đặt
3
21vx= −
ta có phương trình:
( )
( )
33 22
2 2 20x xv v xvx xvv xv⇔ + = + ⇔ − + + + =⇔=
.
Thay trở về thì
3
3
15 15
2 1 2 1 0 1, ,
22
x x x x xx x
−+
= −⇔ − += ⇔ = = =
.
ULưu ý 1:
Không chỉ phương trình chứa căn bậc 3 mới chuyển được về dạng bậc 3 vì
3
()tt t=
.
UVí dụ 2:U Giải phương trình
32
3 4 2 (3 2) 3 1xxx x x+ + += + +
Hướng phân tích:
Ta thấy hệ số trong căn là 3, ở ngoài căn cũng là 3. Như thế ta tách số 2 và biến đổi vế trái
thành hằng đẳng thức:
PT
( )
32
( 3 31)(1)31131xxx x x x⇔ + + + + + = ++ +
33
( 1) ( 1) ( 3 1) 3 1xx x x⇔ + + += + + +
. Đặt
1; 3 1ux v x=+= +
và ta có
phương trình:
( )
( )
33 2 2
10u uv v uvu uvv uv+= +⇔ − + + + =⇔=
...
ULưu ý 2:
Đối với một số bài không phải là có ngay để biến đổi như trên.
UVí dụ 3:U Giải phương trình sau:
3
32 2 3
2 10 17 8 2 5− + − += −x x x x xx
Hướng phân tích:
Rõ ràng ta phát hiện có dạng trên rồi, ở đây có thể b = 2, gần giống ví dụ 1, nhưng vướng
mắc x
P
2
P trước căn. Ta nhận thấy x = 0 không phải là nghiệm, nên chia cả hai vế cho xP
3
P, ta
có:
3
23 2
10 17 8 5
2 21
xx x x
−+ − + = −
. Để cho gọn ta đặt
1
t
x
=
thì ta có:
32 2
3
8 17 10 2 2 5 1ttt t− + −= −
. Đến đây ta biến đổi vế trái thành hằng đẳng thức bậc 3, vế
phải cần thêm
( )
2
51at−
, hệ số a phụ thuộc t vế trái, nói các khác có dạng:
( ) ( )
( )
3
22
3
2 .. 2 2 ... 5 1 2 5 1at t at t− + − = −+ −
. Như thế a = 1 và thử số trong ngoặc dấu ba
chấm là 1, ta có PT
( ) ( )
( )
3
22
3
21 221 5 125 1t tt t⇔ − + −= −+ −
.
Tiếp tục đặt
2
3
2 1; 5 1utv t=−= −
thì ta có
33
22u uv v⇔+=+
( )
( )
22
20u v u uv v u v⇔ − + + + =⇔=
... ĐS:
17 97
12
x
±
=
Lời b
ình:
Đây là bài khó vì qua hai lần ẩn phụ mới đưa được về phương trình cần giải. Nhưng ít ra
có dạng thì cũng có hướng để mò.
Sau đây ta xét thêm một số ví dụ mà người ra đề cố ý lái đi để cho người giải phải mò.
UVí dụ 4:U Giải phương trình sau:
3
24 11 16 2 1 1 0x xx− − −−=
(4).
Hướng phân tich:
Ta nhận thấy phương trình có chứa hai căn thức nên trước hết chuyển vế
PT
3
24 11 1 16 2 1x xx⇔ −=+ −
sau đó cộng thêm một lượng vP
3
P xem thế nào
( )
3
24 11 24 11 16 2 1 24 10x x xx x⇔ − + − = −+ −
, ta cần giảm hệ số trước căn nên đưa bớt vào
căn:
( ) ( )
3
24 11 24 11 8 4 4 8 4 24 10x x x xx⇔ − + − = −+ −+ −
, rõ ràng xuất hiện số 4 nên tách ra
theo hằng đẳng thức:
( ) ( ) ( )
3
24 11 24 11 8 4 3 8 4 3 8 4 8 4 2x x x xxx⇔ − + − = −+ −+ − + −+
.
Đặt
3
24 11, 8 4 1v xux= − = −+
ta có phương trình:
33
v vu u+= +
. Mò được rồi!
Lời giải:
PT (4)
( ) ( )
3
24 11 24 11 16 2 1 24 10 8 8 4 3 8 4 2x x xx x xx x⇔ −+−= −+−= −+−+
( ) ( ) ( )
( )
(
)
3
24 11 24 11 8 4 3 1 8 4 3 8 4 2
84843843841841
x x x xx
xx x x x
⇔ −+−=−++ −+−+
= − −+ − + −++ −+
Đặt
3
24 11, 8 4 1v xux= − = −+
ta có phương trình:
( )
( )
33 2 2
10v v u u u v u uv v+= +⇔ − + + + =
3
24 11 8 4 1uv x x⇔=⇔ − = −+
. Đặt
84 0xy−=≥
suy ra
2
3
31 1yy+= +
lập phương hai vế
ta có
( )
2 32 2
3 1 3 31 30 0y y y y yy y+= + + +⇔ + = ⇔ =
.
Thay trở về ta được
1
2
x =
là nghiệm duy nhất của phương trình đã cho.
Như thế ta gặp hai bài khó gặm rồi! Sau đây ta xét bài dễ một ít.
UVí dụ 5:U Giải phương trình sau:
32 2
3
8 13 7 2 3 3x xx xx− += +−
.
Hướng phân tích:
Đặt
2
3
33xx v+ −=
trước hết ta cộng thêm hai vế một lượng vP
3
P xem sao:
32 2 3 32 3
8 13 7 3 3 2 8 12 10 3 2x xxxx vv x x x vv− + + + −= + ⇔ − + −= +
Bây giờ ghép hằng đẳng thức:
( ) ( )
3
3
21 221 2x x vv⇔ − + −= +
...
ĐS:
5 89
1,
16
xx
±
= =
.
UVí dụ 6:U Giải phương trình sau:
32
3
2 2 1 27 27 13 2x xxx−= − + −
.
Hướng phân tích:
Đặt
3
21vx= −
như thế vế trái là
2v
và ta thử cộng thêm vào lượng
3
21vx= −
vào hai vế, ta
có PT
3 32 32
2 2 1 27 27 13 2 27 27 15 3vvx xxx xxx⇔+=−+−+−=−+−
Tiếp tục biến đổi vế phải
( ) ( )
3
3 3 33
2 3 1 2 3 1 2 ...v v x x u u uv u v+ = − + −= + ⇒⇒=⇒ =
.
Cuối cùng ta được phương trình bậc ba đối với x. Đs:
0x =
.
Sau đây ta xét bài bậc chẵn thử xem
UVí dụ 7:U Giải phương trình sau:
( )
32
2 7 5423131xxx x x+ + += − −
(5)
Hướng phân tích:
Để tạo hằng đẳng thức vế trái hệ số nguyên thì ta nhân hai vế với 4, ta có:
( )
32
8 28 20 16 8 3 1 3 1xxx x x⇔ + + += − −
để giảm bớt hệ số 8 thì đưa vào trong ngoặc và
trong căn:
( )
32
8 28 20 16 12 4 12 4xxx x x+ + += − −
. Đặt
12 4 0xv−=≥
thì vế phải là
3
v
và
ta cần thêm vào vế trái một lượng
2
v
để xem thử:
( ) ( )
32
3 2 23 32
8 28 20 16 12 4 2 2 2 2x x x x vv x x vv⇔ + + + + −= + ⇔ + + + = +
(*).
Đặt
22 0xu+=>
thì (*)
( )
( )
32 32 22
0u u v v u v u v uv u v u v⇔+=+⇔− ++++=⇔=
.
Thay trở về ta có
2
2 2 12 4 1 3 1 2 0x x x x xx+= −⇔+= −⇒ −+=
(vô nghiệm).
UNhận xétU:
Biểu thức chứa căn bậc ba (hoặc căn bậc hai) là ẩn phụ mới
đặt là
( )
3
v k Qx=
(Hoặc
( )
v k Qx=
).
Trong đó k = 1; 2 hoặc 3 mà ta có thể thêm vào (nhân thêm).
Tiếp theo đưa vào căn hay ra căn (nếu có):
( ) ( )
32
3
;v k Qx v k Qx= =
 
 
.
Sau đó là cộng thêm cả hai vế một lượng
32
;av av
để biến đổi vế trái (vế còn lại) theo hằng
đẳng thức bậc ba, hệ số a này cũng là hệ số của
3
au
.
UVí dụ 8:U Giải phương trình sau:
3
32 32
6 12 7 9 19 11xx x xx x−+−=−+−+
Hướng phân tích:
Rõ ràng nếu ta cộng thêm (- x
P
3
P) thì vế trái triệt tiêu mất
3
x
.
Ta nhân cả hai vế với 2 rồi cộng sau thì sử lí được trường hợp này. Cụ thể là:
PT
3 2 32
3
2 12 24 14 2 9 19 11 2x x x xx x v⇔ − + − = −+ − + =
. Cộng thêm hai vế
3
v
ta có
PT
( )
3 2 32 3
2 12 24 14 9 19 11 2x x x xx x vv⇔ − + − +− + − + = +
( ) ( )
3
32 3 3
3 53 2 1 2 1 2xxx vvx x vv⇔− +−=+⇔−+ −=+
. Đặt
1ux= −
. . .
33
uv⇒=
.
Việc còn lại là giải phương trình bậc ba:
32 32
3 5 3 9 19 11xxx xx x− + −=− + − +
32
6 12 7 0xx x⇔ − + −=
. Đs: x = 1.
U3. Hỗ trợ Casio trong giải toán:
Từ các ví dụ và nhận xét trên ta có thể sử dụng Casio hỗ trợ trong giải toán. Ta thấy các
phương trình dẫn đến:
( )
3
Qx x u
αβ
= +=
với
11
1; 2; 3; ;
23
α
=
do vậy ta tiến hành tìm
nhanh u hơn bằng cách: Tìm X trước, sau đó tính
( )
3
Qx x
αβ
−=
(thử
α
tìm được
β
)
Trở về quá khứ xem nào
UVí dụ 5:U Giải phương trình sau:
32 2
3
8 13 7 2 3 3x xx xx− += +−
.
Hướng phân tích:
+ Nhập phương trình
32 2
3
8 13 7 2 3 3X XX XX− += +−
dù
ng Shift Solve ta tìm X = 1.
+ Sửa
thành
2
3
3 32XX X+ −−
bấm = thì kết quả bằng -1 (đẹp). Nên u = 2x -1.
(lấy số 2X từ 8X
P
3
P để thử cho nhanh)
UVí dụ 6:U Giải phương trình sau:
32
3
2 2 1 27 27 13 2x xxx−= − + −
.
Hướng phân tích:
+ N
hập phương trình
32
3
2 2 1 27 27 13 2X XXX−= − + −
dù
ng Shift Solve ta tìm X = 0
+ Sửa thành
3
2 13XX−−
bấm = thì kết quả bằng -1 (đẹp). Nên u = 3x -1.
UVí dụ 8:U Giải phương trình sau:
3
32 32
6 12 7 9 19 11xx x xx x−+−=−+−+
Hướng phân tích:
+ Nhập phương trình
32 32
3
6 12 7 9 19 11XX X XX X−+−=−+−+
dù
ng Shift Solve ta tìm X = 1.
+ Sửa
thành
32
3
9 19 11XX X X− + − +−
bấm = thì kết quả bằng -1 (đẹp). Nên u = x -1.
(Nhiệm vụ còn lại là thêm bớt đển biến đổi các vế trái theo u)
UVí dụ 9:U Giải phương trình
3
33
3
3
2
22
xx x x
x

−+
= +


.
Hướng phân tích:
Quy đồng số 2 cho đẹp:
( )
3
3
33
16 4 4 12xx x x x−= + +
.
+
Làm nháp ta dự đoán được ngay
3
x xu−=
(nếu không lũy thừa và khai triển thì mệt lắm)
Dễ thấy x = 0 là một nghiệm, ta thử nghiệm khác 0 (nếu có)
( )
3
3
33
16 4 4 12XX X X X−=+ +
Shift Solve 2 = kết quả 1.732
(bạn nào làm nhiều với căn thì đoán đây là
3
)
Sửa thành
( )
3
33
4 12XX X X−− +
bấm = ta có kết quả 0.
+ T
rở về phân tích ta có: Đặt
3
x xu−=
,
3
3
4 12x xv+=
và cộng cả hai vế với 4u ta có:
( )
( )
( )
3 3 3 3 22
4164 4 4 4 40u u x x x v u uv v uvu uvv uv+= + −+⇔+=+⇔− +++=⇔=
+ Thay trở về
3
33
4 12xx x x−= +
, đây lại là phương trình chứa căn bậc 3.
Nếu lập phương khử căn thì cũng giải được (Vì đã đoán được nghiệm ở bước nháp)
tuy nhiên ta có cách sau:
- Xét x = 0 là nghiệm
- Xét x khác 0, chia cả hai vế cho x th
ì
2
3
2
12
14x
x
−= +
. Đặt
2
0xt= >
khi đó ta có
( )
32 432
3
12
1 4 3 3 1 4 12 3 3 5 12 0t tttt t tttt
t
−= + ⇒ − +−=+ ⇒− + −− =
đây là phương trình
bậc 4 có nghiệm t = 3 nên ta có
( )
( )
3
3 34 0 3t tt t− + + = ⇒=
ĐS:
0, 3xx= = ±
.
ULưu ý:U Trên đây là mẹo nhỏ để tìm u và tính nghiệm cho việc giải sau này, chỉ áp dụng
được với một số phương trình nhất định.
U4. Một số bài toán khác:
Phần trước ta giải phương trình vô tỉ đưa về dạng đa thức, nhưng ở đây ta xét phương trình
"đa thức" nhưng để giải ta lại đi "khai căn"!
UVí dụ 10:U Giải phương trình sau:
( )
27x811x
3
3
−=+
.
Hướng phân tích:
Rõ ràng đây là phương trình đa thức bậc 9, như thế ta hạ bậc bằng cách khai căn bậc 3
PT
3
33
1 81 27 3 3 1xx x⇔ += − = −
(Đưa hệ số 3 ra ngoài căn trái ngược VD 7).
Đặt
3
3
31 31x vx v−= ⇒ −=
và cộng vào hai vế ta có:
3 3 33 3
1 3 1 3 3 3 ... 3 1 0x x v v x xv v xv x x⇔++−=+⇔+=+⇔⇔=⇔−+=
.
Giả sử phương trình có nghiệm
[ ]
2;2x∈−
thì ta đặt
[ ]
2sin , 0; 2x
αα π
= ∈
và có:
3
1 2 52
8sin 6sin 1 0 sin3 ,
2 18 3 18 3
kk
ππ ππ
αα α α α
− += ⇔ = ⇒ = + = +
.
Cho
[ ]
0;2
απ
∈
thì có k = 0, 1, 2 ta được
13 29
;;
18 18 18
πππ
α
=
và phương trình bậc ba chỉ có tối
đa 3 nghiệm nên PT có nghiệm là:
13 29
2sin , 2sin , 2sin
18 18 18
xx x
πππ
= = =
.
Sau đây ta sử lí trường hợp b < 0.
UVí dụ 11:U Giải phương trình
( )
3
33
3
43
2
−+ − =xx x
.
Hướng phân tích:
PT
3 33 33
33
3 33
43 2 2
2 22

⇔ −+= + ⇔ −=− + + +


xx x xx x x
Đặt
3
3
3
2
xt+=−
ta có phương trình
( )
( )
33 2 2
2 2 2 2 2 10x x t t x t x xt t− = −⇔ − + + − =
.
+ TH1: x =
t
⇔
xP
3
P = tP
3
P
3
33
36
()
22
⇔ =− + ⇔=−xx x
;
+ TH2:
Ta có hệ
33 3
22 2
3/2 ( ) 3 (x t) 3/2
1/2 ( ) 1/2

+=− + − +=−
⇔

++ = +
−=

x t x
t xt
x t xt x
t xt
.
Đặt x + t = S, xt = P,
2
4≥SP
ta có hệ
33
22
3 3 / 2 4 3 3 (*)
1/2 1/2

− =− −=
⇔

−= = −

SSP SS
S P PS
T
a có
2 22
11 2
1
24 3
= −≤ ⇒ ≤⇒ <PS S S S
. Khi đó đặt
( )
os , 0;= ∈Sc
αα π
thay vào (*)
ta được
3
4 os 3 os 3 os3 3−=⇔ =cc c
αα α
(Vô nghiệm).
Vậy phương trình đã cho có nghiệm duy nhất
3
6
2
= −x
.
Dưới đây ta xem một ví dụ đặt ẩn phụ đưa về dạng đa thức.
UVí dụ 12:U Giải phương trình
3
22
6 2 3 4 18 0x x xx+ + ++− =
.
Hướng phân tích:
Ta quan sát bộ (6; 2) và bộ (3; 1) tỉ lệ nên biến đổi sơ lược
PT
( )
3
22
23434300xx xx⇔ ++ + ++− =
. Đặt
3
2
34
txx =++
ta có phương trình
33
1
15
2
2 30 0
tt t
t
=−+
+− = ⇔
. Nhận xét vế trái tăng theo t, vế phải giảm theo t nên phương
trình có nghiệm dương duy nhất 2 < t < 3. Giả sử t = a + b thì ta có:
( ) ( ) ( )
3
33
11
15 3 15
22
ab ab a b ab ab

+ =− ++⇔+++ + =


, đến đây ta chọn a, b thỏa mãn:
33
33
33
15
15
1
1
30
216
2
ab
ab
ab
ab
+=
+=

⇔

= −
+=

như thế
33
;ab
là nghiệm của phương trình
2
1 12151
216 2
216
15
15 0
y yy− − =⇔= ±
suy ra
33
12151 12151
,
2 216 2 216
15 15
ba = =
+−
.
Tiếp đó
33
12151 12151
2 216 2 216
15 15
t
+−= +
. Bây giờ ta còn phải sử lí phương trình ẩn x
2
23
1 1 1 133 1 133 1
3 4 15
2 6 6 36 6 36 6
xx t t x t x t

++= =− + ⇔ + =− + ⇔=−± −


.
Vậy phương trình có hai nghiệm:
33
1 133 1 12151 12151
6 36 6 2 216 2 216
15 15
x


=−± − +
−


+
.
UNhận xétU: Nghiệm "khủng quá" cần kiên trì trong biến đổi!.
Cũng là phương trình có căn bậc ba, nhưng đôi khi biến x vẫn đóng vai trò hệ số.
UVí dụ 13:U Giải phương trình
3
22
1
8 15 9 1 5 2 2x x xx
x

− += + − −


Hướng phân tích:
Điều kiện
0x ≠
, quy đồng mẫu thức ta có:
( )
3
32 2
8 15 9 1 5 2 2x x xx x x− +=+ −−
(2).
Đặt
3
2 23
5 22 5 22xx v xx v−−=⇔ −−=
. Cộng thêm hai vế một lượng vP
3
P thì vế phải là:
3
(x 1).vv++
.
Bây giờ nhiệm vụ của chúng ta là biến đổi vế trái (ẩn x) thành dạng
3
(x 1).uu++
:
VT =
( ) ( )( )
3
32 2 32
8 15 9 5 2 2 8 10 7 2 2 1 1 2 1x x xx x x x x x x x− + + − −= − + −= − + + −
Như vậy phương trình (2) trở thành phương trình hai ẩn u, v mà x + 1 là hệ số:
( )
( )
3 3 22
(x 1). (x 1). 1 0u u v v u v u uv v x++ = ++ ⇔ − + + ++=
+ TH 1:
22
22 2 2
3
10 10
4 3(2x1) 4 40
24 2
uu
u uv v x v
u x v x
 
+ + + += ⇔ + + + += ⇔ + + − + + =
 
 
2
2
4 12x 8 7 0
2
u
vx

+ + − +=


(Vô nghiệm vì
2
12x 8 7x−+
> 0, có
' 16 84 0∆= − <
).
+ TH 2:
33 3 2 2
8 12 6 1 5 2 2uvuv x xx xx=⇔=⇔ − +−= −−
M
ời các bạn thực hành. ĐS:
9 113
1,
16
xx
±
= =
.
Sau đây ta lại xét ví dụ cần phải chia mà không phải quy đồng.
UVí dụ 14:U Giải phương trình
3
32 632
341 2x x x xx+ −= + +
.
Hướng phân tích:
Ta thấy trong căn có bậc cao nên nhận xét x khác 0 và chia cả hai vế cho x ta được
23
3
11
34 2xx x
xx
+ − = ++
. Đặt
3
3
1
2xv
x
++ =
và cộng hai vế với vP
3
P ta có:
( ) ( )
3
32 3 3
3 42 1 1x x x vv x x vv+ + += +⇔ + + + = +
. Đặt
1xu+=
ta có
33
u uv v+= +
...
ĐS:
3
1,
3
xx
±
=−=
.
Sau đây là các bài luyện tập bồi dưỡng cho học sinh.
U5. Luyện tập:
Bài 1: Giải phương trình
3
8 2 ( 2) 1x xx x+=+ +
.
Bài 2: Giải phương trình
3
3
2 33 2+= −xx
.
Bài 3: Giải phương trình
3
3
1
21
2
x
x
+
−=
.
B
ài 4: Giải phương trình
3
3
66 4 4xx= ++
.
Bài 5: Giải phương trình
3
3
6 18 4 1x xx+= − −
.
Bài 6: Giải phương trình
32 2
3
4 56 7 94xxx xx− − += + −
Bài 7: Giải phương trình
32
3
8 36 53 25 3 5xxx x− + −= −
.
Bài 8: Giải phương trình
( )
( )
2
4 1 3 52xx x x+=− −
.
Bài 9: Giải phương trình
222
3
7 1382 (133)x x xx x x− += + −
B
ài 10: Giải phương trình
3
32 2
5 12 6 2 1− + −= −+x x x xx
Bài 11: Giải phương trình
( )
3
2
2 5 2 52x x xx+ += + +
.
Bài 12: Giải phương trình
32
2
2
8 12 8 1
3 24 .
3 25
x xx
xx
xx
+ ++
+ +=
++
MỘT SỐ ĐỊNH HƯỚNG GIẢI PHƯƠNG TRÌNH VÔ TỈ - PHẦN 3
U3. Định hướng khái quát giải một lớp bài toánU:
Ua. Đặt vấn đềU:
Trước hết ta quan sát các bài toán sau: Giải các phương trình
+)
2
55xx
+)
2
2 61 4 5xx x 
+)
2
2 4 23 2 1x x xx− += −
+)
−− = + −
22
12 ( 3) 10xx x x
+)
2
4 6 ( 1) 6 6x x xx+= − −−
+)
2
9 25 ( 1) 2 5 5.x x xx+=− +−
Nhận dạng phương trình:
Ta thấy có sự khác nhau ở trong căn, ở ngoài căn và biểu thức trước căn. Các phương trình có dạng:
( )
22
' ''Ax Bx C mx n A x B x C+ += + + +
với A. A' không đồng thời bằng 0.
Phương pháp chung nhất để giải các phương trình trên là bình phương đưa về phương trình đa thức
bậc 4.
Tuy nhiên việc giải phương trình bậc 4 là được nhưng cũng không đơn giản chút nào mà còn khá dài.
Đôi khi phải hỗ trợ máy tính Casio, nếu không thì việc giải rất vất vả, nhất là phương trình vô nghiệm!
Ưu điểm là: chúng ta chủ động trong việc giải phương trình, dù khó khăn cực nhọc và có hy vọng rất lớn
để giải thành công.
Nếu không đưa về phương trình bậc 4 thì chúng ta tìm cách giải như:
Đặt ẩn phụ hoàn toàn hay không hoàn toàn, chuyển về hệ phương trình, nhân liên hợp trục căn kết hợp
nhẩm nghiệm các loại ... thành thử thiếu định hướng chung, phải loay hoay và xoay các kiểu mới làm
được bài. Tuy nói như vậy nhưng không phải đặt ẩn phụ là đặt được ngay, chuyển về hệ là chuyển được
ngay, nhân liên hợp trục căn được ngay, ...Như thế có nghĩa là phải nắm giữ được "các dạng con" hay là
các nhánh khác nhau thì mới giải tốt được, nếu không chúng ta cứ mò từ dạng này sang dạng khác. Nói
cách khác: chúng ta bị các dạng phương trình chi phối, rơi vào thế bị động trong giải toán.
Chính vì vậy chúng ta đặt ra là: có định hướng giải chung cho tất cả 6 phương trình trên đồng thời
khắc phục được các nhược điểm nào đó, hay nói cách khác: Phương pháp chúng ta đưa ra phải thỏa mãn
các yêu cầu:
+ Dễ hiểu hay tương đối dễ hiểu
+ Không quá cồng kềnh
+ Dễ áp dụng hay tương đối dễ áp dụng.
+ Có thể không cần sử dụng máy tính Casio. Đây chính là điều nói lên: Bạn sử dụng Casio quen rồi, nếu
thiếu công cụ này thì dễ bị lúng túng. Đặc biệt là nghiệm vô tỉ!
Phương pháp chúng ta đưa ra phức tạp và cồng kềnh khó nhớ, khó hiểu, khó áp dụng thì cũng không
mang lại ý nghĩa thực tế bao nhiêu.
Thứ hai ta xét phương trình sau:
22
3 6 2 13 1xx x x+ ++ −= +
, ta viết lại phương trình thành:
22
3 63 1 2 1xx x x+ + = +− −
(Sau khi đặt điều kiện). Bình phương 2 vế và thu gọn ta được phương
trình mới:
22
10 3 6 2(3 1) 2 1 0xx x x+ −− + −=
. Như thế ta lại chuyển về dạng của 6 phương trình đầu,
điều này nói lên: coi như 6 phương trình đầu là hệ quả của các phương trình khác thì việc định hướng
giải chúng lại mang ý nghĩa lớn. Nếu chúng ta làm được điều này thì việc chuyển vế bình phương sẽ
không còn đáng ngại. Nắm thế chủ động trong giải toán!. Dưới đây ta xét cách giải một vài ví dụ sau đó
khái quát cách giải.
Ub. Các ví dụ giải toán:
U Ví dụ 1:U Giải phương trình:
22
3 32(6)3 23xx x xx++=+ −−
(1)
.
Hướng phân tích:
(Nhận xét: nhắc lại 1 tí mà không làm theo cách trừ cả hai vế với 5(x + 6) và trục căn vế phải).
Làm nháp: ta chuyển vế thành
++−+ −−=
22
3 32(6)3 230xx x xx
(*).
Mục tiêu của ta là:
( )
( )( )
*0ax b u cx d u⇔ ++ ++ =
(**). Bây giờ ta lại đi phân tích ngược trở về
(nhân phá ngoặc nhưng không cần phá rời ra - Tách phần đa thức và căn):
( ) ( )( ) ( )
2
** 3 2 3 0axbcxd x x acxbd u⇔ + + + − −+ + ++ =


(***).
Cân bằng các hệ số từ (***) và (*) ta có hai hệ sau:
1 6; 3 2
&
33 23
a c d b bd
ac ad bc
+=− +=− −=


+= + −=

.
Ta chọn a = -1, c = 0 và hệ sau có nghiệm
1, 5bd=−=−
.
Hướng dẫn giải:
( )
(
)
(
)
22
1 13 2353 230x xx xx⇔−−+ − − −+ − − =
.
+ TH1: Với
10 1xx− − ≤ ⇔ ≥−
Ta có phương trình
22
1 3 2 3 2 4 40 1 3x xx xx x+= −−⇒ −−=⇒=±
(Thỏa mãn).
+ TH2:
22
1 85
532332280
3
xx xx x
±
= −−⇒ −−=⇒=
.
Kết luận: nghiệm phương trình là
±
=±= ⋅
1 85
1 3,
3
xx
U Ví dụ 2:U Giải phương trình:
2
55xx
(2)
.
Hướng phân tích:
Làm nháp: ta chuyển vế thành
2
55 0xx 
(*).
Mục tiêu là:
( )
( )
( )
*0ax b u cx d u⇔ ++ ++ =
(**). Bây giờ ta phân tích ngược trở về:
( ) ( )( ) ( )
** 5 0axbcxd x acxbd u⇔ + + +−+ + ++ =


(***).
Cân bằng các hệ số từ (***) và (*) ta có hai hệ sau:
0 1; 5 5
&
1 10
a c d b bd
ac ad bc
+= += +=


=− + −=

.
Ta chọn a = 1, c = -1 và hệ sau có nghiệm
0, 1bd= =
.
Hướng dẫn giải:
( )
( )( )
2 5 15 0x xx x⇔+− −++−=
.
+ TH1: Với
0x ≤
. Ta có phương trình :
5xx−= −
2
1 21
50
2
xx x
−−
⇒ +−=⇒=
(loại nghiệm dương).
+ TH2: Với
10 1xx−+≤ ⇔ ≥
. Ta có phương trình:
15xx
−= −
2
1 17
40
2
xx x
+
⇒ −−=⇒=
(loại nghiệm âm).
Kết luận: phương trình có hai nghiệm là
−− +
= = ⋅
1 21 1 17
,
22
xx
U PHƯƠNG PHÁP PHÂN TÍCH NGƯỢC:
Để giải phương trình:
(
)
22
' ''
Ax Bx C mx n A x B x C+ += + + +
ta thực hiện theo phương pháp
phân tích ngược như sau:
Chuyển vế :
( )
22
' ' '0Ax Bx C mx n A x B x C++− + + +=
Hoặc
( )
22
' ' '0Ax Bx C mx n A x B x C− − −+ + + + =
Khi đó phân tích nhân tử dạng:
( )( )
0ax b u cx d u++ ++ =
.
Làm nháp nhân phá ngoặc và cân bằng hệ số. Đảm bảo hệ số có nghiệm.
U Ví dụ 3:U Giải phương trình:
2
4 6 ( 1) 6 6x x xx+= − −−
.
Hướng phân tích:
Làm nháp: chuyển vế thành
− −+ − −−=
2
4 6 ( 1) 6 6 0x x xx
(*).
Mục tiêu là:
( )
(
)
(
)
*0ax b u cx d u
⇔ ++ ++ =
(**). Bây giờ ta phân tích ngược trở về:
( ) ( )( ) ( )
2
** 6 6 0axbcxd x x acxbd u⇔ + + + −−+ + ++ =


(***).
Cân bằng các hệ số từ (***) và (*) ta có hai hệ sau:
1 1; 6 6
&
60 1 4
a c d b bd
ac ad bc
+= +=− −=−


+ = + −=−

.
Ta chọn a = 3, c = -2 và hệ sau có nghiệm
0, 1bd= = −
.
Hướng dẫn giải:
( )
(
)
(
)
22
*36621660x xx x xx⇔ + −− − −+ −− =
.
+ TH1: Với
30x ≤
.Ta có phương trình :
22 2
966360x xx xx= −−⇒ ++=
(vô nghiệm)
+ TH2: Với
2 1 0 1/2xx− − ≤ ⇔ ≥−
. Ta có phương trình:
2
21 6 6x xx+= −−
2
7
2 5 70
2
xx x⇒ − −=⇒=
(Thỏa mãn) (loại nghiệm -1).
Kết luận: phương trình có một nghiệm là
= ⋅
7
2
x
UNhận xétU:
Cách nhẩm của chúng ta mặc dù chưa được "ngon lành" và hơi chậm khi làm nháp, nhưng ưu điểm là
rèn luyện tư duy, ít ra cũng có hướng để mò, ngoài ra lời giải tương đối ngắn gọn. Hơn nữa không quá
khó cũng như không quá lệ thuộc máy tính Casio, chủ động trong giải toán dạng này.
U Ví dụ 4:U Giải phương trình:
2
6 9 (2 1) 15 9 0x x xx
.
Hướng phân tích:
Làm nháp: Ta cần:
0axbcxd u acxbdu




Ta có:
2 1; 9 9
&
15 0 1
6
a c d b bd
ac ad bc
+= += +=


+= ++=

suy ra hệ có nghiệm:
5, 3, 0, 1ac bd= =−= =
.
Hướng dẫn giải:
(
)
(
)
2 22
6 9 (2 1) 15 9 0 5 15 9 3 1 15 9 0x x xx x xx x xx++ + ++=⇔ + ++ − ++ ++ =
.
+ TH1:
50x ≤
, ta có phương trình:
22
9
5 15 9 10 9 0
10
x xx xx x− = ++⇒ −−=⇒=−
.
+ TH2:
1
3 10
3
xx− +≤ ⇔ ≥
ta có phương trình:
22
3 1 15 9 6 7 8 0x xx x x x−= ++⇒ + +=⇒∈∅
.
Kết luận: Phương trình đã cho có nghiệm duy nhất là
9
10
x =−⋅
U Ví dụ 5:U Giải phương trình:
2
11 ( 3) 2 5 7x x xx
( ).x
Hướng phân tích:
2
11 ( 3) 2 5 7 0x x xx
. Ta cần:
0axbcxd u acxbdu




Ta có
1
2
ac
ac


và
3; 7 11
2, 1, 4, 1
51
d b bd
ac bd
ad bc

 

.
Hướng dẫn giải:
2 22
11(3)2 57 24 2 57 1 2 570x x xx x xx x xx   
+ TH1:
2 40 2xx 
, ta có phương trình:
22
2 4 2 5 7 2 11 23 0x xx x x x  
.
+ TH2:
10 1xx 
, ta có:
2
3 41
1 2 57
2
x xx x


.
Kết luận: Phương trình có một nghiệm là
3 41
2
x

.
U Ví dụ 6:U Giải phương trình:
22
4 19 6 2 4 3.x x xx x 
( ).x
Hướng phân tích:
Nháp:
22
4 19 6 2 4 3 0
x x xx x 
0axbcxd u acxbdu




Ta có
1
24
ac
ac


và
0; 3 6
4 19
d b bd
ad bc


. Hệ có nghiệm
2, 3, 3, 3a cdb 
.
Hướng dẫn giải:
22 2 2
4 196 2 43 232 43332 430.x x xxx x xx x xx   
+ TH1:
2
2
2 30
3/2
4 13
2 16 6 0
23 2 43
x
x
x
xx
x xx









.
+TH2:
2
2
3 30
1
11 79
7 22 6 0
7
33 2 43
x
x
x
xx
x xx










.
Kết luận: Phương trình đã cho có 2 nghiệm là
11 79
4 13,
7
xx
 
U Ví dụ 7:U Giải phương trình:
22
12 ( 3) 10xx x x

.
Hướng phân tích:
Nháp:
22
12 ( 3) 10 0
xx x x 
0axbcxd u acxbdu




Ta có
1
11
ac
ac


và
3; 10 12
1
d b bd
ad bc


. Hệ có nghiệm
1, 0, 1, 2
acdb 
.
Hướng dẫn giải:
2 2 22
12 ( 3) 10 2 10 1 10 0xx x x x x x  
2
2
2
2 10 3.
2 4 60
x
xx x
xx



Kết luận: Phương trình có nghiệm duy nhất
3.x

U Ví dụ 8:U [Toán Học & Tuổi Trẻ số 420] Giải phương trình:
2
4 14 11 4 6 10xx x 
.
Hướng phân tích:
Nháp:
2
4 14 11 4 6 10 0xx x 
0axbcxd u acxbdu




Ta có
0
4
ac
ac


và
4; 10 11
6 14
d b bd
ad bc


. Hệ có nghiệm
2, 2, 3, 7ac d b  
.
Hướng dẫn giải:
2
4 14 11 4 6 10 2 7 6 10 2 3 6 10 0xx x x x x x 
(*).
Vì
6 10 0 2 7 0xx 
nên
3 13
* 2 3 6 10
4
x xx


.
Kết luận: Phương trình có 1 nghiệm là
3 13
4
x

.
U Ví dụ 9:U [Tuyển sinh lớp 10 Chuyên Lam Sơn Thanh Hóa 2014]
Giải phương trình:
22
12 2 2 3 2x x xx x 
.
Hướng phân tích:
Nháp:
22
2 3 2 12 2 0xx x xx 
0axbcxd u acxbdu




Ta có
1
22
ac
ac


và
1; 2
23
d b bd
ad bc
 

. Hệ có nghiệm
1, 0, 1, 2a cdb 
.
Hướng dẫn giải:
22 2 2
122232 222122 0x xxxx x xx xx  
2
2
20
2
3 13
6 40
222
x
x
x
xx
x xx









.
Kết luận: Phương trình có hai nghiệm
3 13x 
.
U Ví dụ 10:U Giải phương trình:
22
4 11 6 ( 1) 2 6 6x x x xx 
.
Hướng phân tích:
Nháp:
22
4 11 6 1 2 6 6 0x x x xx 
Ta cần:
0axbcxd u acxbdu




Ta có
1
24
ac
ac


và
1; 6 6
6 11
d b bd
ad bc
 

. Hệ có nghiệm
3, 2, 3, 4ac db  
.
Hướng dẫn giải:
22 2 2
4 116(1)2 66 34 2 66232 660x x x xx x xx x xx   
+ TH1:
2
2
4
3 40
9 11
3
7
34 2 66
7 18 10 0
x
x
x
x xx
xx








.
+ TH2:
2
2
3
2 30
33
2
2
23 2 66
2 6 30
x
x
x
x xx
xx








.
Kết luận: Phương trình có 2 nghiệm là:
9 11 3 3
,
72
xx


.
U Ví dụ 11:U Giải phương trình:
2
2 4 2 32 1x x xx 
.
Hướng phân tích:
Nháp:
2
2 4 232 1 0x x xx 
0axbcxd u acxbdu




Ta có:
3 0; 1 2
&
2 24
ac db bd
ac ad bc









suy ra hệ vô nghiệm. Vậy để hệ có nghiệm ta chia
cả hai vế cho 2:
2
3
1 21 210
2
x x xx 
và có
3
0; 1 1
&
2
22
1
d b bd
ac
ad bc
ac







như thế:
1
2, , 0
2
a c bd 
.
Hướng dẫn giải:
2
1
2 42321 2 21 210
2
xx xx xx xx

 

. Vì
1
2
x
nên suy ra:
2
1
2 1 8 4 0 4 23
2
x x xx x 
(Thỏa mãn).
Kết luận: Phương trình có hai nghiệm:
4 23x 
.
UChú ý 1U:
+ Tại sao ta không nhân với 2; 3; 4; ... mà ta nhân với
1
2
k =
? Sau đây ta phân tích kỹ hơn một chút:
Lý do ta chia (hay nhân) thêm hằng số để điều chỉnh các tích và tổng
'
a c km
ac A kA
+=
+=
và
'
b d kn
bd C kC
+=
+=
Sao cho đảm bảo hệ có nghiệm thỏa mãn
'ad bc B kB++=
.
Cụ thể
2
2 4 2 3 2 10kx kx k kx x− + − + −=
với
0, 1 2
24
b d bd k
ad bc k
+ = −=−
+ +=
, nếu
1
2
k =
thì b = d = 0
+ Nếu phương trình có dạng
( )
( )
2
2
0ux
α βγ
+ + +=
thì không thể phân tích thành nhân tử.
Bởi vậy trên đây là định hướng phân tích nhưng không tham hy vọng quá lớn để bao toàn bộ các bài
toán nói trên.
U Ví dụ 12:U [Olympic 30/04/2013] Giải phương trình:
2
( 3) 8 48 24x xx x 
.
Hướng phân tích:
2
2 48 (2 6) 8 48 0x x xx 
0axbcxd u acxbdu




Ta có
2
10
ac
ac


và
6; 48 48
82
d b bd
ad bc


. Hệ có nghiệm
1, 1, 0, 6acd b
.
Hướng dẫn giải:
22
( 3) 8 48 24 2 48 (2 6) 8 48 0x xx x x x xx  
22
6 8 48 8 48 0x xx x xx 
+ TH1:
60 6xx 
, ta có
22
6 8 48 2 20 12 0 5 31x xx x x x 
.
+ TH2:
0x
, ta có
22
8 48 2 8 48 0 2 2 7x xx xx x 
.
Kết luận: Phương trình có 2 nghiệm là
2 2 7, 5 31.xx 
(Ở trên nếu không nhân thêm 2 thì a + c = 1, ac = 1 sẽ vô nghiệm! Vậy nếu a = c = 1 thì a + c = 2).
U Ví dụ 13:U Giải phương trình:
22
3
5 3 (1 3 ) 2 1
2
x x xx 
.
Hướng phân tích:
Nháp:
22
5 3 3 13
( )2 1 0
2 4 2 22
x x xx 
0axbcxd u acxbdu




.
Ta có
3
2
5
2
2
ac
ac


và
13
;1
22
3
4
d b bd
ad bc
 

có nghiệm
11
1, , 1,
22
ac db  
.
Hướng dẫn giải:
PT
2 2 22
5 3 3 13 1 1
( )210 21 1210
2 4 2 22 2 2
x x xx x
x x x











+ TH1:
2
2
1
1
0
16
2
2
2
4 4 50
2 1 22 1
x
x
x
xx
xx










.
+ TH2:
2
2
1
2
10
2 2 15
2
7 4 80
7
2 22 1
x
x
x
xx
xx









.
Kết luận: Phương trình có 3 nghiệm là
6 1 2 2 15
,
27
xx


ULời bìnhU:
Qua các ví dụ trên ta cũng đã làm chủ được loại toán này, chủ động trong giải toán cho dù thay đổi các
biểu thức trong căn hay ngoài căn, là bậc nhất hay bậc hai.
U Ví dụ 14:U Giải phương trình:
2
5(8 11 ) 27(2 1) 3 2xx x x

()x ∈
.
Hướng phân tích:
Bài này tổng hai số a + c = 54 khá lớn so với tích nên nhân cả hai vế với 5 và đặt
−=53 2xu
.
2
200 275 54 27 75 50 0x xx x 
Ta cần:
0axbcxd u acxbdu




Ta có
54
200
ac
ac


và
27; 50 0
75 275
d b bd
ad bc


có nghiệm
4, 50, 25, 2ac d b   
.
Hướng dẫn giải:
22
5(8 11 ) 27(2 1) 3 2 200 275 54 27 75 50 0
xx x x x xx x 
4 2 75 50 50 25 75 50 0xx x x

+ TH1:
2
1
4 20
27
2,
2
16
4 2 75 50
16 59 54 0
x
x
xx
xx
xx









.
+ TH2:
2
1
50 25 0
2
10 5 3 2
100 97 27 0
x
x
xx
xx








(Vô nghiệm).
Kết luận: Phương trình có 2 nghiệm là
27
2,
16
xx 
UChú ý 2U:
Câu hỏi đặt ra là: tại sao ta không nhân với 2; 4; 6; .. mà ta nhân với 5?. Như trên đã nói:
54
40
ac
ac k
+=
=
và
2
27;
20
db
bd k
+=
−=
nên ta chọn k để hai hệ có nghiệm đẹp một tí. Ta có thể hình dung như
sau tách 54 = 2 + 52 = 4 + 50 = 6 + 48 .. và thử nhân các cặp xem sao?
Hay là
2.52 4.50
...
40 40 40
ac
k = = = =
và
2
bd
k =
mà ta cũng chọn tổng a + c âm?
Như thế ta vừa chọn được a, c, b, d vừa biết cần nhân như thế nào để thử.
Để củng cố ta xét thêm vài ví dụ nhân thêm.
U Ví dụ 15:U Giải phương trình:
22
15 12 12 10(2 1) 3xx xx

()x
.
Hướng phân tích:
Nếu để nguyên thì a + c = -20 và ac = 14, tách -20 = -2 + -18 = -4 + -16 ...và tích lại thì bằng 36, 64, ...
khi đó nhân thêm cả hai vế với k và đưa vào căn thì
22 2
3kx k
như thế:
2
15ac k k
thử tích 36
trước:
2
36 15 3k kk 
. Nên PT
22
45 36 36 (20 10) 9 27 0xx x x 
.
Ta cần
( )( ) ( )
0axbcxd u acxbd u+ + ++ + ++ =


Nên
20
9 45
ac
ac
+=−
+=
và
10; 27 36
36
d b bd
ad bc
+=− + =
+=
hệ có nghiệm
2, 18, 9, 1ac db=−=− =−=−
.
Hướng dẫn giải:
PT
22
45 36 36 (20 10) 9 27 0xx x x 
22
2 1 9 27 18 9 9 27 0xx xx
+ TH1:
2
2
1
2 10
2
2 1 9 27
5 4 26 0
x
x
xx
xx








(Vô nghiệm).
+ TH2:
2
2
1
18 9 0
18 114
2
35
18 9 9 27
35 36 6 0
x
x
x
xx
xx










Kết luận: Phương trình có 1 nghiệm là
18 114
35
x

.
U Ví dụ 16:U Giải phương trình:
22
3 2 7 3( 1) 3xx x x 
()x
.
Hướng phân tích:
Nếu để nguyên thì a + c = -3 và ac = 2 do đó tách -3 = -2 + -1.và tích lại thì bằng 2 (đẹp), tuy nhiên khi
đó b+ d = -3, bd = 4, nhân cả hai vế với k và đưa vào căn thì
22 2
3kx k
như thế:
2
37bd k k
thử
tích 2 thì:
2
23 7 2k kk 
. Nên PT
22
6 4 14 (3 3) 4 12 0xx x x  
.
Ta cần
( )( ) ( )
0axbcxd u acxbd u+ + ++ + ++ =


Nên
3
46
ac
ac
+=−
+=
và
3; 12 14
4
d b bd
ad bc
+=− + =
+=
hệ có nghiệm
2, 1, 1, 2acdb=−=−=−=−
.
Hướng dẫn giải:
PT
22
6 4 14 (3 3) 4 12 0xx x x  
22
2 2 4 12 1 4 12 0xx xx
+ TH1:
2
2 20
1
1
2 13
2 2 4 12
x
x
x
x
xx








.
+ TH2:
2
2
10
1
3 2 11 0
1 4 12
x
x
xx
xx








(Vô nghiệm).
Kết luận: Phương trình có 1 nghiệm là
1.x =
U Ví dụ 17:U Giải phương trình:
22
10 9 3 8 2 3 1 0x x xx x 
.
Hướng phân tích:
Nếu để nguyên thì a + c = -8 và ac = 8, tách -8 = -2 + -6 = -4 + -4... và tích lại thì bằng 12, 16... , ...
khi đó nhân thêm cả hai vế với k và đưa vào căn
22 2 2
23kx kx k
như thế:
2
2 10ac k k
thử tích
ac = 12 thì:
2
12 2 10 3k kk 
, nên PT
22
30 27 9 8 18 27 9 0xx xxx  
(*).
Ta cần
( )( ) ( )
0axbcxd u acxbd u+ + ++ + ++ =


Nên
8
18 30
ac
ac
+=−
+=
và
0; 9 9
27 27
d b bd
ad bc
+= +=
+−=−
hệ có nghiệm
2, 6, 0, 0a c db=−=−= =
.
Hướng dẫn giải:
PT
22
30 27 9 8 18 27 9 0xx xxx  
22
2 18 27 9 6 18 27 9 0x xx x xx 
+ TH1:
2
2
20
0
33
,
14 27 9 0
72
2 18 27 9
x
x
xx
xx
x xx








.
+ TH2:
2
2
60
0
3 17
18 27 9 0
4
6 18 27 9
x
x
x
xx
x xx









.
Kết luận: Phương trình có 3 nghiệm là
3 3 3 17
,,
72 4
xxx


.
UChú ý 3U:
Chúng ta cũng có thể xét một vài ví dụ mà sự phân tích thành hệ số vô tỉ. Các ví dụ này không nhiều
nhưng không có nghĩa là không làm được, với lưu ý các số
pq
và
pq
có tổng bằng 2p và tích
bằng
2
pq
đều là các số hữu tỉ.
U Ví dụ 18:U Giải phương trình:
22
64 1x x xx 
.
Hướng phân tích:
PT
22
16 4 0 0x x x x ax b u cx d u 
.
Ta cần
0 1; 1
&
61 4 1
a c b d bd
ac ad
bc









. Do đó:
5, 5
15 15
,
22
ac
bd



.
+ TH1:
2 22
51 3 5
64 5 645 55
22
xxx xx
x x

 
2
5 11 2
53
15 0
22
xx x


(loại).
+ TH2:
2 22
51 3 5
64 5 645 55
22
xxx xx
x x


2
51 21
53
15 0
22
xx x


(Thỏa mãn ).
U Ví dụ 19:U Giải phương trình:
2
3
1
1
x
x
x

.
Hướng phân tích:
Điều kiện:
0;1x
. Quy đồng và chuyển vế ta thu được:
2
3 1 10xx x 
.
Nhân hai vế với 6 ta có:
2
18 2 2 9 9 0 0x x x ax b u cx d u 
.
Xét các hệ:
2 2; 9
&
9 18
a c b d bd
ac ad bc


 






ta có
1 10 1 10
&
1 10 1 10
ab
cd











+ TH1:
2
9 9 10 1 1xx
2
1 10 1 0xx 
(cả hai nghiệm đều loại).
+ TH2:
2
9 9 10 1 1xx
2
1 10 1 0xx 
1 10 5 2
2
x


Vậy pt có một nghiệm:
51 21
2
x

.
U MỘT SỐ ỨNG DỤNGU.
U Ví dụ 20:U Giải phương trình:
2
30
1.
2 7 99
x
xx


( ).x
Hướng phân tích:
Điều kiện:
2
2 7 99 0xx 
.
Từ PT suy ra
22
30 ( 1)( 2 7 9 9) 9 39 ( 1) 2 7 9 0x xx x x xx  
(*).
Ta cần
0axbcxd u acxbdu




. Cân bằng hệ số:
Ta có
1
20
ac
ac


và
1; 9 39
79
d b bd
ad bc


. Hệ có nghiệm
2, 1, 5, 6ac d b  
.
Như thế
22
* 26 2 79 5 2 790x xx x xx  
+ TH1:
2
2
2 60
3
2 17 45 0
26 2 79
x
x
xx
x xx








(Vô nghiệm).
+ TH2:
2
2
50
5
3 145
3 34 0
2
5 2 79
x
x
x
xx
x xx









, (
4x
).
Kết luận: Phương trình có 2 nghiệm là
3 145
2
x

U Ví dụ 21:U Giải phương trình:
2 43
3 21 3 0x x xx 
()x
.
Hướng phân tích:
Điều kiện:
43
2
30
1
1
3 2 10
3
xx
x
xx


hoặc
1
0
3
x
+ Nếu
1
0
3
x
thì
2 43 2 2
3 21 3 03 21 3 0xx xx xx xxx  
(*)
Ta cần
0axbcxd u acxbdu




. Cân bằng hệ số:
Ta có
1
33
ac
ac


và
0; 1
12
d b bd
ad bc


. Hệ có nghiệm
1, 0, 1, 1acdb 
.
Nên
22
* 13 13 0x xx xx
2
3 17
13
4
x xxx


.
+ Nếu
1
1
3
x 
thì
2 43 2 2
3 21 3 03 21 3 0xx xx xx xxx 
(**)
Ta cần
0axbcxd u acxbdu




. Cân bằng hệ số:
Ta có
1
33
ac
ac


và
0; 1
12
d b bd
ad bc


. Hệ có nghiệm
1, 0, 1, 1a cd b 
.
Nên
22
** 13 13 0x xx xx
2
1 13
13
6
xxx


.
Kết luận: Phương trình có hai nghiệm
3 17 1 13
,
46
xx


.
U Ví dụ 22:U Giải phương trình sau:
22
3 6 2 13 1xx x x 
.
Hướng phân tích:
Điều kiện:
22
11
210,2131
32
x xx x 
hoặc
1
2
x
.
Ta viết lại phương trình thành:
22
3 63 1 2 1xx x x 
. Bình phương 2 vế và thu gọn ta
được phương trình mới:
22
10 3 6 (3 1) 8 4 0xx x x 
(*) (đưa 2 vào căn).
Ta cần
0axbcxd u acxbdu




. Cân bằng hệ số:
Ta có
3
8 10
ac
ac


và
1; 4 6
3
d b bd
ad bc
 

. Hệ có nghiệm
2, 1, 2, 1acdb  
.
Như thế
22
* 2184 2840x xx x
+ TH1:
2
2
1
2 10
16
2
2
21 8 4
4 4 50
x
x
x
xx
xx









.
+ TH2:
2
2
20
2
2 2 15
7 4 80
7
284
x
x
x
xx
xx









.
Kết luận: Kết hợp điều kiện thì phương trình đã cho có hai nghiệm
1 6 2 2 15
,
27
xx


.
U Ví dụ 23:U Giải phương trình sau:
2
1 4 13x xx x
.
Hướng phân tích:
Điều kiện:
0, 1 3xx x 
. Bình phương 2 vế và thu gọn ta được phương trình mới:
22
2 11 2 ( 1) 4 16 4 0xx x xx 
(*). Ta cần
0axbcxd u acxbdu




. Cân bằng hệ số:
Ta có
1
42
ac
ac


và
1; 4 2
16 11
d b bd
ad bc


. Hệ có nghiệm
2, 1, 2, 1ac db  
.
Như thế
22
* 2 1 4 16 4 2 4 16 4 0x xx x xx  
+ TH1:
2
1
2 10
1
2
4
1 2 4 16 4
12 3
x
x
x
xxx
x







(Thỏa mãn điều kiện).
+ TH2:
2
2
20
2
4
3 12 0
2 4 16 4
x
x
x
xx
x xx








(Thỏa mãn điều kiện).
Kết luận: Phương trình có hai nghiệm
1
, 4.
4
xx
U Ví dụ 24:U Giải phương trình sau:
2
4 1 1 3 21 1x x xx
.
Hướng phân tích:
Điều kiện:
1x
.Viết lại
2
4 1 21 3 1 1x xx x 
. Bình phương 2 vế ta thu được
phương trình mới:
22
8 6 18 (6 18) 1 0xx x x
. Nếu để nguyên thì a + c = 6, ac = 9 nên
a = c = 3, tuy nhiên b + d = 18 và 3b + 3d = - 6 (vô nghiệm). Nhân hai vế với - 2 và đưa 4 vào căn để
cân bằng bậc hai , giảm bớt tổng b +d:
22
16 12 36 (3 9) 16 16 0xx x x
. Ta cần
( )( ) ( )

+ + ++ + ++ =

0axbcxd u acxbd u
.
Cân bằng hệ số:
Ta có
3
16 16
ac
ac
+=−
−=−
và
9; 16 36
12
d b bd
ad bc
+=− + =
+=
. Hệ có nghiệm
3, 0, 4, 5a cd b=−= =−=−
.
Hướng dẫn giải:
Điều kiện:
1; 4 1 1 3x xx 
. Viết lại:
2
4 1 21 3 1 1x xx x 
.
Bình phương 2 vế ta thu được phương trình:
2 22 2
8 6 18 (6 18) 1 0 16 12 36 (3 9) 16 16 0xx x x x x x x 
.
22
3 5 16 16 4 16 16 0
xx x 
.
Trường hợp 1:
2
2
5
3 50
3
3
5
3 5 16 16
25 30 9 0
x
x
x
xx
xx









thỏa mãn điều kiện.
Trường hợp 2:
2
4 16 16 0xx 
(thỏa mãn điều kiện).
Kết luận: Phương trình có hai nghiệm
=−=
3
, 0.
5
xx
U Ví dụ 25:U Giải phương trình sau:
2
2 2 4 4 2 9 16x xx
.
Hướng phân tích:
Điều kiện:
2x
. Bình phương 2 vế ta thu được:
22
9 8 32 8 32 8 0xx x 
.
Ta cần:
0axbcxd u acxbdu




. Cân bằng hệ số:
0
89
ac
ac


và
8; 32 32
8
d b bd
ad bc


có nghiệm
1, 1, 8, 0a cd b
.
Hướng dẫn giải:
Điều kiện:
2x
. Bình phương 2 vế ta thu được:
22
9 8 32 8 32 8 0xx x 
.
22
32 8 8 32 8 0x xx x 
.
Trường hợp 1:
2
2
0
0
42
9 32
3
32 8
x
x
x
x
xx







thỏa mãn điều kiện.
Trường hợp 2:
2
2
80
8
9 16 32 0
8 32 8
x
x
xx
xx








(Vô nghiệm).
Kết luận: Phương trình có 1 nghiệm
42
3
x
.
UNhận xétU:
Với cách làm này nếu kết hợp được máy tính Casio thì việc phân tích thành nhân tử hết sức dễ dàng.
Hy vọng với cách làm này sẽ giúp ích cho học sinh trong giải toán. Ta cũng thấy được một phần ý nghĩa
thông qua các ví dụ từ 20 đến 25.
Mặt khác chúng ta cũng thấy được "không có chìa khóa vạn năng" hay nói cách khác là chúng ta không
nên hy vọng có một công thức đơn giản mà đi giải các bài toán khó!
Sau đây là các bài luyện tập
Uc. Luyện tập:
Bài 1. Giải phương trình:
22
3 (3 ) 4.x x xxx 
Bài 2. Giải phương trình:
2
8 16 20 15xx x 
.
Bài 3. Giải phương trình:
22
1 ( 1) 2 3 0x x xx
.
Bài 4. Giải phương trình:
2
97(27)27xx x x 
.
Bài 5. Giải phương trình:
2
9 25 ( 1) 2 5 5.x x xx 
Bài 6. Giải phương trình:
22
4 11 10 1 2 6 2x x x xx 
.
Bài 7. Giải phương trình:
22
8 26 ( 1) 6 6.xx x xx
Bài 8. Giải phương trình:
22
4 9 1 (4 1) 8 3 1.xx x xx 
Bài 9. Giải phương trình:
22
4 23 23 ( 2) 2 6 12.x x x xx 
Bài 10. Giải phương trình:
22
16 11 1 ( 4) 4 18 4.xx x x x 
Bài 11. Giải phương trình:
2
2 61 4 5xx x 
.
Bài 12. Giải phương trình:
22
2 2 3 (2 3) 5 7.xx x xx 
Bài 13. Giải phương trình:
2
3
4 5 2
8 4.
1
x xx
x

Bài 14. Giải phương trình:
22
4 2 (5 3) 5 6 2.xx x xx 
Bài 15. Giải phương trình:
2
5 3 2 1.x xx x 
Bài 16. Giải phương trình:
2
3 13 37 8( 3) 2xx x x 
.
Bài 17. Giải phương trình:
22
3( 1) 12 9 20 2xx xx 
.
Bài 18. Giải phương trình:
22
7 27 2xx xxx 
.
Bài 19. Giải phương trình:
22
5 4 3 18 5x xx x x 
.
MỘT SỐ ĐỊNH HƯỚNG GIẢI PT VÔ TỈ PHẦN 4
UIII. Giải phương trình theo phương pháp trục căn thức và bình phương
U1. Đặt vấn đề:U Trước hết ta xét 3 ví dụ sau:
U Ví dụ 1:U Giải phương trình:
2
83
24 3 3
x
xx x


(1)
Hướng dẫn giải:
PT(1)
2
21
0 1 2 2 32 1
33 2
22 33
x
x xx
xx
xx







11
2123 0210
2
33 2
xx x x
xx


 




(Do ĐK nên trong ngoặc dương).
Phương trình có nghiệm duy nhất
1
2
x 
.
42TULời bìnhU:
42T Trong ví dụ 1: Phương trình chỉ có một nghiệm đơn nên ta trục căn một lần là xong.
U Ví dụ 2:U Giải phương trình:
2
5 1 12 8 3x xx
(2).
Lời giải: Điều kiện:
23
x
. Ta có
2
2 2 21
5 1 12 8
x xx


2
51 121
10
22
5 12
1 10
22
10
5 12
1 0 *
22
5 1 12 8
5 1 12 8
5 1 12 8
xx
x
x
x
xx
x
xx
x
xx




 








Ta coi
*
như là một phương trình bình thường và tiếp tục
5 12
* 1 2 0
22
2
5 1 12 8
x
xx















42 3 2
3 51
0
22
2
5 1 12 8
x
x
x
xx






52 46 3
0
23 5 1 22 3 2
2
5 1 12 8
xx
xx
x
xx


 


58
2 10
23 5 1 22 3 2
5 1 12 8
x
xx
xx





2x
(Vì
58
10
23 5 1 22 3 2
5 1 12 8
xx
xx

 

).
Vậy phương trình có hai nghiệm phân biệt
1, 2 .xx
ULời bìnhU:
Trong ví dụ 2: Phương trình có hai nghiệm phân biệt và ta trục căn lần lượt hai lần mới
xong, rõ ràng khi trục căn lần thứ hai khó hơn lần thứ nhất. Đối với nhiều bài toán ta trục căn lần
hai sẽ gặp khó khăn rất lớn vì biểu thức chứa căn cồng kềnh, phức tạp, ..
U Ví dụ 3:U Giải phương trình:
2
33 6 2 3 2 7x x xx 
(3).
Lời giải: Điều kiện:
2 3.x
Ta có
2
3 3 5 3 4 3 2 *
3 22x x xxxx




+ Vì
23x
nên
3 3 5 0; 3 2 4 0xx x x
. Do đó:
2
2
2
*
22
2
32
33 5 3 2 4
xx
xx
xx
xx x x



 
2
12
2 3
0 **
33 5 3 2 4
xx
xx x x




+ Vì
23x
nên
3 3 5 2; 3 2 4 2xx x x
1 1 11
3 30
22
33 5 3 2 4xx x x
 

+ Do đó
2
1
** 2
0
2
x
xx
x


Vậy phương trình có 2 nghiệm
1, 2xx
.
42TULời bìnhU:
42T Trong ví dụ 3: Phương trình có hai nghiệm phân biệt và ta trục căn một lần để được nhân tử
chung là tam thức bậc hai. Cách trục căn này khá phổ biến.
42T Vấn đề chúng ta quan tâm hơn là: Có thể dự đoán được phương trình có bao nhiêu nghiệm để
"biết đường" mà "liệu cơm gắp mắm"?. Nếu cứ áp dụng cách giải trong ví dụ 3 vào trong ví dụ 1
thì không ổn!. Nếu cứ áp dụng cách "trục căn dần dần" như ví dụ 2 thì sẽ gặp khó khăn rất lớn, mà
còn dài dòng! Nếu không dùng máy tính Casio thì đây chính là câu hỏi nan giải rồi.
42T Như vậy: chúng ta hãy "dự đoán" hay áng chừng xem phương trình có bao nhiêu nghiệm? Mà
dự đoán của chúng ta phải "tương đối chuẩn" thì sẽ mang lại hiệu quả cao trong giải toán.
U2. Phương pháp nhẩm nghiệm hữu tỉ và trục căn.
Ua. Nhẩm nghiệm hữu tỉU:
Việc chúng ta nghĩ đến đầu tiên là nghiệm nguyên hay nghiệm hữu tỉ đẹp, bởi lí do: phương
trình phức tạp thì nghiệm đơn giản một tí.
+ Các căn bậc hai đẹp như:
; ; ; ; ; ;...
0 1 4 9 16 25
hay các nghich đảo của chúng?.
+ Tìm được
0
x
và thử vào căn khác và cả phương trình xem có phải là nghiệm không?
42TU Ví dụ 2:U Giải phương trình:42T
2
5 1 12 8 3x xx
42T.
Hướng phân tích:
+ Thử x = 1 thì cả hai căn đều là số đẹp và x = 1 là nghiệm của phương trình
+ Thử x = 2 thì cả hai căn đều là số đẹp và x = 2 là nghiệm của phương trình.
42TU Ví dụ 3U: Giải phương trình: 42T
2
33 6 2 3 2 7x x xx 
42T.
Hướng phân tích:
+ Thử x = -1 thì cả hai căn đều là số đẹp và x = -1 là nghiệm của phương trình
+ Thử x = 2 thì cả hai căn đều là số đẹp và x = 2 là nghiệm của phương trình.
Trên quan điểm đồ thị (bản chất): Phương trình ẩn x coi như hoành độ giao điểm của hai đường
cong, từ đó dự đoán khoảng nghiệm và số nghiệm của phương trình.
Nhiều khi nghiệm vô tỉ sẽ khó nhẩm nghiệm, bởi vậy dự đoán khoảng nghiệm và số nghiệm sẽ
góp phần quan trọng khi định hướng giải cũng như trong lập luận và đánh giá.
Việc phác họa đồ thị là không cần thiết đối với HS các lớp 9; 10, 11. Tuy nhiên chúng ta cần "nhìn
thấu bản chất" và thử sơ lược các giá trị để dự đoán khoảng nghiệm, nghiệm đơn -kép -hai nghiệm.
U Ví dụ 1:U Giải phương trình:
2
83
24 3 3
x
xx x


(1)
Hướng phân tích:
Điều kiện
1x 
. Tại x = - 1 thì VT(1) > VP(1) , tại x = 0 thì VT(1) < VP(1) nên dự đoán
nghiệm thuộc (- 1; 0) và nghiệm hữu tỉ đẹp có thể là x = - 1/ 2 . Thử vào phương trình thỏa mãn.
Như thế qua ba ví dụ trên ta thấy việc nhẩm nghiệm cũng không quá khó khăn và không phụ
thuộc nhiều vào máy tính Casio. (Trừ các nghiệm vô tỉ được trình bầy riêng ở phần 5).
Ub. Định hướng trục căn thức:
Chúng ta có hai hướng chính để trục căn thức là:
+ Hướng 1: Tìm biểu thức liên hợp với căn thức sao cho khi trục căn sẽ tạo ra nhân tử mà chúng
ta đã nhẩm nghiệm.
Theo hướng này chúng ta thực hiện đối với hai căn thức nên sẽ khá dài, đa số phải xét dấu nhiều
trước khi trục căn và sau khi trục căn.
+ Hướng 2: Đặt điều kiện. Bình phương hai vế đưa về trường hợp một căn thức, trục căn một
lần để tạo nhân tử mà chúng ta đã nhẩm nghiệm.
Theo hướng này: chúng ta vướng mắc nhỏ ở việc bình phương nhưng cũng không cần lo lắng khi
mà chúng ta đã biết trước nhân tử.
U Ví dụ 4:U Giải phương trình sau:
2
114 3x xx
(4).
Hướng phân tích:
Điều kiện
0.x
42TVới x = 0 thì VT(4) > VP(4), với x = 1 thì VT(4) < VP(4) nên dự đoán phương
trình có một nghiệm thuộc (0; 1) và nghiệm hữu tỉ đẹp có thể là x = 1/2, thử vào thấy thỏa mãn.
Hướng dẫn giải:
42TĐiều kiện 42T
0x
. 42TTa có 42T
22
21
4 41 3 1041
31
0
x
x xx x
xx
  

11
2121 210
2
31
0
xx x x
xx





. (Vì
0x
42T nên trong ngoặc thứ hai
xác định và dương42T)
Vậy phương trình có một nghiệm là
1
2
x
.
U Ví dụ 5:U Giải phương trình sau:
2
3 1 6 3 14 8 0.x xx x
Hướng phân tích:
Điều kiện
1
;6
3
x





. PT có ít nhất một nghiệm x = 5. Khả năng 42Tnghiệm đơn 42Tduy nhất.
Hướng dẫn giải:
Điều kiện
1
;6
3
x





. Ta có
2
314 16 3 1450x xx x
31
5 3 1 0 50 5
3 141 6
x x xx
xx




.
Vậy phương trình có nghiệm duy nhất
5x
.
U Ví dụ 6:U Giải phương trình:
23
10 3 3 26 5 23 xx xxx 
(6).
Hướng phân tích:
Điều kiện:
1 5/2x
. Thử x = 2 thì cả hai căn là số đẹp và x = 2 là nghiệm của phương
trình. Viết lại phương trình thành
32
3 3 5 2 10 263
xx xxx

(*)
42TVới x = 1 thì VT(*) < VP(*), với x = 5/2 thì VT(*) > VP(*) nên phương trình khả năng có
nghiệm đơn duy nhất x = 2.
Hướng dẫn giải:
42TĐiều kiện:42T
1 5/2x
42T. Ta có
32
3 3 3 1 5 2 10 24 0
3
x xx
xx
 
32
2 34
0
3 3 3 1 52
x xx
xx







(6.1).
Dễ thấy
32
34 0
3 3 3 1 52
1 5/2 xx
xx
x



42TNên từ (6.1) suy ra x = 2.
42TVậy phương trình có nghiệm duy nhất x = 2.
42TU Lưu ý 1U:
+ Đối với căn bâc 3: ta có thể ký hiệu
3
3
ux a ux a
để gọn nhẹ, bớt cồng kềnh
trong khi trục căn, x vẫn là ẩn chính mà a có mặt trong phương trình nhưng không phải là ẩn.
+ Để giảm bậc hay giảm hệ số, ... ta có thể đặt ẩn phụ mới
vx t
và khi đó ta cần chuyển đổi
hoàn toàn ẩn x sang ẩn t và cần giới hạn cho t.
U Ví dụ 7:U Giải phương trình:
3
2
92 3 5 11x xx x 
.
Hướng phân tích:
Ta nhẩm được x = 1 là nghiệm, khả năng là nghiệm 42Tnghiệm đơn42T duy nhất.
Hướng dẫn giải:
Điều kiện
1
5
x
. Ký hiệu
3
9xa
ta có phương trình:
2
5 12 2 2 3 5 0x a xx
3
2
51
8
12 5 0
24
5 12
x
a
xx
aa
x



2
51
1 2
5 0 (*)
24
5 12
xx
aa
x





. Vì
1
5
x
nên ngoặc thứ hai âm
Do đó
(*) 1 0 1xx 
.
Vậy phương trình có 1 nghiệm là
1x
.
U Ví dụ 8:U Giải phương trình:
3 2 42
8 6 1 4 21 16 12 2 21xx x x xx 
.
Hướng phân tích:
Ta nhẩm được x = 1 là nghiệm, khả năng là nghiệm đơn duy nhất, đặt t = 2x thì khi đó t = 2.
Hướng dẫn giải:
Đặt
2xt
, ta có phương trình:
3 2 42
3 1 21 3 21t t t t tt 
32 3 2
2
21
3 1 21 21 3 1 21
21
tt t t tt t t
tt
 

2
32
2
6
3 2 3 21 0 2 1 0
3 21
tt t t t t
tt






20 2 1t tx
.
Vậy phương trình có 1 nghiệm là
1x
.
U Ví dụ 9:U Giải phương trình:
6 1 82
2 15
2
31
xx x
x
xx



.
Hướng phân tích:
Nhẩm được nghiệm x = 5. Để giảm độ phức tạp ta đổi biến
2
10 1x t xt
.
Hướng dẫn giải:
Đặt
2
10 1x t xt
, ta có phương trình:
22
2 32 2
22
5 82 1
2 15 2 5 6 2 15
11
22
22
tt t
t ttt t
t t tt

 




2
2
2
2
2
2
0, 1
23
22
1
22
1
2
2
2 13
21 1
2 13
t
tt
tt t
tt
t
tt
t
tt
t
tt
t










2t
. Thay trở về
2
1xt
ta có nghiệm của phương trình là
5x
.
U Ví dụ 10:U Giải phương trình:
33 43
28 4 2 15 2 3 14 16xx xx x 
.
Hướng phân tích:
Ta nhẩm được x = 2 là nghiệm, khả năng là nghiệm đơn duy nhất, ở đây ta đổi biến sang căn bậc
3 để giảm bậc bên ngoài căn.
Đặt
33
3
7 7;2 15 2 1 0 1 / 2xt x t x t t 
thì khi đó:
43 3
3
2 3 14 16 2 7 3 7 16 2 7 3 5x x x x x t t
t t  
.
Hướng dẫn giải:
Đặt
33
3
1
7 7
;2 15 2 1 0
2
xt x t x t t 
, khi đó ta có phương trình:
33
4212 735 5 12 724211 0t t tt t t t t t t  
2
3
28
15 0
1 0 1
2 11
71 3
tt
t tt
t
t





(Vì
1
2
t
).
Thay
1t
trở về
3
7xt
ta có nghiệm của phương trình là
2x
.
U Lưu ý 2U:
Trong một số trường hợp phương trình có nghiệm duy nhất ta cần sử lí tinh tế để tránh độ phức
tạp của phép trục căn. Như đưa về
22
0AB
hoặc bình phương hay đổi biến.
U Ví dụ 11:U Giải phương trình:
22
2 35 2 353xx xx x 
.
Hướng phân tích:
Ta nhẩm được một nghiệm x = 4. Nếu ta biến đổi theo cách:
22
4 32 35 12 350x x xx x xx 
22
22
34 54
40
32 35 12 35
xx xx
x
x xx x xx
 


22
11
41 0
32 35 12 35
xx
x
x xx x xx





. Khi đó ta phải đi đánh
giá biểu thức trong ngoặc khó khăn.
Hướng dẫn giải:
Điều kiện
0x
. Đặt
1
0t
x

, ta có phương trình:
22
22
6
5 32 5 323 3
5 32 5 32
t
tt tt
tt tt


22
5 32 5 322tt tt t 
. Kết hợp
22
5 32 5 323tt tt 
suy ra
22
23 1
5 3 2 16 1
24
t
tt t t

(vì
1
0t
x

)
4x
.
Vậy phương trình có 1 nghiệm là
4x
.
Cách khác
Điều kiện
0x
. Bình phương hai vế ta có:
22 2
22 352 355 10xx xx x 
(*).
Vì
0x
nên ta có điều kiện
2
20 2xx
. Tiếp tục bình phương hai vế của (*):
42 2 4 2 4 2 2
4 4 20 25 9 25 100 100 9 144 0 16xx x x x x x x




Từ đó suy ra phương trình có một nghiệm
4x
.
U Ví dụ 12:U Giải phương trình:
22 21 65xxx 
.
Hướng dẫn giải: (Tương tự ví dụ 11)
Điều kiện
1
2
x 
. PT
41
22
65 21
x
x
xx


6 5 2 12xx 
(*). Từ
đây ta có điều kiện
1
6 52
6
xx 
. Kết hợp
6 5 2 12 2x xx 
suy ra:
2
2 22
6 5 2 2 10
2
x
x x xx

 
. Giải ra lấy nghiệm
12x 
.
Vậy phương trình có 1 nghiệm là
12x 
.
U Ví dụ 13:U Giải phương trình:
2
4 3 3 4 3 22 1x x xx x 
.
Hướng phân tích:
Ta nhẩm được một nghiệm x = 1. Nếu ta biến đổi theo cách:
2
4 5 1 4 2 3 21 2 1 0xx x x x 
44
14 1 0
2 31 2 1
x
xx
xx




. Khi đó ta phải đi đánh giá biểu thức
trong ngoặc khó khăn. Ta có thể biến đổi tiếp tục nhưng cồng kềnh và phức tạp.
Thử tại x = 1/2 thì VT > VP, thử tại x = 2 thì VT > VP nên khả năng Parabol
2
4 33yx x 
luôn nằm trên đường cong
4 3 22 1y xx x 
do đó đoán là nghiệm kép tại x = 1.
Hướng dẫn giải: (đưa về nghiệm kép)
Điều kiện
1
2
x
. Ta có:
2
4 34 3 2 2 1 0x x xx x x
2
2
21
2 30
23 0 1
10
21
x
xx
xx x
x
xx




.
Vậy phương trình có 1 nghiệm là
1x
.
U Ví dụ 14:U Giải phương trình:
2 12 2 1x xx
.
Hướng phân tích:
Thử tại x = 1/2 thì VT > VP, thử tại x = 2 thì VT > VP nên khả năng đường thẳng
21yx
luôn nằm trên đường cong
2 21yxx 
do đó đoán là nghiệm kép tại x = 1.
Hướng dẫn giải: (Tương tự ví dụ 13)
Điều kiện
1
2
x
. Ta có
2 1 12 0xx x x 
22
11
0 10 1
2 1 12
xx
xx
xx x x



(Vì
1
2
x
).
Vậy phương trình có 1 nghiệm là
1x
.
U Ví dụ 15:U Giải phương trình:
3
2
2 11 21 3 4 4xx x 
.
Hướng phân tích:
Nhận xét
2
2 11 21 0, 4 4 0 1x x xx x 
. Nhẩm được nghiệm đẹp x = 3.
Để bớt cồng kềnh ta ký hiệu
3
44xa
, khi x = 3 thì a = 2. Mặt khác viết lại:
3
2
2 12 18 3 3 4 4xx x x 
thì khả năng Parabol tiếp xúc với đường cong!
Hướng dẫn giải:
Dễ thấy
2
2 11 21 0,xx x 
do đó để phương trình có nghiệm thì
4 40 1
xx

.
Ký hiệu
3
44 0
xa

, ta có phương trình
2
2 12 18 3 3 0xx x a 
33
2
22
33
23 0
33 33
xa
x
x ax a



(Với
1, 0xa
)
32
2
22
9 27 27 27 4 4
23 0
33 33
xx x x
x
x ax a



(Với
1, 0
xa
)
2
22
15
32 0 3
33 33
x
xx
x ax a








(Vì
1, 0xa
).
Vậy phương trình có một nghiệm là
3
x
.
ULời bìnhU:
Từ hướng phân tích trên ta có thể giải phương trình theo phương pháp đánh giá ngắn gọn hơn
như sau:
Dễ thấy
2
2 11 21 0,xx x 
do đó để phương trình có nghiệm thì
4 40 1
xx

.
Viết lại phương trình:
3
2
2 12 18 3 3 4 4
xx x x 
(*).
Ta có VT(*) =
2
2 30x 
.
Mà VP(*)
3
3 3 2.2. 1 3 2 2 1 0x xx x

 


.
Dấu bằng xảy ra khi
12 3
xx
. Từ đó phương trình có 1 nghiệm
3x
.
Tương tự ta có thể giải các ví dụ 13, ví dụ 14 hay các các bài toán nghiệm kép theo phương
pháp đánh giá bằng bất đẳng thức AM - GM, B.C.S, ...
Chẳng hạn ví dụ 13, với
1/2x
:
2 22
2. 4 . 3 2 1. 2 1 4 3 1 2 1 4 3 3xx x x x x x x 
.
U Ví dụ 16:U Giải phương trình:
2
1 4 5 2 5 3 3 14 13x x x x xx

.
Hướng phân tích:
Ta nhẩm được một nghiệm x = 1. Nếu x = 0 thì VT > VP, nếu x = 2 thì VT < VP nên khả năng
x = 1 là nghiệm đơn duy nhất.
Hướng dẫn giải:
ĐK
5
4
x 
. Ta có
2
3 7 10 1 3 4 5 2 5 2 3 0xx x x x x  
41 25
1 3 10 0
3 4 52 3
xx
xx
xx








3104555125
1 0 1. 0
3 45 2 3
xx x x
x xM
xx



 





(*).
Ta có
3 10 4 5 5 5 1 4 5 0
5
,
4
0 3 4 5 4 4 12 2 2 3
xx x x
x
xx x



Suy ra:
45 25
5
0,
4
23
22 3
xx
Mx
x
x




. Do đó
(*) 1 0 1xx 
.
Vậy phương trình có một nghiệm là
1x
.
ULời bình:U Ví dụ trên ta gặp khó khăn khi đánh giá biểu thức M trong ngoặc vuông. Đây là bài
khó, ta có thể đổi biến quy về một căn thức như sau:
Cách 2: Phương trình
2
( 1) 4 5 2( 5) 3 3 14 13x x x x xx 
2
(4 4) 4 5 (4 20) 4 12 12 56 52x x x x xx 
.
Đặt
2
4 5 04 5x t xt 
ta có phương trình:
2
2 22 2 2
3
( 1) ( 15) 7 5 14 5 52
4
tt t t t t 
43 2 2 2
3 4 26 4 3 4( 15) 7 0tt tt t t 
43 2 2 2
3 4 10 4 237 4( 15) 4 7 0tt tt t t 
2
32
2
4( 15) 3
3 3 5 25 79 0
3 . 0
47
tt
t tt t t
M
t



 




(*).
Ta có
32 32 2
0 3 5 25 79 3 15 75 ( 15) 3t tt t tt t t t
Kết hợp
2
4 74t 
suy ra
0M
và từ (*) ta có
30 3tt 
.
Thay trở về
2
5
4
t
x
ta có nghiệm của phương trình là
1x
.
Tuy giải được nhưng độ phức tạp và cồng kềnh không giảm hơn bao nhiêu. Ta tiếp tục xét thêm
một vài ví dụ để thấy rõ sự đa dạng của phương trình vô tỉ nhưng trong trường hợp nhẩm được
nghiệm hữu tỉ thì ta vẫn tự tin trong giải toán.
U Ví dụ 17:U Giải phương trình:
2 32
3 5 6 4 19 12 36 2 20 6xx x x x x x
.
Hướng phân tích:
ĐK
2
5 60
6
;4
4 19 12 0
5
x
x
xx







. Ta nhẩm
2x
thì VT < VP, với
3x
là nghiệm
Với
4x
thì VT < VP. Như thế khả năng hai đường cong tiếp xúc nhau tại x = 3.
Hướng dẫn giải:
Điều kiện
6
4
5
x
. Bình phương hai vế và thu gọn ta có phương trình:
2 32
6 5 6 4 19 12 9 56 39 18 0xx x x x x x
2 32
6 5 6 4 19 12 9 9 56 93 18 0xx x x x x x 
2
2
6 20 1
3 92
0 3
5 6 4 19 12 9
xx
x xx
x xx







.
(vì
6
4
5
x
nên ngoặc vuông dương). Vậy phương trình có nghiệm duy nhất
3x
.
Cách khác: (Dùng phương pháp đánh giá)
Ta có điều kiện
2
5 60
6
;4
4 19 12 0
5
x
x
xx







. Bình phương hai vế và thu gọn ta được:
2 32
3 .2 5 6. 4 19 12 9 56 39 18 0xx x x x x x  
(*)
Áp dụng bđt Cô si thì:
22
3 .2 5 6. 4 19 12 3 5 6 4 19 12xx xx xx xx 
2 32
3 .2 5 6. 4 19 12 12 72 54xx xx xxx 
. Dấu bằng có khi và chỉ khi
6
3 ;4
5
x





. Từ đó suy ra: VT(*)
32 32
12 72 54 9 56 39 18x x xx x x  
VT(*)
2
32
6
3 16 15 18 3 3 2 0, ;4
5
xxx x x x





.
Từ đó suy ra phương trình (*) có nghiệm duy nhất x = 3 và là nghiệm của phương trình đã cho.
ULời bìnhU:
Phương pháp bình phương một bước làm cho bài toán ngắn gọn hơn. Các bạn hãy thử giải theo
cách để nguyên trục căn hoặc đánh giá mà không bình phương:?.
U Ví dụ 18:U Giải phương trình:
22
2 3 4 2 3 11 3x x x xx 
.
Hướng phân tích:
Điều kiện
22x 
. Tại
1x 
thì VT< VP, tại
0x
thì VT < VP, x = 1 là nghiệm.
Tại
2x
thì VT < VP nên dự đoán x = 1 là nghiệm kép.
Hướng dẫn giải:
Điều kiện
22x 
. Viết lại
22
2 3 4 2 3 11 3x x xxx 
.
Bình phương hai vế ta được:
2 22
10 5 55 16 3 2 6 11 3 0x x x x x xx 
(18).
Áp dụng bđt Cô si:
2 22
4.2 3 8 4 4 3 8 4 44 4 16x x x x xx 
(18a).
Suy ra: VT(18)
2 22
10 5 55 44 4 16 6 11 3x x x x x xx 
VT(18)
2
22 2 2
9 11 3 6 11 3 3 11 3 0x xx x xx x xx   
(18b).
Từ (18a) và (18b) ta có dấu bằng xảy ra khi và chỉ khi:
2
2
3 84
1
3 11 3
xx
x
x xx



. Vậy phương trình có nghiệm duy nhất
1x
.
U Ví dụ 19:U Giải phương trình:
22
2
2
21
85
2
xx
x
x
x


.
Hướng phân tích:
Điều kiện
2 22x
. Nếu
2 2; 2x




thì VT
2
2
11
85
2
x
x

, mà khi
đó VP
2
1
55
x
x

nên phương trình không có nghiệm
2 2; 2x




.
Xét
2;2 2x



: Ta nhẩm được nghiệm đẹp
2x
, và khi
2x
hay
22x
ta đều có
VT < VP, nên khả năng
2x
là nghiệm kép. Nhân cả hai vế với 2x để khử mẫu thức.
Hướng dẫn giải (Cách phổ biến):
Điều kiện
2 22x
. Nếu
2 2; 2x




thì VT
2
2
11
85
2
x
x

, mà khi
đó VP
2
1
55
x
x

nên phương trình không có nghiệm
2 2; 2x




.
Xét
2;2 2x



, nhân cả hai vế với
2x
ta có phương trình:
22 2
28 242102xx x x x 
2 22
288222424 8xx x x x x 
2 22
2
22
22 22 2
22
22 2 4 4 8
x xx
x
x x xx



2
2
22
220 2
2
1
1 (
*)
2 2 2 44 8
xx
x
x x xx



.
Ta có
2
2
2
2
2
1 4 8 2
0, 2; 2 2
48
x
x xx x
xx





nên (*) vô
nghiệm.
Vậy phương trình có nghiệm duy nhất
2x
.
ULời bìnhU:
Để tránh trục hai căn thức như biểu thức vế phải (*) ta cũng có thể giải theo phương pháp bình
phương quen thuộc đưa về bậc 4 rồi trục căn một lần:
Cách 2: Xét
2;2 2x



, nhân cả hai vế với
2x
ta có phương trình:
22 2
28 242102xx x x x 
. Bình phương hai vế và thu gọn ta được:
22 4 3 2
2 8 2 4 4 20 37 20 4x xx x x x x 
4 3 2 22
4 20 33 20 4 2 2 8 2 4 0x x x x xx x x 
2
22 2
22
42
22 1 0
2 0 2
2 8 24
xx
xx x
x
x xx









.
Từ đó phương trình có nghiệm duy nhất
2x
.
Uc. Trường hợp hai nghiệm hữu tỉU:
Nếu nhẩm được hai nghiệm hữu tỉ thì mục tiêu của ta là trục căn một lần để có nhân tử chung là
tam thức bậc hai. Theo định lý Viet đảo:
2
0x Sx P 
.
U Ví dụ 20:U Giải phương trình:
2
2 3 4 3 5 9 6 13x x xx
.
Hướng phân tích:
Ta thấy phương trình có ít nhất hai nghiệm x = 0 và x = - 1, do đó định hướng trục căn thức sẽ
xuất hiện nhân tử
2
xx
. Cách làm phổ biến là:
2
6 5 13 2 3 2 3 4 3 5 9 0x a x b d ax b x ax d x




Cho x = 0 suy ra
2, 3; 13 2 3 0b d bd 
.
Kiểm tra
65 4 3 6 51 1aa a a 
Cách giải phổ biến là:
Điều kiện:
4
3
x 
. Ta có:
2
2 2 343 3 590xx x x x x 
22
2
23
0
2 34 3 59
xx xx
xx
x xx x



22
23
1 00
2 34 3 59
xx xx
x xx x




Từ đó suy ra phương trình có đúng hai nghiệm
1, 0xx
.
ULời bìnhU:
Đối với bài trên thoạt nhìn theo cách trên không có phức tạp hay sự cồng kềnh trong lời giải, tuy
nhiên theo cách làm ta phải tìm hai biểu thức liên hợp với hai căn sẽ mất thời gian hơn. Cách
ngắn gọn vẫn là bình phương như ví dụ 19. Dùng phép chia đa thức hay lược đồ Hooc - ne để
tìm thương và phần dư.
Hướng dẫn giải (PP bình phương):
Điều kiện
4/3x 
. Bình phương hai vế ta có phương trình:
432
12 3 4 5 9 12 62 99 72x x xxxx 
432
12 62 51 12 4 6 3 4 5 9 0xxxx x x x 
22 2
12
11 51 0 0
46 3459
xxx x xx
x xx







Từ đó suy ra phương trình có đúng hai nghiệm
1, 0xx
.
Cách tìm biểu thức liên hợp là chia đa thức
432
12 62 99 72xxxx 
cho
2
xx
ta
tìm được thương là
2
11 51xx
và dư
48 72x
ghép vào căn là được. Chúng ta sẽ kiểm
chứng khi giải lại VD2.
42TU Ví dụ 2:U Giải phương trình:42T
2
5 1 12 8 3x xx
42T.
Hướng phân tích:
Thử x = 1 và x = 2 là nghiệm của phương trình. Nhân tử của chúng ta là
2
32xx
.
Hướng dẫn giải:
Điều kiện
2/3x
. Bình phương hai vế ta có phương trình:
42
4 5 1 3 2 6 17 18x x xx x 
42
6 33 26 4 4 2 5 1 3 2 0xx x x x x
22
4
3 2 3 13 0
4 2 5 13 2
xx xx
x xx




2
3 2 0 1, 2xx xx 
.
Vậy phương trình có hai nghiệm
1, 2xx
.
U Ví dụ 21:U Giải phương trình:
22
2 92 1 4xx xx x 
.
Hướng phân tích:
Ta dễ nhẩm được một nghiệm
0x
. Khả năng còn nghiệm thứ hai
x
nên mục tiêu là:
nhân tử sau khi trục căn có dạng
2
ax bx
.
Giải theo PP bình phương:
Điều kiện
4x 
. Bình phương hai vế và thu gọn ta có phương trình
2 22
3 8 6 22 92 1x x xx xx 
. Cộng thêm hai vế với
2
46x
ta được
2 22 2
7 8 22 3 2 9 2 1x x x xx xx 
2
22 2
28
7 8 1 0
0,
7
2 3 2 92 1
xx x
x
x xx xx




.
Giải theo cách thông thường:
Điều kiện
4x 
. Nếu
42x 
suy ra VT
15 11
VP nên
42x 
không phải là nghiệm.
Do đó
2x 
và PT
22
22 9 6 22 1 2 0xx x xx x  
2
22
11 8
7 8 0
0,
7
22 9 6 22 1 2
xx x
x
xx x xx x



 
Vậy phương trình có hai nghiệm
8
0,
7
xx
.
ULời bìnhU:
PP bình phương ta không cần lập luận nhiều. Bài trên ta có thể đặt thêm điều kiện và tiếp
tục bình phương lần thứ hai. Ngoài ra ta cũng có thể giải theo cách tương tự VD11, VD12.
Theo phương pháp thứ hai ta cần tách hạng tử hợp lý và xét mẫu thức khác 0 để trục căn.
Đặc biệt ví dụ sau thì PP thông thường sẽ khó khăn
U Ví dụ 22:U Giải phương trình:
22
32 1 5 4 4x x xx
.
Hướng phân tích:
Nhẩm được các nghiệm x = 1/2 và x = 1. Nhân tử chúng ta cần là
2
2 31xx
.
Hướng dẫn giải:
Điều kiện
15
;
22
xD






. Bình phương hai vế ta có phương trình:
2 42
6 2 1 5 4 20 5 18 9xx x x x x 
, trừ cả hai vế một lượng 6x(2x - 1) thuộc tập
xác định ta có phương trình:
2 42
6 2 1 5 4 2 1 20 17 12 9xx x x x x x 
2 42
6 2 1 5 4 2 1 20 17 12 9xx x x x x x 
22
2
21 2 3
6 2 1 2
3 1 10 15 9
54 2 1
xx
xx x
x x x
xx



2
2
12 2 3
1 2 1 2 1 10 15 9 0
54 2 1
x
x x x xx
xx







(Biểu thức trong ngoặc vuông dương vì
xD
)
1
12 1 0 , 1
2
x x xx 
.
Vậy phương trình có hai nghiệm
1
1,
2
xx
.
UChú ýU:
Bài trên nếu ta "trục căn dần dần" thì sẽ phức tạp, còn để nguyên không bình phương mà muốn
tạo ra nhân tử
2
2 31xx
thì chưa biết như thế nào?
Tuy nhiên ta thử đổi biến để quy về một căn xem sao? Đặt
2
21 02 1x t xt
22
2 22 2 2
8 62 1254 0 2 1 6 15 1 0x x x x t tt t  
4 2 2 42
2 4 6 2 14 2 0t tt t tt 
(*). Để giảm cồng kềnh khi trục căn ta
lại ký hiệu
2
1ty
thì
42
2 42 2
2
54
2 14 2 2 5
25
yy
t tt y y
yy



.
Khi đó thì phương trình (*) trở thành:

2
2
1212
(*) 2 1 3 0
25
yyyy
tt t t
yy



2
2
112
12 2 6 0
25
tt y y
tt t t
yy








, vì
0, 0ty
suy ra
1
1 0 0, 1 , 1
2
tt t t x x 
.
Mặc dù giải được nhưng cũng không giảm được độ phức tạp! Tiếp tục ta xét ví dụ 23
U Ví dụ 23:U Giải phương trình sau:
22
2 16 18 1 2 4xx x x 
.
Hướng dẫn:
Điều kiện:
22
1 0, 1 2 4 2 1x xx x 
hoặc
1x
.
Viết lại phương trình:
22
2 16 18 2 4 1xx x x 
.
Bình phương 2 vế và thu gọn ta được phương trình:
22
3 1 2(2 4) 1 0x xx 
2
2
2
1
1
10
32 3 57
7 64 73 0
3 14 8
7
x
x
x
xx
xx x







Kết hợp điều kiện ta có nghiệm phương trình là
32 3 57
1,
7
xx


.
ULời bình:
Theo phương pháp bình phương ta đã giải phương trình tương đối ngắn gọn, lý do là sau
khi bình phương thì phương trình có nhân tử chung dễ dàng nhận ra là
2
1x
.
U Ví dụ 24:U Giải phương trình:
2
4 3 19 3 2 9x xx x
.
Hướng phân tích:
Nhẩm được các nghiệm x = 1 và x = - 2. Nhân tử ta cần là
2
2xx
.
Hướng dẫn giải (PP bình phương):
Điều kiện
19
3;
3
xD





. Bình phương hai vế và thu gọn ta có:
43 2
4 22 23 14 8 3 19 3 0xx x x x x 
43 2
4 22 15 42 8 7 3 19 3 0xx x x x x x 
22
32
2 3 21 0
7 3 19 3
xx x x
xx x







(Vì
xD
nên trong ngoặc thứ hai dương)
2
2 0 2, 1xx x x 
.
Vậy phương trình có hai nghiệm là:
2, 1xx
.
Cách phổ biến:
làm nháp
3ax b x
= 0 và cho x = 1 và x = - 2 để tìm a, b. Kết quả
15
,
33
ab
.
Tương tự: biểu thức liên hợp
19 3 0cx d x
suy ra
1 13
,
33
cd
.
Phương trình:
2
1 5 1 13
4 3 19
3 2 0
33 3 3
x x x xxx











.
Mời các bạn giải tiếp theo cách trên.
ULời bình:
Có thể nói: phương pháp bình phương là "dồn nghiệm" từ hai căn thức vào chung một
căn thức. Tuy nói thế nhưng không phải bài nào ta cũng áp dụng như vậy.
U Ví dụ 25:U Giải phương trình:
22
2 3 21 17 0xx x xx
.
Hướng phân tích:
Nhẩm được các nghiệm x = 1 và x = 2. Nhân tử ta cần là
2
32xx
. Ta thấy trong căn có bậc
hai
2
23xx
nếu trừ đi
2
21xx
sẽ có nhân tử cần tìm (đẹp rồi). Do đó không phải bình
phương.
Hướng dẫn giải:
Điều kiện
2
17
, 21 17
21
x xx x 
. Phương trình tương đương với:
22
2 3 1 3 1 21 17 3 2 0xx x x x x x 
2
2
19
32 10
3 1 21 17
2 31
xx
xx
xx x





( biểu thức
trong ngoặc thứ hai dương)
2
3 2 0 1, 2 .xx xx

Vậy phương trình có hai nghiệm
1, 2xx
.
U Ví dụ 26:U Giải phương trình:
32 2
( 1) 3 1 2 1 2 1 6x x x x xx x   
.
Hướng phân tích:
Nhẩm được các nghiệm x = 0 và x = 1. Nhân tử ta cần là
2
xx
. Vì trong phương trình có bậc 3
nên ta không bình phương mà cố gắng ghép các hạng tử hợp lý.
Hướng dẫn giải:
PT
32 2
2 3 31(1)312 11x x x x x x xx




2
2
31 2
30
1 31
11
x
x xx
xx
xx








(*).
Ta có
2
12
1 0&2 0
3
11
xx
xx


Do đó từ (*) ta có
2
0 0, 1xx x x
.
Cách ghép 2:
PT
32 2 2 2
6 2 1 ( 1) ( 1) ( 1) 3 1 2 1 0xx x x x x x x x




32 2
4 3 1 ( 1) 3 1 2 1 1 0xx x x x x x x




2
2
12
40
1 31
11
x
xx x
xx
xx





(**).
Ta có
2
1
1 3 1 1 0; 1 1 1
3
x x x x xx  
. Suy ra
2
12
4 4
12 1 0
1 31
11
x
x xx
xx
xx




Do đó (**)
2
0 0, 1xx x x 
.
Một lưu ý mà chúng ta có thể quan tâm là: Không chỉ
0
x
làm cho căn thức trở thành số đẹp
mới là nghiệm của phương trình,
0
x
là nghiệm nhưng thay vào căn thức vẫn là số vô tỉ.
U Ví dụ 27:U Giải phương trình
2 6 4 5 2 3 3 1.xx x x x 
Hướng phân tích:
Thử
1, 3, 5xxx
thì đều là nghiệm của phương trình, nếu bình phương hai lần và
chuyển về phương trình bậc 6 thì chắc chắn chúng ta cũng có nhân tử
135xxx
nhưng khá dài dòng. Nhiệm vụ của ta là tách ghép các căn hợp lý sao cho khi trục căn xuất hiện
nhân tử mà ta cần, đồng thời không phải xét dấu mẫu cũng như giải phương trình còn lại là đơn
giản nhất vì mẫu thức lúc này phức tạp. Định hướng các mẫu của ta là
uv
và
av
như
vậy sẽ đơn giản hơn.
Hướng dẫn giải:
Điều kiện
3/2x 
. PT
26 426 1233 1xx xx x x 
26 4 23 1323xx x x x 
2 61 16 2 1 2 6
4 23 323 323
x x x x xx
xx x x
 

  
1
2 61 0
3
4 23323
5
x
xx
x
xx x
x



Vậy phương trình có ba nghiệm
1, 3, 5.xxx
U Ví dụ 28:U Giải phương trình:
2
2 1 2 1 2 2 4 2.x x xx
Hướng phân tích:
Ta thấy trong phương trình xuất hiện số tự do
2
nên hướng nhẩm nghiệm là: một trong hai căn
ở vế trái bằng số này, từ đó ta nhẩm được hai nghiệm
1
0; .
2
xx
Chúng ta lựa chọn phương
pháp trục căn lần lượt hai lần vì trục căn một lần phải xét mẫu thức phức tạp.
Hướng dẫn giải:
+ TH1: Xét
0x
là nghiệm của phương trình;
+TH2: Xét
1
;1 \ 0
2
x





, chuyển vế:
2
2 11 22 2 4 2x x xx
1 1 22 1 2 2 1
21 21
2 11 22 2
2 11 22 2
xx
xx
xx
xx

 


12 12 1 1
22 1 2 2 1 22
1 2 2 1
21 211 0
2 11 22 2 2
11 22 2
xx
xx xx
xx
xx xx





 








1
2 10
2
xx 
.
Vậy phương trình có hai nghiệm
1
0; .
2
xx
Ud. Luyện tập:
Bài 1. Giải phương trình:
2 2 10 2 3xx x
Bài 2. Giải phương trình:
3
41 32
5
x
xx

Bài 3. Giải phương trình:
9( 4 1 3 2) 3x xx
Bài 4. Giải phương trình:
2
3 2 12 3x x xx 
Bài 5. Giải phương trình:
2
2 4 2 51x xx x
Bài 6. Giải phương trình:
2
3 5 2 7 20x xx x 
Bài 7. Giải phương trình:
2
2 32 2xxxx 
Bài 8. Giải phương trình:
3
2
23 1
4
x
xx

Bài 9. Giải phương trình:
2
3
6 11x xx 
Bài 10. Giải phương trình:
3
2
92 3 5 11x xx x 
Bài 11. Giải phương trình:
2
3
3 2 3 2 22 1x xx x 
Bài 12. Giải phương trình:
2
18 (2 9) 3 2 5 1 0xx x x x 
Bài 13. Giải phương trình:
22
4 512 193x x xx x 
Bài 14. Giải phương trình:
2
2 11 2 16 28 5x xx x 
Bài 15. Giải phương trình:
3
234 25416x xx
Bài 16. Giải phương trình:
2
3
4 12 3x xx 
Bài 17. Giải phương trình:
2
3
4 2 7 8 13 0x x xx 
Bài 18. Giải phương trình:
32
3
42 2x x xx 
Bài 19. Giải phương trình:
3
2
10 1 1x x xx 
Bài 20. Giải phương trình:
2
3
2 41 32x x xx x 
Bài 21. Giải phương trình:
22
5 5 23 2x xx x x 
Bài 22. Giải phương trình:
32 2
2 2 5 24 5 5 4xx xx x x 
Bài 23. Giải phương trình:
32
5 1 2 5 10 13 0x x xx x
Bài 24. Giải phương trình:
32
3 17 89327 0x xx x x  
Bài 25. Giải phương trình:
43 2
3 2 1 5 12 15 3 0x x xx x x 
Bài 26. Giải phương trình:
432
3 2 2 2 3 8 80x x xxxx
Bài 27. Giải phương trình:
2
2 3 2 2( 1) 2 3 8 4x x x xx
Bài 28. Giải phương trình:
(54)23(45)322xx xx
Bài 29. Giải phương trình:
2
( 1) 2 ( 6) 7 7 12x x x x xx 
Bài 30. Giải phương trình:
3 29
31 3
xx
x
xx


Bài 31. Giải phương trình:
2
9 14 25 ( 1 1)(2 4)
3 3 42 1
xx x x
x
xx


Bài 32. Giải phương trình:
2
3
2 3 7 34 4 0xx x 
Bài 33. Giải phương trình:
3
2
3 5 2 19 30 2 7 11x x xx
Bài 34. Giải phương trình:
2
( 1) 1 3 2. 2 2x x x xx 
Bài 35. Giải phương trình:
22
2 21 1xx x x 
Bài 36. Giải phương trình:
32
3 8 4 22 1 3 1x x x x xx 
Bài 37. Giải phương trình:
22
2 2 4 5 1 53 .xx x x 
Bài 38. Giải phương trình:
22
(5 4 3). ( 3). 5 4 .xx xx xx 
Bài 39. Giải phương trình:
32
3 2 44 1x x xx x xx 
Bài 40. Giải phương trình:
3
322.(32)211
21
2 (2 1)
x xx
x
x



MỘT SỐ ĐỊNH HƯỚNG GIẢI PT VÔ TỈ PHẦN 5
UIII. Giải phương trình theo phương pháp trục căn thức và bình phương
U3. Trường hợp nghiệm vô tỉ:U
Ua. Nhận xét và ví dụ:U Để giải phương trình có nghiệm là số vô tỉ mà không dựa vào máy tính Casio
là hết sức vất vả. Nếu không nắm được nhiều dạng khác nhau của phương trình vô tỉ thì trong những
trường hợp nhất định và với những cách nhất định chúng ta cũng mò ra nghiệm hay nhân tử.
U Ví dụ 1:U Giải phương trình:
22
2 3 4 1 2 1.xx xx x 
Hướng dẫn giải:
Điều kiện
1
2
x
. Viết lại
22
2 21 3 41xx x xx 
. Bình phương hai vế ta được
22
22 1 1x xx x 
tiếp tục bình phương hai vế ta có:
2
4 32 2 2
15
2 2 10 1 0 10
2
x xx x xx xx x
  
.
Đối chiếu với điều kiện ta có nghiệm của phương trình là
15
2
x
.
ULời bình:
Bài trên ta bình phương hai lần và đưa về phương trình đa thức bậc 4, sau đó chuyển về phương trình
bậc hai. Bài này rất may là chuyển về bình phương đúng khá đơn giản. Ở đây ta muốn nhấn mạnh:
Phương pháp bình phương vẫn tỏ ra hiệu quả. Chúng ta có thể trục căn nhưng khá cồng kềnh.
Hướng phân tích:
+ Giới hạn khoảng nghiệm: Cho
1
2
x
thì VT
5
2
< VP
15
2
, cho
1x
thì
VT
3
< VP
81
, cho
2x
thì VT
8
< VP
21 3
, ... ta thấy vế trái luôn nhỏ
hơn vế phải và độ lệch hai vế ngày càng tăng. Cho
3
2
x
thì hai vế gần bằng nhau, cụ thể:
VT
21
2
và VP
55 8
2
, như thế khả năng phương trình có nghiệm kép! ( xem thêm phần
4). Nghiệm kép vô tỉ thuộc khoảng
1; 2
.
+ Đối với nghiệm kép hữu tỉ
0
xx
thì từ đa thức bậc 4 ta có thể phân tích thành dạng sau
2
2
0
0x x ax bx c 
, nhưng đối với nghiệm vô tỉ ta không phân tích thành dạng trên., mà
thành dạng
2
2
0ax bx c
(là do các hệ số đều là số nguyên).
Từ đó ta mạnh dạn bình phương và có cách giải như trên.
U Ví dụ 2:U Giải phương trình:
22 21 65xxx 
.
Hướng dẫn: (Đã giải trong phần 4)
Điều kiện
1
2
x 
. PT
41
22
65 21
x
x
xx


6 5 2 12xx 
(*). Từ đây
ta có điều kiện
1
6 52
6
xx 
. Từ (*) kết hợp
6 5 2 12 2x xx 
suy ra:
2
2 22
6 5 2 2 10
2
x
x x xx

 
. Giải ra lấy nghiệm
12
x 
.
ULời bìnhU:
Trong ví dụ trên thì nghiệm
12x 
xuất hiện sau khi giải phương trình mà không phải ta dự
kiến trước (đoán trước), nghĩa là xuất hiện sau phương pháp giải: có thể xuất hiện nghiệm hữu tỉ hoặc
nghiệm vô tỉ, phụ thuộc phương trình cuối:
65 2xx
. Đối với nhiều bài toán thì phương
pháp này không thành công, chẳng hạn như phương trình:
1 (2 1) 2 1xx x
. Đây là
những bài toán khó nếu không sử dụng máy tính Casio. Trước hết ta giải lại ví dụ 2 theo các cách
sau:
Cách 2:
Điều kiện
1/2
x

. Bình phương hai vế và rút gọn ta có phương trình:
2
2 1 2 16 5
x xx

. Đến đây ta có điều kiện
2
1
2
x
, kết hợp
1
2
x 
suy ra
2
2
x
.
Bình phương hai vế lần nữa và rút gọn ta có
2
42 2
4 4 10 2 1 1 0xxx xx x 
(vì
2
2
x
)
2
2 10 1 2
xx x 
. Vậy phương trình có 1 nghiệm là
12
x 
.
Cách 3: Điều kiện
1
2
x 
. Xét
1
;0
2
xD





thì:
2121 165 212111650120
x x x xx x  
Do đó phương trình không có nghiệm trên
D
. Xét
0;xE 
khi đó ta có:
PT
265 210x x xx  
22
11
21 0 210 1 2
2 65 21
xx xx x E
x x xx

 


.
ULời bìnhU:
Đối với phương trình tương đối đơn giản ở trên thì còn nhiều cách giải khác, nhưng ta dừng ở các
cách giải đã trình bầy bởi vì ta muốn nhấn mạnh là: Các cách mà chúng ta đã giải đều dựa vào nhân
tử chung
2
2 10xx 
và được suy ngược từ
2
12 1 2xx
.
UNhận xét 1U:
Trong nhiều trường hợp: chúng ta có thể giải được phương trình dựa trên việc đoán được nhân tử
hay một nghiệm vô tỉ của phương trình, dự đoán của ta tương đối chuẩn thì mang lại hiệu quả cao.
+ Trước hết ta giới hạn hay dự đoán khoảng nghiệm
;x 
+ Việc tính giá trị trung bình của các khoảng nghiệm sẽ giúp ta thuận lợi hơn để mò ra nhân tử theo
định lý Viet đảo:
2
0x Sx P 
.
+ Phương pháp bình phương một bước hoặc bình phương hai lần vẫn tỏ ra hiệu quả.
U Ví dụ 3:U Giải phương trình:
22
2 3 38 5 6 4.xx x x x 
Hướng phân tích:
Điều kiện:
2
2
2 3 38 0
1 115 1 115
5 6 0 ; 3 2;
33
40
xx
xx x
x









.
Cho
1 115
3
x
thì VT < VP, cho
3x 
thì VT > VP nên phương trình có 1 nghiệm thuộc
1 115
;3
3



. Cho
2; 1; 0;1
x

thì VT > VP, cho
1 115
2;
3
xx

thì VT < VP nên
phương trình có 1 nghiệm thuộc
1; 2
.
Viết lại phương trình
22
2 3 38 5 6 4
xx x x x

bình phương hai vế ta có:
22
2 2 14 5 6 4xx xx x 
tiếp tục bình phương hai vế và thu gọn ta có
43 2
4 7 61 82 172 0xx x x

. Giả sử một nghiệm là
1
1, 5 1; 2x 
và một nghiệm liên hợp
với nó nhưng bị loại là
2
3, 5 4; 3x

suy ra
1 2 12
2; 5x x xx  
mà ta để ý là
172 4 . 43
nên nhân tử là
2
2 40xx 
. Kết quả:
43 2 2 2
4 7 61 82 172 0 2 4 4 43 0x x x x x x xx 
1 689
1 5,
8
xx

. Đối chiếu điều kiện ta được phương trình có hai nghiệm:
1 689
, 15
8
xx

.
ULời bình:
Khi so sánh giá trị để xác định khoảng nghiệm ta gặp vấn đề số vô tỉ
1 115
3
x
cồng kềnh, nếu
cứ thay vào phương trình mà tính thì khó khăn lớn, tuy nhiên ta không cần thay trực tiếp vì một căn
bằng 0 và vế trái âm.
U Ví dụ 4:U Giải phương trình:
2 22
4 24 35 3 2 7 12
x x xx xx
  
(4)
Hướng dẫn: ĐK
5
;4 ;2 1;
2
x



 




.
Thử các giá trị tại
5, 4, 1, 0, 1
x x x xx
  
không thỏa mãn.
Dự đoán nghiệm thuộc khoảng
5
;2
2



. Viết lại phương trình:
2 22
4 24 35 3 2 7 12x x xx xx 
bình phương hai vế ta có:
2 22
2 14 21 2 3 2 7 12
x x xx xx 
. Đến đây ta bình phương lần nữa thì sẽ thu được
phương trình bậc 3 và hy vọng phương trình có một nghiệm hữu tỉ (loại), hai nghiệm vô tỉ mà trong
đó có nghiệm chúng ta cần.
43 2 2 2
4 56 280 588 441 4 3 2 7 12x x x x xx xx  
32 2
16 140 388 345 0 2 5 8 50 69 0x x x x xx 
5 25 73
,
28
xx


. Dễ thấy
5
2
x 
không là nghiệm vì VT (4) < 0 < VP(4).
Vậy phương trình có 1 nghiệm là
25 73
8
x

.
ULời bìnhU:
Độ dài khoảng nghiệm
51
2
22



là khá nhỏ, nghiệm có dạng
9
84
pq
x

.
U Ví dụ 5:U Giải phương trình:
2 22
9 29 11 2 3 3 2.x x xxxx  
Hướng phân tích: Điều kiện
3x
. Với
3
x
ta có VT > VP, với
4x
ta có VT < VP và do đó
dự đoán phương trình có nghiệm duy nhất
3; 4x
. Bình phương hai vế ta được:
2 22
4 14 9 4 3 3 2x x xxxx 
, bình phương lần nữa ta có:
32 2
16 92 156 81 0 2 3 8 34 27 0xx x x xx 
Giải ra ta có nghiệm cần tìm của phương trình là
17 73
8
x

ULời bình:
Nhận xét được
32
16 92 156 81 0xx x 
không có nghiệm âm, nghĩa là ít nhất còn có một
nghiệm
2
1; 2x
liên hợp với
1
3; 4x
và giả sử
1 2 1 2 12
3, 5; 1, 5 4; 5, 25x x x x xx 
Kết hợp
27
16 2.8; 81 3.27 5
8

là hợp lý để phân tích nhân tử
2
8 34 27xx
.
U Ví dụ 6:U Giải phương trình:
22
2 3 3 1 9 23 19.xx x x x 
Hướng phân tích:
Điều kiện là
x
. Bình phương hai vế ta có:
22
4 9 64 1 3 3xx x xx 
(1).
Ta có
2
4 9 6 0,xx x

nên để
x
là nghiệm thì từ (1) ta phải có
10 1xx 
+ Nếu
0
x
thì
22
4 964 1062 123xx x x x x  
(*)
Mặt khác
2
232 33912x xx

(**) nên kết hợp (*) suy ra (1) vô nghiệm.
+ Do đó ta phải có
1; 0x 
. Nếu ta bình phương thì xuất hiện nghiệm âm thứ hai, ta có:
2
2 22
1 4 9 6 16 2 1 3 3xx xx xx
 
(2).
Cho
2x 
thì VT = VP nên
2x 
là nghiệm, với
1, 5x 
thì VT < VP, với
1x 
thì
VT > VP nên phương trình có thêm nghiệm
3
;1
2
x



.
Giả sử
12
1 5 75
,;
2 4 48
x x SP  
nên khả năng
2
8 14 5 0xx 
.
Ta chú ý
2
16.3 6 12 2.6
suy ra
6
8
P
như thế
2
8 60
x Sx 
.
Ta có
32 2
2 8 31 36 12 0 2 8 15 6 0
xxx x xx 
15 33
2,
16
xx


. So sánh điều kiện ta lấy nghiệm
15 33
16
x

.
ULời bình:
Sau khi bình phương thì phương trình có nghiệm
2
x 
, ngoài ra phương trình trở thành bậc 3 nên
khá dễ dàng. Mặt khác ta cũng có thể giải (1) theo phương pháp đưa về dạng tích như trong phần 3.
ULưu ý 1:
Trong quá trình dò khoảng nghiệm mà ta phát hiện phương trình có nghiệm nguyên thì ta vẫn bình
phương hay trục căn, bài toán sẽ dễ hơn và tiến hành giải bình thường.
U Ví dụ 7:U Giải phương trình:
3
32
3 2 2 6 0.xx x x 
Hướng phân tích:
Điều kiện
2x 
. Với
2x 
ta có VT < VP, với
1x 
ta có VT > VP do đó dự đoán phương
trình có nghiệm
2; 1x 
. Với
0;1x
thì VT > VP,
2x
là một nghiệm, với
3;4;5...x
ta
có VT > VP nên
2x
là nghiệm kép. Ở đây ta lựa chọn trục căn:
PT
3
32
3 42 2 3 2 0xx x x



. Với
1x 
không thỏa mãn
32
32
3
3
3 4 0 ( a)
2
3 41 0
2 3 2 2 (b)
2 32
xx
xx
xx
xx






.
+ Giải (a):
2
2 1 0 2, 1x x xx

.
+ Giải (b):
3
32
2
4
4
2
2
2 34
3
3
3 12 8 0
1 480
x
x
xx
xx x
x xx










2 23
x 
. So sánh các điều kiện ta có nghiệm phương trình là
2; 2 2 3xx 
.
U Ví dụ 8:U Giải phương trình:
22
5 4 3 18 5 .x xx x x 
Hướng phân tích:
Điều kiện
6
x
. Với
6; 7x
ta có VT > VP, với
8x
ta có VT < VP do đó dự đoán phương
trình có nghiệm
7; 8
x
, ngoài ra
9x
là một nghiệm. Chuyển vế bình phương ta được:
22
2 16 9 5 5 4 2 19 9 5 5 4 7xxxx xxxx  
9
25 9
92 1
2 1 5 4 7 25 (*)
5 47
x
xx
xx
xx x
x



.
Giải (*)
32
2 1 5 4 11 7 4 25 33 9 0x x x xxx 
2
7 61
43 730
2
x xx x

(Loại các nghiệm âm).
Vậy phương trình có hai nghiệm là
7 61
9,
2
xx

.
U Ví dụ 9:U Giải phương trình:
22
5 14 9 20 5 1.x x xx x

Hướng dẫn:
Điều kiện
5x
. Với
5; 6x
ta có VT > VP, với
7x
ta có VT < VP do đó dự đoán phương
trình có nghiệm
6; 7x
, ngoài ra
8x
là một nghiệm. Chuyển vế bình phương ta được:
22
2 5 2 5 20 1x x xx x 
. Bình phương lần nữa và rút gọn thành
4 3 2 32
4 45 33 505 504 0 8 4 13 71 63 0xx x x x xxx 
2
5 61
8 4 7 5 9 0 8,
2
x x xx x x

(Loại các nghiệm âm).
Vậy phương trình có hai nghiệm là:
5 61
8,
2
xx

.
ULời bình:
Qua các ví dụ 7, ví dụ 8, ví dụ 9 ta thấy có thể lựa chọn phương pháp bình phương hai bước đưa về
bậc 4 hay bình phương một bước và trục căn như lưu ý đã nêu. Ngoài ra ta cũng có thể sử dụng
phương pháp "Kim thiền thoát xác" ở sau.
U Ví dụ 10:U Giải phương trình:
22
3(9 20 9) 2 6 11 3 2 .xx xx x 
Hướng phân tích:
Điều kiện
2x
. Với
2x
ta có VT < VP, với
3
x
ta có VT > VP và do đó dự đoán phương
trình có nghiệm duy nhất
2; 3x
. Bình phương hai vế ta được:
22
3 17 17 4 6 11 3 2x x xxx 
. Tiếp tục bình phương hai vế lần nữa ta có
432
9 198 759 978 385 0xxxx 
. Đến đây ta thấy phương trình xuất hiện thêm nghiệm
thứ hai
0;1x
và tính
1 2 12
2, 5 0, 5 3; 1, 25x x xx

ngoài ra
385 5.7.11
do đó dự
đoán nhân tử là
2
3 9 50xx 
và kết quả PT
22
3 9 5 3 57 77 0xx x x

.
Giải ra ta có nghiệm cần tìm của phương trình là
9 21
6
x

ULời bình:U Ta có thể bình phương và sau đó trục căn nhưng khá dài dòng, chẳng hạn:
22
3 17 17 4 6 11 3 2 0xx xxx 
22
3 9 5 4 6 11 3 2 2 3 0
xx x x x x 
(với
2
x
)
2
2
2
2
6 11 3 2 2 3
3 9 5 4. 0
6 11 3 2 2 3
xxx x
xx
xxx x



(với
2x
)
2
2
42 3
3 9 51 0
6 11 3 2 2 3
x
xx
xxx x







(với
2x
)
(vì
2x
)
2
9 21
3 9 50
6
xx x

. (Xem thêm về PP "Kim thiền thoát xác" ở sau)
U Ví dụ 11:U Giải phương trình:
22
6 3 1 3 6 19 0.xx x x x 
Hướng phân tích:
Điều kiện
2;xD

. Cho
xD
chạy thì phương trình đổi dấu hai lần và ta đoán được
phương trình có hai nghiệm
1
2; 3x
và
2
20;21x
. Giả sử
12
2, 5 ; 20, 5xx
thì ta có
1 2 12
23, 51x x xx
. Chuyển vế thành
22
3 6 19 6 3 1.x x xx x

Bình
phương hai vế ta có
22
8 17 3 6 1x x xx x

. Ta có
2
17 9.6 235 5.47
nên dự
đoán nhân tử là
2
23 47 0xx 
. Tiếp tục bình phương hai vế ta được:
432 2 2
25 98 209 235 0 23 47 2 5 0x x x x x x xx 
2
23 47 0xx

. Giải ra ta có nghiệm cần tìm của phương trình là
23 341
2
x

ULưu ý 2:U (Phương pháp "Kim thiền thoát xác")
Đối với các tam thức có hai nghiệm như
2
6xx

ta tráo đổi nghiệm với biểu thức khác
22
6 1 23 2xx x x x x 
và ta có phương trình:
22
8 17 3 2 3 2xx xx x 
chia cả hai vế cho
2
2 3 0, 2xx x 
ta được
2
2
10 2
2
13
23
23
x
x
xx
xx



. Đặt
2
2
0
23
x
t
xx


ta có
2
1 10 3tt
suy ra
22
2
1 2 23 341
2 3 25 50 23 47 0
52
23
x
t xx x x x x
xx



.
Phương pháp "Kim thiền thoát xác" ở trên có thể áp dụng với đa thức bậc cao hơn.
U Ví dụ 12:U Giải phương trình:
22
2 1 3 5 2 18 18 5.x xx x x
Hướng dẫn "Kim thiền thoát xác":
Điều kiện
1
3
x
. Bình phương hai vế ta có:
22
15974 1352xx x xx 
(*).
Điều kiện
9 501
30
x

. Viết lại
22
13 5 2 23 2 1x xx x xx 
và chia cả hai
vế của (*) cho
2
9 501
3 2 1 0,
30
xx x


ta có
22
22
*5 4
3 21 3 21
xx
xx xx


 
. Đặt
2
2
0
3 21
x
t
xx


thì có
2
54tt
2
2
2
1 3 30
3 21
x
t xx
xx
 

1 37
6
x


.
Đối chiếu điều kiện ta có nghiệm cần tìm của phương trình là
1 37
6
x


ULưu ý 3:
Trong quá trình dò khoảng nghiệm mà ta phát hiện phương trình vô nghiệm thì ta vẫn tiến hành giải
bình thường.bằng phương pháp bình phương hay trục căn.
U Ví dụ 13:U Giải phương trình:
22
2 3 2 18 16 39 5 1.
xx x x x

Hướng phân tích:
Điều kiện
2
2
2 3 20
18 16 39 0 2
10
xx
xx x
x



. Khi cho
2, 3, 4, ...xxx
ta có VT < VP nên khả
năng phương trình vô nghiệm. Viết lại:
22
2 3 2 5 1 18 16 39xx x x x 
Bình phương hai vế ta có:
22
52 3 2 1 8 3 6
xx x xx 
.
Tiếp tục bình phương hai vế:
2 432
25 2 3 2 1 64 48 87 36 36
xx x x x x x

(*)
Cho
1
2
x

ta có VT < VP, cho
0
x
ta có VT > VP nên (*) có nghiệm thuộc
1
;0
2


và nghiệm
này bị loại. Cho
1
x
ta có VT < VP nên (*) có nghiệm
0;1
cũng bị loại.
11
1
; 0 0, 4
2
xx



và
22
0; 1 0, 8xx 
nên
1 2 12
0, 5 ; 0, 5x x xx

432
* 64 98 38 11 14 0
xx xx

(**). Các tỉ số sinh ra từ
14 14 7
64 32 16

là gần
đúng nhất. Kết quả là:
22 2
17 2081
* * 2 2 1 32 17 14 0 32 17 14 0
64
xx xx xx x
 
cả hai nghiệm đều loại. Vậy phương trình đã cho vô nghiệm.
UNhận xét 2U:
Ta có thể sử dụng phương pháp trục căn trực tiếp, bình phương một lần hay hai lần, đặt ẩn phụ, ...
nhưng nghiệm vô tỉ ta cần cuối cùng dẫn đến nghiệm của phương trình bậc hai:
2
0ax bx c 
.
Nhìn chung ta thường gặp các hệ số
,,abc
và đặc biệt ta luôn chuyển về được
*
a
.
Phương trình trên xem như giao điểm của Parabol
2
y ax bx c 
với trục hoành. Rõ ràng khi
a
càng lớn thì khoảng cách giữa hai nghiệm
21
dxx
càng bé, ngược lại khi
1a
thì Parabol có
xu hướng như "một cái chảo", nghĩa là
21
dxx

càng lớn.
Gọi
;

,
'; '
là các khoảng hữu tỉ gần đúng nhất để phương trình
0fx
đổi dấu.
+ Nếu khoảng cách
'' 5d  
thì nghiệm có dạng
*
,,x p qp q 
và có
thể lấy gần đúng
''
,
44
d
pq


.
+ Nếu tính gần đúng
' ' 13
;
4 22
p


hay tương tự thì
'
22
pq
d
qx

.
U Ví dụ 14:U Giải phương trình:
22 2
( 6 11) 1 2( 4 7) 2
x x xx x x x 
Hướng phân tích:
Điều kiện
2x
. Với
2x
thì VT > VP, với
3x
thì VT < VP, với
4;5;6;7;x
thì VT < VP,
với
8x
thì VT > VP do đó ta đoán phương trình có hai nghiệm
1
2; 3 ,x
2
7; 8x
.
Tính gần đúng:
2378
5
4
p


và
7823
2, 5 6
4
qq


56x
nên nhân tử đoán là
2
10 19 0xx 
.
Nếu bình phương hai vế sẽ dẫn đến phương trình bậc 5, ở đây ta sử dụng phương pháp trục căn và
làm như sau:
Nhân cả hai vế với 3 ta có:
22 2
3( 6 11) 1 2( 4 7) 9 18x x xx x x x 
2 22 2 2
3( 6 11) 2( 4 7) 1 2( 4 7) 9 18 1x x x x xx x x x xx

 


22
22
2
2 4 7 10 19
10 19 1
9 18 1
xx x x
x x xx
x xx



2
22
2
2 47
10 19 1 0
9 18 1
xx
x x xx
x xx









2
10 19 0 5 6xx x 
(thỏa mãn điều kiện)
Vậy nghiệm cần tìm của phương trình là
56x

.
ULời bìnhU:
Nếu nói ta "nhẩm nghiệm vô tỉ" thì quá xạo nhưng "mò ra nghiệm vô tỉ" tương đối chuẩn đấy!
UTrở về ví dụ 11U:
1
5
2; ,
2
x


2
41
;21
2
x


. Tính gần đúng:
21 20, 5 2,5 2 23
42
p


và
20, 5 21 2, 5 2
18,5 341
2
qq


23 341
2
x

nhân tử
2
23 47 0xx 
.
U Ví dụ 15:U Giải phương trình:
23
2( 3 2) 3 8xx x 
.
Hướng phân tích:
Điều kiện:
2x 
. Cho x = -2; -1; 0; 1; 2; ... thì phương trình đổi dấu hai lần trong khoảng (-1; 0) và
(6; 7) nên phương trình có hai nghiệm trái dấu.
Tính gần đúng:
671
3
4
p


và
671
3, 5 13
4
qq


3 13x
nên nhân
tử đoán là
2
6 40xx 
.
Bình phương hai vế ta có:
432
4 33 52 48 56 0xxxx 
.
Và ta được
22
644 9140
xx xx

2
3 13
6 40
3 13
x
xx
x



.
U Ví dụ 16:U Giải phương trình:
22
3 6 4 ( 4) 2 4xx x x 
.
Hướng phân tích:
Bài này có thể có cách nhận dạng khác, tuy nhiên ta thử mò nghiệm và tìm cách giải xem?
Điều kiện
2
3 6 40
3 21
2 40
3
xx
x
x




. Cho
1; 2; 3xxx
ta có VT < VP
Cho
7
2
x
ta có VT > VP nên dự đoán phương trình có nghiệm đơn duy nhất
1
7
3;
2
x


. Để tìm
nghiệm âm liên hợp ta viết lại
22
22
42 4 3 6 4 0x x xx 
với
3
2
x 
là một
nghiệm, cho
1x

ta có VT > 0 nên nghiệm
2
3
;1
2
x



.
Tính
3 3,5 1,5 1
1
4
p


và
3,5 3 1,5 1
2, 25 5
4
qq


như thế dự đoán
nghiệm là
15
x

và nhân tử là
2
2 40
xx

.
Hướng dẫn giải:
Điều kiện
2
3 6 40
3 21
2 40
3
xx
x
x




.
Bình phương hai vế ta có:
4 3 2 42
9 36 12 48 16 ( 8 16) 2 4x x x x xx x 
2
54 3 2 2
2 5 20 20 80 48 0 2 4 2 3 0
xx x x x xx x 
(vì
0x
)
2
2 40xx 
15
x 
.
Vậy phương trình có một nghiệm
15
x 
.
ULời bìnhU:
Vì đã biết nhân tử nên chúng ta cứ mạnh dạn bình phương để khử căn bậc hai! Sau đây
chúng ta sẽ xét thêm ví dụ và trục căn.
U Ví dụ 17:U Giải phương trình:
22
47324121xx xx x 
.
Hướng phân tích:
Bài này có thể có cách nhận dạng khác, tuy nhiên ta thử mò nghiệm và tìm cách giải xem?
Cho
1; 2; 3xxx
ta có VT > VP. Cho
7
2
x
ta có VT < VP nên dự đoán phương trình có
nghiệm duy nhất
1
7
3;
2
x


. Để tìm nghiệm liên hợp
2
x
ta viết lại thành:
22
22
473241210xx xx x
 
. Cho
1
2
x
thì VT > 0, cho
1x
thì VT < 0 do
đó nghiệm
2
1
;1
2
x


. Tính
3 3, 5 0, 5 1
2
4
p


và
3, 5 3 0, 5 1
1, 3
4
q


2
q

22x

. Nhân tử là
2
4 20xx 
.
Hướng dẫn giải:
Điều kiện:
22
4732410
22
1; 3;
2 10
2
xx xx
xD
x

 






.
Lấy
2
2 41 1xx x
trừ đi mỗi vế ta có phương trình:
32 2
2 10 12 4 2 4 1 1 2 1x x x xx x x 
22
2
2 41 42
4 22 2
1 21
xx xx
xx x
xx
 


2
2
420
(*)
2 41
22
1 21
xx
xx
x
xx




Ta có
2
2 41
22
1 21
xx
x
xx



2 22 1 1
xx

(Vô nghiệm vì
xD
).
Do đó
2
(*) 4 2 0xx 
giải ra lấy nghiệm
22
x 
.
U Ví dụ 18:U Giải phương trình:
23
1 4 3 ( 2)x xx x

()x
.
Hướng phân tích:
Điều kiện
1
x 
. Nếu để ba căn để trục căn hay đánh giá thì phức tạp nên bình phương hai vế và
thu gọn ta có:
32
2 1 3 5 74x x xxx 
.
Tại
1x 
thì VT < VP, tại
0x
thì VT < VP, tại
1x
thì VT < VP ... và cả hai vế ngày càng
lớn. Như thế ta đoán phương trình có nghiệm duy nhất
1; 0x 
(nghiệm kép).
Chuyển vế lần nữa ta có
32
2 1 3 5 740x x xxx 
. Cho
3x 
ta có VT = -1,
cho
2x

ta có VT = - 4 như thế có thêm điểm tiếp xúc liên hợp là
3; 2x

.
Tính
3201 3
42
p


và
132
25
2
qq


nên
35
2
x

.
Nhân tử là
2
3 10xx 
.
Hướng dẫn giải:
Điều kiện
1x 
. Bình phương hai vế và thu gọn:
32
2 1 3 5 74x x xxx 
.
32 2
21
3 2 1 2 30 31 0
23
x
x xx x x x x x x
xx







.
2
3 10
21
0
23
xx
x
x
xx



(*). Ta có
21
0
23
x
x
xx


(với
10x
)
2 43 2
4 2 3 7 17 16 4 0x x xx x x x x 
2
2
31 2 0xx x 
2
3 10xx 
(**).
Từ (*) và (**) ta đều có
2
3 10
xx

giải ra lấy nghiệm
35
2
x

.
U Ví dụ 19:U Giải phương trình:
2
4 6 4 27 1xx x x 
.
HƯỚNG PHÂN TÍCH
Với
1x 
thì VT > VP, với
0x
thì VT < VP nên phương trình có nghiệm
1
1; 0x 
như thế
ta đoán phương trình bậc hai còn có nghiệm liên hợp
2
0x
nhưng bị loại. Để chính xác hơn ta thử
tại
1
2
x 
thì VT > VP nên
1
1
;0
2
x



. Để đoán
2
0x
ta viết lại thành:
2
2
2
4 67 1 4 2 0xx x x
và với
2x
thì VT > 0, với
5
2
x
thì VT < 0 nên
phương trình này có nghiệm
2
5
2;
2
x


.
Tính
2 2, 5 0, 5 0
1
4
p


và
2, 5 2 0, 5 0
2, 5 7
2
qq


như thế dự đoán
nghiệm là
27
2
x
và nhân tử là
2
4 8 30xx 
.
Hướng dẫn 1:
Điều kiện
1x 
. Bình phương hai vế và thu gọn
2
12 32 47 28 2 1 1 0
xx xx 
Dễ thấy
1/2x
không là nghiệm nên ta có
1 1/2x
. Mặt khác trở về phương trình đầu
PT
2
4 631212210xx x x x 
2
2
12
4 83 0
12 2 1
4 63 1
xx
xx
xx x





2
4 8 30xx 
giải ra lấy nghiệm
27
2
x
.
Hướng dẫn 2:
Đặt
2
10 1x t xt
, khi đó ta có phương trình:
42 2
7 145
4 7 94 7 60
8
tt tt t


. Bình phương hai vế ta có
42 432 432
4 7 9 16 56 84 36 12 56 8 84 27 0tt tttt tttt  
22
1 7 11 5 7
22362290 ,
26
tt t t t t


.
Đối chiếu điều kiện ta lấy
17 27
22
tx


.
ULời bình:
Khi đã lập luận
1 1/2x

thì
2
12 32 47 14 2 4 1x x xx

tiếp tục bình phương
để đưa về bậc 4, chắc chắn có nhân tử là
2
4 83xx
. Đây là bài toán khó, các bạn thử tìm cách
giải khác xem độ phức tạp thế nào ?
Bình phương để mở rộng tập xác định nhiều khi rất cần thiết để giải!
U Ví dụ 20:U Giải phương trình:
22
10 50 3 2 5 2 3 5.x x xx x

Hướng phân tích:
Điều kiện
25 655
10
x
. Bình phương hai vế:
22
4 27 20 3 2 5 2 5
x x xx x 
(*) .
Điều kiện
25 655 27 409
10 8
x


. Tiếp tục bình phương ta được:
43 2
16 234 1024 1323 490 0xx x x 
(**).
Đến đây ta thấy vấn đề vướng mắc là phân tích đa thức bậc 4 thành nhân tử. Đối với bài toán độc lập
như phương trình (**) thì quả nhiên là khó, tuy nhiên trong bài toán này thì (**) là phương trình hệ
quả của (*) nên ta chú ý viết như sau:
2
22
4 27 20 9 2 5 2 5 0x x xx x 
Phương trình (*) có nghiệm
1
5; 6x
; nhưng phương trình (**) có thêm nghiệm
2
1
;1
2
x


nên ta
suy ra
5 6 0, 5 1
3
4
p


và
5 6 0, 5 1
4, 5 22
2
qq


do đó ta đoán nhân tử
là
2
2 12 7xx
(và kết hợp 490 chia cho 7 là đẹp) kết quả là:
22
* * 2 12 7 8 69 70 0xx xx 
. Đáp số:
6 22
2
x

ULời bình:
Trên đây là bài khó vì phương trình bậc 4 có các hệ số lớn, đòi hỏi tính kiên trì. Hơn nữa nghiệm bị
kẹp trên đoạn vô tỉ cồng kềnh, tuy nhiên sau khi bình phương để khử căn thì ta mở rộng đoạn thêm
một tí để được đoạn hữu tỉ và từ đó dự đoán nhân tử dễ hơn. Xem thêm PP "Kim thiền thoát xác".
U Ví dụ 21:U Giải phương trình:
22
2 8 8 4 19 8 17 3xx xx x x x

Phân tích:
Cho
0x
ta có VT > VP, cho
1
2
x
ta có VT < VP nên phương trình có nghiệm
1
1
0;
2
x


.
Cho
2x
ta có VT < VP, cho
3
x
ta có VT > VP nên phương trình có nghiệm
2
2; 3x
.
Tính
230,5 3
42
p


và
2 3 0, 5
2, 25 5
2
qq


35
2
x

nhân tử là
2
3 10xx 
. Nhiệm vụ bây giờ là trục căn thức để tao ra nhân tử.
Ta có:
22
2 8 8 4 19 8 17 3
xx xx x x x

22 2
5 6 3 1 29 8 3 2 17 3 0xx xx x x xx x x  
2
3198 2 398 1 2730xxxxxxxxx
 
2
21
3 19 8 0
398 273
xx
xx x
xxxx





(ĐK
3
7
x 
)
2
3 10xx 
giải ra ta có hai nghiệm cần tìm là
35
2
x
.
U Ví dụ 22:U Giải phương trình:
32
3 4 3 26 6xxx x x 
.
Phân tích:
Cho
3
4
x 
thì VT > VP, cho
0x
thì VT < VP nên phương trình có nghiệm
1
3
;0
4
x



.
Cho
2x
thì VT < VP, cho
3x
ta có VT > VP nên phương trình có nghiệm
2
2; 3
x
.
Tính
2 3 0, 75
1
4
p


và
230,75
1, 5 3
4
qq


13x 
nhân tử là
2
2 20xx 
. Nhiệm vụ bây giờ là trục căn thức để tao ra nhân tử.
Ta có:
32
3 4 3 26 6xxx x x 
32
42 1 4 32 2 6 6 0xx x x x x x 
2
12
22 1 0
143 2 66
xx x
x xx x




(vì ĐK
3
4
x 
)
2
2 20xx 
giải ra ta có hai nghiệm cần tìm là
13x 
.
U Ví dụ 23:U Giải phương trình:
2
3
24 3 16 4 2 1x xxx x 
.
Phân tích:
Cho
3
4
x 
thì VT > VP, cho
0
x
thì VT < VP nên phương trình có nghiệm
1
3
;0
4
x



.
Cho
2x
thì VT < VP, cho
3x
ta có VT > VP nên phương trình có nghiệm
2
2; 3x
.
Tính
2 3 0, 75
1
4
p


và
230,75
1, 5 3
4
qq


13
x 
nhân tử là
2
2 20xx 
. Nhiệm vụ bây giờ là trục căn thức để tao ra nhân tử.
Ta có
2
2
3
24 3 16 4 2 1 2 4 2x x x x x xx 
3
1 64 2 1430xxx x x x 
32
2
2
3
3
1 64 2 22
0
143
64 64
x xx x xx
xx
x xx x
 



(với
3
4
x 
)
2
2
2
3
3
12 2
22 0
143
64 64
xx x
xx
xx
x xx x











(với
3
4
x 
)
2
2 20xx 
giải ra ta có hai nghiệm cần tìm là
13x 
.
U Ví dụ 24:U Giải phương trình:
3 23
41 1x x xx xx x 
,
x
.
Phân tích:
Cho
1
x 
thì VT > VP, cho
0x
thì VT < VP nên phương trình có nghiệm
1
1; 0x 
. Cho
2x
thì VT < VP, cho
5
2
x
thì VT > VP nên phương trình có nghiệm
2
5
2;
2
x


.
Tính gần đúng
1022,5
0, 88 1
4
p


;
2 2, 5 1
1, 4 2
4
qq


. Như thế ta
đoán nghiệm
12x 
nhân tử là
2
2 10xx 
. Bây giờ phân tích thành nhân tử:
PT
32 3
52 1 1 0x x xx x x xx 
32 2
52 1 1 1 0x x xx x x x xx 
2
22
11
21 2 0
11
x
xx x
xx x xx x



 

(*).
Với
2
1
10
1
x
xx x


và
2
22
1
10
11
x xx
xx x xx x


 
Nên từ (*) suy ra
2
2 10 1 2xx x 
.
U Ví dụ 25:U Giải phương trình:
43 2 2 2
5 11 12 5 2 2 4 3x x x x xx x x  
.
Phân tích:
Cho
0x
thì VT > VP, cho
1x
thì VT < VP nên phương trình có nghiệm
1
0;1x
.
Cho
2x
thì VT < VP, cho
3
x
thì VT > VP nên phương trình có nghiệm
2
2; 3x
.
Tính gần đúng
1023 3
42
p


;
2301
25
2
qq


. Như thế ta đoán nhân tử
là
2
3 10xx 
. Bây giờ ta giải phương trình:
PT
2 2 2 43 2
2 2 4 3 2 5 10 11 3 0xx x x xx x x x x

 



2
22
22
2
31 230
2 43 2
xx
xx xx
x x xx





(*).
Với
2
2
22
22
2
231 23 1 1 0
2 43 2
xx
xx xx x
x x xx



Nên từ (*) suy ra
2
35
3 10
2
xx x

.
U Ví dụ 26:U Giải phương trình:
22
3
11 9 15 7 2 8 3x x x xx x 
,
x
.
Phân tích:
Cho
0x
thì VT < VP, cho
1x
thì VT > VP nên phương trình có nghiệm
1
0;1x
.
Cho
3
x
thì VT > VP, cho
4x
thì VT < VP nên phương trình có nghiệm
2
3; 4
x
.
Tính gần đúng
1034
2
4
p


;
3401
1, 5 3
4
qq


. Như thế ta đoán
nghiệm
23x 
nhân tử là
2
4 10xx 
. Bây giờ ta giải phương trình:
Ký hiệu
2
3
9 15 7xx a 
và với
3
8
x 
khi đó ta có
PT
2
41 83 2 83 2 0xx x x x x a




2
2
2
83 1
4 11 0
283
22
xx
xx
xx
x x aa










(với
3
8
x 
)
2
4 10 2 3xx x 
.
U Ví dụ 27:U Giải phương trình:
2
3 6 7 9 9 14
xx x x

,
x
.
Phân tích:
Cho
6
5
x 
thì VT > VP, cho
1x 
thì VT < VP phương trình có nghiệm
1
6
;1
5
x



.
Cho
4x
thì VT < VP, cho
9
2
x
thì VT > VP nên phương trình có nghiệm
2
9
4;
2
x


.
Tính gần đúng
1, 2 1 4 4, 5 3
42
p


;
44,51,21
5, 4 29
2
qq


. Như thế
ta đoán nghiệm
3 29
2
x
nhân tử là
2
3 50xx 
. Bây giờ phân tích thành nhân tử:
PT
2
279 35 39140xxxxxx 
2
11
35 1 0
279 3914
xx
xx xx




(với
9
7
x

)
2
3 29
3 50
2
xx x

.
U Ví dụ 28:U Giải phương trình:
32
6 2 3 33 2 2 1
x x xx x x 
,
x
.
Phân tích:
Cho
1x
thì VT < VP, cho
2x
thì VT > VP nên phương trình có nghiệm
1
1; 2
x
.
Nếu ta dò tiếp thì không thành công, để đoán nghiệm thứ hai, ta chuyển vế thành:
2
2
32
6 2 3 2 1 33 2 0xxx x x x  
Thử
1x 
thì
2
2
5 1 .2 0 
, với
0x
thì
2
2
2 2.3 0

như thế phương trình này có
nghiệm
2
1; 0x 
liên hợp với
1
1; 2x
.
Tính gần đúng
1012 1
42
p


;
1201
25
2
qq


. nhân tử là
2
10xx
. Bây giờ ta trục căn phân tích thành nhân tử:
Trước hết ta có
2
3
x 
và
32
6 2 30xxx 
nên
1 19 1 19
;0 ;
66
xD













.
PT
32
6 3 93 3 1 322 10x x x x x x xx   
22
32
1 6 3 0 1. 0
132 1
x
xx x xx M
x x xx

 


(*)
+ Nếu
1 19
;0
6
x



thì
6 40x 
;
3 232
10
132 132
xx
xx xx


 
Và
2
0
1xx

suy ra
0M
.
+ Nếu
1 19
;
6
x




thì dễ thấy
0M
.
Do đó ta luôn có
0,
M xD 
nên từ (*)
2
15
10
2
xx x

.
ULời bình:
Trên đây là bài khó vì phải đánh giá biểu thức M. Nếu ta không có điều kiện
xD
mà chỉ
có điều kiện ban đầu
2
3
x

thì
2
1xx
chưa được xác định tại
15
2
x
không
những thế ta cũng không loại được giá trị này vì nó thỏa mãn
2
3
x 
. Đây chính là sai lầm
đối với học sinh khi mà loại
15
2
x
không có cơ sở hoặc lấy làm nghiệm của phương
trình!.
Phương trình vô tỉ rất đa dạng và phong phú, để kết thúc ta xét thêm vài ví dụ liên quan các
phần đã nêu, ở đây ta không nghiên cứu chủ đề đặt ẩn phụ hay lượng giác hóa, phương
pháp hàm số ... vì vượt qua khả năng của HS các lớp 9, lớp 10 và lớp 11 không chuyên.
Qua 5 phần đã nêu: ta tiếp cận và giải phương trình dưới góc độ nhìn nhận phổ thông và tự
nhiên nhất có thể được.
U Ví dụ 29:U Giải phương trình:
1 2 12 1
xx x
,
x
.
Phân tích:
Trước hết đặt ẩn phụ:
10xt
ta có
22
2 12tt t
. Điều kiện
2
2
t
.
Với
1
2
t
thì VT > VP, với
1t
thì VT < VP nên phương trình có nghiệm
1
1
;1
2
t


.
Ta cần dự đoán thêm nghiệm
2
t
liên hợp với
1
t
. Nhận xét
3
1t 
là một nghiệm. Với
9
5
t 
thì VT > VP, với
3
2
t 
thì VT < VP nên phương trình có nghiệm
2
93
;
52
t



.
Tính gần đúng
1, 5 1, 8 0, 5 1 1
42
p


;
1 0, 5 1, 8 1, 5
2, 4 5
2
qq


.
Như thế ta đoán nghiệm
15
2
t

nhân tử là
2
10tt

. Bây giờ ta trục căn phân
tích thành nhân tử:
PT
2
22 2 2
2 11
21212 11
21
tt
tt t t t
t



(với
2
1
2
t
)
22
2 11 2 1 1 2 2 2
t t t t t tt
 
bình phương hai vế ta có:
4 32 2
4 4 7 4 4 12 2
t t t t ttt 
4 32
4 3 7 20
t t tt 
22
1 33 1 5
4 2 10 ,
82
tttttt


. Đối chiếu điều kiện ta lấy
2
1 33 2 1 15 33
1 12
8 4 4 32
t
t xt t x

 
.
Vậy phương trình có một nghiệm
15 33
32
x

.
ULời bình:U Khi đã đoán được nhân tử thì ta có cách khác như sau:
Trước hết đặt ẩn phụ:
10xt
ta có
22
2 12
tt t
. Điều kiện
2
2
t
.
22 2
21 2 42 2 2 4 2
11
22 2
t t t t t t tt
tt t
tt t

 

2
22
4 20
4242
22 2
22 2
tt
tt tt
t t tt
t
t tt

 



(*).
Ta có
2 2 2 22 2 0t t tt t t 
(vô nghiệm vì
2
2
t
). Do đó từ (*) ta
được
2
1 33
4 20
8
tt t

(vì
2
2
t
).
Thay trở về
2
1xt
suy ra phương trình có một nghiệm
15 33
32
x

.
U Ví dụ 30:U Giải phương trình:
2 2 34
4 1 15 4 2xx x x xx
.
Phân tích:
Dễ thấy đây là phương trình có chứa đa thức bậc 4 nên ta hướng đến đặt ẩn phụ để khử
căn hoặc để giảm bậc vì thế ta chia đa thức
2 34
15 4 2x x xx
cho
2
1xx
và có
2
2 34 2 2
1 5 4 2 1 71 5x x x x xx xx  
đến đây ta đặt:
2
10xx t
ta được
42 42
4 7 5 7 4 50tt t tt t  
Cho
1t

thì VT < 0, cho
1
2
t

thì VT > 0 nên phương trình có nghiệm
1
1;
2
t



.
Cho
1
t
thì VT > 0, cho
3
t
thì VT < 0.
Như thế phương trình có các nghiệm
1
1
1;
2
t



và
2
1; 2t
Tính gần đúng
1 2 1 0, 5 1 1 2 1 0, 5
; 2, 25 5
42 2
pq q


do đó nghiệm
15
2
t
nhân tử ta đoán là
2
10tt
.
Kết quả:
42 2 2
7 4 50 1 5 0t t t tt tt 
và giải ra lấy các nghiệm dương
1 5 1 21
,
22
tt


. Ta có
2
2
2
1 3 143
24 2
t
x tx




Từ đó phương trình có 4 nghiệm
1 3 2 5 1 19 2 21
,
22
xx
 

.
ULời bình:
Ta nhận thấy phương trình
42
7 4 50ttt 
có hai nghiệm trái dấu và do hệ số tự do
bằng 5 nên có thể phân tích thành dạng
22
1 50tmt tnt 
đến đây ta cân bằng
hệ số bậc 3 và bậc nhất thì
01
541
mn m
mn n









ta cũng đi đến kết quả cần thiết.
Bài trên có thể nói nghiệm là "hai lần vô tỉ". Khi chuyển về được đa thức bậc 4 "ta nhẹ đi rất
nhiều".
U Ví dụ 31:U Giải phương trình:
22
8 344 2 4x x xx x

.
Phân tích:
Ta thấy phương trình có một nghiệm
0x
do đó ta trục căn để giảm bậc:
PT
2
2
2
42
0
4 2 42
4 4 4*
42
xx x
x
x xx x
xx x
x




Ta chuyển được về phương trình đơn giản hơn và giải (*) theo phương pháp như trong
phần 3 phân tích thành nhân tử:
22
4 4 4 4 4 2 40xx x xx x x 
2 42 1 4 0xx x x 
;
+ TH1:
2
0
0
1 65
4 40
8
24
x
x
x
xx
xx







+ TH2:
2
1
2 10
3 57
2
8
21 4
4 3 30
x
x
x
xx
xx










Vậy phương trình có 3 nghiệm
1 65 3 57
0, ,
88
xx x


.
U Ví dụ 32:U Giải phương trình:
2
32x xx x 
,
()x
.
Phân tích:
Điều kiện
23
x

. Cho
2x
thì VT > VP, cho
3x
thì VT < VP nên phương trình có
nghiệm
1
2; 3x
. Ta viết lại
2
2
2
3 20
x x xx
khi đó:
Cho
0
x
thì VT < 0, cho
1x
thì VT > 0 nên phương trình có nghiệm
2
0;1x
.
Tính gần đúng
231 3 231
; 25
42 2
pq q


do đó nghiệm
35
2
x
nhân tử ta đoán là
2
3 10xx

. Bây giờ ta giải theo phương pháp như trong phần 4
bình phương và trục căn:
2432 432 2
23 2341 2341213 0xx x x x x x x x x xx 
22
2
2
31 1 0
13
x x xx
xx




(*). Vì
2
2 3 10x xx 
nên
(*)
2
3 10xx 
giải ra lấy nghiệm
35
2
x

U Ví dụ 33:U Giải phương trình:
43 2
32
2
2 9 74
3.
3
xx x x
xxx
xx



Phân tích:
Do
0x
không là nghiệm nên ta có điều kiện
0x
. Ta viết lại:
43 2 2 32
2 9 7 43 3xx x x xx xxx 
Cho
0x
thì VT > VP, cho
1x
thì VT < VP nên phương trình có nghiệm
1
0;1x
.
Cho
2x
ta có VT < VP, cho
3x
ta có VT > VP nên phương trình có nghiệm
2
2; 3x
.
Tính
231 3 231
; 25
42 2
pq q


nên ta đoán nghiệm
35
2
x
và
nhân tử là
2
3 10xx 
. Nhiệm vụ của ta là trục căn tạo ra nhân tử: Trừ cả hai vế với
2
63xx x
ta có
432 2 2
2 5 3 11 4 3 3 1 2x x x x xxx xx x   
22
22
2
3 3 31
3 12 4
12
xx x x x
x x xx
xx x



2
2
2
2
3 10
33
24 *
12
xx
xx x
xx
xx x




. Với
2
0 12 3x xx x x 
VP(*) <
2
3xx
< VT (*) nên (*) vô nghiệm. Do đó ta có
2
35
3 10
2
xx x

. Đối chiếu điều kiện phương trình có 2 nghiệm
35
.
2
x
U Ví dụ 34:U Giải phương trình:
11 52 1 2 12 1x x x xx
.
Phân tích:
Điều kiện
1
2
x
. Đổi biến để khử bớt căn thức:
6
1
2
xt
ta có phương trình:
2 22 3 2 22
1 2 4 22 3 3 6 422 3
t t t tt t t t tt
(*).
Cho
1t
thì VT > VP, cho
3
2
t
thì VT < VP nên phương trình có nghiệm
1
3
1;
2
t


.
Viết lại
2
3 2 42
3 6 4 42 3 0t t t tt 
và
4t 
thì VT < 0,
3t 
thì VT > 0 nên
phương trình có nghiệm
2
4; 3
t 
. Tính
11,534
1;
4
p


11,534
2, 3
4
q


5q
nên ta đoán nghiệm
15t

và nhân tử là
2
2 40tt 
. Do đó:
2 2 32
* 2 2 3 1 6 40t t t tt t 
2
2
2
2
24 10
23 1
t
tt t
tt




, vì
6
2
t
nên
2
2 40 1 5tt t 
.
Thay trở về
2
1xt
ta có nghệm của phương trình là
5 25x 
.
U Ví dụ 35:U Giải phương trình:
22
3 562 3 65xx x xx 
,
()x
.
Phân tích:
Đặt
20xt

ta có
22
22 22
32 52 6) 32 62 5ttttt

 



42 42
374 365tt t tt 
. Điều kiện
2
3 26
0;
3
tt

(*).
Dễ thấy nếu trừ vào hai vế một lượng t và trục căn sẽ có nhân tử:
(*)
42
42 42 42
42
375
374 365 375
365
tt
tt tt tt t tt t
tt t

 

42
42
42 2
42
3 7 50
3 7 50
1
3 6 51
365
tt
tt
t
tt t t
tt t





(**).
Do điều kiện (*) nên từ (**)
42
3 7 50tt 
2
7 109
6
t

thay trở về
2
2xt
ta
được nghiệm của phương trình là
5 109
6
x
.
Ub. Luyện tập:
Bài 1. Giải phương trình:
2
13 2 1xx x x
.
Bài 2. Giải phương trình:
22 3
42 1 3 2 2 1 2 5 .x x xx x x 
Bài 3. Giải phương trình:
2
1 7 17 7.x xxx
Bài 4. Giải phương trình:
22
6 3 4 18.xx x x x
Bài 5. Giải phương trình:
22
2 2 5 9 10.x xx x x 
Bài 6. Giải phương trình:
32 3 2
2 3 4 6.x xx x x 
Bài 7. Giải phương trình:
2 2 32
9 11 6 ( 3) 3 8 4x x xx xx x  
.
Bài 8. Giải phương trình:
22
3 2 2 2 3 5 7 13.x xx xx
Bài 9. Giải phương trình:
2
4 3 18 5 6 2xx x x x  
.
| 1/81
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

MỘT SỐ ĐỊNH HƯỚNG GIẢI PT VÔ TỈ - PHẦN 1
I. Giải phương trình đa thức bậc 4 U
1. Sơ lược cách giải: U U
Phương trình bâc 4 dạng: 4 3 2
ax + bx + cx + dx + e = 0 (1), (a, b, c, d, e nguyên).
Nhìn chung phương trình có hai nghiệm (trường hợp vô nghiệm ta nói sau), do đó mục
tiêu và thường hay làm là đưa về phương trình tích của hai tam thức bậc hai: ( ) ⇔ ( 2
mx + nx + p)( 2 1
m ' x + n ' x + p ') = 0 (2).
Trong đó ta chú ý mm' = a, pp' = e và các số m, m’, p, p’ nguyên và thường là nhẩm để thử
tính, kết hợp máy tính cầm tay Casio fx 570 ES, VN.
Đặc biệt nếu hạn chế sử dụng máy tính Casio thì ta chỉ phân tích tự luận. Nếu a khác 1 thì
ta chia cả hai vế cho a để đưa về a = 1. Phương trình (2) là mục tiêu cuối và để giải, bước
trung gian là dựa vào hằng đẳng thức 2 2
M − N = 0 ⇔ (M + N )(M − N ) = 0 . 2 2
Cụ thể hơn ta xét dạng sau: ( 2
x + Bx + C ) − (Dx + E) = 0. Xét ví dụ
Ví dụ 1: Giải phương trình 4 2
x −10x − x + 20 = 0 (1). Hướng phân tích:
Đầu tiên ta định hướng đưa về 2 2 dạng: ( 2
x + Bx + C ) − (Dx + E) = 0. Nhưng vì hệ 2 2
số bậc 3 bằng 0 nên B = 0, còn lại là: ( 2
x + C ) − (Dx + E) = 0 (*). Để ý số e = 20 ta có 2 2 2
C − E = 20 ⇒ E = ± C − 20 , và ta có thể chọn C để E hữu tỉ. 9 11 9 1
20 ≈ 4.47 nên chọn C hữu tỉ chẳng hạn ± ; 5
± ;± ;... và C = ± ⇒ E = ± (đẹp) 2 2 2 2 Hay như C = 6 ± ⇒ E = 4
± . Bây giờ ta thử trừ và nhẩm trực tiếp: 2  9  2  x ± −   ( 4 2
x −10x − x + 20 2 )
(Dx + E) =  2   (x ± 6)2 2 − ( 4 2
x −10x − x + 20) 2 2  1  9
Ta được ( Dx + E ) = x + 
 ứng với C = − .  2  2 Hướng dẫn giải: 2 2 ( )  9   1  2 1 ⇔ x − − x − = 0 ⇔    
( 2x + x −4)( 2x − x −5) = 0 …  2   2 
Ví dụ 2: Giải phương trình 4 3 2
2x −10x + 11x + x −1 = 0 (2). Hướng phân tích: Đầ 11 1 1
u tiên ta chia hai vế cho 2 đưa về a = 1, ta có: 4 3 2 x − 5x + x + x − = 0 . 2 2 2 2  5  2
Tiếp theo định hướng đưa về phương trình sau: 2 x − x + C −   (Dx + E) = 0.  2  Để 1 1 1 ý 2 2 2 e = −
⇒ C − E = − ⇒ E = ± C + . Cho C hữu tỉ chạy để tìm E hữu tỉ, chẳng 2 2 2 1 3
hạn C = ± ⇒ E = ± . Ta trừ thử trực tiếp xem sao: 4 4 2 2  3   5 1   11 1 1  2 4 3 2 Dx ± = x − x ± − x − 5x + x + x −       .  4   2 4   2 2 2  2 Ứ 1 2  1 3 
ng với C = − ⇒ ( Dx + E ) = x +   . 4  2 4  Hướng dẫn giải: 2 2  5 1   1 3   1  PT (2) 2 ⇔ x − x − − x + = 0     2 ⇔ x − 2x +  ( 2 x − 3x − ) 1 = 0 …  2 4   2 4   2 
Ví dụ 3: Giải phương trình 4 3 2
x + 6x + 6x + 11x + 2 = 0 (3). Hướng phân tích: Ở 2 2 đây là ( 2
x + 3x + C ) − (Dx + E) và ta thử chọn C = 2 và tiếp theo là 2 2 2
C − E = e ⇔ 4 − E = 2 ⇔ E = ± 2 . Nói cách khác ( + )2 Dx E
hoặc là bình phương đúng hay hằng số và ta thử trừ trực tiếp : ( 2 Dx + E )2 = ( 2 2
x + x + ) − ( 4 3 2 3 2
x + 6x + 6x + 11x + 2) = 2
2x − 4x + 2 = ( 2x − 2 ) Hướng dẫn giải: 2 2 4 3 2
x + 6x + 6x + 11x + = ⇔ ( 2 2 0
x + 3x + 2) − ( 2x − 2 ) = 0 2 ⇔ x +  ( + ) 2 3
2 x + 2 − 2  x +   (3− 2)x+2+ 2 =0  … Nhận xét : U U
Cách làm cũng không quá khó khăn khi mà hạn chế hay cấm Casio trong phòng thi! 2. Bài luyện tập: U U
Bài 1: Giải phương trình 4 2
x −10x − x + 20 = 0 .
Bài 2: Giải phương trình 4 2
x – 25x + 60x – 36 = 0 .
Bài 3: Giải phương trình 4 3 2 x 8
+ x + 7x – 26x + 7 = 0 .
3. Xét trường hợp vô nghiệm: U U
Từ cách giải phương trình có nghiệm thì ta cũng có hướng khái quát trong trường hợp
phương trình vô nghiệm là:
(Ax + Bx +C)2 2 2
+ A'x + B'x + C ' = 0 Trong đó 2
A' x + B ' x + C ' là tam thức luôn dương hoặc cả hai không đồng thời bằng 0.
Ví dụ 4: Giải phương trình 4 3 2
x + 6x + 15x + 10x + 7 = 0 (4). Hướng phân tích:
Cũng như trên ta nhẩm và trừ trực tiếp: 2 2
A' x + B ' x + C ' = ( 4 3 2
x + 6x + 15x + 10x + 7) − ( 2 x + 3x + 2) 2
= 2x − 2x + 3.
Ta thấy số 3 = 7 – 22 = C’ là cố định, vậy thì để khỏi bình phương và trừ lâu ta làm như P P sau :
x ( A' x + B ') = ( 2 4 3 2
x + 6x + 15x + 10x + 7) − ( 2
x + 3x + 2) − 3
Ta cho x = 1 hai vế ta được A'+ B ' = 0 , cho x = 2 ta có 2(2A'+ B ') = 4 ⇔ 2A'+ B ' = 2
Và dễ dàng tìm được A' = 2; B ' = 2 − . Hướng dẫn giải: 2 4 3 2
x + 6x + 15x + 10x + 7 = 0 ⇔ ( 2 x + 3x + 2) 2
+ 2x − 2x + 3 = 0 … Nhận xét : U U
Các phương trình bậc 4 vô nghiệm thì ít khi gặp. Phương trình bậc 4 cũng đa dạng nên ta
không thể khái quát và nói hết được. Trên đây chỉ là mẹo nhỏ để các bạn tham khảo.
II. Giải một số phương trình vô tỉ chứa căn bậc hai U 1. Dạng 1: U U
Ta để ý đến một số phương trình có thể áp dụng phép khai căn mở rộng:  ( ) 2 u x  = u  (x)
Ví dụ 1: Giải phương trình 2
x + 4x −12x + 9 = 4 . Hướng dẫn giải:  4 − x ≥ 0   7 x =
PT ⇔ x + 2x − 3 = 4 ⇔ 2x − 3 = 4 –x ⇔ 2x − 3 = 4 − x ⇔  3 .  
2x − 3 = x − 4 x = 1 − 7
Vậy phương trình có hai nghiệm là x = , x = 1 − . 3  x + 56 x
Ví dụ 2: Giải phương trình + x −8 = ( )1 16 8 Hướng dẫn giải: 2 x x − 8 + 8 PT ( ) 1 ⇔
x + 56 + 16 x − 8 = ⇔ x − 8 + 8 = (2). 2 2
Đặt x − 8 = t ≥ 0 khi đó (2) 2
⇒ t − 2t − 8 = 0 ⇔ (t − 4)(t + 2) = 0 ⇒ t = 4 (vì t ≥ 0) Thay trở về 2
x = t + 8 suy ra phương trình (1) có một nghiệm x = 24. Nhận xét: U U
Có thể đặt điều kiện x ≥ 8 rồi bình phương hai vế để khử căn theo phương pháp thông
thường, cùng lắm là đưa về bậc 4. 1.1. Luyện tập: U U
Bài 4: Giải phương trình x + 6 − 4 x + 2 + x +11 − 6 x + 2 = 1.
Bài 5: Giải phương trình 5 + x − 4 x +1 + 10 + x − 6 x +1 = 1.
Bài 6: Giải phương trình 1 1 x + x + + x + = a (với a > 0). 2 4 2. Dạng 2: U U
Do trong căn không có hướng như dạng 1 nên ta biến đổi ngoài căn theo trong căn. Nghĩa
là phương trình có một căn thức u(x) thì ta biến đổi các biểu thức ngoài căn theo
hướng: ( u )2 , ( u )3, ( u )4, …đưa về “dạng đa thức”. P P P P P P
Ví dụ 3: Giải phương trình 2 2
7 − x + x x + 5 = 3 − 2x − x . Hướng dẫn giải: Điều kiện: 2
3 − 2x − x ≥ 0 ⇔ x ∈[ 1 − ; ] 3 = D .
Bình phương hai vế ta được phương trình 2 2
7 − x + x x + 5 = 3 − 2x − x ⇔ ( x + 5 − 5) x + 5 + 2( x + 5) − 6 = 0 (*).
Đặt x + 5 = t, x∈ D ⇒ 2 ≤ t ≤ 2 2 thì từ (*) ta có phương trình: 3 2
t − t + t − = ⇔ (t − )( 2 5 2 6 0
2 t + 4t + 3) = 0 ⇒ t = 2 (Vì t ≥ 2) Thay trở về 2
x = t − 5 suy ra phương trình có 1 nghiệm x = - 1.
Ví dụ 4: Giải phương trình 2 x + x + 1 = 1. Hướng dẫn giải:
Ở đây ta biến đổi trước rồi đặt ẩn phụ sau. 2 x + x + = ⇔ ( 2 1 1 x + 2x + ) 1 − 2( x + ) 1 + 1 + x + 1 = 1 (*).
Đặt x +1 = t ≥ 0 thì từ (*) ta có phương trình: 4 2
t − t + + t − =
⇔ t ( 3t − t + ) = ⇔ t(t − )( 2 2 1 1 0 2 1 0 1 t + t − ) 1 = 0 5 −1
⇒ t = 0,t =1,t =
(loại một nghiệm t < 0 ). 2 1 − 5 Thay trở về 2
x = t −1 suy ra phương trình có 3 nghiệm x = - 1, x = 0, x = . 2
Ví dụ 5: Giải phương trình 2
x − 2x = 2 2x −1 . Hướng dẫn giải:
Ở đây ta thấy trong căn có hệ số 2 nên nhân cả hai vế với 4 và biến đổi. 2 x − x = x − ⇔ ( 2 2 2 2 1 4x − 4x + ) 1 − 2(2x − )
1 − 3 = 8 2x −1 (*).
Đặt 2x −1 = t ≥ 0 thì từ (*) ta có phương trình: 4 2 4 2
t − t − = t ⇔ t − t − t − =
⇔ ( 2t − t − )( 2 2 3 8 2 8 3 0 2
1 t + 2t + 3) = 0 (Với t ≥ 0 ) 2
⇔ t − 2t −1 = 0 ⇒ t =1+ 2 (loại t < 0). 2 t + 1 Thay trở về x =
suy ra phương trình có một nghiệm x = 2 + 2 . 2 +  4x 5
Ví dụ 6: Giải phương trình 2 3x + 3x = . 12 Hướng dẫn giải:
Nhân cả hai vế của phương trình với 6 ta có: 2
18x + 18x = 12x + 15 tiếp tục nhân cả hai vế với 8 thì 2
144x + 144x = 8 12x + 15 . Đặt 2
12x + 15 = t ≥ 0 ⇒ 12x = t −15 ta có
phương trình: (t − )2 2 + ( 2t − ) 4 2 15 12
15 = 8t ⇔ t −18t − 8t + 45 = 0 .
⇔ ( 2t + t − )( 2 2
5 t − 2t − 9) = 0 ⇒ t = 6 −1,t = 10 +1 (loại các nghiệm âm). 2 t −15 4 + 6 2 − + 10 Thay trở về x =
suy ra phương trình có 2 nghiệm x = − , x = . 12 6 6 Nhận xét: U U
Việc giải phương trình bậc 4 góp phần quan trọng khi giải phương trình vô tỉ.
 Các ví dụ trên đều có dạng chung khái quát là: ax2 + bx + c = d px + q . P P
Nếu không có hướng giải theo cách trên thì bình phương để giải phương trình bậc 4 như phần I. 2.2. Luyện tập: U U
Bài 7: Giải phương trình 2 x + x + 5 = 5 .
Bài 8: Giải phương trình 2
4x −13x + 5 + 3x + 1 = 0 . x + 3
Bài 9: Giải phương trình 2 2x + 4x = . 2 3. Dạng 3: U U
Trong căn có chứa tam thức bậc hai nhưng không phải bình phương đúng như dạng 1.
Ngoài căn cũng là tam thức bậc hai, ta gọi là đặt ẩn phụ không hoàn toàn.
Nhìn chung ta đều đưa phương trình về ( u − ax −b)( u − cx − d) = 0.
Tuy nhiên ở đây ta giải hơi khác, xét ví dụ sau
Ví dụ 7: Giải phương trình 2
x + x + = ( x + ) 2 6 1 2 1 x + 2x + 3 . Hướng dẫn giải:
Dễ thấy PT xác định với mọi x. PT 2 ⇔ x + x + − x + = ( x + )( 2 6 1 2(2 1) 2 1
x + 2x + 3 − 2) 2  + − x + x x x − =
⇔ x + 2x −1 = (2x + ) 2 2 1 0 (a) 2 1 2 1 ⇔  2 2 x + 2x + 3 + 2
 x + 2x + 3 = 2x −1 (b)
+ Giải (a) ta được các nghiệm: x = 1 − − 2, x = 1 − + 2 1 3 + 15 + Với x ≥ , PT (b) 2
⇒ 3x − 6x − 2 = 0 giải ra lấy nghiệm x = 2 3 3 + 15
Kết luận: phương trình có 3 nghiệm x = 1 − − 2, x = 1 − + 2 , x = . 3
Nhận xét: Phương trình có dạng 2 + + = ( + ) 2 ax px q mx n
ax + bx + c . U U
Ta có PP khái quát: Trừ thêm vào hai vế biểu thức trước căn là α (mx + n) nhằm trục căn vế phải: PT 2 α ( ) ( ) 2 ax px q mx n mx n ax bx c α  ⇔ + + − + = + + + −  
p −αm = b p − b
Số α làm nháp thỏa điều kiện sau: 2  ⇔ α =
, α − α n + q − c = 0 . 2
q −αn = c −α m 6 2 Ở Ví dụ 7 có α − = = 2 . 2
Ví dụ 8: Giải phương trình 2
2x + 2x + 1 = (4x − ) 2 1 x + 1 . Hướng phân tích: p b 2 0 1 Làm nháp ta có α − − = = = và ta thử: m 4 2 1  1  PT 2
⇔ 2x + 2x +1− (4x − ) 1 = (4x − ) 2 1 x + 1 − 
 quy đồng số 2 cho đẹp ta có 2  2  PT 2
⇔ x + x + − ( x − ) = ( x − ) 1 ( 2 4 4 2 4 1 4 4x + 4 − ) 1 4x + 3 2
⇔ 4x + 3 = (4x − ) 2 2 2 1
⇔ 4x + 4 +1 = 4x −1 ⇔ x +1 = 2x −1… 2 4x + 4 + 1
Lạy trời sự may mắn đã đến. Nhận xét: U U
Bình phương hai vế ta cũng đưa về phương trình bậc 4, tuy nhiên đó chỉ là biện pháp cuối
cùng. Để củng cố ta xét thêm ví dụ
Ví dụ 9: Giải phương trình 2 2
x + 4x − 20 = (x + 2) x − 2x + 4 . Hướng phân tích: p − b 4 − ( 2 − ) Làm nháp ta có α = = = 6 và ta thử: m 1 PT 2 ⇔ x + x −
− (x + ) = x + ( 2 4 20 6 2 ( 2)
x − 2x + 4 − 6) 2 2  − −
x − 2x − 32 = 0 x 2x 32 2
⇔ x − 2x − 32 = (x + 2) ⇔  … 2 2 x − 2x + 4 + 6
 x − 2x + 4 + 6 = x + 2
Ồ, sự may mắn lại đến lần nữa!. 3.2. Luyện tập: U U
Bài 10: Giải phương trình 2 x + x + = (x + ) 2 2 3 7 5 2x + 1 .
Bài 11: Giải phương trình 2 2
x + 3x −1 = (x + 2) x + 2 .
Bài 12: Giải phương trình 2 x + = ( x + ) 2 1 1 x − 2x + 3 .
Bài 13: Giải phương trình 2
x + x + = ( x − ) 2 2 4 1 4 1 x + x + 1 .
Bài 14: Giải phương trình 2 x + x − = ( x + ) 2 5 4 2 1 x + x − 2 .
Bài 15: Giải phương trình 2 2
x −1 = 2x x − 2x . Nhận xét: U
Qua các ví dụ 7, ví dụ 8, ví dụ 9 ta lại thấy: sau khi biến đổi thì xuất hiện một phương
trình liên hệ căn thức và biểu thức trước căn, dạng ban đầu là: ( + ) 2 mx n
ax + bx + c Sau biến đổi thì 2
ax + bx + c = mx + n ' Hay là 2 n ' =
ax + bx + c − mx là số hữu tỉ.
Kết hợp máy tính cho ta thêm một hướng nhẩm nghiệm để phân tích thành nhân tử ! + Xét phương trình 2 2
x + 4x − 20 = (x + 2) x − 2x + 4
Dùng máy tính tìm được hai nghiệm của phương trình: 2
x − 2x + 4 = 6 .
Như thế ta thử phương trình 2 2
x − 2x + 4 + 6 = x + 2 ⇔
x − 2x + 4 = x − 4 (VN)
Nếu x là nghiệm thì phép trừ 2
x − 2x + 4 − x phải cho ta kết quả 4 − . + Xét phương trình 2
x + x + = ( x + ) 2 6 1 2 1 x + 2x + 3
Bằng máy tính ta tìm được các nghiệm: x = 2,29 ; x = -2,414 ; x = 0,414.
Không cần gán, ta tính xấp sĩ xem sao: 2
x + 2x + 3 − 2x ≈ 0.9989 − ≈ 1 − và như thế ta có 2 x + x + − x = − ⇔ ( 2 2 3 2 1
x + 2x + 3 − 2x + )
1 = 0 là một nhân tử ứng với x = 2.29. Lưu ý: U
Nếu Hội đồng thi cấm sử dụng máy tính thì cách “tính bo” vẫn tốt hơn cả.
Phương trình vô tỉ cực kì đa dạng và phong phú không kém gì bất đẳng thức. Ngoài ra
phương trình vô tỉ sẽ là khâu quan trọng thứ hai trong giải hệ phương trình. Vì vậy
việc giải PT vô tỉ hết sức cần thiết trước khi giải hệ PT (nâng cao).
MỘT SỐ ĐỊNH HƯỚNG GIẢI PT VÔ TỈ - PHẦN 2
II. Giải một số phương trình vô tỉ chứa căn bậc ba U
1. Cơ sở và định hướng giải: U
Đối với học sinh lớp 10, 11 và học sinh THCS thì chúng ta không sử dụng đạo hàm, nên
có một kiến thức quan trọng và hay thường sử dụng là "Bình phương thiếu": 3 3 − = ( − )( 2 2 A B A B
A + AB + B ) Như thế biểu thức 2 2
A + AB + B là không âm và nếu cộng thêm số dương thì luôn dương.
Mở rộng hơn khi giải một số phương trình vô tỉ thì ta sẽ định hướng đưa về dạng hàm số
bậc ba lẻ như: f (t ) 3
= at + bt,(a,b > 0) . Nếu dùng đạo hàm thì đây là hàm đồng biến trên
R. Như trên đã nói, chúng ta đưa về phương trình f (u) = f (v) và sau đó là chuyển vế đưa về bình phương thiếu: (u − v)( 2 2
au + auv + av + b) = 0 ⇔ u = v .
Chúng ta cũng lưu ý là: không phải bài nào cũng đưa về hàm số kiểu trên!
2. Các ví dụ giải toán: U
Ví dụ 1: Giải phương trình 3 3
x + 1 = 2 2x −1 (1). U U Hướng phân tích:
Ta thấy hệ số trước căn là 2, hay nói như trên ta đoán b = 2 và 3
v = 2x −1 như thế còn thiếu 3
av , mà hệ số vế trái của x3 là 1 nên khả năng a = 1, như vậy ta thêm bớt để tạo ra P P 3
v = 2x −1. Ta có (1) 3 3
⇔ x + 2x = (2x−1) + 2 2x −1 Hướng dẫn giải: Ta có (1) 3 3
⇔ x + 2x = (2x−1) + 2 2x −1 . Đặt 3
v = 2x −1 ta có phương trình: 3 3
⇔ x + x = v + v ⇔ (x − v)( 2 2 2 2
x + xv + v + 2) = 0 ⇔ x = v . 1 − 5 1 + 5 Thay trở về thì 3 3
x = 2x −1 ⇔ x − 2x + 1 = 0 ⇔ x = 1, x = , x = . 2 2 Lưu ý 1: U
Không chỉ phương trình chứa căn bậc 3 mới chuyển được về dạng bậc 3 vì 3 t t = ( t ) .
Ví dụ 2: Giải phương trình 3 2
x + 3x + 4x + 2 = (3x + 2) 3x + 1 U U Hướng phân tích:
Ta thấy hệ số trong căn là 3, ở ngoài căn cũng là 3. Như thế ta tách số 2 và biến đổi vế trái thành hằng đẳng thức: PT 3 2
⇔ (x + 3x + 3x +1) + (x +1) = (3x +1+ ) 1 3x + 1 3 3
⇔ (x +1) + (x +1) = ( 3x +1) + 3x +1. Đặt u = x +1;v = 3x +1 và ta có phương trình: 3 3
u + u = v + v ⇔ (u − v)( 2 2
u + uv + v + )
1 = 0 ⇔ u = v ... Lưu ý 2: U
Đối với một số bài không phải là có ngay để biến đổi như trên.
Ví dụ 3: Giải phương trình sau: 3 2 2 3 3 2
− x +10x −17x + 8 = 2x 5x − x U U Hướng phân tích:
Rõ ràng ta phát hiện có dạng trên rồi, ở đây có thể b = 2, gần giống ví dụ 1, nhưng vướng
mắc x2 trước căn. Ta nhận thấy x = 0 không phải là nghiệm, nên chia cả hai vế cho x3, ta P P P P có: 10 17 8 5 3 2 − + − + = 2
−1 . Để cho gọn ta đặt 1 t = 2 3 2 thì ta có: x x x x x 3 2 3 2
8t −17t + 10t − 2 = 2 5t −1 . Đến đây ta biến đổi vế trái thành hằng đẳng thức bậc 3, vế phải cần thêm a( 2 5t − )
1 , hệ số a phụ thuộc t vế trái, nói các khác có dạng:
a (2t − ..)3 + 2(2t − ...) = a( 2 5t − ) 3 2
1 + 2 5t −1 . Như thế a = 1 và thử số trong ngoặc dấu ba 3
chấm là 1, ta có PT ⇔ (2t − ) 1 + 2(2t − ) 1 = ( 2 5t − ) 3 2 1 + 2 5t −1 . Tiếp tục đặt 3 2
u = 2t −1;v = 5t −1 thì ta có 3 3
⇔ u + 2u = v + 2v ± ⇔ (u − v)( 2 2
u + uv + v + 2) = 0 ⇔ u = v ... ĐS: 17 97 x = 12 Lời bình:
Đây là bài khó vì qua hai lần ẩn phụ mới đưa được về phương trình cần giải. Nhưng ít ra
có dạng thì cũng có hướng để mò.
Sau đây ta xét thêm một số ví dụ mà người ra đề cố ý lái đi để cho người giải phải mò.
Ví dụ 4: Giải phương trình sau: 3 24x −11 −16x 2x −1 −1 = 0 (4). U U Hướng phân tich:
Ta nhận thấy phương trình có chứa hai căn thức nên trước hết chuyển vế PT 3
⇔ 24x −11 = 1+16x 2x −1 sau đó cộng thêm một lượng v3 xem thế nào P P 3
⇔ 24x −11 + (24x − )
11 = 16x 2x −1 + 24x −10 , ta cần giảm hệ số trước căn nên đưa bớt vào căn: 3
⇔ 24x −11 + (24x − )
11 = (8x − 4 + 4) 8x − 4 + 24x −10 , rõ ràng xuất hiện số 4 nên tách ra theo hằng đẳng thức: 3
⇔ 24x −11 + (24x − )
11 = (8x − 4 + 3) 8x − 4 + 3(8x − 4) + 8x − 4 + 2 . Đặt 3 v =
24x −11, u = 8x − 4 +1 ta có phương trình: 3 3
v + v = u + u . Mò được rồi! Lời giải: PT (4) 3
⇔ 24x −11 + (24x − )
11 = 16x 2x −1 + 24x −10 = 8x 8x − 4 + 3(8x − 4) + 2 3
⇔ 24x −11 + (24x − ) 11 = (8x − 4 + 3 + ) 1
8x − 4 + 3(8x − 4) + 2
= (8x − 4) 8x − 4 + 3(8x − 4) + 3 8x − 4 +1+ 8x − 4 +1 Đặt 3 v =
24x −11, u = 8x − 4 +1 ta có phương trình: 3 3
v + v = u + u ⇔ (u − v)( 2 2
u + uv + v + ) 1 = 0 3
⇔ u = v ⇔ 24x −11 = 8x − 4 +1. Đặt 8x − 4 = y ≥ 0 suy ra 2
3 3y +1 = y +1 lập phương hai vế ta có 2 3 2
y + = y + y + y + ⇔ y ( 2 3 1 3 3 1
y + 3) = 0 ⇔ y = 0 . 1
Thay trở về ta được x = là nghiệm duy nhất của phương trình đã cho. 2
Như thế ta gặp hai bài khó gặm rồi! Sau đây ta xét bài dễ một ít.
Ví dụ 5: Giải phương trình sau: 3 2 3 2
8x −13x + 7x = 2 x + 3x − 3 . U U Hướng phân tích: Đặt 3 2
x + 3x − 3 = v trước hết ta cộng thêm hai vế một lượng v3 xem sao: P P 3 2 2 3 3 2 3
8x −13x + 7x + x + 3x − 3 = v + 2v ⇔ 8x −12x + 10x − 3 = v + 2v 3
Bây giờ ghép hằng đẳng thức: ⇔ ( x − ) + ( x − ) 3 2 1 2 2 1 = v + 2v ... ĐS: 5 ± 89 x = 1, x = . 16
Ví dụ 6: Giải phương trình sau: 3 3 2
2 2x −1 = 27x − 27x +13x − 2 . U U Hướng phân tích: Đặt 3 v =
2x −1 như thế vế trái là 2v và ta thử cộng thêm vào lượng 3
v = 2x −1 vào hai vế, ta có PT 3 3 2 3 2
⇔ v + 2v = 2x −1+ 27x − 27x +13x − 2 = 27x − 27x +15x − 3
Tiếp tục biến đổi vế phải v + v = ( x − )3 3 + ( x − ) 3 3 3 2 3 1 2 3
1 = u + 2u ⇒ ... ⇒ u = v ⇒ u = v .
Cuối cùng ta được phương trình bậc ba đối với x. Đs: x = 0 .
Sau đây ta xét bài bậc chẵn thử xem
Ví dụ 7: Giải phương trình sau: 3 2
2x + 7x + 5x + 4 = 2(3x − ) 1 3x −1 (5) U U Hướng phân tích:
Để tạo hằng đẳng thức vế trái hệ số nguyên thì ta nhân hai vế với 4, ta có: 3 2
⇔ 8x + 28x + 20x +16 = 8(3x − ) 1
3x −1 để giảm bớt hệ số 8 thì đưa vào trong ngoặc và trong căn: 3 2
8x + 28x + 20x +16 = (12x − 4) 12x − 4 . Đặt 12x − 4 = v ≥ 0 thì vế phải là 3 v và
ta cần thêm vào vế trái một lượng 2 v để xem thử: ⇔ x + x + x +
+ x − = v + v ⇔ ( x + )3 + ( x + )2 3 2 2 3 3 2 8 28 20 16 12 4 2 2 2 2 = v + v (*).
Đặt 2x + 2 = u > 0 thì (*) 3 2 3 2
⇔ u + u = v + v ⇔ (u − v)( 2 2
u + v + uv + u + v) = 0 ⇔ u = v . Thay trở về ta có 2
2x + 2 = 12x − 4 ⇔ x +1 = 3x −1 ⇒ x − x + 2 = 0 (vô nghiệm). Nhận xét: U U
Biểu thức chứa căn bậc ba (hoặc căn bậc hai) là ẩn phụ mới đặt là 3
v = k Q ( x) (Hoặc v = k Q( x) ).
Trong đó k = 1; 2 hoặc 3 mà ta có thể thêm vào (nhân thêm).
Tiếp theo đưa vào căn hay ra căn (nếu có): 3
v = k Q ( x) 2 3
;v = k Q(x)     .
Sau đó là cộng thêm cả hai vế một lượng 3 2
av ;av để biến đổi vế trái (vế còn lại) theo hằng
đẳng thức bậc ba, hệ số a này cũng là hệ số của 3 au .
Ví dụ 8: Giải phương trình sau: 3 2 3 3 2
x − 6x +12x − 7 = −x + 9x −19x +11 U U Hướng phân tích:
Rõ ràng nếu ta cộng thêm (- x3) thì vế trái triệt tiêu mất 3 x . P P
Ta nhân cả hai vế với 2 rồi cộng sau thì sử lí được trường hợp này. Cụ thể là: PT 3 2 3 3 2
⇔ 2x −12x + 24x −14 = 2 −x + 9x −19x +11 = 2v . Cộng thêm hai vế 3 v ta có PT 3 2 ⇔ x − x + x − + ( 3 2
−x + x − x + ) 3 2 12 24 14 9 19 11 = v + 2v
⇔ x − x + x − = v + v ⇔ (x − )3 3 2 3 + (x − ) 3 3 5 3 2 1 2
1 = v + 2v . Đặt u = x −1. . . 3 3 ⇒ u = v .
Việc còn lại là giải phương trình bậc ba: 3 2 3 2
x − 3x + 5x − 3 = −x + 9x −19x +11 3 2
⇔ x − 6x +12x − 7 = 0 . Đs: x = 1.
3. Hỗ trợ Casio trong giải toán: U
Từ các ví dụ và nhận xét trên ta có thể sử dụng Casio hỗ trợ trong giải toán. Ta thấy các phương trình dẫn đế 1 1
n: 3 Q ( x) = α x + β = u với α = 1;2;3; ; do vậy ta tiến hành tìm 2 3
nhanh u hơn bằng cách: Tìm X trước, sau đó tính 3 Q( x) − α x = β (thử α tìm được β )
Trở về quá khứ xem nào
Ví dụ 5: Giải phương trình sau: 3 2 3 2
8x −13x + 7x = 2 x + 3x − 3 . U U Hướng phân tích: + Nhập phương trình 3 2 3 2
8X −13X + 7 X = 2 X + 3X − 3
dùng Shift Solve ta tìm X = 1. + Sửa thành 3 2
X + 3X − 3 − 2 X bấm = thì kết quả bằng -1 (đẹp). Nên u = 2x -1.
(lấy số 2X từ 8X3 để thử cho nhanh) P P
Ví dụ 6: Giải phương trình sau: 3 3 2
2 2x −1 = 27x − 27x + 13x − 2 . U U Hướng phân tích: + Nhập phương trình 3 3 2
2 2 X −1 = 27 X − 27 X + 13X − 2
dùng Shift Solve ta tìm X = 0
+ Sửa thành 3 2X −1 − 3X bấm = thì kết quả bằng -1 (đẹp). Nên u = 3x -1.
Ví dụ 8: Giải phương trình sau: 3 2 3 3 2
x − 6x +12x − 7 = −x + 9x −19x +11 U U Hướng phân tích: + Nhập phương trình 3 2 3 3 2
X − 6 X + 12 X − 7 =
−X + 9X −19X +11
dùng Shift Solve ta tìm X = 1. + Sửa thành 3 3 2
−X + 9X −19X +11 − X bấm = thì kết quả bằng -1 (đẹp). Nên u = x -1.
(Nhiệm vụ còn lại là thêm bớt đển biến đổi các vế trái theo u) 3 3 3  x − x x + 3x
Ví dụ 9: Giải phương trình 3   = 2x + . U U  2  2 Hướng phân tích:
Quy đồng số 2 cho đẹp: ( 3x − x)3 3 3
=16x + 4 4x +12x .
+ Làm nháp ta dự đoán được ngay 3
x − x = u (nếu không lũy thừa và khai triển thì mệt lắm)
Dễ thấy x = 0 là một nghiệm, ta thử nghiệm khác 0 (nếu có) ( 3 X − X )3 3 3
=16X + 4 4X +12X Shift Solve 2 = kết quả 1.732
(bạn nào làm nhiều với căn thì đoán đây là 3 ) Sửa thành ( 3 X − X ) 3 3
− 4X +12X bấm = ta có kết quả 0.
+ Trở về phân tích ta có: Đặt 3
x − x = u , 3 3
4x +12x = v và cộng cả hai vế với 4u ta có: 3 u + u = x + ( 3 x − x) 3 3
+ v ⇔ u + u = v + v ⇔ (u − v)( 2 2 4 16 4 4 4 4
u + uv + v + 4) = 0 ⇔ u = v + Thay trở về 3 3 3
x − x = 4x +12x , đây lại là phương trình chứa căn bậc 3.
Nếu lập phương khử căn thì cũng giải được (Vì đã đoán được nghiệm ở bước nháp) tuy nhiên ta có cách sau: - Xét x = 0 là nghiệm 12
- Xét x khác 0, chia cả hai vế cho x thì 2 3 x −1 = 4 + . Đặt 2
x = t > 0 khi đó ta có 2 x 12 t −1 = 4 + ⇒ t ( 3 2
t − 3t + 3t − ) 4 3 2 3
1 = 4t +12 ⇒ t − 3t + 3t − 5t −12 = 0 đây là phương trình t
bậc 4 có nghiệm t = 3 nên ta có (t − )( 3
3 t + 3t + 4) = 0 ⇒ t = 3
ĐS: x = 0, x = ± 3 .
Lưu ý: Trên đây là mẹo nhỏ để tìm u và tính nghiệm cho việc giải sau này, chỉ áp dụng U U
được với một số phương trình nhất định.
4. Một số bài toán khác: U
Phần trước ta giải phương trình vô tỉ đưa về dạng đa thức, nhưng ở đây ta xét phương trình
"đa thức" nhưng để giải ta lại đi "khai căn"! 3
Ví dụ 10: Giải phương trình sau: (x3 + ) 1 = x 81 − 27 . U U Hướng phân tích:
Rõ ràng đây là phương trình đa thức bậc 9, như thế ta hạ bậc bằng cách khai căn bậc 3 PT 3 3 3
⇔ x +1 = 81x − 27 = 3 3x −1 (Đưa hệ số 3 ra ngoài căn trái ngược VD 7). Đặt 3 3
3x −1 = v ⇒ 3x −1 = v và cộng vào hai vế ta có: 3 3 3 3 3
⇔ x +1+ 3x −1 = v + 3v ⇔ x + 3x = v + 3v ⇔ ... ⇔ x = v ⇔ x − 3x +1 = 0 .
Giả sử phương trình có nghiệm x ∈[ 2;
− 2] thì ta đặt x = 2sinα,α ∈[0;2π ] và có: 1 π k 2π 5π k 2π 3
8sin α − 6 sin α +1 = 0 ⇔ sin 3α = ⇒ α = + ,α = + . 2 18 3 18 3 π 13π 29π
Cho α ∈[0;2π ] thì có k = 0, 1, 2 ta được α = ; ;
và phương trình bậc ba chỉ có tối 18 18 18 đa 3 nghiệ π 13π 29π
m nên PT có nghiệm là: x = 2sin , x = 2 sin , x = 2 sin . 18 18 18
Sau đây ta sử lí trường hợp b < 0. 3
Ví dụ 11: Giải phương trình (4x − x + 3)3 3 3 − x = . U U 2 Hướng phân tích: 3  3  3 PT 3 3 3 3 3 3 3
⇔ 4x − x + 3 = x + ⇔ 2x − x = 2 − x + + x +   2  2  2 Đặ 3 t 3 3 x + = t − ta có phương trình 3 3
x − x = t − t ⇔ ( x − t )( 2 2 2 2
2x + 2xt + 2t − ) 1 = 0 . 2 3 3 6
+ TH1: x = t ⇔ x3 = t3 3 3
⇔ x = −(x + ) ⇔ x = − ; P P P P 2 2 3 3 3  x + t = 3 − / 2
(x + t) − 3xt(x+ t) = 3 − / 2 + TH2: Ta có hệ  ⇔  . 2 2 2
x + t + xt = 1/ 2 
(x + t) − xt = 1 / 2 3 3 Đặ S − 3SP = 3 − / 2
4S − 3S = 3 (*) t x + t = S, xt = P, 2
S ≥ 4P ta có hệ  ⇔  2 2
S − P = 1/ 2
P = S −1/ 2 1 1 2 Ta có 2 2 2 P = S −
≤ S ⇒ S ≤ ⇒ S < 1. Khi đó đặt S = o
c sα ,α ∈ (0;π ) thay vào (*) 2 4 3 ta được 3 4 os c α − 3 os c α = 3 ⇔ os
c 3α = 3 (Vô nghiệm). 3 6
Vậy phương trình đã cho có nghiệm duy nhất x = − . 2
Dưới đây ta xem một ví dụ đặt ẩn phụ đưa về dạng đa thức.
Ví dụ 12: Giải phương trình 2 3 2
6x + 2x + 3x + x + 4 −18 = 0 . U U Hướng phân tích:
Ta quan sát bộ (6; 2) và bộ (3; 1) tỉ lệ nên biến đổi sơ lược PT ⇔ ( 2 x + x + ) 3 2 2 3
4 + 3x + x + 4 − 30 = 0 . Đặt 3 2
3x + x + 4 = t ta có phương trình 1 3 3
2t + t − 30 = 0 ⇔ t = − t +15 . Nhận xét vế trái tăng theo t, vế phải giảm theo t nên phương 2
trình có nghiệm dương duy nhất 2 < t < 3. Giả sử t = a + b thì ta có: (   a + b)3 1 = − (a + b) 1 3 3
+15 ⇔ a + b + (a + b) 3ab + = 15  
, đến đây ta chọn a, b thỏa mãn: 2  2  3 3 3 3 a + b =15 a + b =15    1 ⇔  1 như thế 3 3
a ;b là nghiệm của phương trình 3 3 3ab + = 0 a b = −    2  216 1 15 12151 15 12151 15 12151 2 y −15 y − = 0 ⇔ y = ± suy ra 3 3 a = + , b = − . 216 2 216 2 216 2 216 15 12151 15 12151 Tiếp đó 3 3 t = + + −
. Bây giờ ta còn phải sử lí phương trình ẩn x 2 216 2 216 2 1  1  1 133 1 133 1 2 3
3x + x + 4 = t = − t +15 ⇔ x + = − t + ⇔ x = − ± − t   . 2  6  6 36 6 36 6   1 133 1 15 12151 15 12151
Vậy phương trình có hai nghiệm: = − ± −  3 3 x + + −  . 6 36 6  2 216 2 216   
Nhận xét: Nghiệm "khủng quá" cần kiên trì trong biến đổi!. U U
Cũng là phương trình có căn bậc ba, nhưng đôi khi biến x vẫn đóng vai trò hệ số.  1 
Ví dụ 13: Giải phương trình 2 3 2
8x −15x + 9 = 1+ 5x − 2x − 2   U U  x Hướng phân tích:
Điều kiện x ≠ 0 , quy đồng mẫu thức ta có: 3 2 x −
x + x = ( x + ) 3 2 8 15 9 1
5x − 2x − 2 (2). Đặt 3 2 2 3
5x − 2x − 2 = v ⇔ 5x − 2x − 2 = v . Cộng thêm hai vế một lượng v3 thì vế phải là: P P 3 v + (x+1).v .
Bây giờ nhiệm vụ của chúng ta là biến đổi vế trái (ẩn x) thành dạng 3 u + (x+1).u : VT = x −
x + x + x − x − = x −
x + x − = ( x − )3 3 2 2 3 2 8 15 9 5 2 2 8 10 7 2 2 1 + ( x + ) 1 (2x − ) 1
Như vậy phương trình (2) trở thành phương trình hai ẩn u, v mà x + 1 là hệ số: 3 3 u +
+ u = v + + v ⇔ (u − v)( 2 2 (x 1). (x 1).
u + uv + v + x + ) 1 = 0 2 2  u  3  u  + TH 1: 2 2 2 2
u + uv + v + x +1 = 0 ⇔
+ v + u + x +1 = 0 ⇔ 4
+ v + 3(2 x−1) + 4x + 4 = 0      2  4  2  2  u  2 4
+ v +12 x − 8x + 7 = 0   (Vô nghiệm vì 2
12 x − 8x + 7 > 0, có ∆ ' = 16 − 84 < 0 ).  2  + TH 2: 3 3 3 2 2
u = v ⇔ u = v ⇔ 8x −12x + 6x −1 = 5x − 2x − 2 9 ± 113
Mời các bạn thực hành. ĐS: x = 1, x = . 16
Sau đây ta lại xét ví dụ cần phải chia mà không phải quy đồng.
Ví dụ 14: Giải phương trình 3 2 3 6 3 2 3x + 4x −1 =
x + 2x + x . U U Hướng phân tích:
Ta thấy trong căn có bậc cao nên nhận xét x khác 0 và chia cả hai vế cho x ta được 1 1 1 2 3 3 3 3x + 4x − = x + 2 + . Đặt 3 3 x + 2 +
= v và cộng hai vế với v ta có: P P x x x
x + x + x + = v + v ⇔ ( x + )3 3 2 3 + (x + ) 3 3 4 2 1
1 = v + v . Đặt x +1 = u ta có 3 3
u + u = v + v ... ĐS ± 3 : x = 1 − , x = . 3
Sau đây là các bài luyện tập bồi dưỡng cho học sinh. 5. Luyện tập: U
Bài 1: Giải phương trình 3
8x + 2x = (x + 2) x +1 .
Bài 2: Giải phương trình 3 3
x + 2 = 3 3x − 2 . x +1
Bài 3: Giải phương trình 3 3 2x −1 = . 2
Bài 4: Giải phương trình 3 3
x = 6 6x + 4 + 4 .
Bài 5: Giải phương trình 3 3
6x + 1 = 8x − 4x −1.
Bài 6: Giải phương trình 3 2 3 2
x − 4x − 5x + 6 = 7x + 9x − 4
Bài 7: Giải phương trình 3 2 3
8x − 36x + 53x − 25 = 3x − 5 .
Bài 8: Giải phương trình ( 2 4x + )
1 x = (3 − x) 5 − 2x .
Bài 9: Giải phương trình 2 2 2 3
7x −13x + 8 = 2x
x(1+ 3x − 3x )
Bài 10: Giải phương trình 3 2 3 2
x − 5x +12x − 6 = 2 x − x +1
Bài 11: Giải phương trình 3 2
2 x + 5x + 2 = x ( x + 5) + 2 . 3 2
8x + 12x + 8x + 1
Bài 12: Giải phương trình 2 3x + 2x + 4 = . 2 3x + 2x + 5
MỘT SỐ ĐỊNH HƯỚNG GIẢI PHƯƠNG TRÌNH VÔ TỈ - PHẦN 3
3. Định hướng khái quát giải một lớp bài toán: U U a. Đặt vấn đề: U U
 Trước hết ta quan sát các bài toán sau: Giải các phương trình +) 2
x  5  5  x +) 2
2x − 4x + 2 = 3x 2x −1 +) 2
4x + 6 = (x − 1) 6x − x − 6 2 2 +) 2
2x  6x  1  4x  5
+) x − x − 12 = (x + 3) 10 − x +) 2
9x + 25 = (x − 1) 2x + 5x − 5.
 Nhận dạng phương trình:
Ta thấy có sự khác nhau ở trong căn, ở ngoài căn và biểu thức trước căn. Các phương trình có dạng: 2
Ax + Bx + C = (mx + n) 2
A ' x + B ' x + C ' với A. A' không đồng thời bằng 0.
 Phương pháp chung nhất để giải các phương trình trên là bình phương đưa về phương trình đa thức bậc 4.
Tuy nhiên việc giải phương trình bậc 4 là được nhưng cũng không đơn giản chút nào mà còn khá dài.
Đôi khi phải hỗ trợ máy tính Casio, nếu không thì việc giải rất vất vả, nhất là phương trình vô nghiệm!
Ưu điểm là: chúng ta chủ động trong việc giải phương trình, dù khó khăn cực nhọc và có hy vọng rất lớn để giải thành công.
 Nếu không đưa về phương trình bậc 4 thì chúng ta tìm cách giải như:
Đặt ẩn phụ hoàn toàn hay không hoàn toàn, chuyển về hệ phương trình, nhân liên hợp trục căn kết hợp
nhẩm nghiệm các loại ... thành thử thiếu định hướng chung, phải loay hoay và xoay các kiểu mới làm
được bài. Tuy nói như vậy nhưng không phải đặt ẩn phụ là đặt được ngay, chuyển về hệ là chuyển được
ngay, nhân liên hợp trục căn được ngay, ...Như thế có nghĩa là phải nắm giữ được "các dạng con" hay là
các nhánh khác nhau thì mới giải tốt được, nếu không chúng ta cứ mò từ dạng này sang dạng khác. Nói
cách khác: chúng ta bị các dạng phương trình chi phối, rơi vào thế bị động trong giải toán.
 Chính vì vậy chúng ta đặt ra là: có định hướng giải chung cho tất cả 6 phương trình trên đồng thời
khắc phục được các nhược điểm nào đó, hay nói cách khác: Phương pháp chúng ta đưa ra phải thỏa mãn các yêu cầu:
+ Dễ hiểu hay tương đối dễ hiểu + Không quá cồng kềnh
+ Dễ áp dụng hay tương đối dễ áp dụng.
+ Có thể không cần sử dụng máy tính Casio. Đây chính là điều nói lên: Bạn sử dụng Casio quen rồi, nếu
thiếu công cụ này thì dễ bị lúng túng. Đặc biệt là nghiệm vô tỉ!
Phương pháp chúng ta đưa ra phức tạp và cồng kềnh khó nhớ, khó hiểu, khó áp dụng thì cũng không
mang lại ý nghĩa thực tế bao nhiêu.
 Thứ hai ta xét phương trình sau: 2 2
x + 3x + 6 + 2x −1 = 3x +1, ta viết lại phương trình thành: 2 2
x + 3x + 6 = 3x +1− 2x −1 (Sau khi đặt điều kiện). Bình phương 2 vế và thu gọn ta được phương trình mới: 2 2
10x + 3x − 6 − 2(3x +1) 2x −1 = 0 . Như thế ta lại chuyển về dạng của 6 phương trình đầu,
điều này nói lên: coi như 6 phương trình đầu là hệ quả của các phương trình khác thì việc định hướng
giải chúng lại mang ý nghĩa lớn. Nếu chúng ta làm được điều này thì việc chuyển vế bình phương sẽ
không còn đáng ngại. Nắm thế chủ động trong giải toán!. Dưới đây ta xét cách giải một vài ví dụ sau đó khái quát cách giải.
b. Các ví dụ giải toán: U
Ví dụ 1: Giải phương trình: 2 2
3x + 3x + 2 = (x + 6) 3x − 2x − 3 (1) . U U Hướng phân tích:
(Nhận xét: nhắc lại 1 tí mà không làm theo cách trừ cả hai vế với 5(x + 6) và trục căn vế phải).
Làm nháp: ta chuyển vế thành 2
x + x + − x + 2 3 3 2 (
6) 3x − 2x − 3 = 0 (*).
Mục tiêu của ta là: (*) ⇔ (ax + b + u )(cx + d + u ) = 0 (**). Bây giờ ta lại đi phân tích ngược trở về
(nhân phá ngoặc nhưng không cần phá rời ra - Tách phần đa thức và căn):
( ) ⇔ (ax +b)(cx + d ) 2 **
+ 3x − 2x − 3 + (a + c) x +b + du = 0  (***). a + c = 1 − d + b = 6; − bd − 3 = 2
Cân bằng các hệ số từ (***) và (*) ta có hai hệ sau:  &  .
ac + 3 = 3 ad + bc − 2 = 3
Ta chọn a = -1, c = 0 và hệ sau có nghiệm b = 1 − , d = 5 − . Hướng dẫn giải: ( ) ⇔ ( 2 −x − + x − x − )( 2 1 1 3 2 3 5
− + 3x − 2x − 3) = 0.
+ TH1: Với −x −1 ≤ 0 ⇔ x ≥ 1 − Ta có phương trình 2 2
x +1 = 3x − 2x − 3 ⇒ 2x − 4x − 4 = 0 ⇒ x = 1± 3 (Thỏa mãn). 1± 85 + TH2: 2 2
5 = 3x − 2x − 3 ⇒ 3x − 2x − 28 = 0 ⇒ x = . 3 1 85
Kết luận: nghiệm phương trình là ± x = 1 ± 3, x = ⋅ 3
Ví dụ 2: Giải phương trình: 2
x  5  5  x (2) . U U Hướng phân tích:
Làm nháp: ta chuyển vế thành 2 x
  5  5  x  0 (*).
Mục tiêu là: (*) ⇔ (ax + b + u )(cx + d + u ) = 0 (**). Bây giờ ta phân tích ngược trở về:
(**) ⇔ (ax +b)(cx + d )+5− x + (a +c)x +b+ du = 0  (***).
a + c = 0 d + b = 1;bd + 5 = 5
Cân bằng các hệ số từ (***) và (*) ta có hai hệ sau:  &  . ac = 1 −
ad + bc −1 = 0
Ta chọn a = 1, c = -1 và hệ sau có nghiệm b = 0, d = 1. Hướng dẫn giải:
(2) ⇔ (x+ 5− x)(−x+1+ 5− x) = 0.
+ TH1: Với x ≤ 0 . Ta có phương trình : −x = 5 − x 1 − − 21 2
⇒ x + x − 5 = 0 ⇒ x = (loại nghiệm dương). 2
+ TH2: Với −x +1 ≤ 0 ⇔ x ≥ 1. Ta có phương trình: x −1 = 5 − x 1+ 17 2
⇒ x − x − 4 = 0 ⇒ x = (loại nghiệm âm). 2 −1 − 21 1 + 17
Kết luận: phương trình có hai nghiệm là x = , x = ⋅ 2 2
PHƯƠNG PHÁP PHÂN TÍCH NGƯỢC: U
Để giải phương trình: 2
Ax + Bx + C = (mx + n) 2
A ' x + B ' x + C ' ta thực hiện theo phương pháp
phân tích ngược như sau: Chuyển vế : 2
Ax + Bx + C − (mx + n) 2
A ' x + B ' x + C ' = 0 Hoặc 2
−Ax − Bx − C + (mx + n) 2
A ' x + B ' x + C ' = 0
Khi đó phân tích nhân tử dạng: (ax +b + u )(cx + d + u ) = 0.
Làm nháp nhân phá ngoặc và cân bằng hệ số. Đảm bảo hệ số có nghiệm.
Ví dụ 3: Giải phương trình: 2
4x + 6 = (x − 1) 6x − x − 6 . U U Hướng phân tích:
Làm nháp: chuyển vế thành − x − + x − 2 4 6 (
1) 6x − x − 6 = 0 (*).
Mục tiêu là: (*) ⇔ (ax + b + u )(cx + d + u ) = 0 (**). Bây giờ ta phân tích ngược trở về:
( ) ⇔ (ax +b)(cx + d ) 2 **
+ 6x − x − 6 + (a + c) x +b + du = 0  (***). a + c = 1 d + b = 1 − ;bd − 6 = 6 −
Cân bằng các hệ số từ (***) và (*) ta có hai hệ sau:  &  .
ac + 6 = 0 ad + bc −1 = 4 −
Ta chọn a = 3, c = -2 và hệ sau có nghiệm b = 0, d = 1 − . Hướng dẫn giải: ( ) ⇔ ( 2 x + x − x − )( 2 * 3 6 6 2
− x −1+ 6x − x − 6 ) = 0.
+ TH1: Với 3x ≤ 0 .Ta có phương trình : 2 2 2
9x = 6x − x − 6 ⇒ 3x + x + 6 = 0 (vô nghiệm) + TH2: Với 2
− x −1 ≤ 0 ⇔ x ≥ 1
− / 2 . Ta có phương trình: 2
2x +1 = 6x − x − 6 7 2
⇒ 2x − 5x − 7 = 0 ⇒ x = (Thỏa mãn) (loại nghiệm -1). 2 7
Kết luận: phương trình có một nghiệm là x = ⋅ 2 Nhận xét: U U
Cách nhẩm của chúng ta mặc dù chưa được "ngon lành" và hơi chậm khi làm nháp, nhưng ưu điểm là
rèn luyện tư duy, ít ra cũng có hướng để mò, ngoài ra lời giải tương đối ngắn gọn. Hơn nữa không quá
khó cũng như không quá lệ thuộc máy tính Casio, chủ động trong giải toán dạng này.
Ví dụ 4: Giải phương trình: 2
6x  9  (2x  1) 15x x  9  0 . U U Hướng phân tích:
Làm nháp: Ta cần: ax
bcx du a c  x b d        u  0   a + c = 2
d + b = 1;bd + 9 = 9 Ta có:  & 
suy ra hệ có nghiệm: a = 5, c = 3,
− b = 0, d = 1.
ac +15 = 0 ad + bc +1 = 6 Hướng dẫn giải: 2 x + + x + x + x + = ⇔ ( 2 x + x + x + )( 2 6 9 (2 1) 15 9 0 5 15 9 3
− x +1+ 15x + x + 9 ) = 0 . 9
+ TH1: 5x ≤ 0 , ta có phương trình: 2 2 5
− x = 15x + x + 9 ⇒ 10x − x − 9 = 0 ⇒ x = − . 10 1 + TH2: 3
− x +1 ≤ 0 ⇔ x ≥ ta có phương trình: 2 2
3x −1 = 15x + x + 9 ⇒ 6x + 7x + 8 = 0 ⇒ x ∈ ∅ . 3 9
Kết luận: Phương trình đã cho có nghiệm duy nhất là x = − ⋅ 10
Ví dụ 5: Giải phương trình: 2
x  11  (x  3) 2x  5x  7 (x  ). U U Hướng phân tích: 2 x
  11  (x  3) 2x  5x  7  0 . Ta cần: ax bcx du a c  x b d        u  0   a  c  1   d
  b  3;bd  7  11  Ta có  và 
a  2,c  1,b  4,d  1 . ac   2   
ad bc  5  1  Hướng dẫn giải: 2 x   x
x x    2 x  
x x   2 11 ( 3) 2 5 7 2 4 2 5 7 x
  1  2x  5x  7  0
+ TH1: 2x  4  0  x  2 , ta có phương trình: 2 2
2x  4  2x  5x  7  2x  11x  23  0  x   .   + TH2: x
  1  0  x  1 , ta có: 2 3 41
x  1  2x  5x  7  x  . 2 3  41
Kết luận: Phương trình có một nghiệm là x  . 2
Ví dụ 6: Giải phương trình: 2 2
4x  19x  6  x 2x  4x  3. (x  ). U U Hướng phân tích: Nháp: 2 2
4x  19x  6  x 2x  4x  3  0
ax bcx du a c  x b d         u  0   a  c  1   d
  b  0;bd  3  6  Ta có  và 
. Hệ có nghiệma  2, 3, c d  3, b  3 . ac   2  4   
ad bc  4  19  Hướng dẫn giải: 2 2
x x   x
x x    2  x  
x x   2 4 19 6 2 4 3 2 3 2 4
3 3x  3  2x  4x  3  0. 2x  3  0 x   3 / 2   + TH1:   
x  4  13 . 2 2 2
x  3  2x  4x  3 2
x  16x  6  0     3  x  3  0 x   1   11  79  +TH2:     x  . 2 2
3x  3  2x  4x  3 7
x  22x  6  0 7     11  79
Kết luận: Phương trình đã cho có 2 nghiệm là x  4  13, x    7
Ví dụ 7: Giải phương trình: 2 2
x x  12  (x  3) 10  x . U U Hướng phân tích: Nháp: 2 2 x
  x  12  (x  3) 10  x  0
ax bcx du a c  x b d         u  0   a  c  1   d
  b  3;bd  10  12  Ta có  và 
. Hệ có nghiệm a  1, c  0, d  1, b  2 . ac   1  1    ad bc  1  Hướng dẫn giải: 2 2 x x   x   x   2 x    x  2 12 ( 3) 10 2 10
1  10  x   0 x   2 2 x 2 10 x          x  3. 2 2
x  4x  6  0 
Kết luận: Phương trình có nghiệm duy nhất x  3.
Ví dụ 8: [Toán Học & Tuổi Trẻ số 420] Giải phương trình: 2
4x  14x  11  4 6x  10 . U U Hướng phân tích: Nháp: 2
4x  14x  11  4 6x  10  0
ax bcx du a c  x b d         u  0   a  c  0   d
  b  4;bd  10  11  Ta có  và 
. Hệ có nghiệm a  2, c  2, d  3, 7 b  . ac   4   
ad bc  6  14  Hướng dẫn giải: 2
4x  14x  11  4 6x  10  2x  7  6x  102x  3  6x  10  0 (*).  
Vì 6x  10  0  2x  7  0 nên   3 13
*  2x  3  6x  10  x  . 4 3  13
Kết luận: Phương trình có 1 nghiệm là x  . 4
Ví dụ 9: [Tuyển sinh lớp 10 Chuyên Lam Sơn Thanh Hóa 2014] U U
Giải phương trình: x   2 2
1 2x  2x  2x  3x  2 . Hướng phân tích: Nháp: 2
x x   x   2 2 3 2
1 2x  2x  0
ax bcx du a c  x b d         u  0   a  c  1   d
  b  1;bd  2  Ta có  và 
. Hệ có nghiệm a  1, c  0, d  1, b  2 . ac   2  2   
ad bc  2  3  Hướng dẫn giải: x   2 2
x x x x    2 x    x x  2 1 2 2 2 3 2 2 2 2
1  2x  2x   0 x   2  0 x   2        x  3  13 . 2 2 x
  2  2x  2x x   6x  4  0    
Kết luận: Phương trình có hai nghiệm x  3  13 .
Ví dụ 10: Giải phương trình: 2 2
4x  11x  6  (x  1) 2x  6x  6 . U U Hướng phân tích: Nháp: 2
x x   x   2 4 11 6
1 2x  6x  6  0 Ta cần:
ax bcx du a c  x b d        u  0   a  c  1   d
  b  1;bd  6  6  Ta có  và 
. Hệ có nghiệm a  3, 2, c   d  3, 4 b   . ac   2  4   
ad bc  6  11  Hướng dẫn giải: 2 2
x x   x
x x    2 x  
x x   2 4 11 6 ( 1) 2 6 6 3 4 2 6
6 2x  3  2x  6x  6  0    4 3  x  4  0  x     9  11  + TH1:    3  x  . 2
3x  4  2x  6x  6  2 7  7
x 18x  10  0     3 2x  3  0     x 3  3  + TH2:   2  x  . 2 2
x  3  2x  6x  6  2 2  2
x  6x  3  0   9  11 3  3
Kết luận: Phương trình có 2 nghiệm là: x  ,x  . 7 2
Ví dụ 11: Giải phương trình: 2
2x  4x  2  3x 2x  1 . U U Hướng phân tích: Nháp: 2
2x  4x  2  3x 2x  1  0
ax bcx du a c  x b d         u  0   a  c  3 d
 b  0;bd 1  2   Ta có:  & 
suy ra hệ vô nghiệm. Vậy để hệ có nghiệm ta chia ac   2 ad   bc  2  4    3 a  c d
 b  0;bd 1  1   cả hai vế cho 2: 2 3
1x  2x  1  x 2x  1  0 và có  2 &  2  a
d bc  2  2 ac   1     như thế 1
: a  2,c   ,b d  0 . 2 Hướng dẫn giải:   2 1
x x   x
x    x x   1 2 4 2 3 2 1 2 2 1  
x  2x  1  0  x   . Vì nên suy ra:  2  2 1 2
x  2x  1  x  8x  4  0  x  4  2 3 (Thỏa mãn). 2
Kết luận: Phương trình có hai nghiệm: x  4  2 3 . Chú ý 1: U U 1
+ Tại sao ta không nhân với 2; 3; 4; ... mà ta nhân với k =
? Sau đây ta phân tích kỹ hơn một chút: 2
a + c = km b  + d = kn
Lý do ta chia (hay nhân) thêm hằng số để điều chỉnh các tích và tổng  và 
ac + A' = kA b
d + C ' = kC
Sao cho đảm bảo hệ có nghiệm thỏa mãn ad + bc + B ' = kB . b
 + d = 0,bd −1 = 2 − k 1 Cụ thể 2 2
− kx + 4kx − 2k + 3kx 2x −1 = 0 với  , nếu k = thì b = d = 0
ad + bc + 2 = 4k 2 2 2
+ Nếu phương trình có dạng (α + u ) + (β x + γ ) = 0 thì không thể phân tích thành nhân tử.
Bởi vậy trên đây là định hướng phân tích nhưng không tham hy vọng quá lớn để bao toàn bộ các bài toán nói trên.
Ví dụ 12: [Olympic 30/04/2013] Giải phương trình: 2 (x  3) x
  8x  48  x  24 . U U Hướng phân tích: 2
2x  48  (2x  6) x   8x  48  0
ax bcx du a c  x b d         u  0   a  c  2   d
  b  6;bd  48  48  Ta có  và 
. Hệ có nghiệm a  1, c  1, d  0, b  6 . ac   1  0   
ad bc  8  2  Hướng dẫn giải: 2 2 (x  3) x
  8x  48  x  24  2x  48  (2x  6) x   8x  48  0  2 x   x   x   2 6 8 48 x x
  8x  48  0
+ TH1: x  6  0  x  6 , ta có 2 2 x   6  x
  8x  48  2x  20x  12  0  x  5  31 .
+ TH2: x  0 , ta có 2 2 x   x
  8x  48  2x  8x  48  0  x  2  2 7 .
Kết luận: Phương trình có 2 nghiệm là x  2  2 7, 5 x    31.
(Ở trên nếu không nhân thêm 2 thì a + c = 1, ac = 1 sẽ vô nghiệm! Vậy nếu a = c = 1 thì a + c = 2). 3
Ví dụ 13: Giải phương trình: 2 2
5x x  3  (1  3x) 2x  1 . U U 2 Hướng phân tích: 5 3 3 1 3 Nháp: 2 2
x x   (  x) 2x  1  0
ax bcx du a c  x b d         u  0 2 4 2 2 2   .  3  1 3 a  c     d
  b   ;bd  1     1 1 Ta có 2  2 2 a  1, c   , d  1, b   và  có nghiệm . 5  3 ac  2 2   2      ad bc  2  4 Hướng dẫn giải: 5 3 3 1 3  1  1     PT 2 2 2 2
x x   (  x) 2x  1  0   x
   2x  1   
x  1  2x  1  0 2 4 2 2 2  2   2   1 1  x    0     x 1  6  + TH1:  2  2  x    . 2 2 2 2
 x 1  2 2x 1 4x  4x  5  0     1   x  1  0 2  x   2  2 15  + TH2:  2    x  2   . 2
7x  4x  8  0 7 x
  2  2 2x 1   6  1 2  2 15
Kết luận: Phương trình có 3 nghiệm là x  , x   2 7 Lời bình: U U
Qua các ví dụ trên ta cũng đã làm chủ được loại toán này, chủ động trong giải toán cho dù thay đổi các
biểu thức trong căn hay ngoài căn, là bậc nhất hay bậc hai.
Ví dụ 14: Giải phương trình: 2
5(8x  11x)  27(2x  1) 3x  2 (x∈ ) . U U Hướng phân tích:
Bài này tổng hai số a + c = 54 khá lớn so với tích nên nhân cả hai vế với 5 và đặt 5 3x − 2 = u . 2
200x  275x  54x  27 75x  50  0 Ta cần: ax bcx du a c  x b d        u  0   a  c  54   d
  b  27;bd  50  0  Ta có  và 
có nghiệm a  4,c  50,d  25,b  2 . ac   200   
ad bc  75  275  Hướng dẫn giải: 2 2
5(8x  11x)  27(2x  1) 3x  2  200x  275x  54x  27 75x  50  0
 4x 2  75x  5050x 25  75x  50  0    1 4x  2  0  x      27  + TH1:    2
x  2,x  . 4
x  2  75x  50  2 16  16
x  59x  54  0     1 50x  25  0       x  + TH2:    2 (Vô nghiệm). 10
x  5  3x  2  2  100 
x  97x  27  0  27
Kết luận: Phương trình có 2 nghiệm là x  2, x   16 Chú ý 2: U U
Câu hỏi đặt ra là: tại sao ta không nhân với 2; 4; 6; .. mà ta nhân với 5?. Như trên đã nói: a + c = 54 d + b = 27;  và 
nên ta chọn k để hai hệ có nghiệm đẹp một tí. Ta có thể hình dung như ac = 40k 2 bd  − 2k = 0
sau tách 54 = 2 + 52 = 4 + 50 = 6 + 48 .. và thử nhân các cặp xem sao? ac 2.52 4.50 bd Hay là k = = = = ...và k =
mà ta cũng chọn tổng a + c âm? 40 40 40 2
Như thế ta vừa chọn được a, c, b, d vừa biết cần nhân như thế nào để thử.
Để củng cố ta xét thêm vài ví dụ nhân thêm.
Ví dụ 15: Giải phương trình: 2 2
15x  12x  12  10(2x  1) x  3 (x  ). U U Hướng phân tích:
Nếu để nguyên thì a + c = -20 và ac = 14, tách -20 = -2 + -18 = -4 + -16 ...và tích lại thì bằng 36, 64, ...
khi đó nhân thêm cả hai vế với k và đưa vào căn thì 2 2 2
k x  3k như thế: 2
ac k  15k thử tích 36 trước: 2
36  k  15k k  3 . Nên PT 2 2
 45x  36x  36  (20x  10) 9x  27  0 .
Ta cần (ax + b)(cx + d ) + u + (a + c) x + b + d u = 0  a + c = 20 − d + b = 10 − ;bd + 27 = 36 Nên  và 
hệ có nghiệm a = 2 − , c = 1 − 8, d = 9 − , b = 1 − . ac + 9 = 45 ad + bc = 36 Hướng dẫn giải: PT 2 2
 45x  36x  36  (20x  10) 9x  27  0   2  x   x   2 2 1 9
27 18x  9  9x  27  0    1 2x  1  0  x       + TH1:    2 (Vô nghiệm). 2 2
x  1  9x  27  2  5
x  4x  26  0      1 18x  9  0  x      18  114  + TH2:    2  x  2 18
x  9  9x  27  2 35  35
x  36x  6  0   18  114
Kết luận: Phương trình có 1 nghiệm là x  . 35
Ví dụ 16: Giải phương trình: 2 2
3x  2x  7  3(x  1) x  3 (x  ). U U Hướng phân tích:
Nếu để nguyên thì a + c = -3 và ac = 2 do đó tách -3 = -2 + -1.và tích lại thì bằng 2 (đẹp), tuy nhiên khi
đó b+ d = -3, bd = 4, nhân cả hai vế với k và đưa vào căn thì 2 2 2
k x  3k như thế: 2
bd  3k  7k thử tích 2 thì: 2
2  3k  7k k  2 . Nên PT 2 2
 6x  4x  14  (3x  3) 4x  12  0 .
Ta cần (ax + b)(cx + d ) + u + (a + c) x + b + d u = 0  a + c = 3 − d + b = 3 − ;bd +12 = 14 Nên  và 
hệ có nghiệm a = 2 − , c = 1 − , d = 1 − , b = 2 − . ac + 4 = 6 ad + bc = 4 Hướng dẫn giải: PT 2 2
 6x  4x  14  (3x  3) 4x  12  0   2  x   x   2 2 2 4 12 x
  1  4x  12  0 2x  2  0  x   1   + TH1:     x  1. 2 2
x  2  4x  12 2  x  1  3      x   1  0 x   1   + TH2:    (Vô nghiệm). 2 2 x   1  4x  12 3
x  2x  11  0    
Kết luận: Phương trình có 1 nghiệm là x = 1.
Ví dụ 17: Giải phương trình: 2 2
10x  9x  3  8x 2x  3x  1  0 . U U Hướng phân tích:
Nếu để nguyên thì a + c = -8 và ac = 8, tách -8 = -2 + -6 = -4 + -4... và tích lại thì bằng 12, 16... , ...
khi đó nhân thêm cả hai vế với k và đưa vào căn 2 2 2 2
2k x  3k x k như thế: 2
ac  2k  10k thử tích ac = 12 thì: 2
12  2k  10k k  3 , nên PT 2 2
 30x  27x  9  8x 18x  27x  9  0 (*).
Ta cần (ax + b)(cx + d ) + u + (a + c) x + b + d u = 0  a + c = 8 −
d + b = 0;bd + 9 = 9 Nên  và 
hệ có nghiệm a = 2, − c = 6, − d = 0, 0 b = . ac +18 = 30
ad + bc − 27 = 27 − Hướng dẫn giải: PT 2 2
 30x  27x  9  8x 18x  27x  9  0   2  x x x   2 2 18 27
9 6x  18x  27x  9  0 2x  0 x   0   3 3  + TH1:   
x  ,x  . 2 2 2
x  18x  27x  9 14
x  27x  9  0 7 2     6x  0 x   0   3  17  + TH2:     x  . 2 2 6
x  18x  27x  9 18
x  27x  9  0 4     3 3 3  17
Kết luận: Phương trình có 3 nghiệm là x  ,x  ,x  . 7 2 4 Chú ý 3: U U
Chúng ta cũng có thể xét một vài ví dụ mà sự phân tích thành hệ số vô tỉ. Các ví dụ này không nhiều
nhưng không có nghĩa là không làm được, với lưu ý các số p q và p q có tổng bằng 2p và tích bằng 2
p q đều là các số hữu tỉ.
Ví dụ 18: Giải phương trình: 2 2
x  6x  4x x  1 . U U Hướng phân tích: PT 2 2
x x  1  6x  4x  0  ax b ucx d u  0.  a  c  0 b
 d  1;bd  1 a   5,c   5    Ta cần  &  . Do đó:  . ac   6  1 ad   bc  4  1     1 5 1 5   b   ,d   2 2 5  1 3  5 + TH1: 2 2 2
6x  4x x  5 
 6x  4x  5x   5  5x 2 2 5  1 1  2  2  x  1  5 5 3    x   0  x  (loại). 2 2 5  1 3  5 + TH2: 2 2 2
6x  4x x 5 
 6x  4x  5x   5  5x 2 2 5  1 2  1  2  x  1 5 5 3    x   0  x  (Thỏa mãn ). 2 2 3x
Ví dụ 19: Giải phương trình: x   1. U U 2 x  1 Hướng phân tích:
Điều kiện: x  0; 
1 . Quy đồng và chuyển vế ta thu được: x  x   2 3 1 x  1  0 .
Nhân hai vế với 6 ta có:
x   x   2 18 2
2 9x  9  0  ax b ucx d u  0. a  c  2 b
 d  2;bd  9     a  1 10 b      1  10 Xét các hệ:  &  ta có  &    ac   9 ad   bc  18      c   1  10 d   1  10   + TH1: 2
9x  9   10   1 x   1 2
x  1 10x 1  0 (cả hai nghiệm đều loại). 1  10  5  2 + TH2: 2
9x  9   10   1 1  x 2
x  1  10x 1  0  x  2  5  1 2  1
Vậy pt có một nghiệm: x  . 2
MỘT SỐ ỨNG DỤNG. U U 30
Ví dụ 20: Giải phương trình:
x  1. (x  ). U U 2
2x  7x  9  9 Hướng phân tích: Điều kiện: 2
2x  7x  9  9  0 . Từ PT suy ra 2 2
30  (x  1)( 2x  7x  9  9)  9x  39  (x  1) 2x  7x  9  0 (*). Ta cần ax
bcx du a c  x b d        u  0   . Cân bằng hệ số: a  c  1   d
  b  1;bd  9  39  Ta có  và 
. Hệ có nghiệm a  2, c  1, d  5, b  6 . ac   2  0   
ad bc  7  9  Như thế     2 x  
x x   2 * 2 6 2 7 9 x
  5  2x  7x  9  0 2  x  6  0 x   3   + TH1:    (Vô nghiệm). 2 2
2x  6  2x  7x  9 2
x  17x  45  0      x   5  0 x   5   3  145  + TH2:     x  , ( x  4 ). 2 2 x
  5  2x  7x  9 x   3x  34  0 2     3  145
Kết luận: Phương trình có 2 nghiệm là x   2
Ví dụ 21: Giải phương trình: 2 4 3
3x  2x  1  3x x  0 (x  ). U U Hướng phân tích: 4 3 3
 x x  0 Điề  1  1 u kiện: 
 1  x   hoặc 0  x   2
3x  2x  1  0 3  3 1 + Nếu 0  x   thì 2 4 3 2 2
3x  2x  1  3x x  0  3x  2x  1  x 3x x  0 (*) 3 Ta cần ax
bcx du a c  x b d        u  0   . Cân bằng hệ số: a  c  1   d
  b  0;bd  1  Ta có  và 
. Hệ có nghiệm a  1, c  0, d  1, b  1 . ac   3  3   
ad bc  1  2    Nên     2 x   x x  2 * 1 3
1  3x x   0 2 3 17
 1  x  3x x x  . 4 1
+ Nếu 1  x   thì 2 4 3 2 2
3x  2x  1  3x x  0  3x  2x  1  x 3x x  0 (**) 3 Ta cần ax
bcx du a c  x b d        u  0   . Cân bằng hệ số: a  c  1   d
  b  0;bd  1  Ta có  và 
. Hệ có nghiệm a  1, c  0, d  1, b  1. ac   3  3   
ad bc  1  2    Nên     2 x    x x  2 * * 1 3
1  3x x   0 2 1 13
 1  3x x x  . 6 3  17 1  13
Kết luận: Phương trình có hai nghiệm x  ,x  . 4 6
Ví dụ 22: Giải phương trình sau: 2 2
x  3x  6  2x  1  3x  1 . U U Hướng phân tích: Điề 1 u kiện: 2 2 1 1
2x  1  0, 2x  1  3x  1    x   hoặc x  . 3 2 2
Ta viết lại phương trình thành: 2 2
x  3x  6  3x  1  2x  1 . Bình phương 2 vế và thu gọn ta
được phương trình mới: 2 2
10x  3x  6  (3x  1) 8x  4  0 (*) (đưa 2 vào căn). Ta cần ax
bcx du a c  x b d        u  0   . Cân bằng hệ số: a  c  3   d
  b  1;bd  4  6  Ta có  và 
. Hệ có nghiệm a  2, c  1, d  2, b  1. ac   8  10    ad bc  3  Như thế     2  x   x   2 * 2 1 8 4 x
  2  8x  4  0    1 2x  1  0  x     1  6  + TH1:    2  x  . 2 2
x 1  8x  4  2 2  4
x  4x  5  0    x   2  0 x   2   2  2 15  + TH2:     x  . 2 2 x   2  8x  4 7
x  4x  8  0 7     1  6 2  2 15
Kết luận: Kết hợp điều kiện thì phương trình đã cho có hai nghiệm x  ,x  . 2 7
Ví dụ 23: Giải phương trình sau: 2
x  1  x  4x  1  3 x . U U Hướng phân tích:
Điều kiện: x  0,x  1  3 x . Bình phương 2 vế và thu gọn ta được phương trình mới: 2 2
2x  11x  2  (x  1) 4x  16x  4  0 (*). Ta cần
ax bcx du a c  x b d        u  0   . Cân bằng hệ số: a  c  1   d
  b  1;bd  4  2  Ta có  và 
. Hệ có nghiệm a  2, c  1, d  2, b  1 . ac   4  2   
ad bc  16  11  Như thế     2 x  
x x   2 * 2 1 4 16 4 x
  2  4x  16x  4  0    1 2  x  1  0  x     1  + TH1:    2
x  (Thỏa mãn điều kiện). 2 1
  2x  4x 16x  4  4  12  x  3    x   2  0 x   2   + TH2:   
x  4 (Thỏa mãn điều kiện). 2 2 x
  2  4x 16x  4 3
x  12x  0     1
Kết luận: Phương trình có hai nghiệm x  ,x  4. 4
Ví dụ 24: Giải phương trình sau: 2
4 x  1  1  3x  2 1  x  1  x . U U Hướng phân tích:
Điều kiện: x  1.Viết lại 2
4 x  1  2 1  x  3x  1  1  x . Bình phương 2 vế ta thu được phương trình mới: 2 2
8x  6x  18  (6x  18) 1  x  0 . Nếu để nguyên thì a + c = 6, ac = 9 nên
a = c = 3, tuy nhiên b + d = 18 và 3b + 3d = - 6 (vô nghiệm). Nhân hai vế với - 2 và đưa 4 vào căn để
cân bằng bậc hai , giảm bớt tổng b +d: 2 2
 16x  12x  36  (3x  9) 16  16x  0 . Ta cần (ax + b)(cx + d) + u + (a + c)x + b + du =   0 . Cân bằng hệ số: a + c = 3 − d + b = 9 − ;bd +16 = 36 Ta có  và 
. Hệ có nghiệm a = 3 − , c = 0, d = 4 − , b = 5 − . ac −16 = 16 −
ad + bc =12 Hướng dẫn giải:
Điều kiện: x  1;4 1  x  1  3x. Viết lại: 2
4 x  1  2 1  x  3x  1  1  x .
Bình phương 2 vế ta thu được phương trình: 2 2 2 2
8x  6x  18  (6x  18) 1  x  0  16x  12x  36  (3x  9) 16  16x  0 .   2  x    x  2 3 5 16 16
4  16  16x   0 .    5 3x  5  0  Trườ  x     3  ng hợp 1:    3
x   thỏa mãn điều kiện. 2 3
x  5  16 16x  2 5  25
x  30x  9  0   Trường hợp 2: 2
4  16  16x x  0 (thỏa mãn điều kiện). 3
Kết luận: Phương trình có hai nghiệm x = − , x = 0. 5
Ví dụ 25: Giải phương trình sau: 2
2 2x  4  4 2  x  9x  16 . U U Hướng phân tích:
Điều kiện: x  2 . Bình phương 2 vế ta thu được: 2 2
9x  8x  32  8 32  8x  0 . Ta cần: ax
bcx du a c  x b d        u  0   . Cân bằng hệ số: a  c  0   d
  b  8;bd  32  32   và 
có nghiệm a  1, c  1, d  8, b  0 . ac   8  9   
ad bc  8  Hướng dẫn giải:
Điều kiện: x  2 . Bình phương 2 vế ta thu được: 2 2
9x  8x  32  8 32  8x  0 .   2 x    x  2 32 8
x  8  32  8x   0.  x   0 x   0 Trườ   4 2  ng hợp 1:     x  thỏa mãn điều kiện. 2 2 x   32  8x 9  x  32 3     x   8  0 x   8 Trườ   ng hợp 2:    (Vô nghiệm). 2 2  x   8  32  8x 9
x  16x  32  0     4 2
Kết luận: Phương trình có 1 nghiệm x  . 3 Nhận xét: U U
Với cách làm này nếu kết hợp được máy tính Casio thì việc phân tích thành nhân tử hết sức dễ dàng.
Hy vọng với cách làm này sẽ giúp ích cho học sinh trong giải toán. Ta cũng thấy được một phần ý nghĩa
thông qua các ví dụ từ 20 đến 25.
Mặt khác chúng ta cũng thấy được "không có chìa khóa vạn năng" hay nói cách khác là chúng ta không
nên hy vọng có một công thức đơn giản mà đi giải các bài toán khó!
Sau đây là các bài luyện tập c. Luyện tập: U
Bài 1. Giải phương trình: 2 2
x  3x  (3  x) x   x  4.
Bài 2. Giải phương trình: 2
8x  16x  20  x  15 .
Bài 3. Giải phương trình: 2 2
x  1  (x  1) x  2x  3  0 .
Bài 4. Giải phương trình: 2
x  9x  7  (2x  7) 2x  7 .
Bài 5. Giải phương trình: 2
9x  25  (x  1) 2x  5x  5.
Bài 6. Giải phương trình: 2 x x   x   2 4 11 10
1 2x  6x  2 .
Bài 7. Giải phương trình: 2 2
x  8x  26  (x  1) x  6x  6.
Bài 8. Giải phương trình: 2 2
4x  9x  1  (4x  1) 8x  3x  1.
Bài 9. Giải phương trình: 2 2
4x  23x  23  (x  2) 2x  6x  12.
Bài 10. Giải phương trình: 2 2
16x  11x  1  (x  4) 4x  18x  4.
Bài 11. Giải phương trình: 2
2x  6x  1  4x  5 .
Bài 12. Giải phương trình: 2 2
2x  2x  3  (2x  3) x  5x  7. 3
Bài 13. Giải phương trình: 2 4x  5 
 2x  8x  4. x  1
Bài 14. Giải phương trình: 2 2
x  4x  2  (5x  3) 5x  6x  2.
Bài 15. Giải phương trình: 2
5x  3  x 2x x  1.
Bài 16. Giải phương trình: 2
3x  13x  37  8(x  3) x  2 .
Bài 17. Giải phương trình: 2 2
3(x  1) x  12  9x  20x  2 .
Bài 18. Giải phương trình: 2 2
7x x  2  7x x x  2 .
Bài 19. Giải phương trình: 2 2
5x  4x x  3x  18  5 x .
MỘT SỐ ĐỊNH HƯỚNG GIẢI PT VÔ TỈ PHẦN 4
III. Giải phương trình theo phương pháp trục căn thức và bình phương U
1. Đặt vấn đề: Trước hết ta xét 3 ví dụ sau: U U
Ví dụ 1: Giải phương trình: 2
x  2  4x  8x  3  3x  3 (1) U U Hướng dẫn giải:  2  2  1
PT(1)  0  2x   2 1      3x 3 x
x  2  2x   3 2x   1  
3x  3  x  2    x  1 1 2 1 2x 3    
 0  2x  1  0  x    
(Do ĐK nên trong ngoặc dương). 
3x  3  x  2 2  Phương trình có nghiệ 1
m duy nhất x   . 2 Lời bình: 4 2 T U U
Trong ví dụ 1: Phương trình chỉ có một nghiệm đơn nên ta trục căn một lần là xong. 4 2 T
Ví dụ 2: Giải phương trình: 2
5x 1  12x  8  x  3 (2). U U
Lời giải: Điều kiện: x  2 3 . Ta có     5x 1   12x  8   2 2 2 2  x 1 5x   1 12x   1    2 x   1  0 5x 1  2 12x  8  2    x   5 12 1    
x  1  0  5x 1  2 12x  8  2   x 1  0    5 12    
x  1  0  *  5x 1  2 12x  8  2 Ta coi  
* như là một phương trình bình thường và tiếp tục  5   12      *   1      2      x  2  0  5x 1  2
  12x 8  2  4  x  2 3x 2 3 5 1    x   2  0 5x 1  2 12x  8  2 52  x 46  3x     x  
5x 1    x    12x 8    x     2 0 2 3 5 1 2 2 3 2      5 8   
 2  x   x  2       
5x 1    x    12x 8    x   1 0 2 3 5 1 2 2 3 2    5 8 (Vì     ).
5x 1    x    12x 8    x   1 0 2 3 5 1 2 2 3 2
Vậy phương trình có hai nghiệm phân biệt x  1,x  2. Lời bình: U U
Trong ví dụ 2: Phương trình có hai nghiệm phân biệt và ta trục căn lần lượt hai lần mới
xong, rõ ràng khi trục căn lần thứ hai khó hơn lần thứ nhất. Đối với nhiều bài toán ta trục căn lần
hai sẽ gặp khó khăn rất lớn vì biểu thức chứa căn cồng kềnh, phức tạp, ..
Ví dụ 3: Giải phương trình: 2
3 3  x  6 x  2  3x  2x  7 (3). U U
Lời giải: Điều kiện: 2  x  3. Ta có   
  3x  x
 2 x 2 x        2 3 3 5 3 4
3 x x   2   *    
+ Vì 2  x  3 nên 3 3  x x  5  0; 3 x  2  x  4  0 . Do đó: 2 2 2 x   x x x     2 2      3 2 * x   x   2
3 3 x x  5
3 x  2  x  4     2 x   x   1 2 2    3  0   * *
3 3 x x  5
3 x  2  x  4 
+ Vì 2  x  3 nên 3 3  x x  5  2; 3 x  2  x  4  2 1 1 1 1    3    3  0
3 3 x x  5 3 x  2  x  4 2 2  + Do đó  x   *  1 2 *  x   x  2  0   x 2 
Vậy phương trình có 2 nghiệm x  1,x  2 . Lời bình: 4 2 T U U
Trong ví dụ 3: Phương trình có hai nghiệm phân biệt và ta trục căn một lần để được nhân tử 4 2 T
chung là tam thức bậc hai. Cách trục căn này khá phổ biến.
 Vấn đề chúng ta quan tâm hơn là: Có thể dự đoán được phương trình có bao nhiêu nghiệm để 4 2 T
"biết đường" mà "liệu cơm gắp mắm"?. Nếu cứ áp dụng cách giải trong ví dụ 3 vào trong ví dụ 1
thì không ổn!. Nếu cứ áp dụng cách "trục căn dần dần" như ví dụ 2 thì sẽ gặp khó khăn rất lớn, mà
còn dài dòng! Nếu không dùng máy tính Casio thì đây chính là câu hỏi nan giải rồi.
 Như vậy: chúng ta hãy "dự đoán" hay áng chừng xem phương trình có bao nhiêu nghiệm? Mà 4 2 T
dự đoán của chúng ta phải "tương đối chuẩn" thì sẽ mang lại hiệu quả cao trong giải toán.
2. Phương pháp nhẩm nghiệm hữu tỉ và trục căn. U
a. Nhẩm nghiệm hữu tỉ: U U
Việc chúng ta nghĩ đến đầu tiên là nghiệm nguyên hay nghiệm hữu tỉ đẹp, bởi lí do: phương
trình phức tạp thì nghiệm đơn giản một tí.
+ Các căn bậc hai đẹp như: 0; ;
1 4; 9; 16; 25;... hay các nghich đảo của chúng?.
+ Tìm được x và thử vào căn khác và cả phương trình xem có phải là nghiệm không? 0
Ví dụ 2: Giải phương trình: 2
5x 1  12x  8  x  3 . 4 2 T U U 4 2 T 4 2 T Hướng phân tích:
+ Thử x = 1 thì cả hai căn đều là số đẹp và x = 1 là nghiệm của phương trình
+ Thử x = 2 thì cả hai căn đều là số đẹp và x = 2 là nghiệm của phương trình.
Ví dụ 3: Giải phương trình: 2
3 3  x  6 x  2  3x  2x  7 . 4 2 T U U 4 2 T 4 2 T Hướng phân tích:
+ Thử x = -1 thì cả hai căn đều là số đẹp và x = -1 là nghiệm của phương trình
+ Thử x = 2 thì cả hai căn đều là số đẹp và x = 2 là nghiệm của phương trình.
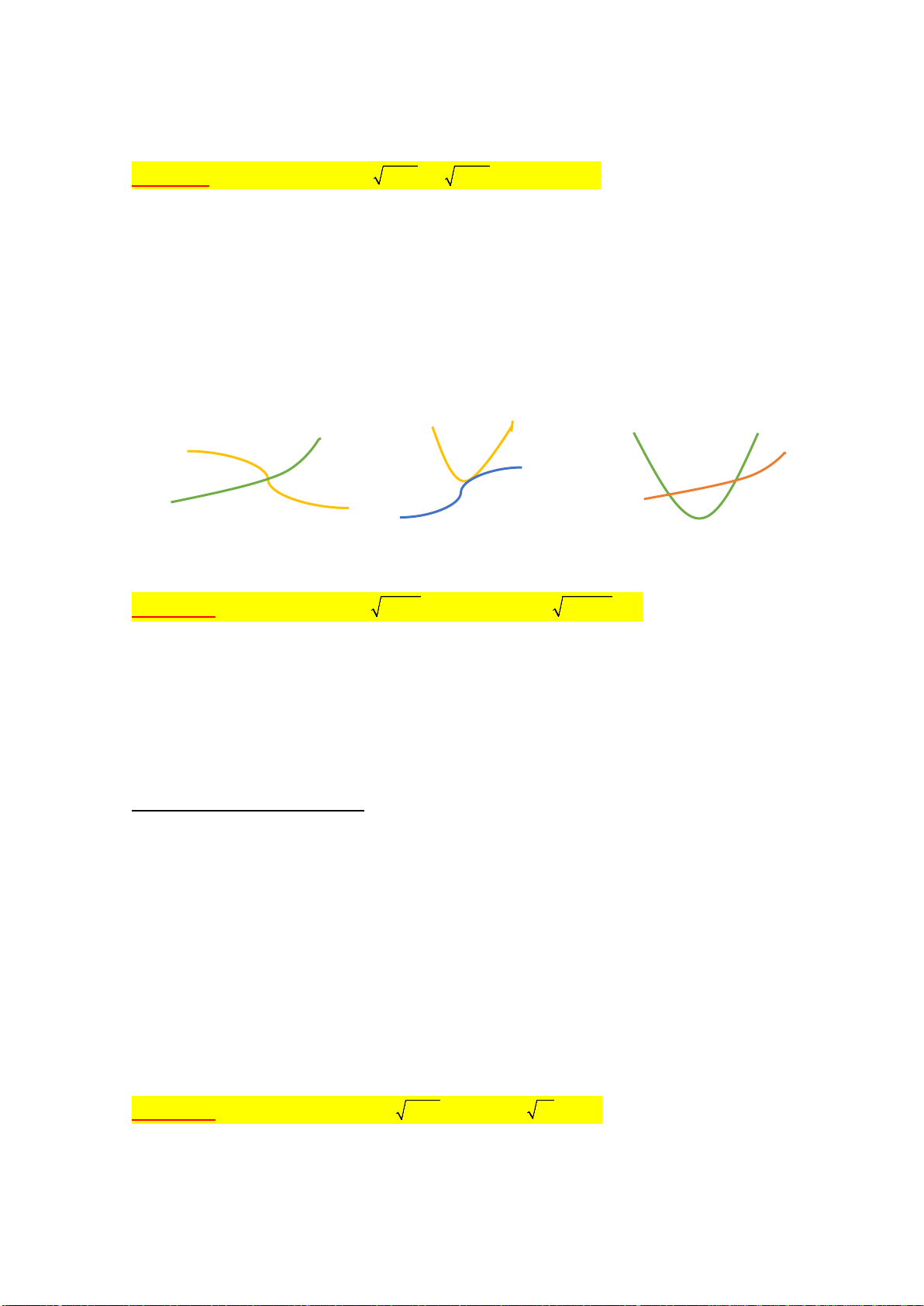
Trên quan điểm đồ thị (bản chất): Phương trình ẩn x coi như hoành độ giao điểm của hai đường
cong, từ đó dự đoán khoảng nghiệm và số nghiệm của phương trình.
Nhiều khi nghiệm vô tỉ sẽ khó nhẩm nghiệm, bởi vậy dự đoán khoảng nghiệm và số nghiệm sẽ
góp phần quan trọng khi định hướng giải cũng như trong lập luận và đánh giá.
Việc phác họa đồ thị là không cần thiết đối với HS các lớp 9; 10, 11. Tuy nhiên chúng ta cần "nhìn
thấu bản chất" và thử sơ lược các giá trị để dự đoán khoảng nghiệm, nghiệm đơn -kép -hai nghiệm.
Ví dụ 1: Giải phương trình: 2
x  2  4x  8x  3  3x  3 (1) U U Hướng phân tích:
Điều kiện x  1. Tại x = - 1 thì VT(1) > VP(1) , tại x = 0 thì VT(1) < VP(1) nên dự đoán
nghiệm thuộc (- 1; 0) và nghiệm hữu tỉ đẹp có thể là x = - 1/ 2 . Thử vào phương trình thỏa mãn.
Như thế qua ba ví dụ trên ta thấy việc nhẩm nghiệm cũng không quá khó khăn và không phụ
thuộc nhiều vào máy tính Casio. (Trừ các nghiệm vô tỉ được trình bầy riêng ở phần 5).
b. Định hướng trục căn thức: U
Chúng ta có hai hướng chính để trục căn thức là:
+ Hướng 1: Tìm biểu thức liên hợp với căn thức sao cho khi trục căn sẽ tạo ra nhân tử mà chúng ta đã nhẩm nghiệm.
Theo hướng này chúng ta thực hiện đối với hai căn thức nên sẽ khá dài, đa số phải xét dấu nhiều
trước khi trục căn và sau khi trục căn.
+ Hướng 2: Đặt điều kiện. Bình phương hai vế đưa về trường hợp một căn thức, trục căn một
lần để tạo nhân tử mà chúng ta đã nhẩm nghiệm.
Theo hướng này: chúng ta vướng mắc nhỏ ở việc bình phương nhưng cũng không cần lo lắng khi
mà chúng ta đã biết trước nhân tử.
Ví dụ 4: Giải phương trình sau: 2
x  1  1  4x  3x (4). U U Hướng phân tích:
Điều kiện x  0.Với x = 0 thì VT(4) > VP(4), với x = 1 thì VT(4) < VP(4) nên dự đoán phương 4 2 T
trình có một nghiệm thuộc (0; 1) và nghiệm hữu tỉ đẹp có thể là x = 1/2, thử vào thấy thỏa mãn. Hướng dẫn giải: Điề 2x  1
u kiện x  0 . Ta có 4   2 4x  
1   3x x 1  0   2 4x   1   0 4 2 T 4 2 T 4 2 T 4 2 T 3x x  1       x   1 1 2 1 2  x  1   
  0  2x 1  0  x  . (Vì x  0 nên trong ngoặc thứ hai  4 2 T 
3x x  1 2 xác định và dương) 42T 1
Vậy phương trình có một nghiệm là x  . 2
Ví dụ 5: Giải phương trình sau: 2
3x  1  6  x  3x  14x  8  0. U U Hướng phân tích:   Điề 1
u kiện x   ;6 
. PT có ít nhất một nghiệm x = 5. Khả năng nghiệm đơn duy nhất. 3  4 2 T 4 2 T   Hướng dẫn giải:   Điề 1
u kiện x   ;6 
. Ta có  x        x  2 3 1 4 1 6
 3x  14x  5  0 3       x   3 1 5    3x  1 
  0  x  5  0  x  5 .
 3x  1  4 1  6  x 
Vậy phương trình có nghiệm duy nhất x  5 .
Ví dụ 6: Giải phương trình: 2 3
3x  10x  3x  3  x  26  5  2x (6). U U Hướng phân tích:
Điều kiện: 1  x  5 / 2. Thử x = 2 thì cả hai căn là số đẹp và x = 2 là nghiệm của phương
trình. Viết lại phương trình thành 3 2
3x  3  5  2x x  3x  10x  26 (*)
Với x = 1 thì VT(*) < VP(*), với x = 5/2 thì VT(*) > VP(*) nên phương trình khả năng có 4 2 T
nghiệm đơn duy nhất x = 2. Hướng dẫn giải:
Điều kiện: 1  x  5 / 2 . Ta có 4 2 T 4 2 T 4 2 T
x      x 3 2 3 3 3 1 5 2
x  3x 10x  24  0   x  3 2 2 
 x 34 x       0  (6.1).
 3x  3  3 1  5  2x  3 2
Dễ thấy 1  x  5 / 2  
 x  34  x  0 3x  3  3 1  5  2x Nên từ (6.1) suy ra x = 2. 4 2 T
Vậy phương trình có nghiệm duy nhất x = 2. 4 2 T  Lưu ý 1: 4 2 T U U
+ Đối với căn bâc 3: ta có thể ký hiệu       3 3 u x a
u x a để gọn nhẹ, bớt cồng kềnh
trong khi trục căn, x vẫn là ẩn chính mà a có mặt trong phương trình nhưng không phải là ẩn.
+ Để giảm bậc hay giảm hệ số, ... ta có thể đặt ẩn phụ mới v x  t và khi đó ta cần chuyển đổi
hoàn toàn ẩn x sang ẩn t và cần giới hạn cho t.
Ví dụ 7: Giải phương trình: 3 2
x  9  2x  3x  5x  1  1. U U Hướng phân tích:
Ta nhẩm được x = 1 là nghiệm, khả năng là nghiệm nghiệm đơn duy nhất. 4 2 T 4 2 T Hướng dẫn giải: Điề 1 u kiện x
. Ký hiệu 3 x  9  a ta có phương trình: 5
x   a   2 5 1 2 2
2x  3x   5  0 5x   3 1 a  8  
x  1 2x  5  0 2    5x  1  2 a  2a  4     1 x   5 1 1  
 2x  5  0 (*)  . Vì x  nên ngoặc thứ hai âm 2 
 5x 1  2 a  2a  4  5
Do đó (*)  x 1  0  x  1.
Vậy phương trình có 1 nghiệm là x  1 .
Ví dụ 8: Giải phương trình:  3 x x   2 4 2 8 6
1 4x  21  16x  12x  2x  21. U U Hướng phân tích:
Ta nhẩm được x = 1 là nghiệm, khả năng là nghiệm đơn duy nhất, đặt t = 2x thì khi đó t = 2. Hướng dẫn giải:
Đặt 2x t , ta có phương trình:  3t t   2 4 2 3
1 t  21  t  3t t  21
  3t  3t  
1  2t  21 t 3 21 2
 21  t  3t  1 
t  21  t 2 t  21  t   t t  t t
t  t 2 3 2 6 3 2 3 21 0 2 1               0  2 
t  3  t  21
t  2  0  t  2  x  1.
Vậy phương trình có 1 nghiệm là x  1 .
x 6 x 1  8 2x 2x  1  5
Ví dụ 9: Giải phương trình:  . U U
x  3  x  1 2 Hướng phân tích:
Nhẩm được nghiệm x = 5. Để giảm độ phức tạp ta đổi biến 2
x  1  t  0  x t  1 . Hướng dẫn giải: Đặt 2
x  1  t  0  x t  1 , ta có phương trình:
 2t  5t  8 2 2t   2 3 2 2 1 2t  1  5
t  2t  5t  6 2t  1  5    1   1 2 2 t  2  t 2 t t  2 2    t   0,t  1 t  2 2 t t   2 t  3
t 2t  2       1   
t  2 t  2  t   1  2    2 t t  2 t   2 2t  1  3     2  2 
 2t  1  t  1  2t  1  3   
t  2 . Thay trở về 2
x t  1 ta có nghiệm của phương trình là x  5 .
Ví dụ 10: Giải phương trình:  3  x  3 4 3 28 4
2x  15  2x  3x  14x  16. U U Hướng phân tích:
Ta nhẩm được x = 2 là nghiệm, khả năng là nghiệm đơn duy nhất, ở đây ta đổi biến sang căn bậc
3 để giảm bậc bên ngoài căn. Đặt 3 3 3
x t  7  x t  7;2x  15  2t  1  0  t  1 / 2 thì khi đó: 4 3
x x x    3
x  x  t   3 2 3 14 16 2 7 3
7  16  2t t  7  3t  5 . Hướng dẫn giải: Đặ 1 t 3 3 3
x t  7  x t  7;2x  15  2t  1  0  t  , khi đó ta có phương trình: 2 3
t t   t t   t   t    t 3 4 2 1 2 7 3 5 5 1 2
t  7  2 4t  2t 1   1  0           2t 8t  1 t 1 5    
  0  t  1  0  t  1  (Vì t  ).  2      t 2 3 2t  1  1 7 1 3     
Thay t  1 trở về 3
x t  7 ta có nghiệm của phương trình là x  2 .  Lưu ý 2: U U
Trong một số trường hợp phương trình có nghiệm duy nhất ta cần sử lí tinh tế để tránh độ phức
tạp của phép trục căn. Như đưa về 2 2
A B  0 hoặc bình phương hay đổi biến.
Ví dụ 11: Giải phương trình: 2 2
2x  3x  5  2x  3x  5  3x . U U Hướng phân tích:
Ta nhẩm được một nghiệm x = 4. Nếu ta biến đổi theo cách:
 x     2 x  
x x    2 4 3 2 3 5
x  1  2x  3x  5  0         x   2 2 x 3x 4 x 5x 4 4    0 2 2
x  3  2x  3x  5
x  1  2x  3x  5       1  x 1  xx 4 1     
  0 . Khi đó ta phải đi đánh  2 2  
x  3  2x  3x  5
x  1  2x  3x  5 
giá biểu thức trong ngoặc khó khăn. Hướng dẫn giải: Điề 1
u kiện x  0 . Đặt t
 0 , ta có phương trình: x 2 2 6t
5t  3t  2  5t  3t  2  3   3 2 2
5t  3t  2  5t  3t  2 2 2
 5t  3t  2  5t  3t  2  2t . Kết hợp 2 2
5t  3t  2  5t  3t  2  3 suy ra  2 2t 3 2 1 1
5t  3t  2 
 16t  1  t  (vì t   0 )  x  4 . 2 4 x
Vậy phương trình có 1 nghiệm là x  4 . Cách khác
Điều kiện x  0. Bình phương hai vế ta có: 2 2 2
2 2x  3x  5 2x  3x  5  5x  10 (*).
Vì x  0 nên ta có điều kiện 2
x  2  0  x  2 . Tiếp tục bình phương hai vế của (*):  4 2 x x    2  4 2 4 2 2 4 4 20
25  9x  25x  100x  100  9x  144x  0  x  16   
Từ đó suy ra phương trình có một nghiệm x  4 .
Ví dụ 12: Giải phương trình: 2x  2  2x  1  6x  5 . U U
Hướng dẫn giải: (Tương tự ví dụ 11) 4x   1 Điề 1
u kiện x   . PT  2x  2 
 6x  5  2x  1  2 (*). Từ 2
6x  5  2x  1 đây ta có điề 1
u kiện 6x  5  2  x   . Kết hợp 6x  5  2x  1  2x  2 suy ra: 6 2x  2  2 2 6x  5 
x  2  x  2x  1  0 . Giải ra lấy nghiệm x  1  2 . 2
Vậy phương trình có 1 nghiệm là x  1  2 .
Ví dụ 13: Giải phương trình: 2
4x  3x  3  4x x  3  2 2x  1 . U U Hướng phân tích:
Ta nhẩm được một nghiệm x = 1. Nếu ta biến đổi theo cách:   2
4x  5x  
1  4x 2  x  3  21 2x 1  0    x   4x 4 1 4x  1     
  0. Khi đó ta phải đi đánh giá biểu thức  2  x  3 1  2x  1
trong ngoặc khó khăn. Ta có thể biến đổi tiếp tục nhưng cồng kềnh và phức tạp.
Thử tại x = 1/2 thì VT > VP, thử tại x = 2 thì VT > VP nên khả năng Parabol 2
y  4x  3x  3
luôn nằm trên đường cong y  4x x  3  2 2x  1 do đó đoán là nghiệm kép tại x = 1.
Hướng dẫn giải: (đưa về nghiệm kép) Điề 1 u kiện x  . Ta có:  2
4x x  3  4x x  3 2x  2x 1  0 2        x x  x 2 2 2 1 2x x 3 0 2 3 0          x  1 . x  2x  1 x  1  0 
Vậy phương trình có 1 nghiệm là x  1 .
Ví dụ 14: Giải phương trình: 2x  1  2 x  2x  1 . U U Hướng phân tích:
Thử tại x = 1/2 thì VT > VP, thử tại x = 2 thì VT > VP nên khả năng đường thẳng y  2x  1
luôn nằm trên đường cong y  2 x  2x  1 do đó đoán là nghiệm kép tại x = 1.
Hướng dẫn giải: (Tương tự ví dụ 13) Điề 1 u kiện x
. Ta có x  2x 1  x  1  2 x   0 2 x  2 x  2 1 1    1
0  x  1  0  x  1 (Vì x  ). x  2x  1 x  1  2 x 2
Vậy phương trình có 1 nghiệm là x  1 .
Ví dụ 15: Giải phương trình: 2 3
2x  11x  21  3 4x  4 . U U Hướng phân tích: Nhận xét 2
2x  11x  21  0, x  4x  4  0  x  1 . Nhẩm được nghiệm đẹp x = 3.
Để bớt cồng kềnh ta ký hiệu 3 4x  4  a , khi x = 3 thì a = 2. Mặt khác viết lại: 2
2x  12x  18  x  3 3
 3 4x  4 thì khả năng Parabol tiếp xúc với đường cong! Hướng dẫn giải: Dễ thấy 2
2x  11x  21  0, x do đó để phương trình có nghiệm thì 4x  4  0  x  1.
Ký hiệu 3 4x  4  a  0 , ta có phương trình 2
2x  12x  18  x  3 3a  0 3 3 x   a  2x  32  3 3  
 0 (Với x  1,a  0 )
x  32  3ax  33a2 3 2 x x x   x   2x  32 9 27 27 274 4 
 0 (Với x  1,a  0 )
x  32  3ax  33a2        x  2 x 15 3 2     0  x  3 x a   (Vì 1, 0 ). 
x 32 3ax 3 3a2        
Vậy phương trình có một nghiệm là x  3 . Lời bình: U U
Từ hướng phân tích trên ta có thể giải phương trình theo phương pháp đánh giá ngắn gọn hơn như sau: Dễ thấy 2
2x  11x  21  0, x do đó để phương trình có nghiệm thì 4x  4  0  x  1. Viết lại phương trình: 2
2x  12x  18  x  3 3  3 4x  4 (*).
Ta có VT(*) = x  2 2 3  0. Mà VP(*) x  3 3 3 2.2.x 1 x 3 2 2  x 1              0   .
Dấu bằng xảy ra khi x  1  2  x  3 . Từ đó phương trình có 1 nghiệm x  3 .
Tương tự ta có thể giải các ví dụ 13, ví dụ 14 hay các các bài toán nghiệm kép theo phương
pháp đánh giá bằng bất đẳng thức AM - GM, B.C.S, ...
Chẳng hạn ví dụ 13, với x  1 / 2 : 2 x x    x   2 2 2. 4 . 3 2 1. 2
1  4x x  3  1  2x  1  4x  3x  3 .
Ví dụ 16: Giải phương trình: x   x   x   2 1 4 5 2
5 x  3  3x  14x  13 . U U Hướng phân tích:
Ta nhẩm được một nghiệm x = 1. Nếu x = 0 thì VT > VP, nếu x = 2 thì VT < VP nên khả năng
x = 1 là nghiệm đơn duy nhất. Hướng dẫn giải: ĐK 5 x   . Ta có 2
3x  7x  10  x  
1 3  4x  5  2x  52  x  3  0 4      x  4  x 1 2x 5 1 3x 10         0  3  4x  5 2  x  3              
x   3x 10 4x 5 5x 5 1 2x 5 1  
  0  x   1 .M  0 (*).  3  4x  5 2  x  3   
3x 10 4x  5  5x  51  4x  5 0 5  Ta có  x   0
  3  4x  5  4  4x 12  2  2 x 3, 4  4x  5 2x  5 5 Suy ra: M  
 x   . Do đó (*)  x  1  0  x  1. 22  x  3 0, 2  x  3 4
Vậy phương trình có một nghiệm là x  1 .
Lời bình: Ví dụ trên ta gặp khó khăn khi đánh giá biểu thức M trong ngoặc vuông. Đây là bài U U
khó, ta có thể đổi biến quy về một căn thức như sau:
Cách 2: Phương trình 2
(x  1) 4x  5  2(x  5) x  3  3x  14x  13 2
 (4x  4) 4x  5  (4x  20) 4x  12  12x  56x  52 . Đặt 2
4x  5  t  0  4x t  5 ta có phương trình: 3
t(t  1)  (t  15) t  7  t  2 2 2 2 2 5  14 2t   5  52 4 4 3 2 2 2
 3t  4t  26t  4t  3  4(t  15) t  7  0 4 3 2 2
t t t t   t   2 3 4 10 4 237 4(
15) 4  t  7  0  2   t t t 3 4( 15) 3  3 2   3t 5t 25t 79       
  0  t  3.M  0 (*). 2  4  t  7    Ta có 3 2 3 2 2
t  0  3t  5t  25t  79  t  3t  15t  75  (t  15)t  3 Kết hợp 2
4  t  7  4 suy ra M  0 và từ (*) ta có t  3  0  t  3 . 2 t  5 Thay trở về x
ta có nghiệm của phương trình là x  1 . 4
Tuy giải được nhưng độ phức tạp và cồng kềnh không giảm hơn bao nhiêu. Ta tiếp tục xét thêm
một vài ví dụ để thấy rõ sự đa dạng của phương trình vô tỉ nhưng trong trường hợp nhẩm được
nghiệm hữu tỉ thì ta vẫn tự tin trong giải toán.
Ví dụ 17: Giải phương trình: 2 3 2
3x 5x  6  4x  19x  12  36x  2x  20x  6 . U U Hướng phân tích: 5  x  6  0   ĐK  6 
x   ;4 . Ta nhẩm x  2 thì VT < VP, với x  3 là nghiệm 2
4x  19x  12  0 5    
Với x  4 thì VT < VP. Như thế khả năng hai đường cong tiếp xúc nhau tại x = 3. Hướng dẫn giải: Điề 6 u kiện
x  4 . Bình phương hai vế và thu gọn ta có phương trình: 5 2 3 2
6x 5x  6 4x  19x  12  9x  56x  39x  18  0  x  2 x   x x     3 2 6 5 6 4 19 12 9
9x  56x  93x  18  0     x 2 6x  20x 1 3  9x 2   
   0  x  3 . 2
 5x  6 4x  19x 12  9    6 (vì
x  4 nên ngoặc vuông dương). Vậy phương trình có nghiệm duy nhất x  3 . 5
Cách khác: (Dùng phương pháp đánh giá) 5  x  6  0   Ta có điề  6  u kiện 
x   ;4 . Bình phương hai vế và thu gọn ta được: 2
4x  19x  12  0 5     2 3 2
3x.2 5x  6. 4x  19x  12  9x  56x  39x  18  0 (*) Áp dụng bđt Cô si thì: 2 x x   x x   x  2 3 .2 5 6. 4 19 12
3 5x  6  4x  19x   12 2 3 2
3x.2 5x  6. 4x  19x  12  12x  72x  54x . Dấu bằng có khi và chỉ khi 6  x  3   ;4  . Từ đó suy ra: VT(*) 3 2 3 2
 12x  72x  54x  9x  56x  39x  18 5    2 6  VT(*) 3 2
 3x  16x  15x  18  x  3 3x  2  0, x   ;4  . 5   
Từ đó suy ra phương trình (*) có nghiệm duy nhất x = 3 và là nghiệm của phương trình đã cho. Lời bình: U U
Phương pháp bình phương một bước làm cho bài toán ngắn gọn hơn. Các bạn hãy thử giải theo
cách để nguyên trục căn hoặc đánh giá mà không bình phương:?.
Ví dụ 18: Giải phương trình: 2 2
x  2 x  3  4 2  x  3 11  x  3x . U U Hướng phân tích:
Điều kiện  2  x  2 . Tại x  1 thì VT< VP, tại x  0 thì VT < VP, x = 1 là nghiệm.
Tại x  2 thì VT < VP nên dự đoán x = 1 là nghiệm kép.
Hướng dẫn giải:
Điều kiện  2  x  2 . Viết lại 2 2
2 x  3  4 2  x  3 11  x  3x x .
Bình phương hai vế ta được: 2 2 2
10x  5x  55  16 x  3 2  x  6x 11  x  3x  0 (18). Áp dụng bđt Cô si: 2 x   x   2
x    x  2 4.2 3 8 4 4 3 8 4
 44  4x  16x (18a). Suy ra: VT(18) 2 2 2
 10x  5x  55  44  4x  16x  6x 11  x  3x
VT(18)   x   x x x
x x    x   x x 2 2 2 2 2 9 11 3 6 11 3 3 11 3  0 (18b).
Từ (18a) và (18b) ta có dấu bằng xảy ra khi và chỉ khi:  2
x  3  8  4x 
x  1. Vậy phương trình có nghiệm duy nhất x  1 . 2 3
 x  11  x  3x  2 2 x  2 1  x
Ví dụ 19: Giải phương trình: 2 8  x   5  . U U 2 2x x Hướng phân tích: Điề  1 1
u kiện 2  x  2 2 . Nếu x   2 2; 2   thì VT 2  8  x    5 , mà khi   2 2 x 2 đó VP 1  x  5   5 
nên phương trình không có nghiệm x   2 2; 2 . x      Xét x   2;2 2 
 : Ta nhẩm được nghiệm đẹp x  2 , và khi x  2 hay x  2 2 ta đều có  
VT < VP, nên khả năng x  2 là nghiệm kép. Nhân cả hai vế với 2x để khử mẫu thức.
Hướng dẫn giải (Cách phổ biến): Điề  1 1
u kiện 2  x  2 2 . Nếu x   2 2; 2   thì VT 2  8  x    5 , mà khi   2 2 x 2 đó VP 1  x  5   5 
nên phương trình không có nghiệm x   2 2; 2 . x      Xét x   2;2 2 
 , nhân cả hai vế với 2x ta có phương trình:   2 2 2
2x 8  x  2x  4  2x  10x  2 2
x x    2 x   x     2 2 8 8 2 2 2 4
2 4  x 8  x  2 2 2 x x x   2x  22 2 2 2 2  2   2 2
2x  2  2x  4 4  x 8  x
2x 22  0  x  2    x  2 1 2 . 1    (*) 2 2 
2x  2  2x  4 4  x 8  xx  22 2   Ta có 2
 1  x  4  8  x  x  2  0, x  2;2 2   nên (*) vô 2 4 x 8 x     nghiệm.
Vậy phương trình có nghiệm duy nhất x  2 . Lời bình: U U
Để tránh trục hai căn thức như biểu thức vế phải (*) ta cũng có thể giải theo phương pháp bình
phương quen thuộc đưa về bậc 4 rồi trục căn một lần:  Cách 2: Xét x   2;2 2 
 , nhân cả hai vế với 2x ta có phương trình:   2 2 2
2x 8  x  2x  4  2x  10x  2 . Bình phương hai vế và thu gọn ta được: 2 2 4 3 2 2x 8  x
2x  4  4x  20x  37x  20x  4   4 3 2 x x
x x    x  2 2 4 20 33 20 4 2 2x  8  x 2x  4  0 2      x x  
x  22 2x  2 4  2 1 
  0  x  22  0  x  2  . 2 2 2x 8 x 2x 4        
Từ đó phương trình có nghiệm duy nhất x  2 .
c. Trường hợp hai nghiệm hữu tỉ: U U
Nếu nhẩm được hai nghiệm hữu tỉ thì mục tiêu của ta là trục căn một lần để có nhân tử chung là
tam thức bậc hai. Theo định lý Viet đảo: 2
x Sx P  0.
Ví dụ 20: Giải phương trình: 2
2 3x  4  3 5x  9  x  6x  13 . U U Hướng phân tích:
Ta thấy phương trình có ít nhất hai nghiệm x = 0 và x = - 1, do đó định hướng trục căn thức sẽ xuất hiện nhân tử 2
x x . Cách làm phổ biến là:  2 x
6 5ax 13 2b 3d       2  
ax b  3x 43ax d  5x 9 0
Cho x = 0 suy ra b  2,d  3;13  2b  3d  0 .
Kiểm tra 6  5a  4a  3  6a  5  1  a  1
Cách giải phổ biến là: Điề 4
u kiện: x   . Ta có:  2
x x  2x  2  3x  4 3x  3  5x  9  0 3 2 2   2 x x 3 x x 2 x x        0
x  2  3x  4
x  3  5x  9     2 x x 2 3  2 1     
  0  x x  0 
x  2  3x  4
x  3  5x  9 
Từ đó suy ra phương trình có đúng hai nghiệm x  1,x  0 . Lời bình: U U
Đối với bài trên thoạt nhìn theo cách trên không có phức tạp hay sự cồng kềnh trong lời giải, tuy
nhiên theo cách làm ta phải tìm hai biểu thức liên hợp với hai căn sẽ mất thời gian hơn. Cách
ngắn gọn vẫn là bình phương như ví dụ 19. Dùng phép chia đa thức hay lược đồ Hooc - ne để
tìm thương và phần dư.
Hướng dẫn giải (PP bình phương):
Điều kiện x  4 / 3 . Bình phương hai vế ta có phương trình: 4 3 2
12 3x  4 5x  9  x  12x  62x  99x  72   4 3 2
x  12x  62x  51x  124x  6  3x  4 5x  9  0    2 x x 2 12 2 x  11x 51      
 0  x x  0   
4x  6  3x  4 5x  9 
Từ đó suy ra phương trình có đúng hai nghiệm x  1,x  0 .
Cách tìm biểu thức liên hợp là chia đa thức 4 3 2
x  12x  62x  99x  72 cho 2 x x ta tìm được thương là 2
x  11x  51 và dư 48x  72 ghép vào căn là được. Chúng ta sẽ kiểm chứng khi giải lại VD2.
Ví dụ 2: Giải phương trình: 2
5x  1  12x  8  x  3 . 4 2 T U U 4 2 T 4 2 T Hướng phân tích:
Thử x = 1 và x = 2 là nghiệm của phương trình. Nhân tử của chúng ta là 2
x  3x  2 . Hướng dẫn giải:
Điều kiện x  2 / 3. Bình phương hai vế ta có phương trình: 4 2
4 5x  1 3x  2  x  6x  17x  18   4 2
x  6x  33x  
26  44x  2  5x 1 3x  2  0     2
x x   2 4 3 2 x   3x  13     0    
4x  2  5x  1 3x  2  2
x  3x  2  0  x  1,x  2 .
Vậy phương trình có hai nghiệm x  1,x  2 .
Ví dụ 21: Giải phương trình: 2 2
2x x  9  2x x  1  x  4 . U U Hướng phân tích:
Ta dễ nhẩm được một nghiệm x  0 . Khả năng còn nghiệm thứ hai x nên mục tiêu là:
nhân tử sau khi trục căn có dạng 2 ax bx .
Giải theo PP bình phương:
Điều kiện x  4. Bình phương hai vế và thu gọn ta có phương trình 2 2 2
3x  8x  6  2 2x x  9 2x x  1 . Cộng thêm hai vế với 2 4x  6 ta được 2
x x   2 2 2 7 8
2 2x  3  2x x  9 2x x  1     2   x x 2 8 7 8 1    
  0  x  0,x  .  2 2 2    7
2x  3  2x x  9 2x x  1
Giải theo cách thông thường:
Điều kiện x  4. Nếu 4  x  2 suy ra VT  15  11  VP nên 4  x  2 không phải là nghiệm.
Do đó x  2 và PT   2
x x   x    2 2 2 9 6
2 2x x  1  x   2  0     2   x x 1 1 8 7 8    
  0  x  0,x   2 2    7
2 2x x  9  x  6
2 2x x  1  x  2 8
Vậy phương trình có hai nghiệm x  0,x  . 7 Lời bình: U U
PP bình phương ta không cần lập luận nhiều. Bài trên ta có thể đặt thêm điều kiện và tiếp
tục bình phương lần thứ hai. Ngoài ra ta cũng có thể giải theo cách tương tự VD11, VD12.
Theo phương pháp thứ hai ta cần tách hạng tử hợp lý và xét mẫu thức khác 0 để trục căn.
Đặc biệt ví dụ sau thì PP thông thường sẽ khó khăn
Ví dụ 22: Giải phương trình: 2 2
3 2x  1  x 5  4x  4x . U U Hướng phân tích:
Nhẩm được các nghiệm x = 1/2 và x = 1. Nhân tử chúng ta cần là 2
2x  3x  1. Hướng dẫn giải:   Điề 1 5  
u kiện x D  ; 
. Bình phương hai vế ta có phương trình: 2 2      2 4 2
6x 2x  1 5  4x  20x  5x  18x  9 , trừ cả hai vế một lượng 6x(2x - 1) thuộc tập
xác định ta có phương trình: x  2 x
x x   4 2 6 2 1 5 4 2
1  20x  17x  12x  9  x x   2  x x   4 2 6 2 1 5 4 2
1  20x  17x  12x  9
21  x2x  3  6x 2x  1   2
2x  3x   1  2
10x  15x   9 2
5  4x  2x  1     x x 1 2x 1  2x 1 12 2 3 2 10x 15x    9           0 2 
5  4x  2x  1   
(Biểu thức trong ngoặc vuông dương vì x D )  x   1
1 2x  1  0  x  ,x  1. 2 1
Vậy phương trình có hai nghiệm x  1,x  . 2 Chú ý: U U
Bài trên nếu ta "trục căn dần dần" thì sẽ phức tạp, còn để nguyên không bình phương mà muốn tạo ra nhân tử 2
2x  3x  1thì chưa biết như thế nào?
Tuy nhiên ta thử đổi biến để quy về một căn xem sao? Đặt 2
2x  1  t  0  2x t  1 x x   x
x   t  2  t t   t  2 2 2 2 2 2 8 6 2 1 2 5 4 0 2 1 6 1 5 1  0   4 2
t t t   2t   4 2 2 4 6 2
1 4  t  2t  0 (*). Để giảm cồng kềnh khi trục căn ta y  5y  4 lại ký hiệu 2
t  1  y thì 2  t   4 2 2 4 2 2
1 4  t  2t  2  y 5  y  . 2 2  y 5  y
Khi đó thì phương trình (*) trở thành: y y y y
(*)  2t t   1  1 2 1 2 2
t t        3   0 2 2  y 5  y     t t y y t t 1  1 1 2  2  2t 2t      6      
  0 , vì t  0,y  0 suy ra 2  2  y 5  y    t t   1
1  0  t  0,t  1  x  ,x  1. 2
Mặc dù giải được nhưng cũng không giảm được độ phức tạp! Tiếp tục ta xét ví dụ 23
Ví dụ 23: Giải phương trình sau: 2 2
2x  16x  18  x  1  2x  4 . U U Hướng dẫn: Điều kiện: 2 2
x  1  0, x  1  2x  4  2  x  1 hoặc x  1. Viết lại phương trình: 2 2
2x  16x  18  2x  4  x  1 .
Bình phương 2 vế và thu gọn ta được phương trình:  2 x   2 3
1  2(2x  4) x  1  0   2 x  1  x  1  0 x   1         2        2 32 3 57 7x 64x 73 0
3 x  1  4x  8  x       7  
Kết hợp điều kiện ta có nghiệm phương trình là 32 3 57 x  1,x  . 7 Lời bình: U
Theo phương pháp bình phương ta đã giải phương trình tương đối ngắn gọn, lý do là sau
khi bình phương thì phương trình có nhân tử chung dễ dàng nhận ra là 2 x  1 .
Ví dụ 24: Giải phương trình: 2
4 x  3  19  3x x  2x  9 . U U Hướng phân tích:
Nhẩm được các nghiệm x = 1 và x = - 2. Nhân tử ta cần là 2 x x  2 .
Hướng dẫn giải (PP bình phương):   Điề 19
u kiện x D  3;  
. Bình phương hai vế và thu gọn ta có: 3    4 3 2
x  4x  22x  23x  14  8 x  3 19  3x  0   4 3 2
x  4x  22x  15x  
42  8x  7  x  3 19  3x   0    2 x x  2 32 2 x  3x 21         0   
x  7  x  3 19  3x 
(Vì x D nên trong ngoặc thứ hai dương) 2
x x  2  0  x  2,x  1.
Vậy phương trình có hai nghiệm là: x  2,x  1 . Cách phổ biến: 1 5
làm nháp ax b  x  3 = 0 và cho x = 1 và x = - 2 để tìm a, b. Kết quả a  ,b  . 3 3 Tương tự 1 13
: biểu thức liên hợp cx d  19  3x  0 suy ra c   ,d  . 3 3     Phương trình: 1 5   1 13   2
 4 x   x  3      x
 19  3x   x x  2  0  . 3 3     3 3 
Mời các bạn giải tiếp theo cách trên. Lời bình: U
Có thể nói: phương pháp bình phương là "dồn nghiệm" từ hai căn thức vào chung một
căn thức. Tuy nói thế nhưng không phải bài nào ta cũng áp dụng như vậy.
Ví dụ 25: Giải phương trình: 2 2
2x x  3  21x  17  x x  0 . U U Hướng phân tích:
Nhẩm được các nghiệm x = 1 và x = 2. Nhân tử ta cần là 2
x  3x  2 . Ta thấy trong căn có bậc hai 2
2x x  3 nếu trừ đi 2
x  2x  1 sẽ có nhân tử cần tìm (đẹp rồi). Do đó không phải bình phương. Hướng dẫn giải: Điề 17 u kiện 2 x
,x x  21x  17 . Phương trình tương đương với: 21
 2x x  x   x   x   2 2 3 1 3 1 21
17  x  3x  2  0     2   x x   1 9 3 2    1    0 ( biểu thức  2 
 2x x  3  x  1 3x 1  21x 17 
trong ngoặc thứ hai dương) 2
x  3x  2  0  x  1,x  2.
Vậy phương trình có hai nghiệm x  1,x  2 .
Ví dụ 26: Giải phương trình: 3 2 2
(x  1) 3x  1  x  2x  1  2 x x  1  6x . U U Hướng phân tích:
Nhẩm được các nghiệm x = 0 và x = 1. Nhân tử ta cần là 2
x x . Vì trong phương trình có bậc 3
nên ta không bình phương mà cố gắng ghép các hạng tử hợp lý. Hướng dẫn giải:   PT   3 2
x x x  x x   x    2 2 3 3 1 ( 1) 3 1
2 x x  1      1     2 x x x   3x 1 2 3        0  (*). 2 
x  1  3x  1
x x  1  1   1 2 Ta có x  
x  1  0 & 2   0 2 3
x x  1  1 Do đó từ (*) ta có 2
x x  0  x  0,x  1. Cách ghép 2:   PT 3 2 2 2 2
 6x x  2x  1  (x  1)  (x  1)  (x  1) 3x  1  2 x x  1  0      3 2 x x x  x  x x                2 4 3 1 ( 1) 3 1
2 x x  1  1  0       2  x xx 1 2 4  x       0 (**).  2 
x  1  3x  1 
x x  1  1 1 Ta có 2
x    x  1  3x  1  x  1  0; x x  1  1  1. Suy ra 3 x  1 2 4  x  
 4  x  1  2  1  x  0 2
x  1  3x  1
x x  1  1 Do đó (**) 2
x x  0  x  0,x  1.
 Một lưu ý mà chúng ta có thể quan tâm là: Không chỉ x làm cho căn thức trở thành số đẹp 0
mới là nghiệm của phương trình, x là nghiệm nhưng thay vào căn thức vẫn là số vô tỉ. 0
Ví dụ 27: Giải phương trình 2x  6 x  4 x  5 2x  3  3x   1 . U U Hướng phân tích: Thử x  1, x  3,
x  5 thì đều là nghiệm của phương trình, nếu bình phương hai lần và
chuyển về phương trình bậc 6 thì chắc chắn chúng ta cũng có nhân tử x  
1 x  3x  5
nhưng khá dài dòng. Nhiệm vụ của ta là tách ghép các căn hợp lý sao cho khi trục căn xuất hiện
nhân tử mà ta cần, đồng thời không phải xét dấu mẫu cũng như giải phương trình còn lại là đơn
giản nhất vì mẫu thức lúc này phức tạp. Định hướng các mẫu của ta là u v và a v như vậy sẽ đơn giản hơn. Hướng dẫn giải:
Điều kiện x  3 / 2 . PT  2x  6 x  4 2x  6  x  
1 2x  3  3x   1
 2x  6 x  4  2x  3  x   1 3  2x  3
2x 61x
x  16 2x 1x2x 6   
x  4  2x  3 3  2x  3 3  2x  3     x  xx 1 2 6 1 0       x     3 
x  4  2x  3  3  2x  3 x     5 
Vậy phương trình có ba nghiệm x  1, x  3, x  5.
Ví dụ 28: Giải phương trình: 2
2x  1  2x  1  2  2x  4x  2. U U Hướng phân tích:
Ta thấy trong phương trình xuất hiện số tự do 2 nên hướng nhẩm nghiệm là: một trong hai căn ở 1
vế trái bằng số này, từ đó ta nhẩm được hai nghiệm x  0;
x  . Chúng ta lựa chọn phương 2
pháp trục căn lần lượt hai lần vì trục căn một lần phải xét mẫu thức phức tạp. Hướng dẫn giải:
+ TH1: Xét x  0 là nghiệm của phương trình;  1 
+TH2: Xét x   ;1 \   0 
, chuyển vế:  x       x   2 2 1 1 2 2 2  4x  2x 2    1 1
2  2x  1  2  2x  1    2x  1    x    x
x     x   2x 1 2 1 1 2 2 2 2 1 1 2 2 2 1 2x 1 2x  1 1        2 2x 1 2 2x 1  2 2x 1 2 2x 1                     
x     x   2x 1 2x
1 1  x     x   0 2 1 1 2 2 2 2 1 1 2 2 2      1
 2x  1  0  x  . 2 1
Vậy phương trình có hai nghiệm x  0; x  . 2 d. Luyện tập: U
Bài 1. Giải phương trình: x  2  2x  10  2x  3 x  3
Bài 2. Giải phương trình: 4x  1  3x  2  5
Bài 3. Giải phương trình: 9( 4x  1  3x  2)  x  3
Bài 4. Giải phương trình: 2
3x  2  x  1  2x x  3
Bài 5. Giải phương trình: 2
x  2  4  x  2x  5x  1
Bài 6. Giải phương trình: 2
x  3  5  x  2x  7x  2  0
Bài 7. Giải phương trình: 2
x  2  x  3x  2  x  2 2  x
Bài 8. Giải phương trình: 3
 2x  3  x  1 4
Bài 9. Giải phương trình: 3 2
x  6  x  1  x  1
Bài 10. Giải phương trình: 3 2
x  9  2x  3x  5x  1  1
Bài 11. Giải phương trình: 3 2
3x  2  x 3x  2  2 2x  1
Bài 12. Giải phương trình: 2
x x  18  (2x  9) x  3  2 5x  1  0
Bài 13. Giải phương trình: 2 2
4x  5x  1  2 x x  1  9x  3
Bài 14. Giải phương trình: 2
2x  11  2x  16x  28  5  x
Bài 15. Giải phương trình: 3
2 3x  4  x  2 5x  4  16
Bài 16. Giải phương trình: 3 2
x  4  x  1  2x  3
Bài 17. Giải phương trình: 3 2
x  4  2x  7  x  8x  13  0
Bài 18. Giải phương trình: 3 3 2
x x  4  2x x  2
Bài 19. Giải phương trình: 3 2
x  10  x  1  x x  1
Bài 20. Giải phương trình: 2 3
x  2x x 4x  1  3x  2
Bài 21. Giải phương trình: 2 2
x x  5x  5  x  2  3x  2
Bài 22. Giải phương trình: 3 2 2
x  2x x  2x  5  2 4x  5  5x  4
Bài 23. Giải phương trình: 3 2
5x  1  x  2  x  5x  10x  13  0
Bài 24. Giải phương trình: 3 2
3x  17x  8x  9  3x  2  7  x  0
Bài 25. Giải phương trình: 4 3 2
3x  2  x  1  x  5x  12x  15x  3  0
Bài 26. Giải phương trình: 4 3 2
3x  2  x  2  x  2x  3x  8x  8  0
Bài 27. Giải phương trình: 2
2 3x  2  2(x  1) x  2  3x  8x  4
Bài 28. Giải phương trình: (5x  4) 2x  3  (4x  5) 3x  2  2
Bài 29. Giải phương trình: 2
(x  1) x  2  (x  6) x  7  x  7x  12 x  3 2 9  x
Bài 30. Giải phương trình: 
3 x  1  x  3 x 2
9x  14x  25
( x  1  1)(2x  4)
Bài 31. Giải phương trình: 
3x  3  4 2x  1 x
Bài 32. Giải phương trình: 2 3
2x  3x  7  3 4x  4  0
Bài 33. Giải phương trình: 3 2
3x  5  2 19x  30  2x  7x  11
Bài 34. Giải phương trình: 2
(x  1) x  1  3  x  2. x  2x  2
Bài 35. Giải phương trình: 2 2
x  2x  2x  1  x  1
Bài 36. Giải phương trình: 3 2
3x x  8x  4  2 2x  1  x 3x  1
Bài 37. Giải phương trình: 2 2
2x  2x  4  5 x  1  5 3  x .
Bài 38. Giải phương trình: 2 2
(5x  4x  3). x  (x  3). 5x  4x .
Bài 39. Giải phương trình: 3 2
3  x x  2  x x  4x  4  x x  1 3x  2
2.(3x  2) 2x  1  1
Bài 40. Giải phương trình:   3 2x  1 2  (2x  1)
MỘT SỐ ĐỊNH HƯỚNG GIẢI PT VÔ TỈ PHẦN 5
III. Giải phương trình theo phương pháp trục căn thức và bình phương U
3. Trường hợp nghiệm vô tỉ: U U
a. Nhận xét và ví dụ: Để giải phương trình có nghiệm là số vô tỉ mà không dựa vào máy tính Casio U U
là hết sức vất vả. Nếu không nắm được nhiều dạng khác nhau của phương trình vô tỉ thì trong những
trường hợp nhất định và với những cách nhất định chúng ta cũng mò ra nghiệm hay nhân tử.
Ví dụ 1: Giải phương trình: 2 2
x  2x  3x  4x  1  2x  1. U U Hướng dẫn giải: Điề 1 u kiện x  . Viết lại 2 2
x  2x  2x  1  3x  4x  1 . Bình phương hai vế ta được 2 2 2
x  2x 2x  1  x  1 tiếp tục bình phương hai vế ta có: 
x x x x    x x  2 4 3 2 2 2 1 5 2 2 1 0
1  0  x x  1  0  x  . 2 Đố 
i chiếu với điều kiện ta có nghiệm của phương trình là 1 5 x  . 2 Lời bình: U
Bài trên ta bình phương hai lần và đưa về phương trình đa thức bậc 4, sau đó chuyển về phương trình
bậc hai. Bài này rất may là chuyển về bình phương đúng khá đơn giản. Ở đây ta muốn nhấn mạnh:
Phương pháp bình phương vẫn tỏ ra hiệu quả. Chúng ta có thể trục căn nhưng khá cồng kềnh. Hướng phân tích: 1 5 15
+ Giới hạn khoảng nghiệm: Cho x  thì VT  < VP  , cho x  1 thì 2 2 2 VT 
3 < VP  8  1 , cho x  2 thì VT  8 < VP  21  3 , ... ta thấy vế trái luôn nhỏ
hơn vế phải và độ lệch hai vế ngày càng tăng. Cho 3
x  thì hai vế gần bằng nhau, cụ thể: 2 21 55  8 VT  và VP 
, như thế khả năng phương trình có nghiệm kép! ( xem thêm phần 2 2
4). Nghiệm kép vô tỉ thuộc khoảng 1;  2 .
+ Đối với nghiệm kép hữu tỉ x x thì từ đa thức bậc 4 ta có thể phân tích thành dạng sau 0
x x 2  2
ax bx c  0 , nhưng đối với nghiệm vô tỉ ta không phân tích thành dạng trên., mà 0 
thành dạng ax bx c2 2
 0 (là do các hệ số đều là số nguyên).
Từ đó ta mạnh dạn bình phương và có cách giải như trên.
Ví dụ 2: Giải phương trình: 2x  2  2x  1  6x  5 . U U
Hướng dẫn: (Đã giải trong phần 4) 4x   1 Điề 1
u kiện x   . PT  2x  2 
 6x  5  2x  1  2 (*). Từ đây 2
6x  5  2x  1 ta có điề 1
u kiện 6x  5  2  x   . Từ (*) kết hợp 6x  5  2x  1  2x  2 suy ra: 6 2x  2  2 2 6x  5 
x  2  x  2x  1  0 . Giải ra lấy nghiệm x  1  2 . 2 Lời bình: U U
Trong ví dụ trên thì nghiệm x  1  2 xuất hiện sau khi giải phương trình mà không phải ta dự
kiến trước (đoán trước), nghĩa là xuất hiện sau phương pháp giải: có thể xuất hiện nghiệm hữu tỉ hoặc
nghiệm vô tỉ, phụ thuộc phương trình cuối: 6x  5  x  2 . Đối với nhiều bài toán thì phương
pháp này không thành công, chẳng hạn như phương trình: x  1  (2x  1) 2  x  1 . Đây là
những bài toán khó nếu không sử dụng máy tính Casio. Trước hết ta giải lại ví dụ 2 theo các cách sau: Cách 2:
Điều kiện x  1 / 2 . Bình phương hai vế và rút gọn ta có phương trình: 2 1 2
2x  1  2x  1 6x  5 . Đến đây ta có điều kiện 2 1
x  , kết hợp x   suy ra x  . 2 2 2
Bình phương hai vế lần nữa và rút gọn ta có x x x    x x  x  2 4 2 2 4 4 1 0 2 1 1  0 2 (vì x  ) 2
x  2x  1  0  x  1  2 . Vậy phương trình có 1 nghiệm là x  1  2 . 2 1  1 
Cách 3: Điều kiện x   . Xét x   ;0  D thì: 2  2   
2x 1 2x 11 6x 5 2x 1 2x 1 11 6x 5 01 2  0
Do đó phương trình không có nghiệm trên D . Xét x  0;  E khi đó ta có:
PT  x  2  6x  5  x  2x  1  0     2
x  2x   1 1  2 1    
  0  x  2x  1  0  x  1  2  E .
x  2  6x  5 x  2x  1 Lời bình: U U
Đối với phương trình tương đối đơn giản ở trên thì còn nhiều cách giải khác, nhưng ta dừng ở các
cách giải đã trình bầy bởi vì ta muốn nhấn mạnh là: Các cách mà chúng ta đã giải đều dựa vào nhân tử chung 2
x  2x  1  0 và được suy ngược từ x    x  2 1 2 1  2 . Nhận xét 1: U U
Trong nhiều trường hợp: chúng ta có thể giải được phương trình dựa trên việc đoán được nhân tử
hay một nghiệm vô tỉ của phương trình, dự đoán của ta tương đối chuẩn thì mang lại hiệu quả cao.
+ Trước hết ta giới hạn hay dự đoán khoảng nghiệm x   ;  
+ Việc tính giá trị trung bình của các khoảng nghiệm sẽ giúp ta thuận lợi hơn để mò ra nhân tử theo định lý Viet đảo: 2
x Sx P  0 .
+ Phương pháp bình phương một bước hoặc bình phương hai lần vẫn tỏ ra hiệu quả.
Ví dụ 3: Giải phương trình: 2 2
2x  3x  38  x  5x  6  x  4. U U Hướng phân tích: 2 2
 x  3x  38  0       Điề  1  115 1  115     u kiện: 2 x   5x  6  0  x  ;3  2;  .   3     3  x  4  0       1  115 Cho x
thì VT < VP, cho x  3 thì VT > VP nên phương trình có 1 nghiệm thuộc 3 1 115     1  115 ;3   x    x  2;x   . Cho 2; 1;0;1 thì VT > VP, cho thì VT < VP nên  3    3
phương trình có 1 nghiệm thuộc 1;2. Viết lại phương trình 2 2
2x  3x  38  x  5x  6  x  4 bình phương hai vế ta có: 2 2
2x  2x  14  x  5x  6 x  4 tiếp tục bình phương hai vế và thu gọn ta có 4 3 2
4x  7x  61x  82x  172  0 . Giả sử một nghiệm là x  1,5  1;2 và một nghiệm liên hợp 1  
với nó nhưng bị loại là x  3, 5  4; 3 suy ra x x  2;x x  5 mà ta để ý là 2   1 2 1 2
172  4.43 nên nhân tử là 2
x  2x  4  0 . Kết quả: 4 3 2
x x x x     2
x x   2 4 7 61 82 172 0 2 4 4x x   43  0 1  689
x  1  5,x
. Đối chiếu điều kiện ta được phương trình có hai nghiệm: 8 1  689 x  ,x  1  5 . 8 Lời bình: U 1  115
Khi so sánh giá trị để xác định khoảng nghiệm ta gặp vấn đề số vô tỉ x  cồng kềnh, nếu 3
cứ thay vào phương trình mà tính thì khó khăn lớn, tuy nhiên ta không cần thay trực tiếp vì một căn bằng 0 và vế trái âm.
Ví dụ 4: Giải phương trình: 2 2 2
4x  24x  35  x  3x  2  x  7x  12 (4) U U   Hướ 5
ng dẫn: ĐK x   ;
 4   ;2   1;     . 2   
Thử các giá trị tại x  5,x  4,x  1,x  0,x  1 không thỏa mãn.  5   
Dự đoán nghiệm thuộc khoảng   ;2 
. Viết lại phương trình:  2  2 2 2
4x  24x  35  x  3x  2  x  7x  12 bình phương hai vế ta có: 2 2 2
2x  14x  21  2 x  3x  2 x  7x  12 . Đến đây ta bình phương lần nữa thì sẽ thu được
phương trình bậc 3 và hy vọng phương trình có một nghiệm hữu tỉ (loại), hai nghiệm vô tỉ mà trong
đó có nghiệm chúng ta cần. 4 3 2 x x x x    2
x x   2 4 56 280 588 441 4 3
2 x  7x   12 3 2  x x x
   x   2 16 140 388 345 0 2 5 8x  50x   69  0 5 25  73 5
x   ,x
. Dễ thấy x   không là nghiệm vì VT (4) < 0 < VP(4). 2 8 2 25  73
Vậy phương trình có 1 nghiệm là x  . 8 Lời bình: U U  5   1 p q 9
Độ dài khoảng nghiệm 2       x    
là khá nhỏ, nghiệm có dạng .  2 2 8 4
Ví dụ 5: Giải phương trình: 2 2 2
9x  29x  11  2 x  3x x  3x  2. U U
Hướng phân tích: Điều kiện x  3. Với x  3 ta có VT > VP, với x  4 ta có VT < VP và do đó
dự đoán phương trình có nghiệm duy nhất x  3;4. Bình phương hai vế ta được: 2 2 2
4x  14x  9  4 x  3x x  3x  2 , bình phương lần nữa ta có: 3 2 x x x
   x   2 16 92 156 81 0 2
3 8x  34x  27  0 17  73
Giải ra ta có nghiệm cần tìm của phương trình là x   8 Lời bình: U Nhận xét được 3 2
16x  92x  156x  81  0 không có nghiệm âm, nghĩa là ít nhất còn có một
nghiệm x  1;2 liên hợp với x  3; 4 và giả sử x  3, 5;x  1, 5  x x  4;x x  5,25 1   2   1 2 1 2 1 2 27
Kết hợp 16  2.8; 81  3.27 
 5 là hợp lý để phân tích nhân tử 2
8x  34x  27 . 8
Ví dụ 6: Giải phương trình: 2 2
2 x  3x  3  x  1  9x  23x  19. U U Hướng phân tích:
Điều kiện là x   . Bình phương hai vế ta có: 2
x x   x   2 4 9 6 4
1 x  3x  3 (1). Ta có 2
4x  9x  6  0, x   nên để x là nghiệm thì từ (1) ta phải có x  1  0  x  1 + Nếu x  0 thì 2 2
4x  9x  6  4x  10x  6  2x   1 2x  3 (*) Mặt khác 2
2x  3  2 x  3x  3  9  12 (**) nên kết hợp (*) suy ra (1) vô nghiệm.
+ Do đó ta phải có x  1;0. Nếu ta bình phương thì xuất hiện nghiệm âm thứ hai, ta có:
    x x  2 2 
 2x x   2 1 4 9 6 16 2
1 x  3x   3 (2).
Cho x  2 thì VT = VP nên x  2 là nghiệm, với x  1, 5 thì VT < VP, với x  1 thì  
VT > VP nên phương trình có thêm nghiệ 3   m x    ;1  .  2  1 5 7 5
Giả sử x   ,x  
S   ;P  nên khả năng 2
8x  14x  5  0 . 1 2 2 4 4 8 6 Ta chú ý 2
16.3  6  12  2.6 suy ra P  như thế 2
8x Sx  6  0 . 8 Ta có   3 2
x x x
  x   2 2 8 31 36 12 0
2 8x  15x   6  0 15  33 15  33
x  2,x
. So sánh điều kiện ta lấy nghiệm x  . 16 16 Lời bình: U
Sau khi bình phương thì phương trình có nghiệm x  2 , ngoài ra phương trình trở thành bậc 3 nên
khá dễ dàng. Mặt khác ta cũng có thể giải (1) theo phương pháp đưa về dạng tích như trong phần 3. Lưu ý 1: U
Trong quá trình dò khoảng nghiệm mà ta phát hiện phương trình có nghiệm nguyên thì ta vẫn bình
phương hay trục căn, bài toán sẽ dễ hơn và tiến hành giải bình thường.
Ví dụ 7: Giải phương trình: x x  x  3 3 2 3 2 2  6x  0. U U Hướng phân tích:
Điều kiện x  2. Với x  2 ta có VT < VP, với x  1 ta có VT > VP do đó dự đoán phương
trình có nghiệm x  2; 
1 . Với x  0;1 thì VT > VP, x  2 là một nghiệm, với x  3;4;5... ta
có VT > VP nên x  2 là nghiệm kép. Ở đây ta lựa chọn trục căn:    
PT  x x     x  3 3 2 3 4 2 2  3x  2  0   x    . Với 1 không thỏa mãn     3 2     x
  3x  4  0 (a)      3 2 x x   2 3 4 1     0   3  .    
x  3  x  
 x  2  3x  2  2 (b) 2 3 2  2
+ Giải (a):  x  2 x  
1  0  x  2,x  1 .  4  4   3   2  x      2  x   
+ Giải (b):  x  2  3x  4   3   3  3 2
x  3x  12x  8  0     x   
1 2x  4x  8  0  
x  2  2 3 . So sánh các điều kiện ta có nghiệm phương trình là x  2;x  2  2 3 .
Ví dụ 8: Giải phương trình: 2 2
5x  4x x  3x  18  5 x . U U Hướng phân tích:
Điều kiện x  6. Với x  6;7 ta có VT > VP, với x  8 ta có VT < VP do đó dự đoán phương
trình có nghiệm x  7;8, ngoài ra x  9 là một nghiệm. Chuyển vế bình phương ta được: 2 2
2x  16x  9  5x 5x  4  2x  19x  9  5x  5x  4  7 25x x  9 x   9  
x  92x     1    . x  
2x  1 5x  4  7  25x (*) 5 4 7 
Giải (*)   x   3 2 2
1 5x  4  11x  7  4x  25x  33x  9  0    x   2 x x   7 61 4 3 7 3  0  x  (Loại các nghiệm âm). 2 7  61
Vậy phương trình có hai nghiệm là x  9,x  . 2
Ví dụ 9: Giải phương trình: 2 2
5x  14x  9  x x  20  5 x  1. U U Hướng dẫn:
Điều kiện x  5. Với x  5;6 ta có VT > VP, với x  7 ta có VT < VP do đó dự đoán phương
trình có nghiệm x  6;7, ngoài ra x  8 là một nghiệm. Chuyển vế bình phương ta được: 2 x x    2 2 5 2 5 x x   20 x  
1 . Bình phương lần nữa và rút gọn thành 4 3 2 x x x x
  x   3 2 4 45 33 505 504 0
8 4x  13x  71x   63  0  
x   x   2 x x   5 61 8 4 7 5
9  0  x  8,x  (Loại các nghiệm âm). 2 5  61
Vậy phương trình có hai nghiệm là: x  8,x  . 2 Lời bình: U
Qua các ví dụ 7, ví dụ 8, ví dụ 9 ta thấy có thể lựa chọn phương pháp bình phương hai bước đưa về
bậc 4 hay bình phương một bước và trục căn như lưu ý đã nêu. Ngoài ra ta cũng có thể sử dụng
phương pháp "Kim thiền thoát xác" ở sau.
Ví dụ 10: Giải phương trình: 2 2
3(9x  20x  9)  2 6x  11x  3  x  2. U U Hướng phân tích:
Điều kiện x  2 . Với x  2 ta có VT < VP, với x  3 ta có VT > VP và do đó dự đoán phương
trình có nghiệm duy nhất x  2;3. Bình phương hai vế ta được: 2 2
3x  17x  17  4 6x  11x  3 x  2 . Tiếp tục bình phương hai vế lần nữa ta có 4 3 2
9x  198x  759x  978x  385  0 . Đến đây ta thấy phương trình xuất hiện thêm nghiệm
thứ hai x  0; 
1 và tính x x  2,5  0,5  3; x x  1,25 ngoài ra 385  5.7.11 do đó dự 1 2 1 2 đoán nhân tử là 2
3x  9x  5  0 và kết quả PT   2
x x   2 3 9
5 3x  57x  77  0 . 9  21
Giải ra ta có nghiệm cần tìm của phương trình là x   6
Lời bình: Ta có thể bình phương và sau đó trục căn nhưng khá dài dòng, chẳng hạn: U U 2 2
3x  17x  17  4 6x  11x  3 x  2  0   2
x x     2 3 9 5
4 6x  11x  3 x  2  2x  
3  0 (với x  2 )  x x x   x
 3x  9x   6 11 3 2 2 32 2 2 5  4.  0 (với x  2 ) 2
6x  11x  3 x  2  2x  3    4 2x  3 2 3x 9x    5 1      
  0 (với x  2 ) 2 
6x  11x  3 x  2  2x  3    (vì x  2 ) 2 9 21
 3x  9x  5  0  x
. (Xem thêm về PP "Kim thiền thoát xác" ở sau) 6
Ví dụ 11: Giải phương trình: 2 2
x x  6  3 x  1  3x  6x  19  0. U U Hướng phân tích: Điều kiện x D 2    ;   
. Cho x D chạy thì phương trình đổi dấu hai lần và ta đoán được
phương trình có hai nghiệm x  2;3 và x  20;21 . Giả sử x  2,5;x  20,5 thì ta có 2   1   1 2
x x  23,x x  51 . Chuyển vế thành 2 2
3x  6x  19  x x  6  3 x  1. Bình 1 2 1 2 phương hai vế ta có 2 2
x  8x  17  3 x x  6 x  1 . Ta có 2
17  9.6  235  5.47 nên dự đoán nhân tử là 2
x  23x  47  0 . Tiếp tục bình phương hai vế ta được: 4 3 2 x x x x     2 x x   2 25 98 209 235 0 23
47 x  2x   5  0 2 
x  23x  47  0 . Giải ra ta có nghiệm cần tìm của phương trình là 23 341 x   2
Lưu ý 2: (Phương pháp "Kim thiền thoát xác") U U
Đối với các tam thức có hai nghiệm như 2
x x  6 ta tráo đổi nghiệm với biểu thức khác 2 2
x x  6 x  1  x  2x  3 x  2 và ta có phương trình: 2 2
x  8x  17  3 x  2x  3 x  2 chia cả hai vế cho 2
x  2x  3  0, x  2 ta được 10x  2 x  2 x  2 1   3 . Đặt  t  0 ta có 2
1  10t  3t suy ra 2 2 x  2x  3 x  2x  3 2 x  2x  3 1 x  2  2 2 23 341 t  
x  2x  3  25x  50  x  23x  47  0  x  . 2 5 2 x  2x  3
Phương pháp "Kim thiền thoát xác" ở trên có thể áp dụng với đa thức bậc cao hơn.
Ví dụ 12: Giải phương trình: 2 2
2 x  1  3x  5x  2  18x  18x  5. U U
Hướng dẫn "Kim thiền thoát xác": Điề 1 u kiện x
. Bình phương hai vế ta có: 2 2
15x  9x  7  4 x  1 3x  5x  2 (*). 3 Điề 9  501 u kiện x  . Viết lại 2 2
x  1 3x  5x  2  x  2 3x  2x  1 và chia cả hai 30   vế của (*) cho 2 9 501
3x  2x  1  0, x  ta có 30   x  2 x  2 x  2 *  5   4 . Đặt  t  0 thì có 2 5  t  4t 2 2 3x  2x  1 3x  2x  1 2 3x  2x  1 x  2   2 1 37  t  1 
 3x x  3  0  x  . 2 3x  2x  1 6 Đố  
i chiếu điều kiện ta có nghiệm cần tìm của phương trình là 1 37 x   6 Lưu ý 3: U
Trong quá trình dò khoảng nghiệm mà ta phát hiện phương trình vô nghiệm thì ta vẫn tiến hành giải
bình thường.bằng phương pháp bình phương hay trục căn.
Ví dụ 13: Giải phương trình: 2 2
2x  3x  2  18x  16x  39  5 x  1. U U Hướng phân tích: 2 2
 x  3x  2  0  Điề  u kiện 2 18
x  16x  39  0  x  2
x x x   . Khi cho 2, 3,
4,... ta có VT < VP nên khả x  1  0 
năng phương trình vô nghiệm. Viết lại: 2 2
2x  3x  2  5 x  1  18x  16x  39
Bình phương hai vế ta có: 2 2
5 2x  3x  2 x  1  8x  3x  6 .
Tiếp tục bình phương hai vế:
 2x x  x   4 3 2 25 2 3 2
1  64x  48x  87x  36x  36 (*) 1  1   
Cho x   ta có VT < VP, cho x  0 ta có VT > VP nên (*) có nghiệm thuộc   ;0 và nghiệm 2  2 
này bị loại. Cho x  1 ta có VT < VP nên (*) có nghiệm 0;  1 cũng bị loại.  1  x    
;0  x  0, 4 và x  0;1  x  0, 8 nên x x  0,5;x x  0,5 2   1   1  2  2 1 2 1 2   14 14 7 4 3 2
*  64x  98x  38x  11x  14  0 (**). Các tỉ số sinh ra từ      là gần 64 32 16
đúng nhất. Kết quả là:      2
x x   2 x x   2 17 2081 * * 2 2 1 32 17
14  0  32x  17x  14  0  x  64
cả hai nghiệm đều loại. Vậy phương trình đã cho vô nghiệm. Nhận xét 2: U U
Ta có thể sử dụng phương pháp trục căn trực tiếp, bình phương một lần hay hai lần, đặt ẩn phụ, ...
nhưng nghiệm vô tỉ ta cần cuối cùng dẫn đến nghiệm của phương trình bậc hai: 2
ax bx c  0 .
Nhìn chung ta thường gặp các hệ số a, ,
b c   và đặc biệt ta luôn chuyển về được * a   .
Phương trình trên xem như giao điểm của Parabol 2
y ax bx c với trục hoành. Rõ ràng khi a
càng lớn thì khoảng cách giữa hai nghiệm d x x càng bé, ngược lại khi a  1 thì Parabol có 2 1
xu hướng như "một cái chảo", nghĩa là d x x càng lớn. 2 1 Gọi  ;
 , ';' là các khoảng hữu tỉ gần đúng nhất để phương trình f x  0 đổi dấu.
+ Nếu khoảng cách d ' '  5 thì nghiệm có dạng *
x p q, p  ,
q   và có
d
thể lấy gần đúng ' ' p  , q . 4 4
d p ' q
+ Nếu tính gần đúng ' ' 1 3 p
  ; hay tương tự thì q   x . 4 2 2 2 2
Ví dụ 14: Giải phương trình: 2 2 2
(x  6x  11) x x  1  2(x  4x  7) x  2 U U Hướng phân tích:
Điều kiện x  2 . Với x  2 thì VT > VP, với x  3 thì VT < VP, với x  4;5;6;7;thì VT < VP,
với x  8 thì VT > VP do đó ta đoán phương trình có hai nghiệm x  2; 3 , x  7; 8 . 2   1      7  8  2  3 Tính gần đúng: 2 3 7 8 p   5 và q
 2,5  q  6  x  5  6 4 4 nên nhân tử đoán là 2
x  10x  19  0 .
Nếu bình phương hai vế sẽ dẫn đến phương trình bậc 5, ở đây ta sử dụng phương pháp trục căn và làm như sau:
Nhân cả hai vế với 3 ta có: 2 2 2
3(x  6x  11) x x  1  2(x  4x  7) 9x  18 2 2 2 2  x x x x       
x x   x x     2 3( 6 11) 2( 4 7) 1 2( 4
7) 9x  18  x x  1 2 2
2 x  4x  7 x  10x  19   2 x  10x   2   
19 x x  1   2
9x  18  x x  1  2   2 x  4x  7 2  
x  10x   2  
19  x x  1    0 2  9x 18 x x 1       2
x  10x  19  0  x  5  6 (thỏa mãn điều kiện)
Vậy nghiệm cần tìm của phương trình là x  5  6 . Lời bình: U U
Nếu nói ta "nhẩm nghiệm vô tỉ" thì quá xạo nhưng "mò ra nghiệm vô tỉ" tương đối chuẩn đấy!  5     41     
Trở về ví dụ 11: x  2  ; , x   ;21   . Tính gần đúng: 21 20,5 2,5 2 23 p   và U U 1  2 2  2  4 2 20,5  21  2,5  2 23  341 q
 18,5  q  341  x  nhân tử 2
x  23x  47  0 . 2 2
Ví dụ 15: Giải phương trình: 2 3
2(x  3x  2)  3 x  8 . U U Hướng phân tích:
Điều kiện: x  2. Cho x = -2; -1; 0; 1; 2; ... thì phương trình đổi dấu hai lần trong khoảng (-1; 0) và
(6; 7) nên phương trình có hai nghiệm trái dấu.   6  7  1 Tính gần đúng: 6 7 1 p   3 và q
 3,5  q  13  x  3  13 nên nhân 4 4 tử đoán là 2
x  6x  4  0 .
Bình phương hai vế ta có: 4 3 2
4x  33x  52x  48x  56  0 . x   3  13 Và ta đượ  c  2
x x   2 6
4 4x  9x  14  0 2
x  6x  4  0   . x   3  13 
Ví dụ 16: Giải phương trình: 2 2
3x  6x  4  (x  4) 2x  4 . U U Hướng phân tích:
Bài này có thể có cách nhận dạng khác, tuy nhiên ta thử mò nghiệm và tìm cách giải xem? 2 3
 x  6x  4  0 Điề  3  21  u kiện   x
. Cho x  1;x  2;x  3 ta có VT < VP 2  x  4  0 3  7  7   Cho x
ta có VT > VP nên dự đoán phương trình có nghiệm đơn duy nhất x  3;  . Để tìm 2 1  2 2 2 3
nghiệm âm liên hợp ta viết lại  2
x    x   2 4 2 4
3x  6x  4  0 với x   là một 2  3   
nghiệm, cho x  1 ta có VT > 0 nên nghiệm x    ;1. 2  2  3  3,5  1,5  1 3,5  3  1,5  1 Tính p   1 và q
 2,25  q  5 như thế dự đoán 4 4
nghiệm là x  1  5 và nhân tử là 2
x  2x  4  0 . Hướng dẫn giải: 2 3
 x  6x  4  0 Điề  3  21  u kiện   x  . 2  x  4  0 3 
Bình phương hai vế ta có: 4 3 2 4 2
9x  36x  12x  48x  16  (x  8x  16)2x  4
x x x x x
  x x  2 5 4 3 2 2 2 5 20 20 80 48 0 2
4 2x  3  0 (vì x  0) 2
x  2x  4  0  x  1  5 .
Vậy phương trình có một nghiệm x  1  5 . Lời bình: U U
Vì đã biết nhân tử nên chúng ta cứ mạnh dạn bình phương để khử căn bậc hai! Sau đây
chúng ta sẽ xét thêm ví dụ và trục căn.
Ví dụ 17: Giải phương trình: 2
x x    2 4 7 3
2x  4x   1 2x  1 . U U Hướng phân tích:
Bài này có thể có cách nhận dạng khác, tuy nhiên ta thử mò nghiệm và tìm cách giải xem? 7
Cho x  1;x  2;x  3 ta có VT > VP. Cho x
ta có VT < VP nên dự đoán phương trình có 2  7  
nghiệm duy nhất x  3;  . Để tìm nghiệm liên hợp x ta viết lại thành: 1  2 2  1
x x  2  x x  2 2 2 4 7 3 2 4 1 2x  
1  0 . Cho x  thì VT > 0, cho x  1 thì VT < 0 do 2   đó 1   3  3,5  0,5  1 3,5  3  0,5  1
nghiệm x   ;1. Tính p   2 và q   1, 3 2 2  4 4
q  2  x  2  2 . Nhân tử là 2
x  4x  2  0 . Hướng dẫn giải:  2
 x x    2 4 7
3 2x  4x   1  0   Điề 2  2   u kiện:  x D 1;      3;    . 2  x 1  0   2      Lấy  2
2x  4x   1 x  
1 trừ đi mỗi vế ta có phương trình: 3 2
x x x    2 2 10 12 4
2x  4x  
1 x 1 2x 1
 2x 4x    2 2 2  0  
2x  4x  1 x  4x  2 2 x  4x      2 2x  2      2
2x  4x   1 (*)
x  1  2x  1 2x 2   
x  1  2x  1  2
2x  4x   1
Ta có 2x  2 
 2x  2 2x  1  1 (Vô nghiệm vì x D ).
x  1  2x  1 Do đó 2
(*)  x  4x  2  0 giải ra lấy nghiệm x  2  2 .
Ví dụ 18: Giải phương trình: 2 3
x  1  x  4x  3  (x  2) (x  ). U U Hướng phân tích:
Điều kiện x  1. Nếu để ba căn để trục căn hay đánh giá thì phức tạp nên bình phương hai vế và
thu gọn ta có: x   3 2 2
1 x  3  x  5x  7x  4 .
Tại x  1 thì VT < VP, tại x  0 thì VT < VP, tại x  1 thì VT < VP ... và cả hai vế ngày càng
lớn. Như thế ta đoán phương trình có nghiệm duy nhất x  1;  0 (nghiệm kép).
Chuyển vế lần nữa ta có x   x    3 2 2 1 3
x  5x  7x  4  0 . Cho x  3 ta có VT = -1,
cho x  2 ta có VT = - 4 như thế có thêm điểm tiếp xúc liên hợp là x  3;   2 . 3  2  0  1 3 1  3  2 3  5 Tính p   và q
 2  q  5 nên x  . 4 2 2 2 Nhân tử là 2
x  3x  1  0 . Hướng dẫn giải:
Điều kiện x  1. Bình phương hai vế và thu gọn: x   3 2 2
1 x  3  x  5x  7x  4 .    2 x  1 3 2 x 3x x 2x
1x 2 x 3 0  2x 3x    1 x                 0 . 
x  2  x  3    2 x   3x  1  0   2x   1  2x   1 (*). Ta có x
 0 (với 1  x  0 ) x    0
x  2  x  3 
x  2  x  3 2 4 3 2
x  4x  2  x
x  3  x  7x  17x  16x  4  0
 x x  x  2 2 3 1 2  0 2
x  3x  1  0 (**). 3  5
Từ (*) và (**) ta đều có 2
x  3x  1  0 giải ra lấy nghiệm x  . 2
Ví dụ 19: Giải phương trình: 2
4x x  6  4x  2  7 x  1 . U U HƯỚNG PHÂN TÍCH
Với x  1 thì VT > VP, với x  0 thì VT < VP nên phương trình có nghiệm x  1; 0 như thế 1  
ta đoán phương trình bậc hai còn có nghiệm liên hợp x  0 nhưng bị loại. Để chính xác hơn ta thử 2 1  1   
tại x   thì VT > VP nên x   
;0 . Để đoán x  0 ta viết lại thành: 2 1  2  2  5 x x  
x  2  x  2 2 4 6 7 1 4
2  0 và với x  2 thì VT > 0, với x  thì VT < 0 nên 2  
phương trình này có nghiệ 5   m x  2  ;  . 2  2 2  2,5  0,5  0 2,5  2  0,5  0 Tính p   1 và q
 2,5  q  7 như thế dự đoán 4 2 2  7 nghiệm là x  và nhân tử là 2
4x  8x  3  0 . 2 Hướng dẫn 1:
Điều kiện x  1. Bình phương hai vế và thu gọn 2
 12x  32x  47  282x   1 x  1  0
Dễ thấy x  1 / 2 không là nghiệm nên ta có 1  x  1 / 2 . Mặt khác trở về phương trình đầu PT   2
4x x  6  3 x  1  212x 2 x 1  0     2   x x   1 2 4 8 3       0  2 
 4x x  6  3 x  1 1 2x  2 x  1 2   2 7
4x  8x  3  0 giải ra lấy nghiệm x  . 2 Hướng dẫn 2: Đặt 2
x  1  t  0  x t  1 , khi đó ta có phương trình:   4 2 2 7 145
4t  7t  9  4t  7t  6  0  t
. Bình phương hai vế ta có 8 4 2 4 3 2 4 3 2
4t  7t  9  16t  56t t  84t  36  12t  56t  8t  84t  27  0       2
t t   2t t   1 7 11 5 7 2 2 3 6 22 9  0  t  ,t  . 2 6 Đố 1  7 2  7
i chiếu điều kiện ta lấy t   x  . 2 2 Lời bình: U
Khi đã lập luận 1  x  1 / 2 thì 2
 12x  32x  47  142  4xx  1 tiếp tục bình phương
để đưa về bậc 4, chắc chắn có nhân tử là 2
4x  8x  3 . Đây là bài toán khó, các bạn thử tìm cách
giải khác xem độ phức tạp thế nào ?
Bình phương để mở rộng tập xác định nhiều khi rất cần thiết để giải!
Ví dụ 20: Giải phương trình: 2 2
10x  50x  3  2x  5x  2  3 x  5. U U Hướng phân tích: Điề 25  655 u kiện x  . Bình phương hai vế: 2 2
4x  27x  20  3 2x  5x  2 x  5 (*) . 10 Điề 25  655 27  409 u kiện  x
. Tiếp tục bình phương ta được: 10 8 4 3 2
16x  234x  1024x  1323x  490  0 (**).
Đến đây ta thấy vấn đề vướng mắc là phân tích đa thức bậc 4 thành nhân tử. Đối với bài toán độc lập
như phương trình (**) thì quả nhiên là khó, tuy nhiên trong bài toán này thì (**) là phương trình hệ 2
quả của (*) nên ta chú ý viết như sau:  2  x x     2 4 27 20
9 2x  5x   2 x  5  0  
Phương trình (*) có nghiệ 1  
m x  5; 6 ; nhưng phương trình (**) có thêm nghiệm x   ;1 nên ta 1   2 2  5  6  0,5  1 5  6  0,5  1 suy ra p   3 và q
 4,5  q  22 do đó ta đoán nhân tử 4 2 là 2
2x  12x  7 (và kết hợp 490 chia cho 7 là đẹp) kết quả là:   6  22   2
x x   2 * * 2 12 7 8x  69x  
70  0 . Đáp số: x   2 Lời bình: U
Trên đây là bài khó vì phương trình bậc 4 có các hệ số lớn, đòi hỏi tính kiên trì. Hơn nữa nghiệm bị
kẹp trên đoạn vô tỉ cồng kềnh, tuy nhiên sau khi bình phương để khử căn thì ta mở rộng đoạn thêm
một tí để được đoạn hữu tỉ và từ đó dự đoán nhân tử dễ hơn. Xem thêm PP "Kim thiền thoát xác".
Ví dụ 21: Giải phương trình: 2
x x    2 2 8 8 x  4x  
1 9x  8  x   1 7x  3 U U Phân tích: 1  1  
Cho x  0 ta có VT > VP, cho x
ta có VT < VP nên phương trình có nghiệm x  0; . 2 1  2
Cho x  2 ta có VT < VP, cho x  3 ta có VT > VP nên phương trình có nghiệm x  2; 3 . 2   2  3  0,5 3 2  3  0,5 3  5 Tính p   và q
 2,25  q  5  x  nhân tử là 4 2 2 2 2
x  3x  1  0 . Nhiệm vụ bây giờ là trục căn thức để tao ra nhân tử. Ta có: 2
x x    2 2 8 8 x  4x  
1 9x  8  x   1 7x  3 2
x x    2
x x   x   2 5 6 3 1
2 9x  8  x  3x  2  x   1 7x  3  0   2 x  3x  
1 9x  8  x  2x  3  9x  8 x  
1 x  2  7x  3  0        2 x x   x 2 x 1 3 1  9x  8        0 (ĐK 3 x   ) 
x  3  9x  8
x  2  7x  3  7 2   3 5
x  3x  1  0 giải ra ta có hai nghiệm cần tìm là x  . 2
Ví dụ 22: Giải phương trình: 3 2
x x x  3  4x  3  2 6x  6 . U U Phân tích: 3  3   
Cho x   thì VT > VP, cho x  0 thì VT < VP nên phương trình có nghiệm x    ;0. 4 1  4 
Cho x  2 thì VT < VP, cho x  3 ta có VT > VP nên phương trình có nghiệm x  2; 3 . 2   2  3  0,75 2  3  0,75 Tính p   1 và q
 1,5  q  3  x  1  3 nhân tử là 4 4 2
x  2x  2  0 . Nhiệm vụ bây giờ là trục căn thức để tao ra nhân tử. Ta có: 3 2
x x x  3  4x  3  2 6x  6   3 2
x x  4x  
2  x  1 4x  3 2x  2  6x  6  0     2
x x   1 2 2 2 x   1        0 (vì ĐK 3 x   ) 
x  1  4x  3
x  2  6x  6  4 2
x  2x  2  0 giải ra ta có hai nghiệm cần tìm là x  1  3 .
Ví dụ 23: Giải phương trình: x   x   x   x   x  2 3 2 4 3 1 6 4 2 1 . U U Phân tích: 3  3   
Cho x   thì VT > VP, cho x  0 thì VT < VP nên phương trình có nghiệm x    ;0. 4 1  4 
Cho x  2 thì VT < VP, cho x  3 ta có VT > VP nên phương trình có nghiệm x  2; 3 . 2   2  3  0,75 2  3  0,75 Tính p   1 và q
 1,5  q  3  x  1  3 nhân tử là 4 4 2
x  2x  2  0 . Nhiệm vụ bây giờ là trục căn thức để tao ra nhân tử. Ta có x  
x   x   3 2 4 3
1 6x  4  2x  2 2
1  2x  4x  2  x   3
1 x  6x  4  x  2x  1 4x  3  0
x  1 3x 6x  4
x  2 2x 2x  2 3  
 0 (với x   ) 4 x x
x    x  2 2 3 3
x  1  4x  3 6 4 6 4         x 1 x 2 x 2 2 3 x 2x       2        0   (với x   )  4 x x xx 2 2 3 3
x  1  4x  3 6 4 6 4          2
x  2x  2  0 giải ra ta có hai nghiệm cần tìm là x  1  3 .
Ví dụ 24: Giải phương trình: 3 2 3
x  4x  1  x x x x x  1 , x   . U U Phân tích:
Cho x  1 thì VT > VP, cho x  0 thì VT < VP nên phương trình có nghiệm x  1; 0 . Cho 1   5  5 x  2  
thì VT < VP, cho x
thì VT > VP nên phương trình có nghiệm x  2  ;  . 2 2  2     2  2,5  1 Tính gần đúng 1 0 2 2,5 p   0, 88  1; q
 1, 4  q  2 . Như thế ta 4 4
đoán nghiệm x  1  2 nhân tử là 2
x  2x  1  0 . Bây giờ phân tích thành nhân tử: PT   3
x x     2
x x x    3 5 2 1
x  1  x x   0   3
x x     2
x x x    x   2 5 2 1 1
x  1  x x   0        2 x x   1 x 1 2 1 x   2       0  (*). 2 2  
x x x  1
x x x  1 1 2 x  1 x x Với x  1   0 và 1    0 2
x x x  1 2 2
x x x  1
x x x  1 Nên từ (*) suy ra 2
x  2x  1  0  x  1  2 .
Ví dụ 25: Giải phương trình: 4 3 2
x x x x    2
x x   2 5 11 12 5
2 2x  4x   3 . U U Phân tích:
Cho x  0 thì VT > VP, cho x  1 thì VT < VP nên phương trình có nghiệm x  0;1 . 1  
Cho x  2 thì VT < VP, cho x  3 thì VT > VP nên phương trình có nghiệm x  2; 3 . 2      2  3  0  1 Tính gần đúng 1 0 2 3 3 p   ; q
 2  q  5 . Như thế ta đoán nhân tử 4 2 2 là 2
x  3x  1  0 . Bây giờ ta giải phương trình:   PT    2
x x   2
x x    2
x x    4 3 2 2 2 4 3 2
x  5x  10x  11x   3  0         x x   x  3x   2 2 2 2 1 
x  2x  3  0   (*). 2 2
 2x  4x  3  x x  2  2 x x  2 2 Với 2 2
x  2x  3  1  x  2x  3  1  x   1  0 2 2
2x  4x  3  x x  2  Nên từ (*) suy ra 2 3 5
x  3x  1  0  x  . 2
Ví dụ 26: Giải phương trình: 3 2 2
11x  9x  15x  7  x  x  2 8x  3 , x   . U U Phân tích:
Cho x  0 thì VT < VP, cho x  1 thì VT > VP nên phương trình có nghiệm x  0;1 . 1  
Cho x  3 thì VT > VP, cho x  4 thì VT < VP nên phương trình có nghiệm x  3; 4 . 2      3  4  0  1 Tính gần đúng 1 0 3 4 p   2 ; q
 1,5  q  3 . Như thế ta đoán 4 4
nghiệm x  2  3 nhân tử là 2
x  4x  1  0 . Bây giờ ta giải phương trình: 3 Ký hiệu 3 2
9x  15x  7  a và với x   khi đó ta có 8   PT   2 x  4x  
1  8x  3 x  2   8x  3  
x  2 a  0     3       2 x x   8x 3 x 1 4 1 1      0 x    (với ) x 2 8x 3 
x 22 x 2 2 a a          8   2
x  4x  1  0  x  2  3 .
Ví dụ 27: Giải phương trình: 2
x  3x  6  7x  9  9x  14 , x   . U U Phân tích: 6  6   
Cho x   thì VT > VP, cho x  1 thì VT < VP phương trình có nghiệm x    ;1. 5 1  5  9  9  
Cho x  4 thì VT < VP, cho x
thì VT > VP nên phương trình có nghiệm x  4;  . 2 2  2      4  4,5  1,2  1 Tính gần đúng 1,2 1 4 4,5 3 p   ; q
 5, 4  q  29 . Như thế 4 2 2 ta đoán nghiệ 3  29 m x  nhân tử là 2
x  3x  5  0 . Bây giờ phân tích thành nhân tử: 2
PT  x   x     2 2 7 9 x  3x  
5  x  3  9x  14  0     2
x x   1 1 3 5   1       0
x  2  7x  9
x  3  9x  14  9  (với x   ) 2 3 29
x  3x  5  0  x  . 7 2
Ví dụ 28: Giải phương trình: 3 2
6x  2x  3x  x  3 3x  2  2 x  1 , x   . U U Phân tích:
Cho x  1 thì VT < VP, cho x  2 thì VT > VP nên phương trình có nghiệm x  1;2 . 1  
Nếu ta dò tiếp thì không thành công, để đoán nghiệm thứ hai, ta chuyển vế thành:
x x x x  2 x  2 3 2 6 2 3 2 1 3 3x  2  0 2
Thử x  1 thì      2 5
1 .2  0 , với x  0 thì  2 2
2  2.3  0 như thế phương trình này có
nghiệm x  1; 0 liên hợp với x  1;2 . 1   2       1  2  0  1 Tính gần đúng 1 0 1 2 1 p   ; q
 2  q  5 . nhân tử là 4 2 2 2
x x  1  0 . Bây giờ ta trục căn phân tích thành nhân tử:     Trướ 2 1  19  1  19 
c hết ta có x   và 3 2
6x  2x  3x  0 nên x D   ;0     ;       . 3  6     6    PT   3 2
6x  3x  9x  
3  x  3x 1 3x  2  2x x  1  0       2 x x   x 3 2 1 6  x  3        0   2 x x   1 .M  0 (*) 
x  1  3x  2
x x  1 1 19    x  3 2  3x  2 + Nếu x   ;0   x    1   0  thì 6 4 0 ;  6   
x  1  3x  2
x  1  3x  2 2 Và  0 suy ra M  0 . x x  1 1 19    + Nếu x   ;     M   thì dễ thấy 0 .  6    Do đó ta luôn có 
M  0, x D nên từ (*) 2 1 5
x x  1  0  x  . 2 Lời bình: U
Trên đây là bài khó vì phải đánh giá biểu thức M. Nếu ta không có điều kiện x D mà chỉ có điề 2 2 1  5
u kiện ban đầu x   thì
chưa được xác định tại x  không 3 x x  1 2 2
những thế ta cũng không loại được giá trị này vì nó thỏa mãn x   . Đây chính là sai lầm 3 đố 1  5
i với học sinh khi mà loại x
không có cơ sở hoặc lấy làm nghiệm của phương 2 trình!.
Phương trình vô tỉ rất đa dạng và phong phú, để kết thúc ta xét thêm vài ví dụ liên quan các
phần đã nêu, ở đây ta không nghiên cứu chủ đề đặt ẩn phụ hay lượng giác hóa, phương
pháp hàm số ... vì vượt qua khả năng của HS các lớp 9, lớp 10 và lớp 11 không chuyên.
Qua 5 phần đã nêu: ta tiếp cận và giải phương trình dưới góc độ nhìn nhận phổ thông và tự
nhiên nhất có thể được.
Ví dụ 29: Giải phương trình: x  1  2x  
1 2  x  1 , x   . U U Phân tích: Trướ 2
c hết đặt ẩn phụ: x  1  t  0 ta có 2 t   2 2t  
1 2  t . Điều kiện t  . 2 1 1   
Với t  thì VT > VP, với t  1 thì VT < VP nên phương trình có nghiệm t   ;1 . 2 1 2 
Ta cần dự đoán thêm nghiệm t liên hợp với t . Nhận xét t  1 là một nghiệm. Với 2 1 3 9 3  9 3 t    
thì VT > VP, với t   thì VT < VP nên phương trình có nghiệm t    ;  . 5 2 2  5 2     1  0,5  1, 8  1,5 Tính gần đúng 1,5 1, 8 0,5 1 1 p    ; q   2, 4  q  5 . 4 2 2 Như thế 1  5
ta đoán nghiệm t  nhân tử là 2
t t  1  0 . Bây giờ ta trục căn phân 2 tích thành nhân tử: 2 2t  1 1  t 2 PT 2  t   2 2t   1   2 2t   1  2 t   2    1  1  t  (với  t  1) 2  t  1 2
  t   t 2
t    t 2 2 1 1 2 1 1
2  t  2t t  2 bình phương hai vế ta có: 4 3 2
t t t t    2 4 4 7 4 4
1  2t t t  2 4 3 2
 4t  3t  7t t  2  0      2
t t   2t t   1 33 1 5 4 2 1  0  t  ,t
. Đối chiếu điều kiện ta lấy 8 2 1  33    2 t 2 1 t
x t     t   15 33 1 1 2  x  . 8 4 4 32 15  33
Vậy phương trình có một nghiệm x  . 32
Lời bình: Khi đã đoán được nhân tử thì ta có cách khác như sau: U U Trướ 2
c hết đặt ẩn phụ: x  1  t  0 ta có 2 t   2 2t  
1 2  t . Điều kiện t  . 2 2 2 2 t 2t  1 2t 4t  2 2t  2  t 4t t  2     1   1   2  t t 2  t t 2  t t 2  2 2
4t t  2  0 4t t  2 4t t  2    (*).       t t tt
2t  2t   2 2 2 2  t t  2
Ta có 2t  2  t  2  t t  2t 2  t  2  0 (vô nghiệm vì t  ). Do đó từ (*) ta 2 đượ  2 c 2 1 33
4t t  2  0  t  (vì t  ). 8 2 15  33 Thay trở về 2
x t  1 suy ra phương trình có một nghiệm x  . 32
Ví dụ 30: Giải phương trình: 2 2 3 4
4 x x  1  1  5x  4x  2x x . U U Phân tích:
Dễ thấy đây là phương trình có chứa đa thức bậc 4 nên ta hướng đến đặt ẩn phụ để khử
căn hoặc để giảm bậc vì thế ta chia đa thức 2 3 4
1  5x  4x  2x x cho 2
x x  1 và có
x x x x    x x 2 2 3 4 2   2 1 5 4 2 1
7 1  x x   5 đến đây ta đặt: 2
x x  1  t  0 ta được 4 2 4 2 4t t
  7t  5  t  7t  4t  5  0 1  1  
Cho t  1 thì VT < 0, cho t   thì VT > 0 nên phương trình có nghiệm t    1;  . 2  2
Cho t  1 thì VT > 0, cho t  3 thì VT < 0.   Như thế 1  
phương trình có các nghiệm t  
 1;  và t  1;2 2   1  2       Tính gần đúng 1 2 1 0,5 1 1 2 1 0,5 p   ; q
 2,25  q  5 do đó nghiệm 4 2 2 1  5 t  nhân tử ta đoán là 2
t t  1  0 . 2 Kết quả: 4 2
t t t     2t t   2 7 4 5 0
1 t t  
5  0 và giải ra lấy các nghiệm dương 2 1  5 1  21 2  1   3 1  4t  3 t  ,t  . Ta có 2 x
    t   x  2 2  2 4 2 1  3  2 5 1  19  2 21
Từ đó phương trình có 4 nghiệm x  ,x  . 2 2 Lời bình: U
Ta nhận thấy phương trình 4 2
t  7t  4t  5  0 có hai nghiệm trái dấu và do hệ số tự do
bằng 5 nên có thể phân tích thành dạng  2
t mt   2
1 t nt  
5  0 đến đây ta cân bằng m   n  0 m   1  
hệ số bậc 3 và bậc nhất thì    
ta cũng đi đến kết quả cần thiết.
5m n  4 n   1  
Bài trên có thể nói nghiệm là "hai lần vô tỉ". Khi chuyển về được đa thức bậc 4 "ta nhẹ đi rất nhiều".
Ví dụ 31: Giải phương trình: 2
x x    2 8 3 4 4x x   2 x  4 . U U Phân tích:
Ta thấy phương trình có một nghiệm x  0 do đó ta trục căn để giảm bậc: 2
x 4x x  2 x   0  PT  x   2 4x x   2  x  4 2      2 x  4  2
4x x  4  x  4   * 
Ta chuyển được về phương trình đơn giản hơn và giải (*) theo phương pháp như trong
phần 3 phân tích thành nhân tử: 2
x x   x    2 4 4 4
4x x  4  2x x  4  0
 2x x  42x 1  x  4  0; x   0 x   0   1  65  + TH1:     x  2 2
x x  4 4
x x  4  0 8        1 2  x  1  0  x      3  57  + TH2:    2  x  
2x  1  x  4  2 8  4
x  3x  3  0  1  65 3  57
Vậy phương trình có 3 nghiệm x  0,x  ,x  . 8 8
Ví dụ 32: Giải phương trình: 2
x  3  x x x  2 , (x  ). U U Phân tích:
Điều kiện 2  x  3. Cho x  2 thì VT > VP, cho x  3 thì VT < VP nên phương trình có 2 2
nghiệm x  2; 3 . Ta viết lại  x   x   2 3 x x   2  0 khi đó: 1  
Cho x  0 thì VT < 0, cho x  1 thì VT > 0 nên phương trình có nghiệm x  0;1 . 2       3  5 Tính gần đúng 2 3 1 3 2 3 1 p   ; q
 2  q  5 do đó nghiệm x  4 2 2 2 nhân tử ta đoán là 2
x  3x  1  0 . Bây giờ ta giải theo phương pháp như trong phần 4
bình phương và trục căn: 2 4 3 2
x x x x x x    4 3 2
x x x x     2 2 3 2 3 4 1 2 3 4 1
2 1  3x x   0     2
x x   2 2 3 1 x   x  1       0 (*). Vì 2
2  x  3  x x  1  0 nên 2 
1  3x x  3  5 (*) 2
x  3x  1  0 giải ra lấy nghiệm x   2 4 3 2
2x x  9x  7x  4
Ví dụ 33: Giải phương trình: 3 2
 3 x x x . U U 2 x x  3 Phân tích:
Do x  0 không là nghiệm nên ta có điều kiệnx  0 . Ta viết lại: 4 3 2
x x x x    2
x x   3 2 2 9 7 4 3
3 x x x
Cho x  0 thì VT > VP, cho x  1 thì VT < VP nên phương trình có nghiệm x  0;1 . 1  
Cho x  2 ta có VT < VP, cho x  3 ta có VT > VP nên phương trình có nghiệm x  2; 3 . 2   2  3  1 3 2  3  1 3  5 Tính p   ; q
 2  q  5 nên ta đoán nghiệm x  và 4 2 2 2 nhân tử là 2
x  3x  1  0 . Nhiệm vụ của ta là trục căn tạo ra nhân tử: Trừ cả hai vế với x  2
6 x x   3 ta có 4 3 2
x x x x   x  2
x x   2 2 5 3 11 4 3 3
x x  1  2 x  2 2  
3 x x x  3 x  3x  1 2 x  3x   1  2
2x x  4     2
x x  1  2 x 2 x   3x  1  0     3 x  2 x x  3 . Với 2
x  0  x x  1  2 x  3 x 2  2
x x  4   *  2 
x x  1  2 x  VP(*) < 2
x x  3 < VT (*) nên (*) vô nghiệm. Do đó ta có   2 3 5 3 5
x  3x  1  0  x
. Đối chiếu điều kiện phương trình có 2 nghiệm x  . 2 2
Ví dụ 34: Giải phương trình:  x 1  
1 x  5  2 x  1  2x   1 2x  1 . U U Phân tích: Điề 1 6
u kiện x  . Đổi biến để khử bớt căn thức: x  1  t  ta có phương trình: 2 2
t   2t t   2 2 3 2 2 2 1 2
4  2t 2t  3  t  3t  6t  4  2t 2t  3 (*). 3  3  
Cho t  1 thì VT > VP, cho t
thì VT < VP nên phương trình có nghiệm t  1;   . 2 1  2 2 Viết lại  3 2
t t t   4  t  2 3 6 4 4 2t  
3  0 và t  4 thì VT < 0, t  3 thì VT > 0 nên phương trình có nghiệ 1  1,5  3  4
m t  4;3 . Tính p   1; 2   4 1  1,5  3  4 q
 2, 3  q  5 nên ta đoán nghiệm t  1  5 và nhân tử là 4 2
t  2t  4  0 . Do đó:   2
t  2t  t   3 2 * 2 2 3
1  t t  6t  4  0 6      t   2 2  2t t 2 4   t  1    0 , vì t  nên 2
t  2t  4  0  t  1  5 . 2
 2t  3  t 1  2 Thay trở về 2
x t  1 ta có nghệm của phương trình là x  5  2 5 .
Ví dụ 35: Giải phương trình:  2 x x   2 3 5
6 2  x  3x  6x  5 , (x  ). U U Phân tích: Đặ 2 2  
t 2  x t  0 ta có   2  t    2
t  t   2  t    2 3 2 5 2 6) 3 2 6 2  t  5      4 2 t t   4 2 3 7
4 t  3t  6t  5 . Điều kiện 2 3 2 6 t  0;t  (*). 3
Dễ thấy nếu trừ vào hai vế một lượng t và trục căn sẽ có nhân tử: 3t  7t  5
(*)  3t  7t  4t t  3t  6t  5  t  3t  7t   4 2 4 2 4 2 4 2 5 t  4 2
3t  6t  5  t 4 2
3t  7t  5  0 4 2 
3t  7t  5  0    1    (**). 4 2 2 t t
 3t  6t  5  1  t 4 2  3t 6t 5 t      
Do điều kiện (*) nên từ (**) 4 2
 3t  7t  5  0 2 7 109  t  thay trở về 2
x  2  t ta 6 đượ 
c nghiệm của phương trình là 5 109 x  . 6 b. Luyện tập: U
Bài 1. Giải phương trình: 2
x x  1  3  x  2 x  1 .
Bài 2. Giải phương trình:  2 x     2
x xx    3 4 2 1 3 2 2 1 2 x  5x.
Bài 3. Giải phương trình: 2
x  1  x  7x  17x  7.
Bài 4. Giải phương trình: 2 2
x x  6  x  3x  4x  18.
Bài 5. Giải phương trình: 2 2
x  2 x x  2  5x  9x  10.
Bài 6. Giải phương trình: 3 2 3 2
x x x  2  3x  4x  6.
Bài 7. Giải phương trình: 2 2 3 2
9x  11x  6  (x x  3) 3x x  8x  4 .
Bài 8. Giải phương trình: 2 2
3x  2  2 x  2x  3  5x  7x  13.
Bài 9. Giải phương trình: 2
x  4x  3  x  
1 8x  5  6x  2 .
Document Outline

  • MỘT SỐ ĐỊNH HƯỚNG GIẢI PT VÔ TỈ
  • MỘT SỐ ĐỊNH HƯỚNG GIẢI PT VÔ TỈ P2
  • MỘT SỐ ĐỊNH HƯỚNG GIẢI PT VÔ TỈ P3
  • MỘT SỐ ĐỊNH HƯỚNG GIẢI PT VÔ TỈ P4
  • MỘT SỐ ĐỊNH HƯỚNG GIẢI PT VÔ TỈ P5