


































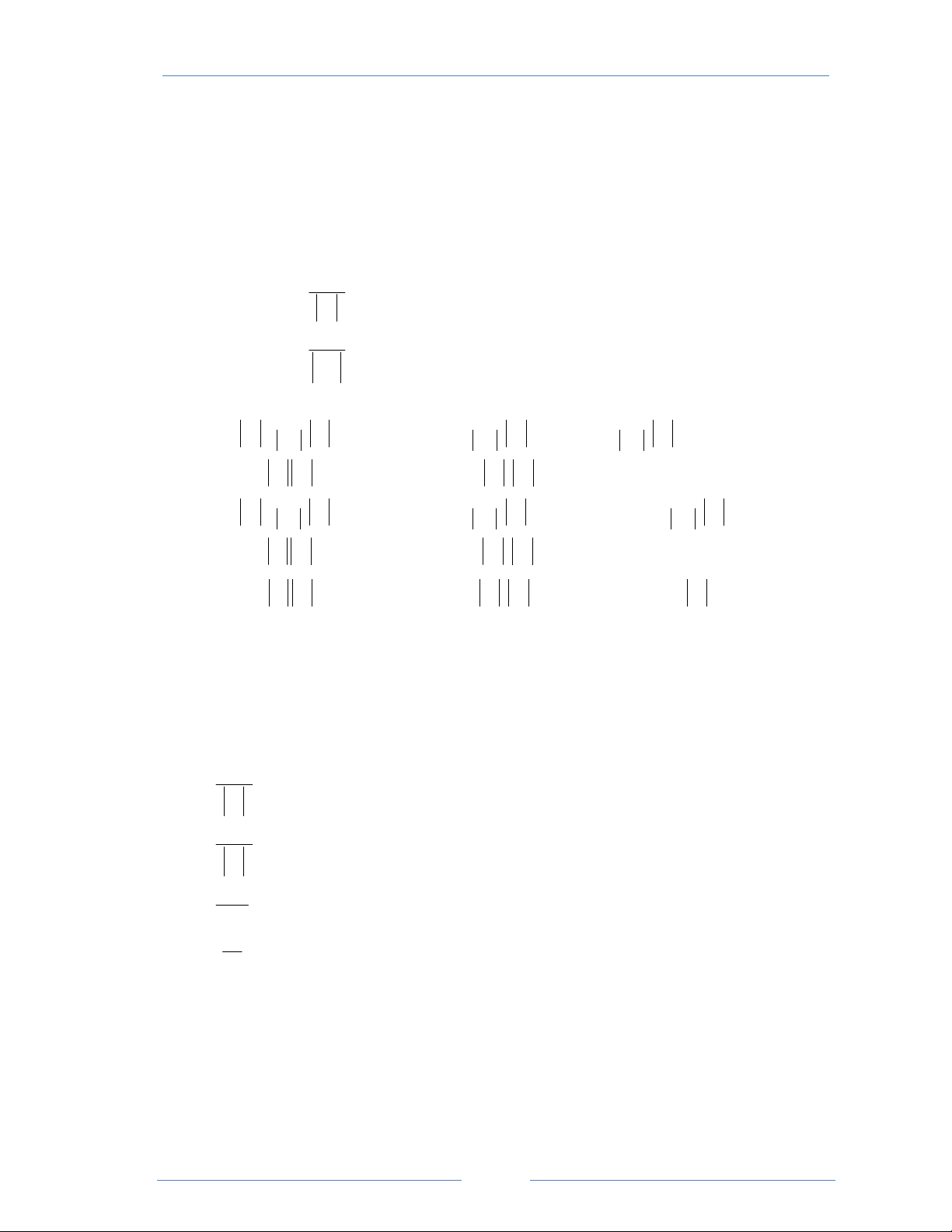




Preview text:
BÀI TẬP LƯỚI ĐIỆN
TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI
Bộ môn Hệ thống điện – Viện Điện
BÀI TẬP LƯỚI ĐIỆN 4/7/2017
Biên soạn: PHẠM NĂNG VĂN 0
BÀI TẬP LƯỚI ĐIỆN BÀI 1
Đường dây 3 pha 765kV dài 300km được hoán vị đầy đủ có tổng trở đơn vị và
tổng dẫn đơn vị thứ tự thuận như sau
Z0 = 0,0165 + j0,03306 Ω / km Y0 = j4,674.10-6 S / km
Tính toán các hệ số A, B, C, D của ma trận mạng hai cửa của đường dây trong 2 trường hợp: a) Tính chính xác b) Tính gần đúng Bài giải
a) Tính chính xác Hệ số truyền sóng γ γ = Z .Y 0 0 6
γ = (0, 0165 + j0, 03306).j4, 674.10− 5 − −4 = 9,533162.10 + j4,044881.10
Tổng trở sóng của đường dây Zc Z (0, 0165 + j0,03306) 0 Z = = c 6 Y j4, 674.10− 0 = 86,540013 − j20,39615
Các thông số A, B, C, D của ma trận L γ = αL + jβL −5 −4 L
γ = (9,533162.10 + j4,044881.10 ).300 L γ = 0,0285995 + j0,1213464 Hệ số A: A = cosh( L γ ) = cosh(αL + jβL)
= cosh(0,0285995).cos(0,1213464) + sinh(0,0285995).sin(0,12134464) = 0, 993053 + j0,003462 Hệ số B: 1
BÀI TẬP LƯỚI ĐIỆN B = Z .sinh( L γ ) c
sinh(0,0285995).cos(0,1213464) + = (86,540012 + j20,39615).
+ sin(0,1213464).cosh(0,0285995) = 4, 927076 + j9, 90074 (Ω) Hệ số C: 1 C =
.sin(γL) = −1, 619831 + j0, 001399 (S) Zc Hệ số D:
D = A = 0, 993053 + j0,003462
b) Tính gần đúng
Z = Z .L = (0,0165 + j0,00306).300 = 4, 95 + j9, 918 0 6
Y = Y .L = j4,674.10− .300 = j0,001402 0
Các thông số của mạng hai cửa: Hệ số A: Y.Z (4, 95 + j9, 918).j0,001402 A = 1 + = 1 + 2 2 = 0, 993047 + j0,003471 Hệ số B: B = Z = 4, 95 + j9, 918 Hệ số C: Y.Z
j0, 001402.(4, 95 + j9, 918) C = Y.1 + = j0,001402. 1 + 4 4 6 − 3
= −2, 433129.10 + j1,397325.10− Hệ số D:
D = A = 0, 993047 + j0, 003471 BÀI 2
Đường dây 3 pha 765kV dài 600km được hoán vị đầy đủ có tổng trở đơn vị và
tổng dẫn đơn vị thứ tự thuận như sau: Z = 0,0165 + j0,03306 Ω / km 0 6 Y = j4,674.10− S / km 0 2
BÀI TẬP LƯỚI ĐIỆN
Lập sơ đồ thay thế của đường dây và tính toán các thông số trong sơ đồ thay thế trong hai trường hợp: a) Mạch PI chuẩn b) Mạch PI tương đương Bài giải
a) Mạch hình PI chuẩn Z = Z .L 0 = (0,0165 + j0,03306).600 = 9, 9 + j19, 836 (Ω) Y = Y .L 0 6
= j4,674.10− .600 = j0,0028044 (S)
b) Mạch PI tương đương 3
BÀI TẬP LƯỚI ĐIỆN Hệ số truyền sóng: γ = Z .Y 0 0 = (0,0165 + j0,03306) 6 .j4, 674.10− 5 − 4
= 9,533162.10 + j4,044881.10−
Tổng trở sóng của đường dây: Z 0, 0165 + j0, 03306 0 ( ) Z = = = 86,540013 − j20,39615 c 6 Y j4, 674.10− 0 −5 −4 L
γ = (9,533162.10 + j4,044881.10 ).600 = 0,057199 + j0,242693 Z.sinh(γL) ' Z = = 9, 717129 + j19, 698033 (Z) γL cosh( L γ ) − 1 ' −6 Y = 2.
= 6,561093.10 + j0,0028175 (S) Z .sinh( L γ ) c BÀI 3
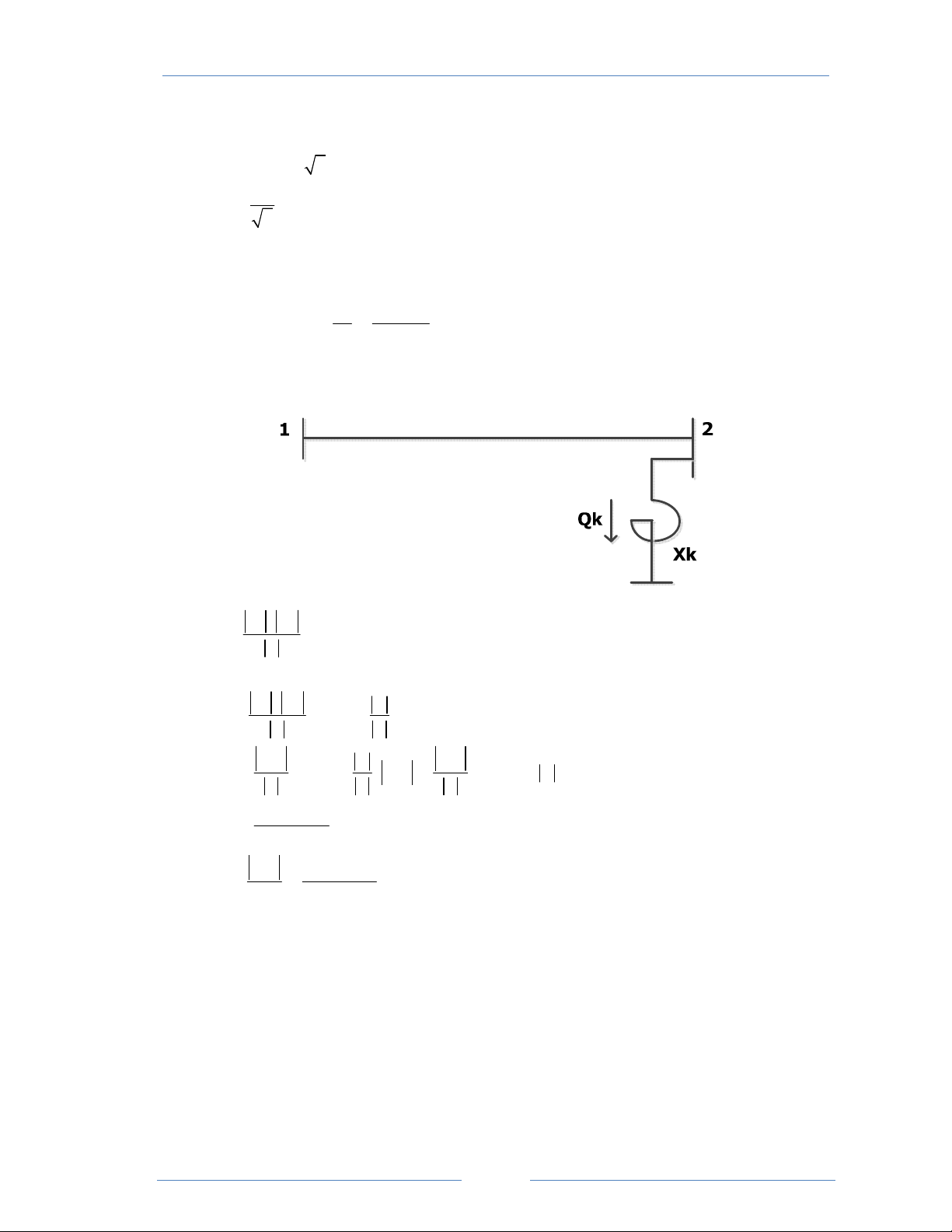
Đường dây 220kV có Z0 = 0,05 + j0,45 Ω / km và tổng dẫn Y0 = j3,4.10-6 A/km.
Điện áp cuối đường dây bằng 220kV. Phụ tải cuối đường dây bằng 150MVA,
cos ϕ = 0, 9 (tải cảm). Tìm điện áp, dòng điện và tổn thất công suất trên đường dây
bằng cách sử dụng mạch Pi chuẩn và mô hình chính xác trong hai trường hợp:
a) Chiều dài đường dây bằng 100km
b) Chiều dài đường dây bằng 300km Bài giải
a) L = 100km
Trường hợp 1: Sử dụng mạch PI chuẩn
Z = Z .L = (0, 05 + j0, 45).100 = 5 + j45 (Ω) 0 −6 −4
Y = Y .L = j3, 4.10 .100 = j3, 4.10 (S) 0
Các thông số của ma trận: 4
BÀI TẬP LƯỚI ĐIỆN −4 Y.Z j3, 4.10 (5 + j45) A = 1 + = 1 + = 0, 99235 + j0,00085 2 2 B = Z = 5 + j45 Y.Z − + 4 − (5 j45) 4 .j3, 4.10 C = Y.1 + = j3, 4.10 1 + 4 4 −7 4 = −1, 445.10 + j3,3870.10− D = A
Điện áp và dòng điện đầu đường dây
Điện áp đầu đường dây . . . 1 U = A. 2 U + 3B.I2 Trong đó: * . S2 I2 = . 3. 2 U .
S2 = 150.cos ϕ + j150.sin ϕ = 135 + j65, 383 . 135 − j65, 383 → I2 = = 0,3543 − j0,1716 3.220 . → 1 U = 236, 2292 6 ∠ ,3959 (kV)
Dòng điện đầu đường dây . . . C 1 I = . 2 U + D. 2 I 3 −7 −1, 445.10 =
.220 + (0, 99235 + j0,00085).(0,3543 − j0,1716) 3 = 373,9115∠ − 19, 85 (A)
Công suất đầu đường dây . . * 1 S = 3. 1 U . 1 I = 3.236, 2292 6 ∠ ,3957.0,3739115 1 ∠ 9, 85 = 137,22 + j67,65 MVA
Tổn thất công suất trên đường dây . . . ∆ S = 1 S − S2 = (137,22 + j67,65) − (135 + j65,383) = 2,22 + j2,267 MVA
Trường hợp 2: Sử dụng mô hình PI tương đương Hệ số truyền sóng 5
BÀI TẬP LƯỚI ĐIỆN γ = Z .Y 0 0 = (0,05 + j0, 45) −6 −5 −3 .j3, 4.10 = 6,8613.10 + j1,23883.10 Z 0, 05 + j0, 45 0 Z = = = 364,3627 − j20,1828 c −6 Y0 j3, 4.10 3 L γ = 6, 8613.10− + j0,123883
Các hệ số của ma trận:
A = cosh(γL) = cosh(αL + βL)
= cosh(0,0068613).cos(0,123883) + j sinh(0,0068613).sin(0,123883) = 0,99236 + j0,000848 B = Z .sinh L γ c ( )
sinh(0,0068613).cos(0,123883) + = (364,3627 − j20,1828).
+j cosh(0,0068613).sin(0,123883) = 4, 9745 + j44,8868 sinh ( L γ ) −8 4 C = = −9,6186.10 + j3,3913.10− Zc D = A
Điện áp và dòng điện đầu đường dây
Điện áp đầu đường dây . . . 1 U = A. 2 U + 3B. 2 I
= (0,9923 + j0,0008).220 + 3.(4,9745 + j44,8868).(0,3543 − j0,1716) 0 = 236,1754 6 ∠ ,382 kV
Dòng điện đầu đường dây . . . C 1 I = . 2 U + D.I2 3 −8 4 ( 9 − ,6186.10 + j3,3913.10− ) =
.220 + (0, 99235 + j0,0008).(0,3543 − j0,1716) 3 = 0,3739∠ − 19, 84 (kA)
Công suất đầu đường dây . . * 1 S = 3. 1 U . 1 I = 3.236,1754 6 ∠ ,382.0,3739 1 ∠ 9, 84 = 137,2113 + j67,5808 MVA
Tổn thất công suất trên đường dây . . . ∆ S = 1
S − S2 = 2, 2113 + j2,1978 MVA 6
BÀI TẬP LƯỚI ĐIỆN
b) L = 300km
Trường hợp 1: Sử dụng mạch PI chuẩn Z = Z .L = 15 + j135 (Ω) 0 −6
Y = Y .L = j3, 4.10 .300 = j0, 00102 (S) 0
Các thông số của ma trận: Y.Z A = 1 + = 0,93115 + j0,00765 2 B = Z = 15 + j135 Y.Z 6 − −4 C = Y.1 + = 3 − , 9015.10 + j9,848865.10 4 D = A
Điện áp và dòng điện đầu đường dây
Điện áp đầu đường dây . . . 1 U = A. 2 U + 3B. 2 I
= (0,93115 + j0,00765).220 + 3.(15 + j135).(0,3542 − j0,1716) 0 = 266, 491 1 ∠ 7, 48 (kV)
Dòng điện đầu đường dây . . . C 1 I = . 2 U + D.I2 3 ( 6 3 − , 9015.10− + j9, 848865) =
.220 + (0, 93115 + j0,00765).(0,3542 − j0,1716) 3 = 0,33∠ − 5,52 (kA)
Công suất đầu đường dây . . * 1 S = 3. 1 U . 1 I = 3.266, 491 1 ∠ 7, 48.0,332 5 ∠ ,52 = 141,1616 + j59, 934 MVA
Tổn thất công suất trên đường dây . . . ∆ S = 1
S − S2 = 6,1616 − j5, 4486
Trường hợp 2: Sử dụng mô hình PI tương đương Hệ số truyền sóng 7
BÀI TẬP LƯỚI ĐIỆN γ = Z .Y 0 0 = (0,05 + j0, 45) −6 −5 −3 .j3, 4.10 = 6,8613.10 + j1,23883.10 Z 0, 05 + j0, 45 0 Z = = = 364,3627 − j20,1828 c −6 Y0 j3, 4.10 L γ = 0,020584 + j0,371650
Các hệ số của ma trận: A = cosh( L γ ) = cosh(αL + βL) = 0,9319268 + j0,007475 B = Z .sinh L γ c ( ) = 14,318550 + j131, 9605 sinh ( L γ ) −6 −4 C = = −2,56535.10 + j9, 9675.10 Zc D = A
Điện áp và dòng điện đầu đường dây
Điện áp đầu đường dây . . . 1 U = A.U2 + 3B.I2 0 = 264, 8857 1 ∠ 7,2082 kV
Dòng điện đầu đường dây . . . C 1 I = .U2 + D.I2 3 6 − −4 (−2,56536.10 + j9, 9675.10 ) (0, 931927 + j0,007476). = .220 + 3 . (0,3543 − j0,1716) = 0,332539∠ − 5,2889 (kA)
Công suất đầu đường dây . . * 1 S = 3. 1 U . 1 I = 3.264, 8857 1 ∠ 7,208.0,332539 5 ∠ ,2889 = 140, 9566 + j58,3778 MVA
Tổn thất công suất trên đường dây . . . ∆ S = 1
S − S2 = 5, 9566 + j7, 0052 MVA 8
BÀI TẬP LƯỚI ĐIỆN BÀI 4
Đường dây 765kV có chiều dài 650km, có tổng trở dọc Z = 0, 02 + j0, 32 Ω / km 0 và tổng dẫn ngang −6 Y = j5.10
S / km . Các dữ liệu tại đầu đường dây: điện áp bằng 0
765kV, công suất bằng 1960MW, hệ số công suất bằng 0,99 (vượt trước). Sử dụng
mô hình hình PI chuẩn và mô hình chính xác hãy xác định:
a) Các thông số: A, B, C, D
b) Xác định điện áp, dòng điện và hệ số công suất tại cuối đường dây Bài giải
a) Sử dụng mô hình PI chuẩn
Z = Z .L = (0,02 + j0,32).650 = 13 + j208 ( ) Ω 0 6
Y = Y .L = j5.10− .650 = j0,00325 (S) 0
Các thông số mạng hai cửa: Y.Z 0, 00325.(13 + j208) A = 1 + = 1 + = 0,662 + j0, 021125 2 2 B = Z = 13 + j208 Y.Z j0, 00325.(13 + j208) C = Y.1 + = j0, 00325. 1 + 4 4 5 = 3 − , 43281.10− + j0,0027008 D = A = 0, 662 + j0, 021125
Xác định điện áp, dòng điện và hệ số công suất cuối đường dây: U D B − U 2 1 = . I C − A I 2 1 Với . . 1 S 1I = = 1, 479224 + j0,2107 . 3. 1 U . 1
S = P + jP .tgϕ = 1960 − j279, 20594 1 1 . . . 2 U = D. 1 U − 3B. 1 I
= (0,662 + j0,021125).765 − 3.(13 + j208).(1, 479224 + j0,210719) = 757,2342∠ − 43,526 (kV) 9
BÀI TẬP LƯỚI ĐIỆN . . . −C − 765 5 I2 = . 1 U + A. 1 I = (3, 43218.10 − j0,0027008). + 3 3 0
+ (0,662 + j0,022125).(1, 479224 + j0,210719) = 1422,9234∠ − 45, 915 kA . . * 0
S2 = 3.U2 .I2 = 3.757, 2342∠ − 43,528 .1422, 9234∠45, 915 = 1864,639 + j77,78985 (MVA) . . . ∆ S = 1
S − S2 = 95, 361 − j356, 9958 (MVA)
b) Sử dụng mô hình PI tương đương −6 −5 3
γ = Z .Y = (0,02 + j0,32).j5.10 = 3,9509.10 + j1,2655.10− 0 0 Z 0, 02 + j0, 32 0 Z = = = 253,1056 − j7, 90184 c −6 Y j5.10 0 −5 −3 L
γ = αL + βL = (3, 9509.10 + j1,2655.10 ).650 = 0,02581 + j0, 8822593
Các thông số mạng hai cửa: A = cosh( L γ )
= cosh(0,02581).cos(0,8822593) + j sinh(0,02581).sin(0, 8822593) = 0,68055 + j0,01882 B = Z .sinh( L γ ) c
sinh(0,02581).cos(0, 8822593) + = (253,1056 − j7,9018).
j sin(0,8822593).cosh(0,02581) = 10,2159 + j185, 4273 1 C = sinh ( L γ ) 5 − −3 = 2 − ,1375.10 + j2, 8959.10 Zc D = A
Ma trận nghịch đảo của ABCD: −1 A B D B − = C D −C A . . . 2 U = D. 1 U − 3B. 1 I
= (0,68055 + j0,01882).765 − 3.(10,2159 + j185, 4273).(1, 47922 + j0,210718) = 729,1480∠ − 39,563 (kV) 10
BÀI TẬP LƯỚI ĐIỆN . . . −C 0 I2 = . 2
U + A.I2 = 1,500576∠ − 47,584 (kA) 3 . . * 0 0 S2 = 3 2
U .I2 = 3.729,1480∠ − 39,5626 .1,500576∠47,584 = 1876,5692 + j264, 4394 (MVA) . . . ∆ S = 1
S − S2 = 83, 4308 − j543, 6453 (MVA) BÀI 5
Một đường dây truyền tải ba pha 500kV, dài 500km. Điện cảm và điện dung trên
một pha của đường dây tương ứng bằng 0,97mH/km; 0,0115µF/km. Giả sử đường dây không tổn thất
1. Xác định điện áp tại cuối đường dây khi không tải (hở mạch) khi điện áp tại
đầu đường dây bằng 500kV
2. Xác định điện kháng và công suất của kháng bù ngang đặt tại cuối đường dây
sao cho điện áp tại đầu và cuối đường dây bằng nhau và bằng điện áp định mức. Bài giải Hệ số truyền sóng: γ = Z .Y = jω L C = j2 f π L C 0 0 0 0 0 0 3 − −6
= j2.3,14.50. 0, 97.10 .0,0115.10 = j, 0010493 (rad / km) −3 Z L 0, 97.10 0 0 Z = = = = 290, 427 (Ω) c 6 Y C 0, 0115.10− 0 0 L γ = j0,0010493.500 = j0,52465
Các thông số của mạng hai cửa
A = cosh(γL) = cos(βL) = 0, 8655 B = Z sinh( L
γ ) = Z j sin(βL) = 290, 427.j sin(0,52465) = j145, 4732 c c 1 1 C = sinh( L γ ) = .j sin(βL) = j0, 001725 Z Z c c D = A 11
BÀI TẬP LƯỚI ĐIỆN
1. Xác định U tại cuối đường dây . . . 1 U = A. 2 U + 3B. 2 I . . . C 1 I = . 2 U + D.I2 3 . . . I2 = 0 → 1 U = A. 2 U Khi không tải . . 1 U 500 2 U = = = 577, 6951 kV A 0, 8655
2. Đặt kháng bù ngang ở cuối đường dây U . U 1 2 P = .sin δ = 0 2 B → δ = 0 U . U 1 2 A 2 Q = .cos δ − .U k 2 B B 2 2 U U dm A 2 dm = .cos δ − . U = . cos δ − dm ( A ) B B B 2 500 =
.(1 − 0, 8655) = 231,1277 MVAr 145, 4732 2 2 U 500 dm X = = = 1081,653 Ω L Q 231,1277 k BÀI 6
Một đường dây truyền tải ba pha 500 kV, dài 300 km. Điện cảm và điện dung trên
một pha của đường dây tương ứng bằng 0,97 mH/km; 0,0115 µF/km. Giả sử đường
dây không tổn thất. Cho đường dây mang tải cảm có công suất bằng 1000 MVA hệ
số công suất bằng 0,95. 12
BÀI TẬP LƯỚI ĐIỆN
a) Xác định điện áp phức tại cuối đường dây nếu điện áp đầu đường dây bằng 500kV.
b) Xác định điện dung và công suất của tụ bù ngang đặt tại cuối đường dây
để giữ biên độ điện áp đầu và cuối đường dây bằng nhau và bằng 500kV. Bài giải a) 3 Z = j L ω = j2 f π .L = j2 . π 50.0,97.10− = j0,3047 0 0 0 −6 −6 Y = jωC = j2 f π .C = j2 . π 50.0,0115.10 = j3,6128.10 0 0 0
Z = Z .L = j0, 3047.300 = j91, 41 0 6 − 3 Y = Y .L = j3, 6128.300.10 = j1,68.10− 0 −3 L 0, 97.10 0 Z = = = 290, 427 (Ω) c 6 C 0, 0115.10− 0 γ = Z .Y = jω L C 0 0 0 0 = j2 3 − 6 .50. 0, 97.10 .0, 0115.10− π = j0,00105 rad / km L
γ = jβL = j0,00105.300 = j0,315
Các hệ số của ma trận mạng hai cửa: A = cosh L γ
= cos βL = cos 0,315 = 0,90796 1 ( ) ( ) ( ) B = Z sinh L γ = Z .j sin βL 1 c ( ) c ( )
= 290, 427.j sin(0,315) = j89, 918064 1 1 C = sinh L γ = .j sin βL 1 ( ) ( ) Z Z c c 1 = .j sin(0, 315) = 0, 001066 290, 427 D = A 1 1
Công suất cuối đường dây: . = 1000 MVA S 2 cos ϕ = 0, 95 → P = S .cos ϕ = 950 MW 2 2 Q = S .sin ϕ = 312, 29 MVAr 2 2 . → S2 = 950 + j312,29 MVA Áp dụng 2 2 sin δ + cos δ = 1 13
BÀI TẬP LƯỚI ĐIỆN 4 4 a U + b U + c = 0 2 2 2 2 a = A = 0, 950796 = 0, 904013 1 2 b = 2 A B Q − U 1 1 2 1 2
= 2.0, 950796.89, 9791.312,29 − 500 = −196572, 9207 2 2 2 2 c = B
.S = 89, 9791 .1000 = 809663844 1 2 2 U = 162245,032 2 1 . → = 402,7965 2 2 U U = 55199,7621 2 2 U U 1 2 P = sin δ 2 B1 B P 89, 9791.950 1 2 0 → δ = arcsin = arcsin = 25,09 U U 500.402, 7965 1 2 . 0 → 2
U = 402, 7965∠ − 25, 02 (kV) Do tải cảm δ < 0 b) 1 2 P2+jQ2 Qc . ' S = P + j(Q − Q ) 2 2 2 c U U 1 2 P = .sin δ (1) 2 B 1 − A U U 1 2 1 2 Q − Q = .U + .cos δ (2) 2 c 2 B B 1 1 950.89, 9791 500.500 sin δ = = 0,3487 2 (1) → 950 = .sin δ → 500 89, 9791 cos δ = 0,9398 2 0, 90796 500 2 (2) → (312, 29 − Q ) = − .500 + .0, 9398 c 89, 9791 89, 9791 → Q = 343,0168 MVAr c 14
BÀI TẬP LƯỚI ĐIỆN BÀI 7
Một đường dây truyền tải ba pha 500kV, dài 700km. Điện cảm và điện dung trên
một pha của đường dây tương ứng bằng 0,97mH/km; 0,0115µF/km. Giả sử đường
dây không tổn thất cho đường dây mang tải cảm có công suất 10000MVA, hệ số công suất bằng 0,95.
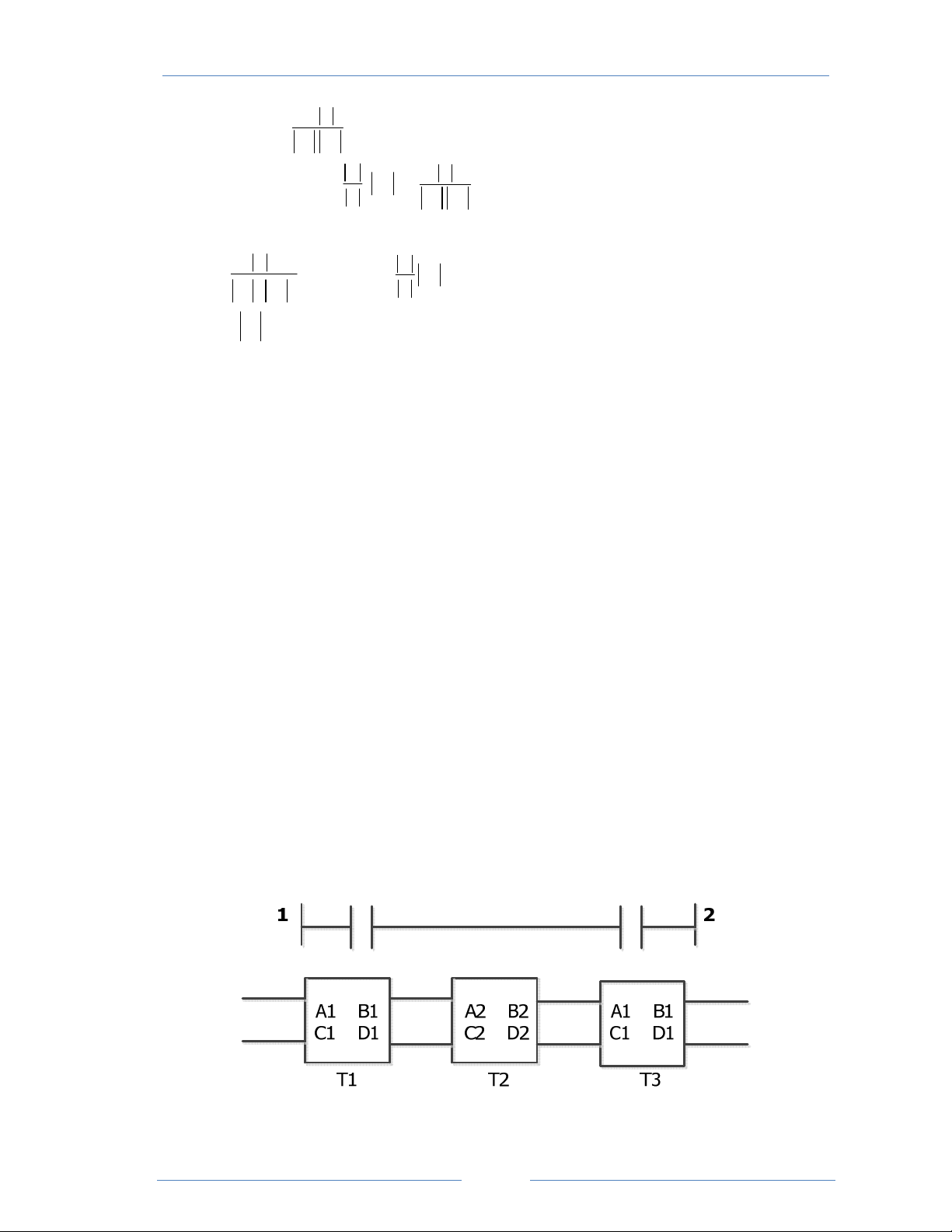
Giả sử có duy nhất một tụ bù dọc được lắp ở điểm giữa của đường dây với mức
độ bù bằng 40%. Biết điện áp cuối đường dây bằng 490kV. Hãy xác định điện áp đầu đường dây. Bài giải
Cần xây dựng các mạng hai cửa nối tiếp nhau như sau: T = T .T .T 1 2 3 S = 1000MVA P
= S .cos ϕ = 1000.0,95 = 950 MW 2 2 2 → cos ϕ = 0, 95
Q = S .sin ϕ = 1000.0,31229 = 312, 29 MVAr 2 2 . S2 = 950 + j312, 290 γ = Z .Y = jω L C = j2 f π L C 0 0 0 o 0 o −3 6 = j2 .
π 50. 0, 97.10 .0,0115.10− = j0,001049 rad / km −3 Z L 0, 97.10 0 0 Z = = = = 290, 4277 Ω c 6 Y C 0, 0115.10− 0 0
Các thông số của ma trận truyền T (A ,B , C ,D ) với một nửa đường dây đầu: 1 1 1 1 1 L γ βL 700 = j = j0,001049. = j0,367242 2 2 2 15
BÀI TẬP LƯỚI ĐIỆN L γ βL A = cosh = cos = cos 0,367242 = 0,933321 1 ( 2) ( 2) ( ) L γ βL B = Z sinh = Z .j sin = 290, 427.j sin(0, 367242) 1 c ( 2) c ( 2) = 104,275767 1 = (γ β − = = Z 2 ) 1 L ( L C sinh j sin Z 2 ) 3 j1, 2368.10 1 c c D = A = 0, 933321 1 1
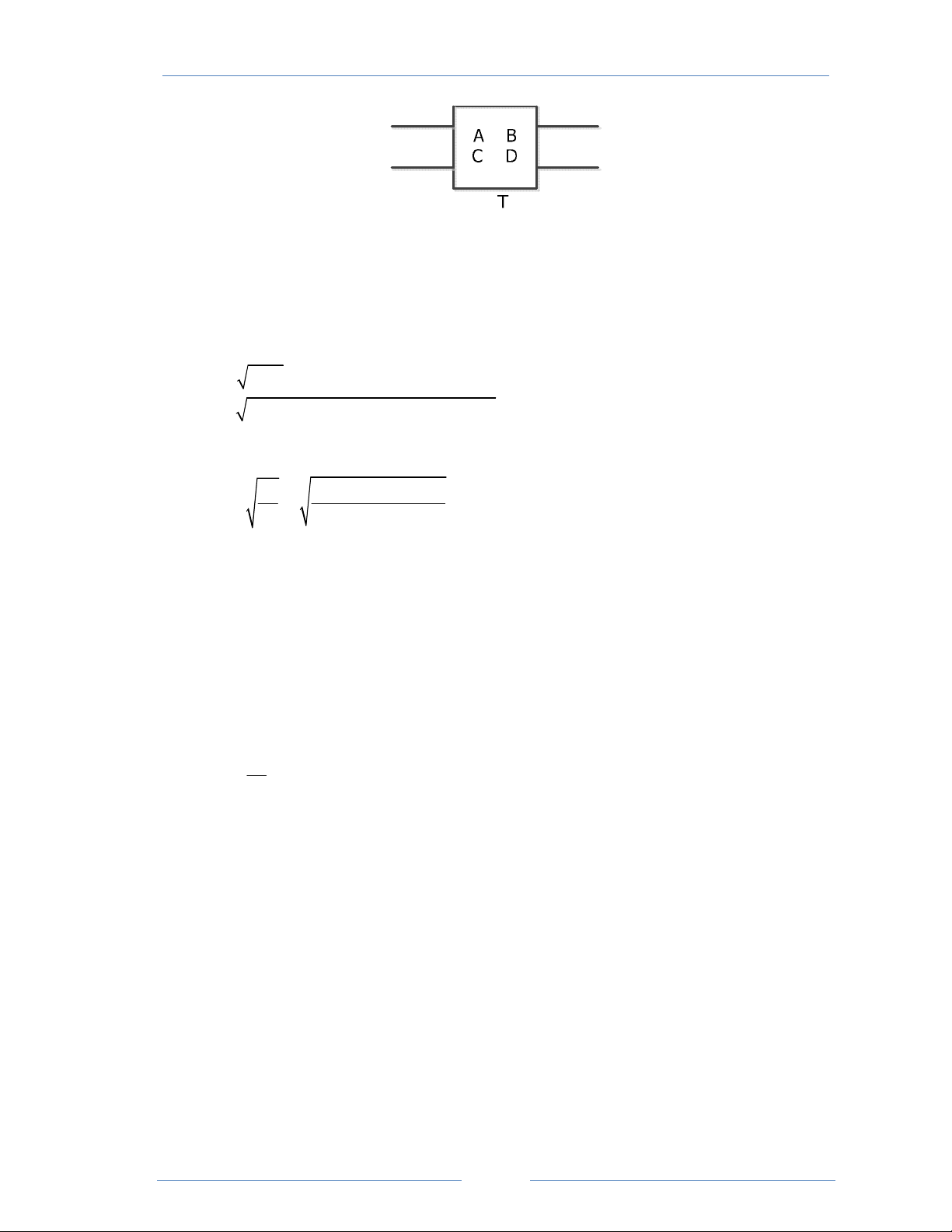
Các thông số của ma trận truyền T (A ,B , C ,D ) của tụ bù dọc 2 2 2 2 2 A = 1 2 B = Z = −jX = −j40%. L ω .L 2 c c 0 3 = −j0, 4.2 .
π 50.0, 97.10− .700 = −j85,3257 C = 0 2 D = 1 2 Ma trận tổng A B A B A B A B 1 1 2 2 1 1 T = = . . C D C D C D C D 1 1 2 2 1 1 t T 1 A B a b A B 1 1 → T = = . C D c d C D 1 1 t T1 a = A .A + B .C = 0, 933321 1 2 1 2 b = A .B + B .D = 24,639538 1 2 1 2 c = C .A + D .C = 0, 0012363 1 2 1 2 d = C .B + D .D = 1,038806 1 2 1 2 Tính T = t.T 1 A = a.A + b.C = 0, 840627 1 1 B = a.B + b.D = 120, 319365 1 1 C = c.A + d.C = 0, 002438 1 1 D = A U U 1 2 P = .sin δ 2 B U U A 2 1 2 1 Q = .cos δ − . U 2 2 B B 16
BÀI TẬP LƯỚI ĐIỆN P2 B sin δ = U U 1 2 → 2 A B cos δ = Q + . U . 2 2 B U U 1 2 2 2 sin δ + cos δ = 1 2 2 B 2 2 A → .P + Q + U = 1 2 2 2 2 2 U U B 1 2 . = 541, 421 1 U
→ sinδ = 0,4308 → δ = 0,4454 rad . → 1 U = 541, 421 0 ∠ , 4454rad (kV) BÀI 8
Đường dây truyền tải ba pha dài 450km có tổng trở dọc đơn vị 0
Z = 0, 8431∠79, 04 Ω / km và tổng dẫn ngang đơn vị −6 0 Y = 5,10510.10 ∠90 S / km 0 0
. Đường dây được đặt tụ bù dọc ở hai đầu đường dây với mức độ bù bằng 70%
(35% tại đầu đường dây, 35% tại cuối đường dây). Hãy xác định:
a) Điện áp tại cuối đường dây trong chế độ không tải khi điện áp tại đầu đường dây bằng 220kV.
b) Công suất tác dụng lớn nhất của phụ tải có thể truyền tải trên đường dây có
đặt bù theo điều kiện ổn định tĩnh khi biên độ điện áp hai đầu đường dây được giữ 220kV. Bài giải a) 17
BÀI TẬP LƯỚI ĐIỆN
Cần xây dựng các mạng hai cửa cho tụ bù và cho đường dây: T = T .T .T 1 2 3
Mạng hai cửa của đường dây γ = Z Y 0 0 0 −6 0 = 0, 8431 7 ∠ 9,04 .5,105.10 ∠90 4 − −3 = 1, 98122.10 + j2,0651.10 0 Z 0 − , 8431 7 ∠ 9,04 0 Z = = = 404,53138 − j38,80942 c 6 − 0 Y 5,105.10 9 ∠ 0 0 L γ = αL + jβL = ( 4 − −3 1, 98122.10 + j2,0651.10 ).450 = 0,089155 + j0,9293097
Các thông số của ma trận truyền T (A ,B , C ,D ) của đường dây: 2 2 2 2 2 A = cosh( L γ ) = 0, 6007669 + j0,0715263 2 B = Z .sinh( L
γ ) = 52, 8280717 + j323,3291905 2 c 1 5 C = .sinh( L
γ ) = −5, 817695.10− + j0,0019829 2 Zc D = A 2 2
Mạng hai cửa của tụ bù:
Điện kháng tổng của đường dây
Z = Z .L = 0,160293 + j0, 827722 .450 0 ( ) = 72,1319599 + j372, 474894 → X = 372, 474894
→ X = 35%.372, 47494 = 130,366213 c Z = −jX − j130, 366213 c c
Các thông số của ma trận truyền T (A ,B , C ,D ) của tụ bù dọc: 1 1 1 1 1 18
BÀI TẬP LƯỚI ĐIỆN A = 1 1
B = Z = −jX = −j130, 366213 1 c c C = 0 1 D = A = 1 1 1 Ma trận tổng T = (T .T ).T = t.T 1 2 1 1 a b A B A B 1 1 2 2 t = T .T = = . 1 2 c d C D C D 1 1 2 2
a = A .B + B .C = 0,959267 + j0,079111 2 1 2 1
b = A .B + B .D = 62,152679 + j245,009481 2 1 2 1 −5
c = C .A + D .C = −5, 817694.10 + j0,001983 2 1 2 1
d = C .B + D .D = 0,600767 + j0,071528 2 1 2 1 a b A B A B 1 1 T = . = c d C D C D 1 1
A = a.A + b.C = 0, 859267 + j0,079111 1 1 B
= a.B + b.D = 72.466 + j132, 9901 1 1 −5
C = c.A + d.C = 5, 817694.10 + j0, 001983 1 1 D = A . Khi không tải 2 I = 0 . . . 1 U = A. 2 U + 3.B.I2 . . . C 1 I = . 2 U + D.I2 3 . I2 = 0 . . 1 U 0 → 2 U = = 254, 9539143∠ − 5,2602 A b)
Để đảm bảo điều kiện dự trữ ổn định tĩnh 0
δ < 35 nên công suất truyền tải lớn
nhất trên đường dây là: 19
BÀI TẬP LƯỚI ĐIỆN . . U U Từ 1 2 P = .sin δ 2 max B P đạt max khi 0 δ = 35 2 max 0 220.220.sin 35 P = = 183,2997215 MW 2 max 151, 452 BÀI 9
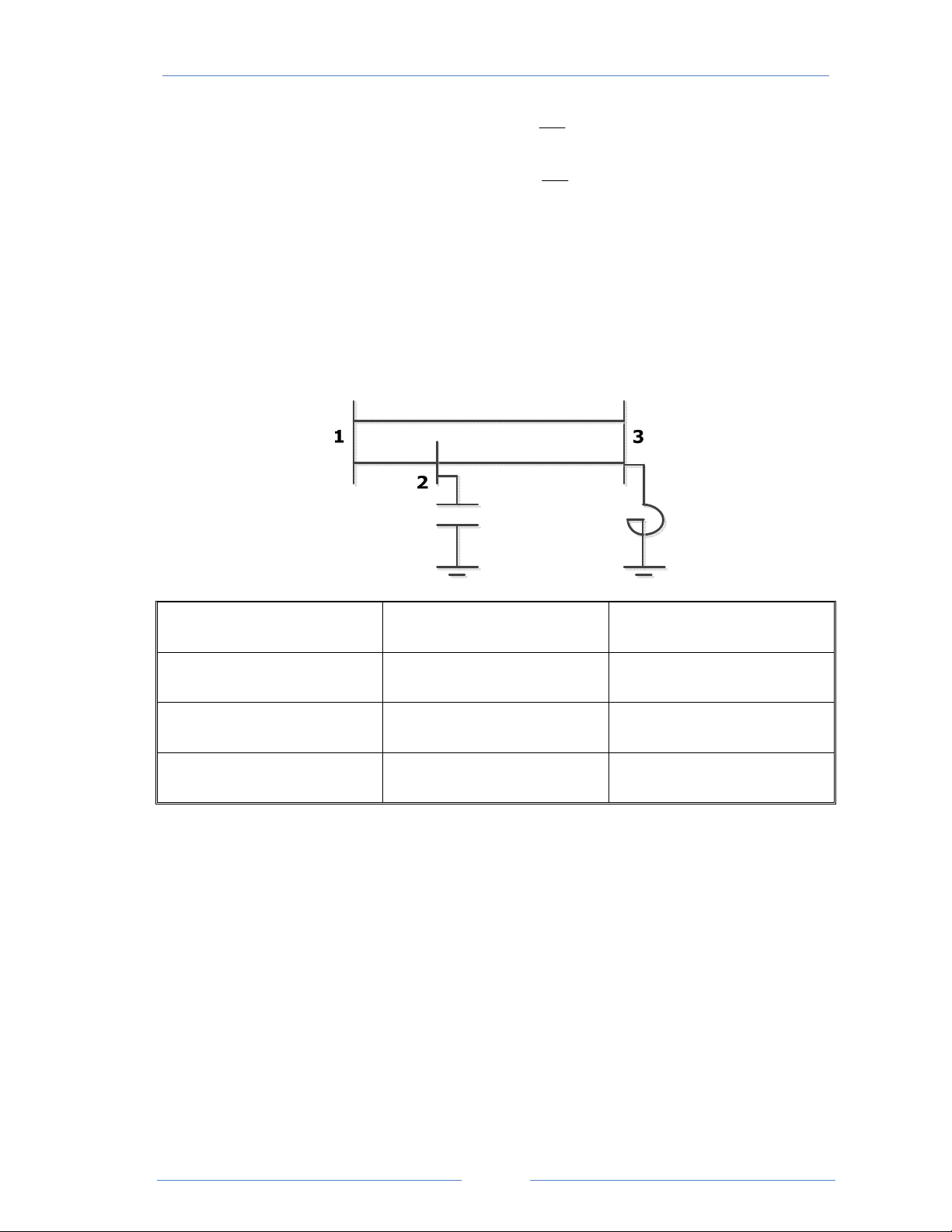
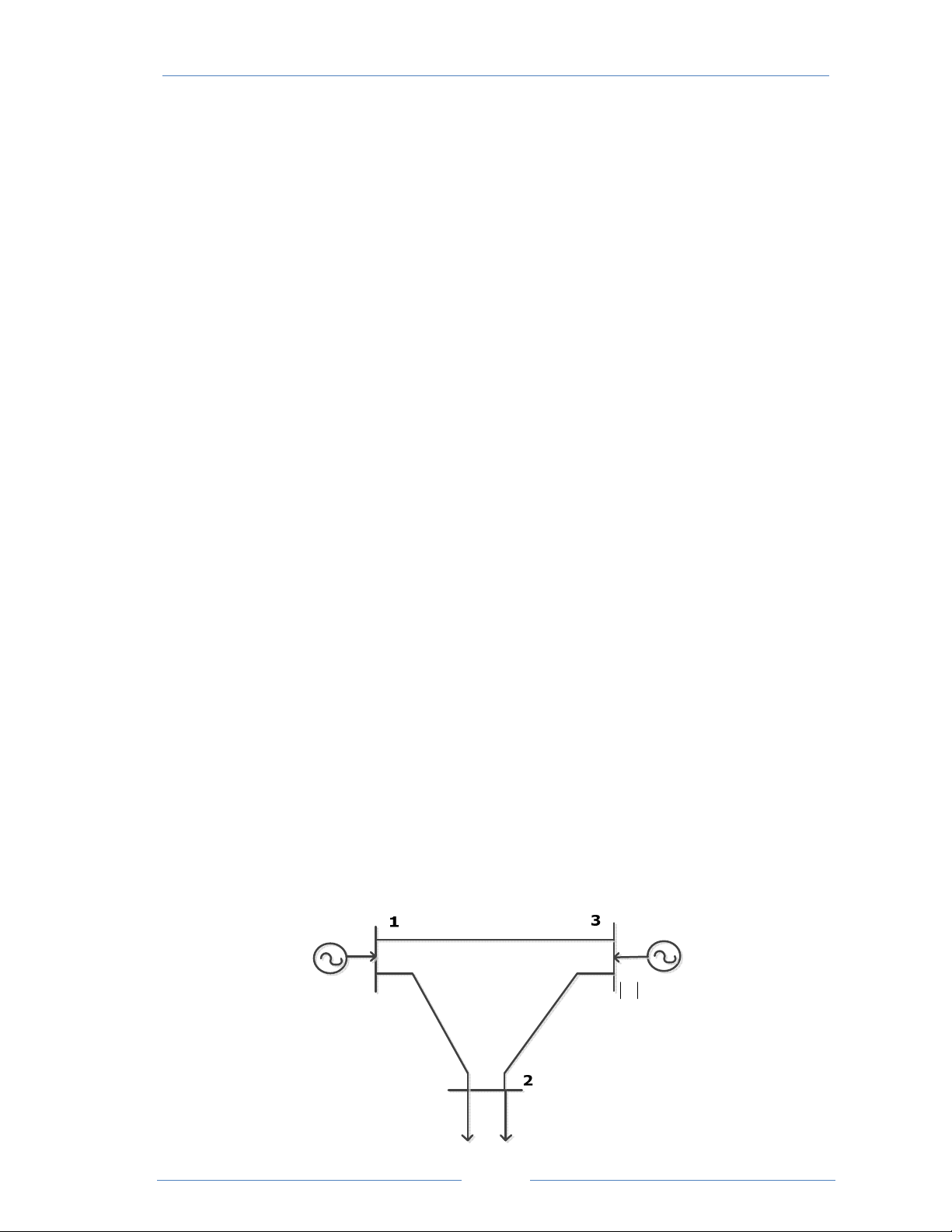
Cho mạng điện như hình vẽ: 1 2 3 6 5 4
Thông số các phần tử được cho như bảng sau: Đường dây
1 – 2 1 – 6 2 – 4 2 – 3 3 – 4 4 – 5 5 – 6 Điện kháng (pu) j0,04 j0,06 j0,03 j0,02 j0,08 j0,06 j0,05
a) Hãy xây dựng ma trận tổng dẫn Ybus
b) Hãy cải biên ma trận tổng dẫn khi có thêm một đường dây với điện kháng
dọc bằng j0,1pu được nối giữa nút 1 và 5 Bài giải
a) Xây dựng ma trận tổng dẫn Ybus Đường dây 1 – 2 1 – 6 2 – 4 2 – 3 3 – 4 4 – 5 5 – 6 Điện kháng (pu) j0,04 j0,06 j0,03 j0,02 j0,08 j0,06 j0,05 Y=1/X -25j -16,667j -33,333j -50j -12,5j -16,667j -20j 20
BÀI TẬP LƯỚI ĐIỆN
Các phần tử của ma trận tổng dẫn Ybus: Y = y + y = −j41,66667 11 12 16 Y = y + y + y = −j108,3333 22 12 23 24 Y = y + y = −j62,5 33 23 34 Y = y + y + y = −j62,5 44 24 34 45 Y = y + y = −j36,66667 55 56 45 Y = y + y = −j36.66667 66 16 56 Y = Y = −y Y = Y = −y Y = Y = 0 12 21 12 23 32 23 35 53 Y = Y = 0 Y = Y = −y Y = Y = 0 15 51 24 42 24 36 63 Y = Y = 0 Y = Y = 0 Y = Y = −y 13 31 25 52 45 54 45 Y = Y = 0 Y = Y = 0 Y = Y = 0 14 41 26 62 46 64 Y = Y = −y Y = Y = −y Y = Y = − y 16 61 16 34 43 34 56 65 56 Ma trận tổng dẫn: Y11 Y12 Y13 Y14 Y15 Y16 Y21 Y22 Y23 Y24 Y25 Y26 Y31 Y32 Y33 Y34 Y35 Y36 Y41 Y42 Y43 Y44 Y45 Y46 Y51 Y52 Y53 Y54 Y55 Y56 Y61 Y62 Y63 Y64 Y65 Y66 −j41,66667 j25 0 0 0 j16, 66667 j25 −j108,3333 j50 j33, 3333 0 0 0 j50 −j62,5 j12,5 0 0 Y = bus 0 j33, 3333 j12,5 −j62,5 j16, 66667 0 0 0 0 j16, 66667 −j36, 66667 j20 j16,66667 0 0 0 j20 −j36,66667 b)
Khi có thêm đường dây nối giữa nút 1 và 5 các thành phần sau trong ma trận bị thay đổi 21
BÀI TẬP LƯỚI ĐIỆN 1 ' Y = y + y + y = −j 25 + 16,66667 + = −j51,66667 11 ( 12 16 15 ) 0,1 1 ' Y = y + y + y = −j 20 + 16,66667 + = −j46,66667 55 ( 56 45 15 ) 0,1 ' ' Y = Y = − y = j10 15 51 ( 15) BÀI 10
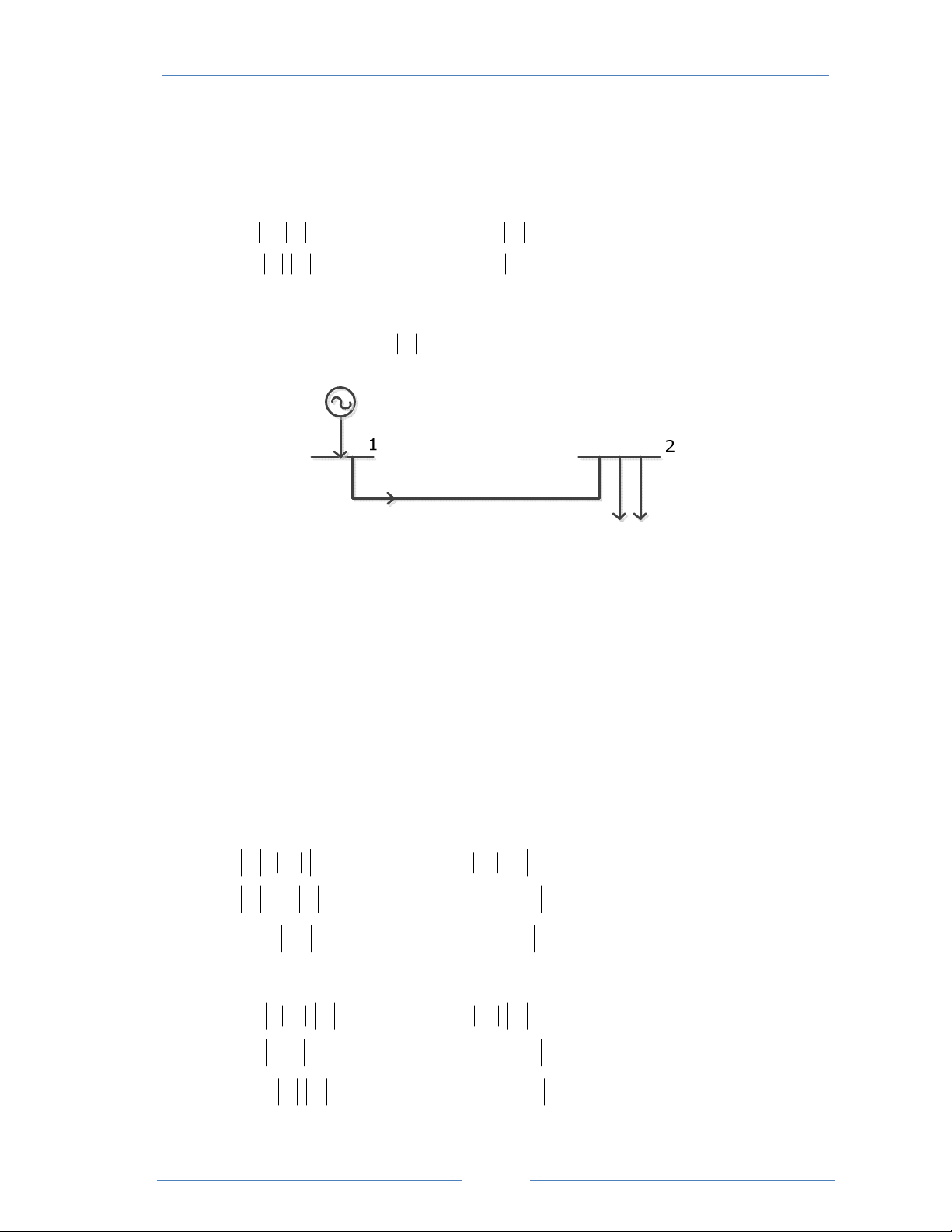
Cho hệ thống như hình vẽ, bỏ qua điện trở tác dụng, thông số của các đường dây được cho ở bảng sau: Đường dây
Tổng trở dọc Z, pu
Tổng dẫn ngang Y, pu 1 – 2 j0,20 j0,24 2 – 3 j0,10 j0,16 1 – 3 j0,25 j0,30
Tụ điện tại nút 2 có y20 = j0,3 pu
Điện kháng tại nút 3 có y30 = -j0,6 pu
a) Xác định ma trận tổng dẫn nút của HTĐ ba nút
b) Hãy cải biên ma trận tổng dẫn khi nút 2 bị loại bỏ 22
BÀI TẬP LƯỚI ĐIỆN Bài giải
a) Xác định ma trận tổng dẫn của HTĐ ba nút Đường dây Z (pu) 1/Z (pu) Y (pu) Y/2 (pu) 1 – 2 j0,2 -j5 j0,24 j0,12 2 – 3 j0,1 -j10 j0,16 j0,08 1 – 3 j0,25 -j4 j0,30 j0,15
Xây dựng ma trận tổng dẫn Ybus Y Y Y 11 12 13 Y = Y Y Y bus 21 22 23 Y Y Y 31 32 33 1 1 1 Y = + + . y + y
= j0,15 + j0,12 − j5 − j4 = −j8,73 11 ( 13 12 ) Z Z 2 13 12 1 1 1 Y = + + . y + y
= −j5 − j10 + j0,12 + j0,08 = −j14,5 22 ( 12 23 ) Z Z 2 12 23 1 1 1 Y = + + . y + y
= −j4 − j10 + j0,15 + j0,08 = −j14,3 33 ( 13 23 ) Z Z 2 13 23 −1 Y = Y = = j5 12 21 Z12 −1 Y = Y = = j4 13 31 Z13 1 Y Y − = = = j10 32 23 Z23 −j8,73 j5 j4 Y = j5 −14,5 j10 bus j4 j10 −j14,37 23
BÀI TẬP LƯỚI ĐIỆN
b) Khi nút 2 bị loại bỏ ma trận Ybus bị thay đổi ' ' Y Y mod 11 13 Y = bus ' ' Y Y 31 33 ' Y = Y + y = −j4 + j0,15 = −j3, 85 11 13 13 ' Y = Y + y + y
= −j4 + j0,15 − j0,6 = −j4, 45 33 13 13 30 −j3,85 j4 mod Y = bus j4 −j4, 45 BÀI 11
Cho hệ thống như hình vẽ:
1. Xác định ma trận tổng dẫn
2. Hãy cải biên ma trận khi có 1 tụ bù ngang với dung lượng 75 MVAr được nối
với nút 4 (điện áp nút giả sử bằng 1pu).
Dữ liệu hệ thống cho như sau (hệ đơn vị tương đối S = 100MVA ) cb Bus to bus R (pu) X (pu) B (pu) 1 – 2 0,02 0,06 0,06 1 – 3 0,08 0,24 0,05 2 – 3 0,06 0,18 0,04 2 – 4 0,08 0,24 0,05 2 – 5 0,02 0,06 0,02 3 – 4 0,01 0,04 0,01 4 – 5 0,03 0,10 0,04 24
BÀI TẬP LƯỚI ĐIỆN Bài giải
1. Xác định các thành phần của tổng dẫn Z = 0,02 + j0,06; y = j0,06 12 12 Z = 0,08 + j0,24; y = j0,05 13 13 Z = 0,06 + j0,18; y = j0,04 23 23 Z = 0,08 + j0,24; y = j0,05 24 24 Z = 0,01 + j0,04; y = j0,01 34 34 Z = 0,03 + j0,10; y = j0,04 45 45 Z = 0,02 + j0,06; y = j0,02 25 25 Đường dây Z 1/Z y y/2 1 – 2 0,02 + j0,06 5 – j15 j0,06 j0,03 1 – 3 0,08 + j0,24 1,25 – j3,75 j0,05 j0,025 2 – 3 0,06 + j0,18 1,667 – j3,75 j0,04 j0,02 2 – 4 0,08 + j0,24 1,25 – j3,75 j0,05 j0,025 2 – 5 0,02 + j0,06 5 – j15 j0,02 j0,01 3 – 4 0,01 + j0,04 5,88 – j23,53 j0,01 j0,005 4 – 5 0,03 + j0,10 2,752 – j9,174 j0,04 j0,02 1 1 1 Y = + + . y + y = 6,25 − j18,695 11 ( 13 12 ) Z Z 2 13 12 1 1 1 1 1 Y = + + + + . y + y + y + y = 12,92 − j38,67 22 ( 12 23 24 25 ) Z Z Z Z 2 12 23 24 25 1 1 1 1 Y = + + + . y + y + y = 8,8 − j32,33 33 ( 13 34 23 ) Z Z Z 2 13 34 23 1 1 1 1 Y = + + + . y + y + y = 9, 88 − j36, 40 44 ( 24 34 45 ) Z Z Z 2 24 34 45 1 1 1 Y = + + .(y + y = 7,75 − j24,14 5 45 ) 55 2 Z Z 2 25 45 Y = Y = −5 + j15 Y = Y = −1, 667 + j5 12 21 23 32 Y = Y = −1, 25 + j3, 75 Y = Y = 1 − ,25 + j3,75 13 31 24 42 Y = Y = 0 Y = Y = 5 − + j15 14 41 25 52 Y = Y = 0 Y = Y = 5 − , 88 + j23,53 15 51 34 43 Y = Y = 2 − ,752 + j9,174 Y = Y = 0 45 54 35 53 Ma trận tổng dẫn: 25
BÀI TẬP LƯỚI ĐIỆN 6,25 − j18,695 5 − + j15 1 − ,25 + j3,75 0 0 5 − + j15 12, 92 − j38,67 1 − ,667 + j5 −1,25 + j3,75 5 − + j15 Y = 1 − ,25 + j3,75 1 − ,667 + j5 8, 8 − j32,33 −5,88 + j23,53 0 bus 0 1 − ,25 + j3,75 5 − ,88 + j23,53 9, 88 − j36, 40 −2,752 + j9,174 0 5 − + j15 0 2 − ,752 + j9,174 7,75 − j24,14
2. Khi có tụ bù ngang tại nút 4
Khi có tụ bù ngang dung lượng 75MVAr nối với nút 4 ta có: 2 U .B 2Q 2.75 c jQ = j → B = = = 1,5 c 2 2 U .S 1.100 cb yc → = j0,75 2
Như vậy so với ma trận Ybus thì ma trận mod Y
chỉ thay đổi ở thành phần Y bus 44 ' Y = Y + y = 9, 88 − j35,65 44 44 c BÀI 12
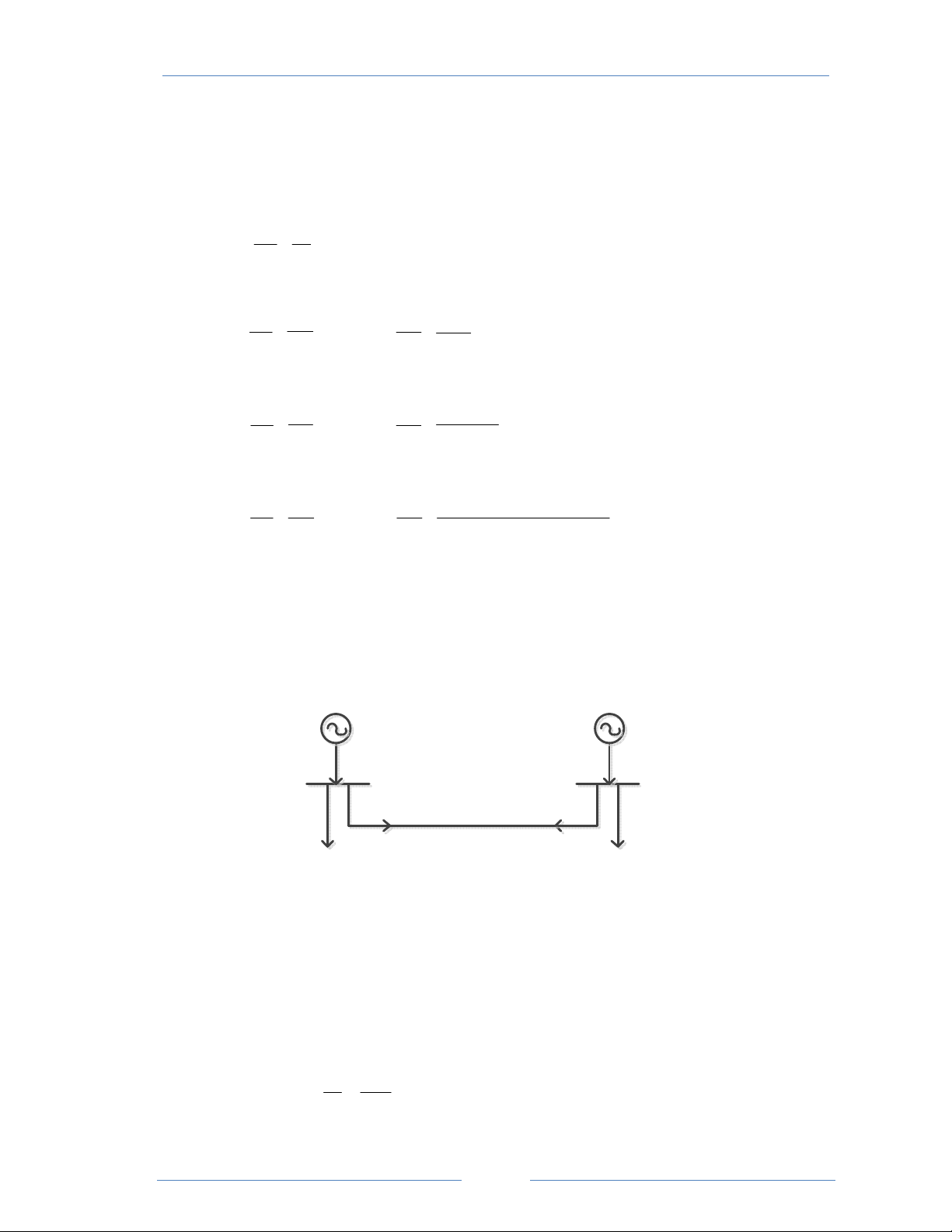
Cho hệ thống như hình vẽ SG1 jQ = j1,0 C2 0 V = 1 0 ∠ 1 Z = j0,5 L S S = 0,5 + j1,0 D1 D2 S S 1 2
Hãy tính điện áp tại nút 2 và công suất S1 sử dụng phương pháp lặp Gause. Xấp xỉ
ban đầu của điện áp các nút được lấy bằng 1,0pu và góc 0
0 . Yêu cầu thực hiện 3 bước lặp. Bài giải . S2 = P + jQ = S − + jQ = 0 − ,5 2 2 D2 G2 1 Z = j0,5 → y = = 2 − j L Z Ma trận tổng dẫn nút 26
BÀI TẬP LƯỚI ĐIỆN −j2 j2 Y = bus j2 − j2 Công thức lặp * * + 1 S 2 k 1 U = . Y . − 1 U 2 k 21 * Y 22 2 U * * ( ) 1 S2 1 0 − ,5 1 U = . Y .U − = . − j2.1 0 ∠ 2 (0) 1 21 * Y −j2 1 0 ∠ 22 2 U
= 1 − j0,25 = 1,030776∠ − 14,036243 * * ( ) 1 S2 1 0 − ,5 2 U = . − Y . 1 U = . − j2.1 0 ∠ 2 ( 1) 21 * Y −j2 1 + j0,25 22 2 U = 0,970143∠ − 14,036249 * * ( ) 1 S2 1 0 − ,5 3 U = . Y .U − = . − j2.1 0 ∠ 2 (2) 1 21 * Y
−j2 0,970143∠ −14,036249 22 2 U = 0,970261∠ − 14,931409 BÀI 13
Cho hệ thống như hình vẽ S S = 0,25 + jQ G1 G1 G2 0 V = 1 0 ∠ 1 Z = j0,5 L S S = 1,0 + j0,5 D1 D2 S S 1 2
Tính điện áp tại nút 2 và công suất S1 sử dụng phương pháp Gauss. Xấp xỉ ban
đầu của điện áp các nút được lấy bằng 1,0pu và góc 00. Yêu cầu thực hiện 4 bước lặp. Bài giải . . .
S2 = P + jQ = − SD2 + SG2 = 0 − ,75 + j(Q − 0,5) 2 2 G2 1 1 Z = j0,5 → y = = = −j2 L Z j0,5 c Ma trận tổng dẫn nút 27
BÀI TẬP LƯỚI ĐIỆN −j2 j2 Y = bus j2 − j2 Công thức lặp ( ) * Q = −I . 2 m U . ( . . . k 2 Y .U + Y . 2 U + Y . 2 U 3 21 1 22 23 ) * . + 1 S2 (k 1) U = . Y . − 1 U 2 (k ) 21 * Y 22 2 U Vậy * ( 0) Q = I − . = − ∠ ∠ + ∠ 2 U . I . 1 0. 2j.1 0 j2.1 0 2 m ( (0) . . Y .U + Y . 2 U 21 1 22 ) m ( ) (0) . P − jQ 1 2 2 1 − − '(1) 0,75 j0 = Y . − 1 U U . = (k ) 21 . − j2.1 0 ∠ 2 * Y 2j − 1 0 ∠ 22 2 U 0
= 1 − j0,375 = 1,0680∠ − 20,5560 (1) '(1) 0 U = U ∠δ = 1∠ − 20,5560 2 2 2 ( * 1) (1) Q = −I . . ( (1) . . = Y .U Y . + 2 U 21 1 22 ) 2 m 2 U = I − . 1 2 ∠ 0,5560. 2j.1 0 ∠ + j2.1 2 ∠ 0,5560 = 0,1273 m ( ) (1) . P − jQ 1 2 2 1 0 − ,75 − j0,1273 '(2) = − Y . 1 U U . = − ∠ (1) 21 . j2.1 0 2 * Y 2 − j 1 2 ∠ 0,5560 22 2 U 0 = 1,0003∠ − 21,9238 (2) '(2) U = U ∠δ = 1∠ − 21,92380 2 2 2 (2) ( ) * Q = I − . = 2 m U . ( (2) 2 . . 2 Y .U Y . + 2 U 21 1 22 ) = I − . 1 2 ∠ 1,9238. 2j.1 0 ∠ + j2.1 2 ∠ 1,9238 = 0,1446 m ( ) (2) . P − jQ 1 2 2 1 0 − ,75 − j0,1446 '(3) 0 = − Y . 1 U U . = − ∠ = ∠ − (2) 21 . j2.1 0 0, 9999 22,0170 2 * Y 2 − j 1 2 ∠ 1,9238 22 2 U (3) '(3 U = U ∠δ ) 0 = 1∠ − 22,0170 2 2 2 (3) ( ) * Q = I − . = 2 m U . ( (3) 3 . . 2 Y .U Y . + 2 U 21 1 22 ) = I − . 1 2 ∠ 2,0170. 2j.1 0 ∠ + j2.1 2 ∠ 2,0170 = 0,1459 m ( ) (3) . P − jQ 1 2 2 1 0 − ,75 − j0,1459 '(4) 0 = − Y . 1 U U . = − ∠ = ∠ − (3) 21 . j2.1 0 1,0 22,0238 2 * Y 2 − j 1 2 ∠ 2,0170 22 2 U ( 4 U ) '(4) 0 = U ∠δ = 1,0∠ − 22,0238 2 2 2 28
BÀI TẬP LƯỚI ĐIỆN BÀI 14
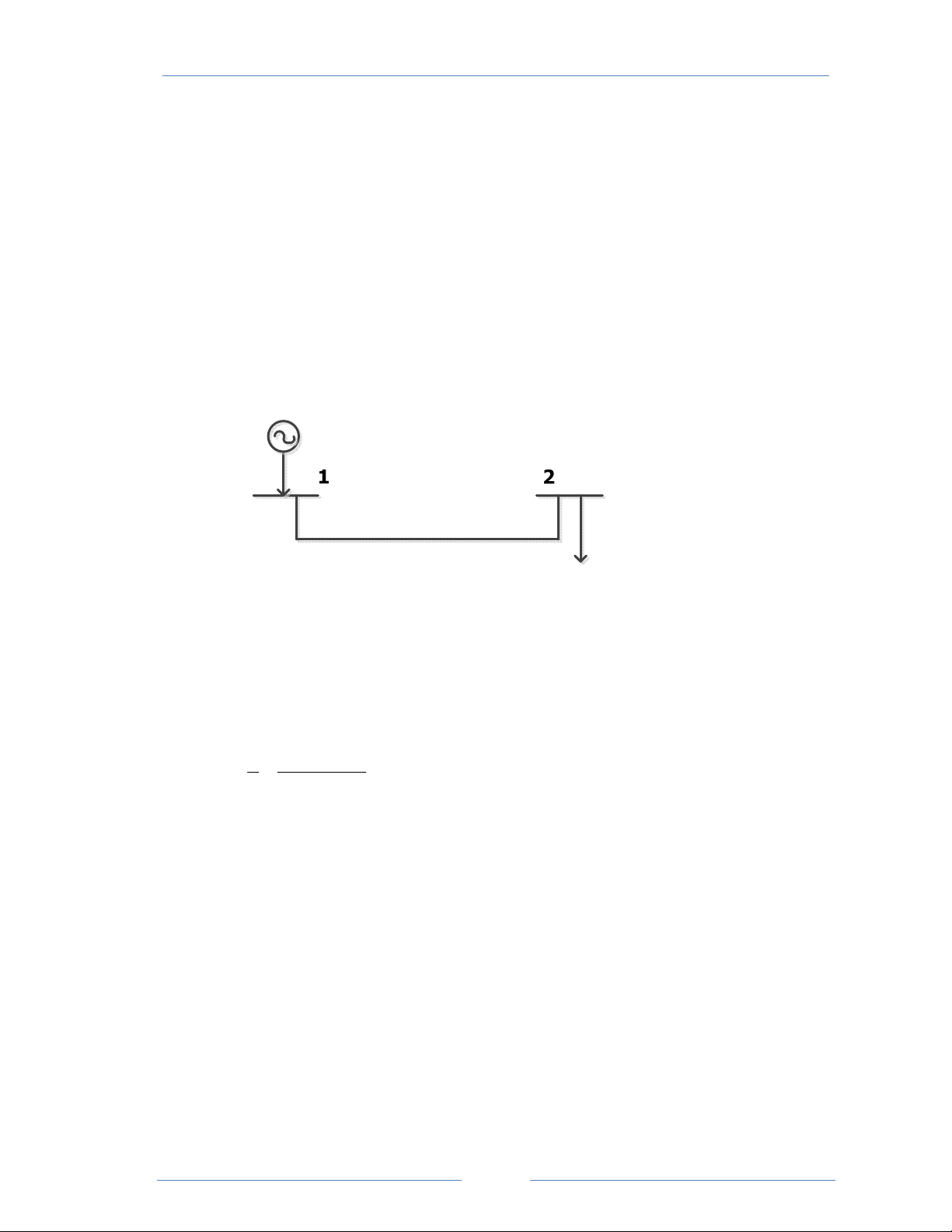
Cho mạng điện như hình vẽ. Nút 1 là nút cân bằng với U = 1 0 ∠ puvà nút 2 là nút 1
tải với S2 = 280 + j60 MVA. Tổng trở đường dây được cho trong hệ đơn vị tương đối
Scb = 100 MVA là Z = 0,02 + j0,04pu.
a) Sử dung phương pháp lặp Gauss – Seidel, hãy xác định điện áp nút 2 U2. Lấy xấp xỉ ban đầu U (0) 2
= 1,0 + j0,0 pu và thực hiện 4 bước lặp.
b) Giả sử sau vài bước lặp, điện áp tại nút 2 hội tụ với trị số U2 = 0,9 – j0,1pu.
Hãy xác định S1, tổn thất công suất tác dụng và tổn thất công suất phản kháng trên đường dây. SG1 Z = 0,02 + j0,04 L S = 280 + j60 MVA D2 Bài giải a) . . S2 = − SD2 = P + jQ = 2 − 80 − j60 MVA = 2 − ,8 − j0,6 pu 2 2 Z = 0,02 + j0,04 12 1 1 = = = − y 10 j20 12 Z 0,02 + j0,04 Y = y = 10 − j20 11 12 Y = y = 10 − j20 22 12 Y = Y = −y = 1 − 0 + j20 12 21 12 Ma trận tổng dẫn: 10 − j20 −10 + j20 Y = bus −10 + j20 10 − j20
Tại nút 2 biết P2 và Q2, Q2 không thay đổi trong các bước lặp 29
BÀI TẬP LƯỚI ĐIỆN Q = − Im{* 2 2 U . Y .U + Y .U 21 1 22 2 } (0) U = 1 0 ∠ 2 P − jQ 1 2 2 1 − + (1) 2, 8 j0,6 − Y .U U = . (0) 21 1 = . − 1 − 0 + j20 .1 0 ∠ 2 * ( ) Y 10 j20 − 1 0 ∠ 22 2 U = (0,92 − j0,1) pu . P − jQ 1 2 2 (2) − Y . 1 U U = . (1) 21 2 * Y 22 2 U 1 2 − ,8 + j0,6 = . − ( 1 − 0 + j20).1 0 ∠ = 0,90238 − j0,09808 10 − j20 0,92 + j0,1 . P − jQ 1 2 2 (3) − Y . 1 U U = . (2) 21 2 * Y 22 2 U 1 2 − ,8 + j0,6 = . − ( 1 − 0 + j20).1 0 ∠ = 0,9005 − j0,1
10 − j20 0,90238 + j0,09808 . P − jQ 1 2 2 (4) − Y . 1 U U = . (3) 21 2 * Y 22 2 U 1 2 − ,8 + j0,6 = . − ( 1 − 0 + j20).1 0 ∠ = 0,9006 − j0,1 10 − j20 0,90005 + j0,1 b) . 2 U = 0, 9 − j0,1 * * . * . . 1 S = 1 U . 1 I = 1 U . Y . 1 U + Y . 2 U 11 12 = 1 0 ∠ .(10 − j20).1 0
∠ + (−10 + j20).(0,9 − j0,1) = 3 − 1j . . 1 S = 3 + 1j → 1 S = 300 + j100 MVA
Tổn thất công suất trên đường dây . . . ∆ S = 1
S − S2 = (300 + j100) − (280 + j60) = 20 + j40 MVA
Tổn thất công suất tác dụng: P ∆ = 20 MW
Tổn thất công suất phản kháng: Q ∆ = 40MVAr 30
BÀI TẬP LƯỚI ĐIỆN BÀI 15
Cho hệ thống như hình vẽ. Hệ đơn vị tương đối có Scb = 100MVA. Bỏ qua điện trở
và điện dẫn phản kháng của đường dây.
a) Sử dụng phương pháp lặp Gausse – Seidel với xấp xỉ ban đầu U (0) 2 = 1,0pu; U (0) 3
= 1,0pu. Xác định điện áp nút 2 và 3. Yêu cầu thực hiện 2 bước lặp.
b) Sau vài bước lặp, điện áp nút hội tụ và có trị số U2 = 0,9 + j0,1pu; U3 =
0,95 – j0,05pu. Hãy xác định:
• Phân bố công suất trong mạng điện
• Tổn thất công suất trong mạng điện
• Công suất phát của nút cân bằng j1 / 30 SG1 400MW 320MW j0,0125 j0,05 300MW 270MW Bài giải a) Đường dây Z (pu) Y=1/Z (pu) 1 – 2 j0,033 -j30 1 – 3 j0,0125 -j80 2 – 3 j0,05 -j20 Y = y + y = −j110 11 12 13 Y = y + y = −j50 22 21 23 Y = y + y = −j100 33 31 32 Y = Y = −y = j30 12 21 12 Y = Y = −y = j80 13 31 13 Y = Y = −y = j20 23 32 23 31
BÀI TẬP LƯỚI ĐIỆN −j110 j30 j80 Y = j30 −j50 j20 bus j80 j20 −j100
Lấy xấp xỉ ban đầu (0) (0) U = 1∠0; U = 1∠0 2 3 . S2 = P + jQ = 400 + j320 MVA 2 2 . sch . S2 400 + j320 S2 = − = − = 4 − − j3,2 pu S 100 cb sch * S2 = P − jQ = 4 − + j3,2 2 2 . S3 = P + jQ = 300 + j270 MVA 3 3 . sch . S3 300 + j270 S3 = − = − = 3 − − j2,7 pu S 100 cb sch * S3 = P − jQ = 3 − + j2,7 2 2 Bước 1: (0) (0) . . P − jQ 1 2 2 (1) = − Y . 1 U − Y . 3 U U . (0) 21 23 2 * Y 22 2 U 1 4 − + j3,2 = . − j30.1 0 ∠ − j20.1 0 ∠ = 0,936 − j0,08 j50 − 1 0 ∠ (0) (1) . . P − jQ 1 3 3 (1) = − Y . 1 U − Y . 2 U U . (0) 31 32 3 * Y 33 3 U 1 3 − + j2,7 = . − j80.1 0 ∠ − j20.
(0,936 − j0,08) = 0,9602 − j0,046 −j100 1 0 ∠ Bước 2: (1) (1) . . P − jQ 1 2 2 (2) = − Y . 1 U − Y . 3 U U . (1) 21 23 2 * Y 22 2 U 1 4 − + j3,2 = . − j30.1 0 ∠ − j20.
(0,9602 − j0,046) = 0,9089 − j0,0974 −j50 0,936 + j0,08 (1) (2) . . P − jQ 1 3 3 (2) = − Y . 1 U − Y . 2 U U . (1) 31 32 3 * Y 33 3 U 1 3 − + j2,7 = . − j80.1 0 ∠ − j20.
(0,9089 − j0,0974) = 0,9522 − j0,0493 − j100 0,9602 + j0,046 32
BÀI TẬP LƯỚI ĐIỆN b) . 1 U = 1 0 ∠ . 2 U = 0, 9 − j0,1 . 3 U = 0, 95 − j0,05 . . U − U = 0,1 + j0,1 ( = − U − U )* . . 1 2 0,1 j0,1 1 2 . . U − U = 0 − ,05 − j0,05 ( = − + U − U )* . . 2 3 0,05 j0,05 2 3 . . * U − U = 0,05 + j0,05 ( . . 1 3 = 0,05 − j0,05 1 U − 3 U ) . . U − U = 0 − ,1 − j0,1 ( = − + U − U )* . . 2 1 0,1 j0,1 2 1 . . U − U = 0 − ,05 − j0,05 ( = − + U − U )* . . 3 1 0,05 j0,05 3 1 . 1 U .( . . . − − 1 U 2 U ) . 0,1 j0,1 1 S 2 = = 1 0 ∠ . = 3 + j3 → 1 S 2 = 300 + j300MVA * 1 − j Z12 30 . 2 U .( . . . − − + 2 U 1 U ) 0,1 j0,1 S21 = = (0,9 − j0,1) . . = 3 − − j2, 4 → S21 = 3 − 00 − j240MVA * 1 − j Z12 30 . 1 U .( . . . − − 1 U 3 U ) . 0,05 j0,05 1 S 3 = = 1 0 ∠ . = 4 + j4 → 1 S 3 = 400 + j400MVA * 0 − ,0125j Z13 . 3 U .( . . − − + 3 U 1 U ) . . 0,05 j0,05 S31 = = 1 0 ∠ . = 4 − − j3,6 → 1 S 3 = 4 − 00 − j360MVA * 0 − ,0125j Z13 . 2 U .( . . . − − + 2 U 3 U ) 0,05 j0,05 S23 = = (0,9 − j0,1) . . = 1 − − j0,8 → 1 S 3 = 1 − 00 − j80MVA * 0 − ,05j Z23 . 3 U .( . . . − − 3 U 2 U ) . 0,05 j0,05 S32 = = 1 0 ∠ . = 1 + j0,9 → 1 S 3 = 100 + j90MVA * 0 − ,05j Z23
Tổn thất công suất trên các đường dây: . . . ∆ 1 S 2 = 1
S 2 + S21 = (3 + j3) + (3 − j2, 4) = −j0,6 . . . ∆ 1 S 3 = 1 S 3 + S31 = (4 + j4) + ( 4 − − j3,6) = j0,4 . . . ∆ S23 = S23 + S32 = ( 1
− − j0,8) + (1 + j0,9) = j0,1
Tổn thất công suất của mạng điện: 33
BÀI TẬP LƯỚI ĐIỆN . . . . ∆ S = ∆ S + ∆ 1 S 3 + ∆ S23 = j1,1 12 . . ∆ S
= ∆ S.S = j1,1.100 = j110 MVA (MVA ) cb
(mạng điện không xét tới điện dẫn tác dụng và điện trở của đường dây)
Công suất của các nút: * * . . 1 S = 1 U .I = 1 U .( . . . 1 Y . 1 U + Y .U + Y . 3 U 11 12 2 13 ) = 1.(−j110.1 0
∠ + j30.(0,9 − j0,1) + j80.(0,95 − j0,05)) = 7 − j7 . 1 S = 7 + j7 . . 1 S (MVA) = 1 S .S = 700 + j700 cb BÀI 16
Cho mạng điện như hình vẽ. Hệ đơn vị tương đối Scb = 100 MVA. Bỏ qua điện trở
và điện dẫn phản kháng của đường dây.
a) Sử dụng phương pháp lặp Gauss – Seidel với xấp xỉ ban đầu U (0) 2 = 1,1pu; U (0) 3
= 1,03pu. Hãy xác định điện áp tại nút 2 và 3. Yêu cầu thực hiện 2 bước lặp.
b) Sau vài bước lặp điện áp hội tụ và có trị số:
V = 1,001243∠ − 2,1 = 1,000571 − j0,0366898 2 V = 1,03 1 ∠ ,36851 = 1,029706 + j0,246 3 Hãy xác định:
Phân bố công suất trong mạng điện
Tổn thất công suất trong mạng điện
Công suất phát của nút cân bằng j0, 05 S P = 300MW G1 3 V = 1, 025 0 ∠ 1 V = 1, 03 3 j0, 025 j0, 025 400MW 200MVAr 34
BÀI TẬP LƯỚI ĐIỆN Bài giải a) Đường dây Z (pu) y = 1/Z (pu) 1 – 2 j0,025 -j40 1 – 3 j0,05 -j20 2 – 3 j0,025 -j40 Y = y + y = −j60 11 12 13 Y = y + y = −j80 22 21 23 Y = y + y = −j60 33 31 32 Y = Y = −y = j40 12 21 12 Y = Y = −y = j20 13 31 13 Y = Y = −y = j40 23 32 23 −j60 j40 j20 → Y = j40 −j80 j40 bus j20 j40 −j60 . S2 = P + jQ = 400 + j200MVA 2 2 . sch * S2 sch = − = − − → = − + S 4 j2 S2 4 j2pu 2 S cb . S3 = P + jQ = 400MVA 3 3 P = 3pu 3 Bước lặp 1 (1) . (P − jQ 1 2 2 ) . . = − Y . 1 U − Y . 3 U 2 U . (0) 21 23 * Y 22 2 U 1 − + 4 j2 = . − j40.1,025 0 ∠ − j40.1,03 0 ∠ j80 − 1 0 ∠
= 1,0025 − j0,05 = 1,003746 2 ∠ ,855279 (0) * (1) . . . Q = − Im 3 3 U . Y . 1 U + Y . 2 U + Y . 3 U 31 32 33 = − Im{ 0 0 1,03 0 ∠ .20j.1,05 0 ∠ + 40j. (1,0025 − j0,05) 0 − j60.1,03 0 ∠ } = 1,236 35
BÀI TẬP LƯỚI ĐIỆN ( (1) P − jQ 1 ) . . 3 3 (1) ' U = . − Y . 1 U − Y . 2 U 3 (0) 31 32 . Y 33 3 U 1 − 3 − j1,236 = . − j20.1,025 0 ∠ − j40. (1,0025 − j0,05) j60 1,03 0 ∠ 0 = 1,03 + j0,0152 = 1,03011 0 ∠ ,846045 (1) (1) ' 0 U = U ∠δ = 1,03 0 ∠ ,846045 = 1,0299 + j0,0152 3 3 3 Bước lặp 2 (P − jQ 1 ) (1) (2) . . . 2 2 = − Y . 1 U − Y . 3 U 2 U . (1) 21 23 * Y 22 2 U 1 4 − + j2 = .
− j40.1,025∠0 − j40.(1,03 + j0,0152) −j80 (1,0025 + j0,05) = 1,0001 − j0,0409 (1) * (2) (1) (2) . . . Q = − Im 3 3 U . Y . 1 U + Y . 2 U + Y . 3 U 31 32 33 0 20j.1,025 0 ∠
+ 40j.(1,0001 − j0,0409)
= − Im (1,0299 − j0,0152). −j60. (1,0299 + j0,0152) = 1,3671 ( (2) P − jQ 1 ) (2) . . 3 3 (2) ' U = . − Y . 1 U − Y . 2 U 3 (1) 31 32 . Y 33 3 U 1 − 3 − j1,3671 = . − j20.1,025 0 ∠ − j40. (1,0001 − j0,0409) j60 1,0299 − j0,0152 0 = 1,0298 + j0,0216 = 1,03 1 ∠ ,20146 (2) (2) ' 0 U = U ∠δ = 1,03 1 ∠ ,20146 3 3 3 b) ( . =1,001243∠ −2,1 U2 ) 0 ( . = ∠ − U ) 0 1,03 1,36851 3 ( = + = − U − U ) 0,0244 j0,0367 (U −U )* . . . . 0,0244 j0,0367 1 2 1 2 ( = − − = − + U − U ) 0,0244 j0,0367 (U −U )* . . . . 0,0244 j0,0367 2 1 1 2 ( = 0 − ,0291 − j0,0613 = 0 − ,0244 + j0,0367 2 U − 3 U ) ( 2U− 3U)* . . . . ( = + = − U − U ) 0,0291 j0,0613 (U −U )* . . . . 0,0291 j0,0613 3 2 3 2 ( * . . = 0 − ,0047 + . . j0,0246 = 0 − ,0047 − j0,0246 1 U − ( 1U− 3U) 3 U ) ( = + = − U − U ) 0,0047 j0,0246 (U −U )* . . . . 0,0047 j0,0246 3 1 3 1 36
BÀI TẬP LƯỚI ĐIỆN (U −U )* . . . . 0,0244 − j0,0367 1 2 0 ( ) 1 S 2 = 1 U . = 1,025 0 ∠ . = 1,5047 + j1,0004 * −j0,025 1 Z 2 (U −U )* . . . . 0 − ,0244 + j0,0367 2 1 0 ( ) S21 = 2 U . = 1,001243∠ − 2,1 . = −1,5047 − j0,9227 * −j0,025 1 Z 2 (U −U )* . . . . 0 − ,0047 + j0,0246 1 2 0 ( ) 1 S 3 = 1 U . = 1,025 0 ∠ . = 0 − ,5043 − j0,0964 * −j0,005 1 Z 3 (U −U )* . . . . 0,0047 − j0,0246 3 1 0 ( ) S31 = 3 U . = 1,03 1 ∠ ,36851 . = 0,5043 + j0,1089 * −j0,005 1 Z 3 (U −U )* . . . . −0,0291 + j0,0613 2 3 0 ( ) S23 = 2 U . = 1,023∠ − 2,1 . = 2 − , 4961 − j1,0747 * −j0,025 Z23 (U −U )* . . . . (0,0291 − j0,0613) 3 2 0 S32 = 3 U . = 1,03 1 ∠ ,36851 . = 2, 4961 + j1,2589 * −j0,025 Z 23 . . . ∆ 1 S 2 = 1 S 2 + S21 = j0,0777 . . . ∆ 1 S 3 = 1 S 3 + S31 = j0,0125 . . . ∆ S23 = S23 + S32 = j0,1842
tổn thất công suất trong mạng điện: . . . . ∆ S = ∆ S + ∆ S + ∆ S 12 13 23 . ∆ S = j27, 44
Công suất phát nút cân bằng: . . * 1 S = 1 U . 1 I * * . * 1 S = 1 U .I = 1 U .( . . . 1 Y . 1 U + Y . 2 U + Y . 3 U 11 12 13 ) = 1,025.( 0 0 0 −j60.1,025 0 ∠
+ j40.1,001243∠ − 2,1 + j20.1,03 1 ∠ ,36851 ) = 1 − j0,9051
Vậy công suất phát nút cân bằng: . → S = 1 + j0,9051 1 . . 1 S (MVA) = 1 S .S = 100 + j90,51 MVA cb 37
BÀI TẬP LƯỚI ĐIỆN BÀI 17
Cho hệ thống điện như hình vẽ. Hệ đơn vị tương đối Scb = 100MVA. Công suất tác
dụng và công suất phản kháng tại nút 2 như sau:
P = 10 V . V .cos (106,26 − δ + δ + 10 V .cos −73,74 2 1 ) 2 0 ( 0 2 1 2 2 )
Q = 10 V . V .sin (106,26 − δ + δ + 10 V .sin −73,74 2 1 ) 2 0 ( 0 2 1 2 2 )
Sử dụng phương pháp Newton – Raphson, hãy xác định điện áp tại nút 2 sau 2
bước lặp. Lấy xấp xỉ ban đầu 0 V = 1, 0pu; δ = 0 2 2 0 V = 1 0 ∠ 1 y = 2,8 − j9,6 12 S = 150MW D1 S = 50MVAr D2 Bài giải
Xác định ma trận tổng dẫn Ybus: Y = y = 2,8 − j9,6 11 12 Y = y = 2,8 − j9,6 22 21 Y = Y = −y = 2 − ,8 + j9,6 12 21 12 0 0 2,8 − j9,6 2 − ,8 + j9,6 1 0∠ − 73,74 10 1 ∠ 06,26 → Y = = bus 0 0 2 − ,8 + j9,6 2, 8 − j9,6 10 1 ∠ 06,26 10∠ − 73,74 . . P . Y . .cos (δ − δ − θ ) . Y . .cos = + δ − δ − θ 2 21 2 1 21 22 ( 2 2 22 ) 2 U 1 U 2 U . . P . 1 0. .cos (δ − δ −106,26 10. .cos 73,74 = + U U 2 1 ) . 0 2 ( ) 2 1 2 U P = 10. . .cos (106,26 − δ + δ + 10. .cos 7 − 3,74 U U 2 1 ) 2 . . . 0 2 ( ) 1 2 2 U . . Q . Y . .sin(δ − δ − θ ) . Y . .sin = + δ − δ − θ 2 21 2 1 21 22 ( 2 2 22 ) 2 U 1 U 2 U . . Q . 1 0. .sin(δ − δ −106,26 10. .sin 73,74 = + U U 2 1 ) . 0 2 ( ) 2 1 2 U Q = 1 − 0. .
.sin (106,26 − δ + δ −10. .sin 7 − 3,74 U U 2 1 ) 2 . . . 0 2 ( ) 1 2 2 U
Xây dựng ma trận Jacobi: 38
BÀI TẬP LƯỚI ĐIỆN P ∂ . . 2 = 10 . .sin (106,26 − δ + δ 2 1 ) 1 U 2 U ∂δ2 P ∂ . = 10 .cos (106,26 − δ + δ ) . 2 + 20 .cos 7 − 3,74 2 1 ( ) 1 U 2 U U ∂ 2 Q ∂ . . 2 = 10 . .cos (106,26 − δ + δ 2 1 ) 1 U 2 U ∂δ2 Q ∂ . = 1 − 0 .sin (106,26 − δ + δ ) . 2 − 20 .sin 7 − 3,74 2 1 ( ) 1 U 2 U U ∂ 2 (0) U = 1
Lấy xấp xỉ ban đầu: 2 (0) δ = 0 2 Bước lặp 1: (0) schd (0) ∆P = P − P = 1 − ,5 − 0 = 1 − ,5 2 2 2 (0) schd (0) Q ∆ = Q − Q = −0,5 − 0 = −0,5 2 2 2 9,6 2, 8 (0) J = −2,8 9,6 (0) (0) (0) P ∆ ∆δ −1,5 9,6 2, 8 ∆δ 2 (0) 2 2 = J . ↔ = . (0) (0) (0) Q ∆ ∆ U 0 − ,5 −2,8 9,6 ∆ U 2 2 2 (0) ∆δ = − (1) (0) (0) 0 0,13
δ = δ + ∆δ = −0,13rad = −7,4485 2 → 2 2 2 → (0) (1) (0) (0) ∆ U = 0 − ,09 U = U + ∆ U = 0,91pu 2 2 2 2 Bước lặp 2: (1) P = 1 − ,340309 2 (1) Q = 0 − ,38219 2 (1) schd (1) P ∆ = P − P = ( − 1 − ,340309) + 1,5 − 0 = 0 − ,159691 2 2 2 (1) schd (1) Q ∆ = Q − Q = 0 − ,5 − ( 0 − ,38219) = −0,117781 2 2 2 8,3319 1,0751 (1) J = 3 − ,6589 8,3159 (1) (1) P ∆ ∆δ (1) 0 − ,159691 8,3319 1,0751 ∆δ 2 (1) 2 = J . 2 ↔ = . (1) Q ∆ ∆ U (1) (1) 0 − ,117781 3 − ,6589 8,3159 ∆ U 2 2 2 (1) (2) (1) (1) ∆δ = 0 − ,0164
δ = δ + ∆δ = −0,15rad 2 2 2 2 → → (1) (2) (1) (1) ∆ U = 0 − ,021 U = U + ∆ U = 0,889pu 2 2 2 2 BÀI 18
Cho mạng điện như hình vẽ. Hệ đơn vị tương đối có Scb = 100MVA. Bỏ qua điện
trở và điện dẫn phản kháng của đường dây.
a) Chứng minh rằng công suất tác dụng tại nút 2 và nút 3 được diễn tả như sau: 39
BÀI TẬP LƯỚI ĐIỆN P = 40 V V cos ( 0
90 − δ + δ + 20 V V cos 90 − δ + δ 2 2 1 2 1 ) 2 3 ( 2 3 ) P = 20 V V cos ( 0
90 − δ + δ + 20 V V cos 90 − δ + δ 3 3 1 3 1 ) 3 2 ( 3 2 ) Q = 2
− 0 V V sin(90 − δ + δ ) + 20 V V sin(90 − δ + δ ) 2 0 + 40 V 3 3 1 3 1 3 2 3 2 3
b) Sử dụng phương pháp Newton – Raphson hãy xác định điện áp tại nút 2 và
nút 3 với xấp xỉ ban đầu (0) (0) δ = 0; V = 1,0; δ = 0 . 2 3 3 y = −j40 S 12 P = 100MW G1 3 y = −j20 y = −j20 13 23 V = 1,05 2 V = 1,0 0 ∠ 1 500MW 400MVAr Bài giải a) . SD3 = 500 + j40 . → S3 = 5 − 00 − j400MVA . → S3 = 5 − − j4(pu) 0 Y = y + y = −j60 = 60∠ − 90 11 12 13 0 Y = y + y = −j60 = 60∠ − 90 22 12 23 0 Y = y + y = −j40 = 40∠ − 90 33 31 32 Y = Y = −y = j40 12 21 12 Y = Y = −y = j20 13 31 13 Y = Y = −y = j20 23 32 23 −j60 j40 j20 60∠ − 90 40∠90 20∠90 Y = j40 −j60 j20 = 40∠90 60∠ − 90 20∠90 bus j20 j20 −j40 20∠90 20∠90 40∠ − 90 Vậy: . P = δ − δ − θ + −θ + δ − δ − θ 2 U . Y U .cos Y U .cos Y U .cos 2 21 1 ( 2 1 21) 22 2 ( 22 ) 23 3 ( 2 3 23 )
P = 40 U U .cos (δ − δ − 90 ) 2 0 + 60 U .cos ( 0 90 ) + 20 U U .cos ( 0 δ − δ − 90 2 1 2 2 1 2 2 3 2 3 ) P = 40 U U .cos ( 0
δ − δ − 90 ) + 20 U U .cos ( 0 90 − δ + δ 2 1 2 2 1 2 3 2 3 ) 40
BÀI TẬP LƯỚI ĐIỆN . P = δ − δ − θ + δ − δ − θ + −θ 3 U . Y U .cos Y U .cos Y U .cos 3 31 1 ( 3 1 31) 32 2 ( 3 2 32 ) 23 3 ( 33)
P = 20 U U .cos δ − δ − 90
+ 20 U U .cos δ − δ − 90 + 40 U .cos 90 3 3 1 ( 3 1 ) 2 3 ( 3 2 ) 2 0 0 ( 0 ) 3 P = 20 U U .cos ( 0
90 − δ + δ ) + 20 U U .cos ( 0 90 − δ + δ 3 1 3 3 1 2 3 3 2 ) . Q = δ − δ − θ + δ − δ − θ + −θ 3 U . Y U .sin Y U .sin Y U .sin 3 31 1 ( 3 1 31) 32 2 ( 3 2 32 ) 23 3 ( 33)
Q = 20 U U .sin δ − δ − 90
+ 20 U U .sin δ − δ − 90 + 40 U .sin 90 3 3 1 ( 3 1 ) 2 3 ( 3 2 ) 2 0 0 ( 0 ) 3 Q = 2
− 0 U U .sin(90 − δ + δ ) − 20 U U .sin(90 − δ + δ ) 2 0 0 + 40 U 3 1 3 3 1 2 3 3 2 3 b) Ma trận Jacobi: P ∂ P ∂ P ∂ 2 2 2 ∂δ ∂δ ∂ U 2 3 3 P P P ∂ ∂ ∂ 3 3 3 J = ∂δ ∂δ ∂ U 2 3 3 Q ∂ Q ∂ Q ∂ 3 3 3 ∂δ ∂δ ∂ U 2 3 3
Các phần tử của ma trận Jacobi: . . P ∂ 2 = 40 1 U 2 U .sin (90 − δ + δ ) . . 0 + 20 2 U 3 U .sin 90 − δ + δ 2 1 ( 0 2 3) ∂δ2 . . P ∂ 2 = 2 − 0 2 U 3 U .sin ( 0 90 − δ + δ 2 3 ) ∂δ3 . P ∂ 2 = 20 2 U .cos ( 0 90 − δ + δ 2 3 ) ∂ U3 . . P ∂ 3 = 2 − 0 2 U 3 U .sin ( 0 90 − δ + δ 3 2 ) ∂δ2 . . P ∂ 3 = 20 1 U 3 U .sin (90 − δ + δ ) . . 0 + 20 2 U 3 U .sin 90 − δ + δ 3 1 ( 0 3 2) ∂δ3 . P ∂ . 3 = 20 ( 0 0 − δ + δ ) + 20 U .cos ( 0 2 90 − δ + δ 3 1 3 2 ) 1 U .cos 9 ∂ U3 . . Q ∂ 3 = 2 − 0 2 U 3 U .cos ( 0 90 − δ + δ 3 2 ) ∂δ2 . . Q ∂ 3 = 20 1 U U3 .cos (90 − δ + δ ) . . 0 + 20 2 U 3 U .cos 90 − δ + δ 3 1 ( 0 3 2 ) ∂δ3 . Q ∂ 3 = 2 − 0 1 U .sin (90 − δ + δ ) . 0 − 20 2 U .sin 90 − δ + δ 3 1 ( 0 3 2 ) . ∂ 3 U Vậy: 41
BÀI TẬP LƯỚI ĐIỆN (1) schd (1) ∆P = P − P = 4 − 3,7696 = 0,2304 2 2 2 (1) schd (1) ∆P = P − P = 5 − + 4,6011 = 0 − ,3989 3 3 3 (1) schd (1) ∆Q = Q − Q = −4 + 3, 4782 = −0,5217 3 3 3 (1) (2) (1) (1) ∆δ = 0,0006 δ = δ + ∆δ = 0,0275 + 0,0006 = 0,0281rad 2 2 2 2 (1) (2) (1) (1) ∆δ = 0 − ,0126 → δ = δ + ∆δ = 0 − ,1078 − 0,0126 = 0 − ,1204rad 2 3 3 3 (1) (2) (1) (1) ∆ U = 0 − ,0175 U = U + ∆ U = 0,9231 − 0,0175 = 0,9056pu 3 3 3 3 BÀI 19 138,6 + j45,2MVA V = 1,05pu 1 305,6MW V = 1,0pu 2 P = 50MW G2
Dữ liệu đường dây cho trong hệ đơn vị tương đối cơ bản với Scb = 100 MVA. Đường dây Tổng trở (pu) 1 – 2 0,02 + j0,04 2 – 3 0,01 + j0,03 1 – 3 0,0125 + j0,025
Sử dụng phương pháp lặp Gause – Seidel với 2 bước lặp với xấp xỉ ban đầu:
U = 1,0pu; δ = 0 . Hãy xác định: 3 2
a) Điện áp tại các nút trong mạng điện
b) Công suất tác dụng và công suất phản kháng của nhà máy điện cân bằng
c) Xác định dòng công suất trên đường dây và tổn thất công suất trong mạng điện. 42
BÀI TẬP LƯỚI ĐIỆN Bài giải a)
Xây dựng ma trận tổng dẫn nút: Z = (0,02 + j0,04) 12 Z = 0,01 + j0,03 12 ( ) Z = 0,0125 + j0,025 12 ( ) 1 1 Y = y + y = + = 26 − j52 11 12 13 0,02 + j0,04 0,0125 + j0,025 1 1 Y = y + y = + = 20 − j50 22 12 23 0,02 + j0,04 0,01 + j0,03 1 1 Y = y + y = + = 26 − j62 33 31 31 0,0125 + j0,025 0,01 + j0,03 Y = Y = −10 + j20 12 21 Y = Y = 1 − 6 + j32 13 31 Y = Y = 1 − 0 + j30 32 23 . .
S3 = 138,6 + j45,2 → S3 = 1,382 + j0, 452(pu) P = 3 − 05,6 + 50 = 2 − 55,6 (MW) → P = 0 − ,2556(pu) 2 2 Bước lặp 1 (0) . . 1 P − jQ (1) 3 3 U = . − Y . 1 U − Y . 2 U 3 (0) 31 32 * Y33 U3 1 −1,386 + j0, 452 (1) U = . − (−16 + j32) 0 .1,05 0 ∠ − (−10 + j30).1 3 0 26 − j62 1 0 ∠ (1) U = 1,0124 − j0,0146 3 Q = − Im{ (0) (0) (1) * . . . (1) 2 U . Y . 1 U + Y . 2 U + Y . 3 U 2 21 22 23 } ( 1 − 0 + j20) 0 .1,05 0 ∠ + (20 − j50) 0 .1 0 ∠ + 0 = − Im 1 0 ∠ . ( + 1
− 0 + j30).(1,012 − j0,0146) = −1,518 (1) (1) . . 1 P − jQ '(1) 2 2 U = . − Y 1 U − Y 3 U 2 (0) 21 23 * Y22 2 U −2,556 + j1,518 1 − ( 1 − 0 + j20) 0 .1,05 0 ∠ − (−10 + j80). = 0 ( 1 0 ∠ − ). 20 j50 . (1,0124 − j0,0146) = 0,984∠ − 2,3788 (1) . (1) 0 2 U = U ∠δ = 1∠ − 2,3788 2 2 43
BÀI TẬP LƯỚI ĐIỆN Bước lặp 2 (1) . . 1 P − jQ (2) 3 3 U = . − Y . 1 U − Y . 2 U 3 (1) 31 32 * Y33 3 U (2) U = 1,0104 − j0,0337 3 Q = − Im{ (1) (1) (2) * . . . (2) 2 U . Y . 1 U + Y . 2 U + Y . 3 U 2 21 22 23 } = 0 − ,791 (2) (2) . . 1 P − jQ '(2) 2 2 U = . − Y 1 U − Y 3 U 2 (1) 21 23 * Y22 2 U 0 = 0,994∠ − 3,21 (2) . (2) 0 2 U = U ∠δ
= 1∠ − 3,21 = 0,9984 − j0,0560 2 2
b) Công suất NMNĐ 1 S = 1 U . 1 I = 1 U .(Y . 1 U + Y . 2 U + Y . 3 U 11 12 13 )* (2) (2) . . * . . . . = 3,515 + j1,259 (pu)
c) Xác định dòng công suất trên đường dây . . . 0 0 0 1 U = 1,05 0 ∠ ; 2 U = 1∠ − 3,21 ; 3 U = 1,011∠ −1,91 (U − U )* . . . . 1 2 = 0,0516 − j0,056 1 U − 2 U = 0,0516 + j0,056 1 U − 3 U = 0,0396 + j0,0337 → ( 1 U − 3 U )* . . . . = 0,0396 − j0,0337 . . U − U = 0 − ,012 − j0,022 ( U − U )* . . 2 3 2 3 = 0 − ,012 + j0,022 (U −U )* . . . . 1 2 (0,0516 − j0,056) 1 S 2 = 1 U . = 1,05. = 1,7178 + j0, 4956 * 0,02 − j0,04 1 Z 2 (U −U )* . . . . 2 1 0 − ,0516 + j0,056 0 ( ) S21 = 2 U . = 1∠ − 3,21 . = 1 − ,6598 − j0,3796 * 0,02 − j0,04 Z21 (U −U )* . . . . 2 3 0 − ,012 + j0,022 0 ( ) S23 = 2 U . = 1∠ − 3,21 . = 0 − ,7866 − j0,0961 * 0,01 − j0,03 Z23 (U −U )* . . . . 3 2 (0,012 − j0,022) S32 = 3 U . = 1,011∠ −1,91. = 0,7929 + j0,1152 * 0,01 − j0,03 Z32 44
BÀI TẬP LƯỚI ĐIỆN (U −U )* . . . . 1 3 (0,0396 − j0,0337) 1 S 3 = 1 U . = 1,05. = 1,7926 + j0,7644 * 0,0125 − j0,025 1 Z 3 (U −U )* . . . . 3 1 0 − ,0396 + j0,0337 0 ( ) S31 = 3 U . = 1,011∠ − 1,91 . = 1 − ,7544 − j0,76779 * 0,0125 − j0,025 Z31 . . . ∆ 1 S 2 = 1 S 2 + S21 = 0,058 + j0,116 . . . ∆ 1 S 3 = 1 S 3 + S31 = 0,0432 + j0,0865 . . .
∆ S23 = S23 + S32 = 0,0063 + j0,0191 . . . . ∆ S = ∆ 1 S 2 + ∆ 1
S 3 + ∆ S23 = 0,1075 + j0,2216 (pu) . .
∆ S(MVA) = ∆ S.S = 10,75 + j22,16 (MVA) cb BÀI 20
Cho mạng điện như hình vẽ (Scb = 100MVA) 1 y = −j40 12 2 S P = 400MW G1 3 y = −j20 y = −j20 13 23 V = 1,05 V = 1,0 0 ∠ 1 3 2 500MW 400MVAr
Sử dụng phương pháp tách biến (FDDF) với 2 bước lặp, xác định điện áp nút 2 và .
3, tổn thất công suất trong mạng điện, lấy xấp xỉ ban đầu 0 U3 = 1,0pu; δ = 0 . 2 Bài giải 0 Y = y + y = −j60 = 60∠ − 90 11 12 13 0 Y = y + y = −j60 = 60∠ − 90 22 21 23 0 Y = y + y = −j40 = 40∠ − 90 33 31 32 0 Y = Y = −y = j40 = 40∠90 12 21 12 0 Y = Y = −y = j20 = 20∠90 13 31 13 0 Y = Y = −y = j20 = 20∠90 23 32 23 45
BÀI TẬP LƯỚI ĐIỆN 0 0 0 60∠ − 90 40 9 ∠ 0 20 9 ∠ 0 0 0 0 Y = 40 9 ∠ 0 60∠ − 90 20 9 ∠ 0 bus 0 0 0 20∠90 20 9 ∠ 0 40∠ − 90 −60 20 ' B = 20 −40 (k ) P ∆ 2 . (k ) ∆δ 2 U ' 2 B − . = (k ) (k ) ∆δ P ∆ 3 3 (k) . 3 U (0) schd (0) ∆P = P − P 2 2 2 . . P = U . Y . U .cos (δ − δ − θ ) . + Y . U .cos (−θ ) . 2 1 2 + Y . 3 U .cos δ − δ − θ 2 21 2 1 21 22 22 23 ( 2 3 23) . .
= 40. U U .cos (90 − δ + δ ) . . 0 1 2 + 20. 2 U . 3 U .cos 90 + δ 2 1 ( 3 ) . . . . P = . 1 U .cos (δ − δ − θ ) + Y . 2
U .cos (δ − δ − θ ) + Y . 3 U .cos −θ 31 3 1 31 32 3 2 32 33 ( 33) 3 U . Y 3 . .
= 20. U U .cos (90 − δ + δ ) . . 0 1 3 + 20. 2 U . 3 U .cos 90 − δ + δ 3 1 ( 3 2 ) 2 . .
Q = 20. U U .sin(90 − δ + δ ) . .
− 20. U . U .sin(90 − δ + δ ) . 0 1 3 2 3 + 40 3 U 3 3 1 3 2 (0) (0) (0) → P = 0; P = 0; Q = 1 2 3 3 (0) schd (0) ∆P = P − P = 4 2 2 2 (0) schd (0) ∆P = P − P = 5 − 3 3 3 (0) schd (0) ∆Q = Q − Q = 3 − 2 3 3 (0) ∆P 2 . (0) 2 U 6 − 0 20 ∆δ 2 = . (0) (0) ∆P 20 4 − 0 ∆δ 3 3 . 3 U 4 (0) (0) 1,05 60 2 − 0 ∆δ ∆δ = 0,0262 2 2 = . → (0) (0) 5 − 2 − 0 40 ∆δ ∆δ = 0 − ,1119 3 3 1 (1) rad 0 δ = 0,0262 = 1,5011 2 (1) rad 0 δ = 0 − ,1119 = 6 − ,4114 3 '' B = [ 4 − 0] 46
BÀI TẬP LƯỚI ĐIỆN (0) ∆Q 3 − 3 '' (0) = B − .∆ U → = −[−40] (0) (0) . U ∆ → ∆U = 0 − ,075 3 3 3 (0) U 1 3 (1) (0) (0) U = U + U ∆ = 0,925 pu 3 3 3 (1) (1) (1) P = 3,7743; P = 4 − ,7399; Q = −3,3994 2 3 3 (1) schd (1) ∆P = P − P = 4 − 3,7743 = 0,2257 2 2 2 (1) schd (1) ∆P = P − P = 5 − + 4,7399 = 0 − ,2601 3 3 3 (1) schd (1) ∆Q = Q − Q = 4 − + 3,3994 = 0 − ,6006 3 3 3 .
Lấy xấp xỉ ban đầu: (0) 0) δ = 0; 3 U = 1,0; δ = 0 2 3 400 schd schd schd P = = 4pu; P = 5 − pu; Q = −4pu 2 3 3 100 (0) (0) (0) P = 0; P = 0; Q = 1 2 3 3 63 2 − 1 0 (0) J = 2 − 1 41 0 0 0 39 (0) schd (0) P ∆ = P − P = 4 − 4 = 0 2 2 2 (0) schd (0) P ∆ = P − P = 5 − − 0 = 5 − 3 3 3 (0) schd (0) Q ∆ = P − P = 4 − − ( 1 − ) = 3 − 3 2 2 (0) (0) (0) P ∆ ∆δ 4 ∆δ 2 2 2 (0) (0) (0) (0) (0) P ∆ = J . ∆δ ⇔ 5 − = J . ∆δ 3 3 3 (0) ∆ (0) ∆ − (0) Q U 3 ∆ 3 U 3 3 (0) (1) (0) (0) rad 0 ∆δ = 0,0275 δ = δ + ∆δ = 0,0275 ≈ 1,5756 2 2 2 2 (0) (1) ( → ∆δ = 0 − ,1078 → δ = δ 0) (0) rad 0 + ∆δ = 0 − ,1078 ≈ 6 − ,1764 3 3 3 3 (0) ∆ U = 0 − ,0769 (1) (0) (0) U = U + ∆ U = 0,9231 pu 3 3 3 3 47
BÀI TẬP LƯỚI ĐIỆN TRƯỜNG ĐỀ THI HỌC PHẦN
Giảng viên phụ trách HP
ĐẠI HỌC BÁCH KHOA HÀ NỘI LƯỚI ĐIỆN VIỆN ĐIỆN SỐ ĐỀ: 1
THỜI GIAN LÀM BÀI: 120 PHÚT PHẠM NĂNG VĂN CÂU 1 (3 điểm)
Đường dây truyền tải điện 3 pha có Uđm = 500 kV, chiều dài L = 1000 km, điện cảm đơn vị Lo = 0,97 mH/km,
điện dung đơn vị Co = 0,0115 μF/km. Điện áp vận hành đầu đường dây U1 = 525 kV. Phụ tải cuối đường dây có
công suất bằng 150 + j35 MVA. Đường dây có đặt kháng bù ngang để giữ điện áp tại các nút m và 2 bằng điện
áp đầu đường dây. Bỏ qua tổn thất.
1) Xác định công suất định mức và điện kháng của các kháng bù ngang.
2) Xác định công suất của nguồn.
3) Vẽ sơ bộ chiều dòng công suất và phân bố điện áp dọc theo chiều dài đường dây có đặt kháng bù. CÂU 2 (7 điểm)
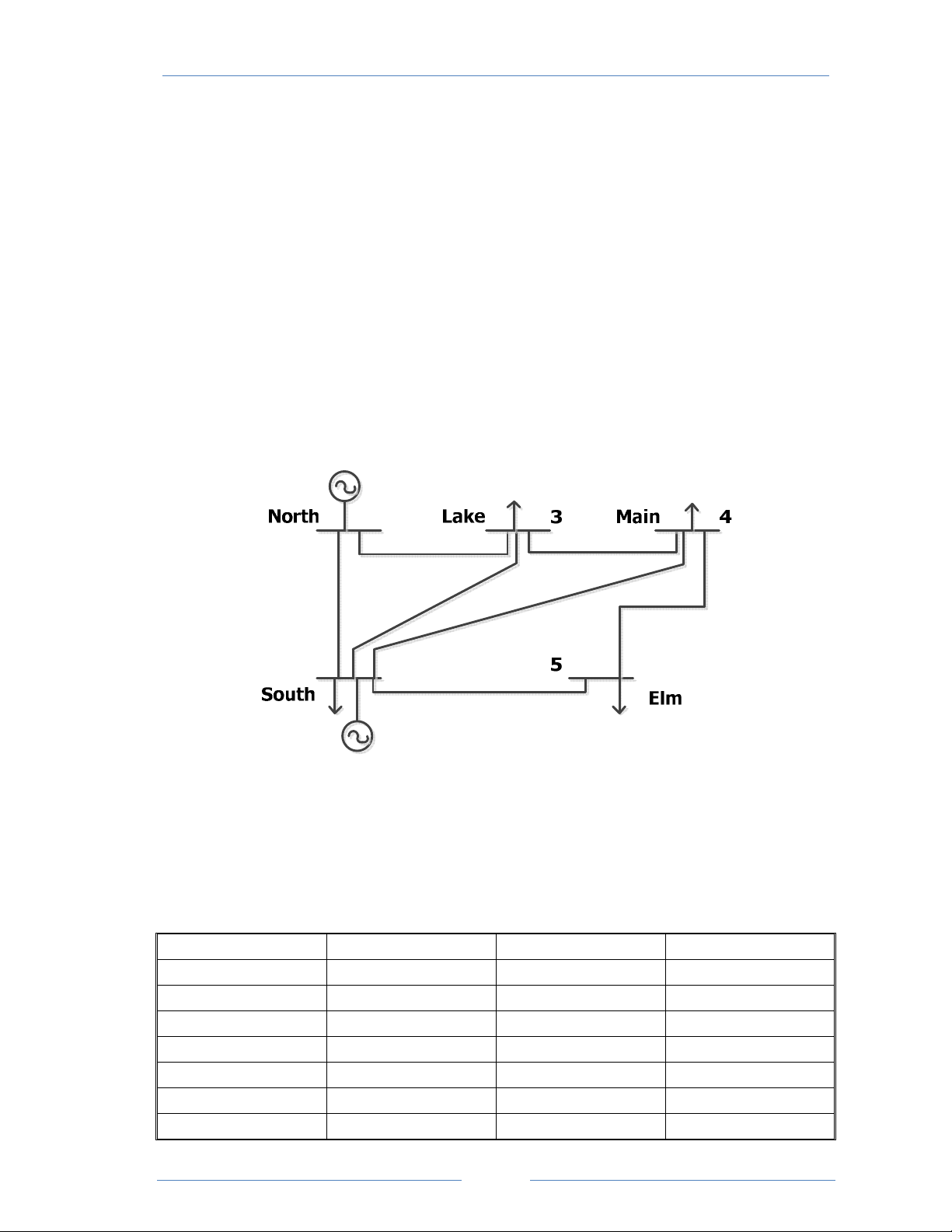
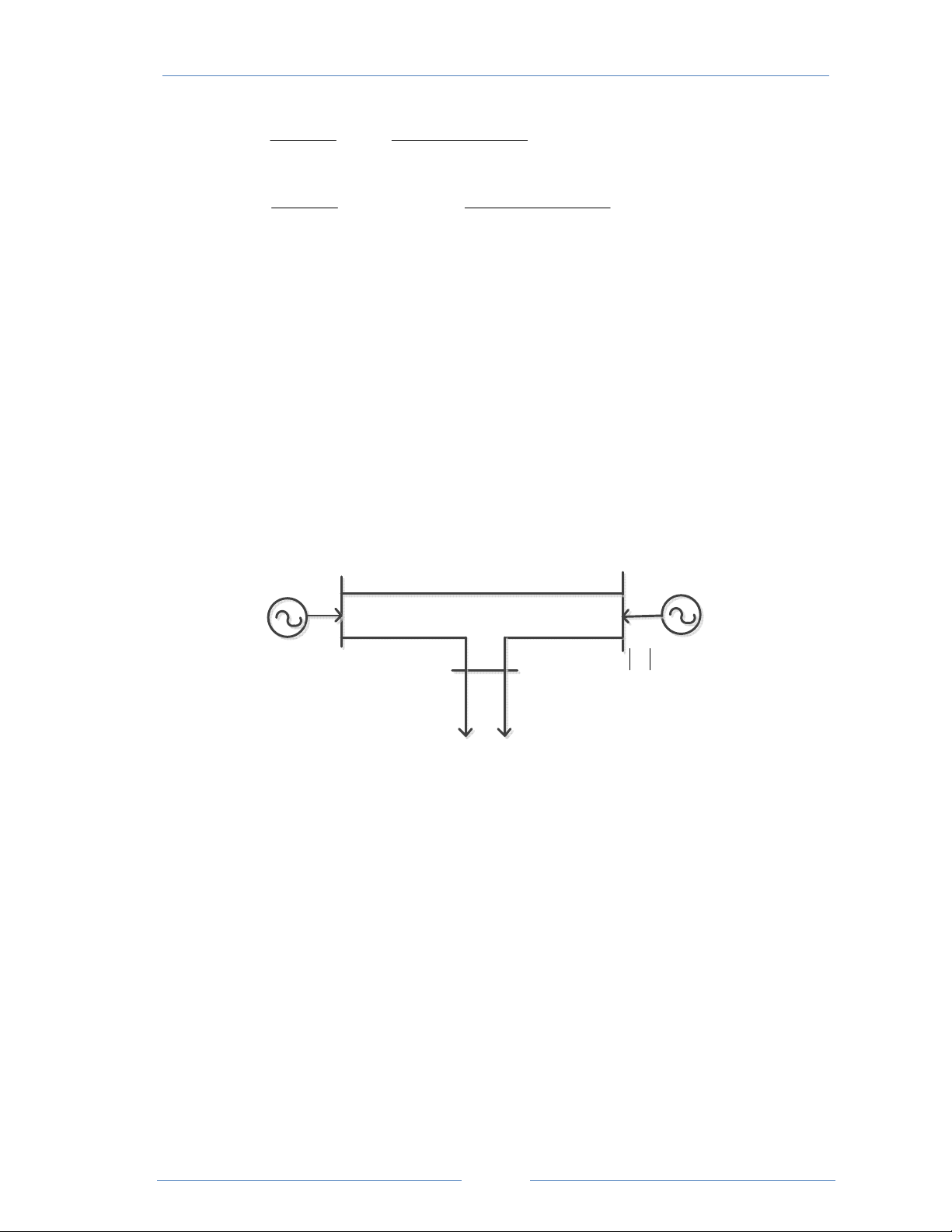
Cho mạng điện gồm 3 nút như hình vẽ. 1 2 L1 L2 3
Dữ liệu của mạng điện được cho trong hệ đơn vị tương đối với công suất cơ bản Scb = 100 MVA, điện áp cơ bản Ucb = 220 kV. Dữ liệu nút: Công suất phụ tải
Công suất tác dụng của nguồn Nút Uɺ (pu) δ (độ) PD (MW) QD (MVAr) PG (MW) 1 90 36 1,05 0 2 90 45 200 1,02 3 350 164 Dữ liệu nhánh: Nhánh R (pu) X (pu) B (pu) Ghi chú 1 - 3
0,01952 0,08662 0,13560 Thông số 1 mạch 2 - 3 0,01392 0,06191 0,10533
1) Thành lập ma trận tổng dẫn nút của mạng điện.
2) Viết công thức lặp để xác định điện áp các nút theo phương pháp Gauss – Seidel (phải thay số tất cả các đại lượng đã biết). (0) (0) ɺ (0)
3) Lấy xấp xỉ ban đầu δ = δ = 0; U
= 1,0 pu , hãy xác định điện áp tại các nút sau 2 bước lặp sử dụng 2 3 3
phương pháp lặp Gauss - Seidel.
4) Sử dụng tiêu chuẩn độ lệch công suất nút (ε = 0,01), hãy chứng minh rằng kết quả điện áp các nút trong bài
toán phân tích chế độ xác lập được cho như sau: o o δ = − δ = − ɺ = 2 1,79663 ; 3 5,30687 ; 3 U 0, 97552 pu
5) Sử dụng trị số điện áp nút cho ở ý 4, xác định phân bố công suất trong mạng điện, tổn thất công suất và
công suất phát của các nguồn điện (quy đổi sang hệ đơn vị có tên).
6) Theo anh (chị), có thể sử dụng phương pháp cộng công suất để phân tích chế độ xác lập của mạng điện trên
hay không? Nếu có thì anh (chị) hãy nêu các bước tính (có giải thích)? 48
BÀI TẬP LƯỚI ĐIỆN
7) So sánh các phương pháp Gauss – Seidel và Newton - Raphson? Tại sao phải có nút cân bằng trong bài toán phân tích CĐXL?
Chú ý câu 2: Các tính toán sử dụng hệ đơn vị tương đối. Kết quả tính điện áp nút được viết ở dạng tọa độ cực
và lấy 5 chữ số phần thập phân. 49
BÀI TẬP LƯỚI ĐIỆN TRƯỜNG ĐỀ THI HỌC PHẦN
Giảng viên phụ trách HP
ĐẠI HỌC BÁCH KHOA HÀ NỘI LƯỚI ĐIỆN VIỆN ĐIỆN SỐ ĐỀ: 1
THỜI GIAN LÀM BÀI: 150 PHÚT PHẠM NĂNG VĂN
Chú ý: Sinh viên phải nộp lại đề thi. Được sử dụng tài liệu. CÂU 1 (3 điểm)
Cho đường dây tải điện dài có điện áp định mức bằng 500 kV, chiều dài 700 km. Các thông số đơn vị của
đường dây xo = 0,27 Ωkm; bo = 4,4.10-6 S/km.
1) Lập sơ đồ thay thế hình PI tương đương của đường dây. 2) Giả sử o
Uɺ = 500 kV, Uɺ = 475 kV, δ = 35 1 2
Hãy xác định điện kháng dung tính và công suất của tụ bù dọc đặt tại vị trí giữa đường để nâng công suất tác
dụng có thể truyền tải trên đường dây theo điều kiện ổn định góc bằng 1000 MW. Từ đó, xác định mức độ bù
dọc và nhu cầu công suất phản kháng ở 2 đầu đường dây. Biết rằng, hệ số công suất của phụ tải bằng 0,95 (chậm sau). CÂU 2 (3 điểm)
Cho lưới điện phân phối đối xứng như hình vẽ:
Dữ liệu được cho như sau:
- Điện áp vận hành đầu nguồn Uo = 11 kV
- Công suất của các phụ tải được cho tại cùng một thời điểm: Sɺ = 1400 + j700 kVA Sɺ = 800 + j500 kVA Sɺ = 2500 + j1200 kVA 1 3 5 Sɺ = 1200 + j450 kVA Sɺ = 1000 + j600 kVA 2 4
- Các đường dây trên không có các thông số đơn vị giống nhau: ro = 0,33 Ω/km; xo = 0,395 Ω/km
1) Viết công thức lặp để xác định điện áp các nút sử dụng phương pháp cộng công suất.
2) Lấy xấp xỉ ban đầu điện áp các nút bằng điện áp định mức của mạng, xác định điện áp các nút của mạng điện
sau 1 bước lặp. Sau đó, xác định tổn thất công suất và tổn thất điện áp lớn nhất của mạng điện. CÂU 3 (3 điểm)
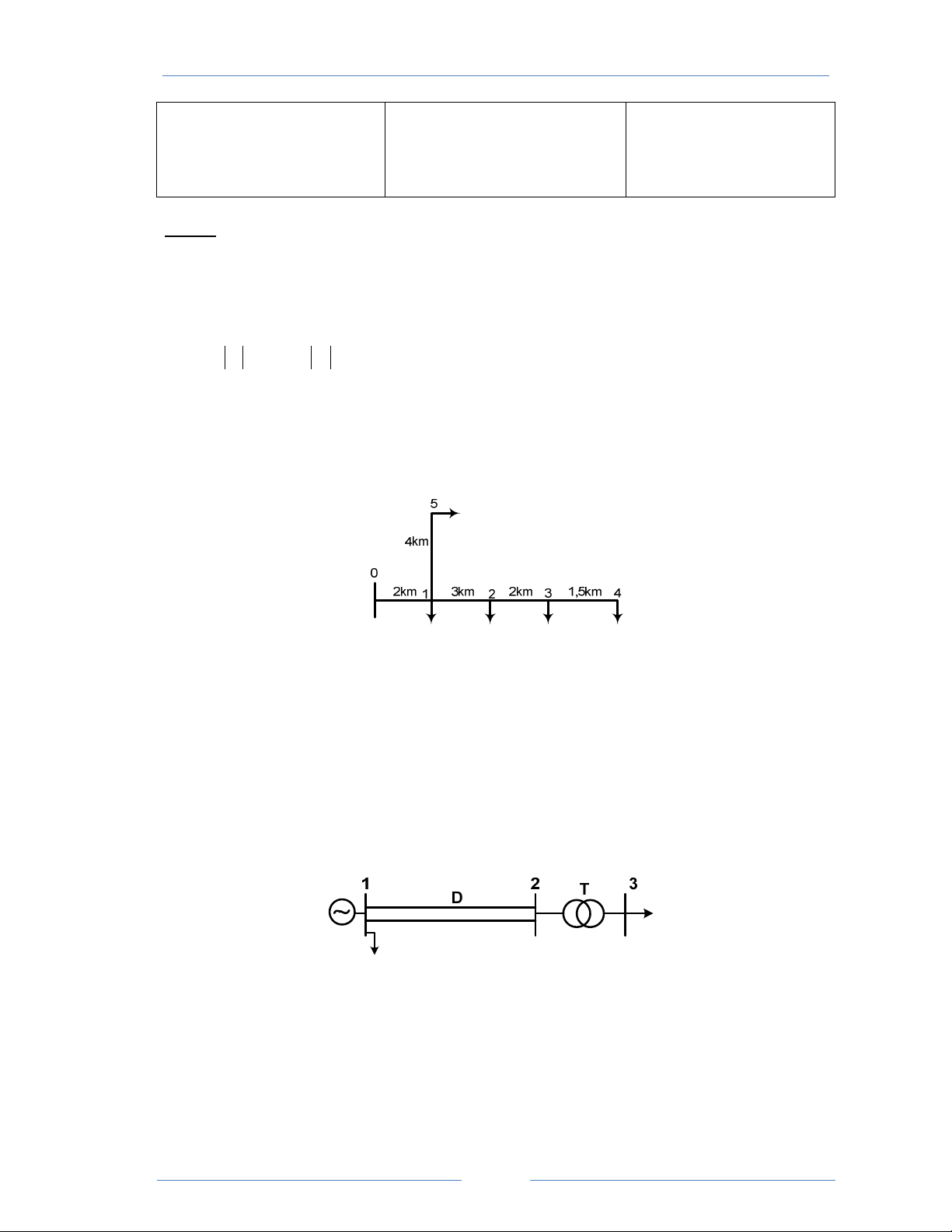
Cho mạng điện như hình vẽ:
Dữ liệu được cho như sau:
- Điện áp vận hành của nguồn điện bằng 121 kV.
- Đường dây 2 mạch D có: ro = 0,17 Ω/km; xo = 0,41 Ω/km; bo = 2,8.10-6 S/km; L = 60 km
- Máy biến áp T có: Sđm = 40 MVA; UCđm = 115 kV; UHđm = 23,5 kV; ΔPo = 29 kW; Io% = 0,75; ΔPN = 145 kW;
uN% = 10,5; eo% = 1,78. Máy biến áp có 19 đầu phân áp đặt ở phía cao áp, đang vận hành với nấc phân áp n = 3.
- Phụ tải tại nút 3: PD3 = 28 MW; cosφ3 = 0,9 (chậm sau)
- Phụ tải tại nút 1: PD1 = 40 MW; cosφ1 = 0,87 (chậm sau) 50
BÀI TẬP LƯỚI ĐIỆN
1) Lấy Scb = 100 MVA, Ucb = 110 kV. Lập sơ đồ thay thế của mạng điện trong hệ đơn vị tương đối (sử dụng sơ đồ
thay thế hình PI cho đường dây và máy biến áp, bỏ qua tổn thất trong mạch từ của máy biến áp).
2) Xây dựng ma trận tổng dẫn nút của mạng điện.
3) Viết công thức lặp để xác định điện áp các nút theo phương pháp Gauss – Seidel (phải thay số tất cả các đại lượng đã biết). (0) (0)
4) Lấy xấp xỉ ban đầu U ɺ = Uɺ
= 1 pu , xác định điện áp các nút của mạng điện sau 2 bước lặp. Lấy 5 chữ số 2 3 phần thập phân. 51




