Nghiệm kép là gì? Phương trình có nghiệm kép khi nào?

Nghiệm kép là gì? Phương trình có nghiệm kép khi nào?
1. Nghiệm kép là gì? Phương trình có nghiệm kép khi nào?
Phương trình có nghiệm kép là phương trình bậc 2 mà có hai nghiệm gần như nhau. Để xác định
một phương trình có nghiệm kép, ta cần tính giá trị của được tính bằng công thức Nếu giá trị của là 0 tức là
= 0 thì phương trình có nghiệm kép
Công thức tính nghiệm kép của phương trình là x =
Phương trình bậc 2 có dạng như sau:
Phương trình bậc 2 là một dạng phương trình đa thức có dạng ax + bx + c = 0 trong đó có a, b, c
là các hằng số và a khác 0. Đây là một loại phương trình bậc hai vì có một số biến số x được bình
phương. Hệ số a đại diện cho hệ số của biến số được bình phương, b là đại diện cho hệ số của
biến số và c là hằng số
Các bước để giải phương trình bậc 2 như sau:
- Xác định các hệ số a, b, c trong phương trình - Tính giá trị của theo công thức
với là một tham số quan trọng trong việc
xác định loại các nghiệm của phương trình - Kiểm tra giá trị của Nếu
> 0 thì tức là phương trình có hai nghiệm phân biệt Nếu
= 0 thì phương trình có một nghiệm kép Nếu
< 0 thì phương trình không có nghiệm thực
Tính giá trị của các nghiệm x:
- Nếu phương trình có hai nghiệm phân biệt thì sử dụng công thức x = để
tính giá trị của hai nghiệm x1, x2
- Nếu phương trình có một nghiệm kép thì sử dụng công thức nghiệm x = để tính giá trị của nghiệm kép
Phương trình có nghiệm kép khi:
Để phương trình bậc 2 có nghiệm kép thì cần đảm bảo những điều kiện sau:
- Hệ số a của phương trình phải khác 0 tức là phương trình không được là phương trình bậc 1 -
của phương trình phải bằng 0.
được tính theo công thức trong đó có a,
b, c là các hệ số của phương trình Nếu
bằng 0 thì phương trình có nghiệm kép Nếu
khác 0 thì phương trình không có nghiệm kép
Ví dụ: Để phương trình ax + bx + c = 0 có nghiệm kép thì ta cần thực hiện các bước sau:
- kiểm tra hệ số a của phương trình: Nếu a = 0 tức là phương trình không phải là phương trình
bậc 2 và không có nghiệm kép - Tính giá trị của
bằng cách sử dụng công thức
= b - 4ac với a,b, c lần lượt là các hệ số phương trình So sánh giá trị với 0: - Nếu
= 0 thì phương trình có nghiệm kép - Nếu
khác 0 thì phương trình không có nghiệm kép
Như vậy để phương trình có nghiệm kép thì cần đảm bảo a khác 0 và = 0
2. Bài tập về phương trình có nghiệm kép
Câu 1: Bạn An kinh doanh hai mặt hàng handmade là vòng tay và vòng đeo cổ. Mỗi vòng tay làm
trong 4 giờ, bán được 40 ngàn đồng. Mỗi vòng đeo cổ làm trong 6 giờ bán được 80 ngàn đồng.
Mỗi tuần bạn An bán được không quá 15 vòng tay và 4 vòng đeo cổ. Tính số giờ tối thiểu trong
tuần An cần dùng để bán được ít nhất 400 ngàn đồng?
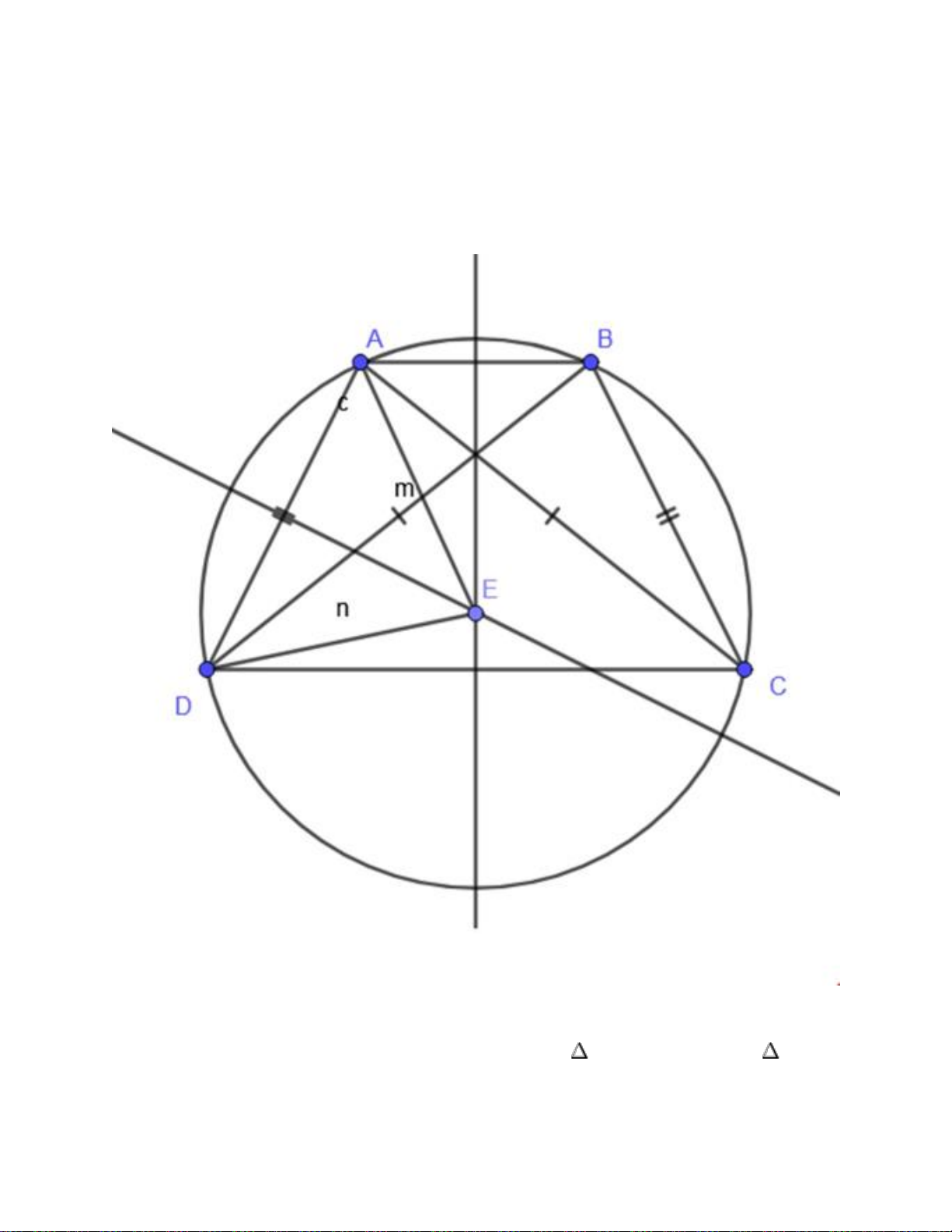
Câu 2: Nêu cách xác định tâm đường tròn ngoại tiếp hình thang cân
Câu 3: Tìm giá trị của m để phương trình mx + 4x + m - 1= 0 có nghiệm kép
Câu 4: khi nào phương trình m2x + 3mx + 5= 0 có nghiệm kép
Câu 5: tìm những giá trị của m để phương trình m2x2 + 5x + m = 0 có nghiệm kép Câu 6:
Diện tích của hình chữ nhật là 36 đơn vị diện tích. Độ dài một cạnh hình chữ nhật là 6 đơn vị.
Tìm chiều dài và chiều rộng của hình chữ nhật đó
Ta gọi chiều dài của hình chữ nhật là x và chiều rộng là y
Theo bài toán ta có phương trình diện tích hình chữ nhật là x * y = 36 và hai cạnh của hình chữ nhật là bao nhiêu?
3. Giải bài tập về phương trình có nghiệm kép Câu 1:
Làm vòng tay mỗi giờ được 10 ngàn đồng
Làm vòng đeo cổ mỗi giờ được: 40 : 3 = 13 ngàn đồng
Vậy làm vòng đeo cổ có lợi hơn nên ưu tiên làm tối đa số vòng cổ trước
Làm 4 vòng đeo cổ hết 4. 6 = 24 giờ bán được 4 . 80 = 320 ngàn đồng
Để làm được ít nhất 400 ngàn đồng cần làm thêm vòng tay để thu về 80 ngàn đồng hay cần làm thêm 2 cái vòng tay
Suy ra cần thêm 2. 4 = 8 giờ
Vậy cần tối thiểu: 24 + 8 = 32 giờ một tuần để An bán được ít nhất 400 ngàn đồng Câu 2:
Xét hình thang cân ABCD có AB // CD AC giao BD tại O Do đó AD = Bc và AC = BD
Xét tam giác ACD và tam giác BDC ta có: AC = BD AD = BC CD chung
Vậy tam giác ACD = tam giác BDC (c. c.c) Suy ra
Mà 2 góc này đều chắn cung CD suy ra A, B, C, D cùng thuộc một đường tròn
Gọi E là tâm đường tròn ngoại tiếp ABCD
Suy ra: EA = EB suy ra E thuộc đường trung trực của AB
EA = ED suy ra E thuộc đường trung trực của AD
Vậy tâm của đường tròn ngoại tiếp hình thang ABCD là giao của đường trung trực cạnh đáy và
đường trung trực cạnh bên Câu 3:
Để phương trình có nghiệm kép ta cần xác định điều kiện để của phương trình = 0. được
tính bằng bình phương của hệ số b (4) trừ tích của 4 lần hệ số a (m) và hệ số c (m2 - 1)
Vậy công thức tính ta có:
Thay vào đây ta có giá trị của a, b, c trong phương trình ta có:
Để phương trình có nghiệm kép thì ta cần xác định điều kiện 16 - 4m + 4m = 0
Đưa hệ số m3 về phía trái và hệ số m về phía phải ta có: 4m - 4m + 16 = 0
Tiến hành giải phương trình này để tìm giá trị của m
Vì phương tình này là phương trình bậc 3 nên để tìm nghiệm chính xác ta có thể sử dụng
phương pháp giải đường cong hoặc sử dụng các phương pháp giải phương trình bậc 3 khác
Tuy nhiên tùy thuộc cụ thể vào m để phương trình ban đầu có nghiệm kép hoặc không có nghiệm kép
Để tìm m sao cho phương trình có nghiệm kép thì ta cần giải phương trình 4m - 4m + 16 = 0
bằng cách sử dụng các phương pháp giải phương trình bậc 3 khác nhau hoặc sử dụng công cụ
giải phương trình trực tuyến Câu 4:
Phương trình m2x + 3mx + 5 = 0 có nghiệm kép khi và chỉ khi = 0 Để tính ta sử dụng công thức = b - 4ac với a = m , b = 3m, c = 5
Thay các giá trị vào công thức ta có: = (3m - 4(m ) (5) = -11m Để
= 0 ta giải phương trình -11m = 0
Giải phương trình này ta được m = 0
Vậy phương trình 2xm + 3mx + 5 = 0 có nghiệm kép khi và chỉ khi m = 0 x - (2m + 3) x + m2 = 0 câu 5:
Để phương trình m2x + 5x + m = 0 có nghiệm kép ta phải kiểm tra xem của phương trình này có bằng 0 hay không
Đầu tiên ta áp dụng công thức tính
của phương trình bậc 2:
Trong phương trình 2xm + 5x + m = 0 với a = m , b = 5 và c = m
Tiếp theo ta tính được giá trị
bằng cách thay các giá trị đã biết vào công thức:
Sau đó ta rút gọn được
Để phương trình có nghiệm kép thì ta phải có = 0
Do đó ta phải giải phương trình
để tìm giá trị của m
Tiếp theo ta chuyển phương trình về dạng 4m = 25
Sau đó ta tìm được m = 25/4
Cuối cùng ta lấy căn bậc ba của cả hai phía để tìm giá trị của m Câu 6:
ta gọi chiều dài của hình chữ nhật là x và chiều rộng là y
Theo bài toán ta có phương trình diện tích x . y = 36 và hai cạnh của hình chữ nhật là x và y đều bằng 6
Sử dụng phương trình diện tích ta có: x * y = 36
Thay x = y = 6 vào phương trình ta có: 6 . 6 = 36
Phương trình đã được chứng minh đúng tức là hai cạnh của hình chữ nhật là 6. Vì vậy, ta có thể
nói rằng trong trường hợp này thì phương trình diện tích hình chữ nhật có nghiệm kép x = y = 6