


















































Preview text:
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
ỨNG DỤNG ĐỊNH LÝ VIÈTE ĐẠI SỐ SƠ CẤP A. LỊCH SỬ.
François Viète, Seigneur de la Bigotière ( tiếng Latinh : Franciscus Vieta ; 1940 - 23
tháng 2 năm 1603) là một nhà toán học người Pháp có công trình về đại số mới là một
bước tiến quan trọng đối với đại số hiện đại, do việc sử dụng sáng tạo các chữ cái làm
tham số trong phương trình và đồng thời ứng dụng chúng trong việc biến đổi và giải
phương trình. Ông là một luật sư về thương mại, và từng là ủy viên hội đồng bí mật cho
cả Henry III và Henry IV của Pháp.
Ông đã phát hiện ra mối liên hệ giữa các nghiệm và các hệ số của phương trình. Ông còn
là một chuyên gia về giải các mật mã trong thế chiến giữa Pháp và Tây Ban Nha. Ông mất năm 1603.
Thành tựu nổi bật: Đại số mới. Nền
Vào cuối thế kỷ 16, toán học được đặt dưới sự bảo trợ kép của người Hy Lạp, họ đã
mượn các công cụ của hình học và người Ả Rập, những người cung cấp các thủ tục cho
phép giải. Vào thời của Viète, đại số do đó dao động giữa số học, điều này làm xuất hiện
một danh sách các quy tắc và hình học có vẻ chặt chẽ hơn.
Đại số biểu tượng của Viète
Viète đã tạo ra nhiều đổi mới: công thức nhị thức , sẽ được Pascal và Newton lấy, và
các hệ số của đa thức thành tổng và tích các gốc của nó , được gọi là công thức Viète .
Đại số hình học
Viète rất thành thạo trong hầu hết các công cụ hiện đại, nhằm mục đích đơn giản hóa các
phương trình bằng cách thay thế các đại lượng mới có mối liên hệ nhất định với các đại
lượng chưa biết ban đầu. Một tác phẩm khác của ông, Recensio canonica effectionum
learningarum , mang dấu ấn hiện đại, sau này được gọi là hình học đại số — một bộ sưu
tập các giới thiệu cách xây dựng các biểu thức đại số chỉ với việc sử dụng thước và compass.
1 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] B. ĐỊNH LÝ VIÈTE.
Trong toán học, định lý Viète hay công thức Viète (có khi viết theo phiên âm tiếng
Việt là Vi-ét), do nhà toán học Pháp François Viète tìm ra, nêu lên mối quan hệ giữa
các nghiệm của một phương trình đa thức (trong trường số phức) và các hệ số của nó.
I. Định lý Viète cho phương trình bậc hai.
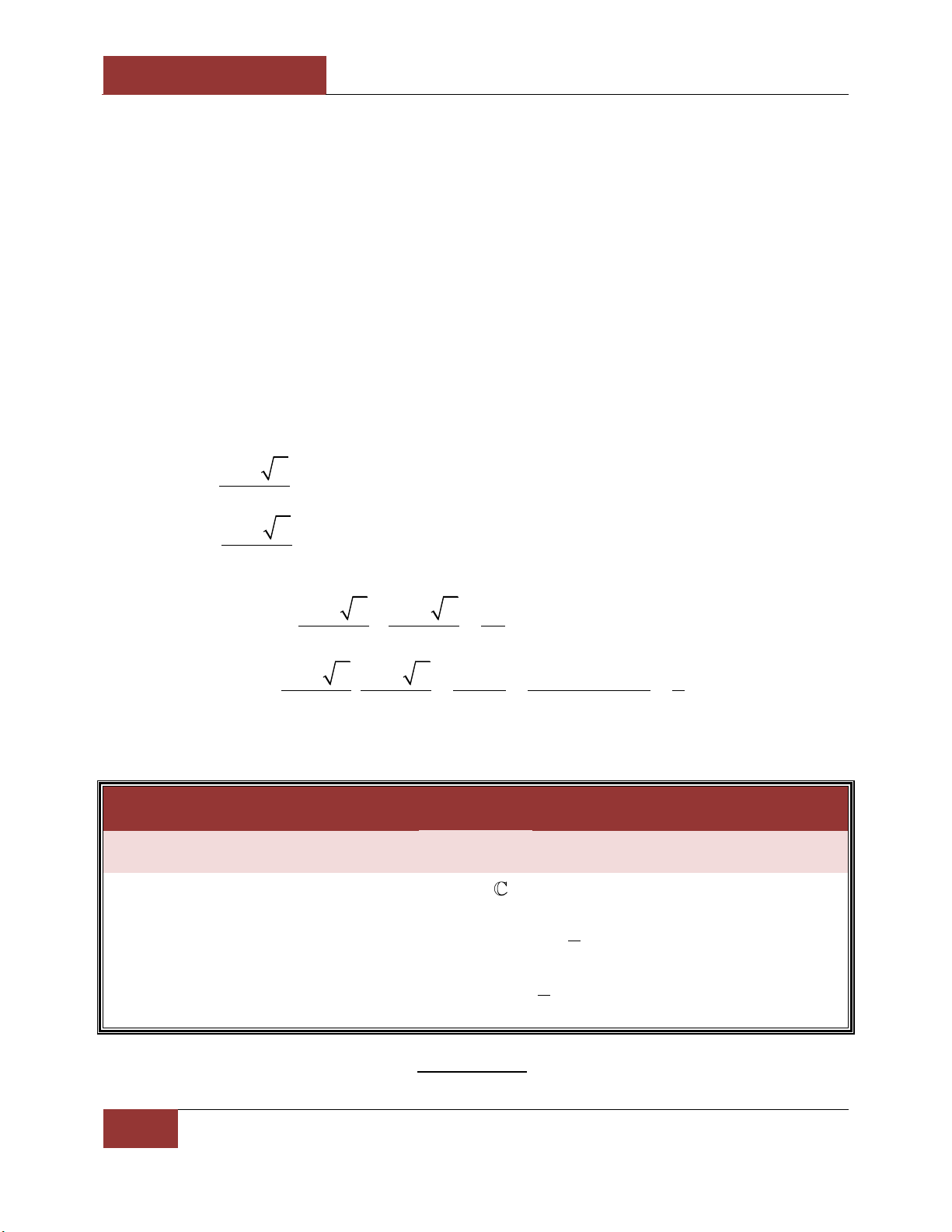
1. Bài toán mở đầu. Xét phương trình bậ 2
c hai: y ax bx c a 0 1 . 2
Giả sử: b 4ac 0 . b x 1 2a Ta có:
là hai nghiệm tổng quát của phương trình 2
ax bx c 0 . b x 2 2a
b b b
S x x 1 2 2a 2a a Khi đó: 2 . b 2 2 b 4ac b b b . c P x x 1 2 2 2 2a 2a 4a 4a a 2. Định lý Viète. Extra Techniques Định lý Viète Nếu x , x 1
2 là hai nghiệm (trên trường số phức
, có thể nghiệm đơn hoặc nghiệm kép) b
x x S 1 2 a của phương trình: 2
ax bx c 0 , thì: . c x x P 1 2 a Chứng minh:
2 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
Giả sử: x , x
ax bx c 1
2 là hai nghiệm của phương trình 2 0 .
Khi đó, phương trình bậc hai
1 tương đương với phương trình y ax x x x 1 2 . Như vậy, ta có đẳ 2
ng thức: ax bx c a x x x x 1 2 . 2 2
Hay: ax bx c ax a x x x ax x 1 2 1 2 . b x x b a x x 1 2 1 2 Đồ a
ng nhất hệ số hai vế, ta thu được: (đpcm). c ax x c 1 2 x x 1 2 a
Như vậy, một câu hỏi được đặt ra: Liệu rằng có hay không một Định lý Viète tổng quát
trên trường số thực cho một đa thức có bậc n ?
Câu trả lời là có và xin được trình bày tiếp ở phần dưới đây.
II. Định lý Viète cho phương trình đa thức bất kỳ.
1. Bài toán mở đầu.
Xét phương trình bậc n theo ẩn x tổng quát như sau: n n 1
y a x a x ... a x a , a 0 2 n n 1 1 0 n n n
Giả sử: x , i 1, n
a x a x ... a x a 0 i
là n nghiệm của phương trình 1 n n 1 1 0 .
Khi đó, phương trình bậc n tương đương với phương trình:
y a x x x x ... x x n 1 2 n Như vậ n n 1
y, ta có: a x a x
... a x a a x x
x x ... x x n n 1 1 0 n 1 2 n n n 1
a x a x ... n
a x a a x n n 1 1 0 n a x x ...x n 1 2 n n elements
3 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] a x x x x ... x x ... x x n 1 2 1 3 k k 1 n 1 n nn 1 elements 2
....................................................................... n 1
1 a x x ...x x x ...x x ... x x ...x n 1 2 n 1 1 2 n2 n 2 3 n n elements 1 n a x x ...x n 1 2 n
Đồng nhất hệ số ở hai vế, ta thu được Định lý Viète mở rộng như sau: Extra Techniques
Định lý Viète mở rộng Nếu x , i 1, , n n i
là hai nghiệm (trên trường số phức , có thể nghiệm đơn hoặc n n
nghiệm kép) của phương trình: 1 a x a x
... a x a 0 n n 1 1 0 , thì: n an 1
x x x ... x i 1 2 n i 1 a n n an2
x x x x x x x x .... x x i j 1 2 1 3 2 3 n 1 n 1
ijn an
........................................ .................... . n a x x ...x
x x ...x x x ...x x ... x x ...x 1 n . 2 3 n 1 1 1 i 2 i n i 1 1 2 n 1 1 2 n2 n 1 a 1 i 2i ... ni 1n n n a
x x x ...x i n n 0 1 . 1 2 i 1 a n
Lưu ý: Trong mỗi hàng k bất kỳ, vế trái của đẳng thức là tổng của các tích từng cụm k
các nghiệm của phương trình trên. Và vế phải của đẳng thức được tính một cách tổng a
quát theo công thức: 1 k nk a . n
4 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
Một số tổng quát thường gặp:
Phương trình bậc ba:
Nếu x , x , x
ax bx cx d 1 2
3 là nghiệm của phương trình: 3 2 0 thì công thức Viète b
x x x 1 2 3 a c
cho ta: x x x x x x 1 2 2 3 3 1 a . d x x x 1 2 3 a
Hệ quả 1 của định lý Viète: n n 1
Giả sử phương trình: a x a x
... a x a 0 3 a i n n n 1 1 0
có các hệ số , 0, i thỏa mãn: n n 1 i 2 2
a a 0 x 3 2k 2k 1 khi và chỉ khi:
1 là một nghiệm của phương trình . k0 k 1 n n 1 ii 2 2
a a 0 x 3 2k 2k 1 khi và chỉ khi:
1 là một nghiệm của phương trình . k0 k 1 Chứng minh i: n n 1 2 2
Giả sử: a a
0 a a a ... a 2k 2k 1 0 n n 1 1 . k0 k 1 Khi đó: 3 n
a x a a x a
a x a n n n 1 . . 0 n 1 n 1 1 1 ;
a x a
x a x n n
1 n n 1 1 ... 1 0 1 1 x
1 a x x a
x x a x a n n 1 n 2 ...
1 n n 2 n 3 ... 1 ... 1 0 1 2 1
5 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
x 1 là một nghiệm. i :
Giả sử: x 1 là một nghiệm của phương trình 3, khi đó, ta có: n n 1 a a a
a a a a a a a n 1 n n 1 n ... 2 2 1 1 0 ... 0 1 1 0 n n 1 1 0 2k 2k 1 . k0 k 1
Vậy: i hoàn toàn được chứng minh. ii: Bài toán phụ: 2 1
x 1 x 1 2 2 1
x x ... 1 k t t t k
x ... 1 x 1. 4 2t 1 Ta có: * k x 1 kx2 2 1 k x 1 kx
1 ... x 1 . 5 2t
Một điều đáng nói, ở đây k hoặc chẵn hoặc lẻ, nhưng điều đó không quan trọng vì nếu k 2 k
thì ta xét x
1 như ở đẳng thức 5 , nếu k 2 1 thì hoàn toàn rút được
lượng nhân tử x
1 theo đẳng thức 4. Như vậy dù k là bội nào đó của 2 , thì đến
một số đủ lớn các bước (sau bước), ta sẽ thu được nhân tử x 1 . n n 1 n n 1 2 2 2 2
Giả sử: a a
0 a a a 2k 2k 1 0 2k 2k 1 . k0 k 1 k 1 k 1 n 1 n Khi đó: 3 n a x a a x a
a x a a x a n n 1 1 n n 1 ... n 2 0 1 1 2 2 1 1 . x
1 a a . . a x 1 a 0 x 1 3 n n n 1 n 1 2 1
là một nghiệm của .
ii : Giả sử: x 1
là một nghiệm của phương trình 3, khi đó, ta có:
6 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] a a
a a a a
a a a n
1n n n 1 1 ... 1 0
1n n n 1 1 ... 1 k ... 0 1 1 0 n 1 k 1 0 n n 1 . 2 2
a a 0 2k 2k 1 k0 k 1
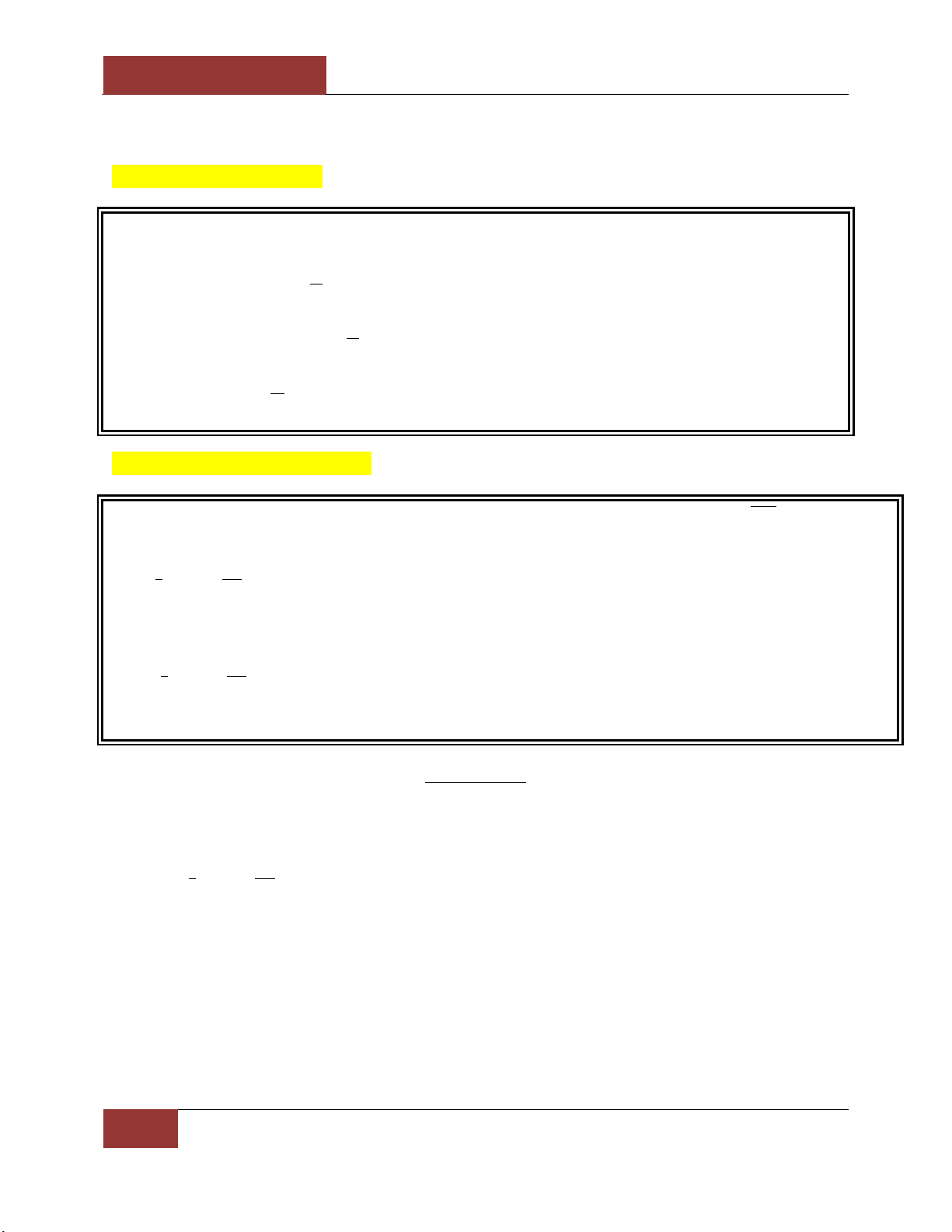
Vậy: ii hoàn toàn được chứng minh. Extra Techniques Study tips Xét phương trình: 2
ax bx c 0 a 0 6 . x 1 1
Nếu phương trình 6 có tổng a b c 0 thì:
c là hai nghiệm của 6 . x 2 a x 1 1
Nếu phương trình 6 có tổng a b c 0 thì:
c là hai nghiệm của 6 . x 2 a
Hệ quả 2 của định lý Viète: n n 1
Giả sử phương trình: a x a x
... a x a 0 3 x i n n n 1 1 0
có n nghiệm, kí hiệu , 1, i . n S x 1 i i 1 n S x x 2 i j
1i jn
Nếu ta đặt: ........................ n S x x ...x n 1 1 i 2 i n i 1 1
1i 2i... ni 1n n S x n i i 1
7 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
Khi đó: x ,i 1,n i
là nghiệm của phương trình:
x S x S x . . 1 k S .x . . S x S k n 1 1 2 1 1 n n n n n k 0 7 1 2 n 1 n . Chứng minh:
Theo định lý Viète mở rộng, ta suy ra:
Nếu x , i 1, n 3 i
là nghiệm của , thì: n an 1
x x x ... x i 1 2 n i 1 a n n an2
x x x x x x x x .... x x i j 1 2 1 3 2 3 n 1 n 1
ijn an
........................................ .................... n a x x ...x
x x ...x x x ...x x ... x x ...x 1 n . 2 3 n 1 1 1 i 2 i n i 1 1 2 n 1 1 2 n2 n 1 a 1 i 2i ... ni 1n n n a
x x x ...x i n n 0 1 . 1 2 i 1 a n an 1 S 1 a n an2 S 2 an
Như vậy, dễ dàng ta có: .................. . a S n n 1 1 1 . 1 an a S n n 0 1 . an a a a a n n 1 n 1 n2 n2
Vậy phương trình 7 tương đương với: 1 0 x x x . . x 0 a a a a . n n n n
8 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
Vì: deg f x , x ,. ., x
n a 0 1 2 n n .
Nhân cả hai vế cho a , ta thu được phương trình 3 n (đpcm). Extra Techniques Study tips
S x x Xét phương trình: 2
ax bx c 0 a 0 6 1 2
với 0 , nếu ta đặt: . P x x 1 2 2 2 Thì: x , x
x Sx P 0, S 4P 1
2 là hai nghiệm của phương trình .
C. MỘT SỐ TIPS GIẢI NHANH CÁC BÀI TOÁN ỨNG DỤNG ĐỊNH LÝ VIÈTE.
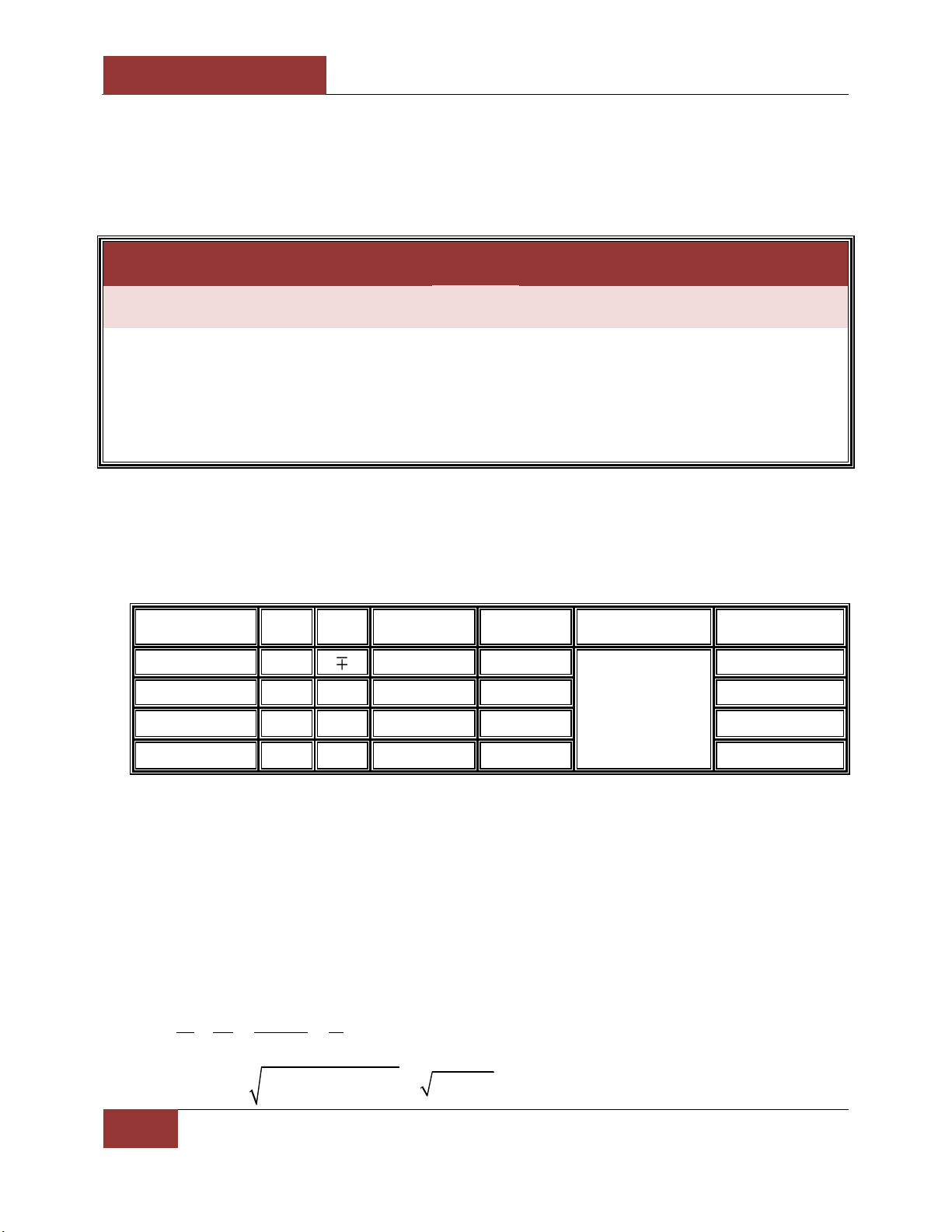
I. Dấu nghiệm của phương trình bậc hai. Dấu nghiệm x x
S x x P x x 1 2 1 2 1 2
Điều kiện cần Điều kiện đủ Trái dấu ? P 0 Cùng dấu P 0 0 Cùng dương
P 0, S 0 Cùng âm
P 0, S 0
II. Một số đẳng thức cần lưu ý.
i x x x x 2 2 2 2
2x x S 2P 1 2 1 2 1 2
ii x x x x x x 2 3 3 3x x S. 2S 3P 1 2 1 2 1 2 1 2
iii x x x x 2 2 2x x 2x x 2 4 4 2S 2P2 2 2P 1 2 1 2 1 2 1 2 iv 1 1 x x P 1 2 x x x x S 1 2 1 2
v x x x x 2 2
4x x S 4P x x 2 1 1 2 1 2 2 1
9 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
III. Ứng dụng đa thức đối xứng để giải quyết các bài tập áp dụng định lý Viète.
1. Định nghĩa. Giả sử A là một vành giao hoán có đơn vị, f x , x ,..., x 1 2
n là một đa thức
của vành A x , x ,..., x
f x , x ,..., x 1 2
n . Đa thức 1 2
n được gọi là một đa thức đối xứng của
n ẩn nếu f x ,x ,. .,x f x ,x ,. .,x 1 2 n
1 2 n
với mọi phép thế 1 2 .... n
1 2 .... n
f x ,x ,. .,x
f x , x ,..., x
f x , x ,..., x x 1 2 n suy ra từ 1 2
n bằng cách thay trong 1 2 n , 1
bởi x ,. . , x x 1
n bởi n .
2. Định lý 1. Bộ phận gồm các đa thức đối xứng của vành A x , x ,..., x 1 2 n là một vành
con của vành A x , x ,..., x 1 2 n . Chứng minh:
Giả sử f x , x ,..., x
g x , x ,..., x 1 2 n và 1 2
n là những đa thức đối xứng của vành
A x , x ,..., x 1 2
n , theo định nghĩa ta có:
f x ,x ,. .,x f x ,x ,. .,x 1 2 n
1 2 n Và
gx ,x ,. .,x g x ,x ,. .,x 1 2 n
1 2 n 1 2 .... n
với mọi phép thế 1 2 .... n . Thế thì:
f x ,x ,. .,x g x ,x ,. .,x f x ,x ,. .,x g x , x ,. ., x 1 2 n 1 2 n
1 2 n 1 2 n ,
f x ,x ,. .,x .g x ,x ,. .,x f x ,x ,. .,x
.g x , x ,. ., x 1 2 n 1 2 n
1 2 n 1 2 n
10 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
với mọi phép thế . Từ đó, suy ra bộ phận gồm các đa thức đối xứng của vành
A x , x ,..., x
A x , x ,..., x 1 2
n là một vành con của vành 1 2 n .
Chú ý: Có thể coi mỗi phần tử của vành A là một đa thức đối xứng đặc biệt. Thật vậy, a A 0 0 0
thì ta có thể viết: a x x ...x 1 2 n .
Các đa thức đối xứng cơ bản: n
x x ... x x 1 1 2 n i i 1 n
x x x x x x .... x x x x 2 1 2 1 3 2 3 n 1 n i j
1i jn
........................................ .................... n
x x ...x x x ...x x ... x x ...x x x ...x n 1 1 2 n 1 1 2 n2 n 2 3 n 1 i 2 i n i 1 1 1i 2i ...
ni1n n
x x ...x x n 1 2 n i i 1
Theo Định lý 1 thì mọi đa thức của các đa thức đối xứng cơ bản , ,..., 1 2 n cũng là
một đa thức đối xứng của n ẩn x , x ,. ., x 1 2
n . Chiều ngược lại cũng đúng, đó chính là nội
dung của định lý cơ bản về đa thức đối xứng dựa trên các Bổ đề sau. a a a
3. Bổ đề 1. Giả sử f x , x ,..., x x x x ... na x 1 2
n là một đa thức đối xứng khác 0 và 1 2 3 1 2 3 n
là hạng tử cao nhất của nó, thế thì: a a ... a 1 2 n . Chứng minh:
Ta phải chứng minh: a a , i 2,n f x ,..., x i 1 i . Vì 1
n là một đa thức đối xứng nên nếu thay x x x x i 1 , ta đượ
bởi i và hoán vị ngược lại thay i bởi i 1 c: 1 a i a 1 x ... i a x x ... na x 1 i i 1 n
cũng là một hạng tử của f x ,..., x 1 n .
Giả sử: a a i i 1 , khi đó:
11 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
a ,...,a ,a ,a ,...,a a ,...,a ,a ,a ,...,a 1 i2 i i 1 n 1 i2 i 1 i n . Điề a a a a
u này mâu thuẫn với giả thuyết 1 i 1 x ... i x x ... n x 1 i 1 i n là hạng tử cao nhất.
4. Bổ đề 2. Giả sử a ,. ., a 1
n là những số tự nhiên sao cho:
a a ... a 1 2 n a a a a a a a
thế thì đa thức f x , x ,. ., x . . n n n 1 2 n 1 2 2 3 1 2 1 2 n 1 n trong đó ,..., 1
n là các đa thức đối xứng cơ bản, có hạng tử cao nhất là 1 a 2 a x x ... na x 1 2 n . Chứng minh:
Các hạng tử cao nhất của , ,. ., , 1 2 n 1
n theo thứ tự là:
x , x x ,. ., x x . .x , x x . .x 1 1 2 1 2 n 1 1 2 n
Ta có hạng tử cao nhất của f x ,..., x 1 n là: a a x
x x 2a 3a . .x x . .x x x x x x x n n a 1 a a 1 2 n . . n n 1 a 2 a . . na 1 1 2 1 2 1 1 2 1 2 n (đpcm).
Sở dĩ ta kết luận được hạng tử như thế là do ta chứng minh được một Định lý sau:
Định lý * . Giả sử f x , x ,..., x
g x , x ,..., x 1 2 n và 1 2
n là hai đa thức khác không của vành
A x , x ,..., x a a b b 11 c x ... n x 11 d x ... n x c d 0 1 2
n có hạng tử cao nhất theo thứ tự là 1 1 1 n và 1 1 1 n . Nếu 1 1 a b a b
thì hạng tử cao nhất của đa thức tích f x , x ,..., x .g x , x ,..., x 11 11 c d x ... n n x 1 2 n 1 2 n là 1 1 1 1 1 n . Chứng minh: f
x , x ,..., a
x c x ... a n x ... l a c x ... a x 1 2 n 11 1 1 ln 1 1 n l 1 n Giả sử:
đã được sắp xếp theo lối từ điển. g
x , x ,..., b
x d x ... b n x ... m b d x ... m b x 1 2 n 11 1 1 n 1 1 n m 1 n Điều đó có nghĩa là:
12 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
a ,. .,a a ,. .,a , i 2,l 11 1n 1i in Và
b ,. .,b b ,. .,b , i 2,m 11 1n 1i in . Ta sẽ chứng minh: 11 a 11 b 1 a 1 c d x ... n b n x 1 1 1 n
là hạng tử cao nhất của đa thức tích f x ,..., x .g x ,..., x 1 n 1 n .
Nhân f x ,..., x g x ,..., x 1 n với 1 n , ta được:
f x ,...,x g x x c d x x
i l j m n . ,..., n i
a 1 bj1 ... ian bjn , 1, ; 1, 1 1 i j 1 n . i, j a b a b Mỗi hạng tử i1 j1 c d x ... in jn x a b ,. ., n a b i j 1 n
cho ta phần tử 1i j1 in jn . Nhưng vì, ta lại có:
+) Nếu a ,...,a b ,...,b
a c ,...,a c b c ,...,b c , c ,..., n c 1 n 1 n 1 n thì 1 1 n n 1 1 n n .
Thật vậy! Vì: a ,...,a b ,...,b i n 1 n 1
n nên có một chỉ số 1, sao cho:
a b ,. .,a b ,a b 1 1 i 1 i 1 i i .
Do đó: a c b c ,. .,a c b c ,a c b c 1 1 1 1 i 1 i 1 i 1 i 1 i i i i (đpcm).
+) Nếu a ,...,a b ,...,b
c ,...,c d ,...,d 1 n 1 n và 1 n 1 n , thì:
a c ,...,a c b d ,...,b d 1 1 n n 1 1 n n . Thật vậy!
Ta có: a c ,...,a c b c ,...,b c b d ,...,b d 1 1 n n 1 1 n n 1 1 n n (đpcm).
Do vậy, ta có các bất đẳng thức sau:
13 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
a b ,...,a b a b ,...,a b , j 2,m 11 11 1n 1n
11 j1 1n jn
a b ,...,a b a b ,...,a b , i 2,l 11 11 1n 1n 1i 11 in 1n
a b ,...,a b a b ,...,a b , i 2,l, j 2,m 11 11 1n 1n
1i j1 in jn a b a b Vậy hạng tử 11 11 1 1 c d x ... n n x 1 1 1 n
chính là hạng tử cao nhất của đa thức tích. 5. Bổ đề 3.
Giả sử g ,..., 1
n là một đa thức của các đa thức đối xứng cơ bản g ,. ., a
c . . a n . . m a c . . m a n 1 n 11 1 1 1 1 n m 1 n
trong đó c 0, i 1,m
a ,. .,a a ,. .,a , i j i , và 1i in j1 jn .
Thế thì: g ,..., 0 1 n . Chứng minh: Trong g ,...,
x x . . x ,. .,
x x ... x 1 n , thay 1 bằng 1 2 n n bằng 1 2
n ta được một đa
thức của các ẩn x , x ,. ., x 1 2 n . g m
x x ... x ,..., x x ...x f x ,..., x f x ,...,x 1 2 n 1 2 n 1 n i 1 n i 1 với
f x ,...,x c x x x x x x i m n ... n i a 1 ... ... i a n , 1, 1 1 1 1 2 1 2 3 .
Hạng tử cao nhất của đa thức f x ,..., x * 1 1
n theo Định lý là: a a 11 a c x x x ... x x ... n i k i k x c x x ... km x 1 1
1 2 12 1 2 n 1 1 2 i 1 2 k
14 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
a a ...a k 1 i i2 in 1 i
a ...a k với: i2 in i2 .
................................. a k in in
Hạng tử cao nhất của mỗi đa thức f x ,..., x k ,k ,..., n k i 1
n , cho ta phần tử 1 i i2 in .
Ta có: k ,k . .,k
k ,k ,. .,k , i j 1 i i2 in
j1 j2 jn .
Vì nếu: k ,k . .,k
k ,k ,. .,k , i j 1 i i2 in
j1 j2 jn , thì:
a k k k k a 1 i 1 i i2 j1 j2 j1
a k k k k a i2 i2 i3 j2 j3 j2
.................................................
a k k a in in jn jn
với i j , mâu thuẫn với giả thuyết. n Vì
sắp thứ tự toàn phần nên bộ phận hữu hạn gồm các phần tử k ,k ...,k i m 1 i i2 in với 1, k k
có phần tử lớn nhất, chẳng hạn k ,k ,...,k 11 c x ... n x 11 12
1n là phần tử lớn nhất. Do đó 1 1 1 n là hạng
tử cao nhất của f x ,..., x 1 n .
Vậy: g ,...,
f x ,..., x 0 1 n 1 n (đpcm).
Hệ quả. Giả sử:
hx ,x ,. ., a
x c x . . a n x . . m a c x . . m a n x 1 2 n 11 1 1 1 1 n m 1 n và
h'x ,x ,. ., a
x c x . . a n x . . m a c x . . m a n x 1 2 n ' 11 1 ' 1 1 1 n 1m 1 n
là hai đa thức trong đó a ,. .,a a ,. .,a 1 i in
j1 jn khi i j, sao cho:
15 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
h ,..., h' ,..., 1 n 1 n
Thế thì c c ', i 1, m i i . Chứng minh:
Giả sử có c c ' i i .
Đặt: g ,..., h ,..., h' ,..., 1 n 1 n 1 n . a a a a
c c ' . . n
. . c c ' m . . mn 1 1 11 1 1 n m m 1 1 n Vì: c c ' c c ' 0 1 1 , nên 1 1 .
Theo Bổ đề 3, ta có: g ,..., 0 1 n .
Nhưng theo giả thuyết thì: g ,..., 0 1 n , mâu thuẫn.
6. Định lý 2. (Định lý cơ bản về đa thức đối xứng).
Giả sử f x , x ,..., x A x , x ,..., x 1 2 n 1 2
n là một đa thức đối xứng khác không, khi đó có một
và chỉ một đa thức h x , x ,..., x A x , x ,..., x
f x , x ,..., x h , ,..., 1 2 n 1 2 n sao cho 1 2 n 1 2 n . Trong đó , ,. ., 1 2
n là các đa thức đối xứng cơ bản. Chứng minh: Sự tồn tại. a a
Ta hãy sắp xếp f x , x ,..., x x x ... na x 1 2
n theo lối từ điển, giả sử 1 2 1 2 n
là hạng tử cao nhất của
f x ,x ,...,x 1 2
n . Theo Bổ đề 1, ta có:
a a ... a 1 2 n
Mặt khác, theo Bổ đề 2, thì đa thức:
16 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] 1 a 2 a 2 a 3 a a 1 ... n n a n a 1 2 n 1 n cũng có hạ a a ng tử cao nhất là: 1 2 x x ... na x 1 2 n . Xét hiệu:
f x ,. ., x f x ,. ., a a a a x . . n a n a n a 1 1 n 1 n 1 2 2 3 1 1 2 n 1 n .
Nếu f x ,..., x 0 1 1 n
, thì ta sắp xếp nó theo lối từ điển và giả sử 1 b 2 b x x ... nb x 1 2 n
là hạng tử cao nhất của nó.
Theo Định lý 1 thì f x , x ,..., x 1 1 2
n cũng là một đa thức đối xứng, và do đó ta có:
b b ... b 1 2 n .
Mặt khác, từ biểu thức của hiệu hai đa thức, ta có:
a ,...,a b ,...,b 1 n 1 n Do đó: a b 1 1 . b b b b b b b Xét hiệu: f
x ,. ., x f x ,. ., x . . n n n 2 1 n 1 1 2 1 2 2 3 1 1 2 n 1 n . Nếu f x ,..., x 0 2 1 n
, ta hãy sắp xếp nó theo lối từ điển và giả sử 1 c x ... nc x 1 n
là hạng tử cao nhất của nó. Cũng lý luận tương tự đối với f x ,..., x , ta đượ 1 1 n c:
c c ... c 1 2 n Với
17 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
b ,b ,...,b c ,c ,...,c 1 2 n 1 2 n .
Ta nhận thấy rằng dãy a ,...,a b ,...,b c ,...,c ... 1 n 1 n
1 n không thể giảm vô hạn, tức là
quá trình lập luận trên diễn ra không thể vô tận. Sau một số hữu hạn bước, ta sẽ có: 0 f x x
x k , ,. ., l l l l . . n l n l n l 1 2 n 1 2 2 3 1 1 2 n 1 n
Vậy, từ các kết quả trên, ta có:
f x ,x ,. .,x n 1 a 2 a 2 a 3 a n a 1 b 2 b 2 b 3 b n b 1 l 2l 2 l 3 . . . . . . l . . nl 1 2 1 2 n 1 2 n 1 2 n .
Vậy đa thức h x , x ,..., x 1 2
n cần tìm là đa thức:
hx ,x ,. .,x x x x x x x x x x n 1 a 2 a 2 a 3 a n a 1 b 2 b 2 b 3 b n b 1 l 2l 2 l 3 . . . . . . l . . nl 1 2 1 2 n 1 2 n 1 2 n Tính duy nhất.
Giả sử có một đa thức h ' x ,..., x
h' ,..., f x ,..., x 1 n sao cho 1 n 1 n .
Thế thì: h ' ,..., h ,..., 1 n 1 n .
Áp dụng hệ quả của Bổ đề 3 ta có:
hx ,...,x h' x ,...,x 1 n 1 n . n n
Hệ quả. Giả sử f x 1 x a x ... a 1
n là một đa thức bậc n trên trường K , có n nghiệm , ,. .,
g x , x ,..., x 1 2
n trong trường E nào đó chứa K như một trường con và giả sử 1 2 n
K x , x ,..., x
g , ,..., K 1 2
n là đa thức đối xứng. Khi đó: 1 2 n . Chứng minh:
Thật vậy! Theo định lý cơ bản về đa thức đối xứng, tồn tại K x , x ,..., x 1 2 n sao cho
gx ,x ,...,x , ,..., 1 2 n 1 2 n .
Mặt khác, theo công thức Viète, ta có:
18 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
, ,..., 1 k a K k 1 2 n k . Bởi vậy
g , ,. ., ,. ., ,. ., ,. ., a ,a ,. ., 1 n a K 1 2 n
1 1 n n 1 n 1 2 n .
Phép chứng minh Định lý 2 cho phép chúng ta biết cách biễu diễn một đa thức đối xứng qua
các đa thức đối xứng cơ bản. Trong thực tế để việc biểu diễn nhanh chóng hơn, chúng ta có
nhận xét rằng đa thức đối xứng f x , x ,..., x 1 2
n có thể không phải là đẳng cấp, nhưng các hạng
tử có cùng một cấp của nó lập thành một đa thức đối xứng đẳng cấp, do đó f x , x ,..., x 1 2 n là
tổng của những đa thức đối xứng đẳng cấp.
Bây giờ giả sử f x , x ,..., x A x , x ,..., x 1 2 n 1 2
n là đa thức đối xứng đẳng cấp bậc k và hạng tử cao nhất là 1 a 2 a x x ... na x 1 2 n .
Bậc của f x , x ,..., x 1 2 n là
a a ... a k 1 2 n .
Các đa thức đối xứng cơ bản ,..., 1
n có bậc theo thứ tự là 1,2,. ., n , nên đa thức tích 1 a 2 a 2 a 3 a a ... n a 1 2 n
cũng là đẳng cấp và có bậc là:
a a 2 a a ... na a a ... a k 1 2 2 3 n 1 2 n .
Do đó theo Định lý 2, ta có:
f x ,x ,. .,x f x x x n , ,. ., n 1 a 2 a 2 a 3 a . . na 1 1 2 1 2 1 2 n
cũng là đẳng cấp bậc k nếu khác 0 .
Sắp xếp f x , x ,..., x 1 1 2
n theo lối từ điển và giả sử hạng tử cao nhất là
19 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] 1 b 2 b x x ... nb x 1 2 n
Thế thì a a . . a b b . . b k
a ,a ,...,a b ,b ,...,b 1 2 n 1 2 n và 1 2 n 1 2 n .
Theo Định lý 2, ta có dãy hữu hạn
a ,a ,...,a b ,b ,...,b c ,c ,...,c ... 8 1 2 n 1 2 n 1 2 n trong đó
a a ... a 1 2 n
b b ... b 1 2 n
c c ... c 1 2 n .........................
và a a . . a b b . . b c c . . c . . k 1 2 n 1 2 n 1 2 n .
Tập hợp các phần tử của dãy * là một bộ phận của tập hợp hữu hạn M
t ,. .,t ,. ., t ,. .,t 11 1n 1m mn
Trong đó t t ... t
t t . . t a a . . a k 1 i i2 in và 1 i i2 in 1 2 n .
Vậy, theo Định lý 2 thì f m
x , x ,..., x n it1 it2 it2 it3 ... itn 1 2 i 1 2 n . i 1
các hệ số A i
tìm được nhờ phương pháp hệ số bất định.
Chú ý: Nếu phần tử t ,...,t 8 1 i
in không có mặt trong dãy thì 0 i . Tập hợp M
t ,. .,t ,. ., t ,. .,tn
f x , x ,..., x 11 1n 1m
gọi là hệ thống số mũ của đa thức 1 2 n .
20 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
D. MỘT SỐ ỨNG DỤNG CỦA ĐỊNH LÝ VIÈTE.
I. Một số ứng dụng.
Dạng 1. Tìm hai số khi biết tổng và tích.
Dạng 2. Tính giá trị biểu thức đối xứng.
Dạng 3. Tìm điều kiện của tham số để hai nghiệm liên hệ với nhau bởi một hệ thức cho trước.
Dạng 4. Tìm hệ thức liên hệ giữa các nghiệm độc lập với tham số.
Dạng 5. Thiết lập phương trình bậc hai.
Dạng 6. Xét dấu các nghiệm.
Dạng 7. Giải hệ phương trình đối xứng loại 1.
Dạng 8. Chứng minh bất đẳng thức.
Dạng 9. Ứng dụng trong bài toán cực trị.
Dạng 10. Ứng dụng trong bài toán tiếp tuyến.
Dạng 11. Ứng dụng hệ thức truy hồi.
Dạng 12. Ứng dụng tính các biểu thức lượng giác.
Dạng 13. So sánh nghiệm.
Dạng 14. Ứng dụng khác.
II. Bài tập áp dụng.
Dạng 1. Tìm hai số khi biết tổng và tích. S 2x
Câu 1. Tìm hai số a và b khi biết tổng S và tích P : . 2 2
P x y Giải Ta có: X ,
a X b là nghiệm của phương trình: 2 2 2
X 2xX x y 0 .
21 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] 2 2 2 2
Ta có: ' x x y y 0 . Khi đó: 2
X x y x y . Vậy: ; a b
x ;yx y,x ;yx y.
Câu 2. Tìm hai số a và b biết:
a b 9 a) . 2 2
a b 41 Giải 2 2 81 a b 2 2 2 81 41
Ta có: a b 9 a b 81 a b
2ab 81 ab 20 2 2 . a b 9 Khi đó, ta có: . ab 20 Như vậy, x ,
a x b là hai nghiệm thực của phương trình: 2
x 9x 20 0 . 2 x 4
Ta có: x 9x 20 0 . x 5 Suy ra: , a b 4;5,5;4. a b 5 b) . ab 36 2 2 2
Ta có: a b 25 a b 4ab 25 a b 25 4ab 25 4.36 169 .
a b 13 Như vậy: . ab 36 2 Suy ra: x ,
a x b là hai nghiệm mỗi phương trình 2
x 13x 36 0 hoặc x 13x 36 0.
22 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] x 4 +) Phương trình 2
x 13x 36 0 có hai nghiệm là: . x 9 Do vậy: , a b 4;9,9;4. x 4 +) Phương trình 2
x 13x 36 0 có hai nghiệm là: . x 9 Do vậy: , a b 9 ; 4 , 4 ; 9 .
Dạng 2. Tính giá trị biểu thức đối xứng.
Câu 1. Giả sử x , x , x
x px q 1 2
3 lần lượt là ba nghiệm của phương trình 3 0 . 2 2 2
Tính giá trị của biểu thức: S x x x x x x 1 2 2 3 1 3 . Giải 2 2 2
Đặt: gx , x , x x x x x x x 1 2 3
1 2 1 3 2 3 2 2 2
Dễ thấy: g x , x , x x x x x x x 1 2 3
1 2 1 3 2 3 là đa thức đối xứng.
Hệ thống số mũ: M 4;2;0;4;1 ;1 ;3;3;0;3;2 ;1 ;2;2;2.
Khi đó: gx , x , x 2 2 3 3 2
a b c d 1 2 3 1 2 1 3 2 1 2 3 3 . Chọn: x 1 0 1 1 +) x 1 1 b 4 2 2 . x 0 0 3 3 0 1 x 2 1 +) 3 d 27 2 . x x 1 2 3 2 3
23 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] 3 1 x 1 1 +) 0 a 4 2 . x x 2 2 3 4 3 1 1 x 1 1 +) 1 c 18 2 .
x x 1 2 3 1 3
Khi đó: gx , x , x 2 2 3 3 2
4 4 18 27 1 2 3 1 2 1 3 2 1 2 3 3 . 0 1
Vì: x , x , x
x px q p 1 2
3 lần lượt là ba nghiệm của phương trình 3 0 nên 2 . q 3 Do đó, 3 2 S 4 p 27q .
Câu 2. Giả sử x, y, z là ba nghiệm của phương trình 3
2021 2022 0 . Tính giá trị 4 4 4
của biểu thức S x y z ? Giải
x y z 0
Theo định lý Viète, ta có: xy yz xz 2021 . xyz 2022 Mặt khác, ta có:
x y z 0 x y z2 2 2 2
0 x y z 2xy yz xz
x y z 2 2
xy yz xz 2 2 2 2 4 4 4 2 2 2 2 2 2
x y z 2x y 2y z 2x z 4 2 2 2 2 2 2 2 2 2
x y y z x z 2xy z 2xyz 2x yz 4 4 4
x y z 2 2 2 2 2 2 2 2 2 2
x y y z x z 2xy z 2xyz 2x yz 4 2 2 2
x yz xy z xyz 4 4 4
x y z 2xy yz xz2 xyzx y z xy yz xz2 2 4 2 2.2021
24 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
Dạng 3. Tìm điều kiện của tham số để hai nghiệm liên hệ với nhau bởi một hệ thức cho trước.
Câu 1. Cho phương trình 2
y my p 0 có hai nghiệm là y y . Đị 1 và 2
nh m và p để 1 1 1 và
cũng là nghiệm của phương trình này. y 1 y 1 2 Giải Xét phương trình 2
y my p 0 * . Phương trình * 2 2
có nghiệm khi và chỉ khi: m 4 p 0 hay m 4 p .
y y m 1 2
Áp dụng hệ thức Viète, ta có: . y y p 1 2 1 1 2 y y 1 2 2 m 1 y 1 y
1 y y y y p m 1 1 2 1 2 Khi đó, ta có: 1 2 . 1 1 1 . 1 y 1 y p m 1 1 2
2 m m 1 1 1 p m 1 Do ; * 1
cũng là nghiệm của phương trình nên: . y 1 y 1 1 2 p 2
p m 1 Từ
1 , 2, suy ra: p2 m m 3 . +) Nếu m 2 . p 0 2 (vô lý). m
+) Nếu m 2 p 2 , ta đượ m , thay vào c: 2 m m m
mm m m 2 2 1 . 1 4 2 2 . m 2 m 2
25 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] m m 1 1 2
m 2m 4 0 . m 1 5 Thử lại: 2
+) Với m 1, thì p 1
thỏa điều kiện m 4p . 3 5 2
+) Với m 1 5 thì p m 4p 2 thỏa điều kiện . 3 5 2
+) Với m 1 5 thì p m 4p 2 thỏa điều kiện .
Vậy các cặp m, p cần tìm là 3 5 3 5 1; 1 ,1 5; ,1 5, 2 2 .
Câu 2. Cho phương trình 2 2
x 2mx m m 6 0 ( m là tham số).
1. Với giá trị nào của m thì phương trình đã cho có hai nghiệm x x 1 và 2 sao cho x x 18 1 2 x x 7 . 2 1
2. Với giá trị nào của m để phương trình đã cho có hai nghiệm x x 1 và 2 sao cho x x 8 1 2 . Giải
1. Để phương trình 2 2
x 2mx m m 6 0 có hai nghiệm thì: 2 m 2 '
m m 6 m 6 0 m 6 1 . Với điều kiện 1 , ta có: x x 18 x x 18 x x 2x x 18 1 2 1 2 2 2 2 1 2 1 2 , x x 0 1 2 x x 7 x x 7 x x 7 . 2 1 1 2 1 2
26 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] 2 4m 2 2 m m 6 2 18 m m 6 9 , m 2, m 3 2 2 . m m 6 7 m m 6 7 m 4 2 1
m 8m 48 0
(thỏa điều kiện
1 và đều khác 2 và 3 ). m 12 2
2. Với điều kiện 1 ,
x x 8 x x 2 x x 64 x x 2 2 2
2x x 2 x x 64 2 1 2 1 2 1 2 1 2 1 2 1 2 . m 6 6 m 2 Nếu x x x x 0 3 1 và 2 cùng dấu thì: 1 2 2 m . m 6
m2m3 0 m 3
Khi đó: 2 x x 2 2
64 4m 64 m 4 3 1 2
(thỏa điều kiện ). 2 Nếu x x
x x 0 m m 6 m 2 m 3 0 2 m 3 4 1 và 2 trái dấu thì: 1 2 . 2
Khi đó: 2 x x 2
4x x 64 4m 4 2
m m 6 64 m 10 1 2 1 2
(không thỏa điều kiện 4 ).
Vậy để x x 8 m 1 2 thì: 4.
Dạng 4. Tìm hệ thức liên hệ giữa các nghiệm độc lập với tham số. 2
Câu 1. Giả sử phương trình mx 2m 3 x m 4 0 ( m là tham số) có hai nghiệm
thực phân biệt là x , x x , x 1
2 . Tìm hệ thức liên hệ giữa 1
2 không phụ thuộc vào m . Giải 2m 3 3 12 x x 2
4 x x 8 1 2 1 2 Theo đị m m m nh lý Viète, ta có: . m 4 4 12 x x 1 3 x x 3 1 2 1 2 m m m
27 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
Suy ra: 4 x x 3x x 11 4x 4x 3x x 11 x , x 1 2 1 2 1 2 1 2
là hệ thức liên hệ giữa 1 2 ,
độc lập với tham số m . 2
Câu 2. Cho phương trình m
1 x 2m
1 x m 0.
a) Giải và biện luận phương trình.
b) Khi phương trình có hai nghiệm phân biệt x , x x , x 1
2 . Tìm một hệ thức liên hệ giữa 1 2 độc lập với m . Giải 1
a) Xét m 1, phương trình đã cho trở thành: 4
x 1 0 x 4 là nghiệm duy nhất. 2
Với m 1, ta có: ' m
1 mm 1 3m 1. 1
+) Với: m , phương trình đã cho có hai nghiệ 3 m phân biệt. 1
+) Với m , phương trình đã cho có mộ 3 t nghiệm kép. 1
+) Với m , phương trình vô nghiệ 3 m. 2m 1 4 x x 2 1 2 m 1 m 1
b) Theo định lý Viète, ta có:
lấy phương trình trên trừ đi m 1 x x 1 1 2 m 1 m 1
4 lần phương trình dưới, ta có: x x 4x x 2 1 2 1 2 .
Vậy hệ thức liên hệ giữa x , x , độ
x x 4x x 2 1 2
c lập với tham số m là: 1 2 1 2 .
Dạng 5. Thiết lập phương trình bậc hai.
Câu 1. Tìm phương trình bậc hai có hai nghiệm x 2021 và x 2022 . Giải
28 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
S x x 4043 1 2 Ta có: .
P x x 4086462 1 2
Như vậy, dễ dàng suy ra được, phương trình bậc hai có hai nghiệm x 2021 và x 2022 là: 2
x 4043x 4086462 0 .
Câu 2. Giả sử x , x
x px q 1
2 là hai nghiệm của phương trình 2 0 . Hãy lập một phương
trình bậc hai có hai nghiệm là x x x x 1 2 và 1 2 . Giải
x x p Theo đị 1 2 nh lý Viète, ta có: . x x q 1 2
X x x Bài toán đã cho đượ 1 1 2
c quy về việc tìm phương trình bậc hai nhận làm nghiệm. X x x 2 1 2
S X X p q Đặ 1 2 t: .
P X X pq 1 2
Như vậy! Phương trình bậ 2
c hai cần tìm là: x p q x pq 0 .
Dạng 6. Xét dấu các nghiệm. x x
Câu 1. Cho hàm số C 2 3 3 : y x . 2
Tìm các giá trị của m để đường thẳng d : y mx m cắt đồ thị tại hai điểm thuộc về hai
nhánh của đồ thị C . Giải 2 x 3x 3
Phương trình hoành độ giao điểm của hai đồ thị d và C: mx m * x . 2
m 2 *
1 x m 3 x 2m 3 0 1 .
29 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
Để d cắt C tại hai điểm thuộc hai nhánh khi và chỉ khi
1 có hai nghiệm x , x 1 2 thỏa mãn x 2 x
x 2 0 x 2 1 2 hay 1 2 .
Đặt: t x 2, ta đưa
1 về phương trình ẩn t : m 2
1 t 3m
1 t 1 0 2 .
Phương trình 2 phải có hai nghiệm trái dấu. Khi đó: m 1 . 1 0 m 1.
Câu 2. Cho phương trình
m 3x m 2 1 3
1 x x 4m 1 0 1 ( m là tham số).
Với giá trị nào của m , thì phương trình
1 có ba nghiệm phân biệt, trong đó có hai nghiệm âm. Giải 3 2 Ta có: m
1 x 3m
1 x x 4m 1 0 1 . m 3
1 x m 2 2
1 x 4mx 4m x 1 0 m 2 1 x x 1 4m 2 x 1 x 1 0 m 2 1 x x
1 4mx 1 x 1 x 1 0 x a
x 1 m 1 2
1 x 4mx 4m 1 0 g
x m 2
1 x 4mx 4m 1 0 b Để phương trình
1 có ba nghiệm thực phân biệt thì phương trình b phải có hai m 1
nghiệm thực phân biệt khác 1, tương đương với: ' m b 1 3 0 . g 1 0
30 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] m 1 1 1 Hay: m m 1
,m 0,m * 3 3 . 9m 0
Với điều kiện * , phương trình
1 có ba nghiệm phân biệt, trong đó có một nghiệm
x 1 0 và hai nghiệm còn lại x , x x x b . Do đó để 1 2 1
2 là nghiệm của 1 có ba
nghiệm phân biệt trong đó có hai nghiệm âm thì: x x 0 , tương đương vớ 1 2 i: m 1 4m 1 P x x 0 1 m 1 1 2 m 1 m 4 1 **. 4m 0 m S x x m 1 1 2 4 m 1 m 0 Để phương trình
1 có ba nghiệm phân biệt, trong đó có hai nghiệm âm thì điều kiện cần 1 1 và đủ là: m 1 hoặc m 4 3 .
Dạng 7. Giải hệ phương trình đối xứng.
x y y x 30
Câu 1. Giải hệ phương trình: .
x x y y 35 Giải
u x 0 Đặt: , hệ đã cho trở thành: v y 0 2 2 uv u v u v uv 30 30 . 3 3
u v 35 u v
3 3uvu v 35
31 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
S u v 2 Tiếp theo ta đặt:
, S 4P. P uv SP 30 SP 30 S 5
Ta thu được một hệ mới: (thỏa mãn). 3 3
S 3SP 35 S 125 P 6
Theo định lý Viète, ta có: u,v là nghiệm của phương trình: 2
t 5t 6 0 . u 2 t 2 v 3 Khi đó: . t 3 u 3 v 2
Dẫn đến nghiệm của hệ là ; x y 4;9;9;4 2 2
x xy y 3 2
Câu 2. Giải hệ phương trình: . 4 4
x y 5 Giải
Ta có: x y x y 2 4 4 2 2 2 2 2x y . 2 2
u x y
u v 3 2 Đặt:
, hệ đã cho trở thành: . v xy 2 2
u 2v 5 u 3 v 2
Giải hệ đã cho, ta được: II . u 9 4 2
v 6 3 2 2 2 2 2
x y 3 x y 3
Với hệ I , thì: . 2 2 xy 2 x y 2
32 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] t 1 Theo đị 2 2
nh lý Viète, thì: x , y là nghiệm của phương trình: 2
t 3t 2 0 , ta được: . t 2 2 x 1 2 y 2 xy 0
Thế vào hệ, ta được: . 2 x 2 2 y 1 xy 0 Suy ra nghiệm ;
x y 1; 2; 1 ; 2 ; 2; 1 ; 2;1.
Trường hợp còn lại vô nghiệm.
Dạng 8. Chứng minh bất đẳng thức. 2
Câu 1. Cho x, y, z khác 0 , thỏa mãn: x y z xyz và x yz . 2
Chứng minh rằng: x 3 . Giải 3
y z x x
Từ giả thuyết, ta có: . 2 yz x Theo đị 2 3 2
nh lý Viète, thì y, z là nghiệm của phương trình: t x xt x 0 .
Do tồn tại các số y, z , nên phương trình trên phải có nghiệm: 2 2 3 2 2 2
Tức là: 0 x x 4x 0 x x 1 4 0 . x 1 2
Vì: x 0 , nên: x 2 2 2 2 1 4 0 x 3 . 2 x 1 2
33 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
x y z 5 7
Câu 2. Cho các số thực x, y, z thỏa mãn:
. Chứng minh rằng: 1 x, y, z .
xy yz xz 8 3 Giải
Từ giả thuyết, ta xem z là tham số, ta có hệ phương trình ẩn x, y :
x y 5 z
x y 5 z xy z . x y 8 xy 8 z 5z Theo đị 2
nh lý Viète thì x, y là nghiệm của phương trình: t 5 zt 8 z5 z 0 .
Do phương trình có nghiệm đối với x, y nên:
z2 z z 7 5 4 8 5
0 1 z 3 .
Do vai trò bình đẳng của x, y,z nên ta có kết luận tương tự đối với x và y .
Dạng 9. Ứng dụng trong bài toán cực trị.
Câu 1. Tìm tất cả các giá trị tham số m để đồ thị hàm số y f x 3
mx m 2
2 x 1 m x 3
có hai điểm cực trị có hoành độ dương là? Giải
Ta có: f x 2
3mx 2m 2 x 1 m .
Để đồ thị hàm số có hai điểm cực trị có hoành độ dương thì:
m 2 m m 1 2 3 1 0 m 4 0 m 2 2 2 1 S 0 0
2 m 0 m 0 . 3m 2 P 0 m 0 1 m 0 m 1 m
Câu 2. Tìm tất cả các giá trị nguyên của tham số m 1
0;10 để hàm số:
34 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] 3 y
x 4mx m 2 3 2 1 x 1 2
có hai điểm cực trị x , x thỏa mãn x x x x là? 1 2 1 2 1 2 Giải 9 Ta có: y
x 8mx m 2 2 1 . 2
Hàm số y có hai điểm cực trị khi phương trình y 0 có hai nhgiệm phân biệt
m23m 18 9 . 2m 2 1 Theo đị 16m
nh lý Viéte ta có: x x ; x x . 1 2 1 2 9 9 2 16 m 5 2 6
x x x x m 2 2 1
m m 10m 1 0 . 1 2 1 2 9 9 m 5 2 6 m 1 0;01 0 .
Dạng 10. Ứng dụng trong bài toán tiếp tuyến. x 2
Câu 1. Cho hàm số y
có đồ thị C và điểm A0;a . Hỏi có tất cả bao nhiêu giá x 1
trị nguyên của a để từ điểm A kẻ được hai tiếp tuyến đến C sao cho hai tiếp điểm nằm
về hai phía của trục hoành? Giải 3 Ta có: y ' . x 2 1 x 2 Gọi tiếp điểm là 0 M x ;
. Khi đó phương trình tiếp tuyến của C tại M là: 0 x 1 0 x
d : y f x x x 3 2 y x x . 2 0 0 0 0 0 x 1 x 1 0 0
35 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] Vì đườ 3 x 2
ng thẳng d : y x x
đi qua điểm A0;a . Khi đó: 2 0 0 x 1 x 1 0 0 3x x 2 0 0 2 2 x a 3x x x 2 ax 2ax a 2 0 0 0 0 0 1 x 1 0 0 a 2
1 x 2 a 2 x a 2 0, x 1 1 0 0 0
Từ A kẻ được 2 tiếp tuyến đến C Phương trình
1 có 2 nghiệm x phân biệt khác 1 0
a 2 2 a 1 a 2 0
3a 6 0 . a
a 1 .1 2 a 2 2 .1 a 2 0 3 0
Khi đó phương trình (1) có hai nghiệm x , x 1. 1 2
Hai tiếp điểm nằm về hai phía của trục hoành a 2 2 a 2 2 4 x 2 x 2
x x 2 x x 4 1 2 1 2 1 2 a 1 a 1
y .y 0 0 0 0 1 2 x 1 x 1
x x x x 1 a 2 2 a 2 1 2 1 2 1 2 1 a 1 a 1
a 2 4a 8 4a 4 9a 6 2 a 1 0
0 3a 2 0 a .
a 2 2a 4 a 1 3 3 a 1 x
Câu 2. Cho hàm số: C 1 : y . Đườ
d y x m 2x ng thẳng :
. Với mọi m ta luôn có 1
d cắt C tại hai điểm phân biệt ,
A B . Gọi k ,k 1
2 lần lượt là hệ số góc của tiếp tuyến với
C tại ,AB. Tìm m để tổng k k 1
2 đạt giá trị lớn nhất. Giải
Phương trình hoành độ giao điểm của d và C là: 1 x 1 x
x m 2 2x . 1 g x 2
2x 2mx m 1 0*
x x m 1 2
Theo định lý Viète, ta có: m 1 . x x 1 2 2
36 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
Giả sử: A x ; y ,B x ; y 1 1 2 2. 1 Ta có: y ' . 2x 2 1 1 k 1 2x 2 1 1
Nên tiếp tuyến của C tại A và B có hệ số góc lần lượt là: . 1 k 2 2x 2 1 2 4 2 2 x x
4 x x 2 1 1 1 2 1 2
Vậy: k k 1 2 . 2x 2 1 2x 2 1 4x x 2 x x 2 1 1 2 1 2 1 2
4 x x 2 2x x
4x x 2 4 2 1 2 1 2 1 2 m m 1 4m 2
k k 1 2 4x x 2 x x 2 1 2
m 2 2m 2 1 1 2 1 2
k k 4
m 8m 6 4
m 2m
1 2 4m 2 2 2 1 2 2 1 2
Vậy tổng k k m 1
2 đạt giá trị lớn nhất bằng 2 khi 1.
Dạng 11. Ứng dụng hệ thức truy hồi.
Phương pháp truy hồi:
Xét phương trình bậc hai: 2 2
ax bx c 0, a 0. Giả sử x , x 1
2 là các nghiệm của nó. Đặ n n
t: S x x , n n 1 2 .
Lúc đó ta có hệ thức truy hồi tuyến tính sau: aS
bS cS 0 1 n2 n 1 n .
37 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] Chứng minh: n2 n2 n 1 n 1 n n Ta có: S x x x x
x x x x x x n2 1 2 1 2 1 2 1 2 1 2 . . b c S S .S aS
bS cS 0 n2 n 1 n n2 n 1 n (đpcm). a a
Câu 1. Tìm số nguyên lớn nhất không vượt quá 7 4 15 Giải x 4 15 Ta đặ 1 t: . x 4 15 2 Khi đó: x , x x x 1
2 là nghiệm của phương trình: 2 8 1 0 . Đặ n n
t: S x x , n S
8S S 0 n 1 2
. Ta có hệ thức: n2 n 1 n . S 8 1 S 62 2 S 488 3
Ta tính được: S 3842 4 . S 30248 5 S 238142 6 S 1874888 7 Như vậ 7 7 7 y: x 1874888 x 0 x 1 1 2 . Mà 2 . 7
Suy ra: 1874887 x 18748888 1 .
Vậy số nguyên lớn nhất không vượt quá 7 4 15 là 1874887 .
Câu 2. Tìm chữ số tận cùng của phần nguyên của số 2021 5 3 3 .
38 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] Giải x 53 3 Ta đặ 1 t: x , x x x 1
2 là nghiệm của phương trình: 2 10 2 0 . x 5 3 3 2 Đặ n n
t: S x x , n n 1 2
. Theo hệ thức truy hồi, ta có: S 10S 2S n2 n 1 n .
Ta có: S 10 10 S 1 2k 1 . Để n n ý rằng: 1 x 0
S x S x S 1 2 , nên suy ra: n 1 n 2 n . n
Vậy nên x S 10 S 1 n . Vì 2021 là số lẻ nên 2021 .
Vậy chữ số tận cùng của phần nguyên của số 2021 5 3 3 là số 0 .
Dạng 12. Ứng dụng tính các biểu thức lượng giác. 9 9 17 17 3
Câu 1. Chứng minh rằng: cos cos cos cos cos cos 12 12 12 12 12 12 4 . Giải 3
Áp dụng công thức nhân ba, ta có: cos3x 4 cos x 3 cos x . 3 2 +) Với x 4cos 3cos 0 1 12 , ta có: . 12 12 2 Nên: cos t t
12 là nghiệm của phương trình: 3 2 4 3 0 2 . 9 17
Lập luận tương tự, ta có: cos cos 12 và
12 cũng là nghiệm của phương trình 1 . 9 9 17 17 3
Theo định lý Viète, ta có: cos cos cos cos cos cos 12 12 12 12 12 12 4 .
39 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
Câu 2. Cho b 0 , giả sử phương trình: 3 2
x ax x b 0
có ba nghiệm là x , x , x 1 2 3 . Chứng minh rằng: 1 1 1 1 1 1 x x x x x x 4 1 2 2 3 3 1 x x x x x x . 1 2 2 3 3 1 Giải
Theo định lý Viète, ta có:
x x x x x x 1 1 2 2 3 3 1 .
Đặt: x tan; x tan ; x tan 1 2 3 , thế thì ta có:
tan tan tan tan tan tan 1.
Suy ra: k , k
k k 2 , suy ra: 2 2 2 , .
Đẳng thức cần chứng minh tương đương với:
tan cottan cot tan cot tan cottan cottan cot 4
Để ý rằng: tan x cot x 2 cot 2x .
Vì thế, đẳng thức cần chứng minh trở thành:
cot 2 cot 2 cot 2 cot 2 cot 2 cot 2 1.
Đẳng thức hiển nhiên đúng, vì: 2 2 2 k , k (đpcm). 1 1 1 1 1 1 Vậy: x x x x x x 4 1 2 2 3 3 1 x x x x x x . 1 2 2 3 3 1
40 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
Dạng 13. So sánh nghiệm.
Định lý về dấu kết hợp định lý Viéte cho tam thức bậc hai:
S x x Đặt: 1 2 .
P x .x 1 2 .
a So sánh nghiệm với hằng số 0 . 0 ' 0
i Điều kiện để: x x 0 là: S 0 1 . 1 2 P 0 0 ' 0
ii Điều kiện để: 0 x x là: S 0 2. 1 2 P 0
iii Điều kiện để: x 0 x là: P 0 3. 1 2 .
b So sánh nghiệm với hằng số , (Với , là các tham số thực cho trước).
i Điều kiện để: x x là: .af 0 4 . 1 2 0 ' 0
ii Điều kiện để: x x là: . a f 0 5. 1 2 S 2 0 ' 0
iii Điều kiện để: x x là: . a f 0 6. 1 2 S 2
41 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] . a f 0
iv Điều kiện để: x x là: 7. 1 2 . a f 0 . a f 0
v Điều kiện để: x x là: 8. 1 2 . a f 0
x x
vi Điều kiện để: 1 2
là: f . f 0 9.
x x 1 2 0 ' 0 .af 0
vii Điều kiện để: x x là: 10 . 1 2 . a f 0 S 2
Để tiết kiệm thời gian cho một số bài toán ta có thể tính trực tiếp dựa trên hàm số bậc ba: 3 2
y ax bx cx d a 0 . Khi đó: a 0
Hàm số đồng biến trên khi và chi khi . ' 2
b 3ac 0 f ' a 0
Hàm số nghịch biến trên khi và chi khi . ' 2
b 3ac 0 f '
42 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] Extra Techniques Study tips
Cơ sở hình thành các điều kiện:
1 :Phương trình có hai nghiệm phân biệt nên 0 hoặc ' 0. Do tổng của hai số âm
là một số âm và tích của hai số âm là một số dương.
2:Phương trình có hai nghiệm phân biệt nên 0 hoặc ' 0. Do tổng của hai số
dương là một số dương và tích của hai số dương là một số dương. c
3 :Sỡ dĩ chỉ cần một điều kiện P 0 là vì khi P 0 P 0 hay a
ac 0 ac 0 . Khi đó: 2
b 4ac 0 . Đã thỏa mãn điều kiện cần và đủ để
phương trình có hai nghiệm thực phân biệt.
4,7,8,9: gx trong khoảng hai nghiệm thì trái dấu với hệ số a và ở ngoài hai
khoảng nghiệm thì cùng dấu với hệ số a . Và tích của một số dương với một số âm là một số âm. S
5 : Vì x x nên x x 2x 2 6 : Vì x x nên 2 1 1 2 1 2 1 2 S
x x 2x 2
6 : Vì x x nên 2x x x 2x . Khi đó: 1 2 2 2 1 2 1 1 2 2 S
2 S 2 . 2
Lưu ý: Ở các điều kiện5,6, 10 thì dấu của các tích . a f , .
a f đều được xét
dấu tương tự với 4, 7,8,9 . Và vì phương trình có hai nghiệm phân biệt nên 0 hoặc ' 0 . 2
Câu 1. Tìm m để hàm số 3 y
x m 2
1 x 2mx 5 đồng biến trên khoảng 0;2 . 3 Giải
43 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] Ta có: 2 y ' 2
x 2m 1 x 2m .
Để hàm số đồng biến trên khoảng 0;2 thì phương trình y ' 0 có hai nghiệm thực phân
biệt x x thỏa mãn: x 0 2 x . Điều đó tương đương với hệ: 1 2 1 2 . a f 0 0 2.2 m 0 m 0 m 0. . a f 2 0 2 m 12 0 m 6
Câu 2. Tìm tất cả các giá trị thực của tham số m để hàm số: 1 3
y x m 2
1 x m 3 x 10 đồng biến trong khoảng 0;3 ? 3 Giải Ta có: 2
y ' x 2m
1 x m 3 .
Để hàm số đồng biến trên 0;3 thì phương trình: y ' 0 có hai nghiệm phân biệt x , x 1 2
thỏa mãn: x 0 3 x . Khi đó: 1 2
m 2 2 ' 1 m 3 0
' m m 4 0 1 . f 0 0 f 0 0 1 . f 3 0 f 3 0 m m 12
m 3 0 m 3 m 7 7m 12 0 12 m 7
Dạng 14. Ứng dụng khác.
Câu 1. Cho parabol P 2
: y x và đường thẳng d đi qua điểm I 0; 1 và có hệ số
góc là k . Gọi A và B là các giao điểm của P và d . Giả sử ,
A B lần lượt có hoành độ là
. Giá trị nhỏ nhất của biểu thức: 3 3 x x là? 1 2 Giải
44 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] Cho parabol 2
y x và đường thẳng d đi qua điểm I 0;
1 và có hệ số góc là k .
Gọi A và B là các giao điểm của P và d . Giả sử A và B lần lượt có hoành độ là x , x . 1 2
+ Đường thẳng d có phương trình: y kx 1.
+ Phương trình tương giao d và P: 2 2
x kx 1 x kx 1 0 * .
+ * luôn có 2 nghiệm phân biệt: x ; x , vì: 2
k 4 0, x . 1 2
Theo định lý Viéte, ta có: x x k, x x 1. 1 2 1 2 Ta có: 3 3 2
x x (x x ) (x x ) x x
x x . (x x ) x x . 1 2 1 2 1 2 1 2 = 2 1 2 1 2 1 2 2 2 Ta có: x x
x x 2
4x x k 4 . 1 2 1 2 1 2 3 3 x x = 2 k 2 4. k 1 4.1 2 , k
. Đẳng thức xảy ra khi k 0 . 1 2
Câu 2. Tìm tất các các giá trị thực m để đường thẳng y x m cắt đồ thị hàm số 1 3 y
x 2 m 2
x 32m 3 x m tại ba điểm phân biệt A0;m, ,
B C sao cho đường 3
thẳng OA là phân giác của góc BOC . Giải
Phương trình hoành độ giao điểm: x 0 1 3
x 2 m 2
x 32m 3 x m x m 1 . 2 3
x 2 m x 6m 8 0 * 3
Để đường thẳng cắt đồ thị tại ba điểm phân biệt thì * phải có hai nghiệm phân biệt khác x 0 Hay:
45 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] 18 8 3 m 44 3 m 4 m 2 2 m 12m 0 2 6 8 0 3 18 8 3 3 m 1 . 4 3 6m 8 0 m 3 4 m 3
Suy ra: Tọa độ các điểm B, C lần lượt là: B x , x m ,C x , x m . 1 1 2 2
x x 3 m 2 1 2
Theo định lý Viéte, ta có: .
x x 3 6m 8 1 2 O 0;0Oy
Để ý: OA Oy (Do
) có véctơ chỉ phương j 0; 1 . A
0;mOy
Vậy để đường thẳng OA là phân giác của góc BOC . m x m x
cos j,OB cos j,OC 1 2 2. 2 2 2 2
x (m x )
x (m x ) 1 1 2 2
2 m x x m x 2 m x x m x 2 2 2 1 2 2 2 1 1
m x 2 x m x 2 m x 2 x m x 2 2 2 1 2 2 2 1 1
m x 2 x m x . m x m x
x m x m x 2 2 2 2 2 2 2 1 1 1 2 2 1 2 2
x (m x ) x m x 2 2 2 2 2 2 2 2 2 2 2 2 2 2
x m 2mx x x .x x m 2mx x x x 2 1 1 2 2 1 2 1 2 1 1 2 1 2 2 m 2 2
x x 2mx x x x 2
0 m x x x x
2mx x x x 0 1 2 1 2 1 2 1 2 1 2 1 2 1 2
mx x m
x x mx mx 1 2 2x x 0 1 2 1 2 1 2
m(x x ) 2x x . 1 2 1 2 m 0 m 0 m 0 m 7 33 2
3m(m 2) 6(6m 8)
3m 42m 48 m 7 33
Đối chiếu điều kiện
1 và A O0;0 nên ta nhận m 7 33 .
46 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
Câu 3. Biết đồ thị hàm số y x x 2 1
1 x 7 m cắt trục hoành tại 4 điểm phân
biệt có hoành độ là x , x , x , x . Tìm tất cả các giá trị nguyên của tham số m để 1 2 3 4 1 1 1 1 1? 1 x 1 x 1 x 1 x 1 2 3 4 Giải
Xét phương trình hoành độ giao điểm:
x x 2x 4 2 1 1
7 m 0 x 8x 7 m 0 1 Đặt: 2
t x ,t 0 . Khi đó phương trình đã cho có dạng: 2
t 8t 7 m 0 2
Vì đồ thị cắt trục hoành tại 4 điểm phân biệt nên phương trình 1 có 4 nghiệm thực
phân biệt hay phương trình 2 có hai nghiệm phân biệt dương. Điều đó tương đương ' 0 16 7 m 0 với: S 0 8 0 9 m 7 . P 0 7 m 0 t t 8
Khi đó phương trình 2 có hai nghiệm dương: 0 t t thoả mãn: 1 2 . 1 2 t t 7 m 1 2 Suy ra phương trình
1 có bốn nghiệm lần lượt là:
x t , x t , x
t , x t . 1 2 2 1 3 1 4 2 Như vậ 1 1 1 1 1 1 1 1 y: 1 1. 1 x 1 x 1 x 1 x 1 t 1 t 1 t 1 t 1 2 3 4 2 1 1 2 1 1 1 1 2 2
4 2t t 1 2 1 1 1 1 t 1 t 1 t 1 t 1 t 1 t 1 t t t t 2 2 1 1 2 1 1 2 1 2 4 2.8 12 12 m 1 1
0 0 m 12 1 8 7 m m m
Kết hợp điều kiện ta được: 0 m 7 m 1;2;3;4;5; 6 .
47 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] Câu 4. Cho hàm số 3
y x m 2 3 2
x 9m 3
1 x 27 7m có đồ thị là C . Biết
rằng ứng với giá trị nguyên m m thì hàm số C cắt trục hoành tại 3 điểm lập thành 1
một cấp số cộng có các phần tử đều nguyên dương và ứng với giá trị nguyên m m thì 2
hàm số cắt trục hoành tại 3 điểm lập thành một cấp số nhân có các phần tử đều nguyên
dương. Tìm giá trị m , m ? 1 2 Giải Từ hàm số: 3
y x m 2 3 2
x 9m 3
1 x 27 7m .
Ta nhận thấy x 1 luôn luôn là một nghiệm của phương trình y 0 .
Bằng phép chia Hoocner ta có: y x 2
1 x 4 2m x 7m 27 . x 1
Giao điểm của hàm số với trục hoành là nghiệm của: . 2 x
4 2mx 7m 27 0
Để hàm số cắt trục hoành tại 3 điểm phân biệt thì: '
2 m2 7m 27 0 22 m .
2 m 5 1 4 2 .1 7m 27 0
Giả sử 3 giao điểm của y f x với trục hoành lần lượt là: 1, x , x . 1 2 Khi đó:
- 3 điểm trên lập thành một cấp số cộng khi và chỉ khi:
2 3d 2m 4 x 1 d
x x 2m 4
2 3d 2m 4 1 1 2 3m 2 2 x 1 2d
x .x 7m 27
2d 3d 1 7m 27
2d 3d 1 7 3 27 2 1 2 2 3d m 3
2 3d 2m 4 2
d;m 2;6 TM 21 d 2 2 d d d d m 7 45 2 3 1 6 ; ; L 2 7 4 8 d 4 Hay: m 6 . 1
- 3 điểm trên lập thành một cấp số nhân khi và chỉ khi:
48 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] 2
d d 2m 4 2 x d 1 x x 2m 4 d d 2m 4 1 2 2
d d 4 . 2 3 3 x d
x .x 7m 27
d 7m 27 d 7 27 2 1 2 2 2 d d 4 m 2
d d 2m 4 2 d 2
d;m 2;5 7 7 TM 3 2 d d d 13 0 2 2 3 113 d L 4 Nên: m 5 . 2 1 3 Câu 5. Cho hàm số 2 y
x mx m 6 x 2021. Tìm tất cả các giá trị nguyên của 3
m thuộc để đồ thị hàm số có 5 điểm cực trị. Giải Đồ 1 3 thị hàm số 2 y
x mx m 6 x 2021 có 5 điểm cực trị khi và chỉ khi đồ thị 3 1 hàm số 3 2 y
x mx m 6 x 2021 có hai điểm cực trị nằm bên phải trục Oy hay 3 1 hàm số 3 2 y
x mx m 6 x 2021 có hai điểm cực trị dương. 3 Ta có: 2
y x 2mx m 6 .
Bài toán đã cho trở thành việc tìm m để phương trình 2
x 2mx m 6 0 có hai
nghiệm dương phân biệt. Khi đó: m 3 0 2
m m 6 0 m 2 b
0 2m 0
m 0 m 3. a m 6 0 m 6 c 0 a
49 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] Câu 6. Cho hàm số 3 2
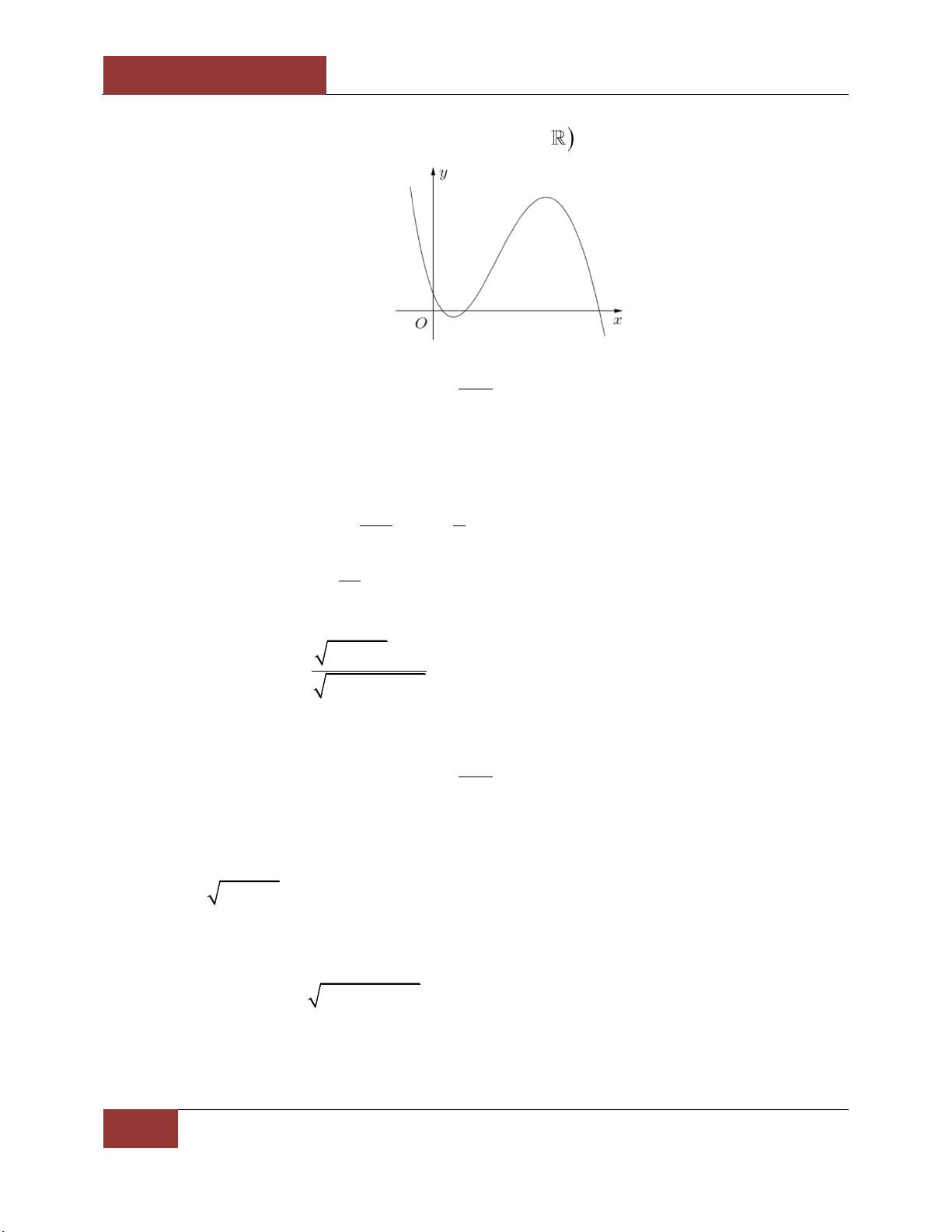
y ax bx cx d a, , b c, d
có đồ thị là đường cong như
hình vẽ. Định dấu của các hệ số , a , b , c d . Giải
Ta có: lim y a 0 . x
Gọi x , x là hoành độ hai điểm cực trị của hàm số suy ra x , x nghiệm phương trình 1 2 1 2 2
y 3ax 2bx c 0 nên theo định lí Viéte, ta có: 2 b b
+) Tổng hai nghiệm: x x
0 0 b 0 . 1 2 3a a c
+) Tích hai nghiệm: x .x 0 c 0 . 1 2 3a
Lại có đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên d 0 . 2 4x x 12
Câu 7. Cho hàm số y
có đồ thị C . Tìm tập hợp S chứa tất cả các giá 2
x 6x 2k
trị thực của thám số k để đồ thị C có đúng hai tiệm cận đứng? Giải 0 x 4 Điều kiện: . 2
x 6x 2k 0 Ta có: 2
12 4x x 0, x D .
Nên để C có hai tiệm cận đứng thì phương trình: 2 2
x 6x 2k 0 x 6x 2k 0 *
có hai nghiệm phân biệt thuộc 0;4.
50 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] Để 9
phương trình * có hai nghiệm phân biệt thì: 9 2k 0 k . 2
Gọi hai nghiệm phân biệt của * là x x , ta có: 0 x x 4 . 1 2 1 2
Theo định lý Viéte ta có: x x 0 2k 0 1 2 x x 6
x x 0 6 0 k 0 1 2 1 2 k 4 x x 2k x 4 x 4 0 2k 24 16 0 2k 8 0 1 2 1 2
x 4 x 4 0 6 8 0 1 2 9
Kết hợp nghiệm ta có: S 4; . 2
Câu 8. Với giá trị nào của tham số m thì phương trình x x 1 4 m2 2m 0 có hai
nghiệm x , x thỏa mãn x x 3 ? 1 2 1 2 Giải 2 Ta có: x x 1 4 2
2 0 2x 2 .2x m m m 2m 0 * .
Xem phương trình * là phương trình bậc hai theo ẩn 2x t 0 . Khi đó: 2
* t 2mt 2m 0 **.
Điều kiện để phương trình
** có hai nghiệm dương phân biệt: 2
' m 2m 0
S 2m 0 m 2 .
P 2m 0
Theo định lý Viéte, ta có: t .t 8 2m 8 m 4 . 1 2 Note:
Để phương trình * có hai nghiệm x , x thỏa mãn yêu cầu đề bài thì ** phải có hai 1 2
nghiệm dương phân biệt thỏa mãn t .t 8 do 1 x 2 x 3 1 x 2 3 2 2 8 2 .2x x x 8. 1 2 1 2 2 x 1 0
Câu 8. Xác định m để bất phương trình sau có nghiệm: . 2 x 2 m
1 x 4m 1 0 Giải 2 x 1 0 1 Đặt: . 2 x 2 m
1 x 4m 1 0 2
51 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] 1 x 1 Từ 1 . 2
m 2m 2
+) Trường hợp 1: 0 hệ phương trình đã cho có nghiệm đúng với mọi x 1 ; 1 2 2
m 2m 0 m0;2 * . m 0
+) Trường hợp 2: 0
hệ phương trình có nghiệm 2 có nghiệm 2 m 2 m 0 m 0 m 2 m 2 0 2 2 f 1 6m 4 0 . 1 0 m a f m 3 2 1 2 S m 2 1 m 0 1 3 x x 1 2 2 1 2 m 2 * . x x 1 1 2 m 0 m 0 m 0 0 2 m 2 a f m 2 . 1 0 f 1 2m 0 m 0 S 1 2 m 1 m 0 2 1 2 2 Từ * * * m . 3
Câu 9. Cho các số thực a, b, c (với a 0) sao cho phương trình 2
ax bx c 0 có hai
(a b)(2a b)
nghiệm thuộc đoạn 0
;1 . Tìm giá trị lớn nhất của biểu thức: P .
a(a b c) Giải b x x 1 2 a
Gọi x , x là nghiệm của phương trình đã cho. Theo định lý Viéte, ta có: . 1 2 c x x 1 2 a
52 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] Do a 0 , nên: b b 1 2 a a
1 x x 2 x x 2 1 x x 1 x x x x 1 2 1 2 1 2 1 2 1 2 P b c
1 x x x x
1 x x x x 1 2 1 2 1 2 1 2 1 a a
2 1 x x x x x x 2
2 1 x x x x 2 2
x x x x 2 2 1 2 1 2 1 2 1 2 x x x x 1 2 1 2 1 2 1 2 1 2 P 2
1 x x x x
1 x x x x
1 x x x x 1 2 1 2 1 2 1 2 1 2 1 2
Giả sử x x do 2 nghiệm thuộc 0 ;1 nên 2 2
x x x x 1 . 1 2 1 1 2 2 2 2
x x x x
x x 1 x x
Và 1 x x x x 0 nên ta có: 1 2 1 2 1 2 1 2 1 P 3 . 1 2 1 2
1 x x x x
1 x x x x 1 2 1 2 1 2 1 2 Vậy max P 3 .
Dấu đẳng thức xảy ra khi và chỉ khi: x 0 1 c 0 2 x x x x 1 1 1 2 2 b a 0 2 x 1 x 1 2 1 b
a c 0 x 1 2 2 2m 1 Câu 10. Cho hàm số 3 2 y x
x 2x 2022
. Biết rằng tồn tại hai giá trị tham số 2
m m ; thỏa mãn hàm số đạt cực trị tại hai điểm x , x sao cho 2x 3x 3 m . Tìm m , m . 1 2 1 2 1 2 1 2 Giải 2m 1 3 2 2 y x
x 2x 2022; y ' 3x 2m 1 x 2 2
Hàm số có hai điểm cực trị khi phương trình y ' 0 có hai nghiệm phân biệt 1
2m 2 1
6 0 2m 2 1 24,(*) 4
53 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG] 2m 1 x x 1 2 Theo đị 3 nh lý Viète ta có: . 2 x x 1 2 3 1 2m 1 x 3m 2 1 x x 5 Vì: 1 2 3 . 1
2x 3x 3 m x m 11 1 2 2 15 2
Thế vào x .x , ta được: 1 2 3 2 1 x x 3m 2 1 . m 2 1 11 2 2
3m 31m 22 . 1 2 3 5 15 3 75 3 1 m 5 73 31 1 2 2 6
3m 31m 22 50 3m 31m 72 0 . 1
m 5 73 31 2 6
Câu 11. Xác định giá trị của tham số m để hàm số
y f x m 3
x m 2 1 3
1 x 2mx 4 đồng biến trên khoảng có độ dài bằng 1 . Giải Ta xét các khả năng:
Trường hợp 1: m 1
, khi đó: y f x 2
x 4 là một đường thẳng có hệ số góc k 2
0 . Nên hàm số nghịch biến trên .
Trường hợp 2: m 1 , khi đó:
Nếu f ' x 0 vô nghiệm hoặc có nghiệm kép thì hàm số luôn đồng biến trên . (Loại)
Nếu f ' x 0 có hai nghiệm thực x , x thì hàm số đồng biến trên hai khoảng ; x 1 1 2
và x ; . (Loại) 2
Như vậy ở Trường hợp 2 không tồn tại giá trị thực m nào để cho hàm số đồng biến trên
khoảng có độ dài bằng 1 .
Trường hợp 3: m 1 , khi đó:
54 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
Nếu f ' x 0 vô nghiệm hoặc có nghiệm kép thì hàm số luôn nghịch biến trên . (Loại)
Nếu f ' x 0 có hai nghiệm thực x , x thì hàm số đồng biến trên khoảng x ; x . 1 2 1 2 m 1
Như vậy để hàm số đồng biến trên khoảng có độ lớn bằng 1 thì: ' . f 0 * ' x
x x 1 1 2
Ta có: f x m 2 ' 3
1 x 6m 1 x 2m . 2 m 1 Suy ra: ' m
m m m m . f 9 1 6 1 1 3 9 0 ' x m 3 x x 2 1 2
Theo định lý Viète, ta có: 2m . x x 1 2 3m 1 2 2
Mà x x 1 x x
1 x x 4x x 1 1 2 1 2 1 2 1 2 m 1 m 3 m 1 * 2m m 9 . 2 m 3 2 4. 3m 1 1 2 2m 2 4. m 1 3 1 ----The End----
55 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com
October 4, 2021 [NGUYỄN THÀNH NHÂN – TRƯỜNG ĐẠI HỌC AN GIANG]
56 Nghiên cứu định lý Viète và ứng dụng | ▫▪ mathvn.com




