Nguyên hàm từng phần (Phần 1)| Trường Đại học Sư phạm Hà Nội

Nguyên hàm từng phần (Phần 1)| Trường Đại học Sư phạm Hà Nộivới những kiến thức và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng, ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả cao cũng như có thể vận dụng tốt những kiến thức mình đã học vào thực tiễn cuộc sống.

11 6 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Chuyên đề Toán

Trường: Đại học Sư Phạm Hà Nội

Thông tin:

3 trang 2 tháng trước

Tác giả:

Profile Kim Oanh
BÀI TẬP VỀ NHÀ
PHẦN 1
Câu 1: Để tính
ln 2 d
x x x
theo phương pháp tính nguyên hàm từng phần, ta đặt
A.
d ln 2 d
u x
v x x
B.
ln 2
d d
u x
v x x
C.
ln 2
d d
u x x
v x
D.
ln 2
d d
u x
v x
Câu 2:
Để tính
2
cos d
x x x
theo phương pháp tính nguyên hàm từng phần, ta đặt
A.
d cos d
u x
v x x x
B.
2
d cos d
u x
v x x
C.
2
cos
d d
u x
v x x
D.
2
cos
d d
u x x
v x
Câu 3: Tính nguyên hàm của hàm số
.
x
f x xe
A.
d
x x
f x x e x e C
B.
2
d
2
x
x
f x x e C
C.
d
x x
f x x x e e C
D.
2
d
2
x x
x
f x x e e C
Câu 4: Họ nguyên hàm của hàm số
2
.
x
f x x e
là
A.
2
1 1
2 2
x
F x e x C
B.
2
1
2
2
x
F x e x C
C.
2
2 2
x
F x e x C
D.
2
1
2
2
x
F x e x C
Câu 5: Họ nguyên hàm của
1
x
e x dx
là:
A.
x
I xe C
B.
1
2
x x
I e xe C
C.
1
2
x x
I e xe C
D. 2
x x
I e xe C
Câu 6: Biết
( )
F x
là một nguyên hàm của hàm số
2
( )
x
f x xe
và
(0) 1
F
. Tính
(4)
F
A.
2
(4) 4 3
F e
B.
(4) 3
F
C.
2
(4) 4 3
F e
D.
2
7 3
(4)
4 4
F e
Câu 7: Gọi
F x
là một nguyên hàm của hàm số
e
x
f x x
. Tính
F x
biết
0 1
F
.
A.
1 e 2
x
F x x
B.
1 e 1
x
F x x
C.
1 e 2
x
F x x
D.
1 e 1
x
F x x
Câu 8: Tính
cos
d
F x x x
x
ta được kết quả
A.
sin cos
F x x x x C
B.
sin cos
F x x x x C
C.
sin cos
F x x x x C
D.
sin cos
F x x x x C
Câu 9: Tìm họ nguyên hàm của hàm số
.sin .
f x x x
A.
.cos sin
F x x x x C
B.
.cos sin
F x x x x C
C.
.cos sin
F x x x x C
D.
.cos sin
F x x x x C
Câu 10: Tìm
cos 2 d .
x x x
A.
1 1
.sin 2 cos2 +C
2 4
x x x
B. .s in2 cos 2
x x x C
C.
1 1
sin 2 cos2
2 2
x x x C
D.
1 1
.sin 2 cos2
2 4
x x x C
Câu 11: Một nguyên hàm của
2
sin
x
f x
x
là :
A. cot ln sinx
x x C
B. cot ln sinx
x x C
C. tan ln cos x
x x C
D. tan ln sin
x x x C
Câu 12: Giả sử
F x
là một nguyên hàm của hàm số
1 sin2 .
f x x x
Biết
1
0 .
2
F
Khi đó
A.
1 1
sin 2 cos 2 .
4 2
x
F x x x
B.
1 1
sin 2 cos 2 1.
4 2
x
F x x x
C.
1 1
sin 2 cos 2 1.
4 2
x
F x x x
D.
1 1 1
sin 2 cos 2 .
4 2 2
x
F x x x
Câu 13: Tìm nguyên hàm
( )
F x
của hàm số
( ) (1 3x)cos2
f x x
, biết
(0) 1
F
A.
3cos2 sin 2 3 sin 2 7
( )
4 2 2 4
x x x x
F x
B.
3cos 2 sin 2 3 sin 2 1
( )
4 2 2 4
x x x x
F x
C.
3cos2 sin 2 3 sin 2 7
( )
4 2 2 4
x x x x
F x
D.
3cos 2 sin 2 3 sin 2 1
( )
4 2 2 4
x x x x
F x
Câu 14: Tìm họ nguyên hàm của hàm số
2
.
cos 2 1
x
f x
x
A.
tan ln cos .
F x x x x C
B.
tan ln cos .
F x x x x C
C.
tan ln cos .
F x x x x C
D.
tan ln cos .
F x x x x C
Câu 15: Tìm
2
sinx
cos
x
I dx
x
A.
2
1 1
tan
cos cos
I x x C
x x
B.
1
tan ln cos
cos
I x x x C
x
C.
1
tan ln cos
cos
I x x x C
x
D.
2
1 1
tan
cos cos
I x x C
x x
Câu 16: Nguyên hàm của ln
I x xdx
bằng với:
A.
2
ln
2
x
x xdx C
. B.
2
1
ln
2 2
x
x xdx C
.
C.
2
1
ln
2
x x xdx C
. D.
2
ln
x x xdx C
.
Câu 17: Tìm tất cả các nguyên hàm của hàm số
2
3 1 .ln
f x x x
.
A.
3
2
1 ln
3
x
f x dx x x x C
. B.
3
3
ln
3
x
f x dx x x C
.
C.
3
2
1 ln
3
x
f x dx x x x x C
. D.
3
3
ln
3
x
f x dx x x x C
.
Câu 18: Tìm
3
ln
x
dx
x
A.
2 2
ln 1
2 2
x
C
x x
B.
2 2
ln 1
2
x
C
x x
C.
2 2
ln 1
2
x
C
x x
D.
2 2
ln 1
2 4
x
C
x x
Câu 19: Tìm ln
I xdx
A. ln
I x x x C
B. ln
I x x C
C. ln
I x x x C
D.
1
I C
x
Câu 20:
2
1 ln( 1)
x
I dx
x
A.
1 ln 1
ln | | ln | 1|
x
x x C
x
B.
1 ln 1
ln | | ln | 1|
x
x x C
x
C.
1 ln 1
ln | | ln | 1|
x
x x C
x
D.
1 ln 1
ln | | ln | 1|
x
x x C
x
Câu 21: Tìm
2
2
1
ln
x
x dx
x
A.
ln 1
ln
x
x x x C
x
B.
ln 1
ln
x
x x x C
x
C.
ln 1
ln
x
x x x C
x
D.
ln
ln
x
x x x C
x
Câu 22: Giả sử
F x
là một nguyên hàm của
2
ln 3
x
f x
x
sao cho
2 1 0
F F
. Giá trị
của
1 2
F F bằng
A.
10 5
ln 2 ln5
3 6
. B.
0
.
C.
7
ln 2
3
.
D.
2 3
ln 2 ln 5
3 6
.
BẢNG ĐÁP ÁN
1.B 2.B 3.C 4.A 5.A 6.C 7.A 8.C 9.A 10.D
11.B 12.C 13.A 14.B 15.B 16.B 17.C 18.D 19.A 20.B
21.C 22.A
| 1/3
| | Tải xuống

Có thể bạn quan tâm:

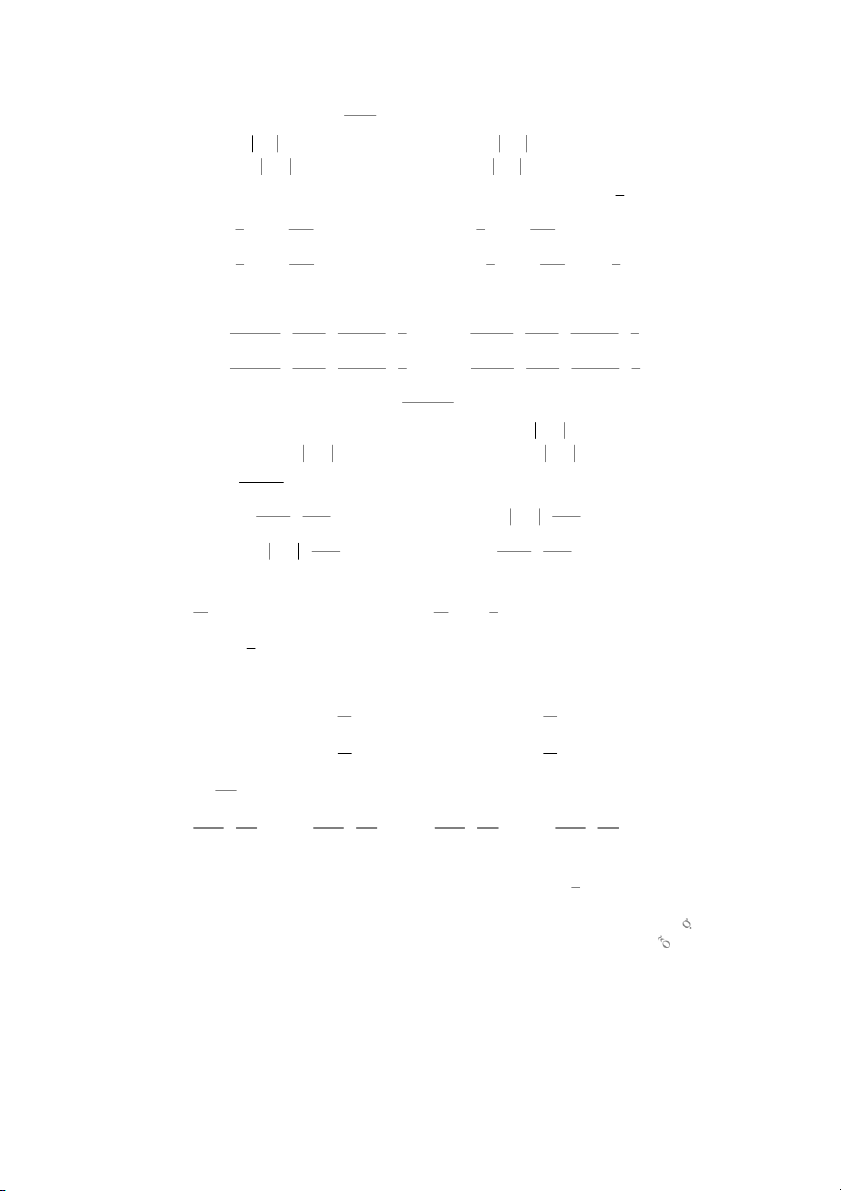
Preview text:

BÀI TẬP VỀ NHÀ PHẦN 1
Câu 1: Để tính x ln 
2 xdx theo phương pháp tính nguyên hàm từng phần, ta đặt u x
u  ln2  xA.B.
dv  ln  2  x dx
dv x dx
u x ln2 x
u  ln2  xC. D.  dv  dx  dv  dxCâu 2: Để tính 2
x cos x dx
theo phương pháp tính nguyên hàm từng phần, ta đặt u x 2  u xu  cos x 2
u x cos x A. B. C. D.
dv xcos x dx
 dv cos xdx 2
dv x dx dv  dx
Câu 3: Tính nguyên hàm của hàm số   x f x x e . 2 x A.   d x x f x
x e x e C B. f   x d x x e C  2 2 x C.   d x x f x
x x e e C
D. f xd x x x
e e C  2
Câu 4: Họ nguyên hàm của hàm số   2  . x f x x e là 1 1 x  1 A. F x 2  e x   C B.   2 x F x
e x  2  C 2  2    2   x 1 C.   2  2 x F x
e x  2 C
D. F x 2  2e x   C  2   
Câu 5: Họ nguyên hàm của x e
 1 xdx là: 1 x 1 A. x
I xe C B. x
I e xe C C. x x
I e xe C D.  2 x x I
e xe C 2 2 x
Câu 6: Biết F (x) là một nguyên hàm của hàm số 2
f (x)  xe và (0 F )  1  . Tính F(4) 7 3 A. 2
F(4)  4e  3 B. (4 F )  3 C. 2
F (4)  4e  3 D. 2 F (4)  e 4 4
Câu 7: Gọi F x  là một nguyên hàm của hàm số   e x f x x  
. Tính F x  biết F0 1 . A.     1 e x F x x      2 B.     1 e x F x x     1
C.    1e x F x x    2 D.    1e x F x x     1
Câu 8: Tính F x  xcos x d 
x ta được kết quả
A. F x  x sin x  cosx C
B. F x   xsin x cos x C
C. F x  x sin x  cos x C
D. F x    xsin x cos x C
Câu 9: Tìm họ nguyên hàm của hàm số f x  . x sin . x
A. F x   .
x cos x sin x C
B. F x  x.cos x sin x C
C. F x  x.cosx  sinx C
D. F x    x.cos x  sin x C
Câu 10: Tìm x cos 2x dx.  1 1 A. .
x sin 2x  cos2x+C
B. x.s in2x  cos 2x C 2 4 1 1 1 1
C. x sin 2x  cos2x C D. .
x sin 2x  cos2x C 2 2 2 4
Câu 11: Một nguyên hàm của   x f x  là : 2 sin x
A. x cot x  ln sinx C
B. x cotx  ln sinx C
C. x tan x  ln cos x  C
D. x tan x ln sin x C
Câu 12: Giả sử Fx là một nguyên hàm của hàm số f x   x 1sin 2 .
x Biết F   1 0  . Khi đó 2 x x
A. F x 1 1  sin 2x  cos 2x .
B. F x 1 1  sin 2 x  cos 2 x 1  . 4 2 4 2 x x
C. F x 1 1  sin 2x  cos 2x 1.
D. F x 1 1 1   sin 2x  cos 2 x  . 4 2 4 2 2
Câu 13: Tìm nguyên hàm ( F )
x của hàm số f ( )
x  (1 3x)cos 2 x , biết F(0)  1
3cos 2x sin 2x 3x sin 2x 7
3cos 2x sin 2x 3x sin 2x 1 A. F( ) x   
B. F (x)     4 2 2 4 4 2 2 4
3cos 2x sin 2x 3x sin 2x 7
3cos 2x sin 2x 3x sin 2x 1
C. F(x)   
D. F (x)     4 2 2 4 4 2 2 4 x
Câu 14: Tìm họ nguyên hàm của hàm số f x 2  . cos 2x 1
A. F x  x tan x  ln cos x C.
B. F x  x tan x  ln cos x C.
C. F x  x tan x ln cos x  . C
D. F x    x tan x ln cos x C. x  sinx
Câu 15: Tìm I dx  2 cos x A. 1 1 1
I x tan x   
B. I x tan x  ln cos   2 C x C cos x cos x cos x 1 1 1
C. I xtan x ln cos x   C
D. I x tan x   C cos x 2 cos x cos x
Câu 16: Nguyên hàm của I x ln xdx  bằng với: 2 x 2 x 1 A. lnx xdx C  ln xxdxC 2  . B. 2  . 2 1 C. 2 x ln x xdx C  . D. 2
x ln x xdx C  . 2
Câu 17: Tìm tất cả các nguyên hàm của hàm số f x   2 3x   1 .lnx . 3 A.        3 2 1 ln x x f x dx x x x   C .
B. f x 3
dx x ln x   C  . 3 3 3 C.        3 2 1 ln x x f x dx x x x
x C . D. f x 3
dx x ln x   x C  . 3 3 ln Câu 18: Tìm xdx 3 x  ln x 1  ln x 1 ln x 1  ln x 1 A.   C B.   C C.   C D.   C 2 2 2 2 2 2 2 2 2 x 2 x x 2x x 2 x 2x 4x
Câu 19: Tìm I  lnxdx  1
A. I x ln x x C B. I x ln x C
C.I x ln x x C D. I   C x 1 ln(x 1) Câu 20: I dx 2 x 1 ln x  1 1  ln x 1 A.
 ln | x |  ln | x  1| C B.
 ln | x | ln | x 1| C x x 1 ln x  1 1 ln x 1 C.
 ln | x |  ln | x  1| C D.
 ln | x |  ln | x 1| C x x 2 x 1 Câu 21: Tìm ln  2 x dx x ln  1 ln 1  A. ln x x x x  C B.  ln x x x x  C x x ln  1 ln C. ln x x x x   C D.  ln x x x x   C x x ln x  3
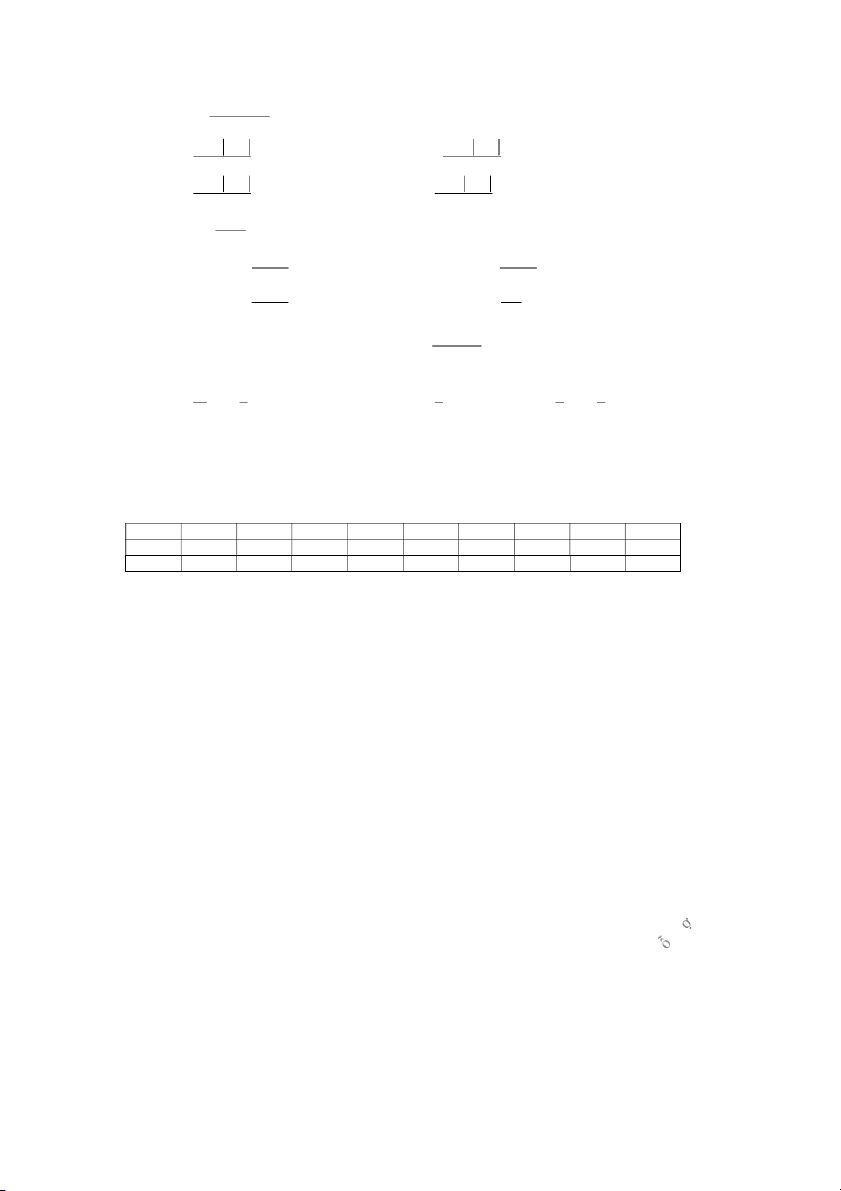
Câu 22: Giả sử F x  là một nguyên hàm của f x    
sao cho F  2  F   1  0 . Giá trị 2 x của F  1
   F 2  bằng 10 5 7 2 3 A. ln 2  ln 5 . B. 0 . C. ln 2 . D. ln 2  ln 5 . 3 6 3 3 6 BẢNG ĐÁP ÁN 1.B 2.B 3.C 4.A 5.A 6.C 7.A 8.C 9.A 10.D 11.B 12.C 13.A 14.B 15.B 16.B 17.C 18.D 19.A 20.B 21.C 22.A