Nguyên lý cực trị rời rạc - Toán rời rác | Đại học Sư Phạm Hà Nội

CHỦ ĐỀ: NGUYÊN LÝ CỰC TRỊ RỜI RẠC
Mục lục
I. Phát biểu nguyên lý ......................................................................................... 2
1. Một số ví dụ đơn giản ................................................................................... 2
II. Chứng minh sự tồn tại của các cấu hình ..................................................... 2
1. Một số ví dụ trong giáo trình ........................................................................ 2
2. Bài tập vận dụng ........................................................................................... 6
𝐈𝐈𝐈. Tìm cực trị rời rạc ........................................................................................ 7
1. Ví dụ minh họa .............................................................................................. 7
2. Bài tập vận dụng: .......................................................................................... 8
IV. Thiết lập thứ tự trên các yếu tố bình đẳng ................................................. 9
1. Ví dụ minh họa ............................................................................................ 10
2. Bài tập vận dụng: ........................................................................................ 11
I. Phát biểu nguyên lý
Nguyên lý cực trị rời rạc được phát biểu như sau: Trong một tập hữu hạn và khác
rỗng các số thực luôn:
(a): tồn tại một số bé nhất và một số lớn nhất
(b): luôn xếp được chúng theo trật tự tăng hoặc giảm
Nguyên lí thật đơn giản nhưng sự vận động của nó đã thấm sâu vào nhiều chứng minh toán học.
1. Một số ví dụ đơn giản
Ví dụ 1: Trong tập hợp các trường sắp thứ tự điều này là hiển nhiên đúng. Ví dụ trong
trường các số thực ℝ, khi cho một tập gồm {−2; 2; 1; 0} ta luôn tìm được số lớn nhất
là 2; số nhỏ nhất là −2 và sắp xếp được chúng theo thứ tự tăng dần {−2; 0; 1; 2} hoặc
thứ tự giảm dần {2; 1; 0; −2}
Ví dụ 2: Trong một lớp học, nếu chúng ta quyết định một yếu tố nào đó của các bạn
học sinh, chúng ta cũng hoàn toàn tìm được điều tương tự. Ví dụ là yếu tố chiều cao,
sẽ luôn có ít nhất một bạn cao nhất, ít nhất một bạn thấp nhất; Và ta cũng luôn sắp thứ
tự tăng dần, hoặc giảm dần chiều cao của các bạn trong một lớp. Ở đây, tôi muốn nhấn
mạnh rằng (i) chỉ ra sự tồn tại, tức là có thể có nhiều hơn 1 số bé nhất hoặc nhiều hơn
1 số lớn nhất (trong lớp có thể có hai bạn cao nhất có cùng chiều cao,…)
Lưu ý: Trong các ví dụ thực tế được nêu ra thì đa số đều có sẵn 2 điều kiện quan
trọng là tập hữu hạn và khác rỗng. Tuy nhiên trong các đối tượng toán học khác, việc
chỉ ra sự thỏa mãn hoặc bóc tách các trường hợp suy biến khi một trong hai điều kiện
không được đáp ứng là quan trọng và cần thiết
II. Chứng minh sự tồn tại của các cấu hình
Việc chứng minh sự tồn tại của các cấu hình là chỉ ra một mô hình, với một tiêu chí
nào đó ăn khớp với nội dung của nguyên lí, từ đó áp dụng nguyên lí đó. Thông thường
chúng ta có thể làm trội đối tượng lên hoặc dùng phản chứng để chứng minh sự tồn tại đó
1. Một số ví dụ trong giáo trình
Ví dụ 1: Cho 2n điểm phân biệt trên một đường tròn, trong đó có n điểm trắng và n
điểm đen n ≥ 2. Chứng minh luôn tồn tại:
(i) Một cách nối tất cả các điểm trắng với các điểm đen bởi n đoạn thẳng sao cho các
đoạn thẳng không có điểm chung
(ii) Một cách nối tất cả các điểm trắng với các điểm đen bởi n đoạn thẳng sao cho các
đoạn thẳng từng đôi một cắt nhau
Lời giải: * Phân tích tình huống:
- Gọi S là tập tổng độ dài các đoạn thẳng nối n điểm trắng và n điểm đen
Nên luôn tồn tại một phần tử của S có tổng độ dài là nhỏ nhất và một phần tử của S có
tổng độ dài là lớn nhất
Trường hợp (N): Khi nối các đoạn thẳng sao cho tổng độ dài các đoạn là nhỏ nhất, ta
sẽ được các đoạn thẳng này sẽ không có điểm chung với nhau
Trường hợp (L): Khi nối các đoạn thẳng sao cho tổng độ dài các đoạn là lớn nhất, ta
sẽ được các đoạn thẳng này sẽ đôi một có điểm chung với nhau
* Chứng minh (i) đúng: Ta chứng minh bằng phản chứng
Giả sử cách nối N tồn tại 1 cặp đường thẳng có điểm chung.
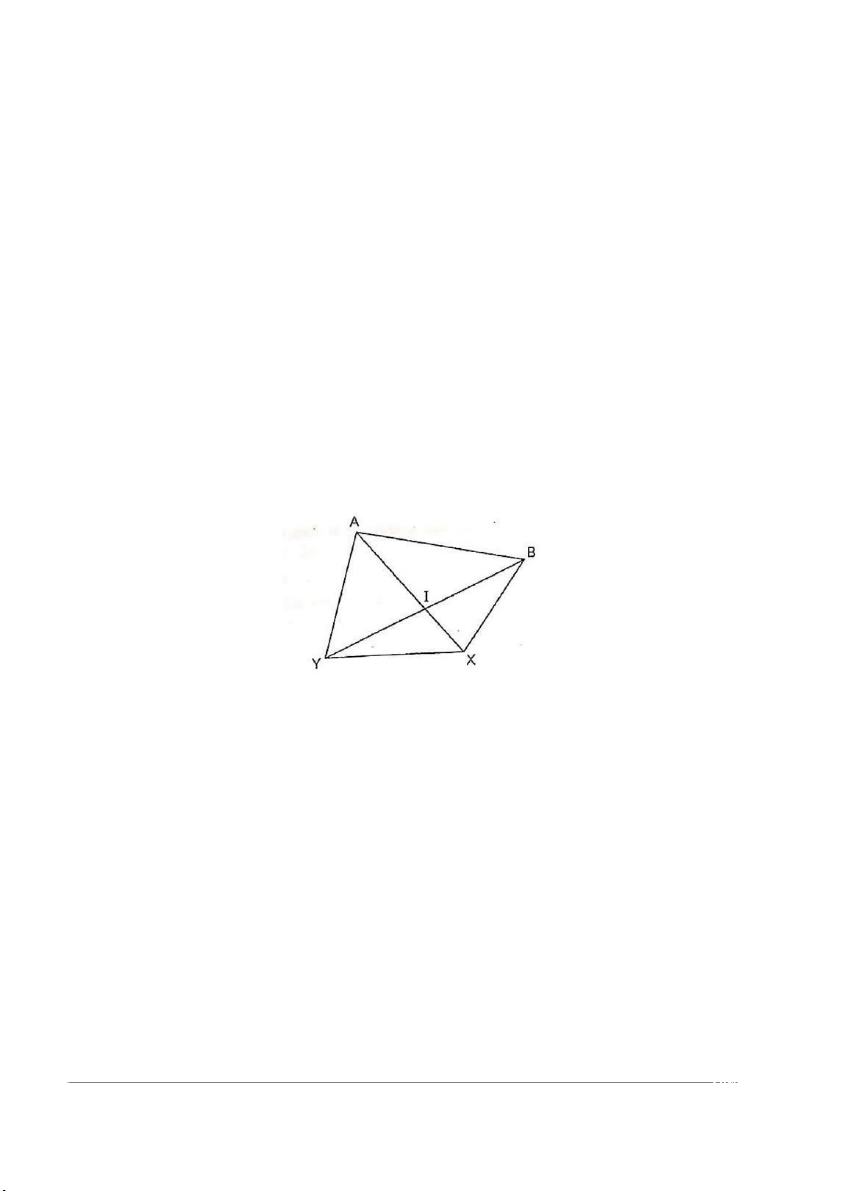
Không mất tính tổng quát, giả sử cặp đường thẳng A X cắt BY tại I.
Theo giả thiết ta có AX + BY là nhỏ nhất.
Ta có: AY + BX < AI + IY + BI + IX = AX + BY (Mâu thuẫn)
Từ đó, ta suy ra được không tồn tại một cặp đoạn thẳng nào có điểm chung
Nên trong trường hợp (N): Khi nối các đoạn thẳng sao cho tổng độ dài các đoạn là nhỏ
nhất, ta sẽ được các đoạn thẳng này sẽ không có điểm chung với nhau
* Chứng minh (ii) đúng: Hoàn toàn tương tự ứng với tr ờ ư ng hợp (L)
Ví dụ 2: Có n đội bóng đấu với nhau theo nguyên lí đấu vòng, tức là mỗi đội phải ấ đ u
với tất cả các đội còn lại. Biết rằng trong mỗi trận đấu không có hòa. Chứng minh
rằng luôn có thể xếp thứ tự tên các đội theo một cột dọc sao cho đội đứng trước thắng đội đứng sau
* Phân tích tình huống: Trong trường hợp nêu trên, ta để ý rằng tiêu chí so sánh ở đây
chỉ là đội xếp trên thắng đội xếp ngay dưới mà không cần đến tính chất bắc cầu.
Tức là nếu A thắng B, B thắng C thì ta sẽ có luôn thứ tự là A > B > C mà không cần
quan tâm đến kết quả của trận đấu giữa A và C. Vì vậy, chúng tôi kiến nghị đổi đề bài
thành: Chứng minh rằng luôn có thể xếp thứ tự tên các đội theo một cột dọc sao cho
đội đứng trước thắng đội đứng ngay sau. * Chứng minh:
- Do trong một bảng đấu, số đội là hữu hạn và khác rỗng (luôn lớn hơn 2 đội) nên thỏa
mãn điều kiện của nguyên lí cực trị.
Ta sẽ chứng minh bằng quy nạp
- Với n = 2 ta xét một cặp đấu bất kì, ta luôn có đội thắng và đội thua nên ta luôn xếp
được thứ tự trong cặp đấu đó. Nên phát biểu đúng với n = 2
- Giả sử phát biểu đúng với k = n − 1. Tức là ta có thể sắp xếp các đội theo thứ tự
thỏa mãn yêu cầu phát biểu, giả sử là A1, A2, … , A ng minh c n. Ta chứ An cũng xếp đượ vào dãy trên. Trường hợp 1: A thua t ộ n
ất cả các đ i còn lại⇒Ta có cách sắp xếp A1, A2, … , An−1, A n Trường hợp 2: A th n ắng ít nhất 1 trận.
Nếu A thắng đội A thì ta có cách x p n 1 ế An, A1, A2, … , An−1 Mặt khác, nếu A i và th i thì ta có cách x p n thua độ A1 ắng độ A2 ế A1, An, A2, … , An−1
Tương tự như vậy cho đến khi A A ếp như trườ n thua đội thì có cách x 1 ng hợp 1
Vậy, trong mọi trường hợp đều có thể xếp A vào dãy trên nên phát bi i m i n ểu đúng vớ ọ n (dpcm)
Ví dụ 3: Chứng minh rằng có vô số số nguyên tố có dạng 4n + 3
Lời giải 1: Ta chứng minh bằng phản chứng
Giả sử chỉ có hữu hạn số nguyên tố có dạng 4n + 3. Đặt S là tập hợp các số nguyên tố có dạng này
Ứng với n = 0 ta có 3 ∈ S ⇒ A ≠ ∅, kết hợp với việc giả sử tập S hữu hạn nên
thỏa mãn điều kiện của nguyên lí cực trị rời rạc
Do S hữu hạn nên luôn tồn tại sắp xếp được theo thứ tự tăng dần p1 < p2 < ⋯ < pn
Xét số A = 2p1p2 … pn + 1
Do A lẻ nên A ≡ 1 (mode 4) hoặc A ≡ 3 (mode 4)
Do p là các s nguyên t nên l ( ) hay A cũng có dạng i ố ố
p1p2 … pn ẻ ⇒ A ≡ 3 mode 4 4n + 3 Hiển nhiên A > p n
TH1: Nếu A là số nguyên tố ⇒ A là số nguyên tố có dạng 4n + 3 và A > p n
(Mâu thuẫn do p là s l n nh t có d ng ) n ố ớ ấ ạ 4n + 3
TH2: Nếu A là hợp số. Do A ≡ 3 (mode 4) nên A phải có một ước nguyên tố chia 4 dư 3.
Thật vậy, do A lẻ, nếu A chỉ có các ước chia 4 dư 1 thì A cũng chia 4 dư 1
(Mâu thuẫn với A ≡ 3 (mode 4))
Nên A phải có một ước nguyên tố chia 4 dư 3. Ta chứng minh ước nguyên tố này
không thể là pi=1,n với i nào đó Thật vậy:
Nếu ước nguyên tố này là pi=1,n
 (với i nào đó) thì hiển nhiên 2p1p2 … pn chia hết cho p i
Mà 1 không chia hết cho p nên không chia hết cho p i 2p1p2 … pn + 1 i (Mâu thuẫn với p c c a ) i là ướ ủ A
⇒ pi > pn, pi cũng có dạng 4n + 3 (Mâu thuẫn do pn là số lớn nhất có dạng 4n + 3 )
Vậy trong trường hợp 1 và trường hợp 2 đều dẫn đến mâu thuẫn nếu như tập S hữu hạn
Vậy tập S có vô hạn phần tử hay có vô số số nguyên tố có dạng 4n + 3 (dpcm)
Lời giải 2: Ta có thể chọnA = 4p1p2 … pn + 1 . Bạn đọc chứng minh tương tự với lập luận như trên
Ví dụ 4: Chứng minh rằng với mọi số nguyên n > 1 thì 2n − 1 không chia hết cho n
Lời giải: Ta chứng minh bằng phản chứng
Giả sử tồn tại một số nguyên n > 1 là ước của 2n − 1
Do 2n − 1 là số lẻ nên n cũng là số lẻ. Gọi p là ước nguyên tố nhỏ nhất của n
Áp dụng định lí Fermat nhỏ 2p−1 − 1 chia hết cho p
(Nhắc lại về định lí Fermat nhỏ: nếu p là một số nguyên tố, thì với số nguyên a bất kỳ
ap − a sẽ chia hết cho p)
Bây giờ ta gọi k là số nguyên dương nhỏ nhất sao cho p chia hết cho 2k − 1. Rõ ràng
k ≤ p − 1 < p. Ta cần chứng minh k cũng chia hết cho n.
Thật vậy, nếu n không chia hết cho k thì n = k. q + r(0 < r < k)
Do 2k − 1 chia hết cho p nên (2k)q ≡ 1 (mode p)
⇒ 2n − 1 = (2k)q. 2r − 1 ≡ 1 (mode p)
Ta có: 2n − 1 chia hết cho p (mâu thuẫn với cách chọn k)
Vậy mọi số nguyên n > 1 thì 2n − 1 không chia hết cho n
2. Bài tập vận dụng
Bài 1: Trên mặt phẳng cho n điểm(n ≥ 3). Biết rằng mỗi đường thẳng đi qua 2 điểm
bất kì đều đi qua 1 điểm thứ ba. Chứng minh rằng n điểm đã cho thẳng hàng. (Bài toán Sylvester, 1814-1897) Giải:
Giả sử n điểm đã cho không thẳng hàng. Suy ra với mỗi điểm A bất kì trong n điểm
thì luôn tồn tại đường thẳng đi qua 2 điểm B, C khác A và không đi qua A.
Xét tập G là tập tất cả các khoảng cách từ A đến các đường thẳng như giả sử
trên. Vì số khoảng cách đó là hữu hạn, nên tồn tại khoảng cách ngắn nhất. Giả sử
khoảng cách ngắn nhất đó là khoảng cách từ A đến BC. Ta hạ AH ⊥ BC.
Gọi S là tập n điểm đã cho. Nếu H ∈ S thì AH = d(A, BC) > d(H, BC)(mâu thuẫn)
Do đó H ∉ S. Theo giả thiết, ∃ D ∈ S nằm trên BC. Giả sử C, D nằm cùng phía so với H. Từ đây t có:
d(A, BC) = AH > d(H, AD) > d(C, AD) (mâu thuẫn với giả thiết)
Vậy n điểm đã cho thẳng hàng.
Chú ý: Có thể mở rộng bài toán Sylvester như sau:
Cho n hình lồi (n ≥ 2) sao cho cứ 3 hình lồi bất kì thì có giao khác rỗng.
Chứng minh rằng n hình lồi đã cho có giao khác rỗng.
Bài 2: Phát biểu và chứng minh bài toán đối ngẫu của bài toán Sylvester.(Bạn đọc tự chứng minh)
Bài 3: Trên mặt phẳng cho n điểm(n ≥ 3), trong đó không có 3 điểm nào thẳng
hàng. Chứng minh rằng tồn tại một hình tròn đi qua 3 điểm mà không chứa điểm còn lại nào bên trong. Giải:
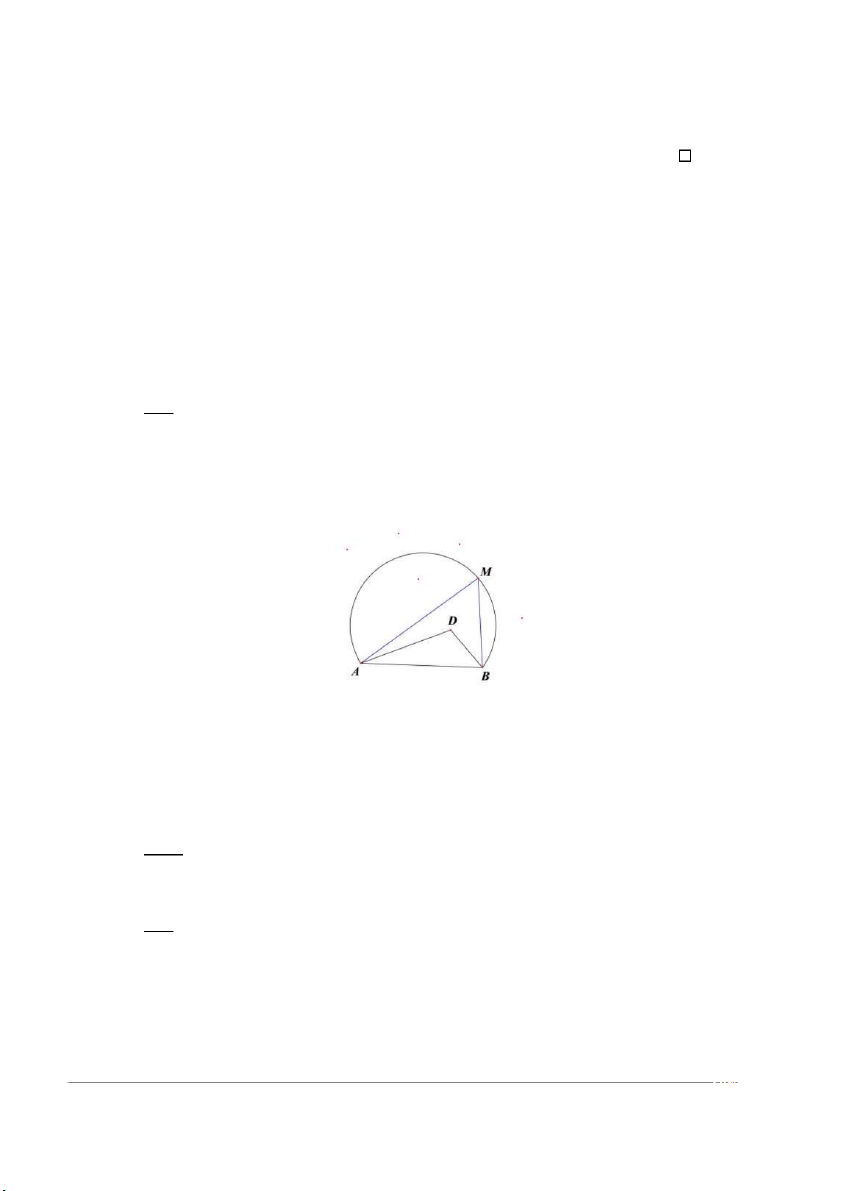
Chọn 2 điểm A, B cố định sao cho n − 2 điểm còn lại nằm về một phía đối với AB.
Với mỗi một điểm C bất kì trong n − 2 điểm còn lại ta xét góc ACB . Do số các góc
này là hữu hạn nên tồn tại diểm M sao cho số đo góc AMB
 là lớn nhất. Ta sẽ chứng
minh đường tròn đi qua 3 điểm A, M, B là đường tròn cần tìm.
Thật vậy, giả sử tồn tại điểm D nằm trong đường tròn (AMB). Khi đó ta có ADB  > AMB
 (mâu thuẫn). Vậy luôn tồn tại một hình tròn đi qua 3 điểm mà không chứa điểm còn lại nào bên trong.
𝐈𝐈𝐈. Tìm cực trị rời rạc
1. Ví dụ minh họa
𝐕𝐃𝟏: Cho m và d là các số nguyên với m ≥ d ≥ 2. Giả sử x1, x2, … , xd là các biến nguyên dương sao cho x 2 2
1+x2 + ⋯ +xd = m. Tìm giá trị nhỏ nhất của S = x1 + x2 + ⋯ + x2d. Giải:
Gọi G là tập tất cả các giá trị của S. Ta thấy G hữu hạn và khác rỗng ( do m ≥ d ≥ 2).
Do đó theo nguyên lý cực trị rời rạc, luôn tồn tại N là số nhỏ nhất của G. Giả sử
(a1,a2, …, ad) làm cho S nhận giá trị N. Ta sẽ chứng minh rằng tất cả các số
a1, a2, … , ad chỉ hơn kém nhau tối đa là 1. Thật vậy, giả sử chẳng hạn a1 − a2 = a > 1. Khi đó lấy b = a 2 2 2 2
1 − 1; c = a2 + 1 thì a1 + a2 = b + c và b + c < a1 + a2. Như
vậy ta tìm được các số nguyên dương b, c, a3, … thỏa mãn b + c + a3 + ⋯ + ad = m
và làm cho giá trị của S nhỏ hơn N (mâu thuẫn). Vậy các số a1, a2, … , ad chỉ hơn kém
nhau tối đa là 1. Bây giờ giả sử a
và m = dn + k (0 ≤ k < d). Do 1 ≤ a2 ≤ ⋯ ≤ ad, đặc điểm của dãy a ta suy ra ngay 1 ≤ a2 ≤ ⋯ ≤ ad a1 = a2 = ⋯ = ad−k = ⋯ = a 2
d = n + 1. Vậy giá trị nhỏ nhất ta cần tìm là N = (d − k)n + k(n + 1)2
𝐕𝐃𝟐: Cho m > 3 là một số nguyên dương. Giả sử x1, x2, … , xd là biến nguyên dương sao cho x 3 3 3
1x2 … xd = m. Tìm giá trị lớn nhất của S = x1 + x2 + ⋯ + xd . Giải
Gọi A là tập tất cả các giá trị của S. Ta có A hữu hạn và khác rỗng. Theo nguyên lý
cực trị rời rạc, tồn tại U là số lớn nhất của A. Giả sử (a1, a2, … , ad) làm cho S nhận giá
trị U. Ta sẽ chứng minh rằng tất cả các số a có m 1, a2, … , ad
ột số là m, còn tất cả các
số khác là 1. Bây giờ giả sử a . Ta c n ch 1 ≥ a2 ≥ ⋯ ≥ ad ầ ỉ ra rằng a còn 1 = m a2 =
a3 = ⋯ = ad = 1. Thật vậy, nếu a1 < m, khi đó a2 > m. Lấy a = a và còn 1a2 b = 1, a. b. a 3 3 3
3 … ad = m. Khi đó a3 + b = (a1a2)3 + 1 > a1 + a2 dẫn đến (a, b, a3, … , ad)
còn làm giá trị của của S lớn hơn U = a3 3 3
1 + a2 + ⋯ + ad (mâu thuẫn). Vậy a1 = m và do đó a 3
2 = ⋯ = ad = 1. Giá trị lớn nhất của S sẽ là U = m + (d − 1)
2. Bài tập vận dụng:
Bài 1: Cho m và d là các số nguyên với m ≥ d ≥ 2. Giả sử x1, x2, … , x là các bi n d ế
nguyên dương sao cho x1 + x2 + ⋯ + xd = m. Tìm giá trị nhỏ nhất và giá trị lớn nhất của S = ∑dk=1kxk. Giải:
Gọi A là tập tất cả các giá trị của S. Ta có A hữu hạn và khác rỗng. Theo nguyên lý
cực trị rời rạc, tồn tại N là số nhỏ nhất của A. Giả sử (a1, a2, … , ad) làm cho S nhận giá
trị N. Ta sẽ chứng minh rằng tất cả các số a1, a2, … , ad có một số là m − d + 1 , còn
tất cả các số khác là 1. Bây giờ giả sử a . Ta c n ch ng còn 1 ≥ a2 ≥ ⋯ ≥ ad ầ ỉ ra rằ a1 = m − d + 1 a2 = a3 = ⋯ = ad = 1. Thật vậy, nếu a . Ta l y và b = a2 − 1. Khi
1 < m − d + 1, khi đó a2 ≠ 1 ấ a = a1 + 1
này a + b + a3 + ⋯ + ad = m, và S = a + 2b + 3x3 + ⋯ + dad = a1 + 1 + 2a2 −
2 + 3a3 + ⋯ + dad = a1 + 2a2 + ⋯ + dad − 1 < a1 + 2a2 + ⋯ + dad(mâu thuẫn). Vậy a
và giá trị nhỏ nhất của S là
1 = m − d + 1, do đó a2 = a3 = ⋯ = ad = 1 N =
m − d + 1 + 2 + 3 + ⋯ + d = m + 1 + 2 + ⋯ + (d − 1) = m + (d−1)d . 2
Làm tương tự ta thu được giá trị lớn nhất của S là L = 1 + 2 + 3 + ⋯ + (d − 1) +
d[m − d + 1] đạt được tại (x1, x2, … , xd−1, xd) = (1,1, … ,1, m − d + 1) Bài 2: Cho a là các h ng s th là
1, a2, … , ad, b1, b2, … , bd ằ
ố ực dương, cho x1, x2, … , xd
các biến không âm sao cho ∑dk=1 akxk = a. Hãy tìm giá trị nhỏ nhất và lớn nhất của
biểu thức A = ∑dk=1 bkxk . Giải:
Giả sử b1 , ≤ b2 ≤ ⋯ ≤ bd . Khi đó, ta có: a1 a2 ad b1a = b1 ∑d bda k=1 a d k=1 ≤ ∑ b d kakxk k=1 (= A) ≤ ∑ b d dadxk a kxk = ∑ b1akxk k=1 = 1 a1 a1 ak ad ad Do đó b1a ≤ A ≤ bda a1 ad Dễ thấy: x1 = a , x thì b1a còn x , x a 2 = ⋯ = xd = 0 A = d = a 1 = ⋯ = xd−1 = 0 thì 1 a1 ad A = bda ad Vậy a là giá tr nh nh t c a ; là giá tr l n nh t c a 1b1 ị ỏ ấ ủ A adbd ị ớ ấ ủ A
Bài 3: Giả sử x1, x2, … , x là các bi . Tìm giá tr d
ến nguyên dương có tích là d! ị nhỏ nhất của S = x5 5 5 1 + x2 + ⋯ + xd . Giải:
Gọi G là tập tất cả các giá trị của S. Ta thấy G hữu hạn và khác rỗng. Do đó theo
nguyên lý cực trị rời rạc, luôn tồn tại N là số nhỏ nhất của G. Giả sử (a1, a2, … , ad)
làm cho S nhận giá trị N. Không làm mất tính tổng quát, ta giả sử rằng a1 ≤ a2 ≤
… ≤ ad. Ta sẽ chứng minh rằng a1 = i tức số sau hơn số trước 1 đơn vị.
Thật vậy, giả sử kết luận trên là sai, tức tồn tại 2 số a là h p i, ai+1(ai > 1, ai+1 = ab ợ
số) hơn kém nhau một lượng lớn hơn 1. Khi đó, dựa vào tính chất a nên 1a2 … ad = d!
sẽ tồn tại ít nhất 2 thừa số a . Khi này xét ′ ′ j = ak = 1
aj = 1,ai+1 = b, dễ thấy rằng
a5 + b5 < (ab)5 nên giả sử trên là sai. Vậy S 5 5 5 min = N = 1 + 2 + ⋯ + d
Mở rộng bài toán tìm giá trị lớn nhất của S
IV. Thiết lập thứ tự trên các yếu tố bình đẳng
Sự thiết lập thứ tự trên các yếu tố bình đẳng đã làm giảm đi rất nhiều trường
hợp xét trong bài toán. Đó chính là tính ưu việt của phương pháp này.
1. Ví dụ minh họa
Ví dụ 1: Tìm các số ngyên tố a,b,c sao cho abc < ab + bc + ca Giải:
Vì vai trò của a, b, c là như nhau, nên không làm mất tính tổng quát, ta có thể giải
thiết a ≤ b ≤ c. Từ đó suy ra ab + bc + ca ≤ 3bc, và do đó abc < 3b. Từ đây suy ra
a < 3 hay a = 2. Từ đó giả thiết trở thành 2bc < 2b + 2c + bc
Từ đây ta nhận được bc < 2(b + c) hay 1 + 1 < 1. b c 2
Lại có 1 + 1 ≥ 1 + 1. Từ đây suy ra b < 4. Mà b nguyên tố suy ra b = 2 hoặc b = 3 b c b b
+) b = 2 thì mọi số nguyên tố c đều thỏa mãn
+) b = 3 thì c = 3 hoặc c = 5.
Hoán vị các nghiệm đã có ta sẽ thu được toàn bộ nghiệm của bài toán
Ví dụ 2: Cho a, b, c, d là các số thực đôi một khác nhau . Giải hệ phương trình sau:
|a − b|y + |a − c|z + |a − d|t = 1
|b − a|x + |b − c|z + |b − d|t = 1
|c − a|x + |c − b|y + |c − d|t = 1 (1)
{|d − a|x + |d − b|y + |d − c|z = 1 Giải:
Do vai trò của a, b, c, d là bình đẳng trong bài toán này, nên ta có thể giả sử a > b >
c > d. Khi đó hệ (1) được chuyển thành hệ sau:
(a − b)y + (a − c)z + (a − d)t = 1
{ (a − b)x + (b − c)z + (b − d)t = 1
(a − c)x + (b − c)y + (c − d)t = 1 (2)
(a − d)x + (b − d)y + (c − d)z = 1
Biến đổi hệ trên bằng cách lấy phương trình thứ nhất trừ phương trình thứ hai;
phương trình thứ 2 trừ phương trình thứ 3; phương trình thứ ba trừ phương trình thứ tư
và giữu nguyên phương trình cuối, ta được hệ mới:
(a − b)(−x + y + z + t) = 0 {
(b − c)(−x − y + z + t) = 0
(c − d)(−x − y − z + t) = 0
(a − d)x + (b − d)y + (c − d)z = 1