Nhiễu xạ ánh sáng |Bài giảng môn Vật lý đại cương 3 | Trường Đại học Bách Khoa Hà Nội

Bμi gi¶ng VËt lý ®¹i c−¬ng
T¸c gi¶: PGS. TS §ç Ngäc UÊn ViÖn VËt lý kü thuËt
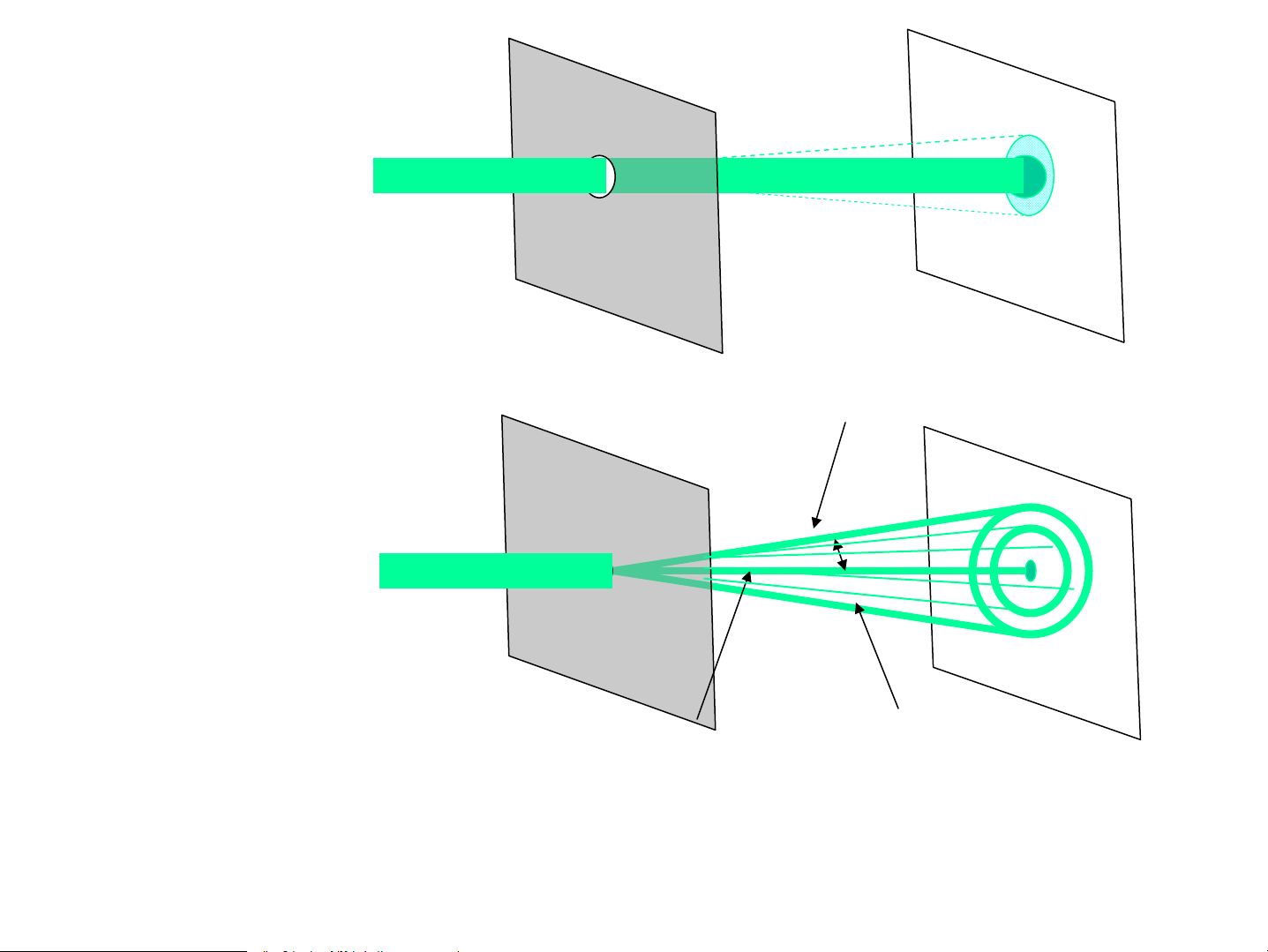
Tr−êng §H B¸ch khoa Hμ néi Ch−¬ng 4 NhiÔu x¹ ¸nh s¸ng 1. HiÖn t−îng Lç to nhiÔu x¹ ¸nh s¸ng gãc nhiÔu x¹ Lç nhá ¶nh ϕ nhiÔu x¹ Tia s¬ cÊp , tia nhiÔu x¹
lμ hiÖn t−îng tia s¸ng lÖch khái ph−¬ng truyÒn khi ®i gÇn ch−íng ng¹i
2. Nguyªn lý Huyghen - Frenen
BÊt k× ®iÓm nμo mμ AS truyÒn qua ®Òu trë thμnh
nguån s¸ng thø cÊp ph¸t AS vÒ phÝa tr−íc nã.
Biªn ®é vμ pha cña nguån thø cÊp lμ biªn ®é vμ
pha cña nguån thùc g©y ra t¹i vÞ trÝ cña nguån thø cÊp
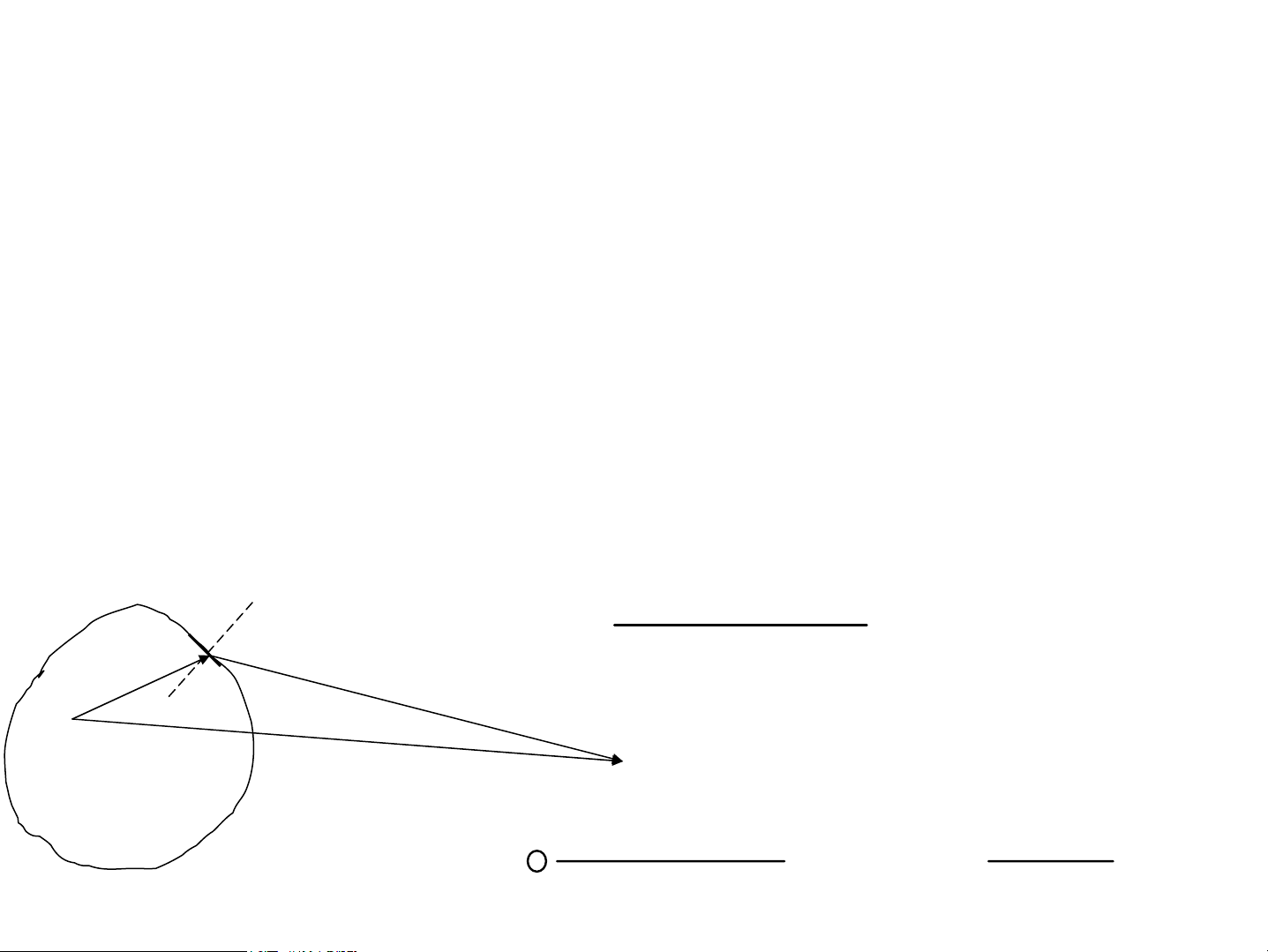
Biªn ®é tõ dS chiÕu ®Õn M dS A(θ , ) θ dS cμng θ 0 a(M) = θ,θ0 r r θ 2 r r nhá A cμng 1 0 1 2 O M lín θ θ + S A( , )dS r r x(M) 0 = cos ( ω t 1 2 − ) ∫ r r v S 1 2
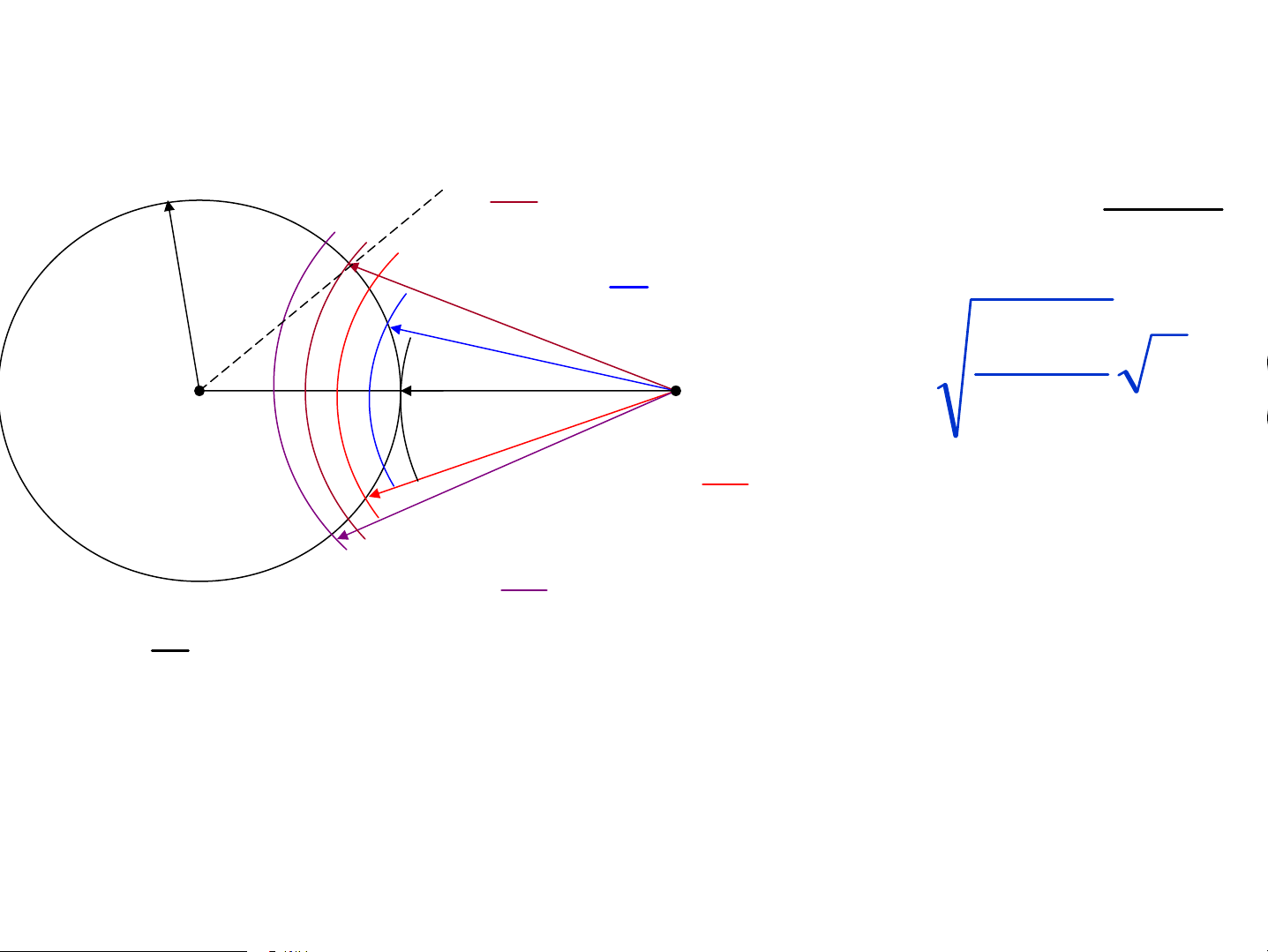
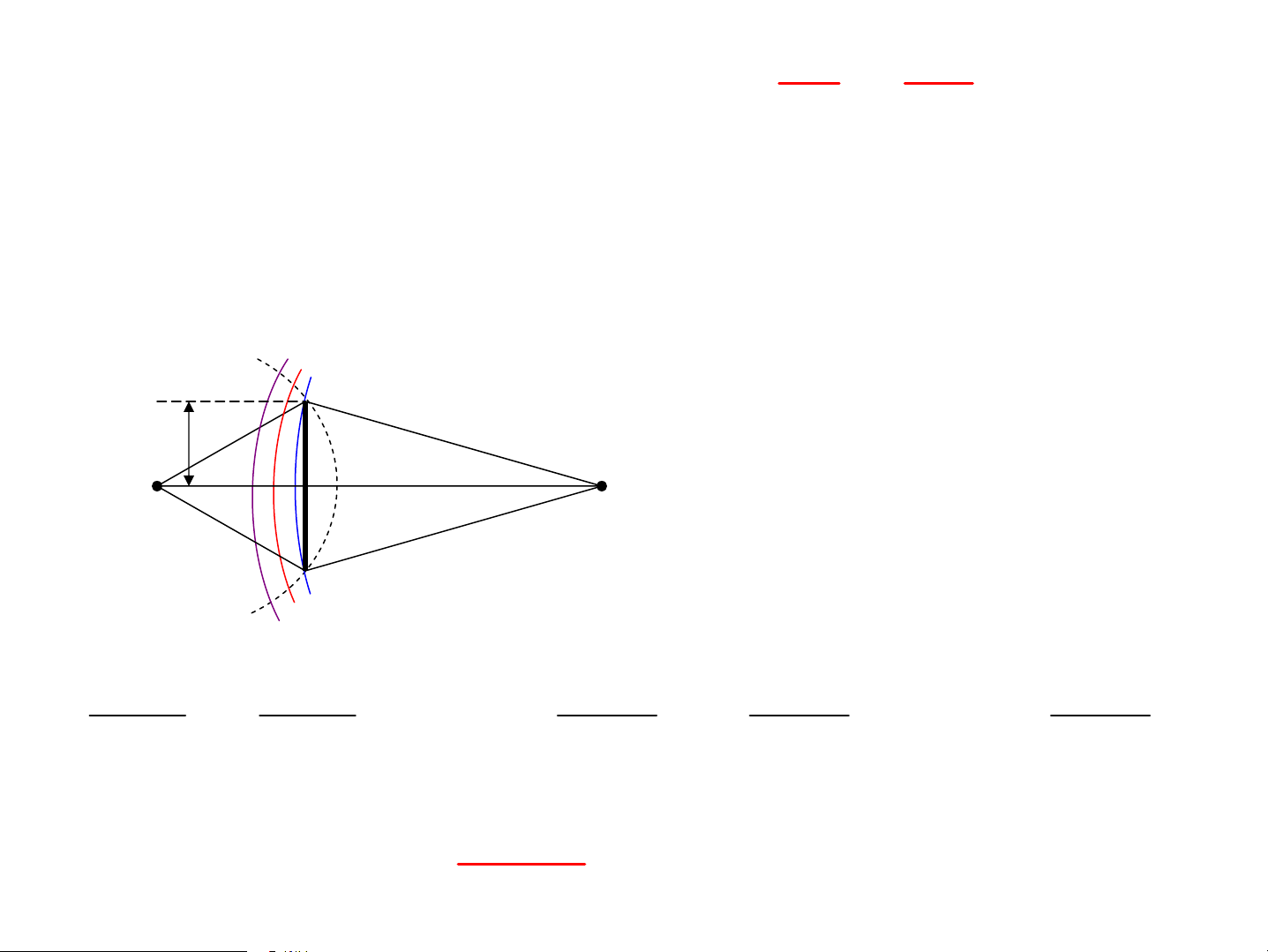
3. Ph−¬ng ph¸p ®íi cÇu Frªnen 3.1 §Þnh λ
nghÜa, tÝnh chÊt ®íi cÇu Frªnen: πRb b + 3 ΔS= λ θ 2 λ R+b R b + Σ3 Σ 2 Rbλ 0 Σ = O 1 M r k k Σ Σ B b R + b 2 4 λ b + 2 k=1, 2,... λ 2 b + 4 a tû lÖ nghÞch víi θ: 1 2 a = (a + a ) k k 1 − k 1 +
a > a > a >...> a >... 1 2 3 n 2
HiÖu quang lé AS tõ 2 ®íi cÇu liªn tiÕp ΔL=λ/2 Biªn ®é s¸ng t¹i M: a=a -a + a - a ... ± a ... 1 2 3 4 n + n lÎ, - n ch½n
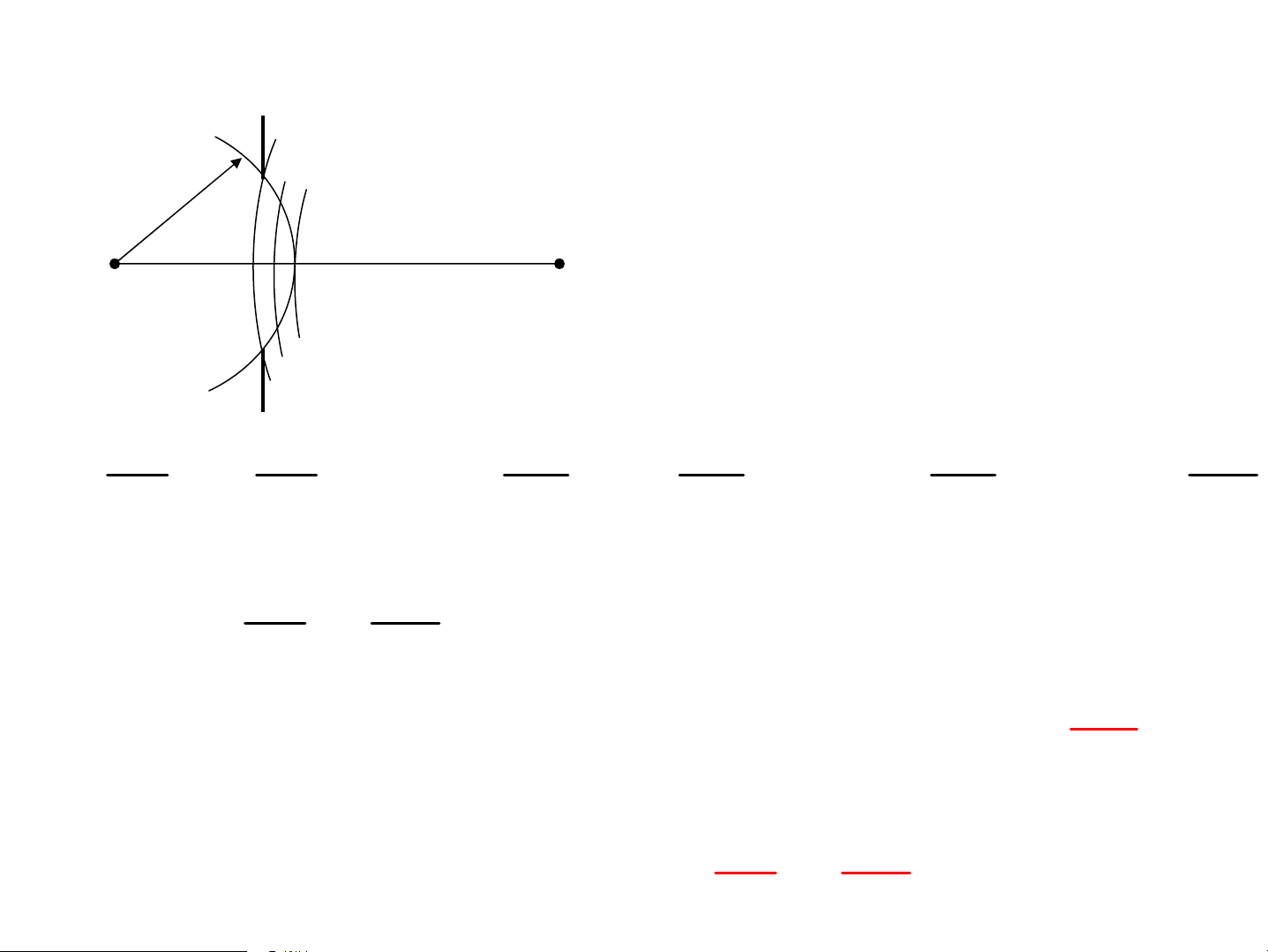
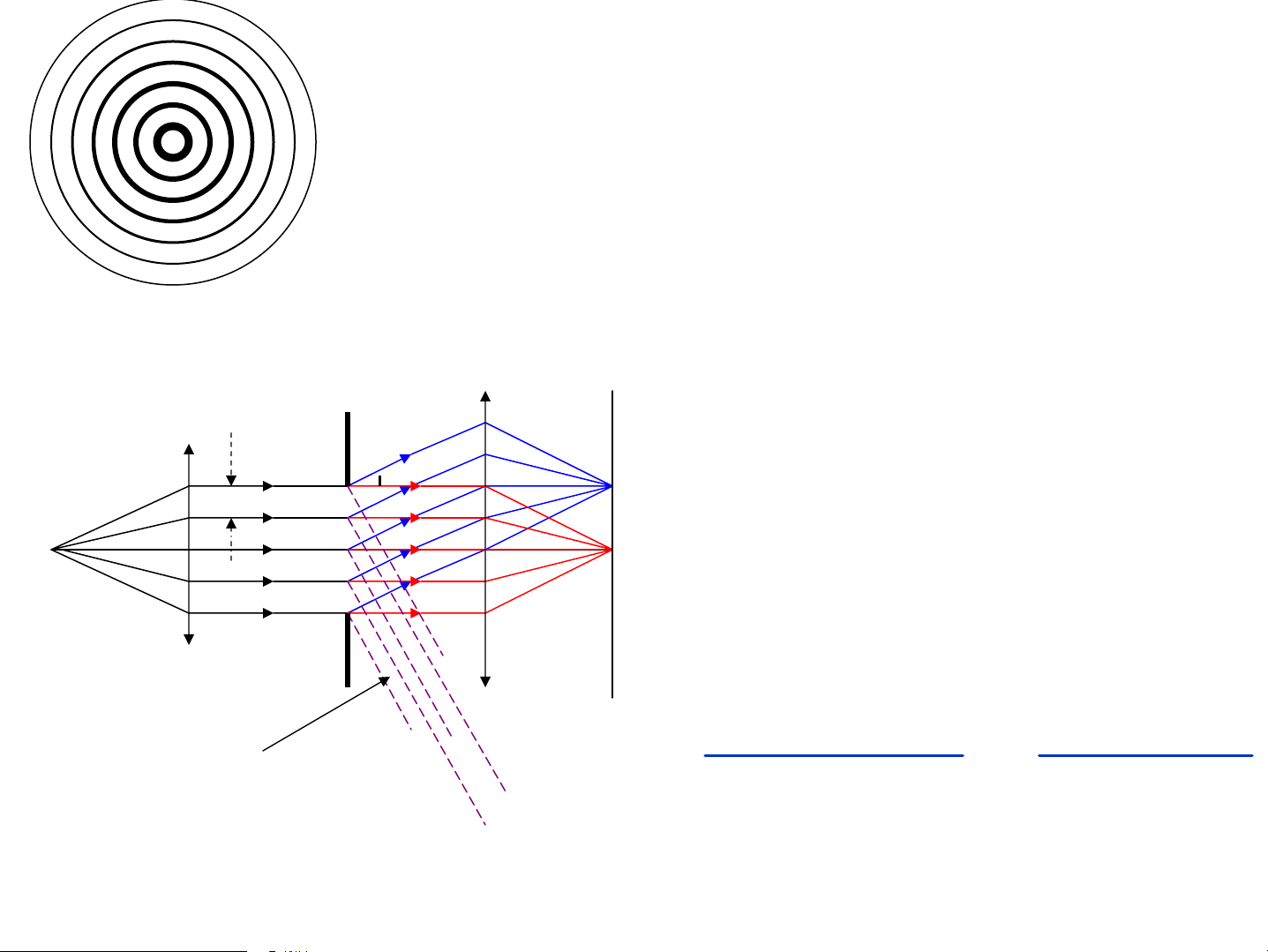
3.2. NhiÔu x¹ qua lç trßn g©y bëi nguån ®iÓm ë gÇn:
Cã n ®íi cÇu, Biªn ®é s¸ng t¹i M R O a=a -a + a - a ... ± a M 1 2 3 4 n + n lÎ, - n ch½n a a a a a a a 1 = + ( 1 − a 3 + ) + ( 3 − a 5 + ) + ... n ± 2 2 2 2 2 4 2 2 a a a 1 n = ± + n lÎ, - n ch½n 2 2 a 2
NhiÒu ®íi cÇu a ->0 => I =a2 I 1 = n 0 0 4 Chøa sè lÎ ®íi cÇu a a 1 n 2 I = ( + ) > I0 2 2 a a Chøa sè ch½n ®íi cÇu 1 n 2 I = ( − ) < I0 2 2 n=2 => I =0 2 2 n=1 => I =a =4I 1 1 0
3.3. NhiÔu x¹ qua ®Üa trßn: m+3 §Üa b¸n kÝnh r che mÊt m+1 0 M r 0 m ®íi cÇu. AS tõ ®íi O cÇu m+1 chiÕu tíi M a = a -a + a - ... m+2 m+1 m+2 m+3 a a a a a a m 1 = + + ( m 1 + − a m+3 + ) + ( m+3 − a m+5 + ) + ... + + 2 2 m 2 2 2 m 4 2 a a m 1 + = 2
Che c¸c ®íi cÇu (hoÆc ch½n hoÆc
lÎ) ®Ó t¨ng c−êng ®é s¸ng a=a -a + a - a ... ± a 1 2 3 4 n -> a=a + a ... +a 1 3 lÎ
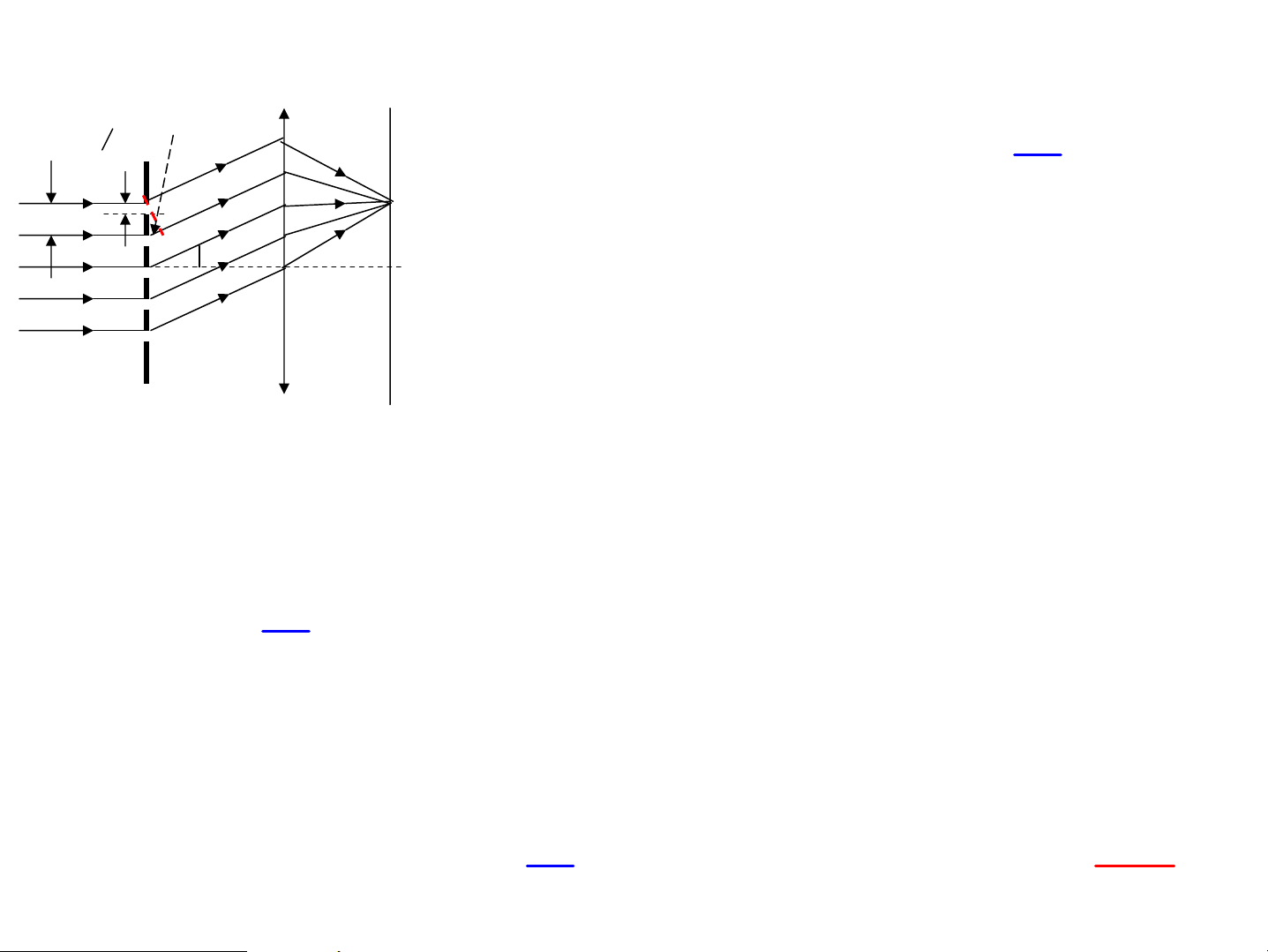
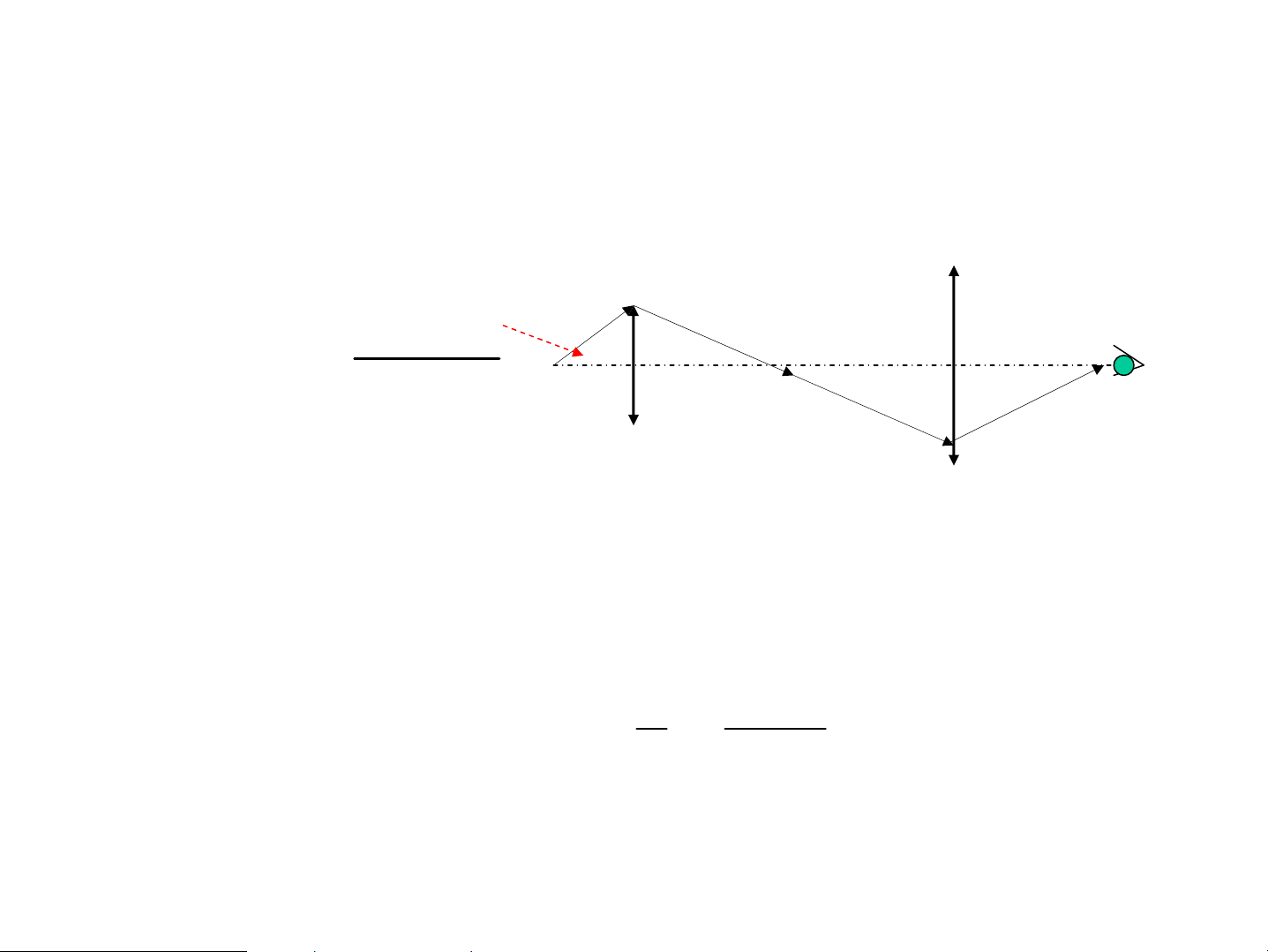
4. NhiÔu x¹ g©y bëi c¸c sãng ph¼ng δ AB=b A ϕ M 4.1.Qua mét khe hÑp BÒ réng O F δ mçi d¶i =λ/2sinϕ B Σ I 0 I 1 Sè d¶i 0 Σ b 2b sin ϕ 4 Σ n = = 2 Σ1 λ/2 Σ λ / 2sin ϕ λ 3
HiÖu quang lé gi÷a 2 tia tõ 2 d¶i liªn tiÕp: Δ
Chóng dËp t¾t nhau tõng ®«i mét L=λ/2 2b sin ϕ
§iÒu kiÖn cùc tiÓu: M tèi n = = 2k λ λ sin ϕ = k k = ±1, ±2... Trõ k=0 b
§iÒu kiÖn cùc ®¹i: M s¸ng λ 2b sin ϕ ϕ = + n = = 2k + 1 sin (2k ) 1 λ 2b
k = 1, ±2, ±3... Trõ k=0 vμ k=-1
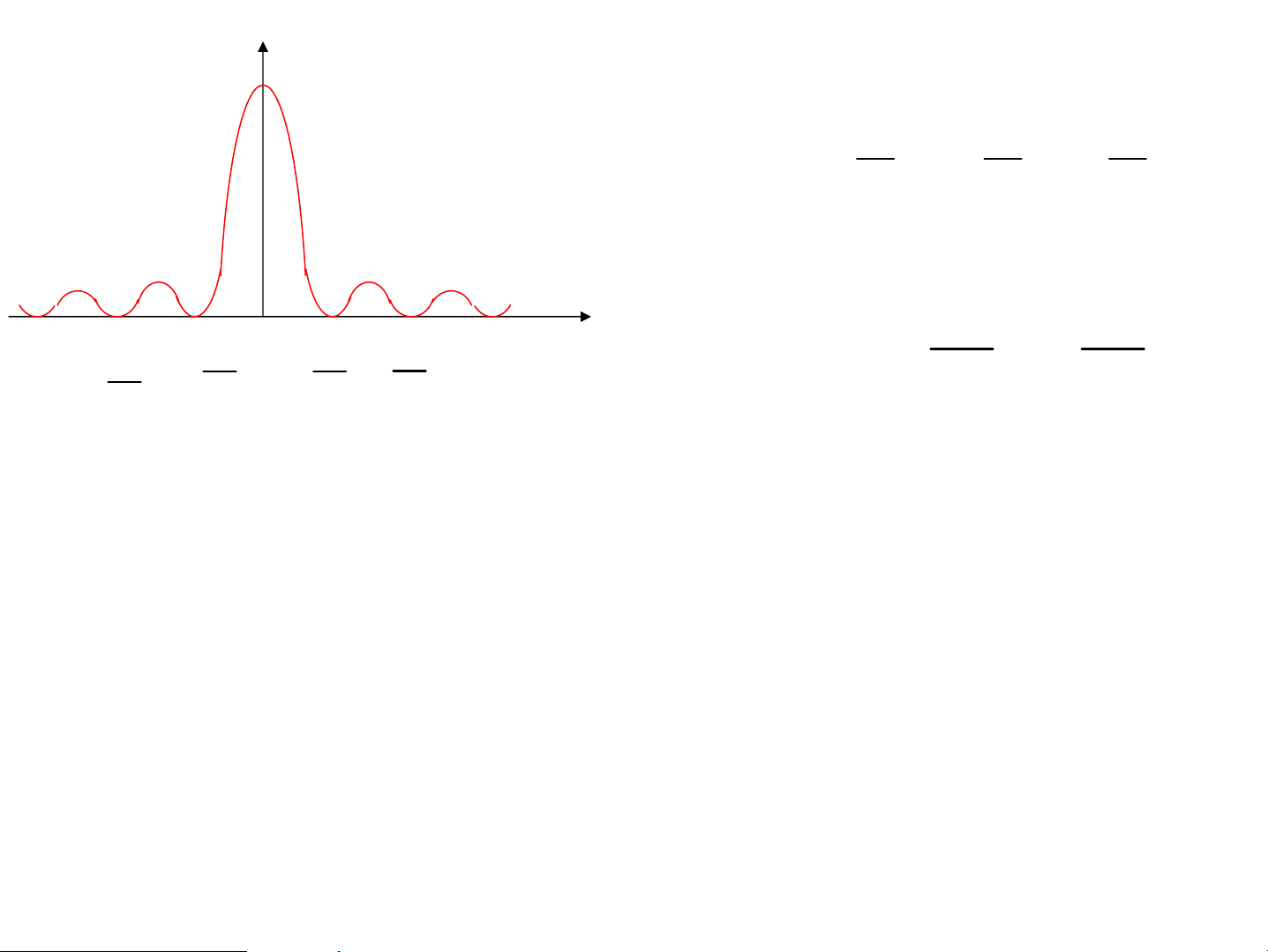
øng víi k=0, -1 trïng víi cùc ®¹i gi÷a I sinϕ=0 cùc ®¹i gi÷a 0 λ λ λ sin ϕ = ± ,±2 ,±3 ... b b b I1 I cã c¸c cùc tiÓu 2 λ λ λ λ λ λ ϕ = ± ± − O sinϕ sin 3 , 5 ,... 2 − 2 b b 2b 2b b b cã c¸c cùc ®¹i
Tû lÖ I :I :I : I ...=1: 0,045:0,016:0,008... 0 1 2 3 NhËn xÐt:
1 Cùc ®¹i gi÷a cã bÒ réng gÊp ®«i c¸c cùc ®¹i bªn.
2 Cùc ®¹i gi÷a cã c−êng ®é gÊp tr¨m lÇn c¸c cùc ®¹i bªn.
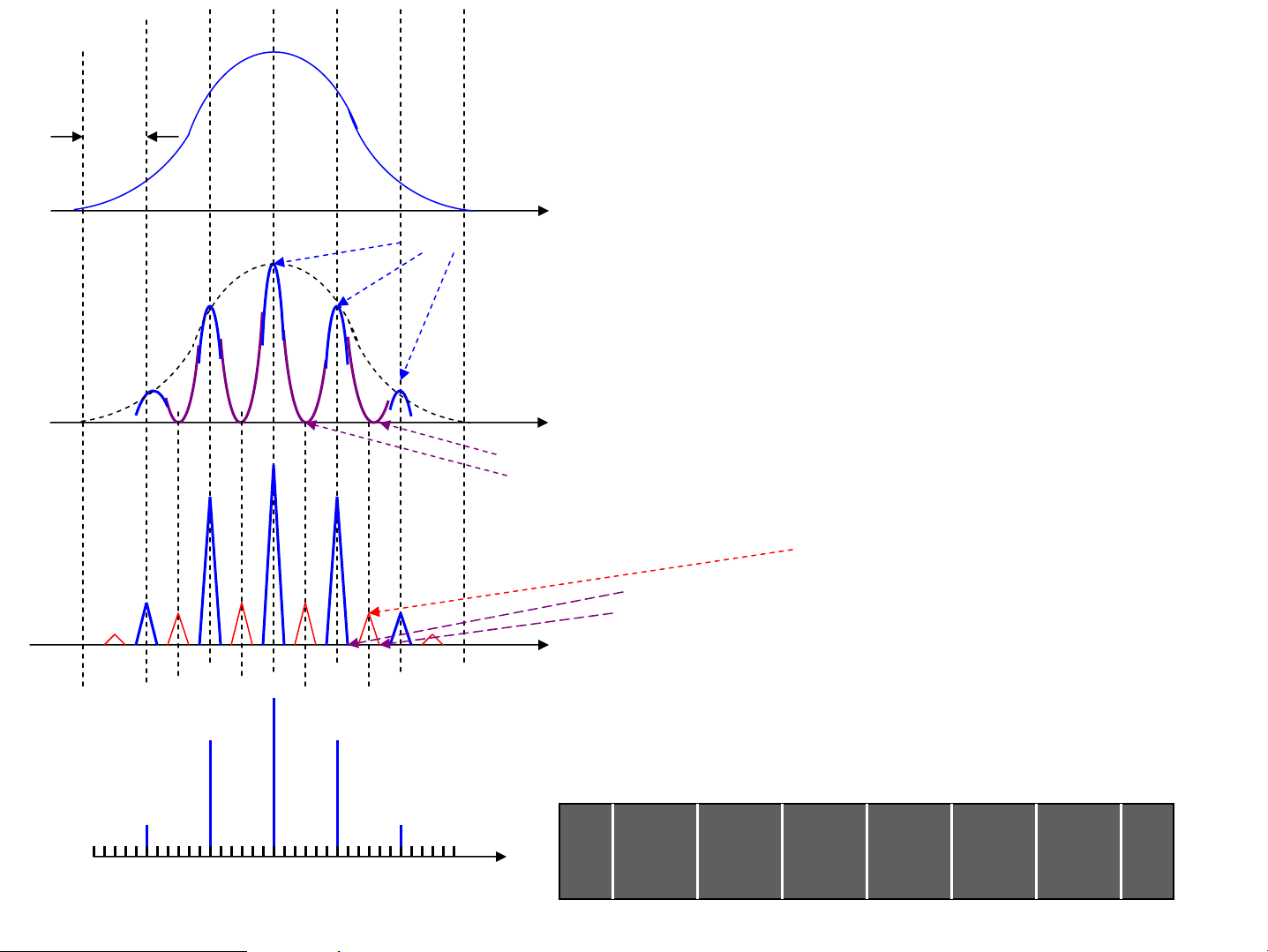
4.2. NhiÔu x¹ qua nhiÒu khe hÑp. C¸ch tö dsinϕ d>b>λ λ d b sin ϕ = k M ϕ b F Cã c¸c cùc tiÓu chÝnh.
N/CPh©n bè c−êng ®é s¸ng I E gi÷a hai cùc tiÓu chÝnh:
HiÖu quang lé gi÷a 2 tia t−¬ng øng tõ 2 khe liªn tiÕp L − L = d sin ϕ = λ k 1 2 λ sin ϕ = k cã c¸c cùc ®¹i chÝnh. d
k =0, ±1, ±2... k=0 cùc ®¹i gi÷a.
Gi÷a c¸c cùc ®¹i chÝnh cã c¸c cùc tiÓu t¹i λ λ d sin ϕ = (2k + ) 1 sin ϕ = (2k + ) 1 2 2d d=3b Hai tia tõ 2 khe liªn tiÕp λ/d khö lÉn nhau -> tèi -λ/b 0
λ/b cßn tuú thuéc vμo sè khe N kλ/d N=1-> 1 Cùc ®¹i gi÷a
N=2 -> C¸c cùc ®¹i chÝnh Sinϕ & Cùc tiÓu (2k+1)λ/2d
N=3-> 1 Cùc ®¹i phô: N-2. 2 cùc tiÓu phô: N-1. N nhiÒu: C¸c cùc ®¹i nÐt • C¸ch tö nhiÔu x¹:
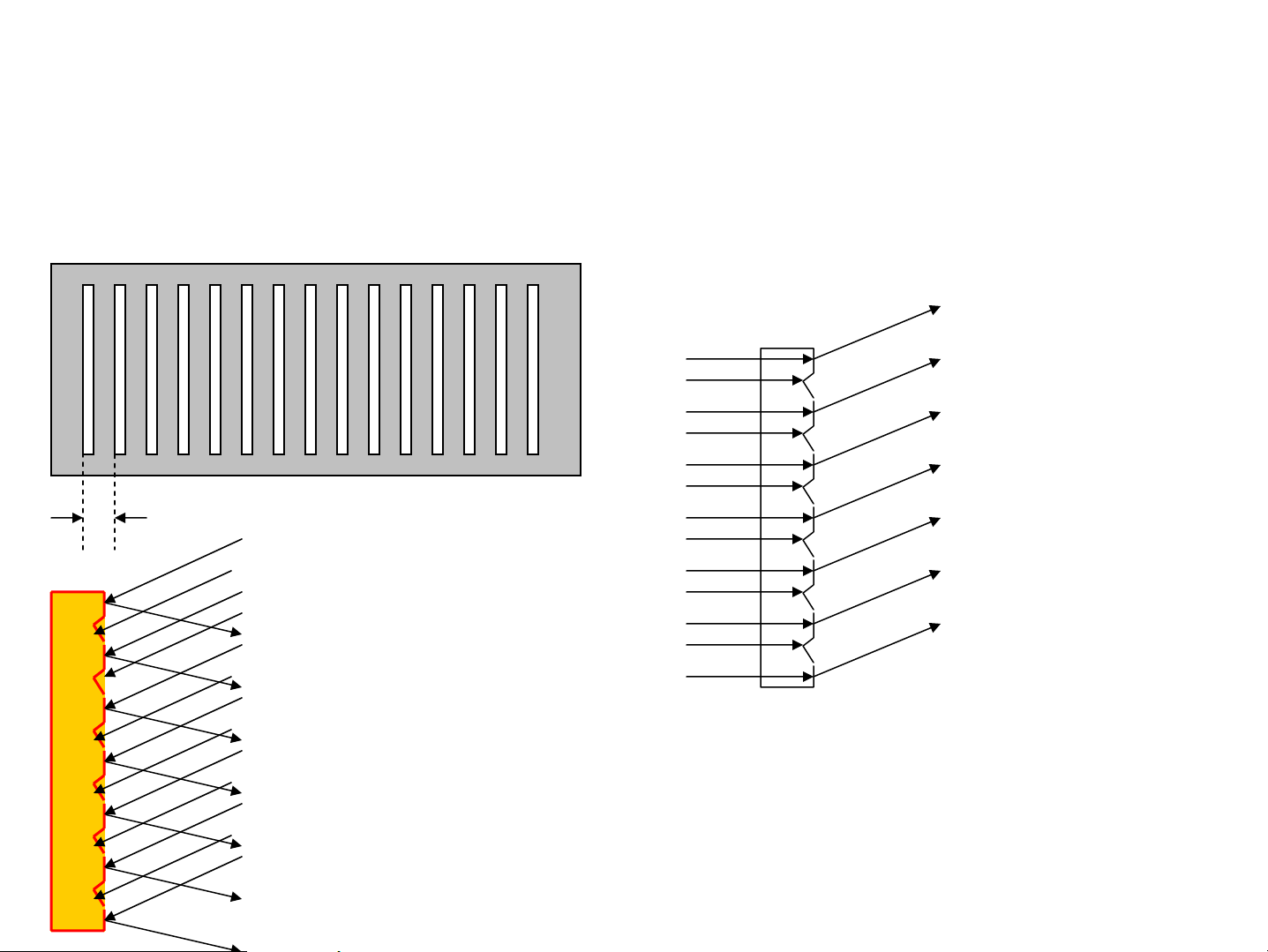
TËp hîp c¸c khe hÑp gièng nhau c¸ch ®Òu nhau
vμ cïng n»m trªn mÆt ph¼ng: d chu k× C¸ch tö truyÒn qua: KÝnh r¹ch n=1/d d 500 - C¸ch tö ph¶n x¹: 1200/mm Kim lo¹i R¹ch KÜ thuËt quang kh¾c
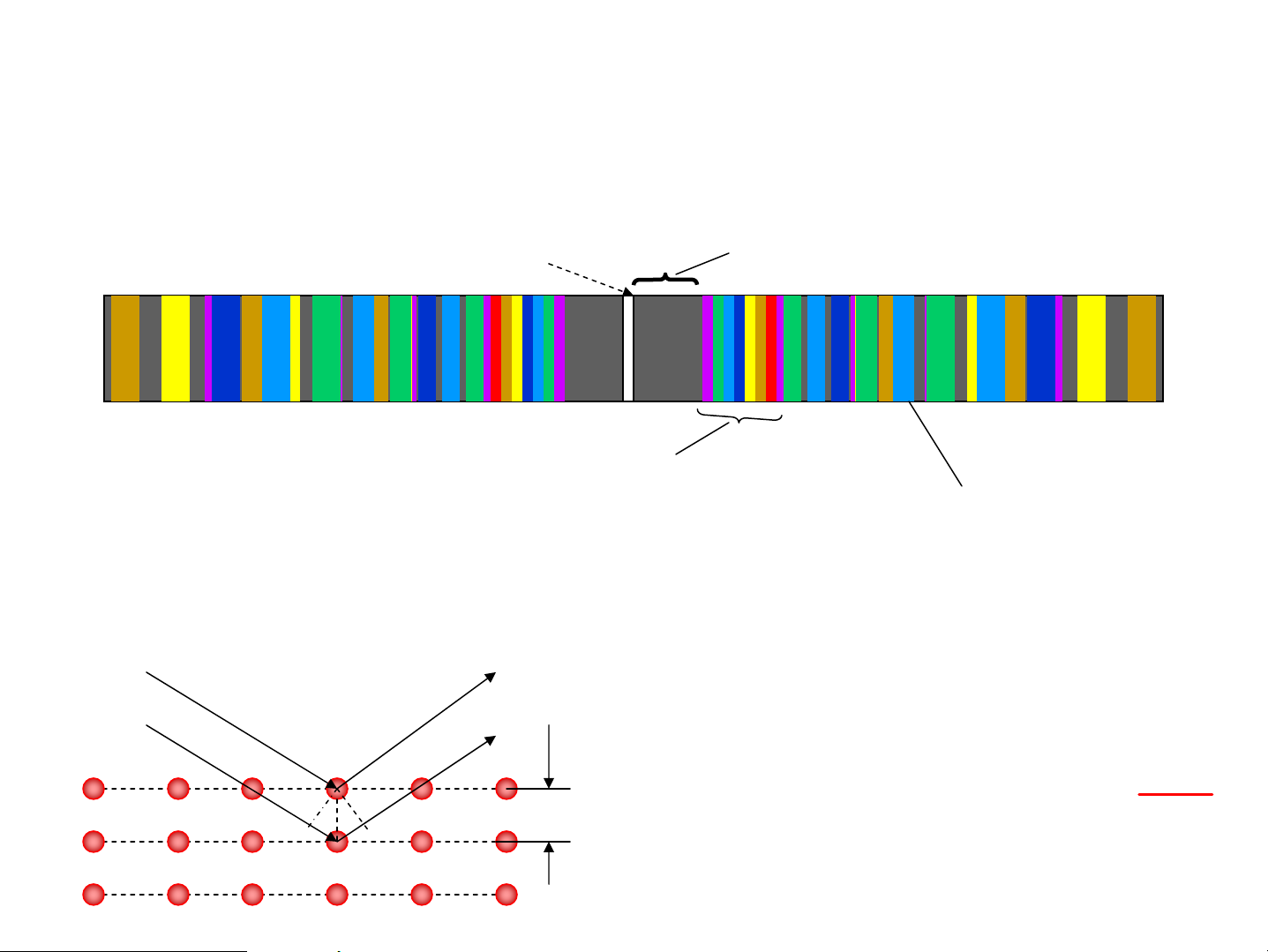
• NhiÔu x¹ ¸nh s¸ng tr¾ng qua c¸ch tö 0,4μm ≤ λ ≤ 0,76μm
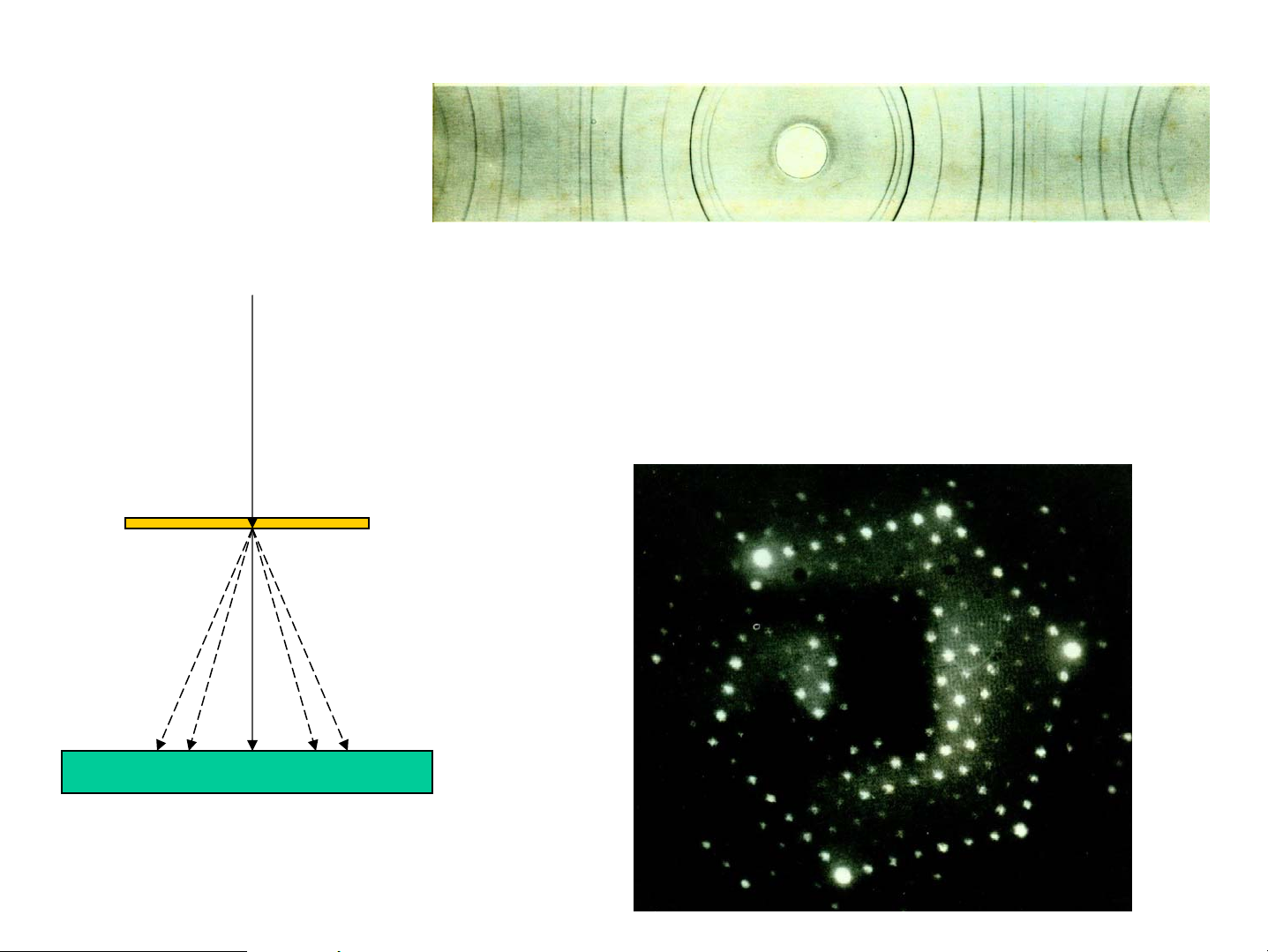
TÝm, Chμm, Lam, Lôc,Vμng,Da cam, §á V©n tr¾ng trung t©m Kho¶ng tèi k=4 7 mÇu,k=1 k=2 k=3 • NhiÔu x¹ trªn tinh thÓ HiÖu quang lé 2 tia Tia X cã λ~10-10m ΔL=2dsinθ=kλ θ λ d~3.10-10m sin θ = k 2d C«ng thøc Wulf-Bragg tia x, e,n Zn Debye (111)Si mÉu tinh thÓ Phim
• N¨ng suÊt ph©n ly cña dông cô quang häc
Kh¶ n¨ng ph©n biÖt chi tiÕt nhá nhÊt
9B»ng nghÞch ®¶o kho¶ng c¸ch nhá nhÊt gi÷a 2
®iÓm cã thÓ ph©n biÖt ®−îc hoÆc cña gãc nhá
nhÊt gi÷a 2 tia tíi 2 ®iÓm cßn ph©n biÖt ®−îc.
9NhiÔu x¹ qua lç trßn cña dông cô → ®iÓm trªn
vËt → vÖt s¸ng trong dông cô
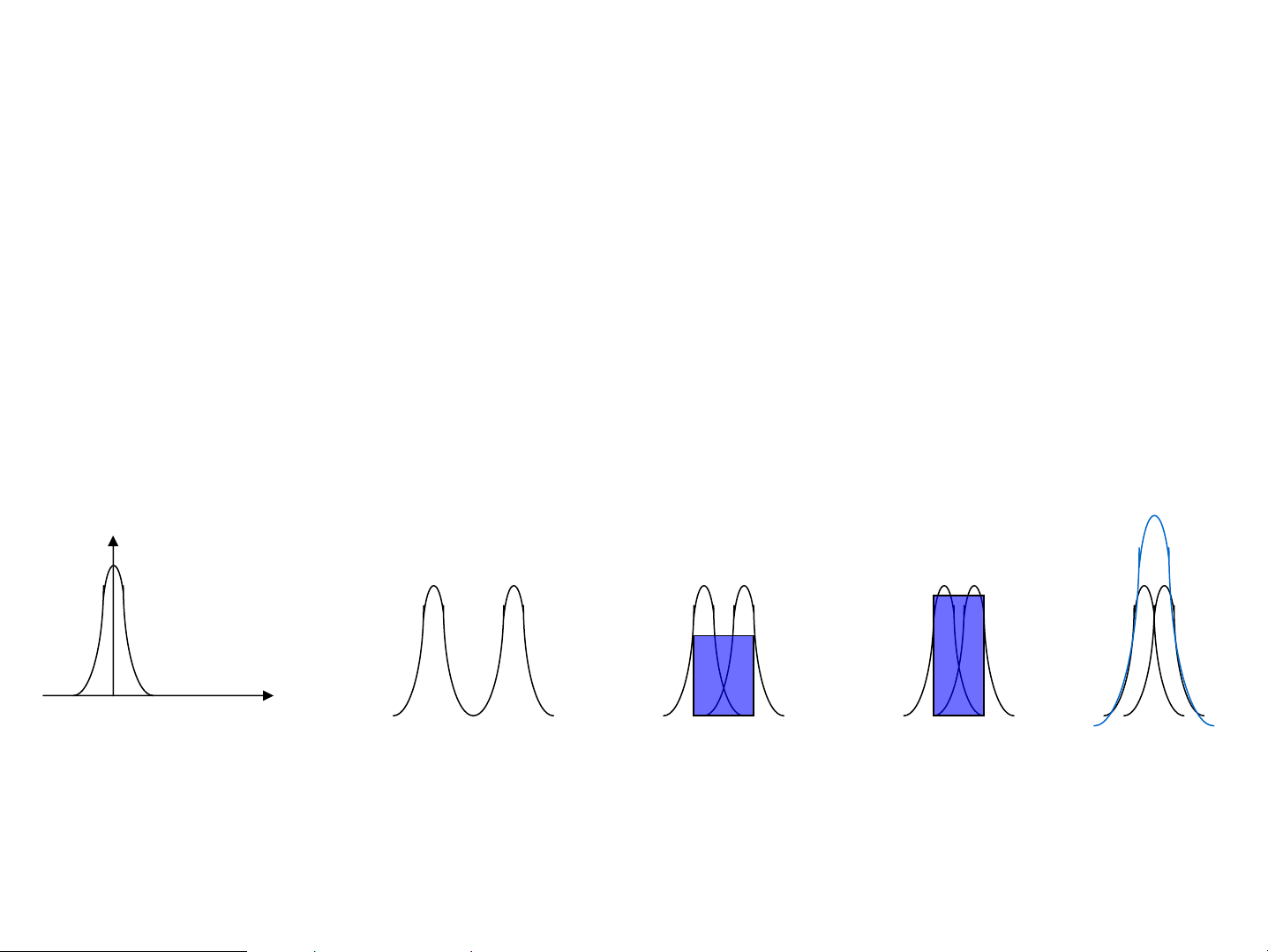
C−êng ®é s¸ng 2 ®iÓm cßn 2 ®iÓm kh«ng trong ¶nh cña
ph©n biÖt ®−îc ph©n biÖt ®−îc mét ®iÓm
N¨ng suÊt ph©n ly cña dông cô quang häc b»ng
nghÞch ®¶o kho¶ng c¸ch nhá nhÊt gi÷a 2 ®iÓm (= b¸n kÝnh cña 1 vÕt ) ¾ VËt kÝnh thÞ kÝnh KÝnh hiÓn vi: S = n sin u , 0 λ 61
n- chiÕt suÊt cña m«I tr−êng, u- gãc nghiªng lín
nhÊt cña chïm s¸ng chiÕu vμo vËt kÝnh, λ- b−íc sãng ¸nh s¸ng ¾ KÝnh thiªn v¨n: 1 d S = = ε , 1 22'
d- ®−êng kÝnh cña kÝnh vËt