Những mã vùng cần biết môn Công nghệ thông tin | Đại học Hoa Sen

Những mã vùng cần biết môn Công nghệ thông tin | Đại học Hoa Sen được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem

16 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Công nghệ thông tin ( 02)

Trường: Đại học Hoa Sen

Thông tin:

40 trang 3 tuần trước

Tác giả:

Profile Kim Oanh
DANH SÁCH LIÊN K T Ế
Định nghĩa
Danh sách liên k là m t danh sách mà các ph n t c k t n i v i nhau nh vào ế ộ ầ ử đượ ế ố ớ ờ
vùng liên k t c a chúng. ế ủ
Một phần t c a DSLK bao g m 2 vùng chính ử ủ ồ
Vùng chứa thông tin
Vùng chứa địa chỉ, còn g i là vùng liên k t ọ ế
Việc lưu trữ hơn DSĐ DSLK tốn bộ nhớ vì ph i ch a thêm ph n liên k t. ả ứ ầ ế
Danh sách liên k ết đơn
DSLK đơn là loại DSLK mà vùng địa chỉ của mỗi phần tử chỉ chứa duy nh t ấ
một địa chỉ của ph n t ti p theo. ầ ử ế
Phần tử cuối cùng c tr ủa DSLK đơn sẽ ỏ đến NULL.
Khởi t o danh sách r ng gán pHead = NULL ạ ỗ
Kiểm tra danh sách có r ng hay không ktra pHead = NULL hay không ỗ
Kiểm tra danh sách có đầy hay chưa không kiểm tra được tính đầy đối với DSLK
Tổ ch ức lưu trữ DSLK đơn
Duyệt danh sách cho con tr p ch y t n cu i ỏ ạ ừ đầu đế ố
danh sách
Tìm ki m m t ph n t trong danh sách n u tìm th y ế ộ ầ ử ế ấ
trả v con tr c l i tr v NULL ề ỏ p, ngượ ạ ả ề
Thêm m t ph n t vào danh sách ộ ầ ử
B1: T o m t ph n t trong b nh ạ ộ ầ ử ộ ớ
B2: G n ph n t v a t o vào danh sách ắ ầ ử ừ ạ
Thêm vào đầu danh sách
Thên vào sau v trí q ị
Thêm vào cu i danh sách ố
Xóa phần t ử ở u danh sách đầ
Xóa phầ ần t ng sau phử đứ n t q ử
Xóa phần t có giá trử ị X
Hủy toàn b danh sách ộ
STACK
ĐỊNH NGHĨA
Stack là m t danh sách ho ng ộ ạt độ
theo cơ chế LIFO ( ast n irst ut). L I F O
Thao tác thêm và h c th c ủy đượ ự
hiện ở cùng m t phía c a Stack ộ ủ
cơ chế LIFO: phần t nào vào sau s ử ẽ
được lấy ra trước.
TỔ CHỨC LƯU TRỮ
LẤY MỘT PH N T KH NH STACK Ầ Ử ỎI ĐỈ
XEM THÔNG TIN PH N T NH STACK Ầ Ử Ở ĐỈ
QUEUE
ĐỊNH NGHĨA
Queue (hàng đợi) là một danh sách ho ạt động theo cơ chế
FIFO ( irst n F I First Out).
Thao tác thêm và h c th c hi n 2 phía c a queue ủy đượ ự ệ ở ủ
cơ chế FIFO: phần t c s c l c. ử nào vào trướ ẽ đượ ấy ra trướ
TỔ CHỨC LƯU TRỮ
KHỞI T O RẠ ỖNG
KIỂM TRA CÓ RỖNG HAY KHÔNG
KIỂM TRA CÓ ĐẦY HAY CHƯA
THÊM M T PH N TỘ Ầ Ử VÀO CU I QUEUE Ố
LẤY MỘT PH N T U QUEUE Ầ Ử Ở ĐẦ
XEM THÔNG TIN PH N T U VÀ CU I QUEUE Ầ Ử Ở ĐẦ Ố
LINEAR SEARCH
Ý TƯỞNG:
Bắt đầ ần lượu từ phần tử đầu tiên của danh sách, so sánh l t
từng ph n t c a danh sách v i giá tr X c n tìm: ầ ử ủ ớ ị ầ
Nếu có ph n tầ ử b ng X, thu t toán dằ ậ ừng l i (thành ạ
công).
Nếu đến cu i danh sách mà không có ph n t nào ố ầ ử
bằng X, thu t toán d ng l i (không thành công). ậ ừ ạ
Trường hợp t t nhố ất: s lố ần so sánh 1
Trường hợp xấ ấu nh t: s lố ần so sánh n
Trường hợp trung binh: s lố ần so sánh (n+1)/2
Độ ph c t p T(n) = O(n) ứ ạ
NGHỊCH TH Ế
Khái ni m ệ
Xét m t m ng các s ộ ả ố a1, a2, … an
Nếu có i<j và ai > aj, thì đó là một nghịch thế.
Mảng chưa sắp xếp sẽ có ngh ch th . ị ế
Mảng đã có thứ tự s không có ngh ch th ẽ ị ế a1≤ a2≤... ≤ an
BINARY SEARCH
Ý TƯỞNG:
Điều kiện: danh sách ph i có th t . ả ứ ự
So sánh giá tr mu n tìm X v i ph n t n m v trí gi a cị ố ớ ầ ử ằ ở ị ữ ủa danh sách:
Nếu bằng, tìm kiếm d ng lừ ại (thành công).
Nếu X lớn hơn thì tiếp tục tìm ki m ph n danh sách bên phế ở ầ ải phần tử
giữa.
Nếu X nh p t c tìm ki m phỏ hơn thì tiế ụ ế ở ần danh sách bên trái phần tử
giữa.
Trường h p t t nh t: s l n so sánh 1 ợ ố ấ ố ầ
Trường h p x u nh t: s l n so sánh log(n) ợ ấ ấ ố ầ
Trường h p trung binh: s l n so sánh log(n/2) ợ ố ầ
Độ ph c t p T(n) = O(log(n)) ứ ạ
INTERCHANGE SORT
Ý TƯỞNG
Xuất phát từ ph n tầ ử đầu danh sách, tìm t t các các c p nghấ ặ ịch
thế chứa ph n tầ ử này. Tri t tiêu chúng b ng cách ệ ằ đổi chỗ 2 ph n ầ
tử trong c p ngh ch th . L p l i x lý trên v i ph n t k ti p trong ặ ị ế ặ ạ ử ớ ầ ử ế ế
danh sách.
Trường h p t t nh t: ợ ố ấ
Số lần so sánh: n(n-1)/2 ; s lố ần hoán v : 0 ị
Trường h p x u nh t: ợ ấ ấ
Số lần so sánh: n(n-1)/2 ; s lố ần hoán v : n(n-1))/2 ị
BUBBLE SORT
Ý TƯỞNG
Thuật toán s p x p bubble sort th c hi n s p x p dãy s b ng cách lắ ế ự ệ ắ ế ố ằ ặp lại
công vi i ch 2 s liên ti p nhau n ng sai th t sau bé ệc đổ ỗ ố ế ếu chúng đứ ứ ự(số
hơn số ới trườ ếp tăng dần) cho đế trước v ng hợp sắp x n khi dãy số được
sắp x p. ế
Trường h p t t nh t: ợ ố ấ
Số lần so sánh: n(n-1)/2 ; s lố ần hoán v : 0 ị
Trường h p x u nh t: ợ ấ ấ
Số lần so sánh: n(n-1)/2 ; s lố ần hoán v : n(n-1))/2 ị
SELECTION SORT
Ý TƯỞNG
Thuật toán selection sort s p x p mắ ế ột m ng b n ả ằng cách đi tìm phầ
tử có giá tr nh nh s v i s p x p m n ị ỏ ất(giả ử ớ ắ ế ảng tăng dần) trong đoạ
đoạn chưa đượ ếp và đổ ất đó vớc sắp x i cho phần tử nhỏ nh i phần
tử ở đầu đoạn chưa được s p x p(không phắ ế ải đầu mảng). Thu t toán ậ
sẽ chia m ng làm 2 m ng con ả ả
Một mảng con đã được sắp xếp
Một mảng con chưa được sắp xếp
Trường h p t t nh t: ợ ố ấ
Số lần so sánh: n(n-1)/2 ; s lố ần hoán v : 0 ị
Trường h p x u nh t: ợ ấ ấ
Số lần so sánh: n(n-1)/2 ; s lố ần hoán v : n-1 ị
INSERTION SORT
Ý TƯỞNG
Thuật toán s p x p chèn th c hi n s p x p dãy s theo cách duy t t ng ắ ế ự ệ ắ ế ố ệ ừ
phần t và chèn t ng phử ừ ần t ử đó vào đúng vị trí trong m ng con(dãy s ả ố
từ đầu đến phần tử phía trước nó) đã sắp xếp sao cho dãy số trong
mảng s m b o tính ch t c a m t dãy s n. ắp đã xếp đó vẫn đả ả ấ ủ ộ ố tăng dầ
Trường h p t t nh t: ợ ố ấ
Số lần so sánh: n-1 ; số lần hoán v : 2(n-1) ị
Trường h p x u nh t: ợ ấ ấ
Số lần so sánh: n(n-1)/2 ; s lố ần hoán v : n(n-1)/2 + 2(n-1) ị
BINARY INSERTION SORT
Ý TƯỞNG
Binary Insertion Sort được sử dụng để tìm ki m nh phân v trí thích hế ị ị ợp để chèn
mục đã chọn ở m i l n l p. ỗ ầ ặ
SO SÁNH CÁC THU T TOÁN S P X P Ậ Ắ Ế
| 1/40
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

DANH SÁCH LIÊN KẾT
Tổ chức lưu trữ DSLK đơn Định nghĩa
Danh sách liên kế là một danh sách mà các phần tử được kết nối với nhau nhờ vào
vùng liên kết của chúng.
 Một phần tử của DSLK bao gồm 2 vùng chính  Vùng chứa thông tin
 Vùng chứa địa chỉ, còn gọi là vùng liên kết
 Việc lưu trữ DSLK tốn bộ nhớ hơn DSĐ vì phải chứa thêm phần liên kết. Danh sách liên kết đơn
 DSLK đơn là loại DSLK mà vùng địa chỉ của mỗi phần tử chỉ chứa duy nhất
một địa chỉ của phần tử tiếp theo.
 Phần tử cuối cùng của DSLK đơn sẽ trỏ đến NULL.
 Khởi tạo danh sách rỗng  gán pHead = NULL
Kiểm tra danh sách có rỗng hay không  ktra pHead = NULL hay không
Kiểm tra danh sách có đầy hay chưa  không kiểm tra được tính đầy đối với DSLK
Duyệt danh sách  cho con trỏ p chạy từ đầu đến cuối
Thêm một phần tử vào danh sách danh sách
B1: Tạo một phần tử trong bộ nhớ
Tìm kiếm một phần tử trong danh sách  nếu tìm thấy
trả về con trỏ p, ngược lại trả về NULL
B2: Gắn phần tử vừa tạo vào danh sách Thêm vào đầu danh sách Thên vào sau vị trí q Thêm vào cuối danh sách
Xóa phần tử đứng sau phần tử q
Xóa phần tử có giá trị X
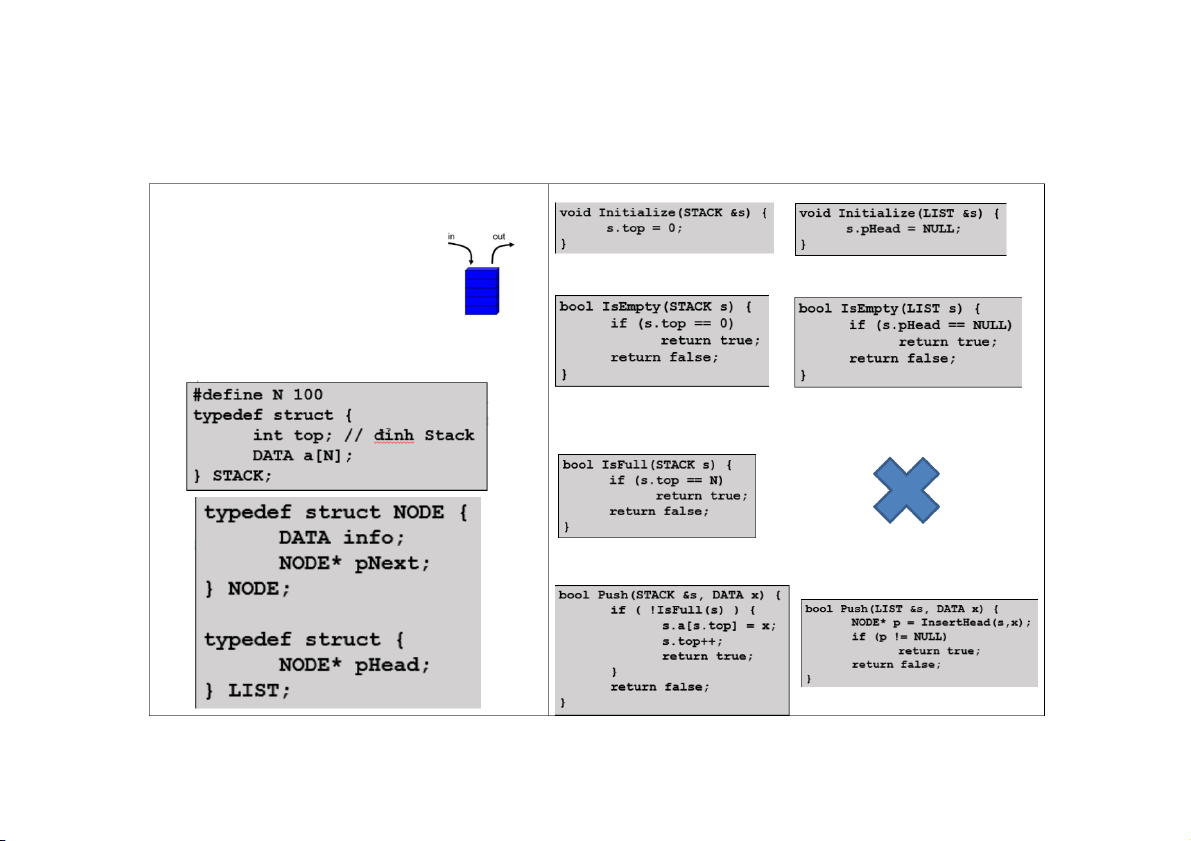
Xóa phần tử ở đầu danh sách Hủy toàn bộ danh sách STACK KHỞI TẠO RỖNG  ĐỊNH NGHĨA
 Stack là một danh sách hoạt động
theo cơ chế LIFO (Last In First Out).
 Thao tác thêm và hủy được thực
hiện ở cùng một phía của Stack 
KIỂM TRA CÓ RỖNG HAY KHÔNG
cơ chế LIFO: phần tử nào vào sau sẽ được lấy ra trước. TỔ CHỨC LƯU TRỮ
KIỂM TRA CÓ ĐẦY HAY CHƯA
THÊM MỘT PHẦN TỬ VÀO ĐỈNH STACK
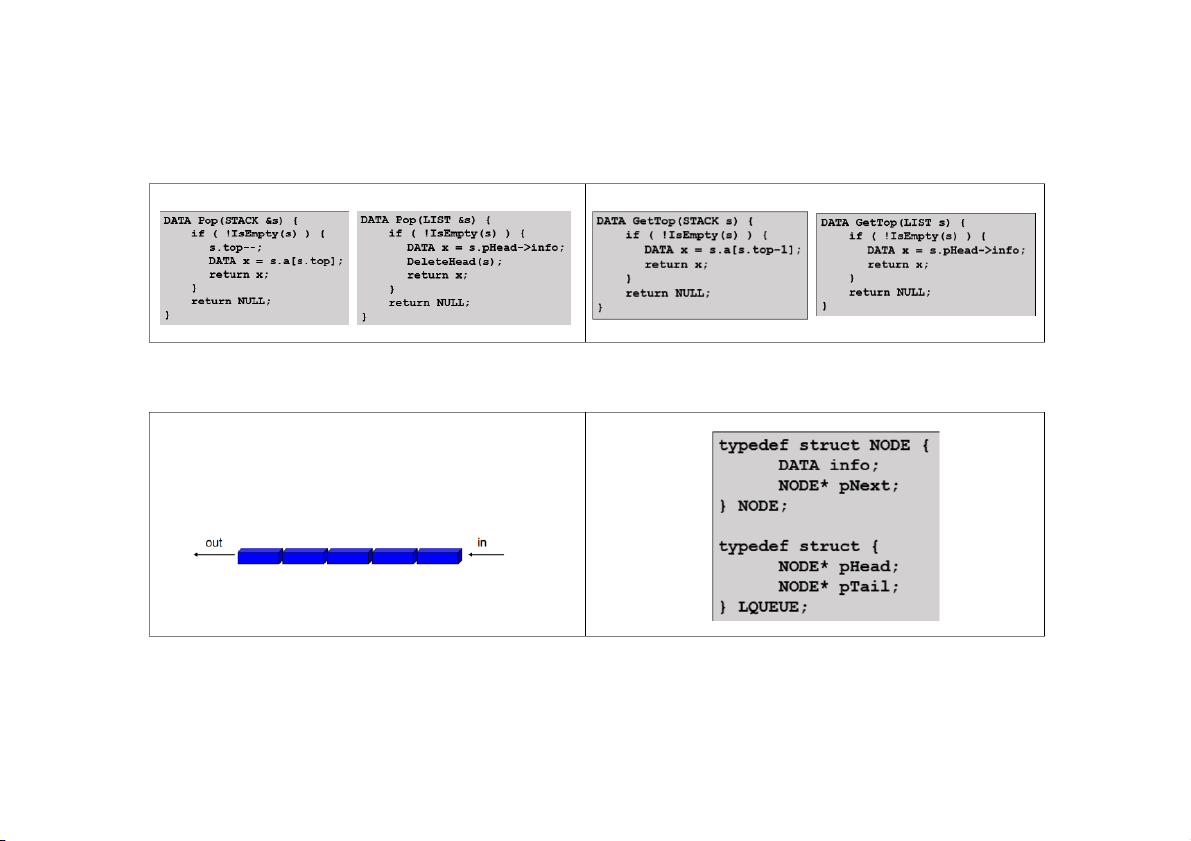
LẤY MỘT PHẦN TỬ KHỎI ĐỈNH STACK
XEM THÔNG TIN PHẦN TỬ Ở ĐỈNH STACK QUEUE TỔ CHỨC LƯU TRỮ ĐỊNH NGHĨA
 Queue (hàng đợi) là một danh sách hoạt động theo cơ chế
FIFO (First In First Out).
 Thao tác thêm và hủy được thực hiện ở 2 phía của queue 
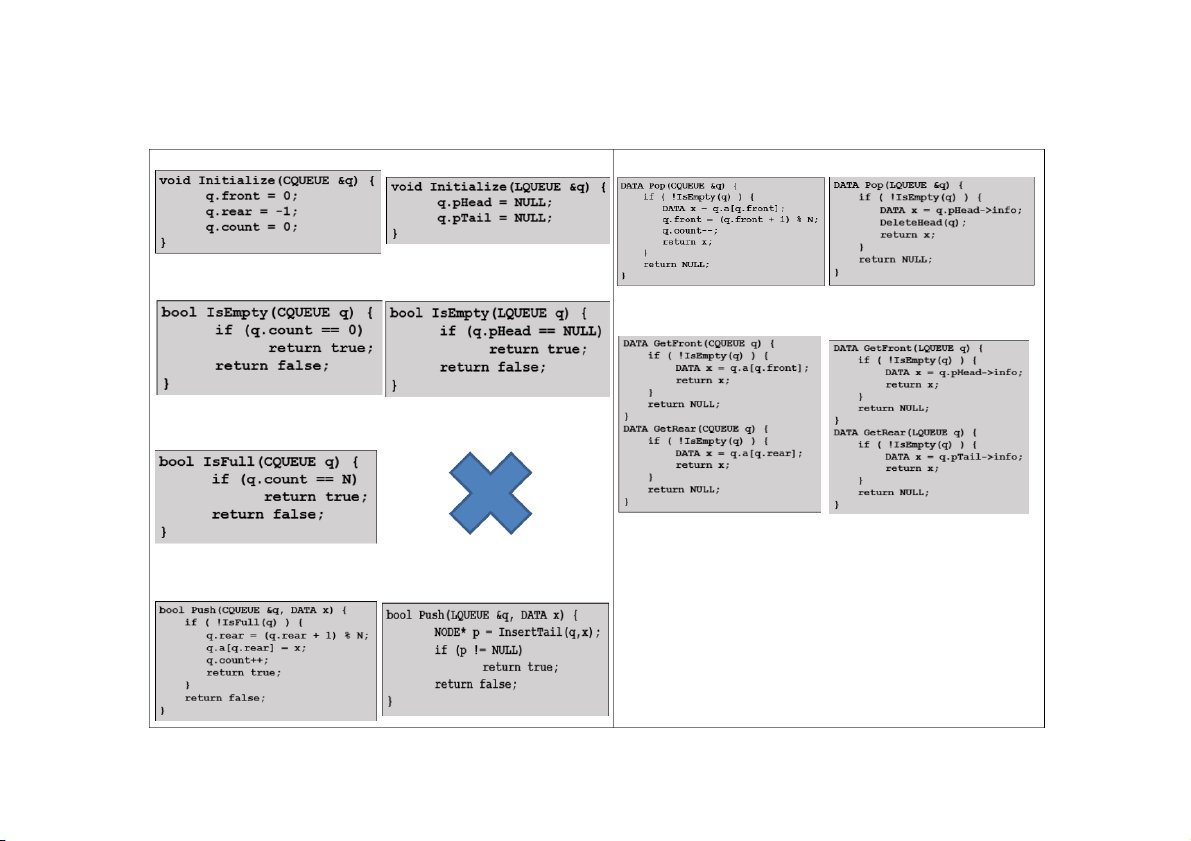
cơ chế FIFO: phần tử nào vào trước sẽ được lấy ra trước. KHỞI TẠO RỖNG
LẤY MỘT PHẦN TỬ Ở ĐẦU QUEUE
KIỂM TRA CÓ RỖNG HAY KHÔNG
XEM THÔNG TIN PHẦN TỬ Ở ĐẦU VÀ CUỐI QUEUE
KIỂM TRA CÓ ĐẦY HAY CHƯA
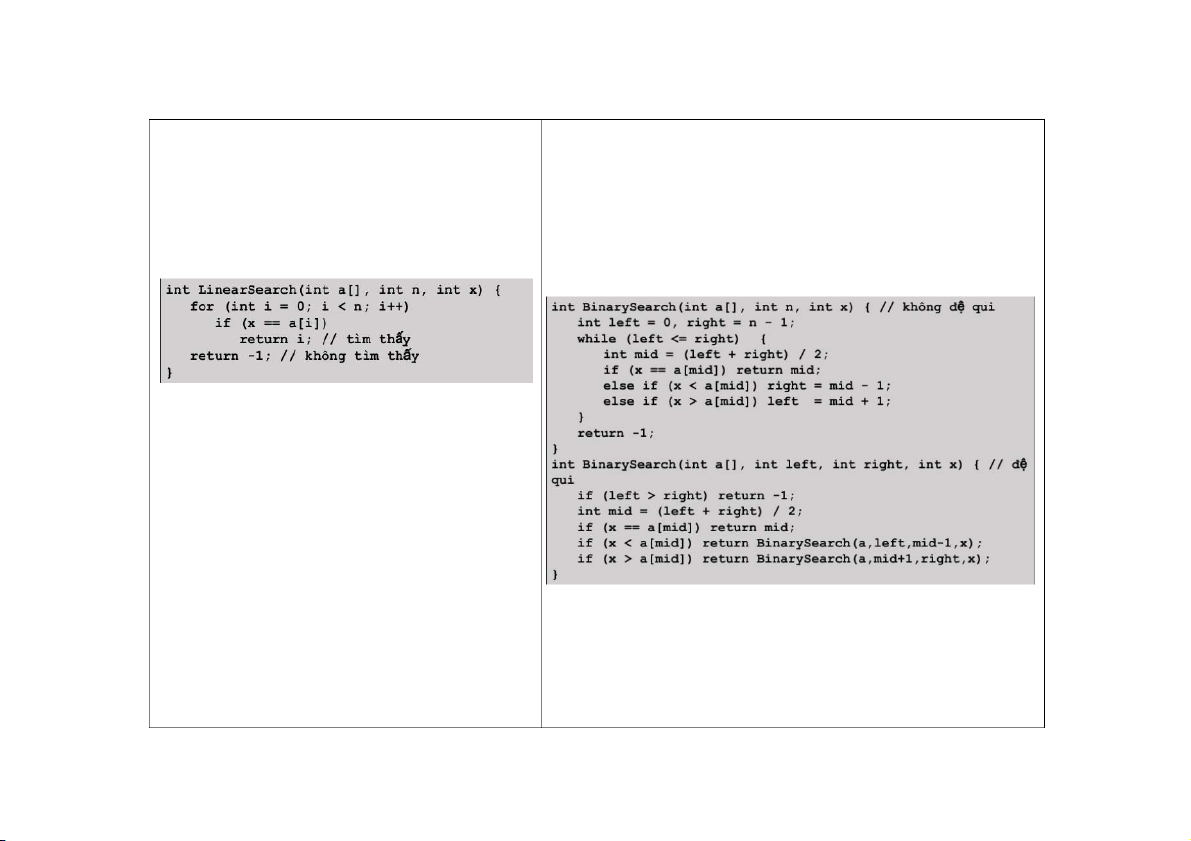
THÊM MỘT PHẦN TỬ VÀO CUỐI QUEUE LINEAR SEARCH BINARY SEARCH Ý TƯỞNG: Ý TƯỞNG:
Bắt đầu từ phần tử đầu tiên của danh sách, so sánh lần lượt Điều kiện: danh sách phải có thứ tự.
từng phần tử của danh sách với giá trị X cần tìm:
So sánh giá trị muốn tìm X với phần tử nằm ở vị trí giữa của danh sách:
 Nếu có phần tử bằng X, thuật toán dừng lại (thành
 Nếu bằng, tìm kiếm dừng lại (thành công). công).
 Nếu X lớn hơn thì tiếp tục tìm kiếm ở phần danh sách bên phải phần tử
 Nếu đến cuối danh sách mà không có phần tử nào giữa.
bằng X, thuật toán dừng lại (không thành công).
 Nếu X nhỏ hơn thì tiếp tục tìm kiếm ở phần danh sách bên trái phần tử giữa.
 Trường hợp tốt nhất: số lần so sánh 1
 Trường hợp xấu nhất: số lần so sánh n
 Trường hợp trung binh: số lần so sánh (n+1)/2
 Độ phức tạp T(n) = O(n) NGHỊCH THẾ Khái niệm
Xét một mảng các số a1, a2, … an
Nếu có i aj, thì đó là một nghịch thế.
Mảng chưa sắp xếp sẽ có nghịch thế.
Mảng đã có thứ tự sẽ không có nghịch thế a1≤ a2≤... ≤ an
 Trường hợp tốt nhất: số lần so sánh 1
 Trường hợp xấu nhất: số lần so sánh log(n)
 Trường hợp trung binh: số lần so sánh log(n/2)
 Độ phức tạp T(n) = O(log(n)) INTERCHANGE SORT BUBBLE SORT Ý TƯỞNG Ý TƯỞNG
Xuất phát từ phần tử đầu danh sách, tìm tất các các cặp nghịch Thuật toán sắp xếp bubble sort thực hiện sắp xếp dãy số bằng cách lặp lại
thế chứa phần tử này. Triệt tiêu chúng bằng cách đổi chỗ 2 phần công việc đổi chỗ 2 số liên tiếp nhau nếu chúng đứng sai thứ tự(số sau bé
tử trong cặp nghịch thế. Lặp lại xử lý trên với phần tử kế tiếp trong hơn số trước với trường hợp sắp xếp tăng dần) cho đến khi dãy số được danh sách. sắp xếp. Trường hợp tốt nhất: Trườ ố ầ ị ng hợp tốt nhất:
 Số lần so sánh: n(n-1)/2 ; s l n hoán v : 0 Trường hợp xấu nhất:
 Số lần so sánh: n(n-1)/2 ; số lần hoán vị: 0 Trườ ố ầ ị ng hợp xấu nhất:
 Số lần so sánh: n(n-1)/2 ; s l n hoán v : n(n-1))/2
 Số lần so sánh: n(n-1)/2 ; số lần hoán vị: n(n-1))/2 SELECTION SORT INSERTION SORT Ý TƯỞNG Ý TƯỞNG
Thuật toán selection sort sắp xếp một mảng bằng cách đi tìm phần Thuật toán sắp xếp chèn thực hiện sắp xếp dãy số theo cách duyệt từng
tử có giá trị nhỏ nhất(giả sử với sắp xếp mảng tăng dần) trong đoạn phần tử và chèn từng phần tử đó vào đúng vị trí trong mảng con(dãy số
đoạn chưa được sắp xếp và đổi cho phần tử nhỏ nhất đó với phần từ đầu đến phần tử phía trước nó) đã sắp xếp sao cho dãy số trong
tử ở đầu đoạn chưa được sắp xếp(không phải đầu mảng). Thuật toán mảng sắp đã xếp đó vẫn đảm bảo tính chất của một dãy số tăng dần.
sẽ chia mảng làm 2 mảng con
 Một mảng con đã được sắp xếp
 Một mảng con chưa được sắp xếp Trường hợp tốt nhất:
 Số lần so sánh: n-1 ; số lần hoán vị: 2(n-1) Trường hợp xấu nhất:
 Số lần so sánh: n(n-1)/2 ; số lần hoán vị: n(n-1)/2 + 2(n-1) Trường hợp tốt nhất:
 Số lần so sánh: n(n-1)/2 ; số lần hoán vị: 0 Trường hợp xấu nhất:
 Số lần so sánh: n(n-1)/2 ; số lần hoán vị: n-1 BINARY INSERTION SORT
SO SÁNH CÁC THUẬT TOÁN SẮP XẾP Ý TƯỞNG
Binary Insertion Sort được sử dụng để tìm kiếm nhị phân vị trí thích hợp để chèn
mục đã chọn ở mỗi lần lặp.