Những nội dung kiến thức cơ bản | Cơ học lượng tử | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Hà Nội
Hàm sóng tương ứng với trạng thái của hạt vi mô gọi là hàm trạng thái, là một hàm phức phụ thuộc vào toạ độ r và thời gian t . - Sự tương ứng giữa trạng thái và hàm sóng là 1-1, ngoại trừ hai hàm sóng khác nhau bởi một thừa số vô hướng có bình phương mô – đun bằng đơn vị thì tương ứng với cùng một trạng thái. - Hàm trạng thái phải đơn trị, liên tục, giới nội. - Khi biết hàm trạng thái thì ta biết đủ thông tin về hạt. Tài liệu được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Cơ học lượng tử (HUS) 10 tài liệu
Trường: Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Hà Nội 687 tài liệu
Tác giả:
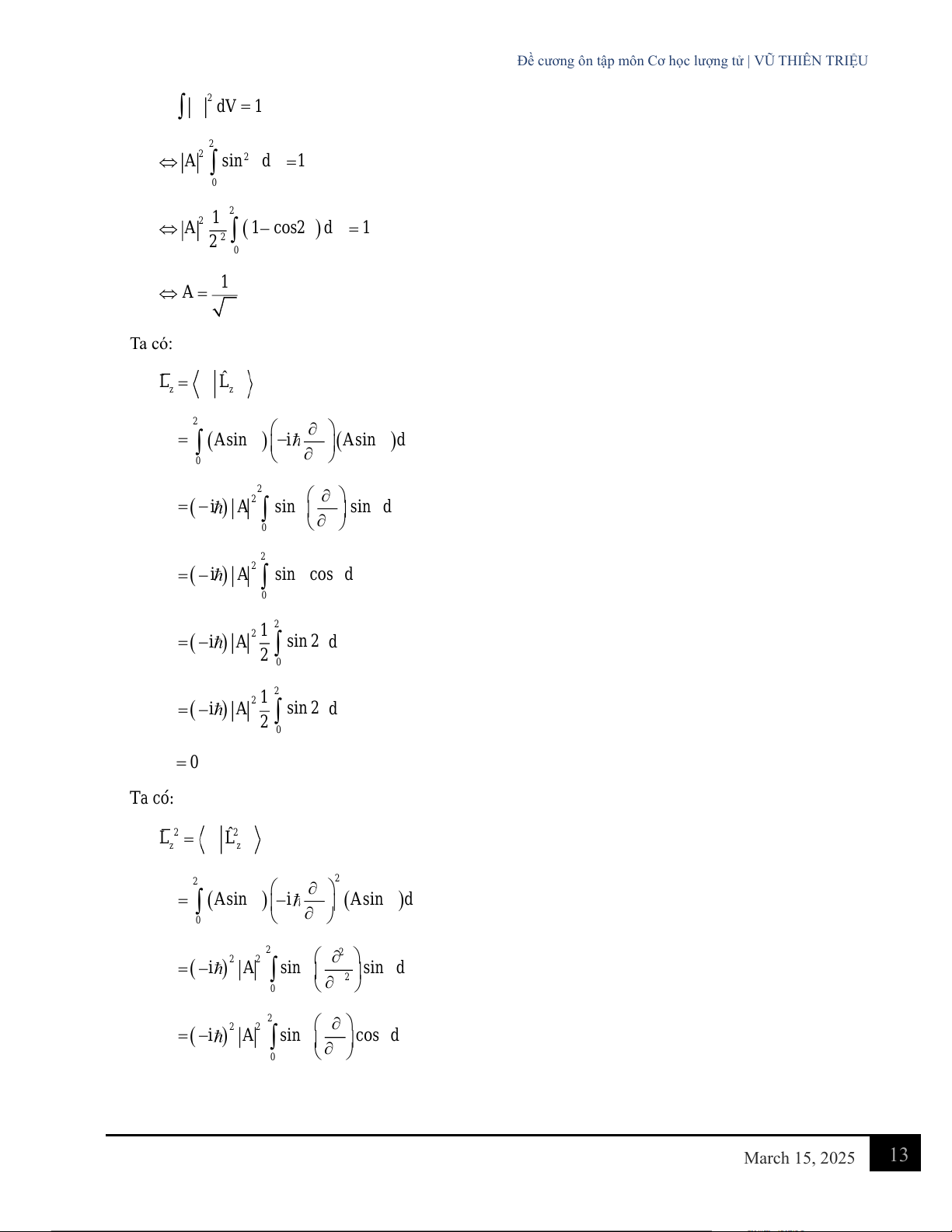
Preview text:
Đề cương ôn tập môn Cơ học lượng tử | VŨ THIÊN TRIỆU
Câu 1: Nguyên lý bất định Heisenberg nói gì? Các công thức của nguyên lý? Tự c ọn h và nêu ý nghĩa một công thức?
Hệ thức bất định Heisenberg chỉ rằng: “Không thể xác định đồng thời chính xác tọa độ và xung lượng của hạt vi mô”. Công thức:
• Toạ độ và xung lượng: . x x p 2
• Năng lượng và thời gian: . E t 2
• Góc và hình chiếu của momen xung lượng: . z L 2
Ví dụ: Tọa độ càng chính xác thì xung lượng càng không chính xác, nghĩa là hạt vi mô không có quỹ đạo xác định.
Câu 2: Chứng minh Hermite, không Hermite
• Nếu hai toán tử ˆA và ˆB là Hermite và giao hoán nhau. Chứng minh rằng ˆ ˆ . A B cũng Hermite. Nếu hai toán tử ˆ
A và ˆB là Hermite và giao hoán nhau thì ˆ ˆ . A B cũng Hermite. ˆ
A : Hermite thì ˆ = ˆ 1 A 2 A 1 2 ˆ
B : Hermite thì ˆ = ˆ 1 B 2 B 1 2 ˆ
A và ˆB giao hoán suy ra ˆ ˆ ˆ ˆ . A B = . B A
Để c ứng minh toán tử tích h ˆ ˆ .
A B cũng là Hermite thì ta chứng minh: ˆ ˆ ˆ ˆ AB = AB 1 2 1 2 Ta có: = ˆ ˆ VT AB 1 2 ˆ = ˆ A B 1 2 ˆ ˆ = BA 1 2 ˆ ˆ = AB 1 2 = VP March 15, 2025 1
Đề cương ôn tập môn Cơ học lượng tử | VŨ THIÊN TRIỆU
• Nếu hai toán tử ˆA và ˆB là Hermite và không giao hoán nhau. Chứng minh rằng ˆ ˆ , A B không Hermite
và trong lúc đó toán tử ˆ ˆ i , A B là Hermite. Nếu hai toán tử ˆ
A và ˆB là Hermite và không giao hoán nhau thì ˆ ˆ , A B
không Hermite nhưng ˆ ˆ i , A B là Hermite. ˆ A : Hermite thì ˆ ˆ A = A 1 2 1 2 ˆ B : Hermite thì ˆ ˆ B = B 1 2 1 2 Để c ứng minh h ˆ ˆ , A B
không Hermite thì ta chứng minh: ˆ ˆ ˆ ˆ , A B , A B 1 2 1 2 Ta có: ˆ ˆ ˆ ˆ ˆˆ , A B = AB − BA 1 2 1 ( ) 2 ˆ ˆ ˆ = ˆ − ˆˆ 1 , A B 2 1 ( AB) 2 1 ( B ) A 2 ˆ ˆ ˆ = ˆ − ˆˆ 1 , A B 2 1 AB 2 1 BA 2 ˆ ˆ 1 , A B 2 = ˆ ˆ 1 , A B 2 = ˆ ˆ 1 , A B 2 = ˆ ˆ , A B = 1 2 ˆ ˆ , A B = 1 2 Vậy ˆ ˆ ˆ ˆ ˆ ˆ , A B , A B , A B 1 2 1 2 không Hermite Ta có: ˆ ˆ = ˆ ˆ ˆ ˆ i , A B i AB − BA 1 2 1 ( ) 2 ˆ ˆ ˆ ˆ ˆˆ i ,
A B = i AB − i BA 1 2 1 ( ) 2 1 ( ) 2 March 15, 2025 2
Đề cương ôn tập môn Cơ học lượng tử | VŨ THIÊN TRIỆU
ˆ ˆ = ˆ ˆ − ˆˆ i , A B iAB iBA 1 2 1 2 1 2 ˆ ˆ i , A B = 1 2 ˆ ˆ i , A B = 1 2 ˆ ˆ i , A B = 1 2 ˆ ˆ i , A B 1 2 = ˆ ˆ = ˆ ˆ i , A B i , A B 1 2 1 2 Vậy toán tử ˆ ˆ i , A B là Hermite.
Câu 3: Phát biểu tiên đề cơ học lượng tử, nêu đặc điểm? • Tiên đề I
Phát biểu: “Trạng thái của một hạt hoặc một hệ hạt lượng tử thì tương ứng với một hàm chuẩn hóa trong không gian Hilbert”. Đặc điểm:
- Hàm sóng tương ứng với trạng thái của hạt vi mô gọi là hàm trạng thái, là một hàm phức phụ
thuộc vào toạ độ r và thời gian t .
- Sự tương ứng giữa trạng thái và hàm sóng là 1-1, ngoại trừ hai hàm sóng khác nhau bởi một
thừa số vô hướng có bình phương mô – đun bằng đơn vị thì tương ứng với cùng một trạng thái.
- Hàm trạng thái phải đơn trị, liên tục, giới nội.
- Khi biết hàm trạng thái thì ta biết đủ thông tin về hạt. • Tiên đề II
Phát biểu: “Tương ứng với mỗi đại lượng động lực A là một toán tử tuyến tính và Hermite ˆA tác dụng
trong không gian Hilbert các hàm trạng thái. Các kết quả đo được về đại lượng A chỉ có thể là các trị riêng của toán tử ˆ A . Đặc điểm:
- Phép đo đại lượng động lực A có thể được biểu diễn bằng cách tác dụng toán tử ˆA lên trạng
thái . Kết quả thu được của một phép đo chính là một trong các trị riêng (phổ trị riêng) của toán tử ˆ
A . Phổ trị riêng này có thể gián đoạn hoặc liên tục. Điều này sẽ tương ứng với hai
phương trình trị riêng của toán tử ˆ A như sau:
ˆA i = a i , đối với trường hợp phổ trị riêng gián đoạn i March 15, 2025 3
Đề cương ôn tập môn Cơ học lượng tử | VŨ THIÊN TRIỆU ˆ
A a = a a , đối với trường hợp phổ trị riêng liên tục
- Nếu khi đo đại lượng động lực A ta được giá trị a thì ngay sau đó hạt (hệ) sẽ ở trạng thái được
biểu diễn bằng hàm sóng = a (phép đo làm nhiễu loạn trạng thái của hạt)
- Tính chất tuyến tính của toán tử ˆA liên quan đến nguyên lý chồng chất các trạng thái, trong
lúc đó tính chất Hermite của ˆA liên quan đến “tính thức” của giá trị đo được của đại lượng động lực A . • Tiên đề III
Phát biểu: “Xác suất để trong phép đo đại lượng động lực A ở trạng thái được giá trị ak là 2 ck , trong đó k
c là hệ số trong khai triển hàm sóng theo hàm riêng k của toán tử ˆA . • Tiên đề IV
Phát biểu: “Toán tử xung lượng trong biểu diễn tọa độ có dạng: ˆ P = i − với i =1,2,3. . = , x , y z i x i • Tiên đề V
Phát biểu: “Phương trình động lực học của cơ học lượng tử là phương trình Schrodinger” i ( t) ˆ , = H (,t) t
Câu 4: Các định luật bảo toàn: phát biểu, so sánh
• Bảo toàn xung lượng Đặc điểm:
- Định luật này liên quan đến tính đồng nhất của không gian. - Các toán tử: ˆ
H , toán tử tịnh tiến ˆT , toán tử xung lượng ˆP
- Phép tịnh tiến giao hoán tử hai toán tử - ˆ ˆ
H, P = 0 nên hai toán tử này giao hoán nhau vì thế xung lượng của hệ bảo toàn
• Bảo toàn mô – men xung lượng Đặc điểm:
- Định luật này liên quan đến tính đằng hướng của không gian. - Các toán tử quay: ˆL - ˆ ˆ H, L = 0
nên hai toán tử này giao hoán nhau, vì thế mô – men xung lượng của hệ bảo toàn.
• Bảo toàn năng lượng Đặc điểm:
- Định luật này liên quan đến tính đồng nhất của thời gian. March 15, 2025 4
Đề cương ôn tập môn Cơ học lượng tử | VŨ THIÊN TRIỆU
- Toán tử tịnh tiến thời gian: ˆ V ˆ H - ˆ ˆ H,V = 0
nên hai toán tử này giao hoán nhau. Suy ra
= 0 vì thế năng lượng của hệ bảo t toàn.
• Bảo toàn chẵn lẻ
Phát biểu: “Khi một hệ kín có số c ẵn lẻ xác định thì số h
chẵn lẻ đó không đổi theo thời gian” Đặc điểm:
- Định luật này liên quan đến tính nghịch đảo của không gian. - Các toán tử: ˆ
H , toán tử nghịch đảo ˆI
- Phép biến đổi không gian: thay đổi tọa độ, phép biến đổi nghịch đảo.
- Trường đối xứng xuyên tâm.
- Phương trình trị riêng – hàm sóng thành: hàm c ẵn, hàm lẻ. h - ˆ ˆ H, I = 0
nên hai toán tử này giao hoán nhau. Tính chẵn lẻ của hàm sóng là một tích phân chuyển động.
• Bảo toàn tính đối xứng
Tính đối xứng phản hạt: Định luật này đúng đối với tương tác mạnh, tương tác điện từ nhưng bị vi
phạm bởi các tương tác yếu. • Bảo toàn spin
Bảo toàn spin đồng vị ( ảo b
toàn tính độc lập điện tích): Các mezon và barion tương tác mạnh với nhau
và có tính độc lập điện. Tính độc lập điện được biểu thị bởi số lượng tử spin đồng vị I được xác định sao 1
cho 2I +1 cho ta số hạt trong từng đa tuyến. Ví dụ: pion có I =1 , nucleon có I = . 2
Định luật: “Trong tương tác mạnh, spin đồng vị tổng cộng (được vận dụng như một vectơ) được bảo
toàn”. Định luật này áp dụng cho tương tác mạnh, điện từ, không áp dụng trong tương tác yếu.
Câu 5: Phương trình Schrodinger không phụ thuộc thời gian với phương trình Schrodinger phụ thuộc
thời gian: đặc điểm, so sánh, ứng dụng?
Không phụ thuộc thời gian
Phụ thuộc thời gian
- Mô tả trạng thái của một hạt có năng lượng - Phương trình có sự biến đổi trạng thái
không đổi theo thời gian. theo thời gian.
Đặc điểm - Có hàm sóng ( , x y, z): ( ) 2 , m r t + E −U r ,t r ,t = 0 2 ( ) ( ) ( ) 2 , , m x y z + E −U x, y,z = 0 2 ( ) ( )
Giống nhau: Cả 2 phương trình đều mô tả sự thay đổi trạng thái của vi hạt Khác nhau So sánh
- Sự phụ thuộc của các hàm sóng vào thời gian - Là phương trình vi phân bậc nhất theo
được xác định đơn trị bởi giá trị năng lượng ở thời gian và bậc hai theo không gian. trạng thái đó. March 15, 2025 5
Đề cương ôn tập môn Cơ học lượng tử | VŨ THIÊN TRIỆU
- Mật độ xác suất và mật độ dòng xác suất không - Mật độ xác suất và mật độ dòng xác
phụ thuộc vào thời gian.
suất phụ thuộc vào thời gian. - T ị
r trung bình của một đại lượng động lực có
toán tử tương ứng không phụ thuộc tường minh - T ị
r trung bình của một đại lượng động
vào thời gian và trùng với toán tử năng lượng.
lực có toán tử tương ứng phụ thuộc vào
- Toán tử Hamilton không phụ thuộc tường minh thời gian thì thay đổi.
vào thời gian và trùng với toán tử năng lượng.
- Toán tử Hamilton phụ thuộc vào thời
gian và không trùng với toán tử năng lượng.
- Hàm sóng (r ) chỉ phụ thuộc vào các toạ độ - Hàm sóng (r,t) là một hàm của toạ không gian. độ và thời gian.
- Vi hạt chuyển động trong trường lực thế U (r ) - Vi hạt chuyển động trong trường ngoài
không đổi theo thời gian biến thiên U (r,t) .
- Nghiệm của phương trình phụ thuộc vào giá trị - Nghiệm của phương trình phụ thuộc E
vào điều kiện biên của hàm sóng cho trước.
- G ải bài toán tìm hạt trong giếng thế i
- H ệu ứng đường ngầm i - Quay tử
Ứng dụng - Dao động tử điều hoà lượng tử
- Hạt trong giếng thế đối xứng cầu
- Hạt trong trường xuyên tâm
- Dao động điều hoà và phép biểu diễn các số lấp đầy
Câu 6: Hiệu ứng đường ngầm Định nghĩa:
Theo cơ học cổ điển, nếu năng lượng của hạt E E : hạt không thể vượt qua hàng rào. max
Theo cơ học lượng tử, nếu năng lượng của hạt E E : hạt có thể xuyên qua hàng rào thế năng, gọi max
là hiệu ứng đường ngầm.
Ví dụ: hiện tượng phát electron lạnh, hiện tượng phân rã alpha,…
Đặc điểm của bài toán về hiệu ứng đường ngầm:
+ Các miền có thể có hạt vì vậy sẽ có hàm sóng và phổ năng lượng của hạt trên cả ba miền.
+ Có thêm hệ số phản xạ R và hệ số truyền qua D.
+ Bài toán phức tạp hơn so với bài toán hạt trong giếng thế một chiều.
Câu 7: Nêu các loại biểu diễn, so sánh?
Biểu diễn: năng lượng, xung lượng, ma trận của toán tử, trị trung bình. Phương trình:
- Trị riêng của toán tử
- Schrodinger dạng ma trận March 15, 2025 6
Đề cương ôn tập môn Cơ học lượng tử | VŨ THIÊN TRIỆU
- Heisenberg dạng ma trận
Các loại biểu diễn: - Biểu diễn Heisenberg - Biểu diễn Schrodinger - Biểu diễn Dirac
- Biểu diễn lượng tử hóa lần thứ hai:
+ Biểu diễn số lắp đầy
+ Biểu diễn qua toán tử sinh hủy
+ Biểu diễn qua toán tử trường
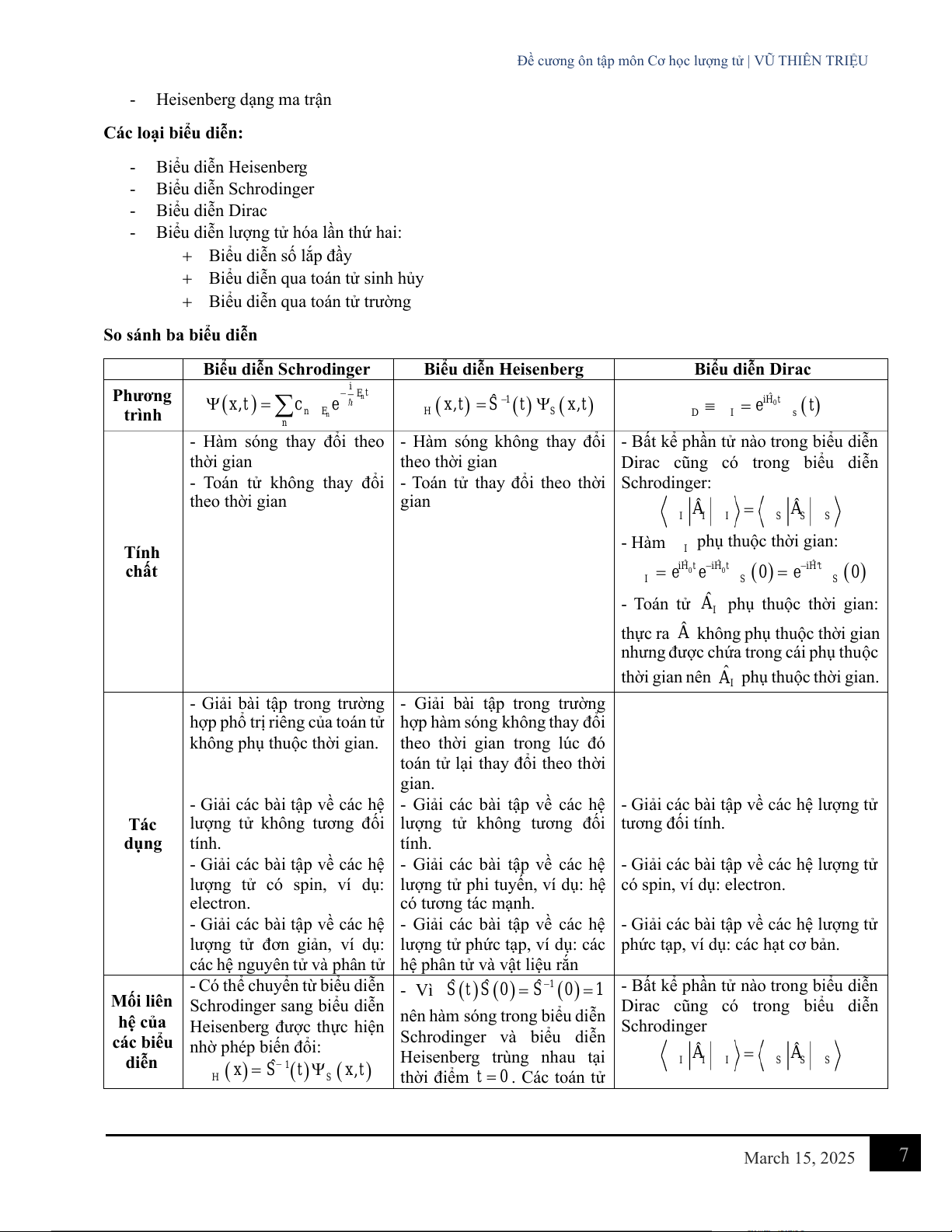
So sánh ba biểu diễn
Biểu diễn Schrodinger
Biểu diễn Heisenberg Biểu diễn Dirac Phương i , − n E t x t = c e − ˆ iH0t = H ( x,t) ˆ 1 = S (t) S ( x,t) e t D I s ( ) trình ( ) n n E n
- Hàm sóng thay đổi theo - Hàm sóng không thay đổi - Bất kể phần tử nào trong biểu diễn thời gian theo thời gian
Dirac cũng có trong biểu diễn
- Toán tử không thay đổi - Toán tử thay đổi theo thời Schrodinger: theo thời gian gian ˆ ˆ A = A I I I S S S
- Hàm phụ thuộc thời gian: Tính I chất ˆ ˆ ˆ i 0 H t i − 0 H t = e e (0) i − H t = e I S S ( 0) - Toán tử ˆ AI phụ thuộc thời gian:
thực ra ˆA không phụ thuộc thời gian
nhưng được chứa trong cái phụ thuộc thời gian nên ˆ AI phụ thuộc thời gian. - G ải
i bài tập trong trường - G ải i bài tập trong trường
hợp phổ trị riêng của toán tử hợp hàm sóng không thay đổi
không phụ thuộc thời gian. theo thời gian trong lúc đó
toán tử lại thay đổi theo thời gian. - G ải
i các bài tập về các hệ - G ải
i các bài tập về các hệ - Giải các bài tập về các hệ lượng tử Tác
lượng tử không tương đối lượng tử không tương đối tương đối tính. dụng tính. tính. - G ải
i các bài tập về các hệ - G ải
i các bài tập về các hệ - Giải các bài tập về các hệ lượng tử
lượng tử có spin, ví dụ: lượng tử phi tuyến, ví dụ: hệ có spin, ví dụ: electron. electron. có tương tác mạnh. - G ải
i các bài tập về các hệ - G ải
i các bài tập về các hệ - Giải các bài tập về các hệ lượng tử
lượng tử đơn giản, ví dụ: lượng tử phức tạp, ví dụ: các phức tạp, ví dụ: các hạt cơ bản.
các hệ nguyên tử và phân tử hệ phân tử và vật liệu rắn
- Có thể chuyển từ biểu diễn - Vì ˆS (t) ˆS (0) ˆ 1 S− =
(0) = 1 - Bất kể phần tử nào trong biểu diễn
Mối liên Schrodinger sang biểu diễn
Dirac cũng có trong biểu diễn hệ của
nên hàm sóng trong biểu diễn
Heisenberg được thực hiện Schrodinger các biểu Schrodinger và biểu diễn nhờ phép biến đổi: ˆ ˆ A = A diễn Heisenberg trùng nhau tại x = S− t x t I I I S S S H ( )
ˆ 1( ) S ( , ) thời điểm t = 0. Các toán tử March 15, 2025 7
Đề cương ôn tập môn Cơ học lượng tử | VŨ THIÊN TRIỆU
- Chuyển được sang biểu trong cả hai biểu diễn cũng diễn Dirac.
trùng nhau tại thời điểm này. - Vì ˆ F nên phương H (0) = FS trình ˆ F (t) ˆ 1 S − = (t) F sẽ H S
xác định sự biến thiên của
toán tử trong biểu diễn
Heisenberg sau thời gian t .
Câu 8: Phương trình thế kỉ n
Cho m =1,2,. .,n ta thu được hệ n phương trình dạng (1) c W − E = với n ẩn s ố c , c ,. ., c . p ( p m mp ) 0 1 2 n p 1 =
Muốn cho các nghiệm không tầm thường thì định th c l ứ ập bởi các hệ s c ố ủa các i b ẩn đó phả ằng không: ( ) 1 W − E W W W 11 12 13 1n ( ) 1 2 W 1 2 W 2 −E 2 W 3 2 W n =0 (1) . . . . . . . . ( ) 1 W W W W − E n1 n 2 n 3 nn Khai triển định th c
ứ (1) ta có một phương trình bậc n của ( )1
E . Phương trình trên được gọi là phương trình thế kỉ.
Câu 9: Quy tắc vàng Fermi
Quy tắc vàng Fermi ra rằng trong trường hợp nhiễu loạn bậc nhất: Tốc độ dịch chuyển chỉ ph thu ụ ộc vào
bình phương của phần tử ma trận của toán tử nhiễu loạn giữa trạng thái đầu và trạng thái cuối và điều kiện bảo toàn năng lượng.
Câu 10: Trong cơ học lượng tử trạng thái của m t
ộ electron trong nguyên tử được đặc trưng các số lượng
tử nào (nêu tóm tắt)? Mục đích? Liên quan đến nguyên lý nào? Có 4 s
ố lượng tử n , l , m , m : l s
- n là số lượng tử chính, có giá trị nguyên ( n =1,2,3,. .). Số lượng tử này tương ứng với số lượng tử trong lý thuyết Bohr. - l là s ố lượng tử qu
ỹ đạo, có giá trị từ 0 đến n −1 . - m là s
ố lượng tử t có giá tr ừ ị t ừ −l đến +l. l - m ng t là lượ
ử spin, có giá trị là +1 2 hoặc −1 2. s
Mục đích: Để mô tả chi tiết trạng thái thực của vi hạt.
Liên quan đến nguyên lý loại trừ Pauli: Không có hai electron trong nguyên t có c ử ùng b s ộ ố lượng t ( ử n , l , m , m ) gi ng nhau. ố l s March 15, 2025 8
Đề cương ôn tập môn Cơ học lượng tử | VŨ THIÊN TRIỆU Câu 11: Nhiễu lo n d ạ ừng: m i,
ục đích, phân loạ ứng dụng
Mục đích: tìm nghiệm ần
g đúng (hàm riêng và trị riêng của năng lượng) của phương trình Schrodinger
trong các hệ th c, không khác nhi ự
ều lắm so với nghiệm chính xác của hệ ng hoá. đã lý tưở Nhiễu loạn dừng gồm:
+ Nhiễu loạn dừng không suy biến: một hàm riêng đối với một trị riêng
+ Nhiễu loạn dừng suy biến: một hàm riêng đối với nhiều trị riêng
Ứng dụng của nhiễu loạn dừng:
+ Giải quyết các bài toán nguyên tử hydro trong điện trường (hiệu ứng Stark)
+ Giải quyết các bài toán nguyên tử heli ở trạng thái cơ bản
Câu 12: Khái niệm trường xuyên tâm
Một trường lực được gọi là đối xứng xuyên tâm khi lực tác d ng t ụ
ại một điểm trong trường thoả mãn các điều kiện sau:
+ Đi qua một điểm cố định gọi là tâm của trường
+ Thế năng ứng với lực chỉ phụ thuộ ả c vào kho ừ ng cách t h ng ạt đến tâm trườ
Khi nghiên cứu chuyển đ ng ộ c a h ủ
ạt trong trường xuyên tâm có một đại lượng ng độ lực đóng vai trò rất
quan trọng đó là mô – men xung lượng. Trước khi khảo sát chi tiết ta cần nghiên c u ứ c ụ thể toán t mô ử – men xung lượng.
Câu 13: Phương trình Schrodinger: viết phương trình 1D, 2D, 3D; viết hàm sóng và phổ năng lượng 1D, 2D, 3D Phụ thu c th ộ ời gian Không phụ thu c th ộ ời gian Tổng 2m 2m quát (r,t)+ E −U r ,t r,t = 0 (r ) + E −U r r = 0 2 ( ) ( ) 2 ( ) ( ) 1D 2m ( ) 2 , m x t + E −U (r ,t ) (x,t ) = 0 (x) + E U − (r ,t ) (x) = 0 2 2 2D 2m ( ) 2 , , m x y t + E U − r ,t x, y,t =0 (x, y ) + E U − r ,t x, y =0 2 ( ) ( ) 2 ( ) ( ) 3D 2m ( ) 2 , , , m x y z t + E U − (r ,t ) (x ,y ,z ,t ) = 0 (x ,y ,z ) + E U − (r ,t ) (x ,y ,z ) = 0 2 2 Hàm sóng và ph ổ năng lượng c a gi ủ ếng lượng tử
• Giếng vuông góc sâu vô hạn 1D, 2D, 3D x L 1D: U (x) 0, khi 0 =
, khi x 0 và x L March 15, 2025 9
Đề cương ôn tập môn Cơ học lượng tử | VŨ THIÊN TRIỆU + Hàm sóng: ( ) 2 sin n x x = L L 2 2 2 n + Phổ năng lượng: E = 2 2mL 0 , khi 0 x Lx, 0 y L 2D: U (x) y =
, khi x 0 và x L , x y Ly n x n y + Hàm sóng: = n ( x y ) 4 , sin x n sin y x y L xLy x L Ly 2 2 2 2 2 2 n n + Phổ năng lượng: x y E = + x n ny 2 2 2mL mL x 2 y 0 , khi 0 x L y L z L x, 0 y, 0 3D: (x) z U = , khi x 0, x L z z L x; y 0, y Ly; 0, z n x n y n z + Hàm sóng: n n ( x y z) 8 , , = sin sin y x z n sin x y z x L L L L L L y z x y z 2 2 2 2 2 2 2 2 2 n n n + Phổ năng lượng: y x z E = + + x n yn zn 2 2 2 2mLx 2mL 2mL y z 0 , khi − L x L
• Giếng đối xứng: U (x) = , khi x L
Đối với lớp nghiệm chẵn: nx + Hàm sóng: 1 chan = cos , trong đó n =1,3,5,. . L 2L 2 2 2 n
+ Phổ năng lượng: Echan = 2 8mL
Đối với lớp nghiệm lẻ: n x + Hàm sóng: 1 le = sin , trong đó n = 2, 4,6,. . L 2L 2 2 2 n + Phổ năng lượng: Ele = 2 8mL
Câu 14: Xác định độ ất
b định về xung lượng c a m ủ i
ỗ photon 6000 Å nếu bước sóng chính xác đến phần triệu. Cho 3 hc =12,310 e Å V Giải March 15, 2025 10
Đề cương ôn tập môn Cơ học lượng tử | VŨ THIÊN TRIỆU
Xung lượng của photon là: 3 hc 12,310 eVÅ p = = = c ( 2,05 eV c 3 610 ) ( ) Å c Độ bất đị ề nh v xung lượng: h hc 6 − 6 p = − = = p = .p10 = 2, 05 1 0 − (eV c ) 2 2 c
Câu 15: Trong nghiên cứu hệ nhiều hạt vi mô, viết biểu th c
ứ hàm sóng trong biểu diễn s ố lấp đầy. Tính ˆ+ 3 C , , và nhận xét 4 123 ( 1 2 3 ) Giải
Hàm sóng trong biểu diễn l y là: ấp đầ N a a a , ,. ., , ,. ., ( 1 2 N) 1 2 N ˆ+ 3 C , , = − , , , 4 ( ) 4 123 1 2 3 1234 ( 1 2 3 4 ) 1 = (−
)1pP a a . . 1 ( 1 ) 2 ( 2 ) aN ( N ) 4! p 1 ( 1) 1 ( 2 ) 1 ( 3 ) 1 ( 4 ) 1 2 ( 1 ) 2 ( 2 ) 2 ( 3 ) 2 ( 4 ) = = 0 4! 3 ( 1) 3 ( 2 ) 3 ( 3 ) 3 ( 4 ) 4 ( 1 ) 4 ( 2 ) 4 ( 3 ) 4 ( 4 ) Nhận xét: Vì ở ng thái và là s trước đó có 3 trạ ố lẻ ọ nên ta ch n dấu “-”
Câu 16: Hạt ở trạng thái được mô tả bởi hàm sóng (x)= Ax(L− x) , với 0 x L . Tính động năng trung bình c a h ủ ạt Giải Tìm A t ừ u ki điề
ện chuẩn hoá c a hàm sóng: ủ 2 dV = 1 L 2 2 A x (L− x)2 dx =1 0 L 2 2 A x ( 2 2 L −2Lx + x )dx =1 0 March 15, 2025 11
Đề cương ôn tập môn Cơ học lượng tử | VŨ THIÊN TRIỆU L L L 2 2 2 3 4
A L x dx − 2L x dx + x dx = 1 0 0 0 30 A = 5 L 2 2 2 ˆ − Với ˆ x p T = = 2 2m 2m x Ta có: ˆ T = T L 2 = A ( 2 Lx − x ) ˆT ( 2 Lx − x )dx 0 L = A (Lx− x ) 2 2 2 − 2 2 Lx− x dx 2 ( ) 2m x 0 2 L − = A (Lx− x ) 2 2 2 ( 2 Lx− x dx 2 ) 2m x 0 2 L − 2 = A ( 2 Lx− x ) (L− 2x )dx 2m x 0 2 L − 2 = A (− )( 2 2 Lx− x ) dx 2m 0 2 L L 2 2 = A Lxdx− x dx m 0 0 2 2 L 3 L 2 x x = A L − m 2 3 0 0 2 5 = 2 mL
Câu 17: Tìm các trị riêng khả dĩ của toán t
ử ˆL và xác suất do các trị riêng ấy i
đố với hạt ở trạng thái z ( ) = Asin . T
ừ đó hãy tính trị trung bình L và 2 L z z Giải Tìm A t ừ u ki điề
ện chuẩn hoá c a hàm sóng: ủ March 15, 2025 12
Đề cương ôn tập môn Cơ học lượng tử | VŨ THIÊN TRIỆU 2 dV = 1 2 2 2 A sin d =1 0 2 2 1 A (1− cos2)d = 1 2 2 0 1 A = Ta có: ˆ L = L z z 2 (Asin ) i = − (Asin )d 0 2 ( i ) 2 A sin = − sin d 0 2 = ( −i ) 2 A sin cos d 0 2 = ( −i ) 2 1 A sin 2d 2 0 2 = ( −i ) 2 1 A sin 2 d 2 0 = 0 Ta có: 2 2 = ˆ L L z z 2 2 (Asin ) − i = (Asin )d 0 2 2 ( −i )2 2 A sin = sind 2 0 2 ( i )2 2 A sin = − cosd 0 March 15, 2025 13
Đề cương ôn tập môn Cơ học lượng tử | VŨ THIÊN TRIỆU 2 2 2 2 = A sin d 0 2 1 = 2 =
Câu 18: Hạt trong giếng thế một chiều vuông góc có bề rộng L. Chứng minh rằng hạt ở trạng thái thứ n thì L 1
xác suất tìm hạt giữa miền x = 0 và x = là n n Giải
Hàm sóng chuẩn hoá có dạng: ( ) 2 = sin n x x n L L
Xác suất tìm hạt trong miền 0 L x là: n L n 2 W = n dx 0 L 2 n 2 sin n x = dx L L 0 L 2 n 2 sin n x = dx L L 0 1 = n
Câu 19: Electron có năng lượng 2,0 eV đi đến một hàng rào thế chiều cao 5,0 eV. Tìm hệ số truyền qua T khi
bề rộng của hàng rào là L =1,5 nm và L = 0,5 nm . Nhận xét kết quả. Cho T = 3,8 − = 0 , 9 1 8,9 10 m Giải E E Ta có: −2 −2 T = 16 1 L L − e T = 0 T e U U 0 0 Khi 9 L 1,5 nm =1,5 10− = m: March 15, 2025 14
Đề cương ôn tập môn Cơ học lượng tử | VŨ THIÊN TRIỆU 9 9 2.8,9 10 .1,5 10 − 2 1 T = 3, . 8 e − − 9,6410 Khi 9 L 0,5 nm = 0,5 0 1 − = m 9 9 2.8,9 10 .0,5 10 −4 T = 3,8.e − − 5,1810 March 15, 2025 15