Ôn kiến thức, luyện kỹ năng bài giảng cực trị của hàm số

Tài liệu gồm 59 trang, được biên soạn bởi thầy giáo Đặng Công Đức (Giang Sơn), tuyển chọn các bài tập trắc nghiệm ôn kiến thức, luyện kỹ năng bài giảng cực trị của hàm số môn Toán 12 THPT (kết hợp ba bộ sách giáo khoa Toán 12 chương trình mới: Cánh Diều, Chân Trời Sáng Tạo, Kết Nối Tri Thức Với Cuộc Sống). Mời bạn đọc đón xem!

23 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

59 trang 1 tháng trước

Tác giả:

Profile Lê Phương
1
T
T
À
À
I
I
L
L
I
I
Ệ
Ệ
U
U
T
T
H
H
A
A
M
M
K
K
H
H
Ả
Ả
O
O
T
T
O
O
Á
Á
N
N
H
H
Ọ
Ọ
C
C
P
P
H
H
Ổ
Ổ
T
T
H
H
Ô
Ô
N
N
G
G
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Ô
Ô
N
N
K
K
I
I
Ế
Ế
N
N
T
T
H
H
Ứ
Ứ
C
C
T
T
O
O
Á
Á
N
N
1
1
2
2
T
T
H
H
P
P
T
T
B
B
À
À
I
I
G
G
I
I
Ả
Ả
N
N
G
G
C
C
Ự
Ự
C
C
T
T
R
R
Ị
Ị
C
C
Ủ
Ủ
A
A
H
H
À
À
M
M
S
S
Ố
Ố
(
(
C
C
Ự
Ự
C
C
Đ
Đ
Ạ
Ạ
I
I
,
,
C
C
Ự
Ự
C
C
T
T
I
I
Ể
Ể
U
U
)
)
(
(
K
K
Ế
Ế
T
T
H
H
Ợ
Ợ
P
P
3
3
B
B
Ộ
Ộ
S
S
Á
Á
C
C
H
H
G
G
I
I
Á
Á
O
O
K
K
H
H
O
O
A
A
)
)
T
T
H
H
Â
Â
N
N
T
T
Ặ
Ặ
N
N
G
G
T
T
O
O
À
À
N
N
T
T
H
H
Ể
Ể
Q
Q
U
U
Ý
Ý
T
T
H
H
Ầ
Ầ
Y
Y
C
C
Ô
Ô
V
V
À
À
C
C
Á
Á
C
C
E
E
M
M
H
H
Ọ
Ọ
C
C
S
S
I
I
N
N
H
H
T
T
R
R
Ê
Ê
N
N
T
T
O
O
À
À
N
N
Q
Q
U
U
Ố
Ố
C
C
C
C
R
R
E
E
A
A
T
T
E
E
D
D
B
B
Y
Y
G
G
I
I
A
A
N
N
G
G
S
S
Ơ
Ơ
N
N
(
(
F
F
A
A
C
C
E
E
B
B
O
O
O
O
K
K
)
)
G
G
A
A
C
C
M
M
A
A
1
1
4
4
3
3
1
1
9
9
8
8
8
8
@
@
G
G
M
M
A
A
I
I
L
L
.
.
C
C
O
O
M
M
(
(
G
G
M
M
A
A
I
I
L
L
)
)
;
;
T
T
E
E
L
L
0
0
3
3
9
9
8
8
0
0
2
2
1
1
9
9
2
2
0
0
T
T
H
H
À
À
N
N
H
H
P
P
H
H
Ố
Ố
T
T
H
H
Á
Á
I
I
B
B
Ì
Ì
N
N
H
H
–
–
T
T
H
H
Á
Á
N
N
G
G
7
7
/
/
2
2
0
0
2
2
4
4
2
Ô
Ô
N
N
K
K
I
I
Ế
Ế
N
N
T
T
H
H
Ứ
Ứ
C
C
T
T
O
O
Á
Á
N
N
1
1
2
2
T
T
H
H
P
P
T
T
C
C
Ự
Ự
C
C
T
T
R
R
Ị
Ị
C
C
Ủ
Ủ
A
A
H
H
À
À
M
M
S
S
Ố
Ố
(
(
C
C
Ự
Ự
C
C
Đ
Đ
Ạ
Ạ
I
I
,
,
C
C
Ự
Ự
C
C
T
T
I
I
Ể
Ể
U
U
)
)
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
DUNG
LƯỢNG
NỘI DUNG
1 FILE
XÁC ĐỊNH CỰC TRỊ CÁC HÀM SỐ THƯỜNG GẶP
1 FILE
XÁC ĐỊNH CỰC TRỊ CÁC HÀM SỐ PHỨC TẠP
1 FILE
CÁC BÀI TOÁN CHỨA THAM SỐ
3
PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI TOÁN KHẢO SÁT HÀM SỐ LỚP 12 THPT
LÝ THUYẾT CỰC TRỊ CỦA HÀM SỐ
ĐIỂM CỰC TRỊ, GIÁ TRỊ CỰC TRỊ CỦA HÀM SỐ
1) Định nghĩa:
Cho hàm số
( )y f x
liên tục trên tập
K
, trong đó
K
là một khoảng, đoạn hoặc nửa khoảng
và
0 1
,
x K x K
.
+)
0
x
được gọi là một điểm cực đại của hàm số đã cho nếu tồn tại một khoảng
;a b
chứa điểm
0
x
sao cho
;
a b K
và
với mọi
;x a b
và
0
x x
.
Khi đó,
0
f x
được gọi là giá trị cực đại của hàm số đã cho, kí hiệu là
C
Đ
f
.
+)
1
x
được gọi là một điểm cực tiểu của hàm số đã cho nếu tồn tại một khoảng
;c d
chứa điểm
1
x
sao cho
;
c d K
và
1
f x f x
với mọi
;x c d
và
1
x x
.
Khi đó,
1
f x
được gọi là giá trị cực tiểu của hàm số đã cho, kí hiệu là
CT
f
.
+) Điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại và giá trị cực tiểu
được gọi chung là giá trị cực trị (hay cực trị).
2) Chú ý
Nếu
0
x
là một điểm cực trị của hàm số
y f x
thì người ta nói rằng hàm số
y f x
đạt cực trị
tại điểm
0
x
. Khi đó, điểm
0 0
;
M x f x
được gọi là điểm cực trị của đồ thị hàm số
y f x
.
3) Cách nhận biết cực trị của hàm số bằng dấu của đạo hàm.
Giả sử hàm số
y f x
liên tục trên khoảng
;a b
chứa điểm
0
x
và có đạo hàm trên các khoảng
0
;a x
và
0
;x b
. Khi đó
a) Nếu
0
f x
với mọi
0
;x a x
và
0
f x
với mọi
0
;x x b
thì hàm số
y f x
đạt cực
tiểu tại điểm
0
x
.
b) Nếu
0
f x
với mọi
0
;x a x
và
0
f x
với mọi
0
;x x b
thì hàm số
f x
đạt cực đại
tại điểm
0
x
.
4) Cách tìm cực trị của hàm số
f x
.
Bước 1: Tìm tập xác định của hàm số
f x
.
Bước 2: Tính đạo hàm
'f x
. Tìm các điểm
i
x
1,2,...i n
mà tại đó hàm số có đạo hàm bằng
0
hoặc không tồn tại.
Bước 3: Sắp xếp các điểm
i
x
theo thứ tự tăng dần và lập bảng biến thiên.
Bước 4: Căn cứ bảng biến thiên, nêu kết luận về các cực trị của hàm số.
4
PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI TOÁN KHẢO SÁT HÀM SỐ LỚP 12 THPT
CỰC TRỊ CỦA HÀM SỐ
XÁC ĐỊNH CỰC TRỊ CỦA CÁC HÀM SỐ THƯỜNG GẶP
_____________________________________
QUAN SÁT ĐỒ THỊ, BẢNG BIẾN THIÊN XÁC ĐỊNH CỰC TRỊ
Bài toán 1. Cho hàm số
f x
có bảng xét dấu của
f x
như hình vẽ
Hàm số đã cho đạt cực đại tại
A.
3
x
. B.
1
x
. C.
1x
. D.
1
y
.
Lời giải. Dựa vào bảng biến thiên thì đạo hàm đổi dấu từ dương sang âm tại
1
x
, đây là điểm cực đại.
Bài toán 2. Cho hàm số
y f x
xác định trên
và có bảng xét dấu của đạo hàm như sau.
Khi đó số điểm cực trị của hàm số
y f x
là
A.
3
. B.
2
C.
4
. D.
1
.
Lời giải. Đạo hàm đổi dấu 3 lần nên ta có 3 cực trị.
Bài toán 3. Cho hàm số
y f x
có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng
A.
4
. B.
0
. C.
1
. D.
3
.
Bài toán 4. Cho hàm số
y f x
có bảng biến thiên như sau:
Số điểm cực trị của hàm số đã cho
A.
3
. B.
2
. C.
1
. D.
4
.
Lời giải. Dựa vào bảng biến thiên thì Số điểm cực trị của hàm số đã cho là
3
.
Bài toán 5. Cho hàm số
y f x
có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng
A.
2
. B.
3
. C.
1
. D.
2
.
Lời giải
Dựa vào bảng biến thiên thì giá trị cực đại của hàm số là
2
.
Bài toán 6. Cho hàm số
f x
có bảng xét dấú
5
Hàm số đạt cực tiểu tại
A.
1
x
. B.
0
x
. C.
1x
. D.
2
x
.
Lời giải. Hàm số đạt cực tiểu tại điểm
y
đổi dấu từ âm sang dương
Bài toán 7. Cho hàm số
y f x
có bảng biến thiên như sau:
Điểm cực đại của hàm số đã cho bằng:
A.
4
27
. B.
4
3
. C.
2
. D.
0
.
Lời giải. Dựa vào bảng biến thiên thì điểm cực đại của hàm số đã cho là:
4
3
x
.
Bài toán 8. Cho hàm số
y f x
có bảng biến thiên như sau
-1
+∞
∞
0 +
+
0
+∞
1
0
-∞
y
y'
x
Mệnh đề nào sau đây đúng?
A.Hàm số có đúng một cực trị.
B. Hàm số đạt cực đại tại
0
x
và đạt cực tiểu tại
1x
.
C.Hàm số có giá trị lớn nhất bằng
0
và giá trị nhỏ nhất bằng
1
.
D.Hàm số có giá trị cực tiểu bằng
1
.
Lời giải
Dựa vào bảng biến thiên ta thấy hàm số đạt cực đại tại
0
x
và đạt cực tiểu tại
1x
.
Bài toán 9. Cho hàm số
y f x
xác định, liên tục trên đoạn
2;2
và có đồ thị là đường cong trong hình vẽ
bên.
x
2
-2
y
1
O
-1
2
4
-2
-4
Hàm số
f x
đạt cực đại tại điểm nào dưới đây ?
A.
2
x
B.
1
x
. C.
1x
. D.
2
x
.
Bài toán 10. Cho hàm số
f x
có đồ thị như hình vẽ
Hàm số có bao nhiêu điểm cực trị
6
A.
0
B.
1
. C.
2
. D.
3
.
Lời giải. Đồ thị hàm số đổi chiều 2 lần ta được 2 điểm cực trị
Bài toán 11. Cho hàm số
f x
có đồ thị như hình vẽ
x
y
O
Hàm số đã cho có bao nhiêu điểm cực tiểu
A.
3
. B.
2
. C.
1
. D.
0
.
Bài toán 12. Cho hàm số
y f x
liên tục trên
và có đồ thị như hình bên.
x
y
-2
-1
-1
O
1
Hỏi hàm số có bao nhiêu điểm cực trị?
A.
2
. B.
3
. C.
4
. D.
5
.
Lời giải
Đồ thị hàm số
y f x
đổi chiều
5
lần nên hàm số có
5
cực trị.
Bài toán 13. Cho hàm số
y f x
liên tục trên
và có bảng xét dấu đạo hàm như sau:
Hỏi hàm số
y f x
có bao nhiêu điểm cực trị?
A.
2
. B.
1
. C.
3
. D.
3
.
Lời giải
Vì hàm số
y f x
liên tục trên
và
f x
đổi dấu 2 lần nên hàm số đó có 2 điểm cực trị.
Bài toán 14. Cho hàm số
f x
có đạo hàm trên
và có bảng xét dấu
f x
như sau
Mệnh đề nào sau đây sai?
A. Hàm số
y f x
đạt cực trị tại
2
x
. B. Hàm số
y f x
đạt cực đại tại
1x
.
C. Hàm số
y f x
đạt cực tiểu tại
1
x
. D. Hàm số
y f x
có hai điểm cực trị.
Lời giải
Đạo hàm đổi dấu tại điểm
2
x
nên hàm số đạt cực trị tại
2
x
.
7
CỰC TRỊ HÀM SỐ ĐA THỨC
Bài toán 1. Tìm giá trị cực tiểu
CT
y
của hàm số
3
3 4
y x x
.
A.
6
CT
y
B.
1
CT
y
C.
2
CT
y
D.
1
CT
y
Lời giải
Tập xác định:
D
;
2
3 3
y x
;
0
y
1
x
. Bảng biến thiên
Vậy
1 2
CD
y y
;
1 6
CT
y y
.
Bài toán 2. Gọi
1
x
là điểm cực đại,
2
x
là điểm cực tiểu của hàm số
3
3 2y x x
. Tính
1 2
2x x
.
A.
2
. B.
1
. C.
1
. D.
0
.
Lời giải. Ta có
2
3 3 0 1; 1y x x x
.
Lập bảng xét dấu đạo hàm ta có cực đại, cực tiểu lần lượt là
1 2 1 2
1; 1 2 1
x x x x
.
Bài toán 3. Hàm số
3 2
1
3 1
3
y x x x
đạt cực tiểu tại điểm
A.
1
x
. B.
1x
. C.
3
x
. D.
3
x
.
Lời giải
Ta có hàm số
3 2
1
3 1
3
y x x x
có tập xác định
D
.
2
2 3y x x
;
1
0
3
x
y
x
.
2 2
y x

;
3 4 0
y
;
1 4 0
y
. Suy ra hàm số đạt cực tiểu tại điểm
1x
.
Bài toán 4. Tìm số điểm cực trị của hàm số
4 2
2y x x
.
A. 2. B. 4. C. 3. D. 1.
Lời giải
Tập xác định:
D
. Đạo hàm
3
0
4 4 0
1
x
y x x
x
.
Bảng biến thiên:
Dựa vào bảng biến thiên suy ra hàm số có 3 điểm cực trị.
Bài toán 5. Điểm cực tiểu của đồ thị hàm số
3 2
5 5 y x x x
là
A.
1; 8
B.
0; 5
C.
5 40
;
3 27
D.
1;0
Lời giải
2
1
3 2 5 0
5
3
x
y x x
x
.
6 2

y x
.
Ta có:
1 8 0
y
Hàm số đạt cực tiểu tại
1
x
;
1 8
CT
y y
.
Vậy điểm cực tiểu của đồ thị hàm số là
1; 8
.
Bài toán 6. Tính tổng các cực trị của hàm số
3
3 6y x x
.
8
A.1 B. 2 C. 0 D. 4
Lời giải
Ta có
2
3 3 0 1; 1y x x x
. Tổng các cực trị bằng 0.
Bài toán 7. Cho hàm số
( )y f x
có đạo hàm
2
( ) ( 2)
f x x x
,
x
. Số điểm cực trị của hàm số đã cho là
A.
0
. B.
3
. C.
2
. D.
1
.
Lời giải
Ta có:
2
0 0
( ) 0 ( 2) 0
2 0 2
x x
f x x x
x x
Bảng biến thiên:
Dựa vào bảng biến thiên, ta thấy hàm số có 1 điểm cực trị
0
x
.
Bài toán 8. Tìm điểm cực tiểu của đồ thị hàm số
3 2
1
2 3 1
3
y x x x
.
A.
3;1
. B.
3
x
. C.
7
1;
3
. D.
1x
.
Lời giải.
3 2 2
1
2 3 1 4 3 0 1;3
3
y x x x y x x x
.
Đạo hàm đổi dấu từ âm sang dương tại điểm
3
x
nên
3
x
là điểm cực tiểu.
Bài toán 9. Tìm giá trị thực của tham số
m
để hàm số
3 2 2
1
4 3
3
y x mx m x
đạt cực đại tại
3
x
.
A.
1
m
B.
7
m
C.
5
m
D.
1
m
Lời giải
Ta có
2 2
2 4
y x mx m
;
2 2y x m

.
Hàm số
3 2 2
1
4 3
3
y x mx m x
đạt cực đại tại
3
x
khi và chỉ khi:
3 0
3 0
y
y
2 2
1
9 6 4 0 6 5 0
5
6 2 0 3
3
m L
m m m m
m TM
m m
m
.
Vậy
5
m
là giá trị cần tìm.
Bài toán 10. Đồ thị hàm số
3 2
3 1
y x x
có điểm cực tiểu là A, tính khoảng cách từ A đến trục hoành
A.2 B. 3 C. 4 D.
2
Lời giải.
3 2 2
0
3 1 3 6 3 ( 2) 0
2
x
y x x y x x x x
x
Điểm cực tiểu của đồ thị là
2; 3
A
. Khoảng cách từ A đến trục hoành bằng 3.
Bài toán 11. Hàm số nào sau đây có hai điểm cực trị cùng dương ?
A.
3 2
3 1
y x x
B.
4 2
4 1
y x x
C.
4 2
2 1
y x x
D.
3 2
4 5 1y x x x
.
Lời giải.
Hàm số
3 2 2
0
3 1 3 6 3 ( 2) 0
2
x
y x x y x x x x
x
, 1 cực trị dương.
9
Hàm số trùng phương
4 2 3 2 2
4 1 4 8 4 ( 2)
y x x y x x x x
, hàm số có 1 cực trị dương.
Hàm số trùng phương
4 2
2 1
y x x
có 3 cực trị, trong đó 1 cực trị dương.
3 2 2
5
4 5 1 3 8 5; 0 1;
3
y x x x y x x y x x
, hàm số có 2 cực trị dương.
Bài toán 12. Khoảng cách giữa hai điểm cực trị của đồ thị hàm số
3
2 1y x x
bằng
A.
10 6
3
. B.
10
3
. C.
10 6
3
. D.
10 6
9
.
Lời giải.
3 2
2 2 9 4 6 2 9 4 6
2 1 3 2 0 ; , ;
3 3 9 3 9
y x x y x x A B
.
Khi đó
2 8 6 10 6
2 ;
3 9 9
AB AB
.
Bài toán 13. Cho hàm số
y
f x
có bảng biến thiên như dưới đây
Tung độ điểm uốn (trung điểm hai điểm cực đại, cực tiểu) của đồ thị hàm số bằng
A.2 B. 1 C. 3 D. 4
Lời giải.
Trung điểm hai điểm cực trị là
1
;2
2
I
. Tung độ bằng 2.
Bài toán 14. Biết đồ thị hàm số
3 2
6 9 2y x x x
có hai điểm cực trị là
1 1
;A x y
và
2 2
;B x y
. Khẳng định
nào sau đây không đúng?
A.
1 2
4
y y
. B.
4 2
AB
. C.
1 2
y y
. D.
1 2
2
x x
.
Lời giải.
3 2 2
1 2
6 9 2 3 12 9 0
3 2
x y
y x x x y x x
x y
.
Hai điểm cực trị là
1;2 , 3; 2 2; 4 4 2
A B AB AB
.
Bài toán 15. Đồ thị hàm số nào sau đây có đúng hai điểm cực trị và hai điểm cực trị nằm khác phía với trục tung
A.
3 2
3 1
y x x
B.
4 2
4 1
y x x
C.
3 2
2 5 5
y x x x
D.
3 2
4 5 1y x x x
.
Lời giải. Hai điểm cực trị trái dấu, hàm số
3 2
2 5 5
y x x x
có đạo hàm
2
3 4 5y x x
nên có hai
nghiệm trái dấu.
Bài toán 16. Đường cong
3 2
3y x x
có các điểm cực trị A, B. Tính khoảng cách
d
từ điểm
3;4
C
đến
đường thẳng AB.
A.
5
d
. B.
2 5
d
. C.
26
d
. D.
4 3
d
.
Lời giải.
3 2 2
0 0
3 3 6 3 ( 2) 0
2 4
x y
y x x y x x x x
x y
Hai điểm cực trị là
0;0 , 2; 2 : 2 2 2 0
A B AB y kx k y x x y
.
Khi đó
2.3 4
,( ) 2 5
5
d d C AB
.
10
CỰC TRỊ HÀM SỐ PHÂN THỨC HỮU TỶ
Bài toán 1. Hàm số
2
2
1
y
x
nghịch biến trên khoảng nào dưới đây?
A.
1
x
. B.
1x
. C.
3
x
. D.
0x
.
Lời giải. Ta có
2
2
4
0 0
1
x
y x
x
. Hàm số đạt cực trị tại điểm
Bài toán 2. Hàm số
2
4
1
x x
y
x
có tổng hai cực trị bằng
A.2 B. 0 C. 1 D. – 2
Lời giải
Tập xác định:
\ 1
D
. Ta có
2
2
2
1
2 3
, 0 2 3 0
3
1
x
x x
y y x x
x
x
.
Bảng xét dấu đạo hàm
Từ bảng xét dấu
y
ta có tổng hai cực trị bằng 2.
Bài toán 3. Cho hàm số
2
2 6
1
x x
f x
x
. Tổng hai giá trị cực trị của hàm số bằng
A.4 B. 3 C. 8 D. – 8
Lời giải
Đạo hàm
2
2
2
2
2 8
0 0 2 8 0
4
1
x
x x
f x x x
x
x
.
Bảng biến thiên:
Vậy hàm số
f x
có tổng 2 giá trị cực trị bằng – 8.
Bài toán 4. Hàm số
2
2 2
1
x x
y
x
có giá trị cực đại bằng
A.3 B. 2 C. – 2 D. 0
Lời giải.
2 2
2
2 2 2
; 0 0; 2
1
( 1)
x x x x
y y y x x
x
x
. Bảng biến thiên
Hàm số có giá trị cực đại bằng – 2.
Bài toán 5. Cho hàm số
2
2 5
1
x x
y
x
có hai giá trị cực trị
1 2
,y y
. Giá trị
1 2
2y y
có thể bằng
A.0 B. 12 C. 10 D. – 14
Lời giải
Tập xác định:
\ 1
D
.
Ta có
2
2
2 2
2 2 1 2 5
2 3
1 1
x x x x
x x
y
x x
. Giải phương trình
1
0
3
x
y
x
.
Bảng biến thiên
11
Từ bảng biến thiên ta thấy
1 2
2y y
có thể bằng 12.
Bài toán 6. Hàm số
2
2x 1
2
x
y
x
có hai điểm cực trị
,A B
. Gọi
,M N
là hình chiếu của
,A B
trên trục hoành.
Tính độ dài đoạn thẳng
MN
.
A.6 B. 4 C. 8 D. 8
Lời giải
Ta có
2
2
4 5
2
x x
y
x
. Giải phương trình
1
0
5
x
y
x
.
Bảng biến thiên như sau. Dựa vào bảng biến thiên, ta thấy
1 ( 5) 6
MN
.
Bài toán 7. Biết đồ thị
C
của hàm số
2
4 5
1
x x
y
x
có hai điểm cực trị. Đường thẳng đi qua hai điểm cực trị
của đồ thị
C
cắt trục hoành tại điểm
M
có hoành độ
M
x
bằng
A.
2
M
x
. B.
1 2
M
x
. C.
1
M
x
. D.
1 2
M
x
.
Lời giải. Ta có
2
2
4 5
4 5
: 2 4; 0 2
1
1
x x
x x
y d y x d Ox y x
x
x
.
Bài toán 8. Đồ thị hàm số
2
2
2
x x m
y
x
có hai điểm cực trị
,A B
. Tính khoảng cách từ gốc tọa độ O đến
đường thẳng đi qua hai điểm
AB
.
A.
2
5
B.
1
5
C.
3
5
D.
4
5
Lời giải.
Phương trình của đường thẳng AB là
/
2
/
2
2 2 2 2 0
2
x x m
y y x x y
x
.
Khoảng cách
2
2
2.0 0 2
2
;
5
2 1
d O AB
.
Bài toán 9. Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
2
2 3
2 1
x x
y
x
.
A.
2 2
y x
. B.
1y x
. C.
2 1y x
. D.
3 1y x
Lời giải. Đường thẳng đi qua hai điểm cực trị là
2
2 3
2 2
1
2
2 1
x x
x
y x
x
.
12
CỰC TRỊ HÀM SỐ CHỨA CĂN
Bài toán 1. Tìm số điểm cực đại của hàm số
2
4 10
y x x
.
A.3 B. 2 C. 1 D. 3
Lời giải.
2
2 2
2 4 2
4 10
2 4 10 4 10
x x
y x x y
x x x x
.
Bài toán 2. Số điểm cực trị của hàm số
2
2 1
y x x
là
A. 1. B. 2. C. 3. D. 0.
Lời giải
Ta có
2
2
2 2
2
2
2 1 1 ;
2 1
2 1 4
1
0 2 1 2
0
2
x
y x x y
x
x x
y x x x
x
Hàm số có 1 cực trị.
Bài toán 3. Tìm số cực tiểu của hàm số
2
2y x x x
A.2 B. 3 C. 1 D. 0
Lời giải
Ta có:
2
2y x x x
2
2
2 2
' 2 .
2 2
x
y x x x
x x
2
2
2 2
2 1
2 3
2 2
x x x x
x x
x x x x
.
Do đó:
0
y
tương đương
2
3
2 3 0 0;
2
x x x x
.
Hai nghiệm đơn và thỏa mãn TXĐ nên hàm có 1 cực tiểu.
Bài toán 4. Hàm số
2
2
y x x
đạt cực đại tại điểm
A.
1
x
. B.
1x
. C.
0
x
. D.
2
x
.
Lời giải
Tập xác định
0;2
.
Ta có
2
2
2 2 2
2
2 2 1
2 ; 0 1
2 2 2 2 2
x x
x x
y x x y y x
x x x x x x
Đạo hàm đổi dấu từ dương sang âm nên
1x
là điểm cực đại.
Bài toán 5. Hàm số
2
8 19
y x x
đạt cực trị tại
A.
2
x
B.
3
x
C.
1x
D.
4
x
Lời giải.
2
2 2 2
( 8 19) 2 8 4
; 0 4
2 8 19 2 8 19 8 19
x x x x
y y x
x x x x x x
.
Bài toán 6. Số điểm cực trị của hàm số
2
2 1
y x x
là
A. 1. B. 2. C. 3. D. 0.
Lời giải
Ta có
2
2
2 2
2
2
2 1 1 ;
2 1
2 1 4
1
0 2 1 2
0
2
x
y x x y
x
x x
y x x x
x
Hàm số có 1 cực trị.
Bài toán 7. Tìm một điểm cực trị của hàm số
2
1
y x
.
A.
1y
. B.
0
x
. C.
0
y
. D.
1x
.
Lời giải
Tập xác định
1;1
. Ta có
2
2
2 2 2
(1 ) 2
1 ; 0 0
2 1 2 1 1
x x x
y x y y x
x x x
.
13
Bài toán 8. Hàm số
2
2 5
y x x
đạt cực trị tại
A.
3
x
. B.
1
x
. C.
1x
. D.
1
y
.
Lời giải
Hàm số luôn xác định.
Ta có đạo hàm
2
1
0 1
2 5
x
y x
x x
. Hàm số đạt cực trị tại
1
x
.
Bài toán 9. Hàm số
2
6 10
y x x
đạt cực trị tại điểm
A.
3
x
B.
3
x
C.
1x
D.
5
x
Lời giải
Hàm số luôn xác định.
2
2
2 2 2
( 6 10) 2 6 3
6 10 ; 0 3
2 6 10 2 6 10 6 10
x x x x
y x x y y x
x x x x x x
.
Bài toán 10. Giá trị cực tiểu của hàm số
3 2 1y x x
bằng
A.
10 5
9
B.
10 3
9
C.
6 3
9
D.
8 2
9
Lời giải.
Tập xác định:
1;D

.
+)
3 2 3.2. 1
1 9 4
. 3 2 3 1
2 1 2 1 2 1
x x
x
y x x
x x x
.
+)
4
0 9 4 0
9
y x x
.
+) Bảng biến thiên
Từ bảng biến thiên suy ra hàm số đạt cực tiểu tại
4 10 5
,
9 9
CT
x y
.
Bài toán 11. Giá trị cực tiểu của hàm số
3 1y x x
bằng
A.
4 5
B.
1
5
C.
3 3
D.
2 2
Lời giải.
Tập xác định:
1;3
D
. Đạo hàm
1 1 3 1
2 3 2 1 2 3 . 1
x x
y
x x x x
.
+)
0 3 1 0 3 1
y x x x x
1 1
1.
3 1 2 2
x x
x
x x x
+) Bảng biến thiên:
Từ bảng biến thiên suy ra hàm số đạt cực tiểu tại
1, 2 2
CT
x y
.
14
CỰC TRỊ HÀM SỐ LƯỢNG GIÁC, HÀM SỐ MŨ, HÀM SỐ LOGARIT
Bài toán 1. Hàm số
2
x x
y e e
đạt cực trị tại điểm
A.
3
x
. B.
ln 2
x
. C.
1
ln 2
2
x
. D.
1
x
.
Lời giải.
2
1
2 0 2 1 0 ln 2
2
x x x x
y e e e e x
.
Bài toán 2. Hàm số
cos siny x x
có cực trị tại
0
x
. Giá trị
0
tan x
khi đó bằng
A.2 B. 1 C. – 1 D. 0
Lời giải
0
cos sin sin cos ; 0 sin cos 0
sin cos ta tann 11
y x x x x y x x
x x x x
Bài toán 3. Tìm số điểm cực trị của hàm số
1 2x
y e
.
A.2 B. 1 C. 3 D. 0
Lời giải. Ta thấy
1 2
2
x
y e
nên hàm số không có cực trị.
Bài toán 4. Tính giá trị cực tiểu của hàm số
2
ln 2 10
y x x
.
A.3 B.
2ln 3
C.
3ln 2
D.
2ln 2
Lời giải
Tập xác định
2
2
2 2
; ln 2 10 0 1
2 10
x
y x x y x
x x
.
Đạo hàm đổi dấu từ âm sang dương nên hàm số đạt cực tiểu tại
1 ln9 3ln 2
x y
.
Bài toán 5. Hàm số
2
5
3
x x
y
tại cực trị tại điểm
A.
5
2
x
. B.
3
x
. C.
1x
. D.
1
x
.
Lời giải
Công thức tổng quát
2 2
2 5 5
. ln 5 3 ln3 2 5 3 ln3
u u x x x x
a u a a y x x x
.
5
0
2
y x
. Đạo hàm đổi dấu tại đây nên hàm số đạt cực trị tại
5
2
x
.
Bài toán 6. Tìm số điểm cực trị của hàm số
2
4
x x
y e e
.
A.2 B. 1 C. 3 D. 4
Lời giải.
2 2 2
1
4 2 4 0 2 2 ln 2 ln 2
2
x x x x x
y e e y e e e x x
0 2
y x
, đạo hàm đổi dấu từ âm sang dương nên hàm số đạt cực tiểu tại
2
x
.
Bài toán 7. Tìm số điểm cực trị của hàm số
2
3
2
log 5
y x x
.
A.3 B. 2 C. 1 D. 4
Lời giải
Ta có
2
2 2
2 5 '
2 2
' ; 0 1
2 5 ln3 2 5 ln 3
x x
x
y y x
x x x x
. Hàm số có 1 cực trị.
Bài toán 8. Tìm số cực tiểu của hàm số
2
ln 4 12
y x x
.
A.2 B. 1 C. 3 D. 4
Lời giải
2
2
2 4
ln 4 12 ; 0 2 4 0 2
4 12
x
y x x y y x x
x x
.
Đạo hàm đổi dấu từ âm sáng dương nên hàm số có 1 cực tiểu.
Bài toán 9. Tìm số cực trị thuộc khoảng
0;2
của hàm số
1
sin
3
y x x
.
A.3 B. 4 C. 2 D. 1
Lời giải.
15
1 1
cos 0 cos
3 3
y x x
. Phương trình này có 2 nghiệm trong khoảng
0;2
. Hàm có 2 cực trị.
Bài toán 10. Có bao nhiêu số nguyên m để hàm số
3sin 4cos 4
y x x mx
có cực trị
A.11 B. 10 C. 9 D. 6
Lời giải.
3sin 4cos 4 3cos 4sin 0 3cos 4siny x x mx y x x m m x x
.
Theo BĐT Bunyakovsky có
2
2 2 2 2
3cos 4sin 3 4 sin cos 25 5 3cos 4sin 5
x x x x x x
.
Bài toán 11. Tìm số điểm cực trị thuộc khoảng
0;4
của hàm số
2sin 2 4
y x x
.
A.3 B. 2 C. 1 D. 4
Lời giải.
2
2sin 2 4 2cos 2 0 cos
2
y x x y x x
.
Trên khoảng
0;4
, vẽ 2 vòng tròn lượng giác ta thu được 4 nghiệm dẫn đến 4 điểm cực trị.
Bài toán 12. Tính độ dài đoạn thẳng OA với A là điểm cực tiểu của đồ thị hàm số
2
ln 8 17
y x x
.
A.
3
OA
B.
4
OA
C.
5
OA
D.
6
OA
Lời giải
Ta có
2
2 8
; 0 4 ln1 0 4;0 4
8 17
x
y y x y A OA
x x
.
Bài toán 13. Tìm số điểm cực trị của hàm số
f x
trên
0; 4
biết rằng
3 sin 2 1
x
f x e x
.
A.3 B. 2 C. 4 D. 1
Lời giải
ln 3 ln 3
0 3 sin 2 1 0
2 2
2 4
x
x x
f x e x
x k x k
Trên
0; 4
(2 vòng tròn lượng giác) ta thu được 5 điểm cực trị.
Bài toán 14. Tìm tất cả cả điểm cực trị của hàm số
cos 3 sin
y x x x
.
A.
2 ; 2
6 2
x k x k k
. B.
2
6
x k k
.
C.
;
6 2
x k x k k
. D.
2 ; 2
3
x k x k k
.
Lời giải
sin 3 cos 1y x x
. Giải phương trình
1 3 1
sin 3 cos 1 sin cos sin sin
2 2 2 3 6
x x x x x
2 2
3 6 6
2 2
3 6
2
x k x k
k
x k x k
.
Bài toán 16. Tính tổng các cực trị của hàm số
2
2 3
x
y e x x
.
A.3 B. – 4 C. – 2 D. 1
Lời giải
Ta có
2 2
2 2
2 3 2 3 2 2
0 4 1 0 4 1 0
x x x
x
y e x x y e x x x e
y e x x x x
Tổng các cực trị bằng – 4 (theo hệ thức Viet).
Bài toán 17. Giá trị cực tiểu của hàm số
ln 2 6
y x x
nằm trong khoảng nào sau đây
A.
1;2
B.
3;4
C.
4;5
D.
2;3
16
Lời giải.
Tập xác định R.
1
1
; 0 1
2 6
x
y y x
x x
.
Bài toán 18. Tìm tất cả các giá trị của tham số m để hàm số
2 cos 2sin 5 20
2 2
x x
y m x
có cực trị
A.
2
2
m
m
B.
2
2
m
m
C.
2 2m
D.
2 2m
Lời giải.
2 cos 2sin 5 20 sin cos 5
2 2 2 2
x x x x
y m x y m
.
0 sin cos 5
2 2
x x
y m
. Điều kiện có cực trị là phương trình có nghiệm (không kép):
2
2
1 5
2
m
m
m
Bài toán 19. Tìm số cực trị của hàm số
2
ln 2f x x x
.
A.2 B. 3 C. 4 D. 1
Lời giải
Điều kiện
2
2
1 1 4
0; ln 2 4
x
x f x x x f x x
x x
. Khi đó
1
0
2
f x x
.
Đạo hàm đổi dấu qua đây nên hàm số có 1 cực trị.
Bài toán 20. Gọi M là điểm cực tiểu của hàm số
2
2 5
x x
y e e
. Điểm M nằm trên đường thẳng nào sau đây
A.
3y x
. B.
7 2
y x
. C.
1 3
2 2
y x
. D.
2 3 0
x y
.
Lời giải
2
2 2
2
2 2 2
2
2 5
2 2
2 5
2 2 5 2 2 5 2 5
0 1 0 2 0;2
x x
x x x x
x x
x x x x x x
x x x
e e
e e e e
y e e y
e e e e e e
y e e e x y M
Đạo hàm đổi dấu từ âm sang dương nên hàm số đạt cực tiểu tại
0
x
.
Điểm M này thuộc đường thẳng
7 2
y x
.
Bài toán 21. Tìm số điểm cực trị của hàm số
3 2
3 3 1x x x
y e
.
A.2 B. 3 C. 1 D. 0
Lời giải
3 2 3 2
2
3 3 1 2 3 3 1
0 3 6 3 0 1 0 1
x x x x x x
e x x e x x
(nghiệm kép).
Hàm số không có cực trị.
Bài toán 22. Hàm số
.sin2
x
y e x
đạt cực trị tại điểm
0
x
. Khi đó
A.
0
1
tan 2
2
x
B.
0
tan 2 2
x
C.
0
1
tan 2
2
x
D.
0
tan 3
x
Lời giải.
Theo công thức đạo hàm tích ta có
.sin 2 .2cos2 .sin 2 sin 2 2cos2
x x x x
y e x y e x e x e x x
.
sin 2
0 sin 2 2cos 2 0 sin 2 2cos 2 2 tan 2 2
cos2
x
x
y e x x x x x
x
. Như vậy
0
tan 2 2
x
.
17
PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI TOÁN KHẢO SÁT HÀM SỐ LỚP 12 THPT
CỰC TRỊ CỦA HÀM SỐ
XÁC ĐỊNH CỰC TRỊ CỦA CÁC HÀM SỐ PHỨC TẠP
_____________________________________
ĐƯỜNG THẲNG ĐI QUA HAI ĐIỂM CỰC TRỊ
Bài toán 1. Đồ thị hàm số
3 2
3 9 1y x x x
có hai cực trị
A
và
B
. Điểm nào dưới đây thuộc đường thẳng
AB
?
A.
0; 1
M
B.
1; 10
N
C.
1;0
P
D.
1;10
Q
Lời giải
Ta có:
2
3 6 9
y x x
thực hiện phép chia
y
cho
y
ta được số dư là
8 2y x
.
Như thế điểm
1; 10
N
thuộc đường thẳng
AB
.
Bài toán 2. Tìm giá trị thực của tham số
m
để đường thẳng
: 2 1 3
d y m x m
vuông góc với đường
thẳng đi qua hai điểm cực trị của đồ thị hàm số
3 2
3 1
y x x
.
A.
3
2
m
B.
3
4
m
C.
1
2
m
D.
1
4
m
Lời giải
Ta có
2
3 6y x x
. Từ đó ta có tọa độ hai điểm cực trị
0;1
A
,
2; 3
B
. Đường thẳng qua hai điểm cực trị có
phương trình
2 1y x
. Đường thẳng này vuông góc với đường thẳng
2 1 3
y m x m
khi và chỉ khi
3
2 1 2 1
4
m m
.
Bài toán 3. Tìm giá trị thực của tham số
m
để đường thẳng
2 1 3
y m x m
song song với đường thẳng
đi qua các điểm cực trị của đồ thị hàm số
3 2
3 1
y x x
A.
3
4
m
. B.
1
2
m
. C.
3
4
m
. D.
1
2
m
.
Lời giải
Hàm số
3 2
3 1
y x x
có TXĐ:
;
2
3 6y x x
;
0
' 0
2
x
y
x
Suy ra đồ thị hàm số có hai điểm cực trị là
0;1
A
,
2; 3 2; 4
B AB
.
Đường thẳng
d
đi qua hai điểm
A
,
B
có phương trình:
1
2 1
2 4
x y
y x
.
Đường thẳng
2 1 3
y m x m
song song với đường thẳng
2 1 2
1
3 1
2
m
d m
m
.
Bài toán 4. Đồ thị của hàm số
3 2
3 9 1y x x x
có hai điểm cực trị
A
và
B
. Điểm nào dưới đây thuộc
đường thẳng
AB
.
A.
1;0
P
. B.
0; 1
M
. C.
1; 10
N
. D.
1;10
Q
.
Lời giải
TXĐ:
D
.
2
' 3 6 9y x x
.
2
1 6
' 0 3 6 9 0
3 26
x y
y x x
x y
Ta có
1;6 , 3; 26
A B
4; 32
AB
nên ) Chọn
8;1
AB
n
.
Phương trình đường thẳng
AB
là:
8 1 1 6 0 8 2 0
x y x y
.
Thay tọa độ các điểm
, , ,P M N Q
vào phương trình đường thẳng
AB
ta có điểm
1; 10
N
thuộc đường thẳng.
Bài toán 5. Tìm giá trị thực của tham số
m
để đường thẳng
: 3 1 3
d y m x m
vuông góc với đường
thẳng đi qua hai điểm cực trị của đồ thị hàm số
3 2
3 1
y x x
.
18
A.
1
3
. B.
1
6
. C.
1
6
m
. D.
1
3
.
Lời giải
Xét hàm số
3 2
3 1
y x x
Có :
2
3 6y x x
,
1 1
2 1
3 3
y x y x
.
Do đó, đường thẳng
qua hai điểm cực trị của đồ thị hàm số này có phương trình là
2 1y x
.
Để
d
vuông góc với
thì
3 1 . 2 1
m
1
6
m
.
Vậy giá trị cần tìm của
m
là
1
6
m
.
Bài toán 6. Biết đồ thị hàm số
3
3 1y x x
có hai điểm cực trị
A
,
B
. Khi đó phương trình đường thẳng
AB
là
A.
2 1y x
. B.
2 1.
y x
C.
2.
y x
D.
2y x
.
Lời giải
Thực hiện phép chia
y
cho
y
ta được:
1
. 2 1
3
y y x x
.
Giả sử hai điểm cực trị của đồ thị hàm số lần lượt là:
1 1
;A x y
và
2 2
;B x y
.
Ta có:
1 1 1 1 1 1
2 2 2 2 2 2
1
. 2 1 2 1
3
1
. 2 1 2 1
3
y y x y x x x x
y y x y x x x x
.
Ta thấy, toạ độ hai điểm cực trị
A
và
B
thoả mãn phương trình
2 1y x
.
Vậy phương trình đường thẳng qua hai điểm cực trị là:
2 1y x
.
Bài toán 7. Giả sử
A
,
B
là hai điểm cực trị của đồ thị hàm số
3 2
f x x ax bx c
và đường thẳng
AB
đi
qua gốc tọa độ. Tìm giá trị nhỏ nhất của
P abc ab c
.
A.
16
25
. B.
9
. C.
25
9
. D.
1
.
Lời giải
TXĐ
D
.
2
3 2
f x x ax b
. Điều kiện để hàm số có hai điểm cực trị là
0
f x
có hai nghiệm phân biệt
2
3 0
a b
.
Lấy
f x
chia cho
f x
. Ta có
1 1 2 2 1
.
3 9 3 9 9
f x f x x a b x c ab
.
Suy ra đường thẳng đi qua
A
,
B
là:
2 2 1
3 9 9
y b x c ab d
.
Theo đầu bài
d
đi qua gốc tọa độ
1
0
9
c ab
9ab c
.
Khi đó
P abc ab c
2
9 10P c c
2
5 25
3
3 9
P c
. Suy ra
25
min
9
P
.
19
CỰC TRỊ HÀM SỐ ĐA THỨC SỬ DỤNG ĐỊNH LÝ VIET VÀ HÌNH HỌC GIẢI TÍCH
Bài toán 1. Cho hàm số
4 2
8 10
y x x
. Tính diện tích của tam giác có ba đỉnh là ba điểm cực trị của đồ thị
hàm số đã cho.
A.32 B. 16 C. 48 D. 40
Lời giải
Tập xác định:
D
.
Ta có
3
4 16y x x
;
0
0
2
x
y
x
.
Suy ra đồ thị hàm số có ba điểm cực trị . Không mất tính tổng quát, giả sử ba điểm cực trị là:
0;10
A
,
2; 6
B
,
2; 6
C
.
Do
A Oy
và
,B C
đối xứng nhau qua
Oy
nên tam giác
ABC
cân tại
A
. Gọi
H
là trung điểm của đoạn thẳng
BC
, khi đó
0; 6
H
;
16;
AH
4
BC
.
Diện tích tam giác
ABC
là:
1 1
. .16.4 32
2 2
ABC
S AH BC
.
Bài toán 2. Cho hàm số
3 2
6 9 2y x x x
có đồ thị là
C
. Đường thẳng đi qua điểm
1,1
A
và vuông góc
với đường thẳng đi qua hai điểm cực trị của
C
là
A.
3y x
. B.
1 3
2 2
y x
. C.
1 3
2 2
y x
. D.
2 3 0
x y
.
Lời giải
2
3 12 9
y x x
,
3 2 2
1 2
6 9 2 3 12 9 2 4
3 3
y x x x x x x x
Khi đó đường thẳng đi qua hai điểm cực trị của
C
có phương trình là
2 4y x
.
Đường thẳng vuông góc với
2 4y x
có phương trình
1
2
y x b
.
Đường thẳng qua
1;1
A
suy ra
1 3
1 . 1
2 2
b b
.
Vậy phương trình đường thẳng cần tìm là
1 3
2 2
y x
.
Bài toán 3. Biết rằng đồ thị hàm số
3 2
1 1
2
3 2
f x x mx x
có giá trị tuyệt đối của hoành độ hai điểm cực trị
là độ dài hai cạnh của tam giác vuông có cạnh huyền là
7
. Hỏi có mấy giá trị của
m
?
A.
3
. B.
1
. C. Không có
m
. D.
2
.
Lời giải.
3 2 2
1
2 2 1
3
f x x mx x f x x mx
.
Hai cực trị là a, b thì
2 ; 1
a b m ab
.
Theo định lý Pytago
2
2 2 2
3
7 2 7 4 2 7
2
a b a b ab m m
. Thử lại ta thu được 2 giá trị m.
Bài toán 4. Đồ thị hàm số
3 2
3 1
y x x
có điểm cực đại B, tính khoảng cách từ điểm B đến đường thẳng
:3 4 1 0
x y
.
A.2 B. 1 C.
1
5
D.
Lời giải
Ta có
3 2 2
0 1
3 1 3 6 3 ( 2) 0
2 3
x y
y x x y x x x x
x y
20
Khi đó
2 2
3.2 4.( 3) 1
0;1 , 2; 3 , 1
3 4
A B d B
.
Bài toán 5. Đường cong
3 2
3 1
y x x
có điểm cực tiểu A và điểm cực đại B. Đường thẳng AB cắt trục
hoành tại C, tính tỷ số
CA
k
CB
.
A.
1
2
k
. B.
1
3
k
. C.
1
3
k
. D.
4
3
k
.
Lời giải.
3 2 2
3 1 3 6 0 0; 2 (0; 1), (2;3)
y x x y x x x x A B
.
Theo định lý Talet
( , ) 1
( , ) 3
A
B
yCA d A Ox
CB d B Ox y
.
Bài toán 6. Với giá trị nào của tham số
m
để đồ thị hàm số
3 2
3
y x x m
có hai điểm cực trị
A
,
B
thỏa
mãn
OA OB
(
O
là gốc tọa độ)?
A.
3
2
m
. B.
3
m
. C.
1
2
m
. D.
5
2
m
.
Lời giải
Tập xác định:
D
.
2
3 6y x x
,
2
0
0 3 6 0
2
x
y x x
x
.
Do đó đồ thị hàm số đã cho luôn có hai điểm cực trị lần lượt có tọa độ là
0;A m
và
2; 4
B m
.
Ta có
2 2
2 2 2 2
0 2 4 4 4
OA OB m m m m
5
20 8 0
2
m m
.
Bài toán 7. Gọi S là tập các giá trị dương của tham số
m
sao cho hàm số
3 2
3 27 3 2
y x mx x m
đạt cực
trị tại
1 2
,x x
thỏa mãn
1 2
5
x x
. Biết
;S a b
. Tính
2
T b a
.
A.
51 6
T
B.
61 3
T
C.
61 3
T
D.
51 6
T
Lời giải
+) Ta có
2
3 6 27
y x mx
,
2
0 2 9 0
y x mx
(1)
+) Theo giả thiết hàm số đạt cực trị tại
1 2
,x x
phương trình
(1)
có
2
nghiệm phân biệt
0
2
3
9 0
3
m
m
m
(*)
+) Với điều kiện (*) thì phương trình
(1)
có
2
nghiệm
1 2
,x x
, theo Vi-ét ta có:
1 2
1 2
2
9
x x m
x x
+) Ta lại có
1 2
5
x x
2 2
1 2 1 2 1 2
25 4 25 0
x x x x x x
2
61 61
4 61 0
2 2
m m
(**)
+) Kết hợp (*), (**) và điều kiện
m
dương ta được:
61
3
2
m
3
2 61 3
61
2
a
T b a
b
.
| 1/59
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


TÀI LIỆU THAM KHẢO TOÁN HỌC PHỔ THÔNG
______________________________________________________________
------------------------------------------------------------------------------------------
ÔN KIẾN THỨC TOÁN 12 THPT BÀI GIẢNG
CỰC TRỊ CỦA HÀM SỐ (CỰC ĐẠI, CỰC TIỂU)
(KẾT HỢP 3 BỘ SÁCH GIÁO KHOA)
THÂN TẶNG TOÀN THỂ QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TRÊN TOÀN QUỐC
CREATED BY GIANG SƠN (FACEBOOK)
GACMA1431988@GMAIL.COM (GMAIL); TEL 0398021920
THÀNH PHỐ THÁI BÌNH – THÁNG 7/2024 1
ÔN KIẾN THỨC TOÁN 12 THPT
CỰC TRỊ CỦA HÀM SỐ (CỰC ĐẠI, CỰC TIỂU)
__________________________ DUNG NỘI DUNG LƯỢNG 1 FILE
XÁC ĐỊNH CỰC TRỊ CÁC HÀM SỐ THƯỜNG GẶP 1 FILE
XÁC ĐỊNH CỰC TRỊ CÁC HÀM SỐ PHỨC TẠP 1 FILE
CÁC BÀI TOÁN CHỨA THAM SỐ 2
PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI TOÁN KHẢO SÁT HÀM SỐ LỚP 12 THPT
LÝ THUYẾT CỰC TRỊ CỦA HÀM SỐ
ĐIỂM CỰC TRỊ, GIÁ TRỊ CỰC TRỊ CỦA HÀM SỐ 1) Định nghĩa:
Cho hàm số y f (x) liên tục trên tập K   , trong đó K là một khoảng, đoạn hoặc nửa khoảng
và x K , x K . 0 1
+) x được gọi là một điểm cực đại của hàm số đã cho nếu tồn tại một khoảng  ;
a b chứa điểm x 0 0 sao cho  ;
a b  K và f x  f x với mọi x  ;
a b và x x . 0  0
Khi đó, f x được gọi là giá trị cực đại của hàm số đã cho, kí hiệu là f . 0  CĐ
+) x được gọi là một điểm cực tiểu của hàm số đã cho nếu tồn tại một khoảng c; d  chứa điểm x 1 1 sao cho  ;
c d   K và f x  f x với mọi x  ;
c d  và x x . 1  1
Khi đó, f x được gọi là giá trị cực tiểu của hàm số đã cho, kí hiệu là f . 1  CT
+) Điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại và giá trị cực tiểu
được gọi chung là giá trị cực trị (hay cực trị). 2) Chú ý
Nếu x là một điểm cực trị của hàm số y f x thì người ta nói rằng hàm số y f x đạt cực trị 0
tại điểm x . Khi đó, điểm M x ; f x
được gọi là điểm cực trị của đồ thị hàm số y f x . 0  0  0
3) Cách nhận biết cực trị của hàm số bằng dấu của đạo hàm.
Giả sử hàm số y f x liên tục trên khoảng  ;
a b chứa điểm x và có đạo hàm trên các khoảng 0  ;
a x và  x ;b . Khi đó 0  0 
a) Nếu f   x  0 với mọi x  ; a x
và f   x  0 với mọi x  x ;b thì hàm số y f x đạt cực 0  0 
tiểu tại điểm x . 0
b) Nếu f   x  0 với mọi x  ; a x
và f   x  0 với mọi x  x ;b thì hàm số f x đạt cực đại 0  0  tại điểm x . 0
4) Cách tìm cực trị của hàm số f x.
Bước 1: Tìm tập xác định của hàm số f x .
Bước 2: Tính đạo hàm f ' x . Tìm các điểm x i  1, 2,...n mà tại đó hàm số có đạo hàm bằng 0 i hoặc không tồn tại.
Bước 3: Sắp xếp các điểm x theo thứ tự tăng dần và lập bảng biến thiên. i
Bước 4: Căn cứ bảng biến thiên, nêu kết luận về các cực trị của hàm số. 3
PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI TOÁN KHẢO SÁT HÀM SỐ LỚP 12 THPT
CỰC TRỊ CỦA HÀM SỐ
XÁC ĐỊNH CỰC TRỊ CỦA CÁC HÀM SỐ THƯỜNG GẶP
_____________________________________
QUAN SÁT ĐỒ THỊ, BẢNG BIẾN THIÊN XÁC ĐỊNH CỰC TRỊ
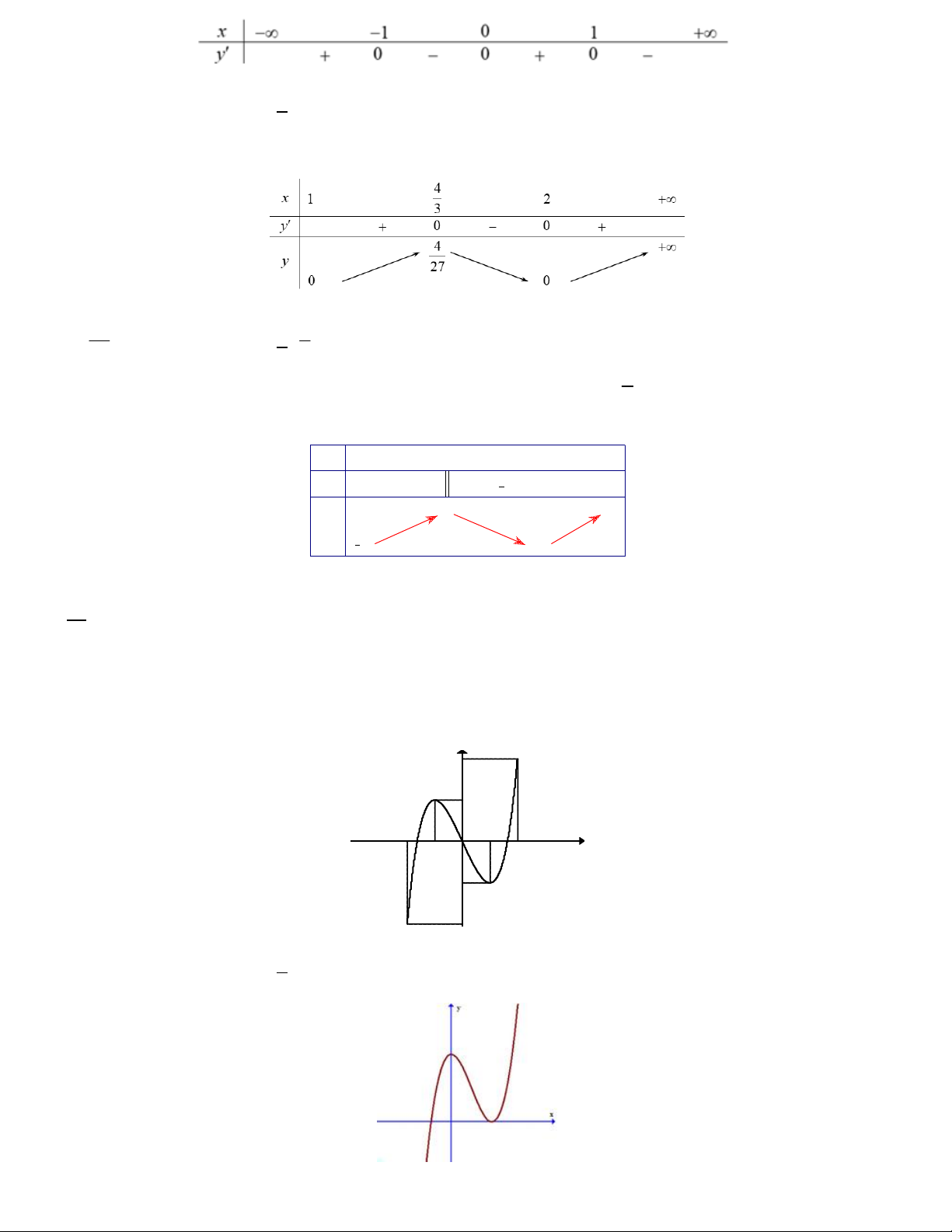
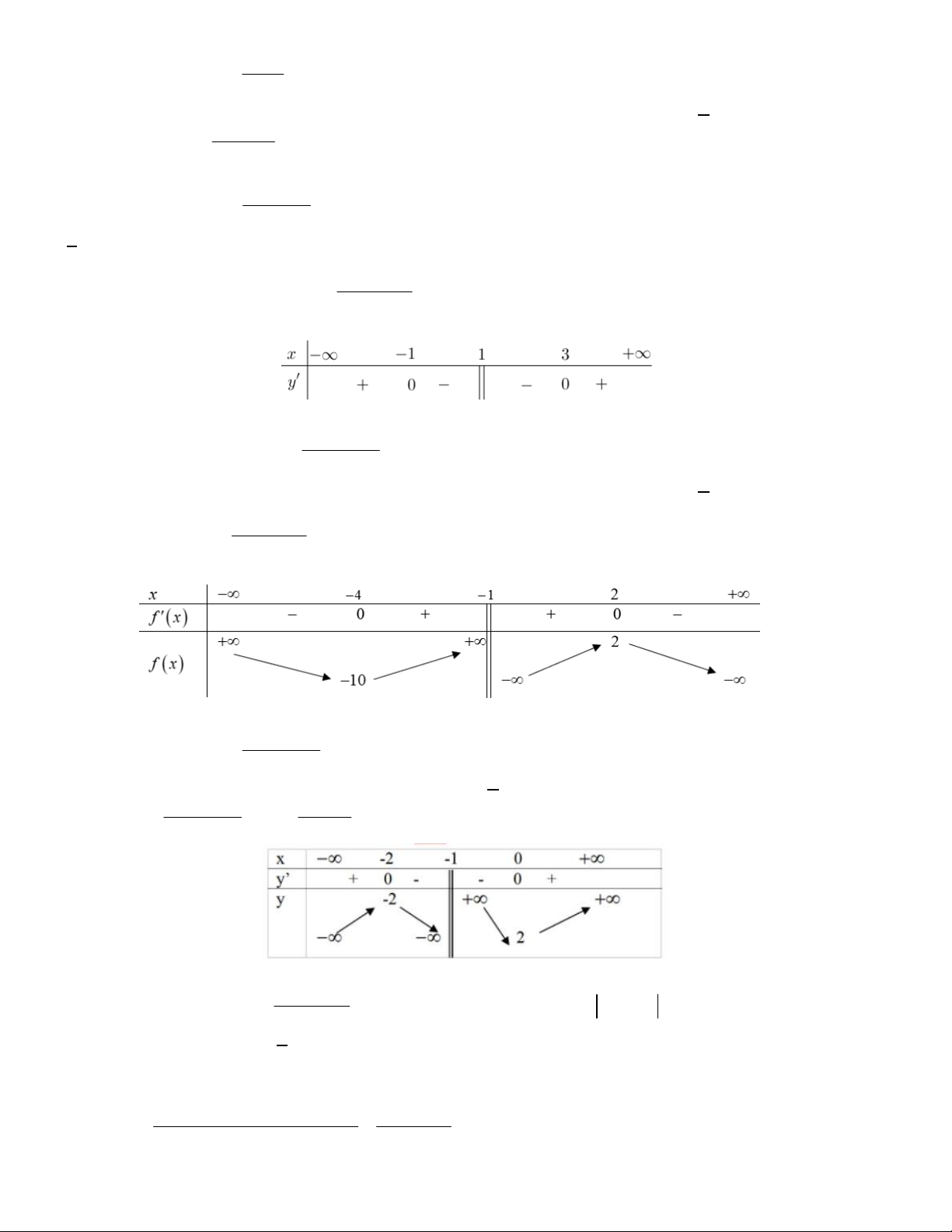
Bài toán 1. Cho hàm số f x có bảng xét dấu của f  x như hình vẽ
Hàm số đã cho đạt cực đại tại A. x  3  . B. x  1  . C. x  1. D. y  1.
Lời giải. Dựa vào bảng biến thiên thì đạo hàm đổi dấu từ dương sang âm tại x  1
 , đây là điểm cực đại.
Bài toán 2. Cho hàm số y f x xác định trên  và có bảng xét dấu của đạo hàm như sau.
Khi đó số điểm cực trị của hàm số y f x là A. 3 . B. 2 C. 4 . D. 1.
Lời giải. Đạo hàm đổi dấu 3 lần nên ta có 3 cực trị.
Bài toán 3. Cho hàm số y f x có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng A. 4  . B. 0 . C. 1. D. 3  .
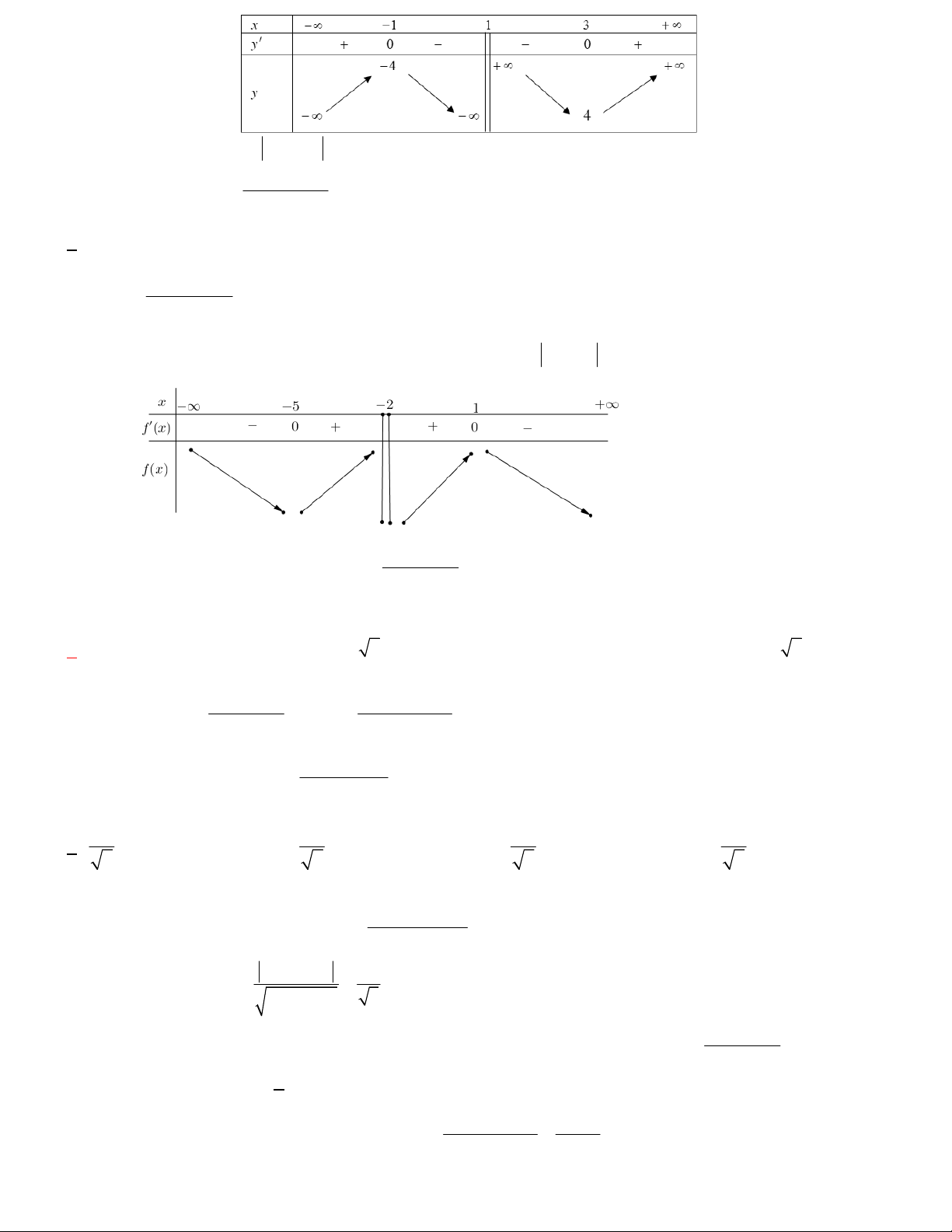
Bài toán 4. Cho hàm số y f x có bảng biến thiên như sau:
Số điểm cực trị của hàm số đã cho A. 3 . B. 2 . C. 1. D. 4 .
Lời giải. Dựa vào bảng biến thiên thì Số điểm cực trị của hàm số đã cho là 3 .
Bài toán 5. Cho hàm số y f x có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng A. 2 . B. 3 . C. 1. D. 2  . Lời giải
Dựa vào bảng biến thiên thì giá trị cực đại của hàm số là 2 .
Bài toán 6. Cho hàm số f x có bảng xét dấú 4
Hàm số đạt cực tiểu tại A. x  1  . B. x  0 . C. x  1. D. x  2 .
Lời giải. Hàm số đạt cực tiểu tại điểm y đổi dấu từ âm sang dương
Bài toán 7. Cho hàm số y f x có bảng biến thiên như sau:
Điểm cực đại của hàm số đã cho bằng: 4 4 A. . B. . C. 2 . D. 0 . 27 3 4
Lời giải. Dựa vào bảng biến thiên thì điểm cực đại của hàm số đã cho là: x  . 3
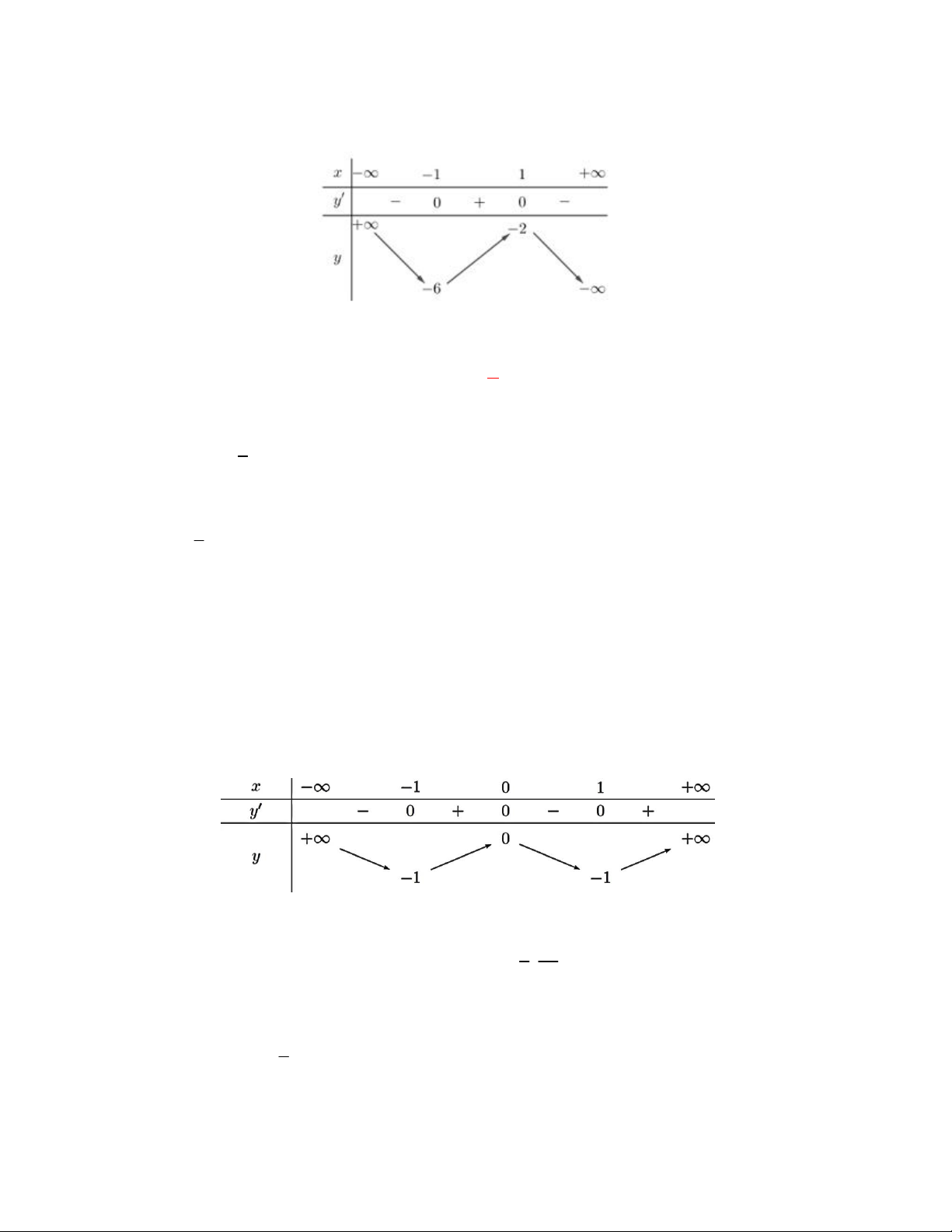
Bài toán 8. Cho hàm số y f x có bảng biến thiên như sau 0 +∞ x 1 -∞ y' 0 + + +∞ 0 y ∞ -1
Mệnh đề nào sau đây đúng?
A.Hàm số có đúng một cực trị.
B. Hàm số đạt cực đại tại x  0 và đạt cực tiểu tại x  1.
C.Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng 1.
D.Hàm số có giá trị cực tiểu bằng 1. Lời giải
Dựa vào bảng biến thiên ta thấy hàm số đạt cực đại tại x  0 và đạt cực tiểu tại x  1.
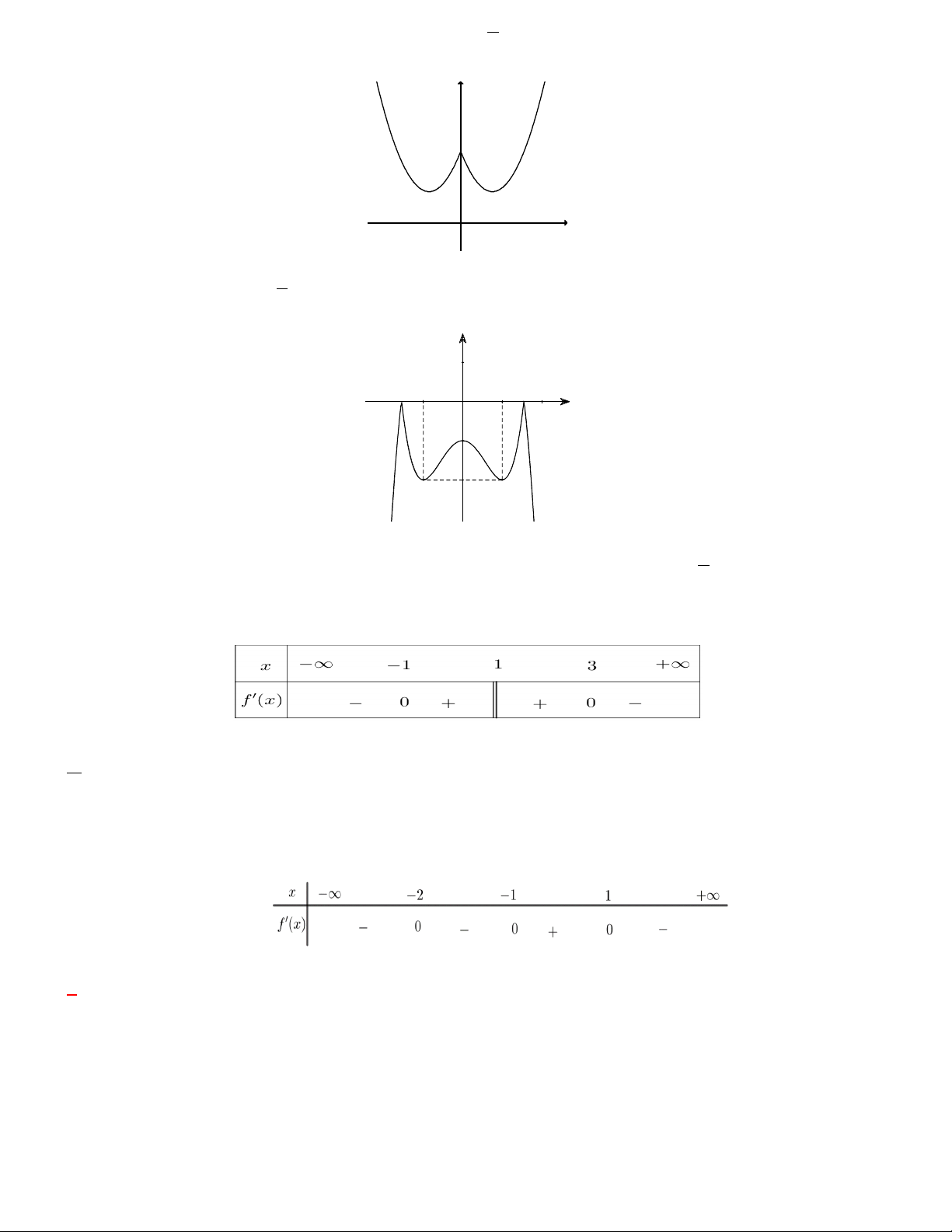
Bài toán 9. Cho hàm số y f x xác định, liên tục trên đoạn 2; 2 và có đồ thị là đường cong trong hình vẽ bên. 4 y 2 x -2 1 -1 O 2 -2 -4
Hàm số f x đạt cực đại tại điểm nào dưới đây ? A. x  2 B. x  1 . C. x  1 . D. x  2 .
Bài toán 10. Cho hàm số f x có đồ thị như hình vẽ
Hàm số có bao nhiêu điểm cực trị 5 A. 0 B.1. C. 2 . D. 3 .
Lời giải. Đồ thị hàm số đổi chiều 2 lần ta được 2 điểm cực trị
Bài toán 11. Cho hàm số f x có đồ thị như hình vẽ y x O
Hàm số đã cho có bao nhiêu điểm cực tiểu A. 3 . B. 2 . C. 1. D. 0 .
Bài toán 12. Cho hàm số y f x liên tục trên  và có đồ thị như hình bên. y -1 O 1 x -1 -2
Hỏi hàm số có bao nhiêu điểm cực trị? A. 2 . B. 3 . C. 4 . D. 5 . Lời giải
Đồ thị hàm số y f x đổi chiều 5 lần nên hàm số có 5 cực trị.
Bài toán 13. Cho hàm số y f x liên tục trên  và có bảng xét dấu đạo hàm như sau:
Hỏi hàm số y f x có bao nhiêu điểm cực trị? A. 2 . B. 1. C. 3. D. 3. Lời giải
Vì hàm số y f x liên tục trên  và f  x đổi dấu 2 lần nên hàm số đó có 2 điểm cực trị.
Bài toán 14. Cho hàm số f x có đạo hàm trên  và có bảng xét dấu f  x như sau
Mệnh đề nào sau đây sai?
A. Hàm số y f x đạt cực trị tại x  2  .
B. Hàm số y f x đạt cực đại tại x  1.
C. Hàm số y f x đạt cực tiểu tại x  1  .
D. Hàm số y f x có hai điểm cực trị. Lời giải
Đạo hàm đổi dấu tại điểm x  2
 nên hàm số đạt cực trị tại x  2  . 6
CỰC TRỊ HÀM SỐ ĐA THỨC
Bài toán 1. Tìm giá trị cực tiểu y của hàm số 3 y x  3x4 . CT A. y  6  B. y  1  C. y  2  D. y 1 CT CT CT CT Lời giải
Tập xác định: D   ; 2 y  3
x 3; y  0  x  1. Bảng biến thiên Vậy yy  1  2 ; yy    . CT   1 6 CD
Bài toán 2. Gọi x là điểm cực đại, x là điểm cực tiểu của hàm số 3
y  x  3x  2 . Tính x  2x . 1 2 1 2 A. 2 . B. 1. C. 1  . D. 0 . Lời giải. Ta có 2 y  3
x  3  0  x  1  ; x  1.
Lập bảng xét dấu đạo hàm ta có cực đại, cực tiểu lần lượt là x  1; x  1
  x  2x  1  . 1 2 1 2 1 Bài toán 3. Hàm số 3 2 y
x x  3x  1 đạt cực tiểu tại điểm 3 A. x  1  . B. x  1 . C. x  3  . D. x  3 . Lời giải 1 Ta có hàm số 3 2 y
x x  3x  1 có tập xác định D   . 3  x  1 2
y  x  2x  3; y  0   . x  3  
y  2x  2 ; y3  4
  0 ; y 
1  4  0 . Suy ra hàm số đạt cực tiểu tại điểm x  1 .
Bài toán 4. Tìm số điểm cực trị của hàm số 4 2
y x  2x . A. 2. B. 4. C. 3. D. 1. Lời giải x  0
Tập xác định: D   . Đạo hàm 3
y  4x  4x  0   . x  1   Bảng biến thiên:
Dựa vào bảng biến thiên suy ra hàm số có 3 điểm cực trị.
Bài toán 5. Điểm cực tiểu của đồ thị hàm số 3 2
y  x x  5x  5 là  5 40  A.  1  ; 8   B. 0; 5   C. ;   D. 1; 0  3 27  Lời giải x  1 2 y 3x 2x 5 0         5 .  x   3
y  6x  2 .
Ta có: y 
1  8  0  Hàm số đạt cực tiểu tại x  1  ; yy . CT   1  8
Vậy điểm cực tiểu của đồ thị hàm số là  1  ; 8 .
Bài toán 6. Tính tổng các cực trị của hàm số 3
y x  3x  6 . 7 A.1 B. 2 C. 0 D. 4 Lời giải Ta có 2
y  3x  3  0  x  1
 ; x  1 . Tổng các cực trị bằng 0.
Bài toán 7. Cho hàm số y f (x) có đạo hàm 2 f (
x)  x(x  2) , x   . Số điểm cực trị của hàm số đã cho là A. 0 . B. 3 . C. 2 . D. 1. Lời giải x  0  x  0 Ta có: 2 f (
x)  0  x(x  2)  0     x  2  0 x  2   Bảng biến thiên:
Dựa vào bảng biến thiên, ta thấy hàm số có 1 điểm cực trị x  0 . 1
Bài toán 8. Tìm điểm cực tiểu của đồ thị hàm số 3 2 y
x  2x  3x 1 . 3  7  A. 3;  1 . B. x  3 . C. 1;   . D. x  1 .  3  1 Lời giải. 3 2 2 y
x  2x  3x 1  y  x  4x  3  0  x 1;  3 . 3
Đạo hàm đổi dấu từ âm sang dương tại điểm x  3 nên x  3 là điểm cực tiểu. 1
Bài toán 9. Tìm giá trị thực của tham số m để hàm số 3 2 y
x mx   2
m  4 x  3 đạt cực đại tại x  3. 3 A. m  1  B. m  7  C. m  5 D. m  1 Lời giải Ta có 2
y  x mx   2 2
m  4 ; y  2x  2m . 1  y  3  0 Hàm số 3 2 y
x mx   2
m  4 x  3 đạt cực đại tại x  3 khi và chỉ khi:  3 y  3  0 
m  1L 2 2 9
  6m m  4  0
m  6m  5  0     
 m  5TM  . 6 2m 0 m 3       m  3 
Vậy m  5 là giá trị cần tìm.
Bài toán 10. Đồ thị hàm số 3 2
y x  3x 1 có điểm cực tiểu là A, tính khoảng cách từ A đến trục hoành A.2 B. 3 C. 4 D. 2 Lời giải. x  0 3 2 2
y x  3x 1  y  3x  6x  3x(x  2)  0   x  2 
Điểm cực tiểu của đồ thị là A2; 3
  . Khoảng cách từ A đến trục hoành bằng 3.
Bài toán 11. Hàm số nào sau đây có hai điểm cực trị cùng dương ? A. 3 2
y x  3x 1 B. 4 2
y x  4x 1 C. 4 2
y x  2x 1 D. 3 2
y x  4x  5x 1. Lời giải. x  0 Hàm số 3 2 2
y x  3x 1  y  3x  6x  3x(x  2)  0   , 1 cực trị dương. x  2  8 Hàm số trùng phương 4 2 3 2 2
y x  4x 1  y  4x  8x  4x (x  2) , hàm số có 1 cực trị dương. Hàm số trùng phương 4 2
y x  2x 1có 3 cực trị, trong đó 1 cực trị dương. 5 3 2 2
y x  4x  5x 1  y  3x  8x  5; y  0  x  1; x
, hàm số có 2 cực trị dương. 3
Bài toán 12. Khoảng cách giữa hai điểm cực trị của đồ thị hàm số 3
y x  2x 1 bằng 10 6 10 10 6 10 6 A. . B. . C. . D. . 3 3 3 9 Lời giải. 2  2 9  4 6   2 9  4 6  3 2
y x  2x 1  y  3x  2  0  x    A ;  , B   ;  . 3  3 9   3 9        2 8 6  10 6
Khi đó AB   2 ;   AB  .  3 9  9  
Bài toán 13. Cho hàm số y f x  có bảng biến thiên như dưới đây
Tung độ điểm uốn (trung điểm hai điểm cực đại, cực tiểu) của đồ thị hàm số bằng A.2 B. 1 C. 3 D. 4 Lời giải.  1 
Trung điểm hai điểm cực trị là I ; 2   . Tung độ bằng 2.  2 
Bài toán 14. Biết đồ thị hàm số 3 2
y x  6x  9x  2 có hai điểm cực trị là Ax ; y và B x ; y . Khẳng định 2 2  1 1  nào sau đây không đúng? A. y y  4  . B. AB  4 2 .
C. y   y .
D. x x  2 . 1 2 1 2 1 2 Lời giải.
x  1  y  2 3 2 2
y x  6x  9x  2  y  3x 12x  9  0   .
x  3  y  2   
Hai điểm cực trị là A1; 2, B 3; 2
   AB  2; 4  AB  4 2 .
Bài toán 15. Đồ thị hàm số nào sau đây có đúng hai điểm cực trị và hai điểm cực trị nằm khác phía với trục tung A. 3 2
y x  3x 1 B. 4 2
y x  4x 1 C. 3 2
y x  2x  5x  5 D. 3 2
y x  4x  5x 1.
Lời giải. Hai điểm cực trị trái dấu, hàm số 3 2
y x  2x  5x  5 có đạo hàm 2
y  3x  4x  5 nên có hai nghiệm trái dấu.
Bài toán 16. Đường cong 3 2
y x  3x có các điểm cực trị A, B. Tính khoảng cách d từ điểm C 3; 4 đến đường thẳng AB. A. d  5 . B. d  2 5 . C. d  26 . D. d  4 3 . Lời giải.
x  0  y  0 3 2 2
y x  3x y  3x  6x  3x(x  2)  0  
x  2  y  4 
Hai điểm cực trị là A0;0, B 2; 2
    AB : y kx k  2  y  2x  2x y  0 . 2.3  4
Khi đó d d C, (AB)   2 5 . 5 9
CỰC TRỊ HÀM SỐ PHÂN THỨC HỮU TỶ 2
Bài toán 1. Hàm số y
nghịch biến trên khoảng nào dưới đây? 2 x  1 A. x  1  . B. x  1 . C. x  3  . D. x  0 . 4x
Lời giải. Ta có y 
 0  x  0 . Hàm số đạt cực trị tại điểm  2 2 x  1 2 x x  4
Bài toán 2. Hàm số y
có tổng hai cực trị bằng x 1 A.2 B. 0 C. 1 D. – 2 Lời giải 2 x  2x  3  x  1
Tập xác định: D   \   1 . Ta có 2 y 
, y  0  x  2x  3  0   .  x  2 1 x  3  Bảng xét dấu đạo hàm
Từ bảng xét dấu y ta có tổng hai cực trị bằng 2. 2 x  2x  6
Bài toán 3. Cho hàm số f x 
. Tổng hai giá trị cực trị của hàm số bằng x 1 A.4 B. 3 C. 8 D. – 8 Lời giải 2 x  2 x  8  x  2
Đạo hàm f   x 2  0 
 0  x  2 x  8  0  .   x  12 x  4  Bảng biến thiên:
Vậy hàm số f x  có tổng 2 giá trị cực trị bằng – 8. 2 x  2x  2
Bài toán 4. Hàm số y
có giá trị cực đại bằng x  1 A.3 B. 2 C. – 2 D. 0 2 x  2x  2 2 x  2x
Lời giải. y   y 
; y  0  x  0; x  2 . Bảng biến thiên x  1 (x  2 1)
Hàm số có giá trị cực đại bằng – 2. 2 x  2x  5
Bài toán 5. Cho hàm số y
có hai giá trị cực trị y , y . Giá trị y  2y có thể bằng x 1 1 2 1 2 A.0 B. 12 C. 10 D. – 14 Lời giải
Tập xác định: D  \  1 .
2x  2 x   1   2
x  2x  5 2 x  2x  3 x  1 Ta có y  
. Giải phương trình y  0   .  x  2 1  x  2 1 x  3  Bảng biến thiên 10
Từ bảng biến thiên ta thấy y  2y có thể bằng 12. 1 2 2 x  2x 1
Bài toán 6. Hàm số y
có hai điểm cực trị A, B . Gọi M, N là hình chiếu của A, B trên trục hoành. x  2
Tính độ dài đoạn thẳng MN . A.6 B. 4 C. 8 D. 8 Lời giải 2
x  4x  5  x  1 Ta có y 
. Giải phương trình y  0   .  x  22 x  5  
Bảng biến thiên như sau. Dựa vào bảng biến thiên, ta thấy MN  1  (5)  6 . 2 x  4x  5
Bài toán 7. Biết đồ thị C  của hàm số y
có hai điểm cực trị. Đường thẳng đi qua hai điểm cực trị x 1
của đồ thị C  cắt trục hoành tại điểm M có hoành độ x bằng M A. x  2 . B. x  1 2 . C. x  1 . D. x  1 2 . M M M Mx x   2 2 x  4x  5 4 5 
Lời giải. Ta có y   d : y
 2x  4; d Ox y  0  x  2 . x 1  x  1   2
x  2x m
Bài toán 8. Đồ thị hàm số y
có hai điểm cực trị A, B . Tính khoảng cách từ gốc tọa độ O đến x  2
đường thẳng đi qua hai điểm AB . 2 1 3 4 A. B. C. D. 5 5 5 5 Lời giải.
x  2x m/ 2
Phương trình của đường thẳng AB là y
y  2x  2  2x y  2  0 .  x  2/ 2.0  0  2 2 Khoảng cách d  ; O AB   .   2 2 5 2 1 2 x  2x  3
Bài toán 9. Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y  . 2x 1
A. y  2x  2 .
B. y x 1.
C. y  2x 1.
D. y  3x 1  2 
x  2x  3 2x  2
Lời giải. Đường thẳng đi qua hai điểm cực trị là y    x 1.  x   2 2 1 11
CỰC TRỊ HÀM SỐ CHỨA CĂN
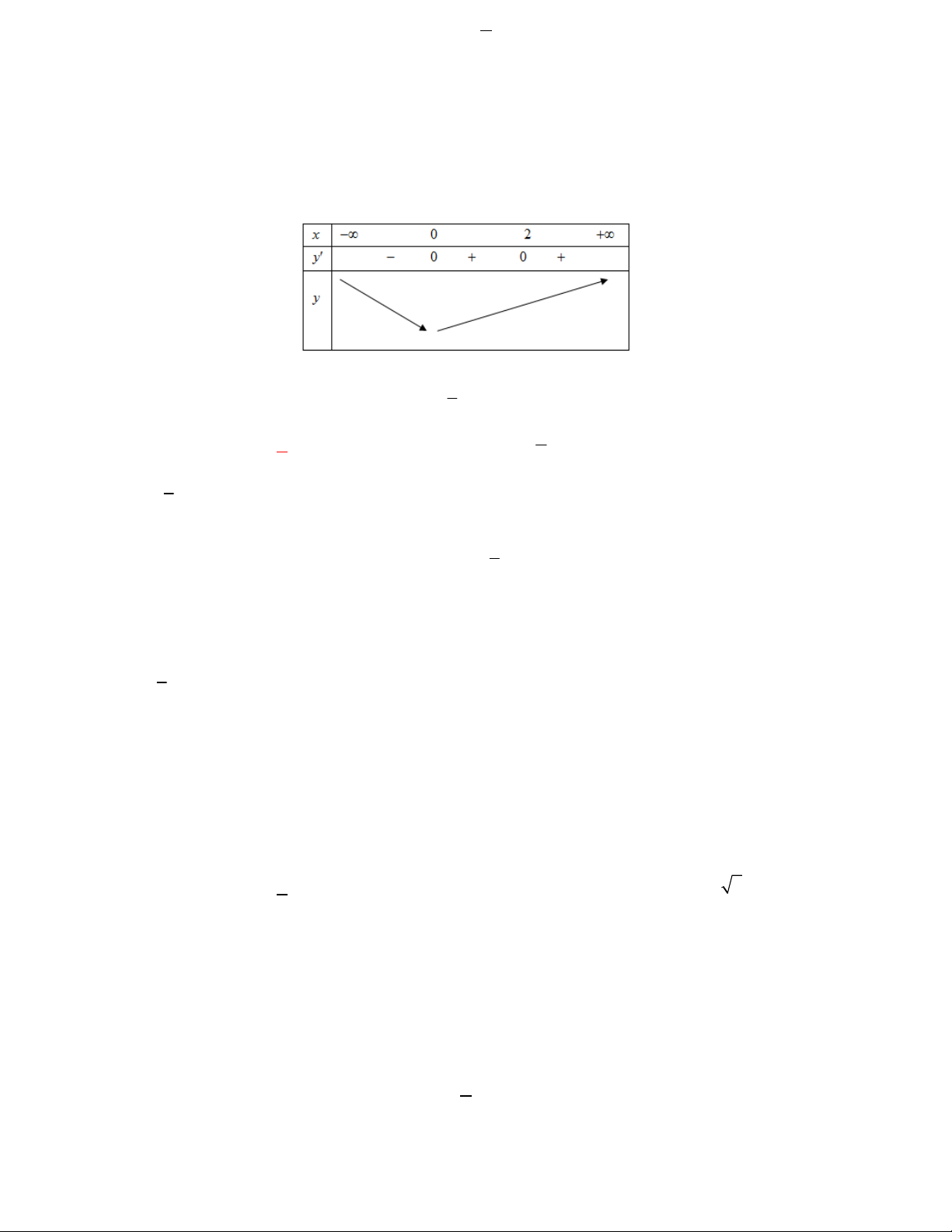
Bài toán 1. Tìm số điểm cực đại của hàm số 2 y
x  4x 10 . A.3 B. 2 C. 1 D. 3 2x  4 x  2 Lời giải. 2 y
x  4x 10  y   . 2 2 2 x  4x 10 x  4x 10
Bài toán 2. Số điểm cực trị của hàm số 2
y x  2x 1 là A. 1. B. 2. C. 3. D. 0. Lời giải Ta có 2x 2
y x  2x 1  y  1 ; 2 2x 1 2 2
2x 1  4x 1 2 y  0 
2x 1  2x    x   x  0 2  Hàm số có 1 cực trị.
Bài toán 3. Tìm số cực tiểu của hàm số 2
y x x  2x A.2 B. 3 C. 1 D. 0 Lời giải 2x  2 2
x  2x x x   2 1 2x  3x Ta có: 2
y x x  2x 2  y '  x  2x  . x   . 2 2 x  2x 2 2 x  2x x  2x 3
Do đó: y  0 tương đương 2
2x  3x  0  x  0; x   . 2
Hai nghiệm đơn và thỏa mãn TXĐ nên hàm có 1 cực tiểu.
Bài toán 4. Hàm số 2
y  2x x đạt cực đại tại điểm A. x  1  . B. x  1 . C. x  0 . D. x  2 . Lời giải
Tập xác định 0;2 .  2  2x x 2  2x 1 x 2  Ta có y
2x x y   
; y  0  x  1 2 2 2 2 2x x 2 2x x 2x x
Đạo hàm đổi dấu từ dương sang âm nên x  1 là điểm cực đại.
Bài toán 5. Hàm số 2 y
x  8x 19 đạt cực trị tại A. x  2 B. x  3 C. x  1 D. x  4  2
(x  8x 19) 2x  8 x  4
Lời giải. y   
; y  0  x  4 . 2 2 2 2 x  8x 19 2 x  8x 19 x  8x 19
Bài toán 6. Số điểm cực trị của hàm số 2
y x  2x 1 là A. 1. B. 2. C. 3. D. 0. Lời giải Ta có 2x 2
y x  2x 1  y  1 ; 2 2x 1 2 2
2x 1  4x 1 2 y  0 
2x 1  2x    x   x  0 2  Hàm số có 1 cực trị.
Bài toán 7. Tìm một điểm cực trị của hàm số 2 y  1 x . A. y  1. B. x  0 . C. y  0 . D. x  1. Lời giải 2 (1 x ) 2  xx Tập xác định  1   ;1 . Ta có 2
y  1 x y   
; y  0  x  0 . 2 2 2 2 1 x 2 1 x 1 x 12
Bài toán 8. Hàm số 2 y
x  2x  5 đạt cực trị tại A. x  3  . B. x  1  . C. x  1. D. y  1. Lời giải
Hàm số luôn xác định. x 1
Ta có đạo hàm y   0  x  1
 . Hàm số đạt cực trị tại x  1  . 2 x  2x  5
Bài toán 9. Hàm số 2 y
x  6x 10 đạt cực trị tại điểm A. x  3  B. x  3 C. x  1 D. x  5 Lời giải
Hàm số luôn xác định. 2
(x  6x 10) 2x  6 x  3 2 y
x  6x 10  y   
; y  0  x  3  . 2 2 2 2 x  6x 10 2 x  6x 10 x  6x 10
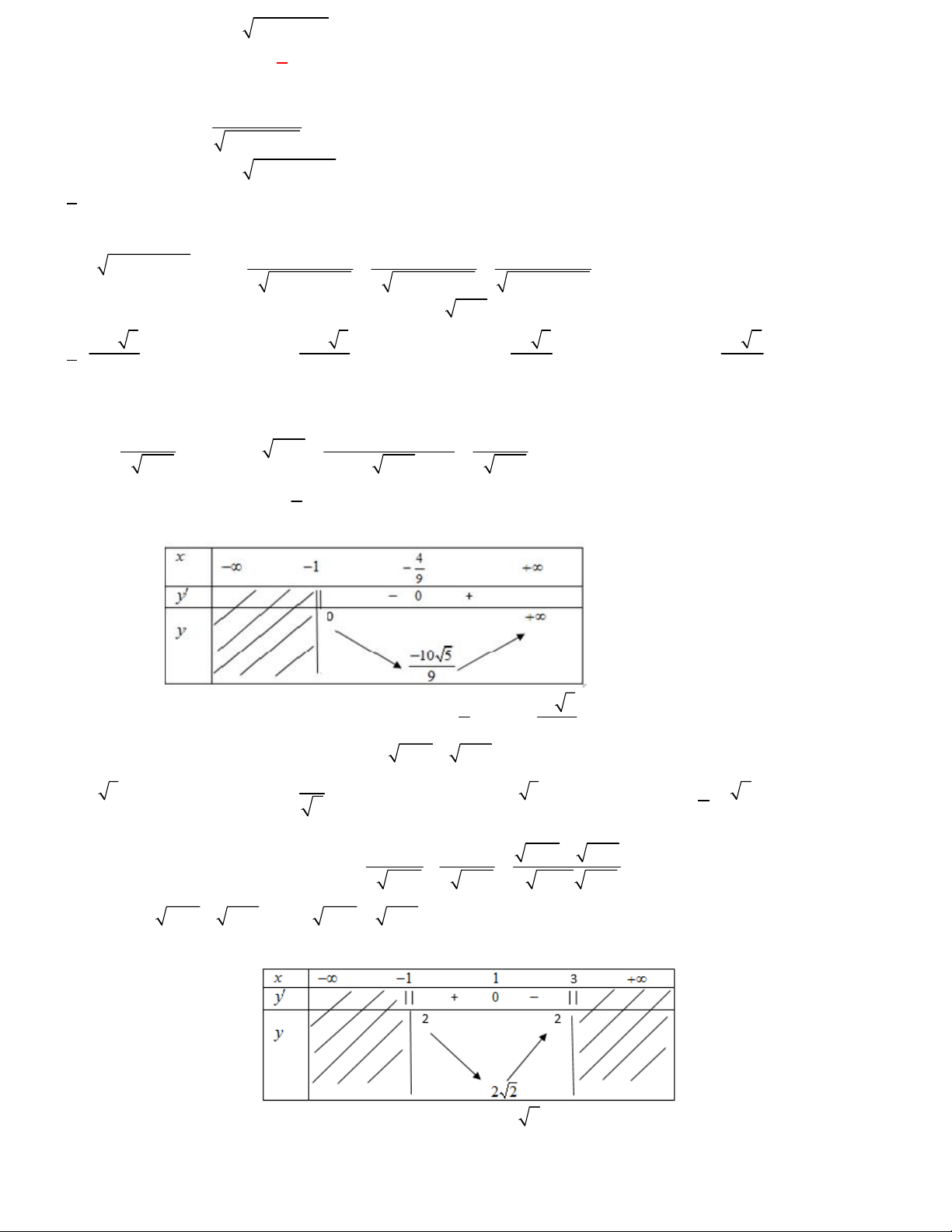
Bài toán 10. Giá trị cực tiểu của hàm số y  3x  2 x 1 bằng 10  5 10  3 6  3 8  2 A. B. C. D. 9 9 9 9 Lời giải.
Tập xác định: D   1  ;  . 1
3x  2  3.2. x   1 9x  4 +) y 
.3x  2  3 x 1   . 2 x 1 2 x 1 2 x 1 4
+) y  0  9x  4  0  x   . 9 +) Bảng biến thiên 4 10 5
Từ bảng biến thiên suy ra hàm số đạt cực tiểu tại x   , y   . 9 CT 9
Bài toán 11. Giá trị cực tiểu của hàm số y  3  x x 1 bằng 1 A. 4 5 B. C. 3 3 D. 2 2 5 Lời giải. 1  1
3  x x 1
Tập xác định: D   1  ; 
3 . Đạo hàm y    . 2 3  x 2 x 1 2 3  . x x 1 x  1  x  1
+) y  0  3  x x 1  0  3  x x 1      x  1.
3  x x 1 2x  2   +) Bảng biến thiên:
Từ bảng biến thiên suy ra hàm số đạt cực tiểu tại x  1, y  2 2 . CT 13
CỰC TRỊ HÀM SỐ LƯỢNG GIÁC, HÀM SỐ MŨ, HÀM SỐ LOGARIT Bài toán 1. Hàm số 2 x x y e
e đạt cực trị tại điểm 1 A. x  3 . B. x   ln 2 . C. x   ln 2 . D. x  1  . 2 x x x x 1 Lời giải. 2 y  2e
e  0  2e 1  0  e
x   ln 2 . 2
Bài toán 2. Hàm số y  cos x  sin x có cực trị tại x . Giá trị tan x khi đó bằng 0 0 A.2 B. 1 C. – 1 D. 0 Lời giải
y  cos x  sin x    sin x  cos ;
x y  0   sin x  cos x  0
 sin x   cos x  tan x  1   tan x  1  0
Bài toán 3. Tìm số điểm cực trị của hàm số 1 2 x y e   . A.2 B. 1 C. 3 D. 0
Lời giải. Ta thấy 1 2 2 x y e    
nên hàm số không có cực trị.
Bài toán 4. Tính giá trị cực tiểu của hàm số y   2
ln x  2x 10 . A.3 B. 2 ln 3 C. 3ln 2 D. 2 ln 2 Lời giải 2x  2 Tập xác định ;  y  ln  2
x  2x 10  y   0  x  1. 2 x  2x 10
Đạo hàm đổi dấu từ âm sang dương nên hàm số đạt cực tiểu tại x  1  y  ln 9  3ln 2 . 2 5
Bài toán 5. Hàm số 3x x y  
tại cực trị tại điểm 5 A. x  . B. x  3  . C. x  1. D. x  1  . 2 Lời giải 2 2 u u 2  x 5x x 5 x
Công thức tổng quát a   u .a ln a y   x  5x 3
ln 3  2x  53 ln 3 . 5 5
y  0  x
. Đạo hàm đổi dấu tại đây nên hàm số đạt cực trị tại x  . 2 2
Bài toán 6. Tìm số điểm cực trị của hàm số 2 x   4 x y e e . A.2 B. 1 C. 3 D. 4 x x x x x 1 Lời giải. 2 2 2 y e
 4e y  2e
 4e  0  e
 2  2x  ln 2  x  ln 2 2
y  0  x  2 , đạo hàm đổi dấu từ âm sang dương nên hàm số đạt cực tiểu tại x  2 .
Bài toán 7. Tìm số điểm cực trị của hàm số y  log  2
x  2x  5 . 3  A.3 B. 2 C. 1 D. 4 Lời giải  2
x  2x  5' 2x  2 Ta có y '  
; y  0  x  1 . Hàm số có 1 cực trị.  2
x  2x  5ln 3  2
x  2x  5ln 3
Bài toán 8. Tìm số cực tiểu của hàm số y   2
ln x  4x 12 . A.2 B. 1 C. 3 D. 4 Lời giải x y  ln  2 4 2
x  4x 12  y 
; y  0  2x  4  0  x  2 . 2 x  4x 12
Đạo hàm đổi dấu từ âm sáng dương nên hàm số có 1 cực tiểu. 1
Bài toán 9. Tìm số cực trị thuộc khoảng 0; 2  của hàm số y  sin x x . 3 A.3 B. 4 C. 2 D. 1 Lời giải. 14 1 1
y  cos x   0  cos x
. Phương trình này có 2 nghiệm trong khoảng 0; 2  . Hàm có 2 cực trị. 3 3
Bài toán 10. Có bao nhiêu số nguyên m để hàm số y  3sin x  4 cos x mx  4 có cực trị A.11 B. 10 C. 9 D. 6 Lời giải.
y  3sin x  4 cos x mx  4  y  3cos x  4 sin x m  0  m  3cos x  4 sin x . 2 Theo BĐT Bunyakovsky có  x x   2 2   2 2 3cos 4 sin 3 4
sin x  cos x  25  5
  3cos x  4 sin x  5 .
Bài toán 11. Tìm số điểm cực trị thuộc khoảng 0; 4  của hàm số y  2sin x x 2  4 . A.3 B. 2 C. 1 D. 4 2
Lời giải. y  2sin x x 2  4  y  2 cos x  2  0  cos x   . 2
Trên khoảng 0; 4  , vẽ 2 vòng tròn lượng giác ta thu được 4 nghiệm dẫn đến 4 điểm cực trị.
Bài toán 12. Tính độ dài đoạn thẳng OA với A là điểm cực tiểu của đồ thị hàm số y   2
ln x  8x 17 . A. OA  3 B. OA  4 C. OA  5 D. OA  6 Lời giải 2x  8 Ta có y 
; y  0  x  4  y  ln1  0  A4;0  OA  4 . 2 x  8x 17
Bài toán 13. Tìm số điểm cực trị của hàm số f x trên 0; 4 x
 biết rằng f  x  e  3sin 2x  1 . A.3 B. 2 C. 4 D. 1 Lời giải x  ln 3 x  ln 3 f x 0
xe 3sin2x 1         0       2x   2kx   k   2  4 Trên 0; 4 
 (2 vòng tròn lượng giác) ta thu được 5 điểm cực trị.
Bài toán 14. Tìm tất cả cả điểm cực trị của hàm số y  cos x  3 sin x x .    A. x  
k 2 ; x
k 2 k   . B. x   k 2 k   . 6 2 6    C. x    k ; x
k k   .
D. x k 2 ; x
k 2 k   . 6 2 3 Lời giải 1 3 1      
y  sin x  3 cos x 1 . Giải phương trình sin x  3 cos x  1  sin x  cos x   sin x   sin     2 2 2  3   6       x    k 2 x    k 2  3 6  6     k  .     xk 2      x   k 2  3 6  2
Bài toán 16. Tính tổng các cực trị của hàm số x y e  2
x  2x  3 . A.3 B. – 4 C. – 2 D. 1 Lời giải Ta có x y e  2
x  2x  3 x
y  e  2
x  2x  3  2x  2 x e y  0 xe  2 x  4x   2
1  0  x  4x 1  0
Tổng các cực trị bằng – 4 (theo hệ thức Viet).
Bài toán 17. Giá trị cực tiểu của hàm số y  ln  x  2 x  6nằm trong khoảng nào sau đây A. 1; 2 B. 3; 4 C. 4;5 D. 2;3 15 Lời giải. 1 1 x
Tập xác định R. y 
; y  0  x  1. x  2 x  6 x x
Bài toán 18. Tìm tất cả các giá trị của tham số m để hàm số y  2m cos  2sin
 5x  20 có cực trị 2 2 m  2 m  2 A.  B.  C. 2  m  2 D. 2  m  2 m  2   m  2   Lời giải. x x x x y  2  m cos  2sin
 5x  20  y  m sin  cos  5 . 2 2 2 2 x x
y  0  m sin  cos
 5 . Điều kiện có cực trị là phương trình có nghiệm (không kép): 2 2 m  2 2 m 1  5   m  2 
Bài toán 19. Tìm số cực trị của hàm số f x 2
 ln x  2x . A.2 B. 3 C. 4 D. 1 Lời giải 2 1 1 4x 1
Điều kiện x  0; f x 2
 ln x  2x f  x   4x
. Khi đó f  x  0  x  . x x 2
Đạo hàm đổi dấu qua đây nên hàm số có 1 cực trị.
Bài toán 20. Gọi M là điểm cực tiểu của hàm số 2 x   2 x y e
e  5 . Điểm M nằm trên đường thẳng nào sau đây 1 3
A. y x  3 . B. y  7x  2 . C. y   x  .
D. x  2 y  3  0 . 2 2 Lời giải ee ee ee x x  2x 2 x 5 2 x x 2 2 2 x x 2 y e
 2e  5  y    2 x x 2 x x 2 2 e  2e  5 2 e  2e  5 x e  2 x e  5 2 y  0 x x xe
e e  1  x  0  y  2  M 0; 2
Đạo hàm đổi dấu từ âm sang dương nên hàm số đạt cực tiểu tại x  0 .
Điểm M này thuộc đường thẳng y  7x  2 . 3 2
Bài toán 21. Tìm số điểm cực trị của hàm số x 3x 3x 1 y e     . A.2 B. 3 C. 1 D. 0 Lời giải  3 2 
x x x        3 2
x x x e x x e     x  2 3 3 1 2 3 3 1 0 3 6 3 0 1
 0  x  1 (nghiệm kép).
Hàm số không có cực trị.
Bài toán 22. Hàm số x
y e .sin 2x đạt cực trị tại điểm x . Khi đó 0 1 1 A. tan 2x  B. tan 2x  2 C. tan 2x   D. tan x  3  0 2 0 0 2 0 Lời giải.
Theo công thức đạo hàm tích ta có x  .sin 2 x    .2cos 2 x  .sin 2 x y e x y e x e
x e sin 2x  2cos 2x . x x sin 2
y  0  e sin 2x  2cos 2x  0  sin 2x  2cos 2x   2
  tan 2x  2 . Như vậy tan 2x  2 . cos 2x 0 16
PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI TOÁN KHẢO SÁT HÀM SỐ LỚP 12 THPT
CỰC TRỊ CỦA HÀM SỐ
XÁC ĐỊNH CỰC TRỊ CỦA CÁC HÀM SỐ PHỨC TẠP
_____________________________________
ĐƯỜNG THẲNG ĐI QUA HAI ĐIỂM CỰC TRỊ
Bài toán 1. Đồ thị hàm số y  3 x  2
3x  9x  1 có hai cực trị A và B . Điểm nào dưới đây thuộc đường thẳng AB ? A. M 0;   1 B. N 1; 10 C. P1;0 D. Q1;10 Lời giải Ta có: y  2
3x  6x  9 thực hiện phép chia y cho y ta được số dư là y  8x  2 .
Như thế điểm N 1; 10 thuộc đường thẳng AB.
Bài toán 2. Tìm giá trị thực của tham số m để đường thẳng d : y  2m 1 x  3  m vuông góc với đường
thẳng đi qua hai điểm cực trị của đồ thị hàm số 3 2
y x  3x 1. 3 3 1 1 A. m  B. m  C. m   D. m  2 4 2 4 Lời giải Ta có 2
y  3x  6x . Từ đó ta có tọa độ hai điểm cực trị A 0;1 , B 2; 3 . Đường thẳng qua hai điểm cực trị có phương trình y  2
x 1. Đường thẳng này vuông góc với đường thẳng y  2m 1 x  3  m khi và chỉ khi 3 2m   1 2  1   m  . 4
Bài toán 3. Tìm giá trị thực của tham số m để đường thẳng y  2m 1 x m  3 song song với đường thẳng
đi qua các điểm cực trị của đồ thị hàm số 3 2
y x  3x 1 3 1 3 1 A. m  . B. m  . C. m   . D. m   . 4 2 4 2 Lời giải x  0 Hàm số 3 2
y x  3x 1 có TXĐ: ; 2
y  3x  6x ; y '  0   x  2  
Suy ra đồ thị hàm số có hai điểm cực trị là A 0;1 , B2;  3  AB  2; 4   . x y 1
Đường thẳng d đi qua hai điểm A , B có phương trình:   y  2  x 1. 2 4 2m 1  2 1
Đường thẳng y  2m 1 x m  3 song song với đường thẳng d    m   . m  3  1 2 
Bài toán 4. Đồ thị của hàm số 3 2
y x  3x  9x 1 có hai điểm cực trị A và B . Điểm nào dưới đây thuộc đường thẳng AB . A. P 1; 0 . B. M 0; 1 . C. N 1; 10 . D. Q 1;10 . Lời giải TXĐ: D   . 2
y '  3x  6x  9 .
x  1  y  6 2
y '  0  3x  6x  9  0  
x  3  y  26   
Ta có A 1; 6, B 3; 26  AB  4; 3
 2 nên ) Chọn n  8  ;1 . AB
Phương trình đường thẳng AB là: 8  x  
1  1 y  6  0  8x y  2  0 .
Thay tọa độ các điểm P, M , N , Q vào phương trình đường thẳng AB ta có điểm N 1; 10 thuộc đường thẳng.
Bài toán 5. Tìm giá trị thực của tham số m để đường thẳng d : y  3m  1 x  3  m vuông góc với đường
thẳng đi qua hai điểm cực trị của đồ thị hàm số 3 2
y x  3x 1. 17 1 1 1 1 A. . B.  . C. m  . D.  . 3 6 6 3 Lời giải Xét hàm số 3 2
y x  3x 1  1 1  Có : 2
y  3x  6x , y x y  2x 1   .  3 3 
Do đó, đường thẳng  qua hai điểm cực trị của đồ thị hàm số này có phương trình là y  2  x 1. 1
Để d vuông góc với  thì 3m 1.2  1  m   . 6 1
Vậy giá trị cần tìm của m là m   . 6
Bài toán 6. Biết đồ thị hàm số 3
y x  3x 1 có hai điểm cực trị A , B . Khi đó phương trình đường thẳng AB là
A. y  2x 1. B. y  2  x 1.
C. y  x  2.
D. y x  2 . Lời giải  1 
Thực hiện phép chia y cho y ta được: y y . x   2  x     1 .  3 
Giả sử hai điểm cực trị của đồ thị hàm số lần lượt là: A x ; y và B x ; y . 2 2  1 1    1 
y y x yx . x  2  x 1  2  x 1  1  1  1   1   1  1   3  Ta có:  .  1 
y y x yx . x  2  x 1  2  x 1 2  2   2   2   2  2    3 
Ta thấy, toạ độ hai điểm cực trị A và B thoả mãn phương trình y  2  x 1.
Vậy phương trình đường thẳng qua hai điểm cực trị là: y  2  x 1.
Bài toán 7. Giả sử A , B là hai điểm cực trị của đồ thị hàm số   3 2
f x x ax bx c và đường thẳng AB đi
qua gốc tọa độ. Tìm giá trị nhỏ nhất của P abc ab c . 16 25 A.  . B. 9 . C.  . D. 1. 25 9 Lời giải TXĐ D   . f   x  2
 3x  2ax b . Điều kiện để hàm số có hai điểm cực trị là f   x   0 có hai nghiệm phân biệt 2
a  3b  0 .  1 1   2 2  1
Lấy f x chia cho f  x . Ta có f x  f  x. x a b
x c ab     .  3 9   3 9  9  2 2  1
Suy ra đường thẳng đi qua A , B là: y b
x c ab   d  .  3 9  9 1
Theo đầu bài d  đi qua gốc tọa độ  c ab  0  ab  9c . 9 2  5  25 25
Khi đó P abc ab c 2
P  9c 10c P  3c     . Suy ra min P   .  3  9 9 18
CỰC TRỊ HÀM SỐ ĐA THỨC SỬ DỤNG ĐỊNH LÝ VIET VÀ HÌNH HỌC GIẢI TÍCH 4 2
Bài toán 1. Cho hàm số y x 8x 10 . Tính diện tích của tam giác có ba đỉnh là ba điểm cực trị của đồ thị hàm số đã cho. A.32 B. 16 C. 48 D. 40 Lời giải
Tập xác định: D .  x  0 3
Ta có y  4x 16x ; y  0   . x  2 
Suy ra đồ thị hàm số có ba điểm cực trị . Không mất tính tổng quát, giả sử ba điểm cực trị là:
A0;10 , B 2; 6   , C  2  ; 6 .
Do A Oy và B,C đối xứng nhau qua Oy nên tam giác ABC cân tại A . Gọi H là trung điểm của đoạn thẳng
BC , khi đó H 0; 6
  ; AH  16; BC  4 . 1 1
Diện tích tam giác ABC là: SAH.BC  .16.4  32 . ABC 2 2
Bài toán 2. Cho hàm số 3 2
y x  6x  9x  2 có đồ thị là C  . Đường thẳng đi qua điểm A1,  1 và vuông góc
với đường thẳng đi qua hai điểm cực trị của C  là 1 3 1 3
A. y x  3 . B. y x  . C. y   x  .
D. x  2 y  3  0 . 2 2 2 2 Lời giải  1 2 2 
y  3x 12x  9 , 3 2
y x  6x  9x  2  x    2
3x 12x  9   2  x  4  3 3 
Khi đó đường thẳng đi qua hai điểm cực trị của C  có phương trình là y  2  x  4 . 1
Đường thẳng vuông góc với y  2
x  4 có phương trình y x b . 2 1 3
Đường thẳng qua A1;  1 suy ra 1  . 
1  b b  . 2 2 1 3
Vậy phương trình đường thẳng cần tìm là y x  . 2 2 1 1
Bài toán 3. Biết rằng đồ thị hàm số f x 3 2  x
mx x  2 có giá trị tuyệt đối của hoành độ hai điểm cực trị 3 2
là độ dài hai cạnh của tam giác vuông có cạnh huyền là 7 . Hỏi có mấy giá trị của m ? A. 3 . B. 1. C. Không có m . D. 2 . Lời giải. 1 f x 3 2 
x mx x  2  f  x 2
x  2mx 1. 3
Hai cực trị là a, b thì a b  2 ; m ab  1. 3
Theo định lý Pytago a b  7  a b2 2 2 2
 2ab  7  4m  2  7  m  
. Thử lại ta thu được 2 giá trị m. 2
Bài toán 4. Đồ thị hàm số 3 2
y x  3x 1 có điểm cực đại B, tính khoảng cách từ điểm B đến đường thẳng
 : 3x  4 y 1  0 . 1 A.2 B. 1 C. D. 5 Lời giải
x  0  y  1 Ta có 3 2 2
y x  3x 1  y  3x  6x  3x(x  2)  0  
x  2  y  3   19 3.2  4.( 3  ) 1 Khi đó A0  ;1 , B 2; 3
   d B,    1. 2 2 3  4
Bài toán 5. Đường cong 3 2
y  x  3x 1có điểm cực tiểu A và điểm cực đại B. Đường thẳng AB cắt trục CA
hoành tại C, tính tỷ số k  . CB 1 1 1 4 A. k  . B. k  . C. k  . D. k  . 2 3 3 3 Lời giải. 3 2 2
y  x  3x 1  y  3
x  6x  0  x  0; x  2  (
A 0; 1), B(2;3) . CA d ( , A Ox) y 1 Theo định lý Talet A    . CB d (B, Ox) y 3 B
Bài toán 6. Với giá trị nào của tham số m để đồ thị hàm số 3 2
y x  3x m có hai điểm cực trị A , B thỏa
mãn OA OB ( O là gốc tọa độ)? 3 1 5 A. m  . B. m  3 . C. m  . D. m  . 2 2 2 Lời giải
Tập xác định: D   .  x  0 2
y  3x  6x , 2
y  0  3x  6x  0   . x  2 
Do đó đồ thị hàm số đã cho luôn có hai điểm cực trị lần lượt có tọa độ là A 0; m  và B 2; 4  m  . 5
Ta có OA OB   m
   m 2  m     m2 2 2 2 2 0 2 4 4 4
 20  8m  0  m  . 2
Bài toán 7. Gọi S là tập các giá trị dương của tham số m sao cho hàm số 3 2
y x  3mx  27x  3m  2 đạt cực
trị tại x , x thỏa mãn x x  5 . Biết S  a;b . Tính T  2b a . 1 2 1 2 A. T  51  6 B. T  61  3 C. T  61  3 D. T  51  6 Lời giải +) Ta có  2
y  3x  6mx  27 ,  2
y  0  x  2mx  9  0 (1)
+) Theo giả thiết hàm số đạt cực trị tại x , x  phương trình (1) có 2 nghiệm phân biệt     0 1 2 m  3 2
m  9  0   (*) m  3 
x x  2m
+) Với điều kiện (*) thì phương trình (1) có 2 nghiệm x , x , theo Vi-ét ta có: 1 2 1 2 x x  9  1 2 2 2
+) Ta lại có x x  5   x x
 25  x x  4x x  25  0 1 2   1 2  1 2 1 2 61 61 2
 4m  61  0    m  (**) 2 2 a  3 61 
+) Kết hợp (*), (**) và điều kiện m dương ta được: 3  m   
T  2b a  61  3 61 . 2 b    2 20