













Preview text:
TÀI LIỆU THAM KHẢO TOÁN HỌC PHỔ THÔNG
______________________________________________________________
--------------------------------------------------------------------------------------------
ÔN KIẾN THỨC, LUYỆN KỸ NĂNG TOÁN 10 THPT CHUYÊN ĐỀ
BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
(KẾT HỢP 3 BỘ SÁCH GIÁO KHOA TOÁN 10)
THÂN TẶNG TOÀN THỂ QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TRÊN TOÀN QUỐC
CREATED BY GIANG SƠN (FACEBOOK)
GACMA1431988@GMAIL.COM (GMAIL); TEL 0398021920
THÀNH PHỐ THÁI BÌNH – THÁNG 7/2024 1
ÔN KIẾN THỨC, LUYỆN KỸ NĂNG TOÁN 10 THPT
BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
CƠ BẢN – VẬN DỤNG – VẬN DỤNG CAO
__________________________________________ DUNG NỘI DUNG BÀI TẬP LƯỢNG 2 FILE
CƠ BẢN BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN 2 trang 2 FILE
CƠ BẢN HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN 2 trang 3 FILE
VẬN DỤNG BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH 2 trang BẬC NHẤT HAI ẨN 3 FILE
VẬN DỤNG CAO: GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT 2 trang
VÀ ỨNG DỤNG THỰC TẾ 1 FILE
TRẮC NGHIỆM ĐÚNG SAI: 6 trang
BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN 3 FILE LUYỆN TẬP CHUNG 4 trang
BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
FILE ĐÁP ÁN CHI TIẾT PDF
BẠN ĐỌC VUI LÒNG LIÊN HỆ TÁC GIẢ 2
BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN LỚP 10 THPT
BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
LỚP BÀI TOÁN CƠ BẢN P1 ______________________
Câu 1. Cặp số nào sau đây là nghiệm của bất phương trình 2x y 6 A. 0 ;1 B. 1;3 C. 1; 1 D. 4; 2
Câu 2. Miền biểu diễn nghiệm của bất phương trình 3x 2 y 5 là
A.Nửa mặt phẳng bên trái đường thẳng 3x 2 y 5 .
B.Nửa mặt phẳng bên phải đường thẳng 3x 2 y 5 .
C.Nửa mặt phẳng bên dưới đường thẳng 3x 2 y 5 .
D.Nửa mặt phẳng bên trên đường thẳng 3x 2 y 5 .
Câu 3. Cặp số nào sau đây không là nghiệm của bất phương trình x y 8 A. 0 ;1 B. 1;3 C. 1; 1 D. 1;9
Câu 4. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn
A. 2x y 5 B. 2
2x y x C. 2
2x y y D. 2 2 x y 5
Câu 5. Tính a b c biết rằng x 3 2(2 y 5) 2(1 x) ax by c . A.3 B. – 4 C. 1 D. – 2
Câu 6. Điểm nào sau đây thuộc miền nghiệm của bất phương trình 2x y 3 3 3 A. 1; 3 B. 1; 1 C. 1 ; D. 1; 2 2
Câu 7. Bất phương trình nào sau đây luôn là bất phương trình bậc nhất hai ẩn A. 2
ax a y 4 B. 2 2 x y 5 C. 2
(a 9)x (a 3) y 8 D. 2 2
(a 2)x (b 3) y 5
Câu 8. Cặp số 2;3 là nghiệm của bao nhiêu bất phương trình bậc nhất hai ẩn sau
2x y 10; 3x y 9; x y 8 A.0 B. 1 C. 2 D. 3
Câu 9. Miền nghiệm của bất phương trình x 2 2( y 1) 2x 4 là nửa mặt phẳng bên trên đường thẳng d ,
hệ số góc đường thẳng d bằng A.0,5 B. 1 C. 0,25 D. 1,5
Câu 10. Bất phương trình nào sau đây không phải phương trình bậc nhất hai ẩn
A. 2x y 5
B. 2x 3y a C. 2
(a 1)x y 9 D. 2 2 x y 5
Câu 11. Tính a b c biết rằng 2 2 2 2
x y 2x 3(2 y x) 15 x y 13 ax by c . A.7 B. 1 C. 2 D. 4
Câu 12. Miền nghiệm của bất phương trình 3x y 2 0 không chứa điểm nào sau đây 1 A. 1; 2 B. 2 ;1 C. D. 1; 2
Câu 13. Tìm điều kiện của m để cặp số 0;
1 là nghiệm của bất phương trình 2x y m . A. m 2 B. m 1 C. m 2 D. 0 m 1
Câu 13. Tìm điều kiện của m để cặp số 0;
1 là nghiệm của bất phương trình 2x y m . A.m < 0 B. m < 1 C. m > 2 D. m = 4
Câu 14. Bất phương trình 2x y 6 có bao nhiêu cặp nghiệm nguyên dương A. 5 B. 6 C. 3 D. 4
Câu 15. Tìm m để bất phương trình 3
(m 1)x (m 1) y 6 là bất phương trình bậc nhất hai ẩn A. m 1 B. m 2 C. m 3 D. m 4
Câu 16. Miền nghiệm (phần tô đậm) sau đây của bất phương trình nào 3
A. x 2 y 1
B. x 2 y 1
C. x y 2
D. x y 2
Câu 17. Có bao nhiêu số nguyên m để bất phương trình 2 2
(m 1)x 2mx y 6 là bất phương trình bậc nhất hai ẩn A.3 B. 2 C. 1 D. 0
Câu 18. Miền nghiệm của bất phương trình x 3y 5 chứa điểm nào sau đây A. 1; 1 B. 5; 2 C. 0 ;1 D. 2 ;1
Câu 19. Cho các bất phương trình 2 2 2 2
x 2 y 9; x 2 y 8; x y 10; ax 2 y 4; (a 1)x y 0 .
Có bao nhiêu bất phương trình luôn là bất phương trình bậc nhất hai ẩn A.2 B. 1 C. 3 D. 4
Câu 20. Bất phương trình 2x 3y 2 0 . Khi đó 2 A. 1 ;1 S B. ; 0 S
C. 1; 2 S D. 1;0 S 2
Câu 21. Cặp số 2;3 là nghiệm của bất phương trình nào sau đây A. 4x 3y
B. x 3y 7 0
C. 2x 3y 1 0 D. x y
Câu 22. Miền nghiệm của bất phương trình x y 3 chứa bao nhiêu điểm nguyên có tọa độ đều là những số tự nhiên A.7 B. 9 C. 8 D. 6
Câu 23. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn A. 2
x y 4m
B. x 6 y 4x y C. 2
2x y 7a
D. 2x y 5a
Câu 24. Có bao nhiêu số nguyên dương m 10 để 2
(m 2)x (m 4) y 6 là bất phương trình bậc nhất hai ẩn A. 6 B. 8 C. 4 D. 5
Câu 25. Cặp số ; a
1 là nghiệm của bất phương trình nào sau đây
A. 2x y 1
B. ax y 1 0 C. 2
(a 1)x y a 2
D. x y 6a
Câu 26. Cặp số 1; a là nghiệm của bao nhiêu bất phương trình sau đây 2 2 2 2
(a 2)x y 1; 2x 3y 5; (1 a )x 2 y 0; (a b 1)x y 0 A.2 B. 1 C. 3 D. 4
Câu 27. Cặp số ;
a a là nghiệm của bất phương trình nào sau đây
A. 2x 3y 1
B. 2x 3y 7a C. 2
x y a 2 0
D. 2x y 4
Câu 28. Cho các bất phương trình: 2
x 2 y z 4;
x 3x 2 0; x 2 y 2000; 2x 3y 2(x y) 1.
Số lượng bất phương trình bậc nhất hai ẩn là A.2 B. 1 C. 3 D. 4
Câu 29. Nửa mặt phẳng không bị tô đậm như hình vẽ dưới là biểu diễn miền nghiệm của bất phương trình nào
A. x y 1.
B. x y 1.
C. x y 1.
D. x y 1.
Câu 30. Tìm điều kiện của a và b để 2 2
(a 1)x (a 1)(b 5) y 5 là bất phương trình bậc nhất hai ẩn.
A. a 1;b
B. a 2;b
C. a 3;b 2
D. a 1;b 2
Câu 31. Có bao nhiêu số nguyên m để cặp số ;
m m là nghiệm của bất phương trình (m 1)x 2 y 6 A.3 B. 4 C. 2 D. 5
Câu 32. Có bao nhiêu bất phương trình sau đây luôn là bất phương trình bậc nhất hai ẩn 2 2 2x y 4 ; a
(a 1)x (b 2) y 0; x my 5; (m 1)x y 5m A.2 B. 1 C. 3 D. 4
Câu 33. Bất phương trình bậc nhất hai ẩn 2
(m 1)x my 0 luôn nhận cặp nghiệm nào sau đây A. 1; 1 B. 0;m C. ; m m D. 1; 2
Câu 34. Miền nghiệm của bất phương trình x y 3 chứa điểm ;
a a với a là số tự nhiên. Tính 2a 5. A.7 B. 11 C. 15 D. 9 4
BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN LỚP 10 THPT
BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
LỚP BÀI TOÁN CƠ BẢN P2 ______________________
Câu 1. Điểm nào dưới đây thuộc miền nghiệm của bất phương trình 2x y 1 0 ? A. Q 1; 1 . B. M 1; 2 . C. P 2 ; 2 . D. N 1; 0 .
Câu 2. Cho bất phương trình x 2 y 5 0 có tập nghiệm là S . Mệnh đề nào sau đây là đúng?
A. 2;2 S . B. 2; 2 S .
C. 2;4 S . D. 1;3 S .
Câu 3. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn? A. 2 2x 3y 0 B. 2 2 x y 2 C. 2 x y 0
D. x y 0
Câu 4. Miền nghiệm của bất phương trình: 3x 2( y 3) 4(x 1) y 3 là nửa mặt phẳng chứa điểm: A. (3;0) B. (3;1) C. (2;1) D. (0;0)
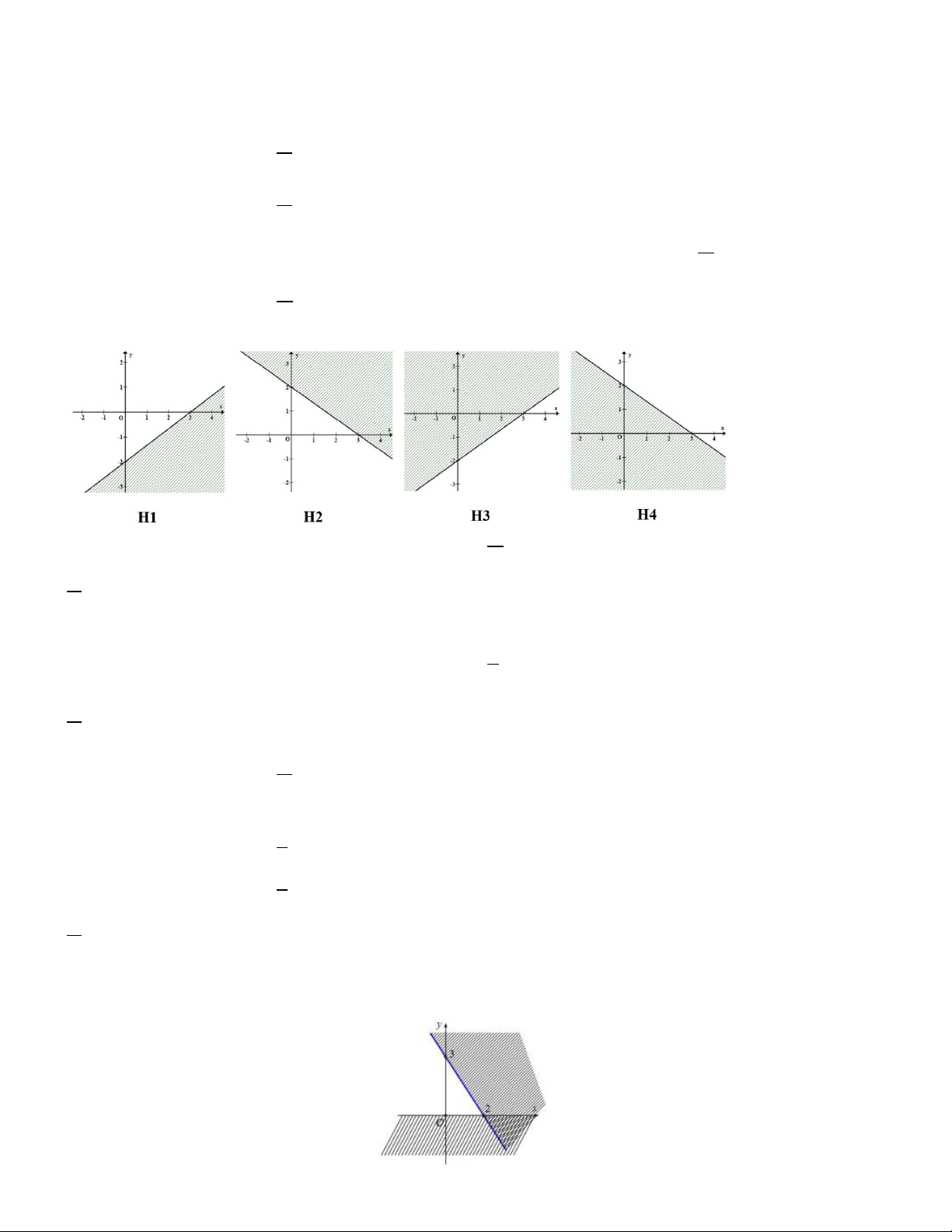
Câu 5. Hình vẽ nào sau đây biểu diễn miền nghiệm của bất phương trình 2x 3y 6 0 (miền không tô đậm kể cả bờ)? A. H1 H1 B. H 2 C. H 3 D. H 4
Câu 6. Miền nghiệm của bất phương trình: 3(x 1) 4( y 2) 5x 3 là nửa mặt phẳng chứa điểm: A. (0;0) B. ( 4 ;2) C. ( 2 ;2) D. ( 5 ;3)
Câu 7. Miền nghiệm của bất phương trình x 2 2 y 2 21 x là nửa mặt phẳng không chứa điểm nào trong các điểm sau? A. 0;0 . B. 1; 1 . C. 4;2 . D. 1; 1 .
Câu 8. Miền nghiệm của bất phương trình 5 x 2 9 2x 2 y 7 không chứa điểm nào trong các điểm sau? A. 2; 3 . B. 2; 1 . C. 2; 1 . D. 0; 0 .
Câu 9. Điểm nào dưới đây thuộc miền nghiệm của bất phương trình x 2 y 1 0 ? A. M 0; 1 . B. Q 1;0 . C. N 1; 2 . D. P 1; 1 .
Câu 10. Cho các bất phương trình 2 2
x 2 y 3; (a 2)x y 5; x(x 2 y) 0; x 3x 2 0 .
Số lượng bất phương trình bậc nhất hai ẩn là A.1 B. 2 C. 3 D. 4
Câu 11. Cho bất phương trình x 2 y 5
có tập nghiệm là S. Mệnh đề nào sau đây đúng? A. (1;3) S . B. (0; 2) S . C. (2; 2) S . D. ( 2 ; 2) S .
Câu 12. Cho bất phương trình 3x y 2 . Khẳng định nào sau đây đúng?
A. Bất phương trình đã cho vô số nghiệm.
B. Bất phương trình đã cho có tập nghiệm (; 2) .
C. Bất phương trình đã cho có một nghiệm duy nhất.
D. Bất phương trình đã cho vô nghiệm.
Câu 13. Miền nghiệm (không gạch chéo) trong hình vẽ dưới đây là nghiệm của hệ bất phương trình nào 5 x 0 x 0 y 0 y 0 A. B. C. D. 3x 2 y 6 3x 2 y 6 3x 2 y 6 3x 2 y 6
Câu 14. Có bao nhiêu số nguyên a để (a 1)x (a 2) y 4 là bất phương trình bậc nhất hai ẩn A.2 B. 10 C. Vô số D. 2000
Câu 15. Bất phương trình nào sau đây luôn là bất phương trình bậc nhất hai ẩn A. 2
ax a y 26 B. 2 2 x y 5 C. 2
(a 9)x 26(a 3) y 5 D. 2 2
(a 2)x (b 3) y 5
Câu 16. Miền nghiệm của bất phương trình 2
x 2a 4( y 1) 3x 4a 26 là nửa mặt phẳng bên trên đường
thẳng , hệ số góc đường thẳng bằng A.0,5 B. 1 C. 0,25 D. 1,5
Câu 17. Bất phương trình nào sau đây không phải phương trình bậc nhất hai ẩn
A. 2x y 5
B. 2x 3y a C. 2
(a 1)x y 9 D. 2 2 x y 5
Câu 18. Tìm điều kiện của tham số m để bất phương trình 3
26(m 1)x 5(m 1) y 2000m là bất phương trình bậc nhất hai ẩn A. m 1 B. m 2 C. m 3 D. m 4
Câu 19. Tìm điều kiện của m để miền nghiệm của bất phương trình (m 3)x 3y 8 chứa điểm (1;1) A. m 7 B. m 5 C. m 8 D. Kết quả khác
Câu 20. Tìm điều kiện của a và b để 2 3 2
(a 1)x (a 1)(b 5) y 26a 5b là bất phương trình bậc nhất hai ẩn.
A. a 1;b
B. a 2;b
C. a 3;b 2
D. a 3;b 4
Câu 21. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn? 3 A.
x y 1 . B. 2 2 x y 0 . C. 2
x 2 y 3 . D. 2
2x 5 y 1. 4
Câu 22. Có bao nhiêu giá trị m để 4
(m 1)x (m 1) y 5 không là bất phương trình bậc nhất hai ẩn A.2 B. 1 C. 3 D. 4
Câu 23. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn? A. 2 2x 3y 0
B. x 4 y 3 C. 2 x y 2 D. 2 2 x 4 y 6
Câu 24. Cho bất phương trình 2x 3y 6 0 (1) . Chọn khẳng định đúng trong các khẳng định sau:
A. Bất phương trình
1 chỉ có một nghiệm duy nhất.
B. Bất phương trình 1 vô nghiệm.
C. Bất phương trình
1 luôn có vô số nghiệm.
D. Bất phương trình
1 có tập nghiệm là .
Câu 25. Cho các hệ bất phương trình x 0
2x ay 2
ax 3y 1
2x y 8 ; ; ; 2 2 2 2 2x y 5
(a 1)x (a 1) y 5
(a 1)x 5 y 7a x y 7
Có bao nhiêu hệ luôn là hệ bất phương trình bậc nhất hai ẩn A.2 B. 3 C. 4 D. 1
2x y 0
Câu 26. Miền nghiệm của hệ bất phương trình x y 1
chứa điểm nào trong các điểm sau x y 2 A. 5;8 B. 6;9 C. 4;7 D. 1;0
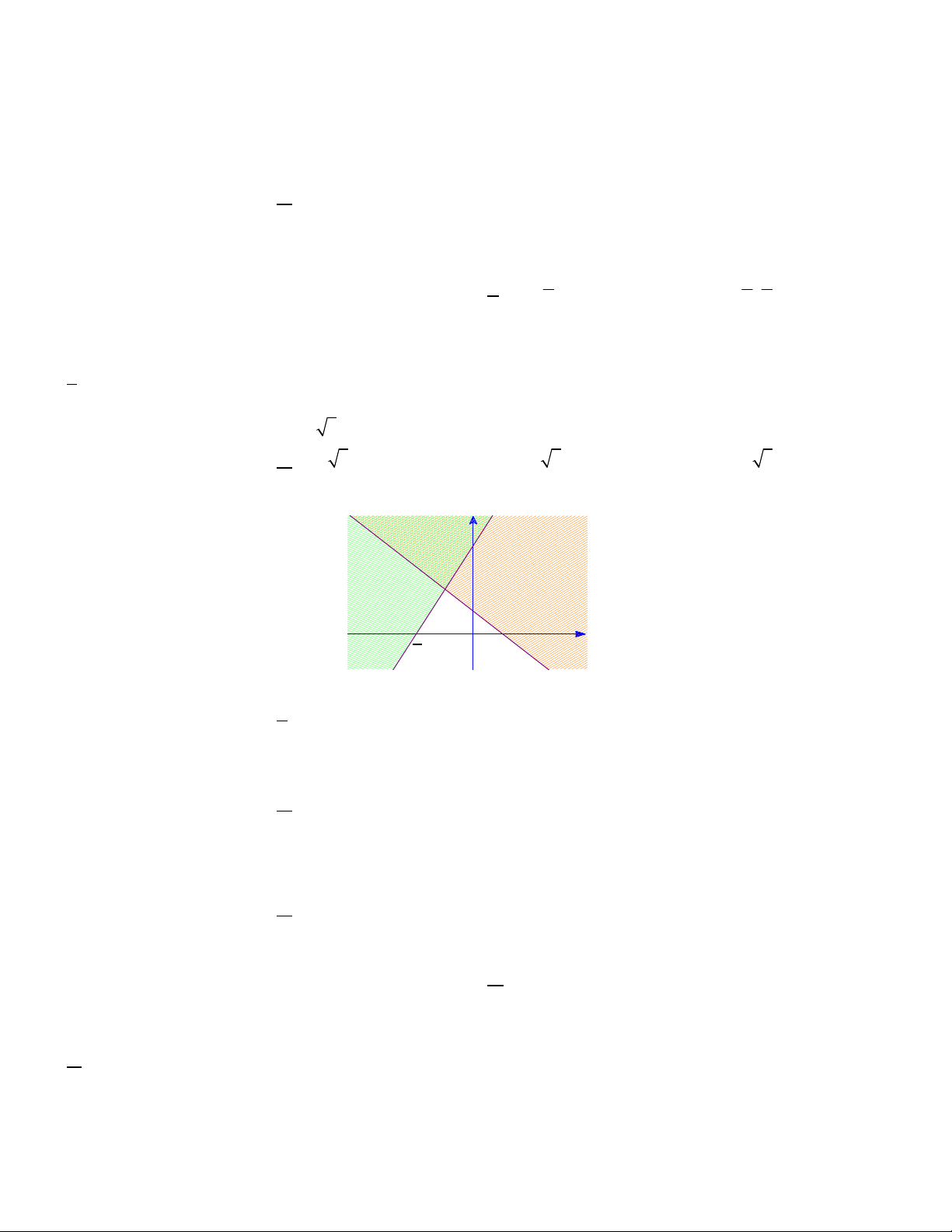
Câu 27. Miền không bị gạch chéo là miền nghiệm của hệ bất phương trình nào sau đây
x y 2 x y 2 x y 2
x y 2 A. B. C. D. 2
x y 2 2
x y 2 2
x y 2
2x y 2 6
BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN LỚP 10 THPT
HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
LỚP BÀI TOÁN CƠ BẢN P1
___________________________________
2x y 6 0
Câu 1. Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình x 3y 5 0 ? x 1 0 A. M 0;7 . B. N 1; 1 . C. P 2;3 . D. Q 1 ; 2 . x y 0
Câu 2. Hệ bất phương trình
có tập nghiệm S. Khẳng định nào sau đây đúng 2x 5 y 0 1 1 2 A. 1 ;1 S B. 1; 1 S C. 1; S D. ; S 2 2 5
2mx y 13
Câu 3. Có bao nhiêu số nguyên dương m để hệ bất phương trình nhận 1; 1 làm nghiệm
3x 2 y 10 A.6 B. 1 C. 2 D. 3 x 0
Câu 4. Hệ bất phương trình
có tập nghiệm S. Khẳng định nào sau đây đúng
x y 3 1 0 A. 1; 1 S B. 1; 3 S C. 1 ; 5 S D. 4 ; 3 S Lời giải
Câu 5. Miền không bị gạch chéo (kể cả các đường thẳng) là miền nghiệm của hệ bất phương trình nào? y d2 d1 4 2 O 1 x x y 1 0 x y 1 0 x y 1 0 x y 1 0 A. . B. . C. . D. .
2x y 4 0
2x y 4 0
2x y 4 0
2x y 4 0 3
x y 3
Câu 6. Tìm điều kiện tham số m để hệ bất phương trình nhận 1 ;1 làm nghiệm
x (m 1) y 10 A. m 7 B. m 8 C. 1 m 10 D. 2 m 5 3
x 4 y 12 0
Câu 7. Miền nghiệm của hệ bất phương trình: x y 5 0
là miền chứa điểm nào trong các điểm sau? x 1 0 A. M 1;3. B. N 4;3. C. P 1;5 . D. Q 2 ; 3 .
Câu 8. Điểm O 0;0 không thuộc miền nghiệm của hệ bất phương trình nào dưới đây?
x 3y 6 0
x 3y 0
x 3y 0
x 3y 6 0 A. . B. . C. . D. .
2x y 4 0
2x y 4 0
2x y 4 0
2x y 4 0
Câu 9. Điểm O 0;0 không thuộc miền nghiệm của hệ bất phương trình nào sau đây?
x 3y 0
x 3y 0
x 3y 6 0
x 3y 6 0 A. . B. . C. . D. .
2x y 4 0
2x y 4 0
2x y 4 0
2x y 4 0
x 2 y 0
Câu 10. Miền nghiệm của hệ bất phương trình x 3y 2
là phần không tô đậm của hình vẽ nào
y x 3 7 A. B. C. D.
x y 2 0
Câu 11. Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phương trình là
2x 3y 2 0 A. 0;0 . B. 1; 1 . C. 1; 1 . D. 1 ; 1 .
2x y 1
Câu 12. Điểm nào dưới đây thuộc miền nghiệm của hệ bất phương trình ?
x y 4 0 A. (0 ; 0). B. (0 ; 2). C. (0 ; 5). D. (0 ; 4).
3x y 9 x y 3
Câu 13. Miền nghiệm của hệ bất phương trình
là phần mặt phẳng chứa điểm 2 y 8 x y 6 A. 0;0 . B. 1;2 . C. 2; 1 . D. 8;4 . 3
x y 1
Câu 14. Trong mặt phẳng Oxy , điểm nào dưới đây thuộc miền nghiệm của hệ ? x 2 y 2 A. P 1 ;0. B. N 1 ;1 . C. M 1; 1 . D. Q 0 ;1 .
2x 5 y 1 0
Câu 15. Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình 2x y 5 0 ?
x y 1 0 A. 0;0 . B. 1;0 . C. 0; 2 . D. 0; 2 . 2
x 2 y 1
x 2 y a
x 2 y 1
x 2 y 1
Câu 16. Cho các hệ bất phương trình ; ; ; 3x 2 y 5 ax 2 y 5
(a 1)x 2 y 8 x 2 y 3
Số lượng hệ bất phương trình bậc nhất hai ẩn là A.2 B. 1 C. 3 D. 4
Câu 17. Cho các hệ bất phương trình x y 1
ax y 2
(a 2)x y 1
x 2 y 5 ; ; ; 2 2 2 2x y 4
(a 1)x (a 1) y 5
(a 2)x (a 4) y 8a x y 6
Số lượng hệ luôn là hệ bất phương trình bậc nhất hai ẩn là A.3 B. 4 C. 1 D. 2
x 2 y 0
Câu 18. Miền nghiệm của hệ bất phương trình x 3y 2
chứa điểm nào sau đây?
y x 3 A. A1 ; 0 . B. B 2 ; 3 . C. C 0 ; 1 . D. D 1 ; 0. 8
BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN LỚP 10 THPT
HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
LỚP BÀI TOÁN CƠ BẢN P2 ______________________
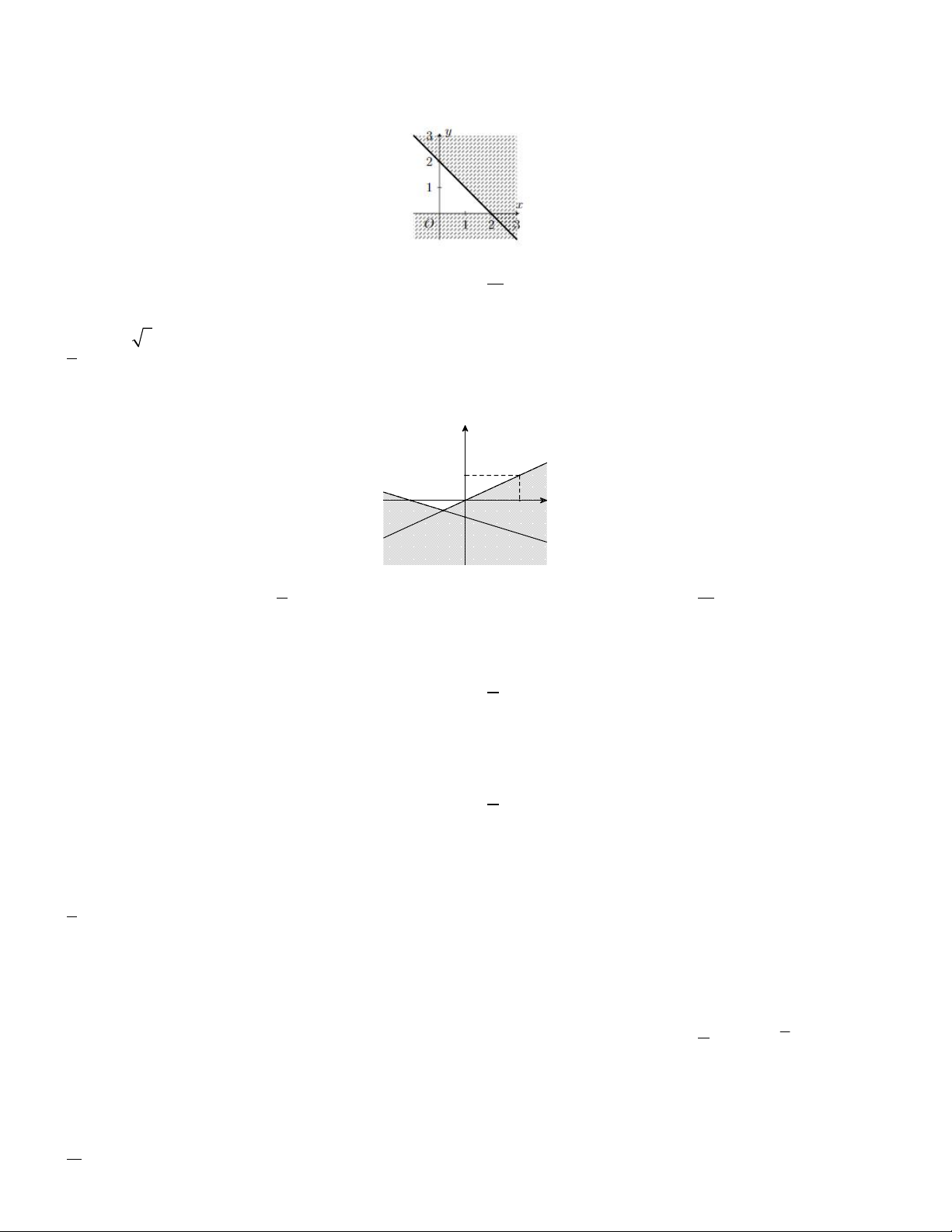
Câu 1. Trong hình vẽ bên, phần mặt phẳng không bị gạch là miền nghiệm của hệ bất phương trình nào y 0 y 0 y 0 y 0 A. B. C. D. x y 2 x y 2 x y 2 x y 2
Câu 2. Trong các hệ bất phương trình sau, hệ nào là hệ bất phương trình bậc nhất hai ẩn? 2
2x 3y 0
2x y 1 2
x 3y 0
x 3y 0 A. . B. . C. . D. . x y 1 y 4 0
x y 4 0 xy y 4
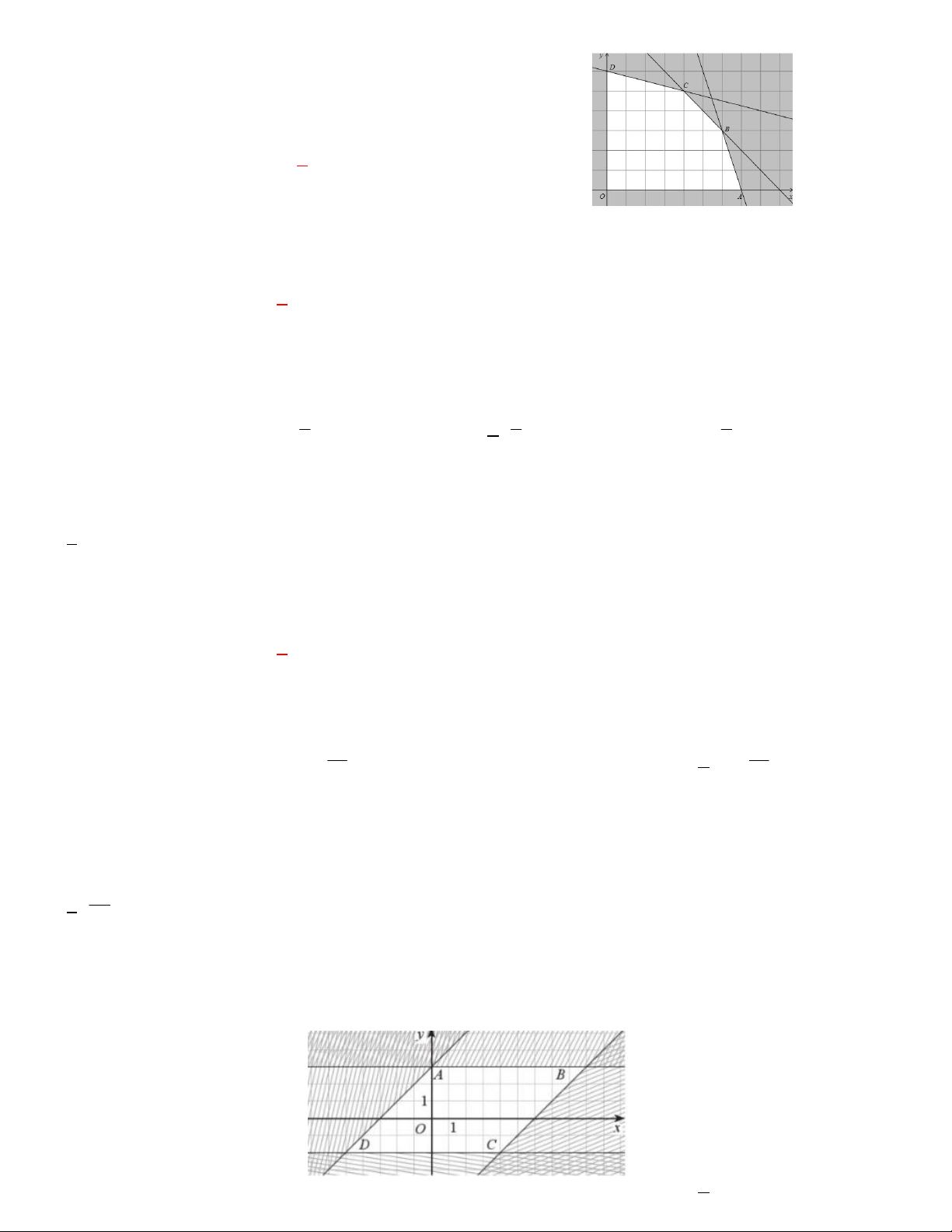
Câu 3. Phần không tô đậm trong hình vẽ dưới đây , biểu diễn tập nghiệm của hệ bất phương trình nào trong các
hệ bất phương trình sau? y 1 x - 2 2
x 2 y 0
x 2 y 0
x 2 y 0
x 2 y 0 A. B. C. D.
x 3y 2
x 3y 2 x 3y 2
x 3y 2
2x 3y 1 0
Câu 4. Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình ?
5x y 4 0 A. 1 ;4 . B. 2 ;4 . C. 0;0 . D. 3 ;4 .
2x 5y 1 0
Câu 5. Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình 2x y 5 0 ?
x y 1 0 A. 0;0 . B. 1;0 . C. 0; 2 . D. 0;2 . x y 0
Câu 6. Miền nghiệm của hệ bất phương trình x 3y 3 0 là phần mặt phẳng chứa điểm
x y 5 0 A. 5;3 . B. 0;0 . C. 1; 1 . D. 2 ;2 .
2x 3y 6 0
Câu 7. Miền nghiệm của hệ bất phương trình x 0
chứa điểm nào sau đây?
2x 3y 1 0 1 A. A1 ; 2. B. B 0 ; 2 . C. C 1 ; 3 . D. D 0 ; . 3 x 0
Câu 8. Điểm nào dưới đây không thuộc miền nghiệm của hệ bất phương trình x 2 y 4 ?
y x 2 0 A. 2; 1 . B. 4; 3 . C. 3; 1 . D. 3; 2 .
Câu 9. Phần không bị gạch, kể cả biên trong hình vẽ là miền nghiệm của hệ bất phương trình nào ? 9 x y 0 x y 0 x y 0 x y 0 A. . B. . C. . D. . y 0 x 0 x 0 x 0
2x 3y 6 0
Câu 10. Miền nghiệm của hệ bất phương trình x 0 có dạng
2x 3y 1 0 A.Lục giác B. Ngũ giác. C. Tứ giác. D. Tam giác
Câu 12. Miền nghiệm của hệ bất phương trình nào sau đây chứa điểm 1; 1 ? x y 0 x y 3
x 4 y 6
x y 0 A. . B. . C. . D. . 2x 3y 0 2 x y 0 2x y 0 x 0
2x 4 y 5
Câu 10. Cho hệ bất phương trình:
. Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình x 2 y 9 đã cho. A. O 0;0 . B. A4; 2 . C. B 4 ; 8 . D. C 10; 2 .
Câu 13. Hệ bất phương trình nào sao đây không phải là hệ bất phương trình bậc nhất hai ẩn ? x 2 x y 1 y 0
x y 0 A. . B. . C. . D. . y 1
x 2 y 3 x 0 x y 2
Câu 14. Điểm O 0;0 thuộc miền nghiệm của hệ bất phương trình nào sau đây?
x 3y 6 0
x 3y 6 0
x 3y 6 0
x 3y 6 0 A. . B. . C. . D. .
2x y 4 0
2x y 4 0
2x y 4 0
2x y 4 0
Câu 15. Miền nghiệm của hệ bất phương trình nào sao đây có chứa điểm 0;3 ?
x y 4
2x 3y 12 10 x y 0
2x 3y 2 A. . B. . C. . D. . 3x 4 y 0 x y 5 3y 8 x y 1
Câu 16. Trong các hệ sau hệ nào không phải là hệ bất phương trình bậc nhất hai ẩn? x y 3 2
x y 2
2x y 2 0 y 2 0 A. . B. . C. . D. .
x 5 y 3 0 x y 2
5x 2 y 3 0 x 5 0
2x 5 y 1 0
Câu 17. Điểm nào sau đây thuộc tập nghiệm của hệ bất phương trình sau: 2x y 5 0
x y 1 0 A. 0;0 . B. 1;0 . C. 0; 2 . D. 0; 2 . x y 3
Câu 18. Cho hệ bất phương trình 1
có tập nghiệm S . Khẳng định nào sau đây là khẳng định 1 x y 0 2 đúng ? A. 1; 2 S . B. 2; 1 S . C. 5; 6 S . D. S .
x 2 y 6
Câu 19. Cho hệ bất phương trình:
. Điểm nào sau đây không thuộc miền nghiệm của hệ bất
3x y 2 phương trình đã cho. A. A 1 ;3 . B. B 1;4 . C. C 2 ; 4 . D. D 1; 2 . 10
BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN LỚP 10 THPT
LỚP BÀI TOÁN VẬN DỤNG P1 __________________________
Câu 1. Có bao nhiêu số nguyên m để cặp số ;
m m là nghiệm của bất phương trình (m 1)x 6 y 6 A.3 B. 8 C. 7 D. 5
Câu 2. Có bao nhiêu số nguyên âm m để điểm Q ; m m
1 nằm trong miền nghiệm bất phương trình 3
x 2 y m 2 . A.0 B. 3 C. 2 D. 1
Câu 3. Bất phương trình 2x 3y 8 có bao nhiêu cặp nghiệm tự nhiên A.8 B. 10 C. 9 D. 7
Câu 4. Để trở thành một thành viên của ban nhạc thì một sinh viên phải đạt điểm trung bình các môn học ít nhất
là 7,0 và phải có 5 lần thực hành sau giờ học. Gọi x là điểm trung bình các môn học và y là số lần thực hành
sau giờ học, hãy chọn hệ bất phương trình thể hiện tốt nhất tình huống này. x 7 x 7 x 7 x 7 A. B. C. D. y 5 y 5 y 5 y 5
Câu 5. Bất phương trình x y 6 có cặp nghiệm tự nhiên ;
x y , giá trị nhỏ nhất của x 2 y bằng A.6 B. 5 C. 8 D. 7
4x y 12a
Câu 6. Biết rằng hệ bất phương trình 5
x y 6a có một hệ quả là 2 x 8 . Tính a b . x 8b A.9 B. 2 C. 3 D. 7
Câu 7. Miền nghiệm của bất phương trình 3x 4 y 5 là nửa mặt phẳng bờ là đường thẳng d , ký hiệu miền H.
Khoảng cách nhỏ nhất từ gốc tọa độ O đến một điểm trên H là A.1 B. 0,5 C. 2 D. 1,5
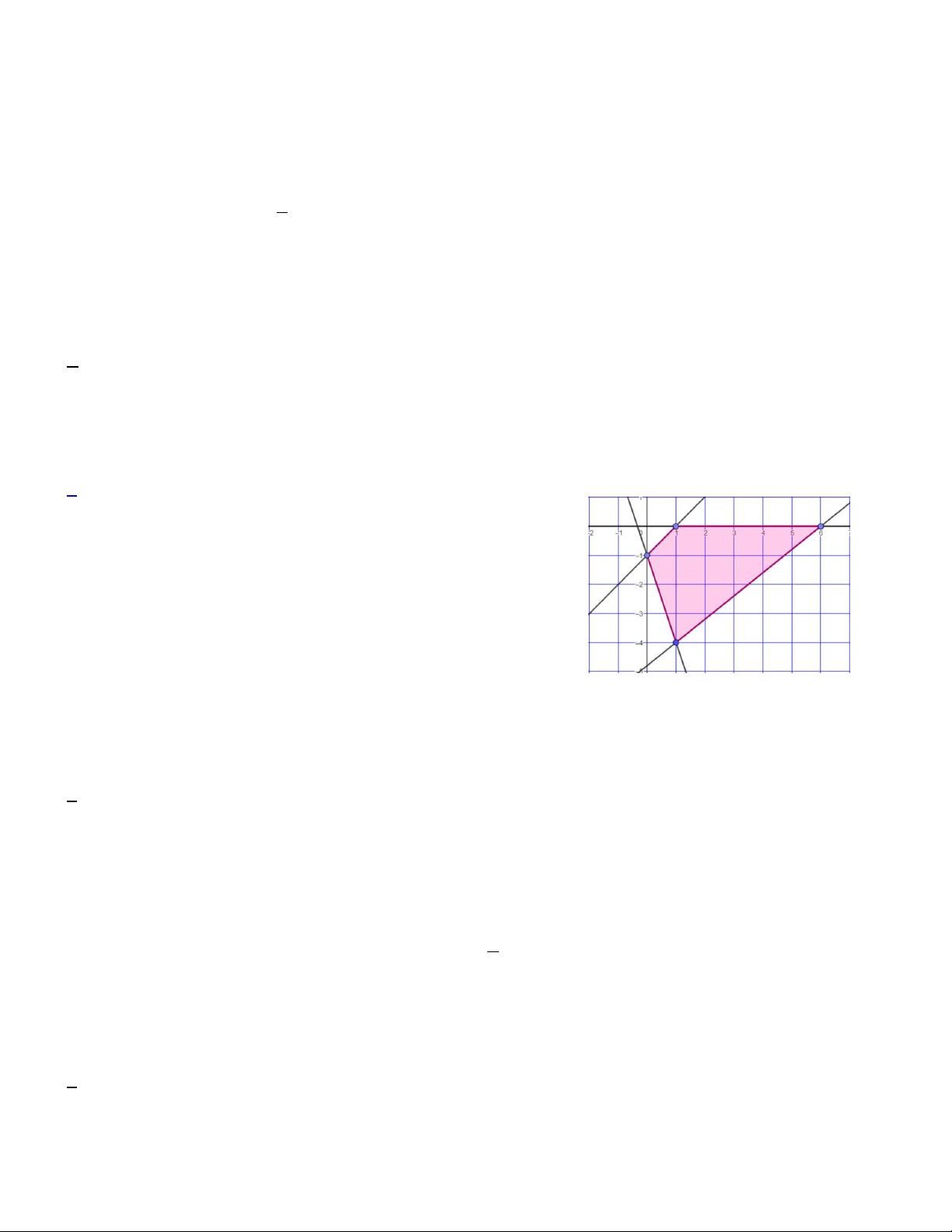
Câu 8. Cho hệ bất phương trình gồm 4 bất phương trình bậc nhất x 0 3
x 2 y a hai ẩn
có miền nghiệm là tứ giác như hình vẽ. Tính giá
x y b
x y c
trị biểu thức a 2b 5c . A. 15. B. 16. C. 17. D. 10.
Câu 9. Cặp số 1; 2 là nghiệm của bao nhiêu bất phương trình sau đây 2 2 2 2
(a 2)x y 4a; 2x 3y 5a; (1 a )x 2 y 3 0; (a b 1)x y 15 A.2 B. 1 C. 3 D. 4
Câu 10. Miền nghiệm của bất phương trình x 2 2( y 1) 2x 4 là nửa mặt phẳng bên trên đường thẳng d,
khoảng cách từ gốc tọa O đến đường thẳng d bằng 8 2 4 A.2 B. C. D. 5 5 5
4x y 6a 1
Câu 11. Với a 0 , tìm một hệ quả của hệ bất phương trình 5
x y 3a 1 x 4a
A. a x 4a
B. 3a x 4a
C. 1 x 4a D. x 2a
x y 0,
Câu 12. Tính diện tích S của tam giác tạo bởi miền nghiệm của hệ x 3y 3 ,
x y 5. A. S 4, 5 B. S 1, 5 C. S 2, 25 D. S 3, 5
Câu 13. Miền nghiệm của bất phương trình x y 3 chứa bao nhiêu điểm nguyên có hoành độ và tung độ đều
là các số nguyên dương nhỏ hơn 2 A.2 B. 1 C. 3 D. 4 11
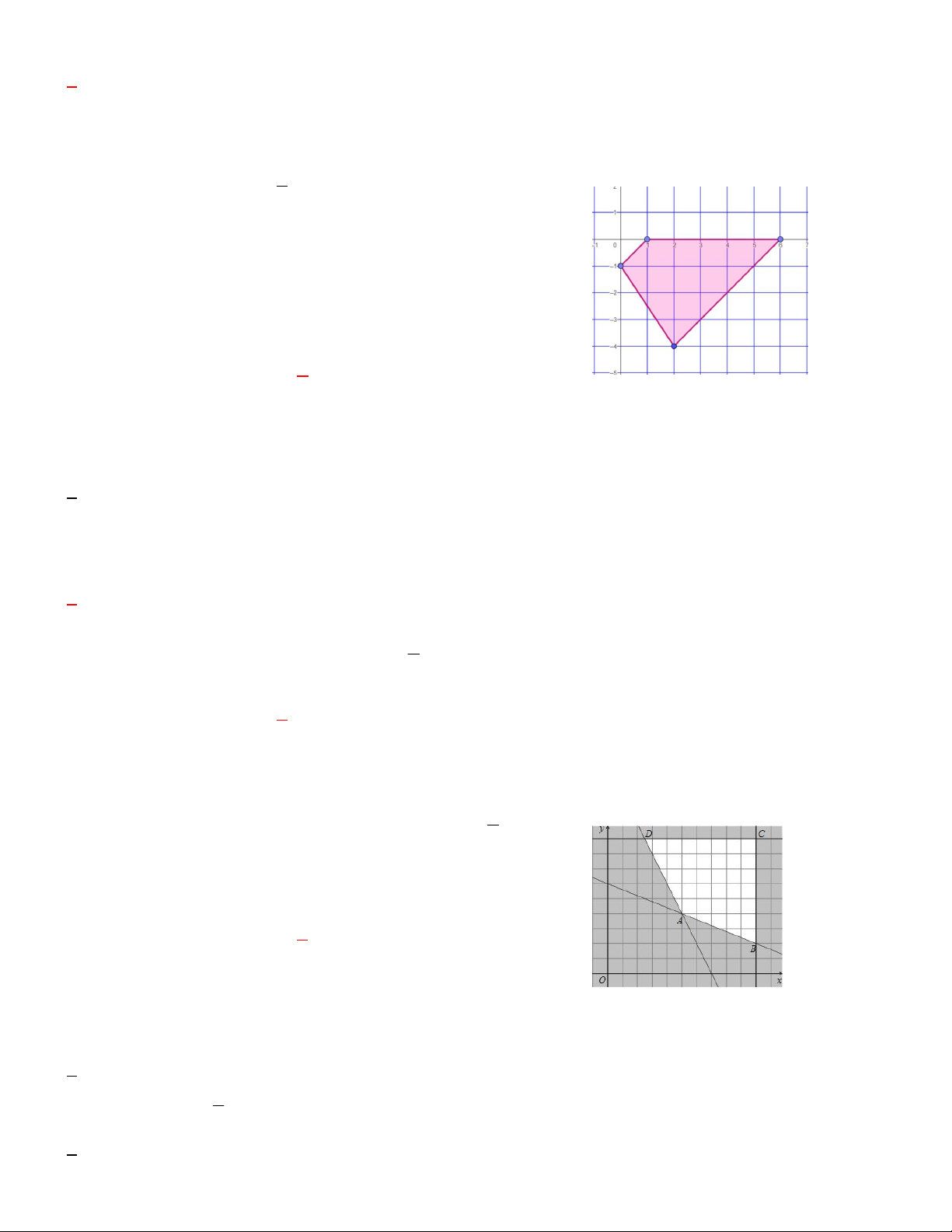
Câu 14. Cho hệ bất phương trình gồm 5 bất phương trình bậc nhất
hai ẩn có miền nghiệm là ngũ giác như hình vẽ. Đường thẳng CB
trong hình vẽ có hệ số góc bằng A. – 2. B. – 1. C. – 3. D. 3.
2x y 2
Câu 15. Miền nghiệm của hệ bất phương trình 3
x y 3 chứa bao nhiêu điểm nguyên x 0 A.6 B. 7 C. 5 D. 4
x 0; y 0
Câu 16. Miền nghiệm của hệ bất phương trình 2x 5y 10 là tứ giác ABCD , một trong bốn đỉnh của tứ giác x y 3 có hoành độ bằng 2 4 7 A.1 B. C. D. 3 3 3
Câu 17. Bạn Khoa làm một bài thi giữa kỳ I môn Toán. Đề thi gồm 35 câu hỏi trắc nghiệm và 3 câu hỏi tự luận.
Khi làm đúng mỗi câu trắc nghiệm được 0,2 điểm, làm đúng mỗi câu tự luận được 1 điểm. Giả sử bạn Khoa làm
đúng x câu trắc nghiệm, y câu tự luận. Viết bất phương trình bậc nhất 2 ẩn x, y để đảm bảo bạn Khoa được ít nhất 9 điểm.
A. 0, 2x y 9
B. x 0, 2 y 9 .
C. x 0, 2y 9 .
D. 0, 2x y 9 .
Câu 18. Cho các điểm A2
;1 , B 2;5,C 1
; 4, D0;5 . Có bao nhiêu điểm thuộc miền nghiệm của hệ bất
2x my 7 phương trình
3x my 2 A.3 B. 2 C. 1 D. 4 3
x 2 y 5
Câu 19. Tính diện tích S của tam giác tạo bởi miền nghiệm của hệ 4x 3y 1 y 0 19 17 A. S 4, 5 B. S C. S 6 D. S 24 24 2
x(x x 1) 0
Câu 20. Miền nghiệm của hệ bất phương trình 2
y( y y 2) 0 là một tam giác vuông có diện tích bằng 3
x 4y 5 25 A. B. 0,375 C. 0,75 D. 0,5 24 2 y 3
Câu 21. Miền đa giác không bị gạch trong hình vẽ là nghiệm của hệ ay x b a 0;b 0;c 0; d 0 .
cy x d
Tính a b c d . A.2 B. 10 C. 3 D. 9 12
BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN LỚP 10 THPT
LỚP BÀI TOÁN VẬN DỤNG P2 _________________________
Câu 1. Tìm điều kiện tham số m để hai điểm O 0; 0, B 1; m cùng nằm trong miền biểu diễn nghiệm của bất
phương trình 2x y 1. A. m 1 B. 1 m 2 C. m 5 D. m 0 5
x 3y a
Câu 2. Một hệ quả của hệ bất phương trình là
2x 3y 8a A. x a B. x 3a C. x 5a D. x 4a
Câu 3. Cho hệ bất phương trình gồm 4 bất phương trình bậc nhất
x 0; y 0
hai ẩn x y a
có miền nghiệm là tứ giác như hình vẽ. Tính giá
x y b trị a b . A. 2. B. 6. C. 7. D. 5.
Câu 4. Có bao nhiêu số nguyên m để điểm A ;
m 2m thuộc miền nghiệm của bất phương trình
mx (m 1) y 5 A.3 B. 2 C. 1 D. 4
Câu 5. Ông An muốn thuê một chiếc ô tô (có lái xe) trong một tuần. Giá thuê xe được cho như bảng sau: Phí cố định (nghìn
Phí tính theo quãng đường di chuyển đồng/ngày) (nghìn đồng/kilômét)
Từ thứ Hai đến thứ Sáu 900 8 Thứ Bảy và Chủ nhật 1500 10
Gọi x và y lần lượt là số kilômét ông An đi trong các ngày từ thứ Hai đến thứ Sáu và trong hai ngày cuối tuần.
Bất phương trình biểu thị mối liên hệ giữa x và y sao cho tổng số tiền ông An phải trả không quá 14 triệu đồng là.
A. 5x 4 y 3250
B. 4x 5 y 3250 .
C. 5x 4 y 3250 .
D. 4x 5 y 3250 .
2x y 8a
Câu 6. Một hệ quả của hệ bất phương trình là
2x y 4a A. x a B. x 3a C. x 5a D. x 4a y 0 Câu 7. Cho hệ
có miền nghiệm S và bốn điểm O 0;0, A2;3, B 1 ; 1 ,C 1 ;3 . 3x 2 y 6
Trong các điểm đã cho, có bao nhiêu điểm thuộc S A.1 B. 2 C. 3 D. 4
x y 2 0,
Câu 8. Cho hệ bất phương trình x y 1 0,
2x y 1 0.
Miền biểu diễn tập hợp nghiệm của hệ đã cho là tam giác ABC. Tính diện tích S của tam giác ABC. A. S 4 B. S 2, 25 C. S 0, 75 D. S 1, 25
Câu 9. Có bao nhiêu số nguyên a 5 ;5để 3 2 2
(a 1) x (a 3a 2) y 26a 5là bất phương trình bậc nhất hai ẩn. A.10 B. 12 C. 8 D. 6
Câu 10. Có bao nhiêu cặp số ;
a b đều thuộc 5;5để hệ sau là hệ bất phương trình bậc nhất hai ẩn 2
(a 1)x (a 1) y 5 . 2
(b 2)x (b 4) y 6 A.100 B. 99 C. 26 D. 80
Câu 11. Một gian hàng trưng bày bàn và ghế rộng 2
60m . Diện tích để kê một chiếc ghế là 2 0,5m , một chiếc 13 bàn là 2
1, 2m . Gọi x là số chiếc ghế, y là số chiếc bàn được kê. Viết bất phương trình bậc nhất hai ẩn cho
phần mặt sàn để kê bàn và ghế, biết diện tích mặt sàn dành cho lưu thông tối thiểu là 2 12m .
A. 5x 12 y 480
B. 5x 12 y 120
C. 5x 12 y 140
D. 5x 12 y 150
x 0; y 0
Câu 12. Tính tổng các giá trị m để miền nghiệm của hệ bất phương trình
m 0 là một tam
3x 4 y 5m
giác có chiều cao (hạ từ gốc tọa độ O) có độ dài bằng 1. A. 2 B. 1 C. 3 D. 4
Câu 13. Cho hệ bất phương trình gồm 4 bất phương trình bậc nhất x 0 3
x 2 y a hai ẩn
có miền nghiệm là tứ giác như hình vẽ. Hệ bất
x y b
x y c
phương trình đã cho có bao nhiêu nghiệm nguyên ; x y ? A. 15. B. 16. C. 17. D. 19.
2x 3y 5 1
Câu 14. Cho hệ bất phương trình
, trong đó S , S lần lượt là miền nghiệm của (1), (2), S là 1 2 x 1,5 y 5 2
miền nghiệm của hệ. Khi đó A. S S B. S S C. S S
D. S S S 1 2 2 1 2 2 1
Câu 15. Trong 1 lạng thịt bò chứa khoảng 26g protein, 1 lạng cá rô phi chứa khoảng 20g protein. Trung bình
một ngày một người phụ nữ cần tối thiểu 46g protein. Gọi x, y lần lượt là số lạng thịt bò và số lạng cá rô phi mà
một người phụ nữ nên ăn trong một ngày. Viết bất phương trình bậc nhất hai ẩn x, y để biểu diễn lượng protein
cần thiết cho một người phụ nữ trong một ngày.
A.13x 10 y 23
B. 13x 10 y 23
C. 13x 10 y 46
D. 26x 20 y 23
Câu 16. Cho các bất phương trình bậc nhất hai ẩn 9
(m 1)x 3y 3
; (m 2)x y
0; mx (m 2) y 1 0;
(m 1)x my 10 . 4 Điểm M ( ;
m m) luôn thuộc miền nghiệm của bao nhiêu bất phương trình đã cho A.2 B. 3 C. 1 D. 4 x y 3
Câu 17. Tính diện tích S của miền nghiệm hệ bất phương trình y x 3 y 1 A.8 B. 25 C. 16 D. 12
Câu 18. Cho hệ bất phương trình gồm 4 bất phương trình bậc nhất hai ẩn ,
x y có miền nghiệm là tứ giác như hình vẽ. Một trong các bất phương trình đó là
A. 2x y 4 .
B. 2x 5 y 30 .
C. 3x 2 y 6 .
D. 4x 3y 10 .
x 0; y 0
Câu 19. Tìm số thực a để miền nghiệm của hệ bất phương trình
là một tam giác có diện tích ax 3y 12 bằng 6 A. a 4 B. a 4 C. a 6 D. a 12 5
Câu 20. Điểm A 0;
luôn thuộc miền nghiệm của bất phương trình nào trong số các bất phương trình sau 3 A. 2
(m 4)x 3y 5 B. 2
(m 4)x 3y 5 C. 2
(m 4)x 3y 5 D. 2
(m 4)x 3y 7 0 14
BẤT PHƯƠNG TRÌNH, HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN LỚP 10 THPT
LỚP BÀI TOÁN VẬN DỤNG P3 _________________________
Câu 1. Tồn tại bao nhiêu cặp số ; a b để 2
(a 1)x (b 3b) y 5 không là bất phương trình bậc nhất hai ẩn A.3 B. 4 C. 2 D. 1 x a
Câu 2. Tìm điều kiện tham số a,b sao cho miền nghiệm của hệ bất phương trình chứa điểm M 1 ; 1 . y b A. a 1 ;b 1 B. a 1 ;b 1 C. a 1 ;b 1 D. a 1 ;b 1
Câu 3. Điểm Am
;1 luôn thuộc miền nghiệm của bất phương trình nào sau đây
A. 2x y 5
B. 4x y m
C. mx 2 y 1 D. 2
(m 1)x y m
x 2 y 1
Câu 4. Điểm M thuộc miền nghiệm của hệ bất phương trình
. Hoành độ của M có thể bằng 3x 2 y 5 A.1 B. 0,5 C. 0,75 D. 2
x 2 y 10
2x y 0
Câu 5. Hệ bất phương trình
có miền nghiệm là tứ giác lồi ABCD , một trong các đỉnh của tứ
2x y 12 y 2 giác có tung độ bằng A.3 B. 4 C. 3,5 D. 6
Câu 6. Bạn Bích có 500g bột gạo để pha hai loại nước hồ tráng bánh đa và bánh xèo. Một lit nước hồ tráng
bánh đa cần 200g bột gạo, còn một lít nước hồ tráng bánh xèo cần 100g bột gạo. Gọi x, y lần lượt là số lít
nước hồ tráng bánh đa và bánh xèo. Thiết lập hệ bất phương trình mô tả điều kiện của x, y .
A. 2x y 5
B. 2x y 5
C. 100x 200 y 500
D. x 2 y 5
Câu 7. Có bao nhiêu số nguyên m để điểm M ( ;
m m) nằm trong miền nghiệm của hệ bất phương trình
mx 2 y 3
(m 1)x 3y 5 A.3 B. 4 C. 5 D. 6
4x 5y 7a
Câu 8. Một hệ quả của hệ bất phương trình 3
x 5y 6a 3 là
x 3a 5 A. x a B. x 2a C. x 2a
D. x 2a 1
Câu 9. Có bao nhiêu cặp số a;b để 3
26(a a 2)x 5(b 2 2 b 1) y 2000 không phải bất phương trình bậc nhất hai ẩn A.3 B. 2 C. 1 D. Vô số
x 2 y 2
Câu 10. Miền nghiệm của hệ bất phương trình 7x 4 y 16 chứa bao nhiêu điểm nguyên
2x y 4 A.3 B. 6 C. 4 D. 5 x 3
Câu 11. Tính diện tích S (theo đvdt) của miền nghiệm của hệ bất phương trình x y 8
y x 2 A.48 B. 64 C. 81 D. 49
Câu 12. Miền nghiệm của bất phương trình (m 1)x 3y 2
không thể chứa điểm nào sau đây A. 1; 2 B. ; m m C. 1; m D. 3;5
x y a
Câu 13. Hình vẽ sau là miền nghiệm (không gạch chéo) của hệ bất phương trình
. Tính a b
2x y b 15 A.3 B. – 2 C. – 3 D. – 1
Câu 14. Ngoài giờ học bạn Nam làm thêm việc phụ bán cơm được 15 nghìn đồng/1 giờ và phụ bán tạp hóa
được 10 nghìn đồng/ 1 giờ. Nam không thể làm thêm việc nhiều hơn 15 giờ mỗi tuần. Gọi x, y lần lượt là số giờ
phụ bán cơm và phụ bán tạp hóa. Hệ bất phương trình nào sau đây xác định số giờ để làm mỗi việc nếu Nam
muốn kiếm được ít nhất 100 nghìn đồng mỗi ngày.
x y 15
x y 15
x y 15
x y 15 A. B. C. D.
15x 10 y 100
15x 10 y 100
15x 10 y 100
15x 10 y 100 y 0
Câu 15. Miền tam giác ABC kể cả ba cạnh là miền nghiệm của hệ bất phương trình ax 3y b
x y c
Tính giá trị a b c . A.6 B. 11 C. 10 D. 7
Câu 16. Có bao nhiêu số nguyên m nhỏ hơn 10 để điểm A 1
; 2nằm trong miền nghiệm của bất phương trình
mx (m 1) y 2 . A.4 B. 6 C. 5 D. 7
Câu 17. Cho bốn điểm A 2
;0, B 0;3,C 3;2, D3; 2 . Đoạn ;
a b gồm tất cả các giá trị m để điểm M ; m m
1 nằm trong miền trong tứ giác ABCD (tính cả biên). Tính b a . 16 13 39 A.3 B. C. D. 7 21 14
x 2 y 2a
Câu 18. Một hệ quả của hệ bất phương trình là
3x 2 y 6a A. x a B. x 2a C. x 2a
D. x 2a 1 2
x(x 1) 0
Câu 19. Miền nghiệm của hệ bất phương trình 2
y( y 2) 0 là một tam giác vuông có chiều cao ứng với cạnh 3
x 4y 5 huyền bằng A.2 B. 1 C. 3 D. 1,5
Câu 20. Ông Minh trồng hai loại hoa gồm hoa hồng và hoa ly để bán vào dịp Tết Nguyên Đán. Hoa hồng có giá
80000 đồng/chậu và hoa ly có giá 120000 đồng/chậu. Ông Minh tính toán rằng, để không phải bù lỗ thì số tiền
bán hoa thu được phải đạt tối thiểu 30 triệu đồng. Gọi x và y lần lượt là số chậu hoa hồng và hoa ly bán
được. Hỏi x và y
thỏa mãn điều kiện nào dưới đây thì ông Minh không phải bù lỗ.
A. 2x 3y 750 B. 2x 3y 750
C. 3x 2 y 750
D. 3x 2 y 750
Câu 21. Miền không bị gạch trong hình vẽ (tính cả bờ) là miền nghiệm của hệ bất phương trình nào sau đây? x 0 y 0 x 0 y 0 x y 2 x y 2 x y 2 x y 2 A. . B. . C. . D. . x y 4 x y 4 x y 4 x 2 y 4
x y 2
x y 2
x y 2
x y 2 16
BPT BẬC NHẤT HAI ẨN + HỆ BPT BẬC NHẤT HAI ẨN LỚP 10 THPT
GIÁ TRỊ LỚN NHẤT, NHỎ NHẤT VÀ BÀI TOÁN THỰC TẾ
LỚP BÀI TOÁN VẬN DỤNG CAO P1
________________________________________ 0 y 4 x 0
Câu 1. Tìm trị lớn nhất của biểu thức F ;
x y x 2y , với điều kiện .
x y 1 0
x 2 y 10 0 A.9 B. 10 C. 8 D. 12
Câu 2. Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24 g hương liệu, 9 lít nước và 210 g
đường để pha chế nước cam và nước táo.
● Để pha chế 1 lít nước cam cần 30 g đường, 1 lít nước và 1 g hương liệu;
● Để pha chế 1 lít nước táo cần 10 g đường, 1 lít nước và 4 g hương liệu.
Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao
nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?
A. 5 lít nước cam và 4 lít nước táo.
B. 6 lít nước cam và 5 lít nước táo.
C. 4 lít nước cam và 5 lít nước táo.
D. 4 lít nước cam và 6 lít nước táo.
x y 2 0,
Câu 3. Cho cặp số ;
x y thỏa mãn hệ bất phương trình x y 1 0,
2x y 1 0.
Tính tổng các giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F 2x 3y . A. – 18 B. – 6 C. – 17 D. – 22
Câu 4. Cho hệ bất phương trình gồm 4 bất phương trình bậc nhất
hai ẩn x, y có miền nghiệm là tứ giác như hình vẽ. Tìm giá trị nhỏ
nhất của biểu thức F 3x 2 y . A. 4. B. – 5. C. – 2. D. 1.
Câu 5. Một phân xưởng sản xuất hai kiểu mũ. Thời gian để làm ra một chiếc mũ kiểu thứ nhất nhiều gấp hai lần
thời gian làm ra một chiếc mũ kiểu thứ hai. Nếu chỉ sản xuất toàn kiểu mũ thứ hai thì trong 1 giờ phân xưởng
làm được 60 chiếc. Phân xưởng làm việc 8 tiếng mỗi ngày và thị trường tiêu thụ tối đa trong một ngày là 200
chiếc mũ kiểu thứ nhất và 240 chiếc mũ kiểu thứ hai. Tiền lãi khi bán một chiếc mũ kiểu thứ nhất là 24 nghìn
đồng, một chiếc mũ kiểu thứ hai là 15 nghìn đồng. Tính số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một
ngày mà phân xưởng cần sản xuất để tiền lãi thu được là cao nhất.
A.240 mũ kiểu 1, 0 mũ kiểu 2
B. 120 mũ kiểu 1, 120 mũ kiểu 2
C. 60 mũ kiểu 1, 100 mũ kiểu 2
D. 150 mũ kiểu 1, 90 mũ kiểu 2.
Câu 6. Tìm điểm M ;
x y trong miền nghiệm S của hệ sao cho biểu thức T 3x 2y 4 có giá trị nhỏ nhất.
x y 1 0
x 4 y 9 0
x 2 y 3 0 A. 5; 4 . B. 1 ; 2 . C. 5 ; 1 . D. 2;5 .
Câu 7. Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilôgam thịt bò
chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilôgam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết
rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn; giá tiền 1 kg thịt bò là 250 nghìn đồng; 1 kg
thịt lợn là 160 nghìn đồng. Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn. Chi phí ít nhất gia đình chi trả là A.91 nghìn đồng B. 80 nghìn đồng C. 75 nghìn đồng D. 95 nghìn đồng
x y 2 0 Câu 8. Cho cặp ;
x y là nghiệm của hệ bất phương trình 2x y 4 0 . y 2 0
Hãy tính giá trị nhỏ nhất của biểu thức f ;
x y 2022x 2021y 2023 17 A. 2018 . B. 2019 . C. 2022 . D. 4041. 0 y 5 x 0
Câu 9. Giá trị nhỏ nhất của biểu thức F ;
x y x2y , với điều kiện là
x y 2 0
x y 2 0 A. 1 2. B. 1 0 . C. 8 . D. 6 .
Câu 10. Một nhà khoa học đã nghiên cứu về tác động phối hợp của hai loại Vitamin A và B đã thu được kết
quả như sau: Trong một ngày, mỗi người cần từ 400 đến 1000 đơn vị Vitamin cả A lẫn B và có thể tiếp nhận
không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B . Do tác động phối hợp của hai loại vitamin
trên nên mỗi ngày một người sử dụng số đơn vị vitamin B không ít hơn một nửa số đơn vị vitamin A và không
nhiều hơn ba lần số đơn vị vitamin A . Tính số đơn vị vitamin mỗi loại ở trên để một người dùng mỗi ngày sao
cho chi phí rẻ nhất, biết rằng mỗi đơn vị vitamin A có giá 9 đồng và mỗi đơn vị vitamin B có giá 7,5 đồng.
A. 600 đơn vị Vitamin A , 400 đơn vị Vitamin . B
B. 600 đơn vị Vitamin A , 300 đơn vị Vitamin . B
C. 500 đơn vị Vitamin A , 500 đơn vị Vitamin . B
D. 100 đơn vị Vitamin A , 300 đơn vị Vitamin . B
y 2x 2
Câu 11. Giá trị nhỏ nhất của biết thức trên miền xác định bởi hệ 2y x 4 là.
x y 5
A. min F 1 khi x 2, y 3 .
B. min F 2 khi x 0, y 2 .
C. min F 3 khi x 1, y 4 .
D. min F 0 khi x 0, y 0 .
Câu 12. Người ta định dùng hai loại nguyên liệu để chiết xuất ít nhất 120 kg hóa chất A và 9 kg hóa chất B. Từ
mỗi tấn nguyên liệu loại I giá 4 triệu đồng có thể chiết xuất được 20 kg chất A và 0,6 kg chất B. Từ mỗi tấn
nguyên liệu loại II giá 3 triệu đồng có thể chiết xuất được 10 kg chất A và 1,5 kg chất B. Biết rằng cơ sở cung
cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II.
Khi chi phí nguyên liệu là ít nhất thì khối lượng nguyên liệu loại 1 là A.3,75 tấn B. 3,25 tấn C. 3,45 tấn D. 3 tấn
Câu 13. Có ba nhóm máy A, B,C dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một đơn vị sản
phẩm mỗi loại phải lần lượt dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và số máy của
từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được cho trong bảng sau:
Số máy trong từng nhóm để sản xuất ra một đơn Số máy trong mỗi Nhóm vị sản phẩm nhóm Loại I Loại II A 10 2 2 B 4 0 2 C 12 2 4
Một đơn vị sản phẩm I lãi ba nghìn đồng, một đơn vị sản phẩm loại II lãi năm nghìn đồng. Hãy lập phương án để
việc sản xuất hai loại sản phẩm trên có lãi cao nhất.
A.4 sản phẩm loại 1, 1 sản phẩm loại 2
B. 3 sản phẩm loại 1, 1 sản phẩm loại 2
C. 2 sản phẩm loại 1, 2 sản phẩm loại 2
D. 2 sản phẩm loại 1, 1 sản phẩm loại 2.
Câu 14. Lượng calo từ tinh bột khuyến nghị hàng ngày cho một người bình thường khoảng 480 đến 1200 calo.
Để nạp đủ chất thì người ta cần nạp cả hai loại tinh bột hấp thu nhanh và tinh bột hấp thu chậm vào cơ thể. Biết
rằng trong 100 g gạo (chứa tinh bột hấp thu nhanh) có khoảng 150 calo và 100 g yến mạch (chứa tinh bột hấp
thu chậm) có khoảng 50 calo. Hôm nay bạn An đã ăn ít nhất là 200 g gạo. Hỏi bạn ấy cần ăn nhiều nhất bao
nhiêu gam yến mạch để có thể nạp vào cơ thể lượng calo tối thiểu cần thiết. A. 800 gam. B. 200 gam. C. 320 gam. D. 360 gam. 0 x 10 0 y 9
Câu 15. Miền nghiệm của hệ 2x y 14
là miền đa giác. Tính diện tích đa giác đó.
2x 5y 30 147 145 A. . B. . C. 35 . D. 36 . 4 4
_________________________________ 18
BPT BẬC NHẤT HAI ẨN + HỆ BPT BẬC NHẤT HAI ẨN LỚP 10 THPT
GIÁ TRỊ LỚN NHẤT, NHỎ NHẤT VÀ BÀI TOÁN THỰC TẾ
LỚP BÀI TOÁN VẬN DỤNG CAO P2
________________________________________
Câu 1. Một hộ nông dân định trồng đậu và cà trên diện tích 800 m2. Nếu trồng đậu thì cần 20 công và thu
3.000.000 đồng trên 100 m2 nếu trồng cà thì cần 30 công và thu 4.000.000 đồng trên 100 m2. Biết rằng tổng số
công không quá 180 , khi hộ nông dân thu được nhiều tiền nhất thì diện tích trồng đậu là A. 2 600m B. 2 400m C. 2 500m D. 2 450m
2x 3y 6 0
Câu 2. Biểu thức L y x , với x và y thỏa mãn hệ bất phương trình x 0
, đạt giá trị lớn nhất là
2x 3y 1 0
a và đạt giá trị nhỏ nhất là b. Hãy chọn kết quả đúng trong các kết quả sau: 25 11 9 A. a và b 2 .
B. a 2 và b .
C. a 3 và b 0 .
D. a 3 và b . 8 12 8
Câu 3. Bạn An kinh doanh hai mặt hàng handmade là vòng tay và vòng đeo cổ. Mỗi vòng tay làm trong 4 giờ,
bán được 40 ngàn đồng. Mỗi vòng đeo cổ làm trong 6 giờ, bán được 80 ngàn đồng. Mỗi tuần bạn An bán được
không quá 15 vòng tay và 4 vòng đeo cổ. Tính số giờ tối thiểu trong tuần An cần dùng để bán được ít nhất 400 ngàn đồng? A.32 giờ B. 30 giờ C. 34 giờ D. 28 giờ
2x 3y 6 0 Câu 4. Cho cặp ;
x y là nghiệm của hệ bất phương trình x 2 y 3 0 . y 2 0
Hãy tính giá trị lớn nhất của biểu thức f ;
x y 2022x 2021y A. 2022 . B. 6066 . C. 4044 . D. 4042 .
Câu 5. Bác Hai có một mảnh đất rộng 6 ha. Bác dự tính trồng cà chua và bắp cho mùa vụ sắp tới. Nếu trồng
bắp thì bác Hai cần mười ngày để trồng một ha. Nếu trồng cà chua thì bác Hai cần hai mươi ngày để trồng một
ha. Biết rằng mỗi ha bắp sau thu hoạch bán được 30 triệu đồng, mỗi ha cà chua sau thu hoạch bán được 50
triệu đồng và bác Hai chỉ còn 100 ngày để canh tác cho kịp mùa vụ. Số tiền nhiều nhất mà bác Hai có thể thu
được sau màu vụ này là bao nhiêu. A. 180 triệu. B. 250 triệu. C. 260 triệu. D. 270 triệu.
Câu 6. Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm I và II . Mỗi sản
phẩm I bán lãi 500 nghìn đồng, mỗi sản phẩm II bán lãi 400 nghìn đồng. Để sản xuất được một sản phẩm I
thì Chiến phải làm việc trong 3 giờ, Bình phải làm việc trong 1 giờ. Để sản xuất được một sản phẩm II thì
Chiến phải làm việc trong 2 giờ, Bình phải làm việc trong 6 giờ. Một người không thể làm được đồng thời hai
sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá 180 giờ và Bình không thể làm việc quá
220 giờ. Tính số tiền lãi lớn nhất trong một tháng của xưởng. A.32 triệu đồng B. 35 triệu đồng C. 36 triệu đồng D. 30 triệu đồng
2x y 14
2x 5y 30
Câu 7. Miền nghiệm của hệ bất phương trình
là miền tứ giác ABCD . 0 x 10 0 y 9
Tìm giá trị nhỏ nhất của biểu thức F x 6 y , với ;
x y là nghiệm của hệ bất phương trình trên. A. 29 . B. 64 . C. 22 . D. 20 .
y 2x 2
Câu 8. Miền nghiệm của hệ bất phương trình 2 y x 4 là miền tam giác ABC .
x y 5
Tìm giá trị lớn nhất của biểu thức F 3x y , với ;
x y là nghiệm của hệ bất phương trình trên. A. 2 . B. 9 . C. 7 . D. 10.
Câu 9. Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kiogam thịt
bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilogam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit.
Biết rằng gia đình này chỉ mua nhiều nhất 1, 6 kg thịt bò và 1,1 kg thịt lợn. Giá tiền một kg thịt bò là 160 nghìn 19
đồng, một kg thịt lợn là 110 nghìn đồng. Gọi x , y lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua.
Tìm tổng số tiền họ phải trả ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn. A.170 nghìn đồng B. 173 nghìn đồng C. 180 nghìn đồng D. 150 nghìn đồng
Câu 10. Một hộ nông dân định trồng dứa và củ đậu trên diện tích 8ha . Trên diện tích mỗi ha , nếu trồng dứa thì
cần 20 công và thu 3 triệu đồng, nếu trồng củ đậu thì cần 30 công và thu 4 triệu đồng. Hỏi cần trồng mỗi loại cây
trên với diện tích tỉ lệ (diện tích trồng đậu: diện tích trồng cà) là bao nhiêu để thu được nhiều tiền nhất, biết rằng
tổng số công không quá 180. A.3 B. 2 C. 4 D. 5
Câu 11. Trên miền tứ giác OABC , phần không bị gạch sọc như hình vẽ bên dưới. Giá trị lớn nhất của biểu
thức F 2x 3 y 2022 bằng A. 2022 . B. 2038 . C. 2040 . D. 4044 .
y 2 x 2
Câu 12. Gọi S là tập hợp các điểm trong mặt phẳng tọa độ có tọa độ thỏa mãn hệ 2 y x 4 . Trong S
x y 5 điểm có tọa độ ,
x y làm cho biểu thức F( ;
x y) y x đạt giá trị nhỏ nhất là A. 2; 3 . B. 1; 4 . C. 2; 0 . D. 4; 1 .
Câu 13. Cho hệ bất phương trình gồm 4 bất phương trình bậc
nhất hai ẩn x, y có miền nghiệm là tứ giác như hình vẽ. Có bao
nhiêu số nguyên m để điểm Q 2 ;
m m nằm trong miền nghiệm của hệ. A. 4. B. 3. C. 1. D. 2. 0 y 4 x 0
Câu 14. Giá trị lớn nhất của biết thức F ;
x y x 2 y với điều kiện là
x y 1 0
x 2 y 10 0 A. 8 . B. 10 . C. 12 . D. 6 .
Câu 15. Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24 g hương liệu, 9 lít nước và 210 g
đường để pha chế nước cam và nước táo. Để pha chế 1 lít nước cam cần 30 g đường và 1 lít nước; pha chế 1
lít nước táo cần 10 g đường, 1 lít nước và 4 g hương liệu. Mỗi lít nước cam nhận được 20 điểm thưởng, mỗi lít
nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để được số tiền thưởng là lớn nhất? A. 7 lít nước cam. B. 6 lít nước táo.
C. 3 lít nước cam, 6 lít nước táo.
D. 6 lít nước cam, 3 lít nước táo.
2x y 9 0
Câu 16. Cho hệ bất phương trình x y 0
. Tìm giá trị lớn nhất của biểu thức F ;
x y 2x y bằng y 1 0 A. 6 . B. 12 . C. 3. D. 9 . 20




