Ôn luyện các nhóm câu hỏi vận dụng cao trong đề thi THPTQG môn Toán (Đề 2)

Tài liệu gồm 35 trang tuyển tập 40 câu hỏi và bài toán vận dụng cao có lời giải chi tiết nhằm ôn luyện kỳ thi THPTQG môn Toán năm 2019, các bài toán được chọn lọc từ nhóm các đề thi thử và đề khảo sát chất lượng môn Toán giai đoạn giữa học kỳ 1 năm học 2018 – 2019

27 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu ôn thi THPTQG môn Toán

Môn: Toán

Thông tin:

35 trang 6 tháng trước

Tác giả:

Profile Nguyễn Vân
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 1
ĐỀ ÔN LUYỆN CÁC NHÓM CÂU HỎI
VẬN DỤNG CAO TRONG ĐỀ THI THPT QUỐC GIA
Đề gồm 40 câu trắc nghiệm
Quà tặng mừng ngày nhà giáo Việt Nam 20/11
Tuyển chọn 40 câu vận dụng cao có lời giải chi tiết là một sản phẩm được biên soạn, sưu
tầm và sáng tác bởi nhóm Chinh Phục Olympic Toán và được đăng trên Fanpage Tạp chí
và tư liệu Toán học. Đồng thời đây cũng là một quà tặng gửi tới các thầy cô nhân ngày nhà
giáo Việt Nam, và cũng nhân dịp này cả nhóm chúc các thầy cô trên cả nước có sức khỏe,
hạnh phúc trong cuộc sống, thành đạt hơn trong cïng việc và có một ngày 20/11 thật ý
nghĩa và vui vẻ. Xin cảm ơn mọi người!
ĐỀ BÀI
Câu 1 : Biết rằng tập hợp các giá trị của
m
để phương trënh sau cî nghiệm là đoạn
;ab
2 3 2 1 1 1 0m x m x m
có nghiệm là đoạn
;ab
. Tính giá trị của biểu
thức
22
3S a b ab
?
A.
1
2
C.
0
D.
3
Câu 2: Gọi
12
,z a bi z c di
là nghiệm của phương trënh
2 2 2 2 6zz
đồng
thời thỏa mãn
0ac bd
. Gọi M, n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
12
1
2
P z z
. Tính giá trị của biểu thức
S M n
A.
14
5
S
13
5
S
C.
12
5
S
D.
11
5
S
Câu 3: Cho hai hàm
fx
và
gx
cî đạo hàm trên
1; 2 ,
thỏa mãn
1 1 0fg
và
2
3
2
2018 1 '
1
, 1; 2 .
' 2019
1
x
g x x x f x
x
x
x
g x f x x
x


Tính
2
1
1
.
1
xx
I g x f x dx
xx




A.
1
.
2
I
1.I
C.
3
.
2
I
D.
2.I
Câu 4: Cho lăng trụ đứng ABC.A’B’C’ có
0
6, 12, 60AB BC ABC
. Thể tích khối chóp
'. ' 'C ABB A
bằng 216. Gọi M là điểm nằm trong tam giác
' ' 'A B C
sao cho tổng diện tích các
mặt bên của hình chóp
.M ABC
đạt giá trị nhỏ nhất. Tính cosin góc giữa 2 đường thẳng
' , 'B M AC
?
A.
2
2
2
3
C.
2
4
D.
1
2
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
2 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Câu 5: Hai người bắn độc lập vào một mục tiêu, mỗi người bắn 1 lần. Xác suất trúng của
người thứ nhất là 0,9; của người thứ hai là 0,7. Tìm giá trị lớn nhất của biểu thức
2
13 10M p p
, trong đî p là xác suất của một biến cố.
A.
169
40
528
125
C.
4221
1000
D. 3
Câu 6: Cho tam giác
ABC
có
60BAC
và
,AB AC
đã biết. Biểu thức
.P k MA MB MC
đạt giá trị nhỏ nhất bằng
AB AC
với mọi giá trị thực
0
kk
. Giá
trị của
0
k
nằm trong khoảng nào dưới đây ?
A.
0; 1
3
;2
2



C.
3
1;
2



D.
2; 3
Câu 7: Cho
tan d
n
n
I x x
với
n
. Khi đî
0 1 2 3 8 9 10
2 ...I I I I I I I
bằng?
A.
9
1
tan
r
r
x
C
r
1
9
1
tan
1
r
r
x
C
r
C.
10
1
tan
r
r
x
C
r
D.
1
10
1
tan
1
r
r
x
C
r
Câu 8: Cho hàm số
fx
cî đạo hàm liên tục trên đoạn
1; 2
thỏa mãn đồng thời 2 điều
kiện
2 2 2 2
22
2 2 1 63;2 ' 27 , 1;2f f f x x f x x x
. Tính giá trị của tích
phân
2
2
1
f x dx


A.
15
18
C.
21
D.
25
Câu 9: Cho hàm số
fx
cî đạo hàm liên tục trên đoạn
0; 1
thỏa mãn
. 1 4 0 4e f f
và đồng thời
11
22
2
00
8
' 4 .
3
xx
e f x f x dx e f x dx

. Tính tích phân
1
0
f x dx
?
A.
4 e 1
e
3 e 1
e
C.
2 e 2
e
D.
5 e 2
e
Câu 10: Cho
,xy
là hai số thực dương thay đổi thỏa mãn điều kiện
1
1 1 1xy xy y x
y
.
Tëm giá trị lớn nhất của biểu thức
22
2
6
3
x y x y
P
xy
x xy y



?
A.
57
3 30
75
30 3
C.
57
3 30
D.
57
30
Câu 11: Cho hàm số
y f x
cî đạo hàm
2
2
12f x x x x
với
x
. Có bao
nhiêu giá trị nguyên dương của tham số
m
để hàm số
2
8f x x m
có
5
điểm cực trị?
A.
15
17
C.
16
D.
18
Câu 12: Biết rằng đồ thị hàm số bậc
4
:
y f x
được cho như hënh vẽ sau:
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 3
Tëm số giao điểm của đồ thị hàm số
2
.y g x f x f x f x


và trục
Ox
.
A.
4
6
C.
2
D.
0
Câu 13: Cho biểu thức
log 2017 log 2016 log 2015 log ... log 3 log 2 ...A
Biểu thức
A
có giá trị thuộc khoảng nào trong các khoảng dưới đây?
A.
log 2017;log 2018
B.
log 2019;log 2020
C.
log 2018;log 2019
D.
log 2020;log 2021
Câu 14: Cho dãy số
n
u
thỏa mãn
21
1
*
2
2
391 1 39
log log 2
40 4 4
21
2
,
11
n
n
uu
nu
n
un
n
nn
.
Giá trị nhỏ nhất của n để
100 2
100 3
51
5
n
n
u
nn

.
A. 235
B. 255
C. 233
D. 241
Câu 15: Xét tập hợp gồm
2 2 2 2
, , ,A ax bx c ax bx ax c ax
(trong đî a, b, c là các số
nguyên dương nhỏ hơn). Lấy ngẫu nhiên ra một tam thức bậc hai thuộc A. Tính xác suất
để lấy được tam thức bậc hai mà khi ghép các hệ số của theo thứ tự từ bậc cao tới bậc
thấp được một số chia hết cho 7 hoặc 11.
A.
220
900
220
999
C.
218
999
D.
218
900
Câu 16 : Tính tổng
2 2 2 2
1 2 2017 2018
2018 2018 2018 2018
1 2 2017 2018
...
2018 2017 2 1
S C C C C
A.
2018
4036
2018
2019
C
2018
4036
2018
2017
C
C.
2018
4036
2019
2018
C
D.
2018
4036
2017
2018
C
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
4 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Câu 17: Cho 2 số phức
1
2
z a bi
z c di


thỏa mãn
29
24
ab
cd


. Tìm
12
zz
khi biểu thức
1 1 2 2
6 4 2 4P z i z z z i
đạt giá trị nhỏ nhất.
A.
4 29
3 29
C.
6 29
D.
3 29
Câu 18: Cho hai số phức
12
,zz
thỏa mãn
12
1
2
3 3 0z i k z i k
z mi m R
zR

Tìm k khi biểu thức
22
12
94
P
zz

đạt giá trị nhỏ nhất.
A.
1k
3k 
C.
4k 
D.
2k
Câu 19: Trong mặt phẳng phức, xét hình bình hành tạo bởi các điểm
0
,
z
,
1
z
và
1
z
z
.
Biết
z
có phần thực dương và diện tích hình bình hành bằng
35
37
. Tìm GTNN của
2
1
z
z
.
A.
53
20
60
37
C.
22
9
D.
50
37
Câu 20: Cho hình chóp
.S ABCD
cî đáy
ABCD
là hình bình hành. Gọi
M
,
N
lần lượt là
trung điểm của các cạnh
AB
,
BC
. Điểm
I
thuộc đoạn
SA
. Biết mặt phẳng
MNI
chia
khối chóp
.S ABCD
thành hai phần, phần chứa đỉnh
S
có thể tích bằng
7
13
lần phần còn
lại. Tính tỉ số
IA
k
IS
?
A.
3
4
1
2
C.
1
3
D.
2
3
Câu 21: Cho đa giác đều gồm 100 đỉnh. Tính số tam giác tù được chọn từ 3 đỉnh của đa
giác trên?
A.
117600
117800
C.
116700
D.
117670
Câu 22: Cho hai số thực
,1xy
thỏa mãn điều kiện:
2 2 2
22
2
log 2 log log 4 1
41
xy
x y xy
xy

Giá trị lớn nhất của biểu thức
22
, 2 2 4f x y xy x y x y
bằng?
A.
1
2
2
3
C.
3
4
D.
3
7
Câu 23. Cho phương trënh
3 tan 1 sin 2 cos sin 3cos .x x x m x x
Có bao nhiêu giá
trị nguyên của tham số
m
thộc đoạn
2018; 2018
để phương trënh trên cî đúng một
nghiệm thuộc
0;
2



?
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 5
A.
2015.
2016.
C.
2018.
D.
4036.
Câu 24: Cho phương trënh
2017 2018 2018
cos 2
2 sin cos sin cos cos .
1 tan
x
x x x x x
x
Nghiệm
dương nhỏ nhất của phương trënh cî dạng
a
b
với
, ab
là các số nguyên và nguyên tố
cùng nhau. Tính
.S a b
A.
2.S
3.S
C.
4.S
D.
7.S
Câu 25: Cho các số thực a,b,c thỏa mãn
0 , , 1a b c
. Khi đî trị nhỏ nhất của biểu thức
2
1
log log log
4
a b c
P b c a
được viết dưới dạng
m
n
, với m,n là các số nguyên dương và
m
n
là phân số tối giản. Hỏi
33
T m n
có giá trị là bao nhiêu?
A. 171
B. 89
C. 195
D. 163
Câu 26: Có bao nhiêu số nguyên
2018; 2018m
để phương trënh
1
2
3
28
2
x
xm
có
đúng 2 nghiệm thực phân biệt?
A.
2013
2012
C.
4024
D.
2014
Câu 27: Giả sử số tự nhiên
2n
thỏa mãn đẳng thức dưới đây hãy tëm n?
2 4 6 2 2 2
0
2 2 2 2 2
2
4096
...
3 5 7 2 1 2 1 13
nn
n n n n n
n
C C C C C
C
nn

A.
4n
5n
C.
6n
D.
7n
Câu 28: Tính tổng
0 3 6 3 15 18
20 20 20 20 20 20
3 6 ... 3 ... 15 18
k
S C C C kC C C
?
A.
20
10.2
13
3
S 
20
10.2
14
3
S 
C.
21
10.2
13
3
S 
D.
19
10.2
13
3
S 
Câu 29: Cho hàm số
fx
cî đạo hàm trên
\ b
và hàm số
gx
cî đạo hàm trên .
Biết đồ thị của hai hàm số
' , 'y f x y g x
như hënh vẽ dưới.
Đặt
2
2
22
, 1 2h x f x g x S h x b h b x h c h c




với a,b,c là các số
thực đã biết. Khẳng định đúng với mọi
0x
là?
y g x
y f x
O
y
x
a
b
c
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
6 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
A.
;S h c h a c


B.
S h c
C.
;S h c h a b


D.
;S h a h c


Câu 30: Cho 3 số thực thỏa mãn
2; 4 ; 0; 4 ; 1; 5x y z
. Khi đî giá trị lớn nhất của
biểu thức
2
3 5 5
5 log 1 2 log 1 4logT x y z x y z
bằng?
A.
10
11
C.
8 5 14
D.
12
Câu 31: Cho
0 1 1a b a
và hàm số
2
1
fx
y g x
fx

cî đạo hàm trên
0;
. Biết đồ thị hàm số
y f x
như hënh vẽ dưới. Khẳng định nào sau đây đúng với
mọi
1; 1x a b


A.
1fb
gx
m
1fa
gx
n
C.
1fb
gx
m
D.
10 0gx
Câu 32: Cho các số thực dương a,b,c,m,n,p thỏa mãn điều kiện
2017 2017
2017
2 2 3 7m n p
và
4 4 3 42a b c
. Đặt
2018 2018
2018
2 2 2 2
3
ab
c
S
m n p
thì khẳng định đúng là?
A.
2018
42 7.6S
2018
6S
C.
2018
7 7.6S
D.
4 42S
Câu 33: Có bao nhiêu cặp số nguyên
, ab
để phương trënh sau đúng với mọi x
22
cos 1 1 1a x b cos ax b
A.
0
1
C.
2
D.
3
O
a
b
x
y
m
n
y f x
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 7
Câu 34: Cho hệ phương trënh
2
2
20
1
p x p x
x
vô nghiệm khi
;;p a b  
.
Tính giá trị của biểu thức
22
A a b
A.
10
9
C.
13
D.
16
Câu 35: Cho dãy số
n
u
được xác định bởi
1
2u
;
1
2 3 1
nn
u u n
. Cïng thức số hạng
tổng quát của dãy số đã cho là biểu thức cî dạng
.2
n
a bn c
, với
a
,
b
,
c
là các số nguyên,
2n
;
n
. Khi đî tổng
a b c
cî giá trị bằng
A.
4
4
C.
3
D.
3
Câu 36: Một ngày đẹp trời, trong lúc đi dạo công viên, cầm một khối cầu trong tay, một
nhà khoa học yêu cái đẹp nảy ra û tưởng muốn tạo ra một khối nón nội tiếp trong một
khối cầu cî bán kình R và đựng một loại dung dịch X do ông chế tạo ra vào trong đî, sao
cho thể tích dung dịch X chứa được trong X là lớn nhất. Sau khi chế tạo xong, trong lúc
mải ngắm tác phẩm của mình, nhà khoa học đã vï tënh làm vỡ cả khối cầu thủy tinh, tuy
vậy ïng đã thu hồi lại được lượng dung dịch X quý giá của mình. Lần này, vì rút kinh
nghiệm, cũng lượng dung dịch X đî, nhà khoa học muốn chế tạo một cái hộp bằng một
loại kim loại chịu lực trong suốt để đựng dung dịch của mình. Ông có hai sự lựa chọn cho
hộp kim loại của mình, có dạng hình hộp chữ nhật hoặc là có dạng khối trụ. Tuy nhiên,
kinh phí còn lại của ông có hạn, còn giá thành kim loại đî lại rất đắt vì nó hiếm. Ông
muốn chi phí sản xuất kim loại cấu thành hộp là bé nhất, nhưng vẫn phải chứa được lượng
dung dịch X đã cî của mình.Hãy giúp nhà khoa học tính toán xem diện tích toàn phần
nhỏ nhất của hộp kim loại là bao nhiêu?
A.
11
2
3
8
2
3
3
R
11
2
3
8
2
3
R
C.
6
2
3
4
2
3
3
R
D.
6
2
3
4
2
3
R
Câu 37:
O
x
y
11
1
2
–1
–2
–1
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
8 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Cho hàm số
fx
cî đồ thị như hënh vẽ đồng thời
1 2 2 1 1 *f x f x x x x
Biết
rằng
42
f x ax bx c
;
2
g x mx nx p
và
2
1f x g x
. Tìm giá trị nhỏ nhất của
hàm số
gx
A.
1
2
1
4
C.
2
D.
4
Câu 38: Cho hàm số
32
51
3
33
y x x C
. Tìm những điểm trên đường thẳng
:d y ax b
đi qua gốc tọa độ và tạo với đường thẳng
1
3
yx
một góc
0
15
mà từ đî kẻ
được đến
C
2 tiếp tuyến .
A.
11
; ; 1;1
55




11
; ; 1;1
55



C.
11
; ; 1;1
55




D.
11
; ; 1; 1
55



Câu 39: Cho hàm số
8 c
3 tan
1 2
x a bx
f x c x
xx
. Biết đồ thị hàm số cî đúng 2
đường tiệm cận (chỉ tính tiệm cận đứng và tiệm cận ngang). Số giá trị nguyên tối đa cî thể
của tham số a thỏa mãn bài toán là?
A.
8
2
C.
10
D.
9
Câu 40: Cho tích phân
11
7
7 11I x x dx
, gọi M và m lần lượt là giá trị lớn nhất và
giá trị nhỏ nhất của I. Tính
S M m
?
A.
54 2 108
B.
36 2 108
C.
6 3 54
D.
6 3 36
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 9
LỜI GIẢI CHI TIẾT ĐỀ VẬN DỤNG CAO
Câu 1 : Biết rằng tập hợp các giá trị của
m
để phương trënh sau cî nghiệm là đoạn
;ab
2 3 2 1 1 1 0m x m x m
có nghiệm là đoạn
;ab
. Tính giá trị của biểu
thức
22
3S a b ab
?
A.
1
B.
2
C.
0
D.
3
Giải
Biến đổi phương trënh đầu tương đương PT
2 3 1 1
3 2 1 1
xx
m
xx

2
Vì
22
3 1 4xx
nên đặt
3 2 sin
0;
2
1 2 os
x
xc






.
Đặt
tan 0;1
2
tt

khi đî
2
trở thành
2
2
22
2
2
2
22
21
4. 2. 1
4sin 2 os 1 8 3 1 20 4
11
21
2 sin 4 os 1 3 4 5 3
3 3 4 5
2. 4. 1
11
tt
c t t t
tt
m
tt
c t t
tt
tt




Xét
2
20 4
3 4 5
t
ft
tt
trên đoạn
0; 1
được:
2
22
60 24 84
0, 0;1
( 3 4 5)
tt
f t t
tt

. Suy ra
4 4 4 1 4 1 1 4 3 5
0 1 4
5 15 3 3 3 15 3 3 3 3 5 3
f t f t
f f t f f t m
Câu 2: Gọi
12
,z a bi z c di
là nghiệm của phương trënh
2 2 2 2 6zz
đồng
thời thỏa mãn
0ac bd
. Gọi M, n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
12
1
2
P z z
. Tính giá trị của biểu thức
S M n
A.
14
5
S
B.
13
5
S
C.
12
5
S
D.
11
5
S
Giải
Gọi
12
, , 0 . 0A z B z ac bd OA OB OA OB
.
Trường hợp 1: Xét A,B lần lượt nằm trên hai trục tọa độ thì ta có:
12
1 1 3
.
2 2 2
P z z OA OB
Trường hợp 2: Xét hai điểm A,B lần lượt nằm trên hai đường vuông góc
1
,y kx y x
k
.
Tọa độ điểm A thỏa mãn
2
2
22
22
2 2 2
1
9 9 1
3
91
9 1 9 1 9 1
AA
y
x
kk
x y OA
k k k
y kx

SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
10 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Tương tự
2
2
1
3
9
k
OB
k
. Theo giả thiết ta có:
2
12
22
91
11
.
22
9 1 9
OAB
k
P z z S
kk

.
Theo AM – GM ta có
2 2 2 2
9
2 9 1 9 10 1 1
10
k k k S k
.
Theo Cauchy – Shwarz ta có
2 2 2
3
9 1 9 3 1
2
k k k S
. Dấu “=” xảy ra khi A,B
là các giao điểm của elip với trục tọa độ và các hoán vị.
Vậy cả hai trường hợp ta có
9
min
10
3
max
2
P
P
.
Câu 3: Cho hai hàm
fx
và
gx
cî đạo hàm trên
1; 2 ,
thỏa mãn
1 1 0fg
và
2
3
2
2018 1 '
1
, 1; 2 .
' 2019
1
x
g x x x f x
x
x
x
g x f x x
x


Tính
2
1
1
.
1
xx
I g x f x dx
xx




A.
1
.
2
I
B.
1.I
C.
3
.
2
I
D.
2.I
Giải
Bài này có vẻ tương đối khî khăn rồi do đây là 2 hàm độc lập, tuy nhiên ta chú ý vẫn bám
sát û tưởng của các bài toán trong mục này!
Từ giả thiết ta có
2
2
1
1
' 2018
1
1
' 2019
1
x
g x f x
x
x
x
g x f x
xx

. Cộng lại vế theo vế ta được:
2
2
1
11
' ' 1
1
1
x
x
g x g x f x f x
x x x
x







11
1.
11
xx
xx
g x f x g x f x x C
x x x x








Mà ta lại có
22
11
11
1 1 0 1 1 .
12
xx
f g C I g x f x dx x dx
xx




Câu 4: Cho lăng trụ đứng ABC.A’B’C’ cî
0
6, 12, 60AB BC ABC
. Thể tích khối chóp
'. ' 'C ABB A
bằng 216. Gọi M là điểm nằm trong tam giác
' ' 'A B C
sao cho tổng diện tích các
mặt bên của hình chóp
.M ABC
đạt giá trị nhỏ nhất. Tính cosin góc giữa 2 đường thẳng
' , 'B M AC
?
A.
2
2
B.
2
3
C.
2
4
D.
1
2
Giải
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 11
B'
A'
C'
A
B
C
K
H
M
Gọi I là hình chiếu của M lên
ABC
;
,,D E F
lần lượt là hình chiếu của I lên AB, BC, CA.
Đặt
, , , 2 , 2 , 2 , 'ID x IE y IF z AB a BC b CA c MI AA h
.
Khi đî
ABC IAB IAC IBC
S S S S ax by cz
. Diện tích toàn phần của hình chóp
.M ABC
nhỏ nhất khi và chỉ khi
MAB MBC MCA
S S S S
nhỏ nhất.
Có
22
2 2 2 2 2 2
1
.
2
MAB
MD MI ID x h S AB MD a h x ah ax
Tương tự ta được
2
2 2 2 2 2
S ah xa bh by hc cz
Theo Mincowski ta có
2
22
22
const
ABC
S ah bh ch ax by cz a b c h S
Dấu “=” xảy ra khi và chỉ khi
by
ax cz
x y z
ah bh ch
.
Khi đî ta cî
' ' '
1
. sin 18 3
2
A B C ABC
S S BA BC ABC
,
2 2 2 2 0
' ' 2 . .cos60 ' ' 6 3A C AC AB BC AB BC A C
Vì
'. ' '
3
324 ' 6 3
2
LT C ABB A
V V AA
. Gọi K là chân đường phân giác trong của tam giác
' ' 'A B C
kẻ từ B , từ K kẻ đường thẳng song song với AC ' cắt AA' tại H , khi đó
' , ' , cos cos 'B M AC B K KH B KH
Ta có
0
' ' ' ' ' ' '
1
' ' ' ' ' sin 30 ' 4 3
2
B C A B KC B KA
S S S B K B A B C B K
' ' ' 1 1
' ' ' 2 3
' ' ' 2 3
A K A B
A K A C
C K C B
Do
' ' 1
// ' ' 2 3
' ' ' 3
A H A K
KH AC A H
A A A C
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
12 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
22
2 6, ' 4 3 cos ' cos
44
KH B H B KH
Câu 5: Hai người bắn độc lập vào một mục tiêu, mỗi người bắn 1 lần. Xác suất trúng của
người thứ nhất là 0,9; của người thứ hai là 0,7. Tìm giá trị lớn nhất của biểu thức
2
13 10M p p
, trong đî p là xác suất của một biến cố.
A.
169
40
B.
528
125
C.
4221
1000
D. 3
Giải
Gọi
1
A
là biến cố người thứ nhất bắn trúng,
2
A
là biến cố người thứ hai bắn trúng.
Khi đî
12
0,9; 0,7.p A p A
Ta có
2
2
169 13
13 10 10
40 20
M p p p



.
Do đî M lớn nhất khi và chỉ khi
13
20
p
nhỏ nhất
Giả sử p là xác suất của biến cố A. Ta quy ước
0.
1.
A
AA

Khi đî
1 2 1 2 1 2 1 2
A xA A yA A zA A tA A
, trong đî
, , , 0;1x y z t
.
1 2 1 2 1 2 1 2
. . . . 0,63 0,07 0,27 0,03p p A x p A A y p A A z p A A t p A A x y z t
13
0,63 0,07 0,27 0,03 0,65 0,63 0,07 0, 27 0,03 0,65
20
p x y z t x y z t
Nếu x = 1:
13
0,07 0,27 0,03 0,02
20
p y z t
Ta có
; ; 0;1y z t
thì
0,07 0,27 0,03 0,02y z t
nhỏ nhất khi
0
0
1
y
z
t
Khi đî
13
0,01
20
p 
Nếu x = 0:
13
0,07 0,27 0,03 0,65
20
p y z t
Ta có
; ; 0;1 0 ; ; 1 0 0,07 0, 27 0,03 0, 37y z t y z t y z t
0,65 0,07 0,27 0,03 0,65 0, 28
13
0,65 0,07 0,27 0,03 0,65 0, 28 0, 28 0,01
20
y z t
y z t p
Từ 2 trường hợp trên ta thấy
min
1
13
0,01
0
20
xt
p
yz


Khi đî
2
max
169 528
10.0,01
40 125
M
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 13
Câu 6: Cho tam giác
ABC
có
60BAC
và
,AB AC
đã biết. Biểu thức
.P k MA MB MC
đạt giá trị nhỏ nhất bằng
AB AC
với mọi giá trị thực
0
kk
. Giá
trị của
0
k
nằm trong khoảng nào dưới đây ?
A.
0; 1
B.
3
;2
2



C.
3
1;
2



D.
2; 3
Giải
Ta có:
. . .
v
u v u v u u
v
và:
..u v u v
. Áp dụng vào bài này, ta có :
. . . . . . .
AB AC AB AC
P k MA MB MC k MA MB MC k MA MA AB MA AC
AB AC AB AC
..
AB AC AB AC
P k MA AB AC MA k MA AB AC MA
AB AC AB AC


AB AC
P MA k AB AC
AB AC




.
Theo giả thiết ta có
AB AC
P MA k AB AC AB AC
AB AC




Suy ra
0
AB AC AB AC
kk
AB AC AB AC




Ta có
2 2 2
2 . 1 1 2.cos 60 3
AB AC AB AC AB AC
AB AC AB AC AB AC
Suy ra:
0
3
AB AC
kk
AB AC
.
Câu 7: Cho
tan d
n
n
I x x
với
n
. Khi đî
0 1 2 3 8 9 10
2 ...I I I I I I I
bằng?
A.
9
1
tan
r
r
x
C
r
B.
1
9
1
tan
1
r
r
x
C
r
C.
10
1
tan
r
r
x
C
r
D.
1
10
1
tan
1
r
r
x
C
r
Giải
Biến đổi tìch phân ban đầu ta có
22
tan .tan d
n
n
I x x x

2
2
1
tan . 1 d
cos
n
xx
x



1
2
tan
1
n
n
x
IC
n
2
2
tan . tan d
n
n
x x x I

1
2
tan
1
n
nn
x
I I C
n
.
Khi đî
0 1 2 3 8 9 10
2 ...I I I I I I I
=
10 8 9 7 3 1 2 0
...I I I I I I I I
9 8 2
tan tan tan
.... tan
9 8 2
x x x
xC
9
1
tan
r
r
x
C
r

.
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
14 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Câu 8: Cho hàm số
fx
cî đạo hàm liên tục trên đoạn
1; 2
thỏa mãn đồng thời 2 điều
kiện
2 2 2 2
22
2 2 1 63; 2 ' 27 , 1;2f f f x x f x x x
. Tính giá trị của tích
phân
2
2
1
f x dx


A.
15
B.
18
C.
21
D.
25
Giải
Theo giả thiết ta có
2 2 2 2
2 2 2
22
1 1 1 1
' 27 63 1f x dx f x dx x f x dx x dx
Xét tích phân
2
2
1
I f x dx


, đặt
2
2'du f x f x
u f x
vx
dv dx




2
22
2
11
1
2 ' 63 2 'I x f x xf x f x dx xf x f x dx



Ta có:
2 2 2 2
2 2 2
2
1 1 1 1
1 2 ' ' 0 ' 0f x dx xf x f x dx x f x dx f x xf x dx
Do đî
1
' 0 ' 0f x xf x f x f x Cx
x



Vậy
2
2
2
2 2 2 2 2
1
2 3 27 3 21Cx x C C x x C f x dx


Câu 9: Cho hàm số
fx
cî đạo hàm liên tục trên đoạn
0; 1
thỏa mãn
. 1 4 0 4e f f
và đồng thời
11
22
2
00
8
' 4 .
3
xx
e f x f x dx e f x dx

. Tính tích phân
1
0
f x dx
?
A.
4 e 1
e
B.
3 e 1
e
C.
2 e 2
e
D.
5 e 2
e
Giải
Xét tích phân
11
22
2
00
8
'4
3
xx
K e f x f x dx e f x dx

Đặt
' ' ' '
x x x x
u x e f x u e f x e f x e f x u u
, khi đî ta được
11
22
2
00
' 4 ' 2 . ' 4 1 4, 0 1K u u u u dx u u u u dx u u

Ta có
1
2
1 1 1 1
1
0
0 0 0 0
0
15
. 'dx , ' 4 '
22
u
u u udx xu xu dx xu dx
.
Suy ra
1
2
0
8
' 4 '
3
K u xu dx


. Đến đây ta chọn
m
sao cho
1 1 1 1
2
22
0 0 0 0
2
' 2 0 ' 4 2 ' 2 0
84
6 2 0 2
33
u x m dx u xu dx m u dx x m dx
m m m m


Vậy ta được
1
2
0
' 2 2 0 ' 2 2
xx
u x dx e f x e f x x
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 15
22
1
01
0
52
2 2 1
' 2 2
f
x
xx
e
x x C x x
e f x x f x f x f x dx
e e e

Câu 10: Cho
,xy
là hai số thực dương thay đổi thỏa mãn điều kiện
1
1 1 1xy xy y x
y
.
Tìm giá trị lớn nhất của biểu thức
22
2
6
3
x y x y
P
xy
x xy y



?
A.
57
3 30
B.
75
30 3
C.
57
3 30
D.
57
30
Giải
Biến đổi giả thiết ta có
1
1 1 1xy xy y x
y
22
1 1 1 0y xy xy y xy y
1 1 1 0xy y y xy xy y


1 0 1xy y xy y
2
2
1 1 1 1 1
42
x
y y y y



1
0
4
x
y
. Dấu bằng đạt được khi
2y
,
1
2
x
.
22
2
6
3
x y x y
P
xy
x xy y


2
12
61
3
tt
t
tt



với
x
t
y
và
1
0;
4
t


.
Ta có
2
15
87
27
3
t
t
tt


với mọi
1
0;
4
t


Thật vậy
2
15
87
27
3
t
t
tt


2
2
2
4 1 20 25 6
1
0
729 3
t t t
tt

với mọi
1
0;
4
t


.
Suy ra
52
87
27 6 6
t
P t f t
t
.
Khi đî
2
2
1 16 5 32 5 16 5 27
.0
54
1
tt
ft
t

với mọi
1
0;
4
t


.
Vậy
52
87
27 6 6
t
P t f t
t
1 7 10 5
4 30
f




, dấu bằng đạt được khi
1
2
x
,
2y
.
Câu 11: Cho hàm số
y f x
cî đạo hàm
2
2
12f x x x x
với
x
. Có bao
nhiêu giá trị nguyên dương của tham số
m
để hàm số
2
8f x x m
có
5
điểm cực trị?
A.
15
B.
17
C.
16
D.
18
Giải
Đặt
2
8g x f x x m
2
2
12f x x x x
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
16 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
2
2 2 2
2 8 8 1 8 8 2g x x x x m x x m x x m
Ta có
0gx
2
2
2
4
8 1 0 1
8 0 2
8 2 0 3
x
x x m
x x m
x x m
Các phương trënh
1
,
2
,
3
không có nghiệm chung từng đïi một và
2
2
8 1 0x x m
với
x
Suy ra
gx
có
5
điểm cực trị khi và chỉ khi
2
và
3
có hai nghiệm phân biệt khác
4
2
3
16 0
16 2 0
16 32 0
16 32 2 0
m
m
m
m
16
18
16
18
m
m
m
m
16m
.
Vì
m
nguyên dương và
16m
nên có
15
giá trị
m
cần tìm.
Câu 12: Biết rằng đồ thị hàm số bậc
4
:
y f x
được cho như hënh vẽ sau:
Tëm số giao điểm của đồ thị hàm số
2
.y g x f x f x f x


và trục
Ox
.
A.
4
B.
6
C.
2
D.
0
Giải
Số giao điểm của đồ thị hàm số
2
.y g x f x f x f x


và trục
Ox
bằng số
nghiệm của phương trënh:
2
.0f x f x f x



2
.f x f x f x




.
Giả sử đồ thị hàm số
4 3 2
y f x ax bx cx dx e
,
, , , , ; 0, 0a b c d e a b
cắt trục
hoành
Ox
tại
4
điểm phân biệt
1
x
,
2
x
,
3
x
,
4
x
.
Đặt
1
A x x
,
2
B x x
,
3
C x x
,
4
D x x
ta có:
1 2 3 4
.f x a x x x x x x x x a ABCD
.
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 17
TH1: Nếu
i
xx
với
1, 2, 3, 4i
thì
2
0
ii
g x f x



.
Do đî
, 1,2,3, 4
i
x x i
không phải nghiệm của phương trënh
0gx
.
TH2: Nếu
i
xx
với
1, 2, 3, 4i
thë ta viết lại
f x a BCD ACD ABD ABC
1 1 1 1
fx
A B C D



.
2 2 2 2
1 1 1 1 1 1 1 1
f x f x f x
A B C D A B C D
2
2 2 2 2
1 1 1 1 1 1 1 1
..f x f x
A B C D A B C D
Suy ra,
2
22
2 2 2 2
1 1 1 1 1 1 1 1
. . .f x f x f x f x
A B C D A B C D

.
Khi đî
2
2
2 2 2 2
1 1 1 1
. . 0g x f x f x f x f x
A B C D





1, 2, 3, 4
i
x x i
.
Từ đî suy ra phương trënh
0gx
vô nghiệm.
Vậy đồ thị hàm số
y g x
khïng cắt trục hoành.
Câu 13: Cho biểu thức
log 2017 log 2016 log 2015 log ... log 3 log 2 ...A
Biểu thức
A
có giá trị thuộc khoảng nào trong các khoảng dưới đây?
A.
log 2017;log 2018
B.
log 2019;log 2020
C.
log 2018;log 2019
D.
log 2020;log 2021
Giải
Đặt
1
log 2017 log 2016 log 2015 log ... log 3 log 2 ...
n n n
A A n A
Ta có
2
32
98
10 9
0 log 2 1 0 1
0 log 3 log 3 log 4 1
...
0 log 9 log 9 log 10 1
1 log 10 log 10 log 11 2
A
AA
AA
AA
11 10
1 log 12 log 11 log 13 2
...
AA
997 996
998 997
999 998
2017 2016
2 log 999 log 997 log 1000 3
3 log 1000 log 998 log 1001 4
3 log 1002 A log 999 log 1003 4
...
3 log 2020 log 2017 log 2021 4
AA
AA
A
AA
Vậy
2017
log 2020;log 2021A
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
18 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Câu 14: Cho dãy số
n
u
thỏa mãn
21
1
*
2
2
391 1 39
log log 2
40 4 4
21
2
,
11
n
n
uu
nu
n
un
n
nn
.
Giá trị nhỏ nhất của n để
100 2
100 3
51
5
n
n
u
nn

.
C. 233
D. 241
Giải
Ta có
22
2
2 2 2 2 2
1 1 1 2 1 1 1 1 1n n n n n n n n
Biến đổi giả thiết tương đương
2
2
2
11
22
22
11
22
22
1 2 1 1
2
2 1 2 1
1 1 1 1 1 1
1 2 1 1 1
2 1 1
1 2 1
1 1 1 1
n n n
n n n n
nn
nn
nu n u n u
n n n n
nu n u n u nu
nn
nn






Đặt
1
2
11
12
n n n n n
v nu v v v
n
là CSN có công bội
1
2
q
Từ đî suy ra
11
1 1 1
31
1 1 1 1 1 1
2 2 2 2 2
nn
nn
n
v v u u u
n n n

Thay
21
11
40 4
uu
vào giả thiết ta được
1 1 1
3
1 39 1 39 1 1
log log 2 1
4 4 4 4 2
n
n
u u u u
n n n
Để
100 2
2
100 3
51
100log 5 233
5
n
n
u n n
nn

Câu 15: Xét tập hợp gồm
2 2 2 2
, , ,A ax bx c ax bx ax c ax
(trong đî a, b, c là các số
nguyên dương nhỏ hơn). Lấy ngẫu nhiên ra một tam thức bậc hai thuộc A. Tính xác suất
để lấy được tam thức bậc hai mà khi ghép các hệ số của theo thứ tự từ bậc cao tới bậc
thấp được một số chia hết cho 7 hoặc 11.
A.
220
900
B.
220
999
C.
218
999
D.
218
900
Giải
Vì tam thức bậc hai có bốn dạng xảy ra:
Dạng đầy đủ:
2
ax bx c
khi đî ta thu được số nguyên
Dạng khuyết c:
2
ax bx
khi đî ta thu được số nguyên
Dạng khuyết b
2
ax c
khi đî ta thu được số nguyên ac
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 19
Dạng khuyết b, c:
2
ax
khi đî ta thu được số nguyên a.
Trong đî
, , 1; 2; 3; 4;5;6;7;8;9a b c
Do cî 729 số cî các chữ số khác 0; 81 số cî hai chữ số cî các chữ số khác 0 và 9 số cî 1 chữ
số khác khïng. Suy ra cî
729 81 2 9 900
tam thức bậc hai. Vë vậy, số phần tử của
khïng gian mẫu là: 900.
Nhận xét: Các số nguyên chia hết cho d đều cî dạng d với k là số nguyên dương. Do đî,
số các số nguyên dương chia hết cho d và khïng vượt quá sẽ bằng số các số nguyên k
với
0nkd
hay
0
n
k
d

Vë vậy cî
n
d



số nguyên khïng vượt quá n chia hết cho d –
n
d



là số nguyên khïng vượt quá n).
Theo nhận xét trên thë:
Số các số cî 1 chữ số (các chữ số khác 0) chia hết cho 7 là 1;
Số các số cî 2 chữ số (các chữ số khác 0) chia hết cho 7 là 12;
Số các số cî 3 chữ số (các chữ số khác 0) chia hết cho 7 là 115;
Số các số cî 1 chữ số (các chữ số khác 0) chia hết cho 11 là 0;
Số các số cî 2 chữ số (các chữ số khác 0) chia hết cho 11 là 9;
Số các số cî 3 chữ số (các chữ số khác 0) chia hết cho 11 là 72;
Số các số cî 1 chữ số (các chữ số khác 0) chia hết cho 77 là 0;
Số các số cî 2 chữ số (các chữ số khác 0) chia hết cho 77 là 1;
Số các số cî 3 chữ số (các chữ số khác 0) chia hết cho 77 là 10;
Suy ra có
1 12 115 0 9 72 12 9 1 0 1 10 218
tam thức bậc hai cî hệ số
ghép (theo thứ tự từ bậc cao tới bậc thấp) tạo thành số chia hết cho 7 hoặc 11. Vậy xác suất
để lấy ra 1 tam thức bậc hai thỏa mãn bài toán là
218
900
P
Câu 16 : Tính tổng
2 2 2 2
1 2 2017 2018
2018 2018 2018 2018
1 2 2017 2018
...
2018 2017 2 1
S C C C C
A.
2018
4036
2018
2019
C
B.
2018
4036
2018
2017
C
C.
2018
4036
2019
2018
C
D.
2018
4036
2017
2018
C
Giải
Ta có
1
1
.
kk
nn
nk
CC
k

với
k
,
n
,
nk
nên:
1 0 2 1 2018 2017
2018 2018 2018 2018 2018 2018
1 2018 2 2017 2018 1
. . ... .
2018 1 2017 2 1 2018
S C C C C C C
1 0 2 1 2017 2016 2018 2017
2018 2018 2018 2018 2018 2018 2018 2018
. . ... . .C C C C C C C C
.
Mà
2018
2018 2018
kk
CC
suy ra
1 2018 2 2017 2017 2 2018 1
2018 2018 2018 2018 2018 2018 2018 2018
. . ... . .S C C C C C C C C
.
Mặt khác ta có
2018
2018 2018 2018
2018
0
1 1 . 1
kk
k
x C x x x
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
20 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
2018 2018 2018
2018 2018 2018 2018
0 0 , 0
. . .
k k l l k l k l
k l k l
C x C x C C x

1
.
Suy ra hệ số của số hạng chứa
2019
x
trong khai triển của
1
là
1 2018 2 2017 2017 2 2018 1
2018 2018 2018 2018 2018 2018 2018 2018
. . ... . .S C C C C C C C C
.
Lại do
2018 2018 4036
1 . 1 1x x x
;
4036
4036
4036
0
1
nn
n
x C x

2
Suy ra hệ số của số hạng chứa
2019
x
trong khai triển của
2
là
2019
4036
C
.
Vậy
1 2018 2 2017 2017 2 2018 1 2019
2018 2018 2018 2018 2018 2018 2018 2018 4036
. . ... . .S C C C C C C C C C
2018
4036
4036! 4036 2018 4036! 2018
2019!. 4036 2019 ! 2019 2018!. 4036 2018 ! 2019
C

.
Câu 17: Cho 2 số phức
1
2
z a bi
z c di


thỏa mãn
29
24
ab
cd


. Tìm
12
zz
khi biểu thức
1 1 2 2
6 4 2 4P z i z z z i
đạt giá trị nhỏ nhất.
A.
4 29
B.
3 29
C.
6 29
D.
3 29
Giải
Gọi
12
6; 4 , 2; 4 , ,A D M z N z
. Mặt khác
1
2
2 9 : 2 9 0
2 4 : 2 4 0
a b M d x y
c d N d x y



Theo bất đẳng thức tam giác ta có:
1 1 2 2
6 4 2 4 4 5P z i z z z i AM MN ND AN ND AD
Phương trënh
: 2 8 0AD x y
. Khi đî
1
2
5;2
4;0
M d AD M
N d AD N
.
Suy ra
12
4 29zz
Câu 18: Cho hai số phức
12
,zz
thỏa mãn
12
1
2
3 3 0z i k z i k
z mi m R
zR

Tìm k khi biểu thức
22
12
94
P
zz

đạt giá trị nhỏ nhất.
A.
1k
B.
3k 
C.
4k 
D.
2k
Giải
Gọi
12
3;1 , ,M A z B z
. Theo giả thiết thì ta có M,A,B thẳng hàng đồng thời A thuộc Oy,
B thuộc Ox. Phương trënh đoạn AB theo đoạn chắn là:
31
: 1, 1 ;0 , 0; , 0
y
x
AB M AB A a B b a b
a b a b
Theo Cauchy – Schwarz ta có:
2
22
9 4 4 3 1 4
55
P
a b a b



.
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 21
Dấu “=” xảy ra khi
15
; 5 4
4
a b k
Câu 19: Trong mặt phẳng phức, xét hình bình hành tạo bởi các điểm
0
,
z
,
1
z
và
1
z
z
.
Biết
z
có phần thực dương và diện tích hình bình hành bằng
35
37
. Tìm GTNN của
2
1
z
z
.
A.
53
20
B.
60
37
C.
22
9
D.
50
37
Giải
Gọi
, , ,O A B C
lần lượt là điểm biểu diễn số phức
1
0, ,z
z
và
1
z
z
.
Khi đî diện tích hình bình hành
OACB
là
. .sinS OA OB
1 35
. .sin
37
z
z
35
sin
37
.
Suy ra
2
12
cos 1 sin
37
.
Áp dụng định lý cosin trong tam giác
OA C
ta có
2
2 2 2
1
2 . .cosz OC OA OB OA OB
z
2
2
11
2 .coszz
zz
2
2
1
2 cosz
z
2
1
z
z

12 50
2 2.
37 37
. Vậy
2
1
z
z
nhỏ nhất bằng
50
37
.
Dấu “
” xảy ra
1z
và
12
cos
37

.
Chẳng hạn như
1 12 1 12
sin arccos cos arccos
2 37 2 37
zi

.
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
22 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Câu 20: Cho hình chóp
.S ABCD
cî đáy
ABCD
là hình bình hành. Gọi
M
,
N
lần lượt là
trung điểm của các cạnh
AB
,
BC
. Điểm
I
thuộc đoạn
SA
. Biết mặt phẳng
MNI
chia
khối chóp
.S ABCD
thành hai phần, phần chứa đỉnh
S
có thể tích bằng
7
13
lần phần còn
lại. Tính tỉ số
IA
k
IS
?
A.
3
4
B.
1
2
C.
1
3
D.
2
3
Giải
Ta có hình vẽ
F
E
H
Q
P
O
N
M
B
J
D
A
S
C
I
F
E
N
M
B
A
D
C
Dễ thấy thiết diện tạo bởi mặt phẳng
MNI
với hënh chîp là hënh ngũ giác
IMNJH
với
//MN JI
. Ta có
MN
,
AD
,
IH
đồng qui tại
E
với
1
3
EA ED
và
MN
,
CD
,
HJ
đồng qui
tại
F
với
1
3
FC FD
, chú ý
E
,
F
cố định.
Dùng định lí Menelaus với tam giác
SAD
ta có
. . 1
HS ED IA
HD EA SI
1
.3. 1
3
HS HS
k
HD HD k
.
Từ đî
,
3
31
,
d H ABCD
HD k
SD k
d S ABCD

. Suy ra
. . .HJIAMNCD H DFE I AEM J NFC
V V V V
.
Đặt
.S ABCD
VV
và
ABCD
SS
,
,h d S ABCD
ta có
1
8
AEM NFC
S S S
và
,
1
,
d I ABCD
IA k
SA k
d S ABCD

Thay vào ta được
1 3 9 1 1
. . 2. . .
3 3 1 8 3 1 8
HJI AMNCD
kk
V h S h S
kk





2
1 21 25
.
8
3 1 1
kk
V
kk

.
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 23
Theo giả thiết ta có
13
20
HJIAMNCD
VV
nên ta cî phương trënh
2
1 21 25 13
.
8 3 1 1 20
kk
kk

, giải
phương trënh này được
2
3
k
.
Câu 21: Cho đa giác đều gồm 100 đỉnh. Tính số tam giác tù được chọn từ 3 đỉnh của đa
giác trên?
A.
117600
B.
117800
C.
116700
D.
117670
Giải
Đánh số các đỉnh là
1 2 100
, ,..., .A A A
Xét đường chéo
1 51
AA
của đa giác là đường kính của đường tròn ngoại tiếp đa giác đều
chia đường tròn ra làm hai phần, mỗi phần có
49
điểm: từ
2
A
đến
50
A
và
52
A
đến
100
A
.
Khi đî, mỗi tam giác có dạng
1 ij
A A A
là tam giác tù nếu
i
A
và
j
A
cùng nằm trong nửa
đường tròn
Chọn nửa đường tròn: có
2
cách chọn.
Chọn hai điểm
,
ij
AA
là hai điểm tùy û được lấy từ
49
điểm
2 3 50
, ,...,A A A
có
2
49
1176C
cách chọn.
Giả sử
i
A
nằm giữa
1
A
và
j
A
thì tam giác
1 ij
A A A
tù tại đỉnh
.
i
A
Mà
11j i i j
A A A A A A
nên kết quả bị lặp hai lần. Có
100
cách chọn đỉnh.
Vậy số tam giác tù là
2.1176.100
117600.
2
Chú ý: Cho đa giác đều có
n
đỉnh. Công thức tổng quát tính số tam giác tù:
Nếu
n
chẵn thì số tam giác tù là
2
2
2
.
n
nC
Nếu
n
lẻ thì số tam giác tù
2
1
2
.
n
nC
Áp dụng công thức nhanh ta có
22
2 49
2
. 100. 117600.
n
n C C

Câu 22: Cho hai số thực
,1xy
thỏa mãn điều kiện:
2 2 2
22
2
log 2 log log 4 1
41
xy
x y xy
xy

Giá trị lớn nhất của biểu thức
22
, 2 2 4f x y xy x y x y
bằng?
A.
1
2
B.
2
3
C.
3
4
D.
3
7
Giải
Áp dụng bất đẳng thức trị tuyệt đối ta có:
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
24 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
22
2 2 2 2
22
22
2 2 2 2
2 2 2 2
2
41
log 2 log log 1 1 log
41
41
log 1 log 1 log 4 1 log 4 1
xy
xy
x y x y
x y x y
xy
x y x y x y
xy


Mặt khác theo bất đẳng thức AM – GM ta lại có
22
22
log 4 1 log 4 1x y xy VP
Dấu “=” xảy ra khi và chỉ khi
22
22
41
1 log log 1
2
xy
xy
xy
xy




Thế vào
,f x y
ta được
2
,2f x y g x x x
Ta có
1;
1 1 1 3
' 0 2 max
2 2 4
2
g x x x g x g
x




Câu 23. Cho phương trënh
3 tan 1 sin 2 cos sin 3cos .x x x m x x
Có bao nhiêu giá
trị nguyên của tham số
m
thộc đoạn
2018; 2018
để phương trënh trên cî đúng một
nghiệm thuộc
0;
2



?
A.
2015.
B.
2016.
C.
2018.
D.
4036.
Giải
Vì
cos 0x
nên phương trënh tương đương với
3 tan 2 tan 1 tan 3 .x x m x
Đặt
tan 1,tx
vì
0; 1; .
2
xt




Khi đî phương trënh trở thành
3
22
2
33
3 1 2 .
2
tt
t t m t m
t
Xét hàm
3
2
33
2
tt
ft
t
với
1; .t 
Ta có
42
2
2
3 5 2
' 0, 1; .
2
tt
f t t
t


Lập bảng biến thiên suy ra phương trënh cî nghiệm khi
2m
2018;2018
3, 4,...,2018
m
m
m


Có
2016
giá trị.
Câu 24: Cho phương trình
2017 2018 2018
cos 2
2 sin cos sin cos cos .
1 tan
x
x x x x x
x
Nghiệm
dương nhỏ nhất của phương trënh cî dạng
a
b
với
, ab
là các số nguyên và nguyên tố
cùng nhau. Tính
.S a b
A.
2.S
B.
3.S
C.
4.S
D.
7.S
Giải
Điều kiện:
cos 0
.
tan 1
x
x
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 25
Ta có
22
cos 2 cos sin
cos cos sin .
sin
1 tan
1
cos
x x x
x x x
x
x
x
Do đî phương trënh
2017 2018 2018
2 sin cos sin cos cos sin cos cosx x x x x x x x
2017 2018 2018
cos sin cos . 2 sin cos 1 0.x x x x x


cos 0xL
sin cos 0 tan 1 .
4
x x x x k k
2017 2018 2018 2017 2018 2018
2 sin cos 1 0 2 sin cos 1x x x x
: Vô nghiệm vì
1009
1009 1009
2018 2018
1008
1
sin cos 2. 2
2 2 2
a b a b
xx







với
22
sin , cos .a x b x
Nghiệm dương nhỏ nhất là
3
3
7
4
4
a
S
b
Câu 25: Cho các số thực a,b,c thỏa mãn
0 , , 1a b c
. Khi đî trị nhỏ nhất của biểu thức
2
1
log log log
4
a b c
P b c a
được viết dưới dạng
m
n
, với m,n là các số nguyên dương và
m
n
là phân số tối giản. Hỏi
33
T m n
có giá trị là bao nhiêu?
A. 171
B. 89
C. 195
D. 163
Giải
Theo bất đẳng thức AM – GM ta có:
2 2 2
1 1 1
log log log 2 log log log 2 log log
4 4 4
a b c a b c a c
P b c a b c a c a
22
1 1 1 1 1 1
2 log log log log log log log
4 4 4 4 4 4
a c a a a a c
c a c c c c a
2
5
1 1 1 1 1 5
5 log . log . log . log . log
4 4 4 4 4 4
a a a a c
c c c c a
Vậy giá trị nhỏ nhất của
5
4
P
, khi đî
189T
Câu 26: Có bao nhiêu số nguyên
2018; 2018m
để phương trënh
1
2
3
28
2
x
xm
có
đúng 2 nghiệm thực phân biệt?
2013
2012
C.
4024
D.
2014
Giải
Phương trënh tương đương với
1
2
3
28
2
x
mx
. Hàm số
1
2
3
28
2
x
f x x
là một
hàm số chẵn do đî ta chỉ cần xét trên nửa khoảng
0;
để suy ra bảng biến thiên của
hàm số
fx
trên cả tập số thực.
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
26 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Xét hàm số
2
1
1
1
2
21
1
3
2 8 2
2 ln 2 3 2
3
2
2 8 '
2
3 2 ln 2 3 0 0 2
2 8 0 2
2
x
x
x
x
x
x
x
g x x x
f x x f x
x x x
x


Ta có
1 2 2
' 2 ln 3 8ln 2 3 0, 2, 2 8ln 2 6 0, 3 16ln 2 9 0
x
g x x x g g
nên
phương trënh
0gx
có nghiệm
0
2;3x
.
Vẽ bảng biến thiên cho hàm số
fx
ta suy ra được phương trënh cî đúng 2 nghiệm thực
khi và chỉ khi
0
2
1
0
0
6
7, 8,...,2018
3
28
2
x
m
m
x
m f x

Câu 27: Giả sử số tự nhiên
2n
thỏa mãn đẳng thức dưới đây hãy tëm n?
2 4 6 2 2 2
0
2 2 2 2 2
2
4096
...
3 5 7 2 1 2 1 13
nn
n n n n n
n
C C C C C
C
nn

4n
5n
C.
6n
D.
7n
Giải
Giả sử số tự nhiên
2n
thỏa mãn
2 4 6 2 2 2
0
2 2 2 2 2
2
8192
...
3 5 7 2 1 2 1 15
nn
n n n n n
n
C C C C C
C
nn

.
Ta có:
2
0 1 2 2 2 2
2 2 2 2
1 ...
n
nn
n n n n
x C C x C x C x
.
1
1
2
0 1 2 2 3 2 2 1
2 2 2 2
0
0
1 1 1
1 d ...
2 3 2 1
n
nn
n n n n
x x C x C x C x C x
n



1
21
1
0 1 2 2 3 2 2 1
2 2 2 2
0
0
1
1 1 1
...
2 1 2 3 2 1
n
nn
n n n n
x
C x C x C x C x
nn




21
0 1 2 2
2 2 2 2
2 2 1
2 2 2
2 ...
2 1 2 3 2 1
n
n
n n n n
C C C C
nn

1
Mặt khác
1
1
2
0 1 2 2 3 2 2 1
2 2 2 2
0
0
1 1 1
1 d ...
2 3 2 1
n
nn
n n n n
x x C x C x C x C x
n



0 1 2 2
2 2 2 2
2 2 2 2
2 ...
2 1 2 3 2 1
n
n n n n
C C C C
nn

2
Lấy
1
trừ
2
, ta được:
1 4 6 2 2 2
21
0
2 2 2 2 2
2
2
2 ...
2 1 3 5 7 2 1 2 1
nn
n
n n n n n
n
C C C C C
C
n n n



21
2 4096
2.
2 1 13
n
n
6n
.
Câu 28: Tính tổng
0 3 6 3 15 18
20 20 20 20 20 20
3 6 ... 3 ... 15 18
k
S C C C kC C C
?
20
10.2
13
3
S 
20
10.2
14
3
S 
C.
21
10.2
13
3
S 
D.
19
10.2
13
3
S 
Giải
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 27
Xét khai triển
20
0 1 2 2 19 19 20 20
20 20 20 20 20
1 ...x C xC x C x C x C
Đạo hàm hai vế ta có
19
1 2 2 3 18 19 19 20
20 20 20 20 20
20 1 2 3 ... 19 20 *x C xC x C x C x C
Nhân hai vế
*
với x ta có
19
1 2 2 3 3 19 19 20 20
20 20 20 20 20
20 1 2 3 ... 19 20x x xC x C x C x C x C
Cho
1x
ta được
19 1 2 3 19 20
20 20 20 20 20
20.2 2 3 ... 19 20 1C C C C C
Đặt
13
a
22
i
. Cho
xa
ta có
19
1 2 2 3 19 2 20
20 20 20 20 20
20 1 2 3 ...19 20 2a a aC a C C aC a C
Cho
2
xa
ta có
19
2 2 2 1 2 3 2 4 2 19 20
20 20 20 20 20 20
20 1 2 3 4 ... 19 20 3a a a C aC C a C a C aC
Cộng vế theo vế
1 , 2 , 3
ta có
19
19
19 2 2 0
20
20 2 1 1 3a a a a S C



Mặt khác
19
19
2 39
19
19
2 2 2 21
11
11
a a a a a
a a a a a
20
10.2
13
3
S
Câu 29: Cho hàm số
fx
cî đạo hàm trên
\ b
và hàm số
gx
cî đạo hàm trên .
Biết đồ thị của hai hàm số
' , 'y f x y g x
như hënh vẽ dưới.
Đặt
2
2
22
, 1 2h x f x g x S h x b h b x h c h c




với a,b,c là các số
thực đã biết. Khẳng định đúng với mọi
0x
là?
A.
;S h c h a c


B.
S h c
C.
;S h c h a b


D.
;S h a h c


Giải
Từ đồ thị đã cho ta suy ra
' ' ' ; ' 0 ' '
xa
h x f x g x h x f x g x
xc
Lập bảng biến thiên ta có
y g x
y f x
O
y
x
a
b
c
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
28 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
x

a
b
c

'hx
0 + + 0
hx
hc
ha
Lại có
2
2 2 2
S h b x h c h b x h x b h c
Câu 30: Cho 3 số thực thỏa mãn
2; 4 ; 0; 4 ; 1; 5x y z
. Khi đî giá trị lớn nhất của
biểu thức
2
3 5 5
5 log 1 2 log 1 4 logT x y z x y z
bằng?
10
11
C.
8 5 14
D.
12
Giải
Theo Cauchy – Schwarz , ta có:
2
2
1 1 5
1 1 2 1 1 2 2
22
2
x y z x y z x y z x y z






Dấu
""
xảy ra khi:
2 4 1x y z x y z
Suy ra
3 5 5
5
T 2 5 log 1 2 log 1 4log
2
x y z x y z
3 5 5
5
T 2z 2 log 1 4 log 1 8log
2
x y x y z
3 5 5
5
T 2z 2 log 1 4 log 1 8log
2
x y x y z
3 5 5
55
T 2 log 1 4 log 1 5 4 log
22
x x y y z z
Áp dụng kết quả quan trọng
1 log 1 0, 1;
a
x a x x a
. Dấu “=” xảy ra khi
1x
hoặc
xa
33
55
55
log 1 1 2 log 1 1 2 2
4log 1 1 4log 1 1 0
4log 4 log 1 1 1
x x x x
y y y y
z z z z
10T
Dấu “=” xảy ra khi
44x y z
.
Câu 31: Cho
0 1 1a b a
và hàm số
2
1
fx
y g x
fx

cî đạo hàm trên
0;
. Biết đồ thị hàm số
y f x
như hënh vẽ dưới. Khẳng định nào sau đây đúng với
mọi
1; 1x a b


TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 29
1fb
gx
m
1fa
gx
n
C.
1fb
gx
m
D.
10 0gx
Giải
Ta có
2
1; 1 1 ;x a b x a b


, dựa vào đồ thị ta có
2
2
1 1 1
1
1
m f x n
nm
fx
Mặt khác
0 1 1a b a
dựa vào đồ thị ta thấy
fx
đồng biến trên
1; 1ab



nên ta có
1
11
fb
f a f x f b g x
m
Câu 32: Cho các số thực dương a,b,c,m,n,p thỏa mãn điều kiện
2017 2017
2017
2 2 3 7m n p
và
4 4 3 42a b c
. Đặt
2018 2018
2018
2 2 2 2
3
ab
c
S
m n p
thì khẳng định đúng là?
2018
42 7.6S
2018
6S
C.
2018
7 7.6S
D.
4 42S
Giải
Đặt
2017 2017 2017
;;m x n y p z
;
2 2 3 7; 2 2 3 21 2x y z a b d c d
Theo AM – GM ta có
2018
2018 2018 2018 2017
2017
2018
2018 2018 2018 2017
2017
2018
2018 2018 2018 2017
2017
2
2. 2 6 6 ... 6 2.2018.6 .2
2
2. 2 6 6 ... 6 2.2018.6 .2
2
3. 3 6 6 ... 6 3.2018.6 .2
a
x x x a
x
a
y y y b
y
a
y y y d
y
Mặt khác
2018 2018
2017.6 2 2 3 2017.7.6x y z
2017 2018 2017 2018 2018
2.2018.6 2 2 3 2017.6 2 2 3 2.2018.6 .3.7 2017.7.6 7.6S a b d x y z
Dấu “=” xảy ra khi
11
3 2 2 6
x y z m n p
a b d a b c



O
a
b
x
y
m
n
y f x
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
30 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Câu 33: Có bao nhiêu cặp số nguyên
, ab
để phương trënh sau đúng với mọi x
22
cos 1 1 1a x b cos ax b
0
1
C.
2
D.
3
Giải
Giả sử phương trënh
1
đúng với mọi x nên cũng đúng với
0x
2
2
10b cos b b
Khi đî phương trình (1) trở thành:
cos 1 cos 1 2a x ax
(
2
đúng với mọi x khi
0a
)
Vậy ta chỉ cần xét khi a
0. Do
2
đúng với mọi x nên đúng khi
2x 
2x
khi ấy có:
2 1 2 2cos ax a k
. Do
03a a k
. Trong
2
thay
2
x
a
( do
0a
) ta có
2 2 2 1
cos 1 0 1 2 4a cos m a
a a a m



Từ
3 , 4
và
,km
nguyên nên
1.a 
Thử lại ta thấy chỉ có
0a
và
0b
hoặc
1a
và
0b
thỏa mãn
Vậy có 2 cặp số nguyên
;ab
để pt
1
đúng với mọi x.
Câu 34: Cho hệ phương trënh
2
2
20
1
p x p x
x
vô nghiệm khi
;;p a b  
.
Tính giá trị của biểu thức
22
A a b
10
9
C.
13
D.
16
Giải
Ta có hệ phương trënh đã cho vï nghiệm
2
20f x p x p x
với mọi
11x
Giả sử
1
đúng , ta cî
2
1 3 0
10
0
0 0 2 0
3
10
10
pp
f
p
f p p
p
f
p



Thử lại, ta có:
)
Nếu
0p
khi đî
2
0px
với mọi x
Do
2
1 2 1 2 0x p x p x p x
với mọi
x
1.
)
Nếu
3p
Do
2
12x p x
và
20px
(do
1x 
)
2
20p x p x
với mọi
1.x
Vậy
0, 3 9a b A
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 31
Câu 35: Cho dãy số
n
u
được xác định bởi
1
2u
;
1
2 3 1
nn
u u n
. Cïng thức số hạng
tổng quát của dãy số đã cho là biểu thức cî dạng
.2
n
a bn c
, với
a
,
b
,
c
là các số nguyên,
2n
;
n
. Khi đî tổng
a b c
cî giá trị bằng
4
4
C.
3
D.
3
Giải
Ta có
1
2 3 1
nn
u u n
1
3 5 2 3 1 5
nn
u n u n


, với
2n
;
n
.
Đặt
35
nn
v u n
, ta có
1
2
nn
vv
với
2n
;
n
.
Như vậy,
n
v
là cấp số nhân với cïng bội
2q
và
1
10v
, do đî
1
10.2 5.2
nn
n
v

.
Do đî
3 5 5.2
n
n
un
, hay
5.2 3 5
n
n
un
với
2n
;
n
.
Suy ra
5a
,
3b 
,
5c 
. Nên
5 3 5 3a b c
.
Câu 36: Một ngày đẹp trời, trong lúc đi dạo công viên, cầm một khối cầu trong tay, một
nhà khoa học yêu cái đẹp nảy ra û tưởng muốn tạo ra một khối nón nội tiếp trong một
khối cầu cî bán kình R và đựng một loại dung dịch X do ông chế tạo ra vào trong đî, sao
cho thể tích dung dịch X chứa được trong X là lớn nhất. Sau khi chế tạo xong, trong lúc
mải ngắm tác phẩm của mình, nhà khoa học đã vï tënh làm vỡ cả khối cầu thủy tinh, tuy
vậy ïng đã thu hồi lại được lượng dung dịch X quý giá của mình. Lần này, vì rút kinh
nghiệm, cũng lượng dung dịch X đî, nhà khoa học muốn chế tạo một cái hộp bằng một
loại kim loại chịu lực trong suốt để đựng dung dịch của mình. Ông có hai sự lựa chọn cho
hộp kim loại của mình, có dạng hình hộp chữ nhật hoặc là có dạng khối trụ. Tuy nhiên,
kinh phí còn lại của ông có hạn, còn giá thành kim loại đî lại rất đắt vì nó hiếm. Ông
muốn chi phí sản xuất kim loại cấu thành hộp là bé nhất, nhưng vẫn phải chứa được lượng
dung dịch X đã cî của mình.Hãy giúp nhà khoa học tính toán xem diện tích toàn phần
nhỏ nhất của hộp kim loại là bao nhiêu?
11
2
3
8
2
3
3
R
11
2
3
8
2
3
R
C.
6
2
3
4
2
3
3
R
D.
6
2
3
4
2
3
R
Giải
Ta tëm lượng dung dịch X lớn nhất mà nhà khoa học đã đựng được trong khối nîn nội tiếp
khối câu bán kình R.
Rõ ràng trong hai khối nîn cî cùng bán kình thë đáy nội tiếp trong một khối cầu thì khối
nón nào có chiều cao lớn hơn thë thể tích, nên ta chỉ xét khối nón có chiều cao lớn hơn
trong hai khối nîn đî.
Giả sử rằng khối nîn cî đáy là hënh trín bán kình r. Gọi x với
0 xR
là khoảng cách từ
tâm khối cầu đến đáy khối nîn. Khi đî chiều cao lớn hơn của khối nón nội tiếp khối cầu
với đáy là hënh trín bán kình r sẽ là
h R x
. Khi đî bán kënh đáy nîn là
22
r R x
, suy
ra thể tích khối nón là
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
32 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
2 2 2
1 1 1 1
22
3 3 3 6
V r h R x R x R x R x R x R x R x R x
.
Theo bất đẳng thức AM – GM ta có
3
3
22
1 1 32
22
6 6 27 81
R x R x R x
V R x R x R x R
.
Đây cũng chình là lượng dung dịch X mà nhà khoa học đã đựng trong khối nón lúc ban
đầu.
Ta tìm diện tìch toàn phần nhỏ nhất của hộp kim loại đựng lượng dung dịch X nîi trên,
với
3
32
81
VR
.
TH1: Hộp kim loại hình trụ. Khi đî
2 2 2
2
2
, 2 2 2
tp
VV
V R h h S R Rh R
RR
Áp dụng bất đẳng thức AM-GM cho bộ ba số dương
2
2 , ,
VV
R
RR
, ta có
3
22
2 3 2
tp
VV
S R V
RR
TH2: Hộp kim loại hình hộp chữ nhật, khi đî
, 2 2 2 2 2 2
tp
V V V V V
V abh h S ab a b h ab a b ab
ab ab ab a b



.
Áp dụng bất đẳng thức AM-GM cho bộ ba số dương
,,
VV
ab
ab
ta có
3
2
2 2.3
tp
VV
S ab V
ab



So sánh
3
2
32V
và
3
2
6 V
ta có
33
22
3 2 6VV
. Vậy diện tích toàn phần nhỏ nhất của hộp
kim loại là
3
2
32V
. Từ đây thay
3
32
81
VR
vào, ta được
11
22
3
3
8
2048 2
33
6561 3
tp
S R R
.
R
R
r
x
O
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 33
Vậy đáp án đúng là A.
Câu 37:
Cho hàm số
fx
cî đồ thị như hënh vẽ đồng thời
1 2 2 1 1 *f x f x x x x
Biết
rằng
42
f x ax bx c
;
2
g x mx nx p
và
2
1f x g x
. Tìm giá trị nhỏ nhất của
hàm số
gx
1
2
1
4
C.
2
D.
4
Giải
Từ
*
ta thay
0 1 0x f f
Ta có
0
0 1 1
1
ab
x y c
c


và
42
2, 11 1x y f x x x
Mặt khác
2
4 2 2 2 2
1 1 1 1x x g x m x n x p
4 2 2
2mx mx m nx n p
1
21
1
m
n
np
2
1
1
1 ; ' 2 1; ' 0
2
0
m
n g x x x g x x g x x
p
Vậy giá trị nhỏ nhất
1
4
gx
Câu 38: Cho hàm số
32
51
3
33
y x x C
. Tìm những điểm trên đường thẳng
:d y ax b
đi qua gốc tọa độ và tạo với đường thẳng
1
3
yx
một góc
0
15
mà từ đî kẻ
được đến
C
2 tiếp tuyến .
11
; ; 1;1
55




11
; ; 1;1
55



C.
11
; ; 1;1
55




D.
11
; ; 1; 1
55



Giải
O
x
y
11
1
2
–1
–2
–1
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
34 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Ta có
1
3
yx
tạo với Ox một góc
0
30
d
tạo với
Ox
góc
0
45
1a y x
(qua O)
Md
và
00
;M x x
Phương trënh đường thẳng
qua
00
: k ,M x x x
tiếp xúc với
C
khi
32
00
3 2 2
00
2
3 2 2
0 0 0 0 0
51
3
51
3 5 6
33
33
56
10 1
3 5 6 0 1 10 15 3 1 0
33
x x k x x x
x x x x x x x
x x k
x x x x x x x x x x x x
Suy ra để kẻ được 2 tiếp tuyến thì
2
00
10 15 3 1x x x x x
có 1 nghiệm duy nhất
2
00
10 15 1 3 1 0x x x x
Ta có
2
00
1
225 1 30 120 40 0
5
13
1
15
xN
x x x
x
xL


12
11
; ; 1;1
55
MN




Câu 39: Cho hàm số
8 c
3 tan
1 2
x a bx
f x c x
xx
. Biết đồ thị hàm số cî đúng 2
đường tiệm cận (chỉ tính tiệm cận đứng và tiệm cận ngang). Số giá trị nguyên tối đa cî thể
của tham số a thỏa mãn bài toán là?
8
2
C.
10
D.
9
Giải
Hàm
tanyx
là một hàm có vô số tiệm cận đứng. vì vậy muốn có hàm số
fx
cî đúng
hai tiệm cận thì ít nhất hệ số của hàm tanx phải bằng 0
3c
. Khi này hàm số trở thành:
20 20
88
3 tan
11
x a bx c x a bx c
f x c x
x x x x

Hàm số trên có một TCN:
0y
(khi
x 
). Yêu cầu bài toán tương đương hàm số có
đúng một đường TCĐ nữa. Xảy ra các trường hợp sau:
Trường hợp 1: Tử số có nghiệm
0x
3 0 9aa
Trường hợp 2: Tử số có nghiệm kép
1x
. Suy ra
8 3 0
81
4
8 3 0
84
0
8
8 4 8
2 8 8
ab
a VN
a
bb
a
aa
aa

Trường hợp 3: Điều kiện xác định của căn thức chỉ chứa một nghiệm ở mẫu số. Cụ thể là:
8 0 .
8
a
x a x
Suy ra
0
8
80
1
8
a
a
a


TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 35
Kết hợp cả 3 trường hợp thì các giá trị nguyên của a thỏa mãn bài toán là
9
8
81
a
a
a
Suy ra có tất cả 10 giá trị nguyên của tham số a thỏa mãn.
Câu 40: Cho tích phân
11
7
7 11I x x dx
, gọi M và m lần lượt là giá trị lớn nhất và
giá trị nhỏ nhất của I. Tính
S M m
?
A.
54 2 108
B.
36 2 108
C.
6 3 54
D.
6 3 36
Giải
Đặt
7 11y x x
với
7;11x
. Ta có
11
02
2 7 2 11
yx
xx

Nhận thấy y’ khïng xác định tại
7;11
, vẽ bảng biến thiên ta có
18 6y
11 11 11
7 7 7
18 7 11 dx 6dx x x dx
11
7
54 2 7 11 108x x dx
| 1/35
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


ĐỀ ÔN LUYỆN CÁC NHÓM CÂU HỎI
VẬN DỤNG CAO TRONG ĐỀ THI THPT QUỐC GIA
Đề gồm 40 câu trắc nghiệm
Quà tặng mừng ngày nhà giáo Việt Nam 20/11
Tuyển chọn 40 câu vận dụng cao có lời giải chi tiết là một sản phẩm được biên soạn, sưu
tầm và sáng tác bởi nhóm Chinh Phục Olympic Toán và được đăng trên Fanpage Tạp chí
và tư liệu Toán học. Đồng thời đây cũng là một quà tặng gửi tới các thầy cô nhân ngày nhà
giáo Việt Nam, và cũng nhân dịp này cả nhóm chúc các thầy cô trên cả nước có sức khỏe,
hạnh phúc trong cuộc sống, thành đạt hơn trong cïng việc và có một ngày 20/11 thật ý
nghĩa và vui vẻ. Xin cảm ơn mọi người! ĐỀ BÀI
Câu 1 : Biết rằng tập hợp các giá trị của m để phương trënh sau cî nghiệm là đoạn a;b
m 2 x  3 2m1 1 x m1  0 có nghiệm là đoạn a;b . Tính giá trị của biểu thức 2 2
S a b  3ab ? A. 1 B. 2 C. 0 D. 3
Câu 2: Gọi z a bi, z c di là nghiệm của phương trënh z  2 2  z  2 2  6 đồng 1 2
thời thỏa mãn ac bd  0 . Gọi M, n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của 1
P z z . Tính giá trị của biểu thức S M n 1 2 2 A. 14 S B. 13 S C. 12 S D. 11 S 5 5 5 5
Câu 3: Cho hai hàm f x và gx cî đạo hàm trên 1;2, thỏa mãn f 1  g1  0 và  x
g x  2018x x  1 f ' x  2       x  1 2  x x  1   , x
 1;2. Tính I g  x
f xd . x   3  xx  1 x
g'x  f x 2  2019x 1 x  1 A. 1 I  .
B. I  1. C. 3 I  .
D. I  2. 2 2
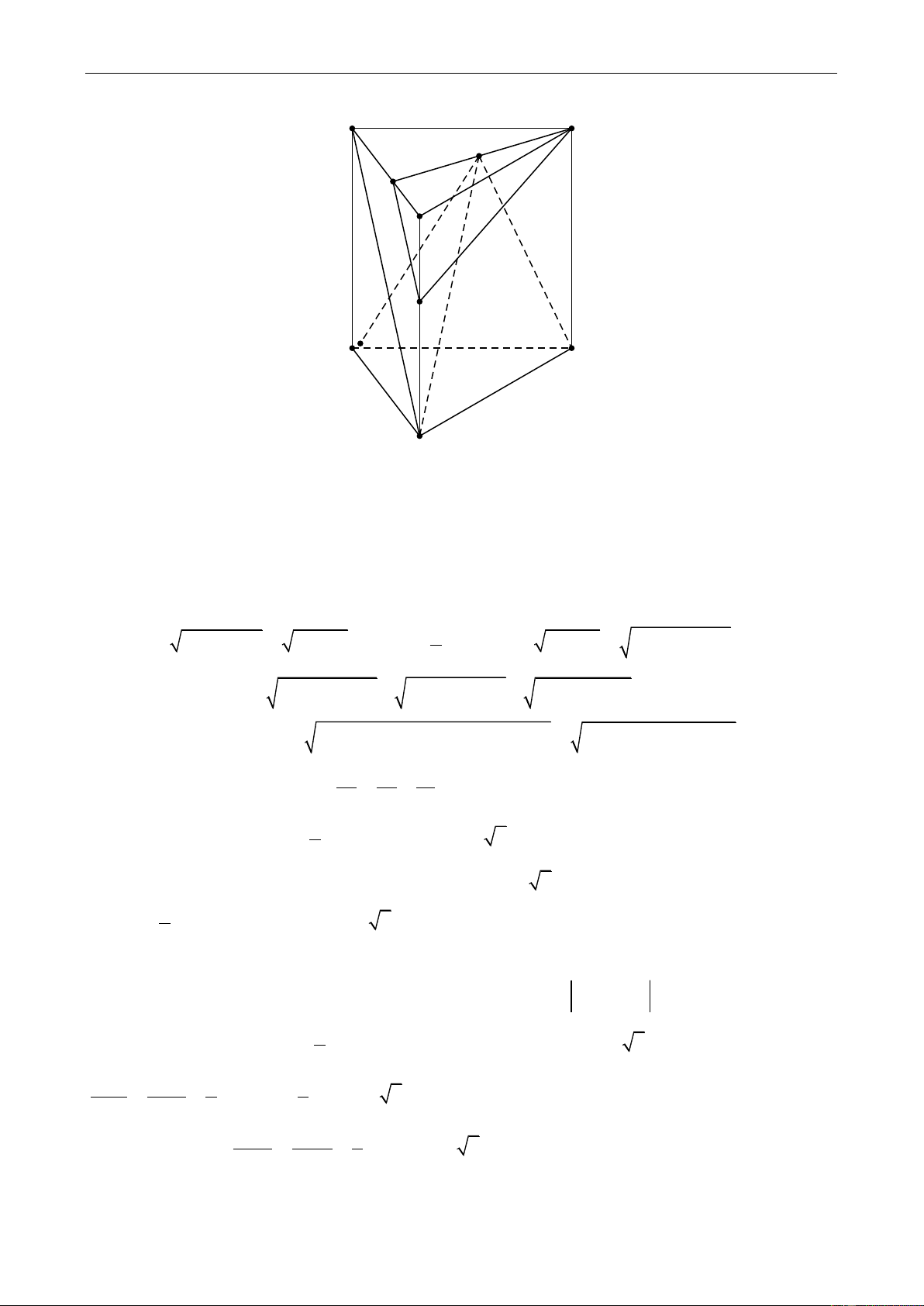
Câu 4: Cho lăng trụ đứng ABC.A’B’C’ có 0
AB  6, BC  12, ABC  60 . Thể tích khối chóp
C '.ABB' A' bằng 216. Gọi M là điểm nằm trong tam giác A'B'C ' sao cho tổng diện tích các
mặt bên của hình chóp M.ABC đạt giá trị nhỏ nhất. Tính cosin góc giữa 2 đường thẳng
B'M, AC ' ? A. 2 B. 2 C. 2 D. 1 2 3 4 2
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 1
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
Câu 5: Hai người bắn độc lập vào một mục tiêu, mỗi người bắn 1 lần. Xác suất trúng của
người thứ nhất là 0,9; của người thứ hai là 0,7. Tìm giá trị lớn nhất của biểu thức 2
M  13p  10p , trong đî p là xác suất của một biến cố. A. 169 B. 528 C. 4221 D. 3 40 125 1000
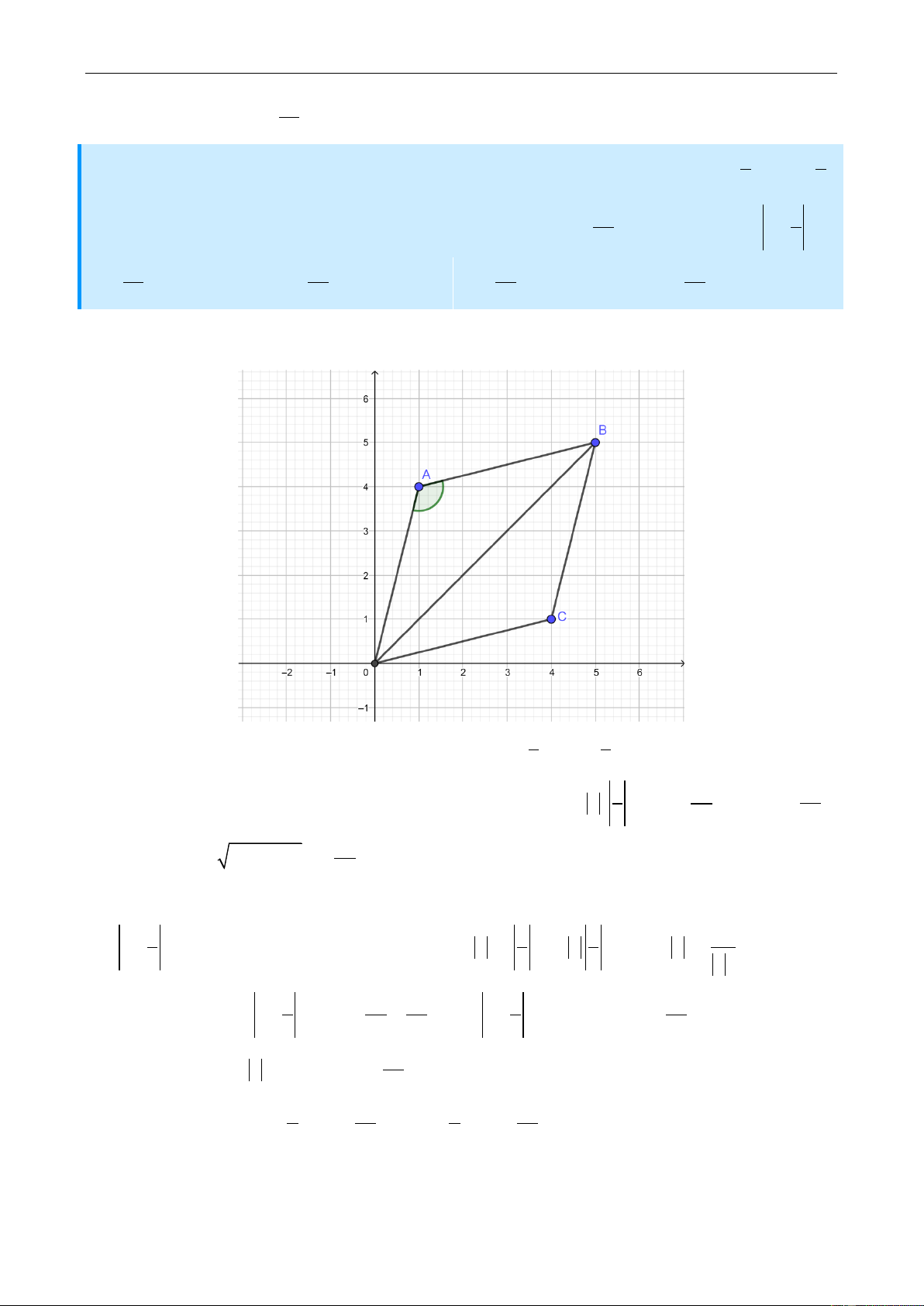
Câu 6: Cho tam giác ABC có BAC  60 và AB, AC đã biết. Biểu thức
P k.MA MB MC đạt giá trị nhỏ nhất bằng  AB AC với mọi giá trị thực k k . Giá 0
trị của k nằm trong khoảng nào dưới đây ? 0 A.      0;1 B. 3  ; 2 C. 3  1; D. 2;3 2      2 
Câu 7: Cho I  tann xdx
I I  2 I I  ... I I I bằng? n
với n . Khi đî 0 1  2 3 8  9 10 9 tan xr tanxr1 9 10 tan xr tanxr1 10 A.  C B.  C C.  C D.  C   r1 r r1 r 1 r1 r r1 r 1
Câu 8: Cho hàm số f x cî đạo hàm liên tục trên đoạn 1;2 thỏa mãn đồng thời 2 điều kiện  f    2    f     2    f   x 2   x f   x 2 2 2 2 2 1 63; 2 '   27x , x   
1;2. Tính giá trị của tích phân 2  f
  x 2 dx  1 A. 15 B. 18 C. 21 D. 25
Câu 9: Cho hàm số f x cî đạo hàm liên tục trên đoạn 0;1 thỏa mãn .ef 1  4 f 0  4 và đồng thời 1 x 1 e
  f x 2  f   x 2 2 x 8 '
dx  4 e . f x dx   
. Tính tích phân f xdx  ? 0  1   0 3 0 4e  1 3e  1 2 e  2 5e  2 A. B. C. D. e e e e
Câu 10: Cho x, y là hai số thực dương thay đổi thỏa mãn điều kiện
xy   xy   y 1 1 1  1  x  . y  
Tëm giá trị lớn nhất của biểu thức x y x 2y P   ? 2 2
x xy  3y 6x yA. 5 7   B. 7 5  C. 5 7  D. 5 7 3 30 30 3 3 30 30
Câu 11: Cho hàm số y f x cî đạo hàm f x  x  2  2 1
x  2x với x  . Có bao
nhiêu giá trị nguyên dương của tham số m để hàm số f  2
x  8x m có 5 điểm cực trị? A. 15 B. 17 C. 16 D. 18
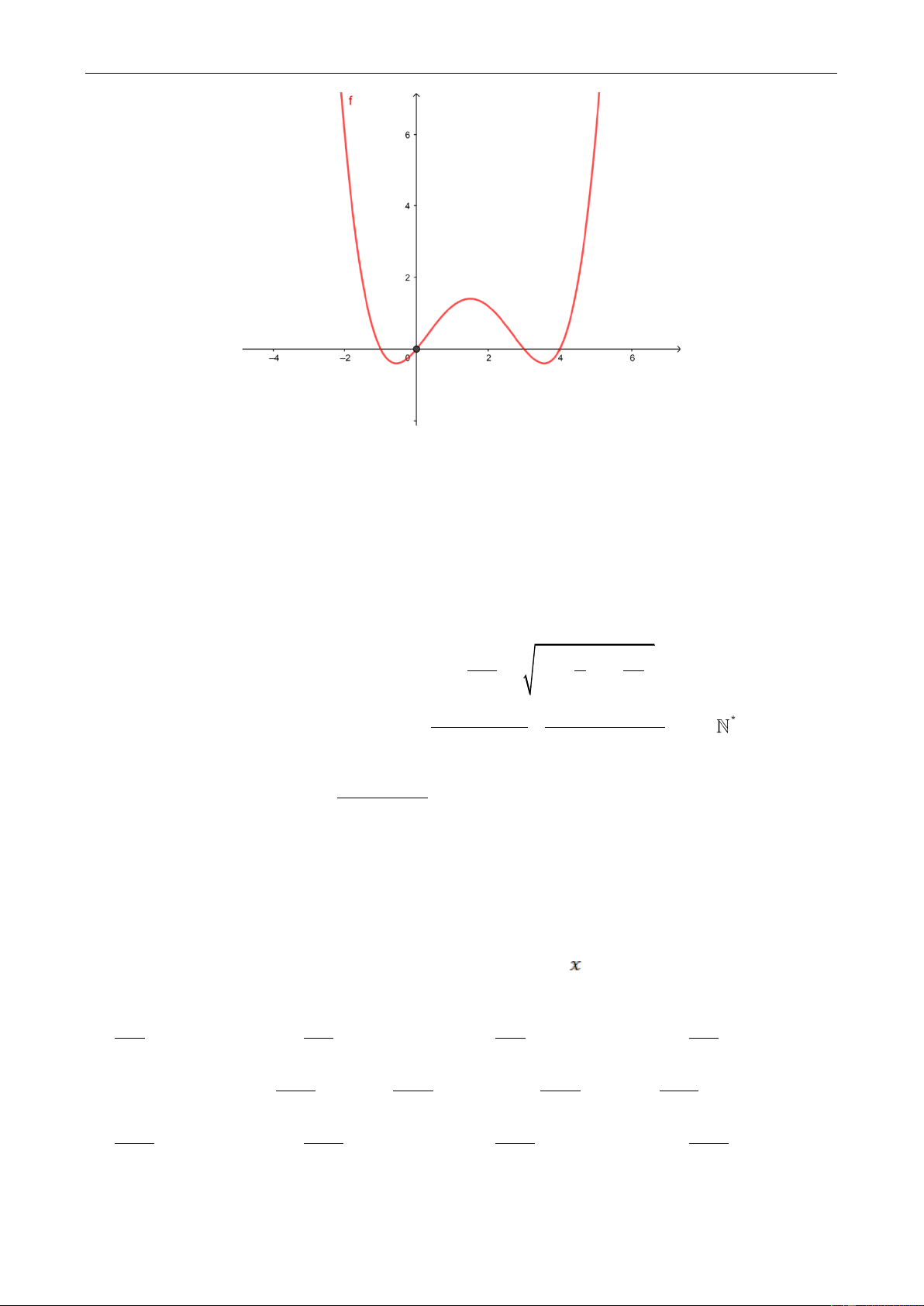
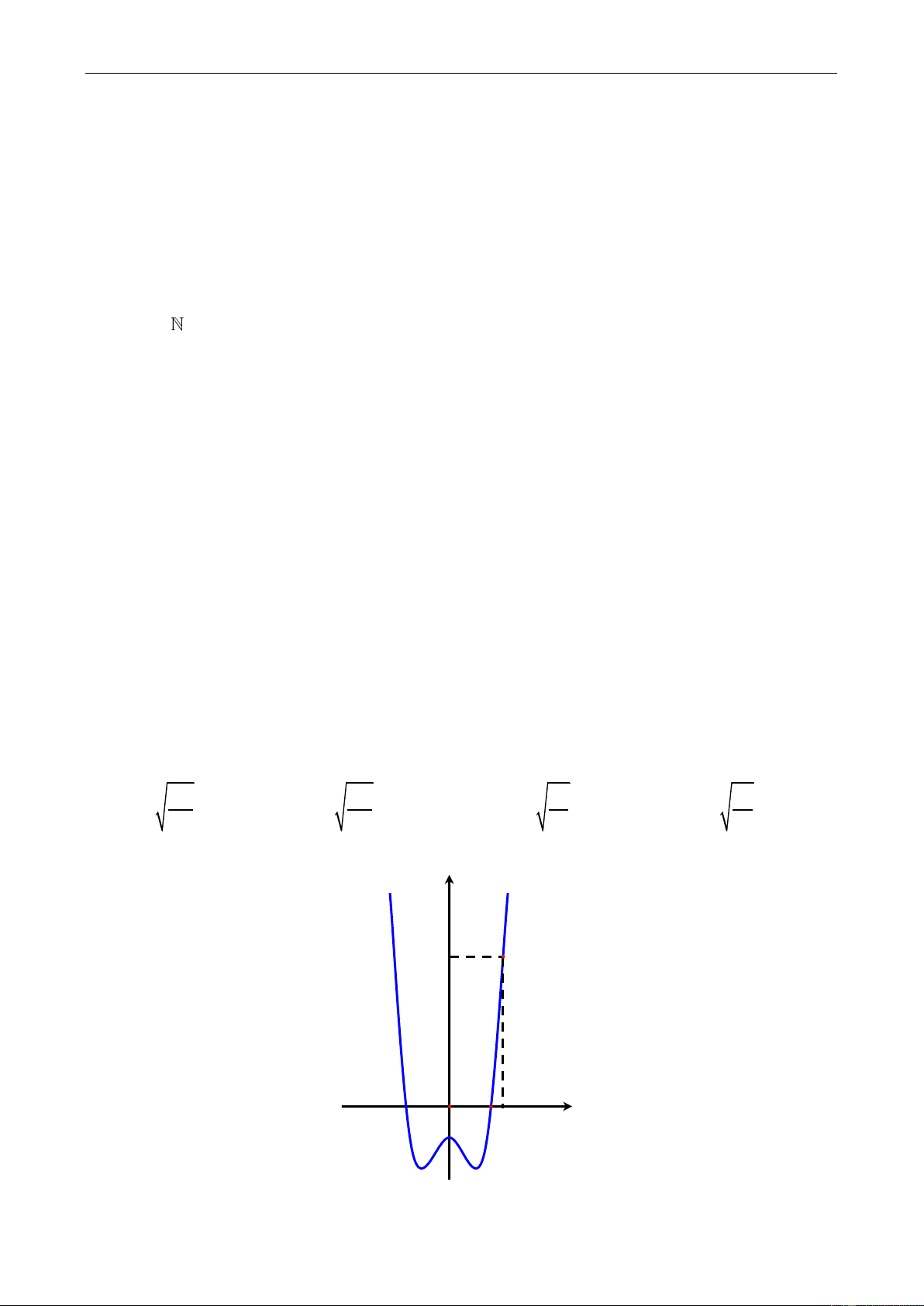
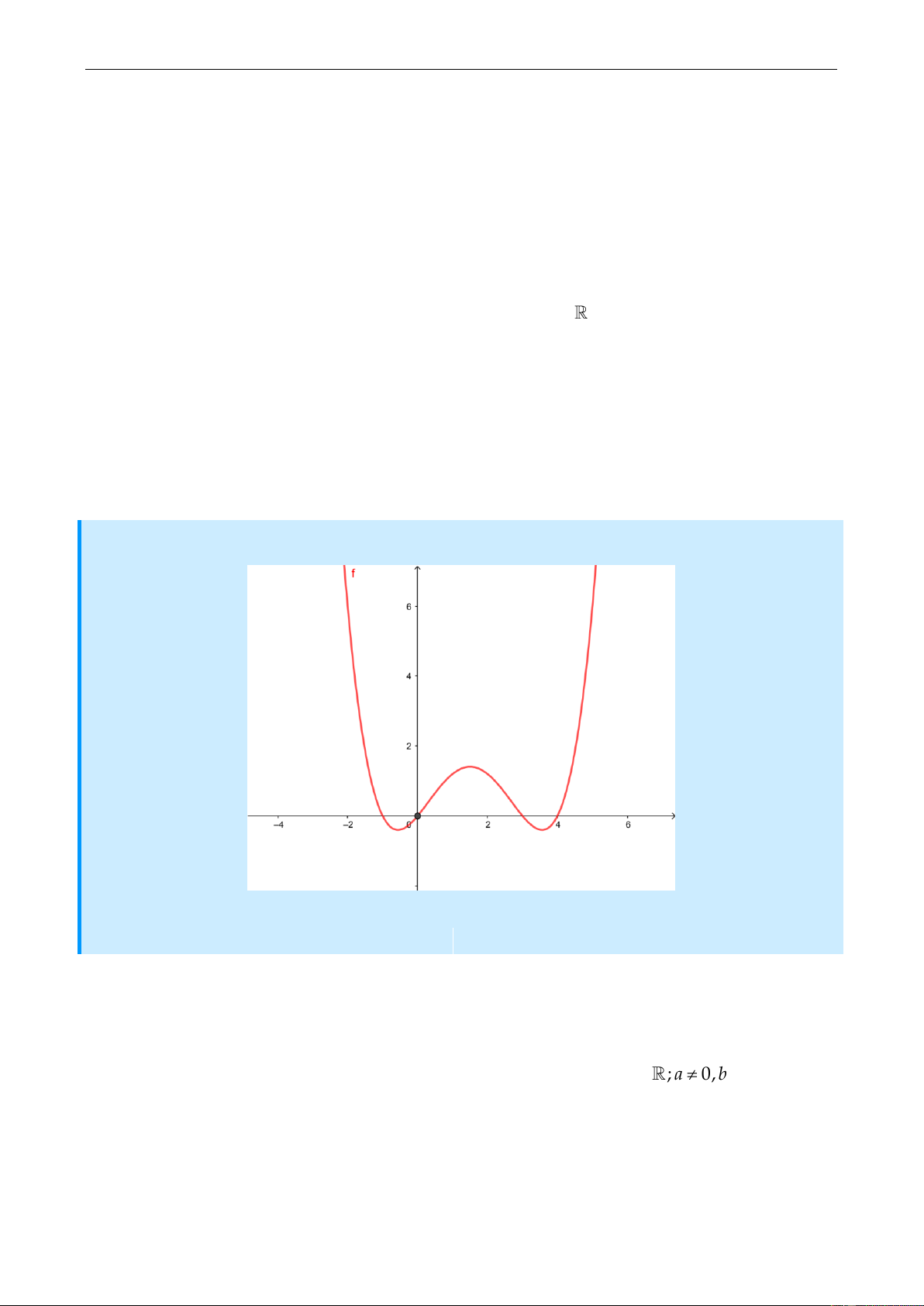
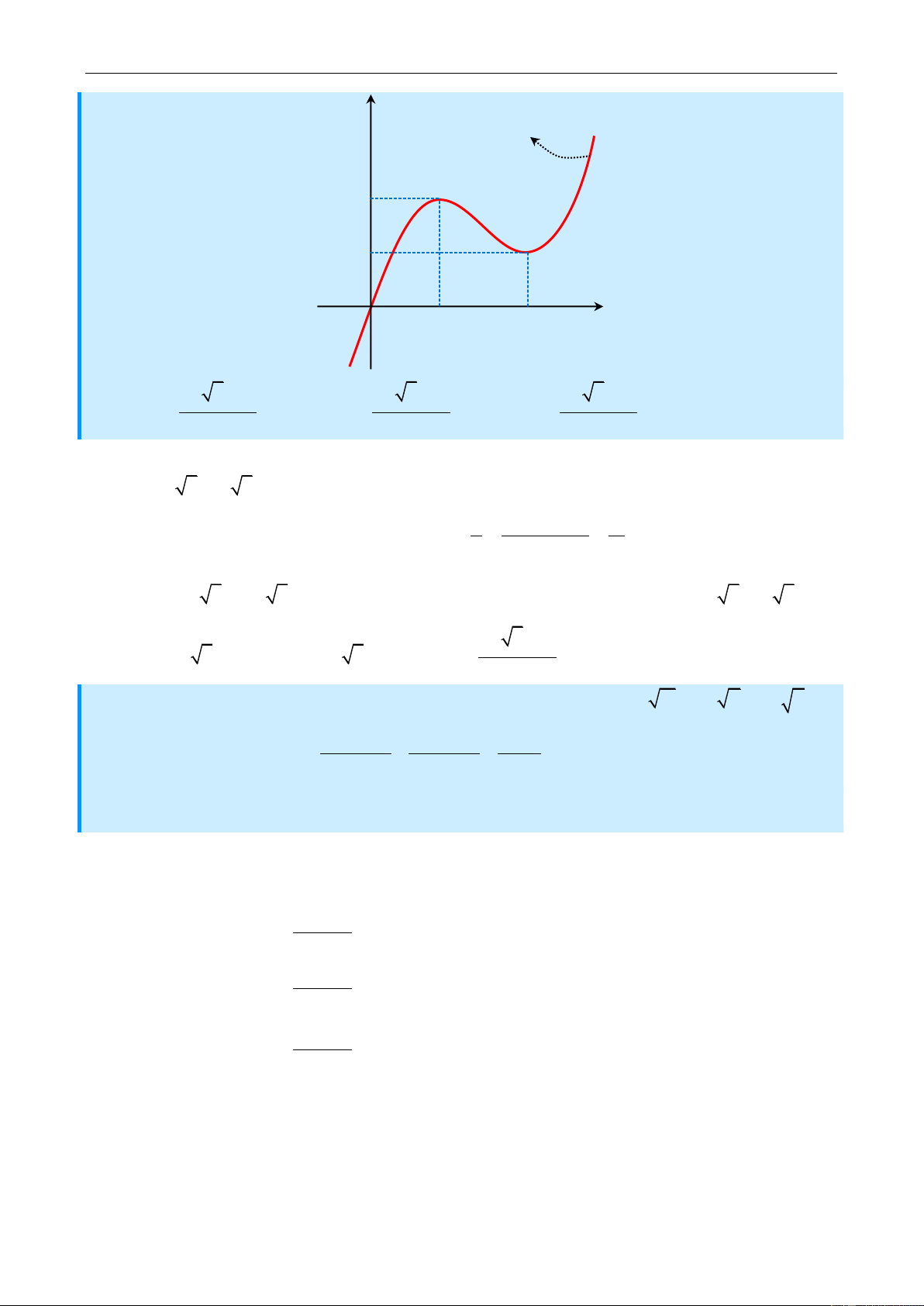
Câu 12: Biết rằng đồ thị hàm số bậc 4 : y f x được cho như hënh vẽ sau:
2 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tëm số giao điểm của đồ thị hàm số y gx   f   x 2   f
x.f  x và trục Ox . A. 4 B. 6 C. 2 D. 0
Câu 13: Cho biểu thức A  log2017 log2016 log2015 log... lo  g 3 log  2 ... 
Biểu thức A có giá trị thuộc khoảng nào trong các khoảng dưới đây?
A. log 2017;log 2018
B. log 2019;log 2020
C. log 2018;log 2019
D. log 2020;log 2021   391   1 39  log u    log  u    2 2 1   40   4 4 
Câu 14: Cho dãy số u thỏa mãn . n   2 n  1un1 2 n * u   n   nn  n n1 , 2 2  1 100 2
Giá trị nhỏ nhất của n để 5  n  1 u  . n 100 5  3 n nA. 235 B. 255 C. 233 D. 241
Câu 15: Xét tập hợp gồm A   2 2 2 2
ax bx c,ax bx,ax c,ax  (trong đî a, b, c là các số
nguyên dương nhỏ hơn). Lấy ngẫu nhiên ra một tam thức bậc hai thuộc A. Tính xác suất
để lấy được tam thức bậc hai mà khi ghép các hệ số của theo thứ tự từ bậc cao tới bậc
thấp được một số chia hết cho 7 hoặc 11. A. 220 B. 220 C. 218 D. 218 900 999 999 900 Câu 16 : Tính tổng 1 S  C 2 2  C 2 2017   C 2 2018 ...  C 2 1 2 2017 2018 2018 2018 2018 2018 2018 2017 2 1 A. 2018 2018 2018 2019 2017 C B. 2018 C C. 2018 C D. 2018 C 4036 2019 4036 2017 4036 2018 4036 2018
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 3
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
z a bi
a  2b  9
Câu 17: Cho 2 số phức 1  thỏa mãn 
. Tìm z z khi biểu thức z c   di c  2d   4 1 2 2
P z  6  4i z z z  2  4i đạt giá trị nhỏ nhất. 1 1 2 2 A. 4  29 B. 3  29 C. 6  29 D. 3  29
z  3  i k z  3  i k  0 1  2   
Câu 18: Cho hai số phức z , z thỏa mãn z mi mR 1   1 2  z R 2 Tìm k khi biểu thức 9 4 P  
đạt giá trị nhỏ nhất. 2 2 z z 1 2
A. k  1
B. k  3
C. k  4
D. k  2
Câu 19: Trong mặt phẳng phức, xét hình bình hành tạo bởi các điểm 0 , z , 1 và 1 z  . z z 2
Biết z có phần thực dương và diện tích hình bình hành bằng 35 . Tìm GTNN của 1 z  . 37 z A. 53 B. 60 C. 22 D. 50 20 37 9 37
Câu 20: Cho hình chóp .
S ABCD cî đáy ABCD là hình bình hành. Gọi M , N lần lượt là
trung điểm của các cạnh AB , BC . Điểm I thuộc đoạn SA . Biết mặt phẳng MNI chia khối chóp .
S ABCD thành hai phần, phần chứa đỉnh S có thể tích bằng 7 lần phần còn 13 lại. Tính tỉ số IA k  ? IS A. 3 B. 1 C. 1 D. 2 4 2 3 3
Câu 21: Cho đa giác đều gồm 100 đỉnh. Tính số tam giác tù được chọn từ 3 đỉnh của đa giác trên? A. 117600 B. 117800 C. 116700 D. 117670
Câu 22: Cho hai số thực x, y  1 thỏa mãn điều kiện: 2 x y
log 2 x y  log  log 4xy  1 2     2 2 2 2   x  4y  1
Giá trị lớn nhất của biểu thức f x y 2 2 ,
 2xy x  2y x  4y bằng? A. 1 B. 2 C. 3 D. 3 2 3 4 7
Câu 23. Cho phương trënh 3 tan x  1 sin x  2 cos x  msin x  3cos x. Có bao nhiêu giá
trị nguyên của tham số m thộc đoạn  2018 
; 2018 để phương trënh trên cî đúng một nghiệm thuộc     0; ? 2   
4 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN A. 2015. B. 2016. C. 2018. D. 4036.
Câu 24: Cho phương trënh 2017  2018 2018 x x x x cos 2x 2 sin cos sin cos cos x  . Nghiệm 1  tan x
dương nhỏ nhất của phương trënh cî dạng a
 với a, b là các số nguyên và nguyên tố b
cùng nhau. Tính S a  . b A. S  2. B. S  3. C. S  4. D. S  7.
Câu 25: Cho các số thực a,b,c thỏa mãn 0  a,b,c  1 . Khi đî trị nhỏ nhất của biểu thức 1 2 P  log b c
a được viết dưới dạng m , với m,n là các số nguyên dương và m a logb log 4 c n n
là phân số tối giản. Hỏi 3 3
T m n có giá trị là bao nhiêu? A. 171 B. 89 C. 195 D. 163
Câu 26: Có bao nhiêu số nguyên x  3 m 20
 18;2018 để phương trënh 1 2 2
 8  x m có 2
đúng 2 nghiệm thực phân biệt? A. 2013 B. 2012 C. 4024 D. 2014
Câu 27: Giả sử số tự nhiên n  2 thỏa mãn đẳng thức dưới đây hãy tëm n? 2 4 6 2n2 2n 0 C C C C C n n n n n 4096 2 2 2 2 2 C        n ... 2 3 5 7
2n  1 2n  1 13 A. n  4 B. n  5 C. n  6 D. n  7
Câu 28: Tính tổng 0 3 6 3k 15 18
S C  3C  6C  ...  3kC  ...  15C  18C ? 20 20 20 20 20 20 20 20 21 19 A. 10.2 10.2 10.2 10.2 S   13 B. S   14 C. S   13 D. S   13 3 3 3 3
Câu 29: Cho hàm số f x cî đạo hàm trên \ 
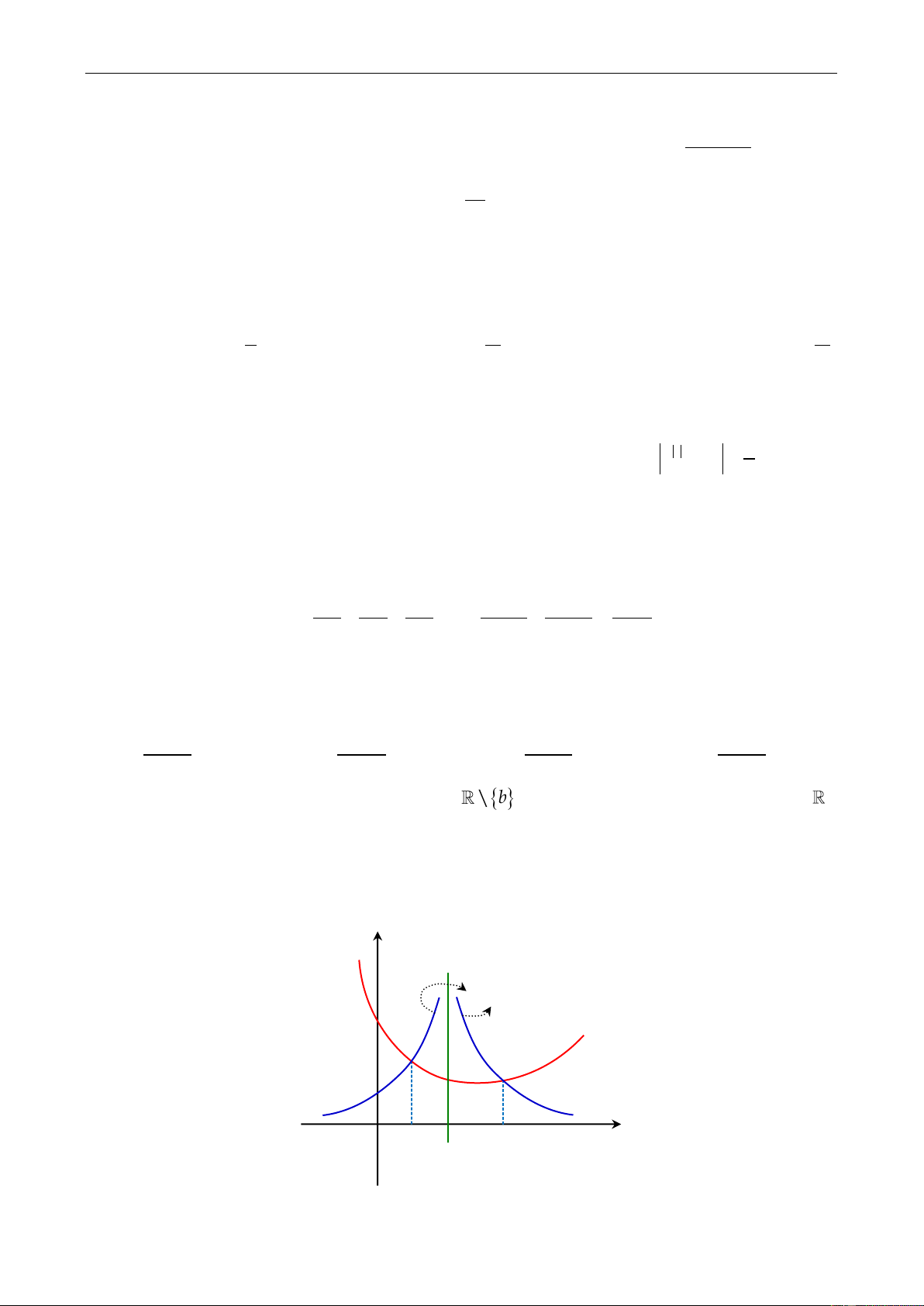
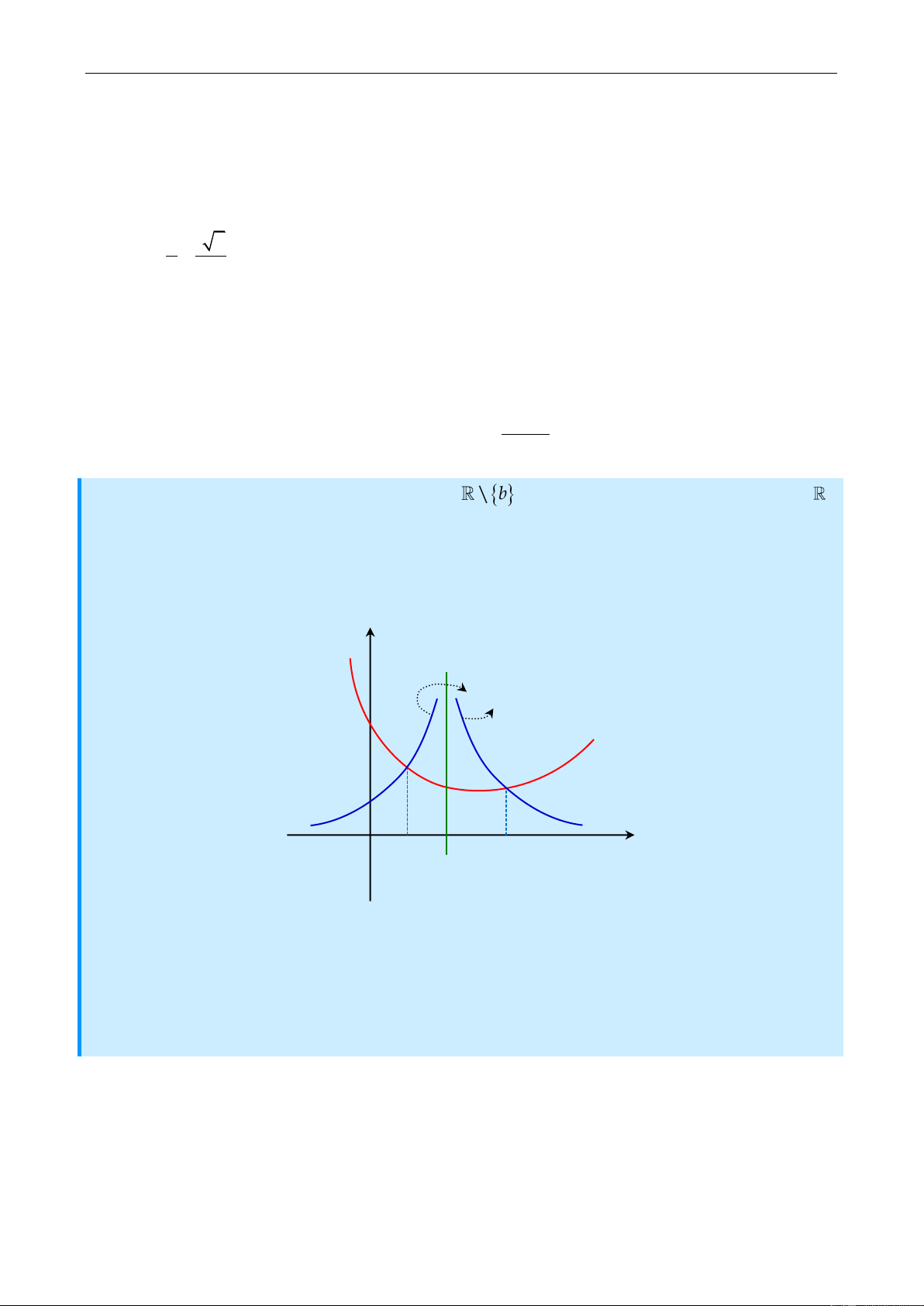
b và hàm số g x cî đạo hàm trên .
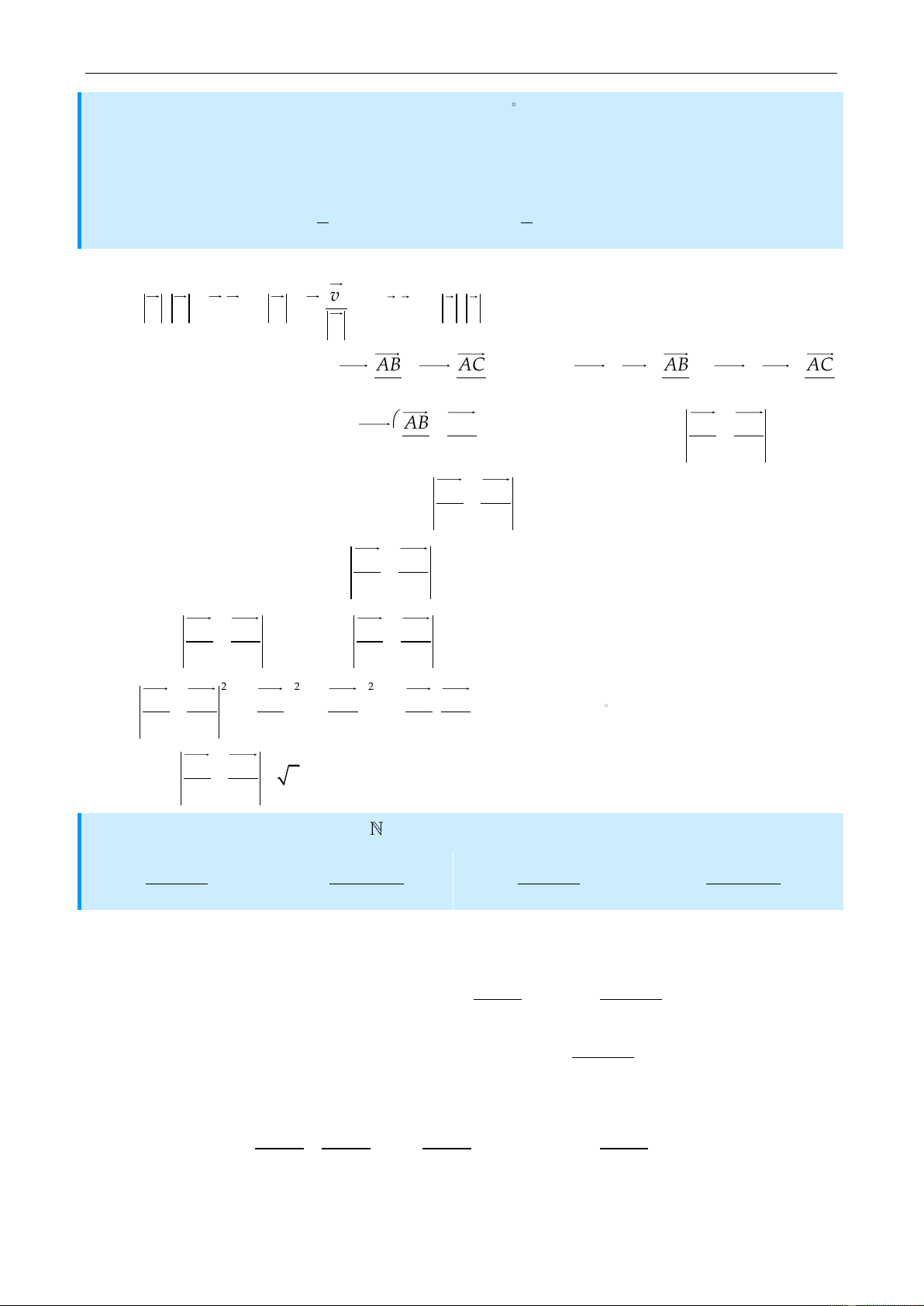
Biết đồ thị của hai hàm số y f 'x ,y g'x như hënh vẽ dưới.
Đặt hx  f x  gxS   h
 x b 2   h
bx   hchc 2 2 2 , 1 2  
 với a,b,c là các số
thực đã biết. Khẳng định đúng với mọi x  0 là? y
y f x
y gxO a b c x
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 5
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
A. S hc ;ha c  
B. S hc
C. S  hc ;ha b  
D. S ha ;hc  
Câu 30: Cho 3 số thực thỏa mãn x 2;4;y 0;4; z1;5 . Khi đî giá trị lớn nhất của
biểu thức T   x y z2  5log x 1  2log y 1  4log z bằng? 3   5   5  A. 10 B. 11 C. 8 5  14 D. 12 Câu 31: Cho f x
0  a  1  b  1  a và hàm số y g x    cî đạo hàm trên
f x  2 1 
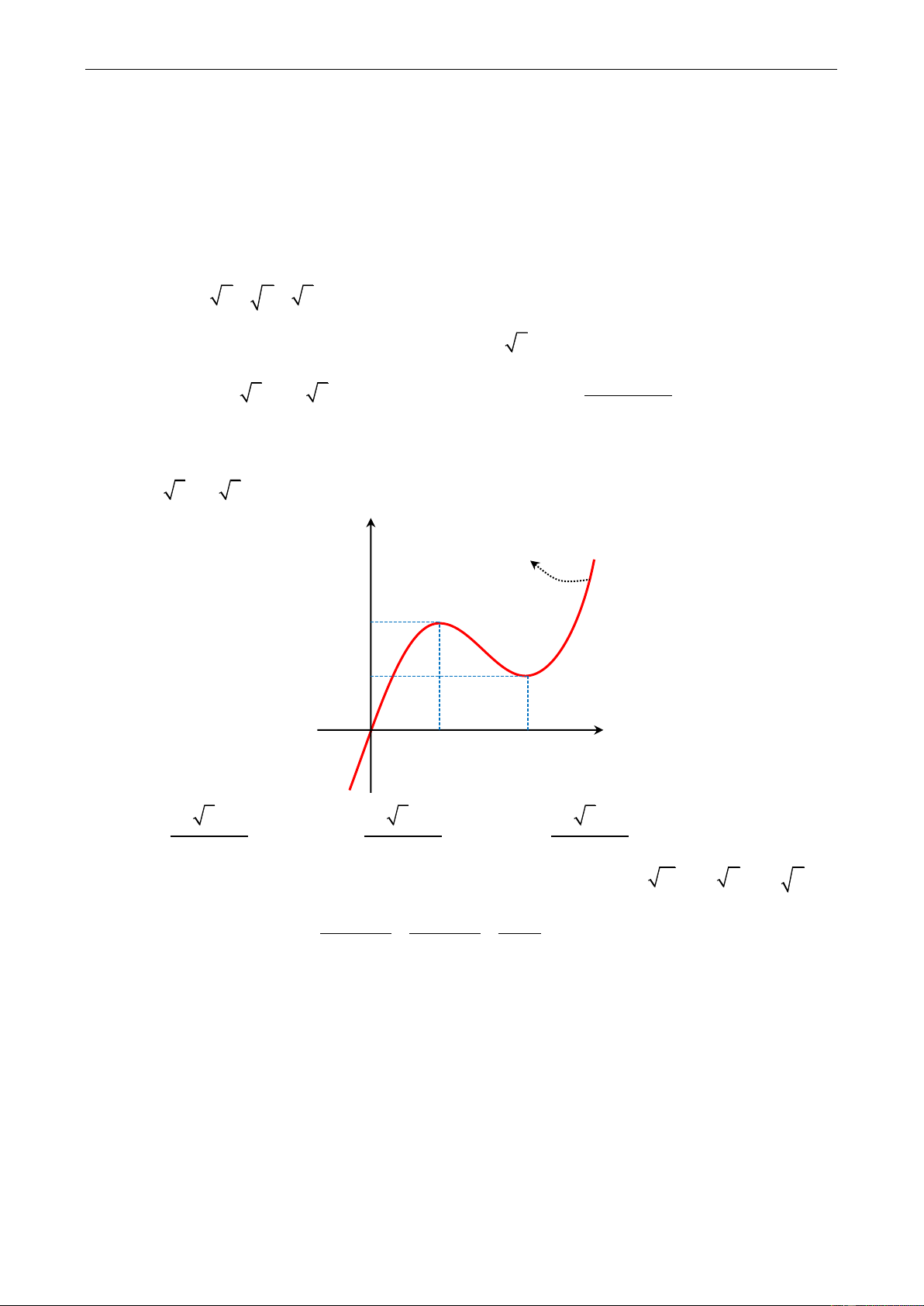
0;. Biết đồ thị hàm số y f x như hënh vẽ dưới. Khẳng định nào sau đây đúng với
mọi x   a  1; b  1   y
y f xn m O a b x f b 1 f a 1 f b 1
A. gx 
B. gx 
C. gx  D. 10 
gx  0 m n m
Câu 32: Cho các số thực dương a,b,c,m,n,p thỏa mãn điều kiện 2017 2017 2017 2 m  2 n  3 p  7  a2018  b2018 2018 2 2 2 2 và 3c
4a  4b  3c  42 . Đặt S   
thì khẳng định đúng là? m n p A. 2018 42  S  7.6 B. 2018 S  6 C. 2018 7  S  7.6
D. 4  S  42
Câu 33: Có bao nhiêu cặp số nguyên a, b để phương trënh sau đúng với mọi x ax   2  b cos 2 cos 1
ax b   11 A. 0 B. 1 C. 2 D. 3
6 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN  2
 p x p x  2  0
Câu 34: Cho hệ phương trënh 
vô nghiệm khi p;ab; . 2 x  1
Tính giá trị của biểu thức 2 2
A a b A. 10 B. 9 C. 13 D. 16
Câu 35: Cho dãy số u được xác định bởi u  2 ; u u
 . Cïng thức số hạng  n n 2 n 3 1 n  1 1
tổng quát của dãy số đã cho là biểu thức cî dạng .2n a
bn c , với a , b , c là các số nguyên,
n  2 ; n  . Khi đî tổng a b c cî giá trị bằng A. 4 B. 4 C. 3  D. 3
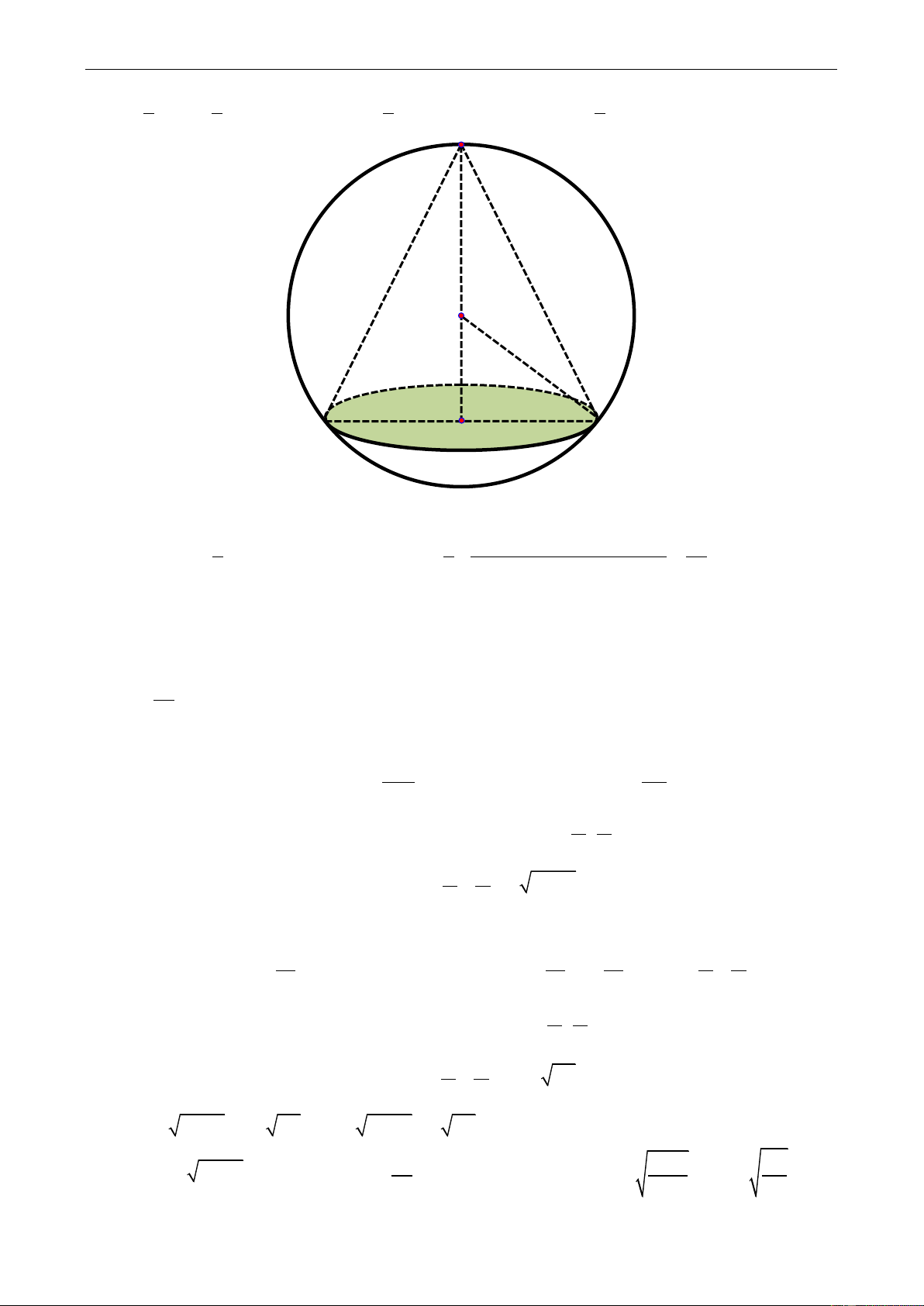
Câu 36: Một ngày đẹp trời, trong lúc đi dạo công viên, cầm một khối cầu trong tay, một
nhà khoa học yêu cái đẹp nảy ra û tưởng muốn tạo ra một khối nón nội tiếp trong một
khối cầu cî bán kình R và đựng một loại dung dịch X do ông chế tạo ra vào trong đî, sao
cho thể tích dung dịch X chứa được trong X là lớn nhất. Sau khi chế tạo xong, trong lúc
mải ngắm tác phẩm của mình, nhà khoa học đã vï tënh làm vỡ cả khối cầu thủy tinh, tuy
vậy ïng đã thu hồi lại được lượng dung dịch X quý giá của mình. Lần này, vì rút kinh
nghiệm, cũng lượng dung dịch X đî, nhà khoa học muốn chế tạo một cái hộp bằng một
loại kim loại chịu lực trong suốt để đựng dung dịch của mình. Ông có hai sự lựa chọn cho
hộp kim loại của mình, có dạng hình hộp chữ nhật hoặc là có dạng khối trụ. Tuy nhiên,
kinh phí còn lại của ông có hạn, còn giá thành kim loại đî lại rất đắt vì nó hiếm. Ông
muốn chi phí sản xuất kim loại cấu thành hộp là bé nhất, nhưng vẫn phải chứa được lượng
dung dịch X đã cî của mình.Hãy giúp nhà khoa học tính toán xem diện tích toàn phần
nhỏ nhất của hộp kim loại là bao nhiêu? 11 11 6 6 A. 2 2 2 2 2 3 3 RB. 2 3 RC. 2 3 3 RD. 2 3 R  8 3 8 3 4 3 4 3 Câu 37: y 11 –2 – O 1 1 2 x –1
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 7
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
Cho hàm số f xcî đồ thị như hënh vẽ đồng thời f x  1  f x  2x2x  1x  1* Biết rằng   4 2
f x ax bx c ;   2
g x mx nx p và f x  g  2
x  1 . Tìm giá trị nhỏ nhất của
hàm số gxA. 1  B. 1  C. 2 D. 4 2 4 Câu 38: Cho hàm số 5 3 2 1
y   x  3x  C . Tìm những điểm trên đường thẳng 3 3
d : y ax b đi qua gốc tọa độ và tạo với đường thẳng 1 y x một góc 0 15 mà từ đî kẻ 3
được đếnC 2 tiếp tuyến . A.  1  1    1 1   1  1    1  1   ;  ;1;1 B.  ; ;1;1 C. ; ; 1    ;1 D. ; ;1; 1      5 5   5 5   5 5   5 5  Câu 39: Cho hàm số    f x 8x a bx c  
. Biết đồ thị hàm số cî đúng 2  
c  3tan x x x 1 2
đường tiệm cận (chỉ tính tiệm cận đứng và tiệm cận ngang). Số giá trị nguyên tối đa cî thể
của tham số a thỏa mãn bài toán là? A. 8 B. 2 C. 10 D. 9
Câu 40: Cho tích phân 11 I
x  7  11  x dx
, gọi M và m lần lượt là giá trị lớn nhất và 7   
giá trị nhỏ nhất của I. Tính S M m ?
A. 54 2  108
B. 36 2  108 C. 6 3  54 D. 6 3  36
8 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
LỜI GIẢI CHI TIẾT ĐỀ VẬN DỤNG CAO
Câu 1 : Biết rằng tập hợp các giá trị của m để phương trënh sau cî nghiệm là đoạn a;b
m 2 x  3 2m1 1 x m1  0 có nghiệm là đoạn a;b . Tính giá trị của biểu thức 2 2
S a b  3ab ? A. 1 B. 2 C. 0 D. 3 Giải
Biến đổi phương trënh đầu tương đương PT
2 x  3  1  x  1  m  2
x  3  2 1  x  1
 x  3  2sin Vì     
x  2    x 2 3 1  4 nên đặt     0;    .  1  x  2 o c s   2   Đặt 
t  tan t 0; 
1  khi đî 2 trở thành 2 2 2t 1  t 4.  2.  1 2 2 2 4sin   2 o c s  1 1  t 1  t t   8t  3 1 20t  4 m      2 2 2 sin   4 o c s  1 2t 1  t 3
t  4t  5 3 3 2 3
t  4t  5 2.  4.  1 2 2 1  t 1  t 2 Xét 
60t  24t  84 f t 20t 4 
trên đoạn 0;1được: f t   0, t   0;1 . Suy ra 2 2   2 3
t  4t  5 ( 3
t  4t  5)
f    f t  f   4
  f t 4 f t 4 1 4 1 f t 1 4 3 5 0 1  4            m  5 15 3 3 3 15 3 3 3 3 5 3
Câu 2: Gọi z a bi, z c di là nghiệm của phương trënh z  2 2  z  2 2  6 đồng 1 2
thời thỏa mãn ac bd  0 . Gọi M, n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của 1
P z z . Tính giá trị của biểu thức S M n 1 2 2 A. 14 S B. 13 S C. 12 S D. 11 S 5 5 5 5 Giải
Gọi Az ,B z ,ac bd  0  O .
A OB  0  OA OB . 1   2 
Trường hợp 1: Xét A,B lần lượt nằm trên hai trục tọa độ thì ta có: 1 1 3 P z z O . A OB  1 2 2 2 2
Trường hợp 2: Xét hai điểm A,B lần lượt nằm trên hai đường vuông góc 1
y kx, y   x . k 2 2 x y 2 2
Tọa độ điểm A thỏa mãn    1 2 9 2 9k k  1  9 1  x   y   OA A A 3 2 2 2 9k  1 9k  1 9k  1 y   kx
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 9
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11 2 9 2 k  1 1 1  Tương tự k  1 OB  3
. Theo giả thiết ta có: P z z S  . OAB . 2 9  k 1 2 2 2  2 9k  1 2 k  9 Theo AM – GM ta có 2  2 9k  1 2 k  9  10 2 k  1 9 2  S   k  1. 10
Theo Cauchy – Shwarz ta có  2 k   2 k     2 k   3 9 1 9 3
1  S  . Dấu “=” xảy ra khi A,B 2
là các giao điểm của elip với trục tọa độ và các hoán vị.  9 min P  
Vậy cả hai trường hợp ta có 10  . 3 max P   2
Câu 3: Cho hai hàm f x và gx cî đạo hàm trên 1;2, thỏa mãn f 1  g1  0 và  x
g x  2018x x  1 f ' x  2       x  1 2  x x  1   , x
 1;2. Tính I g  x
f xd . x   3  xx  1 x
g'x  f x 2  2019x 1 x  1 A. 1 I  .
B. I  1. C. 3 I  .
D. I  2. 2 2 Giải
Bài này có vẻ tương đối khî khăn rồi do đây là 2 hàm độc lập, tuy nhiên ta chú ý vẫn bám
sát û tưởng của các bài toán trong mục này!  1 x  1 g x f ' x  20   18 2      
Từ giả thiết ta có x  1 x
. Cộng lại vế theo vế ta được:
x g x 1 ' 
f x  2019  2 x  1 x  1 x   x  1 1   g x g' x    f ' x f x   1 2           x  1 2 x  1   x x     x       g x x 1  f xx x  1  g x  1 
f x  x      C.  x  1   xx  1 x 2 2 Mà ta lại có   
f    g  x
  C    I g  xx 1 
f xdx  x   1 1 1 0 1 1 dx  .  x 1 x    2 1 1
Câu 4: Cho lăng trụ đứng ABC.A’B’C’ cî 0
AB  6, BC  12, ABC  60 . Thể tích khối chóp
C '.ABB' A' bằng 216. Gọi M là điểm nằm trong tam giác A'B'C ' sao cho tổng diện tích các
mặt bên của hình chóp M.ABC đạt giá trị nhỏ nhất. Tính cosin góc giữa 2 đường thẳng
B' M, AC ' ? A. 2 B. 2 C. 2 D. 1 2 3 4 2 Giải
10 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN C' B' M K A' H C B A
Gọi I là hình chiếu của M lên ABC; D,E,F lần lượt là hình chiếu của I lên AB, BC, CA.
Đặt ID x, IE y, IF z, AB  2a, BC  2b,CA  2c, MI AA'  h. Khi đî SS SS
ax by cz . Diện tích toàn phần của hình chóp M.ABC ABC IAB IAC IBC
nhỏ nhất khi và chỉ khi S SSS nhỏ nhất. MAB MBC MCA Có 1
MD MI ID x h S
AB MD a h x ah ax MAB .  2  2 2 2 2 2 2 2 2
Tương tự ta được   2   2   2   2   2   2 S ah xa bh by hc cz
Theo Mincowski ta có S  ah bh ch2  ax by cz2  a b c2 2 2 h SABC const
Dấu “=” xảy ra khi và chỉ khi ax by cz  
x y z . ah bh ch Khi đî ta cî 1 SSBA BC ABC  , A B C ABC . sin 18 3 ' ' ' 2 2 2 2 2 0
A'C '  AC AB BC  2A .
B BC.cos 60  A'C '  6 3 Vì 3 V V   AA  . LT C ABB A 324 ' 6 3 '. ' '
Gọi K là chân đường phân giác trong của tam giác 2
A'B'C ' kẻ từ B , từ K kẻ đường thẳng song song với AC ' cắt AA' tại H , khi đó
  B'M, AC  B'K,KH  cos  cosB'KH Ta có 1 SSS
B K B A B CB K B C A B KC B KA '  ' ' ' ' 0 sin 30 ' 4 3 ' ' ' ' ' ' ' 2 A'K A'B' 1 1 
  A'K A'C '  2 3 C 'K C 'B' 2 3 Do A'H A'K 1 KH //AC '  
  A'H  2 3 A' A A'C ' 3
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 11
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11 2 2
KH  2 6,B'H  4 3  cos B'KH   cos  4 4
Câu 5: Hai người bắn độc lập vào một mục tiêu, mỗi người bắn 1 lần. Xác suất trúng của
người thứ nhất là 0,9; của người thứ hai là 0,7. Tìm giá trị lớn nhất của biểu thức 2
M  13p  10p , trong đî p là xác suất của một biến cố. A. 169 B. 528 C. 4221 D. 3 40 125 1000 Giải
Gọi A là biến cố người thứ nhất bắn trúng, A là biến cố người thứ hai bắn trúng. 1 2 2 Khi đî  
pA  0,9; p A  0,7. Ta có 2 169 13
M  13p  10p   10 p  . 1   2  40 20   
Do đî M lớn nhất khi và chỉ khi 13 p  nhỏ nhất 20 0.A  
Giả sử p là xác suất của biến cố A. Ta quy ước  1.A   A
Khi đî A xA A yA A zA A tA A , trong đî x, y, z,t 0;  1 . 1 2 1 2 1 2 1 2
p pA  .
x pA A y.p A A  .
z p A A t.p A A  0,63x  0,07y  0, 27z  0,03t 1 2   1 2  1 2  1 2  13 p
 0,63x  0,07y  0,27z  0,03t  0,65  0,63x  0,07y  0,27z  0,03t  0,65 20 Nếu x = 1: 13 p
 0,07y  0,27z  0,03t  0,02 20 y  0 Ta có 
y; z;t 0; 
1 thì 0,07y  0,27z  0,03t  0,02 nhỏ nhất khi z  0 t   1 Khi đî 13 p   0,01 20 Nếu x = 0: 13 p
 0,07y  0,27z  0,03t  0,65 20
Ta có y; z;t 0; 
1  0  y; z;t  1  0  0,07y  0, 27z  0,03t  0, 37 0
 ,65  0,07y  0,27z  0,03t  0,65  0  ,28  13
 0,65  0,07y  0,27z  0,03t  0,65  0,28 p   0,28  0,01 20 13 x t  1
Từ 2 trường hợp trên ta thấy p   0,01   20 y z   0 min Khi đî 169 2 528 M   10.0,01  max 40 125
12 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Câu 6: Cho tam giác ABC có BAC  60 và AB, AC đã biết. Biểu thức
P k.MA MB MC đạt giá trị nhỏ nhất bằng  AB AC với mọi giá trị thực k k . Giá 0
trị của k nằm trong khoảng nào dưới đây ? 0 A.      0;1 B. 3  ; 2 C. 3  1; D. 2;3 2      2  Giải Ta có: v
u . v u .v u u . và: .
u v   u . v . Áp dụng vào bài này, ta có : v AB AC AB AC
P k.MA MB MC k.MA M . BMC.  .
k MA  MAAB.
 MAAC. AB AC AB AC    AB AC AB AC
P k.MA AB AC MA 
  k.MA ABAC MAAB AC AB AC      AB AC
P MAk  
  AB AC  . AB AC      Theo giả thiết ta có AB AC
P MAk  
  AB AC AB ACAB AC      Suy ra AB AC AB ACk     0  k    AB AC AB AC   2 2 2     Ta có AB AC AB AC AB AC         2 .  1  1  2.cos60  3 AB AC AB AC AB AC     Suy ra: AB AC k    3  k . 0 AB AC
Câu 7: Cho I  tann xdx
I I  2 I I  ... I I I bằng? n
với n . Khi đî 0 1  2 3 8  9 10 9 tan xr tanxr1 9 10 tan xr tanxr1 10 A.  C B.  C C.  C D.  C   r1 r r1 r 1 r1 r r1 r 1 Giải
Biến đổi tìch phân ban đầu ta có n1 n2 2 n  1  tan x I  tan . x tan d x x  tan . x    1dx   I   C n  2 2  cos xn 2 n  1 n1 n2 tan x tan . x  tan x  dx II I   .  C n2 n n 2 n  1
Khi đî I I  2 I I  ... I I I =I I I I ... I I I I 10 8   9 7   3 1  2 0  0 1  2 3 8  9 10 9 8 2 tan x tan x tan x 9    tanr x ....
 tan x C   C . 9 8 2 r1 r
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 13
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
Câu 8: Cho hàm số f x cî đạo hàm liên tục trên đoạn 1;2 thỏa mãn đồng thời 2 điều kiện  f    2    f     2    f   x 2   x f   x 2 2 2 2 2 1 63; 2 '   27x , x   
1;2. Tính giá trị của tích phân 2  f
  x 2 dx  1 A. 15 B. 18 C. 21 D. 25 Giải Theo giả thiết ta có 2  f   x 2 2  dx   f    x 2 2 2
dx x f '    x 2 2 2
dx  27x dx  63   1 1 1 1 1
u   f  x 2 
du  2 f 'xf x Xét tích phân 2 I   f    x 2  dx  , đặt    1 dv dx v x
I x f  x 2 2 2   2 xf '  
xf x 2
dx  63  2 xf ' 
xf xdx 1 1 1 Ta có: 1 2   f   x 2 2
dx  2 xf '  
xf x 2
dx x f '   x 2 2
dx  0   f
  xxf 'x 2 2  dx  0  1 1 1 1 Do đî  
f x  xf x 1 '  0 
f x '  0  f x    Cx x  Vậy 2Cx 2 2 2 2 2 2 2
x C  3C x  27x C  3   f
  x 2 dx  21  1
Câu 9: Cho hàm số f x cî đạo hàm liên tục trên đoạn 0;1 thỏa mãn .ef 1  4 f 0  4 và đồng thời 1 x 1 e
  f x 2  f   x 2 2 x 8 '
dx  4 e . f x dx   
. Tính tích phân f xdx  ? 0  1   0 3 0 4e  1 3e  1 2 e  2 5e  2 A. B. C. D. e e e e Giải Xét tích phân 1 x K e
  f x 2  f   x 2 2 x 8 '
dx  4 e f x dx    0  1   0 3 Đặt   x     ' x    x  '  x u x e f x u e f x
e f x e f 'x  u' u , khi đî ta được 1 K    u'u 1
2  u  4udx    u'2 2  2 .
u u' 4udx u1  4,u0  1 0   0   1 2 Ta có 1 1 1 1 u 15 1 . u u'dx  
, udx xu xu'dx  4  xu'dx     . 0 0 0 0 0 2 2 0 Suy ra 1 K    u 2 8
'  4xu' dx  . Đến đây ta chọn m  sao cho 0   3 1
 u'2x m 1 dx  0    u' 1 1 2
2  4xudx  2m u'dx  
 2x m2 dx  0 0 0   0 0 8 2 4
  6m m  2m   0  m  2 3 3 Vậy ta được 1   '2 22  0 x    x u x dx
e f x e f 'x  2x  2 0
14 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN   2 2
x x C     x x e x
e f x  x   f x 2     f x   f x dx   x   1 0 1 2 1 ' 2 2 f x   5 2 0 e e e
Câu 10: Cho x, y là hai số thực dương thay đổi thỏa mãn điều kiện
xy   xy   y 1 1 1  1  x  . y
Tìm giá trị lớn nhất của biểu thức x y x  2y P   ? 2 2
x xy  3y 6x yA. 5 7   B. 7 5  C. 5 7  D. 5 7 3 30 30 3 3 30 30 Giải
Biến đổi giả thiết ta có xy   xy   y  1 1 1  1  x y
y xy   xy   y  2 2 1 1
xy  1  y   0
  xy  1  y yxy  1 
xy1 y 0  2    x 1 1 1 1 1
xy  1  y  0  xy  1  y         2  y y y 4  y 2  x 1
 0   . Dấu bằng đạt được khi y  2 , 1 x  . y 4 2 x y x  2y    t 1 t 2   P     với x t  và 1 t 0; . 2 2 
x xy  3y 6x y 2
t t  3 6t  1 y  4 Ta có t  1 5    
8t  7 với mọi 1 t 0; 2  t t  3 27  4 1 4t  12  2
20t  25t  6 Thật vậy t  1 5     8t  7    0 với mọi 1 t 0; . 2  t t  3 27 2 729 t t  3  4 Suy ra 5  P
t   t 2 8 7   f t . 27 6t  6 2 Khi đî      f t 1 16 5t 32 5t 16 5 27  .  với mọi 1 t 0; . 54 t 1 0 2 4   Vậy 5   1  7  10 5 P
t   t 2 8 7 
f t  f
, dấu bằng đạt được khi 1
x  , y  2 . 27 6t  6  4    30 2
Câu 11: Cho hàm số y f x cî đạo hàm f x  x  2  2 1
x  2x với x  . Có bao
nhiêu giá trị nguyên dương của tham số m để hàm số f  2
x  8x m có 5 điểm cực trị? A. 15 B. 17 C. 16 D. 18 Giải
Đặt gx  f  2
x  8x m  f x  x  2  2 1 x  2x
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 15
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
gx   x  x x m  2 2
 2x xm 2 2 8 8 1 8
x  8x m  2 x  4  2
x  8x m  1  0  1
Ta có gx  0   2
x  8x m  0 2  2
x  8x m  2  0  3
Các phương trënh 1 , 2 , 3 không có nghiệm chung từng đïi một và
x xm 2 2 8 1  0 với x
Suy ra gx có 5 điểm cực trị khi và chỉ khi 2 và 3 có hai nghiệm phân biệt khác 4
  16  m  0 m  16 2  
  16  m  2  0 m  18 3      m  16 . 16  32  m  0  m  16 
16  32  m  2   0 m   18
Vì m nguyên dương và m  16 nên có 15 giá trị m cần tìm.
Câu 12: Biết rằng đồ thị hàm số bậc 4 : y f x được cho như hënh vẽ sau:
Tëm số giao điểm của đồ thị hàm số y gx   f   x 2   f
x.f  x và trục Ox . A. 4 B. 6 C. 2 D. 0 Giải
Số giao điểm của đồ thị hàm số y gx   f   x 2   f
x.f  x và trục Ox bằng số
nghiệm của phương trënh:  f  2  x 2   f
x.f  x  0   f
 x  f
x.f  x.
Giả sử đồ thị hàm số    4 3 2 y
f x ax bx cx dx e , a,b ,c,d, e  ; a  0,b  0 cắt trục
hoành Ox tại 4 điểm phân biệt x , x , x , x . 1 2 3 4
Đặt A x x , B x x , C x x , D x x ta có: 1 2 3 4
f x  ax x x x x x x x  . a ABCD . 1   2   3   4 
16 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN 
TH1: Nếu x x với i  1,2,3, 4 thì gx   f x   i    i  2 0 i  .
Do đî x x i
không phải nghiệm của phương trënh gx  0 . i , 1, 2, 3, 4 
TH2: Nếu x x với i  1,2,3, 4 thë ta viết lại i  
f x  aBCD ACD ABD ABC    1 1 1 1 f x     . A B C D   
      1 1 1 1        1 1 1 1  f x f x f x       2 2 2 2 A B C D A B C D      2    
f x 1 1 1 1     f x 1 1 1 1 . .       2 2 2 2 A B C D A B C D      2 Suy ra,    
f xf x 2
f x 1 1 1 1 2     f x 1 1 1 1 . . .       . 2 2 2 2 A B C D A B C D      Khi đî  
gx   f   x 2   f  
xf x 2  f x 1 1 1 1 . .       0 x   x i  . i  1, 2, 3, 4 2 2 2 2  A B C D
Từ đî suy ra phương trënh gx  0 vô nghiệm.
Vậy đồ thị hàm số y gx khïng cắt trục hoành.
Câu 13: Cho biểu thức A  log 2017 log2016log2015log...log3log2... 
Biểu thức A có giá trị thuộc khoảng nào trong các khoảng dưới đây?
A. log 2017;log 2018
B. log 2019;log 2020
C. log 2018;log 2019
D. log 2020;log 2021 Giải Đặt A      
A n A n
log 2017 log2016 log2015 log... log 3 log  2 .. .  nn1  Ta có
0  log 2  1  0  A  1 2
 0  log 3  A  log 3  A  log 4  1 3  2  ...
 0  log 9  A  log 9  A  log 10  1 9  8 
 1  log 10  A  log 10  A  log 11  2 10  9 
 1  log 12  A  log 11  A  log 13  2 11  10  ...
 2  log 999  A  log 997  A  log 1000  3 997  996 
 3  log 1000  A  log 998  A  log 1001  4 998  997 
 3  log 1002  A  log 999  A  log 1003  4 999  998  ...
 3  log 2020  A  log 2017  A  log 2021  4 2017  2016  Vậy A  log 2020;log 2021 2017  
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 17
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11   391   1 39  log u    log  u    2 2 1   40   4 4 
Câu 14: Cho dãy số u thỏa mãn . n   2 n  1un1 2 n * u   n   nn  n n1 , 2 2  1 100 2
Giá trị nhỏ nhất của n để 5  n  1 u  . n 100 5  3 n nA. 235 B. 255 C. 233 D. 241 Giải
Ta có n n  2   n  2  nn   n   n   n 2 2 2 2 2 2 1 1 1 2 1 1 1 1  1
Biến đổi giả thiết tương đương 2n n
n  12  2 2 2 n  1  nu n u      n u n 2  1 1 n 2 1 1  n
n  1 n  12  1 
 1 n 1 n12 2 2  1  
nu n u         n u  nu n   1 2 1 1 1 2 1 n 1 1 2 2   n 1    n  1 n 1  1 n 12 n 2  1 2  n  1  Đặt 1 1 v nu   v   là CSN có công bội 1  v v q n n 2 n 1 nn n  1 2 2 n1 n1 Từ đî suy ra  1   1   1  1 1  1 
v    v    u    u   u n 1 1 n 3 n1 1  2   2   2  n n 2 n  2    Thay 1 1 u  
u vào giả thiết ta được 2 1 40 4  1 39   1 39  1 1 log u    log  u  
 2  u  1  u    1 1 1 n 3  4 4   4 4 
n n 2nn 100 2 Để 5  n  1 u   n   n n 100log 5 233 100 5  3 n n 2
Câu 15: Xét tập hợp gồm A   2 2 2 2
ax bx c, ax bx, ax c, ax  (trong đî a, b, c là các số
nguyên dương nhỏ hơn). Lấy ngẫu nhiên ra một tam thức bậc hai thuộc A. Tính xác suất
để lấy được tam thức bậc hai mà khi ghép các hệ số của theo thứ tự từ bậc cao tới bậc
thấp được một số chia hết cho 7 hoặc 11. A. 220 B. 220 C. 218 D. 218 900 999 999 900 Giải
Vì tam thức bậc hai có bốn dạng xảy ra:  Dạng đầy đủ: 2
ax bx c khi đî ta thu được số nguyên  Dạng khuyết c: 2
ax bx khi đî ta thu được số nguyên  Dạng khuyết b 2
ax c khi đî ta thu được số nguyên ac
18 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN  Dạng khuyết b, c: 2
ax khi đî ta thu được số nguyên a.
Trong đî a,b,c 1;2;3;4;5;6;7;8;  9
Do cî 729 số cî các chữ số khác 0; 81 số cî hai chữ số cî các chữ số khác 0 và 9 số cî 1 chữ
số khác khïng. Suy ra cî 72981 2  9  900 tam thức bậc hai. Vë vậy, số phần tử của khïng gian mẫu là: 900.
Nhận xét: Các số nguyên chia hết cho d đều cî dạng d với k là số nguyên dương. Do đî,
số các số nguyên dương chia hết cho d và khïng vượt quá sẽ bằng số các số nguyên k với n  
0  kd  n hay 0  k
Vë vậy cî n số nguyên khïng vượt quá n chia hết cho d – dd   n 
là số nguyên khïng vượt quá n). d    Theo nhận xét trên thë:
 Số các số cî 1 chữ số (các chữ số khác 0) chia hết cho 7 là 1;
 Số các số cî 2 chữ số (các chữ số khác 0) chia hết cho 7 là 12;
 Số các số cî 3 chữ số (các chữ số khác 0) chia hết cho 7 là 115;
 Số các số cî 1 chữ số (các chữ số khác 0) chia hết cho 11 là 0;
 Số các số cî 2 chữ số (các chữ số khác 0) chia hết cho 11 là 9;
 Số các số cî 3 chữ số (các chữ số khác 0) chia hết cho 11 là 72;
 Số các số cî 1 chữ số (các chữ số khác 0) chia hết cho 77 là 0;
 Số các số cî 2 chữ số (các chữ số khác 0) chia hết cho 77 là 1;
 Số các số cî 3 chữ số (các chữ số khác 0) chia hết cho 77 là 10;
Suy ra có 1 12  115  0  9  72  12  9  1  0  1  10  218 tam thức bậc hai cî hệ số
ghép (theo thứ tự từ bậc cao tới bậc thấp) tạo thành số chia hết cho 7 hoặc 11. Vậy xác suất
để lấy ra 1 tam thức bậc hai thỏa mãn bài toán là 218 P  900 Câu 16 : Tính tổng 1 S  C 2 2  C 2 2017   C 2 2018 ...  C 2 1 2 2017 2018 2018 2018 2018 2018 2018 2017 2 1 A. 2018 2018 2018 2019 2017 C B. 2018 C C. 2018 C D. 2018 C 4036 2019 4036 2017 4036 2018 4036 2018 Giải Ta có   k n k 1 k1 C C
với k  , n , n k nên: n . n k 1 1 2018 0 2 2 2017 1 2018 2018 1 2017 S C . CC . C  ... C . C 2018 2018 2018 2018 2018 2018 2018 1 2017 2 1 2018 1 0 2 1 2017 2016 2018 2017  C .CC .C  ...C .CC .C . 2018 2018 2018 2018 2018 2018 2018 2018 Mà k 2018 k C C   suy ra 1 2018 2 2017 2017 2 2018 1 S C .CC .C  ...C .CC .C . 2018 2018 2018 2018 2018 2018 2018 2018 2018 2018 2018
Mặt khác ta có 1 x2018 k k
 C x  1 x2018 .1 x2018 2018 k0
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 19
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11 2018 2018 2018 k k  C x . l l k
C x   C . l C . k l x  1 . 2018 2018 2018 2018 k0 l0 k,l0
Suy ra hệ số của số hạng chứa 2019 x
trong khai triển của 1 là 1 2018 2 2017 2017 2 2018 1 S C .CC .C  ...C .CC .C . 2018 2018 2018 2018 2018 2018 2018 2018 4036
Lại do   x2018   x2018    x4036 1 . 1 1 ;1 x4036 n n  C x 2 4036 n0
Suy ra hệ số của số hạng chứa 2019 x
trong khai triển của 2 là 2019 C . 4036 Vậy 1 2018 2 2017 2017 2 2018 1 2019 S C .CC .C  ... C .CC .CC 2018 2018 2018 2018 2018 2018 2018 2018 4036 4036! 4036  2018 4036! 2018 2018    C . 2019!.4036  2019! 2019 2018!.4036  2018 4036 ! 2019
z a bi
a  2b  9
Câu 17: Cho 2 số phức 1  thỏa mãn 
. Tìm z z khi biểu thức z c   di c  2d   4 1 2 2
P z  6  4i z z z  2  4i đạt giá trị nhỏ nhất. 1 1 2 2 A. 4  29 B. 3  29 C. 6  29 D. 3  29 Giải
a  2b  9
M d : x  2y  9  0
Gọi A6;4 ,D2; 4
  , M z ,N z . Mặt khác 1   1   2   c  2d  4
N d : x  2y  4    0 2
Theo bất đẳng thức tam giác ta có:
P z  6  4i z z z  2  4i AM MN ND AN ND AD  4 5 1 1 2 2
M d AD M 5;2 1  
Phương trënh AD : 2x y  8  0 . Khi đî  .
N d AD N 4;0  2  
Suy ra z z  4  29 1 2
z  3  i k z  3  i k  0 1  2   
Câu 18: Cho hai số phức z , z thỏa mãn z mi mR 1   1 2  z R 2 Tìm k khi biểu thức 9 4 P  
đạt giá trị nhỏ nhất. 2 2 z z 1 2
A. k  1
B. k  3
C. k  4
D. k  2 Giải
Gọi M 3;1, Az ,B z . Theo giả thiết thì ta có M,A,B thẳng hàng đồng thời A thuộc Oy, 1   2 
B thuộc Ox. Phương trënh đoạn AB theo đoạn chắn là: x y 3 1
AB :   1, M AB    1Aa;0,B0;ba,b  0 a b a b 2
Theo Cauchy – Schwarz ta có: 9 4 4  3 1  4 P      . 2 2 a b 5  a b    5
20 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN Dấu “=” xảy ra khi 15 a
;b  5  k  4  4
Câu 19: Trong mặt phẳng phức, xét hình bình hành tạo bởi các điểm 0 , z, 1 và 1 z  . z z 2 Biết 1
z có phần thực dương và diện tích hình bình hành bằng 35 . Tìm GTNN của z  . 37 z A. 53 B. 60 C. 22 D. 50 20 37 9 37 Giải
Gọi O, A,B,C lần lượt là điểm biểu diễn số phức 1 0, z, và 1 z  . z z
Khi đî diện tích hình bình hành OACB là S O . A O . B sin  1 35  z . .sin   35  sin   . z 37 37 Suy ra 2 12
cos   1  sin    . 37
Áp dụng định lý cosin trong tam giác OAC ta có 2 1 2 2 2 2 1 z
OC OA OB  2O . A O . B cos 2 1 1  z   2 z .cos 2  z   2 cos z z z 2 z 2 1 2  1 z  12 50  2  2.  . Vậy z  nhỏ nhất bằng 50 . z 37 37 z 37
Dấu “ ” xảy ra  z  1 và 12 cos  . 37 Chẳng hạn như  1 12   1 12  z  sin arccos    i cos arccos . 2 37 2 37     
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 21
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
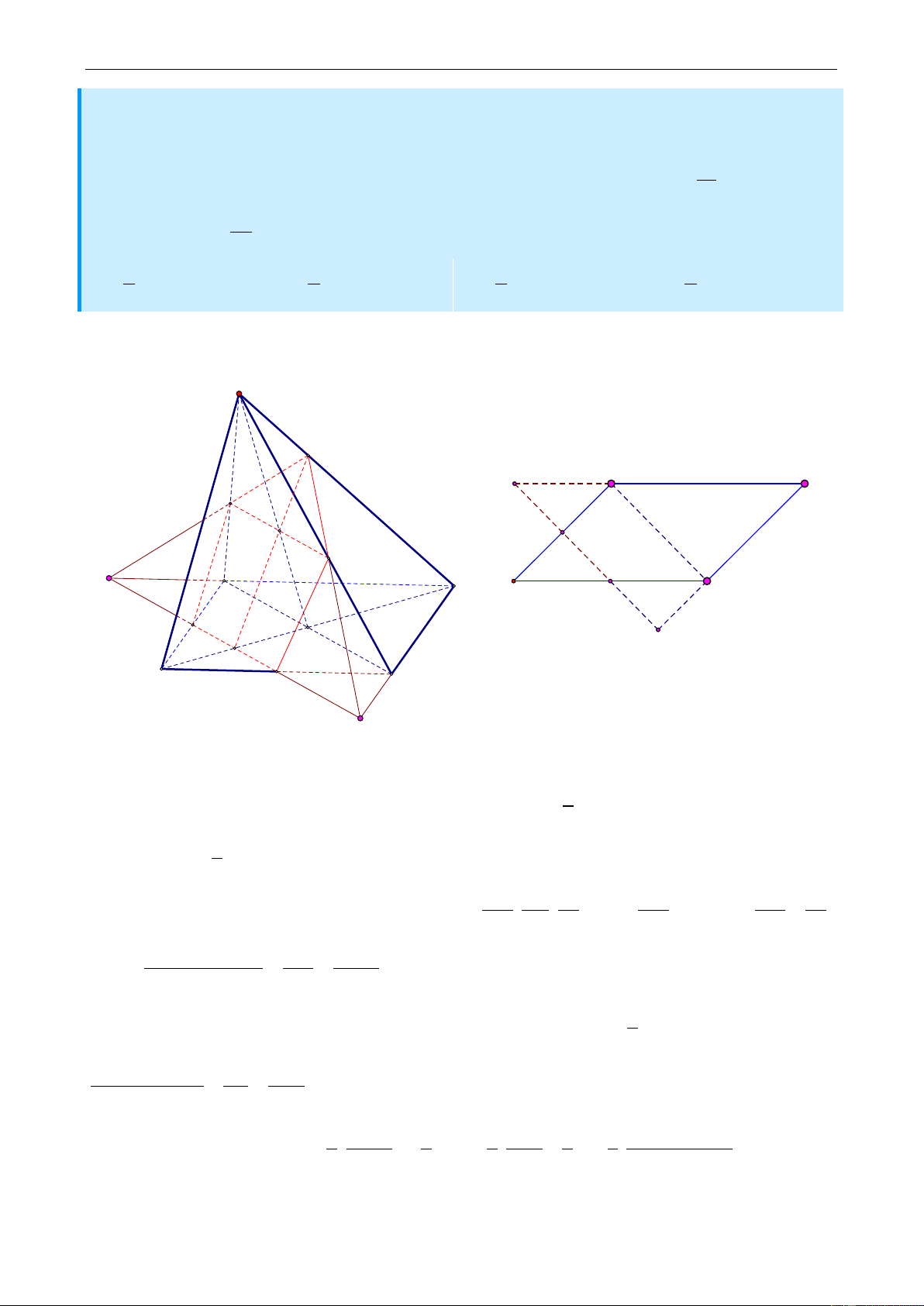
Câu 20: Cho hình chóp .
S ABCD cî đáy ABCD là hình bình hành. Gọi M , N lần lượt là
trung điểm của các cạnh AB , BC . Điểm I thuộc đoạn SA . Biết mặt phẳng MNI chia khối chóp .
S ABCD thành hai phần, phần chứa đỉnh S có thể tích bằng 7 lần phần còn 13 lại. Tính tỉ số IA k  ? IS A. 3 B. 1 C. 1 D. 2 4 2 3 3 Giải Ta có hình vẽ S H A E D I Q M J N A E B D C M P O F B N C F
Dễ thấy thiết diện tạo bởi mặt phẳng MNI với hënh chîp là hënh ngũ giác IMNJH với
MN //JI . Ta có MN , AD , IH đồng qui tại E với 1
EA ED và MN , CD , HJ đồng qui 3 tại F với 1
FC FD , chú ý E , F cố định. 3
Dùng định lí Menelaus với tam giác HS ED IA HS HS SAD ta có . .  1 1  .3.k  1   . HD EA SI HD HD 3k
dH,ABCD Từ đî HD 3k   . Suy ra VVVV .
dS,ABCD SD 3k  1 HJIAMNCD H.DFE I.AEM J.NFC Đặt V V và S S
, h dS,ABCD ta có 1 SSS và S.ABCD ABCD AEM NFC 8
dI,ABCD IA k  
dS,ABCD SA k  1 2 Thay vào ta được 1 3k  9  1 k 1 1 21k  25k V  . . h S    2. . . h S  . V . HJIAMNCD 3 3k  1  8  3 k  1 8 8 3k   1 k   1
22 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN 2 Theo giả thiết ta có 13 1 21k  25k 13 V
V nên ta cî phương trënh .  , giải HJIAMNCD 20
8 3k  1k  1 20 phương trënh này được 2 k  . 3
Câu 21: Cho đa giác đều gồm 100 đỉnh. Tính số tam giác tù được chọn từ 3 đỉnh của đa giác trên? A. 117600 B. 117800 C. 116700 D. 117670 Giải
Đánh số các đỉnh là A , A ,..., A . 1 2 100
Xét đường chéo A A của đa giác là đường kính của đường tròn ngoại tiếp đa giác đều 1 51
chia đường tròn ra làm hai phần, mỗi phần có 49 điểm: từ A đến A và A đến A . 2 50 52 100
Khi đî, mỗi tam giác có dạng A A A là tam giác tù nếu A và A cùng nằm trong nửa 1 i j i j đường tròn
 Chọn nửa đường tròn: có 2 cách chọn.
 Chọn hai điểm A A là hai điểm tùy û được lấy từ 49 điểm A , A ,..., A có i , j 2 3 50 2
C  1176 cách chọn. 49
Giả sử A nằm giữa A và A thì tam giác A A A tù tại đỉnh A Mà AA A AA A i . i 1 j 1 i j j i 1 1 i j
nên kết quả bị lặp hai lần. Có 100 cách chọn đỉnh.
Vậy số tam giác tù là 2.1176.100  117600. 2
Chú ý: Cho đa giác đều có n đỉnh. Công thức tổng quát tính số tam giác tù:
 Nếu n chẵn thì số tam giác tù là 2 . n C n2 2
 Nếu n lẻ thì số tam giác tù 2 . n C n1 2
Áp dụng công thức nhanh ta có 2 2 . n C    C n 100. 117600. 2 49 2
Câu 22: Cho hai số thực x, y  1 thỏa mãn điều kiện: 2 x y
log 2 x y  log  log 4xy  1 2     2 2 2 2   x  4y  1
Giá trị lớn nhất của biểu thức f x y 2 2 ,
 2xy x  2y x  4y bằng? A. 1 B. 2 C. 3 D. 3 2 3 4 7 Giải
Áp dụng bất đẳng thức trị tuyệt đối ta có:
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 23
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11 2 2 2 x y x  4y  1
log 2 x y  log
 log x y  1  1  log 2     2 2 2 2   2 x  4y  1 x y 2 2     x yx 4y 1 log  1  log  1  log  2 2
x  4y  1  log  2 2 x  4y  1 2 2 2 2  x y
Mặt khác theo bất đẳng thức AM – GM ta lại có log  2 2
x  4y  1  log 4xy  1  VP 2  2   2 2 
x  4y  1  1  log
 log x y  1 2  2   
Dấu “=” xảy ra khi và chỉ khi  x y  x   2y
Thế vào f x,y ta được f x y  gx 2 ,  2x x Ta có   g x 1 1  
x x   g x 1 3 ' 0 2 max  g     1; 2x 2  2  4
Câu 23. Cho phương trënh 3 tan x  1 sin x  2 cosx  msin x  3cos x. Có bao nhiêu giá
trị nguyên của tham số m thộc đoạn  2018 
; 2018 để phương trënh trên cî đúng một nghiệm thuộc     0; ? 2    A. 2015. B. 2016. C. 2018. D. 4036. Giải
Vì cos x  0 nên phương trënh tương đương với  3tan x  2 tan x  1  mtan x  3. Đặt   
t  tan x  1, vì x  0;  t 1;   .  2 
Khi đî phương trënh trở thành 
t t    mt   3 2 2 3t 3t 3 1 2  m  . 2 t  2 3 3 4 2
t  5t  2
Xét hàm   3t  3t f t
với t 1;. Ta có f 't   0, t   1;  . 2   2 t  2  2t 2
Lập bảng biến thiên suy ra phương trënh cî nghiệm khi m  2 m   2  018;2018 m  Có 2016 giá trị. m 3,4,...,201  8
Câu 24: Cho phương trình 2017  2018 2018 x x x x cos 2x 2 sin cos sin cos cos x  . Nghiệm 1  tan x
dương nhỏ nhất của phương trënh cî dạng a
 với a, b là các số nguyên và nguyên tố b
cùng nhau. Tính S a  . b A. S  2. B. S  3. C. S  4. D. S  7. Giải cos x  0 Điều kiện:  . tan x   1
24 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN 2 2 Ta có cos 2x cos x  sin x
 cos xcos x  sin x. 1  tan x sin x 1  cosx Do đî phương trënh 2017   2018 2018 2 sin x  cos
xsin x  cosxcosx  sin x  cos xcos x xx x 2017   2018 2018 cos sin cos . 2 sin x  cos x  1  0. 
 cos x  0L 
 sin x  cos x  0  tan x  1
  x    k k  . 4  2017  2018 2018 x x 2017     2018 2018 2 sin cos 1 0 2 sin x  cos
x  1: Vô nghiệm vì 1009 1009 1009      2018 2018 a b a b  1 sin x  cos x  2.   2    với 2 2
a  sin x, b  cos . x 1008  2   2  2 3 a  3
Nghiệm dương nhỏ nhất là    S  7 4 b   4
Câu 25: Cho các số thực a,b,c thỏa mãn 0  a,b,c  1 . Khi đî trị nhỏ nhất của biểu thức 1 2 P  log b c
ađược viết dưới dạng m , với m,n là các số nguyên dương và m a logb log 4 c n n
là phân số tối giản. Hỏi 3 3
T m n có giá trị là bao nhiêu? A. 171 B. 89 C. 195 D. 163 Giải
Theo bất đẳng thức AM – GM ta có:  1 1 1 2 2 2 P  log b c a b c a c a a logb logc 2 loga logb logc 2 loga log 4 4 4 c  1 1 1 1 1 1 2 2 2 log c a c c c c a a logc loga loga loga loga log 4 4 4 4 4 4 c 1 1 1 1 1 2 5  5 5 log c. log c. log c.
log c. log a  4 a 4 a 4 a 4 a 4 c 4
Vậy giá trị nhỏ nhất của 5
P  , khi đî T  189 4
Câu 26: Có bao nhiêu số nguyên x  3 m 20
 18;2018 để phương trënh 1 2 2
 8  x m có 2
đúng 2 nghiệm thực phân biệt? A. 2013 B. 2012 C. 4024 D. 2014 Giải
Phương trënh tương đương với x 1 3 2 x  3 m  2
 8  x . Hàm số f x 1 2  2  8  x là một 2 2
hàm số chẵn do đî ta chỉ cần xét trên nửa khoảng 0; để suy ra bảng biến thiên của
hàm số f x trên cả tập số thực.
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 25
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11 Xét hàm số 2  x1 3x 2  8  x   2   g x    x x x  3   x 1 2 ln 2 3 2 1   f x 2 2  2  8  x  
f 'x   2 x1 2       x1 3x x x 2  8  0  x  2 2 ln 2 3 0  0 2  2 Ta có g xx1 2 2 '
 2 ln x  3  8ln 2  3  0, x
  2, g2  8ln 2  6  0, g3  16ln 2  9  0 nên
phương trënh gx  0 có nghiệm x  2;3 . 0  
Vẽ bảng biến thiên cho hàm số f x ta suy ra được phương trënh cî đúng 2 nghiệm thực m  6 khi và chỉ khi  2    x mx 3 7,8,...,201 
m f x  8 0 1 0  2  8   0  2
Câu 27: Giả sử số tự nhiên n  2 thỏa mãn đẳng thức dưới đây hãy tëm n? 2 4 6 2n2 2n 0 C C C C C n n n n n 4096 2 2 2 2 2 C        n ... 2 3 5 7
2n  1 2n  1 13 A. n  4 B. n  5 C. n  6 D. n  7 Giải 2 4 6 2n2 2n Giả sử số tự nhiên C C C C C n n n n n 8192 n  2 thỏa mãn 0 2 2 2 2 2 C        . n ... 2 3 5 7
2n  1 2n  1 15
Ta có: 1 x2n 0 1 2 2 2n 2
C C x C x  C x . n n n ... n 2 2 2 2n 1 1     1  x2n 0 1 1 2 1 2 3 1 2n 2n1
dx C x C x C x    C x n n n ... 2 2 2 2  2 3 2n 1 n    0 0 1 x 1 2n1 1   0 1 1 2 1 2 3 1 2n 2n1 
C x C x C x    C x n n n ... 2 2 2 2 2n 1  2 3 2n 1 n     0 0 2 2n1 2  1  0 2 1 2 2 2 2
 2C C C  ... nC 1 2n 2n 2n 2 2n  1 2 3 2n  1 n 1  1  Mặt khác     1  x2n 0 1 1 2 1 2 3 1 2n 2n1
dx C x C x C x    C x n n n ... 2 2 2 2  2 3 2n 1 n    0 0   2 0 2 1 2 2 2 2  2
C C C   C 2 n n n ... n 2 2 2 2 2n  1 2 3 2n  1 n
Lấy 1 trừ 2 , ta được: 2n1 1 4 6 2n2 2 2 n   2n1 0 C C C C C 2 4096 2n 2n 2n 2n 2  2C         2.  n  6 . n ... n 2  2n  1 3 5 7 2n  1 2n   1  2n  1 13
Câu 28: Tính tổng 0 3 6 3k 15 18
S C  3C  6C  ...  3kC  ...  15C  18C ? 20 20 20 20 20 20 20 20 21 19 A. 10.2 10.2 10.2 10.2 S   13 B. S   14 C. S   13 D. S   13 3 3 3 3 Giải
26 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Xét khai triển x  120 0 1 2 2 19 19 20 20
C xC x C  ... x C x C 20 20 20 20 20
Đạo hàm hai vế ta có 20x  119 1 2 2 3 18 19 19 20
C  2xC  3x C  ... 19x C  20x C * 20 20 20 20 20  
Nhân hai vế * với x ta có 20xx  119 1 2 2 3 3 19 19 20 20
xC  2x C  3x C  ... 19x C  20x C 20 20 20 20 20
Cho x  1 ta được 19 1 2 3 19 20
20.2  C  2C  3C  ...  19C  20C 1 20 20 20 20 20   Đặt 1 i 3 a   
. Cho x a ta có 2 2
20a1  a19 1 2 2 3 19 2 20
aC  2a C  3C  ...19aC  20a C 2 20 20 20 20 20   Cho 2
x a ta có 20a 1 a 19 2 2 2 1 2 3 2 4 2 19 20
a C  2aC  3C  4a C  ... 19a C  20aC 3 20 20 20 20 20 20  
Cộng vế theo vế 1 ,2 ,3 ta có 20 2  a1 a19 19 2  a  2 1  a 19  0  3S C 20   a
 1  a19  a 2 a 19 39  a  1 20 Mặt khác 10.2   S   13
a 1 a 19  a a19 2 2 2 21  a  1  3 
Câu 29: Cho hàm số f x cî đạo hàm trên \ 
b và hàm số g x cî đạo hàm trên .
Biết đồ thị của hai hàm số y f 'x ,y g'x như hënh vẽ dưới.
Đặt hx  f x  gxS   h
 x b 2   h
bx   hchc 2 2 2 , 1 2  
 với a,b,c là các số
thực đã biết. Khẳng định đúng với mọi x  0 là? y
y f x
y gxO a b c x
A. S hc ;ha c  
B. S hc
C. S  hc ;ha b  
D. S ha ;hc   Giải x a
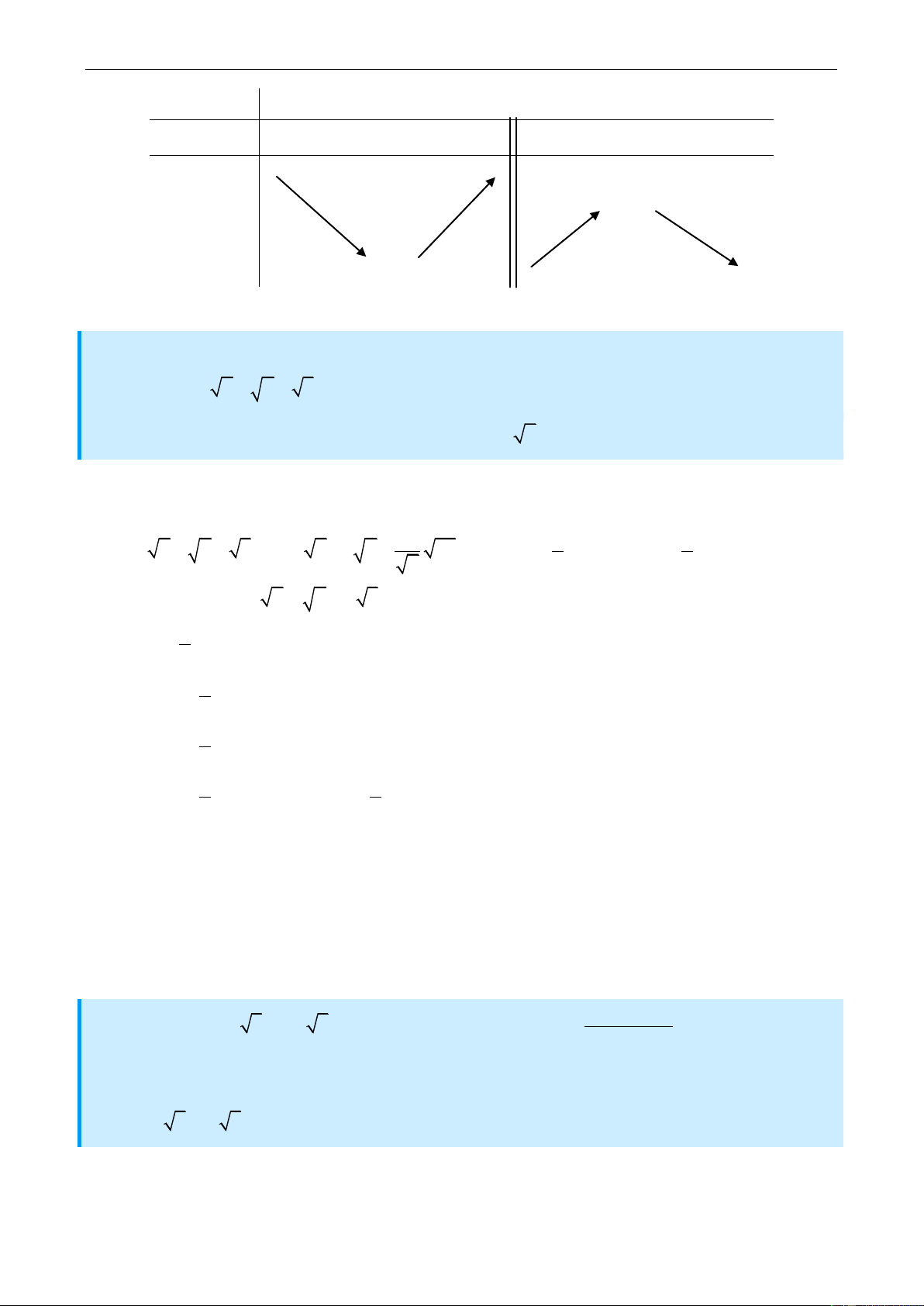
Từ đồ thị đã cho ta suy ra h'x  f 'x  g'x;h'x  0  f 'x  g'x   x   c
Lập bảng biến thiên ta có
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 27
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11 x
 a b c  h'x  0 + + 0  hch xha
Lại có       2 2   2     2 S h b x h c h b x
h x b  hc
Câu 30: Cho 3 số thực thỏa mãn x 2;4;y 0;4; z1;5 . Khi đî giá trị lớn nhất của
biểu thức T   x y z2  5log x 1  2log y 1  4log z bằng? 3   5   5  A. 10 B. 11 C. 8 5  14 D. 12 Giải
Theo Cauchy – Schwarz , ta có:     
x y z  2 2 1 1  x y z     
x y z 5 1 1 2 1 1
2  x y    2z  2   2  2
Dấu "  " xảy ra khi: x y  2 z x y  4z 1 Suy ra 5
T  x y  2z  5log x  1  2log y  1  4log z 3   5   5  2 5
 T  x y  2z  2log x  1  4 log y  1  8log z 3   5   5  2 5
 T  x y  2z  2log x  1  4 log y  1  8log z 3   5   5  2 5    5 T
x  2 log x  1 
y  4 log y  1  5 z  4log z 3    5    5  2 2
Áp dụng kết quả quan trọng x  a  1log x   x  
a . Dấu “=” xảy ra khi x  1 a 1 0, 1; 
x  log x  1  x  1  2log x  1  1  2  2 3     3     hoặc 
x a  y  4log y  1  y  1  4log y  1  1  0  T  10 5     5   
z4log z z4log z1 1 1  5  5  
Dấu “=” xảy ra khi x y  4z  4. Câu 31: Cho f x
0  a  1  b  1  a và hàm số y g x    cî đạo hàm trên
f x  2 1 
0;. Biết đồ thị hàm số y f x như hënh vẽ dưới. Khẳng định nào sau đây đúng với
mọi x   a  1; b  1  
28 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN y
y f xn m O a b x f b 1 f a 1 f b 1
A. gx 
B. gx 
C. gx  D. 10 
gx  0 m n m Giải
Ta có x   a
b    x  2 1; 1 1 a;b  
, dựa vào đồ thị ta có
m f x  2  1 1 1 1  n    n
f x  12  m
Mặt khác 0  a  1  b  1  a dựa vào đồ thị ta thấy f x đồng biến trên  a  1; b  1   f b 1
nên ta có f a 1  f x  f b 1  gx  m
Câu 32: Cho các số thực dương a,b,c,m,n,p thỏa mãn điều kiện 2017 2017 2017 2 m  2 n  3 p  7
22a2018 22b2018 2018 và 3c
4a  4b  3c  42 . Đặt S   
thì khẳng định đúng là? m n p A. 2018 42  S  7.6 B. 2018 S  6 C. 2018 7  S  7.6
D. 4  S  42 Giải Đặt 2017 2017 2017 m x ;n y ; p z
; 2x  2y  3z  7;2a  2b  3d  21c  2d  2a2018 2.  2 2018 2018 2018 6 x  6 x  ...  6 x 2017  2.2018.6 .2a 2017  x  2a2018 Theo AM – GM ta có 2.  2 2018 2018 2018 6 y  6 y  ...  6 y 2017  2.2018.6 .2b 2017 y   2a2018 3.  3 2018 2018 2018 6 y  6 y  ...  6 y 2017  3.2018.6 .2d 2017  y Mặt khác 2018 
x y z 2018 2017.6 2 2 3  20  17.7.6 2017  S
a b d 2018 
x y z 2017 2018 2018 2.2018.6 2 2 3 2017.6 2 2 3  2.2018.6 .3.7  2017.7.6  7.6
x y z  1
m n p  1 Dấu “=” xảy ra khi   
a b d  3
2a  2b c    6
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 29
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11
Câu 33: Có bao nhiêu cặp số nguyên a, b để phương trënh sau đúng với mọi x ax   2  b cos 2 cos 1
ax b   11 A. 0 B. 1 C. 2 D. 3 Giải
Giả sử phương trënh1 đúng với mọi x nên cũng đúng với x  0
  b cosb2 2 1  b  0
Khi đî phương trình (1) trở thành:
acos x  1  cos ax  12 ( 2 đúng với mọi x khi a  0 )
Vậy ta chỉ cần xét khi a  0. Do 2 đúng với mọi x nên đúng khi x  2 x  2 khi ấy có: 
cos2ax  1  2a  2k . Do a  0  a k 3 . Trong 2 thay 2 x  ( do a  0 ) ta có a  2  2 2 1 a cos  1  0  cos  1 
 2m  a    4  aa a m
Từ 3 ,4 và k,m nguyên nên a  1.
Thử lại ta thấy chỉ có a  0 và b  0 hoặc a  1 và b  0 thỏa mãn
Vậy có 2 cặp số nguyên a;b để pt 1 đúng với mọi x.  2
 p x p x  2  0
Câu 34: Cho hệ phương trënh 
vô nghiệm khi p;ab; . 2 x  1
Tính giá trị của biểu thức 2 2
A a b A. 10 B. 9 C. 13 D. 16 Giải
Ta có hệ phương trënh đã cho vï nghiệm  f x   2
p x p x  2  0 với mọi x  11  f  1    0
p 1p 3  0    p  0
Giả sử 1 đúng , ta cî  f 0  0  pp  2  0       f    p 3 1  0 p1  2  0 Thử lại, ta có:
) Nếu p  0 khi đî 2
p x  0 với mọi x
Do x   p x      2 1 2 1
p x p x  2  0 với mọi x  1. ) Nếu p  3 Do 2
x  1  p x  2 và p x  2  0 (do x  1 )   2
p x p x  2  0 với mọi x  1.
Vậy a  0,b  3  A  9
30 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Câu 35: Cho dãy số u được xác định bởi u  2 ; u u
 . Cïng thức số hạng  n n 2 n 3 1 n  1 1
tổng quát của dãy số đã cho là biểu thức cî dạng .2n a
bn c , với a , b , c là các số nguyên,
n  2 ; n  . Khi đî tổng a b c cî giá trị bằng A. 4 B. 4 C. 3  D. 3 Giải
Ta có u u
  u  3n  5  2 u      n  ; n  .  3 n 1 5 n n 1    n n 2 n 3 1 1  , với 2
Đặt v u n  , ta có v v với n  2 ; n . n 2 n n 3 5 n1
Như vậy, v là cấp số nhân với cïng bội q  2 và v  10 , do đî n1 v  10.2  5.2n . n  1 n
Do đî u  3n  5  5.2n , hay u  5.2n n  với n  2 ; n . n 3 5 n
Suy ra a  5 , b  3 , c  5 . Nên a b c  5   3     5    3  .
Câu 36: Một ngày đẹp trời, trong lúc đi dạo công viên, cầm một khối cầu trong tay, một
nhà khoa học yêu cái đẹp nảy ra û tưởng muốn tạo ra một khối nón nội tiếp trong một
khối cầu cî bán kình R và đựng một loại dung dịch X do ông chế tạo ra vào trong đî, sao
cho thể tích dung dịch X chứa được trong X là lớn nhất. Sau khi chế tạo xong, trong lúc
mải ngắm tác phẩm của mình, nhà khoa học đã vï tënh làm vỡ cả khối cầu thủy tinh, tuy
vậy ïng đã thu hồi lại được lượng dung dịch X quý giá của mình. Lần này, vì rút kinh
nghiệm, cũng lượng dung dịch X đî, nhà khoa học muốn chế tạo một cái hộp bằng một
loại kim loại chịu lực trong suốt để đựng dung dịch của mình. Ông có hai sự lựa chọn cho
hộp kim loại của mình, có dạng hình hộp chữ nhật hoặc là có dạng khối trụ. Tuy nhiên,
kinh phí còn lại của ông có hạn, còn giá thành kim loại đî lại rất đắt vì nó hiếm. Ông
muốn chi phí sản xuất kim loại cấu thành hộp là bé nhất, nhưng vẫn phải chứa được lượng
dung dịch X đã cî của mình.Hãy giúp nhà khoa học tính toán xem diện tích toàn phần
nhỏ nhất của hộp kim loại là bao nhiêu? 11 11 6 6 A. 2 2 2 2 2 3 3 RB. 2 3 RC. 2 3 3 RD. 2 3 R  8 3 8 3 4 3 4 3 Giải
Ta tëm lượng dung dịch X lớn nhất mà nhà khoa học đã đựng được trong khối nîn nội tiếp khối câu bán kình R.
Rõ ràng trong hai khối nîn cî cùng bán kình thë đáy nội tiếp trong một khối cầu thì khối
nón nào có chiều cao lớn hơn thë thể tích, nên ta chỉ xét khối nón có chiều cao lớn hơn trong hai khối nîn đî.
Giả sử rằng khối nîn cî đáy là hënh trín bán kình r. Gọi x với0  x R là khoảng cách từ
tâm khối cầu đến đáy khối nîn. Khi đî chiều cao lớn hơn của khối nón nội tiếp khối cầu
với đáy là hënh trín bán kình r sẽ là h R x . Khi đî bán kënh đáy nîn là 2 2
r R x , suy
ra thể tích khối nón là
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 31
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11 1 2 1 V r
h  R x 2 2 R x  1
 R xR xR x 1
 R xR x2R  2x . 3 3 3 6 R O R x r
Theo bất đẳng thức AM – GM ta có 1
     
R x R x R x V
R x R x 2R  2x 1  2 2 3 32 3    R  . 6 6 27 81
Đây cũng chình là lượng dung dịch X mà nhà khoa học đã đựng trong khối nón lúc ban đầu.
Ta tìm diện tìch toàn phần nhỏ nhất của hộp kim loại đựng lượng dung dịch X nîi trên, với 32 3 V R  . 81
 TH1: Hộp kim loại hình trụ. Khi đî 2 V 2 2 2V V Rh h  ,S R   Rh R   tp 2 2 2 2 RR
Áp dụng bất đẳng thức AM-GM cho bộ ba số dương 2 V V 2 R  , , , ta có R R 2 V V 3 2 S R     Vtp 2 3 2 R R
 TH2: Hộp kim loại hình hộp chữ nhật, khi đî V V VV V
V abh h
,S  2ab  2a bh  2ab  2a  2b  2ab   . tp ab ab ab a b   
Áp dụng bất đẳng thức AM-GM cho bộ ba số dương V V ab, , ta có a bV V  3 2
S  2 ab      2.3 V tpa b  So sánh 3 2 3 2 V  và 3 2 6 V ta có 3 2 3 2 3 2 V
 6 V . Vậy diện tích toàn phần nhỏ nhất của hộp 11 kim loại là 3 2 32 2048 2 3 2 V  . Từ đây thay 3 V R  vào, ta được 2 2   3 3 S 3 R  3 R  . 81 tp 8 6561 3
32 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
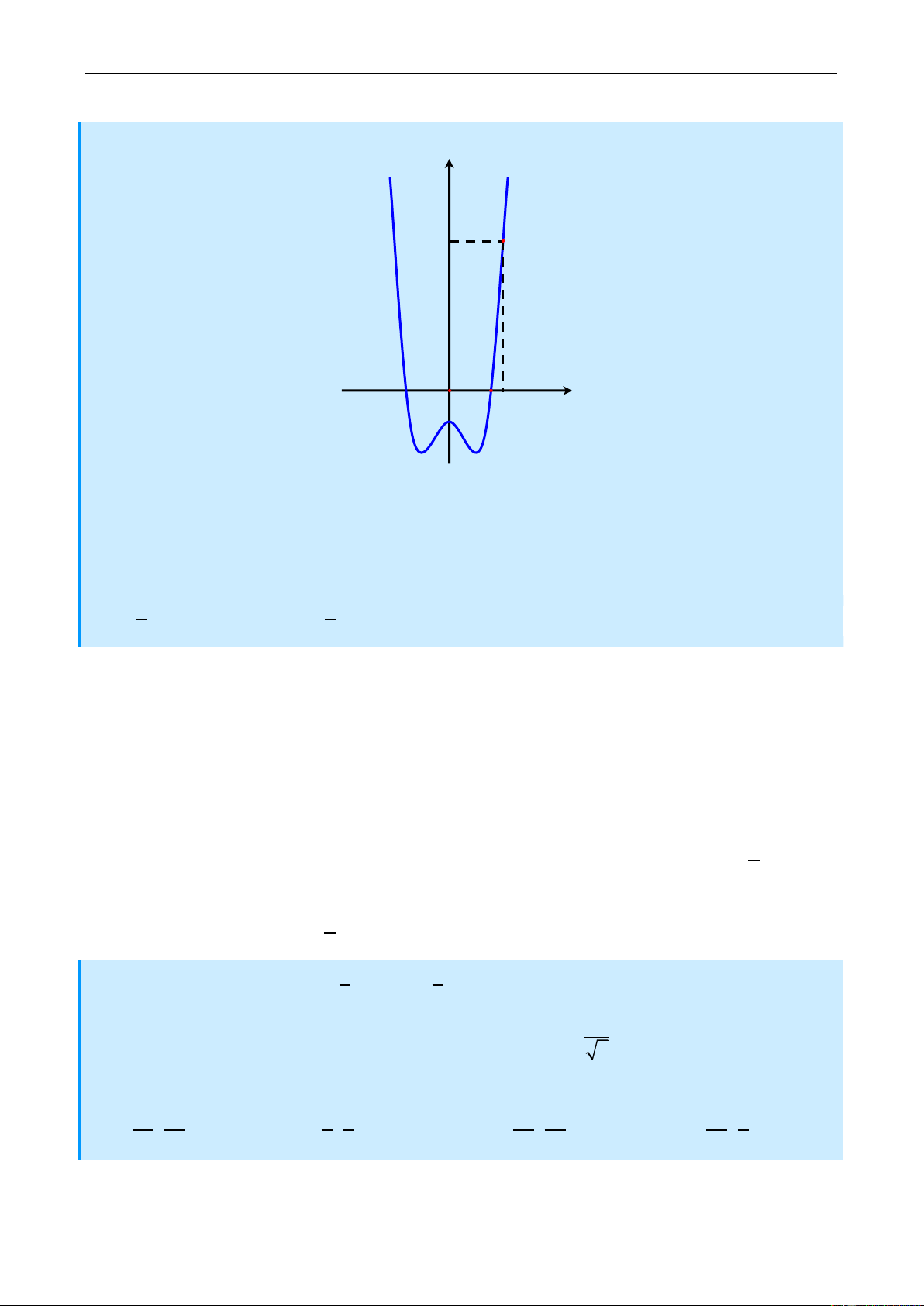
Vậy đáp án đúng là A. Câu 37: y 11 –2 – O 1 1 2 x –1
Cho hàm số f xcî đồ thị như hënh vẽ đồng thời f x  1  f x  2x2x  1x  1* Biết rằng   4 2
f x ax bx c ;   2
g x mx nx p và f x  g 2
x  1 . Tìm giá trị nhỏ nhất của
hàm số gxA. 1  B. 1  C. 2 D. 4 2 4 Giải
Từ * ta thay x  0  f 1  f 0 a b  0
Ta có x  0  y  1   c  1    và x y   f x 4 2 2, 11
x x  1 c  1  
Mặt khác x x   gx    mx  2 4 2 2 2  n 2 1 1 1 x  1  p 4 2 2
mx  2mx m nx n p m  1 m  1    1  2   n  1
  n  1  gx 2
x x; g'x  2x  1; g'x  0  x    2 1   n    p p   0
Vậy giá trị nhỏ nhất gx 1   4 Câu 38: Cho hàm số 5 3 2 1
y   x  3x  C . Tìm những điểm trên đường thẳng 3 3
d : y ax b đi qua gốc tọa độ và tạo với đường thẳng 1 y x một góc 0 15 mà từ đî kẻ 3
được đếnC 2 tiếp tuyến . A.  1  1    1 1   1  1    1  1   ;  ;1;1 B.  ; ;1;1 C. ; ; 1    ;1 D. ; ;1; 1      5 5   5 5   5 5   5 5  Giải
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 33
SẢN PHẨM KỶ NIỆM NGÀY NHÀ GIÁO VIỆT NAM 20/11 Ta có 1 y
x tạo với Ox một góc 0
30  d tạo với Ox góc 0
45  a  1  y x (qua O) 3
M d và M x ;x 0 0 
Phương trënh đường thẳng  qua M : k x x x , tiếp xúc với C khi 0  0  5 3 2 1
 x  3x   k x x x 0  0 5 3 2 1  3 3
  x  3x    2
5x  6xx x x 0  0 2 3 3  5  x  6x   k 10 3 
x    x  2 1 3 5
x  6x x x   0  x  1 2
10x  15x x  3x x  1  0 0 0 0 0 0  3 3
Suy ra để kẻ được 2 tiếp tuyến thì 2
10x  15x x  3x x  1 có 1 nghiệm duy nhất 0 0 2  10x   1
 5x  1 x  3x  1  0 0  0  1 2
x   N          Ta có 225x 1 30x 120x 40 0     0 0 5 1 1    
M  ; ;N 1;1 1 2   x   1 13 x  L  5 5   15 Câu 39: Cho hàm số    f x 8x a bx c  
. Biết đồ thị hàm số cî đúng 2  
c  3tan x x x 1 2
đường tiệm cận (chỉ tính tiệm cận đứng và tiệm cận ngang). Số giá trị nguyên tối đa cî thể
của tham số a thỏa mãn bài toán là? A. 8 B. 2 C. 10 D. 9 Giải
Hàm y  tan x là một hàm có vô số tiệm cận đứng. vì vậy muốn có hàm số f x cî đúng
hai tiệm cận thì ít nhất hệ số của hàm tanx phải bằng 0 c  3 . Khi này hàm số trở thành:  
8x a bx c
8x a bx c f x
c  3 tan x  20   xx  1 xx  120
Hàm số trên có một TCN: y  0 (khi x   ). Yêu cầu bài toán tương đương hàm số có
đúng một đường TCĐ nữa. Xảy ra các trường hợp sau:
Trường hợp 1: Tử số có nghiệm x  0  a  3  0  a  9
Trường hợp 2: Tử số có nghiệm kép x  1 . Suy ra
 8  a b  3  0  4  8  a  1  VN  8 4  8  a   3  0    
b  0  b  8  a
 8  a  4  a  8 2 8  a 8  a
Trường hợp 3: Điều kiện xác định của căn thức chỉ chứa một nghiệm ở mẫu số. Cụ thể là:  a    0 a 
8x a  0  x  . Suy ra 8   8   a  0 8 a 1    8
34 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN a  9
Kết hợp cả 3 trường hợp thì các giá trị nguyên của a thỏa mãn bài toán là a  8   8   a    1
Suy ra có tất cả 10 giá trị nguyên của tham số a thỏa mãn.
Câu 40: Cho tích phân 11 I
x  7  11  x dx
, gọi M và m lần lượt là giá trị lớn nhất và 7   
giá trị nhỏ nhất của I. Tính S M m ?
A. 54 2  108
B. 36 2  108 C. 6 3  54 D. 6 3  36 Giải
Đặt y x  7  11  x với x  7  ;11 . Ta có 1 1 y    0  x  2
2 x  7 2 11  x
Nhận thấy y’ khïng xác định tại 7;11, vẽ bảng biến thiên ta có 18  y  6 11 11  18dx            x 7 11 x  11 dx 6dx 7 7 7  11  54 2 
x  7  11  x dx  108  7   
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 35