Thông tin
Quiz

Ôn luyện các nhóm câu hỏi vận dụng cao trong đề thi THPTQG môn Toán (Đề 3)

Giới thiệu đến bạn đọc đề thi số 3, loạt đề do các tác giả nhóm Chinh Phục Olympic Toán tổng hợp và biên soạn, đây là các bài toán thuộc mức độ khó và rất khó được trích dẫn từ các đề thi thử THPT Quốc gia môn Toán của các trường THPT, sở GD&ĐT.

Chủ đề:

Tài liệu ôn thi THPTQG môn Toán 257 tài liệu

Môn:

Toán 1.9 K tài liệu

Thông tin:

42 trang 1 năm trước

Tác giả:

Nguyễn Vân

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Ôn luyện các nhóm câu hỏi vận dụng cao trong đề thi THPTQG môn Toán (Đề 3)

66 33 lượt tải Tải xuống

Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 1

ĐỀ ÔN LUYỆN CÁC NHÓM CÂU HỎI

VẬN DỤNG CAO TRONG ĐỀ THI THPT QUỐC GIA

Đề gồm 40 câu trắc nghiệm

Sản phẩm được thực hiện bởi nhóm

Chinh Phục Olympic Toán

Câu 1: Có bao nhiêu giá tr nguyên ca tham s

 

m x m x

   



Ct nghim nh 

D. Vô s.

Câu 2: Cho 2 dãy cp s cng

; ;...

u u u u

có công sai

và

; ;...

v v v v

có công sai

. Gi tng ca n s h u ca mi cp s theo th t là

... 7 1

S u u u n     

và

... 14 27

T v v v n     

. Tính t s ca

Câu 3: Cho hình chóp

.S ABC

có

, , 1.SA x BC y AB AC SB SC     

Th tích khi chóp

.S ABC

t giá tr ln nht khi tng

 

xy

bng :

4 3.

Câu 4: Giá tr nh nht c h m :

   

log log 2 2

x y xy

x y xy m



   





  





Câu 5: Cho

   

2 sin cos , .a b a b a b k     

Tính giá tr ca biu thc

1 2 sin 2 1 2 sin 2







Câu 6: Cho dãy

 

tha mãn

5 1 5 5

2 1 2

25.2 15.2 5.2 15.2 4 0

u u u u

  

    

và





Giá tr nh nht ca



2019.

u 

512.

258.

511.

257.

Câu 7: Cho hình chóp

.S ABCD



ABCD

là hình vuông,

1AB 

, cnh bên

1SA 

và

vuông góc vi mt ph

 

ABCD

. Kí hiu

n

và

là

n

sao cho

45MAN 

. Th tích nh nht ca khi chóp

.S AMN

là ?

60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT

2 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor









Câu 8: Cho mt cp s cng :

1 2 3 4

, , ,u u u u

tha

1 4 2 3

6u u u u

. Tìm tnh D ca

hàm

      

1 2 3 4

9f x x u x u x u x u     

 

;6D  

 

6;D  

D 

 

6;6D 

Câu 9: Cho hàm s

 

sin sin 1



    





. Tìm





 



sao cho khong cách

gim ci và cc tiu là ln nht ?



    



    



    



    

Câu 10: Cho t din

ABCD

có tt c các cu bng

Gi

là trng tâm ca tam giác

.BC D

Mt phng

 



ct

,BC BD

lt ti

,.IK

Tính th

tích nh nht ca

.ABIK

Câu 11: Cho hai s phc

,zz

tha mãn

2 3 17 ; 1 5z i z    

. Bit rng

  

1 1 0z i k z i k     

. Tìm k khi

P z z

t giá tr ln nht.

1k 

2k 

3k 

5k 

Câu 12: Gi

là tp hp các s t nhiên gm 5 ch s. Chn ngu nhiên mt s t tp

Tính xác su chc s chia ht cho 7 và có ch s  bng 2.

257

90000

257

18000

127

90000

127

30000

Câu 13: Cho s phc z tha mãn

15zi  

. Tìm GTLN ca

2 8 7 9P z i z i    

109P 

1 109P   

109 2P 

109 1P 

Câu 14: Cho s phc z tha mãn

4 1 2 1z z i z i     

. Tìm giá tr ln nht ca biu

thc

22P z i  

P 

Câu 15: Bit tng

2 2 2

1 1 1

2 2 ... 2

2 2 2

     

      

     

     

. Giá tr nh nht c  

3 2 4





n 

TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN

Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 3

Câu 16: Cho 3 s phc

0 1 2

,,z z z

thng thi

1 3 3 2

2 2 8zz

z z z z

    











, vi

zi  

. Bit

rng

 

, , ,

z z a bi

a b c d R

z z c di

  







  



. Tìm giá tr ln nht ca biu thc

P a d bc

17P 

18P 

19P 

20P 

Câu 17: Cho hàm s

 

y f x

o hàm trên . Gi

     

1 2 3

,,C C C

l th

ca các hàm s

   

 

, , 1y f x y f f x y f x   

. Các tip tuyn

   

,CC

t m

2x 

t là

2 1, 4 3y x y x   

, hi tip tuyn ca

 

tm

2x 



 

2; 11Q 

 

2;11M 

 

2; 21N 

 

2; 21P 

Câu 18: Cho dãy

()

tha mãn

5, 2, 1

x x x n



    

. Tính giá tr ca

1 1 2 1 2

1 1 1

lim ........

...

x x x x x x



   





5 21





5 21





3 31





3 15





Câu 19: Có bao nhiêu cp s nguyên

 

;ab

tha mãn

0 , 100ab

 th ca 2 hàm

s



và



ct nhau tm phân bit?

A. 9704

B. 9702

C. 9698

D. 9700

Câu 20: Xét các hình chóp

.S ABCD

thu ki

ABCD

là hình vuông, cnh

bên

vuông góc và khong cách t n mt phng

 

SBC

bng a. Bit

rng th tích khi chóp

.S ABCD

t giá tr nh nht

khi cosin góc ging thng

và mt phng

 

ABCD

bng



,pq

là các s 

là

ti gin. Tính

 

..T p q V

3 3 .Ta

6.Ta

2 3 .Ta

Ta

Câu 21: Cho s phc

1 2 3

,,z z z

lt tha mãn

3zi

là s thun o vi thun o

không âm,

là s thc không âm. Bit rng

2 3 2 1 3 1

z z z z z z    

. Gi M,n ln

t là giá tr ln nht và nh nht ca biu thc

2 1 3 1

P z z z z  

ng?

. 90Mn

. 80Mn

. 100Mn

. 70Mn

Câu 22: Cho các s th

,,x y z

tha mãn

 

2 2 2

5 9 2x y z xy yz zx    

. Tìm giá

tr ln nht ca biu thc:

 

x y z







60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT

4 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor

Câu 23: Gieo mt con súc sng cht hai ln. Gi s

là tích s chm mà con

súc sc xut hin sau hai ln gieo. Tính xác sut sao cho hàm s

   

3 41 2 2y m x m x    

ng bin trên khong

 

0;

Câu 24: Cho hàm s

 

ln 1y f x



  







     

2 3 ... 2018 ln ln ln lnf f f a b c d      



, , a c d



a b c d  

. Tính

P a b c d   

1986

1698

1689

1989

Câu 25: Cho hàm s

     

2 1 2 2y f x x m x m x      

. Tìm tt c các giá tr ca tham

s

 hàm s

 

y f x

m cc tr.

m

m  

m

Câu 26: Cho hàm s

 

y f x

o hàm liên tn

 

1; 2

thng thc:

 

   

 

 

' , 1; 2

x f x

f x x x

f x xf x x

   







và

 

f 

. Tính

 

7 7 1





 

7 7 1





 

2 7 1





 

2 7 1





Câu 27:

Cho hàm s  c bc ba

 

y f x

  th    m sau

     

2;4 , 3;9 , 4;16A B C

. ng thng

,,AB AC BC

li c th ti l t ti các

m

,,D E F

(

khác

và

khác

và

khác

và

). Bit rng tng các

 ca

,,D E F

bng

. Tính

 

02f 

 

00f 

 

f 

 

02f 

Câu 28: Cho hàm s

 

   

sin cosg x f x f x



thu kin :

 

cot sin 2 cos 2 ,f x x x

 

0;x  

Tích ca giá tr ln nht và giá tr nh nht ca

 

bng:



Câu 29: Cho hàm s

 

liên tn

 

1; 4

tha mãn

   

1 1, 4 8ff   

ng

thi

   

 

' 9 3 , 1; 4f x x f x x x x x     





. Tích phân

 

f x dx



bng

7



8

TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN

Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 5

 

'y h x

 

'y f x

 

'y g x

Câu 30:   

 

2 2 2

log 2 2 2 2

x x y x x     

. Hi có bao nhiêu cp s



 

;xy

, vi

0 500x

th

Câu 31: Cho hình chóp

.S ABCD



ABCD

là hình bình hành. Gi



m trên

sao cho

A A A S





. Mt phng

 



qua



ct các cnh

,,SB SC SD

lt ti

, , .B C D

  

Tính giá tr ca biu thc

SB SD SC

  

  

T 

2T 

T 

Câu 32: Gi

là công bi ca mt cp s nhân , bit tng ba s hu bng

ng

thi theo th t , chúng là s hng th nht , th  tám ca mt cp s cng . Hi

thuc kho

 

3; 4q 

 

1; 2q 

 

2;3q

 

0;1q 

Câu 33: Cho tích phân







, bit rng tng giá tr ln nht và giá tr nh

nht cc vii dng





 ng

là phân s ti gin. Tính

S a b c d   

Câu 34: Cho 3 hàm s

     

,,y f x y g x y h x  

  th ca 3 hàm s

     

,,y f x y g x y h x

  

  

 th  

th ca hàm s

 

y f x





. Hàm s

     

7 5 1 4

k x f x g x h x



     





ng bin trên

kho

60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT

6 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor

;0 .

















;1 .















Câu 35: Cho 2 s phc

tha mãn

7 5 9 3

4 4 4 4

zz    

z a bi

vi

 

3 2 1 0ab   

Bit rng

2z i z i  

. Tìm GTNN ca

3 2 3P z i z i     

38P 

39P 

2 38P 

2 39P 

Câu 36: Cho ba s th

,,a b c

tha mãn

abc a c b  

. Tìm giá tr ln nht ca biu

thc

2 2 2

2 2 3

1 1 1

a b c

  

  

max

P 

max

P 

max

P 

max

P 

Câu 37: Cho hàm s

 

liên tc trên n cp hai trên và tha mãn

   

 

   

. 4 ' . '' ,

f x f x f x f x e x



   



, bit

 

00f 



 

5ln 2

f x dx



bng?

25ln 2

5 31 5ln 2









1 355ln 2









1 25ln 2

31 5ln 2









355ln 2

5 31









Câu 38: Cho hàm s

 

y f x

 th hàm s

 

y f x





:

Xét hàm s

   

2 2 4 3 6 5g x f x x x m    

vi

là s th 

 

0gx

5; 5x



  



u kin ca

là

 

mf

 

mf

 

0 2 5

mf

 

5 4 5

mf  

13

5

 

'fx

TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN

Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 7

Câu 39: Cho 4 s nguyên

, , ,a b c d

i tha:

1 50a b c d    

. Tìm giá tr nh nht

ca biu thc



min

175

P 

min

200

P 

min

175

P 

min

200

P 

Câu 40: Cho các s t nhiên t n 100 . Chn ra 6 s bt k. Tính xác su chn ra 6

s sao cho chúng có th xp thành 1 cp s cng.

7528752

1254792

2509584

3764376

Câu 41: Cho các s thc x,y tha mãn

 

log 3 2 log 2 3 log 3 2 log 3 2x y y x        

Giá tr nh nht ca biu thc

 

4 15P x y xy  

là?

min 80P 

min 91P 

min 83P 

min 63P 

Câu 42 : Cho hàm s

 

và

 

tha mãn

         

' 1 1 1; 2 . 2 1f g f g f  

ng

thi

           

1 ' ' '' ' , \ 0f x g x g x f x f x x



    





. Tính tích phân

   

'I f x g x dx



ln 2



ln 2



ln 2



ln 2



Câu 43: Có tc to bi các ô vuông ca bàn c 8x8 khi bt

t ô vuông?

204

196

150

Câu 44: Gi R là bán kính mt cu ngoi ti   ng

1 1 1

.ABC A B C

. Gi s

BC a

, AA h

. Khi R ngn nht thì tam giác

ABC

A. u.

B. Cân ti A.

C. Vuông ti A.

D. Nhn

Câu 45: Cho hai s phc

,zz

tha mãn

2 , 5zz

. Bit rng

z i a bi

z i c di

  





  



Tìm GTLN ca biu thc

P a d bc

1P 

2P 

3P 

4P 

Câu 46: Cho t din ABCD ni tip trong mt mt cu bán kính R và thu kin

,AB CD

,BC AD AC BD

là m   i trong không gian. t

,P MA MB MC MD   

giá tr nh nht ca

là?

min

2 3.PR

min

4.PR

min

3.PR

min

P 

Câu 47: Cho 2 s thu kin

 

2 2 2

log 2 log 4 1 log

x y xy   

60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT

8 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor

t

P x y

. Hc s nguyên?

Câu 48:  

 

3 3 3 10 2 3 10 2m m x x x x      

. Có bao nhiêu

giá tr nguyên ca tham s  m?

Câu 49: Cho hàm s

 

sin cos cos sin

sin cos

x x x x

y f x







. Hi có bao nhiêu giá tr

 

2019;2019x 

tha mãn hàm s

 

t giá tr ln nht.

2453

5142

2571

4906

Câu 50: Cho 2 hàm s

     

 

1 6 2 1, h 6

f x m m x x



      

. Tìm tham s  

hàm s

     

.g x h x f x

có giá tr nh nht là 0 vi mi

 

0;1x 

1m 

m 









1m 

Câu 51: Cho cp s nhân

1 2 3

, , ,..,

u u u u

   

0, 1,2,...,

u i n  

. Bit rng

1 2 3

... 2018

S u u u u     

1 2 3

1 1 1 1

... 2019

u u u u

     

và

1 2 3

. . ....

100

P u u u u

Hi s t nhiên nh nht tha mãn P là:

9295

9296

18592

18591

Câu 52: 

{0,1,2,3, 4,5,6,7,8,9}A 















1 2 3 4 5

a a a a a

sao cho

1 2 3

a a a



3 4 5

a a a



Câu 53: Cho b





 

3 1 3

log 11 log 3 10 4 log 3 12 0

x ax x ax



      





Giá tr thc ca tham s  bm duy nht thuc khong nào



 

1; 0

 

1; 2

 

0; 1

 

2;

Câu 54: Cho hai s thu kin

 

2 log 1

y y x x



  

   



Tìm giá tr ln nht ca biu thc

 

log .2

P y x







TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN

Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 9

Câu 55: Gi

là tp hp các s t nhiên gm 5 ch s. Chn ngu nhiên mt s t tp

Tính xác su chc s chia ht cho 7 và có ch s  bng 2.

257

90000

257

18000

127

90000

127

30000

Câu 56 : Có tt c bao nhiêu cp s thc

 

;xy

thng thi u kin

 

2 3 log 5

4 1 3 8

y y y

  











    





Câu 57: Cho

()



31y x mx  



0m 



là

        

( ).

 

   

 

1; 0I 

bán kính

3R 



,.AB







IAB

 



A. 1

B. 2

C. 3

D. 0

Câu 58: Cho 3 s tha mãn

2zy

. Khi biu tht giá tr nh

nht, hãy tính

log xyz

 

2 3 3 3 3 4 2 2

log log 2 2P xy x y x z y xy zy xz       

1

Câu 59: Cho phương trình

sin 2 cos 2 sin cos 2 cos 0.x x x x x m m      

Có bao

nhiêu giá trị nguyên của tham số

để phương trình có nghiệm ?

Câu 60: Gi s

là s thc ln nht sao cho bng thc

2 2 2

sin

  



i











 ca

là?

60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT

10 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor

LỜI GIẢI CHI TIẾT ĐỀ 3

Câu 1: Có bao nhiêu giá tr nguyên ca tham s

  trình

m x m x

   



Ct nghim nh 

D. Vô s.

Lời giải



 

m x m m x m x



    













Xét

0m 

 

x x x

















mi

0x 

u là nghim c

Xét

0m 

 

x m x m x



  













  

x m x m x



  















  















vô nghim.

Xét

0m 

 

2 2 .

m x m x m x



   













    

m x m x m x



   



  

















  









2xm  

Vì

2 10xm  

 

5 4, 3, 2, 1





        

Câu 2: Cho 2 dãy cp s cng

; ;...

u u u u

có công sai

và

; ;...

v v v v

có công sai

. Gi tng ca n s h u ca mi cp s theo th t là

... 7 1

S u u u n     

và

... 14 27

T v v v n     

. Tính t s ca

Lời giải

T gi thit, ta có

 

n u n d









và

 

n v n d









 

11 1 1 1 1

11 1 2 1 2

2 1 4 27

10 2 20

u n d

T v n d n

u u d u d

v v d v d

  







  



















TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN

Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 11

So sách (1) và (2) bng nht

148 4

1 20 21

111 3

       

Câu 3: Cho hình chóp

.S ABC

có

, , 1.SA x BC y AB AC SB SC     

Th tích khi chóp

.S ABC

t giá tr ln nht khi tng

 

xy

bng :

4 3.

Lời giải

Gi

,HK

lm

,.BC SA

t

2 , 2 .BC x SA y

Có

2 2 2 2 2 2

1 ; 1 .SH SC CH x AH AB BH x       



SAH

cân ti

Hay

.HK SA

Có

 

, 1 .d BC SA HK x y   

Th tích khi chóp

.S AB C

là

   

2 2 2 2

. . , sin ,

2 2 2 3

1 . .

6 3 3 3 27

S ABC

BC SA d BC SA BC SA

x y x y

V xy x y



   

     





Du bng xy ra khi và ch khi

x y x y x y x y         

Ch

Câu 4: Giá tr nh nht c h m :

   

log log 2 2

x y xy

x y xy m



   





  





Lời giải

t

   

log , log 2x y a xy b   



2ab

Li có:

 

4x y xy  

     

2 4 3 2 4 3 2 12 8.3 36 0

a b a a a

       

Xét hàm

 

12 8.3 36

ga  

ng bin trên ,

 

1 0 1ga  

   

     

 

3 2 2 3 3 2 .2 2 3 2

a a a a

m x y xy x y xy f a



          

ng bin trên





1;

suy ra

(1) 1mf

Vy h m khi và ch  2 có nghim

11am  

Câu 5: Cho

   

2 sin cos , .a b a b a b k     

Tính giá tr ca biu thc

1 2 sin 2 1 2 sin 2







Lời giải

60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT

12 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor

D dàng chc:

     

sin 2 2 sin cos sina a b a b a b    

     

           

1 2 sin 2 a 1 4 sin 2 cos sin

1 cos 2 cos sin

sin 2 cos sin sin sin 2 cos

a b a b a b

a b a b a b a b a b a b

       

     

         





 ta có:

     

1 2 sin 2 b sin sin 2 cosa b a b a b     





Suy ra:

 

2 2 2 2

2 sin

sin sin ( ) 4 cos ( ) sin ( ) 4 sin ( ) 4

sin ( ) cos ( ) 4 3

a b a b a b a b a b

a b a b





       

  

   

Câu 6: Cho dãy

 

tha mãn

5 1 5 5

2 1 2

25.2 15.2 5.2 15.2 4 0

u u u u

  

    

và





Giá tr nh nht ca



2019.

u 

512.

258.

511.

257.

Lời giải

T

 

n n n

u u u



  

là CSC công sai

 

1 5 1

8 8 1 32

d u u n u u       

Thay vào gi thic:

   

32 32

2 5.2 3 2 5.2 3 2 4 0



    



Có dc 2 suy ra:

 

1 33 1 33

5.2 3 2 log

4 5.2 3



   



   







 

1 min

2019

8 1 2019 1 257,63 258

u u n n n



         

Câu 7: Cho hình chóp

.S ABCD



ABCD

là hình vuông,

1AB 

, cnh bên

1SA 

và

vuông góc vi mt ph

 

ABCD

. Kí hiu

n

và

là

ng trên

sao cho

45MAN 

. Th tích nh nht ca khi chóp

.S AMN

là ?









Lời giải

t

DM x

BN y

ta có

 

tan tan

tan 45 tan

1 tan .tan

DAM BAN



    



. Suy ra







và

2 2 2

1AM AD DM x   

 

2 2 2

AN AB BN y







      







Vì vy

 

1 1 1 2 1

. . . sin 45 2 1

3 6 6 1 3

AMN

V SA S SA AM AN f x f



       



TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN

Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 13

Câu 8: Cho mt cp s cng :

1 2 3 4

, , ,u u u u

tha

1 4 2 3

6u u u u

. Tìm tnh D ca

hàm

      

1 2 3 4

9f x x u x u x u x u     

 

;6D  

 

6;D  

D 

 

6;6D 

Lời giải

Theo tính cht ca cp s cng , ta có :

1 4 2 3

u u u u  



        

1 2 3 4 1 4 1 4 2 3 2 3

x u x u x u x u x u u x u u x u u x u u

   

          

   

 

t

   

1 4 2 3

t x u u x x u u x     



 

    

1 4 2 3 1 4 2 3 1 4 2 3

( ) 9 9f t t u u t u u t u u u u t u u u u         

Vi :

   

1 4 1 3 1 2 3 4 1 4 2 3

4 36 36

u u u u u u u u u u u u       

Rõ ràng

1 4 2 3

6 0 ( ) 0,

u u u u f t t        

 

i mi x.

Câu 9: Cho hàm s

 

sin sin 1



    





. Tìm





 



sao cho khong cách

gim ci và cc tiu là ln nht ?



    



    



    



    

Lời giải

Hàm s

 

sin sin 1

x V x

    





có minh

 

\1D 

ng thi ta

có

 

2 sin sin 1

x x x

     





u ki hàm s có ci, cc tiu là



hay

sin sin 0 sin 0      

60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT

14 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor

Gi

,xx

l m ci, cc tiu ca

 



th

 

max 1 min 2

2 sin , 2 sin

U x U x

y x y x

V x V x

       

Gi

   

1 1 2 2

,2 sin , ,2 sinA x x B x x   

m ci, cc ting ca

 





,xx

là 2 nghim c

'0y 

nên

sin sin 1 2sin 1

  







       





Ta có

 

5 40sin

B A B A

AB x x y y x x        

Do vy AB ln nht khi

 



     

Câu 10: Cho t din

ABCD

có tt c các cu bng

Gi

là trng tâm ca tam giác

.BCD

Mt phng

 



ct

,BC BD

lt ti

,.IK

Tính th

tích nh nht ca

.ABIK

Lời giải

t

,BK x BI y

S dng công thc tính t s th tích ta có

. . . .

. . .BCD .

A BKG A BKG A BGI A BIK

A BHD A BCD A A BCD

V V V V

   

Mt khác ta có

. . .

A BHD A BCH A BCD

V V V

nên

 

6 6 9

x y xy

xy xy



   

Ta có

12 27

A BIK

V 

. Dy ra khi và ch khi

xy

Ch

TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN

Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 15

Câu 11: Cho hai s phc

,zz

tha mãn

2 3 17 ; 1 5z i z    

Bit rng

  

1 1 0z i k z i k     

. Tìm k khi

P z z

t giá tr ln nht.

1k 

2k 

3k 

5k 

Lời giải

Gi

       

, , 2;3 , 0; 1M z N z I J 

. Theo gi thit ta có:

 m M thung tròn

 

tâm I bán kính

17R 

 m N thung tròn

 

tâm J bán kính

5R 

Ta thy rng s phc

1zi

u tha mãn

2 3 17



  











u này chng t

 

1; 1A 

m ca

   

,CC

và theo gi thic

,,A M N

thng hàng.

Gi H,K lt là hình chiu ca I,J lên MN

22P MN HK IJ   

Dy ra khi và ch khi

MN IJ

m A và có

vector pháp tuyn

 

3; 3IJ 

là

: 2 0MN x y  

. T m

   

6; 4 , 0; 2MN

Vy

6 4 1

1 2 1

z i i i



  

   

    

. Chn ý D.

Câu 12: Gi

là tp hp các s t nhiên gm 5 ch s. Chn ngu nhiên mt s t tp

Tính xác su chc s chia ht cho 7 và có ch s n v bng 2.

257

90000

257

18000

127

90000

127

30000

Lời giải

Gi s t nhiên gm 5 ch s là

abcde

Chn

0a 

có 9 cách.

Chn

, , ,b c d e

mi s có 10 cách.

Nên

9.10A 

Gi

là bin c "chc t nhiên gm 5 ch s chia ht cho 7 và có ch s 

bng 2''.

Gi s t nhiên gm 5 ch s chia ht cho 7 và có ch s  bng 2 là

2ab cd

Ta có

2 10. 2 7 3 2abcd abcd abcd abcd    

60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT

16 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor

2ab cd

chia ht cho 7 nên

32abcd 

chia ht cho 7 hay

3 2 7 ,( )abcd t t  

7 2 2

3 2 7 2

abcd t abcd abcd t



      

Suy ra

( 2) 3t 

hay

2 3 3 2t n t n    



74abcd n

mà

1000 9999abcd

nên

996 9995

1000 7 4 9999

nn     

Mt khác

là s nguyên

 

143;144;145;...;1427n

Nên

1285B 



1285 257

()

9.10 18000

PB 

Câu 13: Cho s phc z tha mãn

15zi  

. Tìm GTLN ca

2 8 7 9P z i z i    

109P 

1 109P   

109 2P 

109 1P 

Lời giải



     

1;1 , 7;9 , 1;8I A B





2P MB MA





m

    

2MA MK

  











 

2 2 2 2 2 2

2 2 2

4 4 4

3 4 2 4 0

MA MK MA MK MI IA MI IK

MI IK IA MI IK IA

      

     

 tn t m K thì

2 2 2

3 4 0

MI IK IA

IK IA



  





  













. D th u này luôn

n tm K c nh tha mãn

2MA MK

m K này nm trên IC.

Lm K thuc IC sao cho

IK 

Ta có:

 

. . . 2IK IA IM IAM IMK c g c MA MK     

Vi thì

2MA MK

. Theo bng thc tam giác thì ta có:

 

2 2 2P MB MA MB MK BK    

Ta có:

;3 2 109

K P BK



  





TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN

Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 17

Câu 14: Cho s phc z tha mãn

4 1 2 1z z i z i     

. Tìm giá tr ln nht ca biu

thc

22P z i  

P 

Lời giải

S dng bng thc Cauchy – Schwarz ta có:

 

   

2 2 2 2 2

16 1 2 1 1 4 1 1 5 2 2 1z z i z i z i z i z i               

T  dng bng thc tr tuyi ta có

P  

Câu 15: Bit tng

2 2 2

1 1 1

2 2 ... 2

2 2 2

     

      

     

     

. Giá tr nh nht c  

3 2 4





n 

Lời giải

Ta có

2 4 2

1 1 1

2 2 2 2 ... 2 2

2 2 2

     

         

     

     

 

2 4 2

1 1 1

2 2 .. 2 2 ..

2 2 2



        





Áp dng công thc tính tng ca n s hu ca mt cp s nhân :







  

4 1 4 1

4 1 1

4. 2 . 2

3 4 3.4

S n n















    



 bài ta có:

  

1 100

min

4 1 4 1

3 2 4

2 4 1 4 1 3 39,124... 40

3.4 4

n n n







         

Câu 16: Cho 3 s phc

0 1 2

,,z z z

thng thi

1 3 3 2

2 2 8zz

z z z z

    











, vi

zi  

. Bit

rng

 

, , ,

z z a bi

a b c d R

z z c di

  







  



. Tìm giá tr ln nht ca biu thc

P ad bc

17P 

18P 

19P 

20P 

Lời giải

Gi

       

1 2 3 0

, , ,A z B z M z C z

. Theo gi thit ta có

1 3 3 2

z z z z AM MB    

, suy ra

i xng vm M. Mt khác

 

;

CA a b

z z a bi

z z c di

CB c d





  









  









60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT

18 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor

Vy

ABC

P ad bc S  

. Do

35AB z z  

n din tích ln nht thì

 

max

;d C AB

Gi

   

; , 2 ; 3A x y B x y   

mà A,B thuc elip nên ta có:

   

4;0 , 2; 3 : 2 4 0A B AB x y     

S dng tip gi thit

2 2 8zz   

m C thu

 

: 1 4sin ;2 3 cos



    





Ta có

 

max

8 1 12 5

; sin 18

3 2 5 6

d C AB P





        





Câu 17: Cho hàm s

 

y f x

o hàm trên . Gi

     

1 2 3

,,C C C

l th

ca các hàm s

   

 

, , 1y f x y f f x y f x   

. Các tip tuyn

   

,CC

t m

2x 

t là

2 1, 4 3y x y x   

, hi tip tuyn ca

 

tm

2x 



 

2; 11Q 

 

2;11M 

 

2; 21N 

 

2; 21P 

Lời giải

Theo gi thit ta có

 

   

 

' . ' 4

' 5 2

5 11

f x f f x

f f x



























 s góc ca tip tuyn t

2x 

c th hàm s

 

là

 

2 . ' 1 4 ' 5 8k x f x f   

t      p tuyn c  th

 

là

 

8 2 11 8 5y x x    

Câu 18: Cho dãy

()

tha mãn

5, 2, 1

x x x n



    

. Tính giá tr ca

1 1 2 1 2

1 1 1

lim ........

...

x x x x x x



   





5 21





5 21





3 31





3 15





Lời giải

u tiên d thy

x 

Ta có

   

 

2 2 2 2 2 2

1 1 1 2 1

2 4 4 ... . .... 4

n n n n n n

x x x x x x x x x



        

   

1 2 1 2

21 lim lim 21 21

. .... . ....

x x x x x x



      

Li có

1 2 1 2 1 1 1 2 1 1 2 1 2

2 1 1 1

... 2 ........

... ... ... ... ...

n n n

n n n n n

x x x

x x x x x x x x x x x x x x x x x









        





TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN

Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 19

1 1 2 1 2 1 2

1 1 1 1

........

... 2 ...

1 1 1 1 5 21

lim ........ 5 lim

... 2 ... 2

x x x x x x x x x





     





   



      

   

   

Câu 19: Có bao nhiêu cp s nguyên

 

;ab

tha mãn

0 , 100ab

 th ca 2 hàm

s



và



ct nhau tm phân bit?

A. 9704

B. 9702

C. 9698

D. 9700

Lời giải

Ta thy

1; 1ab

, nu

ab

ng cong trùng nhau nên có vô s m chung, loi.

Vì vai trò cên ta ch cn tìm cp s nguyên

 

;ab

vi

1ab

sao cho



1 1 1 1 1 1 1 1

x x x x

a b b a a b a b

       

có 2 nghim phân bit.

Xét hàm s

     

1 1 1 1 1 1

' ln , 1 0

f x f x a f

a b a b a b

   

        

   

   

Ta có

 

' 0 log

lna

f x x x



   





 

'0fx

khi

xx

 

'0fx

khi

xx

Nu

   

ln ln lnb

1 log 1 ; 4; 2

lna

x a b



      





Chú ý xét hàm s

 

lnt ln 3 ln 2 ln 4 ln 5 ln 100

...

3 2 4 5 100

      



       

10f x f x f f x   

m

1x 

Nu

1x 

 bng bin thiên cho hàm s ta th

 

0fx

luôn có 2

nghim phân bit.

Vi mi

   

2,3,...,99 1,...,100b k a k    

tc có

100 k

cách chn a.

Vy có

 

100 4851







cp

  

;1a b a b

và lop

 

4; 2

ta có 4850 cp.

 vng hp

1ba

ta có tt c 9700 cách chn.

Câu 20: Xét các hình chóp

.S ABCD

thiu ki

ABCD

là hình vuông, cnh

bên

vuông góc vng cách t n mt phng

 

SBC

bng a. Bit

rng th tích khi chóp

.S ABCD

t giá tr nh nht

khi cosin góc ging thng

và mt phng

 

ABCD

bng



,pq

là các s 

là

ti gin. Tính

 

..T p q V

3 3 .Ta

6.Ta

2 3 .Ta

Ta

Lời giải

60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT

20 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor

Ta có

;BC AB BC SA

nên

 

BC SAB

Gi H là hình chiu vuông góc ca A trên SB. 

 

AH SBC

và

 

,.d A S BC AH

Ta có góc ging thng SB và mt phng

 

ABCD

là góc

SBA

t

SBA 

.Theo gi thit ta có

sin cos

AB SA



Th tích khi chóp

.S ABCD

là

. . .

3 3sin cos

ABCD

V SA S a



Áp dng bng thc AM  GM , ta có

2 2 2

sin sin 2 cos 8

sin .sin .2 cos

3 27



    

    





sin cos

   



Va

Du bng xy ra khi

sin 2 cos cos .

     

Vy th tích khi chóp

.S ABCD

y giá tr nh nht bng

khi

cos



Suy ra

;p 1,q 3

Va  

 

2 3 .T p q V a   

Câu 21: Cho s phc

1 2 3

,,z z z

lt tha mãn

3zi

là s thun o vi thun o

không âm,

là s thc không âm. Bit rng

2 3 2 1 3 1

z z z z z z    

. Gi M,n ln

t là giá tr ln nht và nh nht ca biu thc

2 1 3 1

P z z z z  

ng?

. 90Mn

. 80Mn

. 100Mn

. 70Mn

Lời giải

Gi

     

3;1 , ,M A z B z

. Theo gi thit ta có:

2 2 2

2 3 2 1 3 1

z z z z z z AB MA MB MA MB         

là s thun o vi thun o không âm,

là s thu kin

là

    

;0 , 0; , 0A a B b a b 

. 0 10 3 0

MA MB b a a



     





Ta có:

 

 

2 1 3 1

. 3 6 10 3;30P z z z z MA MB a a       

Vy

min 3,max 30PP

Câu 22: Cho các s th

,,x y z

tha mãn

 

2 2 2

5 9 2x y z xy yz zx    

. Tìm giá

tr ln nht ca biu thc:

 

x y z







Lời giải

Ta có:

 

       

2 2 2

5 9 2 5 9 2 10x y z xy yz zx x y z xy yz zx xy yz zx             

TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN

Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 21

       

 

5 19 28 19 7

5 1 19 7 2 2

x y z x y z yz x y z y z

x x x

x y z

y z y z y z

         



        



  



Mc khác ta có:

 





 

2 3 3

1 4 1

y z y z



    





  

Xét hàm s

   

max

, 0 max 16 16

f t t f t P

      

Dy ra khi và ch khi

















Câu 23: Gieo mt con súc sng cht hai ln. Gi s

là tích s chm mà con

súc sc xut hin sau hai ln gieo. Tính xác sut sao cho hàm s

   

3 41 2 2y m x m x    

ng bin trên khong

 

0;

Lời giải

Ta có

 

 

 

; | , ;1 , 6 36a b a b a b n       

Gi bin c  ng bin trên khong

 

0;

ng hp sau:

 ng hp 1:

3 0 3mm   

  c:

35 2yx

ng bin trên nên



ng bin trên

 

0;

ng hp 2:

3m 

: Hàm s ng bin trên

 

0;

0 3 0

0 41 2 0





  





  

  

  









m  

T ng hp ta suy ra

3 20.m

                 

 

 

1;1 , 1;2 , 2;1 , 4;6 , 6; 4 , 5;5 , 5;6 , 6; 5 , 6;6 9A n A   

 

p A p A

     



Câu 24: Cho hàm s

 

ln 1y f x



  







     

2 3 ... 2018 ln ln ln lnf f f a b c d      



, , a c d



a b c d  

. Tính

P a b c d   

1986

1698

1689

1989

Lời giải

60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT

22 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor

Ta có

   

ln ln 1 ln 1 2 ln

y x x x





     







 

         

2 ln 1 ln 3 2 ln 2

3 ln 2 ln 4 2 ln 3

4 ln 3 ln 5 2 ln 4

..........

2017 ln 2016 ln 2018 2 ln 2017

2018 ln 2017 ln 2019 2 ln 2018

2 3 4 ... 2017 2018

ln 2 ln 2018 ln 2019 ln 3 ln 4 ln 673 ln 1019

f f f f f

  

     

       

Câu 25: Cho hàm s

     

2 1 2 2y f x x m x m x      

. Tìm tt c các giá tr ca tham

s

 hàm s

 

y f x

m cc tr.

m

m  

m

Lời giải

Ta có:

 

3 2 2 1 2y x m x m



    

Hàm s

 

y f x

m cc tr khi chi khi hàm s

 

m cc tr 

















   

 

2 1 3 2 0

2 2 1



   























4 5 0



  















m  

Câu 26: Cho hàm s

 

y f x

o hàm liên tn

 

1; 2

thng thc:

 

   

 

 

' , 1;2

x f x

f x x x

f x xf x x

   







và

 

f 

. Tính

 

7 7 1





 

7 7 1





 

2 7 1





 

2 7 1





Lời giải

Bii gi thit ta có:

 

   

         

       

 

3 3 3

' 3 ' ' '

3 ' 3 1 '

x f x

f x x x f x f x x f x xf x x

f x xf x x

x f x f x x x f x f x x



      

   

   









       

     

     



TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN

Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 23

 

   

 

2 2 2

1 1 1

3 1 3

3 1 3 1

2 3 2

dx xdx f x d f x



      







  

     

   

2 2 2

3 3 3

1 3 3

. 3 1 3 2 1 3 1 1 3

3 2 2

7 7 1

3 2 1 7 2

f x f f

       

     

     



    





Câu 27:

Cho hàm s  c bc ba

 

y f x

  th    m sau

     

2;4 , 3;9 , 4;16A B C

ng thng

,,AB AC BC

li c th ti l t ti các

m

,,D E F

(

khác

và

khác

và

khác

và

). Bit rng tng các

 ca

,,D E F

bng

. Tính

 

02f 

 

00f 

 

f 

 

02f 

Lời giải

Gi s

     

2 3 4f x a x x x x    

 

0a 

Ta có

qua

 

2; 4A

và nhn

 

1; 5AB 

là mt VTCP

 

: 5 2 4 0AB x y    

56yx  



: 6 8AC y x

và

: 7 12BC y x

 cm

là nghim c

   

2 3 4 5 6a x x x x x     

      

2 3 4 2 3a x x x x x       

 

4 1 4a x x

       

 cm

và

lt là

  

và

  

Bài ra ta có

1 1 1

2 3 4 24

a a a

     

        

     

     

a  



       

0 . 2 . 3 . 4 0

fa     

Câu 28: Cho hàm s

 

   

sin cosg x f x f x



thu kin :

 

cot sin 2 cos2 ,f x x x

 

0;x  

Tích ca giá tr ln nht và giá tr nh nht ca

 

bng:



Lời giải

t

cottx

2 2 2 2

2 tan 2 cot 2 1

sin 2 ; 2

1 tan 1 cot 1 1

x x t t

x cos x

x x t t



    

   

60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT

24 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor

 

2 2 2

2 1 2 1

1 1 1

t t t t

t t t

  

   

  

hay

 







 

  

4 2 4 2

4 4 2 2

sin 2 sin 1 cos 2 cos 1

sin .cos 8sin .cos 2

sin .cos 2 sin .cos 2

1 sin 1 cos

x x x x

   



  





t

sin .cos 0

u x x u   

 trình tr thành:

 

8 2 1

, 0;

2 2 4

h u u













D c

 

max

4 25

h u h

















và

   

min 0 1

h u h









  

Câu 29: Cho hàm s

 

liên tn

 

1; 4

tha mãn

   

1 1, 4 8ff   

vng

thi

   

 

' 9 3 , 1; 4f x x f x x x x x     





. Tích phân

 

f x dx



bng

7



8

Lời giải

Gi thi

 

   





Ly tích phân 2 v n

 

1; 4

c:

 

4 4 4

1 1 1

' 9 21 2 ln 2

f x dx dx dx



     









  

S dng tích phân tng phc:

 

dx f x d a



  







, a s nh sau

     

2 2 1

' 7 6 2 '

a f x a f x dx a f x dx

x x x

     

       

     

     



T ng thc:

 

' 7 6 2 ' 21 2 ln 2

f x dx a f x dx



     







 

' 2ln 2 9 6 21 2 ln 2

f x dx a



        







Ta d c

3a 



2 ln 2 9 6 21 2 ln 2

a     



 

 

 

' 3, 1; 4 2 3f x x f x x x

      

Vy

 

f x dx x x dx   



TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN

Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 25

Câu 30:   

 

2 2 2

log 2 2 2 2

x x y x x     

. Hi có bao nhiêu cp s



 

;xy

, vi

0 500x

th

Lời giải

Bii gi thic:

   

2 2 2 2 2 2

log 2 2 2 2 log 1 1 2

x x y x x x x x x y             

 

   

log 1

2 2 2 2

2 log 1 2 log 1

x x y x x y



         

 

0 500 log 1 0;18 0 5x y x x y         

. Vy ta có 4 giá tr nguyên ca y

tha mãn yêu c p s

 

,xy

tho.

Câu 31: Cho hình chóp

.S ABCD



ABCD

là hình bình hành. Gi



m trên

sao cho

A A A S





. Mt phng

 



qua



ct các cnh

,,SB SC SD

lt ti

, , .B C D

  

Tính giá tr ca biu thc

SB SD SC

  

  

T 

2T 

T 

Lời giải

Gi

là giao ca

và

. Ta có

m cn thng

n thng



ng quy ti

Ta có

'SA I SC I SA C

S S S

  



SA I SC I SA C

SAC SAC SAC

S S S

   

  

SA I SC I SA C

SAO SCO SAC

S S S

   

  

. . .

SA SI SC SI SA SC

SA SO SC SO SA SC

   

  

SI SA SC SA SC

SO SA SC SA SC

   



  





SA SC SO

SA SC SI

  



:

SB SD SO

SB SD SI





. Suy ra:

SB SD SC

  

  





Câu 32: Gi

là công bi ca mt cp s nhân , bit tng ba s hu bng

ng

thi theo th t , chúng là s hng th nht , th  tám ca mt cp s cng . Hi

thuc kho

 

3; 4q 

 

1; 2q 

 

2;3q 

 

0;1q 

Lời giải

Gi :

1 2 3

,,u u u

là 3 s hu tiên ca cp s nhân , vi công bi

. Gi

 

là cp s

cng vi công sai là d . Theo gi thit ta có :

60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT

26 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor

 

1 2 3

1 1 1

2 4 1

381

16 1

3 2

7 3

u u u

u u q u q

u q u d

u v v d

u q u d

u v v d



  





  





  





  





Kh d t c :

 

3 7 4 0 4u q q  

Do (1) nên :

 







  









1q 

, do vy

q 

Câu 33: Cho tích phân







, bit rng tng giá tr ln nht và giá tr nh

nht cc vii dng





 

là phân s ti gin. Tính

S a b c d   

Lời giải

Ta có

1 1 1

2 2 2

0 0 0

1 1 1 1

1 1 1

n n n

x dx dx dx

x x x

      

  

  

Dy ra khi

0x 

Ta thy

1 1 1

*, 0;

n x x x dx dx



     









t

2 6 6

0 0 0

sin cos

costdt

dx dx dt

x sin

x t dx t t



  





   

  

Dy ra khi

1x 

Câu 34: Cho 3 hàm s

     

,,y f x y g x y h x  

  th ca 3 hàm s

     

,,y f x y g x y h x

  

  

 th  m 

th ca hàm s

 

y f x





. Hàm s

     

7 5 1 4

k x f x g x h x



     





ng bin trên

kho

;0 .

















;1 .















Lời giải

TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN

Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 27

 

'y h x

 

'y f x

 

'y g x

Ta cn gii b

   

15 3

' ' 7 2 ' 2 4 ' 4 0

k x f x g x h x

   

      

   

   

Không th gii trc tip b        th ca các hàm s

     

' , ' , 'y f x y g x y h x  

ta nhn thy

         

' 10, 3;8 ; ' 5, , ' 5, 3;8f x x g x x h x x       



       

' 2 ' 4 ' 10 2.5 4.5 0, , 3;8 ,f a g b h c a c b        

Vì vy ta ch cn chn

3 7 8

3 4 8

  





  



  





i chiu vn ý C.

Câu 35: Cho 2 s phc

tha mãn

7 5 9 3

4 4 4 4

zz    

z a bi

vi

 

3 2 1 0ab   

Bit rng

2z i z i  

. Tìm GTNN ca

3 2 3P z i z i     

38P 

39P 

2 38P 

2 39P 

Lời giải

Theo gi thim

 

: 1 0M z d x y   

 

: 3 2 1 0N z d x y    

m ca

,dd

là

 

0; 1I 

. Theo gi thit ta có

2MI NI



 

3;1 2A P MA NA  

. . .2 . .P IN AM IN AN IN AM IN AN IM    

Ptolemy ta có:

. . .

AM IN AN IM AI MN

AI MN

P AM AN



   

Ta có

 

cos ,

dd 

Cosine

ta có:

60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT

28 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor

2 2 2

2 . .cos

5 4 cos 3 3 39

MN MI NI MI NI MIN

MIN P AI

  

      

D xy ra khi AMIN ni ting tròn và

MIN 

Chn ý B.

Câu 36: Cho ba s th

,,a b c

tha mãn

abc a c b  

. Tìm giá tr ln nht ca biu

thc

2 2 2

2 2 3

1 1 1

a b c

  

  

max

P 

max

P 

max

P 

max

P 

Lời giải

Ta có:

 

10a c b ac   

. D thy

10ac a

   



  



 

   

 

  

2 2 2 2

2 1 2

2 3 2 3

1 1 1 1

ac a c

a c a c

a c ac



      

   



  

Xét hàm s

 

  

 

  

2 2 2

2 2 2 2

2 2 2 1

2 3 3

1 1 1

1 1 1 1

x cx c

x c c

x c x c

  



      

  

   

Vi

0 xa

  

Tính

 

   

4 2 1

c x cx

  





Trên khong







 

'0fx

có nghim

1x c c   

và

 

'fx

i du t 

sang âm khi

qua

, suy ra

 

t ci ti

xx

   

2 2 2

1 2 3 2 3

0; : 2

1 1 1

f x g c

c c c

c c c c



      







   

Kho sát hàm s

 

vi

 

max

1 10 10

0 max

c g c g P





     





Câu 37: Cho hàm s

 

liên tc trên n cp hai trên và tha mãn

   

 

   

. 4 ' . '' ,

f x f x f x f x e x



   



, bit

 

00f 



 

5ln 2

f x dx



bng?

25ln 2

5 31 5ln 2









1 355ln 2









1 25ln 2

31 5ln 2









355ln 2

5 31









Lời giải

TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN

Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 29

Gi thi

   

 

   

. ' ' '

f x f x e f x f x e C   

mà

 

0 0 1fC   

         

 

4 4 5

' 1 ' 5

x x x

f x f x e f x f x dx e x D f x e x D          



Mt khác

   

 

0 0 1 5 1

f D f x e x       

 

5ln 2 5ln2

25ln 2

5 1 5 31 5ln 2

f x dx e x dx



      







Câu 38: Cho hàm s

 

y f x

 th hàm s

 

y f x





:

Xét hàm s

   

2 2 4 3 6 5g x f x x x m    

vi

là s th 

 

0gx

5; 5x



  



u kin ca

là

 

mf

 

mf

 

0 2 5

mf

 

5 4 5

mf  

Lời giải

Ta có

       

0 2 2 4 3 6 5 0 3 2 2 4 6 5g x g x f x x x m m f x x x            

t

   

2 2 4 6 5h x f x x x   

. Ta có

   

2 6 4h x f x x



  

Suy ra

   

5 2 5 6.5 4 0

0 2 0 0 4 0

1 2 1 6.1 4 0





     





   





   







   





     





T  có bng bin thiên

13

5

 

'fx

60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT

30 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor

5





 

5h 

 

T bng bin thiên ta có

 

35mh

 

mf

Câu 39: Cho 4 s nguyên

, , ,a b c d

thay i tha:

1 50a b c d    

. Tìm giá tr nh nht

ca biu thc



min

175

P 

min

200

P 

min

175

P 

min

200

P 

Lời giải

Vì

1 50a b c d    

và

, , ,a b c d

là các s nguyên nên

1cb

Suy ra:

a c b

b d b



   

D thy

2 48b

nên xét hàm s

 

 

, 2; 48

f x x



  

Ta có

   

' ' 0 5 2

f x f x x

      

Lp bng bic

 

 

2;48

min 5 2f x f

7x 

và

8x 

là 2 giá tr gn

52x 

nht, vì vy:

 

     

 

2;48

53 61 53

min min 7 ; 8 min ;

175 200 175

f x f f



  





Vy GTNN ca

175

P 

Câu 40: Cho các s t nhiên t n 100 . Chn ra 6 s bt k. Tính xác su chn ra 6

s sao cho chúng có th xp thành 1 cp s cng.

7528752

1254792

2509584

3764376

Lời giải

Gi 6 s 

1 2 3 4 5 6

;u ; ; ; ; .u u u u u

Vit theo cp s cng s là

1 1 1 1 1 1

; ; 2 ; 3 ;u 4 ; 5u u d u d u d d u d    



d u u



  

chia ht cho 5

Nc

;uu

ta s c d và t c các s còn li .Vy bài toán

chuyn thành chn ra hai s sao cho chúng có cùng s 

T n 100 có 20 s chia ht cho 5 ta có

cách chn

TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN

Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 31

T n 100 có 20 s 

cách chn

T n 100 có 20 s 

cách chn

T n 100 có 20 s 

cách chn

T n 100 có 20 s 

cách chn

Vy ta có

.5C

cách chn

Xác sut s là

100

.5C

Câu 41: Cho các s thc x,y tha mãn

 

log 3 2 log 2 3 log 3 2 log 3 2x y y x        

Giá tr nh nht ca biu thc

 

4 15P x y xy  

là?

min 80P 

min 91P 

min 83P 

min 63P 

Lời giải

Gi thit 

 

log 3 log 2 3 log 3 log 3 2

x y y x        

   

 

log 3 log 3 2 log 3 log 2 3

3 3 2 3 3 2

3 2 3 3 2 3 2 3 3

x x y y

x x y y x y x y

         

        

              

Ta có

 

     

2 3 3 4 8 3. 3 4

x y x y x y x y x y x y





              







Mt khác

 

 

2 3 3 2 2 8 4;8x y x y x y x y x y            

Xét biu thc

 

     

4 15 4 7 16 7 7 3 16 5P x y xy x y xy x y xy x y y x            

Mà

 

16 4 5 64 21

P x x x





     







Kt hp vi

 

4 3;7 64 21 83x y x x       



là

83

Câu 42 : Cho hàm s

 

và

 

tha mãn

         

' 1 1 1; 2 . 2 1f g f g f  

ng

thi

           

1 ' ' '' ' , \ 0f x g x g x f x f x x



    





Tính tích phân

   

'I f x g x dx



ln 2



ln 2



ln 2



ln 2



Lời giải

Bin i gi thi

60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT

32 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor

           

   

 

   

' 1 1 1

' ' '' '

' ' f'' '

' ' '

2 2 2

1 3 1

' ln 2

2 2 4 2

x xf x g x xg x f x g x f x

x x g x f x g x x g x f x

x xf x g x xf x g x C

x C x

f x g x f x g x

f x g x dx dx



  

   





    

     



    







S dng tích phân tng phn ta có

           

   

' ' ln 2

' ln 2

I f x g x dx g x f x f x g x dx

f x g x dx

    

   





Chn ý D.

Câu 43: Có tc to bi các ô vuông ca bàn c 8x8 khi bt

t ô vuông?

204

196

150

Lời giải

 có t hình vuông



Bt 1 ô vuông  góc vuông ca bàn c

S c to thành t các ô vuông trong bàn c là

204





(hình vuông)

S hình vuông cht là 8



S c to thành sau khi bt

204 8 196

Câu 44: Gi R là bán kính mt cu ngoi ti   ng

1 1 1

.ABC A B C

. Gi s

BC a

, AA h

. Khi R ngn nht thì tam giác

ABC

A. u.

B. Cân ti A.

C. Vuông ti A.

D. Nhn

Lời giải

Gi

,OO

lng tròn ngoi tip tam giác

ABC

và

1 1 1

A B C



là

trc cng tròn ngoi tit phng

()AOO A

ng trung trc cnh

TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN

Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 33

ct

ti I. Ta chc I m

t cu ngoi

ti

1 1 1

.ABC A B C



R IA

Ta có

2 2 2 2 2

IA OA OI OA OA



     





(1)

Mt khác, áp dnnh lý hàm sin trong tam giác

ABC

c

     

Sin 2 Sin 2 Sin

BC BC a

A OA

BAC BAC BAC

   

(2)

T (1) và (2) suy ra

 

sin

IA h

BAC













R IA

ngn nht



bé nht



 

sin BAC

ln nht



 

sin 1 90

BAC BAC  

Hay tam giác ABC vuông ti A.

Câu 45: Cho hai s phc

,zz

tha mãn

2 , 5zz

. Bit rng

z i a bi

z i c di

  





  



Tìm GTLN ca biu thc

P ad bc

1P 

2P 

3P 

4P 

Lời giải

Gi

     

0;1 , ,A B z C z

thì

   

0; 2 , 0; 5BC

Bổ đề:      

 

;C O R

và

 

;'C O R

 

'RR

B và C 

   

,CC

O 

tam giác ABC và O Thật vậy, nếu cố

định B thì đường thẳng AB cố định. Giả sử AB cắt

 

M

và N, diện tích lớn nhất khi CO  AB. Tương tự nếu cố định

C. Tức O là trực tâm của ABC. Khi đó C là điểm chính giữa

cung lớn MN hay O nằm trong tam giác ABC.

Áp dng vi

 

0;1A BC Ox

i xng nên có th gi









 

2 ; , 5 ; 0B b b C b b b   

Ta có

  

 

2; 1

. 0 2 5 1 1

1; 1

ABCO b b b b b







         









Vy

max max

ABC

P ad bc S   

60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT

34 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor

Câu 46: Cho t din ABCD ni tip trong mt mt cu bán kính R và thu kin

,AB CD

,BC AD AC BD

là m   i trong không gian. t

,P MA MB MC MD   

giá tr nh nht ca

là?

min

2 3.PR

min

4.PR

min

3.PR

min

P 

Lời giải

Gi G là trng tâm ca t din; E, F, K, L lm ca các cnh AB, CD, BC,

AD. Ta có tam giác ACD bng tam giác BCD nên

AF BF

suy ra

EF AB

 ta

chc

EF CD

ng thng PQ vuông góc vi c ng thng BC,

AD. T 

.GA GB GC GD R   

Ta có

. . . .MA GA MB GB MC GC MD GD

MA MB MC MD

  

   

. . . .MA GA MB GB MC GC MD GD

  



 

. 4.

4 4 .

MG GA GB GC GD GA

GA R

   

  

Du bng xy ra khi và ch khi

trùng vm G.

Vy

min

4.PR

Câu 47: Cho 2 s thu kin

 

2 2 2

log 2 log 4 1 log

x y xy   

t

P x y

. Hc s nguyên?

Lời giải

t

 

2 2 2

log 2 ,log 4 ,log , , 4x y a b c a b c



    





TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN

Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 35

Gi thit tr thành

. Nhn thy 2 gi thii xng theo 2 bin

,ab

nên

d xy ra ti

,a b x c y  

 tham s  

Theo bng thc AM  GM ta có:

 

2 2 2 2 3 2 3 2

3 3 3 2

2 2 3 2 2

a x ax

b x bx a b c x a b y c y x

c y y y c







         





  



n tìm

,xy

tha mãn























. Vy P không phi là s nguyên



Câu 48:  

 

3 3 3 10 2 3 10 2m m x x x x      

. Có bao nhiêu

giá tr nguyên ca tham s  rình có nghim?

Lời giải

t

 

3 3 10 2 ; 3 10 2 , 0, 0a m x x b x x a b        

u kin

05x

Ta có:

m a b m a b

m b a



   













    

3 3 0

3 0 ( )

a b b a a b a b

a b L





         



  



Vi

 

33a b m b b m b b f b       

(*)



 

3 10 2 10 2 3 10 2 10 10b x x b x x x b          

(1)



 

  

3 10 2 3 2 5 3 2 5 25 5b x x b x x x x b             

(2)

T (1) và (2) suy ra

10; 5b







Xét hàm s

 

3f b b b

n

10 ;5





ta có

 

   

10 ;5

min 10 10 3 10, max 5 10f b f f b f





    



 

có nghim khi

   

10 ;5

min max 10 3 10 10f b m f b m





     

mà

m 

nên có 10 giá tr nguyên ca m tha mãn.

60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT

36 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor

Câu 49: Cho hàm s

 

sin cos cos sin

sin cos

x x x x

y f x







. Hi có bao nhiêu giá tr

 

2019;2019x 

tha mãn hàm s

 

t giá tr ln nht.

2453

5142

2571

4906

Lời giải

Ta có

 

sin cos cos sin

sin cos

x x x x







. Vì

sin cos sin cos 1,x x x x x    

Nên

 

sin cos sin cos

sin cos 1 sin cos sin co

sin cos

x x x x

f x x x x x x x



   



 

1 1 1

sin 2 sin 2 sin 2

8 4 2

f x x x x    

t

 

sin 2 , 0;1t x t

Xét hàm s

 

1 1 1

8 4 2

f x t t t   

liên tc trên

 

0; 1

Kho sát hàm s trên, suy ra

 

 

0;1

max

3 27

f t f









c khi

 

2019;2019

2 1 1 1

sin 2 cos 4 arccos

3 9 4 9 2

x x x





       

có 5142 giá tr

Câu 50: Cho 2 hàm s

     

 

1 6 2 1, h 6

f x m m x x



      

. Tìm tham s  

hàm s

     

.g x h x f x

có giá tr nh nht là 0 vi mi

 

0;1x 

1m 

m 









1m 

Lời giải

Ta thy rng vi mi m, ta luôn có

   

1 1 0hf

nên bài toán tr  cho hàm

s

     

 

. 0 0;1g x h x f x x   

. D thy vi

1x 

thì bng th

s xét trên





0; 1

Ta d thy

 

ng bin trên





0; 1

   





1 0 0 0;1h h x x    

i

rút gn bài toán tr 

 





0 0;1f x x  

t





 

6 1;6

tt

ta có

     

0 1 6 2 1 0 1 2 2 0

f x m m m t mt t m



              



 thành bài toán rn, ta cn

 

1;6

min







TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN

Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 37

Câu 51: Cho cp s nhân

1 2 3

, , ,..,

u u u u

   

0, 1,2,...,

u i n  

. Bit rng

1 2 3

... 2018

S u u u u     

1 2 3

1 1 1 1

... 2019

u u u u

     

và

1 2 3

. . ....

100

P u u u u

Hi s t nhiên nh nht tha mãn P là:

9295

9296

18592

18591

Lời giải

Ta có

 

1 2 3

... 2018

S u u u u



      



 

Và

 

1 2 3 1

1 1 1 1

... 2019

u u u u u q q



      



 

T

   

1 , 2

suy ra

2018

2019





Ta có

 

   

 

2 1 2 1

1 2 3 1 1 1 1 1 1

2018

. . .... . . . . .... .

2019

n n n

Q u u u u u u q u q u q u q u q







    







2018 min

2019

2018 1 1

2 log 18591,1 18592

2019 100 100

   

     

   

   



1285 257

()

9.10 18000

PB 

Câu 52: 

{0,1,2,3, 4,5,6,7,8,9}A 















1 2 3 4 5

a a a a a

sao cho

1 2 3

a a a



3 4 5

a a a



Lời giải





|S| 9.9.8.7.6 27216

i



1 2 3 4 5

a a a a a

sao cho

1 2 3

a a a



3 4 5

a a a



















1 2 3 4 5

a a a a a

















756CC 





60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT

38 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor













1 2 3 4 5

a a a a a

















378CC 







| | 756 378 1134B   





1134

27216





Câu 53: Cho b





 

3 1 3

log 11 log 3 10 4 log 3 12 0

x ax x ax



      





Giá tr thc ca tham s  btrên có nghim duy nht thuc khong nào



 

1; 0

 

1; 2

 

0; 1

 

2;

Lời giải

u kinh

a

Bii b





 





 





 

3 1 3

3 7 3

7 3 3

log 11 log 3 10 4 log 3 12 0

log 11 log 3 10 4 .log 3 12 0

log 3 10 4 .log 3 12 log 11

x ax x ax



      





       

      

t

2 2 2 2

3 10 0 3 12 3 10 2 2t x ax x ax x ax t            



tr thành

 

log 4 log 2 *

log 3

  

 Nu

0 log 3 0

aa   

b

 

tr thành

 

7 11 3 7 11

log 4 log 3 log 2 1 log 4 log 2 1

t a t t t      

Xét hàm s

   

 

7 11

f log 4 log 2 0t t t t   

ng bing thi

 

31f 

nên

   

3 3 3 1 0f t f t x ax      

     m duy nht thì ta có

a 

, nghim này không tha mãn.

 Nu

log 3 0

aa  

 ng hp 1 ta s c

a 

TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN

Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 39

Câu 54: Cho hai s thu kin

 

2 log 1

y y x x



  

   



Tìm giá tr ln nht ca biu thc

 

log .2

P y x







Lời giải

Bii gi thic:

 

  

2 2 1

2 log 1 2

2 1 2 1 log 1

x y x y

y y x x

x y y x



  



      

    

   

2 1 2 1

2 1 log 1 2 1 log 1

x y x y

y x y x



   

     

     

t li thành

 

log . 2

P y x







 n t

 

log

2 1 1

1 1 2

a y x

b a b













     











Th c

   

2 2 8

b b b b



  

Câu 55: Gi

là tp hp các s t nhiên gm 5 ch s. Chn ngu nhiên mt s t tp

Tính xác su chc s chia ht cho 7 và có ch s  bng 2.

257

90000

257

18000

127

90000

127

30000

Lời giải

Gi s t nhiên gm 5 ch s là

abcde

Chn

0a 

có 9 cách.

Chn

, , ,b c d e

mi s có 10 cách. Nên

9.10A 

Gi

là bin c "chc t nhiên gm 5 ch s chia ht cho 7 và có ch s 

bng 2''.

Gi s t nhiên gm 5 ch s chia ht cho 7 và có ch s  bng 2 là

2abcd

Ta có

2 10. 2 7 3 2abcd abcd abcd abcd    

2ab cd

chia ht cho 7 nên

32abcd 

chia ht cho 7 hay

3 2 7 ,( )abcd t t  

7 2 2

3 2 7 2

abcd t abcd abcd t



      

Suy ra

( 2) 3t 

hay

2 3 3 2t n t n    



74abcd n

mà

1000 9999abcd

nên

996 9995

1000 7 4 9999

nn     

Mt khác

là s nguyên

 

143;144;145;...;1427n

Nên

1285B 

60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT

40 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor

Câu 56 : Có tt c bao nhiêu cp s thc

 

;xy

thng thi u kin

 

2 3 log 5

4 1 3 8

y y y

  











    





Lời giải

T gi thit ta suy ra

     

2 3 2 3

4 4 3

log 5

5 5 3 5 1 3

x x x x

y y y

   



     

        

         

       

2 2 2

4 1 3 4 1 3 3 1 3 8 3

4 1 3 4 1 3 3 1 3 8

y y y y y y y y y

y y y y y y y y

                  

                

Dy ra khi và ch khi

3y 

. Th vào gi thic

2 3 0





   







Vy tn ti 2 b s tha mãn yêu c bài

Câu 57: Cho

()



31y x mx  



0m 



là

        

( ).

 

   

 

1; 0I 

bán kính

3R 



,.AB







IAB

 



A. 1

B. 2

C. 3

D. 0

Lời giải

Ta có

: 2 1.d y mx



 

2 2 2

1 1 2 1

, 2 , 2 2 9 .

4 1 4 1

x d I d AB R x x

  



       



Vì vy



 

0; 2

. 9 max 9 2 14.

IAB

S AB x x x x x y





      

Du bt ti

2 1 1 1

1 1 2 2





      





Câu 58: Cho 3 s tha mãn

2zy

. Khi biu tht giá tr nh

nht, hãy tính

log xyz

 

2 3 3 3 3 4 2 2

log log 2 2P xy x y x z y xy zy xz       

1

Lời giải

Ta có

 

2 3 3 3 3 4 2 2

log log 2 2P xy x y x z y xy zy xz       

   

 

2 3 3 3 3 2 2 3 3 3 3

2 2 2 2

log log 2 log logxy x y x z z y x y xy x y x z        

Theo bng thc AM  GM ta có

3 3 3 3 3 3 3

2x y z x x y z

TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN

Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 41

   

2 2 2 2

log log 2 log log 1

P xy x yz xy x yz



     





 ng hp 1:

log 3log 1

y z P xy xy      

 ng hp 2:

log 3log 1

y z P xz xz      

Vy

min

P 

, dy ra khi và ch khi

, 4 log 1

x y z xyz     

Câu 59: Cho phương trình

sin 2 cos 2 sin cos 2 cos 0.x x x x x m m      

Có bao

nhiêu giá trị nguyên của tham số

để phương trình có nghiệm ?

Lời giải

Điều kiện:

2 cos 0.xm

Phương trình đã cho tương đương với

1 sin 2 sin cos 1 cos2 2 cosx x x x m x m       

 

sin cos sin cos 2 cos 2 cosx x x x x m x m       

 





sin cos sin cos 2 cos 2 cosx x x x x m x m       

Xét hàm

 

f t t t

với

0.t 

Ta có

 

' 2 1 0, 0f t t t     

Hàm số

 

đồng biến.

Mà

 





sin cos 2 cos ,f x x f m  

suy ra

sin cos cosx x x m  

 

sin cos 2 cos 1 sin 2 2 cos sin 2 cos 2 .x x x m x x m x x m          

Vì

sin 2 cos2 2 sin 2 2; 2

x x x







    









Phương trình đã cho có nghiệm

 

2 2 1;0;1 .



      

Câu 60: Gi s

là s thc ln nht sao cho bng thc

2 2 2

sin

  



i











 ca

là?

Lời giải

Ta có

2 2 2 2 2 2

1 1 1 1

sin sin

x x x x

      



Xét

 

sin













Ta s chng minh

 

2 cos 2

sin



   











60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT

42 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor

Tht vy:

 

2 sin 2 cos

sin

x x x







sin cos 0x x x  











sin cosx x x











 

sin

cos

g x x

   











Ta có

 

   

2 cos 3 cos 1

2 cos 1

3cos . cos 3 cos . cos

x x x x







  

   

cos 1 2 cos 1

3cos . cos

   



   

   















   

00g x g

. Suy ra

 

0fx















V bng bin thiên ta suy ra

 

fx











1 1 4

k     



Bấm Tải xuống để xem toàn bộ.

| 1/42

| | Tải xuống

Preview text:

ĐỀ ÔN LUYỆN CÁC NHÓM CÂU HỎI
VẬN DỤNG CAO TRONG ĐỀ THI THPT QUỐC GIA
Đề gồm 40 câu trắc nghiệm
Sản phẩm được thực hiện bởi nhóm
Chinh Phục Olympic Toán
Câu 1: Có bao nhiêu giá trị nguyên của tham số m để phương trình 2 m m  x   2m  x m  x
Có đúng một nghiệm nhỏ hơn 10 . A. 5 B. 4 C. 9 D. Vô số.
Câu 2: Cho 2 dãy cấp số cộng u  u u u d v  v v v n ; ;... n ; ;... 1 2 n có công sai 1 và 1 2 n có công sai
d2 . Gọi tổng của n số hạng đầu của mỗi cấp số theo thứ tự là u
S  u  u   u  n 
T  v  v   v  n  n ... n 14 27 n ... n 7 1 1 2 và 1 2
. Tính tỉ số của 11 v11 5 4 9 5 A. B. C. D. 3 3 4 4
Câu 3: Cho hình chóp S.ABC có SA  x, BC  y, AB  AC  SB  SC  1. Thể tích khối chóp
S.ABC đạt giá trị lớn nhất khi tổng x  y bằng : 2 4 A. . . 3 B. 3. C. 3 D. 4 3.
Câu 4: Giá trị nhỏ nhất của m để hệ phương trình sau có nghiệm :
log x  y  log xy  2  2 2   3    3 3
x  y  2xy  m A. 1. B. 2. C. 3. D. 4.
Câu 5: Cho 2 sin a  b  cosa  b , a  b  k .
 Tính giá trị của biểu thức 1 1 E  
1  2 sin 2a 1  2 sin 2b 2 1 A.  . B. . C. 2. D. 0. 3 2
Câu 6: Cho dãy u 2u 1 u u 2 25.2  15.2
 5.2u  15.2u  4  0 u    u n n 8. n thỏa mãn 5 1 5 5 1 và 1
Giá trị nhỏ nhất của n để u  n 2019. A. 512. B. 258. C. 511. D. 257.
Câu 7: Cho hình chóp .
S ABCD có đ{y ABCD là hình vuông, AB  1 , cạnh bên SA  1 và
vuông góc với mặt phẳng đ{y  ABCD . Kí hiệu M l| điểm di động trên đoạn CD và N là
điểm di động trên đoạn CB sao cho MAN  45 . Thể tích nhỏ nhất của khối chóp S.AMN là ?
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 1
60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT 2  1 2  1 2  1 2  1 A. B. C. D. 9 3 6 9
Câu 8: Cho một cấp số cộng : u , u , u , u
u u  u u  6 1 2 3 4 thỏa 1 4 2 3
. Tìm tập x{c định D của
hàm f x  x  u x  u x  u x  u  9 1   2   3   4 
A. D  ;6
B. D  6;  C. D  D. D   6  ;6 2
x  sin x  sin   1
Câu 9: Cho hàm số y  C C   . Tìm  để 
  sao cho khoảng cách x  1
giữa 2 điểm cực đại và cực tiểu là lớn nhất ?    
A.     k2 . 
B.     k . 
C.     k2 . 
D.     k .  4 4 2 3
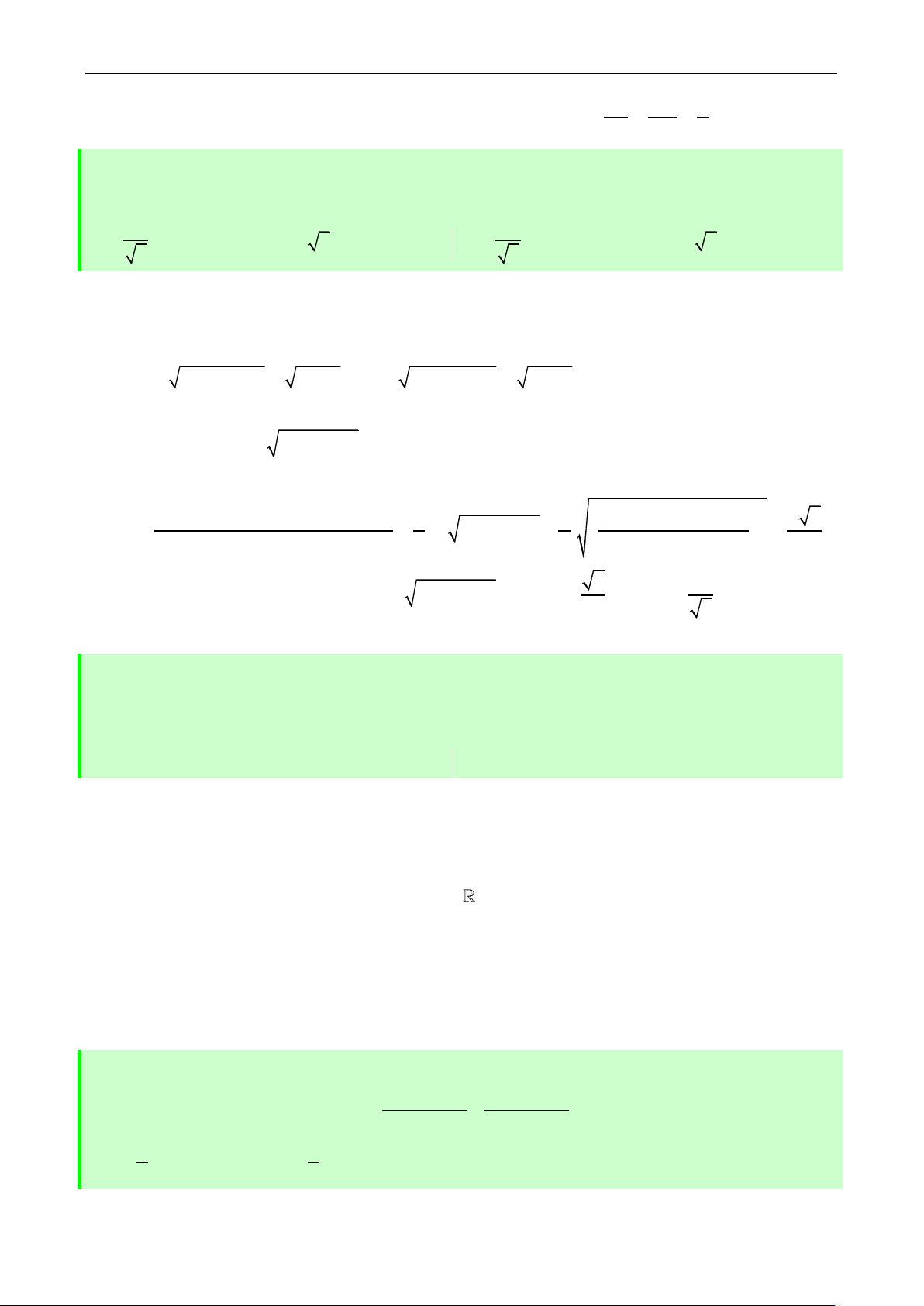
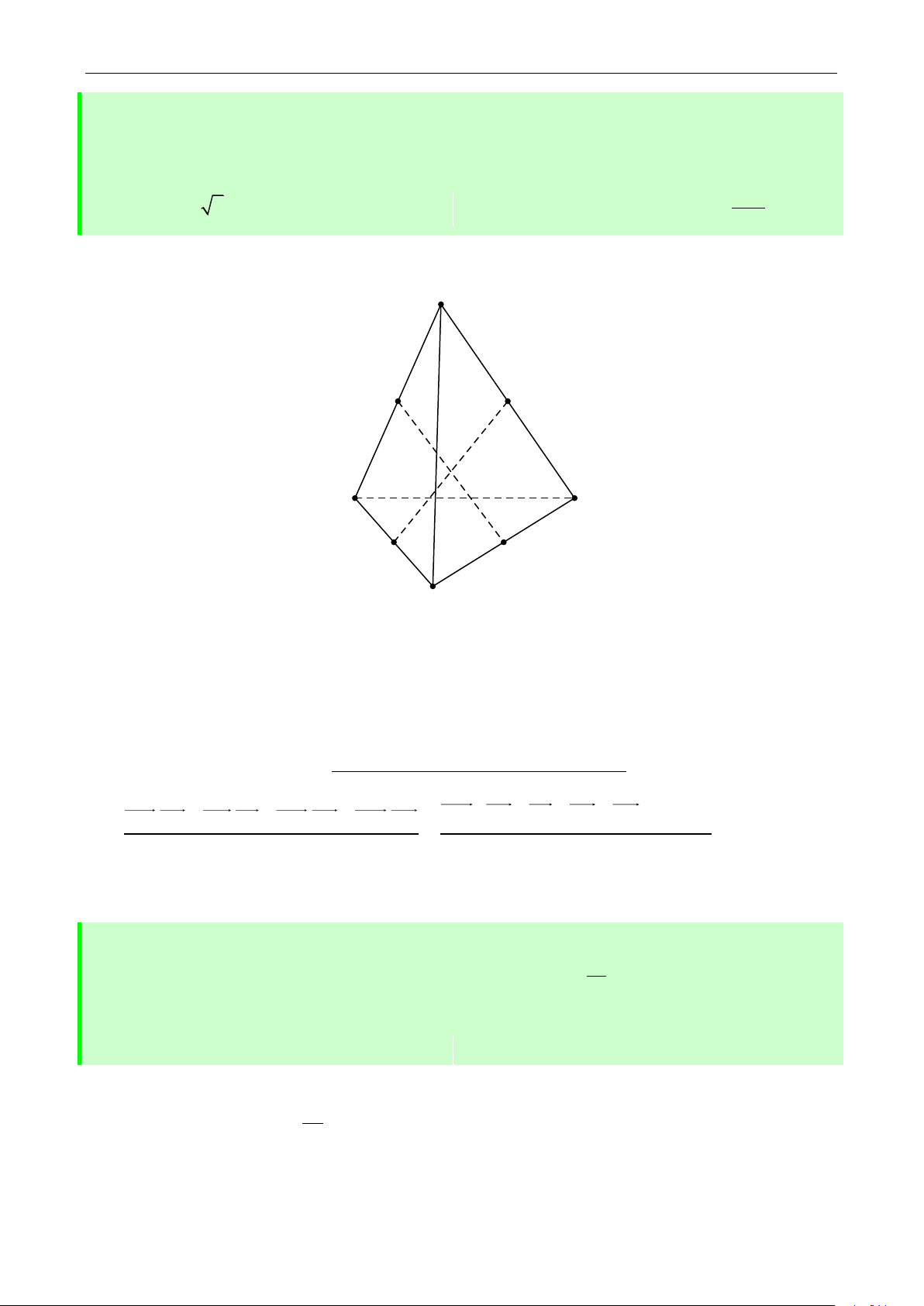
Câu 10: Cho tứ diện ABCD có tất cả các cạnh đều bằng 1. Gọi G là trọng tâm của tam giác BC .
D Mặt phẳng P thay đổi luôn luôn đi qua AG cắt BC, BD I K
lần lượt tại , . Tính thể
tích nhỏ nhất của ABIK. 2 2 4 2 A. . B. . C. . D. . 27 18 9 36
Câu 11: Cho hai số phức z , z
z  2  3i  17 ; z  1  5 1 2 thỏa mãn 1 2 . Biết rằng
z  1  i  k z  1  i k  0
P  z  z 1  2  . Tìm k khi 1
2 đạt giá trị lớn nhất.
A. k  1
B. k  2 C. k  3
D. k  5
Câu 12: Gọi A là tập hợp các số tự nhiên gồm 5 chữ số. Chọn ngẫu nhiên một số từ tập A .
Tính xác suất để chọn được số chia hết cho 7 và có chữ số h|ng đơn vị bằng 2. 257 257 127 127 A. B. C. D. 90000 18000 90000 30000
Câu 13: Cho số phức z thỏa mãn z  1  i  5 . Tìm GTLN của P  2 z  8i  z  7  9i .
A. P  109
B. P  1  109
C. P  109  2
D. P  109  1
Câu 14: Cho số phức z thỏa mãn 4 z  z  i  1  2 z  i  1 . Tìm giá trị lớn nhất của biểu
thức P  z  2  2i 30 30 30 30 A. P   2 2 B. P   3 2 C. P   4 2 D. P   5 2 3 4 5 6 2 2 2  1   1   n 1 
Câu 15: Biết tổng 2 S        n  2   2  ... 2
. Giá trị nhỏ nhất của n để 2 2 2 2n        99 3  2n4n S  n , * n  4n A. 41 B. 40 C. 51 D. 50
2 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
 z  2  z  2  8 3
Câu 16: Cho 3 số phức z , z , z z  1   i 0 1
2 thỏa mãn đồng thời  , với . Biết  3
z  z  z  z 2 1 3 3 2
z  z  a  bi 1 rằng 0 1 
a,b,c,dR . Tìm giá trị lớn nhất của biểu thức P  ad bc
z  z  c   di 2 0 2
A. P  17
B. P  18
C. P  19
D. P  20
Câu 17: Cho hàm số y  f x có đạo hàm trên
. Gọi C , C , C 1   2  
3  lần lượt l| đồ thị
của các hàm số y  f x y  f  f x y  f  2 , ,
x  1. Các tiếp tuyến C , C 1   2  tại điểm x  2
y  x  y  x  C 0
có phương trình lần lượt là 2 1, 4
3 , hỏi tiếp tuyến của  3  tại điểm x  2 0
đi qua điểm n|o sau đ}y? A. Q 2; 11   B. M  2  ;11 C. N  2  ; 21   D. P 2; 21  
Câu 18: Cho dãy (x x  5, x      x n n n 2, 1 n ) thỏa mãn 2 1 1 . Tính giá trị của  1 1 1  M  lim   ........   x x x x x ...x 1 1 2 1 2 n  5  21 5  21 3  31 3  15 A. M  B. M  C. M  D. M  2 2 3 3
Câu 19: Có bao nhiêu cặp số nguyên a; b thỏa mãn 0  a, b  100 sao cho đồ thị của 2 hàm 1 1 1 1 số y   và y 
 cắt nhau tại đúng 2 điểm phân biệt? x a b x b a A. 9704 B. 9702 C. 9698 D. 9700
Câu 20: Xét các hình chóp .
S ABCD thỏa mãn điều kiện: đ{y ABCD là hình vuông, cạnh
bên SA vuông góc với đ{y và khoảng cách từ điểm A đến mặt phẳng SBC  bằng a. Biết
rằng thể tích khối chóp .
S ABCD đạt giá trị nhỏ nhất V0 khi cosin góc giữa đường thẳng SB p p
và mặt phẳng  ABCD bằng
, trong đó p,q là các số nguyên dương v| ph}n số là q q
tối giản. Tính T   p  q.V . 0 5 3 A. 3 T  3 3a . B. 3 T  6a . C. 3 T  2 3a . D. 3 T  a . 2
Câu 21: Cho số phức z , z , z z  3  i z 1 2 3 lần lượt thỏa mãn 1
, 2 là số thuần ảo với thuần ảo 2 2 không âm, z
z  z  z  z  z  z
3 là số thực không âm. Biết rằng 2 3 2 1 3 1 . Gọi M,n lần
lượt là giá trị lớn nhất và nhỏ nhất của biểu thức P  z  z z  z 2 1 3 1 . Khi đó M.n bằng?
A. M.n  90
B. M.n  80
C. M.n  100
D. M.n  70
Câu 22: Cho các số thực dương x, y, z thỏa mãn  2 2 2
5 x  y  z   9xy  2yz  zx . Tìm giá x 1
trị lớn nhất của biểu thức: P   . 2 2 y  z
x  y  z3
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 3
60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT A. 14 B. 16 C. 12 D. 18
Câu 23: Gieo một con súc sắc c}n đối đồng chất hai lần. Giả sử m là tích số chấm mà con
súc sắc xuất hiện sau hai lần gieo. Tính xác suất sao cho hàm số
y  m   2
3 x  41  2mx  2 đồng biến trên khoảng 0;   . 1 2 3 17 A. B. C. D. 2 3 4 36  1 
Câu 24: Cho hàm số y  f x  ln 1   . Biết rằng : 2 x   
f 2  f 3  ... f 2018  ln a  ln b  ln c  ln d
trong đó a, c, d l| c{c số nguyên tố v| a  b  c  d . Tính P  a  b  c  d A. 1986 B. 1698 C. 1689 D. 1989
Câu 25: Cho hàm số y  f x 3
 x   m   2 2
1 x  2  mx  2 . Tìm tất cả các giá trị của tham
số m để hàm số y  f  x  có 5 điểm cực trị. 5 5 5 5 A.  m  2 B. 2   m  C.   m  2 D.  m  2 4 4 4 4
Câu 26: Cho hàm số y  f x có đạo hàm liên tục trên đoạn 1; 2 thỏa mãn đẳng thức: 3 3x f x
 f ' x  x, x   1;2 f  f 2 2     và   7 1 . Tính   .  f '
 x  xf '  x 2  x 3    
A. f   7 7 1 2 
B. f   7 7 1 2 
C. f   2 7 1 2 
D. f   2 7 1 2  3 3 3 3
Câu 27: Cho hàm số đa thức bậc ba y  f x có đồ thị đi qua c{c điểm sau
A2; 4 ,B3;9 ,C 4;16 . C{c đường thẳng AB, AC, BC lại cắt đồ thị tại lần lượt tại các
điểm D, E, F ( D khác A và B , E khác A và C , F khác B và C ). Biết rằng tổng các
ho|nh độ của D, E, F bằng 24 . Tính f 0 .
A. f 0  2 
B. f 0  0 C. f   24 0 
D. f 0  2 5
Câu 28: Cho hàm số g x  f  2 x f  2 sin
cos x trong đó f thỏa mãn điều kiện :
f cot x  sin 2x  cos 2x, x  0; .
Tích của giá trị lớn nhất và giá trị nhỏ nhất của g x bằng: 1 1 1 1 A. . B. . C.  . D.  . 25 5 5 25
Câu 29: Cho hàm số f x liên tục trên đoạn 1; 4 thỏa mãn f 1  1  , f 4  8  v| đồng 2 4 thời  f  x 3  x  f  x 3 '
 9 x  x  3x, x
 1;4 . Tích phân f xdx  bằng 1 89 79 A. 7 B.  C.  D. 8  6 6
4 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Câu 30: Cho phương trình log 2  2  2 2 2 2 2  2y x x
 y  x  x 2
. Hỏi có bao nhiêu cặp số
nguyên dương x; y , với 0  x  500 thỏa mãn phương trình đã cho? A. 4. B. 2. C. 3. D. 1.
Câu 31: Cho hình chóp .
S ABCD có đ{y ABCD là hình bình hành. Gọi A l| điểm trên SA 1 sao cho A A   A S
 . Mặt phẳng  qua A cắt các cạnh SB,SC,SD lần lượt tại B,C,D . 2 SB SD SC
Tính giá trị của biểu thức T   
SB SD SC . 3 1 1 A. T  B. T 
C. T  2 D. T  2 3 2 4
Câu 32: Gọi q là công bội của một cấp số nhân , biết tổng ba số hạng đầu bằng 16 , đồng 9
thời theo thứ tự , chúng là số hạng thứ nhất , thứ tư v| thứ tám của một cấp số cộng . Hỏi
q thuộc khoảng n|o sau đ}y?
A. q 3; 4
B. q 1; 2
C. q 2; 3
D. q 0;1 1 2 dx
Câu 33: Cho tích phân * I  ,n  
, biết rằng tổng giá trị lớn nhất và giá trị nhỏ 2 0 1 n  x a c a c
nhất của I được viết dưới dạng
 , trong đó a, b, c, d l| c{c số nguyên dương v| , b d b d
là phân số tối giản. Tính S  a  b  c  d ? A. 9 B. 10 C. 11 D. 12
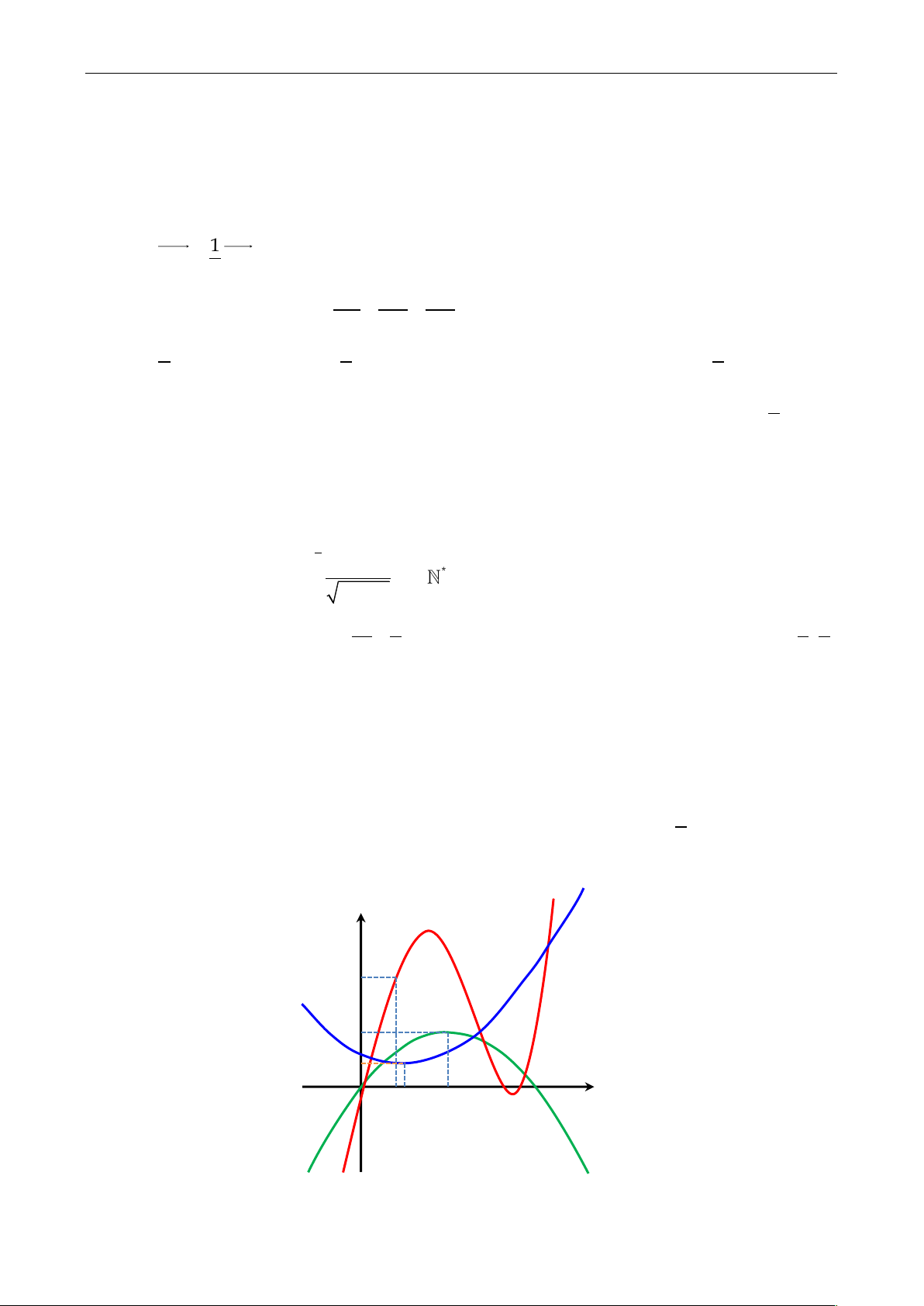
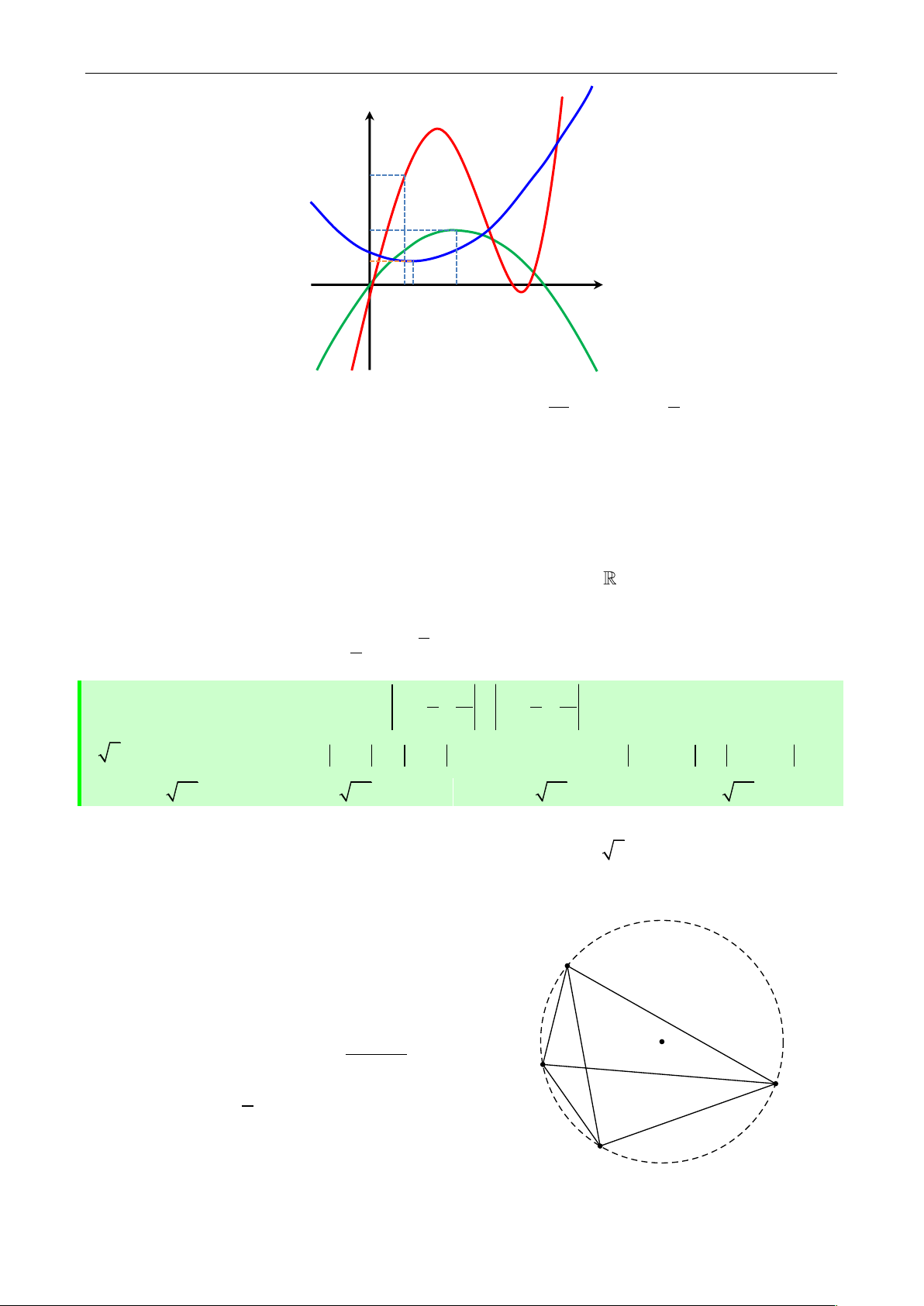
Câu 34: Cho 3 hàm số y  f x , y  g x , y  h x . Đồ thị của 3 hàm số
y  f x , y  gx , y  hx có đồ thị như hình vẽ dưới, trong đó đường đậm hơn l| đồ  
thị của hàm số y  f x . Hàm số k x  f x    g  x   3 7 5 1  h 4x   đồng biến trên 2    khoảng n|o dưới đ}y ? y
y  g'x 10
y  f 'x 5 O 3 4 8 x
y  h'x
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 5
60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT  15   1   3   3  A.   ;0. B.   ; . C.  ;1. D. ;  .  4   4   8   8  7 5i 9 3i
Câu 35: Cho 2 số phức z z    z  
z  a  bi 1 thỏa mãn 1 1 , với 4 4 4 4 2
 3 2ab1 0Biết rằng z i  2 z i
P  z  3  i  2 z  3  i 1 2 . Tìm GTNN của 1 2
A. P  38
B. P  39
C. P  2 38
D. P  2 39
Câu 36: Cho ba số thực dương a, b,c thỏa mãn abc  a  c  b . Tìm giá trị lớn nhất của biểu 2 2 3 thức P    . 2 2 2
a  1 b  1 c  1 5 10 7 14 A. P  . P  . P  . P  . max B. C. D. 3 max 3 max 2 max 3
Câu 37: Cho hàm số f x liên tục trên
, có đạo h|m đến cấp hai trên và thỏa mãn 5ln 2      2 3 . 4 '   . '   x f x f x
f x f x  e , x    5  
, biết f 0 0 . Khi đó
f xdx  bằng? 0 2  25ln 2  1  355ln 2  A. 5 31   5ln 2 B. 31     2  5  2  2 1  25ln 2   355ln 2  C.  31   5ln 2 D. 5 31    5  2   2 
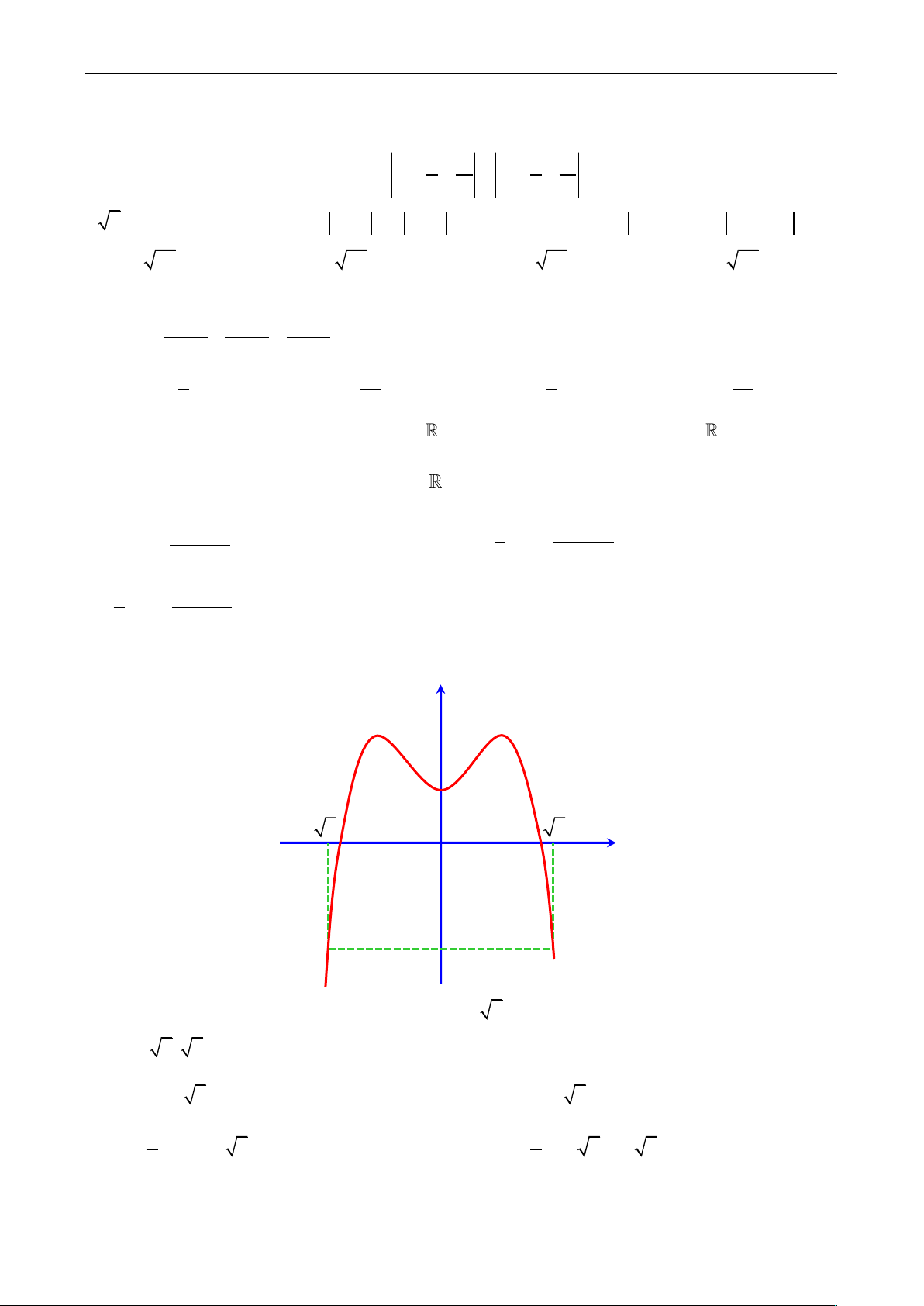
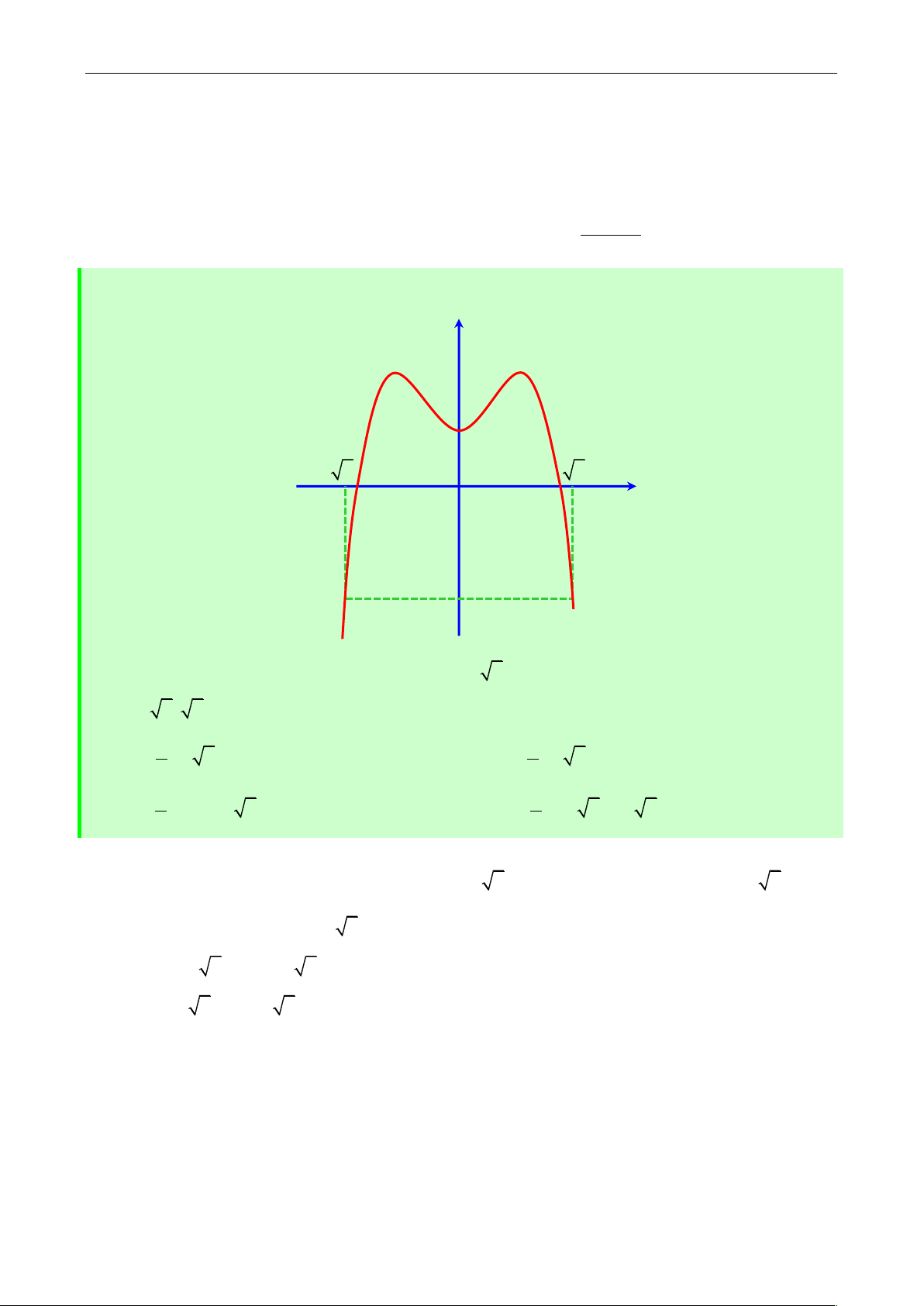
Câu 38: Cho hàm số y  f x có đồ thị hàm số y  f x như hình vẽ: y f 'x 2  5 O 5 x B A 13
Xét hàm số g x  f x 3 2
 2x  4x  3m  6 5 với m là số thực. Để g x  0 x    5; 5 
 thì điều kiện của m là 2 2 A. m  f  5 B. m  f  5 3 3 2 2 C. m  f 0  2 5 D. m  f  5  4 5 3 3
6 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Câu 39: Cho 4 số nguyên a, b,c, d thay đổi thỏa: 1  a  b  c  d  50 . Tìm giá trị nhỏ nhất a c
của biểu thức P   . b d 53 61 58 73 A. P  P  P  P  min B. C. D. 175 min 200 min 175 min 200
Câu 40: Cho các số tự nhiên từ 1 đến 100 . Chọn ra 6 số bất kỳ. Tính xác suất để chọn ra 6
số sao cho chúng có thể xếp thành 1 cấp số cộng. 95 95 95 95 A. B. C. D. 7528752 1254792 2509584 3764376
Câu 41: Cho các số thực x,y thỏa mãn
log x  3  2 log 2  y  3  log y  3  2 log x  3  2 . 2 2     2   2
Giá trị nhỏ nhất của biểu thức P   2 2
4 x  y   15xy là?
A. min P  80
B. min P  91
C. min P  83
D. min P  63
Câu 42 : Cho hàm số f x và g x thỏa mãn f '1  g 1  1; f 2.g 2  f 1 v| đồng  1 
thời 1  f 'x g'x   g x  f ' x   f ' x  , x   \0  . Tính tích phân x    2 I  f
 xg'xdx ? 1 3 1 3 1 3 1 3 1 A.  ln 2
B.   ln 2 C.  ln 2
D.   ln 2 4 2 4 2 4 2 4 4
Câu 43: Có tối đa bao nhiêu hình vuông được tạo bởi các ô vuông của bàn cờ 8x8 khi bớt đi một ô vuông? A. 204 B. 63 C. 196 D. 150
Câu 44: Gọi R là bán kính mặt cầu ngoại tiếp lăng trụ đứng ABC.A B C 1 1 1 . Giả sử
BC  a , AA  h 1
. Khi R ngắn nhất thì tam giác ABC A. Đều.
B. Cân tại A.
C. Vuông tại A. D. Nhọn
z  i  a  bi
Câu 45: Cho hai số phức z , z
z  2 , z  5 1 2 thỏa mãn 1 2 . Biết rằng 1  .
z  i  c   di 2 1
Tìm GTLN của biểu thức P  ad  bc . 2
A. P  1
B. P  2
C. P  3
D. P  4
Câu 46: Cho tứ diện ABCD nội tiếp trong một mặt cầu bán kính R và thỏa mãn điều kiện AB  C , D BC  ,
AD AC  BD. M là một điểm thay đổi trong không gian. Đặt
P  MA  MB  MC  ,
MD giá trị nhỏ nhất của P là? 16R A. P  2R 3. P  4 . R P  3 . R P  . min B. min C. min D. min 3
Câu 47: Cho 2 số thực x,y dương thỏa mãn điều kiện x  y    xy3 2 2 11 log 2 log 4 1 log  2 2 2 2
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 7
60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT Đặt 3 3
P  x  y . Hỏi P có bao nhiêu ước số nguyên? A. 1 B. 2 C. 5 D. 0
Câu 48: Cho phương trình m  3 m  3 3x  10  2x   3x  10  2x . Có bao nhiêu
giá trị nguyên của tham số m để phương trình có nghiệm? A. 10 B. 11 C. 9 D. 12 6 6
sin x cos x  cos x sin x
Câu 49: Cho hàm số y  f x 
. Hỏi có bao nhiêu giá trị sin x  cos x x  20
 19;2019 thỏa mãn hàm số f x đạt giá trị lớn nhất. A. 2453 B. 5142 C. 2571 D. 4906 x 2
Câu 50: Cho 2 hàm số f x  m  16 
 2m  1,h x   1
x  6 x . Tìm tham số m để x  6
hàm số g x  h x. f x có giá trị nhỏ nhất là 0 với mọi x 0;1 1  1  A. m  1 B. m  C. m ;1 D. m  1 2 2   
Câu 51: Cho cấp số nhân u , u , u ,.., u u  i   n 1 2 3 n ; trong đó i 0, 1, 2,..., . Biết rằng 1 1 1 1 1
S  u  u  u   u  T      
P  u .u .u ....u  n ... 2019 n ... n 2018 1 2 3 , và . u u u u 1 2 3 n 100 1 2 3 n
Hỏi số tự nhiên nhỏ nhất thỏa mãn P là: A. 9295 B. 9296 C. 18592 D. 18591
Câu 52: Cho tập A  {0, 1, 2, 3, 4, 5, 6,7, 8, 9} . ọi S l| tập hợp tất cả c{c số có 5 năm chữ số
ph}n biệt được lập từ A . Chọn ngẫu nhiên một số từ S . Khi đó x{c suất để chọn được số có dạng a a a a a
a  a  a
a  a  a 1 2 3 4 5 sao cho 1 2 3 v| 3 4 5 l|? 5 1 5 1 A. B. C. D. 7 12 12 24  
Câu 53: Cho bất phương trình log   x  ax    x  ax   a 11 log  2 3 10 4 log a  2 3 12 0 3 1 3  .  7 
Giá trị thực của tham số a để bất phương trình trên có nghiệm duy nhất thuộc khoảng nào sau đ}y? A. 1; 0 B. 1; 2 C. 0; 1 D. 2; 
Câu 54: Cho hai số thực dương x,y thỏa mãn điều kiện 2  2  log x  y  1 2 2 x2y   2  1
y yx x
Tìm giá trị lớn nhất của biểu thức P  log     y x 2 4 .2 x y x y 1 1 1 1 1 A. B. C. D. 2 4 8 16
8 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Câu 55: Gọi A là tập hợp các số tự nhiên gồm 5 chữ số. Chọn ngẫu nhiên một số từ tập A .
Tính xác suất để chọn được số chia hết cho 7 và có chữ số h|ng đơn vị bằng 2. 257 257 127 127 A. B. C. D. 90000 18000 90000 30000
Câu 56 : Có tất cả bao nhiêu cặp số thực x; y thỏa mãn đồng thời 2 điều kiện 2
x 2x3 log  3 5 y4 3  5  ?
4 y  y  1   y  32  8 A. 3 B. 2 C. 1 D. 0
Câu 57: Cho (C )
y  x  mx  m 
m l| đồ thị của h|m số 3 3 1 (với
0 l| tham số thực). ọi d là
đường thẳng đi qua hai điểm cực trị của (C ). m
Đường thẳng d cắt đường tròn t}m
I 1;0 bán kính R  3 tại hai điểm ph}n biệt A, .
B ọi S l| tập hợp tất cả c{c gi{ trị của
m sao cho diện tích tam gi{c IAB đạt gi{ trị lớn nhất. Hỏi S có tất cả bao nhiêu phần tử ? A. 1 B. 2 C. 3 D. 0
Câu 58: Cho 3 số thực dương x,y,z thỏa mãn 2
2z  y . Khi biểu thức sau đạt giá trị nhỏ nhất, hãy tính log xyz 2 ? 2
P  log xy  log  3 3 3 3 x y  x z  4 2 2
 y  xy  2zy  2xz 2 2 A. 3 B. 2 C. 1 D. 0
Câu 59: Cho phương trình 2
sin 2x  cos 2x  sin x  cos x  2 cos x  m  m  0. Có bao
nhiêu giá trị nguyên của tham số m để phương trình có nghiệm ? A. 2. B. 3. C. 5. D. 9. 1 1 k
Câu 60: Giả sử k là số thực lớn nhất sao cho bất đẳng thức   1  đúng với 2 2 2 sin x x     x  0;
. Khi đó gi{ trị của k là? 2    A. 5 B. 2 C. 4 D. 6
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 9
60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT
LỜI GIẢI CHI TIẾT ĐỀ 3
Câu 1: Có bao nhiêu giá trị nguyên của tham số m để phương trình 2 m m  x   2m  x m  x
Có đúng một nghiệm nhỏ hơn 10 . A. 5 B. 4 C. 9 D. Vô số. Lời giải
m x  m  2m x. m x Phương trình   I
m  x  0 x  x x Xét m  0 :   . I  
mọi x  0 đều là nghiệm của phuơng trình đã cho.  x  0  2m 2
x  2m  xm  x x    0  x 
m  x m  x  3  Xét m  0 :   2 . I    x  0  x  0  vô nghiệm. m  x  0 m x  0   m  x  0     m  x2 2
 2m  xm  x
 m  x  m  x m  x  Xét m  0 :   2 2 . I  
 m  x  0  m  x  0 2m x  0  x  2  m 
 2m  x  0  x  2m . m x   0
Vì x  2m  10  m  5 m   m 4  , 3  , 2  , 1  . m0  
Câu 2: Cho 2 dãy cấp số cộng u  u u u d v  v v v n ; ;... n ; ;... 1 2 n có công sai 1 và 1 2 n có công sai
d2 . Gọi tổng của n số hạng đầu của mỗi cấp số theo thứ tự là u
S  u  u   u  n 
T  v  v   v  n  n ... n 14 27 n ... n 7 1 1 2 và 1 2
. Tính tỉ số của 11 v11 5 4 9 5 A. B. C. D. 3 3 4 4 Lời giải
n 2u  n  1 d  
n 2v  n  1 d   1   1     Từ giả thiết, ta có 1 S  2 T  n và 2 n 2 S
2u  n  1 d n  n 1   1 7 1    1 T
v  n  d n  n 2 1 4 27 1     2   . u u  10d 2u   20d 11 1 1 1 1   2  v v  10d 2v   20d 11 1 2 1 2
10 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN u 148 4
So sách (1) và (2) bằng c{ch đồng nhất 11
 n  1  20  n  21    v 111 3 11
Câu 3: Cho hình chóp S.ABC có SA  x, BC  y, AB  AC  SB  SC  1. Thể tích khối chóp
S.ABC đạt giá trị lớn nhất khi tổng x  y bằng : 2 4 A. . . 3 B. 3. C. 3 D. 4 3. Lời giải
Gọi H , K lần lượt l| trung điểm BC ,S . A
Đặt BC  2x, SA  2y. Có 2 2 2 2 2 2
SH  SC CH  1  x ; AH  AB  BH  1  x .
Do đó SAH cân tại H. Hay HK  S . A
Có d BC SA 2 2 ,
 HK  1  x  y .
Thể tích khối chóp S.ABC là BC.S .
A d BC,SAsin BC,SA 3 2 2 2 2 2       2 2 2 x y 1 x y 2 3 V   xy  x  y     S ABC 1 . . . 6 3 3  3  27
Dấu bằng xảy ra khi và chỉ khi 2 2 3 2
x  y  1  x  y  x  y   x  y  . 3 3 Chọn đ{p {n A.
Câu 4: Giá trị nhỏ nhất của m để hệ phương trình sau có nghiệm :
log x  y  log xy  2  2 2   3    3 3
x  y  2xy  m A. 1. B. 2. C. 3. D. 4. Lời giải
Đặt log x  y  a, log xy  2  b a  b  2   3   khi đó 2 2
Lại có: x  y2  4xy   a    b     2 2 4 3 2
4 3 a  2  12a  8.3a  36  0
Xét hàm   12a 8.3a g a  
 36 đồng biến trên , g1  0  a  1    3    
  a 3   2a   a   2 3 2 2 3 3 2 .2 2 3 a m x y xy x y xy
 2  f a
H|m f đồng biến trên 1;  suy ra m  f (1)  1
Vậy hệ phương trình có nghiệm khi và chỉ khi phương trình thứ 2 có nghiệm
a  1  m  1
Câu 5: Cho 2 sin a  b  cosa  b , a  b  k .
 Tính giá trị của biểu thức 1 1 E  
1  2 sin 2a 1  2 sin 2b 2 1 A.  . B. . 3 2 C. 2. D. 0. Lời giải
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 11
60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT
Dễ dàng chứng minh được: 2
sin 2a  2 sin a  b  cosa  bsin a  b 2
 1  2 sin 2 a  1  4sin a  b  2 cosa  bsin a  b 2
 1  cos a  b  2 cosa  bsin a  b 2
 sin a  b  2 cosa  bsin a  b  sin a  b sin a  b  2 cosa  b  
Tương tự ta có: 1  2 sin 2 b  sin a  b sin a  b  2 cos a  b   Suy ra: 1
2 sin a  b 2 E  
sin a  b . 2 2 2 2
sin (a  b)  4 cos (a  b) sin (a  b)  4 sin (a  b)  4 2 2    2 2
sin (a  b)  cos (a  b)  4 3
Câu 6: Cho dãy u 2u 1 u u 2 25.2  15.2
 5.2u  15.2u  4  0 u    u n n 8. n thỏa mãn 5 1 5 5 1 và 1
Giá trị nhỏ nhất của n để u  n 2019. A. 512. B. 258. C. 511. D. 257. Lời giải Từ u             u u d 8 u u n u u n 8 1 32 n n 8. 1
 n  là CSC công sai 1   5 1
Thay vào giả thiết ta được:    2 32 1 u    32 2 5.2 3 2 5.2  3 1 2u    4  0       u 1 33 1 33
Có dạng phương trình bậc 2 suy ra:  32 5.2  3 1 2   u  log   1 2 4  4 32 5.2  3    u
u  u  n    n     n  n 8 1 2019 1 2019 1 257,63 258 1 min 8
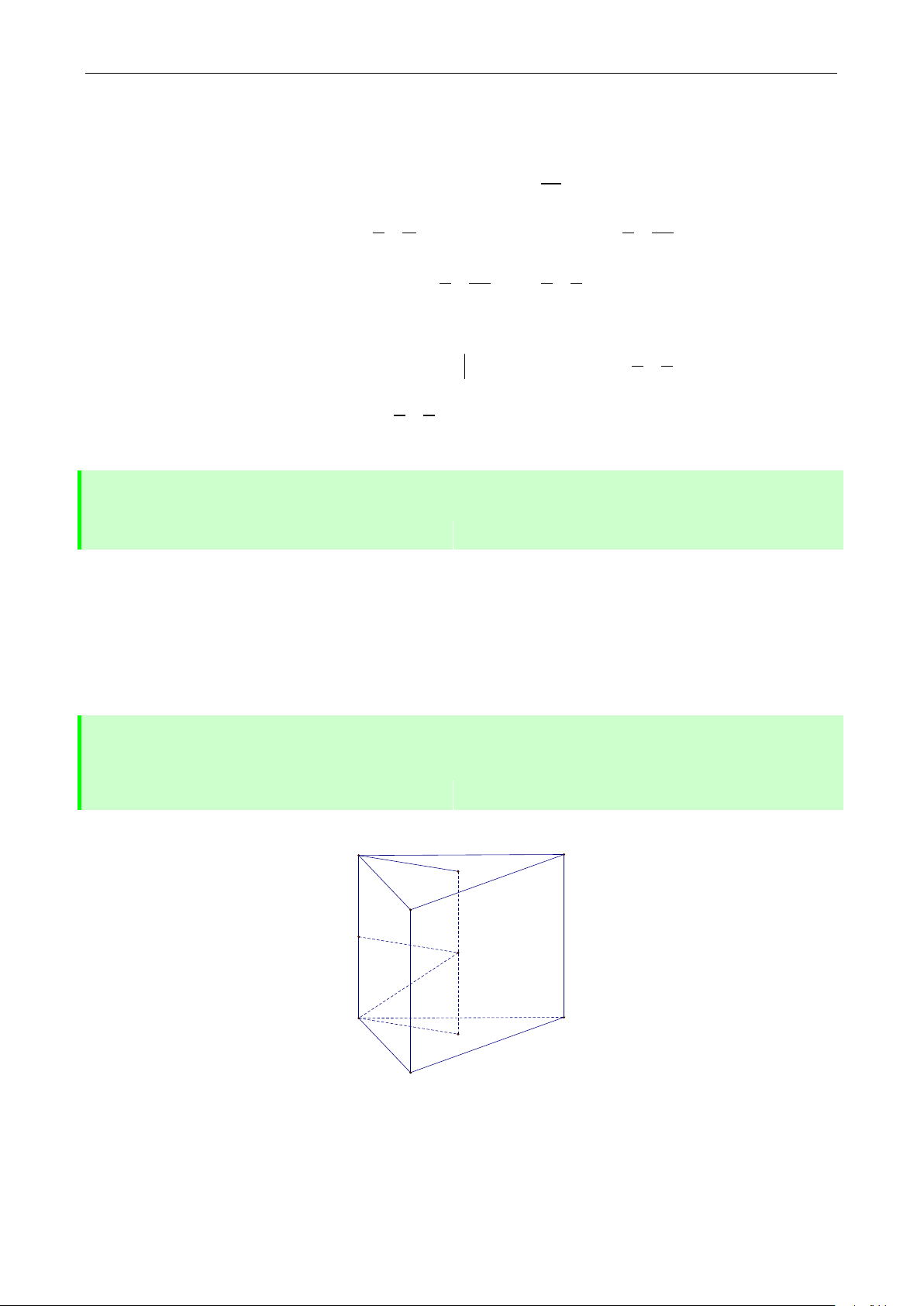
Câu 7: Cho hình chóp .
S ABCD có đ{y ABCD là hình vuông, AB  1 , cạnh bên SA  1và
vuông góc với mặt phẳng đ{y  ABCD . Kí hiệu M l| điểm di động trên đoạn CD và N là
điểm di động trên đoạn CB sao cho MAN  45 . Thể tích nhỏ nhất của khối chóp S.AMN là ? 2  1 2  1 2  1 2  1 A. B. C. D. 9 3 6 9 Lời giải
Đặt DM  x , BN  y ta có       1 x DAM  BAN tan DAM tan BAN x y tan 45 tan   . Suy ra y  .
1  tan DAM.tan BAN 1  xy 1  x 2  x   2 2 x   1 1  và 2 2 2
AM  AD  DM  x  1 , 2 2 2
AN  AB  BN  1  y     1  .  1  x  x  1 2 1 1 x  1 2  1
Vì vậy V  S . A S  SA AM AN   f x   f   AMN . . sin 45    2   . x   1 3 6 6 1 3
12 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN S A D M B N C
Câu 8: Cho một cấp số cộng : u , u , u , u
u u  u u  6 1 2 3 4 thỏa 1 4 2 3
. Tìm tập x{c định D của
hàm f x  x  u x  u x  u x  u  9 1   2   3   4 
A. D  ;6
B. D  6;  C. D  D. D   6  ;6 Lời giải
Theo tính chất của cấp số cộng , ta có : u  u  u  u 1 4 2 3
Do đó x  u x  u x  u x  u  2
 x  u  u  2
x  u u  x  u  u x  u u  * 1 2 3 4  1 4 1 4    2 3  2 3    Đặt 2
t  x  u  u  2
x  x  u  u x 1 4  2 3 , khi đó :
*  f (t)  t  u u t  u u  2
 9  t  u u  u u t  u u u u  9 1 4 2 3  1 4 2 3 1 4 2 3 2 2
Với :   u u  u u  u u u u   u u  u u  t  4 36 36 1 4 1 3  1 2 3 4  1 4 2 3  .
Rõ ràng u u  u u  6     f t  t
  f x t 0 ( ) 0, 1 4 2 3 có nghĩa với mọi x. 2
x  sin x  sin   1
Câu 9: Cho hàm số y  C C   . Tìm  để 
  sao cho khoảng cách x  1
giữa 2 điểm cực đại và cực tiểu là lớn nhất ?    
A.     k2 . 
B.     k . 
C.     k2 . 
D.     k .  4 4 2 3 Lời giải 2
x  sin x  sin   1 U x Hàm số y  
có miền x{c định D  \  1 v| đồng thời ta x  1 V x 2
x  2x  sin x  sin   1 có y '    0 
. Điều kiện để hàm số có cực đại, cực tiểu là ' hay x  12 y'
sin   sin   0  sin   0 .
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 13
60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT Gọi x , x C 1
2 lần lượt l| ho|nh độ c{c điểm cực đại, cực tiểu của    thì khi đó: U 'x U ' x 1   2  y 
 2x  sin , y   2x  sin  max V 'x  1 min V 'x  2 1 2
Gọi Ax , 2x  sin  , B x , 2x sin  C 1 1   2 2
 l| c{c điểm cực đại, cực tiểu tương ứng của    ,
x  x  2  1 2 khi đó x , x y  1
2 là 2 nghiệm của phương trình ' 0 nên 
x x  sin   sin   1  2 sin   1  1 2 2 2 2 Ta có 2
AB  x  x  y  y  x  x    B A   B A 5 40 sin 2 1  
Do vậy AB lớn nhất khi     k2k   2
Câu 10: Cho tứ diện ABCD có tất cả các cạnh đều bằng 1. Gọi G là trọng tâm của tam giác BC .
D Mặt phẳng P thay đổi luôn luôn đi qua AG cắt BC, BD I K
lần lượt tại , . Tính thể
tích nhỏ nhất của ABIK. 2 2 4 2 A. . B. . C. . D. . 27 18 9 36 Lời giải A K B D G O H I C
Đặt BK  x, BI  y V 2V x V y V A BKG A BKG 2 2 2
Sử dụng công thức tính tỷ số thể tích ta có . . A.BGI A.   ,  , BIK  xy V V 3 V 3 V A.BHD A.BCD A.BCD A.BCD 1 2x  y 4 xy 4 Mặt khác ta có V  V  V  xy   xy  A.BHD A.BCH A. nên 2 BCD 6 6 9 xy 2 2 2 Ta có V   x  y  . A.BIK
. Dấu “=” xảy ra khi và chỉ khi Chọn đ{p {n A. 12 27 3
14 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
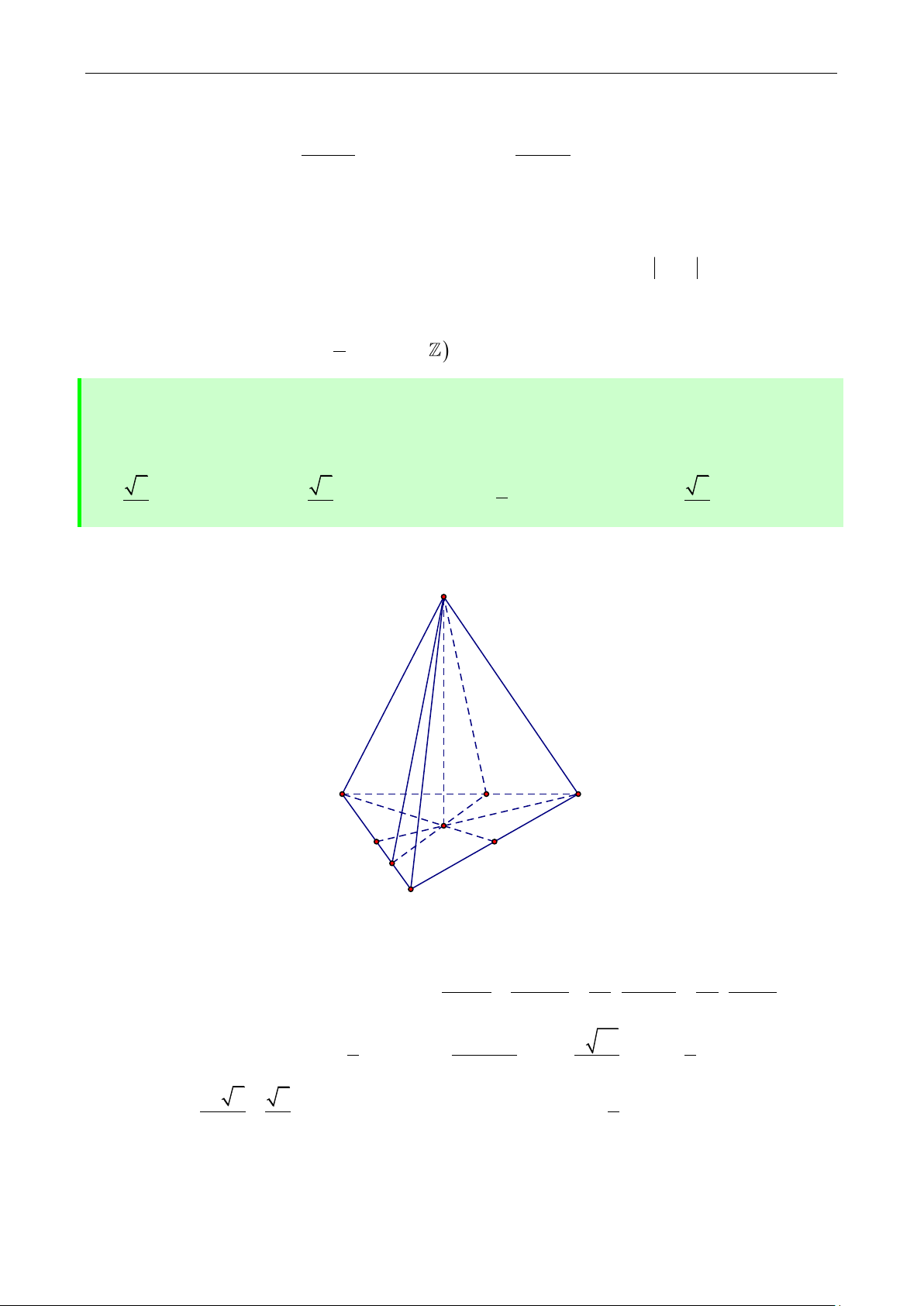
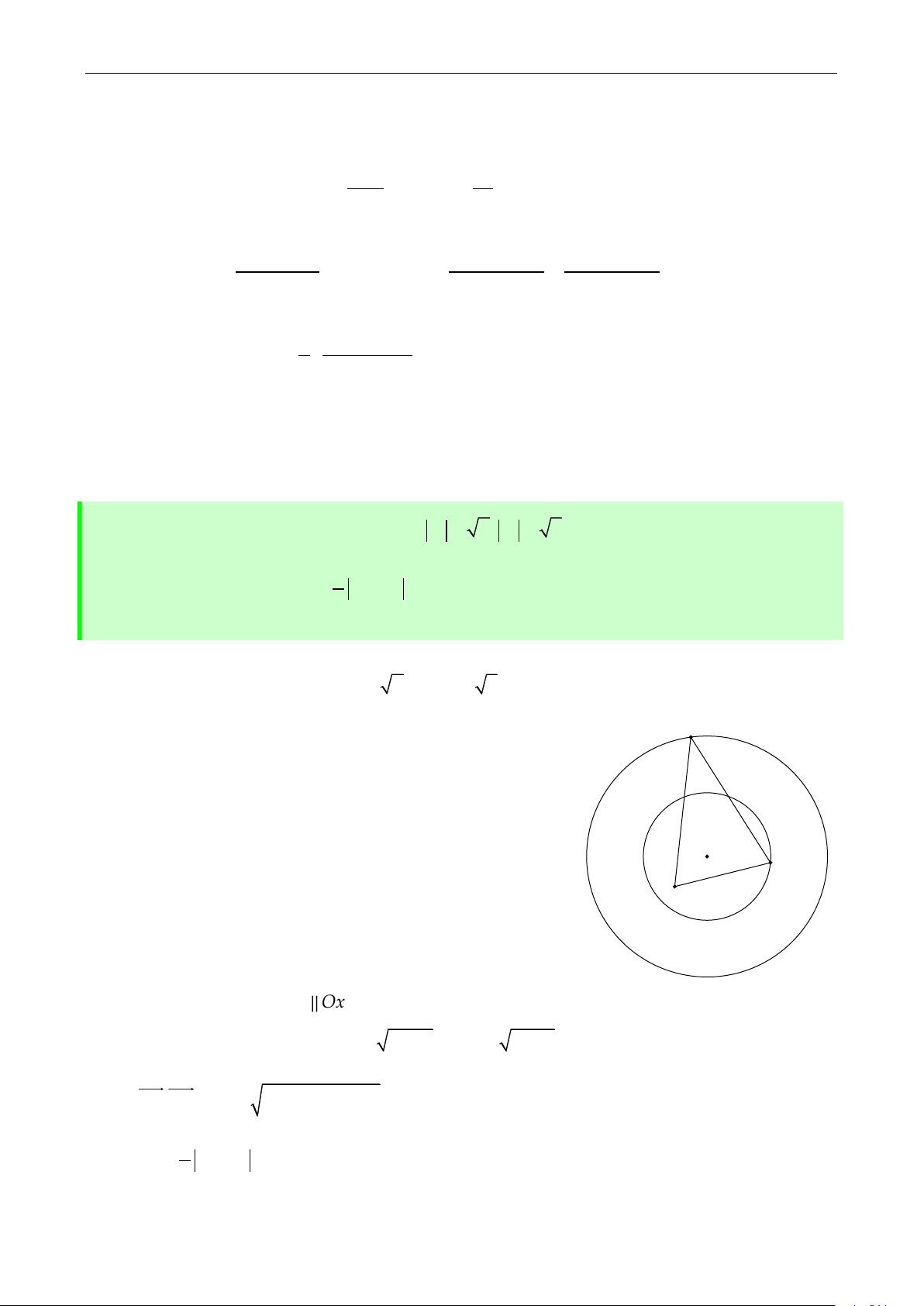
Câu 11: Cho hai số phức z , z
z  2  3i  17 ; z  1  5 1 2 thỏa mãn 1 2 .
Biết rằng z  1  i  k z  1  i k  0
P  z  z 1  2  . Tìm k khi 1
2 đạt giá trị lớn nhất.
B. k  1
B. k  2 C. k  3
D. k  5 Lời giải I J M H A K N
Gọi M z , N z , I 2; 3 , J 0; 1  1   2    
. Theo giả thiết ta có:
 Điểm M thuộc đường tròn C R  17 1  tâm I bán kính 1
 Điểm N thuộc đường tròn C R  5 2  tâm J bán kính 2
 z  2  3i   17
Ta thấy rằng số phức z  1  i đều thỏa mãn 
. Điều này chứng tỏ A1; 1  z  1  5 
l| giao điểm của C , C A M N 1  
2  và theo giả thiết ta suy ra được , , thẳng hàng.
Gọi H,K lần lượt là hình chiếu của I,J lên MN  P  MN  2HK  2IJ .
Dấu “=” xảy ra khi và chỉ khi MN IJ . Khi đó phương trình MN đi qua điểm A và có
vector pháp tuyến IJ  3  ; 3
  là MN : x  y  2  0 . Từ đ}y suy ra điểm M 6; 4, N 0; 2  
z  1  i 6  4i  1  i Vậy 1 k    5  . Chọn ý D. z  1  i 2  i  1 i 2
Câu 12: Gọi A là tập hợp các số tự nhiên gồm 5 chữ số. Chọn ngẫu nhiên một số từ tập A .
Tính xác suất để chọn được số chia hết cho 7 và có chữ số h|ng đơn vị bằng 2. 257 257 127 127 A. B. C. D. 90000 18000 90000 30000 Lời giải
Gọi số tự nhiên gồm 5 chữ số là abcde
Chọn a  0 có 9 cách.
Chọn b,c, d, e mỗi số có 10 cách. Nên 4 A  9.10 .
Gọi B là biến cố "chọn được tự nhiên gồm 5 chữ số chia hết cho 7 và có chữ số h|ng đơn vị bằng 2''.
Gọi số tự nhiên gồm 5 chữ số chia hết cho 7 và có chữ số h|ng đơn vị bằng 2 là abcd2
Ta có abcd2  10.abcd  2  7abcd  3abcd  2
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 15
60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT
abcd2 chia hết cho 7 nên 3abcd  2 chia hết cho 7 hay 3abcd  2  7t,(t  ) 7t  2 t  2
3abcd  2  7t  abcd 
 abcd  2t  3 3
Suy ra (t  2) 3 hay t  2  3n  t  3n  2 996 9995
Khi đó abcd  7n  4 mà 1000  abcd  9999 nên 1000  7n  4  9999   n  7 7
Mặt khác n là số nguyên  n 143;144;145;...;14  27 Nên B  1285 . 1285 257 Khi đó, ( P ) B   . 4 9.10 18000
Câu 13: Cho số phức z thỏa mãn z  1  i  5 . Tìm GTLN của P  2 z  8i  z  7  9i .
A. P  109
B. P  1  109
C. P  109  2
D. P  109  1 Lời giải
ọi I 1;1 , A7;9 , B1;8 . M
Yêu cầu b|i to{n chuyển về tìm gi{ trị lớn
nhất của biểu thức P  2MB  MA .
Ý tưởng cho b|i to{n n|y l| ta sẽ sử dụng D I A
bất đẳng thức tam gi{c, nhưng do có số 2 K C
ở giữa nên ta sẽ nảy ý tưởng tìm một điểm
K cố định thỏa mãn MA  2MK . iả sử
tồn tại một điểm K như thế thì ta có: B 2 2
MA  4MK  MA  4MK   2 2
MI  IA   4 2 2 MI  IK  2 2 2
 3MI  4IK  IA  2MI 4IK  IA  0 2 2 2 2
3MI  4IK  IA  0  IA 
Để tồn tại điểm K thì 2   3 R 
  0 . Dễ thấy điều này luôn
4IK  IA  0  4 
đúng do đó luôn tồn tại điểm K cố định thỏa mãn MA  2MK v| điểm K này nằm trên IC. R
Lấy điểm K thuộc IC sao cho IK  . 2 Ta có: 2
IK.IA  IM  I  AM I
 MK c.g.c  MA  2MK
Vậy khi M thay đổi thì MA  2MK . Theo bất đẳng thức tam giác thì ta có:
P  2MB  MA  2 MB  MK  2BK  5  Ta có: K
;3  P  2BK    109 .  2 
16 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Câu 14: Cho số phức z thỏa mãn 4 z  z  i  1  2 z  i  1 . Tìm giá trị lớn nhất của biểu
thức P  z  2  2i 30 30 30 30 A. P   2 2 B. P   3 2 C. P   4 2 D. P   5 2 3 4 5 6 Lời giải
Sử dụng bất đẳng thức Cauchy – Schwarz ta có: 2
z   z  i   z  i  2     2 2 z  i   z  i    2 2 16 1 2 1 1 4 1 1
5 2 z  2 i  1  30
Từ đ}y sử dụng bất đẳng thức trị tuyệt đối ta có  P   2 2 . 3 2 2 2  1   1   n 1 
Câu 15: Biết tổng 2 S        n  2   2  ... 2
. Giá trị nhỏ nhất của n để 2 2 2 2n        99 3  2n4n S  n , * n  4n A. 41 B. 40 C. 51 D. 50 Lời giải  1   1   n 1  Ta có 2 4 2 S  2  2     2  2    ...   2  2  n 2 4 2 2 2 2 n         2 4 2n      1 1 1   2 2 .. 2  2n    ..  2 4 2 2 2 2 n    n q  1
Áp dụng công thức tính tổng của n số hạng đầu của một cấp số nhân : S  u n 1 : q  1  1 n   n   1 4  1 1   4 
4n 1 n 1 4  1 S   n   n  n 4. 2 . 2 3 4 1 3.4n  1 4 Theo đề bài ta có:
4n 1 n1 4  1 99 3  2n4n 2n         n   n  n n
4n 1 n 1 4 1 100 3 39,124... 40 min 3.4 4
 z  2  z  2  8 3
Câu 16: Cho 3 số phức z , z , z z  1   i 0 1
2 thỏa mãn đồng thời  , với . Biết  3
z  z  z  z 2 1 3 3 2
z  z  a  bi 1 rằng 0 1 
a,b,c,dR . Tìm giá trị lớn nhất của biểu thức P  ad bc
z  z  c   di 2 0 2
A. P  17
B. P  18
C. P  19
D. P  20 Lời giải
Gọi Az ,B z , M z ,C z
z  z  z  z  AM  MB 1 
 2   3   0 . Theo giả thiết ta có 1 3 3 2 , suy ra
z  z  a  bi C
 A  a;b 0 1  
được A đối xứng với B qua điểm M. Mặt khác    .
z  z  c  di 0 2 C  B   c;d
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 17
60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT 1 Vậy P 
ad  bc  S
. Do AB  z  z  3 5 nên để diện tích lớn nhất thì d C; AB . 2 ABC 1 2 max
Gọi Ax; y  ,B 2   x; 3
  y  mà A,B thuộc elip nên ta có: A 4  ;0 ,B2; 3
   AB : x  2y  4  0
Sử dụng tiếp giả thiết z  2  z  2  8 ta suy ra điểm C thuộc v|o elip có phương trình l| 2 2      E x y : 
 1  C 4sin;2 3 cos       4   2 3  8    1 12 5 
Ta có d C; AB  sin         P    18 max 5  3  2 5 6
Câu 17: Cho hàm số y  f x có đạo hàm trên
. Gọi C , C , C 1   2  
3  lần lượt l| đồ thị
của các hàm số y  f x y  f  f x y  f  2 , ,
x  1. Các tiếp tuyến C , C 1   2  tại điểm x  2
y  x  y  x  C 0
có phương trình lần lượt là 2 1, 4
3 , hỏi tiếp tuyến của  3  tại điểm x  2 0
đi qua điểm n|o sau đ}y? A. Q 2; 11   B. M  2  ;11 C. N  2  ; 21   D. P 2; 21   Lời giải
 f 'x  2 0 
 f 'x  2 0    f x 5   0   f x  5 0  Theo giả thiết ta có   
f 'x . f ' f x  4   0    0 f '  5 2  f   f x  11  f 5  11 0    
Do đó hệ số góc của tiếp tuyến tại điểm có ho|nh độ x  2 C 0
của đồ thị hàm số  3  là
k  2x . f ' 2
x  1  4 f ' 5  8 C 0 0   
từ đ}y suy ra phương trình tiếp tuyến của đồ thị  3  là
y  8x  2  11  8x  5.
Câu 18: Cho dãy (x x  5, x      x n n n 2, 1 n ) thỏa mãn 2 1 1 . Tính giá trị của  1 1 1  M  lim   ........   x x x x x ...x 1 1 2 1 2 n  5  21 5  21 3  31 3  15 A. M  B. M  C. M  D. M  2 2 3 3 Lời giải
Đầu tiên dễ thấy x   n 2 2 Ta có 2 x           x x  x x x x x x n  2n 2 2 2 n 4 n  2n
4 ...  . .... n   2 4 1 1 1 2 1  x  x n 4 n 4 1 1        x x x x x x x x x n  21 lim lim 21 21 . .... . .... . .... x x x n n . .... 1 2 2  1 2 n2 1 2 1 2 2 x     x x n n 2 n 2 1 1 1 Lại có 1   
 ...  x  2   ........ 1  x x ...x x x x x x  x x x  x x x x x x n ... n ... n ... n ... 1 2 1 2 1 1 1 2 1 1 2 1 2 n 
18 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN 1 1 1 1  x  n1    ........  x  1  x x x x x ...x  x x x n 2 ... 1 1 2 1 2 1 2 n   1 1 1  1  x   n 5 21 1  lim    ........    5  lim    x x x x x ...x   x x x n 2 ... n  2 1 1 2 1 2 1 2
Câu 19: Có bao nhiêu cặp số nguyên a; b thỏa mãn 0  a, b  100 sao cho đồ thị của 2 hàm 1 1 1 1 số y   và y 
 cắt nhau tại đúng 2 điểm phân biệt? x a b x b a A. 9704 B. 9702 C. 9698 D. 9700 Lời giải
Ta thấy a  1; b  1 , nếu a  b 2 đường cong trùng nhau nên có vô số điểm chung, loại.
Vì vai trò của a,b như nhau nên ta chỉ cần tìm cặp số nguyên a; b với a  b  1 sao cho 1 1 1 1 1 1 1 1 phương trình     
   0 có 2 nghiệm phân biệt. x x x x a b b a a b a b 1 1 1 1  1 x   1 x 
Xét hàm số f x  
   f ' x    a    f  x x   ln , 1 0 a b a b  a   b   ln b 
Ta có f 'x  0  x  x  log f ' x  0 x  x f ' x  0 x  x 0 b  ,   khi ,   khi . lna    0 0 a  ln b  ln a lnb Nếu x  1  log       a b  b 1 ; 4;2 0     .  lna  a b a
Chú ý xét hàm số f t lnt ln 3 ln 2 ln 4 ln 5 ln 100       ...  t 3 2 4 5 100
Khi đó f x  f x  f 1  0  f x x  1 0   
  có đúng 1 nghiệm 0 Nếu x  1 f x  0
, khi đó vẽ bảng biến thiên cho hàm số ta thấy phương trình   0 luôn có 2 nghiệm phân biệt.
Với mỗi b  k 2, 3,...,99  ak 1,...,100  tức có 100  k cách chọn a. 99
Vậy có 100  k  4851 cặp a;ba  b  1 và loại đi cặp 4;2 ta có 4850 cặp. k2
Xét tương tự với trường hợp b  a  1 ta có tất cả 9700 cách chọn.
Câu 20: Xét các hình chóp .
S ABCD thỏa mãn điều kiện: đ{y ABCD là hình vuông, cạnh
bên SA vuông góc với đ{y v| khoảng cách từ điểm A đến mặt phẳng SBC  bằng a. Biết
rằng thể tích khối chóp .
S ABCD đạt giá trị nhỏ nhất V0 khi cosin góc giữa đường thẳng SB p p
và mặt phẳng  ABCD bằng
, trong đó p,q là các số nguyên dương v| ph}n số là q q
tối giản. Tính T   p  q.V . 0 5 3 A. 3 T  3 3a . B. 3 T  6a . C. 3 T  2 3a . D. 3 T  a . 2 Lời giải
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 19
60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT
Ta có BC  AB; BC  SA nên BC  SAB .
Gọi H là hình chiếu vuông góc của A trên SB. Khi đó AH  SBC  và d  A,SBC   AH.
Ta có góc giữa hai đường thẳng SB và mặt phẳng  ABCD là góc SBA . a a
Đặt SBA   .Theo giả thiết ta có AB  ;SA  . sin  cos 1 1 Thể tích khối chóp . S ABCD là 3 V  . . SA S  a ABCD . 2 3 3sin  cos 
Áp dụng bất đẳng thức AM – GM , ta có 3 2 2 2        2 2 2 sin sin 2 cos 8 sin .  sin .  2 cos      2 2 3  sin  cos   3  27 9 3 Do đó 3 V 
a . Dấu bằng xảy ra khi 2 2 1
sin   2 cos   cos  . 2 3 3 1
Vậy thể tích khối chóp .
S ABCD đạy giá trị nhỏ nhất bằng 3 a khi cos  2 3 3 Suy ra 3 V 
a ;p  1,q  3  T  p  q V  2 3a . 0   3 2 0
Câu 21: Cho số phức z , z , z z  3  i z 1 2 3 lần lượt thỏa mãn 1
, 2 là số thuần ảo với thuần ảo 2 2 không âm, z
z  z  z  z  z  z
3 là số thực không âm. Biết rằng 2 3 2 1 3 1 . Gọi M,n lần
lượt là giá trị lớn nhất và nhỏ nhất của biểu thức P  z  z z  z 2 1 3 1 . Khi đó M.n bằng?
A. M.n  90
B. M.n  80
C. M.n  100
D. M.n  70 Lời giải
Gọi M 3;1 , Az , B z 2 
 3. Theo giả thiết ta có: 2 2 2 2 2
z  z  z  z  z  z
 AB  MA  MB  MA  MB 2 3 2 1 3 1 Do z z
2 là số thuần ảo với thuần ảo không âm, 3 là số thực không }m nên ta có điều kiện  10 
là Aa;0 , B0; ba, b  0 . M .
A MB  0  b  10  3a 0  a   3   
Ta có: P  z  z z  z  M . A MB  3 2
a  6a  10  3; 30 2 1 3 1   .
Vậy min P  3, max P  30
Câu 22: Cho các số thực dương x, y, z thỏa mãn  2 2 2
5 x  y  z   9xy  2yz  zx . Tìm giá x 1
trị lớn nhất của biểu thức: P   . 2 2 y  z
x  y  z3 A. 14 B. 16 C. 12 D. 18 Lời giải 2 Ta có:  2 2 2
5 x  y  z   9xy  2yz  zx  5x  y  z  9xy  2yz  zx  10xy  yz  zx
20 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
 5x  y  z2  19xy  z  28yz  19xy  z  7 y  z2 2  x  x x  5  1  19  7 
 2  x  2y  z y  z y  z y    z y  z 2 y  z 2 2  2 1 4 1
Mặc khác ta có: y  z   P     2
y  z2 2y  z y  z3 y  z 27y  z3 2 4 1
Xét hàm số f t  
, t  0  max f t  16  P  16 3 max t 27t  1 x   3
Dấu “=” xảy ra khi và chỉ khi  1 y  z   12
Câu 23: Gieo một con súc sắc c}n đối đồng chất hai lần. Giả sử m là tích số chấm mà con
súc sắc xuất hiện sau hai lần gieo. Tính xác suất sao cho hàm số
y  m   2
3 x  41  2mx  2 đồng biến trên khoảng 0;   . 1 2 3 17 A. B. C. D. 2 3 4 36 Lời giải Ta có   
 a;b|a,b ;1  a,b  
6  n  36 .
Gọi biến cố A: “ h|m số đã cho đồng biến trên khoảng 0;   .
Ta xét c{c trường hợp sau:
+ Trường hợp 1: m  3  0  m  3 , ta được: y  35x  2 đồng biến trên nên y cũng
đồng biến trên 0;   .
+ Trường hợp 2: m  3 : Hàm số đồng biến trên 0;   a  0  a  0 m  3  0  41  b      3  m    0  b  0 41  2m  0 2  2a
Từ hai trường hợp ta suy ra 3  m  20.  A  
 1;1,1;2,2;1,4;6,6;4,5;5,5;6,6;5,6;6 nA  9 .
 pA   pA nA 3 1  1  . n 4  1 
Câu 24: Cho hàm số y  f x  ln 1   . Biết rằng : 2 x   
f 2  f 3  ... f 2018  ln a  ln b  ln c  ln d
trong đó a, c, d l| c{c số nguyên tố v| a  b  c  d . Tính P  a  b  c  d A. 1986 B. 1698 C. 1689 D. 1989 Lời giải
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 21
60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT 2  x  1  Ta có y  ln 
  ln x  1  ln x  1  2 ln x 2  x  Khi đó:
f 2  ln 1  ln 3  2 ln 2
f 3  ln 2  ln 4  2 ln 3
f 4  ln 3  ln 5  2 ln 4 ..........
f 2017  ln 2016  ln 2018  2 ln 2017
f 2018  ln 2017  ln 2019  2 ln 2018
 f 2  f 3  f 4  ... f 2017  f 2018
  ln 2  ln 2018  ln 2019  ln 3  ln 4  ln 673 ln 1019
Câu 25: Cho hàm số y  f x 3
 x   m   2 2
1 x  2  mx  2 . Tìm tất cả các giá trị của tham
số m để hàm số y  f  x  có 5 điểm cực trị. 5 5 5 5 A.  m  2 B. 2   m  C.   m  2 D.  m  2 4 4 4 4 Lời giải Ta có: 2
y  3x  2 2m  1x  2  m
Hàm số y  f  x  có 5 điểm cực trị khi chi khi hàm số f x có hai điểm cực trị dương.   m  2 2
1  32  m  0 2
4m  m  5  0   0   22m1   1 5 S   0    0  m    m  2  3 2 4 P     0 2  m    m 2 0    3
Câu 26: Cho hàm số y  f x có đạo hàm liên tục trên đoạn 1; 2 thỏa mãn đẳng thức: 3 3x f x
 f ' x  x, x   1;2 f  f 2 2     và   7 1 . Tính   .  f '
 x  xf '  x 2  x 3    
A. f   7 7 1 2 
B. f   7 7 1 2 
C. f   2 7 1 2 
D. f   2 7 1 2  3 3 3 3 Lời giải
Biến đổi giả thiết ta có: 3 3x f x f ' x x 3x f x  f ' x x 
  f ' x  xf ' x x         2  
         2 3    2  f '  x xf '  x 2 x     f x
 3x f x   f '  x 3
  x  x 3 f  
x 1   f '   x 3 ' 3 3 3      x 
3 3 f x  1
22 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN 2 f 'x 2 2 3 1 
dx  xdx   3 f    x 1  3 3  1 d 
3f x1  3 3 f x  1 2 3 2 1   1 1 2 1 3   f  x 2 3 . 3  1   3 f   2 2  1  3 f   1 2 3 3 3  1  3 3 2 2  1   3 f  2 2 7 7 1 3  1  7  f  2  3
Câu 27: Cho hàm số đa thức bậc ba y  f x có đồ thị đi qua c{c điểm sau
A2; 4 ,B3;9 ,C 4;16 . C{c đường thẳng AB, AC, BC lại cắt đồ thị tại lần lượt tại các
điểm D, E, F ( D khác A và B , E khác A và C , F khác B và C ). Biết rằng tổng các
ho|nh độ của D, E, F bằng 24 . Tính f 0 .
A. f 0  2 
B. f 0  0 C. f   24 0 
D. f 0  2 5 Lời giải
Giả sử f x  ax  x  x   2 2 3
4  x a  0 .
Ta có AB qua A2; 4 và nhận AB  1; 5 là một VTCP
 AB : 5x  2  y  4  0  y  5x  6 .
Tương tự AC : y  6x  8 và BC : y  7x  12 .
Ho|nh độ của điểm D là nghiệm của phương trình
ax  x  x   2 2 3
4  x  5x  6  ax  2x  3x  4  x  2x  3
 ax   1 4  1
  x    4 . a 1 1
Tương tự, ho|nh độ của điểm E và F lần lượt là x    3 và x    2 . a a  1   1   1  1
Bài ra ta có   2    3    4        24  a   .  a   a   a  5
Do đó f    a       2 24 0 . 2 . 3 . 4  0  . 5
Câu 28: Cho hàm số g x  f  2 x f  2 sin
cos x trong đó f thỏa mãn điều kiện :
f cot x  sin 2x  cos 2x, x  0; .
Tích của giá trị lớn nhất và giá trị nhỏ nhất của g x bằng: 1 1 1 1 A. . B. . C.  . D.  . 25 5 5 25 Lời giải
Đặt t  cot x 2 2 tan x 2 cot x 2t t  1  sin 2x    ; cos2x  2 2 2 2
1  tan x 1  cot x 1  t 1  t
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 23
60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT 2 2    2    x 2x 1 f t 2t t 1 t 2t 1   
hay f x  2 2 2 1  t 1  t t  1 2 x  1  4 2
sin x  2 sin x  1 4 2
cos x  2 cos x  1 4 4 2 2    gx sin . x cos x 8sin . x cos x 2    4 1  sin x 4 1  cos x 4 4 2 2 sin .
x cos x  2 sin . x cos x  2 Đặt 2 2 1 u  sin .
x cos x  0  u  , khi đó phương trình trở thành: 4 2    
hu u 8u 2 1  , u 0; 2 u 2u 2  4      1  1
Dễ d|ng tìm được max h u  h   
và min h u  h 0  1   1  1 u 0;  4  25  u 0; 4    4  
Câu 29: Cho hàm số f x liên tục trên đoạn 1; 4 thỏa mãn f 1  1  , f 4  8  v| đồng 2 4 thời  f  x 3  x  f  x 3 '
 9 x  x  3x, x
 1;4 . Tích phân f xdx  bằng 1 89 79 A. 7 B.  C.  D. 8  6 6 Lời giải 2 f x 1 3
Giả thiết đã cho tương đương  f '  x      9    3 x x x
Lấy tích phân 2 vế trên đoạn 1; 4 ta được: 4    f   x 2 4 f x 4 1 3 '  dx  dx   
 9  dx  212ln2 1 1 3 1 x  x x 
Sử dụng tích phân từng phần ta được: 4 f x 4   dx  f   x 2 d   
a , a sẽ được x{c định sau 1 3 1 x  x  4  2      4  2            x 4 1 a a f x a f '
dx  7a  6  2  f    'xdx 1 1  x   x   x 2  1
Từ đ}y ta có đẳng thức: 1      x2 4 1 a f '
dx  7a  6  2  f ' 
xdx  21   2 ln 2 1 1  x 2  2 2 4      x 1 a 3a f '  
dx  2 ln 2  9a   6  21   2 ln 2 1  x 2  4 2 3a
Ta dễ tìm được a  3 để 2  ln 2  9a 
 6  21  2 ln 2 , khi đó 4 f x 1 '   3, x
 1;4  f x  2 x  3x x 4 4 79 Vậy
f xdx 
2 x  3x dx     1 1   6
24 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Câu 30: Cho phương trình log 2  2  2 2 2 2 2  2y x x
 y  x  x 2
. Hỏi có bao nhiêu cặp số
nguyên dương x; y , với 0  x  500 thỏa mãn phương trình đã cho? A. 4. B. 2. C. 3. D. 1. Lời giải
Biến đổi giả thiết ta được:
log 2x  2x  2 2
 2y  y  x  x  log x  x  1 2 2 2 2 2 2 y 2
 x  x  1  2  y 2 2 log  2 x x1  2  log  2 x  x  1 2 2 y 2
 2  y  log  2 x  x  1 2  y 2 2 Do 2
0  x  500  y  log  2
x  x  1  0;18  0  y  5 2   
. Vậy ta có 4 giá trị nguyên của y
thỏa mãn yêu cầu đề b|i đồng nghĩa có 4 cặp số x, y thỏa mãn phương trình đã cho.
Câu 31: Cho hình chóp .
S ABCD có đ{y ABCD là hình bình hành. Gọi A l| điểm trên SA 1 sao cho A A   A S
 . Mặt phẳng  qua A cắt các cạnh SB,SC,SD lần lượt tại B,C,D . 2 SB SD SC
Tính giá trị của biểu thức T   
SB SD SC . 3 1 1 A. T  B. T 
C. T  2 D. T  2 3 2 Lời giải
Gọi O là giao của AC và BD . Ta có O l| trung điểm của đoạn thẳng AC , BD .
C{c đoạn thẳng SO , A C
  , BD đồng quy tại I . S  S  S S  S  S Ta có S  S  SA I SC I SA C      SA I SC I SA C       S SA'I SC I SA C   S S S 2S 2S S SAC SAC SAC SAO SCO SAC SA SI SC SI SA SC        SI SA SC SA SC SA SC SO .  .  .      .    2. 2SA SO 2SC SO SA SC
2SO  SA SC  SA SC SA SC . SI SB SD SO SB SD SC SA 3 Tương tự:   2.     SB SD . Suy ra: SI
SB SD SC SA . 2 4
Câu 32: Gọi q là công bội của một cấp số nhân , biết tổng ba số hạng đầu bằng 16 , đồng 9
thời theo thứ tự , chúng là số hạng thứ nhất , thứ tư v| thứ tám của một cấp số cộng . Hỏi
q thuộc khoảng n|o sau đ}y?
A. q 3; 4
B. q 1; 2
C. q 2; 3
D. q 0;1 Lời giải
Gọi : u , u , u v 1 2
3 là 3 số hạng đầu tiên của cấp số nhân , với công bội q . Gọi  n  là cấp số
cộng tương ứng với công sai là d . Theo giả thiết ta có :
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 25
60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT  4  2 4
u  u  u  16     1 2 3 u u q u q 16 1  1 1 1   9 9   u  v  1 1
 u q  u  3d 2 1 1  
u  v  v  3d  2 2 4 1
u q  u  7d 3   1 1  
u  v  v  7d 3 8 1 
Khử d từ (2) v| (3) ta được : u  2
3q  7q  4  0 4 1   . q  1 4 Do (1) nên : u 0 4     q  q  1   4  . Theo định nghĩa thì 1 , do vậy q  3  3 1 2 dx
Câu 33: Cho tích phân * I  ,n  
, biết rằng tổng giá trị lớn nhất và giá trị nhỏ 2 0 1 n  x a c a c
nhất của I được viết dưới dạng
 , trong đó a, b, c, d l| c{c số nguyên dương v| , b d b d
là phân số tối giản. Tính S  a  b  c  d ? A. 9 B. 10 C. 11 D. 12 Lời giải 1 1 1 n 1 1 1 1 Ta có 2 2 2 2 x  0  1   dx  dx  dx     2n 0 0 2n 0 2 1  x 1  x 1 n  x 2
Dấu “=” xảy ra khi x  0 1 1  1 n 1 1 Ta thấy 2 2 2 2 n *,x  0;  x  x  dx  dx     0 2n 0 2  2  1  x 1  x 1 1  costdt   Đặt 2 6 6
x  sin t  dx  cost t d  dx  dx  dt     0 2 0 2 0 1  x 1  sin t 6
Dấu “=” xảy ra khi x  1
Câu 34: Cho 3 hàm số y  f x , y  g x , y  h x . Đồ thị của 3 hàm số
y  f x , y  gx , y  hx có đồ thị như hình vẽ dưới, trong đó đường đậm hơn l| đồ  
thị của hàm số y  f x . Hàm số k x  f x    g  x   3 7 5 1  h 4x   đồng biến trên 2    khoảng n|o dưới đ}y ?  15   1   3   3  A.   ;0. B.   ; . C.  ;1. D. ;  .  4   4   8   8  Lời giải
26 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN y
y  g'x 10
y  f 'x 5 O 3 4 8 x
y  h'x    
Ta cần giải bất phương trình k x  f x   15 3 ' ' 7  2g' 2x   4h' 4x       0  2   2 
Không thể giải trực tiếp bất phương trình n|y. Quan s{t c{c đồ thị của các hàm số
y  f 'x , y  g'x , y  h'x ta nhận thấy
f 'x  10, x
 3;8; g'x  5, x
 , h'x  5, x  3;8
Do đó f 'a  2g'b  4h'c  10  2.5  4.5  0, a
 ,c 3;8,b 3  x  7  8  3
Vì vậy ta chỉ cần chọn  3
  x  1 . Đối chiếu với đ{p {n ta chọn ý C. 3  4x   8 8  2 7 5i 9 3i
Câu 35: Cho 2 số phức z z    z  
z  a  bi 1 thỏa mãn 1 1 , với 4 4 4 4 2
 3 2ab10Biết rằng z i  2 z i
P  z  3  i  2 z  3  i 1 2 . Tìm GTNN của 1 2
A. P  38
B. P  39
C. P  2 38
D. P  2 39 Lời giải
Theo giả thiết ta có điểm M z  d : x  y  1  0 N z  d :
3  2 x  y  1  0 1  1 ,  2  2  
iao điểm của d , d I 0; 1 MI  NI 1 2 là 
 . Theo giả thiết ta có 2 .
ọi điểm A3;1  P  MA  2NA .  .
P IN  AM.IN  AN.2IN  AM.IN  AN.IM M
Theo bất đẳng thức Ptolemy ta có:
AM.IN  AN.IM  AI.MN AI.MN
 P  2AM  2AN  IN A 1 I
Ta có cosd , d  1 2 
. Theo định lý h|m số Cosine 2 ta có: N
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 27
60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT 2 2 2
MN  MI  NI  2MI.NI.cos MIN MN 
 5  4 cos MIN  3  P  AI 3  39 NI
Dấu “=” chỉ xảy ra khi AMIN nội tiếp đường tròn và 60o MIN  Chọn ý B.
Câu 36: Cho ba số thực dương a, b,c thỏa mãn abc  a  c  b . Tìm giá trị lớn nhất của biểu 2 2 3 thức P    . 2 2 2
a  1 b  1 c  1 5 10 7 14 A. P  . P  . P  . P  . max B. C. D. 3 max 3 max 2 max 3 Lời giải 1
Ta có: a  c  b 1  ac  0 . Dễ thấy ac  1  0  a  c a  c 2 2 1  ac2 3 2 2 a  c2  3 b   P        2 1  ac 2
a  1 a  c2  1 ac2 2 2
c  1 a  1  2 a  1 2 c  1 2 c  1 2 2 2 x  c 3 2  2 2
x  2cx  2c  1 3
Xét hàm số f x       2    2 2 x  1  2 x  1 2 c  1 2 c  1
 2x 1 2c 1 2 c  1 1
Với 0  x  a  c 4  c  2
x  2cx  1
Tính f 'x   x  12 2  2c 1  1  Trên khoảng 0;
: f 'x  0 có nghiệm 2 x  c
  c  1 và f 'x đổi dấu từ dương c    0
sang âm khi x qua x f x x  x 0 , suy ra
  đạt cực đại tại 0  1   f x 2 3 2c 3 0; :    2      gc 2 2 2 2 2  c 
c  1  c c  1 c  1 c  1 c  1  1  10 10
Khảo sát hàm số g c với c  0  max g c  g   P      max 0;  2 2  3 3
Câu 37: Cho hàm số f x liên tục trên
, có đạo h|m đến cấp hai trên và thỏa mãn 5ln 2      2 3 . 4 '   . '   x f x f x
f x f x  e , x    5  
, biết f 0 0 . Khi đó
f xdx  bằng? 0 2  25ln 2  1  355ln 2  A. 5 31   5ln 2 B. 31     2  5  2  2 1  25ln 2   355ln 2  C.  31   5ln 2 D. 5 31    5  2   2  Lời giải
28 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Giả thiết tương đương  4     x 4 . ' '     '  x f x f x e
f x f x  e C mà f 0  0  C  1  4      x 4         x 5 ' 1 '        5 x f x f x e f x f x dx e x D f x
e  x  D Mặt khác   5 0  0   1      5 x f D f x
e  x  1          x f x dx e  x   2 5ln 2 5ln 2 5 25ln 2 5 1 dx  531  5ln 2 0 0  2 
Câu 38: Cho hàm số y  f x có đồ thị hàm số y  f x như hình vẽ: y f 'x 2  5 O 5 x B A 13
Xét hàm số g x  f x 3 2
 2x  4x  3m  6 5 với m là số thực. Để g x  0 x    5; 5 
 thì điều kiện của m là 2 2 A. m  f  5 B. m  f  5 3 3 2 2 C. m  f 0  2 5 D. m  f  5  4 5 3 3 Lời giải
Ta có g x   g x  f x 3
 x  x  m 
  m  f x 3 0 2 2 4 3 6 5 0 3 2
 2x  4x  6 5 .
Đặt h x  f x 3 2
 2x  4x  6 5 . Ta có hx  f x 2 2  6x  4 .
h 5  2 f  56.5 4  0  h
  5   2 f  5   6.5  4  0 
Suy ra h0  2 f 0  0  4  0
h1  2 f 16.14  0  h 1
   2 f  1    6.1 4  0 
Từ đó ta có bảng biến thiên
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 29
60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT x  5 0 5 h  0  h  5 h h 0 h  5 2
Từ bảng biến thiên ta có 3m  h  5  m  f  5 . 3
Câu 39: Cho 4 số nguyên a, b,c, d thay đổi thỏa: 1  a  b  c  d  50 . Tìm giá trị nhỏ nhất a c
của biểu thức P   . b d 53 61 58 73 A. P  P  P  P  min B. C. D. 175 min 200 min 175 min 200 Lời giải
Vì 1  a  b  c  d  50 và a, b,c, d là các số nguyên nên c  b  1 a c 1 b  1 Suy ra: P     b d b 50 1 x  1
Dễ thấy 2  b  48 nên xét hàm số f x   ,x 2; 48 x 50 1 1
Ta có f 'x   
 f 'x  0  x  5 2 2 x 50
Lập bảng biến thiên ta được min f x  f 5 2  2;48
Do x  7 và x  8 là 2 giá trị gần x  5 2 nhất, vì vậy:   f x 
f   f   53 61 53 min min 7 ; 8  min  ;   2;48 175 200  175 53 Vậy GTNN của P  175
Câu 40: Cho các số tự nhiên từ 1 đến 100 . Chọn ra 6 số bất kỳ. Tính xác suất để chọn ra 6
số sao cho chúng có thể xếp thành 1 cấp số cộng. 95 95 95 95 A. B. C. D. 7528752 1254792 2509584 3764376 Lời giải
Gọi 6 số đó l| u ; u ; u ; u ; u ; u . 1 2 3 4 5
6 Viết theo cấp số cộng sẽ là
u ;u  d;u  2d;u  3d; u  4d;u  5d 1 1 1 1 1 1 u  u Do đó 6 1 d   u  u 6 1 chia hết cho 5 5
Nếu ta x{c định được u ; u 6
1 ta sẽ tìm được d và từ đó tìm được các số còn lại .Vậy bài toán
chuyển thành chọn ra hai số sao cho chúng có cùng số dư khi chia cho 5
Từ 1 đến 100 có 20 số chia hết cho 5 ta có 2 C20 cách chọn
30 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Từ 1 đến 100 có 20 số chia 5 dư 1 ta có 2 C20 cách chọn
Từ 1 đến 100 có 20 số chia 5 dư 2 ta có 2 C20 cách chọn
Từ 1 đến 100 có 20 số chia 5 dư 3 ta có 2 C20 cách chọn
Từ 1 đến 100 có 20 số chia 5 dư 4 ta có 2 C20 cách chọn Vậy ta có 2 C .5 20 cách chọn 2 C .5 Xác suất sẽ là 20 5 C100
Câu 41: Cho các số thực x,y thỏa mãn
log x  3  2 log 2  y  3  log y  3  2 log x  3  2 . 2 2     2   2
Giá trị nhỏ nhất của biểu thức P   2 2
4 x  y   15xy là?
A. min P  80
B. min P  91
C. min P  83
D. min P  63 Lời giải 1 1
Giả thiết tương đương log x  3  log 2  y  3  log y  3  log x  3  2 2 2     2   2 2 2  log          2
x 3 log  x 3 2 log y 3 log 2 y 3 2   2 2
 x  3  x  3  2   y  3  y  3  2
 x  3  2 x  3  y  3  2 y  3  x  y  2 x  3  y  3    2 x y 4
Ta có x  y  2  x  3  y  3  x  y  4x  y  8 x  3. y  3  4x  y   x  y   0
Mặt khác x  y  2  x  3  y  3  2 2x  y  x  y  8  x  y 4;8 2
Xét biểu thức P   2 2
4 x  y   15xy  4x  y  7xy  16x  y  7xy  7xy  3  16y  5x . y  3  0 Mà 
 P  164  x  5x  64  21x y  4   x
Kết hợp với x  y  4  x 3;7 64  21x  83 
Vậy gi{ trị nhỏ nhất của biểu thức P là 83
Câu 42 : Cho hàm số f x và g x thỏa mãn f '1  g 1  1; f 2.g 2  f 1 v| đồng  1 
thời 1  f 'x g'x  g x f ' x 
f 'x , x   \  0  . x    2 Tính tích phân I  f
 xg'xdx ? 1 3 1 3 1 3 1 3 1 A.  ln 2
B.   ln 2 C.  ln 2
D.   ln 2 4 2 4 2 4 2 4 4 Lời giải
Biến đổi giả thiết tương đương
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 31
60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT
x  xf 'x g'x  xg x f ' x  g x f 'x
 x  x g'
 x f 'x  g x f' x  g 
x f 'x    2 x x
xf 'x g x'  xf 'x gx  C 2
 f x gx x C
f '1g11   
 f x gx x 1 ' '   2 x 2 2x 2    f
 xgx 2 x 1 3 1 ' dx   dx      ln 2 1 1  2 2x  4 2
Sử dụng tích phân từng phần ta có 2 I  f
 xgxdx  gx f x 2 2  f
 xg x 3 1 ' ' dx   ln 2 1 1 1 4 2 2  f
 xg x 3 1 ' dx    ln 2 1 4 4 Chọn ý D.
Câu 43: Có tối đa bao nhiêu hình vuông được tạo bởi các ô vuông của bàn cờ 8x8 khi bớt đi một ô vuông? A. 204 B. 63 C. 196 D. 150 Lời giải
Để có tối đa số hình vuông Bớt 1 ô vuông ở góc vuông của bàn cờ 8
Số hình vuông được tạo thành từ các ô vuông trong bàn cờ là 2
x  204 (hình vuông) x1
Số hình vuông chứa ô vuông đã bớt là 8
 Số hình vuông được tạo thành sau khi bớt 204  8  196
Câu 44: Gọi R là bán kính mặt cầu ngoại tiếp lăng trụ đứng ABC.A B C 1 1 1 . Giả sử
BC  a , AA  h 1
. Khi R ngắn nhất thì tam giác ABC A. Đều.
B. Cân tại A.
C. Vuông tại A. D. Nhọn Lời giải A1 C1 O1 B1 I A C O B Gọi O,O A B C OO
1 lần lượt l| t}m đường tròn ngoại tiếp tam giác ABC và 1 1 1 . Khi đó, 1 là
trục của đường tròn ngoại tiếp đ{y. Trong mặt phẳng (AOO A ) 1
1 , đường trung trực cạnh
32 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN AA OO OO 1 cắt
1 tại I. Ta chứng minh được I l| trung điểm
1 v| cũng l| t}m mặt cầu ngoại
tiếp lăng trụ ABC.A B C  1 1 1 . Do đó, R IA . 2 2  OO  h Ta có 2 2 2 2 1 2
IA  OA  OI  OA    OA   (1)  2  4
Mặt khác, áp dụng định lý hàm sin trong tam giác ABC , ta được BC BC a      (2) BAC  2OA OA Sin
2 Sin BAC 2 SinBAC   2 1  a Từ (1) và (2) suy ra 2 IA h    . 4  sin BAC 2 2     
Do đó, R  IA ngắn nhất  2 IA bé nhất  2
sin BAC lớn nhất 2 sin  1  90o BAC BAC
Hay tam giác ABC vuông tại A.
z  i  a  bi
Câu 45: Cho hai số phức z , z
z  2 , z  5 1 2 thỏa mãn 1 2 . Biết rằng 1  .
z  i  c   di 2 1
Tìm GTLN của biểu thức P  ad  bc . 2
A. P  1
B. P  2
C. P  3
D. P  4 Lời giải
Gọi A0;1 , Bz ,C z
B 0; 2 ,C  0; 5 1   2  thì    .
Bổ đề: Cho hai đường tròn đồng t}m C O; R 1   và C
C O; R' R  R' 2  
. C{c điểm B và C lần lượt di động trên C , C 1  
2  tương ứng. Khi đó S đạt max khi O l| trực t}m
tam giác ABC và O nằm trong tam gi{c. Thật vậy, nếu cố O
định B thì đường thẳng AB cố định. Giả sử AB cắt C2  tại M B
và N, diện tích lớn nhất khi CO  AB. Tương tự nếu cố định A
C. Tức O là trực tâm của ABC. Khi đó C là điểm chính giữa
cung lớn MN hay O nằm trong tam giác ABC.
Áp dụng với A0;1  BC Ox .
Do tính đối xứng nên có thể gọi B 2  b b C 2 2 ; ,
 5  b ;bb  0 B 2  ; 1   Ta có A . BCO  0   2 2  b  2
5  b   bb  1  b  1    . C  1; 1   1 Vậy P
 ad  bc  S  1 max max 2 ABC
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 33
60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT
Câu 46: Cho tứ diện ABCD nội tiếp trong một mặt cầu bán kính R và thỏa mãn điều kiện
AB  CD, BC  AD, AC  BD . M là một điểm thay đổi trong không gian. Đặt
P  MA  MB  MC  MD, giá trị nhỏ nhất của P là? 16R A. P  2R 3. P  4 . R P  3 . R P  . min B. min C. min D. min 3 Lời giải A E L B D K F C
Gọi G là trọng tâm của tứ diện; E, F, K, L lần lượt l| trung điểm của các cạnh AB, CD, BC,
AD. Ta có tam giác ACD bằng tam giác BCD nên AF  BF suy ra EF  AB , tương tự ta
chứng minh được EF  CD v| đường thẳng PQ vuông góc với cả hai đường thẳng BC,
AD. Từ đó suy GA  GB  GC  GD  . R M . A GA  M .
B GB  MC.GC  M . D GD
Ta có MA  MB  MC  MD  GA M . A GA  M .
B GB  MC.GC  M . D GD
MG GAGBGC GD 2 .  4.GA    4GA  4 . R GA GA
Dấu bằng xảy ra khi và chỉ khi M trùng với điểm G. Vậy P  4 . R min
Câu 47: Cho 2 số thực x,y dương thỏa mãn điều kiện x  y    xy3 2 2 11 log 2 log 4 1 log  2 2 2 2 Đặt 3 3
P  x  y . Hỏi P có bao nhiêu ước số nguyên? A. 1 B. 2 C. 5 D. 0 Lời giải  2 
Đặt log 2x,log 4y,log
  a,b,c  a  b  c  4 2 2 2    xy 
34 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN 11 Giả thiết trở thành
. Nhận thấy 2 giả thiết đều l| đa thức đối xứng theo 2 biến a, b nên 2
dấu “=” sẽ xảy ra tại a  b  x,c  y đến đ}y ta sẽ tham số hóa để tìm điểm rơi.
Theo bất đẳng thức AM – GM ta có: 2 2
a  x  2ax  2 2 2 2 3
b  x  2bx
 a  b  c  2xa  b 2 3 2
 3y c  2y  2x  3 3 3 2
c  y  y  3y c    2 y 1 2x  3y 
Đến đ}y ta cần tìm x, y thỏa mãn   
3 . Vậy P không phải là số nguyên 2x  y  4 x    2
nên không có ước nguyên dương.
Câu 48: Cho phương trình m  3 m  3 3x  10  2x   3x  10  2x . Có bao nhiêu
giá trị nguyên của tham số m để phương trình có nghiệm? A. 10 B. 11 C. 9 D. 12 Lời giải
Đặt a  m  3 3x  10  2x ;b  3x  10  2x ,a  0,b  0 .
Điều kiện 0  x  5 . 2
 m  3a  b
m  3a  b Ta có:    2
 m  3b  a
m  3b  a     a  b a b 2 2 3
 b  a  a  ba  b  3  0  
a  b  3   0 (L) Với 2
a  b  m  3b  b  m  b  3b  f b (*)  2
b  3x  10  2x  b  x  10  2 3x 10  2x  10  b  10 (1) 2  2
b  3x  10  2x  b   3x  25 x  3 2x  5 x  25  b  5 (2)
Từ (1) và (2) suy ra b   10 ; 5  
Xét hàm số f b 2
 b  3b trên đoạn  10 ;5   ta có
min f b  f  10  10  3 10, max f b  f 5  10  10 ;5  10 ;5    
Phương trình * có nghiệm khi min f b  m  max f b  10  3 10  m  10 mà m   10 ;5  10 ;5    
nên có 10 giá trị nguyên của m thỏa mãn.
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 35
60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT 6 6
sin x cos x  cos x sin x
Câu 49: Cho hàm số y  f x 
. Hỏi có bao nhiêu giá trị sin x  cos x x  20
 19;2019 thỏa mãn hàm số f x đạt giá trị lớn nhất. A. 2453 B. 5142 C. 2571 D. 4906 Lời giải 6 6
sin x cos x  cos x sin x
Ta có f x  . Vì 2 2
sin x  cos x  sin x  cos x  1, x  sin x  cos x sin x cos x  5 5
sin x  cos x 
Nên f x 
 sin x cos x  2 2
1  sin x cos x  sin x co x sin x  cos x  f x 1 3 1 2 1
  sin 2x  sin 2x  sin 2x 8 4 2
Đặt t  sin 2x ,t 0;  1 1 1 1
Xét hàm số f x 3 2
  t  t  t liên tục trên 0;1 8 4 2  2  5
Khảo sát hàm số trên, suy ra max f t  f     0;  1  3  27 2 1 1
1 k x  2019;2019
Đạt được khi sin 2x 
 cos 4x   x   arccos 
 có 5142 giá trị 3 9 4 9 2 x 2
Câu 50: Cho 2 hàm số f x  m  16 
 2m  1,h x   1
x  6 x . Tìm tham số m để x  6
hàm số g x  h x. f x có giá trị nhỏ nhất là 0 với mọi x 0; 1 1  1  A. m  1 B. m  C. m ;1 D. m  1 2 2    Lời giải
Ta thấy rằng với mọi m, ta luôn có h 1 f 1  0 nên bài toán trở th|nh tìm m để cho hàm
số g x  h x. f x  0 x
 0;1 . Dễ thấy với x  1 thì bất đẳng thức luôn đúng, do đó ta sẽ xét trên 0; 1 .
Ta dễ thấy h x l| h|m đồng biến trên 0; 1 , h 1  0  h x  0 x
 0;1 . Đến đ}y lại
rút gọn bài toán trở th|nh tìm m để f x  0 x
 0;1. Đặt  6x t
t1;6 ta có 2          x 2 t t f x m 
 m    m  t  mt   t   m  x   2 2 0 1 6 2 1 0 1 2 2 0 2 6 t  2t 2 t  t  2 1
Đến đ}y b|i to{n trở thành bài toán rất đơn giản, ta cần m  min    2 1;6 t  2t 2
36 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Câu 51: Cho cấp số nhân u , u , u ,.., u u  i   n 1 2 3 n ; trong đó i 0, 1, 2,..., . Biết rằng 1 1 1 1 1
S  u  u  u   u  T      
P  u .u .u ....u  n ... 2019 n ... n 2018 1 2 3 , và . u u u u 1 2 3 n 100 1 2 3 n
Hỏi số tự nhiên nhỏ nhất thỏa mãn P là: A. 9295 B. 9296 C. 18592 D. 18591 Lời giải n u q  1 1  
Ta có S  u  u  u   u   1 n ... n 2018 1 2 3   q  1 1 1 1 1 1 n  q  Và T        2 n ... 2019   n1 u u u u u q  q n 1 1 2 3 1   Tn n 2018 Từ 1 ,2 suy ra 2 1  u q  1 S 2019 n n n n1 n 2 n n n  2018 
Ta có Q  u u u u  u u q u q u q  u q  u q  n . . .... n . . . 2 . .... 1 .     2 1 2 2 1 2 3 1 1 1 1 1 1  2019    n 2  2018  1  1  Theo đề   n  2 log  18591,1  n      18592 2018 min  2019  100  100  2019 1285 257 đó, ( P ) B   . 4 9.10 18000
Câu 52: Cho tập A  {0, 1, 2, 3, 4, 5, 6,7, 8, 9} . ọi S l| tập hợp tất cả c{c số có 5 năm chữ số
ph}n biệt được lập từ A . Chọn ngẫu nhiên một số từ S . Khi đó x{c suất để chọn được số có dạng a a a a a
a  a  a
a  a  a 1 2 3 4 5 sao cho 1 2 3 v| 3 4 5 l|? 5 1 5 1 A. B. C. D. 7 12 12 24 Lời giải
Số phần tử của tập hợp S l| |S| 9.9.8.7.6  27216 .
ọi B l| tập hợp c{c số có dạng a a a a a
a  a  a
a  a  a 1 2 3 4 5 sao cho 1 2 3 v| 3 4 5 .
Ta x{c định số phần tử của tập B như sau: Trường hợp 1
Chọn 5 chữ số bất kỳ không có chữ số 0 có 5
C9 c{ch, sau đó xếp 5 chữ số v|o 5 vị trí a a a a a 1 2 3 4 5 . Vị trí a a
3 có 1 c{ch chọn, vì 3 lớn nhất. Có 2 C a a
4 c{ch chọn hai số để xếp v|o hai vị trí 1 2 .
Có 1 c{ch chọn hai số để xếp v|o hai vị trí a a 4 5 . Suy ra có 5 2 C C  756 9 4 (số). Trường hợp 2
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 37
60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT
Chọn 5 chữ số bất kỳ phải có chữ số 0 có 4
C9 c{ch, sau đó xếp 5 chữ số v|o 5 vị trí a a a a a 1 2 3 4 5 . Vị trí a a
3 có 1 c{ch chọn, vì 3 lớn nhất. Có 2 C a a
3 c{ch chọn hai số để xếp v|o hai vị trí 1 2 .
Có 1 c{ch chọn hai số để xếp v|o hai vị trí a a 4 5 . Suy ra có 4 2 C C  378 9 3 (số).
Do đó số phần tử của tập B l| | |
B  756  378  1134 (số). 1 C 1
Vì vậy x{c suất cần tìm l| 1134  . 1 C 24 27216 Suy ra chọn D.  
Câu 53: Cho bất phương trình log   x  ax    x  ax   a 11 log  2 3 10 4 log a  2 3 12 0 3 1 3  .  7 
Giá trị thực của tham số a để bất phương trình trên có nghiệm duy nhất thuộc khoảng nào sau đ}y? A. 1; 0 B. 1; 2 C. 0; 1 D. 2;  Lời giải 1
Điều kiện x{c định 0  a  . 3
Biến đổi bất phương trình tương đương   log   x  ax    x  ax   a 11 log  2 3 10 4 log a  2 3 12 0 3 1 3   7   log  x  ax   x  ax   a 11 log  2 3 10 4.log a  2 3 12 0 3 7 3 
 log  2x  3ax 10  4.log x  ax   a  2 3 12 log a 11 7 3  3 Đặt 2 2 2 2
t  x  3ax  10  0  x  3ax  12  x  3ax  10  2  t  2 . Khi đó bất phương trình 1
trở thành log t  4log t   a  2 2 * 7 3    . log 3a 11  1 Nếu 0  a   log 3a  0 * 11
bất phương trình   trở thành 3
log t  4log 3alog t    t  t   a  2 2 1 log  4log  2 2 1 7 11 3 7 11 
Xét hàm số f t  log t  4 log  2 t  2 t  0 f 3  1 7 11 
 l| h|m đồng biến đồng thời   nên
f t  f   2
3  t  3  x  3ax  1  0 . Để phương trình có nghiệm duy nhất thì ta có 2
a  , nghiệm này không thỏa mãn. 3  1 2 Nếu a   log 3a  0 a  11
. Đến đ}y xét tương tự trường hợp 1 ta sẽ tìm được 3 3
38 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Câu 54: Cho hai số thực dương x,y thỏa mãn điều kiện 2  2  log x  y  1 2 2 x2y   2  1
y yx x
Tìm giá trị lớn nhất của biểu thức P  log     y x 2 4 .2 x y x y 1 1 1 1 1 A. B. C. D. 2 4 8 16 Lời giải
Biến đổi giả thiết ta được: 2 2 1  2  log
x  y  1   2  2 2 x2y  
y yx x x2 2  1 2 y  1 log      x y y x x y 1 1    2 1 2 1   2     2 x2 2 y  1 log         y x x2 1 2 y   y x x y 1 logx y 1 1 1  
Khi đó P viết lại thành P  log     y
x.2x y x y 2 2 1 a  log    y x x y 1   2 1 b  1
Để đơn giản ta đặt     2  a   1 x2 b  2 y b  1 a  1 2b 2
b 1  b b1  b 1
Thế v|o ta được P    2b 2 8
Câu 55: Gọi A là tập hợp các số tự nhiên gồm 5 chữ số. Chọn ngẫu nhiên một số từ tập A .
Tính xác suất để chọn được số chia hết cho 7 và có chữ số h|ng đơn vị bằng 2. 257 257 127 127 A. B. C. D. 90000 18000 90000 30000 Lời giải
Gọi số tự nhiên gồm 5 chữ số là abcde
Chọn a  0 có 9 cách.
Chọn b,c, d, e mỗi số có 10 cách. Nên 4 A  9.10 .
Gọi B là biến cố "chọn được tự nhiên gồm 5 chữ số chia hết cho 7 và có chữ số h|ng đơn vị bằng 2''.
Gọi số tự nhiên gồm 5 chữ số chia hết cho 7 và có chữ số h|ng đơn vị bằng 2 là abcd2
Ta có abcd2  10.abcd  2  7abcd  3abcd  2
abcd2 chia hết cho 7 nên 3abcd  2 chia hết cho 7 hay 3abcd  2  7t,(t  ) 7t  2 t  2
3abcd  2  7t  abcd 
 abcd  2t  3 3
Suy ra (t  2) 3 hay t  2  3n  t  3n  2 996 9995
Khi đó abcd  7n  4 mà 1000  abcd  9999 nên 1000  7n  4  9999   n  7 7
Mặt khác n là số nguyên  n 143;144;145;...;14  27 Nên B  1285 .
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 39
60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT
Câu 56 : Có tất cả bao nhiêu cặp số thực x; y thỏa mãn đồng thời 2 điều kiện 2
x 2x3 log  3 5 y4 3  5  ?
4 y  y  1   y  32  8 A. 3 B. 2 C. 1 D. 0 Lời giải 2 2 x 2x3 x 2x3 3 y4 3 y4 2 x 2x3 y3 Từ giả thiết ta suy ra  5   5  3  5  1  y  3  log3 5 3 5
 4 y  y  1  y  32  4y  1  y  y  32  3y  1 y  32  8y  3
 4 y  y  1  y  32  4y  1  y  y  32  3y  1 y  32  8 x  1 
Dấu “=” xảy ra khi và chỉ khi y  3 . Thế vào giả thiết ta được 2
x  2x  3  0   x   3
Vậy tồn tại 2 bộ số thỏa mãn yêu cầu đề bài
Câu 57: Cho (C )
y  x  mx  m 
m l| đồ thị của h|m số 3 3 1 (với
0 l| tham số thực). ọi d là
đường thẳng đi qua hai điểm cực trị của (C ). m
Đường thẳng d cắt đường tròn t}m
I 1;0 bán kính R  3 tại hai điểm ph}n biệt A, .
B ọi S l| tập hợp tất cả c{c gi{ trị của
m sao cho diện tích tam gi{c IAB đạt gi{ trị lớn nhất. Hỏi S có tất cả bao nhiêu phần tử ? A. 1 B. 2 C. 3 D. 0 Lời giải
Ta có d : y  2mx  1.  m 
1 1  2m2 2 2 2  1 2 1 
Do đó x  d I, d 2 2 2  
 2 , AB  2 R  x  2 9  x . 2 2 4m  1 4m  1 1 Vì vậy 2 2 S  AB x  x  x  x  x  y  IAB . 9 max 9  2 14. 2 0; 2 2  m 1 1  1  Dấu bằng đạt tại
  m    S   . 1 1 2  2 
Câu 58: Cho 3 số thực dương x,y,z thỏa mãn 2
2z  y . Khi biểu thức sau đạt giá trị nhỏ nhất, hãy tính log xyz 2 ? 2
P  log xy  log  3 3 3 3 x y  x z  4 2 2
 y  xy  2zy  2xz 2 2 A. 3 B. 2 C. 1 D. 0 Lời giải Ta có 2
P  log xy  log  3 3 3 3 x y  x z  4 2 2
 y  xy  2zy  2xz 2 2 2
 log xy  log  3 3 3 3
x y  x z    2
2z  y x  y 2
 log xy  log  3 3 3 3 x y  x z 2 2 2 2 
Theo bất đẳng thức AM – GM ta có 3 3 3 3 3 3 3
x y  z x  2x y z
40 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN    P  xy   x yz3 2 2 2 3 log log 2
  log xy  log  2 2 x yz  1 2 2 2 2    2  5 Trường hợp 1: 2
y  z  P  log xy  3log xy  1   2 2 4  5 Trường hợp 2: 2
y  z  P  log xz  3log xz  1   2 2 4 5 2
Vậy min P   , dấu “=” xảy ra khi và chỉ khi x 
, y  z  4  log xyz  1  4 2 16
Câu 59: Cho phương trình 2
sin 2x  cos 2x  sin x  cos x  2 cos x  m  m  0. Có bao
nhiêu giá trị nguyên của tham số m để phương trình có nghiệm ? A. 2. B. 3. C. 5. D. 9. Lời giải Điều kiện: 2
2 cos x  m  0.
Phương trình đã cho tương đương với 2
1  sin 2x  sin x  cos x  1  cos 2x  m  2 cos x  m   x  x2 2 2 sin cos
 sin x  cos x  2 cos x  m  2 cos x  m   x  x   x  x   x  m 2 2 2 2 sin cos sin cos 2 cos
 2 cos x  m Xét hàm   2
f t  t  t với t  0. Ta có f 't  2t  1  0, t
  0  Hàm số f t đồng biến. Mà f  x  x   f  2 sin cos
2 cos  m , suy ra 2
sin x  cos x  cos x  m   x  x2 2 2 sin cos
 2 cos x  m  1  sin 2x  2 cos x  m  sin 2x  cos 2x  . m Vì   
sin 2x  cos 2x  2 sin 2x      2 ; 2  4    
 Phương trình đã cho có nghiệm 2 2 m m       m 1  ;0;  1 . 1 1 k
Câu 60: Giả sử k là số thực lớn nhất sao cho bất đẳng thức   1  đúng với 2 2 2 sin x x     x  0;
. Khi đó gi{ trị của k là? 2    A. 5 B. 2 C. 4 D. 6 Lời giải 1 1 k 1 1 k Ta có   1     1 . 2 2 2 2 2 2 sin x x  sin x x  1 1   
Xét f x   , x  0; . 2 2 sin x x 2    2 cos x 2   
Ta sẽ chứng minh f x     0 , x  0; . 3 3 sin x x 2   
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 41
60 CÂU VẬN DỤNG CAO CÓ LỜI GIẢI CHI TIẾT 3 3
2 sin x  2x cos x
Thật vậy: f x   0 3 3 x sin x   3 3  
sin x  x cos x  0 , x  0; 2      sin x   3   
sin x  x cos x , x  0;  gx   x  0 , x  0; . 2     3 cos x  2  2 
 cosx6 3 cosx x 4 3 3 2  1 2 cos 1
Ta có gx   1  3 3 3 cos . x cos x 3 cos . x cos x  cosx 2 2 1 2  cosx 2 3 3 1            0 , x  0;  . 3 3 cos . x cos x  2    
Do đó g x  g 0  0 . Suy ra f x  0 , x  0; . 2    k    4 k
Vẽ bảng biến thiên ta suy ra f x  1  , x  0;  1   1   k  4 . 2  2    2 2  
42 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor