Ôn tập bài tập môn xác suất thống kê| Đại học Kinh tế Quốc Dân

Bài tập luyện tập Bài 1
Một nhóm gồm 10 sinh viên trong đó có 1 sinh viên học lực giỏi, 6 sinh viên khá và 3 sinh viên trung bình.
Chọn ngẫu nhiên 2 sinh viên, tính xác suất để chọn được 1 sinh viên khá. Giải.
Gọi C ”chọn được 1 sinh viên khá” 1 1 C C 24 8 6 4 P(C ) = = = = 0,533 2 C 45 15 10 Bài 2
Cho số liệu về người lao động ở một cơ quan:
Chọn ngẫu nhiên một người thì khả năng để người đó không mua một loại bảo hiểm nào trong hai loại trên là bao nhiêu? Giải
Gọi A ”người được chọn không mua bảo hiểm loại nào trong 2 loại” 𝟒𝟒𝟒𝟒 P(A) = ,
𝟐𝟐𝟒𝟒𝟒𝟒+𝟏𝟏𝟒𝟒𝟒 + 𝟒 𝟔𝟔𝟒𝟒+ = 𝟒𝟒 𝟏𝟏 𝟒𝟒𝟒𝟒 Bài 3
Một người đấu thầu hai dự án. Xác suất trúng thầu dự án thứ nhất và thứ hai lần lượt là 0,5
và 0,4; xác suất trúng thầu cả hai là 0,1. Tính xác suất:
(a) Trúng thầu ở ít nhất một dự án
(b) Trúng thầu dự án thứ hai, biết rằng trúng thầu dự án thứ n t hấ Giải: a)
A1 ” trúng thầu dự án 1”
A2 ” trung thaầu dư󰈨 an 2”
A” trung thaầu ơ󰈖 ıt nhaất 1 d
ư󰈨 an” => A=A1 ∪ A2
P(A) = P(A1) + P(A2) - P(A1∩ A2) = 0,5 + 0,4 – 0,1 = 0 8 , 0,1
b) P(A2 | A1) = P(A1∩A2)/ P(A1) = 0 = 0,2 ,5 Bài 4
Tỷ lệ sản phẩm loại II do một máy sản suất là 40%. Vậy trong số 5 sản phẩm do máy này sản xuất thì xác
suất để có ít nhất là 1 sản phẩm loại II bằng bao nhiêu? Giải:
Gọi A” có ít nhất 1 sản phẩm loại II ”
Ā” không có sản phẩm loại II nào” P(Ā) = 0 0 5 5
P(x = 0 n = 5, p = 0, 4) = C (0, 4) (1− 0, 4) = 0,6 = 0, 0778 5 P(A) = 1 – 0,0778 = 0,9222 Bài 5
Sinh viên tốt nghiệp tại một trường đại học có 60% là nữ và 40% là nam. Tỷ lệ có việc làm sau nửa năm
tốt nghiệp ở nữ là 80% và ở nam là 70%.
(a) Tìm tỉ lệ sinh viên có việc làm sau nửa năm tốt nghiệp
(b) Trong số sinh viên có việc làm sau nửa năm tốt nghiệp thì sinh viên nữ chiếm bao nhiêu phần trăm?
Giải: a) Đặt A “ sinh viên có việc làm sau nửa năm”.
A1 ” sinh viên là nữ ” A2 ” sinh viên là nam ”
P(A) = P(A1)P(A | A1) + P(A2) P(A | A2)
= 0,6 × 0,8 + 0,4 × 0,7 = 0 76 , b) Theo công thức Bayes thì: 0,6 × 0,8 P( A1/A) = 0,76 = 0,63 Bài 6
Trên một chuyến bay người ta thống kê được có 0,8% số hành khách bị mất hành lý. Trung bình
mỗi khách bị mất hành lý đòi bồi thường 5 triệu đồng. Công ty hàng không muốn tăng giá vé để
bù đắp số tiền phải bồi thường nói trên thì công ty nên tăng thêm giá vé là bao nhiều? Gi i ả .
Số tiền tăng thêm trên giá của 1 vé chính bằng số tiền bồi thường trung bình cho m t khách. ộ
Gọi X là số tiền bồi thường cho 1 khách bất kì, đơn vị triệu đồng
Nếu khách bị mất hành lý thì X = 5. Theo đề bài P(X = 5) = P(khách mất hành lý) = 0,008
Nếu khách không bị mất hành lý thì X = 0 và P(X = 0) = 1 – P(X=5) = 0,992
E(X) = 5.0,008 + 0.0,992 = 0,04 (triệu đồng) = 40 (nghìn ng) đồ
Vậy công ty nên tăng giá vé thêm 40 nghìn đồng để bù vào số tiề ồi thườ n b ng nói trên. Bài 7
Cho biết doanh thu một ngày của cửa hàng là biến ngẫu nhiên rời rạc X có bảng phân phối xác suất: X (triệu đồng) 8 9 10 11 12 P 0,15 0,3 0,4 0,1 0,05
a. Tìm xác suất doanh thu một ngày của cửa hàng ít nhất là 10 triệu đồng.
b. Tìm trung bình và phương sai về doanh thu một ngày của cửa hàng.
c. Biết lãi của cửa hàng bằng 10% doanh thu. Tính trung bình và phương sai về lãi một ngày của cửa hàng. Giải
a. Doanh thu một ngày của cửa hàng ít nhất
là 10 triệu đồng nghĩa là doanh thu X ≥ 10
P(X ≥ 10) = P(X = 10) + P(X = 11) + P(X = 12) = 0,4 + 0,1 + 0,05 = 0,55
b. E(X) = 8.0,15 + 9.0,3 + 10.0,4 + 11.0,1 + 12.0,05 = 9,6 (triệu đồng)
V(X) = 82.0,15 + 92.0,3 + 102.0,4 + 112.0,1 + 122.0,05 - 9,62 = 1,04 (triệu đồng2)
c. Gọi Y là lãi một ngày của cửa hàng thì Y = 10%.X = 0,1X (triệu đồng)
E(Y) = 0,1.E(X) = 0,1.9,6 = 0,96 (triệu đồng)
V(Y) = 0,11.V(X) = 0,01.1,04 = 0,0104 (triệu đồng2) Bài 8
Cho biết lương nhân viên một công ty lớn là biến ngẫu nhiên liên tục X (đơn vị: nghìn USD) có hàm mật độ x ác suất:
0 𝑣𝑣ớ𝑖𝑖 𝑥𝑥 ∉ (5; 9) 𝑓𝑓(𝑥𝑥) = � 𝑥𝑥− 5
𝑣𝑣ớ𝑖𝑖 𝑥𝑥 ∈ (5; 9) 8 8
a. Tìm tỷ lệ nhân viên có lương thấp hơn 7 nghìn USD.
b. Tìm lương trung bình của nhân viên công ty này. Giải
a. Lương thấp hơn 7 nghìn USD nghĩa là (X < 7)
Tỷ lệ nhân viên có lương thấp hơn 7 nghìn USD là P(X < 7) 7 7
𝑃𝑃(𝑋 𝑋 < 7) = � 𝑓𝑓(𝑥𝑥) =𝑑𝑑𝑥𝑥
� �𝑥𝑥 − 5� 𝑑𝑑𝑥𝑥 = 0,25 8 8 −∞ 5
b. Lương trung bình của nhân viên công ty này là E(X) (nghìn USD) +∞ 9 23
𝐸𝐸(𝑋𝑋) = � 𝑥𝑥𝑓𝑓(𝑥𝑥) = 𝑑𝑑𝑥𝑥
� 𝑥𝑥 �𝑥𝑥− 5� 𝑑𝑑𝑥𝑥= 8 8 3 −∞ 5 Bài 9
Một công ty A, theo quy định mỗi tháng trả lương cho công nhân n 1 lầ vào cu i ố tháng. Xác suất
để công ty trả chậm lương cho công nhân trong một tháng là 0,4.
a) Hãy cho biết quy luật phân phối xác suất của số lần trả chậm lương cho công nhân trong 12 tháng c a công ty ủ A.
b) Tính xác suất để trong 12 tháng có không quá 2 lần công ty A trả chậm lương cho công nhân. c) Tính s l
ố ần trả chậm lương trung bình của công ty A trong 12 tháng.
d) Tìm số lần trả chậm lương có thể ả x ề y ra nhi ấ
u nh t trong 12 tháng của công ty A. Hướ ẫ ả ng d n gi i
a) Số tháng trả chậm lương trong 12 tháng là X ~ B(12; 0,4) b) Pb = P(x = 0 | n = 2; p = 1
0,4) + P(x = 1 | n = 12; p = 0,4) + P(x = 2 | n = 12; p = 0,4) = …
c) E(X) = np = 12.0,4 = 4,8 lần
d) Cầm tìm mốt m0 là số nguyên thỏa mãn np + p – 1 ≤ m0 ≤ np + p ⇒ 4,2 ≤ m0 ≤ 5,2 ⇒ m0 = 5 Bài 10
Thu nhập của nhân viên văn phòng trên địa bàn Hà Nội là biến ngẫu nhiên có phân phối ch ẩ u n,
với thu nhập trung bình là 10 tri l
ệu/tháng, độ ệch chuẩn là 2 triệu/tháng. a) Tính xác suất để m p nhi
ột nhân viên văn phòng có thu nhậ ều hơn 14 triệu/tháng.
b) Tìm tỷ lệ nhân viên văn phòng có thu nhập không quá 8 triệu/ tháng.
c) Tìm tỷ lệ nhân viên văn phòng có thu nhập từ 7,5 triệu/ tháng đến 15 triệu/tháng.
d) Trong một 100 nhân viên văn phòng thì có trung bình bao nhiêu nhân viên có mức thu nhập cao hơn trung bình? Hướ ẫ ả ng d n gi i
Thu nhập của m t nhân viên là X ~ N(10; 2 ộ 2)
a) P(X > 14) = 1 – Ф[(1 -1
4 0)/2] = 1 – Ф(2) = – 0,9772 = 0,0228 1
b) P(X ≤ 8) = Ф[(8-10)/2] = Ф(-1) = 0,1587
c) P(7,5 ≤ X ≤ 15) = … = Ф(2,5) – Ф(-1,25) = 0,9938 – 0,1056 = 0,888 2
d) Xác suất một nhân viên bất kì có lương vao hơn mức trung bình là 0,5 (tính chất của phân phối Chuẩn)
Số nhân viên có lương cao hơn mức trung bình trong số 100 người là Y ~ B(100; 0,5) E(Y) = 100.0,5 = 50 người. Bài 11
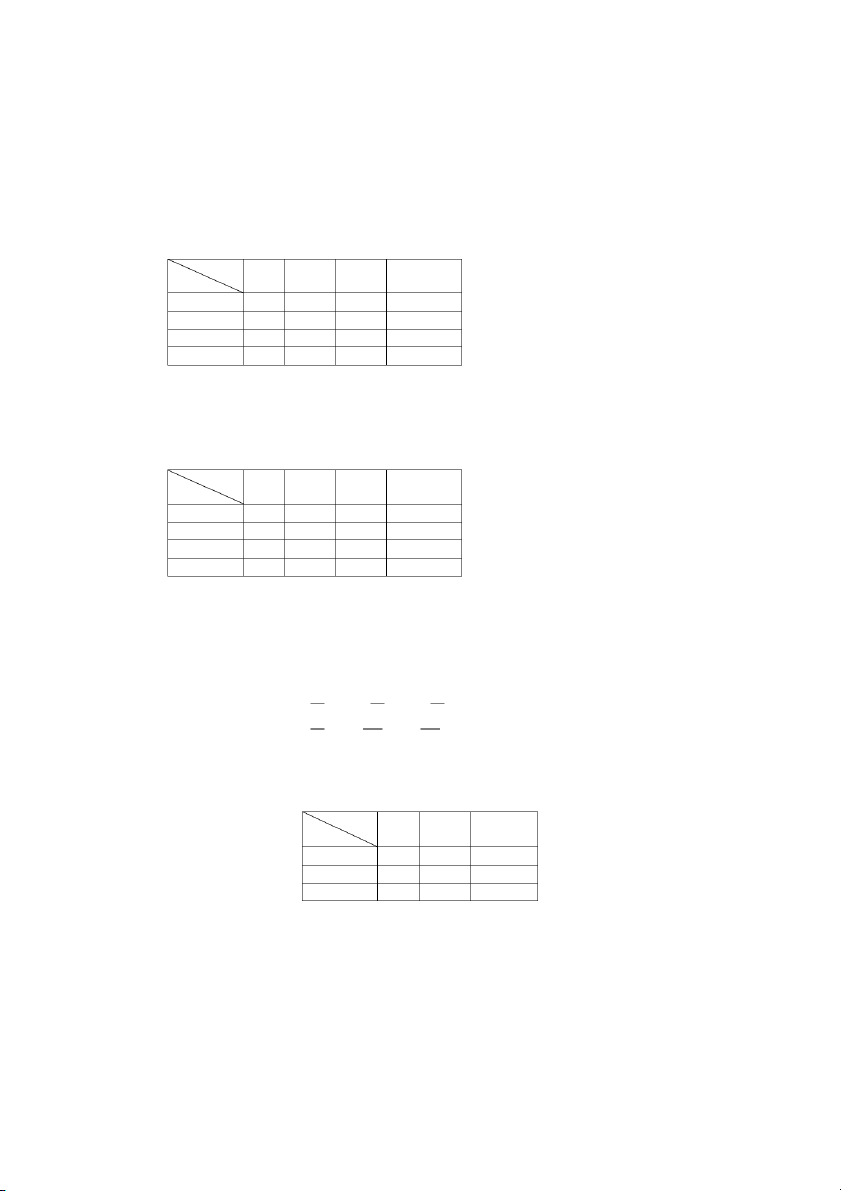
Cho X là doanh thu và Y là chi phí quảng cáo của một công ty (đơn vị: triệu đồng) 𝑌𝑌 10 20 30 𝑃𝑃(𝑋𝑋) 𝑋𝑋 600 0,1 0,14 0,3 800 0,1 0,1 900 0,4 𝑃𝑃(𝑌𝑌) 0,4 0,2 1
a) Hãy điền vào các giá trị còn thiếu trong bảng.
b) Tính chi phí quảng cáo trung bình và doanh thu trung bình của công ty.
c) Tính doanh thu trung bình khi chi phí quảng cáo là 10 triệu.
d) Tính chi phí quảng cáo trung bình khi doanh thu là 900 triệu. Hướng dẫn giải
Kí hiệu giá trị ở các ô như sau 𝑌𝑌 10 20 30 𝑃𝑃(𝑋𝑋) 𝑋𝑋 600 0,1 0,14 0,3 800 0,1 0,1 0,3 900 0,4 𝑃𝑃(𝑌𝑌) 0,4 0,4 0,2 1
a) a = 0,3 – 0,1 – 0,14 = 0,06
b = (1 – 0,3 – 0,4) – 0,1 – 0,1 = 0,1
c = 0,4 – 0,1 – 0,1 = 0,2
d = (1 – 0,4 – 0,2) – 0,14 – 0,1 = 0,16
e = 0,2 – 0,06 – 0,1 = 0,04
b) E(X) = 600.0,3 + 800.0,3 + 900.0,4 = 780
E(Y) = 10.0,4 + 20.0,4 + 30.0,2 = 18 0,1 0,1 0,2
c) 𝐸𝐸(𝑋𝑋|𝑌 𝑌 = 10) = 600.
0,4 + 800. 0,4 + 900. 0,4 = 800 0,2 0,16 0,04
d) 𝐸𝐸(𝑌𝑌|𝑋 𝑋 = 900) = 10. 0,4 + 20. 0,4 + 30. 0,4 = 16 Bài 12
Cho X, Y lần lượt là thu nhập trong một tháng của chồng và vợ trong gia đình (đơn vị: triệu đồng) Y 6 9 15 X 7 0,1 0,2 0,1 15 0,2 0 0,1 20 0,2 0,1 0
a) Thu nhập của hai vợ chồng có phụ thuộc nhau không?
b) Tính thu nhập trung bình của cả hai vợ chồng.
c) Thu nhập của hai vợ chồng tương quan dương hay âm? Hướng ẫ d n giải
a) Từ bảng có P(X = 7) = 0,1 + 0,2 + 0,2 = 0,4
P(Y = 6) = 0,1 + 0,2 + 0,2 = 0,5
P(X = 7, Y = 6) = 0,1 ≠ 0,4.0,5 = P(X = 7).P(Y = 6) ⇒ X và Y phụ thuộc nhau
b) E(X + Y) = E(X) + E(Y) = (7.0,4 + 15.0,3 + 20.0,3) + (6.0,5 + 9.0,3 + 15.0,2) = 13,3 + 8,7 = 22
c) E(X.Y) = 7.6.0,1 + 7.9.0,2 + 7.15.0,1 + 15.6.0,2 + 15.15.0,1 + 20.6.0,2 + 20.9.0,1 = 109,8
Cov(X, Y) = 109,8 – 13,3.8,7 = - 5,91, nghĩa là tương quan âm