Ôn Tập CT - Thống Kê Kinh Doanh Chi Tiết và Công Thức Xác Suất | Đại học Văn Lang

lOMoARcPSD| 61538472 lOMoARcPSD| 61538472
CHƯƠNG 2 BIẾN NGẪU NHIÊN
I. Biến ngẫu nhiên rời rạc
II. Biến ngẫu nhiên liên tục
5.Giá trị tin chắc nhất
5. Giá trị tin chắc nhất
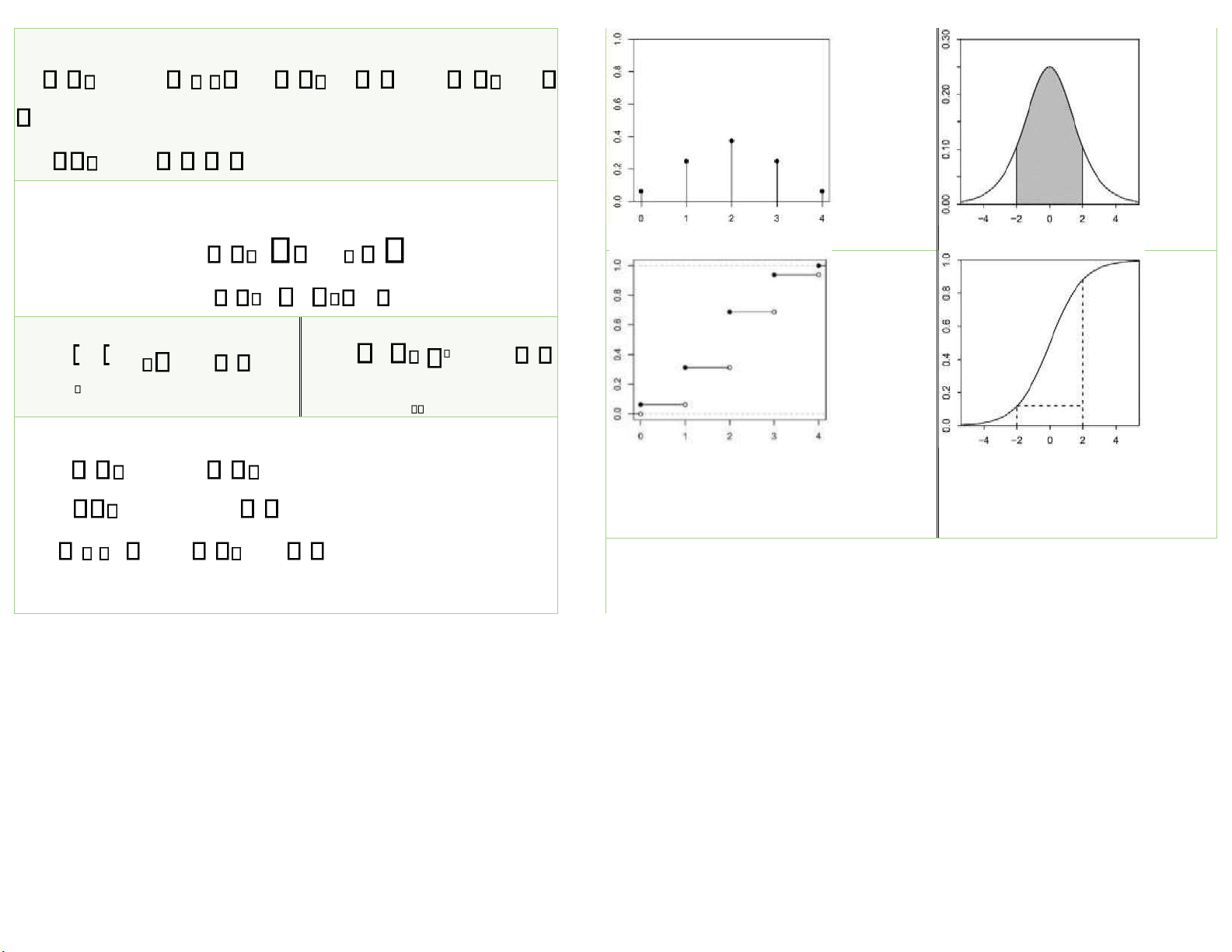
1. Bảng phân phối xác suất Bảng
1. Hàm mật độ xác suất
phân phối xác suất của biến ngẫu
Hàm mật độ xác suất của biến Mod X x Mod X x if x
i Max f xi 1;n 0 f x 0 Max f nhiên X ngẫu nhiên X x i x 
f x là hàm mật độ khi 6. Trung vị 6. Trung vị i 0,5 X x1 x2 … xn f x 0 x 
MedX x0 P X x0 P … MedX x i 0,5 i P X x f x f x f x n 0,5 x P X x 1 2
xi pi và n 0 f x dx 0,5 f x dx 1
Trong đó f x i P
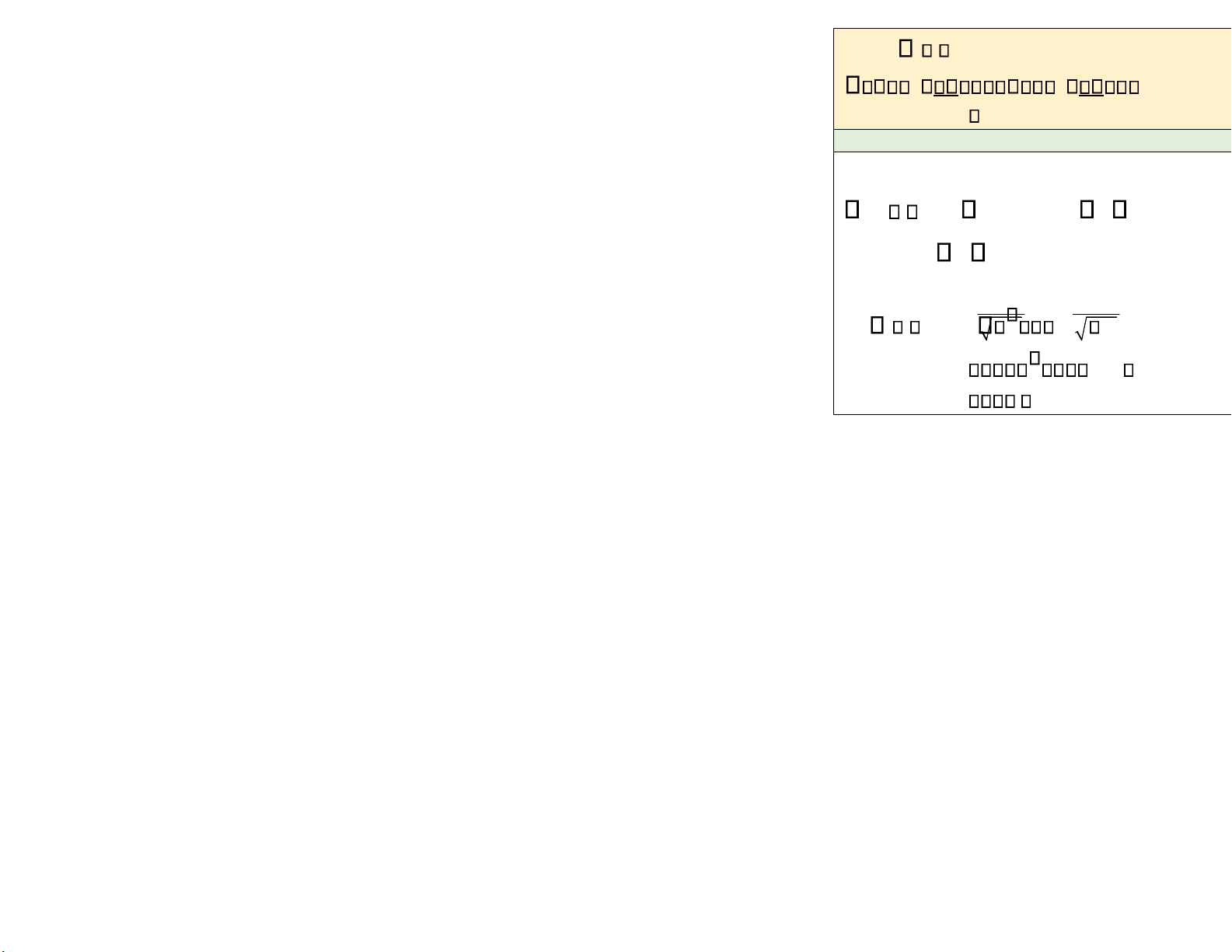
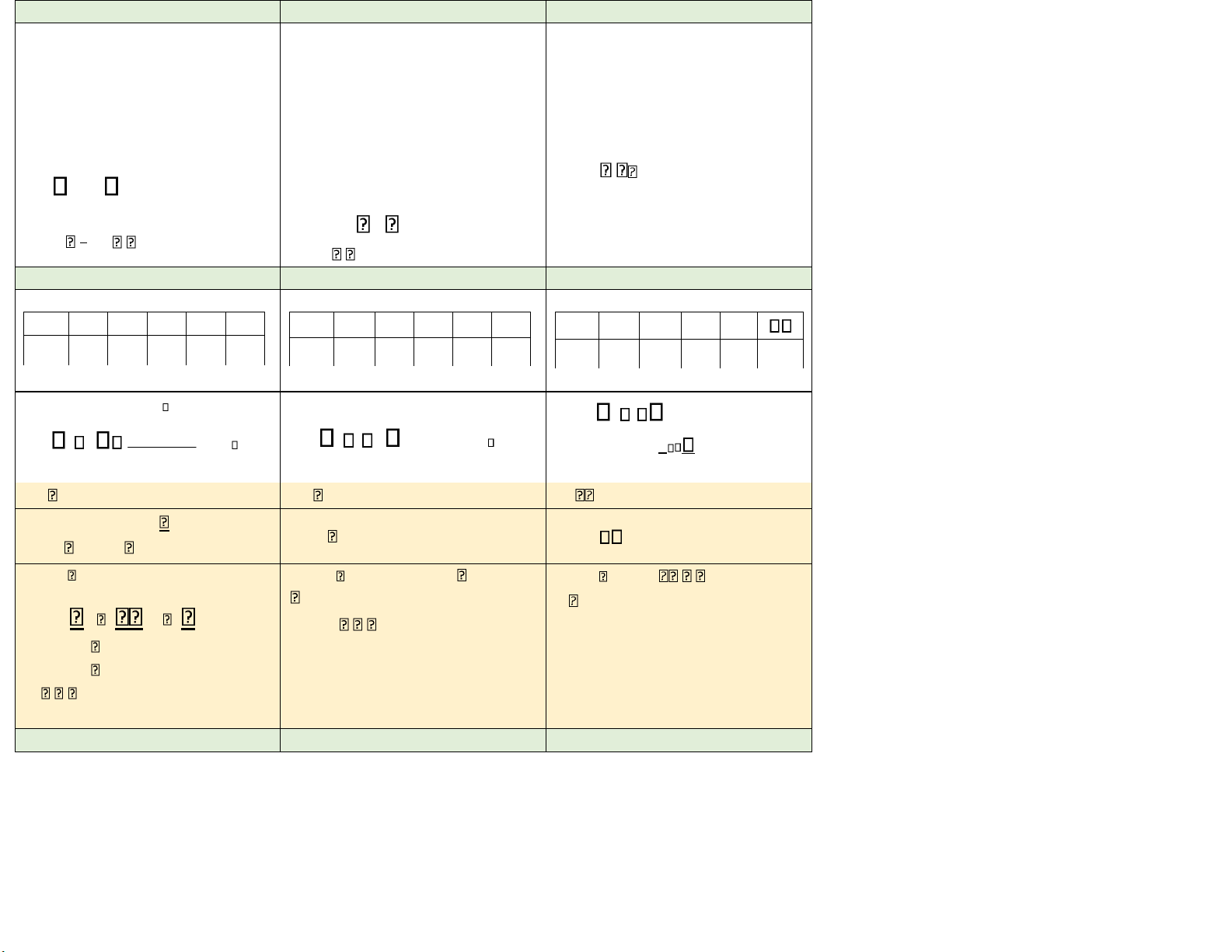
Hàm mật độ và hàm phân phối f x X i i 1 1 F x P X x 0 x x 1 2. Xác suất 2.Xác suất p 0 x 1 x x x1 2 b x x 2 x x3
P a Xb f x i P a Xb f x dx p p 1 2 ... f t dt x a x ib F x xn x a F x 3. Kỳ vọng 3. Kỳ vọng ...
Kỳ vọng biến ngẫu nhiên X :
Kỳ vọng hàm biến ngẫ nhiên X : n 1 x 1 E X x f x i i E X xf x dx i 1 P a x b F b
Kỳ vọng hàm biến ngẫu nhiên
Kỳ vọng hàm biến ngẫu nhiên F a F ' E g X n g x
x f x i f E g X g x f x x i i 1 dx lOMoARcPSD| 61538472
Tính chất kỳ vọng E C
C ; E X Y
E X E Y ; E CX CE X
với C là hằng số. E XY
E X E Y khi XY; là hai biến ngẫu nhiên độc lập. 4. Phương sai Var X E X EX 2 Var X E X2 EX 2 n Với E X 2 x f x Với E X 2 x f x dx2 i2 i i 1
Tính chất phương sai Var C 0 ; Var X
0 với mọi biến ngẫu nhiên X . Var CX C Var X2
Var X Y Var X
Var Y khi XY; là hai biến ngẫu nhiên độc lập lOMoARcPSD| 61538472
Phân phối chuẩn đơn giản
Y ~N 0;1 EY 0 ; VarY 1 ; ModY 0 ( ) a t2 1 e 2 P 0 ta a 2 dt 0
x : Hàm Lapace 0,5 ; 0,5 x x
Phân phối chuẩn tổng quát EX X ~N ; ; 2 VarX 2 ModX a 1 e x2 2 2dx P X a a 2 lOMoARcPSD| 61538472
CHƯƠNG 3: CÁC QUY LUẬT PHÂN PHỐI THÔNG DỤNG P a X b b a
pp Nhị thức xấp xỉ pp chuẩn
Nếu n lớn và p không quá gần 0 và 1
0,1 p 0,9 thì X ~ B n p ; xấp xỉ bằng X ~N np npq ; và P a X b b np npq a np npq lOMoARcPSD| 61538472
Phân phối siêu bội
Phân Phối nhị thức Phân phối Poisson Miêu tả Miêu tả Miêu tả
Cho một tập gồm N phần tử, trong Thực hiện phép thử trong đó chỉ Phân phối nhị thức khi số lần thực đó có N
quan tâm biến cố A xảy ra hay hiện n lớn và xác suất xảy ra biến
A phần tử loại A, từ tập này không xảy ra. Với xác suất xảy ra cố A lại nhỏ.
chọn ra n phần tử ngẫu nhiên.
biến cố A là p . Thực hiện phép thử X : biến ngẫu nhiên chỉ số lần A
X : biến ngẫu nhiên chỉ số phần tử lặp lại n độc lập với nhau. thành công
loại A có trong n phần tử X ~H N X : biến ngẫu nhiên chỉ số lần biến X ~ P N n ; cố A thành công. A; N X B n p~ ,
Đặt p A ; q 1 p N Đặt q 1 p Đặc trưng số Đặc trưng số Đặc trưng số
Bảng phân phối xác suất
Bảng phân phối xác suất
Bảng phân phối xác suất X … k … X 0 … k … n X 0 … k … P … pk … P
p0 … pk … pn P p0 … pk … 0 C Ck n k P X k P X k N
P X k C p q A nN N A nk k n k e k CN k! EX np EX np EX N n VarX npq VarX VarX npq N 1
ModX k thỏa với
ModX k thỏa với M ModX k thỏa 1 np q thì k 1 1 n NA M k M 1 M thì N 2 M 1 k M
Pp siêu bội xấp xỉ pp nhị thức
Pp Nhị thức Xấp xỉ pp Poisson lOMoARcPSD| 61538472
Nếu N lớn và n rất nhỏ so với
Nếu n lớn và p có giá trị rất gần N n 5%.N
0 hoặc 1 p 0,1 p0,9
X H N N n~ ; A; xấp xỉ bằng
X B n p~ ; xấp xỉ bằng X P~ với np N
X B n p~ ; với p A N
CHƯƠNG 4 : THỐNG KÊ MÔ TẢ
Tổ chứa trung vị là tổ chứa ½ tổng lượng quan sát. X x1 x2 … xk X
X1MIN X1MAX
X2MIN X2MAX … XkMIN XkMAX Me X Me Min nhMeMe S2 SMe 1 n n1 n2 … nk X x1 x2 … xk n n1 n2 … nk n n k (1) Trung bình cộng.
(2) Trung bình cộng có trọng số. x nx (3) x X Trung bình nhân i d 1 X i 1 i 1 i ;
2 X i 1k i i ; 3 X n xx x1 (X liên tục : n x i XiMIN XiMAX ) 2... n n ni 1 S 1 X 1 i 1 2 n xi 2 ; 2S2 n n X M
i ; Tổ chức Mod là tổ có lớn nhất. i Mi Mo Min
: cận dưới tổ chứa Mod. xi X 2 hi n i 1 n 1 i 1
h : chiều dài tổ chứa Mod. Mo
Hệ số biến thiên V S .100% M ; ;
: mật độ tổ chứa Mod, tổ trước X Mo MMo 1 MMo 1 ModX X Mo Min hMo M Mo MMMoMo 1 và sau tổ chứa Mod.
Phân phối mẫu Giả sử mẫu X X1; MMMoMo 1 M Mo 1
2;. .;Xn lấy từ tổng thể có quy luật
phân phối chuẩn X ~ N ; lOMoARcPSD| 61538472 Phân phối Student
. Trong một tổng thể quan sát tỷ lệ phần tử loại A xác suất chọn được phần tử loại A trong tổng thể là p .  X ~ N ; 2 X n N~ 0;1 
n 12 S2 ~ n2 1  XS n T~ n 1
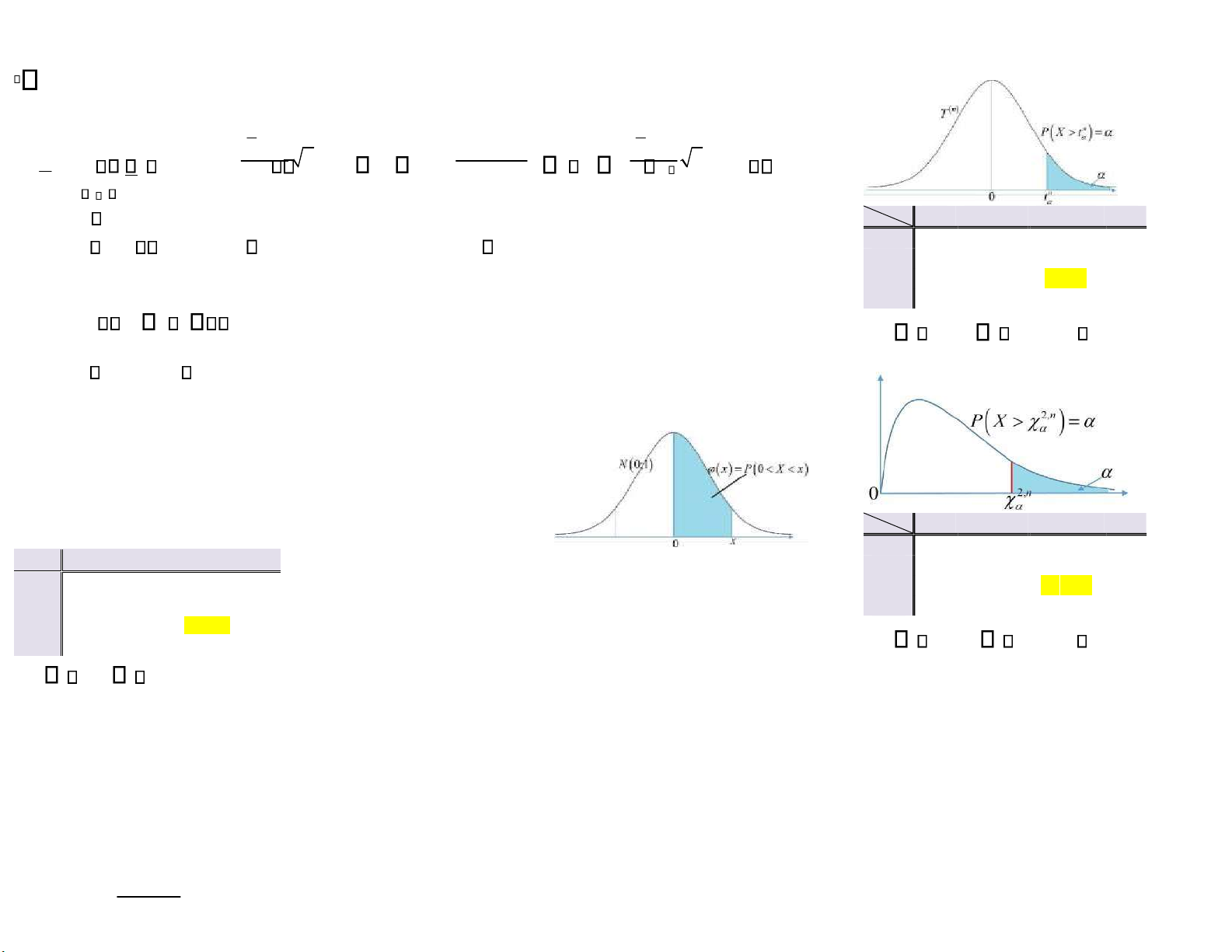
n α … 0 ,02 , 0 025 … … … … … … n 9 … 2,398 2,262 … 10 … 2,359 2 ,228 … … … … … … f ~N p ;p 1 p
P X 2,228 0,025 ;n 10 
Phân phối Chi bình phương n
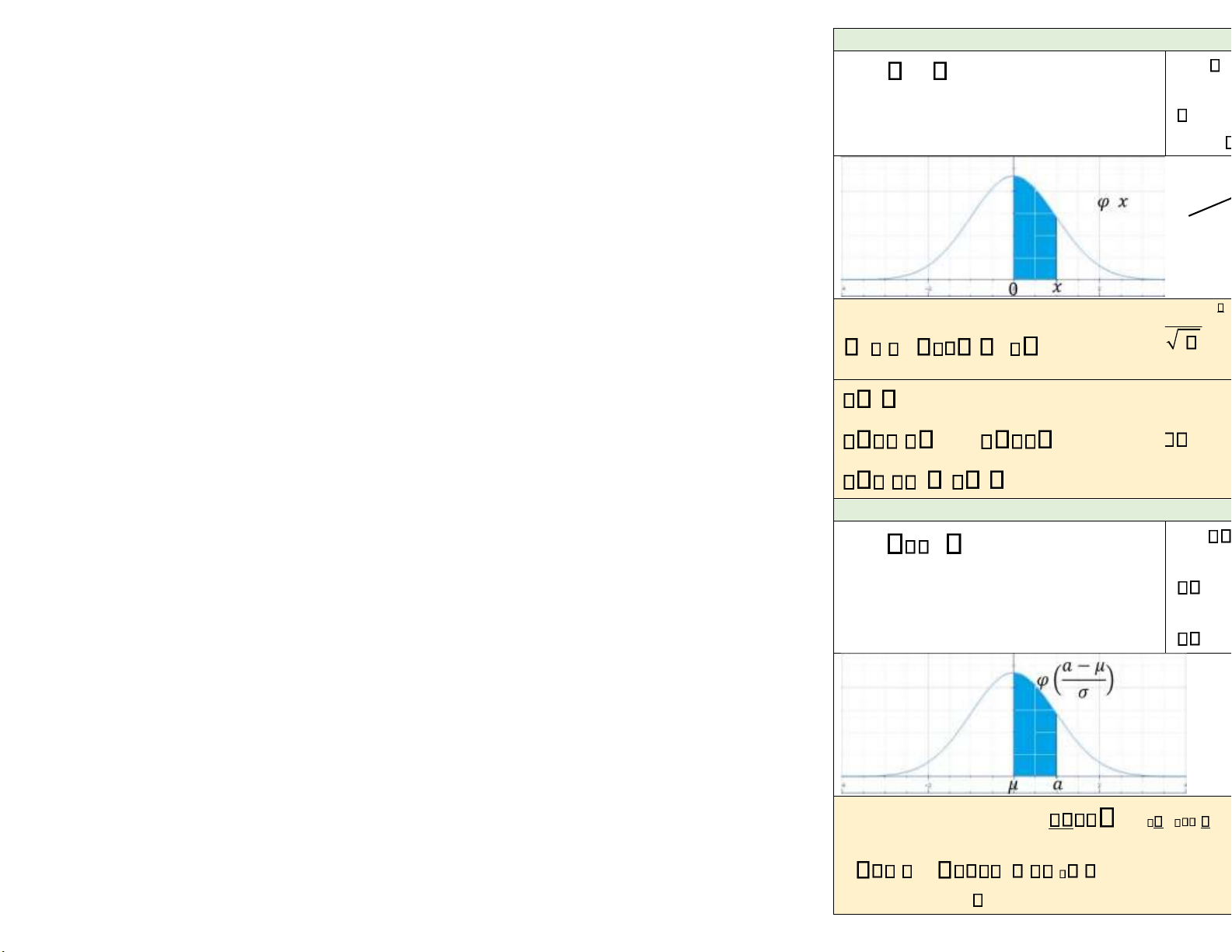
Các quy luật phân phối liên tục Phân phối chuẩn
n α … 0 ,95 , 0 05 … … … … … … x … 0.05 0.06 … 9 … 3,325 16,919 … … … … … … 10 … 3,940 18 ,307 … 1.8
… 0.4678 0.4686 … … … … … … 1.9
… 0.4744 0.4750 … … … … … …
P X 18,307 0,05 ; n 10 P X 1,96 0,475
DÙNG MÁY TÍNH CASIO TÍNH TOÁN QUY LUẬT PHÂN PHỐI. lOMoARcPSD| 61538472 lOMoARcPSD| 61538472 lOMoARcPSD| 61538472 Trường hợp Trị thống kê Đối thiết Kết luận
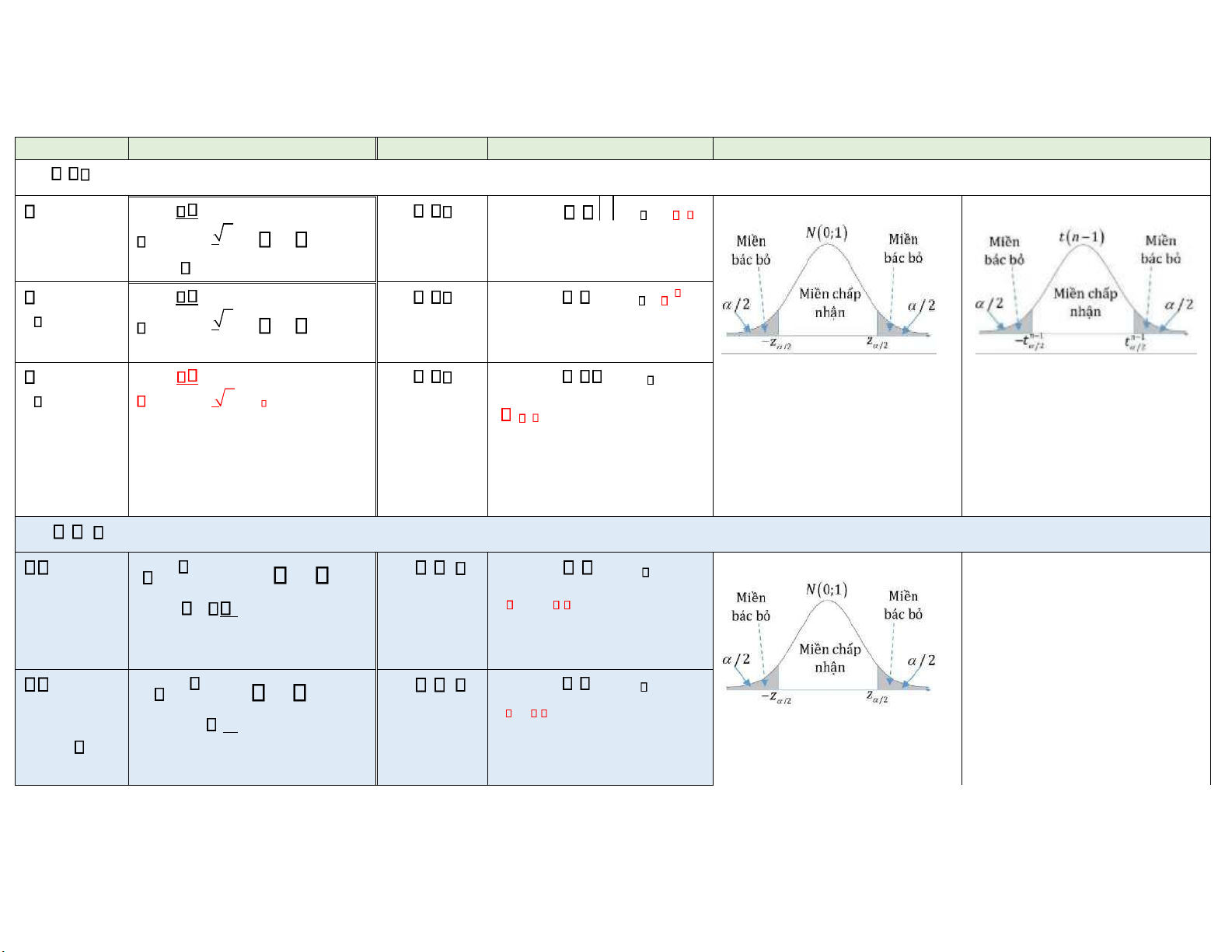
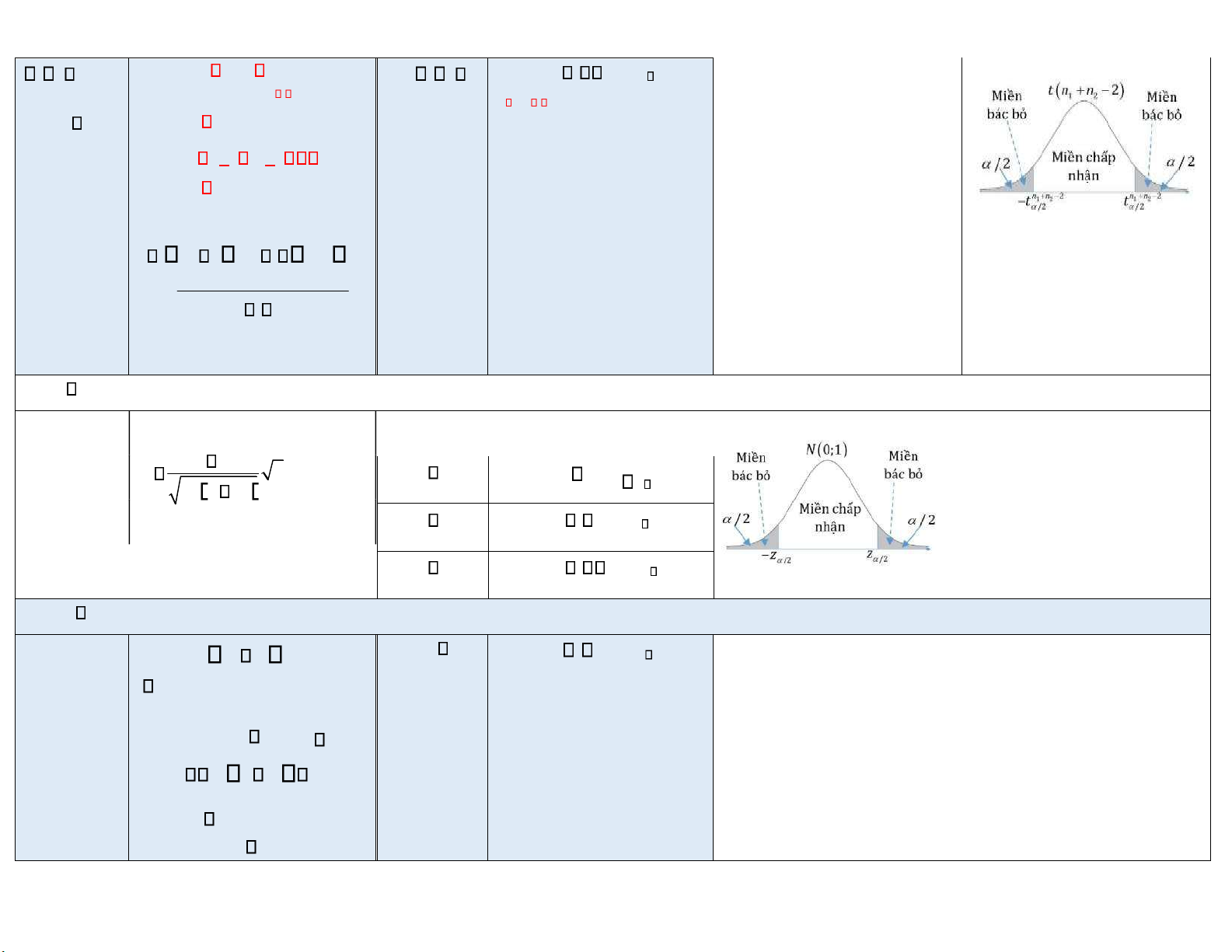
Miền bác bỏ kiểm định hai phía H0 : 0 : đã biết X H1 :
0 Bác bỏ H0 z z /2;t n /21 z 0 n N~ 0;1 : chưa biết X H1 :
0 Bác bỏ H0 z z ; t n 1 n 30 z 0 n N~ 0;1 S Theo phân phối chuẩn Theo phân phối Student : chưa biết X H1 : 0 Bác bỏ H0 z z ; n 30 z 0 n T~ n 1 t S n 1 H0 : 1 2 Theo phân phối Chuẩn 1; 2 : đã z X H 1 X2 ~ N 0;1 1 :
1 2 Bác bỏ H0 z z /2 ; biết t 12 22 n n1 2/2 2 n1 n2 1; 2 : chưa z X H 1 X2 ~N 0;1 1 :
1 2 Bác bỏ H0 z z ; biết t n n S 1 2 2 12 S22 n n1 2; 30 n1 n2 lOMoARcPSD| 61538472 X X z 1 2 : 1
H1 : 1 2 Bác bỏ H0 z z ; chưa biết 2 ~Tn 2 1 n2 t n n1 2 2 n n1 2; 30
S2 n11 n12
Với phương sai chung 2 mẫu: Theo phân phối Student
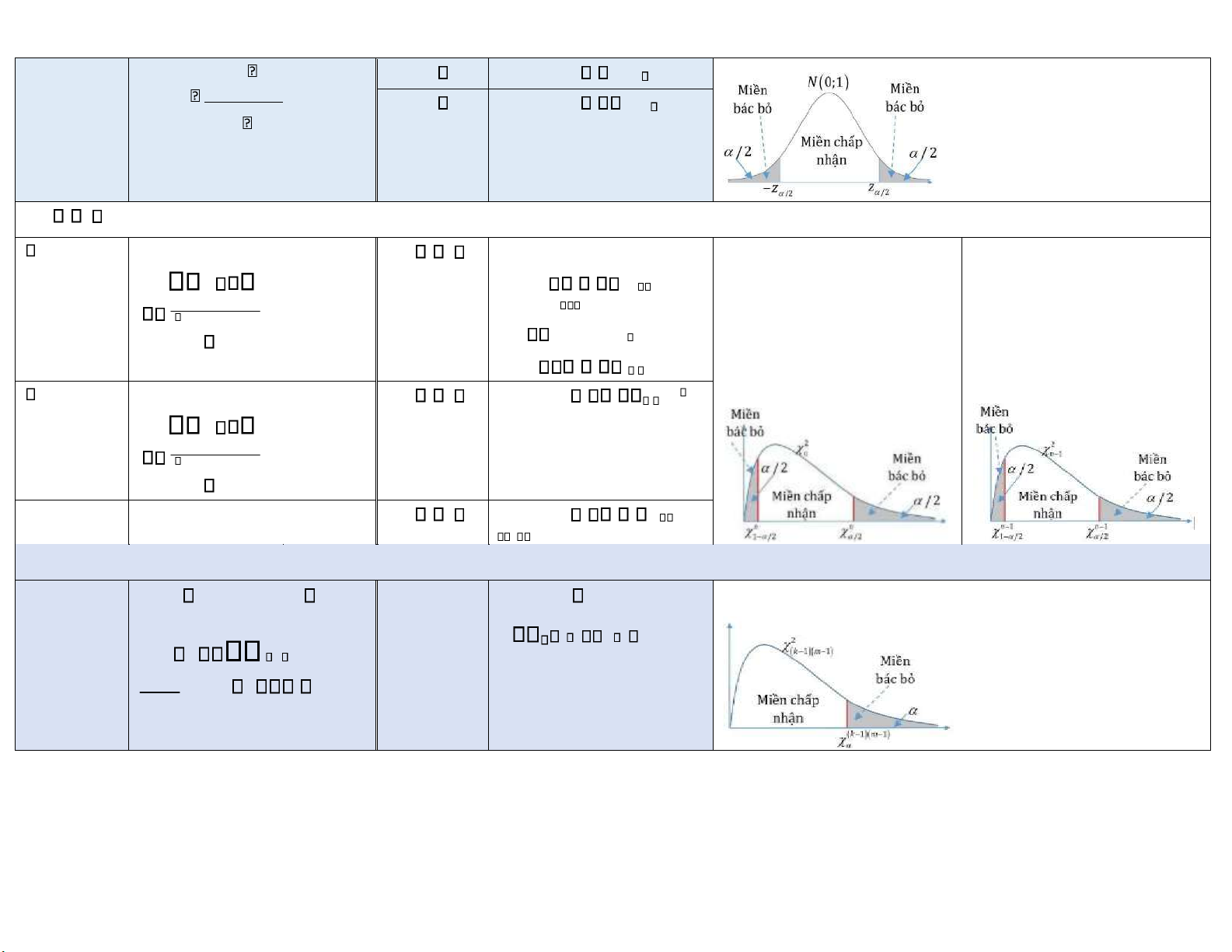
S2 n1 1 S12 n21 S22 n1 n2 2 H0 : p p0 f p 0 z n
H1 : p p0
Bác bỏ H0 z z /2 p 1 p 0 0 H1 : p p0 Bác bỏ H0 z z H 1 : p p0 Bác bỏ H0 z z
H0 : p1 p2 f f H 1 : p1 p2 Bác bỏ H0 z z /2 z 1 2 1 1 f 1 f n1 n2 lOMoARcPSD| 61538472
Chương 6 : KIỂM ĐỊNH GIẢ THIẾT THỐNG KÊ lOMoARcPSD| 61538472 n f n f : tỷ lệ
H1 : p1 p2 Bác bỏ H0 z z Với f 1 1 2 2
H1 : p1 p2 Bác bỏ H0 z z n1 n2
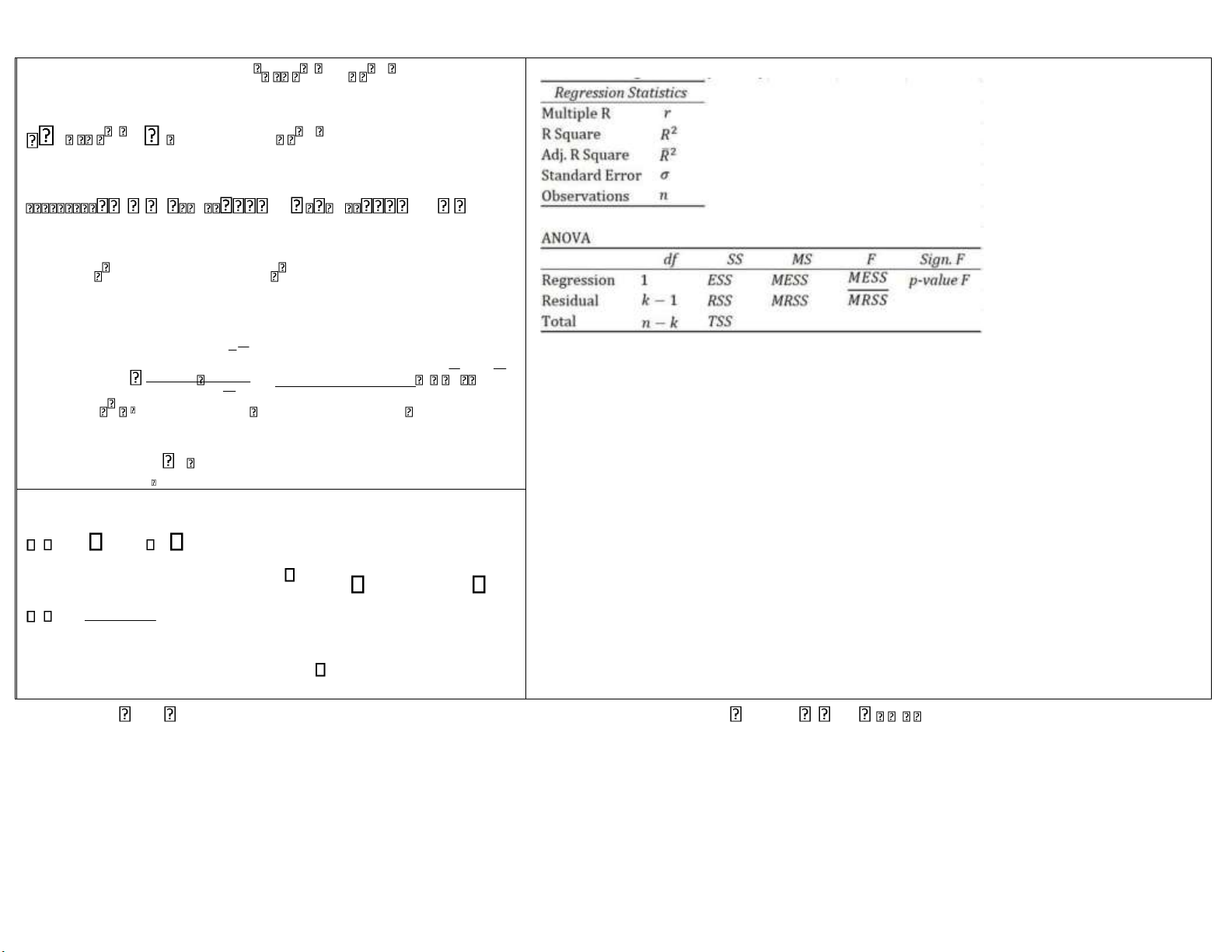
phần tử loại A chung của hai mẫu H0 : 2 02 : đã biết n H1 : 2 02 Bác bỏ xi 2 1n /2; 1n 1/2 i 1 2 H0 n ; n /21 0 /2 : chưa biết n
H1 : 2 02 Bác bỏ H0 n; n 1 xi 2 i 1 2 0
H1 : 2 02 Bác bỏ H0 1n ; n 1
H0 : X Y; độc l ập với nhau. k m n2 H1 : X Y; Bác bỏ H0 phụ thuộc G k 1 m 1 G n i 1 1j p qi .ij j 1
pi : tổng dòng i. qj : tổng cột j.
Chương 7: TƯƠNG QUAN - MÔ HÌNH HỒI QUY lOMoARcPSD| 61538472
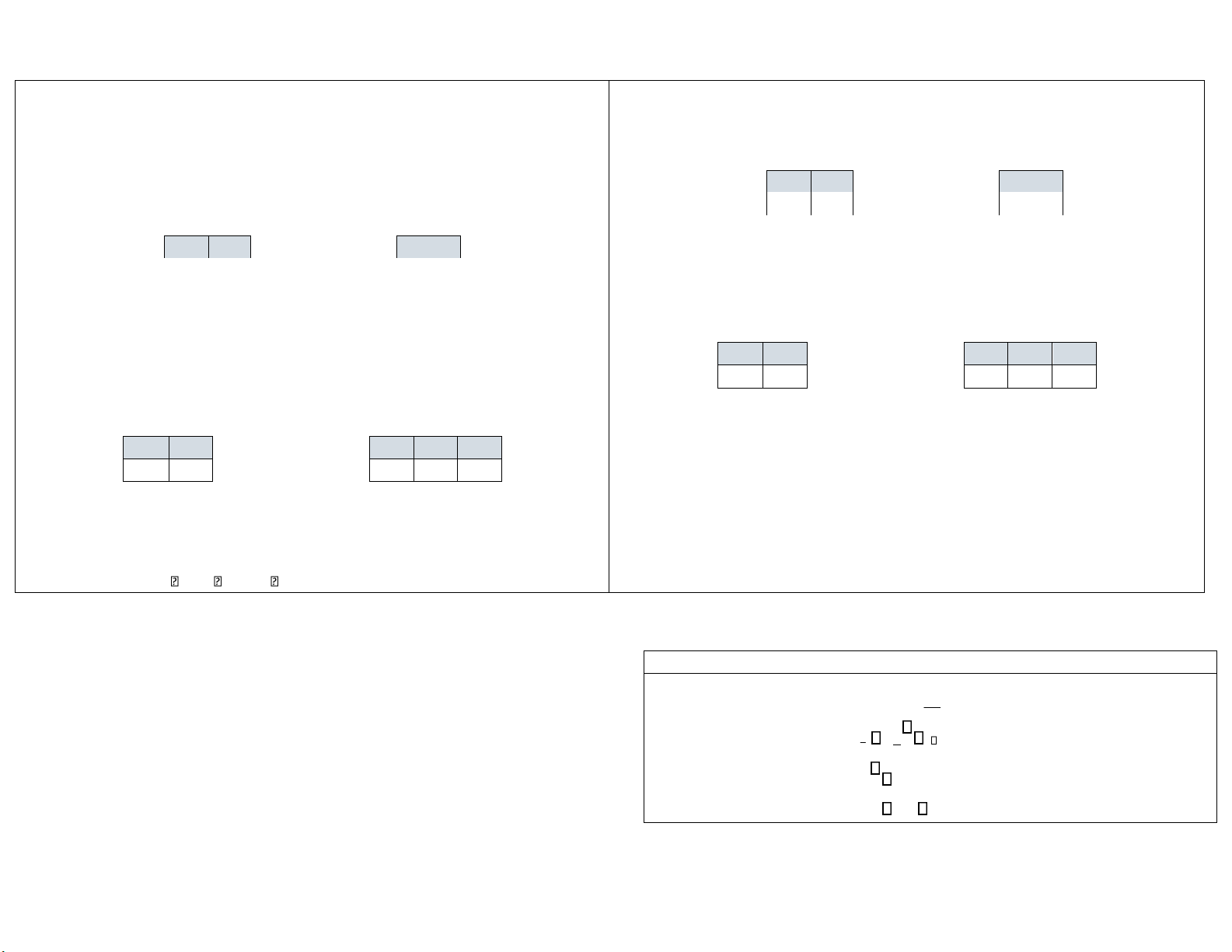
Các đại lượng tổng tích chéo Bảng ANOVA. Bậc tự Tổng bình phương Cách tính Ý nghĩa do SXY XYi i nXY ; SXX X nXi2 2 ; SYY Y nYi2 2
Sự biến động của biến phụ thuộc do
Hệ số tương quan giữa 2 biến XY; . TSS S
tất cả các yếu tố. YY n 1 TSS Yi Y 2
Sự biến động của biến phụ thuộc do RSS Y 2 i Y i RSS TSS ESS
n 2 các yếu tố ngoài mô hình.
Sự biến động của biến phụ thuộc do ESS
các yếu tố trong mô hình hồi quy. 22SXX 1 ESS Y i Y 2 XX YY 1 Với trong đó
Phương sai của phần dư : 2
RSS ; với phương sai của sai số ngẫu nhiên : 2 2 XY 0,2;0,2 : XY;
không có tương quan tuyến tính n 2 XY
1; 0,8 : XY; tương quan tuyến tính nghịch biến mạnh ESS RSS
Hệ số phù hợp : R2 1 TSS TSS XY 0,8;1
: XY; tương quan tuyến tính đồng biến mạnh VarVar 12 S nS1XXXXX i22 2 ;Se i Var i .
Phương sai của hệ sồ hồi quy : lOMoARcPSD| 61538472
Hàm hồi quy mẫu (đơn biến) : Y ; thỏa 1 2xi 1; 2 Y 2 thỏa hệ i 1 2Xi
MIN và từ đó 1; 2 X in 11 XXi2 i 2 2 XYYii i Trong đó
: gọi là hệ số chặn và gọi là hệ số góc 1 2
Công thức tính hệ số hồi quy n
Cấu trúc bảng ANOVA (EXCEL) 2 i 1n XYi i nXY2 SXY 1 Y 2X Hệ số góc và Hệ số chặn 2 S Xi nX XX i 1
Ý nghĩa hệ số hồi quy đơn. 1 E Y X
| 0 : khi biến độc lập tiến về 0 thì trung bình của
biến phụ thuộc phản ánh bởi giá trị 1 . dE Y X |
: khi biến độc lập thay đổi 1 lượng 2 dX thì trung dX
bình biến phụ thuộc thay đổi 1 lượng là 2dX .
Với bộ dữ liệu X Y , trong đó . i; i
X là biến độc lập và Y là biến phụ thuộc, mô hình hồi quy tổng thể PRF E Y X : | i 1 2Xi lOMoARcPSD| 61538472
PHỤ LỤC BẤM MÁY CASIO.
Cách bấm máy tính cho phần thống kê (máy 570)
Cách bấm máy tính cho phần thống kê (máy 580)
Bước 1. Vào chế độ thống kê; tạo bảng có tần số hoặc không tần số.
Bước 1. Vào chế độ thống kê; tạo bảng có tần số hoặc không tần số. qwR4, trong đó
qwR3, trong đó: 1: Bảng số liệu có tần số. 2: Bảng số liệu không tần
1: Bảng số liệu có tần số. 2: Bảng số.
số liệu không tần số.
Bước 2. Chọn loại X n Hoặc X thống kê:
Bước 2. Chọn loại thống kê:  Nếu là bài … … … toán ước lượng
 Nếu là bài toán ước lượng và kiểm định chọn: w31 và kiểm định chọn: w61 X n Hoặc X
Sau khi nhập dữ liệu xong bấm Cvà chọn T2 Đọc bảng … … …
kết quả thống kê mô tả:
Sau khi nhập dữ liệu xong bấm C, để xuất các đại lượng thống kê mô tả chọn q14, trong đó
 Nếu là bài toán tương quan hồi quy (mô hình hồi quy đơn biến dạng  Trung bình mẫu q142 tuyến tính) chọn : w62
 độ lệch chuẩn mẫu hiệu chỉnh q144 X Y Hoặc X Y n … … … … …
 Nếu là bài toán tương quan hồi quy (mô hình hồi quy đơn biến dạng
 Tính tổng của các đại lượng giữa x y : i; i T2 tuyến tính) chọn : w32
 Tính hệ số hồi quy : T3 X Y Hoặc X Y n … … … … …
 Tính tổng của các đại lượng giữa x y :
i; i q13, trong đó:
 Đưa ra các đặc trưng của dữ liệu x y : i; i q14
 Đưa ra giá trị của hệ số mô hình hồi quy: q15 Trong đó ,1: ; và 1 2 : 2 3 :
2. Dự báo bằng tốc độ phát triển bình quân 1 Yn n 1
Tốc độ phát triển bình quân t Y1 lOMoARcPSD| 61538472  Dự báo Y n L Yn. t L
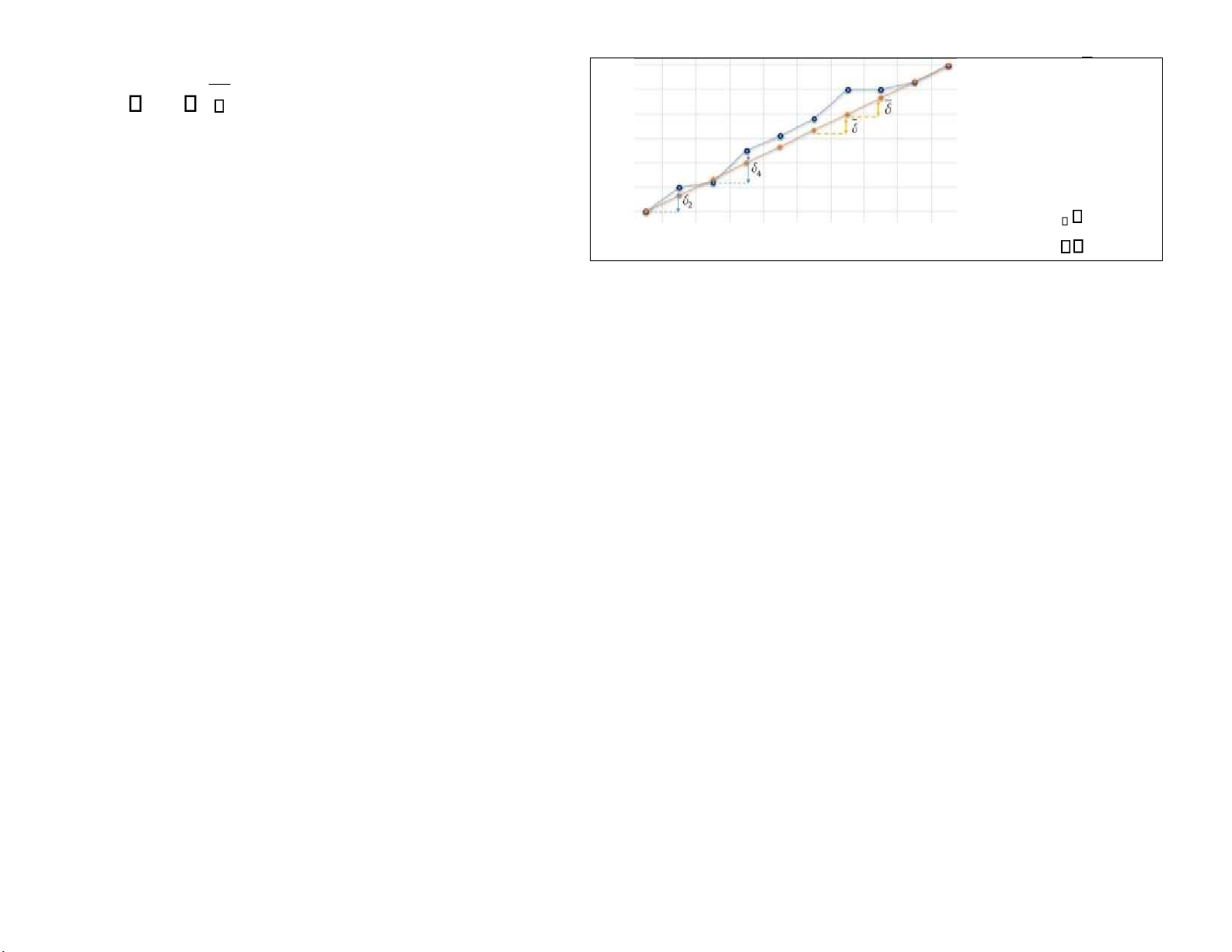
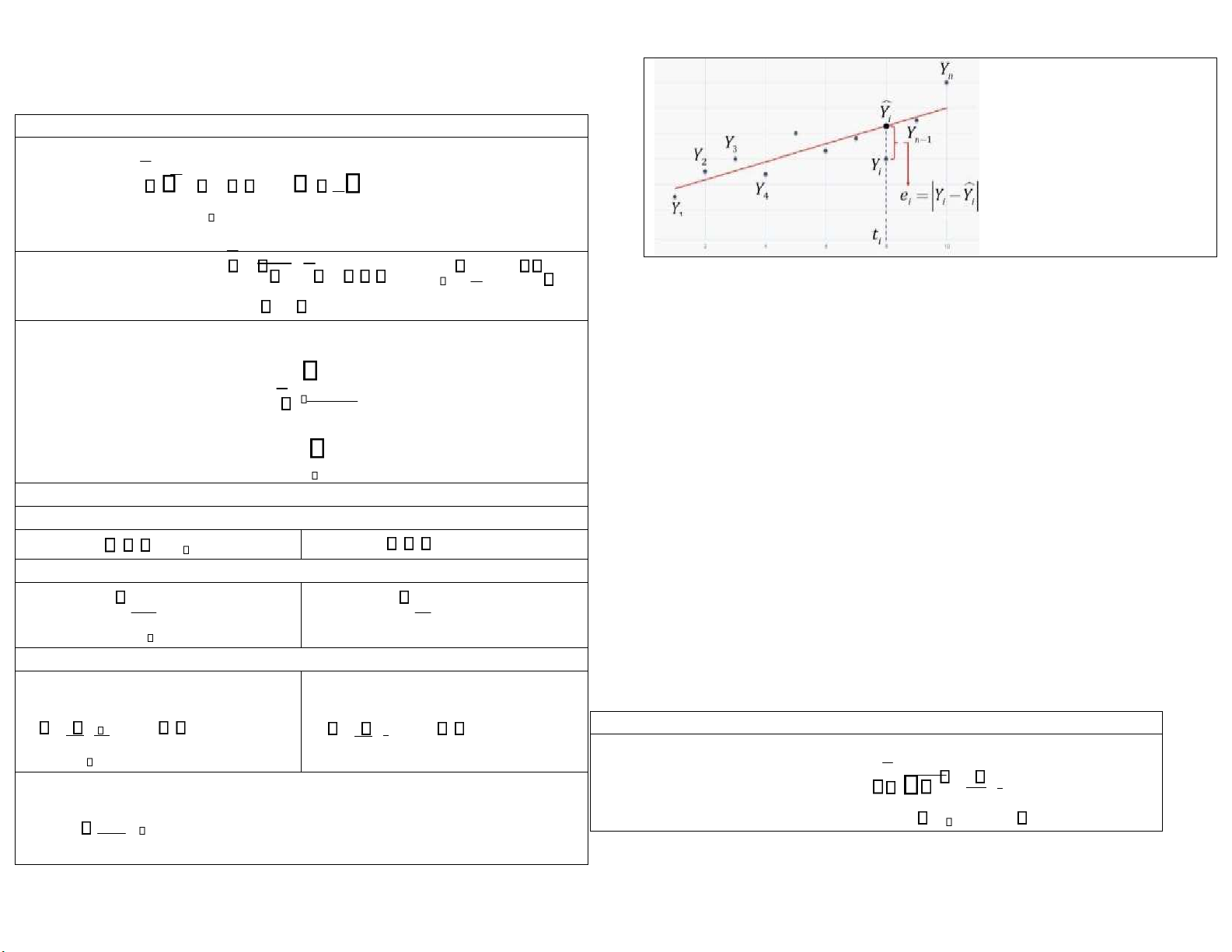
3. Dự báo bằng hàm ngoại suy xu thế dạng tuyến tính
Hàm hồi quy mẫu (đơn biến): Y ; thỏa 1 2ti 1; 2 Y 2 thỏa hệ i 1 2ti
MIN và từ đó 1; 2 ti n 1 1 ti2 t i 2 2 tYi Yi i ; Trong đó 1
và 2 gọi là hệ số hồi quy n 2 i 1n XYi i nXY2 SXY 1 Y 2X Hệ số góc và Hệ số chặn 2 S Xi nX XX i 1 lOMoARcPSD| 61538472
1. Trung bình chuỗi thời gian: 1 1 n
Chuỗi thời kỳ: Y Y 1 Y2 ... Yn Yi n n i 1
Chuỗi thời điểm cách đều: 1 1 Y 1Y 1 Y2 Y3 ... Yn 1 2Yn n 1 2 k Yni i
Chuỗi thời điểm không cách đều: Y i 1 k ni i 1
2. Các đặc trưng biến động của chuỗi thời gian:
Lượng tăng giảm tuyệt đối (đơn vị : là đơn vị lượng biến) Liên hoàn: i Y Yii 1
Định gốc : i Y Yi 1
Tốc độ phát triển (đơn vị : %) Liên hoàn: Y Y t i Định gốc: i i 100% Ti 100% Yi 1 Y1
Tốc độ tăng giảm (đơn vị : %) Liên hoàn: Định gốc: a
1. Dự báo bằng lượng tăng giảm tuyệt đối bình quân i
Yi Yi 1100% ti 100% A i
Yi Y1100% Ti 100% 1 n Yi 1 Y1
Lượng tăng giảm tuyệt đối ứng với 1% tốc độ tăng giảm (đơn vị của lượng
Lượng tăng giảm tuyệt đối bình quân Yn Y1 i biến) n 1 g i 1 n 1 i Yi 1 100 lOMoARcPSD| 61538472
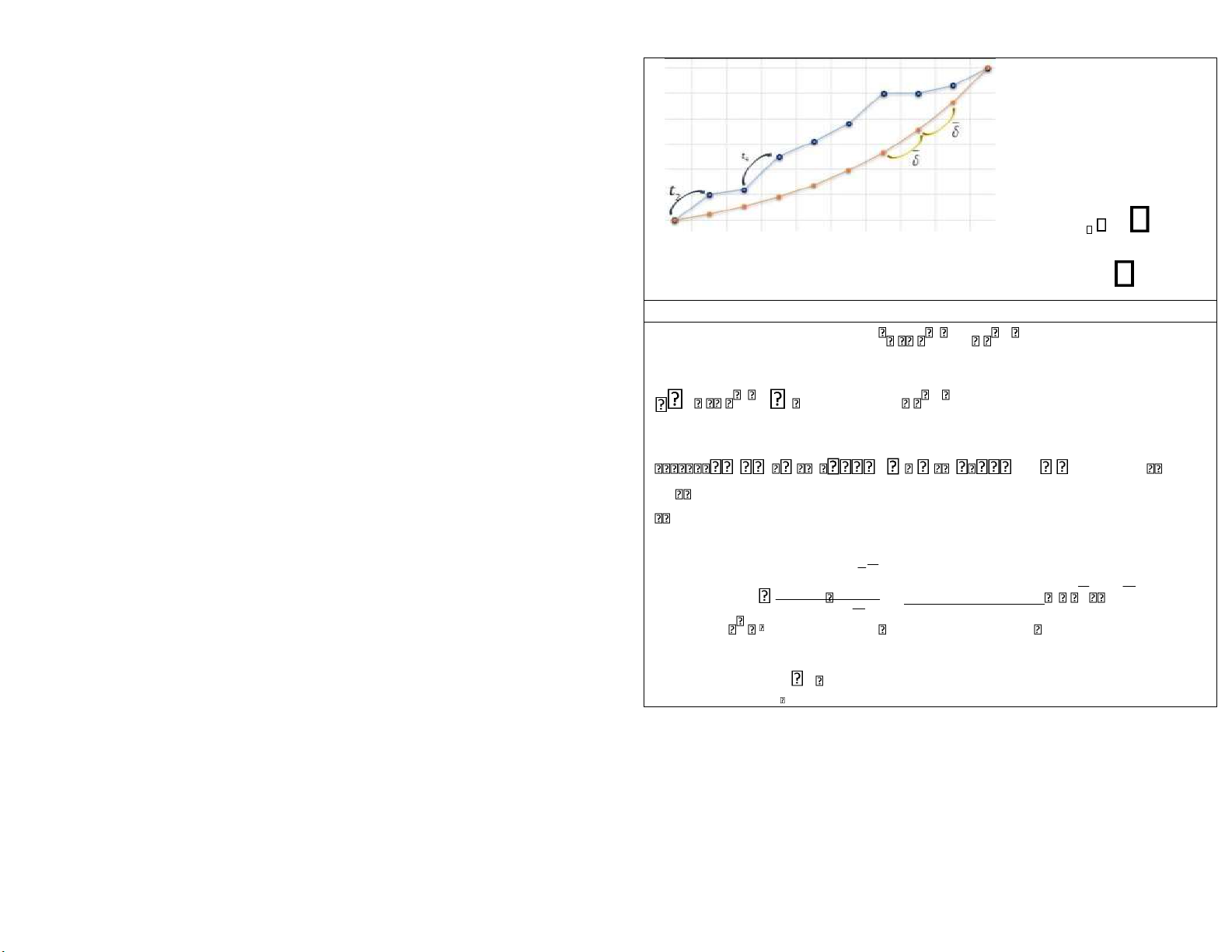
Chương 8 : CHUỖI THỜI GIAN VÀ DỰ BÁO
Chuỗi thời gian t Yi; i ;i 1,n
Mô hình dự báo đơn giản 
Dự báo : Y n L Yn .L