Định hướng ôn tập thi cuối kỳ trường điện từ môn Vật lý đại cương | Đại học Bách Khoa Hà Nội

VIỆN ĐIỆN TỬ VIỄN THÔNG
TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI TRƯỜNG ĐIỆN TỪ ÔN TẬP CUỐI KỲ GV. TẠ SƠN XUẤT TRƯỜNG ĐIỆN TỪ
Chương 2: Điện trường tĩnh và từ trường tĩnh
2.3. HỆ THỐNG PT CỦA ĐIỆN TRƯỜNG TĨNH Phương trình Ý nghĩa vật lý
Biểu thị tính chất không xoáy của điện trường. Điện trường là 𝑟𝑜𝑡 ത 𝐸 = 0
một trường thế, cường độ trường có thể biểu thị qua gradient của
Hay 𝑔𝑟𝑎𝑑 𝑈 = − ത 𝐸 một hàm thế vô hướng
Điện trường là một trường có nguồn. Nguồn của điện trường chính 𝑑𝑖𝑣 ഥ 𝐷 = 𝜌 với ഥ 𝐷 = 𝜀 ത 𝐸 là các điện tích
Điều kiện bờ tổng quát
Thành phần tiếp tuyến của điện trường liên tục khi chuyển dịch từ 𝐸𝑡2 = 𝐸𝑡1
môi trường này sang môi trường kia
𝐷𝑛1 − 𝐷𝑛2 = 𝜎 (khi có tồn
Thành phần pháp tuyến của
tại điện tích mặt tại bờ
vec-tơ điện cảm liên tục khi chuyển từ )
môi trường này sang môi trường khác nếu tại bờ không có điện
𝐷𝑛1 − 𝐷𝑛2 = 0 (khi không tích tự
tồn tại điện tích mặt tại bờ
do, và bị gián đoạn nếu ở bờ có điện tích tự do )
𝜀1𝐸𝑛1 = 𝜀2𝐸𝑛2
Thành phần pháp tuyến của điện trường luôn bị gián đoạn tại bờ Mật độ năng lượng: 1 𝜔 ത 𝑒 = 𝐸 ഥ 𝐷 2 1 TRƯỜNG ĐIỆN TỪ
Chương 2: Điện trường tĩnh và từ trường tĩnh
2.6. HỆ THỐNG PT CỦA TỪ TRƯỜNG TĨNH Phương trình Ý nghĩa vật lý
Nguyên lý liên tục của từ thông
Từ trường là trường không có nguồn. Trong tự nhiên không 𝑑𝑖𝑣𝐵 = 0
න 𝑑𝑖𝑣𝐵𝑑𝑉 = 0
có từ tích là nguồn của từ trường 𝑉
Định luật toàn dòng điện
Từ trường là trường xoáy. Đường sức từ trường là những
đường khép kín. Tại mỗi điểm, cường độ xoáy bằng mật độ ׯ ഥ
𝐻 ҧ𝑙 = 𝐼 hay 𝑟𝑜𝑡 ഥ 𝐻 = 𝐽ҧ 𝑙
dòng điện tại điểm ấy
Điều kiện bờ tổng quát
- Thành phần pháp tuyến của ഥ
𝑩 liên tục khi chuyển từ môi
trường này sang môi trường khác. B và n1 = Bn2
𝐻𝑡1 − 𝐻𝑡2 = 𝐽𝑠
- Thành phần tiếp tuyến của ഥ
𝑯 gián đoạn tại bờ điện môi và
(bờ giữa điện môi và kim loại)
kim loại, khoảng gián đoạn có giá trị bằng mật độ dòng điện 𝐻𝑡1 = 𝐻𝑡2
- Thành phần tiếp tuyến của ഥ
𝑯 liên tục khi chuyển qua bờ (bờ giữa 2 điện môi) giữa 2 điện môi Mật độ năng lượng: 1 𝜔 ത 𝑀 = 𝐵 ഥ 𝐻 2 2 TRƯỜNG ĐIỆN TỪ
Chương 3: Trường điện từ biến thiên
3.4.1. HỆ THỐNG PHƯƠNG TRÌNH MAXWELL Dạng vi phân Dạng tích phân Ý nghĩa vật lý
Định luật toàn dòng điện
- Trong việc tạo ra từ trường, dòng điện dịch cũng
có vai trò tương đương như dòng điện dẫn. Chúng 𝜕 ത 𝐸 𝑑 ഥ ഥ 𝑟𝑜𝑡 ഥ 𝐻 = 𝐽ҧ + 𝜀 ර 𝐻 ഥ 𝑑𝑙 = 𝐼 + න 𝐷 𝑑𝑆 tạo ra từ trường xoáy. 𝜕𝑡 𝑑𝑡 𝑆 𝑆
- Quy luật biến thiên của điện trường theo thời gian
xác định quy luật phân bố của từ trường trong không gian
Định luật tổng quát về cảm ứng điện từ
Từ trường biến thiên tạo ra điện trường xoáy. Quy 𝜕 ഥ 𝐻 𝑑𝜙 ത 𝑟𝑜𝑡 ത 𝐸 = −𝜇 ර 𝐸 ഥ 𝑑𝑙 = −
luật biến thiên của từ trường theo thời gian xác 𝜕𝑡 𝑑𝑡 𝑙
định quy luật phân bố của điện trường trong không gian 𝑑𝑖𝑣 𝜀 ത 𝐸 = 𝜌 න 𝜀 ത 𝐸 𝑑𝑆 = ෍ 𝑞
Điện trường có thể có nguồn. Nguồn của điện
trường là các điện tích. 𝑆 𝑑𝑖𝑣 𝜇 ഥ 𝐻 = 0 න 𝜀 ഥ 𝐻 𝑑𝑆 = 0
Từ trường không có nguồn. Trong tự nhiên không có các từ tích tự do. 𝑆 3 TRƯỜNG ĐIỆN TỪ
Chương 4: Sóng điện từ phẳng
4.1. KHÁI NIỆM SÓNG ĐIỆN TỪ PHẲNG
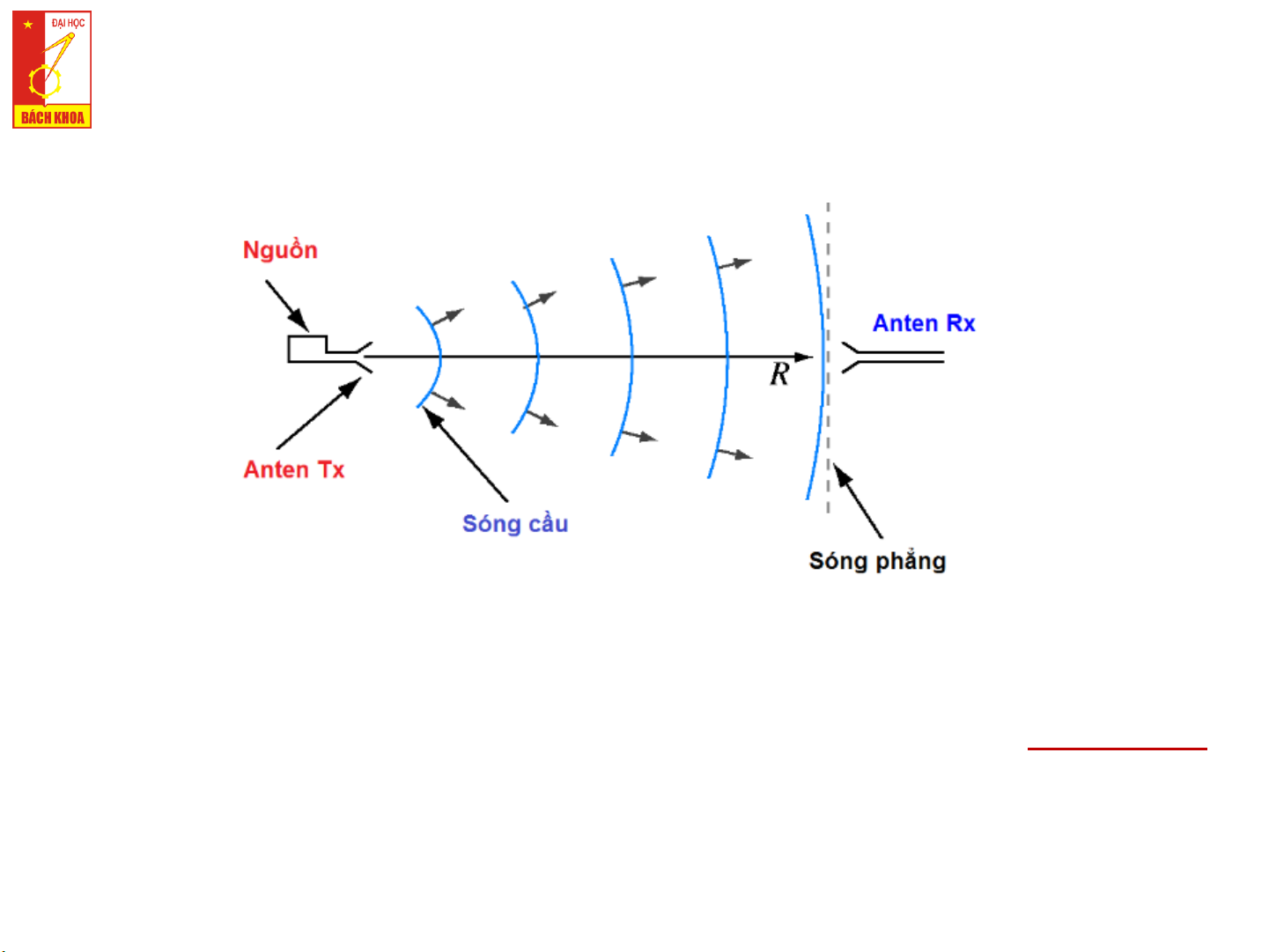
❑ Tại mỗi điểm trong không gian, ത 𝐸 và ഥ
𝐻 có biên độ và pha xác định.
❑ Mặt đồng biên: là tập hợp các điểm của trường có biên độ giống nhau.
❑ Mặt đồng pha: là tập hợp các điểm của trường có pha giống nhau. Vận tốc pha
của sóng là vận tốc dịch chuyển của các mặt đồng pha.
❑ Mặt đồng nhất hay mặt sóng là các điểm có pha và biên độ giống nhau.
❑ Nếu mặt sóng là mặt phẳng, ta có sóng điện từ phẳng. 4 TRƯỜNG ĐIỆN TỪ
Chương 4: Sóng điện từ phẳng
4.2.1. SÓNG PHẲNG ĐIỀU HÒA
❑ Pt Maxwell đối với môi trường điện môi lý tưởng (𝜎 = 0, 𝐽ҧ = 0, 𝜌 = 0) 𝜕 ത 𝐸 𝑟𝑜𝑡 ഥ 𝐻 = 𝜀 (I) 𝑑𝑖𝑣 ത 𝐸 = 0 (III) 𝜕𝑡 𝜕 ഥ 𝐻 𝑟𝑜𝑡 ത 𝐸 = −𝜇 (II) 𝑑𝑖𝑣 ഥ 𝐻 = 0 (IV) 𝜕𝑡
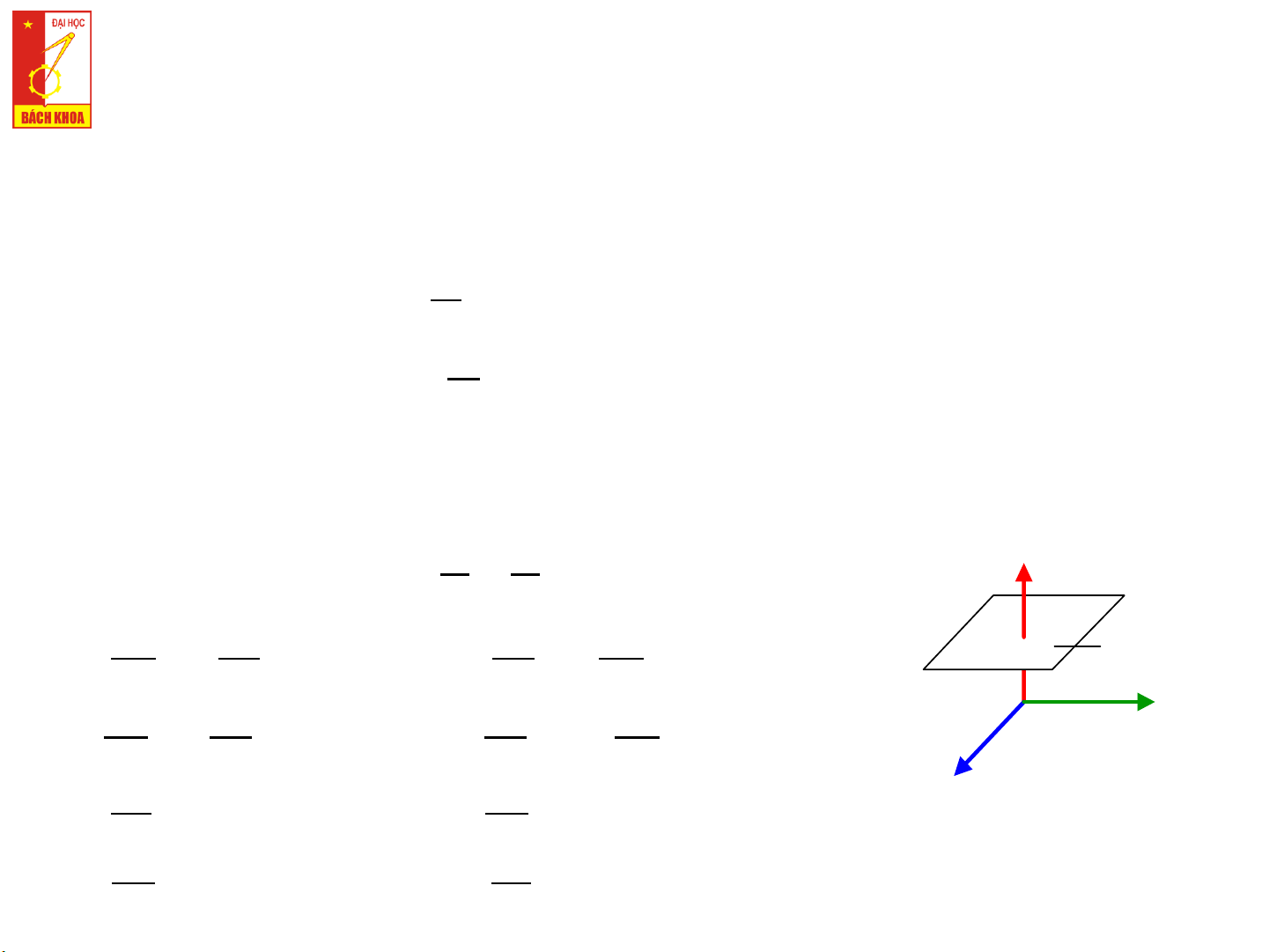
❑ Chọn để trục z vuông góc với mặt sóng => ത 𝐸 và ഥ
𝐻 chỉ phụ thuộc (𝑧, 𝑡) Hướng truyền sóng ❑ Triển 𝜕
khai pt (I) và (II) với 𝜕 = = 0, ta được z 𝜕𝑥 𝜕𝑦 𝜕𝐻𝑦 𝜕𝐸𝑥 𝜕𝐸𝑦 𝜕𝐻𝑥 Mặt sóng − = 𝜀 (I.a) = 𝜇 (II.a) 𝜕𝑧 𝜕𝑡 𝜕𝑧 𝜕𝑡 y 𝜕𝐻𝑥 𝜕𝐸 𝜕𝐸 𝜕𝐻 = 𝜀 𝑦 (I.b) 𝑥 = −𝜇 𝑦 (II.b) 𝜕𝑧 𝜕𝑡 𝜕𝑧 𝜕𝑡 𝜕𝐸 𝜕𝐻 x 𝑧 = 0 (I.c) 𝑧 = 0 (II.c) 𝜕𝑡 𝜕𝑡 𝜕𝐻𝑧 𝜕𝐸 = 0 (IV.a) 𝑧 = 0 (III.a) 𝜕𝑥 𝜕𝑧 5 TRƯỜNG ĐIỆN TỪ
Chương 4: Sóng điện từ phẳng
4.2.1. SÓNG PHẲNG ĐIỀU HÒA
❑ Từ (I.c) và (III.a) – (II.c) và (IV.a) => 𝐸𝑧 = 0 và 𝐻𝑧 = 0 ❑ Suy ra: ത 𝐸 = 𝐸 ഥ ഥ ഥ ഥ
𝑥𝑖𝑥 + 𝐸𝑦𝑖𝑦 và ഥ
𝐻 = 𝐻𝑥𝑖𝑥 + 𝐻𝑦𝑖𝑦
❑ Sóng này thuộc loại sóng điện từ ngang (Transverse Electromagnetic - TEM) ❑ Hệ thống 𝜕𝐸 𝜕𝐻 𝜕𝐻 A: 𝜀 𝑥 = − 𝑦 và 𝜕𝐸𝑥 = −𝜇 𝑦 𝜕𝑡 𝜕𝑧 𝜕𝑧 𝜕𝑡 ❑ Hệ thống 𝜕𝐸 𝜕𝐻 𝜕𝐻 B: 𝜀 𝑦 = 𝑥 và 𝜕𝐸𝑦 = 𝜇 𝑥 𝜕𝑡 𝜕𝑧 𝜕𝑧 𝜕𝑡 ❑ Lấy 𝜕2𝐸 1 𝜕2𝐸 𝜕2𝐸 𝜕2𝐸 1
vi phân theo 𝑡 pt 1A ta có: 𝜀 𝑥 = 𝑥 <=> 𝜀𝜇 𝑥 = 𝑥 , đặt 𝑣 = 𝜕𝑡2 𝜇 𝜕𝑧2 𝜕𝑡2 𝜕𝑧2 𝜀𝜇 ❑ 𝜕2𝐸 1 𝜕2𝐸 𝜕2𝐸 𝑧 Ta có: 𝑥 − 𝑥 = 0  𝜕2𝐸𝑥 − 𝑥 = 0 với 𝜉 = 𝜕𝑧2 𝑣2 𝜕𝑡2 𝜕𝜉2 𝜕𝑡2 𝑣 ❑ 𝑧 𝑧
𝐸𝑥 = 𝐹1 𝑡 − 𝜉 + 𝐹2(𝑡 + 𝜉) hay 𝐸𝑥 = 𝐹1 𝑡 − + 𝐹 ) 𝑣 2(𝑡 + 𝑣 Ở đây 𝑧 𝑧 , 𝐹1 𝑡 −
biểu diễn sóng truyền theo hướng +z, sóng thuận, 𝐹 biểu 𝑣 2 𝑡 + 𝑣
diễn sóng truyền theo hướng -z, sóng nghịch 6 TRƯỜNG ĐIỆN TỪ
Chương 4: Sóng điện từ phẳng
4.2.1. SÓNG PHẲNG ĐIỀU HÒA ❑ 𝑧 𝑧
𝐸𝑥 = 𝐹1 + 𝑡 − 𝜉 𝐹2(𝑡 + 𝜉) hay 𝐸𝑥 = 𝐹1 𝑡 − + 𝐹 ) 𝑣 2(𝑡 + 𝑣 ❑ Tương tự với 𝜕2𝐻 1 𝜕2𝐻 𝑧 𝑧 𝐻 𝑦 𝑦 𝑦, − = 0 hay 𝐻 + 𝐺 ) 𝜕𝑧2 𝑣2 𝜕𝑡2 𝑦 = 𝐺1 𝑡 − 𝑣 2(𝑡 + 𝑣 ❑ Tại thời điểm 𝑧 𝑧 𝑡 giá trị của 𝐹 1 2 1 𝑡 − và 𝐹 sẽ khác nhau 𝑣 1 𝑡 − 𝑣 ❑ Có thể chọn 𝑧 𝑧 𝑧 𝑧 𝑧 : 𝐹 1 2 1 2 2−𝑧1 1 𝑡1 − = 𝐹  𝑡 = 𝑡 𝑡 𝑣 1 𝑡2 − 𝑣 1 − 𝑣 2 − 𝑣 2 − 𝑡1 = 𝑣 Δ𝑧 1
=> Giá trị 𝐹1 đã được truyền đi dọc theo trục +𝑧 với vận tốc 𝑣 = = Δ𝑡 𝜀𝜇
❑ Các hàm đang xét là các hàm sóng, 𝑣 là vận tốc truyền sóng x F1(t1 - z/v) F1(t2 - z/v) z z1 z2 y 7 TRƯỜNG ĐIỆN TỪ
Chương 4: Sóng điện từ phẳng
4.2.1. SÓNG PHẲNG ĐIỀU HÒA ❑ 𝑧 𝑧 𝑧 𝑧
Ta có : 𝐸𝑥 = 𝐹1 𝑡 − + 𝐹 ) và 𝐻 + 𝐺 ) 𝑣 2(𝑡 + 𝑣 𝑦 = 𝐺1 𝑡 − 𝑣 2(𝑡 + 𝑣 ❑ Sóng thuận 𝑧 𝑧 𝜕𝐸 𝜕𝐻 𝐸 𝑥 𝑦 𝑥 = 𝐹1 𝑡 − và 𝐻 thay vào 𝜀 = − ta được 𝑣 𝑦 = 𝐺1 𝑡 − 𝑣 𝜕𝑡 𝜕𝑧 𝑧 1 𝑧 𝑧 𝑧 1 𝑧 𝜀𝐹′1 𝑡 − = 𝐺′
lấy tích phân theo τ = 𝑡 − => 𝜀𝐹 = 𝐺 𝑣 𝑣 1 𝑡 − 𝑣 𝑣 1 𝑡 − 𝑣 𝑣 1 𝑡 − 𝑣 ❑ 𝑧 𝜇 𝑧 1 𝐸 𝐹 𝜇 Hay 𝐹 𝑥 1 𝑡−𝑧/𝑣 1 𝑡 − = 𝐺 với 𝑣 = => = = 𝑣 𝜀 1 𝑡 − 𝑣 𝜀𝜇 𝐻𝑦 𝐺 𝜀 𝑡ℎ𝑢ậ𝑛 1 𝑡−𝑧/𝑣
❑ Tương tự với sóng ngược 𝐸 𝐹 𝜇 : 𝑥 = 2 𝑡+𝑧/𝑣 = − 𝐻𝑦 𝐺 𝜀 𝑛𝑔ượ𝑐 2 𝑡+𝑧/𝑣 ❑ Ký hiệu 𝜇 𝑍0 =
là trở kháng sóng, có thứ nguyên là Ohm (Ω) 𝜀 ❑ Tổng quát 1 1
: 𝐸𝑥 = 𝐹1 𝑡 − 𝑧/𝑣 + 𝐹2(𝑡 + 𝑧/𝑣) và 𝐻𝑦 = 𝐹 𝐹 𝑍 1 𝑡 − 𝑧/𝑣 − 2 𝑡 + 𝑧/𝑣 0 𝑍0 𝐸 𝐸 𝑯𝟐 𝝁 𝑬𝟐 𝑬𝟐 => 𝑥 = − 𝑥 = 𝑍 = = 𝜺 𝐻 0, Năng lượng: 𝝁 𝟐 𝑦 𝐻 𝟐 𝟐 𝒁 𝟐 𝑡ℎ𝑢ậ𝑛 𝑦 𝑛𝑔ượ𝑐 𝟎 8 TRƯỜNG ĐIỆN TỪ
Chương 4: Sóng điện từ phẳng
4.2.2. PHÂN CỰC SÓNG ĐIỆN TỪ
❑ Một sóng phẳng điều hòa: ത
𝐸 = 𝐸𝑥, 𝐸𝑦, 0 =(𝐴𝑥cos(𝜔𝑡 − 𝑘𝑧), 𝐴𝑦cos 𝜔𝑡 − 𝑘𝑧 + Փ , 0)
❑ Ở đây, 𝐴𝑥, 𝐴𝑦 là các biên độ dao động theo trục 𝑥 và 𝑦, Փ là độ lệch pha giữa dao
động theo trục 𝑥 và 𝑦.
❑ Xét trong mặt phẳng bất kỳ vuông góc với phương truyền sóng 𝑧
➢ Nếu Փ = 0 hoặc 𝜋, vec-tơ ത
𝐸 sẽ vạch ra đường thẳng, ta có trạng thái phân cực
thẳng hay phân cực tuyến tính.
➢ Nếu Փ = ±90° và 𝐴𝑥 = 𝐴𝑦 vec-tơ ത𝐸 sẽ vạch ra đường tròn, ta có trạng thái
phân cực tròn. Nếu Փ = 90° là phân cực tròn trái (LHCP), Փ = −90° là phân cực tròn phải (RHCP).
➢ Với các Փ khác, ta có trạng thái phân cực elip.
Phân cực tuyến tính theo trục x 9 TRƯỜNG ĐIỆN TỪ
Chương 4: Sóng điện từ phẳng
4.3. SÓNG PHẲNG TRONG MÔI TRƯỜNG BÁN DẪN
Phân loại môi trường:
❑ Trong tự nhiên không có môi trường điện môi lý tưởng (𝜎 = 0, 𝐽ҧ = 0, 𝜌 = 0)=> môi
trường truyền sóng thực tế là môi trường bán dẫn điện. Điện môi hay dẫn điện là
các trường hợp đặc biệt của bán dẫn điện. ❑ Phân loại môi 𝜕 ത 𝐸
trường sẽ dựa vào giá trị tương đối của 𝐽ҧ𝑑ẫ𝑛 = 𝜎 ത
𝐸 và 𝐽ҧ𝑑ị𝑐ℎ = 𝜀 𝜕𝑡 ❑ Nếu 𝜕𝐸 𝜎𝐸 ≫ 𝜀
thì môi trường được coi là dẫn điện 𝜕𝑡 ❑ Nếu 𝜕𝐸 𝜀
≫ 𝜎𝐸 thì môi trường được coi là điện môi 𝜕𝑡 ❑ Nếu 𝜕𝐸 𝜎𝐸 ~ 𝜀
thì môi trường được coi là bán dẫn điện. 𝜕𝑡
=> Tính chất của môi trường không chỉ phụ thuộc vào 𝜎 và 𝜀, mà còn phụ thuộc vào
tốc độ biến thiên của trường theo thời gian (hay tần số của sóng điều hòa). 10 TRƯỜNG ĐIỆN TỪ
Chương 4: Sóng điện từ phẳng
4.3. SÓNG PHẲNG TRONG MÔI TRƯỜNG BÁN DẪN
Các hệ thức của sóng phẳng điều hòa trong môi trường bán dẫn Điện môi Bán dẫn Hệ số điện môi 𝜀 𝜎 𝜀𝑝 = 𝜀 − 𝑖 𝜔
Hệ số pha (hằng số sóng)
𝑘 = 𝜔/𝑣 = 𝜔 𝜀𝜇
𝑘′ = 𝜔/𝑣′ = 𝜔 𝜀𝑝𝜇 (phức) Trở kháng sóng 𝑍0 = 𝜇/𝜀 𝑍′0 = 𝜇/𝜀𝑝 (𝑝ℎứ𝑐)
Thành phần điện trường
𝐸 = 𝐸0𝑒−𝑖𝑘𝑧𝑒𝑖𝜔𝑡
𝐸 = 𝐸0𝑒−𝑖𝑘′𝑧𝑒𝑖𝜔𝑡 Thành phần từ trường 𝐸 𝐸
𝐻 = 0 𝑒−𝑖𝑘𝑧𝑒𝑖𝜔𝑡
𝐻 = 0 𝑒−𝑖𝑘′𝑧𝑒𝑖𝜔𝑡 𝑍0 𝑍0′ Vận tốc pha 𝜔 𝑣 = 𝑘 11 TRƯỜNG ĐIỆN TỪ
Chương 4: Sóng điện từ phẳng
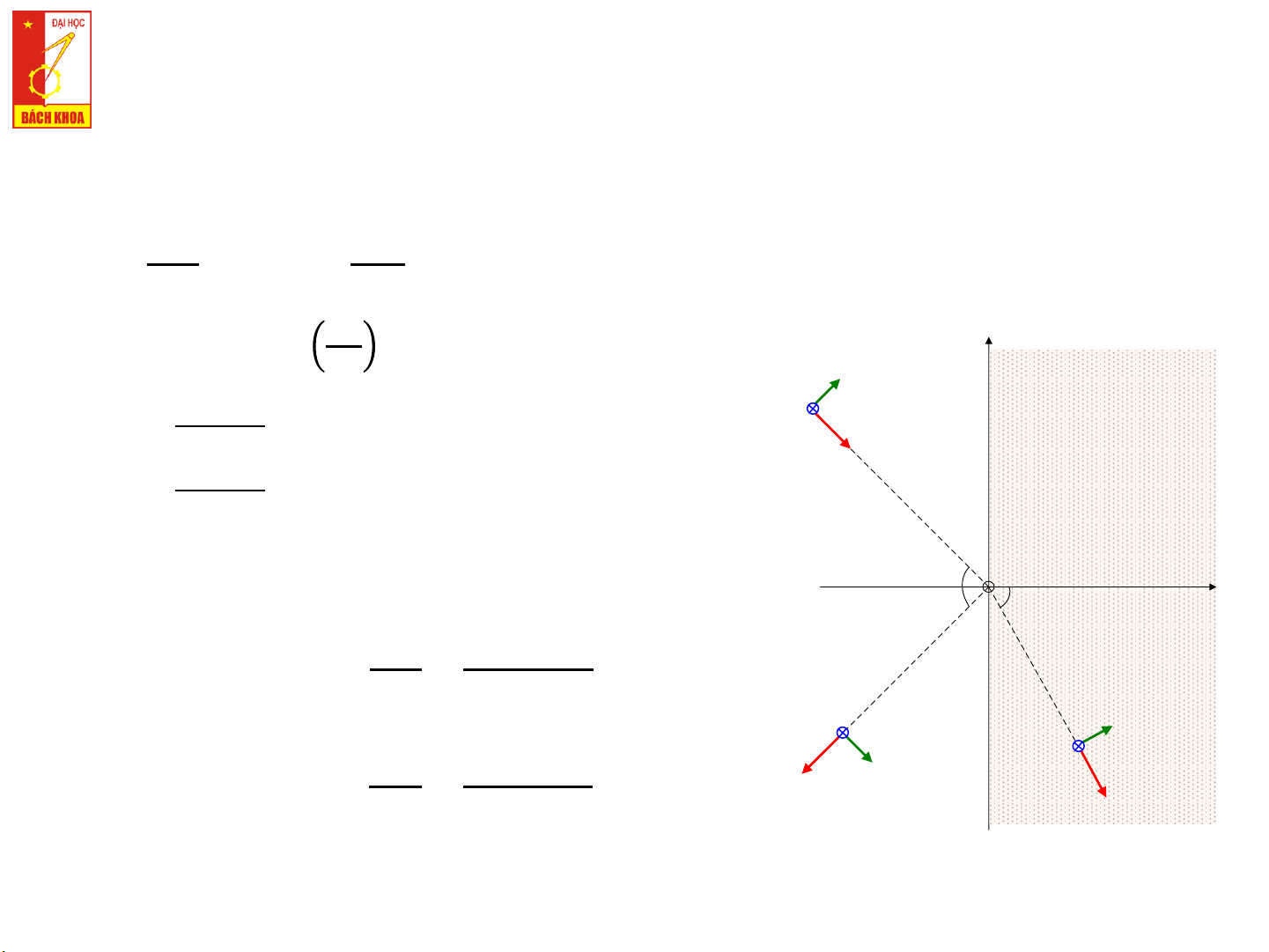
4.4. PHẢN XẠ VÀ KHÚC XẠ CỦA SÓNG PHẲNG TẠI MẶT PHÂN CÁCH 2 MÔI TRƯỜNG ❑ Đặt 𝑍′ 𝑍′ : 01 = 𝑍 02 = 𝑍 𝑐𝑜𝑠𝜃 01 𝑣à 𝑐𝑜𝑠𝜓
02 trở kháng sóng quy đổi 𝑍 z =>𝐸 01
𝑡ớ𝑖 − 𝐸𝑝𝑥 = 𝐸𝑘𝑥 Sóng tới 𝑍02 ഥ 𝐻′1 𝑍 𝐸 02−𝑍01 ത 𝐸′ 𝑝𝑥 = 𝐸 1 𝑍 𝑡ớ𝑖 ഥ′ => 02+𝑍01 ቑ Π1 2𝑍 𝐸 02 𝑘𝑥 = 𝐸 𝑍 𝑡ớ𝑖 02+𝑍01 I(γ
❑ Hệ số phản xạ và hệ số khúc xạ 1,Z’01) II(γ2,Z’02) : θ x y θ' ψ 𝐸𝑝𝑥 𝑍 𝑅 02 − 𝑍01 𝑝𝑥 = = 𝐸𝑡ớ𝑖 𝑍02 + 𝑍01 ത 𝐸"1 ഥ 𝐻2 𝐸 2𝑍 ത 𝐸 " 2 𝑅 𝑘𝑥 02 ഥ Π ഥ 1 𝐻" ഥ Π 𝑘𝑥 = = 1 𝐸 2 𝑡ớ𝑖 𝑍02 + 𝑍01 Sóng phản xạ Sóng khúc xạ 12 TRƯỜNG ĐIỆN TỪ
Chương 4: Sóng điện từ phẳng
4.4. PHẢN XẠ VÀ KHÚC XẠ CỦA SÓNG PHẲNG TẠI MẶT PHÂN CÁCH 2 MÔI TRƯỜNG
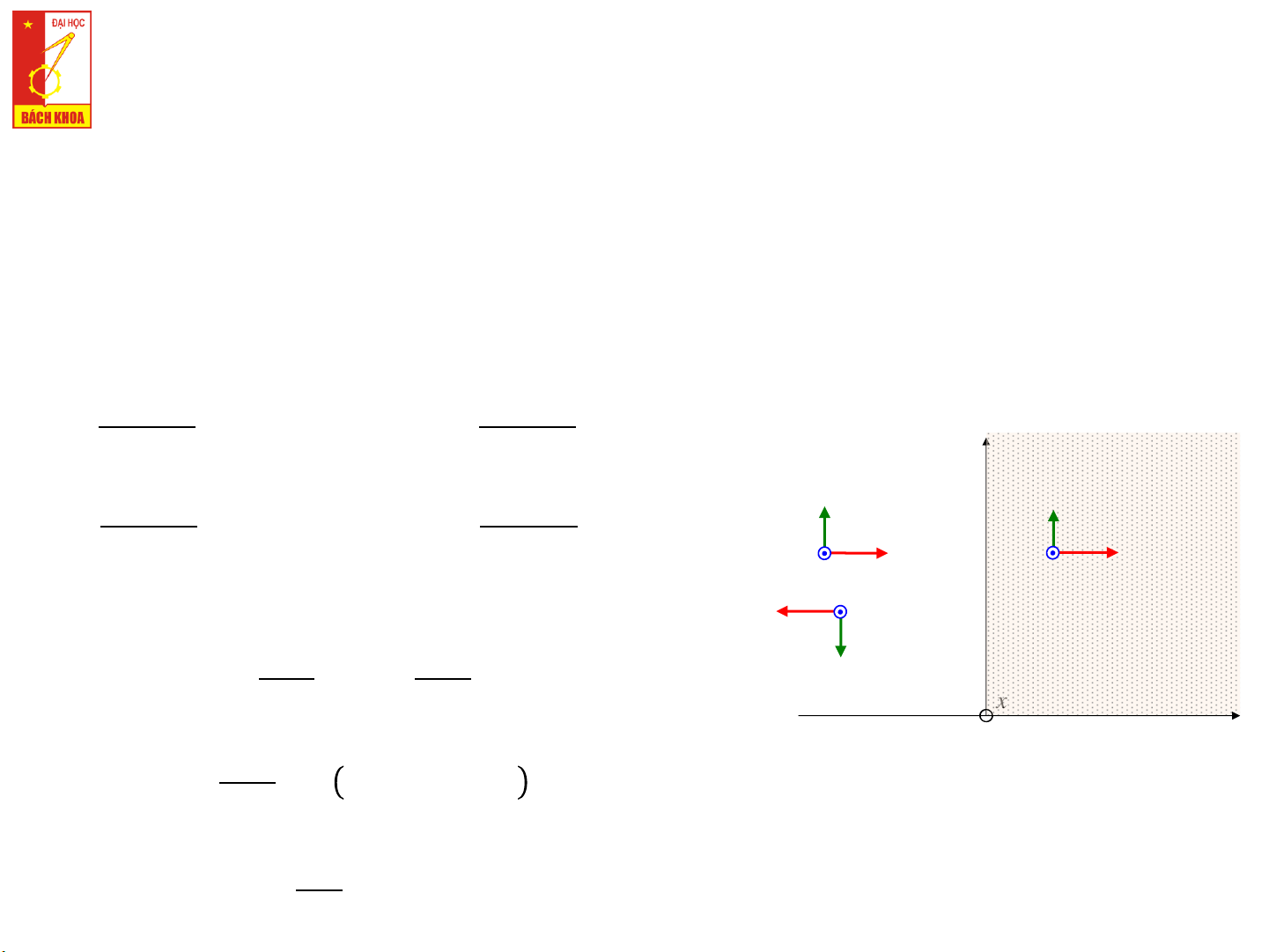
b) Sóng phẳng truyền vuông góc tới mặt ngăn cách
giữa 2 môi trường I và II.
𝜃 = 0°, ψ = 0°, 𝑍𝑛1 = 𝑍′01, 𝑍𝑛2 = 𝑍′02, 𝛾𝑛1 = 𝛾1, 𝛾𝑛2 = 𝛾2 𝑍′ 2𝑍′ 𝐸 02−𝑍′01 02 𝑝𝑥 = 𝐸 𝐸 z 𝑍′ 𝑡ớ𝑖 𝐸𝑘𝑥 = 𝑡ớ𝑖 I(γ 02+𝑍′01 𝑍′02+𝑍′01 1,Z’01) II(γ2,Z’02) Sóng tới ഥ ′ 𝐻2 𝑍′ 2𝑍′ ഥ 𝐻 𝑅 02−𝑍′01 02 1 𝑝𝑥 = 𝑅 𝑍′ 𝑘𝑥 = 02+𝑍′01 𝑍′02+𝑍′01 ത ′ ഥ 𝐸′ ഥ Π ത Π2 1 1 𝐸2 𝐸 " Sóng khúc xạ
1 = 𝐸𝑡ớ𝑖𝑒𝛾1𝑦 + 𝐸𝑝𝑥𝑒−𝛾1𝑦 = 𝐸𝑡ớ𝑖𝑒𝛾1𝑦(1 + 𝑅𝑝𝑥𝑒−2𝛾1𝑦) ത 𝐸1 ഥ Π"1 𝐸 𝐸 ഥ" 𝑝𝑥 𝐻1 𝐻 𝑡ớ𝑖 1 = . 𝑒𝛾1𝑦 − . 𝑒−𝛾1𝑦 𝑍′ Sóng phản xạ 01 𝑍′01 x y 𝐸 =
𝑡ớ𝑖 𝑒𝛾1𝑦 1 − 𝑅 𝑍′ 𝑝𝑥𝑒−2𝛾1𝑦 01 𝐸 𝐸 𝑘𝑥
2 = 𝐸𝑘𝑥𝑒𝛾2𝑦 và 𝐻2 = . 𝑒𝛾2𝑦 𝑍′02 13 TRƯỜNG ĐIỆN TỪ
Chương 6: Hệ định hướng
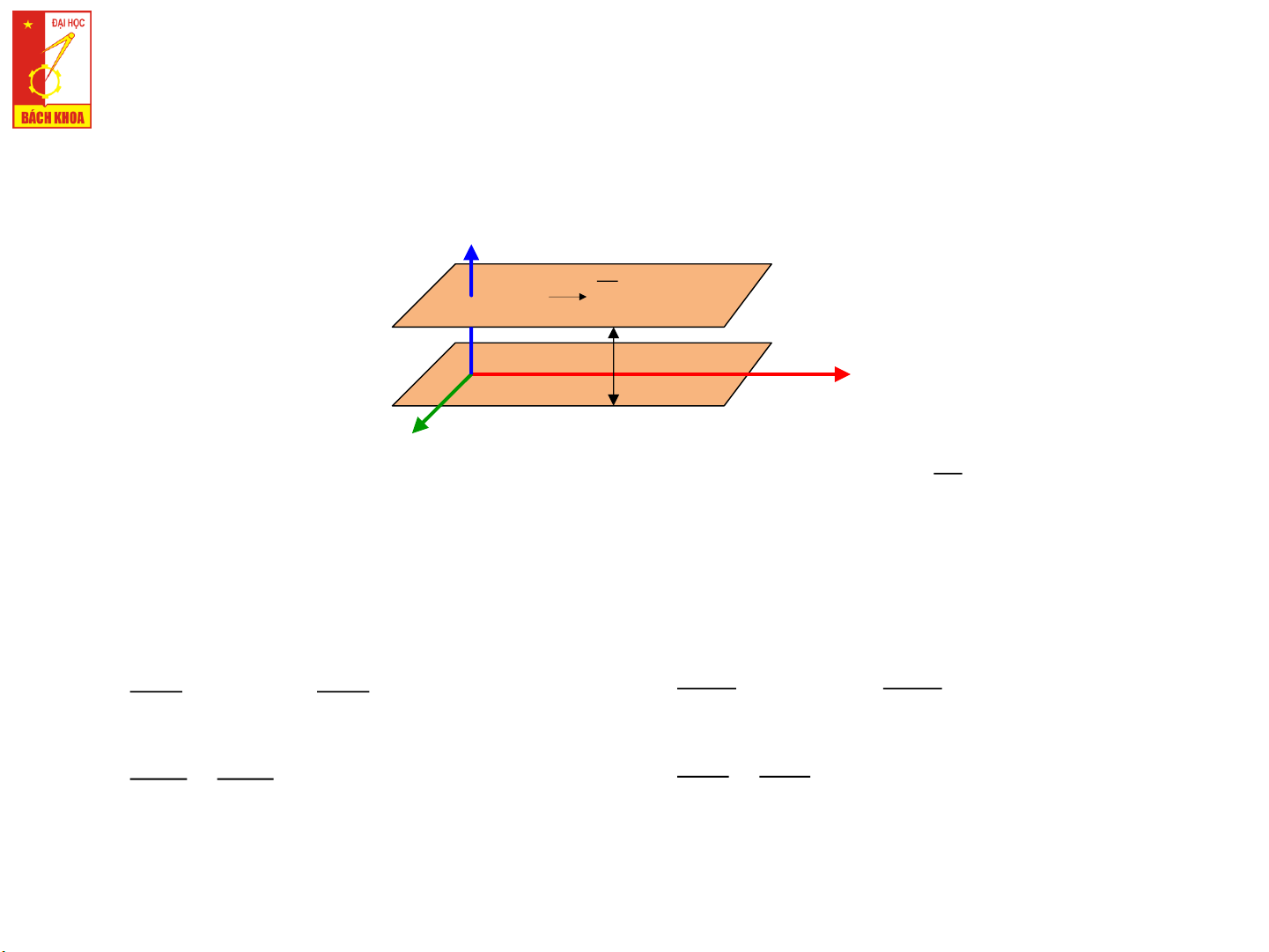
6.2. SÓNG ĐIỆN TỪ ĐỊNH HƯỚNG GIỮA 2 MẶT DẪN ĐIỆN SONG SONG x Et a 0 z y
❑ Cho hệ thống gồm 2 mặt dẫn điện song song vô cùng lớn => E = 0 t
❑ Giả thiết nguồn trường được đặt ngoài miền khảo sát, và sóng truyền theo trục 𝑧, các vec-tơ ത 𝐸 và ഥ
𝐻 không phụ thuộc vào tọa độ 𝑦 và có dạng: E  E   H  H   y = y y i H , y = i − H = −i E , = i E  x z  x z z  x       z x  H  H  E  E   x z  − = i E x z − = −iH y y z  x   z  x  
Trường điện ngang (TE)
Trường từ ngang (TM) 14 TRƯỜNG ĐIỆN TỪ
Chương 6: Hệ định hướng
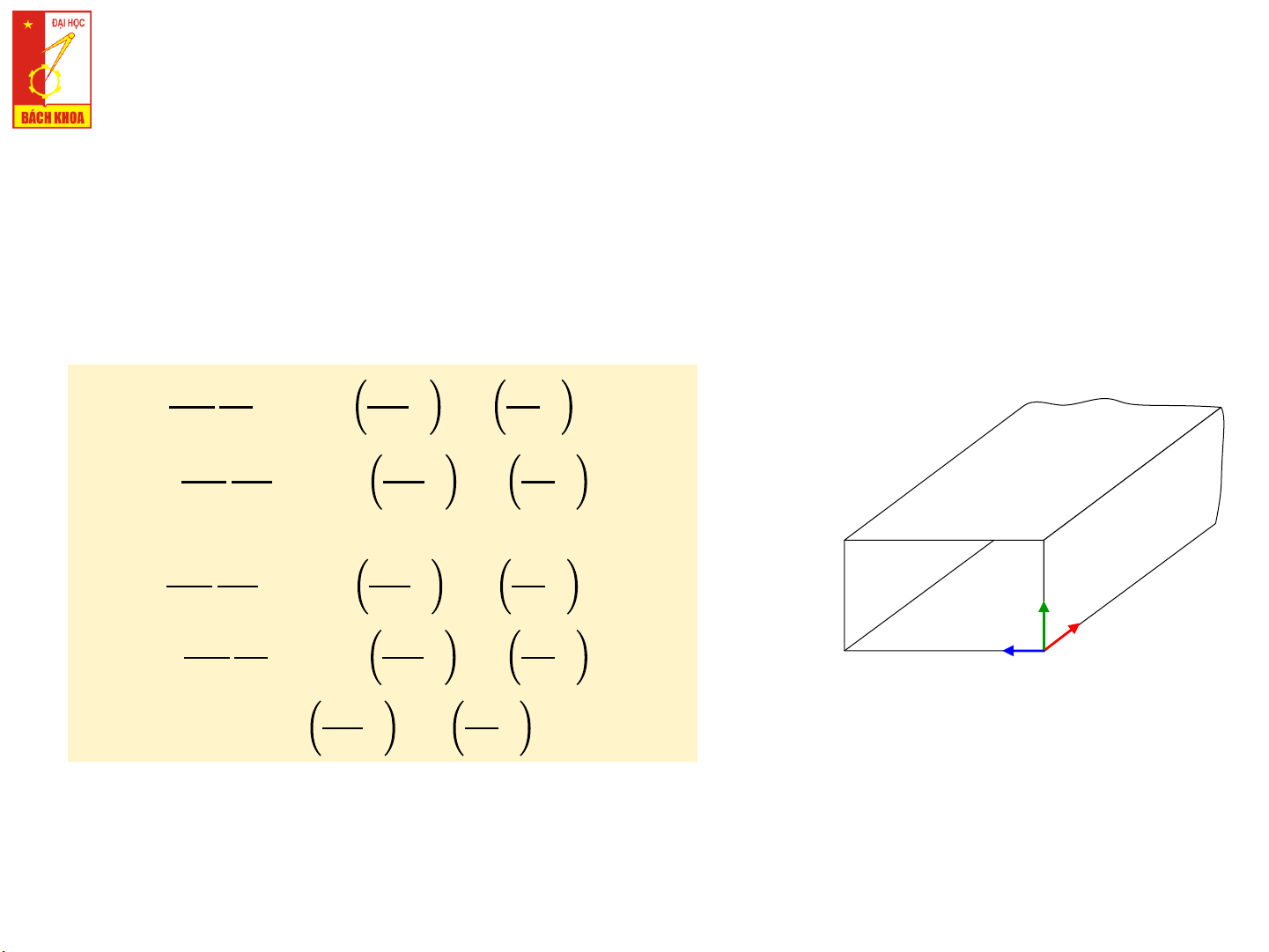
6.4.1. SÓNG TE TRONG ỐNG DẪN SÓNG CHỮ NHẬT
❑ Từ H => các biểu thức của các vec-tơ trường TE trong ống dẫn sóng chữ nhật z 𝑖𝜔𝜇 𝑛𝜋 𝑚𝜋 𝑛𝜋 𝐸𝑥 = 𝐴 𝑥 sin 𝑦 𝑒−𝛾𝑚𝑛𝑧 𝑘2 𝑚𝑛cos 𝑐 𝑏 𝑎 𝑏 𝑖𝜔𝜇 𝑚𝜋 𝑚𝜋 𝑛𝜋 𝐸𝑦 = − 𝐴 𝑥 cos 𝑦 𝑒−𝛾𝑚𝑛𝑧 𝑘2 𝑚𝑛sin 𝑐 𝑎 𝑎 𝑏 𝐸 a 𝑧 = 0 𝛾 𝑚𝜋 𝑚𝜋 𝑛𝜋 𝐻 𝑚𝑛 𝑥 = 𝐴 𝑥 cos 𝑦 𝑒−𝛾𝑚𝑛𝑧 b y 𝑘2 𝑚𝑛sin 𝑐 𝑎 𝑎 𝑏 z 𝛾 𝑛𝜋 𝑚𝜋 𝑛𝜋 𝐻 𝑚𝑛 𝑦 = − 𝐴 𝑥 sin 𝑦 𝑒−𝛾𝑚𝑛𝑧 x 𝑘2 𝑚𝑛cos 𝑐 𝑏 𝑎 𝑏 𝑚𝜋 𝑛𝜋 𝐻𝑧 = 𝐴𝑚𝑛cos 𝑥 cos 𝑦 𝑒−𝛾𝑚𝑛𝑧 𝑎 𝑏 15 TRƯỜNG ĐIỆN TỪ
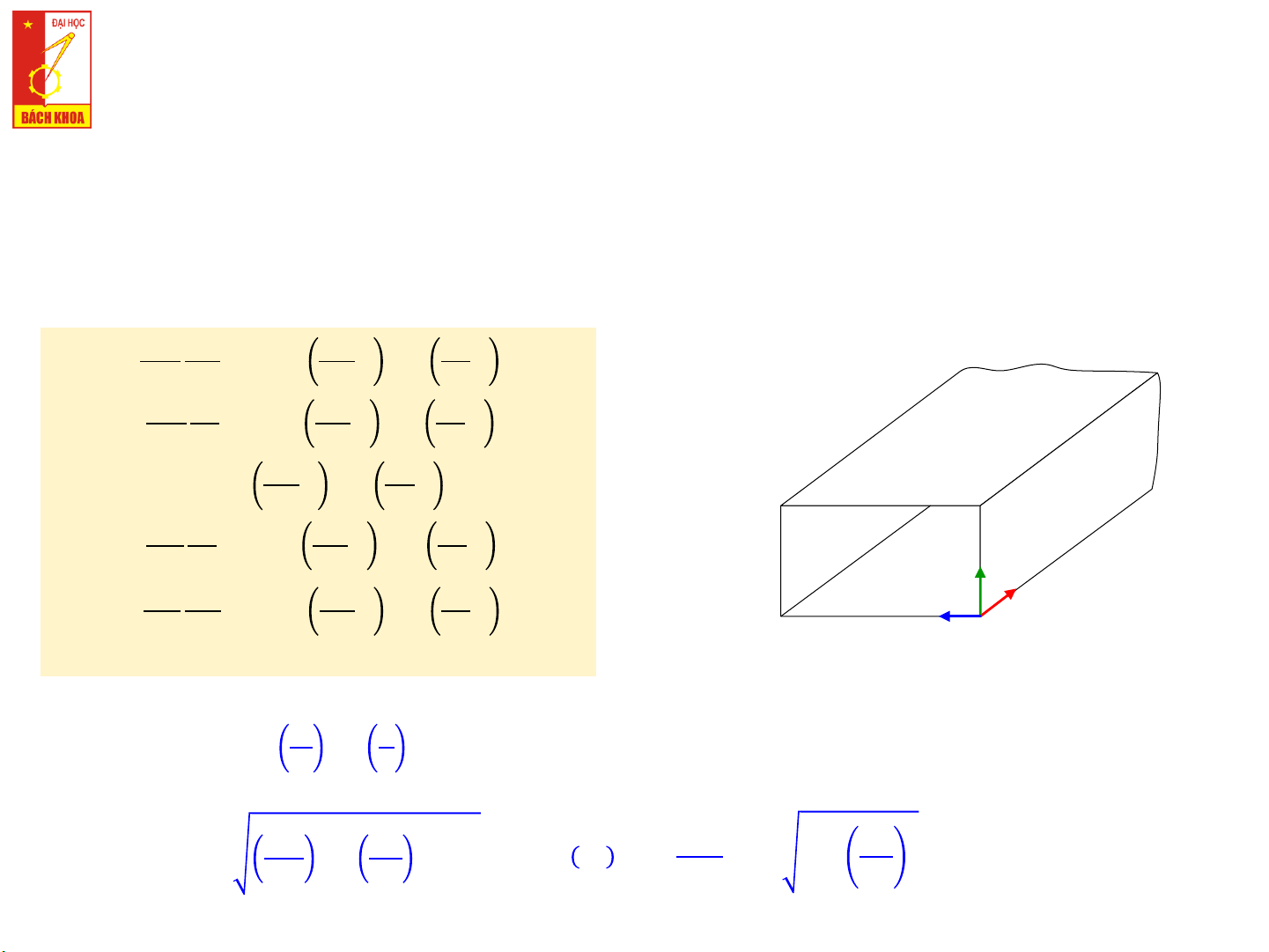
Chương 6: Hệ định hướng
6.4.2. SÓNG TM TRONG ỐNG DẪN SÓNG CHỮ NHẬT Các thành phần trường: 𝛾 𝑚𝜋 𝑚𝜋 𝑛𝜋 𝐸 𝑚𝑛 𝑥 = − 𝐵 𝑥 sin 𝑦 𝑒−𝛾𝑚𝑛𝑧 𝑘2 𝑚𝑛cos 𝑐 𝑎 𝑎 𝑏 𝛾 𝑛𝜋 𝑚𝜋 𝑛𝜋 𝐸 𝑚𝑛 𝑦 = − 𝐵 𝑥 cos 𝑦 𝑒−𝛾𝑚𝑛𝑧 𝑘2 𝑚𝑛sin 𝑐 𝑏 𝑎 𝑏 𝑚𝜋 𝑛𝜋 𝐸𝑧 = 𝐵𝑚𝑛sin 𝑥 sin 𝑦 𝑒−𝛾𝑚𝑛𝑧 𝑎 𝑏 a 𝑖𝜔𝜀 𝑛𝜋 𝑚𝜋 𝑛𝜋 𝐻𝑥 = − 𝐵 𝑥 cos 𝑦 𝑒−𝛾𝑚𝑛𝑧 𝑘2 𝑚𝑛sin b y 𝑐 𝑏 𝑎 𝑏 z 𝑖𝜔𝜀 𝑚𝜋 𝑚𝜋 𝑛𝜋 𝐻𝑦 = − 𝐵 𝑥 sin 𝑦 𝑒−𝛾𝑚𝑛𝑧 𝑘2 𝑚𝑛cos x 𝑐 𝑎 𝑎 𝑏 𝐻𝑧 = 0 𝒎 𝟐 𝒏 𝟐 𝒌𝟐𝒄 = + 𝒂 𝒃 𝟐 𝒎𝝅 𝟐 𝒏𝝅 𝟐 𝜷𝒎𝒏 𝒇𝒕𝒉 𝜸𝒎𝒏 = + − 𝒌𝟐 𝒁 = 𝒁 𝒂 𝒃 𝒄 𝑻𝑴 = 𝝎𝜺 𝒐 𝟏 − 𝒇 16 TRƯỜNG ĐIỆN TỪ
Chương 6: Hệ định hướng
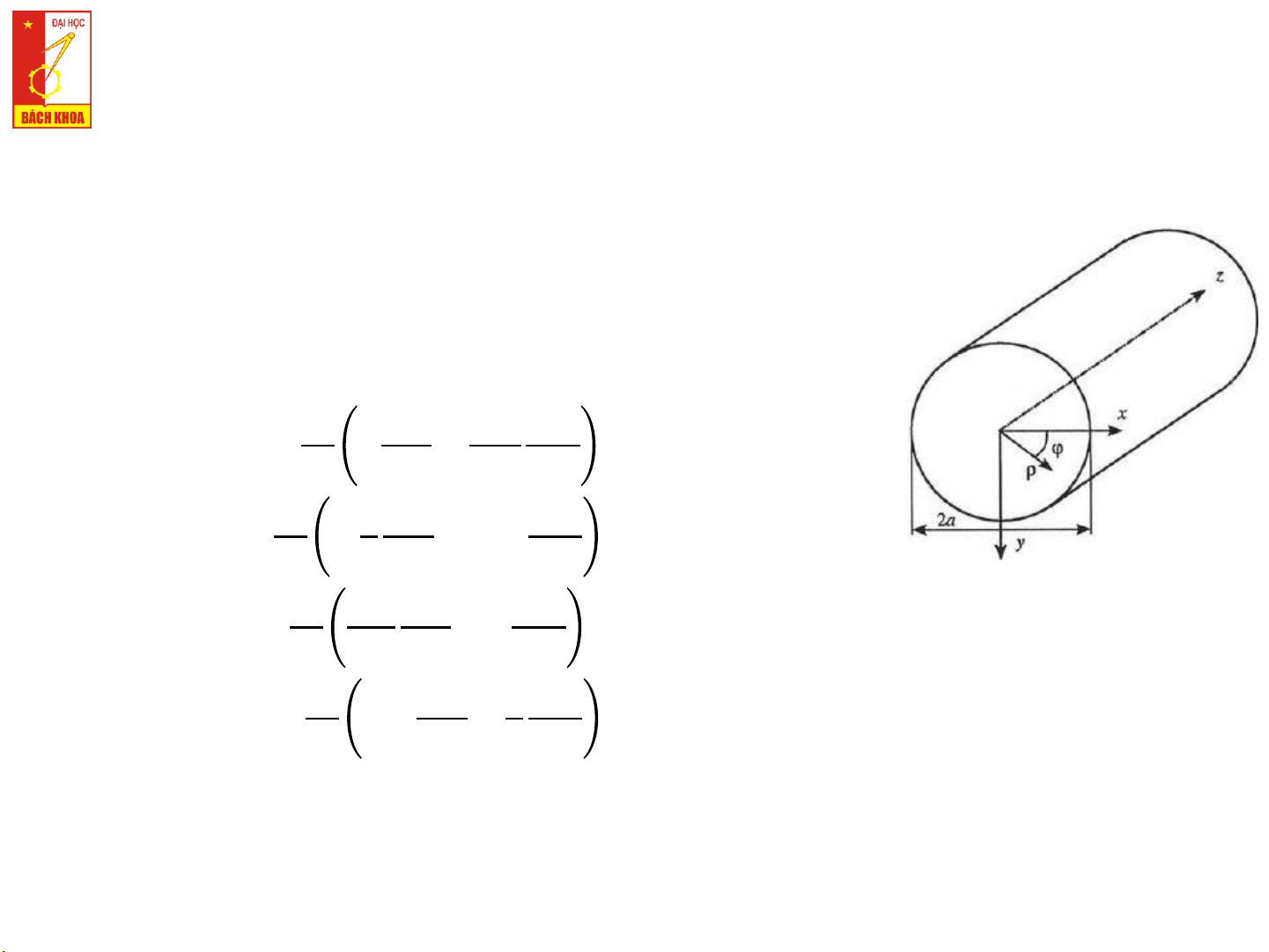
6.5. ỐNG DẪN SÓNG HÌNH TRỤ TRÒN
❑ Biên độ phức của các vec-tơ ത 𝐸 và ഥ 𝐻 trong miền không gian
không chứa nguồn thỏa mãn các pt vi phân sau:
❑ Các thành phần của trường là: 1 𝜕𝐸 𝑖𝜔𝜇 𝜕𝐻 𝐸 𝑧 𝑧 𝜌 = − 𝛾 + 𝑘2𝑐 𝜕𝜌 𝜌 𝜕𝜑 1 𝛾 𝜕𝐸 𝜕𝐻 𝐸 𝑧 𝑧 𝜑 = − + 𝑖𝜔𝜇 𝑘2𝑐 𝜌 𝜕𝜑 𝜕𝜌 1 𝑖𝜔𝜀 𝜕𝐸 𝜕𝐻 𝐻 𝑧 𝑧 𝜌 = − 𝛾 𝑘2𝑐 𝜌 𝜕𝜑 𝜕𝜌 1 𝜕𝐸 𝛾 𝜕𝐻 𝐻 𝑧 𝑧 𝜑 = − 𝑖𝜔𝜀 + 𝑘2𝑐 𝜕𝜌 𝜌 𝜕𝜑 17 TRƯỜNG ĐIỆN TỪ
Chương 6: Hệ định hướng
6.5.1. SÓNG TE TRONG ỐNG DẪN SÓNG HÌNH TRỤ TRÒN ❑ Để 𝜕𝐻𝑧 (𝑘𝑐𝜌)
= 0 tại 𝜌 = 𝑎 được thỏa mãn nếu 𝑑𝐽𝑚
= 0 tại 𝜌 = 𝑎 hoặc 𝐽′ 𝜕𝜌 𝜕𝜌 𝑚 𝑘 𝑎 = 0 𝑐 ❑ Lý thuyết 𝑣
Bessel cho biết có vô số nghiệm 𝑣 𝑎 = 𝑣 = 𝑚𝑛 𝑚𝑛 , ta có 𝑘𝑐 𝑚𝑛 hay 𝑘𝑐 𝑎 2 2 ❑ 𝑣 𝑣 Thay 𝑘 vào 𝑚𝑛 − 𝑘2 và 𝛽 𝑚𝑛 𝑐 ta được: 𝛾𝑚𝑛 = 𝑎 𝑚𝑛 = 𝑘2 − 𝑎
❑ Các thành phần của các vec-tơ trường TE 1 𝑣𝑚𝑛 𝑖𝜔𝜇 𝑣 𝑓𝑡ℎ 𝑇𝐸 = 𝑘𝑐𝑣 = 𝐸 𝑚𝑛 2𝜋 2𝜋𝑎 𝜀𝜇 𝜌 = 𝐴
𝜌 sin 𝑚𝜑 𝑒−𝛾𝑚𝑛𝑧 𝑘2 𝑚𝑛𝐽𝑚 𝑐 𝑎 𝑖𝜔𝜇 𝑣 𝑍 𝐸 𝑚𝑛 0 𝜑 = 𝐴
𝜌 cos 𝑚𝜑 𝑒−𝛾𝑚𝑛𝑧 2𝜋 𝜀𝜇 𝑍 = 𝑘2 𝑚𝑛𝐽′𝑚 𝑐 𝑐 𝑎 𝜆𝑡ℎ 𝑇𝐸 = 𝑎 2 𝐸 𝑣𝑚𝑛 𝜀𝑜𝜇𝑜 𝑓 𝑧 = 0 1 − 𝑡ℎ 𝛾 𝑣 𝑓 𝐻 𝑚𝑛 𝑚𝑛 𝜌 = − 𝐴
𝜌 cos 𝑚𝜑 𝑒−𝛾𝑚𝑛𝑧 𝑘2 𝑚𝑛𝐽′𝑚 𝑐 𝑎 𝛾 𝑚 𝑣 2 𝐻 𝑚𝑛 𝑚𝑛 𝑣 𝑓 𝜑 = 𝐴
𝜌 sin 𝑚𝜑 𝑒−𝛾𝑚𝑛𝑧 𝑡ℎ 𝑘2 𝑚𝑛𝐽′𝑚 𝑣 ; 𝑣 𝑐 𝜌 𝑎 𝑓 = 𝑛ℎ = 𝑣 1 − 𝑓 𝑣 𝑓 2 𝐻 𝑚𝑛 𝑡ℎ 𝑧 = 𝐴𝑚𝑛𝐽𝑚
𝜌 cos 𝑚𝜑 𝑒−𝛾𝑚𝑛𝑧 1 − 𝑎 𝑓 18 TRƯỜNG ĐIỆN TỪ
Chương 6: Hệ định hướng
6.5.2. SÓNG TM TRONG ỐNG DẪN SÓNG HÌNH TRỤ TRÒN
❑ Các thành phần của các vec-tơ trường TM: 𝛾 𝜒 𝐸 𝑚𝑛 𝑚𝑛 𝜌 = − 𝐵
𝜌 cos 𝑚𝜑 𝑒−𝛾𝑚𝑛𝑧 𝑘2 𝑚𝑛𝐽′𝑚 𝑐 𝑎 𝛾 𝑚 𝜒 𝐸 𝑚𝑛 𝑚𝑛 𝜑 = 𝐵
𝜌 sin 𝑚𝜑 𝑒−𝛾𝑚𝑛𝑧 𝑘2 𝑚𝑛𝐽𝑚 𝑐 𝜌 𝑎 1 𝜒𝑚𝑛 𝜒 𝑓𝑡ℎ 𝑇𝑀 = 𝑘𝑐𝑣 = 𝐸 𝑚𝑛 2𝜋 2𝜋𝑎 𝜀𝜇 𝑧 = 𝐵𝑚𝑛𝐽𝑚
𝜌 cos 𝑚𝜑 𝑒−𝛾𝑚𝑛𝑧 𝑎 𝑖𝜔𝜀 𝜒 𝐻 𝑚𝑛 𝜌 = − 𝐵
𝜌 sin 𝑚𝜑 𝑒−𝛾𝑚𝑛𝑧 𝑘2 𝑚𝑛𝐽𝑚 2𝜋𝑎 𝜀𝜇 𝑐 𝑎 𝜆𝑡ℎ 𝑇𝑀 = 𝑖𝜔𝜀 𝜒 𝜒𝑚𝑛 𝜀𝑜𝜇𝑜 𝐻 𝑚𝑛 𝜑 = − 𝐵
𝜌 cos 𝑚𝜑 𝑒−𝛾𝑚𝑛𝑧 𝑘2 𝑚𝑛𝐽′ 𝑚 𝑐 𝑎
𝐻𝑧 = 0; 𝑚 = 0,1,2, . . . , 𝑛 = 1,2,3, . . . 𝜒 2 𝛾 𝑚𝑛 𝑚𝑛 = − 𝑘2 𝑎 19