Ôn tập giữa học kì I | Giáo án Toán 11 Kết nối tri thức

Ôn tập giữa học kì I | Giáo án Toán 11 Kết nối tri thức được soạn dưới dạng file PDF gồm 18 trang. Các bạn xem và tải về ở bên dưới.

42 21 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Giáo án Toán 11

Môn: Toán 11

Sách: Kết nối tri thức

Thông tin:

18 trang 8 tháng trước

Tác giả:

Profile Thùy Dương (H)
1
Trường ………………………..
Tổ ………………….
Họ và tên giáo viên: ……………………
KẾ HOẠCH BÀI DẠY
TÊN BÀI DẠY: ÔN TẬP GIỮA HỌC KÌ I
Môn học/Hoạt động giáo dục: Toán; lớp: 11
Thời gian thực hiện: (01 tiết)
I. MỤC TIÊU
1. Kiến thức
- Cung và góc lượng giác, giá trị lượng giác của một cung, công thức lượng giác.
- Công thức nghiệm của phương trình lượng giác cơ bản.
- Cách giải một số phương trình lượng giác đơn giản
- Định nghĩa và các tính chất của dãy số.
- Định nghĩa, các công thức số hạng tổng quát, tính chất của cấp số cộng và cấp số nhân.
- Mẫu số liệu ghép nhóm
- Các số đặc trưng đo xu thế trung tâm
2. Về năng lực
- Năng lực tư duy và lập luận Toán học: Trong quá trình giải bài tập.
- Năng lực mô hình hóa Toán học: Trong các bài toán thực tế.
- Năng lực giải quyết vấn đề Toán học: Trong các lời giải của các bài tập.
- Năng lực giao tiếp Toán học: Trong các định lý, ví dụ, bài tập.
- Năng lực sử dụng công cụ, phương tiện để học Toán: Sử dụng máy tính cầm tay.
3. Về phẩm chất
- Chăm chỉ, hoàn thành các nhiệm vụ được giao.
- Trách nhiệm, cố gắng chiếm lĩnh kiến thức mới, cố gắng làm đúng các bài tập.
- Có thế giới quan khoa học
II. THIẾT BỊ DẠY HỌC
- Kế hoạch bài dạy, SGK, phiếu học tập, phấn, thước kẻ, máy chiếu.
III. TIẾN TRÌNH DẠY HỌC
1. HOẠT ĐỘNG 1: LUYỆN TẬP
a) Mục tiêu: HS biết áp dụng các kiến thức đã học vào các dạng bài tập cụ thể
b) Nội dung: Nêu ND bài tập / Phiếu học tập
Phiếu học tập 1
Câu 1. Trong các khẳng định sau, khẳng định nào sai?
A. . B. .
C. . D. .
Câu 2. Trong các khẳng định sau, khẳng định nào sai?
( )
sin sin
pa a
-=
( )
cos cos
pa a
-=
( )
sin sin
pa a
+=-
( )
cos cos
pa a
+=-
2
A. . B. .
C. . D. .
Câu 3. Trong các khẳng định sau, khẳng định nào đúng?
A. . B. .
C. . D. .
Câu 4. Trong các khẳng định sau, khẳng định nào là sai?
A. . B. .
C. . D. .
Câu 5. Khẳng định nào sau đây là sai?
A. Hàm số đồng biến trên khoảng .
B. Hàm số có đồ thị nhận trục tung làm trục đối xứng.
C. Hàm số có giá trị nhỏ nhất là .
D. Hàm số nghịch biến trên .
Câu 6. Trong các hàm số sau đây, hàm số nào không phải là hàm tuần hoàn?
A. . B. . C. . D.
.
Câu 7. Tìm tập xác định của hàm số .
A. . B. .
C. . D. .
Câu 8. Giải các phương trình sau:
a) .
b)
( )
sin sin
pa a
-=-
( )
cos cos
pa a
-=-
( )
sin sin
pa a
+=-
( )
cos cos
pa a
+=-
sin sin
2
p
aa
æö
+=-
ç÷
èø
sin sin
2
p
aa
æö
+=
ç÷
èø
sin cos
2
p
aa
æö
+=-
ç÷
èø
22
cos 2 sin cosaaa=-
2
cos 2 2 cos 1aa=-
2
cos 2 1 2sinaa=-
sin 2 2 sin cosaaa=
sinyx=
;0
2
p
æö
-
ç÷
èø
cosyx=
sinyx=
1
cosyx=
0;
2
p
æö
ç÷
èø
tanyx=
2
2024yx=+
sinyx=
cosyx=
cos
sin 1
x
y
x
=
+
{ }
\2,kk
p
Î!"
\,
2
kk
p
p
ìü
-+ Î
íý
îþ
!"
\2,
2
kk
p
p
ìü
-+ Î
íý
îþ
!"
{ }
\,kk
p
Î!"
3
cos 2
62
x
p
æö
-=
ç÷
èø
2
2sin 2 1 cos 6 0xx-+ =
3
c)
Phiếu học tập 2
Câu 1. Khẳng định nào sau đây là sai?
A. Mỗi hàm số xác định trên tập các số nguyên dương được gọi là một dãy số.
B. Dãy số với là dãy số không tăng cũng không giảm.
C. Dãy số với là dãy số tăng.
D. Dãy số với là dãy số giảm.
Câu 2. (Tương tự) Dãy số với là dãy số:
A. Bị chặn. B. Không bị chặn.
C. Bị chặn trên bởi . D. Bị chặn dưới bởi .
Câu 3. Cho dãy số (số hạng sau bằng một phần ba số hạng liền trước nó). Công
thức tổng quát của dãy số đã cho là
A. . B. . C. . D.
.
Câu 4. Cho dãy số (số hạng sau bằng âm hai lần số hạng liền trước nó).
Công thức tổng quát của dãy số đã cho là
A. . B. . C. . D.
.
Câu 5. Trong các dãy số cho bởi công thức sau đây, dãy số nào là cấp số cộng?
A. . B. . C. . D.
.
Câu 6. Cho dãy số được xác định như sau: . Biết dãy số là cấp số nhân.
Tính số hạng thứ 5 của cấp số nhân đó.
A. . B. . C. . D.
.
Câu 7. Tổng 100 số hạng đầu của dãy số với là
ππ
tan tan
35
xx
æöæö
+= -
ç÷ç÷
èøèø
( )
n
u
1
1
2
n
n
u
-
æö
=-
ç÷
èø
( )
n
u
21
n
un=-
( )
n
u
32
n
un=+
( )
n
u
21
2
n
n
u
n
+
=
+
1
2
11 1
1, , , , .. .
3927
1
3
n
n
u
æö
=
ç÷
èø
1
1
3
n
n
u
-
æö
=
ç÷
èø
1
3
n
u
n
=
( )
1
1
3
n
n
n
u
-
-
=
3, 6,12, 24, ...--
( )
3. 2
n
n
u =-
( )
1
3. 2
n
n
u
-
=-
1
3.2
n
n
u
-
=-
52
n
un=-
( )
n
u
2
n
n
u =
( )
2
n
unn=+
72
n
un=-
2
1
n
un=+
( )
n
u
1
1
2
5
nn
u
uu
+
=-
ì
í
=
î
( )
n
u
5
1250u =-
5
1250u =
5
6250u =
5
6250u =-
( )
n
u
32
n
un=- +
4
A. . B. . C. . D.
.
Câu 8. Biết tổng số hạng đầu tiên của dãy số với bằng . Tìm ?
A. . B. . C. . D. .
Phiếu học tập 3
Câu 1. Theo số liệu thông kê điểm Giữa học kì I môn toán khối 10 của một trường THPT được
cho bởi bảng số liệu sau:
Điểm nào đại diện cho nhiều học sinh đạt được nhất?
A. . B. . C. . D. .
Câu 2. Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối thu được mẫu
số liệu ghép nhóm sau:
Mẫu số liệu ghép nhóm này có số mốt là
A. . B. . C. . D. .
Câu 3. Bảng số liệu ghép nhóm sau cho biết chiều cao của 45 học sinh lớp .
Mẫu số liệu ghép nhóm này có số mốt là
A. . B. . C. . D. .
Câu 4. Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu
số liệu ghép nhóm sau:
Nhóm chứa mốt của mẫu số liệu này là
298-
( )
100
32-+
14 950-
14 948-
n
( )
n
u
21
n
un=-
2500
n
50n =
49n =
51n =
52n =
6, 5
7, 25
7,5
8
11
0
1
2
3
( )
cm
11A
0
1
2
3
5
A. . B. . C. . D. .
Câu 5. Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 50 học sinh lớp
Nhóm chứa mốt của mẫu số liệu này là
A. . B. . C. . D. .
Câu 6. Khảo sát vận tốc (dặm/h; dặm ) của xe ô tô chạy trên con đường
thu được mẫu số liệu ghép nhóm như sau:
Nhóm chứa tứ phân vị thứ nhất là
A. . B. . C. . D.
.
Câu 7. Khảo sát số phần trăm của trẻ sơ sinh có trọng lượng dưới của một số tỉnh thành
thu được mẫu số liệu ghép nhóm như sau:
Nhóm chứa tứ phân vị thứ ba là
A. . B. . C. . D. .
Câu 8. Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số
liệu ghép nhóm sau:
Nhóm chứa trung vị là
A. . B. . C. . D. .
c) Sản phẩm:
Phiếu học tập 1
Câu 1. Trong các khẳng định sau, khẳng định nào sai?
A. . B. .
[
)
0;15
[
)
45;60
[
)
15;30
[
)
60; 75
10 A
[
)
160 ;165
[
)
155;160
[
)
165;170
[
)
145;150
1
1, 609km=
300
A
[
)
27,5 ;32,5
[
)
32,5 ;37,5
[
)
37,5 ; 42,5
[
)
42,5 ; 47, 5
2500g
[
)
5, 5; 6, 5
[
)
6, 5 ; 7, 5
[
)
7,5; 8,5
[
)
8, 5; 9, 5
[
)
15;30
[
)
30; 45
[
)
45;60
[
)
60; 75
( )
sin sin
pa a
-=
( )
cos cos
pa a
-=
6
C. . D. .
Lời giải
Chọn B
Vì nên sai.
Câu 2. Trong các khẳng định sau, khẳng định nào sai?
A. . B. .
C. . D. .
Lời giải
Chọn A
Vì nên sai.
Câu 3. Trong các khẳng định sau, khẳng định nào đúng?
A. . B. .
C. . D. .
Lời giải
Chọn A
.
Câu 4. Trong các khẳng định sau, khẳng định nào là sai?
A. . B. .
C. . D. .
Lời giải
Chọn A
Ta có :
;
.
Câu 5. Khẳng định nào sau đây là sai?
A. Hàm số đồng biến trên khoảng .
( )
sin sin
pa a
+=-
( )
cos cos
pa a
+=-
( )
cos cos
pa a
-=-
( )
cos cos
pa a
-=
( )
sin sin
pa a
-=-
( )
cos cos
pa a
-=-
( )
sin sin
pa a
+=-
( )
cos cos
pa a
+=-
( )
sin sin
pa a
-=
( )
sin sin
pa a
-=-
sin sin
2
p
aa
æö
+=-
ç÷
èø
sin sin
2
p
aa
æö
+=
ç÷
èø
sin cos
2
p
aa
æö
+=-
ç÷
èø
sin sin sin cos
222
ppp
apa aa
éù
æö æö æö
+= -+ = -=
ç÷ ç÷ ç÷
êú
èø èø èø
ëû
22
cos 2 sin cosaaa=-
2
cos 2 2 cos 1aa=-
2
cos 2 1 2sinaa=-
sin 2 2 sin cosaaa=
sin 2 2 sin cosaaa=
22
cos 2 cos sinaaa=-
2
2cos 1a=-
2
1 2sin a=-
sinyx=
;0
2
p
æö
-
ç÷
èø
7
B. Hàm số có đồ thị nhận trục tung làm trục đối xứng.
C. Hàm số có giá trị nhỏ nhất là .
D. Hàm số nghịch biến trên .
Lời giải
Chọn C
Hàm số đồng biến trên mỗi khoảng nên án A đúng.
Hàm số là hàm số chẵn nên nhận trục tung làm trục đối xứng nên đáp án B đúng.
Hàm số có tập giá trị là
nên giá trị nhỏ nhất của hàm số là , giá trị lớn nhất
là nên C sai.
Hàm số nghịch biến trên mỗi khoảng nên nên đáp án D đúng.
Câu 6. Trong các hàm số sau đây, hàm số nào không phải là hàm tuần hoàn?
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có hàm số là hàm số tuần hoàn với chu kỳ . Hàm số là hàm số tuần
hoàn với chu kỳ . Hàm số là hàm số tuần hoàn với chu kỳ .
Câu 7. Tìm tập xác định của hàm số .
A. . B. .
C. . D. .
Lời giải
Chọn C
Điều kiện .
Tập xác định .
Câu 8. Giải các phương trình sau:
cosyx=
sinyx=
1
cosyx=
0;
2
p
æö
ç÷
èø
sinyx=
2; 2 ,
22
kkk
pp
pp
æö
-+ + Î
ç÷
èø
!
cosyx=
sinyx=
[ ]
1; 1-
1-
1
cosyx=
( )
2; 2 ,kkk
pp p
+Î!
tanyx=
2
2024yx=+
sinyx=
cosyx=
sinyx=
2
p
cosyx=
2
p
tanyx=
p
cos
sin 1
x
y
x
=
+
{ }
\2,kk
p
Î!"
\,
2
kk
p
p
ìü
-+ Î
íý
îþ
!"
\2,
2
kk
p
p
ìü
-+ Î
íý
îþ
!"
{ }
\,kk
p
Î!"
sin 1 2 ,
2
xxkk
p
p
¹- Û ¹- + Î!
\2,
2
kk
p
p
ìü
-+ Î
íý
îþ
!"
8
a) .
b)
c)
Lời giải
a)
b)
c)
Phiếu học tập 2
Câu 1 Khẳng định nào sau đây là sai?
A. Mỗi hàm số xác định trên tập các số nguyên dương được gọi là một dãy số.
B. Dãy số với là dãy số không tăng cũng không giảm.
C. Dãy số với là dãy số tăng.
D. Dãy số với là dãy số giảm.
Lời giải
Chọn D
Phương án A: Mỗi hàm số xác định trên tập các số nguyên dương được gọi là một
dãy số là khẳng định đúng.
Phương án B: Dãy số với có nên dãy
không tăng cũng không giảm, suy ra phương án B đúng.
3
cos 2
62
x
p
æö
-=
ç÷
èø
2
2sin 2 1 cos 6 0xx-+ =
ππ
tan tan
35
xx
æöæö
+= -
ç÷ç÷
èøèø
( )
22
22
3
66
cos 2
36
62
22
22
66
xk
xk xk
xk
xk xk
xk
pp
pp
p
pp
p
pp
pp
p
é
-=+
éé
ê
=+ =+
æö
êê
-= Û Û Û Î
ê
ç÷
êê
èø
ê
==
-=-+
ëë
ê
ë
!
( )
22
2sin 2 1 cos 6 0 1 2sin 2 cos 6 0xx xx-+ = Û- - + =
( )
cos 6 cos 4 0 cos 6 cos 4
64 2 2 2
6 4 2 10 2
5
5
xx x x
xk
xxk xk
k
xk
k
xxk xk
x
p
pp
p
p
pp
Û-=Û=
=
é
=+ =
éé
ê
ÛÛÛÛ=Î
êê
ê
=- + =
=
ëë
ë
!
( )
ππ ππ 2π ππ
tan tan π2 π
35 35 15 152
xxxxkxkxkk
æöæö
+= -Û+=-+Û=-+Û=-+ Î
ç÷ç÷
èøèø
!
( )
n
u
1
1
2
n
n
u
-
æö
=-
ç÷
èø
( )
n
u
21
n
un=-
( )
n
u
32
n
un=+
( )
n
u
1
1
2
n
n
u
-
æö
=-
ç÷
èø
12 3
11
1; ; ; . . .
24
uu u==- =
( )
n
u
9
Phương án C: Dãy số thỏa nên dãy là dãy số
tăng, suy ra phương án C đúng.
Phương án D: Dãy số thỏa nên dãy là dãy số
tăng, suy ra phương án D sai. Vậy chọn D làm đáp án.
Câu 2. (Tương tự) Dãy số với là dãy số:
A. Bị chặn. B. Không bị chặn.
C. Bị chặn trên bởi . D. Bị chặn dưới bởi .
Lời giải
Chọn A
Với ta có với nên dãy số bị chặn dưới bởi .
Lại có: với nên dãy số bị chặn trên bởi .
Từ và suy ra dãy số bị chặn.
Câu 3. (Đổi số) Cho dãy số (số hạng sau bằng một phần ba số hạng liền trước
nó). Công thức tổng quát của dãy số đã cho là
A. . B. . C. . D. .
Lời giải
Chọn B
Phương án A: , do đó loại.
Phương án B: (thỏa mãn). Các số hạng tiếp theo khi tăng mỗi đơn
vị, số hạng thứ bằng số hạng liền trước nhân thêm (thỏa dãy số đề bài).
Phương án C: , do đó loại.
Phương án D: , do đó loại.
( )
n
u
1
20, *
nn
uu n
+
-=>"Ε
( )
n
u
( )
n
u
1
30, *
nn
uu n
+
-=>"Ε
( )
n
u
( )
n
u
21
2
n
n
u
n
+
=
+
1
2
*
n Î •
21
1
2
n
n
u
n
+
=³
+
*
n Î •
( )
n
u
1
( )
1
21 3
22
22
n
n
u
nn
+
==-<
++
*
n Î •
( )
n
u
2
( )
2
( )
1
( )
2
( )
n
u
11 1
1, , , , .. .
3927
1
3
n
n
u
æö
=
ç÷
èø
1
1
3
n
n
u
-
æö
=
ç÷
èø
1
3
n
u
n
=
( )
1
1
3
n
n
n
u
-
-
=
1
1
11
1
33
u
æö
==¹
ç÷
èø
0
1
1
1
3
u
æö
==
ç÷
èø
n
n
u
1
3
1
11
1
3.1 3
u ==¹
( )
1
1
11
1
11
3
u
-
-
==-¹
10
Vậy đán án là B.
Câu 4. (Tương tự) Cho dãy số (số hạng sau bằng âm hai lần số hạng liền
trước nó). Công thức tổng quát của dãy số đã cho là
A. . B. . C. .D. .
Lời giải
Chọn B
Phương án A: , do đó loại.
Phương án B: (thỏa mãn). Các số hạng tiếp theo khi tăng mỗi đơn vị, số
hạng thứ bằng số hạng liền trước nhân thêm (thỏa dãy số đề bài).
Phương án C: , do đó loại.
Phương án D: (thỏa mãn), , do đó loại.
Vậy đáp án là B.
Câu 5. Trong các dãy số cho bởi công thức sau đây, dãy số nào là cấp số cộng?
A. . B. . C. . D. .
Lời giải
Chọn C
Xét các dãy số với:
Dãy này không phải cấp số cộng
.
Dãy này không phải cấp số cộng
..
Dãy này không phải cấp số cộng.
.
.
, ta có: .
Dãy này là cấp số cộng với công sai .
Câu 6. Cho dãy số được xác định như sau: . Biết dãy số là cấp số nhân.
Tính số hạng thứ 5 của cấp số nhân đó.
A. . B. . C. . D. .
3, 6,12, 24, ...--
( )
3. 2
n
n
u =-
( )
1
3. 2
n
n
u
-
=-
1
3.2
n
n
u
-
=-
52
n
un=-
1
63u =- ¹
1
3u =
n
n
u
2-
1
33u =- ¹
1
3u =
2
16u =¹-
( )
n
u
2
n
n
u =
( )
2
n
unn=+
72
n
un=-
2
1
n
un=+
( )
n
u
123
22;4;8
n
n
uuuu=Þ= = =Þ
( )
21 32
uuuu-¹-
( )
123
23;8;15
n
unn u u u=+Þ= = =Þ
( )
21 32
uuuu-¹-
2
123
1 2; 5; 10
n
unuuu=+ Þ = = = Þ
( )
21 32
uuuu-¹-
72
n
un=-
*
n"Ε
( ) ( )
1
72 1 72 2
nn
uu n n
+
-=- + -- =-
éù
ëû
Þ
2d =-
( )
n
u
1
1
2
5
nn
u
uu
+
=-
ì
í
=
î
( )
n
u
5
1250u =-
5
1250u =
5
6250u =
5
6250u =-
11
Lời giải
Chọn A
Ta có: , . Vì dãy số là cấp số nhân nên công bội
. Do đó .
Câu 7 Tổng 100 số hạng đầu của dãy số với là
A. . B. . C. . D. .
Lời giải
Chọn C
Ta có:
.
Câu 8. Biết tổng số hạng đầu tiên của dãy số với bằng . Tìm ?
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có:
.
Theo bài ra ta có
1
2u =-
2
2.5 10u =- =-
( )
n
u
2
1
5
u
q
u
==
4
51
.1250uuq==-
( )
n
u
32
n
un=- +
298-
( )
100
32-+
14 950-
14 948-
1
2
100 1 2 100
100
3.1 2
3.2 2
.
... 3.(1 2 ... 100) 100.2.
.
.
3.100 2
u
u
Suu u
u
=- +
ü
ï
=- +
ï
ï
ï
Þ=+++=-+++ +
ý
ï
ï
ï
=- +
ï
þ
100
1100
3. .100 200 14 950
2
S
+
=- + =-
n
( )
n
u
21
n
un=-
2500
n
50n =
49n =
51n =
52n =
1
2
12
2.1 1
2.2 1
.
... 2.(1 2 ... ) .
.
.
2. 1
nn
n
u
u
Suu u nn
un
=-
ü
ï
=-
ï
ï
ï
Þ=+++= +++-
ý
ï
ï
ï
=-
ï
þ
2
1
2. .
2
n
n
Snnn
+
=-=
2
2500 50.nn=Þ=
12
Phiếu học tập 3
Câu 1. Theo số liệu thông kê điểm Giữa học kì I môn toán khối 10 của một trường THPT được
cho bởi bảng số liệu sau:
Điểm nào đại diện cho nhiều học sinh đạt được nhất?
A. . B. . C. . D. .
Lời giải
Chọn B
Từ bảng số liệu ta thấy nhóm có nhiều học sinh đạt được nhất (60 học
sinh).
Giá trị đại diện của nhóm là: .
Câu 2. Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối thu được mẫu
số liệu ghép nhóm sau:
Mẫu số liệu ghép nhóm này có số mốt là
A. . B. . C. . D. .
Lời giải
Chọn B
Tần số lớn nhất là nên nhóm chứa mốt là nhóm . Vậy mẫu số liệu có
một mốt.
Câu 3. Bảng số liệu ghép nhóm sau cho biết chiều cao của 45 học sinh lớp .
Mẫu số liệu ghép nhóm này có số mốt là
A. . B. . C. . D. .
Lời giải
Chọn C
6, 5
7, 25
7,5
8
[
)
6, 5;8
4
6, 5 8
7, 25
2
X
+
==
11
0
1
2
3
18
[
)
45;60
( )
cm
11A
0
1
2
3
13
Tần số lớn nhất là nên có hai nhóm chứa mốt là nhóm và .
Vậy mẫu số liệu có hai mốt.
Câu 4. Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu
số liệu ghép nhóm sau:
Nhóm chứa mốt của mẫu số liệu này là
A. . B. . C. . D. .
Lời giải
Chọn B
Nhóm có tần số lớn nhất là . Nên nhóm chứa mốt.
Câu 5. Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 50 học sinh lớp
Nhóm chứa mốt của mẫu số liệu này là
A. . B. . C. . D. .
Lời giải
Chọn B
Nhóm có tần số lớn nhất là . Nên nhóm chứa mốt.
Câu 6. Khảo sát vận tốc (dặm/h; dặm ) của xe ô tô chạy trên con đường
thu được mẫu số liệu ghép nhóm như sau:
Nhóm chứa tứ phân vị thứ nhất là
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có .
12
[
)
150 ;155
[
)
155;160
[
)
0;15
[
)
45;60
[
)
15;30
[
)
60; 75
[
)
45;60
14
[
)
45;60
10 A
[
)
160 ;165
[
)
155;160
[
)
165;170
[
)
145;150
[
)
155;160
13
[
)
155;160
1
1, 609km=
300
A
[
)
27,5 ;32,5
[
)
32,5 ;37,5
[
)
37,5 ; 42,5
[
)
42,5 ; 47, 5
300n =
14
Gọi là vận tốc của ô tô và sắp xếp theo thứ tự tăng dần. Khi đó
trung vị là . Do hai giá trị đều thuộc nhóm
nên số trung vị thuộc nhóm này. Suy ra tứ phân vị thứ nhất là
. Do thuộc nhóm nên tứ phân vị thứ nhất thuộc
nhóm này.
Câu 7. Khảo sát số phần trăm của trẻ sơ sinh có trọng lượng dưới của một số tỉnh thành
thu được mẫu số liệu ghép nhóm như sau:
Nhóm chứa tứ phân vị thứ ba là
A. . B. . C. . D. .
Lời giải
Chọn C
Ta có .
Gọi là số phần trăm của trẻ sơ sinh có trọng lượng dưới của
tỉnhthành và sắp xếp theo thứ tự tăng dần. Khi đó trung vị là . Do giá trị thuộc
nhóm nên số trung vị thuộc nhóm này. Suy ra tứ phân vị thứ ba là
. Do thuộc nhóm nên tứ phân vị thứ ba thuộc nhóm này.
Câu 8. Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số
liệu ghép nhóm sau:
Nhóm chứa trung vị là
A. . B. . C. . D. .
Lời giải
Chọn B
Cỡ mẫu .
12 300
,,...,xx x
300
150 151
2
xx+
[
)
37,5 ; 42,5
1
Q
75 76
2
xx+
75 76
,xx
[
)
32,5 ;37,5
2500g
[
)
5, 5; 6, 5
[
)
6, 5 ; 7, 5
[
)
7,5; 8,5
[
)
8, 5; 9, 5
9 6 17 8 3 43n =++ ++=
12 43
,,...,xx x
2500g
43
22
x
22
x
[
)
6, 5 ; 7, 5
3
Q
33
x
33
x
[
)
7,5; 8,5
[
)
15;30
[
)
30; 45
[
)
45;60
[
)
60; 75
9 5 15 14 7 50n =++ + +=
15
Gọi là thời gian tập thể dục của 50 học sinh và giả sử dãy này đã được
sắp xếp theo thứ tự không giảm. Khi đó trung vị là . Do hai giá trị
thuộc nhóm nên nhóm này chứa trung vị.
d) Tổ chức thực hiện
Chuyển giao
GV: Chia lớp thành 6 nhóm, tổ chức, giao nhiệm vụ
Nhóm 1,2 làm phiếu 1.Nhóm 3,4 phiếu 2. Nhóm 5,6 làm phiếu 3
HS:Nhận
Thực hiện
GV: điều hành, quan sát, hướng dẫn
HS: phân công nhiệm vụ trong nhóm, trao đổi, thảo luận và đưa ra kết quả
cuối cùng của nhóm mình
Báo cáo thảo luận
GV đưa đáp án, các nhóm thu phiếu chấm chéo
Gv gọi đại diện nhóm báo cáo, giải thích câu đúng của nhóm mình. Câu nào
sai nhóm khác có thể bổ sung thỏa luận và GV chốt kết quả
Đánh giá, nhận xét,
tổng hợp
GV nhận xét thái độ làm việc, phương án trả lời của các nhóm học sinh, ghi
nhận và tuyên dương nhóm học sinh có câu trả lời tốt nhất.
Hướng dẫn HS chuẩn bị cho nhiệm vụ tiếp theo
2. HOẠT ĐỘNG 2: VẬN DỤNG.
a)Mục tiêu: Vận dụng các kiến thức đã học giải quyết bài toán trong thực tế hoặc liên môn
b) Nội dung: Nêu ND bài tập / Phiếu học tập / Yêu cầu thực tế cần tìm hiểu/ nghiên cứu/
trảinghiệm
Câu 1. Huyết áp là áp lực cần thiết tác động lên thành của động mạch để đưa máu từ tim đến
nuôi dưỡng các mô trong cơ thể. Huyết áp được tạo ra do lực co bóp của cơ tim và
sức cản của thành động mạch. Mỗi lần tim đập, huyết áp của chúng ta tăng rồi giảm
giữa các nhịp. Huyết áp tối đa và huyết áp tối thiểu được gọi tương ứng là huyết áp
tâm thu và tâm trương. Chỉ số huyết áp của chúng ta được viết là huyết áp tâm
thu/huyết áp tâm trương. Chỉ số huyết áp là bình thường. Giả sử huyết áp của
một người nào đó được mô hình hóa bởi hàm số
,
Trong đó là huyết áp tính theo đơn vị (milimét thủy ngân) và thời gian
tính theo phút.
a) Tìm chu kì của hàm số .
b) Tìm số nhịp tim mỗi phút.
c) Tìm chỉ số huyết áp. So sánh huyết áp của người này và huyết áp bình thường.
Câu 2. Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu. Khi
người chơi nhún đều, cây đu sẽ đưa người đu dao động quanh vị trí cân bằng. Nghiên
cứu trò chơi này người ta thấy khoảng cách từ vị trí người đu đến vị trí cân
bằng được biểu diễn qua thời gian bởi hệ thức với
12 50
,,...,xx x
25 26
2
xx+
25 26
,xx
[
)
30; 45
120/80
( ) ( )
85 20sin 140pt t
p
=+
( )
pt
mmHg
t
( )
pt
( )
mh
( )
st
hd=
16
, trong đó ta quy ước khi vị trí cân bằng ở phía sau lưng
người đu và trong trường hợp ngược lại (Nguồn: Đại số và Giải tích 11 Nâng
cao, NXBGD Việt Nam năm 2020).
a) Tìm chu kì của hàm số .
b) Hỏi mỗi phút người chơi qua vị trí cân bằng theo chiều dương (tức là từ
sang ) bao nhiêu lần?
c) Khoảng cách lớn nhất của người đu so với vị trí cân bằng là bao nhiêu?
Câu 3. Từ giờ đến giờ trưa, chuông của một chiếc đồng hồ quả lắc sẽ đánh bao nhiêu
tiếng, biết rằng nó chỉ đánh chuông báo giờ và số tiếng chuông bằng số giờ?
Câu 4. Tế bào E.Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần. Hỏi
sau 12 giờ, tế bào ban đầu sẽ phân chia thành bao nhiêu tế bào?
c) Sản phẩm: Sản phẩm trình bày của cá nhân/ nhóm học sinh
Câu 1. Huyết áp là áp lực cần thiết tác động lên thành của động mạch để đưa máu từ tim đến
nuôi dưỡng các mô trong cơ thể. Huyết áp được tạo ra do lực co bóp của cơ tim và
sức cản của thành động mạch. Mỗi lần tim đập, huyết áp của chúng ta tăng rồi giảm
giữa các nhịp. Huyết áp tối đa và huyết áp tối thiểu được gọi tương ứng là huyết áp
tâm thu và tâm trương. Chỉ số huyết áp của chúng ta được viết là huyết áp tâm
thu/huyết áp tâm trương. Chỉ số huyết áp là bình thường. Giả sử huyết áp của
một người nào đó được mô hình hóa bởi hàm số
,
Trong đó là huyết áp tính theo đơn vị (milimét thủy ngân) và thời gian
tính theo phút.
a) Tìm chu kì của hàm số .
b) Tìm số nhịp tim mỗi phút.
c) Tìm chỉ số huyết áp. So sánh huyết áp của người này và huyết áp bình thường.
Lời giải
a) Áp dụng định lý: Nếu hàm số có chu kì thì hàm số với
có chu kì
Vì hàm số có chu kì nên hàm số
có chu kì
Vậy hàm số tuần hoàn với chu kì .
( )
2
3cos
33
dt t
pp
æö
=-
ç÷
èø
0d >
0d <
( )
dt
0d <
0d >
0
10
120/80
( ) ( )
85 20sin 140pt t
p
=+
( )
pt
mmHg
t
( )
pt
( )
fx
0
T
( )
fax b+
0a ¹
0
T
T
a
=
( )
85 20 sinft t=+
0
2T
p
=
( ) ( )
85 20sin 140pt t
p
=+
0
221
140 140 70
T
T
a
pp
pp
== = =
( )
pt
1
70
T =
17
b) Do mỗi lần tim đập, huyết áp của chúng ta tăng rồi giảm giữa các nhịp nên số nhịp
tim mỗi phút là: (lần/phút).
c) Ta có
.
Vậy chỉ số huyết áp là . Chỉ số huyết áp của người này so với huyết áp bình
thường là thấp hơn.
Câu 2. Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu. Khi
người chơi nhún đều, cây đu sẽ đưa người đu dao động quanh vị trí cân bằng. Nghiên
cứu trò chơi này người ta thấy khoảng cách từ vị trí người đu đến vị trí cân
bằng được biểu diễn qua thời gian bởi hệ thức với
, trong đó ta quy ước khi vị trí cân bằng ở phía sau lưng
người đu và trong trường hợp ngược lại (Nguồn: Đại số và Giải tích 11 Nâng
cao, NXBGD Việt Nam năm 2020).
a) Tìm chu kì của hàm số .
b) Hỏi mỗi phút người chơi qua vị trí cân bằng theo chiều dương (tức là từ
sang ) bao nhiêu lần?
c) Khoảng cách lớn nhất của người đu so với vị trí cân bằng là bao nhiêu?
Lời giải
a) Áp dụng định lý: Nếu hàm số có chu kì thì hàm số với
có chu kì
Vì hàm số có chu kì nên hàm số có
chu kì
Vậy hàm số tuần hoàn với chu kì .
b) Trong một phút số lần người chơi qua vị trí cân bằng theo chiều dương (tức là từ
sang ) là: (lần).
c) Ta có:
.
1
70
T
=
( ) ( ) ( )
1sin140 1 20 20sin140 20 658520sin140 105tt t
pp p
-£ £ Û- £ £ Û £ + £
105/65
( )
mh
( )
st
hd=
( )
2
3cos
33
dt t
pp
æö
=-
ç÷
èø
0d >
0d <
( )
dt
0d <
0d >
( )
fx
0
T
( )
fax b+
0a ¹
0
T
T
a
=
( )
3cosft t=
0
2T
p
=
( )
2
3cos
33
dt t
pp
æö
=-
ç÷
èø
0
22
3
2
2
3
3
T
T
a
pp
p
p
== = =
( )
dt
3T =
0d <
0d >
60
20
3
=
222
,1 cos 1 3 3cos 3 0 3cos 3
33 33 33
tt t t
pp pp pp
æö æö æö
"Î - £ - £ Û- £ - £ Þ £ - £
ç÷ ç÷ ç÷
èø èø èø
!
18
Vậy khoảng cách lớn nhất của người chơi so với vị trí cân bằng là .
Câu 3. Từ giờ đến giờ trưa, chuông của một chiếc đồng hồ quả lắc sẽ đánh bao nhiêu
tiếng, biết rằng nó chỉ đánh chuông báo giờ và số tiếng chuông bằng số giờ?
Lời giải
Từ giờ đến giờtrưa có tiếng đồng hồ (tính cả giờ)
Ta có số tiếng chuông của đồng hồ tăng theo cấp số cộng
Số tiếng chuông của đồng hồ là tổng của số hạng đầu tiên của cấp số cộng
Chuông của một chiếc đồng hồ quả lắc sẽ đánh tiếng.
Câu 4. Tế bào E.Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần. Hỏi
sau 12 giờ, tế bào ban đầu sẽ phân chia thành bao nhiêu tế bào?
Lời giải
Vì ban đầu có một tế bào và mỗi tế bào phân chia thành hai tế bào nên ta có cấp số
nhân với .
Vì cứ 20 phút tế bào lại phân đôi một lần nên sau 12 giờ sẽ có 36 lần phân chia tế
bào.
Số tế bào nhận được sau 12 giờ là tế bào.
d) Tổ chức thực hiện
Chuyển giao
GV: tổ chức, giao nhiệm vụ
HS:Nhận
Thực hiện
GV: điều hành, quan sát, hướng dẫn HS chuẩn bị
HS: Đọc, nghe, nhìn, làm ( cách thức thực hiện: cá nhân)
thực hiện ở nhà
Báo cáo thảo luận
HS báo cáo, theo dõi, nhận xét / hình thức báo cáo vở bài tập
Đánh giá, nhận xét,
tổng hợp
Hướng dẫn HS xây dựng sơ đồ tư duy các kiến thức trong bài học
• Tự ôn tập lại toàn bộ kiến thức chương I, II, III. Xem lại tất cả các bài
tập được hướng dẫn.
• Chuẩn bị tốt kiến thức để làm bài kiểm tra giữa Học kì I theo đề
chung của nhà trường.
( )
3m
0
10
0
10
11
0
1
0
1
u
d
=
ì
í
=
î
11
( )
11
11 11 1 .1
0.11 55
2
S
-
=+ =
55
1
1, 2uq==
36 36
37 1
.2uuq==
| 1/18
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


Trường ………………………..
Họ và tên giáo viên: ……………………
Tổ ………………….
KẾ HOẠCH BÀI DẠY
TÊN BÀI DẠY: ÔN TẬP GIỮA HỌC KÌ I
Môn học/Hoạt động giáo dục: Toán; lớp: 11
Thời gian thực hiện: (01 tiết) I. MỤC TIÊU 1. Kiến thức
- Cung và góc lượng giác, giá trị lượng giác của một cung, công thức lượng giác.
- Công thức nghiệm của phương trình lượng giác cơ bản.
- Cách giải một số phương trình lượng giác đơn giản
- Định nghĩa và các tính chất của dãy số.
- Định nghĩa, các công thức số hạng tổng quát, tính chất của cấp số cộng và cấp số nhân.
- Mẫu số liệu ghép nhóm
- Các số đặc trưng đo xu thế trung tâm 2. Về năng lực
- Năng lực tư duy và lập luận Toán học: Trong quá trình giải bài tập.
- Năng lực mô hình hóa Toán học: Trong các bài toán thực tế.
- Năng lực giải quyết vấn đề Toán học: Trong các lời giải của các bài tập.
- Năng lực giao tiếp Toán học: Trong các định lý, ví dụ, bài tập.
- Năng lực sử dụng công cụ, phương tiện để học Toán: Sử dụng máy tính cầm tay. 3. Về phẩm chất
- Chăm chỉ, hoàn thành các nhiệm vụ được giao.
- Trách nhiệm, cố gắng chiếm lĩnh kiến thức mới, cố gắng làm đúng các bài tập.
- Có thế giới quan khoa học
II. THIẾT BỊ DẠY HỌC
- Kế hoạch bài dạy, SGK, phiếu học tập, phấn, thước kẻ, máy chiếu.
III. TIẾN TRÌNH DẠY HỌC
1. HOẠT ĐỘNG 1: LUYỆN TẬP
a) Mục tiêu: HS biết áp dụng các kiến thức đã học vào các dạng bài tập cụ thể
b) Nội dung: Nêu ND bài tập / Phiếu học tập Phiếu học tập 1
Câu 1. Trong các khẳng định sau, khẳng định nào sai? A. sin(p -a ) = sina . B. cos(p -a ) = cosa .
C. sin(p +a ) = -sina .
D. cos(p +a ) = -cosa .
Câu 2. Trong các khẳng định sau, khẳng định nào sai? 1
A. sin(p -a ) = -sina .
B. cos(p -a ) = -cosa .
C. sin(p +a ) = -sina .
D. cos(p +a ) = -cosa .
Câu 3. Trong các khẳng định sau, khẳng định nào đúng? æ p ö æ p ö A. sin a + = cosa . B. sin a + = -sina . ç ÷ ç ÷ è 2 ø è 2 ø æ p ö æ p ö C. sin a + = sina . D. sin a + = -cosa . ç ÷ ç ÷ è 2 ø è 2 ø
Câu 4. Trong các khẳng định sau, khẳng định nào là sai? A. 2 2
cos 2a = sin a - cos a. B. 2
cos 2a = 2cos a - . 1 C. 2
cos 2a =1- 2sin a .
D. sin 2a = 2sin a cos a .
Câu 5. Khẳng định nào sau đây là sai? æ p ö
A. Hàm số y = sin x đồng biến trên khoảng - ; 0 . ç ÷ è 2 ø
B. Hàm số y = cos x có đồ thị nhận trục tung làm trục đối xứng.
C. Hàm số y = sin x có giá trị nhỏ nhất là 1. æ p ö
D. Hàm số y = cos x nghịch biến trên 0; . ç ÷ è 2 ø
Câu 6. Trong các hàm số sau đây, hàm số nào không phải là hàm tuần hoàn?
A. y = tan x. B. 2
y = x + 2024.
C. y = sin x . D.
y = cos x . cos x
Câu 7. Tìm tập xác định của hàm số y = . sin x +1 ì p ü
A. ! \{k2p,k Î } " .
B. ! \ í- + kp ,k Î"ý. î 2 þ ì p ü
C. ! \ í- + k2p ,k Î"ý.
D. ! \{kp,k Î } " . î 2 þ
Câu 8. Giải các phương trình sau: æ p ö 3 a) cos 2x - = ç ÷ . è 6 ø 2 b) 2
2sin 2x -1+ cos 6x = 0 2 æ π ö æ π ö c) tan x + = tan - x ç ÷ ç ÷ è 3 ø è 5 ø Phiếu học tập 2
Câu 1. Khẳng định nào sau đây là sai?
A. Mỗi hàm số xác định trên tập các số nguyên dương được gọi là một dãy số. n 1 1 - æ ö B. Dãy số (u u = - n ) với
là dãy số không tăng cũng không giảm. n ç ÷ è 2 ø C. Dãy số (u u = 2n -1 n ) với là dãy số tăng. n D. Dãy số (u u = 3n + 2 n ) với là dãy số giảm. n 2n +1
Câu 2. (Tương tự) Dãy số (u u = n ) với là dãy số: n n + 2 A. Bị chặn. B. Không bị chặn.
C. Bị chặn trên bởi 1.
D. Bị chặn dưới bởi 2 . 1 1 1
Câu 3. Cho dãy số 1, , ,
,... (số hạng sau bằng một phần ba số hạng liền trước nó). Công 3 9 27
thức tổng quát của dãy số đã cho là æ 1 n ö n 1 1 - æ ö 1 A. u = . B. u = . C. u = . D. n ç ÷ ç ÷ è 3 ø n è 3 ø n 3n (- )1n u = . n n 1 3 -
Câu 4. Cho dãy số 3, - 6,12, - 24,... (số hạng sau bằng âm hai lần số hạng liền trước nó).
Công thức tổng quát của dãy số đã cho là A. u = 3. - u - = - 1 u 3.2n- = - n ( ) 1 3. 2 n n ( 2)n. B. . C. . D. n u = 5 - 2n . n
Câu 5. Trong các dãy số (un ) cho bởi công thức sau đây, dãy số nào là cấp số cộng?
A. u = 2n .
B. u = n(n + 2 u = 7 - 2n n ). C. . D. n n 2 u = 1+ n . n u ì = 2 -
Câu 6. Cho dãy số (u 1 (un)
n ) được xác định như sau: í . Biết dãy số là cấp số nhân. u = 5u î n 1+ n
Tính số hạng thứ 5 của cấp số nhân đó. A. u = 1250 - . B. u =1250 . C. u = 6250 . D. 5 5 5 u = 6250 - . 5
Câu 7. Tổng 100 số hạng đầu của dãy số (u u = 3 - n + 2 n ) với là n 3 A. 298 - . B. (- )100 3 + 2. C. 14 - 950 . D. 14 - 948.
Câu 8. Biết tổng n số hạng đầu tiên của dãy số (u u = 2n -1 2500 n n ) với bằng . Tìm ? n A. n = 50 . B. n = 49 . C. n = 51. D. n = 52 . Phiếu học tập 3
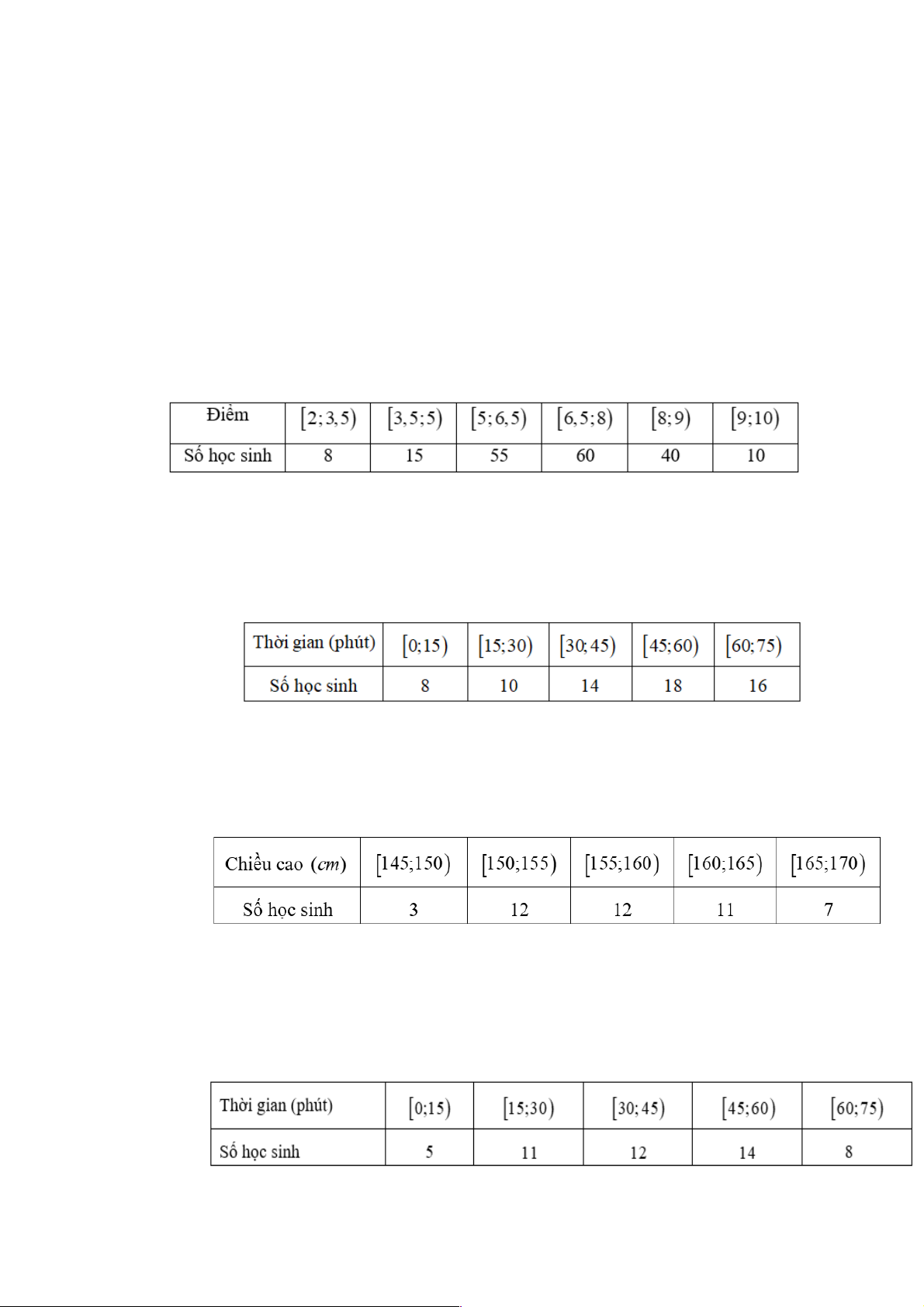
Câu 1. Theo số liệu thông kê điểm Giữa học kì I môn toán khối 10 của một trường THPT được
cho bởi bảng số liệu sau:
Điểm nào đại diện cho nhiều học sinh đạt được nhất? A. 6,5. B. 7, 25. C. 7,5. D. 8 .
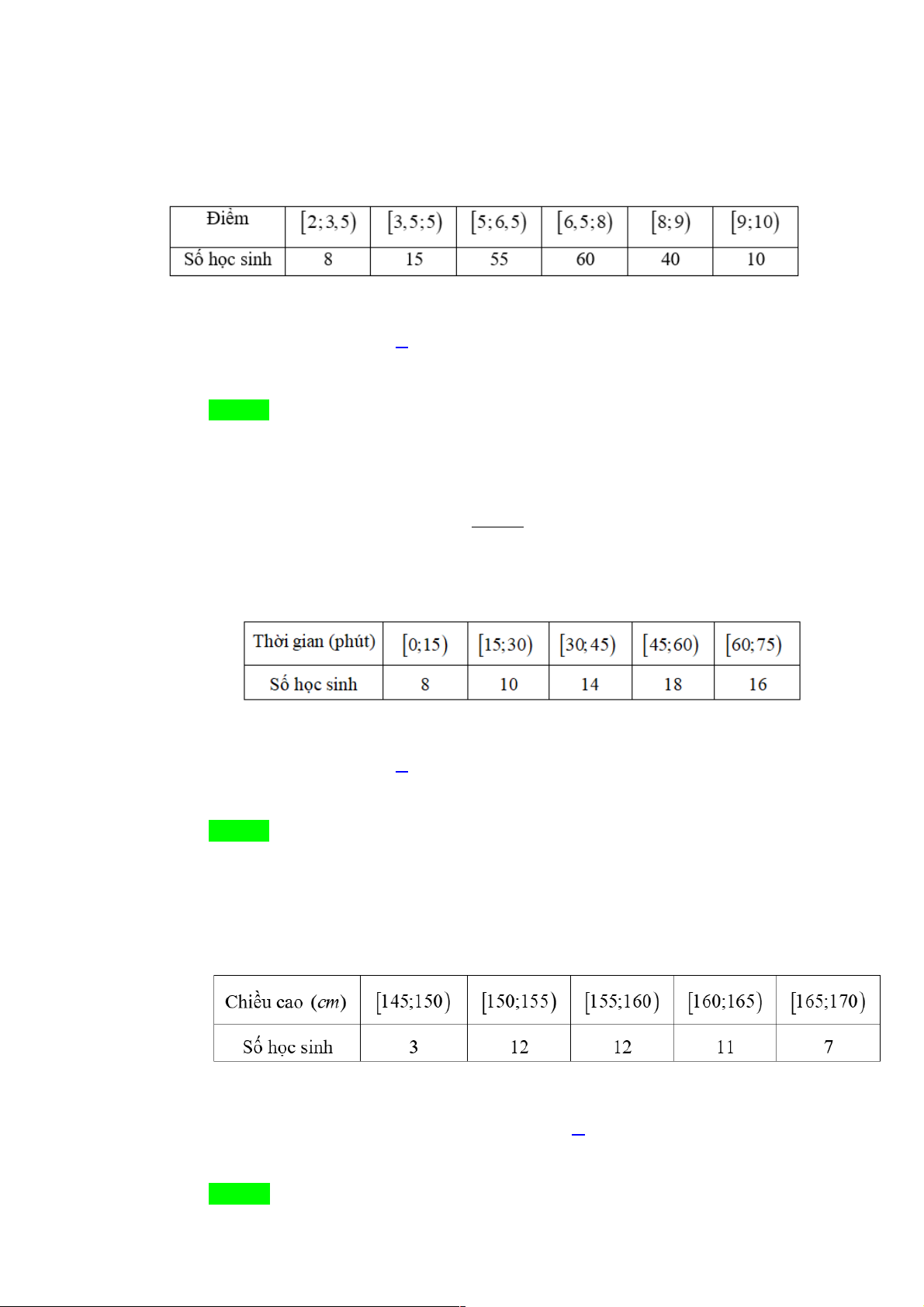
Câu 2. Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Mẫu số liệu ghép nhóm này có số mốt là A. 0 . B. 1. C. 2 . D. 3.
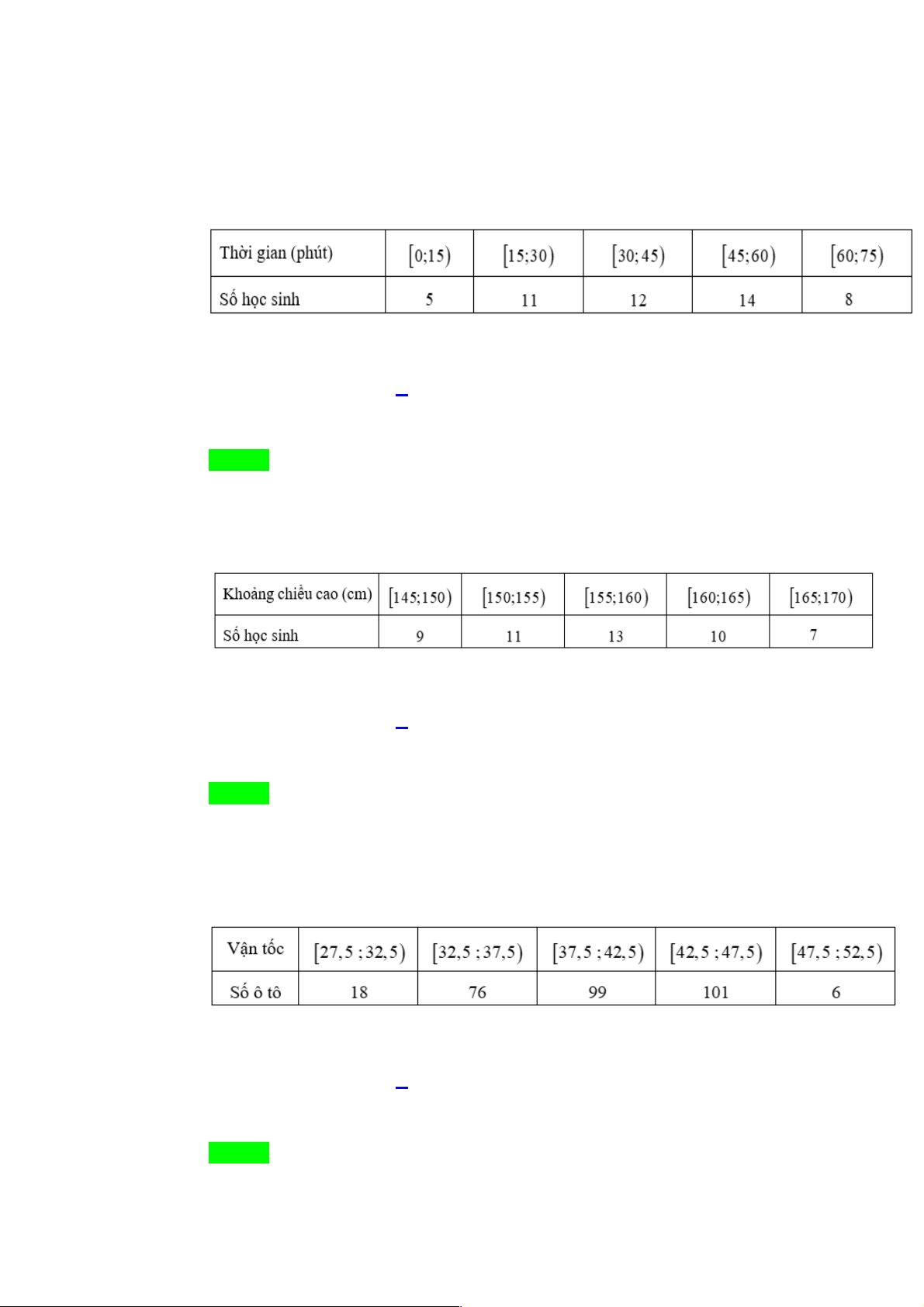
Câu 3. Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 45 học sinh lớp 11A.
Mẫu số liệu ghép nhóm này có số mốt là A. 0 . B. 1. C. 2 . D. 3.
Câu 4. Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa mốt của mẫu số liệu này là 4 A. [0;15). B. [45;60).
C. [15;30). D. [60;75).
Câu 5. Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 50 học sinh lớp 10A
Nhóm chứa mốt của mẫu số liệu này là A. [160;165). B. [155;160).
C. [165;170). D. [145;150).
Câu 6. Khảo sát vận tốc (dặm/h; 1 dặm = 1,609km) của 300 xe ô tô chạy trên con đường A
thu được mẫu số liệu ghép nhóm như sau:
Nhóm chứa tứ phân vị thứ nhất là A. [27,5 ;32,5). B. [32,5 ;37,5).
C. [37,5 ;42,5). D. [42,5 ;47,5) .
Câu 7. Khảo sát số phần trăm của trẻ sơ sinh có trọng lượng dưới 2500g của một số tỉnh thành
thu được mẫu số liệu ghép nhóm như sau:
Nhóm chứa tứ phân vị thứ ba là A. [5,5; 6,5). B. [6,5; 7,5).
C. [7,5; 8,5). D. [8,5; 9,5).
Câu 8. Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Nhóm chứa trung vị là A. [15;30). B. [30;45).
C. [45;60). D. [60;75). c) Sản phẩm: Phiếu học tập 1
Câu 1. Trong các khẳng định sau, khẳng định nào sai? A. sin(p -a ) = sina . B. cos(p -a ) = cosa . 5
C. sin(p +a ) = -sina .
D. cos(p +a ) = -cosa . Lời giải Chọn B
Vì cos(p -a ) = -cosa nên cos(p -a ) = cosa sai.
Câu 2. Trong các khẳng định sau, khẳng định nào sai?
A. sin(p -a ) = -sina .
B. cos(p -a ) = -cosa .
C. sin(p +a ) = -sina .
D. cos(p +a ) = -cosa . Lời giải Chọn A
Vì sin(p -a ) = sina nên sin(p -a ) = -sina sai.
Câu 3. Trong các khẳng định sau, khẳng định nào đúng? æ p ö æ p ö A. sin a + = cosa . B. sin a + = -sina . ç ÷ ç ÷ è 2 ø è 2 ø æ p ö æ p ö C. sin a + = sina . D. sin a + = -cosa . ç ÷ ç ÷ è 2 ø è 2 ø Lời giải Chọn A æ p ö é æ p öù æ p ö sin a + = sin p - a + = sin -a = cosa . ç ÷ ê ç ÷ú ç ÷ è 2 ø ë è 2 øû è 2 ø
Câu 4. Trong các khẳng định sau, khẳng định nào là sai? A. 2 2
cos 2a = sin a - cos a. B. 2
cos 2a = 2cos a - . 1 C. 2
cos 2a =1- 2sin a .
D. sin 2a = 2sin a cos a . Lời giải Chọn A Ta có :
sin 2a = 2sin a cos a ; 2 2
cos 2a = cos a - sin a 2 = 2cos a - 1 2 =1- 2sin a.
Câu 5. Khẳng định nào sau đây là sai? æ p ö
A. Hàm số y = sin x đồng biến trên khoảng - ; 0 . ç ÷ è 2 ø 6
B. Hàm số y = cos x có đồ thị nhận trục tung làm trục đối xứng.
C. Hàm số y = sin x có giá trị nhỏ nhất là 1. æ p ö
D. Hàm số y = cos x nghịch biến trên 0; . ç ÷ è 2 ø Lời giải Chọn C æ p p ö
Hàm số y = sin x đồng biến trên mỗi khoảng - + k2p ; + k2p , k Î ! nên án A đúng. ç ÷ è 2 2 ø
Hàm số y = cos x là hàm số chẵn nên nhận trục tung làm trục đối xứng nên đáp án B đúng.
Hàm số y = sin x có tập giá trị là [ 1 - ; ]
1 nên giá trị nhỏ nhất của hàm số là 1 - , giá trị lớn nhất là 1 nên C sai.
Hàm số y = cos x nghịch biến trên mỗi khoảng (k2p;p + k2p ),k Î! nên nên đáp án D đúng.
Câu 6. Trong các hàm số sau đây, hàm số nào không phải là hàm tuần hoàn?
A. y = tan x. B. 2
y = x + 2024.
C. y = sin x . D. y = cos x . Lời giải Chọn B
Ta có hàm số y = sin x là hàm số tuần hoàn với chu kỳ 2p . Hàm số y = cos x là hàm số tuần
hoàn với chu kỳ 2p . Hàm số y = tan x là hàm số tuần hoàn với chu kỳ p . cos x
Câu 7. Tìm tập xác định của hàm số y = . sin x +1 ì p ü
A. ! \{k2p,k Î } " .
B. ! \ í- + kp ,k Î"ý. î 2 þ ì p ü
C. ! \ í- + k2p ,k Î"ý.
D. ! \{kp,k Î } " . î 2 þ Lời giải Chọn C p
Điều kiện sin x ¹ 1
- Û x ¹ - + k2p,k Î!. 2 ì p ü
Tập xác định ! \ í- + k2p , k Î"ý. î 2 þ
Câu 8. Giải các phương trình sau: 7 æ p ö 3 a) cos 2x - = ç ÷ . è 6 ø 2 b) 2
2sin 2x -1+ cos 6x = 0 æ π ö æ π ö c) tan x + = tan - x ç ÷ ç ÷ è 3 ø è 5 ø Lời giải é p p 2x - = + k2p é p é p æ p ö 3 ê 6 6 2x = + k2p x = + kp a) cos 2x ê ç ÷ ê 3 ê - = Û Û Û 6 (k Î!) è 6 ø 2 p p ê ê ê2x - = - + k2p ë2x = k2p ëx = kp êë 6 6 b) 2 x - + x = Û -( 2 2sin 2 1 cos6 0
1- 2sin 2x)+cos6x = 0
Û cos 6x - cos 4x = 0 Û cos 6x = cos 4x é x = kp
é 6x = 4x + k2p é 2x = k2p kp ê Û Û Û kp Û x = (k Î ê ê !)
ë6x = -4x + k2p 10 ë x = k2p êx = 5 ë 5 æ π ö æ π ö π π 2π π π c) tan x + = tan
- x Û x + = - x + π k Û 2x = - + π k Û x = - + k (k Î ç ÷ ç ÷ !) è 3 ø è 5 ø 3 5 15 15 2 Phiếu học tập 2
Câu 1 Khẳng định nào sau đây là sai?
A. Mỗi hàm số xác định trên tập các số nguyên dương được gọi là một dãy số. n 1 1 - æ ö B. Dãy số (u u = - n ) với
là dãy số không tăng cũng không giảm. n ç ÷ è 2 ø C. Dãy số (u u = 2n -1 n ) với là dãy số tăng. n D. Dãy số (u u = 3n + 2 n ) với là dãy số giảm. n Lời giải Chọn D
Phương án A: Mỗi hàm số xác định trên tập các số nguyên dương được gọi là một
dãy số là khẳng định đúng. n 1 1 - æ ö 1 1
Phương án B: Dãy số (u u = -
u = 1;u = - ;u = ;... n ) với có nên dãy n ç ÷ è 2 ø 1 2 3 2 4
(un) không tăng cũng không giảm, suy ra phương án B đúng. 8
Phương án C: Dãy số (u
u - u = 2 > 0, n " Ε * (un) n ) thỏa nên dãy là dãy số n 1 + n
tăng, suy ra phương án C đúng.
Phương án D: Dãy số (u
u - u = 3 > 0, n " Ε * (un) n ) thỏa nên dãy là dãy số n 1 + n
tăng, suy ra phương án D sai. Vậy chọn D làm đáp án. 2n +1
Câu 2. (Tương tự) Dãy số (u u = n ) với là dãy số: n n + 2 A. Bị chặn. B. Không bị chặn.
C. Bị chặn trên bởi 1.
D. Bị chặn dưới bởi 2 . Lời giải Chọn A 2n +1 Với *
n Î • ta có u = ³ 1 với *
n Î • nên dãy số (u 1
n ) bị chặn dưới bởi . n n + 2 ( ) 1 2n +1 3 Lại có: u = = 2 - < 2 với *
n Î • nên dãy số (u 2
n ) bị chặn trên bởi . n n + 2 n + 2 (2) Từ ( )
1 và (2) suy ra dãy số (un ) bị chặn. 1 1 1
Câu 3. (Đổi số) Cho dãy số 1, , ,
,... (số hạng sau bằng một phần ba số hạng liền trước 3 9 27
nó). Công thức tổng quát của dãy số đã cho là æ 1 n ö n 1 1 - æ ö 1 (- )1n A. u = . B. u = . C. u = . D. u = . n ç ÷ ç ÷ è 3 ø n è 3 ø n 3n n n 1 3 - Lời giải Chọn B 1 æ 1 ö 1 Phương án A: u = = ¹ 1, do đó loại. 1 ç ÷ è 3 ø 3 0 æ 1 ö Phương án B: u =
=1 (thỏa mãn). Các số hạng tiếp theo khi n tăng mỗi đơn 1 ç ÷ è 3 ø 1
vị, số hạng thứ u bằng số hạng liền trước nhân thêm (thỏa dãy số đề bài). n 3 1 1 Phương án C: u = = ¹ 1, do đó loại. 1 3.1 3 (- )1 1 Phương án D: u = = 1 - ¹ 1, do đó loại. 1 1 1 3 - 9 Vậy đán án là B.
Câu 4. (Tương tự) Cho dãy số 3, - 6,12, - 24,... (số hạng sau bằng âm hai lần số hạng liền
trước nó). Công thức tổng quát của dãy số đã cho là A. u = 3. - u - = - 1 u 3.2n- = - u = 5 - 2n n ( ) 1 3. 2 n n ( 2)n. B. . C. .D. . n n Lời giải Chọn B Phương án A: u = 6 - ¹ 3, do đó loại. 1
Phương án B: u = 3 (thỏa mãn). Các số hạng tiếp theo khi n tăng mỗi đơn vị, số 1
hạng thứ u bằng số hạng liền trước nhân thêm 2
- (thỏa dãy số đề bài). n Phương án C: u = 3 - ¹ 3, do đó loại. 1
Phương án D: u = 3 (thỏa mãn), u =1 ¹ 6 - , do đó loại. 1 2 Vậy đáp án là B.
Câu 5. Trong các dãy số (un ) cho bởi công thức sau đây, dãy số nào là cấp số cộng?
A. u = 2n .
B. u = n(n + 2 u = 7 - 2n 2 u = 1+ n n ). C. . D. . n n n Lời giải Chọn C
Xét các dãy số (un ) với:
u = 2n Þ u = 2;u = 4;u = 8 Þ Dãy này không phải cấp số cộng n 1 2 3
(u -u ¹ u -u 2 1 3 2 ) . u = n n +
Þ u = u = u = Þ n ( 2) 3; 8; 15
Dãy này không phải cấp số cộng 1 2 3
(u -u ¹ u -u 2 1 3 2 ) .. 2
u = 1+ n Þ u = 2;u = 5;u = 10 ÞDãy này không phải cấp số cộng. n 1 2 3
(u -u ¹ u -u 2 1 3 2 ) . u = 7 - 2n. n * n
" Ε , ta có: u -u = é7 - 2 n +1 ù - 7 - 2n = 2 - n 1 + n ë ( )û ( ) .
Þ Dãy này là cấp số cộng với công sai d = 2 - . u ì = 2 -
Câu 6. Cho dãy số (u 1 (un)
n ) được xác định như sau: í . Biết dãy số là cấp số nhân. u = 5u î n 1+ n
Tính số hạng thứ 5 của cấp số nhân đó. A. u = 1250 - . B. u =1250 .
C. u = 6250 . D. u = 6250 - . 5 5 5 5 10 Lời giải Chọn A Ta có: u = 2 - , u = 2. - 5 = 10
- . Vì dãy số (un ) là cấp số nhân nên công bội 1 2 u2 q = = 5. Do đó 4
u = u .q = 1 - 250. u 5 1 1
Câu 7 Tổng 100 số hạng đầu của dãy số (u u = 3 - n + 2 n ) với là n A. 298 - . B. (- )100 3 + 2. C. 14 - 950 . D. 14 - 948. Lời giải Chọn C Ta có: u = 3 - .1+ 2 ü 1 u 3.2 2 ï = - + 2 ï . ï
ý Þ S = u + u +...+ u = 3 - .(1+ 2 + ...+100) +100.2. 100 1 2 100 . ï . ï ï u = 3 - .100 + 2ï 100 þ 1+100 S = 3. - .100 + 200 = 14 - 950. 100 2
Câu 8. Biết tổng n số hạng đầu tiên của dãy số (u u = 2n -1 2500 n n ) với bằng . Tìm ? n A. n = 50 . B. n = 49 . C. n = 51. D. n = 52 . Lời giải Chọn A Ta có: u = 2.1-1 ü 1 u 2.2 1ï = - 2 ï . ï
ý Þ S = u + u +...+ u = 2.(1+ 2 +...+ n) - . n n 1 2 . n ï . ï ï u = 2.n -1ï n þ 1+ n 2 S = 2.
.n - n = n . n 2 Theo bài ra ta có 2
n = 2500 Þ n = 50. 11 Phiếu học tập 3
Câu 1. Theo số liệu thông kê điểm Giữa học kì I môn toán khối 10 của một trường THPT được
cho bởi bảng số liệu sau:
Điểm nào đại diện cho nhiều học sinh đạt được nhất? A. 6,5. B. 7, 25. C. 7,5. D. 8 . Lời giải Chọn B
Từ bảng số liệu ta thấy nhóm [6,5;8) có nhiều học sinh đạt được nhất (60 học sinh).
Giá trị đại diện của nhóm là: 6,5 + 8 X = = 7, 25. 4 2
Câu 2. Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Mẫu số liệu ghép nhóm này có số mốt là A. 0 . B. 1. C. 2 . D. 3. Lời giải Chọn B
Tần số lớn nhất là 18 nên nhóm chứa mốt là nhóm [45;60). Vậy mẫu số liệu có một mốt.
Câu 3. Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 45 học sinh lớp 11A.
Mẫu số liệu ghép nhóm này có số mốt là A. 0 . B. 1. C. 2 . D. 3. Lời giải Chọn C 12
Tần số lớn nhất là 12 nên có hai nhóm chứa mốt là nhóm [150;155) và [155;160).
Vậy mẫu số liệu có hai mốt.
Câu 4. Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa mốt của mẫu số liệu này là A. [0;15). B. [45;60).
C. [15;30). D. [60;75). Lời giải Chọn B
Nhóm [45;60) có tần số lớn nhất là 14. Nên nhóm [45;60) chứa mốt.
Câu 5. Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 50 học sinh lớp 10A
Nhóm chứa mốt của mẫu số liệu này là A. [160;165). B. [155;160).
C. [165;170). D. [145;150). Lời giải Chọn B
Nhóm [155;160) có tần số lớn nhất là 13. Nên nhóm [155;160) chứa mốt.
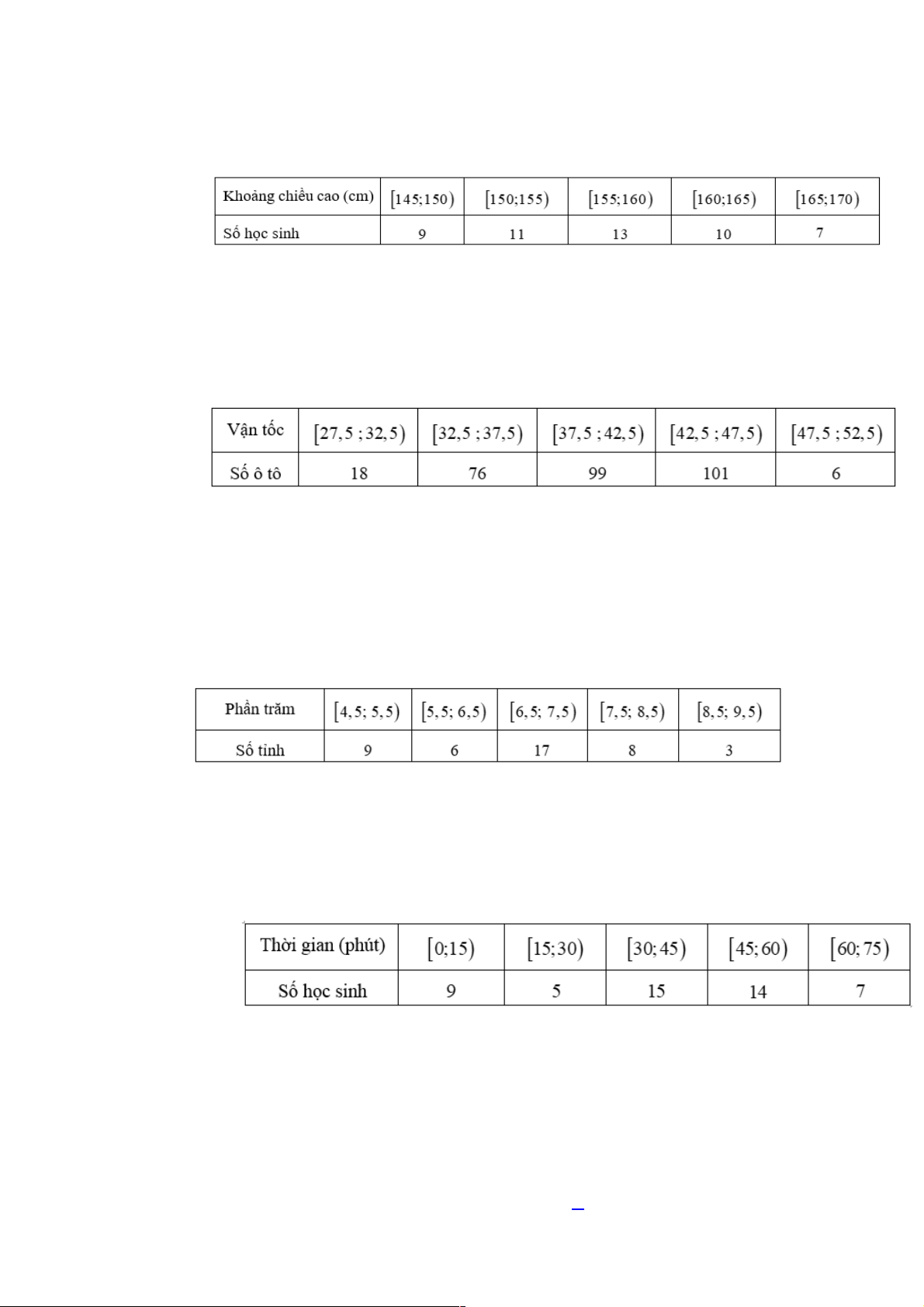
Câu 6. Khảo sát vận tốc (dặm/h; 1 dặm = 1,609km) của 300 xe ô tô chạy trên con đường A
thu được mẫu số liệu ghép nhóm như sau:
Nhóm chứa tứ phân vị thứ nhất là A. [27,5 ;32,5). B. [32,5 ;37,5).
C. [37,5 ;42,5). D. [42,5 ;47,5). Lời giải Chọn B Ta có n = 300 . 13
Gọi x , x ,. ., x là vận tốc của 300 ô tô và sắp xếp theo thứ tự tăng dần. Khi đó 1 2 300 x + x 150 151 trung vị là
. Do hai giá trị đều thuộc nhóm 2 [37,5 ;42,5) Q
nên số trung vị thuộc nhóm này. Suy ra tứ phân vị thứ nhất 1 là x + x 75 76 x , x [32,5 ;37,5) . Do 75 76 thuộc nhóm
nên tứ phân vị thứ nhất thuộc 2 nhóm này.
Câu 7. Khảo sát số phần trăm của trẻ sơ sinh có trọng lượng dưới 2500g của một số tỉnh thành
thu được mẫu số liệu ghép nhóm như sau:
Nhóm chứa tứ phân vị thứ ba là A. [5,5; 6,5). B. [6,5; 7,5).
C. [7,5; 8,5). D. [8,5; 9,5). Lời giải Chọn C
Ta có n = 9 + 6 +17 + 8 + 3 = 43.
Gọi x , x ,. ., x là số phần trăm của trẻ sơ sinh có trọng lượng dưới 2500g của 43 1 2 43
tỉnhthành và sắp xếp theo thứ tự tăng dần. Khi đó trung vị là x . Do giá trị x thuộc 22 22
nhóm [6,5; 7,5) nên số trung vị thuộc nhóm này. Suy ra tứ phân vị thứ ba Q là x 3 33
. Do x thuộc nhóm [7,5; 8,5) nên tứ phân vị thứ ba thuộc nhóm này. 33
Câu 8. Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Nhóm chứa trung vị là A. [15;30). B. [30;45).
C. [45;60). D. [60;75). Lời giải Chọn B
Cỡ mẫu n = 9 + 5 +15 +14 + 7 = 50 . 14
Gọi x , x ,. ., x là thời gian tập thể dục của 50 học sinh và giả sử dãy này đã được 1 2 50 x + x 25 26 x , x
sắp xếp theo thứ tự không giảm. Khi đó trung vị là . Do hai giá trị 25 26 2 [30;45) thuộc nhóm
nên nhóm này chứa trung vị.
d) Tổ chức thực hiện
GV: Chia lớp thành 6 nhóm, tổ chức, giao nhiệm vụ Chuyển giao
Nhóm 1,2 làm phiếu 1.Nhóm 3,4 phiếu 2. Nhóm 5,6 làm phiếu 3 HS:Nhận
GV: điều hành, quan sát, hướng dẫn Thực hiện
HS: phân công nhiệm vụ trong nhóm, trao đổi, thảo luận và đưa ra kết quả
cuối cùng của nhóm mình
GV đưa đáp án, các nhóm thu phiếu chấm chéo
Báo cáo thảo luận Gv gọi đại diện nhóm báo cáo, giải thích câu đúng của nhóm mình. Câu nào
sai nhóm khác có thể bổ sung thỏa luận và GV chốt kết quả
GV nhận xét thái độ làm việc, phương án trả lời của các nhóm học sinh, ghi
Đánh giá, nhận xét, nhận và tuyên dương nhóm học sinh có câu trả lời tốt nhất. tổng hợp
Hướng dẫn HS chuẩn bị cho nhiệm vụ tiếp theo
2. HOẠT ĐỘNG 2: VẬN DỤNG.
a)Mục tiêu: Vận dụng các kiến thức đã học giải quyết bài toán trong thực tế hoặc liên môn
b) Nội dung: Nêu ND bài tập / Phiếu học tập / Yêu cầu thực tế cần tìm hiểu/ nghiên cứu/ trảinghiệm
Câu 1. Huyết áp là áp lực cần thiết tác động lên thành của động mạch để đưa máu từ tim đến
nuôi dưỡng các mô trong cơ thể. Huyết áp được tạo ra do lực co bóp của cơ tim và
sức cản của thành động mạch. Mỗi lần tim đập, huyết áp của chúng ta tăng rồi giảm
giữa các nhịp. Huyết áp tối đa và huyết áp tối thiểu được gọi tương ứng là huyết áp
tâm thu và tâm trương. Chỉ số huyết áp của chúng ta được viết là huyết áp tâm
thu/huyết áp tâm trương. Chỉ số huyết áp 120/80 là bình thường. Giả sử huyết áp của
một người nào đó được mô hình hóa bởi hàm số
p(t) = 85+ 20sin(140pt) ,
Trong đó p(t) là huyết áp tính theo đơn vị mmHg (milimét thủy ngân) và thời gian t tính theo phút.
a) Tìm chu kì của hàm số p(t).
b) Tìm số nhịp tim mỗi phút.
c) Tìm chỉ số huyết áp. So sánh huyết áp của người này và huyết áp bình thường.
Câu 2. Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu. Khi
người chơi nhún đều, cây đu sẽ đưa người đu dao động quanh vị trí cân bằng. Nghiên
cứu trò chơi này người ta thấy khoảng cách h(m) từ vị trí người đu đến vị trí cân
bằng được biểu diễn qua thời gian t (s) bởi hệ thức h = d với 15 æ p p ö d (t) 2 = 3cos t -
, trong đó ta quy ước d > 0 khi vị trí cân bằng ở phía sau lưng ç ÷ è 3 3 ø
người đu và d < 0 trong trường hợp ngược lại (Nguồn: Đại số và Giải tích 11 Nâng
cao, NXBGD Việt Nam năm 2020).
a) Tìm chu kì của hàm số d (t).
b) Hỏi mỗi phút người chơi qua vị trí cân bằng theo chiều dương (tức là từ d < 0
sang d > 0 ) bao nhiêu lần?
c) Khoảng cách lớn nhất của người đu so với vị trí cân bằng là bao nhiêu?
Câu 3. Từ 0 giờ đến 10 giờ trưa, chuông của một chiếc đồng hồ quả lắc sẽ đánh bao nhiêu
tiếng, biết rằng nó chỉ đánh chuông báo giờ và số tiếng chuông bằng số giờ?
Câu 4. Tế bào E.Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần. Hỏi
sau 12 giờ, tế bào ban đầu sẽ phân chia thành bao nhiêu tế bào?
c) Sản phẩm: Sản phẩm trình bày của cá nhân/ nhóm học sinh
Câu 1. Huyết áp là áp lực cần thiết tác động lên thành của động mạch để đưa máu từ tim đến
nuôi dưỡng các mô trong cơ thể. Huyết áp được tạo ra do lực co bóp của cơ tim và
sức cản của thành động mạch. Mỗi lần tim đập, huyết áp của chúng ta tăng rồi giảm
giữa các nhịp. Huyết áp tối đa và huyết áp tối thiểu được gọi tương ứng là huyết áp
tâm thu và tâm trương. Chỉ số huyết áp của chúng ta được viết là huyết áp tâm
thu/huyết áp tâm trương. Chỉ số huyết áp 120/80 là bình thường. Giả sử huyết áp của
một người nào đó được mô hình hóa bởi hàm số
p(t) = 85+ 20sin(140pt) ,
Trong đó p(t) là huyết áp tính theo đơn vị mmHg (milimét thủy ngân) và thời gian t tính theo phút.
a) Tìm chu kì của hàm số p(t).
b) Tìm số nhịp tim mỗi phút.
c) Tìm chỉ số huyết áp. So sánh huyết áp của người này và huyết áp bình thường. Lời giải
a) Áp dụng định lý: Nếu hàm số f (x) có chu kì T thì hàm số f (ax + b) với a ¹ 0 0 T có chu kì 0 T = a Vì hàm số
f (t) = 85+ 20sint có chu kì T = 2p nên hàm số 0 T 2p 2p 1
p(t) = 85+ 20sin(140pt) có chu kì 0 T = = = = a 140p 140p 70 1
Vậy hàm số p(t) tuần hoàn với chu kì T = . 70 16
b) Do mỗi lần tim đập, huyết áp của chúng ta tăng rồi giảm giữa các nhịp nên số nhịp 1 tim mỗi phút là: = 70 (lần/phút). T c) Ta có 1 - £ sin(140pt) £1Û 2
- 0 £ 20sin(140pt) £ 20 Û 65 £ 85+ 20sin(140pt) £105.
Vậy chỉ số huyết áp là 105/65 . Chỉ số huyết áp của người này so với huyết áp bình thường là thấp hơn.
Câu 2. Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu. Khi
người chơi nhún đều, cây đu sẽ đưa người đu dao động quanh vị trí cân bằng. Nghiên
cứu trò chơi này người ta thấy khoảng cách h(m) từ vị trí người đu đến vị trí cân
bằng được biểu diễn qua thời gian t (s) bởi hệ thức h = d với æ p p ö d (t) 2 = 3cos t -
, trong đó ta quy ước d > 0 khi vị trí cân bằng ở phía sau lưng ç ÷ è 3 3 ø
người đu và d < 0 trong trường hợp ngược lại (Nguồn: Đại số và Giải tích 11 Nâng
cao, NXBGD Việt Nam năm 2020).
a) Tìm chu kì của hàm số d (t).
b) Hỏi mỗi phút người chơi qua vị trí cân bằng theo chiều dương (tức là từ d < 0
sang d > 0 ) bao nhiêu lần?
c) Khoảng cách lớn nhất của người đu so với vị trí cân bằng là bao nhiêu? Lời giải
a) Áp dụng định lý: Nếu hàm số f (x) có chu kì T thì hàm số f (ax + b) với a ¹ 0 0 T có chu kì 0 T = a æ p p ö
Vì hàm số f (t) = 3cost có chu kì T = 2p nên hàm số d (t) 2 = 3cos t - có 0 ç ÷ è 3 3 ø T 2p 2p chu kì 0 T = = = = 3 a 2p 2p 3 3
Vậy hàm số d (t) tuần hoàn với chu kì T = 3.
b) Trong một phút số lần người chơi qua vị trí cân bằng theo chiều dương (tức là từ 60
d < 0 sang d > 0 ) là: = 20 (lần). 3 c) Ta có: æ 2p p ö æ 2p p ö æ 2p p ö t " Î! , 1 - £ cos t - £1 Û 3 - £ 3cos t - £ 3 Þ 0 £ 3cos t - £ 3 ç ÷ ç ÷ ç ÷ è 3 3 ø è 3 3 ø è 3 3 ø . 17
Vậy khoảng cách lớn nhất của người chơi so với vị trí cân bằng là 3(m).
Câu 3. Từ 0 giờ đến 10 giờ trưa, chuông của một chiếc đồng hồ quả lắc sẽ đánh bao nhiêu
tiếng, biết rằng nó chỉ đánh chuông báo giờ và số tiếng chuông bằng số giờ? Lời giải
Từ 0 giờ đến 10 giờtrưa có 11 tiếng đồng hồ (tính cả 0 giờ) u ì = 0
Ta có số tiếng chuông của đồng hồ tăng theo cấp số cộng 1 í î d =1
Số tiếng chuông của đồng hồ là tổng của 11 số hạng đầu tiên của cấp số cộng 11(11- ) 1 .1 S = 0.11+ = 55 11 2
Chuông của một chiếc đồng hồ quả lắc sẽ đánh 55 tiếng.
Câu 4. Tế bào E.Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần. Hỏi
sau 12 giờ, tế bào ban đầu sẽ phân chia thành bao nhiêu tế bào? Lời giải
Vì ban đầu có một tế bào và mỗi tế bào phân chia thành hai tế bào nên ta có cấp số
nhân với u =1, q = 2. 1
Vì cứ 20 phút tế bào lại phân đôi một lần nên sau 12 giờ sẽ có 36 lần phân chia tế bào.
Số tế bào nhận được sau 12 giờ là 36 36
u = u .q = 2 tế bào. 37 1
d) Tổ chức thực hiện Chuyển giao
GV: tổ chức, giao nhiệm vụ HS:Nhận
GV: điều hành, quan sát, hướng dẫn HS chuẩn bị Thực hiện
HS: Đọc, nghe, nhìn, làm ( cách thức thực hiện: cá nhân) thực hiện ở nhà
Báo cáo thảo luận HS báo cáo, theo dõi, nhận xét / hình thức báo cáo vở bài tập
Hướng dẫn HS xây dựng sơ đồ tư duy các kiến thức trong bài học
Đánh giá, nhận xét,
• Tự ôn tập lại toàn bộ kiến thức chương I, II, III. Xem lại tất cả các bài tổng hợp
tập được hướng dẫn.
• Chuẩn bị tốt kiến thức để làm bài kiểm tra giữa Học kì I theo đề chung của nhà trường. 18