











Preview text:
KẾ HOẠCH BÀI DẠY
TÊN BÀI DẠY: ÔN TẬP KIỂM TRA GIỮA HỌC KỲ II
Môn học/Hoạt động giáo dục: Toán 11
Thời gian thực hiện: 01 tiết I. MỤC TIÊU
1. Kiến thức
- Ôn tập lại các kiến thức: Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm. Biến cố
hợp và biến cố giao, Biến cố độc lập. Các quy tắc tính xác suất. Phép tính luỹ thừa với số mũ thực, Phép tính
lôgarit. Hai đường thẳng vuông góc. Đường thẳng vuông góc với mặt phẳng. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
- Đối với học sinh khá giỏi: Vận dụng các kiến thức: Các số đặc trưng đo xu thế trung tâm cho
mẫu số liệu ghép nhóm. Biến cố hợp và biến cố giao, Biến cố độc lập. Các quy tắc tính xác suất. Phép tính luỹ
thừa với số mũ thực, Phép tính lôgarit. Hai đường thẳng vuông góc. Đường thẳng vuông góc với mặt phẳng.
Góc giữa đường thẳng và mặt phẳng. Góc nhị diện 2. Năng lực
- Năng lực tự học: Học sinh xác định đúng đắn động cơ, thái độ học tập; tự đánh giá và điều
chỉnh được kế hoạch học tập; tự nhận ra những sai sót và khắc phục.
- Năng lực giao tiếp: Tiếp thu kiến thức, trao đổi học hỏi bạn bè thông qua việc thực hiện nhiệm
vụ trong các hoạt động cặp đôi, nhóm; có thái độ tôn trọng, lắng nghe, có phản ứng tích cực trong giao tiếp.
- Năng lực hợp tác: Học sinh xác định được nhiệm vụ của tổ/nhóm, trách nhiệm của bản thân đề
xuất được những ý kiến đóng góp, góp phần hoàn thành nhiệm vụ học tập.
- Năng lực giải quyết vấn đề: Học sinh tiếp cận hệ thống câu hỏi và bài tập, những tình huống
có vấn đề. Phân tích được các vấn đề để đưa ra những giải pháp xử lí tình huống, những vấn
đề liên quan đến bộ môn và trong thực tế.
- Năng lực sáng tạo: Học sinh biết vận dụng tính sáng tạo để giải quyết tình huống của từng bài toán cụ thể.
- Năng lực sử dụng ngôn ngữ: Học sinh nói và viết chính xác bằng ngôn ngữ Toán học.
3. Phẩm chất
- Trách nhiệm: Biết chịu trách nhiệm với thành quả của cá nhân, tập thể; không đổ lỗi cho người
khác. Chủ động phát hiện, chiếm lĩnh tri thức mới, biết quy lạ về quen, có tinh thần trách
nhiệm hợp tác xây dựng cao.
- Trung thực: Học sinh biết tôn trọng kết quả của bản thân, tôn trọng lẽ phải; thật thà, ngay
thẳng trong học tập và làm việc, lên án sự gian lận.
- Chăm chỉ: Chăm làm, ham học, có tinh thần tự học, chăm chỉ tích cực xây dựng bài, nhiệt tình
tham gia các công việc của tập thể, tinh thần vượt khó trong công việc.
- Nhân ái: Yêu con người, yêu cái đẹp của toán học, tôn trọng sự khác biệt, ý kiến trái chiều;
sẵn sàng học hỏi, hòa nhập và giúp đỡ mọi người
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU Page 1
1. Về phía giáo viên:
- Thước thẳng có chia khoảng, compa, bảng phụ ghi bài tập, phiếu học tập, máy chiếu, sách giáo khoa, bài soạn...
2. Về phía học sinh:
- Dụng cụ học tập, sách giáo khoa, chuẩn bị bài trước khi đến lớp...
III. TIẾN TRÌNH DẠY HỌC:
1. HOẠT ĐỘNG 1: KHỞI ĐỘNG a) Mục tiêu:
- HS chuẩn bị tâm thế tốt cho tiết ôn tập giữa học kỳ II
- Nắm bắt việc chuẩn bị và làm đề cương của học sinh. b) Nội dung:
Câu hỏi 1: Trong các bài học của giữa học kì II lớp 11 em thích học bài nào nhất vì sao?
Câu hỏi 2: Trình bày khó khăn của em khi làm đề cương, e đã làm gì để giải quyết khó khăn đó
c) Sản phẩm: Câu trả lời của học sinh d) Tổ chức thực hiện: Chuyển giao
Giáo viên cho học sinh các tổ kiểm tra việc làm đề cương của nhau sau đó báo cáo kết quả. Thực hiện
- HS di chuyển để kiểm tra, thống nhất đáp án một số câu hỏi
- HS suy nghĩa trả lời câu hỏi
- Mong đợi: HS chỉ ra được một nhóm câu hỏi cần giúp đỡ trong tiết học này
Báo cáo thảo luận
HS đưa ra những nhận xét về việc làm đề cương của các bạn, nêu được một số
câu hỏi cần đưa ra thảo luận, giải đáp trong tiết học
Đánh giá, nhận xét,
- Giáo viên đánh giá thái độ làm việc, phương án trả lời của học sinh, ghi nhận tổng hợp và tổng hợp kết quả.
- Hướng học sinh vào các câu hỏi trọng tâm của đề cương.
2. HOẠT ĐỘNG 2: LUYỆN TẬP a) Mục tiêu:
§ Hệ thống kiến thức, ôn tập các bài tập chuẩn bị kiểm tra.
b) Nội dung: Chữa đề cương cho học sinh
c) Sản phẩm: HS so sánh kết quả của việc làm đề cương tại nhà với kết quả của cô giáo và các bạn
chữa. sửa chữa bài tập để được Đề cương chữa hoàn thiện SỞ GD & ĐT LÀO CAI
ĐỀ CƯƠNG KIỂM TRA GIỮA HỌC KỲ II TRƯỜNG THPT …. NĂM HỌC 2022-2023 Môn: Toán. Khối 11
PHẦN I- TRẮC NGHIỆM
CHƯƠNG 5. BÀI 1: MẪU SỐ LIỆU GHÉP NHÓM
Câu 1: Điều tra về chiều cao của học sinh khối lớp 11, ta được mẫu số liệu sau: Chiều cao (cm) Số học sinh [150;152) 5 [152;154) 18 Page 2 [154;156) 40 [156;158) 26 [158;160) 8 [160;162) 3 Tổng N = 100
Mẫu số liệu ghép nhóm đã cho có tất cả bao nhiêu nhóm? A. 5 . B. 6 . C. 7 . D. 12 . Lời giải
Mẫu số liệu ghép nhóm đã cho có tất cả 6 nhóm.
Câu 2: Điều tra về chiều cao của học sinh khối lớp 11, ta có kết quả sau: Nhóm Chiều cao (cm) Số học sinh 1 [150;152) 5 2 [152;154) 18 3 [154;156) 40 4 [156;158) 26 5 [158;160) 8 6 [160;162) 3 N = 100
Giá trị đại diện của nhóm thứ tư là A. 156,5. B. 157 . C. 157,5. D. 158 . Lời giải 156 +158
Giá trị đại diện của nhóm thứ tư là =157. 2
Câu 3: Đo chiều cao (tính bằng cm ) của 500 học sinh trong một trường THPT ta thu được kết quả như sau: [ [ [ [ [ Chiều cao 150;154) 154;158) 158;162) 162;166) 166;170) Số học sinh 25 50 200 175 50
Mẫu số liệu ghép nhóm đã cho có tất cả bao nhiêu nhóm? A. 5 . B. 6 . C. 7 . D. 12 . Lời giải
Mẫu số liệu ghép nhóm đã cho có tất cả 5 nhóm.
Câu 4: Đo chiều cao (tính bằng cm ) của 500 học sinh trong một trường THPT ta thu được kết quả như sau: [150;154) [154;158) [158;162) [162;166) [166;170) Chiều cao Số học sinh 25 50 200 175 50 Page 3
Giá trị đại diện của nhóm [162;166)là A. 162 . B. 164 . C. 166 . D. 4 . Lời giải Ta có bảng sau Lớp chiều cao Giá trị đại diện Số học sinh [150;154) 152 25 [154;158) 156 50 [158;162) 160 200 [162;166) 164 175 [166;170) 168 50
Câu 5: Đo cân nặng của một số học sinh lớp 11D cho trong bảng sau: Cân nặng (kg) [40,5; 45,5) [45,5; 50,5) [50,5; 55,5) [55,5; 60,5) [60,5; 65,5) [65,5; 70,5) Số học sinh 10 7 16 4 2 3
Giá trị đại diện của nhóm [60,5;65,5)là A. 55,5. B. 58 . C. 60,5. D. 5 . Lời giải
Trong mỗi khoảng cân ặng, giá trị đại diện trung bình cộng của giá trị hai đầu mút nên ta có bảng sau: Cân nặng (kg)
[40,5; 45,5) [45,5; 50,5) [50,5; 55,5) [55,5; 60,5) [60,5; 65,5) [65,5; 70,5) Giá trị đại diện 43 48 53 58 63 68 Số họ sinh 10 7 16 4 2 3
CHƯƠNG 5. BÀI 1: CÁC SỐ ĐẶC TRƯNG ĐO XU THẾ TRUNG TÂM
Câu 1: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Giá trị đại diện của nhóm [20; 40) là A. 10 . B. 20 . C. 30 . D. 40 . Lời giải
Giá trị đại diện của nhóm [20; 40) là 20 + 40 c = = 30 2
Câu 2: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép Page 4 nhóm sau:
Nhóm chứa mốt của mẫu số liệu trên là A. [40;60). B. [20; 40) . C. [60;80) . D. [80;100) . Lời giải
Mốt M chứa trong nhóm [40;60) 0
Câu 3: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Mốt của mẫu số liệu trên là A. 42 . B. 52 . C. 53 . D. 54 . Lời giải
Mốt M chứa trong nhóm [40;60) 0
Do đó: u = 40;u
= 60 Þ u -u = 60 - 40 = 20 m m 1 + m 1 + m n = 9;n =12;n =10 m 1 - m m 1 + 12 - 9 M = 40 + (60 - 20) = 52 0 12 ( - 9) + (12 -10)
Câu 4: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa trung vị của mẫu số liệu trên là A. [40;60). B. [20; 40) . C. [60;80) . D. [80;100) . Lời giải Ta có: n = 42 x + x
Nên trung vị của mẫu số liệu trên là 21 22 Q = 2 2
Mà x , x Î 40;60 21 22 [ )
Vậy nhóm chứa trung vị của mẫu số liệu trên là nhóm [40;60)
Câu 5: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa tứ phân vị thứ nhất của mẫu số liệu trên là Page 5 A. [40;60). B. [20; 40) . C. [60;80) . D. [80;100) . Lời giải Ta có: n = 42
Nên tứ phân vị thứ nhất của mẫu số liệu trên là Q = x 1 11 Mà x Î 20;40 11 [ )
Vậy nhóm chứa tứ phân vị thứ nhất của mẫu số liệu trên là nhóm [20; 40)
CHƯƠNG 5. BÀI 2: CÔNG THỨC CỘNG XÁC SUẤT
Câu 1: Nếu hai biến cố A và B xung khắc thì xác suất của biến cố P( AÈ B) bằng
A. 1- P( A) - P(B).
B. P( A).P(B).
C. P( A).P(B) - P( A) - P(B).
D. P( A) + P(B). Lời giải
Vì hai biến cố A và B xung khắc nên A Ç B = Æ. Theo công thức cộng xác suất ta có
P( AÈ B) = P( A) + P(B)
Câu 2: Một hộp đựng 10 viên bi trong đó có 4 viên bi đỏ, 3 viên bi xanh, 2 viên bi vàng và 1 viên
bi trắng. Lấy ngẫu nhiên từ hộp đó 2 viên bi. Xác suất của biến cố C : “lấy được 2 viên bi cùng màu” là:
A. P (C) 1 = .
B. P (C) 2 = .
C. P (C) 4 = .
D. P (C) 1 = . 9 9 9 3 Lời giải Chọn B Ta có: n(W) 2 = C = 45 10 Gọi các biến cố:
D : “lấy được 2 viên đỏ” Þ n(D) 2 = C = 6 4
E : “lấy được 2 viên xanh” Þ n(E) 2 = C = 3 3
F : “lấy được 2 viên vàng” Þ n(F) 2 = C = 1 2 Ta có ,
D E, F là các biến cố đôi một xung khắc và C = D ! E ! F
P (C) = P(D) + P(E) + P(F ) 6 3 1 2 = + + = . 45 45 45 9
Câu 3: Một hộp đựng 8 quả cầu trắng, 12 quả cầu đen. Lấy ngẫu nhiên 2 quả cầu trong hộp. Tính
xác suất để lấy được 2 quả cầu cùng màu. 47 81 47 14 A. . B. . C. . D. . 190 95 95 95 Lời giải Chọn C Page 6 Ta có: n(W) 2 = C =190. 20
Gọi A là biến cố “Lấy được 2 quả cầu cùng màu”
A là biến cố “Lấy được 2 quả cầu màu trắng” 1
A là biến cố “Lấy được 2 quả cầu màu đen” 2
Do A ; A là hai biến cố xung khắc nên 1 2 n A n A C 1 ( 2 ) 2 2 C 47
theo quy tắc cộng xác suất, ta có: P ( A) = P ( A + P A = + = + = 1 ) ( 2) ( ) 8 12 n(W) n(W) 2 2 C C 95 20 20
Câu 4: Hai xạ thủ bắn mỗi người một viên đạn vào bia, biết xác suất bắn trúng vòng 10 của xạ thủ
thứ nhất là 0,75 và của xạ thủ thứ hai là 0,85. Tính xác suất để có ít nhất một xạ thủ bắn trúng vòng 10. A. 0,325. B. 0,6375. C. 0,0375. D. 0,9625. Lời giải
Gọi A là biến cố: “có ít nhất một viên trúng vòng 10”.
Do đó A là biến cố: “không có viên nào trúng vòng 10”
Þ P( A) = (1-0,75).(1-0,85) = 0,0375
Þ P( A) =1- P(A) =1-0,0375 = 0,9625.
Câu 5: Có 4 học sinh muốn tham gia sự kiện từ thiện vào hai ngày cuối tuần, họ có thể chọn tham gia
vào thứ Bảy hoặc Chủ nhật. Tính xác suất để vào cả hai ngày thứ Bảy và Chủ nhật có ít nhất một học sinh tham dự. 3 7 1 5 A. . B. . C. . D. . 8 8 8 8 Lời giải
Vì mỗi học sinh có thể tham gia sự kiện từ thiện vào một trong hai ngày thứ Bảy hoặc chủ Nhật nên 1 1
xác suất để học sinh tham gia trong mỗi ngày là
và xác suất không tham gia trong mỗi ngày là . 2 2
Gọi A : ' Cả hai ngày thứ Bảy và chủ Nhật có ít nhất một học sinh tham dự. "
Ta có: P ( A) 1 1 1 1 1 1 1 1 1 = . . . + . . . = . 2 2 2 2 2 2 2 2 8
Xác suất cần tìm là: P ( A) = - P( A) 1 7 1 =1- = . 8 8
Câu 6: Hai người cùng bắn độc lập vào một mục tiêu. Xác suất bắn trúng của từng người lần lượt là
0,8 và 0,9. Tìm xác suất của biến cố A : “ Chỉ có một người bắn trúng mục tiêu ”.
A. P( A) = 0,26.
B. P( A) = 0,74.
C. P( A) = 0,72.
D. P( A) = 0,3. Lời giải
Gọi A1 là biến cố “ Người 1 bắn trúng mục tiêu ”. Page 7 Gọi A
A ; A ; A ; A
2 là biến cố “ Người 2 bắn trúng mục tiêu ” (
là các biến cố độc lập). 1 2 1 2
Từ giả thiết ta có P( A = 0,8; P A = 0,9. 1 ) ( 2 )
Mà A = A A ! A A 1 2 1 2
Þ P( A) = P( A .P A + P A .P A = 0,8. 1- 0,9 + 1- 0,8 .0,9 = 0,26 1 ) ( 2) ( 1) ( 2) ( ) ( ) .
Câu 7: Hộp thứ nhất chứa 3 bi đỏ và 4 bi xanh, hộp thứ hai chưa 2 bi đỏ và 5 bi xanh. Chuyển ngẫu
nhiên 1 viên bi từ hộp thứ nhất sang hộp thứ hai rồi lấy ngẫu nhiên một viên bi từ hộp thứ hai
ra. Tính xác suất để viên bi lấy ra ở hộp thứ hai có màu đỏ. 3 17 2 9 A. . B. . C. . D. 7 56 7 56 Lời giải Xảy ra hai trường hợp:
TH1: Viên bi lấy ra từ hộp thứ nhất màu đỏ và đưa vào hộp thứ hai, khi đó hộp thứ hai có 3 bi đỏ và 3 3 9
5 bi xanh. Xác suất để lấy ra 1 bi đỏ từ hộp thứ hai là: P = . = . 1 7 8 56
TH2: Viên bi lấy ra từ hộp thứ nhất màu xanh và đưa vào hộp thứ hai, khi đó hộp thứ hai có 2 bi đỏ 4 2 8
và 6 bi xanh. Xác suất để lấy ra 1 bi đỏ từ hộp thứ hai là: P = . = . 2 7 8 56 17
Vậy xác suất cần tìm là P = P + P = . 1 2 56
CHƯƠNG 6. BÀI 1: LŨY THỪA VỚI SỐ MŨ THỰC
DẠNG 1. RÚT GỌN BIỂU THỨC LŨY THỪA
Câu 1: Cho a > 0, ,
m n Î ! . Khẳng định nào sau đây đúng? m a n-m = a . m n m n m n m n m n n m A. a a a + + = . B. a .a a - = .
C. (a ) = (a ) . D. n a Lời giải Tính chất lũy thừa 1
Câu 2: Với a là số thực dương tùy ý, 4 2
a .a bằng 7 9 A. 8 a . B. 2 a . C. 2 a . D. 2 a . Lời giải 1 1 9 4+ Ta có 4 2 2 2 a .a = a = a .
Câu 3: Cho số thực dương a và số nguyên dương n tùy ý. Mệnh đề nào dưới đây đúng? 2 n A. n 2+ = n a a . B. n 2 = n a a . C. n = n a a . D. n 2 a = a . Lời giải n Ta có: n 2 a = a .
Câu 4: Cho a là số thực dương. Biểu thức 3 3 2
a . a được viết dưới dạng lũy thừa với số mũ hữu tỉ là Page 8 11 5 8 A. 3 a B. 2 a C. 3 a D. 3 a Lời giải 2 2 11 3+ 3 3 2 3 3 3 3
a . a = a .a = a = a .
Câu 5: Viết biểu thức 3 4 P = .
x x , ( x > 0) dưới dạng lũy thừa với số mũ hữu tỷ 5 1 1 5 A. 4 P = x . B. 12 P = x . C. 7 P = x . D. 12 P = x . Lời giải 1 5 5 3 3 Ta có 3 4 4 4 12 P = . x x = .
x x = x = x . 2
Câu 6: Rút gọn biểu thức 5 6
P = x . x với x > 0 . 1 17 17 A. 15 P = x . B. 15 P = x . C. 30 P = x .
D. P = x . Lời giải 2 2 1 2 1 17 + 5 6 5 6 5 6 30
P = x . x = x .x = x = x .
DẠNG 2. TÍNH GIÁ TRỊ BIỂU THỨC Câu 7: Biểu thức 5 5 P = 4. - 8 có giá trị bằng A. 4 2 . B. 2 - . C. 2. D. 4 - 2 . Lời giải Ta có 5 5 5 P = 4. - 8 = ( 3 - 2) = 2 - . Câu 8: Giá trị 3 5
2021. 2021viết dưới dạng lũy thữa với số mũ hữu tỷ là 2 1 8 1 A. 5 2021 . B. 15 2021 . C. 15 2021 . D. 10 2021 Lời giải 1 1 1 1 8 + 3 5 3 5 3 5 15 2021. 2021 = 2021 .2021 = 2021 = 2021 . 1
Câu 9: Giá trị của 3 27 bằng A. 6. B. 81. C. 9. D. 3. Lời giải 1 Ta có 3 3 27 = 27 = 3. 1 3 4 - - Câu 10: Cho a = 1 và b = . Tính 4 3
A = a + b 256 27 A. 23. B. 89 . C. 145 . D. 26 . Lời giải 1 3 4 - - Thay a = 1 , b = vào 4 3
A = a + b ta được 256 27 Page 9 3 4 3 4 - æ 1 - ö æ 1 - - - - ö 4
A = a + b = + = ç ÷ ç ÷ (4- ) 34 +(3- ) 4 4 3 4 3 3 4 3 3 = 4 + 3 = 145. è 256 ø è 27 ø
DẠNG 3. SO SÁNH CÁC BIỂU THỨC CHỨA LŨY THỪA 1 1 Câu 11: Nếu 3 6 a > a và 3 5
b > b thì
A. a < 1;0 < b < 1.
B. a > 1;b < 1.
C. 0 < a < 1;b < 1
D. a > 1;0 < b < . 1 Lời giải 1 1 1 1 Ta có: > , lại có 3 6
a > a Þ a > 1. 3 6 Ta có: 3 < 5 , lại có 3 5
b > b Þ 0 < b < 1.
Câu 12: Cho a > 1. Mệnh đề nào dưới đây đúng? 1 1 1 3 2 - 1 a A. < . B. 3
a > a . C. 3 a > . D. >1. 2016 2017 a a 5 a a Lời giải 1 1 - 1 Vì a > 1nên 3 5 a < a Þ > Þ 3 a > . 3 5 a a 5 a
Câu 13: Trong các mệnh đề sau, mệnh đề nào SAI? 2018 2017 A. ( 3 - ) 1 > ( 3 - )1 . B. + > 3 2 1 2 2 . 2019 2018 2017 2018 æ 2 ö æ 2 ö C. ( 2 - ) 1 > ( 2 - )1 . D. ç1- ÷ < ç1- ÷ . ç 2 ÷ ç 2 ÷ è ø è ø Lời giải 2018 2017 A. ( 3 - ) 1
> ( 3 - )1 . Cùng cơ số, 0 < 3 -1< ,
1 hàm nghịch biến, số mũ lớn hơn nên bé hơn. Sai 2 2 B. + > 3 2 1 2
2 . Cùng cơ số, 2 > 1, hàm đồng biến, số mũ ( 2 + )
1 = 3+ 2 2 > ( 3) = 3 nên lớn hơn. Đúng 2017 2018 C. ( 2 - ) 1
> ( 2 - )1 . Cùng cơ số, 0 < 2 -1< ,
1 hàm nghịch biến, số mũ bé hơn nên lớn hơn. Đúng. 2019 2018 æ 2 ö æ 2 ö 2 D. ç1- ÷ < ç1- ÷ . Cùng cơ số, 0 < 1-
<1, hàm nghịch biến, số mũ lớn hơn nên ç 2 ÷ ç 2 ÷ è ø è ø 2 bé hơn. Đúng
Câu 14: Tìm tập tất cả các giá trị của a để 21 5 7 2
a > a ? 5 2
A. a > 0 .
B. 0 < a < 1.
C. a > 1. D. < a < . 21 7 Lời giải 7 2 21 6 a = a . Page 10 Ta có 21 5 7 2 21 5 21 6
a > a Û a > a mà 5 < 6 vậy 0 < a < 1.
DẠNG 4. BÀI TOÁN LÃI SUẤT – DÂN SỐ
Câu 15: Ông An gửi tiết kiệm 50 triệu đồng vào ngân hàng với kỳ hạn 3 tháng, lãi suất 8, 4% một
năm theo hình thức lãi kép. Ông gửi được đúng 3 kỳ hạn thì ngân hàng thay đổi lãi suất, ông
gửi tiếp 12 tháng nữa với kỳ hạn như cũ và lãi suất trong thời gian này là 12% một năm thì
ông rút tiền về. Số tiền ông An nhận được cả gốc lẫn lãi là: A. 62255910 đồng. B. 59895767 đồng. C. 59993756 đồng. C. 63545193 đồng. Lời giải
Đợt I, ông An gửi số tiền P = 50 triệu, lãi suất 8, 4% một năm tức là 2,1% mỗi kỳ hạn. Số tiền cả 0
gốc và lãi ông thu được sau 3 kỳ hạn là: P = 50000000. 1.021 3 ( )3.
Đợt II, do ông không rút ra nên số tiền P được xem là số tiền gửi ban đầu của đợt II, lãi suất đợt II 3
là 3% mỗi kỳ hạn. Ông gửi tiếp 12 tháng bằng 4 kỳ hạn nên số tiền thu được cuối cùng là:
P = P 1.03 = 50000000. 1.021 . 1.03 » 59895767 3 ( )4 ( )3 ( )4 đồng.
Câu 16: Dân số thế giới được ước tính theo công thức = . ni
S A e , trong đó A là dân số của năm lấy làm
mốc, S là dân số sau n năm, i là tỉ lệ tăng dân số hằng năm. Dân số Việt Nam năm 2019 là
95,5triệu người, tỉ lệ tăng dân số hằng năm từ 2009 đến nay là 1,14% . Hỏi dân số Việt Nam
năm 2009 gần với số nào nhất trong các số sau?
A. 94, 4 triệu người.
B. 85, 2triệu người.
C. 86, 2triệu người.
D. 83,9 triệu người. Lời giải
Áp dụng công thức = . ni
S A e trong đó: S = 95,5triệu người, n = 10 năm, i = 1,14% S 95,5
Ta có số dân Việt Nam năm 2009 là: A = = » 85,2triệu người ni 10.1,14% e e
CHƯƠNG 6. BÀI 2: LOGARIT
Câu 1: Cho a,b, c là các số thực dương và a,b ¹ 1. Khẳng định nào sau đây là sai? c A. log . b log a = . 1 B. log c = - log log a . C. log b c = . D. a b a c a log a b log c = log . b log c. a a b Lời giải 1 Ta có log c =
¹ -log a. Suy ra đáp án B sai. a log c a c
Câu 2: Cho 0 < a ¹ 1, x > 0. Mệnh đề nào sau đây là sai? A. log a = . 1 B. log x a = x . C. log 1 = 0. D. loga x x = x. a a a Lời giải
Với 0 < a ¹ 1, x > 0 ta có: log a = 1 Þ Phương án A đúng. a Page 11 log x
a = x Þ Phương án B đúng. a
log 1 = 0 Þ Phương án C đúng. a loga x a = x Þ loga x x
= x sai Þ Phương án D sai.
Câu 3: Cho ba số thực dương a,b,c và a ¹ 1. Khẳng định nào sau đây là sai? A. log bc = b + c loga b a ( ) log log . B. a = b. a a a
C. log b = a log b . D. ln a log b = . a a a ln b Lời giải ln b Ta có log b = , nên đáp án D sai. a ln a
Câu 4: Cho a là số thực dương khác 1. Mệnh đề nào sau đây đúng với mọi số thực dương x, y ? x x A. log
= log x + log y. B. log = log x - y a a ( ). a a a y y x x x C. log = log x - log log y . D. log a = . a a a y a y log y a Lời giải x
Theo quy tắc tính logarit của một thương ta có log
= log x - log y, x " > 0, y > 0. a a a y
Câu 5: Có bao nhiêu số thực dương n ¹ 1để log 265 là một số nguyên? n A. 2 . B. 4 . C. 6 . D. 8 . Lời giải 8 Ta có: 8 log 256 = log 2 = 8log 2 = . n n n log n 2
Để log 265 là một số nguyên thì n log nÎ{ 1 ± ;± 2;± 4;± ì1 1 1 1 8} ü Û n Î í ;2; ;4; ;16; ; 256ý 2 î2 4 16 256 þ
Vậy có tất cả 8 số thực dương n ¹ 1thỏa mãn điều kiện bài toán. 1
Câu 6: Giá trị của log bằng 2 16 1 1 A. 4. B. . C. . D. - 4. 4 8 Lời giải 1 4 log log 2- = = 4 - . 2 2 16
CHƯƠNG 8. BÀI 1: HAI ĐƯỜNG THẲNG VUÔNG GÓC
DẠNG 1: XÁC ĐỊNH GÓC GIỮA HAI ĐƯỜNG THẲNG Page 12
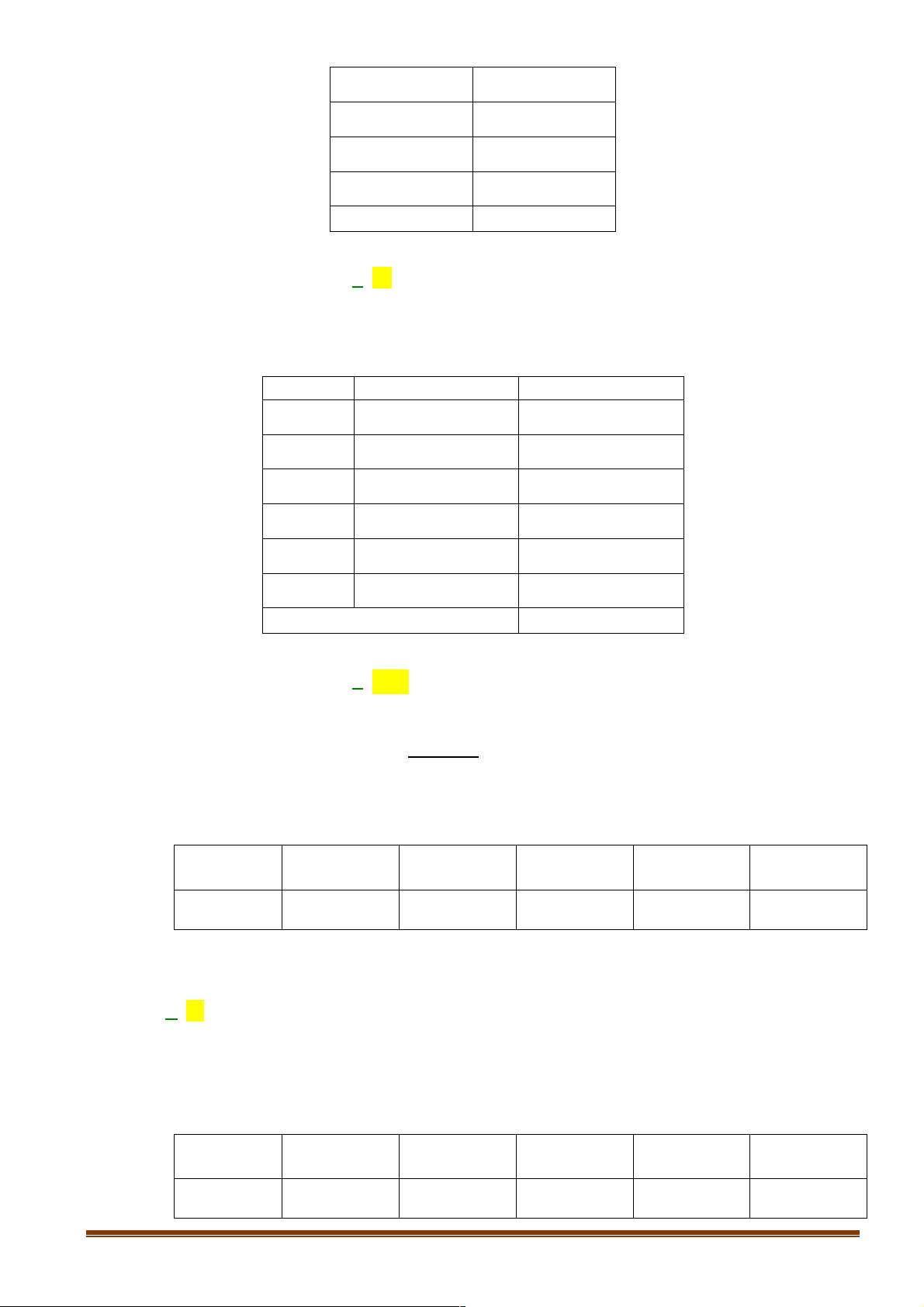
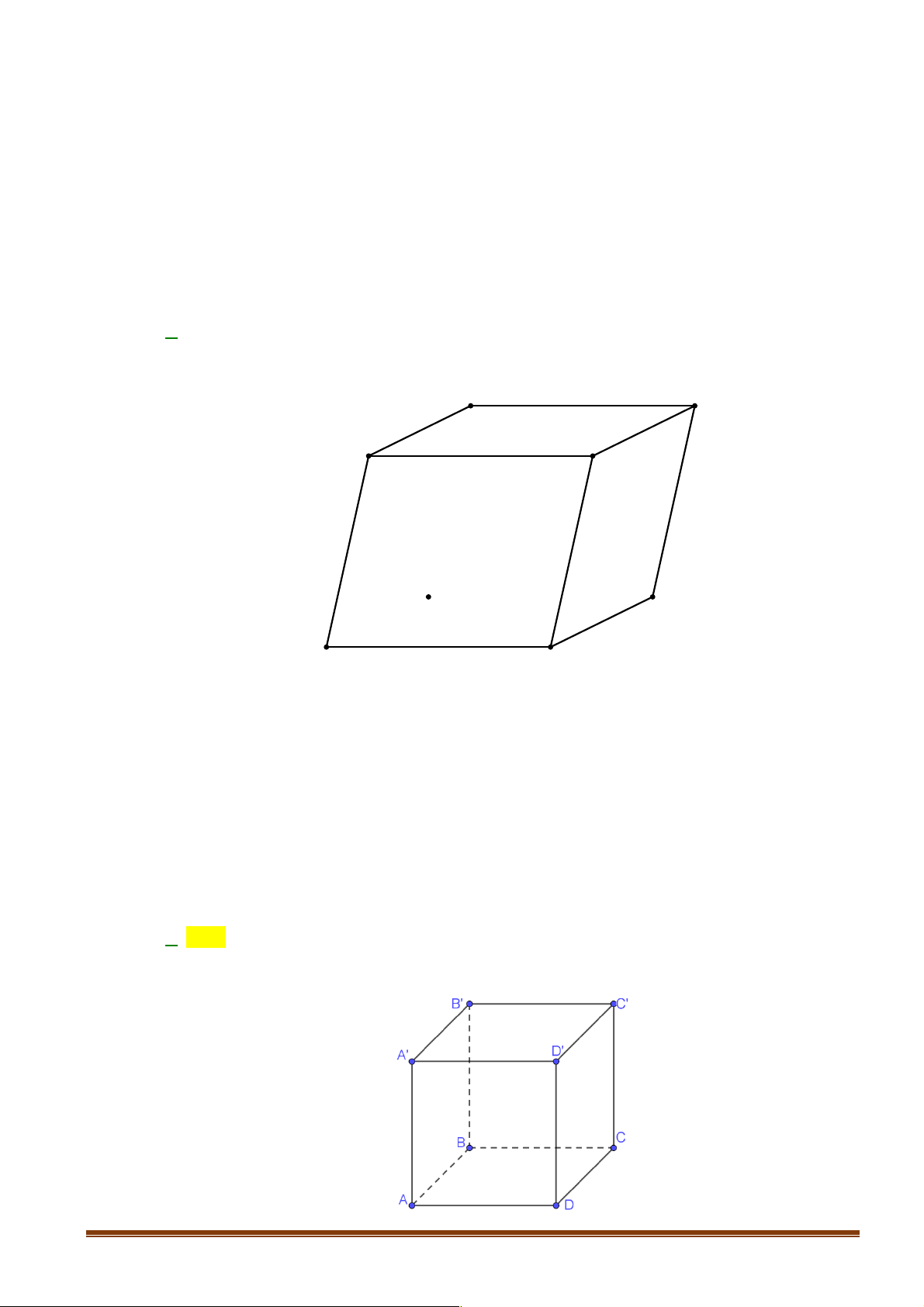
Câu 1: Cho hình lập phương ABC . D A B ¢ C ¢ D ¢ . G
¢ óc giữa hai đường thẳng BA ¢ và CD bằng A. 60 . ∞ B. 90 . ∞ C. 45 . ∞ D. 30 . ∞ Lời giải
Ta có AB PCD nên ∑
BA ,¢CD = BA ,¢ AB . ( ) ∑ ( ) Vì ABB A ¢ ¢là hình vuông nên ∑
BA¢ AB = ABA¢= . ∞ ( ) ∑ , 45
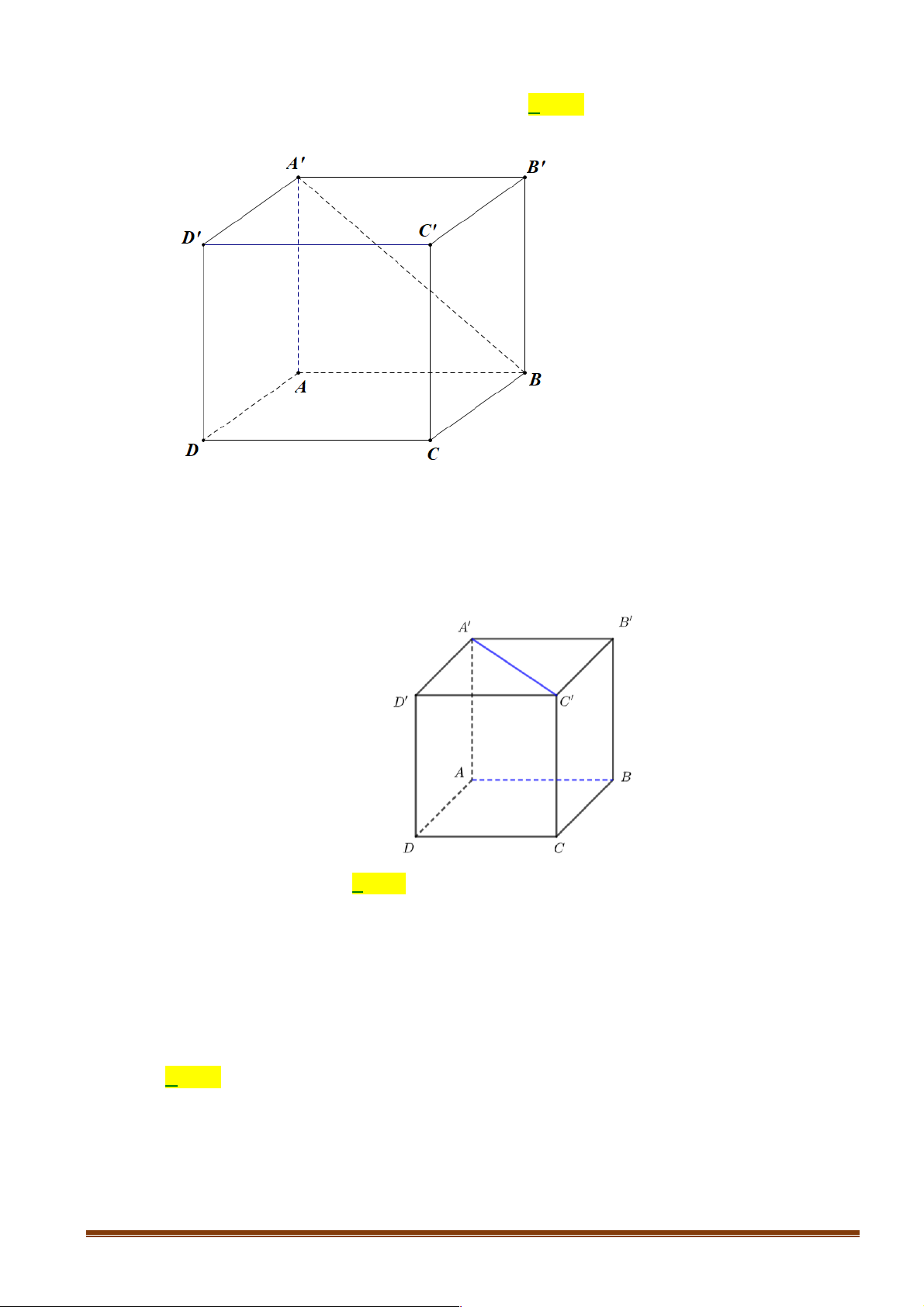
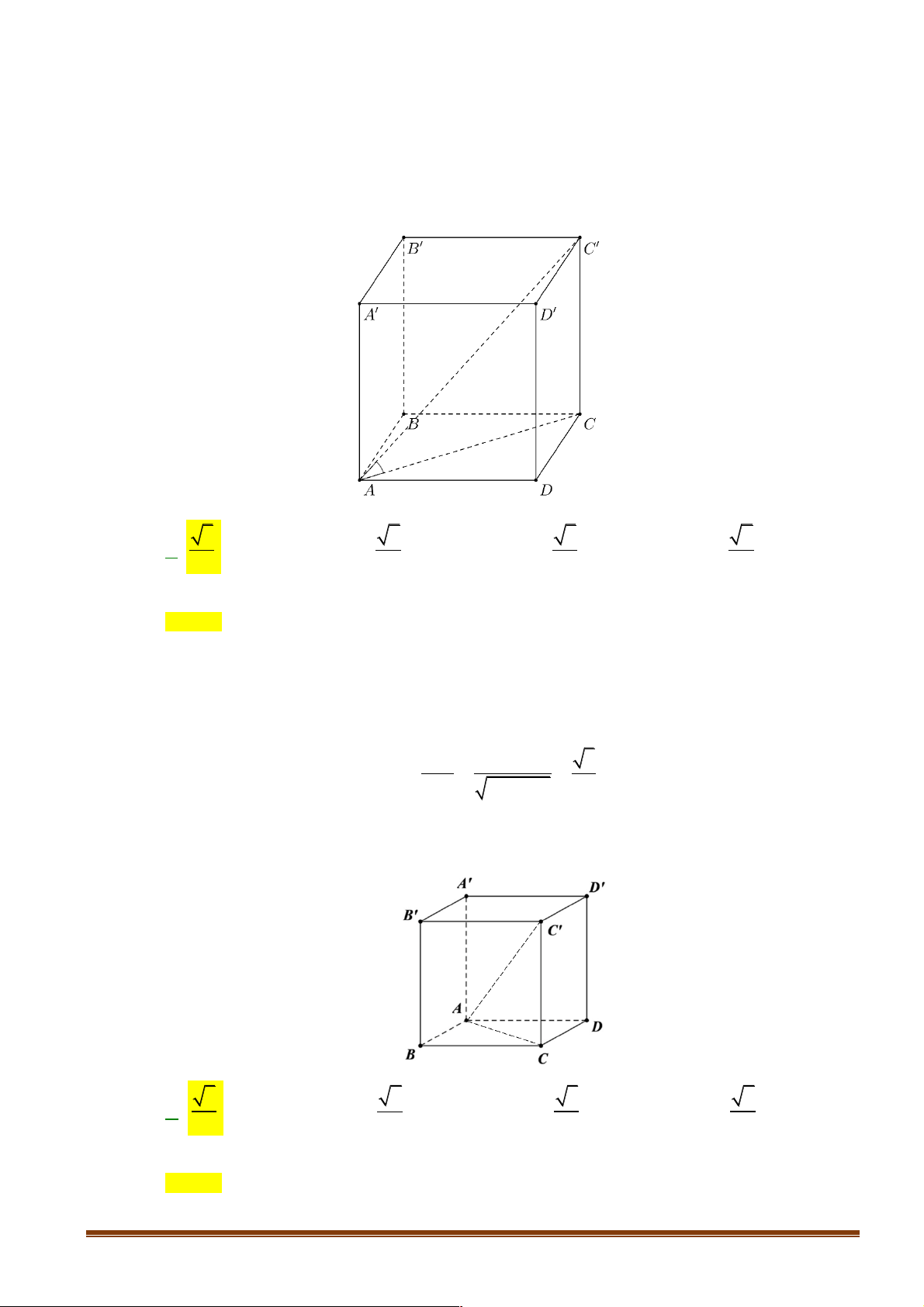
Câu 2: Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ . Góc giữa hai đường thẳng AB và A¢C¢ bằng A. 60° . B. 45°. C. 90° . D. 30° . Lời giải Vì AB // A B ¢ ¢ nên ∑ (AB AC¢¢) ∑ = (A B
¢ ¢ A¢C¢) ∑ , , = B A ¢ ¢C¢. Tam giác A¢B C
¢ ¢ vuông cân tại B¢ nên ∑ B A ¢ C ¢ ¢ = 45°.
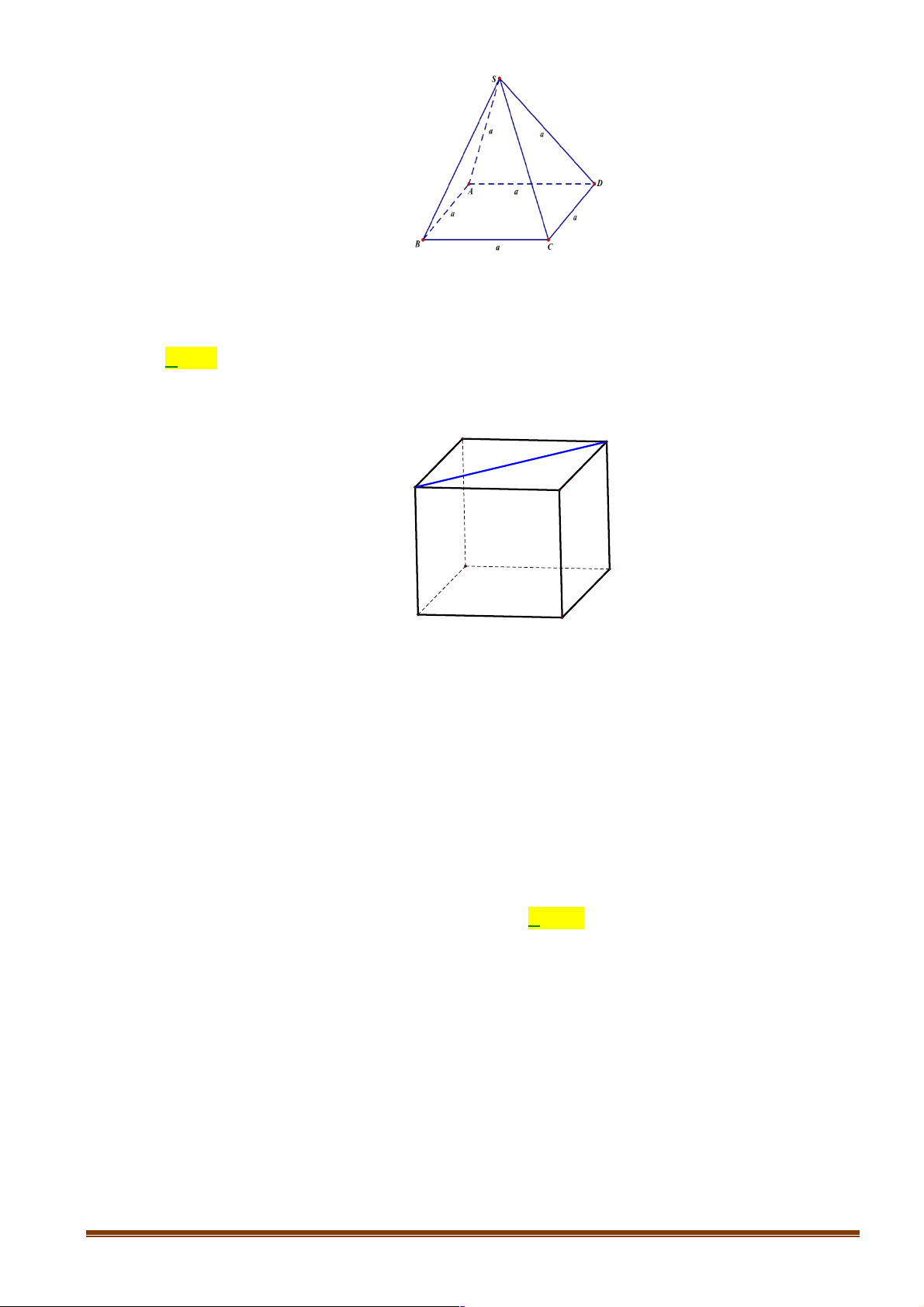
Câu 3: Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a , tam giác SAD đều. Góc giữa BC và SA là: A. 60° . B. 30° . C. 90° . D. 45° . Lời giải Page 13
Vì BC ! AD nên (BC, SA) = ( , AD SA) = 60°
Câu 4: Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ . Tính góc giữa hai đường thẳng B D ¢ ¢ và AA¢ . A. 90° . B. 45° . C. 60° . D. 30° . Lời giải A ' D ' B ' C ' A D B C Vì ABC . D A¢B C ¢ D
¢ ¢ là hình lập phương nên các tứ giác AA¢D D ¢ và AA¢B B ¢ đều là hình vuông. !!!" !!!!" !!!" !!!!"
Do đó AA .¢A D ¢ = AA.¢A B ¢ ¢ = 0 !!!" !!!!" !!!" !!!!" !!!!" !!!" !!!!" !!!" !!!!"
Vậy : AA .¢B D
¢ ¢ = AA .¢(A¢D - A¢B¢) = AA .¢A D ¢ - AA .¢A B ¢ ¢ = 0 !!!" !!!!" !!!" !!!!"
Do đó AA¢ ^ B D
¢ ¢ nên (AA ,¢B D
¢ ¢) = 90°. Suy ra (AA ,¢B D ¢ ¢) = 90°
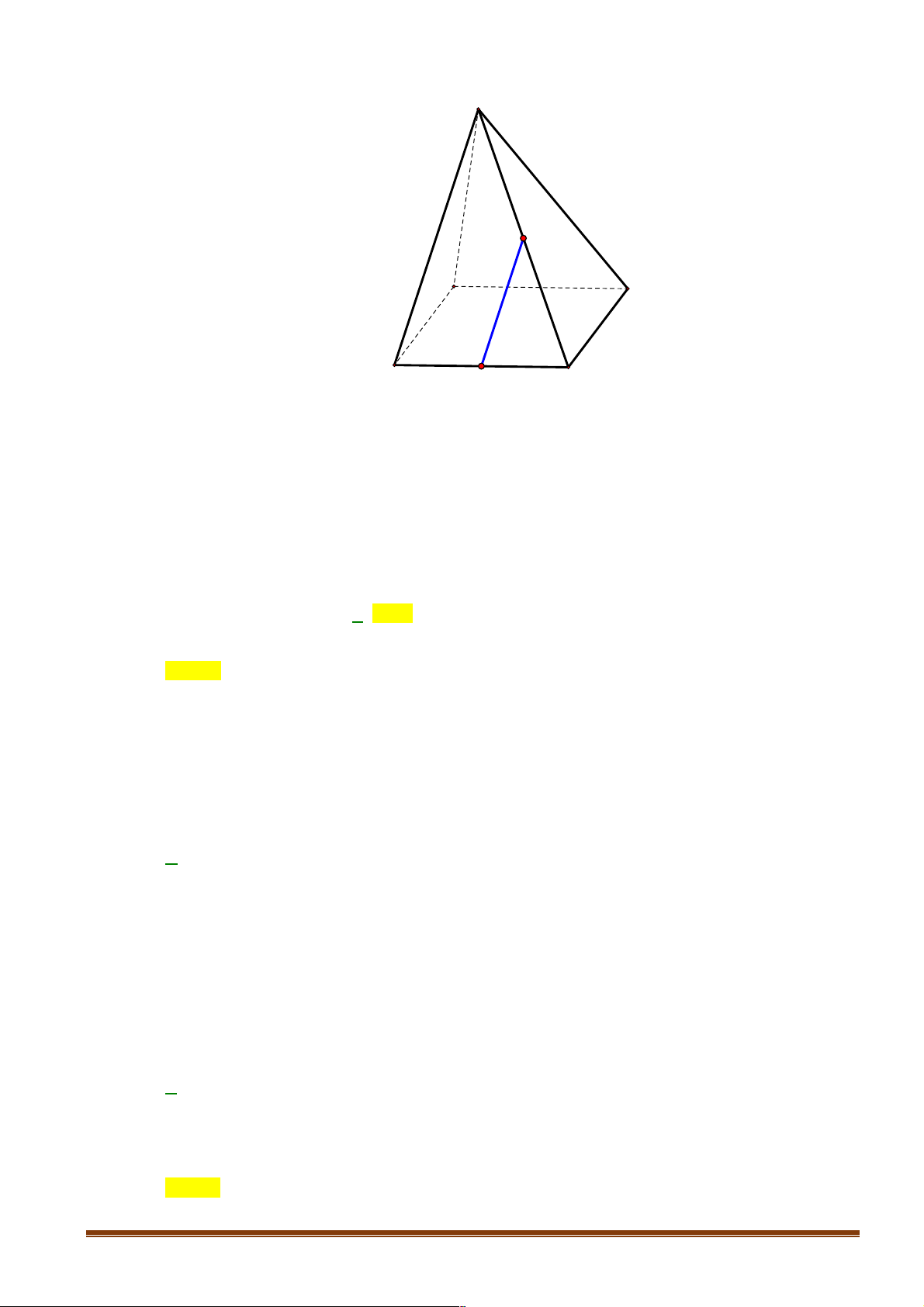
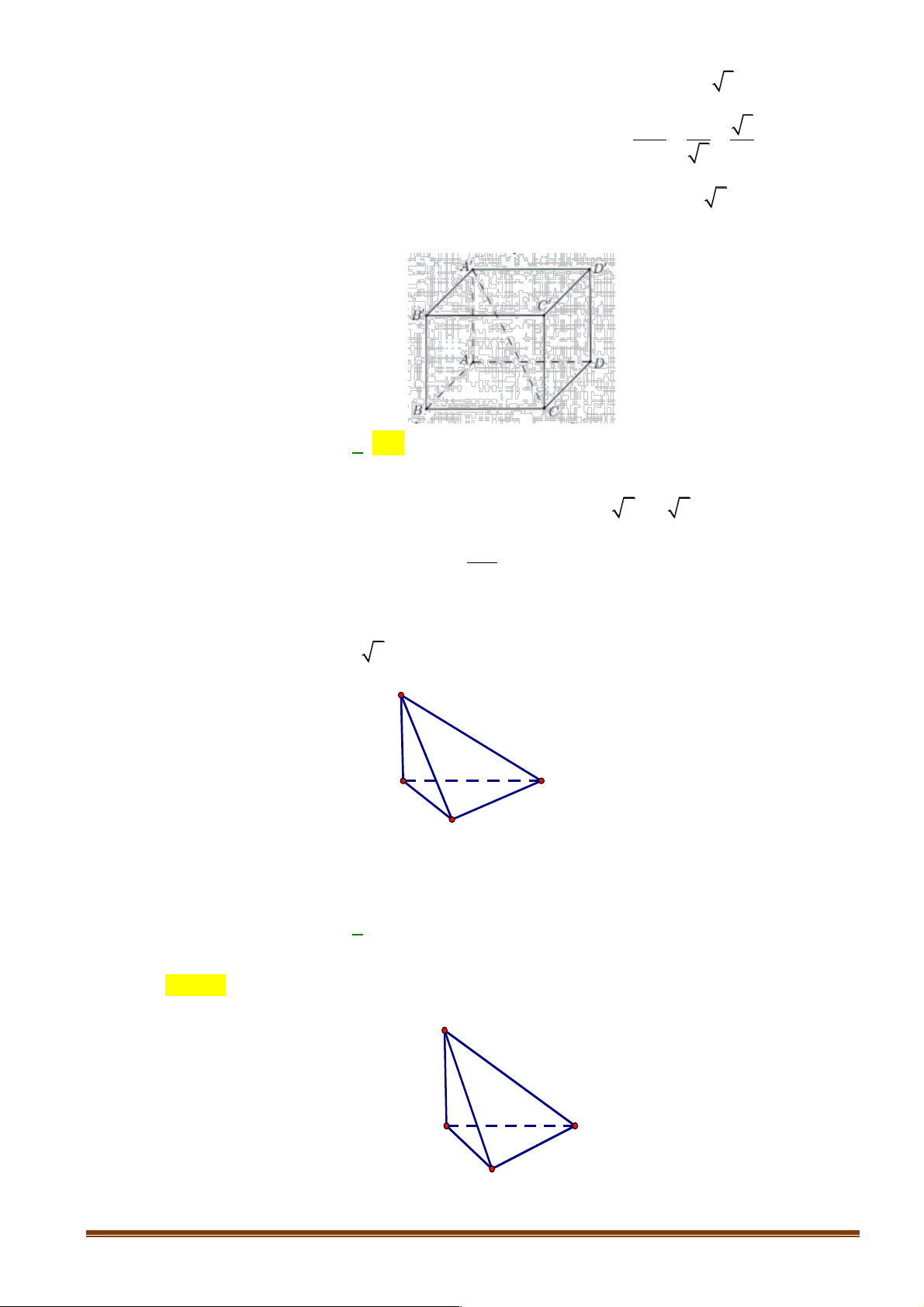
Câu 5: Cho hình chóp S.ABCD có tất cả các cạnh đều bằng nhau. Gọi I và J lần lượt là trung điểm
của SC và BC . Số đo của góc (IJ,CD) bằng: A. 90° . B. 45°. C. 60° . D. 30° . Lời giải Page 14 S I A D B J C
Theo giả thiết ta có IJ là đường trung bình của SB
D C nên IJ // SB .
Vì IJ // SB và CD // AB nên (IJ,CD) = (S , B AB) ∑ = SBA = 60°.
DẠNG 2. HAI ĐƯỜNG THẲNG VUÔNG GÓC
Câu 6: Trong không gian, cho đường thẳng d và điểm O . Qua O có bao nhiêu đường thẳng vuông
góc với đường thẳng d ? A. 3. B. vô số. C. 1. D. 2. Lời giải Chọn B
Trong không gian, có vô số đường thẳng qua một điểm cho trước và vuông góc với một đường thẳng
cho trước. Vì vậy chọn đáp án B
Câu 7: Trong không gian, cho các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
A. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì vuông góc với đường thẳng còn lại.
B. Hai đường thẳng cùng song song với đường thẳng thứ ba thì song song với nhau
C. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.
D. Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau. Lời giải ìa ^ b Sử dụng định lí í Þ a ^ . c b î //c
Câu 8: Chọn khẳng định đúng trong các khẳng định sau:
A. Trong không gian hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
B. Trong không gian hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau.
C. Trong không gian hai mặt phẳng cùng vuông góc với một đường thẳng thì song song với nhau.
D. Trong không gian hai đường thẳng không có điểm chung thì song song với nhau. Lời giải Chọn B Page 15
Đáp án A sai do hai đường thẳng phân biệt cùng vuông góc với một đường thẳng có thể cắt nhau hoặc chéo nhau. ì ¢ ^
Ví dụ: Cho lập phương ABC . D A¢B C ¢ D ¢ ¢ AA AB ta có í
. Dễ thấy AA¢ và AD cắt nhau. îAD ^ AB
Đáp án C sai do hai mặt phẳng cùng vuông góc với một đường thẳng có thể trùng nhau.
Đáp án D sai do trong không gian hai đường thẳng không có điểm chung thì có thể chéo nhau.
Câu 9: Trong hình hộp AB . CD ¢
A B¢C¢D¢ có tất cả các cạnh đều bằng nhau. Trong các mệnh đề sau, mệnh đề nào sai?
A. BB¢ ^ BD . B. ¢ A C¢ ^ BD. C. ¢ A B ^ DC¢ . D. BC¢ ^ ¢ A D. Lời giải A' D' B' C' A D B C Vì hình hộp AB . CD ¢
A B¢C¢D¢ có tất cả các cạnh đều bằng nhau nên các tứ giác ABCD , ¢ A B¢BA,
B¢C¢CB đều là hình thoi nên ta có
AC ^ BD mà AC // A C ¢ ¢ Þ ¢ A C¢ ^ BD. ¢
A B ^ AB¢ mà AB¢ // DC¢ Þ ¢ A B ^ DC¢.
BC¢ ^ B¢C mà B C ¢ // A D ¢ Þ BC¢ ^ ¢ A D .
Câu 10: Cho hình lập phương AB . CD A¢B C ¢ D
¢ ¢. Đường thẳng nào sau đây vuông góc với đường thẳng BC¢ ?
A. A¢D . B. AC . C. BB¢ . D. AD¢ . Lời giải Page 16
Ta có: A¢D / /B C ¢ , B C
¢ ^ BC¢ Þ A¢D ^ BC¢
CHƯƠNG 8. BÀI 2: PHÉP CHIẾU VUÔNG GÓC. GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG
Câu 1: Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ (tham khảo hình bên). Giá trị sin của góc giữa đường
thẳng AC¢ và mặt phẳng ( ABCD) bằng 3 6 3 2 A. . B. . C. . D. . 3 3 2 2 Lời giải Chọn A Ta có AC¢ ( ∑
( ABCD) = AC¢ AC =CAC ¢ = a . ) ∑ ( ) ∑ , ,
Giả sử hình lập phương có cạnh là a CC¢ a 3
Trong tam giác A¢AC ta có sin a = = = . 2 2 AC¢ 2a + a 3
Câu 2: Cho hình lập phương ABC . D ¢
A B¢C¢D¢ (tham khảo hình bên). Giá trị sin của góc giữa đường
thẳng AC ' và mặt phẳng ( ABCD)bằng 3 2 3 6 A. . B. . C. . D. . 3 2 2 3 Lời giải Chọn A Page 17
- Ta có AC ' là đường chéo hình lập phương ABC . D ¢
A B¢C¢D¢ Þ AC ' = . AB 3 ì CC ' ^ (ABCD) ∑ CC í
Þ (AC ',(ABCD)) ∑ = C ' AC , ∑ ' 1 3 sin C ' AC = = = .
îAC 'Ç (ABCD) = A AC ' 3 3
Câu 3: Cho hình hộp chữ nhật ABC .
D A' B 'C ' D ' có AB = AD = 2 và AA' = 2 2 (tham khảo hình
bên). Góc giữa đường thẳng CA' và mặt phẳng ( ABCD) bằng A. 30 .! B. 45 .! C. 60 .! D. 90 .! Lời giải Góc cần tìm là A C
¢ A = a . Vì đáy là hình vuông nên AC = AB 2 = 2 2 và AA¢ tan a = = 1 fi a = 45 . ∞ AC
Câu 4: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng ( ABC), SA = 2a , tam giác ABC
vuông cân tại B và AB = 2a.(minh họa như hình vẽ bên). S A C B
Góc giữa đường thẳng SC và mặt phẳng ( ABC) bằng A. 60° . B. 45° . C. 30° . D. 90° . Lời giải Chọn B S A C B Page 18 ìSC Ç ï ( ABC) = {C} Ta có: ∑ Þ (SC ABC ) ∑ ∑ ,(
) = (SC , AC) = SCA. í ïSA ^ î ( ABC) Mà: 2 2 2 2
AC = AB + BC = 2a + 2a = 2a = SA. Vì SA
D C vuông cân tại A nên ta có ∑ SCA = 45°.
Câu 5: Cho hình chóp S.ABC có đáy là tam giác vuông tại B , AB = 3a , BC = 3a; SA vuông góc
với mặt phẳng đáy và SA = 2a . S A C B
Góc giữa đường thẳng SC và mặt phẳng đáy bằng A. ο 60 . B. ο 45 . C. ο 30 . D. ο 90 . Lời giải
Ta có SA ^ ( ABC) nên góc giữa SC và ( ABC) bằng ∑ SCA. 2 2 2 2
AC = AB + BC = 9a + 3a = 2a 3. SA a Suy ra ∑ 2 1 tan ASC = = = ∑ ο Þ SAC = 30 . AC 2a 3 3 PHẦN II- TỰ LUẬN
I- Đại số và Giải tích
Câu 1: Có ba chiếc hộp: hộp I có 4 bi đỏ và 5 bi xanh, hộp II có 3 bi đỏ và 2 bi đen, hộp III có 5 bi
đỏ và 3 bi vàng. Lấy ngẫu nhiên ra một hộp rồi lấy một viên bi từ hộp đó. Xác suất để viên bi
lấy được màu đỏ bằng Lời giải
Lấy ngẫu nhiên một hộp.
Gọi C là biến cố lấy được hộp I; 1
Gọi C là biến cố lấy được hộp II; 2
Gọi C là biến cố lấy được hộp III. 3 1
Suy ra P (C = P C = P C = 1 ) ( 2) ( 3) . 3 Page 19
Gọi C là biến cố “lấy ngẫu nhiên một hộp, trong hộp đó lại lấy ngẫu nhiên một viên bi và được bi màu đỏ”.
Ta có: C = (C ÇC È C ÇC È C ÇC 1 ) ( 2 ) ( 3 )
Þ P(C) = P(C ÇC + P C ÇC + P C ÇC 1 ) ( 2 ) ( 3 ) 1 4 1 3 1 5 = . + . + 601 . = . 3 9 3 5 3 8 1080
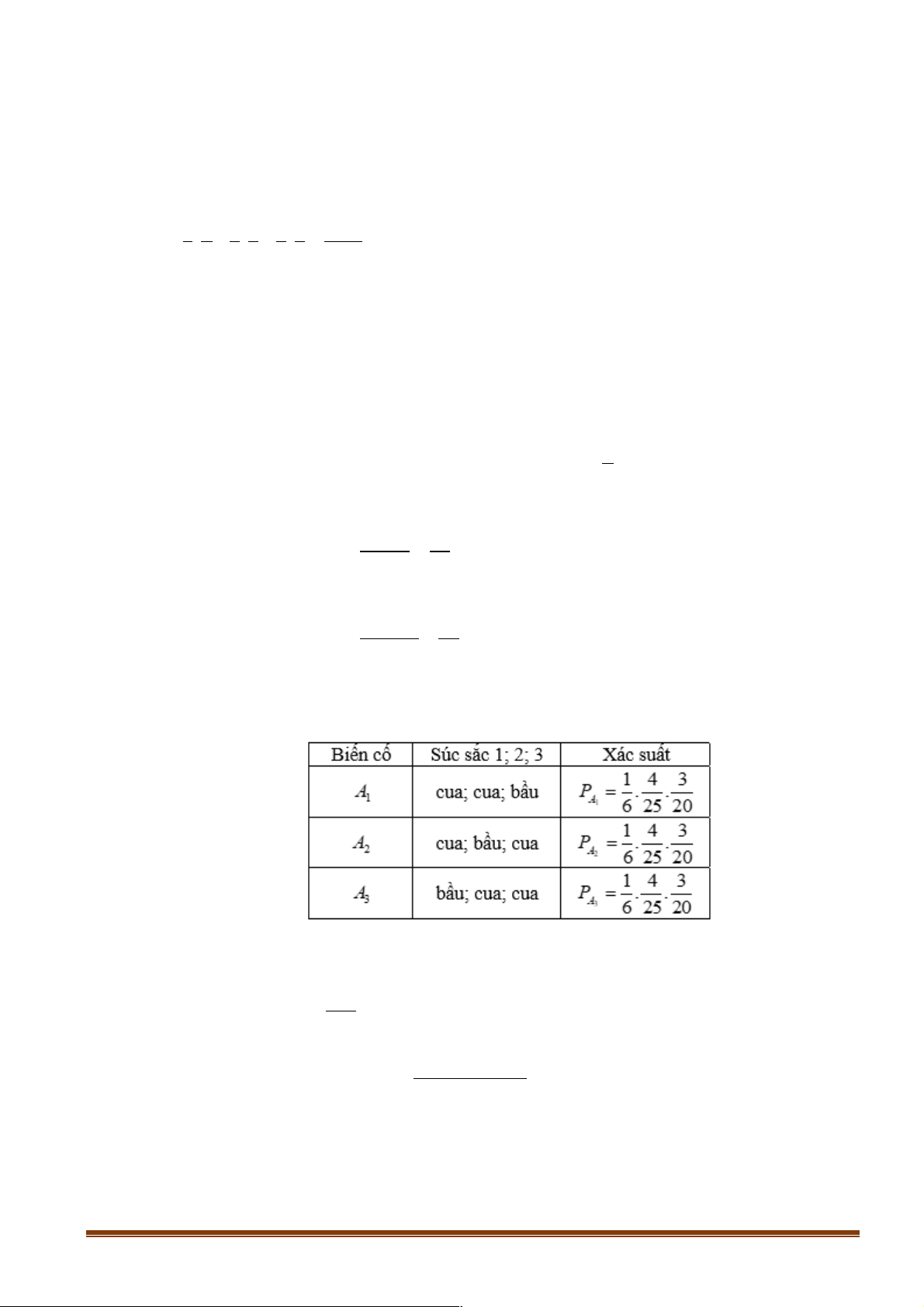
Câu 2: Có 3 con súc sắc hình lập phương làm bằng giấy, các mặt của súc sắc in các hình bầu, cua,
tôm, cá, gà, nai. Súc sắc thứ nhất cân đối. Súc sắc thứ hai không cân đối, có xác suất mặt tôm
là 0,2; các mặt còn lại có xác suất bằng nhau. Súc sắc thứ ba không cân đối, có xác suất mặt
nai là 0,25; các mặt còn lại có xác suất bằng nhau. Gieo một lần ba con súc sắc đã cho. Tính
xác suất để hai súc sắc xuất hiện mặt cua và một súc sắc xuất hiện mặt bầu. Lời giải 1
Con súc sắc thứ nhất cân đối nên xác suất xuất hiện mỗi mặt là . 6
Súc sắc thứ hai không cân đối, có xác suất mặt tôm là 0,2; các mặt còn lại có xác suất bằng nhau nên 1- 0, 2 4
xác suất mỗi mặt còn lại là: = . 5 25
Súc sắc thứ ba không cân đối, có xác suất mặt nai là 0,25; các mặt còn lại có xác suất bằng nhau nên 1- 0, 25 3
xác suất mỗi mặt còn lại là: = . 5 20
Gọi A là biến cố “Gieo một lần 3 con súc sắc, hai súc sắc xuất hiện mặt cua và một súc sắc xuất hiện
mặt bầu.”. Ta có các trường hợp sau:
Do A = A È A È A và các biến cố A ; A ; A đôi một xung khắc nên ta có: 1 2 3 1 2 3 3
P = P + P + P = . A 1 A 2 A 3 A 250 x -x + +
Câu 3: Cho 4x + 4-x = 5 2 2 7. Biểu thức P = có giá trị bằng 8 - 4.2x - 4.2-x Lời giải x -x + = Û ( x -x + )2 4 4 7 2 2
= 9 Û 2x + 2-x = 3. Page 20 5 + 2x + 2-x 5 + 3 Suy ra P = = = 2. - . 8 - 4.2x - 4.2-x 8 -12 x + 3
Câu 4: Tìm tập xác định của hàm số y = log là: 2021 2 - x Lời giải x + 3 x + 3 Hàm số y = log xác định khi > 0 Û 3
- < x < 2. 2021 2 - x 2 - x
Suy ra tập xác định của hàm số: D = ( 3; - 2).
Câu 5: Tất cả các giá trị thực của tham số m để hàm số y = ( 2
log x - 2x - m + ) 1 có tập xác định là R . Lời giải Điều kiện: 2
x - 2x - m +1 > 0.
Để hàm số có tập xác định là 2
R Û x - 2x - m +1 > 0 x " ÎR Û (- )2 1 -( m - + ) 1 < 0 Û m < 0. II- Hình học
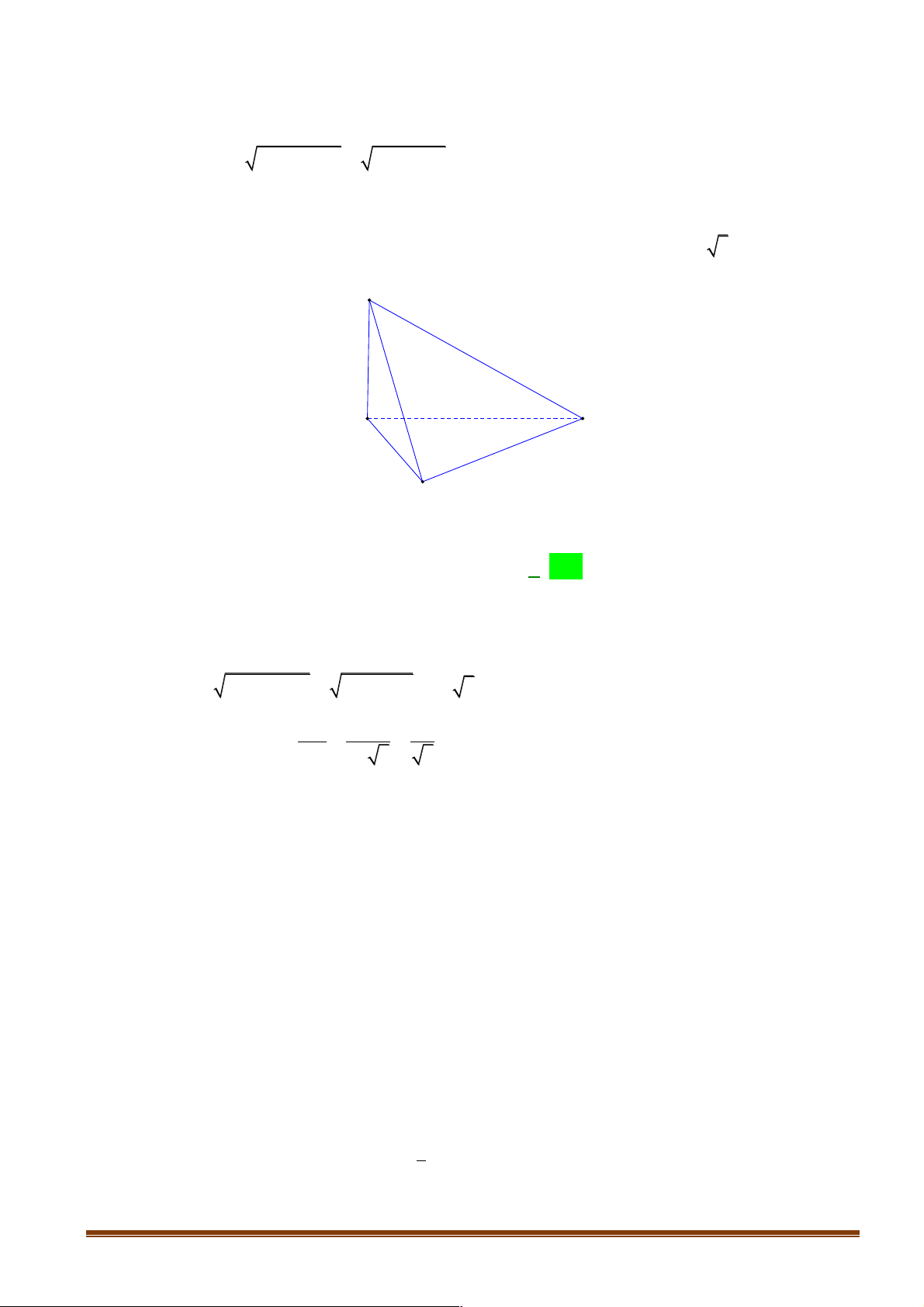
Câu 6: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a . Gọi M là trung điểm của SD
. Tang của góc giữa đường thẳng BM và mặt phẳng ( ABCD) bằng S M A D B C Lời giải S M A D H O B C 2 a a 2
Gọi O là tâm của hình vuông. Ta có SO ^ ( ABCD) và 2 SO = a - = 2 2 Page 21
Gọi M là trung điểm của OD ta có MH / /SO nên H là hình chiếu của M lên mặt phẳng (ABCD) 1 a 2 và MH = SO = . 2 4
Do đó góc giữa đường thẳng BM và mặt phẳng (ABCD) là ∑ MBH . a 2 MH 1 Khi đó ta có ∑ 4 tan MBH = = = . BH 3a 2 3 4 1
Vậy tang của góc giữa đường thẳng BM và mặt phẳng ( ABCD) bằng 3
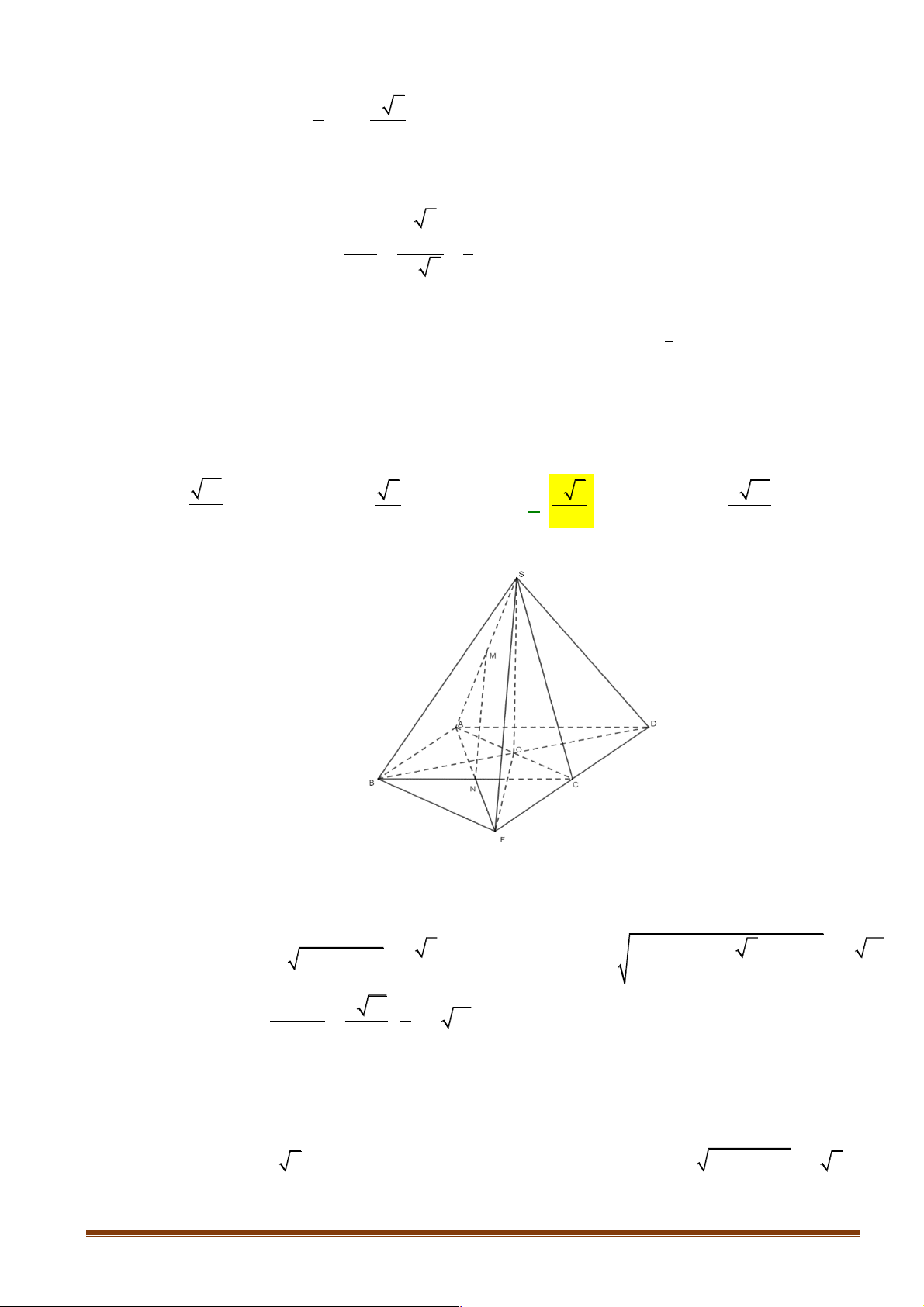
Câu 7: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , tâm O . Gọi M và N lần lượt là
trung điểm của SA và BC . Biết rằng góc giữa MN và ( ABCD) bằng 0 60 , cosin góc giữa
MN và mặt phẳng (SBD) bằng: 41 5 2 5 2 41 A. . B. . C. . D. . 41 5 5 41 Lời giải
Ta có AN Ç CD = F Þ MN / /SF ; (MN ( ABCD)) = (SF ( ABCD)) ∑ , , = SFO = 60°. Với 2 1 1 a 2 a a 2 a 10 2 2 2 OC = AC = AB + BC =
;CF = CD = a Þ OF = a + - 2a cos135° = 2 2 2 2 2 2 OF a 10 1 . Khi đó SF = = : = a 10 . cos 60° 2 2 Ta có OC ^ B ,
D OC ^ SO Þ OC ^ (SBD), lại có OC / /BF Þ BF ^ (SBD), do vậy
(MN (SBD)) =(SF (SBD)) ∑ , , = FSB.
BF = 2OC = a 2 ( OC là đường trung bình trong tam giác BDF ), 2 2
SB = SF - BF = 2 2a. Page 22 SB Vậy ∑ 2 5 cos BSF = = . SF 5
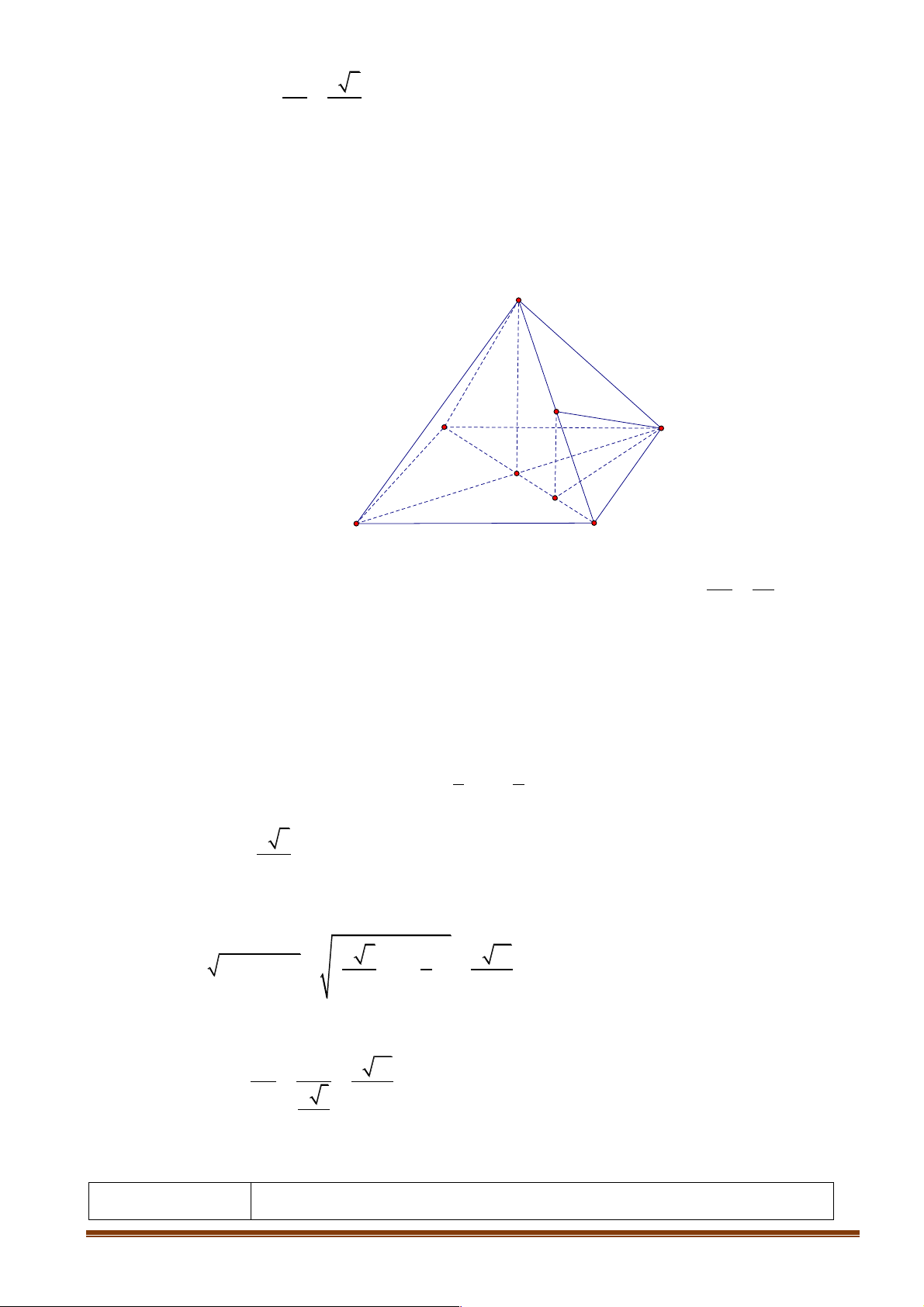
Câu 8: Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và tam giác ABD đều. SO
vuông góc mặt phẳng ( ABCD)và SO = 2a . M là trung điểm của SD . Tang góc giữa CM và (ABCD)là: Lời giải S M C B O I A D SO 2a
Gọi I là trung điểm OD Þ MI là đường trung bình tam giác SOD Þ MI = = = a và 2 2
MI // SO Þ MI ^ ( ABCD).
IC là hình chiếu của MC lên mặt phẳng ( ABCD).
Góc giữa MC với ( ABCD)là ∑ MCI . 1 a
Tam giác ABD đều Þ BD = a Þ OI = BD = . 4 4 a 3 OC = OA = . 2
Xét tam giác OCI vuông tại O : 2 2
æ a 3 ö æ a ö a 13 2 2
CI = CO + OI = ç ÷ + = . ç ÷ ç ÷ 2 è ø è 4 ø 4
Xét tam giác CMI vuông tại I: ∑ MI a 4 13 tan MCI = = = . CI a 1 13 4
d) Tổ chức thực hiện:
Chuyển giao
GV: Giáo viên chia lớp thành 4 nhóm Page 23
Giáo viên giao nhiệm vu chữa các câu hỏi cho các nhóm.
GV: Quan sát các nhóm và đôn đốc các nhóm thực hiện theo yêu cầu
Thực hiện
HS: Thực hiện yêu cầu của GV
GV: học sinh lên bảng trình bày vắn tắt lời giải và đáp án của câu hỏi mà
Báo cáo thảo luận nhóm được giao
Đánh giá, nhận xét, GV nhận xét câu trả lời của các đội, đánh giá thái độ làm việc, ghi nhận, tổng
tổng hợp hợp kết quả Page 24




