Ôn tập kiểm tra giữa kỳ - Toán cao cấp c2 | Trường Đại Học Duy Tân

1. Cho m×n k×p;A B. Điều kiện để phép cộng A B thực hiện được là: A. m = n; k = p B. m = k, n = p C. m = p; n = k D. Với mọi m, n, k, p. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

10 5 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Toán cao cấp c2 (mth 102)

Trường: Đại học Duy Tân

Thông tin:

6 trang 1 tháng trước

Tác giả:

Profile Mai Nguyệt
DTU – Khoa Khoa học Tự nhiên A Thân Thị Quỳnh Dao
Họ và tên: ……………………………………………. Lớp: …… 1
Kiểm tra
1. Cho
m×n k×p
;
A B
. Điều kiện để phép cộng
A B
thực hiện được là:
A. m = n; k = p B m = k, n = p C. m = p; n = k D. Với mọi m, n, k, p .
2. Ma trận con
23
M
của ma trận
2 1 9
5 0 3
A
là ma trận:
A.
2 1
1 4
B.
2 9
1 6
C.
0 3
4 6
D.
1 9
0 3
3. Cho ma trận
5 5
A
. Khi đó,
A. 2
A A
B.
2 2
A A
C.
5
2 2
D. đáp án khác
4. Cho phép biến đổi ma trận sau:
1 2 1
2 3h h h
A B

. Khi đó:
1
2
A B
B.
1
3
A B
C.
1
6
A B
D. 3
A B
5. Cho phép biến đổi ma trận sau
ij 4 4
( )
h h h h h
A a B

. Khi đó:
A.
A B
B.
A B
C.
4
B A
D.
4
B A
6. Cho
2 n 3 5 2 p
A B C
. Xác định n, p?
A. n = 3, p = 5 B. n = 5, p = 3 C. n = 2, p = 5 D. n = 5, p = 2
7. Xác định ma trận , biết ?
A. B. C D. .
8. Xác định ma trận , biết A ?
A. B. C. D.
Câu 1 2 3 4 5 6 7 8
Đáp án
DTU – Khoa Khoa học Tự nhiên A Thân Thị Quỳnh Dao
2
Họ và tên: ……………………………………………. Lớp: ……
9. Cho hai ma trận
1 2 3
1 0 6
4 2 0
A
,
1 2 3
0 2 9
4 2 0
B
. Khi đó,
A.
A B
B.
A B
C.
2
A B
D. đáp án khác
10. Xác định giá trị của định thức ?
A. B. C D. .
11. Cho
1 m
m 4
A
,
det 0
A
khi:
A. m > 2 B. m = 2 C. m > -2 D. với mọi
m
12. Cho hai ma trận:
1 2 3 1 2 3
1 ; 0 2 3
0 5 2 0 10
A b c B b c
a a
. Khẳng định nào sau đây đúng?
A.
1
2
A B
B.
2
A B
C.
A B
D.
A B
13. Cho hai ma trận:
1 4 5 1 4 5
2 0 8 ; 0 8 2
3 1 9 3 1 9
A B
. Khẳng định nào sau đây đúng?
A.
1
2
A B
B.
A B
C.
1
2
A B
D .
A B
14. Cho hai định thức:
1 2
0 2 1 3 2 5
D 3 2 5 ; D 0 2 1
a b c a b c
. Khẳng định nào sau đây đúng?
A.
2 1
D D
B.
2 1
D 3D
C.
1 2
D 3D
D.
1 2
D D
15. Cho
T
0 1 3
1 2 5
4 6 8
A
.
Tính giá trị của
?
A
A.
0 2 6
1 2 5
4 6 8
B .
0 1 3
2 1 2 5
2 3 4
C.
0 2 6
1 2 5
4 6 8
D.
0 1 3
1 2 5
2 3 4
16. Ma trận nào sau đây là ma trận khả nghịch?
A. B C. D. .
Câu 9 10 11 12 13 14 15 16
Đáp án
DTU – Khoa Khoa học Tự nhiên A Thân Thị Quỳnh Dao
3
Họ và tên: ……………………………………………. Lớp: ……
1. Cho hai định thức:
1 2
1 2 3 4 2 5 4 7
2 5 4 7 1 2 3 4
D ; D
3 6 8 4 4 8 12 17
4 8 12 17 3 6 8 4
. Khẳng định nào sau đây đúng?
A.
1 2
D D
B.
1 2
D D
C.
2 1
D 2D
D.
2 1
D 2D
2. Xác định hạng của ma trận
0 1 2
0 0 3
0 2 7
A
?
A. r(A) = 0 B r(A) = 1 C. r(A) = 2 D. r(A) = 3 .
3. Cho ma trận
2 1 3
0 m 0
0 5 0
A
. Tìm giá trị của m để
2
r A
?
A. m = 0 B. m =1 C. m = 2 D .
m
4. Ma trận nào sau đây là ma trận không khả nghịch?
A.
4 8
3 5
B.
1 0
4 5
C.
2 8
3 0
D .
1 2
3 6
5. Ma trận nghịch đảo của ma trận
1 1
0 1
A
là:
A.
1
1 1
0 1
A
B.
1
1 0
1 1
A
C.
1
1 1
0 1
A
D.
1
1 0
1 1
A
6. Cho ma trận
4 2 1
0 m + 1 0
0 3 0
A
. Tìm giá trị m để ma trận
A
khả nghịch?
A.
m = -1
B.
m -1
C. với mọi m D không tồn tại giá trị của m .
7. Ma trận hệ số mở rộng của hệ phương trình
3 0
2 2
x y
x y
là
A.
1 3
2 1
B.
1 3 0
2 1 2
C.
3 0
1 2
D .
0
2
8. Cho ma trận
1 2 3
2 4 6
3 6 9
A
. Khẳng định nào sau đây đúng?
A.
2
r A
B .
0
A
C. tồn tại
1
A
D. A.,B.,C. đều đúng
Câu 1 2 3 4 5 6 7 8
Đáp án
DTU – Khoa Khoa học Tự nhiên A Thân Thị Quỳnh Dao
4
Họ và tên: ……………………………………………. Lớp: ……
9. Cho hệ phương trình tuyến tính
1
x y
x my m
. Khẳng định nào sau đây đúng?
A. Hệ phương trình trên có duy nhất nghiệm với mọi . m
B. Hệ phương trình trên có vô số nghiệm với mọi . m
C. Hệ phương trình trên có nghiệm với mọi . m
D. Hệ phương trình trên vô nghiệm khi và chỉ khi
1.
m
10. Tập nghiệm của một hệ phương trình Cramer là tập hợp:
A. Rỗng B. có 1 phần tử C. có ít nhất 1 phần tử D. có vô số các phần tử
11. Hệ phương trình tuyến tính thuần nhất có ma trận hệ số có vô số nghiệm khi:
A. m B. m C. m hoặc m D . .
12. Tìm giá trị m để hệ phương trình có ma trận hệ số mở rộng là vô nghiệm?
A. m B. m C. D không có giá trị m .
13. Cho hệ phương trình , có thể chọn ẩn nào làm ẩn không cơ bản?
A. B. C . D.
14. Cho hai ma trận . Khẳng định nào sau đây đúng?
A. B. C. D cả A.B.C. đều sai .
15. Cho , hãy tìm công thức tính ma trận X của phương trình ?
A. B. C. D không tồn tại ma trận X .
16. Trong các hệ phương trình sau đây, hệ nào là hệ Cramer?
A. B. C D. .
Câu 9 10 11 12 13 14 15 16
Đáp án
DTU – Khoa Khoa học Tự nhiên A Thân Thị Quỳnh Dao
5
Họ và tên: ……………………………………………. Lớp: ……
1. Cho phép biến đổi ma trận sau:
2 1 2 2 2
2
3 4
'
h h h h h
A B B

. Khi đó:
A.
A B
B.
2
A B
C. 2
A B
D.
2
A B
2. Cho phép biến đổi ma trận sau:
2 2 2 1
3
3 5
'
h h h h
A B B
. Khi đó:
A.
3
A B
B.
3
A B
C .
3
B A
D.
3
B A
.
3. Xác định , biết ?
A. B. C D. .
4. Cho hai định thức:
1 2
1 2 3 4 2 4 6 8
2 2b 2 2
D ; D
3 6 8 4 6 12 16 8
4 8 12 17 4 8 12 17
a b c d a c d
. Khẳng định nào sau đây đúng?
A.
2 1
D 2D
B.
2 1
D 4D
C .
2 1
D 8D
D.
2 1
D 16D
5. Cho hệ phương trình tuyến tính
4 1
10 3 6 3
x y m
x y m
. Khẳng định nào sau đây đúng?
A. Hệ vô nghiệm, m
B Hệ có nghiệm,. m
C. Hệ có vô số nghiệm, m
D. tất cả đều sai
6. Cho ma trận
2
7 1 0
0 0 m
0 0 m 1
A
. Tìm giá trị của m để
2
r A
?
A. m = 0 B. m = 1 C A.,B. đều đúng D. A.,B. đều sai .
7. Cho ma trận
1 0 m
0 0 m
0 m m 1 0
A
. Tìm giá trị của m để
1
r A
?
A. m = 0 B. m =1 C. m = 0 hoặc m = 1 D. đáp án khác
8. Hệ phương trình tuyến tính thuần nhất có ma trận hệ số là có vô số nghiệm
khi:
A. m = 0 B. m = 1 C. m = 0 hoặc m = 1 D. không có giá trị m
DTU – Khoa Khoa học Tự nhiên A Thân Thị Quỳnh Dao
6
Họ và tên: ……………………………………………. Lớp: ……
9. Hệ phương trình có ma trận hệ số mở rộng là vô nghiệm khi:
A. m = 0 B m = 1 C. m = 0 hoặc m = 1 D. không có giá trị m .
10. Hệ phương trình có ma trận hệ số mở rộng là vô số nghiệm khi:
A. m = 2 B m = -2 C. m =. D. không có giá trị m
11. Hệ phương trình có ma trận hệ số mở rộng là có nghiệm duy nhất khi:
A. m B. m C. m hoặc m D m. và m
| 1/6
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

DTU – Khoa Khoa học Tự nhiên A Thân Thị Quỳnh Dao Kiểm tra 1. Cho A ;  m×n
Bk×p . Điều kiện để phép cộng A B thực hiện được là: A. m = n; k = p B. m = k, n = p C. m = p; n = k D. Với mọi m, n, k, p  2 1 9 2.  
Ma trận con M23 của ma trận A  5 0 3 là ma trận:    1  4 6    2 1  2 9 0 3 1 9 A.  B. C. D. 1 4           1  6   4 6   0 3   3. Cho ma trận . Khi đó, 5 A 5  A. 2A  A B. 2A  2 A C. 5 2A  2 A D. đáp án khác 4. 2h 3  h h 
Cho phép biến đổi ma trận sau: 1 2 1
A  B . Khi đó: 1 1 1 A  B B. A  B C. A  B D. 3 A  B 2 3 6 5.    
Cho phép biến đổi ma trận sau  ( ) h h h h h A a   . Khi đó: ij 44 B A. A  B B. A   B C. B  4 A D. B  4  A 6. Cho   . Xác định n, p? 2 A n B3 5 C   2 p  A. n = 3, p = 5 B. n = 5, p = 3 C. n = 2, p = 5 D. n = 5, p = 2
7. Xác định ma trận , biết ? A. B. C. D.
8. Xác định ma trận A, biết ? A. B. C. D. Câu 1 2 3 4 5 6 7 8 Đáp án
Họ và tên: ……………………………………………. Lớp: …… 1
DTU – Khoa Khoa học Tự nhiên A Thân Thị Quỳnh Dao  1 2 3 1  2 3 9. Cho hai ma trận   ,   . Khi đó, A  1  0 6   B  0 2 9    4 2 0   4  2 0    A. A  B B. A   B C. A  2 B D. đáp án khác
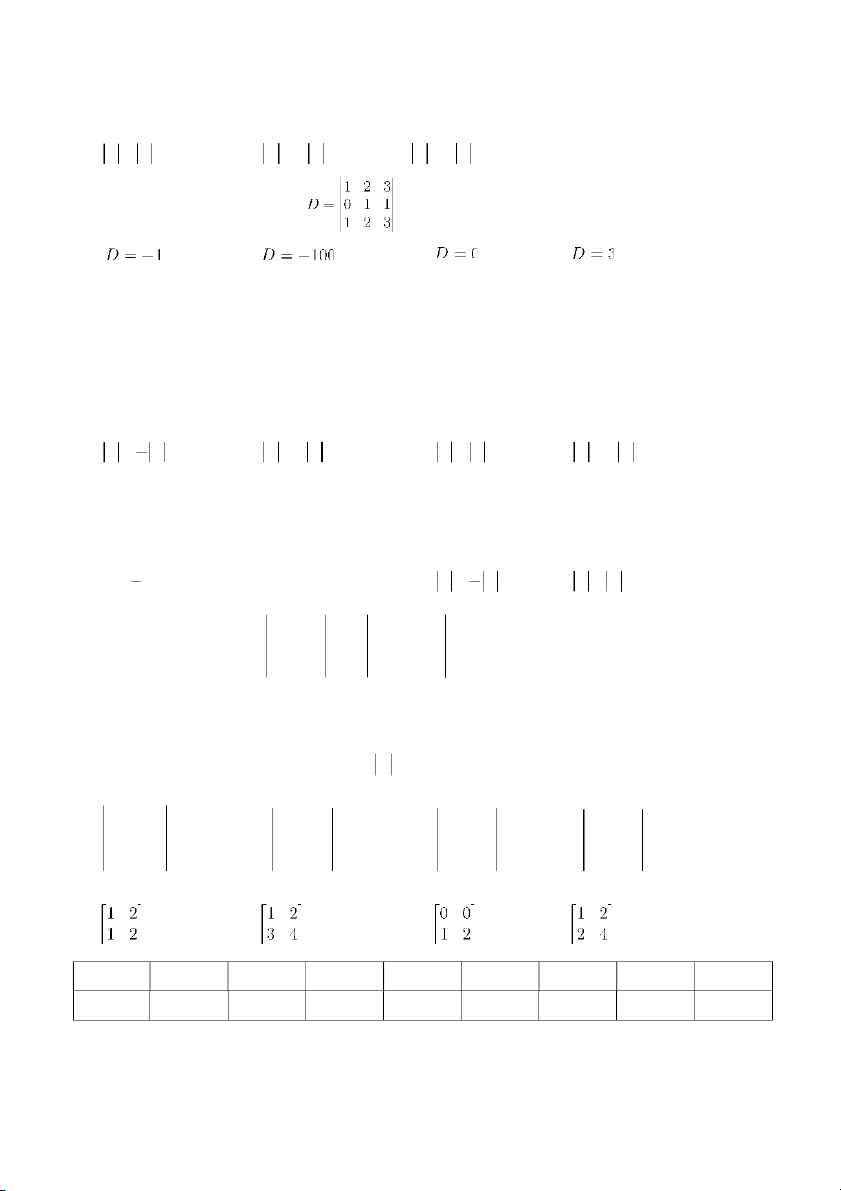
10. Xác định giá trị của định thức ? A. B. C. D.  1 m 11. Cho A   , det  A  0 khi: m 4    A. m > 2 B. m = 2 C. m > -2 D. với mọi m  1 2 3  1 2 3  12. Cho hai ma trận:     A  1 b c ; B  0
b  2 c  3 . Khẳng định nào sau đây đúng?     a 0 5 2a 0 10      1 A. A  B B. A  2 B C. A  B D. A   B 2 1  4 5  1  4 5  13. Cho hai ma trận:   
 . Khẳng định nào sau đây đúng? A  2 0 8 ; B  0 8  2      3  1 9  3  1 9      1 1 A. A  B B. A  B C. A  B D. A  B 2 2 0 2 1 3  2 5
14. Cho hai định thức: D  3 2 5 ; D  0 2
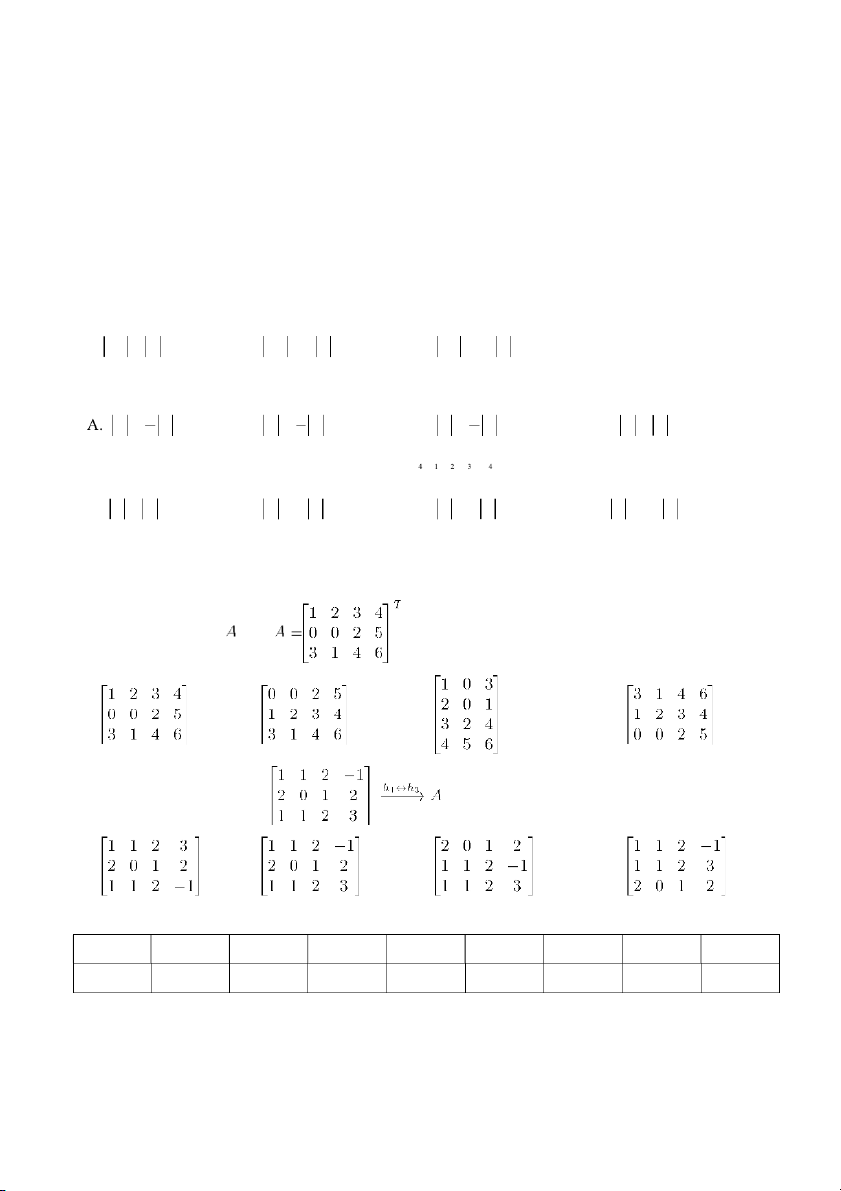
1 . Khẳng định nào sau đây đúng? 1 2 a b c a  b  c  A. D  D B. D  3D C. D  3D D. D  D 2 1 2 1 1 2 1 2 T  0 1 3 15.   Cho A  1 2 5 
 . Tính giá trị của A  ?  4 6 8   0 2 6 0 1 3 0 2 6 0 1 3 A. 1  2 5 B. 2 1 2 5 C. 1 2 5 D.  1 2 5 4 6 8 2 3 4 4 6 8 2 3 4
16. Ma trận nào sau đây là ma trận khả nghịch? A. B. C. D. Câu 9 10 11 12 13 14 15 16 Đáp án 2
Họ và tên: ……………………………………………. Lớp: ……
DTU – Khoa Khoa học Tự nhiên A Thân Thị Quỳnh Dao 1 2 3 4 2 5 4 7 2 5 4 7 1 2 3 4
1. Cho hai định thức: D  ; D 
. Khẳng định nào sau đây đúng? 1 2 3 6 8 4 4 8 12 17 4 8 12 17 3 6 8 4 A. D  D B. D   D C. D  2D D. D  2  D 1 2 1 2 2 1 2 1 0 1 2  
2. Xác định hạng của ma trận A  0 0 3   ? 0 2 7   A. r(A) = 0 B. r(A) = 1 C. r(A) = 2 D. r(A) = 3 2 1 3 3.   Cho ma trận A  0 m 0 
 . Tìm giá trị của m để r A  2 ? 0 5   0 A. m = 0 B. m =1 C. m = 2 D. m  
4. Ma trận nào sau đây là ma trận không khả nghịch? 4 8 1 0  2  8 1 2 A.  B. C. D. 3 5         4 5   3 0   3 6   1  1
5. Ma trận nghịch đảo của ma trận A  là: 0  1   1 1 1  0 1 1  1 0 A.     1 A   B. 1 A  C. 1 A  D. 1 A  0 1         1 1   0 1   1 1   4 2 1 6. Cho ma trận   A  0
m + 1 0 . Tìm giá trị m để ma trận   A khả nghịch? 0  3 0   A. m = -1 B. m  -1 C. với mọi m
D. không tồn tại giá trị của m  x  3y  0
7. Ma trận hệ số mở rộng của hệ phương trình  là 2x  y  2  1 3 1 3 0   3 0 0 A.      B. C. D. 2 1          2 1 2  1 2 2 1 2 3 8. Cho ma trận   A  2
4 6 . Khẳng định nào sau đây đúng?   3 6 9   A. r  A  2 B. A  0 C. tồn tại 1 A  D. A.,B.,C. đều đúng Câu 1 2 3 4 5 6 7 8 Đáp án 3
Họ và tên: ……………………………………………. Lớp: ……
DTU – Khoa Khoa học Tự nhiên A Thân Thị Quỳnh Dao  x  y 1
9. Cho hệ phương trình tuyến tính 
. Khẳng định nào sau đây đúng? x  my  m
A. Hệ phương trình trên có duy nhất nghiệm với mọi m.
B. Hệ phương trình trên có vô số nghiệm với mọi m.
C. Hệ phương trình trên có nghiệm với mọi m.
D. Hệ phương trình trên vô nghiệm khi và chỉ khi m 1.
10. Tập nghiệm của một hệ phương trình Cramer là tập hợp: A. Rỗng B. có 1 phần tử
C. có ít nhất 1 phần tử
D. có vô số các phần tử
11. Hệ phương trình tuyến tính thuần nhất có ma trận hệ số có vô số nghiệm khi: A. m B. m C. m hoặc m D. .
12. Tìm giá trị m để hệ phương trình có ma trận hệ số mở rộng là vô nghiệm? A. m B. m C. D. không có giá trị m 13. Cho hệ phương trình
, có thể chọn ẩn nào làm ẩn không cơ bản? A. B. C. D. 14. Cho hai ma trận
. Khẳng định nào sau đây đúng? A. B. C. D. cả A.B.C. đều sai 15. Cho
, hãy tìm công thức tính ma trận X của phương trình ? A. B. C.
D. không tồn tại ma trận X
16. Trong các hệ phương trình sau đây, hệ nào là hệ Cramer? A. B. C. D. Câu 9 10 11 12 13 14 15 16 Đáp án 4
Họ và tên: ……………………………………………. Lớp: ……
DTU – Khoa Khoa học Tự nhiên A Thân Thị Quỳnh Dao 1. h  h  h 2 h  h
Cho phép biến đổi ma trận sau: 2 1 2 2 2 A 
 B '  B . Khi đó: 3 4  A. A  B B. A  2 B C. 2 A  B D. A  2  B 2. 3  
Cho phép biến đổi ma trận sau: 2 h 2 h 2 h 1 A   . Khi đó:  B ' h 3 5 B A. A  3 B B. A  3  B C. B  3 A D. B  3 A . 3. Xác định , biết ? A. B. C. D. 1 2 3  4 2 4 6  8 a b c  d 2a 2b 2  c 2d
4. Cho hai định thức: D  ; D 
. Khẳng định nào sau đây đúng? 1 2 3 6 8  4 6 12 1  6 8 4 8 1  2 17 4 8 1  2 17 A. D  2D B. D  4D C. D  8D D. D 16D 2 1 2 1 2 1 2 1  4x  y  m 1
5. Cho hệ phương trình tuyến tính 
. Khẳng định nào sau đây đúng? 10  x  3y  6m  3 A. Hệ vô nghiệm, m  
B. Hệ có nghiệm,m 
C. Hệ có vô số nghiệm, m   D. tất cả đều sai 7 1 0  6.   Cho ma trận A  0 0 m
. Tìm giá trị của m để r   ?   A  2 2 0 0 m   1 A. m = 0 B. m = 1 C. A.,B. đều đúng D. A.,B. đều sai 1  0 m  7.   Cho ma trận A  0 0 m 
 . Tìm giá trị của m để r  A  1? 0 m  m 1 0  A. m = 0 B. m =1
C. m = 0 hoặc m = 1 D. đáp án khác
8. Hệ phương trình tuyến tính thuần nhất có ma trận hệ số là có vô số nghiệm khi: A. m = 0 B. m = 1
C. m = 0 hoặc m = 1 D. không có giá trị m 5
Họ và tên: ……………………………………………. Lớp: ……
DTU – Khoa Khoa học Tự nhiên A Thân Thị Quỳnh Dao
9. Hệ phương trình có ma trận hệ số mở rộng là vô nghiệm khi: A. m = 0 B. m = 1
C. m = 0 hoặc m = 1 D. không có giá trị m
10. Hệ phương trình có ma trận hệ số mở rộng là vô số nghiệm khi: A. m = 2 B. m = -2 C. m = D. không có giá trị m
11. Hệ phương trình có ma trận hệ số mở rộng là có nghiệm duy nhất khi: A. m B. m C. m hoặc m D. m và m 6
Họ và tên: ……………………………………………. Lớp: ……