Ôn tập kiểm tra học kì 1 | Giáo án Toán 11 Cánh diều

Ôn tập kiểm tra học kì 1 | Giáo án Toán 11 Cánh diều được biên soạn rất cẩn thận, trình bày khoa học giúp giáo viên có một cách dạy mạch lạc, rõ ràng, dễ hiểu từ đó giúp học sinh tiếp thu kiến thức tốt nhất. Thầy cô và các bạn xem, tải về ở bên dưới.

121 61 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Giáo án Toán 11

Môn: Toán 11

Sách: Cánh diều

Thông tin:

38 trang 8 tháng trước

Tác giả:

Profile Thùy Dương (H)
Trường ………………………..
Tổ ………………….
Họ và tên giáo viên: ……………………
Tiết
KẾ HOẠCH BÀI DẠY
TÊN BÀI DẠY: ÔN TẬP KIỂM TRA HỌC KỲ 1
Môn học/Hoạt động giáo dục: Toán 11
Thời gian thực hiện: 01 tiết
I. MỤC TIÊU
1. Kiến thức
- Ôn tập lại các kiến thức: Hàm số lượng giác và phương trình lượng giác. Dãy số, cấp số cộng,
cấp số nhân. Giới hạn của dãy số, giới hạn của hàm số, hàm số liên tục. Đường thẳng và mặt phẳng
trong không gian, hai đường thẳng song song, đường thẳng song song với mặt phẳng, hai mặt phẳng
song song.
- Đối với học sinh khá giỏi: Vận dụng các kiến thức: Hàm số lượng giác và phương trình lượng
giác. Dãy số, cấp số cộng, cấp số nhân. Giới hạn của dãy số, giới hạn của hàm số, hàm số liên tục.
Đường thẳng và mặt phẳng trong không gian, hai đường thẳng song song, đường thẳng song song với
mặt phẳng, hai mặt phẳng song song vào một số bài toán thực tế đơn giản.
2. Năng lực
- Năng lực tự học: Học sinh xác định đúng đắn động cơ, thái độ học tập; tự đánh giá và điều
chỉnh được kế hoạch học tập; tự nhận ra những sai sót và khắc phục.
- Năng lực giao tiếp: Tiếp thu kiến thức, trao đổi học hỏi bạn bè thông qua việc thực hiện nhiệm
vụ trong các hoạt động cặp đôi, nhóm; có thái độ tôn trọng, lắng nghe, có phản ứng tích cực
trong giao tiếp.
- Năng lực hợp tác: Học sinh xác định được nhiệm vụ của tổ/nhóm, trách nhiệm của bản thân đề
xuất được những ý kiến đóng góp, góp phần hoàn thành nhiệm vụ học tập.
- Năng lực giải quyết vấn đề: Học sinh tiếp cận hệ thống câu hỏi và bài tập, những tình huống có
vấn đề. Phân tích được các vấn đề để đưa ra những giải pháp xử lí tình huống, những vấn đề
liên quan đến bộ môn và trong thực tế.
- Năng lực sáng tạo: Học sinh biết vận dụng tính sáng tạo để giải quyết tình huống của từng bài
toán cụ thể.
- Năng lực sử dụng ngôn ngữ: Học sinh nói và viết chính xác bằng ngôn ngữ Toán học.
3. Phẩm chất
- Trách nhiệm: Biết chịu trách nhiệm với thành quả của cá nhân, tập thể; không đổ lỗi cho người
khác. Chủ động phát hiện, chiếm lĩnh tri thức mới, biết quy lạ về quen, có tinh thần trách
nhiệm hợp tác xây dựng cao.
- Trung thực: Học sinh biết tôn trọng kết quả của bản thân, tôn trọng lẽ phải; thật thà, ngay
thẳng trong học tập và làm việc, lên án sự gian lận.
- Chăm chỉ: Chăm làm, ham học, có tinh thần tự học, chăm chỉ tích cực xây dựng bài, nhiệt tình
tham gia các công việc của tập thể, tinh thần vượt khó trong công việc.
- Nhân ái: Yêu con người, yêu cái đẹp của toán học, tôn trọng sự khác biệt, ý kiến trái chiều;
sẵn sàng học hỏi, hòa nhập và giúp đỡ mọi người
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Về phía giáo viên:
- Thước thẳng có chia khoảng, compa, bảng phụ ghi bài tập, phiếu học tập, máy chiếu, sách
giáo khoa, bài soạn...
2. Về phía học sinh:
- Dụng cụ học tập, sách giáo khoa, chuẩn bị bài trước khi đến lớp...
III. TIẾN TRÌNH DẠY HỌC:
1. HOẠT ĐỘNG 1: KHỞI ĐỘNG
a) Mục tiêu:
- HS chuẩn bị tâm thế tốt cho tiết ôn tập cuối học kỳ 1
- Nắm bắt việc chuẩn bị và làm đề cương của học sinh.
b) Nội dung:
Câu hỏi 1: Trong các bài học của kỳ 1 lớp 11 em thích học bài nào nhất vì sao?
Câu hỏi 2: Trình bày khó khăn của em khi làm đề cương, e đã làm gic để giải quyết khó khăn đó
c) Sản phẩm: Câu trả lời của học sinh
d) Tổ chức thực hiện:
Chuyển giao
Giáo viên cho học sinh các tổ kiểm tra việc làm đề cương của nhau sau
đó báo cáo kết quả.
Thực hiện
- HS di chuyển để kiểm tra, thống nhất đáp án một số câu hỏi
- HS suy nghĩa trả lời câu hỏi
- Mong đợi: HS chỉ ra được một nhóm câu hỏi cần giúp đỡ trong tiết
học này
Báo cáo thảo luận
HS đưa ra những nhận xét về việc làm đề cương của các bạn, nêu được
một số câu hỏi cần đưa ra thảo luận, giải đáp trong tiết học
Đánh giá, nhận xét,
tổng hợp
- Giáo viên đánh giá thái độ làm việc, phương án trả lời của học sinh,
ghi nhận và tổng hợp kết quả.
- Hướng học sinh vào các câu hỏi trọng tâm của đề cương.
2. HOẠT ĐỘNG 2: LUYỆN TẬP
a) Mục tiêu:
§ Hệ thống kiến thức, ôn tập các bài tập chuẩn bị kiểm tra.
b) Nội dung: Chữa đề cương cho học sinh
c) Sản phẩm: HS so sánh kết quả của việc làm đề cương tại nhà với kết quả của cô giáo và các bạn
chữa. sửa chữa bài tập để được Đề cương chữa hoàn thiện
SỞ GD & ĐT LÀO CAI
TRƯỜNG THPT ….
ĐỀ CƯƠNG KIỂM TRA HỌC KỲ I
NĂM HỌC 2022-2023
Môn: Toán. Khối 11
I, PHẦN TRẮC NGHIỆM
Chương 1: Hàm số lượng giác – Phương trình lượng giác
Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác
Câu 1: Đổi số đo của góc sang đơn vị radian.
A. B. C. D.
Lời giải
Chọn C
Áp dụng công thức với tính bằng radian, tính bằng độ.
Ta có .
Câu 2: Đổi số đo của góc sang đơn vị độ, phút, giây.
A. B. C. D.
Lời giải
Chọn C
0
70
70
.
p
7
.
18
7
.
18p
.
180
a p
a =
a
a
.707
180 180 18
a ppp
a == =
3
rad
16
p
-
0
33 45'.
0
29 30 '.-
0
33 45'.-
0
32 55.-
Ta có
Câu 3: Tính độ dài của cung trên đường tròn có số đo
và bán kính bằng .
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có cm.
Câu 4: Cho thuộc góc phần tư thứ hai của đường tròn lượng giác. Hãy chọn kết quả đúng trong
các kết quả sau đây.
A. B.
C. D.
Lời giải
Chọn C
thuộc góc phần tư thứ hai
Câu 5: Cho Khẳng định nào sau đây đúng?
A. B.
C. D.
Lời giải
Chọn D
Ta có
Câu 6: Biết là các góc của tam giác mệnh đề nào sau đây đúng:
A. B.
C. D.
Lời giải
Chọn B
Vì là ba góc của một tam giác suy ra
Khi đó
Câu 7: Cho góc thỏa mãn và . Tính
A. B. C. D.
Lời giải
Chọn B
0
00
0
3
.180
.180 135
16
33 45'.
4
a
p
a
pp
ʈ
˜
Á
-
˜
Á
˜
ʈ ʈ
Á
˜
˜˜
ÁÁ
Á
˜
== =-=-
˜˜
ÁÁ
Á
˜
Á
˜˜
ÁÁ
˯
˯ ˯
1, 5
20 cm
30cm
40cm
20cm
60cm
1,5.20 30Ra== =l
a
sin 0; 0.cos
aa
>>
sin 0; 0.cos
aa
<<
sin 0; 0.cos
aa
><
sin 0; 0.cos
aa
<>
a
sin 0
cos 0
a
a
Ï
>
Ô
Ô
Æ
Ì
Ô
<
Ô
Ó
0.
2
p
a
<<
cot 0.
2
p
a
æö
+>
ç÷
èø
cot 0.
2
p
a
æö
+³
ç÷
èø
( )
tan 0.
ap
+<
( )
tan 0.
ap
+>
( )
0 cot 0
22 2 2
.
3
0tan0
22
pp p p
aapa
pp
apap ap
ì
æö
<< ® <+<¾¾® + <
ç÷
ï
ï
èø
í
ï
<< ®<+< ¾¾® + >
ï
î
,,ABC
,ABC
( )
sin sin .AC B+=-
( )
cos cos .AC B+=-
( )
tan tan .AC B+=
( )
cot cot .AC B+=
,,ABC
.AC B
p
+=-
( ) ( ) ( ) ( )
sin sin sin ; co s cos cos .AC B B AC B B
pp
+= -= += -=-
( ) ( ) ( ) ( )
tan ta n tan ;cot cot c o t .AC B B AC B B
pp
+= -=- += -=-
a
5
cos
3
a
=-
3
2
p
pa
<<
tan .
a
3
tan .
5
a
=-
2
tan .
5
a
=
4
tan .
5
a
=-
2
tan .
5
a
=-
Ta có
Bài 2: Các phép biến đổi lượng giác.
Câu 1: Rút gọn biểu thức
A. B. C. D.
Lời giải
Chọn B
Ta có
Câu 2: Giá trị của biểu thức bằng
A. B. C. D.
Lời giải
Chọn D
Ta có và .
Do đó
Câu 3: Công thức nào sau đây sai?
A. B.
C. D.
Lời giải
Chọn B
Ta có .
Câu 4: Khẳng định nào đúng trong các khẳng định sau?
A. B.
C. D.
Lời giải
Chọn B
Câu 5: Rút gọn
A. B. C. D.
2
2
sin 1 cos
22
3
tan .
3
3cos
5
2
sin
sin
aa
a
aa
p
a
pa
ì
=± - =±
ï
ï
¾¾® = - ¾¾® = =
í
ï
<<
ï
î
4o 4o
cos 15 sin 15 .M =-
1.M =
3
.
2
M =
1
.
4
M =
0.M =
( ) ( )
22
4o 4o 2o 2o
cos 15 sin 15 cos 15 sin 15M =-= -
( )( )
2o 2o 2o 2o
cos 15 sin 15 cos 15 sin 15=- +
( )
2o 2o o o
3
cos 15 sin 15 cos 2.15 cos 30 .
2
=-= ==
5711
sin sin sin sin
24 24 24 24
M
ppp p
=
1
.
2
1
.
4
1
.
8
75
sin cos
24 24
pp
=
11
sin cos
24 24
pp
=
55 1 5 5
sin sin cos cos . 2.sin .cos . 2.sin .cos
24 24 24 24 4 24 24 24 24
M
pppp pp p p
æöæ ö
==
ç÷ç ÷
èøè ø
15116 111
.sin .sin . cos cos . 0 .
412 1242 12 38 216
pp pp
æöæö
==+=+=
ç÷ç÷
èøèø
( )
cos sin sin cos cos .ab a b a b-= +
( )
cos sin sin cos cos .ab a b a b+= -
( )
sin sin cos cos sin .ab a b a b-= -
( )
sin sin cos cos sin .ab a b a b+= +
( )
cos cos cos sin sinab a b a b+= -
sin cos 2 sin .
4
aa a
p
æö
+= -
ç÷
èø
sin cos 2 sin .
4
aa a
p
æö
+= +
ç÷
èø
sin cos 2 sin .
4
aa a
p
æö
+=- -
ç÷
èø
sin cos 2 sin .
4
aa a
p
æö
+=- +
ç÷
èø
( ) ( ) ( ) ( )
cos cos sin sin .=+ --+ -Mabababab
2
12cos .Ma=-
2
1 2 sin .Ma=-
cos 4 .Ma=
sin 4 .Ma=
Lời giải
Chọn B
Áp dụng công thức , ta được
Câu 6: Chọn công thức đúng trong các công thức sau:
A. B.
C. D.
Lời giải
Chọn B
Câu 7: Cho biểu thức . Mệnh đề nào sau đây là đúng?
A. B.
C. D.
Lời giải
Chọn C
Ta có
Câu 8: Rút gọn biểu thức .
A. B. C. D.
Lời giải
Chọn D
Ta có: .
Câu 9: Cho góc thỏa mãn Tính
A. B. C. D.
Lời giải
Chọn A
Áp dụng công thức , ta được
Ta có
Thay vào , ta được
( )
cos cos sin sin cosxy xy xy-=+
( ) ( ) ( ) ( ) ( )
2
cos cos sin sin cos cos 2 1 2 sin .Mabababab abab a a=+ --+ -=++-= =-
( ) ( )
1
sin .sin cos cos .
2
ab ab ab=- + - -
éù
ëû
sin sin 2sin .cos .
22
ab ab
ab
+-
-=
2 tan
tan 2 .
1 tan
a
a
a
=
-
22
cos 2 sin cos .aaa=-
2 sin 2
3
Px
p
æö
=- + +
ç÷
èø
4, .Px³- " Î!
4, .Px³"Î!
0, .Px³"Î!
2, .Px³"Î!
1 sin 1 2 2 sin 2
33
xx
pp
æö æö
-£ + £Þ ³- + ³-
ç÷ ç÷
èø èø
4 2 sin 2 0 4 0.
3
xP
p
æö
Þ³- + +³Þ³ ³
ç÷
èø
2
sin 3 sin
2cos 1
xx
M
x
-
=
-
tan 2x
sin .x
2 tan .x
2 sin .x
2
sin 3 sin 2 cos 2 sin
2sin
2cos 1 cos2
xx xx
x
xx
-
==
-
a
3
sin .
5
a
=
sin sin .
66
P
pp
aa
æöæö
=+ -
ç÷ç÷
èøèø
11
.
100
P =
11
.
100
P =-
7
.
25
P =
10
.
11
P =
( ) ( )
1
sin .sin cos cos
2
ab ab ab=--+
éù
ëû
1
sin sin cos cos 2 .
6623
P
pp p
aa a
æöæöæ ö
=+ -= -
ç÷ç÷ç ÷
èøèøè ø
2
2
37
cos 2 1 2 sin 1 2. .
5 25
aa
æö
=- =- =
ç÷
èø
P
11 7 11
.
22 25 100
P
æö
=-=
ç÷
èø
Bài 3: Hàm số lượng giác và đồ thị
Câu 1: Tìm tập xác định của hàm số
A. B.
C. D.
Lời giải
Chọn D
Hàm số xác định khi và chỉ khi
Vậy tập xác định
Câu 2: Tìm tập xác định của hàm số
A. B.
C. D.
Lời giải
Chọn C
Hàm số xác định
Vậy tập xác định
Câu 3: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. B. C. D.
Lời giải
Chọn B
Nhắc lại kiến thức cơ bản:
= Hàm số là hàm số lẻ.
= Hàm số là hàm số chẵn.
= Hàm số là hàm số lẻ.
= Hàm số là hàm số lẻ.
Vậy B là đáp án đúng.
Câu 4: Trong các hàm số sau, hàm số nào là hàm số lẻ?
A. B. C. D.
Lời giải
Chọn D
Ta kiểm tra được đáp án A và C là các hàm số chẵn. Đáp án B là hàm số không chẵn, không lẻ. Đáp
án D là hàm số lẻ.
Câu 5: Tìm chu kì của hàm số
A. B. C. D.
Lời giải
Chọn A
D
1 sin
.
cos 1
+
=
-
x
y
x
D.= °
D\ , .
2
kk
p
p
ϸ
ÔÔ
ÔÔ
=+Œ
Ì˝
ÔÔ
ÔÔ
Ó˛
°¢
{ }
D\, .kkp=Œ°¢
{ }
D\2, .kkp=Œ°¢
cos 1 0 cos 1 2 , .xxxkkp-π € π€ π Œ¢
{ }
D\2, .kkp=Œ°¢
D
cot 2 sin 2 .
4
yx x
p
ʈ
˜
Á
=-+
˜
Á
˜
Á
˯
D\ , .
4
kk
p
p
ϸ
ÔÔ
ÔÔ
=+Œ
Ì˝
ÔÔ
ÔÔ
Ó˛
°¢
D.=∆
D\ , .
82
kk
pp
ϸ
ÔÔ
ÔÔ
=+Œ
Ì˝
ÔÔ
ÔÔ
Ó˛
°¢
D.= °
sin 2 0 2 , .
4482
k
xxkxk
pppp
p
ʈ
˜
Á
-π€ -π€π+ Œ
˜
Á
˜
Á
˯
¢
D\ , .
82
kk
pp
ϸ
ÔÔ
ÔÔ
=+Œ
Ì˝
ÔÔ
ÔÔ
Ó˛
°¢
sin .yx=
cos .yx=
tan .yx=
cot .yx=
sinyx=
cosyx=
tanyx=
cotyx=
2
cos sin .yx x=+
sin cos .yxx=+
cos .yx=-
sin .cos3 .yxx=
T
sin 5 .
4
yx
p
ʈ
˜
Á
=-
˜
Á
˜
Á
˯
2
.
5
T
p
=
5
.
2
T
p
=
.
2
T
p
=
.
8
T
p
=
Hàm số tuần hoàn với chu kì .
Áp dụng: Hàm số tuần hoàn với chu kì
Bài 4: Phương trình lượng giác cơ bản
Câu 1: Nghiệm của phương trình là:
A. . B. . C. . D. .
Lời giải
Chọn D
.
Câu 2: Nghiệm của phương trình là:
A. .
B. . C. . D. .
Lời giải
Chọn C
.
Câu 3: Nghiệm của phương trình là:
A. . B. . C. . D. .
Lời giải
Chọn C
.
Câu 4: Nghiệm của phương trình là:
A. . B. . C. . D. .
Lời giải
Chọn B
.
Câu 5: Phương trình lượng giác: có nghiệm là:
A. . B. . C. . D. .
Lời giải
( )
sinyaxb=+
2
T
a
p
=
sin 5
4
yx
p
ʈ
˜
Á
=-
˜
Á
˜
Á
˯
2
.
5
T
p
=
1
sin
2
x =
2
3
xk
p
p
=+
6
xk
p
p
=+
xk
p
=
2
6
xk
p
p
=+
( )
22
1
66
sin sin sin
5
26
22
66
xk xk
xx k
xkxk
pp
pp
p
pp
pp p
éé
=+ =+
êê
=Û = Û Û Î
êê
êê
=-+ = +
êê
ëë
!
33tan 0x+=
3
xk
p
p
=+
2
2
xk
p
p
=+
6
xk
p
p
=- +
2
xk
p
p
=+
( )
3
3 3 tan 0 tan
36
xx xkk
p
p
+=Û=-Û=-+Î !
cot 3 0 x +=
2
3
xk
p
p
=+
6
xk
p
p
=+
6
xk
p
p
=- +
3
xk
p
p
=- +
cot 3 0 x +=
( )
cot 3
6
xxkk
p
p
Û=-Û=-+ Î!
1
sin –
2
x =
p
p
=+2
3
xk
p
p
-
=+2
6
xk
p
p
=+2
6
xk
p
p
=+
5
2
6
xk
(k Z).
2
1
6
–
7
2
2
6
p
p
p
p
-
é
=+
ê
=Û
ê
ë
Î
ê
=+
ê
xk
sinx
xk
cos 3 cos12
o
x =
2
15
xk
p
p
=± +
2
45 3
k
x
pp
=± +
2
45 3
k
x
pp
-
=+
2
45 3
k
x
pp
=+
Chọn B
.
Chương 2: Dãy số, cấp số cộng, cấp số nhân
Bài 1: Dãy số
Câu 1: Cho dãy số , biết Năm số hạng đầu tiên của dãy số đó lần lượt là những số
nào dưới đây?
A. B.
C. D.
Lời giải
Chọn A
Ta có
Nhận xét: (i) Dùng MTCT chức năng CALC để kiểm tra (tính) nhanh.
Câu 2: Cho dãy số , biết với . Ba số hạng đầu tiên của dãy số đó là lần lượt
là những số nào dưới đây?
A. B. C. D.
Lời giải
Chọn A
Ta có
Câu 3: Cho dãy số biết Mệnh đề nào sau đây sai?
A. B. C. D.
Lời giải
Chọn D
Thay trực tiếp hoặc dùng chức năng CALC:
.
Nhận xét: Dễ thấy khi chẵn và ngược lại nên đáp án D sai.
Câu 4: Cho các dãy số sau. Dãy số nào là dãy số tăng?
A. B.
C. D.
Lời giải
Chọn C
Xét đáp án A: đây là dãy hằng nên không tăng không giảm.
Xét đáp án B: loại B
Xét đáp án C:
cos 3 cos12
o
x =
cos 3 cos
15
x
p
Û=
32
15
xk
p
p
Û=±+
2
45 3
k
x
pp
Û=± +
( )
n
u
.
1
n
n
u
n
-
=
+
12345
;;;;.
23456
-----
23456
;;;;.
34567
-----
12345
;;;;.
23456
23456
;;;;.
34567
12345
12345
;;;;.
23456
uu u u u=- =- =- =- =-
( )
n
u
1
1
1
3
nn
u
uu
+
=-
ì
í
=+
î
0n ³
1;2;5.-
1; 4; 7 .
4;7;10.
1;3;7.-
121 32
1; 3 2; 3 5 .uuu uu=- = + = = + =
( )
,
n
u
( )
1.2.
n
n
un=-
1
2.u =-
2
4.u =
3
6.u =-
4
8.u =-
( ) ( ) ( )
23 4
12 3 4
2.1 2; 1 .2.2 4, 1 2.3 6; 1 2.4 8uu u u=- =- = - = = - =- = - =
0
n
u >
n
1; 1; 1; 1; 1; 1; !
11 1 1
1; ; ; ; ;
24 816
--!
1; 3; 5; 7; 9; !
111 1
1; ; ; ; ;
24816
!
1; 1; 1; 1; 1; 1;L
123
11 1 1
1; ; ; ; ;
24 816
uu u-- ææÆ><ææÆL
1
*
1; 3; 5; 7 ; 9; ,
nn
uu n
+
ææÆ < Œ•L
Xét đáp án D: loại D
Câu 5: Trong các dãy số
cho bởi số hạng tổng quát sau, dãy số nào là dãy số tăng?
A. B. C. D.
Lời giải
Chọn D
Vì là các dãy dương và tăng nên là các dãy giảm, do đó loại A,B
Xét đáp án C: loại C
Xét đáp án D:
Câu 6: Trong các dãy số
cho bởi số hạng tổng quát sau, dãy số nào là dãy số giảm?
A. B. C. D.
Lời giải
Chọn A
Vì là dãy dương và tăng nên là dãy giảm
Xét B: loại B
Hoặc
nên là dãy tăng.
Xét C: loại C
Xét D: loại D
Câu 7: Cho dãy số , biết Dãy số bị chặn trên bởi số nào dưới đây?
A. B. C. D.
Lời giải
Chọn B
Ta có Mặt khác: nên suy ra dãy bị chặn trên bởi số 1.
Bài 2: Cấp số cộng
Câu 1: Dãy số nào sau đây không phải là cấp số cộng?
A. B.
C. D.
Lời giải
123
111 1
1; ; ; ; ;
24816
n
uuu uææÆ > > º> >ºææÆL
( )
n
u
n
u
1
.
2
n
n
u =
1
.
n
u
n
=
5
.
31
n
n
u
n
+
=
+
21
.
1
n
n
u
n
-
=
+
2;
n
n
11
;
2
n
n
1
12
2
3
5
2
7
31
6
n
u
n
uuu
n
u
Ï
Ô
Ô
=
Ô
+
Ô
Ô
=ææÆ ææÆ>ææÆ
Ì
Ô
+
Ô
=
Ô
Ô
Ô
Ó
1
21 3 1 1
230
11 12
nnn
n
uuu
nn nn
+
ʈ
-
˜
Á
==-fi-= - >
˜
Á
˜
Á
˯
++ ++
( )
n
u
n
u
1
.
2
n
n
u =
31
.
1
n
n
u
n
-
=
+
2
.
n
un=
2.
n
un=+
2
n
1
2
n
ææÆ
1
12
2
1
31
5
1
3
n
u
n
uuu
n
u
Ï
=
Ô
Ô
-
Ô
=ææÆ ææÆ<ææÆ
Ì
Ô
+
=
Ô
Ô
Ó
( )( )
1
3231 4
0
21 12
nn
nn
uu
nn nn
+
+-
-= - = >
++ ++
( )
n
u
( )
2
22
1
1210
nnn
un u u n n n
+
=ææÆ -=+- =+>ææÆ
1
1
2320
32
nnn
un uun n
nn
+
=+ææÆ -=+- += >ææÆ
++ +
( )
n
u
31
.
31
n
n
u
n
-
=
+
( )
n
u
1
.
3
1.
1
.
2
0.
31 2
11.
31 31
n
n
u
nn
-
==- <
++
2
511
0
722
u =>>>
( )
n
u
21 124
; ; 0; ; ;1; ....
33 333
--
15 2;12 2;9 2;6 2;....
47911
;1; ; ; ;....
5555
123 435
; ; 3; ; ;...
33
33
Chọn C
Chỉ cần tồn tại hai cặp số hạng liên tiếp của dãy số có hiệu khác nhau: thì ta kết
luận ngay dãy số đó không phải là cấp số cộng.
Xét đáp án A: loại A
Xét đáp án B:
loại B
Xét đáp án C: Chọn C
Xét đáp án D: loại D
Câu 2: Cho cấp số cộng có số hạng đầu công sai Năm số hạng liên tiếp đầu tiên của
cấp số này là:
A. B. C. D.
Lời giải
Chọn D
Ta dùng công thức tổng quát , hoặc để
tính các số hạng của một cấp số cộng.
Ta có
Nhận xét: Dùng chức năng “lặp” của MTCT để tính:
Nhập: (nhập ).
Bấm CALC: nhập (nhập ).
Để tính 5 số hạng đầu ta bấm dấu “=” liên tiếp để ra kết quả 4 lần nữa!
Câu 3: Cho cấp số cộng có và Khẳng định nào sau đây đúng?
A. B.
C. D.
Lời giải
Chọn C
Ta có
1 1mmkk
u uu u
+ +
=/ --
21 32 43
21124 1
;;0;;;1;....
33333 3
uuuu uu-- ææÆ=-=-=-=ææÆL
21 3 2 43
15 2;12 2;9 2; 6 2;.... 3 3 uu uu uuææÆ- = - = - = - = ææÆL
1 32 2
47911 1
;1; ; ; ;....
555 5
2
55
uuuuææÆ = /- =- =ææÆ
21 32 43
123 435 3
;;3;;;...
33 3
33
uu uu uuææÆ = - = - = - ææÆ
1
1
,
2
u =-
1
.
2
d =
11
;0;1; ;1.
22
-
111
;0; ;0; .
222
-
13 5
;1; ; 2; .
22 2
113
;0; ;1; .
222
-
( ) ( )
1
11
111
222
n
n
uu n d n=+- =-+- =-+
1
1
2
nn n
uudu
+
=+=+
1
21
132
43
54
1
2
0
11 1
;
22 2
1
3
2
u
uud
ud uud
uud
uud
Ï
Ô
Ô
=-
Ô
Ô
Ô
Ô
Ô
=+=
Ô
Ô
Ô
Ô
Ô
=- = ææÆ - + =
Ì
Ô
Ô
Ô
Ô
=+=
Ô
Ô
Ô
Ô
Ô
=+=
Ô
Ô
Ô
Ó
1
2
XX=+
XXd=+
1
2
-
1
u
( )
n
u
1
3u =-
1
.
2
d =
( )
1
31.
2
n
un=- + +
1
31.
2
n
un=- + -
( )
1
31.
2
n
un=- + -
( )
1
31.
4
n
un=- + -
( ) ( )
1
1
3
1
13 1
1
2
2
CTTQ
n
u
uun d n
d
Ï
=-
Ô
Ô
Ô
æææÆ = + - =- + -
Ì
Ô
=
Ô
Ô
Ó
Câu 4: Trong các dãy số được cho dưới đây, dãy số nào là cấp số cộng?
A. B. C. D.
Lời giải
Chọn A
Dãy là cấp số cộng ( là hằng số).
Câu 5: Cho cấp số cộng có và . Khi đó bằng:
A. B. C. D.
Lời giải
Chọn C
Câu 6: Cho cấp số cộng thỏa mãn Chọn khẳng định đúng trong các khẳng
định sau?
A. B. C. D.
Lời giải
Chọn B
Ta có
Câu 7: Một rạp hát có 30 dãy ghế, dãy đầu tiên có 25 ghế. Mỗi dãy sau có hơn dãy trước 3 ghế. Hỏi
rạp hát có tất cả bao nhiêu ghế?
A. 1635. B. 1792. C. 2055. D. 3125.
Lời giải
Chọn C
Số ghế của mỗi dãy (bắt đầu từ dãy đầu tiên) theo thứ tự đó lập thành một cấp số cộng có 30 số hạng
có công sai và
Tổng số ghế là
Câu 8: Người ta trồng 3003 cây theo một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng thứ
hai trồng 2 cây, hàng thứ ba trồng 3 cây,.Hỏi có tất cả bao nhiêu hàng cây?
A. 73. B. 75. C. 77. D. 79.
Lời giải.
Chọn C
Số cây mỗi hàng (bắt đầu từ hàng thứ nhất) lập thành một cấp số cộng có Giả sử có
hàng cây thì
Ta có
Câu 9: Một chiếc đồng hồ đánh chuông, kể từ thời điểm 0 (giờ) thì sau mỗi giờ thì số tiếng chuông
được đánh đúng bằng số giờ mà đồng hồ chỉ tại thời điểm đánh chuông. Hỏi một ngày đồng
hồ đó đánh bao nhiêu tiếng chuông?
A. 78. B. 156. C. 300. D. 48.
73.
n
un=-
73.
n
n
u =-
7
.
3
n
u
n
=
7.3 .
n
n
u =
( )
n
u
n
uanb€=+
,ab
( )
n
u
2
2001u =
5
1995u =
1001
u
1001
4005.u =
1001
4003.u =
1001
3.u =
1001
1.u =
21
1
1001 1
51
2001
2003
1000 3
1995 4
2
uud
u
uu d
uu d
d
Ï
Ï
==+
=
Ô
Ô
ÔÔ
€ææÆ=+=
ÌÌ
ÔÔ
==+
=-
Ô
Ô
Ó
Ó
( )
n
u
135
16
15
.
27
uu u
uu
-+ =
ì
í
+=
î
1
21
.
3
u
d
=
ì
í
=
î
1
21
.
3
u
d
=
ì
í
=-
î
1
18
.
3
u
d
=
ì
í
=
î
1
21
.
4
u
d
=
ì
í
=
î
( ) ( )
( )
11 1
13 5
16
11
2415
15
27
527
Ï
Ï
Ô
-+++ =
-+=
Ô
Ô
Ô
€
ÌÌ
ÔÔ
+=
++ =
ÔÔ
Ó
Ó
uu d u d
uu u
uu
uu d
1
1
1
215
21
.
2527
3
Ï
Ï
+=
=
Ô
Ô
ÔÔ
€€
ÌÌ
ÔÔ
+=
=-
Ô
Ô
Ó
Ó
ud
u
ud
d
3d =
1
25.u =
12 130 30
30.29
30 2055
2
uS uduu += ++=+=L
( )
n
u
1
1, 1.ud==
n
12
3003 .
nn
uu uS+++= =L
( )
2
1
1
3003 6006 0 77
2
n
nn
Snu dnn n
-
== + € +- =€=
Lời giải
Chọn C
Kể từ lúc 1 (giờ) đến 24 (giời) số tiếng chuông được đánh lập thành cấp số cộng có 24 số hạng với
công sai Vậy số tiếng chuông được đánh trong 1 ngày là:
Câu 10: Trên một bàn cờ có nhiều ô vuông, người ta đặt 7 hạt dẻ vào ô đầu tiên, sau đó đặt tiếp vào ô
thứ hai số hạt nhiều hơn ô thứ nhất là 5, tiếp tục đặt vào ô thứ ba số hạt nhiều hơn ô thứ hai là
5,… và cứ thế tiếp tục đến ô thứ . Biết rằng đặt hết số ô trên bàn cờ người ta phải sử dụng
25450 hạt. Hỏi bàn cờ đó có bao nhiêu ô vuông?
A. 98. B. 100. C. 102. D. 104.
Lời giải
Chọn B
Số hạt dẻ trên mỗi ô (bắt đầu từ ô thứ nhất) theo thứ tự đó lập thành cấp số cộng có
Gọi là số ô trên bàn cờ thì Ta có
Câu 11: Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng nước đến để
khoan giếng nước. Biết giá của mét khoan đầu tiên là 80.000 đồng, kể từ mét khoan thứ 2 giá
của mỗi mét khoan tăng thêm 5000 đồng so với giá của mét khoan trước đó. Biết cần phải
khoan sâu xuống 50m mới có nước. Vậy hỏi phải trả bao nhiêu tiền để khoan cái giếng đó?
A. 5.2500.000 đồng. B. 10.125.000 đồng. C. 4.000.000 đồng. D. 4.245.000 đồng.
Lời giải
Chọn B
Giá tiền khoang mỗi mét (bắt đầu từ mét đầu tiên) lập thành cấp số cộng có
Do cần khoang 50 mét nên tổng số tiền cần trả là
.
Bài 3: Cấp số nhân
Câu 1: Trong các dãy số sau, dãy số nào không phải là một cấp số nhân?
A. B.
C. D.
Lời giải
Chọn C
Xét đáp án C:
Các đáp án A, B, D đều là các cấp số nhân.
Nhận xét: Dãy với là cấp số nhân , tức là các số hạng của nó đều được biểu
diễn dưới dạng lũy thừa của cùng một cơ số (công bội), các số hạng liên tiếp (kể từ số hạng
thứ hai) thì số mũ của chúng cách đều nhau. Ví dụ
là cấp số nhân và
là cấp số nhân và
1
1,u =
1.d =
( ) ( )
24 1 24
24
12 1 24 300
2
SS uu== + = +=
n
( )
n
u
1
7, 5.ud==
n
12
25450 .
nn
uSuu += =++L
( )
2
1
1
25450 7 .5
22
-
-
== + =+
n
nn
nn
Snu d n
2
5 9 50900 0 100nn n€+- =€=
( )
n
u
1
80000, 5000.ud==
01 502 51
50.49
50 50.80 000 1225.5 000 10125 000
2
uu uS u d+= = + = + =++L
2; 4; 8; 16; K
1; 1; 1; 1; --L
2222
1; 2; 3; 4; L
( )
357
; ; ; ; 0 .aa a a aπL
2222
3
2
2
1
1; 2; 3; 4;
9
4
4
u
uu
u
æ =/ =æÆ =L
( )
n
u
0
n
u =/
.
n
n
uaq€=
q
2; 4; 8; 16; ææÆK
2.
n
n
u =
1; 1; 1; 1; --ææÆL
( )
1.
n
n
u =-
là cấp số nhân và
Câu 2: Dãy số nào sau đây không phải là cấp số nhân?
A. B. C. D.
Lời giải
Chọn D
Các đáp án A, B, C đều là các cấp số nhân công bội lần lượt là
Xét đáp án D:
Câu 3: Cho cấp số nhân với và Viết bốn số hạng đầu tiên của cấp số nhân.
A. B.
C. D.
Lời giải.
Chọn B
Câu 4: Tìm để ba số theo thứ tự đó lập thành một cấp số nhân.
A. B. C. D.
Lời giải
Chọn B
Cấp số nhân
Câu 5: Trong các dãy số cho bởi số hạng tổng quát sau, dãy số nào là một cấp số nhân?
A. B. C. D.
Lời giải
Chọn D
Dãy là cấp số nhân có
Câu 6: Một cấp số nhân có 6 số hạng, số hạng đầu bằng 2 và số hạng thứ sáu bằng 486. Tìm công bội
của cấp số nhân đã cho.
A. B. C. D.
Lời giải
Chọn A
Theo giải thiết ta có:
Câu 7: Tìm số hạng đầu và công bội của cấp số nhân biết
( )
357
; ; ; ; 0aa a a aπææÆL
( )
21 2
1
..
n
n
n
ua a
a
-
==
1; 2; 4; 8; L
234
3; 3 ; 3 ; 3 ; L
11
4; 2; ; ;
24
L
246
11 1 1
; ; ; ;
p
ppp
L
1
2; 3 ; .
2
2
246
3
2
21
11 1 1 1
; ; ; ;
1
u
u
uup
ppp
p
p
æ =/ =æÆ =L
( )
n
u
1
2u =-
5.q =-
2; 10; 50; 250.--
2; 10; 50; 250.--
2; 10; 50; 250.-- - -
2; 10; 50; 250.-
1
21
1
32
43
2
10
2
50
5
250
u
uuq
u
uuq
q
uuq
Ï
=-
Ô
Ô
Ô
Ô
Ï
==
=-
Ô
Ô
ÔÔ
ææÆ
ÌÌ
ÔÔ
==-
=-
Ô
Ô
Ó
Ô
Ô
==
Ô
Ô
Ó
x
1; 9; 33xx x++ +
1.x =
3.x =
7.x =
3; 7.xx==
( )( ) ( )
2
1; 9; 33 1 33 9 3.xx x x x xx++ +ææÆ+ +=+€=
( )
n
u
n
u
73.
n
un=-
73.
n
n
u =-
7
.
3
n
u
n
=
7.3 .
n
n
u =
7.3
n
n
u =
1
21
3
u
q
Ï
=
Ô
Ô
Ì
Ô
=
Ô
Ó
q
3.q =
3.q =-
2.q =
2.q =-
1
555
61
6
2
486 2 243 3.
486
u
uuq q q q
u
Ï
=
Ô
Ô
ææÆ = = = € = € =
Ì
Ô
=
Ô
Ó
1
u
q
( )
,
n
u
6
7
192
.
384
u
u
Ï
=
Ô
Ô
Ì
Ô
=
Ô
Ó
A. B. C. D.
Lời giải
Chọn B
Chương 3 : Giới hạn – Hàm số liên tục
Câu 1: Kết quả của bằng:
A. . B. . C. . D. .
Lời giải
Chọn C
Câu 2: Giá trị đúng của là:
A. . B. . C. . D. .
Lời giải
Chọn B
.
Vì .
Câu 3: Cho dãy số có . Tính giới hạn .
A. B. C. D.
Lời giải
Chọn C
Từ ta có .
Câu 4: Biết với là tham số. Khi đó bằng
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có .
1
5
.
2
u
q
Ï
=
Ô
Ô
Ì
Ô
=
Ô
Ó
1
6
.
2
u
q
Ï
=
Ô
Ô
Ì
Ô
=
Ô
Ó
1
6
.
3
u
q
Ï
=
Ô
Ô
Ì
Ô
=
Ô
Ó
1
5
.
3
u
q
Ï
=
Ô
Ô
Ì
Ô
=
Ô
Ó
( )
5
61
65
1
5
71 1
2
192
.
192
6
384 192
q
uuq
u
uuq uqq q
q
Ï
=
Ô
Ï
Ô
Ô
==
Ô
Ô
ÔÔ
€
ÌÌ
ÔÔ
==
== = =
ÔÔ
Ô
Ó
Ô
Ô
Ó
1
34.2 3
lim
3.2 4
nn
nn
-
--
+
0
1
1
311
2. 3.
3 4.2 3 3 2.2 3
424
lim lim lim 0
3.2 4 3.2 4
1
3. 1
2
nnn
nn nn
n
nn nn
-
æö æö æö
--
ç÷ ç÷ ç÷
-- --
èø èø èø
== =
++
æö
+
ç÷
èø
(
)
22
lim 1 3 2nn-- +
0
1
(
)
22
22
12
lim 1 3 2 lim 1 3nn n
nn
æö
-- + = - - + =-¥
ç÷
ç÷
èø
22
12
lim ; lim 1 3 1 3 0n
nn
æö
=+¥ - - + = - <
ç÷
ç÷
èø
( )
n
u
lim 2
n
u =
31
lim
25
n
n
u
u
-
+
1
5
-
3
2
5
9
lim 2
n
u =
31
lim
25
n
n
u
u
-
+
3.2 1
2.2 5
-
=
+
5
9
=
32
3
241
lim
22
nn
an
+-
=
+
a
2
aa-
12-
2-
0
6-
3
32
3
3
3
3
14
2
24 21
lim lim
2
22
n
nn
nn
an a
na
n
æö
+-
ç÷
+-
èø
===
+
æö
+
ç÷
èø
Suy ra . Khi đó .
Câu 5: Trong các giới hạn hữu hạn sau, giới hạn nào có giá trị khác với các giới hạn còn lại?
A. B. C. D.
Lời giải
Chọn C
Ta có
vì ; vì
vì ; vì .
Câu 6: Giới hạn bằng
A. . B. . C. . D. .
Lời giải
Chọn C
.
Câu 7: Tính giới hạn
A. B. C. D.
Lời giải
Chọn B
Ta có .
Câu 8: bằng
A. B. C. D.
Lời giải
Chọn D
.
Câu 9:
bằng
A. . B. . C. . D. .
Lời giải
4a =
22
44 12aa-=-=-
31
lim
31
n
n
-
+
21
lim
21
n
n
+
-
41
lim
31
n
n
+
-
1
lim
1
n
n
+
-
1
3
31 3
lim lim 1
1
31 3
3
n
n
n
n
-
-
===
+
+
1
lim 0
n
=
1
2
21 2
lim lim 1
1
21 2
2
n
n
n
n
+
+
===
-
-
1
lim 0
n
=
1
4
41 4
lim lim
1
31 3
3
n
n
n
n
+
+
==
-
-
1
lim 0
n
=
1
1
1
lim lim 1
1
1
1
n
n
n
n
+
+
==
-
-
1
lim 0
n
=
2
2
2
lim
4
x
x
x
®
-
-
2
4
1
4
0
( )( )
2
22 2
2211
lim lim lim
42224
xx x
xx
xxxx
®® ®
--
===
--++
3
3
lim
3
x
x
L
x
®
-
=
+
L = -¥
0L =
L = +¥
1L =
3
3
lim
3
x
x
L
x
®
-
=
+
33
0
33
-
==
+
41
lim
1
x
x
x
®-¥
+
-+
2
4
1-
4-
41
lim
1
x
x
x
®-¥
+
-+
1
4
lim
1
1
x
x
x
®-¥
+
=
-+
4=-
32
lim
24
x
x
x
®-¥
+
-
1
2
-
3
4
-
1
3
2
Chọn D
Ta có: .
Câu 10: Trong các mệnh đề sau, mệnh đề nào sai?
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có: do và . Vậy đáp án A đúng.
Suy ra đáp án B sai.
Các đáp án C và D đúng. Giải thích tương tự đáp án .
Câu 11: Tính giới hạn .
A. . B. . C. . D. .
Lời giải
Chọn C
.
Câu 12: Cho số thực thỏa mãn . Khi đó giá trị của là
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có: .
Câu 13: Cho các giới hạn: ; , hỏi bằng
A. . B. . C. . D. .
Lời giải
Chọn C
Ta có .
Câu 14: Giới hạn bằng
32
lim
24
x
x
x
®-¥
+
-
2
3
lim
4
2
x
x
x
®-¥
+
=
-
3
2
=
0
1
lim
x
x
+
®
=+¥
0
1
lim
x
x
+
®
=-¥
5
0
1
lim
x
x
+
®
=+¥
0
1
lim
x
x
+
®
=+¥
0
1
lim
x
x
+
®
=+¥
0
lim 0
x
x
+
®
=
0x >
A
21
lim
1
x
x
x
®-¥
+
+
1
2
1
2
1-
21
lim
1
x
x
x
®-¥
+
+
1
2
lim 2
1
1
x
x
x
®-¥
+
==
+
a
2
2320171
lim
22018 2
x
ax
x
®+¥
++
=
+
a
2
2
a =
2
2
a
-
=
1
2
a =
1
2
a =-
2
2320171
lim
22018 2
x
ax
x
®+¥
++
=
+
2
32017
2
1
lim
2018
2
2
x
a
xx
x
®+¥
++
Û=
+
21
22
a
Û=
2
2
aÛ=
( )
0
lim 2
xx
fx
®
=
( )
0
lim 3
xx
gx
®
=
( ) ( )
0
lim 3 4
xx
fx gx
®
-
éù
ëû
5
2
6-
3
( ) ( )
0
lim 3 4
xx
fx gx
®
-
éù
ëû
( ) ( )
00
lim 3 lim 4
xx xx
fx gx
®®
=-
( ) ( )
00
3 lim 4 lim
xx xx
fx gx
®®
=-
6=-
( )
2
2
1
lim
2
x
x
x
®-
+
+
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có: .
Do và .
Câu 15: Tìm giới hạn
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có vì , , khi .
Câu 16: bằng
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có .
Câu 17: bằng.
A. . B. . C. . D. .
Lời giải
Chọn C
Ta có: .
Câu 18: Tính .
A. . B. . C. . D. .
Lời giải
Chọn D
Ta có:
.
.
3
16
0
( ) ( )
( )
22
22
11
lim lim . 1
22
xx
x
x
xx
®- ®-
+
= + = -¥
++
( )
2
2
1
lim
2
x
x
®-
= +¥
+
( )
2
lim 1 1 0
x
x
®-
+=-<
1
43
lim
1
x
x
x
+
®
-
-
+¥
2
-¥
2-
1
43
lim
1
x
x
x
+
®
-
=+¥
-
( )
1
lim 4 3 1
x
x
+
®
-=
( )
1
lim 1 0
x
x
+
®
-=
10x ->
1x
+
®
2
2
2
232
lim
4
x
xx
x
®-
+-
-
5
4
5
4
-
1
4
2
2
2
2
232
lim
4
x
xx
x
®-
+-
-
( )( )
( )( )
2
21 2
lim
22
x
xx
xx
®-
-+
=
-+
2
215
lim
24
x
x
x
®-
-
==
-
2
2
4
34
lim
4
x
xx
xx
®-
+-
+
1
1-
5
4
5
4
-
2
2
4
34
lim
4
x
xx
xx
®-
+-
+
4
1
lim
x
x
x
®-
-
=
5
4
=
2
23
lim
23
x
x
x
®-¥
+
-
1
2
1
2
-
2
2-
2
23
lim
23
x
x
x
®-¥
+
-
2
3
2
lim
3
2
x
x
x
x
x
®-¥
æö
+
ç÷
èø
=
-
2
3
2
lim
3
2
x
x
x
x
x
®-¥
æö
+
ç÷
èø
=
--
2
3
2
2
lim 2
32
2
x
x
x
®-¥
+
==-=-
--
Câu 19: Tính giới hạn .
A. . B. . C. . D. .
Lời giải
Chọn A
Ta có .
Câu 20: Cho hàm số . Để hàm số đã cho có đạo hàm tại thì
bằng:
A. . B. . C. . D. .
Lời giải
Chọn A
;
Theo yêu cầu bài toán: .
Câu 21: bằng
A. . B. . C. . D. .
Lời giải
Chọn B
• Ta có .
Câu 22: Tính
A. . B. . C. . D. .
Lời giải
Chọn B
.
2
0
411
lim
3
x
x
K
xx
®
+-
=
-
2
3
K =-
2
3
K =
4
3
K =
0K =
2
0
411
lim
3
x
x
K
xx
®
+-
=
-
( )
( )
0
4
lim
3411
x
x
xx x
®
=
-++
( )
( )
0
4
lim
3411
x
xx
®
=
-++
2
3
=-
2
khi 1
()
21 khi 1
ax bx x
fx
xx
ì
+³
=
í
-<
î
1x =
2ab+
2
5
2-
5-
( ) ( )
1
1
lim
1
x
fx f
x
-
®
-
=
-
1
211
lim 2
1
x
x
x
-
®
--
=
-
( ) ( )
1
1
lim
1
x
fx f
x
+
®
-
-
2
1
lim
1
x
ax bx a b
x
+
®
+--
=
-
( )
( )
2
1
11
lim
1
x
ax bx
x
+
®
-+ -
=
-
( ) ( )
1
11
lim
1
x
xax b
x
+
®
-++
éù
ëû
=
-
( )
1
lim 1
x
ax b
+
®
=++
éù
ëû
2ab=+
( ) ( ) ( ) ( )
11
11
lim lim
11
xx
fx f fx f
xx
-+
®®
--
=
--
22abÛ+=
1
lim
62
x
x
x
®-¥
+
-
1
2
1
6
1
3
1
1
lim
62
®-¥
+
=
-
x
x
x
1
1
lim
2
6
® -¥
+
=
-
x
x
x
1
6
(
)
2
lim 4 2
x
xx x
®+¥
-+-
4-
2-
4
2
(
)
2
lim 4 2
x
xx x
®+¥
-+-
22
2
42
lim
42
x
xx x
xx x
®+¥
-+-
=
-++
2
42
lim
42
x
x
xx x
®+¥
-+
=
-++
2
2
4
lim
42
11
x
x
xx
®+¥
-+
=
-+ +
2=-
Câu 23: Cho hàm số . Khẳng định nào sau đây đúng nhất ?
A. Hàm số liên tục tại .
B. Hàm số liên tục tại mọi điểm trên tập xác định nhưng gián đoạn tại .
C. Hàm số không liên tục tại .
D. Tất cả đều sai.
Lời giải
Chọn A
Ta có :
Hàm số liên tục tại điểm .
Chương 4: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
Bài 1: Đường thẳng và mặt phẳng trong không gian
Câu 1: Trong các khẳng định sau, khẳng định nào đúng?
A. Qua 2 điểm phân biệt có duy nhất một mặt phẳng
B. Qua 3 điểm phân biệt bất kì có duy nhất một mặt phẳng
C. Qua 3 điểm không thẳng hàng có duy nhất một mặt phẳng
D. Qua 4 điểm phân biệt bất kì có duy nhất một mặt phẳng
Lời giải
Chọn C
" A sai. Qua 2 điểm phân biệt, tạo được 1 đường thẳng, khi đó chưa đủ điều kiện để lập một mặt
phẳng xác định. Có vô số mặt phẳng đi qua 2 điểm đã cho.
" B sai. Trong trường hợp 3 điểm phân biệt thẳng hàng thì chỉ tạo được đường thẳng, khi đó có vô số
mặt phẳng đi qua 3 điểm phân biệt thẳng hàng.
" D sai. Trong trường hợp 4 điểm phân biệt thẳng hàng thì có vô số mặt phẳng đi qua 4 điểm đó hoặc
trong trường hợp 4 điểm mặt phẳng không đồng phẳng thì sẽ tạo không tạo được mặt phẳng
nào đi qua cả 4 điểm.
Câu 2: Trong các mệnh đề sau đây, mệnh đề nào sai?
A. Hai mặt phẳng có một điểm chung thì chúng có vô số điểm chung khác nữa
B. Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất
C. Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất
D. Hai mặt phẳng cùng đi qua 3 điểm không thẳng hàng thì hai mặt phẳng đó trùng nhau
Lời giải
Chọn B
Nếu 2 mặt phẳng trùng nhau, khi đó 2 mặt phẳng có vô số điểm chung và chung nhau vô số đường
thẳng.
Câu 3: Cho hình chóp S.ABCD có đáy là hình thang Khẳng định nào sau đây
sai?
A. Hình chóp S.ABCD có 4 mặt bên.
B. Giao tuyến của hai mặt phẳng và là SO là giao điểm của AC và
C. Giao tuyến của hai mặt phẳng và là SI là giao điểm của AD và
2
khi 4
4
()
1
khi 4
4
x
x
x
fx
x
ì
-
¹
ï
ï
-
=
í
ï
=
ï
î
4x =
4x =
4x =
44 4
211
lim ( ) lim lim (4)
44
2
xx x
x
fx f
x
x
®® ®
-
====
-
+
4x =
.
.
.
.
.
.
.
,,ABC
.
( )
.ABCD AB CD!
( )
SAC
( )
SBD
(O
).BD
( )
SAD
( )
SBC
(I
).BC
D. Giao tuyến của hai mặt phẳng và là đường trung bình của ABCD
Lời giải
Chọn D
Hình chóp S.ABCD có 4 mặt bên: Do đó A đúng.
là điểm chung thứ nhất của hai mặt phẳng và
là điểm chung thứ hai của hai mặt phẳng và
Do đó B đúng.
Tương tự, ta có Do đó C đúng.
mà SA không phải là đường trung bình của hình thang ABCD
Do đó D sai.
Câu 4: Cho tứ diện Gọi là trọng tâm của tam giác Giao tuyến của mặt phẳng
và là:
A. là trung điểm của B. là trung điểm của
C. là hình chiếu của trên D. là hình chiếu của trên
Lời giải
Chọn B
là điểm chung thứ nhất giữa hai mặt phẳng và
Ta có là điểm chung thứ hai giữa hai mặt
phẳng và
Vậy
( )
SAB
( )
SAD
I
O
A
B
D
C
S
•
( ) ( ) ( ) ( )
,,,.SAB SBC SCD SAD
•
S
( )
SAC
( )
.SBD
( ) ( )
( ) ( )
O AC SAC O SAC
O
O BD SBD O SBD
ì
ÎÌ ÞÎ
ï
Þ
í
ÎÌ ÞÎ
ï
î
( )
SAC
( )
.SBD
( ) ( )
.SAC SBD SO¾¾® Ç =
•
( ) ( )
.SAD SBC SIÇ=
•
( ) ( )
SAB SAD SAÇ=
.ABCD
G
.BCD
( )
ACD
( )
GAB
(AM M
).AB
(AN N
).CD
(AH H
B
).CD
(AK K
C
).BD
G
N
A
C
D
B
∑
A
( )
ACD
( )
.GAB
∑
( ) ( )
( ) ( )
NBG ABG N ABG
BG CD N N
NCD ACD N ACD
Ï
Ô
ŒÃ fi Œ
Ô
«=ææÆ fi
Ì
Ô
ŒÃ fi Œ
Ô
Ó
( )
ACD
( )
.GAB
( ) ( )
.ABG ACD AN«=
Câu 5: Cho hình chóp có đáy là hình bình hành. Gọi lần lượt là trung điểm
và Giao tuyến của hai mặt phẳng và là:
A.
B. là tâm hình bình hành
C. là trung điểm
D. là trung điểm
Lời giải
Chọn B
là điểm chung thứ nhất giữa hai mặt phẳng và
Gọi là tâm của hình hình hành.
Trong mặt phẳng gọi
là điểm chung thứ hai giữa hai mặt phẳng và
Vậy
Bài 2: Hai đường thẳng song song trong không gian
Câu 1: Trong các mệnh đề sau, mệnh đề nào sai?
A. Hai đường thẳng không có điểm chung thì chéo nhau.
B. Hai đường thẳng chéo nhau thì không có điểm chung.
C. Hai đường thẳng phân biệt không cắt nhau và không song song thì chéo nhau.
D. Hai đường thẳng phân biệt không chéo nhau thì hoặc cắt nhau hoặc song song.
Lời giải
Chọn A
Hai đường thẳng không có điểm chung thì chúng song song (khi chúng đồng phẳng) hoặc chéo nhau
(khi chúng không đồng phẳng).
Câu 2: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song với nhau.
B. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì trùng nhau.
C. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song với nhau hoặc trùng
nhau.
D. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì chúng lần lượt nằm trên hai mặt
phẳng song song.
Lời giải
Chọn C
Câu 3: Cho ba mặt phẳng phân biệt có ; ;
. Khi đó ba đường thẳng :
A. Đôi một cắt nhau. B. Đôi một song song.
.S ABCD
ABCD
, MN
( )
SMN
( )
SAC
(SO O
).ABCD
(SG G
).AB
(SF F
).CD
T
º
O
N
M
D
B
C
A
S
∑
S
( )
SMN
( )
.SAC
∑
OACBD=«
( )
ABCD
TACMN=«
( ) ( )
( ) ( )
OAC SAC O SAC
O
OMN SMN O SMN
Ï
Ô
ŒÃ fiŒ
Ô
fifi
Ì
Ô
ŒÃ fiŒ
Ô
Ó
( )
SMN
( )
.SAC
( ) ( )
.SMN SAC SO«=
( ) ( ) ( )
, ,
abg
( ) ( )
1
d
ab
Ç=
( ) ( )
2
d
bg
Ç=
( ) ( )
3
d
ag
Ç=
123
,,dd d
C. Đồng quy. D. Đôi một song song hoặc đồng quy.
Lời giải
Chọn D
Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyền ấy hoặc đồng quy
hoặc đôi một song song.
Câu 4: Trong không gian, cho 3 đường thẳng , biết , và chéo nhau. Khi đó hai đường
thẳng và :
A. Trùng nhau hoặc chéo nhau. B. Cắt nhau hoặc chéo nhau.
C. Chéo nhau hoặc song song. D. Song song hoặc trùng nhau.
Lời giải
Chọn B
Giả sử (mâu thuẫn với giả thiết).
Câu 5: Trong không gian, cho ba đường thẳng phân biệt trong đó . Khẳng định nào sau
đây sai?
A. Nếu thì .
B. Nếu cắt thì cắt .
C. Nếu và thì ba đường thẳng cùng ở trên một mặt phẳng.
D. Tồn tại duy nhất một mặt phẳng qua và .
Lời giải
Chọn B
Nếu cắt thì cắt hoặc chéo .
Câu 6: Cho tứ diện Gọi lần lượt là trọng tâm các tam giác và Chọn khẳng
định đúng trong các khẳng định sau?
A. song song với
B. song song với
C. chéo
D. cắt
Lời giải
Chọn A
Gọi lần lượt là trung điểm của
là đường trung bình của tam giác
lần lượt là trọng tâm các tam giác và
Từ và suy ra:
Câu 7: Cho hình chóp có đáy là hình bình hành. Gọi lần lượt là trung điểm
Trong các đường thẳng sau, đường thẳng nào không song song với
,,abc
ab
!
a
c
b
c
bc cafi
!!
,,abc
ab
!
ca
!
cb
!
c
a
c
b
AaŒ
BbŒ
,,abAB
a
b
c
a
c
b
c
b
.ABCD
,IJ
ABC
.ABD
IJ
.CD
IJ
.AB
IJ
.CD
IJ
.AB
J
I
N
M
A
D
C
B
,MN
,.BC BD
fi
MN
BCD
( )
// 1MN CDfi
,IJ
ABC
ABD
( )
2
2
3
AI AJ
IJ MN
AM AN
fi==fiP
( )
1
( )
2
.IJ CDP
.S ABCD
ABCD
,, ,IJEF
,,, .SA SB SC SD
?IJ
A. B. C. D.
Lời giải
Chọn C
Ta có (tính chất đường trung bình trong tam giác ) và (tính chất đường trung
bình trong tam giác ).
Mà (đáy là hình bình hành)
Câu 8: Cho hình chóp có đáy là hình bình hành. Gọi là giao tuyến của hai mặt
phẳng và Khẳng định nào sau đây đúng?
A. qua và song song với B. qua và song song với
C. qua và song song với D. qua và song song với
Lời giải
Chọn A
Ta có (với ).
Bài 3: Đường thẳng và mặt phẳng song song
Câu 1: Cho đường thẳng và mặt phẳng trong không gian. Có bao nhiêu vị trí tương đối của
và ?
A. B. C. D.
Lời giải
Chọn B
Có 3 vị trí tương đối của và , đó là: nằm trong , song song với và cắt .
.EF
.DC
.AD
.AB
E
J
F
I
C
A
D
B
S
IJ ABP
SAB
EF CDP
SCD
CD ABP
.CD AB EF IJææÆ PPP
.S ABCD
ABCD
d
( )
SAD
( )
.SBC
d
S
.BC
d
S
.DC
d
S
.AB
d
S
.BD
d
C
A
D
B
S
( ) ( )
( ) ( )
,
SAD SBC S
AD SAD BC SBC
AD BC
Ï
Ô
«=
Ô
Ô
Ô
ÃÃ
Ì
Ô
Ô
Ô
Ô
Ó
P
ææÆ
( ) ( )
SAD SBC Sx AD BC«=PP
dSx∫
a
( )
P
a
( )
P
2.
3.
1.
4.
(P)
a
A
a
(P)
a
(P)
a
( )
P
a
( )
P
a
( )
P
a
( )
P
Câu 2: Cho hai đường thẳng phân biệt và mặt phẳng . Giả sử , . Khi đó:
A. B.
C. cắt D. hoặc
Lời giải
Chọn D
Câu 3: Cho hai đường thẳng phân biệt và mặt phẳng . Giả sử , . Khi đó:
A. B. chéo nhau.
C. hoặc chéo nhau. D. cắt nhau.
Lời giải
Chọn C
Vì nên tồn tại đường thẳng thỏa mãn Suy ra đồng phẳng và xảy ra các trường
hợp sau:
" Nếu song song hoặc trùng với thì .
" Nếu cắt thì cắt nên không đồng phẳng. Do đó chéo nhau.
Câu 4: Cho đường thẳng nằm trong mặt phẳng . Giả sử . Mệnh đề nào sau đây đúng?
A. Nếu thì
B. Nếu cắt thì cắt
C. Nếu thì
D. Nếu cắt và chứa thì giao tuyến của và là đường thẳng cắt cả và
Lời giải
Chọn C
" A sai. Nếu thì hoặc chéo nhau.
" B sai. Nếu cắt thì cắt hoặc chéo nhau.
" D sai. Nếu cắt và chứa thì giao tuyến của và là đường thẳng cắt hoặc song
song với .
Câu 5: Cho hai đường thẳng phân biệt và mặt phẳng . Giả sử và . Mệnh đề nào
sau đây đúng?
A. và không có điểm chung.
B. và hoặc song song hoặc chéo nhau.
C. và hoặc song song hoặc chéo nhau hoặc cắt nhau.
D. và chéo nhau.
Lời giải
Chọn C
Câu 6: Cho mặt phẳng và hai đường thẳng song song và . Khẳng định nào sau đây đúng?
A. Nếu song song với thì cũng song song với
B. Nếu cắt thì cũng cắt
,ab
( )
a
ab
!
( )
b a
!
( )
.a a
!
( )
.a aÃ
a
( )
.a
( )
a a
!
( )
.a aÃ
,ab
( )
a
( )
a a
!
( )
b aÃ
.ab
!
,ab
ab
!
,ab
,ab
c
a
a
b
b
a
a
( )
a a
!
( )
c aÃ
.ac
!
,bc
b
c
ab
!
b
c
b
( ) ( )
,acb ∫
,ab
,ab
a
( )
a
( )
b aÀ
( )
b a
!
.ba
!
b
( )
a
b
.a
ba
!
( )
.b a
!
b
( )
a
( )
b
b
( )
a
( )
b
a
.b
( )
b a
!
ba
!
,ab
b
( )
a
b
a
,ab
b
( )
a
( )
b
b
( )
a
( )
b
a
a
,ab
( )
a
( )
a a
!
( )
b a
!
a
b
a
b
a
b
a
b
( )
P
a
b
( )
P
a
( )
P
.b
( )
P
a
( )
P
.b
C. Nếu chứa thì cũng chứa
D. Các khẳng định A, B, C đều sai.
Lời giải
Chọn B
Gọi .
" A sai. Khi .
" C sai. Khi .
" Xét khẳng định B, giả sử không cắt khi đó hoặc . Khi đó, vì nên
hoặc cắt (mâu thuẫn với giả thiết cắt ).
Vậy khẳng định B đúng.
Câu 7: Cho , mặt phẳng qua cắt theo giao tuyến . Khi đó:
A. B. cắt . C. và chéo nhau. D.
Lời giải
Chọn A
Ta có: . Do và cùng thuộc nên cắt hoặc .
Nếu cắt . Khi đó, cắt (mâu thuẫn với giả thiết).
Vậy .
Câu 8: Có bao nhiêu mặt phẳng song song với cả hai đường thẳng chéo nhau?
A. B. C. D. Vô số.
Lời giải
Chọn D
Gọi và là 2 đường thẳng chéo nhau, là đường thẳng song song với và cắt .
Gọi . Do .
Giả sử . Mà .
Mặt khác, .
Có vô số mặt phẳng . Vậy có vô số mặt phẳng song song với 2 đường thẳng chéo nhau.
Câu 9: Cho hai đường thẳng chéo nhau và . Khẳng định nào sau đây sai?
A. Có duy nhất một mặt phẳng song song với và
B. Có duy nhất một mặt phẳng qua và song song với
C. Có duy nhất một mặt phẳng qua điểm , song song với và (với là điểm cho trước).
D. Có vô số đường thẳng song song với và cắt
Lời giải
Chọn A
Có có vô số mặt phẳng song song với 2 đường thẳng chéo nhau.
Do đó A sai.
( )
P
a
( )
P
.b
( ) ( )
,Qab∫
( ) ( ) ( )
bPQ bP=«fiÃ
( ) ( ) ( )
PQbPπfi
!
( )
P
b
( )
bPÃ
( )
bP
!
ba
!
( )
aPÃ
a
( )
P
( )
P
a
( )
d a
!
( )
b
d
( )
a
d
¢
.dd
¢
!
d
d
¢
d
d
¢
.dd
¢
∫
( ) ( )
d ab
¢
=«
d
d
¢
( )
b
d
d
¢
dd
¢
!
d
d
¢
d
( )
a
dd
¢
!
1.
2.
3.
c
a
a
b
a
b
c
a
b
( ) ( )
,bca ∫
( )
ac a afi
!!
( ) ( )
ba
!
( ) ( )
bbabŒfi
!
( ) ( )
aaabfi
!!
( ) ( )
ba
!
a
b
a
.b
a
.b
M
a
b
M
a
.b
Câu 10: Cho ba đường thẳng đôi một chéo nhau . Gọi là mặt phẳng qua , là mặt phẳng
qua sao cho giao tuyến của và song song với . Có nhiều nhất bao nhiêu mặt phẳng
và thỏa mãn yêu cầu trên?
A. Một mặt phẳng , một mặt phẳng
B. Một mặt phẳng , vô số mặt phẳng
C. Một mặt phẳng , vô số mặt phẳng
D. Vô số mặt phẳng và
Lời giải
Chọn A
Vì song song với giao tuyến của và nên và .
Khi đó, là mặt phẳng chứa và song song với mà và chéo nhau nên chỉ có một mặt phẳng
như vậy.
Tương tự cũng chỉ có một mặt phẳng chứa và song song với .
Vậy có nhiều nhất một mặt phẳng và một mặt phẳng thỏa yêu cầu bài toán.
Câu 11: Cho hình chóp tứ giác . Gọi và lần lượt là trung điểm của và Khẳng
định nào sau đây đúng?
A. // B. // C. // D. //
Lời giải
Chọn A
Xét tam giác có lần lượt là trung điểm của
Suy ra // mà //
Câu 12: Cho hai hình bình hành và không cùng nằm trong một mặt phẳng. Gọi
lần lượt là tâm của là trung điểm của Khẳng định nào sau đây sai?
A. // B. //
C. // D. cắt
Lời giải
Chọn D
Xét tam giác có lần lượt là trung điểm của
,,abc
( )
P
a
( )
Q
b
( )
P
( )
Q
c
( )
P
( )
Q
( )
P
( )
.Q
( )
P
( )
.Q
( )
Q
( )
.P
( )
P
( )
.Q
c
(Q)
(P)
b
a
c
( )
P
( )
Q
( )
cP
!
( )
cQ
!
( )
P
a
,c
a
c
( )
Q
b
c
( )
P
( )
Q
.S ABCD
M
N
SA
.SC
MN
( )
.mp ABCD
MN
( )
.mp SAB
MN
( )
.mp SCD
MN
( )
.mp SBC
SAC
,MN
,.SA SC
MN
AC
( )
AC ABCD M NÃææÆ
( )
.mp ABCD
ABCD
ABEF
1
,OO
,.ABCD ABEF
M
.CD
1
OO
( )
.BEC
1
OO
( )
.AFD
1
OO
( )
.EFM
1
MO
( )
.BEC
O
1
O
E
F
C
D
B
A
ACE
1
,OO
,.AC AE
Suy ra là đường trung bình trong tam giác //
Tương tự, là đường trung bình của tam giác nên //
Vậy // , // và // . Chú ý rằng:
Câu 13: Cho tứ diện Gọi theo thứ tự là trung điểm của các cạnh
Bốn điểm nào sau đây không đồng phẳng?
A. B. C. D.
Lời giải
Chọn C
Theo tính chất của đường trung bình của tam giác ta có
// // suy ra đồng phẳng
Tương tự, ta có được // // suy ra đồng phẳng.
Và // // suy ra đồng phẳng.
Bài 4,5: Hai mặt phẳng song song - Hình lăng trụ và hình hộp
Câu 1: Trong các điều kiện sau, điều kiện nào kết luận
A. và là mặt phẳng nào đó
B. và với là hai đường thẳng phân biệt thuộc
C. và với là hai đường thẳng phân biệt cùng song song với
D. và với là hai đường thẳng cắt nhau thuộc
Lời giải
Chọn D
Trong trường hợp: và là mặt phẳng nào đó) thì và có thể trùng nhau
Loại A
và với là hai đường thẳng phân biệt thuộc thì và vẫn có thể cắt nhau
(hình 1) Loại B
và với là hai đường thẳng phân biệt cùng song song với thì và vẫn có
thể cắt nhau (hình 2) Loại C
Câu 2: Trong các mệnh đề sau, mệnh đề nào đúng?
1
OO
ACE
1
OOfi
.EC
1
OO
BFD
1
OO
.FD
1
OO
( )
BEC
1
OO
( )
AFD
1
OO
( )
EFC
( ) ( )
.EFC EFM=
.ABCD
,,,,,MNPQRS
,,,,,.AC BD AB CD AD BC
,,,.PQRS
,,,.MPRS
,,, .MRSN
,,,.MNPQ
Q
P
N
S
R
M
B
C
D
A
PS
AC
QR
,,,PQRS
PM
BC
NQ
,,,PMNQ
NR
CD
SN
,,,MRSN
( ) ( )
?mp mpabP
( ) ( )
agP
( ) ( ) ( )
(bggP
).
( )
aa P
( )
ba P
,ab
( )
.b
( )
aa P
( )
ba P
,ab
( )
.b
( )
aa P
( )
ba P
,ab
( )
.b
a
b
a
b
b
a
b
a
( ) ( )
agP
( ) ( ) ( )
(bggP
( )
a
( )
b
fi
( )
aa P
( )
ba P
,ab
( )
b
( )
a
( )
b
fi
( )
aa P
( )
ba P
,ab
( )
b
( )
a
( )
b
fi
A. Nếu mặt phẳng thì mọi đường thẳng nằm trong đều song song với
B. Nếu hai mặt phẳng và song song với nhau thì bất kì đường thẳng nào nằm trong cũng
song song với bất kì đường thẳng nào nằm trong
C. Nếu hai đường thẳng phân biệt và song song lần lượt nằm trong hai mặt phẳng và
phân biệt thì
D. Nếu đường thẳng song song với thì nó song song với mọi đường thẳng nằm trong
Lời giải
Chọn A
Nếu hai mặt phẳng và song song với nhau thì hai đường thẳng bất kì lần lượt thuộc và
có thể chéo nhau (Hình 1) Loại B
Nếu hai đường thẳng phân biệt và song song lần lượt nằm trong hai mặt phẳng và phân
biệt thì hai mặt phẳng và có thể cắt nhau (Hình 2) Loại C
Nếu đường thẳng song song với thì nó có thể chéo nhau với một đường thẳng nào đó nằm
trong (Hình 3).
Câu 3: Cho đường thẳng và đường thẳng Mệnh đề nào sau đây đúng?
A. B.
C. và D. và chéo nhau.
Lời giải
Chọn C
Với đường thẳng và đường thẳng
Khi hoặc chéo nhau A sai.
Khi hoặc cắt nhau theo giao tuyến song song với và B sai.
và có thể chéo nhau, song song hoặc cắt nhau D sai.
Câu 4: Hai đường thẳng và nằm trong Hai đường thẳng và nằm trong
Mệnh đề nào sau đây đúng?
A. Nếu và thì
B. Nếu thì và
C. Nếu và thì
D. Nếu cắt và thì
Lời giải
Chọn D
( )
a
P
( )
b
( )
a
( )
.b
( )
a
( )
b
( )
a
( )
.b
a
b
( )
a
( )
b
( ) ( )
.a bP
d
( )
mp a
( )
.mp a
Hình 3
Hình 2
Hình 1
a
b
b
a
b
a
b
a
a
a
d
( )
a
( )
b
( )
a
( )
b
fi
a
b
( )
a
( )
b
( )
a
( )
b
fi
d
( )
mp a
( )
.a
( )
ampPÃ
( )
.bmpQÃ
( ) ( )
.PQabfiPP
( ) ( )
.ab P QfiPP
( ) ( ) ( )
PQaQfiPP
( )
.bPP
a
b
( )
ampPÃ
( )
bmpQÃ
( ) ( )
PQabfiPP
,ab
fi
( ) ( )
ab P QfiPP
( ) ( )
,PQ
a
b
fi
a
b
fi
a
b
( )
.mp a
a
¢
b
¢
( )
.mp b
aa
¢
P
bb
¢
P
( ) ( )
.abP
( ) ( )
abP
aa
¢
P
.bb
¢
P
abP
ab
¢¢
P
( ) ( )
.abP
a
b
,aabb
¢¢
PP
( ) ( )
.abP
Nếu và thì hoặc cắt (Hình 1) A sai.
Nếu thì hoặc chéo nhau (Hình 2) B sai.
Nếu và thì hoặc cắt (Hình 1) C sai.
Câu 5: Cho hai mặt phẳng và cắt nhau theo giao tuyến Hai đường thẳng và lần lượt
nằm trong và Trong các mệnh đề sau, mệnh đề nào đúng?
A. và cắt nhau. B. và chéo nhau.
C. và song song. D. Cả ba mệnh đề trên đều sai.
Lời giải
Chọn D
Ta có và có thể cắt nhau, song song, chéo nhau (hình vẽ).
Câu 6: Cho hình chóp có đáy là hình bình hành tâm Gọi theo thứ tự là
trung điểm của và Khẳng định nào sau đây đúng?
A. cắt B. //
C. D. //
Lời giải
Chọn B
Ta có là đường trung bình của tam giác suy ra //
Và là đường trung bình của tam giác suy ra //
Từ suy ra // // đồng phẳng.
Hình 1
Hình 2
a
b
a
b
b'
a'
a
a'
b
a
aa
¢
P
bb
¢
P
( ) ( )
abP
( )
a
( )
b
fi
( ) ( )
abP
aa
¢
P
,aa
¢
fi
abP
ab
¢¢
P
( ) ( )
abP
( )
a
.CC
¢
fi
.D
p
q
( )
.Q
p
q
p
q
p
q
D
P
Q
p
q
D
q
p
P
Q
q
p
Q
P
D
p
q
.S ABCD
ABCD
.O
,,MNP
,SA SD
.AB
( )
NOM
( )
.OPM
( )
MON
( )
.SBC
( ) ( )
.PO N M NP N P«=
( )
NMP
( )
.SBD
P
N
M
O
A
B
D
C
S
MN
SAD
MN
.AD
( )
1
OP
BAD
OP
.AD
( )( )
1,2
MN
OP
AD
,,,MNOPfi
Lại có // // suy ra // hay //
Bài 5: Hình lăng trụ và hình hộp
Câu 7: Trong các mệnh đề sau, mệnh đề nào sai?
A. Hình lăng trụ có các cạnh bên song song và bằng nhau.
B. Hai mặt đáy của hình lăng trụ nằm trên hai mặt phẳng song song.
C. Hai đáy của lăng trụ là hai đa giác đều.
D. Các mặt bên của lăng trụ là các hình bình hành.
Lời giải
Chọn C
Xét hình lăng trụ có đáy là một đa giác (tam giác, tứ giác,… ), ta thấy rằng
Hình lăng trụ luôn có các cạnh bên song song và bằng nhau.
Hai mặt đáy của hình lăng trụ nằm trên hai mặt phẳng song song.
Hai đáy của lăng trụ là hai đa giác bằng nhau (tam giác, tứ giác,… )
Các mặt bên của lăng trụ là các hình bình hành vì có hai cạnh là hai cạnh bên của hình lăng trụ, hai
cạnh còn lại thuộc hai đáy song song.
Câu 8: Trong các mệnh đều sau, mệnh đề nào sai?
A. Các cạnh bên của hình lăng trụ bằng nhau và song song với nhau.
B. Các mặt bên của hình lăng trụ là các hình bình hành.
C. Các mặt bên của hình lăng trụ là các hình bình hành bằng nhau.
D. Hai đáy của hình lăng trụ là hai đa giác bằng nhau.
Lời giải
Chọn C
Các mặt bên của hình lăng trụ là các hình hình hành, chúng bằng nhau nếu hình lăng trụ có đáy là tam
giác đều.
Câu 9: Trong các mệnh đều sau, mệnh đề nào đúng?
A. Các cạnh bên của hình chóp cụt đôi một song song.
B. Các cạnh bên của hình chóp cụt là các hình thang.
C. Hai đáy của hình chóp cụt là hai đa giác đồng dạng.
D. Cả 3 mệnh đề trên đều sai.
Lời giải
Chọn C
Xét hình chóp cụt có đáy là đa giác (tam giác, tứ giác,… ) ta thấy rằng:
Các cạnh bên của hình chóp cụt đôi một cắt nhau.
Các mặt bên của hình chóp cụt là các hình thang cân.
Hai đáy của hình chóp cụt là hai đa giác đồng dạng.
Câu 10: Trong các mệnh đều sau, mệnh đề nào sai?
A. Trong hình chóp cụt thì hai đáy là hai đa giác có các cạnh tương ứng song song và các tỉ số các
cặp cạnh tương ứng bằng nhau.
B. Các mặt bên của hình chóp cụt là các hình thang.
C. Các mặt bên của hình chóp cụt là các hình thang cân.
D. Đường thẳng chứa các cạnh bên của hình chóp cụt đồng quy tại một điểm.
Lời giải
Chọn C
Với hình chóp cụt, các mặt bên của hình chóp cụt là các hình thang.
Câu 11: Cho hình lăng trụ Trong các khẳng định sau, khẳng định nào sai?
MP
,SB OP
( )
MNOP
( )
SBC
( )
MON
( )
.SBC
111
..ABC A B C
A. // B. //
C. // D. là hình chữ nhật.
Lời giải
Chọn D
Vì mặt bên là hình bình hành, còn nó là hình chữ nhật nếu là hình lăng trụ đứng.
Câu 12: Cho hình hộp Khẳng định nào dưới đây là sai?
A. là hình bình hành.
B. Các đường thẳng đồng quy.
C. //
D. là hình chữ nhật.
Lời giải
Chọn D
Dựa vào hình vẽ và tính chất của hình hộp chữ nhật, ta thấy rằng:
Hình hộp có đáy là hình bình hành.
Các đường thẳng cắt nhau tại tâm của
Hai mặt bên đối diện và song song với nhau.
và là hai đường thẳng chéo nhau suy ra không phải là hình chữ nhật.
Câu 13: Cho hình hộp có các cạnh bên Khẳng định nào dưới đây
sai?
A. // B. //
C. là hình bình hành. D. là một tứ giác.
Lời giải
Chọn B
Dựa vào hình vẽ dưới và tính chất của hình hộp, ta thấy rằng:
( )
ABC
( )
111
.ABC
1
AA
( )
1
.BCC
( )
111
.ABC
11
AA B B
11
AA B B
111
.ABC A B C
111 1
..ABCD A B C D
ABCD
1111
,,,AC AC DB D B
( )
11
ADD A
( )
11
.BCC B
1
AD CB
D
C
A
B
B
1
A
1
C
1
D
1
∑
ABCD
∑
1111
,,,AC AC DB D B
11 11
,.AA C C BDD B
∑
( ) ( )
11 11
,ADD A BCC B
∑
1
AD
CB
1
AD CB
.ABCD A B C D
¢¢¢¢
,,, .AA BB CC DD
¢¢¢ ¢
( )
AA B B
¢¢
( )
.DD C C
¢¢
( )
BA D
¢¢
( )
.ADC
¢
A B CD
¢¢
BB D D
¢¢
D'
C'
A'
B'
B
A
C
D
Hai mặt bên và đối diện, song song với nhau.
Hình hộp có hai đáy là hình bình hành và // suy ra
là hình hình hành.
// suy ra đồng phẳng là tứ giác.
Mặt phẳng chứa đường thẳng mà cắt suy ra không song song với
Bài 6: Phép chiếu song song. Hình biểu diễn của 1 hình trong không gian
Câu 1: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hình chiếu song song của hai đường thẳng cắt nhau là hai đường thẳng song song.
B. Hình chiếu song song của một hình bình hành là một hình bình hành.
C. Phép chiếu song song biến một tam giác thành một tam giác nếu mặt phẳng chứa tam giác không
cùng phương với phương chiếu.
D. Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng.
Lời giải
Chọn C
Câu 2: Trên hình có và hình có
Hình
Hình
Hãy Chọn mệnh đề đúng trong các mệnh đề sau:
A. ABC là tam giác đều.
B. ABC là tam giác cân tại A
C. ABCD là hình thoi.
D. B và C đúng.
Lời giải
Chọn D
Nhìn hình vẽ, ta thấy:
- Tam giác ABC có AH vừa là đường cao vừa là trung tuyến nên cân tại A à B đúng.
- Tứ giác ABCD có nên là hình bình hành. Mặt khác hai đường chéo của nó vuông
góc nên ABCD là hình thoi à C đúng.
Câu 3: Trên hình , ta có phép chiếu song song theo phương d và mặt phẳng chiếu (P); và
; A’, B’, C’, D’, E’, G’ lần lượt là hình chiếu của A, B, C, D, E, G qua phép chiếu
nói trên.
∑
( )
AA B B
¢¢
( )
DD C C
¢¢
∑
( )
( )
,ABCD A B C D
¢¢¢¢
AB CD
¢¢
fi=
AB
¢¢
CD
A B CD
¢¢
∑
BD
¢¢
,, ,BB D D
¢¢
BB D D
¢¢
fi
∑
( )
BA D
¢¢
CD
¢
CD
¢
CD
¢
( )
BA D
¢¢
( )
.ADC
¢
A
ì
^
í
=
î
AH BC
HB HC
B
ì
í
^
î
AB CD, AD BC
AC BD
∥∥
H
A
B
C
A
O
D
A
B
C
B
AB CD, AC BD∥∥
C
AB CG∥
=AB DG
d
P
B'
A'
G'
E'
D'
C'
B
A
C
D
E
G
Hình
Mệnh đề nào sau đây đúng?
A. . B. .
C. . D. Tất cả A, B, C đều đúng.
Lời giải
Chọn D
The định lí 2, ta thấy câu A và câu B đúng. Từ câu A đúng suy ra câu C đúng.
Câu 4: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hình chiếu song song của hai đường thẳng chéo nhau có thể song song với nhau.
B. Hình chiếu song song của hai đường thẳng cắt nhau thì song song.
C. Hình chiếu song song của hai một hình vuông là một hình vuông.
D. Hình chiếu song song của một lục giác đều là một lục giác đều.
Lời giải
Chọn A
Dựng mặt phẳng (P) qua a và song song với b. Dựng mặt phẳng (Q) qua b và song song với a. Giả sử
(P) song song với (Q). Ta Chọn phương chiếu d song song với (P) và mặt phẳng chiếu (R) sao
cho (R) cắt (P) và (Q) lần lượt theo hai giao tuyến a’ và b’. Khi đó hình chiếu a’, b’ song song
với nhau.
Câu 5: Qua phép chiếu song song lên mặt phẳng (P), hai đường thẳng chéo nhau a và b có hình chiếu
là hai đường thẳng a’ và b’. Mệnh đề nào sau đây đúng?
A. a’ và b’ luôn luôn cắt nhau.
B. a’ và b’ có thể trùng nhau.
C. a và b không thể song song.
D. a’ và b’ có thể cắt nhau hoặc song song với nhau.
Lời giải
Chọn D
Gọi l là phương chiếu, và là các mặt phẳng song song với l và lần lượt đi qua a và b. Khi đó
nếu và cắt nhau thì a’ và b’ cắt nhau, nếu và song song thì a’ và b’ song
song.
Câu 6: Qua phép chiếu song song lên mặt phẳng (P), hai đường thẳng a và b có hình chiếu là hai
đường thẳng song song a’ và b’. Khi đó:
A. a và b phải song song với nhau.
B. a và b phải cắt nhau.
C. a và b có thể chéo nhau hoặc song song với nhau.
D. a và b không thể song song.
Lời giải
Chọn C
C
==
DG D' G'
1
AB A' B'
=
C' D' CD
D' E' DE
=D'G' A' B'
a'
b'
a
b
Q
R
P
( )
a
( )
a
( )
a
Nếu thì . Bởi vậy a và b có thể song song hoặc chéo nhau.
Câu 7: Cho bốn điểm không đồng phẳng A, B, C, D có hình chiếu song song trên mặt phẳng (P) lần
lượt là bốn điểm A’, B’, C’, D’. Những trường hợp nào sau đây không thể xảy ra?
A. A’B’C’D’ là bốn đỉnh của một hình bình hành.
B. D’ là trọng tâm tam giác A’B’C’.
C. D’ là trung điểm cạnh A’B’.
D. Hai điểm B’, C’ nằm giữa hai điểm A’ và D’.
Lời giải
Chọn D
Bốn điểm không đồng phẳng A’, B’, C’, D’ không thể thẳng hàng.
Câu 8: Hình chiếu song song của một hình thang ABCD không thể là hình nào dưới đây?
A. Hình bình hành. B. Hình tam giác cân.
C. Đoạn thẳng. D. Bốn điểm thẳng hàng.
Lời giải
Chọn B
II. PHẦN TỰ LUẬN.
Phần: Đại số
Câu 1: Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ của năm được cho
bởi một hàm số với và . Vào ngày nào trong năm thì
thành phố A có nhiều giờ có ánh sáng mặt trời nhất?
A. 28 tháng 5. B. 29 tháng 5. C. 30 tháng 5. D. 31 tháng 5.
Lời giải
Chọn B
Vì
Ngày có ánh sáng mặt trời nhiều nhất
Do .
Với rơi vào ngày 29 tháng 5 (vì ta đã biết tháng 1 và 3 có 31 ngày, tháng 4 có 30
ngày, riêng đối với năm 2017 thì không phải năm nhuận nên tháng 2 có 28 ngày hoặc dựa vào
dữ kiện thì ta biết năm này tháng 2 chỉ có 28 ngày).
Câu 2: Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu (mét) của mực nước
trong kênh được tính tại thời điểm (giờ) trong một ngày bởi công thức
Mực nước của kênh cao nhất khi:
A. (giờ). B. (giờ). C. (giờ). D. (giờ).
Lời giải
. Chọn B
Mực nước của kênh cao nhất khi lớn nhất
a' b'∥
( ) ( )
mp a,a' mp b, b'∥
t
2017
( )
4 sin 60 10
178
yt
p
È˘
Í˙
=-+
Í˙
Î˚
t ΢
0365t<£
( ) ( )
sin 60 1 4 sin 60 10 14.
178 178
tyt
pp
È˘ È˘
Í˙ Í˙
-£ææÆ= -+£
Í˙ Í˙
Î˚ Î˚
( )
14 sin 60 1
178
yt
p
È˘
Í˙
€=€ - =
Í˙
Î˚
( )
60 2 149 356 .
178 2
tktk
pp
p€-=+€=+
149 54
03650149356365 0
356 89
k
tkkk
Œ
<£ ææÆ< + £ €- < £ æææÆ=
¢
0149kt=ææÆ=
0365t<£
h
t
3cos 12.
84
t
h
pp
ʈ
˜
Á
=++
˜
Á
˜
Á
˯
13t =
14t =
15t =
16t =
h
với và
Lần lượt thay các đáp án, ta được đáp án B thỏa mãn
Vì với (đúng với ).
Câu 3: Chu vi của một đa giác là 45 cm, số đo các cạnh của nó lập thành một cấp số cộng với công
sai . Biết cạnh lớn nhất là 15 cm, tính số cạnh của đa giác đó.
Lời giải
Gọi cạnh nhỏ nhất của đa giác là và số cạnh của đa giác là n.
Ta có hay .
Tổng các cạnh là 45 cm, ta có
hay .
Giải phương trình với , ta được .
Câu 4: Tìm ba số hạng liên tiếp của một cấp số cộng, biết rằng:
a) Tổng của chúng bằng 15 và tích của chúng bằng 105.
b) Tổng của chúng bằng 21 và tổng bình phương của chúng bằng 155.
Lời giải
Gọi ba số hạng liên tiếp của cấp số cộng là .
a) Theo bài ra, ta có , kết hợp với , ta được
hoặc .
b) Theo bài ra, ta có , kết hợp với , ta được
hoặc .
Câu 5: Tính
Giải
Câu 6: Tổng có kết quả bằng bao nhiêu?
cos 1 2
84 84
tt
k
pp pp
p
ʈ
˜
Á
€+=€+=
˜
Á
˜
Á
˯
024t<£
.k ΢
14 2
84
t
t
pp
p=ææÆ€ +=
1k =΢
3dcm=
1
u
( )
1
15 1 .3un=+-
1
18 3 0 6unn=- >®<
( )
15 18 3
45
2
nn+-
=
2
333900nn-+=
*
;6nNnÎ<
5n =
( )
,, 2 *abc a c bÞ+=
15
105
abc
abc
++=
ì
í
=
î
( )
*
15
2
105
abc
ac b
abc
++=
ì
ï
+=
í
ï
=
î
( )
315 5 3
210 5
105 7
510 105
bb a
ac b c a b
abc c
aa
ì
== =
ìì
ï
ïï
Û+=Û=- Û=
íí í
ïï ï
==
-=
îî
î
7
5
3
a
b
c
=
ì
ï
=
í
ï
=
î
222
21
155
abc
abc
++=
ì
í
++=
î
( )
*
222
21
2
155
abc
ac b
abc
ì
++=
ï
+=
í
ï
++=
î
( )
222 2
22
321 7 5
214 7
9
155
14 7 155
bb a
ac b c a b
c
abc
aa
ì
ì
== =
ì
ï
ïï ï
Û+= Û=- Û=
íí í
ïï ï
=
++=
î
+-+=
î
ï
î
9
7
5
a
b
c
=
ì
ï
=
í
ï
=
î
22
lim n 7 n 5
æö
+- +
ç÷
èø
22
22
22 22
n7n5 2
lim n 7 n 5 lim lim 0
n7 n5 n7 n5
+- -
æö
+- + = = =
ç÷
èø
++ + ++ +
( ) ( ) ( )
-
=+ + + + + +
23 n1
n
S 1 0,9 0,9 0,9 ... 0,9 ...
Hướng dẫn giải
Đây là tổng của cấp số nhân lùi vô hạng có
Câu 7: Cho Tính
Lời giải
Ta luôn có:
Do đó
Câu 8: Tính
Hướng dẫn giải
Cách 1: Giải bằng tự luận
Cách 2: Giải nhanh bằng máy tính
Nhập vào màn hình ấn ta được kết quả
Lưu ý: Để ra kết quả chính xác ta có thể tính theo quy tắc Lô-pi-tan như sau:
Nhập rồi ấn phím ta được kết quả chính xác
( ) ( ) ( )
-
=+ + + + + +
23 n1
S 1 0,9 0,9 0,9 ... 0,9 ...
1
u1,q0,9.==
1
u
1
S10.
1 q 1 0,9
== =
--
( )( )
n
111 1
u....
3.5 5.7 7.9
2n 1 2n 1
=++++
-+
n
lim u
( )( )
1111
.
22k 1 2k 1
2k 1 2k 1
æö
=-
ç÷
-+
-+
èø
( )( )
n
111 1
u...
3.5 5.7 7.9
2n 1 2n 1
11 1 11 1 11 1 1 1 1
...
23 5 25 7 27 9 22n 1 2n 1
11 1
.
23 2n 1
=++++
-+
æöæöæö æ ö
=-+-+-++ -
ç÷ç÷ç÷ ç ÷
-+
èøèøèø è ø
æö
=-
ç÷
+
èø
n
11 1 1
lim u lim .
23 2n 1 6
æö
=-=
ç÷
+
èø
2
x4
x6x8
lim
x2
®
-+
-
( )( )
( )
( )
( )
2
x4 x4 x4
x2x4 x 2
x6x8
lim lim lim x 2 x 2 2 4 8.
x4
x2
®® ®
-- +
-+
==-+=´=
-
-
2
x6x8
x2
-+
-
5
CALC 4 10
-
+=
8.»
8
( )
( )
2
x4
x4
d
X6X8
dx
d
X2
dx
=
=
-+
-
=
8.
Câu 9: Tính
Hướng dẫn giải
Cách 1: Giải bằng tự luận
Cách 2: Giải nhanh bằng máy tính
Nhập vào màn hình ấn ta được kết quả
Câu 10: Tìm các giá trị của để các hàm số sau liên tục trên tập xác định của chúng:
a) b)
Lời giải
a) Hàm số liên tục với .
• Do đó liên tục trên liên tục tại
• Ta có
• Khi đó .
b) Ta có:
• Từ
Phần hình học:
Ví dụ 1. Cho hình chóp S.ABCD có đáy ABCD không là hình thang. Gọi O là giao điểm của AC và
BD, K là một điểm trên cạnh SD.
a. Tìm giao điểm E của mặt phẳng (ABK) với CD.
b. Tìm giao điểm F của mặt phẳng (ABK) với SC.
c. Chứng minh các đường thẳng AF, BK và SO đồng quy.
Lời giải
2
x
2
x2x3x
Llim .
4x 1 x 2
®-¥
++
=
+- +
2
xx x
2
22
22
x1 3x 1 3
x2x3x 2
xx
lim lim lim .
3
112
4x 1 x 2
x4 x2 4 1
x
xx
®-¥ ®-¥ ®-¥
++ -++
++
===
-
+- +
+-+ -+-+
2
2
x2x3x
4x 1 x 2
++
+- +
15
CALC 10-=
2
.
3
m
( )
2
2
2
2
2
xx
khi x
fx
x
m khi x
ì
--
¹-
ï
=
-
í
ï
=-
î
( )
2
1
2 1
1 1
xx khix
fx khix
mx khi x
ì
+<
ï
==
í
ï
+>
î
( )
fx
2x"¹
( )
fx
( )
fxÛ!
( ) ( )
2
2lim 2
x
xfxf
®
=Û =
( )
1
( )
( )( )
( )
( ) ( )
2
22 2 2
21
2
lim lim lim lim 1 2 1 3; 2 .
22
xx x x
xx
xx
fx x f m
xx
®® ® ®
-+
--
== =+=+==
--
( )
1 Û
33mm=Û=
( ) ( ) ( )
( )
( )
2
11 11
lim lim 1 1; lim lim 1 1 2; 1 2.
xx xx
fx mx m fx x x f
++ --
®® ®®
=+=+ =+=+==
( ) ( ) ( )
11
YCBT lim lim 1 1 2 1.
xx
fx fx f m m
+-
®®
Û==Û+=Û=
a. Trong mp(ABCD): .
Mà nên .
b. Ta có:
Trong mp(SCD): .
Mà nên .
c. Trong mp(ABK): .
Mà
nên .
Vậy ba đường thẳng AF, BK và SO đồng quy.
Ví dụ 2. Cho hình chóp S.ABCD. Gọi M, N là hai điểm bất kì trên SB, CD. Mặt phẳng qua MN và
song song với SC.
Tìm các giao tuyến của với các mặt phẳng , , .
Lời giải
Trong mặt phẳng , từ M kẻ đường thẳng song song với SC cắt
BC tại Q.
Trong mặt phẳng , từ N kẻ đường thẳng song song với SC cắt
SD tại P.
Khi đó giao tuyến của với và lần lượt là MQ và
NP.
Gọi . Từ I kẻ đường thẳng song song với SC cắt SA tại
H.
Khi đó .
d) Tổ chức thực hiện:
Chuyển giao
GV: Giáo viên chia lớp thành 4 nhóm
Giáo viên giao nhiệm vu chữa các câu hỏi cho các nhóm.
Thực hiện
GV: Quan sát các nhóm và đôn đốc các nhóm thực hiện theo yêu cầu
HS: Thực hiện yêu cầu của GV
Báo cáo thảo luận
GV: học sinh lên bảng trình bày vắn tắt lời giải và đáp án của câu hỏi mà
nhóm được giao
Đánh giá, nhận xét,
tổng hợp
GV nhận xét câu trả lời của các đội, đánh giá thái độ làm việc, ghi nhận, tổng
hợp kết quả
{ }
AB CD EÇ=
( )
AB ABKÌ
( )
EABK CDÎÇ
( ) ( )
ABK AEKº
{ }
EK SC FÇ=
( )
EK ABKÌ
( )
FABK SCÎÇ
{ }
AF BK GÇ=
( ) ( )
AF SAC , BK SBDÌÌ
( ) ( )
GSAC SBDSOÎÇ=
F
G
E
O
A
D
B
S
C
K
( )
P
( )
P
( )
SBC
( )
SCD
( )
SAC
( )
SBC
( )
SCD
( )
P
( )
SBC
( )
SCD
IACNQ=Ç
( ) ( )
PSACIHÇ=
| 1/38
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Trường ………………………..
Họ và tên giáo viên: ……………………
Tổ …………………. Tiết
KẾ HOẠCH BÀI DẠY
TÊN BÀI DẠY: ÔN TẬP KIỂM TRA HỌC KỲ 1
Môn học/Hoạt động giáo dục: Toán 11
Thời gian thực hiện: 01 tiết I. MỤC TIÊU 1. Kiến thức
- Ôn tập lại các kiến thức: Hàm số lượng giác và phương trình lượng giác. Dãy số, cấp số cộng,
cấp số nhân. Giới hạn của dãy số, giới hạn của hàm số, hàm số liên tục. Đường thẳng và mặt phẳng
trong không gian, hai đường thẳng song song, đường thẳng song song với mặt phẳng, hai mặt phẳng song song.
- Đối với học sinh khá giỏi: Vận dụng các kiến thức: Hàm số lượng giác và phương trình lượng
giác. Dãy số, cấp số cộng, cấp số nhân. Giới hạn của dãy số, giới hạn của hàm số, hàm số liên tục.
Đường thẳng và mặt phẳng trong không gian, hai đường thẳng song song, đường thẳng song song với
mặt phẳng, hai mặt phẳng song song vào một số bài toán thực tế đơn giản. 2. Năng lực
- Năng lực tự học: Học sinh xác định đúng đắn động cơ, thái độ học tập; tự đánh giá và điều
chỉnh được kế hoạch học tập; tự nhận ra những sai sót và khắc phục.
- Năng lực giao tiếp: Tiếp thu kiến thức, trao đổi học hỏi bạn bè thông qua việc thực hiện nhiệm
vụ trong các hoạt động cặp đôi, nhóm; có thái độ tôn trọng, lắng nghe, có phản ứng tích cực trong giao tiếp.
- Năng lực hợp tác: Học sinh xác định được nhiệm vụ của tổ/nhóm, trách nhiệm của bản thân đề
xuất được những ý kiến đóng góp, góp phần hoàn thành nhiệm vụ học tập.
- Năng lực giải quyết vấn đề: Học sinh tiếp cận hệ thống câu hỏi và bài tập, những tình huống có
vấn đề. Phân tích được các vấn đề để đưa ra những giải pháp xử lí tình huống, những vấn đề
liên quan đến bộ môn và trong thực tế.
- Năng lực sáng tạo: Học sinh biết vận dụng tính sáng tạo để giải quyết tình huống của từng bài toán cụ thể.
- Năng lực sử dụng ngôn ngữ: Học sinh nói và viết chính xác bằng ngôn ngữ Toán học.
3. Phẩm chất
- Trách nhiệm: Biết chịu trách nhiệm với thành quả của cá nhân, tập thể; không đổ lỗi cho người
khác. Chủ động phát hiện, chiếm lĩnh tri thức mới, biết quy lạ về quen, có tinh thần trách
nhiệm hợp tác xây dựng cao.
- Trung thực: Học sinh biết tôn trọng kết quả của bản thân, tôn trọng lẽ phải; thật thà, ngay
thẳng trong học tập và làm việc, lên án sự gian lận.
- Chăm chỉ: Chăm làm, ham học, có tinh thần tự học, chăm chỉ tích cực xây dựng bài, nhiệt tình
tham gia các công việc của tập thể, tinh thần vượt khó trong công việc.
- Nhân ái: Yêu con người, yêu cái đẹp của toán học, tôn trọng sự khác biệt, ý kiến trái chiều;
sẵn sàng học hỏi, hòa nhập và giúp đỡ mọi người
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Về phía giáo viên:
- Thước thẳng có chia khoảng, compa, bảng phụ ghi bài tập, phiếu học tập, máy chiếu, sách giáo khoa, bài soạn...
2. Về phía học sinh:
- Dụng cụ học tập, sách giáo khoa, chuẩn bị bài trước khi đến lớp...
III. TIẾN TRÌNH DẠY HỌC:
1. HOẠT ĐỘNG 1: KHỞI ĐỘNG a) Mục tiêu:
- HS chuẩn bị tâm thế tốt cho tiết ôn tập cuối học kỳ 1
- Nắm bắt việc chuẩn bị và làm đề cương của học sinh. b) Nội dung:
Câu hỏi 1: Trong các bài học của kỳ 1 lớp 11 em thích học bài nào nhất vì sao?
Câu hỏi 2: Trình bày khó khăn của em khi làm đề cương, e đã làm gic để giải quyết khó khăn đó
c) Sản phẩm: Câu trả lời của học sinh d) Tổ chức thực hiện: Chuyển giao
Giáo viên cho học sinh các tổ kiểm tra việc làm đề cương của nhau sau đó báo cáo kết quả. Thực hiện
- HS di chuyển để kiểm tra, thống nhất đáp án một số câu hỏi
- HS suy nghĩa trả lời câu hỏi
- Mong đợi: HS chỉ ra được một nhóm câu hỏi cần giúp đỡ trong tiết học này
Báo cáo thảo luận
HS đưa ra những nhận xét về việc làm đề cương của các bạn, nêu được
một số câu hỏi cần đưa ra thảo luận, giải đáp trong tiết học
Đánh giá, nhận xét,
- Giáo viên đánh giá thái độ làm việc, phương án trả lời của học sinh, tổng hợp
ghi nhận và tổng hợp kết quả.
- Hướng học sinh vào các câu hỏi trọng tâm của đề cương.
2. HOẠT ĐỘNG 2: LUYỆN TẬP a) Mục tiêu:
§ Hệ thống kiến thức, ôn tập các bài tập chuẩn bị kiểm tra.
b) Nội dung: Chữa đề cương cho học sinh
c) Sản phẩm: HS so sánh kết quả của việc làm đề cương tại nhà với kết quả của cô giáo và các bạn
chữa. sửa chữa bài tập để được Đề cương chữa hoàn thiện SỞ GD & ĐT LÀO CAI
ĐỀ CƯƠNG KIỂM TRA HỌC KỲ I TRƯỜNG THPT …. NĂM HỌC 2022-2023 Môn: Toán. Khối 11 I, PHẦN TRẮC NGHIỆM
Chương 1: Hàm số lượng giác – Phương trình lượng giác
Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác
Câu 1: Đổi số đo của góc 0 70 sang đơn vị radian. A. 70 7 7p 7 . B. . C. . D. . p 18 18 18p Lời giải Chọn C Áp dụng công thức . a p a =
với a tính bằng radian, a tính bằng độ. 180 Ta có . a p 70p 7p a = = = . 180 180 18
Câu 2: Đổi số đo của góc 3p -
rad sang đơn vị độ, phút, giây. 16 A. 0 33 45'. B. 0 - 29 30'. C. 0 - 33 45'. D. 0 - 32 55. Lời giải Chọn C 0 Ê 3p ˆ Á ˜ 0 - Á .180 0 ˜ Ta có a Ê .180ˆ Á = Á ˜ 16 ˜ Ê 135ˆ Á ˜ = Á ˜ 0 a ˜ = Á ˜ - Á ˜ Á ˜ Á ˜ = - 33 45'. Ë p ¯ Ë p ¯ Á Ë 4 ˜¯
Câu 3: Tính độ dài của cung trên đường tròn có số đo 1,5 và bán kính bằng 20 cm .
A. 30cm .
B. 40cm .
C. 20cm . D. 60cm . Lời giải Chọn A
Ta có l = a R = 1,5.20 = 30 cm.
Câu 4: Cho a thuộc góc phần tư thứ hai của đường tròn lượng giác. Hãy chọn kết quả đúng trong các kết quả sau đây.
A. sina > 0; cosa > 0 .
B. sina < 0; cosa < 0.
C. sina > 0; cosa < 0.
D. sina < 0; cosa > 0. Lời giải Chọn C Ï sin Ô a > 0
a thuộc góc phần tư thứ hai Ô Æ Ì co Ô sa < 0 Ô Ó p
Câu 5: Cho 0 < a < . Khẳng định nào sau đây đúng? 2 æ p ö æ p ö A. cot a + > 0. B. cot a + ³ 0. ç ÷ ç ÷ è 2 ø è 2 ø
C. tan (a +p ) < 0 . D. tan (a +p ) > 0 . Lời giải Chọn D ì p p p æ p ö 0 < a < ® < a + < p ¾¾ ®cot a + < 0 ï ç ÷ ï Ta có 2 2 2 è 2 ø í . ï p 3p 0 < a < ® p < a + p < ¾¾ ® tan (a +p ) > 0 ïî 2 2 Câu 6: Biết ,
A B,C là các góc của tam giác ABC,mệnh đề nào sau đây đúng:
A. sin ( A+C) = si - n . B
B. cos( A+C) = -cos . B
C. tan ( A+C) = tan . B
D. cot ( A+C) = cot . B Lời giải Chọn B Vì ,
A B,C là ba góc của một tam giác suy ra A + C = p - . B
Khi đó sin ( A+C) = sin(p - B) = sin ;
B cos( A+C) = cos(p - B) = c - os . B
tan( A+C) = tan(p - B) = -tan ;
B cot ( A+C) = cot(p - B) = -cot . B p Câu 7: Cho góc a 5 thỏa mãn cosa = - 3 và p < a < . Tính tana. 3 2 3 A. tana = - 2 . B. tana = 4 . C. tana = - 2 . D. tana = - . 5 5 5 5 Lời giải Chọn B ì 2 2 sina = ± 1- cos a = ± ïï 3 2 sina 2 Ta có í ¾¾ ®sina = - ¾¾ ®tana = = . 3p 3 cosa 5 p ï ïî 2
Bài 2: Các phép biến đổi lượng giác.
Câu 1: Rút gọn biểu thức 4 o 4 o M = cos 15 - sin 15 . A. M = 3 1. B. M = 1 . C. M = . D. M = 0. 2 4 Lời giải Chọn B 2 2 Ta có 4 o 4 o M = - = ( 2 o ) -( 2 o cos 15 sin 15 cos 15 sin 15 ) = ( 2 o 2 o - )( 2 o 2 o cos 15 sin 15 cos 15 + sin 15 ) 3 2 o 2 o = cos 15 - sin 15 = cos( o 2.15 ) o = cos30 = . 2 p 5p 7p 11p
Câu 2: Giá trị của biểu thức M = sin sin sin sin bằng 24 24 24 24 1 1 1 1 A. . B. . C. . D. . 2 4 8 16 Lời giải Chọn D 7p 5p p p Ta có sin = 11 cos và sin = cos . 24 24 24 24 p 5p 5p p 1 æ p p ö æ 5p 5p ö Do đó M = sin sin cos cos = . 2.sin .cos . 2.sin .cos ç ÷ ç ÷ 24 24 24 24 4 è 24 24 ø è 24 24 ø 1 p 5p 1 1 æ 6p p ö 1 æ 1 ö 1 = .sin .sin = . cos + cos = . 0 + = . ç ÷ ç ÷ 4 12 12 4 2 è 12 3 ø 8 è 2 ø 16
Câu 3: Công thức nào sau đây sai?
A. cos(a -b) = sin asinb + cosacosb .
B. cos(a +b) = sin asinb -cosacosb .
C. sin (a -b) = sin acosb -cosasinb .
D. sin(a +b) = sin acosb + cosasin . b Lời giải Chọn B
Ta có cos(a +b) = cosacosb -sin asinb.
Câu 4: Khẳng định nào đúng trong các khẳng định sau? æ p ö æ p ö
A. sin a + cos a = 2 sin a - .
B. sin a + cos a = 2 sin a + . ç ÷ ç ÷ è 4 ø è 4 ø æ p ö æ p ö
C. sin a + cos a = - 2 sin a - .
D. sin a + cos a = - 2 sin a + ç ÷ . ç ÷ è 4 ø è 4 ø Lời giải Chọn B
Câu 5: Rút gọn M = cos(a +b)cos(a -b) -sin(a +b)sin(a -b). A. 2 M = 1- 2cos . a B. 2 M = 1- 2sin . a C. M = cos 4 . a D. M = sin 4 . a Lời giải Chọn B
Áp dụng công thức cos xcos y -sin xsin y = cos(x + y), ta được M =
(a+b) (a-b)- (a+b) (a-b) = (a+b+a-b) 2 cos cos sin sin cos = cos2a =1- 2sin . a
Câu 6: Chọn công thức đúng trong các công thức sau: 1 a + b a - b A. sin .
a sin b = - écos ë
(a +b)-cos(a -b)ù. B. a - b = 2 û sin sin 2sin .cos . 2 2 2 tan a C. tan 2a = . D. 2 2
cos 2a = sin a - cos . a 1- tan a Lời giải Chọn B æ p ö
Câu 7: Cho biểu thức P = 2 - sin x +
+ 2. Mệnh đề nào sau đây là đúng? ç ÷ è 3 ø A. P ³ 4, - x " Î ! .
B. P ³ 4, x " Î! .
C. P ³ 0, x " Î! .
D. P ³ 2, x " Î! . Lời giải Chọn C æ p ö æ p ö Ta có 1 - £ sin x + £1Þ 2 ³ 2 - sin x + ³ 2 - ç ÷ ç ÷ è 3 ø è 3 ø æ p ö Þ 4 ³ 2 - sin x +
+ 2 ³ 0 Þ 4 ³ P ³ 0. ç ÷ è 3 ø sin 3x - sin x
Câu 8: Rút gọn biểu thức M = . 2 2cos x -1
A. tan 2x B. sin . x C. 2 tan . x D. 2sin . x Lời giải Chọn D sin 3x - sin x 2cos 2xsin x Ta có: = = 2sin x. 2 2cos x -1 cos 2x æ p ö æ p ö Câu 9: Cho góc a 3
thỏa mãn sina = . Tính P = sin a + sin a - . ç ÷ ç ÷ 5 è 6 ø è 6 ø 11 A. P = 11 . B. P = - 7 . C. P = 10 . D. P = . 100 100 25 11 Lời giải Chọn A 1 Áp dụng công thức sin . a sin b = écos ë
(a -b)-cos(a +b)ù, ta được 2 û æ p ö æ p ö 1 æ p ö P = sin a + sin a - = cos - cos 2a . ç ÷ ç ÷ ç ÷ è 6 ø è 6 ø 2 è 3 ø 2 3 7 Ta có 2 cos 2a 1 2sin a æ ö = - =1- 2. = . ç ÷ è 5 ø 25 1 æ 1 7 ö 11
Thay vào P , ta được P = - = . ç ÷ 2 è 2 25 ø 100
Bài 3: Hàm số lượng giác và đồ thị
Câu 1: Tìm tập xác định 1+ sin x D của hàm số y = . cos x - 1 A. Ï p Ô ¸ D = ° . B. D ° \Ô Ì k Ô p,k ¢ ˝ . Ô = + Œ 2 Ô Ô Ô Ó Ô ˛
C. D= ° \{kp,k Œ¢}.
D. D= ° \{k2p,k Œ¢ }. Lời giải Chọn D
Hàm số xác định khi và chỉ khi cos x - 1 π 0 € cos x π 1 € x π k2p, k Œ¢.
Vậy tập xác định D = ° \{k2p,k Œ¢ }.
Câu 2: Tìm tập xác định Ê p ˆ
D của hàm số y = cot 2 Á Á x ˜ - ˜ + sin 2x. Á Ë 4 ˜¯ A. Ï p Ô ¸ D ° \Ô Ì k Ô p,k ¢ ˝ . Ô = + Œ B. D = ∆. 4 Ô Ô Ô Ó Ô ˛ C. Ï p Ô p ¸ D ° \Ô Ì k ,k ¢ ˝ . Ô = + Œ D. D = ° . 8 Ô Ó 2 Ô Ô Ô ˛ Lời giải Chọn C Hàm số xác định Ê p ˆ p p kp sin 2 Á Á x ˜ - ˜ π 0 € 2x - π kp € x π + , k Œ¢. Á Ë 4 ˜¯ 4 8 2 Vậy tập xác định Ï p Ô p ¸ D ° \Ô Ì k ,k ¢ ˝ . Ô = + Œ 8 Ô Ó 2 Ô Ô Ô ˛
Câu 3: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. y = sin x.
B. y = cos x.
C. y = tan x.
D. y = cot x. Lời giải Chọn B
Nhắc lại kiến thức cơ bản:
= Hàm số y = sin x là hàm số lẻ.
= Hàm số y = cos x là hàm số chẵn.
= Hàm số y = tan x là hàm số lẻ.
= Hàm số y = cot x là hàm số lẻ.
Vậy B là đáp án đúng.
Câu 4: Trong các hàm số sau, hàm số nào là hàm số lẻ? A. 2
y = cos x + sin x.
B. y = sin x + cos x.
C. y = - cos x.
D. y = sin x.cos3x. Lời giải Chọn D
Ta kiểm tra được đáp án A và C là các hàm số chẵn. Đáp án B là hàm số không chẵn, không lẻ. Đáp án D là hàm số lẻ. Câu 5: Tìm chu kì Ê p ˆ
T của hàm số y = sin 5 Á Á x ˜ - ˜. Á Ë 4 ˜¯ A. 2p 5p p p T = . B. T = . C. T = . D. T = . 5 2 2 8 Lời giải Chọn A Hàm số 2p
y = sin(ax + b
) tuần hoàn với chu kì T = . a Áp dụng: Hàm số Ê p ˆ 2p y = sin 5 Á Á x ˜ -
˜ tuần hoàn với chu kì T = . Á Ë 4 ˜¯ 5
Bài 4: Phương trình lượng giác cơ bản 1
Câu 1: Nghiệm của phương trình sin x = là: 2 p p p A. x = + k2p . B. x = + kp .
C. x = kp . D. x = + k2p . 3 6 6 Lời giải Chọn D é p é p x = + k2p x = + k2p 1 p ê 6 ê 6
sin x = Û sin x = sin Û ê Û ê (k Î!). 2 6 p 5p êx p k2p ê = - + x = + k2p êë 6 êë 6
Câu 2: Nghiệm của phương trình 3 + 3tan x = 0 là: p p p p A. x = + kp . B. x = + k2p .
C. x = - + kp . D. x = + kp . 3 2 6 2 Lời giải Chọn C 3 p
3 + 3tan x = 0 Û tan x = -
Û x = - + kp (k Î!). 3 6
Câu 3: Nghiệm của phương trình cot x + 3 = 0 là: p p p p A. x = + k2p . B. x = + kp .
C. x = - + kp .
D. x = - + kp . 3 6 6 3 Lời giải Chọn C p
cot x + 3 = 0 Û cot x = - 3 Û x = - + kp (k Î!). 6 1
Câu 4: Nghiệm của phương trình sin x = – là: 2 p p - p p 5 A. x = + k p 2 . B. x = + k p 2 . C. x = + k p 2 . D. x = + k p 2 . 3 6 6 6 Lời giải Chọn B é p - x = + k2p 1 ê 6 sinx = – Û ê (k Î Z).. 2 7p êx = + k2p ëê 6
Câu 5: Phương trình lượng giác: cos3 cos12o x = có nghiệm là: p p k p p - k p p k p A. x = ± + 2 k2p . B. x = ± + 2 . C. x = + 2 . D. x = + . 15 45 3 45 3 45 3 Lời giải Chọn B p p p k p cos3 cos12o x = Û cos3x = cos Û 3x = ± + 2 k2p Û x = ± + . 15 15 45 3
Chương 2: Dãy số, cấp số cộng, cấp số nhân Bài 1: Dãy số -n
Câu 1: Cho dãy số (u u = . n ) , biết
Năm số hạng đầu tiên của dãy số đó lần lượt là những số n n +1 nào dưới đây? 1 2 3 4 5 A. - ;- ;- ;- ;- 2 3 4 5 6 . B. - ;- ;- ;- ;- . 2 3 4 5 6 3 4 5 6 7 1 2 3 4 5 2 3 4 5 6 C. ; ; ; ; . D. ; ; ; ; . 2 3 4 5 6 3 4 5 6 7 Lời giải Chọn A 1 2 3 4 5
Ta có u = - ;u = - ;u = - ;u = - ;u = - . 1 2 3 4 5 2 3 4 5 6
Nhận xét: (i) Dùng MTCT chức năng CALC để kiểm tra (tính) nhanh. u ì = 1 -
Câu 2: Cho dãy số (u 1 n ³ 0 n ) , biết í với
. Ba số hạng đầu tiên của dãy số đó là lần lượt u = u + 3 î n 1+ n
là những số nào dưới đây? A. 1 - ;2;5. B. 1;4;7. C. 4;7;10 . D. 1 - ;3;7. Lời giải Chọn A
Ta có u = - 1; u = u + 3= 2; u = u + 3= 5. 1 2 1 3 2
Câu 3: Cho dãy số (u u = - n n ( )1n.2 . n ) , biết
Mệnh đề nào sau đây sai? A. u = 2. - B. u = 4. C. u = 6. - D. u = - 8. 1 2 3 4 Lời giải Chọn D
Thay trực tiếp hoặc dùng chức năng CALC:
u = - 2.1= - 2; u = - 1 .2.2 = 4, u = - 1 2.3 = - 6; u = - 1 2.4 = 8 1 2 ( )2 3 ( )3 4 ( )4 .
Nhận xét: Dễ thấy u > 0 khi n chẵn và ngược lại nên đáp án D sai. n
Câu 4: Cho các dãy số sau. Dãy số nào là dãy số tăng? 1 1 1 1
A. 1; 1; 1; 1; 1; 1;! B. 1; - ; ; - ; ;! 2 4 8 16 1 1 1 1
C. 1; 3; 5; 7; 9; ! D. 1; ; ; ; ;! 2 4 8 16 Lời giải Chọn C
Xét đáp án A: 1; 1; 1; 1; 1; 1;L đây là dãy hằng nên không tăng không giảm. Xét đáp án B: 1 1 1 1 1; - ; ; - ;
;L æ æÆ u > u < u æ æÆ loại B 1 2 3 2 4 8 16 Xét đáp án C: *
1; 3; 5; 7; 9;L æ æÆ u < u , n Œ• n n+1 Xét đáp án D: 1 1 1 1 1; ; ; ;
;L æ æÆ u > u > u º > u > º æ æÆ loại D 1 2 3 2 4 8 16 n
Câu 5: Trong các dãy số (u u
n ) cho bởi số hạng tổng quát n sau, dãy số nào là dãy số tăng? A. 1 1 n + 5 2n - 1 u = . B. u = . C. u = . D. u = . n 2n n n n 3n + 1 n n + 1 Lời giải Chọn D Vì 1 1
2n ; n là các dãy dương và tăng nên
; là các dãy giảm, do đó loại A,B 2n n ÏÔ 3 u Ô = Ô 1 Xét đáp án C: n + 5 Ô Ô 2 u = æ æÆ Ì
æ æÆ u > u æ æÆ loại C n 1 2 3n + 1 Ô 7 u Ô Ô = 2 Ô Ô Ó 6 Xét đáp án D: 2n- 1 3 Ê 1 1 ˆ u = = 2- fi u - u = 3Á ˜ Á - ˜ > 0 n n+ 1 n + 1 n + 1 n n Á Ë + 1 n + 2˜¯
Câu 6: Trong các dãy số (u u
n ) cho bởi số hạng tổng quát
sau, dãy số nào là dãy số giảm? n A. 1 3n - 1 u = . B. u = . C. 2 u = n .
D. u = n+ 2. n 2n n n + 1 n n Lời giải Chọn A Vì 1
2n là dãy dương và tăng nên là dãy giảm æ æÆ 2n Ï u Ô = 1 1 - Ô Xét B: 3n 1 u Ô = æ æÆ Ì
æ æÆ u < u æ æÆ n 5 loại B 1 2 n + 1 u Ô = Ô 2 Ô Ó 3 Hoặc 3n + 2 3n- 1 4 u - u = - = > 0 nên (u n ) là dãy tăng. n+ 1 n n + 2 n + 1 (n + ) 1 (n + ) 2
Xét C: u = n æ æÆ u - u = n + 1 - n = 2n + 1> 0 æ æÆ n n+ 1 n ( )2 2 2 loại C Xét D: 1
u = n + 2 æ æÆ u - u = n + 3 - n + 2 =
> 0 æ æÆ loại D n n+ 1 n n + 3 + n + 2 Câu 7: Cho dãy số ( 3n - 1 u , bi u = . (un ) n ) ết Dãy số
bị chặn trên bởi số nào dưới đây? n 3n + 1 A. 1 1 . B. 1. C. . D. 0. 3 2 Lời giải Chọn B Ta có 3n- 1 2 5 1 1 u = = 1-
< 1. Mặt khác: u = > >
> 0 nên suy ra dãy (u
n ) bị chặn trên bởi số 1. n 3n + 1 3n + 1 2 7 2 2 Bài 2: Cấp số cộng
Câu 1: Dãy số nào sau đây không phải là cấp số cộng? 2 1 1 2 4 A. - ;- ;0; ; ;1; ....
B. 15 2;12 2;9 2;6 2;.... 3 3 3 3 3 4 7 9 11 1 2 3 4 3 5 C. ;1; ; ; ;.... D. ; ; 3; ; ;.. . 5 5 5 5 3 3 3 3 Lời giải Chọn C
Chỉ cần tồn tại hai cặp số hạng liên tiếp của dãy số có hiệu khác nhau: u - u =/ u - u thì ta kết m+ 1 m k+ 1 k
luận ngay dãy số đó không phải là cấp số cộng. Xét đáp án A: 2 1 1 2 4 1 - ;-
;0; ; ;1; .... æ æÆ = u - u = u - u = u - u = L æ æÆ loại A 2 1 3 2 4 3 3 3 3 3 3 3 Xét đáp án B:
15 2;12 2;9 2;6 2;.... æ æÆ - 3 3 = u - u = u - u = u - u = L æ æÆ loại B 2 1 3 2 4 3 Xét đáp án C: 4 7 9 11 1 2
;1; ; ; ;.... æ æÆ = u - u /= u - u = æ æÆ Chọn C 2 1 3 2 5 5 5 5 5 5 Xét đáp án D: 1 2 3 4 3 5 3 ; ; 3; ; ;... æ æÆ
= u - u = u - u = u - u æ æÆ loại D 2 1 3 2 4 3 3 3 3 3 3 1
Câu 2: Cho cấp số cộng có số hạng đầu u = - 1
, công sai d = . Năm số hạng liên tiếp đầu tiên của 1 2 2 cấp số này là: 1 1 1 1 3 A. - 1 1 1 ;0;1; ;1. B. - 1 3 5 ;0; ;0; . C. ;1; ;2; . D. - ;0; ;1; . 2 2 2 2 2 2 2 2 2 2 2 Lời giải Chọn D
Ta dùng công thức tổng quát 1 1 n 1
u = u + n- 1 d = - + n- 1 = - 1+ u
= u + d = u + n 1 ( ) ( ) , hoặc để 2 2 2 n+ 1 n n 2
tính các số hạng của một cấp số cộng. ÏÔ 1 u Ô = - Ô 1 Ô 2
ÔuÔÔ = u + d = 0 Ô 2 1 Ô Ô Ta có 1 1 Ô 1 u ; d Ì u Ô = - = æ æÆ - u + d = 1 3 2 2 2 Ô 2 Ô Ôu Ô = u + d = 1 Ô 4 3 Ô Ô Ô 3 u Ô Ô = u + d = 5 4 Ô Ô Ó 2
Nhận xét: Dùng chức năng “lặp” của MTCT để tính: Nhập: 1 X = X +
(nhập X = X + d ). 2 Bấm CALC: nhập 1 - (nhập u ). 2 1
Để tính 5 số hạng đầu ta bấm dấu “=” liên tiếp để ra kết quả 4 lần nữa! 1
Câu 3: Cho cấp số cộng (u u = 3 - d = . n ) có và
Khẳng định nào sau đây đúng? 1 2 1 A. u = 3 - + n + 1 u = 3 - + n -1. n ( )1. B. 2 n 2 1 1 C. u = 3 - + n - u = 3 - + n - n ( )1. n ( )1. D. 2 4 Lời giải Chọn C Ï u Ô = - 3 1 Ô Ta có Ô CTTQ 1 Ì
1 æ æ æÆ u = u + n- 1 d = - 3+ n- 1 n 1 ( ) ( ) d Ô = 2 Ô Ô Ó 2
Câu 4: Trong các dãy số được cho dưới đây, dãy số nào là cấp số cộng?
A. u = 7 - 3n . B. u = 7 - 7 3n. C. u = .
D. u = 7.3 .n n n n 3n n Lời giải Chọn A Dãy (u
€ u = an+ b a,b
n ) là cấp số cộng ( là hằng số). n
Câu 5: Cho cấp số cộng (u u = 2001 u =1995 u n ) có và . Khi đó bằng: 2 5 1001 A. u = 4005. B. u = 4003. C. u = 3. D. u =1. 1001 1001 1001 1001 Lời giải Chọn C Ï 2001 Ô
= u = u + d Ï u Ô = 2003 Ô 2 1 Ô 1 Ì € Ì æ æÆ u
= u + 1000d = 3 1001 1 1995 Ô
= u = u + 4d d Ô = - 2 Ô Ó 5 1 Ô Ó u ì - u + u =15
Câu 6: Cho cấp số cộng (u 1 3 5 í . n ) thỏa mãn
Chọn khẳng định đúng trong các khẳng u + u = 27 î 1 6 định sau? u ì = 21 u ì = 21 u ì =18 u ì = 21 A. 1 í . B. 1 í . C. 1 í . D. 1 í . îd = 3 îd = 3 - îd = 3 îd = 4 Lời giải Chọn B
ÏÔu - u + u = 15
ÏÔu - u + 2d + u + 4d = 15 ÏÔu + 2d = 15 ÏÔu = 21 1 3 5 1 ( 1 ) ( 1 ) Ta có Ô Ô Ô Ô Ì € Ì 1 1 € Ì € Ì . Ôu + u = 27
Ôu + u + 5d = 27 Ô Ó 2 Ô u + 5d = 27 Ôd = - 3 1 6 Ô 1 ( 1 ) Ó Ô Ó 1 Ô Ó
Câu 7: Một rạp hát có 30 dãy ghế, dãy đầu tiên có 25 ghế. Mỗi dãy sau có hơn dãy trước 3 ghế. Hỏi
rạp hát có tất cả bao nhiêu ghế? A. 1635. B. 1792. C. 2055. D. 3125. Lời giải Chọn C
Số ghế của mỗi dãy (bắt đầu từ dãy đầu tiên) theo thứ tự đó lập thành một cấp số cộng có 30 số hạng
có công sai d = 3 và u = 25. 1 Tổng số ghế là 30.29
S = u + u + L + u = 30u + d = 2055 30 1 2 30 1 2
Câu 8: Người ta trồng 3003 cây theo một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng thứ
hai trồng 2 cây, hàng thứ ba trồng 3 cây,.Hỏi có tất cả bao nhiêu hàng cây? A. 73. B. 75. C. 77. D. 79. Lời giải. Chọn C
Số cây mỗi hàng (bắt đầu từ hàng thứ nhất) lập thành một cấp số cộng (u u = 1, d = 1. n ) có Giả sử có 1
n hàng cây thì u + u + L + u = 3003 = S . 1 2 n n n(n- ) 1 Ta có 2 3003 = S = nu +
d € n + n- 6006 = 0 € n = 77 n 1 2
Câu 9: Một chiếc đồng hồ đánh chuông, kể từ thời điểm 0 (giờ) thì sau mỗi giờ thì số tiếng chuông
được đánh đúng bằng số giờ mà đồng hồ chỉ tại thời điểm đánh chuông. Hỏi một ngày đồng
hồ đó đánh bao nhiêu tiếng chuông? A. 78. B. 156. C. 300. D. 48. Lời giải Chọn C
Kể từ lúc 1 (giờ) đến 24 (giời) số tiếng chuông được đánh lập thành cấp số cộng có 24 số hạng với
u = 1, công sai d = 1. Vậy số tiếng chuông được đánh trong 1 ngày là: 1 24 S = S = u + u = 12 1+ 24 = 300 24 ( 1 24 ) ( ) 2
Câu 10: Trên một bàn cờ có nhiều ô vuông, người ta đặt 7 hạt dẻ vào ô đầu tiên, sau đó đặt tiếp vào ô
thứ hai số hạt nhiều hơn ô thứ nhất là 5, tiếp tục đặt vào ô thứ ba số hạt nhiều hơn ô thứ hai là
5,… và cứ thế tiếp tục đến ô thứ n . Biết rằng đặt hết số ô trên bàn cờ người ta phải sử dụng
25450 hạt. Hỏi bàn cờ đó có bao nhiêu ô vuông? A. 98. B. 100. C. 102. D. 104. Lời giải Chọn B
Số hạt dẻ trên mỗi ô (bắt đầu từ ô thứ nhất) theo thứ tự đó lập thành cấp số cộng (u u = 7, d = 5. n ) có 1 Gọi n là số ô trên bàn cờ thì
u + u + L + u = 25450 = S . Ta có 1 2 n n n(n- ) 2 1 n - n 25450 = S = nu + d = 7n + .5 n 1 2 2 2
€ 5n + 9n - 50900 = 0 € n = 100
Câu 11: Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng nước đến để
khoan giếng nước. Biết giá của mét khoan đầu tiên là 80.000 đồng, kể từ mét khoan thứ 2 giá
của mỗi mét khoan tăng thêm 5000 đồng so với giá của mét khoan trước đó. Biết cần phải
khoan sâu xuống 50m mới có nước. Vậy hỏi phải trả bao nhiêu tiền để khoan cái giếng đó? A. 5.2500.000 đồng.
B. 10.125.000 đồng. C. 4.000.000 đồng. D. 4.245.000 đồng. Lời giải Chọn B
Giá tiền khoang mỗi mét (bắt đầu từ mét đầu tiên) lập thành cấp số cộng (u
u = 80000, d = 5000. n ) có 1
Do cần khoang 50 mét nên tổng số tiền cần trả là 50.49
u + u + L + u = S = 50u +
d = 50.80000+ 1225.5000 = 10125000. 1 2 50 0 5 1 2 Bài 3: Cấp số nhân
Câu 1: Trong các dãy số sau, dãy số nào không phải là một cấp số nhân?
A. 2; 4; 8; 16; K
B. 1; - 1; 1; - 1; L C. 2 2 2 2 1 ; 2 ; 3 ; 4 ; L D. 3 5 7 ;
a a ; a ; a ; L (a π ) 0 . Lời giải Chọn C Xét đáp án C: u 9 u 2 2 2 2 2 3 1 ; 2 ; 3 ; 4 ; L æ æÆ = 4 =/ = u 4 u 1 2
Các đáp án A, B, D đều là các cấp số nhân.
Nhận xét: Dãy (u v u =/ 0 € u = . n a q n ) ới là cấp số nhân
, tức là các số hạng của nó đều được biểu n n
diễn dưới dạng lũy thừa của cùng một cơ số q (công bội), các số hạng liên tiếp (kể từ số hạng
thứ hai) thì số mũ của chúng cách đều nhau. Ví dụ
2; 4; 8; 16; K æ æÆ là cấp số nhân và u = 2n . n
1; - 1; 1; - 1; L æ æÆ là cấp số nhân và u = - n ( ) 1 n . n- 1 n 3 5 7 ;
a a ; a ; a ; L (a π )
0 æ æÆ là cấp số nhân và 2 1 u = a = a n ( 2 . ) . a
Câu 2: Dãy số nào sau đây không phải là cấp số nhân? A. 1 1 1; 2; 4; 8; L B. 2 3 4 3; 3 ; 3 ; 3 ; L C. 4; 2; ; ; L D. 2 4 1 1 1 1 ; ; ; ; L 2 4 6 p p p p Lời giải Chọn D
Các đáp án A, B, C đều là các cấp số nhân công bội lần lượt là 1 2;3; . 2 Xét đáp án D: 1 1 1 1 u 1 1 u 2 3 ; ; ; ; L æ æÆ = =/ = 2 4 6 2 p p p p u p p u 1 2
Câu 3: Cho cấp số nhân (u u = - 2 q = - 5. n ) với và
Viết bốn số hạng đầu tiên của cấp số nhân. 1
A. - 2; 10; 50; - 250.
B. - 2; 10; - 50; 250.
C. - 2; - 10; - 50; - 250.
D. - 2; 10; 50; 250. Lời giải. Chọn B Ï u Ô = - 2 1 Ô Ô Ï u Ô = - 2 u Ô = u q = 10 Ô 1 Ô 2 1 Ô Ì æ æÆ Ì q Ô = - 5 u Ô = u q = - 50 Ô Ó Ô 3 2 Ôu Ô Ô = u q = 250 Ô Ó 4 3
Câu 4: Tìm x để ba số 1+ x; 9 + x; 33+ x theo thứ tự đó lập thành một cấp số nhân. A. x = 1. B. x = 3. C. x = 7.
D. x = 3; x = 7. Lời giải Chọn B
Cấp số nhân + x + x
+ x æ æÆ ( + x)( + x)= ( + x)2 1 ; 9 ; 33 1 33 9 € x = 3.
Câu 5: Trong các dãy số (u u
n ) cho bởi số hạng tổng quát
sau, dãy số nào là một cấp số nhân? n A. 7 u = 7- 3 . n
B. u = 7- 3n. C. u = .
D. u = 7.3n. n n n 3n n Lời giải Chọn D Ï u Ô = 21
Dãy u = 7.3n là cấp số nhân có Ô 1 Ì n q Ô = 3 Ô Ó
Câu 6: Một cấp số nhân có 6 số hạng, số hạng đầu bằng 2 và số hạng thứ sáu bằng 486. Tìm công bội
q của cấp số nhân đã cho. A. q = 3. B. q = - 3. C. q = 2. D. q = - 2. Lời giải Chọn A Ï
Theo giải thiết ta có: u Ô = 2 Ô 1 5 5 5 Ì
æ æÆ 486 = u = u q = 2q € q = 243 € q = 3. 6 1 u Ô = 486 Ô Ó 6 Ï u Ô = 192
Câu 7: Tìm số hạng đầu u q Ô Ì . 1 và công bội
của cấp số nhân (u 6 n ), biết u Ô = 384 Ô Ó 7 Ï u Ô = 5 Ï u Ô = 6 Ï u Ô = 6 Ï u Ô = 5 A. Ô 1 Ì . B. Ô 1 Ì . C. Ô 1 Ì . D. Ô 1 Ì . q Ô = 2 Ô Ó q Ô = 2 Ô Ó q Ô = 3 Ô Ó q Ô = 3 Ô Ó Lời giải Chọn B Ï 5 q Ô = 2 Ï192 Ô = u = u q Ô Ô 6 1 Ô Ô Ì € Ì 192 . 6 384 Ô
= u = u q = u q q = 192q u Ô = = 6 Ô 7 1 ( 5 1 ) Ô 1 5 Ô Ó Ô q Ô Ó
Chương 3 : Giới hạn – Hàm số liên tục n n 1 3 4.2 - - - 3
Câu 1: Kết quả của lim bằng: 3.2n + 4n A. +¥ . B. -¥ . C. 0 . D. 1. Lời giải Chọn C æ 3 n ö æ 1 n ö æ 1 n ö ç ÷ - ç ÷ - n n 1 - n n 2. 3. 3 4.2 3 3 2.2 3 ç ÷ - - - - è 4 ø è 2 ø è 4 lim lim lim ø = = = 0 3.2n + 4n 3.2n + 4n æ 1 n ö 3.ç ÷ +1 è 2 ø
Câu 2: Giá trị đúng của 2 2 lim
n -1 - 3n + 2 là: ( ) A. +¥ . B. -¥ . C. 0 . D. 1. Lời giải Chọn B æ 1 2 ö 2 2 lim
n -1 - 3n + 2 = lim nç 1- - 3+ ÷ = -¥. ( ) 2 2 ç n n ÷ è ø æ ö Vì 1 2 lim n = + ; ¥ limç 1- - 3+ ÷ =1- 3 < 0. 2 2 ç n n ÷ è ø 3u -1 Câu 3: Cho dãy số (u limu = 2 lim n n ) có . Tính giới hạn . n 2u + 5 n -1 3 5 A. B. C. D. +¥ 5 2 9 Lời giải Chọn C 3u -1 3.2 -1 5
Từ limu = 2 ta có lim n = = . n 2u + 5 2.2 + 5 9 n 3 2 2n + n - 4 1 Câu 4: Biết lim
= với a là tham số. Khi đó 2 a - a bằng 3 an + 2 2 A. -12 . B. -2. C. 0 . D. -6. Lời giải Chọn A 3 æ 1 4 ö ç + - 3 2 n 2 ÷ 3 Ta có 2n + n - 4 è n n ø 2 1 lim = lim = = . 3 an + 2 3 æ 2 ö a 2 n ç a + ÷ 3 è n ø
Suy ra a = 4 . Khi đó 2 2
a - a = 4 - 4 = 1 - 2. Câu 5:
Trong các giới hạn hữu hạn sau, giới hạn nào có giá trị khác với các giới hạn còn lại? 3n -1 2n +1 4n +1 n +1 A. lim B. lim C. lim D. lim 3n +1 2n -1 3n -1 n -1 Lời giải Chọn C Ta có 1 1 3 - + 3n -1 3 1 2 2n +1 2 1 lim = lim n = =1 vì lim = 0; lim = lim n = =1 vì lim = 0 3n +1 1 3 2n -1 1 3 + n 2 2 - n n n 1 1 4 + + 4n +1 4 1 1 n +1 1 lim = lim n = vì lim = 0; lim = lim n = 1vì lim = 0. 3n -1 1 3 n -1 1 3 - n 1- n n n x - 2
Câu 6: Giới hạn lim bằng 2 x®2 x - 4 1 A. 2 . B. 4 . C. . D. 0 . 4 Lời giải Chọn C x - 2 x - 2 1 1 lim = lim = lim = . 2 x®2 x®2 x - 4
(x-2)(x+ 2) x®2 x+ 2 4 x - 3
Câu 7: Tính giới hạn L = lim x®3 x + 3 A. L = -¥ B. L = 0 C. L = +¥ D. L = 1 Lời giải Chọn B x - 3 3 - 3 Ta có L = lim = = 0. x®3 x + 3 3 + 3 4x +1 Câu 8: lim bằng x®-¥ -x +1 A. 2 B. 4 C. 1 - D. 4 - Lời giải Chọn D 1 4x +1 4 + lim = lim x = 4 - . x®-¥ -x +1 x®-¥ 1 -1+ x 3x + 2 Câu 9: lim x®-¥ bằng 2x - 4 1 3 A. - 3 . B. - . C. 1. D. . 2 4 2 Lời giải Chọn D 2 + 3x + 2 3 3 Ta có: lim = lim x = . x®-¥ x®-¥ 4 2x - 4 2 - 2 x
Câu 10: Trong các mệnh đề sau, mệnh đề nào sai? 1 1 1 1 A. lim = +¥. B. lim = -¥. C. lim = +¥. D. lim = +¥. x 0+ ® x x 0+ ® x + 5 x®0 x x 0+ ® x Lời giải Chọn B 1 Ta có: lim
= +¥ do lim x = 0và x > 0 . Vậy đáp án A đúng. x 0+ ® x x 0+ ® Suy ra đáp án B sai.
Các đáp án C và D đúng. Giải thích tương tự đáp án A . 2x +1
Câu 11: Tính giới hạn lim . x®-¥ x +1 1 A. . B. 1. C. 2 . D. 1 - . 2 Lời giải Chọn C 1 2x +1 2 + lim = lim x = 2. x®-¥ x +1 x®-¥ 1 1+ x 2 a 2x + 3 + 2017 1
Câu 12: Cho số thực a thỏa mãn lim
= . Khi đó giá trị của a là x®+¥ 2x + 2018 2 2 - A. a = 2 . B. a = 1 . C. a = 1 . D. a = - . 2 2 2 2 Lời giải Chọn A 3 2017 + + 2 a 2 a 2x + 3 + 2017 1 2 x x 1 a 2 1 Ta có: lim = Û lim = Û = 2 Û a = . x®+¥ 2x + 2018 2 x®+¥ 2018 2 2 + 2 2 2 x
Câu 13: Cho các giới hạn: lim f ( x) = 2; lim g ( x) = 3, hỏi lim 3 é f ë
(x)-4g(x)ù bằng û x® ® 0 x x 0 x x® 0 x A. 5 . B. 2 . C. 6 - . D. 3 . Lời giải Chọn C Ta có lim 3 é f ë
(x)-4g(x)ù = lim 3 f x - lim 4g x = 3lim f (x)- 4 lim g (x) = 6 - . û ( ) ( ) x® ® ® ® ® 0 x x 0 x x 0 x x 0 x x 0 x x +1
Câu 14: Giới hạn lim bằng x®- ( x + 2)2 2 3 A. -¥ . B. . C. 0 . D. +¥ . 16 Lời giải Chọn A x +1 1 Ta có: lim = lim . x +1 = -¥ 2 2 ( ) . x 2 ®- ( x + 2) x 2 ®- ( x + 2) 1 Do lim = +¥ và lim (x + ) 1 = 1 - < 0. x®- ( x + 2)2 2 x 2 ®- 4x - 3
Câu 15: Tìm giới hạn lim x 1+ ® x -1 A. +¥ . B. 2 . C. -¥ . D. 2 - . Lời giải Chọn A 4x - 3 Ta có lim
= +¥ vì lim (4x -3) =1, lim (x - )
1 = 0, x -1 > 0 khi x 1+ ® . x 1+ ® x -1 x 1+ ® x 1+ ® 2 2x + 3x - 2 Câu 16: lim bằng 2 x 2 ®- x - 4 5 5 A. . B. - 1 . C. . D. 2 . 4 4 4 Lời giải Chọn A 2 2x + 3x - 2 (2x - )1(x + 2) 2x -1 5 Ta có lim = lim = lim = . 2 x 2 ®- x - 4 x 2
®- ( x - 2)( x + 2) x 2 ®- x - 2 4 2 x + 3x - 4 Câu 17: lim bằng. 2 x 4 ®- x + 4x 5 5 A. 1. B. 1 - . C. . D. - . 4 4 Lời giải Chọn C 2 x + 3x - 4 x -1 Ta có: lim = 5 lim = . 2 x 4 ®- x + 4x x 4 ®- x 4 2x + 3 Câu 18: Tính lim . x®-¥ 2 2x - 3 1 1 A. . B. - . C. 2 . D. - 2 . 2 2 Lời giải Chọn D æ 3 ö æ 3 ö x 2 + x 2 + 3 + 2x + 3 ç ÷ ç ÷ 2 2 Ta có: lim è x è x lim ø = lim ø = = lim x = - = - 2 x®-¥ 2 2x - 3 x®-¥ 3 x®-¥ 3 x®-¥ 3 2 . x 2 - -x 2 - - 2 - 2 x 2 x 2 x . 4x +1 -1
Câu 19: Tính giới hạn K = lim . 2 x®0 x - 3x 2 A. K = - 2 . B. K = 4 . C. K = . D. K = 0 . 3 3 3 Lời giải Chọn A 4x +1 -1 4x 4 2 Ta có K = lim = lim = lim = - . 2 x®0 x - 3x
x®0 x ( x - ) 3 ( 4x +1 + ) 1 x®0 ( x - ) 3 ( 4x +1 + ) 1 3 2
ìax + bx khi x ³1
Câu 20: Cho hàm số f (x) = í
. Để hàm số đã cho có đạo hàm tại x = 1 thì 2a + b
î2x -1 khi x <1 bằng: A. 2 . B. 5 . C. 2 - . D. 5 - . Lời giải Chọn A
f (x)- f ( ) 1 2x -1-1 lim = lim = 2; x 1- ® x -1 x 1- ® x -1
f (x)- f ( ) 1 2
ax + bx - a - b a ( 2 x - ) 1 + b(x - ) 1 (x - )1éa ë (x + ) 1 + bù lim = lim = lim lim û = x 1+ ® x -1 x 1+ ® x -1 x 1+ ® x -1 x 1+ ® x -1 = lim éa ë ( x + ) 1 + bù = + û 2a b x 1+ ®
f (x)- f ( ) 1
f (x)- f ( ) 1
Theo yêu cầu bài toán: lim = lim Û 2a + b = 2. x 1- - x 1 x 1 + ® ® x -1 x + 1 Câu 21: lim bằng x®-¥ 6x - 2 1 1 1 A. . B. . C. . D. 1. 2 6 3 Lời giải Chọn B 1 + x + 1 1 • 1 Ta có lim = lim x = . x®-¥ 6x - 2 x ® -¥ 2 6 - 6 x Câu 22: Tính 2 lim
x - 4x + 2 - x x®+¥ ( ) A. 4 - . B. 2 - . C. 4 . D. 2 . Lời giải Chọn B 2 2 2 4 - x + 2 4 - + 2
x - 4x + 2 - x lim
x - 4x + 2 - x = lim = lim = lim x = 2 - . x®+¥ (
) x®+¥ 2x-4x+2+x x®+¥ 2x-4x+2+x x®+¥ 4 2 1- + +1 2 x x ì x - 2 ï khi x ¹ 4 ï Câu 23: Cho hàm số x - 4 f (x) = í
. Khẳng định nào sau đây đúng nhất ? 1 ï khi x = 4 ïî4
A. Hàm số liên tục tại x = 4 .
B. Hàm số liên tục tại mọi điểm trên tập xác định nhưng gián đoạn tại x = 4 .
C. Hàm số không liên tục tại x = 4 .
D. Tất cả đều sai. Lời giải Chọn A x - 2 1 1
Ta có : lim f (x) = lim = lim = = f (4) x®4 x®4 x®4 x - 4 x + 2 4
Hàm số liên tục tại điểm x = 4 .
Chương 4: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
Bài 1: Đường thẳng và mặt phẳng trong không gian
Câu 1: Trong các khẳng định sau, khẳng định nào đúng?
A. Qua 2 điểm phân biệt có duy nhất một mặt phẳng.
B. Qua 3 điểm phân biệt bất kì có duy nhất một mặt phẳng.
C. Qua 3 điểm không thẳng hàng có duy nhất một mặt phẳng.
D. Qua 4 điểm phân biệt bất kì có duy nhất một mặt phẳng. Lời giải Chọn C
A sai. Qua 2 điểm phân biệt, tạo được 1 đường thẳng, khi đó chưa đủ điều kiện để lập một mặt
phẳng xác định. Có vô số mặt phẳng đi qua 2 điểm đã cho.
B sai. Trong trường hợp 3 điểm phân biệt thẳng hàng thì chỉ tạo được đường thẳng, khi đó có vô số
mặt phẳng đi qua 3 điểm phân biệt thẳng hàng.
D sai. Trong trường hợp 4 điểm phân biệt thẳng hàng thì có vô số mặt phẳng đi qua 4 điểm đó hoặc
trong trường hợp 4 điểm mặt phẳng không đồng phẳng thì sẽ tạo không tạo được mặt phẳng nào đi qua cả 4 điểm.
Câu 2: Trong các mệnh đề sau đây, mệnh đề nào sai?
A. Hai mặt phẳng có một điểm chung thì chúng có vô số điểm chung khác nữa.
B. Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.
C. Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất.
D. Hai mặt phẳng cùng đi qua 3 điểm ,
A B, C không thẳng hàng thì hai mặt phẳng đó trùng nhau . Lời giải Chọn B
Nếu 2 mặt phẳng trùng nhau, khi đó 2 mặt phẳng có vô số điểm chung và chung nhau vô số đường thẳng.
Câu 3: Cho hình chóp S.ABCD có đáy là hình thang ABCD ( AB ! CD). Khẳng định nào sau đây sai?
A. Hình chóp S.ABCD có 4 mặt bên.
B. Giao tuyến của hai mặt phẳng (SAC) và (SBD) là SO (O là giao điểm của AC và BD).
C. Giao tuyến của hai mặt phẳng (SAD) và (SBC) là SI (I là giao điểm của AD và BC).
D. Giao tuyến của hai mặt phẳng (SAB) và (SAD) là đường trung bình của ABCD Lời giải Chọn D S A B O D C I
• Hình chóp S.ABCD có 4 mặt bên: (SAB), (SBC), (SCD), (SAD). Do đó A đúng.
• S là điểm chung thứ nhất của hai mặt phẳng (SAC) và (SBD). O
ì Î AC Ì (SAC) Þ OÎ ï (SAC) í
Þ O là điểm chung thứ hai của hai mặt phẳng (SAC) và (SBD). O ï Î BD Ì î
(SBD) Þ OÎ(SBD) ¾¾ ®(SAC)Ç(SBD) = . SO Do đó B đúng.
• Tương tự, ta có (SAD)Ç(SBC) = SI. Do đó C đúng.
• (SAB)Ç(SAD) = SA mà SA không phải là đường trung bình của hình thang ABCD Do đó D sai.
Câu 4: Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác BCD. Giao tuyến của mặt phẳng (ACD ) và (GAB là: )
A. AM (M là trung điểm của AB).
B. AN (N là trung điểm của CD).
C. AH (H là hình chiếu của B trên CD).
D. AK (K là hình chiếu củaC trên BD). Lời giải Chọn B A B D G N C
∑ A là điểm chung thứ nhất giữa hai mặt phẳng (ACD ) và (GAB). Ï N Ô B
Œ G à (ABG)fi N ( Œ ABG) ∑ Ta có BG CD N Ô « = æ æÆ Ì
fi N là điểm chung thứ hai giữa hai mặt N Ô C
Œ D à (ACD)fi N ( Œ Ô ACD) Ó phẳng (ACD ) và (GAB).
Vậy (ABG)« (ACD)= AN.
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm AD
và BC. Giao tuyến của hai mặt phẳng (SMN )và (SAC ) là: A. SD.
B. SO (O là tâm hình bình hành ABCD).
C. SG (G là trung điểm AB).
D. SF (F là trung điểm CD). Lời giải Chọn B S A M D T º O B N C
∑ S là điểm chung thứ nhất giữa hai mặt phẳng (SMN )và (SAC).
∑ Gọi O = AC « BD là tâm của hình hình hành.
Trong mặt phẳng (ABCD
) gọi T = AC « MN ÏO Ô A
Œ C à (SAC)fi O ( Œ SAC) Ô fi Ì
fi O là điểm chung thứ hai giữa hai mặt phẳng (SMN )và (SAC). O Ô M
Œ N à (SMN )fi O ( Œ Ô SMN ) Ó
Vậy (SMN)« (SAC)= . SO
Bài 2: Hai đường thẳng song song trong không gian
Câu 1: Trong các mệnh đề sau, mệnh đề nào sai?
A. Hai đường thẳng không có điểm chung thì chéo nhau.
B. Hai đường thẳng chéo nhau thì không có điểm chung.
C. Hai đường thẳng phân biệt không cắt nhau và không song song thì chéo nhau.
D. Hai đường thẳng phân biệt không chéo nhau thì hoặc cắt nhau hoặc song song. Lời giải Chọn A
Hai đường thẳng không có điểm chung thì chúng song song (khi chúng đồng phẳng) hoặc chéo nhau
(khi chúng không đồng phẳng).
Câu 2: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song với nhau.
B. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì trùng nhau.
C. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song với nhau hoặc trùng nhau.
D. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì chúng lần lượt nằm trên hai mặt phẳng song song. Lời giải Chọn C
Câu 3: Cho ba mặt phẳng phân biệt (a ), (b ), (g ) có (a )Ç(b ) = d ; (b )Ç(g ) = d ; 1 2
(a)Ç(g ) = d . Khi đó ba đường thẳng d , d , d : 3 1 2 3
A. Đôi một cắt nhau.
B. Đôi một song song. C. Đồng quy.
D. Đôi một song song hoặc đồng quy. Lời giải Chọn D
Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyền ấy hoặc đồng quy hoặc đôi một song song.
Câu 4: Trong không gian, cho 3 đường thẳng , a ,
b c , biết a ! b, a và c chéo nhau. Khi đó hai đường
thẳng b và c :
A. Trùng nhau hoặc chéo nhau. B. Cắt nhau hoặc chéo nhau.
C. Chéo nhau hoặc song song. D. Song song hoặc trùng nhau. Lời giải Chọn B
Giả sử b ! c fi c ! a (mâu thuẫn với giả thiết).
Câu 5: Trong không gian, cho ba đường thẳng phân biệt , a ,
b c trong đó a ! b. Khẳng định nào sau đây sai?
A. Nếu a ! c thì b ! c.
B. Nếu c cắt a thì c cắt b . C. Nếu A a Œ và B b Œ thì ba đường thẳng , a ,
b AB cùng ở trên một mặt phẳng.
D. Tồn tại duy nhất một mặt phẳng qua a và b . Lời giải Chọn B
Nếu c cắt a thì c cắt b hoặc c chéo b .
Câu 6: Cho tứ diện ABCD. Gọi I,J lần lượt là trọng tâm các tam giác ABC và ABD. Chọn khẳng
định đúng trong các khẳng định sau?
A. IJ song song với CD.
B. IJ song song với AB.
C. IJ chéo CD.
D. IJ cắt AB. Lời giải Chọn A A J I N B C M D
Gọi M,N lần lượt là trung điểm của BC, BD.
fi MN là đường trung bình của tam giác BCD fi MN //CD (1 ) AI AJ 2
I, J lần lượt là trọng tâm các tam giác ABC và ABD fi = = fi IJ P MN (2 ) AM AN 3 Từ ( ) 1 và (2 ) suy ra: IJ P CD .
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I,J ,E, F lần lượt là trung điểm ,
SA SB,SC,SD. Trong các đường thẳng sau, đường thẳng nào không song song với IJ ?
A. EF. B. DC. C. AD. D. AB. Lời giải Chọn C S F I J E A D B C
Ta có IJ P AB (tính chất đường trung bình trong tam giác SAB ) và EF P CD (tính chất đường trung
bình trong tam giác SCD ).
Mà CD P AB (đáy là hình bình hành) æ æÆ CD P AB P EF P IJ.
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi d là giao tuyến của hai mặt phẳng (SAD và
) (SBC).Khẳng định nào sau đây đúng?
A. d qua S và song song với BC.
B. d qua S và song song với DC.
C. d qua S và song song với AB.
D. d qua S và song song với BD. Lời giải Chọn A S d A D B C Ï(
ÔSAD)« (SBC)= S Ô Ô Ta có Ì AD Ô
à (SAD),BC à (SBC
) æ æÆ (SAD)« (SBC)= Sx P AD P BC (với d ∫ Sx ). ÔAD Ô Ô BC Ô Ó P
Bài 3: Đường thẳng và mặt phẳng song song
Câu 1: Cho đường thẳng a và mặt phẳng (P
) trong không gian. Có bao nhiêu vị trí tương đối của a và (P ? ) A. 2. B. 3. C. 1. D. 4. Lời giải Chọn B a a a A (P) (P) (P)
Có 3 vị trí tương đối của a và (P , đó l )
à: a nằm trong (P ,
) a song song với (P
) và a cắt (P . )
Câu 2: Cho hai đường thẳng phân biệt ,
a b và mặt phẳng (a . G )
iả sử a ! b, b ! (a . K ) hi đó:
A. a ! (a ).
B. a Ã(a ).
C. a cắt (a ).
D. a ! (a
) hoặc a à (a ). Lời giải Chọn D
Câu 3: Cho hai đường thẳng phân biệt ,
a b và mặt phẳng (a .
) Giả sử a ! (a , ) b à (a . K ) hi đó: A. a ! . b B. , a b chéo nhau.
C. a ! b hoặc , a b chéo nhau. D. , a b cắt nhau. Lời giải Chọn C a a b c a a b Vì a ! (a
) nên tồn tại đường thẳng c à (a
) thỏa mãn a ! c. Suy ra b, c đồng phẳng và xảy ra các trường hợp sau:
Nếu b song song hoặc trùng với c thì a ! b.
Nếu b cắt c thì b cắt (b)∫ ( , a c ) nên ,
a b không đồng phẳng. Do đó , a b chéo nhau.
Câu 4: Cho đường thẳng a nằm trong mặt phẳng (a . G )
iả sử b À(a . M )
ệnh đề nào sau đây đúng?
A. Nếu b ! (a ) thì b ! . a
B. Nếu b cắt (a )thì b cắt . a
C. Nếu b ! a thì b ! (a).
D. Nếu b cắt (a )và (b )chứa b thì giao tuyến của (a )và (b )là đường thẳng cắt cả a và .b Lời giải Chọn C
A sai. Nếu b ! (a
) thì b ! a hoặc , a b chéo nhau.
B sai. Nếu b cắt (a )thì b cắt a hoặc , a b chéo nhau.
D sai. Nếu b cắt (a )và (b )chứa b thì giao tuyến của (a )và (b )là đường thẳng cắt a hoặc song song với a .
Câu 5: Cho hai đường thẳng phân biệt ,
a b và mặt phẳng (a .
) Giả sử a ! (a ) và b ! (a . ) Mệnh đề nào sau đây đúng?
A. a và b không có điểm chung.
B. a và b hoặc song song hoặc chéo nhau.
C. a và b hoặc song song hoặc chéo nhau hoặc cắt nhau.
D. a và b chéo nhau. Lời giải Chọn C
Câu 6: Cho mặt phẳng (P
) và hai đường thẳng song song a và b . Khẳng định nào sau đây đúng? A. Nếu (P
) song song với a thì (P ) cũng song song với . b B. Nếu (P
) cắt a thì (P ) cũng cắt . b C. Nếu (P
) chứa a thì (P ) cũng chứa . b
D. Các khẳng định A, B, C đều sai. Lời giải Chọn B Gọi (Q)∫ ( , a b . )
A sai. Khi b = (P)« (Q)fi b Ã(P . )
C sai. Khi (P)π (Q)fi b ! (P . )
Xét khẳng định B, giả sử (P
) không cắt b khi đó b Ã(P
) hoặc b ! (P .
) Khi đó, vì b ! a nên a Ã(P )
hoặc a cắt (P
) (mâu thuẫn với giả thiết (P ) cắt a ).
Vậy khẳng định B đúng.
Câu 7: Cho d ! (a , m )
ặt phẳng (b )qua d cắt (a )theo giao tuyến d . K ¢ hi đó:
A. d ! d .¢
B. d cắt d . ¢
C. d và d
¢ chéo nhau. D. d ∫ d .¢ Lời giải Chọn A
Ta có: d¢= (a)« (b . D ) o d và d ¢ cùng thuộc (b
) nên d cắt d
¢ hoặc d ! d .¢
Nếu d cắt d . K ¢
hi đó, d cắt (a )(mâu thuẫn với giả thiết). Vậy d ! d .¢
Câu 8: Có bao nhiêu mặt phẳng song song với cả hai đường thẳng chéo nhau? A. 1. B. 2. C. 3. D. Vô số. Lời giải Chọn D a c a b
Gọi a và b là 2 đường thẳng chéo nhau, c là đường thẳng song song với a và cắt b . Gọi (a )∫ ( , b c . D )
o a ! c fi a ! (a . )
Giả sử (b)! (a . M ) à b (
Πa )fi b ! (b . )
Mặt khác, a ! (a)fi a ! (b . )
Có vô số mặt phẳng (b)! (a . V )
ậy có vô số mặt phẳng song song với 2 đường thẳng chéo nhau.
Câu 9: Cho hai đường thẳng chéo nhau a và b . Khẳng định nào sau đây sai?
A. Có duy nhất một mặt phẳng song song với a và . b
B. Có duy nhất một mặt phẳng qua a và song song với . b
C. Có duy nhất một mặt phẳng qua điểm M , song song với a và b (với M là điểm cho trước).
D. Có vô số đường thẳng song song với a và cắt . b Lời giải Chọn A
Có có vô số mặt phẳng song song với 2 đường thẳng chéo nhau. Do đó A sai.
Câu 10: Cho ba đường thẳng đôi một chéo nhau , a , b c . Gọi (P
) là mặt phẳng qua a , (Q ) là mặt phẳng
qua b sao cho giao tuyến của (P ) và (Q
) song song với c . Có nhiều nhất bao nhiêu mặt phẳng (P ) và (Q
) thỏa mãn yêu cầu trên?
A. Một mặt phẳng (P , m )
ột mặt phẳng (Q).
B. Một mặt phẳng (P , vô s )
ố mặt phẳng (Q).
C. Một mặt phẳng (Q , vô s ) ố mặt phẳng (P).
D. Vô số mặt phẳng (P ) và (Q). Lời giải Chọn A a c b (Q) (P)
Vì c song song với giao tuyến của (P ) và (Q ) nên c ! (P ) và c ! (Q . ) Khi đó, (P
) là mặt phẳng chứa a và song song với c, mà a và c chéo nhau nên chỉ có một mặt phẳng như vậy.
Tương tự cũng chỉ có một mặt phẳng (Q
) chứa b và song song với c .
Vậy có nhiều nhất một mặt phẳng (P
) và một mặt phẳng (Q
) thỏa yêu cầu bài toán.
Câu 11: Cho hình chóp tứ giác S.ABCD . Gọi M và N lần lượt là trung điểm của SA và SC . Khẳng
định nào sau đây đúng?
A. MN // mp (ABCD).
B. MN // mp (SAB).
C. MN // mp (SCD).
D. MN // mp (SBC). Lời giải Chọn A
Xét tam giác SAC có M, N lần lượt là trung điểm của , SA SC .
Suy ra MN // AC mà AC Ã(ABCD) æ æÆ MN // mp(ABCD).
Câu 12: Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi O, O 1
lần lượt là tâm của ABCD, ABEF . M là trung điểm của CD. Khẳng định nào sau đây sai?
A. OO //(BEC).
B. OO //(AFD). 1 1
C. OO //(EFM).
D. MO cắt (BEC). 1 1 Lời giải Chọn D D C O A B O1 F E
Xét tam giác ACE có O, O lần lượt là trung điểm của AC, AE . 1
Suy ra OO là đường trung bình trong tam giác ACE fi OO // EC . 1 1
Tương tự, OO là đường trung bình của tam giác BFD nên OO // FD. 1 1
Vậy OO //(BEC , ) OO // (AFD
) và OO // (EFC . Chú ý r )
ằng: (EFC)= (EFM). 1 1 1
Câu 13: Cho tứ diện ABCD. Gọi M, N, P, Q, ,
R S theo thứ tự là trung điểm của các cạnh
AC, BD, AB, CD, AD, BC . Bốn điểm nào sau đây không đồng phẳng?
A. P, Q, , R S.
B. M, P, , R S. C. M, , R S, N.
D. M, N, P, Q. Lời giải Chọn C A R M P B C Q S N D
Theo tính chất của đường trung bình của tam giác ta có
PS // AC // QR suy ra P, Q, , R S đồng phẳng
Tương tự, ta có được PM // BC // NQ suy ra P, M, N, Q đồng phẳng.
Và NR //CD // SN suy ra M, ,
R S, N đồng phẳng.
Bài 4,5: Hai mặt phẳng song song - Hình lăng trụ và hình hộp
Câu 1: Trong các điều kiện sau, điều kiện nào kết luận mp(a )P mp(b)?
A. (a )P (g
) và (b)P (g) ( ( g
) là mặt phẳng nào đó ).
B. (a )P a và (a )P b với ,ab là hai đường thẳng phân biệt thuộc (b).
C. (a )P a và (a )P b với ,ab là hai đường thẳng phân biệt cùng song song với (b).
D. (a )P a và (a )P b với ,ab là hai đường thẳng cắt nhau thuộc (b). Lời giải Chọn D a a b b a b a b
Trong trường hợp: (a )P (g
) và (b)P (g) ( ( g
) là mặt phẳng nào đó) thì (a ) và (b ) có thể trùng nhau fi Loại A
(a )P a và (a )P b với ,
a b là hai đường thẳng phân biệt thuộc (b ) thì (a ) và (b ) vẫn có thể cắt nhau (hình 1) fi Loại B
(a )P a và (a )P b với ,
a b là hai đường thẳng phân biệt cùng song song với (b ) thì (a ) và (b ) vẫn có
thể cắt nhau (hình 2) fi Loại C
Câu 2: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu mặt phẳng (a ) P (b )thì mọi đường thẳng nằm trong (a )đều song song với (b).
B. Nếu hai mặt phẳng (a )và (b
) song song với nhau thì bất kì đường thẳng nào nằm trong (a ) cũng
song song với bất kì đường thẳng nào nằm trong (b).
C. Nếu hai đường thẳng phân biệt a và b song song lần lượt nằm trong hai mặt phẳng (a ) và (b )
phân biệt thì (a)P (b).
D. Nếu đường thẳng d song song với mp(a
) thì nó song song với mọi đường thẳng nằm trong mp(a ). Lời giải Chọn A a a d a a b b a b b a Hình 1 Hình 2 Hình 3
Nếu hai mặt phẳng (a )và (b )song song với nhau thì hai đường thẳng bất kì lần lượt thuộc (a ) và (b )
có thể chéo nhau (Hình 1) fi Loại B
Nếu hai đường thẳng phân biệt a và b song song lần lượt nằm trong hai mặt phẳng (a ) và (b ) phân
biệt thì hai mặt phẳng (a )và (b )có thể cắt nhau (Hình 2) fi Loại C
Nếu đường thẳng d song song với mp(a
) thì nó có thể chéo nhau với một đường thẳng nào đó nằm trong (a ). (Hình 3).
Câu 3: Cho đường thẳng a à mp(P
) và đường thẳng b à mp(Q). Mệnh đề nào sau đây đúng?
A. (P)P (Q)fi a P . b
B. a P b fi (P)P (Q).
C. (P)P (Q)fi a P (Q
) và b P (P). D. a và b chéo nhau. Lời giải Chọn C
Với đường thẳng a à mp(P
) và đường thẳng b à mp(Q )
Khi (P)P (Q)fi a P b hoặc ,ab chéo nhau fi A sai.
Khi a P b fi (P)P (Q
) hoặc (P),(Q
) cắt nhau theo giao tuyến song song với a và b fi B sai.
a và b có thể chéo nhau, song song hoặc cắt nhau fi D sai.
Câu 4: Hai đường thẳng a và b nằm trong mp(a ). Hai đường thẳng a
¢ và b¢ nằm trong mp(b).
Mệnh đề nào sau đây đúng? A. Nếu a P a
¢ và b P b ¢thì (a)P (b).
B. Nếu (a )P (b )thì a P a ¢và b P b .¢
C. Nếu a P b và a¢P b
¢ thì (a)P (b).
D. Nếu a cắt b và a P a ,¢ b P b ¢thì (a)P (b). Lời giải Chọn D a a a a b b a' b' a' b Hình 1 Hình 2 Nếu a P a
¢ và b P b ¢thì (a )P (b )hoặc (a )cắt (b )(Hình 1) fi A sai.
Nếu (a )P (b )thì a P a ¢hoặc , a a
¢chéo nhau (Hình 2) fi B sai.
Nếu a P b và a¢P b
¢ thì (a )P (b )hoặc (a )cắt CC .¢ (Hình 1) fi C sai.
Câu 5: Cho hai mặt phẳng (P ) và (Q
) cắt nhau theo giao tuyến D. Hai đường thẳng p và q lần lượt nằm trong (P
) và (Q). Trong các mệnh đề sau, mệnh đề nào đúng?
A. p và q cắt nhau.
B. p và q chéo nhau.
C. p và q song song.
D. Cả ba mệnh đề trên đều sai. Lời giải Chọn D P P p P p p Q D q Q q Q D D q
Ta có p và q có thể cắt nhau, song song, chéo nhau (hình vẽ).
Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P theo thứ tự là trung điểm của ,
SA SD và AB. Khẳng định nào sau đây đúng? A. (NOM ) cắt (OPM ). B. (MON // ) (SBC).
C. (PON)« (MNP)= NP. D. (NMP // ) (SBD). Lời giải Chọn B S M P N A B O D C
Ta có MN là đường trung bình của tam giác SAD suy ra MN // AD. ( ) 1
Và OP là đường trung bình của tam giác BAD suy ra OP // AD. (2 ) Từ ( ) 1 ,(2
) suy ra MN //OP // AD fi M, N, O, P đồng phẳng.
Lại có MP // SB, OP // BC suy ra (MNOP // ) (SBC ) hay (MON // ) (SBC).
Bài 5: Hình lăng trụ và hình hộp
Câu 7: Trong các mệnh đề sau, mệnh đề nào sai?
A. Hình lăng trụ có các cạnh bên song song và bằng nhau.
B. Hai mặt đáy của hình lăng trụ nằm trên hai mặt phẳng song song.
C. Hai đáy của lăng trụ là hai đa giác đều.
D. Các mặt bên của lăng trụ là các hình bình hành. Lời giải Chọn C
Xét hình lăng trụ có đáy là một đa giác (tam giác, tứ giác,… ), ta thấy rằng
Hình lăng trụ luôn có các cạnh bên song song và bằng nhau.
Hai mặt đáy của hình lăng trụ nằm trên hai mặt phẳng song song.
Hai đáy của lăng trụ là hai đa giác bằng nhau (tam giác, tứ giác,… )
Các mặt bên của lăng trụ là các hình bình hành vì có hai cạnh là hai cạnh bên của hình lăng trụ, hai
cạnh còn lại thuộc hai đáy song song.
Câu 8: Trong các mệnh đều sau, mệnh đề nào sai?
A. Các cạnh bên của hình lăng trụ bằng nhau và song song với nhau.
B. Các mặt bên của hình lăng trụ là các hình bình hành.
C. Các mặt bên của hình lăng trụ là các hình bình hành bằng nhau.
D. Hai đáy của hình lăng trụ là hai đa giác bằng nhau. Lời giải Chọn C
Các mặt bên của hình lăng trụ là các hình hình hành, chúng bằng nhau nếu hình lăng trụ có đáy là tam giác đều.
Câu 9: Trong các mệnh đều sau, mệnh đề nào đúng?
A. Các cạnh bên của hình chóp cụt đôi một song song.
B. Các cạnh bên của hình chóp cụt là các hình thang.
C. Hai đáy của hình chóp cụt là hai đa giác đồng dạng.
D. Cả 3 mệnh đề trên đều sai. Lời giải Chọn C
Xét hình chóp cụt có đáy là đa giác (tam giác, tứ giác,… ) ta thấy rằng:
Các cạnh bên của hình chóp cụt đôi một cắt nhau.
Các mặt bên của hình chóp cụt là các hình thang cân.
Hai đáy của hình chóp cụt là hai đa giác đồng dạng.
Câu 10: Trong các mệnh đều sau, mệnh đề nào sai?
A. Trong hình chóp cụt thì hai đáy là hai đa giác có các cạnh tương ứng song song và các tỉ số các
cặp cạnh tương ứng bằng nhau.
B. Các mặt bên của hình chóp cụt là các hình thang.
C. Các mặt bên của hình chóp cụt là các hình thang cân.
D. Đường thẳng chứa các cạnh bên của hình chóp cụt đồng quy tại một điểm. Lời giải Chọn C
Với hình chóp cụt, các mặt bên của hình chóp cụt là các hình thang.
Câu 11: Cho hình lăng trụ ABC.A B C . Trong các khẳng định sau, khẳng định nào sai? 1 1 1 A. (ABC // ) (A B C . AA (BCC . 1 ) 1 1 1 ) B. // 1
C. AB //(A B C . AA B B 1 1 1 ) D. là hình chữ nhật. 1 1 Lời giải Chọn D
Vì mặt bên AA B B là hình bình hành, còn nó là hình chữ nhật nếu ABC.A B C là hình lăng trụ đứng. 1 1 1 1 1
Câu 12: Cho hình hộp ABC .
D A B C D . Khẳng định nào dưới đây là sai? 1 1 1 1
A. ABCD là hình bình hành.
B. Các đường thẳng AC, AC , DB , D B đồng quy. 1 1 1 1
C. (ADD A //(BCC B . 1 1 ) 1 1 )
D. AD CB là hình chữ nhật. 1 Lời giải Chọn D D C A B D1 C1 A1 B1
Dựa vào hình vẽ và tính chất của hình hộp chữ nhật, ta thấy rằng:
∑ Hình hộp có đáy ABCD là hình bình hành.
∑ Các đường thẳng AC, AC , DB , D B cắt nhau tại tâm của AAC C, BDD B . 1 1 1 1 1 1 1 1
∑ Hai mặt bên (ADD A , BCC B 1 1 ) (
1 1 ) đối diện và song song với nhau.
∑ AD và CB là hai đường thẳng chéo nhau suy ra AD CB không phải là hình chữ nhật. 1 1
Câu 13: Cho hình hộp ABCD.A B ¢ C ¢ D ¢
¢ có các cạnh bên AA ,¢ BB ,¢ CC ,¢ DD .¢ Khẳng định nào dưới đây sai? A. (AA B ¢ B ¢ // ) (DD C ¢ C ¢ ). B. (BA D ¢ ¢ // ) (ADC )¢. C. A B ¢ CD ¢
là hình bình hành. D. BB D ¢ D ¢ là một tứ giác. Lời giải Chọn B D C A B D' C' A' B'
Dựa vào hình vẽ dưới và tính chất của hình hộp, ta thấy rằng:
∑ Hai mặt bên (AA B ¢ B ¢ ) và (DD C ¢ C ¢
) đối diện, song song với nhau.
∑ Hình hộp có hai đáy (ABCD), (A B ¢ C ¢ D ¢ )
¢ là hình bình hành fi A B
¢ ¢= CD và A B ¢ //
¢ CD suy ra A B ¢ CD ¢ là hình hình hành. ∑ BD // B D ¢
¢ suy ra B, B ,¢ D ,¢ D đồng phẳng fi BB D ¢ D ¢ là tứ giác. ∑ Mặt phẳng (BA D ¢ ¢
) chứa đường thẳng CD ¢mà CD ¢cắt C D ¢ suy ra (BA D ¢ ¢ ) không song song với (ADC )¢.
Bài 6: Phép chiếu song song. Hình biểu diễn của 1 hình trong không gian
Câu 1: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hình chiếu song song của hai đường thẳng cắt nhau là hai đường thẳng song song.
B. Hình chiếu song song của một hình bình hành là một hình bình hành.
C. Phép chiếu song song biến một tam giác thành một tam giác nếu mặt phẳng chứa tam giác không
cùng phương với phương chiếu.
D. Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng. Lời giải Chọn C ìAH ^ BC ìAB C ∥ D,AD B ∥ C
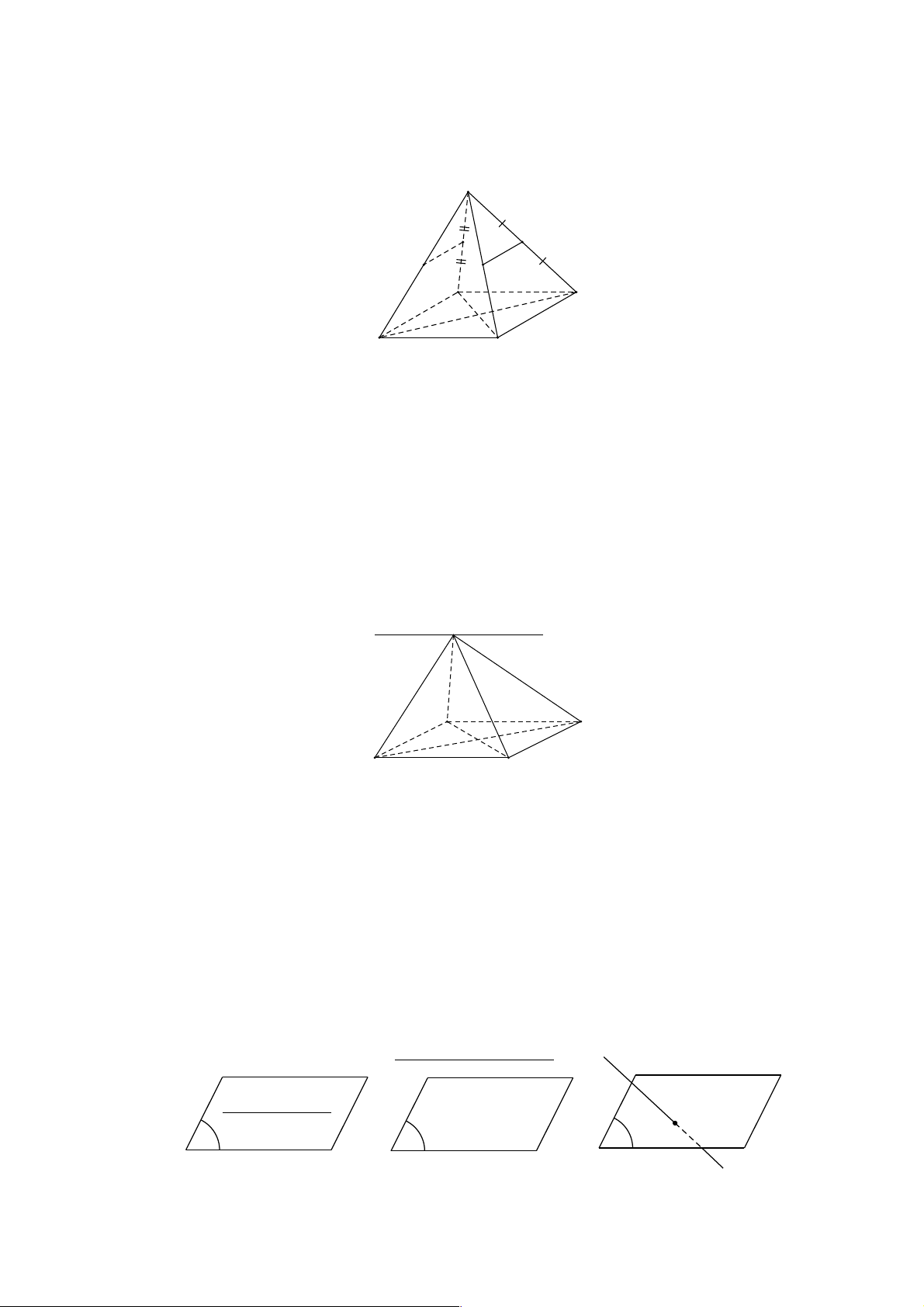
Câu 2: Trên hình A có í và hình B có í HB = î HC AC ^ î BD A A D O B H C B C Hình A Hình B
Hãy Chọn mệnh đề đúng trong các mệnh đề sau:
A. ABC là tam giác đều.
B. ABC là tam giác cân tại A C. ABCD là hình thoi. D. B và C đúng. Lời giải Chọn D Nhìn hình vẽ, ta thấy:
- Tam giác ABC có AH vừa là đường cao vừa là trung tuyến nên cân tại A à B đúng. - Tứ giác ABCD có AB C ∥ D, AC B
∥ D nên là hình bình hành. Mặt khác hai đường chéo của nó vuông
góc nên ABCD là hình thoi à C đúng.
Câu 3: Trên hình C, ta có phép chiếu song song theo phương d và mặt phẳng chiếu (P); AB C ∥ G và
AB = DG ; A’, B’, C’, D’, E’, G’ lần lượt là hình chiếu của A, B, C, D, E, G qua phép chiếu nói trên. D E G C B d A C' D' G' E' P A' B' Hình C
Mệnh đề nào sau đây đúng? A. DG = D'G' = 1. B. C'D' = CD . AB A'B' D'E' DE C. D'G' = A'B' .
D. Tất cả A, B, C đều đúng. Lời giải Chọn D
The định lí 2, ta thấy câu A và câu B đúng. Từ câu A đúng suy ra câu C đúng.
Câu 4: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hình chiếu song song của hai đường thẳng chéo nhau có thể song song với nhau.
B. Hình chiếu song song của hai đường thẳng cắt nhau thì song song.
C. Hình chiếu song song của hai một hình vuông là một hình vuông.
D. Hình chiếu song song của một lục giác đều là một lục giác đều. Lời giải P Q a b a' b' R Chọn A
Dựng mặt phẳng (P) qua a và song song với b. Dựng mặt phẳng (Q) qua b và song song với a. Giả sử
(P) song song với (Q). Ta Chọn phương chiếu d song song với (P) và mặt phẳng chiếu (R) sao
cho (R) cắt (P) và (Q) lần lượt theo hai giao tuyến a’ và b’. Khi đó hình chiếu a’, b’ song song với nhau.
Câu 5: Qua phép chiếu song song lên mặt phẳng (P), hai đường thẳng chéo nhau a và b có hình chiếu
là hai đường thẳng a’ và b’. Mệnh đề nào sau đây đúng?
A. a’ và b’ luôn luôn cắt nhau.
B. a’ và b’ có thể trùng nhau.
C. a và b không thể song song.
D. a’ và b’ có thể cắt nhau hoặc song song với nhau. Lời giải Chọn D
Gọi l là phương chiếu, (a) và (b) là các mặt phẳng song song với l và lần lượt đi qua a và b. Khi đó
nếu (a) và (b) cắt nhau thì a’ và b’ cắt nhau, nếu (a) và (b) song song thì a’ và b’ song song.
Câu 6: Qua phép chiếu song song lên mặt phẳng (P), hai đường thẳng a và b có hình chiếu là hai
đường thẳng song song a’ và b’. Khi đó:
A. a và b phải song song với nhau.
B. a và b phải cắt nhau.
C. a và b có thể chéo nhau hoặc song song với nhau.
D. a và b không thể song song. Lời giải Chọn C Nếu a' b ∥ ' thì mp(a,a') mp ∥
(b,b'). Bởi vậy a và b có thể song song hoặc chéo nhau.
Câu 7: Cho bốn điểm không đồng phẳng A, B, C, D có hình chiếu song song trên mặt phẳng (P) lần
lượt là bốn điểm A’, B’, C’, D’. Những trường hợp nào sau đây không thể xảy ra?
A. A’B’C’D’ là bốn đỉnh của một hình bình hành.
B. D’ là trọng tâm tam giác A’B’C’.
C. D’ là trung điểm cạnh A’B’.
D. Hai điểm B’, C’ nằm giữa hai điểm A’ và D’. Lời giải Chọn D
Bốn điểm không đồng phẳng A’, B’, C’, D’ không thể thẳng hàng.
Câu 8: Hình chiếu song song của một hình thang ABCD không thể là hình nào dưới đây? A. Hình bình hành.
B. Hình tam giác cân. C. Đoạn thẳng.
D. Bốn điểm thẳng hàng. Lời giải Chọn B II. PHẦN TỰ LUẬN. Phần: Đại số
Câu 1: Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ t của năm 2017 được cho bởi một hàm số Èp ˘ y = 4 sin Í
(t - 60)˙+ 10 với t Œ¢ và 0 < t £ 365 . Vào ngày nào trong năm thì 178 Í ˙ Î ˚
thành phố A có nhiều giờ có ánh sáng mặt trời nhất? A. 28 tháng 5. B. 29 tháng 5. C. 30 tháng 5. D. 31 tháng 5. Lời giải Chọn B Vì Èp ˘ Èp ˘ sin Í
(t - 60)˙£ 1 æ æÆ y = 4 sin Í (t - 60)˙+ 10 £ 14. 178 Í ˙ 178 Í ˙ Î ˚ Î ˚
Ngày có ánh sáng mặt trời nhiều nhất Èp ˘ € y = 14 € sin Í (t - 60)˙= 1 178 Í ˙ Î ˚ p € ( p t - 60)=
+ k2p € t = 149 + 356 . k 178 2 Do 149 54 0 365 0 149 356 365 k t k k Œ < £ æ æÆ < + £ € - < £ æ ææ ¢ Æ k = 0. 356 89
Với k = 0 æ æÆ t = 149 rơi vào ngày 29 tháng 5 (vì ta đã biết tháng 1 và 3 có 31 ngày, tháng 4 có 30
ngày, riêng đối với năm 2017 thì không phải năm nhuận nên tháng 2 có 28 ngày hoặc dựa vào
dữ kiện 0 < t £ 365 thì ta biết năm này tháng 2 chỉ có 28 ngày).
Câu 2: Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực nước
trong kênh được tính tại thời điểm p Ê t p ˆ
t (giờ) trong một ngày bởi công thức h = 3cosÁ ˜ Á + ˜ + 12. 8 Á Ë 4 ˜¯
Mực nước của kênh cao nhất khi:
A. t = 13 (giờ).
B. t = 14 (giờ).
C. t = 15 (giờ).
D. t = 16 (giờ). Lời giải . Chọn B
Mực nước của kênh cao nhất khi h lớn nhất p Ê t p ˆ pt p € cosÁ ˜ Á + ˜ = 1 € +
= k2p với 0 < t £ 24 và k Œ¢ . 8 Á Ë 4 ˜¯ 8 4
Lần lượt thay các đáp án, ta được đáp án B thỏa mãn Vì với pt p t = 14 æ æÆ € +
= 2p (đúng với k = 1Œ¢ ). 8 4
Câu 3: Chu vi của một đa giác là 45 cm, số đo các cạnh của nó lập thành một cấp số cộng với công
sai d = 3cm . Biết cạnh lớn nhất là 15 cm, tính số cạnh của đa giác đó. Lời giải
Gọi cạnh nhỏ nhất của đa giác là u và số cạnh của đa giác là n. 1
Ta có 15 = u + n -1 .3
u =18 - 3n > 0 ® n < 6 1 ( ) hay . 1
Tổng các cạnh là 45 cm, ta có n(15 +18 -3n) 45 = hay 2
3n - 33n + 90 = 0. 2 Giải phương trình với *
nÎ N ;n < 6, ta được n = 5.
Câu 4: Tìm ba số hạng liên tiếp của một cấp số cộng, biết rằng:
a) Tổng của chúng bằng 15 và tích của chúng bằng 105.
b) Tổng của chúng bằng 21 và tổng bình phương của chúng bằng 155. Lời giải
Gọi ba số hạng liên tiếp của cấp số cộng là , a ,
b c Þ a + c = 2b( ) * .
ìa + b + c = 15
ìa + b + c =15 ï a) Theo bài ra, ta có í , kết hợp với ( )
* , ta được ía + c = 2b îabc =105 ïabc =105 î 3 ì b =15 b ì = 5 ìa = 3 ìa = 7 ï ï ï Û ï
ía + c = 2b Û íc =10 - a Û b í = 5 hoặc b í = 5 . ïabc 105 ï î 5 ï a î (10 - a) =105 ï = c = 7 î c = 3 î
ìa + b + c = 21
ìa + b + c = 21 ï b) Theo bài ra, ta có , kết hợp với ( )
* , ta được ía + c = 2b í 2 2 2
îa + b + c =155 ï 2 2 2
îa + b + c =155 3b 21 b ì ì = = 7 ìa = 5 ìa = 9 ï ï ï Û ï
ía + c = 2b Û íc =14 - a Û b í = 7 hoặc b í = 7. ï 2 2 2 ï
îa + b + c =155 ï ï ïa + î (14-a)2 2 2 c = 9 + 7 =155 î c = 5 î Câu 5: Tính æ 2 2 limç n 7 n 5 ö + - + ÷ è ø Giải 2 2 æ 2 2 ö n + 7 - n - 5 2 limç n + 7 - n + 5 ÷ = lim = lim = 0 è ø 2 2 2 2 n + 7 + n + 5 n + 7 + n + 5 Câu 6: Tổng S 1 0,9 0,9 0,9 ... 0,9 ... n ( )2 ( )3 ( )n- = + + + + +
1 + có kết quả bằng bao nhiêu? Hướng dẫn giải ( )2 ( )3 ( )n- = + + + + + 1 S 1 0,9 0,9 0,9 ... 0,9 + ...
Đây là tổng của cấp số nhân lùi vô hạng có u =1, q = 0,9. 1 u1 1 S = = = 10. 1- q 1- 0,9 Câu 7: Cho 1 1 1 1 u = + + + ... + . Tính lim u n 3.5 5.7 7.9 (2n - )1(2n + )1 n Lời giải æ ö Ta luôn có: 1 1 1 1 = ç - ÷.
(2k - )1(2k + )1 2è 2k -1 2k +1ø 1 1 1 1 u = + + + ... + n 3.5 5.7 7.9 (2n - )1(2n + )1
1 æ 1 1 ö 1 æ 1 1 ö 1 æ 1 1 ö 1 æ 1 1 ö
= ç - ÷ + ç - ÷ + ç - ÷ + ...+ ç - ÷
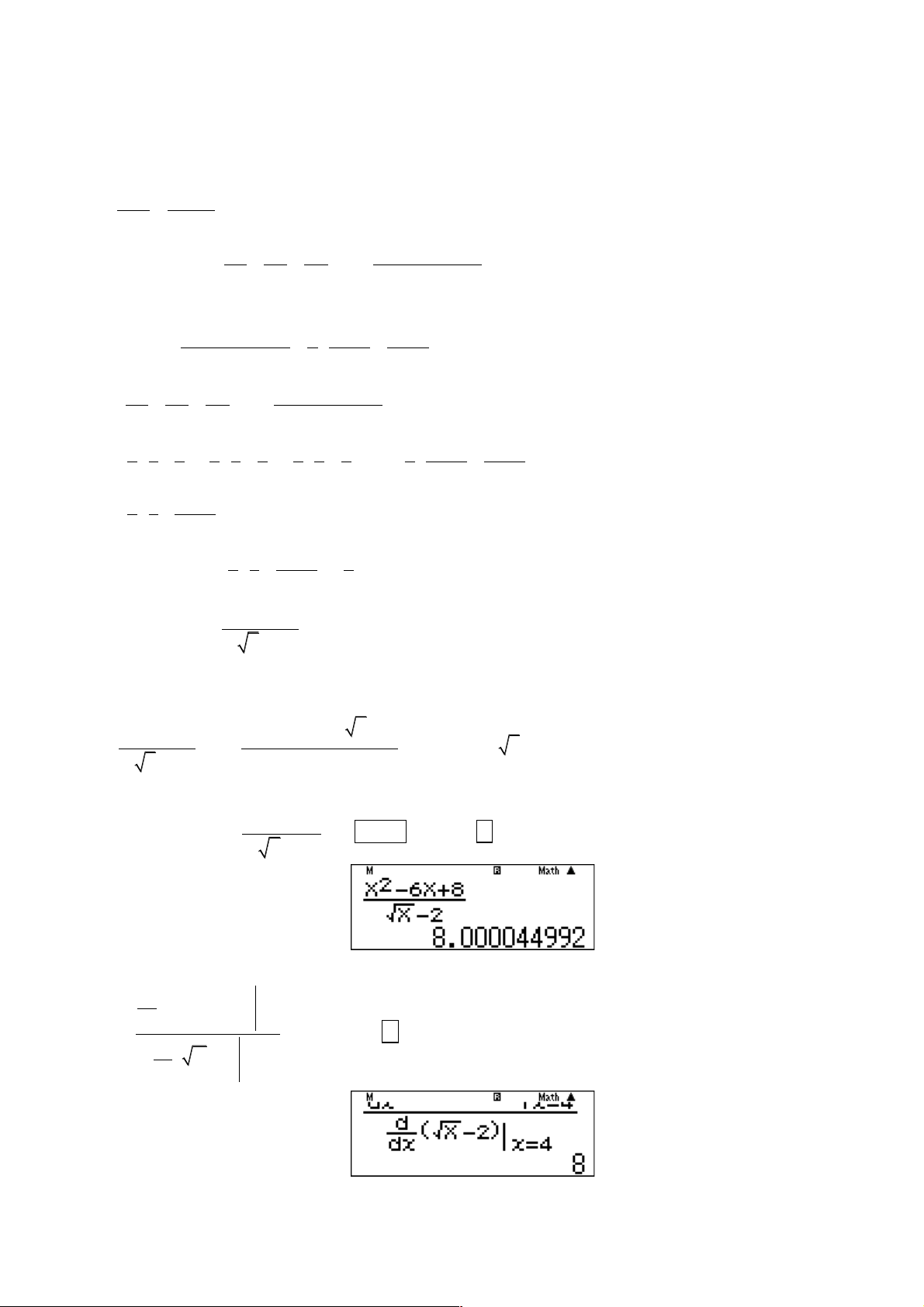
2 è 3 5 ø 2 è 5 7 ø 2 è 7 9 ø 2 è 2n -1 2n +1ø 1 æ 1 1 ö = ç - ÷. 2 è 3 2n +1ø 1 æ 1 1 ö 1 Do đó lim u = lim ç - ÷ = . n 2 è 3 2n +1ø 6 2 x - 6x + 8 Câu 8: Tính lim x®4 x - 2 Hướng dẫn giải
Cách 1: Giải bằng tự luận 2 - + (x -2)(x -4)( x +2 x 6x 8 ) lim = lim
= lim (x - 2)( x + 2) = 2´4 = 8. x®4 x®4 x - 2 x - 4 x®4
Cách 2: Giải nhanh bằng máy tính 2 x - 6x + 8 Nhập vào màn hình ấn 5 CALC 4 10- +
= ta được kết quả » 8. x - 2
Lưu ý: Để ra kết quả chính xác 8 ta có thể tính theo quy tắc Lô-pi-tan như sau: d ( 2 X - 6X + 8) dx Nhập
x=4 rồi ấn phím = ta được kết quả chính xác 8. d ( X -2) dx x=4 2 Câu 9: Tính x + 2x + 3x L = lim . x®-¥ 2 4x +1 - x + 2 Hướng dẫn giải
Cách 1: Giải bằng tự luận 2 2 2 x 1+ + 3x - 1+ + 3 x + 2x + 3x x x 2 lim = lim = lim = . x®-¥ 2 x®-¥ x 4x 1 x 2 1 ®-¥ 1 2 3 - + - + x 4 + - x + 2 - 4 + -1+ 2 2 x x x
Cách 2: Giải nhanh bằng máy tính 2 2 Nhập vào màn hình x + 2x + 3x ấn 15 CALC -10 = ta được kết quả . 2 4x +1 - x + 2 3
Câu 10: Tìm các giá trị của m để các hàm số sau liên tục trên tập xác định của chúng: 2 ì 2 x - x - 2
ìx + x khi x <1 ï khi x ¹ 2 - ï
a) f ( x) = í x - 2
b) f (x) = í2 khi x =1
ïîm khi x = -2
ïmx +1 khi x >1 î Lời giải
a) Hàm số f (x) liên tục với x " ¹ 2 .
• Do đó f (x) liên tục trên ! Û f (x) liên tục tại x = 2 Û lim f (x) = f (2) ( ) 1 x®2 2 - - - + • x x 2 x 2 x 1
Ta có lim f (x) ( )( ) = lim = lim
= lim x +1 = 2 +1 = 3; f 2 = . m x®2 x®2 x®2 x - 2 (x - 2) ( ) ( ) x®2 • Khi đó ( )
1 Û 3 = m Û m = 3.
b) Ta có: lim f ( x) = lim (mx + )
1 = m +1; lim f (x) = lim + = + = = + + - - ( 2 x x) 1 1 2; f ( ) 1 2. x 1 ® x 1 ® x 1 ® x 1 ®
• Từ YCBT Û lim f (x) = lim f (x) = f ( )
1 Û m +1 = 2 Û m =1. x 1+ x 1- ® ® Phần hình học:
Ví dụ 1. Cho hình chóp S.ABCD có đáy ABCD không là hình thang. Gọi O là giao điểm của AC và
BD, K là một điểm trên cạnh SD.
a. Tìm giao điểm E của mặt phẳng (ABK) với CD.
b. Tìm giao điểm F của mặt phẳng (ABK) với SC.
c. Chứng minh các đường thẳng AF, BK và SO đồng quy. Lời giải a. Trong mp(ABCD): ABÇCD ={ } E . S
Mà AB Ì (ABK) nên EÎ(ABK)ÇCD. K b. Ta có: (ABK) º (AEK) Trong mp(SCD): EK ÇSC ={ } F . G F
Mà EK Ì (ABK) nên FÎ(ABK)ÇSC. D A c. Trong mp(ABK): AFÇ BK ={ } G . O Mà AF Ì (SAC), BK Ì (SBD) C B nên GÎ(SAC)Ç(SBD) = SO. E
Vậy ba đường thẳng AF, BK và SO đồng quy.
Ví dụ 2. Cho hình chóp S.ABCD. Gọi M, N là hai điểm bất kì trên SB, CD. Mặt phẳng (P) qua MN và song song với SC.
Tìm các giao tuyến của (P) với các mặt phẳng (SBC), (SCD), (SAC). Lời giải
Trong mặt phẳng (SBC), từ M kẻ đường thẳng song song với SC cắt BC tại Q.
Trong mặt phẳng (SCD), từ N kẻ đường thẳng song song với SC cắt SD tại P.
Khi đó giao tuyến của (P) với (SBC) và (SCD) lần lượt là MQ và NP.
Gọi I = AC Ç NQ. Từ I kẻ đường thẳng song song với SC cắt SA tại H.
Khi đó (P) Ç(SAC) = IH .
d) Tổ chức thực hiện:
GV: Giáo viên chia lớp thành 4 nhóm
Chuyển giao
Giáo viên giao nhiệm vu chữa các câu hỏi cho các nhóm.
GV: Quan sát các nhóm và đôn đốc các nhóm thực hiện theo yêu cầu
Thực hiện
HS: Thực hiện yêu cầu của GV
GV: học sinh lên bảng trình bày vắn tắt lời giải và đáp án của câu hỏi mà
Báo cáo thảo luận nhóm được giao
Đánh giá, nhận xét, GV nhận xét câu trả lời của các đội, đánh giá thái độ làm việc, ghi nhận, tổng
tổng hợp hợp kết quả