ÔN TẬP TOÁN RỜI RẠC | Đại học Kinh tế Kỹ thuật Công nghiệp
Toán rời rạc là một phần quan trọng trong toán học và khoa học máy tính, với nhiều ứng dụng thực tiễn. Nắm vững các khái niệm và phương pháp trong toán rời rạc sẽ giúp sinh viên phát triển tư duy logic và giải quyết các vấn đề phức tạp trong lĩnh vực kỹ thuật và công nghệ.
Môn: Công nghệ phần mềm (KTKTCN)
Trường: Đại học Kinh tế kỹ thuật công nghiệp
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
lOMoAR cPSD| 40190299
ÔN TẬP TOÁN RỜI RẠC PHẦN 1
Câu 1 Giải các hệ thức truy hồi với các điều kiện đầu sau: an = 6an-1 - 8an-2
với n ≥ 2, a0 = 4, a1 = 10.
Câu 2: Giải các hệ thức truy hồi với các điều kiện đầu sau: an = 5an-1 + 6an-2
với n ≥ 2, a0 = 4, a1 = 1. Câu 3
Giải các hệ thức truy hồi với các điều kiện đầu sau:
an 10an 1 11an 2 với n 2, a0 1, a1 4
Câu 4 Có bao nhiêu xâu khác nhau có thể lập được từ các chữ cái trong từ
MISSISSIPI, COMPUTER yêu cầu phải dùng tất cả các chữ? PHẦN 2
Câu 1 Áp dụng thuật toán nhánh cận giải bài toán người du lịch với
ma trận chi phí như sau: ∞ 14 10 40 08 ∞ 18 24 30 12 ∞ 24 10 40 34 ∞
Câu 2 Áp dụng thuật toán nhánh cận giải bài toán cái túi sau:
5x1 + x2 + 9 x3 -> max,
4 x1 + 2 x2 + 6 x3 ≤ 10,
Với xj >=0 nguyên, j = 1,2,3 Câu 3
Cho thời gian gia công các chi tiết trên 2 máy A và B trong bảng
sau. Hãy lập lịch gia công cho các chi tiết này sao cho thời gian gia
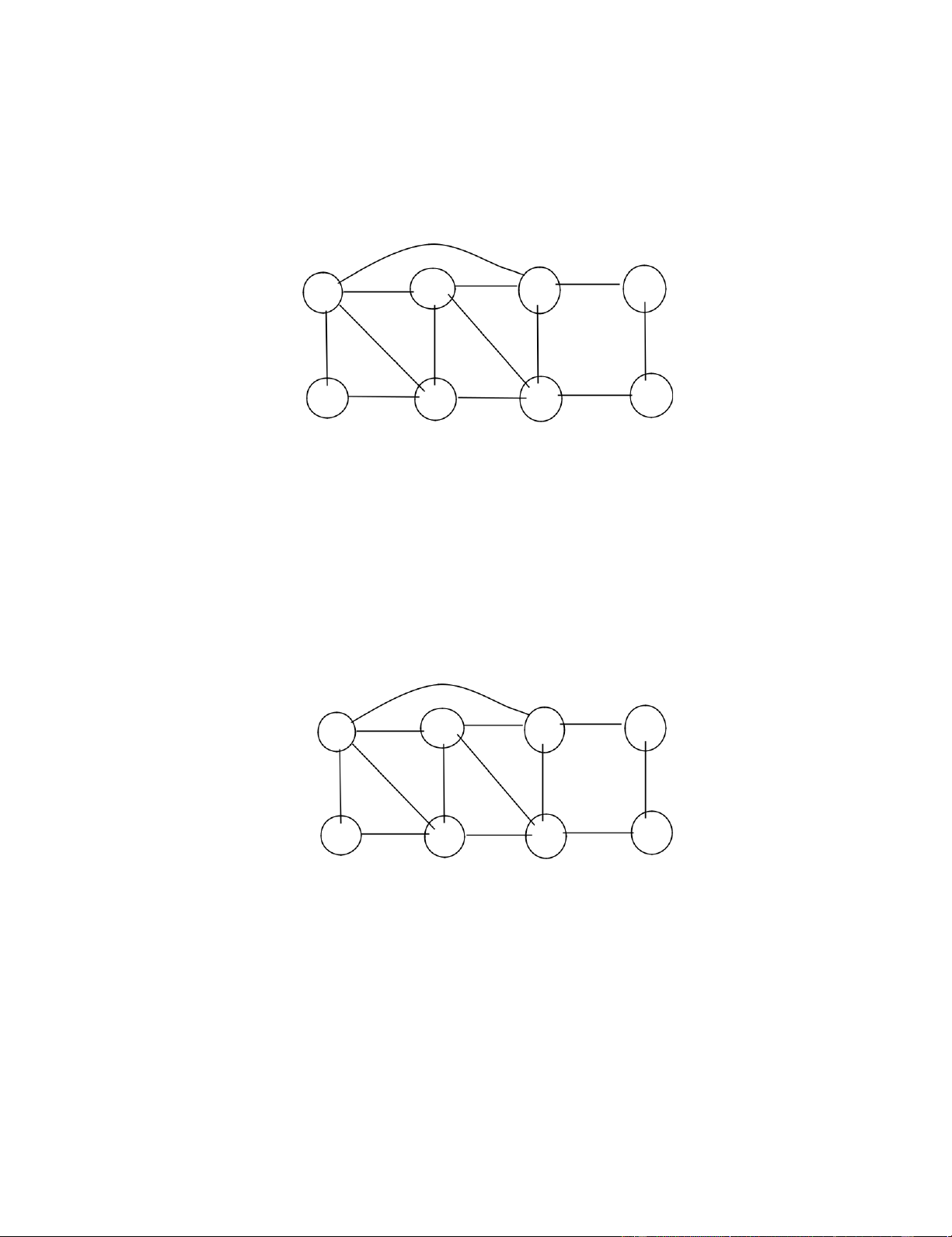
công là ít nhất. Vẽ sơ đồ Gantt cho lịch gia công tối ưu. Chi tiết D1 D2 D3 D4 D5 Máy A 5 7 7 8 4 B 8 5 7 6 2 PHẦN 3 Câu 1 Cho đồ thị sau: 1 3 5 7 2 4 6 8
1. Lập ma trận kề biểu diễn đồ thị trên?
2. Định nghĩa đồ thị Euler, đồ thị nửa Euler?
3. Đồ thị trên có chu trình Euler không? Vì sao? Nếu có hãy tìm chu trình Euler đó? Câu 2 Cho đồ thị sau 1 3 5 7 2 4 6 8
1. Lập ma trận kề biểu diễn đồ thị trên?
2. Định nghĩa đồ thị Hamilton, đồ thị nửa Hamilton?
3. Đồ thị trên có chu trình Hamilton không? Vì sao? Nếu có hãy
tìm chu trình Hamilton đó?
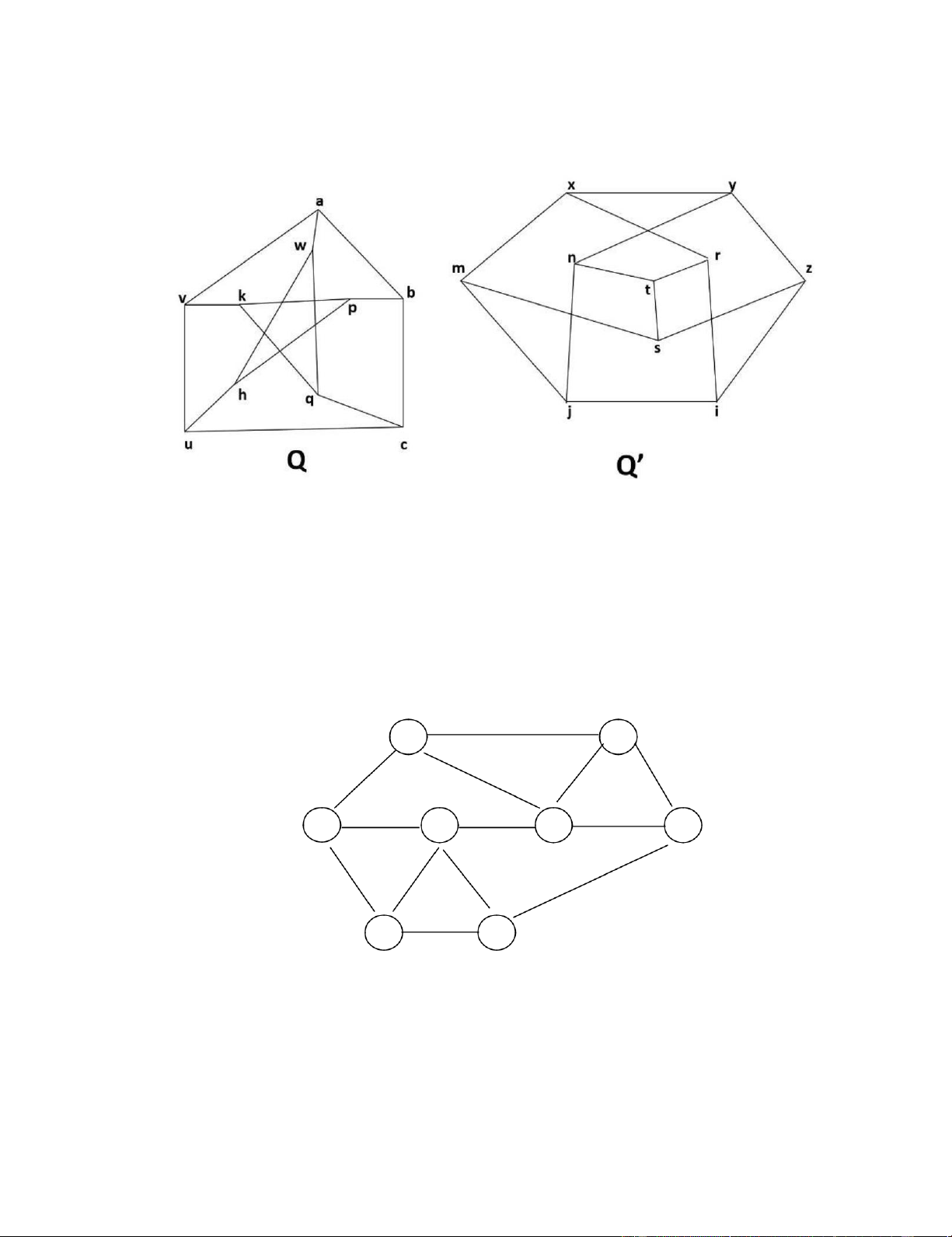
Câu 3 Cho 2 đồ thị sau: lOMoAR cPSD| 40190299
1. Nêu khái niệm đồ thị đẳng cấu?
2. Lập danh sách kề biểu diễn 2 đồ thị trên?
3. Hai đồ thị này có đẳng cấu với nhau không? Vì sao? PHẦN 4
Câu 1 Cho đồ thị sau 42 a b 4 10 14 3 3 1 11 c d e f 5 20 9 15 7 g h
1. Duyệt đồ thị trên theo phương pháp Duyệt theo chiều sâu
– DFS trên (Đỉnh bắt đầu là đỉnh a)
2. Dùng thuật toán Prim tìm cây khung nhỏ nhất của đồ thị
trên (Đỉnh bắt đầu là đỉnh d)
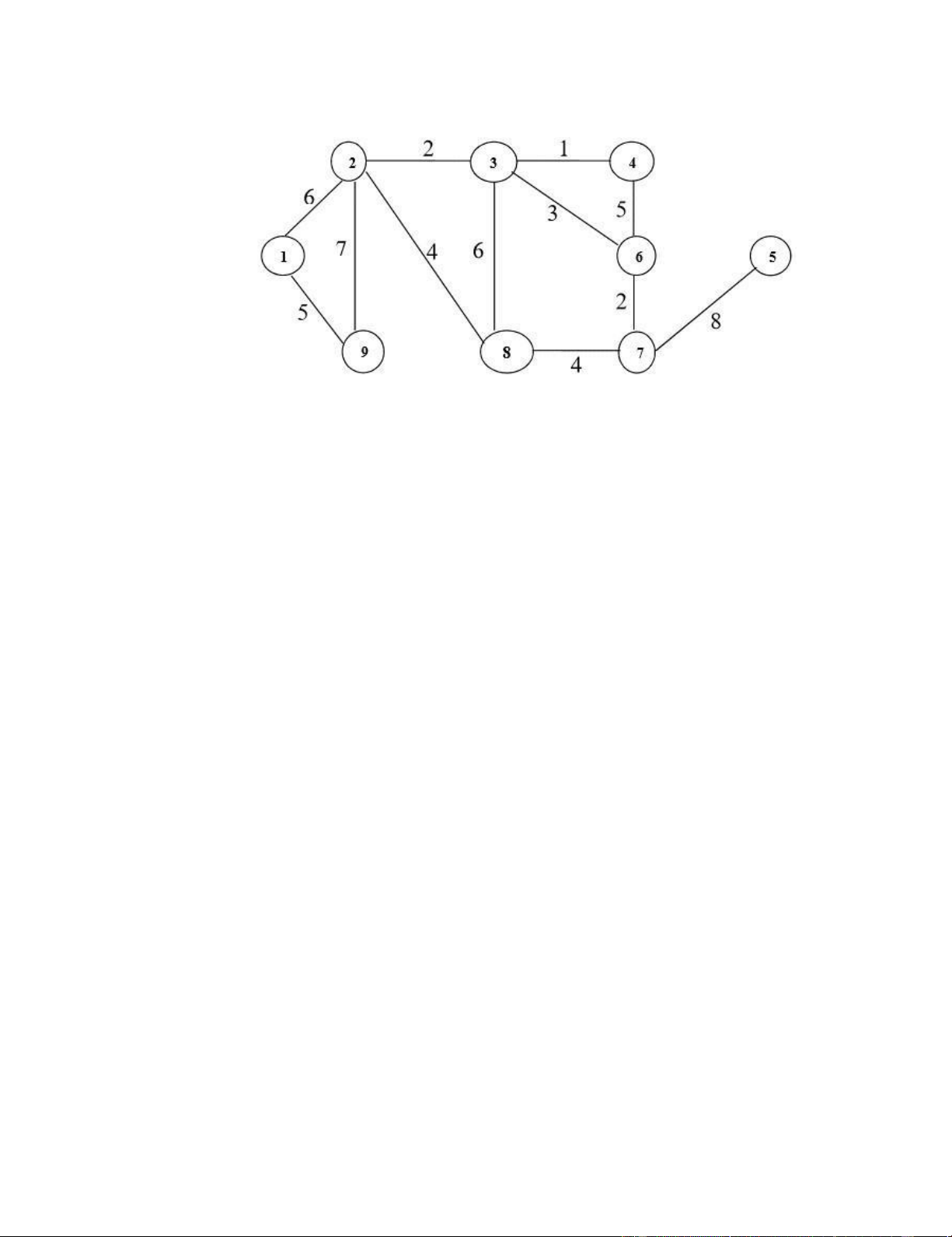
Câu 42 Cho đồ thị sau lOMoAR cPSD| 40190299
1. Duyệt đồ thị trên theo phương pháp Duyệt theo chiều rộng –
BFS (Đỉnh bắt đầu là đỉnh 1)
2. Dùng thuật toán Dijkstra tìm đường đi ngắn nhất từ đỉnh 4
đến tất cả các đỉnh còn lại của đồ thị. Ý Nội dung Điểm 1
Bài toán giải hệ thức truy hồi 2,0
- Lập đúng phương trình đặc trưng 0,25
- Giải phương trình đặc trưng 0,5
- Lập công thức nghiệm tổng quát 0,5
- Lập đúng phương trình từ điều kiện ban đầu 0,25
- Giải đúng nghiệm phương trình, tìm được hệ số A,B 0.25
- Kết luận đúng nghiệm riêng của hệ thức 0,25 2 Bài toán tối ưu 3,0
a. Dạng bài toán Người du lịch và Cái túi
- Tính đúng cận đầu tiên 0,5
- Chọn đúng phương án ban đầu 0,5
- Chọn các phương án thứ 2 0,5
- Chọn các phương án thứ 3 0,25
- Chọn các phương án thứ các lần kế tiếp 0.25
- Tính đúng giá trị tối ưu 0,5
- Chọn đúng phương án tối ưu 0,5
b. Dạng bài toán gia công chi tiết máy
- Chia các chi tiết gia công thành 2 nhóm N1, N2 0,5 - Sắp sếp nhóm N1 0,25 - Sắp xếp nhóm N2 0,25
- Đưa ra lịch gia công tối ưu đúng 0,5
- Vẽ đúng thời gian thực hiện gia công của máy A 0,5
- Vẽ đúng thời gian thực hiện gia công của máy B 0,5
- Kết luận đúng thời gian tối ưu 0,5 3
Lý thuyết đồ thị 2,0 1
- Biểu diễn đúng ma trận kề 0,5 2
- Trả lời đúng định nghĩa đồ thị 0,5 3
- Trả lời đúng loại đồ thị 0,5 4
- Giải thích đúng tại sao 0,5 lOMoAR cPSD| 40190299 Ý Nội dung Điểm 4 Bài tập đồ thị 3 1 Duyệt đồ thị 1
- Xây dựng đúng bảng mô tả thuật toán 0,25
- Chọn thứ tự đúng các đỉnh trong các lần duyệt 0,25
- Kết luận đúng thứ tự các đỉnh đã duyệt 0,25 - Vẽ đúng cây 0.25 2
Thuật toán Prim hoặc Dijkstra 2
- Lập bảng và gán nhãn ban đầu cho các đỉnh 0,25
- Chọn đúng đỉnh ở bước 1 0,25
- Tính đúng nhãn cho các đỉnh ở bước 2 0,25
- Tính đúng nhãn cho các đỉnh ở bước 3 0,25
- Tính đúng nhãn cho các đỉnh ở bước 4 0,25
- Tính đúng nhãn cho các đỉnh ở bước tiếp theo 0,25
- Kết luận đúng số đỉnh và cạnh đã chọn hoặc kết luận 0,25
đường đi ngắn nhất từ đỉnh xuất phát đến các dỉnh còn lại.
- Vẽ đúng cây khung hoặc cây đường đi ngắn nhất 0,25