Ôn Toán Kinh Tế | Đại học Tây Đô

lOMoAR cPSD| 45474828 Cấu trúc đề thi:
1. Bài toán quy hoạch tuyến tính a) Lập mô hình (2đ)
b) Giải bài toán quy hoạch tuyến tính (max, min - ẩn gốc, ẩn phụ, ẩn giả) ( (4đ)
(không có bài toán tiền về max có ẩn giả)
2. Bài toán vận tải (4đ) -F(x) -> max / min
(không thi bài toán có ô cấm)
(Thầy spoiled đề thi không có số lẻ, 3 bảng ra kết quả; Bài toán vận tải 1 - 2 bảng là
ra kết quả; bài tập về mô hình thì có dạng như ví dụ 1.1 trong tài liệu)
ÔN THI TOÁN KINH TẾ
I. Bài toán quy hoạch tuyến tính I.1 Lập mô hình
Mục tiêu của bài toán lập mô hình là để đạt được các kết quả tốt nhất theo các điều kiện tiêu chuẩn nào đó.
xj là ẩn số của phương trình (không âm) thường là đối tượng cần để quan sát. lOMoAR cPSD| 45474828
F(x) được gọi là hàm mục tiêu của phương trình hay còn gọi là phương án tối ưu. Được lấy
dựa trên mục tiêu của đề như lợi nhuận tối đa > max chi phí tối thiểu > min.
Hệ phương trình ràng buộc thường dựa trên các chỉ số được đưa ra có sự trên lệch và giới
hạn trong đề. j là thứ tự các loại đối tượng quan sát
I.2 Giải bài toán quy hoạch tuyến tính
I.2.1 Biến đổi dạng bài toán quy hoạch tuyến tính lOMoAR cPSD| 45474828 lOMoAR cPSD| 45474828 Vd lOMoAR cPSD| 45474828
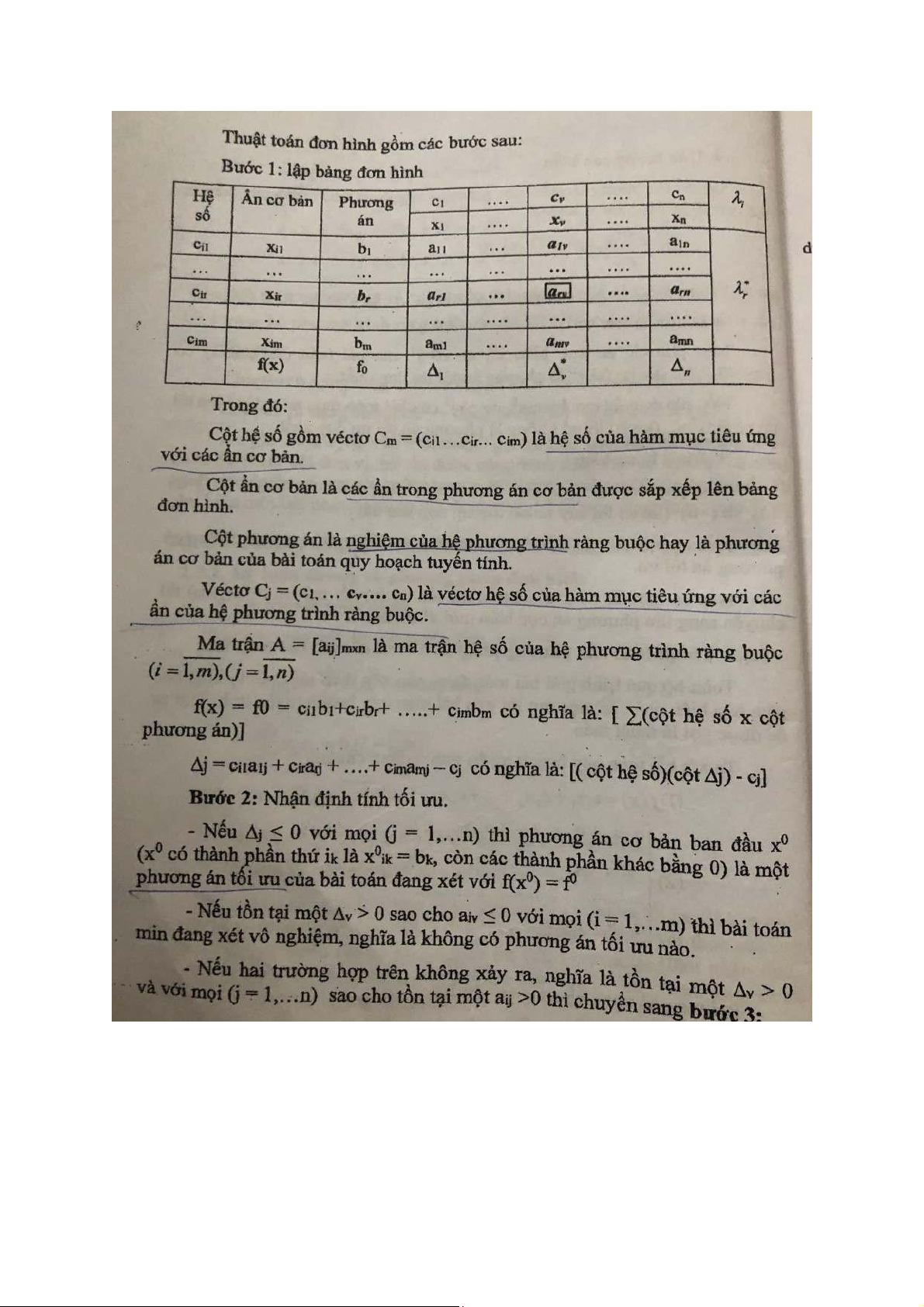
I.2.2 Thực hiện theo phương pháp đơn hình Các thực hiện:
1.Lập mô hình và đưa hết về dạng chuẩn.
(xem như thế nào là dạng chuẩn ở phía trên mỗi hàng phải có ít nhất một ẩn cơ bản. Khi
chuyển từ dạng tổng quát về dạng chuẩn nếu các hàng còn là bất phương trình thì thêm các
ẩn phụ tương ứng (làm như phía trên) còn nếu như đưa về dạng chuẩn nhưng các hàng
vẫn chưa có ẩn cơ bản thì cần phải thêm ẩn giả) 2.Vẽ bảng:
Gồm các cột hệ số, biến cơ bản, phương án và các cột ẩn.
+Cột biến cơ bản là các biến cơ bản của các phương trình trong phương trình ràng buộc.
(mỗi phương trình trong phương trình ràng buộc chỉ có một biến duy nhất)
+Cột hệ số là các hệ số trong hàm mục tiêu của các biến cơ bản bên cột biến cơ bản.
+Cột phương án là các hệ số tự do “b” trong phương trình ràng buộc.
+Các cột ẩn đi từ x1 đến xn với các hệ số của từng ẩn phía trên.
3.Tính F(x) và các delta:
F(x) bằng cột hệ số nhân với cột phương án rồi cộng lại với nhau.
Delta bằng cột phương án nhân cột ẩn của delta đó rồi trừ cho hệ số của ẩn đó. (riêng các
cột ẩn cơ bản (cột đơn vị) thì có thể cho luôn bằng 0 vì bản chất nó bằng 0)
Nếu tất cả các delta đều âm ở bài toán min hoặc đều dương ở bài toán max thì đi đến kết luận.
Còn nếu tồn tại từ một delta dương ở bài toán min hoặc delta âm ở bài toán max thì chuyển sang bước 4
4.Tìm ẩn đưa vào hệ ẩn cơ bản. F(x) => min
Chọn delta dương lớn nhất ẩn này sẽ là ẩn được đưa vào hệ ẩn cơ bản. F(x) => max
Chọn delta âm bé nhất ẩn này sẽ là ẩn được đưa vào hệ ẩn cơ bản.
5.Tìm ẩn cơ bản được thay thế.
Để tìm ẩn cơ bản được thay thế trong hệ ẩn cơ bản ta tính lamda: lOMoAR cPSD| 45474828
lamda bằng cột phương án chia cho cột ẩn của delta mà mới đánh dấu ở bước 4.
Chọn lamda dương bé nhất.
=> đây là hàng chứa ẩn cơ bản nằm trong hệ ẩn cơ bản cần được thay thế. Và cần phải
khoanh tròn phần tử giao giữa cột delta và cột lamda này gọi là phần từ chốt.
6.Tiến hành lập bảng thứ hai
+Cột ẩn cơ bản được viết lại với ẩn cơ bản được thay thế từ bước 4 và 5.
+Cột hệ số được viết lại dựa trên cột ẩn cơ bản được viết lại.
+Cột phương án được tính lại hoàn toàn phần tử nằm cùng hàng với phần từ chốt thì được
tính lại như phần tử chốt còn các phần từ còn lại thì được tính theo phương pháp hình chữ nhật.
Các cột ẩn được viết lại và các hệ số trong các cột được tính lại như sau:
+Từ phần tử chốt ta làm sao để phần từ chốt trở về 1, cột phần từ chốt cũng được đưa về
cột đơn vị với phần tử chốt là 1 và các phần từ còn lại trong cột là 0. +Hàng chứa ẩn cơ
bản cũng được tính theo cách tính phần tử chốt trở về 1.
+Các phần tử còn lại thì được tính theo phương pháp hình chữ nhật phía bên dưới. Các cột
đơn vị thì ghi lại như cũ.
Sau đó làm như bước 3
-Đối với bài toán có ẩn phụ thì các cột ẩn của ẩn phụ có hệ số bằng 0.
-Đối với bài toán có ẩn giả thì tất cả các ẩn khác đều bằng 0 và ẩn giả thì bằng 1. Sau khi
tính ra giá trị chuyển qua bảng tiếp theo có thể bỏ khỏi tính các hệ số trong cột. Đặc biệt khi
đã bỏ hết các cột ẩn giả (các ẩn giả đã được thay thế hết trong cột hệ số cơ bản) thì ta viết
lại bảng và ghi các giá trị lại như tính bình thường không còn các hệ số bằng 0 nữa. Ta có
thể loại bỏ hoàn toàn cột ẩn giả. Lưu ý: Khi F(x) => min +Đktu các delta âm
+Chọn delta dương lớn nhất
+Chọn tỷ số lamda bé nhất
(bảng phía sau luôn có F(x) bé hơn bảng phía trước, trừ trường hợp bài toán ẩn giả) Khi F(x) => max +Đktu các delta dương +Chọn delta âm bé nhất
+Chọn tỷ số lamda bé nhất
(bảng phía sau luôn có F(x) lớn hơn bảng phía trước, trừ trường hợp bài toán ẩn giả) lOMoAR cPSD| 45474828 lOMoAR cPSD| 45474828
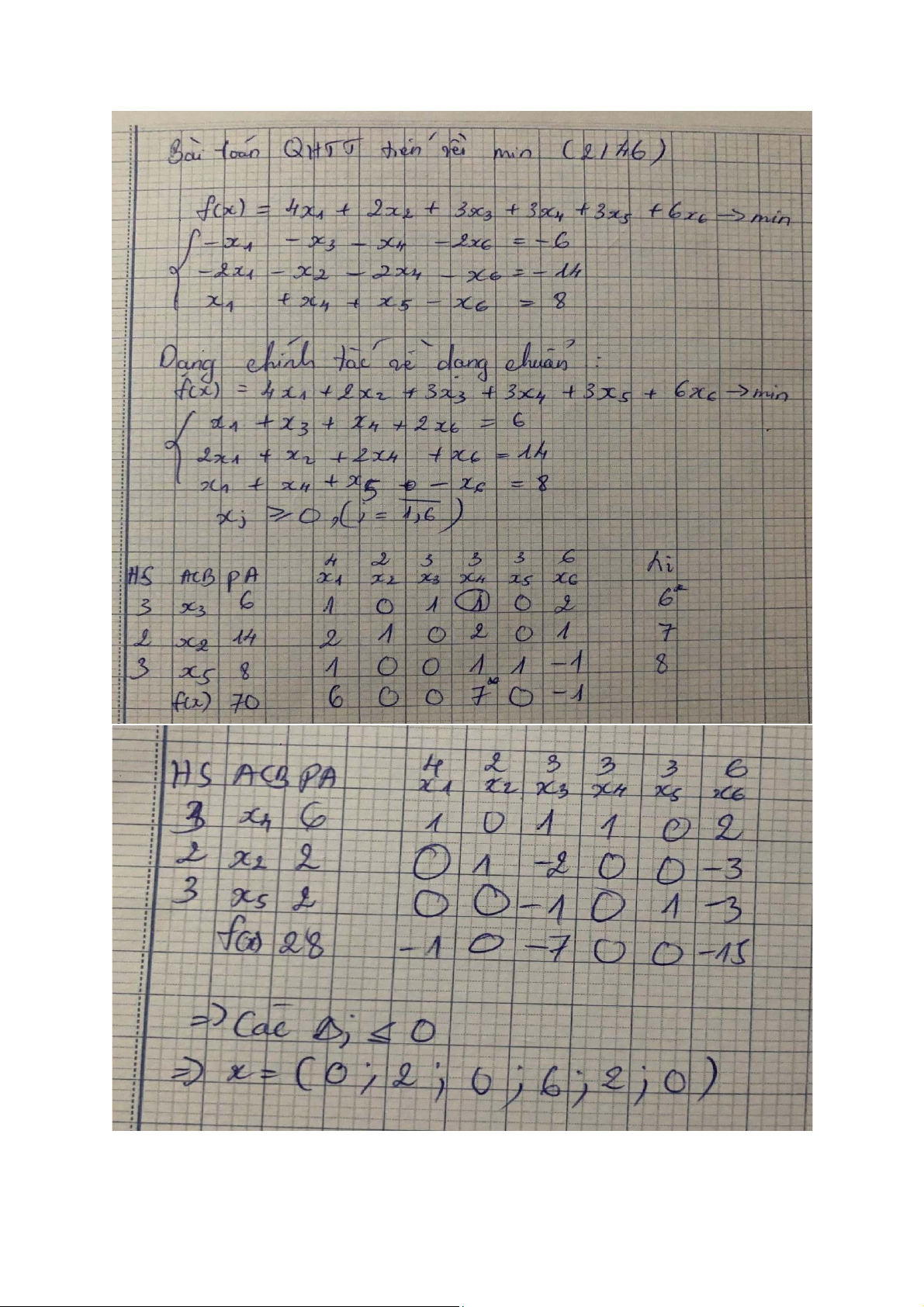
Vd bài toán qhtt với ẩn gốc tiến về min: lOMoAR cPSD| 45474828
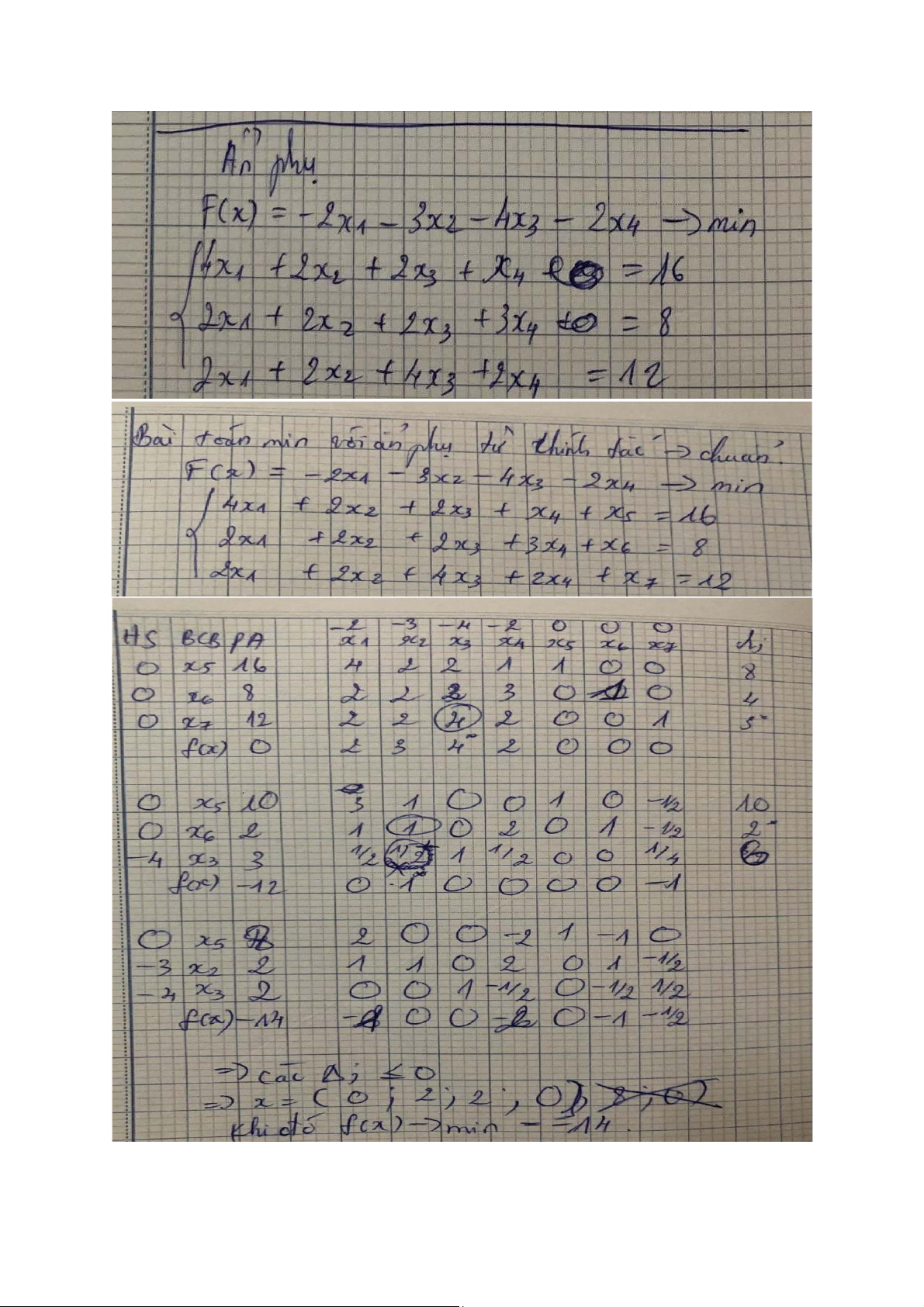
Vd bài toán qhtt với ẩn phụ tiến về min: lOMoAR cPSD| 45474828
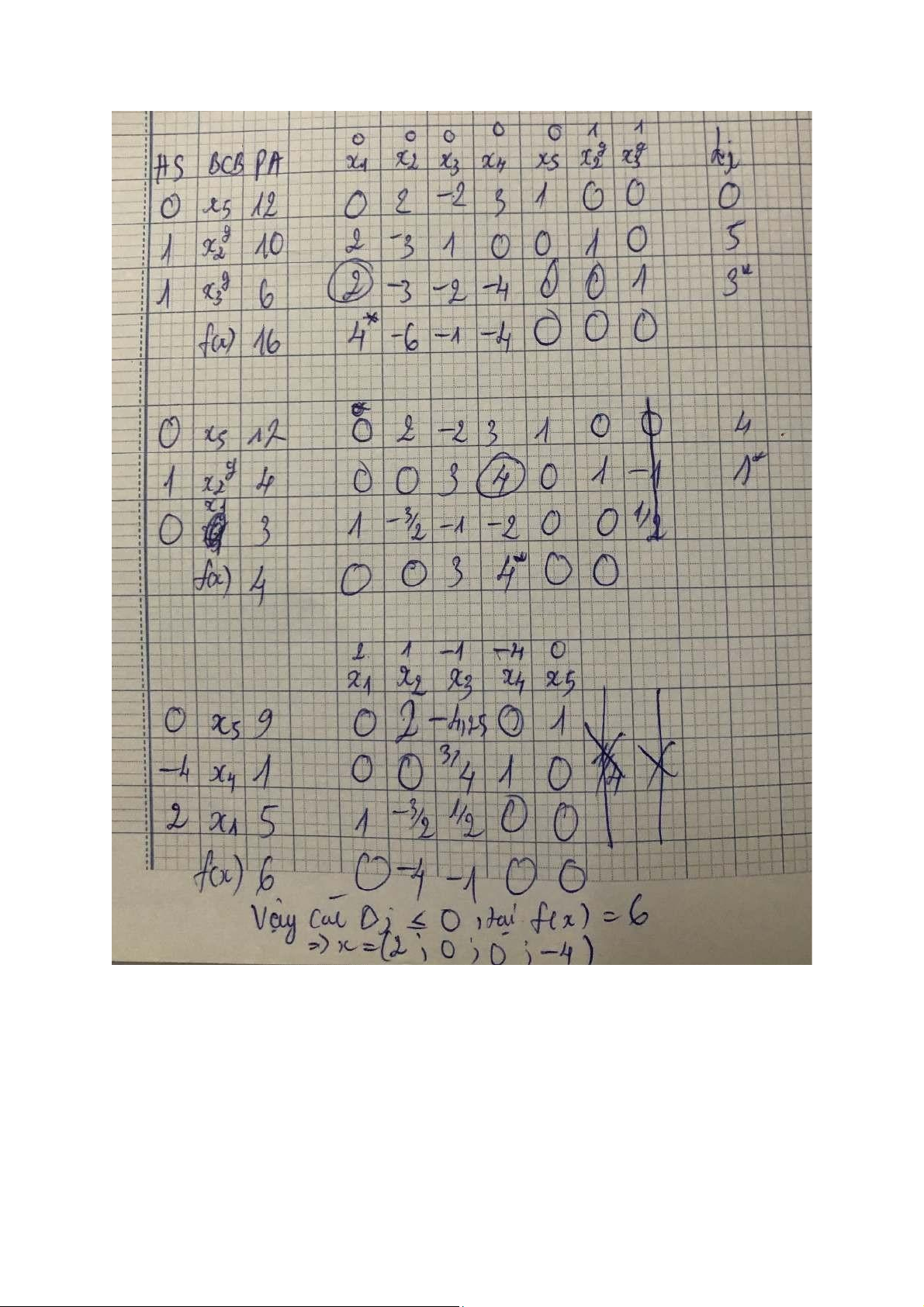
Vd bài toán qhtt với ẩn giả tiến về min: lOMoAR cPSD| 45474828 lOMoAR cPSD| 45474828
II.Bài toán vận tải
II.1 Mô hình bài toán cực tiểu hóa tổng tấn*km xe không
(Đây là bài toán tổng quát nhất về bài toán vận tải)
Bài toán vận tải được tính như sau:
1.Khi đã có số liệu (cij) của bảng chi phí phân phối và Ai và Bj ta thực hiện viết vào bảng.
2.Bắt đầu phân phối (tổng thu = tổng phát): lOMoAR cPSD| 45474828
Bài toán vận tải tiến về Min (chi phí bé nhất,...)
Bài toán vận tải tiến về Max (lợi nhuận,...)
Chọn chi phí (cij) bé nhất (min)/ lớn nhất (max) để phân phối đầu tiên, sau đó căn cứ vào số
lượng giữa cột Ai và Bj có đủ chưa để phân phối tiếp, nếu đã đủ ta đi tìm chi phí (cij) bé
(min)/ lớn (max) tiếp theo để phân phối còn nếu chưa ta dò theo hàng hoặc theo cột từ ô
vừa phân phối xem vị trí có chi phí (cij) bé nhất (min)/lớn nhất (max) tiếp theo trên cột và
hàng đó rồi phân phối tiếp sao cho tổng thu bằng tổng phát.
3.Tính thế vị (Ui đại diện cho các hàng và Vj đại diện cho các cột):
Để tính được thế vị ta cần thỏa mãn điều kiện số cột (m) + số hàng (n) - 1 <= số lượng ô được phân phối.
Nếu m + n - 1 > số ô được phân phối ta cần phải chọn ra một ô bất kỳ (lưu ý ô đó không
được tạo thành vòng với các ô còn lại có nghĩa là không thể nối lại thành vòng để cải tiến
phương án) gán cho giá trị bằng không rồi bắt đầu tính thế vị.
Cách tính thế vị như sau:
+Cho Ui bất kỳ bằng 0 (thông thường là Ui nằm trên cùng) áp dụng theo công thức Vj = Cij
Ui và ngược lại Ui = Cij - Vj. Giống qua các hàng và các cột chứa ô được phân phối tính
các Ui và Vj còn lại. 4.Kiểm tra tính tối ưu
Tính Δij = Ui + Vj - Cij
Đối với bài toán chi phí min thì Δij <= 0 là phương án tối ưu còn bài toán max thì Δij >= 0 là
phương án tối ưu. Nếu tất cả Δij đều tối ưu thì đi đến kết luận tính F(x) = giá trị ô phân phối x Cij cộng tất cả lại.
Nếu tồn tại nhiều hơn một giá trị Δij > 0 trong bài toán min hoặc nhiều hơn một giá trị Δij < 0
trong bài toán max thì ta tiến hành thực hiện cải tiến phương án.
5.Cải tiến phương án:
Chọn ra Δij > 0 lớn nhất trong bài toán min và Δij < 0 bé nhất trong bài toán max. Tiến hành lập
vòng điều chỉnh. Từ ô Δij đó ta xuất phát vẽ vòng điều chỉnh đến các ô phân phối khác theo hàng
ngang và dọc không được đi xéo sau đó quay lại ô Δij. Đánh dấu + tại ô Δij và xen kẽ - rồi cộng cho đến hết vòng.
Từ các ô được đánh dấu - chọn ra ô có giá trị phân phối bé nhất được gọi là q sau đó tiến hành vẽ bảng mới.
Vẽ lại các giá trị như Ai, Vj, các Cij và các ô phân phối nằm ngoài vòng điều chỉnh.
Các ô trong vòng điều chỉnh được viết lại như sau từ giá trị q tìm phía trên những ô có dấu + ta
tiến hành cộng thêm một lượng q những ô có dấu - ta trừ đi một lượng q từ đó ô Δij lớn nhất ban
nảy sẽ có giá trị phân phối là q còn ô - có bé giá trị bé nhất sẽ được trừ còn 0.
Sau đó quay lại bước 3.
5 bước trên đây là cách giải các bài toán vận tải thông thường
(Trường hợp bài toán vận tải có ô cấm ta cần chú ý phân phối tránh vị trí có m (Lưu ý m
là một số rất lớn số nào trừ cho m cũng âm số nào cộng cho m cũng dương) nếu bắt buộc
phải phân phối vô m thì tiến hành cải tiến phương pháp sao cho không còn phân phối vào m
nữa, nếu khi bài toán đã tối ưu nhưng vẫn còn phân phối vào m thì bài toán không có phương án tối ưu.)
Trường hợp bài toán vận tải có xe không:
Sau khi thực hiện 5 bước trên đã tìm được phương án tối ưu. Ta tiến hành kết luận và tính F(x) để so sánh.
6. Tiến hành vẽ các giá trị cần phải giao trên đề bài vào (Lưu ý các ô nhận hàng là các ô
hình tròn còn các ô cần phải giao hàng là các ô hình vuông) 7.Bắt đầu vẽ đường đi (“=>” là
xe có hàng; “->” là xe không có hàng)
Những ô vừa có ô vuông và ô tròn ta tiến hành vẽ đường đi xuất phát từ hàng chứa hai ô đó
đến vị trí ô đó (ta ký hiệu là cột chứa hai ô đó) và quay về hàng chứa hai ô đó. Tấn km xe lOMoAR cPSD| 45474828
không được tính bằng số hàng được giao và nhận nhân cho Cij của ô đó (có nghĩa là chọn
giá trị bé nhất trong hai ô tròn và vuông là số hàng được giao và nhận được)
Sau khi đã đi hết các ô đồng thời chứa hai ô tròn vuông rồi ta tiến hành vẽ lại bảng như cũ
riêng các ô chứa đồng thời hai ô tròn vuông sẽ được trừ đi lượng vừa giao bên trên, ô tròn
hay ô vuông còn dư hàng ra thì vẽ lại (tròn hoặc vuông).
8. Vẽ lại đường đi
Ta đi theo quy tắc bắt đầu bằng một ô vuông và kết thúc bằng một ô tròn. Ta đi làm sao cho
số hàng giao từ đầu đến cuối là như nhau. Tấn Km xe không bằng số hàng hóa đó nhân với
các giá trị Cij của các ô chứa ô tròn cộng lại.
Sau đó đi đến kết luận: Vậy tổng tấn * Km xe không bằng cộng tất cả các đường đi lại bao gồm từ bước 7.
Ví dụ về bài toán xe không: lOMoAR cPSD| 45474828
thế vị bị sau sửa lại như sau lOMoAR cPSD| 45474828 lOMoAR cPSD| 45474828
II.2 Bài toán phân công lao động
(Nhằm mục đích phân công sao cho chi phí hoặc khối lượng công việc phải đảm nhận là ít nhất)
Ban đầu ta sẽ chọn ra các số bé nhất của mỗi hàng và mỗi cột xem xét chúng nhưng có khi
chúng sẽ không phải là phương án tối ưu nên ta cần thực hiện bài toán phân công lao động.
Bài toán phân công lao động được tính như sau: lOMoAR cPSD| 45474828
Đầu tiên ở mỗi hàng ta chọn ra hằng số bé nhất sau đó lấy tất cả các số trong hàng đó trừ
cho hằng số bé nhất sao cho mỗi hàng xuất hiện ít nhất một phần tử bằng 0.
Sau đó xem các cột sao cho đảm bảo mỗi cột đều xuất hiện ít nhất một phần từ bằng không
nếu có cột không có phần từ bằng 0, ta tiến hành chọn ra hằng số bé nhất trong cột đó lấy
tất cả các số trừ đi sao cho xuất hiện phần tử bằng 0.
Tiếp đến ta tiến hành phân bố sao cho hàng chịu trách nhiệm thực hiện một cột có nghĩa là
mỗi hàng và mỗi cột chỉ chấp nhận giao nhau ở một phần tử bằng 0, nếu có một hàng và
một cột không có ô giao nhau thì tiến hành bước tiếp theo.
Ta kẻ thêm các đường thẳng vào các phần từ bằng 0 một đường đi qua ít nhất hai phần từ bằng 0.
Sau đó ta chọn các phần tử ở ngoài đường kẻ chọn ra số bé nhất và trừ tất cả các số cho
số bé nhất để xuất hiện phần tử bằng 0. Tiến hành cộng số bé nhất đó vào những ô giao
nhau của các đường kẻ.
Cuối cùng ta có thể phân bố lại chắc chắn chi phí sẽ thấp hơn so với ban đầu phân bố.