Pha và cách tính số pha | Bài giảng môn Hóa lý | Đại học Bách khoa hà nội

PHA VÀ ĐIỀU KIỆN CÂN BẰNG PHA - Cách tính số pha
- Điều kiện cân bằng pha
- Biểu diễn trên giản đồ pha
Pha và cách tính số pha Số pha: f
f = số pha rắn + số pha lỏng + số pha khí Số pha Số pha rắn khí Hợp kim vàng, f= 1 Fe-Cu…
2 hay nhiều khí chứa trong
các không gian khác nhau à f ≥ 2
Hỗn hợp rắn, f ≥ 2
2 hay nhiều khí chứa trong 1 kim loại không gian à f=1
Pha và cách tính số pha
(f) = số pha rắn + số pha lỏng + số pha khí
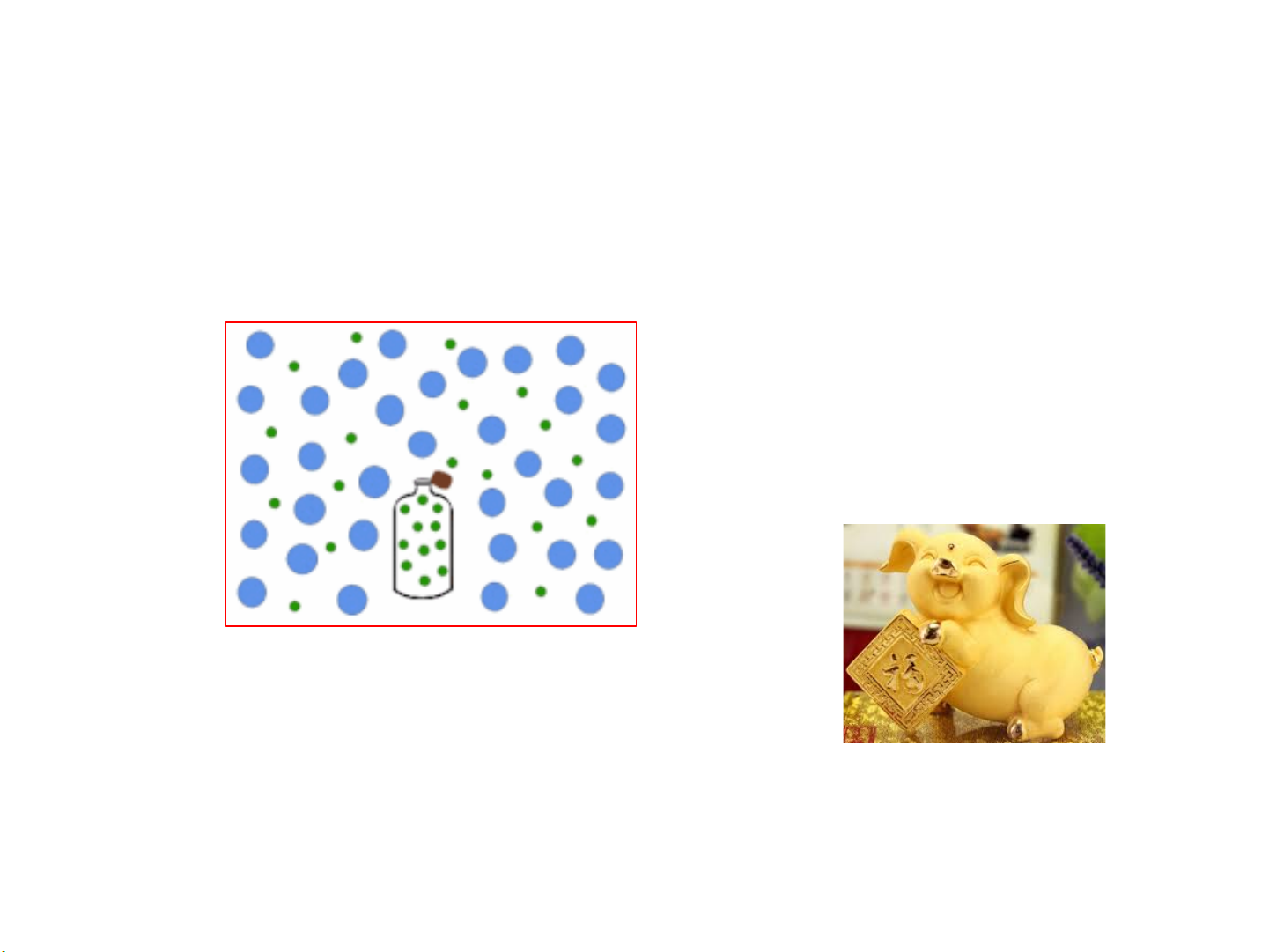
Số pha lỏng phụ thuộc vào khả năng tan của CL
ü Các chất lỏng tan f = 1 đồng nhất với nhau
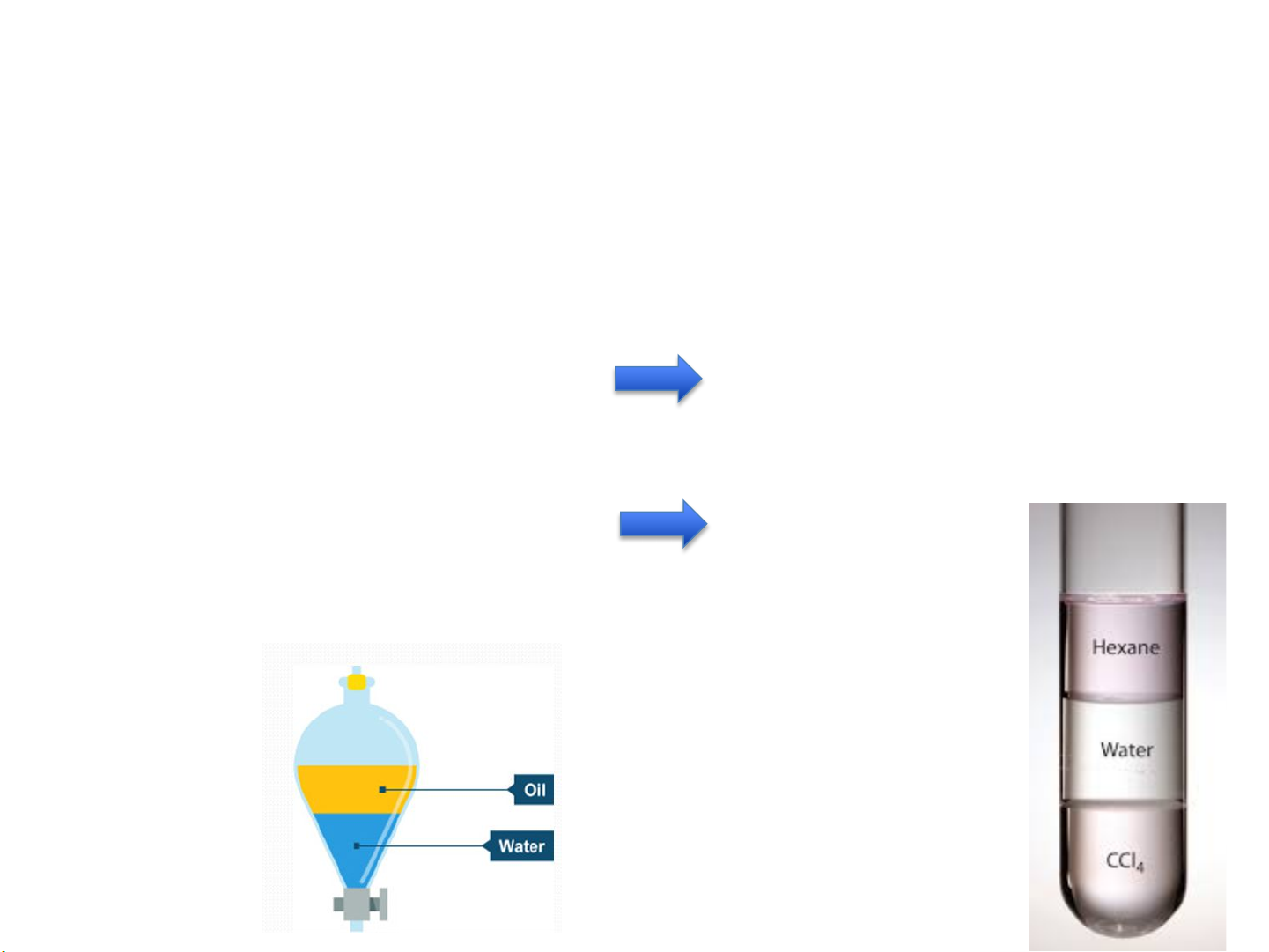
ü Các chất lỏng ko tan f ≥ 2 hoàn toàn vào nhau Dầu- H C 2O 6H12-H2O-CCl4
Hợp phần - Cấu tử
Hợp phần (r): là các chất tạo thành hệ, có thể tồn tại độc lập
Ví dụ: dd NaCl có 2 hợp phần là muối ăn và nước
Số pt liên hệ (r): = số p.ư hoá học + pt liên hệ giữa các thông số
Cấu tử (k): số hợp phần độc lập (tối thiểu) à đủ để x/đ hệ tại CB.
Mối liên hệ giữa r, q, k:
Số cấu tử (k) = số hợp phần (r) – số pt liên hệ (q) Bậc tự do
Cân bằng pha: Là TTCB của quá trình chuyển pha
(ko có sự biến đổi về mặt hoá học)
Bậc tự do (C): số TSNĐ tối thiểu ĐỦ để x/đ hệ tại CB Thông số ngoài: T, P
Thông số trong: nồng độ, số mol...
Ý nghĩa của C: số TSNĐ biến thiên tuỳ ý mà không ảnh hưởng đến CB pha Điều kiện CB pha
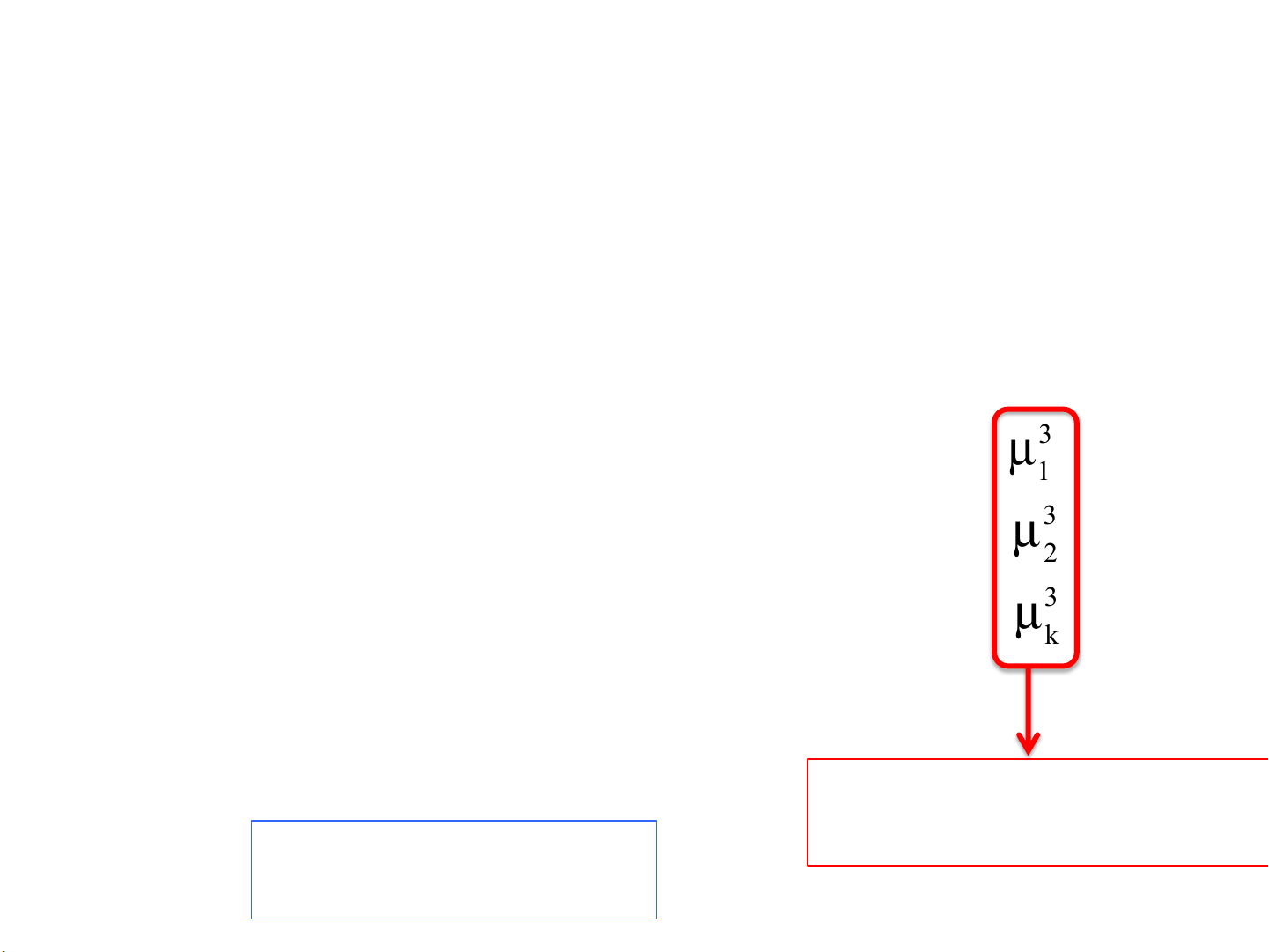
f pha, mỗi pha có k cấu tử pha 1 ! pha 2... ! pha3... ! pha f
(1,2,3..k) (1,2,3..k) (1,2,3..k) (1,2,3..k) ĐK CB pha T1 = T2 = T3 = ... = Tf P1 = P2 = P3 = ... = Pf Cân bằng nhiệt và cơ µ học 1 = µ2 = µ3 = ... = µf 1 1 1 1 µ1 = µ2 = µ3 = ... = µf Cân bằng hoá học 2 2 2 2 1 2 3 f µ = µ = µ = ... = µ k k k k
Động lực của qt chuyển pha
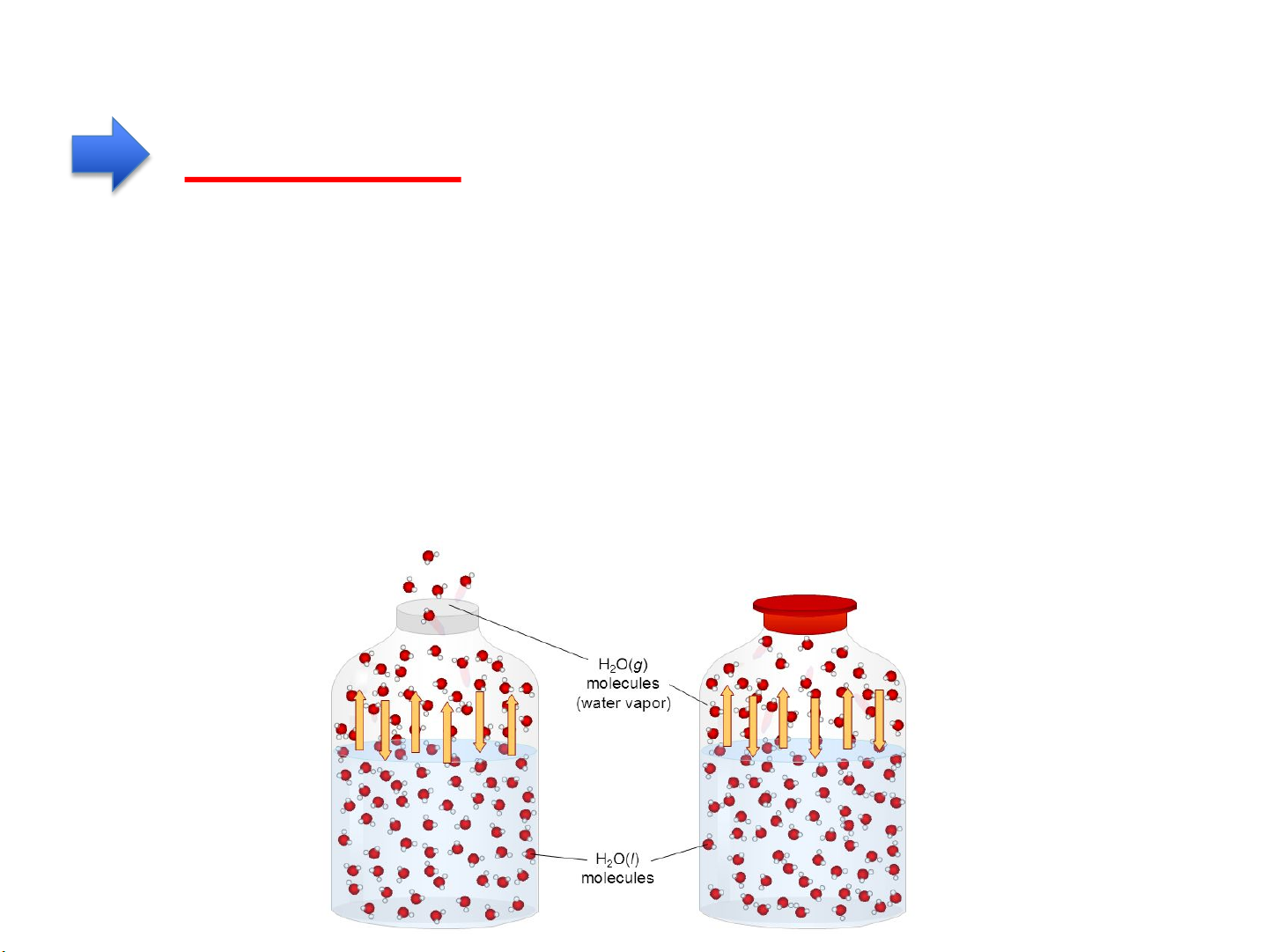
SAN BẰNG về T, P và hoá thế giữa các pha VD H2O(l) = H2O (h)
μ(H2O,l) > μ(H2O,h) à quá trình hoá hơi H O(ℓ) " H O(h) 2 2
μ(H2O,l) < μ(H2O,h) à quá trình ngưng tụ H O(ℓ) "H O(h) 2 2
μ(H2O,l) = μ(H2O,h) à cân bằng lỏng-hơi H O(ℓ) " H O(h) 2 2 Hệ kín Hệ mở
Thiết lập quy tắc pha Gibbs
Quy tắc pha Gibbs: qui tắc để x/đ bậc tư do C k+2 dòng
C = ΣTSTT – Σ số pt liên hệ T1 = T2 = T3 = ... = Tf pha 1 !
pha 2... ! pha ... ! pha f P1 = P2 = P3 = ...= Pf
(1,2,3..k) (1,2,3..k) (1,2,3..k) (1,2,3..k) µ1 = µ2 = µ3 = ... = µf 1 1 1 1
Tổng số TSTT = k.f + 2.f µ1 = µ2 = µ3 = ... = µf 2 2 2 2 = (k+2).f 1 2 3 f µ = µ = µ = ... = µ k k k k
Tổng số pt liên hệ = (k+2)(f-1) + f (1)
Suy ra C = (k+2)f – (k+2)(f-1) –f 1 pt liên hệ giữa các xi à
1 pt liên hệ giữa các μi C = k - f + 2
Áp dụng quy tắc pha Gibbs C = k - f +2 Ví dụ: CaCO (r) ! CaO(r) + CO (k) 3 2
Số pha: f = 3 (1 pha khí + 2 pha rắn)
Số hợp phần: r = 3
Số pt liên hệ: q = 1. Suy ra k = 3 -1 = 2 àC = 2-3+2 = 1
“ 1 trong 2 thông số T, P biến đổi tuỳ ý, thông số
kia phụ thuộc hàm của thông số kia”
Nghĩa là: T= f(P) hoặc P= f(T) Giản đồ pha
Giản đồ pha: sự phụ thuộc các TSTT của 1 hệ trong CB pha
+ Các đường: T=f(x), P=f(x) (2 thông số)
+ Các mặt: T=f(x,y); P= f(V,x);.. (3 thông số)
+ Các vùng: T, P, x biến thiên tuỳ ý trong 1 giới hạn xác định mà
số pha, trạng thái pha ko đổi P, atm B C 218 atm T! P! T! Rắn Lỏng (P-T-V)! (P-T-V)! (T-x-x)! V! P! 4,579 mmHg C! O Hơi D B! T! T! A A! 0,0099°C 374°C t°C P! T! P! x(h) ! B P-T! T-x! P-x! P-x! T! x! x! x(h) ! B
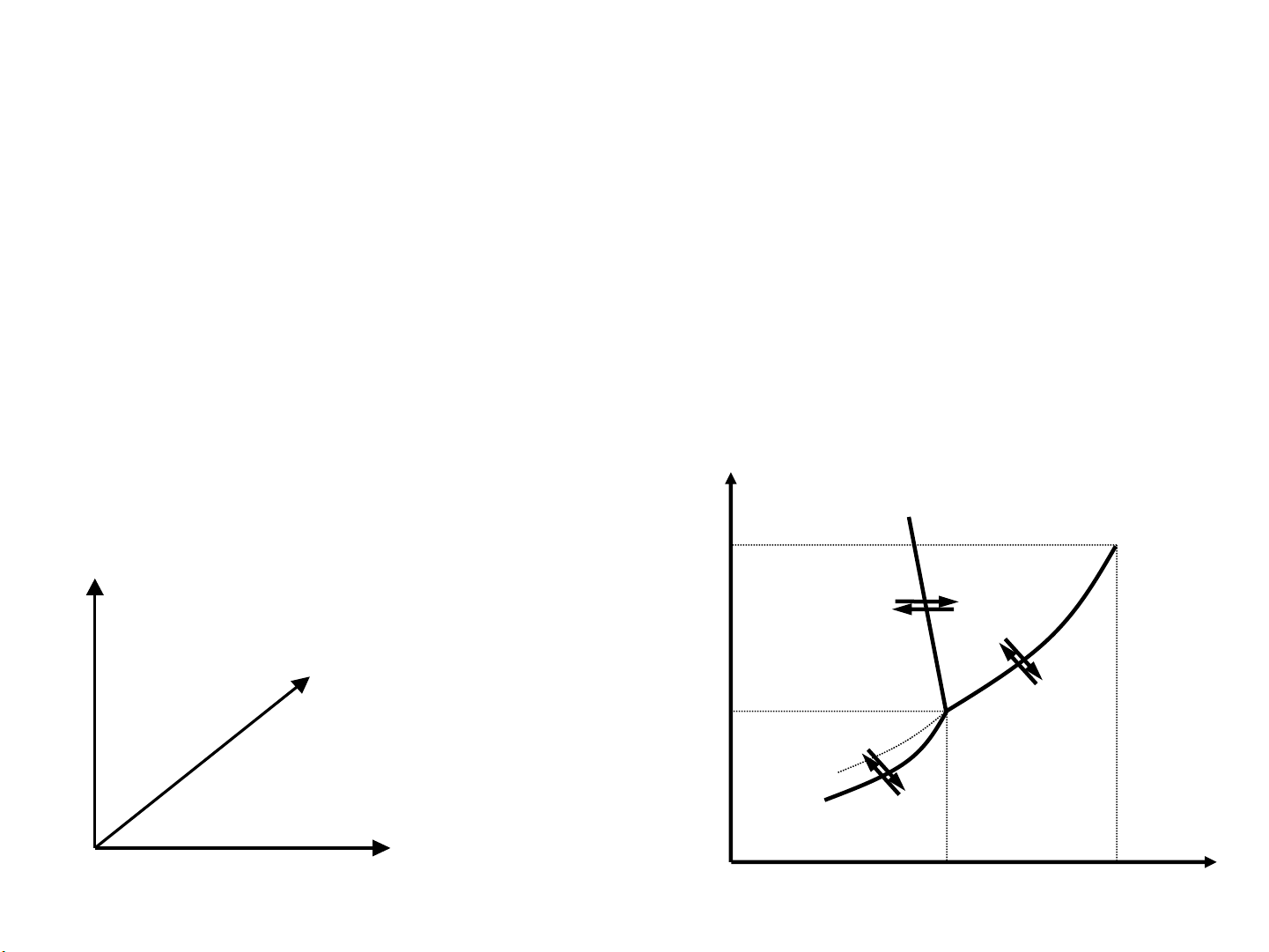
Cách biểu diễn thành phần trên giản đồ pha Hệ 2 cấu tử ß A tăng à B tăng A M1! M2 B 0
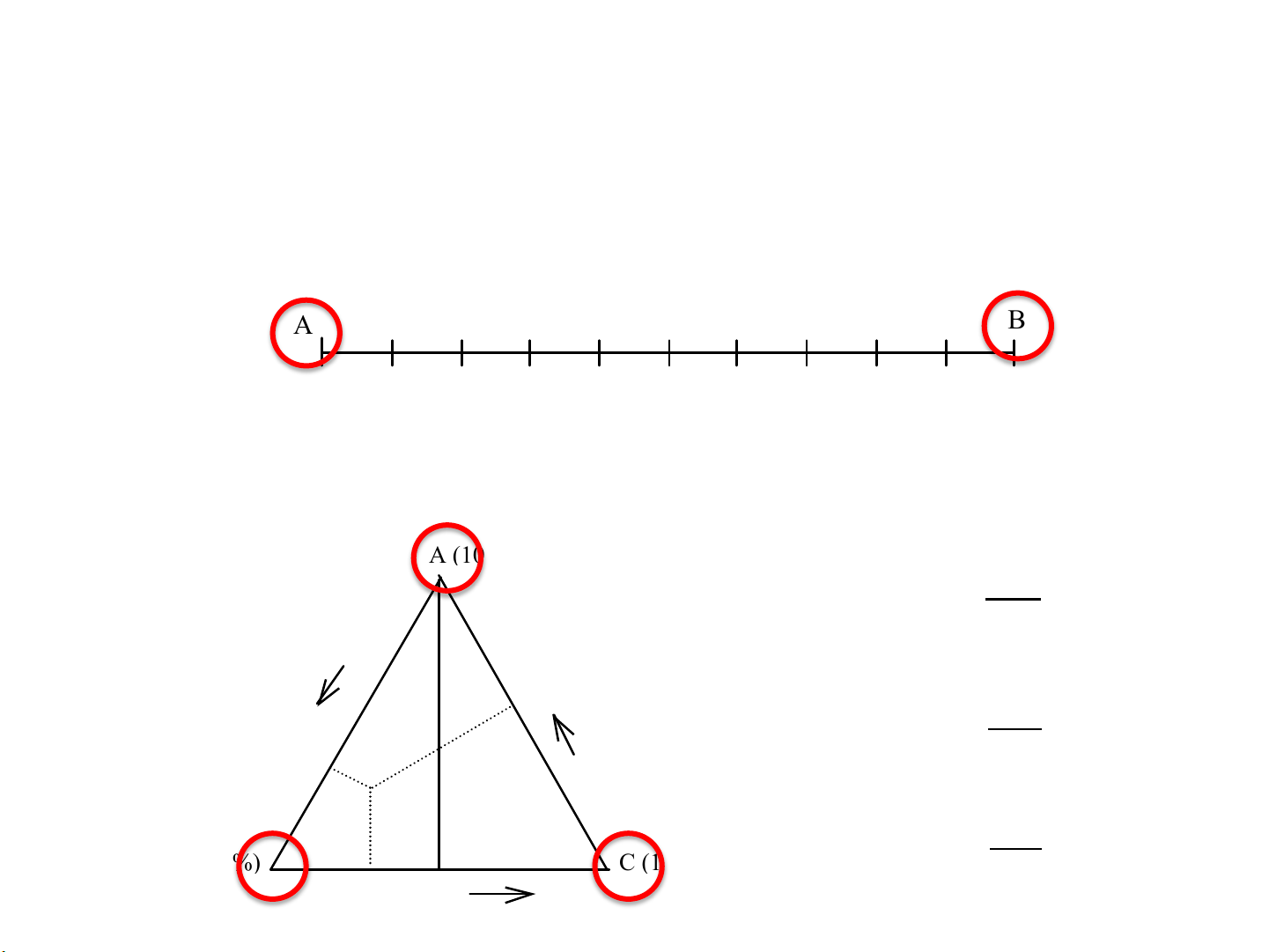
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 xB→ 0 10 20 30 40 50 60 70 80 90 100 %yB→ ! Hệ 3 cấu tử A (100%) %A = Pa % h %B b h %A c %B = Pb % P h %C = Pc % B (100%) C (100%) a H h %C !
Các quy tắc trên giản đồ pha
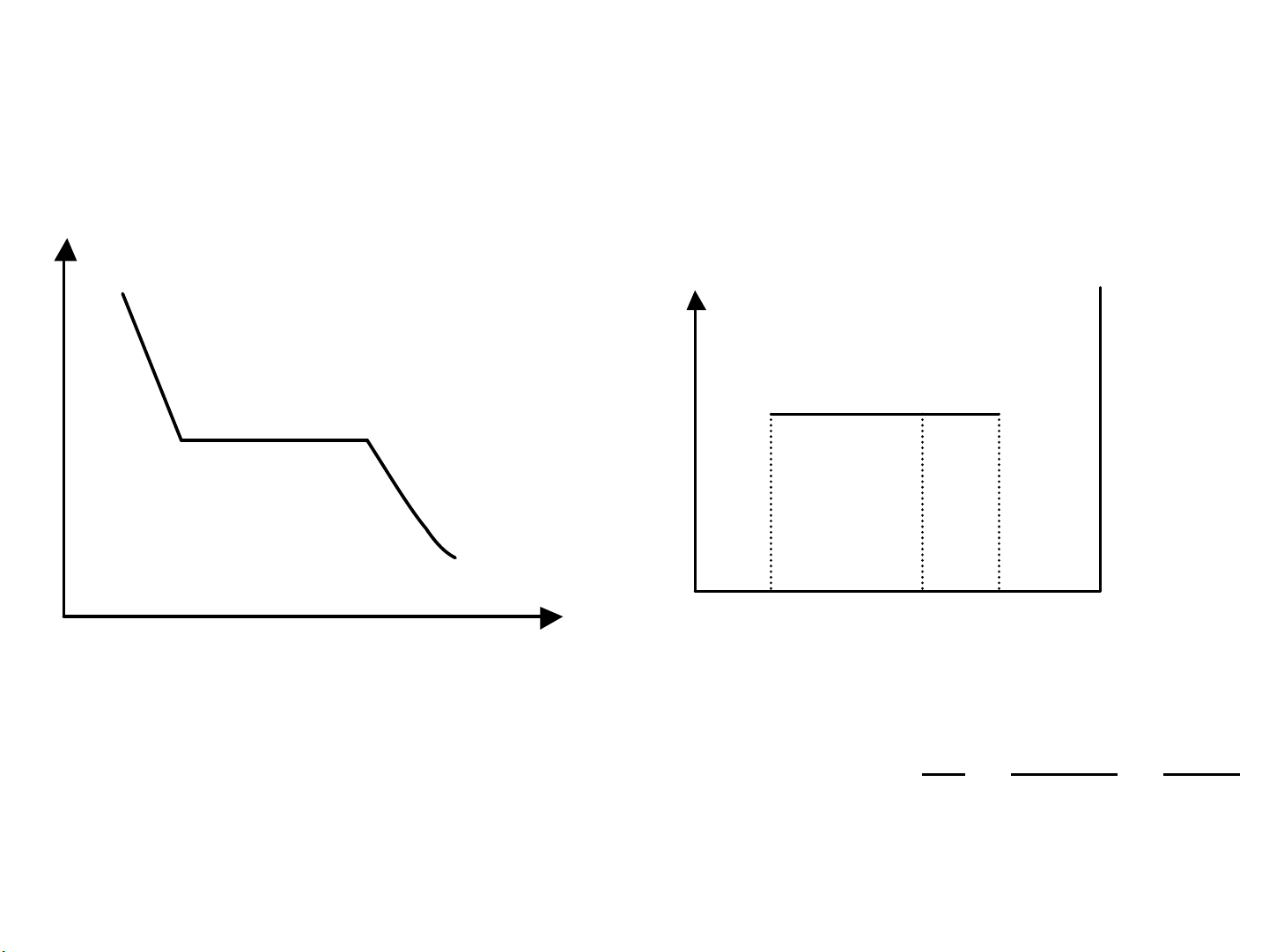
Quy tắc liên tục Quy tắc liên hợp P Hệ H = hệ H1 + hệ H2 Lỏng !T H Lỏng = Hơi 1 H H2 (1) (2) Hơi V A x1 x x2 B ! Điểm 1: chuyển 1 pha Quy tắc đòn bẩy → 2 pha g x − x HH 1 = 2 = 2 Điểm 2: chuyển 2 pha g x − x HH 2 1 1 g → 1 pha 1: khối lượng hệ H1 g2: khối lượng hệ H2 KẾT LUẬN - Cách tính số pha
- Điều kiện cân bằng pha
- Các quy tắc của giản đồ pha