













Preview text:
Phần 2
Các quá trình truyền nhiệt GV: TS. Nguyễn Minh Tân
Bộ môn QTTB CN Hóa – Thực phẩm
Các phương thức truyền nhiệt
• Dẫn nhiệt/Conduction: Quá trình truyền nhiệt từ phần tử
này đến phần tử khác của vật chất khi chúng tiếp xúc trực tiếp với nhau
• Đối lưu/Convection: Quá trình truyền nhiệt do các phần
tử chất lỏng hoặc chất khí đổi chỗ cho nhau, do chúng có
nhiệt độ khác nhau hoặc là do bơm, quạt, khuấy trộn,…
• Bức xạ/Radiation: Qua trình truyền nhiệt dưới dạng các
sóng điện từ. Nhiệt năng biến thành các tia bức xạ rồi
truyền đi, khi gặp vật thể nào đó thì một phần năng lượng
bức xạ đố được biến thành nhiệt năng, một phần phản xạ
lại, và một phần xuyên qua vật thể QTTB II 01 TS. Nguyễn Minh Tân 2 Đối lưu
Dòng đối lưu được hình thành khi trong nồi có nước được đun nóng Dòng không khí đối lưu hình thành do chênh lệch nhiệt độ
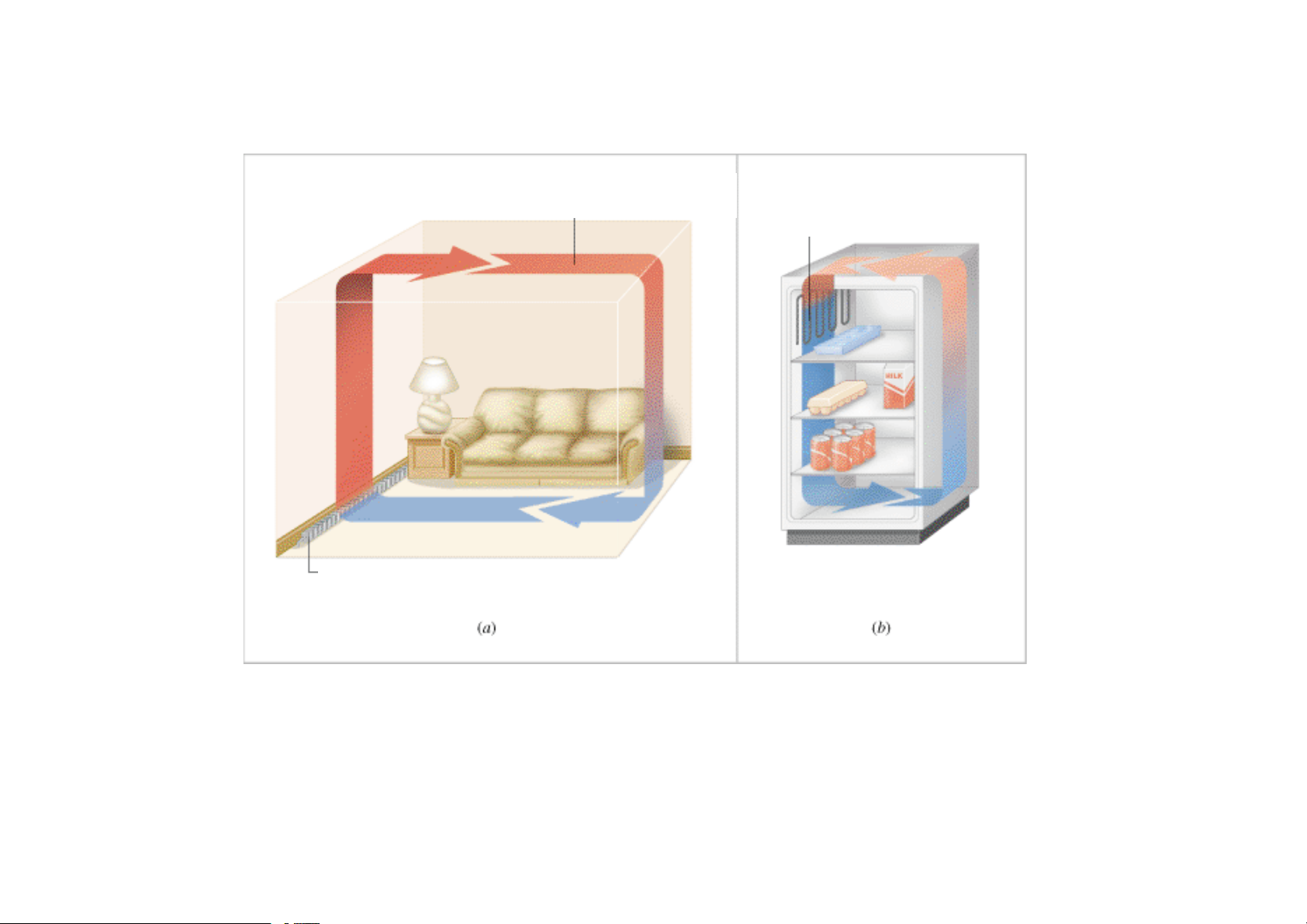
giữa đại dương và lục địa QTTB II 01 TS. Nguyễn Minh Tân 3 Dòng đối lưu Giàn lạnh Bộ phận sưởi
Tại sao bộ phận sưởi được đặt dưới sàn, còn giàn lạnh của tủ lạnh được đặt phía trên? QTTB II 01 TS. Nguyễn Minh Tân 4 1.2. Nhiệt đối lưu
1.2.1. ĐỊNH LUẬT CẤP NHIỆT NEWTON
Quá trình cấp nhiệt rất phức tạp, để đơn giản hóa, người ta dùng định luật cấp nhiệt của NEWTON
Lượng nhiệt dQ do một phân tố bề mặt dF của vật rắn cấp cho môi trường xung
quanh (hoặc ngược lại) trong khoảng thời gian dτ thì tỉ lệ với hiệu số nhiệt độ giữa
vật thể và môi trường, với dF và dτ dQ =α(t t T − )dF τ d
Với quá trình ổn định: Q=α(t −t , T )F W QTTB II 01 TS. Nguyễn Minh Tân 5 1.2. Nhiệt đối lưu
Hệ số cấp nhiệt α: là lượng nhiệt do một đơn vị bề mặt của tường
cấp cho môi trường xung quanh(hoặc ngược lại) trong khoảng thời
gian một giây khi hiệu số nhiệt độ giữa tường và môi trường (hoặc ngược lại) là 1 độ. Q W [α] ⎡ ⎤ ⎡ ⎤ = = ⎢ 2 ⎣(tT − t) ⎥ ⎢ ⎥
Fτ ⎦ ⎣m °C ⎦
Hệ số cấp nhiệt α là một đại lượng rất phức tạp, phụ thuộc vào nhiều yếu tố:
• Loại chất tải nhiệt (khí, lỏng, hơi)
• Chế độ chuyển động của chất tải nhiệt
• Tính chất vật lý của chất tải nhiệt
• Kích thước, hình dạng, trạng thái của bề mặt trao đổi nhiệt,… QTTB II 01 TS. Nguyễn Minh Tân 6 1.2. Nhiệt đối lưu
1.2.2. PHƯƠNG TRÌNH VI PHÂN CỦA NHIỆT ĐỐI LƯU
- Cơ sở Định luật cân bằng nhiệt
- Tách phân tố thể tích dV=dxdydz từ dòng chảy
- Chỉ xét trường hợp trao đổi nhiệt ổn định
Lượng nhiệt đi vào và đi ra khỏi phân tố dV do các phần tử của môi
trường chuyển động mang vào và mang ra
Lượng nhiệt mang vào tính trên trục ox trong một đơn vị thời gian: Q = C t W ρ dydz x p x
Trong cùng thời gian đó, lượng nhiệt mang ra khổi mặt đối diện là: ∂(C t W p ρ x ) Q
= Q + dQ = C t W ρ dydz + dxdydz x+dx x x p x x ∂ QTTB II 01 TS. Nguyễn Minh Tân 7 1.2. Nhiệt đối lưu
1.2.2. PHƯƠNG TRÌNH VI PHÂN CỦA NHIỆT ĐỐI LƯU ⎡ ∂( W ρ x ) t Q
= Q + dQ = C t W ρ dydz + C t + W ∂ ⎤ ρ dxdydz x+dx x x p x p ⎢ x x ∂ x ⎥ ⎣ ∂ ⎦
Lượng nhiệt do đối lưu tích theo phương Ox tích lại trong phân tố dV: ⎡ ∂( W ρ x ) t dQ = Q − Q = C t + W ∂ ⎤ ρ dxdydz x x+dx x p ⎢ x x ∂ x ⎥ ⎣ ∂ ⎦
Lượng nhiệt do đối lưu tích theo phương Oy tích lại trong phân tố dV: ⎡ ∂( W ρ y ) t ∂ ⎤ dQ = Q − Q = C t + W ρ dxdydz y y+dy y p ⎢ y y ∂ y ⎥ ⎢⎣ ∂ ⎥⎦
Lượng nhiệt do đối lưu tích theo phương Ox tích lại trong phân tố dV: ⎡ ∂( W ρ z ) t dQ = Q − Q = C t + W ∂ ⎤ ρ dxdydz z z+dz z p ⎢ z z ∂ z ⎥ ⎣ ∂ ⎦ QTTB II 01 TS. Nguyễn Minh Tân 8 1.2. Nhiệt đối lưu
1.2.2. PHƯƠNG TRÌNH VI PHÂN CỦA NHIỆT ĐỐI LƯU
Lượng nhiệt toàn phần:
dQ = dQ + dQ + dQ x y z + " - ∂ ρW ( ) ∂ ρW ( ) ∂ ρW ( )% ∂t ∂t ∂t ( dQ x y z = C ,t$ + + '+ρW + ρW + ρW d V p x y z ) $ ∂x ∂y ∂z .- # &' ∂x ∂y ∂z * ⎡∂( W ρ ρ x ) ∂( Wy ) ∂( W ρ z )⎤
Với dòng liên tục có: ⎢ + + ⎥ = 0 ⎢ x y z ⎣ ∂ ∂ ∂ ⎥⎦ Nên: % ∂t ∂t ∂t " dQ = ρC W & + W + W d V p x # ' ∂x y ∂y z ∂z$ QTTB II 01 TS. Nguyễn Minh Tân 9 1.2. Nhiệt đối lưu
1.2.2. PHƯƠNG TRÌNH VI PHÂN CỦA NHIỆT ĐỐI LƯU
Với quá trình truyền nhiệt ổn định, lượng nhiệt ở trong nguyên tố dV là không
đổi. Lượng nhiệt này phải bằng lượng nhiệt dẫn qua các mặt của dV là dQ: % ∂t ∂t ∂t " dQ = ρC W & + W + W d V = λ ∇2t p x # ( )dV ' ∂x y ∂y z ∂z$
Phương trình vi phân cấp nhiệt đối lưu Fourier- Kirchhoff: % ∂t ∂t ∂t " λ ρC W & + W + W = λ ∇2t ∇2t p x # ( ); ( ) = a ∇2t ( ) ' ∂x y ∂y z ∂z$ C ρ p QTTB II 01 TS. Nguyễn Minh Tân 10 1.2. Nhiệt đối lưu
1.2.3. ĐỒNG DẠNG CỦA CÁC QUÁ TRÌNH NHIỆT
Quá trình đối lưu nhiệt được mô tả bởi một hệ phương trình:
- Phương trình vi phân cân bằng của Ơle
- Phương trình dòng liên tục
- Phương trình vi phân cấp nhiệt đối lưu Fourier- Kirchhoff
Phải dựa vào lý thuyết đồng dạng để chuyển pt vi phân thành pt chuẩn số QTTB II 01 TS. Nguyễn Minh Tân 11 1.2. Nhiệt đối lưu Chuẩn số Nuxen
Trong quá trình truyền nhiệt ổn định, lượng nhiệt truyền do dẫn nhiệt phải
bằng lượng nhiệt truyền do cấp nhiệt: dt α (t − t T )= −λ dn
Đưa chuẩn số đồng dạng vào: a dt a a a tα (t − t T ) = −a t a λ a dn l a a t a a = a a l = idem Nu l a t a a a = a α = Nu l λ λ
Chuẩn số Nuxen đặc trưng cho quá trình cấp nhiệt trên bề mặt phân giới QTTB II 01 TS. Nguyễn Minh Tân 12 1.2. Nhiệt đối lưu Chuẩn số Pecle
Được rút ra từ phương trình Fourier- Kirchhoff
Ví dụ đối với trục ox: Rút ra: l l w 1 1 = w 2 2 = idem a a 1 2 2 t ∂ ∂ t w = a x 2 wl x∂ x ∂ = Pe a
Ngoài các chuẩn số trên, từ các pt chuyển động có các chuẩn số Eu, Fr,
Re, nên có thể biểu diễn: F(Nu, , Pe Eu,Pr,Re)= 0 QTTB II 01 TS. Nguyễn Minh Tân 13 1.2. Nhiệt đối lưu Trong khi Eu = f (Re)
Kết hợp Pe và Nu có chuẩn số Prandtl đặc trưng cho tính chất vật lý của môi trường wl Pe a µ µ µCp Pr = = Re wl = = = ρ ρ a λρ λ µ ρ 2 3
gl ⎛ wlρ ⎞ gl
Kết hợp Re và Fr có chuẩn số Galile, Ga: 2 Ga = Fr.Re = = 2 ⎜⎜ ⎟⎟ 2 w ⎝ µ ⎠ γ
Chuẩn số Gratkov, đặc trưng cho truyền nhiệt khi đối lưu tự nhiên: gl3 Gr = β t Δ γ 2 QTTB II 01 TS. Nguyễn Minh Tân 14 1.2. Nhiệt đối lưu
Phương trình cấp nhiệt tổng quát được biểu diễn dưới dạng phương trình chuẩn số
là F(Nu,Pe,Eu,Pr,Re)=0⇔ Nu = f '(Re,Pr,Gr)
Quá trình cấp nhiệt xảy ra trong dòng đối lưu tự nhiên:
Nu = f '(Pr,Gr)
Với các chất khí, chuẩn số Pr không biến đổi nhiều theo nhiệt độ:
Chuyển động cưỡng bức Nu = f (Re 3 )
Đối lưu tự nhiên Nu = f (Re 3 )
Dạng cụ thể ở dạng hàm số mũ k m n
Nu = C Re Pr Gr QTTB II 01 TS. Nguyễn Minh Tân 15 1.2. Nhiệt đối lưu
Hệ số α được xác định theo quan hệ : C λ α = ( k m n Re Pr Gr ) l
Hệ số cấp nhiệt α chỉ có thể được xác định với từng trường
hợp cụ thể với mỗi thiết bị riêng biệt QTTB II 01 TS. Nguyễn Minh Tân 16




