Phân cực ánh sáng | Bài giảng môn Vật lý đại cương 3 | Trường Đại học Bách Khoa Hà Nội

Bμi gi¶ng VËt lý ®¹i c−¬ng
T¸c gi¶: PGS. TS §ç Ngäc UÊn ViÖn VËt lý kü thuËt
Tr−êng §H B¸ch khoa Hμ néi Ch−¬ng 5 Ph©n cùc ¸nh s¸ng
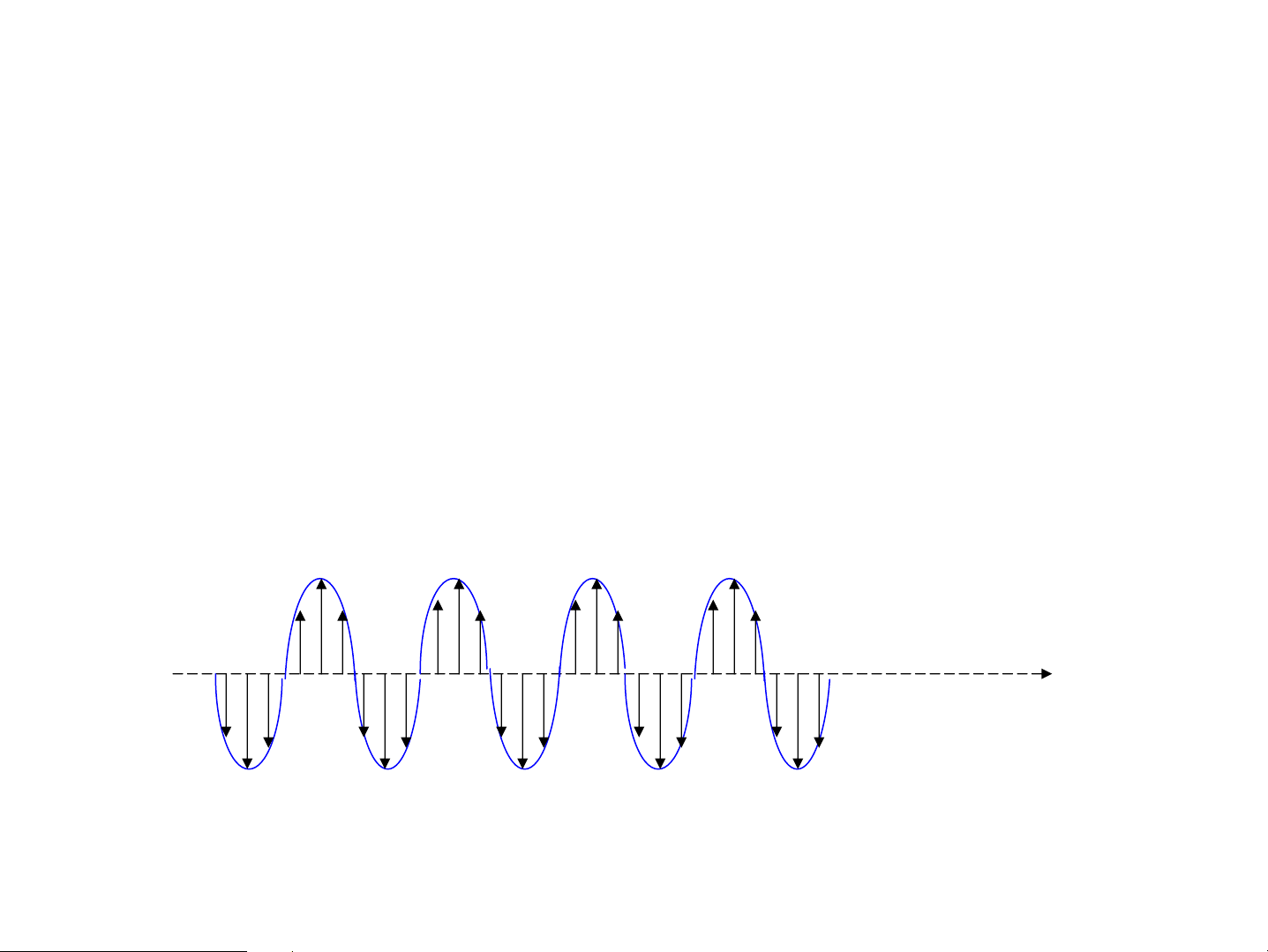
¸nh s¸ng lμ sãng ngang: dao ®éng s¸ng
vu«ng gãc víi ph−¬ng truyÒn sãng rE rv
1. ¸nh s¸ng tù nhiªn vμ ¸nh s¸ng ph©n cùc 1. ¸nh s¸ng tù nhiªn:
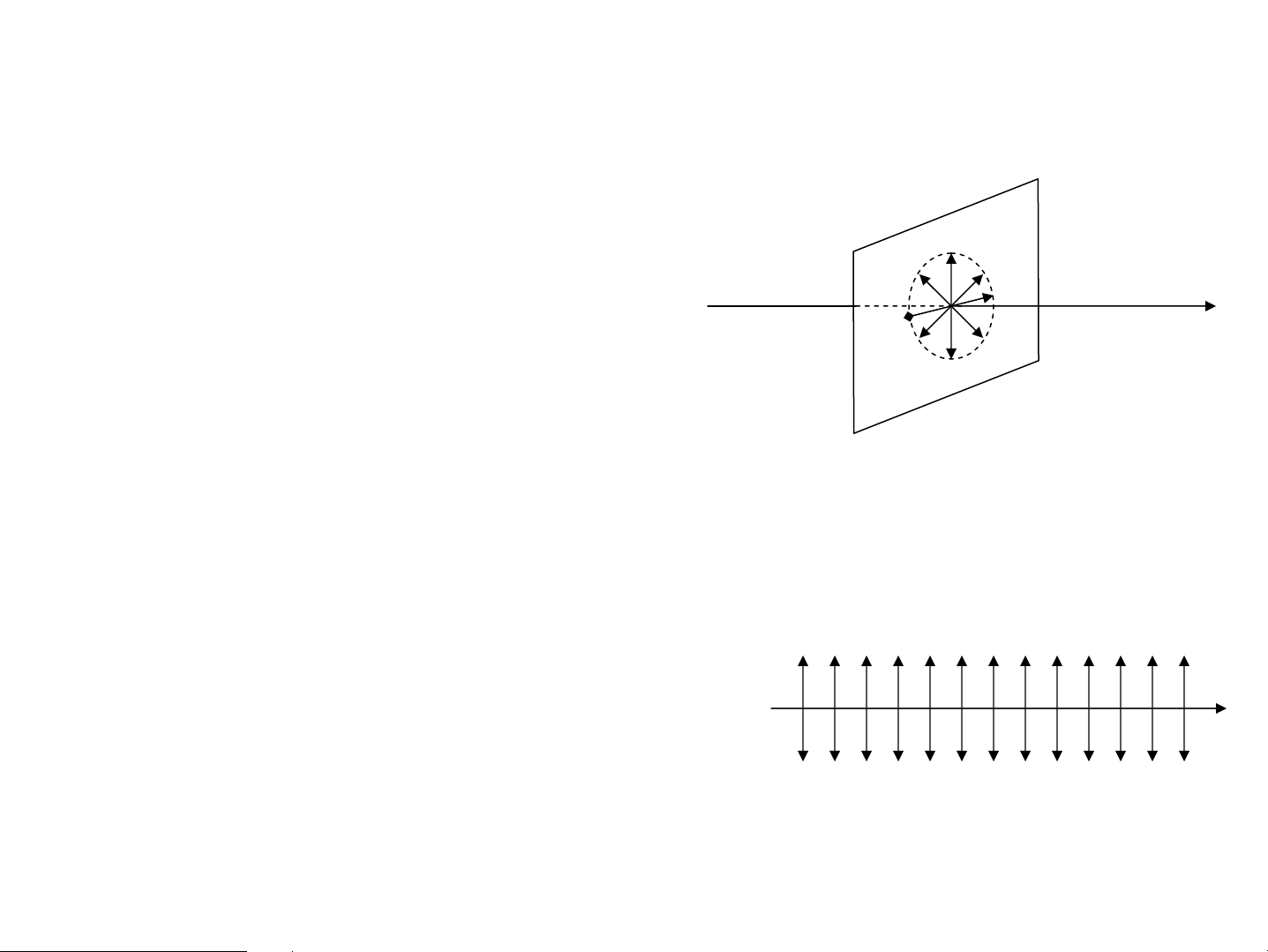
VÐc t¬ c−êng ®é ®iÖn tr−êng rE r dao ®éng theo tÊt c¶ c¸c v ph−¬ng vu«ng gãc víi tia s¸ng 1. ¸nh s¸ng ph©n cùc:
Cã vÐc t¬ c−êng ®é ®iÖn tr−êng chØ dao ®éng theo
mét ph−¬ng x¸c ®Þnh gäi lμ AS ph©n cùc th¼ng hay AS ph©n cùc toμn phÇn r MÆt ph¼ng dao ®éng E rv MÆt ph¼ng ph©n cùc
MÆt ph¼ng chøa ph−¬ng dao ®éng -> MÆt ph¼ng dao ®éng
MÆt ph¼ng chøa tia s¸ng vμ vu«ng gãc víi mÆt
ph¼ng dao ®éng -> MÆt ph¼ng ph©n cùc AS tù nhiªn ph©n cùc mét phÇn toμn phÇn
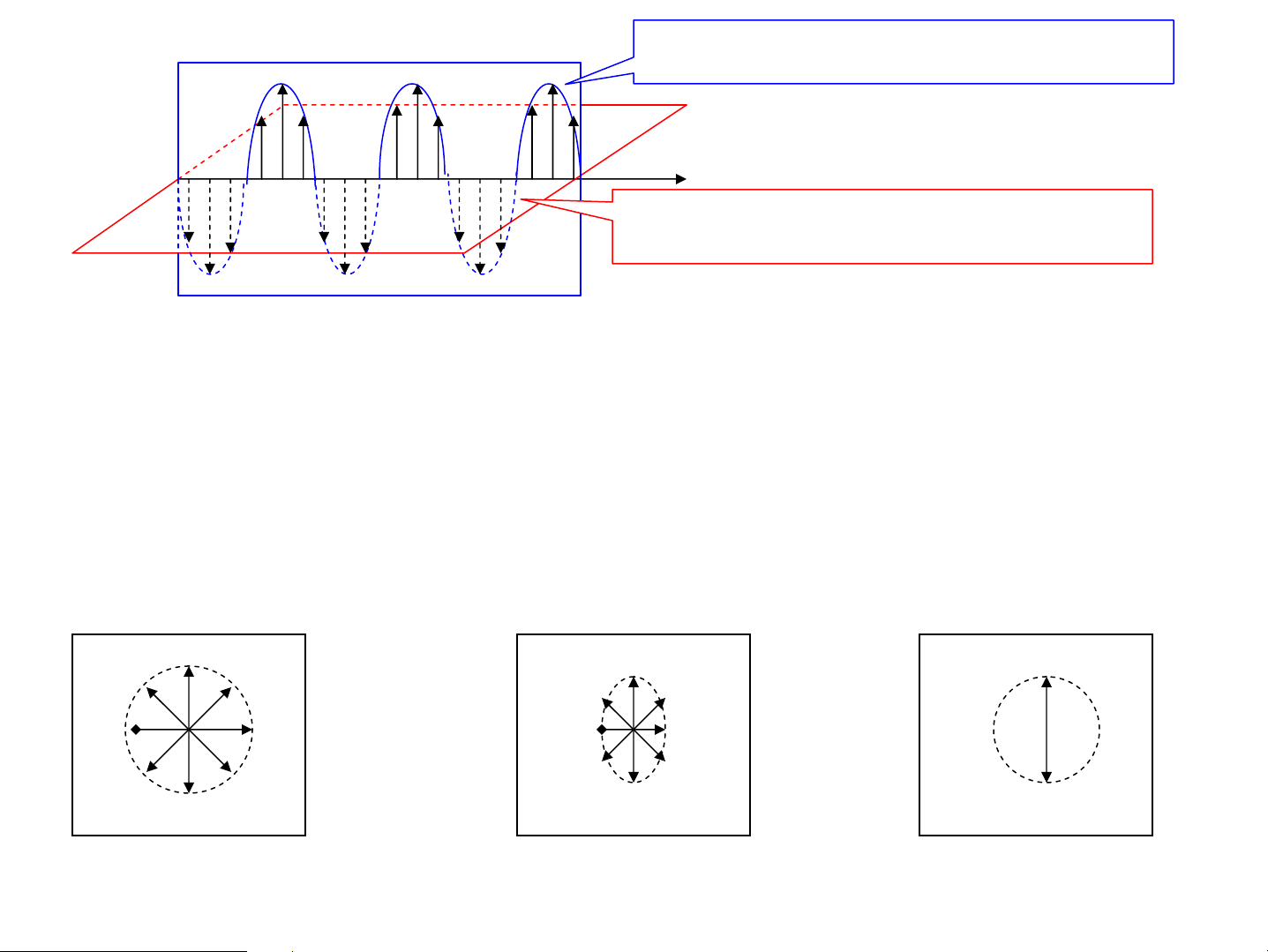
Ph©n cùc mét phÇn: AS cã vÐc t¬ c−êng ®é ®iÖn
tr−êng dao ®éng theo mäi ph−¬ng vu«ng gãc víi
tia s¸ng, nh−ng cã ph−¬ng m¹nh, ph−¬ng yÕu.
AS tù nhiªn cã thÓ coi lμ tËp hîp nhiÒu AS ph©n
cùc toμn phÇn dao ®éng ®Òu ®Æn theo tÊt c¶ c¸c
ph−¬ng vu«ng gãc víi tia s¸ng.
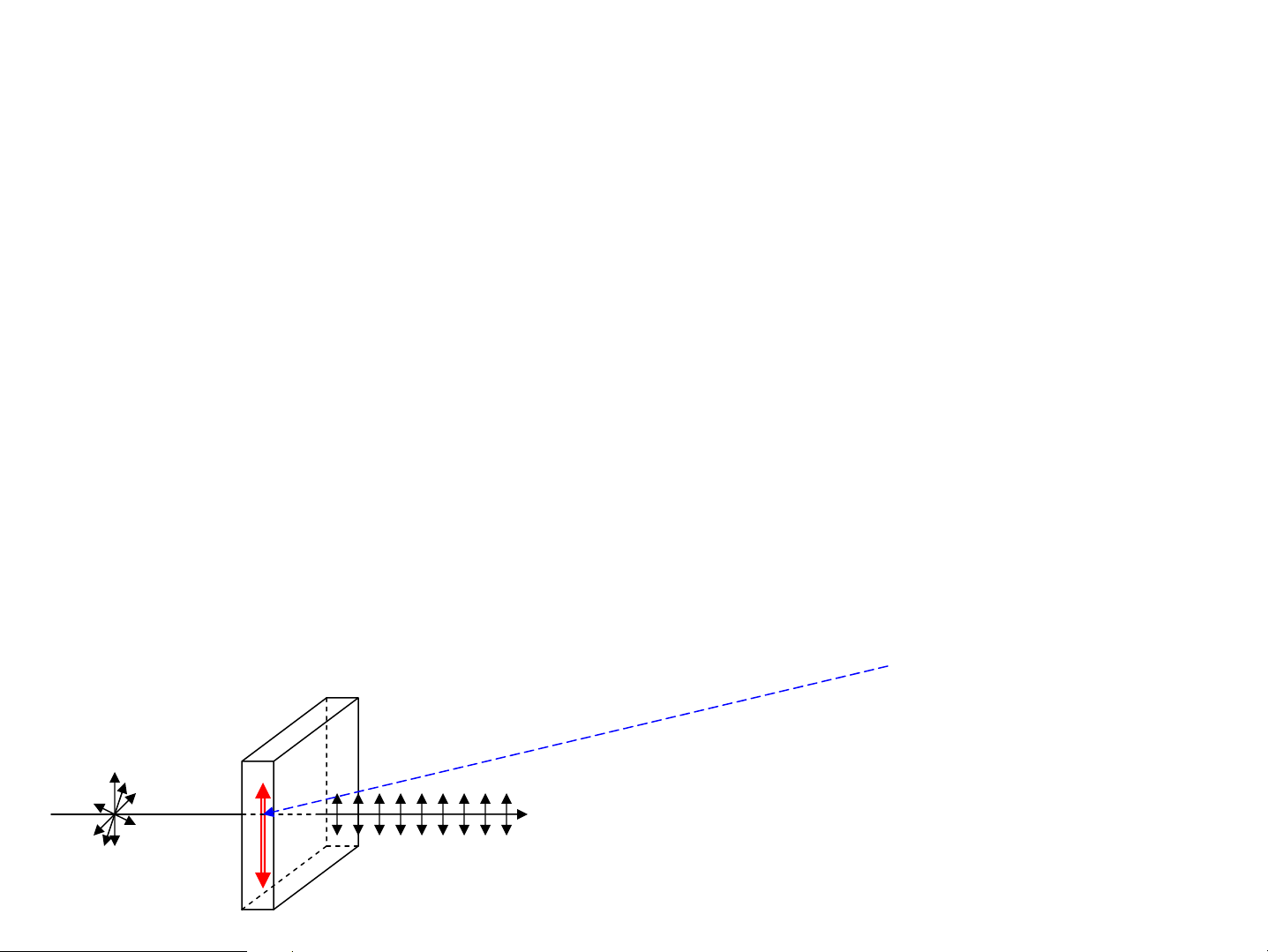
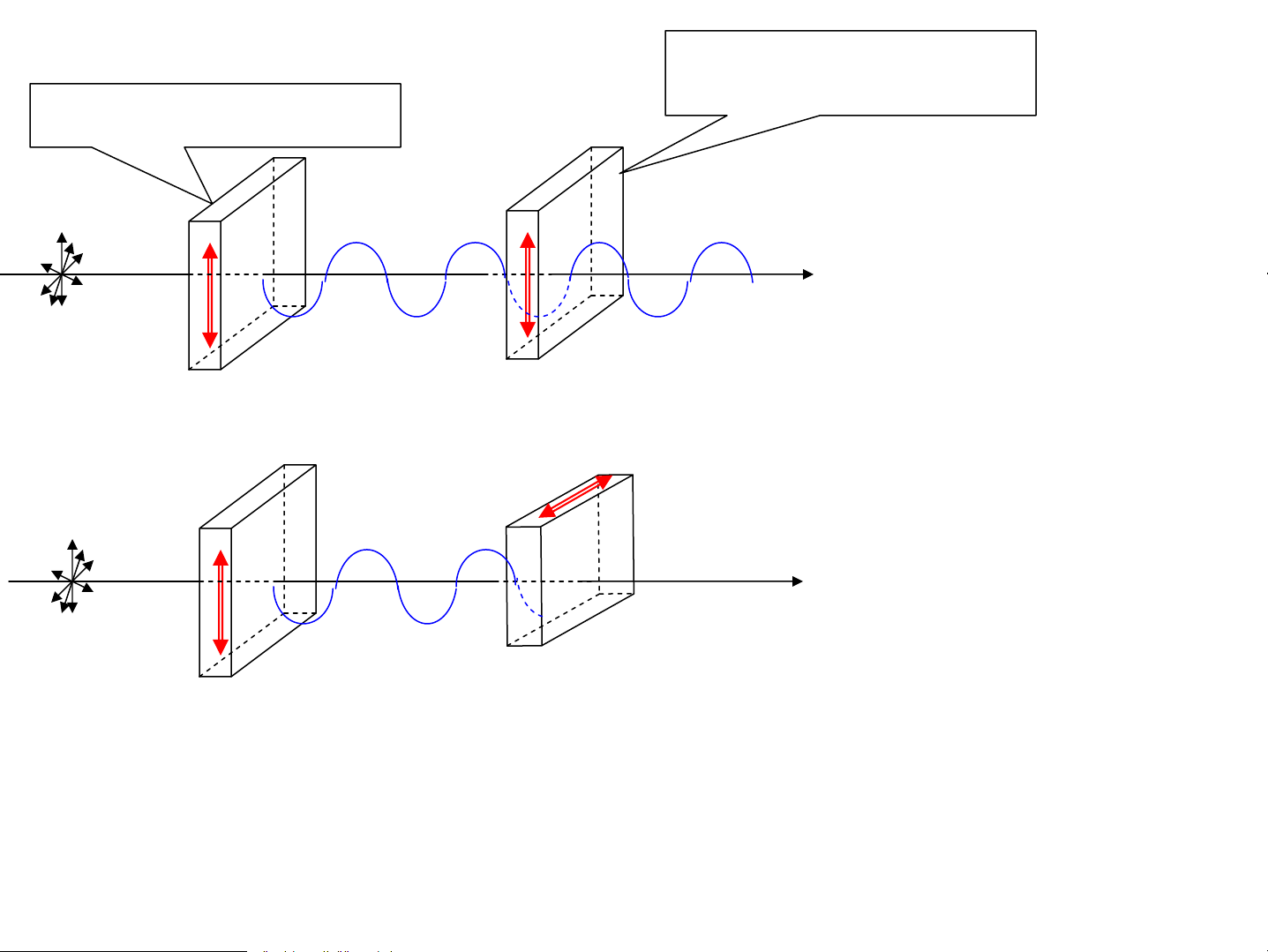
AS tù nhiªn qua b¶n Tuamalin (Alumini
Silicorobat AlSiBO ) bÞ ph©n cùc toμn phÇn cã 5
E dao ®éng trªn mÆt ph¼ng chøa quang trôc rE song song víiquang trôc
2.§Þnh lý Maluýt (Malus)kÝnh ph©n tÝch kÝnh ph©n cùc a =a cosα 2 1 α gãc gi÷a hai a , I a , I quang trôc 1 1 2 2 I = 2 a = 2 I cos α 2 2 1
Khi cho mét chïm tia s¸ng tù nhiªn räi qua hai
b¶n tuamalin cã quang trôc hîp víi nhau gãc α
th× c−êng ®é ¸nh s¸ng thu ®−îc tû lÖ víi cos2α
øng dông: Dïng b¶n tuamalin kiÓm tra xem AS
cã ph¶i lμ ph©n cùc hay kh«ng?
KÝnh chèng n¾ng, trong dông cô quang häc.
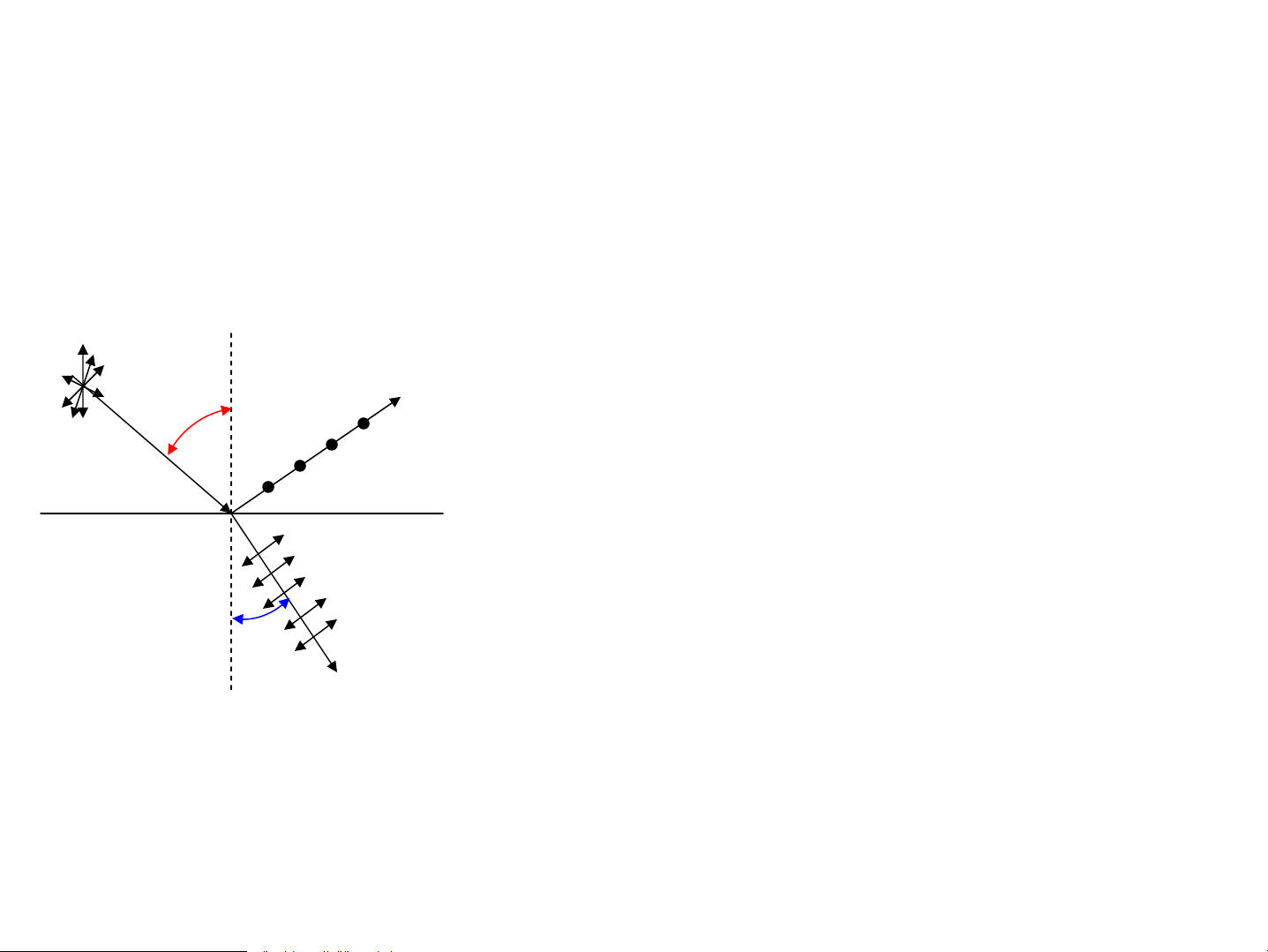
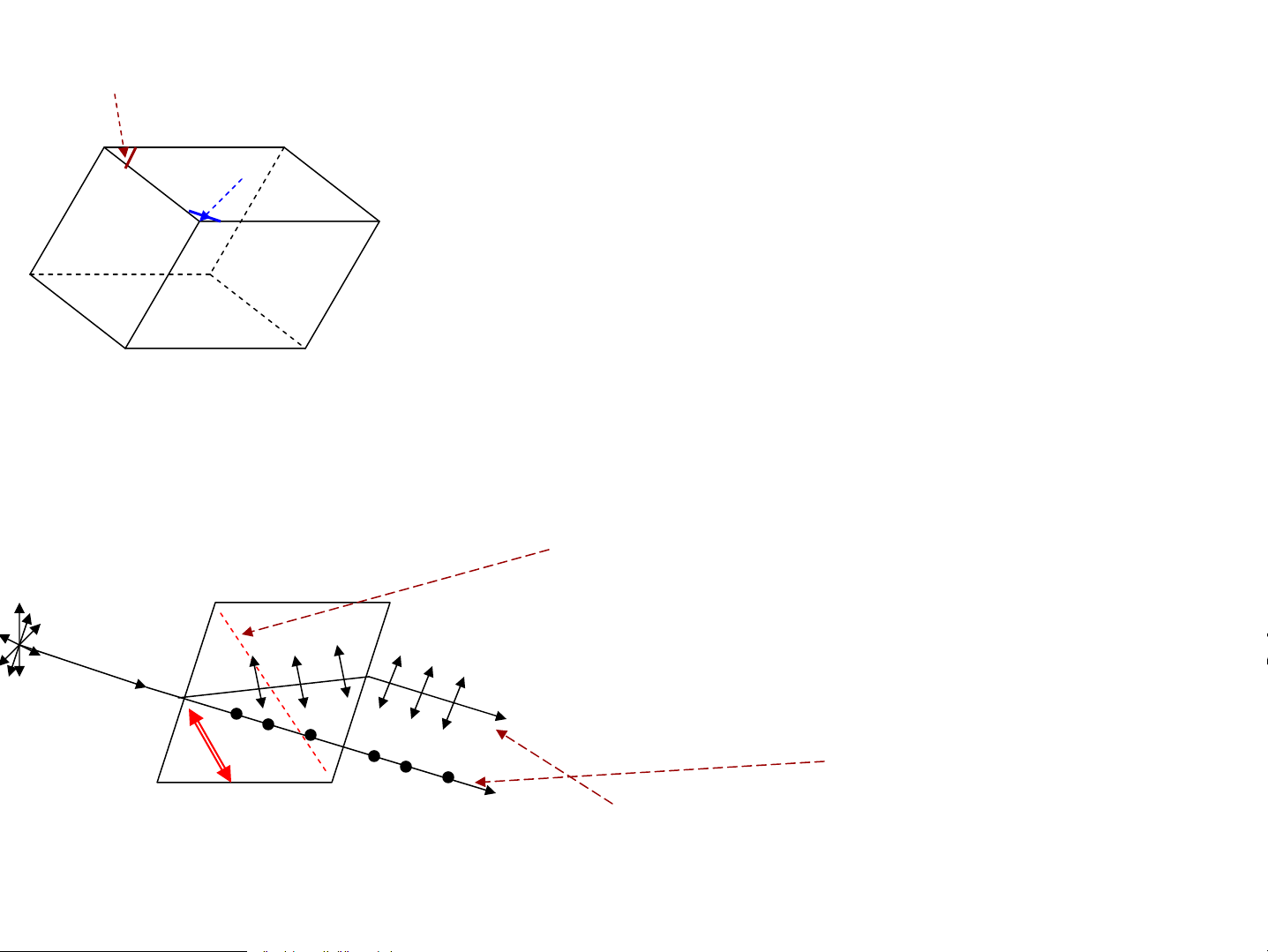
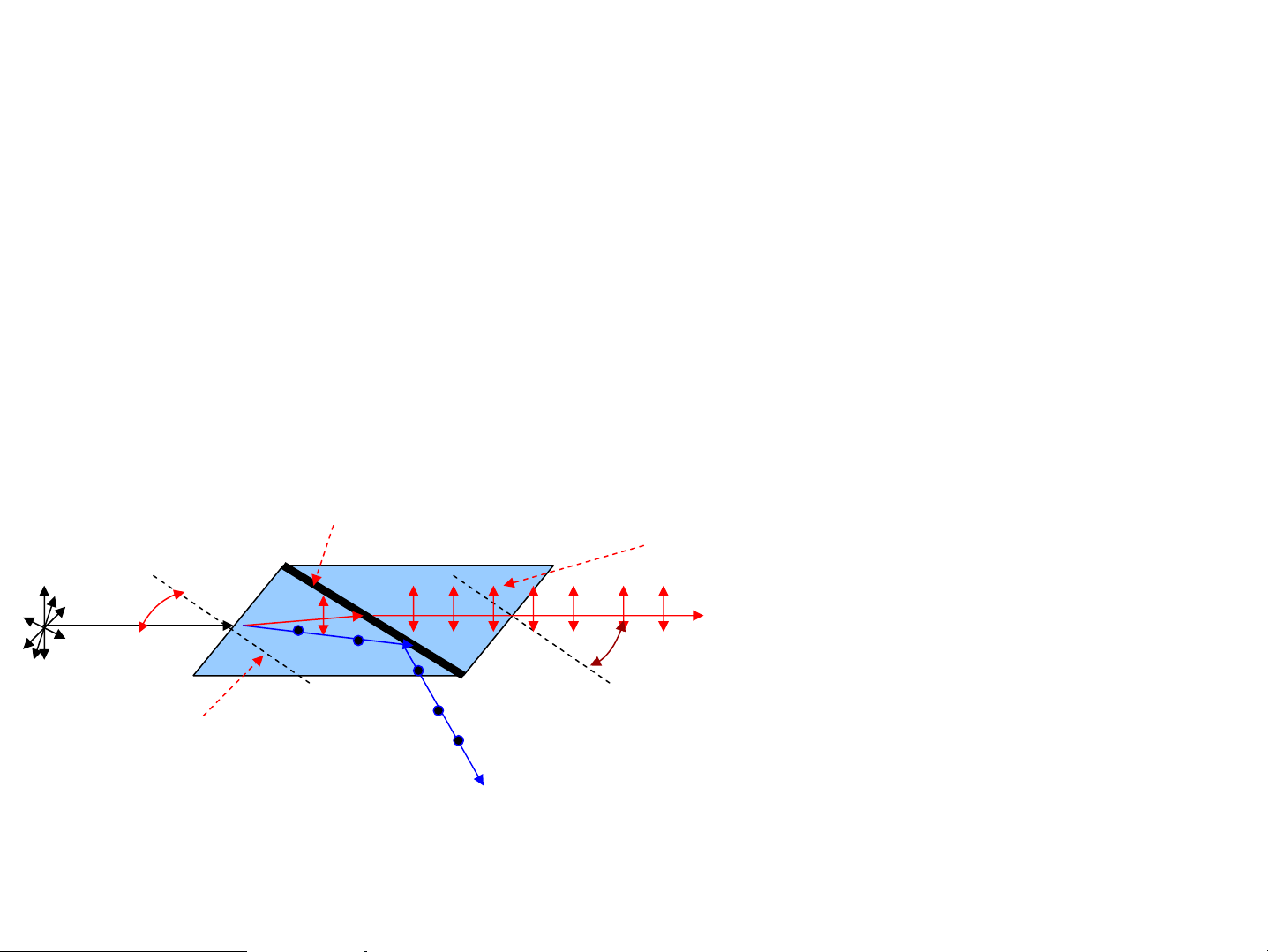
2. Ph©n cùc AS do ph¶n x¹ vμ khóc x¹ AS kh«ng khÝ Tia ph¶n x¹ vμ tia khóc i1 x¹ ph©n cùc mét phÇn t¨ng i møc ®é ph©n cùc 1 thuû tinh
cña tia ph¶n x¹ thay ®æi, khi i =i tia ph¶n x¹ 1 B tgi =n ph©n cùc toμn phÇn B 21 n
lμ chiÕt suÊt tû ®èi gi÷a 2 m«i tr−êng 21 i lμ gãc Briut¬ B
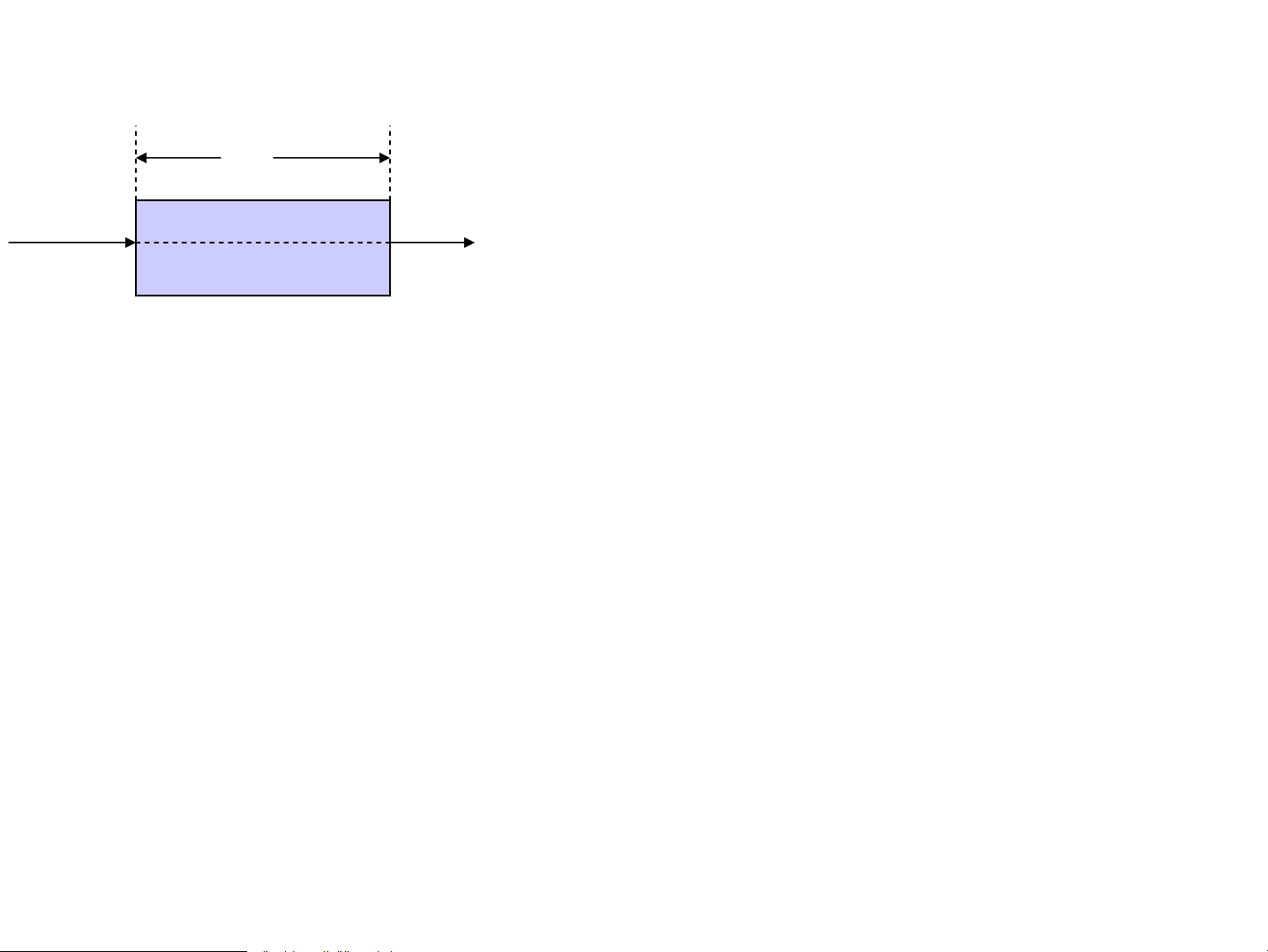
4. Ph©n cùc do l−ìng chiÕt 78o08 B1 D
TÝnh l−ìng chiÕt cña tinh thÓ:
101o52’Tinh thÓ cã tÝnh dÞ h−íng -> Khi A C1 C A
chiÕu 1 tia vμo TT thu ®−îc 2 tia 1 B D1 truyÒn qua: L−ìng chiÕt TT b¨ng lan
NÕu chiÕu tia s¸ng däc theo Thoi-CaCO3 quang trôc tia kh«ng bÞ A C1 t¸ch thμnh 2 tia NÕu chiÕu tia s¸ng ⊥ABCD
e t¸ch thμnh tia th−êng (0) vμ C A 0 tia bÊt th−êng (e-Kh«ng 1
tu©n theo ®Þnh luËt khóc x¹)
sin i = n = const MÆt ph¼ng chøa tia th−êng vμ sin i 0 0
quang trôc lμ mÆt ph¼ng chÝnh
sin i = n ≠ const ChiÕt suÊt cña tinh thÓ ®èi sin i e e víi 2 tia
C¶ 2 tia e & 0 ®Òu ph©n cùc toμn phÇn
B¨ng lan cã n < n : tinh thÓ ©m, e 0
Th¹ch anh cã n > n : tinh thÓ d−¬ng e 0
n kh«ng ®æi, n phô thuéc vμo gãc tíi i 0 e
5. Sù quay mÆt ph¼ng ph©n cùc
C¸c tinh thÓ ®¬n trôc: Th¹ch anh, NaClO3
ChiÕu tia s¸ng ph cùc däc theo quang trôc-> MÆt
ph¼ng dao ®éng & MP ph©n cùc quay ®i gãc α α ρ =[α]ρd khèi l−îng riªng d
[α] HÖ sè tû lÖ phô thuéc vμo λ ®iÒu kiÖn thÝ nghiÖm [α]=21,7 ®é.cm3/(mm.gam)
®èi víi th¹ch anh ë 200C vμ λ =5893A0 vμng
Tr−êng hîp c¸c chÊt v« ®Þnh h×nh: Dung dÞch
cã chøa chÊt quang ho¹t nh− ®−êng, r−îu
α=[α]Cd C nång ®é quang ho¹t trong dung dÞch
[α]=65,6 ®é.cm3/(dm.gam) ®èi víi ®−êng Saccaro ë 200C vμ λ =5893A0 vμng
øng dông: ®−êng kÕ ®o nång ®é dung dÞch
6. C¸c lo¹i kÝnh ph©n cùc:
c B¶n l−ìng chiÕt hÊp thô tia th−êng chØ cho tia
bÊt th−êng ®i qua - b¶n tuamalin dμy cì 1mm.
Mμng xenluyloit cã phñ líp polaroit cã tÝnh hÊp thô kh«ng ®Òu. d L¨ng kÝnh nicol n < n e 0 nhùa canada n =1,55 nh tt l−ìng chiÕt b¨ng lan i1 n e nh i1 tt l−ìng chiÕt ®i qua b¨ng lan n >n tia th−êng 0 nh kh«ng ®i qua
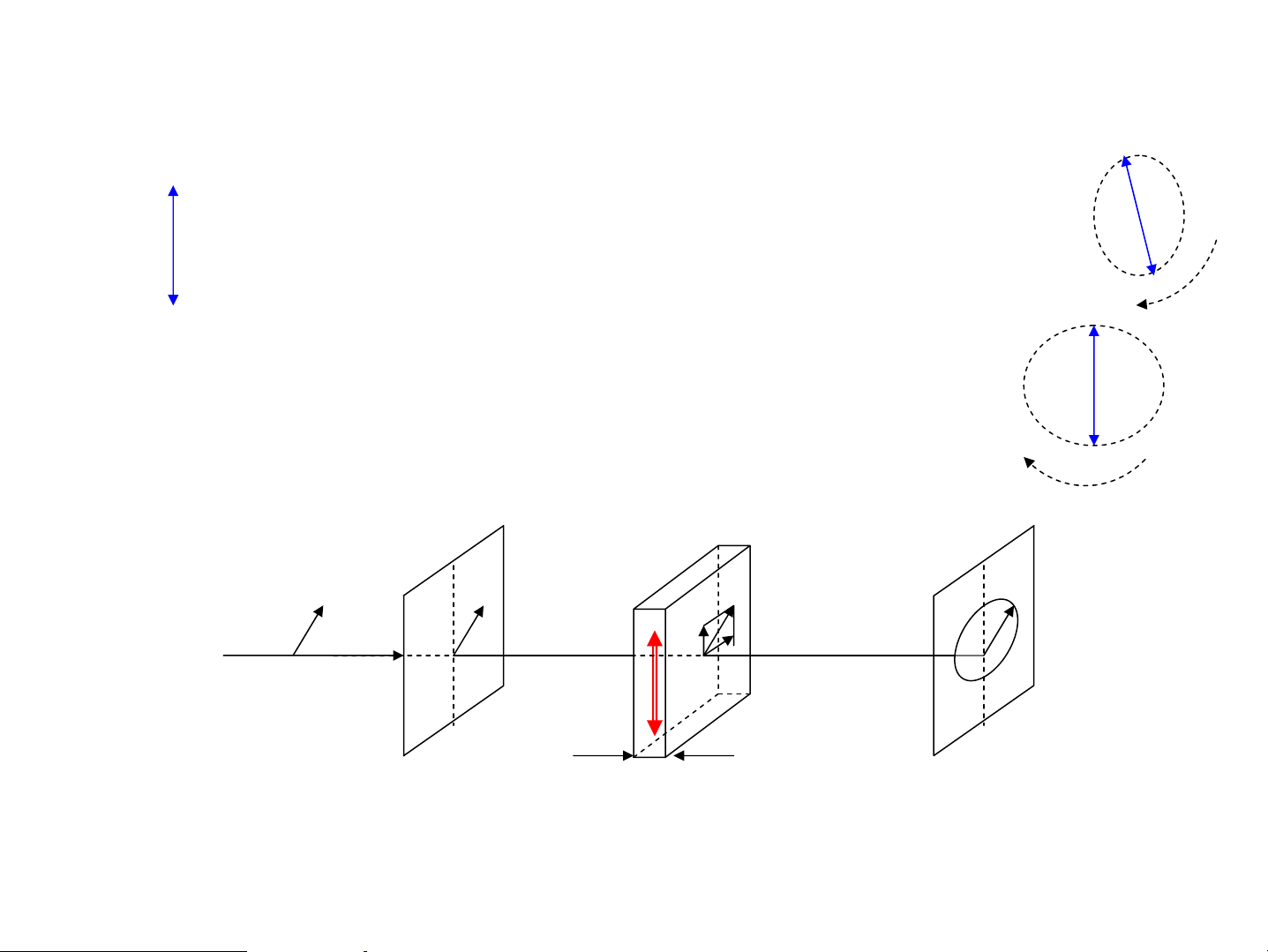
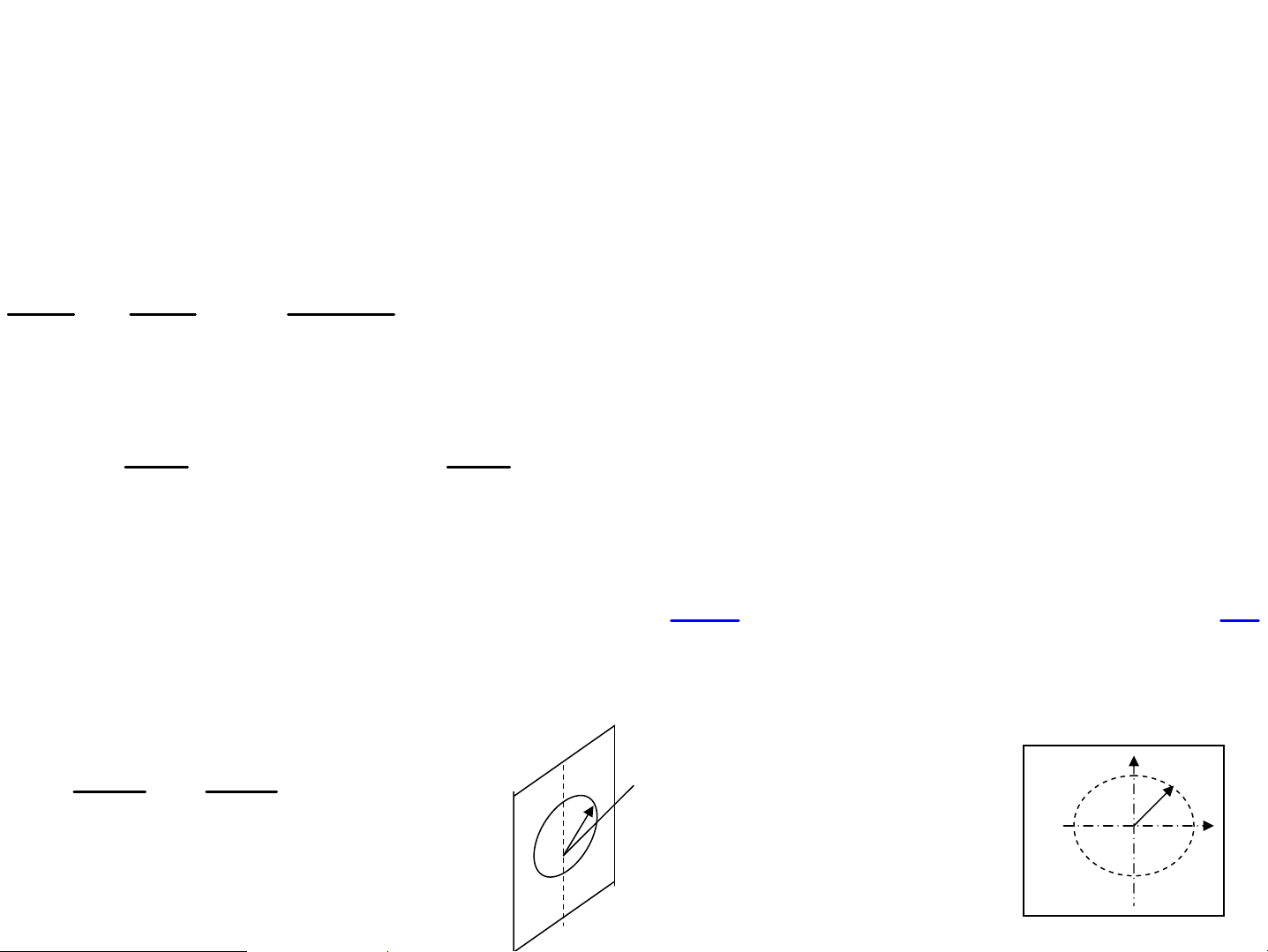
7. Ph©n cùc elip, ph©n cùc trßn
• Ph©n cùc th¼ng • Ph©n cùc elip: mòi vÐc t¬ c−êng ®é ®iÖn tr−êng quay trªn elip
• Ph©n cùc trßn: mòi vÐc t¬ c−êng
®é ®iÖn tr−êng quay trªn vßng trßn Tinh thÓ l−ìng chiÕt r as ph©n cùc α Ee rEo d
Trong b¶n tinh thÓ l−ìng chiÕt as t¸ch thμnh 2 r r tia: e( )v E E e μ o ( )cã o vËn tèc kh¸c nhau.
Ra khái b¶n tinh thÓ l−ìng chiÕt 2 tia e vμ o cã
vËn tèc b»ng nhau nhau vμ kÕt hîp víi nhau nh− r r r
2 dao ®éng vu«ng gãc, cïng tÇn sè: E = E + E e o 2 2 x + y − xy 2 cos ϕ Δ = 2 sin ϕ Δ 2 2 a a a a 1 2 1 2 a =a.cosα, a =A.sinα 2π 2π 1 2 ϕ Δ = (L − L ) = (n − n )d e o e o λ λ c (n -n )d=(2k+1)λ/4 e o 2π π ϕ Δ = (n − n )d = (2k + ) 1 e o → λ 2 elip x2 y2 α=46o → + = 1 a 2 a 2 a =a =R 1 2 1 2 → trßn d (n -n )d=(2k+1)λ/2 2π e o ϕ Δ = (n − n )d = (2k + ) 1 π λ e o → x y y + = 0 ®o¹n th¼ng a2 a a 1 2 -a a x 1 1 -a2 2π e (n -n )d=kλ ϕ Δ = (n − n )d = 2 π k e o λ e o y a → x y 2 − = 0 ®o¹n th¼ng a a -a a 1 2 1 1 x -a2