Phân dạng và phương pháp giải trắc nghiệm chuyên đề hàm số – Nguyễn Vũ Minh (Tập 1) Toán 12

Phân dạng và phương pháp giải trắc nghiệm chuyên đề hàm số – Nguyễn Vũ Minh (Tập 1) Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

112 56 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Phân dạng và phương pháp giải

trắc nghiệm Toán 12

BIÊN HÒA – Ngày 07 tháng 06 năm 2017

TÀI LIỆU LƯU HÀNH NỘI BỘ

 Tính đơn điệu

 Cực trị

 GTLN-GTNN

Tập 1

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

► Hàm số

()y f x

đồng biến trên khoảng (a;b)

' 0, ( ; ).y x a b   

► Hàm số

()y f x

nghịch biến trên khoảng (a;b)

' 0, ( ; ).y x a b   

☺ Chú ý :

♣ Điều kiện để tam thức bậc hai

()f x ax bx c  

i du trên :

ax bx c 0,





     







ax bx c 0,





     







Nếu hệ số a và b có chứa tham số m thì phải xét trường hợp a = 0

♣ Hàm số

()y f x

đồng biến trên khoảng (a,b) thì với

( ) ( ) ( ).a x b f a f x f b    

♣ u c :

♥ B1 : Tìm TXĐ , tính đạo hàm cấp 1 ( y’)

♥ B2 : Cho y’ = 0 tìm x

♥ B3 : Lập bảng biến thiên và kết luận

♣ Vi d  n iu mt chi 

bng

ta gi

Bước 1: Tính

 

y f x m ax bx c



   

Bước 2: Hàm số đơn điệu trên

 

x x y





có

nghiệm phân biệt

















 

Bước 3: Hàm số đơn điệu trên khoảng có độ dài bằng

 

x x l x x x x l

1 2 1 2 1 2

4      

4  S P l

 

Bước 4: Giải

 

và giao với

 

để suy ra giá trị m cần tìm.

BÀI TẬP TỰ LUẬN PHẦN TÍNH ĐƠN ĐIỆU

Bài 1 : Xét tính đơn điệu của các hàm số sau đây :

y 2x 3x 12x 13   

y 3x 6x 2  

y x 5x 1  

PHẦN 1 : TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

..............................................................................................................................................................................

y x 6x 8   

y x 3x 1  

y x 3x 3x 5   

..............................................................................................................................................................................

.............................................................................................................................................................................

y x 3x 24x 25    

y x x 3x

    

2x 2







..............................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

y x x 4x 1

    







x 11

y x 3x

    

..............................................................................................................................................................................

Bài 2 (soạn) : Xét tính đơn điệu của các hàm số sau đây :

y x 2x

  

y 2x 3x 1

    

y 2x 3x 1  

3x 1

x 2







 

y x 2 3x 4   

y x 2x 2

  

y x 2x 1

   

y x 4x 2

    

y x 3x 4  

10/

y x 3x 9x

   

11/

y x 8x 16x

   

12/

y 2x 3x

  

13/

y x 9x 9x

   

14/

1 3 7

y x x

3 2 2

   

15/







Bài 3 : Xét tính đơn điệu của các hàm số sau đây :

y 2x 9x 12x 3   

y 5x 3x 4x 5    

4 3 2

y 3x 4x 24x 48x 3    

 

y x 1 x

..............................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

..............................................................................................................................................................................

Bài 4 : Tìm m để các hàm số sau luôn giảm trên từng khoảng xác định :

mx 1







m x 1

4x 1







 

x 11

y x m 3 x

     

..............................................................................................................................................................................

Bài 5 : Tìm m để các hàm số sau luôn tăng trên từng khoảng xác định :

mx 4







 

y m 1 x 2 m 2 x 4

     

     

y m 2 m 2 x 3m 1 x m

      

     

y m 2 2m 3 x 5m 6 x 2

      

..............................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

..............................................................................................................................................................................

Bài 6 (soạn): Tìm m để các hàm số sau :

mx 1







luôn giảm trên từng khoảng xác định







luôn tăng trên từng khoảng xác định

y x 3mx 3x 1   

luôn tăng trên R (Đs :

11m  

)

 

3 2 2

y x m 1 x m 4 x 9     

luôn tăng (Đs :

1 3 3





hoặc

1 3 3





)

 

y x 3x 2m 1 x 4    

Đồng biến trên R (Đs :

1m 

)

2x 1







nghịch biến trên từng khoảng xác định (Đs :

m 

)

   

y x m 2 x m 1 x 3      

nghịch biến trên R (Đs:

7 3 5 7 3 5

   



)

 

y x x m 1 x 9

    

đồng biến vói mọi x (Đs :

3m 

)

y x mx 4x 1

   

luôn tăng trên R (Đs :

22m  

)

y x mx 4x 3   

luôn tăng trên R (Đs :

2 3 2 3m  

)

Bài 7 : Tìm m để :

a/ (ĐHQG Tp.HCM – 2000) Hàm số

y x 3x mx m   

nghịch biến trên đoạn có độ dài bằng 1

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

b/ Hàm số

   

y x m 1 x m 1 x 3

     

nghịch biến trên đoạn có độ dài bằng 5

c/ Hàm số

3 2 2

y x m x mx 3m 5     

đồng biến trên đoạn có độ dài bằng 3

..............................................................................................................................................................................

Bài 8 : Tìm a để hàm số

 

2 3 2

y a 1 x a 1 x 3x 5

     

luôn đồng biến trên từng khoảng xác

định ? (Đs:

12aa   

)

..............................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

..............................................................................................................................................................................

Bài 9 : Tìm m để hàm số

   

y m 1 x mx 3m 2 x

    

luôn đồng biến với mọi x (Đs:

2m 

)

..............................................................................................................................................................................

Bài 10 : CMR hàm số

 

3 2 2

y x m 1 x m 2 x m      

luôn nghịch biến

..............................................................................................................................................................................

Bài 11 : Tìm m để hàm số

 

3 2 2

y x 2 m 1 x 2m m 2 x m 3       

luôn đồng biến

..............................................................................................................................................................................

Bài 12 : Tìm a để hàm số sau đây luôn giảm

   

y x a 1 x 2a 1 x 3      

ax a 7

5x a 3







..............................................................................................................................................................................

Bài 13 (ĐH Thủy lợi – 1997) : tìm m để hàm số sau đồng biến trên R

y .x m.x (3m 2).x



   

..............................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

..............................................................................................................................................................................

Bài 14) : Cho hàm số

2 3 1y x mx   

. Tìm các giá trị m để hàm số đồng biến trên khoảng

 

,xx

với

1xx

..............................................................................................................................................................................

BÀI TẬP MINH HỌA PHẦN TÍNH ĐƠN ĐIỆU

Ví dụ 1 : Xác định m để hàm số

3y x x mx m   

luôn luôn đồng biến trên

3m 

3m 

m

m

♠ Giải : Tập xác định : D =

Làm tự luận ! Đạo hàm :

' 3 6y x x m  

Hàm số luôn đồng biến trên





  







9 3 0 3mm    

Vậy: với

3m 

thì hàm số luôn đồng biến trên D hay (chọn A)

Làm trắc nghiệm !

Khi làm bài trắc nghiệm chúng ta không thể giải như vậy vì sẽ có nhiều bài phức tạp “số

xấu”

☻Phương pháp “BÓC ĐẠI”

► “Bóc đại” m = 2 ở câu B thì ta thấy

' 3 6 2 0y x x   

, phương trình này có 2 nghiệm (bấm

máy là thấy nha)

Mà hàm số luôn đồng biến thì ∆ < 0, a > 0 mà !! (Loại B)

► “Bóc đại” m = 4 ở câu A thì ta thấy

' 3 6 4 0y x x   

, phương trình này vô nghiệm (bấm

máy là thấy nha )thì ∆ < 0 và a > 0

(thỏa mãn để hs đồng biến) Nên chọn A

Ví dụ 2 : Cho hàm số

 

1 1 3 1

y m m x x     

 

.Tìm

để hàm số

 

luôn đồng

biến.

♠ Giải : Đạo hàm

 

' 1 2 1 3y m x m x    

. Yêu cầu bài toán

' 0, .yx   

Với

1m 

thì

' 4 3 0

y x x     

: không thỏa mãn.

Với

1m 

thì

' 3 0,yx   

: thỏa mãn.

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

Với

1m 

, ta có

 

' 0, .

1 3 1 0











    







   







Vậy

1m 

hoặc

2m 

thỏa mãn yêu cầu bài toán.

Ví dụ 3 : Cho hàm số

43mx m







là tham số. Tìm tất cả các giá trị của

để hàm số

giảm trên từng khoảng xác định.

♠ Giải : MXĐ:

 

\.Dm

Đạo hàm:

 







Hàm số đã cho giảm trên từng khoảng xác định



hàm số nghịch biến trên từng khoảng xác

định

' 0,y x m    

3 4 0 4 1.m m m       

Vậy với

41m  

thì thỏa mãn yêu cầu bài toán.

Ví dụ 4 : Cho hàm số

 

y x m x mx     

(

là tham số).

Xác định

để hàm số nghch bin trên tập xác định.

♠ Giải : Tập xác định:

D 

Đạo hàm

 

' 2 2y x m x m    

. Hàm số nghịch biến trên

' 0, yx   

 

2 2 0, x m x m x       

5 4 0

4 1.





  



      









Vậy

41m   

thỏa mãn yêu cầu bài toán.

Ví dụ 5 : Cho hàm số

   

y m 1 x m 1 x x m     

. Tìm m để hàm số đồng biến trên R

m 4,m 1

1 m 4

1 m 4

1 m 4

♠ Giải : Đáp án D

+ TH 1: Khi

m1

thì

y x 1

hàm số đồng biến trên R.

+ TH 2: Khi

m1

. Ta có

   

y' 3 m 1 x 2 m 1 x 1    

   

 





y' 0 x m 1;4

m 1;4

m 1 3 m 1 0















       

  





   









Vậy

 

m 1;4

Ví dụ 6 : Hàm số

y 2x x

nghịch biến trên khoảng nào?

 

1;2

 

0;2

 

0;1

 

1; 

♠ Giải : Đáp án A . Ta có

y 2x x ,TXD:0 x 2   

   

2 2x 1 x

f ' x f ' x 0 x 1

2 2x x 2x x



     



Lập bảng biến thiên ta nhận thấy Đạo hàm

 

f ' x

khi đi qua điểm có

x1

thì đổi dấu từ dương

sang âm. Nên hàm số nghịch biến trên khoảng

 

1;2

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

Ví dụ 7 : Hàm số nào sau đây đồng biến trên R.







y x x 2

  

y x x 2x 3   

y x x 3x 1   

♠ Giải : Đáp án C

Các hàm số đa thức bậc chẵn không đồng biến trên R vì có đạo hàm

 

f ' x

là đa thức bậc lẻ nên

điều kiện

 

f ' x 0 x  

không xảy ra => Loại B.

Hàm số bậc 1 trên bậc 1 không liên tục trên R (bị gián đoạn tại

x2

) nên loại A.

3 2 2

y x x 3x 1 y' 3x 2x 3       

nhận thấy

y' 0

có nghiệm thực nên điều kiện

 

f ' x 0 x  

không xảy ra => Loại D

 

3 2 2 2

y x x 2x 3 y' 3x 2x 2 2x x 1 1 0 x              

. Nên đồ thị hàm số đồng biến

trên .

Ví dụ 8 : Cho hàm số

y 2x 4x 2  

. Hàm số đồng biến trên khoảng nào?

 

1; 

 

;1

 

0;

 

;0

♠ Giải : Đáp án C.

 

f ' x 8x 8x, x   

 

f ' x 0 x 0  

Mặt khác trên bảng biến thiên đạo hàm

 

f ' x

đổi dấu từ âm sang dương khi đi qua

x0

Vậy hàm số đồng biến trên khoảng

 

0;

Ví dụ 9 : Cho hàm số

 

y x 2x m 1 x 3m

    

. Hàm số đã cho đồng biến trên R với giá trị

là

m3

m3

m3

m3

♠ Giải : Đáp án C;

y' x 4x m 1   

;

 

f ' x 0; x x 4x m 1 0; x         

   

m 1 x 2 4; x 2 4 4 x           

m 1 4 m 3    

Ví dụ 10 : Hàm số

2x 5







đồng biến trên khoảng:

   

; 3 ; 3;  



   

;4 ; 4; 

   

; 3 ; 3;   

♠ Giải : Đáp án D; Ta có:

 

   

y' 0 x ; 3 3;

        



Suy ra hàm số đồng biến trên từng khoảng

   

; 3 , 3;   

Ví dụ 11 : Hàm số

y 3x 6x 15  

đồng bến trên khoảng:

   

1;0 ; 1; 

   

1;0 ; 0;1

   

;1 ; 0;1

 

1; 

♠ Giải : Đáp án A;

y' 12x 12x

;

 

y' 0 x 1;0;1   

Vẽ bảng biến thiên hoặc xét dấu y’ suy ra đáp án

Ví dụ 12 :

     

y m 2 x 3 m 2 x 3 m 3 x 9      

. Hàm số sau đồng biến trên R khi m bằng

m2

m2

m2

m2

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

♠ Giải : Đáp án B;

     

y' 3 m 2 x 6 m 1 x 3 m 3     

+) TH1:

m2

Khi đó:

y' 3 0 x  

suy ra hàm số đồng biến trên R ( thỏa mãn)

+) TH2:

m2

Xét phương trình

y' 0

. Ta có:

 

' 9 m 2   

Để hàm số đồng biến trên R thì

y' 0 x

' 0 m 2     

Kết hợp 2 TH suy ra

m2

Ví dụ 13 : Cho hàm số

y x 4x 5x 2   

. Xét các mệnh đề sau:

(i) Hàm số đồng biến trên khoảng

;









(ii) Hàm số nghịch biến trên khoảng

 

1;2

(iii) Hàm số đồng biến trên khoảng

;









Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng ?

A. 3 B. 1 C. 2 D. 0

♠ Giải : Đáp án C

Ta có:

y' 3x 8x 5;y' 0







    







. Do đó hàm số đồng biến trên

 

;1

và

;









, hàm số

nghịch biến trên







. Do đó mệnh đề (i) và (iii) đúng

Ví dụ 14 : Hàm số

y 2x x

đồng biến trên khoảng nào?

 

0;2

 

1;2

 

0;1

 

;1

♠ Giải : Đáp án C; TXĐ:

 

D 0;2

; Có

y' 0 x 1;y' 0 0 x 1

2x x



       



Hàm số đồng biến trên (0;1)

Ví dụ 15 : Hàm số

y x 2x x 1   

nghịch biến trên khoảng nào?

;



 





 

;1 

 

; 









♠ Giải : Đáp án D; Có

y' 3x 6x 1  

. Phương trình

y' 0

có 2 nghiệm phân biệt.

Hàm số đã cho nghịch biến trên khoảng giữa hai nghiệm của phương trình

y' 0

nên khoảng

đó không thể chứa



hoặc



=> Loại A, B, C

Ví dụ 16 : Hàm số

y 3x 2

đồng biến trên khoảng nào sau đây ?

 

0;

;



 





;



 





 

;0

♠ Giải : Đáp án A; Ta có:

y' 12x y' 0 x 0    

;

y' 0 x 0  

Ví dụ 17 : Tất cả các giá trị của tham số m để hàm số

y x mx 3x 4   

đồng biến trên R là:

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

2 m 2  

3 m 3  

m3

m3

♠ Giải : Đáp án B; Ta có:

y' 3x 2mx 3  

Để hàm số đã cho đồng biến trên R thì

 

y' x 0 x  

' 0 x m 9 0 x         

 

m 3;3  

Ví dụ 18 : Tìm các khoảng đồng biến của hàm số

 

y 2 x 2 3  

 

;0

 

0;

 

;2 

 

2; 

♠ Giải : Đáp án D; Có

   

y' x 8 x 2

;

 

y' x 0 x 2   

Xét dấu của

y':y' 0

khi

x2

;vậy hàm số đồng biến trên khoảng

 

2; 

Ví dụ 19 : Cho hàm số

y x 8x 4  

. Các khoảng đồng biến của hàm số là:

 

2;0

và

 

2;

 

;2 

và

 

2;

 

;2 

và

 

0;2

 

2;0

và

 

0;2

♠ Giải : Đáp án A; Tập xác định:

D 

;

Sự biến thiên:

lim y



 

;

lim y



 

 

y' 4x 16x 4x x 4   

;y' 0 x 2







  







BBT:

Vậy hàm số đồng biến trên

 

2;0

và

 

2;

Ví dụ 20 : Bảng biến thiên sau là của hàm số nào:

y x 2x 3   

y x 2x 1   

y x 2x 3  

y x 2x 1  

♠ Giải : Đáp án B. Ta có y’ có dạng:

 

a x 1 x 0

thì cả 4 đáp án đều thỏa mãn.

Tại

x1

ta loại đáp án A và C do không thỏa mãn

 

f x 2

Tại

 

x 0,5 0;1

ta có:

 

 

y x 2x 1 0 1;2 , tm

      

;

 

 

y x 2x 1 0 1;2 ktm

     

Ví dụ 21 : Cho hàm số

 

y x mx 3m 2 x 1

     

. Tìm tất cả các giá trị của tham số m để

hàm số nghịch biến trên khoảng

 

; 

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017











m2

2 m 1   

1 m 0  

♠ Giải : Đáp án C . Ta có:

y' x 2mx 3m 2    

Có

 

' m 3m 2 0, x m 2; 1          

(điều kiện để hàm số nghịch biến)

Ví dụ 22 : Cho hàm số

 

m 1 x 2







. Tìm tất cả các giá trị của tham số m để hàm số đồng biến

trên từng khoảng xác định.

2 m 1  











2 m 1  











♠ Giải : Đáp án C. TXĐ:

 

D \ m

    

   

m 1 x m m 1 x 2

m m 2

x m x m

    

  





. Để hàm số đồng biến trên

   

;m m;  

thì:

 

y' 0; x D m m 2 0 x D m 2;1            

Ví dụ 23 : Hàm số

y x mx x 1

    

nghịch biến trên khi và chỉ khi

 

m \ 1;1

 

m \ 1;1

 

m 1;1

 

m 1;1

♠ Giải : Đáp án C

Ta có:

y' x 2mx 1   

Nhận thấy hàm số đã cho là hàm số bậc ba có hệ số

  

nên để hàm số đã cho nghịch

biến trên thì phương trình

y' 0

vô nghiệm hoặc có nghiệm kép, hay

' m 1 0 1 m 1       

Ví dụ 24 : Điều kiện cần và đủ của m để hàm số

mx 5







đồng biến trên từng khoảng xác

định là

m5

m5

m5

m5

♠ Giải : Đáp án D

Ta có:

 







để hàm số đã cho luôn đồng biến trên từng khoảng xác định thì

m 5 0 m 5   

Ví dụ 26 : Hàm số nào trong các hàm số sau có bảng biến thiên như hình dưới đây

y x 3x 1  

y 2x 6x 1  

y x 3x 1  

y 2x 9x 1  

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

♠ Giải : Đáp án C

Nhận xét nhìn vào BBT ta thấy đây là bảng biến thiên của hàm số bậc ba có hệ số

a0

Hàm số có hai điểm cực trị là

x 2;x 0  

. Do đó

x 2;x 0  

là nghiệm của phương trình

y' 0

. Tức là

 

y' 0 x x 2 0 x 2x 0 3x 6x 0         

. Đến đây ta loại được B và D.

Với

x0

thì

y1

do đó chọn C

Ví dụ 27 : Cho hàm số

 

3 2 1

y x mx m x     

. Tìm tất cả các giá trị của m để hàm số

nghịch biến trên .











21m   











21m   

♠ Giải : Đáp án B;

y' x 2mx 3m 2    

+ Xét TH

m0

ta có:

   

y' x 2 0, x ; 2 2;         

Suy ra tại m = 0 hàm số ko nghịch biến trên R

+ Xét TH

m0

Để hàm số đã cho nghịch biến trên khoảng R thì

y' 0 x  

x 2mx 3m 2 0, x       

 

m 2; 1

m 3m 2 0







     





  



Ví dụ 28 : Tìm tất cả các giá trị của m để hàm số :

 

12mx







đồng biến trên từng khoảng

xác định.

21m  

21m  





















♠ Giải : Đáp án B ;

   

m 1 x 2 m m 1 2

m m 2

y ,y'

x m x m

    

  

  





Yêu cầu

y' 0 m m 2 0      

m m 2 0 2 m 1       

Ví dụ 29: Cho hàm số

y x x 2x

  

. Phát biểu nào sau đây đúng ?

A. Hàm số nghịch biến trên khoảng

 

2;

B. Hàm số nghịch biến trên khoảng

C. Hàm số đồng biến trên khoảng

 

1;2

D. Hàm số đồng biến trên khoảng

 

;1 

♠ Giải : Đáp án D. Có

y' x x 2 0 x 2     

hoặc

x1

y' 0 x 2  

hoặc

x 1;y' 0 1 x 2      

Hàm số đồng biến trên

 

;1 

và

 

2;

, nghịch biến trên

 

1;2

Ví dụ 30 : Với giá trị nào của m thì hàm số







đồng biến trên mỗi khoảng xác định?

m1

m1

m1

m1

♠ Giải : Đáp án B. Điều kiện cần tìm là

 

y' 0 1 m 0 m 1



        



Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

Ví dụ 31 : Hàm số

y x 2x 3x 2

   

nghịch biến trên khoảng nào?

 

1;3

 

;1

 

3; 

 

1; 

♠ Giải : Đáp án A. Có

y' x 4x 3 0 x 1     

hoặc

x 3;y' 0 1 x 3    

Hàm số nghịch biến trên

 

1;3

Ví dụ 32 : Cho hàm số

y x x mx 3

   

. Tìm m để hàm số luôn đồng biến trên R ?

m1

m1

m1

m1

♠ Giải : Đáp án A

y' x 2x m  

Hàm số đã cho luôn đồng biến trên

x 2x m 0 x ' 1 m 0 m 1             

Ví dụ 33 : Hàm số nào sau đây đồng biến trên







y x 4x 1  

y x 4x 1   

yx

♠ Giải : Đáp án B

Các kết quả cần nhớ

Hàm số phân thức bậc nhất trên bậc nhất không đồng biến hay nghịch biến trên ℝ (chỉ trên

từng khoảng xác định)

Hàm số đa thức bậc chẵn không đồng biến trên ℝ vì đạo hàm của chúng là đa thức bậc lẻ,

không thể luôn dương hoặc luôn âm

Điều kiện cần để hàm số bậc lẻ đồng biến trên ℝ là có hệ số cao nhất dương

– Cách giải

Dựa vào các kết quả trên, loại A, D

Vì hàm số

y x 4x 1   

có hệ số của

là âm nên không thể đồng biến trên ℝ  Loại C

Ví dụ 34 : Hỏi hàm số

y x 4x 3  

đồng biến trên khoảng nào ?

 

2;

 

;3

 

;1

 

3; 

♠ Giải : Đáp án D. Tập xác định của hàm số là

   

;1 3;  

Ta có:

y' ;y' 0 x 2;y' 0 x 2

x 4x 3



      



Kết hợp với điều kiện xác định của hàm số, suy ra khoảng đồng biến của hàm số là

 

3; 

Ví dụ 35 : Tìm tất cả các giá trị của m để hàm số:

   

2 3 1 6 2 3y x m x m x     

nghịch biến

trên khoảng có độ dài lớn hơn 3

0m 

hoặc

6m 

0m 

9m 

♠ Giải : Đáp án A;

   

y' 6x 6 m 1 x 6 m 2 x    

   

' 9 m 1 36 m 2 9m 54m 81 0        

; Dấu bằng xảy ra khi

m3

Gọi

x ,x

là 2 nghiệm của phương trình

 

y' 0 x x

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

Theo viet:

x x 1 m

x .x m 2

  









Ta có BBT

Vậy hàm số đồng biến trên khoảng

 

x ,x pt y' 0

phải có 2 nghiệm phân biệt

m3

Gọi Độ dài khoảng nghịch biến của hàm số là D

D x x

     

x x 1 m 4 m 2 m 6m 9        

D 3 D 9  

m 6m 9 9 m 6m 0      

m0

hoặc

m6

(thỏa mãn)

BÀI TẬP TRẮC NGHIỆM PHẦN TÍNH ĐƠN ĐIỆU

Câu 1 : Cho hàm số

2 3 36 10y x x x   

. Chọn đáp án đúng

A. Hàm số luôn đồng biến trên B. Hàm số luôn nghịch biến trên

C. Hàm số nghịch biến trên

 

3;2

D. Hàm số nghịch biến trên

 

\ 3;2

Câu 2 : Đề minh họa thi THPT Quốc Gian lần 1 năm 2017) Hàm số

21yx

đồng biến trên

khoảng nào?



  





 

0;



  





 

;0 .

Câu 3 : (THPTLê Hồng Phong lần 1)Khoảng đồng biến của hàm số

34y x x  

là

   

; 2 2; .   

 

2;0 .

   

;0 2; .  

 

0;2 .

Câu 4 : (Thi thử chuyên KHTN –HN lần 2 năm 2017) Cho hàm số

21y x x   

. Mệnh đề nào

dưới đây là đúng.

A. Hàm số đồng biến trên khoảng

 

;1  

B. Hàm số đồng biến trên khoảng

 

;0

C. Hàm số đồng biến trên khoảng

 

0;

D. Hàm số đồng biến trên khoảng

 

1; 

Câu 5 : Cho hàm số







(2). Hàm số đồng biến trên khoảng

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

 





 

2; 

 

;0

 

0;

Câu 6 : Hàm số

34y x x  

nghịch biến trên khoảng:

 

2;0

 

;2 

 

0;

 

;2 

và

 

0;

Câu 7 : Hàm số

3 3 2y x x x   

đồng biến trên :

A. B.

 

1; 

 

;1

 

;1

và

 

1; 

Câu 8 : Hàm số

3 4 2y x x x    

nghịch biến trên khoảng:

A. B.

 

1; 

 

;1

 

;1

và

 

1; 

Câu 9 : Cho hàm số







. Phát biểu nào sau đây là đúng

A. Hàm số có đạo hàm

 







B. Hàm số tăng trên

 

;1

và

 

5;

C. Hàm số tăng trên

 

1;5

D. Cả A, B, C đều đúng.

Câu 10 : Hỏi có bao nhiêu số nguyên

để hàm số

2 3 2

( 1) ( 1) 4y m x m x x     

nghịch biến trên

khoảng

 

; 

A. 2.

B. 1.

C. 0.

D. 3.

Câu 11 : Hàm số

   

3 , 0y x x x  

đồng biến trên khoảng nào trong các khoảng nào sau đây:

 

0;1

 

1; 

 

0;2

 

2;

Câu 12 : Cho hàm số

 

có đạo hàm trên khoảng

 

;ab

. Chọn phương án t

     

0, ;f x x a b f x



   

đồng biến trên khoảng

 

;ab

     

0, ;f x x a b f x



   

nghịch biến trên khoảng

 

;ab

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

 

đồng biến trên khoảng

 

;ab

   

0, ;f x x a b



   

D. Cả A và C.

Câu 13 : Hàm số

siny x bx c  

đồng biến trên thì b thuộc khoảng nào sau đây:

 

1; 





1; 

 

;1





;1

Câu 14 : Trong các hàm số sau, hàm số nào luôn nghịch biến trên :

2 10 6y x x x    

8 432y x x  

1yx







Câu 15 : Cho hàm số







. Kết luận nào sau đây là đúng

A. Hàm số luôn đồng biến với mọi x thuộc

B. Hàm số luôn nghịch biến với mọi x thuộc

C. y(2) = 5

D. Tất cả đáp án đều sai

Câu 16 : Cho hàm số

3y x x  

. Khẳng định nào sau đây là đúng ?

A. Hàm số tăng trên khoảng

 

0;1

B. Hàm số giảm trên khoảng

 

4;5

C. Hàm số giảm trên khoảng

 

4;0

D. Tất cả đáp án đều đúng

Câu 17 : (THPT Kim Liên lần 1) Cho hàm số







. Trong các khẳng định sau, khẳng định

nào là đúng.

A. Hàm số nghịch biến trên .

B. Hàm số đồng biến trên từng khoảng xác định.

C. Hàm số đồng biến trên .

D. Hàm số có duy nhất một cực trị.

Câu 18 : ( Chuyên KHTN lần 3) Cho hàm số





. Mệnh đề nào đúng.

A. Hàm số đồng biến trên khoảng

 

0;1 .

B. Hàm số nghịch biến trên

 

\ 1 .

C. Hàm số nghịch biến trên

   

;1 1; .  

D. Hàm số nghịch biến trên từng khoảng

 

;1

và

 

1; .

Câu 19 : (THPT AMSTERDAM HÀ NỘI) Trong tất cả các giá trị của tham số m để hàm số

y x mx mx m   

đồng biến trên

giá trị nhỏ nhất của m là:

1.

Câu 20 : (Sở GD và ĐT Vĩnh Phúc lần 2) Hàm số

2y x x

đồng biến trên khoảng nào?

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

 

0;2 .

 

1;2 .

 

0;1 .

 

;1

Câu 21 : Hàm số

2y x x

nghịch biến trên khoảng

 

1;2

 

2; 

 

0;1

 

0;2

Câu 22 : Hàm số

3y x x

(1). Kết luận nào sau đây là sai khi nói về tính đơn điệu của hàm số

A. Hàm số nghịch biến trên khoảng

 

;0

và

 

2;3

B. Hàm số đồng biến trên khoảng

 

0;2

C. Hàm số nghịch biến trên khoảng

 

;2

và

 

2;3

D. A và B đều đúng

Câu 23 : Cho hàm số

21x







có đạo hàm là

 







thì giá trị m là

A. 4 B. 3

C. 2 D. 1

Câu 24 : Cho hàm số







có đạo hàm là

 





thì giá trị m là

A. 4 B. 3

C. 2 D. 1

Câu 25 : Cho hàm số







có đạo hàm là

 







thì giá trị k là

A. 4 B. 3

C. 2 D. 1

Câu 26 : Cho hàm số

y x 3mx 3x 1   

. Giá trị m để hàm số luôn tăng trên là

 

1;2m

31m  

11m  

12m  

Câu 27 : Cho hàm số







. Giá trị m để hàm số luôn giảm trên từng khoảng xác định là

 

1;2m

31m  

11m  

12m  

Câu 28 : Cho hàm số

2x 1







. Giá trị m để hàm số luôn nghịch biến trên từng khoảng xác định

là

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

m 

m 

Câu 29 : Cho hàm số

 

6 2 1

y mx m x m     

. Giá trị nhỏ nhất và lớn nhất của tham số m để

hàm số sẽ tăng trên là

2, 3

2, 4

6; 9

1; 4

Câu 30 : (KHTN lân 4) Cho hàm số

 

có đạo hàm

       

1 1 2f x x x x



   

. Hàm số

 

đồng biến trên khoảng nào dưới đây?

 

; 1 . 

 

1;1 .

(2; ).

(1;2).

Câu 31 : Cho hàm số

y 3 cosxx  

. Kết luận nào dưới đây là đúng

A. Hàm số luôn nghịch biến với mọi x thuộc

B. Hàm số luôn tăng với mọi x thuộc

C. Chưa thể xác định tính đơn điệu của hàm số này

D. Cả ba đều sai

Câu 32 : Cho hàm số

mx 1







. Giá trị m để hàm số luôn đồng biến trên từng khoảng xác định là

1m 

1m 

hoặc

1m 

1m 

 

1;1m

Câu 33 : Cho hàm số

mx 1







. Giá trị m để hàm số luôn nghịch biến trên từng khoảng xác định

là

1m 

m 

m 

 

1;m  

Câu 34 : Cho hàm số







. Giá trị m để hàm số luôn nghịch biến trên từng khoảng xác định là

0m 

m 

m 

 

;0m 

Câu 35 : Cho hàm số





. Khoảng đồng biến của hàm số đã cho là

 

;1 

 

1; 

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

 

1;1

 

1; 

Câu 36 : Cho hàm số

y cos 4x x x   

. Phát biểu nào sau đây là đúng

A. Hàm số luôn nghịch biến với mọi x thuộc

B. Hàm số luôn đồng biến với mọi x thuộc

C. Chưa thể xác định tính đơn điệu của hàm số này

D. Cả ba đều sai

Câu 37 : Cho hàm số

y cosx

. Phát biểu nào sau đây là đúng

A. Hàm số tăng trên khoảng

π 3π

;







B. Hàm số giảm trên khoảng

π 3π

;







C. Hàm số tăng trên khoảng

;π







D. Cả ba đều sai

Câu 38 : Giá trị α để hàm số sau đây luôn tăng

 

y sinα 4sin α 3

xx   

là

α 2π

k

απ

k

α 2π

k  

α 2π

k

Câu 39 : Cho hàm số

 

y f x







. Trong các mệnh đề sau, tìm mệnh đề đúng

 

nghịch biến trên B.

 

nghịch biến trên

   

;2 2;  

 

nghịch biến trên

 

;2

và

 

2;

 

đồng biến trên

 

;2

và

 

2;

Câu 40 : Cho hàm số

 

y fx

xác định trên

và có đồ thị như hình vẽ bên.

Chọn khẳng định đúng trong các khẳng định sau

(ở đây





A. Hàm số tăng trên khoảng

 

; 

B. Hàm số giảm trên khoảng

 

; 

C. Cả A và B đều đúng

D. Cả A và B đều sai

Câu 41 : Cho hàm số

3 3 1 (1)y x x mx    

, với m là tham số thực.

Giá trị nào của m để hàm số (1) nghịch biến trên khoảng (0; +



)

1m 

m 

O x

y = f(x)

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

m 

 

;1m 

Câu 42 : Cho hàm số

2 2 1y x x mx   

, với m là tham số thực.

Giá trị nào của m để hàm số đã cho đồng biến trên khoảng

 

1; 

2m 

1m 

2m 

2m 

Câu 43 : Hàm số

y x x   

A. Nghịch biến trên

B. Nghịch biến trên khoảng

 

;1

và đồng biến trên khoảng

 

1; 

C. Đồng biến trên

D. Đồng biến trên khoảng

 

;1

và nghịch biến trên khoảng

 

1; 

Câu 44 : Hàm số

()





A. Đồng biến trên \{-1}

B. Nghịch biến trên \{-1}

C. Đồng biến trên mỗi khoảng xác định

D. Nghịch biến trên mỗi khoảng xác định

Câu 45 : Hàm số

()







A. Đồng biến trên \{

3

} B. Nghịch biến trên \{

3

}

C. Đồng biến trên mỗi khoảng xác định D. Nghịch biến trên mỗi khoảng xác định

Câu 46 : Cho hàm số

()







Chọn đáp án sai :

A. Hàm số không xác định khi x =

3

B. Nghịch biến trên

C. Đồ thị hàm số cắt trục hoành tại điểm







D. Đạo hàm cấp 1 trên tập

 

\3

là

 

'( )







Câu 47 : Cho hàm số

( ) 6 3

f x x x   

A. Hàm số luôn giảm trên B. Hàm số luôn tăng trên

C. Hàm số luôn tăng trên

 

2;

D. Hàm số luôn giảm trên

 

2;2

Câu 48 : Cho hàm số







(C). Nghiệm của bất phương trình y’ < - 4 là

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017













































Câu 49 : Khoảng nghịch hàm số

y x x   

là

 

;1 

 

1;3

 

3; 

 

;1 

và

 

3; 

Câu 50 : Khoảng nghịch hàm số

yx  

là

 

;3 

và

 

0; 3









và

;









 

3;

 

3;0

và

 

3;

Câu 51 : Trong các hàm số sau, hàm số nào đồng biến trên

cotyx

3 3 2017y x x x   

2017y x x  







Câu 52 : Trong các hàm số sau, hàm số nào đồng biến trên

 

1;3

 







 







 

2f x x x

 

45f x x x  

Câu 53 : Cho hàm số

 

32y f x x x   

. Tìm mệnh đề sai

 

giảm trên khoảng

 

1;1

 

giảm trên khoảng









 

tăng trên khoảng

 

1;3

 

giảm trên khoảng







Câu 54 : Cho hàm số

 

7 6 5

9 7 12

y f x x x x    

. Khi đó

 

giảm trên khoảng

 

1;1

 

giảm trên

 

tăng trên

 

1;1

 

tăng trên

Câu 55 : Cho các hàm số

   

;y f x y g x

là các   trên

 

;ab

và

   

' 0; ' 0f x g x

trên

 

;ab

. Khi đó hàm số nào sau đây đồng biến trên

 

;ab

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

   

f x g x

 

   

f x g x

Câu 56 : Biết rằng hàm số

   

y x x mx m

nghịch biến trên đoạn dài 1 đơn vị khi



Hỏi biểu diển số nào sau đây và

trên cùng trục số là gần nhau nhất?

A. -4,57

B. -3,76

C. -5,74

D. -6,5

Câu 57 : Có bao nhiêu số nguyên m thỏa mãn điều kiện hàm số







luôn nghịch biến trên

khoảng

 

;1

Câu 58 : Tìm m để hàm số







4mx

luôn nghịch biến trên khoảng

 

;1

1 m

02m

 2m

12m

Câu 59 : Hàm số y =

1mx



đồng biến trên khoảng (1 ; +



) khi

A. m > 1 hoặc m < - 1

B. m < - 1

C. m > - 1

D. m > 1

Câu 60 : Hàm số y =

1mx



nghịch biến trên khoảng (-



; 0) khi:

A. m > 0

10m  

C. m < - 1

D. m > 2

Câu 61 : Hàm số:

31y x x mx   

nghịch biến trên một đoạn có độ dài 2 đơn vị khi:

2m 

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

2m 

0m 

0m 

Câu 62 : Hàm số:

y x x mx m   

nghịch biến trên một đoạn có độ dài 1 đơn vị khi:

1m 

1m 

m 

m 

Câu 63 : Hàm số:

21y x x mx    

đồng biến trên một đoạn có độ dài 1 đơn vị khi:

m 

m 

m 

Câu 64 : Hàm số:

 

y x mx m x     

đồng biến trên một đoạn có độ dài

đơn vị khi:

3m 

4m 

34m  

3, 4mm  

Câu 65 : Biết rằng hàm số

 

3 1 9 1

y m x x    

nghịch biến trên

 

;xx

và đồng biến trên các

khoảng còn lại của tập xác định. Nếu

6xx

thì giá trị m là:

4

hoặc

2

hoặc

Câu 66 : Biết rằng hàm số

3( 1) 9 1

y x m x x    

nghịch biến trên khoảng (x1; x2) và đồng biến

trên các khoảng còn lại của tập xác định. Nếu

63xx

thì giá trị của m bằng bao nhiêu?

1m 

3m 

3; 1mm  

1; 3mm  



Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU

2017

☻  Cho

   

u u x v v x C; ; :

là hằng số .

☻ 

 





  u v u v .

☻ 

   



  

   u v u v v u C u C u. . . . . .



 



   

  



    

   

   

u u v v u C C u

. . .

Bảng công thức tính đạo hàm:

Đạo hàm của hàm sơ cấp

Đạo hàm của hàm hợp

 





(C là hằng số).

 

.xx











 

.xx











( 0)x





 





 





 

..u u u











 





 





 





 

sin cosxx





 

sin .cosu u u





 

cos sinxx





 

cos .sinu u u





 

tan

cos





 

tan

cos





 

cot

sin





 

cot

sin





Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

► Hàm số

y f(x)

đạt cực trị tại

nếu

y'(x ) 0

► Hàm số

y f(x)

đạt cực đại tại

nếu đạo hàm

đổi dấu từ + sang – khi đi qua

► Hàm số

y f(x)

đạt cực tiểu tại

nếu đạo hàm

đổi dấu từ – sang + khi đi qua

Các phương pháp tìm cực trị của hàm số

Phương pháp 1.

♥ B1 : MXĐ, Tìm

 

'xf

♥ B2 : Tìm các điểm

 

x i 1,2,...

mà tại đó đạo hàm của hàm số bằng 0 hoặc hàm số liên tục

nhưng không có đạo hàm.

♥ B3 : Lập bảng xét dấu

 

'xf

. Nếu

 

'xf

đổi dấu khi x qua

thì hàm số đạt cực trị tại

Phương pháp 2.

♥ B1 : Tìm

 

'fx

. giải phương trình

 

'0fx

tìm các nghiệm

 

x i 1,2,...

♥ B2 : Tính

 

'' xf

☺ nếu

 

'' x 0f 

thì hàm số đạt cực đại tại điểm

☺ nếu

 

'' x 0f 

thì hàm số đạt cực tiểu tại điểm

Cho hàm số

 

yxf

,đồ thị là (C). Các vấn đề về cực trị cần nhớ:

◙ Nghiệm của phương trình

 

' x 0f 

là hoành độ của điểm cực trị.

◙ Nếu

 

'' 0















thì hàm số đạt cực đại tại

xx

◙ Nếu

 

'' 0















thì hàm số đạt cực tiểu tại

xx

Chú ý:

PHẦN 2 : CỰC TRỊ CỦA HÀM SỐ

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

☻ Quy tắc 2 thường dùng với hàm số lượng giác hoặc việc giải phương trình f’(x) = 0 phức tạp.

☻ Hàm số

 

y f x

có 2 cực trị

a 











Ví dụ : Tìm cực trị của hàm số

y 2x 3x 36x 10   

Phương pháp I.

TXĐ:

.D 

y' 6x 6x 36

y' 0 6x 6x 36 0

  





     







Vậy x = -3 là điểm cực đại và ycđ = 71

x = 2 là điểm cực tiểu và yct = - 54

Phương pháp II.

TXĐ:

.D 

y' 6x 6x 36

y' 0 6x 6x 36 0

  





     







y”= 12x + 6

y’’(2) = 30 > 0

nên hàm số đạt cực tiểu tại x = 2 và yct = - 54

y’’(-3) = - 30 < 0

nên hàm số đạt cực đại tại x = -3 và ycđ =71

BÀI TẬP TỰ LUẬN PHẦN CỰC TRỊ

Bài 1 : Tìm cực trị các hàm số sau (dấu hiệu 1):

y x 6x 1   

y 2x 3x 12x 5    

y x 2x 3  

85y x x   

6 8 1y x x x    

  

..............................................................................................................................................................................



- 54

-3



Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

..............................................................................................................................................................................

Vận dụng 01 : Cho hàm số

 

y f x

có đạo hàm

      

' 1 2 3 1f x x x x   

. Số điểm cực trị của

hàm số là:

A. 4 B. 3 C. 1 D. 2

Vận dụng 02 : Cho hàm số

 

y f x

có đạo hàm

          

8 3 2 5

' 3 2 3 1 6 4f x x x x x x     

. Số

điểm cực trị của hàm số là:

A. 4 B. 3 C. 1 D. 2

Vận dụng 03 : Cho hàm số

 

y f x

có đạo hàm

   

 

' 1 1f x x x  

. Số điểm cực trị của hàm số

là:

A. 4 B. 3 C. 1 D. 2

Bài 2 : Tìm cực trị các hàm số sau (dấu hiệu 2):

y x 3x 1

    

y 2cos2x 5

..............................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

Bài 3 : Tỉm để hàm số sau có cực đại và cực tiểu

 

3 2 2

y m 2 x 3x mx 2m    

 

3 2 2 2

y x 3 m 1 x 2 m 7m 2 x 2m      

 

y x 2m 3 x 8m

    

 

2 2 4

y 2x m 2m 3 x m

      

..............................................................................................................................................................................

e) (soạn)

y x m x 5

   

( ĐS :

1 m 1  

)

f) (soạn)

 

y x 2m 2 x

    

( ĐS :



)

g) (soạn)

 

y m 2 mx 8m

    

( ĐS :

m0

)

h) (soạn)

   

y 2m 1 x 4m 3 x 8

     

( ĐS :

   

)

Bài 4 : Cho hàm số

y x mx x m    

. Tìm tất cả các giá trị của m để đồ thị hàm số có hai điểm cực

trị là

   

; , ;

A A B B

A x y B x y

thỏa mãn

xx

3m 

0m 

2m 

1m 

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

..............................................................................................................................................................................

Bài 5 (Khối D – 2012): Cho hàm số y =

– mx

– 2(3m

– 1)x +

(1), m là tham số thực. Tìm m

để hàm số (1) có hai điểm cực trị x1 và x2 sao cho x1.x2 + 2(x1 + x2) = 1

..............................................................................................................................................................................

Bài 6 : CMR hàm số

3 2 2

y x (m 2)x (m 3)x 2m

     

luôn luôn có 2 cực trị

 

3 2 2 6

y x mx m 4 x m

    

luôn luôn có cực đại và cực tiểu

..............................................................................................................................................................................

c) (soạn)

 

3 2 2 10 8

y x 3mx 3 1 m x m 7m      

luôn luôn có cực đại và cực tiểu

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

d) (soạn)

   

y x m 1 x m 3 x

     

luôn luôn có cực đại và cực tiểu

Bài 7 : Tìm m để hàm số

a/ (Khối B – 2002)

4 2 2

y mx (m 9)x 10   

có ba cực trị

y x 2(m 1)x m   

có ba cực trị

4 2 2

y x 2 x 1m  

có ba cực trị

..............................................................................................................................................................................

Soạn :

4 2 4

y x 2 x 2m m m   

có ba cực trị e/

 

y x 1 x 1m   

có ba cực trị

 

y x 2 5 x 2m   

có ba cực trị g/

   

y 1 x 1 x 2mm    

có ba cực trị

   

y x 1 x 1

mm     

có ba cực trị

   

4 2 2

y f x x 2 m 2 x m 5m 5      

có ba cực trị

Bài 8 : Tìm m để hàm số

a/ (TN–THPT – 2005)

 

3 2 2

y x 3mx m 1 x 2    

đạt cực đại tại x = 2

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

b/ (TN–THPT – 2011)

y x 2x mx 1   

đạt cực tiểu tại x = 1

 

y x mx m 1 x 2    

đạt cực tiểu tại x = 1

..............................................................................................................................................................................

d/ (Soạn)

 

2 3 2

y m 2 x 3m 4 x mx

    

đạt cực tiểu tại x = 1

e/ (Soạn)

y x 3x 3mx 3m 4    

đạt cực trị tại x = 2 ? Cực trị đó là cực đại hay cực tiểu ?

f/ (Soạn)

 

y x m 3 x mx m 2     

đạt cực tiểu tại x = 2 (ĐS : m = 0 )

g/(Soạn)

 

2 3 2

y m 5m x 6mx 6x 6     

đạt cực đại tại x = 1 (ĐS : m = 1 )

h/(Soạn)

 

y 2m 1 x 3mx 4m 2    

đạt cực đại tại x = –1 (ĐS : m = –2 )

Bài 9 : Tìm m để hàm số

a/ Đồ thị hàm số

y x mx (2m 1)x 2

    

có hai điểm cực trị dương (



)

b/ (Cao Đẳng – 2009)

y f(x) x (2m 1)x (2 m)x 2      

có cực đại và cực tiểu có hoành độ

dương

 

y x (m 1)x (2m 6)x 8



     

có cực đại và cực tiểu có hoành độ dương. (ĐS :

3 m 11

)

..............................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

..............................................................................................................................................................................

Bài 10 : Tìm m để hàm số

3 2 2

1 (2m 3)

y x x (m 2m 2)x 11



     

có cực trị có hoành độ x1, x2 thỏa mãn x1 =2x2 (ĐS :

m 0, 6

)

b/ (soạn)

3 2 2

1 (3m 2)

y x x m x 15



   

có cực đại và cực tiểu có hoành độ x1, x2 thỏa mãn x1 =9x2

(ĐS :

m6

)

..............................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

c/ (soạn)

y x (m 1)x (2m 1)x 1

     

có cực đại và cực tiểu có hoành độ x1, x2 thỏa mãn x2 =9x1

(ĐS :

m 4,



)

 

m 1 11

y x mx m 5 x



    

có cực đại và cực tiểu có hoành độ đều lớn hơn 2 (ĐS :



)

 

2 11

y x 2x 3 4m x

3 1200

    

có cực đại và cực tiểu có hoành độ đều lớn hơn –1 (ĐS :



)

Bài 11 : a/ (ĐHQG-HN-1997)

y 2x mx 12x 13   

có cực đại và cực tiểu trong và các điểm này

cách đều trục tung (ĐS :

m0

)

b/ (ĐH Đà Nẵng – 2000)

 

3 2 2

y x 2m 1 x m 3m 2 x 4      

có cực đại và cực tiểu nằm về hai

phía trục tung (ĐS :

1 m 2

)

..............................................................................................................................................................................

Bài 12: Cho hàm số

 

3 2 2

2m 1

y x x m 2 x 1



    

. Xác định tham số m để hàm số có cực đại,

cực tiểu có hoành độ x1, x2 thỏa mãn hệ thức

 

1 2 1 2

3x .x 5 x x 7 0   

(ĐS :

m2

)

..............................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

Bài 13 : Cho hàm số

 

2m 1

y x x mx m



   

.Xác định tham số m để hàm số có cực đại, cực

tiểu có hoành độ x1, x2 thỏa mãn hệ thức

1 2 1 2

x x 6x x 8   

(ĐS :



)

..............................................................................................................................................................................

(Soạn) Cho hàm số

 

y x mx m 1 x m



    

a/ CMR hàm số luôn có cực trị.

b/ Gọi x1, x2 là hoành độ cực trị. Tìm m để

x x 2

  

(ĐS :



)

Bài 14: Tìm điểm cực tiểu của đồ thị hàm số

56y x x  

5 1 5 1

;;;

2 4 2 4

   

  

   

   

 

0;6 ; ;









 

; ; 0;6









 

0;6

..............................................................................................................................................................................

BÀI TẬP MINH HỌA PHẦN CỰC TRỊ

Ví dụ 01 : Cho hàm số

32y x x mx m    

. Giá trị nào của tham số

thì hàm số có hai điểm

cực trị.

3m 

3m 

m

m

♥ Giải : Tập xác định:

.D 

; Đạo hàm:

' 3 6y x x m  

Làm tự luận !

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

'0y 

3 6 0x x m   

Hàm số có hai điểm cực trị



'0y 

có hai nghiệm phân biệt

' 3 3 0





  



   



; Vậy giá trị

cần tìm là

3m 

Làm trắc nghiệm !

Khi làm bài trắc nghiệm chúng ta không thể giải như vậy vì sẽ có nhiều bài phức tạp “số xấu”

☻Phương pháp “BÓC ĐẠI”

► “Bóc đại” m = 2 ở câu B thì ta thấy

' 3 6 2 0y x x   

, phương trình này có 2 nghiệm (bấm máy

là thấy nha) – Vậy nhận luôn B

Vì còn đáp án C là m thuộc R nữa nên ta phải xét thêm đáp án A kiểm tra

► “Bóc đại” m = 4 ở câu A thì ta thấy

' 3 6 4 0y x x   

, phương trình này vô nghiệm (bấm máy

là thấy nha) thì rõ ràng A không hợp lý

Kết thúc vấn đề - chọn B

Ví dụ 02 : Cho hàm số

 

3 2 2

1 4 3 1

y x m x m m x      

. Tìm

để hàm số có cực đại, cực tiểu

và các điểm cực trị của đồ thị hàm số có hoành độ dương.

♥ Giải : Tập xác định:

D 

; Đạo hàm:

 

' 2 2 1 4 3y x m x m m     

Hàm số có hai điểm cực trị có hoành độ dương



'0y 

có hai nghiệm phân biệt dương

 

' 1 2 4 3 0

1 0 5 3

m m m

S m m





      



         















; Vậy giá trị

cần tìm là

53m   

Ví dụ 03 : Tìm

để hàm số

 

3 1 9y x m x x m    

có 2 điểm cực trị

,xx

thỏa mãn

2.xx

♥ Giải : Tập xác định:

.D 

; Ta có:

 

' 3 6 1 9y x m x   

;

   

' 0 2 1 3 0 1y x m x     

Yêu cầu bài toán tương đương với

 

có 2 nghiệm phân biệt

,xx

thỏa mãn

2.xx

 

' 1 3 0



    













 

1 2 1 2

2 2 0

1 3 1 3

x x x x



  

      









  





 

1 3 1 3

4 1 4.3 4



      















  







Vậy giá trị cần tìm của

là

3m 

hoặc

1m 

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

Ví dụ 04 : Cho hàm số

 

1 7 2y x m x x    

là tham số. Chứng minh rằng với mọi giá trị

, hàm số luôn luôn có một giá trị cực đại và một giá trị cực tiểu.

♥ Giải : Tập xác định:

D 

. Đạo hàm

 

' 3 2 1 7y x m x   

Ta có

 

' 1 21 0,mm      

, suy ra phương trình

'0y 

luôn có hai nghiệm phân biệt với

mọi giá trị

hay với mọi giá trị của

thì hàm số luôn có một giá trị cực đại và một giá trị cực

tiểu.

Ví dụ 05 : Cho các hàm số

32y x mx  

(

 

2 y x d  

, với

là tham số thực. Tìm các

giá trị của

để (

) có hai điểm cực trị và khoảng cách từ điểm cực tiểu của (

) đến đường thẳng

 

bằng

♥ Giải : Tập xác định:

.D 

Đạo hàm :

 

' 3 6 3 2y x mx x x m   













Điều kiện để hàm số có hai cực trị là

0m 

Tọa độ hai điểm cực trị:

 

0;2

2 ;2 4

B m m













Đường thẳng

 

: 2 2 0d y x x y      

Với :

0:m 

là điểm cực tiểu. Khi đó

 

0 2 2

, 0 2

d A d



  



(loại).

Với :

0:m 

là điểm cực tiểu. Khi đó:

 

, 2 2 1d B d m m   

2 1 1

m m m



  



   





  



( m > 0)

► Khoảng cách cũng là một chủ đề hay xuất hiện trong các đề thi , ta cần nắm vững công thức

tính khoảng cách từ điểm

 

;

M x y

đến đường thẳng

:0ax by c   

là

 

;

ax by c







Ví dụ 06 : Cho hàm số

   

2 1 2 2y x m x m x     

, với m là tham số thực. Tìm các giá trị của m

để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số có hoành độ dương.

♥ Giải : Tập xác định:

.D 

;

   

' 0 3 2 2 1 2 0 *y x m x m      

Yêu cầu bài toán



Phương trình

 

có hai nghiệm dương phân biệt

Làm sao: xác định đâu là hoành độ cực đại , hoành độ cực tiểu ?

Làm vậy nè : “ dựa vào dạng đồ thị hoặc bảng biến thiên.”

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

 

4 5 0

0 0 2 2

2 2 1

m hay m

P m m





  

  













        

  

  



















Vậy

m

là giá trị cần tìm

Ví dụ 07 : Cho hàm số

 

3 2 2 2

3 3 1 3 1y x x m x m      

, m là tham số. Tìm m để hàm số có cực đại,

cực tiểu và các điểm cực trị của đồ thị hàm số cách đều gốc tọa độ O.

♥ Giải : Tập xác định:

D 

 

' 3 6 3 1y x x m    

Hàm số

 

có cực trị

'0y

có 2 nghiệm phân biệt

' 0 0mm     

Khi đó













Gọi

,AB

là hai điểm cực trị của đồ thị hàm số

 

thì:

   

1 ; 2 2 , 1 ; 2 2 .A m m B m m     

cách đều

và

2 2 3

OA OB m m m      

(vì

0m 

)

Ví dụ 08 : Tìm tất cả các giá trị tham số

để hàm số

     

2 –1 – 2 1–y f x x m x m x m    

đạt cực đại tại

2x 

♥ Giải : Tập xác định:

D 

; Đạo hàm

   

' 3 2 2 1 2f x x m x m    

(Điều kiện cần) Để hàm số đạt cực đại tại

2x 

thì

       

' 2 0 3. 2 2 2 1 . 2 2 0 2.f m m m           

(Điều kiện đủ) Với

2m 

, ta được

 

31f x x x  

Đạo hàm

   

' 3 6 3 2 ;f x x x x x   

   

' 0 3 2 0 .

f x x x





    







Lập bảng biến thiên ta thấy

 

đạt cực đại tại

2x 

(có thể giải bài toán bằng y’’ thay vì lập BBT)

Vậy

2m 

thỏa yêu cầu bài toán.

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

Ví dụ 09 : Cho hàm số

( 1) 2 1y x m x m    

Tìm tất cả các giá trị của m để hàm số đã cho có

ba điểm cực trị.

♥ Giải : Tập xác định:

D 

; Đạo hàm

' 4 2( 1) 2 (2 1);y x m x x x m     

(1)

















Hàm số đã cho có ba điểm cực trị

'y

có ba nghiệm phân biệt

(1)

có hai nghiệm phân biệt khác

1 0 1mm      

Vậy với

1m 

hàm số đã cho có ba điểm cực trị.

Chú ý, đây là tình huống đặc biệt :

♥ Phương trình





có hai nghiệm phân biệt khác 0





Đó chỉ là cách làm tự luận “cho vui”, khi làm trắc nghiệm là “bế tắc”

Vậy làm sao ???

☻Cách khác :

Hàm số đã cho có ba điểm cực trị tương đương a.b < 0

hay 1.(m + 1) < 0, Suy ra m < -1 ???

☻ Ứng dụng 1 : Cho hàm số

3y x ax  

.Với giá trị nào của tham

số a thì hàm số đã cho có 3 cực trị

A. a = 0 B. a < 0

C. a > 0 D. Không có

☻ Ứng dụng 2 : Cho hàm số

4 2 2

3y x a x  

.Với giá trị nào của

tham số a thì hàm số đã cho có 3 cực trị

A. a khác 0 B. a < 0

C. a > 0 D. Không có

Hàm số trùng phương

y ax bx c  

Có 3 cực trị

Có 1 cực trị

a.b 0

a.b 0

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

☻ Ứng dụng 3 : Cho hàm số

 

1 2 1y a x ax a    

.Với giá trị nào của tham số a thì hàm số

đã cho có đúng 1 cực trị

a

a

01a

 

\ 0;1

☻ Ứng dụng 4 : Cho hàm số

y x ax  

.Với giá trị nào của tham số a thì hàm số đã cho

có cực tiểu mà không có cực đại

a

0a 

01a

 

\ 0;1

Đáp án : Ứng dụng 1 : C Ứng dụng 2 : A

Ứng dụng 3 : D Ứng dụng 4 : B

Ví dụ 10 : Cho hàm số

y x 3x 5x 1   

Viết phương trình đường thẳng đi qua hai

điểm cực trị của đồ thị hàm số.

♥ Giải :

☻Cách 1 : Ta vẽ bảng biến thiên rồi suy ra hai điểm cực trị là

   

1 1 2 2

M x ; y , N x ; y

rồi

dùng công thức đường thẳng qua 2 điểm bất kì

2 1 2 1

x x y y







sẽ ra.

Nhưng trong bài này điểm cực đại và cực tiểu không phải là “số đẹp” nên ta phải dùng cách 2

được trình bày sau đây

☻Cách 2 : (ở đây thầy không chứng minh – trong các sách nâng cao điều có chứng minh)

◙ Mô tả :

Suy ra đường thẳng qua 2 điểm cực trị là (d) : y = mx + n

Lời khuyên : chia cẩn thận dùm cái !!!

Chia y / y’ thì “phần dư” chính là đường thẳng cần tìm

y y’

mx + n

dx + e

Phần dư nè !!

Phần chia được ☺

Chú ý nhỏ :

00AA  

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

◙ Thực hiện : Ta có

3 5 1y x x x   

;

Suy ra

' 3 6 5y x x  

Thực hiện phép chia y / y’ như bảng sau :

Ví dụ 11 : Cho hàm số

32y x x  

Gọi A, B lần lượt là hai điểm cực trị của đồ thị hàm số

và C(1;1). Khi đó diện tích tam giác ABC bằng bao nhiêu ?

♥ Giải : Tập xác định:

D 

; Đạo hàm

' 3 6y x x

;













Khi đó tọa độ hai điểm cực trị là A(0;2) và B(2; -2)

☻ Đặt vấn đề tính diện tích S

∆ABC

của tam giác ABC ??

☺ với

1 2 1 2

AB (a ;a ), AC (b ;b ).

x 3x 5x 1  

3x 6x 5



x 2x x



0 x x 1

  



x 2x



16 8



Phần dư

Phần chia

được dđược

được

Suy ra đường thẳng qua hai

điểm cực trị của đồ thị hàm

số đã cho là

16 8

(d): y x

  

∆ABC

Thuần túy tam giác (cạnh nhân đường cao

tương ứng)

 

ABC

S AB.d C;AB





Công thức giải nhanh

ABC 1 2 2 1

1 1 1

S det(AB,AC) a b a b

2 2 2



   

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

Tiến hành làm !!

♥ Cách thuần túy :

(2; 4), (1; 3)AB AC   

Đường thẳng AB :

B A B A

x x y y







ta được

2 2 0xy  

 

2 4 2 5AB AB    

;

 

;

d C AB







; Suy ra

 

. ; 1

ABC

S AB d C AB





♥ Cách chơi chiêu :

   

1 1 1

det( , ) 3 2 1 4 1

2 2 2

ABC

S AB AC





        



☻ Ứng dụng : Cho tam giác ∆ABC có A(1; 2), B(3; -2), C(2;4). Tính diện tích tam giác ∆ABC.

(ĐS : S = 4)

..............................................................................................................................................................................

............................................................................................................................................................................

BÀI TẬP TRẮC NGHIỆM PHẦN CỰC TRỊ

Câu 1 : Hàm số

12y x x  

có mấy điểm cực trị

A. 4 B. 3 C. 2 D. 1

Câu 2 : Hàm số

sinyx

có bao nhiêu điểm cực trị

A. 4 B. 3 C. 2 D. Vô số

Câu 3 : Hàm số

8 12y x x  

có mấy điểm cực trị

A. 4

B. 3

C. 2

D. 1

Câu 4 : Cho hàm số :

3 4 14y x x x   

. Hàm số đạt cực trị tại hai điểm x1, x2 . Khi đó x1.x2 =



Câu 5 : (THPT Chuyên Lê Hồng Phong-Tp.Hồ Chí Minh) Cho có hai

điểm cực trị nằm về hai phía của trục tung. Khi đó giá trị của là

A. . B. .

C. . D. .

Câu 6 : Cho hàm số :

3 4 14y x x x   

. Hàm số đạt cực trị tại hai điểm x1, x2 . Khi đó x1 + x2 =

 

2 3 5

y x mx m x    

m 

m 

m 

m 

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017



Câu 7 : Cho hàm số

 

2 1 1 (1)y x m x m    

. Với giá trị nào của m thì hàm số (1) có 1 cực trị ?

1m 

1m 

C. Cả A, B đều đúng D. Cả A, B đều sai

Câu 8 : Hàm số

33y x x  

có điểm cực tiểu là

 

0;3

 

2;1

 

1;1

 

1; 6

Câu 9 : Hàm số

 

1y x x

đạt cực đại tại

1x 

x 

1x 

D. Đáp án khác

Câu 10 : Hàm số

34y x x  

. Đường thẳng đi qua 2 điểm cực trị của hàm số là

24yx  

3yx  

1y 

3yx  

Câu 11 : Hàm số

6 8 1y x x x    

có điểm cực đại là

 

7;3

 

2;24

 

2;25

 

1; 6

Câu 12 : Hàm số

2 3 36 10y x x x   

có điểm cực trị lần lượt là A và B. Với M(2; 3). Diện tích

tam giác ∆MAB là

285

S 

287

S 

78S 

S 

Câu 13 : Hàm số

41y x x  

có điểm cực tiểu là

 

2; 15

 

1;2

 

2;11

 

4; 6

Câu 14 : Đồ thị hàm số nào sau đây chỉ có 1 điểm cực trị :

2 4 2y x x  

 

2 4 2

4 9 1y m x x   

21y x x   

 

4 2 2

11y x m x    

Câu 15 : Hàm số

4y x x

có điểm cực tiểu là

 

2;2

 

2;1

 

2; 2

 

2;2

Câu 16 : Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số

3 9 2y x x x   

có phương

trình

y 

18yx

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

18yx

13yx

Câu 17 : Với giá trị nào của tham số m thì hàm số

y m x   

có cực trị

D. Cả A, B, C

Câu 18 : Với giá trị nào của tham số m thì hàm số

2 2 1y x mx m    

có 3 cực trị

1

2

Câu 19 : Với giá trị nào của tham số m thì hàm số

4 2 4

22y x mx m m   

có 3 cực trị

2m 

1m 

2m 

Câu 20 : Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số

31y x x  

có phương trình

21yx  

13yx

17yx

1yx

Câu 21 : Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số

 

3 2 2 3 2

3 3 1y x mx m x m m      

có phương trình

3y x m m  

5y x m

21y x m  

2y x m m  

Câu 22 : Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số

35y x x x  

có hệ số góc là

k 

k 

Câu 23 : Hàm số

10 15 6y x x x   

đạt cực tiểu tại:

5x 

1x 

1x 

5x 

Câu 24 : Hàm số

   

12y x x  

đạt cực trị tại hai điểm A và B.

Cho M(1; -3). Diện tích tam giác ∆MAB bằng

D. Đáp án khác

Câu 25 : (Trường THPT Nguyễn Bỉnh Khiêm) Cho hàm số

32y x x  

. Điểm cực đại của đồ

thị là?

 

2;2

. B.

 

0;2

 

0; 2

. D.

 

2; 2

Câu 26 : Cho hàm số :

y x x   

. Hàm số đạt cực trị tại hai điểm x1, x2 . Khi đó

xx

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

-2

Câu 27 : Cho hàm số . Hàm số có

A. Một cực đại. B. Một cực tiểu.

C. Một cực đại và một cực tiểu . D. Không có cực trị.

Câu 28 : Cho hàm số . Tích các giá trị cực đại và cực tiểu của hàm số bằng:

A. . B. . C. . D. .

Câu 29 : Giả sử hàm số

y ax bx cx d   

có cực trị.

Xác định chính xác số cực trị của hàm số đã cho:

A. Có 2 điểm cực đại

B. Chỉ có 1 điểm cực đại

C. Chỉ có 1 điểm cực tiểu

D. Cả 3 phương án B, C, D đều sai

Câu 30 : Hàm số

54y x x  

có bao nhiêu điểm cực tiểu

A. 0 B. 1

C. Không có điểm cực tiểu D. 2

Câu 31 : Hàm số

3 2cos cos2y x x  

đạt cực tiểu tại

2πxk

πxk

2π

xk

Câu 32 : Hàm số

3 12 2y mx x x   

đạt cực đại tại điểm x = 2 khi

1m 

2m 

3m 

4m 

Câu 22 : Hàm số

 

3 2 2

6 4 1 2y x mx m x    

đạt cực đại tại điểm x = 2 khi

0m 

m 

4m 

4m 

Câu 34 : Hàm số

 

y x m 3 x mx m 2     

đạt cực tiểu tại điểm x = 2 khi

0m 

m 

4m 

4m 

Câu 35 : Hàm số

   

y 1 2f x x m x m      

đạt cực

đại tại điểm x0 = 2 khi

0m 

m 

4m 

4m 

Câu 36 : Hàm số

 

y f x

xác định trên và có đồ thị

như hình bên.

Phương trình đường thẳng d đi qua 2 điềm cực đại và

cực tiểu của đồ thị hàm số là







1 1 1

4 2 2

y x x  



1

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

yx

2yx

yx

2yx

Câu 37 : Đường thẳng (d)

 

y 1 3m x m  

đi qua điểm cực đại K của đồ thị hàm số

y x x 6

   

khi :

1m 



2m 

D. Đáp án khác

Câu 38 : Hàm số

y x m x 5

   

có cực đại và cực tiểu khi :

1m 

1 m 1  

1m 

D. Đáp án khác

Câu 39 : Hàm số

 

y x 2m 2 x

    

có cực đại và cực tiểu khi :



  

1m 

1m 

Câu 40 : Hàm số

 

2 2 4

y 2x m 2m 3 x m

      

có cực đại và cực tiểu khi :

m1

  

1m 

1m 

Câu 41 : Hàm số

   

y 2m 1 x 4m 3 x 8

     

có cực đại và cực tiểu khi :



  

m haym

  

D. Đáp án khác

Câu 42 : Hàm số

 

y x 3 x 2mx 2m     

có cực đại và cực tiểu khi :

m3

6 3 3 m 6 3 3   

m 6 3 3 hay m > 6 3 3  

m 6 3 3 hay m = 6 3 3  

Câu 43 : Cho hàm số

   

y x m 2 x m 3 x 1



     

Với giá trị nào của m thì hàm số có cực trị có hoành độ x1, x2 thỏa mãn

  

4x 1 4x 1 18  

m1

m8

m7

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

m4

Câu 44 : Cho hàm số

 

3 2 2

y x 2m 1 x m 2 x m

     

Với giá trị nào của m thì hàm số có cực trị có hoành độ x1, x2 thỏa mãn





m8



m4

Câu 45 : Cho hàm số

y x mx x

  

. Với giá trị nào của m thì hàm số có cực trị có hoành độ x1,

x2 thỏa mãn

1 2 1 2

x x x x 7  

m1

m2

m3

m4

Câu 46 : Cho hàm số

 

3 2 2

2m 1

y x x m 2 x 1



    

. Với giá trị nào của m thì hàm số có cực trị

có hoành độ x1, x2 thỏa mãn

 

1 2 1 2

3x .x 5 x x 7 0   



m8

m2

m4

Câu 47 : Cho hàm số

 

3 2 2

3m 1

y x x m m 6 x 1



     

. Với giá trị nào của m thì hàm số có

cực trị nằm về 2 phía Oy

2 m 3  

2 m 1  

m2

m4

Câu 48 : Cho hàm số

4 2 2

2( 2) 5 5y x m x m m     

. Với giá trị nào của m thì hàm số có 3 cực trị ?

m2

m1

m2

m1

Câu 49 : Cho hàm số

4 2 2 2

2( 3)y x m x m   

. Với giá trị nào của m thì hàm số có 3 cực trị ?

m3

m3

m3

m

Câu 50 : Cho hàm số

3 2 3

3 4 (1)y x mx m  

. Với giá trị nào của m thì đồ thị hàm số có 2 điểm cực

trị A và B

m0

m3

m1

 

m \ 0

Câu 51 : Cho hàm số

10000yx

. Số điểm cực trị ứng với hàm số là

A. 0 B. 1

C. 2 D. 3

Câu 5 2: Cho hàm số

32y x x  

. Số điểm cực trị ứng với hàm số là

A. 0 B. 1

C. 2 D. 3

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

Câu 51 : Cho hàm số

 

3 2 2

3y x m x m    

Số điểm cực trị ứng với hàm số là

A. 0 B. 1

C. 2 D. 3

Câu 52 : Cho hàm số

31y x x  

. Khoảng cách từ điểm cực đại của đồ thị hàm số đến đường

phân giác của góc phần tư thứ hai trong hệ trục Oxy là

Câu 53 : Cho hàm số

35y x x  

. Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số có hệ

số góc là

2

Câu 54 : Cho hàm số

 

1 1 2y kx k x k    

. Với giá trị nào của k thì đồ thị hàm số chỉ có một

điểm cực trị

A. 7 B. -2

C. 4 D. 1

Câu 55 : Cho hàm số

 

y f x

có bảng biến thiên như sau :



1















Khoảng cách giữa hai điểm cực tiểu của đồ thị hàm số là

Câu 56 : Cho hàm số

 

y f x

có bảng biến thiên như sau :



3















Khoảng cách giữa hai điểm cực tiểu của đồ thị hàm số là

Câu 57 : Cho hàm số

.sin sin3

y m x x

. Với giá trị nào của m thì hàm số đạt cực trị tại

x 

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

2m 

2m 

0m 

3m 

Câu 58 : Cho hàm số

 

y f x

có bảng biến thiên như sau :



x















Và khoảng cách giữa hai điểm cực tiểu của đồ thị hàm số là 8. Giá trị của

là

4

Câu 59 : Xét hàm số

( ) 2 3 1y f x x x   

Chọn đáp án đúng :

A. Hàm số không có cực đại và cực tiểu

B. Nghịch biến trên

 

lim



 

D. Cả A, B, C đều đúng.

Câu 60 : Xét hàm số

()

y f x x   

. Gọi hoành độ các điểm cực trị của đồ thị hàm số là x1 và

x2 thì x1 + x2 =

A. – 1 B. 2

C. – 2 D. 3

Câu 61 : Xét hàm số

 

4 2 2

( ) 9 10y f x mx m x    

(m là tham số) . Giá trị nào của tham số m thì

hàm số có 3 cực trị.

3 0 3m hay m   

m

m

3m 

Câu 62 : Cho hàm số

   

y x 3 2 1 x 12m 5 x 2m     

. Với giá trị nào của m thì hàm số có cực trị

  

hay m  

m

Câu 63 : Cho hàm số

 

2 1 3

y mx m x    

. Với

1m 

thì hàm số có cực trị có hoành độ x1 và

x2 . Với giá trị nào của m thì

.6xx

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

m 

7m 

Câu 64 : Cho hàm số

 

52y f x x

   

. Mệnh đề sai là

 

đạt cực đại tại x = -1 B.

 

đạt cực tiểu tại x = 1

 

có giá trị cực đại là 8 D.

 

1;8M

là điểm cực tiểu

Câu 65 : Cho hàm số

 

6 9 ( )y f x x x x C   

. Phương trình đường thẳng đi qua hai điểm cực

trị của (C) là

26yx

26yx

26yx  

3yx

Câu 66 : Với điều kiện nào của a và b để hàm số sau có cực đại và cực tiểu

     

y f x x a x b x     

.0ab

.0ab

.0ab

.0ab

Câu 67 : Giá trị của m để hàm số

 

21y x m x x m    

có hai điểm cực trị x1 và x2 thỏa mãn

.1xx 

là

4m 

2m 

3m 

D. Cả A và B

Câu 68 : Giá trị của m để hàm số

1y x mx  

có hai điểm cực trị là

0m 

0m 

4m 

D. Một kết quả khác

Câu 69 : Giá trị của m để hàm số

2017

y mx x  

có ba điểm cực trị là

0m 

0m 

0m 

0m 

Câu 70 : Giá trị của m để hàm số

2018

y mx x  

có ba điểm cực trị là

0m 

0m 

0m 

0m 

Câu 71 : Giá trị m để hàm số

y x mx

có ba điểm cực trị là 3 đỉnh của một tam giác vuông

0m 

1m 

0m 

3m 

Câu 72 : Hàm số







có hai điểm cực trị A, B nằm trên đường thẳng có phương trình y =

ax + b, với a + b =

1

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

Câu 73 : Đồ thị hàm số







có hai điểm cực trị A, B nằm trên đường thẳng có phương

trình y = ax + b, với a + b =

1

Câu 74 : Hàm số

2 3000







có hai điểm cực trị A, B nằm trên đường thẳng d. Hệ số góc của d

là

1

Một số dạng toán cơ bản về CỰC TRỊ hàm số

y ax bx c  

lập TAM GIÁC (luôn là tam giác cân)

Giả sử hàm số

y ax bx c  

có

cực trị:

(0; ), ; , ;

2 4 2 4

A c B C

a a a a

   



    

   

   

tạo thành tam giác

ABC

thỏa mãn dữ kiện:

Dữ kiện

Công thức thỏa

0ab 

1). Tam giác

ABC

vuông cân tại

80ab

2). Tam giác

ABC

đều

24 0ab

3). Tam giác

ABC

có góc

BAC





8 .tan 0





4). Tam giác

ABC

có diện tích

0ABC





3 2 5

32 ( ) 0a S b

5). Tam giác

ABC

có độ dài cạnh

BC m

20am b

6). Tam giác

ABC

có độ dài

AB AC n

2 2 4

16 8 0a n b ab  

7). Tam giác

ABC

có cực trị

,B C Ox

40b ac

8). Tam giác

ABC

có

là tâm đường tròn nội tiếp

8 4 0b a abc  

PHỤ LỤC

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

Ví dụ 01 : Tìm tất cả giá trị tham số thực

để hàm số

( 2015) 2017y x m x    

có

cực trị tạo

thành tam giác vuông cân tại

2017m 

2014m 

2016m 

2015m 

Hướng dẫn: Với

1, 2015a b m   

Hàm số có

cực trị là

0ab 

, tức là phải có:

( 2015) 0 2015mm    

Tam giác

ABC

vuông cân tại

khi:

8 0 8.( 1) ( 2015) 0 2015 2 2017a b m m m           



Chọn đáp án A.

Ví dụ 02 : Tìm tất cả giá trị tham số thực

để hàm số

2( 2016) 2017 2016y x m x m    

có

cực

trị tạo thành tam giác vuông cân tại

2017m 

2017m 

2018m 

2015m 

Hướng dẫn: Với

1, 2( 2016)a b m  

Hàm số có

cực trị là

0ab 

, tức là phải có:

2( 2016) 0 2016mm    

Từ

8 0 8.1 8( 2016) 0 2016 1 2017a b m m m            



Chọn đáp án A.

Ví dụ 03 : Tìm tất cả giá trị tham số

để hàm số

3( 2017) 2016

y x m x   

có

cực trị tạo

thành tam giác đều.

2015m 

2016m 

2017m 

2017m 

Hướng dẫn: Với

, 3( 2017)

a b m  

Hàm số có

cực trị là

0ab 

, tức là phải có:

.3( 2017) 0 2017

mm   

Tam giác

ABC

đều , thì :

 

24 0 24 3( 2017) 0 2017 1 2016

a b m m m



           







Chọn đáp án B.

Ví dụ 04 : Nếu đồ thị hàm số

9 2( 2020) 2017 2016y x m x m    

có

cực trị tạo thành tam giác

đều thì giá trị tham số

thuộc khoảng nào?.

(2015;2017)

(2016;2018)

(2017;2019)

(2017;2020)

Hướng dẫn: Với

9, 2( 2020)a b m  

Hàm số có

cực trị là

0ab 

, tức là phải có:

9.2( 2020) 0 2020mm   

 

24 0 24.9 2( 2020) 0 2020 3 2017a b m m m           



Chọn đáp án B.

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ

2017

Ví dụ 05 : Tìm tất cả giá trị tham số

để hàm số

3 ( 2015) 2016y x m x    

có

cực trị tạo

thành tam giác có một góc

120

2017m 

2015m 

2017m 

2016m 

Hướng dẫn: Với

3, 2015a b m   

Hàm số có

cực trị là

0ab 

, tức là phải có:

3.( 2015) 0 2015mm    

Tam giác

ABC

có một góc

120

, thì phải có:

8 .tan 0





với

120 tan 3

BAC

BAC   

Nên có

8 3 0ab

8.( 3) 3( 2015) 0 2015 2 2017m m m         



Chọn đáp án C.

Ví dụ 06 : Tìm tất cả giá trị tham số

để hàm số

3 2( 2018) 2017y x m x   

có

cực trị tạo

thành tam giác có một góc

120

2018m 

2017m 

2017m 

2018m 

Hướng dẫn: Với

3, 2( 2018)a b m  

Hàm số có

cực trị là

0ab 

, tức là phải có:

3.2( 2018) 0 2018mm   

Từ

3 2 0 3

8 .tan 60 0 8.3 8.( 2018) .3 0 2018 1 2017a b m m m           



Chọn đáp án C.

Ví dụ 07 : Tìm tất cả giá trị tham số

để hàm số

22y mx x m   

có

cực trị tạo thành tam

giác có diện tích bằng

2m 

2m 

1m 

1m 

Hướng dẫn: Với

,2a m b

Hàm số có

cực trị là

0ab 

, tức là phải có:

.2 0 0mm  

Tam giác

ABC

có diện tích bằng

, thì :

3 2 5 3 5 3

32 ( ) 0 32. .1 2 0 1 0 1a S b m m m          



Chọn đáp án D.

Ví dụ 08 : Tìm tất cả giá trị tham số

để hàm số

4 2017 2016

y mx x   

có

cực trị tạo thành

tam giác có diện tích bằng

2m 

4m 

1m 

1m 

Hướng dẫn: Với

,4a m b

. Hàm số có

cực trị là

0ab 

, tức là phải có:

.4 0 0mm  

3 2 5 3 2 5 3

32 ( ) 0 32. (4 2) 4 0 1 0 1a S b m m m          



Chọn đáp án D

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN

2017

1/Định nghĩa 

Nu

f(x) M, x D  



f(x ) M,x D



u Max y = M ti x = x0

Nu

f(x) M, x D  



f(x ) M,x D



u Min y = M ti x = x0

2/ Tìm GTLN & GTNN:

♥ Dạng 1: nđọan [a,b]





m ti hn

0 1 2

x , x , x ... [a, b]

y



0 1 2

f(x ), f(x ), f(x ), ....., f(a), f(b)

 l nht

lu

♥ Dạng 2 : nkhoảng (a,b) (vẽ bảng biến thiên)



B2 : lp BBT , suy ra GTLN , GTNN

PHỤ LỤC PHƯƠNG PHÁP CASIO GIẢI QUYẾT BÀI TOÁN GTLN – GTNN

Ví dụ 1.[Thi thử chuyên KHTN –HN lần 2 năm 2017]

 ln nht c

2 4 1y x x x   

n

 

1;3

PHẦN 3 : GIÁ TRỊ LỚN NHẤT – NHỎ NHẤT

- Bước 1:   ln nh nh nht c

 

y f x

n

 

;ab

ta s

di lnh MODE 7 (Lp b)

- Bước 2:  n th ln nht xut hin  nh

nht xut hi

- Chú ý:

Ta thit lp mi ca bin

Start

End

Step

ba

  p)

 u t 

sin ,cos ,tan ...x x x

ta chuy chế độ Radian

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN

2017



max

max 2

max 7

max 4

Hướng dẫn giải

S dng chi thit lp Start 1 End

Step





 

ta th ln nht

 

 

 

32f 

Vy

max 2

, dc khi

3x 



 B

Ví dụ 2. [Thi Học sinh giỏi tỉnh Ninh Bình năm 2017]

 ln nht

c

36y x x   

 3M

 32M

23M 

23M 

Hướng dẫn giải







   









36y x x   



3

End

Step

0.5



4.2421 3 2M 



1x 



2.6x10 0m







Casio



B

Ví dụ 3. [Thi thử chuyên Vị Thanh – Hậu Giang lần 1 năm 2017]

 nh nht c

 

2 3 7y x x   

min 5y

min 7y

min 3y 

D n ti

min

Hướng dẫn giải





9

End

Step



 

2 3 7y x x   



Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN

2017



min 3y 



1x 



C

Ví dụ 4. [Thi thử THPT Lục Ngạn – Bắc Giang lần 1 năm 2017]



 

4mx







 ln nht b

 

2;6





m 

Hướng dẫn giải



m 





A sai



34m 





C 

BÀI TẬP TỰ LUẬN PHẦN GTLN – GTNN

Bài tập 01 :  ln nh nh nht c

5 4 3

y x 5x 5x 2   

n [–1;2]

♥ Giải:

..............................................................................................................................................................................

Bài tập 02 :  ln nh nh nht c

 

2x 3x 3







n [0;2]

(Trích đề thi ĐH Khối D – 2013)

♥ Giải:

..............................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN

2017

Bài tập 03 :  sau:

y x 3x 9x 1   

n [– 4; 4]. b)

y f(x) 2x 3x 4

    

n

[ 4;0]

y x 8x 16  

n [–1; 3]. d)

y x 5x 4  

n [–3; 1].

♥ Giải:

..............................................................................................................................................................................

Bài tập 04 : a)

y x 2 6 x   

y x 5 9 x   

y x 7 11 x   

y x 2x 5  

n [–2; 3].

♥ Giải:

..............................................................................................................................................................................

Bài tập 05 :  sau:

2sinx 1

sinx 2







y cos x 6cos x 9cosx 5   

♥ Giải: .............................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN

2017

..............................................................................................................................................................................

Bài tập 06 : a)

y x 4 x  

(ĐH Khối B – 2003) b)









 

1; 2

(ĐH Khối D – 2003)

c) Đề Thi THPT Quốc Gia 2015:

 

f x x



n

 

1;3 .

y 2x 3x 12x 1, x 2;



     





 

y x 3x 5, x 1; 4    

 

y 5 4x, x 1; 1   

♥ Giải:............................................................................................................................................................

..............................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN

2017

Bài tập 07 :  ca tham s

  nh nht c

 

x m m









n

 

0;1

bng

2

♥ Giải:

..............................................................................................................................................................................

Bài tập 08 :  ln nht c

21mx









 

2;3





khi m nh bng:



5 B. 1 C. 0 D. -2

♥ Giải:

..............................................................................................................................................................................

Bài tập 09 : Mt vt chuyng theo quy lut

s t t  

, vng th

t t bu chuyng vc trong khong th

Hi trong khong thkể từ lúc bắt đầu chuyển động, vn tc ln nht ca vt

c b ?

A. 512 (m/s) B. 90 (m/s) C. 700 (m/s). D. 96 (m/s).

♥ Giải:

..............................................................................................................................................................................

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN

2017

Bài tập 10 : Mt vt chuyng theo quy lut

s t t  

, vi t ng th

t t bu chuyng vc trong khong th

Hi trong khong thkể từ lúc bắt đầu chuyển động, vn tc ln nht ca vt

c b

A. 216 (m/s) B. 30 (m/s) C. 400 (m/s) D. 54 (m/s)

♥ Giải:

..............................................................................................................................................................................

.............................................................................................................................................................................

Bài tập 11 :T mt b tn, ngi ta mut vi mt s vt liu cho

tr  t  nh

din nhu r nh





♥ Giải:.................................................................................................................................................................

.............................................................................................................................................................................

..............................................................................................................................................................................

.............................................................................................................................................................................

BÀI TẬP MINH HỌA PHẦN GTLN – GTNN

Ví Dụ 01 : 

y x 3x 2  

n [1,3]

c chung khi gii m 

► Bước 1: ng vi tnh

 

;ab

c

 

y f x

, ta tính đạo hàm

 

' ' xyf

► Bước 2: Gii phng trnh

 

'0fx

► Bước 3: Nu gii ra m

0 1 2

; ; ;...

x x x x 

ta nhn (long

 

;ab



 

? 0,

f x i n













  





 t lun:

 

 

 

 

;

max

min

x a b

















(☻ không phải hàm số nào cũng tồn tại cả GTLN và GTNN).

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN

2017

* Lưu ý rằng, nu pt

 

'0fx

vô nghiệm hoc các nghiệm tìm được không thuộc

 

;ab



GTLN  GTNN c sẽ đạt được tại x = a, x = b (tạm gọi là 2 biên).

♥ Giải: hàm số xác định và liên tục trên [1,3]

y' 3x 6x, y' 0 3x 6x 0





      







 đoạn [1,3] ta ch nhn x = 0



f(2) y(2) 2 3.2 2 2

f(1) y(1) 0

f(3) y(3) 2



     













Kết luận : - 2 khi x = 2

[1,3] [1,3]

Ví Dụ 02 : 

y f(x) x 2 8 x    

♥ Gi c 

1 1 8 x x 2

y'(x) 0

2 x 2 2 8 x 2. 8 x. x 2

  

   

   

8 x x 2 0    

8 x x 2   

ng













)

x 2 0

x 5 D

8 x 2 x





   



  



f(2) 6; f(5) 2 3; f(8) 6  

Kt lun : Max y =



khi x = 2 hay x = 8

[2, 8] [2, 8]

 

u u u







 





   

.u v v u















 

sin .cosu u u





 

cos .sinu u u





 

tan '. 1 tan

cos

u u u



  

 

. .lna

a u a





 

log

.ln





 

cot '. 1 cot

sin

u u u







   

Ví Dụ 03 :  ln nh nht c :

( ) . (5 )f x x x

n

 

0;5

♥ Giải: f(x) =

(5 )xx

 

BẢNG ĐẠO HÀM

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN

2017



50x

; 

3/2

(5 ) (0;5)x x x   



5 (5 )

xx

; 

5; 2xx  

.  : f(2) =

, f(0) = f(5) = 0

Vy

[0;5]



f(x)= f(2) = 6 3

[0;5]x

Min



f(x) = f(0) = 0

Ví Dụ 04 :  ln nht, nh nht c







n

 

0;1

♥ Giải:  n

 

0;1



 

 

' 4 0, 0;1



    



.  nghch bin

 

0;1

Vy

 

 

0;1

max 0 3yy

;

 

 

0;1

min 1

yy  

Ví Dụ 05 :  ln nh nh nht c

 

f x x



n

 

2; 4

♥ Giải: 

 

n

 

2; 4

;

 





  

. Vi

 

2; 4x

 

 

3 2;4

0 9 0

3 2;4

f x x



  



    











     

13 25

2 , 3 6, 4

f f f  

 ln nh nh nht ca

 

n

 

2; 4

l



Ví Dụ 06 :  ln nh nh nht c

 

2sin 1 2yx  

n

;











♥ Giải: t

sintx



;













 

1;1t 

 tr 

 

2 1 2 4 4 3y t t t     

 

1;1t 

. 

' 8 4yt

Suy ra

 

' 0 8 4 0 1;1

y t t        



   

1 3; 2; 1 11.

y y y



    





Vy

 

 

1;1

max 11ft





khi

1t 

, suy ra





;

 

 

1;1

min 2ft





khi

t 

, suy ra





Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN

2017

Ví Dụ 07 :  ln nh nht c

 

2sin sin

f x x x

n

 

0;π

♥ Giải: t

sintx

. Do

 

0;x







 

0;1t 

 tr 

 

f t t t

n

 

0;1



 

' 2 4f t t

. Suy ra

 

 

0;1

' 0 2 4 0

0;1

f t t







    



  







   

2 2 2 2

0 0; ; 1

2 3 3

f f f



  





Vậy:

► GTLN c bng

khi

t 

, suy ra











;

► GTNN c bng

khi

0t 

, suy ra

0x 







Ví Dụ 08 :  ln nh nht c

 







n







♥ Giải: 

 









 







 

0 ;2

2 ;2





















  









. 









;

 

f 

Vy

 

min











khi

x 

;

 

max











khi

2.x 

Ví Dụ 09 :  ln nh nh nht c

21y x x  

n

 

1;0

♥ Giải: Minh:

D 



 

16 64







Suy ra

' 0 16 64 0 2y x x       

Gii hn tc

lim lim 0

 



Bảng biến thiên

Vy

 

1;0

max 4





khi

2x 

 

1;0

min 4





khi

2x 



2



 

f ' x







 

4

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN

2017

Ví Dụ 10 :  ln nh nh nht c

21y x x  

n

 

1;0

♥ Giải:

 n

 

1;0



2 2 1 2

2 1 2 1

x x x



  



Suy ra

' 0 2 1 2 0y x x    



2 1 2xx  

 

1;0

2 1 4





     









   

1 1 3; ; 0 1

y y y



      





Vy

 

1;0

max 1y





khi

0x 

;

 

1;0

min





khi

x 

Ví Dụ 11 :  ln nht c

 

3 72 90f x x x x   



 

5;5 .

♥ Giải: 

 

3 72 90g x x x x   



 

5;5

; 

 



n

 

5;5

; 

 

' 3 6 72g x x x  

 

 

4 5;5

6 5;5



  





   







     

5 70, 5 400, 4 86.g g g     

Suy ra

     

5 70; 5 400; 4 86g g g   

Vy

 

 

 

     

 

5;5

5 , 4 , 5 400

Max f x Max g g g



  

khi

5.x 

Ở đây các em chú ý công

thức













Và đạo hàm :

 



Lấy giá trị “bự” nhất

trong các giá trị này

!!!

Ghi chú : 

 

y f x



 

;ab

  GTNN c

 

y f x



 

;ab

c :

◙ 

 

y f x

 

GTLN  GTNN.

◙ 

 

, ... ;

x x x a b

◙ 

         

, ... , ,

f x f x f x f a f b

◙ S ln nh  nh 

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN

2017

Ví Dụ 12 : Gi

,Mm

tng  ln nh nht c

 

1y x k k x   

n

 

1;2

. Khi tham s   nh nht ca M



m bng:

 

♥ Giải: Chọn B.



 

2 2 2

' 3 1 3 0, ,

y x k k x k x k



         





. Do v n

 

1;2

V

Mm

   

3 2 2

2 1 2 2 1 1 1y y k k k k



          



1 45 45

3 3 12 3 .

2 4 4

k k k



      





Ví Dụ 13 : 

33y x x  

n

 

1;3

. Gi



ln l ln nht

 nh nht c

Mn

bng:

A. 1 B. 2 C. 3 D. 4

♥ Giải: Chọn B. 

 

3 3, 1;3y x x D   

 

3 6 3 2y x x x x



    

Khi















(loi

0.x 

)

     

1 1; 2 1; 3 3

GTLN M

f f f

GTNN n





     







Vy t nh nh ln nht bng 2.

Ví Dụ 14 :  ln nht c

44y x x



A. 3 B. 1 C. 4 D. 2

♥ Giải: Chọn B

 

3 4 2 3 2

4 3 , 12 12 12 1 ; 0

y x x D R y x x x x y







         







ng bi



0 1



+ 0 + 0





Câu 15: Cho parabol

( ): 2P y x x  

m

(7; 2)A 





()P

sao cho kho

n nh

(1;0), 10M AM 

(1;1), 10M AM 

(1;0), 2 10M AM 

(1;1), 2 10M AM 

♥ Giải: Chọn C.

( ) ( , 2)M P M x x x   

;

ngn nht

AM

ngn nht.

2 2 2 2 4 3 2

( ) ( 7) ( ) 2 2 14 49f x AM x x x x x x x         

3 2 2

'( ) 4 3 4 14 ( 1)(4 10 14) 0 1f x x x x x x x x          

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN

2017





()fx





'( )fx

Dng bi

min ( ) 40fx

ti

10xy  

. Vy

min 2 10AM 

ti

(1;0)M

BÀI TẬP TRẮC NGHIỆM PHẦN GTLN – GTNN

Câu 1 : 

32y x x  

.  ln nht, nh nht c n

 

1;5

ln



2; 2

552;



553;



552;



Câu 2 : 

4 3 2

2 5 2y x x x   

. Hiu c ln nh nht c 

n

 

0;3

 ng

117

375

Câu 3 :  ln nh nh nht c

 

f x x



n

 

2;5



Câu 4 :  ln nh nh nht c

 

f x x



n

 

4; 2



1





1











Câu 5 :  ln nht c

y x x

n

 

2; 1

m c



20xx

9xx

9 sinxx

81 0x 

Câu 6 : 







 :

(I)

 

0;2

max

y 

(II)

 

0;2

min 5y 

Chn khnh sau :

A. (I) (II) sai B. (I) sai (II) 

C. (I), (II)  D. (I), (II) u sai

Câu 7 : 

23y x x  

 :

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN

2017

(I)

 

3;2

max 66y





 (II)

 

3;2

min 11y





Chn khnh sau :

A. (I) (II) sai B. (I) sai (II) 

C. (I), (II)  D. (I), (II) u sai

Câu 8 :  tr ln nht c

 

y f t







Câu 9 :  ln nht t c

4y x x  



Câu 10 :  ln nh nh nht c

 

2sin 2sin 1y f x x x   

theo th t 



B. 











Câu 11 :  ln nh nh nht c

32y x x  

n

 

10;10





132







D. 10 

Câu 12 :  nh nht c

4y x x

n

 

1;3



A. 1 B. 3

D. 2

Câu 13 :  ln nht c

23y x x  

n

 

0;2



A. 1

B. 0

C. 3

D. 2

Câu 14 :  ln nh nh nht c

 

20 10 3

3 2 1

y f x







theo th t 

 

B. 



C. 





Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN

2017

Câu 15 : T c cc tiu c







A. 4 B. 8

C. 6 D. 2

Câu 16 : Mt chm chuy

   

3 9 2 ;x t t t m s  

. Vn tc ca vt

 cc ti

A. 1 B. 2

C. 3 D. 4

Câu 17 :  ln nh nh nht c

2 2 8







n

 

2;0

ln 

 

14

3

Câu 18 :  ln nh nh nht c

 

y f x x

  



n

 

3;0

ln

 M

+ n



107

144

106

Câu 19 :  ln nht c

 

4 2x 4f x x   

n

 

2;1

 s ng

th

2 3 0yx  

23yx  

yx

30yx   

Câu 20 :  ln nh nht c

 

y f x







n

 

2;4



Biu thc A = X + 2Y

Câu 21 :  ln nh nh nht c

 

   

22f x x x  

n









m c

2 3 0xx  

23xx  

40xx

24xx  

Câu 22 :  nh nhn nht c

 

3 9 35f x x x x   

n

 

4; 4



 

 

4; 4

min 41fx







 

 

4; 4

max 40fx





 

 

4; 4

min 1fx







 

 

4; 4

max 40fx





Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN

2017

 

 

4; 4

min 4fx







 

 

4; 4

max 10fx





 

 

4; 4

min 1fx







 

 

4; 4

max 9fx





Câu 23 :  nh nhn nht c

 

32f x x x  

n

 

2; 2



 

 

2; 2

min 2fx







 

 

2; 2

max 4fx





 

 

2; 2

min 2fx







 

 

2; 2

max 0fx





 

 

2; 2

min 2fx







 

 

2; 2

max 8fx





 

 

2; 2

min 2fx







 

 

2; 2

max 6fx





Câu 24 :  nh nhn nht c

 







 

 

min 4







 

max





 

min 3







 

max





 

min 4







 

max





 

min 3







 

max 5





Câu 25 :  nh nhn nht c

 









 

min 0







 

max 1





 

min







 

max 3





 

min







 

max 5





 

min 3







 

max 3





Câu 26 :  nh nht c

 

33f x x x  

n











A. 6 B. -75

C. 4 D. -35

Câu 27 : Cao huyết áp còn gọi là tăng huyết áp 

b(tension). bệnh lý thuờng gặp trong ci, chiếm

8-12% dân số. Mt s yu t ing, thu

    n. Độ giảm huyết áp ca mt b  c cho b  c

   

0,025 30G x x x

x (mg) > 0 ng thuc c  huyt

giảm nhiều nhất t ling bng :

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN

2017

A. 20 mg B. 15 mg

C. 30 mg c

Câu 28 : 

 

25y f x x x   

. GTLN c 

 

2;2

t nghim ca



13 0xx

12 0xx

13 14 0xx  

16 0x 

Câu 29 : 

 

25y f x x x   

. GTNN c 

 

2;2

 

5

4

Câu 30 : 

 

24y f x x x    

 



Câu 31 : 

cosy x x

 sau

(I) :

Maxy













(II) :

Miny













A. (I) 

 

C. C  

D. C u sai

Câu 32 :  GTNN c

sin cosy x x

.Mt h

(I) : Vi m

0 sin 1 (1)x



0 cos 1 (2)x

(II) : C c

0 sin cos 2xx  

(III) : Vy GTLN c bGTNN c 



A. Sai t c (I)

B. Sai t c (II)

C. Sai t c (III)

D. C u sai

Câu 33 : (CHUYÊN LÊ HỒNG PHONG)  ln nht c

2 3 12 2y x x x   



n

 

1;2



A. B.

C. D.

1;2

max 11.y

 





1;2

max 6.y

 





1;2

max 15.y

 





1;2

max 10.y

 





Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN

2017

Câu 34 : (SỞ BẮC NINH)  ln nht c





n

 

1;4



A. B.

C. D.

Câu 35 : (TRƯỜNG THPT CHUYÊN LONG AN) tr ln nh nh nht c









 

1;3



A. B.

C. D.

Câu 36 : (TRƯỜNG THPT CHUYÊN PHAN BỘI CHÂU) 

57y x x  

 ln

nht c n

 

5;0

b

A. . B. . C. . D. .

Câu 37 : m  

4mx







 ln nht bng 5 n

 

2;6

A. B.

C. D.

Câu 38 : m   nh nht c

36y x mx  

n

 

0;3

bng

A. B.

C. D.

Câu 39 : t c  ca   nh nht c

3y x x m   

n

 

1;1

bng .

A. .

B. .

C. .

D. .

Câu 40 : (TRƯỜNG THPT CHUYÊN SƯ PHẠM)  ln nht c

sin siny x x



A. .

B. .

C. .

D. .

1;4

max 11.y







1;4

max .







1;4

max 10.y







1;4

max 6.y







1;3

max 0; min





  

1;3

max ; min 0







1;3

max 3; min 1yy







1;3

max 1; min 0yy







143

26.m 

m 

34.m 

m 

2.m 

m 

m 

1.m 

4m 

2m 

6m 

0m 

1

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN

2017

Câu 41 : (TRƯỜNG THPT CHUYÊN LÝ TỰ TRỌNG - CẦN THƠ)  ln nht c

9y x x m  



 

1;1

b ca tham s thc bng

8

B. 8.

C. 0.

3

hoc

Câu 42 : (TRƯỜNG THPT CHUYÊN PHAN BỘI CHÂU) t c  ca  

 

1mx







 ln nh

 

1;2

bng .

A. .

B. .

C. .

D. .

Câu 43 : Trong tt c  nh nh nht

b

2 S

4 S

Câu 44 :  nh nhn nh

ding.

36 cmS 

24 cmS 

49 cmS 

40 cmS 

Câu 45 : Cho mt tnh

a nh hnh v. Ngi ta ct  bn

ng nhau, ri gp ti

 c m th 

ca khi hn nhnh c

 ct ra bng:

2

3m 

2m 

4m 

3m 

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN

2017

Câu 46 : Cho mt t nh 48cm . Ngi ta ct  ng nhau

p t c m th i hp ln nh

 c

A. 8 cm. B.

24 cm

. D.

Câu 47 : Th c ca mt b bi sau t m tnh theo cng thc

 

100 4

V t t









 

0 90t

. T bm nc ti thm t i

   

'f t V t

nh sau,

khđúng ?

A. T m t   90.

B. T   75.

C. T m.

D. T 

Câu 48 (Trích đề thi thử lần 1, k2pi.net.vn) : Ngt loi thum 

tay phi ca mt b, n thuc  ma b

c cho bc

   

0,28

0 24

C t t

  



. H  thuc  mch

a bn nht ?

A. 12 gi. B.8 gi.

C. 6 gi. D.2 gi.

Câu 49 :  ln nht c







n

 

0;2



. B.

5

. C.

. D.

Câu 50 : Lu lng hc cho bc

 

209,4

0,36 13,2 264







 

/v km h

n tng hn tc

ng hm sao cho lu ln nh ln nht



 

264

0,6

8,9















 

264

0,5

6,3















 

260

0,6

6,4















 

264

1,6

4,9















Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIỆM CẬN

2017

KIẾN THỨC CĂN BẢN

ng tim cn c th c

A. Tiệm cận ngang

ng thng

yy

c gm cn ngang c th 

 

y f x

nu

 

l im f x y





hoc

 

l im f x y





B. Tiệm cận đứng

ng thng

xx

c gm cng c th 

 

y f x

nt mt

u kic th

 

lim f x





 

 

lim f x





 

 

lim f x





 

 

lim f x





 

Chú ý : Mphân thức hữu tỉ bậc nhất trên bậc nhất







ax b

cx d

u có hai tiệm cận

 Tim cng





 Tim cn ngang



  th  nhng tim ci xng.



PHẦN 4 : TIỆM CẬN

Ví dụ :

2 4x

3x 3







Số x = 1 không xác định

tử (- 4x) / mẫu(3x) = - 4/3

TCĐ : x = 1

không xác

định

TCN : y = -4/3

không xác

định

Đối với dạng này thì

chỉ cần chú ý

Các số làm cho mẫu bằng 0

chính là TCĐ

Lấy bậc cao nhất tử chia cho

bậc cao nhất mẫu sẽ ra TCN

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIỆM CẬN

2017

BÀI TẬP TỰ LUẬN PHẦN TIỆM CẬN

Bài 1 : m c sau

2 1 3 4 4

) ; ) ; ) ; ) .

2 1 1 2 6

x x x

a y b y c y d y

x x x x

  

   

   

..............................................................................................................................................................................

Bài 2 :  nht to bi 2 tim cn, 2 trc t c sau













..............................................................................................................................................................................

Bài 3 :  ca tham s

 th 

2 2 1xm







m cm

 

3;1M 

..............................................................................................................................................................................

Bài 4 : S tim cn c th 









A. 0 B. 1 C. 2 D. 3

Bài 5 : 







Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIỆM CẬN

2017

 

1;2

 

2;1

 

1;1

 

1; 1

..............................................................................................................................................................................

Bài 6 : 









 th  m cng, tim c

m ci hai trc t t nhng 8.

..............................................................................................................................................................................

Bài 7 : i xng c th 







 d

 

1;2

 

1; 1

 

1;10

 

1;5

Bài 8 : 







A. 0 B. 1

C. 2 D. 3

Bài 9 :  th 







ng tim cn?

 ng  ng

 ng  ng

Bài 10 : t c  thc ca tham s   th 

45x







m cng nm

i trc Oy .

  B.

0m 

0m 

0m 

..............................................................................................................................................................................

Bài 11 : Cho 







 th  nhn trm cn ngang

m cng

mn

bng:



D. 0

..............................................................................................................................................................................

Bài 12 : 

1mx



n ng

 

1;1m

1m 

1m 

 

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIỆM CẬN

2017

..............................................................................................................................................................................

BÀI TẬP MINH HỌA PHẦN TIỆM CẬN

Bài 1 : Tim cn ngang c th 







ng thng

()y x m d

trng qui ti mm khi m bng:

A. 0 B.

C. 1 D. 2

☻ Hướng dẫn giải : Tim cng thng

y 

Giao ca tim cn ngang vi trm

(0; )

(0; ) ( )

A d m  

Bài 2 : 

( 1) 1

()







. Gm cng tim cn c

gc t -ba điểm O, I, A thẳng hàng khi m bng:

A. -2 B. -1 C. 1 D. 2

☻ Hướng dẫn giải :

; , (4; 6), ;

2 2 2 2

m m m m

I OA OI



   

    

   

   

O, I, A th

4. 6 0 2



    

Bài 3 : 

2016 2016





 ng thng

x 

m cng c

th ?

A. 1 B. 2 C.



☻ Hướng dẫn giải :

xm

m cng c th  

lim





 

 ng thng

x 

m cng c th  

















Bài 4 : 

 

2 1 1

x m x m



   

 th  m c

khi: A. m > 1 B. m < 1 C. m = 1 D. m = -1

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIỆM CẬN

2017

☻ Hướng dẫn giải :

 th  m c khi:

 

2 1 1x m x m   

m hay

' 0 1m   

BÀI TẬP TRẮC NGHIỆM PHẦN TIỆM CẬN

Câu 1 : Phng trnh cc ng tim cn c th 







xy

;

xy

;

xy

;

xy

Câu 2 : Phng trnh cc ng tim cn c th 







3; 1xy  

1; 3xy  

;

xy  

Câu 3 : Phng trnh ng tim cn ngang c th 







4y 





y 

y 

Câu 4 : Gng tim cn c th 







. T c :

A. (1; 3) B. (1; 2) C. (2; 1) D. (2; 7)

Câu 5 : Ch 

 





m cn ngang

 

y x x

 m vng thng y = 1

 

1yx



\{ 1}D 

  th 

2y x x x  

ct trc tung tm

Câu 6 : ng cong (C):







ng thng

 

:5 12 4 0xy   

. Kho giao

m hai tim cn cng thng

Câu 7 : ng cong (C):







i x









i x ng

Câu 8 : ng cong (C):







:

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIỆM CẬN

2017

 m cng

1x 

 m cng

x 

m cn ngang

y 

Chn khnh sau:

A. Ch  B. Ch 

C. Ch  D. C 

Câu 9 : ng cong (C):







ng thng

 

:3 4 4 0xy   

. Kho giao

m hai tim cn ca ng thng

Câu 10 : ng cong (C):

 







 ca tham s  ng tim cn ngang ca

 th  m

 

1; 5M 

7

Câu 11 : ng cong (C):

 

y f x

ng bi



2











11.1 : Phng trnh ng tim c

4x 

3x 

3x 

2x 

11.2 : Phng trnh ng tim c

3y 

2y 

x 

3y 

Câu 12 : ng cong (C):

 

, , 0; 1; 2

mx n

y m n m n



   



m cng tim cn

 th (C) v th 

1yx



Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIỆM CẬN

2017

 

2; 4M 

 

2; 7M 

 

2;0M 

 

2;0M 

Câu 13 : ng cong (C):





Phng tim c

y 

1y 

2y 

3y 

Câu 14 : ng cong (C):

x x m







 tham s   th  m cng

2m 

3m 

1m 

1m 

Câu 15 : ng cong (C):

x x m







 tham s   th  t tim cn

ng

2m 

3m 

1m 

1m 

Câu 16 : ng cong (C):

x x m







 tham s   th  m

cng

2m 

3m 

1m 

1m 

Câu 17 : ng cong (C):







Phng trnh ng tim c

y 

1y 

2y 

3y 

Câu 18 : S ng tim cn c th 





Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIỆM CẬN

2017

Câu 19 : S ng tim cn c th 





Câu 20 : S ng tim cn c th 





D. .

Câu 21 :  tham s  th  m cn







0m 

1m 

C. C 

m

Câu 22 : 

()







 ng tim c

Tp h

 ng thng

2yx

 ng thng

2yx  

 ng thng

2yx  

ngoi tr m

   

1;3 , 3; 1

 ng thng

2yx

ngoi tr m

   

1; 1 , 3;1

Câu 23 : Tim cn ngang c th 









3y 

2y 

1y 

1y 

Câu 24 :  th 

 

9 1 1

3 7 2







A. Nhng thng

3x 

m cng

B. Nhng thng

2x 

m cng

C. Nhng thng

0y 

m cn ngang

D. Nhng thng

3 10yx

m c

Câu 25 : S ng tim cn c th 









A. 1 B. 2 C. 3 D. 0

Câu 26 :  th 

2 3 4







A. Nhng thng

3x 

m cng

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIỆM CẬN

2017

B. Nhng thng

x 

m cng

C. Nhng thng

1y 

m cn ngang

D. Nhng thng

2yx

m c

Câu 27 : ng thng

1x 

m cng c th  















2 3 2







Câu 28 : ng thng

2y 

m cn ngang c th  





















Câu 29 :  ca m  tim cng c th 

21x







m M

2

B. 2 C. 3 D. 0

Câu 30 : S ng tim cn c









A. 1 B. 2 C. 0 D. 3

Câu 31 : 







 sau, m 

  th  m cng

2x 

  th  m cn ngang

1y 

 i xm I(2 ; 1)  u sai.

Câu 32 : Tim cn ngang c th 







ng thng:

x 

y 

Câu 33 : Tim cng c th 







ng thng:

2x 

3y 

x 

 m cng

Câu 34 :  th 







t c ng tim cn:

A. 2 B. 1 C. 3 D. 0

Câu 35 : V  th 







ng tim cng

thng

y 

A. m = 0 B. m = 3 C. m = 6 D. m = 9

Câu 36 :  th  ng tim c-3:

















32y x x  

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIỆM CẬN

2017

Câu 37 : V  th 







ng tim cng

thng x = 2:

A. m = 1 B. m = 2 C. m = 4 D. m = 6

Câu 38 :  th  ng tim c

















2 2 1







Câu 39 :  th 

2 2 1







ng tim c

y 

x 

y 

x 

Câu 40 : 







 th (C). Kh

  th m c-m c

  th m cm c-5

  th m cm c-5

  th m cn

Câu 41 :  th 







t c ng tim cng:

A. 4 B. 3 C. 2 D. 1

Câu 42 : S ng tim cn c th 









A. 0 B. 1 C. 2 D. 3

Câu 43 : ng tim cng c th 









2x 

3x 

C. y = 2 D. y = 3

Câu 44 : ng tim cn ngang ca  th 









x 

x 

y 

y 

Câu 45 : 



. S ng tim cn c th  

A. 0 B. 1 C. 2 D. Kt qu 

Câu 46 : 



. Tim cn ngang c th  ng thng

trnh: A. y = -1 B. y = 1 C. y = -2 D.

y 

Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIỆM CẬN

2017

Câu 47 : 





. Tim cng c th  ng thng

trnh:

A. x = -2 B.

x 

C. x = -1 D. x = 3

Câu 48 : 



. Tim cm cn ngang c th  ng

thng ln lng trnh:

xy  

xy  

xy

Câu 49 : 

x 

. Tim cm cn ngang ca  th  ng

thng ln lng trnh:

xy

Câu 50 :  th c ng thm cng:

2yx

















Câu 51 : Tim cn ngang c th 

1mx







m A(1;-2) khi m bng

A. -2 B. -1 C. 1 D. 2

Câu 52 :  th c ng thm cn ngang:



















2yx

Bấm Tải xuống để xem toàn bộ.

| 1/86

| | Tải xuống

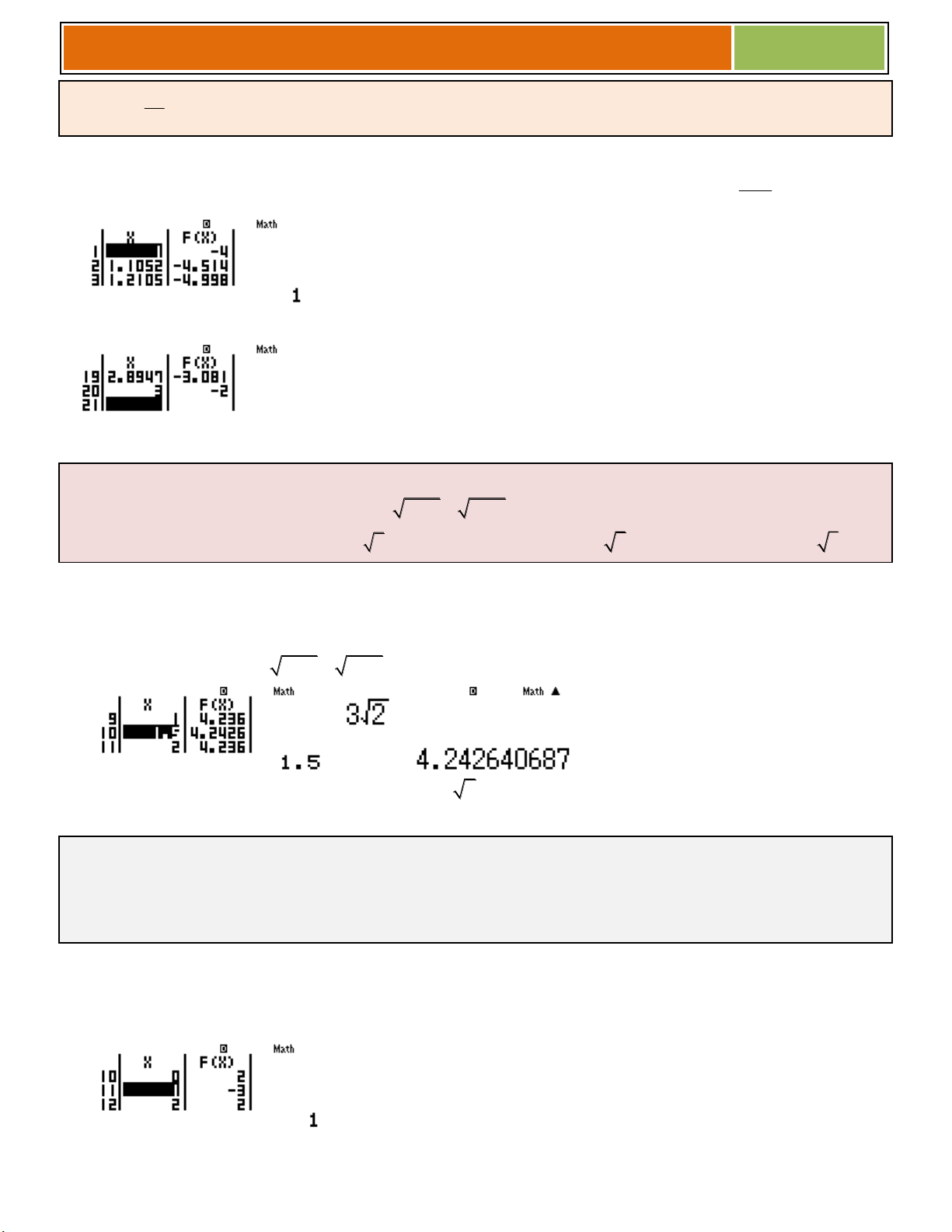
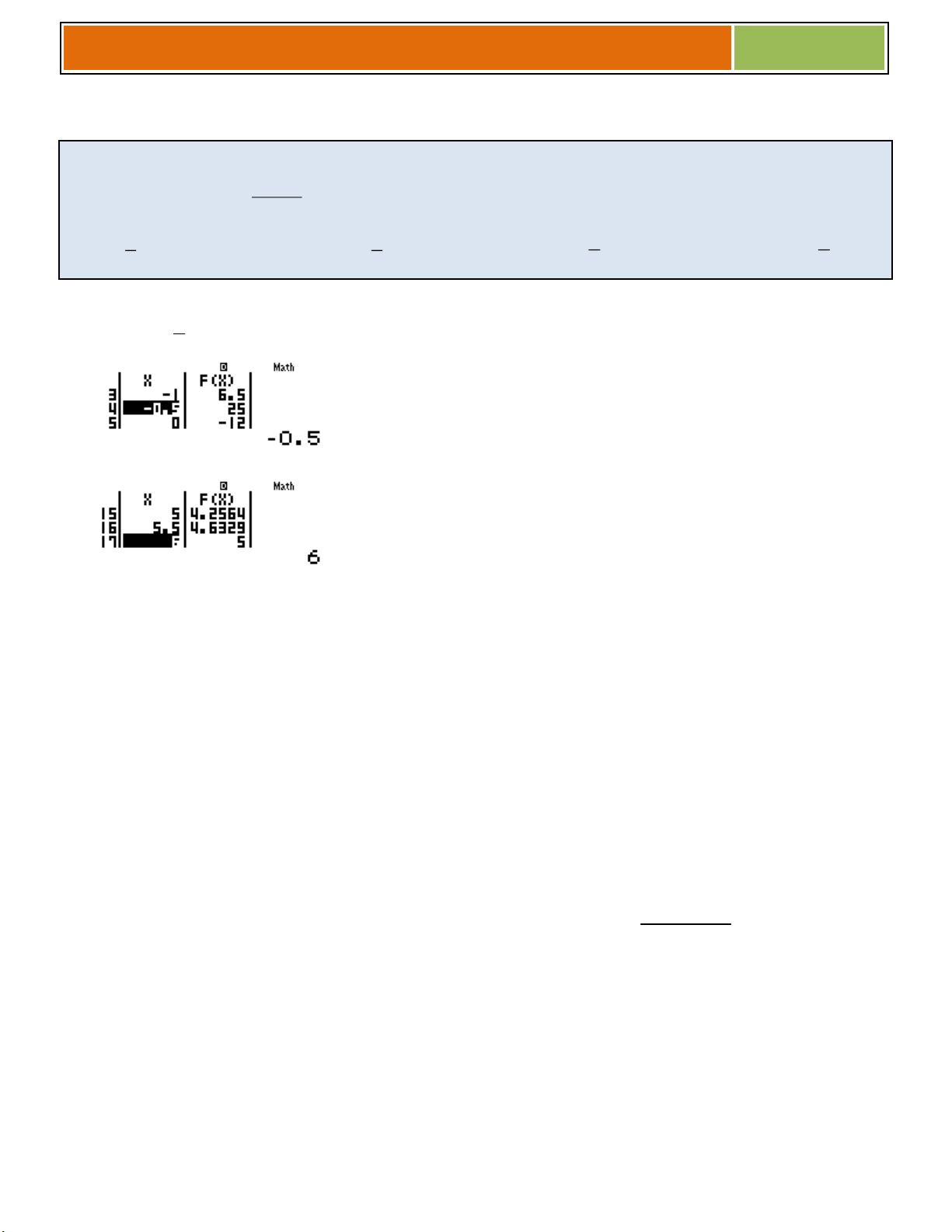
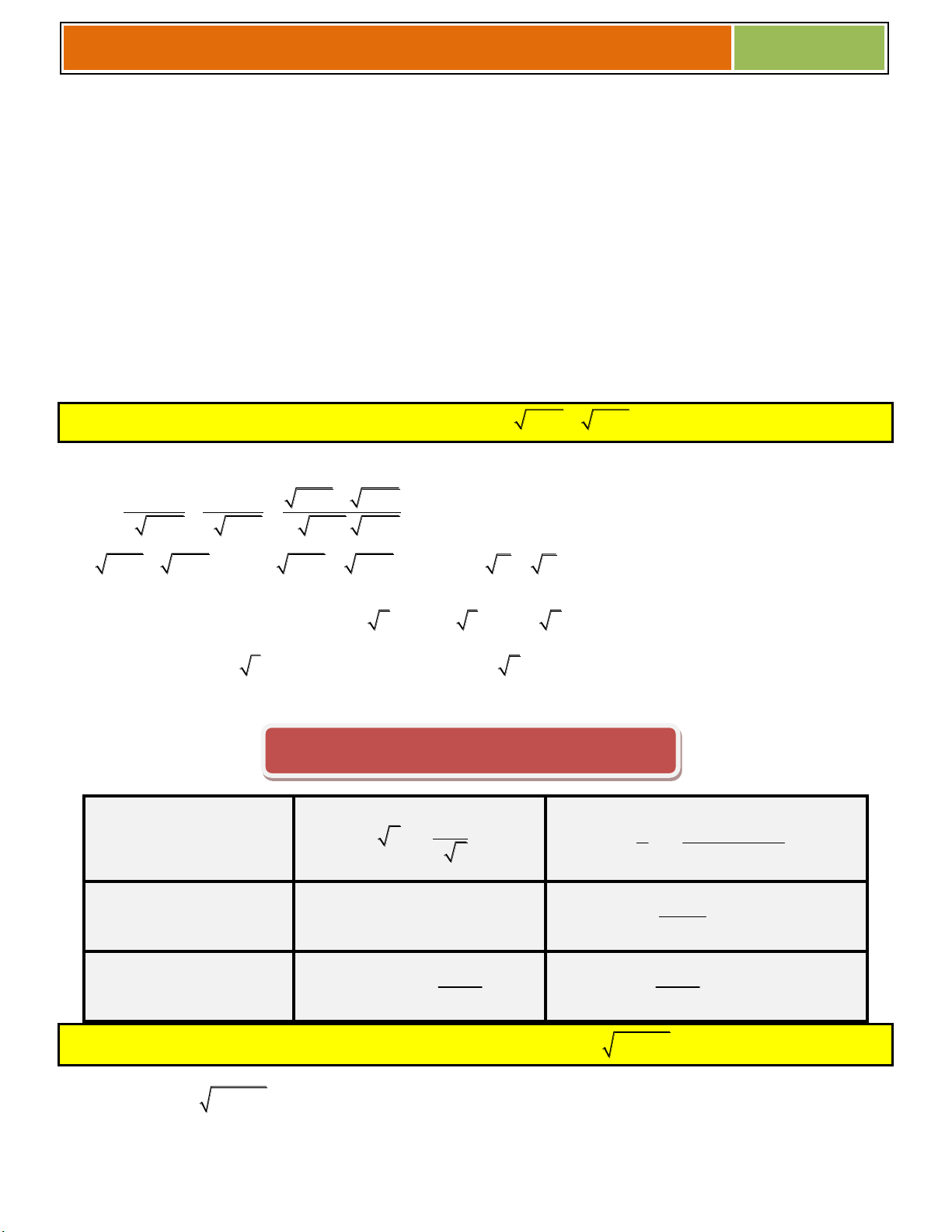
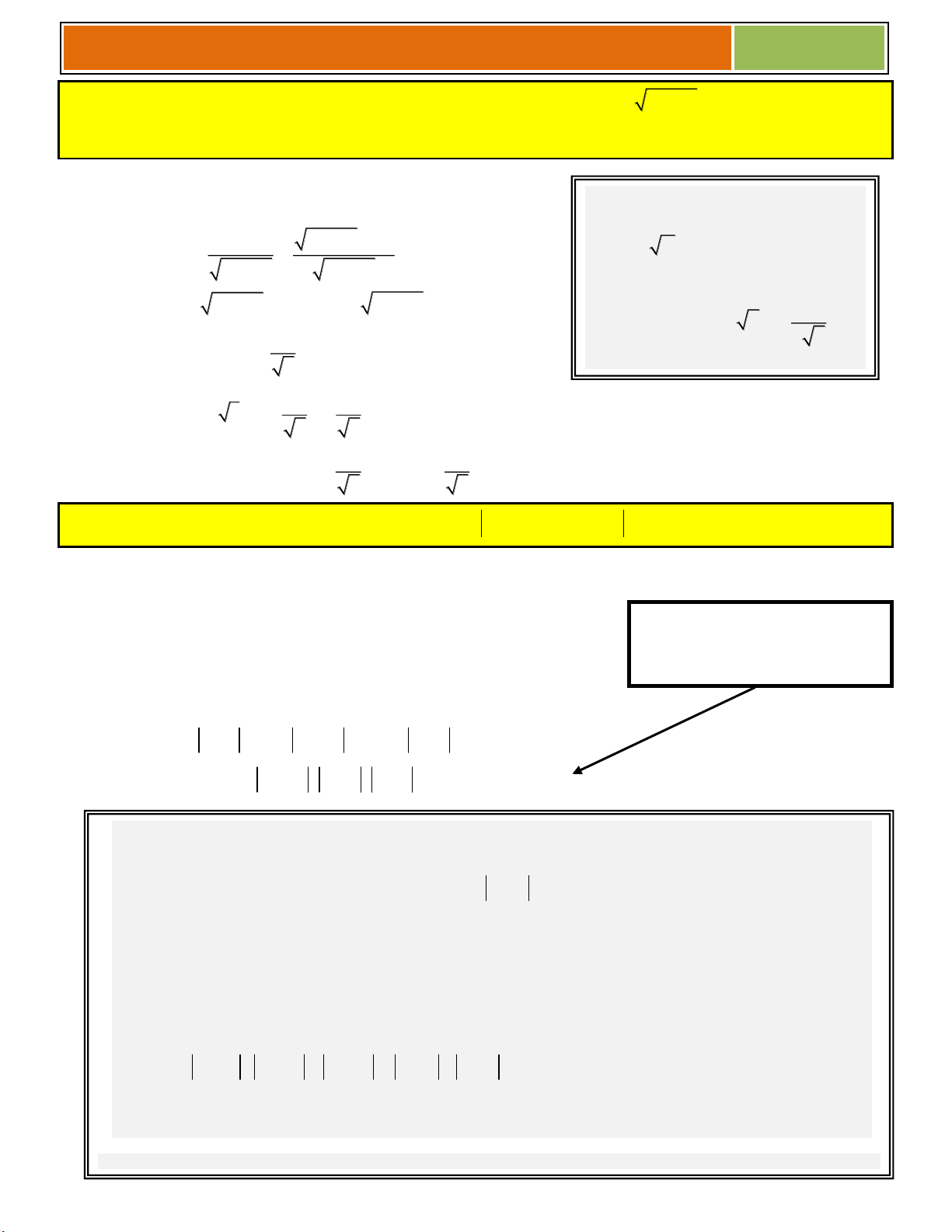
Preview text:

Phân dạng và phương pháp giải
trắc nghiệm Toán 12 Tập 1
 Tính đơn điệu  Cực trị  GTLN-GTNN
BIÊN HÒA – Ngày 07 tháng 06 năm 2017
TÀI LIỆU LƯU HÀNH NỘI BỘ
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017
PHẦN 1 : TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
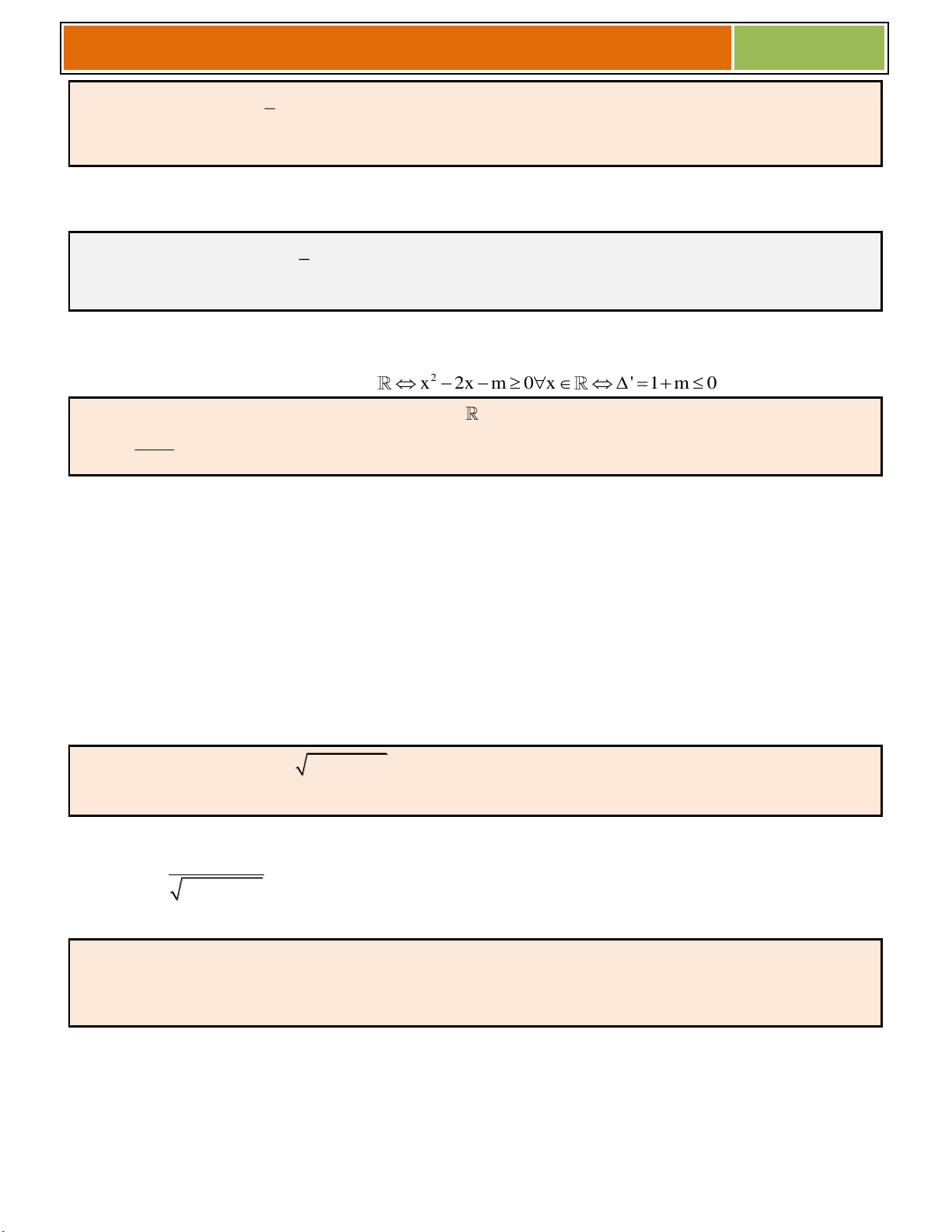
► Hàm số y  f (x) đồng biến trên khoảng (a;b)  y '  0, x  ( ; a ) b .
► Hàm số y  f (x) nghịch biến trên khoảng (a;b)  y '  0, x  ( ; a ) b . ☺ Chú ý :
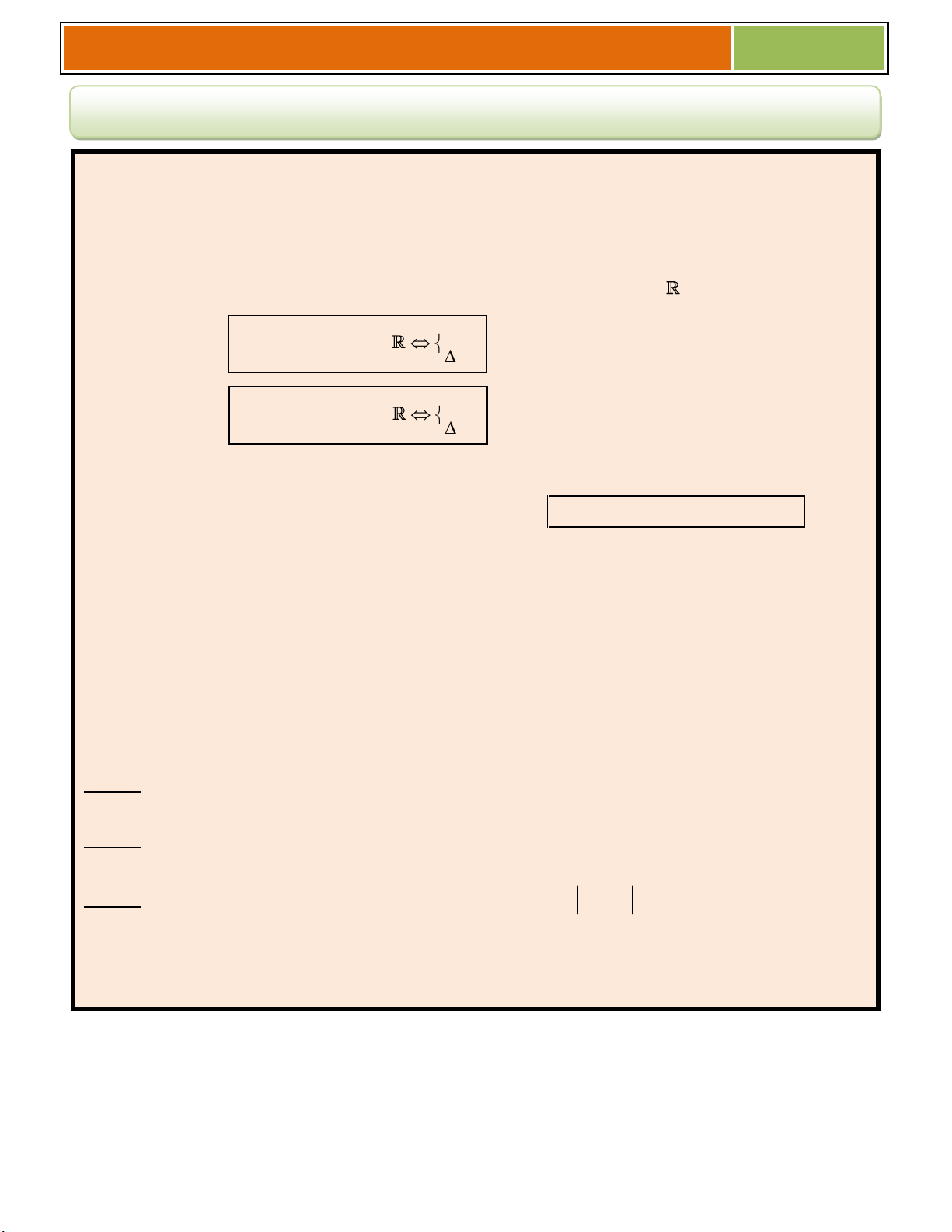
♣ Điều kiện để tam thức bậc hai 2
f (x)  ax  bx  c không đổi dấu trên : a  0 2
ax  bx  c  0, x    0 a  0 2
ax  bx  c  0, x    0
Nếu hệ số a và b có chứa tham số m thì phải xét trường hợp a = 0
♣ Hàm số y  f (x) đồng biến trên khoảng (a,b) thì với a  x  b  f (a)  f (x )  f ( ) b . 1 1
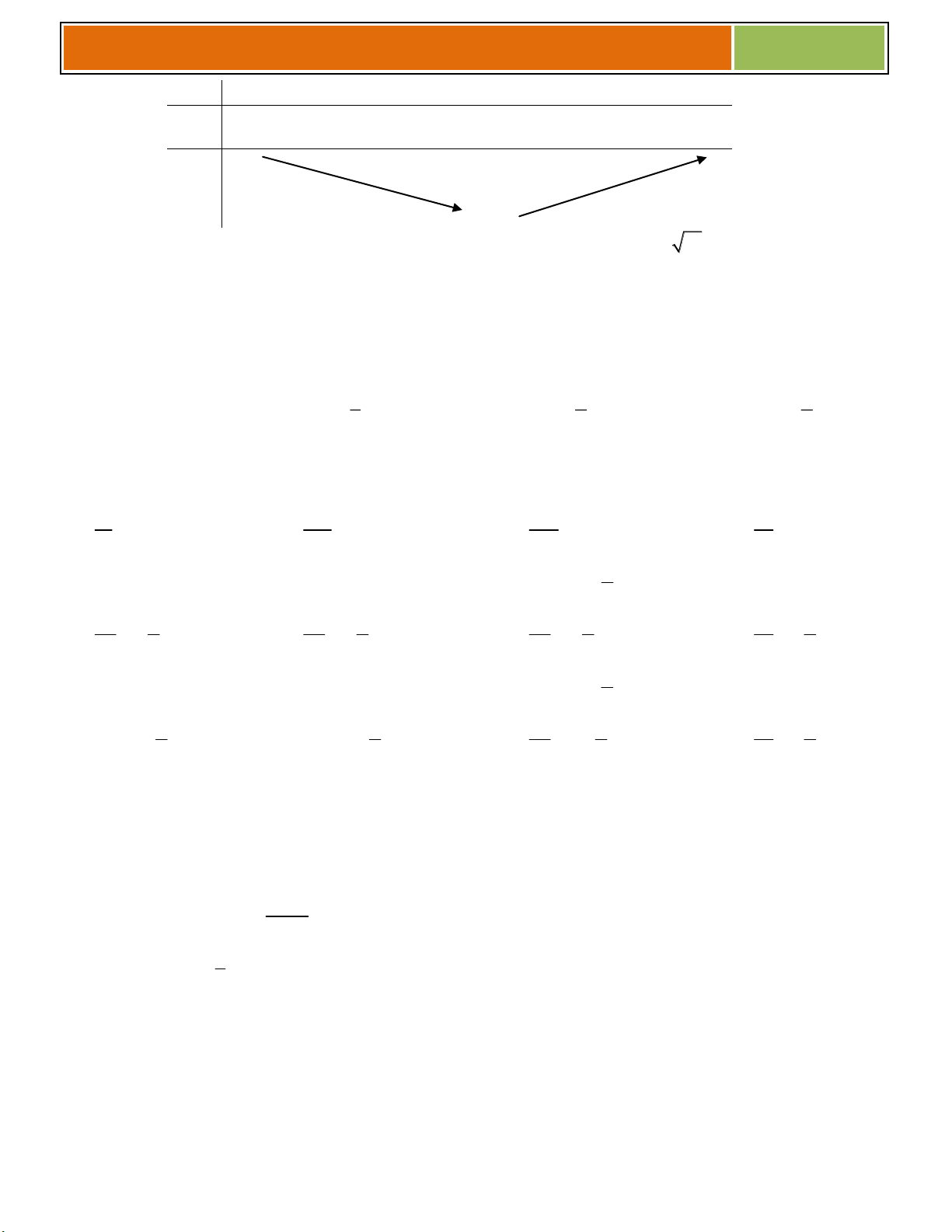
♣ Các bước xét tính đơn điệu của hàm số :
♥ B1 : Tìm TXĐ , tính đạo hàm cấp 1 ( y’) ♥ B2 : Cho y’ = 0 tìm x
♥ B3 : Lập bảng biến thiên và kết luận
♣ Với dạng toán tìm tham số m để hàm số b c ba đơn điệu một chiều trên khoảng có độ dài
bằng l ta giải như sau:
Bước 1: Tính y  f  x m  ax2 ;
 bx  c.   0
Bước 2: Hàm số đơn điệu trên x ;x   y  0 có 2 nghiệm phân biệt   * 1 2 a  0  2
Bước 3: Hàm số đơn điệu trên khoảng có độ dài bằng l  x  x  l  x  x   x 4 x  l2 1 2 1 2 1 2 2 2
 S  4P  l * *
Bước 4: Giải * và giao với * * để suy ra giá trị m cần tìm.
BÀI TẬP TỰ LUẬN PHẦN TÍNH ĐƠN ĐIỆU
Bài 1 : Xét tính đơn điệu của các hàm số sau đây : a/ 3 2 y  2x  3x 12x 13 b/ 4 2 y  3x  6x  2 c/ 4 2 y  x  5x 1 1
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. d/ 4 2 y  x  6x  8 e/ 3 y  x  3x 1 f/ 3 2 y  x  3x  3x  5
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
............................................................................................................................................................................. 1 2x  2 g/ 3 2
y  x  3x  24x  25 h/ 3 2 y  x  x  3x  k/ y  3 x 1
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 2
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017 1 x 1 3 x 11 l/ 4 3 y   x  x  4x 1 m/ y  n/ 2 y    x  3x  4 3  x 3 3
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 2 (soạn) : Xét tính đơn điệu của các hàm số sau đây : 3 3 x 1/ 4 2 y  x  2x  2/ 2 y    2x  3x 1 3/ 3 y  2x  3x 1 2 3 3x 1 1 4/ y  5/    3 y x 2 3x  4 6/ 4 2 y  x  2x  2 x  2 4 3 x 3 2x 7/ 2 y   x  2x 1 8/ 2 y    x  4x  2 9/ 3 2 y  x  3x  4 3 3 2 2 1 10/ 3 2 y  x  3x  9x  11/ 3 2 y  x  8x 16x  12/ 3 2 y  2x  3x  3 5 4 7 1 3 7 x  3 13/ 3 2 y  x  9x  9x  14/ 3 2 y   x  x  15/ y  4 3 2 2 2  x
Bài 3 : Xét tính đơn điệu của các hàm số sau đây : a/ 3 2 y  2x  9x 12x  3 b/ 3 2 y  5  x 3x  4x 5 c/ 4 3 2
y  3x  4x  24x  48x  3 d/    2 3 2 y x 1 x
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 3
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 4 : Tìm m để các hàm số sau luôn giảm trên từng khoảng xác định : mx 1 2 m x 1 3 x 11 a/ y  b/ y  c/ 2 y    x  m 3x  x  2 4  x 1 3 5
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 5 : Tìm m để các hàm số sau luôn tăng trên từng khoảng xác định : mx  4 3 x a/ y  b/ y   m   2 1 x  2 2 m  2 x  4 x  4 3 3 x 3 x c/ y  m  2 m  2 2 x  3m   2 1 x  m d/ y  m  2  2m 3 2 x  5m  6 x  2 3 3
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 4
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 6 (soạn): Tìm m để các hàm số sau : mx 1 a/ y 
luôn giảm trên từng khoảng xác định x  m x  m b/ y 
luôn tăng trên từng khoảng xác định x  3 c/ 3 2
y  x  3mx  3x 1 luôn tăng trên R (Đs : 1   m 1) 1   3 3 1   3 3 d/ 3      2   2 y x m 1 x
m  4 x  9 luôn tăng (Đs : m  hoặc m  ) 2 2 e/ 3 2
y  x  3x  2m  
1 x  4 Đồng biến trên R (Đs : m  1) 2x 1 1 f/ y 
nghịch biến trên từng khoảng xác định (Đs : m  ) x  m 2 7   3 5 7   3 5 g/ 3       2 y x m 2 x  m  
1 x  3 nghịch biến trên R (Đs:  m  ) 2 2 1 h/ 3 2 y  x  x  m  
1 x  9 đồng biến vói mọi x (Đs : m  3 ) 3 1 k/ 3 2 y 
x  mx  4x 1 luôn tăng trên R (Đs : 2   m  2 ) 3 l/ 3 2
y  x  mx  4x  3 luôn tăng trên R (Đs : 2  3  m  2 3 )
Bài 7 : Tìm m để :
a/ (ĐHQG Tp.HCM – 2000) Hàm số 3 2
y  x  3x  mx  m nghịch biến trên đoạn có độ dài bằng 1 5
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017 1 1 b/ Hàm số 3 y  x  m  2 1 x  m  
1 x  3 nghịch biến trên đoạn có độ dài bằng 5 3 2 c/ Hàm số 3 2 2
y  x  m x  mx  3m  5 đồng biến trên đoạn có độ dài bằng 3
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 1
Bài 8 : Tìm a để hàm số y   2 a   3 1 x  a   2
1 x  3x  5 luôn đồng biến trên từng khoảng xác 3 định ? (Đs: a  1   a  2 )
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 6
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017
..............................................................................................................................................................................
.............................................................................................................................................................................. 1
Bài 9 : Tìm m để hàm số y  m   3 2
1 x  mx  3m  2 x luôn đồng biến với mọi x (Đs: m  2 ) 3
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 10 : CMR hàm số 3
      2  2 y x m 1 x
m  2 x  m luôn nghịch biến
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 11 : Tìm m để hàm số 3      2  2 y x 2 m 1 x
2m  m  2 x  m 3 luôn đồng biến
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 12 : Tìm a để hàm số sau đây luôn giảm ax  a  7 a/ 3       2 y x a 1 x  2a   1 x  3 b/ y  5x a 3
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 13 (ĐH Thủy lợi – 1997) : tìm m để hàm số sau đồng biến trên R m 1 3 2 y  .x  m.x  (3m  2).x 3
..............................................................................................................................................................................
.............................................................................................................................................................................. 7
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 14) : Cho hàm số 3 2 y  2
 x  3mx 1. Tìm các giá trị m để hàm số đồng biến trên khoảng x , x 1 2 
với x  x  1. 2 1
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
BÀI TẬP MINH HỌA PHẦN TÍNH ĐƠN ĐIỆU
Ví dụ 1 : Xác định m để hàm số 3 2
y  x  3x  mx  m
luôn luôn đồng biến trên A. m  3 B. m  3 C. m D. m
♠ Giải : Tập xác định : D =
Làm tự luận ! Đạo hàm : 2
y '  3x  6x  m  '  0
Hàm số luôn đồng biến trên  y '  0  
 93m  0  m  3 a 1  0
Vậy: với m  3 thì hàm số luôn đồng biến trên D hay (chọn A) Làm trắc nghiệm !
Khi làm bài trắc nghiệm chúng ta không thể giải như vậy vì sẽ có nhiều bài phức tạp “số xấu”
☻Phương pháp “BÓC ĐẠI”
► “Bóc đại” m = 2 ở câu B thì ta thấy 2
y '  3x  6x  2  0 , phương trình này có 2 nghiệm (bấm máy là thấy nha)
Mà hàm số luôn đồng biến thì ∆ < 0, a > 0 mà !! (Loại B)
► “Bóc đại” m = 4 ở câu A thì ta thấy 2
y '  3x  6x  4  0 , phương trình này vô nghiệm (bấm
máy là thấy nha )thì ∆ < 0 và a > 0
(thỏa mãn để hs đồng biến) Nên chọn A 3 x
Ví dụ 2 : Cho hàm số y   2 m    m   2 1
1 x  3x 1 C
.Tìm m để hàm số C luôn đồng m  m  3 biến.
♠ Giải : Đạo hàm y   2 m   2 '
1 x  2m  
1 x  3 . Yêu cầu bài toán  y '  0, x   . 3
Với m  1 thì y '  4x  3  0  x   : không thỏa mãn. 4 Với m  1
 thì y'  3  0, x   : thỏa mãn. 8
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017 2 m 1  0  m  2 Với m  1
 , ta có y '  0, x       m    . 2 1  3   2 m   1  0 m  1  Vậy m  1
 hoặc m  2 thỏa mãn yêu cầu bài toán. mx  4  3m
Ví dụ 3 : Cho hàm số y 
, m là tham số. Tìm tất cả các giá trị của m để hàm số x  m
giảm trên từng khoảng xác định. 2   ♠ m 3m 4
Giải : MXĐ: D  \  
m . Đạo hàm: y '  xm . 2
Hàm số đã cho giảm trên từng khoảng xác định  hàm số nghịch biến trên từng khoảng xác
định  y '  0, x   m 2
 m  3m  4  0  4   m 1. Vậy với 4
  m 1 thì thỏa mãn yêu cầu bài toán. 1
Ví dụ 4 : Cho hàm số 3
y   x  m  2 2
x  mx  7 ( m là tham số). 3
Xác định m để hàm số nghịch biến trên tập xác định.
♠ Giải : Tập xác định: D  . Đạo hàm 2
y '  x  2m  2 x  m . Hàm số nghịch biến trên  y '  0, x   2  '  0
m  5m  4  0 2
 x  2m 2 x  m  0, x        4   m  1  . a  0  1   0 Vậy 4   m  1
 thỏa mãn yêu cầu bài toán.
Ví dụ 5 : Cho hàm số     3     2 y m 1 x
m 1 x  x  m . Tìm m để hàm số đồng biến trên R A. m  4, m 1 B. 1 m  4 C. 1 m  4 D. 1 m  4
♠ Giải : Đáp án D
+ TH 1: Khi m 1 thì y  x 1 hàm số đồng biến trên R. + TH 2: Khi m  1. Ta có     2 y ' 3 m 1 x  2m   1 x 1   m 1 m 1  m 1  y '  0 x            '  0   m    m 1; 4 2 1  3m   1  0 m  1;4   Vậy m 1;  4 Ví dụ 6 : Hàm số 2 y  2x  x
nghịch biến trên khoảng nào? A. 1;2 B. 0; 2 C. 0  ;1 D. 1;
♠ Giải : Đáp án A . Ta có 2
y  2x  x , TXD : 0  x  2   2  2x 1 x f ' x  
 f 'x  0  x 1 2 2 2 2x  x 2x  x
Lập bảng biến thiên ta nhận thấy Đạo hàm f 'x khi đi qua điểm có x 1 thì đổi dấu từ dương
sang âm. Nên hàm số nghịch biến trên khoảng 1;2 9
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017
Ví dụ 7 : Hàm số nào sau đây đồng biến trên R. x 1 1 A. y  B. 4 2 y  x  x  2 C. 3 2 y  x  x  2x  3 D. 3 2 y  x  x  3x 1 x  2 4
♠ Giải : Đáp án C
Các hàm số đa thức bậc chẵn không đồng biến trên R vì có đạo hàm f 'x là đa thức bậc lẻ nên
điều kiện f 'x  0 x
  không xảy ra => Loại B.
Hàm số bậc 1 trên bậc 1 không liên tục trên R (bị gián đoạn tại x  2) nên loại A. 3 2 2
y  x  x  3x 1 y '  3x  2x  3 nhận thấy y '  0 có nghiệm thực nên điều kiện f 'x  0 x
  không xảy ra => Loại D             2 3 2 2 2 y x x 2x 3 y ' 3x 2x 2 2x x 1 1  0 x
  . Nên đồ thị hàm số đồng biến trên .
Ví dụ 8 : Cho hàm số 4 2
y  2x  4x  2 . Hàm số đồng biến trên khoảng nào? A. 1; B.   ;1  C. 0; D.  ;  0
♠ Giải : Đáp án C.   3 f ' x  8x  8x, x  
. f 'x  0  x  0
Mặt khác trên bảng biến thiên đạo hàm f 'x đổi dấu từ âm sang dương khi đi qua x  0 .
Vậy hàm số đồng biến trên khoảng 0; 1
Ví dụ 9 : Cho hàm số 3 2 y  x  2x  m  
1 x  3m . Hàm số đã cho đồng biến trên R với giá trị 3 m là A. m  3 B. m  3 C. m  3 D. m  3
♠ Giải : Đáp án C; 2
y '  x  4x  m 1 ;   2 f ' x  0; x
   x  4x  m 1 0; x  
     2    2 m 1 x 2 4; x 2  4  4 x    m 1 4  m  3 2x  5
Ví dụ 10 : Hàm số y 
đồng biến trên khoảng: x  3 A.  ;  3  ;3; B.  C.  ;  4;4; D.  ;  3  ; 3  ; ♠ 1
Giải : Đáp án D; Ta có: y '   0 x    ;  3   3  ; 2     x 3
Suy ra hàm số đồng biến trên từng khoảng  ;  3  , 3  ;
Ví dụ 11 : Hàm số 4 2
y  3x  6x 15 đồng bến trên khoảng: A.  1  ;0;1; B.  1  ;0;0;  1 C.  ;   1 ;0;  1 D.  1  ;
♠ Giải : Đáp án A; 3
y '  12x 12x ; y '  0  x  1  ;0;  1
Vẽ bảng biến thiên hoặc xét dấu y’ suy ra đáp án
Ví dụ 12 :     3     2 y m 2 x
3 m 2 x  3m  3 x 9 . Hàm số sau đồng biến trên R khi m bằng A. m  2  B. m  2  C. m  2  D. m  2  10
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017
♠ Giải : Đáp án B;     2 y ' 3 m 2 x  6m   1 x  3m  3 +) TH1: m  2  Khi đó: y'  3  0 x
 suy ra hàm số đồng biến trên R ( thỏa mãn) +) TH2: m  2 
Xét phương trình y '  0 . Ta có:  '  9  m  2
Để hàm số đồng biến trên R thì y '  0 x   '  0  m  2 
Kết hợp 2 TH suy ra m  2 
Ví dụ 13 : Cho hàm số 3 2
y  x  4x  5x  2 . Xét các mệnh đề sau:  5 
(i) Hàm số đồng biến trên khoảng ;     3 
(ii) Hàm số nghịch biến trên khoảng 1;2  1 
(iii) Hàm số đồng biến trên khoảng ;     2 
Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng ? A. 3 B. 1 C. 2 D. 0
♠ Giải : Đáp án C x 1  5  Ta có: 2 
y '  3x  8x  5; y '  0  5  
. Do đó hàm số đồng biến trên   ;1  và ;   , hàm số x   3   3  5  nghịch biến trên 1; 
 . Do đó mệnh đề (i) và (iii) đúng  3 
Ví dụ 14 : Hàm số 2 y  2x  x
đồng biến trên khoảng nào? A. 0; 2 B. 1;2 C. 0  ;1 D.   ;1   ♠ 1 x
Giải : Đáp án C; TXĐ: D  0;2; Có y ' 
 0  x 1; y'  0  0  x 1 2 2x  x
Hàm số đồng biến trên (0;1)
Ví dụ 15 : Hàm số 3 2
y  x  2x  x 1 nghịch biến trên khoảng nào?  1   1  A.  ;    B.  ;    1 C.  ;   D. 1  ;    3   3 
♠ Giải : Đáp án D; Có 2
y '  3x  6x 1. Phương trình y '  0 có 2 nghiệm phân biệt.
Hàm số đã cho nghịch biến trên khoảng giữa hai nghiệm của phương trình y '  0 nên khoảng
đó không thể chứa  hoặc  => Loại A, B, C
Ví dụ 16 : Hàm số 4
y  3x  2 đồng biến trên khoảng nào sau đây ?  2   2  A. 0;  B.  ;     C.  ;    D.  ;  0  3   3 
♠ Giải : Đáp án A; Ta có: 3
y ' 12x  y '  0  x  0 ; y'  0  x  0
Ví dụ 17 : Tất cả các giá trị của tham số m để hàm số 3 2
y  x  mx  3x  4 đồng biến trên R là: 11
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017 A. 2   m  2 B. 3   m  3 C. m  3 D. m  3 
♠ Giải : Đáp án B; Ta có: 2 y '  3x  2mx  3
Để hàm số đã cho đồng biến trên R thì y 'x  0 x   2  '  0 x    m 9  0 x    m 3  ;  3
Ví dụ 18 : Tìm các khoảng đồng biến của hàm số    4 y 2 x 2  3 A.  ;0   B. 0; C.  ;  2   D.  2;  
♠ Giải : Đáp án D; Có      3 y ' x 8 x
2 ; y 'x  0  x  2  .
Xét dấu của y ' : y'  0 khi x  2
 ;vậy hàm số đồng biến trên khoảng  2;  
Ví dụ 19 : Cho hàm số 4 2
y  x  8x  4 . Các khoảng đồng biến của hàm số là: A.  2  ;0 và2; B.  ;  2   và 2; C.  ;  2   và 0;2 D.  2  ;0 và 0;2
♠ Giải : Đáp án A; Tập xác định: D  ; Sự biến thiên: lim y   ; lim y   x x x  0  3     2 y ' 4x 16x
4x x  4 ; y '  0  x  2  x  2   BBT:
Vậy hàm số đồng biến trên  2  ;0 và 2;
Ví dụ 20 : Bảng biến thiên sau là của hàm số nào: A. 4 2 y  x  2x  3 B. 4 2 y  x  2x 1 C. 4 2 y  x  2x  3 D. 4 2 y  x  2x 1
♠ Giải : Đáp án B. Ta có y’ có dạng:  2 a x  
1 x  0 thì cả 4 đáp án đều thỏa mãn. Tại x  1
 ta loại đáp án A và C do không thỏa mãn f x  2 23 9 Tại x  0,5 0;  1 ta có: 4 2 y  x  2x 1   01;2,tm ; 4 2 y  x  2x 1   01;2ktm 16 16 1
Ví dụ 21 : Cho hàm số 3 2
y   x  mx  3m  2 x 1. Tìm tất cả các giá trị của tham số m để 3
hàm số nghịch biến trên khoảng  ;   12
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017 m  2 A.  B. m  2 C. 2   m  1  D. 1   m  0 m  1 
♠ Giải : Đáp án C . Ta có: 2
y '  x  2mx  3m  2 Có 2
'  m  3m  2  0, x    m 2  ; 
1 (điều kiện để hàm số nghịch biến) m 1x 2
Ví dụ 22 : Cho hàm số y  x 
. Tìm tất cả các giá trị của tham số m để hàm số đồng biến m
trên từng khoảng xác định. m 1 m 1 A. 2   m 1 B.  C. 2   m 1 D.  m  2  m  2 
♠ Giải : Đáp án C. TXĐ: D  \  m m 
1 x  m  m   2 1 x  2 m  m  2 y '      
. Để hàm số đồng biến trên  ; m m;  thì: x  m2 x m2 2 y '  0; x
 D  m  m  2  0 x  D  m 2  ;  1 1
Ví dụ 23 : Hàm số 3 2
y   x  mx  x 1nghịch biến trên khi và chỉ khi 3 A. m \  1  ;  1 B. m \  1  ;  1 C. m  1  ;  1 D. m  1  ;  1
♠ Giải : Đáp án C Ta có: 2 y '  x  2mx 1 1
Nhận thấy hàm số đã cho là hàm số bậc ba có hệ số a    0 nên để hàm số đã cho nghịch 3 biến trên
thì phương trình y '  0 vô nghiệm hoặc có nghiệm kép, hay 2 '  m 1 0  1   m 1 mx  5
Ví dụ 24 : Điều kiện cần và đủ của m để hàm số y 
đồng biến trên từng khoảng xác x 1 định là A. m  5  B. m  5  C. m  5 D. m  5
♠ Giải : Đáp án D m  5 Ta có: y '  
để hàm số đã cho luôn đồng biến trên từng khoảng xác định thì x  2 1 m  5  0  m  5
Ví dụ 26 : Hàm số nào trong các hàm số sau có bảng biến thiên như hình dưới đây A. 3 2 y  x  3x 1 B. 3 2 y  2x  6x 1 C. 3 2 y  x  3x 1 D. 3 2 y  2x  9x 1 13
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017
♠ Giải : Đáp án C
Nhận xét nhìn vào BBT ta thấy đây là bảng biến thiên của hàm số bậc ba có hệ số a  0
Hàm số có hai điểm cực trị là x  2  ;x  0 . Do đó x  2
 ;x  0 là nghiệm của phương trình y '  0 . Tức là      2 2 y ' 0 x x
2  0  x  2x  0  3x  6x  0 . Đến đây ta loại được B và D. Với x  0 thì y  1  do đó chọn C 1
Ví dụ 27 : Cho hàm số 3 2
y   x  mx  3m  2 x 1 . Tìm tất cả các giá trị của m để hàm số 3 nghịch biến trên . m  1  m  1  A.  B. 2   m  1  C.  D. 2   m  1  m  2  m  2 
♠ Giải : Đáp án B; 2
y '  x  2mx  3m  2
+ Xét TH m  0 ta có: 2 y '  x  2  0, x   ;
  2  2;
Suy ra tại m = 0 hàm số ko nghịch biến trên R + Xét TH m  0
Để hàm số đã cho nghịch biến trên khoảng R thì y'  0 x   a   0  1   0 2
 x  2mx  3m  2  0, x        m 2  ;  1 2  '  0 m  3m  2  0
m 1 x 2
Ví dụ 28 : Tìm tất cả các giá trị của m để hàm số : y  x 
đồng biến trên từng khoảng m xác định.  m 1  m 1 A. 2   m 1 B. 2   m 1 C.  D.  m  2  m  2  m  1 x  2 mm   2 1  2    ♠ m m 2
Giải : Đáp án B ; y  , y '   x  m x  m2 x m2 Yêu cầu 2
 y'  0  m  m  2  0 2  m  m  2  0  2   m 1 1 1
Ví dụ 29: Cho hàm số 3 2 y  x 
x  2x . Phát biểu nào sau đây đúng ? 3 2
A. Hàm số nghịch biến trên khoảng 2;
B. Hàm số nghịch biến trên khoảng
C. Hàm số đồng biến trên khoảng  1  ;2
D. Hàm số đồng biến trên khoảng  ;    1
♠ Giải : Đáp án D. Có 2
y '  x  x  2  0  x  2 hoặc x  1 
y '  0  x  2 hoặc x  1  ; y'  0  1   x  2
Hàm số đồng biến trên  ;   
1 và 2; , nghịch biến trên  1  ;2 x  m
Ví dụ 30 : Với giá trị nào của m thì hàm số y 
đồng biến trên mỗi khoảng xác định? x 1 A. m  1  B. m  1  C. m  1  D. m  1    ♠ 1 m
Giải : Đáp án B. Điều kiện cần tìm là y '          x   0 1 m 0 m 1 2 1 14
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017 1
Ví dụ 31 : Hàm số 3 2 y 
x  2x  3x  2 nghịch biến trên khoảng nào? 3 A. 1;3 B.   ;1  C. 3; D. 1;
♠ Giải : Đáp án A. Có 2
y '  x  4x  3  0  x 1 hoặc x  3; y'  0 1  x  3
Hàm số nghịch biến trên 1;3 1
Ví dụ 32 : Cho hàm số 3 2 y 
x  x  mx  3 . Tìm m để hàm số luôn đồng biến trên R ? 3 A. m  1  B. m  1  C. m 1 D. m  1 
♠ Giải : Đáp án A 2 y '  x  2x  m
Hàm số đã cho luôn đồng biến trên 2  x  2x  m  0 x
   ' 1 m  0  m  1 
Ví dụ 33 : Hàm số nào sau đây đồng biến trên x 1 A. y  B. 3 y  x  4x 1 C. 3 y  x  4x 1 D. 4 y  x x  2
♠ Giải : Đáp án B
Các kết quả cần nhớ
Hàm số phân thức bậc nhất trên bậc nhất không đồng biến hay nghịch biến trên ℝ (chỉ trên từng khoảng xác định)
Hàm số đa thức bậc chẵn không đồng biến trên ℝ vì đạo hàm của chúng là đa thức bậc lẻ,
không thể luôn dương hoặc luôn âm
Điều kiện cần để hàm số bậc lẻ đồng biến trên ℝ là có hệ số cao nhất dương – Cách giải
Dựa vào các kết quả trên, loại A, D Vì hàm số 3
y  x  4x 1 có hệ số của 3
x là âm nên không thể đồng biến trên ℝ  Loại C
Ví dụ 34 : Hỏi hàm số 2
y  x  4x  3 đồng biến trên khoảng nào ? A. 2; B.  ;3   C.   ;1  D. 3;
♠ Giải : Đáp án D. Tập xác định của hàm số là  ;   1  3; x  2 Ta có: y ' 
; y '  0  x  2; y '  0  x  2 2 x  4x  3
Kết hợp với điều kiện xác định của hàm số, suy ra khoảng đồng biến của hàm số là 3;
Ví dụ 35 : Tìm tất cả các giá trị của m để hàm số: 3
y  x  m   2 2 3
1 x  6m  2 x  3 nghịch biến
trên khoảng có độ dài lớn hơn 3
A. m  0 hoặc m  6 B. m  6 C. m  0 D. m  9
♠ Giải : Đáp án A; 2 y '  6x  6m   1 x  6m  2 x
    2     2 ' 9 m 1
36 m 2  9m  54m  81  0 ; Dấu bằng xảy ra khi m  3
Gọi x , x là 2 nghiệm của phương trình y '  0x  x 1 2  1 2 15
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017 x  x 1 m Theo viet: 1 2 x .x  m2  1 2 Ta có BBT
Vậy hàm số đồng biến trên khoảng x , x  pt y'  0 phải có 2 nghiệm phân biệt  m  3 1 2 
Gọi Độ dài khoảng nghịch biến của hàm số là D 2 2 D  x  x  x  x
 1 m  4 m  2  m  6m  9 1 2      2 1 2 2 D  3  D  9 2 2
 m  6m  9  9  m  6m  0  m  0 hoặc m  6 (thỏa mãn)
BÀI TẬP TRẮC NGHIỆM PHẦN TÍNH ĐƠN ĐIỆU Câu 1 : Cho hàm số 3 2
y  2x  3x  36x 10 . Chọn đáp án đúng
A. Hàm số luôn đồng biến trên
B. Hàm số luôn nghịch biến trên
C. Hàm số nghịch biến trên  3  ;2
D. Hàm số nghịch biến trên \  3  ;2
Câu 2 : Đề minh họa thi THPT Quốc Gian lần 1 năm 2017) Hàm số 4
y  2x 1 đồng biến trên khoảng nào?  1  A.  ;   .   B. 0;  .  2   1  C.  ;   .   D.  ;  0.  2 
Câu 3 : (THPTLê Hồng Phong lần 1)Khoảng đồng biến của hàm số 3 2
y  x  3x  4 là A.  ;  2  2;. B.  2  ;0. C.  ;  02;. D. 0; 2.
Câu 4 : (Thi thử chuyên KHTN –HN lần 2 năm 2017) Cho hàm số 4 2
y  x  2x 1. Mệnh đề nào
dưới đây là đúng.
A. Hàm số đồng biến trên khoảng  ;    1 .
B. Hàm số đồng biến trên khoảng  ;  0 .
C. Hàm số đồng biến trên khoảng 0;  .
D. Hàm số đồng biến trên khoảng 1;  . 2x 1
Câu 5 : Cho hàm số y 
(2). Hàm số đồng biến trên khoảng x 1 16
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017 A.  2;    B.  2;   C.  ;0   D. 0; Câu 6 : Hàm số 3 2
y  x  3x  4 nghịch biến trên khoảng: A.  2  ;0 B.  ;  2   C. 0; D.  ;  2  và0; Câu 7 : Hàm số 3 2
y  x  3x  3x  2 đồng biến trên : A. B. 1; C.   ;1  D.   ;1  và 1; Câu 8 : Hàm số 3 2
y  x  3x  4x  2 nghịch biến trên khoảng: A. B. 1; C.   ;1  D.   ;1  và 1; 2 x  x  2
Câu 9 : Cho hàm số y  x 
. Phát biểu nào sau đây là đúng 3 2 x  6x 1
A. Hàm số có đạo hàm y '  x32 B. Hàm số tăng trên   ;1  và 5;
C. Hàm số tăng trên 1;5 D. Cả A, B, C đều đúng.
Câu 10 : Hỏi có bao nhiêu số nguyên m để hàm số 2 3 2
y  (m 1)x  (m 1)x  x  4 nghịch biến trên khoảng  ;   A. 2. B. 1. C. 0. D. 3.
Câu 11 : Hàm số y  x  x  3, x  0 đồng biến trên khoảng nào trong các khoảng nào sau đây: A. 0  ;1 B. 1; C. 0; 2 D. 2;
Câu 12 : Cho hàm số f  x có đạo hàm trên khoảng  ;
a b . Chọn phương án đúng nhất
A. f  x  0, x   ;
a b  f  x đồng biến trên khoảng  ; a b
B. f  x  0, x   ;
a b  f  x nghịch biến trên khoảng  ; a b 17
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017
C. f  x đồng biến trên khoảng  ;
a b  f  x  0, x   ; a b D. Cả A và C.
Câu 13 : Hàm số y  sin x  bx  c đồng biến trên
thì b thuộc khoảng nào sau đây: A. 1; B. 1; C.   ;1  D.   ;1 
Câu 14 : Trong các hàm số sau, hàm số nào luôn nghịch biến trên : A. 3 2
y  x  2x 10x  6 B. 4 3
y  x  8x  432 x 1 C. y  x 1 D. y  x 9 x  2
Câu 15 : Cho hàm số y 
. Kết luận nào sau đây là đúng x 1
A. Hàm số luôn đồng biến với mọi x thuộc
B. Hàm số luôn nghịch biến với mọi x thuộc C. y(2) = 5
D. Tất cả đáp án đều sai
Câu 16 : Cho hàm số 3 2
y  x  3x . Khẳng định nào sau đây là đúng ?
A. Hàm số tăng trên khoảng 0  ;1
B. Hàm số giảm trên khoảng 4;5
C. Hàm số giảm trên khoảng  4  ;0
D. Tất cả đáp án đều đúng x  2
Câu 17 : (THPT Kim Liên lần 1) Cho hàm số y 
. Trong các khẳng định sau, khẳng định x 1 nào là đúng.
A. Hàm số nghịch biến trên .
B. Hàm số đồng biến trên từng khoảng xác định.
C. Hàm số đồng biến trên .
D. Hàm số có duy nhất một cực trị. x
Câu 18 : ( Chuyên KHTN lần 3) Cho hàm số y  x  . Mệnh đề nào đúng. 1
A. Hàm số đồng biến trên khoảng 0;  1 .
B. Hàm số nghịch biến trên \   1 .
C. Hàm số nghịch biến trên  ;   1  1;.
D. Hàm số nghịch biến trên từng khoảng   ;1  và 1;.
Câu 19 : (THPT AMSTERDAM HÀ NỘI) Trong tất cả các giá trị của tham số m để hàm số 1 3 2 y 
x  mx  mx  m đồng biến trên , giá trị nhỏ nhất của m là: 3 A. 4. B. 1.  C. 0. D. 1.
Câu 20 : (Sở GD và ĐT Vĩnh Phúc lần 2) Hàm số 2
y  2x  x
đồng biến trên khoảng nào? 18
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017 A. 0; 2. B. 1;2. C. 0  ;1 . D.   ;1  . Câu 21 : Hàm số 2
y  2x  x
nghịch biến trên khoảng A. 1;2 B.  2;   C. 0  ;1 D. 0; 2 Câu 22 : Hàm số 2 3
y  3x  x
(1). Kết luận nào sau đây là sai khi nói về tính đơn điệu của hàm số
A. Hàm số nghịch biến trên khoảng  ;0  và 2;3
B. Hàm số đồng biến trên khoảng 0; 2
C. Hàm số nghịch biến trên khoảng  ;  2 và 2;3 D. A và B đều đúng 2x 1 5 
Câu 23 : Cho hàm số y 
có đạo hàm là y '  thì giá trị m là x  m x  m2 A. 4 B. 3 C. 2 D. 1 4x  m 6
Câu 24 : Cho hàm số y 
có đạo hàm là y '  thì giá trị m là x 1 x  2 1 A. 4 B. 3 C. 2 D. 1 kx 1 3 
Câu 25 : Cho hàm số y 
có đạo hàm là y '  thì giá trị k là x  2 x  2 1 A. 4 B. 3 C. 2 D. 1
Câu 26 : Cho hàm số 3 2
y  x  3mx  3x 1 . Giá trị m để hàm số luôn tăng trên là A. m 1;2 B. 3   m 1 C. 1   m 1 D. 1   m  2 mx  2
Câu 27 : Cho hàm số y 
. Giá trị m để hàm số luôn giảm trên từng khoảng xác định là x  m  3 A. m 1;2 B. 3   m 1 C. 1   m 1 D. 1   m  2 2x 1
Câu 28 : Cho hàm số y 
. Giá trị m để hàm số luôn nghịch biến trên từng khoảng xác định x  m là 19
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017 1 1 A. m  B. m  2 4 1 1 C. m  D. m  2 4 3 x
Câu 29 : Cho hàm số 2 y 
 mx  m  6 x  2m 1 . Giá trị nhỏ nhất và lớn nhất của tham số m để 3 hàm số sẽ tăng trên là A. 2  , 3 B. 2  , 4 C. 6; 9 D. 1  ; 4
Câu 30 : (KHTN lân 4) Cho hàm số 2 3
f  x có đạo hàm f  x   x   1  x  
1 2  x . Hàm số f  x
đồng biến trên khoảng nào dưới đây? A.  ;    1 . B.  1   ;1 . C. (2; )  . D. (1; 2).
Câu 31 : Cho hàm số y  3
 x  cos x . Kết luận nào dưới đây là đúng
A. Hàm số luôn nghịch biến với mọi x thuộc
B. Hàm số luôn tăng với mọi x thuộc
C. Chưa thể xác định tính đơn điệu của hàm số này D. Cả ba đều sai mx 1
Câu 32 : Cho hàm số y 
. Giá trị m để hàm số luôn đồng biến trên từng khoảng xác định là x  m A. m  1 B. m  1  hoặc m 1 C. m  1  D. m 1  ;  1 mx 1
Câu 33 : Cho hàm số y 
. Giá trị m để hàm số luôn nghịch biến trên từng khoảng xác định x  2 là 1 A. m  1 B. m   2 1 C. m   D. m 1  ; 2 x  m
Câu 34 : Cho hàm số y 
. Giá trị m để hàm số luôn nghịch biến trên từng khoảng xác định là x  m 1 A. m  0 B. m   2 1 C. m   D. m ;0   2 x
Câu 35 : Cho hàm số y 
. Khoảng đồng biến của hàm số đã cho là 2 x 1 A.  ;    1 B.  1  ; 20
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017 C.  1   ;1 D. 1;
Câu 36 : Cho hàm số 3
y  x  x  cos x  4 . Phát biểu nào sau đây là đúng
A. Hàm số luôn nghịch biến với mọi x thuộc
B. Hàm số luôn đồng biến với mọi x thuộc
C. Chưa thể xác định tính đơn điệu của hàm số này D. Cả ba đều sai
Câu 37 : Cho hàm số y  cos x . Phát biểu nào sau đây là đúng  π 3π 
A. Hàm số tăng trên khoảng ;    2 2   π 3π 
B. Hàm số giảm trên khoảng ;    2 2   π 
C. Hàm số tăng trên khoảng ; π    2  D. Cả ba đều sai 3 x
Câu 38 : Giá trị α để hàm số sau đây luôn tăng 2   x   2 y sin α 4sin α  3 x là 3 π π A. α   k2π B. α   π k 3 2 π π C. α    k2π D. α   k2π 2 2 x 
Câu 39 : Cho hàm số y  f  x 1 
. Trong các mệnh đề sau, tìm mệnh đề đúng x  2
A. f  x nghịch biến trên
B. f  x nghịch biến trên  ;  22;
C. f  x nghịch biến trên  ;  2 và 2;
D. f  x đồng biến trên  ;  2 và 2;
Câu 40 : Cho hàm số y  f  x xác định trên
và có đồ thị như hình vẽ bên.
Chọn khẳng định đúng trong các khẳng định sau y
(ở đây   ,  0 ): α y = f(x)
A. Hàm số tăng trên khoảng  ;  
B. Hàm số giảm trên khoảng  ;   C. Cả A và B đều đúng O x D. Cả A và B đều sai
Câu 41 : Cho hàm số 3 2
y  x  3x  3mx 1 (1) , với m là tham số thực.
Giá trị nào của m để hàm số (1) nghịch biến trên khoảng (0; +  ) 1 A. m  1  B. m   2 21
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017 1 C. m   D. m  ;1 2
Câu 42 : Cho hàm số 3 2
y  2x  2x  mx 1 , với m là tham số thực.
Giá trị nào của m để hàm số đã cho đồng biến trên khoảng 1; A. m  2  B. m  1 C. m  2  D. m  2 3 4 x Câu 43 : Hàm số 5 4 y  x  x  1 5 3 A. Nghịch biến trên
B. Nghịch biến trên khoảng   ;1
 và đồng biến trên khoảng 1; C. Đồng biến trên
D. Đồng biến trên khoảng   ;1
 và nghịch biến trên khoảng 1; 2x
Câu 44 : Hàm số f (x)  x 1 A. Đồng biến trên \{-1} B. Nghịch biến trên \{-1}
C. Đồng biến trên mỗi khoảng xác định
D. Nghịch biến trên mỗi khoảng xác định 2  x  3
Câu 45 : Hàm số f (x)  x 3 A. Đồng biến trên \{ 3  } B. Nghịch biến trên \{ 3  }
C. Đồng biến trên mỗi khoảng xác định
D. Nghịch biến trên mỗi khoảng xác định 2  x  3
Câu 46 : Cho hàm số f (x)  Chọn đáp án sai : x  3
A. Hàm số không xác định khi x = 3  B. Nghịch biến trên  3 
C. Đồ thị hàm số cắt trục hoành tại điểm M ; 0    2  9 
D. Đạo hàm cấp 1 trên tập \   3 
là f '(x)  x32 2 3x
Câu 47 : Cho hàm số 3
f (x)  x   6x  3 2
A. Hàm số luôn giảm trên B. Hàm số luôn tăng trên
C. Hàm số luôn tăng trên 2;
D. Hàm số luôn giảm trên  2  ;2 2x 1
Câu 48 : Cho hàm số y 
(C). Nghiệm của bất phương trình y’ < - 4 là x 1 22
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017 1 5    1 3 x    x  A. 2 2 B. 2 2 x 1 x 1  5 1   x  C.  2 D.  x 1 3 x 5
Câu 49 : Khoảng nghịch hàm số 2 y 
 x  3x  là 3 3 A.  ;    1 B.  1  ;3 C. 3; D.  ;    1 và 3; 4 x 3
Câu 50 : Khoảng nghịch hàm số 2 y   3x  là 2 2  3   3  A.  ;   3 và 0; 3 B.   ; 0    và  ;     2   2   C.  3;
D.  3;0 và  3;
Câu 51 : Trong các hàm số sau, hàm số nào đồng biến trên A. y  cot x B. 3 2
y  x  3x  3x  2017 x 1 C. 4 2
y  x  x  2017 D. y  x 2
Câu 52 : Trong các hàm số sau, hàm số nào đồng biến trên 1;3 x  x  x  A. f  x 3  B. f  x 2 4 8  x 1 x  2 C. f  x 2 4  2x  x D. f  x 2
 x  4x  5
Câu 53 : Cho hàm số y  f  x 3
 x 3x  2 . Tìm mệnh đề sai  1 
A. f  x giảm trên khoảng  1   ;1
B. f  x giảm trên khoảng 1  ;    2   1 
C. f  x tăng trên khoảng 1;3
D. f  x giảm trên khoảng ;3    2  7
Câu 54 : Cho hàm số y  f  x 7 6 5
 9x  7x  x 12 . Khi đó 5
A. f  x giảm trên khoảng  1   ;1
B. f  x giảm trên
C. f  x tăng trên  1   ;1
D. f  x tăng trên
Câu 55 : Cho các hàm số y  f  x; y  g  x là các hàm số dương trên  ;
a b và f ' x  0; g ' x  0 trên  ;
a b . Khi đó hàm số nào sau đây đồng biến trên  ; a b 23
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017 f  x
A. f  x g  x B. gx g  x C.
D. f  x  g  x f  x 1 3 2
Câu 56 : Biết rằng hàm số y  x  2x  mx  2m m m 3
nghịch biến trên đoạn dài 1 đơn vị khi  0 .
Hỏi biểu diển số nào sau đây và 0
m trên cùng trục số là gần nhau nhất? A. -4,57 B. -3,76 C. -5,74 D. -6,5 mx  2
Câu 57 : Có bao nhiêu số nguyên m thỏa mãn điều kiện hàm số y  x  m luôn nghịch biến trên  3 khoảng   ;1 . A. 0 B. 2 C. 5 D. 4 mx  4
Câu 58 : Tìm m để hàm số y  ;1
x  m luôn nghịch biến trên khoảng  . A. 1  m B. 0  m  2 C. m  2 D. 1  m  2 mx 1
Câu 59 : Hàm số y =
đồng biến trên khoảng (1 ; +  ) khi x  m A. m > 1 hoặc m < - 1 B. m < - 1 C. m > - 1 D. m > 1 mx 1
Câu 60 : Hàm số y =
nghịch biến trên khoảng (-  ; 0) khi: x  m A. m > 0 B. 1   m  0 C. m < - 1 D. m > 2 Câu 61 : Hàm số: 3 2
y  x  3x  mx 1 nghịch biến trên một đoạn có độ dài 2 đơn vị khi: A. m  2 24
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017 B. m  2 C. m  0 D. m  0 1 Câu 62 : Hàm số: 3 2 y 
x  2x  mx  2m nghịch biến trên một đoạn có độ dài 1 đơn vị khi: 3 A. m  1 B. m  1 15 C. m   4 15 D. m   4 Câu 63 : Hàm số: 3 2
y  x  2x  mx 1 đồng biến trên một đoạn có độ dài 1 đơn vị khi: 3 A. m  4 3 B. m   4 3 C. m   4 7 D. m  12 1 Câu 64 : Hàm số: 3 2
y   x  mx  m  6 x 1 đồng biến trên một đoạn có độ dài 24 đơn vị khi: 3 A. m  3  B. m  4 C. 3   m  4 D. m  3  ,m  4 3 x
Câu 65 : Biết rằng hàm số y   m   2 3
1 x  9x 1 nghịch biến trên  x ; x và đồng biến trên các 1 2  3
khoảng còn lại của tập xác định. Nếu x  x  6 thì giá trị m là: 1 2 A. 2 B. 4  C. 4  hoặc 2 D. 2  hoặc 4 1
Câu 66 : Biết rằng hàm số 3 2 y 
x  3(m 1)x  9x 1 nghịch biến trên khoảng (x1; x2) và đồng biến 3
trên các khoảng còn lại của tập xác định. Nếu x  x  6 3 thì giá trị của m bằng bao nhiêu? 1 2 A. m  1  B. m  3 C. m  3  ;m 1 D. m  1  ;m  3 LƯU Ý 25
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TÍNH ĐƠN ĐIỆU 2017
☻ Quy tắc tính đạo hàm: Cho u  u x ; v  v x ; C : là hằng số .
☻ Tổng, hiệu: u  v  u  v.  
☻ Tích: u v.  uv.  vu . C u .   C u . . 
 u  uv .  vu . C  C u . 
Thương:    , 0 2
v         v  v  u  u2
Bảng công thức tính đạo hàm:
Đạo hàm của hàm sơ cấp
Đạo hàm của hàm hợp   
C   0 (C là hằng số).    x  1  .x         x  1  .x  u  1
.u  .u    1  1      1 u (x  0)     u  0   2   2  x  x  u  u    u x  1  x  0  u  u  0 2 x 2 u   
sin x  cos x
sinu u .cosu   
cos x  sin x cosu  u  .sin u   u  x 1 tan  tanu  2 cos x 2 cos u   u  x 1 cot   cotu   2 sin x 2 sin u 26
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017
PHẦN 2 : CỰC TRỊ CỦA HÀM SỐ
► Hàm số y  f(x) đạt cực trị tại x nếu y'(x )  0 . 0 0
► Hàm số y  f(x) đạt cực đại tại x nếu đạo hàm y ' đổi dấu từ + sang – khi đi qua x . 0 0
► Hàm số y  f(x) đạt cực tiểu tại x nếu đạo hàm y ' đổi dấu từ – sang + khi đi qua x . 0 0
Các phương pháp tìm cực trị của hàm số
Phương pháp 1.
♥ B1 : MXĐ, Tìm f 'x .
♥ B2 : Tìm các điểm x i 1,2,... mà tại đó đạo hàm của hàm số bằng 0 hoặc hàm số liên tục i  
nhưng không có đạo hàm.
♥ B3 : Lập bảng xét dấu f 'x . Nếu f 'x đổi dấu khi x qua x thì hàm số đạt cực trị tại x . i i
Phương pháp 2.
♥ B1 : Tìm f ' x . giải phương trình f 'x  0 tìm các nghiệm x i 1,2,... . i  
♥ B2 : Tính f ' x . i 
☺ nếu f ' x  0 thì hàm số đạt cực đại tại điểm x . i  i
☺ nếu f ' x  0 thì hàm số đạt cực tiểu tại điểm x . i  i
Cho hàm số y  f x ,đồ thị là (C). Các vấn đề về cực trị cần nhớ:
◙ Nghiệm của phương trình f 'x  0 là hoành độ của điểm cực trị.  f '   x  0 0  ◙ Nếu 
thì hàm số đạt cực đại tại x  x .  0 f '  x  0 0   f '   x  0 0  ◙ Nếu 
thì hàm số đạt cực tiểu tại x  x .  0 f '  x  0 0  Chú ý: 27
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017
☻ Quy tắc 2 thường dùng với hàm số lượng giác hoặc việc giải phương trình f’(x) = 0 phức tạp. a  0
☻ Hàm số y  f x có 2 cực trị    0  y'
Ví dụ : Tìm cực trị của hàm số 3 2 y  2x  3x  36x 10 Phương pháp I. Phương pháp II. TXĐ: D  . TXĐ: D  . 2 y'  6x  6x  36 2 y'  6x  6x  36 x  2 x  2 y”= 12x + 6 2
y'  0  6x  6x  36  0   2
y'  0  6x  6x  36  0   x  3  x  3  x -3 2 + - y' + - 0 0 + y’’(2) = 30 > 0 + 71
nên hàm số đạt cực tiểu tại x = 2 và yct = - 54 y - - 54 y’’(-3) = - 30 < 0
Vậy x = -3 là điểm cực đại và ycđ = 71
nên hàm số đạt cực đại tại x = -3 và ycđ =71
x = 2 là điểm cực tiểu và yct = - 54
BÀI TẬP TỰ LUẬN PHẦN CỰC TRỊ
Bài 1 : Tìm cực trị các hàm số sau (dấu hiệu 1): a) 3 2 y  x  6x 1 b) 3 2 y  2  x  3x 12x 5 c) 4 2 y  x  2x  3 5 3 x x d) 4 2
y  x  8x  5 e) 4 2
y  x  6x  8x 1 f) y    2 5 3
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 28
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Vận dụng 01 : Cho hàm số 2
y  f  x có đạo hàm f ' x   x  
1  x  23x  
1 . Số điểm cực trị của hàm số là: A. 4 B. 3 C. 1 D. 2
Vận dụng 02 : Cho hàm số 8 3 2 5
y  f  x có đạo hàm f ' x   x  3  x  2 3x  
1  x  6 4  x . Số
điểm cực trị của hàm số là: A. 4 B. 3 C. 1 D. 2
Vận dụng 03 : Cho hàm số y  f  x có đạo hàm f  x   x   2 ' 1 x  
1 . Số điểm cực trị của hàm số là: A. 4 B. 3 C. 1 D. 2
Bài 2 : Tìm cực trị các hàm số sau (dấu hiệu 2): 3 x a) 2 y    x  3x 1 b) y  2cos 2x 5 3
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 29
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017
Bài 3 : Tỉm để hàm số sau có cực đại và cực tiểu a)     3 2 2 y m 2 x  3x  mx  2m b) 3 
    2   2    2 y x 3 m 1 x 2 m 7m 2 x  2m 3 x m 3 x c) 2 y   x  2m  3 4 x  8m d) 2 y   2x   2 m  2m  3 4 x  m 3 2 3
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 3 x e) (soạn) 2 2 y   x  m x  5 ( ĐS : 1   m 1 ) 3 3 x 7 2 f) (soạn) 2 y   x  2m  2x  ( ĐS : m  ) 3 9 3 3 2 x x g) (soạn) y   m  2
 mx  8m ( ĐS : m  0 ) 3 2 3 x 2 2 h) (soạn) y   2m   2
1 x  4m  3 x  8 ( ĐS : m    m  ) 3 2 2 1 Bài 4 : Cho hàm số 3 2 y 
x  mx  x  m 1 . Tìm tất cả các giá trị của m để đồ thị hàm số có hai điểm cực 3
trị là A x ; y , B  x ; y thỏa mãn 2 2 x  x  2 A A B B  A B A. m  3  B. m  0 C. m  2 D. m  1  30
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 2 2
Bài 5 (Khối D – 2012): Cho hàm số y = x3 – mx2 – 2(3m2 – 1)x +
(1), m là tham số thực. Tìm m 3 3
để hàm số (1) có hai điểm cực trị x1 và x2 sao cho x1.x2 + 2(x1 + x2) = 1
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. Bài 6 : CMR hàm số 2 a) 3 2 2 y 
x  (m  2)x  (m  3)x  2m luôn luôn có 2 cực trị 3 1 5 b) 3 2 y  x  mx   2 m  4 6 x 
m luôn luôn có cực đại và cực tiểu 3 4
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. c) (soạn) 3 2      2   10 8 y x 3mx 3 1 m
x  m  7m luôn luôn có cực đại và cực tiểu 31
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017 1 5 d) (soạn) 3 y  x  m   2 1 x  m  3 x 
luôn luôn có cực đại và cực tiểu 3 4
Bài 7 : Tìm m để hàm số a/ (Khối B – 2002) 4 2 2
y  mx  (m  9)x 10 có ba cực trị b/ 4 2
y  x  2(m 1)x  m có ba cực trị c/ 4 2 2
y  x  2m x 1 có ba cực trị
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. Soạn : d/ 4 2 4 y  x  2 x m
 2m  m có ba cực trị e/ 4   m   2 y x 1 x 1 có ba cực trị f/ 4   m  2 y x 2 5 x  2 có ba cực trị
g/  m   4  m   2 y 1 x 1 x  2 có ba cực trị m h/ 4    m   2 y x 1 x  m   1 có ba cực trị 4 k/    4      2 2 y f x x
2 m 2 x  m  5m  5 có ba cực trị
Bài 8 : Tìm m để hàm số
a/ (TN–THPT – 2005) 3 2     2 y x 3mx m  
1 x  2 đạt cực đại tại x = 2 32
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017
b/ (TN–THPT – 2011) 3 2
y  x  2x  mx 1 đạt cực tiểu tại x = 1 c/ 3 2
y  x  mx  m  
1 x  2 đạt cực tiểu tại x = 1
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 1 d/ (Soạn) y   2 m  2 3 x  3m  4 2
x  mx đạt cực tiểu tại x = 1 2 e/ (Soạn) 3 2
y  x  3x  3mx  3m  4 đạt cực trị tại x = 2 ? Cực trị đó là cực đại hay cực tiểu ? f/ (Soạn) 3     2 y x
m 3 x  mx  m  2 đạt cực tiểu tại x = 2 (ĐS : m = 0 ) g/(Soạn)   2   3 2 y m
5m x  6mx  6x  6 đạt cực đại tại x = 1 (ĐS : m = 1 ) h/(Soạn)     4 2 y
2m 1 x  3mx  4m  2 đạt cực đại tại x = –1 (ĐS : m = –2 )
Bài 9 : Tìm m để hàm số 1 1 a/ Đồ thị hàm số 3 2 y 
x  mx  (2m 1)x  2 có hai điểm cực trị dương (  m  1) 3 2
b/ (Cao Đẳng – 2009) 3 2
y  f(x)  x  (2m 1)x  (2  m)x  2 có cực đại và cực tiểu có hoành độ dương m2 c/ 3 2 y 
x  (m 1)x  (2m  6)x  8 có cực đại và cực tiểu có hoành độ dương. (ĐS : 3  m 11) 3
..............................................................................................................................................................................
.............................................................................................................................................................................. 33
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 10 : Tìm m để hàm số 1 (2m  3) a/ 3 2 2 y  x 
x  (m  2m  2)x 11 có cực trị có hoành độ x1, x2 thỏa mãn x1 =2x2 (ĐS : m  0, 6 ) 3 2 1 (3m  2) b/ (soạn) 3 2 2 y  x 
x  m x 15 có cực đại và cực tiểu có hoành độ x1, x2 thỏa mãn x1 =9x2 3 2 (ĐS : m  6 )
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 34
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017 1 c/ (soạn) 3 2 y 
x  (m 1)x  (2m 1)x 1 có cực đại và cực tiểu có hoành độ x1, x2 thỏa mãn x2 =9x1 3 4 (ĐS : m  4,  ) 9 m 1 11 5 d/ 3 2 y 
x  mx  m  5 x 
có cực đại và cực tiểu có hoành độ đều lớn hơn 2 (ĐS : 1  m  ) 3 7 4 2 11 1 9 e/ 3 2 y 
x  2x  3  4m x 
có cực đại và cực tiểu có hoành độ đều lớn hơn –1 (ĐS :  m  ) 3 1200 4 4
Bài 11 : a/ (ĐHQG-HN-1997) 3 2
y  2x  mx 12x 13 có cực đại và cực tiểu trong và các điểm này
cách đều trục tung (ĐS : m  0 )
b/ (ĐH Đà Nẵng – 2000) 3     2   2 y x 2m 1 x
m  3m  2 x  4 có cực đại và cực tiểu nằm về hai
phía trục tung (ĐS : 1 m  2 )
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 1 2m 1 3   Bài 12: Cho hàm số 2 y  x  x   2
m  2 x 1. Xác định tham số m để hàm số có cực đại, 3 2
cực tiểu có hoành độ x1, x2 thỏa mãn hệ thức 3x .x 5 x  x  7  0 (ĐS : m  2 ) 1 2  1 2
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 35
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017 1 2m 1 3  
Bài 13 : Cho hàm số 2 y  x 
x  mx  m .Xác định tham số m để hàm số có cực đại, cực 3 2 3
tiểu có hoành độ x1, x2 thỏa mãn hệ thức 2 2 x  x  6x x  8  (ĐS : m  ) 1 2 1 2 2
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. m 1 (Soạn) Cho hàm số 3 2 y  x  mx  m   1 x  m 3
a/ CMR hàm số luôn có cực trị. x x 5 1
b/ Gọi x1, x2 là hoành độ cực trị. Tìm m để 1 2    (ĐS : m   ) x x 2 3 2 1
Bài 14: Tìm điểm cực tiểu của đồ thị hàm số 2
y  x  5 x  6 ?  5 1   5 1     5 1  A. ;  ;  ;          ;  ; 0; 6   0; 6  C.   2 4   2 4  B.   5 1 0; 6 ; ;  2 4   2 4  D.  
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
BÀI TẬP MINH HỌA PHẦN CỰC TRỊ
Ví dụ 01 : Cho hàm số 3 2
y  x  3x  mx  m  2 . Giá trị nào của tham số m thì hàm số có hai điểm cực trị. A. m  3 B. m  3 C. m D. m
♥ Giải : Tập xác định: D  .; Đạo hàm: 2
y '  3x  6x  m , Làm tự luận ! 36
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017 y '  0 2
 3x  6x  m  0
Hàm số có hai điểm cực trị  y '  0 có hai nghiệm phân biệt 3   0  
 m  3 ; Vậy giá trị m cần tìm là m  3 . 2
 '  3  3m  0 Làm trắc nghiệm !
Khi làm bài trắc nghiệm chúng ta không thể giải như vậy vì sẽ có nhiều bài phức tạp “số xấu”
☻Phương pháp “BÓC ĐẠI”
► “Bóc đại” m = 2 ở câu B thì ta thấy 2
y '  3x  6x  2  0 , phương trình này có 2 nghiệm (bấm máy
là thấy nha) – Vậy nhận luôn B
Vì còn đáp án C là m thuộc R nữa nên ta phải xét thêm đáp án A kiểm tra
► “Bóc đại” m = 4 ở câu A thì ta thấy 2
y '  3x  6x  4  0 , phương trình này vô nghiệm (bấm máy
là thấy nha) thì rõ ràng A không hợp lý
Kết thúc vấn đề - chọn B 2
Ví dụ 02 : Cho hàm số 3 y 
x  m   2 1 x   2
m  4m  3 x 1. Tìm m để hàm số có cực đại, cực tiểu 3
và các điểm cực trị của đồ thị hàm số có hoành độ dương.
♥ Giải : Tập xác định: D  ; Đạo hàm: 2
y  x  m   2 ' 2 2
1 x  m  4m  3 ,
Hàm số có hai điểm cực trị có hoành độ dương  y '  0 có hai nghiệm phân biệt dương 
 '  m  2 1  2  2
m  4m  3  0 
 S  m   1  0  5
  m  3 ; Vậy giá trị m cần tìm là 5   m  3  .  2 m  4m  3 P   0  2
Ví dụ 03 : Tìm m để hàm số 3
y  x  m   2 3
1 x  9x  m có 2 điểm cực trị x , x thỏa mãn 1 2 x  x  2. 1 2
♥ Giải : Tập xác định: D  .; Ta có: 2
y '  3x  6m   1 x  9 ; 2
y '  0  x  2m   1 x  3  0   1
Yêu cầu bài toán tương đương với  
1 có 2 nghiệm phân biệt x , x thỏa mãn x  x  2. 1 2 1 2  2 '  m  2 1  3  0
m  2m  2  0   m  1   3  m  1   3        2 2 x  x  2    x  x  4   x  x  4x x  4 1 2    1 2  1 2 1 2 m  1   3  m  1   3 m  3        m  2   m 1 4 1 4.3 4
Vậy giá trị cần tìm của m là m  3  hoặc m 1 37
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017
Ví dụ 04 : Cho hàm số 3
y  x  m   2
1 x  7x  2 , m là tham số. Chứng minh rằng với mọi giá trị m
, hàm số luôn luôn có một giá trị cực đại và một giá trị cực tiểu.
♥ Giải : Tập xác định: D  . Đạo hàm 2
y '  3x  2m   1 x  7 .
Ta có   m  2 ' 1  21  0, m
  , suy ra phương trình y '  0 luôn có hai nghiệm phân biệt với
mọi giá trị m hay với mọi giá trị của m thì hàm số luôn có một giá trị cực đại và một giá trị cực tiểu.
Ví dụ 05 : Cho các hàm số 3 2
y  x  3mx  2 ( C ), y  x  2 d  , với m là tham số thực. Tìm các m
giá trị của m để ( C ) có hai điểm cực trị và khoảng cách từ điểm cực tiểu của (C ) đến đường thẳng m m d  bằng 2 .
Làm sao: xác định đâu là hoành độ cực đại , hoành độ cực tiểu ?
Làm vậy nè : “ dựa vào dạng đồ thị hoặc bảng biến thiên.”
♥ Giải : Tập xác định: D  . x  0 Đạo hàm : 2
y '  3x  6mx  3x  x  2m , y '  0  x  2m
Điều kiện để hàm số có hai cực trị là m  0 A0;2 
Tọa độ hai điểm cực trị:  . B   3 2 ; m 2  4m 
Đường thẳng d  : y  x  2  x  y  2  0 0  2  2
Với : m  0 : A là điểm cực tiểu. Khi đó d  , A d    0  2 (loại). 2 2 1 1
Với : m  0 : B là điểm cực tiểu. Khi đó: d B d  3 ,
 2  2m  m 1 3 2m  m 1 m 1     m 1  ( m > 0) 3
2m  m  1  m  1 
► Khoảng cách cũng là một chủ đề hay xuất hiện trong các đề thi , ta cần nắm vững công thức
tính khoảng cách từ điểm M  x ; y
đến đường thẳng  : ax  by  c  0 là M M  
ax  by  c d M ;  M M  2 2 a  b
Ví dụ 06 : Cho hàm số 3
y  x   m   2 2
1 x  2  m x  2 , với m là tham số thực. Tìm các giá trị của m
để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số có hoành độ dương.
♥ Giải : Tập xác định: D  . ; 2
y '  0  3x  22m  
1 x  2  m  0   *
Yêu cầu bài toán  Phương trình * có hai nghiệm dương phân biệt 38
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017   2 5
4m  m 5  0 m  1  hay m   '  0   4  2  m  5  P  0    0  m  2   m  2 3 4    S  0    m   1 2 2 1 m    0  2  3 5 Vậy
 m  2 là giá trị cần tìm 4
Ví dụ 07 : Cho hàm số 3 2
y  x  x   2 m   2 3 3
1 x  3m 1, m là tham số. Tìm m để hàm số có cực đại,
cực tiểu và các điểm cực trị của đồ thị hàm số cách đều gốc tọa độ O.
♥ Giải : Tập xác định: D  , 2
y   x  x   2 ' 3 6 3 m   1 Hàm số  
1 có cực trị  y '  0 có 2 nghiệm phân biệt x 1 m 2
 '  m  0  m  0 Khi đó y '  0  x 1m Gọi ,
A B là hai điểm cực trị của đồ thị hàm số   1 thì: A 3
 m   m  B 3 1 ; 2 2 , 1 ;
m  2  2m . 1
O cách đều A và B 2 2 3
 OA  OB  8m  2m  m   (vì m  0 ) 2
Ví dụ 08 : Tìm tất cả các giá trị tham số m để hàm số y  f  x 3
 x   m  2
2 –1 x  m – 2 x 1– m
đạt cực đại tại x  2  .
♥ Giải : Tập xác định: D  ;
Đạo hàm f  x 2 '
 3x  22m 
1 x  m  2 .
(Điều kiện cần) Để hàm số đạt cực đại tại x  2  thì
f      2 ' 2 0 3. 2  22m   1 . 2
   m  2  0  m  2.
(Điều kiện đủ) Với m  2 , ta được f  x 3 2
 x  3x 1. x 
Đạo hàm f  x 2 '
 3x  6x  3xx  2; f x   xx   0 ' 0 3 2  0  .  x  2 
Lập bảng biến thiên ta thấy f  x đạt cực đại tại x  2  .
(có thể giải bài toán bằng y’’ thay vì lập BBT)
Vậy m  2 thỏa yêu cầu bài toán. 39
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017
Ví dụ 09 : Cho hàm số 4 2
y  x  (m 1)x  2m 1. Tìm tất cả các giá trị của m để hàm số đã cho có ba điểm cực trị.
♥ Giải : Tập xác định: D  ; Đạo hàm 3 2
y '  4x  2(m 1)x  2x(2x  m 1); x  0 y ' 0    m 1 2 x  (1)  2
Hàm số đã cho có ba điểm cực trị  y 'có ba nghiệm phân biệt  (1) có hai nghiệm phân biệt khác 0  m
 1 0  m  1  Vậy với m  1
 hàm số đã cho có ba điểm cực trị.
Chú ý, đây là tình huống đặc biệt : ♥ Phương trình 2
x   có hai nghiệm phân biệt khác 0    0
Đó chỉ là cách làm tự luận “cho vui”, khi làm trắc nghiệm là “bế tắc” Vậy làm sao ??? ☻Cách khác : Có 3 cực trị a.b  0
Hàm số trùng phương 4 2 y  ax  bx  c Có 1 cực trị a.b  0
Hàm số đã cho có ba điểm cực trị tương đương a.b < 0
hay 1.(m + 1) < 0, Suy ra m < -1 ???
☻ Ứng dụng 1 : Cho hàm số 4 2
y  x  ax  3 .Với giá trị nào của tham
số a thì hàm số đã cho có 3 cực trị A. a = 0 B. a < 0 C. a > 0 D. Không có
☻ Ứng dụng 2 : Cho hàm số 4 2 2
y  x  a x  3 .Với giá trị nào của
tham số a thì hàm số đã cho có 3 cực trị A. a khác 0 B. a < 0 C. a > 0 D. Không có 40
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017
☻ Ứng dụng 3 : Cho hàm số y    a 4 2 1
x  ax  2a 1 .Với giá trị nào của tham số a thì hàm số
đã cho có đúng 1 cực trị A. a  B. a  C. 0  a 1 D. \ 0;  1 ☻ 1 3
Ứng dụng 4 : Cho hàm số 4 2 y  x  ax 
.Với giá trị nào của tham số a thì hàm số đã cho 2 2
có cực tiểu mà không có cực đại A. a  B. a  0 Chú ý nhỏ : C. 0  a 1 D. \ 0;  1 2
A  0  A  0
Đáp án : Ứng dụng 1 : C Ứng dụng 2 : A
Ứng dụng 3 : D Ứng dụng 4 : B 3 2
Ví dụ 10 : Cho hàm số y  x  3x  5x 1. Viết phương trình đường thẳng đi qua hai
điểm cực trị của đồ thị hàm số. ♥ Giải :
☻Cách 1 : Ta vẽ bảng biến thiên rồi suy ra hai điểm cực trị là Mx ; y , N x ; y rồi 1 1   2 2 x  x y  y 1 1
dùng công thức đường thẳng qua 2 điểm bất kì  x  x y  sẽ ra. y 2 1 2 1
Nhưng trong bài này điểm cực đại và cực tiểu không phải là “số đẹp” nên ta phải dùng cách 2
được trình bày sau đây
☻Cách 2 : (ở đây thầy không chứng minh – trong các sách nâng cao điều có chứng minh)
Chia y / y’ thì “phần dư” chính là đường thẳng cần tìm ◙ Mô tả : y y’
Phần chia được ☺ Phần dư nè !! dx + e !! mx + n
Suy ra đường thẳng qua 2 điểm cực trị là (d) : y = mx + n
Lời khuyên : chia cẩn thận dùm cái !!! 41
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017
◙ Thực hiện : Ta có 3 2
y  x  3x  5x 1 ; Suy ra 2
y '  3x  6x  5 Thực hiện phép chia y / y’ như bảng sau : 3 2 x  3x  5x 1 2 3x  6x  5 
Suy ra đường thẳng qua hai 5
điểm cực trị của đồ thị hàm 3 2 x  2x  x x 1  3 số đã cho là 3 3 10 2 0  x  x 1 Phần chia 16 8    3  đượ (d) : y x c dđược 5 3 3 2 x  2x  được 3 Phần dư 16 8  x  3 3
Ví dụ 11 : Cho hàm số 3 2
y  x  3x  2 . Gọi A, B lần lượt là hai điểm cực trị của đồ thị hàm số
và C(1;1). Khi đó diện tích tam giác ABC bằng bao nhiêu ? x  0
♥ Giải : Tập xác định: D  ; Đạo hàm 2
y '  3x  6x ; y '  0  x  2
Khi đó tọa độ hai điểm cực trị là A(0;2) và B(2; -2)
☻ Đặt vấn đề tính diện tích S∆ABC của tam giác ABC ??
☺ với AB  (a ;a ), AC  (b ;b ). 1 2 1 2 Công thức giải nhanh 1 1 a a 1 2 1 S  det(AB,AC)   a b  a b A  BC 1 2 2 1 2 2 b b 2 1 2 S∆ABC
Thuần túy tam giác (cạnh nhân đường cao tương ứ 1 ng) S  AB.d C;AB A  BC   2 42
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017
Tiến hành làm !!
♥ Cách thuần túy : AB  (2; 4  ), AC  (1; 3  ) x  x y  y Đường thẳng AB : A A 
ta được 2x  y  2  0 AB  AB    2 2 2 4  2 5 ; x  x y  y B A B A   1 d C AB 2x y 2 C C 1 ;   ; Suy ra S  A . B d C AB  ABC   ;  1 2 2 2 1 5 2 1 1 2 4  ♥ 1
Cách chơi chiêu : S
 det(AB, AC)         ABC   3 2 1  4 1 2 2 1 3  2
☻ Ứng dụng : Cho tam giác ∆ABC có A(1; 2), B(3; -2), C(2;4). Tính diện tích tam giác ∆ABC. (ĐS : S = 4)
..............................................................................................................................................................................
............................................................................................................................................................................
BÀI TẬP TRẮC NGHIỆM PHẦN CỰC TRỊ Câu 1 : Hàm số 4 2
y  x  x 12 có mấy điểm cực trị A. 4 B. 3 C. 2 D. 1
Câu 2 : Hàm số y  sin x có bao nhiêu điểm cực trị A. 4 B. 3 C. 2 D. Vô số Câu 3 : Hàm số 4 3
y  x  8x 12 có mấy điểm cực trị A. 4 B. 3 C. 2 D. 1
Câu 4 : Cho hàm số : 3 2
y  3x  4x  x 14 . Hàm số đạt cực trị tại hai điểm x1, x2 . Khi đó x1.x2 = 1 A. B. 3 9 1 C. D. 1 7 1
Câu 5 : (THPT Chuyên Lê Hồng Phong-Tp.Hồ Chí Minh) Cho 3 2 y 
x  mx  2m  3 x  5 có hai 3
điểm cực trị nằm về hai phía của trục tung. Khi đó giá trị của m là 3 A. m   3 . B. m   . 2 2 3 C. m   3 . D. m   . 2 2
Câu 6 : Cho hàm số : 3 2
y  3x  4x  x 14 . Hàm số đạt cực trị tại hai điểm x1, x2 . Khi đó x1 + x2 = 43
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017 1 8 1 A. B. C. D. 1 9 9 7 Câu 7 : Cho hàm số 4
y  x  m   2 2
1 x  m 1 (1) . Với giá trị nào của m thì hàm số (1) có 1 cực trị ? A. m  1  B. m  1  C. Cả A, B đều đúng D. Cả A, B đều sai Câu 8 : Hàm số 3 2
y  x  3x  3 có điểm cực tiểu là A. 0;3 B.  2   ;1 C. 1  ;1 D. 1; 6  
Câu 9 : Hàm số y  x   x2 3 1 đạt cực đại tại 3 A. x  1 B. x  5 C. x  1  D. Đáp án khác Câu 10 : Hàm số 3 2
y  x  3x  4 . Đường thẳng đi qua 2 điểm cực trị của hàm số là A. y  2  x  4
B. y  x  3 C. y  1 
D. y  x  3 Câu 11 : Hàm số 4 2
y  x  6x  8x 1có điểm cực đại là A. 7;3 B.  2  ;24 C.  2  ;25 D. 1; 6   Câu 12 : Hàm số 3 2
y  2x  3x  36x 10 có điểm cực trị lần lượt là A và B. Với M(2; 3). Diện tích tam giác ∆MAB là 285 287 A. S  B. S  2 2 87 C. S  78 D. S  3 Câu 13 : Hàm số 4 3
y  x  4x 1 có điểm cực tiểu là A. 2; 1  5 B. 1;2 C.  2  ;1  1 D. 4; 6  
Câu 14 : Đồ thị hàm số nào sau đây chỉ có 1 điểm cực trị : A. 4 2
y  2x  4x  2 B. y   2 m   4 2 4 x  9x 1 C. 4 2
y  x  2x 1 D. 4
y  x   2 m   2 1 x 1 Câu 15 : Hàm số 2
y  x 4  x có điểm cực tiểu là A.  2;2 B.  2  ;1 C.  2; 2   D.  2;2
Câu 16 : Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 3 2
y  x  3x  9x  2 có phương trình x A. y   3 B. y 18x 3 44
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017 C. y 1 8x D. y 1 3x 3 2 x x
Câu 17 : Với giá trị nào của tham số m thì hàm số y   m
 2x 1 có cực trị 3 2 A. 3 B. 4 C. 0 D. Cả A, B, C
Câu 18 : Với giá trị nào của tham số m thì hàm số 4 2
y  x  2mx  2m 1 có 3 cực trị A. 1 B. 1  C. 0 D. 2 
Câu 19 : Với giá trị nào của tham số m thì hàm số 4 2 4
y  x  2mx  2m  m có 3 cực trị A. m  2  B. m  1  C. 0 D. m  2
Câu 20 : Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 3
y  x  3x 1 có phương trình A. y  2  x 1 B. y 1 3x C. y 1 7x D. y 1 x
Câu 21 : Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 3 2
y  x  mx   2  m  3 2 3 3 1
x  m  m có phương trình A. 2
y  3x  m  m B. 2
y  5x  m C. 2
y  2x  m 1 D. 2
y  2x  m  m
Câu 22 : Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số 3 2
y  x  3x  5x có hệ số góc là 16 3 A. k   B. k   3 16 1 1 C. k   D. k  3 3 Câu 23 : Hàm số 2 3
y  10 15x  6x  x đạt cực tiểu tại: A. x  5 B. x  1  C. x  1 D. x  5 
Câu 24 : Hàm số y   x  2
1 2  x đạt cực trị tại hai điểm A và B.
Cho M(1; -3). Diện tích tam giác ∆MAB bằng 3 A. 7 B. 5 8 C. D. Đáp án khác 3
Câu 25 : (Trường THPT Nguyễn Bỉnh Khiêm) Cho hàm số 3 2
y  x  3x  2 . Điểm cực đại của đồ thị là? A. 2; 2 . B. 0; 2 . C. 0; 2   . D. 2; 2   . x
Câu 26 : Cho hàm số : 3 2
y  x  3x 
. Hàm số đạt cực trị tại hai điểm x1, x2 . Khi đó 2 2 x  x  2 1 2 11 13 1 3 A. B. C. D. 3 3 7 2 45
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017 x 1
Câu 27 : Cho hàm số y  . Hàm số có x 1 A. Một cực đại. B. Một cực tiểu.
C. Một cực đại và một cực tiểu . D. Không có cực trị. 1 1 1
Câu 28 : Cho hàm số 4 2 y  x  x 
. Tích các giá trị cực đại và cực tiểu của hàm số bằng: 4 2 2 1 1 A.  . B. 1  . C. 1. D. . 32 32
Câu 29 : Giả sử hàm số 3 2
y  ax  bx  cx  d có cực trị.
Xác định chính xác số cực trị của hàm số đã cho: A. Có 2 điểm cực đại
B. Chỉ có 1 điểm cực đại
C. Chỉ có 1 điểm cực tiểu
D. Cả 3 phương án B, C, D đều sai Câu 30 : Hàm số 4 2
y  x  5x  4 có bao nhiêu điểm cực tiểu A. 0 B. 1
C. Không có điểm cực tiểu D. 2
Câu 31 : Hàm số y  3 2cos x  cos 2x đạt cực tiểu tại A. x  k2π B. x  π k π π C. x   k2π D. x   π k 2 2 Câu 32 : Hàm số 3 2
y  mx  3x 12x  2 đạt cực đại tại điểm x = 2 khi A. m  1  B. m  2  C. m  3  D. m  4  Câu 22 : Hàm số 3 2
y  x  mx   2 6 4m  
1 x  2 đạt cực đại tại điểm x = 2 khi 11 A. m  0 B. m  2 C. m  4 D. m  4  Câu 34 : Hàm số 3     2 y x
m 3 x  mx  m  2 đạt cực tiểu tại điểm x = 2 khi 11 A. m  0 B. m  2 C. m  4 D. m  4 
Câu 35 : Hàm số  f  x 3
 x  m  2 y
1 x  m  2 đạt cực y
đại tại điểm x0 = 2 khi 11 4 A. m  0 B. m  2 C. m  4 D. m  4 
Câu 36 : Hàm số y  f  x 2 xác định trên và có đồ thị như hình bên.
Phương trình đường thẳng d đi qua 2 điềm cực đại và O
cực tiểu của đồ thị hàm số là 2 3 x 46
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – z-a 2 lo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017 A. y  x B. y  2x C. y  x D. y  2  x
Câu 37 : Đường thẳng (d) y  m  
1 x  3m đi qua điểm cực đại K của đồ thị hàm số 9 3 2 y  x  x  6 khi : 2 7 A. m  1 B. m  4 C. m  2  D. Đáp án khác 3 x Câu 38 : Hàm số 2 2 y 
 x  m x  5 có cực đại và cực tiểu khi : 3 A. m  1 B. 1   m 1 C. m  1  D. Đáp án khác 3 x 7 Câu 39 : Hàm số 2 y 
 x  2m  2x  có cực đại và cực tiểu khi : 3 9 2 3 A. m  B. 1   m  3 2 C. m  1  D. m  1  3 x Câu 40 : Hàm số 2 y   2x   2 m  2m  3 4
x  m có cực đại và cực tiểu khi : 3 3 A. m 1 B. 1   m  2 C. m  1  D. m  1 3 x
Câu 41 : Hàm số y   2m   2
1 x  4m  3 x  8 có cực đại và cực tiểu khi : 3 2 3 A. m   B. 1   m  2 2 2 2 C. m   hay m  D. Đáp án khác 2 2 Câu 42 : Hàm số 3
     m 2 y x 3
x  2mx  2 có cực đại và cực tiểu khi : A. m  3
B. 6  3 3  m  6  3 3
C. m  6  3 3 hay m > 6  3 3
D. m  6  3 3 hay m = 6  3 3 m 1
Câu 43 : Cho hàm số 3 y  x  m  2 2 x  m  3 x 1 3
Với giá trị nào của m thì hàm số có cực trị có hoành độ x1, x2 thỏa mãn 4x 1 4x 1 18 1  2  A. m 1 B. m  8 C. m  7 47
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017 D. m  4 1 1
Câu 44 : Cho hàm số 3 y  x  2m  2 1 x   2 m  2 x  m 3 2 81
Với giá trị nào của m thì hàm số có cực trị có hoành độ x1, x2 thỏa mãn 2 2 x  x  1 2 8 1 A. m  B. m  8 4 7 C. m  D. m  4 4 1
Câu 45 : Cho hàm số 3 2 y 
x  mx  x . Với giá trị nào của m thì hàm số có cực trị có hoành độ x1, 3 x2 thỏa mãn 2 2 x  x  x x  7 1 2 1 2 A. m  1  B. m  2  C. m  3  D. m  4  1 2m 1 3  
Câu 46 : Cho hàm số 2 y  x  x   2
m  2 x 1. Với giá trị nào của m thì hàm số có cực trị 3 2
có hoành độ x1, x2 thỏa mãn 3x .x  5 x  x  7  0 1 2  1 2 1 A. m  B. m  8 4 C. m  2 D. m  4 2 3m 1 3  
Câu 47 : Cho hàm số 2 y  x  x   2
m  m  6 x 1. Với giá trị nào của m thì hàm số có 3 2
cực trị nằm về 2 phía Oy A. 2   m  3 B. 2   m 1 C. m  2 D. m  4
Câu 48 : Cho hàm số 4 2 2
y  x  2(m  2)x  m  5m  5 . Với giá trị nào của m thì hàm số có 3 cực trị ? A. m  2 B. m 1 C. m  2 D. m 1
Câu 49 : Cho hàm số 4 2 2 2
y  x  2(m  3) x  m . Với giá trị nào của m thì hàm số có 3 cực trị ? A. m  3 B. m  3 C. m  3 D. m
Câu 50 : Cho hàm số 3 2 3
y  x  3mx  4m (1) . Với giá trị nào của m thì đồ thị hàm số có 2 điểm cực trị A và B A. m  0 B. m  3 C. m  1 D. m  \   0
Câu 51 : Cho hàm số 4
y  x 10000 . Số điểm cực trị ứng với hàm số là A. 0 B. 1 C. 2 D. 3 Câu 5 2: Cho hàm số 3
y  x  3x  2 . Số điểm cực trị ứng với hàm số là A. 0 B. 1 C. 2 D. 3 48
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017
Câu 51 : Cho hàm số 3
y  x   2 m   2 3 x  m .
Số điểm cực trị ứng với hàm số là A. 0 B. 1 C. 2 D. 3
Câu 52 : Cho hàm số 3
y  x  3x 1. Khoảng cách từ điểm cực đại của đồ thị hàm số đến đường
phân giác của góc phần tư thứ hai trong hệ trục Oxy là A. 0 B. 1 C. 2 D. 3
Câu 53 : Cho hàm số 3
y  x  3x  5 . Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số có hệ số góc là A. 2  B. 1 C. 2 D. 5
Câu 54 : Cho hàm số 4
y  kx  k   2
1 x 1 2k . Với giá trị nào của k thì đồ thị hàm số chỉ có một điểm cực trị A. 7 B. -2 C. 4 D. 1
Câu 55 : Cho hàm số y  f  x có bảng biến thiên như sau : x  1  0 1  y  0  0  0  y  
Khoảng cách giữa hai điểm cực tiểu của đồ thị hàm số là A. 0 B. 1 C. 2 D. 4
Câu 56 : Cho hàm số y  f x có bảng biến thiên như sau : x   3 0 3  y  0  0  0  y  
Khoảng cách giữa hai điểm cực tiểu của đồ thị hàm số là 2 3 A. 0 B. 2 3 C. D. 1 3 1 π
Câu 57 : Cho hàm số y  .
m sin x  sin 3x . Với giá trị nào của m thì hàm số đạt cực trị tại x  3 3 49
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017 A. m  2 B. m  2  C. m  0 D. m  3
Câu 58 : Cho hàm số y  f  x có bảng biến thiên như sau : x  x 0 x  0 0 y  0  0  0  y  
Và khoảng cách giữa hai điểm cực tiểu của đồ thị hàm số là 8. Giá trị của 2 x là 0 A. 4 B. 8 C. 16 D. 4 
Câu 59 : Xét hàm số 3 2
y  f (x)  2x  3x 1. Chọn đáp án đúng :
A. Hàm số không có cực đại và cực tiểu B. Nghịch biến trên
C. lim f  x   x D. Cả A, B, C đều đúng. 3 2 x x
Câu 60 : Xét hàm số y  f (x)  
 x . Gọi hoành độ các điểm cực trị của đồ thị hàm số là x1 và 3 2 x2 thì x1 + x2 = A. – 1 B. 2 C. – 2 D. 3
Câu 61 : Xét hàm số 4
y  f x  mx   2 m   2 ( )
9 x 10 (m là tham số) . Giá trị nào của tham số m thì hàm số có 3 cực trị. A. m  3
 hay 0  m  3 B. m C. m D. m  3
Câu 62 : Cho hàm số 3    m  2 y x 3 2
1 x  12m  5 x  2 . Với giá trị nào của m thì hàm số có cực trị 1 1 1 1 A.   m  B. m   hay m  6 6 6 6 1 C. m= D. m 6 3 x
Câu 63 : Cho hàm số 2 y 
 mx  2m  
1 x  3 . Với m  1 thì hàm số có cực trị có hoành độ x1 và 3
x2 . Với giá trị nào của m thì x .x  6 1 2 50
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017 7 1 A. m  B. m  2 2 5 C. m  D. m  7 2
Câu 64 : Cho hàm số y  f  x 5
 5x   2 . Mệnh đề sai là x
A. f  x đạt cực đại tại x = -1
B. f  x đạt cực tiểu tại x = 1
C. f  x có giá trị cực đại là 8
D. M 1;8 là điểm cực tiểu
Câu 65 : Cho hàm số y  f  x 3 2
 x  6x  9x (C) . Phương trình đường thẳng đi qua hai điểm cực trị của (C) là
A. y  2x  6
B. y  2x  6 C. y  2  x  6 D. y  3x
Câu 66 : Với điều kiện nào của a và b để hàm số sau có cực đại và cực tiểu
      3   3 3 y f x x a x b  x A. . a b  0 B. . a b  0 C. . a b  0 D. . a b  0
Câu 67 : Giá trị của m để hàm số y   x  m 2
x  2x  m  
1 có hai điểm cực trị x1 và x2 thỏa mãn x .x  1 là 1 2 A. m  4 B. m  2  C. m  3  D. Cả A và B
Câu 68 : Giá trị của m để hàm số 3 2
y  x  mx 1 có hai điểm cực trị là A. m  0 B. m  0 C. m  4 D. Một kết quả khác 25
Câu 69 : Giá trị của m để hàm số 4 2 y  mx 
x  2017 có ba điểm cực trị là 7 A. m  0 B. m  0 C. m  0 D. m  0 3
Câu 70 : Giá trị của m để hàm số 4 2 y  mx 
x  2018 có ba điểm cực trị là 7 A. m  0 B. m  0 C. m  0 D. m  0
Câu 71 : Giá trị m để hàm số 4 2
y  x  mx có ba điểm cực trị là 3 đỉnh của một tam giác vuông A. m  0 B. m  1 C. m  0 D. m  3 2 x  2x  4
Câu 72 : Hàm số y  x 
có hai điểm cực trị A, B nằm trên đường thẳng có phương trình y = 2 ax + b, với a + b = A. 0 B. 1 C. 1  D. 2 51
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017 2 3x  x  5
Câu 73 : Đồ thị hàm số y 
có hai điểm cực trị A, B nằm trên đường thẳng có phương x  2
trình y = ax + b, với a + b = A. 3 B. 1 C. 1  D. 5 2 5x  x  5
Câu 74 : Hàm số y 
có hai điểm cực trị A, B nằm trên đường thẳng d. Hệ số góc của d 2x  3000 là A. 3 B. 1 C. 1  D. 5 PHỤ LỤC
Một số dạng toán cơ bản về CỰC TRỊ hàm số 4 2
y  ax  bx  c lập TAM GIÁC (luôn là tam giác cân) Giả sử hàm số 4 2
y  ax  bx  c có 3 cực trị:  b    b   (
A 0;c), B    ;  ,C   ;   2a 4a 2a 4a    
tạo thành tam giác ABC thỏa mãn dữ kiện: Dữ kiện
Công thức thỏa ab  0
1). Tam giác ABC vuông cân tại A 3 8a  b  0
2). Tam giác ABC đều 3 24a  b  0 
3). Tam giác ABC có góc BAC   3 2 8a  b . tan  0 2
4). Tam giác ABC có diện tích S  S 3 2 5
32a (S )  b  0 ABC  0 0
5). Tam giác ABC có độ dài cạnh BC  m 2 am  2b  0 0 0
6). Tam giác ABC có độ dài AB  AC  n 2 2 4
16a n  b  8ab  0 0 0
7). Tam giác ABC có cực trị , B C Ox 2 b  4ac  0
8). Tam giác ABC có O là tâm đường tròn nội tiếp 3
b  8a  4abc  0 52
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017
Ví dụ 01 : Tìm tất cả giá trị tham số thực m để hàm số 4 2
y  x  (m  2015)x  2017 có 3 cực trị tạo
thành tam giác vuông cân tại A . A. m  2017 B. m  2014 C. m  2016 D. m  2015
Hướng dẫn: Với a  1
 ,b  m  2015 .
Hàm số có 3 cực trị là ab  0, tức là phải có: (
 m  2015)  0  m  2015.
Tam giác ABC vuông cân tại A khi: 3 3
8a  b  0  8.( 1
 )  (m  2015)  0  m  2015  2  m  2017 Chọn đáp án A.
Ví dụ 02 : Tìm tất cả giá trị tham số thực m để hàm số 4 2
y  x  2(m  2016)x  2017m  2016 có 3 cực
trị tạo thành tam giác vuông cân tại A . A. m  2017  B. m  2017 C. m  2018  D. m  2015
Hướng dẫn: Với a  1,b  2(m  2016) .
Hàm số có 3 cực trị là ab  0, tức là phải có: 2(m  2016)  0  m  2  016 Từ 3 3
8a  b  0  8.1 8(m  2016)  0  m  2016  1   m  2
 017 Chọn đáp án A. 9
Ví dụ 03 : Tìm tất cả giá trị tham số m để hàm số 4 2 y 
x  3(m  2017)x  2016 có 3 cực trị tạo 8 thành tam giác đều. A. m  2015 B. m  2016 C. m  2017 D. m  2017  9
Hướng dẫn: Với a  ,b  3(m  2017) . 8 9
Hàm số có 3 cực trị là ab  0, tức là phải có: .3(m  2017)  0  m  2017 8  9 
Tam giác ABC đều , thì : 24a  b  0  24 
  3(m  2017)3 3
 0  m  2017  1   m  2016  8 
Chọn đáp án B.
Ví dụ 04 : Nếu đồ thị hàm số 4 2
y  9x  2(m  2020)x  2017m  2016 có 3 cực trị tạo thành tam giác
đều thì giá trị tham số m thuộc khoảng nào?. A. (2015;2017) B. (2016;2018) C. (2017;2019)
D. (2017;2020)
Hướng dẫn: Với a  9,b  2(m  2020) .
Hàm số có 3 cực trị là ab  0, tức là phải có: 9.2(m  2020)  0  m  2020 a  b     m  3 3 24 0 24.9 2( 2020)
 0  m  2020  3   m  2017
Chọn đáp án B. 53
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – CỰC TRỊ 2017
Ví dụ 05 : Tìm tất cả giá trị tham số m để hàm số 4 2 y  3
 x  (m  2015)x  2016có 3 cực trị tạo
thành tam giác có một góc 0 120 . A. m  2017  B. m  2015 C. m  2017 D. m  2016
Hướng dẫn: Với a  3
 ,b  m  2015 .
Hàm số có 3 cực trị là ab  0 , tức là phải có: 3
 .(m  2015)  0  m  2015  BAC
Tam giác ABC có một góc 0 120 , thì phải có: 3 2 8a  b . tan  0 với 0 BAC  120  tan  3 2 2 Nên có 3 8a  3b  0 3  8.( 3
 )  3(m  2015)  0  m  2015  2  m  2017
Chọn đáp án C.
Ví dụ 06 : Tìm tất cả giá trị tham số m để hàm số 4 2
y  3x  2(m  2018)x  2017 có 3 cực trị tạo
thành tam giác có một góc 0 120 . A. m  2018  B. m  2017  C. m  2017 D. m  2018
Hướng dẫn: Với a  3,b  2(m  2018) .
Hàm số có 3 cực trị là ab  0, tức là phải có: 3.2(m  2018)  0  m  2018 Từ 3 2 0 3
8a  b . tan 60  0  8.3  8.(m  2018) .3  0  m  2018  1   m  2017 Chọn đáp án C.
Ví dụ 07 : Tìm tất cả giá trị tham số m để hàm số 4 2
y  mx  2x  m  2 có 3 cực trị tạo thành tam
giác có diện tích bằng 1 . A. m  2  B. m  2 C. m  1 D. m  1 
Hướng dẫn: Với a  , m b  2 .
Hàm số có 3 cực trị là ab  0, tức là phải có: .
m 2  0  m  0
Tam giác ABC có diện tích bằng 1 , thì : 3 2 5 3 5 3
32a (S )  b  0  32.m .1 2  0  m 1  0  m  1
 Chọn đáp án D. 0
Ví dụ 08 : Tìm tất cả giá trị tham số m để hàm số 4 2   4  2017m y mx x
 2016 có 3 cực trị tạo thành
tam giác có diện tích bằng 4 2 . A. m  2  B. m  4 C. m  1 D. m  1 
Hướng dẫn: Với a  ,
m b  4 . Hàm số có 3 cực trị là ab  0, tức là phải có: .
m 4  0  m  0 3 2 5 3 2 5 3
32a (S )  b  0  32.m (4 2)  4  0  m 1  0  m  1
 Chọn đáp án D 0 54
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN 2017
PHẦN 3 : GIÁ TRỊ LỚN NHẤT – NHỎ NHẤT
1/Định nghĩa: cho hàm số y = f(x) ,TXĐ: D Nếu f(x)  M, x
 D và f(x )  M,x D thì M là GTLN của hs trên D 0 0 Kí hiệu Max y = M tại x = x0 D Nếu f(x)  M, x
 D và f(x )  M,x D thì M là GTNN của hs trên D 0 0 Kí hiệu Min y = M tại x = x0 D
2/ Tìm GTLN & GTNN:
♥ Dạng 1: nếu D là đọan [a,b]
B1 : Tính y’ ,cho y’ = 0  các điểm tới hạn x , x , x ... [
 a, b], không thuộc *a,b+ ta không lấy 0 1 2
B2 : Tính các giá trị f(x ), f(x ), f(x ), ....., f(a), f(b) so sánh tìm ra giá trị lớn và nhỏ nhất và kết 0 1 2 luận Min và Max
♥ Dạng 2 : nếu D là khoảng (a,b) (vẽ bảng biến thiên) B1 : Tính đạo hàm
B2 : lập BBT , suy ra GTLN , GTNN
PHỤ LỤC PHƯƠNG PHÁP CASIO GIẢI QUYẾT BÀI TOÁN GTLN – GTNN - Bước 1: Đ
ể tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số y  f  x trên miền  ; a b ta sử
dụng máy tính Casio với lệnh MODE 7 (Lập bảng giá trị)
- Bước 2: Quan sát bảng giá trị máy tính hiển thị, giá trị lớn nhất xuất hiện là max , giá trị nhỏ
nhất xuất hiện là min - Chú ý: b  a
Ta thiết lập miền giá trị của biến x Start a End b Step
(có thể làm tròn để Step đẹp) 19
Khi đề bài liên có các yếu tố lượng giác sin , x cos , x tan .
x .. ta chuyển máy tính về chế độ Radian
Ví dụ 1.[Thi thử chuyên KHTN –HN lần 2 năm 2017]
Tìm giá trị lớn nhất của hàm số 3 2
y  x  2x  4x 1 trên đoạn 1;  3 55
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN 2017 A.  67 max B. max  2 C. max  7  D. max  4  27 Hướng dẫn giải 3 1
Sử dụng chức năng MODE 7 của máy tính Casio với thiết lập Start 1 End 3 Step 19
Quan sát bảng giá trị F  X  ta thấy giá trị lớn nhất F  X  có thể đạt được là f 3  2  Vậy max  2
 , dấu = đạt được khi x  3  Đáp số chính xác là B
Ví dụ 2. [Thi Học sinh giỏi tỉnh Ninh Bình năm 2017]
Tìm giá trị lớn nhất M của hàm số y  x  3  6  x A. M  3 B. M  3 2 C. M  2 3 D. M  2  3 Hướng dẫn giải x  3  0
Theo điều kiện xác định thì   3   k  6 6  x  0
Lập bảng giá trị cho y  x  3  6  x với lệnh MODE 7 Start 3  End 6 Step 0.5
Quan sát bảng giá trị thấy ngay 
M  4.2421  3 2 đạt được khi x  1  và 3
m  2.6x10  0 Sử dụng
Casio  Đáp số chính xác là B
Ví dụ 3. [Thi thử chuyên Vị Thanh – Hậu Giang lần 1 năm 2017]
Tìm giá trị nhỏ nhất của hàm số y  x  x  2 2 2 3  7
A. min y  5
B. min y  7 C. min y  3 
D. Không tồn tại min Hướng dẫn giải
Đề bài không nói gì đến miền giá trị của x . Khi đó ta chọn Start 9  End 10 Step 1
Lập bảng giá trị cho y  x  x  2 2 2 3  7 với lệnh MODE 7 56
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN 2017
Quan sát bảng giá trị thấy ngay min y  3
 đạt được khi x 1
 Đáp số chính xác là C
Ví dụ 4. [Thi thử THPT Lục Ngạn – Bắc Giang lần 1 năm 2017] mx  4
Tìm m để hàm số y  2  ;6 x 
đạt giá trị lớn nhất bằng 5 trên   m 3 6 A. m  2 B. m   4 C. m  D. m  6 5 4 7 Hướng dẫn giải 2 Thử với m 
thì giá trị lớn nhất là 25  A sai 6
Tương tự như vậy với m  34 thì giá trị lớn nhất là 5.  Đáp số C chính xác
BÀI TẬP TỰ LUẬN PHẦN GTLN – GTNN
Bài tập 01 : Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 5 4 3 y  x  5x  5x  2
trên đoạn [–1;2] ♥ Giải:
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................  
Bài tập 02 : Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số   2 2x 3x 3 f x  x  trên đoạn [0;2] 1
(Trích đề thi ĐH Khối D – 2013) ♥ Giải:
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 57
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN 2017
Bài tập 03 : Tìm GTLN và GTNN của các hàm số sau: 3 x a) 3 2
y  x  3x  9x 1 trên đoạn [– 4; 4]. b) 2 y  f(x) 
 2x  3x  4 trên đoạn [ 4  ;0] 3 c) 4 2
y  x  8x 16 trên đoạn [–1; 3]. d) 3
y  x  5x  4 trên đoạn [–3; 1]. ♥ Giải:
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài tập 04 : a) y  x  2  6  x b) y  x  5  9  x c) y  x  7  11 x d) 4 2
y  x  2x  5 trên đoạn [–2; 3]. ♥ Giải:
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài tập 05 : Tìm GTLN và GTNN của các hàm số sau: 2sinx 1 a) y      sinx  b) 3 2 y cos x 6cos x 9cosx 5 2
♥ Giải: ............................................................................................................................................................. 58
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN 2017
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. x 1 Bài tập 06 : a) 2
y  x  4  x (ĐH Khối B – 2003) b) y  trên  1
 ; 2 (ĐH Khối D – 2003) 2 x 1
c) Đề Thi THPT Quốc Gia 2015:   4 f x  x  trên đoạn 1;  3 . x  5  d) 3 2
y  2x  3x 12x 1, x  2  ; 3 2 
 e) y  x 3x  5, x  1
 ; 4 f) y  5 4x, x  1  ;  1  2 
♥ Giải:............................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 59
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN 2017
x  m  m
Bài tập 07 : Tìm các giá trị của tham số m để giá trị nhỏ nhất của hàm số f  x 2  x  trên 1 đoạn 0  ;1 bằng 2  . ♥ Giải:
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 2mx 1 1
Bài tập 08 : Giá trị lớn nhất của hàm số y  2;3 là 
khi m nhận giá trị bằng: m  trên   x 3 A.  5 B. 1 C. 0 D. -2 ♥ Giải:
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 1
Bài tập 09 : Một vật chuyển động theo quy luật 3 2
s   t 12t , với t (giây) là khoảng thời gian tính 2
từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong khoảng thời gian đó.
Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu ? A. 512 (m/s) B. 90 (m/s) C. 700 (m/s). D. 96 (m/s). ♥ Giải:
..............................................................................................................................................................................
.............................................................................................................................................................................. 60
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN 2017 1
Bài tập 10 : Một vật chuyển động theo quy luật 3 2
s   t  9t , với t (giây) là khoảng thời gian tính 2
từ lúc vật bắt đầu chuyển động và s (mét) là quảng đường vật đi được trong khoảng thời gian đó.
Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu ? A. 216 (m/s) B. 30 (m/s) C. 400 (m/s) D. 54 (m/s) ♥ Giải:
..............................................................................................................................................................................
.............................................................................................................................................................................
Bài tập 11 :Từ một bờ tường có sẵn, người ta muốn rào quanh một khu đất với một số vật liệu cho
trước là 100 m thẳng hàng rào . Vậy làm thế nào để rào khu đất ấy theo hình chữ nhật sao cho có
diện tích lớn nhất. Khi đó: chiều dài và chiều rộng hình chữ nhật là A. 50 và 25 B. 35 và 35 C. 75 và 25 D. 50 và 50
♥ Giải:.................................................................................................................................................................
.............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................
BÀI TẬP MINH HỌA PHẦN GTLN – GTNN
Ví Dụ 01 : tìm GTLN & GTNN của hàm số 3 2
y  x  3x  2 trên đoạn [1,3]
Các bước chung khi giải một bài toán tìm GTLN – GTNN là
► Bước 1: Ứng với tập xác định  ;
a b của hàm y  f  x , ta tính đạo hàm y '  f 'x .
► Bước 2: Giải phương trình f ' x  0 .
► Bước 3: Nếu giải ra được các nghiệm x ; x ; x ;...x  ta nhận (loại) các nghiệm này trên khoảng 0 1 2 n
 f a     ;
a b đang xét. Khi đó ta có:  f b  
 f  x   ?   i  0,n i 
max f x 
x a;b
Sau đó, so sánh các giá trị và kết luận:  min f x  x  a;b
(☻ không phải hàm số nào cũng tồn tại cả GTLN và GTNN). 61
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN 2017
* Lưu ý rằng, nếu pt f ' x  0 vô nghiệm hoặc các nghiệm tìm được không thuộc  ; a b thì khi đó
GTLN – GTNN của hàm số sẽ đạt được tại x = a, x = b (tạm gọi là 2 biên).
♥ Giải: MXĐ : D = R , hàm số xác định và liên tục trên [1,3] x  0 2 2
y'  3x  6x, y'  0  3x  6x  0  
nhìn vào đoạn [1,3] ta chỉ nhận x = 2 không nhận x = 0 x  2 3 2
f(2)  y(2)  2  3.2  2  2  
Tính các giá trị f(1)  y(1)  0 , f(3)  y(3)  2 
Kết luận : Max y = 2 khi x = 3 và Min y = - 2 khi x = 2 [1,3] [1,3]
Ví Dụ 02 : Tìm GTLN & GTNN của hàm số y  f (x)  x  2  8  x
♥ Giải: MXĐ : D = *2, 8+ , hàm số xác định và liên tục trên *2,8+ 1 1 8  x  x  2 y'(x)     0 2 x  2 2 8  x 2. 8  x. x  2    B 0
8  x  x  2  0  8  x  x  2 (có dạng A  B   ) A  B x  2  0  
 x  5D , f(2)  6; f(5)  2 3; f(8)  6 8   x  2  x
Kết luận : Max y = 2 3 khi x = 5 và Min y = 6 khi x = 2 hay x = 8 [2, 8] [2, 8] BẢNG ĐẠO HÀM    u     u 
u .v  v u n u  n 1   u u  .u         2 u 2  v  v     u  2
sin u  u .cosu cosu  u  .sin u tanu 
 u '. 1 tan u 2   cos u   u  u    u   2 . u a u a .lna log u  cotu   u  '. 1 cot u 2   a  . u ln a sin u
Ví Dụ 03 : Tìm giá trị lớn nhất và nhỏ nhất của hàm số : 3 f (x)  .
x (5  x) trên đoạn 0;5 ♥ Giải: f(x) = 3
x (5  x) hàm số xác định và liên tục trên *0; 5+ 62
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN 2017
trên *0; 5+ thì 5  x  0 ; Nên f(x) 3/2  x(5 x) x  (0;5) 5
f ’(x) = 5  x(5  x) ; f ’(x) = 0  x  5; x  2 . Tính các giá trị : f(2) = 6 3 , f(0) = f(5) = 0 2 Vậy ax M
f(x) = f(2) = 6 3 , Min f(x) = f(0) = 0 x [  0;5] x [  0;5] 2x  3
Ví Dụ 04 : Tìm giá trị lớn nhất, nhỏ nhất của hàm số y   4x 0;1 . x  trên đoạn   1
♥ Giải: Hàm số xác định và liên tục trên đoạn 0  ;1 . 1  Đạo hàm y '   4  0, x
  0;1 . Suy ra hàm số nghịch biến trên đoạn 0  ;1 2   x   1 3
Vậy max y  y 0  3; min y  y   1   . 0; 1 0; 1 2
Ví Dụ 05 : Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số   9
f x  x  x trên đoạn 2; 4 .
♥ Giải: Ta có f  x xác định và liên tục trên đoạn 2; 4 ;  x  3  2;4 f   x 2 9 x 9 1 
. Với x 2; 4 , f   x 2
 0  x  9  0   . 2 2 x x x  3  2;4 13 25 Ta có f 2 
, f 3  6, f 4  . 2 4 13
Suy ra : giá trị lớn nhất và giá trị nhỏ nhất của f  x trên đoạn 2; 4 lần lượt là và 6 . 2
Ví Dụ 06 : Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y   x  2 2sin 1  2 trên đoạn      ;    2 2     
♥ Giải: Đặt t  sin x . Vì x   ;   nên t  1  ;  1 .  2 2 
Hàm số trở thành y   t  2 2 2
1  2  4t  4t  3 , t  1  ; 
1 . Đạo hàm y '  8t  4 . 1
Suy ra y '  0  8t  4  0  t    1  ;  1 . 2  1  Ta có y   1  3; y   2; y     1  11.  2   1 
Vậy max f t   11 khi t  1, suy ra x 
; min f t   2 khi t   , suy ra x   .  1  ;  1 2  1  ;  1 2 6 63
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN 2017 4
Ví Dụ 07 : Tìm giá trị lớn nhất và nhỏ nhất của hàm số f  x 3
 2sin x  sin x trên đoạn 0;π. 3
♥ Giải: Đặt t  sin x . Do x 0;  nên t 0;  1 . 4
Hàm số trở thành f t  3
 2t  t xác định và liên tục trên đoạn 0  ;1 . 3  2 t  0  ;1 Đạo hàm 2 f t  2 '
 2  4t . Suy ra f 't 2
 0  2  4t  0   .  2 t   0  ;1  2  2  2 2 2
Ta có f 0  0; f    ; f   1    . 2 3 3   Vậy:   ► 2 2 2 3 GTLN của hàm số bằng khi t  , suy ra x  và x  ; 3 2 4 4
► GTNN của hàm số bằng 0 khi t  0, suy ra x  0 và x   . x  x  1 
Ví Dụ 08 : Tìm giá trị lớn nhất và nhỏ nhất của hàm số f  x 2 1  ; 2   x  trên đoạn 1 2    ♥ 1
Giải: Hàm số f  x xác định và liên tục trên đoạn ; 2   2   1  x  0  ; 2      2   1  7 x 2 x 2x f '        , f ' x 0
. Tính các giá trị f   ; f   7 2 x  2 1  1   2  6 3 x  2   ; 2     2  7 1 7
Vậy min f  x  khi x 
; m ax f  x  khi x  2. 1  6 2 1  3 x ;2   x ;2    2  2 
Ví Dụ 09 : Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y  x  2x 1 trên đoạn  1  ;0.
♥ Giải: Miền xác định: D  . 2 1  6x  64 x  2  2  Đạo hàm y '   . x  42 2 f 'x  0  0  Suy ra 0 4 2 y '  0  1
 6x  64  0  x  2  f x Giới hạn tại vô cực
lim y  lim y  0 . x x 4  0
Bảng biến thiên
Vậy max y  4 khi x  2 min y  4  khi x  2  . x   1  ;0 x   1  ;0 64
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN 2017
Ví Dụ 10 : Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y  x  2x 1 trên đoạn  1  ;0. ♥ Giải:
Hàm số xác định và liên tục trên đoạn  1  ;0.
Ở đây các em chú ý công   2 B 0 2x 2x 1  2x   Đạo hàm thức y '  1  . A B  2   2 2 A B 2x 1 2x 1 Suy ra 2
y '  0  2x 1  2x  0  2 2x 1  2  x
Và đạo hàm : u u ' '   2  x  0 1 2 u    x    1  ;0 2 2
2x 1  4x 2  1  1 Ta có y   1  1   3; y   ; y   0 1.  2  2 1 1
Vậy max y  1 khi x  0 ; min y  khi x    1  ;  0  1  ;0 2 2
Ví Dụ 11 : Tìm giá trị lớn nhất của hàm số f  x 3 2
 x  3x  72x  90 trên  5  ;  5 .
♥ Giải: Xét hàm số g x 3 2
 x  3x  72x  90 trên  5  ; 
5 ; Hàm số g  x xác định và liên tục trên đoạn  5  ; 
5 ; Đạo hàm g  x 2 '
 3x  6x  72 
Lấy giá trị “bự” nhất x  4  5  ;  g  x 5 '  0   trong các giá trị x  6     5  ;  5 này !!!
Tính các giá trị g 5  7  0, g  5
   400, g 4  8  6.
Suy ra g 5  70; g  5
   400; g 4  86
Vậy Max f  x  Max  g  5
  , g4 , g5  400 khi x  5.    x     x  5;  5 5;5
Ghi chú : Cho hàm số y  f  x liên tục trên  ; a b
Để tìm GTLN – GTNN của hàm số y  f  x trên  ;
a b ta làm các bước :
◙ Xét hàm số y  f x và tìm GTLN – GTNN bình thường như các bài tìm GTLN – GTNN.
◙ Tìm các x , x ...x  ; a b 1 2 n  
◙ Tính f x , f x ... f x , f a , f b 1   2  n     
◙ Số lớn nhất trong các số trên là max và nhỏ nhất trong các số trên là min 65
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN 2017
Ví Dụ 12 : Gọi M , m tương ứng là giá trị lớn nhất và nhỏ nhất của hàm số 3
y  x   2 k  k   1 x trên đoạn  1
 ;2. Khi tham số k thay đổi trên , giá trị nhỏ nhất của M  m bằng: 33 45 A. B. C. 12 D. Kết quả khác. 4 4 ♥ Giải: Chọn B. 2  1  3 Ta có 2
y '  3x   2 k  k   2
1  3x  k    0,  
 ,xk. Do vậy hàm số đã cho tăng trên đoạn  1  ;2.  2  4
Vậy ta có: M  m = y    y   3    2
k  k       2 2 1 2 2 1 1 k  k   1 2  1  45 45 2
 3k  3k 12  3 k    .    2  4 4
Ví Dụ 13 : Cho hàm số 3 2
y  x  3x  3 xác định trên đoạn1; 
3 . Gọi M và n lần lượt là giá trị lớn nhất
và giá trị nhỏ nhất của hàm số, giá trị M  n bằng: A. 1 B. 2 C. 3 D. 4
♥ Giải: Chọn B. Ta có 3 2
y  x  3x  3, D  1;  3 2
 y  3x  6x  3xx  2 x  0 G  TLN M  Khi y  0  
(loại x  0.)  f    f     f   : 3 1 1; 2 1; 3  3   x  2 G
 TNN : n  1 
Vậy tổng giá trị nhỏ nhất và giá trị lớn nhất bằng 2.
Ví Dụ 14 : Giá trị lớn nhất của hàm số 3 4
y  4x  4x là: A. 3 B. 1 C. 4 D. 2 x  0 ♥ Giải: Chọn B 3 4 2 3 2
y  4x  3x , D  R  y  12x 12x  12x 1 x; y  0  x 1 Ta có bảng biến thiên: x 0 1  y ' + 0 + 0  1 y   Câu 15: Cho parabol 2
(P) : y  x  x  2 và điểm (7 A ; 2
 ) . Tìm M trên (P) sao cho khoảng cách AM
là ngắn nhất và tính khoảng cách đó:
A. M (1;0), AM  10
B. M (1;1), AM  10
C. M (1;0), AM  2 10
D. M (1;1), AM  2 10 ♥ Giải: Chọn C. 2
M (P)  M ( ,
x x  x  2) ; AM ngắn nhất 2
 AM ngắn nhất. 2 2 2 2 4 3 2 f ( )
x  AM  (x  7)  (x  x)  x  2x  2x 14x  49 3 2 2
f '(x)  4x  3x  4x 14  (x 1)(4x 10x 14)  0  x 1 66
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN 2017 x  1  f (x)  0  f '(x) 40
Dựa vào bảng biến thiên: min f (x)  40 tại x 1 y  0 . Vậy min AM  2 10 tại M (1;0) .
BÀI TẬP TRẮC NGHIỆM PHẦN GTLN – GTNN Câu 1 : Cho hàm số 4 2
y  x  3x  2 . Giá trị lớn nhất, nhỏ nhất của hàm số này trên đoạn 1;5 lần lượt là 1 1 1 A. 2; 2  B. 552;  C. 553;  D. 552;  3 4 4 Câu 2 : Cho hàm số 4 3 2
y  x  2x  5x  2 . Hiệu của giá trị lớn nhất và nhỏ nhất của hàm số này trên đoạn 0; 
3 có giá trị là M. Khi đó M bằng 11 117 375 91 A. B. C. D. 5 56 16 4
Câu 3 : Giá trị lớn nhất và giá trị nhỏ nhất của hàm số   1 f x  x  trên đoạn 2;5 x 26 5 26 5 26 5 91 5 A. và B. và C. và D. và 5 2 5 4 7 2 4 2
Câu 4 : Giá trị lớn nhất và giá trị nhỏ nhất của hàm số   2 f x  x  trên đoạn  4  ; 2là x 5 7 26 7 91 5 A. 1  và  B. 1  và  C. và  D. và 2 2 7 2 4 2
Câu 5 : Giá trị lớn nhất của hàm số 3 2
y  x  x trên đoạn  2  ; 
1 là nghiệm của phương trình nào sau đây A. 4 2 x  2x  0 B. 3 x  9  x C. 2
x  9  sin x D. 4 x  81  0 3x 1
Câu 6 : Cho hàm số y  x  . Xét các mệnh đề : 3 1 (I) max y  (II) min y  5  0;2 3 0;2
Chọn khẳng định đúng trong các khẳng định sau :
A. (I) đúng (II) sai
B. (I) sai (II) đúng
C. (I), (II) đều đúng
D. (I), (II) đều sai Câu 7 : Cho hàm số 4 2
y  x  2x  3 . Xét các mệnh đề : 67
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN 2017 (I) max y  66 và
(II) min y  11  3  ;2  3  ;2
Chọn khẳng định đúng trong các khẳng định sau :
A. (I) đúng (II) sai
B. (I) sai (II) đúng
C. (I), (II) đều đúng
D. (I), (II) đều sai 4
Câu 8 : Giá trị lớn nhất của hàm số y  f t   2 t  là: 2 A. 3 B. 2 C. 25 D. 0
Câu 9 : Giá trị lớn nhất t của hàm số 2
y  x  4  x là A. 3 2 B. 2 2 C. 3 D. 2
Câu 10 : Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  f  x 2
 2sin x  2sin x 1 theo thứ tự là 3 7 A. 3 và B. 3 và  2 2 3 91 5 C. 3 và  D. và  2 4 2
Câu 11 : Giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y  x  3x  2 trên đoạn  1  0;10 là 5 A. 1 và B. 132 và 0 2 26 7 C. và  D. 10 và 0 7 2
Câu 12 : Giá trị nhỏ nhất của hàm số 2
y  x  4x trên đoạn  1  ;  3 là A. 1 B. 3 7 C. D. 2 2
Câu 13 : Giá trị lớn nhất của hàm số 2
y  x  2x  3 trên đoạn 0; 2 là A. 1 B. 0 C. 3 D. 2 20x 10x  3
Câu 14 : Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  f  x 2  2 3x  2x  theo thứ tự là 1 3 7 A. 3 và B. 3 và  2 2 5 91 5 C. 7 và D. và  2 4 2 68
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN 2017 2 x  2x  2
Câu 15 : Tổng giá trị cực đại và giá trị cực tiểu của hàm số y  x 1 A. 4 B. 8 C. 6 D. 2
Câu 16 : Một chất điểm chuyển động theo phương trình xt 3 2
 3t 9t  2  ;
m s . Vận tốc của vật
đạt giá trị cực tiểu khi t(s) có giá trị A. 1 B. 2 C. 3 D. 4 2 2x  2x  8
Câu 17 : Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  2  ;0 lần lượt là x  trên đoạn   1
M và n, tổng giá trị M + n là : A. 3 B. 14  C. 14 D. 3 
Câu 18 : Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  f  x 9  x  3  ;0 lần 1 trên đoạn   x
lượt là M và n, tổng giá trị M2 + n2 là : A. 107 B. 60 C. 144 D. 106
Câu 19 : Giá trị lớn nhất của hàm số f  x 2
 4  x  2x  4 trên đoạn  2  
;1 là hệ số góc của đường thẳng nào sau đây
A. y  2x  3  0 B. y  2  x  3 C. y  x
D. y  x  3  0 x  x 
Câu 20 : Giá trị lớn nhất và nhỏ nhất của hàm số y  f  x 2 3 6  2; 4 là X và Y. x  trên đoạn   1
Biểu thức A = X + 2Y A. 9 B. 10 C. 3 D. 2 2 2  1 
Câu 21 : Giá trị lớn nhất và giá trị nhỏ nhất của hàm số f  x  x  2 x  2 trên đoạn  ;2    2 
là nghiệm của phương trình A. 2
x  2x  3  0 B. 3 x  2  x  3 C. 2 x  4x  0 D. 3 x  2  x  4
Câu 22 : Giá trị nhỏ nhất và lớn nhất của hàm số f  x 3 2
 x 3x 9x  35 trên đoạn  4  ; 4 là
A. min f  x  4
 1 và max f x  40  4  ; 4  4  ; 4
B. min f  x  1
 và max f x  40  4  ; 4  4  ; 4 69
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN 2017
C. min f  x  4
 và max f x 10  4  ; 4  4  ; 4
D. min f  x 1 và max f  x  9  4  ;  4  4  ; 4
Câu 23 : Giá trị nhỏ nhất và lớn nhất của hàm số f  x 4 2
 x 3x  2 trên đoạn  2  ; 2 là
A. min f  x  2 và max f  x  4  2  ; 2  2  ; 2
B. min f  x  2
 và max f x  0  2  ; 2  2  ; 2
C. min f  x  2 và max f  x  8  2  ; 2  2  ; 2
D. min f  x  2 và max f  x  6  2  ; 2  2  ; 2 8x  3
Câu 24 : Giá trị nhỏ nhất và lớn nhất của hàm số f  x  2
x  x  trên là 1
A. min f  x  4  và f  x 17 max  x x 3
B. min f  x  3  và f  x 16 max  x x 3
C. min f  x  4  và f  x 16 max  x x 3
D. min f  x  3
 và max f x  5 x x x  x 1
Câu 25 : Giá trị nhỏ nhất và lớn nhất của hàm số f  x 2  2 x  x  là 1
A. min f  x  0 và max f  x 1 x x B. f  x 1 min 
và max f  x  3 x 3 x C. f  x 1 min 
và max f  x  5 x 3 x
D. min f  x  3
 và max f x  3 x x  3 
Câu 26 : Tích giá trị nhỏ nhất của hàm số f  x 3
 x 3x  3 trên đoạn 3;    là  2  A. 6 B. -75 C. 4 D. -35
Câu 27 : Cao huyết áp còn gọi là tăng huyết áp và khái niệm thường dùng trong dân chúng là
bệnh tăng xông (tension). Đây là bệnh lý thuờng gặp trong cộng đồng và gia tăng theo tuổi, chiếm
8-12% dân số. Một số yếu tố nguy cơ làm gia tăng nguy cơ cao huyết áp như tiểu đường, thuốc lá,
tăng lipid máu, di truyền. Độ giảm huyết áp của một bệnh nhân được cho bởi công thức G  x 2
 0,025x 30  x , trong đó x (mg) > 0 là liều lượng thuốc cần tiêm cho bệnh nhân. Để huyết
áp giảm nhiều nhất thì cần tiêm cho bệnh nhân một liều lượng bằng : 70
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN 2017 A. 20 mg B. 15 mg C. 30 mg
D. Không xác định được
Câu 28 : Cho hàm số y  f  x 4 2
 x  2x  5 . GTLN của hàm số trên  2
 ;2là một nghiệm của phương trình nào sau đây A. 2 x 13x  0 B. 2 x 12x  0 C. 2
x 13x 14  0 D. 2 x 16  0
Câu 29 : Cho hàm số y  f  x 4 2
 x  2x  5 . GTNN của hàm số trên  2
 ;2có giá trị đối là A. 5 B. 5  C. 4 D. 4 
Câu 30 : Cho hàm số y  f  x  x  2  4  x . Tích GTNN và GTLN của hàm số trên miền xác định là A. 2 B. 2 2 C. 4 D. 4 2
Câu 31 : Cho hàm số 2
y  x  cos x . Xét các mệnh đề sau  2 (I) : Maxy  
(II) : Miny  1    4 2    x 0;   x 0;    4   4  A. (I) đúng và (II) sai B. (I) sai và (II) đúng
C. Cả (I) và (II) đề đúng
D. Cả (I) và (II) đều sai
Câu 32 : Khi tìm GTLN – GTNN của hàm số 4 2
y  sin x  cos x .Một học sinh làm như sau
(I) : Với mọi x ta đều có 4
0  sin x  1 (1) và 2 0  cos x  1 (2)
(II) : Cộng (1) và (2) theo vế ta được 4 2
0  sin x  cos x  2
(III) : Vậy GTLN của hàm số bằng 2 và GTNN của hàm số là 0 Cách giải trên A. Sai từ bước (I) B. Sai từ bước (II) C. Sai từ bước (III)
D. Cả ba bước (I), (II) và (III) đều sai
Câu 33 : (CHUYÊN LÊ HỒNG PHONG) Giá trị lớn nhất của hàm số 3 2
y  2x  3x 12x  2 trên đoạn  1  ;2là A. max y  11. B. max y  6.  1  ;2    1  ;2   C. max y  15. D. max y  10.  1  ;2    1  ;2   71
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN 2017 2 x  9
Câu 34 : (SỞ BẮC NINH) Giá trị lớn nhất của hàm số y  trên đoạn 1;4 là x 25 A. max y  11. B. max y  . 1;  4   1  ;4   4 C. max y  10. D. max y  6. 1;  4   1  ;4  
Câu 35 : (TRƯỜNG THPT CHUYÊN LONG AN) Giá trị lớn nhất, giá trị nhỏ nhất của hàm số x 1 y  1;3 là 2x  trên   1 2 2
A. max y  0; min y  
B. max y  ; min y  0 1  ;3 1  ;3     7 1  ;3 1  ;3   7   
C. max y  3; min y  1
D. max y  1; min y  0 1;  3 1;  3     1;  3 1;  3    
Câu 36 : (TRƯỜNG THPT CHUYÊN PHAN BỘI CHÂU) Cho hàm số 3
y  x  5x  7 . Giá trị lớn
nhất của hàm số trên đoạn  5  ;0 bằng bao nhiêu? A. 80 . B. 143  . C. 5 . D. 7 . mx  4
Câu 37 : Tìm m để hàm số y  2  ;6 . x 
đạt giá trị lớn nhất bằng 5 trên đoạn   m A. m  4 26. B. m   . 5 C. m  6 34. D. m  . 7
Câu 38 : Tìm m để giá trị nhỏ nhất của hàm số 3 2
y  x  3mx  6 trên đoạn 0;  3 bằng 2 A. m  31 2. B. m  . 27 3 C. m  . D. m  1. 2
Câu 39 : Tìm tất cả các giá trị của m để giá trị nhỏ nhất của hàm số 3 2
y  x  3x  m trên đoạn  1   ;1 bằng 0 . A. m  4 . B. m  2 . C. m  6 . D. m  0 .
Câu 40 : (TRƯỜNG THPT CHUYÊN SƯ PHẠM) Giá trị lớn nhất của hàm số 4 3
y  sin x  sin x là A. 1  . B. 2 . C. 0 . D. 3 . 72
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN 2017
Câu 41 : (TRƯỜNG THPT CHUYÊN LÝ TỰ TRỌNG - CẦN THƠ) Giá trị lớn nhất của hàm số 3
y  x  9x  m trên  1  
;1 bằng 0 khi giá trị của tham số thực m bằng A. 8  B. 8. C. 0. D.  3 hoặc 3
Câu 42 : (TRƯỜNG THPT CHUYÊN PHAN BỘI CHÂU) Tìm tất cả các giá trị của m để hàm số  f  x mx 1  1; 2 bằng 2  . x 
có giá trị lớn nhất trên   m A. m  3  . B. m  2 . C. m  4 . D. m  3 .
Câu 43 : Trong tất cả các hình chữ nhật có diện tích S, chu vi của hình chữ nhật có chu vi nhỏ nhất bằng bao nhiêu: A. 2 S B. 2S C. 4S D. 4 S
Câu 44 : Trong số các hình chữ nhật có chu vi 24cm. Hình chữ nhật có diện tích lớn nhất là hình có diện tích bằng. A. 2 S  36 cm B. 2 S  24 cm C. 2 S  49 cm D. 2 S  40 cm
Câu 45 : Cho một tấm nhôm hình vuông cạnh
a như hình vẽ. Người ta cắt ở bốn góc bốn
hình vuông bằng nhau, rồi gập tấm nhôm lại
để được một cái hộp không nắp. Để thể tích
của khối hộp là lớn nhất thì cạnh của hình vuông bị cắt ra bằng: a A. . 6 a B. . 8 a C. . 12 a D. . 24 73
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – GTLN – GTNN 2017
Câu 46 : Cho một tấm nhôm hình vuông cạnh 48cm . Người ta cắt ở 4 góc 4 hình vuông bằng nhau
và gập tấm nhôm lại để được một cái hộp không nắp. Để thể tích khối hộp lớn nhất thì cạnh hình vuông bị cắt dài: 8 A. 8 cm. B. cm . 92 48 C. 24 cm . D. cm . 3 1  t 
Câu 47 : Thể tích nước của một bể bơi sau t phút bơm tính theo công thức V t  4 3  30t   , 100  4 
0  t  90 . Tốc độ bơm nước tại thời điểm t được tính bởi f t V 't. Trong các khẳng định sau,
khẳng định nào đúng ?
A. Tốc độ bơm giảm từ phút thứ 60 đến phút thứ 90.
B. Tốc độ bơm tăng từ phút 0 đến phút thứ 75.
C. Tốc độ bơm luôn giảm.
D. Tốc độ bơm luôn tăng.
Câu 48 (Trích đề thi thử lần 1, k2pi.net.vn) : Người ta tiêm một loại thuốc vào mạch máu ở cách
tay phải của một bệnh nhân. Sau thời gian là t giờ, nồng độ thuốc ở mạch máu của bệnh nhân đó 0, 28t
được cho bởi công thức C t   0  t  24 2   t 
. Hỏi sau bao nhiêu giờ thì nồng độ thuộc ở mạch 4
máu của bệnh nhân là lớn nhất ? A. 12 giờ. B.8 giờ. C. 6 giờ. D.2 giờ. 3x 1
Câu 49 : Tìm giá trị lớn nhất của hàm số y  trên đoạn 0;2 x  3 1 1 A.  . B. 5  . C. 5 . D. . 3 3 209, 4v
Câu 50 : Lưu lượng xe ôtô vào đường hầm được cho bởi công thức f v  2
0,36v 13, 2v  264
(xe/giây), trong đó v km / h là vận tốc trung bình của các xe khi vào đường hầm. Tính vận tốc
trung bình của các xe khi vào đường hầm sao cho lưu lượng xe là lớn nhất và tìm giá trị lớn nhất đó.  264  264  260  264 v  v  v  v   0, 6 B.  0, 5 C.  0, 6 D.  1, 6     f  v  8,9 f  v  6,3 f  v  6, 4 f  v  4,9 74
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIỆM CẬN 2017
PHẦN 4 : TIỆM CẬN
KIẾN THỨC CĂN BẢN
Định nghĩa đường tiệm cận của đồ thị của hàm số A. Tiệm cận ngang
Đường thẳng y  y được gọi là tiệm cận ngang của đồ thị hàm số y  f xnếu 0
lim f x  y hoặc lim f x  y 0 0 x x B. Tiệm cận đứng
Đường thẳng x  x được gọi là tiệm cận đứng của đồ thị hàm số y  f xnếu ít nhất một 0
trong các điều kiện sau được thỏa mãn + lim f x   + lim f x     xx  0 x x0 + lim f x   + lim f x     xx  0 x x0
Đối với dạng này thì chỉ cần chú ý
Lấy bậc cao nhất tử chia cho Các số
làm cho mẫu bằng 0
bậc cao nhất mẫu sẽ ra TCN chính là TCĐ
Số x = 1 không xác định TCĐ : x = 1 không xác 2  4x Ví dụ đị : y  nh 3x  3
tử (- 4x) / mẫu(3x) = - 4/3 TCN : y = -4/3 không xác ax  b
Chú ý : Mọi hàm phân thức hữu tỉ bậc nhất trên bậc nhất y  đều có đ h
ị ai tiệm cận nh cx  d 
 Tiệm cận đứng  d x . c
 Tiệm cận ngang  a y . c
 Đồ thị hàm số nhận giao điểm hai đường tiệm cận làm tâm đối xứng.  75
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIỆM CẬN 2017
BÀI TẬP TỰ LUẬN PHẦN TIỆM CẬN
Bài 1 : Tìm tiệm cận các hàm số sau 2x 1 3  4x x 4  a) y  ; ) b y  ; c) y  ; d ) y  . x  2 x 1 1 2x x  6
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 2 : Tính diện tích của hình chữ nhật tạo bởi 2 tiệm cận, 2 trục tọa độ của các hàm số sau 5x 1 2x 1 a/ y  y  x  b/ 1 x  5
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 2x  2m 1
Bài 3 : Tìm giá trị của tham số m sao cho đồ thị hàm số y  x 
có tiệm cận đứng qua điểm m M  3  ;  1 .
.............................................................................................................................................................................. x  2
Bài 4 : Số tiệm cận của đồ thị hàm số y  là: x  3 A. 0 B. 1 C. 2 D. 3 2x 1
Bài 5 : Tìm tâm đối ứng của đồ thị hàm số y  x 1 76
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIỆM CẬN 2017 A. 1;2 B. 2  ;1 C.  1   ;1 D. 1;  1 
.............................................................................................................................................................................. 2x  m
Bài 6 : Cho hàm số y  mx  . Tìm m sao cho đồ thị hàm số có tiệm cận đứng, tiệm cận ngang và 1
các tiệm cận cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng 8.
..............................................................................................................................................................................
.............................................................................................................................................................................. 5x 1
Bài 7 : Tâm đối xứng của đồ thị hàm số y  x  là điểm nào trong các điểm có tọa độ dưới đây? 1 A. 1;2 B. 1;  1  C.  1  ;10 D. 1;5 x
Bài 8 : ố tiệm cận ngang của hàm số y  là: 2 x 1 A. 0 B. 1 C. 2 D. 3 x  4
Bài 9 : Đồ thị hàm số y  2 x 
có bao nhiêu đường tiệm cận? 16 A. 3 đường B. 4 đường C. 1 đường D. 2 đường 4x  5
Bài 10 : Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y  x  có tiệm cận đứng nằm m bên phải trục Oy . A. Đáp án khác B. m  0 C. m  0 D. m  0
.............................................................................................................................................................................. mx 1
Bài 11 : Cho hàm số y  x 3n . Đồ thị hàm số nhận trục hoành và trục tung làm tiệm cận ngang 1
và tiệm cận đứng. Khi đó tổng m  n bằng: 1 1 2 A.  B. C. D. 0 3 3 3
..............................................................................................................................................................................
.............................................................................................................................................................................. mx 1
Bài 12 : Tìm m để hàm số x  có tiệm cận đứng m A. m 1  ;  1 B. m  1 C. m  1  D. kh ng có m 77
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIỆM CẬN 2017
..............................................................................................................................................................................
..............................................................................................................................................................................
BÀI TẬP MINH HỌA PHẦN TIỆM CẬN 2 x  2x  3
Bài 1 : Tiệm cận ngang của đồ thị hàm số y 
y  x  m d , 2 2x  và các đường thẳng ( ) 1
trục Oy đồng qui tại một điểm khi m bằng: 1 A. 0 B. C. 1 D. 2 2 ☻ 1
Hướng dẫn giải : Tiệm cận ngang là đường thẳng y  , 2 1
Giao của tiệm cận ngang với trục Oy là điểm ( A 0; ) . 2 1 1 (0
A ; )  (d )  m  2 2 (m 1)x 1
Bài 2 : Cho hàm số y  (C) 2x 
. Gọi I là giao điểm của hai đường tiệm cận của (C), O là m
gốc tọa độ và A(4;-6). Khi đó ba điểm O, I, A thẳng hàng khi m bằng: A. -2 B. -1 C. 1 D. 2
☻ Hướng dẫn giải :  m m 1  m m 1 I  ; , OA  (4; 6  ), OI   ;      2 2   2 2  m 1 m O, I, A thẳng hàng  4.  6  0  m  2  . 2 2 3 1
Bài 3 : Cho hàm số y  x 
là tiệm cận đứng của đồ 2016x 
. Tìm m để đường thẳng 2016m 2 thị hàm số? 1 1 A. 1 B. 2 C. D.  2 2
☻ Hướng dẫn giải :
x  m là tiệm cận đứng của đồ thị hàm số vì lim y    xm  1 1 x  1
Để đường thẳng x 
là tiệm cận đứng của đồ thị hàm số thì  2  m  2 2 x  m 1
Bài 4 : Cho hàm số y  2
x  2m   2
1 x  m  . Đồ thị hàm số kh ng có tiệm cận đứng khi và chỉ 1 khi: A. m > 1 B. m < 1 C. m = 1 D. m = -1 78
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIỆM CẬN 2017 ☻ Hướng dẫn giải :
Đồ thị hàm số kh ng có tiệm cận đứng khi và chỉ khi: 2
x  m   2 2
1 x  m 1=0 v nghiệm hay '  0  m 1
BÀI TẬP TRẮC NGHIỆM PHẦN TIỆM CẬN x 1
Câu 1 : Phương trình các đường tiệm cận của đồ thị hàm số y  4x 5 5 5 1 1 5 1 1
A. x  ; y  4 B. x  ; y  C. x  ; y 
D. x  ; y  4 4 4 4 4 4 5 3x  2
Câu 2 : Phương trình các đường tiệm cận của đồ thị hàm số y  x 1 2 1 1
A. x  3; y  1  B. x  1  ; y  3
C. x   ; y  D. x  1  ; y  3 2 3 7 x  2x
Câu 3 : Phương trình đường tiệm cận ngang của đồ thị hàm số y  7 6 4  x  x 1  1 1 A. y  4  B. y  C. y   D. y  4 2 3 2x  3
Câu 4 : Gọi I là giao điểm hai đường tiệm cận của đồ thị hàm số y  x  . Tọa độ của I là : 1 A. (1; 3) B. (1; 2) C. (2; 1) D. (2; 7)
Câu 5 : Chọn phát biểu đúng trong các phát biểu sau đây: 1
A. Hàm số y  2x  kh ng có tiệm cận ngang 1 B. Hàm số 4 2
y  x  x
kh ng có giao điểm với đường thẳng y = 1 C. Hàm số 2 y 
x 1 có tập ác định là D  \{1} D. Đồ thị hàm số 3 2
y  x  x  2x cắt trục tung tại 1 điểm 3x 1
Câu 6 : Cho đường cong (C): y   x 
y   . Khoảng cách từ giao x 
và đường thẳng   : 5 12 4 0 2
điểm hai tiệm cận của (C) đến đường thẳng (∆) bằng 46 37 A. B. 3 13 41 50 C. D. 3 13 x 1 2x 1
Câu 7 : Cho đường cong (C): y  y 
x  có tâm đối xứng là I và đường cong (C’): 1 x  có tâm 3
đối xứng là J. Khi đó độ dài IJ bằng A. 2 B. 3 C. 5 D. 6 2 x  3x  2
Câu 8 : Cho đường cong (C): y  2
2x  x  . Xét các mệnh đề: 1 79
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIỆM CẬN 2017
(I) (C) có tiệm cận đứng x  1 
(II) (C’) có tiệm cận đứng 1 x  2 1
(III) (C) có tiệm cận ngang y  2
Chọn khẳng định đúng trong các khẳng định sau: A. Chỉ (I) và (II) đúng B. Chỉ (I) và (III) đúng C. Chỉ (II) và (III) đúng
D. Cả (I), (II) và (III) đều đúng x 1
Câu 9 : Cho đường cong (C): y  
x  y   . Khoảng cách từ giao
x  và đường thẳng   : 3 4 4 0 2
điểm hai tiệm cận của (C) đến đường thẳng (∆) bằng 14 21 A. B. 5 5 41 50 C. D. 3 13
m 2 x 1
Câu 10 : Cho đường cong (C): y  x 
. Giá trị của tham số m để đường tiệm cận ngang của 2
đồ thị hàm số đi qua điểm M 1; 5   A. 5 B. 1 C. 7  D. 12
Câu 11 : Cho đường cong (C): y  f  x có bảng biến thiên : x  2   y    y  3 3 
11.1 : Phương trình đường tiệm cận đứng là A. x  4  B. x  3  C. x  3 D. x  2 
11.2 : Phương trình đường tiệm cận ngang là 3 A. y  3 B. y  2  C. x  D. y  3  2 mx  n
Câu 12 : Cho đường cong (C): y  , ,
m n  0; m  1; n  2 x 
. Giao điểm của đường tiệm cận 2
đứng đồ thị (C) với đồ thị hàm số 3
y  x 1 là 80
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIỆM CẬN 2017 A. M  2  ; 4   B. M  2  ; 7   C. M  2  ;0 D. M  2  ;0 x
Câu 13 : Cho đường cong (C): y  , 2 
Phương trình đường tiệm cận ngang là x 1 A. y  B. y  1  C. y  2 D. y  3  2 2 x  x  2
Câu 14 : Cho đường cong (C): y  . 2
x  2x  m
Giá trị tham số m để đồ thị hàm số có hai tiệm cận đứng A. m  2 B. m  3 C. m  1  D. m  1 2 x  x  2
Câu 15 : Cho đường cong (C): y  . 2 x  2x 
Giá trị tham số m để đồ thị hàm số có một tiệm cận m đứng A. m  2 B. m  3 C. m  1  D. m  1 2 x  x  2
Câu 16 : Cho đường cong (C): y  . 2 x  2x 
Giá trị tham số m để đồ thị hàm số kh ng có tiệm m cận đứng A. m  2 B. m  3  C. m  1  D. m  1 4  3x
Câu 17 : Cho đường cong (C): y  , 2 
Phương trình đường tiệm cận ngang là x 1 A. y  B. y  1  2 C. y  2 D. y  3 5
Câu 18 : Số đường tiệm cận của đồ thị hàm số y  4x 5 A. 2 B. 0 C. 1 D. 3 81
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIỆM CẬN 2017 5x
Câu 19 : Số đường tiệm cận của đồ thị hàm số y  2 4x  5 A. 2 B. 0 C. 1 D. 3 5
Câu 20 : Số đường tiệm cận của đồ thị hàm số y  2 4x  5 A. 2 B. 0 C. 1 D. . 3 . x 1
Câu 21 : Giá trị tham số m thì đồ thị hàm số sau có tiệm cận y  3 mx 1 A. m  0 B. m  1 C. Cả A và B D. m mx  3
Câu 22 : Cho hàm số y  (C) x  m  , 2
(C) có giao điểm hai đường tiệm cận là I.
Tập hợp các điểm I khi m thay đổi là
A. Đường thẳng y  x  2
B. Đường thẳng y  x  2
C. Đường thẳng y  x  2 ngoại trừ hai điểm  1  ;3, 3;  1
D. Đường thẳng y  x  2 ngoại trừ hai điểm 1;  1 , 3;  1 x  3
Câu 23 : Tiệm cận ngang của đồ thị hàm số y  là: 2 x 1 A. y  3 B. y  2 C. y  1 D. y  1  9 2 x   1  x   1
Câu 24 : Đồ thị hàm số y  2 3x  7x  2
A. Nhận đường thẳng x  3 làm tiệm cận đứng
B. Nhận đường thẳng x  2  làm tiệm cận đứng
C. Nhận đường thẳng y  0 làm tiệm cận ngang
D. Nhận đường thẳng y  3x 10 làm tiệm cận iên 1 x
Câu 25 : Số đường tiệm cận của đồ thị hàm số y  1 là: x A. 1 B. 2 C. 3 D. 0 2 2x  3x  4
Câu 26 : Đồ thị hàm số y  2x 1
A. Nhận đường thẳng x  3 làm tiệm cận đứng 82
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIỆM CẬN 2017 1
B. Nhận đường thẳng x   làm tiệm cận đứng 2
C. Nhận đường thẳng y  1 làm tiệm cận ngang
D. Nhận đường thẳng y  x  2 làm tiệm cận iên
Câu 27 : Đường thẳng x  1 là tiệm cận đứng của đồ thị hàm số nào sao đây? 1 x 2x  2 2 1 x 2 2x  3x  2 A. y  y  y  y  1 B. x x  C. 2 1 D. x 2  x
Câu 28 : Đường thẳng y  2 là tiệm cận ngang của đồ thị hàm số nào sao đây? 1 x 2x  2 2 x  2x  2 2 2x  3 A. y  y  y  y  1 B. 2x x  C. 2 1 D. x 2  x 2x 1
Câu 29 : Giá trị của m để tiệm cận đứng của đồ thị hàm số y  x  đi qua điểm M(2 ; 3) là: m A. 2  B. 2 C. 3 D. 0 2 x  2x
Câu 30 : Số đường tiệm cận của hàm số y  x  là. 2 A. 1 B. 2 C. 0 D. 3 x 1
Câu 31 : Cho hàm số y  x  . Trong các mệnh đề sau, mệnh đề nào sai ? 2
A. Đồ thị hàm số trên có tiệm cận đứng x  2
B. Đồ thị hàm số trên có tiệm cận ngang y  1
C. Tâm đối xứng là điểm I(2 ; 1)
D. Các câu A, B, C đều sai. 2x 1
Câu 32 : Tiệm cận ngang của đồ thị hàm số y  3x  là đường thẳng: 2 2 1 2 3 A. x  B. y  C. y  D. y  3 2 3 2 3x  2
Câu 33 : Tiệm cận đứng của đồ thị hàm số y  x  là đường thẳng: 2 3 A. x  2 B. y  3 C. x 
D. Kh ng có tiệm cận đứng 2 x 1
Câu 34 : Đồ thị hàm số y  5x  có tất cả bao nhiêu đường tiệm cận: 3 A. 2 B. 1 C. 3 D. 0 mx 1
Câu 35 : Với giá trị nào của m thì đồ thị hàm số y  6x  có đường tiệm cận ngang là đường 3 1 thẳng y  2 A. m = 0 B. m = 3 C. m = 6 D. m = 9
Câu 36 : Đồ thị hàm số nào có đường tiệm cận ngang là y = -3: x  2 6x 1 6x 1 A. y  y  y 
y  x  x  3  x  B. 1 2x  C. 6 2  x  D. 3 2 3 2 3 83
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIỆM CẬN 2017 2x 1
Câu 37 : Với giá trị nào của m thì đồ thị hàm số y  3x có đường tiệm cận đừng là đường m thẳng x = 2: A. m = 1 B. m = 2 C. m = 4 D. m = 6
Câu 38 : Đồ thị hàm số nào có đường tiệm cận đứng là = 2: x  2 2x 1 x 1 2 2x  2x 1 A. y  y  y  y  3x  B. 1 x  C. 3 2x  D. 4 x  2 2 2x  2x 1
Câu 39 : Đồ thị hàm số y  3x 
có đường tiệm cận đứng là 2 2 2 3 3 A. y  B. x  C. y  D. x  3 3 2 2 4x  3
Câu 40 : Cho hàm số y  x  có đồ thị (C). Khẳng định nào sau đây là đúng: 5
A. Đồ thị (C) có tiệm cận đứng là = -5 và tiệm cận ngang là y = 4
B. Đồ thị (C) có tiệm cận đứng là y = 4 và tiệm cận ngang là = -5
C. Đồ thị (C) có tiệm cận đứng là = 4 và tiệm cận ngang là y = -5
D. Đồ thị (C) kh ng có tiệm cận 2  x
Câu 41 : Đồ thị hàm số y  2 9 
có tất cả bao nhiêu đường tiệm cận đứng: x A. 4 B. 3 C. 2 D. 1 2  x
Câu 42 : Số đường tiệm cận của đồ thị hàm số y  x  là: 3 A. 0 B. 1 C. 2 D. 3 4  2x
Câu 43 : Đường tiệm cận đứng của đồ thị hàm số y  x  là: 3 A. x  2 B. x  3 C. y = 2 D. y = 3 3x  7
Câu 44 : Đường tiệm cận ngang của đồ thị hàm số y  4x  là: 2 4 1 4 1 A. x  B. x   C. y  D. y   3 2 3 2 x 1
Câu 45 : Cho hàm số y = x  . Số đường tiệm cận của đồ thị hàm số là: 2 A. 0 B. 1 C. 2 D. Kết quả khác. x 1
Câu 46 : Cho hàm số y = x  . Tiệm cận ngang của đồ thị hàm số là đường thẳng có phương 2 1 trình: A. y = -1 B. y = 1 C. y = -2 D. y  2 84
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook
Gv.ThS Nguyễn Vũ Minh – HÀM SỐ – TIỆM CẬN 2017 3  2x
Câu 47 : Cho hàm số y = x  . Tiệm cận đứng của đồ thị hàm số là đường thẳng có phương 1 trình: 2 A. x = -2 B. x  C. x = -1 D. x = 3 3 3  2x
Câu 48 : Cho hàm số y = 2x  . Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là các đường 1
thẳng lần lượt có phương trình: 1 1 3 1 1 3
A. x  , y  1  B. x  1,  y  C. x  , y 
D. x  , y  2 2 2 2 2 2 1
Câu 49 : Cho hàm số y = 2x  . Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là các đường 3
thẳng lần lượt có phương trình: 1 3 3 3 1
A. x  1, y 
B. x  , y  1
C. x  , y  0
D. x  , y  2 2 2 2 2
Câu 50 : Đồ thị của hàm số nào kh ng nhận đường thẳng = 2 làm tiệm cận đứng: x 1 x  3 1 A. y  2  x B. y  C. y  y  x  2 x  D. 2 2  x mx 1
Câu 51 : Tiệm cận ngang của đồ thị hàm số y  x  đi qua điểm A(1;-2) khi m bằng m A. -2 B. -1 C. 1 D. 2
Câu 52 : Đồ thị của hàm số nào kh ng nhận đường thẳng y = 1 làm tiệm cận ngang: 2  x x 1 x  3 A. y   y  y   x  y C. x  B. 3 x  2 x  D. 2 2 85
Đăng kí học thêm Toán tại Biên Hòa qua sđt : 0914449230 – zalo – facebook

Phân dạng và phương pháp giải trắc nghiệm chuyên đề hàm số – Nguyễn Vũ Minh (Tập 1) Toán 12

Thông tin :

Tài liệu liên quan:

Chuyên đề giá trị lớn nhất và giá trị nhỏ nhất của hàm số từ cơ bản đến nâng cao

Chuyên đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số Toán 12

Chuyên đề khảo sát sự biến thiên và vẽ đồ thị hàm số từ cơ bản đến nâng cao

Ôn kiến thức, luyện kỹ năng bài giảng tính đơn điệu của hàm số

Ôn kiến thức, luyện kỹ năng bài giảng cực trị của hàm số