Phân loại dạng và phương pháp giải nhanh chuyên đề mũ và logarit – Nguyễn Vũ Minh

Tài liệu phân dạng và hướng dẫn cách giải các bài toán trắc nghiệm trong chuyên đề phương trình mũ và logarit. Nội dung tài liệu gồm các phần:

+ Phần I: Lũy thừa – Hàm số lũy thừa

67 34 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

170 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
PHÂN LOAI DANG V
PHƯƠNG PHP GIAI NHANH
BIÊN HO – Ngy 31 thng 08 năm 2017
TI LIỆU LƯU HNH NỘI BỘ
Chuyeân ñeà
1
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
A. LŨY THỪA
1. Định nghĩa: Với
a
, lũy thừa bậc n của a là tích của n thừa số a.
thua so
. . . ... .
n
n
a a a a a
2. Lũy thừa với số mũ hữu tỉ
Cho số thực a dương và số hữu tỉ
m
r
n
, trong đó
, , 2m n n
.
Lũy thừa của a với số mũ r là số
xác định bởi
m
n
rm
n
a a a
.
Hay ta chú ý công thức :
2k
x
xác định khi
0x
(k )
21k
x
xác định x (k )
2. Các tính chất : Tất cả các loại lũy thừa đều có tính chất tương tự sau đây (chỉ khác điều kiện):
Cho
0; 0ab
và
,.m n R
Ta có:
Ví dụ tham khảo
0
21
1
77
2
2
1
2
2
1
2
55
1
7
7
aa
4
5
4
5
aa
3
3
3
22
55



Phần I: LŨY THỪA – HÀM SỐ LŨY THỪA
Chú ý
1
a a a
0
1a
1
;0
n
n
aa
a
0
0
và
0
n
không có nghĩa.
0; ,
m
n
m
n
a a a m n
và
11
0; ,
m
n
m
n
m
n
a a m n
a
a
2
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Điền vào bảng :
Bài 01 : Viết các biểu thức sau về dạng lũy thừa của
a
0a
:
a/
3
.aa
b/
7
8
4
.aa
c/
3
0,75
aa
a
d/
5
3
. , , 0a a a b
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 02 : Viết các biểu thức sau về dạng lũy thừa biết a, b > 0:
a/
5
3
8
..a a a
b/
3
5
aa
c/
4
32
4
3
12 6
.
.
ab
ab
d/
35
4
....a a a a a
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
1
9
0
(4,72)
2
( 2)
3
( 2)
4
3
3
( 4)
3
5
a
4
3
1
a
=
3
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
..............................................................................................................................................................................
Bài 03 : Viết các biểu thức sau về dạng lũy thừa :
a/
xxx
b/
21
2
1
.a
a



c/
2
4
3
xx
d/
5
3
222
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 04 : Rút gọn :
3
4
5
4
3
4. 64.( 2)
A
32
3 5 3
2
3
5
243. 3. 9. 12
B
( 3) . 18. 27. 6
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 05 : Chứng minh:
a/
4 2 3 4 2 3 2
b/
33
7 5 2 7 5 2 2
c/
33
9 80 9 80 3
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
4
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 04 (THPT chuyên Vĩnh Phúc lần 5) : Cho biểu thức
3
3
4
.P x x x
, với
0.x
Mệnh đề nào
dưới đây đúng? A.
1
2
Px
. B.
7
24
Px
. C.
15
24
Px
. D.
7
12
Px
.
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 05 (SỞ GDĐT HƯNG YÊN) : Biểu thức
6
5
3
..Q x x x
với
0x
viết dưới dạng lũy thừa với
số mũ hữu tỷ là. A.
2
3
Qx
. B.
5
3
Qx
. C.
5
2
Qx
. D.
7
3
Qx
.
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 06 (THPT chuyên Lê Thánh Tông) : Cho biểu thức
3
23
k
P x x x
0x
. Xác định
k
sao cho
biểu thức
23
24
Px
. A.
2k
. B.
6k
. C.
4k
. D. Không tồn tại
k
.
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
5
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
..............................................................................................................................................................................
Bài 07 : Với giá trị thực nào của
a
thì
24
5
3
4
1
1
. . 2 .
2
aaa
A.
0a
B.
1a
C.
2a
D.
3a
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 08 (THPT Ngô Sĩ Liên lần 3) : Rút gọn biểu thức:
11
16
: , 0x x x x x x
ta được.
A.
4
x
. B.
6
x
. C.
8
x
. D.
x
.
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 09 (Sở GD – ĐT Hưng Yên) : Giá trị của biểu thức
2 1 2 1 2
3 .9 .27E

bằng:
A. 3 B. 27 C. 9 D. 1
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài tập mẫu tham khảo 01 : Rút gọn biểu thức
41
1
2
33
3
3
22
3
33
8
. 1 2
24
a a b b
Aa
a
a ab b





(giả thiết biểu
thức có nghĩa) được kết quả là (nguồn : thầy CAO TUẤN)
A.
1.
B.
.ab
C.
0.
D.
2.ab
♥ Hướng dẫn giải :
Cách 1 : Ta có:
1 1 1
1
22
3 3 3
3
33
2 1 1 2 1 1 3 3
11
3 3 3 3 3 3
33
8 . 8
.
2 4 2
2
a a b a a a b
a
A a a
a a b b a b
ab

6
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
2
2 2 2
3
3 3 3
8
0
8
a a b
a a a
ab
Cách 2: Ta sẽ gán cho
a
và
b
những giá trị cụ thể
(sao cho thỏa mãn điều kiện có nghĩa của biểu thức A).
Ở đây ta gán
1
1
a
b

, khi đó
41
1
2
33
3
3
22
3
33
1 8.1 .1 1 1 8
. 1 2 1 . 1 2 1 1 1 0
17
1 2 1.1 4.1
A






Chọn C.
Bài tập mẫu tham khảo 02 : Cho
33
2 4 2 2 2 4
M a a b b a b
và
3
33
22
N a b
. Ta có kết
luận A.
.MN
B.
0.MN
C.
.MN
D.
.MN
♥ Hướng dẫn giải :
Nhập
3
3 3 3 3
2 4 2 2 2 4 2 2
1; 1
0
CALC a b
a a b b a b a b M N


Chọn D.
Bài tập mẫu tham khảo 03 : Rút gọn biểu thức
44
1 1 1 , 0C x x x x x x x
ta
được (nguồn : thầy CAO TUẤN)
A.
2
1.x
B.
2
1.xx
C.
2
1.xx
D.
2
1.x
♥ Hướng dẫn giải :
Cách 1 : Ta có:
44
1 1 1M x x x x x x
2
1 1 1 1x x x x x x x x



2
2
1 1 1 1x x x x x x x x
Chọn B.
Cách 2 : Nhập
44
100
1 1 1 10101
CALC X
X X X X X X

Ta có:
22
100
10101 100 100 1 1
x
xx

Chọn đáp án B.
Cách 3 : Thử lần lượt với 4 đáp án. Cơ sở lí thuyết:
1, 0
A
A B B
B
7
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Lần 1: Nhập
2
44
3
1 1 1 : 1
1
2
CALC
X X X X X X X
X

loại A.
Lần 2: Bấm phím ! để sửa biểu thức thành:
2
44
1 1 1 : 1 1
1
CALC
X X X X X X X X
X

Chọn B.
Bài tập mẫu tham khảo 04 : Rút gọn biểu thức
1
2
11
22
1 2 , , 0,
yy
D x y x y x y
xx







ta
được A.
.x
B.
2.x
C.
1.x
D.
1.x
♥ Hướng dẫn giải :
Cách 1 :
2
2
2
22
1
1
xy
y
D x y x y x
x
xx











Chọn A.
Cách 2 : Thử lần lượt với 4 đáp án.
Nhập
1
2
11
22
1 2 : 1
1; 0
YY
CALC
D X Y X
XY
XX









Chọn A.
Bài tập mẫu ứng dụng CASIO 01: Giá trị của biểu thức
41
1
2
33
3
3
22
3
33
8
. 1 2
24
a a b b
Pa
a
a ab b





là
A.
1.P
B.
0.P
C.
.
a
P
b
D.
.
b
P
a
Bài tập mẫu ứng dụng CASIO 02: Giá trị của biểu thức
2
11
2
22
:2
bb
Q a b b b
aa







là
A.
.Qa
B.
.Qb
C.
1.Q
D.
.
a
Q
b
Bài tập mẫu ứng dụng CASIO 03 (THPT Trần Cao Vân - Khánh Hòa)
Rút gọn biểu thức
3 1 2 3
22
22
.aa
a

(với
0a
) được kết quả:
A.
4
a
B.
C.
3
a
D.
a
Bài tập mẫu ứng dụng CASIO 04 (THPT QG - 2017)
Rút gọn biểu thức
5
3
3
:Q b b
với
0b
.
Nhập máy
Nhập máy
Nhập máy
Nhập máy
8
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
A.
2
Qb
B.
4
3
Qb
C.
4
3
Qb
D.
5
9
Qb
Bài tập mẫu ứng dụng CASIO 05 (Sở GD và ĐT Long An)
Cho
x
là số thực dương, viết biểu thức
3
2
6
.Q x x x
dưới dạng lũy thừa với số mũ hữu tỉ.
A.
2
Qx
. B.
2
3
Qx
.
C.
Qx
. D.
5
36
Qx
.
Trắc nghiệm phần lũy thừa
Câu 01 : Các căn bậc hai của
4
là
A.
2
. B.
2
. C.
2
. D.
16
Câu 02 : Các căn bậc bốn của
là
A.
3
. B.
3
. C.
3
. D.
9
Câu 03 (THPT Nguyễn Chí Thanh - Khánh Hòa) : Giá trị của
4
0,75
3
11
81 27
K


bằng.A.
180K
. B.
108K
. C.
54K
. D.
18K
.
Câu 04 : Viết biểu thức
aa
0a
về dạng lũy thừa của
a
, ta được:
A.
5
4
a
. B.
1
4
a
. C.
3
4
a
. D.
1
2
a
Câu 05 : Giá trị của biểu thức
2 3 3 2 3
9 :27A
là:
A. 9 B.
4 5 3
3
C. 81 D.
4 12 3
3
Câu 06 : Tính:
11
3
1
2
2
0
33
2
0,001 2 .64 8 9

kết quả là:
A.
115
16
B.
109
16
C.
1873
16
D.
111
16
Câu 07 : Tính:
13
35
0,75
11
81
125 32

kết quả là:
A.
80
27
B.
79
27
C.
80
27
D.
352
27
Nhập máy
9
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Câu 08 (THPT Hoàng Văn Thụ - Khánh Hòa) : Cho biểu thức
5
4
.A a b
, điều kiện xác định của
biểu thức
A
là.
A.
a
tùy ý,
0b
. B.
0; 0ab
. C.
a
tùy ý,
0b
. D.
0; 0ab
.
Câu 9 : Các căn bậc bảy của 128 là
A.
2
. B.
2
. C.
2
. D.
8
Câu 10 : Viết biểu thức
5
3
, , 0
ba
ab
ab
về dạng lũy thừa
m
a
b



, với giá trị của
m
là
A.
2
15
. B.
4
15
. C.
2
5
. D.
2
15
.
Câu 11 : Cho
36
( ) .f x x x
khi đó
(0,09)f
bằng :
A.
0,09
. B.
0,9
. C.
0,03
. D.
0,3
Câu 12 : Cho
3
2
6
xx
fx
x
khi đó
1,3f
bằng:
A.
0,13
. B.
1,3
. C.
0,013
. D.
13
.
Câu 13 : Rút gọn biểu thức:
2
31
3
:bb
A.
34
b
B.
34
b

C.
34
b
D.
2 3 4
b
Câu 14 : Đơn giản biểu thức
4
8
4
1xx
, ta được:
A.
2
1xx
. B.
2
1xx
. C.
2
1xx
. D.
2
1xx
.
Câu 15 : Đơn giản biểu thức
9
3
3
1xx
, ta được:
A.
3
1xx
. B.
3
1xx
. C.
3
1xx
. D.
3
1xx
.
Câu 16 (THPT Chuyên Quang Trung) : Cho các số thực
, , ,a b m n
với
,0ab
. Tìm mệnh đề sai.
A.
2
aa
. B.
.
m
mm
a
ab
b



. C.
n
m m n
aa
. D.
.
m
mm
ab a b
.
Câu 17 : Đơn giản biểu thức
21
2
1
.Pa
a



được kết quả là
A.
2
a
. B.
2 2 1
a
. C.
12
a
. D.
a
.
10
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Câu 18 : Cho
a
,
b
là các số dương. Rút gọn biểu thức
4
32
4
3
12 6
.
.
ab
P
ab
được kết quả là
A.
2
ab
. B.
2
ab
. C.
ab
. D.
22
ab
.
Câu 19 : Căn bậc 4 của 3 là
A. . B. . C. . D. .
Câu 20 : Căn bậc 3 của – 4 là
A. . B. . C. . D. Không có.
Câu 21 : Cho
a
là số thực dương. Biểu thức
4
3
8
a
được viết dưới dạng lũy thừa với số mũ hữu tỉ
là
A.
3
2
a
. B.
2
3
a
. C.
3
4
a
. D.
4
3
a
.
Câu 22 : Cho
x
là số thực dương. Biểu thức
2
4
3
xx
được viết dưới dạng lũy thừa với số mũ hữu tỉ
là
A.
7
12
x
. B.
5
6
x
. C.
12
7
x
. D.
6
5
x
.
Câu 23 : Cho
b
là số thực dương. Biểu thức
2
5
3
bb
bb
được viết dưới dạng lũy thừa với số mũ hữu
tỉ là
A. – 2. B. – 1. C. 2. D. 1.
Câu 24 (Đề minh họa lần 2 – Bộ GDĐT) : Cho biểu thức
4
3
23
..P x x x
, với
0x
. Mệnh đề nào
dưới đây đúng ?
A.
2
3
Px
. B.
1
4
Px
. C.
13
24
Px
. D.
1
2
Px
.
Câu 25 (Đề thi thử Cụm 1 – HCM) : Cho biểu thức
5
4
Px
, với
0x
. Mệnh đề nào dưới đây là
mệnh đề đúng?
A.
4
5
Px
. B.
9
Px
. C.
20
Px
. D.
5
4
Px
.
Câu 26 : Với số dương
a
và các số nguyên dương
m
,
n
bất kì. Mệnh đề nào dưới đây đúng?
A.
()
n
m m n
aa
. B.
n
m
n
m
aa
. C.
m
m
nn
aa
. D.
.
.
m n m n
a a a
.
3
4
4
3
4
3
4
3
3
4
3
4
3
4
11
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Câu 27 : Cho các số thực dương
a
và
b
. Rút gọn biểu thức
4
4 4 4 4
a b a ab
P
a b a b



được kết quả là
A.
4
b
. B.
44
ab
. C.
ba
. D.
4
a
.
Câu 28 : Cho
0, 0ab
. Biểu thức thu gọn của biểu thức
1 1 1 1 1 1
4 4 4 4 2 2
P a b a b a b
là
A.
10 10
ab
. B.
ab
. C.
ab
. D.
88
ab
.
Câu 29 : Cho các số thực dương
a
và
b
. Rút gọn biểu thức
2
3 3 3
33
:
ab
P ab a b
ab



được
kết quả là
A.
1
. B.
1
. C.
2
. D. 3
Câu 30 (THPT CHUYÊN VINH) : Giả sử
a
là số thực dương, khác
1
. Biểu thức
3
aa
được viết
dưới dạng
a
. Khi đó.
A.
2
3
. B.
5
3
. C.
1
6
. D.
11
6
.
Câu 31 (THPT Lê Hồng Phong) : Cho
1
2
11
22
12
yy
P x y
xx







. Biểu thức rút gọn của
P
là
.
A.
.x
. B.
.xy
.
C.
.xy
. D.
2.x
.
Câu 32 (THPT Hà Huy Tập) : Viết biểu thức
3
4
.P x x
(
0x
) dưới dạng luỹ thừa với số mũ hữu
tỷ.
A.
5
4
Px
. B.
5
12
Px
. C.
1
7
Px
. D.
1
12
Px
.
Câu 33 (THPT Đặng Thúc Hứa) : Cho biểu thức
6
4
5 3
. . ,P x x x
với
0x
. Mệnh đề nào dưới đây
đúng?
A.
15
16
Px
. B.
7
16
Px
. C.
5
42
Px
. D.
47
48
Px
.
Câu 34 (Đề thi thử Cụm 1 – HCM) : Cho biểu thức
2
4
3
P x x
,
0x
. Mệnh đề nào dưới đây
đúng?
A.
6
12
Px
. B.
8
12
Px
. C.
9
12
Px
. D.
7
12
Px
.
12
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Câu 35 : Giả sử với biểu thức B có nghĩa, Rút gọn biểu thức
1 9 1 3
4 4 2 2
1 5 1 1
4 4 2 2
a a b b
B
a a b b



ta được:
A.
2
B.
ab
C.
ab
D.
22
ab
Câu 36 : Cho hai số thực
0, 0, 1, 1a b a b
, Rút gọn biểu thức
7 1 5 1
3 3 3 3
4 1 2 1
3 3 3 3
a a b b
B
a a b b



ta được:
A.
2
B.
ab
C.
ab
D.
22
ab
Câu 37 : Rút gọn biểu thức
24
4
:x x x

(x > 0), ta được:
A.
4
x
B.
3
x
C.
x
D.
2
x
Câu 38 : Biểu thức
0x x x x x x
được viết dưới dạng lũy thừa với số mũ hữu tỉ là:
A.
31
32
x
B.
15
8
x
C.
7
8
x
D.
15
16
x
Câu 39 : Rút gọn biểu thức:
11
16
: , 0A x x x x x x
ta được:
A.
8
x
B.
6
x
C.
4
x
D.
x
Câu 40 : Rút gọn
3
5
3
22222P
, ta đuợc:
A.
13
18
2
B.
13
15
2
C.
13
18
2
D.
13
18
2
Câu 41 (Trích đề Minh họa lần 3): Tính giá trị của biểu thức
2017 2016
7 4 3 4 3 7P
.
A.
1P
B.
7 4 3P 
C.
7 4 3
D.
2016
7 4 3P 
Câu 42 (Trích đề Minh họa lần 2): Cho biểu thức
4
3
23
..P x x x
, với
0x
. Mệnh đề nào dưới đây
đúng?
A.
1
2
Px
B.
13
24
Px
C.
1
4
Px
D.
2
3
Px
13
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
B. HÀM SỐ LŨY THỪA
1. Định nghĩa: Hàm số
yx
với
được gọi là hàm số lũy thừa
2. Tập xác định: Tập xác định của hàm số
yx
là:
3. Đạo hàm: Hàm số
, ( )yx

có đạo hàm với mọi
0x
và công thức đạo hàm chính là :
4. Tính chất của hàm số lũy thừa trên khoảng
(0; )
.
, 0yx

, 0yx

Tập khảo sát:
(0; )
Tập khảo sát:
(0; )
Sự biến thiên:
+
1
0, 0.y x x
+ Giới hạn đặc biệt:
0
lim 0, lim .
x
x
xx



+ Tiệm cận: không có
Sự biến thiên:
+
1
0, 0.y x x
+ Giới hạn đặc biệt:
0
lim , lim 0.
x
x
xx



+ Tiệm cận:
Ox là TCN. Oy là TCĐ.
Bảng biến thiên:
x
0

y
y

0
Bảng biến thiên:
x
0

y
y

0
Đồ thị:
α
O
y
x
1
1
01

Nhận xét :
14
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Bài 01: Tìm miền xác định của các hàm số sau :
a/
3
2
y x 3x 4
b/
1
2
7
y x x 2
c/
4
5
y 2 5x

d/
8
2
5
y 5 x
e/
3
y 12 x
f/
8
2
y x 7x 8
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Chú ý : Mở rộng cho hàm :
y u x


Nếu
nguyên dương thì hàm số xác định
x
Nếu
0
hoặc
(nguyên âm) thì hàm số xác định khi
0ux
I
1
1
0
0
15
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Nếu
(không nguyên) thì hàm số xác định khi
0ux
Bài 02: Tìm miền xác định của các hàm số sau :
a/
3
2
y 3 2xx
b/
15
42
y2xx
c/
7
y 2 6xx
d/
1
2
9
y x 3x 4
e/
6
2
y x 3x 2
f/
9
5
y 7 6x

☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 03: Tìm miền xác định của các hàm số sau :
a/
9
2
5
y 16 3x
b/
3
y 5 4x
c/
6
2
y x 7x 8
d/
5
2
y 2 3xx
e/
8
42
y 3 4xx
f/
8
y 2 3x
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
16
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 04: Tìm tập xác định của hàm số
a/ (Sở GD – ĐT Bình Phước) :
2
2
23y x x
.
A.
3;1
B.
; 3 1; 
C.
3;1
D.
; 3 1; 
b/ (THPT Nguyễn Tất Thành) :
2
3
( 2)yx
A.
\2
B.
( 2; ) 
C.
(0; )
D.
c/ (THPT chuyên Lê Thánh Tông) :
12
2
1yx

A.
\1D
B.
\1D
C.
1,1D 
D.
;1 1;D  
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 05 (THPT chuyên Lê Hồng Phong – Nam Định) : Tính đạo hàm của hàm số
6
1 cos3yx
A.
5
' 18sin3 cos3 1y x x
B.
5
' 18sin3 1 cos3y x x
C.
5
' 6sin3 1 cos3y x x
D.
5
' 6sin3 cos3 1y x x
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
17
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Bài 06 (Sở GD – ĐT Hưng Yên) : hàm số
4
2
3
3yx

có đạo hàm trên khoảng
3; 3
là:
A.
7
2
3
8
3
3
y x x

B.
7
2
3
8
3
3
y x x
C.
7
22
3
4
3
3
y x x
D.
7
2
3
4
3
3
yx
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 07 (THPT Lạc Long Quân – Khánh Hòa ) : Tìm tập xác định
D
của hàm số
3
2
1
x
y
x



A.
\1D
B.
\2D
C.
\ 1;2D
D.
D
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Trắc nghiệm phần lũy thừa
Câu 01 : Tìm
x
để biểu thức
2
21x
có nghĩa.
A.
1
2
x
B.
1
2
x
C.
1
;2
2
x




D.
1
2
x
Câu 02 : Tìm
x
để biểu thức
2
2
3
1xx

có nghĩa.
A.
x
B. Không tồn tại
x
C.
1x
D.
\0x
Câu 03 (THPT Chuyên Sơn La) : Hàm số
4
1yx

có tập xác định là.
A.
;1
. B.
1; 
. C. . D.
\1
.
Câu 04 (THPT Nguyễn Quang Diệu) : Tìm tập xác định của hàm số
2
2
23y x x
.
A.
; 3 1; 
B.
3;1
C.
3;1
D.
; 3 1; 
Câu 05 (THPT Chuyên Vinh) : Tập xác định của hàm số
2
2y x x

là.
18
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
A.
;0 2; 
B.
1
0;
2



C.
0;2
D.
0;2
Câu 06 (Sở GD – ĐT Hà Tĩnh) : Hàm số
1/3
yx
có tập xác định là.
A. B.
\0
C.
0;
D.
0;
Câu 07 (Sở GD – ĐT Hà Tĩnh) : Điều kiện xác định của hàm số
3
22
x
y

là.
A.
0x
B.
1x
C.
1x
D.
0x
Câu 08 (THPT Lương Tài) : Tập xác định của hàm số
2
yx
là.
A.
0;D
B.
0;1D
C.
*
D
D.
D
Câu 09 : Tập xác định của hàm số
1
3
(1 2 )yx
là.
A.
1
;
2



B.
1
;
2




C. D.
0; 
Câu 10 (THPT Thuận Thành 2) : Tìm tập xác định
D
của hàm số
1
3
(2 1)yx
.
A.
1
;
2
D


B.
D
C.
1
\
2
DR



D.
1
;
2
D



Câu 11 (Sở GDĐT Lâm Đồng) : Hàm số y =
4
2
41x
có tập xác định là:
A.
0;
B.
11
\;
22


C.
11
;
22



D.
Câu 12 (TT Tân Hồng Phong) : Tìm tập xác định
D
của hàm số
1
3
f x x
A.
D
B.
0;D
C.
0;D
D.
\0D
Câu 13 (THPT Thanh Thủy) : Tập xác định của hàm số
5
2
26y x x
là.
A.
3
;2
2
D




B.
3
; 2;
2
D

 


C.
3
\ 2;
2
D


D.
D
Câu 14 (THPT Nguyễn Huệ-Huế) : Tìm tập xác định của hàm số
4
2
41yx

.
A. B.
11
;
22



C.
0;
D.
11
\;
22


19
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Câu 15 (THPT Hoàng Văn Thụ - Hòa Bình) : Tập xác định của hàm số
1
2
3
32y x x
.
A.
\ 1;2
B.
;1 2; 
C.
;1 2;
D.
Câu 16 : Tập xác định của hàm số
1
3
(1 2 )yx
là.
A.
1
;
2



B.
1
;
2




C. D.
0; 
Câu 17 (THPT Trần Phú - HP) : Hàm số
4
2
41yx

có tập xác định là.
A.
11
\;
22


B. C.
11
;;
22
 
D.
11
;
22



Câu 18 (THPT Tiên Du 1) : Tập xác định của hàm số
5
23yx
là.
A.
2
\
3
D



B.
2
;
3
D



C.
2
;
3
D




D.
2
;
3
D



Câu 19 : Cho các hàm số
1
1
4
3
2
1 2 3 4
( ) , ( ) , ( ) , ( ) .f x x f x x f x x f x x
Trong các hàm số trên, hàm số
nào có tập xác định là nữa khoảng
0; ?
.
A.
1
()fx
và
2
()fx
B.
12
( ), ( )f x f x
và
3
()fx
C.
3
()fx
và
4
()fx
D. Cả 4 hàm số trên
Câu 20 (THPT Hoàng Văn Thụ - Khánh Hòa) : Hàm số
15
2
4yx

có tập xác định là.
A.
; 2 2;D  
B.
D
C.
; 2 2;D 
D.
2;2D 
Câu 21 (TTGDTX Nha Trang - Khánh Hòa) : Hàm số
3
2
5
4yx
có tập xác định là:
A. B.
; 2 2;
C.
( 2;2)
D.
\2
Câu 22 (TTGDTX Cam Lâm - Khánh Hòa) : Trong các hàm số sau đây, hàm số nào đồng biến trên
các khoảng xác định?
A.
4
yx
B.
4
yx
C.
3
4
yx
D.
3
yx
Câu 23 (THPT Nguyễn Thị Minh Khai - Khánh Hòa) : Cho
3
22
.f x x x
Giá trị của
1f
bằng:
A.
2
. B.
8
3
C.
4
D.
3
8
20
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Câu 24 (TTLT ĐH Diệu Hiền) : Tập xác định của hàm số
4
2
6y x x
là.
A.
\ 2;3D
B.
\0D
C.
;2 3;D  
D.
D
Câu 25 (TTGDTX Cam Lâm - Khánh Hòa) : Một chuyển động có phương trình là
(t) (m)s f t t t
. Tính gia tốc tức thời của chuyển động tại thời điểm
1ts
.
A.
2
7
( / )
64
ms
B.
2
7
( / )
8
ms
C.
7
( / )
64
ms
D.
2
7
( / )
64
ms
Câu 26 (THPT Hai Bà Trưng- Huế) : Tập xác định của hàm số
3
3
27yx

là.
A.
D
B.
3;D
C.
\3D
D.
3;D
Câu 27 (THPT Ngô Quyền) : Tìm tập xác định
D
của hàm số
4
2
1yx

.
A.
D
B.
; 1 1;D  
C.
0;D
D.
\ 1;1D
Câu 28 : Tìm tập xác định của hàm số
2
32
6 11 6y x x x
.
A.
D
B.
\ 1;2;3D
C.
1;2 3;D 
D.
;1 2;3D 
Câu 29 (THPT Chuyên Vinh) : Tập xác định của hàm số
1
2
1yx

là.
A.
;1D 
B.
1;D 
C.
0;1D
D.
1;D 
Câu 30 (THPT Nguyễn Đăng Đạo) : Đạo hàm của hàm số
1
3
21yx

trên tập xác định là.
A.
1
3
2 2 1 ln 2 1xx

B.
1
3
2 1 ln 2 1xx

C.
4
3
2
21
3
x

D.
4
3
1
21
3
x

Câu 31 (THPT Lý Nhân Tông) : Hàm số
2
2
5
1yx
có đạo hàm là.
21
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
A.
2
2
5
4
1
y
x
B.
2
21y x x

C.
5
2
41y x x

D.
3
2
5
4
51
x
y
x
Câu 32 (THPT Thái Phiên – HP) : Tìm tập xác định
D
của hàm số
1
2
3
68y x x
.
A.
D
B.
2;4D
C.
;2 4;D 
D.
;2 4;D 
C. SO SÁNH MŨ – LŨY THỪA
Ví Dụ 01 : Hãy so sánh các cặp số sau :
a/
1,7 0,8
22
♥ ta có
1,7 0,8
a 2 1
22
1,7 0,8


Cơ sở lý thuyết
22
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
b/
1,7 0,8
11
22
♥ ta có
1,7 0,8
1,7 0,8
11
1
22
0 a 1
2

c/
1,2 2
33
22
♥ ta có
1,2 2
1,2 2
33
3
22
0 a 1
2

d/
35
30 20
♥ ta có
15 15
55
3
35
15 15
33
5
30 30 243.10
30 20
20 20 8.10



e/
3
4
57
♥ ta có
3
12
4 12
3
4
4
12
3
12
5 5 125
75
7 7 2401



f/
3
17 28
♥ ta có
6
3
6
3
6
2
36
17 17 4913
17 28
28 28 784



Ví Dụ 02 : Cho
2 1 2 1 .

Kết luận nào sau đây đúng?
A.
.

B.
.

C.
.

D.
.

♥ Hướng dẫn giải :
Cách 1: Do
2 1 0 2 1 0;1
(có nghĩa ta sẽ đổi chiều)
nên
2 1 2 1 .


Chọn B
Cách 2: Cho hai giá trị cụ thể ví dụ
1 ; 2XY

sau đó lập hiệu
1; 2
2 1 2 1
XY
CALC
XY

đáp án B
Bài 01 : So sánh các cặp số sau :
a/
65
77

b/
2 3 3 2
55
c/
5 3 3 5
77
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
23
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Bài 02 : So sánh các cặp số sau :
d/
2 1,4
10 10
e/
300 200
23
f/
3,14
11
44
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 03 (THPT Cẩm Bình) : Nếu
8
3
9
4
aa
thì cơ số
a
phải thỏa điều kiện
A.
0a
. B.
01a
. C.
0a
. D.
1a
.
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Trắc nghiệm phần so sánh mũ – lũy thừa
Câu 01 : Khẳng định nào sau đây đúng?
A.
0
1,aa
B.
2
11aa
C.
2 3 3 2
D.
12
11
44
Câu 02 : Nếu
2
2 3 1 2 3 1
a
thì
A.
1a 
. B.
1a
.
C.
1a 
. D.
1a 
.
Câu 03 : Trong các khẳng định sau đây, khẳng định nào sai?
A.
22
0,01 10

. B.
22
0,01 10

.
C.
22
0,01 10

. D.
0
1, 0aa
.
Câu 04 : Trong các khẳng định sau đây, khẳng định nào đúng?
A.
34
2 2 2 2
. B.
6
11 2 11 2
.
C.
34
4 2 4 2
. D.
4
3 2 3 2
.
24
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Câu 05 : Nếu
22
3 2 3 2
m
thì
A.
3
2
m
. B.
1
2
m
.
C.
1
2
m
. D.
3
2
m
.
Câu 06 : So sánh hai số
m
và
n
nếu
11
99
mn
.
A. Không so sánh được B.
mn
C.
mn
D.
mn
Câu 07 : So sánh hai số
m
và
n
nếu
33
22
mn
.
A.
mn
. B.
mn
. C.
mn
. D. Không so sánh được.
Câu 08 : So sánh hai số
m
và
n
nếu
5 1 5 1
mn
.
A.
mn
. B.
mn
. C.
mn
. D. Không so sánh được.
Câu 09 : So sánh hai số
m
và
n
nếu
3,2 3,2
mn
thì:
A.
mn
. B.
mn
. C.
mn
. D. Không so sánh được.
Câu 10 : So sánh hai số
m
và
n
nếu
22
mn
A
mn
. B.
mn
. C.
mn
. D. Không so sánh được.
Câu 11 : So sánh hai số
m
và
n
nếu
2 1 2 1
mn
A.
mn
B.
mn
C.
mn
D. Không so sánh được
Câu 12 : Kết luận nào đúng về số thực
a
nếu
21
33
( 1) ( 1)aa

A.
2a
B.
0a
C.
1a
D.
12a
Câu 13 : Kết luận nào đúng về số thực
a
nếu
31
(2 1) (2 1)aa

A.
1
0
2
1
a
a

. B.
1
0
2
a
.
C.
01
1
a
a


. D.
1a 
.
25
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Câu 14 : Kết luận nào đúng về số thực
a
nếu
0,2
2
1
a
a



?
A.
01a
. B.
0a
. C.
1a
. D.
0a
.
Câu 15 : Kết luận nào đúng về số thực
a
nếu
1
1
3
2
11aa
?
A.
1a
. B.
0a
. C.
01a
. D.
1a
.
Câu 16 : Kết luận nào đúng về số thực
a
nếu
3
2
4
22aa
?
A.
1a
. B.
01a
. C.
12a
. D.
1a
.
Câu 17 : Kết luận nào đúng về số thực
a
nếu
11
22
11
aa
?
A.
12a
. B.
1a
. C.
1a
. D.
01a
.
Câu 18 : Kết luận nào đúng về số thực
a
nếu
37
aa
?
A.
1a
. B.
01a
. C.
1a
. D.
12a
.
Câu 19 : Kết luận nào đúng về số thực
a
nếu
11
17 8
aa

?
A.
1a
. B.
1a
. C.
01a
. D.
12a
.
Câu 20 : Kết luận nào đúng về số thực
a
nếu
0,25 3
aa

?
A.
12a
. B.
1a
. C.
01a
. D.
1a
.
Câu 21 : Điều kiện của cơ số
a
là gì ? Biết rằng
1
1
3
2
aa
.
A.
01a
B.
1a
C.
a
D.
0a
Câu 22 (THPT Lạc Long Quân – Khánh Hòa) : Cho
01a
. Tìm mệnh đề sai trong các mệnh đề
sau
A.
1 khi 0
x
ax
. B.
0 1 khi 0
x
ax
.
C.
12
xx
thì
12
xx
aa
. D.
12
12
xx
a a x x
.
Câu 23 (THPT Tôn Đức Thắng – Khánh Hòa) : Khẳng định nào sau đây SAI ?
A.
2016 2017
2 1 2 1
B.
2018 2017
22
11
22
C.
2017 2016
3 1 3 1
D.
2 1 3
22
26
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
A. HÀM SỐ MŨ
1. Hàm số mũ :
, ( 0, 1).
x
y a a a
Tập xác định :
D
Tập giá trị :
(0, )T
2. Tính đơn điệu :
☻Khi
1a
thì hàm số
x
ya
đồng biến, khi đó ta luôn có:
( ) ( )
( ) ( ).
f x g x
a a f x g x
☻Khi
01a
thì hàm số
x
ya
nghịch biến, khi đó ta luôn có:
( ) ( )
( ) ( ).
f x g x
a a f x g x
3. Đồ thị : Nhận trục hoành làm đường tiệm cận ngang.
Chú ý : đồ thị hàm số luôn cắt Oy tại điểm I( ; )
Bài 01 (Đề thi Cụm 8 – HCM) : Tọa độ giao điểm của đồ thị hàm số
23
x
y

và đường thẳng
11y
là. A.
4;11
. B.
3;11
. C.
3;11
. D.
4;11
.
x
y
O
x
ya
y
O
x
x
ya
Giá trị a :
Giá trị a :
1
1
Phần II : HÀM SỐ MŨ – HÀM SỐ LOGARIT – ĐẠO HÀM
27
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 02 : Hình bên là đồ thị của ba hàm số
x
ya
,
x
yb
,
x
yc
0 , , 1abc
được vẽ trên cùng một hệ trục tọa độ.
Khẳng định nào sau đây là khẳng định đúng?
A.
a c b
B.
abc
C.
bac
D.
c b a
☻ Giải :
..............................................................................................................................................................................
Bài 03 a/ (THPT Ngô Quyền) : Hàm số nào dưới đây đồng biến trên tập xác định của nó?
A.
31
x
y 
. B.
0,25
x
y
. C.
3
4
x
y



. D.
x
y
.
b/ (THPT Ngô Quyền) : Trong các hàm số sau đây hàm số nào không phải là hàm số mũ
A.
4
x
y
. B.
4
yx
. C.
3
x
y
. D.
3
5
x
y
.
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 04 (THPT Nguyễn Huệ-Huế) : Cho


. Kết luận nào sau đây là đúng?
A.
.1

. B.
0


. C.

. D.

.
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 05: a/ Khảo sát và vẽ ĐTHS
3
x
y
b/ Từ đó suy ra các đồ thị hàm số : (C1) :
3
x
y 
(C2) :
1
3
x
y



(C3) :
3
x
y
☻ Giải :
a/ Tập xác định : ...................
x
y
y =
c
x
y =
b
x
y =
a
x
O
Oy
28
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Sự biến thiên : .y’ = ................ nên hàm số ................................trên ........
Các giới hạn ............................... và ...............................
Đồ thị hàm số có tiệm cận..........................là trục....................
Bảng biến thiên :
b/
Bài tập mẫu tham khảo 01 : Hàm số nào dưới đây đồng biến trên ?
A.
4
x
y



. B.
1
75
x
y
. C.
1
5
x
y
. D.
3
x
e
y



.
♥ Hướng dẫn giải :
Hàm số
x
ya
đồng biến trên khi và chỉ khi
1a
.
Oy
Ox
O
Oy
Ox
O
Oy
Ox
O
29
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Bấm máy :
1
2,441 1
75

nên hàm số
11
75
75
x
x
y




đồng biến trên .
Chọn B
Bài tập mẫu tham khảo 02 : Cho đồ thị ba hàm số
x
ya
,
x
yb
,
x
yc
như trong hình vẽ sau.
Khẳng định nào sau đây đúng
A.
c a b
.
B.
c b a
.
C.
a c b
.
D.
b a c
.
♥ Hướng dẫn giải :
Do hàm số
x
yb
giảm nên
01b
(1)
Hai hàm số
,
xx
y a y c
tăng nên
,1ac
Ta chọn ngẫu nhiên x, ở đây chọn x = 1
thì đường thẳng
1x
cắt đồ thị của 2 hàm số
,
xx
y a y c
tại 2 điểm (1; a) và (1; b).
Suy ra (từ hình vẽ)
ac
Vậy
.b a c
Chọn A
Trắc nghiệm hàm số mũ
Câu 01 : Tập giá trị của hàm số
( 0; 1)
x
y a a a
là:
A.
(0; )
B.
[0; )
C.
\{0}
D.
Câu 02 : Cho hàm số
21
x
y 
. Phát biểu nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng
( ; )
.
B. Hàm số đồng biến trên khoảng
(0; )
C. Đồ thị hàm số có đường tiệm cận ngang là trục tung.
D. Đồ thị hàm số có đường tiệm cận đứng là trục hoành.
x
y
2
1
2
O
y = a
x
y = b
x
y = c
x
1
x
y
O
y = a
x
y = b
x
y = c
x
1
x
y
O
c
a
1
30
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
x
y
1
3
O
Câu 02 : Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
2
x
y
B.
yx
C.
2
x
y
D.
2
x
y
Câu 03 : Gọi
C
là đồ thị của hàm số
1
2017
x
y
. Phát biểu nào sau đây là sai ?
A.
C
nhận trục
Ox
làm tiệm cận ngang.
B.
C
không có điểm chung với trục
Ox
.
C.
C
nhận trục
Oy
làm tiệm cận đứng.
D.
C
cắt trục tung tại điểm
0;1M
.
Câu 04 (THPT Lương Tài) : Trong các khẳng định sau, khẳng định nào sai?
A.
33
ab
ab
. B.
11
22
ab
ab
.
C.
22
22
ab
x x a b
. D.
2.3 3 0.5 0
b
a

.
Câu 05 : Biết hàm số
2
x
y
có đồ thị là hình bên.
Khi đó, hàm số
2
x
y
có đồ thị là hình nào trong bốn hình được liệt kê ở
bốn A, B, C, D dưới đây ?
Hình 1
Hình 2
x
y
1
3
O
x
y
y =
2
x
1
3
O
31
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Hình 3
Hình 4
A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4
Ghi chú : cách vẽ đồ thị hàm số
y f x
là :
Câu 06 (THPT Thái Phiên – HP) : Cho
,,abc
là các số thực
đương phân biệt, khác
1
và đồ thị các hàm số
,,
x x x
y a y b y c
như hình vẽ.
Mệnh đề nào sau đây đúng?
A.
a c b
. B.
c a b
.
C.
abc
. D.
bac
.
Câu 07 (THPT Ngô Quyền) : Cho hàm số
2
x
y
. Mệnh đề nào dưới đây đúng?
A. Tập giá trị của hàm số là . B. Hàm số đồng biến trên .
C. Đạo hàm của hàm số là
2
ln2
x
y
. D. Đồ thị hàm số nhận trục
Oy
làm tiệm cận đứng.
Câu 08 (Đề Thử Nghiệm – Bộ GD&ĐT) : Cho ba số thực dương
,,abc
khác 1.
Đồ thị các hàm số
,,
x x x
y a y b y c
được cho trong hình
vẽ bên. Mệnh đề nào dưới đây đúng?
A.
abc
. B.
a c b
.
C.
b c a
. D.
c a b
.
x
y
-4
4
3
O
1
x
y
-4
4
1
3
O
32
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Câu 09 (THPT An Lão – lần 2) : Hàm số nào dưới đây đồng biến trên tập xác định của nó ?
A.
2
3
x
y



. B.
0,5
x
y
. C.
1
x
y



. D.
3
x
y
.
Câu 10 (THPT Chuyên Võ Nguyên Giáp) : Gọi
C
là đồ thị của hàm số
4
x
y
. Mệnh đề nào sau
đây sai?
A. Đồ thị
C
nằm phía dưới trục hoành. B. Đồ thị
C
luôn đi qua điểm
0;1
.
C. Đồ thị
C
luôn đi qua điểm
1;4
. D. Trục
Ox
là tiệm cận ngang của
C
.
Câu 11 (THPT Chuyên Thái Bình) : Chọn kết quả sai trong các kết quả sau?
A.
52
1
4



. B.
83
1
1
3



.
C.
5
1
3



. D.
2
1e
.
Câu 12 (THPT Thái Phiên – HP) : Cho
a
là một số thực dương khác 1. Mệnh đề nào dưới đây sai?
A. Đồ thị hàm số
x
ya
nhận trục
Ox
làm tiệm cận ngang.
B. Hàm số
x
ya
nghịch biến trên với
1a
.
C. Hàm số
x
ya
đồng biến trên với
1a
.
D. Đồ thị hàm số
x
ya
luôn đi qua điểm cố định
1;0
.
Câu 13 (THPT Quế Võ 1) : Tìm mệnh đề đúng trong cá mệnh đề sau.
A. Đồ thị của hàm số
x
ya
và
1
x
y
a



với
01a
thì đối xứng nhau qua trục tung.
B. Hàm số
x
ya
với
1a
là một hàm số nghịch biến trên
;
.
C. Hàm số
x
ya
với
01a
là một hàm số đồng biến trên
;
.
D. Đồ thị của hàm số
x
ya
với
01a
luôn đi qua điểm
; 1a
.
Câu 14 (Sở GDĐT Lâm Đồng lần 03) : Trong các hàm số sau, hàm số nào đồng biến trên R ?
A.
2
x
y
e



B.
4
x
y



C.
1
3
x
y



D.
3
x
y



33
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Câu 15 (THPT Lệ Thủy – Quảng Bình) : Tìm mệnh đề đúng trong các mệnh đề sau?
A. Đồ thị hàm số
01
x
y a a
luôn đi qua điểm
;1Ma
.
B. Hàm số
01
x
y a a
luôn đồng biến trên
; 
.
C. Hàm số
01
x
y a a
luôn nghịch biến trên
; 
.
D. Hàm số
01
x
y a a
luôn đồng biến trên
;1
.
Câu 16 : Cho các số thực dương
,ab
khác
1.
Biết rằng bất kì đường thẳng nào song song với
Ox
mà cắt các đường
,,
xx
y a y b
trục tung lần lượt tại
,MN
và
A
thì
2AN AM
(hình vẽ). Mệnh đề nào sau đây đúng ?
A.
2ba
B.
2
1ab
C.
2
ab
D.
1
2
ab
Câu 17 : Cho đồ thị
C
như hình vẽ. Hỏi
C
có thể là đồ
thị của hàm số nào dưới đây?
A.
5 2
x
y
B.
5 2
x
y
C.
1
5
x
y
D.
25
x
y 
Câu 18 : Cho hàm số
10
x
y
. Khẳng định nào sau đây là sai?
A. Đồ thị hàm số luôn ở phía trên trục hoành .
B. Hàm số luôn đồng biến trên .
C. Đồ thị hàm số luôn đi qua điểm
1;10
D. Đồ thị nhận trục tung làm tiệm cận ngang.
34
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
B. CÔNG THỨC LOGARIT
1. Định nghĩa :
Cho
,b 0a

1a

2. Tính chất và quy tắc :
Vi mi s dng
,ab

1a

Quy tắc :
Hệ quả :
log .log 1
ab
ba
hoc
1
log
log
a
b
b
a
Tính chất gì ?
?
Đó là....
cho
Giáo viên cần file word vui lòng liên hệ
Zalo / đt / facebook : 0914 449 230
35
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
3. Logarit thập phân – logarit tự nhiên.
a) Logarit th. Logarit cơ số 10 c glogarit thập phân. Hay :
10
log b
logb
b) Logarit t . S
1
lim 1 2,71828...
n
n
e
n




Logarit cơ số e c glogarit tự nhiên. Hay :
log
e
b
lnb.
1/
3
log 27
2/
1
9
log 3
3/
3
2
1
3
1
log
81
4/
10
log 100
5/
3
log 81
6/
1
2
log 16
7/
33
1
log
27
8/
3
1
55
log 25
9/
3
243
log
3
10/
3
log 5
3
11/
2
log 5
16
12/
3
2
1
log
a
a
13/
5
log 3
1
25



14/
2
4
log
a
a
36
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Bài 01 (THPT QG – 2017) : Cho
a
 s thc dng khc
2

2
2
log
4
a
a
I



.
A.
1
2
I
. B.
1
2
I 
. C.
2I
. D.
2I 
.
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 02 : Cho
,a
b
 thc dng tha
2
5
b
a

6
2a 4
b
K 
.
A.
226K
. B.
202K
. C.
246K
. D.
242K
.
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 03 (THPT Trần Cao Vân - Khánh Hòa) :  ca biu thc
2
log 3
4A
bng:
A.
6
. B.
2
. C.
12
. D.
9
.
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 04 (THPT An Lão lần 2) : Cho
,,abc
 thc dng
( , 1)ab

log 5,log 7
ab
bc
.
15/
2
2
128
log
2
16/
55
log 3
5
17/
3
log 4
3
18/
3
2 log 6
1
3



19/
3
2 log 5
1
3



20/
3
2
1
1
log
a
a
37
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
 ca biu thc
log
a
b
P
c



.
A.
2
7
P
. B.
15P 
. C.
1
14
P
. D.
60P 
.
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 05 (THPT chuyên Tuyên Quang) : Cho
a
c d
1a
.
c
2
4log 5
a
a
.
A.
125 5
B.
7
5
C.
14
5
D.
75
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 06 (THPT Lương Tài) : Cho
2
log 3a
;
2
log 5b
 ca
2
log 360A

A.
3 2 .ab
B.
3 2 .ab
C.
2.ab
D.
1 3 2 .ab
☻ Giải (theo tự luận lẫn bấm máy tính) :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 07 (Sở GD&ĐT Bình Phước) : Cho
,ab
 thc dng v khc 1. M 

A.
2
1
log
b
a
a a b
. B.
2
1
log
b
a
ab
C.
2
1
log
2
b
a
ab
. D.
2
1
log
b
a
a b a
.
☻ Giải (theo tự luận lẫn bấm máy tính) :
..............................................................................................................................................................................
..............................................................................................................................................................................
Giáo viên cân file word vui lòng liên hệ
Zalo / đt / facebook : 0914 449 230
38
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Bài 08 (THPT chuyên Lam Sơn lần 2) : Bit
2
2
16
1
a
b
x
xx
x


2ab
.  ca biu thc
M a b
. A.
8
. B.
14
. C.
18
. D.
16
.
☻ Giải (theo tự luận lẫn bấm máy tính) :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 09 (Sở GD – ĐT Hà Tĩnh) : Cho
,ab
 thc thu kin
34
45
aa

4
5
3
4
bb
.Chn
khnh sau?
A.
0a

1b
. B.
0a

01b
. C.
0a

01b
. D.
0a

1b
.
☻ Giải (theo tự luận lẫn Casio) :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 10 (THPT Chuyên LHP Nam Định) : Cho hai s thc dng
a

,b
vi
1.a
Kh
d
A.
2
log 2 2log
a
a
ab b
B.
2
1
log log
2
a
a
ab b
C.
2
11
log log
22
a
a
ab b
D.
2
1
log log
4
a
a
ab b
☻ Giải ( tự luận lẫn casio):
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
39
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Bài 11 (Trích đề Minh họa lần 2) : V thc dng
, ba
b 
A.
3
2 2 2
2
log 1 3log log
a
ab
b



. B.
3
2 2 2
21
log 1 log log
3
a
ab
b



.
C.
3
2 2 2
2
log 1 3log log
a
ab
b



. D.
3
2 2 2
21
log 1 log log
3
a
ab
b



.
☻ Giải ( tự luận lẫn casio):
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 12 (Trích đề Minh họa lần 3) : Cho
a
 thc dng,
1a

3
3
log
a
Pa
. M 
 A.
3P
. B.
1P
. C.
9P
. D.
1
3
P
.
☻ Giải ( tự luận lẫn casio):
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 13 (THPT QG 2017) : Vi
a
,
b
 thc dng ty v
a

1
t
2
36
log log
a
a
P b b
.
M 
A.
9log
a
Pb
. B.
27log
a
Pb
. C.
15log
a
Pb
. D.
6log
a
Pb
☻ Giải ( tự luận lẫn casio):
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 14 (THPT QG 2017) : Cho
log 2
a
b

log 3
a
c

23
log
a
P b c
.
A.
31P
. B.
13P
. C.
30P
. D.
108P
.
☻ Giải ( tự luận lẫn casio):
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
40
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Bài 15 (THPT QG 2017) : Cho
3
log 2a

2
1
log
2
b

2
3 3 1
4
2log log 3 logI a b


.
A.
5
4
I
. B.
4I
. C.
0I
. D.
3
2
I
.
☻ Giải ( tự luận lẫn casio):
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 16 : Cho
2
log 5a
c
4
log 1000 , , ,
m a n
m n k
k

. 
2 2 2
m n k
A. 13. B. 10. C. 22. D.
14
.
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài tập mẫu tham khảo 01(Trích Đề minh họa 2017) : t
25
log 3, log 3ab
. Biu din
6
log 45
theo
, ab
c
A.
6
2
log 45 .
a ab
ab
B.
2
6
22
log 45 .
a ab
ab
C.
6
2
log 45 .
a ab
ab b
D.
2
6
22
log 45 .
a ab
ab b
♥ Hướng dẫn giải (nguồn : thầy Cao Tuấn) :
Cách 1 : 
23
1
log 3 log 2a
a

53
1
log 3 log 5 .a
b

3 3 3 3
6
3 3 3 3
1
2
12
log 45 log 9 log 5 2 log 5
2
log 45 .
1
log 6 log 3 log 2 1 log 2 1
1
ab
a ab
b
b a b ab
a

Chọn C.
Cách 2 : Với những bài toán dạng như thế này, HS khi có thể sử dụng MTBT (casio hay vinacal)
để giải như sau: Cơ sở lí thuyết:
0A B A B
Bước 1:  d 
2
log 3
,
5
log 3
cho A, B.
41
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018

2
log 3 A
.
Bm
2
log 3
= q J z

5
log 3 B
.
Bm
5
log 3
= q J x
Bước 2: Nhp biu thc:
6
log 45 ...
Lần 1: Nhp
6
2
log 45 1,34... 0
A AB
AB
loi A.
Lần 2: Bm !  sa biu th
2
6
22
log 45 0,51... 0
A AB
AB
loi B.
Lần 3: Bm !  sa biu th
6
2
log 45 0
A AB
AB B

(hợp lý)
Chọn C.
Bài tập mẫu tham khảo 02 (trích từ tài liệu thầy Cao Tuấn) : Nu
15
log 3a

A.
25
3
log 15 .
51 a
B.
25
5
log 15 .
31 a
C.
25
1
log 15 .
21 a
D.
25
1
log 15 .
51 a
♥ Hướng dẫn giải :
Cách 1 : 
15 3
3
3
1 1 1 1
log 3 log 5 1
1 log 5
log 3.5
a
a
aa

25 5 5 5
3
1 1 1 1 1
log 15 log 15 log 5.3 1 log 3 1
2 2 2 2 log 5



1 1 1 1
11
1
2 2 1
21
a
a
a
a
a









Chọn C.
Cách 2 : Bây giờ, ta sẽ sử dụng casio – vinacal theo cơ sở lí thuyết
0A B A B
42
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Bước 1:  d 
15
log 3
cho A.

15
log 3 A
.
Bm
15
log 3
= q J z
Bước 2: Nhp biu thc:
25
log 15 ...
Lần 1: Nhp
25
3
log 15 0,16... 0
51 A
loi A.
Lần 2: Bm !  sa biu th
25
5
log 15 1,96... 0
31 A
loi B.
Lần 3: Bm !  sa biu th
25
1
log 15 0
21 A
Chọn C.
Bài tập mẫu tham khảo 03 (trích từ tài liệu thầy Cao Tuấn) : Nu
27
log 5 a
;
8
log 7 b
;
2
log 3 c

12
log 35
bng A.
32
.
2
b ac
c
B.
33
.
2
b ac
c
C.
32
.
3
b ac
c
D.
33
.
1
b ac
c
♥ Hướng dẫn giải :
Bước 1:  d tr
27
log 5
,
8
log 7
,
2
log 3
cho A, B, C.

27
log 5 A
.
Bm
27
log 5
= q J z

8
log 7 B
.
Bm
8
log 7
= q J x

2
log 3 C
.
43
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Bm
2
log 3
= q J c
Bước 2: Nhp biu thc:
12
log 35 ...
Lần 1: Nhp
12
32
log 35 ... 0
2
B AC
C
loi A.
Lần 2: Bm !  sa biu th
12
33
log 35 0
2
B AC
C

Chọn B.
Bài tập tương tự 1: Nu
log 3 a

81
1
log 100
bng
A.
4
.a
B.
16 .a
C.
.
8
a
D.
2.a
Bài tập tương tự 2: Biu din
36
log 24
theo
12
log 27a
c
A.
36
9
log 24 .
62
a
a
B.
36
9
log 24 .
62
a
a
C.
36
9
log 24 .
62
a
a
D.
36
9
log 24 .
62
a
a
Bài tập tương tự 3: Nu
30
log 3a

30
log 5b

A.
30
log 1350 2 2.ab
B.
30
log 1350 2 1.ab
C.
30
log 1350 2 1.ab
D.
30
log 1350 2 2.ab
Bài tập tương tự 4: Nu
2
log 3a

2
log 5b

A.
6
2
1 1 1
log 360 .
3 4 6
ab
B.
6
2
1 1 1
log 360 .
2 6 3
ab
C.
6
2
1 1 1
log 360 .
2 3 6
ab
D.
6
2
1 1 1
log 360 .
6 2 3
ab
44
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Bài tập mẫu tham khảo 04 (TT Toán học Tuổi trẻ lần 3) :   
gim (nghch bi : A.
3
x
y



B.
5
3
x
y
e



C.
3x
y
D.
1
22
x
y



♥ Hướng dẫn giải :
Cách 1 :  v
x
ya
ch ca ; n gim, chọn D
Cách 2 :  nghch bin trn tc l lun gim
Kich bin
3
x
y



ci MODE 7
Start
9
End 10 Step 1
w7(aqKR3$)^Q)==p9=10=1=
Ta thy
fx

A sai
Tng t nh vy , v
1
22
x
y



ta thy
fx
m
D
w7(a1R2s2$$)^Q)==p9=10=1=
Bài tập mẫu tham khảo 05 : t
ln2a

ln3b
. Biu din
1 2 3 71
ln ln ln .... ln
2 3 4 72
S
theo
a

b
: A.
3a 2bS 
B.
3a 2bS 
C.
3a 2bS
D.
3a 2bS
♥ Hướng dẫn giải :
1 2 3 71 1 2 71 1
ln ln ln .... ln ln . ... ln
2 3 4 72 2 3 72 72
S



32
ln72 ln(2 .3 ) (3ln2 2ln3) (3a 2b)
. Chọn C
Bài tập mẫu tham khảo 06 (Đề minh họa lần 1) :  thc
,ab
vi
1a
. Khnh

A.
2
1
log log
2
a
a
ab b
B.
2
log 2 2log
a
a
ab b
45
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
C.
2
1
log log
4
a
a
ab b
D.
2
11
log log
22
a
a
ab b
♥ Hướng dẫn giải (sưu tầm):
Ta hiu, nng trnh
2
1
log log 0
2
a
a
ab b
(1) vi m ca
,ab
thu kin
,ab
th
1a
.
Ta chn b
1.15A

0.73B
ch hn. Nhp v 
l
CALC
iQzd$QzQx$pa1R2$iQz$Qxr1.
15=0.73=
t qu một số khác 0 vy v A sai.
Tng t ta thit lp phng trnh cho p 
2
log 2 2log 0
a
a
ab b
S dng ch CALC 
1.15A

0.73B
cho v a (2)
iQzd$QzQx$p2p2iQ
z$Qxr1.15=0.73=
Tip tc ra mt s B cũng sai
Tip t  . Chọn D
iQzd$QzQx$pa1R2$
pa1R2$iQz$Qxr1.
15=0.73=
Giáo viên cần file word vui lòng liên hệ
Zalo / đt / facebook : 0914 449 230
46
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Trắc nghiệm phần công thức LOGARIT
Câu 01 : Cho
0, 1aa
, biu thc
3
log
a
Da
 b
A. 3. B.
1
3
. C.
3
. D.
1
3
.
Câu 02 :  ca biu thc
3
7 7 7
1
log 36 log 14 3log 21
2
C
b ?
A.
2
. B. 2. C.
1
2
. D.
1
2
.
Câu 03 : Cho
0, 1aa
, biu thc
2
4log 5
a
Ea
 b
A.
5
. B.
625
. C.
25
. D.
8
5
.
Câu 04 : Cho
,0ab

,1ab
. Biu thc
2
2
2
log
log
a
a
b
Pb
a

 bng 
A. 6. B. 3. C. 4. D. 2.
Câu 05 : Cho
,0ab

,1ab
, biu thc
34
log .log
b
a
P b a
 bng bao 
A. 6. B. 24. C. 12. D. 18.
Câu 06 :  ca biu thc
8 16
3log 3 2log 5
4

A. 20. B. 40. C. 45. D. 25 .
Câu 07 :  ca biu thc
3
5
log
a
P a a a

A.
53
30
. B.
37
10
. C. 20. D.
1
15
.
Câu 08 :  ca biu thc
35
3 2 3
1
4
log
a
a a a
aa





A.
1
5
B.
3
4
C.
211
60
D.
91
60
Câu 09 : Trong 2 s
3
log 2

2
log 3
, s n hn 1?.
A.
2
log 3
. B.
3
log 2
. C. C hai s . 
Câu 10 (THPT Nguyễn Khuyến –NĐ) : Cho
,,a x y
 thc dng,
1.a
M 

A.
log log
y
aa
x y x
B.
log log
aa
x y x y
47
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
C.
log log log
a a a
x
xy
y

D.
log log .log
a a a
xy x y
Câu 11 (THPT chuyên Nguyễn Trãi – lần 2) : Cho
2
log 3 a
;
2
log 7 b

2
log 2016
theo
a

b
.
A.
52ab
B.
2 3 2ab
. C.
5 3 2ab
D.
2 2 3ab
Câu 12 (THPT Ngô Sĩ Liên – lần 3) : Nu
2 2 2
log 5log 4logx a b
(
,0ab

x
bng.
A.
45
ab
. B.
54ab
.
C.
45ab
. D.
54
ab
.
Câu 13 (Sở GDĐT Lâm Đồng – lần 07) : Cho
12
log 27 a
.Biu din
6
log 16
theo a.
A.
6
8
log 16
3
a
a
. B.
6
4(3 )
log 16
3
a
a
.
C.
6
4
log 16
3 a
. D.
6
3
log 16
3
a
a
.
Câu 14 (THPT chuyên Lê Thánh Tông) : Bit
3
log 2 a

3
log 5 b
.

6
log 30M
theo
a

b
.
A.
1
1
ab
M
b

. B.
1
1
b
M
a
.
C.
1 ab
M
ab
. D.
1
1
ab
M
a

.
Câu 15 (THPT Tiên Lãng) : Cho
2 2 2
a log 3 b log 5 log 7, ,c
. Biu thc biu din
60
log 1050

A.
60
12
log 1050
2
a b c
ab

B.
60
12
log 1050
12
a b c
ab

C.
60
12
log 1050
2
abc
ab

D.
60
12
log 1050
12
a b c
ab

Câu 16 (THPT Hàm Long) : Cho
33
log 15, log 10ab

3
log 50
theo
,ab
.
A.
21ab
B.
31ab
C.
1ab
D.
41ab
Câu 17 (THPT Gia Lộc 2) : Cho
2
log 3a
,
2
log 5b

a
,
b
biu thc
2
log 30P
.
A.
1P a b
B.
P a b
C.
P ab
D.
1P ab
Câu 18 (THPT chuyên Vĩnh Phúc) : Cho
23
log 3 ;log 5ab

12
log 90

,ab

48
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
A.
21
2
ab a
a

B.
21
2
ab a
a

C.
21
2
ab a
a

D.
21
2
ab a
a

Câu 19 (THPT Lý Văn Thịnh) : Cho
3
log 5 a

45
log 75
.
A.
24
2
a
a
B.
22
2
a
a
C.
22
2
a
a
D.
24
2
a
a
Câu 20 (THPT Lý Thường Kiệt) : t
23
log 5 ; log 5ab
u din
6
log 5
theo a b.
A.
22
ab
B.
ab
ab
C.
1
ab
D.
ab
Câu 21 (THPT Lý Thái Tổ) : Cho
log2 a

log25
theo a?
A.
3 5 2a
B.
2 a
C.
2 2 3a
D.
21 a
Câu 22 (THPT Lý Nhân Tông) : Cho
22
log 3; log 5ab

6
log 45

a
;
b

A.
62ab
B.
2
1
ab
a
C.
2
1
ba
a
D.
6 – 2ab
Câu 23 (THPT Lương Tài 2) : t
log5, log3ab
u din
30
log 8
theo
,ab
.
A.
30
3
log 8
1
ab
b
B.
30
31
log 8
1
a
b
C.
30
2
log 8
ab
ab
D.
30
21
log 8
a
ab
Câu 24 (THPT Tiên Du 1) : Cho
23
log 5 ; log 5ab

6
log 5

a

b
.
A.
22
ab
. B.
ab
ab
. C.
1
ab
. D.
ab
.
Câu 25 (THPT Thuận Thành) : Biu thc
49 7
11
log 5 log 5
P 
bng.
A.
7
log 5
. B.
2
. C.
5
log 7
. D.
1
2
.
Câu 26 (THPT Thuận Thành) : Cho
33
log 15; log 10ab
vy
3
log 50 ?
.
A.
41ab
. B.
21ab
. C.
1ab
. D.
31ab
.
Câu 27 (THPT Thuận Thành) : Cho
30 30
log 3, log 5.ab
Biu din
30
log 1350
theo
a

.b
.
49
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
A.
21ab
. B.
21ab
. C.
21ab
. D.
2 ab
.
Câu 28 (THPT Thuận Thành 3) : t
12 12
log 6, log 7ab
u din
2
log 7
theo
a

b
.
A.
1
b
a
. B.
1
a
b
. C.
1
b
a
. D.
1
a
b
.
Câu 29 (THPT Thuận Thành 3) : t
2
log 3a
u din
6
log 24
theo
a
.
A.
1
3
a
a
. B.
3
1
a
a
. C.
1
a
a
. D.
3
1
a
a
.
Câu 30 (THPT Thuận Thành 2) : 
4
M log 1250
theo
a
bit
2
log 5a
.
A.
2 1 4Ma
. B.
2 1 2Ma
. C.
1
2
Ma
. D.
1
2
2
Ma
.
Câu 31 (THPT Quế Vân 2) : Cho
23
log 5 ;log 5mn

6
log 5

m

n

A.
mn
. B.
22
mn
. C.
1
mn
. D.
mn
mn
.
Câu 32 (Sở GDĐT Lâm Đồng lần 03) : Bit
log2, log3ab

log0,018
a b bng.
A.
22ba
. B.
22ab
. C.
2
2
ba
. D.
23ba
.
Câu 33 (Sở GDĐT Lâm Đồng lần 02) : t
2
log 7a
;
7
log 3b
u din
42
log 147
theo
a

b
A.
42
2
log 147
1
b
ab a

. B.
42
2
log 147
1
ba
ab a

.
C.
42
2
log 147
1
ab
ab

. D.
42
2
log 147
1
ab
ab a

.
Câu 34 (Sở GDĐT Hưng Yên) : t
33
log 15; log 10.ab
u din
3
log 50
theo
a

b
.
A.
3
log 50 1ab
. B.
3
log 50 4 1ab
.
C.
3
log 50 2 1ab
. D.
3
log 50 3 1ab
.
Câu 35 (Sở GDĐT Lâm Đồng lần 01) : Cho bit
log3 ;log2ab
. Biu din
125
log 30
theo
a

b

A.
125
1
log 30
1
a
b
. B.
125
2
log 30
1
a
b
.
C.
125
1
log 30
3(1 )
a
b
. D.
125
12
log 30
a
b
.
50
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Câu 36 (THPT Trần Cao Vân - Khánh Hòa) : Cho
30
log 3a
,
30
log 5b

30
log 1350

a

b

A.
21ab
. B.
21ab
C.
21ab
D.
21ab
Câu 37 (THPT Hoàng Văn Thụ - Khánh Hòa) : t
12 12
log 6 ;log 7ab
u din
2
log 7
theo
a

b
.
A.
2
log 7
1
b
a
B.
2
log 7
1
b
a
C.
2
log 7
1
a
b
D.
2
log 7
1
a
b
Câu 38 (THPT Hoàng Hoa Thám - Khánh Hòa) : n biu thc
3
2log
2
5
3 log .log 25
a
a
Pa
, vi
a
 thc dng khc
1
c :
A.
2
4Pa
B.
2
4Pa
C.
2
2Pa
D.
2
2Pa
Câu 39 (THPT Hoàng Hoa Thám - Khánh Hòa) : Cho
33
2 ; 5log a log b

3
log 40
bng :
A.
3ab
. B.
3a b
. C.
3ab
. D.
3a b
.
Câu 40 (Sở GDĐT Lâm Đồng lần 7) : Cho
12
log 27 a
.Biu din
6
log 16
theo a.
A.
6
8
log 16
3
a
a
. B.
6
4(3 )
log 16
3
a
a
.
C.
6
4
log 16
3 a
. D.
6
3
log 16
3
a
a
.
Câu 41 (TTGDTX Vạn Ninh - Khánh Hòa) : Cho
23
log 5 ; log 5ab
.

6
log 5

a

b

A.
ab
ab
. B.
1
ab
. C.
22
ab
. D.
ab
.
Câu 42 (THPT Nguyễn Thị Minh Khai - Khánh Hòa) : Cho
log2 a
. 
125
log
4
theo
a
?
A.
41 a
. B.
25a
. C.
35a
. D.
67a
.
Câu 43 (THPT Nguyễn Thái Học) : Cho
12
log 27 a
u din
6
log 24
theo
a
.
A.
6
9
log 24
3
a
a
. B.
6
9
log 24
3
a
a
.
C.
6
9
log 24
3
a
a
. D.
6
9
log 24
3
a
a
.
Câu 44 (THPT TH Cao Nguyên) : t
ln2a
,
ln3b
u din
ln36
theo
a

b
.
51
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
A.
ln36 2 2ab
. B.
ln36 ab
.
C.
ln36 ab
. D.
ln36 2 2ab
.
Câu 45 (THPT chuyên Nguyễn Bỉnh Khiêm) : Nu
8
log 3 p

3
log 5 q
, th 
log5
bng.
A.
13pq
pq
. B.
22
pq
.
C.
3
13
pq
pq
. D.
3
5
pq
.
Câu 46 : 
4
log 1250
theo
a
bit
2
log 5a
.
A.
4
log 1250 2 1 2a
. B.
4
1
log 1250 2a
2

.
C.
4
log 1250 2 1 4a
. D.
4
1
log 1250
2
a
.
Câu 47 : Cho
33
log 15 ,log 10ab

9
log 50
theo
và ab
.
A.
9
log 50 2ab
. B.
9
log 50 1ab
.
C.
9
1
log 50 1
2
ab
. D.
9
log 50 ab
.
Câu 48 : Cho
,ab
 thc dng khc 1 v th
log 3
a
b
 ca biu thc
3
T log
b
a
b
a
A.
1T
. B.
3
4
T 
. C.
4T 
. D.
4T
.
Câu 49 (THPT Hùng Vương-PT) : Bit
log 3
a
b
 ca biu thc
3
log
b
a
b
P
a
.
A.
3
2
P 
. B.
3P 
.
C.
1
3
P 
. D.
3
3
P 
.
Câu 50 : Cho
6
log 9 .a

3
log 2
theo
a
.
A.
2a
a
B.
2a
a
C.
2 a
a
D.
2
a
a
Câu 51 : Cho hai s thc
a
,
b
bi
01a

log
b
a
Sa
.
52
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
A.
a
Sb
B.
Sa
C.
Sb
D.
a
Sb
Câu 52 (thi thử cụm 4 – Tp.HCM): Cho
0, 1,aa
kh
A.
2
log 2
a
a
B.
log 2 1 log 2
aa
a 
C.
log 2 2
a
a
D.
2
1
log
2
a
a
Câu 53 (THPT Hà Huy Tập) : Cho
log
a
b
. Kh
A.
a
ab
. B.
.ba
. C.
a
b
. D.
ba
Câu 54 (THPT Hà Huy Tập) :  thc dng
,ab
vi
1a

log 0
a
b
. Kh

A.
01
01
ba
ab
B.
01
1,
ba
ab
C.
0 , 1
1,
ab
ab

D.
0 , 1
01
ba
ab

Câu 55 (Sở GDĐT Lâm Đồng lần 07) : Cho
0a

1; ;a x y
 dng. Tm m 
 sau:
A.
log
log
log
a
a
a
x
x
yy
B.
log log .log
b b a
x a x
C.
11
log
log
a
a
xx
D.
log log log
a a a
x y x y
Câu 56 (THPT Đặng Thúc Hứa) : V thc dng
,,abc
b 
A.
ln ln ln
b
c
ab
a
c
B.
ln ln lnabc a bc
C.
ln nl lna
a
b
bc
c
D.
1
ln ln lna bc
abc

Câu 57 (THPT Đặng Thúc Hứa) : V thc dng
;ab
b 
A.
3
27 3
ln
3ln3
log log
a
a
bb




B.
73
3
2
ln
3ln
log log
3
a
b
b
a




C.
3
27 3
ln
3ln3
log log
a
a
bb




D.
73
3
2
ln
3ln
log log
3
a
b
b
a




53
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Câu 58 (THPT chuyên Lương Thế Vinh) :  thc
0a
,
0b

. Kh

A.
ln lnaa
B.
ln ln ln
a
ba
b




C.
ln ln lna b a b
D.
ln . ln .lnab a b
Câu 59 (THPT chuyên Lê Thánh Tông) : nh
a
sao cho
2 2 2
log log 3 log 3aa
.
A.
2a
B.
3
2
a
C.
2a
D.
2
3
a
Câu 60 (THPT chuyên Lam Sơn lần 2) : Cho
,,a b x
c d:
 (I) :
log log
b
b
a
a
xx
 (II) :
log 1 log
log
log
bb
a
b
ax
ab
xa




.
i  ?
   D. (I) 
Câu 61 : Cho
,,abc
 dng
,1ab
. M 
A.
log
b
a
ab
. B.
log log 0
a
a
bb


.
C.
log log .log
a b a
c c b
D.
3
1
log log
3
aa
b
b
a



.
Câu 62 (THPT chuyên Nghuyễn Quang Diêu) : Cho
25
log 7a
;
2
log 5b

5
49
log
8
theo
a
,
b
.
A.
43ab
b
B.
43ab
b
C.
45ab
b
D.
53ab
b
Câu 63 (THPT chuyên KHTN) : Nu
2
84
log log 5ab

2
48
log log 7ab
 ca
ab

A.
8
B.
9
2
C.
2
. D.
18
2
Câu 64 (Trích đề minh họa lần 2) : V thc dng
a
,
b
b 
A.
ln ln ln
a
ba
b

B.
ln ln lnab a b
54
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
C.
ln ln .lnab a b
D.
ln
ln
ln
aa
bb
Câu 65 : Gi s  thc dng. M 
A.
2 2 2
log log logxy x y
B.
2 2 2
1
log log log
2
xy x y
C.
2 2 2
log log log
x
xy
y

D.
2 2 2
log log logx y x y
Câu 66 (THPT chuyên Vinh) :  thc
0ab
. M 
A.
2
22
ln ln lnab a b
B.
2
22
ln ln ln
a
ab
b




C.
ln ln ln
a
ab
b




D.
1
ln ln ln
2
ab a b
Câu 67 (Sở GDĐT Hưng Yên) : 
2 4 1
2
3log log 16 log 2P 
t qu.
A. 2 B. 4 C. 1 D. 3
Câu 68 (Sở GDĐT Hà Tĩnh lần 2) : Cho
1 0, 0, 0a x y
nh sau, khnh
nh sai?
A.
1
log log
2
a
a
xx
B.
log log
aa
xx
C.
1
log log
2
aa
xx
D.
log ( . ) log log
a a a
x y x y
Câu 69 (Sở GDĐT Hà Tĩnh) : S 
0,x

A.
2
22
log 2log .xx
B.
2
22
1
log log
2
xx
C.
2
22
log 2logxx
D.
2
24
log logxx
Câu 70 (THPT Thuận Thành 3) : Cho
0a

1a
  sau.
A.
log log .log
a a a
xy x y
. B.
log log
n
aa
x n x
0, 0xn
.
C.
log
a
x
i
x
. D.
log 1
a
a

log 1
a
a
.
Câu 71 (THPT Chuyên Phan Bội Châu) :  dng
a
,
x
,
y
;
0}{1; ; 1ae

1x
. M

,xy
55
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
A.
log
ln
ln
x
a
x
a
.
B.
log
ln
log
a
a
x
x
e
C.
log
ln
log 10
a
a
e
x
D.
log
ln
log
a
x
x
e
Câu 72 : Cho
a
 thc dng khc 1
log
a
Ia
.
A.
1
2
I
. B.
0I
. C.
2I 
. D.
2I
.
Câu 73 : Cho
,,abc
 thc dng ty v
1.a
 sau, m 
A.
log . log .log .
a a a
bc b c
B.
log log log .
a a a
b
bc
c




C.
log log .
aa
bb
D.
log
b.
a
b
a
Câu 74 (THPT ISCHOOL Nha Trang) : Cho
0a
,
0b
,
, 1; 1a b ab
. 

A.
1
log ( ) 1 log
a
a
ab b
. C.
1
log
1 log
ab
a
a
b
.
B.
1
log ( ) 1 log
a
a
ab b
. D.
2
1
log
2log
a
b
b
a
.
Câu 75 : Cho
42
log 1250 .log 5ab
vi
,ab
 hu t
.ab
?
A.
1.
B.
2.
C.
1.
D.
2.
Câu 76 : Cho
3
log ma
u kin
0m

1m

A log 27
m
m
theo
a
A.
(3 )aa
B.
3 a
a
C.
(3 )aa
D.
3 a
a
Câu 77 (THPT Lạng Giang số 2) : Cho
,0ab

,1ab
,
x

y
 dng. Tm m
 sau
A.
2 2 2
1
log 4log
a
a
xx
B.
log log log
a a a
xy x y
C.
2016
log 2016log
aa
xx
D.
log
log
log
b
a
b
x
x
a
Câu 78 (THPT Lạng Giang số 2) : Cho
log3 m
,
ln3 n
u din
ln30
theo
m

n
Giáo viên cần file word vui lòng liên hệ
Zalo / đt / facebook : 0914 449 230
56
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
A.
ln30 1
n
m

. B.
ln30
m
n
n

.
C.
ln30
nm
n
. D.
ln30
n
n
m

.
Câu 79 (THPT Đông Sơn 1) : Bit
22
2
log (log 10)
log 10
a
 ca
10
a

A. 1 B.
2
log 10
C. 4 D. 2
57
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
C. HÀM SỐ LOGARIT
1. Hàm số logarit:
log , ( 0, 1)
a
y x a a
Tập xác định: ............................................. Tập giá trị: .....................................................
Hàm số đồng biến khi ............................. Hàm số nghịch biến khi .............................
2. Đồ thị: Nhận trục tung làm đường tiệm cận đứng.
 th  cắt trục hoành ti : ..................
Bài tập mẫu tham khảo 01 (THPT Nguyễn Chí Thanh - Khánh Hòa) : 
2
ln( 4 3)y x x


A.
;0
. B.
1;3
. C.
0;
. D.
;1 3; 
♥ Hướng dẫn giải :
Áp dụng vô bài này !

2
ln( 4 3)y x x
nh
2
4 3 0 1 3x x x
. Hay
1;3D
Chọn B.
Bài tập mẫu tham khảo 02 (THPT Nguyễn Chí Thanh - Khánh Hòa) : nh
D
c
s
2
2
log 4 3y x x
.
A.
;1 3;D  
. B.
;1 3;D  
. C.
1;3D
. D.
1;3D
.
♥ Hướng dẫn giải :

2
2
log 4 3y x x
nh
2
4 3 0 1 3x x x hay x
.
O
1
1
O
Phương pháp làm dạng tập xác định này cũng đơn giản lắm !
  khi
58
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Hay
;1 3;D  
Chọn B.
Bài tập mẫu tham khảo 03 (THPT TH Cao Nguyên) : Tnh
D
c
2
lnyx

A.
D
B.
0;D
C.
;0 0;D  
D.
;0D 
♥ Hướng dẫn giải :

2
lnyx
nh
2
00xx
Hay
\0D
ho ghi
;0 0;D  
. Chọn C

2
A 0 A 0
ch không phải
2
A 0 A 0
Bài tập mẫu tham khảo 04 (THPT Lê Hồng Phong) : nh
D
c
3
2
2
2 log 8y x x

A.
2;8D
B.
2;2 2D
C.
2 2;D 
D.
2;D
♥ Hướng dẫn giải :

3
2
2
2 log 8y x x
nh
2
2
20
80
2 2 2 2
x
x
x
x




2 2 2.x
Chọn B
Bài tập mẫu tham khảo 05 : t c  thc ca
m
 
2
2
log 4y x x m

 . A.
4m
B.
4m
C.
4m
D.
4m
♥ Hướng dẫn giải :
 
2
40D x x m x
0 4 0 4mm
. Chọn A
Bài 01 (TTGDTX Vạn Ninh - Khánh Hòa) : nh c
2
ln 2 7 3y x x
.
A.
1
;3
2
D



B.
1
;3
2
D



C.
1
= ; 3;
2
D

 

D.
1
= ; 3;
2
D

 


☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 02 (Sở GDĐT Lâm Đồng lần 2) : nh
D
c
3
2
2
log 8 5 3y x x
.
A.
8
1;
3
D




B.
8
1;
3
D



C.
8
1;
3
D




D.
8
1;
3
D



59
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 03 (Sở GDĐT Lâm Đồng lần 5) : nh D c:
2
3
log 4yx
A.
; 2 2;
B.
; 2 2; 
C.
2;2
D.
2;2
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 04 (THPT Nguyễn Tất Thành) : nh D c
2
log 6 5y x x
A.
;1 5;D  
B.
1;5D
C.
;1 5;D  
D.
1;5D
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 05 (THPT chuyên Lê Hồng Phong - Nam Định) : nh
D
c
1000
3
2
log 8yx
A.
2;D
B.
\2D
C.
2; ;2D 
D.
;2D 
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 06 (THPT Lệ Thủy-Quảng Bình) : nh
D
c
2017
2
log
1
x
y
x
.
A.
\1D
B.
\ 1;2D
C.
;1 2;D 
D.
1;2D
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 07 (Thi thử Cụm 1 – Tp.HCM) : Tnh c
1
log 2
x
yx


A.
;2 \ 0
B.
;2
C.
1;2 \ 0
D.
;1 2;
☻ Giải :
60
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 08 (THPT Võ Nguyên Giáp) : nh
D
c
2
3
log 3y x x
.
A.
;0 3;D 
B.
0;3D
C.
;0 3;D  
D.
0;3D
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 09 (THPT Lương Tài 2) :  thc ca tham s m 
2
ln 1y x mx

t ? A.
22m
B.
2
2
m
m

C.
11m
D.
22m
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 10 :  sau
a/ y =
2
2
2 3 1
log
13
xx
x




b/
22
y x ln 1 2x 3x
c/
32
2
5
y log x x 2x
d/
x
1
y log
2x 1



e/
42
1
2
y log x 3x 4
f/
2
x2
y log x 1

☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
61
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 11 (THPTQG – 2017) : nh
D
c
1
3
( 1)yx
.
A.
( ;1)D
B.
(1; )D
C.
D
D.
\{1}D
☻ Giải :
..............................................................................................................................................................................
.............................................................................................................................................................................
Bài 12 (THPTQG – 2017) : nh c
5
3
log
2
x
y
x
A.
\2D
B.
; 2 3;D 
C.
2;3D 
D.
; 2 3;D 
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 13 : 
m
 
2
2
log 2 2 1y x mx m

.
A.
1;m
B.
\1m
C.
m
D.
m
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 14: :
22
ln 2y x e
. Tnh c 
A.
D
B.
1
;
2
D
e




C.
;
2
e
D



D.
1
D;
2




☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 15 (THPT Tôn Đức Thắng – Khánh Hòa) : t c  c 
2
3
log 5y x x m
 .
62
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
A.
25
4
m
B.
0m
. C.
0m
. D.
25
4
m
.
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Trắc nghiệm phần hàm số LOGARIT
Câu 01 : Tnh c
2
2
log 2y x x

A.
;2D 
B.
\ 1; 2D
C.
; 2 (1; )D  
D.
; 2 1;D 
Câu 02 (THPT chuyên Vĩnh Phúc) : 
2
2
log 6y x x
A.
; 2 3;
B.
2;3
C.
2;3
D.
; 2 3; 
Câu 03 (THPT chuyên Lê Khiết) : 
2
ln 2 7 3y x x
A.
1
;3
2
D



B.
1
; 3;
2
D

 


C.
1
;3
2
D



D.
1
; 3;
2
D

 

Câu 04 (Sở GDĐT Hưng Yên) : 
2
2
log 5 6y x x

A.
2;3
B.
;2 3;
C.
3; 
D.
;2
Câu 05 : nh
D
c
2
2
log 2y x x
A.
0;2D
B.
\1D
C.
;0 2;D  
D.
0;2D
Câu 06 (THPT Chuyên Phan Bội Châu) : nh
D
c
2
2
log 2y x x
.
A.
;0 2;D 
B.
;0 2;D  
C.
0;D 
D.
;0 2;D 
Câu 07 : nh
D
c
2
2
logy x x
A.
1;3D 
B.
;0 1;D  
C.
; 1 3;D  
D.
; 1 3;D  
63
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Câu 08 (THPT Lý Thường Kiệt) : nh
D
c
2
1
5
log 4 .y x x
.
A.
0; 4D
B.
; 0 4;D 
C.
; 0 4;D  
D.
0 ; 4D
Câu 09 (THPT chuyên Lam Sơn lần 2) : 
3
logyx
M  sai?
 th  m cn ngang
 nh
\0D
 th  t tim cc
Oy
 ng binh
Câu 10 : 
2
logyx
.M 
A. Tnh c 
; 
 th  nhn trc
Oy
m cng
 
1
ln2
y
x
 ng bing
0;
Câu 11 (Sở GDĐT Hà Tĩnh) : Cho
0, 1aa
  sau.
A. Tnh c
x
ya
ng
(0; )
B. Tnh c
y log
a
x

C. T c
x
ya

D. T c
log
a
yx

Câu 12 (THPT Lý Nhân Tông) :  ng bi .
A.
– x
ye
. B.
lnyx
. C.
3
x
y
. D.
e
yx
.
Câu 13 (THPT Quế Võ 1) :   sau.
A. 
log
a
yx
vi
01a
 ng bi
0; 
.
B. th c
log
a
yx

1
log
a
yx
vi
01a
i xng nhau qua tr
64
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
x
y
1
2
1
4
-4
3
O
C. 
log
a
yx
vi
01a
 .
D. 
log
a
yx
vi
1a
 nghch bi
0; 
.
Câu 14 : Vi
0a

1a
không đúng ?

x
ya

log
a
yx


x
ya

log
a
yx
u
 th 
x
ya

log
a
yx
i xng thng
yx
 th 
x
ya

log
a
yx
ng tim cn
Câu 15 : ng cong  th ca m trong
b c li bn phng n A, B, C, D di
  
A.
2
logyx
B.
1
2
logyx
C.
2
logyx
D.
2
log 2yx
Câu 16 : tt c  thc ca a 
log
a
yx
01a
 th  
A.
2a
B.
2a
C.
1
2
a
D.
1
2
a
Câu 17 : 
2
log 2yx
. 
2
log 2yx
 th n
c li bn phng n A, B, C, D d
Hình 1
Hình 2
x
y
O
x
y
1
O
x
y
1
2
2
O
65
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Hình 3
Hình 4
   4
Câu 18 (THPT Lý Thái Tổ) : Tp h ca
x

32
5
log 2x x x

A.
0;2 4;
B.
1;0 2; 
C.
1; 
D.
0;1
Câu 19 : nh
D
c
2
ln 2 8yx
A.
; 2 2;D 
B.
2;2D 
C.
2;2D 
D.
; 2 2;D 
Câu 20 (THPT Trần Cao Vân - Khánh Hòa) : 
2
ln 5 6y x x

A.
;2 3: 
. B.
;0
C.
2;3
D.
0;
Câu 21 :  th ca m trong
b c li bi
  
A.
0,8
logyx
B.
2
logyx
C.
2
x
y
D.
0,5
logyx
Câu 22 (THPT Ngô Sĩ Liên lần 3) : p hp tt c  ca
tham s thc
m
 
2
3
1
log 2 3
y
x x m

nh ?
A.
2
;
3




B.
2
;
3



x
y
O
x
y
O
x
y
1
1
4
2
O
66
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
C.
1
;
3




D.
2
;10
3



Câu 23 :  th c
log
a
yx
,
log
b
yx
,
log
c
yx
0 , , 1abc
c v t
h trc t. Khnh

A.
bac
B.
abc
C.
b c a
D.
a c b
Câu 24 :  th
1
:
x
C y a

2
: log
b
C y x

th nh hnh v. Nh
A.
01
1
b
a

B.
1
1
a
b
C.
0
1
1
0
a
b
D.
1
1
0
b
a
Câu 25 (THPT Quế Vân 2) : 
2
21
log
aa
yx

nghch bin trong khong
0;
khi.
A.
0a
B.
1a
C.
1a

02a
D.
1a

1
2
a
Câu 26 (Sở GD-ĐT Hà Tĩnh lần 2) : Cho  khnh sau:
:I
 th 
log (1 0)
a
y x a
i trc tung.
:II
 th 
log (1 0)
a
y x a
m
1;0
.
:III
 th 
log (1 0)
a
y x a
nhn trm cng.
y kh
A.
1
B.
3
C.
0
D.
2
Câu 27 (đề thi thử Cụm 1 – Tp.HCM) : Cho
a
,
b
,
c
 thc dng v khc
1
 th 
s
log
a
yx
,
log
b
yx
,
log
c
yx
  

x
y
y
= log
c
x
y
= log
b
x
y
= log
a
x
4
-4
O
1
67
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
A.
abc
B.
c a b
C.
b c a
D.
c b a
Câu 28 (đề thi thử Cụm 4 – Tp.HCM) : 
d th ca m trong b c li bn
phng n A, B, C, D d  
A. B.
C. D.
Câu 29 (THPT Chuyên Vinh) : 
log
a
yx

log
b
yx
 th nh hnh v ng
thng
7x
ct tr th 
log
a
yx

log
b
yx
ln lt ti
H
,
M
,
N
.
Bit rng
HM MN
.
M 
A.
7ab
B.
2
ab
C.
7
ab
D.
2ab
Câu 30 (THPT chuyên ĐHKH Huế) :   c tr?
A.
2
3
x
y
x
B.
31yx
C.
logyx
D.
x
ye
ln 1 ln2yx
lnyx
ln 1 ln2yx
lnyx
log
a
yx
log
b
yx
log
c
yx
O
1
x
y
O
7
M
N
x
y
log
b
yx
log
a
yx
H
68
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
D. SO SÁNH LOGARIT
c :
........................................................................................................................................................................
........................................................................................................................................................................
........................................................................................................................................................................
........................................................................................................................................................................
+ Ncùng cơ số n c s trong hai trng hp (0; n
hn m u thc b i nhau
+ Trong trng hkhác cơ số u thc b n mt s b
i s b . T t qu
Ví dụ :  :
34
1
log 4 log
3
. 
3 3 4 4 3 4
11
log 4 log 3 1;log log 4 1 log 4 log
33
Ví dụ : 
66
log 1,1 log 0,99
37

6 6 6 6 6 6
log 1,1 log 1 log 0,99 log 1 log 1,1 log 0,99
3 3 1;7 7 1 3 7
Ví Dụ : p s sau :
a/
0,4 0,2
log 2 log 0,34

0,4 0,4
0,2 0,2
2 1 log 2 log 1 0
0,3 1 log 0,3 log 1 0
0,2 0,4
log 0,3 log 2
b/
53
34
32
log log
45

55
33
33
44
5 3 3
1 0 1 log log 1 0
3 4 4
3 2 2
0 1,0 1 log log 1 0
4 5 5
35
43
23
log log
54

c/
25
log 10 log 30

22
55
log 10 log 8 3
log 30 log 36 3


25
log 10 log 30
d/
37
log 5 log 4

33
77
log 5 log 3 1
log 4 log 7 1


37
log 5 log 4
69
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
e/
3
1
2ln 8 lne
e


3
2ln 2.3 6
1
8 ln 8 1 9
e
e

3
1
8 ln 2lne
e
f/
33
65
log log
56

33
33
65
log log 0
55
56
log log 0
66


33
65
log log
56

g/
11
33
log 9 log 17

1
01
3
9 17

11
33
log 9 log 17
h/
11
22
log loge

1
01
2
e

11
22
log loge

Bài 01 :  p s sau
a/
22
53
log log
22
b/
0,1 3
log 8 log 0,98
c/
4 0,2
log 7 log 9
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 02 :  p s sau
a/
37
log 4 log 6
e/
0,2 0,5
log 0,3 log 0,4
d/
34
1
log 4 log
3
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
70
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Trắc nghiệm phần hàm số LOGARIT
Câu 01 (THPT Hoàng Văn Thụ) : Chn khnh sau:
A.
11
33
log log 0a b a b
B.
ln 0 1xx
.
C.
11
22
log log 0a b a b
. D.
2
log 0 0 1xx
.
Câu 02 (THPT chuyên Vĩnh Phúc) : 
A.
2016
10
2017
x
x



B.
2016
log 2017 1
C.
2017
log 2016 1
D.
2017
10
2016
x
x



Câu 03 (THPT chuyên Vĩnh Phúc lần 5) : M 
A.
ln 1 0x x e
B.
log 0 1xx
C.
2
42
log log 0x y x y
D.
11
33
log log 0x y x y
Câu 04 : Cha
, ab
nu
13 15
78
aa

log 2 5 log 2 3
bb
.
A.
1,0 1ab
B.
0 1, 1ab
C.
1, 1ab
D.
0 1,0 1ab
Câu 05 : Cho
01a
. M 
A.
log 2 log .
2
aa
a
B.
11
log log .
23
aa
C.
log 2 log 3.
aa
D.
log log .
32
aa
aa
Câu 06 : Cho
2
3
3
4
aa

23
log log
34
bb
. Chn kh
A.
0 , 1.ab
B.
0 1 .ab
C.
0 1 .ba
D.
, 1.ab
71
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Câu 07 : Cho
4
3
5
4
aa

34
log log
45
bb
. Chn kh
A.
log 1
a
b
B.
log 0
a
b
C.
log 0
b
a
D.
log log
aa
bb
E. ĐẠO HÀM MŨ - LOGARIT
Đạo hàm của hàm số sơ cấp
Đạo hàm của hàm số hợp
1.
1
( )' .xx

1
( )' . . 'u u u

2.
( )'
xx
ee
( )' . '
uu
e e u
3.
( )' .ln
xx
a a a
( )' . '.ln
uu
a a u u
4.
1
(ln )'x
x
'
(ln )'
u
u
u
5.
1
(log )'
ln
a
x
xa
'
(log )'
ln
a
u
u
ua
Bài tập mẫu tham khảo 01 :  sau :
a/
2
22
x
y x x e
b/
2
sinx cosx
x
ye
c/
xx
xx
ee
y
ee
d/
2
ln 1yx
e/
ln x
y
x
f/
1 ln lny x x
♥ Hướng dẫn giải :
a/
2 2 2
2 2 ' 2 2 2 2
x x x x
y x x e y x e x x e x e
b/
2 2 2
' cosx sinx 2 sinx cosx 3sin osx
x x x
y e e x c e
c/
22
4
'
x x x x x x x x
xx
xx
x x x x
e e e e e e e e
ee
yy
ee
e e e e


d/
2
2
2
ln 1 '
1
x
y x y
x
72
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
e/
22
ln 1 1 1 ln
' . ln
xx
y y x x
x x x x



f/
ln 1 ln 1 2ln
1 ln ln '
x x x
y x x y
x x x

Bài tập mẫu tham khảo 02 :  sau
a/
22
ln 1y x x
b/
2
2
log 1y x x
c/
3
2
lnyx
d/
2
4
log
4
x
y
x



e/
2
3
9
log
5
x
y
x



f/
1
log
2
x
y
x




♥ Hướng dẫn giải :
a/
23
2 2 2 2
22
ln 1 ' 2 .ln 1 2 .ln 1
2 1 2 1
x x x
y x x y x x x x
xx

b/
2
2
2
21
log 1 '
1 ln2
x
y x x y
xx

c/
21
3
2
33
3
2 1 2
ln ' ln ' ln
3
3 ln
y x y x x
x
xx



d/
2
2
2
4 1 16 4 16
log ' :
4 ln2 4
4 ln2
4
xx
yy
xx
x
x









e/
2
3
9
log
5
x
y
x



2
22
2
2
2 5 9
1 9 10 9
':
ln3 5
5 9 ln3
5
x x x
x x x
y
x
xx
x





f/
11
1 1 1
log ' :
ln10
2 16 2
8 ln10 1
xx
xx
yy
x x x x
xx










Bài tập mẫu tham khảo 03 : giá trị lớn nhất – giá trị nhỏ nhất  sau :
a/
2
cos2 2sin 1 ln f x x x x e
n
0;e
.
b/
.lny x x
n
1; e
.
♥ Hướng dẫn giải : 
2
cos2 2sin 1 ln 2 ln . f x x x x e x e
♠ Lu :  ta   thc lng   
2
cos2 1 2sinxx
 n
0;e
.

1
' 0, 0; .
f x x e
xe

fx
ng bin
0;e
.
73
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Vy
0;
max 3 ln2
e
fx
khi
xe
;
0;
min 3
e
fx
khi
0x
.
 n
1; e
.

' ln 1yx
. Suy ra
1
' 0 ln 1 0 ln 1 1; . y x x x e
e

1 0; .y y e e
Vy
1;
max
e
f x e
khi
xe
;
1;
min 0
e
fx
khi
1x
.
Bài tập mẫu tham khảo 04 : GTLN - GTNN c :
2ln 1 y f x x x

1;3
.
♥ Hướng dẫn giải :  n
1;3
.

22
'1
x
fx
xx
. Suy ra
' 2 0 2 1;3 . f x x x

1 2; 2 3 2ln2; 3 4 2ln3. f f f
Vy
2;4
max 2fx
khi
1x
;
2;4
min 3 2ln2fx
khi
2x
Bài tập mẫu tham khảo 05 (thầy Cao Tuấn) : 
cos sin
ln
cos sin
xx
y
xx

A.
cos2 .yx
B.
2
.
sin2
y
x
C.
2
.
cos2
y
x
D.
sin2 .yx
♥ Hướng dẫn giải : Cơ sở lý thuyết
1, 0
A
A B B
B
.
Thử với lần lượt các đáp án (khi nào chọn được đáp án đúng thì dừng lại).
Bước 1: Bm q w 4  chuyn v n v rađian,
Bước 2: Nhp
cos sin
ln :.....
cos sin
3
xx
d
dx x x
x








Nhp
cos sin
ln :cos
cos sin 3
6
xx
d
dx x x
x








81Kq
Loại A.
Bm !  nhp li
Giáo viên cân file word vui lòng liên hệ
Zalo / đt / facebook :
0914 449 230
74
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
cos sin
2
ln :
cos sin
sin
6
3
xx
d
dx x x
x








1,73 1Kq
Loại B.
Bm !  nhp li
cos sin
2
ln :
cos sin
cos
6
3
xx
d
dx x x
x








1Kq
Chọn C.
Bài tập mẫu tham khảo 06 (thầy Cao Tuấn) : 
x
e
fx
x
m ca phng
trnh
0fx
 A.
2.
B.
0.
C.
1.
D.
.e
♥ Hướng dẫn giải : Nhp
X
de
xX
dx
X




 chn X tng
r vi
2 0,301.. 0X Kq
loi A.
Bm !  th li
r vi
2 X Math Error
loi B.
Bm !  th li
r vi
10X Kq
Chọn C
Bài tập mẫu tham khảo 07 :  c
2
9
x
x
y
.
A.
2
1 2 2 ln3
3
x
x
y

B.
2
1 2 2 ln3
3
x
x
y

C.
2
1 2 2 ln3
3
x
x
y

D.
2
1 2 2 ln3
3
x
x
y

♥ Hướng dẫn giải :
2
9 9 .ln9 2 1 2 ln9
2
9 9 9
xx
x x x
xx
x
yy
chọn D
75
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Bài tập mẫu tham khảo 08 (THPT Gia Lộc 2) :  ln nht c
2
2x
y xe

1;2
A.
3
2
e
B.
2
1
e
C.
1
2 e
D.
3
1
2e
♥ Hướng dẫn giải :
2
22
14
x
y e x

;
11
0
22
y x hay x
( không thõa mãn )

2
1
1y
e
,
8
1
2y
e
. Vy GTLN c 
1;2

2
1
e
chọn B
Bài tập mẫu tham khảo 09 :  nh nht c
2 lny x x
n
2;3
.
A.
2;3
min 1y
. B.
2;3
min 4 2ln2y 
. C.
2;3
min ye
. D.
2;3
min 2 2ln2y
.
♥ Hướng dẫn giải :
Cách 1:
2 lny x x x
1
2 ln . 1 lny x x x
x



.
0 ln 1 2;3y x x e

y e e
;
2 4 2ln2y 
;
3 6 3ln3y 
. chọn B
 
2;3
min 4 2ln2y 
.
Cách 2: S d
570Casio fx VN PLUS
:
w7Q)(2phQ)))
==2=3=0.1=
D c ta kt lun
2;3
min 4 2ln2y 
ti
2x
. chọn B
Bài 01 :  sau
a/
2
2x 1
ye
b/
sinx
y3
c/
2
3
y log 7x 8x
d/
2
3
y log 7x 8x
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Giáo viên cân file word vui lòng liên hệ
Zalo / đt / facebook :
0914 449 230
76
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Bài 02 :  sau
a/
2
y ln 7x 8x
b/
32
y ln 8x
c/
3
ln x
y
x
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 03 a/(Trích Đề minh họa 2017) : a 
13 .
x
y
A.
1
.13 .
x
yx
B.
13 .ln13.
x
y
C.
13 .
x
y
D.
13
.
ln13
x
y
b/ (Sở GDĐT Hưng Yên) : 
10
x
y

A.
10
x
B.
10
ln10
x
C.
1
.10
x
x
D.
10 .ln10
x
c/ (THPT Thuận Thành 2) : 
2
x
y
.
A.
2
x
yx
. B.
2
x
y
C.
1
2
x
yx
D.
,
2 ln2
x
y
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 04 a/ (THPT Quảng Xương 1 lần 2) : 
2x
(2 5 2)ey x x

A.
x
4 5 ex
B.
x
ex
C.
2x
2 3 exx
D.
2x
2ex
b/  y =
2
22
x
x x e

A.
2 x
y x e
B.
2
44
x
y x x e
C.
2
x
y xe

D.
22
x
y x e

77
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 05 (THPT Gia Lộc 2) : 
.2
x
f x x
A.
1
.2
x
f x x
B.
1 ln2 2
x
f x x

C.
1
2
x
fx
D.
2
x
fx
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 06 (THPT Nguyễn Văn Cừ) : 
2
2
7
xx
y

A.
2
2
( 1).7 .ln7
xx
yx


B.
2
2
(7 1).7 .ln7
xx
yx


C.
2
2
(2 1).7 .ln7
xx
yx


D.
2
2
(2 7).7 .ln7
xx
yx


☻ Giải :
..............................................................................................................................................................................
Bài 07 (THPT Quảng Xương 1 lần 2) : 
2
3
(x) log (x 2x)f 
. Tp nghim
S
ca phng
trnh
'(x) 0f

A.
1 2;1 2S
B.
1S
C.
0;2S
D.
S 
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 08 (Sở GD&ĐT Bình Phước) : Gi
M

m
ln l ln nh nh nht ca

22
ln 2y x e

0;e
. M 
A.
4 ln2Mm
B.
5Mm
C.
4 ln3Mm
D.
2 ln3Mm
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
78
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
..............................................................................................................................................................................
Bài 09 (TN THPT – 2009) :  GTNN
2
y x ln 1 2x
n
2; 0
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 10 :  GTNN f(x) = (x
2
3x +1)e
x
n [0;3]
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 11 : Cho
x
y e .x
; CMR :
y'' 2y' y 0
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 12 : Cho
sinx
ye
; CMR :
y'.cosx y.sin x y'' 0
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 13 : GTNN – GTLN c :
2
2 6 5ln 2 1y f x x x x
n
0;3
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
79
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Bài 14 : GTNN – GTLN c :
2
1.
x
y x e

n
0;2
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 15 : 
sin cos
x
y e x x

A.
e sin2
x
x
B.
2 sin
x
ex
C.
2 .cosx
x
e
D.
sin cos
x
e x x
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 16 : o  c
2
ln 1y x x
 
A.
2
21
1
x
y
xx

B.
2
1
1
y
xx

C.
2
21
1
x
y
xx


. D.
2
1
1
y
xx

☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 17 : a  s
2
()y x x


A.
21
2 ( )xx
B.
21
( ) (2 1)x x x

C.
21
( ) (2 1)x x x

D.
21
()xx
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 18 : Mng
st
km
n
t
c sau
2
4 2 3
2.
tt
s t e t e


km
. Hi vn tc c
A.
5
6e
/km s
B.
5
10e
/km s
C.
5
7e
/km s
D.
5
8e
/km s
☻ Giải :
80
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
..............................................................................................................................................................................
Trắc nghiệm phần đạo hàm hàm số MŨ - LOGARIT
Câu 01 (THPT Hoàng Quốc Việt) : o 
12x
ye

A.
12
2
x
ye
B.
12
2
x
ye

C.
x
ye
D.
12x
ye
Câu 02 : 
31
2
x
fx

A.
31
3.2 ln2
x
fx
B.
31
2 ln2
x
fx
C.
31
2 log2
x
fx
D.
32
3 1 2
x
f x x

Câu 03 (thi thử Cụm 4 – Tp.HCM) :  nh nh ln nht c
2
x
x
y
e

n
1;1
.
A.
0
;
1
e
B.
1
;
e
C.
1
e
;
e
D.
0
;
e
Câu 04 (THPT Hùng Vương – PT) : 
2x
ye

y

A.
2
2
x
xe
B.
21
2
x
xe
C.
2
2
x
e
D.
21
1
2
x
e
Câu 05 (thi thử Cụm 7 – Tp.HCM) : 
1
2
x
y
.
A.
1 2 ln2
x
yx

B.
1
2 log2
x
y
C.
1
2 ln2
x
y
D.
1
2
ln2
x
y
Câu 06 (THPT chuyên Vinh) : 
2 x
y x e
. Nghim ca bt phng trnh
0y

A.
0;2x
B.
; 2 0;x  
C.
2;0x
D.
;0 2;x  
Câu 07 (thi thử Cụm 4 – Tp.HCM) : 
2 x
y x e
nghch bi
A.
2;0
B.
1; 
C.
;1
D.
;2
Câu 08 (THPT Lương Tài 2) : 
xx
y xe e
.
A.
2
x
xe
B.
2
x
e
C.
2
x
xe
D.
1
x
xe
81
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Câu 09 (THPT Thuận Thành) :  
6
3 ln3 7
x
yx

?
A.
7
3
x
yx
B.
37
y x x
C.
3
7
x
yx
D.
37
xx
y 
Câu 10 : 
sinx
2y
A.
sinx
cos .2 .ln2yx

B.
sinx
cos .2 .ln2yx
C.
sinx
2 .ln2y
D.
sinx
cos .2
ln2
x
y
Câu 11 (Sở GDĐT Lâm Đồng lần 03) : 
tan2x
ye
 ca
'
6
f



bng.
A.
3
8e
B.
3
2e
C.
4
D.
3
4e
Câu 12 (Sở GDĐT Lâm Đồng lần 05) : :
25
3.5
xx
ye
.
A.
25
' 2 5 .ln5
xx
ye
B.
25
' 2 3.5
xx
ye
C.
2 5 1
' 2 3.5 .ln5
xx
ye

D.
25
' 2 3.5 .ln5
xx
ye
Câu 13 (THPT Trần Cao Vân - Khánh Hòa) :  s
2 .3
xx
y

A.
6 ln6
x
B.
6
x
C.
11
23
xx
D.
23
xx
Câu 14 (THPT Trần Cao Vân - Khánh Hòa) : 
2
3
x
y e x
 s b
triệt tiêu tm:
A.
0x
B.
1; 3xx
C.
1; 3xx
D.
1; 3xx
Câu 15 (Sở GDĐT Lâm Đồng lần 05) : :
2
51xx
ye

A.
2
51
' 2 4
xx
y x e


B.
2
51
' 2 5
xx
y x e


C.
2
2 5 1
' 5 1
xx
y x x e

D.
2
51
' 2 5
xx
y x e


Câu 16 : 
4
1
5
x
ye
.
A.
4
1
20
x
ye
B.
4
4
5
x
ye

C.
4
4
5
x
ye
D.
4
1
20
x
ye

Câu 17 : 
2016
x
y
.
A.
1
.2016
x
yx
B.
2016
ln2016
x
y
C.
2016 .ln2016
x
y
D.
2016
x
y
Câu 18 (THPT Thanh Thủy) : 
y
c
2
2
x
y x e
.
A.
2
25
x
y x e

B.
2
24
x
y x e

C.
24
x
y x e

D.
25
x
y x e

82
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Câu 19 : đạo hàm cấp 2 c
2016
x
fx
.
A.
2
" 1 2016
x
f x x x

B.
2
" 2016 ln 2016
x
fx
C.
" 2016
x
fx
D.
2
" 2016 log 2016
x
fx
Câu 20 (Sở GD và ĐT Long An) : 
2
2
x
yx
.
A.
2
' 2 2
ln2
x
x
yx




B.
2
' 2 2 ln2
x
y x x
C.
' 2 2 ln2
x
yx
D.
2
' 2 2 ln2
x
y x x
Câu 21 (Sở GD và ĐT Long An) :   ng bi
?
.
A.
1
2
logyx
B.
2
logyx
C.
2
x
y



D.
3
2
x
y




Câu 22 (THPT Gia Lộc 2) : 
.2
x
f x x
.
A.
1
.2
x
f x x
B.
1 ln2 2
x
f x x

C.
1
2
x
fx
D.
2
x
fx
Câu 23 (THPT Chuyên Quang Trung) : 
xx
y e e


1?y

.
A.
1
e
e
B.
1
e
e

C.
1
e
e

D.
1
e
e
Câu 24 (THPT Yên Lạc – VP) :   .
A. B. C. D.
1
Câu 25 : 
17
x
y 

A.
7
'
2 1 7
x
x
y
B.
7 ln7
'
17
x
x
y
C.
7 ln7
'
2 1 7
x
x
y
D.
7
'
1 7 .ln3
x
x
y
Câu 26 (thi thử Cụm 8 – Tp.HCM) :  ln nht c
3
33xx
f x e

n
0;2
bng.
A.
e
B.
3
e
C.
2
e
D.
5
e
Câu 27 (THPT Lê Hồng Phong) :  nh nht c
22
2
x
f x x e

1;2
1
x
f x x e
0f
0
2e
2
Giáo viên cân file word vui lòng liên hệ
Zalo / đt / facebook :
0914 449 230
83
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
A.
4
1;2
min 2f x e
B.
2
1;2
min f x e

C.
2
1;2
min 2f x e
D.
2
1;2
min 2f x e

Câu 28 (Sở GD và ĐT Bình Phước) : 
sin2x
ye
A.
sin2
1
' cos2 .
2
x
y x e
B.
sin2
' 2cos2 .
x
y x e
C.
sin2
' cos2 .
x
y x e
D.
sin2
' cos2 .
x
y x e
Câu 29 :  th c
1
2
yx
lm
0
M

2
0
2x
. Tip tuyn ca
C
ti
m
0
M
 s ng.
A.
2
B.
2
C.
21
D.
3
Câu 30 :  o  ca 
1
2
x
y
A.
1
2
21
x
y
x
B.
1
ln2
2
21
x
y
x
C.
1
ln2
2
21
x
y
x
D.
1
2
21
x
y
x
Câu 32 : Cho  s
1
3
x
y
. Khnh sai?
b  th  
B.
'
11
.ln
33
x
y
.
 ng bing
;
.
 th  t tim cc
Ox
.
Câu 33 (Đề Minh họa lần 2) : 
ln 1 1 yx
.
A.
1
2 1 1 1
y
xx
B.
1
11

y
x
C.
1
1 1 1
y
xx
D.
2
1 1 1
y
xx
Câu 34 :  
1
x
e
y
x
?
 nghch bing
;0
 ng bing
0;
84
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
 t ci ti
0x
 m cc tr
Câu 35 : Biu thc
2
3 3 1
24 12 .2 .ln2
xx
x

 
A.
2
3 3 1
2
xx
y

B.
2
3 3 1
8
xx
y

C.
2
1
2
xx
y

D.
2
1
8
xx
y

Câu 36 :  ng bing khonh c
A.
4
21f x x
B.
lnf x x
C.
1
x
f x e
x
D.
23
1
x
fx
x
Câu 37 : 
ln x
y
x

 t cc tiu  t ci
 c tr  c tiu
Câu 38 : 
fx
c
21
1
x
x
f x e

A.
21
1
x
x
f x e
B.
2
1
21
1
x
x
x
f x e
x
C.
21
1
21
1
x
x
x
f x e
x
D.
21
1
2
3
1
x
x
e
fx
x

Câu 39 : 
x
f x x

A.
1
ln
x
f x x x x

B.
1 ln
x
f x x x

C.
x
f x x
D.
ln
x
f x x x
Câu 40 : Cho 
2
ln 1 2y x x
t lut lun không đúng ?
 c tr  t cc tiu ti
1
2
x
  cc tiu bng
1
ln2
4
 ng bin ng
1
;
2




Câu 41 : 
21
1
2
x
x
y
A.
21
1
' 2 ln2
x
x
y
B.
2
21
1
3
'2
1 ln2
x
x
y
x
85
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
C.
2
1
2
1
3
'2
1
x
x
y
x
D.
21
2
1
ln8
'2
1
x
x
y
x
Câu 42 : 
y f x
 
2
5 3 3
12
x
f x e x x x
.

y f x
m cc tr?

3
m cc tr. 
1
m cc tr.
c tr. 
2
m cc tr.
Câu 43 (THPT Tôn Đức Thắng – Khánh Hòa ) : 
2ln ln – ln 2y x x
 ca
ye
.
A.
1
e
B.
2
e
C.
2
e
D.
1
2e
Câu 44 (THPT Nguyễn Thiện Thuật – Khánh Hòa ) : 
2
3
log 3 5y x x
.
A.
(2 3)ln5yx

B.
2
1
( 3 5)ln3
y
xx

C.
2
( 3 5)ln5y x x
D.
2
23
( 3 5)ln3
x
y
xx

Câu 45 (THPT Trần Quý Cáp – Khánh Hòa ) : 
ln 2 1yx

m

21y e m

.
A.
12
42
e
m
e
B.
12
42
e
m
e
C.
12
42
e
m
e
D.
12
42
e
m
e
Câu 46 (THPT Nguyễn Thiện Thuật – Khánh Hòa) : 
1
ln
2
x
y
x
A.
3
( 1)( 2)
y
xx

B.
3
( 1)( 2)
y
xx

C.
2
3
( 1)( 2)
y
xx

D.
2
3
( 1)( 2)
y
xx

Câu 47 :  ln nht c
3 2 2
45
x
y e x x

n
13
;
22



bng
A.
13
2
3
2
e
B.
12
5
4
5
e
86
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
C.
11
4
5
2
e
D.
14
3
2
3
e
Câu 48 (THPT Nguyễn Thiện Thuật – Khánh Hòa) : 
2
ln 4f x x x
chn khng
nh sau
A.
1
5
2
f
B.
21f
C.
20f
D.
6
1
5
f

Câu 49 : a  s
.5
x
yx
A.
5 1 ln5
x
yx

. B.
5 1 ln5
x
y

.
C.
5 ln5
x
y
. D.
51
x
yx

.
Câu 50 :  ln nht c
2
55
x
y x x e
n
3;0
A.
2
3;0
9
x
Max y e

.
B.
3
3;0
19
x
Max y e

.
C.
2
3;0
8
x
Max y e

.
D.
3;0
0
x
Max y

.
Câu 51 : 
lny x x x

A.
' lnyx
. B.
1
'1y
x

. C.
'1y
. D.
' lnyx
.
Câu 52 (THPT Lạng Giang số 2) : 
2
log 4
x
y
. 
2y
A.
2
log 4
B.
1
ln 4
C.
1
ln2
D.
1
ln4
Giáo viên cần file word vui lòng liên hệ
Zalo / đt / facebook : 0914 449 230
87
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
A. PHƢƠNG TRÌNH MŨ
1. Phƣơng trình mũ cơ bản :
0, 1
x
a b a a
2. Biến đổi, quy về cùng cơ số :
uv
aa
Ví dụ : Gi
1 2 1
9 27
xx
.
HD Giải:
21
1 2 1 6 3
9 27 3 3
x
x x x
(Ở đây ta đƣa về cùng cơ số a = 3 > 1)
1
2 2 6 3 4 1
4
x x x x
3. Logarit hóa:
☻ Phng trnh
0 1, 0
log
u
a
ab
ab
ub

Ví dụ : Gi
39
x
; HD Giải:
3
3 9 log 9 2
x
x
.
☻ Phng trnh
log log .log
f x g x f x g x
a a a
a b a b f x g x b
hoc
log log .log
f x g x
b b b
a b f x a g x
Ví dụ : Gi
2
12
3 2 8.4
x x x
.
HD Giải:  2 hai v 
2
12
22
log 3 2 log 8.4
x x x
2
2
1 log 3 2 1x x x
2
22
2
1
1 log 3 1 0 1 1 log 3 0
1 log 3
x
x x x x
x

4. Đƣa về phƣơng trình tích : Gom s h  chung.
Ví dụ : Gi
25.2 10 5 25 0
x x x
Phần III : PHƢƠNG TRÌNH MŨ - LOGARIT
Phng trnh c một nghiệm duy nhất khi
0b
Phng trnh vô nghiệm khi
0b
.
Giáo viên cần file word vui lòng liên hệ
Zalo / đt / facebook : 0914 449 230
88
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
HD Giải:
25.2 10 5 25 0 25.2 2 .5 25 5 0 2 25 5 25 5 0
x x x x x x x x x x
5 25 2
25 5 2 1 0
0
21
x
xx
x
x
x

Bài tập mẫu tham khảo 01 : Gii phng trnh sau :
a/
x 1 x x 1
5 6.5 3.5 52

b/
1
3 .2 72
xx
♥ Hƣớng dẫn giải :
11
33
a /5 6.5 3.5 52 5.5 6.5 .5 52 5 (5 6 ) 52
55
x x x x x x x
52
.5 52 5 5 1
5
xx
x
. Vy phng trnh c nghim x = 1.
12
b/ 3 .2 72 3 .2 .2 72 2.6 72 6 36 6 6 2.
x x x x x x x
x
Vy phng trnh c nghim x = 2.
Bài tập mẫu tham khảo 02 : Gii phng trnh: a/
2
2x 4
x 3x 5
1
9
3





b/
2
26
2 64.4
x x x
♥ Hƣớng dẫn giải : a/ Nhận xét: Hai v ca phng trnh c th bi a v  s 3.
2
22
24
2 4 3 5
3 5 1 2 2 4 2 6 10
22
1
9 3 3 3 3
3
1
2 4 2 6 10 2 4 6 0
3
x
x x x
x x x x x
x
x x x x x
x





Vy phng trnh c hai nghim: x = 1; x = –3.
b/ phng trnh cho 4
x +3
=
2
6
4
xx
2
63x x x
22
30
6 ( 3)
x
x x x

2
3
2 7 3 0
x
xx

3
3
1
2
x
x
x



x = 3 hay x =
1
2
.
Bài tập mẫu tham khảo 03 : Ging trnh sau y:
a/
2
3
5 625
xx
b/
1
57
2
(1,5)
3
x
x



c/
1
2 .5 200
xx
♥ Hƣớng dẫn giải :
a)
22
3 3 4 2 2
5 625 5 5 3 4 3 4 0
x x x x
x x x x

1x
hoc
89
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
Vy phng trnh  cho c 2 nghim:
1x
hoc
x4
b)
1 5 7 1
57
2 3 3
(1,5) 5 7 1 1
3 2 2
x x x
x
x x x
Vy phng trnh  cho c nghim duy nht:
1x
c)
1
2 .5 200 2.2 .5 200 10 100 2
x x x x x
x
Vy phng trnh  cho c nghim duy nht:
2x
Bài tập mẫu tham khảo 04 (đề Minh họa lần 2) : m ca phng trnh
1
3 27
x
A.
9x
B.
3x
C.
4x
D.
10x
♥ Hƣớng dẫn giải :
Cách 1 : 
1 1 3
3
3 27 3 3 1 log 27 1 3 4.
xx
x x x

Chọn C
Cách 2 : Trc nghi d
Nhp
1
3 27
x
 dr  ki
 Chọn C

3^Q)p1$p27r4=
Bài 01 : Ging trnh sau
a)
4
3
24
x
b)
2
5
6
2
2 16 2
xx
c)
2
2 3 3 5
39
x x x
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
90
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
Bài 02 : Ging trnh sau
a)
2
x x 8 1 3x
24
b) 5
2x + 1
3. 5
2x 1
= 110 c)
5 17
73
1
32 128
4
xx
xx


☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 03 : Ging trnh sau
a) 2
x
+ 2
x 1
+ 2
x 2
= 3
x
3
x 1
+ 3
x 2
b) (1,25)
1 x
=
2(1 )
(0,64)
x
c)
2 2 2 2
x x 1 x 1 x 2
5 3 2 5 3
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Giáo viên cần file word vui lòng liên hệ
Zalo / đt / facebook : 0914 449 230
91
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 04 : a/ (THPT Phù Cát) : Tp nghim ca phng trnh
2
4
1
2
16
xx

A.
B.
2;4
C.
0; 1
D.
2; 2
b/ (THPT Phan Bội Châu) : Phng trnh
21
51
x

A.
1.x
B.
1
.
2
x
C.
1
.
3
x
D.
0.x
c/ (THPT Quy Nhơn) : Phng trnh
32
4 16
x

A.
4
3
x
B.
3
4
x
C.
3x
D.
5x
.
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 05 : a/ (THPT chuyên Nguyễn Trãi lần 2) : m ca phng trnh
2 5 2
42
xx
A.
3
B.
8
5
C.
12
5
D.
8
5
b/ (Sở GD&ĐT Bình Phƣớc) : m ca phng trnh
36
21
x
A.
1
3
x
B.
3x
C.
1
2
x
D.
2x
c/ (THPT chuyên Lƣơng Thế Vinh) : Phng trnh
84
x

A.
2x 
B.
2
3
x
C.
1
2
x 
D.
1
2
x
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
92
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
Bài 06 : Ging trnh sau :
a/
1
11
28
x



b/
2
2 3 2 3
xx
c/
2
4
3 2 2 3 2 2
x x x
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 07 (THPT Trần Hƣng Đạo – Nam Định) : u
12
,xx
m ca phng trnh
2
log 243
4
3
x
 ca biu thc
12
.M x x
A.
3M 
B.
9M
C.
25M 
D.
9M 
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 08 : Ging trnh sau : a/
32
1
8
2
x
x



b/
2
3
24
xx
c/
2
23
22
xx
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 09 :  th
C
c
lny f x x
ct trm A, tip tuyn ca
C
ti A
ng trnh l
93
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
A.
1.yx
B.
2 1.yx
C.
3.yx
D.
4 3.yx
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 10 (THPT Đoàn Thị Điểm – Khánh Hòa) : S lng ca loi vi khun A trong m
nghic
( ) (0)2
t
s t s

(0)s
 lng vi khuu,
()st
 lng vi khu
t
 lng vi khu
con. H t u, s lng vi khuu con?
   
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 11 (Đƣa về dạng tích) : Gi a/
8.3 3.2 24 6
x x x
b/
2 2 2
3 2 6 5 2 3 7
4 4 4 1
x x x x x x
c/
1
12.3 3.15 5 20
x x x
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài tập trắc nghiệm phƣơng trình mũ dạng CƠ BẢN
Câu 01 : p nghim
S
ca phng trnh
2
2
55
xx
.
94
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
A.
1
0;
2
S



B.
0;2S
C.
1
1;
2
S




D.
S 
Câu 02 (THPT Tiên Lãng) : Nghim ca phng trnh
2
48
x m x

A.
2m
B.
m
C.
m
D.
2m
Câu 03 (THPT Võ Nguyên Giáp) : S nghim ca phng trnh
2
21
21
xx

A.
2
B.
0
C.
1
D.
4
Câu 04 (thi thử Cụm 1 – Tp.HCM) : Phng trnh
8 16
x
.
A.
2x
B.
3x
C.
3
4
x
D.
4
3
x
Câu 05 (THPT Lý Thƣờng Kiệt) : Gii phng trnh
2
3 27
x
A.
1x 
B.
0x
C.
2x 
D.
1x
Câu 06 (THPT Lƣơng Tài 2) : Gii phng trnh
21
3 27
x
.
A.
5x
B.
1x 
C.
3
1
log 30
2
x
D.
2x
Câu 07 : Cho phng trnh
2
45
39
xx
tng lp phng cc nghim thc ca phng trnh l:
A.
28
B.
27
C.
26
D.
25
Câu 08 : Cho phng trnh :
2
3 8 2x 1
39
xx
p nghim ca phng tr
A.
2;5S
B.
5 61 5 61
;
22
S





C.
5 61 5 61
;
22
S






D.
2; 5S
.
Câu 09 (TT Tân Hồng Phong) : Gii phng trnh
2
3
2 16
xx
.
A.
4x
B.
1x
hoc
4x 
C.
1x 
D.
1x 
hoc
4x
Câu 10 : Nghim ca phng trnh
23
2
0,125.4
8
x
x





A.
4x
B.
5x
C.
6x
D.
7x
Câu 11 (THPT Lê Hồng Phong) : m ca phng trnh
2 100
28
x
.
A.
204x
B.
102x
C.
202x
D.
302x
95
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
Câu 12 (thi thử Cụm 4 – Tp.HCM) : Gii phng trnh
31
4
1
3
9
x
x



A.
6
7
x
B.
1
3
x
C.
1x
D.
7
6
x
Câu 13 (THPT Ngô Gia Tự) : Gii phng trnh
2
1
1
8 .5
8
xx
A.
5
1; 1 log 8xx
B.
8
1; 1 log 5xx
C.
5
1; 1 log 8xx
D. Kt qu 
Câu 14 (THPT Nguyễn Thái Học) : Gii phng trnh:
2(1 )
16 8
xx
A.
3x 
B.
2x
C.
3x
D.
2x 
Câu 15 (THPT Hoàng Văn Thụ - Hòa Bình) : S nghim ca phng trnh
2
2
21
xx

A.
2
B.
3
C.
1
m
Câu 16 (THPT Ngô Quyền) : p nghim
S
ca phng trnh
2
2
33
xx
A.
1
1;
2
S




B.
1;2S 
C.
1
1;
2
S




D.
S 
Câu 17 : Nu
x

y
th
3 27
x

2 64
xy

y
bng.
A.
1
B.
3
log 8
C.
2
log 8
D.
2
Câu 18 (thi thử Cụm 7 – Tp.HCM) : Phng trnh
44
2
0.2 5
x
x
tng ng vi phng
trnh:
A.
2 2 4
55
xx
B.
2 2 2
55
xx
C.
2 2 4
55
xx
D.
2 2 2
55
xx
Câu 19 (THPT Ngô Sĩ Liên lần 3) : Tp nghim ca phng trnh
2
4
1
2
16
xx

A.
2;4
B.
C.
0;1
D.
2; 2
Câu 20 (THPT chuyên Lê Thánh Tông) : Phng trnh
1
34
x
.
A.
4
log 3x
B.
3
log 2x
C.
2
log 3x
D.
3
log 4x
Câu 21 (THPT Trần Quý Cáp - KH) : S lng ca mt s n sau
t
(gic xp x bi
ng thc
0,195t
o
Q Q e

o
Q
 lng vi khuu. Nu s lng vi khuu

5000

100 000
con?
96
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
A.
3,5
B.
20
C.
15,36
D.
24
PHƢƠNG PHÁP ĐẶT ẨN PHỤ
Cơ sở lý thuyết :
0
0 0 1
0
gx
gx
ta
f a a
ft



Dạng 1: ng t
0
fx
Fa
.
Vi dt
, 0
fx
t a t
n v phng trnh
0Ft
, gim dng t
ca phng trnh, t c x. Ta thƣờng gặp dng:
2
. . 0
f x f x
ma n a p
.
Ví dụ : Gi
2 5 2
3 3 2
xx

.
HD Giải:
2 5 2 5 2 2
3 3 2 3 .3 3 .3 2 0
x x x x
.
t
30
x
t 
; pt cho tr :
52
1
3 9 2 0
9
t t t
1
32
9
x
x
Với bất phƣơng trình ta cũng làm tƣơng tự.
Dạng 2:
. . 0
f x f x
ma nb p

.1ab
. t
1
, 0
f x f x
t a t b
t
.
Dạng 3:
22
. . . . 0
fx
f x f x
ma n a b pb
.
Chia 2 v phng trnh cho
2 fx
b
t
, 0
fx
a
tt
b




ng trnh :
2
0mt nt p
.
Ví Dụ 1 : Ging trnh sau y:
a)
11
4 6.2 8 0
xx
b)
9 5.3 6 0
xx
c)
11
4 2 21 0
xx
d)
2
5 2.5 5 0
xx
e)
6.9 13.6 6.4 0
x x x
f)
13
5 5 26
xx

☺ Giải :
a)
1 1 1 2 1
4 6.2 8 0 (2 ) 6.2 8 0
x x x x
Khi không quy về đƣợc
dạng cơ bản ta nghĩ tiếp đến
là đặt ẩn phụ
97
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
Dạng 1: t
1
t2
x
u kin t > 0. 
2
2
6 8 0
4
t
tt
t
► V
1
2
x
=2
0x
► V
1
2
x
= 4
1x
. Vy phng trnh  cho c hai nghim:
0x
;
1x
b)
2
9 5.3 6 0 3 5.3 6 0
x x x x
t
3
x
t
(t > 0), phng trnh trn tr 
2
5 6 0tt
t = 3 hoc t = 2 (nhận)

3 3 1
x
x

3
3 2 log 2
x
x
. Vy phng trnh  cho c nghim: x = 1 hoc x =
3
log 2
c)
11
4 2 21 0
xx




d)
2
5 2.5 5 0
xx
(dạng 2)




e)
6.9 13.6 6.4 0
x x x
(dạng 3)
Chia hai v ca phng trnh cho c:




f)
13
5 5 26
xx


98
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018


Ví Dụ 2 : Ging trnh sau y:
a/
1
17
4 .2 16 0
2
xx
b/
22
22
9 28.3 27 0
xx
c/
3.16 2.81 5.36
x x x

☺ Giải : a/ u kin:
0x
.
i
2
4 17
.2 16 0 2 34.2 64 0.
42
x
x x x
t
20
x
t 
 
2
32
34 64 0 .
2
t
tt
t
i
32t
c
5
2 32 2 2 5 25
xx
xx
(th
i
2t
c
2 2 1 1
x
xx
(th
Vp nghim
1;25S
.
i
22
2
22
3 28.3 27 0
xx
.
t
2
2
30
x
t

 
2
1
28 27 0 .
27
t
tt
t
i
1t
c
2
22
3 1 2 0
x
x
m.
i
27t
c
22
2 2 3 2 2
3 27 3 3 2 3 1 1.
xx
x x x

Vy tp nghim c
1;1 .S 
i
2
44
3.16 5.36 2.81 0 3. 5. 2 0
99
xx
x x x
.
t
4
0
9
x
t




 
2
1
3 5 2 0
2
3
t
tt
t
.
i
1t
c
4
1 0.
9
x
x



i
5
;4
3
S




c
2
4 2 2 2 1
2 1 .
9 3 3 3 2
xx
xx
Vp nghim
1
0;
2
S



99
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
Ví Dụ 3 : PHƢƠNG PHÁP LIÊN HỢP
Lƣu ý: Mt s nhng cp s o ca nhau:
2 1 ; 2 3 ; 3 8 ,...
Gii phng trnh
( 7 48) ( 7 48) 14
xx
(1)
☺ Giải : 
( 7 48) ( 7 48) 1
xx
. t
1
( 7 48) ;( 0) ( 7 48)
xx
tt
t
g trnh (1) tr 
2
7 48
1
14 14 1 0
7 48
t
t t t
t
t


Vi
7 48t 

( 7 48) 7 48 2
x
x
.
Vi
7 48t 

( 7 48) 7 48 2
x
x
.
Bài 01 : Gii phng trnh: a/
21
5 5 6
xx

b/
21
5 24.5 1 0
xx
c/
1
9 8.3 1 0
xx
☺ Giải :






Bài 02 : Ging trnh sau
a/
x 1 x 4 x 2
4 2 2 16
(ĐH TCKT – 99) b/
x 2 x 2
4 16 10. 2


(ĐH Hàng Hải – 98)
c/
25 6.5 5 0
xx
(TN – 2009) d/
8 2.4 2 2 0
x x x
e/
2002 2003
8.4 5.2 2 0
xx
☺ Giải :




100
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018






Bài 03 : Ging trnh sau
a/
6x 3x
e 3.e 2 0
b/
2
2.2 2 2
xx

c/
22
1 x 1 x
5 5 24


d/
22
2
2 2 3
x x x x

(ĐH Khối D-2003)
☺ Giải :










Bài 04 : Ging trnh sau a/
x x 3x 1
125 50 2

(ĐHQG-HN-98)
b/
2 2 2
2 2 2
2.4 6 9
x x x x x x

c/
3.8 4.12 18 2.27
x x x x
(ĐH Khối A-2006)
☺ Giải :


101
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018








Bài 05 : Ph
9 5.3 6 0
xx
tổng các nghiệm 
A.
3
log 6
B.
3
2
log
3
C.
3
3
log
2
D.
3
log 6
☺ Giải :



Bài 06 : Cho phng trnh
12
2 15.2 8 0
xx
, kh
A. t nghim m m dng D. 
☺ Giải :



Bài 07 : Phng trnh
1
5 25 6
xx


A.
5
1 21
log
2




B.
5
1 21
log
2




C. 5 D.
5
1 21
5log
2




☺ Giải :

102
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018



Bài 08 : Ph
7 4 3 2 3 6
xx

A.
23
log 2x
B.
2
log 3x
C.
2
log 2 3x 
D.
1x
☺ Giải :




Bài 09 : Gi s a m dng ca phng trnh:
23
2 33.2 4 0
xx
 ca
2
37
a
Ma
 A.
6
B.
55
27
C.
29
D.
26
9
☺ Giải :




Bài 10 : Ging trnh sau
a)
2 3 2 3 4
xx
(CĐ Hải Quan – 1998)
b)
xx
7 48 7 48 14
c/
4 15 4 15 2
xx
☺ Giải :



103
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018







Bài 11 (THPT Nguyễn Trãi Lần 1) : tích các nghiệm ca phng trnh
( 2 1) 2 1 2 2 0
x
x
A.
0
B.
2
C.
1
D.
1
☺ Giải :



Bài 12 (THPT Chuyên Bình Long) : trnh m 
ca . A.
1P 
B.
3P
C.
2P
D.
4P
☺ Giải :



Bài 13 (THPT Chuyên Vinh) : Bit rng phng trnh
2
11
23
xx

,ab

a b ab
 bng.
A.
2
1 2log 3
B.
1
C.
2
1 log 3
D.
2
1 2log 3
☺ Giải :

2
22
2 3 7 4 3
xx
12
,xx
12
P x x
104
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018


Bài 14 (THPT Chuyên Bình Long) : Gi
1
x
,
2
x
12
xx
m thc ca phng trnh
21
3 4.3 1 0
xx
. Chn m 
A.
12
20xx
B.
12
22xx
C.
21
22xx
D.
12
22xx
☺ Giải :



Câu 15 (THPT Tôn Đức Thắng – Khánh Hòa) : V tha
m
ng trnh
2
4 2 0
xx
m
m tht?
A.
0m
. B.
04m
. C.
4m
. D.
0m
.
☺ Giải :





Câu 16 (THPT Tôn Đức Thắng – Khánh Hòa) : Tm ca phng trnh
9 9 10.3
xx


A.
5
. B.
. C.
2
. D.
3
.
☺ Giải :



Câu 17 (THPT Huỳnh Thúc Kháng – Khánh Hòa) : Tnh
D
c
5
5 125
x
y


A.
D
. B.
3;D
. C.
\3D
. D.
3;D 
.
☺ Giải :

105
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018

Bài tập trắc nghiệm phƣơng trình mũ dạng ĐỔI BIẾN SỐ
Câu 01 (THPT chuyên Vĩnh Phúc) : 
4 2 .2 2 0
xx
mm
n bit
12
;xx
sao cho
12
3xx

A.
3m
B.
1m 
C.
2m 
D.
4m
Câu 02 (THPT Lƣơng Tài) : Phng trnh
4 2 1 2 3 4 0
xx
mm
m
12
,xx
sao cho
12
3xx
khi.
A.
1
2
m 
B.
4m
C.
5
2
m
D.
2m
Câu 03 : Tng tt c m ca phng trnh
21
2 5.2 2 0
xx
b
A.
1
B.
3
2
C.
5
2
D.
0
Câu 04 : Cho phng trnh:
1
3.25 2.5 7 0
xx
u sau:
(1)
0x
m duy nht ca phng trnh.
(2) Phng trnh c nghim dng.
(3) C hai nghim ca phng trnh u nh hn 1.
(4) Phng trnh trn c tng hai nghim bng
5
3
log
7



S  A.
2
B.
1
C.
4
D.
3
Câu 05 (Sở GD và ĐT Long An) : Gi
1
x
,
2
x
m ca phng trnh
2 3 2 2 3 3
xx
. 
12
P x x
.
A.
3P 
B.
0P
C.
2P
D.
3P
Câu 06 : Tng tt c m ca phng trnh
21
2 5.2 2 0
xx
b
A.
1
. B.
3
2
C.
5
2
D.
0
Câu 07 (THPT Nguyễn Huệ - Huế) : Phng trnh
3 5 3 5 3.2
xx
x
m
12
,xx
.

22
12
A x x
.
A.
1
B.
2
C.
9
D.
13
106
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
Câu 08 (THPT chuyên Biên Hòa lần 2) : tp nghim thc ca phng trnh
2
3 .2 1
x x
.
A.
2
0;log 3S
B.
0S
C.
0;log6S
D.
2
1
0;log
3
S



Câu 09 (THPT Lý Thái Tổ) : Phng trnh:
3 4 5
x x x


A.
1
B.
4
C.
2
D.
3
Câu 10 : Nu
2
3 9 10.3
xx

 ca
21x

A.
1
hoc
5
B.
5
C.
1
D.
0
hoc
2
.
Câu 11 (THPT chuyên Lê Hồng Phong) : t c  thc ca tham s
m
sao cho phng
trnh
9 2 2 3 3 4 0
xx
mm
t
12
,xx
thu kin
12
3xx
.
A.
31
3
m 
B.
5
2
m 
C.
3m 
D.
7
3
m 
Câu 12 (thi thử Cụm 8 – Tp.HCM) : Nu phng trnh
2
3 4.3 1 0
xx
t
12
;xx

12
xx

A.
12
21xx
B.
12
21xx
C.
12
0xx
D.
12
.1xx
Câu 13 (TTGDTX Nha Trang - Khánh Hòa) : Gi
12
,xx
m ca phng trnh
2
61
1
5
5
xx
x



.

12
xx
bng.
A.
7
B.
5
log 2 1
C.
5
D.
10
Câu 14 (THPT Hùng Vƣơng – PT) : Bit phng trnh
2.16 17.4 8 0
xx

2
nghim
12
,xx

tng
12
xx
.
A.
12
2xx
B.
12
4xx
C.
12
1xx
D.
12
17
4
xx
Câu 15 : Phng trnh
11
9 6 3.4
x x x

m:
A.
1
B.
4
C.
3
D.
2
107
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
Câu 16 : S nghim ca phng trnh
1
3 3 2
xx


A.
0
B.
2
C.
3
D.
1
Câu 17 : Tp nghim ca phng trnh trnh
1
2
1
125
25
x
x




A.
1
{}
8
B.
{4}
C.
{1}
D.
1
{}
4
Câu 18 : Tp nghim cu phng trnh
22
11
9 3 6 0
xx

A.
{ 1;1}
B.
{ 2;0;2}
C.
{ 1;0;1}
D.
{0}
Câu 19 : Phng trnh
22
sin cos
2 5.2 7
xx


A.
2
xk

B.
x
C.
3xk

D.
2
2
3
xk

Câu 20 : Tp nghim ca phng trnh
13
5 5 26
xx


A.
{1;3}
B.
{3;5}
C.
D.
{2;4}
Câu 21 : S nghim ca phng trnh
22
2 2 15
xx


A.
0
. B.
3
. C.
2
. D.
1
.
Câu 22 : Phng trnh
9 3.3 2 0
xx
m
1 2 1 2
,x x x x
 ca
12
23A x x

A.
2
B.
2
4log 3
C.
0
D.
3
3log 2
Câu 23 : Cho phng trnh
21
81 4.3 27 0
xx
. Tm ca phng trnh l bao nhiu?
A.
1
2
B.
3
2
C.
1
D.
2
Câu 24 : Phng trnh
1
2 2 4
xx


A.
2
1 log 3
B.
2
3 log 3
C.
2
log 3 2
D.
2
log 3 1
Câu 25 (THPT Nguyễn Văn Trỗi – Khánh Hòa) : t c  ca tham s
m
 phng
trnh
4 2 .2 2 0
xx
mm
t
12
,xx
sao cho
12
3xx
.
A.
;4
B.
0;4
108
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
C.
2;4
D.
;0 2;4
Câu 26 : Nghim ca phng trnh
25 2.5 15 0
xx

A.
3; 5xx
B.
5
log 3x 
C.
5
log 3x
D.
3
log 5x
Câu 27 : Gi
M
m ca phng trnh
12
3 3 2 0
xx

M
.
A.
0M
B.
1M
C.
2M
D.
3M
Câu 28 : Cho
4 4 3
xx


22
xx
A

A.
5
B.
25
C.
10
D.
5
Câu 29 : Bit phng trnh
3.25 2.49 5.35
x x x

t nghi
0
dng
7
5
log
a
x
b
, vi
,ab

 ng v
a
b
 ti gi
ab
.
A.
1
B.
1
C.
0
D.
2
109
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
B. PHƢƠNG TRÌNH LOGARIT
Phƣơng trình LOGARIT cơ bản :
log ( )
a
f x b
Ví dụ : Phng trnh
3
log (3 2) 3x 

A.
29
3
x
B.
11
3
x
C.
25
3
x
D.
87x
Giải : ...........................................................................................................................................................
Chú ý :
log ( ) log ( )
aa
f x g x
Bài tập mẫu tham khảo 01 : Gii phng trnh sau :
a/
2
2
log (3x x) 2
b/
22
log (x 5) log (x 2) 3
♥ Hƣớng dẫn giải :
a/ Điều kiện:
2
3x x 0
(Đối với phương trình này, ta có thể đặt điều kiện mà không cần giải điều kiện đó.
Sau khi giải phương trình tìm được kết quả, ta đối chiếu điều kiên sau cũng được).

2 2 2
2
x1
log (3x x) 2 3x x 4 3x x 4 0
4
x
3

So với điều kiện, ta thy phng trnh c hai nghim:
4
x 1;x .
3
b/
22
log (x 5) log (x 2) 3
u kin:
x5
ng trnh (1)
2
log x 5 x 2 3 x 5 x 2 8


2
x 3x 18 0 x 3 x 6hay
So với điều kiện, ta thy phng trnh c hai nghim:
x6
Bài tập mẫu tham khảo 02 : Gii phng trnh sau :
a)
22
log 4 log 1 1xx
b)
2
3
3
log ( 2) log ( 4) 0xx
c)
48
2
log x 4log x log x 13
d)
48
2
log 1 4log 1 log 1 13x x x
110
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
♥ Hƣớng dẫn giải : a)
22
log 4 log 1 1xx
(1) Điều kiện:
4 0 4
4
1 0 1
xx
x
xx



ng trnh(1)
2
log ( 4)( 1) 1 ( 4)( 1) 2x x x x
2
( 4)( 1) 4 5 0 0x x x x x
hoc x = 5
So vu kin x > 4 ta ch nhn nghim x = 5
Vy phng trnh  cho c nghim duy nh
b)
2
3
3
log ( 2) log ( 4) 0xx
(2) Điều kiện:
2
20
2
4
( 4) 0
x
x
x
x



(I)
ng trnh (2)
2
3
2log ( 2) log( 4) 0xx
2
22
3 3 3
log ( 2) log ( 4) 0 log ( 2)( 4) 0x x x x
2
( 2)( 4) 1
( 2)( 4) 1
( 2)( 4) 1
xx
xx
xx
(hc sinh t gii tip)
Vy phng trnh  cho c nghim x = 3 hoc
32x 
c)
48
2
log x 4log x log x 13 (3)
Điều kiện:
x0
1/2 2 3
48
2
2 2 2
(3) log x 4log x log x 13 log x 4log x log x 13
2 2 2
1
2log x 2log x log x 13
3
22
13
log x 13 log x 3 x 8 (Thoûa ñieàu kieän).
3
Vy phng trnh c nghim duy nht:
x 8.
u kin:
1.x
Vu ki 
2 2 2
1
2log 1 2log 1 log 1 13
3
x x x
2
log 1 3 1 8 9.x x x
Đối chiếu điều kiệnm duy nht
9.x
Bài tập mẫu tham khảo 03 : Gii phng trnh
2
33
log 6 log 2 1xx
.
A.
0x
B.
1x
C.
2x
D.
3x
♥ Hƣớng dẫn giải :
Cách 1:
2
33
log 6 log 2 1xx
2
33
log 6 log 3 2xx
2
3 2 0
6 3 2
x
xx

2
0
3
x
x
x
3x
Chọn D
111
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
Cách 2: S d
570Casio fx VN PLUS
.
Nhấn :
w1i3$Q)dp6$pi3
$Q)p2$p1r0=
Màn hình hiển thị
!
!r1=
!
!r2=
!
!r3=. Chọn D
Bài 1: Ging trnh
a/
2 4 8
log log log 33x x x
b/
2
log [ .( 1)] 1xx
c/
22
log ( 3) log ( 1) 3xx
☺ Giải :







Bài 02 : Gi
a/
2
22
log 3 3 log 2 3x x x
b/
log( 2) log( 3) 1 log5xx
☺ Giải :

Giáo viên cần file word vui lòng liên hệ
Zalo / đt / facebook : 0914 449 230
112
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018





Bài 03 : Gi
a/
4 4 4
log ( 3) log ( 1) 2 log 8xx
b/
2 2 2
log ( 1) log ( 3) log 10 1xx
☺ Giải :





Bài 04 : a/ Phng trnh
2
log (3 2) 2x

A.
4
3
x
B.
2
3
x
C.
1x
D.
2x
b/ Phng trnh
2 2 2
log ( 3) log ( 1) log 5xx

A.
2x
B.
1x
C.
3x
D.
0x
c/ Phng trnh
22
log log ( 1) 1xx
p nghi
A.
1;3
B.
1;3
C.
2
D.
1
d/ Phng 
2
31
3
log (5 3) log ( 1) 0xx
m
12
,xx

12
xx
 ca
12
23P x x

A. 5. B. 14. C. 3. D. 13.
☺ Giải :



113
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018




Bài 05 : Gia/
2
33
log ( 6) log ( 2) 1xx
b/
4 3 2 2
log 2log 1 log (1 3log ) 1x
c/
42
2
ln .log ( 2 ) 3lnx x x x
☺ Giải :









Bài 06 : Gi
21
8
log ( 2) 6log 3 5 2xx
b/
93
log ( 8) log ( 26) 2 0xx
c/
2 3 2
1
log 4 log 5 .log 1
3
xx
☺ Giải :




114
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018





Bài 07 : a/ (THPT Hoàng Hoa Thám - Khánh Hòa) : 
6
log 5 1xx


p nghim
 A.
2;3S
B.
1;6S 
C.
4;6S
D.
1; 6S 
b/ (THPT Hoàng Hoa Thám - Khánh Hòa) : Gi
44
log 1 log 3 3xx
.
A.
1 2 17x 
B.
1 2 17x 
C.
33x
D.
5x
☺ Giải :




Bài 08 : Nghim c
2
3
3
log 1 log 2 1 2xx

m B.
1.x
C.
2.x
D.
3.x
☺ Giải :



Bài 09 : a/ (THPT Nguyễn Trãi Lần 1) m c
2
log (3 2) 3x 
.
A.
10
3
x
B.
16
3
x
C.
8
3
x
D.
11
3
x
b/ (THPT Đặng Thúc Hứa) m c
3
log 1 0.x 
.
A.
1
3
x
B.
1
3
x 
C.
1x 
D.
1x
c/ (THPT chuyên KHTN lần 1) : S nghim c
2
log 1 2x 
.
115
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
A. mt s  B.
2
C.
0
D.
1
d/ (THPT Nguyễn Đăng Đạo) : Gi
3
log 4 1 4x 
A.
21
2
x
B.
63
4
x
C.
20x
D.
11
4
x
☺ Giải :





Bài 10 : a/ (THPT Nguyễn Thị Minh Khai – Khánh Hòa) : 
22
log ( 3) log ( 1) 3xx

nghiA.
11x
B.
7x
C.
5x
D.
9x
b/ (THPT QG – 2017 ) : nghim c
25
1
log 1
2
x 
.
A.
23
2
x
B.
6x 
C.
4x
D.
6x
☺ Giải :


Bài 11 : Gi
1/
2
1
log 4 5 1
x
xx
:
3x
.
2/
2
log 5 8 3 2
x
xx
; :
13
;
22
xx
.
3/
32
1
log 2 2 3 1 3
x
x x x
; :
3x
.
BT Tƣơng tự : a/
3
log 1 2

x
x
; :
5x
. b/
2
35
log 9 8 12 2
x
xx
; :
13
22
x
.
☺ Giải :



116
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018






Bài 12 : Gi
1)
2
log (9 2 ) 3
x
x
2)
3
log (3 8) 2
x
x
3)
1
33
log (3 1).log (3 3) 6
xx
4)
1
2
log (5 25 ) 2
xx

☺ Giải :












Bài 13 : ng ca mc
A.
rx
f x e

A

ng vi khuu, r  l ng
0r
, x ng.
117
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
Bing vi khung
vi khup 25 ln?
A. 50 gi. B. 25 gi. C. 15 gi. D. 20 gi.
☺ Giải :



Bài 14 : p s nhc mng nh cacbon 14 (mt
ng v ca cacbon). Khi mt b phn c chng quang h
d ng cacbon 14 ca b ph y mt
m cht rng nu gi
Nt
 
i trong mt b phn ca mng t
t

Nt

c
500
100. 0,5 %
t
Nt
u g t mi ta thy
i trong mu g 
65%
i c
   
☺ Giải :




Bài 15 : Khi cho d nhi
0
219 C
 l biu th s gim
nhi ca d

0,17 0
( ) . 6, ), 0(
t
T t k e C t

k
ng sm
0
t

nhi gim ti
0
0 C
A.
0
0,17 ln 37,5t
. B.
0
2
0,17 ln
75
t
. C.
0
100ln 37,5
17
t
. D.
0
2
100ln
75
17
t
☺ Giải :



118
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018

Bài 16 (Đề thi ĐH năm 2012) : Gii h 
32
1
2 5 4
42
22
x
xx
x
yy
y


☺ Giải :






Bài 17 (THPT Lạc Long Quân – Khánh Hòa) : C mt trt
M
c cho b
thc
0
log – logM A A
, vi
A
 rung chn t
0
A
 chun (hằng số).
Đầu thế kỉ XX , mt trt 
8,3
 
t tr Nam Đại Tây Dƣơng c c
7,3
 Richter. Hi trt
 gp bao  ca trt ng ?
A.
5
B.
10
C.
13,1
D.
11,2
☺ Giải :




Bài 18 (THPT Ischool Nha Trang) : S ng ca mc
()
rx
f x Ae

A
 lng vi khuu,
r
 l ng
0r
,
x

ging. Bit s vi khu
1000

10
gi 
5000
con. Hi
 lng vi khup
10
ln?
A.
5ln20
(gi). B.
5ln10
(gi). C.
5
10log 10
(gi). D.
5
10log 20
(gi).
☺ Giải :

119
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018


Bài 19 : Cho phng trnh
3
2
2
2
log 2 5
33
x
m x x
, vi
m
t c  ca
m
 phng trt nghi
A.
34 2
22m

B.
4m
hoc
34
02m

C.
4m
hoc
34
02m

D.
2m
☺ Giải :





Bài tập trắc nghiệm phƣơng trình LOGARIT dạng CƠ BẢN
Câu 01 : 
2
2 2 2
log log log 4x x x
m chia ht cho
A. 5 B. 2
C. 3 D. 4
Câu 02 (THPT Lƣơng Tài) : Nghim c
2
log 1 3x 

A.
9x
B.
2x
C.
5x
D.
12x
Câu 03 (THPT Hoàng Quốc Việt) : Nu
log 243 5
x

x
bng:
A.
3
. B.
2
C.
4
D.
5
Câu 04 (THPT Thuận Thành 2) : Gi
2
log 2 1 3x 
A.
5x
B.
8x
C.
9
2
x
D.
3
2
x
Câu 05 (Sở GDĐT Lâm Đồng lần 2) : Gi
2
log 3 11 4x 
.
A.
17
3
x
B.
13
3
x
C.
20
3
x
D.
5x
Câu 06 (THPT Trần Cao Vân - Khánh Hòa) : 
3
log 3 2 3x 

120
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
A.
25
3
B.
87
C.
11
3
D.
29
3
Câu 07 (THPT Hoàng Văn Thụ - Khánh Hòa) :  thc
x
bit
3
log 2 2x
.
A.
4x 
B.
7x 
C.
6x
D.
6x 
Câu 08 (TTGDTX Vạn Ninh - Khánh Hòa) : 
log 1 2x 

A.
21
e
B.
2
1e
C.
101
D.
1025
Câu 09 (THPT Yên Lạc) : 
2
ln 2lnxx

A.
0;
B. C.
0;
D.
\0
Câu 10 (thi thử Cụm 7 – Tp.HCM) : m c
2
log 3 1 3x 
A.
5x
B.
1x
C.
3x
D.
4x
Câu 11 (THPT Nguyễn Tất Thành) :  nghim c
2
3
3
log ( 1) log 2 1 2xx
A.
2
B.
0
C.
1
D.
3
Câu 12 (THPT Nguyễn Quang Diêu) : m c
32
log log 1x
.
A.
2x
. B.
6x
. C.
8x
. D.
9x
.
Câu 13 : Gi
3
log 3 2 3x 
.
A.
25
3
x
B.
29
3
x
C.
87x
D.
11
3
x
Câu 14 (THPT Thái Phiên – HP) : 
2
222
log 2 1 log 3 log 3x x x

nghim?
A.
2
. B.
4
C.
1
D.
3
Câu 15 (THPT chuyên Lê Hồng Phong) : p nghim
S
c
2
0,5 2
log 10 23 log 5 0x x x
A.
7S
. B.
2;9S
.
C.
9S
. D.
4;7S
Câu 16 (Sở GDĐT Hà Tĩnh lần 2) : S nghim c
2
33
log log (3 )xx

A.
1
. B.
0
. C.
3
. D.
2
.
Câu 17 (Sở GDĐT Hà Tĩnh lần) : S nghim ca p
2 4 8
log log log 11x x x
.
Giáo viên cần file word vui lòng liên hệ
Zalo / đt / facebook : 0914 449 230
121
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
A.
2
. B.
3
C.
1
D.
0
Câu 18 (THPT Lý Nhân Tông) : 
5 5 5
log log 6 log 2x x x

A.
2
B.
3
C.
2
D.
3
Câu 19 (THPT Lý Nhân Tông) : Tng tt c m ca ph
2 7 2 7
log 2log 2 log .log x x x x
bng.
A.
10
B.
13
C.
11
D.
15
Câu 20 (THPT Tiên Du 1) : S nghim c
2
2
log 1 1x 

A.
2
B.
1
C.
3
D.
4
Câu 21 (Sở GDĐT Lâm Đồng lần 3) : 
2
log 2 7 1 logx x x
p nghi
A.
1;7
B.
7
C.
1;7
D.
1
Câu 22 (THPT Nguyễn Chí Thanh - Khánh Hòa) : Tp nghim c
22
log ( 3) log ( 1) 3xx

A.
5
B.
1;5
C.
7
2



D.
6
Câu 23 : Gi
2
log 2 2 3x 
.
A.
4x
B.
5x
C.
2x
D.
3x
Câu 24 (THPT Kim Liên - HN) : p nghim
S
c
2
2
log 3 8x 
.
A.
1;5S 
B.
1;5S
C.
7; 1S
D.
1;7S 
Câu 25 : 
2
24
log log 1 0xx
m thc ?
A.
4
B.
2
C.
3
D.
1
Câu 26 : Nghim c
33
log log 2 1xx
.
A.
3x 
. B.
1x
hoc
3x 
.
C.
1, 3xx
. m.
Câu 27 (THPT Gia Lộc 2) : Gi
2
2
2
2log 1 log 1x x x
.
A.
0, 2xx
B.
0x
C.
2x
m
122
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
Câu 28 (Sở GDĐT Lâm Đồng lần 1) : Nghim c
2
3
3
log ( 1) log (2 1) 2xx

A.
1
B. m C.
3
D.
2
Câu 29 (THPT Hoàng Văn Thụ - Khánh Hòa) : S nghim thc c
3 2 2
31
3
log 3 log 0x x x x

A. 0 B. 2 C. 3 D. 1
Câu 30 (THPT Nguyễn Thái Học) : Nu
1
log log 9 log 5 log 2
2
a a a a
x
(
0a
;
1a

x
bng:
A.
3
5
B.
3
C.
2
5
D.
6
5
Câu 31 : S nghim c
2
33
log 6 log 2 1xx

A.
3
B.
2
C.
0
D.
1
Câu 32 (THPT chuyên Lê Khiết) :  
4
log 3.2 1 1
x
x
m
12
,x x
ng
12
x x

A.
4
. B.
2
log 6 4 2
C.
6 4 2
D.
2
Câu 33 (THPT Nguyễn Huệ - Huế) : m c
3
log 1 2x 
A.
8
B.
6
C.
20
D.
3
Câu 34 : 
2
1lnyx
. Nghim c
0'y
:
A.
01xx hay
B.
1x
C.
1x 
D.
0x
Câu 35 : 
57
log log 2xx
 :
A.
1
5
x
B.
1
7
x
C.
7x
D.
5x
Câu 36 : Nghim c
24
1log log x
 :
A.
8
B.
4
C.
16
D.
2
Câu 37 : Phng trnh
log 3 log 2 1 log5xx
m ?
A. 1 B. 3 C. 2 D. 0
123
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
Câu 38 : Phng trnh
2
88
4
2log 2 log 1
3
xx
m ?
A. 1 B. 2
C. 3 D. 4
Câu 39 : m ca phng trnh
3
log 3 2 3x 
.
A.
25
3
B.
29
3
C.
87
D.
11
3
Câu 40 : S nghim c
2 3 2
log .log 2 1 2logx x x

A
0
B.
1
C.
2
D.
3
.
Câu 41 : Phng trnh
3
log 2 1 0x
m ?
A. 0. B. 2. C. 1. D. 3.
Câu 42 : Cho biy ca ch 
239
t lng
Pu
239
 i mt na). S c
S = Ae
rt
ng ch  l y (r < 0) i
i sau thy t. H
239
s  gn nht v 
A. 82135
B. 82335
C. 82235
D. 82435
Câu 43 (THPT Đoàn Thị Điểm – Khánh Hòa) : Gi
S
ng tt c m ca phng trnh
2
log 3.2 1 2 1
x
x

S
.
A.
0S
B.
1S 
C.
3
2
S
D.
1
2
S
Câu 44 (THPT Tôn Đức Thắng – Khánh Hòa) : Phng trnh
2
log 5 – 2 2 –
x
x
m
12
,xx
 ca
1 2 1 2
A x x x x

A.
2
B.
3
C.
9
D.
1
124
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
Câu 45 (THPT Huỳnh Thúc Kháng – Khánh Hòa) :
Nghim ca phng trnh
33
log 2 5 log 2 5 1
xx

A.
log2x
B.
3x
C.
2
log 10x
D.
4x
Câu 46 (THPT Nguyễn Thiện Thuật – Khánh Hòa) : Cho
3
log 4x
 biu thc
4
2
3
33
3
log log logK x x x
A.
23
2
K
B.
23
3
K
C.
23
3
K 
D.
23
2
K 
Câu 47 (THPT Nguyễn Thiện Thuật – Khánh Hòa) : m phng trnh
log 2x
.
A.
100x
B.
x
xe
C.
4x
D.
1x
Câu 48 (Trƣờng PT Hermann Gmeiner– Khánh Hòa) : Vi
01a
, nghim ca phng trnh
42
3
log log log
4
a
aa
x x x

A.
4
a
x
B.
3
a
x
C.
2
a
x
D.
xa
Câu 49 (THPT Lai Vung 2 – Đồng Tháp) : c sinh gii
lp
6
, do c tp t
a hai
tng phng ti
nh em cm thy hi kh th c b gi
 gic sinh lp
12
b
  cao
3000 m
khong bao
 t r
P mmHg

milimet
thu m so v cao
x mét
c
0
PP
xi
e
,

0
760P mmHg
,
i
 s suy gi  cao
1000 m
t c
672,71 mmHg
.
A.
500P mmHg
. B.
512P mmHg
.
C.
527P mmHg
. D.
540P mmHg
.
125
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
Câu 50 : Cho ph
2
1
2016
log 5 2020 1 0xx

12
,xx

22
12
xx
.
A.
51
. B.
16
.
C.
17
. D.
18
.
Câu 51 : C ca mt tr  ng
c
0
log logM A A

A
 rung tc ba chn k 
 chun (hng s
3 12 2016
, mt trt c
2,4
 Richter xy
ra khu vc huyn Bnh Qu
16 10 2016
xy ra mt trng
t c
3,1
 Richter khu vc huyn Phc Sn, tnh Qung Nam. Bit r
chucho c tnh Qung Nam, h ta trt Phc Sn
ngy
16 10
gp khong my l ta trt B
3 12?
A.
7
ln.
B.
5
ln.
C.
4
ln.
D.
3
ln.
Câu 52 (THPT Lạng Giang 2) : Phng trnh
2
log 1 log 2x x x m
m duy nht khi
 khi
A.
5
4
1
m
m
B.
5
4
1
m
m
C.
5
4
m
D.
5
4
1
m
m
Câu 53 (THPT Đa Phúc – HN) : Phng trnh
22
4
16 log 16 2 0x x x
m?
A.
4
B.
2
C.
3
D.
1
126
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
PHƢƠNG PHÁP ĐẶT ẨN SỐ
Bài tập mẫu tham khảo 01 : Gii pt :
2 2 3
22
log ( 1) log ( 1) 7 (*)xx
♥ Hƣớng dẫn giải : u kin:
1x
 (*)
2
22
4log 1 3log 1 7 0xx
t
2
t log 1x

2
t1
4t 3t 7 0
7
t
4
Vi t =1 : 
2
log 1 1 1 2 3x x x
Vi
7
t
4

77
44
2
7
log 1 1 2 1 2
4
x x x

Bài tập mẫu tham khảo 02 : Gi
2
33
3log 8log 3 5 0 xx
♥ Hƣớng dẫn giải : 
0.x
Vu ki
2
33
3log 8log 3 5 0 xx
tr 
22
3 3 3 3
3log 8 1 log 5 0 3log 8log 3 0 x x x x
.
t
3
logtx
 
2
3
3 8 3 0
1
3
t
tt
t

i
3t
c
3
3
log 3 3 27 xx
(th
i
1
3
t
c
1
3
3
2
11
log 3
3
3
xx
(thỏa mãn)
Vp nghim
2
1
;27
3
S



Bài tập mẫu tham khảo 02 (THPT Nguyễn Trãi Lần 1) : p nghim ca phng trnh
3
9
1
log 3
log
x
x

A.
1
;3
3



B.
3;9
C.
1
;9
3



D.
1;2
♥ Hƣớng dẫn giải : u kin :
0, 1xx
Với điều kiện trên t
33
93
12
log 3 log 3
log log
xx
xx
.
2
3
33
3
log 1
3
log 3log 2 0
log 2 9
x
x
xx
xx

(thõa điều kiện). Chọn B
Casio : S dng  r
Thao tác :
Giáo viên cần file word vui lòng liên hệ
Zalo / đt / facebook : 0914 449 230
127
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
Bài 01 : Gi
a/
3
3
22
4
log log
3
xx
b/
22
log 10log 6 9xx
c/
2
22
log 4 log 8 0xx
d/
22
33
log log 1 5 0xx
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 02 (THPT TH Cao Nguyên) : S nghim ca ph
2
33
log 4log 3 7 0xx

A.
2
B.
0
C.
3
D.
1
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 03 (THPT Lý Thái Tổ) :Gii phng trnh
2
2 2 2
2
log 3.log 2 log 2 x x x
c my
nghim.
A.
2
B.
1
C.
3
D.
0
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
128
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 04 (THPT Thanh Thủy) : Cho phng trnh
2
33
2 log 5log 9 3 0xx
m
12
;xx
tr biu thc
12
.P x x

A.
27 5P
. B.
93P
. C.
27 3P
. D.
27
5
P
.
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 05 : Phng trnh
2
2
2
log 4 3log 7 0xx
m ?
A. 0 B. 2 C. 1 D. 3
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 06 : Phng trnh
22
12
1
5 log 1 logxx



A.
12
B.
66
C.
33
64
D.
5
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 07 : S nghim ca phng trnh
32
ln 3ln 4ln 12 0x x x

A.
2
B.
0
C.
3
D.
1
129
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài tập trắc nghiệm phƣơng trình LOGARIT dạng ĐỔI BIẾN SỐ
Câu 01 (Sở GD – ĐT Hà Tĩnh lần 2) : Phng 
2
log log 2 0xx
m thuc
khong
1;100
?
A.
0
B.
2
C.
1
D.
3
Câu 02 (THPT chuyên Nguyễn Bỉnh Khiêm) : Phng trnh
33
3 log log 3 1 0xx

nghim bng.
A.
81
B.
3
C.
78
D.
84
Câu 03 (THPT ISCHOOL Nha Trang) : t c  ca m  phng trnh
2
33
log 2 .log 3 1 0x m x m
m
12
,xx
sao cho
12
. 27xx
A.
4
3
m
B.
25m
C.
28
3
m
D.
1m
Câu 04 (THPT Đa Phúc – HN) : m ca phng trnh
2
33
log 6log 8 0xx
bng
A.
90
B.
729
C.
8
D.
6
Câu 05 (THPT Quảng Xƣơng 1) : Cho phng trnh
2
log(100 ) log(10 ) 1 log
4.5 25.4 29.10
x x x

. Gi
a

b
ln l
2
nghim ca phng trnh. Khi  tch
ab
bng:
A.
0
B.
1
C.
1
100
D.
1
10
130
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
Câu 06 (THPT chuyên ĐH Vinh) : Bit r
4
2
33
log log
3
x
x




a
,
b
.

.ab
?
A.
81
. B.
9
.
C.
8
. D.
64
.
Câu 07 : 
3
log log 9 3,
x
x 
m
12
,.xx
Tng hai
nghing.
A.
6
B.
9
C.
15
D.
12
Câu 08 : 
m
 phng trnh
22
22
log log 3xxm
m
1;8 .x
A.
36m
B.
69m
C.
26m
D.
23m
Câu 09 : Vu kin
0x
ng trnh tng ng vi 
22
2
2
log log 2xx
A.
2
22
2log 2log 2 0xx
B.
2
22
1
2log log 2 0
2
xx
C.
2
22
4log 2log 2 0xx
D.
2
22
1
4log log 2 0
2
xx
Câu 10 : Cho phng trnh
2
12
4
log log 3 0xx
t
2
logtx
ng trnh  cho tr 
phng trnh no?
A.
2
1
30
4
tt
B.
2
2 3 0tt
C.
2
4 3 0tt
D.
2
1
30
2
tt
Câu 11 : Gi
12
,xx
m c
16
log 2 log 0
x
x

12
.xx
bng:
A.
1
B. 1
C. 2 D.
2
Câu 12 : Nt
2
logtx

22
12
1
5 log 1 logxx


tr 
131
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
A.
2
5 6 0tt
B.
2
5 6 0tt
C.
2
6 5 0tt
D.
2
6 5 0tt
Câu 13 : Nt
logtx

12
1
4 log 2 logxx


tr 
A.
2
2 3 0tt
B.
2
3 2 0tt
C.
2
2 3 0tt
D.
2
3 2 0tt
Câu 14 : Nghit c
32
2 2 2
log 2log log 2x x x

A.
4x
B.
1
4
x
C.
2x
D.
1
2
x
Câu 15 : Nt
2
logtx

2
log 4 log 2 3
x
x 
tr 
A.
2
10tt
. B.
2
4 3 1 0tt
.
C.
1
1t
t

. D.
1
23t
t

.
Câu 16 : Nt
logtx

23
log 20log 1 0xx
tr 
A.
2
9 20 1 0tt
. B.
2
3 20 1 0tt
.
C.
2
9 10 1 0tt
. D.
2
3 10 1 0tt
.
Câu 17 : 
12
1
4 ln 2 lnxx



A.
3
e
. B.
1
e
.
C.
e
. D.
2
.
Câu 18 : Bi
9 9 3
log log log 27
4 6.2 2 0
xx
m
12
,xx

22
12
xx
bng :
A.
6642
B.
82
6561
C.
20
D.
90
132
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
A. BẤT PHƢƠNG TRÌNH MŨ
Cơ sở lý thuyết : Khi giải các bất phương trình mũ ta cần chú ý tính đơn điệu của hàm số mũ.
Xét BPT ; Giải tương tự với các dấu
;;
Ví dụ : Giải bất phương trình:
2
2
11
3 27
xx



HD Giải:
22
2 2 3
1 1 1 1
3 27 3 3
x x x x
22
2 3 2 3 0 ; 1 3;x x x x x 
Ta cũng sử dụng các phương pháp giải tương tự như đối với phương trình mũ:
Đƣa về cùng cơ số. Đặt ẩn phụ. Logarit hóa ...
Bài tập mẫu tham khảo 01 : Giải bất phương trình:
2
3 6 3 7
11
7 49
x x x
♥ Hƣớng dẫn giải :
Bất phương trình đã cho tương đương với
2
2
3 6 3 7
1 2 3 6 6 14
7 7 7 7
x x x
x x x
2
5
3 7 20 0 4
3
x x x
(vì cơ số a = 7 > 1 nên ta giữ nguyên chiều BPT)
Vậy bất phương trình có tập nghiệm
5
;4
3
S




.
Bài tập mẫu tham khảo 02 : Giải bất phương trình:
a/
21
3 10.3 3 0
xx
b/
1
2 2 3 0
xx
c /
1
3 4.3 1 0
xx
d/
4 3.2 2 0
xx
♥ Hƣớng dẫn giải : (sử dụng pp đặt ẩn phụ nhƣ bên phƣơng trình)
a/ Bất phương trình tương đương với
2
3.3 10.3 3 0
xx
.
Phần IV : BẤT PHƢƠNG TRÌNH MŨ - LOGARIT
Ở đây cơ số a = 1/3 nên ta đổi chiều là xong
Giáo viên cần file word vui lòng liên hệ
Zalo / đt / facebook : 0914 449 230
133
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
Đặt
30
x
t 
, bất phương trình trở thành
2
1
3 10 3 0 3.
3
t t t
Với
1
3
3
t
, ta được
1
1
3 3 3 3 3 1 1.
3
xx
x
Vậy bất phương trình đã cho có tập nghiệm
1;1S 
b/ Bất phương trình tương đương với
2
2 3 0
2
x
x
Đặt
20
x
t 
, bất phương trình trở thành
2
2
2 3 2
3 0 0 3 2 0 1 2
tt
t t t t
tt

.
Với
12t
, ta được
1 2 2 0 1.
x
x
Vậy tập nghiệm của bất phương trình là
0;1S
.
c/ Bất phương trình tương đương với
2
12
3 1 0 3 3 12 0.
3
x x x
x
Đặt
30
x
t 
, bất phương trình trở thành
2
3
12 0 .
4
t
tt
t

thoaû maõn
loaïi
Với
3t
, ta được
3 3 1
x
x
. Vậy bất phương trình có tập nghiệm
1; .S 
.
d/ Đặt
20
x
t 
, bất phương trình trở thành
2
3 2 0 1 2t t t
.
Với
12t
, ta được
1 2 2 0 1
x
x
.Vậy bất phương trình có tập nghiệm
0;1S
Bài 01 : Giải các bất phương trình sau
a/
3 2 9
33
10 10
x
b/
2
23
1
1
7
7
xx
x




c/
2
32
24
xx
d/
2
6
1
1
4
xx



e/
2 2 2
3 27
28
xx
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
134
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 02 : a/ Bất phương trình
36
0,5 1
x
có tập nghiệm là
A.
2;
B.
1
;
2




C.
1
;
2




D.
3; 
b/ (THPT Đoàn Thị Điểm – Khánh Hòa) : Giải bất phương trình
2
2 3 2 3
xx
.
A.
1x 
B.
2x 
C.
2x 
D.
1x 
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 03 : a/ Các số thực
x
thỏa mãn
1
( ) 1
2
xx
aa

A.
1x
B.
0x
C.
0x
D. Không có
x
nào
b/ Bất phương trình
5.4 2.25 7.10 0
x x x
có nghiệm là
A.
21x
. B.
10x
C.
01x
. D.
12x
c/ Tìm tập nghiệm của bất phương trình
2 1 2 2 2 3
2 2 2 448
x x x
A.
9
;
2
S



B.
;2S 
C.
9
;
2
S



D.
9
;
2
S



☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
135
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 04 : a/ Giải bất phương trình
2.49 5.14 7.4 0
x x x
.
A.
; 1 .S 
B.
;1 .S 
C.
1; .S
D.
1; .S 
b/ Giải bất phương trình
1
1
2
x



.
A.
0.x
B.
1.x 
C.
0.x
D.
1.x
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 05 : a/ Giải bất phương trình
2 3 2 3 14
xx
.
A.
2
2
x
x

B.
11x
C.
1
1
x
x

D.
22x
b/ Giải bất phương trình sau
3 8 3 8 34
xx
A.
44x
B.
22x
C.
66x
D.
88x
136
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 06 : a/ (Sở GDĐT Hà Tĩnh) : Tập nghiệm của bất phương trình
2
0,3 0,09
xx
là
A.
; 2 1; 
B.
2;1
C.
;2
D.
1; 
b/ Tập nghiệm của bất phương trình
2
1
3
9
x
là
A.
;4
B.
;4
C.
0;
D.
4; 
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 07 : a/ (Trƣờng PT Hermann Gmeiner– Khánh Hòa) : Tập nghiệm của bất phương trình:
4 3.2 2 0
xx
là
A.
( 1;0)
B.
0;1
C.
(0;1)
D.
( ;0) (1; )
b/ (THPT Nguyễn Chí Thanh– Khánh Hòa) : Nghiệm của bất phương trình
32.4 18.2 1 0
xx
là
A.
41x
B.
11
16 2
x
C.
24x
D.
14x
137
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Trắc nghiệm phần bất phƣơng trình mũ
Câu 01 : Nghiệm của bất phương trình
13
9 36.3 3 0
xx
là
A.
13x
B.
12x
C.
1x
D.
3x
Câu 02 (THPT Đoàn Thị Điểm – Khánh Hòa) : Tìm tất cả các giá trị của tham số m sao cho
phương trình
1
93
xx
m

có nghiệm.
A.
9
4
m 
B.
0m
C.
1m 
D.
5
8
m
Câu 03 : Giải bất phương trình
1
5
22
55
x
.Một học sinh làm như sau:
Bƣớc 1. Điều kiện:
0*x
.
Bƣớc 2.Vì
2
1
5
nên
1
5
2 2 1
5.
55
x
x
Bƣớc 3. Từ đó suy ra
1
15
5
xx
.
138
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
Vậy tập nghiệm của bất phương trình đã cho là
1
; \ 0 .
5
S



Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào?
A. Đúng. B. Sai ở bước 1. C. Sai ở bước 2. D. Sai ở bước 3
Câu 04 : Tìm tập nghiệm
S
của bất phương trình
2
2 1 5
25
52
x x x
.
A.
; 4 1;S  
B.
1;4S 
C.
; 1 4;S  
D.
4;1S 
Câu 05 : Tập nghiệm của bất phương trình
1
3
1
0,25
2
x
x



là
A.
5;
. B.
;5
.
C.
;5
. D.
5;
.
Câu 06 : Giải bất phương trình
3
2 2 9
xx

.
A.
03x
. B.
3
01
x
x

.
C.
3
1
x
x
. D.
3x
.
Câu 07 (THPT Lai Vung 1 – Đồng Tháp) : Tập nghiệm của bất phương trình
4 2.25 10
x x x

là
A.
2
5
log 2;




. B.
5
2
log 2;




.
C.
2
2
; log
5




. D.
.
Câu 08 (Sở GDĐT Hà Tĩnh) : Nghiệm của bất phương trình
2
11
3 27
x



là:
A.
5x
. B.
5x
. C.
1x 
. D.
1x 
Câu 09 (Sở GDĐT Hà Tĩnh) Bất phương trình
2
2
2 2 2
xx
có tập nghiệm là
A.
3;1
. B.
3;1
. C.
1;3
. D.
1;3
.
Câu 10 (Sở GDĐT Hà Tĩnh) Bất phương trình
9 3 6 0
xx
có tập nghiệm là
139
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
A.
1; 
. B.
;1
.
C.
1;1
. D.
;1
.
Câu 11 (THPT Nguyễn Thiện Thuật – Khánh Hòa) : Tập nghiệm của bất phương trình
3.9 10.3 3 0
xx
có dạng
[ ; ]S a b
. Tính
P b a
.
A.
1P
B.
3
2
P
C.
2P
D.
5
2
P
B. BẤT PHƢƠNG TRÌNH LOGARIT
Cơ sở lý thuyết : Khi giải các bất phương trình LOGARIT ta cần chú ý tính đơn điệu của hàm số
LOGARIT
Xét BPT ; Giải tương tự với các dấu
;;
Ví dụ : Giải bất phương trình:
5
log 3 1 1x 
HD Giải:
1
5 5 5
1
1
3 1 0
1
log 3 1 1 log 3 1 log 5 ;2
3
3
3 1 5
2
x
x
x x x
x
x






Ví dụ : Giải bất phương trình:
2
0,5 0,5
log 4 11 log 6 8x x x
.
HD Giải:
2
22
0,5 0,5
2
2
4 11 0
6 8 0
log 4 11 log 6 8 6 8 0
2 3 0
4 11 6 8
x
xx
x x x x x
xx
x x x


; 4 2;
2;1
3;1
x
x
x
 

Ta cũng sử dụng các phương pháp giải tương tự như đối với phương trình mũ:
Đƣa về cùng cơ số. Đặt ẩn phụ. ...
Bài tập mẫu tham khảo 01 : Giải bất phương trình
a/
2
2
log 2 2 0xx
b/
11
55
log 1 log 8 1xx
.
Chú ý công thức : M = logaa
M
140
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
♥ Hƣớng dẫn giải : a/ Bất phương trình
2
2
log 2 2 0xx
2
22
2
2 2 0 1
2 2 1 2 3 0
3
2 2 1
x x x
x x x x
x
xx
Vậy tập nghiệm của bất phương trình là
; 1 3;S  
b/ Điều kiện:
10
18
80
x
x
x


Với điều kiện trên bất phương trình trở thành :
55
log 1 log 8 1xx
5 5 5
2
log 1 log 8 1 log 1 8 1
9 29 9 29
1 8 5 9 13 0 .
22
x x x x
x x x x x



Đối chiếu điều kiện, ta được tập nghiệm của bất phương trình là
9 29
1;
2
S


.
Bài tập mẫu tham khảo 02 : Giải bất phương trình:
4
7
log 2 log 0
6
x
x
♥ Hƣớng dẫn giải : Điều kiện:
01x
.
Với điều kiện trên, bất phương trình trở thành
2
17
log 2 log 0
26
x
x
2
2
1 1 7
log 0
log 2 6
x
x
.
Đặt
2
logtx
, bất phương trình trở thành
2
1 1 7 6 3 7
00
2 6 6
tt
t
tt

2
2
0
3 7 6
0
3
3
t
tt
t
t

.
● Với
2
0
3
t
, ta được
2 2 2 2
33
2 1 1
log 0 log log log 1 1
3
44
x x x



.
● Với
3t
, ta được
2
log 3 8xx
.
Đối chiếu điều kiện, ta được tập nghiệm của bất phương trình là
3
1
;1 8; .
4
S



Bài tập mẫu tham khảo 03 : Giải bất phương trình:
3 1 3
27
log 1 3log 13 2 1 log 5 1x x x
♥ Hƣớng dẫn giải : Điều kiện:
1 13
52
x
.
Giáo viên cần file word vui lòng liên hệ
Zalo / đt / facebook : 0914 449 230
141
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
Với điều kiện trên, bất phương trình đã cho trở thành
3 3 3 3
log 1 log 13 2 log 3 log 5 1x x x
33
2
log 1 13 2 log 3 5 1 1 13 2 3 5 1
4
2 4 16 0 .
2
x x x x x x
x
xx
x

Kết hợp điều kiện, bất phương trình có tập nghiệm
13
2;
2
S


.
Bài tập mẫu tham khảo 04 : Giải bất phương trình:
33
2log 1 log 3 2xx
♥ Hƣớng dẫn giải : Điều kiện:
3.x
Với điều kiện trên, bất phương trình trở thành
2
33
log 1 log 3 2xx
22
2
2
3
4
11
log 2 9 1 9 3 11 28 0 .
7
33
x
xx
x x x x
x
xx


Kết hợp điều kiện, bất phương trình có tập nghiệm
3;4 7;S 
Bài tập mẫu tham khảo 05 : Giải bất phương trình
22
log 3 2 log 6 5xx
A. (0; +). B.
6
1;
5



. C.
1
;3
2



. D.
3;1
.
♥ Hƣớng dẫn giải :
6
6 5 0
26
5
3 2 0 2
35
3
x
x
x
x
x



22
log 3 2 log 6 5 3 2 6 5 1x x x x x
Vậy nghiệm của bất phương trình là:
6
1
5
x
.
Bài 01 : Giải bất phương trình
a/
2
2
log (2 5 3) 2xx
b/
33
log ( 1) log (11 ) 3xx
c/
1
3
31
log 1
2
x
x
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
142
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 02 : Giải bất phương trình
a/
log log .ln 3 1x e x
b/
3
log 1 0x
. c/
3
log 4 1 4x 
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 03 : Giải bất phương trình : a/
2
log (3 2) 3x 
. b/
0,3 0,3
log 5 log 1 1xx
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Câu 08 (THPT Quế Vân2 ) : Giải bất phương trình
2
log 9 2 3
x
x
ta được tập nghiệm là ?
A.
;0 3;S  
. B.
2
;0 3;2log 3S 
.
C.
2
;0 3;2log 3S 
. D.
0x
hoặc
3x
.
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
143
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
..............................................................................................................................................................................
Câu 09 : Tìm tập nghiệm của bất phương trình
2
ln 3ln 2 0xx
.
A.
2
; ; .ee

B.
2
;.e

C.
2
0; ; .ee

D.
;1 2; . 
☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Câu 10 (THPT Phan Bội Châu – Khánh Hòa) : Tập xác định của hàm số
2
y ln 3ln 2xx
là
A.
2
0; ;ee

B.
;1 2; 
C.
2
;;ee
D.
2
;e

☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Trắc nghiệm phần bất phƣơng trình Logarit
Câu 01 : Giải bất phương trình
1
2
log 2 1 1x 
.
A.
1
2
x
B.
3
4
x
C.
3
0
4
x
D.
13
24
x
Câu 02 : Giải bất phương trình
3
log 2 1 4x
.
A.
5x
. B.
5
2
x
. C.
5
2
x
. D.
5x
.
Câu 03 (Trƣờng PT Hermann Gmeiner– Khánh Hòa) : Giải bất phương trình
1
3
log 4 2x 
A.
4x
. B.
37
4
9
x
. C.
37
9
x
. D.
14
4
3
x
.
Câu 04 : Giải bất phương trình
21
2
log (2 ) log 1xx
.
A.
1;2 .x
B.
1;2 .x
C.
;2 .x 
D.
1; .x 
Câu 05 : Tập nghiệm của bất phương trình
2
ln ln 4 4xx
là
A.
2; .
B.
\ 2 .
C.
1; 
. D.
1; \ 2 .
144
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
Câu 06 : Có bao nhiêu số nguyên
a
là nghiệm bất phương trình
2
0,5 0,5
log logaa
?
A. 1. B. 0. C. Vô số. D. 2.
Câu 29 (THPT Huỳnh Thúc Kháng – Khánh Hòa) :
Tập nghiệm
S
của bất phương trình
2
22
log 5log 6 0xx
là:
A.
1
;64
2
S



B.
1
0;
2
S


C.
64;S 
D.
1
0; 64;
2
S



Câu 08 : Tập nghiệm của bất phương trình
2
0,8 0,8
log ( ) log ( 2 4)x x x
là
A.
4;1
B.
; 4 1;2
C.
; 4 1; 
D.
;4 6;
Câu 09 (THPT Đoàn Thị Điểm – Khánh Hòa) : Xét các số thực dương
, ab
thỏa mãn
22
4log log 1ab
. Tìm giá trị lớn nhất của
a
.
A.
1
10
. B.
1
. C.
10
. D.
2
10
Câu 10 : Tìm tập nghiệm của bất phương trình
22
2log ( 1) log (5 ) 1xx
.
A.
3;3 .
B.
1;5 .
C.
1;3 .
D.
3;5 .
Câu 11 : Tìm tập nghiệm của bất phương trình
12
2
log log 2 1 0x 


.
A.
3
0; .
2



B.
3
1; .
2



C.
0;1 .
D.
3
;2 .
2



Câu 12 (THPT Nguyễn Thái Học – Khánh Hòa) : Tập Giải bất phương trình
2
1
2
log 2 8 4xx
A.
6
4
x
x

B.
6
4
x
x

C.
64
24
x
x

D.
64
24
x
x

Câu 13 (THPT Đông Sơn 1) : Bất phương trình
2
12
2
3
log 2 log 5
4
xx



có nghiệm là:
A.
; 2 1;x 
B.
2;1x
145
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
C.
1;2x
D.
; 1 2;x  
Câu 14 (THPT Tôn Đức Thắng – Khánh Hòa) : Tập nghiệm của bất phương trình
2
log ² –1 3x
là
A.
–3; –1 1; 3S
. B.
–2; –1 1;2S
.
C.
– ; –1 1;S  
. D.
– ; –2 2;S
.
Câu 15 : Một nghiên cứu cho thấy một nhóm học sinh được cho xem cùng một danh sách các loài
động vật và được kiểm tra lại xem họ nhớ bao nhiêu % mỗi tháng. Sau t tháng, khả năng nhớ
trung bình của nhóm học sinh được cho bởi công thức
75 20ln 1 , 0M t t t
(đơn vị %). Hỏi
sau khoảng bao lâu thì nhóm học sinh nhớ được danh sách đó dưới 10%?
A. 24.79 tháng
B. 23 tháng
C. 24 tháng
D. 22 tháng
Câu 16 : Một công ty vừa tung ra thị trường sản phẩm mới và họ tổ chức quảng cáo trên truyền
hình mỗi ngày. Một nghiên cứu thị trường cho thấy, nếu sau x quảng cáo được phát thì số %
người xem mua sản phẩm là
0.015
100
( ) , 0
1 49
x
P x x
e

. Hãy tính số quảng cáo được phát tối thiểu
để số người mua đạt hơn 75%.
A. 333 B. 343
C. 330 D. 323
Câu 17 (THPT Lý Tự Trọng – Khánh Hòa) : Tập xác định của hàm số
ln 2yx
là:
A.
2
;e

. B.
0;
.
C. . (22). D.
2
1
;
e



.
Câu 18 (THPT Phan Bội Châu – Khánh Hòa) : Tìm tập nghiệm
S
của bất phương trình:
42
log 7 log 1xx
:
A.
[ 1;2]S
. B.
[ 7;2)S
.
C.
1; 2S 
. D.
( 7;2)S
.
Giáo viên cần file word vui lòng liên hệ
Zalo / đt / facebook : 0914 449 230
146
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
Câu 19 (THPT Trần Bình Trọng – Khánh Hòa) : Tập nghiệm của bất phương trình
22
2log ( 1) log (5 ) 1xx
là
A.
1;3
. B.
1;5
.
C.
3;3
. D.
1;3
Câu 20 (THPT Nguyễn Trãi Lần 1) : Tìm tập nghiệm của bất phương trình
2
1
2
log 3 2 1.xx
.
A.
0;2
. B.
;1
. C.
0;1 2;3
. D.
0;2 3;7
.
Câu 21 (THPT Nguyễn Tất Thành) : Giải bất phương trình
3
log 2 1 3x 
. .
A.
1
14
2
x
. B.
5x
. C.
1
5
2
x
. D.
14x
.
Câu 22 (THPT Nguyễn Tất Thành) : Tập nghiệm của bất phương trình
1
2
log 2 1 1x
là:
A.
3
;
2




. B.
3
1;
2



. C.
3
;
2




. D.
13
;
22



.
Câu 23 : Bất phương trình
11
22
log 2 1 log 5xx
có tập nghiệm là:
A.
2;
. B.
2;5
. C.
;2
. D.
1
;2
2


.
Câu 24 (THPT An Lão lần 2) : Tìm tập nghiệm
S
của bất phương trình
33
log 2 3 log 1xx
.
A.
2
;
3




. B.
32
;
23




. C.
3
;1
2



. D.
2
;
3




.
Câu 25 (THPT Lý Thái Tổ) : Bất phương trình:
22
log 3 2 log 6 5xx
có tập nghiệm là.
A.
0;
. B.
1
;3
2



. C.
3;1
. D.
6
1;
5



.
Câu 26 (THPT Lƣơng Tài 2) : Giải bất phương trình
1
2
log 3 4 4x
. Tập nghiệm
T
của bất
phương trình là.
A.
;4T 
. B.
4;T 
. C.
4
;4
3
T




. D.
4
;4
3
T



.
Câu 27 (TTGDTX Cam Ranh - Khánh Hòa) : Tập nghiệm của bất phương trình
2
log 4 3x
là:
A.
2;
. B.
0;2
. C.
;2
. D.
0;
.
147
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT
2018
Câu 28 (THPT Trần Hƣng Đạo – Nam Định) : Tìm tập nghiệm
S
của bất phương trình
0,5
log 2 1 2x
.
A.
5
;
2
S




. B.
5
;
2
S



. C.
15
;
22
S


. D.
15
;
22
S



.
Câu 29 : Cho hàm số
2
4 .3
xx
y
, khẳng định nào sau đây sai?
A.
2
3 2 ln2 ln3f x x x
.
B.
2
3
3 log 4 1f x x x
.
C.
2
3 log3 2 log2 log3f x x x
.
D.
2
3
3 2 log 2 1f x x x
.
Câu 30 (Trích Đề minh họa 2017) : Cho hàm số
2
2 .7 .
xx
fx
Khẳng định nào sau đây là khẳng
định sai?
A.
2
2
1 log 7 0.f x x x
B.
2
1 ln2 ln7 0.f x x x
C.
2
7
1 log 2 0.f x x x
D.
2
1 1 log 7 0.f x x
Câu 31 (THPT Lê Hồng Phong – Khánh Hòa) : Cho hàm số
5
1
( ) 5 .7
xx
fx
. Khẳng định nào sau đây
là khẳng định sai ?
A.
5
55
( ) 1 log 7 log 7 0f x x x
.
B.
5
( ) 1 ln5 ln7 ln7 0f x x x
.
C.
5
7
( ) 1 log 5 1f x x x
.
D.
4
55
( ) 1 1 log 7 log 7f x x
.
148
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
CƠ SỞ LÝ THUYẾT
Lãi đơn: Lãi được tính theo tỉ lệ phần trăm trong một khoảng thời gian cố định trước.
Ví dụ: Khi ta gửi tiết kiệm 50 (triệu đồng) vào một ngân hàng với lãi suất 6,9%/năm thì sau một
năm ta nhận được số tiền lãi là:
50 6,9% 3,45
(triệu đồng).
Số tiền lãi này như nhau được cộng vào hằng năm. Kiểu tính lãi này được gọi là lãi đơn.
Sau hai năm số tiền cả gốc lẫn lãi là:
50 2. 3,45 56,9
(triệu đồng).
Sau n năm số tiền cả gốc lẫn lãi là:
50 . 3,45n
(triệu đồng).
Lãi kép: Sau một đơn vị thời gian (kỳ hạn), tiền lãi được gộp vào vốn và được tính lãi. Loãi lãi
này được gọi là lãi kép.
Ví dụ: Khi ta gửi tiết kiệm 50 (triệu đồng) vào một ngân hàng với lãi suất 6,9%/năm thì sau một
năm, ta nhận được số tiền cả gốc lẫn lãi là:
50 3,45 53,45
(triệu đồng).
Toàn bộ số tiền này được gọi là gốc.
Tổng số tiền cuối năm thứ hai là:
53,45 53,45 6,9% 53,45 1 6,9%
C[C DẠNG B\I TO[N ĐIỂN HÌNH
Bài toán 1: (Lãi kép gửi 1 lần)
Một người, gửi vào ngân hàng số tiền là a đồng, với lãi suất kép hàng tháng là r% (Kỳ hạn một tháng).
Tính cả vốn lẫn lãi Tn sau n tháng?
Phương pháp: Gọi Tn là tiền vốn lẫn lãi sau n tháng, ta có:
Tháng 1 (
1n
):
1
1T a ar a r
Tháng 2 (
2n
):
2
2
1 1 1T a r a r r a r
……………………………………………………..
Tháng n :
11
1 1 1
n n n
n
T a r a r r a r

Phần V : TO[N LÃI SUẤT - ỨNG DỤNG
149
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Vậy:
1
n
n
T a r
(1)
Trong đó: a là số tiền vốn có ban đầu, , r lã lãi suất (%) hàng tháng (kỳ hạn 1 tháng), n là số tháng,
n
T
là số tiền vốn lẫn lãi sau n tháng.
Bài tập mẫu tham khảo 01 : Bác An muốn gửi số tiền tiết kiệm 50000000 đồng vào ngân hàng
BIDV với lãi suất kép kì hạn 1 tháng là 0,35% /tháng. Hỏi sau 5 tháng số tiền cả gốc lẫn lãi của bác
An là bao nhiêu, biết rằng lãi suất hàng tháng không thay đổi?
♥ Hướng dẫn giải : Từ công thức :
1
n
n
T a r
Số tiền cả gốc lẫn lãi của bác An là :
5
50000000 1 0,35% 50881146T
(đồng)
Bài tập mẫu tham khảo 02 : Chị Trang có số tiền là 100000000 đồng, chị muốn gửi tiền tiết kiệm
vào ngân hàng SML với lãi suất kép kỳ hạn 1 tháng là 0,36% / tháng. Để được 110000000 đồng chị
Trang phải mất bao nhiêu tháng gửi, biết rằng lãi suất hàng tháng không thay đổi?
♥ Hướng dẫn giải :
Từ công thức :
1
n
n
T a r
ta suy ra
1
ln
1 log
ln 1
n
n
nn
r
T
TT
a
rn
a a r



Số tháng tối thiểu phải gửi là:
110000000
ln
100000000
26,52267649
ln 1 0,36%
n 
(tháng)
Vậy thời gian tối thiểu chị Trang phải gửi là 27 tháng trong ngân hàng SML
Bài tập mẫu tham khảo 03 : Bà Thu có số tiền là 100000000 đồng gởi tiết kiệm ngân hàng trong
vòng 13 tháng thì lãnh về được 105000000 đồng. Hỏi lãi kép hàng tháng với kỳ hạn 1 tháng của
ngân hàng là bao nhiêu, biết rằng lãi suất hàng tháng không thay đổi (làm tròn đến số thập phân
thứ 4)?
♥ Hướng dẫn giải :
Từ công thức :
1
n
n
T a r
ta suy ra
1 1
n
n
n
n
T
r
a
T
r
a

Lãi suất hàng tháng là:
15
105000000
1 0,38%
100000000
r
Giáo viên cần file word vui lòng liên hệ
Zalo / đt / facebook : 0914 449 230
150
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Bài toán 2: (Lãi kép gửi một lần)
Một người, gửi vào ngân hàng số tiền là a đồng, với lãi suất kép là r%(Tính theo kỳ). Tính cả vốn lẫn
lãi Tn sau n kỳ?
Phương pháp:
Gọi Tn là tiền vốn lẫn lãi sau n kỳ, ta có:
Kỳ 1 (
1n
):
1
1T a ar a r
Kỳ 2 (
2n
):
2
2
1 1 1T a r a r r a r
……………………………………………………..
Kỳ n :
11
1 1 1
n n n
n
T a r a r r a r

Vậy:
1
n
n
T a r
(2)
Trong đó: a : số tiền vốn ban đầu, r : lãi suất (%) hàng kỳ, n là số kỳ, Tn : tiền vốn lẫn lãi sau n kỳ.
Từ công thức (2) ta tính được các đại lượng khác như sau:
1)
ln
ln 1
n
T
a
n
r
2)
1
n
n
T
r
a

3)
1
n
n
T
a
r
Bài tập mẫu tham khảo 01 : Một người gửi tiền tiết kiệm 100000000 đồng vào một ngân hàng
a/ Hỏi sau 10 năm, người đó nhận được bao nhiêu tiền cả vốn lẫn lãi, biết rằng người đó gửi theo
kỳ hạn 6 tháng, lãi suất kép là 5,3%/năm và người đó không rút lãi ở tất cả các định kỳ trước đó.
b/ Hỏi sau 10 năm, người đó nhận được bao nhiêu tiền cả vốn lẫn lãi, biết rằng người đó gửi theo
kỳ hạn 3 tháng, lãi suất kép là 4,8%/năm và người đó không rút lãi ở tất cả các định kỳ trước đó.
♥ Hướng dẫn giải : a/ 1 kỳ là 6 tháng, suy ra 10 năm là
10.12
20
6
kỳ
lãi suất của 1 năm là 5,3%, suy ra lãi suất 1 tháng là:
5,3
%
12
. Khi đó lãi suất theo định kỳ 6 tháng là:
5,3
6. % 2,65%
12
Vậy số tiền nhận được sau 10 năm là:
20
20
100000000. 1 2,65 168724859,1T
đồng.
151
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
b/ 1 kỳ là 3 tháng, suy ra 10 năm là
10.12
40
3
kỳ
lãi suất của 1 năm là 4,8%, suy ra lãi suất 1 tháng là:
4,8
%
12
. Khi đó, lãi suất theo định kỳ 3 tháng
là:
4,8
3. % 1,2%
12
Vậy số tiền nhận được sau 10 năm là:
40
40
100000000. 1 1,2% 161146360T
đồng.
Bài tập mẫu tham khảo 02 : Một anh sinh viên được gia đình gửi vào sổ tiết kiệm ngân hàng là
80000000 đồng vỡi lãi suất kép kỳ hạn 1 năm là 6,9%/năm. Hỏi sau đúng 5 năm số tiền trong sổ sẽ
là bao nhiêu, biết rằng trong suốt thời gian đó anh sinh viên không rút một đồng nào cả vốn lẫn
lãi?
♥ Hướng dẫn giải :
Từ công thức
1
n
n
T a r
Số tiền trong sổ sau 5 năm là:
5
5
80000000. 1 6,9% 111680799,2T
đồng
Bài toán 3: (Lãi kép gửi theo định kỳ - gửi đầu tháng)
Một người, hàng tháng gửi vào ngân hàng a đồng , với lãi suất kép hàng tháng là r%. Hỏi sau n tháng,
người ấy có bao nhiêu tiền ?
Phương pháp:
Gọi T
n
là số tiền người đó có được ở cuối tháng n , ta có :
Cuối tháng thứ nhất, người đó có số tiền là :
1
1T a ar a r
Đầu tháng thứ hai, người đó có số tiền là :
22
1 1 1 1 1 1 1
11
aa
a r a a r r r
r
r





Cuối tháng thứ hai, người đó có số tiền là :
2 2 2
2
1 1 1 1 . 1 1 1
a a a
T r r r r r
r r r
……………………………………………………………….
Cuối tháng thứ n , người đó có số tiền là :
1 1 1
n
n
a
T r r
r


Vậy :
1 1 1
n
n
a
T r r
r


(3)
152
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Trong đó : a là tiền vốn gửi vào ngân hàng hàng tháng , r là lãi suất %
hàng tháng , n là số tháng,
T
n
là tiền vốn lẫn lãi sau n tháng.
Bài tập mẫu tham khảo 01 : Một người, hàng tháng gửi vào ngân hàng số tiền là 3000000 đồng với
lãi suất kép là 0.36%/tháng. Hỏi sau 2 năm, người ấy có bao nhiêu tiền, biết rằng lãi suất hàng
tháng không thay đổi ?
♥ Hướng dẫn giải : Áp dụng công thức :
1 1 1
n
n
a
T r r
r


.
Với
3000000a
đồng,
0,36%r
,
24n
tháng.
Ta được:
24
24
3000000
1 0,36% 1 1 0,36% 75331221,69
0,36%
T


đồng
Bài tập mẫu tham khảo 02 : Muốn có 50000000 đồng sau 1 năm thì phải gửi quỹ tiết kiệm ngân
hàng hàng tháng là bao nhiêu ? Biết rằng lãi suất kép gửi hàng tháng là 0,35%/tháng, lãi suất hàng
tháng không thay đổi.
♥ Hướng dẫn giải : Áp dụng công thức :
.
1 1 1
n
n
Tr
a
rr


.
Với
50000000
n
T
đồng,
0,35%r
,
12n
tháng
Ta được:
12
50000000 0,35%
4072810,663
0,35% 0,3
.
1 1 15%
a 


đồng
Bài tập mẫu tham khảo 03 : Nếu ông A muốn có 100000000 đồng thì ông phải phải mất bao nhiêu
tháng gửi tiền tiết kiệm ngân hàng , biết rằng lãi suất kép gửi ngân hàng hàng tháng là 0,36%
/tháng, số tiền ông gửi tiết kiệm hàng tháng là 7000000 đồng?
♥ Hướng dẫn giải : Áp dụng công thức:
.
ln 1
1
ln 1
n
Tr
r
a
n
r





.
Với
100000000
n
T
đồng,
0,36%r
,
7000000a
đồng
153
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Ta được:
.0,36%
ln 1 0,36%
11
100000
3,9067
000
7000000
2580
ln 1 0,36%
n




tháng
Vậy ông A phải mất 14 tháng
Bài toán 4: (Vay theo định kỳ - Trả cuối tháng)
Một người, vay ngân hàng A đồng , với lãi suất kép hàng tháng là r%. Hỏi người ấy phải trả hàng tháng
bao nhiêu tiền để sau n tháng thì hết nợ ?
Phương pháp :
Gọi a là số tiền phải trả hàng tháng.
Cuối tháng thứ nhất, người đó nợ :
1Ar
Đã trả a đồng tiền nợ:
1A r a
Cuối tháng thứ hai, người đó còn nợ:
2
1 1 1 1A r a r a A r a r a


Cuối tháng thứ ba, người đó còn nợ :
2 3 2
1 1 1 1 1 1A r a r a r a A r a r a r a


…………………………………………………………………………..
Cuối tháng thứ n , người đó còn nợ:
12
11
1 1 1 ... 1 .
n
n n n n
r
A r a r a r a A r a
r


Vậy để người đó trả hết nợ sau n tháng thì số tiền phải trả hàng tháng là:
. . 1
11
n
n
Ar r
a
r

(4)
Trong đó : a là tiền trả ngân hàng hàng tháng , r là lãi suất (%) hàng tháng , n là số tháng, A là số
tiền vay ban đầu.
Bài tập mẫu tham khảo 01 (Đề thi minh họa năm 2017) : Ông A vay ngắn hạn ngân hàng 100 triệu
đồng, với lãi suất 12%/năm. Ông muốn hoàn nợ cho ngân hàng theo cách : Sau đúng một tháng kể
từ ngày vay, ông bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền
hoàn nợ ở mỗi lần là như nhau và trả hết tiền nợ sau đúng 3 tháng kể từ ngày vay. Hỏi, theo cách
đó, số tiền m mà ông A phải trả cho ngân hàng trong mỗi lần hoàn nợ là bao nhiêu ? Biết rằng, lãi
suất ngân hàng không thay đổi trong thời gian ông A hoàn nợ.
154
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
♥ Hướng dẫn giải : Sau một tháng ông A hoàn nợ lần 1, các lần hoàn nợ tiếp theo sau đó một
tháng. Ông A trả hết tiền nợ sau 3 tháng, tức là ông A hoàn nợ 3 lần.
Lãi suất 1 năm là 12% suy ra lãi suất hàng tháng là : 1%
Gọi m đồng là số tiền ông A hoàn nợ mỗi tháng
Cuối tháng thứ nhất, ông A nợ:
100 1 1%
(triệu đồng)
Đã trả m đồng nên còn nợ:
100 1 1% m
(triệu đồng)
Cuối tháng thứ hai, ông A còn nợ:
2
100 1 1% 1 1% 100 1 1% 1 1%m m m m


(triệu đồng)
Cuối tháng thứ ba, ông A còn nợ:
2 3 2
100 1 1% 1 1% 1 1% 100 1 1% 1 1% 1 1%m m m m m m


3
3
1 1% 1
100 1 1% .
1%
m

(triệu đồng)
Vậy ông A trả hết nợ sau 3 tháng thì số tiền phải trả hàng tháng là :
33
33
100.1%. 1 1% 1,01
1 1% 1 1,01 1
m

(triệu đồng)
Bài tập mẫu tham khảo 02 : Một người vay 50 triệu, trả góp theo tháng trong vòng 48 tháng, lãi
suất kép là 1,15%/tháng.
a/ Hỏi hàng tháng phải trả bao nhiêu?
b/ Nếu lãi suất kép là 0,75%/tháng thì mỗi tháng phải trả bao nhiêu, lợi hơn bao nhiêu so với lãi
suất kép 1,15%/tháng.
♥ Hướng dẫn giải : a/ Số tiền người ấy phải trả hàng tháng là :
48
48
50000000.1,15%. 1 1,15%
1
13
1,
61
15%
3 ,807
1
12

(đồng)
b/ Số tiền người ấy phải trả hàng tháng là :
48
48
50000000.0,75%. 1 0,75%
1
12
0,
44
75%
2 ,119
1
52

(đồng)
Lợi hơn :
1361312,807 1244252,119 117060
(đồng)
155
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Bài tập mẫu tham khảo 03 : Một người vay ngân hàng với số tiền là 20000000 đồng , mỗi tháng trả
góp cho ngân hàng 300000 đồng và phải chịu lãi suất kép của số tiền chưa trả là 0,4%/tháng. Hỏi
sau bao lâu người đó trả hết nợ ?
♥ Hướng dẫn giải : Gọi A là số tiền vay ngân hàng, a là số tiền trả nợ hàng tháng, r là lãi suất
(%) hàng tháng, n là số tháng trả hết nợ.
Ta có:
20000000A
đồng,
300000a
đồng,
0,4%r
. Số tiền còn nợ trong ngân hàng sau n tháng
là:
11
1 . 0
n
n
n
r
T A r a
r

1
300000
log 77,69370636
. 300000 20000000.0, 4%
r
a
n
a Ar

Số tháng trả hết nợ là 78 tháng
Bài toán 5: Một người gửi ngân hàng với số tiền là A đồng với lãi suất kép là r%/tháng(kỳ hạn một tháng).
Mỗi tháng người ấy rút ra X đồng vào ngày ngân hàng tính lãi. Hỏi sau n tháng số tiền của người ấy còn
bao nhiêu?
Phương pháp:
Gọi Bn là số tiền còn lại sau tháng thứ n
Sau tháng thứ nhất, số tiền vốn và lãi là:
1Ar
(đồng)
Sau khi rút ra X đồng, số tiền còn lại là:
1
1B A r X
(đồng)
Sau tháng thứ hai, số tiền vốn và lãi là:
2
1
1 1 1 1 1B r A r X r A r X r


(đồng)
Sau khi rút ra X đồng, số tiền còn lại là:
2
2 2 2
2
11
1 1 1 1 1 1 .
11
r
B A r X r X A r X r A r X
r




(đồng)
……………………………………………………………………………………….
Bằng cách quy nạp, ta suy ra được sau tháng thứ n , số tiền còn lại là:
11
1.
n
n
n
r
B A r X
r

(đồng) (5)
Từ công thức (5) ta tính được các đại lượng khác như sau:
156
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
1.
11
n
n
n
A r B r
X
r




1
.
log
.
n
r
B r X
n
Ar X
Trong đó : X là số tiền rút ra hàng tháng , r là lãi suất (%) hàng tháng , n là số tháng, A là số tiền
gửi ban đầu.
Bài tập mẫu tham khảo 01 : Giả sử một người gửi vào ngân hàng với số tiền 50000000 đồng theo
kỳ hạn 1 tháng với lãi suất kép là 0,36%/tháng. Mỗi tháng người đó rút ra 1000000 đồng vào ngày
ngân hàng tính lãi. Hỏi sau 2 năm số tiền của người ấy còn lại bao nhiêu ?
♥ Hướng dẫn giải : Áp dụng công thức (5) với:
50000000A
đồng,
0,36%r
,
1000000X
đồng,
24n
tháng. Ta có:
24
24
24
1 0,36% 1
50000000. 1 0,36% 1000000. 29483326,1
0,36%
B

(đồng)
Bài tập mẫu tham khảo 02 : Một sinh viên đi học được gia đình cho gửi tiền tiết kiệm vào ngân
hàng với số tiền là 50000000 đồng theo mức kỳ hạn một tháng với lãi suất kép là 0,35% /tháng.
Nếu mỗi tháng anh sinh viên rút ra một số tiền như nhau vào ngày ngân hàng tính lãi thì hàng
tháng anh ấy rút ra bao nhiêu tiền để sau 4 năm, số tiền vừa hết ?
♥ Hướng dẫn giải : Sau 4 năm tức là sau 48 tháng, anh sinh viên rút vừa hết tiền, có nghĩa là
48
0B
Áp dụng công thức
1.
11
n
n
n
A r B r
X
r




Với:
50000000A
đồng,
0,35%r
,
0
n
B
đồng,
48n
tháng. Ta có:
48
48
50000000 0,35% 0,35%1.
11
1133433,099
0,35%
X


(đồng)
Vậy hàng tháng anh sinh viên rút ra một số tiền là : 1133433,099 (đồng)
157
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Bài tập mẫu tham khảo 03 : Một người gửi tiền tiết kiệm vào ngân hàng với số tiền là 20000000
đồng theo mức kỳ hạn một tháng với lãi suất kép là 0,36%/tháng. Nếu mỗi tháng người ấy rút ra
một số tiền là 300000 đồng vào ngày ngân hàng tính lãi thì sau bao lâu số tiền gửi vừa hết ?
♥ Hướng dẫn giải : Áp dụng công thức:
1
.
log
.
n
r
B r X
n
Ar X
Với
20000000A
đồng,
0,36%r
,
0
n
B
đồng,
300000X
đồng. Ta có:
1 0,36%
300000
76,36959338
20000000 0,36%
log
. 300000
n

(tháng)
Vậy tối thiểu sau 76 tháng thì số tiền gửi sẽ hết
Bài tập trắc nghiệm
Câu 01 : Một khu rừng có trữ lượng gỗ
5
4.10
mét khối. Biết tốc độ sinh trưởng của các cây ở khu
rừng đó là 4% mỗi năm. Hỏi sau 5 năm, khu rừng đó sẽ có bao nhiêu mét khối gỗ?
A.
53
4,8666.10 m
.
B.
53
3.866.10 m
.
C.
53
2,8666.10 m
.
D.
53
0,16.10 m
.
Câu 02 : Một điện thoại đang nạp pin, dung lượng nạp được tính theo công thức
3
2
0
1
t
Q t Q e




với
t
là khoảng thời gian tính bằng giờ và
0
Q
là dung lượng nạp tối đa (pin đầy).
Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là 0%) thì sau bao lâu
sẽ nạp được 90% (kết quả làm tròn đến hàng phần trăm)?
A.
1,54th
.
B.
1,2th
.
C.
1th
.
D.
1,34th
.
158
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
Câu 03 : Biểu đồ bên cho thây kết quả
thống kê sự tăng trưởng về số lượng của
một đàn vi khuẩn: cứ sau
12
tiếng thì số
lượng của một đàn vi khuẩn tăng lên gâp
2
tan. Số lượng vi khuẩn ban đầu của đàn
là
250
con. Công thức nào dưới đây thể
hiện sự tăng trưởng về số lượng của đàn
vi khuẩn
N
tại thời điểm
t
?.
A.
12
500.Nt
.
B.
250.2
t
N
.
C.
2
250.2N
.
D.
2
250.2
t
N
.
Câu 04 (THPT Lê Hồng Phong – Khánh Hòa) : Hàm Một nhà côn trùng học khảo sát thấy số côn
trùng ban đầu ở một đàn là
500
con, tỉ lệ tăng trưởng của côn trùng này là
14%
mỗi tuần. Hỏi sau
22
tuần, số côn trùng sẽ có là bao nhiêu?
A. Khoảng
1248
con.
B. Khoảng
8931
con.
C. Khoảng
9635
con.
D. Khoảng
6915
con.
Câu 05 : Một nguời gửi tiết kiệm với lãi suất
8,4%
năm và lãi hàng năm đuợc nhập vào vốn, hỏi
sau bao nhiêu năm người đó thu được gấp đôi số tiền ban đầu?
A.
6
B.
7
C.
8
D.
9
Câu 06 (THPT Phan Bội Châu – Khánh Hòa) : Bác Ba gửi số tiền 7 triệu đồng vào ngân hàng với
lãi suất
8,5%
năm. Biết rằng nếu không rút tiền thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào số
159
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
vốn ban đầu. Hỏi sau
12
năm Bác Ba rút được bao nhiêu tiền, nếu trong thời gian này Bác Ba
không rút tiền ra và lãi suất không thay đổi?
A.
18 631 803
.
B.
18 631 804
.
C.
7 995 692
.
D.
11 2501 62
.
Câu 07 : Năm 2001, dân số Việt Nam là 78685800 người. Tỷ lệ tăng dân số năm đó là 1,7%. Biết
rằng sự sự tăng dân số ước tính theo thức
r
e
N
SA
, trong đó A là dân số của năm lấy làm mốc
tính, S: dân số sau N năm, r: tỉ lệ tăng dân số hàng năm. Tăng dân số với tỉ lệ tăng như vậy thì đến
năm nào dân số nước ta ở mức 120 triệu người.
A.
2025.
B.
2030
C.
2026
D.
2035
Câu 08 (THPT Tôn Đức Thắng – Khánh Hòa) : Giả sử cứ sau một năm diện tích rừng của nước ta
giảm
x
phần trăm diện tích hiện có. Hỏi sau
4
năm diện tích rừng của nước ta sẽ là bao nhiêu
phần diện tích hiện nay?
A.
4
1
100
x



.
B.
100%.
C.
4
1
100
x
.
D.
4
1
100
x



Câu 09 : Năm 1994, tỉ lệ khí CO2 trong không khí là
6
358
10
. Biết rằng tỉ lệ thể tích khí CO2 trong
không khí tăng
0,4%
hàng năm. Hỏi năm 2016, tỉ lệ thể tích
T
khí CO2 trong không khí là bao
nhiêu (kết quả gần nhất)? Giả sử tỉ lệ tăng hàng năm không đổi.
A.
6
391
10
T
.
160
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN
2018
B.
6
390
.
10
T
C.
6
7907
.
10
T
D.
6
7908
.
10
T
Câu 10 : Ông
A
đi gửi tiết kiệm ngân hàng với số tiền là
m
đồng. Gửi trong
n
tháng với lãi suất
hàng tháng là
r
. Tính số tiền cả vốn lẫn lãi
T
mà Ông
A
nhận được sau cuối tháng thứ
n
là :
A.
1T m nr
. B.
1()
n
T m r
.
C.
1
1()
n
T m r

. D.
11
n
m
T r r
r


.
Câu 11 : Một người dự định sẽ mua xe Honda
2016 150SH i
với giá
80 990 000
đồng. Người đó
gửi tiết kiệm vào ngân hàng với số tiền 60 000 000 đồng với lãi suất hàng tháng là
0,8%
. Vậy sau
bao lâu người đó sẽ đủ tiền mua xe máy :
A.
37
tháng.
B.
36
tháng.
C.
38
tháng.
D.
35
tháng.
Câu 12 : Với số tiền
80 000 000
đồng hiện có , một người lấy một nửa số tiền đó gửi tiết kiệm vào
ngân hàng
A
với lãi suất
4,8%
một năm. Còn một nửa thì gửi vào ngân hàng
B
với lãi suất
0,4%
một tháng. Hỏi sau
36
tháng người đó đồng thời đi rút tiền trong hai ngân hàng thì ngân hàng
nào sẽ trả cả vốn lẫn lãi nhiều nhất và số tiền
T
nhận được từ ngân hàng đó là bào nhiêu?:
A. Ngân hàng
A
,
46040904T
đồng.
B. Ngân hàng
B
,
46040904T
đồng.
C. Ngân hàng
A
,
46182097T
đồng.
D. Ngân hàng
B
,
46182097T
đồng.
161 (SƯU TẦM VÀ BIÊN SOẠN)
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – ÔN TẬP
2018
Câu 1: Gi
21
16 8 .
x
x
A.
2x
. B.
3x
. C.
2x 
. D.
3x 
.
Câu 2: Gi
44
log 1 log 3 3.xx
A.
33.x
B.
1 2 17.x 
C.
5.x
D.
1 2 17.x 
Câu 3: nh c
5
.
ln 3
x
y
x
A.
3;5 .D
B.
3;5 \ 4 .D
C.
3;5 .D
D.
3;5 \ 4D
Câu 4: Gii b
500
1
3
log 9 1000.x
A.
0.x
B.
0.x
C.
500
9.x 
D.
1000
3 0.x
Câu 5: 
4
1
5
x
ye
.
A.
4
1
'
20
x
ye
. B.
4
4
'
5
x
ye
. C.
4
4
'
5
x
ye
. D.
4
1
'
20
x
ye
.
Câu 6: Cho
33
2 ; 5log a log b
340 bng:
A.
3a b
B.
3ab
C.
3a b
D.
3ab
Câu 7: 
2
2
x
y
bng:
A.
2
1
2
'
ln2
x
x
y
. B.
2
1
' 2 ln2
x
yx
. C.
' 2 ln2
xx
y
. D.
1
2
'
ln2
x
x
y
.
Câu 8: nh
D
c
1000
3
2
log 8 .yx
A.
;2 .D 
B.
2; .D 
C.
\ 2 .D
D.
2; ;2D 
Câu 9: Tm tp nghim S ca bt phng trnh
11
55
log 3 5 log 1xx

A.
5
;
3
S




. B.
;3S 
. C.
3
;3
5
S



. D.
5
;3
3
S



Câu 10: Cho
a
t s u thc
2
3
aa
vii dng lu tha vi s u t 
Phần VI : BÀI TẬP ÔN
162 (SƯU TẦM VÀ BIÊN SOẠN)
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – ÔN TẬP
2018
A.
7
6
.a
B.
3
.a
C.
1
6
.a
D.
2
.a
Câu 11: nh c
2
23
5
xx
y
?
A.
1; 3 .
B.
1;3 .
C.
\ 1;3 .
D.
.
Câu 12: m c
4 2 2 0
xx
A.
0x
. B.
2x
. C.
3x
D.
1x
.
Câu 13: Cho biu thc
31
31
5 3 4 5
,
.
a
P
aa

vi
0a
. M 
A.
Pa
. B.
3
2
Pa
. C.
1
2
Pa
. D.
3
Pa
Câu 14: 
3
log x
y
x
A.
22
1 ln
ln 3
x
y
x
. B.
2
1 ln
ln3
x
y
x
C.
1 ln
ln3
x
y
x
. D.
2
1 ln x
y
x
.
Câu 15: 
2
logyx

A.
1
.
ln2x
B.
1
.
x
C.
1
.
ln2
D.
1
.ln2.
x
Câu 16: V thc
, ab
 
A.
log( ) log log .a b a b
B.
log( ) log .log .ab a b
C.
log
log .
log
a
b
b
a
D.
log
log
log
aa
bb
Câu 17: t c m c
2
log( 2 2) logx x x
?
A.
2.x 
B.
1; 2.xx
m. D.
1.x
Câu 18: nh c y =
2
2
34xx

?
A.
.
B.
4
; 1 ; .
3




C.
4
\ ; 1 .
3


D.
4
; 1 ; .
3



Câu 19: Biu thc
6
5
3
. . 0x x x x
vii dng lu tha vi s u t 
A.
5
3
.x
B.
2
3
.x
C.
7
3
.x
D.
5
2
.x
Câu 20: Cho
>
. Kt lu
163 (SƯU TẦM VÀ BIÊN SOẠN)
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – ÔN TẬP
2018
A.
.

B.
0.


C.
.

D.
.1

.
Câu 21: Cho
0;3 3
log 0,07; log 0,2MN
. Khnh 
A.
0MN
. B.
0MN
. C.
0NM
. D.
0 NM
.
Câu 22: p hnh
D
c
2
log 4 1yx
A.
2; 4 .D
B.
;2 .D 
C.
;2 .D 
D.
;4 .D 
Câu 23: Tp  nh c
1
2
3
(1 )yx


A.
1;1 .
B.
;1.
C.
1;1 .
D.
1; .
Câu 24: Cho u thc K =  bng:
A.
2.
B.
3
.
2
C.
5
.
2
D.
1
.
2
Câu 25: Tp nghim ca b
2.4 5.2 2 0
xx
ng
;S a b

ba
.
A.
3
.
2
B.
5
.
2
C.
1.
D.
2.
Câu 26: 
1
1 ln
y
xx

n h th
A.
ln 1 .xy y y x

B.
ln 1 .xy y y x

C.
ln 1 .xy y y x

D.
ln 1 .xy y y x

Câu 27: Chn m  sau:
A.
22
33
e
. B.
32
44

. C.
1,4 2
11
.
33
D.
3 1,7
33
.
Câu 28: S nghim c
9 2.3 3 0
xx

A.
3.
B.
1.
C.
0.
D.
2.
Câu 29: Cho
49 2
log 32; log 14ab
u din
a
theo
b
.
A.
5
.
22
a
b
B.
1
1
a
b
. C.
32ab
. D.
31ab
.
Câu 30: T
2
1yx


A.
\1
. B.
1; 
. C.
;1
. D. .
xx
9 9 23

xx
xx
5 3 3
1 3 3


164 (SƯU TẦM VÀ BIÊN SOẠN)
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – ÔN TẬP
2018
Câu 31: u kin ca
a
tha
4
3
5
4
aa

A.
01a
B.
0a
. C.
0a
. D.
1a
.
Câu 32: 
x
e
y
x

A.
2
( 1)
'
x
ex
y
x
. B.
'
x
ye
. C.
2
( 1)
'
x
ex
y
x
. D.
2
'
x
e
y
x

.
Câu 33: Cho
a
 
b
 
 thc b 
m 
A.
log log .
a
a
bb

B.
1
log log .
a
a
bb
C.
log log .
aa
bb
D.
1
log log .
aa
bb
Câu 34: Chn m  sau:

0 1
x
y a a


x
ya
vi
1a


log
a
yx
vi
01a


, 1log
a
yxa

Câu 35: p nghim
S
c
2
22
log ( 4 3) log (4 4)x x x
A.
3;7 .S
B.
1.S
C.
7.S
D.
1;7 .S
Câu 36:
2 3 6
37
73
xx

A.
2x 
. B.
1x
. C.
1x 
. D.
4x
.
Câu 37: 
cos2x
ye

A.
cos2
2sin2 .
x
xe
. B.
cos2
2sin2 .
x
xe
. C.
cos2
sin2 .
x
xe
. D.
cos2
sin2 .
x
xe
.
Câu 38: Tp nghim c
log(3 3) log(2 5)xx

A.
5
;8
2


. B.
;8
. C.
1;8
. D.
1;8
.
Câu 39: Tnh c
2
log(9 )yx

165 (SƯU TẦM VÀ BIÊN SOẠN)
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – ÔN TẬP
2018
A.
; 3 3; 
. B.
; 3 3;
. C.
\ 3;3 .
D.
3;3
.
Câu 40: Cho
0, 1aa
 ca
log 4
a
a

A. 4. B. 8. C. 2 . D. 16.
Câu 41: Chn m  sau:
A.
32
44

. B.
1,4 2
11
.
33
C.
22
33
e
. D.
3 1,7
33
.
Câu 42: Cho s thn biu thc
5
4
3
P a a a a
c:
A.
1
14
a
. B.
1
120
a
C.
11
40
a
.
D.
13
60
.a
Câu 43: Cho
x
 th
2
3 9 10.3
xx

 ca
2
1x
?
A. 5. B. 1.  
Câu 44: S nghim c
9 2.3 3 0
xx

A.
1.
B.
2.
C.
0.
D.
3.
Câu 45: Cho
,xy
 th
,mn
 tht lu
A.
m n m n
xxx

B.
n
mn
m
m
xx
yy







C.
n
n
mm
xx
D.
.
n
mn
m
m
xy
yx






Câu 46: Tnh c
2
ln 3 4y x x

A.
\ 1;4DR
B.
1;4D 
C.
; 1 4; .D  
D.
; 1 4;D  
Câu 47: 
2
2
3
23y x x

A.
\ 1;3
B.
.
C.
; 1 3; 
D.
; 1 3; 
Câu 48: Biu thc
6
5
3
. . 0x x x x
vii dng lu tha vi s u t 
A.
7
3
.x
B.
5
2
.x
C.
2
3
.x
D.
5
3
.x
Câu 49:  ca biu thc
3 1 3 1 3
5 .25 .125B

bng:
A.
25
. B.
5
. C.
125
. D.
625
.
Giáo viên cần file word vui lòng liên hệ
Zalo / đt / facebook : 0914 449 230
166 (SƯU TẦM VÀ BIÊN SOẠN)
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – ÔN TẬP
2018
Câu 50: Cho
a
 thn biu thc
1 1 2
3 3 3
1 3 1
4 4 4
a a a
P
a a a






A.
( 1)P a a
. B.
1Pa
. C.
1Pa
. D.
1P
.
Câu 51: B
22
log 3 2 log 6 5xx
p nghi
A.
0; .
B.
6
1;
5



. C.
1
;3
2



. D.
3;1
.
Câu 52:  s
2
y ln 5 6xx

A.
;2 3;D  
. B.
2;3D
. C.
;0D 
. D.
0;D
.
Câu 53:   ch bi ?
A.
3
x
y
B.
1
3
logyx
C.
8
3
x
y




D.
3
8
x
y



Câu 54: Cho
1
1
2
x
x
fx
. 
0f
bng
A.
ln2
. B.
2ln2
. C.
1
. D.
2
.
Câu 55:  
3
4 2 3
xx
m
m
1;3x
A.
93m
. B.
39m
.
C.
13 3m
. D.
13 9m
.
Câu 56: 
x
thng thc
23
7 7 7
log 8log 2logx ab a b
,0ab
.
A.
2 14
.x a b
B.
46
.x a b
C.
6 12
.x a b
D.
8 14
.x a b
Câu 57: Gi
2 4 8
log log log 11x x x
c nghim
A.
24x
. B.
36x
. C.
45x
. D.
64.x
Câu 58: nh c
2
9
log 1 ln 3 2y x x
:
A.
3;D 
. B.
;3D 
. C.
; 1 1;3D
. D.
1;3D 
.
Câu 59: Bt  
22
log 3 2 log 6 5xx
p nghi
A.
3;1
. B.
6
1; .
5



C.
1
;3
2



. D.
0; .
167 (SƯU TẦM VÀ BIÊN SOẠN)
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – ÔN TẬP
2018
Câu 60:  
12
1
4 log 2 logxx


p nghi
A.
1; 20
. B.
1
; 10
10



. C.
.
D.
10; 100
.
t
3 3 3
log 4log 7logx a b

x
.
A.
37
x a b
. B.
36
x a b
. C.
46
x a b
. D.
47
x a b
.
Câu 62: t
ln2, ln5,ab
u din
16
ln
25

A.
16
ln 4 2
25
ab
. B.
16
ln 4 2 .
25
ab
C.
16
ln 2 4
25
ab
. D.
16
ln 2 4
25
ab
.
Câu 63: p nghim ca b
33
log ( 3) log ( 5) 1xx
.
A.
(5;6)
. B.
(2;6)
. C.
6;
. D.
(0;6)
Câu 64: Cho
2
log 8
8
(log 2)x
. Khnh 
A.
3
log 3x 
. B.
3
log 2x 
. C.
3
log 2x 
. D.
3
log 3x
.
Câu 65:  biu thc
2,4
0,1
3log 10P
.
A.
7,2P 
. B.
2,4P
. C.
7,2P
. D.
3P
.
Câu 66: Bit
log 3, log 2
aa
bc

4
3
3
log
a
ab
I
c
.
A.
15I
. B.
9I
. C.
13I
. D.
11I
.
Câu 67: Hi
2x
m c
A.
2
39
log 5 1 log 3 1x x x
. B.
13
3
log 1 log 1xx
.
C.
2
4 2 2
log 5log 2 4 log 4 8x x x
. D.
2
33
log 5 log 3 1xx
.
Câu 68:  thn biu thc
11
33
33
a b b a
P
ab
A.
3
P ab
. B.
3
a
P
b
. C.
3
1
P
ab
. D.
3
22
P a b
.
Câu 69: m c
3 27
9 81
1 log 1 log
1 log 1 log
xx
xx


168 (SƯU TẦM VÀ BIÊN SOẠN)
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – ÔN TẬP
2018
A.
1
1; ;
243
B.
11
;
9 27
C.
1 1 1
;;
9 27 81
D.
11
1; ;
27 243
Câu 70: Nu
, 0 à ; 9
ba
a b v a b b a
  sau ?
A.
4
3
. B.
4
27
. C.
3
. D.
33
.
Câu 71: Gi
4
log 1 3x 
A.
63x
B.
65x
C.
82x
D.
80x
Câu 72: 
2
2017
log 1yx
A.
2
1
'
1
y
x
B.
2
1
'
1 ln2017
y
x
C.
2
'
2017
x
y
D.
2
2
'
1 ln2017
x
y
x
Câu 73: Cho
2
log 14 a

49
log 32
theo a:
A.
10
1a
B.
2
51a
C.
5
22a
D.
5
21a
Câu 74: Cho hai s thc
a

b
, vi
1 ab
. Kh ?
A.
log 1 log
ba
ab
B.
log 1 log
ab
ba
C.
1 log log
ab
ba
D.
log log 1
ba
ab
Câu 75:  th
,ab
vi
1a
. Kh ?
A.
2
11
log log
22
a
a
ab b
B.
2
1
log log
4
a
a
ab b
C.
2
log 2 2log
a
a
ab b
D.
2
1
log log
2
a
a
ab b
Câu 76: Nu
12
log 8 a

2
log 3
bng:
A.
1
2
a
a
B.
21
2
a
a
C.
1
22
a
a
D.
12
2
a
a
Câu 77: B
42
25 5
log 1 logxx
i b
A.
4 4 2
25 25 5
log log 1 logxx
B.
24
5 25
log 1 logxx
C.
22
55
2log 1 logxx
D.
22
55
log 1 2logxx
Câu 78: nh c
2
9
log 1 ln 3 2y x x
169 (SƯU TẦM VÀ BIÊN SOẠN)
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – ÔN TẬP
2018
A.
; 1 1;3D 
B.
3;D 
C.
;3D 
D.
1;3D 
Câu 79: Gi
1
24
log 2 1 .log 2 2 1
xx
m:
A.
12xx
B.
2
log 3x

2
5
log
4
x
C.
2
log 3x

2
log 5x
D.
12xx
Câu 80: t
25
log 3, log 3ab
u din
6
log 45

A.
2
6
22
log 45
a ab
ab
B.
2
6
22
log 45
a ab
ab b
C.
6
2
log 45
a ab
ab
D.
6
2
log 45
a ab
ab b
Câu
ĐA
Câu
ĐA
Câu
ĐA
Câu
ĐA
1
B
21
B
41
C
61
D
2
D
22
B
42
C
62
B
3
B
23
A
43
A
63
A
4
C
24
C
44
A
64
A
5
C
25
D
45
D
65
A
6
C
26
B
46
C
66
D
7
B
27
A
47
D
67
B
8
C
28
B
48
D
68
A
9
D
29
A
49
A
69
A
10
A
30
B
50
D
70
A
11
D
31
D
51
B
71
B
12
A
32
C
52
B
72
D
13
A
33
C
53
B
73
C
14
B
34
C
54
A
74
B
15
D
35
C
55
C
75
D
16
C
36
B
56
A
76
C
17
D
37
A
57
D
77
D
18
C
38
C
58
C
78
A
19
A
39
D
59
B
79
B
20
C
40
D
60
D
80
D
| 1/170
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

PHÂN LOẠI DẠNG VÀ PHƯƠNG PHÁP GIẢI NHANH Chuyeân ñeà
BIÊN HOÀ – Ngày 31 tháng 08 năm 2017
TÀI LIỆU LƯU HÀNH NỘI BỘ
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Phần I: LŨY THỪA – HÀM SỐ LŨY THỪA A. LŨY TH ỪA
1. Định nghĩa: Với a  , lũy thừa bậc n của a là tích của n thừa số a. n a  . a . a . a ... .a n thua so Chú ýn 1 a  ; a   0 n 0 a  1 a 0  1 aa a  
0 và 0 n không có nghĩa.
2. Lũy thừa với số mũ hữu tỉ m
Cho số thực a dương và số hữu tỉ r
, trong đó m , n , n  2 . n m
Lũy thừa của a với số mũ r là số r
a xác định bởi r n m n a a a .
Hay ta chú ý công thức : m m  1 1 n m n a aa  0; , m n   và n a   a  0; , m n   m n m a n a 2kk  
x xác định khi x  0 (k  ) 2
1 x xác định x  (k  )
2. Các tính chất : Tất cả các loại lũy thừa đều có tính chất tương tự sau đây (chỉ khác điều kiện):
Cho a  0; b  0 và , m n  . R Ta có:
Ví dụ tham khảo 3  3   1 1 1 4  2  2 0 2 2  1 1 7  7 2  7 5 4  2 2  7  5    2 5 5 a a a a 3  5  5 1
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Điền vào bảng : 1 1 9 0 (4, 72) 2 ( 2  ) 3 ( 2  ) 4 3 3 ( 4)  3 5 a 4 3 a =
Bài 01 : Viết các biểu thức sau về dạng lũy thừa của a a  0 : 7 3 a a a/ 3 a . a b/ 8 4 a . a c/ d/ 5 3 . a a ,  , a b  0 0,75 a ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 02 : Viết các biểu thức sau về dạng lũy thừa biết a, b > 0: 5 4 a .b 4 3 2 a/ 8
a . a. 3 a  b/ 3 5 a a c/ d/ 3 4 5 .
a a. a. a. a 3 12 6 a .b ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 2
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
..............................................................................................................................................................................
Bài 03 : Viết các biểu thức sau về dạng lũy thừa : 2 1   1  2 a/ x x x b/ a .  4 3  x x d/ 5 3 2 2 2 a  c/ 2 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 5 4 3 4 4. 64.( 2 ) 3 5 3 243. 3. 9. 12
Bài 04 : Rút gọn : A  B  3 32 3 2 5 ( 3 ) . 18. 27. 6 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 05 : Chứng minh:
a/ 4  2 3  4  2 3  2 b/ 3 3
7  5 2  7  5 2  2 c/ 3 3 9  80  9  80  3 ☻ Giải :
..............................................................................................................................................................................
.............................................................................................................................................................................. 3
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 04 (THPT chuyên Vĩnh Phúc lần 5) : Cho biểu thức 3 4 3 P  . x x
x , với x  0. Mệnh đề nào 1 7 15 7 dưới đây đúng? A. 2 P x . B. 24 P x . C. 24 P x . D. 12 P x . ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 05 (SỞ GDĐT HƯNG YÊN) : Biểu thức 3 6 5 Q
x. x. x với  x  0 viết dưới dạng lũy thừa với 2 5 5 7 số mũ hữu tỷ là. A. 3 Q x . B. 3 Q x . C. 2 Q x . D. 3 Q x . ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 06 (THPT chuyên Lê Thánh Tông) : Cho biểu thức 3 2 k 3 P x x x
x  0. Xác định k sao cho biểu thức 23 24 P x . A. k  2 . B. k  6 . C. k  4 .
D. Không tồn tại k . ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 4
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
.............................................................................................................................................................................. 1
Bài 07 : Với giá trị thực nào của a thì 3 4 24 5 . a . a a  2 . 1 2 A. a  0 B. a  1 C. a  2 D. a  3 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 11
Bài 08 (THPT Ngô Sĩ Liên lần 3) : Rút gọn biểu thức: 16
x x x x : x , x  0 ta được. A. 4 x . B. 6 x . C. 8 x . D. x . ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 09 (Sở GD – ĐT Hưng Yên) : Giá trị của biểu thức 2 1  2 1 2 E  3 .9 .27 bằng: A. 3 B. 27 C. 9 D. 1 ☻ Giải :
..............................................................................................................................................................................
.............................................................................................................................................................................. 4 1 1  2 3 3 a  8a bb
Bài tập mẫu tham khảo 01 : Rút gọn biểu thức 3 3 A  .1  2
  a (giả thiết biểu 2 2  a  3 3 3 a 2 ab 4b    
thức có nghĩa) được kết quả là (nguồn : thầy CAO TUẤN) A. 1. B. a  . b C. 0. D. 2a  . b
♥ Hướng dẫn giải : 1 3
a a  8b 1 1 1 2 3 3 3 a
a .a a  8b 2 Cách 1 : Ta có: 3 3 A  .  a   a 2 1 1 2 1 1 3 3 1 1     3 3 3 3 3 3
a  2a b  4b a  2b 3 3
a    2b      5
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 2 3
a a  8b 2 2 2 3 3 3 
a a a  0  a  8b
Cách 2: Ta sẽ gán cho a và b những giá trị cụ thể
(sao cho thỏa mãn điều kiện có nghĩa của biểu thức A). a  1 Ở đây ta gán  , khi đó b   1 4 1 1  2 3 3 1  8.1 .1  1  1  8 3 3 A  .1  2  1 
. 1  2  1  1  1  0  Chọn C. 2 2    1  7 3 3 3 1 2 1.1 4.1    
Bài tập mẫu tham khảo 02 : Cho 2 3 4 2 2 3 2 4
M a a b b a b và   2 2 N a b 3 3 3 . Ta có kết
luận A. M N.
B. M N  0. C. M N. D. M N.
♥ Hướng dẫn giải :
CALC a  1; b  1 Nhập 2 4 2 2 2 4
a a b b a b   2 2 a b 3 3 3 3 3 
0  M N Chọn D.
Bài tập mẫu tham khảo 03 : Rút gọn biểu thức C   4
x x   4 1 x x  
1 x x   1 ,  x  0 ta
được (nguồn : thầy CAO TUẤN) A. 2 x 1. B. 2 x x 1. C. 2 x x 1. D. 2 x 1.
♥ Hướng dẫn giải :
Cách 1 : Ta có: M    x   4
x   x   4 1
1  x  x x      1    x  2
1  x x x  
1  x x   1 x x    1    
x   x x   x  x  2 2 1 1
1  x x x 1     Chọn B. CALC X  100 Cách 2 : Nhập  4 X X   1  4 X X  
1  X X   1  1  0101 x  100 Ta có: 2 2
10101  100 100 1 x x 1 Chọn đáp án B. A
Cách 3 : Thử lần lượt với 4 đáp án. Cơ sở lí thuyết: A B
1, B  0 B 6
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 CALC 3
Lần 1: Nhập  4 X X   1  4 X X  
1  X X   1 :  2 X   1   X  loại A. 1 2
Lần 2: Bấm phím ! để sửa biểu thức thành:  CALC 4 X X   4 1 X X  
1  X X   1 :  2 X X   1  1   X Chọn B. 1 2 1  1 1    y y
Bài tập mẫu tham khảo 04 : Rút gọn biểu thức 2 2
D   x y  1 2   ,  ,
x y  0, x y   ta x x     được A. . x B. 2 . x C. x 1. D. x 1.
♥ Hướng dẫn giải : 2  2  2  2   2 yx y   1 
Cách 1 : D   x y  1    
x y     x     
Chọn A. x x      x
Cách 2 : Thử lần lượt với 4 đáp án. 2 1  1 1    Y Y CALC Nhập 2 2
D   X Y  1 2 
 : X  1     Chọn A. X X X  1;Y  0     4 1 1  2 3 3 a  8a bb
Bài tập mẫu ứng dụng CASIO 01: Giá trị của biểu thức 3 3 P  .1 2   a là 2 2   a   3 3 3
a  2 ab  4b A. P  1. B. P  0. a b C. Nhập máy P  . D. P  . b a 2 1 1 2    b b
Bài tập mẫu ứng dụng CASIO 02: Giá trị của biểu thức 2 2
Q   a b  : b  2b     là a a     A. Q  . a B. Q  . b Nhập máy a C. Q  1. D. Q  . b
Bài tập mẫu ứng dụng CASIO 03 (THPT Trần Cao Vân - Khánh Hòa) 3 1  2 3 a .a Rút gọn biểu thức 
(với a  0 ) được kết quả:  a   2 2 2 2 A. 4 a B. 5 a Nhập máy C. 3 a D. a
Bài tập mẫu ứng dụng CASIO 04 (THPT QG - 2017) 5 Rút gọn biểu thức 3 3
Q b : b với b  0 . 7 Nhập máy
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 4  A. 2 Q b B. 3 Q b 4 5 C. 3 Q b D. 9 Q b
Bài tập mẫu ứng dụng CASIO 05 (Sở GD và ĐT Long An)
Cho x là số thực dương, viết biểu thức 3 2 6 Q x x . x
dưới dạng lũy thừa với số mũ hữu tỉ. 2 A. 2 Q x . B. 3 Q x . Nhập máy 5 C. Q x . D. 36 Q x .
Trắc nghiệm phần lũy thừa
Câu 01 : Các căn bậc hai của 4 là A. 2  . B. 2 . C. 2  . D. 16
Câu 02 : Các căn bậc bốn của 81 là A. 3 . B. 3  . C. 3  . D. 9  4 0  ,75  3  1   1 
Câu 03 (THPT Nguyễn Chí Thanh - Khánh Hòa) : Giá trị của K       bằng.A.  81  27  K  180 . B. K 108 . C. K  54 . D. K 18 .
Câu 04 : Viết biểu thức a a a  0 về dạng lũy thừa của a , ta được: 5 1 3 1 A. 4 a . B. 4 a . C. 4 a . D. 2 a
Câu 05 : Giá trị của biểu thức 23 3 2 3 A  9 : 27 là: A. 9 B. 4 5 3 3  C. 81 D. 4 12 3 3  1 3 1  1   2 Câu 06 : Tính:    2 2 0, 001 2 .64  8   0 3 3 9  kết quả là: 115 109 1873 111 A. B. C.  D. 16 16 16 16 1 3   3 5   1   1  Câu 07 : Tính: 0,75 81        kết quả là: 125   32  80 79 80 352 A.  B.  C. D. 27 27 27 27 8
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Câu 08 (THPT Hoàng Văn Thụ - Khánh Hòa) : Cho biểu thức 5 4
A a. b , điều kiện xác định của biểu thức A là.
A. a tùy ý, b  0 .
B. a  0;b  0 .
C. a tùy ý, b  0 .
D. a  0;b  0 .
Câu 9 : Các căn bậc bảy của 128 là A. 2  . B. 2  . C. 2 . D. 8 m b aa
Câu 10 : Viết biểu thức 5 3
, a,b  0 về dạng lũy thừa   , với giá trị của m là a bb  2 4 2 2 A. . B. . C. . D. . 15 15 5 15 Câu 11 : Cho 3 6 f (x) 
x. x khi đó f (0, 09) bằng : A. 0, 09 . B. 0,9 . C. 0, 03. D. 0,3 x x
Câu 12 : Cho f x 3 2 
khi đó f 1,3 bằng: 6 x A. 0,13. B. 1,3 . C. 0,013. D. 13 .   3  2 3 1
Câu 13 : Rút gọn biểu thức: b : b  34  34  34 2 34 A. b B. b C. b D. b
Câu 14 : Đơn giản biểu thức x x  4 8 4 1 , ta được: A. 2 x x   1 . B. 2
x x   1 . C. 2 x x   1 . D. 2 x x 1 .
Câu 15 : Đơn giản biểu thức x x  9 3 3 1 , ta được:
A. x x  3 1 .
B. x x  3 1 .
C. x x  3 1 .
D. x x  3 1 .
Câu 16 (THPT Chuyên Quang Trung) : Cho các số thực , a , b ,
m n với a,b  0 . Tìm mệnh đề sai. ma  A. 2 m a a . B. ma . m b   . C.  n m m n a a   . D.   m  . m ab a b .  b  2 1   1 
Câu 17 : Đơn giản biểu thức 2 P a .  được kết quả là  a  A. 2 a . B. 2 2 1 a  . C. 1 2 a  . D. a . 9
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 4 a .b 4 3 2
Câu 18 : Cho a , b là các số dương. Rút gọn biểu thức P  được kết quả là 3 12 6 a .b A. 2 ab . B. 2 a b . C. ab . D. 2 2 a b .
Câu 19 : Căn bậc 4 của 3 là A. 3 4 . B. 4 3 . C. 4  3 . D. 4  3 .
Câu 20 : Căn bậc 3 của – 4 là A. 3  4  . B. 3 4  . C. 3  4  . D. Không có.
Câu 21 : Cho a là số thực dương. Biểu thức 4 3 8
a được viết dưới dạng lũy thừa với số mũ hữu tỉ là 3 2 3 4 A. 2 a . B. 3 a . C. 4 a . D. 3 a .
Câu 22 : Cho x là số thực dương. Biểu thức 4 2 3 x
x được viết dưới dạng lũy thừa với số mũ hữu tỉ là 7 5 12 6 A. 12 x . B. 6 x . C. 7 x . D. 5 x . 5 2 b b
Câu 23 : Cho b là số thực dương. Biểu thức
được viết dưới dạng lũy thừa với số mũ hữu 3 b b tỉ là A. – 2. B. – 1. C. 2. D. 1.
Câu 24 (Đề minh họa lần 2 – Bộ GDĐT) : Cho biểu thức 4 3 2 3 P  . x
x . x , với x  0 . Mệnh đề nào dưới đây đúng ? 2 1 13 1 A. 3 P x . B. 4 P x . C. 24 P x . D. 2 P x .
Câu 25 (Đề thi thử Cụm 1 – HCM) : Cho biểu thức 4 5 P
x , với x  0 . Mệnh đề nào dưới đây là mệnh đề đúng? 4 5 A. 5 P x . B. 9 P x . C. 20 P x . D. 4 P x .
Câu 26 : Với số dương a và các số nguyên dương m , n bất kì. Mệnh đề nào dưới đây đúng? n m n
A. m  ( m )n a a . B. m n m a a . C. m n n a a . D. m n . . m n a a a . 10
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 4 a b a ab
Câu 27 : Cho các số thực dương a và b . Rút gọn biểu thức P   được kết quả là 4 4 4 4 a b a b A. 4 b . B. 4 4 a b . C. b a . D. 4 a .   1 1   1 1   1 1 4 4 4 4 2 2 P a b a b a b
Câu 28 : Cho a  0,b  0 . Biểu thức thu gọn của biểu thức là A. 10 10 a b . B. a b . C. a b . D. 8 8 a b .  a b
Câu 29 : Cho các số thực dương a và b . Rút gọn biểu thức P
ab : a b 2 3 3 3   được 3 3  a b  kết quả là A. 1  . B. 1. C. 2 . D. 3
Câu 30 (THPT CHUYÊN VINH) : Giả sử a là số thực dương, khác 1. Biểu thức 3 a a được viết dưới dạng  a . Khi đó. 2 5 1 11 A.   . B.   . C.   . D.   . 3 3 6 6 2 1  1 1    y y
Câu 31 (THPT Lê Hồng Phong) : Cho 2 2
P   x y  1 2   
 . Biểu thức rút gọn của P là x x     . A. . x . B. x  . y C. x  . y . D. 2 . x . .
Câu 32 (THPT Hà Huy Tập) : Viết biểu thức 3 4 P  . x
x ( x  0 ) dưới dạng luỹ thừa với số mũ hữu tỷ. 5 5 1 1 A. 4 P x . B. 12 P x . C. 7 P x . D. 12 P x .
Câu 33 (THPT Đặng Thúc Hứa) : Cho biểu thức 6 4 5 3 P  . x
x . x , với x  0 . Mệnh đề nào dưới đây đúng? 15 7 5 47 A. 16 P x . B. 16 P x . C. 42 P x . D. 48 P x .
Câu 34 (Đề thi thử Cụm 1 – HCM) : Cho biểu thức 4 2 3 P x
x ,  x  0 . Mệnh đề nào dưới đây đúng? 6 8 9 7 A. 12 P x . B. 12 P x . C. 12 P x . D. 12 P x . 11
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 1 9 1 3  4 4 2 2 a a bb
Câu 35 : Giả sử với biểu thức B có nghĩa, Rút gọn biểu thức B   ta được: 1 5 1 1  4 4 2 2 a a b b A. 2 B. a b C. a b D. 2 2 a b 7 1 5 1  3 3 3 3 a a b b
Câu 36 : Cho hai số thực a  0, b  0, a 1, b 1 , Rút gọn biểu thức B   ta được: 4 1 2 1  3 3 3 3 a a b b A. 2 B. a b C. a b D. 2 2 a b
Câu 37 : Rút gọn biểu thức  4 2 4 x x : x (x > 0), ta được:  A. 4 x B. 3 x C. x D. 2 x
Câu 38 : Biểu thức x x x x x
x  0 được viết dưới dạng lũy thừa với số mũ hữu tỉ là: 31 15 7 15 A. 32 x B. 8 x C. 8 x D. 16 x 11
Câu 39 : Rút gọn biểu thức: 16 A
x x x x : x , x  0 ta được: A. 8 x B. 6 x C. 4 x D. x Câu 40 : Rút gọn 3 5 3 P  2 2 2 2 2 , ta đuợc: 13 13  13 A.  1318 2 B. 15 2 C. 18 2 D. 18 2 2017 2016
Câu 41 (Trích đề Minh họa lần 3): Tính giá trị của biểu thức P  7  4 3 4 37 . A. P 1 B. P  7  4 3 C. 7  4 3 D. P    2016 7 4 3
Câu 42 (Trích đề Minh họa lần 2): Cho biểu thức 4 3 2 3 P  . x
x . x , với x  0 . Mệnh đề nào dưới đây đúng? 1 13 1 2 A. 2 P x B. 24 P x C. 4 P x D. 3 P x 12
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
B. HÀM SỐ LŨY THỪA
1. Định nghĩa: Hàm số 
y x với  
được gọi là hàm số lũy thừa
2. Tập xác định: Tập xác định của hàm số  y x là: α
3. Đạo hàm: Hàm số 
y x , (  ) có đạo hàm với mọi x  0
và công thức đạo hàm chính là :
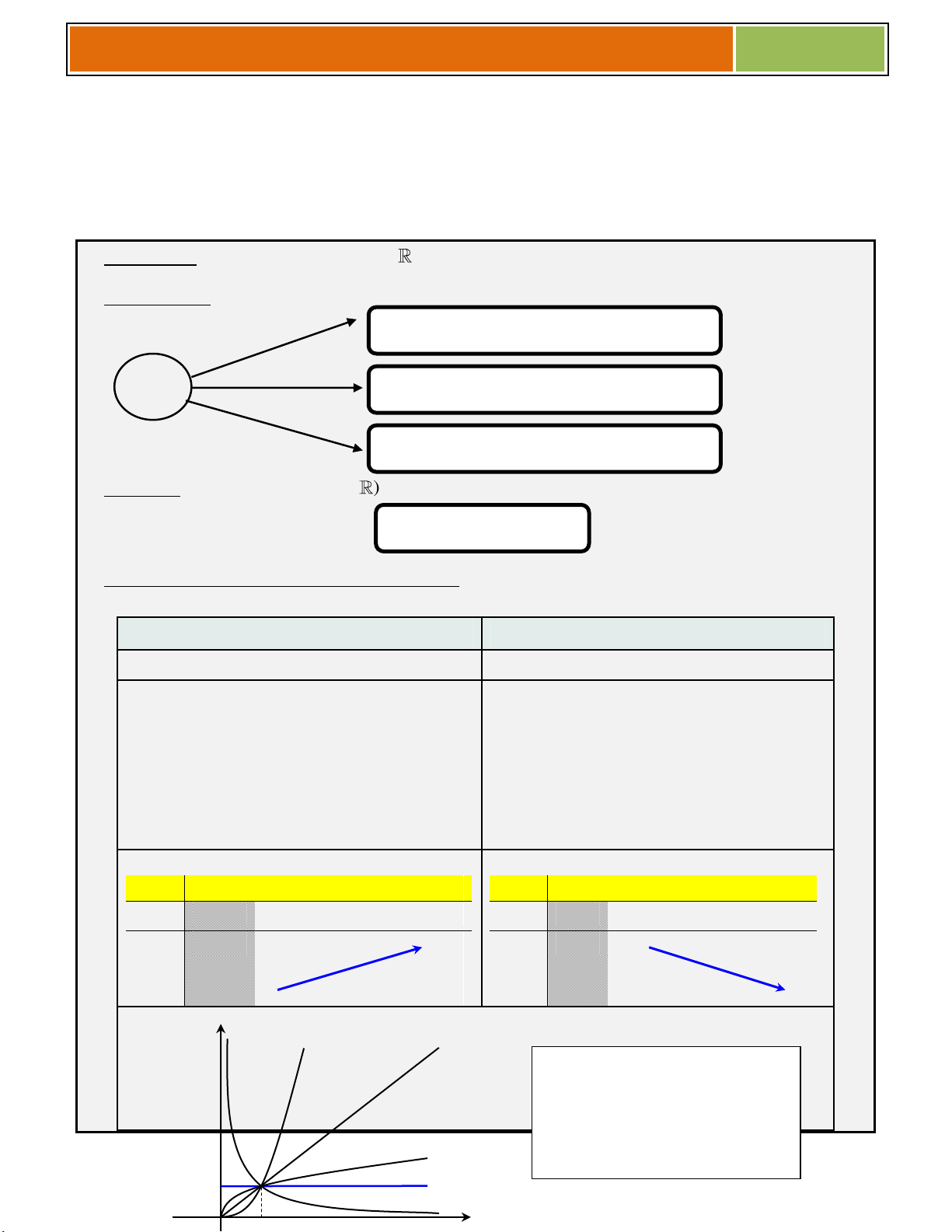
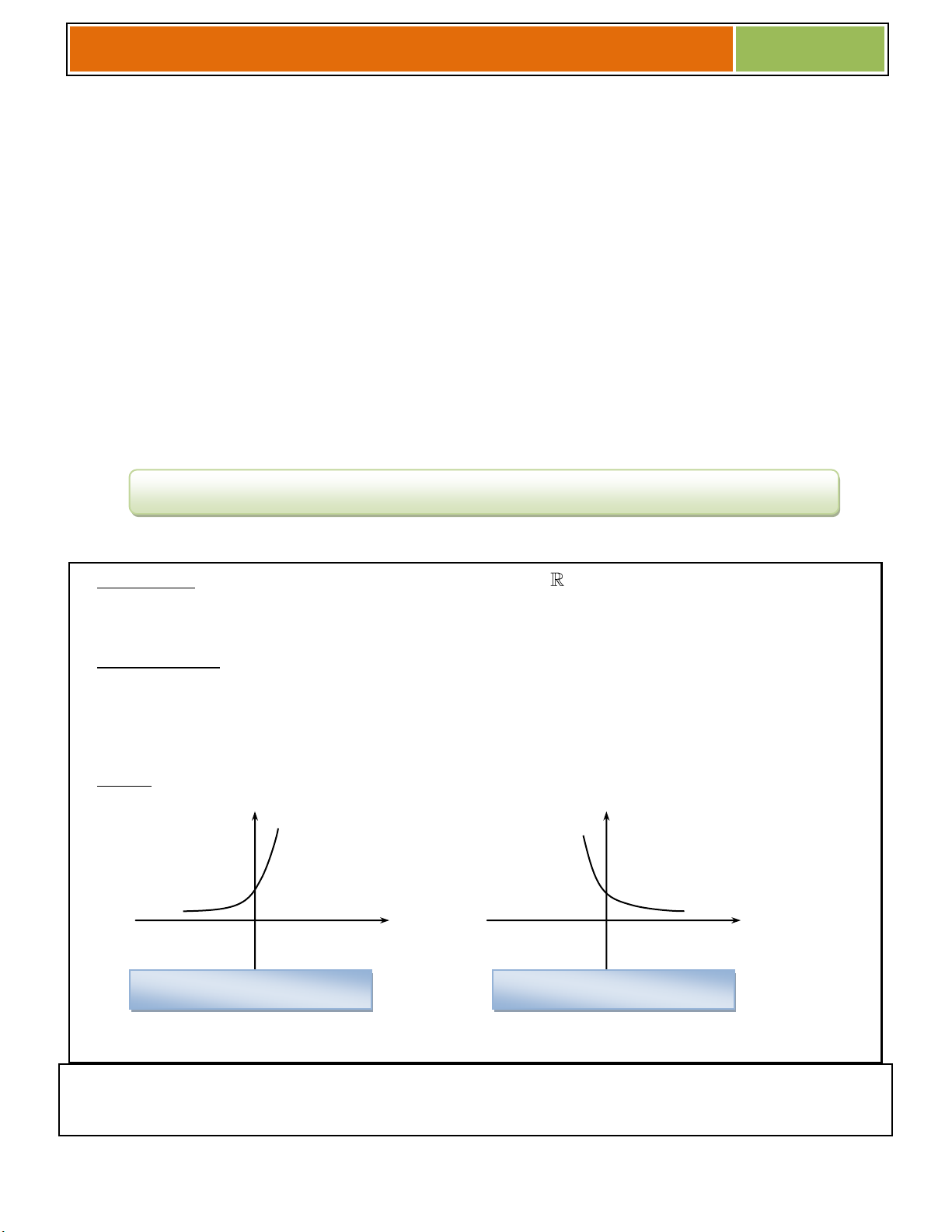
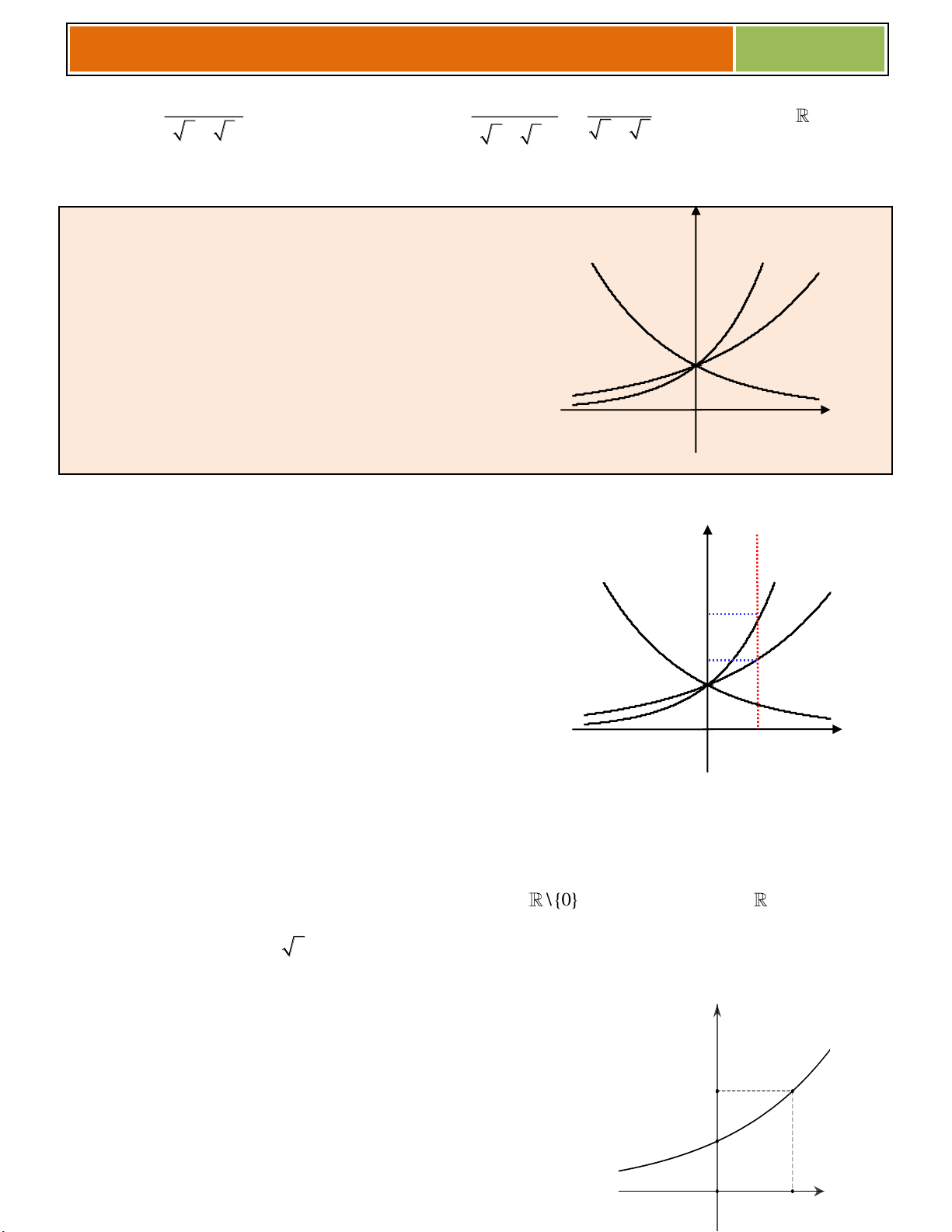
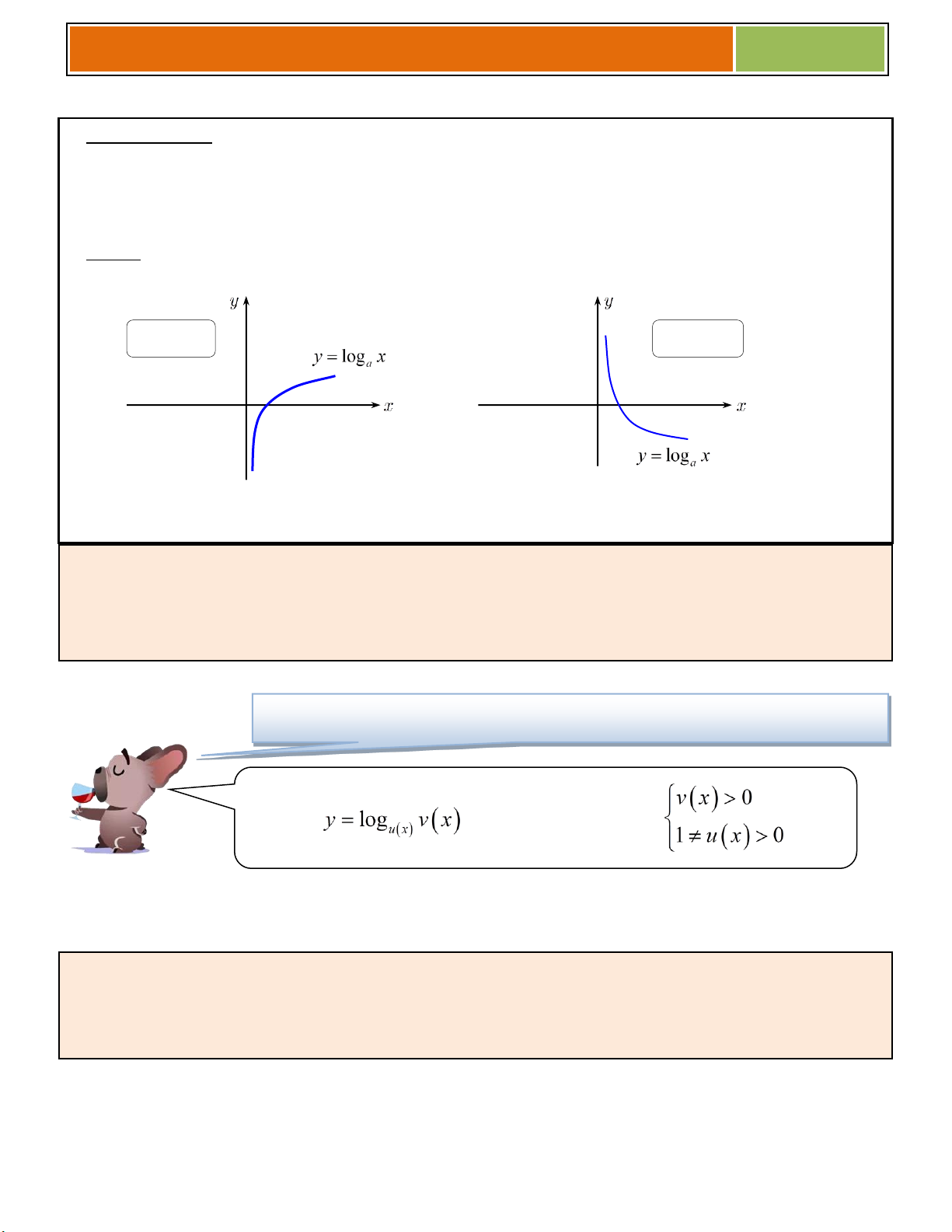
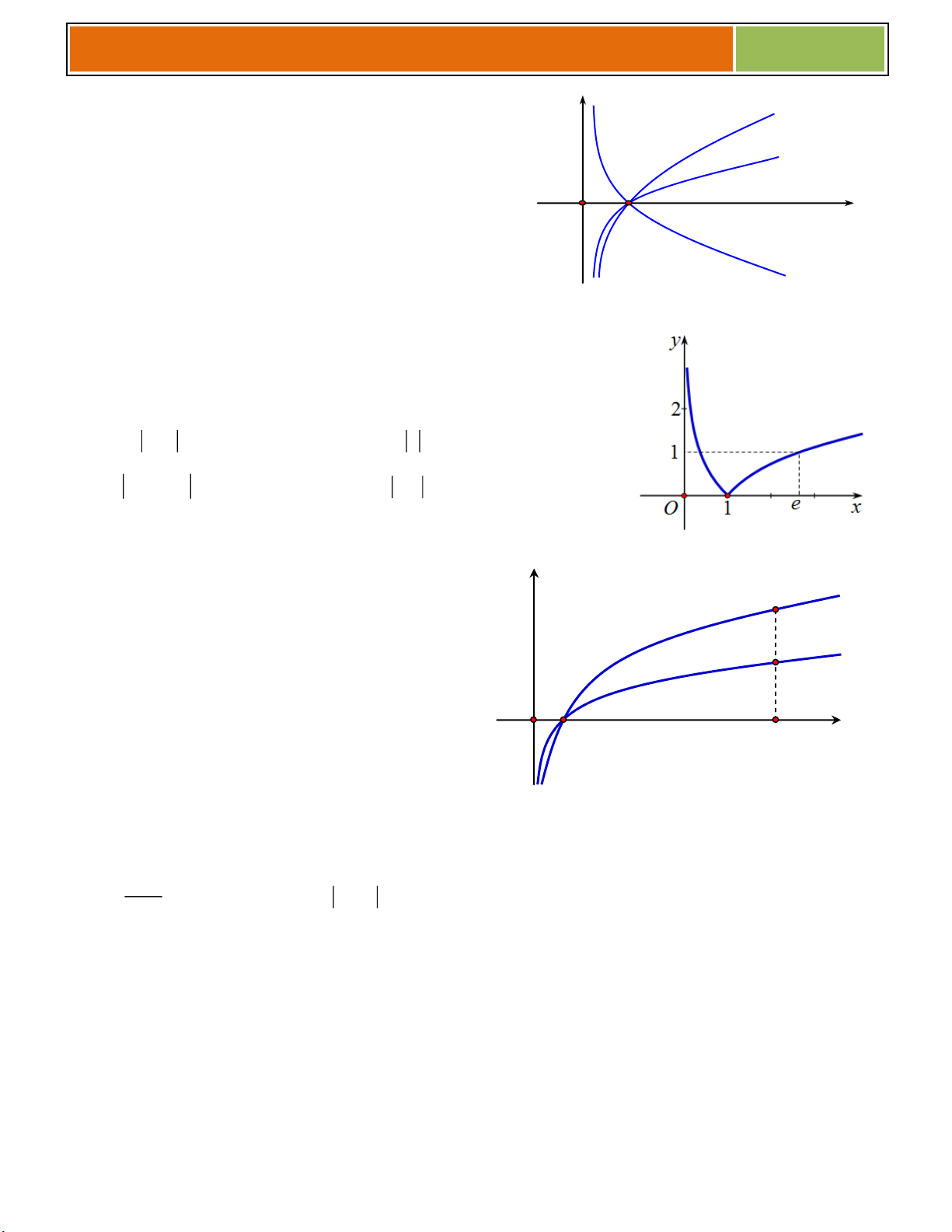
4. Tính chất của hàm số lũy thừa trên khoảng (0; )  .  
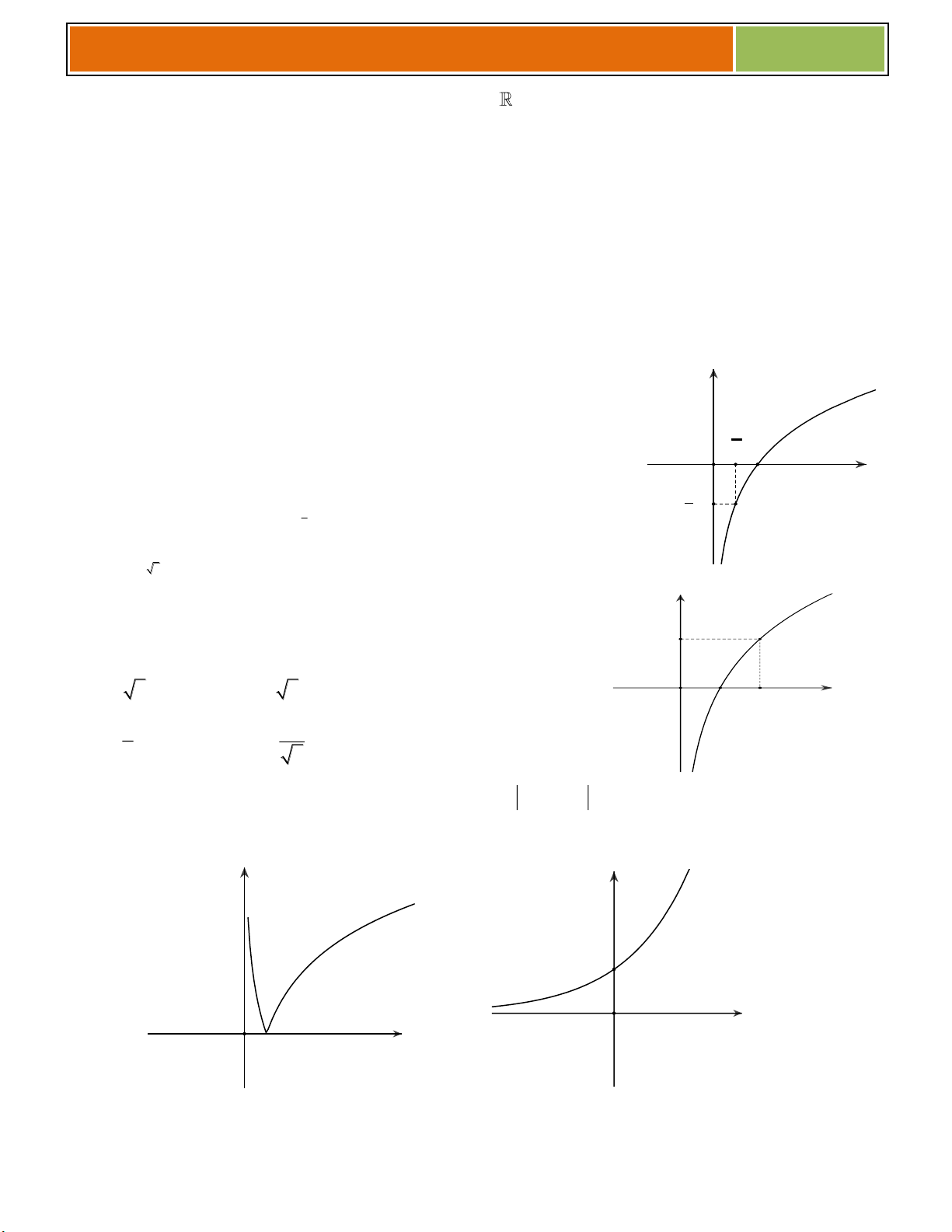
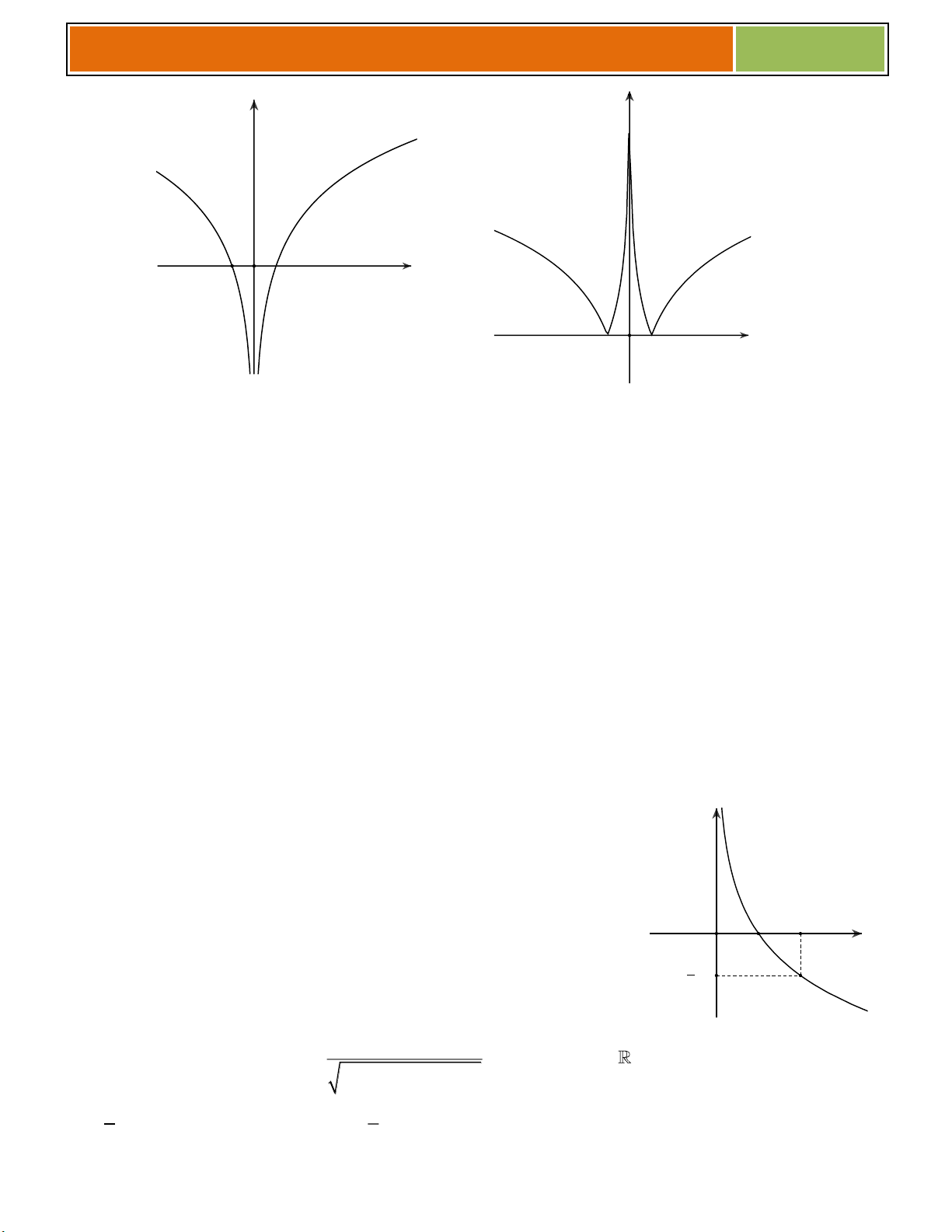
y x ,   0
y x ,   0 Tập khảo sát: (0; )  Tập khảo sát: (0; )  Sự biến thiên: Sự biến thiên:   +  1 yx     0, x   0. + 1 y   x  0, x   0. + Giới hạn đặc biệt:
+ Giới hạn đặc biệt:    
lim x  0, lim x   .  lim x   ,  lim x  0.   x 0  x x 0  x
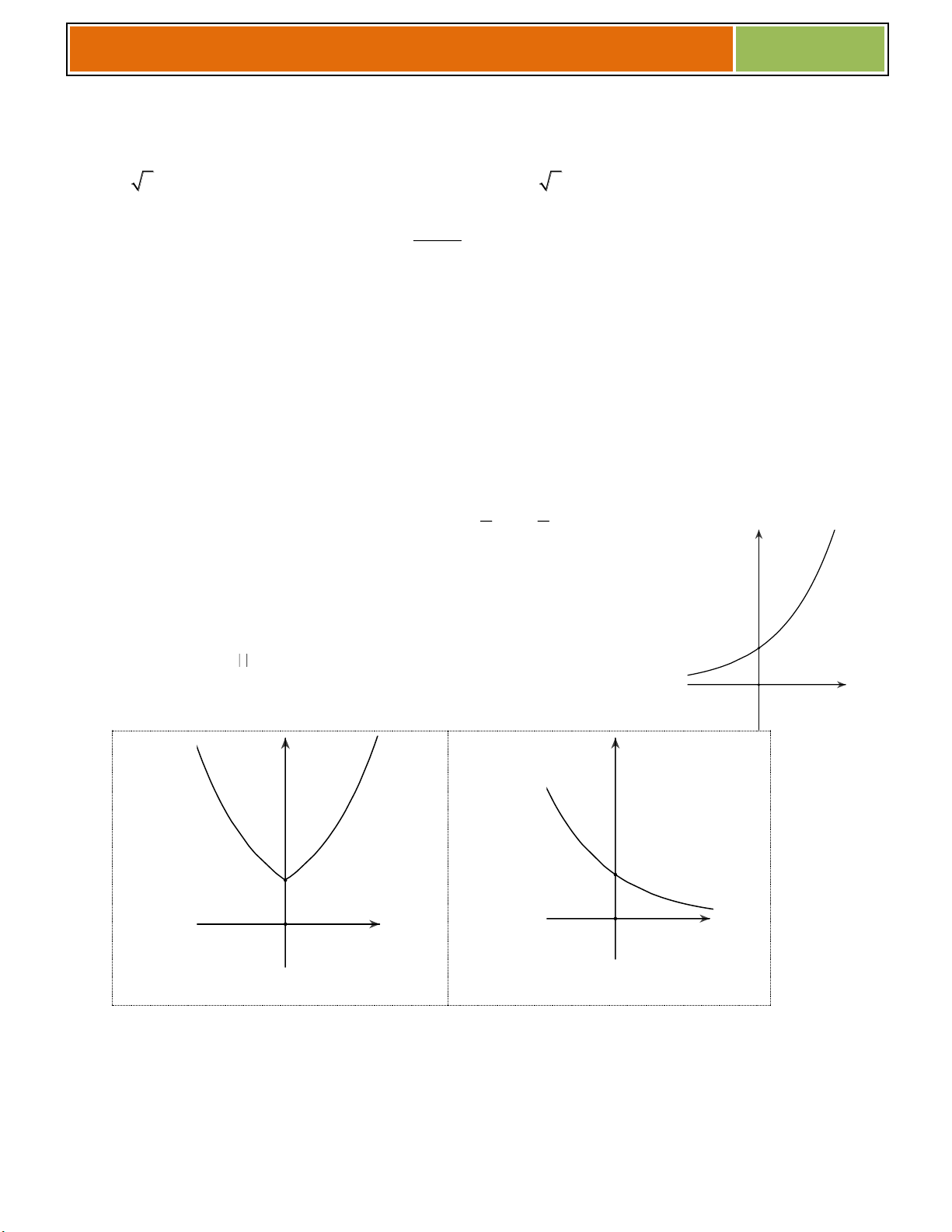
+ Tiệm cận: không có + Tiệm cận: Ox là TCN. Oy là TCĐ. Bảng biến thiên: Bảng biến thiên: x 0  x 0  y  y    y y 0 0 Đồ thị: y  1  1 Nhận xét : 0    1 13
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook) x O
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 I   1 0   0 1
Bài 01: Tìm miền xác định của các hàm số sau :   a/      3 2 y x 3x 4 b/     1 2 7 y x x 2
c/   x   45 y 2 5 d/    8 2 5 y 5 x e/ 3 y  12  x f/ 8 2 y  x  7x  8 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 
Chú ý : Mở rộng cho hàm : y  u x  
Nếu  nguyên dương thì hàm số xác định x   Nếu   0 hoặc   
(nguyên âm) thì hàm số xác định khi u x  0 14
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Nếu   (không nguyên) thì hàm số xác định khi u x  0
Bài 02: Tìm miền xác định của các hàm số sau : 
a/   x x   3 2 y 3 2
b/  x x   15 4 2 y 2 c/ 7
y  2x  6 x   d/     1 2 9 y x 3x 4 e/      6 2 y x 3x 2
f/   x   95 y 7 6 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 03: Tìm miền xác định của các hàm số sau : a/    9 2 5 y 16 3x b/ 3 y  5  4x c/ 6 2 y  x  7x  8 
d/   x x   5 2 y 2 3
e/  x x   8 4 2 y 3 4
f/   x  8 y 2 3 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 15
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 04: Tìm tập xác định của hàm số
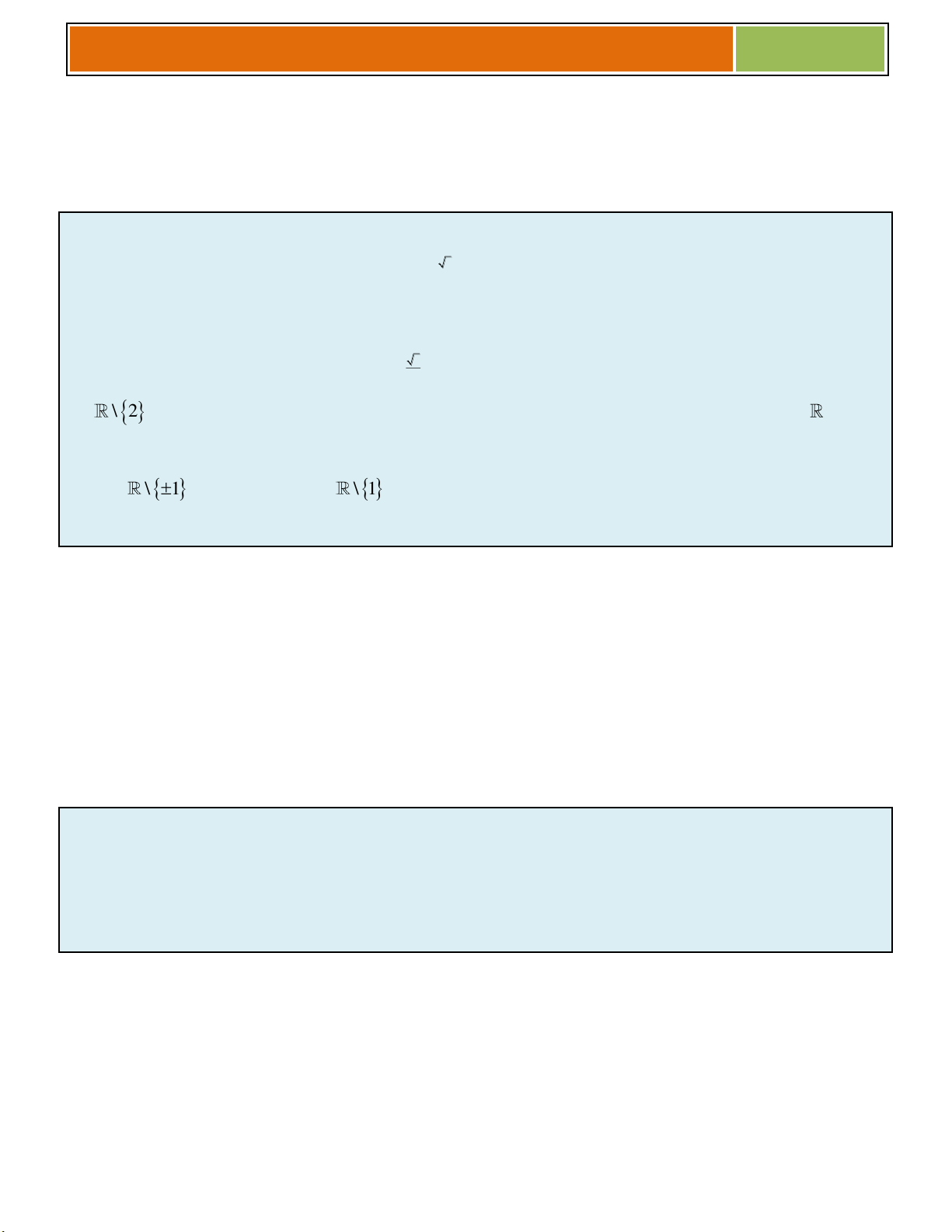
a/ (Sở GD – ĐT Bình Phước) : y  x x   2 2 2 3 . A.  3   ;1 B.  ;    3 1; C.  3   ;1 D.  ;  3  1; 2
b/ (THPT Nguyễn Tất Thành) : 3 y  (x  2) A. \   2 B. ( 2  ; )  C. (0; )  D. 
c/ (THPT chuyên Lê Thánh Tông) : y   x   12 2 1 A. D  \   1 B. D  \   1 C. D   1  ,  1 D. D   ;   1  1; ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 05 (THPT chuyên Lê Hồng Phong – Nam Định) : Tính đạo hàm của hàm số y    x6 1 cos 3 A. y x x  5 ' 18sin 3 cos 3 1 B. y x   x5 ' 18sin 3 1 cos 3 C. y x   x5 ' 6sin 3 1 cos 3 D. y x x  5 ' 6sin 3 cos 3 1 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 16
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Bài 06 (Sở GD – ĐT Hưng Yên) : hàm số y    x  4 2 3 3
có đạo hàm trên khoảng  3; 3 là:     8 8 4 4
A. y x 3 x  7 2 3
B. y   x 3 x  7 2 3
C. y   x 3 x  7 2 2
3 D. y   3 x  7 2 3 3 3 3 3 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
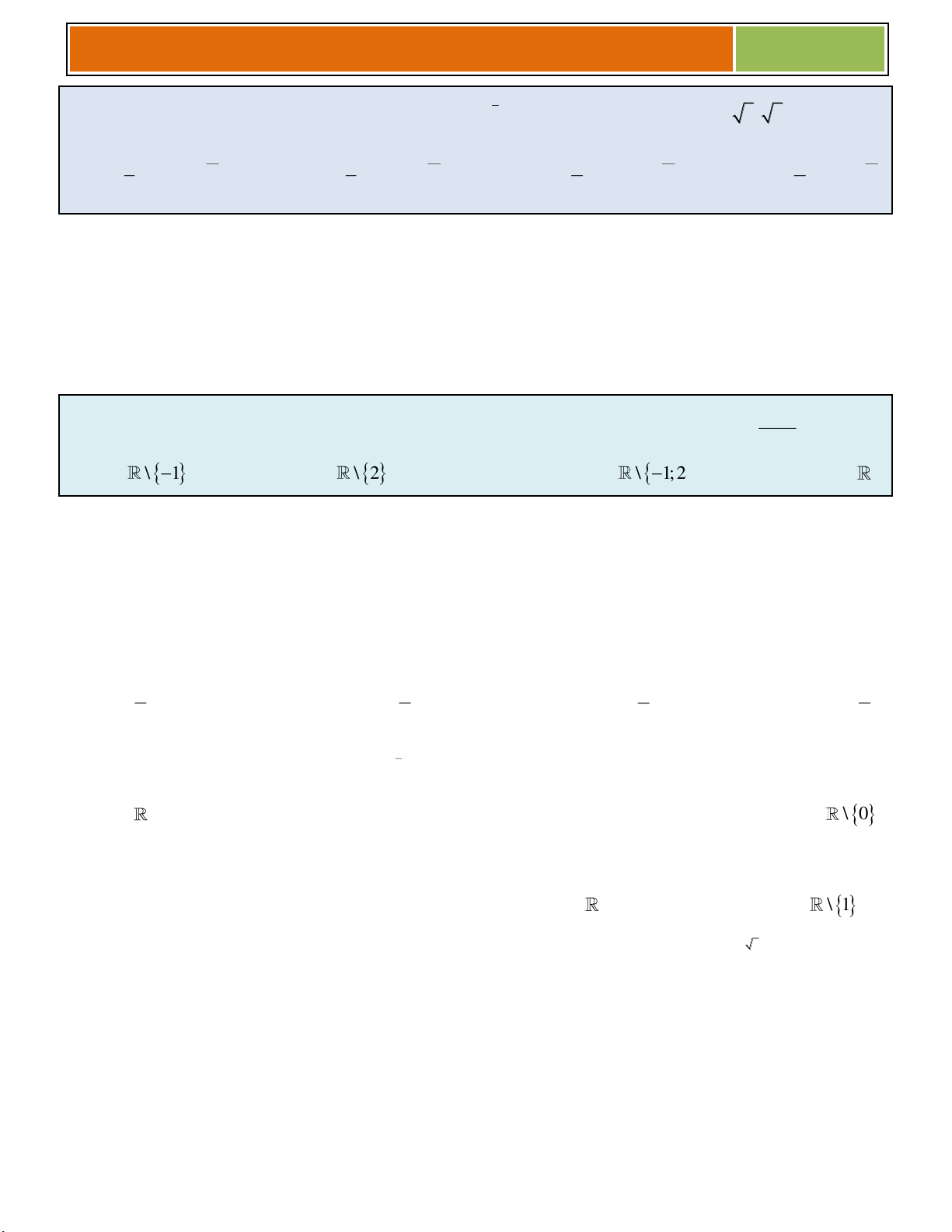
.............................................................................................................................................................................. 3   x  2 
Bài 07 (THPT Lạc Long Quân – Khánh Hòa ) : Tìm tập xác định D của hàm số y    x 1  A. D  \   1 B. D  \   2 C. D  \  1  ;  2 D. D ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Trắc nghiệm phần lũy thừa
Câu 01 : Tìm x để biểu thức  x   2 2 1 có nghĩa. 1 1  1  1 A. x   B. x   C. x   ; 2   D. x   2 2  2  2 
Câu 02 : Tìm x để biểu thức  x x   2 2 3 1 có nghĩa. A. x
  B. Không tồn tại x C. x  1 D. x   \  0 
Câu 03 (THPT Chuyên Sơn La) : Hàm số y   x   4 1 có tập xác định là. A.   ;1  . B. 1; . C. . D. \   1 .
Câu 04 (THPT Nguyễn Quang Diệu) : Tìm tập xác định của hàm số y  x x   2 2 2 3 . A.  ;    3 1; B.  3   ;1 C.  3   ;1 D.  ;  3  1; 
Câu 05 (THPT Chuyên Vinh) : Tập xác định của hàm số y   2
2x x  là. 17
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018  1  A.  ;  02; B. 0;   C. 0;2 D. 0;2  2 
Câu 06 (Sở GD – ĐT Hà Tĩnh) : Hàm số 1/3 y x
có tập xác định là. A. B. \   0 C. 0; D. 0; 
Câu 07 (Sở GD – ĐT Hà Tĩnh) : Điều kiện xác định của hàm số   x y   3 2 2 là. A. x  0 B. x  1 C. x  1 D. x  0
Câu 08 (THPT Lương Tài) : Tập xác định của hàm số 2 y x là.
A. D  0; B. D  0;  1 C. * D  D. D  1
Câu 09 : Tập xác định của hàm số 3
y  (1 2x) là.  1   1  A. ;    B. ;    C. D. 0;    2   2  1
Câu 10 (THPT Thuận Thành 2) : Tìm tập xác định D của hàm số 3
y  (2x 1) . 1  1  1  A. D  ;     B. D
C. D R \   D. D  ;     2  2  2  
Câu 11 (Sở GDĐT Lâm Đồng) : Hàm số y =  x   4 2 4 1 có tập xác định là:  1 1   1 1  A. 0; B. \  ;  C.  ;   D.  2 2  2 2  1 
Câu 12 (TT Tân Hồng Phong) : Tìm tập xác định D của hàm số   3 f x x A. D
B. D  0;  
C. D  0;   D. D  \   0 
Câu 13 (THPT Thanh Thủy) : Tập xác định của hàm số y   x x   5 2 2 6 là.  3   3  A. D   ; 2   B. D   ;   2;     2   2   3  C. D  \ 2;  D. D   2  
Câu 14 (THPT Nguyễn Huệ-Huế) : Tìm tập xác định của hàm số y   x   4 2 4 1 .  1 1   1 1 A. B.  ;   C. 0; D. \  ;   2 2   2 2 18
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Câu 15 (THPT Hoàng Văn Thụ - Hòa Bình) : Tập xác định của hàm số y  x x   1 2 3 3 2 . A. \ 1;  2 B.  ;   1 2; C.  ;   1  2; D. 1
Câu 16 : Tập xác định của hàm số 3
y  (1 2x) là.  1   1  A. ;    B. ;    C. D. 0;    2   2  
Câu 17 (THPT Trần Phú - HP) : Hàm số y   x   4 2 4 1 có tập xác định là.  1 1  1   1   1 1  A. \  ;  B. C.  ;    ;      D.  ;    2 2  2   2   2 2 
Câu 18 (THPT Tiên Du 1) : Tập xác định của hàm số y    x 5 2 3 là. 2  2   2   2  A. D  \   B. D   ;   C. D   ;    D. D  ;      3   3   3   3  1 1
Câu 19 : Cho các hàm số 4 3 2 f (x) 
x, f (x) 
x, f (x)  x , f (x)  x . Trong các hàm số trên, hàm số 1 2 3 4
nào có tập xác định là nữa khoảng 0;? .
A. f (x) và f (x)
B. f (x), f (x) và f (x) 1 2 1 2 3
C. f (x) và f (x) D. Cả 4 hàm số trên 3 4 
Câu 20 (THPT Hoàng Văn Thụ - Khánh Hòa) : Hàm số y  x  1 5 2 4 có tập xác định là. A. D   ;  2  2; B. D  C. D   ;  2
 2; D. D   2  ;2
Câu 21 (TTGDTX Nha Trang - Khánh Hòa) : Hàm số y    x 3 2 5 4 có tập xác định là: A. B.  ;  2   2; C. ( 2  ;2) D. \   2 
Câu 22 (TTGDTX Cam Lâm - Khánh Hòa) : Trong các hàm số sau đây, hàm số nào đồng biến trên các khoảng xác định? 3 A. 4 y x B. 4 y x C. 4 y x D. 3 y x
Câu 23 (THPT Nguyễn Thị Minh Khai - Khánh Hòa) : Cho f x 2 3 2
x . x Giá trị của f   1 bằng: 8 3 A. 2 . B. C. 4 D. 3 8 19
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Câu 24 (TTLT ĐH Diệu Hiền) : Tập xác định của hàm số y  x x   4 2 6 là. A. D  \  2  ;  3 B. D  \   0 C. D   ;  23; D. D
Câu 25 (TTGDTX Cam Lâm - Khánh Hòa) : Một chuyển động có phương trình là
s f (t)  t t t (m) . Tính gia tốc tức thời của chuyển động tại thời điểm t  1s . 7 7 A. 2 (m / s ) B. 2 (m / s ) 64 8 7 7 C.  (m / s) D. 2  (m / s ) 64 64 
Câu 26 (THPT Hai Bà Trưng- Huế) : Tập xác định của hàm số y   3 x  3 27 là. A. D
B. D  3;  C. D  \   3
D. D  3;  
Câu 27 (THPT Ngô Quyền) : Tìm tập xác định D của hàm số y   x   4 2 1 . A. D  B. D   ;    1  1;
C. D  0; D. D  \  1  ;  1 
Câu 28 : Tìm tập xác định của hàm số y  x x x   2 3 2 6 11 6 . A. D  B. D  \ 1;2;  3
C. D  1;2 3; D. D   ;   1  2;3 
Câu 29 (THPT Chuyên Vinh) : Tập xác định của hàm số y   x   12 1 là. A. D    ;1
B. D  1; C. D  0;  1
D. D  1; 
Câu 30 (THPT Nguyễn Đăng Đạo) : Đạo hàm của hàm số y   x   13 2 1
trên tập xác định là. 1  1  A.  x   3 2 2 1 ln 2x   1 B.  x   3 2 1 ln 2x   1 2  1  C.  2x   43 1 D.  2x   43 1 3 3
Câu 31 (THPT Lý Nhân Tông) : Hàm số y   x  2 2 5 1 có đạo hàm là. 20
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 4 A. y  B. 2
y  2x x 1 x  2 2 5 1 4x C. 5 2
y  4x x 1 D. y  5  x  3 2 5 1
Câu 32 (THPT Thái Phiên – HP) : Tìm tập xác định D của hàm số y  x x  1 2 3 6 8 . A. D  B. D  2;4 C. D   ;  24; D. D   ;  24;
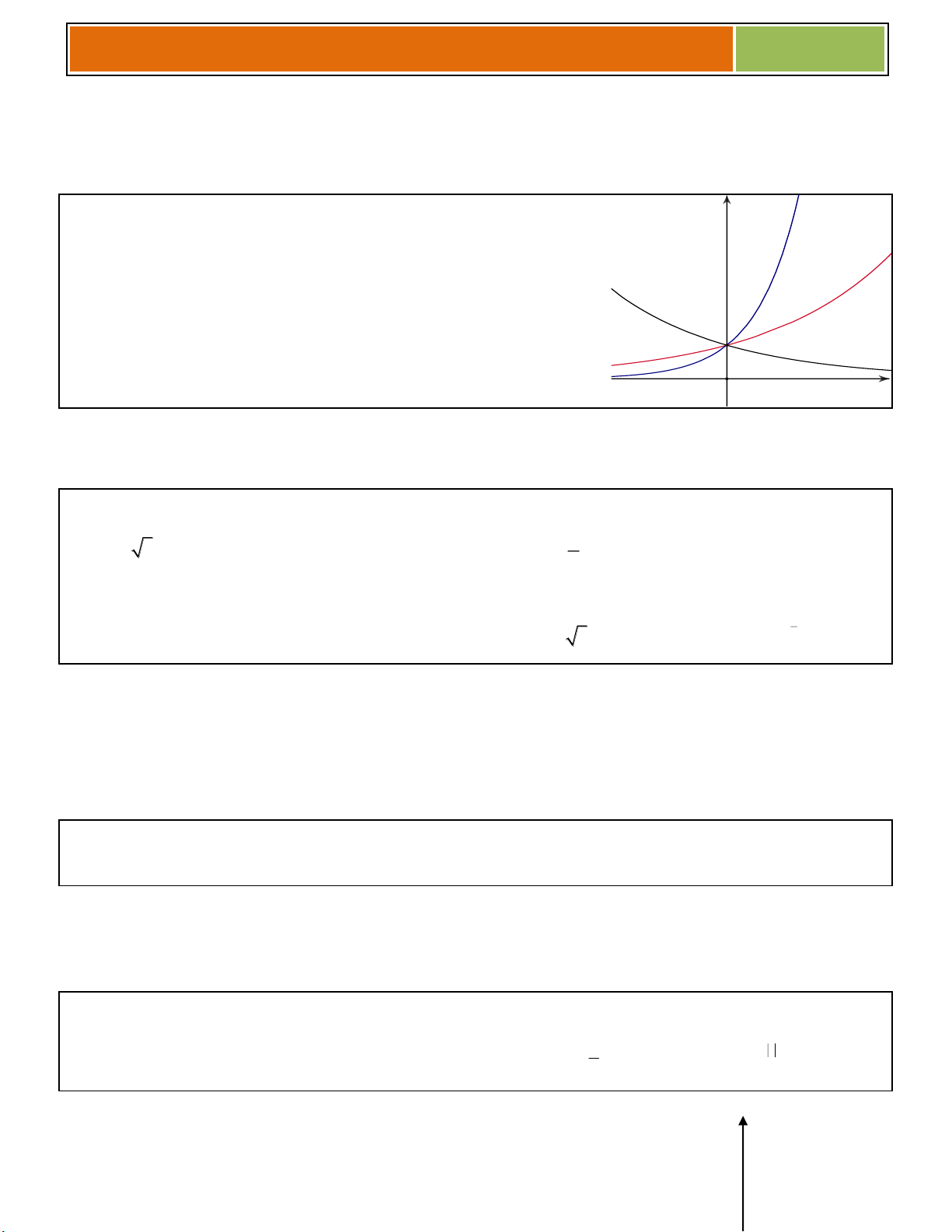
C. SO SÁNH MŨ – LŨY THỪA Cơ sở lý thuyết
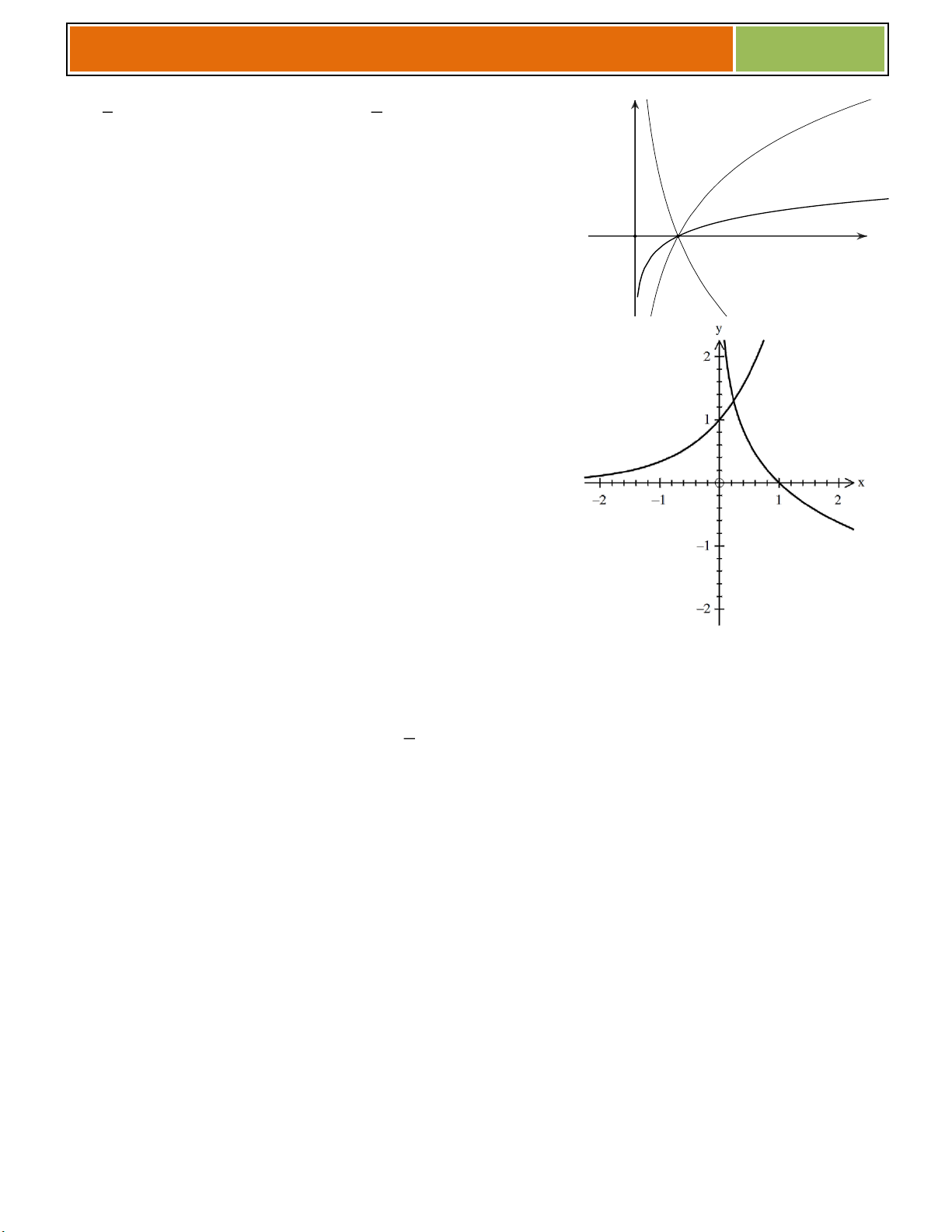
Ví Dụ 01 : Hãy so sánh các cặp số sau : a  2 1 1,7 0,8 a/ 2  2 ♥ ta có 1,7 0,8   2  2 1  ,7  0,8 21
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 1  ,7  0,8 1,7 0,8  1,7 0,8 1   1    1   1  b/      ♥ ta có  1        2   2  0  a  1   2   2   2  1,2 2   1,2 2 1, 2 2 3   3    3   3  c/               ♥ ta có 3       2 2     2 2 0  a  1      2 3 15 5 15 5  30  30  243.10 d/ 3 5 30  20 ♥ ta có 3 5   30  20 5 15 3 15 3  20  20  8.10 4 12 3 12  5  5  125 e/ 4 3 5  7 ♥ ta có 3 4   7  5 3 12 4 12  7  7  2401 6 3  6  17  17  4913 f/ 3 3 17  28 ♥ ta có   17  28 3 6 2 6  28  28  784  
Ví Dụ 02 : Cho  2   1   2  
1 . Kết luận nào sau đây đúng? A.   . B.   . C.   . D.   .
♥ Hướng dẫn giải :
Cách 1: Do 2  1  0   2   1 0; 
1 (có nghĩa ta sẽ đổi chiều)   nên  2   1   2   1
   . Chọn B
Cách 2: Cho hai giá trị cụ thể ví dụ  1  X ;   2  Y X Y
sau đó lập hiệu  2   1  2   1 CALC   đáp án B X 1  ;Y 2
Bài 01 : So sánh các cặp số sau :   a/ 6 5 7  7 b/ 2 3 3 2 5  5 c/ 5 3 3 5 7  7 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 22
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Bài 02 : So sánh các cặp số sau :  3,14  1   1  d/ 2 1,4 10  10 e/ 300 200 2  3 f/       4   4  ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 3 8
Bài 03 (THPT Cẩm Bình) : Nếu 4 9
a a thì cơ số a phải thỏa điều kiện A. a  0 . B. 0  a  1. C. a  0 . D. a  1. ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Trắc nghiệm phần so sánh mũ – lũy thừa
Câu 01 : Khẳng định nào sau đây đúng? 1  2  1   1  A. 0 a  1, a  B. 2
a  1  a  1 C. 2 3  3 2 D.       4   4  aCâu 02 : Nếu    2 2 3 1  2 3 1 thì A. a  1  . B. a  1. C. a  1  . D. a  1  .
Câu 03 : Trong các khẳng định sau đây, khẳng định nào sai?     A.   2    2 2 2 0, 01 10 . B. 0,0  1  10 .   C.   2    2 0, 01 10 . D. 0 a  1, a   0 .
Câu 04 : Trong các khẳng định sau đây, khẳng định nào đúng? 3 4 6 
A. 2  2  2  2 .
B.  11  2   11  2 . 3 4 4 
C. 4  2  4  2 .
D.  3  2   3  2 . 23
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 mCâu 05 : Nếu   2 2 3 2  3  2 thì 3 1 A. m  . B. m  . 2 2 1 3 C. m  . D. m  . 2 2 m n  1   1 
Câu 06 : So sánh hai số m và n nếu      .  9   9  A. Không so sánh được B. m n C. m n D. m n m n  3   3 
Câu 07 : So sánh hai số m và n nếu      .  2   2  A. m n . B. m n . C. m n . D. Không so sánh được. m n
Câu 08 : So sánh hai số m và n nếu  5   1   5   1 . A. m n . B. m n . C. m n . D. Không so sánh được.
Câu 09 : So sánh hai số m và n nếu 3, 2m 3, 2n  thì: A. m n . B. m n . C. m n . D. Không so sánh được. m n
Câu 10 : So sánh hai số m và n nếu  2    2  A m n . B. m n . C. m n . D. Không so sánh được. m n
Câu 11 : So sánh hai số m và n nếu  2   1   2   1 A. m n B. m n C. m n D. Không so sánh được 2 1  
Câu 12 : Kết luận nào đúng về số thực a nếu 3 3 (a 1)  (a 1) A. a  2 B. a  0 C. a  1 D. 1 a  2
Câu 13 : Kết luận nào đúng về số thực a nếu 3  1 (2a 1) (2a 1)     1   a  0 1 A.  2     . B. a 0 . 2 a  1  0  a 1 C.  . D. a  1  . a  1  24
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 0  ,2  1 
Câu 14 : Kết luận nào đúng về số thực a nếu 2    a ?  a  A. 0  a 1. B. a  0 . C. a  1. D. a  0 . 1 1  
Câu 15 : Kết luận nào đúng về số thực a nếu   a 3   a 2 1 1 ? A. a  1. B. a  0 . C. 0  a 1. D. a  1. 3
Câu 16 : Kết luận nào đúng về số thực 2
a nếu   a 4 2  2  a ? A. a  1. B. 0  a 1. C. 1 a  2. D. a  1. 1 1  2 2  1   1 
Câu 17 : Kết luận nào đúng về số thực a nếu      ?  a   a  A. 1 a  2. B. a  1. C. a  1. D. 0  a 1.
Câu 18 : Kết luận nào đúng về số thực a nếu 3 7 aa ? A. a  1. B. 0  a 1. C. a  1. D. 1 a  2. 1 1  
Câu 19 : Kết luận nào đúng về số thực a nếu 17 8 aa ? A. a  1. B. a  1. C. 0  a 1. D. 1 a  2.
Câu 20 : Kết luận nào đúng về số thực a nếu 0  ,25  3 aa ? A. 1 a  2. B. a  1. C. 0  a 1. D. a  1. 1 1
Câu 21 : Điều kiện của cơ số a là gì ? Biết rằng 2 3 a a . A. 0  a 1 B. a  1 C. a  D. a  0
Câu 22 (THPT Lạc Long Quân – Khánh Hòa) : Cho 0  a  1. Tìm mệnh đề sai trong các mệnh đề sau A. x
a  1 khi x  0 . B. 0 x
a 1 khi x  0 .
C. x x thì 1x 2  x a a . D. 1x 2  x a ax x . 1 2 1 2
Câu 23 (THPT Tôn Đức Thắng – Khánh Hòa) : Khẳng định nào sau đây SAI ? 2018 2017 2016 2017  2   2  A.  2   1   2   1 B. 1   1      2 2     2017 2016 C.   3   1   3   1 D. 2 1 3 2  2 25
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Phần II : HÀM SỐ MŨ – HÀM SỐ LOGARIT – ĐẠO HÀM A. HÀM SỐ MŨ 1. Hàm số mũ : x
y a , (a  0, a  1). Tập xác định : D
Tập giá trị : T  (0,  ) 
2. Tính đơn điệu :
☻Khi a 1 thì hàm số x
y a đồng biến, khi đó ta luôn có: f (x) g ( x) aa
f (x)  g(x).
☻Khi 0  a 1 thì hàm số x
y a nghịch biến, khi đó ta luôn có: f (x) g ( x) aa
f (x)  g(x).
3. Đồ thị : Nhận trục hoành làm đường tiệm cận ngang. y y x y a x y a 1 1 x x O O Giá trị a : Giá trị a :
Chú ý : đồ thị hàm số luôn cắt Oy tại điểm I( ; )
Bài 01 (Đề thi Cụm 8 – HCM) : Tọa độ giao điểm của đồ thị hàm số 2 x y    3 và đường thẳng y  11 là. A.  4  ;1  1 . B.  3  ;1  1 . C. 3;1  1 . D. 4;1  1 . 26
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
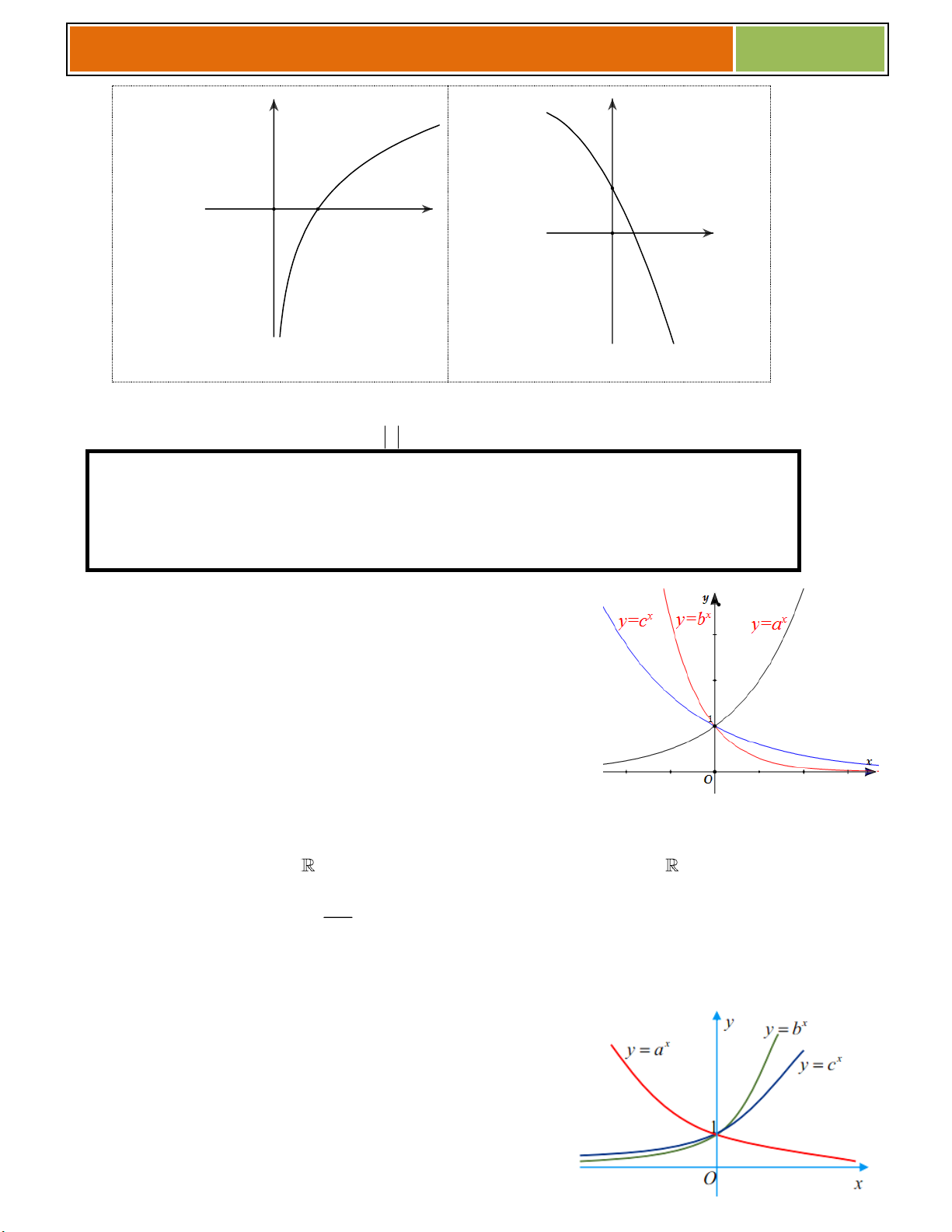
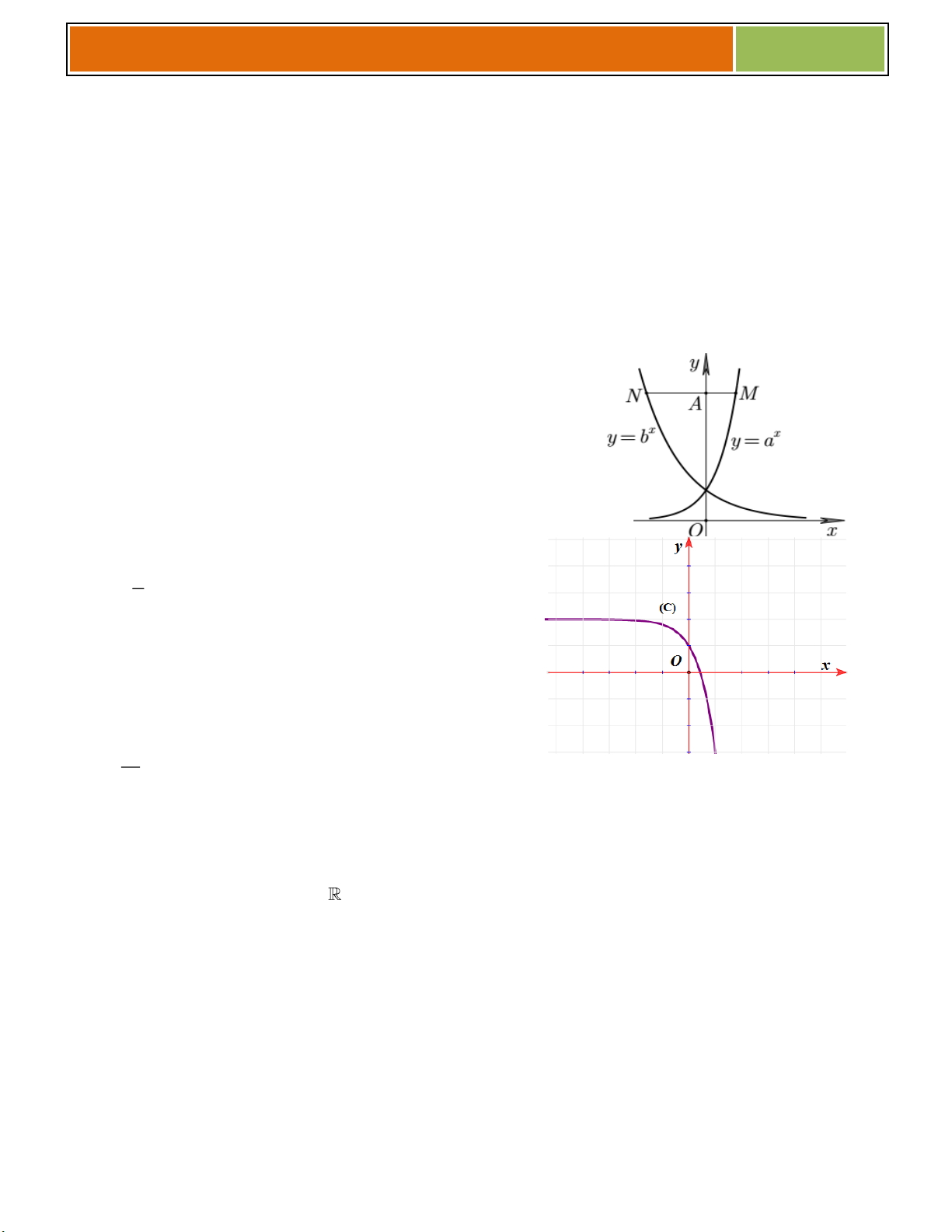
Bài 02 : Hình bên là đồ thị của ba hàm số x y y a , x y b , x
y c 0  , a , b c   1 y = bx
được vẽ trên cùng một hệ trục tọa độ.
Khẳng định nào sau đây là khẳng định đúng? y = cx
A. a c b y = ax
B. a b c
C. b a c
D. c b a O x ☻ Giải :
..............................................................................................................................................................................
Bài 03 a/ (THPT Ngô Quyền) : Hàm số nào dưới đây đồng biến trên tập xác định của nó? x x  3  A. x y   3   1 . B. y  0, 25 . C. y    . D.   x y  .  4 
b/ (THPT Ngô Quyền) : Trong các hàm số sau đây hàm số nào không phải là hàm số mũ x x A. 4 x y   . B. 4 y x  . C. y   3 . D. 3 y  5 . ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 04 (THPT Nguyễn Huệ-Huế) : Cho  
   . Kết luận nào sau đây là đúng? A. .  1. B.     0 . C.    . D.    . ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 05: a/ Khảo sát và vẽ ĐTHS 3x y x  1 
b/ Từ đó suy ra các đồ thị hàm số : (C1) : 3x y    (C2) : y    3  (C3) : 3x y ☻ Giải : Oy
a/ Tập xác định : ................... 27
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Sự biến thiên : .y’ = ................ nên hàm số ................................trên ........
Các giới hạn ............................... và ...............................
Đồ thị hàm số có tiệm cận..........................là trục.................... Bảng biến thiên : b/ Oy Oy Oy O Ox O Ox O Ox
Bài tập mẫu tham khảo 01 : Hàm số nào dưới đây đồng biến trên ? x    x 1 1  e  A. y    . B. y  . C. y  . D. y    .  4   x 7  5 5x  3 
♥ Hướng dẫn giải : Hàm số x
y a đồng biến trên
khi và chỉ khi a  1. 28
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 x 1 1  1  Bấm máy :  nên hàm số y  
đồng biến trên .   2,4411 x   7 5     7  5 7 5  Chọn B
Bài tập mẫu tham khảo 02 : Cho đồ thị ba hàm số y x y a , x y b , x
y c như trong hình vẽ sau.
y = bx
Khẳng định nào sau đây đúng
y = cx
A. c a b .
y = ax
B. c b a . 1
C. a c b .
D. b a c . x O
♥ Hướng dẫn giải : y Do hàm số x
y b giảm nên 0  b  1 (1)
y = bx Hai hàm số x  , x y a
y c tăng nên , a c  1
y = cx c
y = ax
Ta chọn ngẫu nhiên x, ở đây chọn x = 1 a
thì đường thẳng x  1 cắt đồ thị của 2 hàm số x  , x y a y c 1
tại 2 điểm (1; a) và (1; b). O x
Suy ra (từ hình vẽ) a c 1
Vậy b a  .
c Chọn A
Trắc nghiệm hàm số mũ
Câu 01 : Tập giá trị của hàm số x y a
(a  0; a  1) là: A. (0; )  B. [0; )  C. \{0} D. x
Câu 02 : Cho hàm số y   2  
1 . Phát biểu nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng ( ;   )  . y
B. Hàm số đồng biến trên khoảng (0; ) 
C. Đồ thị hàm số có đường tiệm cận ngang là trục tung. 2
D. Đồ thị hàm số có đường tiệm cận đứng là trục hoành. 1 29
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook) O 2 x
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Câu 02 : Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? x x A. y   2 B. y x C. 2x y  D. y   2 1
Câu 03 : Gọi C  là đồ thị của hàm số y
. Phát biểu nào sau đây là sai ? 2017x
A. C  nhận trục Ox làm tiệm cận ngang.
B. C  không có điểm chung với trục Ox .
C. C  nhận trục Oy làm tiệm cận đứng.
D. C  cắt trục tung tại điểm M 0;  1 .
Câu 04 (THPT Lương Tài) : Trong các khẳng định sau, khẳng định nào sai? a b  1   1 
A. 3a  3b a b . B.   a b     .  2   2  y a b y = 2x C.  2 b x     2 2
x  2  a b .
D. 2.3a  30.5  0 .
Câu 05 : Biết hàm số 2x y
có đồ thị là hình bên. 1
Khi đó, hàm số 2 x y
có đồ thị là hình nào trong bốn hình được liệt kê ở O x 3
bốn A, B, C, D dưới đây ? y y 1 1 x O 3 O x 3 Hình 1 Hình 2 30
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook) 4
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 4 2018 3 y y 1 O 1 x x O 3 Hình 3 Hình 4 A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4 -4
Ghi chú : cách vẽ đồ thị hàm số y f x  là : -4
Câu 06 (THPT Thái Phiên – HP) : Cho a, ,
b c là các số thực
đương phân biệt, khác 1 và đồ thị các hàm số x  , x  , x y a y
b y c như hình vẽ.
Mệnh đề nào sau đây đúng?
A. a c b .
B. c a b .
C. a b c .
D. b a c .
Câu 07 (THPT Ngô Quyền) : Cho hàm số 2x y
. Mệnh đề nào dưới đây đúng?
A. Tập giá trị của hàm số là .
B. Hàm số đồng biến trên . 2x
C. Đạo hàm của hàm số là y  .
D. Đồ thị hàm số nhận trục Oy làm tiệm cận đứng. ln 2
Câu 08 (Đề Thử Nghiệm – Bộ GD&ĐT) : Cho ba số thực dương a, , b c khác 1. Đồ thị các hàm số x  , x  , x y a y
b y c được cho trong hình
vẽ bên. Mệnh đề nào dưới đây đúng?
A. a b c .
B. a c b .
C. b c a .
D. c a b . 31
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Câu 09 (THPT An Lão – lần 2) : Hàm số nào dưới đây đồng biến trên tập xác định của nó ? xx 2   1  x A. x y    . B. y  0,5 . C. y    . D. y   3 .  3    
Câu 10 (THPT Chuyên Võ Nguyên Giáp) : Gọi C  là đồ thị của hàm số 4x y  . Mệnh đề nào sau đây sai?
A. Đồ thị C  nằm phía dưới trục hoành.
B. Đồ thị C  luôn đi qua điểm 0  ;1 .
C. Đồ thị C  luôn đi qua điểm 1;4 .
D. Trục Ox là tiệm cận ngang của C  .
Câu 11 (THPT Chuyên Thái Bình) : Chọn kết quả sai trong các kết quả sau? 5 2     8 3  1  A. 1   . B. 1   .  4   3  5     C. 1   . D. 2 e  1 .  3 
Câu 12 (THPT Thái Phiên – HP) : Cho a là một số thực dương khác 1. Mệnh đề nào dưới đây sai? A. Đồ thị hàm số x
y a nhận trục Ox làm tiệm cận ngang. B. Hàm số x
y a nghịch biến trên với a  1. C. Hàm số x
y a đồng biến trên với a  1. D. Đồ thị hàm số x
y a luôn đi qua điểm cố định 1;0 .
Câu 13 (THPT Quế Võ 1) : Tìm mệnh đề đúng trong cá mệnh đề sau. x  1 
A. Đồ thị của hàm số x
y a và y    với 0  a 1 
thì đối xứng nhau qua trục tung. a  B. Hàm số x
y a với a  1 là một hàm số nghịch biến trên  ;   . C. Hàm số x
y a với 0  a  1 là một hàm số đồng biến trên  ;   .
D. Đồ thị của hàm số x
y a với 0  a  1 luôn đi qua điểm  ; a  1 .
Câu 14 (Sở GDĐT Lâm Đồng lần 03) : Trong các hàm số sau, hàm số nào đồng biến trên R ? xx 2     A. y    B. y     e   4  xx 1     C. y    D. y     3   3  32
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Câu 15 (THPT Lệ Thủy – Quảng Bình) : Tìm mệnh đề đúng trong các mệnh đề sau? A. Đồ thị hàm số x
y a 0  a  
1 luôn đi qua điểm M a  ;1 . B. Hàm số x
y a 0  a  
1 luôn đồng biến trên  ;   . C. Hàm số x
y a 0  a  
1 luôn nghịch biến trên  ;   . D. Hàm số x
y a 0  a  
1 luôn đồng biến trên   ;1  .
Câu 16 : Cho các số thực dương a,b khác 1. Biết rằng bất kì đường thẳng nào song song với Ox mà cắt các đường x  , x y a
y b , trục tung lần lượt tại M , N
và A thì AN  2AM (hình vẽ). Mệnh đề nào sau đây đúng ? A. b  2a B. 2 ab  1 C. 2 a b 1 D. ab  2
Câu 17 : Cho đồ thị C  như hình vẽ. Hỏi C  có thể là đồ
thị của hàm số nào dưới đây? A. 5x y   2 B. 5x y   2 1 C. y  D. 2 5x y   5x
Câu 18 : Cho hàm số 10x y
. Khẳng định nào sau đây là sai?
A. Đồ thị hàm số luôn ở phía trên trục hoành .
B. Hàm số luôn đồng biến trên .
C. Đồ thị hàm số luôn đi qua điểm 1;10
D. Đồ thị nhận trục tung làm tiệm cận ngang. 33
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
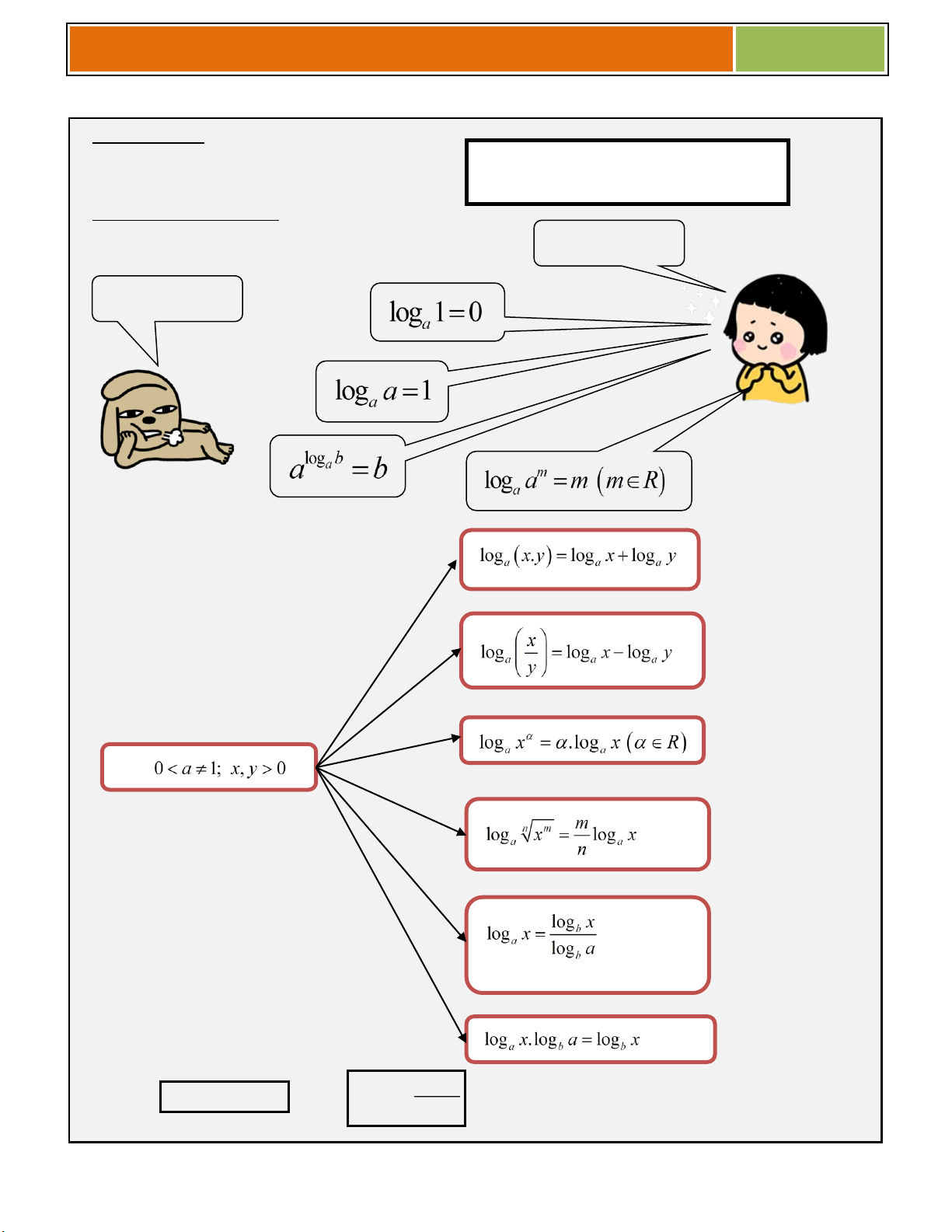
B. CÔNG THỨC LOGARIT 1. Định nghĩa : Cho ,
a b  0 và a  1 thì ta có định nghĩa sau :
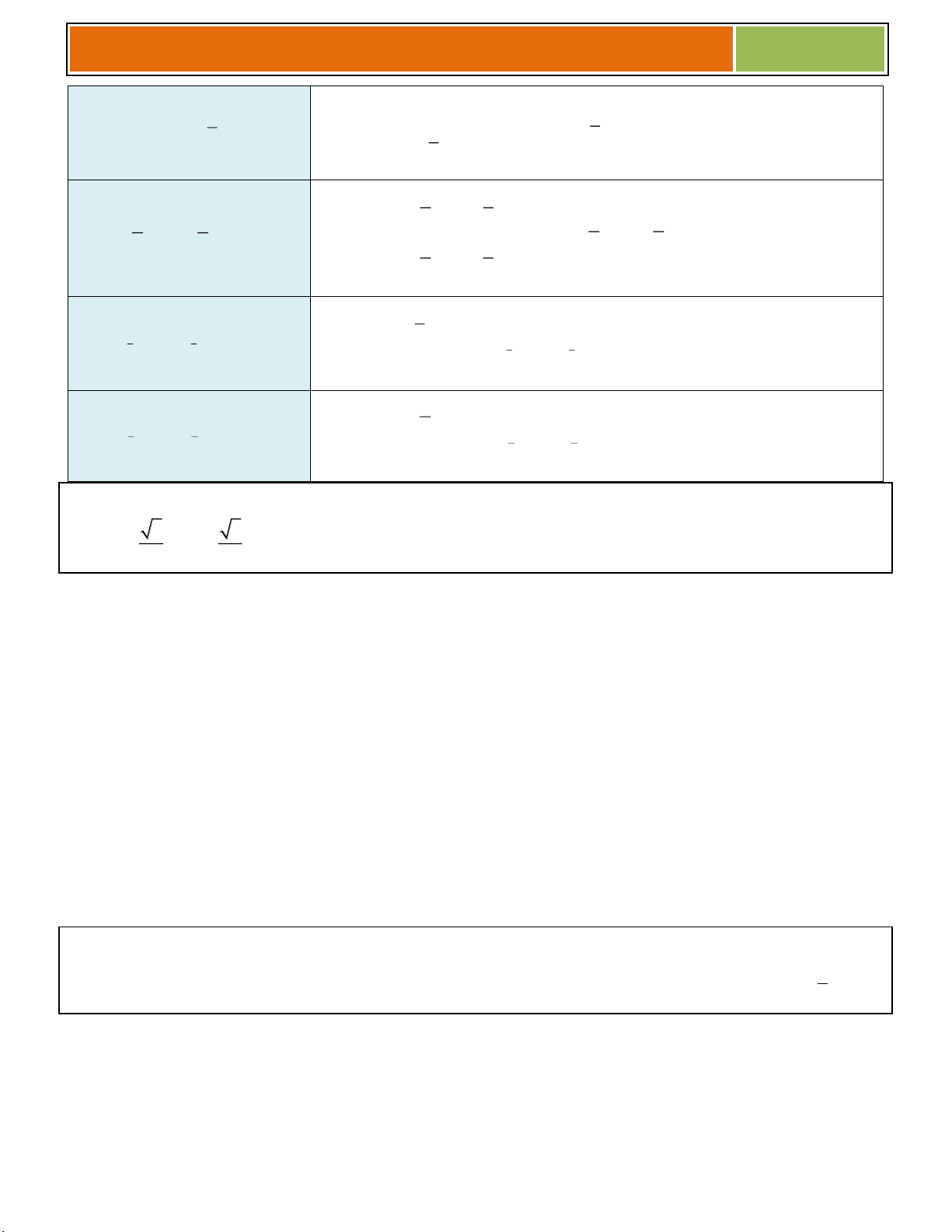
2. Tính chất và quy tắc :
Với mọi số dương a,b và a  1, ta có : Đó là....
Tính chất gì ? ? Quy tắc : cho
Giáo viên cần file word vui lòng liên hệ
Zalo / đt / facebook : 0914 449 230 1 Hệ quả : log . b log a  1 log b a b hoặc a log a b 34
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
3. Logarit thập phân – logarit tự nhiên.
a) Logarit thập phân. Logarit cơ số 10 được gọi là logarit thập phân. Hay : log b kí hiệu là logb 10 n  1 
b) Logarit tự nhiên. Số e  lim 1  2,71828...   n  n
Logarit cơ số e được gọi là logarit tự nhiên. Hay : log b kí hiệu là lnb. e 1/ log 27 3 2/ log 3 1 9 1 3/ log 1 81 3 2 3 4/ log 100 10 5/ log 81 3 6/ log 16 1 2 1 7/ log 3 3 27 8/ 3 log 25 1 5 5 243 9/ log 3 3 10/ log35 3 11/ log 5 2 16 12/ 2 log a 1 3 a log 5 3  1  13/    25  14/ 4 log a 2 a 35
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 128 15/ log 2 2 2 16/ log 3 5 5 5 log 4 17/  3 3 2log 6 3  1  18/    3  2log 5 3  1  19/    3  1 20/ log 1 a 3 2 a 2  a
Bài 01 (THPT QG – 2017) : Cho a là số thực dương khác 2 . Tính I  log   . a  4  2 1 1 A. I  . B. I   . C. I  2 . D. I  2  . 2 2 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 02 : Cho a, b là các số thực dương thỏa 2b a  5 . Tính 6 2a b K   4 . A. K  226. B. K  202. C. K  246. D. K  242. ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 03 (THPT Trần Cao Vân - Khánh Hòa) : Giá trị của biểu thức log 3 2 A  4 bằng: A. 6 . B. 2 . C. 12 . D. 9 . ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 04 (THPT An Lão lần 2) : Cho a, ,
b c là các số thực dương ( ,
a b  1) và log b  5,log c  7 . a b 36
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 b
Tính giá trị của biểu thức P  log   . a c  2 1 A. P  . B. P  15  . C. P  . D. P  60  . 7 14 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 05 (THPT chuyên Tuyên Quang) : Cho a là số thực dương và a  1. 4log 5
Tính giá trị của iểu thức 2 a a . A. 125 5 B. 7 5 C. 14 5 D. 7 5 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 06 (THPT Lương Tài) : Cho a  log 3; b  log 5 . Giá trị của A  log 360 là. 2 2 2 A. 3 a  2 . b B. 3 2a  . b C. 2  a  . b D. 1 3a  2 . b
☻ Giải (theo tự luận lẫn bấm máy tính) :
..............................................................................................................................................................................
.................................................................................
Giáo viên cân file word vui lòng liên h ............................................................... ệ
..............................
Zalo / đt / facebook : 0914 449 230
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 07 (Sở GD&ĐT Bình Phước) : Cho a, b là các số thực dương và khác 1. Mệnh đề nào dưới đây là đúng. 1 1 1 1 2 2 2 2 A. logb a aa b . B. logb a ab C. log 2 log b a ab . D. b a ab a .
☻ Giải (theo tự luận lẫn bấm máy tính) :
..............................................................................................................................................................................
.............................................................................................................................................................................. 37
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 2 a x
Bài 08 (THPT chuyên Lam Sơn lần 2) : Biết 16  x
x  1 và a b  2 . Tính giá trị của biểu thức 2   b x
M a b . A. 8 . B. 14 . C. 18 . D. 16 .
☻ Giải (theo tự luận lẫn bấm máy tính) :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. a a  3   4  5 4
Bài 09 (Sở GD – ĐT Hà Tĩnh) : Cho a,b là các số thực thỏa điều kiện      và 4 3 b b .Chọn  4   5 
khẳng định đúng trong các khẳng định sau?
A. a  0 và b  1.
B. a  0 và 0  b 1.
C. a  0 và 0  b 1.
D. a  0 và b  1.
☻ Giải (theo tự luận lẫn Casio) :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 10 (THPT Chuyên LHP Nam Định) : Cho hai số thực dương a và b, với a  1. Khẳng định nào
dưới đây là khẳng định đúng? 1 A. log
ab  2  2log b B. log ab  log b 2   2   a a 2 a a 1 1 1 C. log ab   log b D. log ab  log b 2   2   2 2 a a 4 a a
☻ Giải ( tự luận lẫn casio):
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 38
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Bài 11 (Trích đề Minh họa lần 2) : Với các số thực dương a, b bất kì. Mệnh đề nào dưới đây đúng? 3  2a  3  2a  1 A. log 
 1 3log a  log b . B. log 
 1 log a  log b . 2 2 2  b  2 2 2  b  3 3  2a  3  2a  1 C. log 
 1 3log a  log b . D. log 
 1 log a  log b . 2 2 2  b  2 2 2  b  3
☻ Giải ( tự luận lẫn casio):
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 12 (Trích đề Minh họa lần 3) : Cho a là số thực dương, a  1 và 3 P  log
a . Mệnh đề nào dưới đây 3 a 1 đúng? A. P  3 . B. P 1. C. P  9 . D. P  . 3
☻ Giải ( tự luận lẫn casio):
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 13 (THPT QG 2017) : Với a , b là các số thực dương tùy ý và a khác 1, đặt 3 6
P  log b  log b . 2 a a
Mệnh đề nào dưới đây đúng ?
A. P  9log b .
B. P  27 log b .
C. P  15log b .
D. P  6log b a a a a
☻ Giải ( tự luận lẫn casio):
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 14 (THPT QG 2017) : Cho log b  2 và log c  3 . Tính P   2 3 log b c . aa a A. P  31. B. P 13. C. P  30 . D. P 108.
☻ Giải ( tự luận lẫn casio):
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 39
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 1
Bài 15 (THPT QG 2017) : Cho log a  2 và log b  . Tính I  2log log 3a   log b 3  3   2 3 2  . 2 1 4 5 3 A. I  . B. I  4 . C. I  0 . D. I  . 4 2
☻ Giải ( tự luận lẫn casio):
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. ma n
Bài 16 : Cho a  log 5 . Ta phân tích được log 1000  , , m , n k  . Tính 2 2 2
m n k 4   2 k A. 13. B. 10. C. 22. D. 14 . ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài tập mẫu tham khảo 01(Trích Đề minh họa 2017) : Đặt a  log 3, b  log 3 . Biểu diễn log 45 2 5 6
theo a, b ta được a  2ab 2 2a  2ab a  2ab 2 2a  2ab A. log 45  . B. log 45  . C. log 45  . log 45  . 6 ab 6 ab 6 ab  D. b 6 ab b
♥ Hướng dẫn giải (nguồn : thầy Cao Tuấn) : 1 1
Cách 1 : Ta có: log 3  a  log 2 
và log 3  a  log 5  . 2 3 a 5 3 b 1 2  log 45 log 9  log 5 2  log 5 a 1 2ba  2ab Khi đó: 3 3 3 3 log 45 b       . 6 log 6 log 3  log 2 1 log 2 1 b 1 a b ab 3 3 3 3   1 aChọn C.
Cách 2 : Chú ý: Với những bài toán dạng như thế này, HS khi có thể sử dụng MTBT (casio hay vinacal)
để giải như sau: Cơ sở lí thuyết: A B A B  0
Bước 1: Để dễ dàng ấm máy ta gán các giá trị log 3 , log 3 cho A, B. 2 5 40
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
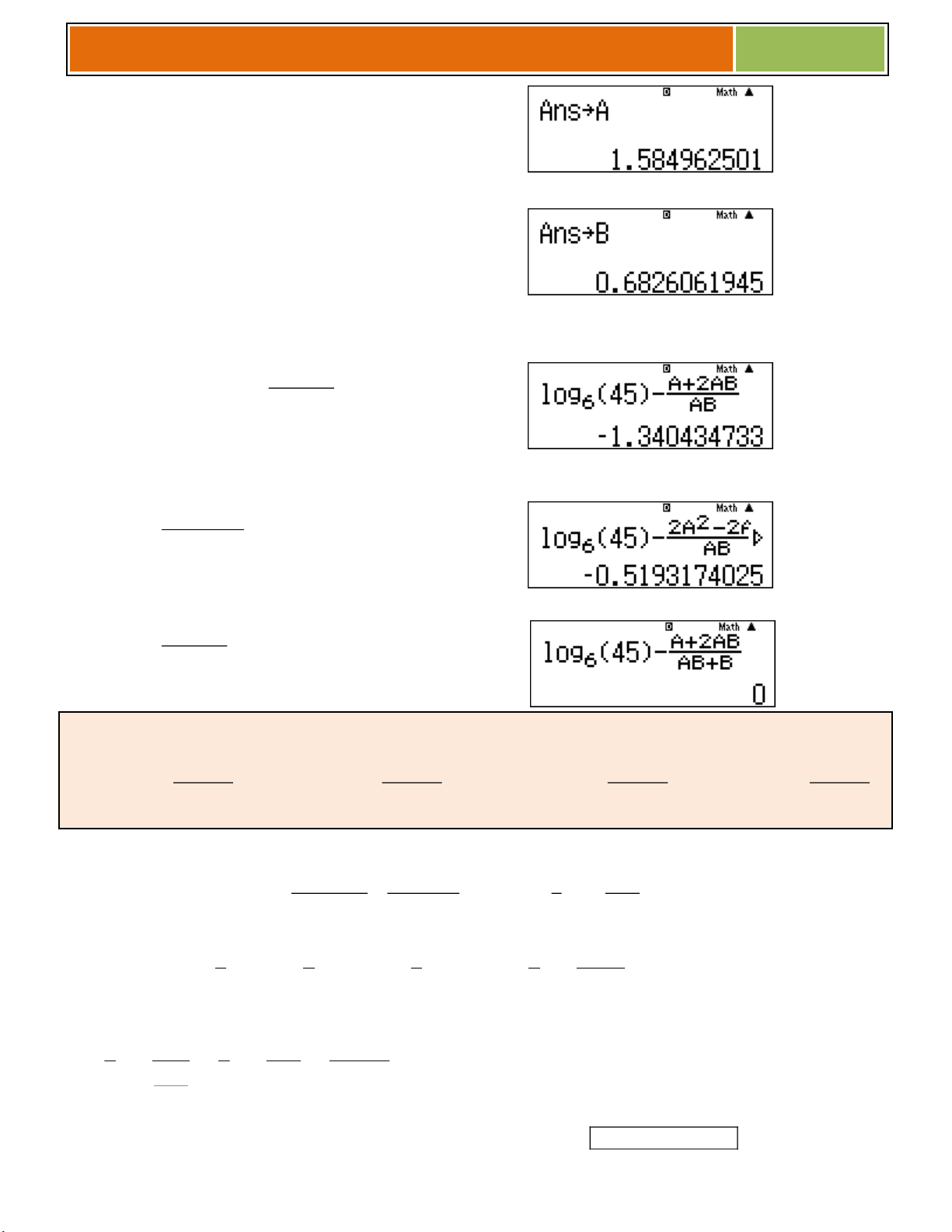
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 Gán log 3  A . 2 Bấm log 3 = q J z 2 Gán log 3  B . 5 Bấm log 3 = q J x 5
Bước 2: Nhập biểu thức: log 45  ... 6   A  2AB
Lần 1: Nhập log 45   1  ,34...  0 6 AB  loại A.
Lần 2: Bấm ! để sửa biểu thức thành 2 2A  2AB log 45   0  ,51...  0 6 AB  loại B.
Lần 3: Bấm ! để sửa biểu thức thành A  2AB log 45   0 6 AB (hợp lý) BChọn C.
Bài tập mẫu tham khảo 02 (trích từ tài liệu thầy Cao Tuấn) : Nếu a  log 3 thì 15 3 5 1 1 A. log 15  . B. log 15  . C. log 15  . D. log 15  . 25 51 a 25 31 a 25 21 a 25 51 a
♥ Hướng dẫn giải : 1 1 1 1  a
Cách 1 : Ta có: a  log 3    log 5  1  15 log 3.5 1 log 5 a a 3   3 3 1 1 1 1  1 
Khi đó: log 15  log 15  log 5.3  1 log 3  1  25 5 5    5  2 2 2 2  log 5 3    1  1  1  a  1  1   1    Chọn C. 2 1 a   2 
1  a  21 a    a
Cách 2 : Bây giờ, ta sẽ sử dụng casio – vinacal theo cơ sở lí thuyết A B A B  0 41
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Bước 1: Để dễ dàng ấm máy ta gán các giá trị log 3 cho A. 15 Gán log 3  A . 15 Bấm log 3 = q J z 15
Bước 2: Nhập biểu thức: log 15 ... 25 3
Lần 1: Nhập log 15   0  ,16...  0 25 51 A  loại A.
Lần 2: Bấm ! để sửa biểu thức thành 5 log 15   1  ,96...  0 25 31 A  loại B.
Lần 3: Bấm ! để sửa biểu thức thành 1 log 15 
 0  Chọn C. 25 21 A
Bài tập mẫu tham khảo 03 (trích từ tài liệu thầy Cao Tuấn) : Nếu log 5  a ; log 7  b ; log 3  c 27 8 2 3b  2ac 3b  3ac 3b  2ac 3b  3ac thì log 35 bằng A. . . . . 12 c  B. 2 c  C. 2 c  D. 3 c  1
♥ Hướng dẫn giải :
Bước 1: Để dễ dàng ấm máy ta gán các giá trị log 5 , log 7 , log 3 cho A, B, C. 27 8 2 Gán log 5  A . 27 Bấm log 5 = q J z 27 Gán log 7  B . 8 Bấm log 7 = q J x 8 Gán log 3  C . 2 42
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 Bấm log 3 = q J c 2
Bước 2: Nhập biểu thức: log 35  ... 12   3B  2AC
Lần 1: Nhập log 35   ...  0 12 C  2  loại A.
Lần 2: Bấm ! để sửa biểu thức thành 3B  3AC log 35   0 12 C  2  Chọn B. 1
Bài tập tương tự 1: Nếu log 3  a thì bằng log 100 81 a A. 4 a . B. 16 . a C. . D. 2 . a 8
Bài tập tương tự 2: Biểu diễn log 24 theo a  log 27 ta được 36 12 9  a 9  a A. log 24  . B. log 24  . 36 6  2a 36 6  2a 9  a 9  a C. log 24  . D. log 24  . 36 6  2a 36 6  2a
Bài tập tương tự 3: Nếu a  log 3 và b  log 5 thì 30 30
A. log 1350  2a b  2.
B. log 1350  a  2b 1. 30 30
C. log 1350  2a b 1.
D. log 1350  a  2b  2. 30 30
Bài tập tương tự 4: Nếu a  log 3 và b  log 5 thì 2 2 1 1 1 1 1 1 A. 6 log 360   a  . b B. 6 log 360   a  . b 2 3 4 6 2 2 6 3 1 1 1 1 1 1 C. 6 log 360   a  . b D. 6 log 360   a  . b 2 2 3 6 2 6 2 3 43
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Bài tập mẫu tham khảo 04 (TT Toán học Tuổi trẻ lần 3) : Trong các hàng số sau, hãy chỉ ra hàm số x     xx 5   1 
giảm (nghịch biến) trên : A. y    B. y    C.   3x y  D. y     3   3e   2 2 
♥ Hướng dẫn giải :
Cách 1 : Dĩ nhiên với hàm số x
y a chỉ cần xét a ; nếu 0 < a < 1 là iết hàm số giảm, chọn D
Cách 2 : Hàm số nghịch biến trên tức là luôn giảm x   
Kiểm tra tính nghịch biến y    của hàm với MODE 7  3  Start 9  End 10 Step 1 w7(aqKR3$)^Q)==p9=10=1=
Ta thấy f x luôn tăng  A sai x  1 
Tương tự như vậy , với hàm y  
 ta thấy f x luôn giảm  Đáp án chính xác là D  2 2  w7(a1R2s2$$)^Q)==p9=10=1= 1 2 3 71
Bài tập mẫu tham khảo 05 : Đặt a  ln 2 và b  ln 3 . Biểu diễn S  ln  ln  ln ....  ln theo a 2 3 4 72
và b : A. S  3a 2b B. S  3a 2b C. S  3  a 2b D. S  3  a 2b
♥ Hướng dẫn giải : 1 2 3 71  1 2 71  1 S  ln  ln  ln .... ln  ln . ...  ln    2 3 4 72  2 3 72  72 3 2
 ln 72  ln(2 .3 )  (  3ln 2  2ln3)  (
 3a 2b) . Chọn C
Bài tập mẫu tham khảo 06 (Đề minh họa lần 1) : Cho các số thực a,b với a  1. Khẳng định
nào sau đây là khẳng định đúng ? 1 A. log ab  log b B. log
ab  2  2log b 2   2   2 a a a a 44
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 1 1 1 C. log ab  log b D. log ab   log b 2   2   4 a a 2 2 a a
♥ Hướng dẫn giải (sưu tầm): 1
Ta hiểu, nếu đáp án A đúng thì phương trình log ab
log b  0 (1) với mọi giá trị của 2   2 a a
a,b thỏa mãn điều kiện a,b thực và a  1 .
Ta chọn bất kì A 1.15 và B  0.73chả hạn. Nhập vế trái của (1) vào máy tính Casio rồi dùng
lệnh tính giá trị CALC iQzd$QzQx$pa1R2$iQz$Qxr1. 15=0.73=
Giáo viên cần file word vui lòng liên hệ
Zalo / đt / facebook : 0914 449 230
Máy tính áo kết quả là một số khác 0 vậy vế trái của (1) khác 0 hay đáp án A sai.
Tương tự ta thiết lập phương trình cho đáp án B là log
ab  2  2log b  0 2   a a
Sử dụng chức năng CALC gán giá trị A 1.15 và B  0.73 cho vế trái của (2) iQzd$QzQx$p2p2iQ z$Qxr1.15=0.73=
Tiếp tục ra một số khác 0 vậy đáp án B cũng sai
Tiếp tục phép thử này và ta sẽ tìm được đáp án D là đáp án chính xác . Chọn D iQzd$QzQx$pa1R2$ pa1R2$iQz$Qxr1. 15=0.73= 45
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Trắc nghiệm phần công thức LOGARIT
Câu 01 : Cho a  0, a  1, biểu thức D  log a có giá trị bằng ao nhiêu? 3 a 1 1 A. 3. B. . C. 3  . D.  . 3 3 1
Câu 02 : Giá trị của biểu thức 3 C  log 36  log 14 3log 21 bằng ao nhiêu ? 7 7 7 2 1 1 A. 2  . B. 2. C.  . D. . 2 2 4log 5
Câu 03 : Cho a  0, a  1, biểu thức 2 a E a
có giá trị bằng ao nhiêu? A. 5 . B. 625. C. 25 . D. 8 5 . 2 Câu 04 : Cho , a b  0 và ,
a b  1. Biểu thức 2 P  log b
có giá trị bằng ao nhiêu? a log a a 2 b A. 6. B. 3. C. 4. D. 2. Câu 05 : Cho , a b  0 và ,
a b  1, biểu thức 3 4 P  log
b .log a có giá trị bằng bao nhiêu? b a A. 6. B. 24. C. 12. D. 18.
Câu 06 : Giá trị của biểu thức 3log 32log 5 8 16 4 là: A. 20. B. 40. C. 45. D. 25 .
Câu 07 : Giá trị của biểu thức P   3 5 log a a a là a  53 37 1 A. . B. . C. 20. D. . 30 10 15 3 3 2 5 3  a a a
Câu 08 : Giá trị của biểu thức log   là:. 1  4 a aa   1 3 211 91 A. B. C.  D. 5 4 60 60
Câu 09 : Trong 2 số log 2 và log 3 , số nào lớn hơn 1?. 3 2 A. log 3 . B. log 2 . C. Cả hai số . D. Đáp án khác 2 3
Câu 10 (THPT Nguyễn Khuyến –NĐ) : Cho , a ,
x y là các số thực dương, a  1. Mệnh đề nào sau đây sai? A. log y
x y log x
B. log x  log y x y a a a a 46
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 x C. log
 log x  log y D. log xy  log . x log y a a a y a a a
Câu 11 (THPT chuyên Nguyễn Trãi – lần 2) : Cho log 3  a ; log 7  b . Tính log 2016 theo a và b . 2 2 2
A. 5  2a b
B. 2  3a  2b .
C. 5  3a  2b
D. 2  2a  3b
Câu 12 (THPT Ngô Sĩ Liên – lần 3) : Nếu log x  5log a  4log b ( ,
a b  0 ) thì x bằng. 2 2 2 A. 4 5 a b . B. 5a  4b . C. 4a  5b . D. 5 4 a b .
Câu 13 (Sở GDĐT Lâm Đồng – lần 07) : Cho log 27  a .Biểu diễn log 16 theo a. 12 6 8a 4(3  a) A. log 16  . B. log 16  . 6 3  a 6 3  a 4 3  a C. log 16  . D. log 16  . 6 3  a 6 3  a
Câu 14 (THPT chuyên Lê Thánh Tông) : Biết log 2  a và log 5  b . 3 3
Tính M  log 30 theo a và b . 6 1 a b 1 b A. M  . B. M  . 1 b 1 a 1 ab 1 a b C. M  . D. M  . a b 1 a
Câu 15 (THPT Tiên Lãng) : Cho a  log 3,b  log 5,c  log 7 . Biểu thức biểu diễn log 1050 là: 2 2 2 60
1 a  2b c
1 a  2b c A. log 1050  B. log 1050  60 2  a b 60 1 2a b
1 2a b c
1 a b  2c C. log 1050  D. log 1050  60 2  a b 60 1 2a b
Câu 16 (THPT Hàm Long) : Cho a  log 15,b  log 10 . Tính log 50 theo a,b . 3 3 3
A. 2a b   1
B. 3a b   1 C. a b 1
D. 4a b   1
Câu 17 (THPT Gia Lộc 2) : Cho a  log 3, b  log 5 . Tính theo a , b biểu thức P  log 30 . 2 2 2
A. P 1 a b
B. P a b C. P ab
D. P 1 ab
Câu 18 (THPT chuyên Vĩnh Phúc) : Cho log 3  ;
a log 5  b . Khi đó log 90 tính theo a,b ằng: 2 3 12 47
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 ab  2a 1 ab  2a 1 A. B. a  2 a  2 ab  2a 1 ab  2a 1 C. D. a  2 a  2
Câu 19 (THPT Lý Văn Thịnh) : Cho log 5  a . Tính log 75 . 3 45 2  4a 2  2a 2  2a 2  4a A. B. C. D. 2  a 2  a 2  a 2  a
Câu 20 (THPT Lý Thường Kiệt) : Đặt log 5  ;
a log 5  b . Hãy iểu diễn log 5 theo a và b. 2 3 6 ab 1 A. 2 2 a b B. C. D. a b a b a b
Câu 21 (THPT Lý Thái Tổ) : Cho log 2  a .Tính log 25 theo a? A. 35  2a B. 2  a C. 22  3a D. 21 a
Câu 22 (THPT Lý Nhân Tông) : Cho a  log 3;b  log 5 . Khi đó log 45 tính theo a ; b là. 2 2 6 2a b 2b a A. 6a  2b B. C. D. 6a – 2b 1 a 1 a
Câu 23 (THPT Lương Tài 2) : Đặt a  log5, b  log3. Hãy iểu diễn log 8 theo a,b . 30 3a b 31 a A. log 8  log 8  30 1 B. b 30 1 b 2a b 21 a C. log 8  log 8  30 a  D. b 30 a b
Câu 24 (THPT Tiên Du 1) : Cho log 5  ;
a log 5  b . Khi đó log 5 tính theo a và b là. 2 3 6 ab 1 A. 2 2 a b . B. . C. . D. ab . a b a b 1 1
Câu 25 (THPT Thuận Thành) : Biểu thức P   bằng. log 5 log 5 49 7 1 A. log 5 . B. 2 . C. log 7 . D. . 7 5 2
Câu 26 (THPT Thuận Thành) : Cho a  log 15;b  log 10 vậy log 50  ? . 3 3 3
A. 4a b   1 .
B. 2a b   1 .
C. a b 1.
D. 3a b   1 .
Câu 27 (THPT Thuận Thành) : Cho a  lo  3
g 0 3, b log30 5. Biểu diễn log301350 theo a và . b . 48
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
A. 2a b 1.
B. 2a b 1.
C. a  2b 1.
D. 2a b .
Câu 28 (THPT Thuận Thành 3) : Đặt a  log 6, b  log 7 . Hãy iểu diễn log 7 theo a và b . 12 12 2 b a b a A. . B. . C. . D. . a 1 b 1 1 a b 1
Câu 29 (THPT Thuận Thành 3) : Đặt a  log 3. Hãy iểu diễn log 24 theo a . 2 6 a 1 a  3 a a  3 A. . B. . C. . D. . a  3 a 1 a 1 a 1
Câu 30 (THPT Thuận Thành 2) : Tính M  log 1250 theo a biết a  log 5 . 4 2 1 1
A. M  21 4a .
B. M  21 2a . C. M   a . D. M   2a . 2 2
Câu 31 (THPT Quế Vân 2) : Cho log 5  ;
m log 5  n . Khi đó log 5 tính theo m và n là. 2 3 6 1 mn A. m n . B. 2 2 m n . C. . D. . m n m n
Câu 32 (Sở GDĐT Lâm Đồng lần 03) : Biết a  log 2, b  log3 thì log0,018 tính theo a và b bằng. 2b a
A. 2b a  2 .
B. 2a b  2 . C. .
D. 2b a  3 . 2
Câu 33 (Sở GDĐT Lâm Đồng lần 02) : Đặt a  log 7 ; b  log 3 . Hãy iểu diễn log 147 theo a và b 2 7 42 2  b b 2  a A. log 147  . B. log 147  . 42 1 ab a 42 1 ab a a 2  ba 2  b C. log 147  log 147  42 a b  . D. 1 42 1 ab  . a
Câu 34 (Sở GDĐT Hưng Yên) : Đặt a  log 15; b  log 10. Hãy iểu diễn log 50 theo a và b . 3 3 3
A. log 50  a b   1 .
B. log 50  4a b   1 . 3 3
C. log 50  2a b   1 .
D. log 50  3a b   1 . 3 3
Câu 35 (Sở GDĐT Lâm Đồng lần 01) : Cho biết log 3  ;
a log 2  b . Biểu diễn log
30 theo a và b là. 125 1 a 2a A. log 30  . B. log 30  . 125 1 b 125 1 b 1 a 1 2a C. log 30  . D. log 30  . 125 3(1 b) 125 b 49
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Câu 36 (THPT Trần Cao Vân - Khánh Hòa) : Cho a  log 3 , b  log 5 . Khi đó log 1350 tính theo 30 30 30 a và b là:
A. 2a b 1.
B. a  2b 1
C. 2a b 1
D. 2a b 1
Câu 37 (THPT Hoàng Văn Thụ - Khánh Hòa) : Đặt log 6  ;
a log 7  b . Hãy iểu diễn log 7 theo 12 12 2 a và b . b b a a A. log 7  B. log 7  C. log 7  D. log 7  2 1 a 2 1 a 2 1 b 2 1 b
Câu 38 (THPT Hoàng Hoa Thám - Khánh Hòa) : Rút gọn biểu thức 2log3 a 2 P  3  log a .log 25 5 a , với
a là số thực dương khác 1 ta được : A. 2 P a  4 B. 2 P a  4 C. 2 P a  2 D. 2 P a  2
Câu 39 (THPT Hoàng Hoa Thám - Khánh Hòa) : Cho log 2  ;
a log 5  b , khi đó log 40 bằng : 3 3 3 A. a  3b . B. 3a  b . C. a  3b . D. 3a  b .
Câu 40 (Sở GDĐT Lâm Đồng lần 7) : Cho log 27  a .Biểu diễn log 16 theo a. 12 6 8a 4(3  a) A. log 16  . B. log 16  . 6 3  a 6 3  a 4 3  a C. log 16  . D. log 16  . 6 3  a 6 3  a
Câu 41 (TTGDTX Vạn Ninh - Khánh Hòa) : Cho log 5  ; a log 5  b . 2 3
Khi đó log 5 tính theo a và b là. 6 ab 1 A. . B. . C. 2 2 a b . D. a b . a b a b 125
Câu 42 (THPT Nguyễn Thị Minh Khai - Khánh Hòa) : Cho log 2  a . Tính log theo a ? 4 A. 41 a . B. 2a  5 . C. 3  5a . D. 6  7a .
Câu 43 (THPT Nguyễn Thái Học) : Cho log 27  a Hãy iểu diễn log 24 theo a . 12 6 9  a a  9 A. log 24  . B. log 24  . 6 a  3 6 a  3 a  9 9  a C. log 24  . D. log 24  . 6 a  3 6 a  3
Câu 44 (THPT TH Cao Nguyên) : Đặt a  ln 2 , b  ln 3 . Hãy iểu diễn ln 36 theo a và b . 50
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
A. ln 36  2a  2b .
B. ln 36  a b .
C. ln 36  a b .
D. ln 36  2a  2b .
Câu 45 (THPT chuyên Nguyễn Bỉnh Khiêm) : Nếu log 3  p và log 5  q , thể thì log 5 bằng. 8 3 1 3 pq A. . B. 2 2 p q . p q 3 pq 3 p q C. . D. . 1 3 pq 5
Câu 46 : Tính log 1250 theo a biết a  log 5 . 4 2 1 A. log 1250  2 1 2a . B. log 1250   2a . 4   4 2 1 C. log 1250  2 1 4a . D. log 1250   a . 4   4 2
Câu 47 : Cho log 15  ,
a log 10  b . Tính log 50 theo a và b . 3 3 9
A. log 50  2a b .
B. log 50  a b 1. 9 9 1 C. log 50  a b 1 .
D. log 50  a b . 9   2 9
Câu 48 : Cho a,b là các số thực dương khác 1 và thỏa mãn log b  3 . Tính giá trị của biểu thức a 3 b T  log b a a 3 A. T  1. B. T   . C. T  4  . D. T  4 . 4 3 b
Câu 49 (THPT Hùng Vương-PT) : Biết log b  3 . Tính giá trị của biểu thức P  log . a b a a 3 A. P   . B. P   3 . 2 1 3 C. P   . D. P   . 3 3
Câu 50 : Cho log 9  .
a Tính log 2 theo a . 6 3 a  2 a  2 2  a a A. B. C. D. a a a 2  a
Câu 51 : Cho hai số thực a , b bất kì với 0  a  1. Tính S  log b a . a 51
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 A. a S b B. S a C. S b D. a S b
Câu 52 (thi thử cụm 4 – Tp.HCM): Cho a  0, a  1, khẳng định nào sau đây sai? A. 2 log a  2
B. log 2a 1 log 2 a a a 1 C. log 2a  2 D. log a a 2 a 2
Câu 53 (THPT Hà Huy Tập) : Cho log b   . Khẳng định nào sau đây là khẳng định đúng? a A. aa b .
B. b  .a . C. a b   . D. b a
Câu 54 (THPT Hà Huy Tập) : Cho các số thực dương a,b với a  1 và log b  0 . Khẳng định nào a sau đây là đúng?
0  b 1 a
0  b 1 a A.  B. 
0  a 1 b 1   a,b
0  a,b 1 0  , b a  1 C.  D.  1   a,b
0  a 1 b
Câu 55 (Sở GDĐT Lâm Đồng lần 07) : Cho a  0 và a  1; ;
x y là hai số dương. Tìm mệnh đề đúng trong các mệnh đề sau: x log x A. log a  B. log x  log . a log x a y log y b b a a 1 1 C. log 
D. log x y x y a   log log a x log x a a a
Câu 56 (THPT Đặng Thúc Hứa) : Với các số thực dương a, ,
b c bất kì. Mệnh đề nào dưới đây là sai ab b A. ln  ln a  ln
B. ln abc  ln a  ln bc c c a 1 C. ln  n l a  ln bc D. ln
 ln a  ln bc bc abc
Câu 57 (THPT Đặng Thúc Hứa) : Với các số thực dương ;
a b bất kì. Mệnh đề nào dưới đây đúng? 3  a  3ln 3 3  a  ln b A. log    log a  B. log    log a  27 3  b  ln b 7 2 3  b  3ln 3 3  a  3ln 3 3  a  ln b C. log    log a  D. log    log a  27 3  b  ln b 7 2 3  b  3ln 3 52
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Câu 58 (THPT chuyên Lương Thế Vinh) : Cho các số thực a  0 , b  0 và   . Khẳng định nào sau đây đúng ?  a  A. 
ln a   ln a B. ln
 ln b  ln a    b
C. ln a b  ln a  ln b D. ln  . a b  ln . a ln b
Câu 59 (THPT chuyên Lê Thánh Tông) : Xác định a sao cho log a  log 3  log a  3 . 2 2 2   3 A. a  2 B. a  2 2 C. a  2 D. a  3
Câu 60 (THPT chuyên Lam Sơn lần 2) : Cho , a ,
b x là các số thực dương và khác 1 và các mệnh đề:
ab  log a 1 log x Mệnh đề (I) : log b x
x Mệnh đề (II) : log b b  . b loga   a a x  log a b
Khẳng định nào dưới đây là đúng ? A. (II) đúng, (I) sai. B. (I), (II) đều sai.
C. (I), (II) đều đúng. D. (I) đúng, (II) sai.
Câu 61 : Cho a, ,
b c là các số dương a,b  
1 . Mệnh đề nào dưới đây đúng? A. logb a ab . B. log      b log b 0 . aab  1 C. log c  log . c log b D. log  log b . a b a a   3  a  3 a 49
Câu 62 (THPT chuyên Nghuyễn Quang Diêu) : Cho a  log 7 ; b  log 5 . Tính log theo a , b . 25 2 5 8 4ab  3 4ab  3 4ab  5 5ab  3 A. B. C. D. b b b b
Câu 63 (THPT chuyên KHTN) : Nếu 2
log a  log b  5 và 2
log a  log b  7 thì giá trị của ab là. 8 4 4 8 A. 8 B. 9 2 C. 2 . D. 18 2
Câu 64 (Trích đề minh họa lần 2) : Với các số thực dương a , b bất kì. Mệnh đề nào dưới đây đúng a A. ln
 ln b  ln a
B. ln ab  ln a  ln b b 53
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 a ln a C. ln ab  ln . a ln b D. ln  b ln b Câu 65 : Giả sử ,
x y là các số thực dương. Mệnh đề nào sau đây sai? 1
A. log xy  log x  log y B. log xy
log x  log y 2  2 2  2 2 2 2 x C. log
 log x  log y
D. log x y  log x  log y 2   2 2 2 y 2 2
Câu 66 (THPT chuyên Vinh) : Cho các số thực a b  0 . Mệnh đề nào sau đây sai? 2 2  a  A.
ab   2a  2 ln ln ln b  B.   2 a      2 ln ln ln b   b   a  1 C. ln
 ln a  ln b  
D. ln  ab   ln a  lnb  b  2
Câu 67 (Sở GDĐT Hưng Yên) : Tính P  3log log 16  log 2 có kết quả. 2  4  1 2 A. 2 B. 4 C. 1 D. 3
Câu 68 (Sở GDĐT Hà Tĩnh lần 2) : Cho 1  a  0, x  0, y  0. Trong các khẳng định sau, khẳng định nào là khẳng định sai? 1 A.  log x  log x
B. log x   log x 2 a a a a 1 C. log x  log x D. log ( .
x y)  log x  log y a 2 a a a a
Câu 69 (Sở GDĐT Hà Tĩnh) : SỞ GD ĐT HÀ TĨNH] Cho x  0, ta có. 1 A. 2 log x  2log . x B. 2 log x  log x 2 2 2 2 2 C. 2
log x  2log x D. 2
log x  log x 2 2 2 4
Câu 70 (THPT Thuận Thành 3) : Cho a  0 và a  1. Tìm mệnh đề đúng trong các mệnh đề sau.
A. log  xy  log . x log y . B. log n
x n log x x  0, n  0 . a a a a a
C. log x có nghĩa với x  .
D. log 1  a và log a  1. a a a
Câu 71 (THPT Chuyên Phan Bội Châu) : Cho các số dương a , x , y ; a {1; ; e 0} 1
và x  1. Mệnh đề nào dưới đây đúng? 54
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 log a log x log e log x A. ln x x  B. ln a x  C. ln a x  D. ln a x  ln a . log e log 10 log e a a
Câu 72 : Cho a là số thực dương khác 1. Tính I  log a . a 1 A. I  . B. I  0 . C. I  2  . D. I  2 . 2
Câu 73 : Cho a, ,
b c là các số thực dương tùy ý và a  1. Trong các mệnh đề sau, mệnh đề nào sai?  b  A. log  . b c  log . b log . c B. log  log b  log . c a a a a   a ac  C.  log b   log . b D. loga b a  b. a a
Câu 74 (THPT ISCHOOL Nha Trang) : Cho a  0 , b  0 , ,
a b  1; ab  1 . Mệnh đề nào dưới đây đúng ? 1 A. log (ab)  1   log b . C. log a  . 1 a ab 1 log b a a 1 B. log (ab)  1   log b . D. log b  . 1 a 2 a 2 log a a b
Câu 75 : Cho log 1250  a  .
b log 5 với a,b là các số hữu tỉ. Tính . a b ? 4 2 A. 1. B. 2. C. 1.  D. 2. 
Câu 76 : Cho log m a ( điều kiện m  0 và m  1 ), tính A  log 27m theo a m  3 3  a A. (3  a)a B.
Giáo viên cần file word vui lòng liên hệ a 3  a
Zalo / đt / facebook : 0914 449 230 C. (3  a)a D. a
Câu 77 (THPT Lạng Giang số 2) : Cho , a b  0 và ,
a b  1, x và y là hai số dương. Tìm mệnh đề
sai trong các mệnh đề sau A. 2 2 2 log x  4  log x B. log xy x y a   log log 1 a a a a log x C. 2016 log x  2016log x D. log b x a a a log a b
Câu 78 (THPT Lạng Giang số 2) : Cho log 3  m , ln 3  n . Hãy iểu diễn ln 30 theo m và n 55
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 n m A. ln 30  1. B. ln 30   n . m n n m n C. ln 30  . D. ln 30   n . n m log (log 10)
Câu 79 (THPT Đông Sơn 1) : Biết 2 2 a
. Giá trị của 10a là: log 10 2 A. 1 B. log 10 2 C. 4 D. 2 56
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 C. HÀM SỐ LOGARIT
1. Hàm số logarit: y  log ,
x (a  0, a  1) a
Tập xác định: ............................................. Tập giá trị: .....................................................
Hàm số đồng biến khi ............................. Hàm số nghịch biến khi .............................
2. Đồ thị: Nhận trục tung làm đường tiệm cận đứng. 1 O 1 O
Đồ thị hàm số luôn cắt trục hoành tại : ..................
Bài tập mẫu tham khảo 01 (THPT Nguyễn Chí Thanh - Khánh Hòa) : Hàm số 2
y  ln(x  4x  3) có tập xác định là. A.  ;  0. B. 1;3 . C. 0; . D.  ;   1  3;
♥ Hướng dẫn giải :
Phương pháp làm dạng tập xác định này cũng đơn giản lắm ! Hàm số
xác định khi và chỉ khi
Áp dụng vô bài này ! Hàm số 2
y  ln(x  4x  3) xác định 2
 x  4x 3  0 1 x  3. Hay D  1;3 Chọn B.
Bài tập mẫu tham khảo 02 (THPT Nguyễn Chí Thanh - Khánh Hòa) : Tìm tập xác định D của hàm số y  log  2
x  4x  3 . 2  A. D   ;  
1 3; . B. D   ;  
1 3; . C. D  1;  3 . D. D  1;3 .
♥ Hướng dẫn giải :
Hàm số y  log  2
x  4x  3 xác định 2
x  4x  3  0  x 1 hay x  3 . 2  57
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 Hay D   ;  
1 3; Chọn B.
Bài tập mẫu tham khảo 03 (THPT TH Cao Nguyên) : Tập xác định D của hàm số 2
y  ln x là. A. D
B. D  0; C. D   ;  00; D. D   ;0  
♥ Hướng dẫn giải : Hàm số 2
y  ln x xác định 2
x  0  x  0 Hay D  \  
0 hoặc có thể ghi D   ;
 00;. Chọn C Ở đây chúng ta chú ý 2
A  0  A  0 chứ không phải 2 A  0  A  0
Bài tập mẫu tham khảo 04 (THPT Lê Hồng Phong) : Tìm tập xác định D của hàm số
y   x  23  log  2 8  x là. 2  A. D  2;8 B. D  2;2 2
C. D  2 2;
D. D  2;
♥ Hướng dẫn giải : x  2  0 x  2 3 
Hàm số y   x  2  log  2 8  x xác định     2  2 8   x  0  2  2  x  2 2
 2  x  2 2.Chọn B
Bài tập mẫu tham khảo 05 : Tìm tất cả các giá trị thực của m để hàm số y  log  2
x  4x m xác 2  định trên . A. m  4 B. m  4 C. m  4 D. m  4
♥ Hướng dẫn giải : Hàm số có TXĐ là 2 D
x  4x m  0 x    
  0  4  m  0  m  4. Chọn A
Bài 01 (TTGDTX Vạn Ninh - Khánh Hòa) : Tìm tập xác định của hàm số y   2 ln 2
x  7x 3 . 1   1   1   1  A. D  ;3   B. D  ;3   C. D=  ;  3;   D. D=  ;  3;      2   2   2   2  ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 02 (Sở GDĐT Lâm Đồng lần 2) : Tìm tập xác định D của hàm số 2 y  log 8  5x  3x . 3 2    8   8   8   8  A. D  1;    B. D  1  ;   C. D  1  ;   D. D  1;    3   3   3   3  58
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 03 (Sở GDĐT Lâm Đồng lần 5) : Tìm tập xác định D của hàm số: y  log  2 4  x 3  A.  ;  2  2; B.  ;  2  2; C.  2  ;2 D.  2  ;2 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 04 (THPT Nguyễn Tất Thành) : Tìm tập xác định D của hàm số y   2
log x  6x  5 A. D   ;   1 5; B. D  1;5 C. D   ;   1 5; D. D  1;  5 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 05 (THPT chuyên Lê Hồng Phong - Nam Định) : Tìm tập xác định D của hàm số
y  log  x 81000 3 2
A. D  2; B. D  \   2 C. D   2  ; ;
 2 D. D   ;  2 ☻ Giải :
..............................................................................................................................................................................
.............................................................................................................................................................................. x  2
Bài 06 (THPT Lệ Thủy-Quảng Bình) : Tìm tập xác định D của hàm số y  log . 2017 1 x A. D  \   1 B. D  \ 1;  2 C. D   ;   1 2; D. D  1;2 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 07 (Thi thử Cụm 1 – Tp.HCM) : Tập xác định của hàm số y  log 2  x là: x 1    A.  ;  2 \  0 B.  ;  2 C.  1  ;2 \  0 D.  ;   1  2; ☻ Giải : 59
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 08 (THPT Võ Nguyên Giáp) : Tìm tập xác định D của hàm số y  log  2 x  3x . 3  A. D   ;  03; B. D  0;3 C. D   ;  03; D. D  0;  3 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 09 (THPT Lương Tài 2) : Tìm giá trị thực của tham số m sao cho hàm số y   2
ln x mx   1 có m  2  tập xác định là ? A. 2   m  2 B.  C. 1   m 1 D. 2   m  2 m  2 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 10 : Tìm tập xác định các hàm số sau 2
 2x  3x 1 a/ y = log   b/ 2    2 y x
ln 1 2x  3x  c/ y  log  3 2 x  x  2x 2  2  13x  5  1  d/ y  log e/ y  log  4 2 x  3x  4 f/ y  log    2 x 1 x 2  1  x    2x 1 2 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 60
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 1
Bài 11 (THPTQG – 2017) : Tìm tập xác định D của hàm số 3
y  (x 1) . A. D  ( ;  1) B. D  (1; )  C. D  D. D  \{1} ☻ Giải :
..............................................................................................................................................................................
............................................................................................................................................................................. x  3
Bài 12 (THPTQG – 2017) : Tìm tập xác định của hàm số y  log 5 x  2 A. D  \   2 B. D   ;
  23;  C. D   2  ;3 D. D   ;
  23;  ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 13 : Tìm m để hàm số 2 y log2 x 2mx
2m 1 có tập xác định là . A. m 1; B. m \ 1 C. m D. m ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 14: Cho hàm số: y   2 2
ln 2x e  . Tập xác định của hàm số là  1   e   1  A. D  B. D   ;    C. D  ;    D. D   ;     2e   2   2  ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 15 (THPT Tôn Đức Thắng – Khánh Hòa) : Tìm tất cả các giá trị của m để hàm số y  log  2
x  5x m xác định trên . 3  61
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 25 25 A. m  B. m  0 . C. m  0 . D. m  . 4 4 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Trắc nghiệm phần hàm số LOGARIT
Câu 01 : Tập xác định của hàm số y  log  2
x x  2 là. 2  A. D   ;  2   B. D  \ 1;  2 C. D   ;  2  (1; )  D. D   ;  2  1;
Câu 02 (THPT chuyên Vĩnh Phúc) : Tìm tập xác định của hàm số y  log  2 x x  6 2  A.  ;  2  3; B.  2  ;3 C.  2  ;  3 D.  ;  2  3;
Câu 03 (THPT chuyên Lê Khiết) : Tìm tập xác định của hàm số y   2 ln 2
x  7x 3  1   1  A. D  ;3   B. D   ;  3;     2   2  1   1  C. D  ;3   D. D   ;  3;     2   2 
Câu 04 (Sở GDĐT Hưng Yên) : Hàm số y  log  2
x  5x  6 có tập xác định là: 2  A. 2;3 B.  ;  23; C. 3; D.  ;  2
Câu 05 : Tìm tập xác định D của hàm số y  log  2 x  2x 2  A. D  0;2 B. D  \   1 C. D   ;  02; D. D  0;2
Câu 06 (THPT Chuyên Phan Bội Châu) : Tìm tập xác định D của hàm số y  log  2 x  2x . 2  A. D   ;  02; B. D   ;  02;
C. D  0; D. D   ;  02;
Câu 07 : Tìm tập xác định D của hàm số y  log  2 x x 2  A. D   1  ;3 B. D   ;  01; C. D   ;    1 3; D. D   ;    1  3; 62
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Câu 08 (THPT Lý Thường Kiệt) : Tìm tập xác định D của hàm số y  log  2 4x x . . 1  5 A. D  0; 4 B. D   ;  04;   C. D   ;  04; D. D  0 ; 4
Câu 09 (THPT chuyên Lam Sơn lần 2) : Cho hàm số y  log x 3
Mệnh đề nào dưới đây là mệnh đề sai?
A. Đồ thị hàm số đã cho không có tiệm cận ngang
B. Hàm số đã cho có tập xác định D  \   0
C. Đồ thị hàm số đã cho có một tiệm cận đứng là trục Oy
D. Hàm số đã cho đồng biến trên tập xác định
Câu 10 : Cho hàm số y  log x .Mệnh đề nào dưới đây sai ? 2
A. Tập xác định của hàm số là  ;  
B. Đồ thị hàm số nhận trục Oy làm tiệm cận đứng 1
C. Đạo hàm của hàm số là y  x ln 2
D. Hàm số đồng biến trên khoảng 0; 
Câu 11 (Sở GDĐT Hà Tĩnh) : Cho a  0, a  1. Tìm mệnh đề đúng trong các mệnh đề sau.
A. Tập xác định của hàm số x
y a là khoảng (0; ) 
B. Tập xác định của hàm số y  log x là a
C. Tập giá trị của hàm số x y a là
D. Tập giá trị của hàm số y  log x là a
Câu 12 (THPT Lý Nhân Tông) : Hàm số nào dưới đây đồng biến trên . A. – x y e . B. y  ln x . C. 3x y  . D. e y x .
Câu 13 (THPT Quế Võ 1) : Tìm mệnh đề đúng trong cá mệnh đề sau.
A. Hàm số y  log x với 0  a 1 là một hàm số đồng biến trên 0;   . a
B. Đồ thị của hàm số y  log x và y  log x với 0  a   1 a 1
thì đối xứng nhau qua trục hoành. a 63
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
C. Hàm số y  log x với 0  a 1 có tập xác định là . a
D. Hàm số y  log x với a  1 là một hàm số nghịch biến trên 0;   . a
Câu 14 : Với a  0 và a  1. Phát iểu nào sau đây không đúng ? A. Hai hàm số x
y a và y  log x có cùng tập giá trị a B. Hai hàm số x
y a và y  log x có cùng tính đơn điệu a C. Đồ thị hai hàm số x
y a và y  log x đối xứng nhau qua đường thẳng y 4  x a 3 D. Đồ thị hai hàm số x
y a và y  log x đều có đường tiệm cận a y
Câu 15 : Đường cong trong hình ên là đồ thị của một hàm số trong 1
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi x O 2
hàm số đó là hàm số nào? A. y  log x B. y  log x 1 2 1 2 C. y  log x
D. y  log 2x 2   2
Câu 16 : Tìm tất cả các giá trị thực của a để hàm số y  log x y a 2 -4 0  a  
1 có đồ thị là hình ên ? O x A. a  2 B. a  2 1 2 1 1 C. a  D. a  2 2
Câu 17 : Cho hàm số y  log 2x . Khi đó, hàm số y  log 2x có đồ thị là hình nào trong ốn 2   2  
hình được liệt kê ở bốn phương án A, B, C, D dưới đây: y y 1 x O O x Hình 1 Hình 2 64
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 y y x O O x Hình 3 Hình 4 A. Hình 3 B. Hình 2 C. Hình 1 D. Hình 4
Câu 18 (THPT Lý Thái Tổ) : Tập hợp các giá trị của x để log  3 2
x x  2x có nghĩa là. 5 
A. 0;2 4; B.  1  ;02; C. 1; D. 0  ;1
Câu 19 : Tìm tập xác định D của hàm số y   2 ln 2  x 8 A. D   ;  2  2; B. D   2  ;2 C. D   2  ;2 D. D   ;  2  2;
Câu 20 (THPT Trần Cao Vân - Khánh Hòa) : Hàm số y   2
ln x  5x  6 có tập xác định là: A.  ;  23:  . B.  ;  0 C. 2;3 4 D. 0;
Câu 21 : Đường cong trong hình ên là đồ thị của một hàm số trong y
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi
hàm số đó là hàm số nào? O 2 x 1 A. y  log x B. y  log x 0,8 2 C. 2x y  D. y  log x 1 0,5
Câu 22 (THPT Ngô Sĩ Liên lần 3) : Tìm tập hợp tất cả các giá trị của 1
tham số thực m để hàm số y  có tập xác định ? log  2
x  2x  3m 3   2  2  A. ;    B. ;     3  3  65
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 4  1  2  C. ;    D. ;10 y    3  3  y = logax
Câu 23 : Hình ên là đồ thị của a hàm số y  log x , a
y  log x , y  log x 0  , a , b c  
1 được vẽ trên cùng một y = logbx b c
hệ trục tọa độ. Khẳng định nào sau đây là khẳng định O 1 x đúng? y = logcx
A. b a c
B. a b c
C. b c a
D. a c b
Câu 24 : Cho hai đồ thị  : x C
y a , và C : y  log x có đồ 2  1  b -4
thị như hình vẽ. Nhận xét nào ên dưới là đúng? a 1 a  1 A.  B.  0  b 1 b   1 0  a 1 0  a 1 C.  D.  0  b 1 b  1
Câu 25 (THPT Quế Vân 2) : Hàm số y  log
x nghịch biến trong khoảng 0;  khi. 2 a 2a 1  A. a  0 B. a  1 1
C. a  1 và 0  a  2
D. a  1 và a  2
Câu 26 (Sở GD-ĐT Hà Tĩnh lần 2) : Cho các khẳng định sau:
I :Đồ thị hàm số y  log x (1 a  0) luôn nằm ên phải trục tung. a
II :Đồ thị hàm số y  log x (1 a  0) đi qua điểm 1;0 . a
III :Đồ thị hàm số y  log x (1 a  0) nhận trục tung làm tiệm cận đứng. a
Trong các khẳng định trên có mấy khẳng định đúng? A. 1 B. 3 C. 0 D. 2
Câu 27 (đề thi thử Cụm 1 – Tp.HCM) : Cho a , b , c là a số thực dương và khác 1. Đồ thị các hàm
số y  log x , y  log x , y  log x được cho trong hình vẽ ên. Mệnh đề nào dưới đây là mệnh đề a b c đúng? 66
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
A. a b c y y  log x a
B. c a b
C. b c a y  log x b
D. c b a O 1 x y  log x c
Câu 28 (đề thi thử Cụm 4 – Tp.HCM) : Đường cong trong hình ên
dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A. y  ln x 1  ln 2 B. y  ln x
C. y  ln  x   1  ln 2 D. y  ln x
Câu 29 (THPT Chuyên Vinh) : Cho các hàm số y  log x và a
y  log x có đồ thị như hình vẽ ên. Đường y b N
thẳng x  7 cắt trục hoành, đồ thị hàm số y  log x b
y  log x và y  log x lần lượt tại H , M , N . M a b y  log x a
Biết rằng HM MN . H
Mệnh đề nào sau đây là đúng? O 7 x A. a  7b B. 2 a b C. 7 a b D. a  2b
Câu 30 (THPT chuyên ĐHKH Huế) : Trong các hàm số sau, hàm số nào có cực trị? x  2 A. y y x  C. y  log x   D. x y e x  B. 3 1 3 67
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 D. SO SÁNH LOGARIT Công thức :
........................................................................................................................................................................
........................................................................................................................................................................
........................................................................................................................................................................
........................................................................................................................................................................
+ Nếu so sánh hai loga rít có cùng cơ số thì ta chú ý đến cơ số trong hai trường hợp (0; 1) và lớn
hơn một để so sánh hai iểu thức bị lo ga rít hóa với nhau
+ Trong trường hợp hai lo ga rít khác cơ số , khác iểu thức bị lo ga rít hóa thì ta chọn một số b
nào đó . Sau đó ta so sánh hai lo ga rít với số b . Từ đó suy ra kết quả 1
Ví dụ : so sánh hai số : log 4  log . Ta có : 3 4 3 1 1 log 4  log 3  1;log
 log 4 1 log 4  log 3 3 4 4 3 4 3 3
Ví dụ : So sánh : log61,1 log6 0,99 3  7 . Ta có : log 1,1 log 1 log 0,99 log 1 log 1,1 log 0,99 6 6 6 6 6 6 3  3 1; 7  7 1 3  7
Ví Dụ : Hãy so sánh các cặp số sau :  2 1 log 2  log 1  0 a/ log 2  log 0,34 Ta có : 0,4 0,4   log 0,3  log 2 0,4 0,2  0,2 0,4 0,3  1  log 0,3  log 1  0  0,2 0,2 5 3 3 1 0  1  log  log 1  0  5 5 3 2 3 4 4 2 3 b/ log  log 3 3  log  log 5 3 Ta có :  4 5 3 2 2 3 5 5 4 3 4
0  1,0  1 log  log 1  0 4 3 3 3  4 5 5  4 4 log 10  log 8  3 c/ log 10  log 30 Ta có : 2 2   log 10  log 30 2 5 log 30  log 36  3  2 5 5 5 log 5  log 3 1 d/ log 5  log 4 Ta có : 3 3   log 5  log 4 3 7 log 4  log 7  1  3 7 7 7 68
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 3 2ln e  2.3  6 1  1 e/ 3 2 ln e  8  ln Ta có :  1 3  8  ln  2ln e e 8  ln  8 1  9  ee  6 5 log  log  0 6 5  3 3  5 5 6 5 f/ log  log Ta có :   log  log 3 3 3 3 5 6 5 6  5 6 log  log  0 3 3  6 6  1    g/ log 9  log 17 0 1 1 1 Ta có :  3  log 9  log 17 1 1 3 3 9  17 3 3  1    h/ log e  log  0 1 1 1 Ta có :  2  log e  log  1 1 2 2 e   2 2
Bài 01 : So sánh các cặp số sau 5 3 a/ log  log
b/ log 8  log 0,98 c/ log 7  log 9 2 2 2 2 0,1 3 4 0,2 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 02 : So sánh các cặp số sau 1 a/ log 4  log 6 e/ log 0,3  log 0, 4 d/ log 4  log 3 7 0,2 0,5 3 4 3 ☻ Giải :
..............................................................................................................................................................................
.............................................................................................................................................................................. 69
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Trắc nghiệm phần hàm số LOGARIT
Câu 01 (THPT Hoàng Văn Thụ) : Chọn khẳng định sai trong các khẳng định sau:
A. log a  log b a b  0
B. ln x  0  x 1. 1 1 3 3
C. log a  log b a b  0 .
D. log x  0  0  x 1. 1 1 2 2 2
Câu 02 (THPT chuyên Vĩnh Phúc) : Khẳng định nào sau đây là đúng: x  2016  A. 1  x  0   B. log 2017  1  2017  2016 x  2017  C. log 2016  1 D. 1  x  0 2017    2016 
Câu 03 (THPT chuyên Vĩnh Phúc lần 5) : Mệnh đề nào dưới đây sai?
A. ln x 1  0  x e
B. log x  0  x 1 C. 2
log x  log y x y  0
D. log x  log y x y  0 4 2 1 1 3 3 13 15
Câu 04 : Chọn điều đúng của a, b nếu 7 8 a
a và log  2  5  log 2 3 . b b
A. a 1,0  b 1
B. 0  a 1,b 1
C. a 1,b 1
D. 0  a 1,0  b 1 Câu 05 : Cho 0 a
1. Mệnh đề nào sau đây là đúng? a 1 1 a a A. log 2 log . B. log log . C. log 2 log 3. D. log log . a a 2 a 2 a 3 a a a 3 a 2 2 3 2 3 Câu 06 : Cho 3 4 a a và log log b b
. Chọn khẳng định đúng ? 3 4 A. 0 , a b 1. B. 0 a 1 . b C. 0 b 1 . a D. , a b 1. 70
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 3 4 3 4 Câu 07 : Cho 4 5 a a và log log b b
. Chọn khẳng định đúng ? 4 5 A. log 1 a b B. log 0 a b b b C. log 0 b a D. log log a a
E. ĐẠO HÀM MŨ - LOGARIT
Đạo hàm của hàm số sơ cấp
Đạo hàm của hàm số hợp 1.   1   (x ) ' .x   1 (u ) ' .u   .u ' 2. ( x ) ' x ee ( u ) ' u e
e .u ' 3. ( x ) ' x a
a .ln a ( u ) ' u a
a .u '.lnu 1 u ' 4. (ln x) '  (ln u) '  x u 1 u ' 5. (log x) '  (log u) '  a x ln a a u ln a
Bài tập mẫu tham khảo 01 : Tính đạo hàm các hàm số sau : xx e e
a/   2  2  2 x y x x e b/     2 s inx cosx x y e c/ y xx e e ln x d/ y   2 ln x   1 e/ y
f/ y  1 ln xln x x
♥ Hướng dẫn giải : a/   2 
  x      x  2    x   2 2 2 ' 2 2 2 2  x y x x e y x e x x e x e b/     2x     2x     2 ' cosx sinx 2 s inx cosx 3sin osx x y e e x c e    x x
e e  xx
e e    xx
e e  xx x x e e e e  4 c/ y   y '   xx e ex x e e 2  x x e e 2 2x d/ y  ln  2 x   1  y '  2 x  1 71
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 ln x 1  1  1 ln x e/ y   y '  .x  ln x    2 2 x x xx xxx f/ y    x ln 1 ln 1 2 ln 1 ln ln x y '    x x x
Bài tập mẫu tham khảo 02 : Tính đạo hàm các hàm số sau a/ 2 y x  2 ln x 1 b/ y  log  2 x x 1 c/ 3 2 y  ln x 2   x  4  2  x  9  1 x  d/ y  log e/ y  log   f/ y  log   2      x  4  3  x  5  2 x  
♥ Hướng dẫn giải : 2 3 x x x a/ 2 y x ln  2
x 1  y '  2 .xln 2 x 1   x x  
2 x   2 .ln  2 1 2  1 2 2 x   1 2x 1 b/ y  log  2
x x 1  y '  2 
 2x x 1ln2 2 1   2  1 2 c/ 3 2
y  ln x y '  ln x3 '  ln x 3    3   3 x 3x ln xx 4  1  16 x 4    16 d/ y  log  y '   :   2    x  4 
ln 2  x  42 x  4   2 x  4ln 2 2  x  9 
1  2x x  5 2 2 2
x  9 x 9 x 10x  9 e/ y  log    y '   :   3  x  5  ln 3  x 52
x  5   x  5   2x 9ln3      x  1    x x x 1 1 1 1 f/ y  log    y '   :     2 x ln10  16x x 2 x    8x ln10   1 x
Bài tập mẫu tham khảo 03 : Tìm giá trị lớn nhất – giá trị nhỏ nhất các hàm số sau : a/ f x 2
 cos 2x  2sin x 1 ln x e trên đoạn 0;e . b/ y  .
x ln x trên đoạn 1;e .
♥ Hướng dẫn giải : a/ Ta có f x 2
 cos 2x  2sin x 1 lnx e  2 lnx e.
♠ Lưu ý : ở đây ta chú ý công thức lượng giác nhân đôi 2
cos 2x 1 2sin x
Hàm số xác định và liên tục trên đoạn 0;e . 1
Đạo hàm f ' x 
 0, x0;e. Suy ra hàm số f x đồng biến trên đoạn 0;e . x e 72
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Vậy max f x  3  ln 2 khi x e ; min f x  3 khi x  0 . 0;e 0;e
/ Hàm số xác định và liên tục trên đoạn 1;e . 1
Đạo hàm y '  ln x 1. Suy ra y '  0  ln x 1  0  ln x  1
  x  1;e. e Ta có y  
1  0; y e  .
e Vậy max f x  e khi x e ; min f x  0 khi x 1. 1;e 1;e
Bài tập mẫu tham khảo 04 : Tìm GTLN - GTNN của hàm số : y f x  x  2ln x 1 trên 1;  3 .
♥ Hướng dẫn giải : Hàm số xác định và liên tục trên đoạn 1;  3 .  Đạo hàm   2 2 ' 1  x f x
. Suy ra f ' x  x  2  0  x  21;  3 . x x Ta có f  
1  2; f 2  3 2ln 2; f   3  4  2ln 3.
Vậy max f x  2 khi x 1; min f x  3  2ln 2 khi x  2 2;  4 2;4 cos x  sin x
Bài tập mẫu tham khảo 05 (thầy Cao Tuấn) : Hàm số y  ln có đạo hàm là cos x  sin x 2 2 A. y  cos 2 . x B. y  . C. y  . D. y  sin 2 . x sin 2x cos 2x ♥ A
Hướng dẫn giải : Cơ sở lý thuyết A B
1, B  0 . B
Thử với lần lượt các đáp án (khi nào chọn được đáp án đúng thì dừng lại).
Bước 1: Bấm q w 4 để chuyển về tính theo đơn vị rađian,
Giáo viên cân file word vui lòng liên hệ     d
cos  x sin  xBước 2: Nhập ln    dx  
x x : ..... cos sin  x    
Zalo / đt / facebook : 0914 449 230 3     d
cos  x sin  x  Nhập ln    dx  
x x : cos cos sin  x  3    6
Kq  8 1 Loại A.
Bấm ! để nhập lại 73
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018     d
cos  x sin  x 2 ln    dx  
x x : cos sin  x      sin 6 3
Kq 1,73 1 Loại B.
Bấm ! để nhập lại     d
cos  x sin  x 2 ln    dx  
x x : cos sin  x      cos 6 3
Kq 1 Chọn C.
Bài tập mẫu tham khảo 06 (thầy Cao Tuấn) : Cho hàm số   x e f x
. Khi đó, nghiệm của phương x
trình f  x  0 là A. 2. B. 0. C. 1. D. . e X   ♥ d e
Hướng dẫn giải : Nhập  
sau đó chọn X tại các đáp án đến khi ra 0 thì dừng dx   X x X  
r với X  2  Kq  0,301..  0  loại A. Bấm ! để thử lại
r với X  2  Math Error  loại B. Bấm ! để thử lại
r với X 1 Kq  0  Chọn C x  2
Bài tập mẫu tham khảo 07 : Tính đạo hàm của hàm số y  . 9x
1 2 x  2ln 3
1 2 x  2 ln 3
1 2 x  2 ln 3
1 2 x  2 ln 3 A. y  B. y  C. y  D. y  2 2 3x 3x 2 3 x 2 3 x x  2 9x  9 .
x ln 9 x  2 1  x  2ln 9
♥ Hướng dẫn giải : y   y   chọn D x 2 9 9 x 9x 74
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 2
Bài tập mẫu tham khảo 08 (THPT Gia Lộc 2) : Giá trị lớn nhất của hàm số 2 x y xe  trên 1;2 2 1 1 1 A. B. C. D. 3 e 2 e 3 2 e 2e 1 1 ♥ 2
Hướng dẫn giải : 2  x y  e  2
1 4x  ; y  0  x hay x  
( không thõa mãn ) 2 2 1 1 1 Ta có: y   1  , y 2 
. Vậy GTLN của hàm số trên 1;2 là chọn B 2 e 8 e 2 e
Bài tập mẫu tham khảo 09 : Tìm giá trị nhỏ nhất của hàm số y x 2  ln x trên đoạn 2;  3 . A. min y  1.
B. min y  4  2ln 2 .
C. min y e . D. min y  2   2ln 2 . 2; 3 2; 3 2; 3 2; 3
♥ Hướng dẫn giải :  
Cách 1: y  2x  1
x ln x y  2  ln x  . x 1 ln x   . x
y  0  ln x  1  x e 2;  3
Ta có y e  e ; y 2  4  2ln 2 ; y 3  6  3ln 3 . chọn B
So sánh a giá trị trên ta có min y  4  2ln 2 . 2; 3
Cách 2: Sử dụng máy tính Casio fx  570VN PLUS : w7Q)(2phQ))) ==2=3=0.1=
Dựa vào ảng giá trị thu được ta kết luận min y  4  2ln 2 tại x  2 . chọn B 2; 3
Bài 01 : Tính các đạo hàm của các hàm số sau 2 a/ 2x 1 y e   b/ sinx y  3 c/ y  log  2 x  7x  8 d/ y  log  2 x  7x  8 3  3  ☻ Giải :
Giáo viên cân file word vui lòng liên hệ
..............................................................................................................................................................................
Zalo / đt / facebook : 0914 449 230
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 75
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Bài 02 : Tính các đạo hàm của các hàm số sau 3 ln x a/   2 y ln x  7x  8 b/ 3   2 y ln x  8 c/ y  x ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 03 a/(Trích Đề minh họa 2017) : Tính đạo hàm của hàm số 13 . x y 13x A. x 1 y . x 13    . B. 13 . x y  ln13. C. 13 . x y  D. y  . ln13
b/ (Sở GDĐT Hưng Yên) : Đạo hàm của hàm số 10x y  là: 10x A. 10x B. C. 1 .10x x  D. 10 . x ln10 ln10
c/ (THPT Thuận Thành 2) : Tính đạo hàm hàm số 2x y  . A.   2x y x . B. 2x y  C. 1 2x y x    D. , 2x y  ln 2 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 04 a/ (THPT Quảng Xương 1 lần 2) : Đạo hàm của hàm số 2 x
y  (2x  5x  2)e là: A.  x   x 4 5 e B. x e x C.  2
x x   x 2 3 e D. 2 x 2x e
b/ Hàm số y =  2  2  2 x x x
e có đạo hàm là: A. 2 x y  x e B.    2   4  4 x y x x e C.   2 x yxe
D.   2  2 x y x e 76
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 05 (THPT Gia Lộc 2) : Tính đạo hàm của hàm số    .2x f x x A.   1 .2x f x x   
B.    1 ln 2 2x f x x C.   1 2x f x    D.    2x f x ☻ Giải :
..............................................................................................................................................................................
.............................................................................................................................................................................. 2
Bài 06 (THPT Nguyễn Văn Cừ) : Tính đạo hàm của hàm số 2 7x x y    2 2 A. x x2
y  (x 1).7 .ln 7 B. x x2
y  (7x 1).7 .ln 7 2 2 C. x x2
y  (2x 1).7 .ln 7 D. x x2
y  (2x  7).7 .ln 7 ☻ Giải :
..............................................................................................................................................................................
Bài 07 (THPT Quảng Xương 1 lần 2) : Cho hàm số 2
f (x)  log (x  2 x) . Tập nghiệm S của phương 3
trình f '(x)  0 là:
A. S  1 2;1 2 B. S    1 C. S  0;  2 D. S   ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 08 (Sở GD&ĐT Bình Phước) : Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y   2 2
ln 2x e  trên 0;e . Mệnh đề nào sau đây ĐÚNG ?
A. M m  4  ln 2
B. M m  5
C. M m  4  ln 3
D. M m  2  ln 3 ☻ Giải :
..............................................................................................................................................................................
.............................................................................................................................................................................. 77
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
..............................................................................................................................................................................
Bài 09 (TN THPT – 2009) : Tìm GTLN – GTNN 2
y  x  ln 1 2x trên đoạn  2  ; 0 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 10 : Tìm GTLN – GTNN f(x) = (x2 – 3x +1)ex trên đoạn [0;3] ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. Bài 11 : Cho x
y  e .x ; CMR : y '  2y ' y  0 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. Bài 12 : Cho sinx y  e
; CMR : y'.cosx  y.sin x  y'  0 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 13 : Tìm GTNN – GTLN của hàm số : y f x 2
 2x  6x 5ln2x   1 trên đoạn 0;  3 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 78
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Bài 14 : Tìm GTNN – GTLN của hàm số :  2 1. x y x e   trên đoạn 0;2 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. Bài 15 : Hàm số x
y e sin x  cos x có đạo hàm là: A. ex sin 2x B. 2 x e sin x C. 2 x e .cosx D. x
e sin x  cos x☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 16 : Đạo hàm của hàm số y   2
ln x x  
1 là hàm số nào sau đây? 2x 1 1 2x   1 1  A. y  y  y  . D. y  2 x x  B. 1 2 x x  C. 1 2 x x 1 2 x x  1 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 17 : Đạo hàm của hàm số 2 
y  (x x) là: A. 2  1    2 (x x)   B. 2 1 (x x)   (2x 1) C. 2 1 (x x)   (2x 1) D. 2 1 (x x)   ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 18 : Một tên lửa ay vào không trung đi được quãng đường s t  km là hàm theo iến t  
(giây) theo qui tắc sau s t  2 t 4 2t 3  e  2t.e
km . Hỏi vận tốc của tên lửa sau 1 giây là ao nhiêu? A. 5
6e km / s B. 5
10e km / s C. 5
7e km / s D. 5
8e km / s☻ Giải : 79
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
..............................................................................................................................................................................
Trắc nghiệm phần đạo hàm hàm số MŨ - LOGARIT
Câu 01 (THPT Hoàng Quốc Việt) : Đạo hàm của hàm số 1 2 x y e   là. A. 1 2 2 x y e    B. 1 2 2 x y e     C. x y  e D. 1 2 x y e   
Câu 02 : Tính đạo hàm của hàm số   3 1 2 x f x  
thì khẳng định nào sau đây đúng? A. f x 3x 1 3.2    ln 2 B. f x 3x 1 2    ln 2 C. f x 3x 1 2    log 2 D.     3 2 3 1 2 x f x x     2 x
Câu 03 (thi thử Cụm 4 – Tp.HCM) : Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số y  trên x e đoạn  1   ;1 . 1 A. 0 ; B. 1; e e 1 C. ; e D. 0 ; e e
Câu 04 (THPT Hùng Vương – PT) : Cho hàm số 2 x
y e khi đó y là: 1 A. 2 2 x xe B. 2 1 2 x xe  C. 2 2 x e D. 2 x 1 e  2
Câu 05 (thi thử Cụm 7 – Tp.HCM) : Tính đạo hàm của hàm số 1 2x y   . x 1 2  A.      1 2x y x ln 2 B. x 1 y 2    log 2 C. x 1 y 2    ln 2 D. y  ln 2
Câu 06 (THPT chuyên Vinh) : Cho hàm số 2 x
y x e . Nghiệm của bất phương trình y  0 là: A. x 0;2 B. x  ;  2  0; C. x  2  ;0 D. x  ;  02;
Câu 07 (thi thử Cụm 4 – Tp.HCM) : Hàm số 2 x
y x e nghịch biến trên khoảng nào? A.  2  ;0 B. 1; C.   ;1  D.  ;  2  
Câu 08 (THPT Lương Tài 2) : Tính đạo hàm của hàm số x x
y xe e . A.   2 x x e B. 2 x e C. 2 x xe D.    1 x x e 80
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Câu 09 (THPT Thuận Thành) : Hàm số nào sau đây có đạo hàm là x 6
y  3 ln 3  7x ? A. 7  3x yx B. 3 7
y x x C. 3   7x y x D. 3x 7x y  
Câu 10 : Tính đạo hàm của hàm số sinx y  2 sinx cos . x 2 A. sinx y   cos . x 2 .ln 2 B. sinx y  cos . x 2 .ln 2 C. sinx y  2 .ln 2 D. y  ln 2   
Câu 11 (Sở GDĐT Lâm Đồng lần 03) : Cho hàm số tan 2 x y e
, giá trị của f '  bằng.  6  A. 3 8e B. 3 2e C. 4 D. 3 4  e
Câu 12 (Sở GDĐT Lâm Đồng lần 05) : Tính đạo hàm của hàm số: 2 x 5  3.5 x y e . A. 2 x 5 '  2 5 .x y e ln 5 B. 2 x 5 '  2 3.5 x y e C. 2 x 5x 1 y ' 2e 3.5    .ln 5 D. 2 x 5 '  2 3.5 .x y e ln 5
Câu 13 (THPT Trần Cao Vân - Khánh Hòa) : Đạo hàm của hàm số 2 . x 3x y  là: A. 6x ln 6 B. 6x C. x 1  x 1 2 3   D. 2x 3x
Câu 14 (THPT Trần Cao Vân - Khánh Hòa) : Cho hàm số x y e  2
3  x  . Đạo hàm của hàm số bị
triệt tiêu tại các điểm: A. x  0
B. x 1; x  3  C. x  1  ; x  3
D. x 1; x  3 2
Câu 15 (Sở GDĐT Lâm Đồng lần 05) : Tính đạo hàm của hàm số: x 5x 1 y e    2 A.   2 5 1 ' 2 4 x x y x e     B.   2 5 1 ' 2 5 x x y x e     C.   2 2 5 1 ' 5 1 x x y x x e      D. 5 1 ' 2 5 x x y x e     1
Câu 16 : Tính đạo hàm của hàm số 4 x y e . 5 1 4 4 1 A. 4 x y  e B. 4 x y   e C. 4 x y  e D. 4 x y   e 20 5 5 20
Câu 17 : Tính đạo hàm của hàm số 2016x y  . 2016x A. 1 .2016x y x    B. y  C. 2016 . x y  ln 2016 D. 2016x y  ln 2016
Câu 18 (THPT Thanh Thủy) : Đạo hàm y của hàm số     2 2 x y x e là. A.      2 2 5 x y x e B.      2 2 4 x y x e
C.   2  4 x y x e
D.   2  5 x y x e 81
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Câu 19 : Tính đạo hàm cấp 2 của hàm số   2016x f x  . A.     2 " 1 2016x f x x x    B. f xx 2 "  2016 ln 2016 C. "  2016x f x  D. f xx 2 "  2016 log 2016
Câu 20 (Sở GD và ĐT Long An) : Tính đạo hàm của hàm số 2  2x y x . 2  x
A. y '  2x  2x   B. x y   2 ' 2
2x x ln 2  ln 2  C. '  2 2x y x ln 2 D. x y   2 ' 2
2x x ln 2
Câu 21 (Sở GD và ĐT Long An) : Trong các hàm số sau, hàm số nào đồng biến trên ? . x x     3  A. y  log x B. y  log x C. y  D. y    1 2      2  2 2  
Câu 22 (THPT Gia Lộc 2) : Tính đạo hàm của hàm số    .2x f x x . A.   1 .2x f x x   
B.    1 ln 2 2x f x x C.   1 2x f x    D.    2x f x
Câu 23 (THPT Chuyên Quang Trung) : Cho hàm số x x y e e   . Tính y   1  ? . 1 1 1 1 A. e  B. e  C. e  D. e e e e e
Câu 24 (THPT Yên Lạc – VP) : Cho hàm số       1 x f x x
e . Tính f 0 . A. 0 B. 2e C. 2 D. 1 Câu 25 : Hàm số 1 7x y   có đạo hàm là: 7x 7x ln 7 A. y '  B. y '  2 1 7x 1 7x 7x ln 7 7x C. y '  D. y '  2 1 7x 1 7 . x ln 3
Câu 26 (thi thử Cụm 8 – Tp.HCM) : Giá trị lớn nhất của hàm số f x 3 x 3x 3 e    trên đoạn 0;2 bằng.
Giáo viên cân file word vui lòng liên hệ A. e B. 3 e
Zalo / đt / facebook : 0914 449 230 C. 2 e D. 5 e
Câu 27 (THPT Lê Hồng Phong) : Tìm giá trị nhỏ nhất của hàm số     2   2 2 x f x x e trên  1  ;2 82
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
A. min f x 4  2e
B. min f x 2  e   1  ;2  1  ;2
C. min f x 2  2e
D. min f x 2  2  e  1  ;2  1  ;2
Câu 28 (Sở GD và ĐT Bình Phước) : Tính đạo hàm của hàm số sin 2 x y e 1 A. sin 2 '  cos 2 . x y x e B. sin 2 '  2cos 2 . x y x e C. sin 2 '  cos 2 . x y x e D. sin 2 '   cos 2 . x y x e 2  2 1 
Câu 29 : Trên đồ thị của hàm số 2 y x
lấy điểm M có hoành độ x 2 
. Tiếp tuyến của C  tại 0 0
điểm M có hệ số góc ằng. 0 A. 2 B.  2 C. 2 1 D. 3 1
Câu 30 : Tính đạo hàm của hàm số 2 x y   1 2 x   ln 2 ln 2 1 2 x  A. y  B. 1   2 x y C. 1   2 x y D. y  2 1 x 2 1 x 2 1 x 2 1 x 1
Câu 32 : Cho hàm số y
. Khẳng định nào dưới đây là khẳng định sai? 3x
A. Toàn bộ đồ thị hàm số đã cho nằm phía trên trục hoành. 1 1 B. ' y  .ln . 3x 3
C. Hàm số đã cho đồng biến trên khoảng  ;    .
D. Đồ thị hàm số đã cho có một tiệm cận ngang là trục Ox .
Câu 33 (Đề Minh họa lần 2) : Tính đạo hàm của hàm số y  ln 1 x 1 . 1 1 A. y  B. y 
2 x 11 x 1 1 x 1 1 2 C. y  D. y 
x 11 x 1
x 11 x 1 x e
Câu 34 : Phát iểu nào sau đây đúng khi nói về hàm số y  ? x 1
A. Hàm số nghịch biến trên khoảng  ;  0
B. Hàm số đồng biến trên khoảng 0;  83
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
C. Hàm số đạt cực đại tại x  0
D. Hàm số có hai điểm cực trị
Câu 35 : Biểu thức  x  2 3x 3x 1 24 12 .2  
.ln 2 là đạo hàm của hàm số nào sau đây ? 2 2 2 2 A. 3 3 1 2 x x y    B. 3 3 1 8 x x y    C. 1 2x x y    D. 1 8x x y   
Câu 36 : Hàm số nào sau đây đồng biến trên từng khoảng xác định của nó ? x  A.  f x 4  2x 1
B. f x  ln x C. f xx 1  e  D. f x 2 3  x x  1 ln x
Câu 37 : Cho hàm số y
. Trong các phát iểu sau, đâu là phát iểu đúng ? x
A. Hàm số có một cực tiểu
B. Hàm số có một cực đại
C. Hàm số không có cực trị
D. Hàm số có 1 cực đại và 1 cực tiểu 2 x 1 
Câu 38 : Đạo hàm f  x của hàm số f xx 1 e   là ? 2 x 1  x2 2x 1 A. f xx 1 e    B. f  xx 1  e x 1 2 x 1  2 x 1  2x 1 x 1 3e  C. f  xx 1  e
D. f  x   x 1 x  2 1
Câu 39 : Đạo hàm của hàm số   x f x x là A. f xx 1 x    x ln x B.   x f
x x 1 ln x C.   x f x x D.   x f
x x ln x
Câu 40 : Cho hàm số 2
y x  ln 1 2x . Trong các kết luận sau, đâu là kết luận không đúng ? 1
A. Hàm số có hai cực trị
B. Hàm số đạt cực tiểu tại x  2 1  1 
C. Hàm số có giá trị cực tiểu bằng  ln 2
D. Hàm số đồng biến trên khoảng ;     4  2  2 x 1 
Câu 41 : Tìm đạo hàm của hàm số x 1 y 2   2 x 1  2 x 1  3 A. x 1 y ' 2   ln 2 B. x 1 y ' 2    x  2 1 ln 2 84
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 2 x 1   3 2 x 1 ln 8 C. x 1 y ' 2   x 1    D. y ' 2 2 x  2 1 x  1
Câu 42 : Cho hàm số 2
y f x liên tục trên
và có đạo hàm f  x 5x3 3  e x x   1  x  2 .
Hàm số y f x có ao nhiêu điểm cực trị? A. Có 3 điểm cực trị. B. Có 1 điểm cực trị. C. Không có cực trị. D. Có 2 điểm cực trị.
Câu 43 (THPT Tôn Đức Thắng – Khánh Hòa ) : Cho hàm số y  2ln ln x – ln 2x . Tính giá trị của ye . 1 2 e 1 A. B. C. D. e e 2 2e
Câu 44 (THPT Nguyễn Thiện Thuật – Khánh Hòa ) : Tính đạo hàm của hàm số y  log  2
x  3x  5 . 3  1
A. y  (2x  3) ln 5 B. y  2
(x  3x  5) ln 3 2x  3 C. 2
y  (x  3x  5) ln 5 D. y  2
(x  3x  5) ln 3
Câu 45 (THPT Trần Quý Cáp – Khánh Hòa ) : Cho hàm số y  ln 2x  
1 . Tìm m để ye  2m 1. 1 2e 1 2e A. m  B. m  4e  2 4e  2 1 2e 1 2e C. m  D. m  4e  2 4e  2 x 1
Câu 46 (THPT Nguyễn Thiện Thuật – Khánh Hòa) : Tính đạo hàm của hàm số y  ln x  2 3 3  A. y  B. y 
(x 1)(x  2)
(x 1)(x  2) 3  3 C. y  D. y  2
(x 1)(x  2) 2
(x 1)(x  2) 1 3
Câu 47 : Giá trị lớn nhất của hàm số 3x2 y e  2
4x  5x trên đoạn ;   bằng 2 2 13 3 12 4 A. 2 e B. 5 e 2 5 85
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 11 5 14 2 C. 4 e D. 3 e 2 3
Câu 48 (THPT Nguyễn Thiện Thuật – Khánh Hòa) : Cho hàm số f x   2
ln 4x x  chọn khẳng
định đúng trong các khẳng định sau A. f   1 5  B. f 2  1 C. f 2  0 D. f   6 1  2 5
Câu 49 : Tính đạo hàm của hàm số  .5x y x A.   5x y 1 xln5. B. 5x y  1ln5 . C. 5x y  ln 5 . D.   5x y 1 x.
Câu 50 : Tìm giá trị lớn nhất của hàm số   2 5  5 x y x x e trên đoạn  3  ;0 A. 2
Max y  9e . x   3  ;  0 B. 3
Max y  19e .
Giáo viên cần file word vui lòng liên hệ x   3  ;0
Zalo / đt / facebook : 0914 449 230 C. 2
Max y  8e . x   3  ;0 D. Max y  0 . x   3  ;0
Câu 51 : Đạo hàm của hàm số y x ln x x là 1
A. y '  ln x . B. y '  1. C. y '  1.
D. y '  ln x . x
Câu 52 (THPT Lạng Giang số 2) : Cho hàm số y  log 4 . Tính y2 2 x 1 1 1 A. log 4 B. C.  D.  2 ln 4 ln 2 ln 4 86
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
Phần III : PHƢƠNG TRÌNH MŨ - LOGARIT A. PHƢƠNG TR ÌNH MŨ
1. Phƣơng trình mũ cơ bản :
Phương trình có một nghiệm duy nhất khi b  0 x
a ba  0, a   1
● Phương trình vô nghiệm khi b  0 .
2. Biến đổi, quy về cùng cơ số : u v
a a
Ví dụ : Giải phương trình: x 1  2 x 1 9 27   . x 1  2 x 1   2 x  HD Giải: 1 6 x3 9  27  3  3
(Ở đây ta đƣa về cùng cơ số a = 3 > 1) 1 
 2x  2  6x  3  4x  1   x 4 3. Logarit hóa:
Giáo viên cần file word vui lòng liên hệ     ☻ 0 a 1, b 0 Phương trình u a b  
Zalo / đt / facebook : 0914 449 230 u  log ba
Ví dụ : Giải phương trình: 3x  9 ; HD Giải: 3x  9  x  log 9  2 . 3 ☻ f xgxf xg x Phương trình ab  log a  log bf x g x b a a    .loga f xgx hoặc log a  log bf x a g x b b  .logb   2
Ví dụ : Giải phương trình: x 1  x x2 3 2  8.4 . 2
HD Giải: Lôgarit cơ số 2 hai vế ta có: log  x 1
3  2x   log  x2 8.4   x   2
1 log 3  x  2x 1 2 2  2     x    x  2 x 1 1 log 3 1
 0  x 1 x 1 log 3  0  2   2  x 1log 3  2
4. Đƣa về phƣơng trình tích : Gom số hạng thích hợp để thu được nhân tử chung.
Ví dụ : Giải phương trình: 25.2x 10x 5x    25  0 87
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
HD Giải: 25.2x 10x 5x 25 0 25.2x 2 .
x 5x 25 5x  0
2x 25 5x  25 5x                0     x x   x   5x 25 2 25 5 2 1  0     2x 1 x  0
Bài tập mẫu tham khảo 01 : Giải các phương trình sau :    a/ x 1 x x 1 5  6.5 3.5  52 b/ x x 1 3 .2  72 ♥ xx xx x 3 x x 3
Hƣớng dẫn giải : 1 1 a / 5
 6.5 3.5  52  5.5  6.5  .5  52  5 (5  6  )  52 5 5 52 
.5x  52  5x  5  x  1. Vậy phương trình có nghiệm x = 1. 5 x x 1  x x x x x 2 b / 3 .2
 72  3 .2 .2  72  2.6  72  6  36  6  6  x  2.
Vậy phương trình có nghiệm x = 2. 2  x4 2  1  2
Bài tập mẫu tham khảo 02 : Giải phương trình: a/ x 3x5     9   b/ 2x x x 6 2  64.4  3 
♥ Hƣớng dẫn giải : a/ Nhận xét: Hai vế của phương trình có thể biến đổi để đưa về cùng cơ số 3. 2  x4  1  xx x  x 3x5  9     1 3  2 4   2 3  2 2 3 5 2 2 x4 2 x 6 x 1  0  3  3  3  x 1 2 2
 2x  4  2x  6x 10  2x  4x  6  0  x  3
Vậy phương trình có hai nghiệm: x = 1; x = –3. 2
b/ phương trình cho  4x +3 =   6 4 x x  2
x x  6  x  3 x  3  0 x  3      2 2
x x  6  (x  3) 2
2x  7x  3  0 x  3    x  3 1   x = –3 hay x =  .  1  2 x    2
Bài tập mẫu tham khảo 03 : Giải các phương trình sau đây: x 1  2  x  2  a/ x 3 5 x  625 b/ 5 7 (1, 5)    c/ x 1 2 .5x  200  3 
♥ Hƣớng dẫn giải : 2 2
a) x 3x x 3x 4 2 2 5  625  5
 5  x  3x  4  x  3x  4  0  x 1 hoặc 88
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
Vậy phương trình đã cho có 2 nghiệm: x  1hoặc x  4  x 1  5 x7 x 1       x  2 3 3 b) 5 7 (1,5)   
 5x  7  x 1  x 1        3   2   2 
Vậy phương trình đã cho có nghiệm duy nhất: x  1  c) x 1 2 .5x  200  2.2 .
x 5x  200 10x 100  x  2
Vậy phương trình đã cho có nghiệm duy nhất: x  2 
Bài tập mẫu tham khảo 04 (đề Minh họa lần 2) : Tìm nghiệm của phương trình x 1 3  27 A. x  9 B. x  3 C. x  4 D. x 10
♥ Hƣớng dẫn giải :
Cách 1 : Ta có x 1  x 1  3 3
 27  3  3  x 1 log 27  x 1 3  x  4.Chọn C 3
Cách 2 : Trắc nghiệm có sử dụng máy tính.  Nhập x 1 3
 27 vào máy tính, sau đó sử dụng phím r để kiểm tra các đáp án
Được đáp án đúng là C. Chọn C Cách bấm máy tính 3^Q)p1$p27r4=
Bài 01 : Giải các phương trình sau 2 5 x 6 x 2 a) x4 3 2  4 b) 2 2 16 2 c) 2x3 x 3x5 3  9 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 89
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
Bài 02 : Giải các phương trình sau x5 x 1  7 2 1 a) x x 8  1 3  x 2  4
b) 52x + 1 – 3. 52x –1 = 110 c) x7 x3 32  128 4 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.................................................................................
Giáo viên .............................................................................................
cần file word vui lòng liên hệ
Zalo / đt / facebook : 0914 449 230
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 03 : Giải các phương trình sau 2 2 2 2 a) 2x  x x 1  x 1  x 2
+ 2x –1 + 2x – 2 = 3x – 3x – 1 + 3x – 2 b) (1,25)1 – x = 2(1 ) (0, 64) x c) 5  3  25 3  ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 90
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 2 x x 1
Bài 04 : a/ (THPT Phù Cát) : Tập nghiệm của phương trình 4 2  là: 16 A.  B. 2;  4 C. 0;  1 D.  2  ;  2 
b/ (THPT Phan Bội Châu) : Phương trình 2x 1 5 1 có nghiệm là 1 1 A. x 1. B. x  . C. x  . D. x  0. 2 3
c/ (THPT Quy Nhơn) : Phương trình 3x2 4 16 có nghiệm là: 4 3 A. x  B. x  C. x  3 D. x  5. 3 4 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 05 : a/ (THPT chuyên Nguyễn Trãi lần 2) : Tìm nghiệm của phương trình 2x5 2 4  2 x 8 12 8 A. 3 B. C. D.  5 5 5
b/ (Sở GD&ĐT Bình Phƣớc) : Tìm nghiệm của phương trình 36 2 x 1 1 1 A. x  B. x  3 C. x  D. x  2 3 2
c/ (THPT chuyên Lƣơng Thế Vinh) : Phương trình 8x  4 có nghiệm là. 2 1 1 A. x  2  B. x  C. x   D. x  3 2 2 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 91
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
Bài 06 : Giải các phương trình sau : x 1   1  1 2 x xx x 4x a/    b/       2 2 3 2 3 c/ 3 2 2  3 2 2  2  8 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 07 (THPT Trần Hƣng Đạo – Nam Định) : Kí hiệu x , x là nghiệm của phương trình 1 2 2 4 log 243 3x   
. Tính giá trị của biểu thức M x x . 1 2 A. M  3  B. M  9 C. M  25  D. M  9  ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 3 x2  1  2  2 x 2 x 3
Bài 08 : Giải các phương trình sau : a/    8x   b/ x 3 2 x  4 c/  2    2  2  ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 09 : Đồ thị C  của hàm số y f x  ln x cắt trục hoành tại điểm A, tiếp tuyến của C  tại A có phương trình là 92
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
A. y x 1.
B. y  2x 1. C. y  3 . x
D. y  4x  3. ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 10 (THPT Đoàn Thị Điểm – Khánh Hòa) : Số lượng của loại vi khuẩn A trong một phòng thí
nghiệm được tính theo công thức ( )  (0)2t s t s
, trong đó s(0) là số lượng vi khuẩn A lúc ban đầu,
s(t) là số lượng vi khuẩn A có sau t phút. Biết sau 3 phút thì số lượng vi khuẩn A là 625 nghìn
con. Hỏi sau bao lâu, kể từ lúc bắt đầu, số lượng vi khuẩn A là 10 triệu con? A. 48 phút. B. 19 phút. C. 7 phút. D. 12 phút. ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 11 (Đƣa về dạng tích) : Giải các phương trình sau : a/ 8.3x 3.2x 24 6x    2 2 2 b/ x 3  x2 x 6x5 2x 3x7 4  4  4 1 c/ x x x 1 12.3 3.15 5     20 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài tập trắc nghiệm phƣơng trình mũ dạng CƠ BẢN 2
Câu 01 : Tìm tập nghiệm 
S của phương trình 2 5 x x  5 . 93
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018  1   1  A. S  0;  B. S  0;  2 C. S  1  ;  D. S    2  2  
Câu 02 (THPT Tiên Lãng) : Nghiệm của phương trình 2
4 x m  8x là: A. 2m B. m C. m D. 2  m 2
Câu 03 (THPT Võ Nguyên Giáp) : Số nghiệm của phương trình x 2x 1 2  1 là: A. 2 B. 0 C. 1 D. 4
Câu 04 (thi thử Cụm 1 – Tp.HCM) : Phương trình 8x 16 có nghiệm là. 3 4 A. x  2 B. x  3 C. x  D. x  4 3 
Câu 05 (THPT Lý Thƣờng Kiệt) : Giải phương trình 2 3 x  27 A. x  1  B. x  0 C. x  2  D. x  1 
Câu 06 (THPT Lƣơng Tài 2) : Giải phương trình 2x 1 3  27 . 1 A. x  5 B. x  1  C. x  log 30 D. x  2 3 2 2
Câu 07 : Cho phương trình x 4x5 3
 9 tổng lập phương các nghiệm thực của phương trình là: A. 28 B. 27 C. 26 D. 25 2
Câu 08 : Cho phương trình : x 3x8 2x 1 3 9  
, khi đó tập nghiệm của phương trình là:  5   61 5   61 A. S  2;  5 B. S   ;   2 2   5 61 5 61 C. S   ;  D. S   2  ;  5 .  2 2   2
Câu 09 (TT Tân Hồng Phong) : Giải phương trình x 3 2 x 16 . A. x  4
B. x  1 hoặc x  4  C. x  1  D. x  1  hoặc x  4 x  2 
Câu 10 : Nghiệm của phương trình 2 x3    0,125.4   là 8   A. x  4 B. x  5 C. x  6 D. x  7
Câu 11 (THPT Lê Hồng Phong) : Tìm các nghiệm của phương trình x2 100 2  8 . A. x  204 B. x 102 C. x  202 D. x  302 94
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018 3x 1   x  1
Câu 12 (thi thử Cụm 4 – Tp.HCM) : Giải phương trình 4 3     9  6 1 7 A. x  B. x  C. x  1 D. x  7 3 6 2 x x  1
Câu 13 (THPT Ngô Gia Tự) : Giải phương trình 1 8 .5  8 A. x  1  ; x 1 log 8 B. x  1  ; x 1 log 5 5 8 C. x  1  ; x 1 log 8 D. Kết quả khác 5  
Câu 14 (THPT Nguyễn Thái Học) : Giải phương trình: x 2(1 x) 16  8 A. x  3  B. x  2 C. x  3 D. x  2  2
Câu 15 (THPT Hoàng Văn Thụ - Hòa Bình) : Số nghiệm của phương trình x x2 2 1 là A. 2 B. 3 C. 1 D. Vô nghiệm 2
Câu 16 (THPT Ngô Quyền) : Tìm tập nghiệm 
S của phương trình 2 3 x x  3  1   1  A. S  1  ;  B. S   1  ;  2 C. S   1  ;  D. S    2   2  
Câu 17 : Nếu x và y thỏa mãn 3x  27 và 2x y  64 thì y bằng. A. 1 B. log 8 C. log 8 D. 2 3 2 xx
Câu 18 (thi thử Cụm 7 – Tp.HCM) : Phương trình     4 4 2 0.2 5
tương đương với phương trình:             A. x 2 2x 4 5  5 B. x 2 2x 2 5  5 C. x 2 2x 4 5  5 D. x 2 2x 2 5  5 2 x x 1
Câu 19 (THPT Ngô Sĩ Liên lần 3) : Tập nghiệm của phương trình 4 2  là. 16 A. 2;  4 B.  C. 0  ;1 D.  2  ;  2 1
Câu 20 (THPT chuyên Lê Thánh Tông) : Phương trình 3x  4 có nghiệm là. A. x  log 3 B. x  log 2 C. x  log 3 D. x  log 4 4 3 2 3
Câu 21 (THPT Trần Quý Cáp - KH) : Số lượng của một số loài vi khuẩn sau t (giờ) được xấp xỉ bởi đẳng thức 0,195t Q Q e
, trong đó Q là số lượng vi khuẩn ban đầu. Nếu số lượng vi khuẩn ban đầu o o
là 5000 con thì sau bao lâu có 100 000 con? 95
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018 A. 3,5 B. 20 C. 15,36 D. 24
PHƢƠNG PHÁP ĐẶT ẨN PHỤ
Khi không quy về đƣợc
dạng cơ bản ta nghĩ tiếp đến là đặt ẩn phụ gxt   a gx 0
Cơ sở lý thuyết : f a   0 0  a   1     f  t  0 f x
Dạng 1: Ta có dạng tổng quát của bài toán trên là: F a 0. f x
Với dạng này ta đặt t a
, t  0 và chuyển về phương trình F t   0 , giải tìm nghiệm dương t 2 f xf x
của phương trình, từ đó ta tìm được x. Ta thƣờng gặp dạng: . m a  . n ap  0 .
Ví dụ : Giải phương trình: 2x5 x2 3  3  2.
HD Giải: 2x5 x2 5 2 x 2 3  3
 2  3 .3 3 .3x  2  0 . 1 x 1 Đặt 3x t
 0 ; pt cho trở thành : 5 2
3 t  9t  2  0  t   3   x  2  9 9
Với bất phƣơng trình ta cũng làm tƣơng tự. f xf xf xf x 1 Dạng 2: . m a  . n b
p  0 , trong đó .
a b  1. Đặt t a , t  0  b  . t 2 f xf x Dạng 3: . m a  . n  . a b   2 f x  . p b  0 . f x   2 f xa
Chia 2 vế phương trình cho b và đặt t  , t  0   . Ta có phương trình : 2
mt nt p  0 .  b
Ví Dụ 1 : Giải các phương trình sau đây:     a) x 1 x 1 4 6.2 8  0 b) 9x 5.3x  6  0 c) x 1 x 1 4  2  21 0    d) x 2
5  2.5 x  5  0
e) 6.9x 13.6x 6.4x    0 f) x 1 3 5 5 x  26 ☺ Giải : a) x 1  x 1  x 1  2 x 1 4 6.2 8 0 (2 ) 6.2       8  0 96
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018 t  2 Dạng 1: Đặt 1 t 2x 
. Điều kiện t > 0. Ta có 2
t  6t  8  0   t  4 ► Với t = 2 ta có 1
2x =2  x  0 ► Với t = 4 ta có 1
2x = 4  x  1. Vậy phương trình đã cho có hai nghiệm: x  0 ; x 1 b) x x 2 9 5.3 6 0 3 x 5.3x      6  0 Đặt 3x t
(t > 0), phương trình trên trở thành: 2
t  5t  6  0  t = 3 hoặc t = 2 (nhận)
 t = 3 thì 3x  3  x 1
 t = 2 thì 3x  2  x  log 2 . Vậy phương trình đã cho có nghiệm: x = 1 hoặc x = log 2 3 3   c) x 1 x 1 4  2  21 0
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<  d) x 2
5  2.5 x  5  0 (dạng 2)
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
e) 6.9x 13.6x 6.4x  
 0 (dạng 3)
Chia hai vế của phương trình cho ..............ta được:
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<   f) x 1 3 5 5 x  26
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 97
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Ví Dụ 2 : Giải các phương trình sau đây: x  17 2 2 a/ 1   4  .2 x 16  0 b/ x 2 x 2 9  28.3
 27  0 c/ 3.16x 2.81x 5.36x   2
☺ Giải : a/ Điều kiện: x  0 . x
Phương trình tương đương với xx2 4 17 .2 16 0 2 34.2 x      64 0. 4 2 t  32 Đặt 2 x t
 0 , phương trình trở thành 2
t  34t  64  0  .  t  2
● Với t  32 , ta được x x 5 2
 32  2  2  x  5  x  25 (thỏa mãn).
● Với t  2, ta được 2 x  2  x 1  x 1 (thỏa mãn).
Vậy phương trình đã cho có tập nghiệm S  1;2  5 . 2 2 2
b/ Phương trình tương đương với  x 2  x 2 3  28.3  27  0.   2 t 1 Đặt x 2 t  3
 0, phương trình trở thành 2
t  28t  27  0  .  t  27 2 ● Với 
t  1, ta được x 2 2 3
1 x  2  0: vô nghiệm. 2 2 ● Với  
t  27 , ta được x 2 x 2 3 2 2 3  27  3
 3  x  2  3  x 1 x  1  .
Vậy tập nghiệm của phương trình là S   1  ;  1 . 2 x x     x x x 4 4
c/ Phương trình tương đương với 3.16  5.36  2.81  0  3.  5.  2  0     .  9   9    x t 1  4  Đặt  t   0  
, phương trình trở thành 2
3t  5t  2  0  .  2 9  t   3 x  4 
● Với t  1, ta được 1  x  0.    9   x 2 x 5   4  2  2  2 1 ● Với S   ; 4   , ta được  
  2x 1  x  .      3   9  3  3  3 2  1 
Vậy phương trình có tập nghiệm S  0;   2 98
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
Ví Dụ 3 : PHƢƠNG PHÁP LIÊN HỢP
Lƣu ý: Một số những cặp số là nghịch đảo của nhau: 2 1 ; 2  3 ; 3  8 ,... Giải phương trình ( 7 48 )x ( 7 48 )x    14 (1) ☺ x x 1 Giải : Ta có ( 7 48 )x ( 7 48 )x  
1. Đặt t  ( 7  48 ) ;(t  0)  ( 7 48 )  t 1 t  7  48
Khi đó phươg trình (1) trở thành: 2
t   14  t 14t 1  0   t t  7  48
 Với t  7  48 ta có: ( 7  48 )x  7  48  x  2  .
 Với t  7  48 ta có: ( 7  48 )x  7  48  x  2 .   
Bài 01 : Giải phương trình: a/ 2x x 1 5  5  6 b/ 2x x 1 5  24.5 1 0 c/ x 1 9 8.3x 1 0 ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 02 : Giải các phương trình sau    a/ x 1 x 4 x 2 4  2
 2 16 (ĐH TCKT – 99) b/ x2    x2 4 16 10. 2
(ĐH Hàng Hải – 98)   c/ 25x 6.5x
5  0 (TN – 2009) d/ 8x 2.4x 2x    2  0 e/ x 2002 x 2003 8.4 5.2  2  0 ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 99
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 03 : Giải các phương trình sau a/ 6x 3x e  3.e  2  0 b/ x 2 2.2  2  x  2 2 2 2 2 c/ 1x 1x 5  5  24 d/ x x 2 2
 2 xx  3(ĐH Khối D-2003) ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 04 : Giải các phương trình sau a/ x x 3x 1 125 50 2    (ĐHQG-HN-98) 2 2 2 b/ x 2x x 2x x 2 2.4  6  9 x
c/ 3.8x 4.12x 18x 2.27x   
(ĐH Khối A-2006) ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 100
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 05 : Phương trình 9x 5.3x
 6  0 có tổng các nghiệm là: 2 3 A. log 6 B. log C. log D.  log 6 3 3 3 3 2 3 ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 
Bài 06 : Cho phương trình 1 2
2 x 15.2x 8  0 , khẳng định nào sau dây đúng? A. Có một nghiệm B. Vô nghiệm
C. Có hai nghiệm dương D. Có hai nghiệm âm ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 
Bài 07 : Phương trình x 1
5  25 x  6 có tích các nghiệm là : 1 21  1 21  1 21  A. log   B. log   C. 5 D. 5log   5       2   5 2   5 2   ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 101
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< x x
Bài 08 : Phương trình 7  4 3  2  3  6 có nghiệm là: A. x  log 2 B. x  log 3 C. x  log 2  3 D. x  1 2   2 3 2 ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 
Bài 09 : Giả sử a là nghiệm dương của phương trình: 2x 3 2
33.2x  4  0. Khi đó, giá trị của 2   55 26 3a M a 7 là A. 6 B. C. 29 D.  27 9 ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 10 : Giải các phương trình sau x x
a)  2 3   2 3   4 (CĐ Hải Quan – 1998) x x x x
b)  7  48   7  48  14
c/ 4  15  4  15  2 ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 102
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 11 (THPT Nguyễn Trãi Lần 1) : Tìm tích các nghiệm của phương trình x ( 2 1)x    2   1  2 2  0 A. 0 B. 2 C. 1 D. 1  ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< x x
Bài 12 (THPT Chuyên Bình Long) : trình    2 2 2 2 3
 7  4 3 có hai nghiệm x , x 1 2 . Tính giá trị
của P x x 1 2 . A. P  1  B. P  3 C. P  2 D. P  4 ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 2
Bài 13 (THPT Chuyên Vinh) : Biết rằng phương trình x 1  x 1 2 3  
có 2 nghiệm là a,b . Khi đó
a b ab có giá trị bằng. A. 1 2log 3 B. 1  C. 1 log 3 1   2log 3 2 2 D. 2 ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 103
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 14 (THPT Chuyên Bình Long) : Gọi x , x x x là hai nghiệm thực của phương trình 1 2  1 2 2x 1
3   4.3x 1  0 . Chọn mệnh đề đúng?
A. x  2x  0
B. 2x x  2
C. 2x x  2 
D. 2x x  2  1 2 1 2 2 1 1 2 ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Câu 15 (THPT Tôn Đức Thắng – Khánh Hòa) : Với giá trị thực nào của m thì phương trình x x2 4  2
m  0 có hai nghiệm thực phân biệt? A. m  0 . B. 0  m  4 . C. m  4 . D. m  0 . ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Câu 16 (THPT Tôn Đức Thắng – Khánh Hòa) : Tổng các nghiệm của phương trình 9x 9 10.3x   là A. 5 . B. 10 . C. 2 . D. 3 . ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 
Câu 17 (THPT Huỳnh Thúc Kháng – Khánh Hòa) : Tập xác định D của hàm số   x y   5 5 125 là: A. D  .
B. D  3; . C. D  \   3 .
D. D  3; . ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 104
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài tập trắc nghiệm phƣơng trình mũ dạng ĐỔI BIẾN SỐ
Câu 01 (THPT chuyên Vĩnh Phúc) : iá trị của tham số m để phương trình. 4x  2 .2x m
 2m  0 có hai nghiệm phân biệt x ; x sao cho x x  3 là: 1 2 1 2 A. m  3 B. m  1  C. m  2  D. m  4
Câu 02 (THPT Lƣơng Tài) : Phương trình 4x  2   1 2x m
3m 4 0 có 2 nghiệm x ,x 1 2 sao cho x x  3 1 2 khi. 1 5 A. m   B. m  4 C. m  D. m  2 2 2 
Câu 03 : Tổng tất cả các nghiệm của phương trình 2x 1 2
5.2x  2  0 bằng bao nhiêu? 3 5 A. 1 B. C. D. 0 2 2 
Câu 04 : Cho phương trình: x x 1 3.25  2.5
 7  0 và các phát biểu sau:
(1) x  0 là nghiệm duy nhất của phương trình.
(2) Phương trình có nghiệm dương.
(3) Cả hai nghiệm của phương trình đều nhỏ hơn 1.  3 
(4) Phương trình trên có tổng hai nghiệm bằng  log 5    7 
Số phát biểu đúng là: A. 2 B. 1 C. 4 D. 3
Câu 05 (Sở GD và ĐT Long An) : Gọi x , x là hai nghiệm của phương trình 1 2  x x
2  3  22  3  3 . Tính P x x . 1 2 A. P  3  B. P  0 C. P  2 D. P  3 
Câu 06 : Tổng tất cả các nghiệm của phương trình 2x 1 2
5.2x  2  0 bằng bao nhiêu? 3 5 A. 1. B. C. D. 0 2 2 x x
Câu 07 (THPT Nguyễn Huệ - Huế) : Phương trình 3 5  3 5 3.2x    
có hai nghiệm x , x . 1 2 Tính 2 2
A x x . 1 2 A. 1 B. 2 C. 9 D. 13 105
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018 2
Câu 08 (THPT chuyên Biên Hòa lần 2) : Tìm tập nghiệm thực của phương trình 3 .x2x 1. A. S  0;log 3 B. S    0 2   1 C. S  0;log  6 D. S  0;log  2  3
Câu 09 (THPT Lý Thái Tổ) : Phương trình: 3x 4x 5x   có nghiệm là. A. 1 B. 4 C. 2 D. 3 Câu 10 : Nếu 2 3 x 9 10.3x  
thì giá trị của 2x 1 là: A. 1 hoặc 5 B. 5 C. 1 D. 0 hoặc 2 .
Câu 11 (THPT chuyên Lê Hồng Phong) : Tìm tất cả các giá trị thực của tham số m sao cho phương
trình 9x  2  2 3x m
3m  4  0 có hai nghiệm phân biệt x , x thỏa mãn điều kiện x x  3 . 1 2 1 2 31 A. m   3 5 B. m   2 C. m  3  7 D. m   3
Câu 12 (thi thử Cụm 8 – Tp.HCM) : Nếu phương trình 2 3 x 4.3x
1 0 có hai nghiệm phân biệt
x ; x và x x thì. 1 2 1 2
A. 2x x  1 B. x 2  x  1  C. x x  0 D. x .x  1 1 2 1 2 1 2 1 2 2 xx  1 
Câu 13 (TTGDTX Nha Trang - Khánh Hòa) : Gọi 
x , x là nghiệm của phương trình 6 x 1  5 . 1 2    5 
Khi đó x x bằng. 1 2 A. 7 B. log 2 1 5 C. 5  D. 10
Câu 14 (THPT Hùng Vƣơng – PT) : Biết phương trình 2.16x 17.4x
8  0 có 2 nghiệm x , x . Tính 1 2
tổng x x . 1 2
A. x x  2
B. x x  4 1 2 1 2 17
C. x x  1
D. x x   1 2 1 2 4  
Câu 15 : Phương trình x 1 x 1 9
6  3.4x có bao nhiêu nghiệm: A. 1 B. 4 C. 3 D. 2 106
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
Câu 16 : Số nghiệm của phương trình x 1 3  3 x  2 là A. 0 B. 2 C. 3 D. 1 x 1   1 
Câu 17 : Tập nghiệm của phương trình trình 2 125 x   là:  25  1 1 A. {  } B. {4} C. {1} D. {  } 8 4 2 2
Câu 18 : Tập nghiệm cảu phương trình x 1  x 1 9 3    6  0 là: A. { 1  ;1} B. { 2  ;0;2} C. { 1  ;0;1} D. {0} 2 2
Câu 19 : Phương trình sin x cos 2 5.2 x   7 có nghiệm là:  A. x   k B. x   2 2 C. x  3  k D. x   k2 3  
Câu 20 : Tập nghiệm của phương trình x 1 3 5 5 x  26 là: A. {1;3} B. {3;5} C.  D. {2;4}  
Câu 21 : Số nghiệm của phương trình 2 x 2 2  2 x 15 là A. 0 . B. 3 . C. 2 . D. 1.
Câu 22 : Phương trình 9x 3.3x
 2  0 có hai nghiệm x , x x x . iá trị của A  2x 3x là: 1 2  1 2  1 2 A. 2 B. 4log 3 C. 0 D. 3log 2 2 3 
Câu 23 : Cho phương trình x 2x 1 81  4.3
 27  0. Tổng các nghiệm của phương trình là bao nhiêu? 1 3 A. B. C. 1 D. 2 2 2
Câu 24 : Phương trình x x 1 2 2    4 có nghiệm là A. 1 log 3 B. 3  log 3 C. log 3  2 D. log 3 1 2 2 2 2
Câu 25 (THPT Nguyễn Văn Trỗi – Khánh Hòa) : Tìm tất cả các giá trị của tham số m để phương
trình 4x  2 .2x m
 2m  0 có hai nghiệm phân biệt x , x sao cho x x  3. 1 2 1 2 A.  ;  4 B. 0;4 107
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018 C. 2;4 D.  ;  02;4
Câu 26 : Nghiệm của phương trình 25x 2.5x  15  0 là:
A. x  3; x  5  B. x   log 3 C. x  log 3 D. x  log 5 5 5 3
Câu 27 : Gọi M là tổng các nghiệm của phương trình x 1  2 3
3 x  2  0. Tìm M . A. M  0 B. M 1 C. M  2 D. M  3
Câu 28 : Cho 4x  4x  3. Tính 2x 2 x A    A. 5 B. 2 5 C.10 D. 5 a
Câu 29 : Biết phương trình 3.25x 2.49x 5.35x  
có một nghiệm khác 0 dạng x  log
, với a,b là 7 b 5 a
các số nguyên dương và là phân số tối giản. Tính a b . b A. 1  B.1 C. 0 D. 2 108
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
B. PHƢƠNG TRÌNH LOGARIT
Phƣơng trình LOGARIT cơ bản :
log f (x)  b a
Ví dụ : Phương trình log (3x  2)  3 có nghiệm là: 3 29 11 25 A. x  B. x  C. x  D. x  87 3 3 3
Giải : ........................................................................................................................................................... Chú ý :
log f (x)  log g( ) x a a
Bài tập mẫu tham khảo 01 : Giải các phương trình sau : a/ 2 log (3x  x)  2
b/ log (x  5)  log (x  2)  3 2 2 2
♥ Hƣớng dẫn giải : a/ Điều kiện: 2
3x  x  0 (Đối với phương trình này, ta có thể đặt điều kiện mà không cần giải điều kiện đó.
Sau khi giải phương trình tìm được kết quả, ta đối chiếu điều kiên sau cũng được). x 1 Phương trình 2 2 2 
log (3x  x)  2  3x  x  4  3x  x  4  0  2 4  x    3 4
So với điều kiện, ta thấy phương trình có hai nghiệm: x  1; x   . 3
b/ log (x  5)  log (x  2)  3  2 2 (1) ; Điều kiện: x 5
Khi đó phương trình (1)  log  x  5 x  2   3  x  5 x  2  8 2       2
 x 3x18  0  x  3  hay x  6
So với điều kiện, ta thấy phương trình có hai nghiệm: x  6
Bài tập mẫu tham khảo 02 : Giải các phương trình sau : a) log x  4  log x 1  1 b) 2
log (x  2)  log ( x  4)  0 2 2 3 3
c) log x  4log x  log x 13 d) log  x   1  4log x 1  log x 1  13 4   8   4 8 2 2 109
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018 x  4  0 x  4
♥ Hƣớng dẫn giải : a) log x  4  log
x 1  1 (1) Điều kiện:     x  4 2 2 x 1  0 x 1
Khi đó phương trình(1)  log
(x  4)(x 1)  1  (x  4)(x 1)  2 2 2
 (x  4)(x 1)  4  x 5x  0  x  0 hoặc x = 5
So với điều kiện x > 4 ta chỉ nhận nghiệm x = 5
Vậy phương trình đã cho có nghiệm duy nhất là x = 5 x  2  0 x  2 b) 2
log (x  2)  log ( x  4)  0 (2) Điều kiện:    (I) 3 3 2 (x  4)  0 x  4 Khi đó phương trình (2) 2
 2log (x  2)  log(x  4)  0 3
 log (x  2)  log (x  4)  0  log (x  2)(x  4)2 2 2  0 3 3 3       x x  2 (x 2)(x 4) 1 ( 2)( 4) 1  
(học sinh tự giải tiếp)
(x  2)(x  4)  1 
Vậy phương trình đã cho có nghiệm x = 3 hoặc x  3  2
c) log x  4log x  log x 13 (3) Điều kiện: x  0 4 8 2 (3)  log
x  4log x  log x  13  log x  4log x  log x  13 1/2 2 3 4 8 2 2 2 2 1  13
2 log x  2 log x  log x  13 
log x  13  log x  3  x  8 (Thoûa ñieàu kieän). 2 2 2 3 2 2 3
Vậy phương trình có nghiệm duy nhất: x  8.
d) Điều kiện: x 1.Với điều kiện trên, phương trình trở thành 1 2 log x 1  2 log x 1  log x 1  13 2   2   2   3
 log x 1  3  x 1 8  x  9. Đối chiếu điều kiện, phương trình có nghiệm duy nhất x  9. 2  
Bài tập mẫu tham khảo 03 : Giải phương trình log  2 x  6  log x  2 1. 3  3   A. x  0 B. x  1 C. x  2 D. x  3
♥ Hƣớng dẫn giải : Cách 1: log  2 x  6  log
x  2 1  log  2
x  6  log 3 x  2 3  3   3  3   x  2 3
 x  2  0   
 x  0  x  3 Chọn D 2 x  6  3  x  2  x  3 110
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
Cách 2: Sử dụng máy tính Casio fx  570VN PLUS . Nhấn :
Màn hình hiển thị w1i3$Q)dp6$pi3 $Q)p2$p1r0=
Thay đổi giá trị nghiệm bằng phím !qua thao tác !r1=
Giáo viên cần file word vui lòng liên hệ
Thay đổi giá trị nghiệm bằng phím !qua thao tác !r2=
Zalo / đt / facebook : 0914 449 230
Thay đổi giá trị nghiệm bằng phím !qua thao tác !r3=. Chọn D
Bài 1: Giải các phương trình
a/ log x  log x  log x  33 b/ log [ .
x (x 1)] 1 c/ log (x  3)  log (x 1)  3 2 4 8 2 2 2 ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 02 : Giải phương trình sau đây: a/ log  2
x  3x  3  log 2x  3
b/ log(x  2)  log(x 3) 1log5 2  2   ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 111
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 03 : Giải phương trình sau đây:
a/ log (x  3)  log (x 1)  2  log 8
b/ log (x 1)  log (x 3)  log 10 1  4 4 4 2 2 2 ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 04 : a/ Phương trình log (3x  2)  2 có nghiệm là: 2 4 2 A. x  B. x  C. x  1 D. x  2 3 3
b/ Phương trình log (x  3)  log (x 1)  log 5 có nghiệm là: 2 2 2 A. x  2 B. x  1 C. x  3 D. x  0
c/ Phương trình log x  log (x 1) 1 có tập nghiệm là: 2 2 A.  1  ;  3 B. 1;  3 C.   2 D.   1 d/ Phương trình 2
log (5x  3)  log (x 1)  0 có 2 nghiệm x , x trong đó x x . iá trị của 3 1 1 2 1 2 3
P  2x  3x là 1 2 A. 5. B. 14. C. 3. D. 13. ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 112
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 05 : Giải phương trình sau đây: a/ 2
log (x  6)  log (x  2) 1 3 3
b/ log 2log 1 log (1 3log ) x 1 c/ 4 2 ln .
x log (x  2x )  3ln x 4  3  2 2  2 ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 06 : Giải phương trình sau đây: a/ log (x  2)  6log 3x  5  2 2 1 8 1
b/ log (x  8)  log (x  26)  2  0
c/ log x  4  log x  5 .log 1 2   3   9 3 2 3 ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 113
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 07 : a/ (THPT Hoàng Hoa Thám - Khánh Hòa) : Phương trình log x 5  x   1 6    có tập nghiệm là. A. S  2;  3 B. S   1  ;  6 C. S  4;  6 D. S  1;  6
b/ (THPT Hoàng Hoa Thám - Khánh Hòa) : Giải phương trình log x 1  log x  3  3 4   4   . A. x 1 2 17 B. x 1 2 17 C. x  33 D. x  5 ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 2
Bài 08 : Nghiệm của phương trình log x 1  log 2x 1  2 là 3     3 A. Vô nghiệm B. x 1. C. x  2. D. x  3. ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 09 : a/ (THPT Nguyễn Trãi Lần 1) Tìm nghiệm của phương trình: log (3x  2)  3 . 2 10 16 8 11 A. x  B. x  C. x  D. x  3 3 3 3
b/ (THPT Đặng Thúc Hứa) Tìm nghiệm của phương trình log x 1  0.. 3 1 1 A. x  B. x   C. x  1  D. x  1 3 3
c/ (THPT chuyên KHTN lần 1) : Số nghiệm của phương trình x  2 log 1  2 . 114
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018 A. một số khác B. 2 C. 0 D. 1
d/ (THPT Nguyễn Đăng Đạo) : Giải phương trình log 4x 1  4 3   21 63 11 A. x  B. x  C. x  20 D. x  2 4 4 ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 10 : a/ (THPT Nguyễn Thị Minh Khai – Khánh Hòa) : Phương trình log (x  3)  log (x 1)  3 có 2 2
nghiệm là: A. x 11 B. x  7 C. x  5 D. x  9 1
b/ (THPT QG – 2017 ) : Tìm nghiệm của phương trình log x 1  . 25   2 23 A. x  B. x  6  C. x  4 D. x  6 2 ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 11 : Giải các phương trình 1/ log x x   Đáp số: x  3 . x  2 4 5 1 1  1 3 2/ x x ; Đáp số: x  ; x  . x  2 log 5 8  3  2 2 2 3/ log
x x x
 ; Đáp số: x  3. x  3 2 2 2 3 1 3 1  13
BT Tƣơng tự : a/ log
x 1  2 ; Đáp số: x  5. b/ log x x
 ; Đáp số: x   . x  2 9 8 12 2 3 5  x3   22 ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 115
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 12 : Giải các phương trình
1) log (9  2x )  3  x
2) log (3x  8)  2  x 2 3 3) x x 1 log (3 1).log (3   3)  6 4) x 1
log (5   25x )  2 3 3 2 ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 13 : ự t ng trưởng của một loài vi khuẩn tuân theo công thức    A. rx f x
e , trong đó A là số
lượng vi khuẩn ban đầu, r là tỉ lệ t ng trưởng r  0 , x (tính thoe giờ) là thời gian t ng trưởng. 116
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
Biết số lượng vi khuẩn ban đầu có 1000 con và sau 10 giờ là 5000 con. ỏi sau bao lâu thì số lượng
vi khuẩn t ng gấp 25 lần? A. 50 giờ. B. 25 giờ. C. 15 giờ. D. 20 giờ. ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 14 : Các loại cây xanh trong quá trình quang hợp sẽ nhận được một lượng nhỏ cacbon 14 (một
đồng vị của cacbon). Khi một bộ phận của cây xanh đó bị chết thì hiện tượng quang hợp cũng
dừng và nó sẽ không nhận thêm cacbon 14 nữa. Lượng cacbon 14 của bộ phận đó sẽ phân hủy một
cách chậm chạp và chuyển hóa thành nitơ 14. Biết rằng nếu gọi N t  là số phân tr m cacbon 14
còn lại trong một bộ phận của một cây sinh trưởng từ t n m trước đây thì N t  được tính theo t
công thức N t    500 100. 0,5
%. Phân tích mẫu gỗ từ một công trình kiến trúc cổ, người ta thấy
lượng cacbon 14 còn lại trong mẫu gỗ đó là 65% . ãy xác định niên đại của công trình đó A. 3656 n m. B. 3574 n m. C. 3475 n m. D. 3754 n m ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 15 : Khi cho dầu n đang sôi ở nhiệt độ 0
219 C vào tủ lạnh thì ta có hàm số biểu thị sự giảm
nhiệt độ của dầu n là   0,17t T t k e  0 ( ) .
6, ( C),t  0 , trong đó k là hằng số. Tìm thời điểm t mà 0 nhiệt độ giảm tới 0 0 C 2 100 ln A. 2 100 ln 37, 5 t  . B. t  . C. t  . D. t  75 0 0,17 ln 37,5 0 0,17 ln 75 0 17 0 17 ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 117
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 3x 2
2  5y  4y
Bài 16 (Đề thi ĐH năm 2012) : Giải hệ phương trình x x 1 4  2    y  2x  2 ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 17 (THPT Lạc Long Quân – Khánh Hòa) : Cường độ một trận động đất M được cho bởi công
thức M  log A – log A , với A là biên độ rung chấn tối đa và A là một biên độ chuẩn (hằng số). 0 0
Đầu thế kỉ XX , một trận động đất ở an Francisco có cường độ 8,3 độ Richter. Trong cùng n m
đó, một trận động đất khác ở Nam Đại Tây Dƣơng có cường độ 7,3 độ Richter. Hỏi trận động đất
ở an Francisco có biên độ gấp bao nhiêu lần biên độ của trận động đất ở Nam Đại Tây Dương ? A. 5 B. 10 C. 13,1 D. 11, 2 ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài 18 (THPT Ischool Nha Trang) : Sự t ng trưởng của một loài vi khuẩn được tính theo công thức ( ) rx
f x Ae , trong đó A là số lượng vi khuẩn ban đầu, r là tỷ lệ t ng trưởng r  0 , x (tính theo
giờ) là thời gian t ng trưởng. Biết số vi khuẩn ban đầu có 1000 con và sau 10 giờ là 5000 con. Hỏi
sao bao lâu thì số lượng vi khuẩn t ng gấp 10 lần? A. 5ln 20 (giờ). B. 5ln10 (giờ). C. 10log 10 (giờ). D. 10log 20 (giờ). 5 5 ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 118
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< 3 x 2
Bài 19 : Cho phương trình 2 log m
 2x  5x  , với m là tham số. Tìm tất cả các giá trị của m 2 3 3
để phương trình trên có một nghiệm là A. 3  4 2 2  m  2 B.  m  4 hoặc 34 0  m  2 C.  m  4 hoặc 34 0  m  2 D. m  2 ☺ Giải :
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<
Bài tập trắc nghiệm phƣơng trình LOGARIT dạng CƠ BẢN
Câu 01 : Phương trình 2
log x  log x  log
4x có nghiệm chia hết cho 2 2 2   A. 5 B. 2 C. 3 D. 4
Câu 02 (THPT Lƣơng Tài) : Nghiệm của phương trình log x 1  3 là. 2   A. x  9 B. x  2 C. x  5 D. x 12
Câu 03 (THPT Hoàng Quốc Việt) : Nếu log 243  5 thì x bằng: x A. 3 . B. 2 C. 4 D. 5
Câu 04 (THPT Thuận Thành 2) : Giải phương trình log 2x 1  3 2   9 3 A. x  5 B. x  8 C. x  D. x  2 2
Câu 05 (Sở GDĐT Lâm Đồng lần 2) : Giải phương trình : log 3x 1  1  4 . 2 17 13 20 A. x  B. x  C. x  D. x  5 3 3 3
Câu 06 (THPT Trần Cao Vân - Khánh Hòa) : Phương trình log 3x  2  3 có nghiệm là: 3   119
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018 25 11 29 A. B. 87 C. D. 3 3 3
Câu 07 (THPT Hoàng Văn Thụ - Khánh Hòa) : Tìm số thực x biết log 2  x  2 . 3   A. x  4  B. x  7  C. x  6 D. x  6 
Câu 08 (TTGDTX Vạn Ninh - Khánh Hòa) : Nghiệm của phương trình log  x   1  2 là. A. 2e 1 B. 2 e 1 C. 101 D. 1025
Câu 09 (THPT Yên Lạc) : Tập nghiệm của phương trình 2
ln x  2ln x là: A. 0; B. C. 0; D. \   0
Câu 10 (thi thử Cụm 7 – Tp.HCM) : Tìm nghiệm của phương trình: log 3x 1  3 2   A. x  5 B. x  1 C. x  3 D. x  4
Câu 11 (THPT Nguyễn Tất Thành) : Tìm số nghiệm của phương trình 2 log (x 1)  log 2x 1  2 3   3 A. 2 B. 0 C. 1 D. 3
Câu 12 (THPT Nguyễn Quang Diêu) : Tìm nghiệm của phương trình log log x 1. 3  2  A. x  2 . B. x  6 . C. x  8 . D. x  9 .
Câu 13 : Giải phương trình log 3x  2  3 . 3   25 29 11 A. x  B. x  C. x  87 D. x  3 3 3
Câu 14 (THPT Thái Phiên – HP) : Phương trình log 2x 1  log x  3  log x  3 có bao nhiêu 2      2 2 2  nghiệm? A. 2 . B. 4 C. 1 D. 3
Câu 15 (THPT chuyên Lê Hồng Phong) : Tìm tập nghiệm S của phương trình log
 2x 10x23 log x5 0 0,5  2  
Giáo viên cần file word vui lòng liên hệ A. S    7 . B. S  2;  9 .
Zalo / đt / facebook : 0914 449 230 C. S    9 . D. S  4;  7
Câu 16 (Sở GDĐT Hà Tĩnh lần 2) : Số nghiệm của phương trình 2
log x  log (3x) là. 3 3 A. 1. B. 0 . C. 3 . D. 2 .
Câu 17 (Sở GDĐT Hà Tĩnh lần) : Số nghiệm của phương trình: log x  log x  log x 11 là. 2 4 8 120
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018 A. 2 . B. 3 C. 1 D. 0
Câu 18 (THPT Lý Nhân Tông) : Phương trình log x  log x  6  log x  2 có nghiệm là. 5 5   5   A. 2  B. 3  C. 2 D. 3
Câu 19 (THPT Lý Nhân Tông) : Tổng tất cả các nghiệm của phương trình
log x  2log x  2  log . x log x bằng. 2 7 2 7 A. 10 B. 13 C. 11 D. 15
Câu 20 (THPT Tiên Du 1) : Số nghiệm của phương trình 2 log x 1  1 là. 2   A. 2 B. 1 C. 3 D. 4
Câu 21 (Sở GDĐT Lâm Đồng lần 3) : Phương trình  2
log x  2x  7 1 log x có tập nghiệm là. A. 1;  7 B.   7 C.  1  ;  7 D.   1
Câu 22 (THPT Nguyễn Chí Thanh - Khánh Hòa) : Tập nghiệm của phương trình
log (x  3)  log (x 1)  3 là 2 2 7  A.   5 B.  1  ;  5 C.   D.   6 2 
Câu 23 : Giải phương trình log 2x  2  3 . 2   A. x  4 B. x  5 C. x  2 D. x  3
Câu 24 (THPT Kim Liên - HN) : Tìm tập nghiệm S của phương trình log  x  32  8. 2 A. S   1  ;  5 B. S  1;  5 C. S   7  ;  1 D. S   1  ;  7
Câu 25 : Phương trình 2 log x  log
x 1  0 có bao nhiêu nghiệm thực ? 2 4 A. 4 B. 2 C. 3 D. 1
Câu 26 : Nghiệm của phương trình log x  log x  2 1. 3 3   A. x  3  .
B. x  1 hoặc x  3  .
C. x 1, x  3.
D. Phương trình vô nghiệm.
Câu 27 (THPT Gia Lộc 2) : Giải phương trình 2log  2
x x 1  log x 1 . 2    2
A. x  0, x  2 B. x  0 C. x  2 D. vô nghiệm 121
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
Câu 28 (Sở GDĐT Lâm Đồng lần 1) : Nghiệm của phương trình 2
log (x 1)  log (2x 1)  2 là: 3 3 A. 1 B. Vô nghiệm C. 3 D. 2
Câu 29 (THPT Hoàng Văn Thụ - Khánh Hòa) : Số nghiệm thực của phương trình log  3 2
x  3x   log  2 x x  0 là. 3 1  3 A. 0 B. 2 C. 3 D. 1 1
Câu 30 (THPT Nguyễn Thái Học) : Nếu log x  log 9  log 5  log 2 ( a  0 ; a  1) thì x bằng: a 2 a a a 3 2 6 A. B. 3 C. D. 5 5 5
Câu 31 : Số nghiệm của phương trình log  2 x  6  log x  2 1 là: 3  3   A. 3 B. 2 C. 0 D. 1
Câu 32 (THPT chuyên Lê Khiết) : phương trình log 3.2x 1  x 1 có hai nghiệm x , x thì tổng 4   1 2 x x là. 1 2 A. 4 . B. log 6  4 2 2   C. 6  4 2 D. 2
Câu 33 (THPT Nguyễn Huệ - Huế) : Tính tích các nghiệm của phương trình log x 1  2 3 A. 8  B. 6  C. 20  D. 3
Câu 34 : Cho hàm số y  ln 2 x  
1 . Nghiệm của phương trình y'  0 : A. x  0 hay x 1 B. x  1 C. x  1  D. x  0
Câu 35 : Phương trình log x  log x  2 có nghiệm là : 5 7   1 1 A. x  B. x  C. x  7 D. x  5 5 7
Câu 36 : Nghiệm của phương trình log log x  1 là : 2  4  A. 8 B. 4 C. 16 D. 2
Câu 37 : Phương trình log  x 3  log  x  2 1log5 có bao nhiêu nghiệm ? A. 1 B. 3 C. 2 D. 0 122
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018 4
Câu 38 : Phương trình 2log 2x  log  x  2 1  có bao nhiêu nghiệm ? 8 8 3 A. 1 B. 2 C. 3 D. 4
Câu 39 : Tìm nghiệm của phương trình log 3x  2  3 . 3   25 29 11 A. B. C. 87 D. 3 3 3
Câu 40 : Số nghiệm của phương trình log .
x log 2x 1  2log x là : 2 3   2 A 0 B. 1 C. 2 D. 3 .
Câu 41 : Phương trình log x  2 1  0 có bao nhiêu nghiệm ? 3   A. 0. B. 2. C. 1. D. 3.
Câu 42 : Cho biết chu kì bán hủy của chất phóng xạ Plutôni Pu239 là 24360 n m (tức là một lượng
Pu239 sau 24360 n m phân hủy thì chỉ còn lại một nửa). Sự phân hủy được tính theo công thức
S = Aert, trong đó A là lượng chất phóng xạ ban đầu, r là tỉ lệ phân hủy hàng n m (r < 0) , t là thời
gian phân hủy, là lượng còn lại sau thời gian phân hủy t. Hỏi sau bao nhiêu n m thì 10 gam Pu239
sẽ phân hủy còn 1 gam có giá trị gần nhất với giá trị nào sau? A. 82135 B. 82335 C. 82235 D. 82435
Câu 43 (THPT Đoàn Thị Điểm – Khánh Hòa) : Gọi S là tổng tất cả các nghiệm của phương trình log
3.2x 1  2x 1 . Tính S . 2   A. S  0 B. S  1  3 1 C. S  D. S  2 2
Câu 44 (THPT Tôn Đức Thắng – Khánh Hòa) : Phương trình log 5 – 2x  2 – x có hai nghiệm x , x 2   1 2
Tính giá trị của A x x x x là 1 2 1 2 A. 2 B. 3 C. 9 D. 1 123
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
Câu 45 (THPT Huỳnh Thúc Kháng – Khánh Hòa) : Nghiệm của phương trình log 2x 5 log 2x   5 1 là: 3   3   A. x  log 2 B. x  3 C. x  log 10 D. x  4 2
Câu 46 (THPT Nguyễn Thiện Thuật – Khánh Hòa) : Cho log x  4 3
Tính giá trị biểu thức 2 3
K  log x  log x  log x 4 3 3 3 23 23 23 23 A. K  B. K  C. K   D. K   2 3 3 2
Câu 47 (THPT Nguyễn Thiện Thuật – Khánh Hòa) : Tìm nghiệm phương trình log x  2 . A. x 100 B. x x e C. x  4 D. x  1
Câu 48 (Trƣờng PT Hermann Gmeiner– Khánh Hòa) : Với 0  a  1, nghiệm của phương trình 3 log x  log x  log x  là: 4 2 a a a 4 a a a A. x  B. x  C. x  D. x a 4 3 2
Câu 49 (THPT Lai Vung 2 – Đồng Tháp) : An là học sinh giỏi
lớp 6 , do thành tích học tập tốt nên hè qua An được gia đình
cho đi tham quan đỉnh núi Fansipan nằm giáp ranh giữa hai
tỉnh Lào Cai và Lai Châu, bằng phương tiện cáp treo. Khi lên
đến đỉnh em cảm thấy hơi khó thở và được bố giải thích là do
áp suất không khí bị giảm. Là học sinh lớp 12 bạn hãy giúp
An tính xem áp suất không khí ở độ cao 3000m khoảng bao
nhiêu milimet thuỷ ngân? Biết rằng áp suất không khí
PmmHg  , đọc là milimet thuỷ ngân) suy giảm so với độ cao x mét  theo công thức P  P xi e , 0
trong đó P  760 mmHg , i là hệ số suy giảm và ở độ cao 1000m thì áp suất của không khí là 0   672, 7  1 mmHg  .
A. P  500mmHg  .
B. P  512mmHg  .
C. P  527mmHg  .
D. P  540mmHg  . 124
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
Câu 50 : Cho phương trình log
 2x 5x2020 1 0 có hai nghiệm là x ,x . Tính 2 2 x x . 1  1 2 1 2 2016 A. 51. B. 16 . C. 17 . D. 18 .
Câu 51 : Cường độ của một trận động đất được đo bằng độ Richter. Độ Richter được tính bằng
công thức M  log A  log A , trong đó A là biên độ rung tối đa đo được bằng địa chấn kế và là 0
biên độ chuẩn (hằng số). Vào ngày 312  2016 , một trận động đất cường độ 2, 4 độ Richter xảy
ra ở khu vực huyện Bắc Trà My, tỉnh Quảng Nam; còn ngày 16 10  2016 xảy ra một trận động
đất cường độ 3,1 độ Richter ở khu vực huyện Phước Sơn, tỉnh Quảng Nam. Biết rằng biên độ
chuẩn được dùng chung cho cả tỉnh Quảng Nam, hỏi biên độ tối đa của trận động đất Phước Sơn
ngày 16 10 gấp khoảng mấy lần biên độ tối đa của trận động đất Bắc Trà My ngày 3 12? A. 7 lần. B. 5 lần. C. 4 lần. D. 3 lần.
Câu 52 (THPT Lạng Giang 2) : Phương trình x     2 log 1
log x  2x m có nghiệm duy nhất khi và chỉ khi  5  5 m m  A.   4  B. 4  m  1 m  1  5 5 m  C.  m  D. 4 4  m  1
Câu 53 (THPT Đa Phúc – HN) : Phương trình 4 2 16  x log  2
16  2x x   0 có bao nhiêu nghiệm? A. 4 B. 2 C. 3 D. 1 125
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
PHƢƠNG PHÁP ĐẶT ẨN SỐ
Bài tập mẫu tham khảo 01 : Giải pt : 2 2 3
log (x 1)  log (x 1)  7 (*) 2 2
♥ Hƣớng dẫn giải : Điều kiện: x 1 khi đó pt (*) 2
 4log x 1  3log x 1  7  0 2   2   t 1
Đặt t  log x 1 , ta được phương trinh: 2  4t  3t  7  0   2   7 t   4
 Với t =1 : ta có log x 1 1  x 1  2  x  3 2        7 7 Với t  ta có log x 1 
x 1  2  x 1 2 2   7 7 4 4 4 4
Bài tập mẫu tham khảo 02 : Giải phương trình : 2
3log x  8log 3x  5  0 3 3
♥ Hƣớng dẫn giải : Điều kiện: x  0.
Với điều kiện trên phương trình 2
3log x  8log 3x  5  0 trở thành 3 3 2
3log x  81 log x 2
 5  0  3log x 8log x 3  0 . 3 3 3 3 t  3 
Đặt t  log x , phương trình trở thành 2
3t  8t  3  0  3 1 t    3
● Với t  3 , ta được 3
log x  3  x  3  27 (thỏa mãn). 3 1 1 1  1
● Với t   , ta được 3 log x    x  3  (thỏa mãn) 3 3 2 3 3
Giáo viên cần file word vui lòng liên hệ  1 
Vậy phương trình đã cho có tập nghiệm S   ; 27
Zalo / đt / facebook : 0914 449 230 2  3 
Bài tập mẫu tham khảo 02 (THPT Nguyễn Trãi Lần 1) : Tìm tập nghiệm của phương trình 1 1  1  log x   3 là A.  ;3 B. 3;  9 C.  ;9 D. 1;  2 3 log x 3  3  9
♥ Hƣớng dẫn giải : Điều kiện : x  0, x 1 1 2
Với điều kiện trên ta có: log x   3  log x   3 . 3 3 log x log x 9 3    x  x  log x log 1 2 3 3
 3log x  2  0  
(thõa điều kiện). Chọn B 3 3   log x  2  x  9 3
Casio : Sử dụng phím r Thao tác : 126
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
Bài 01 : Giải các phương trình 4 a/ 3 3 log x  log x
b/ log x  10log x  6  9 2 2 3 2 2 c/ 2
log 4x  log x  8  0 d/ 2 2
log x  log x 1  5  0 2 2 3 3 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 02 (THPT TH Cao Nguyên) : Số nghiệm của phương trình 2
log x  4log 3x  7  0 là. 3 3   A. 2 B. 0 C. 3 D. 1 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 03 (THPT Lý Thái Tổ) :Giải phương trình 2 2
log x  3.log x  2  log x  2 . Ta được mấy 2 2 2 nghiệm. A. 2 B. 1 C. 3 D. 0 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 127
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 04 (THPT Thanh Thủy) : Cho phương trình 2log x2  5log 9x  3  0 có các nghiệm x ; x . iá 3 3   1 2
trị biểu thức P x .x là 1 2 27 A. P  27 5 . B. P  9 3 . C. P  27 3 . D. P  . 5 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 05 : Phương trình log 4x2 3log x  7  0 có bao nhiêu nghiệm ? 2 2 A. 0 B. 2 C. 1 D. 3 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 1 2
Bài 06 : Phương trình 
1 có tổng các nghiệm là: 5  log x 1 log x 2 2 33 A. 12 B. 66 C. D. 5 64 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 07 : Số nghiệm của phương trình 3 2
ln x  3ln x  4ln x 12  0 là : A. 2 B. 0 C. 3 D. 1 128
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài tập trắc nghiệm phƣơng trình LOGARIT dạng ĐỔI BIẾN SỐ
Câu 01 (Sở GD – ĐT Hà Tĩnh lần 2) : Phương trình 2
log x  log x  2  0 có bao nhiêu nghiệm thuộc khoảng 1;100 ? A. 0 B. 2 C. 1 D. 3
Câu 02 (THPT chuyên Nguyễn Bỉnh Khiêm) : Phương trình 3 log x  log 3x 1  0 có tổng các 3 3 nghiệm bằng. A. 81 B. 3 C. 78 D. 84
Câu 03 (THPT ISCHOOL Nha Trang) : Tìm tất cả các giá trị của m để phương trình 2
log x m  2 .log x  3m 1  0 có 2 nghiệm x , x sao cho x .x  27 3   3 1 2 1 2 4 A. m  B. m  25 3 28 C. m  D. m  1 3
Câu 04 (THPT Đa Phúc – HN) : Tích hai nghiệm của phương trình 2
log x  6log x  8  0 bằng 3 3 A. 90 B. 729 C. 8 D. 6 2
Câu 05 (THPT Quảng Xƣơng 1) : Cho phương trình log(100 x ) log(10 x) 1 l  og 4.5  25.4  29.10
x . Gọi a và b
lần lượt là 2 nghiệm của phương trình. Khi đó tích ab bằng: A. 0 B. 1 1 1 C. D. 100 10 129
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018 4  x
Câu 06 (THPT chuyên ĐH Vinh) : Biết rằng phương trình 2 log x  log 
 có hai nghiệm là a , b . 3 3  3  Khi đó . a b  ? A. 81. B. 9 . C. 8 . D. 64 .
Câu 07 : Cho phương trình log x  log 9  3, phương trình này có hai nghiệm x , x . Tổng hai 3 x 1 2 nghiệm này bằng. A. 6 B. 9 C. 15 D. 12
Câu 08 : Tìm m để phương trình 2 2
log x  log x  3  m có nghiệm x 1;  8 . 2 2 A. 3  m  6 B. 6  m  9 C. 2  m  6 D. 2  m  3
Câu 09 : Với điều kiện x  0 .Tìm phương trình nào dưới đây tương đương với phương trình 2 2 log x  log x  2 2 2 1 A. 2 2log
x  2log x  2  0 B. 2 2 log x  log x  2  0 2 2 2 2 2 1 C. 2 4log
x  2log x  2  0 D. 2 4 log x  log x  2  0 2 2 2 2 2
Câu 10 : Cho phương trình 2
log x  log x  3  0 .Đặt t  log x thì phương trình đã cho trở thành 1 2 2 4 phương trình nào? 1 A. 2
t t  3  0 B. 2
2t t  3  0 4 1 C. 2
4t t  3  0 D. 2
t t  3  0 2
Câu 11 : Gọi x , x là nghiệm của phương trình log 2  log x  0 . Khi đó tích x .x bằng: 1 2 x 16 1 2 A. 1  B. 1 C. 2 D. 2  1 2
Câu 12 : Nếu đặt t  log x thì phương trình  1 2 5  log x 1
trở thành phương trình nào? log x 2 2 130
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018 A. 2
t  5t  6  0 B. 2
t  5t  6  0 C. 2
t  6t  5  0 D. 2
t  6t  5  0 1 2
Câu 13 : Nếu đặt t  log x thì phương trình 
1 trở thành phương trình nào? 4  log x 2  log x A. 2
t  2t  3  0 B. 2
t  3t  2  0 C. 2
t  2t  3  0 D. 2
t  3t  2  0
Câu 14 : Nghiệm bé nhất của phương trình 3 2 log x  2log
x  log x  2 là: 2 2 2 1 A. x  4 B. x  4 1 C. x  2 D. x  2
Câu 15 : Nếu đặt t  log x thì phương trình log 4x  log 2  3 trở thành phương trình nào? 2   2 x A. 2
t t 1  0 . B. 2
4t  3t 1  0 . 1 1 C. t   1 . D. 2t   3 . t t
Câu 16 : Nếu đặt t  log x thì phương trình 2 3
log x  20log x 1  0 trở thành phương trình nào? A. 2
9t  20 t 1  0 . B. 2
3t  20t 1  0 . C. 2
9t 10t 1  0 . D. 2
3t 10t 1  0 . 1 2
Câu 17 : Phương trình  1 4  ln x 2  có tích các nghiệm là: ln x 1 A. 3 e . B. . e C. e . D. 2 .
Câu 18 : Biết phương trình log9 x log9 x log3 27 4 6.2  2
 0 có hai nghiệm x , x . Khi đó 2 2
x x bằng : 1 2 1 2 82 A. 6642 B. 6561 C. 20 D. 90 131
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
Phần IV : BẤT PHƢƠNG TRÌNH MŨ - LOGARIT A. BẤT PHƢƠNG T RÌNH MŨ
Cơ sở lý thuyết : Khi giải các bất phương trình mũ ta cần chú ý tính đơn điệu của hàm số mũ.
Xét BPT ; Giải tương tự với các dấu ; ;  2 x 2 x  1  1
Giáo viên cần file word vui lòng liên hệ
Ví dụ : Giải bất phương trình:     3  27
Zalo / đt / facebook : 0914 449 230 2 2 x 2 x x 2 x 3  1  1  1   1 
HD Giải:       
  Ở đây cơ số a = 1/3 nên ta đổi chiều là xong  3  27  3   3  2 2
x  2x  3  x  2x 3  0  x ;   
1 3;
Ta cũng sử dụng các phương pháp giải tương tự như đối với phương trình mũ:
Đƣa về cùng cơ số.
Đặt ẩn phụ.
Logarit hóa ... 2 3x x6 3x7  1   1 
Bài tập mẫu tham khảo 01 : Giải bất phương trình:       7   49 
♥ Hƣớng dẫn giải : 2 3x x6 3x7 2
Bất phương trình đã cho tương đương với  1     2  3  x x6 6  x 1  4 7 7  7  7 5 2  3
x  7x  20  0    x  4 (vì cơ số a = 7 > 1 nên ta giữ nguyên chiều BPT) 3  5 
Vậy bất phương trình có tập nghiệm S   ; 4   .  3 
Bài tập mẫu tham khảo 02 : Giải bất phương trình: a/ 2x 1
3  10.3x  3  0 b/ xx 1 2 2   3  0 c / x 1
3  4.3 x 1  0 d/ 4x 3.2x   2  0
♥ Hƣớng dẫn giải : (sử dụng pp đặt ẩn phụ nhƣ bên phƣơng trình)
a/ Bất phương trình tương đương với 2 3.3 x 10.3x  3 0 . 132
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018 1 Đặt 3x t
 0 , bất phương trình trở thành 2
3t 10t  3  0   t  3. 3 1 1
Với  t  3, ta được x 1 3 3 3     3x  3  1   x 1. 3 3
Vậy bất phương trình đã cho có tập nghiệm S   1  ;  1 x 2
b/ Bất phương trình tương đương với 2   3  0 2x 2 2 t  3t  2 Đặt 2x t
 0, bất phương trình trở thành 2 t   3  0 
 0  t  3t  2  0 1 t  2 . t t
Với 1  t  2 , ta được 1 2x  2  0  x 1.
Vậy tập nghiệm của bất phương trình là S  0;  1 . x 12
c/ Bất phương trình tương đương với 2 3 
1 0  3 x  3x 12  0. 3x
t  3 thoaû maõn Đặt 3x t
 0 , bất phương trình trở thành 2
t t 12  0   t    loaïi . 4
Với t  3 , ta được 3x  3  x 1. Vậy bất phương trình có tập nghiệm S  1; .   . d/ Đặt 2x t
 0, bất phương trình trở thành 2
t  3t  2  0  1  t  2 .
Với 1  t  2 , ta được 1 2 x 2  0  x 1.Vậy bất phương trình có tập nghiệm S  0;  1
Bài 01 : Giải các bất phương trình sau 3x2 9 2 2  x 2 x3 x x6 22 x 2x 3   3    1   3   27  x  1 2 a/      b/ 1   7    c/ x 3x 2 2  4 d/ 1   e/      10  10   7   4   2   8  ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 133
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 02 : a/ Bất phương trình 36 0,5
x 1 có tập nghiệm là  1   1  A. 2; B. ;    C. ;    D.  3;    2   2  x x
b/ (THPT Đoàn Thị Điểm – Khánh Hòa) : Giải bất phương trình       2 2 3 2 3 . A. x  1  B. x  2  C. x  2  D. x  1  ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 1
Bài 03 : a/ Các số thực x thỏa mãn ( x x a a  )  1 2 A. x  1 B. x  0 C. x  0 D. Không có x nào
b/ Bất phương trình 5.4x 2.25x 7.10x    0 có nghiệm là A. 2   x  1  . B. 1   x  0 C. 0  x 1. D. 1 x  2
c/ Tìm tập nghiệm của bất phương trình 2x 1  2x2 2 x 3 2 2 2     448 9   9   9  A. S  ;    B. S   ;  2   C. S   ;    D. S   ;      2   2   2  ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 134
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 04 : a/ Giải bất phương trình 2.49x 5.14x 7.4x    0. A. S   ;    1 . B. S   ;   1 .
C. S  1;. D. S   1  ;.  x  1 
b/ Giải bất phương trình 1   .  2  A. x  0. B. x  1.  C. x  0. D. x  1. ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. x x
Bài 05 : a/ Giải bất phương trình 2  3  2  3 14. x  2  x  1  A.  B. 1   x 1 C.  D. 2   x  2     x 2 x 1 x x
b/ Giải bất phương trình sau  3 8   3 8   34 A. 4   x  4 B. 2   x  2 C. 6   x  6 D. 8   x  8 135
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. x x
Bài 06 : a/ (Sở GDĐT Hà Tĩnh) : Tập nghiệm của bất phương trình   2 0,3  0,09 là A.  ;  2  1; B.  2   ;1 C.  ;  2   D. 1; x 1
b/ Tập nghiệm của bất phương trình 2 3  là 9 A.  ;  4 B.  ;  4   C. 0; D.  4;   ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 07 : a/ (Trƣờng PT Hermann Gmeiner– Khánh Hòa) : Tập nghiệm của bất phương trình: 4x 3.2x   2  0 là A. ( 1  ;0) B.0  ;1 C. (0;1) D. ( ;  0) (1; ) 
b/ (THPT Nguyễn Chí Thanh– Khánh Hòa) : Nghiệm của bất phương trình 32.4x 18.2x  1 0 là 1 1 A. 4   x  1  B.  x  C. 2  x  4 D. 1 x  4 16 2 136
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Trắc nghiệm phần bất phƣơng trình mũ
Câu 01 : Nghiệm của bất phương trình x 1  x 3 9 36.3   3  0 là A. 1 x  3 B. 1 x  2 C. x  1 D. x  3
Câu 02 (THPT Đoàn Thị Điểm – Khánh Hòa) : Tìm tất cả các giá trị của tham số m sao cho phương trình x x 1 9 3    m có nghiệm. 9 A. m   4 B. m  0 C. m  1  5 D. m  8 1 5 2 x    2 
Câu 03 : Giải bất phương trình    
 .Một học sinh làm như sau:  5   5 
Bƣớc 1. Điều kiện: x  0   * . 1 5 2  2 x   2  1 Bƣớc 2.Vì 1 nên    5.     5  5   5  x 1
Bƣớc 3. Từ đó suy ra 1  5x x  . 5 137
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018  1 
Vậy tập nghiệm của bất phương trình đã cho là S   ;  \    0 .   5
Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào? A. Đúng. B. Sai ở bước 1. C. Sai ở bước 2. D. Sai ở bước 3 2 x 2 x 1  x5  2   5 
Câu 04 : Tìm tập nghiệm S của bất phương trình      .  5   2  A. S   ;  4  1; B. S   1  ;4 C. S   ;    1 4; D. S   4  ;  1 x 1   1  
Câu 05 : Tập nghiệm của bất phương trình     x 0, 25 3 là  2  A.5; . B.   ;5  . C.  ;5   . D. 5; .
Câu 06 : Giải bất phương trình x 3 2  2 x  9 . x  3 A. 0  x  3 . B.  . 0  x 1 x  3 C.  . D. x  3 . x  1
Câu 07 (THPT Lai Vung 1 – Đồng Tháp) : Tập nghiệm của bất phương trình 4x 2.25x 10x   là     A.  log 2;   . B.  log 2;   . 2  5 5   2   2  C. ;  log  . D.  . 2   5  x2  1  1
Câu 08 (Sở GDĐT Hà Tĩnh) : Nghiệm của bất phương trình    là:  3  27 A. x  5 . B. x  5. C. x  1  . D. x  1  x x
Câu 09 (Sở GDĐT Hà Tĩnh) Bất phương trình   2 2 2
 2 2 có tập nghiệm là A.  3   ;1 . B. 3   ;1 . C. 1  ;  3 . D.  1  ;3 .
Câu 10 (Sở GDĐT Hà Tĩnh) Bất phương trình 9x 3x
 6  0có tập nghiệm là 138
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018 A. 1; . B.   ;1  . C.  1   ;1 . D.  ;    1 .
Câu 11 (THPT Nguyễn Thiện Thuật – Khánh Hòa) : Tập nghiệm của bất phương trình 3.9x 10.3x
 3  0 có dạng S  [ ; a ]
b . Tính P b a . 3 A. P 1 B. P  2 5 C. P  2 D. P  2
B. BẤT PHƢƠNG TRÌNH LOGARIT
Cơ sở lý thuyết : Khi giải các bất phương trình LOGARIT ta cần chú ý tính đơn điệu của hàm số LOGARIT Xét BPT
; Giải tương tự với các dấu ; ; 
Ví dụ : Giải bất phương trình: log 3x 1 1 5  
Chú ý công thức : M = logaaM  1 3  x 1  0 x   1 
HD Giải: log 3x  
1  1  log 3x   1 1  log 5     3  x  ; 2 5 5 5   1 3  x 1 5   3  x  2
Ví dụ : Giải bất phương trình: log 4x 1  1  log
 2x 6x8 . 0,5 0,5  4x 11  0 
x  6x 8  0
HD Giải: log 4x 1  1  log
x 6x8 2 2 2
 x  6x 8  0   0,5 0,5 2 
x  2x 3  0 2
4x 11  x  6x  8  x    ;  4   2  ;    x  2   x     ;1 3;1
Ta cũng sử dụng các phương pháp giải tương tự như đối với phương trình mũ:
Đƣa về cùng cơ số.
Đặt ẩn phụ. ...
Bài tập mẫu tham khảo 01 : Giải bất phương trình a/ log  2
x  2x  2  0 b/ log x 1  log 8  x  1  . 1   1   2  5 5 139
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
♥ Hƣớng dẫn giải : a/ Bất phương trình log  2
x  2x  2  0 2  2
x  2x  2  0 x  1  2 2  
x  2x  2 1  x  2x  3  0   2
x  2x  2 1 x  3
Vậy tập nghiệm của bất phương trình là S   ;    1  3; 
Giáo viên cần file word vui lòng liên hệ x 1  0 b/ Điều kiện:   1 x  8 8   x  0
Zalo / đt / facebook : 0914 449 230
Với điều kiện trên bất phương trình trở thành : log x 1  log 8  x  1  5   5  
 log x 1  log 8  x 1  log  x 1 8  x  1 5   5   5        x   1 8  x 9 29 9 29 2
 5  x  9x 13  0   x  . 2 2  9  29 
Đối chiếu điều kiện, ta được tập nghiệm của bất phương trình là S  1;   . 2   7
Bài tập mẫu tham khảo 02 : Giải bất phương trình: log 2  log x   0 x 4 6
♥ Hƣớng dẫn giải : Điều kiện: 0  x 1. 1 7 1 1 7
Với điều kiện trên, bất phương trình trở thành log 2  log x   0   log x   0 . x 2 2 6 2 log x 2 6 2 2 1 1 7 6  3t  7t
Đặt t  log x , bất phương trình trở thành  t   0   0 2 t 2 6 6t  2 2 3t  7t  6   t  0    0  3 . t  t  3 2 2  1  1
● Với   t  0 , ta được   log x  0  log  log x  log 1  x 1   . 3 2 2 2 2 3 3 3  4  4
● Với t  3 , ta được log x  3  x  8 . 2  1 
Đối chiếu điều kiện, ta được tập nghiệm của bất phương trình là S  ;1   8;  . 3  4 
Bài tập mẫu tham khảo 03 : Giải bất phương trình: log x 1  3log
13  2x  1 log 5x 1 3   1   3   27 ♥ 1 13
Hƣớng dẫn giải : Điều kiện:  x  . 5 2 140
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
Với điều kiện trên, bất phương trình đã cho trở thành log x 1  log 13  2x  log 3  log 5x 1 3   3   3 3  
 log  x 1 13 2x   log 3 5x 1   x 1 13 2x  3 5x 1 3    3         x  4  2  2
x  4x 16  0  .  x  2  13 
Kết hợp điều kiện, bất phương trình có tập nghiệm S  2;   .  2 
Bài tập mẫu tham khảo 04 : Giải bất phương trình: 2log x 1  log x  3  2 3   3  
♥ Hƣớng dẫn giải : Điều kiện: x  3.
Với điều kiện trên, bất phương trình trở thành log  x  2 1  log x  3  2 3 3   x  2 1 x  2 1   2 x 4  log  2   9  x   1  9x 3 2
x 11x  28  0  . 3  x  3 x  3 x  7
Kết hợp điều kiện, bất phương trình có tập nghiệm S  3;47; 
Bài tập mẫu tham khảo 05 : Giải bất phương trình log 3x  2  log 6  5x 2 2  6   1  A. (0; +). B. 1;  . C.  ;3 . D.  3  ;  1 .  5   2   6 x  6  5x  0  ♥ 5 2 6
Hƣớng dẫn giải :      x 3  x  2  0 2 3 5 x   3
log 3x  2  log 6  5x  3x  2  6  5x x  1 2 2 6
Vậy nghiệm của bất phương trình là: 1  x  . 5
Bài 01 : Giải bất phương trình 3x 1 a/ 2
log (2x  5x  3)  2
b/ log (x 1)  log (11 ) x  3 c/ log 1 2 3 3 1 x  2 3 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 141
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 02 : Giải bất phương trình a/ log x  log .
e ln  x  3 1 b/ log x 1  0 . c/ log 4x 1  4 3   3 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Bài 03 : Giải bất phương trình : a/ log (3x  2)  3 . b/ log 5  x  log x 1  1 0,3   0,3   2 ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Câu 08 (THPT Quế Vân2 ) : Giải bất phương trình log 9 2x x  
 3 ta được tập nghiệm là ? 2   A. S   ;  03; . B. S   ;  03;2log 3 . 2  C. S   ;  03;2log 3 .
D. x  0 hoặc x  3 . 2  ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
.............................................................................................................................................................................. 142
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
..............................................................................................................................................................................
Câu 09 : Tìm tập nghiệm của bất phương trình 2
ln x  3ln x  2  0 . A.  e 2 ;  e ;  . B. 2 e ;  . C.  e 2 0;  e ;  . D.  ;   1 2;. ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Câu 10 (THPT Phan Bội Châu – Khánh Hòa) : Tập xác định của hàm số 2
y  ln x  3ln x  2 là A.  e 2 0;  e ;   B.  ;   1 2; C.  e 2 ;  e ;   D. 2 e ;   ☻ Giải :
..............................................................................................................................................................................
..............................................................................................................................................................................
..............................................................................................................................................................................
Trắc nghiệm phần bất phƣơng trình Logarit
Câu 01 : Giải bất phương trình log 2x 1  1. 1   2 1 3 3 1 3 A. x  B. x  C. 0
x  D.  x  2 4 4 2 4
Câu 02 : Giải bất phương trình log 2x   1  4 . 3 5 5 A. x  5. B. x  . C. x  . D. x  5 . 2 2
Câu 03 (Trƣờng PT Hermann Gmeiner– Khánh Hòa) : Giải bất phương trình log x  4  2 1   3 37 37 14 A. x  4 . B. 4  x  . C. x  . D. 4  x  . 9 9 3
Câu 04 : Giải bất phương trình log (2  x)  log x 1 . 2 1   2 A. x  1  ;2. B. x  1  ;2. C. x  ;  2. D. x  1  ;.
Câu 05 : Tập nghiệm của bất phương trình 2
ln x  ln 4x  4 là A. 2; . B. \   2 . C. 1; . D. 1; \  2 . 143
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
Câu 06 : Có bao nhiêu số nguyên a là nghiệm bất phương trình 2 log a  log a ? 0,5 0,5 A. 1. B. 0. C. Vô số. D. 2.
Câu 29 (THPT Huỳnh Thúc Kháng – Khánh Hòa) : Tập nghiệm S của bất phương trình 2
log x  5log x  6  0 là: 2 2 1   1  A. S  ; 64   B. S  0;    2   2  1
C. S  64; D. S  0; 64;     2
Câu 08 : Tập nghiệm của bất phương trình 2
log (x x)  log ( 2  x  4) là 0,8 0,8 A.  4   ;1 B.  ;  4  1;2 C.  ;  4
 1; D. ;  46;
Câu 09 (THPT Đoàn Thị Điểm – Khánh Hòa) : Xét các số thực dương a, b thỏa mãn 2 2
4log a  log b  1. Tìm giá trị lớn nhất của a . 1 A. . B. 1. C. 10 . D. 2 10 10
Câu 10 : Tìm tập nghiệm của bất phương trình 2log (x 1)  log (5  ) x 1. 2 2 A.  3  ;  3 . B. 1;5. C. 1;  3 . D. 3;5.
Câu 11 : Tìm tập nghiệm của bất phương trình log log 2x 1   0 1  2   . 2  3   3   3  A. 0; .   B. 1; .   C. 0  ;1 . D. ; 2 .    2   2   2 
Câu 12 (THPT Nguyễn Thái Học – Khánh Hòa) : Tập Giải bất phương trình log  2
x  2x  8  4  1  2 x  6  x  6  A.  B.  x  4 x  4  6   x  4   6   x  4  C.  D.  2  x  4 2  x  4  3 
Câu 13 (THPT Đông Sơn 1) : Bất phương trình 2 log x x
 2  log 5 có nghiệm là: 1   2  4  2 A. x  ;  2  1; B. x  2  ;  1 144
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018 C. x  1  ;2 D. x  ;    1 2;
Câu 14 (THPT Tôn Đức Thắng – Khánh Hòa) : Tập nghiệm của bất phương trình log x² –1  3 là 2  
A. S  –3; –  1 1;  3 .
B. S  –2; –  1 1;  2 . C. S  – ;  –  1 1; . D. S  – ;
 –22; .
Câu 15 : Một nghiên cứu cho thấy một nhóm học sinh được cho xem cùng một danh sách các loài
động vật và được kiểm tra lại xem họ nhớ bao nhiêu % mỗi tháng. Sau t tháng, khả năng nhớ
trung bình của nhóm học sinh được cho bởi công thức M t   75  20ln t  
1 , t  0 (đơn vị %). Hỏi
sau khoảng bao lâu thì nhóm học sinh nhớ được danh sách đó dưới 10%? A. 24.79 tháng B. 23 tháng
Giáo viên cần file word vui lòng liên hệ C. 24 tháng Z alo / đt /
facebook : 0914 449 230 D. 22 tháng
Câu 16 : Một công ty vừa tung ra thị trường sản phẩm mới và họ tổ chức quảng cáo trên truyền
hình mỗi ngày. Một nghiên cứu thị trường cho thấy, nếu sau x quảng cáo được phát thì số % 100
người xem mua sản phẩm là P(x)  , x  0 0.015 1
. Hãy tính số quảng cáo được phát tối thiểu 49 x e
để số người mua đạt hơn 75%. A. 333 B. 343 C. 330 D. 323
Câu 17 (THPT Lý Tự Trọng – Khánh Hòa) : Tập xác định của hàm số y  ln x  2 là: A. 2 e ;  . B. 0; .  1  C. . (22). D. ;    . 2 e
Câu 18 (THPT Phan Bội Châu – Khánh Hòa) : Tìm tập nghiệm S của bất phương trình:
log  x  7  log  x   1 : 4 2 A. S  [ 1  ;2]. B. S  [ 7  ;2) . C. S   1  ; 2 . D. S  ( 7  ;2) . 145
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
Câu 19 (THPT Trần Bình Trọng – Khánh Hòa) : Tập nghiệm của bất phương trình
2log (x 1)  log (5  ) x 1 là 2 2 A. 1;  3 . B. 1;5 . C.  3  ;  3 . D. 1;  3
Câu 20 (THPT Nguyễn Trãi Lần 1) : Tìm tập nghiệm của bất phương trình log  2
x  3x  2  1  . . 1  2 A. 0;2 . B.   ;1  . C. 0;  1  2;  3 . D. 0;2 3;7 .
Câu 21 (THPT Nguyễn Tất Thành) : Giải bất phương trình log 2x 1  3. . 3   1 1 A.  x 14 . B. x  5. C.  x  5 . D. x 14 . 2 2
Câu 22 (THPT Nguyễn Tất Thành) : Tập nghiệm của bất phương trình log 2x 1  1  là: 1   2  3   3   3   1 3  A. ;    . B. 1;   . C. ;    . D. ;   .  2   2   2   2 2 
Câu 23 : Bất phương trình log 2x 1  log
5  x có tập nghiệm là: 1   1   2 2  1  A. 2; . B. 2;5 . C.  ;  2. D. ; 2   .  2 
Câu 24 (THPT An Lão lần 2) : Tìm tập nghiệm S của bất phương trình log 2x  3  log 1 x . 3   3    2    3  2    3    2   A. ;    . B. ;   . C. ;1   . D. ;    .  3   2 3   2   3 
Câu 25 (THPT Lý Thái Tổ) : Bất phương trình: log 3x  2  log 6  5x có tập nghiệm là. 2 2  1   6  A. 0; . B.  ;3 . C.  3  ;  1 . D. 1;  .  2   5 
Câu 26 (THPT Lƣơng Tài 2) : Giải bất phương trình log 3x  4  4
 . Tập nghiệm T của bất 1   2 phương trình là.  4   4  A. T   ;  4 .
B. T  4; . C. T   ; 4   . D. T   ; 4   .  3   3 
Câu 27 (TTGDTX Cam Ranh - Khánh Hòa) : Tập nghiệm của bất phương trình log 4x  3 là: 2 A. 2; . B. 0;2 . C.  ;  2 . D. 0; . 146
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – PHƢƠNG TRÌNH MŨ - LOGARIT 2018
Câu 28 (THPT Trần Hƣng Đạo – Nam Định) : Tìm tập nghiệm S của bất phương trình log 2x   1  2  . 0,5  5   5  1 5   1 5  A. S    ;  .
B. S   ;   . C. S  ; . D. S   ;  .    2   2  2 2   2 2  2
Câu 29 : Cho hàm số 4 . x 3x y
, khẳng định nào sau đây sai? A. f x 2
 3  x  2xln 2  ln3 . B. f x 2
 3  x xlog 4 1. 3 C. f x 2
 3  x log3 2xlog 2  log3. D. f x 2
 3  x  2xlog 2 1 . 3
Câu 30 (Trích Đề minh họa 2017) : Cho hàm số   2 2 . x 7x f x
. Khẳng định nào sau đây là khẳng định sai? A. f x 2
1 x x log 7  0. 2 B. f x 2
1 xln 2  x ln 7  0. C. f x 2
1 xlog 2  x  0. 7
D. f x 1 1 x log 7  0. 2 5
Câu 31 (THPT Lê Hồng Phong – Khánh Hòa) : Cho hàm số x x 1 f (x) 5 .7  
. Khẳng định nào sau đây là khẳng định sai ? A. 5      f (x) 1 x x log 7 log 7 0 . 5 5 B. 5      f (x) 1 x ln 5 x ln 7 ln 7 0 . C. 5
f (x)  1  x log 5  x  1  . 7 D. 4
f (x)  1  1 x log 7   log 7 . 5 5 147
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Phần V : TO[N LÃI SUẤT - ỨNG DỤNG CƠ SỞ LÝ THUYẾT
Lãi đơn: Lãi được tính theo tỉ lệ phần trăm trong một khoảng thời gian cố định trước.
Ví dụ: Khi ta gửi tiết kiệm 50 (triệu đồng) vào một ngân hàng với lãi suất 6,9%/năm thì sau một
năm ta nhận được số tiền lãi là: 506,9%  3, 45 (triệu đồng).
Số tiền lãi này như nhau được cộng vào hằng năm. Kiểu tính lãi này được gọi là lãi đơn.
Sau hai năm số tiền cả gốc lẫn lãi là: 50  2.3, 45  56,9 (triệu đồng).
Sau n năm số tiền cả gốc lẫn lãi là: 50  .
n 3, 45 (triệu đồng).
Lãi kép: Sau một đơn vị thời gian (kỳ hạn), tiền lãi được gộp vào vốn và được tính lãi. Loãi lãi
này được gọi là lãi kép.
Ví dụ: Khi ta gửi tiết kiệm 50 (triệu đồng) vào một ngân hàng với lãi suất 6,9%/năm thì sau một
năm, ta nhận được số tiền cả gốc lẫn lãi là:
50  3, 45  53, 45 (triệu đồng).
Toàn bộ số tiền này được gọi là gốc.
Tổng số tiền cuối năm thứ hai là: 53, 45  53, 456,9%  53, 451 6,9%
C[C DẠNG B\I TO[N ĐIỂN HÌNH
Bài toán 1: (Lãi kép gửi 1 lần)
Một người, gửi vào ngân hàng số tiền là a đồng, với lãi suất kép hàng tháng là r% (Kỳ hạn một tháng).
Tính cả vốn lẫn lãi Tn sau n tháng?
Phương pháp: Gọi Tn là tiền vốn lẫn lãi sau n tháng, ta có:
Tháng 1 ( n  1): T a ar a 1 r 1  
Tháng 2 ( n  2 ): T a 1 r  a 1 rr a 1 r 2 2
……………………………………………………..  
Tháng n : T a ra r r ar n  n 1  n 1 n 1 1 1  148
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 n Vậy:
T a r n 1  (1)
Trong đó: a là số tiền vốn có ban đầu, , r lã lãi suất (%) hàng tháng (kỳ hạn 1 tháng), n là số tháng,
T là số tiền vốn lẫn lãi sau n tháng. n
Bài tập mẫu tham khảo 01 : Bác An muốn gửi số tiền tiết kiệm 50000000 đồng vào ngân hàng
BIDV với lãi suất kép kì hạn 1 tháng là 0,35% /tháng. Hỏi sau 5 tháng số tiền cả gốc lẫn lãi của bác
An là bao nhiêu, biết rằng lãi suất hàng tháng không thay đổi? ♥ n
Hướng dẫn giải : Từ công thức : T a r n 1 
Số tiền cả gốc lẫn lãi của bác An là : T    5 50000000 1 0,35%  50881146 (đồng)
Bài tập mẫu tham khảo 02 : Chị Trang có số tiền là 100000000 đồng, chị muốn gửi tiền tiết kiệm
vào ngân hàng SML với lãi suất kép kỳ hạn 1 tháng là 0,36% / tháng. Để được 110000000 đồng chị
Trang phải mất bao nhiêu tháng gửi, biết rằng lãi suất hàng tháng không thay đổi?
♥ Hướng dẫn giải : T  ln n   n T Ta
Từ công thức : T a r n n n      n 1  ta suy ra 1 rn log 1r a a ln 1 r  110000000 ln
Số tháng tối thiểu phải gửi là: 100000000 n   (tháng)    26,52267649 ln 1 0,36%
Vậy thời gian tối thiểu chị Trang phải gửi là 27 tháng trong ngân hàng SML
Bài tập mẫu tham khảo 03 : Bà Thu có số tiền là 100000000 đồng gởi tiết kiệm ngân hàng trong
vòng 13 tháng thì lãnh về được 105000000 đồng. Hỏi lãi kép hàng tháng với kỳ hạn 1 tháng của
ngân hàng là bao nhiêu, biết rằng lãi suất hàng tháng không thay đổi (làm tròn đến số thập phân thứ 4)?
♥ Hướng dẫn giải :
Giáo viên cần file word vui lòng liên hệ n
Từ công thức : T a r n 1 
Zalo / đt / facebook : 0914 449 230 T n T
ta suy ra n  1 rn nr  1 a a 105000000 Lãi suất hàng tháng là: 15 r  1  0,38% 100000000 149
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Bài toán 2: (Lãi kép gửi một lần)
Một người, gửi vào ngân hàng số tiền là a đồng, với lãi suất kép là r%(Tính theo kỳ). Tính cả vốn lẫn
lãi Tn sau n kỳ? Phương pháp:
Gọi Tn là tiền vốn lẫn lãi sau n kỳ, ta có:
Kỳ 1 ( n  1): T a ar a 1 r 1  
Kỳ 2 ( n  2 ): T a 1 r  a 1 rr a 1 r 2 2
……………………………………………………..   n
Kỳ n : T a ra r r a
r Vậy: T a r n 1  (2) n  n 1  n 1 n 1 1 1 
Trong đó: a : số tiền vốn ban đầu, r : lãi suất (%) hàng kỳ, n là số kỳ, Tn : tiền vốn lẫn lãi sau n kỳ.
Từ công thức (2) ta tính được các đại lượng khác như sau: T ln n T T 1) a n  2) n n r  1 3) n a  ln 1 r n a 1 r
Bài tập mẫu tham khảo 01 : Một người gửi tiền tiết kiệm 100000000 đồng vào một ngân hàng
a/ Hỏi sau 10 năm, người đó nhận được bao nhiêu tiền cả vốn lẫn lãi, biết rằng người đó gửi theo
kỳ hạn 6 tháng, lãi suất kép là 5,3%/năm và người đó không rút lãi ở tất cả các định kỳ trước đó.
b/ Hỏi sau 10 năm, người đó nhận được bao nhiêu tiền cả vốn lẫn lãi, biết rằng người đó gửi theo
kỳ hạn 3 tháng, lãi suất kép là 4,8%/năm và người đó không rút lãi ở tất cả các định kỳ trước đó. ♥ 10.12
Hướng dẫn giải : a/ 1 kỳ là 6 tháng, suy ra 10 năm là  20 kỳ 6 5, 3
lãi suất của 1 năm là 5,3%, suy ra lãi suất 1 tháng là:
% . Khi đó lãi suất theo định kỳ 6 tháng là: 12 5,3 6. %  2, 65% 12
Vậy số tiền nhận được sau 10 năm là: T 100000000.1 2,6520 168724859,1 đồng. 20 150
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 10.12
b/ 1 kỳ là 3 tháng, suy ra 10 năm là  40 kỳ 3 4,8
lãi suất của 1 năm là 4,8%, suy ra lãi suất 1 tháng là:
% . Khi đó, lãi suất theo định kỳ 3 tháng 12 4,8 là: 3. %  1, 2% 12
Vậy số tiền nhận được sau 10 năm là: T 100000000.11, 2%40 161146360 đồng. 40
Bài tập mẫu tham khảo 02 : Một anh sinh viên được gia đình gửi vào sổ tiết kiệm ngân hàng là
80000000 đồng vỡi lãi suất kép kỳ hạn 1 năm là 6,9%/năm. Hỏi sau đúng 5 năm số tiền trong sổ sẽ
là bao nhiêu, biết rằng trong suốt thời gian đó anh sinh viên không rút một đồng nào cả vốn lẫn lãi?
♥ Hướng dẫn giải : n
Từ công thức T a r n 1 
Số tiền trong sổ sau 5 năm là: T  80000000.1 6,9%5 111680799, 2 đồng 5
Bài toán 3: (Lãi kép gửi theo định kỳ - gửi đầu tháng)
Một người, hàng tháng gửi vào ngân hàng a đồng , với lãi suất kép hàng tháng là r%. Hỏi sau n tháng,
người ấy có bao nhiêu tiền ? Phương pháp:
Gọi Tn là số tiền người đó có được ở cuối tháng n , ta có :
Cuối tháng thứ nhất, người đó có số tiền là : T a ar a 1 r 1  
Đầu tháng thứ hai, người đó có số tiền là :
a   r   a a   ra 2 a 2 1 1 1             r 1 r 1 1 r 1 1 1    r     
Cuối tháng thứ hai, người đó có số tiền là : a   a a T
 1 r2 1  1 r2 1.r  1 r2 1 1 r 2   r   r   r  
……………………………………………………………….
Cuối tháng thứ n , người đó có số tiền là : a a n      T
  r    r Vậy : T rr n 1  1 1  nn 1  1 1    (3) r   r 151
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Trong đó : a là tiền vốn gửi vào ngân hàng hàng tháng , r là lãi suất % hàng tháng , n là số tháng,
Tn là tiền vốn lẫn lãi sau n tháng.
Bài tập mẫu tham khảo 01 : Một người, hàng tháng gửi vào ngân hàng số tiền là 3000000 đồng với
lãi suất kép là 0.36%/tháng. Hỏi sau 2 năm, người ấy có bao nhiêu tiền, biết rằng lãi suất hàng tháng không thay đổi ? ♥ a
Hướng dẫn giải : Áp dụng công thức : T
  r    r nn 1  1 1  r   .
Với a  3000000 đồng, r  0,36% , n  24 tháng. 3000000 Ta được: T
10,36%24 1 10,36%  75331221,69 24   0,36%   đồng
Bài tập mẫu tham khảo 02 : Muốn có 50000000 đồng sau 1 năm thì phải gửi quỹ tiết kiệm ngân
hàng hàng tháng là bao nhiêu ? Biết rằng lãi suất kép gửi hàng tháng là 0,35%/tháng, lãi suất hàng tháng không thay đổi. T .r
♥ Hướng dẫn giải : Áp dụng công thức : n a   . n
1 r  1 r  1  
Với T  50000000 đồng, r  0,35% , n  12 tháng n 50000000 0 . ,35% Ta được: a    đồng
1 0,35% 1 0,35% 4072810, 663 12 1  
Bài tập mẫu tham khảo 03 : Nếu ông A muốn có 100000000 đồng thì ông phải phải mất bao nhiêu
tháng gửi tiền tiết kiệm ngân hàng , biết rằng lãi suất kép gửi ngân hàng hàng tháng là 0,36%
/tháng, số tiền ông gửi tiết kiệm hàng tháng là 7000000 đồng?  T .r  ln n 1 r   ♥a
Hướng dẫn giải : Áp dụng công thức: n    .  r 1 ln 1
Với T 100000000 đồng, r  0,36% , a  7000000 đồng n 152
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 100000 . 000 0,36%  ln 1 0,36%    7000000  Ta được: n   tháng   1 13,90672580 ln 1 0,36%
Vậy ông A phải mất 14 tháng
Bài toán 4: (Vay theo định kỳ - Trả cuối tháng)
Một người, vay ngân hàng A đồng , với lãi suất kép hàng tháng là r%. Hỏi người ấy phải trả hàng tháng
bao nhiêu tiền để sau n tháng thì hết nợ ? Phương pháp :
Gọi a là số tiền phải trả hàng tháng.
Cuối tháng thứ nhất, người đó nợ : A1 r
Đã trả a đồng tiền nợ: A1 r  a 2
Cuối tháng thứ hai, người đó còn nợ:  A1 r  a 
1 r  a A1 r  a1 r  a
Cuối tháng thứ ba, người đó còn nợ :
A  r2 a  ra  ra A  r3 a  r2 1 1 1 1 1
a1 r a  
………………………………………………………………………….. n n n 1  n   2 n 1 r 1
Cuối tháng thứ n , người đó còn nợ: A1 r   a 1 r
a1 r ... a A1 r    . a r n .
A r.1 r
Vậy để người đó trả hết nợ sau n tháng thì số tiền phải trả hàng tháng là: a   (4) n 1 r  1
Trong đó : a là tiền trả ngân hàng hàng tháng , r là lãi suất (%) hàng tháng , n là số tháng, A là số tiền vay ban đầu.
Bài tập mẫu tham khảo 01 (Đề thi minh họa năm 2017) : Ông A vay ngắn hạn ngân hàng 100 triệu
đồng, với lãi suất 12%/năm. Ông muốn hoàn nợ cho ngân hàng theo cách : Sau đúng một tháng kể
từ ngày vay, ông bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền
hoàn nợ ở mỗi lần là như nhau và trả hết tiền nợ sau đúng 3 tháng kể từ ngày vay. Hỏi, theo cách
đó, số tiền m mà ông A phải trả cho ngân hàng trong mỗi lần hoàn nợ là bao nhiêu ? Biết rằng, lãi
suất ngân hàng không thay đổi trong thời gian ông A hoàn nợ. 153
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
♥ Hướng dẫn giải : Sau một tháng ông A hoàn nợ lần 1, các lần hoàn nợ tiếp theo sau đó một
tháng. Ông A trả hết tiền nợ sau 3 tháng, tức là ông A hoàn nợ 3 lần.
Lãi suất 1 năm là 12% suy ra lãi suất hàng tháng là : 1%
Gọi m đồng là số tiền ông A hoàn nợ mỗi tháng 10011%
Cuối tháng thứ nhất, ông A nợ: (triệu đồng)
Đã trả m đồng nên còn nợ: 10011%  m (triệu đồng)
Cuối tháng thứ hai, ông A còn nợ:    m    m    2 100 1 1% 1 1% 100 1 1%
m11% m (triệu đồng)
Cuối tháng thứ ba, ông A còn nợ: 
  2 m  m  m
  3 m  2 100 1 1% 1 1% 1 1% 100 1 1% 1 1%
m11% m         3  3 1 1% 1 100 1 1%  . m (triệu đồng) 1%
Vậy ông A trả hết nợ sau 3 tháng thì số tiền phải trả hàng tháng là : 100.1%.11%3 1,0 3 1 m    (triệu đồng) 11%3 1 1,0 3 1 1
Bài tập mẫu tham khảo 02 : Một người vay 50 triệu, trả góp theo tháng trong vòng 48 tháng, lãi suất kép là 1,15%/tháng.
a/ Hỏi hàng tháng phải trả bao nhiêu?
b/ Nếu lãi suất kép là 0,75%/tháng thì mỗi tháng phải trả bao nhiêu, lợi hơn bao nhiêu so với lãi suất kép 1,15%/tháng.
♥ Hướng dẫn giải : a/ Số tiền người ấy phải trả hàng tháng là :
50000000.1,15%.11,15%48   13613 , 12 807 (đồng) 11,15%48 1
b/ Số tiền người ấy phải trả hàng tháng là :
50000000.0, 75%.1 0,75%48   12442 , 52 119 (đồng) 1 0, 75%48 1
Lợi hơn : 1361312,807 1244252,119 117060 (đồng) 154
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Bài tập mẫu tham khảo 03 : Một người vay ngân hàng với số tiền là 20000000 đồng , mỗi tháng trả
góp cho ngân hàng 300000 đồng và phải chịu lãi suất kép của số tiền chưa trả là 0,4%/tháng. Hỏi
sau bao lâu người đó trả hết nợ ?
♥ Hướng dẫn giải : Gọi A là số tiền vay ngân hàng, a là số tiền trả nợ hàng tháng, r là lãi suất
(%) hàng tháng, n là số tháng trả hết nợ.
Ta có: A  20000000 đồng, a  300000 đồng, r  0, 4% . Số tiền còn nợ trong ngân hàng sau n tháng n   n 1 r 1 a 300000
là: T A ra   n  log   77,69370636 n 1    . 0  r 1 r a  . A r 300000  20000000.0, 4%
Số tháng trả hết nợ là 78 tháng
Bài toán 5: Một người gửi ngân hàng với số tiền là A đồng với lãi suất kép là r%/tháng(kỳ hạn một tháng).
Mỗi tháng người ấy rút ra X đồng vào ngày ngân hàng tính lãi. Hỏi sau n tháng số tiền của người ấy còn bao nhiêu? Phương pháp:
Gọi Bn là số tiền còn lại sau tháng thứ n
Sau tháng thứ nhất, số tiền vốn và lãi là: A1 r (đồng)
Sau khi rút ra X đồng, số tiền còn lại là: B A 1 r X (đồng) 1   2
Sau tháng thứ hai, số tiền vốn và lãi là: B 1 r   A 1 r X  1 r A 1 r X 1 r (đồng) 1 
         
Sau khi rút ra X đồng, số tiền còn lại là: 2 1 r 1
B A 1 r
X 1 r X A 1 r X  1 r 1  A 1 r X. (đồng) 2  2    2     2   1 r1
……………………………………………………………………………………….
Bằng cách quy nạp, ta suy ra được sau tháng thứ n , số tiền còn lại là: nr B Ar X n  n 1  1 1 . (đồng) (5) r
Từ công thức (5) ta tính được các đại lượng khác như sau: 155
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 An
1 r   B .r n  
B .r X X n   n log n 1r 1 r  1 . A r X
Trong đó : X là số tiền rút ra hàng tháng , r là lãi suất (%) hàng tháng , n là số tháng, A là số tiền gửi ban đầu.
Bài tập mẫu tham khảo 01 : Giả sử một người gửi vào ngân hàng với số tiền 50000000 đồng theo
kỳ hạn 1 tháng với lãi suất kép là 0,36%/tháng. Mỗi tháng người đó rút ra 1000000 đồng vào ngày
ngân hàng tính lãi. Hỏi sau 2 năm số tiền của người ấy còn lại bao nhiêu ?
♥ Hướng dẫn giải : Áp dụng công thức (5) với: A  50000000 đồng, r  0,36% , X 1000000 đồng,
n  24 tháng. Ta có:   B     1 0,36%24 24 1 50000000. 1 0,36% 1000000.  29483326,1 (đồng) 24 0,36%
Bài tập mẫu tham khảo 02 : Một sinh viên đi học được gia đình cho gửi tiền tiết kiệm vào ngân
hàng với số tiền là 50000000 đồng theo mức kỳ hạn một tháng với lãi suất kép là 0,35% /tháng.
Nếu mỗi tháng anh sinh viên rút ra một số tiền như nhau vào ngày ngân hàng tính lãi thì hàng
tháng anh ấy rút ra bao nhiêu tiền để sau 4 năm, số tiền vừa hết ?
♥ Hướng dẫn giải : Sau 4 năm tức là sau 48 tháng, anh sinh viên rút vừa hết tiền, có nghĩa là B  0 48 An
1 r   B .r n  
Áp dụng công thức X   n 1 r  1
Với: A  50000000đồng, r  0,35% , B  0 đồng, n  48 tháng. Ta có: n 500000001 0,35%48 0 . ,35% X    1133433, 099 (đồng) 1 0,35%48 1
Vậy hàng tháng anh sinh viên rút ra một số tiền là : 1133433,099 (đồng) 156
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Bài tập mẫu tham khảo 03 : Một người gửi tiền tiết kiệm vào ngân hàng với số tiền là 20000000
đồng theo mức kỳ hạn một tháng với lãi suất kép là 0,36%/tháng. Nếu mỗi tháng người ấy rút ra
một số tiền là 300000 đồng vào ngày ngân hàng tính lãi thì sau bao lâu số tiền gửi vừa hết ?  ♥ B .r X
Hướng dẫn giải : Áp dụng công thức: n  log n 1r . A r X
Với A  20000000 đồng, r  0,36% , B  0 đồng, X  300000 đồng. Ta có: n 300000  n  log  76,36959338 (tháng) 10,36% 20000000 0 . ,36%  300000
Vậy tối thiểu sau 76 tháng thì số tiền gửi sẽ hết
Bài tập trắc nghiệm
Câu 01 : Một khu rừng có trữ lượng gỗ 5
4.10 mét khối. Biết tốc độ sinh trưởng của các cây ở khu
rừng đó là 4% mỗi năm. Hỏi sau 5 năm, khu rừng đó sẽ có bao nhiêu mét khối gỗ? A. 5  3 4,8666.10 m  . B. 5  3 3.866.10 m  . C. 5  3 2,8666.10 m  . D. 5  3 0,16.10 m  .
Câu 02 : Một điện thoại đang nạp pin, dung lượng nạp được tính theo công thức 3  t   Q t  2
Q 1e  với t là khoảng thời gian tính bằng giờ và Q là dung lượng nạp tối đa (pin đầy). 0   0
Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là 0%) thì sau bao lâu
sẽ nạp được 90% (kết quả làm tròn đến hàng phần trăm)? A. t 1,54h . B. t 1, 2h . C. t 1h . D. t 1,34h . 157
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
Câu 03 : Biểu đồ bên cho thây kết quả
thống kê sự tăng trưởng về số lượng của
một đàn vi khuẩn: cứ sau 12 tiếng thì số
lượng của một đàn vi khuẩn tăng lên gâp
2 tan. Số lượng vi khuẩn ban đầu của đàn
là 250 con. Công thức nào dưới đây thể
hiện sự tăng trưởng về số lượng của đàn
vi khuẩn N tại thời điểm t ?. A. 12 N  500.t . B. 250.2t N  . C. 2 N  250.2 . D. 2 250.2 t N  .
Câu 04 (THPT Lê Hồng Phong – Khánh Hòa) : Hàm Một nhà côn trùng học khảo sát thấy số côn
trùng ban đầu ở một đàn là 500 con, tỉ lệ tăng trưởng của côn trùng này là 14% mỗi tuần. Hỏi sau
22 tuần, số côn trùng sẽ có là bao nhiêu? A. Khoảng 1248 con. B. Khoảng 8931 con. C. Khoảng 9635 con. D. Khoảng 6915 con.
Câu 05 : Một nguời gửi tiết kiệm với lãi suất 8, 4% năm và lãi hàng năm đuợc nhập vào vốn, hỏi
sau bao nhiêu năm người đó thu được gấp đôi số tiền ban đầu? A. 6 B. 7 C. 8 D. 9
Câu 06 (THPT Phan Bội Châu – Khánh Hòa) : Bác Ba gửi số tiền 7 triệu đồng vào ngân hàng với
lãi suất 8,5% năm. Biết rằng nếu không rút tiền thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào số 158
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018
vốn ban đầu. Hỏi sau 12 năm Bác Ba rút được bao nhiêu tiền, nếu trong thời gian này Bác Ba
không rút tiền ra và lãi suất không thay đổi? A. 18 631 803 . B. 18 631 804 . C. 7 995 692 . D. 11 2501 62 .
Câu 07 : Năm 2001, dân số Việt Nam là 78685800 người. Tỷ lệ tăng dân số năm đó là 1,7%. Biết
rằng sự sự tăng dân số ước tính theo thức r  eN S A
, trong đó A là dân số của năm lấy làm mốc
tính, S: dân số sau N năm, r: tỉ lệ tăng dân số hàng năm. Tăng dân số với tỉ lệ tăng như vậy thì đến
năm nào dân số nước ta ở mức 120 triệu người. A. 2025. B. 2030 C. 2026 D. 2035
Câu 08 (THPT Tôn Đức Thắng – Khánh Hòa) : Giả sử cứ sau một năm diện tích rừng của nước ta
giảm x phần trăm diện tích hiện có. Hỏi sau 4 năm diện tích rừng của nước ta sẽ là bao nhiêu
phần diện tích hiện nay? 4  x  A. 1   . 100  B.100%. 4x C. 1 . 100 4  x  D. 1    100  358
Câu 09 : Năm 1994, tỉ lệ khí CO2 trong không khí là
. Biết rằng tỉ lệ thể tích khí CO2 trong 6 10
không khí tăng 0, 4% hàng năm. Hỏi năm 2016, tỉ lệ thể tích T khí CO2 trong không khí là bao
nhiêu (kết quả gần nhất)? Giả sử tỉ lệ tăng hàng năm không đổi. 391 A. T  . 6 10 159
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – SƯU TẦM VÀ BIÊN SOẠN 2018 390 B. T  . 6 10 7907 C. T  . 6 10 7908 D. T  . 6 10
Câu 10 : Ông A đi gửi tiết kiệm ngân hàng với số tiền là m đồng. Gửi trong n tháng với lãi suất
hàng tháng là r . Tính số tiền cả vốn lẫn lãi T mà Ông A nhận được sau cuối tháng thứ n là :
A. T m1 nr . B.  1 (  )n T m r . m C. 1 n 1 ( )n T m r    . D. T  r   1  r   1  r   .
Câu 11 : Một người dự định sẽ mua xe Honda SH 2016 150i với giá 80 990 000 đồng. Người đó
gửi tiết kiệm vào ngân hàng với số tiền 60 000 000 đồng với lãi suất hàng tháng là 0,8% . Vậy sau
bao lâu người đó sẽ đủ tiền mua xe máy : A. 37 tháng. B. 36 tháng. C. 38 tháng. D. 35 tháng.
Câu 12 : Với số tiền 80 000 000 đồng hiện có , một người lấy một nửa số tiền đó gửi tiết kiệm vào
ngân hàng A với lãi suất 4,8% một năm. Còn một nửa thì gửi vào ngân hàng B với lãi suất 0, 4%
một tháng. Hỏi sau 36 tháng người đó đồng thời đi rút tiền trong hai ngân hàng thì ngân hàng
nào sẽ trả cả vốn lẫn lãi nhiều nhất và số tiền T nhận được từ ngân hàng đó là bào nhiêu?:
A. Ngân hàng A , T  46040904 đồng.
B. Ngân hàng B , T  46040904 đồng.
C. Ngân hàng A , T  46182097 đồng.
D. Ngân hàng B , T  46182097 đồng. 160
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – ÔN TẬP 2018
Phần VI : BÀI TẬP ÔN x  2 1x
Câu 1: Giải phương trình 16  8 . A. x  2 . B. x  3. C. x  2  . D. x  3  .
Câu 2: Giải phương trình log x 1  log x  3  3. 4   4   A. x  33. B. x 1 2 17. C. x  5. D. x 1 2 17. 5  x
Câu 3: Tìm tập xác định của hàm số y   x   . ln 3 A. D  3;  5 . B. D  3;  5 \   4 . C. D  3;5.
D. D  3;5 \  4
Câu 4: Giải bất phương trình log  500 x  9  1  000. 1  3 A. x  0. B. x  0. C. 500 x  9  . D. 1000 3   x  0. 1
Câu 5: Tính đạo hàm của hàm số 4 x y e . 5 1 4 4 1 A. 4 ' x y e . B. 4 ' x y   e . C. 4 ' x y e . D. 4 ' x y   e . 20 5 5 20
Câu 6: Cho log 2  ;
a log 5  b , khi đó log 3 3 340 bằng: A. 3a  b B. a  3b C. 3a  b D. a  3b 2
Câu 7: Đạo hàm của hàm số 2x y  bằng: 2 1  2 x x 1 x 2 x2 A. y '  . B. 1 ' 2 x y x   ln 2 . C. ' 2x ln 2x y  . D. y '  . ln 2 ln 2
Câu 8: Tìm tập xác định D của hàm số y  log  x 81000 3 . 2 A. D   ;
 2. B. D  2;. C. D  \   2 . D. D   2  ; ;  2
Câu 9: Tìm tập nghiệm S của bất phương trình log 3x  5  log x 1 là 1   1   5 5  5   3   5  A. S  ;    . B. S   ;3  . C. S  ;3   . D. S  ;3    3   5   3  2
Câu 10: Cho a là một số dương, biểu thức 3 a
a viết dưới dạng luỹ thừa với số mũ hữu tỉ là
161 (SƯU TẦM VÀ BIÊN SOẠN)
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – ÔN TẬP 2018 7 1 A. 6 a . B. 3 a . C. 6 a . D. 2 a . 2
Câu 11: Tìm tập xác định của hàm số 2 3 5 x x y     ? A.  1  ; 3. B.  1  ;  3 . C. \  1  ;  3 . D. .
Câu 12: Tìm nghiệm của phương trình 4x 2x   2  0 A. x  0 . B. x  2 . C. x  3 D. x  1.   a   3 1 3 1
Câu 13: Cho biểu thức P
, với a  0 . Mệnh đề nào dưới đây đúng ? 5 3 4 5 a .a 3 1 A. P a . B. 2 P a . C. 2 P a . D. 3 P a log x
Câu 14: Tính đạo hàm của hàm số 3 y x 1 ln x 1 ln x 1 ln x 1 ln x A. y  . B. y  C. y  . D. y  . 2 2 x ln 3 2 x ln 3 x ln 3 2 x
Câu 15: Tính đạo hàm số y  log x có đạo hàm 2 1 1 1 1 A. . B. . C. . D. .ln 2. x ln 2 x ln 2 x
Câu 16: Với các số thực a, b dương, khác 1. Mệnh đề nào dưới đây đúng? A. log(a  )
b  log a  log . b B. log(a ) b  log . a log . b log b a log a C. log b  . D. log  a log a b log b
Câu 17: Tìm tất cả các nghiệm của phương trình 2
log(x  2x  2)  log x ? A. x  2. 
B. x 1; x  2  . C. vô nghiệm. D. x  1. 
Câu 18: Tìm tập xác định của hàm số y =  x x   2 2 3 4 ?    4    A. . B.    4 ; 1  ;   .   C. \  ; 1. D.    4 ; 1  ;   .    3   3  3  Câu 19: Biểu thức 3 6 5
x. x. x x  0 viết dưới dạng luỹ thừa với số mũ hữu tỷ là: 5 2 7 5 A. 3 x . B. 3 x . C. 3 x . D. 2 x .
Câu 20: Cho  > . Kết luận nào sau đây là đúng?
162 (SƯU TẦM VÀ BIÊN SOẠN)
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – ÔN TẬP 2018 A.   . B.     0. C.   . D. .  1.
Câu 21: Cho M  log 0,07; N  log 0, 2 . Khẳng định nào sau đây là khẳng định đúng? 0;3 3
A. M N  0 .
B. M  0  N .
C. N  0  M .
D. 0  N M .
Câu 22: Tìm tập hợp xác định D của hàm số y  log 4  x 1 2  
A. D  2; 4. B. D   ;  2. C. D   ;  2. D. D   ;  4. 1 
Câu 23: Tập xác định của hàm số 2 3 y  (1  x ) là: A.  1  ;  1 . B.  ;    1 . C.  1  ;  1 . D. 1; . x x 5  3  3 Câu 24: Cho x x 9  9
 23. Khi đó biểu thức K = có giá trị bằng: x x 1 3  3 3 5 1 A. 2. B. . C.  . D. . 2 2 2
Câu 25: Tập nghiệm của bất phương trình 2.4x 5.2x
 2  0 có dạng S   ;
a b. Tính b a . 3 5 A. . B. . C. 1. D. 2. 2 2 1
Câu 26: Cho hàm số y
. Hãy chọn hệ thức đúng. 1 x  ln x
A. xy y yln x   1 .
B. xy  y y ln x   1 .
C. xy  y y ln x   1 .
D. xy y y ln x   1 .
Câu 27: Chọn mệnh đề đúng trong các mệnh đề sau:  e  1,4 2 2   2   1   1  A.      . B.  3  2 4  4 . C.  .     D. 3 1,7 3  3 .  3   3   3   3 
Câu 28: Số nghiệm của phương trình 9x 2.3x  3  0 là A. 3. B. 1. C. 0. D. 2.
Câu 29: Cho a  log 32; b  log 14 . Hãy biểu diễn a theo b . 49 2 5 1 A. a  . B. a  .
C. a  3b  2 .
D. a  3b 1. 2b  2 b 1 
Câu 30: Tập xác định hàm số y   x   2 1 là A. \   1 . B. 1; . C.   ;1  . D. .
163 (SƯU TẦM VÀ BIÊN SOẠN)
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – ÔN TẬP 2018 3 4  
Câu 31: Điều kiện của a thỏa 4 5 aa là A. 0  a 1 B. a  0 . C. a  0 . D. a  1 . x e
Câu 32: Đạo hàm của hàm số y  là x x e (x 1) x e (x 1) x e A. y '  . B. ' x y e . C. y '  . D. y '   . 2 x 2 x 2 x
Câu 33: Cho a là số dương khác 1, b là số dương và  là số thực bất kì. Mệnh đề nào dưới đây là mệnh đề đúng ? 1 A. log      b log . b B. log  b log . b a a a a   1 C.  log b   log . b D. log b  log . b a a a a
Câu 34: Chọn mệnh đề đúng trong các mệnh đề sau: A. Hàm số x
y a  0  a  
1 luôn đ ng biến tr n tập xác định. B. Hàm số x
y a với a  1 luôn nghịch biến tr n tập xác định.
C. Hàm số y  log x với 0  a 1 luôn nghịch biến tr n tập xác định. a D. Hàm số y  log , x a
luôn nghịch biến tr n tập xác định. a   1
Câu 35: Tìm tập nghiệm S của phương trình 2
log (x  4x  3)  log (4x  4) 2 2 A. S   3;  7 . B. S  1. C. S   7 . D. S  1 ;  7 . x2 3x6  3   7 
Câu 36: hương trình      có nghiệm là  7   3  A. x  2  . B. x  1 . C. x  1  . D. x  4 .
Câu 37: Đạo hàm của hàm số cos2x y e là A. cos 2 2  sin 2 . x x e . B. cos 2 2sin 2 . x x e . C. cos 2 sin 2 . x x e . D. cos 2 sin 2 . x x e .
Câu 38: Tập nghiệm của bất phương trình log(3x  3)  log(2x  5) là  5  A.  ;8   . B.   ;8  . C. 1;  8 . D. 1;  8 .  2 
Câu 39: Tập xác định của hàm số 2
y  log(9  x ) là
164 (SƯU TẦM VÀ BIÊN SOẠN)
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – ÔN TẬP 2018 A.  ;  3  3; . B.  ;    3 3; . C. \  3  ;  3 . D.  3  ;3 .
Câu 40: Cho a  0, a  1. Giá trị của log 4 a a là A. 4. B. 8. C. 2 . D. 16.
Câu 41: Chọn mệnh đề đúng trong các mệnh đề sau: 1,4 2   e 1   1   2   2  A.  3  2 4  4 . B.  .     C.  . D. 3 1,7 3  3 .      3   3   3   3 
Câu 42: Cho số thực a dương. Rút gọn biểu thức 5 4 3 P a a a a ta được: 1 1 11 13 A. 14 a . B. 120 a C. 40 a . D. 60 a .
Câu 43: Cho x là số thực dương thỏa mãn 2 3 x 9 10.3x   . Tính giá trị của 2 x 1? A. 5. B. 1. C. 1 và 5. D. 0 và 2.
Câu 44: Số nghiệm của phương trình 9x 2.3x  3  0 là A. 1. B. 2. C. 0. D. 3. Câu 45: Cho ,
x y là hai số thực dương và ,
m n là hai số thực tùy ý. Kết luận nào sau đây là đúng? n mnn mmn x   x m nx   y  A. m n m n x x x    B.      C.  m n m xx D.    .   my   y my   x
Câu 46: Tập xác định của hàm số 2
y  ln x  3x  4 là:
A. D R \  1  ;  4 B. D   1  ;4 C. D   ;    1  4;. D. D   ;    1 4;
Câu 47: Hàm số y   x x  2 2 3 2 3
có tập xác định là: Giáo viên cần file word vui lòng liên hệ A. \  1  ;  3 B. . Z
alo / đt / facebook : 0914 449 230 C.  ;    1 3; D.  ;    1  3; Câu 48: Biểu thức 3 6 5
x. x. x x  0 viết dưới dạng luỹ thừa với số mũ hữu tỷ là: 7 5 2 5 A. 3 x . B. 2 x . C. 3 x . D. 3 x .
Câu 49: Giá trị của biểu thức 3 1  3 1 3 B  5 .25 .125 bằng: A. 25 . B. 5 . C. 125 . D. 625 .
165 (SƯU TẦM VÀ BIÊN SOẠN)
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – ÔN TẬP 2018 1 1  2   3 3 3
a a a   
Câu 50: Cho a là số thực dương. Đơn giản biểu thức P  1 3 1    4 4 4
a a a   
A. P a(a 1) .
B. P a 1.
C. P a 1. D. P 1.
Câu 51: Bất phương trình: log 3x  2  log 6  5x có tập nghiệm là 2 2  6   1  A. 0;. B. 1;  . C.  ;3 . D.  3  ;  1 .  5   2  Câu 52: Hàm số   2 y
ln x  5x  6 có tập xác định là A. D   ;
 23; . B. D  2;3 . C. D   ;0   .
D. D  0; .
Câu 53: Trong các hàm số sau, hàm số nào nghịch biến tr n ? xx 8   3  A. 3x y  B. y  log x C. y    D. y  1     3  8  3   x 1 
Câu 54: Cho f xx 1 2  
. Đạo hàm f 0 bằng A. ln 2 . B. 2ln 2 . C. 1. D. 2 .
Câu 55: Tìm m để phương trình x x3 4  2
 3  m có đúng 2 nghiệm x1;3 A. 9   m  3. B. 3  m  9 . C. 1  3  m  3 . D. 1  3  m  9  .
Câu 56: Tìm x thỏa đẳng thức 2 3
log x  8log ab  2log a b a,b  0 . 7 7 7 A. 2 14 x a b . B. 4 6 x a b . C. 6 12 x a b . D. 8 14 x a b .
Câu 57: Giải phương trình log x  log x  log x 11, ta được nghiệm 2 4 8 A. x  24 . B. x  36 . C. x  45 . D. x  64.
Câu 58: Tìm tập xác định của hàm số y  log  x  2
1  ln 3  x  2 : 9  
A. D  3; . B. D   ;3  . C. D   ;    1  1;3 . D. D   1  ;3.
Câu 59: Bất phương trình log 3x  2  log 6  5x có tập nghiệm là 2 2  6   1  A.  3  ;  1 . B. 1; .   C.  ;3 0;  .  5   2  . D.  
166 (SƯU TẦM VÀ BIÊN SOẠN)
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – ÔN TẬP 2018 1 2
Câu 60: hương trình  1 có tập nghiệm là 4  log x 2  log x  1  A. 1; 2  0 . B.  ; 10 . C. .  D. 10; 10  0 . 10  
Câu 61: Biết log x  4log a  7 log b . Tìm x . 3 3 3 A. 3 7 x a b . B. 3 6 x a b . C. 4 6 x a b . D. 4 7 x a b . 16
Câu 62: Đặt a  ln 2,b  ln 5, hãy biểu diễn ln theo a và b. 25 16 16 16 16 A. ln  4a  2b . B. ln  4a  2 . b C. ln  2a  4b . D. ln  2a  4b . 25 25 25 25
Câu 63: Tìm tập nghiệm của bất phương trình log (x  3)  log (x  5) 1. 3 3 A. (5;6) . B. (2;6) . C. 6; . D. (0;6) Câu 64: Cho log2 8 x  (log 2) . Khẳng định đúng? 8 A. log x  3  . B. log x  2  . C. log x  2  . D. log x  3 . 3 3 3 3
Câu 65: Tính giá trị biểu thức 2,4 P  3log 10 . 0,1 A. P  7  ,2 . B. P  2, 4 . C. P  7, 2 . D. P  3 . 4 3 a b
Câu 66: Biết log b  3, log c  2 . Tính I  log . a a a 3 c A. I  15 . B. I  9 . C. I  13 . D. I 11.
Câu 67: Hỏi x  2 là nghiệm của phương trình nào trong các phương trình sau? A. log 5x   1  log  2
x x  3  1 . B. log x 1  log x 1 . 1   3   3 9  3 2 2
C. log x  5log 2x  4  log 4x  8 .
D. log x  5  log x  3 1. 3   3   4 2   2   1 1 3 3 a b b a
Câu 68: Cho a, b là các số thực dương. Rút gọn biểu thức P  3 3 a b a 1 A. 3 P ab . B. 3 P  . C. P  . D. 3 2 2 P a b . b 3 ab 1 log x 1 log x
Câu 69: Tìm nghiệm của phương trình 3 27  1 log x 1 log x 9 81
167 (SƯU TẦM VÀ BIÊN SOẠN)
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – ÔN TẬP 2018 1 1 1 1 1 1 1 1 A. 1; ; B. ; C. ; ; D. 1; ; 243 9 27 9 27 81 27 243
Câu 70: Nếu ,  0 à b a a b
v a b ;b  9a thì a nhận giá trị nào trong các giá trị sau ? A. 4 3 . B. 4 27 . C. 3 . D. 3 3 .
Câu 71: Giải phương trình log x 1  3 4   A. x  63 B. x  65 C. x  82 D. x  80
Câu 72: Tính đạo hàm của hàm số y  log  2x 1 2017  1 1 2x 2x A. y '  B. y '  C. y '  D. y '  2 x 1  2x  1ln2017 2017  2x  1ln2017
Câu 73: Cho log 14  a . Tính log 32 theo a: 2 49 10 2 5 5 A. B. C. D. a 1 5a   1 2a  2 2a 1
Câu 74: Cho hai số thực a và b , với 1 a b . Khẳng định nào dưới đây là khẳng định đúng ?
A. log a 1 log b
B. log b 1 log a b a a b
C. 1  log b  log a
D. log a  log b 1 a b b a
Câu 75: Cho các số thực dương a,b với a  1. Khẳng định nào sau đây là khẳng định đúng ? 1 1 1 A. log ab   log b B. log ab  log b 2   2   2 2 a a 4 a a 1 C. log
ab  2  2log b D. log ab  log b 2   2   a a 2 a a
Câu 76: Nếu log 8  a thì log 3 bằng: 12 2 1 a 2a 1 a 1 1 2a A. B. C. D. a  2 a  2 2a  2 a  2
Câu 77: Bất phương trình log
x 1  log x tương đương với bất phương trình nào dưới đây: 4   2 25 5
A. log x  log 1  log x B. log x 1  log x 2   4 4 2 4 25 25 5 5 25 C. 2log
x 1  log x D. log
x 1  2 log x 2   2   2 2 5 5 5 5
Câu 78: Tìm tập xác định của hàm số y  log  x  2 1  ln 3  x  2 9  
168 (SƯU TẦM VÀ BIÊN SOẠN)
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)
Gv. ThS Nguyễn Vũ Minh – ÔN TẬP 2018 A. D   ;    1  1  ;3
B. D  3; C. D   ;3   D. D   1  ;3
Câu 79: Giải phương trình log 2x 1.log  x 1 2    2 1. Ta có nghiệm: 2 4  5
A. x 1 x  2 
B. x  log 3 và x  log 2 2 4
C. x  log 3 và x  log 5
D. x 1 x  2 2 2
Câu 80: Đặt a  log 3,b  log 3. Hãy biểu diễn log 45 theo a và b: 2 5 6 2 2a  2ab 2 2a  2ab A. log 45  B. log 45  6 ab 6 ab b a  2ab a  2ab C. log 45  D. log 45  6 ab 6 ab b Câu ĐA Câu ĐA Câu ĐA Câu ĐA 1 B 21 B 41 C 61 D 2 D 22 B 42 C 62 B 3 B 23 A 43 A 63 A 4 C 24 C 44 A 64 A 5 C 25 D 45 D 65 A 6 C 26 B 46 C 66 D 7 B 27 A 47 D 67 B 8 C 28 B 48 D 68 A 9 D 29 A 49 A 69 A 10 A 30 B 50 D 70 A 11 D 31 D 51 B 71 B 12 A 32 C 52 B 72 D 13 A 33 C 53 B 73 C 14 B 34 C 54 A 74 B 15 D 35 C 55 C 75 D 16 C 36 B 56 A 76 C 17 D 37 A 57 D 77 D 18 C 38 C 58 C 78 A 19 A 39 D 59 B 79 B 20 C 40 D 60 D 80 D
169 (SƯU TẦM VÀ BIÊN SOẠN)
Đăng kí học thêm Toán tại Biên Hòa – Đồng Nai qua sđt 0914 449 230 (Zalo – facebook)