


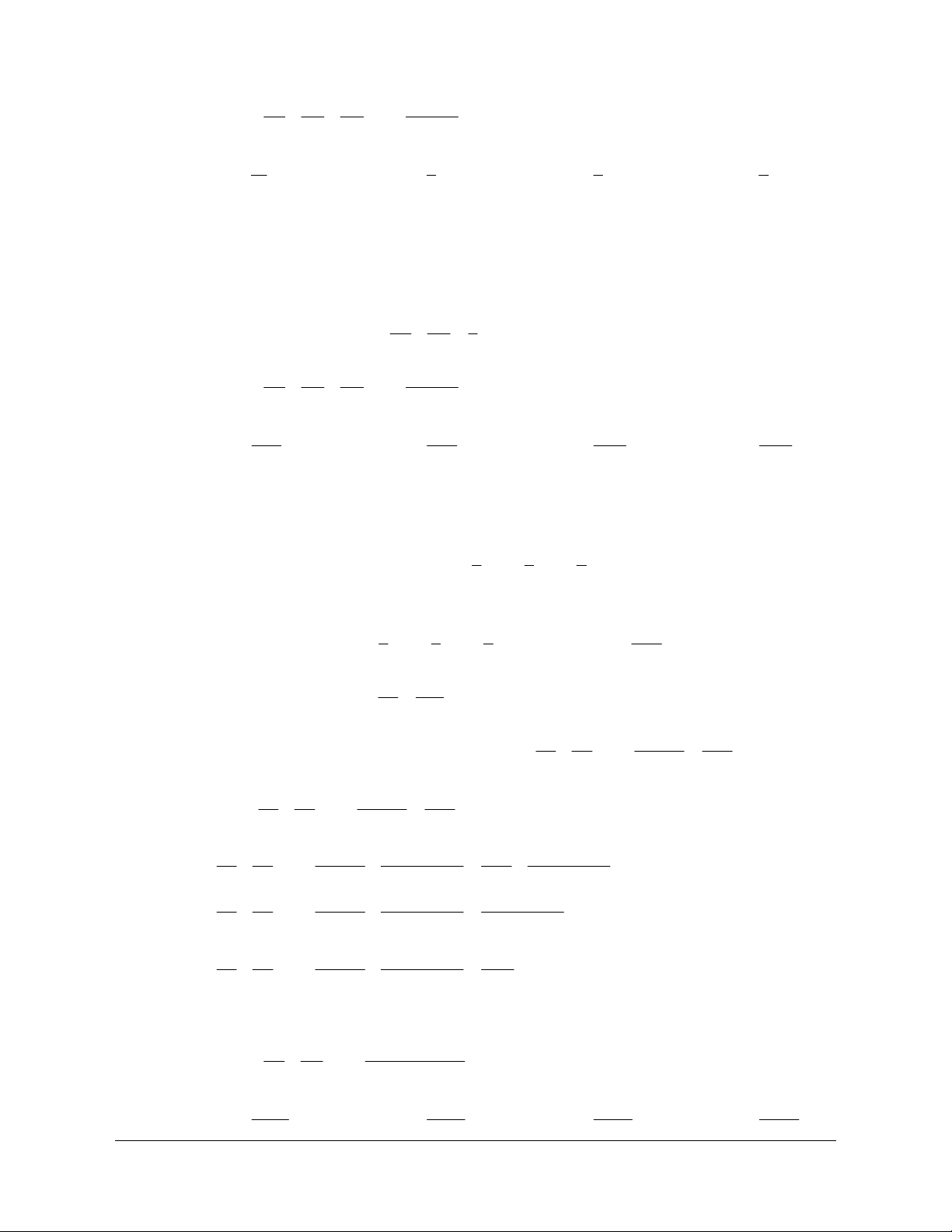
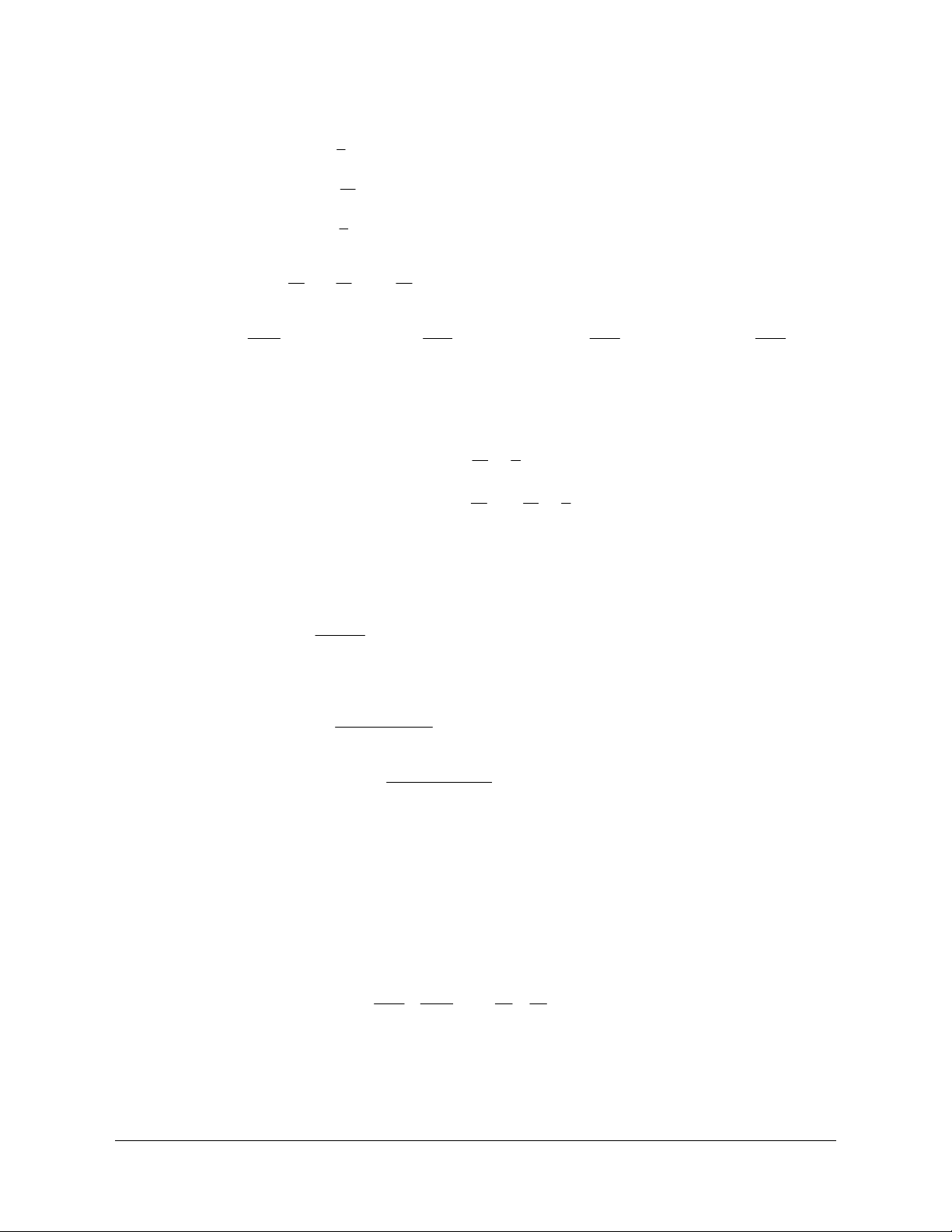






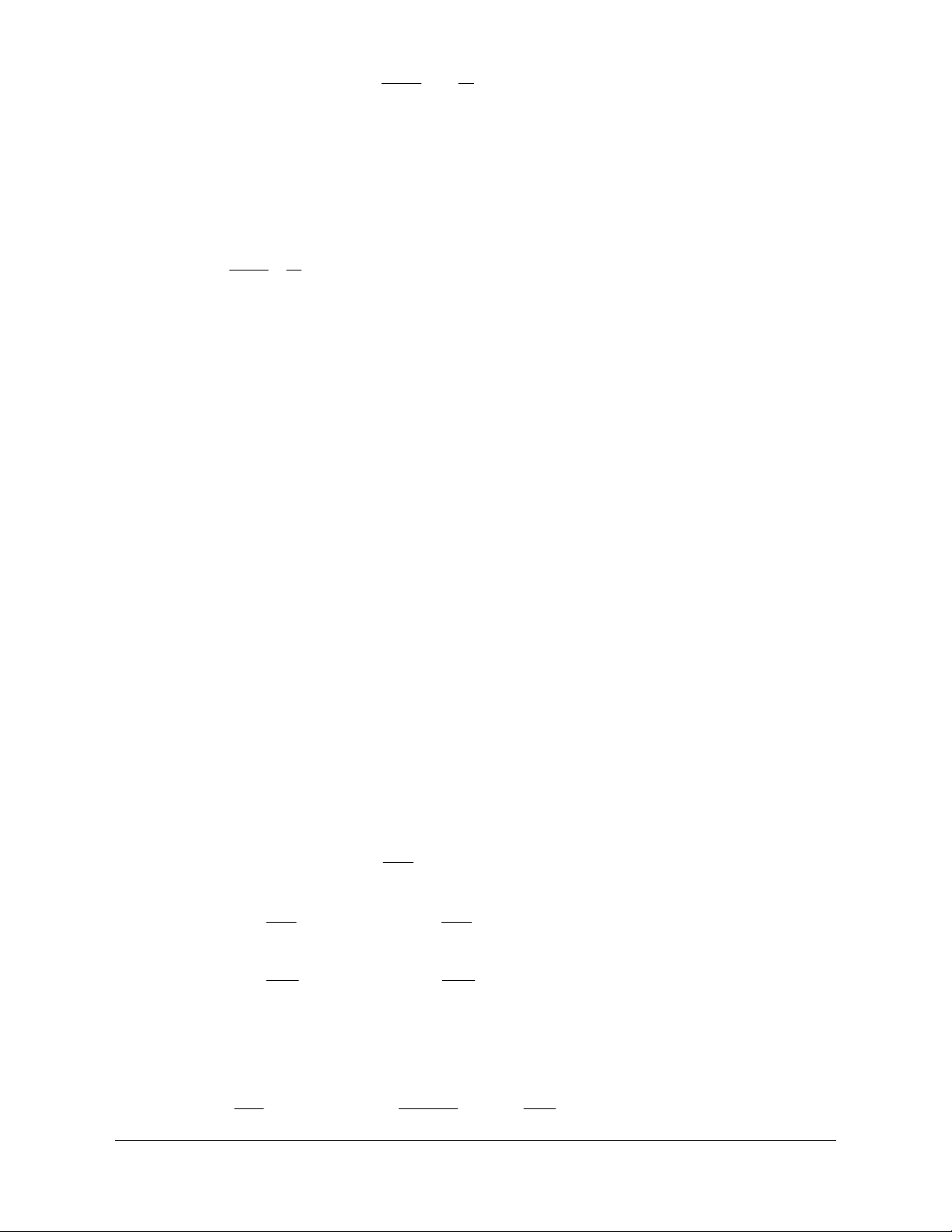







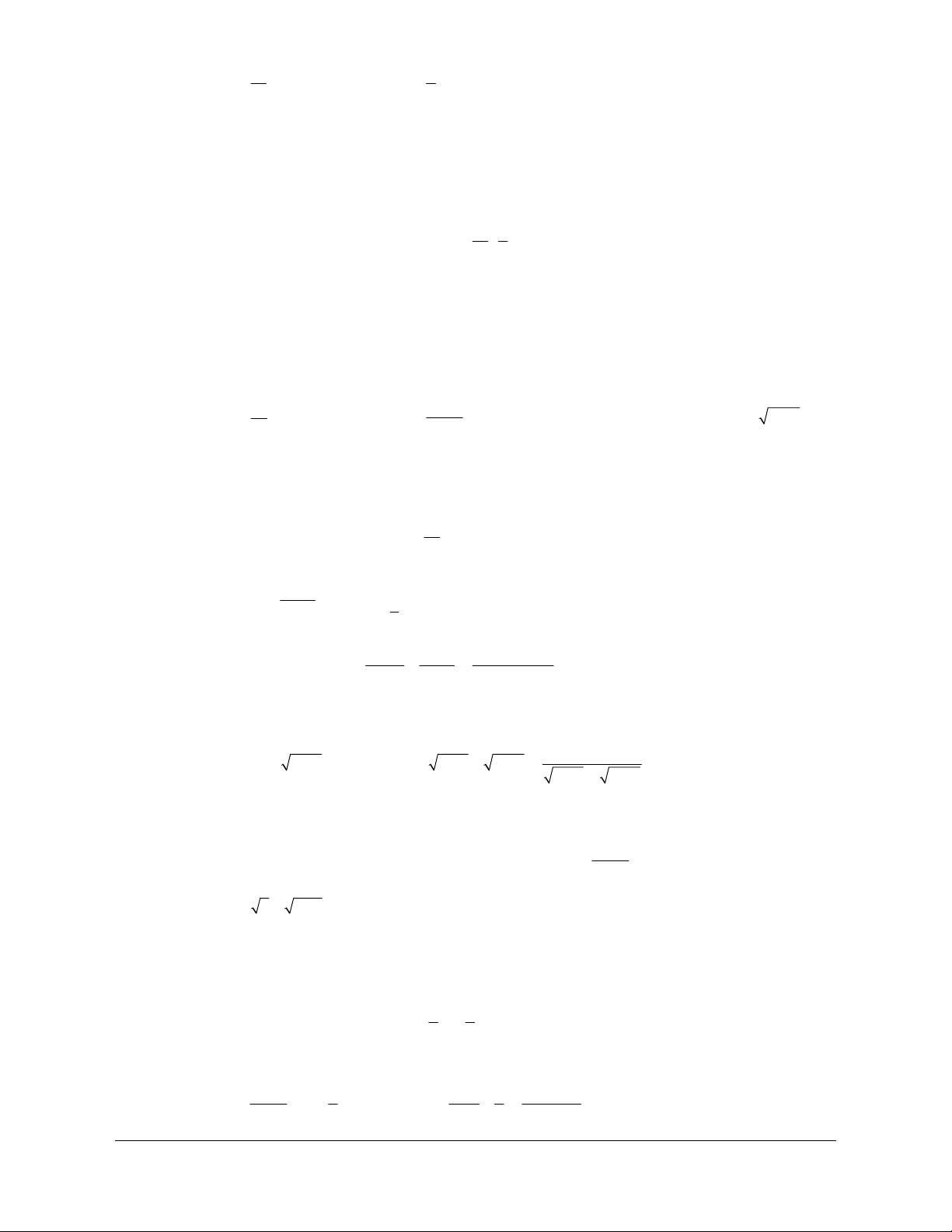

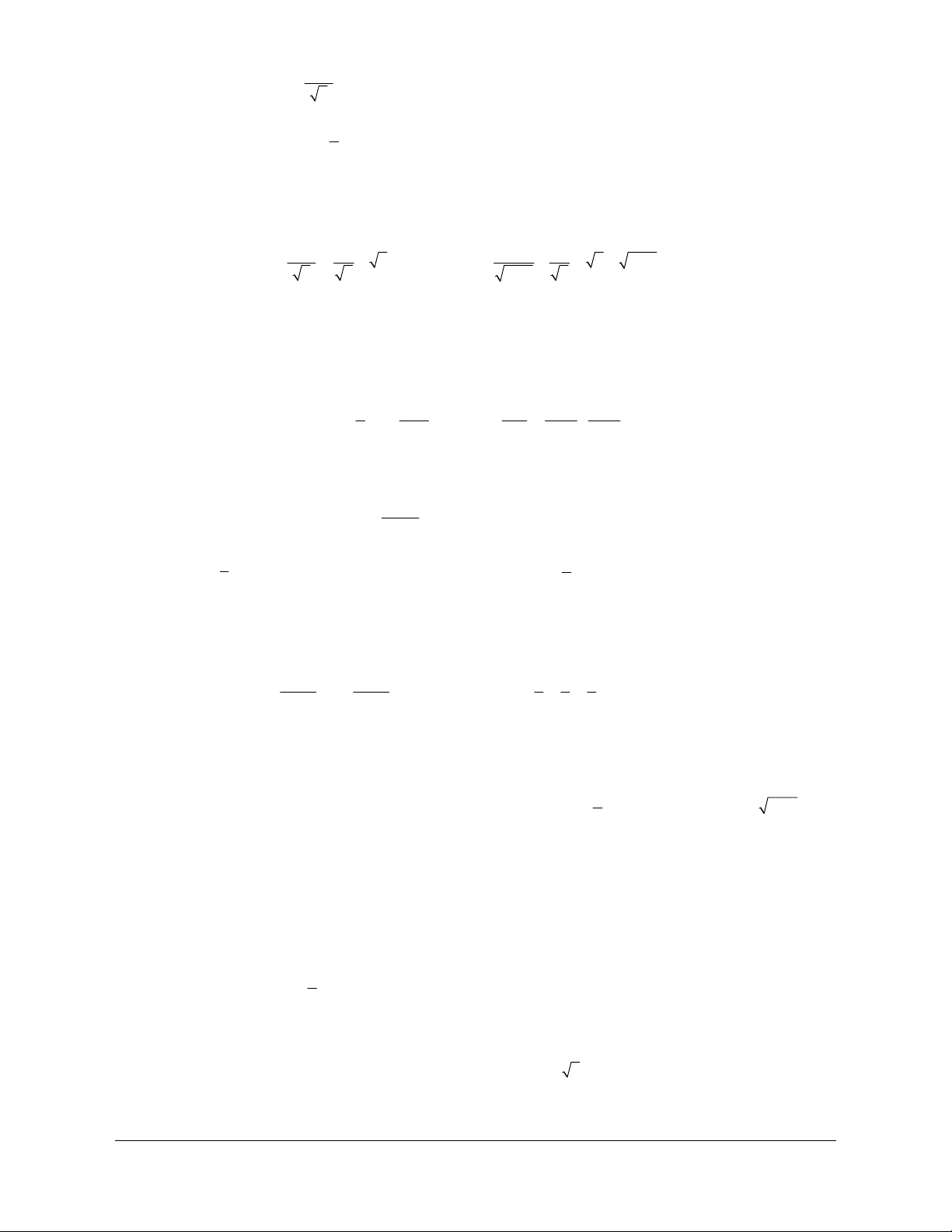













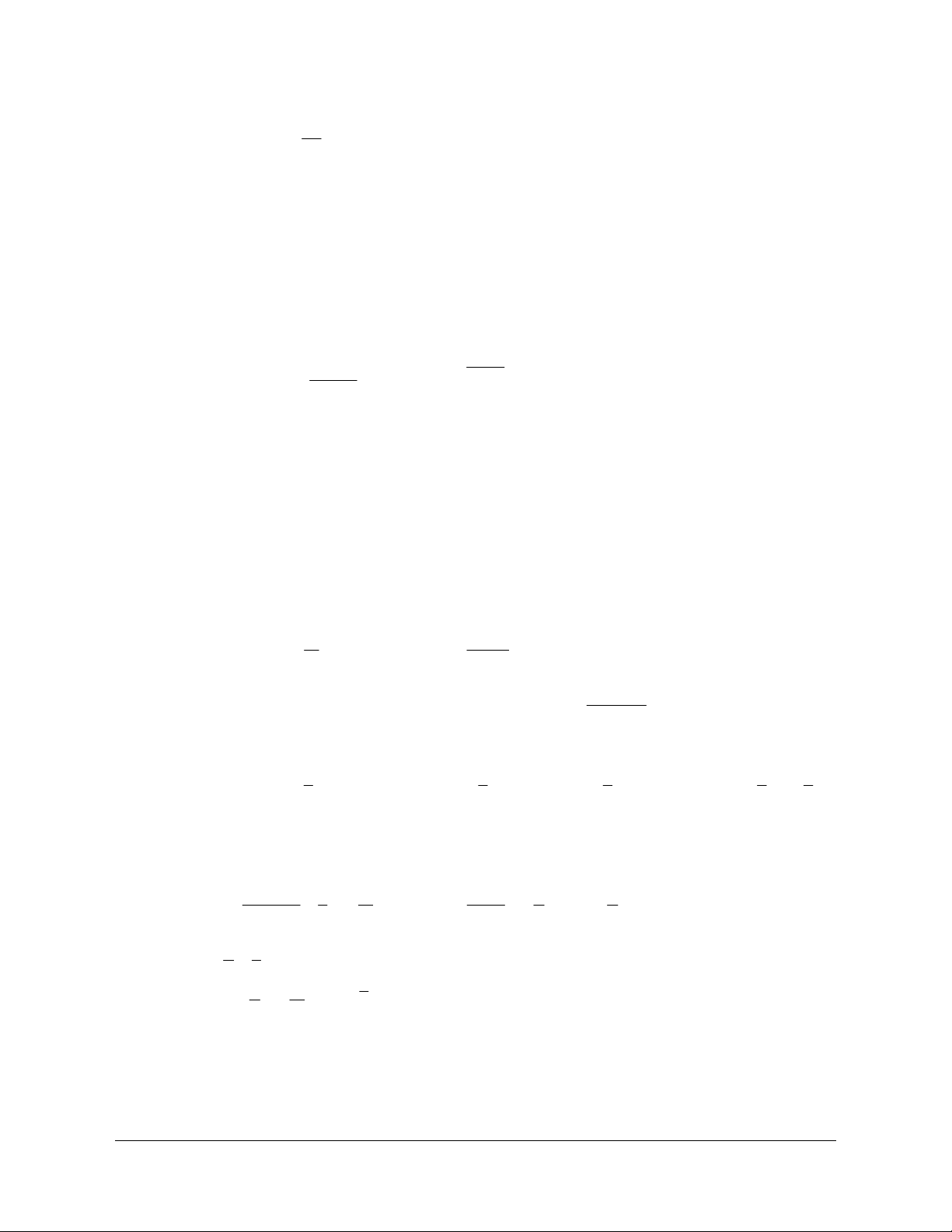



























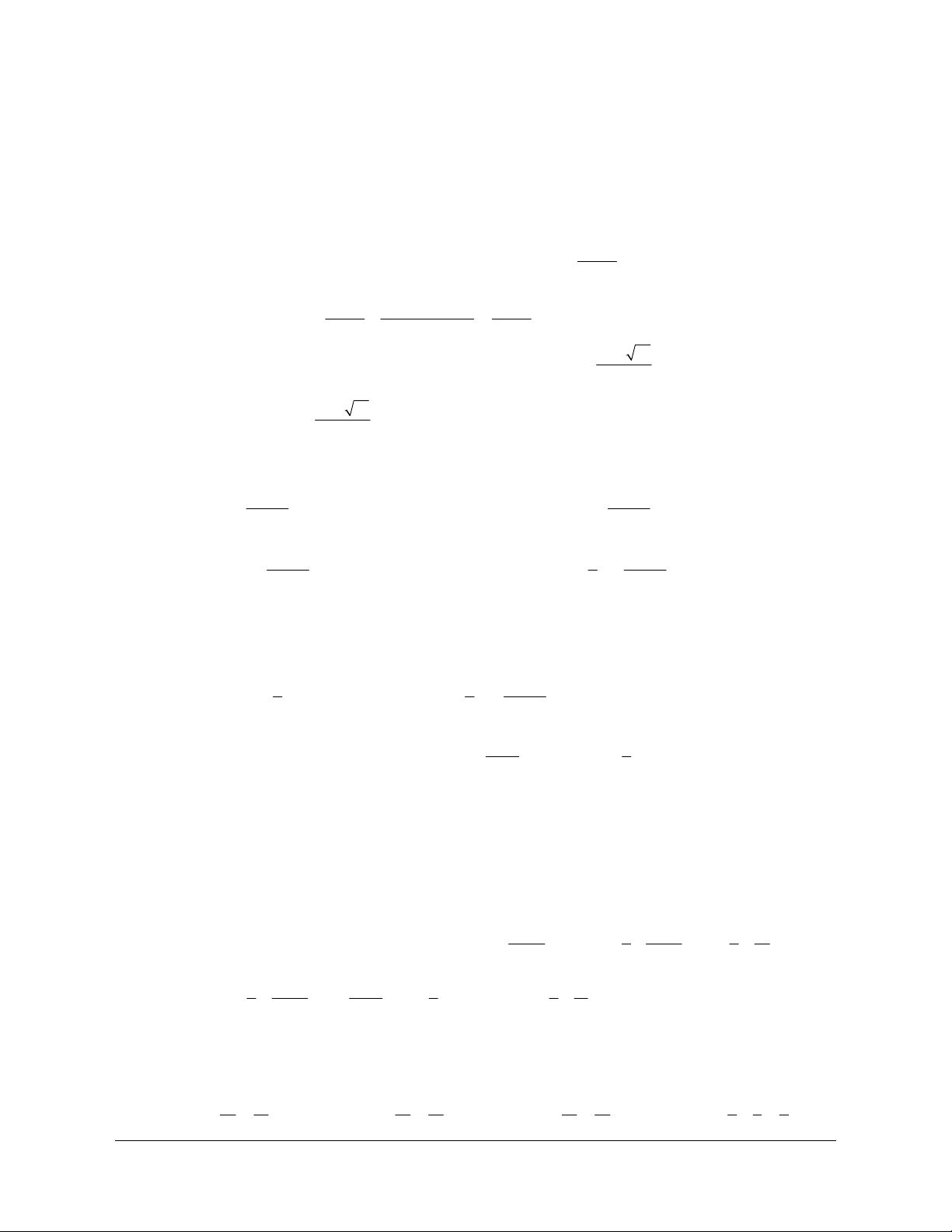

Preview text:
CHƯƠNG 3. DÃY SỐ- CẤP SỐ CỘNG – CẤP SỐ NHÂN
BÀI 1. PHƯƠNG PHÁP QUY NẠP TOÁN HỌC
A. KIẾN THỨC CƠ BẢN CẦN NẮM
Để chứng minh những mệnh đề liên quan đến số tự nhiên *
n Î là đúng với mọi n mà không thể
thử trực tiếp thì có thể làm như sau:
· Bước 1. Kiểm tra rằng mệnh đề đúng với n = 1.
· Bước 2. Giả thiết mệnh đề đúng với một số tự nhiên bất kì n = k ³1 (gọi là giả thiết quy nạp),
chứng minh rằng nó cũng đúng với n = k +1.
Đó là phương pháp quy nạp toán học, hay còn gọi tắt là phương pháp quy nạp.
Một cách đơn giản, ta có thể hình dung như sau: Mệnh đề đã đúng khi n =1 nên theo kết quả ở
bước 2, nó cũng đúng với n = 1+1 = 2. Vì nó đúng với n = 2 nên lại theo kết quả ở bước 2, nó đúng
với n = 2 +1 = 3,... Bằng cách ấy, ta có thể khẳng định rằng mệnh đề đúng với mọi số tự nhiên * n Î .
Chú ý: Nếu phải chứng minh mệnh đề là đúng với mọi số tự nhiên n ³ p ( p là một số tự nhiên) thì:
· Bước 1, ta phải kiểm tra mệnh đề đúng với n = ; p
· Bước 2, giả thiết mệnh đề đúng với số tự nhiên bất kì n = k ³ p và phải chứng minh rằng nó cũng
đúng với n = k +1.
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1. Chứng minh đẳng thức
Ví dụ 1 . Chứng minh rằng:
2 * 1.2 2.5 3.8 ... n 3n 1 n n 1 ,vôùin N (1) Lời giải
Bước 1: Với n=1, vế trái bằng 1.2=2, vế phải bằng 2. hệ thức (1) đúng
Bước 2: Đăt vế trái bằng Sn.
Giả sử hệ thức (1) đúng vơi n k 1 , tức là :
S 1.2 2.5 ... k(3k 1) 2 k (k k 1)( giaû thieát quy naïp)
Ta phaûi chöùng minh raèng (1) cuõng ñuùng vôùi n=k+1, töùc laø : S k 2 1 k k 2 1
Thaä vaäy, töø giaû thieát quy naïp ta coù: S
S k 1 3 k 11 2 k k 1 k 1 3k k 2 1 k
(k 1)(k 3k 2) k 2 2 1 k 2
Vaäy heä thöùc (1) ñuùng vôùi moïi n * N
Dạng 2. Chứng minh bất đẳng thức
Ví dụ 1. Chứng minh rằng với mọi n 3 ta có: n 2
3 n 4n 5 (1) Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 214
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Vôùi n=3, veá traùi baèng 27, coøn veá phaûi baèng 26.
Baát ñaúng thöùc (4) ñuùng.
Giaûi söû baát ñaúng thöùc (4) ñuùng vôùi n=k 3. töùc laø: k 3 2 k 4k 5. (1')
Ta phaûi chöùng minh noù cuõng ñuùng vôùi n=k+1, töùc laø: 3 k 2 k+1 1 4k 1 5
Thaät vaäy, nhaân hai veá cuûa baát ñaúng thöùc (1') vôùi 3 ta coù: 3
3k 12k 15 k 2 k 1 2 1 4k 1 5 2 2k 6k 5
Vì 2k 6k 5 0neân 3 k 2 2 k 1 1 4k 1 5
Ñaêng thöùc (1) ñaõ ñöôïc chöùng minh
Dạng 3. Chứng minh một tính chất
Ví dụ. Chứng minh rằng: 7 * n
n chia heát cho 7 vôùi moïi n N Giải Ñaët A 7 n n n. Khi n=1 thì A 1 0 chia heát cho 7 Giaû söû ñaõ coù: A k 7k k7
Thaät vaây, aùp duïng coâng thöùc nhò thöùc Niu-ton ta coù: A k+1 k 7 1 k 1 7 k 6 7k 5 21k 4 35k 3 35k 2 21k 7k 1 k 1 7 k k 6 7k 5 3k 4 5k 5k3 2 3k k
Theo giaû thieát quy naïp thì A 7
k k chia heát cho 7, do ñoùA k k+1 7 7
Vaäy n n chia heát cho 7 vôùi moïi n * N
Dạng 4. Một số bài toán khác
Ví dụ. Chứng minh rằng: 2 2 ... 2 2cos n+1 2 Giải
Ñaët veá traùi cuûa heä thöùc (1) baèng Cn.
Khi n=1, veá traùi baèng 2, veá phaûi baèng 2cos 2; heä thöùc (1) ñuùng 4
Giaû söû heä thöùc (1) ñuùng vôùi n=k 1, töùc laø C k 2cos k+1 2 ta phaûi chöùng minh: C k+1 2cos k+2 2
Thaät vaäy, töø giaû thieát quy naïp ta coù: C 2 C 2 2cos k+1 k k1 2 2 4cos 2cos ( vì cos ) k2 k2 k2 2 2 2
Vaäy heä thöùc (1) ñaõ ñöôïc chöùng minh
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 215
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
C. CÂU HỎI TRẮC NGHIỆM
Câu 1: Dùng quy nạp chứng minh mệnh đề chứa biến A(n) đúng với mọi số tự nhiên n ³ p ( p là
một số tự nhiên). Ở bước 1 (bước cơ sở) của chứng minh quy nạp, bắt đầu với n bằng: A. n =1. B. n = . p C. n > . p D. n ³ . p Lời giải. Chọn B
Câu 2: Dùng quy nạp chứng minh mệnh đề chứa biến A(n) đúng với mọi số tự nhiên n ³ p ( p là
một số tự nhiên). Ở bước 2 ta giả thiết mệnh đề A(n) đúng với n = k . Khẳng định nào sau đây là đúng? A. k > . p B. k ³ . p C. k = . p D. k < . p Lời giải. Chọn B
Câu 3: Khi sử dụng phương pháp quy nạp để chứng minh mệnh đề chứa biến A(n) đúng với mọi
số tự nhiên n ³ p ( p là một số tự nhiên), ta tiến hành hai bước:
· Bước 1, kiểm tra mệnh đề A (n) đúng với n = . p
· Bước 2, giả thiết mệnh đề A (n) đúng với số tự nhiên bất kỳ n = k ³ p và phải chứng
minh rằng nó cũng đúng với n = k +1. Trong hai bước trên:
A. Chỉ có bước 1 đúng. B. Chỉ có bước 2 đúng. C. Cả hai bước đều đúng. D. Cả hai bước đều sai. Lời giải. Chọn C
Câu 4: Một học sinh chứng minh mệnh đề ''8n +1 chia hết cho * 7, ' "n Î ' ( ) * như sau: · Giả sử ( )
* đúng với n = k , tức là 8k +1 chia hết cho 7. · Ta có: k 1 8 + +1 = 8(8k + )
1 -7 , kết hợp với giả thiết 8k +1 chia hết cho 7 nên suy ra được k 1
8 + +1 chia hết cho 7. Vậy đẳng thức ( ) * đúng với mọi * n Î .
Khẳng định nào sau đây là đúng?
A. Học sinh trên chứng minh đúng.
B. Học sinh chứng minh sai vì không có giả thiết qui nạp.
C. Học sinh chứng minh sai vì không dùng giả thiết qui nạp.
D. Học sinh không kiểm tra bước 1 (bước cơ sở) của phương pháp qui nạp. Lời giải. Chọn D
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 216
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Thiếu bước 1 là kiểm tra với n =1 , khi đó ta có 1
8 +1 = 9 không chi hết cho 7. Câu 5: 1 1 1 1 Cho S = + + +... + với *
n Î . Mệnh đề nào sau đây đúng? n 1⋅2 2⋅3 3⋅ 4 . n (n + ) 1 A. 1 1 2 1 S = . B. S = . C. S = . D. S = . 3 12 2 6 2 3 3 4 Lời giải. Chọn C
Lưu ý rằng S là tổng n số hạng đầu tiên nên. n Do đó với 1 1 2
n = 2 , ta có S = + = . 2 1⋅2 2⋅3 3 Câu 6: 1 1 1 1 Cho S = + + +... + với *
n Î . Mệnh đề nào sau đây đúng? n 1⋅2 2⋅3 3⋅ 4 . n (n + ) 1 A. n -1 n n + n + S = . B. S = . C. 1 S = . D. 2 S = . n n n n +1 n n + 2 n n + 3 Lời giải. Chọn B
Cách trắc nghiệm: Ta tính được 1 2 3 S = , S = ,
= . Từ đó ta thấy quy luật là từ nhỏ 1 2 S3 2 3 4
hơn mẫu đúng 1 đơn vị.
Cách tự luận. Ta có 1 2 3 n S = , S = , = ¾¾ dự đoán S = . 1 2 S3 2 3 4 n n +1 1 1
· Với n =1 , ta được S = = : đúng. 1 1.2 1+1 1 1 1
· Giả sử mệnh đề đúng khi k
n = k (k ³ ) 1 , tức là + +... + = . 1.2 2.3 k (k + ) 1 k +1 1 1 1 · Ta có + +... k + = 1.2 2.3 k (k + ) 1 k +1 1 1 1 1 k 1 + +... + + = + 1.2 2.3 k (k + ) 1 (k + ) 1 (k + 2) k +1 (k + ) 1 (k + 2) 2 1 1 1 1 k + 2k +1 + +... + + = 1.2 2.3 k (k + ) 1 (k + ) 1 (k + 2) (k + ) 1 (k + 2) 1 1 1 1 k +1 + +... + + = . S 1.2 2.3 k (k + ) 1 (k + ) 1 (k + 2) k + 2
uy ra mệnh đề đúng với n = k +1 . Câu 7: 1 1 1 Cho S = + +... + với *
n Î . Mệnh đề nào sau đây đúng? n 1⋅3 3⋅5 (2n - ) 1 ⋅(2n + ) 1 A. n -1 n n n + S = . B. S = . C. S = . D. 2 S = . n 2n -1 n 2n +1 n 3n -2 n 2n + 5
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 217
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải. Chọn B ìï 1 n ï =1 ¾¾ S = ï 1 ï 3 ïïï Cho 6 ïn í = 2 ¾¾ S =
. Kiểm tra các đáp án chỉ cho B thỏa. 2 ï 15 ïïï 3 ïn ï = 3 ¾¾ S = 3 ïïî 7 æ öæ ö æ ö Câu 8: 1 1 1 Cho P = 1 ç ÷ ç - ÷ 1 çç - . ÷÷ .. 1 ç ÷ ç ÷
với n ³ 2 và n Î .
Mệnh đề nào sau đây đúng? è ç ÷ ç - ÷ n 2 2 2 2 øè 3 ø ç ÷ è n ø A. n +1 n - n + n + P = . B. 1 P = . C. 1 P = . D. 1 P = . n + 2 2n n 2n Lời giải. Chọn D ìï æ 1 ö 3 n ïï = 2 ¾¾P = 1 ç ÷ ç - ÷ = 2 2 ï ç ÷ è ø Vì ï 2 4 ï n ³ 2 nên ta cho í . ï æ 1 ö æ 1 ö ï 2 n ï = 3 ¾¾ P = 1 ç ÷ ç - ÷. 1 ç ÷ ï ç ÷ ç - ÷ = 3 2 2 ï è ï 2 ø çè 3 ÷ø 3 î
Kiểm tra các đáp án chỉ cho D thỏa. Câu 9: Với mọi *
n Î , hệ thức nào sau đây là sai? n (n + ) 1
A. 1+ 2 +...+ n = 2
B. + + + +( n - ) 2 1 3 5 ... 2 1 = n . n (n + ) 1 (2n + ) 1 C. 2 2 2 1 + 2 +... + n = 6 + + 2 2n(n ) 1 (2n ) 1 D. 2 2 2 2 + 4 + 6 ++(2n) = . 6 Lời giải. Chọn D
Bẳng cách thử với n =1 , n = 2 , n = 3 là ta kết luận được.
Câu 10: Xét hai mệnh đề sau: I) Với mọi * n Î , số 3 2
n + 3n + 5n chia hết cho 3. II) Với mọi * n Î , ta có 1 1 1 13 + +... + > . n +1 n + 2 2n 24 Mệnh đề nào đúng? A. Chỉ I. B. Chỉ II. C. Không có. D. Cả I và II. Lời giải.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 218
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn A
Ta chứng minh I) đúng. Với n =1 , ta có 3 2
u = 1 + 3.1 + 5.1 = 93 : đúng. 1
Giả sử mệnh đề đúng khi n = k (k ³ ) 1 , tức là 3 2
u = k + 3k + 5k 3 . k Ta có u = ( 3 2
k + 3k + 5k ) 2
+ 3k + 9k + 9 = u + 3 k + k + Kết thúc chứng minh. + k ( 2 3 3 3. k 1 )
Mệnh đề II) sai vì với n = 1, ta có 1 1 12 13 VT = = = > : Vô lý. 1+1 2 24 24
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 219
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 BÀI 2. DÃY SỐ
A. KIẾN THỨC CƠ BẢN CẦN NẮM I – ĐỊNH NGHĨA
1. Định nghĩa dãy số
Mỗi hàm số u xác định trên tập các số nguyên dương *
được gọi là một dãy số vô hạn (gọi tắt là dãy số). Kí hiệu: * u :
n u(n).
Người ta thường viết dãy số dưới dạng khai triển u , , u u , ..., u , ..., 1 2 3 n
trong đó u = u n hoặc viết tắt là (u và gọi
u là số hạng thứ n và là số hạng n ), n ( ) 1
u là số hạng đầu, n tổng quát của dãy số.
2. Định nghĩa dãy số hữu hạn
Mỗi hàm số u xác định trên tập M = {1,2,3,...,m} với *
m Î được gọi là một dãy số hữu hạn.
Dạng khai triển của nó là u , u , u , ..., u , trong đó 1 2 3
u là số hạng cuối. n 1
u là số hạng đầu, m
II –CÁCH CHO MỘT DÃY SỐ
1. Dãy số cho bằng công thức của số hạng tổng quát
2. Dãy số cho bằng phương pháp mô tả
3. Dãy số cho bằng phương pháp truy hồi
Cách cho một dãy số bằng phương pháp truy hồi, tức là:
a) Cho số hạng đầu (hay vài số hạng đầu).
b) Cho hệ thức truy hồi, tức là hệ thức biểu thị số hạng thứ n qua số hạng (hay vài số hạng) đứng trước nó.
III – DÃY SỐ TĂNG, DÃY SỐ GIẢM VÀ DÃY SỐ BỊ CHẶN
1. Dãy số tăng, dãy số giảm Định nghĩa 1
Dãy số (u ) được gọi là dãy số tăng nếu ta có u > u với mọi * n Î . n n 1 + n
Dãy số (u ) được gọi là dãy số giảm nếu ta có u < u với mọi * n Î . n n 1 + n
Chú ý: Không phải mọi dãy số đều tăng hoặc giảm. Chẳng hạn, dãy số ( n u ) với u = - tức là n ( 3) n dãy -3,9, 2
- 7,81,... không tăng cũng không giảm.
2. Dãy số bị chặn Định nghĩa 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 220
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Dãy số (u ) được gọi là bị chặn trên nếu tồn tại một số M sao cho n * u £ M, . "n Î n
Dãy số (u ) được gọi là bị chặn dưới nếu tồn tại một số m sao cho n * u ³ m, . "n Î n
Dãy số (u ) được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m, M n sao cho *
m £ u £ M, . "n Î n
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1. Tìm số hạng của dãy số 1. Phương pháp 2. Các ví dụ
Ví dụ 1. Cho dãy số un , tìm un u 5 u 3 a) u 1 n : ; b) un 1 : u n 1 un 3 u 4u n 1 n Hướng dẫn giải a) Ta có: u 5 1 u 5 1.3 2 u 5 2.3 3 u 5 3.3 4 ... u 5 n 1 .3 * n b) Ta có u 3 1 u 3.4 2 2 u 3.4 3 3 u 3.4 4 ... n 1 u 3.4 * n
Ví dụ 2. Cho dãy số un , tìm un u 1 u 3 a) u 1 n : ; b) un 1 : u 2 n 1 2un 3 u n 1 1 u n Hướng dẫn giải a) Ta có:
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 221
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 u 1 2 3 1 3 u 5 2 3 2 4 u 13 2 3 3 5 u 29 2 3 4 ... n 1 u 2 3 * n b) Ta có 2 u 3 3 0 1 2 u 10 3 1 2 2 u 11 3 2 3 2 u 12 3 3 4 ... 3 u 3 n 1 * n 3. Bài tập trắc nghiệm Câu 1: n -
Cho dãy số (u , biết u =
. Năm số hạng đầu tiên của dãy số đó lần lượt là những số n ) n n +1 nào dưới đây? A. 1 2 3 4 5 - ;- ;- ;- ;- . B. 2 3 4 5 6
- ;- ;- ;- ;- . C. 1 2 3 4 5 ; ; ; ; . D. 2 3 4 5 6 ; ; ; ; . 2 3 4 5 6 3 4 5 6 7 2 3 4 5 6 3 4 5 6 7 Lời giải. Chọn A Ta có 1 2 3 4 5
u = - ; u = - ; u = - ; u = - ; u = - . 1 2 3 4 5 2 3 4 5 6
Nhận xét: (i) Dùng MTCT chức năng CALC để kiểm tra (tính) nhanh.
(ii) Ta thấy dãy (u ) là dãy số âm nên loại các phương án C, D . Đáp án đúng là A hoặc n
B. Ta chỉ cần kiểm tra một số hạng nào đó mà cả hai đáp án khác nhau là được. Chẳng hạng kiểm tra 1 1 u thì thấy 1 u = - 2 Câu 2: n
Cho dãy số (u ) , biết u =
. Ba số hạng đầu tiên của dãy số đó lần lượt là những số n n 3n -1 nào dưới đây? A. 1 1 1 ; ; . B. 1 1 3 ; ; . C. 1 1 1 ; ; . D. 1 2 3 ; ; . 2 4 8 2 4 26 2 4 16 2 3 4 Lời giải. Chọn B
Dùng MTCT chức năng CALC: ta có
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 222
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 1 2 2 1 3 3 u = ; u = = = ; u = = . 1 2 2 3 3 2 3 -1 8 4 3 -1 26 u ìï = 1 - Câu 3: Cho dãy số ( ï u ) , biết 1 í
với n ³ 0 . Ba số hạng đầu tiên của dãy số đó là lần lượt n u ï = u + 3 ïî n 1 + n
là những số nào dưới đây? A. -1;2;5. B. 1;4;7. C. 4;7;10. D. 1; - 3;7. Lời giải. Chọn A Ta có u = 1
- ; u = u +3 = 2; u = u +3 = 5. 1 2 1 3 2
Nhận xét: (i) Dùng chức năng “lặp” của MTCT để tính:
Nhập vào màn hình: X = X +3.
Bấm CALC và cho X = -1 (ứng với u = -1) 1
Để tính u cần bấm “=” ra kết quả liên tiếp n-1 lần. Ví dụ để tính u ta bấm “=” ra kết n 2
quả lần đầu tiên, bấm “=” ra kết quả thứ hai chính là u ,... 3
(ii) Vì u = -1 nên loại các đáp án B, C. Còn lại các đáp án A, C; để biết đáp án nào ta chỉ 1
cần kiểm tra u (vì
u = u + 3 = 2 2
u ở hai đáp án là khác nhau): 2 2 1 2 Câu 4: 2n -1
Cho dãy số (u ), biết u =
. Tìm số hạng u . n n 2 5 n + 3 A. 1 17 7 71 u = . B. u = . C. u = . D. u = . 5 4 5 12 5 4 5 39 Lời giải. Chọn C 2
Thế trực tiếp hoặc dùng chức năng CALC: 2.5 -1 49 7 u = = = . 5 2 5 + 3 28 4 Câu 5: Cho dãy số ( n
u ), biết u = -
n Mệnh đề nào sau đây sai? n ( ) 1 .2 . n A. u = -2. B. u = 4. C. u = -6. D. u = -8. 1 2 3 4 Lời giải. Chọn D
Thay trực tiếp hoặc dùng chức năng CALC: u = 2.1 - = -2; u = (- )2 1 .2.2 = 4, u = (- )3 1 2.3 = -6; u = (- )4 1 2.4 = 8 . 1 2 3 4
Nhận xét: Dễ thấy u > 0 khi n chẵn và ngược lại nên đáp án D sai. n n Câu 6: Cho dãy số ( n
u ), biết u = - Tìm số hạng u . n ( ) 2 1 . . n 3 n
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 223
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. 8 8 u = . B. u = 2. C. u = -2. D. u = - . 3 3 3 3 3 3 Lời giải. Chọn D 3
Thay trực tiếp hoặc dùng chức năng CALC: u = (- )3 2 8 1 . = - . 3 3 3 u ìï = 2 1 ï Câu 7: Cho dãy số ( ï u xác định bởi í 1
. Tìm số hạng u . n ) 4 u ï = u +1 ï n 1 + ( n ) ïî 3 A. 5 2 14 u = . B. u = 1. C. u = . D. u = . 4 9 4 4 3 4 27 Lời giải. Chọn A Ta có 1 1 1 2 1 1æ2 ö 5 u = u +1 = 2 +1 = 1; u = u +1 = ; u = u +1 = çç +1÷÷ = . 2 ( 1 ) ( ) 3 ( 2 ) 4 ( 3 ) 3 3 3 3 3 3çè3 ÷ø 9
Nhận xét: Có thể dùng chức năng “lặp” trong MTCT để tính nhanh. u ìï = 3 1 ï Câu 8: Cho dãy ( ï
u ) xác định bởi í u
. Mệnh đề nào sau đây sai? n n u ï = + ï 2 n 1 + ïî 2 A. 5 15 31 63 u = . B. u = . C. u = . D. u = . 2 2 3 4 4 8 5 16 Lời giải. Chọn A ìï u 3 7 u 7 15 1 2 u ï = + 2 = + 2 = ; u = + 2 = + 2 = ï 2 3 Ta có ïï 2 2 2 2 4 4 í ï u 15 31 u 31 63 ï 3 4 u ï = + 2 = + 2 = ; u = + 2 = + 2 = . 4 5 ïïî 2 8 8 2 16 16
Nhận xét: Dùng chức năng “lặp” trong MTCT để tính nhanh. Câu 9: n +
Cho dãy số (u ), biết 1 u =
. Số 8 là số hạng thứ mấy của dãy số? n n 2n +1 15 A. 8. B. 6. C. 5. D. 7. Lời giải. Chọn D Ta cần tìm n + n sao cho 1 8 u = =
15n +15 =16n +8 n = 7. n 2n +1 15
Nhận xét: Có thể dùng chức năng CALC để kiểm tra nhanh.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 224
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Câu 10: n +
Cho dãy số (u ), biết 2 5 u =
. Số 7 là số hạng thứ mấy của dãy số? n n 5n - 4 12 A. 8. B. 6. C. 9. D. 10. Lời giải. Chọn A
Dùng chức năng “lặp” để kiểm tra đáp án. Hoặc giải cụ thể như sau: 2n + 5 7 u = =
24n + 60 = 35n- 28 11n = 88 n = 8. n 5n - 4 12
Câu 11: Cho dãy số (u ), biết u = 2n. Tìm số hạng u . n n n 1 + A. u = 2n.2. B. u = 2n +1. C. u = 2 n +1 . D. u = 2n + 2. n 1 + ( ) n 1 + n 1 + n 1 + Lời giải. Chọn A
Thay n bằng n +1 trong công thức u ta được: n 1 u = 2 + = 2.2n . n n 1 +
Câu 12: Cho dãy số (u , biết u = 3n. Tìm số hạng u . n ) n 2n 1 - A. 2 2 n 1 - u = 3 .3n -1. B. n n 1 u = 3 .3 - . C. 2 u = 3 n -1. D. ( ) u = 3 . 2n 1 - 2n 1 - 2n 1 - 2n 1 - Lời giải. Chọn B Ta có n n«2n 1 - 2n 1 - n n 1 u = 3 ¾¾¾¾ u = 3 = 3 .3 - . n 2n 1 -
Câu 13: Cho dãy số ( + u ), với n 1 u = 5 . Tìm số hạng u . n n n 1 - A. n 1 u = 5 - .
B. u = 5n. C. n 1 u = 5.5 + . D. n 1 u = 5.5 - . n 1 - n 1 - n 1 - n 1 - Lời giải. Chọn B n 1 + n«n 1 - (n- ) 1 1 + u = 5 ¾¾¾u = 5 = 5n. n n 1 - 2n+3 æ - ö Câu 14: n 1
Cho dãy số (u ), với u = ç ÷ ç ÷ . Tìm số hạng u . n n ç ÷ è n 1 + n +1ø 2(n+ ) 1 +3 æ - ö 2(n- ) 1 +3 æ - ö A. n 1 n 1 u = ç ÷ ç ÷ . B. u = ç ÷ ç ÷ . n 1 + ç ÷ è n 1 + ç ÷ n +1ø èn +1ø 2n+3 æ ö 2n+5 æ ö C. n n u = ç ÷ ç ÷ . D. u = ç ÷ ç ÷ . n 1 + ç ÷ è n 1 + ç ÷ n + 2 ø èn + 2ø Lời giải. Chọn D n+ + + + æ - ö æ + - ö n 1 n = ç ÷ ç ÷ æ ö « + (n ) ( 2 ) 1 3 2 3 2n 5 1 1 n n n 1 u ç ÷ ¾¾¾u = ç ÷ ç ÷ ç ÷ = ç ÷ ç ÷ . n n 1 + è + ø çè + + ÷ ç ÷ n 1 (n ) 1 1ø èn + 2ø
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 225
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 15: Dãy số có các số hạng cho bởi: 1 2 3 4 0; ; ; ; ; .
có số hạng tổng quát là công thức nào dưới 2 3 4 5 đây? 2 A. n +1 n n - n - n u = . B. u = . C. 1 u = . D. u = . n n n n +1 n n n n +1 Lời giải. Chọn C Vì 1
u = 0 nên loại các đáp án A và B. Ta kiểm tra 1 u = ở các đáp án C, D: 2 2 Xét đáp án C: n -1 1 u = ¾¾ u = n 2 n 2 2 Xét đáp án D: n - n 2 1 u = ¾¾ u = = / ¾¾ loại n 2 n +1 3 2 Nhận xét: 1-1 1 2-1 2 3-1 n - u = 0 = ; u = = ; u = = ,... nên đoán 1 u = . 1 2 3 1 2 2 3 3 n n
Câu 16: Dãy số có các số hạnh cho bởi: -1;1;-1;1;-1; .
có số hạng tổng quát là công thức nào dưới đây? A. n n+ u = 1. B. u = -1. C. u = (- ) 1 . D. u = (- ) 1 1 . n n n n Lời giải. Chọn C
Vì dãy số đa cho không phải là dãy hằng nên loại các đáp án A và B. Ta kiểm tra u = -1 1 ở các đáp án C, D:
Xét đáp án C: u = - ¾¾ u = - n ( ) 1 n 1 1 Xét đáp án D: + u = (- )n 1 1 ¾¾ u = (- )2 1 = 1 = / -1 ¾¾ loại D. n 1
Câu 17: Cho dãy số có các số hạng đầu là: -2;0;2;4;6; .
Số hạng tổng quát của dãy số này là
công thức nào dưới đây? A. u = -2 . n
B. u = n -2.
C. u = -2(n + ) 1 .
D. u = 2n -4. n n n n Lời giải. Chọn D
Kiểm tra u = -2 ta loại các đáp án B, C. Ta kiểm tra u = 0 ở các đáp án A, D: 1 2
Xét đáp án A: u = 2n u = 4 =/ 0 ¾¾ loại A. n 2
Xét đáp án D: u = 2n-4 = 2.2-4 = 0 n
Nhận xét: Dãy 2;4;6;... có công thức là ( *
2n n Î ) nên dãy -2;0;2;4;6; . có được bằng
cách “tịnh tiến” 2n sang trái 4 đớn vị, tức là 2n-4.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 226
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 u ìï = 2
Câu 18: Cho dãy số ( ï
u ), được xác định 1 í
. Số hạng tổng quát u của dãy số là số hạng n u ï = 2u n ïî n 1 + n nào dưới đây? A. n 1 u n - = .
B. u = 2n. C. n 1 u 2 + = . D. u = 2. n n n n Lời giải. Chọn B u ìï = 2 1 u ìï = 2 ï Từ công thức 1 ï ï ï í ¾¾ u í = 2u = 2.2 = 4. 2 1 u ï = 2u ï ïî n 1 + n ïu ï = 2u = 2.4 = 8 ïî 3 2 Xét đáp án A với 1 1 - 0 n = 1 ¾¾ u = 1 = 1 = 1 ¾¾ A loại. 1
Xét đáp án B, ta thấy đều thỏa mãn. Xét đáp án C với 1 1 + 2 n = 1 ¾¾ u = 2 = 2 = 4 ¾¾ C loại. 1
Dễ thấy đáp án D không thỏa mãn. ìï 1 ï = Câu 19: u Cho dãy số ( ï
u ), được xác định 1 í 2
. Số hạng tổng quát u của dãy số là số hạng n ï n u ïï = u -2 ïî n 1 + n nào dưới đây? A. 1 1 u = + 2 n -
B. u = -2 n - C. 1 u = -2 . n D. 1 u = + 2 . n n ( ) 1 . n ( ) 1 . 2 2 n 2 n 2 Lời giải. Chọn B ìï 1 ï = ï 1 u ï 2 ìï 1 ïï ï = ï Từ công thức ï 1 u 1 3 í 2 ï ¾¾ u í = u -2 = -2 = - . 2 1 ï ï 2 2 u ïï u 2 ï = - ïî ï n 1 + n ï 3 7 ïu ï = u -2 = - -2 = - 3 2 ïïî 2 2 Xét đáp án A với 1 5 n = 2 ¾¾ u = + 2 2 -1 = ¾¾ A loại. 2 ( ) 2 2
Xét đáp án B, ta thấy đều thỏa mãn. Xét đáp án C với 1 1 7 n = 2 ¾¾
u = -2.2 = - 4 = - ¾¾ C loại. 2 2 2 2 Xét đáp án D với 1 5 n = 1 ¾¾ u = + 2.1 = ¾¾ D loại. 1 2 2 u ìï = 2
Câu 20: Cho dãy số ( ï
u ), được xác định 1 í
. Số hạng tổng quát u của dãy số là số n u ï -u = 2n -1 n ïî n 1 + n hạng nào dưới đây?
A. u = +(n - )2 2 1 . B. 2 u = 2 + n . n n
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 227
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
C. u = +(n + )2 2 1 .
D. u = -(n - )2 2 1 . n n Lời giải. Chọn A
Kiểm tra u = 2 ta loại các đáp án B và C. Ta có u = u + 2.1-1= 3. 1 2 1
Xét đáp án A: u = 2+(n- )2 1 ¾¾ u = 3 n 2
Hoặc kiểm tra: u -u = n - n- = n- + n ( )2 2 1 2 1. n 1
Xét đáp án D: u = 2-(n- )2 1 ¾¾ u =1 ¾¾
loại D. Hoặc kiểm tra: n 2 u -u = n - - n = - n + = / n - + n ( )2 2 1 2 1 2 1. n 1 u ìï = 1
Câu 21: Cho dãy số ( ï
u ), được xác định 1 í
. Số hạng tổng quát u của dãy số là số n 2 n u ï = u + n ïî n 1 + n hạng nào dưới đây? A.
n(n +1)(2n +1) u = 1+ . B. n 6
n(n -1)(2n + 2) u = 1+ . n 6 C.
n(n -1)(2n -1) u = 1+ . D. n 6
n(n +1)(2n - 2) u = 1+ . n 6 Lời giải. Chọn C
Kiểm tra u =1 ta loại đáp án A. Ta có 2 u = u +1 = 2. 1 2 1 Xét đáp án B:
n(n -1)(2n + 2) 2.1.6 u = 1+ ¾¾ u =1+ = 3 = / 2 ¾¾ B loại. n 2 6 6 Xét đáp án C:
n(n -1)(2n -1) 2.1.3 u = u = 1+ ¾¾ u = 1+ = 2 n n 2 6 6 Xét đáp án D:
n(n +1)(2n - 2) 2.3.2 u = 1+ . ¾¾ u =1+ = 3 = / 2 ¾¾ D loại. n 2 6 6 u ìï = -2 1 ï Câu 22: ï
Cho dãy số (u ), được xác định í
1 . Số hạng tổng quát u của dãy số là số n u ï = -2 - n ï n 1 + ï u ïî n hạng nào dưới đây? A. n - +1 n + n + n u = . B. 1 u = . C. 1 u = - . D. u = - . n n n n n n n n +1 Lời giải. Chọn C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 228
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Kiểm tra 1 3
u = -2 ta loại các đáp án A, B. Ta có u = -2 - = - . 1 2 u 2 1 Xét đáp án C: n +1 3 u = - ¾¾ u = - n 2 n 2 Xét đáp án D : n 2 u = - ¾¾ u = - ¾¾ D loại. n 2 n +1 3 u ìï = 1 Câu 23: 1 Cho dãy số ( ï
u ), được xác định í
. Số hạng tổng quát u của dãy số là số n n u ïï = u + - ï + n ( )2 1 n n 1 î hạng nào dưới đây? A. n u = 1+ . n B. u = 1- . n C. u = +(- )2 1 1 . D. u = . n n n n n Lời giải. Chọn D
Kiểm tra u =1 ta loại đáp án A, B và C 1
Câu 24: Cho dãy số (u ) có số hạng tổng quát là u = 2(3n với *
n Î . Công thức truy hồi của dãy n ) n số đó là: u ìï = 6 u ìï = 6 A. ï 1 í . B. ï 1 í . u
ï = 6u , n >1 ïî u
ï = 3u , n >1 n n 1 - ïî n n 1 - u ìï = 3 u ìï = 3 C. ï 1 í . D. ï 1 í . u
ï = 3u , n >1 ïî u
ï = 6u , n >1 n n 1 - ïî n n 1 - Lời giải. Chọn B Vì 1
u = 2.3 = 6 nên ta loại các đáp án C và D. Ta có 2 u = 2.3 = 18. 1 2 u ìï = 6 Xét đáp án A: ï 1 í ¾¾
u = 6u = 6.6 = 36 ¾¾ A loại. 2 1 u
ï = 6u , n >1 ïî n n 1 - u ìï = 6 Xét đáp án B: ï 1 í ¾¾
u = 3u = 3.6 =18 2 1 u
ï = 3u , n >1 ïî n n 1 - a ìï = 3 1 ï
Câu 25: Cho dãy số ( ï
a ), được xác định í 1
. Mệnh đề nào sau đây sai? n a ï = a , n ³ 1 ï n 1 + ïî 2 n A. 93 3
a + a + a + a + a = . B. a = . 1 2 3 4 5 16 10 512 C. 9 a + a = . D. 3 a = . n 1 + n 2n n 2n Lời giải. Chọn D
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 229
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Ta có u u u u u u 3 1 2 1 3 1 1 a = 3; a = ; a = = ; a = = ,... ¾¾ = = nên suy ra đáp án D 1 2 3 u 2 4 3 n n 1 - n 1 2 2 2 2 2 2 2 - sai. Xét đáp án A: 5 æ1ö 1-ç ÷ ç ÷ æ 1 1 1 1 ö çè2÷ø 93
a + a + a + a + a = 3 1 ç ÷ ç + + + + ÷ = 3. = ¾¾ A đúng. 1 2 3 4 5 2 3 4 çè 2 2 2 2 ÷ø 1 16 1- 2 Xét đáp án B: 3 3 10 a = = ¾¾ B đúng. 9 2 512 Xét đáp án C. 3 3 3+ 3.2 9 a + a = + = = ¾¾ C đúng. n 1 + n n n 1 2 2 - 2n 2n
Dạng 2. Tính tăng giảm và bị chặn của dãy số 1. Phương pháp
Xét tính tăng giảm
(un) là dãy số tăng un+1 > un, n N*. u u n
n+1 – un > 0 , n N*
1 1,n N* ( un > 0). n u
(un) là dãy số giảm
un+1 < un với n N*. u u n
n+1 – un< 0 , n N*
1 1, n N* (un > 0). n u
Dãy số bị chặn
(un) là dãy số bị chăn trên M R: un M, n N*.
(un) là dãy số bị chặn dưới m R: un m, n N*.
(un) là dãy số bị chặn m, M R: m un M, n N*. 1. Phương pháp 2. Các ví dụ
Ví dụ 1. Xét tính tăng giảm của dãy số un biết 2n 1 a)u 2 n n ; u 3n b) 2 n n Hướng dẫn giải 7 2n 1 2 3 a)u ; u u 0, n * n 3n . Vậy dãy giảm 2 3 3n n 1 1 n 2
Lưu ý: Ta không cần phải chia như vậy, làm cũng rất nhanh. b)
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 230
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 n 2 u n n n n . 2 u u n n 1 1 0,n * n1 n n n 1 Vậy dãy giảm
Ví dụ 2. Xét tính tăng giảm của dãy số un biết n 5 n2 a)u 2 n ; b) u . n 1 3 n n Hướng dẫn giải 2n 5 0,n 2k 1 2n 5 n 3 n 2 n 1 a) Xét u u 1 . n 1 n n 3n 2 2n 5 0,n 2k n 3 n 2
Vậy dãy đã cho không tăng không giảm 1 0,n 2k 1 1 n 4 n 5 n 1 b) Xét u u 1 . n 1 n n 4n 5 1 0,n 2k n 4 n 5
Vậy dãy đã cho không tăng không giảm
Ví dụ 3. Xét tính bị chặn của dãy số un 2 n 2n a)u n n ; b) u 2 n n 1 n 2 n 2n n Hướng dẫn giải 2 n 2n n 1 a)u 1 n 2 n n 2 1 n n 1 Ta có: n 1 0 1,n * . Suy ra: * 1 u 2, n . 2 n n 1 n
Vậy dãy số đã cho bị chặn n 1 1 b) u 0 u ,n* n n 2 n 2n n 2 2 1 1 n
Ví dụ 4. Xét tính bị chặn của dãy số un 4sinn 4cos 2 3n 1 a)u n n 1 cos ; u 2n b) n 2 5n n Hướng dẫn giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 231
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 a)un n 1 cos un n 1 cos cos 1 2n 2n 2n 1 u n 1
Vậy dãy đã cho bị chặn. 4sinn 4cos 2 3n 1 4sinn 4cos 2 3n 1 5 b) u u n 1 2 5n n 2 n 5n 2 n 5n Suy ra: * 1 u 1, n n .
Vậy dãy đã cho bị chặn. 3. Bài tập trắc nghiệm
Câu 1: Cho các dãy số sau. Dãy số nào là dãy số tăng?
A. 1; 1; 1; 1; 1; 1; B. 1 1 1 1 1; - ; ; - ; ; 2 4 8 16
C. 1; 3; 5; 7; 9; D. 1 1 1 1 1; ; ; ; ; 2 4 8 16 Lời giải. Chọn C
Xét đáp án A: 1; 1; 1; 1; 1; 1; đây là dãy hằng nên không tăng không giảm. Xét đáp án B: 1 1 1 1 1; - ; ; - ; ; ¾¾ > < ¾¾ loại B 1 u u2 3 u 2 4 8 16 Xét đáp án C: * 1; 3; 5; 7; 9; ¾¾
u < u , n Î n n 1 + Xét đáp án D: 1 1 1 1 1; ; ; ; ; ¾¾ > > ¼> >¼ ¾¾ loại D. 1 u u2 3 u u 2 4 8 16 n
Câu 2: Trong các dãy số (u ) cho bởi số hạng tổng quát u sau, dãy số nào là dãy số tăng? n n A. 1 n + n - u = . B. 1 u = . C. 5 u = . D. 2 1 u = . n 2n n n n 3n +1 n n +1 Lời giải. Chọn D
Vì 2n;n là các dãy dương và tăng nên 1 1 ;
là các dãy giảm, do đó loại A,B. 2n n ìï 3 ï = ï 1 u Xét đáp án C: n + 5 ï 2 u = ¾¾ í ¾¾ u > u ¾¾ loại C n 1 2 3n +1 ï 7 ïu ï = 2 ïïî 6 - æ ö Xét đáp án D: 2n 1 3 1 1 u = = 2- u -u = 3ç ÷ ç - ÷ > 0 n n 1 + ç ÷ n +1 n +1 n èn +1 n + 2ø
Câu 3: Trong các dãy số (u ) cho bởi số hạng tổng quát u sau, dãy số nào là dãy số tăng? n n
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 232
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. 2 n u = . B. 3 u = .
C. u = 2n. D. u = (-2) . n 3n n n n n Lời giải. Chọn C Xét đáp án C: n n 1 u = 2 ¾¾ u
-u = 2 + - 2n = 2n > 0 ¾¾ n n 1 + n
Vì 2n;n là các dãy dương và tăng nên 1 1 ;
là các dãy giảm, do đó loại các đáp án A và 2n n B. u ìï = n 4 Xét đáp án D: ï u = - ¾¾ í ¾¾ u > u ¾¾ loại D. n ( 2) 2 2 3 u ï = -8 ïî 3
Câu 4: Trong các dãy số (u cho bởi số hạng tổng quát u sau, dãy số nào là dãy số giảm? n ) n A. 1 n - u = . B. 3 1 u = . C. 2 u = n .
D. u = n + 2. n 2n n n +1 n n Lời giải. Chọn A
Vì 2n là dãy dương và tăng nên 1 là dãy giảm ¾¾ 2n u ìï =1 1 - ï Xét B: 3n 1 ï u = ¾¾ í ¾¾ u < u ¾¾ loại B. Hoặc n 5 1 2 n +1 u ï = ï 2 ïî 3 3n + 2 3n -1 4 u -u = - =
> 0 nên (u ) là dãy tăng. n 1 + n n + 2 n +1 (n + ) 1 (n + 2) n
Xét C: u = n ¾¾ u -u = n +
-n = n + > ¾¾ loại C. + n ( )2 2 2 1 2 1 0 n n 1 Xét D: 1 u = n + 2 ¾¾ u
-u = n + 3 - n + 2 = > 0 ¾¾ loại D. n n 1 + n n + 3 + n + 2
Câu 5: Trong các dãy số (u cho bởi số hạng tổng quát u sau, dãy số nào là dãy số giảm? n ) n 2 A. n +1 u = sin . n B. u = . n n n C. n
u = n - n -1. D. u = (- ) 1 .(2n + n ) 1 . n Lời giải. Chọn C æ ö A. 1 1
u = sin n u -u = 2 cosççn ÷
+ ÷sin có thể dương hoặc âm phụ thuộc n nên đáp án A n n 1 + n çè 2÷ø 2
sai. Hoặc dễ thấy sin n có dấu thay đổi trên *
nên dãy sin n không tăng, không giảm. 2 2 B. n +1 1 1 1 n + n -1 u = = n + u -u = 1+ - =
> 0 nên dãy đã cho tăng nên B sai. n n 1 + n n n n +1 n n (n + ) 1
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 233
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 C. 1
u = n - n -1 =
, dãy n + n -1 > 0 là dãy tăng nên suy ra u giảm. n n n + n +1 D. u = (- )
1 n (2n + là dãy thay dấu nên không tăng không giảm. n ) 1 Cách trắc nghiệm.
A. u = sin n có dấu thay đổi trên *
nên dãy này không tăng không giảm. n n ìï =1 u = 2 2 1 2 ï B. n +1 ï n +1 u = , ta có í 5 ¾¾ u < u ¾¾ u = không giảm. n 1 2 n n ï = 2 n u = n ï 2 ïî 2 n ìï =1 u =1 C. ï
u = n - n -1 , ta có 1 í ¾¾
u > u nên dự đoán dãy này giảm. n 1 2 n ïï = 2 u = 2 -1 î 2 D. u = (- )
1 n (2n + là dãy thay dấu nên không tăng không giảm. n ) 1 Cách CASIO. Các dãy sin ; ( ) 1 n (2n n - + )
1 có dấu thay đổi trên *
nên các dãy này không tăng không
giảm nên loại các đáp án A, D.
Còn lại các đáp án B, C ta chỉ cần kiểm tra một đáp án bằng chức năng TABLE. 2
Chẳng hạn kiểm tra đáp án B, ta vào chức năng TABLE nhập + F (X ) X 1 = với thiết lập X
Start = 1, End = 10, Step = 1.
Nếu thấy cột F (X ) các giá trị tăng thì loại B và chọn C, nếu ngược lại nếu thấy cột F (X )
các giá trị giảm dần thị chọn B và loại C.
Câu 6: Mệnh đề nào sau đây đúng? A. Dãy số 1 n u = - 2 là dãy tăng.
B. Dãy số u = (- )
1 (2n + là dãy giảm. n )1 n n C. Dãu số n -1 u = là dãy giảm. D. Dãy số 1 u = 2n + cos là dãy tăng. n n +1 n n Lời giải. Chọn D Xét đáp án A: 1 1 1 u = - 2 ¾¾ u -u = - < 0 ¾¾ loại A. n n 1 + n n n +1 n
Xét đáp án B: u = (- )
1 n (2n + là dãy có dấu thay đổi nên không giảm nên loại B. n )1 - æ ö Xét đáp án C: n 1 2 1 1 u = = 1- ¾¾ u -u = 2ç ÷ ç - ÷ > 0 ¾¾ loại C. n n 1 + ç ÷ n +1 n +1 n èn +1 n + 2ø æ ö Xét đáp án D: 1 1 1 u = 2n + cos ¾¾ u -u = çç2-cos ÷÷+cos > 0 nên n n 1 + n ç ÷ n è n +1ø n + 2
Câu 7: Mệnh đề nào sau đây sai?
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 234
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. Dãy số 1- n u = là dãy giảm. B. Dãy số 2
u = 2n - 5 là dãy tăng. n n n n æ ö C. Dãy số 1 u = 1 ç ÷ ç + ÷ là dãy giảm. D. Dãy số 2
u = n + sin n là dãy tăng. n ç ÷ è nø n Lời giải. Chọn C Xét A: 1- n 1 1 1 u = = - n ¾¾ u -u = -
+ n - n +1 < 0 nên dãy (u ) là dãy n n 1 + n n n n n +1 n giảm nên C đúng. Xét đáp án B: 2
u = 2n - 5 là dãy tăng vì 2
n là dãy tăng nên B đúng. Hoặc n u
-u = 2 2n +1 > 0 nên (u là dãy tăng. n ) n 1 + n ( ) n n n æ ö æ + ö + æ + ö Xét đáp án C: 1 n 1 u + n 2 n 2 = ç ÷ ç + ÷ = ç ÷ n 1 u 1 ç ÷ > 0 ¾¾ = .ç ÷ ç ÷ >1 ¾¾
u là dãy tăng nên n ( n) ç ÷ è ø ç ÷ è ø ç ÷ n n u n +1 è n ø n Xét đáp án D: 2
u = n + sin n ¾¾ u -u = - n + +
n > nên D đúng. + n ( 2 1 sin ( ) 1 ) 2 sin 0 n n 1 Câu 8: n -
Cho dãy số (u ) , biết 3 1 u =
. Dãy số (u ) bị chặn trên bởi số nào dưới đây? n n 3n +1 n A. 1. B. 1. C. 1 . D. 0. 3 2 Lời giải. Chọn B Ta có 3n-1 2 5 1 1 u = =1-
<1. Mặt khác: u = > > > 0 nên suy ra dãy (u ) bị chặn n 3 2 n +1 3n +1 7 2 2 n trên bởi số 1.
Câu 9: Trong các dãy số (u ) cho bởi số hạng tổng quát u sau, dãy số nào bị chặn trên? n n A. 2 u = n .
B. u = 2n. C. 1 u = .
D. u = n +1. n n n n n Lời giải. Chọn C Các dãy số 2; 2n n
; n +1 là các dãy tăng đến vô hạn khi n tăng lên vô hạn nên chúng không
bị chặn trên (có thể dùng chức năng TABLE của MTCT để kiểm tra). Nhận xét: 1 u = £1 với mọi *
n Î nên dãy (u ) bị chặn trên bởi 1. n n n
Câu 10: Cho dãy số (u ) , biết u = cosn + sin .
n Dãy số (u ) bị chặn trên bởi số nào dưới đây? n n n A. 0. B. 1. C. 2. D. Không bị chặn trên. Lời giải.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 235
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn C Ta có MTCT u ¾¾ ¾
u = sin1+ cos1>1> 0 nên loại các đáp án A và B (dùng TABLE của n 1
MTCT để kiểm tra, chỉ cần 1 số hạn nào đó của dãy số lớn hơn a thì dãy số đó không thể bị chặn trên bởi . a ) æ ö Ta có p
u = cos n + sin n = 2 sinççn ÷ + ÷ £ 2 n çè 4 ÷ø
Câu 11: Cho dãy số (u ) , biết u = sin n -cos .
n Dãy số (u ) bị chặn dưới bởi số nào dưới đây? n n n A. 0. B. -1. C. - 2. D. Không bị chặn dưới. Lời giải. Chọn C MTCT u ¾¾ ¾
u = sin 5-cos5 < -1< 0 ¾¾
loại A và B (dùng TABLE của MTCT để kiểm tra, n 5
chỉ cần có một số hạng nào đó của dãy số nhỏ hơn a thì dãy số đó không thể bị chặn dưới với số . a ) æ ö Ta có p u = 2 sinççn ÷ - ÷ ³ - 2 n çè 4 ÷ø
Câu 12: Cho dãy số (u , biết u = 3 cosn -sin . n Dãy số (u
bị chặn dưới và chặn trên lần lượt n ) n ) n
bởi các số m và M nào dưới đây? A. m = 2; - 2 M = . B. 1 m = - ; M = 3 +1. 2 C. m = - 3 +1; M = 3 -1. D. 1 1 m = - ; M = . 2 2 Lời giải. Chọn A MTCT (TABLE) 1 u ¾¾¾¾¾ u > 3 -1> ¾¾
loại C và D. n 1 2 MTCT (TABLE) 1 u ¾¾¾¾¾ u < - ¾¾ loại B. Vậy n 4 2 æ ö ç ÷ æ ö Nhận xét: 3 1 p u = 2ç sin n - cos n÷ ç ÷ = 2sinççn ÷ - ÷ ¾¾ 2 - £ u £ 2. n çè 2 2 ÷ ç ø è 6 n ÷ø
Câu 13: Cho dãy số ( n u ), biết u + = -
Mệnh đề nào sau đây đúng? n ( ) 2n 5 1 .5 . n
A. Dãy số (u ) bị chặn trên và không bị chặn dưới. n
B. Dãy số (u bị chặn dưới và không bị chặn trên. n )
C. Dãy số (u ) bị chặn. n
D. Dãy số (u không bị chặn. n )
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 236
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải. Chọn D
Nếu n chẵn thì 2n 1 u 5 + =
> 0 tăng lên vô hạn (dương vô cùng) khi n tăng lên vô hạn nên n
dãy (u ) không bị chặn trên. n Nếu n lẻ thì 2n 1 u 5 + = -
< 0 giảm xuống vô hạn (âm vô cùng) khi n tăng lên vô hạn nên n
dãy (u không bị chặn dưới. n )
Vậy dãy số đã cho không bị chặn. Câu 14: 1 1 1
Cho dãy số (u ), với u = + +... + , "n = 1; 2; 3 .
Mệnh đề nào sau đây n n 1.4 2.5 n (n + 3) đúng?
A. Dãy số (u ) bị chặn trên và không bị chặn dưới. n
B. Dãy số (u bị chặn dưới và không bị chặn trên. n )
C. Dãy số (u ) bị chặn. n
D. Dãy số (u ) không bị chặn. n Lời giải. Chọn C Ta có 1 1 1 1 u > 0 ¾¾
(u ) bị chặn dưới bởi 0. Mặt khác < = - ( * k Î ) n n k (k + ) 3 k (k + ) 1 k k +1 nên suy ra: 1 1 1 1 1 1 1 1 1 1 1 1 u < + + ++ =1- + - + - ++ - = 1- <1 n 1.2 2.3 3.4 n(n + ) 1 2 2 3 2 4 n n +1 n +1
nên dãy (u ) bị chặn trên, do đó dãy (u ) bị chặn. n n Câu 15: 1 1 1
Cho dãy số (u ), với u = + +... + , "n = 2; 3; 4; .
Mệnh đề nào sau đây đúng? n n 2 2 2 2 3 n
A. Dãy số (u ) bị chặn trên và không bị chặn dưới. n
B. Dãy số (u bị chặn dưới và không bị chặn trên. n )
C. Dãy số (u ) bị chặn. n
D. Dãy số (u không bị chặn. n ) Lời giải. Chọn C Ta có 1 1 1 1 u > 0 ¾¾
(u ) bị chặn dưới bởi 0. Mặt khác * < = -
k Î , k ³ 2 2 ( ) n n k (k - ) 1 k k -1 k nên suy ra:
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 237
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 1 1 1 1 1 1 1 1 1 1 1 1 u < + + ++ =1- + - + - ++ - = 1- <1 n 1.2 2.3 3.4 n(n + ) 1 2 2 3 2 4 n n +1 n +1
nên dãy (u ) bị chặn trên, do đó dãy (u ) bị chặn. n n
Câu 16: Trong các dãy số (u ) sau đây, dãy số nào là dãy số bị chặn? n A. 2 n u = n +1. B. 1 u = n + .
C. u = 2n +1. D. u = . n n n n n n +1 Lời giải. Chọn D Các dãy số 2; ; 2n n n
dương và tăng lên vô hạn (dương vô cùng) khi n tăng lên vô hạn, nên các dãy 1 2 +1; + ; 2n n n
+1 cũng tăng lên vô hạn (dương vô cùng), suy ra các dãy này n
không bị chặn trên, do đó chúng không bị chặn. Nhận xét: n 1 0 < u = =1- <1. n n +1 n +1
Câu 17: Trong các dãy số (u ) cho bởi số hạng tổng quát u sau, dãy số nào bị chặn? n n A. 1 u = .
B. u = 3n.
C. u = n +1. D. 2 u = n . n 2n n n n Lời giải. Chọn A Các dãy số 2; ; 3n n n
dương và tăng lên vô hạn (dương vô cùng) khi n tăng lên vô hạn nên các dãy 2; 1; 3n n n +
cũng tăng lên vô hạn (dương vô cùng), suy ra các dãy này không bị
chặn trên, do đó chúng không bị chặn. Nhận xét: 1 1 0 < u = £ . n 2n 2 u ìï = 6
Câu 18: Cho dãy số ( ï
u ), xác định bởi 1 í
. Mệnh đề nào sau đây đúng? n * u ï = 6 + u , "n Î ï n 1 + n î A. 5 6 £ u < .
B. 6 £ u < 3. n 2 n
C. 6 £ u < 2.
D. 6 £ u £ 2 3. n n Lời giải. Chọn D Ta có 5 u = 12 > 3 >
> 2 nên loại các đáp án A, B, C. 2 2 Nhận xét: Ta có u ìï = 6 u ìï = 6 u ìï = 6 1 ï ï 1 1 ï í ¾¾ í ¾¾ u ³ 0 ¾¾ í ¾¾ u ³ 6. u ï = 6 + ï u u ï ³ 0 n ï = + ³ + î ïî + u ï u n n 6 6 n n 1 1 n 1 + n î
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 238
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ta chứng minh quy nạp u £ 2 3. n
u £ 2 3;u £ 2 3 ¾¾ u = 6 +u £ 6 + 2 3 < 6 + 6 = 2 3. 1 k k 1 + k 1 + Câu 19: p
Cho dãy số (u ), với u = sin
. Khẳng định nào sau đây là đúng? n n n +1 A. Số hạng thứ p
n +1 của dãy là u = sin . n 1 + n +1
B. Dãy số (u là dãy số bị chặn. n )
C. Dãy số (u ) là một dãy số tăng. n
D. Dãy số (u không tăng không giảm. n ) Lời giải. Chọn B p p p u = sin ¾¾ u = sin = sin ¾¾ A sai. n n 1 + n +1 (n + ) 1 +1 n + 2 p u = sin ¾¾ -1£ u £1 ¾¾ B đúng. n n +1 n p p æ p p pö u -u = sin -sin < 0 çç0 ÷ < < £ ÷ ¾¾ C, D sai. n 1 + n ç ÷ n + 2 n +1 è n + 2 n +1 2 ø
Câu 20: Cho dãy số ( n
u ), với u = (- )
1 . Mệnh đề nào sau đây đúng? n n
A. Dãy số (u ) là dãy số tăng.
B. Dãy số (u ) là dãy số giảm. n n
C. Dãy số (u là dãy số bị chặn.
D. Dãy số (u là dãy số không bị chặn. n ) n ) Lời giải. Chọn C u = (- )
1 n là dãy thay dấu nên không tăng, không giảm ¾¾ A, B sai. n
Tập giá trị của dãy u = (- ) 1 n là { 1; - } 1 ¾¾ 1 - £ u £1 ¾¾ C đúng. n n
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 239
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
BÀI 3. CẤP SỐ CỘNG
A. KIẾN THỨC CƠ BẢN CẦN NẮM I – ĐỊNH NGHĨA
Cấp số cộng là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều
bằng số hạng đứng ngay trước nó cộng với một số không đỗi d.
Số d được gọi là công sai của cấp số cộng.
Nếu (u ) là cấp số cộng với công sai d, ta có công thức truy hồi u = u + d với * n Î . n n 1 + n
Đặc biệt khi d = 0 thì cấp số cộng là một dãy số không đỗi (tất cả các số hạng đều bằng nhau).
II – SỐ HẠNG TỔNG QUÁT Định lí 1
Nếu cấp số cộng (u ) có số hạng đầu
u được xác định bởi n 1
u và công sai d thì số hạng tổng quát n công thức:
u = u + n -1 d với n ³ 2. n 1 ( )
III – TÍNH CHẤT CÁC SỐ HẠNG CỦA CẤP SỐ CỘNG Định lí 2
Trong một cấp số cộng, mỗi số hạng (trừ số hạng đầu và cuối) đều là trung bình cộng của hai số
hạng đứng kề với nó, nghĩa là u + u k 1 k 1 u - + = với k ³ 2. k 2
IV – TỔNG n SỐ HẠNG ĐẦU CỦA MỘT CẤP SỐ CỘNG Định lí 3 n ( + 1 u un )
Cho cấp số cộng (u ). Đặt S = u +u +u +...+u . Khi đó S = . n n 1 2 3 n n 2 n (n - ) 1
Chú ý: Vì u = u + n -1 d nên công thức trên có thể viết lại là S = nu + d. n 1 ( ) n 1 2
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1. Xác định cấp số cộng, công sai và số hạng của cấp số cộng 1. Phương pháp
Xác định một cấp số cộng là xác định số hạng đầu u1 và công sai d
Từ những giải thiết ta thường lập hệ phương trình theo ẩn số u1 và d rồi giải hệ đó.
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Trong các dãy số sau, dãy số nào là một cấp số cộng?
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 240
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
A. 1;-3;-7;-11;-15; B. 1;-3;-6;-9;-12; C. 1;-2;-4;-6;-8; D. 1;-3;-5;-7;-9; Lời giải Chọn A
Ta lần lượt kiểm tra: u -u = u -u = u -u =? 2 1 3 2 4 3 Xét đáp án A: 1;-3; 7 - ;-11;-15; ¾¾ u - = - = - = 2 1 u 3 u u2 u4 3 u Xét đáp án B: 1; 3 - ;-6;-9;-12; ¾¾ u -u = -4 = / -3 = - ¾¾ loại 2 1 3 u u2 Xét đáp án C: 1;-2; 4 - ;-6;-8; ¾¾ u -u = -3 = / -2 = - ¾¾ loại 2 1 3 u u2 Xét đáp án D: 1;-3; 5 - ;-7;-9; ¾¾ u -u = -4 = / -2 = - ¾¾ loại 2 1 3 u u2
Ví dụ 2: Cho dãy số 1 1 3
;0;- ;-1;- ;..... là cấp số cộng với: 2 2 2
A. Số hạng đầu tiên là 1 , công sai là 1 . 2 2
B. Số hạng đầu tiên là 1 , công sai là 1 - . 2 2
C. Số hạng đầu tiên là 0 , công sai là 1 . 2
D. Số hạng đầu tiên là 0 , công sai là 1 - . 2 Lời giải: Chọn B
Nếu dãy số (u ) là một cấp số cộng thị công sai d của nó là hiệu của một cặp số hạng n
liên tiếp bất kì (số hạng sau trừ cho số hạng trước) của dãy số đó. ìï 1 ï = ï 1 u Ta có 1 1 3 ï
;0;- ;-1;- ;..... là cấp số cộng 2 ¾¾ í 2 2 2 ï 1 ïu ï - = - = 2 1 u d ïïî 2
Ví dụ 4: Cho cấp số cộng (u có u = -5 và d = 3. Số 100 là số hạng thứ mấy của cấp số cộng? n ) 1 A. Thứ 15. B. Thứ 20. C. Thứ 35. D. Thứ 36. Lời giải. Chọn D
Ví dụ 5: Cho cấp số cộng (u ) có u =15 và d = 2 - . Tìm u . n 3 n A. 3 u = 2 - n + 21. B. 3 u = - n +12.
C. u = -3n -17. D. 2 u = n - 4. n n 2 n n 2 Lời giải.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 241
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn A 15
ìï = u = u + 2d ìïu =19 Ta có ï 3 1 ï 1 í í
u = u + n-1 d = 2 - n + 21. n 1 ( ) ïd = -2 ïd = 2 - ïî ïî
Ví dụ 6: Một cấp số cộng có 8 số hạng. Số hạng đầu là 5, số hạng thứ tám là 40. Khi đó công sai d
của cấp số cộng đó là bao nhiêu?
A. d = 4. B. d = 5. C. d = 6. D. d = 7. Lời giải. Chọn B u ìï = 5 ï 1 í ¾¾ d = 5 ï40 = u = u + 7 ïî 8 1 d
Dạng 2. Tính tổng các số hạng trong một cấp số cộng 1. Phương pháp nu u n 2u n 1 d 1 n 1
Tính tổng n số hạng đầu tiên nhờ công thức: S n 2 2
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Số hạng tổng quát của một cấp số cộng là u = 3n + 4 với *
n Î . Gọi S là tổng n số hạng n n
đầu tiên của cấp số cộng đã cho. Mệnh đề nào sau đây đúng? n 7(3n - ) 1 2 2 A. 3 -1 3n + 5n 3n +11n S = . B. S = . C. S = . D. S = . n 2 n 2 n 2 n 2 Lời giải. Chọn D ìï = + Câp số cộng ï 1 u a b
u = an + b ¾¾ í . n ïd = a ïî ìïu = 7 n(n - ) 1 3( 2 n - n) 2 n + ï 1 3 11 = 3 + 4 n u n S nu d n n í = + = 7 + = . n 1 ïd = 3 2 2 2 ïî
Ví dụ 2: Cho cấp số cộng (u ) có u = 4 và d = 5.
- Tính tổng 100 số hạng đầu tiên của cấp số n 1 cộng.
A. S = 24350. B. S = -24350. C. S = -24600. D. S = 24600. 100 100 100 100 Lời giải. Chọn B n(n - ) 1 100.99 S = nu + d ¾¾ S =100u + d = 2 - 4350 n 1 100 1 2 2
Ví dụ 3: Xét các số nguyên dương chia hết cho 3. Tổng số 50 số nguyên dương đầu tiên đó bằng:
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 242
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. 7650. B. 7500. C. 3900. D. 3825. Lời giải. Chọn D
Số nguyên dương chia hết cho 3 có dạng ( *
3n n Î ) nên chúng lập thành cấp số cộng u ìï = 3 ï 1 50 u = 3n ¾¾ í ¾¾ S = u + u = 3825 n 50 ( 1 50 ) u ï =150 2 ïî 50 n n(n - ) 1
Chú ý: S = u +u = nu + d n ( . 1 n ) 1 2 2
Ví dụ 4: Tính tổng S = 1-2 +3-4 +5+...+(2n - )
1 -2n với n ³1 và n Î . A. S = 0. B. S = -1. C. S = . n D. S = - . n Lời giải. Chọn D Với mọi *
n Î thì (2n - ) 1 - 2n = -1 .
Ta có S = (1-2)+(3-4)+(5-6)++ ( ( 2n- )
1 - 2n). Do đó ta xem S là tổng của n số hạng,
mà mỗi số hạng đều bằng -1 nên S = - . n
Nhận xét: Ta có 1;3;5;;2n-1 và 2;4;6; ;
2n là các cấp số cộng có n số hạng nên
S = (1+ 3 + 5 ++ 2n - )
1 -(2 + 4 + 6 ++ 2n) = n ( + - )- n n ( + n) 2 = n -( 2 1 2 1 2 2 n + n) = - . n 2 2
Ví dụ 5: Cho cấp số cộng (u ) thỏa mãn u +u +u +u =100. Tính tổng 16 số hạng đầu tiên của n 2 8 9 15 cấp số cộng đã cho. A. S =100. B. S = 200. C. S = 300. D. S = 400. 16 16 16 16 Lời giải. Chọn D
Ta có u +u +u +u =100 4u +30d =100 2u +15d = 50. 2 8 9 15 1 1 Khi đó 16 S = u + u
= 8 2u +15d = 8.50 = 400 16 ( 1 16 ) ( 1 ) 2
Dạng 3. Chứng minh một hệ thức trong cấp số cộng: 1. Phương pháp
Sử dụng các tính chất của cấp số cộng
2. Các ví dụ rèn luyện kĩ năng Ví dụ 1: Nếu ; a ;
b c theo thứ tự lập thành cấp số cộng thì dãy số nào sau đây lập thành cấp số cộng?
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 243
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. 2 2 2
2b ; a ; c . B. -2 ; b -2 ; a -2 . c C. 2 ; b ; a . c D. 2 ; b - ; a - . c Lời giải. Chọn B
Ta có c + a = 2b -2(c + a) = -2(2b) (-2c)+(-2a)= 2(-2b). Ví dụ 2: Nếu 1 1 1
; ; theo thứ tự lập thành cấp số cộng thì dãy số nào sau đây lập thành b + c c + a a + b cấp số cộng? A. 2 2 2 b ; a ; c . B. 2 2 2 c ; a ; b . C. 2 2 2 a ; b ; c . D. 2 2 2 a ; c ; b . Lời giải. Chọn C 2 1 1 c + a
(b+ c)(b+ a) Theo giả thiết ta có = + = c + a b + c a + b 2
2b + a + c
(a + c)2 + b(c + a) = ( 2 2
2 b + ab + bc + ac) 2 2
a + c + ac + bc + bc = ( 2
b + ab + bc + ac) 2 2 2 2 2 2 2
a + c = 2b . Ví dụ 3: Cho ; a ;
b c theo thứ tự lập thành cấp số cộng. Mệnh đề nào sau đây đúng? A. 2 2 2
a + c + 2ac = 4b . B. 2 2
a + c = 2ab - 2b . c C. 2 2
a - c = ab - b . c D. 2 2
a - c = 2ab - 2b . c Lời giải. Chọn A
Ta có: a + c = b (a +c)2 2 2 2 2 2
= 4b a + c + 2ac = 4b
Dạng 4. Giải phương trình ( tìm x trong cấp số cộng) 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Cho các số -4; 1; 6; x theo thứ tự lập thành một cấp số cộng. Tìm x. A. x = 7. B. x = 10. C. x =11. D. x =12. Lời giải. Chọn C Vì các số 4;
- 1; 6; x theo thứ tự u , u , u , 1 2
3 u lập thành cấp số cộng nên 4
u -u = u -u ¾¾
x -6 = 6-1 x =11 4 3 3 2
Ví dụ 2: Nếu các số 5+m ; 7 +2m ; 17 +m theo thứ tự lập thành cấp số cộng thì m bằng bao nhiêu? A. m = 2. B. m = 3. C. m = 4. D. m = 5. Lời giải.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 244
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn C
Ba số 5+ m ; 7 + 2m ; 17 + m theo thứ tự u , u , 1 2 3
u lập thành cấp số cộng nên
u + u = 2u 5 + m + 17 + m = 2 7 + 2m m = 4 1 3 2 ( ) ( ) ( )
Nhận xét: Ta có thể dùng tính chất u -u = u = u . 3 2 2 1
Ví dụ 3: Với giá trị nào của x và y thì các số -7; ; x
11; y theo thứ tự đó lập thành một cấp số công?
A. x =1; y = 21.
B. x = 2; y = 20.
C. x = 3; y -19.
D. x = 4; y =18. Lời giải. Chọn B Bốn số -7; ; x
11; y theo thứ tự u , u , u , 1 2
3 u lập thành cấp số cộng nên 4 u
ìï -u = u -u ìïy -11=11- x ìïx + y = 22 ìïx = 2 ï 4 3 3 2 ï ï ï í í í í u
ï -u = u -u ïy -11= x + 7 ïx- y = -18 ïy = 20 ïî 4 3 2 1 ïî ïî ïî
C. CÂU HỎI TRẮC NGHIỆM
Câu 1: Dãy số nào sau đây không phải là cấp số cộng? A. 2 1 1 2 4 - ;- ;0; ; ;1; ....
B. 15 2;12 2;9 2;6 2;.... 3 3 3 3 3 C. 4 7 9 11 ;1; ; ; ;.... D. 1 2 3 4 3 5 ; ; 3; ; ;... 5 5 5 5 3 3 3 3 Lời giải. Chọn C
Chỉ cần tồn tại hai cặp số hạng liên tiếp của dãy số có hiệu khác nhau: u -u = / u -u m 1 + m k 1 + k
thì ta kết luận ngay dãy số đó không phải là cấp số cộng. Xét đáp án A: 2 1 1 2 4 1 - ;- ;0; ; ;1; .... ¾¾ = u - = - = - = ¾¾ loại A 2 1 u 3 u u2 u4 3 u 3 3 3 3 3 3 Xét đáp án B: 15 2;12 2;9 2;6 2;.... ¾¾ 3 - 3 = u - = - = - = ¾¾ loại B 2 1 u 3 u u2 u4 3 u Xét đáp án C: 4 7 9 11 1 2 ;1; ; ; ;.... ¾¾ = u - / = - = ¾¾ Chọn C 2 1 u 3 u u2 5 5 5 5 5 5 Xét đáp án D: 1 2 3 4 3 5 3 ; ; 3; ; ;... ¾¾ = u - = - = - ¾¾ loại D 2 1 u 3 u u2 u4 3 u 3 3 3 3 3 Câu 2: 1
Cho cấp số cộng có số hạng đầu u = - , công sai 1 d =
. Năm số hạng liên tiếp đầu tiên 1 2 2 của cấp số này là: A. 1 1 - ;0;1; ;1. B. 1 1 1 - ;0; ;0; . C. 1 3 5 ;1; ;2; . D. 1 1 3 - ;0; ;1; . 2 2 2 2 2 2 2 2 2 2 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 245
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải: Chọn D
Ta dùng công thức tổng quát 1 1 = + -1 = - + -1 = 1 n u u n d n - + , hoặc n 1 ( ) ( ) 2 2 2 1 u
= u + d = u + để tính các số hạng của một cấp số cộng. n 1 + n n 2 ìï 1 ï = - ï 1 u ï 2
ïïuï =u +d =0 ï 2 1 ïï Ta có 1 1 ï 1 ï u = - ; = ¾¾ í - + = 1 d 3 u u2 d 2 2 ï 2
ïïuï =u +d =1 ï 4 3 ïïï 3 ïï = + = 5 u u4 d ïïî 2
Nhận xét: Dùng chức năng “lặp” của MTCT để tính: Nhập: 1 X = X +
(nhập X = X + d ). 2 Bấm CALC: nhập 1 - (nhập 2 1 u ).
Để tính 5 số hạng đầu ta bấm dấu “=” liên tiếp để ra kết quả 4 lần nữa!
Câu 3: Viết ba số hạng xen giữa các số 2 và 22 để được một cấp số cộng có năm số hạng. A. 7; 12; 17, B. 6; 10; 14. C. 8; 13; 18. D. 6; 12; 18. Lời giải. Chọn A
Giữa 2 và 22 có thêm ba số hạng nữa lập thành cấp số cộng, xem như ta có một cấp số
cộng có 5 số hạng với u = 2; u = 22; ta cần tìm u , u , u . 1 5 2 3 4 u ìï = u + d = 7 2 1 ï Ta có u -u 22- 2 ï 5 1 ï
u = u + 4d d = = = 5 ¾¾ u
í = u + 2d =12 5 1 3 1 4 4
ïïuï =u +3d =17 ïî 4 1
Câu 4: Cho hai số -3 và 23. Xen kẽ giữa hai số đã cho n số hạng để tất cả các số đó tạo thành
cấp số cộng có công sai d = 2. Tìm . n A. n =12. B. n =13. C. n =14. D. n =15. Lời giải. Chọn A
Theo giả thiết thì ta được một cấp số cộng có n + 2 số hạng với u = 3, - u = 23. 1 n+2 u -u 23-(- ) 3 Khi đó u
= u + n + d n + = n = = n = ¾¾ A n+ ( ) +2 1 1 1 13 12 2 1 d 2
Câu 5: Biết các số 1 2 3 C ; ; C
C theo thứ tự lập thành một cấp số cộng với n > 3. Tìm . n n n n
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 246
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. n = 5. B. n = 7. C. n = 9. D. n =11. Lời giải. Chọn B Ba số 1 2 3 C ; ; C
C theo thứ tự u , u , u lập thành cấp số cộng nên n n n 1 2 3 (n-2)(n- ) 1 n (n- ) 1 n 1 3 2
u + u = 2u C + C = 2C n ³ 3 n + = 2. 1 3 2 n n n ( ) 6 2 2 n -3n + 2 én = 2 2 1+
= n-1 n -9n +14 ê n = 7(n ) 3 . 6 ê ³ n = 7 ë
Nhận xét: Nếu u , u , u là ba số hạng liên tiếp của một cấp số cộng thì ta có k 1 - k k 1 + u + u = 2u . k 1 - k 1 + k
Câu 6: Cho cấp số cộng (u ) có các số hạng đầu lần lượt là 5; 9; 13; 17; . Tìm số hạng tổng n
quát u của cấp số cộng. n
A. u = 5n +1. B.
u = 5n -1. C.
u = 4n +1. D.
u = 4n -1. n n n n Lời giải. Chọn C
Các số 5; 9; 13; 17; theo thứ tự đó lập thành cấp số cộng (u ) nên n u ìï = 5 ï 1 CTTQ í ¾¾¾
u = u + n-1 d = 5+ 4 n -1 = 4n +1 n 1 ( ) ( )
ïd = u -u = 4 ïî 2 1
Câu 7: Cho cấp số cộng (u ) có u = -3 và 1 d =
. Khẳng định nào sau đây đúng? n 1 2 A. 1 u = -3 + n + B. 1 u = -3 + n -1. n ( ) 1 . 2 n 2 C. 1 1 u = 3 - + (n - ) 1 .
D. u = -3+ (n - ) 1 . n 2 n 4 Lời giải. Chọn C u ìï = 3 - 1 ï Ta có ï CTTQ 1 í 1 ¾¾¾
u = u + n -1 d = 3 - + n -1 n 1 ( ) ( ) ïd = 2 ïïî 2
Câu 8: Trong các dãy số được cho dưới đây, dãy số nào là cấp số cộng? A. u = 7-3 . n
B. u = 7-3n. C. 7 u = .
D. u = 7.3n. n n n 3n n Lời giải. Chọn A
Dãy (u là cấp số cộng u = an +b ( a,b là hằng số). n ) n
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 247
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 9: Trong các dãy số được cho dưới đây, dãy số nào là cấp số cộng? u ìï =1 u ìï = 1 A. p ï ï u = (- ) 1 n n + B. u = sin . C. 1 í . D. 1 í . n (2 ) 1 . n n u ï = u -1 ïî u ï = 2u n n 1 - ïî n n 1 - Lời giải. Chọn C
Dãy (u ) là một cấp số cộng u = u + d ( d là hằng số). n n n 1 -
Câu 10: Trong các dãy số được cho dưới đây, dãy số nào không phải là cấp số cộng? A. u = 4 - n + 9.
B. u = -2n +19. C. u = 2 - n -21.
D. u = -2n +15. n n n n Lời giải. Chọn D
Dãy số u = -2n +15 không có dạng an +b nên có không phải là cấp số cộng. n
Câu 11: Cho cấp số cộng (u ) có u = -5 và d = 3. Mệnh đề nào sau đây đúng? n 1 A. u = 34. B. u = 45. C. u = 31. D. u = 35. 15 15 13 10 Lời giải. Chọn C u ìï = 37 15 u ìï = -5 ï 1 ï ï ï í ¾¾ u = 3n-8 ¾¾ u í = 31 n 13 ïd = 3 ï ïî ïu ï = 22 ïî 10 Câu 12: 1
Cho cấp số cộng (u ) có u = và 1
d = - . Gọi S là tổng 5 số hạng đầu tiên của cấp số n 1 4 4 5
cộng đã cho. Mệnh đề nào sau đây đúng? A. 5 4 5 4 S = - . B. S = . C. S = . D. S = - . 5 4 5 5 5 4 5 5 Lời giải. Chọn A ìï 1 ï = ï 1 u ïï 4 5.4 1 æ 1ö 5 í ¾¾ S = 5u + d = 5. +10.ç ÷ - ç ÷ = - 5 1 ï 1 2 4 çè 4÷ø 4 ïïd = - ïïî 5
Câu 13: Cho cấp số cộng (u ) có d = -2 và S = 72. Tìm số hạng đầu tiên u . n 8 1 A. 1 1 u = 16. B. u = -16. C. u = . D. u = - . 1 1 1 16 1 16 Lời giải.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 248
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn A ìïd = -2 ïïí 8.7 ¾¾
72 = 8u + 28. -2 u = 16 1 ( ) 1 72 ï = S = 8 + ï 8 1 u d ïî 2
Câu 14: Một cấp số cộng có số hạng đầu là 1, công sai là 4, tổng của n số hạng đầu là 561. Khi đó
số hạng thứ n của cấp số cộng đó là u có giá trị là bao nhiêu? n A. u = 57. B. u = 61. C. u = 65. D. u = 69. n n n n Lời giải. Chọn C u ìï =1, d = 4 1 ï 2 ï - ïí n(n - ) n n 2 1 ¾¾ 561= n +
.4 2n - n -561 = 0 n = 17. 561 ïï = S = nu + d 2 n 1 ïïî 2
u = u = u +16d = 1+16.4 = 65 ¾¾ C n 17 1
Câu 15: Một cấp số cộng có 12 số hạng. Biết rằng tổng của 12 số hạng đó bằng 144 và số hạng
thứ mười hai bằng 23. Khi đó công sai d của cấp số cộng đã cho là bao nhiêu? A. d = 2. B. d = 3. C. d = 4. D. d = 5. Lời giải. Chọn A u ìï +11d = 23 u ìï =1 1 1 u ìï = 23 ï ï ï 12 ï ï í ¾¾ 12 í í - ï = 144 ï î ( + ) 23 1 = 144 u S u u ïd = = ï ï ï 2 12 1 12 ïî 2 ïî 11 2 Câu 16: 3n -19n
Tổng n số hạng đầu tiên của một cấp số cộng là S = với *
n Î . Tìm số hạng n 4 đầu tiên 1
u và công sai d của cấp số cộng đã cho. A. 1 3 3 5 1 u = 2; . = - B. u = -4; . = C. u = - ; d = -2. D. u = ; d = . 1 d d 2 1 2 1 2 1 2 2 Lời giải. Chọn B 2 2 n - n n - n d æ d ö Ta có 3 19 3 19 2 2 = n -
n = S = nu + d = n +ç ÷ u n n ç - ÷ 1 1 4 4 4 2 2 çè 2 ÷ø ìïd 3 ï = ìïu = -4 ï 1 ï 2 4 ï ï ï í í 3 . ï d 19 ïd = ï ï ïu - = - ï 1 ï î 2 ïî 2 4
Câu 17: Tổng n số hạng đầu tiên của một cấp số cộng là 2
S = n + 4n với *
n Î . Tìm số hạng n
tổng quát u của cấp số cộng đã cho. n
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 249
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 n 1 - æ ö A. 8
u = 2n + 3. B. u = 3n + 2. C. n 1 u 5.3 - = . D. u = 5.ç ÷ ç ÷ . n n n n çè5÷ø Lời giải. Chọn A ìïïd =1 ï d æ d ö Ta có ï 2 2
n + n = S = n +ç ÷ 2 4 u n n ç - ÷ í 1 2 çè 2 ÷ø ïï d ïu - = 4 1 ïïî 2 u ìï = 5 ï 1 í ¾¾ u = 2n + 3 ïd = 2 n ïî
Câu 18: Cho cấp số cộng (u ) có u = 2001 và u =1995 . Khi đó u bằng: n 2 5 1001 A. u = 4005. B. u = 4003. C. u = 3. D. u = 1. 1001 1001 1001 1001 Lời giải. Chọn C
ìï2001= u = u + d u ìï = 2003 ï 2 1 ï 1 í í ¾¾ u
= u +1000d = 3 1001 1 19
ï 95 = u = u + 4d ïd = -2 ïî 5 1 ïî
Câu 19: Cho cấp số cộng (u ) , biết: u = -1,u = 8 . Tính công sai d cảu cấp số cộng đó. n n n 1 + A. d = -9. B. d = 7. C. d = -7. D. d = 9. Lời giải. Chọn D d = u -u = 8- -1 = 9 n 1 + n ( )
Câu 20: Cho cấp số cộng (u ). Hãy chọn hệ thức đúng trong các hệ thức sau: n A. + u . 10 u u20 = u u + u .
B. u +u = 2u .
C. u .u = u . D. 10 30 = u . 5 10 2 90 210 150 10 30 20 20 2 Lời giải. Chọn B ìïu +u
u + 9d + u + 29 10 30 1 1 d ï = = + Xét đáp án A: u 19 ï 1 d í 2 2 ¾¾ loại ïu
ïï +u = u +4d +u +9d = 2u +13 ïî 5 10 1 1 2 d u ìï + u
= 2u + 298d = 2 u +149 90 210 2 ( 1 d ) Xét đáp án B: ïí ï2u = 2 u + ï 159 150 ( 1 d ) î
Nhận xét: Có thể lấy một cấp số cộng cụ thể để kiểm tra, ví dụ u = n ( * n Î ). n
Câu 21: Cho cấp số cộng (u thỏa mãn u +u = 60. Tính tổng S của 24 số hạng đầu tiên của n ) 2 23 24 cấp số cộng đã cho.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 250
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. S = 60. B. S =120. C. S = 720. D. S =1440. 24 24 24 24 Lời giải. Chọn C
u + u = 60 u + d + u + 22d = 60 2u + 23d = 60. 2 23 ( 1 ) ( 1 ) 1 Khi đó 24 S = u + u
= 12 u + u + 23d = 12 2u + 23d = 12.60 = 720. 24 ( 1 24 ) ( 1 ( 1 )) ( 1 ) 2
Câu 22: Một cấp số cộng có 6 số hạng. Biết rằng tổng của số hạng đầu và số hạng cuối bằng 17;
tổng của số hạng thứ hai và số hạng thứ tư bằng 14. Tìm công sai d của câp số cộng đã cho.
A. d = 2. B. d = -3. C. d = 4. D. d = 5. Lời giải. Chọn B u ìï +u =17 ìï2u +5d =17 u ìï =16 ï 1 6 ï 1 ï 1 í í í u ï +u =14 ï2u + 6d =14 ïd = -3 ïî 2 4 ïî 1 ïî u ìï -u = 8
Câu 23: Cho cấp số cộng ( ï u thỏa mãn 7 3 í
. Tìm công sai d của câp số cộng đã cho. n ) u ï u = 75 ïî 2 7 A. 1 1 d = . B. d = . C. d = 2.
D. d = 3. 2 3 Lời giải. Chọn C u ìï -u = 8 (
ìï u + 6d - u + 2d = 8 ìïd = 2 ï 7 3 ï 1 ) ( 1 ) ï í í í u ï u = 75
ï u + d u + 6d = ïî ï 75
ï u + 2 u +12 = 75 2 7 ( 1 )( 1 ) ( î ï 1 )( 1 ) î u ìï +u = 26
Câu 24: Cho cấp số cộng ( ï u ) thỏa mãn 1 7 í
. Mệnh đề nào sau đây đúng? n 2 2 u ï + u = 466 ïî 2 6 u ìï =13 u ìï =10 u ìï =1 u ìï =13 A. ï 1 í . B. ï 1 í . C. ï 1 í . D. ï 1 í . d ï = 3 - ïî d ï = -3 ïî d ï = 4 ïî d ï = 4 - ïî Lời giải. Chọn C u ìï +u = 26 2 ìï u + 6d = 26 u ìï =13-3d (1) Ta có 1 7 1 1 ï ï ï í í í . 2 2 u ï +u = 466 ï ïî
ï u + d + u + 5d = 466 ï ïî
ï u + d + u +5d = 466 2 2 6 ( 1 )2 ( 1 )2 ( ï 1 )2 ( 1 )2 ( ) î
Thay (1) và (2) ta được: ( - d)2 +( + d)2 2 13 2 13 2
= 466 8d + 338 = 466 éd = 4 u =1 1 êê d = 4 - u = 25 ë 1
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 251
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 u ìï -u +u =15
Câu 25: Cho cấp số cộng ( ï u ) thỏa mãn 1 3 5 í
. Chọn khẳng định đúng trong các khẳng n u ï +u = 27 ïî 1 6 định sau? u ìï = 21 u ìï = 21 u ìï =18 u ìï = 21 A. ï 1 í . B. ï 1 í . C. ï 1 í . D. ï 1 í . d ï = 3 ïî d ï = -3 ïî d ï = 3 ïî d ï = 4 ïî Lời giải. Chọn B
ìïu -u +u =15
ìïu - u + 2d + u + 4d =15 ï ìïu + 2d =15 ìïu = 21 1 3 5 1 ( 1 ) ( 1 ) Ta có ï í í ï 1 ï 1 í í . ïu +u = 27
ïu + u +5d = ïî ï 27 ï2u +5d = 27 ïd = -3 1 6 1 ( 1 ) î ïî 1 ïî u ìï +u +u = 36
Câu 26: Cho cấp số cộng ( ï u thỏa 2 4 6 í
. Tìm công sai d của cấp số cộng (u biết n ) n ) u ï u = 54 ïî 2 3 d <10. A. d = 3. B. d = 4. C. d = 5. D. d = 6. Lời giải. Chọn A u ìï +u +u = 36 (
ìï u +d + u +3d + u +5d = 36 ï 2 4 6 1 ) ( 1 ) ( 1 ) Ta có ï í í u ï u = 54
ï u +d u +2d = ïî ï 54 2 3 ( 1 )( 1 ) î u ìï +3d =12 1 ï 1 ( ) í . Từ ( )
1 suy ra u = 12 -3 . Thay vào (2) , ta được ( ï 1 d
u + d u + 2d = 54 2 ï 1 )( 1 ) ( ) î ( - d)( -d) 2 12 2 12
= 54 d -18d + 45 = 0 d = 3 hoặc d =15 . u ìï +u +u = 27
Câu 27: Cho cấp số cộng ( ï u ) thỏa 1 2 3 í . Tính u . n 2 2 2 2 u ï +u +u = 275 ïî 1 2 3 A. u = 3. B. u = 6. C. u = 9. D. u =12. 2 2 2 2 Lời giải. Chọn C u ìï +u +u = 27 u
ìï + u +d + u + 2d = 27 1 2 3 ï ï 1 ( 1 ) ( 1 ) Ta có ï í í 2 2 2 2 u ï +u +u = 275 ï ïî ï + + + + = 1 2 3 u u d u 2d 275 ï 1 ( 1 )2 ( 1 )2 î u ìï + d = 9 1 ï 1 ( ) ïí . u
ïï +(u d)2 (u 2d)2 2 275 2 ï 1 1 1 ( ) î + + + = Từ ( )
1 suy ra d = 9 - . Thay vào (2) , ta được 1 u
u +(u + 9 -u )2 2
+ éu + 2(9 -u ) 2 2
ù = 275 u -18u + 65 = 0 u = 13 u = 5 . 1 1 1 1 1 1 1 1 ë û hoặc 1 u ìï =13 u ìï = 5 Vậy ï 1 í hoặc ï 1 í ¾¾
u = u + d = 9 2 1 d ï = -4 ïî ïd = 4 ïî
Câu 28: Tính tổng T =15+ 20+ 25+...+ 7515.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 252
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. T = 5651265. B. T = 5651256. C. T = 5651625. D. T = 5651526. Lời giải. Chọn A
Ta thấy các số hạng của tổng T tạo thành một cấp số cộng với số hạng đầu u = 15 và 1 công sai d = 5.
Giả sử tổng trên có n số hạng thì u = 7515 n
u + n -1 d = 7515 15 + n -1 5 = 7515 n = 1501 . 1 ( ) ( ) (2u +1500d .1501 2.15 +1500.5 .1501 1 ) ( ) Vậy T = S = = = 5651265 1501 2 2 Câu 29: Tính tổng 2 2 2 2 2 2
T = 1000 - 999 + 998 - 997 + ...+ 2 -1 . A. T = 500500. B. T = 500005. C. T = 505000. D. T = 500050. Lời giải. Chọn A
Ta có T = 1.(1000 +999)+1.(998 +997)+...+1.(2 + )
1 = 1999 +1995 +... + 3.
Ta thấy các số hạng của tổng T tạo thành một cấp số cộng với số hạng đầu u =1999 và 1 công sai d = -4.
Giả sử tổng trên có n số hạng thì
u = 3 u + n -1 d = 3 1999 + n -1 -4 = 3 n = 500. n 1 ( ) ( )( ) (u +u .500 1999 + 3 .500 1 500 ) ( ) Vậy T = S = = = 500500 500 2 2
Câu 30: Cho cấp số cộng u ; u ; u ;
; có công sai d, các số hạng của cấp số cộng đã cho đều 1 2 3 un khác 1 1 1 1
0. Với giá trị nào của d thì dãy số ; ; ;
; là một cấp số cộng? 1 u u2 3 u un A. d = -1. B. d = 0. C. d = 1. D. d = 2. Lời giải. Chọn B ìï 1 1 d ï - = - ï ìï - = ï Ta có u ï 2 1 u d u ï 2 1 u 1 u u2 í í . u ï -u = d ï 1 1 ïî 3 2 d ïï - = - ïïî 3u u2 u2 3 u
Theo yêu cầu bài toán thì ta phải có 1 1 1 1 - = - u2 1 u 3 u u2 éd = 0 ê éd = 0 ê 1 1 ê d = 0 ê =
êu = u = u + 2 ê ë 1 3 1 d ë 1 u 3 u
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 253
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 31: Ba góc của một tam giác vuông tạo thành cấp số cộng. Hai góc nhọn của tam giác có số đo (độ) là: A. 20 và 70. B. 45 và 45. C. 20 và 45. D. 30 và 60. Lời giải. Chọn D Ba góc ,
A B, C của một tam giác vuông theo thứ tự đó ( A < B < C ) lập thánh cấp số cộng
nên C = 90, C + A = 2B .
ìïA+ B +C =180 3 ìï B =180 ìïB = 60 ï ï ï Ta có ï ï ï
íA+ C = 2B
íA+C = 2B íA = 30 ï ï ï ï ï ï C ï = 90 C ï = 90 C ï = 90 ïî ïî ïî
Câu 32: Ba góc A, B, C (A < B <C) của tam giác tạo thành cấp số cộng, biết góc lớn nhất gấp đôi
góc bé nhất. Hiệu số đo độ của góc lớn nhất với góc nhỏ nhất bằng: A. 40. B. 45. C. 60. D. 80. Lời giải. Chọn A Ba góc ,
A B, C của một tam giác theo thứ tự đó lập thành cấp số cộng thỏa yêu cầu, thì C = 2 ,
A C + A = 2B . Ta có 0 0 0 0 ìï + + = ì ì ï = ï = ì A B C 180 3B 180 B 60 ïA = 40 ï ï ï ï ï ï ï ï ï ï ï 0 ï 0 0
íA +C = 2B
íA +C = 2B íA +C = 120 ¾¾ íB = 60 ¾¾
C - A = 40 . ï ï ï ï ï ï ï ï 0 C ï = 2A C ï = 2A C ï = 2A C ï = 80 ïî ïî ïî ïî
Câu 33: Một tam giác vuông có chu vi bằng 3 và độ dài các cạnh lập thành một cấp số cộng. Độ
dài các cạnh của tam giác đó là: A. 1 3 ; 1; . B. 1 5 ; 1; . C. 3 5 ; 1; . D. 1 7 ; 1; . 2 2 3 3 4 4 4 4 Lời giải. Chọn C Ba cạnh a, ,
b c (a < b < c) của một tam giác theo thứ tự đó lập thành một cấp số cộng thỏa 2 2 2 2 2 2 2 2 2
ìïa +b = c
ìïa +b = c
ìïa +b = c ï ï ï ï ï ï yêu cầu thì ï ï ï
ía + b + c = 3 3 í b = 3 b í =1 . ï ï ï ï ï ï
ïa + c = 2b
ïa + c = 2b
ïa = 2b-c -2-c ïî ïî ïî ìï 3 ïa = ïï 4 ï Ta có b= a b c ( ï 2 c)2 5 2 2 2 1 2 1 c 4c 5 0 + = ¾¾¾ - + =
- + = c = íb =1 . a=2-c 4 ïïï 5 ïïc = ïïî 4
Câu 34: Một rạp hát có 30 dãy ghế, dãy đầu tiên có 25 ghế. Mỗi dãy sau có hơn dãy trước 3 ghế.
Hỏi rạp hát có tất cả bao nhiêu ghế?
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 254
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. 1635. B. 1792. C. 2055. D. 3125. Lời giải. Chọn C
Số ghế của mỗi dãy (bắt đầu từ dãy đầu tiên) theo thứ tự đó lập thành một cấp số cộng có
30 số hạng có công sai d = 3 và u = 25. 1 Tổng số ghế là 30.29 S
= u +u ++ u = 30u + d = 2055 30 1 2 30 1 2
Câu 35: Người ta trồng 3003 cây theo một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng
thứ hai trồng 2 cây, hàng thứ ba trồng 3 cây,.Hỏi có tất cả bao nhiêu hàng cây? A. 73. B. 75. C. 77. D. 79. Lời giải. Chọn C
Số cây mỗi hàng (bắt đầu từ hàng thứ nhất) lập thành một cấp số cộng (u có n )
u = 1, d = 1. Giả sử có
u + u ++ u = 3003 = S . 1 n hàng cây thì 1 2 n n n(n - ) 1 Ta có 2 3003 = S = nu +
d n + n - 6006 = 0 n = 77 n 1 2
Câu 36: Một chiếc đồng hồ đánh chuông, kể từ thời điểm 0 (giờ) thì sau mỗi giờ thì số tiếng
chuông được đánh đúng bằng số giờ mà đồng hồ chỉ tại thời điểm đánh chuông. Hỏi một
ngày đồng hồ đó đánh bao nhiêu tiếng chuông? A. 78. B. 156. C. 300. D. 48. Lời giải. Chọn C
Kể từ lúc 1 (giờ) đến 24 (giời) số tiếng chuông được đánh lập thành cấp số cộng có 24 số
hạng với u =1, công sai d =1. Vậy số tiếng chuông được đánh trong 1 ngày là: 1 24 S = S = u + u = 12 1+ 24 = 300 24 ( 1 24 ) ( ) 2
Câu 37: Trên một bàn cờ có nhiều ô vuông, người ta đặt 7 hạt dẻ vào ô đầu tiên, sau đó đặt tiếp
vào ô thứ hai số hạt nhiều hơn ô thứ nhất là 5, tiếp tục đặt vào ô thứ ba số hạt nhiều hơn ô
thứ hai là 5,… và cứ thế tiếp tục đến ô thứ n . Biết rằng đặt hết số ô trên bàn cờ người ta
phải sử dụng 25450 hạt. Hỏi bàn cờ đó có bao nhiêu ô vuông? A. 98. B. 100. C. 102. D. 104. Lời giải. Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 255
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Số hạt dẻ trên mỗi ô (bắt đầu từ ô thứ nhất) theo thứ tự đó lập thành cấp số cộng (u ) có n
u = 7, d = 5. Gọi
u + u ++ u = 25450 = S . Ta có 1
n là số ô trên bàn cờ thì 1 2 n n n(n - ) 2 1 n - 25450 = = + = 7 + n S nu d n .5 n 1 2 2 2
5n +9n -50900 = 0 n =100
Câu 38: Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan giếng nước
đến để khoan giếng nước. Biết giá của mét khoan đầu tiên là 80.000 đồng, kể từ mét
khoan thứ 2 giá của mỗi mét khoan tăng thêm 5000 đồng so với giá của mét khoan trước
đó. Biết cần phải khoan sâu xuống 50m mới có nước. Vậy hỏi phải trả bao nhiêu tiền để khoan cái giếng đó? A. 5.2500.000 đồng.
B. 10.125.000 đồng. C. 4.000.000 đồng. D. 4.245.000 đồng. Lời giải. Chọn B
Giá tiền khoang mỗi mét (bắt đầu từ mét đầu tiên) lập thành cấp số cộng (u ) có n
u = 80 000, d = 5 000. Do cần khoang 50 mét nên tổng số tiền cần trả là 1 50.49
u + u ++ u = S = 50u +
d = 50.80 000 +1225.5 000 = 10125 000 1 2 50 0 5 1 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 256
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
BÀI 4. CẤP SỐ NHÂN
A. KIẾN THỨC CƠ BẢN CẦN NẮM I – ĐỊNH NGHĨA
Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều
là tích của số hạng đứng ngay trước nó với một số không đổi . q
Số q được gọi là công bội của cấp số nhân.
Nếu (u ) là cấp số nhân với công bội ,
q ta có công thức truy hồi: n u = u q với * n Î . n 1 + n Đặc biệt:
· Khi q = 0, cấp số nhân có dạng u , 0, 0, ..., 0, ... 1
· Khi q =1, cấp số nhân có dạng u , u , u , ..., u , ... 1 1 1 1
· Khi u = 0 thì với mọi , 1
q cấp số nhân có dạng 0, 0, 0, ..., 0, ...
II - SỐ HẠNG TỔNG QUÁT Định lí 1
Nếu cấp số nhân có số hạng đầu 1
u và công bội q thì số hạng tổng quát u được xác định bởi công n thức 1 u u . n q - = với n ³ 2. n 1
III – TÍNH CHẤT CÁC SỐ HẠNG CỦA CẤP SỐ NHÂN Định lí 2
Trong một cấp số nhân, bình phương của mỗi số hạng (trừ số hạng đầu và cuối) đều là tích của hai
số hạng đứng kề với nó, nghĩa là 2 u = u .u với k ³ 2. k k 1 - k 1 +
IV – TỔNG n SỐ HẠNG ĐẦU TIÊN CỦA MỘT CẤP SỐ NHÂN Định lí 3
Cho cấp số nhân (u với công bội q ¹1. Đặt S = u +u +...+u . Khi đó n ) n 1 2 n u 1 n - 1 ( q ) S = . n 1-q
Chú ý: Nếu q = 1 thì cấp số nhân là u , u , u , ..., u ,
... khi đó S = nu . 1 1 1 1 n 1
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 257
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1. Xác định cấp số nhân, số hạng , công bội của cấp số nhân 1. Phương pháp
Xác định một cấp số nhân là xác định số hạng đầu u1 và công bội q
Từ những giải thiết ta thường lập hệ phương trình theo ẩn số u1 và q rồi giải hệ đó.
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Trong các dãy số sau, dãy số nào là một cấp số nhân?
A. 128; -64; 32; -16; 8; ...
B. 2; 2; 4; 4 2; ....
C. 5; 6; 7; 8; ... D. 1 15; 5; 1; ; ... 5 Lời giải. Chọn A Dãy ( u u u
u ) là cấp số nhân u = qu Î = = = = = / - ( * n ) 2 3 4 q u 0 , q gọi là công n n 1 ( ) n n 1 u u2 3 u bội. Xét đáp án A: u 1 2 3 u u4 128; -64; 32; -16; 8; ... ¾¾ = - = = u 2 1 u2 3 u Xét đáp án B: u 1 2 3 u 2; 2; 4; 4 2; .... ¾¾ = = / 2 = ¾¾ loại B. 1 u 2 u2
Tương tự, ta cũng loại các đáp án C, D.
Ví dụ 2: Với giá trị x nào dưới đấy thì các số 4; - ;
x - 9 theo thứ tự đó lập thành một cấp số nhân? A. x = 36. B. 13 x = - . C. x = 6. D. x = -36. 2 Lời giải. Chọn C
Nhận xét: ba số a; b; c theo thứ tự đó lấp thành cấp số nhân 2 ac = b .
Ví dụ 3: Tìm b > 0 để các số 1 ; b; 2 theo thứ tự đó lập thành một cấp số nhân. 2 A. b = 1. - B. b = 1. C. b = 2. D. b = -2. Lời giải. Chọn B Cấp số nhân b ¾¾ = ( b)2 1 1 ; ; 2 . 2 b =1 2 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 258
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ví dụ 4: Cho cấp số nhân 1 1 1 1 ; ; ; ;
. Hỏi số 1 là số hạng thứ mấy trong cấp số nhân đã 2 4 8 4096 4096 cho? A. 11. B. 12. C. 10. D. 13. Lời giải. Chọn B ìï 1 ï = ï 1 u n 1 - ï æ ö Cấp số nhân: 1 1 1 1 2 1 1 1 ; ; ; ; ï ¾¾ í u = .ç ÷ ç ÷ = . 2 4 8 4096 ï u 1 n ç ÷ n è ø 2 2 2 2 ïïq = = ï u 2 ïî 1 1 1 1 u = = n =12 n n 12 4096 2 2 u ìï +u +u = 14
Ví dụ 5: Cho cấp số nhân ( ï u ) thỏa 1 2 3 í . Tính u . n 2 u ï .u .u = 64 ïî 1 2 3 A. u = 4. B. u = 6. C. u = 8. D. u =10. 2 2 2 2 Lời giải. Chọn A
Từ u .u .u = 64 u .u .
q u q = 64 (u q)3 2
= 64 u q = 4 hay u = 4 . 1 2 3 1 1 1 1 1 2 u ìï + 4 +u =14 u ìï +u =10 u ìï = 8 u ìï = 2
Thay vào hệ ban đầu ta được ï 1 3 ï 1 3 ï 1 í í í hoặc ï 1 í . u ï .4.u = 64 u ï .u =16 u ï = 2 ïî u ï = 8 1 3 ïî 1 3 ïî 3 ïî 3 u ìï = 8 1 ï u ìï = 2 Vậy ïí ï 1 hoặc 1 í ¾¾ u = u q = 4. 2 1 q ï = ï ïq = 2 ï ïî î 2 u ìï -u +u = 65
Ví dụ 6: Cho cấp số nhân ( ï u ) thỏa 1 3 5 í . Tính u . n 3 u ï +u = 325 ïî 1 7 A. u =10. B. u =15. C. u = 20. D. u = 25. 3 3 3 3 Lời giải. Chọn C ìï u ìï -u +u = 65 u
ìï -u q +u q = 65 u ï ( 2 4 2 4 1-q + q = 65 1 1 ) ( ) Ta có ï 1 3 5 ï 1 1 1 í í ïí . 6 u ï +u = 325 ïî u ïï +u q = 325 u î ïï ( 6 1 7 1+ q = 325 2 1 1 1 ) ( ) ïî 6 Lấy ( 1+ q 325 2) chia ( ) 1 , ta được 2 =
1+ q = 5 q = 2 . 2 4 1-q + q 65 u ìï = 5 u ìï = 5 Vậy ï 1 í hoặc ï 1 2 í ¾¾
u = u q = 5.4 = 20. 3 1 q ï = 2 ïî ïq = 2 - ïî
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 259
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Dạng 2. Tính tổng của cấp số nhân 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Cho cấp số nhân (u ) có u = -2 và u = 54. Tính tổng 1000 số hạng đầu tiên của cấp số n 2 5 nhân đã cho. 1000 1000 1000 1000 A. 1-3 3 -1 3 -1 1-3 S = . B. S = . C. S = . D. S = . 1000 4 1000 2 1000 6 1000 6 Lời giải. Chọn D ìï 2 ì- ï 2 = = ï = Ta có u2 1 u q ï ï 1 u í í 3 . Khi đó 4 3 3 54 ï
= u = u q = u . q q = -2 ï ïî 5 1 1 q ïïq = -3 î 1- q 2 1-(- )100 100 100 3 1-3 S = u . = . = 100 1 1- q 3 1-(- ) 3 6
Ví dụ 2: Cho cấp số nhân có các số hạng lần lượt là 1 1 ; ; 1; ;
2048. Tính tổng S của tất cả các số 4 2
hạng của cấp số nhân đã cho.
A. S = 2047,75. B.
S = 2049, 75. C.
S = 4095, 75. D. S = 4096, 75. Lời giải. Chọn A Cấp số nhân đã cho có ìï 1 u ï = ï n- 1 1 11 1 n 1 - n-2 í 4 ¾¾ 2048 = 2 = u q = .2 = 2 n =13. 1 ï 2 ïïq = 2 î
Vậy cấp số nhân đã cho có tất cả 13 số hạng. Vậy 13 13 1- q 1 1- 2 S = u . = . = 2047,75 13 1 1- q 4 1- 2 -
Ví dụ 3: Tính tổng = - + - + - + - +(- )n 1 2 4 8 16 32 64 ... 2 +(-2)n S với n ³1, . n Î A. S = 2 . n B. 2n S = . -2(1-2n ) 1-(-2)n C. S = . D. S = 2. - . 1-2 3 Lời giải. Chọn D Các số hạng ( )n 1 2; 4; 8; 16; 32; 64;...; 2 - - - - -
; (-2)n trong tổng S gồm có n số hạng theo
thứ tự đó lập thành cấp số nhân có u = -2, q = -2. Vậy 1
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 260
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 1- q 1-(-2)n 1-(-2)n n
S = S = u . = -2. = -2. n 1 1-q 1-(-2) 3
Ví dụ 4: Gọi S = 9 +99 +999 +...+999...9 ( n số 9 ) thì S nhận giá trị nào sau đây? n n æ - ö A. 10 -1 ç ÷ S = . B. 10 1 S = 10ç ÷. 9 çè 9 ÷÷ø n æ - ö n æ - ö C. 10 1 ç ÷ ç ÷ S = 10ç ÷- . n ç D. 10 1 S = 10ç ÷+ . ç n è 9 ÷÷ø çè 9 ÷÷ø Lời giải. Chọn C Ta có 9 99 999 ... 99...9 (10 ) 1 ( 2 10 ) 1 ... (10n S = + + + + = - + - + + - ) 1 n so 9 - n 1 10n 2
= 10 +10 +... +10 -n = 10. - . n 1-10
Ví dụ 5 : Cho cấp số nhân (u ) có tổng của hai số hạng đầu tiên bằng 4 , tổng của ba số hạng đầu n
tiên bằng 13 . Tính tổng của năm số hạng đầu tiên của cấp số nhân đã cho, biết công bội của cấp số nhân là một số dương. A. 181 35 S = . B. S =141. C. S = 121. D. S = . 5 16 5 5 5 16 Lời giải. Chọn C
ìï4 = S = u +u = u 1+ 2 1 2 1 ( q) ïí 4( 2 1+ q + q ) = + q q = q > u = 13
ï = S = u (1+q + ï q ) 13(1 ) 3 ( 0) 1. 1 2 3 1 ïî 5 5 Khi đó 1- q 1-3 S = u . =1. =121 5 1 1-q 1-3
Dạng 3. Các bài toán thực tế 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nữa
diện tích của mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích
của đế tháp (có diện tích là 2
12 288 m ). Tính diện tích mặt trên cùng. A. 2 6 m . B. 2 8 m . C. 2 10 m . D. 2 12 m . Lời giải. Chọn A
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 261
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Diện tích bề mặt của mỗi tầng (kể từ 1) lập thành một cấp số nhân có công bội 1 q = và 2 12 288 u =
= 6 144. Khi đó diện tích mặt trên cùng là 1 2 6144 10 u = u q = = 6 11 1 10 2
Ví dụ 2: Một du khách vào chuồng đua ngựa đặt cược, lần đầu đặt 20000 đồng, mỗi lần sau tiền đặt
gấp đôi lần tiền đặt cọc trước. Người đó thua 9 lần liên tiếp và thắng ở lần thứ 10. Hỏi du khác trên thắng hay thua bao nhiêu? A. Hòa vốn. B. Thua 20000 đồng.
C. Thắng 20000 đồng. D. Thua 40000 đồng. Lời giải. Chọn C
Số tiền du khác đặt trong mỗi lần (kể từ lần đầu) là một cấp số nhân có u = 20 000 và 1 công bội q = 2.
Du khách thua trong 9 lần đầu tiên nên tổng số tiền thua là: u ( 9 1- 1 p )
S = u + u +... + u = = 10220000 9 1 2 9 1- p
Số tiền mà du khách thắng trong lần thứ 10 là 9
u = u . p = 10240000 10 1
Ta có u -S = 20 000 > 0 nên du khách thắng 20 000. 10 9
C. CÂU HỎI TRẮC NGHIỆM
Câu 1: Trong các dãy số sau, dãy số nào không phải là một cấp số nhân?
A. 2; 4; 8; 16; B. 1; 1; - 1; 1; - C. 2 2 2 2 1 ; 2 ; 3 ; 4 ; D. 3 5 7 ; a a ; a ; a ; (a ¹ 0). Lời giải. Chọn C Xét đáp án C: u 9 2 2 2 2 2 3 u 1 ; 2 ; 3 ; 4 ; ¾¾ = 4 = / = u 4 1 u2
Các đáp án A, B, D đều là các cấp số nhân.
Nhận xét: Dãy (u ) với u =/ 0 là cấp số nhân u = . n
a q , tức là các số hạng của nó đều n n n
được biểu diễn dưới dạng lũy thừa của cùng một cơ số q (công bội), các số hạng liên tiếp
(kể từ số hạng thứ hai) thì số mũ của chúng cách đều nhau. Ví dụ 2; 4; 8; 16; ¾¾
là cấp số nhân và u = 2n. n 1; 1; - 1; -1; ¾¾
là cấp số nhân và u = - n ( ) 1 n .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 262
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 n- 1 3 5 7 n a; a ; a ; a ; (a ¹ 0) ¾¾ là cấp số nhân và 2 1 u = a = a n ( 2 . ) . a
Câu 2: Dãy số nào sau đây không phải là cấp số nhân? A. 1; 2; 4; 8; B. 2 3 4 3; 3 ; 3 ; 3 ; C. 1 1 1 1 1 1 4; 2; ; ; D. ; ; ; ; 2 4 2 4 6 p p p p Lời giải. Chọn D
Các đáp án A, B, C đều là các cấp số nhân công bội lần lượt là 1 2;3; . 2 Xét đáp án D: 1 1 1 1 u 1 1 2 3 u ; ; ; ; ¾¾ = = / = 2 4 6 2 p p p p p p 1 u u2
Câu 3: Dãy số 1; 2; 4; 8; 16; 32; là một cấp số nhân với:
A. Công bội là 3 và số hạng đầu tiên là 1.
B. Công bội là 2 và số hạng đầu tiên là 1.
C. Công bội là 4 và số hạng đầu tiên là 2.
D. Công bội là 2 và số hạng đầu tiên là 2. Lời giải. Chọn B u ìï =1 1 ï Cấp số nhân: ï 1; 2; 4; 8; 16; 32;¼ ¾¾ í u 2 ïq = = 2 ïïïî 1 u
Câu 4: Cho cấp số nhân (u ) với u = -2 và q = -5. Viết bốn số hạng đầu tiên của cấp số nhân. n 1
A. -2; 10; 50; -250. B. -2; 10; -50; 250. C. -2; 10 - ; -50; -250.
D. -2; 10; 50; 250. Lời giải. Chọn B u ìï = -2 1 ïï u ìï = -2 u ï ï ï = u q =10 1 ï 2 1 í ¾¾ í ïq = 5 - u ï = u q = 50 - ïî ï 3 2
ïïuï =u q = 250 ïî 4 3
Câu 5: Một cấp số nhân có hai số hạng liên tiếp là 16 và 36. Số hạng tiếp theo là: A. 720. B. 81. C. 64. D. 56. Lời giải. Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 263
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ta có cấp số nhân (u có: n ) u ìï =16 u ï k k + 9 1 í q = = ¾¾ u = u q = 81 k +2 k 1 + u ï = 36 ïî + u 4 k 1 k
Câu 6: Tìm x để các số 2; 8; x; 128 theo thứ tự đó lập thành một cấp số nhân. A. x =14. B. x = 32. C. x = 64. D. x = 68. Lời giải. Chọn B
Cấp số nhân 2; 8; x; 128 theo thứ tự đó sẽ là u ; u ; u ; 1 2 3 u , ta có 4 ìïu2 3 u ì ï ï8 x = ï ï ì = ïx = 32 ïu u ï ì ï ï ïx = 32 ïï 1 2 ï2 8 ï ï í í í
íéx = 32 x = 32 2 ïu u 12 ï 8 x ïx =1024 ïê ï 3 4 ï ïî ï ï = ï = ïêx = -32 ï ï ïîë ïu u ïî x 8 ïî 2 3
Câu 7: Tìm tất cả giá trị của x để ba số 2x -1; x; 2x +1 theo thứ tự đó lập thành một cấp số nhân. A. 1 x = . B. 1 x = . C. x = 3. D. x = 3. 3 3 Lời giải. Chọn A
Cấp số nhân 2x-1 ; x ; 2x +1¾¾ (2x- ) 1 (2x + ) 1 2 2
1 = x 3x = 1 x = . 3
Câu 8: Tìm x để ba số 1+ x ; 9 + x ; 33+ x theo thứ tự đó lập thành một cấp số nhân. A. x = 1. B. x = 3. C. x = 7. D. x = 3; 7 x = . Lời giải. Chọn B
Cấp số nhân + x + x + x ¾¾
( + x)( + x) = ( + x)2 1 ; 9 ; 33 1 33 9 x = 3.
Câu 9: Với giá trị x, y nào dưới đây thì các số hạng lần lượt là -2; ; x -18;
y theo thứ tự đó lập thành cấp số nhân? ìïx = 6 ìïx = 10 - ìïx = 6 - ìïx = 6 - A. ïí . B. ïí . C. ïí . D. ïí . ïy = -54 ïî ïy = 26 - ïî ïy = 54 - ïî ïy = 54 ïî Lời giải. Chọn C ìï x 18 - ï = ì ï ïx = 6 ï Cấp số nhân: ïï-2 -2; ; -18; x ï x y ¾¾ í í 324 . Vậy ï-18 y ïy = = 5 4 ï ï ï = ï ï î x ïî x 18 - ( ;
x y) = (6;54) hoặc ( ; x y) = ( 6 - ; 5 - 4)
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 264
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 10: Cho cấp số nhân có các số hạng lần lượt là x; 12; y; 192. Mệnh đề nào sau đây là đúng?
A. x = 1; y = 144. B. x = 2; y = 72.
C. x = 3; y = 48.
D. x = 4; y = 36. Lời giải. Chọn C 12 ìï y ï = ìï 144 ï ï ï x ï x = ì ï ïx = 3 Câp số nhân: 12 ; ï ï
x 12; y; 192 ¾¾ í í y í . ï y 192 ï ïy = 48 ï ï = ï 2 ïî ïy = 2304 12 ïï y ïî î
Câu 11: Thêm hai số thực dương x và y vào giữa hai số 5 và 320 để được bốn số 5; x; y; 320
theo thứ tự đó lập thành cấp số nhận. Khẳng định nào sau đây là đúng? ìïx = 25 ìïx = 20 ìïx = 15 ìïx = 30 A. ïí . B. ïí . C. ïí . D. ïí . ïy =125 ïî ïy = 80 ïî ïy = 45 ïî ïy = 90 ïî Lời giải. Chọn B u ìï = 5 1 ïïïï x ïq = ïï 5 ï ìïx = 20 Cấp số nhân: ï 2 5; ; ï x y; 320 ¾¾ í x í . 2
ïy = u = u q = ïy = 80 ï 3 1 ïî ï 5 ïï 3 ïï 3 32 ï 0 x = u = = ï 4 1 u q ïî 25
Câu 12: Ba số hạng đầu của một cấp số nhân là x -6; x và y. Tìm y , biết rằng công bội của cấp số nhân là 6.
A. y = 216. B. 324 y = . C. 1296 y = . D. y = 12. 5 5 Lời giải. Chọn C
Cấp số nhân x -6; x và y có công bội q = 6 nên ta có ì ì ï ï 36
u = x - 6, q = 6 ï 1 ïx = ï ï ï ïï 5
íx = u = u q = 6 x -6 2 1 ( ) í ï ï 36 1296 ï ï 2 ï ïy = 36. =
ïy = u = u q = 36 î 3 2 x ïïî 5 5
Câu 13: Hai số hạng đầu của của một cấp số nhân là 2x +1 và 2
4x -1. Số hạng thứ ba của cấp số nhân là:
A. 2x -1. B. 2x +1. C. 3 2
8x - 4x -2x +1. D. 3 2
8x + 4x -2x -1. Lời giải. Chọn C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 265
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2
Công bội của cấp số nhân là: 4x -1 q =
= 2x -1. Vậy số hạng thứ ba của cấp số nhân là: 2x +1 ( 2x - )( x- ) 3 2 4 1 2
1 = 8x - 4x - 2x +1
Câu 14: Dãy số nào sau đây là cấp số nhân? u ìï = 1 u ìï = -1 A. ï 1 í . B. ï 1 í . u ï = u +1, 1 n ³ ïî u ï = -3u , n ³ 1 n 1 + n ïî n 1 + n ìï p u ï = ï u ìï = -2 1 ï C. ï 1 2 í . D. ïí . u ï = 2u +3, n ³1 ïî ï æ p ö n 1 + n u ïï = sinç ÷ ç ÷, 1 n ³ n ï ç ÷ è ï n -1ø î Lời giải. Chọn B
(u ) là cấp số nhân u = qu ¾¾ n n 1 + n
Câu 15: Cho dãy số (u ) với 3 u =
.5n. Khẳng định nào sau đây đúng? n n 2
A. (u ) không phải là cấp số nhân. n B. ( 3
u ) là cấp số nhân có công bội q = 5 và số hạng đầu u = . n 1 2 C. ( 15
u ) là cấp số nhân có công bội q = 5 và số hạng đầu u = . n 1 2
D. (u ) là cấp số nhân có công bội 5 q =
và số hạng đầu u = 3. n 2 1 Lời giải. Chọn C 3 15 u =
.5n là cấp số nhân công bội q = 5 và u = n 2 1 2
Câu 16: Trong các dãy số (u ) cho bởi số hạng tổng quát u sau, dãy số nào là một cấp số nhân? n n A. 1 1 u = . B. 1 u = -1. C. 1 u = n + . D. 2 u = n - . n n-2 3 n 3n n 3 n 3 Lời giải. Chọn A u ìï = 3 n æ ö 1 ï Dãy 1 1 ï u = = 9.ç ÷
ç ÷ là cấp số nhân có í 1 n n-2 3 çè3÷ø ïq = ïïî 3
Câu 17: Trong các dãy số (u cho bởi số hạng tổng quát u sau, dãy số nào là một cấp số nhân? n ) n A. u = 7-3 . n
B. u = 7-3n. C. 7 u = .
D. u = 7.3n. n n n 3n n
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 266
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải. Chọn D u ìï = 21 Dãy ï
u = 7.3n là cấp số nhân có 1 í ¾¾ n ïq = 3 ïî
Câu 18: Cho dãy số (u ) là một cấp số nhân với * u ¹ 0, .
n Î Dãy số nào sau đây không phải là n n cấp số nhân? A. u ; ; ; u u ...
B. 3u ; 3u ; 3u ; ... 1 3 5 1 2 3 C. 1 1 1 ; ; ; ... D. u +2; 2 u + ; u + 2; ... 1 2 3 1 u u2 3 u Lời giải. Chọn D
Giả sử (u ) là cấp số nhân công bội q, thì n Dãy u ; ; ; u u
... là cấp số nhân công bội 2 q . 1 3 5
Dãy 3u ; 3u ; 3u ; ... là cấp số nhân công bội 2 . 1 2 3 q Dãy 1 1 1 ; ; ;
... là cấp số nhân công bội 1 . 1 u u2 3 u q Dãy u + 2; 2 u + ; u + 2;
... không phải là cấp số nhân. 1 2 3
Nhận xét: Có thể lấy một cấp số nhân cụ thể để kiểm tra, ví dụ u = 2n. n
Câu 19: Cho cấp số nhân có các số hạng lần lượt là 3; 9; 27; 81; ... . Tìm số hạng tổng quát u của n cấp số nhân đã cho. A. n 1 u 3 - = .
B. u = 3n. C. n 1 u 3 + = .
D. u = 3+3n. n n n n Lời giải. Chọn B u ìï = 3 1 ï Câp số nhân ï n 1 - n 1 3; 9; 27; 81; ... ¾¾ í 9 u = u q = 3.3 - = 3n . n 1 ïq = = 3 ïïî 3
Câu 20: Một cấp số nhân có 6 số hạng, số hạng đầu bằng 2 và số hạng thứ sáu bằng 486. Tìm
công bội q của cấp số nhân đã cho. A. q = 3. B. q = -3. C. q = 2. D. q = -2. Lời giải. Chọn A u ìï = 2
Theo giải thiết ta có: ï 1 5 5 5 í ¾¾
486 = u = u q = 2q q = 243 q = 3. 6 1 u ï = 486 ïî 6
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 267
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 21: Cho cấp số nhân (u có u = -3 và 2 q =
. Mệnh đề nào sau đây đúng? n ) 1 3 A. 27 16 16 27 u = - . B. u = - . C. u = . D. u = . 5 16 5 27 5 27 5 16 Lời giải. Chọn B u ìï = -3 4 1 ï æ2ö ï 16 16 4 í 2 ¾¾
u = u q = -3.ç ÷ ç ÷ = -3. = - . 5 1 ï ç ÷ q = è3ø 81 27 ïïî 3
Câu 22: Cho cấp số nhân (u ) có u = 2 và u = -8 . Mệnh đề nào sau đây đúng? n 1 2 A. S = 130. B. u = 256. S = 256. D. q = -4. 6 5 C. 5 Lời giải. Chọn D ìïïïïuï =2 1 ïïïïq=-4 ïïï u ìï = 2 ï 1- q 1-(-4)5 5 ï 1 ï í íS = u . = 2. = 410 5 1 u
ï = -8 = u q = 2q ï 1- q 1+ 4 ïî 2 1 ïïïïï 1-(-4)6 ïS = 2. = -1638 ï 6 ï 1+ 4
ïïïuï =u q = (2.-4)4 4 = 512. ï 5 1 î
Câu 23: Cho cấp số nhân (u có u = 3 và q = -2 . Số 192 là số hạng thứ mấy của cấp số nhân đã n ) 1 cho?
A. Số hạng thứ 5.
B. Số hạng thứ 6.
C. Số hạng thứ 7.
D. Không là số hạng của cấp số đã cho. Lời giải. Chọn C 192 n - - u u q - 3 - = = = - - = = - n = n (. 2)n 1 ( )n 1 1 .2n 64 ( )6 1 1 6 1 .2 7. 1 Câu 24: 1
Cho cấp số nhân (u có u = -1 và 1 q = - . Số
là số hạng thứ mấy của cấp số n ) 1 10 103 10 nhân đã cho?
A. Số hạng thứ 103.
B. Số hạng thứ 104.
C. Số hạng thứ 105.
D. Không là số hạng của cấp số đã cho. Lời giải. Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 268
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 n 1 1 - æ ö - ìïn chan n- 1 ( ) 1 n 1 = = = - ç ÷ ï u u q 1. - ç ÷ = í n =104. 103 n 1 ç ÷ n 1 10 è 10ø 10 - ïn-1=103 ïî
Câu 25: Một cấp số nhân có công bội bằng 3 và số hạng đầu bằng 5. Biết số hạng chính giữa là
32805. Hỏi cấp số nhân đã cho có bao nhiêu số hạng? A. 18. B. 17. C. 16. D. 9. Lời giải. Chọn B n 1 - n 1 - n 1 - 8 32805 = u = u q = 5.3 3
= 6561 = 3 n = 9. Vậy n 1 9
u là số hạng chính giữa của cấp
số nhân, nên cấp số nhân đã cho có 17 số hạng.
Câu 26: Cho cấp số nhân (u ) có u = 81 và u
= 9. Mệnh đề nào sau đây đúng? n n n 1 + A. 1 q = . B. q = 9. C. q = -9. D. 1 q = - . 9 9 Lời giải. Chọn A Công bội u + 9 1 n 1 q = = = u 81 9 n Câu 27: 1
Một dãy số được xác định bởi u = 4 - và u = - u ,
n ³ 2. Số hạng tổng quát 1 u của n n 1 2 - n dãy số đó là: A. n 1 n- u 2 - = . B. u = - n ( ) 1 2 . n n 1 - æ ö C. 1 u - + = - D. u = 4 - ç ÷ - ç ÷ . n ( n 1 4 2 ). n çè 2÷ø Lời giải. Chọn D u ìï = -4 u ìï = -4 n 1 1 1 - ï ï æ ö ï ï n- 1 1 í 1 ¾¾ í 1 u = u q = -4.ç ÷ - ç ÷ . n 1 ï = - ï ç ÷ u u q = - è 2ø ï n 1 + ï ïî 2 n ïî 2
Câu 28: Cho cấp số nhân (u ) có u = 3
- và q = -2. Tính tổng 10 số hạng đầu tiên của cấp số n 1 nhân đã cho. A. S = 511. - B. S = -1025. C. S =1025. D. S =1023. 10 10 10 10 Lời giải. Chọn D u ìï = -3 1- q 1- -2 ï 1 ( )10 10 í ¾¾ S = u . = 3 - . =1023. 10 1 ïq = -2 1- q 1-( 2 - ïî )
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 269
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 29: Cho cấp số nhân có các số hạng lần lượt là 1; 4; 16; 64; Gọi S là tổng của n số hạng n
đầu tiên của cấp số nhân đó. Mệnh đề nào sau đây đúng? n( n 1 1 4 - + ) n 4(4n - ) 1 A. - n 1 S 4 - = . B. S = . C. 4 1 S = . D. S = . n n 2 n 3 n 3 Lời giải. Chọn C u ìï =1 n n n
Cấp số nhân đã cho có - - - ï 1 1 q 1 4 4 1 í ¾¾ S = u . =1. = . n 1 ïq = 4 1-q 1-4 3 ïî
Câu 30: Một cấp số nhân có 6 số hạng với công bội bằng 2 và tổng số các số hạng bằng 189. Tìm
số hạng cuối u của cấp số nhân đã cho. 6 A. u = 32.
B. u =104. C. u = 48. D. u = 96. 6 6 6 6 Lời giải. Chọn D ìïq = 2 ï ì ï ïq = 2 Theo giả thiết: ï 6 6 ï 5 5 í 1- q 1- 2 í
u = u q = 3.2 = 96. 6 1 ïS =189 = u = u . u ï = 3 ï 6 1 1 ïî 1 ï 1- q 1- 2 ïî
Câu 31: Cho cấp số nhân (u ) có u = -6 và q = -2. Tổng n số hạng đầu tiên của cấp số nhân đã n 1 cho bằng 2046. Tìm . n A. n = 9.
B. n =10. C. n = 11. D. n = 12. Lời giải. Chọn B 1- q 1-(-2)n n
Ta có 2046 = S = u . = 6 - .
= 2 -2 n -1 -2 n =1024 n = 10. n 1 ( ( ) ) ( ) 1- q 1-(-2)
Câu 32: Cho cấp số nhân (u ) có tổng n số hạng đầu tiên là S = 5n -1. Tìm số hạng thứ 4 của cấp n n số nhân đã cho. A. u = 100.
B. u =124. C. u = 500. D. u = 624. 4 4 4 4 Lời giải. Chọn C - ìï = - ìï = - q u u q u n 1 n 1 4 Ta có 1 1 5 1 ï ï - = S = u . n = q -1 í í . Khi đó n 1 ( ) 1 1 1- q q -1 ïq = 5 ïq = 5 ïî ïî 3 3
u = u q = 4.5 = 50 4 1 n Câu 33: 3 -1
Cho cấp số nhân (u ) có tổng n số hạng đầu tiên là S =
. Tìm số hạng thứ 5 của n n n 1 3 -
cấp số nhân đã cho.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 270
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. 2 1 5 u = . B. u = . C. 5 u = 3 . D. u = . 5 4 3 5 5 3 5 5 5 3 Lời giải. Chọn A ìï = - ìï = n u 3 1 q u 2 n æ ö 1 ( ) - æ ö ï 1 ï Ta có 3 1 ç 1 ÷ = ç -ç ÷ 1 u ï 3 1 ÷ ï ç ç ÷ ÷ = S = 1 n - q í í Khi đó n- n ç ç ÷ 1 1 . 1 ( ) 3 è è 3ø ÷÷ø 1- q ïïq ï = q = ï ïïî 3 ïî 3 2 4 = = 5 u 1 u q 4 3
Câu 34: Một cấp số nhân có số hạng thứ bảy bằng 1 , công bội bằng 1 . Hỏi số hạng đầu tiên của 2 4
cấp số nhân bằng bào nhiêu? A. 4096. B. 2048. C. 1024. D. 1 . 512 Lời giải. Chọn B ìï 1 ïq = ï 6 Ta có ïï 4 4 í u = = 2048 1 ï1 u 2 ï 6 1 ï = u = = 7 1 u q 6 ïïî2 4
Câu 35: Cho cấp số nhân (u ) có u = -6 và u = -486. Tìm công bội q của cấp số nhân đã cho, n 2 6
biết rằng u > 0. 3 A. q = -3. B. 1 q = - . C. 1 q = . D. q = 3. 3 3 Lời giải. Chọn D ì- ï 6 = u = 2 1 u q ï 4 4 í
q = 81= 3 q = 3. 5 4 4
ï-486 = u = u q = u . q q = -6. ïî 6 1 1 q
Câu 36: Cho cấp số nhân u ; u ; u ;
với u = 1. Tìm công bội 4 5 1 2 3 1 q để u + 2 3
u đạt giá trị nhỏ nhất? A. 2 q = - .
B. q = 0. C. 2 q = . D. q = 1. 5 5 Lời giải. Chọn A 2 æ ö Ta có 2 4 4 2 2
4u + 5u = 4u q +5u q = 5q + 4q = 5ççq ÷ + ÷ - ³ . Vậy 2 3 1 1 5÷ - çè ø 5 5 ( 4 min 4u + 5 = - khi 2 2 3 u ) q = - 5 5
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 271
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 37: Một cấp số nhân có số hạng thứ hai bằng 4 và số hạng thứ sáu bằng 64, thì số hạng tổng
quát của cấp số nhân đó có thể tính theo công thức nào dưới đây? A. n 1 u 2 - = .
B. u = 2n C. n 1 u 2 + = . D. u = 2 . n n n n n Lời giải. Chọn B ìï4 = u = u q u ìï = 2 Ta có 2 1 ï ï 1 n 1 - n 1 í í u = u q = 2.2 - = 2n. 5 4 4 n 1 64 ï
= u = u q = u . q q = 4q ïq = 2 ïî 6 1 1 ïî
Câu 38: Cho cấp số nhân (u ) có công bội .
q Mệnh đề nào sau đây đúng? n + A. u u k 1 u u .q - = . B. k 1 k 1 u - + = . k 1 k 2
C. u = u .u .
D. u = u + k –1 . q k 1 ( ) k k 1 + k +2 Lời giải. Chọn A
Câu 39: Cho cấp số nhân (u ) có u ¹ 0 và q ¹ 0. Đẳng thức nào sau đây là đúng? n 1 A. 3
u = u .q . B. 4
u = u .q . C. 5
u = u .q . D. 6
u = u .q . 7 4 7 4 7 4 7 4 Lời giải. Chọn A 3 ìï = u ï 4 1 u q í ¾¾ u = ( 3 u q ) 3 3 . = 7 1 q u4q 6 u ïï = î 7 1 u q
Câu 40: Cho cấp số nhân (u ) có u ¹ 0 và q ¹ 0. Với 1< k < m, đẳng thức nào dưới đây là đúng? n 1
A. u = u . k q .
B. u = u . m q . C. u u . m k q - = .
D. u = u .qm+k . m k m k m k m k Lời giải. Chọn C k 1 - m 1 u u q u u q - u q - q - u q - = ¾¾ = = = m ( k 1 . m k m k k 1 1 1 ) k
Câu 41: Cho một cấp số nhân có n số hạng (n > k > 55). Đẳng thức nào sau đây sai?
A. u .u = u .u .
B. u .u = u .u . 1 n 2 n 1 - 1 n 5 n-4
C. u .u = u .u .
D. u .u = u .u . 1 n 55 n 5 - 5 1 n k n-k 1 + Lời giải. Chọn C n 1 u u u .u q - u q - u q - = =
= u u với k + m = n +1. n ( k 1) ( m 1 . . 1 1 1 1 1 ) k m u ìï =192
Câu 42: Tìm số hạng đầu biết ï 6 í . 1
u và công bội q của cấp số nhân (u ), n u ï = 384 ïî 7
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 272
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 u ìï = 5 u ìï = 6 u ìï = 6 u ìï = 5 A. ï 1 í . B. ï 1 í . C. ï 1 í . D. ï 1 í . q ï = 2 ïî q ï = 2 ïî q ï = 3 ïî q ï = 3 ïî Lời giải. Chọn B ì 5 ïq = 2 19 ìï 2 = u = u q ï ï 6 1 ï ï í í 192 . 6 384 ï
= u = u q = u q q =192q u ï = = 6 ï 7 1 ( 5 1 ) ï 1 5 ïî ï q ïî u ìï -u = 36
Câu 43: Cho cấp số nhân ( ï u thỏa mãn 4 2 í
. Chọn khẳng định đúng? n ) u ï -u = 72 ïî 5 3 u ìï = 4 u ìï = 6 u ìï = 9 u ìï = 9 A. ï 1 í . B. ï 1 í . C. ï 1 í . D. ï 1 í . q ï = 2 ïî q ï = 2 ïî q ï = 2 ïî q ï = 3 ïî Lời giải. Chọn B ì ì ï = ï
= u -u = u q ï ( 2 q 2 36 q -1 ï 4 2 1 ) ï ï ï í í 36 . ï 2 72 é ù ï = = ï
= u -u = u q ( 2 q - ) 1 = u q( 2 q - ) u 6 1 1 q = 36q ï ï ê î ë úû ï q( 2 5 3 1 1 q - ) 1 ïî u ìï = 8 Câu 44: u Cho cấp số nhân ( ï u ) thỏa mãn 20 17 í
. Chọn khẳng định đúng? n u ï +u = 272 ïî 1 5 A. q = 2. B. q = -4. C. q = 4. D. q = -2. Lời giải. Chọn A 3 ì 19 16 ïq = 8 ì u ìï = 8u u ï q = 8u q ï ì ï ï ï ïq = 2 1 1 20 17 ï í í í 272 ï í . u ï +u = 272 u ï 1+ q = 272 u ï = u ï =16 ïî 1 5 ï 1 ( 4 ) ï 1 4 ïî 1 ïî ï 1+ q ïî
Câu 45: Một cấp số nhân có năm số hạng mà hai số hạng đầu tiên là các số dương, tích của số
hạng đầu và số hạng thứ ba bằng 1, tích của số hạng thứ ba và số hạng cuối bằng 1 . Tìm 16 số hạng đầu 1
u và công bội q của cấp số nhân đã cho. ìï 1 ì ì ì ï u ï = 2 u ï = -2 ï 1 1 ï 1 ï ï A. = ï = - 1 u u í ï ï 2 . B. í ï 1 . C. í 1 . D. 1 í 2 . ï q ï = q ï = - ï q ïï = 2 ï ï ï î ïî 2 ïî 2 q ï = -2 î Lời giải Chọn B u ìï , u ìï > 0, 1 1 ï ï ï ï ìï 1 u ïï > 0 ïïq > 0 ïq = 2 ï ï ï ï ï ï ï 2 2 2 u í .u =1 í = í . u q 1 1 3 1 ï ï ï 1 ï ï ï ï u ïï = = 2 ï 1 ï 1 ï u ï .u = ï = u q = ï ï (u q ) 1 2 6 2 2 4 4 q = ïî 3 5 1 1 q q ïî 16 16 ïî
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 273
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 46: Cho cấp số nhân (u ) có công bội q và thỏa n ìï æ 1 1 1 1 1 ö ï ç ÷ u
ï + u + u + u +u = 49ç + + + + ÷ ï 1 2 3 4 5 ç ÷ í ç ÷ è ø . 1 u u2 3 u u4 5 u ïïuï +u =35 ïî 1 3 Tính 2
P = u + 4q . 1 A. P = 24. B. P = 29. C. P = 34. D. P = 39. Lời giải. Chọn B
Nhận xét: Nếu 1 1 1 1 1 u , u , u , u , , , , , 1 2 3 4 5
u là một cấp số nhân với công bội q thì 1 u u2 3 u u4 5 u
cũng tạo thành cấp số nhân với công bội 1 . q ìï æ 1 ö ï ç ï ç -1÷÷ 5 5 ï q -1 ç 1 ÷ ï ç ÷ ï . = 49ç . q u ÷÷ 1 1 ( )
Do đó từ giả thiết ta có ï ç í q 1 çu 1 ÷ - ÷ . 1 ï ç -1 ÷ ï ç ÷ çè q ï ÷ø ïï 2 u ï +u q = 35 2 ï 1 1 ( ) î 5 æ 5 ö Phương trình ( ) q -1 49 ç q -1 ÷ 2 4 2 1 u . = ç ÷ ç
÷ u q = 49 u q = 7 . 1 4 q -1 u çèq q -1 ÷ 1 ( ) 1 1 ø Với 7 2
u q = -7 . Thay vào (2) , ta được u -7 = 35 u = 42 . Suy ra 2 1 1 1 q = - : vô lý. 42 u ìï = 28 u ìï = 28 1 ï 1 ï Với 2 ï ï
u q = 7 . Thay vào (2) , ta được u + 7 = 35 u = 28 . Vậy í hoặc í . Khi 1 1 1 1 1 q ï = ï ï = - ï q ï î 2 ïî 2 đó 2
u + 4q = 29. 1 u ìï +u +u = 26
Câu 47: Cho cấp số nhân ( ï u
có công bội q và thỏa 1 2 3 í
. Tìm q biết rằng q >1. n ) 2 2 2 u ï +u +u = 364 ïî 1 2 3 A. 5 q = . B. q = 4. C. 4 q = . D. q = 3. 4 3 Lời giải. Chọn D ì 2 ìï 2 2 2 u ìï +u +u = 26 u ïï ( 2 1+ q + q = 26 u ï 1+ q + q = 26 1 1 ( ) ( ) 1 1 2 3 ) Ta cóï ï í í ïí . 2 2 2 ï + + = ï 2 u u u 364 ïî u ï ( 2 4 ï 2 2 4 1 2 3 1+ q + q = 364 u ï 1+ q q = 364 2 1 ( ) ( ) 1 ) ïî ïî + Lấy ( ) 1 chia (2) , ta (1+q+q )2 2 2 æ ö æ ö được 26 1 1 4 3 2 ç 2 = 3 ÷ ç ÷
q -7q - 4q -7q + 3 = 0 3çq + ÷-7 ç ÷
çq + ÷- 4 = 0 . 2 4 2 1+ + ç ÷ ç ÷ q q 364 è q ø çè q÷ø
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 274
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ét = -1 (loaïi) ê Đặt 1 t = q +
, t ³ 2 . Phương trình trở thành 2
3t -7t -10 = 0 ê 10 . q êt = - êë 3 Với 10 1 10 t = - , suy ra 2 q + = -
3q -10q + 3 = 0 q = 3 hoặc 1 q =
. Vì q >1 nên q = 3. 3 q 3 3
Câu 48: Các số x + 6y, 5x + 2y, 8x + y theo thứ tự đó lập thành một cấp số cộng; đồng thời các số x -1, 2 y + ,
x -3 y theo thứ tự đó lập thành một cấp số nhân. Tính 2 2 x + y . A. 2 2 x + y = 40. B. 2 2 x + y = 25. C. 2 2 x + y = 100. D. 2 2 x + y = 10. Lời giải. Chọn A (
ìï x +6y)+(8x + y)= 2(5x +2y)
Theo giả thiết ta có ïí ( ïï x - )
1 (x -3y) = (y + 2)2 ïî ìïx = 3y ìïx = 3y ì ï ï ïx = 6 - ï í í í . ( ïï 3y - )
1 (3y -3y) = (y + 2)2 0 ï î ï = (y + 2)2 ïy = 2 - î ïî Suy ra 2 2
x + y = 40.
Câu 49: Ba số x; y; z theo thứ tự lập thành một cấp số nhân với công bội q khác 1; đồng thời các
số x; 2y; 3z theo thứ tự lập thành một cấp số cộng với công sai khác 0. Tìm giá trị của q . A. 1 q = . B. 1 q = . C. 1 q = - . D. q = -3. 3 9 3 Lời giải. Chọn A 2
ìïy = xq; z = xq éx = 0 ï 2 í
x + 3xq = 4xq x( 2 3q - 4q + ) 1 = 0 ê . ïx +3z = 2 ï (2y) ê 2 3q - 4q +1 = 0 î ë
Nếu x = 0 y = z = 0 công sai của cấp số cộng: ;
x 2 y; 3z bằng 0 (vô lí). éq =1 ê Nếu 1 2
3q - 4q +1 = 0 ê 1 q = (q = / ) 1 . êq = 3 êë 3
Câu 50: Cho dãy số tăng a, ,
b c (c Î ) theo thứ tự lập thành cấp số nhân; đồng thời , a b + 8, c theo
thứ tự lập thành cấp số cộng và , a b + 8,
c + 64 theo thứ tự lập thành cấp số nhân. Tính giá
trị biểu thức P = a-b+ 2 .c A. 184 P = . B. P = 64. C. 92 P = . D. P = 32. 9 9 Lời giải. Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 275
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìï 2 ì 2 ïac = b ïïac = b ( ) 1 ï ï Ta có ï ï ï ï
ía + c = 2(b + ) 8
ía -2b =16-c (2) . ï ï ï ï ï ï
ïa(c + 64) = (b + )2 8
ïac + 64a = (b + )2 8 ( ) 3 ïî ïî
Thay (1) vào (3) ta được: 2 2
b + 64a = b +16b + 64 4a -b = 4 (4). ìï c -8 ï = ìïa-2b =16 a ï -
Kết hợp (2) với (4) ta được: c ï ï 7 í í ( ) 5 ï4a -b = 4 ï 4c -60 ïî ïb ï = ïïî 7
Thay (5) vào (1) ta được: éc = 36 ê 7(c - ) 8 c = (4c -60)2 2
9c -424c + 3600 = 0 ê
100 c = 36 (c Î ). êc = êë 9
Với c = 36 a = 4, b =12 P = 4-12+ 72 = 64.
Câu 51: Số hạng thứ hai, số hạng đầu và số hạng thứ ba của một cấp số cộng với công sai khác 0
theo thứ tự đó lập thành một cấp số nhân với công bội q . Tìm . q A. q = 2. B. q = -2. C. 3 q = - . D. 3 q = . 2 2 Lời giải. Chọn B Giả sử ba số hạng ; a ;
b c lập thành cấp số cộng thỏa yêu cầu, khi đó ;
b a; c theo thứ tự đó
lập thành cấp số nhân công bội . q Ta có
ìïa + c = 2b éb = 0 ï 2 í
bq + bq = 2b ê . 2 ï ê 2
a = bq; c = bq q + q - 2 = 0 ïî ë
Nếu b = 0 a = b = c = 0 nên ; a ;
b c là cấp số cộng công sai d = 0 (vô lí). Nếu 2
q + q - 2 = 0 q = 1 hoặc q = 2.
- Nếu q =1 a = b = c (vô lí), do đó q = -2.
Câu 52: Cho bố số a, ,
b c, d biết rằng a, b, c theo thứ tự đó lập thành một cấp số nhân công bội
q > 1 ; còn b, c, d theo thứ tự đó lập thành cấp số cộng. Tìm q biết rằng a + d = 14 và b + c = 12. A. 18 + 73 + + + q = . B. 19 73 q = . C. 20 73 q = . D. 21 73 q = . 24 24 24 24 Lời giải. Chọn B
Giả sử a,b,c lập thành cấp số cộng công bội .
q Khi đó theo giả thiết ta có:
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 276
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 b
ìï = aq, c = aq ì 2 ï ï ï
ïaq + d = 2aq ( ) 1 ï ï b ï + d = 2c ï ï ï í ía + d =14 (2) ïa + d =14 ï ï ï ï ï ï ïa( 2 q + q ) = 12 ( ) 3 b ï + c = 12 ïî ïî
Nếu q = 0 b = c = 0 = d (vô lí) Nếu q = 1 - b = a
- ;c = a b + c = 0 (vô lí). Vậy 12 q = / 0, q = / 1
- , từ (2) và (3) ta có: d =14-a và a = thay vào (1) ta được: 2 q + q 2 3 12q 14q +14q -12 24q 3 2 + =
12q -7q -13q + 6 = 0 2 2 2 q + q q + q q + q (q + ) 73 1 ( 19 2
12q -19q + 6) = 0 q = 24 Vì + q > 1 nên 19 73 q = . 24
Câu 53: Gọi S =1+11+111+...+111...1 ( n số 1) thì S nhận giá trị nào sau đây? n n æ - ö A. 10 -1 ç ÷ S = . B. 10 1 S = 10ç . ÷ 81 çè 81 ÷÷ø n æ - ö é n æ - ö ù C. 10 1 ç ÷ ê ç ÷ S = 10ç ÷- . n = ç ÷ ú ç D. 1 10 1 S 10 -n . çè 81 ÷÷ø 9 ê ç ê è 9 ÷÷ ú ø ë úû Lời giải. Chọn D n æ ö é - ù Ta có 1 1 1 10 ç ÷ S = ç9 + 99 + 999 +... + 99...9÷ = . 1 ê 0. -nú . 9 ç ÷ è ø ê ú - n so 9 9 1 10 ë û b Câu 54: 21.3 b Biết rằng 2 10
S = 1+ 2.3 + 3.3 +...+11.3 = a +
. Tính P = a + . 4 4 A. P =1. B. P = 2. C. P = 3. D. P = 4. Lời giải. Chọn C Từ giả thiết suy ra 2 3 11
3S = 3+ 2.3 +3.3 +...+11.3 . Do đó 11 11 1-3 1 21.3 1 21 2 10 11 11 11
-2S = S -3S =1+ 3+ 3 +...+ 3 -10.3 = -11.3 = - - S = + .3 . 1-3 2 2 4 4 11 b Vì 1 21.3 21.3 1 1 11 S = + = a +
a = , b =11 ¾¾ P = + = 3. 4 4 4 4 4 4
Câu 55: Một cấp số nhân có ba số hạng là , a ,
b c (theo thứ tự đó) trong đó các số hạng đều khác
0 và công bội q ¹ 0. Mệnh đề nào sau đây là đúng? A. 1 1 1 1 1 1 = . B. = . C. = . D. 1 1 2 + = . 2 a bc 2 b ac 2 c ba a b c
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 277
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải. Chọn B Ta có 1 1 2 ac = b = 2 b ac
Câu 56: Bốn góc của một tứ giác tạo thành cấp số nhân và góc lớn nhất gấp 27 lần góc nhỏ nhất.
Tổng của góc lớn nhất và góc bé nhất bằng: A. 0 56 . B. 0 102 . C. 0 252 . D. 0 168 . Lời giải. Chọn C
Giả sử 4 góc A, B, C, D (với A < B < C < D ) theo thứ tự đó lập thành cấp số nhân thỏa yêu cầu với công bội . q Ta có ìïq = ì ìï + + + = ï ï A B C D 360 A ï ï ( 3 2 3
1+ q + q + q ) = 360 ï ï ï í í íA = 9 A+ D = 252. ï = ï 3 D 27 A ï ïî ïAq = 27A ï 3 ïî ïD = Aq = 243 ïî
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 278
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Document Outline
- Pages from [toanthaycu.com]Bài giảng toán 11_Thầy Trần Đình Cư-9.pdf
- Pages from [toanthaycu.com]Bài giảng toán 11_Thầy Trần Đình Cư-10.pdf
- Pages from Pages from [toanthaycu.com]Bài giảng toán 11_Thầy Trần Đình Cư-9.pdf




