Phân loại và phương pháp giải bài tập phương trình – hệ phương trình

Tài liệu gồm 78 trang, được biên soạn bởi thầy giáo Trần Đình Cư, tóm tắt lý thuyết, phân loại và phương pháp giải bài tập phương trình – hệ phương trình, giúp học sinh lớp 10 tham khảo khi học chương trình Đại số 10 chương 3 (Toán 10).

176 88 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 10

Môn: Toán 10

Thông tin:

78 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang183
BÀI 1. ĐẠI CƯƠNG VỀ PHƯƠNG TRÌNH
A. KIẾN THỨC CƠ BẢN CẦN NẮM
I – KHÁI NIỆM PHƯƠNG TRÌNH
1. Phương trình một ẩn
Phương trình ẩn
x
là mệnh đề chứa biến có dạng
 
f
xgx
1
trong đó

f
x
và
g
x
là những biểu thức của
.
x
Ta gọi
f
x
là vế trái,
x
là vế phải của
phương trình

1.
Nếu có số thực
0
x
sao cho
00
f
xgx là mệnh đề đúng thì
0
x
được gọi là một nghiệm của
phương trình

1.
Giải phương trình
()
1
là tìm tất cả các nghiệm của nó .
Nếu phương trình không có nghiệm nào cả thì ta nói phương trình vô nghiệm .
2. Điều kiện của một phương trình
Khi giải phương trình
1
, ta cần lưu ý với điều kiện đối với ẩn số
x
để
f
x
và
x
có nghĩa .
Ta cũng nói đó là điều kiện xác định của phương trình .
3. Phương trình nhiều ẩn
Ngoài các phương trình một ẩn, ta còn gặp những phương trình có nhiều ẩn số, chẳng hạn

2
222
32 2 8, 2
4232.3
xyx xy
xxyz z xzy


Phương trình
2
là phương trình hai ẩn (
x
và y ), còn
3
là phương trình ba ẩn ( ,
x
y và z ).
Khi
2, 1
x
y thì hai vế của phương trình
2 có giá trị bằng nhau, ta nói cặp
;2;1xy là
một nghiệm của phương trình
2.
Tương tự, bộ ba số
;; 1;1;2xyz là một nghiệm của phương trình
3.
4. Phương trình chứa tham số
Trong một phương trình , ngoài các chữ đóng vai trò ẩn số còn có thể có các chữ khác được xem
như những hằng số và được gọi là
tham số.
II – PHƯƠNG TRÌNH TƯƠNG ĐƯƠNG VÀ PHƯƠNG TRÌNH HỆ QUẢ
1. Phương trình tương đương
Hai phương trình được gọi là tương đương khi chúng có cùng tập nghiệm.
2. Phép biến đổi tương đương
Định lí
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang184
Nếu thực hiện các phép biển đổi sau đây trên một phương trình mà không làm thay đổi điều kiện
của nó thì ta được một phương trình mới tương đương
a) Cộng hay trừ hai vế với cùng một số hoặc cùng một biểu thức;
b) Nhân hoặc chia hai vế với cùng một số khác
0
hoặc với cùng một biểu thức luôn có giá trị khác
0.
Chú ý: Chuyển vế và đổi dấu một biểu thức thực chất là thực hiện phép cộng hay trừ hai vế với
biểu thức đó.
3. Phương trình hệ quả
Nếu mọi nghiệm của phương trình
f
xgx đều là nghiệm của phương trình
11
f
xgx thì
phương trình
11
f
xgx
được gọi là phương trình hệ quả của phương trình
 
.
f
xgx
Ta viết
11
.
f
xgx fxgx
Phương trình hệ quả có thể có thêm nghiệm không phải là nghiệm của phương trình ban đầu. Ta gọi
đó là
nghiệm ngoại lai.
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Điều kiện xác định của phương trình
1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1.
Tìm điều kiện xác định của phương trình
22
23
5
11
x
xx

Lời giải
Chọn D
Do
2
10,xx nên điều kiện xác định của phương trình là
D
.
Ví dụ 2. Tìm điều kiện xác định của phương trình 12 3xx x

Lời giải
Điều kiện xác định của phương trình là:
10 1
20 2 3
30 3
xx
xxx
xx








.
Ví dụ 3. Tìm điều kiện xác định của phương trình
6
24
3
x
x

Lời giải
Điều kiện xác định của phương trình:
20 2
30 3
xx
xx





Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang185
Ví dụ 4. Cho phương trình
3
2
1
11 .
4
xx
x

Tìm điều kiện xác định của phương trình
đã cho.
Lời giải
Điều kiện xác định của phương trình
3
2
10
10 2.
40
x
xx
x



3. Bài tập trắc nghiệm
Câu 1.
Tìm tập xác định của phương trình
5
1
3 2017 0
x
x
x

.
A.
1;
. B.
1; \ 0
. C.
1; \ 0
. D.
1;
.
Hướng dẫn giải
Chọn C.
Điều kiện
10 1
00
xx
xx





.
Tập xác định của phương trình là
1; \ 0
.
Câu 2. Điều kiện xác định của phương trình
132
24
x
x
x
x

là
A.
2x 
và
3
2
x .
B.
3
2
2
x
.
C.
2x 
và
0x
. D.
3
2
2
0
x
x

.
Hướng dẫn giải
Chọn C.
Điều kiện xác định của phương trình là
32 0
240
0
x
x
x
3
2
2
0
x
x
x

3
2
2
0
x
x

Câu 3. Cho phương trình
2
1
1
1
x
x

. Tập giá trị của x để phương trình xác định là
A.
1; 
. B. . C.
1; )
. D.
\1
.
Hướng dẫn giải
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang186
Chọn A.
2
1
1
1
x
x

xác định 10x 1
x
.
Câu 4: Điều kiện xác định của phương trình 28
x
x
 là
A.

2;8x. B.
8x
. C.
2x
. D.
8x
.
Lời giải
Chọn C
ĐK:
20 2xx
Câu 5. Giá trị 2x là điều kiện của phương trình nào sau đây?
A.
1
21
2

x
x
x
. B.
1
20
xx
x
.
C.
1
2
4

xx
x
. D.
1
0
2
x
x
.
Hướng dẫn giải
Chọn B.
Phương trình
1
21
2

x
x
x
có điều kiện là 20 2
xx.
Phương trình
1
20 xx
x
có điều kiện là
20
2
0

x
x
x
.
Phương trình
1
2
4

xx
x
có điều kiện là
20
40
x
x
2
4
x
x
.
Phương trình
1
0
2

x
x
có điều kiện là
20 2
xx
.
Câu 6. Điều kiện xác định của phương trình
2
23
2
5
x
xx
x
là
A.
\0;2x
. B.
2;5 \ 0x
.
C.
2;5 \ 0; 2
. D.
;5 \ 0; 2

.
Hướng dẫn giải
Chọn B.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang187
Phương trình
2
23
2
5
x
xx
x
có nghĩa khi
2
20
2
20 0; 2
50 5
x
x
xx xx
xx






2;5 \ 0x
.
Câu 7. Điều kiện xác định của phương trình
2
42
1
3
x
x
x
là
A.
4;x
. B.
4;3 \ 1x

. C.
;3x
. D.
\1x
.
Hướng dẫn giải
Chọn
B.
Phương trình đã cho xác định khi
2
40
4
43
10 1
1
30 3
x
x
x
xx
x
xx








.
Câu 8. Tập xác định của phương trình
2
3
1
2
1
x
xx
x

là
A.
2;D 
. B.
0; \ 1D 
.
C.
0;D 
. D.
0; \ 1; 2D 
.
Hướng dẫn giải
Chọn B.
Điều kiện xác định:
00
10 1
xx
xx





. Vậy đáp án
0; \ 1D 
.
Câu 9. Điều kiện xác định của phương trình
5
1
2
x
x
+
=
-
là
A.
5.x ³- B.
5
.
2
x
x
ì
>-
ï
ï
í
ï
¹
ï
î
C.
5
.
2
x
x
ì
³-
ï
ï
í
ï
¹
ï
î
D.
2.x>
Lời giải
Chọn C
Phương trình xác định khi và chỉ khi
50 5
.
20 2
xx
xx
ìì
+³ ³-
ïï
ïï
íí
ïï
-¹ ¹
ïï
îî
Câu 10. Điều kiện xác định của phương trình 21 1
x
xx
 là
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang188
A.
1
1
2
x

. B.
1
1
2
x

. C.
1
2
x 
. D.
1
x
.
Lời giải
Chọn B
Điều kiện xác định của phương trình là
210
10
x
x
1
2
1
x
x

1
1
2
x

.
Câu 11. Điều kiện xác định của phương trình
2
5
20
7
x
x
x

?
A.
2;7 . B.
2;
. C.
2;7 . D.
7;  .
Lời giải
Chọn A
Điều kiện xác định của phương trình đã cho là:
20 2
27
70 7
xx
x
xx






.
Câu 12. Điều kiện xác định của phương trình
2
42
1
3
x
x
x
là:
A.
4;x
. B.
4;3 \ 1x

. C.
;3x
. D.
\1x
.
Lời giải:
Chọn B
Phương trình đã cho xác định khi
2
40
4
43
10 1
1
30 3
x
x
x
xx
x
xx








.
Dạng 2: Sử dụng điêu kiện xác định của phương trình để tìm gghiệm của phương trình
1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1 :
Giải phương trình
()
2
110xx x--=
có bao nhiêu nghiệm?
Lời giải
Vì :
()
2
2
10
1
0
110 1
0
1
10
x
x
x
xx x x
x
x
x
ì
é
-³
³
ï
ï
ê
ï
ï
ê
é
é
=
--= =
=
í
ê
ê
ê
ï
ï
ê
ê
ê
ï
=
-=
ê
ë
ë
ë
ï
î
Ví dụ 2 : Giải phương trình 2222xx x+-=-+
Lời giải
Vì : Điều kiện của pt
20 2
2
20 2
xx
x
xx






. Thay x = 2 vào phương trình thấy
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang189
thỏa mãn nên x = 2 là nghiệm phương trình.
Ví dụ 3: Giải phương trình
32
452 2
x
xx x x-+-+=-
Lời giải
Vì:
32 2
452 2 (2)(1) 2
x
xxxxxxxx-+-+=- - -+=-
.
Điều kiện của phương trình:
2
20 2
2
(2)(1)0
11
1
20
202
xx
x
xx
xx
x
x
xx
ìì
é
é
ïï
-³ ³
ïï
ì
êê
é
=
ï
--³
ïï
ïïï
êê
ê

==
ííí
ëë
ê
ïïï
=
-³
ïïïë
î
ïï
-³ £
ïï
îî
Ví dụ 4: Giải phương trình
()
2
32 30xx x-+ -=
Lời giải
Vì :
()
2
2
3
30
1
32 30 3
320
2
30
3
x
x
x
xx x x
xx
x
x
x
ì
³
ï
ï
ì
-³
ï
ï
ï
ï
é
=
ï
ï
ïï
êé
-+ -= =
-+=
íí
ê
ê
ïï
=
ïï
ê
ê
ïï
-=
ë
ïï
ê
î
=
ï
ë
ï
î
+ Thay
2
1
x
x
é
=
ê
ê
=
ë
vào phương trình thì thấy chỉ có x = 1 thỏa mãn. Nên x = 1 là nghiệm pt
3. Bài tập trắc nghiệm
Câu 1.
Cặp số
;
xy
nào sau đây không là nghiệm của phương trình
23 5
xy
?
A.

5
;;0
2



xy
. B.
;1;1
xy
.
C.

5
;0;
3



xy
. D.
;2;3
xy
.
Hướng dẫn giải
Chọn C.
Thay các bộ số
;
xy
vào phương trình, ta thấy bộ số đáp án C không thỏa mãn:
5
2.0 3. 5 5
3

.
Câu 2. Số nghiệm của phương trình
2
11
2
11
xx
xx

là
A. 0 . B.
1
. C.
2
. D. 3.
Hướng dẫn giải
Chọn
B.
Điều kiện: 1x  . Khi đó phương trình đã cho

2
0
20
2
x
xx x
xL


.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang190
Câu 3. Số nghiệm của phương trình
1
23 3
x
xx
là:
A. 2 . B.
0
. C. 1. D.
3
.
Hướng dẫn giải
Chọn B.
Đkxđ:
3x
Với điều kiện
3x phương trình đã cho trở thành
123
2
x
x

Vậy phương trình không có nghiệm.
Câu 4. Tập nghiệm của phương trình
1
x
xx

là
A.
S
. B.
S
. C.
0S
. D.
1S 
.
Lời giải
Chọn B
Điều kiện:
0x
.
11xx x x.
Vây tập nghiệm của phương trình đã cho là
S
.
Câu 5. Phương trình nào sau đây nhận
2
làm nghiệm ?
A.
42
430.xx
B.
2
430.xx

C.
112xx x . D.
42
540.xx

Lời giải
Chọn D
- Xét PT:
42
430xx

2
2
1
3
x
x
1
3
x
x
Vậy
2x
không phải nghiệm của PT đã cho.
- Xét PT:
2
430xx

1
3
x
x
Vậy
2x
không phải nghiệm của PT đã cho.
- Xét PT:
112xx x
 .
Điều kiện
10 1
x
x
Vậy
2x không phải nghiệm của PT đã cho.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang191
- Xét PT:
42
540xx

2
2
1
4
x
x
1
2
x
x
Vậy 2x là nghiệm của PT đã cho.
Câu 6. Phương trình
()
2
110xx x--=
có bao nhiêu nghiệm?
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải
Chọn B
Vì :
()
2
2
10
1
0
110 1
0
1
10
x
x
x
xx x x
x
x
x
ì
é
-³
³
ï
ï
ê
ï
ï
ê
é
é
=
--= =
=
í
ê
ê
ê
ï
ï
ê
ê
ê
ï
=
-=
ê
ë
ë
ë
ï
î
Câu 7. Phương trình
23
69 27xx x-+ -+ =
có bao nhiêu nghiệm?
A. 0. B. 1. C. 2. D. 3.
Lời giải
Chọn B
Vì
23 23
69 27 (3) 27
x
xx x x-+ -+ = -- = -
Đk :
2
(3)0 3xx-- ³=
. Thay x = 3 vào phương trình thấy thỏa mãn nên x = 3 là
nghiệm pt
Câu 8. Phương trình
()( )
2
353 2 3 54xxxx--+=-+
có bao nhiêu nghiệm?
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải
Chọn B
Vì điều kiện của phương trình: :
2
5
53 0
3
3
(3)(53)0
33
5
350
3
350 5
3
x
x
x
xx
xx
x
x
x
x
ì
é
ï
ï
ê
£
ï
ì
é
ï
-³
ï
é
ê
=
ï
ï
ì
ê
ê
ï
ê
--³
ï
ï
ïïï
ê
ê

=ê=
ííí
ëë
ïïï
ê
=
-³
ïïï
î
ê
ïï
-³
ë
ï
î
ï
³
ï
ï
ï
î
+ Thay
3
5
3
x
x
é
=
ê
ê
ê
=
ê
ë
vào phương trình thì thấy chỉ có x = 3 thỏa mãn. Nên x = 3 là nghiệm pt
Câu 9. Phương trình 11
x
xx+-=- có bao nhiêu nghiệm?
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải
Chọn A
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang192
Vì : Điều kiện của pt :
10 1
1
10 1
xx
x
xx






. Thay x = 1 vào phương trình thấy vô
lí nên pt vô nghiệm.
+ Thay
2
1
x
x
é
=
ê
ê
=
ë
vào phương trình thì thấy chỉ có x = 1 thỏa mãn. Nên x = 1 là nghiệm pt
Câu 10. Phương trình
()
2
210xx x-- +=
có bao nhiêu nghiệm?
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải
Chọn C
Vì :
()
2
2
10
1
1
210
1
20
2
2
10
x
x
x
xx x
x
xx
x
x
x
ì
ì
+³
³-
ï
ï
ï
ï
é
=-
ï
ï
ïï
é
ê
é
-- +=
=-
--=
íí
ê
ê
ê
ïï
=
ïïë
ê
ê
ïï
=
+=
ë
ï
ë
î
ï
î
Dạng 3: Phương trình tương đương, phương trình hệ quả
1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1.
Cho phương trình
0fx
có tập nghiệm
1
;2 1Smm
và phương trình
0gx
có tập nghiệm

2
1; 2S
. Tìm tất cả các giá trị m để phương trình
0gx
là
phương trình hệ quả của phương trình
0fx
.
A.

3
1
2
m
. B.
12m
. C.
.m
. D.

3
1
2
m
.
Lời giải
Chọn D
Gọi
1
S ,
2
S lần lượt là tập nghiệm của hai phương trình
0fx và
0gx .
Ta nói phương trình

0gx
là phương trình hệ quả của phương trình
0fx
khi
12
SS .
Khi đó ta có






12
12
3
1
3
12 12
2
1
2
m
m
m
m
m
.
3. Bài tập trắc nghiệm
Câu 1.
Trong các phương trình sau, phương trình nào tương đương với phương trình
10x
?
A.
20x 
. B.
10x
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang193
C.
220x 
. D.
120xx

.
Hướng dẫn giải
Chọn C.
Ta có
10x 
220x
.
Câu 2. Cho phương trình
2
1–1 10xxx
. Phương trình nào sau đây tương đương với
phương trình đã cho?
A.
2
10x  . B.
10x
. C.
–1 1 0xx
. D.
10x 
.
Hướng dẫn giải
Chọn C.
Hai phương trình tương đương khi chúng có cùng tập nghiệm.
Phương trình
2
1–1 10xxx
có tập nghiệm
1; 1S 
.
Phương trình
–1 1 0xx
có tập nghiệm
1; 1S 
.
Câu 3. Phương trình
231x 
tương đương với phương trình nào dưới đây?
A.
32 3 3
x
xx
. B.
42 3 4xxx

.
C. 23
x
xx. D. 3231 3xx x
.
Hướng dẫn giải
Chọn C.
231 2xx.
Xét

2
3
32 3 3
30
231
x
xxx
x
x


3
2
x
x
nên phương trình này không tương
đương với phương trình đã cho.
Xét
42 3 4xxx
2
3
40
231
x
x
x

4
2
x
x
nên phương trình này không
tương đương với phương trình đã cho.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang194
Xét
23
x
xx
2
3
0
231
x
x
x

2x
phương trình tương đương với phương trình đã cho.
Xét
3231 3xx x
3
231
x
x
x

nên phương trình này không
tương đương với phương trình đã cho.
Câu 4: Cho phương trình:
2
0xx (1) . Phương trình nào tương đương với phương trình (1) ?
A.
10xx
. B.
10x
. C.
22
(1)0xx
. D.
0x
Lời giải
Chọn A
2
0
(1) 0
1
x
xx
x


Ý A:

0
10
1
x
xx
x

Câu 5. Phương trình nào dưới đây tương đương với phương trình
2
30xx
?
A.
2
213 21
x
xxx. B.
2
33 3xx xx
.
C.
2
33
33 3xx xx
. D.
2
11
2xx x
x
x

.
Lời giải
Chọn C
Phương trình
2
30xx
có tập nghiệm là
0;3S
nên phương trình tương đương
cũng phải có tập nghiệm như vậy. Chọn C
Chú ý lý thuyết:
+ Phép biến đổi tương đương cho hai phương trình tương đương
+ Phép biến đổi cộng hai vế một biểu thức hoặc nhân 2 vế với một biểu thức khác 0 là
phép biến đổi tương đương khi chúng không làm thay đổi điều kiện
Do đó dựa và điều kiện của các phương trình ta cũng có th
ể chọn C
Câu 6. Phép biến đổi nào sau đây là phép biến đổi tương đương?
A.
222 2
22
x
xxx xx
. B.
2
22
x
xxx

.
C.
22
22
x
xxx xx
. D.
222 2
33
x
xxx xx
 
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang195
Lời giải
Chọn D
* Xét phương án A:
2
2
222
2
2
20
20
22
0
1
0
1
x
x
xx x x x
x
xx
x
x
xx
x





2 phương trình không có cùng tập nghiệm nên phép biến đổi không tương đương.
* Xét phương án B:
2
2
0
0
21
2
2
1
2
2
1
x
x
x
xx
x
xx
x
x
xx
x

 





2 phương trình không có cùng tập nghiệm nên phép biến đổi không tương đương.
* Xét phương án C:
22
2
2
2
20
22
0
1
0
1
x
x
xx x x xx x
x
xx
x
x
xx
x





2 phương trình không có cùng tập nghiệm nên phép biến đổi không tương đương.
* Xét phương án D:
2
222 2
2
2
30 0
33
1
0
1
xx
xx x x xx
x
xx
x
xx
x



2 phương trình có cùng tập nghiệm nên phép biến đổi là tương đương.
Câu 7. Tìm giá trị thực của tham số
m
để cặp phương trình sau tương đương:
2
220xmx+-=
()
1
và
() ()
32
242140xm x mx++ + - -=
(
)
2
.
A. 2.m = B. 3.m = C.
1
.
2
m =
D. 2.m =-
Lời giải
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang196
Chọn B
Xét phương trình
() ()
32
242140xm x mx++ + - -=
2
2
2
(2)(2x 2)0
2x 2 0(1)
x
xmx
mx
é
=-
ê
+ + -=
ê
+-=
ë
để hai phương trình trên tương đương thì x = - 2 phải là nghiệm của phương trình (1) từ
đó suy ra m = 3.
Cách khác : có thể thử ngược đáp án.
Câu 8. Tìm tất cả các giá trị thực của tham số
m
để cặp phương trình sau tương đương:
()
2
21 20mx m x m--+-=
()
1
và
()
22
23 150mxxm--+-=
()
2
.
A. 5.m =- B.
5; 4.mm=- =
C.
4.m =
D. 5.m =
Lời giải
Chọn C
Vì xét phương trình:
()
2
1
21 20(1)( 2)0
20
x
mx m x m x mx m
mx m
é
=
ê
--+-=- -+=
ê
-+=
ë
Để hai phương trình tương đương thì điều kiện cần x = 1 phải là nghiệm của phương trình
(2).
Thay x = 1 vào (2) ta được:
2
4
20 0
5
m
mm
m

+ Với m = 4 :
2
(1) 4 6 2 0xx
2
(2) 2 3 1 0xx suy ra m = 4 thỏa mãn
+ Với m = -5:
2
(1) 5 12 7 0xx
2
(2) 7 3 10 0xx
suy ra m = -5 (loại)
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang197
BÀI 2. PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC NHẤT VÀ PHƯƠNG TRÌNH
BẬC HAI
A. KIẾN THỨC CƠ BẢN CẦN NẮM
I – ÔN TẬP VỀ PHƯƠNG TRÌNH BẬC NHẤT, BẬC HAI
1. Phương trình bậc nhất
Cách giải và biện luận phương trình dạng
0ax b+=
được tóm tắt trong bảng sau
()
01ax b+=
Hệ số Kết luận
0a ¹
(
)
1
có nghiệm duy nhất
b
x
a
=-
0a =
0b ¹
(
)
1
vô nghiệm
0b =
(
)
1
nghiệm đúng với mọi
x
Khi
0a ¹
phương trình
0ax b+=
được gọi là phương trình bậc nhất một ẩn.
2. Phương trình bậc hai
Cách giải và công thức nghiệm của phương trình bậc hai được tóm tắt trong bảng sau
() ()
2
0 0 2ax bx c a++= ¹
2
4bacD= -
Kết luận
0D>
()
2
có hai nghiệm phân biệt
1, 2
2
b
x
a
-D
=
0D=
()
2
có nghiệm kép
2
b
x
a
=-
0D<
()
2
vô nghiệm
3. Định lí Vi–ét
Nếu phương trình bậc hai
()
2
00ax bx c a++= ¹
có hai nghiệm
12
,
x
x thì
12 12
,.
bc
xx xx
aa
+=- =
Ngược lại, nếu hai số
u và v có tổng uvS+= và tích uv P= thì u và v là các nghiệm của phương
trình
2
0.xSxP-+=
II – PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC NHẤT, BẬC HAI
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang198
Có nhiều phương trình khi giải có thể biến đổi về phương trình bậc nhất hoặc bậc hai.
Sau đây ta xét hai trong các dạng phương trình đó.
1. Phương trình chứa ẩn trong dấu giá trị tuyệt đối
Để giải phương trình chứa ẩn trong dấu giá trị tuyệt đối ta có thể dùng định nghĩa của giá trị tuyệt
đối hoặc bình phương hai vế để khử dấu giá trị tuyệt đối.
Ví dụ
1. Giải phương trình
32 1.xx-= +
()
3
Giải
Cách 1
a) Nếu
3x ³
thì phương trình
()
3
trở thành
32 1.xx-= +
Từ đó 4.x =-
Giá trị
4x =-
không thỏa mãn điều kiện
3x ³
nên bị loại.
b) Nếu
3x <
thì phương trình
()
3
trở thành 32 1.xx-+= + Từ đó
2
.
3
x =
Giá trị này thỏa mãn điều kiện
3x <
nên là nghiệm.
Kết luận. Vậy nghiệm của phương trình là
2
.
3
x =
Cách 2. Bình phương hai vế của phương trình
()
3
ta đưa tới phương trình hệ quả
() ( ) ( )
22
22
2
3321
694 41
31080.
xx
xx xx
xx
- = +
-+= ++
+-=
Phương trình cuối có hai nghiệm là
4x =- và
2
.
3
x =
Thử lại ta thấy phương trình
()
3
chỉ có nghiệm là
2
.
3
x =
2. Phương trình chứa ẩn dưới dấu căn
Để giải các phương trình chứa ẩn dưới dấu căn bậc hai, ta thường bình phương hai vế để đưa về một
phương trình hệ quả không chứa ẩn dưới dấu căn.
Ví dụ 2. Giải phương trình
23 2.xx-=-
()
4
Giải.
Điều kiện của phương trình
()
4
là
3
.
2
x ³
Bình phương hai vế của phương trình
()
4
ta đưa tới phương trình hệ quả
()
2
2
423 44
670.
xxx
xx
-=-+
-+=
Phương trình cuối có hai nghiệm là
32x =+ và 32.x =- Cả hai giá trị này đều thỏa mãn điều
kiện của phương trình
()
4,
nhưng khi thay vào phương trình
()
4
thì giá trị 32x =- bị loại , còn
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang199
giá trị
32x =+
là nghiệm .
Kết luận. Vậy nghiệm của phương trình
()
4
là 32.x =+
Dạng 1: Phương trình tích
1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Giải phương trình

2
43 20xx x
Hướng dẫn giải

2
43 20xx x
2
1
3
2
x
x
x
x
2
3
x
x
.
Vây phương trình đã cho có
2
nghiệm.
Ví dụ 2. Giải phương trình

2
22 7 4xxx
Hướng dẫn giải
Điều kiện xác định của phương trình
2
2.7
7
0xx³³-+
Ta có
() () ()()
2
22 7 4 22 7 2 2xxx xxxx-+=--+=-+
() ()
() ()
27
27 27
20 2
220 .
20 21
xx
xx
xx
x
xx
+-
+-
é
é
-= =
éù
êê
- +=
êú
êê
ëû
+= +
ê
ê
ë
ë
+=
Giải phương trình
()
()
2
2
27
2
1: 2
72
x
x
x
x
x
ì
ï
ï
+
í
ï
+
+=
=+
³
î
-
ï
2
2
2
1
3
3
1.
20
x
x
x
x
xx
x
³-
³-
ì
ï
ï
ì
ï
ï
ïï
=
íí
ïï
ïï
î
ï
ï
é
=
ê
+
ê
=-
ë
î
-=
Vậy phương trình đã cho có hai nghiệm
1, 2xx==
3. Bài tập trắc nghiệm
Câu 1.
Cho phương trình
32
44 0xmx x m. Tìm
m
để có đúng hai nghiệm
A.
2m
. B.
2m
. C.
2; 2m
. D.
0m
.
Hướng dẫn giải
Chọn C.
32 2 2 2
44 0 4 40 4 0xmx x m xx mx x xm
2x
x
m
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang200
Để phương trình có đúng hai nghiệm thì
2m
.
Câu 2. Phương trình
432
581040xxx x
có bao nhiêu nghiệm nguyên?
A.
4
. B.
1
. C.
2
. D.
0
.
Hướng dẫn giải
Chọn D.
432
581040xxx x
22
2420xx x x

Phương trình không có nghiệm nguyên.
Câu 3. Phương trình
42
450xx có bao nhiêu nghiệm thực?
A.
4
. B.
2
. C.
1
. D.
3
.
Hướng dẫn giải
Chọn B.
Phương trình
22
150 xx
2
11
 xx.
Vậy phương trình có
2
nghiệm thực.
Câu 4. Phương trình
222
617 6
x
xxxx
có bao nhiêu nghiệm thực phân biệt?
A.
2
. B.
1
. C.
4
. D. 3.
Hướng dẫn giải
Chọn D.
Điều kiện:
2
17 0 17 17xx
.
Ta có:
222
617 6
x
xxxx
22
617 10xx x

2
2
60
17 1
xx
x


2
60
16 0
xx
x




0
6
4
x
T
x
L
x
T


. Vậy phương trình có 3 thực phân
biệt.
Câu 5. Phương trình

2
54 30xx x có bao nhiêu nghiệm?
A. 0 . B.
1
. C.
2
. D. 3.
Hướng dẫn giải
Chọn C.
Điều kiện xác định của phương trình là 3x  .
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang201
Phương trình tương đương với
3
1
4
3
x
x
x
x

1
3
x
x
.
Câu 6. Số nghiệm của phương trình:
2
41 7 6 0xxx

là
A.
0
. B.
3
. C.
1
. D.
2
.
Hướng dẫn giải
Chọn D.
Điều kiện xác định của phương trình
4x
.
Phương trình tương đương với
2
41
760
x
xx


5
1
6
x
x
x
kết hợp điều kiện suy ra
5
6
x
x
.
Dạng 2: Phương trình chứa ẩn trong giá trị tuyệt đối
1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1.
Giải phương trình
3221
x
x
Hướng dẫn giải
Ta có
3221
x
x

22
210
32 21
x
xx


2
1
2
5830
x
xx

1
3
5
x
x
Ví dụ 2. Giải phương trình
2
232 2xx x
Hướng dẫn giải
Phương trình
2
2
232 2
232 2


xx x
x
xx
2
2
13
2440
0
220
1




x
xx
x
xx
x
.
3. Bài tập trắc nghiệm
Câu 1.
Phương trình
231
x
x
có tổng các nghiệm là
A.
1
2
.
B.
1
4
. C.
1
4
.
D.
3
4
.
Hướng dẫn giải
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang202
Chọn C.
Ta có:
231
x
x
23 1
213
x
x
x
x


1
2
3
4
x
x
. Vậy tổng các nghiệm là
1
4
.
Câu 2. Phương trình
2
28 2
x
xx
có số nghiệm là
A.
0
. B.
2
. C.
3
. D.
1
.
Hướng dẫn giải
Chọn D.
Ta có


2
2
2
2
2
20
28 2
28 2
28 2
28 2
x
x
xx x
xx x
xx x
xx x






2
2
2
2
60 2, 3
2
2
2
2, 5
3100
x
x
xx x x
x
x
x
xx
xx








.
Câu 3. Phương trình
24240xx
có bao nhiêu nghiệm?
A.
0
. B.
1
. C.
2
. D. vô số.
Hướng dẫn giải
Chọn D.
24240 2424240 2xx x x x x 
.
Câu 4. Phương trình
2
23 5
x
xx
có tổng các nghiệm nguyên là
A.
2
. B.
3
. C.
1
. D.
4
.
Hướng dẫn giải
Chọn B.
TH1:
2
230xx
3
1
x
x
. Khi đó phương trình trở thành:
2
23 5
x
xx
2
80xx
133
2
133
2
x
x


.
TH2:
2
230xx
31
x

. Khi đó phương trình trở thành:
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang203
2
23 5
x
xx
2
320xx
1
2
x
x
.
Vậy tổng các nghiệm nguyên là
12 3T

.
Câu 5. Tập nghiệm của phương trình:
235xx

là tập hợp nào sau đây?
A.
73
;
42




. B.
37
;
24

. C.
73
;
42

. D.
37
;
24



.
Hướng dẫn giải
Chọn B.
235xx
23 3
233
xx
x
x


3
2
7
4
x
x
Vậy tập nghiệm của phương trình đã cho là
37
;
24
S

.
Câu 6. Tổng nghiệm bé nhất và lớn nhất của phương trình
13 3 42
x
xx
là
A.
0
. B.
1
. C.
2
. D.
3
.
Hướng dẫn giải
Chọn A.
Ta có:
13 3 42
x
xx

2
2
13 3 42
x
xx
22 2
10 16 10 2 3 3 16 16 4
x
xx xx
22
6166
x
x
22
11
x
x
2
1011
x
x
. Vậy tổng nghiệm lớn nhất và bé nhất bằng
0
.
Câu 8. Tính tổng tất cả các nghiệm của phương trình
22 2xx

.
A.
1
2
.
B.
2
3
.
C.
6
. D.
20
3
.
Hướng dẫn giải
Chọn D.
6
22 4
22 2
2
224
3
x
xx
xx
xx
x



.
Vậy tổng các nghiệm là
20
3
.
Câu 10. Để giải phương trình
22 31xx
, một học sinh đã lập luận như sau:
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang204
I
Bình phương
2
vế:
22
1 4 4 4 12 9 2xx x x
2
II 3 8 5 0 3xx
.

5
III 1
3
xx.
IV
Vậy
1
có hai nghiệm
1
1x
và
2
5
3
x
Cách giải trên sai từ bước nào?
A.
IV
. B.
II
. C.
III
. D.
I
.
Hướng dẫn giải
Chọn D.
Muốn bình phương hai vế của phương trình thì hai vế phải không âm
Để giải phương trình này ta áp dụng công thức
230
22 3
22 3
223
x
xx
xx
x
x




Hoặc ta giải bằng phương pháp hệ quả thì
22
1 4 4 4 12 9 2xx x x
.
Câu 11. Cho phương trình:
22
x
x
1
. Tập hợp các nghiệm của phương trình
1
là tập
hợp nào sau đây?
A.
;2
. B.
. C.
2;
. D.
0;1; 2
.
Hướng dẫn giải
Chọn A.
Phương trình
22 20 2xxx x
.
Phương trình có tập nghiệm
;2S 
.
Câu 12. Giải phương trình
13 3 1 0xx
.
A.
1
;
3




. B.
1
2

. C.
1
;
3



. D.
1
;
3



.
Hướng dẫn giải
Chọn D.
Ta có
1
13 3 1 0 13 3 1 13 0
3
xx x x x x
.
Câu 13. Phương trình
2
3325
x
xx
có tích của tất cả các nghiệm nguyên là
A.
4
. B.
1
. C.
56
. D.
0
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang205
Hướng dẫn giải
Chọn B.
Phương trình
2
3325
x
xx
2
3325
x
xx

*
.
Điều kiện
2
25 0xx
16 16x 
.
TH1:
316x
. Phương trình
*
2
157
14 0
2
xx x


.
TH2:
16 3x. Phương trình
*
2
540 1
x
xx

.
Câu 14. Phương trình
2
23 5
x
xx có tổng các nghiệm nguyên là
A.
2
. B.
3
. C.
1
. D.
4
.
Hướng dẫn giải
Chọn D.
+ Với
50 5xx
ta có
VP 0
,
VP 0
suy ra phương trình vô nghiệm
+ Với
50 5xx
Phương trình


2
2
22
22
23 5 23 5xx x xx x
2
2
133
80
2
320
133
2
x
xx
xx
x





hoặc
1
2
x
x
Tổng các nghiệm bằng
4
.
Dạng 3: Phương trình chứa ẩn ở mẫu
1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1:
Giải phương trình
33
2
11
x
x
xx
+=
--
Lời giải
Điều kiện
1.x =/
Khi đó phương trình
()
31
33 3
22
11 1 2
x
x
xxx
xx x
-
+ = = =
-- -
thỏa mãn điều kiện
Ví dụ 2. Giải phương trình
2
2
210
3
5
xx
x
xx
-
=-
-
.
Lời giải
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang206
()
()
2
2
2
2
0
0
.
25
3
5
5
210
3
5
23
5
xx
xx
xx
xS
xx
x
xx
x
xx
ì
ï
-
ï
ì
ï
=
ï
-
-
ïï
=- =
íí
ïï
-
=-
ïï
î
/
=/
-
=-
ï
ï
Æ
-
î
Ví dụ 3.
Giải phương trình
()()
210 50
1
232 3xx xx
-=-
-+-+
.
Lời giải
()()()()
()
()
thoaû maõn
loaïi
2
10
2 3 2 3 10 2 50 7 30 0 .
3
x
xx x x x x
x
é
=
ê
- +- += -- -- =
ê
=-
ê
ë
3. Bài tập trắc nghiệm
Câu 1.
Gọi
n
là các số các giá trị của tham số
m
để phương trình

12
0
2
xmx
x

có
nghiệm duy nhất. Khi đó
n
là:
A.
2
. B.
1
. C.
0
. D.
3
.
Hướng dẫn giải
Chọn A.
Điều kiện:
2x
.
Phương trình có nghiệm duy nhất khi xảy ra hai trường hợp:
TH 1: tử thức có đúng một nghiệm thỏa điều kiện, suy ra
20 2mm

.
TH 2: tử thức có hai nghiệm và một nghiệm
2x
, suy ra
220 1mm

.
Vậy
2n
.
Câu 2. Tìm phương trình tương đương với phương trình
2
61
0
2
xx x
x

trong các
phương trình sau:
A.
2
43
0
4
xx
x

. B. 21
x
x
.
C.
3
10x  . D.

2
3
2
x
x
x

.
Hướng dẫn giải
Chọn C.
Xét phương trình
2
61
0
2
xx x
x

1
. ĐK:
1x 
và
2x
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang207
Với điều kiện ở trên, ta có

2
1
10
13
60
2
x
x
x
xx
x



.
Đối chiếu điều kiện, phương trình
1
có nghiệm
1x
.
Xét phương trình
2
43
0
4
xx
x

2
. ĐK:
4x 
.

2
1
2430
3
x
xx
x



.
Loại A
Xét phương trình
21
x
x. ĐK:
0x
. Loại B
Xét phương trình
3
10 1xx .
Xét phương trình

2
3
2
x
x
x

. ĐK:
2x
. Loại D
Đã sửa đáp án C từ
2
1x
thành
3
10x
.
Câu 3. Cho phương trình:
2
32
3
xx
x
x

có nghiệm
a
. Khi đó
a
thuộc tập:
A.
1
;3
3



. B.
11
;
22



. C.
1
;1
3



. D.
.
Hướng dẫn giải
Chọn B.
Điều kiện:
3x
.
Ta có:

2
2
2
313
32 3
32
2
02 620
33
313
2
x
xx xx
xx
xxx
xx
x




.
Ta có:
13 13
0
22

. Vậy nghiệm của phương trình đã cho thuộc tập
11
;
22



.
Dạng 4: Phương trình chứa ẩn ở trong dấu căn
1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1.
Giải phương trình
2
235 1
x
xx
Lời giải
Ta có :
2
235 1
x
xx

2
2
10
235 1
x
xx x


2
1
60
x
xx


2x
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang208
Ví dụ 2. Giải phương trình: 22
x
x
?
Hướng dẫn giải
Điều kiện:
20
20
x
x


2
2
x
x
2x
.
Thay
2x vào phương trình ta được 00
hay 2x
là nghiệm của phương trình.
Ví dụ 3. Giải phương trình
2
284 2xx x
.
A.
4x
. B.
0
4
x
x
. C.
422x
. D.
6x
.
Hướng dẫn giải
Chọn A.
2
284 2xx x

2
2
20
284 2


x
xx x
2
0
4
x
x
x
4
x
.
Ví dụ 4. Giải phương trình:
22
522 5100xx xx 
Hướng dẫn giải
Điều kiện xác định
2
5100xx x
.
Khi đó phương trình
22
5102 51080xx xx 
2
2
5102
510 4
xx
xx


22
3
5102 560
2
x
xx xx
x



.
3. Bài tập trắc nghiệm
Câu
1. Số nghiệm nguyên dương của phương trình 13
x
x
 là
A.
0
. B.
1
. B.
2
. D.
3
.
Hướng dẫn giải
Chọn
B.

2
2
3
3
3
13 5
2
7100
13
5
x
x
x
xx x
x
xx
xx
x





.
Câu 2. Số các nghiệm nguyên của phương trình

32
52 522xx x x
 là
A.
0
. B.
1
. C.
2
. D.
3
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang209
Hướng dẫn giải
Chọn C.
Đặt
32 2 3
52 5 2txx xxt.
Phương trình đã cho trở thành:
32
2
240 2 5 60
3
x
tt t xx
x



.
Vậy phương trình đã cho có hai nghiệm nguyên.
Câu 3. Cho phương trình
2
42
2
2
xx
x
x

. Số nghiệm của phương trình này là
A.
0
. B.
2
. C.
4
. D.
1
.
Hướng dẫn giải
Chọn D.
ĐKXĐ:
2x
khi đó phương trình trở thành
22
1
42 2 540
4
x
xx x xx
x
 
.
Đối chiếu điề kiện suy ra phương trình có một nghiệm
4x
.
Câu 5. Tổng các nghiệm của phương trình 37 12xx
 là
A.
2
. B.
–1
. C.
2
. D.
4
.
Hướng dẫn giải
Chọn A.
1
37 12
372 1
x
xx
x
x



11
374 14 1 12 1
xx
x
xxx x
 







2
1
1
3
230
x
x
x
xx




.
Vậy tổng các nghiệm của phương trình là
2
.
Câu 6. Số nghiệm nguyên của phương trình: 35 7
x
xx
 là
A.
0
. B.
2
. C.
3
. D.
1
.
Hướng dẫn giải
Chọn B.
+ Điều kiện:
30
70
x
x


3
7
x
x
.
+ Thay
x
lần lượt bằng
3
,
4
,
5
,
6
,
7
vào phương trình ta thấy các số
3
,
7
là nghiệm.
+ Vậy phương trình có hai nghiệm nguyên.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang210
Câu 7. Số nghiệm của phương trình:
2
11
6
11
xx
xx


là
A.
0
. B.
2
. C.
1
. D.
3
.
Hướng dẫn giải
Chọn C.
2
11
6
11
xx
xx


2
10
60
x
xx


1
23
x
xx

3x
.
Vập phương trình đã cho có một nghiệm
3x
.
Câu 8. Phương trình sau có bao nhiêu nghiệm 11
x
x
?
A. 0 . B. vô số. C. 1. D. 2 .
Hướng dẫn giải
Chọn C.
Điều kiện xác định:
1
1
x
x
1
x
.
Với
1
x
thay vào phương trình thỏa mãn. Vậy phương trình có một nghiệm.
Câu 9. Tổng tất cả các nghiệm của phương trình:
2
32 1
x
xx

là
A. 3. B. 3
. C.
2
. D.
1
.
Hướng dẫn giải
Chọn D.
2
32 1
x
xx
2
10
321
x
x
xx


2
1
1
230
x
x
xx



.
Câu 10. Phương trình
2
41 3
x
xx có nghiệm là
A.
1
x
hoặc
3x
. B. Vô nghiệm. C.
1
x
. D.
3x
.
Hướng dẫn giải
Chọn B.
2
41 3
x
xx
22
30
41 69
x
x
xxx


3
1
x
x
.
Câu 11. Biết phương trình
2
31 3 7 310xxxx
có một nghiệm có dạng
ab
x
c
,
trong đó
a
,
b
,
c
là các số nguyên tố. Tính
Sabc

.
A.
14S
. B.
21S
. C.
10S
. D.
12S
.
Hướng dẫn giải
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang211
Chọn C.
Điều kiện:

2
370
1
*
3
310
xx
x
x



Với điều kiện trên, phương trình tương đương

2
21 3 7 31 0xxxxx






22
2
31 31
0
31
21 3 7
xx xx
xx
xxx
 




2
2
11
31 0
31
21 3 7
xx
xx
xxx






2
310xx
35
2
x

hoặc
35
2
x
Theo yêu cầu đề bài ta chọn nghiệm
35
2
x
Vậy
3a
,
5b
,
2c
10Sabc
.
Câu 12. Phương trình
33 3
56211xx x
có bao nhiêu nghiệm.
A.
2
. B. 3. C.
1
. D. 0 .
Hướng dẫn giải
Chọn B.
33 3
56211xx x
33 3 3
56356 5 6211xx xx x x x
333
3562110xx x
5
6
11
2
x
x
x

Thử lại ta được các nghiệm đều thỏa mãn
Câu 13. Tập nghiệm của phương trình
4
22
112xx xx

là
A.
. B.
7
;1
2

. C.
0
. D.
1
.
Hướng dẫn giải
Chọn D.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang212
Đặt
4
2
1, 0txx t
2
2
1
1xx
t

Ta có pt:
2
1
2t
t

32
210tt
1
15
2
15
2
t
t
t

So sánh với điều kiện
0t
ta tìm được
1,t
15
2
t
Trường hợp 1:
4
2
1: 1 1txx
2
11xx

2
11xx
22
1
1
21 1
x
x
xx x


Trường hợp 2:
15
2
t
4
2
15
1
2
xx

2
735
1
2
xx

2
735
1
2
xx

2
2
735
2
735
1
2
x
xx





735
2
7
2
x
x
x
Câu 14. Số nghiệm của phương trình

2
2844 2xx xx

là
A.
3
. B.
1
. C.
4
. D.
2
.
Hướng dẫn giải
Chọn D.
Điều kiện:

420 2;4xx x
.

2
2844 2xx xx

22
284 281xx xx 
.
Đặt
2
28txx
, 0t
22
28txx

22
28
x
xt

.

2
14tt
2
40tt

0
4
tn
tl

2
280xx


2
280xx


2
4
x
n
x
n

. Vậy phương trình đã cho có hai nghiệm.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang213
Câu 15. Tổng các bình phương các nghiệm của phương trình

2
133 4520xx xx
là
A.
17
. B.
4
. C.
16
. D.
8
.
Hướng dẫn giải
Chọn B.
Ta có

2
133 4520xx xx
22
453 4540xx xx
2
451xx

2
451xx
2
440 2xx x
.
Câu 16. Phương trình 3221 2xx x có bao nhiêu nghiệm?
A. 0 . B.
1
. C.
2
. D. 3.
Hướng dẫn giải
Chọn A.
ĐKXĐ:
30
220
10
x
x
x


0
11
1
x
x
x
x

.
Thay
1
x
vào
3221 2xx x
, ta được:
32
.
Vậy phương trình vô nghiệm.
Câu 17. Số nghiệm của phương trình
82 7 2 1 7xx xx

là
A.
2
. B. 3. C. 0 . D.
1
.
Hướng dẫn giải
Chọn D.
82 7 2 1 7xx xx
71 2 73 72
73
xxx
x



73 73 72 0
2
xxx
x
 
73 73 72 0
2
xx x
x
  
2
730
2
2
2
x
x
x
x
x



.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang214
Dạng 5: Định lý viet và ứng dụng
1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1.
Tìm tham số
m
để phương trình
2
12 20mxmxm

có hai nghiệm trái dấu
Hướng dẫn giải
Phương trình
2
12 20mxmxm
có hai nghiệm trái dấu khi và chỉ khi

10
120
m
mm


21m .
Ví dụ 2. Cho phương trình
22
30mx m x m
. Tìm tất cả các giá trị của tham số
m
để
phương trình có hai nghiệm
1
x
,
2
x
thỏa mãn
12
13
4
xx
.
Hướng dẫn giải
Phương trình có
2
nghiệm
1
x
,
2
x
thỏa mãn
12
13
4
xx
0
0
13
4
a
b
a



2
22
2
0
34 0
313
4
m
mm
m
m



22
2
0
32 32 0
413120
m
mmmm
mm
 

 
0
;3 1;1 3;
3
4
4
m
m
m
m
 

3
4
4
m
m
.
Vậy tổng bình phương các giá trị của
m
là
265
16
.
Ví dụ 3. Tìm tham số
m
để phương trình
2
220xmxm

có hai nghiệm dương phân biệt
Hướng dẫn giải
Để phương trình
2
220xmxm
có hai nghiệm dương phân biệt
0
0
0
S
P



2
1. 2 0
20
20
mm
m
m



2
20
0
2
mm
m
m



1v 2
0
2
mm
m
m



2m
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang215
3. Bài tập trắc nghiệm
Câu 1.
Phương trình
2
0 0ax bx c a có hai nghiệm phân biệt cùng dấu khi và chỉ khi:
A.
0
0P

.
B.
0
0S
.
C.
0
0P
.
D.
0
0S

.
Hướng dẫn giải
Chọn A.
Phương trình
2
0 0ax bx c a có hai nghiệm phân biệt cùng dấu khi và chỉ
0
0P

.
Câu 2. Biết phương trình
2
0ax bx c
, (0)a
có hai nghiệm
1
x
,
2
x
. Khi đó:
A.
12
12
a
xx
b
a
xx
c

. B.
12
12
b
xx
a
c
xx
a
.
C.
12
12
2
2
b
xx
a
c
xx
a

. D.
12
12
b
xx
a
c
xx
a

.
Hướng dẫn giải
Chọn D.
Theo Hệ thức Viet, ta có
12
12
b
xx
a
c
xx
a

.
Câu 3. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn
7;7
để phương trình
2
22 10mx m x m
có hai nghiệm phân biệt?
A. 14. B.
8
. C.
7
. D.
15
.
Hướng dẫn giải
Chọn C.
 TH1:
0m 410x
1
4
x

; phương trình chỉ có một nghiệm duy nhất nên
loại
0m
 TH2:
0m
Để
2
22 10mx m x m
với
7;7m 
có hai nghiệm phân biệt thì
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang216

2
210mmm

54m

4
5
m

đồng thời

7;7m 
Vậy
1; 2;3; 4;5;6; 7m
có
7
giá trị nguyên của
m
thỏa mãn.
Câu 4. Tìm tất cả giá trị của tham số
m
để phương trình
2
210xmxm
 có 2 nghiệm
phân biệt
1
x
,
2
x
sao cho
22
12
2xx
.
A.
1
2
0
m
m

. B.
0m
. C.
1
2
m
. D.
1
2
0
m
m
.
Hướng dẫn giải
Chọn A.
Phương trình:
2
210xmxm.
Để phương trình có
2
nghiệm phân biệt thì
0
2
10mm

, luôn đúng với
x
.
Khi đó, theo định lí Vi-ét ta có:
12
12
2
1
x
xm
xx m


.
Ta có:
22
12
2xx

2
12 12
22xx xx
2
4222mm

1
2
0
m
m

.
Câu 5. Phương trình

22
45 0mxxm
có hai nghiệm trái dấu, giá trị
m
là
A.
;2 0;2m
. B.
;2 0;2m
.
C.
2;0 2;m
. D.
2; 2m
.
Hướng dẫn giải
Chọn B
Phương trình có hai nghiệm trái dấu
2
0
4
m
m
2
02
m
m


hay
;2 0;2m 
.
Câu 6. Tìm
m
để phương trình
22
30
xmxm
có hai nghiệm
1
x
,
2
x
là độ dài các cạnh
góc vuông của một tam giác vuông với cạnh huyền có độ dài bằng
2
là
A.
0; 2m
. B. 3
m . C.
2;0m
. D.
m
.
Hướng dẫn giải
Chọn D.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang217
Phương trình
22
30xmxm
có hai nghiệm
1
x
,
2
x
là độ dài các cạnh góc vuông của
một tam giác với cạnh huyền có độ bài bằng
2 khi và chỉ khi:
22
12
12
22
12
4120
0
.0
4




mm
Sxx m
Pxx
xx

2
2
12 12
34
0
24



m
m
xx xx

22
32
234


m
mm
2
32
2
m
m
m .
Câu 7. Cho hàm số
2
43 yx x, có đồ thị
P
. Giả sử
d
là dường thẳng đi qua
0; 3
A
và có hệ số góc
k
. Xác định
k
sao cho
d
cắt đồ thị
P
tại
2
điểm phân biệt
E
,
F
sao
cho
OEF
vuông tại
O (O là gốc tọa độ). Khi đó
A.
1
3

k
k
. B.
1
2
k
k
. C.
1
2
k
k
. D.
1
3
k
k
.
Hướng dẫn giải
Chọn D.
Phương trình đường thẳng
:3
d
y
kx
Phương trình hoành độ giao điểm của
P
và
d
:
2
43 3
x
xkx
2
40 xkx
40
 xx k
1
.
d cắt đồ thị
P
tại
2
điểm phân biệt khi
1 có
2
nghiệm phân
biệt
40k 4k
.
Ta có
11
;3Exkx
,
22
;3
Fxkx
với
1
x
,
2
x
là nghiệm phương trình

1
.
OEF
vuông tại
O
.0
 
OE OF
12 1 2
.330 x x kx kx

2
12 1 2
.1 3 90
 xx k k x x


2
0. 1 3 4 9 0 kkk
2
430kk
1
3
k
k
.
Câu 8. Giả sử phương trình
2
2410xmx

có hai nghiệm
1
x
,
2
x
. Tìm giá trị nhỏ nhất của
biểu thức
12
Txx
.
A.
2
min
3
T
. B.
min 2T
. C.
min 2T
. D.
2
min
2
T
.
Hướng dẫn giải
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang218
Chọn B.
Phương trình
2
2410xmx
có
2
420m

nên phương trình có hai nghiệm phân
biệt
1
x
,
2
x
với
12
2Sxx m
,
12
1
2
Pxx

.
Ta có

2
2
12
Txx
2
4SP
2
422m
 2T
. Dấu bằng xảy ra khi 0m
.
Vậy
min 2T
.
Câu 9. Gọi
S
là tập hợp các giá trị của tham số
m
sao cho parabol
P
:
2
4yx xm cắt
Ox
tại hai điểm phân biệt
A
,
B
thỏa mãn
3OA OB
. Tính tổng
T
các phần tử của
S
.
A.
3T
. B.
15T
. C.
3
2
T
. D.
9T 
.
Hướng dẫn giải
Chọn D.
Phương trình hoành độ giao điểm của
P
và
Ox
:
2
40xxm

Để

P
cắt Ox tại hai điểm phân biệt thì có hai nghiệm phân biệt
1
x
,
2
x
0
0a

40
10
m
4m
. Giả sử
1
;0Ax ,
2
;0Bx và
12
4xx
,
12
x
xm
.
Ta có
3OA OB
12
3
x
x
12
12
3
3
x
x
x
x

.
Trường hợp 1:
12
3
x
x
1
2
3
1
x
x
3m
Trường hợp 2:
12
3
x
x
1
2
6
2
x
x
12m
Vậy
12 3 9S  
.
Câu 10. Cho hàm số
2
22yx x có đồ thị
P
, và đường thẳng

d
có phương trình
y
xm
. Tìm
m
để

d cắt
P
tại hai điểm phân biệt
A
,
B
sao cho
22
OA OB
đạt
giá trị nhỏ nhất.
A.
5
2
m 
. B.
5
2
m
. C.
1m
. D.
2m
.
Hướng dẫn giải
Chọn A.
Phương trình hoành độ giao điểm:
2
22
x
xxm

2
32 0xx m

Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang219

d
cắt

P
tại hai điểm phân biệt
A
,
B
0174 0m

17
4
m
.
11
;
A
xx m
11
;OA x x m


22
;Bx x m

22
;OB x x m


22
2222
12 1 2
OA OB x x x m x m
 
2
2
12 12 12
242 2
x
xxxmxxm

2
18 4 2 6 2mmm
2
21010mm

2
51515
2
222
m




với
17
4
m 
Vậy giá trị nhỏ nhất của
22
OA OB
là
15
2
khi
5
2
m
.
Câu 11. Số giá trị nguyên của tham số
m
thuộc
5;5
để phương trình
22
40xmxm
có hai
nghiệm âm phân biệt là
A. 5. B. 6 . C. 10. D. 11
Hướng dẫn giải
Chọn A.
Phương trình có hai nghiệm âm phân biệt
0
0
0
S
P
2
2
30
40
0
m
m
m

0m
.
Vậy trong đoạn
5;5
có
5
giá trị nguyên của
m
thỏa mãn yêu cầu bài toán.
Câu 12. Với giá trị nào của m thì phương trình
2
122 30mx m xm
 có hai nghiệm
1
x
,
2
x
thỏa mãn
1212
1xxxx
?
A.
13m
. B.
12m
. C.
2m
. D.
3m
.
Hướng dẫn giải
Chọn A.
Phương
2
122 30mx m xm có hai nghiệm
1
x
,
2
x
khi và chỉ khi
10
0
m 


2
1
2130
m
mmm

1
10
m
1m
.
Theo định lí Vi-et ta có:
12
24
1
m
xx
m

,
12
3
1
m
xx
m
.
Theo đề ta có:
1212
1xxxx
24 3
1
11
mm
mm

26
0
1
m
m
13m
.
Vậy
13m
là giá trị cần tìm.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang220
Câu 13. Cho phương trình

2
521 0mx mxm
1 . Với giá trị nào của
m
thì
1 có
2
nghiệm
1
x
,
2
x
thỏa
12
2
x
x ?
A.
5m
. B.
8
3
m
. C.
8
5
3
m
. D.
8
5
3
m.
Hướng dẫn giải
Chọn C.
Phương trình
1 có hai nghiệm phân biệt

2
50
150
m
mmm


5
1
3
m
m

* .
Khi đó theo định lý Viète, ta có:
12
12
21
5
5
m
xx
m
m
xx
m

.
Với
12
2
x
x
12
220xx
12 1 2
240xx x x

41
40
55
m
m
mm


924
0
5
m
m

8
5
3
m
. Kiểm tra điều kiện
* ta được
8
5
3
m
.
Câu 14. Gọi
S
là tập hợp tất các giá trị thực của tham số
m
để đường thẳng
:dymx
cắt
parabol

2
:23
P
yx x
tại hai điểm phân biệt
A
và
B
sao cho trung điểm
I
của
đoạn thẳng
A
B
thuộc đường thẳng
:3yx

. Tính tổng tất cả các phần tử của
S
.
A.
2
. B.
1
. C.
5
. D.
3
.
Hướng dẫn giải
Chọn D.
Phương trình hoành độ giao điểm:

22
23 2 301xx mxxmx
.
Để

d
cắt
P
tại hai điểm phân biệt
1
có hai nghiệm phân biệt

2
10
2120
a
m
m



.
Khi đó

d
cắt

P
tại hai điểm phân biệt
11
;
A
xmx
,
22
;Bx mx
, với
1
x
,
2
x
là nghiệm
phương trình

1
. Theo Viét, có:
12
2
x
xm
 ,
12
3xx
.
I
là trung điểm
2
12 1 2
22
;;
22 22
x x mx mx
mm m
AB I









.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang221
Mà

2
1
2
2
1
22
:3 3 340
4
22
mm
mm m
Iyx mm
mm


 

12
3mm.
Dạng 6: Giải và biện luận phương trình
1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1.
Tìm tham số
m
để phương trình
2
2320xmxm
 có nghiệm là
Hướng dẫn giải
Chọn B.
Để phương trình
2
2320xmxm có nghiệm
0


2
320mm
2
320mm

1
2
m
m
.
Ví dụ 2. Cho phương trình

2
1175mx mxm. Tìm tham số
m
để phương trình đã cho
vô nghiệm là
Hướng dẫn giải
Ta có:

2
1175 1mx mxm
2
56 1mm xm
23 12mmxm
Để phương trình

1
vô nghiệm
phương trình
2
vô nghiệm
230
2v 3
2v 3
1
10
mm
mm
mm
m
m





Ví dụ 3. Xác định
m
để phương trình
2
67mx x

có
4
nghiệm phân biệt.
Hướng dẫn giải
2
67mx x
là phương trình hoành độ giao điểm của đường thẳng
ym
và đồ thị
2
:67Cyx x
.
Vẽ
2
:67
P
yx x
, lấy đối xứng phần phía dưới
Ox
của
P
lên trên
Ox
và xóa đi
phần phía dưới
Ox
, ta được đồ thị
C
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang222
Dựa vào đồ thị: phương trình
2
67mx x

có 4 nghiệm phân biệt khi
0;16m
.
Ví dụ 4. Tìm m để phương trình
2
22 2 4230xxxm

có nghiệm.
A.
1
. B.
3
. C.
0
. D.
2
.
Hướng dẫn giải
Chọn D.
Đặt
22tx x
22
424tx
2
2
4
4
2
t
x

, Điều kiện
222t
Phương trình trở thành:
2
4
2230
2
t
tm

2
210(*)tt m
Xét hàm số
2
1
f
ttt
, có bảng biến thiên
7+2 2
5
22
2
-
1
4
-
1
2
y
x
+∞
-∞
Phương trình có nghiệm thỏa
222t
khi
52 722m
5722
22
m

Ví dụ 5. Tìm tham số
m
để phương trình
2
2
11
23210xxm
xx




có nghiệm
Hướng dẫn giải
Điều kiện xác định:
0x
. Đặt
1
tx
x
22
2
1
22tx
x

2t
2
2
t
t

.
Phương trình đã cho trở thành
2
223210ttm

2
23230ttm

Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang223
2
2332tt m
Xét hàm số
2
233yft t t
có bảng biến thiên
có nghiệm t thỏa
2
2
t
t

khi
21
211
m
m

1
2
m

.
3. Bài tập trắc nghiệm
Câu 1.
Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
để phương trình

2
22mx m m x m x
có tập nghiệm là
. Tính tổng tất cả các phần tử của
S
.
A.
1
. B.
1
. C.
2
. D.
0
.
Hướng dẫn giải
Chọn A.
Biến đổi phương trình đã cho thành
2
0
x
mm
.
Phương trình có tập nghiệm là
thì
2
0
0
1
m
mm
m

.
Suy ra
0;1S
. Do đó ta có
011
.
Câu 2. Cho phương trình
2
24mx m
. Có bao nhiêu giá trị của tham số m để phương
trình có tập nghiệm là
?
A. vô số. B.
2
. C.
1
. D.
0
.
Hướng dẫn giải
Chọn C.
Phương trình bậc nhất đã cho có tập nghiệm là
khi và chỉ khi
2
20
2
2
40
m
m
m
m




2m
.
Vậy có duy nhất một giá trị của tham số
m
để phương trình đã cho có tập nghiệm là
.
Câu 3. Cho phương trình
31 13mm x m
(
m
là tham số). Khẳng định nào sau đây là
đúng?
A.
1
3
m
thì phương trình có tập nghiệm là
1
m

.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang224
B.
0m
và
1
3
m thì phương trình có tập nghiệm là
1
m

.
C.
0m
thì phương trình có tập nghiệm là
.
D.
0m
và
1
3
m thì phương trình vô nghiệm.
Hướng dẫn giải
Chọn B.
Giải và biện luận phương trình:
31 13mm x m
như sau:
+ Khi

0
310
1
3
m
mm
m

.
0m
: phương trình trở thành
01
x
.
1
3
m : phương trình trở thành
00x
.
+ Khi

0
310
1
3
m
mm
m

: phương trình có nghiệm duy nhất
1
x
m
 .
Câu 4. Tìm
m
để phương trình
2
–2 1 1 0mx m x m

vô nghiệm.
A.
1m 
. B.
1m
hoặc
0m
.
C.
0m
và
1m 
. D.
0m
và
1m 
.
Hướng dẫn giải
Chọn A.
Xét
0m
phương trình thành
1
210
2
xx
 nên ta loại
0m
.
Xét
0m
phương trình có biệt thức

2
111mmmm

.
Phương trình đã cho vô nghiệm khi
01m

thỏa
0m
.
Câu 5. Cho phương trình
2
0ax bx c
0a
. Phương trình có hai nghiệm âm phân biệt
khi và chỉ khi:
A.
0
0
0
S
P

. B.
0
0P
. C.
0
0
0
S
P
. D.
0
0
0
S
P

.
Hướng dẫn giải
Chọn C.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang225
Phương trình có hai nghiệm âm phân biệt thì tổng hai nghiệm âm và tích hai nghiệm
dương.
Câu 6. Phương trình
2
0ax bx c có nghiệm duy nhất khi và chỉ khi:
A.
0a
và
0b
. B.
0
0
a
hoặc
0
0
a
b
.
C.
0ab
. D.
0
0
a
.
Hướng dẫn giải
Chọn B.
Nếu
0a
thì phương trình đã cho là PTB2 nên có nghiệm duy nhất khi
0
.
Nếu
0a
ta được phương trình
0bx c
. Phương trình này có nghiệm duy nhất khi và
chỉ khi
0b
.
Câu 7. Phương trình
42
2210(1)xmx m
có 4 nghiệm phân biệt khi và chỉ khi:
A.
1
2
m .
B.
1
2
m và
1m
. C.
m
. D.
1m
.
Hướng dẫn giải
Chọn B.
Đặt
2
,0txt, khi đó phương trình trở thành:
2
2210tmtm


*
.
Để phương trình đã cho có bốn nghiệm phân biệt khi và chỉ khi
*
có hai nghiệm dương
phân biệt
0
0
0
S
P


2
210
20
210
mm
m
m



1
0
1
2
m
m
m
1
2
1
m
m
.
Câu 8. Vậy
1
2
m và
1m
thỏa mãn yêu cầu bài toán. Tìm tất cả các tham số
m
để phương
trình

2
93mxm
nghiệm đúng với mọi
x
.
A.
3m
. B.
3
m
. C. Không tồn tại
m
. D.
3m
.
Hướng dẫn giải
Chọn D.
Phương trình

2
93mxm
nghiệm đúng với mọi
x
khi
2
30
3
90



m
m
m
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang226
Câu 9. Tìm tất cả các giá trị của tham số
m
để hai đồ thị hàm số
2
23yx x
và
2
yx m có điểm chung.
A.
7
2
m 
.
B.
7
2
m 
.
C.
7
2
m 
.
D.
7
2
m 
.
Hướng dẫn giải
Chọn C.
Phương trình hoành độ giao điểm
22
23
x
xxm


2
22 30*xxm
có nghiệm khi
7
270
2
mm
 .
Câu 10. Có tất cả bao nhiêu giá trị nguyên của tham số
10;10m
để phương trình
2
93 3mxmm
có nghiệm duy nhất?
A.
2
. B.
21
. C.
19
. D.
18
.
Hướng dẫn giải
Chọn C.
Phương trình
2
93 3mxmm
có nghiệm duy nhất khi và chỉ khi
2
90m 
3m 
.
Vì

10;10m
nên
10;10 \ 3m 
.
Vậy có 19 giá trị nguyên của
m
để
2
93 3mxmm

có nghiệm duy nhất.
Câu 11. Tìm giá trị của tham số m để phương trình
22
23mx m m x m vô nghiệm.
A.
2m
. B.
0m
. C.
1
2
m
. D.
1m
.
Hướng dẫn giải
Chọn B.
22
23mx m m x m
22
32mmxm m
*
.
Xét
2
001mm m m.
Với
0m
,
*02x
, phương trình vô nghiệm.
Với
1m
,
*00x
, phương trình có vô số nghiệm.
Với
0;1m
,

2
2
32
*
mx
x
mm

2m
m
, nên
*
có nghiệm duy nhất.
Vậy
0m
thì phương trình đã cho vô nghiệm.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang227
Câu 12. Điều kiện cần và đủ để phương trình
2
21 0mx m x m
 có hai nghiệm phân biệt là
A. 0m ,
1
2
m 
.
B.
1
2
m
. C.
1
2
m 
. D. 0m .
Hướng dẫn giải
Chọn A.
Phương trình có hai nghiệm phân biệt
0
'0
m
.
Ta có:

2
2
'1mm
21m
.
Hệ có nghiệm:
0
'0
m

0
1
2
m
m

.
Vậy
0
1
2
m
m

cần tìm.
Câu 13. Phương trình
2
1310mxx
có nghiệm khi và chỉ khi
A.
5
4
m 
. B.
5
4
m 
. C.
5
4
m
. D.
5
4
m 
,
1m
.
Hướng dẫn giải
Chọn A.
Trường hợp 1: Xét
1m , phương trình có nghiệm
1
3
x
.
Trường hợp 2: Xét
1m ,
94 1m

45m
. Phương trình có nghiệm khi 0
450m
5
4
m
.
Vậy phương trình đã cho có nghiệm khi
5
4
m 
.
Câu 14. Với
m
bằng bao nhiêu thì phương trình 10
mx m vô nghiệm?
A. 0m . B. 0
m và 1
m . C. 1
m . D. 1m .
Hướng dẫn giải
Chọn A.
Phương trình
10mx m vô nghiệm khi
0
10
m
m
0
1
m
m
0
m .
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang228
Câu 15. Có bao nhiêu giá trị thực của
m
để phương trình
22
21mmx xm
 vô nghiệm?
A. 2. B. Đáp án khác. C.
3
. D. 1.
Hướng dẫn giải
Chọn D.
Ta có
22
21mmx xm
22
21mm xm

.
Để phương trình vô nghiệm thì
2
2
20
10
mm
m


2m
.
Câu 16. Cho phương trình
2
110mxm
1
. Trong các kết luận sau kết luận nào đúng?
A. Với 1m  phương trình
1
có nghiệm duy nhất.
B. Với
1m
phương trình
1
có nghiệm duy nhất.
C. Với 1m  phương trình
1
có nghiệm duy nhất.
D. Cả ba kết luận trên đều đúng.
Hướng dẫn giải
Chọn C.
2
111mxm
Phương trình

1
có nghiệm duy nhất khi
2
11mm
.
Câu 17. Tất cả các giá trị của tham số
m
để phương trình
2
2
11
210xmx
xx




có
nghiệm là
A.
3
;
4
m



. B.
33
;;
44
m

 



.
C.
3
;
4
m



. D.
33
;
44
m




.
Hướng dẫn giải
Chọn B.
Ta có
2
2
11
210xmx
xx




2
11
210xmx
xx
 

 
 
Đặt
1
x
t
x

,
2t
ta được
2
210tmt

.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang229
Phương trình luôn có hai nghiệm
12
0tt
phương trình có nghiệm khi và chỉ khi
phương trình có ít nhất một nghiệm
t
sao cho
2t
, hay ít nhất một trong hai số
2; 2
phải nằm giữa hai nghiệm
12
,;tt hay

20
20
f
f
03
0
4
34
m
m
3
4
3
4
m
m

.
Câu 18. Tìm tất cả các giá trị thực của
m
để phương trình
2
463 0xx m

có nghiệm thuộc
đoạn
1; 3
.
A.
211
33
m
. B.
11 2
33
m

.
C.
2
1
3
m
. D.
11
1
3
m

.
Hướng dẫn giải
Chọn B.
Ta có:
2
463 0xx m
2
346mx x

.
Số nghiệm của phương trình
2
463 0xx m

là số nghiệm của đường thẳng
3ym
và parabol
2
46yx x .
Bảng biến thiên của hàm số
2
46yx x
 trên đoạn
1; 3
:
Phương trình có nghiệm thuộc đoạn
1; 3
11 3 2m

11 2
33
m

.
Câu 19. Số giá trị nguyên của tham số thực
m
thuộc đoạn
10;10
để phương trình
2
0xxm
vô nghiệm là
A.
21
. B.
9
. C.
20
. D.
10
.
Hướng dẫn giải
Chọn B.
Để phương trình
2
0xxm

vô nghiệm

2
1
14.1.0140
4
mmm
.
Vậy số các trị nguyên của tham số thực
m
thuộc đoạn
10;10
để phương trình
2
0xxm
vô nghiệm là
1; 2;3; 4;5; 6;7;8;9;10m
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang230
Câu 20. Có bao nhiêu giá trị nguyên của m để phương trình

22
41 10xx m
 có
4
nghiệm phân biệt
A.
1
. B.
0
. C.
2
. D. Vô số.
Hướng dẫn giải
Chọn B.
Điều kiện xác định
x
.
Đặt
2
1tx
,
1t
.
Phương trình trở thành
2
14 10ttm
2
4ttm

.
2
Để phương trình có
4
nghiệm phân biệt thì phương trình
2
có hai nghiệm phân biệt
lớn hơn
1
.
Vẽ BBT ta có
Dựa BBT ta có
43m
. Vậy không có giá trị nguyên của
m
thỏa mãn yêu cầu bài
toán.
Câu 21. Để phương trình sau có
4
nghiệm phân biệt:
22
10 2 8 5
x
xxxa

. Giá trị của
tham số
a
là
A.

1; 10a
. B.
1a
. C.
43
4
4
a
. D.
45
4;
4
a



.
Hướng dẫn giải
Chọn C.
Phương trình đã cho tương đương:
22
254 5
x
xxxa

,
1
.
Đặt
2
5tx xa
.
Phương trình

1
trở thành:
24tat

,
2
Phương trình
2
0
28
28
3
t
ta
a
t

, để phương trình
1
có
4
nghiệm phân biệt thì
2
phải có
2
nghiệm phân biệt, tức là
280a
4a
,
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang231
Khi đó, thay lại ta có:
2
2
528
3 153 28
xxaa
xxaa


2
2
58 0
315 80
xx a
xxa


. Điều kiện để
1
có
4
nghiệm phân biệt là mỗi phương trình bậc
2
ở trên có
2
nghiệm phân biệt.
Vậy

1
2
2
25 4 8 0
15 4.3. 8 0
a
a


7
4
43
4
a
a
743
44
a
.
So với điều kiện
, suy ra
43
4
4
a
.
Câu 22. Có tất cả bao nhiêu giá trị nguyên không dương của tham số
m
để phương trình
21
x
mx có nghiệm duy nhất?
A.
4
. B.
3
. C.
1
. D.
2
.
Hướng dẫn giải
Chọn B.
21
x
mx

2
10
21
x
xm x



2
1
41 0*
x
xx m

.
Phương trình có nghiệm duy nhất khi hệ có nghiệm duy nhất.
Xét
2
41 0xx m
;
3 m

TH1:
03m

thì có nghiệm kép
21x
.
TH2:
03m
 thì phương trình có nghiệm duy nhất khi có 2 nghiệm thỏa
12
1
x
x
12 1212
110 10xx xxxx
1410 2mm

.
m
không dương nên
3; 1; 0m
.
Câu 23. Phương trình
22
43 32mmxmm
có nghiệm duy nhất khi:
A.
3m
. B.
1m
và
3m
. C.
1m
. D.
1m
hoặc
3m .
Hướng dẫn giải
Chọn B.
Phương trình
22
43 32mmxmm
có nghiệm duy nhất
2
430mm
1
3
m
m
.
Câu 24. Tìm m để phương trình
422
110mxmxm

có ba nghiệm phân biệt.
A.
1m 
. B.
1m
. C.
1m
. D.
0m
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang232
Hướng dẫn giải
Chọn C.
+ Khi
10m  1m
phương trình cho trở thành:
2
0x
0x
Do đó:
1m không thỏa mãn đề bài.
+ Khi
10m  1m
Đặt
2
tx
0t
.
Phương trình cho trở thành
22
1101mtmtm .
Phương trình cho có ba nghiệm phân biệt
1
có hai nghiệm
12
,tt thoả
12
0tt
Khi
1
01tm
. Do có hai nghiệm phân biệt nên 1m
.
Với
2
1
1
2
mt
.
Do đó phương trình

1 có nghiệm khi
5
4
1
m
m

**
Từ
*
và
**
phương trình
1
có nghiệm
5
4
m 
.
Câu 25. Có tất cả bao nhiêu giá trị của
m
để phương trình
23
0
1
xmx
x

có nghiệm duy
nhất?
A. 0 . B.
2
. C. 3. D.
1
.
Hướng dẫn giải
Chọn C.
Điều kiện:
1
x
.
23
0
1
xmx
x


230xmx
2
3
x
x
m
Vậy để phương trình có nghiệm duy nhất thì
0m
hoặc
3
1
m
3m 
hoặc
3
2
m

6m
Câu 26. Tìm tất cả các giá trị của
m
để phương trình
2
23 0xx m

có nghiệm
0; 4x
.
A.
;5m 
. B.
4; 3m

. C.
4;5m 
. D.
3;m 
Hướng dẫn giải
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang233
Chọn C.
Cách 1: Phương trình có nghiệm khi
40 4mm

1
.
Khi đó, phương trình có nghiệm
1
14
x
m
,
2
14
x
m
.
Để phương trình có nghiệm
0; 4x
thì
1
2
04
04
x
x
41
43
01 4 4 4 1 3
5
5
01 4 4 4 3
41
43
m
m
mmm
m
m
mm
m
m



 


 




.
So với điều kiện

1
,
4;5m 
thì phương trình đã cho có nghiệm
0; 4x
.
Cách 2: Phương trình đã cho tương đương
2
23mx x

.
Đặt
2
23yfx x x.
Ta có đồ thị hàm số
yfx
như sau:
Dựa vào đồ thị. Để phương trình
2
23yfx x x m

có nghiệm

0; 4x
thì
45m
Câu 27. Tìm
m
để phương trình
22 2
2
1
mx
x
m
x


có
2
nghiệm phân biệt.
A.
5
2
m
và
1m
. B.
5
2
m
và
3
2
m
. C.
5
2
m
và
1
2
m
. D.
5
2
m
.
Hướng dẫn giải
Chọn B.
Điều kiện:
1x 
. Với điều kiện đó, phương trình đã cho tương đương với:
O
x
y
5
4
1
4
1
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang234
21222
x
mx mx
2
22442
x
mx x m m x

2
23 240*xmxm .
Phương trình đã cho có
2
nghiệm phân biệt khi và chỉ khi phương trình
*
có hai
nghiệm phân biệt khác
1

 
2
2
234240
123.1240
mm
mm


2
420250
460
mm
m



2
25 0
46
m
m

5
2
3
2
m
m
.
Câu 28. Có bao nhiêu giá trị nguyên của m để phương trình
2
232 0xx m

có đúng một
nghiệm

0; 4x .
A.
5
. B.
4
. C.
6
. D.
9
.
Hướng dẫn giải
Chọn A.
Ta có
2
232 0xx m
2
232
x
xm
.
Để phương trình đã cho có đúng một nghiệm
0; 4x
thì đường thẳng
2ym
cắt đồ thị
hàm số
2
23yx xtrên
0; 4
tại một điểm duy nhất.
Lập bảng biến thiên
Dựa vào bảng biến thiên ta có:
24
32 5
m
m


2
35
22
m
m


.
Vậy các giá trị nguyên của
m
thỏa mãn là
2; 1;0;1; 2m
Câu 29. Cho phương trình
32
21 41 210xmxmxm
. Số các giá trị của
m
để
phương trình có một nghiệm duy nhất?
A.
0
. B. vô số. C. 1. D. 2 .
Hướng dẫn giải
Chọn C.
Tập xác định
D
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang235
Phương trình tương đương với
2
12210xxmxm

2
1
2210*
x
xmxm

.
Ta có, phương trình
* có

2
2
21 1 0mm m

.
Phương trình đã cho có duy nhất một nghiệm nếu phương trình
*
có nghiệm kép
1
x
0

1m
.
Thay
1m vào phương trình
* , ta được
2
210xx

1
x
.
Vậy với
1m
thì phương trình đã cho có một nghiệm duy nhất.
Câu 30. Tập hợp các giá trị của
m
để phương trình
2
1
11
x
mm
x
xx

có nghiệm là
A.
1
;
3



. B.
1;
. C.
1
;
3



. D.
1
;
3




.
Hướng dẫn giải
Chọn C.
Điều kiện
1
x
. Khi đó, ta có
2
1
11
x
mm
x
x
x


12
x
xm m 231xm

31
2
m
x

.
Phương trình đã cho có nghiệm khi
31
1
2
m
1
3
m
.
Câu 31. Cho hàm số

3
f
xmx m
, với
m
là tham số thực. Có bao nhiêu giá trị nguyên của
m
để phương trình
0fx
không có nghiệm thuộc đoạn
0; 2
?
A. vô số B. 5. C. 3. D.
4
.
Hướng dẫn giải
Chọn D.
Ta có
030 3fx mx m mx m 
Với
0m
thì phương trình tương đương:
03
.
Với 0m thì phương trình có nghiệm
3m
x
m
Để phương trình không có nghiệm thuộc đoạn
0; 2
thì
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang236
33
00
03
3330
20
mm
m
mm
mm m
mm












Mà
2; 1; 1; 2mm
.
Vậy có 4 giá trị của
m
thỏa mãn yêu cầu bài toán.
Câu 32. Tìm các giá trị của
m
để phương trình 21
x
xm
 có nghiệm:
A.
2m
. B.
2m
. C.
2m
. D.
2m
.
Hướng dẫn giải
Chọn C.
21
x
xm

1
Phương trình tương đương:

22
0
41 2
xm
x
xmxm



22
22 402
xm
xmxm


Phương trình

1
có nghiệm
p
t2
có ít nhất một nghiệm lớn hơn hoặc bằng
m
.
84m

Phương trình

1
có nghiệm
0
 2m
1
2
284
284
xm m
x
mmm


.
Vậy
2m
.
Câu 33. Cho biết tập hợp tất cả các giá trị của tham số
m
để phương trình
2
2
11
23510xxm
xx




có nghiệm là
;
a
S
b

, với
a
,
b
là các số
nguyên dương và
a
b
là phân số tối giản. Tính .Tab
A.
5T 
. B.
5T
. C.
11T
. D.
55T
.
Hướng dẫn giải
Chọn B.
Đặt
1
x
t
x

,
2t
khi đó phương trình trở thành
2
23530ttm

Phương trình
2
2
11
23510xxm
xx




có nghiệm khi và chỉ khi phương trình
có nghiệm t thỏa mãn
2t
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang237
Số nghiệm của phương trình bằng số giao điểm của parabol
2
:233
P
yt t và
đường thẳng
:5d
y
m
.
Xét parabol
2
:233
P
yt t
ta có bảng biến thiên như sau
Từ bảng biến thiên ta có phương trình có nghiệm khi và chỉ khi
51m 
1
5
m
.
Vậy khi
1
;
5
m



thì phương trình có nghiệm
1
5
a
b
5T
.
t

2
3
4
2
2
233yt t

11
33
8
1

Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang238
BÀI 3. PHƯƠNG TRÌNH VÀ HỆ PHƯƠNG TRÌNH BẬC NHẤT NHIỀU ẨN
A. KIẾN THỨC CƠ BẢN CẦN NẮM
I – ÔN TẬP VỀ PHƯƠNG TRÌNH VÀ HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
1. Phương trình bậc nhất hai ẩn
Phương trình bậc nhất hai ẩn
,
x
y
có dạng tổng quát là
()
1ax by c+=
, trong đó ,,abc là các
hệ số, với điều kiện
a
và
b
không đồng thời bằng
0.
CHÚ Ý
a) Khi
0ab==
ta có phương trình 00 .
x
yc+= Nếu
0c ¹
thì phương trình này vô nghiệm, còn nếu
0c =
thì mọi cặp số
(
)
00
;
x
y
đều là nghiệm.
b) Khi
0,b ¹ phương trình ax by c+= trở thành
()
2
ac
yx
bb
=- +
Cặp số
(
)
00
;
x
y
là một nghiệm của phương trình
()
1
khi và chỉ khi điểm
()
00
;
M
xy
thuộc đường thẳng
(
)
2.
Tổng quát, người ta chứng minh được rằng phương trình bậc nhất hai ẩn luôn luôn có vô số nghiệm.
Biểu diễn hình học tập nghiệm của phương trình của phương trình
()
1
là một đường thẳng trong mặt
phẳng tọa độ
.Oxy
2. Hệ hai phương trình bậc nhất hai ẩn
Hệ phương trình bậc nhất hai ẩn có dạng tổng quát là
()
11 1
22 2
3
ax by c
ax by c
ì
+=
ï
ï
í
ï
+=
ï
î
Trong đó
,
x
y
là hai ẩn; các chữ số còn lại là hệ số.
Nếu cặp số
(
)
00
;
x
y
đồng thời là nghiệm của cả hai phương trình của hệ thì
(
)
00
;
x
y
được gọi là một
nghiệm của hệ phương trình
()
3.
Giải hệ phương trình
()
3
là tìm tập nghiệm của nó.
II – HỆ BA PHƯƠNG TRÌNH BẬC NHẤT BA ẨN
Phương trình bậc nhất ba ẩn có dạng tổng quát là
,ax by c z d++=trong đó
,,
x
yz
là ba ẩn; ,,,abcd
là các hệ số và
,,abc không đồng thời bằng
0.
Hệ phương trình bậc nhất ba ẩn có dạng tổng quát là
()
111 1
222 2
333 3
4
ax by cz d
ax by cz d
ax by cz d
ì
++=
ï
ï
ï
ï
++=
í
ï
ï
ï
++=
ï
î
Trong đó
,,
x
yz
là ba ẩn; các chữ còn lại là các hệ số.
Mỗi bộ ba số
()
000
;;
x
yz
nghiệm đúng ba phương trình của hệ được gọi là một nghiệm của hệ
phương trình
(
)
4.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang239
Dạng 1: Giải và biện luận hệ phương trình bậc nhất hai ẩn
1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Giải hệ phương trình
24
4250
xy
xy


Lời giải
Ta có:

24
24 24
422450
4250 130
xy
x
yxy
xx
xy

 




 

.
Vậy hệ phương trình đã cho vô nghiệm.
Ví dụ 2: Giải hệ phương trình
65
3
910
1
xy
xy
ì
ï
ï
+=
ï
ï
ï
í
ï
ï
-=
ï
ï
ï
î
Lời giải
Điều kiện:
0, 0xy
.
Ta có
65
3
910
1
xy
xy
ì
ï
ï
+=
ï
ï
ï
í
ï
ï
-=
ï
ï
ï
î
11
65 3
11
910 1
xy
xy












11
3
11
5
x
y
3
5
x
y
.
Vậy
53 2yx
.
Ví dụ 3: Giải hệ phương trình
41
5
2
52
3
2
xy
xy
Lời giải
Ta có:
41
1
5
1
3
2
2
1
52 1
1
3
2
x
xy
x
y
y
xy







.
Ví dụ 3: Tìm m để hệ phương trình
2
46
mx y m
xmym


vô nghiệm
Lời giải
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang240
Cách 1.
Từ phương trình đầu ta có
2*ymx m
.
Thế

*
vào phương trình thứ hai ta được:
22
426426**xmmx m m mx m m
.
Hệ phương trình vô nghiệm khi và chỉ khi phương trình
**
vô nghiệm.

**
vô nghiệm khi và chỉ khi:
2
2
40
2
260
m
m
mm



.
Cách 2.

2
1
422
4
m
Dmmm
m

.

2
21
26223
6
x
m
Dmmmm
mm


.

2
2
22
46
y
mm
Dmmmm
m

.
Hệ phương trình vô nghiệm khi và chỉ khi:
0
0
2
0
x
y
D
D
m
D

.
Ví dụ 4. Tìm m để hệ phương trình
21
22
mx y
xy
có nghiệm
Lời giải
21(1)
22(2)
mx y
xy


Từ pt
22yx
. Thế vào pt ta được:
2(2 2 ) 1 ( 4) 5 (3)mx x m x
4m
thì pt có nghiệm duy nhất Hệ đã cho có nghiệm duy nhất.
Ví dụ 5.
Tìm m để hệ phương trình:
(1)3
22
24
mx m y m
xmym
xy



có nghiệm
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang241
Lời giải
Xét hệ


(1)31
222
243
mx m y m
xmym
xy



,
Trừ theo vế hai phương trình
2 và
3 ta được:
212 4my m
Nếu
1m  thì
4 vô nghiệm nên hệ vô nghiệm.
Nếu
1m 
thì


2
4
21
m
y
m

, thay vào
3
được
52
1
m
x
m
.
Thế các giá trị
,
x
y
tìm được vào
1
ta được phương trình:


 
2
52 2
.1.3
121
25 2 12 6 1
1
5320
2
5
mm
mm m
mm
mm m m mm
m
mm
m






Ví dụ 6. Tìm tất cả các giá trị của
m
để hệ phương trình
3
21
mx y
xmy m


có nghiệm duy nhất
00
;
x
y
thỏa mãn
22
00
10xy
.
Lời giải
Hệ phương trình có nghiệm duy nhất khi
2
10 1mm

.
Khi đó

2
1
3
3
3
1
1
321
21 23
1
1
ymx
x
ymx
mx y
m
m
xm mx m
xmy m m
x
y
m
m









.
Vậy hệ phương trình có nghiệm duy nhất là:
0
0
1
1
23
1
x
m
m
y
m
.
Nên:

22
22
00
10 1 2 3 10. 1xy m m 
2
0
680 ()
4
3
m
mm TM
m

.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang242
3. Bài tập trắc nghiệm
Câu 1.
Hệ phương trình
23
13
32
12
xy
xy


có nghiệm là
A.
1
2
x ;
1
3
y  .
B.
1
2
x
;
1
3
y
. C.
1
2
x
;
1
3
y
. D.
1
2
x ;
1
3
y
.
Hướng dẫn giải
Chọn D.
Điều kiện
0
0
x
y
.
Đặt
1
a
x
và
1
b
y
thì hệ trở thành
2313
3212
ab
ab
2
3
a
b
.
Vậy nghiệm của hệ là
1
2
x ;
1
3
y
.
Câu 2. Cho hệ phương trình
1
1

xmy
mx y
I
,
m
là tham số. Mệnh đề nào sai?
A. Hệ

I
có nghiệm duy nhất
1
m
.
B. Khi
1m
thì hệ

I
có vô số nghiệm.
C. Khi
1m
thì hệ
I
vô nghiệm.
D. Hệ

I
có vô số nghiệm.
Hướng dẫn giải
Chọn D.
Hệ
I
có nghiệm duy nhất
1
1
1

m
m
m
,
A đúng.
Hệ
I
vô số nghiệm
1
11
1

m
m
m
,
B đúng. Hệ
I
vô nghiệm
1
11
1

m
m
m
, C đúng.
D sai.
Câu 3. Cho hệ phương trình
21
341
xym
xy m


. Giá trị
m
thuộc khoảng nào sau đây để hệ
phương trình có nghiệm duy nhất
00
;
xy
thỏa mãn
00
231xy
?
A.
5; 9m
. B.
5; 1m
. C.
0; 3m
. D.
4;1m
.
Hướng dẫn giải
Chọn B.
21
341
xym
xy m


1
xm
ym

. Vậy phương trình có nghiệm duy nhất

;1mm
mà
00
231xy

23 11mm
4m
 . Vậy
5; 1m
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang243
Câu 4. Có bao nhiêu giá trị
m
nguyên dương để hệ phương trình
3
29
mx y
xmy
có nghiệm duy
nhất
;
x
y
sao cho biểu thức
3
A
xy
nhận giá trị nguyên
A.
4.
B.
2.
C.
3.
D.
1.
Hướng dẫn giải
Chọn B.
Ta có
2
1
20
2
m
Dm
m

,
m
nên hệ phương trình luôn có nghiệm duy nhất.
31
39
9
x
Dm
m

;
3
96
29
y
m
Dm

.
Vậy hệ luôn có nghiệm duy nhất là
2
2
39
2
96
2
m
x
m
m
y
m
.
Ta có
3
A
xy
22
33 9
96
22
m
m
mm


2
33
2m
.
Để
A
nguyên thì
2
2m
là ước của 33 mà
2
22m
nên ta có các trường hợp sau:
+ TH1:
2
23m 
1m
.
+ TH2:
2
211m 
3m.
+ TH3:
2
233m 
31m .
Vậy có
2 giá trị nguyên dương của
m
để
A
nguyên.
Câu 5. Gọi S là tập hợp các giá trị của tham số
m
để hệ phương trình
(1) 2
(1) 2
mxym
mx m y


có
nghiệm là
0
(2; )y . Tổng các phần tử của tập S bằng
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải
Chọn B
Ta có:



2
2
2
2
110,
122 34
21 2 42
x
y
Dm mmm m
Dmm mm
Dmmm mm
 
 
 
Suy ra với mọi giá trị của
m
thì hệ có nghiệm duy nhất:
2
2
2
2
34
1
42
1
x
y
D
mm
x
Dmm
D
mm
y
Dmm






Để
0
(2; )y là nghiệm của hệ thì
2
2
2
1
34
220
2
1
m
mm
mm
m
mm


 

Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang244
Vậy
1; 2S 
Câu 6. Hệ phương trình
2
46
mx y m
xmym


vô nghiệm khi giá trị
m bằng
A.
2m
. B.
2m
. C.
1m
. D.
1m 
.
Lời giải
Chọn B
Ta có
2
1
4
4
m
Dm
m

;
2
21
26
6
x
m
Dmm
mm


;
2
2
2
46
y
mm
Dmm
m

Xét
2
04 0 2Dmm 
Khi
20
xy
mDD
hệ phương trình có vô số nghiệm
Khi 2 4 0
x
mD  hệ phương trình vô nghiệm
Câu 7. Gọi
0
m
là giá trị của m để hệ phương trình
3
2
9
xym
mx y m


có vô số nghiệm. Khi đó:
A.
0
1
1;
2
m




. B.
0
1
0;
2
m



.
C.
0
1
;2
2
m



. D.
0
1
;0
2
m




.
Lời giải
Chọn B
Ta có
13
13
1
Dm
m
.
Để hệ phương trình vô số nghiệm thì
0
xy
DD D

Ta có
1
013 0
3
Dmm 
Thay
1
3
m
vào hệ phương trình ta có:
111
333
333
11211 1
3
33939 3
xy xy xy
xy xy x y







 


Vậy
1
3
m
hệ phương trình vô số nghiệm.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang245
Câu 8. Cho hệ phương trình:
22
21
x
ya
xya


. Gọi
0
a
là giá trị của tham số
a để tổng bình phương
hai nghiệm của hệ phương trình đạt giá trị nhỏ nhất. Chọn khẳng định đúng trong các khẳng định
sau:
A.

0
10;0a 
B.
5;8
C.
0
0;5a
D.

8;12
Lời giải
Chọn C.
Ta có :
22
21
x
ya
xya


42 42
21
x
ya
xya


5
5
3
5
a
x
a
y

2
2
22
22 2
5910 110 25
25
1199
22
525 25 5 5 210
2
aaa
a
a
yaxa












Đẳng thức xảy ra khi và chỉ khi
1
2
a
.
Dạng 2: Giải và biện luận hệ phương trình bậc nhất ba ẩn
1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1.
Giải hệ phương trình
23
3
22 2
xyz
xyz
xyz



Lời giải
238
31
22 2 12
xyz x
xyz y
xyz z
 







Vậy nghiệm duy nhất của hệ phương trình là
;; 8;1;12xyz 
Ví dụ 2. Tìm giá trị thực của tham số
m
để hệ phương trình
2340
310
25 0
xy
xy
mx y m



có duy nhất một
nghiệm
Lời giải
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang246
2340 1
310 2 10
25 02.25.2 0
xy x
xy y m
mx y m m m








.
Vậy
10m
.
Ví dụ 3. Cho

;;
x
yz
là nghiệm của hệ phương trình
6
23 1
710 15
mx ny pz
mx ny pz
mx ny pz



biết hệ có nghiệm

;; 1;2;3xyz . Tìm ,,mnp
Lời giải
Hệ phương trình
6
23 1
710 15
mx ny pz
mx ny pz
mx ny pz



có nghiệm

;; 1;2;3xyz
nên ta có
23 6
263 1
14 30 15
mnp
mnp
mn p



1
1
1
m
n
p

Vậy
111 3Smnp
.
3. Bài tập trắc nghiệm
Câu 1. Khi hệ phương trình

21
222
41
xmyz
xmy z
x
myz



có nghiệm
;;
x
yz
với
0
4
3
m
m

, giá trị
2017 2018 2017Tx
y
z
là
A.
2017T 
. B.
2018T
. C.
2017T
. D.
2018T 
.
Hướng dẫn giải
Chọn C.
Kí hiệu


211
2222
413
xmyz
xmy z
xm yz



.
Do
0
4
3
m
m

, từ

1
và
3
ta có
1
0
x
z
y
.
Ta có
2017 2018 2017Txyz
2017
x
z
2017
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang247
Dạng 3: Giải và biện luận hệ phương trình bậc cao
1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1.
Giải hệ phương trình:
2
1
2220
xy
xxy


Lời giải

2
11
2220 2
xy
xxy


Ta có:
11yx
Thế vào phương trình
2 ;ta được :
22
221 20 440 2xx x xx x 
Với
21xy
Hệ có 1 nghiệm :

;2;1xy 
Ví dụ 2. Giải hệ phương trình:
2
22
2
29
xxy
xxyy


Lời giải
Chọn D
Đặt
ytx
thay vào hệ ta được

2
22
1 2 (1)
2 9 (2)
xt
xtt


.
Do
1t
không thỏa mãn nên suy ra
2
2
5
29
21150
1
12
2
t
tt
tt
t
t


.
+ Với
5t
thay vào ta được
2
42x
.
+ Với
1
2
t
thay vào ta được
2
21
4
21
x
x
x


.
Vậy
00 00
21 3xySxy
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang248
Ví dụ 3. Giải hệ phương trình
22
3
1
xxyy
xxyy
ì
ï
++=
ï
í
ï
++=-
ï
î
Lời giải
Hệ phương trình
(
)
(
)
2
3
1
xy xy
xy xy
ì
ï
+-=
ï
ï
í
ï
++=-
ï
ï
î
.
Đặt
,.SxyPxy=+ =
()
2
4SP³
Ta được hệ mới
2
2
2
2
3
3
3
1
1
20
2
PS
PS
SP
S
SP
SS
S
ì
ï
=-
ï
ì
ì
ï
=-
ï
ï
-=
ïï ï
é

=
íí í
ïï ï
ê
+=-
+-=
ïï ï
î
î
ê
ï
=-
ë
ï
î
Với
12SP= =-
Với
21SP=- =
2
.1
xy
xy
ì
+=-
ï
ï
í
ï
=
ï
î
2
2
1
1
210
xy
y
x
xx
ì
ì
=- -
=-
ï
ï
ïï

íí
ïï
=-
++=
ï
î
ï
î
.
Vậy hệ phương trình có nghiệm
()( )
;1;1xy=- - .
Ví dụ 4. Các nghiệm của hệ
22
3216
24 33
xy x y
xy xy


là
Hướng dẫn giải
Ta có:

22
3216
1
24 33
xy x y
xy xy



22
221221
21 4 438
xy x y x y
xx yy




22
12 1 221
2
1238
xy x y
xy


Đặt
1ux
;
2vy
ta được hệ phương phương
22
21
38
uv u v
uv



2
21
238
uv u v
uv uv


Đặt
Suv
;
P
uv
ta được hệ phương phương
2
21
238
PS
SP

2
21
2800
PS
SS


8
13
S
P

v
10
31
S
P
.
+ Khi
8
13
S
P

thì
u
;
v
là nghiệm của phương trình:
2
8130XX

43
43
u
v


v
43
43
u
v


Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang249
143
243
x
y


v
143
243
x
y


33
23
x
y


v
33
v
23
x
y


.
+ Khi
10
31
S
P
thì
u
;
v
là nghiệm của phương trình:
2
10 31 0XX

Ví dụ 5. Giải hệ phương trình
22
2
283129
4186 72310
xxyxy y
xy x xy


Hướng dẫn giải
Điều kiện

7
*
1
3
x
y



22
2
283129 1
4186 723102
xxyxy y
xy x xy


.
Có:
22
12431290xyxyy
, ta coi
1
là phương trình bậc hai ẩn
x
và
y
là tham số, giải
x
theo
y
ta được
39
1
xy
xy


,
Với
39
xy

thì

39 7
*
1
3
x
y


2
3
1
3
y
y

.
Với
1
x
y
thì

2
2467232140xx x xx 
22
32 73 0xx x

32
73
xx
x


2x
1
y

.
3. Bài tập trắc nghiệm
Câu 1. Hệ phương trình
22
22
7
3
xyxy
xyxy


có tất cả các nghiệm là
A.

;1;2;xy

;2;1;xy 
;1;2;xy 
;2;1xy
.
B.

;1;2;xy
;2;1xy

.
C.
;1;2;xy

;2;1xy
.
D.

;1;2;xy
;2;1xy

;
;1;2;xy
;2;1xy
.
Hướng dẫn giải
Chọn D.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang250
22
22
7
3
xyxy
xyxy


22
5
2
xy
xy


2
25
2
xy xy
xy


2
93
2
xy xy
xy

Với
3
2
xy
xy

thì

;1;2;xy
;2;1xy
.
Với
3
2
xy
xy

thì

;1;2;xy
;2;1xy

.
Câu 2. Hệ phương trình
2
2
3
3
x
xy
yyx


có bao nhiêu nghiệm?
A.
3
. B.
2
. C.
1
. D.
4
.
Hướng dẫn giải
Chọn B.

2
2
3 1
3 2
xxy
yyx


.
Lấy
1
trừ
2
theo vế ta được:
22
44
x
yxy
40xyxy
4
yx
yx
.
TH1:
2
3
x
xy
yx

2
20xx
yx
0
2
xy
xy
.
TH2:
2
3
4
x
xy
yx


2
440
4
xx
yx


2xy

.
Vậy hệ có hai nghiệm.
Câu 3. Hệ phương trình

2
22 2 2
254 644 0
1
23
2


xy x y x xyy
xy
xy
có một nghiệm

00
;
x
y
. Khi đó
2
00
Px
y
có giá trị là
A.
1
. B.
17
16
. C.
3
. D.
2
.
Hướng dẫn giải
Chọn A.
Ta có



2
22 2 2
254 644 01
1
232
2
 

xy x y x xyy
xy
xy
.
22
181220 0 xyxy
23 0
xy x y
23
xy
xy
.
Với
xy
ta có

1
23 3x
x
2
3310
xx
: phương trình vô nghiệm.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang251
Với
23
xy
ta có

1
24 3
2
 y
y
2
8610
yy
1
2
1
4
y
y
.
Với
1
2
y
3
4
x
1P .
Với
1
4
y
3
8
x
7
16
P
.
Câu 4. Cho hệ phương trình
222
2
42
xy
x
yxy m m


. Tìm tất cả các giá trị của
m
để hệ trên có
nghiệm.
A.
1
;1
2



. B.
1;
. C.
0; 2
. D.
1
;
2



.
Hướng dẫn giải
Chọn A.
222
2
42
xy
x
yxy m m



2
2
42
xy
x
yx y m m


2
2
242
xy
x
ym m



2
2
2. 2 4 2 (*)
xy
yy m m



*
22
244 20yymm
Hệ phương trình có nghiệm
(*)
có nghiệm
'0

2
42.4 2 0mm

2
8440mm
1
1
2
m

.
Câu 5. Hệ phương trình
2
22
3
4


xxy
yxym
có nghiệm khi
A.
1
1

m
m
. B. 1m . C. 1
m . D. 1m .
Hướng dẫn giải
Chọn A.
2
22
3
4


xxy
yxym
22 2
21 xy xym

2
2
1 xy m .
Phương trình này có nghiệm khi
2
10
m
1
1
m
m
.
Câu 6: Gọi
(;)
x
y
là nghiệm dương của hệ phương trình
22
4
128
xy xy
xy


. Tổng
x
y
bằng.
A.
12
. B.
8
. C.
16
. D.
0
.
Lời giải
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang252
Chọn C
ĐK:
0
x
y
Ta có :
22
2
8
48
16 64
x
xy xy x y x
yx
  
Thay
2
16 64yx
vào PT
22
128xy
ta được PT:
2
8
16 192 0
24
x
xx
x


.
Suy ra PT có nghiệm
8
8
x
y
. Vậy
16
x
y
Câu 7. Hệ phương trình
3
3
2019
2019
x
yx
yxy


có số nghiệm là:
A.
4
. B.
6
. C.
1
. D.
3
.
Lời giải
Chọn D
Trừ hai phương trình theo vế ta được:
33
2019 2019
x
yy xxy

22
2018 0xyx xyy

2
2
13
2018 0
24
xy x y y








x
y
vì biểu thức
2
2
13
2018 0, ,
24
x
yyxy




.
Với
y
x
ta được:
3
2020 0xx
2
2020 0xx

00
2020 2020
2020 2020
xy
xy
xy


 
.
Vậy hệ đã cho có
3
nghiệm.
Câu 8. Giả sử
;
x
y
là nghiệm của hệ
3
114
xy xy
xy


Tính
2
x
y
A. 2 . B.
3
. C. 1. D. 2
.
Lời giải
Chọn B
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang253
. Điều kiện:
0
1
1
xy
x
y


.
33
114 2 114
xy xy xy xy
x y xy xyxy

 


 


.
Đặt

2, 0
axy
ab
bxy


ta được hệ phương trình:
2
3
2114
ab
aab





2
2
2
2
2
2
14 0
23114251014
451014
14
14
6
63.
381560
26
3
a
a
aaa aa a
aa a
a
a
a
ab
aa
a


 





6
66
39
3
xy
axy
bxy
xy







.
x
, y
là nghiệm của phương trình:
2
3
690 3
3
x
XX X
y

.
Vậy
23xy
.
Câu 9: Tìm
a
để biểu thức
2( )
F
x
y
x
y

đạt giá trị nhỏ nhất, biết
(; )
xy
là nghiệm của hệ
phương trình
22 2
.
6
xya
xy
a


A.
0a
. B.
3a
. C.
1a
. D.
2a 
.
Lời giải
Chọn C
Ta có:

2
22 2 2
2
63
26
xya
x
ya xya
xy a xya
xy xy a

 






Điều kiện tồn tại
,
x
y
:

2
22 2
443422.xy xy a a a a
Khi đó:

2
2
23 1 4 4Fa a a
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang254
min 4 1( / )
F
atm
Do đó chọn đáp án C
Câu 10. Gọi
11 2 2
;;;
x
yxy là hai nghiệm phân biệt của hệ phương trình
22
8
3( ) 1
xyxyxy
xy x y


. Tính
12
x
x
.
A. 3. B. 2. C. 1. D. 0.
Lời giải
Chọn A
Ta có

2
22
8
38
3( ) 1
3( ) 1
xyxyxy
xy xyxy
xy x y
xy x y





Đặt
2
;4
xyS
SP
xy P

, hệ đã cho trở thành

2
22
1
()
2
31 3 8
38 10110
31 13
11
13
()
34
S
N
P
SS S
SSP S S
SP P S
S
PS
L
P












Với
1; 2SP
ta có
;
x
y
là nghiệm của phương trình
2
1
20
2
t
tt
t


Vậy hệ phương trình có nghiệm
12
1; 2 ; 2; 1 1 ( 2) 2 1 3xx

, chọn A.
Câu 11. Tìm giá trị nguyên dương nhỏ nhất của tham số m để hệ
3
3
2
2
x
yxm
yxym


có nghiệm duy
nhất.
A.
m2
. B.
m3
. C.
m4
. D.
m1
.
Lời giải
Chọn B
Trừ vế với vế của hai phương trình ta được:
33
xyyx xy

.
Thay y bởi x vào một trong hai phương trình của hệ ta được:
3
mx 3x
.
Xét hàm số

3
fx x 3x
trên R, ta có
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang255
 
2
x1
f' x 3x 3,f' x 0
x1

.
Bảng biến thiên
2
- 2
-
+
+0
+
f(x)
-
+
0
1-1
-
f'(x)
x
Từ bảng biến thiên suy ra: Phương trình có đúng một nghiệm
m;22;

.
Chọn B.
Câu 12. Cho hệ phương trình
43 2 2
4222 2
6 ( ) ( 12) 6
5(1).11 5
xxxyy x
xx y x


. Biết hệ có 2 nghiệm
là:
11 2 2
(x ;y ) ,(x ;y ).
Đặt S =
12
yy
. Khi đó S bằng:
A.
0 B. 1 C. 2 D. 3
Lời giải
Chọn D
Ta có
22 2
43 2 2
4222 2
222222
6( 1) ( 1)
6( )(12) 6
5(1).11 5
5( 1) ( 1)
x
x
yy
xx
xxxyy x
xx y x
xy
xx






Dễ thấy
0x
hoặc
0y
đều không là nghiệm của hệ phương trình.
Với
0; 0xy
ta có: Hệ
22 2
22
22 22
22 2 2
6( 1) 1 1
5( 1) ( 1) 1
xx
xy x y
xx
x
yxy




Đặt
2
11
;
x
uv
x
y

.
Khi đó hệ trở thành:
22 22 22
22 2 2 22 2 22 44
66 6
55()25362
uv u v uv u v uv u v
uv u v uv u v uv uv uv uv

  






Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang256


22
22
22
33
0; ,
3
6
6
2
2136 920
1
536 2
2
uv
uv u v
uv
uv u v
uv u v uv
uv u v
uv










Giải hệ được

11
;1;;;1
22
uv






. Khi đó
12
2; 1yy
S =
12
3.Syy
Câu 13. Tìm các giá trị của m để hệ phương trình sau có nghiệm:
222
2
42


xy
x
yxy m m
có
nghiệm:
A.
1
1;
2



. B.
1
;1
2
. C.
1
0;
2
. D.
1; 
Lời giải
Chọn B
222
2
42


xy
x
yxy m m
2
2
2

xy
x
ymm
Hệ có nghiệm khi và chỉ khi

22
1
442 2 10 1
2
mm mm m
Câu 14. Cho hệ phương trình
332 2
22
0(1)
29214(2)
xyxyxyxy
xy yx x

 
. Gọi nghiệm dương
của hệ phương trình là
;
ac
bd



trong đó
;
ac
bd
là các phân số tối giản. Khi đó biểu thức

2018 2019
Pab cd
bằng
A.
0
. B.
2
. C.
1
. D.
1
.
Lời giải
Chọn B
Điều kiện xác định:
2
290xy;
2
210yx
 .
Ta có
22
(1) ( )( ) ( ) 0xyx xyy xyxy xy 
22
()( 1)0xyx y
xy

.
Thế
x
y
vào
(2)
ta được
22
29214xx xx x

(3)
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang257
Đặt
2
29
x
xu;
2
21
x
xv
 thì 4uvx
 .
Mặt khác
22
2( 4) 2(u v)uv x

.
Suy ra
0
()( 2)0
2
uv
uvuv
uv

Với
0uv. Suy ra
40 4 (3)xx
vô nghiệm.
Với
2uv
ta có
4
26
2
uvx
ux
uv



Khi đó ta được phương trình
2
22 9 6
x
xx

22
4(2 9) ( 6)xx x
2
0
780 (78)0
8
7
x
xx xx
x

.
Với
00xy
;
88
77
xy
.
Vậy hệ phương trình đã cho có 2 nghiệm là

88
;0;0,;
77
xy




.
Do đó
8; 7; 8; 7 2abcd P
Dạng 4: Các bài toán thực tế phương trình, hệ phương trình
1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1.
Hiện nay tuổi của mẹ gấp 7 lần tuổi con. Sau 2 năm nữa tuổi của mẹ gấp 5 lần tuổi con.
Hỏi mẹ sinh con lúc đó mẹ bao nhiêu tuổi ?
Lời giải
Gọi
*xx
là tuổi mẹ hiện nay,
*yy
là tuổi con hiện nay.
Theo đề bài ta có:

7
25 2
xy
xy

70 28
58 4
xy x
xy y






.
Vậy mẹ sinh con năm
28 4 24
tuổi.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang258
Ví dụ 2: Một khách hàng vào cửa hàng bách hóa mua một đồng hồ treo tường, một đôi giày và
một máy tính bỏ túi. Đồng hồ và đôi giày giá
420.000 đ; máy tính bỏ túi và đồng hồ giá
570.000đ; máy tính bỏ túi và đôi giày giá 750.000 đ. Hỏi mỗi thứ giá bao nhiêu?
Lời giải
Gọi giá của đồng hồ, máy tính bỏ túi và đôi giá lần lượt là
,,
x
yz
.
Khi đó ta có hệ phương trình
420.000
570.000
750.000
xz
xy
yz



. Giải hệ này ta được
120.000
450.000
300.000
x
y
z
Ví dụ 3: Cho hai người Avà
B
xuất phát cùng một lúc ngược chiều từ thành phố M và N. Khi họ
gặp nhau, người ta nhận thấy A đã đi nhiều hơn B là 6km. Nếu mỗi người tiếp tục đi theo
hướng cũ với cùng vận tốc ban đầu thì
A
sẽ đến N sau 4,5 giờ, còn B đến M sau 8 giờ
tính từ thời điểm họ gặp nhau. Gọi ,
A
B
vvlần lượt là vận tốc của người A và người
B
.
Tìm vận tốc của mỗi người
Lời giải
Gọi P là điểm mà hai người A và B gặp nhau. Gọi đoạn
M
Px
là quãng đường A đi
được,
NP
y
là quảng đường B đi được.
Khi họ gặp nhau, người ta nhận thấy A đã đi nhiều hơn B 6km có nghĩa là đoạn MP dài
hơn NP là 6km và thời gian đi của hai người cho đến lúc gặp nhau là bằng nhau. Ta có hệ
6
(1)
AB
xy
xy
vv

Nếu mỗi người tiếp tục đi theo hướng cũ với cùng vận tốc ban đầu thì A sẽ đến N sau 4,5
giờ,
còn B đến M sau 8 giờ tính từ thời điểm họ gặp nhau nên ta có hệ:
4,5
4,5
8
8
A
A
B
B
y
vyv
xxv
v

Thế vào ta có hệ :
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang259
84,56
84,56
3
84,5
4
84,5
BA
BA
B
BA
A
BA
SB
vv
vv
v
vv
v
vv
vv





3. Bài tập trắc nghiệm
Câu 1.
Hai bạn Vân và Lan đi mua trái cây. Vân mua
10
quả quýt,
7
quả cam với giá tiền là
17800
. Lan mua
12
quả quýt,
6
quả cam hết
18000
. Hỏi giá tiền mỗi quả quýt, quả cam
là bao nhiêu?
A. Quýt
1400
, cam
800
. B. Quýt
700
, cam
200
.
C. Quýt
800
, cam
1400
. D. Quýt
600
, cam
800
.
Hướng dẫn giải
Chọn C.
Cách 1: Gọi số tiền để mua một quả quýt là
x
đồng ; số tiền để mua một quả cam là
y
đồng.
Theo bài ra ta có hệ phương trình:
10 7 17 800
12 6 18 000
xy
xy


800
1400
x
y
.
Vậy giá tiền mỗi quả quýt là
800
đồng, mỗi quả cam là
1400
đồng.
Cách 2: Thử các đáp án,
Chọn C.
Câu 2. Một xe hơi khởi hành từ Krông Năng đi đến Nha Trang cách nhau
175
km. Khi về xe
tăng vận tốc trung bình hơn vận tốc trung bình lúc đi là
20
km/giờ. Biết rằng thời gian
dùng để đi và về là
6
giờ; vận tốc trung bình lúc đi là
A.
60
km/giờ. B.
45
km/giờ. C.
55
km/giờ. D.
50
km/giờ.
Hướng dẫn giải
Chọn D.
Gọi
x
,
y
0 lần lượt là vận tốc trung bình lúc đi và vận tốc trung bình lúc về.
Theo đề bài ta có hệ phương trình:

20 1
20
175 175
175 175
6
62
yx
yx
xy
xy







.
Thế

1
vào
2
ta được
2
50
175 175
6 6 230 3500 0 50
35
20
3
x
xx x
xx
x


vì
0x
.
Vậy vận tốc lúc đi là
50
km/giờ.
Câu 3. Một đoàn xe tải chở
290
tấn xi măng cho một công trình xây đập thủy điện. Đoàn xe có 57
chiếc gồm ba loại, xe chở
3
tấn, xe chở 5 tấn và xe chở
7,5
tấn. Nếu dùng tất cả xe
7,5
tấn chở ba
chuyến thì được số xi măng bằng tổng số xi măng do xe
5 tấn chở ba chuyến và xe
3
tấn chở hai
chuyến. Hỏi số xe mỗi loại?
A.
18
xe chở
3
tấn,
19
xe chở 5 tấn và
20
xe chở
7,5
tấn.
B.
20
xe chở
3
tấn,
19
xe chở
5
tấn và
18
xe chở
7,5
tấn.
C.
19
xe chở
3
tấn,
20
xe chở
5
tấn và
18
xe chở
7,5
tấn.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang260
D.
20
xe chở
3
tấn,
18
xe chở 5 tấn và
19
xe chở
7,5
tấn.
Lời giải
Chọn B
Gọi
x
là số xe tải chở 3 tấn, y là số xe tải chở 5 tấn và z là số xe tải chở 7,5 tấn.
Điều kiện:
, ,
x
yz nguyên dương.
Theo giả thiết của bài toán ta có
57
3 5 7,5 290.
22,5 6 15
xyz
xy z
zx y
ì
++=
ï
ï
ï
ï
++ =
í
ï
ï
ï
=+
ï
î
Giải hệ ta được
20, 19, 18.xyz===
Câu 4:
Có ba lớp học sinh 10 , 10 , 10ABC gồm
128
em cùng tham gia lao động trồng cây. Mỗi em
lớp
10
A
trồng được
3
cây bạch đàn và
4
cây bàng. Mỗi em lớp
10B
trồng được
2
cây bạch đàn và
5
cây bàng. Mỗi em lớp
10C
trồng được
6
cây bạch đàn. Cả ba lớp trồng được là
476
cây bạch đàn
và
375
cây bàng. Hỏi mỗi lớp có bao nhiêu học sinh?
A.
10
A
có
40
em, lớp
10B
có
43
em, lớp
10C
có
45
em.
B.
10
A
có
45
em, lớp
10B
có
43
em, lớp
10C
có
40
em.
C.
10
A
có
45
em, lớp
10B
có
40
em, lớp
10C
có
43
em.
D.
10
A
có
43
em, lớp
10B
có
40
em, lớp
10C
có
45
em.
Lời giải
Chọn A
Gọi số học sinh của lớp 10 , 10 , 10
A
BC lần lượt là , , .
x
yz
Điều kiện:
, ,
x
yz nguyên dương.
Theo đề bài, ta lập được hệ phương trình
128
3 2 6 476.
45375
xyz
xyz
xy
ì
++=
ï
ï
ï
ï
++=
í
ï
ï
ï
+=
ï
î
Giải hệ ta được
40, 43, 45.xyz===
| 1/78
| | Tải xuống

Có thể bạn quan tâm:

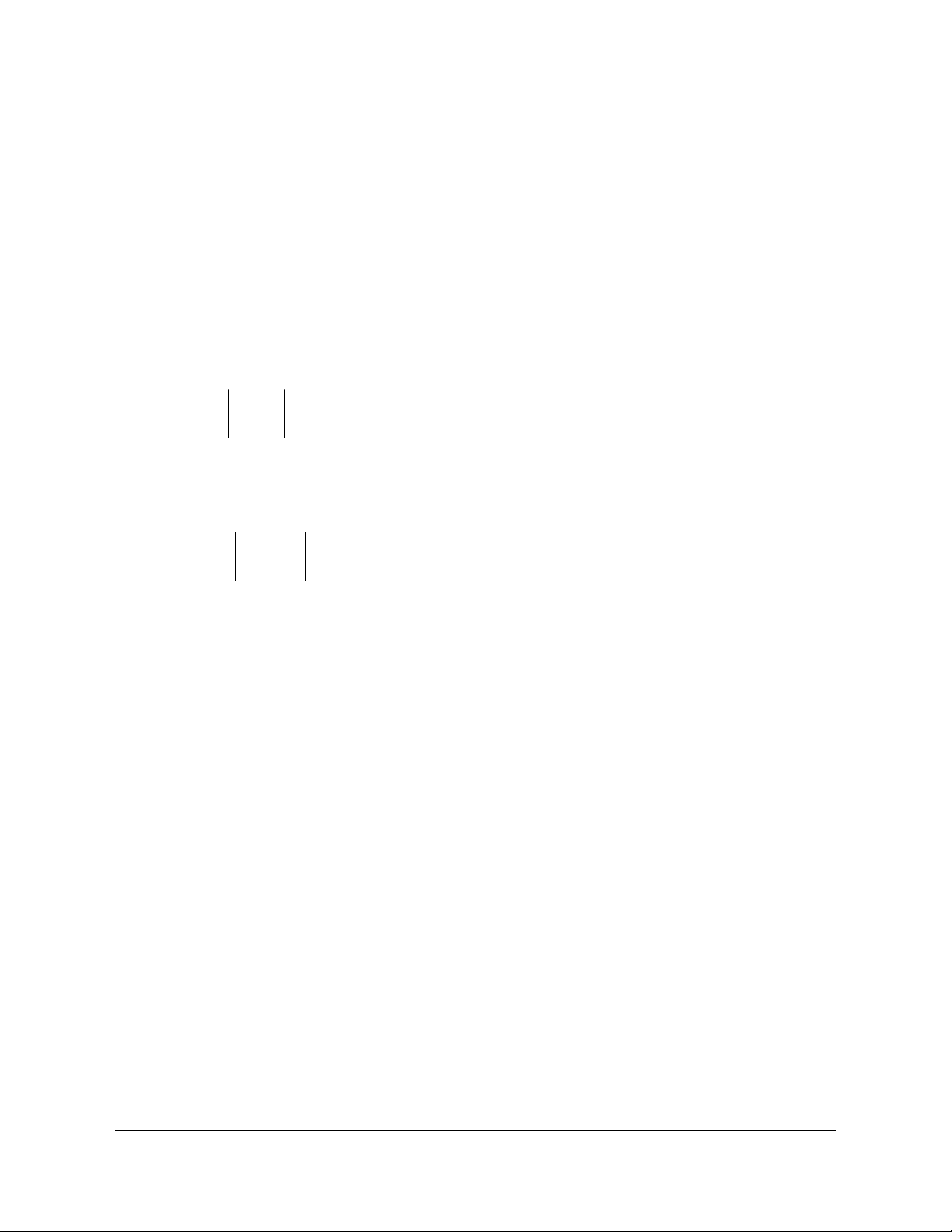
Preview text:

BÀI 1. ĐẠI CƯƠNG VỀ PHƯƠNG TRÌNH
A. KIẾN THỨC CƠ BẢN CẦN NẮM
I – KHÁI NIỆM PHƯƠNG TRÌNH
1. Phương trình một ẩn
Phương trình ẩn x là mệnh đề chứa biến có dạng
f x  g x   1
trong đó f x và g x là những biểu thức của .
x Ta gọi f x là vế trái, g x là vế phải của phương trình   1 . Nếu có số thực  là mệnh đề đúng thì 0
x sao cho f  0 x g  0 x  0
x được gọi là một nghiệm của phương trình   1 . Giải phương trình ( )
1 là tìm tất cả các nghiệm của nó .
Nếu phương trình không có nghiệm nào cả thì ta nói phương trình vô nghiệm .
2. Điều kiện của một phương trình
Khi giải phương trình  
1 , ta cần lưu ý với điều kiện đối với ẩn số x để f x và g x có nghĩa .
Ta cũng nói đó là điều kiện xác định của phương trình .
3. Phương trình nhiều ẩn
Ngoài các phương trình một ẩn, ta còn gặp những phương trình có nhiều ẩn số, chẳng hạn 2
3x  2y x  2xy  8, 2 2 2 2
4x xy  2z  3z  2xz y . 3
Phương trình 2 là phương trình hai ẩn ( x và y ), còn 3 là phương trình ba ẩn ( x,y và z ).
Khi x  2, y  1 thì hai vế của phương trình 2 có giá trị bằng nhau, ta nói cặp  ; x y   2;  1 là
một nghiệm của phương trình 2.
Tương tự, bộ ba số  ;
x y; z    1
 ;1;2 là một nghiệm của phương trình 3.
4. Phương trình chứa tham số
Trong một phương trình , ngoài các chữ đóng vai trò ẩn số còn có thể có các chữ khác được xem
như những hằng số và được gọi là tham số.
II – PHƯƠNG TRÌNH TƯƠNG ĐƯƠNG VÀ PHƯƠNG TRÌNH HỆ QUẢ
1. Phương trình tương đương
Hai phương trình được gọi là tương đương khi chúng có cùng tập nghiệm.
2. Phép biến đổi tương đương Định lí
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 183
Trần Đình Cư. SĐT: 0834332133
Nếu thực hiện các phép biển đổi sau đây trên một phương trình mà không làm thay đổi điều kiện
của nó thì ta được một phương trình mới tương đương
a) Cộng hay trừ hai vế với cùng một số hoặc cùng một biểu thức;
b) Nhân hoặc chia hai vế với cùng một số khác 0 hoặc với cùng một biểu thức luôn có giá trị khác 0.
Chú ý: Chuyển vế và đổi dấu một biểu thức thực chất là thực hiện phép cộng hay trừ hai vế với biểu thức đó.
3. Phương trình hệ quả
Nếu mọi nghiệm của phương trình f x  g x đều là nghiệm của phương trình  thì 1 f x 1 g x phương trình 
được gọi là phương trình hệ quả của phương trình f x  g x. 1 f x 1 g x Ta viết
f x  g x  f x g x . 1   1  
Phương trình hệ quả có thể có thêm nghiệm không phải là nghiệm của phương trình ban đầu. Ta gọi
đó là nghiệm ngoại lai.
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Điều kiện xác định của phương trình 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng 2x 3
Ví dụ 1. Tìm điều kiện xác định của phương trình  5  2 2 x 1 x 1 Lời giải Chọn D Do 2 x 1  0, x
   nên điều kiện xác định của phương trình là D   .
Ví dụ 2. Tìm điều kiện xác định của phương trình x 1  x  2  x  3 Lời giải x 1  0 x 1  
Điều kiện xác định của phương trình là: x  2  0  x  2  x  3.   x  3  0 x  3   6
Ví dụ 3. Tìm điều kiện xác định của phương trình x  2   4 x  3 Lời giải x  2  0 x  2
Điều kiện xác định của phương trình:    x  3  0 x  3
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 184
Trần Đình Cư. SĐT: 0834332133 1
Ví dụ 4. Cho phương trình 3 x 1  x 1 
. Tìm điều kiện xác định của phương trình 2 x  4 đã cho. Lời giải 3 x 1  0 
Điều kiện xác định của phương trình x 1  0  x  2.  2 x  4  0 
3. Bài tập trắc nghiệm x 1 Câu 1.
Tìm tập xác định của phương trình 5
 3x  2017  0 . x A.  1  ;. B.  1  ; \  0 . C.  1  ; \  0 . D.  1  ;. Hướng dẫn giải Chọn C. x 1 0 x  1  Điều kiện    . x  0 x  0
Tập xác định của phương trình là  1  ; \  0 . 1 3  2 Câu 2.
Điều kiện xác định của phương trình x x   là 2x  4 x 3 3
A. x  2 và x  . B. 2   x  . 2 2  3  2   x
C. x  2 và x  0 . D.  2 . x  0 Hướng dẫn giải Chọn C.  3  3   2 x x  0  2  3   2  x
Điều kiện xác định của phương trình là 2x  4  0  x  2    2    x  0  x  0 x  0   1 Câu 3. Cho phương trình 2 x 1 
. Tập giá trị của x để phương trình xác định là x 1 A. 1; . B.  . C. 1;) . D.  \   1 . Hướng dẫn giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 185
Trần Đình Cư. SĐT: 0834332133 Chọn A. 1 2 x 1 
xác định  x 1  0  x  1. x 1
Câu 4: Điều kiện xác định của phương trình x  2  8  x là
A. x 2;  8  . B. x  8 . C. x  2 . D. x  8 . Lời giải Chọn C
ĐK: x  2  0  x  2 Câu 5.
Giá trị x  2 là điều kiện của phương trình nào sau đây? 1 1 A. x   2x 1.
B. x   x  2  0 . x  2 x 1 1 C. x   x  2 . D. x   0 . 4  x x  2 Hướng dẫn giải Chọn B. 1 Phương trình x
 2x 1 có điều kiện là x  2  0  x  2 . x  2 1 x  2  0
Phương trình x   x  2  0 có điều kiện là   x  2. xx  0 1 x  2  0 x  2 Phương trình x
x  2 có điều kiện là    . 4  x 4  x  0 x  4 1 Phương trình x
 0 có điều kiện là x  2  0  x  2 . x  2 x  2 3 Câu 6.
Điều kiện xác định của phương trình  là 2 x  2x 5  x
A. x   \0;  2 . B. x  2;  5 \  0 . C.  2;  5\0;  2 . D.  ;5   \0;  2 . Hướng dẫn giải Chọn B.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 186
Trần Đình Cư. SĐT: 0834332133 x  2 3 Phương trình  có nghĩa khi 2 x  2x 5  xx  2  0 x  2    2
x  2x  0  x  0; x  2   x  2;  5 \  0 . 5    x  0 x  5   x  4 2 Câu 7.
Điều kiện xác định của phương trình  là 2 x 1 3  x A. x  4;    . B. x  4;  3 \ 
1 . C. x  ;3  .
D. x  \  1 . Hướng dẫn giải Chọn B.x  4  0 x  4     4   x  3
Phương trình đã cho xác định khi 2
x 1  0  x  1    .   x  1  3  x  0 x  3   2 x 1 Câu 8.
Tập xác định của phương trình 3 x   x  2 là x 1
A. D  2;  .
B. D  0;  \  1 .
C. D  0;  .
D. D  0;  \1;  2 . Hướng dẫn giải Chọn B. Điều kiện xác định: x  0 x  0   
. Vậy đáp án D  0;  \  1 . x 1  0 x  1 x + 5 Câu 9.
Điều kiện xác định của phương trình =1 là x - 2 x ìï > 5 - ìïx 5 ³- A. ï ï x ³ -5. B. í . C. í . D. x > 2. x ï ¹ 2 ïî ïx ¹ 2 ïî Lời giải Chọn C ìïx +5 ³ 0 ìïx ³ 5 -
Phương trình xác định khi và chỉ khi ï ï í  í . ïx-2 ¹ 0 ïx ¹ 2 ïî ïî
Câu 10. Điều kiện xác định của phương trình x  2x 1  1 x là
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 187
Trần Đình Cư. SĐT: 0834332133 1 1 1
A.   x  1.
B.   x  1. C. x   . D. x  1. 2 2 2 Lời giải Chọn B  1 2x 1 0 x   1
Điều kiện xác định của phương trình là    2    x  1. 1   x  0  2 x 1 2 x  5
Câu 11. Điều kiện xác định của phương trình x  2   0 ? 7  x
A. 2;7. B. 2; . C. 2;7. D. 7; . Lời giải Chọn Ax  2  0 x  2
Điều kiện xác định của phương trình đã cho là:     2  x  7 . 7  x  0 x  7 x  4 2
Câu 12. Điều kiện xác định của phương trình  là: 2 x 1 3 x A. x  4;    . B. x  4;  3 \ 
1 . C. x  ;3  .
D. x   \   1 . Lời giải: Chọn B x  4  0 x  4     4   x  3
Phương trình đã cho xác định khi 2
x 1  0  x  1    .   x  1  3  x  0 x  3  
Dạng 2: Sử dụng điêu kiện xác định của phương trình để tìm gghiệm của phương trình 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1 : Giải phương trình x ( 2 x - ) 1
x -1 = 0 có bao nhiêu nghiệm? Lời giải ìïx-1³ 0 éx ³1 ï ê Vì : ïï x( 2 x - ) 1 x -1 = 0  é í x = 0 ê
 éx = 0  x = 1 ïê êê ïê 2 ê ï x -1= 0 ê ïîë ê x = 1 ëë
Ví dụ 2 : Giải phương trình 2x + x -2 = 2- x + 2 Lời giải x  2  0 x  2
Vì : Điều kiện của pt   
x  2 . Thay x = 2 vào phương trình thấy 2  x  0 x  2
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 188
Trần Đình Cư. SĐT: 0834332133
thỏa mãn nên x = 2 là nghiệm phương trình.
Ví dụ 3: Giải phương trình 3 2
x - 4 x + 5x - 2 + x = 2 - x Lời giải Vì: 3 2 2
x - 4x + 5x - 2 + x =
2- x  (x - 2)(x -1) + x = 2- x .
ìïéx-2 ³ 0ìïéx ³ 2 2 ì ï ï - - ³ ê ïê ï ï é =
Điều kiện của phương trình: (x 2)(x 1) 0 x 2 ï ï í  ê ï í x = 1 ê ë í x = 1  ê ï2 ë - x ³ 0 ï ï êx =1 ïî ïï2 ï ë
- x ³ 0 ïx £ 2 ïî ïî
Ví dụ 4: Giải phương trình ( 2
x - 3x + 2) x -3 = 0 Lời giải ìïx ³ 3 ìïx-3 ³ 0 ïï ï ï ï é ï ï x =1 Vì : ( 2 ï x -3x + 2) 2 x -3 = 0  é
í x -3x + 2 = 0  ê í  x = 3 ïê ïêx = 2 ïê ïê ï x-3 = 0 ï ïîë ïê ï x = 3 ïîë é = + Thay x 2 ê
vào phương trình thì thấy chỉ có x = 1 thỏa mãn. Nên x = 1 là nghiệm pt êx =1 ë
3. Bài tập trắc nghiệm Câu 1. Cặp số  ;
x y nào sau đây không là nghiệm của phương trình 2x  3y  5?   A. x y 5 ;  ; 0   . B.  ;
x y  1;   1 .  2    C. x y 5 ;  0;   . D.  ; x y   2  ;  3 .  3  Hướng dẫn giải Chọn C. Thay các bộ số  ;
x y vào phương trình, ta thấy bộ số đáp án C không thỏa mãn: 5 2.0  3.  5   5 . 3 1 1 Câu 2.
Số nghiệm của phương trình 2 2x   x  là x 1 x 1 A. 0 . B. 1. C. 2 . D. 3. Hướng dẫn giải
Chọn B. x  0
Điều kiện: x  1 . Khi đó phương trình đã cho 2
 2x  x     . x    Lx 0 2
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 189
Trần Đình Cư. SĐT: 0834332133 x 1 Câu 3.
Số nghiệm của phương trình  là: 2 x  3 x  3 A. 2 . B. 0 . C. 1. D. 3. Hướng dẫn giải
Chọn B. Đkxđ: x  3 Với điều kiện x
x  3 phương trình đã cho trở thành
 1  x  2  3 2
Vậy phương trình không có nghiệm. Câu 4.
Tập nghiệm của phương trình x x x 1 là A. S   .
B. S   . C. S    0 . D. S    1 . Lời giải Chọn B
Điều kiện: x  0 . x x
x 1  x  1  .
Vây tập nghiệm của phương trình đã cho là S   .
Câu 5. Phương trình nào sau đây nhận 2 làm nghiệm ? A. 4 2
x  4 x  3  0. B. 2
x  4 x  3  0.
C. 1 x x  1 x  2 . D. 4 2
x  5x  4  0. Lời giải Chọn D 2  x 1  x  1  - Xét PT: 4 2
x  4 x  3  0     2 x  3 x   3
Vậy x  2 không phải nghiệm của PT đã cho.  x 1 - Xét PT: 2
x  4 x  3  0   x  3
Vậy x  2 không phải nghiệm của PT đã cho.
- Xét PT: 1 x x  1 x  2 .
Điều kiện 1 x  0  x 1
Vậy x  2 không phải nghiệm của PT đã cho.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 190
Trần Đình Cư. SĐT: 0834332133 2  x  1  x  1  - Xét PT: 4 2
x  5x  4  0     2 x  4 x  2 
Vậy x  2 là nghiệm của PT đã cho.
Câu 6. Phương trình x ( 2 x - ) 1
x -1 = 0 có bao nhiêu nghiệm? A. 0. B. 1. C. 2. D. 3. Lời giải Chọn B ìïx-1³ 0 éx ³1 ï ê ï Vì : ï x( 2 x - ) 1 x -1 = 0  é í x = 0 ê
 éx = 0  x = 1 ïê êê ïê 2 ê ï x -1= 0 ê ïîë ê x = 1 ëë
Câu 7. Phương trình 2 3
-x + 6x - 9 + x = 27 có bao nhiêu nghiệm? A. 0. B. 1. C. 2. D. 3. Lời giải Chọn B Vì 2 3 2 3
-x + 6x -9 + x = 27  (
- x -3) = 27- x Đk : 2 (
- x -3) ³ 0  x = 3 . Thay x = 3 vào phương trình thấy thỏa mãn nên x = 3 là nghiệm pt
Câu 8. Phương trình (x - )2
3 (5-3x) + 2x = 3x -5 + 4 có bao nhiêu nghiệm? A. 0. B. 1. C. 2. D. 3. Lời giải Chọn B ìïé 5 ï ì ïê £ ïé5-3 ³ 0 x x ïê ì ï ï - - ³ ê ï 3 éx = 3 2 ï ï ï ïê ê
Vì điều kiện của phương trình: : (x 3) (5 3x) 0 í  ê ï í x = 3 ë íêx = 3  ê ë 5 3 ï x-5 ³ 0 ï ï êx = ïî ï ï 3 ï x-5 ³ 0 ï 5 ê ï ë 3 î ïïx ³ ïïî 3 éx = 3 ê + Thay ê
5 vào phương trình thì thấy chỉ có x = 3 thỏa mãn. Nên x = 3 là nghiệm pt êx = êë 3
Câu 9. Phương trình x + x -1 = 1- x có bao nhiêu nghiệm? A. 0. B. 1. C. 2. D. 3. Lời giải Chọn A
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 191
Trần Đình Cư. SĐT: 0834332133 x 1  0 x 1
Vì : Điều kiện của pt :   
x  1. Thay x = 1 vào phương trình thấy vô 1   x  0 x 1 lí nên pt vô nghiệm. é = + Thay x 2 ê
vào phương trình thì thấy chỉ có x = 1 thỏa mãn. Nên x = 1 là nghiệm pt êx =1 ë
Câu 10. Phương trình ( 2
x - x - 2) x +1 = 0 có bao nhiêu nghiệm? A. 0. B. 1. C. 2. D. 3. Lời giải Chọn C ìïx +1³ 0 ìïx ³ -1 ï ï ï ï é = - Vì : ( x 1 2 ï ï x - x - 2) 2 x +1 = 0  é
í x - x - 2 = 0  íéx = -1  ê ïê ïê êx = 2 ïê ï ë ï x +1= 0 ïêx = 2 ïîë ïîë
Dạng 3: Phương trình tương đương, phương trình hệ quả 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Cho phương trình f x  0 có tập nghiệm S  m; 2m 1 và phương trình 1 
g x  0 có tập nghiệm S  1; 2 . Tìm tất cả các giá trị m để phương trình g x  0 là 2  
phương trình hệ quả của phương trình f x  0 . A. m  3 1 .
B. 1  m  2 . C. m. . D. m  3 1 . 2 2 Lời giải Chọn D Gọi
và g x  . 1
S , S lần lượt là tập nghiệm của hai phương trình f x  2 0 0
Ta nói phương trình g x  0 là phương trình hệ quả của phương trình f x  0 khi  . 1 S S2 1  m    m   2 1 2 Khi đó ta có 3   
 1  m  . 1  2m  1  3  2 1  m   2  2
3. Bài tập trắc nghiệm Câu 1.
Trong các phương trình sau, phương trình nào tương đương với phương trình x 1  0 ?
A. x  2  0 .
B. x 1  0 .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 192
Trần Đình Cư. SĐT: 0834332133
C. 2x  2  0 . D. x  
1  x  2  0 . Hướng dẫn giải Chọn C.
Ta có x 1  0  2x  2  0 . Câu 2.
Cho phương trình  2 x   1  x –  1  x  
1  0 . Phương trình nào sau đây tương đương với phương trình đã cho? A. 2 x 1  0 .
B. x 1  0 . C. x  –1  x  
1  0 . D. x 1  0 . Hướng dẫn giải Chọn C.
Hai phương trình tương đương khi chúng có cùng tập nghiệm. Phương trình  2 x   1  x –  1  x  
1  0 có tập nghiệm S   1  ;  1 . Phương trình  x  –1  x  
1  0 có tập nghiệm S   1  ;  1 . Câu 3.
Phương trình 2x  3  1 tương đương với phương trình nào dưới đây?
A.x 3 2x 3  x 3.
B.x  4 2x  3  x  4 .
C. x 2x  3  x .
D. x  3  2x  3  1 x  3 . Hướng dẫn giải Chọn C.
2x  3 1  x  2 .  2 x   3  x  3
Xét  x  3 2x  3  x  3    
nên phương trình này không tương x  3  0   x  2   2x 3 1
đương với phương trình đã cho.  2 x   3  x  4
Xét  x  4 2x 3  x  4    
nên phương trình này không x  4  0   x  2   2x 3 1
tương đương với phương trình đã cho.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 193
Trần Đình Cư. SĐT: 0834332133  2 x   3 
Xét x 2x  3  x  x  0  x  2  2x 3 1  
 phương trình tương đương với phương trình đã cho. x  3 
Xét x  3  2x  3  1 x  3  
x  nên phương trình này không  2x  3 1
tương đương với phương trình đã cho.
Câu 4: Cho phương trình: 2
x x  0 (1) . Phương trình nào tương đương với phương trình (1) ?
A. x x   1  0 .
B. x 1  0 . C. 2 2
x  (x 1)  0 . D. x  0 Lời giải Chọn A x  0 2
(1)  x x  0   x  1  x
Ý A: x x   0 1  0   x 1
Câu 5. Phương trình nào dưới đây tương đương với phương trình 2
x  3x  0 ? A. 2 x
2x 1  3x  2x 1 . B. 2 x
x  3  3x x  3 . 1 1 C. 2 3 3 x
x  3  3x x  3 . D. 2 x x   2x  . x x Lời giải Chọn C Phương trình 2
x  3x  0 có tập nghiệm là S  0; 
3 nên phương trình tương đương
cũng phải có tập nghiệm như vậy. Chọn C Chú ý lý thuyết:
+ Phép biến đổi tương đương cho hai phương trình tương đương
+ Phép biến đổi cộng hai vế một biểu thức hoặc nhân 2 vế với một biểu thức khác 0 là
phép biến đổi tương đương khi chúng không làm thay đổi điều kiện
Do đó dựa và điều kiện của các phương trình ta cũng có thể chọn C Câu 6.
Phép biến đổi nào sau đây là phép biến đổi tương đương? A. 2 2 2 2 x
x  2  x
x  2  x x . B. 2
2  x x  2  x x . C. 2 2
x x  2  x x  2  x x . D. 2 2 2 2 x
x  3  x
x  3  x x .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 194
Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn D * Xét phương án A: 2  2 x  2  0    2 2 2 x 2 0  x
x  2  x x  2    x  0  x  2 x x  x  1   2 x 0
x x  x 1
2 phương trình không có cùng tập nghiệm nên phép biến đổi không tương đương. * Xét phương án B: x  0 x  0  
2  x x    x  2   x 1 2
2  x x  x 1    2 x 2
2  x x  x 1
2 phương trình không có cùng tập nghiệm nên phép biến đổi không tương đương. * Xét phương án C: x  2 x  2  0 2 2   x
x  2  x
x  2  x x  
 x  0  x  2 x x  x  1   2 x 0
x x  x 1
2 phương trình không có cùng tập nghiệm nên phép biến đổi không tương đương. * Xét phương án D: 2      2 2 2 2 x 3 0 x 0 x
x  3  x
x  3  x x     2   x  1 x x   2 x 0
x x  x 1 2
phương trình có cùng tập nghiệm nên phép biến đổi là tương đương.
Câu 7. Tìm giá trị thực của tham số m để cặp phương trình sau tương đương: 2
2x + mx -2 = 0 ( ) 1 và 3 x +(m + ) 2 2 4 x + 2(m - ) 1 x -4 = 0 (2) . A. m = 2. B. m = 3. C. 1 m = . D. m = -2. 2 Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 195
Trần Đình Cư. SĐT: 0834332133 Chọn B Xét phương trình éx = -2 3 x +(m + ) 2 2 4 x + 2(m- ) 1 x -4 = 0 2
 (x + 2)(2 x + mx -2) = 0  êê 2 2 x + mx - 2 = 0(1) ë
để hai phương trình trên tương đương thì x = - 2 phải là nghiệm của phương trình (1) từ đó suy ra m = 3.
Cách khác : có thể thử ngược đáp án.
Câu 8. Tìm tất cả các giá trị thực của tham số m để cặp phương trình sau tương đương: 2 mx - 2(m - )
1 x + m -2 = 0 ( ) 1 và (m - ) 2 2
2 x -3x + m -15 = 0 (2) . A. m = -5. B. m = 5; - 4 m = . C. m = 4. D. m = 5. Lời giải Chọn C é = Vì xét phương trình: x 1 2 mx - 2(m - )
1 x + m - 2 = 0  (x -1)(mx - m + 2) = 0  ê êmx-m + 2 = 0 ë
Để hai phương trình tương đương thì điều kiện cần x = 1 phải là nghiệm của phương trình (2). m  4
Thay x = 1 vào (2) ta được: 2
m m  20  0   m  5  + Với m = 4 : 2
(1)  4x  6x  2  0 2
(2)  2x  3x 1  0 suy ra m = 4 thỏa mãn + Với m = -5: 2 (1)  5
x 12x  7  0 2 (2)  7
x  3x 10  0 suy ra m = -5 (loại)
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 196
Trần Đình Cư. SĐT: 0834332133
BÀI 2. PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC NHẤT VÀ PHƯƠNG TRÌNH BẬC HAI
A. KIẾN THỨC CƠ BẢN CẦN NẮM
I – ÔN TẬP VỀ PHƯƠNG TRÌNH BẬC NHẤT, BẬC HAI
1. Phương trình bậc nhất
Cách giải và biện luận phương trình dạng ax + b = 0 được tóm tắt trong bảng sau ax +b = 0 ( ) 1 Hệ số Kết luận a ¹ 0 ( ) 1 có nghiệm duy nhất b x = - a b ¹ 0 ( ) 1 vô nghiệm a = 0 b = 0 ( )
1 nghiệm đúng với mọi x
Khi a ¹ 0 phương trình ax + b = 0 được gọi là phương trình bậc nhất một ẩn.
2. Phương trình bậc hai
Cách giải và công thức nghiệm của phương trình bậc hai được tóm tắt trong bảng sau 2
ax +bx +c = 0 (a ¹ 0) (2) 2 D = b -4ac Kết luận -b  D D > 0
(2) có hai nghiệm phân biệt x = 1, 2 2a b D = 0
(2) có nghiệm kép x = - 2a D < 0 (2) vô nghiệm
3. Định lí Vi–ét
Nếu phương trình bậc hai 2
ax +bx + c = 0 (a ¹ 0) có hai nghiệm x , x thì 1 2 b c x + x = - , x x = . 1 2 1 2 a a
Ngược lại, nếu hai số u và v có tổng u +v = S và tích uv = P thì u và v là các nghiệm của phương trình 2
x -Sx + P = 0.
II – PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC NHẤT, BẬC HAI
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 197
Trần Đình Cư. SĐT: 0834332133
Có nhiều phương trình khi giải có thể biến đổi về phương trình bậc nhất hoặc bậc hai.
Sau đây ta xét hai trong các dạng phương trình đó.
1. Phương trình chứa ẩn trong dấu giá trị tuyệt đối
Để giải phương trình chứa ẩn trong dấu giá trị tuyệt đối ta có thể dùng định nghĩa của giá trị tuyệt
đối hoặc bình phương hai vế để khử dấu giá trị tuyệt đối.
Ví dụ 1. Giải phương trình x -3 = 2x +1. ( ) 3 Giải Cách 1
a) Nếu x ³ 3 thì phương trình ( )
3 trở thành x - 3 = 2x +1. Từ đó x = -4.
Giá trị x = -4 không thỏa mãn điều kiện x ³ 3 nên bị loại.
b) Nếu x < 3 thì phương trình ( )
3 trở thành -x +3 = 2x +1. Từ đó 2 x = . 3
Giá trị này thỏa mãn điều kiện x < 3 nên là nghiệm.
Kết luận. Vậy nghiệm của phương trình là 2 x = . 3
Cách 2. Bình phương hai vế của phương trình ( )
3 ta đưa tới phương trình hệ quả
(3) (x -3)2 = (2x + )2 1 2 2
x -6x + 9 = 4x + 4x +1 2
 3x +10x -8 = 0.
Phương trình cuối có hai nghiệm là x = -4 và 2 x = . 3
Thử lại ta thấy phương trình ( ) 3 chỉ có nghiệm là 2 x = . 3
2. Phương trình chứa ẩn dưới dấu căn
Để giải các phương trình chứa ẩn dưới dấu căn bậc hai, ta thường bình phương hai vế để đưa về một
phương trình hệ quả không chứa ẩn dưới dấu căn.
Ví dụ 2. Giải phương trình 2x -3 = x -2. (4) Giải.
Điều kiện của phương trình (4) là 3 x ³ . 2
Bình phương hai vế của phương trình (4) ta đưa tới phương trình hệ quả (4) 2
 2x -3 = x - 4x + 4 2
x -6x +7 = 0.
Phương trình cuối có hai nghiệm là x = 3 + 2 và x = 3- 2. Cả hai giá trị này đều thỏa mãn điều
kiện của phương trình (4), nhưng khi thay vào phương trình (4) thì giá trị x = 3- 2 bị loại , còn
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 198
Trần Đình Cư. SĐT: 0834332133
giá trị x = 3 + 2 là nghiệm .
Kết luận. Vậy nghiệm của phương trình (4) là x = 3 + 2.
Dạng 1: Phương trình tích 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Giải phương trình  2
x  4x  3 x  2  0 Hướng dẫn giảix  2   x  1 x  2 2
x  4x  3 x  2  0    . x  3   x  3 x  2 
Vây phương trình đã cho có 2 nghiệm.
Ví dụ 2. Giải phương trình  x   2 2
2x  7  x  4 Hướng dẫn giải
Điều kiện xác định của phương trình 7
2x +7 ³ 0  x ³ - . 2 Ta có (x - ) 2 2
2x +7 = x -4  (x -2) 2x +7 = (x -2)(x + 2) éx -2 = 0 éx = 2
(x 2)é 2x +7 -(x 2)ù 0 ê ê  - + =   . ê ë úû ê 2x +7 - ê (x +2)= 0 ê 2x 7 x +2 ë ê ( ) 1 ë + = Giải phương trình ì ì ïx ³ -2 ïx ³ 2 - ìïx ³ -2 ï ( ) ï 1 : 2x +7 = x 2 ï +  í ï ï  í
 íéx = 1  x = 1. 2
ïï x +7 =(x +2)2 2 ï + - = ïê î x 2x 3 0 ïî ïïêx = -3 ïîë
Vậy phương trình đã cho có hai nghiệm x =1, x = 2
3. Bài tập trắc nghiệm Câu 1. Cho phương trình 3 2
x mx  4x  4m  0 . Tìm m để có đúng hai nghiệm A. m  2 . B. m  2 .
C. m2;  2 . D. m  0 . Hướng dẫn giải Chọn C. x  2  3 2
x mx x m   x 2
x    m 2 x      2 4 4 0 4 4 0
x  4x m  0   x m
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 199
Trần Đình Cư. SĐT: 0834332133
Để phương trình có đúng hai nghiệm thì m  2 .
Câu 2. Phương trình 4 3 2
x  5x  8x 10x  4  0 có bao nhiêu nghiệm nguyên? A. 4 . B. 1. C. 2 . D. 0 .
Hướng dẫn giải Chọn D. 4 3 2
x  5x  8x 10x  4  0   2
x x   2
2 x  4x  2  0
Phương trình không có nghiệm nguyên. Câu 3. Phương trình 4 2
x  4x  5  0 có bao nhiêu nghiệm thực? A. 4 . B. 2 . C. 1. D. 3 . Hướng dẫn giải Chọn B. Phương trình   2 x   2 1 x  5  0 2
x 1  x  1  .
Vậy phương trình có 2 nghiệm thực. Câu 4. Phương trình  2 x x 2 2 6
17  x x  6x có bao nhiêu nghiệm thực phân biệt? A. 2 . B. 1. C. 4 . D. 3. Hướng dẫn giải Chọn D. Điều kiện: 2
17  x  0   17  x  17 . Ta có:  2 x x 2 2 6
17  x x  6x   2 x x 2 6 17  x   1  0
x  0 T  2
x  6x  0
xx  6  0     
 x  6 L . Vậy phương trình có 3 thực phân 2  17  x 1 2 16   x  0 x  4  T  biệt. Câu 5. Phương trình  2
x  5x  4 x  3  0 có bao nhiêu nghiệm? A. 0 . B. 1. C. 2 . D. 3. Hướng dẫn giải Chọn C.
Điều kiện xác định của phương trình là x  3  .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 200
Trần Đình Cư. SĐT: 0834332133 x  3   x  1 x  1 
Phương trình tương đương với    . x  4   x  3  x  3  Câu 6.
Số nghiệm của phương trình:  x    2
4 1 x  7x  6  0 là A. 0 . B. 3. C. 1. D. 2 . Hướng dẫn giải Chọn D.
Điều kiện xác định của phương trình x  4 .    x 5 x  4  1
Phương trình tương đương với  
x  1 kết hợp điều kiện suy ra 2  
x  7x  6  0 x  6  x  5  . x  6
Dạng 2: Phương trình chứa ẩn trong giá trị tuyệt đối 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Giải phương trình 3x  2  2x 1 Hướng dẫn giải 2x 1  0  1 x 1  x
Ta có 3x  2  2x 1       2  3  3x  2  2  2x  2 1   2  x
5x  8x  3  0  5
Ví dụ 2. Giải phương trình 2
2x  3x  2  x  2 Hướng dẫn giảix 1 3 2
2x  3x  2  x  2 2
2x  4x  4  0  Phương trình      x  0  . 2
2x  3x  2  x  2 2
2x  2x  0 x 1 
3. Bài tập trắc nghiệm Câu 1.
Phương trình x  2  3x 1 có tổng các nghiệm là 1 1 1 3 A.  . B.  . C. . D.  . 2 4 4 4 Hướng dẫn giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 201
Trần Đình Cư. SĐT: 0834332133 Chọn C.  1
x  2  3x 1 x    1
Ta có: x  2  3x 1  2   
. Vậy tổng các nghiệm là .
x  2 1 3x 3  4 x   4 Câu 2. Phương trình 2
x  2x  8  x  2 có số nghiệm là A. 0 . B. 2 . C. 3 . D. 1. Hướng dẫn giải Chọn D. x  2 x  2  0   Ta có 2
x  2x  8  x  2  
 x x   x x  2x  8   2 2 8 2 2   x  2  2
x  2x  8  x  2 x  2 x  2   2
x x  6  0
x  2, x  3     x  2  . x  2 x  2     2
x 3x 10  0 x  2, x  5  Câu 3.
Phương trình 2x  4  2x  4  0 có bao nhiêu nghiệm? A. 0 . B. 1. C. 2 . D. vô số. Hướng dẫn giải Chọn D.
2x  4  2x  4  0  2x  4  2x  4  2x  4  0  x  2 . Câu 4. Phương trình 2
x  2x  3  x  5 có tổng các nghiệm nguyên là A. 2  . B. 3 . C. 1  . D. 4  . Hướng dẫn giải Chọn B. x  3  TH1: 2
x  2x  3  0  
. Khi đó phương trình trở thành: x 1  1   33 x  2
x  2x  3  x  5 2
x x 8  0 2   .  1   33 x   2 TH2: 2
x  2x  3  0  3  x  1. Khi đó phương trình trở thành:
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 202
Trần Đình Cư. SĐT: 0834332133 x  1  2
x  2x  3  x  5 2
x  3x  2  0   . x  2 
Vậy tổng các nghiệm nguyên là T  1 2  3 . Câu 5.
Tập nghiệm của phương trình: x  2  3x  5 là tập hợp nào sau đây?  7 3  3 7   7 3   3 7  A.  ;   . B.  ;  . C.  ;  . D.  ;  .  4 2  2 4   4 2   2 4  Hướng dẫn giải Chọn B.  3
x  2  3x  3 x  
x  2  3x  5  2    x  2  3  x  3 7 x   4 3 7 
Vậy tập nghiệm của phương trình đã cho là S   ;  . 2 4  Câu 6.
Tổng nghiệm bé nhất và lớn nhất của phương trình x 1  3x  3  4  2x là A. 0 . B. 1. C. 2 . D. 3. Hướng dẫn giải Chọn A.
Ta có: x 1  3x  3  4  2x   x   x  2    x2 1 3 3 4 2 2 2 2
 10x 16x 10  2 3x  3  16 16x  4x 2 2
 6 x 1  6  6x 2 2
x 1  1 x 2
 1 x  0  1  x  1. Vậy tổng nghiệm lớn nhất và bé nhất bằng 0 . Câu 8.
Tính tổng tất cả các nghiệm của phương trình x  2  2 x  2 . 1 2 20 A. . B. . C. 6 . D. . 2 3 3 Hướng dẫn giải Chọn D. x  6
x  2  2x  4 x 2 2 x 2        2 .
x  2  2x  4 x   3 20
Vậy tổng các nghiệm là . 3
Câu 10. Để giải phương trình x  2  2x  3 
1 , một học sinh đã lập luận như sau:
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 203
Trần Đình Cư. SĐT: 0834332133
IBình phương 2 vế:   2 2
1  x  4x  4  4x 12x  9 2   2
II  3x 8x  5  0 3 .   5
III  x  1 x  . 3  5 IV Vậy  
1 có hai nghiệm x  1 và x  1 2 3
Cách giải trên sai từ bước nào? A. IV . B. II . C. III . D. I . Hướng dẫn giải Chọn D.
Muốn bình phương hai vế của phương trình thì hai vế phải không âm 2x  3  0 
Để giải phương trình này ta áp dụng công thức x  2  2x  3  x  2  2x  3  x  2  2  x  3
Hoặc ta giải bằng phương pháp hệ quả thì   2 2
1  x  4x  4  4x 12x  9 2 .
Câu 11. Cho phương trình: x  2  2  x  
1 . Tập hợp các nghiệm của phương trình   1 là tập hợp nào sau đây? A.  ;  2. B.  . C. 2;   . D. 0;1;  2 . Hướng dẫn giải Chọn A.
Phương trình x  2  2  x x  2  0  x  2 .
Phương trình có tập nghiệm S   ;  2.
Câu 12. Giải phương trình 1 3x  3x 1  0 .  1  1   1  1  A. ;    . B.   . C. ;  . D. ;    .  3  2  3   3  Hướng dẫn giải Chọn D. 1
Ta có 1 3x  3x 1  0  1 3x  3x 1  1 3x  0  x  . 3
Câu 13. Phương trình 2
x  3 x  3  2x  5 có tích của tất cả các nghiệm nguyên là A. 4 . B. 1. C. 56  . D. 0 .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 204
Trần Đình Cư. SĐT: 0834332133 Hướng dẫn giải Chọn B. Phương trình 2
x  3 x  3  2x  5 2
 3 x  3  2x  5  x   * . Điều kiện 2
2x  5  x  0  1 6  x  1 6 . 1 57
TH1: 3  x  1 6 . Phương trình   * 2
x x 14  0  x  . 2
TH2: 1 6  x  3 . Phương trình   * 2
x  5x  4  0  x  1 .
Câu 14. Phương trình 2
x  2x  3  x  5 có tổng các nghiệm nguyên là A. 2  . B. 3  . C. 1  . D. 4  . Hướng dẫn giải Chọn D.
+ Với x  5  0  x  5
 ta có VP  0 , VP  0 suy ra phương trình vô nghiệm
+ Với x  5  0  x  5  2 2
Phương trình  x x
 x  2  x x    x  2 2 2 2 3 5 2 3 5  1   33 2     8  0 x x xx  1  2     hoặc  2
x  3x  2  0  1   33 x  2  x   2 Tổng các nghiệm bằng 4  .
Dạng 3: Phương trình chứa ẩn ở mẫu 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Giải phương trình 3 3x 2x + = x -1 x -1 Lời giải
Điều kiện x =/ 1. Khi đó phương trình 3 3x 3(x - ) 1 3  2x + =  2x =
x = thỏa mãn điều kiện x -1 x -1 x -1 2 2
Ví dụ 2. Giải phương trình 2x -10x = x -3 . 2 x -5x Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 205
Trần Đình Cư. SĐT: 0834332133 2 ìïx -5x =/ 0 2 ï 2 2x -10x ï ìïx -5x =/ 0 x 3 ïí2x x -5 ï = -   í  S = . Æ 2 ( ) x -5x ï = x -3 2 ï = x - ï ï 3 ï x (x -5) î ïî
Ví dụ 3. Giải phương trình 2 10 50 1- = - . x -2
x + 3 (2 - x)(x + 3) Lời giải éx =10(thoaû maõn) (2 x)(x ) 3 2(x 3) 10(2 x) 2 50 x 7x 30 0 ê  - + - + = - -  - - =  . ê x = - ê 3(loaïi) ë
3. Bài tập trắc nghiệm
x  1mx  2 Câu 1.
Gọi n là các số các giá trị của tham số m để phương trình  0 x  2 có
nghiệm duy nhất. Khi đó n là: A. 2 . B. 1. C. 0 . D. 3 . Hướng dẫn giải Chọn A.
Điều kiện: x  2 .
Phương trình có nghiệm duy nhất khi xảy ra hai trường hợp:
TH 1: tử thức có đúng một nghiệm thỏa điều kiện, suy ra m  2  0  m  2 .
TH 2: tử thức có hai nghiệm và một nghiệm x  2 , suy ra 2m  2  0  m  1. Vậy n  2 .
 2x x6 x1 Câu 2.
Tìm phương trình tương đương với phương trình  0 trong các x  2 phương trình sau: 2 x  4x  3 A.  0 .
B. x  2  x  1. x  4 x C. 3 x 1  0 .
D. x  2 3  . x  2 Hướng dẫn giải Chọn C.
 2x x6 x1 Xét phương trình  0  
1 . ĐK: x  1 và x  2 . x  2
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 206
Trần Đình Cư. SĐT: 0834332133 x  1   x 1  0
Với điều kiện ở trên, ta có   1     x  3  . 2 x x 6 0     x  2 
Đối chiếu điều kiện, phương trình  
1 có nghiệm x  1 . 2 x  4x  3 x  1  Xét phương trình
 0 2 . ĐK: x  4  . 2 2
x  4x  3  0   . x  4 x  3  Loại A
Xét phương trình x  2  x  1. ĐK: x  0 . Loại B Xét phương trình 3
x 1  0  x  1  . x
Xét phương trình  x  2 3 
. ĐK: x  2 . Loại D x  2 Đã sửa đáp án C từ 2 x  1 thành 3 x 1  0 . 2 x  3x  2 Câu 3. Cho phương trình:
 x có nghiệm a . Khi đó a thuộc tập: x  3  1   1 1   1  A. ;3   . B.  ;   . C. ;1   . D.  .  3   2 2   3  Hướng dẫn giải Chọn B.
Điều kiện: x  3.  3  13 x  2 2 x  3x  2
x  3x  2  x x  3 Ta có: 2 2  x
 0  2x  6x  2  0   . x  3 x  3  3  13 x   2 1 3  13  1 1  Ta có:  
 0 . Vậy nghiệm của phương trình đã cho thuộc tập  ;   . 2 2  2 2 
Dạng 4: Phương trình chứa ẩn ở trong dấu căn 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Giải phương trình 2
2x  3x  5  x 1 Lời giải x 1 0  x  1  Ta có : 2
2x  3x  5  x 1      x  2.
2x  3x  5  2  x  2 2 1
x x  6  0
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 207
Trần Đình Cư. SĐT: 0834332133
Ví dụ 2. Giải phương trình: x  2  2  x ?
Hướng dẫn giảix  2  0 x  2 Điều kiện:     x  2 . 2  x  0 x  2
Thay x  2 vào phương trình ta được 0  0 hay x  2 là nghiệm của phương trình.
Ví dụ 3. Giải phương trình 2
2x 8x  4  x  2 . x  0 A. x  4 . B.  .
C. x  4  2 2 . D. x  6 . x  4
Hướng dẫn giải Chọn A.x  2 x  2  0 2  
2x 8x  4  x  2  
 x  0  x  4.
2x 8x  4   x 22 2  x  4
Ví dụ 4. Giải phương trình: 2 2
x  5x  2  2 x  5x 10  0 Hướng dẫn giải Điều kiện xác định 2
x  5x 10  0  x   . Khi đó phương trình 2 2
x  5x 10  2 x  5x 10 8  0 2
x  5x 10  2 x  3    2 2
x  5x 10  2  x  5x  6  0   . 2
 x 5x 10  4  x  2 
3. Bài tập trắc nghiệm
Câu 1. Số nghiệm nguyên dương của phương trình x 1  x  3 là A. 0 . B. 1. B. 2 . D. 3 .
Hướng dẫn giải
Chọn B. x  3 x  3  x  3 
x 1  x  3    
 x   x  . x 1   x 3 2 5 2 2
x  7x 10  0  x  5
Câu 2. Số các nghiệm nguyên của phương trình x x   3 2
5  2 x  5x  2  2 là A. 0 . B. 1. C. 2 . D. 3 .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 208
Trần Đình Cư. SĐT: 0834332133
Hướng dẫn giải Chọn C. Đặt 3 2 2 3
t x  5x  2  x  5x t  2 . x  2 
Phương trình đã cho trở thành: 3 2
t  2t  4  0  t  2
  x  5x  6  0   . x  3 
Vậy phương trình đã cho có hai nghiệm nguyên. 2 x  4x  2
Câu 3. Cho phương trình
x  2 . Số nghiệm của phương trình này là x  2 A. 0 . B. 2 . C. 4 . D. 1.
Hướng dẫn giải Chọn D.
ĐKXĐ: x  2 khi đó phương trình trở thành x 1 2 2
x  4x  2  x  2  x  5x  4  0   . x  4
Đối chiếu điề kiện suy ra phương trình có một nghiệm x  4 .
Câu 5. Tổng các nghiệm của phương trình 3x  7  x 1  2 là A. 2 . B. –1. C. 2  . D. 4 .
Hướng dẫn giải Chọn A.x  1  
3x  7  x 1  2   3x7  2 x1 x  1   x  1   x  1 x  1          . 3
 x  7  4  x 1 4 x 1
x 1  2 x 1 2
x  2x  3  0 x  3
Vậy tổng các nghiệm của phương trình là 2 .
Câu 6. Số nghiệm nguyên của phương trình: x  3  5  7  x x là A. 0 . B. 2 . C. 3 . D. 1.
Hướng dẫn giải Chọn B.x  3  0 x  3 + Điều kiện:    . 7  x  0 x  7
+ Thay x lần lượt bằng 3 , 4 , 5 , 6 , 7 vào phương trình ta thấy các số 3 , 7 là nghiệm.
+ Vậy phương trình có hai nghiệm nguyên.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 209
Trần Đình Cư. SĐT: 0834332133 1 1 Câu 7.
Số nghiệm của phương trình: 2 x x    6 là x 1 x 1 A. 0 . B. 2 . C. 1. D. 3 .
Hướng dẫn giải Chọn C. 1 1 x 1  0 x 1 2 x x    6      x  3 . x 1 x 1 2
x x  6  0 x  2   x  3
Vập phương trình đã cho có một nghiệm x  3 .
Câu 8. Phương trình sau có bao nhiêu nghiệm x 1  1 x ? A. 0 . B. vô số. C. 1. D. 2 .
Hướng dẫn giải
Chọn C. x 1
Điều kiện xác định:   x 1. x 1
Với x  1thay vào phương trình thỏa mãn. Vậy phương trình có một nghiệm.
Câu 9. Tổng tất cả các nghiệm của phương trình: 2
x  3x  2  1 x là A. 3. B. 3 . C. 2  . D. 1.
Hướng dẫn giải Chọn D. 1   x  0 x  1  2
x  3x  2  1 x      x 1. 2
x  3x  2 1 x 2
x  2x  3  0
Câu 10. Phương trình 2
x  4x 1  x  3 có nghiệm là
A. x  1 hoặc x  3. B. Vô nghiệm. C. x  1. D. x  3.
Hướng dẫn giải Chọn B.x  3  0 x  3 2
x  4x 1  x  3     2 2 .
x  4x 1  x  6x  9 x 1 a b
Câu 11. Biết phương trình 2
3x 1 3x  7x  3x 1  0 có một nghiệm có dạng x  , c
trong đó a , b , c là các số nguyên tố. Tính S a b c . A. S 14 . B. S  21. C. S 10 . D. S 12 . Hướng dẫn giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 210
Trần Đình Cư. SĐT: 0834332133 Chọn C. 2 3
x  7x  0 1 Điều kiện:   x  * 3  x 1  0 3
Với điều kiện trên, phương trình tương đương  x   2 2
1  3x  7x   x  3x 1  0     2 2 x  3x 1 x  3x 1    0 2x   2 1  3x  7x x  3x 1    1 1  2 x  3x   1     0 2
 2x 1 3x  7x x  3x 1  2
x  3x 1  0 3  5   3 5 x  hoặc x  2 2 3  5
Theo yêu cầu đề bài ta chọn nghiệm x  2
Vậy a  3, b  5 , c  2  S a b c  10 .
Câu 12. Phương trình 3 3 3
x  5  x  6  2x 11 có bao nhiêu nghiệm. A. 2 . B. 3. C. 1. D. 0 . Hướng dẫn giải Chọn B. 3 3 3
x  5  x  6  2x 11 3 3
x   x   x x   3 3 5 6 3 5 6
x  5  x  6   2x 11  x  5  3 3 3
 3 x  5 x  6 2x 11  0  x  6   11 x    2
Thử lại ta được các nghiệm đều thỏa mãn
Câu 13. Tập nghiệm của phương trình 4 2 2
x x 1  x x 1  2 là 7  A.  . B.  ;1. C.   0 . D.   1 . 2  Hướng dẫn giải Chọn D.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 211
Trần Đình Cư. SĐT: 0834332133 1 Đặt 4 2
t x x 1,t  0 2
x x 1  2 t  t  1  1  1 5 Ta có pt: t   2 3 2
t  2t 1  0  t  2 t  2   1 5 t   2 
So sánh với điều kiện t  0 ta tìm được t  1 5 1, t  2 Trường hợp 1: 4 2
t  1: x x 1  1 2
x x 1 1 x 1 2
x 1  x 1    x 1 2 2
x  2x 1  x 1 1 5 1 5
Trường hợp 2: t  4 2
x x 1  2 2 7  3 5 7  3 5 2
x x 1  2  x   x 1 2 2  7  3 5 x   7  3 5 2  x     2 2   x     7  3 5  7 2  x    x 1    x  2       2
Câu 14. Số nghiệm của phương trình 2
x  2x  8  4 4  x x  2 là A. 3. B. 1. C. 4 . D. 2 . Hướng dẫn giải Chọn D.
Điều kiện: 4  x x  2  0  x  2  ;4. 2
x  2x  8  4 4  x x  2 2
x x     2 2 8 4
x  2x  8   1 . Đặt t   2
x  2x  8 , t  0 2  t   2
x  2x  8 2 2
x  2x  8  t .
t  0n   2 1  t   4t 2
t  4t  0     2
x  2x  8  0   2
x  2x  8  0 t  4   l x  2  n  
. Vậy phương trình đã cho có hai nghiệm. x  4  n
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 212
Trần Đình Cư. SĐT: 0834332133
Câu 15. Tổng các bình phương các nghiệm của phương trình
x  x   2 1
3  3 x  4x  5  2  0 là A. 17 . B. 4 . C. 16 . D. 8. Hướng dẫn giải Chọn B.
Ta có  x   x   2 1
3  3 x  4x  5  2  0 2 2
x  4x  5  3 x  4x  5  4  0  2
x  4x  5  1  2
x  4x  5  1  2
x  4x  4  0  x  2 .
Câu 16. Phương trình 3x  2x  2  1 x  2 có bao nhiêu nghiệm? A. 0 . B. 1. C. 2 . D. 3. Hướng dẫn giải Chọn A. 3  x  0 x  0  
ĐKXĐ: 2x  2  0  x 1  x 1. 1   x  0   x  1 
Thay x  1 vào 3x  2x  2  1 x  2 , ta được: 3  2 .
Vậy phương trình vô nghiệm.
Câu 17. Số nghiệm của phương trình x  8  2 x  7  2  x 1 x  7 là A. 2 . B. 3. C. 0 . D. 1. Hướng dẫn giải Chọn D.
x  7 1  2   x  7  3 x  7  2
x  8  2 x  7  2  x 1 x  7    x  7  3
 x 7 3  x7 3 x7 2  0  x2  x 7 3
 x  7 3  0 x  2 
x73 x720       x  2 .  x  2 x  2 x  2
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 213
Trần Đình Cư. SĐT: 0834332133
Dạng 5: Định lý viet và ứng dụng 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Tìm tham số m để phương trình m   2
1 x  2mx m  2  0 có hai nghiệm trái dấu Hướng dẫn giải
Phương trình m   2
1 x  2mx m  2  0 có hai nghiệm trái dấu khi và chỉ khi m 1  0   2   m 1.  m   1m 2  0
Ví dụ 2. Cho phương trình 2 mx   2
m  3 x m  0 . Tìm tất cả các giá trị của tham số m để 13
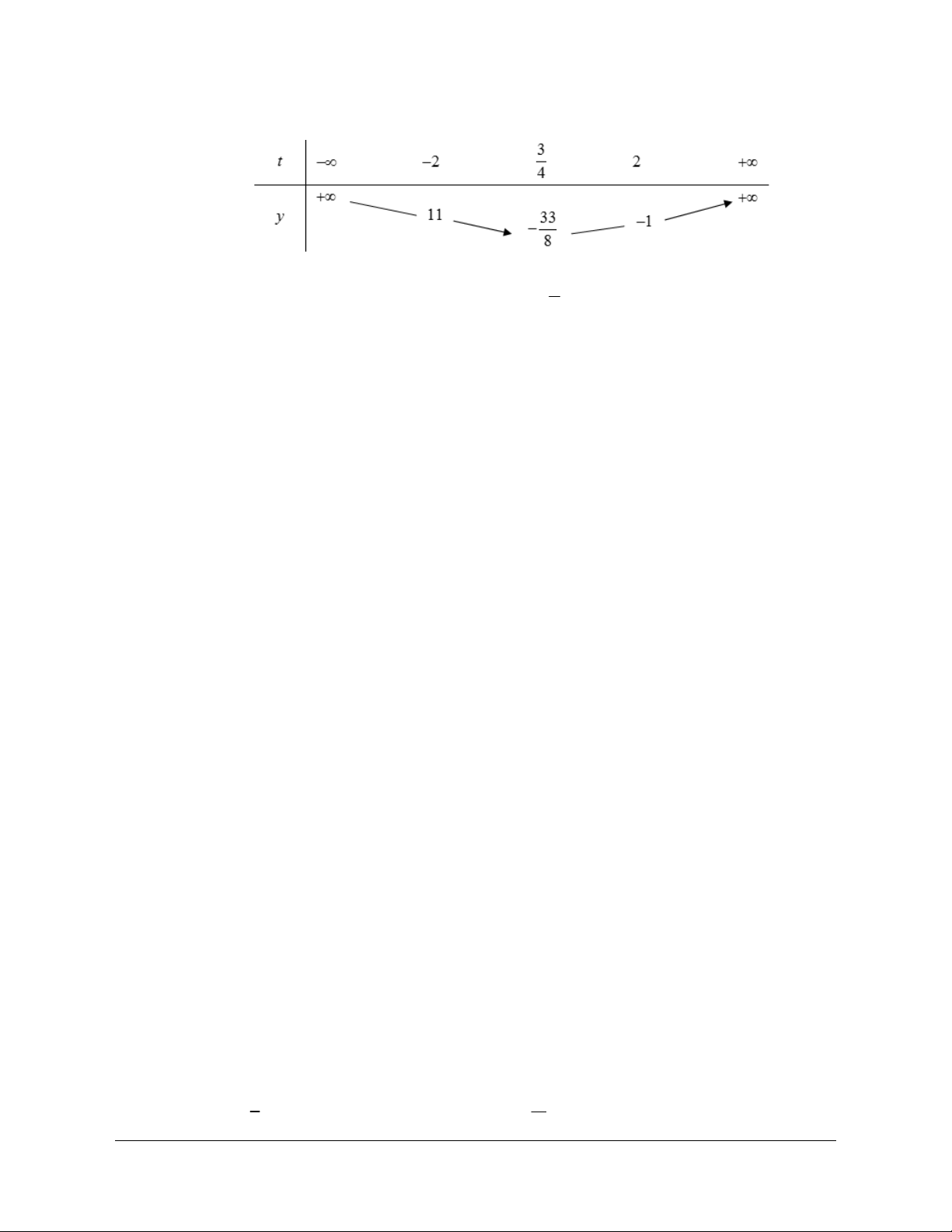
phương trình có hai nghiệm x , x thỏa mãn x x  . 1 2 1 2 4 Hướng dẫn giải 13
Phương trình có 2 nghiệm x , x thỏa mãn x x  1 2 1 2 4   a  0 m  0 m  0        0    m  32 2 2  4m  0   2
m  3  2m 2
m  3  2m  0  b 13     2  m  3 13 2
4m 13m 12  0  a 4    m 4    m  0  3  m   m ;    3  1  ;  1 3;   4 .    3 m  4   m    4   m  4  265
Vậy tổng bình phương các giá trị của m là . 16
Ví dụ 3. Tìm tham số m để phương trình 2
x  2mx m  2  0 có hai nghiệm dương phân biệt Hướng dẫn giải Để phương trình 2
x  2mx m  2  0 có hai nghiệm dương phân biệt   0 
 m2 1.m  2  0 2
m m  2  0 m  1  v m  2      
S  0  2m  0  m  0  m  0  m  2 . P  0     m  2  0       m 2  m 2 
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 214
Trần Đình Cư. SĐT: 0834332133
3. Bài tập trắc nghiệm Câu 1. Phương trình 2
ax bx c   0 0
a   có hai nghiệm phân biệt cùng dấu khi và chỉ khi:   0   0   0   0 A.  . B.  . C.  . D.  . P  0 S  0 P  0 S  0 Hướng dẫn giải Chọn A. Phương trình 2
ax bx c   0 0
a   có hai nghiệm phân biệt cùng dấu khi và chỉ   0  . P  0 Câu 2.
Biết phương trình 2
ax bx c  0 , (a  0) có hai nghiệm x , x . Khi đó: 1 2  ab x x    x x  1 2   1 2  A. b a  . B.  . ac x x  x x  1 2  c 1 2  abb x x    x x   1 2   1 2  C. 2a a  . D.  . cc x x  x x  1 2  2a 1 2  a Hướng dẫn giải Chọn D.b x x    1 2  Theo Hệ thức Viet, ta có a  . cx x  1 2  a Câu 3.
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn  7;
 7 để phương trình 2
mx  2m  2 x m 1  0 có hai nghiệm phân biệt? A. 14 . B. 8 . C. 7 . D. 15 . Hướng dẫn giải Chọn C. TH1: m  0  4  x 1  1
0  x   ; phương trình chỉ có một nghiệm duy nhất nên 4 loại m  0 TH2: m  0 Để 2
mx  2m  2 x m 1  0 với m 7;
 7 có hai nghiệm phân biệt thì
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 215
Trần Đình Cư. SĐT: 0834332133
  m  2
2  m m   1  0  5m  4  4
m   đồng thời m 7;  7 5
Vậy m  1;2;3;4;5;6; 
7  có 7 giá trị nguyên của m thỏa mãn. Câu 4.
Tìm tất cả giá trị của tham số m để phương trình 2
x  2mx m 1  0 có 2 nghiệm
phân biệt x , x sao cho 2 2 x x  2 . 1 2 1 2  1  1 m   1 m A.  2 . B. m  0 . C. m   . D.  .  2 2  m  0 m  0 Hướng dẫn giải Chọn A. Phương trình: 2
x  2mx m 1  0 .
Để phương trình có 2 nghiệm phân biệt thì   0 2
m m 1  0 , luôn đúng với x    .
x x  2m
Khi đó, theo định lí Vi-ét ta có: 1 2  .
x x  m 1  1 2  1 m   Ta có: 2 2
x x  2   x x  2x x  2 2
 4m  2m  2  2   . 1 2 2 1 2 1 2 2  m  0 Câu 5. Phương trình  2 m   2
4 x  5x m  0 có hai nghiệm trái dấu, giá trị m là A. m ;  2  0;2. B. m ;  2   0;2. C. m 2;  0 2;. D. m  2;  2 . Hướng dẫn giải Chọn B mm  2 
Phương trình có hai nghiệm trái dấu   0  hay 2 m  4  0  m  2 m ;  2   0;2. Câu 6.
Tìm m để phương trình 2 2
x mx m  3  0 có hai nghiệm x , x là độ dài các cạnh 1 2
góc vuông của một tam giác vuông với cạnh huyền có độ dài bằng 2 là
A. m0;2 .
B. m   3 . C. m 2;  0 . D. m . Hướng dẫn giải Chọn D.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 216
Trần Đình Cư. SĐT: 0834332133 Phương trình 2 2
x mx m  3  0 có hai nghiệm x , x là độ dài các cạnh góc vuông của 1 2
một tam giác với cạnh huyền có độ bài bằng 2 khi và chỉ khi: 2 2
  m  4m 12  0  2 3   m  4
S x x m  0  1 2   m  0
P x .x  0  1 2  2    x x  2x x  4  1 2  2 2 x x  4  1 2 1 2  3  m  2   3  m  2      m. 2 m  2  2   2 m  3  4 m  2 Câu 7. Cho hàm số 2
y  x  4x  3 , có đồ thị P . Giả sử d là dường thẳng đi qua A0;3
và có hệ số góc k . Xác định k sao cho d cắt đồ thị P tại 2 điểm phân biệt E , F sao
cho OEF vuông tại O (O là gốc tọa độ). Khi đó k  1  k  1  k 1 k 1 A.  . B.  . C.  . D.  . k  3 k  2 k  2 k  3 Hướng dẫn giải Chọn D.
Phương trình đường thẳng d : y kx  3
Phương trình hoành độ giao điểm của P và d : 2
x  4x  3  kx  3 2
 x  4  kx  0  xx  4  k  0   1 .
d cắt đồ thị P tại 2 điểm phân biệt khi   1 có 2 nghiệm phân
biệt  4  k  0  k  4 .
Ta có E x ;kx 3 , F x ;kx  3 với x , x là nghiệm phương trình   1 . 2 2  1 1  1 2 OEF vuông tại  
O OE.OF  0  x .x kx  3 kx  3  0  x .x  2
1 k  3k x x  9  0 1 2   1 2 1 2  1  2    2
0. 1 k   3k 4  k   9  0 k 1 2
k  4k  3  0   . k  3 Câu 8.
Giả sử phương trình 2
2x  4mx 1  0 có hai nghiệm x , x . Tìm giá trị nhỏ nhất của 1 2
biểu thức T x x . 1 2 2 2 A. minT  .
B. min T  2 . C. minT  2 . D. min T  . 3 2 Hướng dẫn giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 217
Trần Đình Cư. SĐT: 0834332133 Chọn B. Phương trình 2
2x  4mx 1  0 có 2
  4m  2  0 nên phương trình có hai nghiệm phân 1
biệt x , x với S x x  2m , P x x   . 1 2 1 2 1 2 2
Ta có T   x x 2 2 2  S  4P 2
 4m  2  2  T  2 . Dấu bằng xảy ra khi m  0. 1 2 Vậy min T  2 . Câu 9.
Gọi S là tập hợp các giá trị của tham số m sao cho parabol P : 2
y x  4x m cắt
Ox tại hai điểm phân biệt A , B thỏa mãn OA  3OB . Tính tổng T các phần tử của S . 3 A. T  3. B. T  15  . C. T  . D. T  9 . 2 Hướng dẫn giải Chọn D.
Phương trình hoành độ giao điểm của P và Ox : 2
x  4x m  0
Để P cắt Ox tại hai điểm phân biệt thì có hai nghiệm phân biệt x , x 1 2   0 4  m  0    
m  4 . Giả sử Ax ;0 , Bx ;0 và x x  4, x x m . 2  1  a  0 1   0 1 2 1 2 x  3x
Ta có OA  3OB x  3 x 1 2  . 1 2 x  3  x  1 2 x  3
Trường hợp 1: x  3x 1   m  3 1 2 x 1  2 x  6
Trường hợp 2: x  3  x 1   m  12  1 2 x  2   2 Vậy S  12   3  9  . Câu 10. Cho hàm số 2
y x  2x  2 có đồ thị P , và đường thẳng d  có phương trình
y x m . Tìm m để d  cắt P tại hai điểm phân biệt A , B sao cho 2 2
OA OB đạt giá trị nhỏ nhất. 5 5 A. m   . B. m  . C. m 1. D. m  2 . 2 2 Hướng dẫn giải Chọn A.
Phương trình hoành độ giao điểm: 2
x  2x  2  x m 2
x  3x  2  m  0
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 218
Trần Đình Cư. SĐT: 0834332133  17
d  cắt P tại hai điểm phân biệt A , B    0 17  4m  0  m   . 4 
Ax ; x m OA   x ; x m 1 1  1 1  
B x ; x m OB   x ; x m 2 2  2 2 
OA OB x x   x m2   x m2 2 2 2 2  2x x
 4x x  2m x x  2m 1 2 2 1 2  1 2  2 1 2 1 2 2      5  15 15 17 m 2 18 4 2  6m  2m 2
 2m 10m 10  2 m      với m    2  2 2 4 15 5
Vậy giá trị nhỏ nhất của 2 2 OA OB là khi m   . 2 2
Câu 11. Số giá trị nguyên của tham số m thuộc  5;  5 để phương trình 2 2
x  4mx m  0 có hai nghiệm âm phân biệt là A. 5. B. 6 . C. 10 . D. 11 Hướng dẫn giải Chọn A.   0 2 3  m  0  
Phương trình có hai nghiệm âm phân biệt  S  0   4
m  0  m  0 . P  0   2 m  0  Vậy trong đoạn  5; 
5 có 5 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Câu 12. Với giá trị nào của m thì phương trình m   2
1 x  2m  2 x m  3  0 có hai nghiệm
x , x thỏa mãn x x x x 1? 1 2 1 2 1 2
A. 1  m  3.
B. 1 m  2 . C. m  2 . D. m  3 . Hướng dẫn giải Chọn A. Phương m   2
1 x  2m  2 x m  3  0 có hai nghiệm x , x khi và chỉ khi 1 2 m 1 0  m  1  m  1     m  1.       0   m  2  2 m   1 m  3  0 1 0 2m  4 m  3
Theo định lí Vi-et ta có: x x  , x x  . 1 2 m 1 1 2 m 1 m m  2m  6
Theo đề ta có: x x x x  2 4 3 1   1 
 0  1 m  3 . 1 2 1 2 m 1 m 1 m 1
Vậy 1  m  3 là giá trị cần tìm.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 219
Trần Đình Cư. SĐT: 0834332133
Câu 13. Cho phương trình m   2
5 x  2m  
1 x m  0  
1 . Với giá trị nào của m thì   1 có 2
nghiệm x , x thỏa x  2  x ? 1 2 1 2 8 8 8 A. m  5 . B. m  .
C. m  5 .
D. m  5 . 3 3 3 Hướng dẫn giải Chọn C. m  5  0 m  5   Phương trình  
1 có hai nghiệm phân biệt   *    1 .  m   2
1  mm  5  0 m    3  2m   1 x x    1 2 
Khi đó theo định lý Viète, ta có: m  5  . mx x  1 2  m  5 Với m 4m   1
x  2  x   x  2 x  2  0  x x  2 x x  4  0    4  0 1 2  1 2 1  2  1 2 m  5 m  5 9m  24   8 8
0   m  5 . Kiểm tra điều kiện * ta được  m  5 . m  5 3 3
Câu 14. Gọi S là tập hợp tất các giá trị thực của tham số m để đường thẳng d  : y mx cắt parabol P 2
: y  x  2x  3 tại hai điểm phân biệt A và B sao cho trung điểm I của
đoạn thẳng AB thuộc đường thẳng  : y x  3. Tính tổng tất cả các phần tử của S . A. 2 . B. 1. C. 5. D. 3. Hướng dẫn giải Chọn D.
Phương trình hoành độ giao điểm: 2 2
x  2x  3  mx x  m  2 x 3  0   1 .
Để d  cắt P tại hai điểm phân biệt a  1  0    
1 có hai nghiệm phân biệt   .      mm  22 12  0
Khi đó d  cắt P tại hai điểm phân biệt Ax ;mx , Bx ;mx , với x , x là nghiệm 2 2  1 1  1 2 phương trình  
1 . Theo Viét, có: x x  2  m , x x  3  . 1 2 1 2 2
x x mx mx   2  m m  2m I là trung điểm 1 2 1 2 AB I  ;  ;     .  2 2   2 2 
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 220
Trần Đình Cư. SĐT: 0834332133 Mà 2        I  m 2m 2 m m 1 m 2 1
: y x  3  
 3  m  3m  4  0  
m m  3. 2 2 m  4  m  1 2 2
Dạng 6: Giải và biện luận phương trình 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Tìm tham số m để phương trình 2
x  2mx  3m  2  0 có nghiệm là Hướng dẫn giải Chọn B. Để phương trình 2
x  2mx  3m  2  0 có nghiệm m 1
   0  m2  3m  2  0 2
m  3m  2  0   . m  2
Ví dụ 2. Cho phương trình m  2
1 x 1  7m  5 x m . Tìm tham số m để phương trình đã cho vô nghiệm là Hướng dẫn giải Ta có: m  2
1 x 1  7m  5 x m   1   2
m  5m  6 x m 1
 m  2m 3 x m 1 2 Để phương trình  
1 vô nghiệm  phương trình 2 vô nghiệm 
 m  2m 3  0
m  2 v m  3    
m  2 v m  3 m 1 0 m  1
Ví dụ 3. Xác định m để phương trình 2
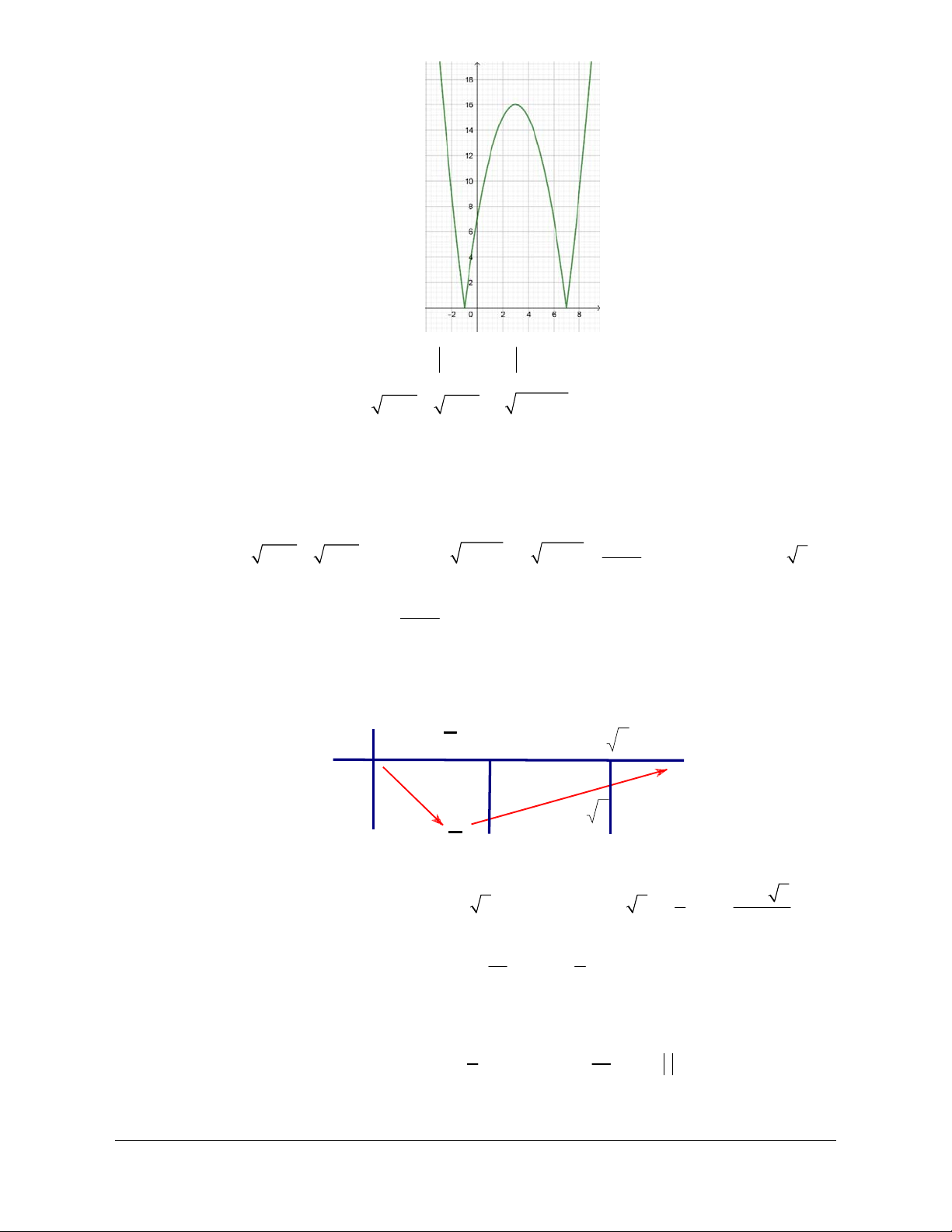
m x  6x  7 có 4 nghiệm phân biệt. Hướng dẫn giải 2
m x  6x  7 là phương trình hoành độ giao điểm của đường thẳng y m và đồ thị C 2
: y x  6x  7 . Vẽ P 2
: y x  6x  7 , lấy đối xứng phần phía dưới Ox của P lên trên Ox và xóa đi
phần phía dưới Ox , ta được đồ thị C  .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 221
Trần Đình Cư. SĐT: 0834332133
Dựa vào đồ thị: phương trình 2
m x  6x  7 có 4 nghiệm phân biệt khi m0;16 .
Ví dụ 4. Tìm m để phương trình 2
x  2  2  x  2 x  4  2m  3  0 có nghiệm. A. 1. B. 3. C. 0 . D. 2 . Hướng dẫn giải Chọn D. 2 t  4
Đặt t x  2  2  x 2 2
t  4  2 4  x 2  4  x
, Điều kiện 2  t  2 2 2 2 t  4
Phương trình trở thành: t  2  2m  3  0 2
t t  2m 1  0 (*) 2
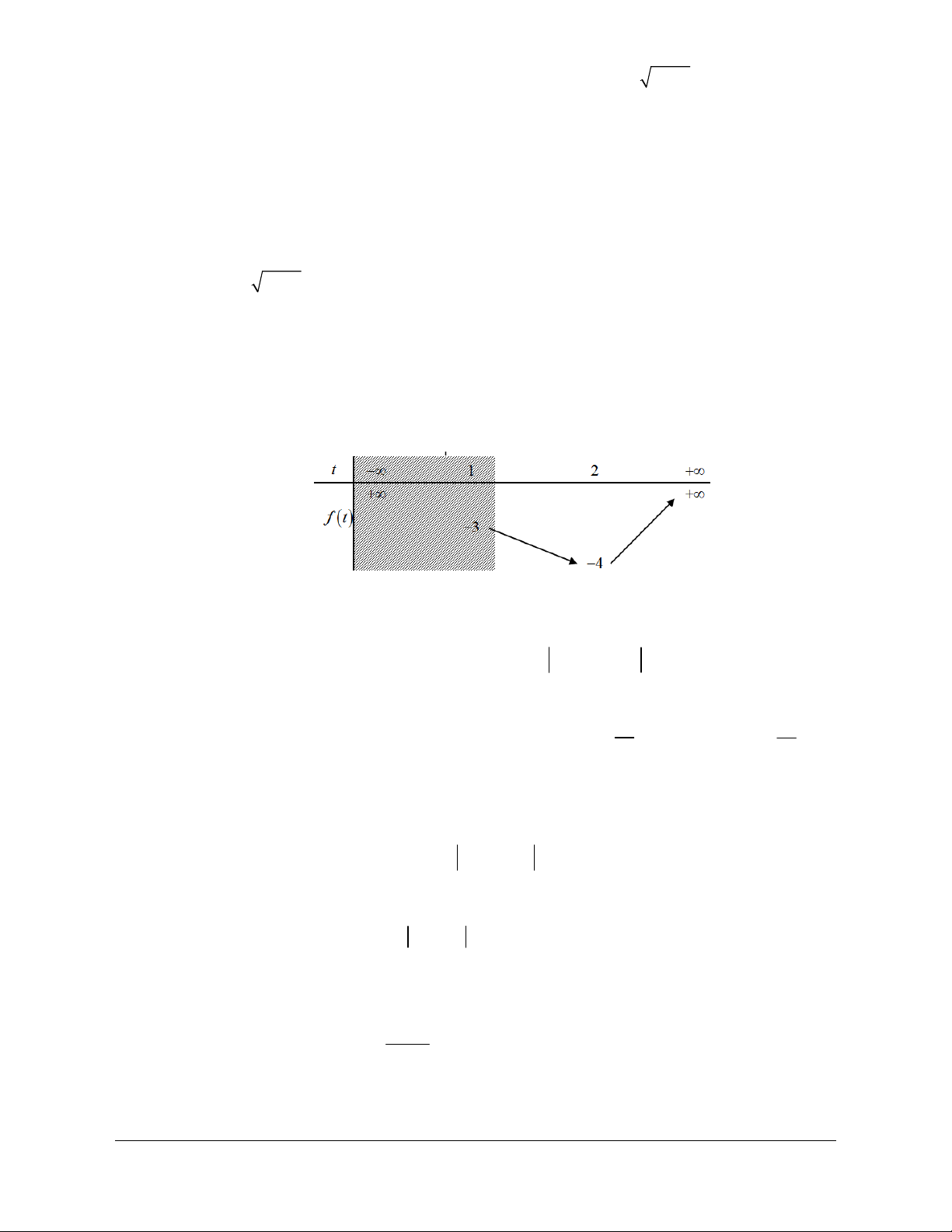
Xét hàm số f t 2
t t 1, có bảng biến thiên 1 - 2 2 2 x -∞ 2 +∞ y 7+2 2 1 5 - 4
Phương trình có nghiệm thỏa 2  t  2 2 khi 5  2m  7  5 7 2 2 2 2   m  2 2  1   1 
Ví dụ 5. Tìm tham số m để phương trình 2 2 x   3 x   2m 1  0  có nghiệm 2     x   x Hướng dẫn giải 1 1 t  2
Điều kiện xác định: x  0 . Đặt t x  2 2
t  2  x   2  t  2  . x 2 x  t  2 
Phương trình đã cho trở thành  2
2 t  2  3t  2m 1  0 2
 2t  3t  2m  3  0
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 222
Trần Đình Cư. SĐT: 0834332133 2
 2t  3t  3  2m
Xét hàm số y f t 2
 2t  3t  3 có bảng biến thiên t  2 2m  1  1
có nghiệm t thỏa  khi   m   . t  2  2m 11 2
3. Bài tập trắc nghiệm Câu 1.
Gọi S là tập hợp tất cả các giá trị thực của tham số m để phương trình
mx m  m   2
2 x m  2x có tập nghiệm là  . Tính tổng tất cả các phần tử của S . A. 1. B. 1  . C. 2 . D. 0 . Hướng dẫn giải Chọn A.
Biến đổi phương trình đã cho thành 2
0x m m . m  0
Phương trình có tập nghiệm là  thì 2
m m  0   . m 1 Suy ra S  0; 
1 . Do đó ta có 0 1  1 . Câu 2.
Cho phương trình   m 2 2
x m  4 . Có bao nhiêu giá trị của tham số m để phương
trình có tập nghiệm là  ? A. vô số. B. 2 . C. 1. D. 0 . Hướng dẫn giải Chọn C.
Phương trình bậc nhất đã cho có tập nghiệm là  khi và chỉ khi 2  m  0 m  2     m  2 . 2 m  4  0 m  2 
Vậy có duy nhất một giá trị của tham số m để phương trình đã cho có tập nghiệm là  . Câu 3.
Cho phương trình m3m  
1 x 1 3m ( m là tham số). Khẳng định nào sau đây là đúng? 1  1 
A. m  thì phương trình có tập nghiệm là   . 3  m
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 223
Trần Đình Cư. SĐT: 0834332133 1  1 
B. m  0 và m  thì phương trình có tập nghiệm là   . 3  m
C. m  0 thì phương trình có tập nghiệm là  . 1
D. m  0 và m  thì phương trình vô nghiệm. 3 Hướng dẫn giải Chọn B.
Giải và biện luận phương trình: m3m  
1 x 1 3m như sau: m  0
+ Khi m 3m  1 0     1 . m   3
m  0 : phương trình trở thành 0x  1 . 1
m  : phương trình trở thành 0x  0 . 3 m  0  1
+ Khi m 3m   1  0  
1 : phương trình có nghiệm duy nhất x   . m   m  3 Câu 4.
Tìm m để phương trình 2
mx – 2m  
1 x m 1  0 vô nghiệm. A. m  1.
B. m  1 hoặc m  0 .
C. m  0 và m  1.
D. m  0 và m  1. Hướng dẫn giải Chọn A. 1
Xét m  0 phương trình thành 2
x 1  0  x  nên ta loại m  0 . 2
Xét m  0 phương trình có biệt thức   m  2
1  mm   1  m 1.
Phương trình đã cho vô nghiệm khi   0  m  1 thỏa m  0 . Câu 5. Cho phương trình 2
ax bx c  0 a  0 . Phương trình có hai nghiệm âm phân biệt khi và chỉ khi:   0   0   0    0   A. S  0 . B.  . C. S  0 . D. S  0 .  P  0 P  0    P  0  P  0  Hướng dẫn giải Chọn C.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 224
Trần Đình Cư. SĐT: 0834332133
Phương trình có hai nghiệm âm phân biệt thì tổng hai nghiệm âm và tích hai nghiệm dương. Câu 6. Phương trình 2
ax bx c  0 có nghiệm duy nhất khi và chỉ khi: a  0 a  0
A. a  0 và b  0 . B.  hoặc  .   0 b   0 a  0
C. a b  0 . D.  .   0 Hướng dẫn giải Chọn B.
Nếu a  0 thì phương trình đã cho là PTB2 nên có nghiệm duy nhất khi   0 .
Nếu a  0 ta được phương trình bx c  0 . Phương trình này có nghiệm duy nhất khi và chỉ khi b  0 . Câu 7. Phương trình 4 2
x  2mx  2m  
1  0 (1) có 4 nghiệm phân biệt khi và chỉ khi: 1 1 A. m  .
B. m  và m  1.
C. m   . D. m  1. 2 2 Hướng dẫn giải Chọn B. Đặt 2
t x ,t  0 , khi đó phương trình trở thành: 2
t  2mt  2m   1  0   * .
Để phương trình đã cho có bốn nghiệm phân biệt khi và chỉ khi   * có hai nghiệm dương phân biệt    0 2
m  2m 1  0 m  1  1   m   
S  0  2m  0  m  0   2 . P  0     2m 1  0  1 m  1 m   2 1 Câu 8.
Vậy m  và m  1 thỏa mãn yêu cầu bài toán. Tìm tất cả các tham số m để phương 2 trình  2
m  9 x m 3 nghiệm đúng với mọi x . A. m  3 . B. m  3 .
C. Không tồn tại m . D. m  3 . Hướng dẫn giải Chọn D. m  3  0 Phương trình  2
m  9 x m 3 nghiệm đúng với mọi x khi   m  3 . 2 m  9  0
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 225
Trần Đình Cư. SĐT: 0834332133 Câu 9.
Tìm tất cả các giá trị của tham số m để hai đồ thị hàm số 2
y  x  2x  3 và 2
y x m có điểm chung. 7 7 7 7 A. m   . B. m   . C. m   . D. m   . 2 2 2 2 Hướng dẫn giải Chọn C.
Phương trình hoành độ giao điểm 2 2
x  2x  3  x m 2
 2x  2x m 3  0  * 7 
có nghiệm khi   2m  7  0  m  . 2
Câu 10. Có tất cả bao nhiêu giá trị nguyên của tham số m 10
 ;10 để phương trình  2
m  9 x  3mm 3 có nghiệm duy nhất? A. 2 . B. 21. C. 19 . D. 18 . Hướng dẫn giải Chọn C. Phương trình  2
m  9 x  3mm 3 có nghiệm duy nhất khi và chỉ khi 2
m  9  0  m  3 . Vì m 10
 ;10 nên m 10  ;10\  3 .
Vậy có 19 giá trị nguyên của m để  2
m  9 x  3mm 3 có nghiệm duy nhất.
Câu 11. Tìm giá trị của tham số m để phương trình 2 2
mx  2  m m x  3m vô nghiệm. 1 A. m  2 . B. m  0 . C. m   . D. m  1. 2 Hướng dẫn giải Chọn B. 2 2
mx  2  m m x  3m   2 m m 2
x m  3m  2   * . Xét 2
m m  0  m  0  m  1. Với m  0 ,  
*  0x  2 , phương trình vô nghiệm. Với m  1,  
*  0x  0, phương trình có vô số nghiệm. 2 m  3x  2 m  2 Với m0;  1 ,   *  x   , nên   * có nghiệm duy nhất. 2 m m m
Vậy m  0 thì phương trình đã cho vô nghiệm.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 226
Trần Đình Cư. SĐT: 0834332133
Câu 12. Điều kiện cần và đủ để phương trình 2
mx  2m  
1 x m  0 có hai nghiệm phân biệt là 1 1 1
A. m  0 , m   . B. m  . C. m   . D. m  0 . 2 2 2 Hướng dẫn giải Chọn A. m  0
Phương trình có hai nghiệm phân biệt   . '  0
Ta có:   m  2 2 '
1  m  2m 1.    m  0 m 0  Hệ có nghiệm:    1 . '  0 m    2 m  0  Vậy  1 cần tìm. m    2
Câu 13. Phương trình m   2
1 x  3x 1  0 có nghiệm khi và chỉ khi 5 5 5 5 A. m   . B. m   . C. m   . D. m   , 4 4 4 4 m  1. Hướng dẫn giải Chọn A. 1
Trường hợp 1: Xét m  1, phương trình có nghiệm x  . 3
Trường hợp 2: Xét m  1,   9  4m  
1  4m  5 . Phương trình có nghiệm khi   0  4m  5  5 0  m   . 4 5
Vậy phương trình đã cho có nghiệm khi m   . 4
Câu 14. Với m bằng bao nhiêu thì phương trình mx m 1  0 vô nghiệm? A. m  0 .
B. m  0 và m  1. C. m  1. D. m  1. Hướng dẫn giải Chọn A.m  0 m  0
Phương trình mx m 1  0 vô nghiệm khi     m  0 . m 1  0 m 1
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 227
Trần Đình Cư. SĐT: 0834332133
Câu 15. Có bao nhiêu giá trị thực của m để phương trình  2 m m 2
x  2x m 1 vô nghiệm? A. 2 . B. Đáp án khác. C. 3. D. 1. Hướng dẫn giải Chọn D. Ta có  2 m m 2
x  2x m 1   2 m m   2 2 x m 1. 2
m m  2  0
Để phương trình vô nghiệm thì   m  2 . 2 m 1  0
Câu 16. Cho phương trình  2 m  
1 x m 1  0  
1 . Trong các kết luận sau kết luận nào đúng?
A. Với m  1 phương trình   1 có nghiệm duy nhất.
B. Với m  1 phương trình   1 có nghiệm duy nhất.
C. Với m  1 phương trình   1 có nghiệm duy nhất.
D. Cả ba kết luận trên đều đúng. Hướng dẫn giải Chọn C.     2 1 m  
1 x  m 1 Phương trình  
1 có nghiệm duy nhất khi 2
m 1  m  1  .  1   1 
Câu 17. Tất cả các giá trị của tham số m để phương trình 2 x   2m x  1  0  có 2     x   x  nghiệm là 3   3 3  A. m ;   . B. m ;    ;     . 4   4 4   3  3 3  C. m  ;    . D. m  ;  . 4    4 4  Hướng dẫn giải Chọn B.  1   1  2  1   1  Ta có 2 x   2m x  1  0   x   2m x  1  0 2     x   x       x   x  1
Đặt x   t , t  2 ta được 2
t  2mt 1  0 . x
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 228
Trần Đình Cư. SĐT: 0834332133
Phương trình luôn có hai nghiệm t  0  t  phương trình có nghiệm khi và chỉ khi 1 2
phương trình có ít nhất một nghiệm t sao cho t  2 , hay ít nhất một trong hai số 2;  2  3  f 2  0 3 4m  0 m  
phải nằm giữa hai nghiệm t , t ; hay   4   . 1 2   f   2    0 3 4m  0 3 m     4
Câu 18. Tìm tất cả các giá trị thực của m để phương trình 2
x  4x  6  3m  0 có nghiệm thuộc đoạn  1  ;  3 . 2 11 11 2 A. m  . B.   m   . 3 3 3 3 2 11 C. 1   m   . D.   m  1  . 3 3 Hướng dẫn giải Chọn B. Ta có: 2
x  4x  6  3m  0 2
 3m  x  4x  6 .
Số nghiệm của phương trình 2
x  4x  6  3m  0 là số nghiệm của đường thẳng y  3m và parabol 2
y  x  4x  6 .
Bảng biến thiên của hàm số 2
y  x  4x  6 trên đoạn  1  ;  3 :
Phương trình có nghiệm thuộc đoạn  1  ;  3  11   3m  2  11 2    m   . 3 3
Câu 19. Số giá trị nguyên của tham số thực m thuộc đoạn  10
 ;10 để phương trình 2
x x m  0 vô nghiệm là A. 21. B. 9. C. 20 . D. 10 . Hướng dẫn giải Chọn B. Để phương trình 2
x x m  0 vô nghiệm     2 1
1  4.1.m  0  1 4m  0  m  . 4
Vậy số các trị nguyên của tham số thực m thuộc đoạn  10
 ;10 để phương trình 2
x x m  0 vô nghiệm là m 1;2;3;4;5;6;7;8;9;1  0
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 229
Trần Đình Cư. SĐT: 0834332133
Câu 20. Có bao nhiêu giá trị nguyên của m để phương trình 2 2
x  4 x 1  m   1  0 có 4 nghiệm phân biệt A. 1. B. 0 . C. 2 . D. Vô số. Hướng dẫn giải Chọn B.
Điều kiện xác định x   . Đặt 2
t x 1 , t  1. Phương trình trở thành 2
t 1 4t m 1  0 2
t  4t m . 2
Để phương trình có 4 nghiệm phân biệt thì phương trình 2 có hai nghiệm phân biệt lớn hơn 1. Vẽ BBT ta có Dựa BBT ta có 4   m  3
 . Vậy không có giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Câu 21. Để phương trình sau có 4 nghiệm phân biệt: 2 2
10x  2x  8  x  5x a . Giá trị của tham số a là 43  45
A. a 1;10. B. a 1. C. 4  a  . D. a  4; . 4  4    Hướng dẫn giải Chọn C.
Phương trình đã cho tương đương: 2 2
2 x  5x  4  x  5x a ,   1 . Đặt 2
t x  5x a . Phương trình  
1 trở thành: 2 t  4  a t , 2 t  0
t  2a 8
Phương trình 2  
, để phương trình  
1 có 4 nghiệm phân biệt thì 2  2a  8 t   3
phải có 2 nghiệm phân biệt, tức là 2a  8  0  a  4 ,  .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 230
Trần Đình Cư. SĐT: 0834332133 2
x  5x a  2a 8 2
x  5x  8  a  0
Khi đó, thay lại ta có:    . Điều kiện để   1 2
3x 15x  3a  2a 8 2
3x 15x a  8  0
có 4 nghiệm phân biệt là mỗi phương trình bậc 2 ở trên có 2 nghiệm phân biệt.  7
  25  4 8  a  0   a  1    7 43 Vậy  4     a  . 2
  15  4.3. a  8  0  43 4 4 2   a   4 43
So với điều kiện  , suy ra 4  a  . 4
Câu 22. Có tất cả bao nhiêu giá trị nguyên không dương của tham số m để phương trình
2x m x 1 có nghiệm duy nhất? A. 4 . B. 3. C. 1. D. 2 . Hướng dẫn giải Chọn B. x 1 0  x 1 
2x m x 1     . 2x m  2  x  2 1
x  4x 1 m  0  *
Phương trình có nghiệm duy nhất khi hệ có nghiệm duy nhất. Xét 2
x  4x 1 m  0 ;    3 m TH1:    0  m  3
 thì có nghiệm kép x  2 1 . TH2:    0  m  3
 thì phương trình có nghiệm duy nhất khi có 2 nghiệm thỏa
x  1  x   x 1 x 1  0  x x x x 1 0 1 m  4 1 0  m  2  . 1  2  1 2  1 2 1 2
m không dương nên m  3;  1  ;  0 .
Câu 23. Phương trình  2 m m   2 4
3 x m  3m  2 có nghiệm duy nhất khi: A. m  3 .
B. m  1 và m  3. C. m  1.
D. m  1 hoặc m  3 . Hướng dẫn giải Chọn B. Phương trình  2 m m   2 4
3 x m  3m  2 có nghiệm duy nhất m 1 2
m  4m  3  0   . m  3
Câu 24. Tìm m để phương trình m   4 2 2
1 x mx m 1  0 có ba nghiệm phân biệt. A. m  1  . B. m 1. C. m  1  . D. m  0 .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 231
Trần Đình Cư. SĐT: 0834332133 Hướng dẫn giải Chọn C.
+ Khi m 1  0  m 1 phương trình cho trở thành: 2
x  0  x  0
Do đó: m 1 không thỏa mãn đề bài.
+ Khi m 1  0  m  1 Đặt 2
t x t  0 .
Phương trình cho trở thành m   2 2
1 t mt m 1  0   1 .
Phương trình cho có ba nghiệm phân biệt   
1 có hai nghiệm t ,t thoả t  0  t 1 2 1 2
Khi t  0  m  1 . Do có hai nghiệm phân biệt nên m  1. 1 1 Với m  1   t  . 2 2  5 m  
Do đó phương trình   1 có nghiệm khi  4   ** m 1 5 Từ   * và   ** phương trình  
1 có nghiệm m   . 4
x  2mx 3
Câu 25. Có tất cả bao nhiêu giá trị của m để phương trình  0 có nghiệm duy x 1 nhất? A. 0 . B. 2 . C. 3. D. 1. Hướng dẫn giải Chọn C.
Điều kiện: x  1.  x  2 
x  2mx  3  0  x2mx3  0   3  x 1 x   m 3 
Vậy để phương trình có nghiệm duy nhất thì m  0 hoặc 1  m  3  m 3  hoặc  2   m  6 m
Câu 26. Tìm tất cả các giá trị của m để phương trình 2
x  2x  3  m  0 có nghiệm x 0;4.
A. m   ;5 . B. m  4;    3 . C. m  4;  5.
D. m 3; Hướng dẫn giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 232
Trần Đình Cư. SĐT: 0834332133 Chọn C.
Cách 1: Phương trình có nghiệm khi   4  m  0  m  4    1 .
Khi đó, phương trình có nghiệm x  1 4  m , x  1 4  m . 1 2 0  x  4
Để phương trình có nghiệm x 0;4 thì 1  0  x  4  2  4 m 1 
0 1 4  m  4
 4  m  3  4  m 1 m  3         m  5  .
0 1 4  m  4
 4  m  1  4  m  3 m  5 
 4  m  3
So với điều kiện   1 , m  4; 
5 thì phương trình đã cho có nghiệm x0;4.
Cách 2: Phương trình đã cho tương đương 2
m x  2x  3.
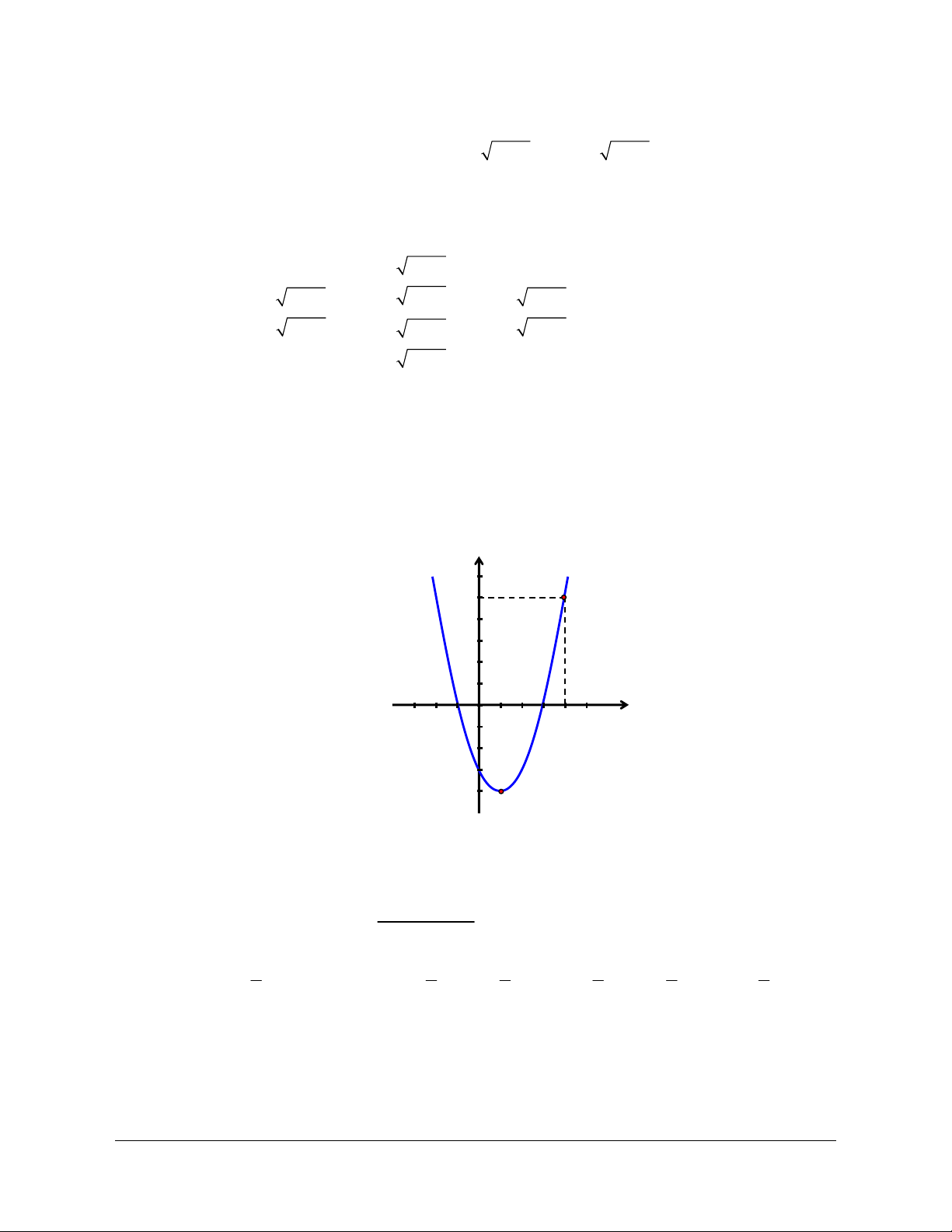
Đặt y f x 2
x  2x  3.
Ta có đồ thị hàm số y f x như sau: y 5 1 O x 1 4 4
Dựa vào đồ thị. Để phương trình y f x 2
x  2x  3  m có nghiệm x 0;4 thì 4   m  5
22  2m x
Câu 27. Tìm m để phương trình
x  2m có 2 nghiệm phân biệt. x 1 5 5 3 5 1 5
A. m  và m  1.
B. m  và m  . C. m  và m  . D. m  . 2 2 2 2 2 2 Hướng dẫn giải Chọn B. Điều kiện: x  1
 . Với điều kiện đó, phương trình đã cho tương đương với:
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 233
Trần Đình Cư. SĐT: 0834332133
x 2mx  1  222mx  2x  2mx x  2m  4 4m  2x  2
x  2m  3 x  2m  4  0   * .
Phương trình đã cho có 2 nghiệm phân biệt khi và chỉ khi phương trình   * có hai   
2m32 42m 4  0 nghiệm phân biệt khác 1         2
1  2m  3.  1  2m  4  0 2
4m  20m  25  0  4m  6  0  5     m m  2 2 5  0     2  . 4m  6 3 m   2
Câu 28. Có bao nhiêu giá trị nguyên của m để phương trình 2
x  2x  3  2m  0 có đúng một
nghiệm x 0;4. A. 5. B. 4. C. 6 . D. 9. Hướng dẫn giải Chọn A. Ta có 2
x  2x  3  2m  0 2
x  2x  3  2m .
Để phương trình đã cho có đúng một nghiệm x 0;4 thì đường thẳng y  2m cắt đồ thị hàm số 2
y x  2x  3 trên 0;4 tại một điểm duy nhất. Lập bảng biến thiên    2m  4  m 2
Dựa vào bảng biến thiên ta có:    3 5 .  3   2m  5   m   2 2
Vậy các giá trị nguyên của m thỏa mãn là m  2;  1  ;0;1;  2
Câu 29. Cho phương trình 3
x   m   2 2
1 x  4m  
1 x  2m 1  0 . Số các giá trị của m để
phương trình có một nghiệm duy nhất? A. 0 . B. vô số. C. 1. D. 2 . Hướng dẫn giải Chọn C.
Tập xác định D   .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 234
Trần Đình Cư. SĐT: 0834332133
Phương trình tương đương với    x 1 x   2
1 x  2mx  2m   1  0   . 2
x  2mx  2m 1  0  *
Ta có, phương trình  
* có   m m   m  2 2 2 1 1  0 .
Phương trình đã cho có duy nhất một nghiệm nếu phương trình  
* có nghiệm kép x 1
   0  m 1.
Thay m 1 vào phương trình   * , ta được 2
x  2x 1  0  x 1 .
Vậy với m 1 thì phương trình đã cho có một nghiệm duy nhất. x m 2m
Câu 30. Tập hợp các giá trị của m để phương trình x 1   có nghiệm là x 1 x 1 1   1   1  A. ;    . B. 1; . C. ;    . D. ;    . 3   3   3  Hướng dẫn giải Chọn C.
Điều kiện x  1. Khi đó, ta có x m 2m m x 1  
x 1 x m  2m  2x  3m  3 1 1  x  . x 1 x 1 2 3m 1
Phương trình đã cho có nghiệm khi  1 1  m  . 2 3
Câu 31. Cho hàm số f x  mx  3 m , với m là tham số thực. Có bao nhiêu giá trị nguyên của
m để phương trình f x  0 không có nghiệm thuộc đoạn 0;2 ? A. vô số B. 5. C. 3. D. 4 . Hướng dẫn giải Chọn D.
Ta có f x  0  mx  3 m  0  mx m 3
Với m  0 thì phương trình tương đương: 0  3  . m  3
Với m  0 thì phương trình có nghiệm x m
Để phương trình không có nghiệm thuộc đoạn 0;2 thì
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 235
Trần Đình Cư. SĐT: 0834332133 m  3 m  3  0  0  m  m 0  m  3      m  3 m  3   3  m  0  2  0  m  m
Mà m  m 2  ; 1  ;1;  2 .
Vậy có 4 giá trị của m thỏa mãn yêu cầu bài toán.
Câu 32. Tìm các giá trị của m để phương trình 2 x 1  x m có nghiệm: A. m  2 . B. m  2 . C. m  2 . D. m  2 . Hướng dẫn giải Chọn C.
2 x 1  x m   1
Phương trình tương đương: x m  0  x  m     4   x   2 2
1  x  2mx m 2 x   m  2 2
2 x m  4  02 Phương trình  
1 có nghiệm  pt 2 có ít nhất một nghiệm lớn hơn hoặc bằng m .    8 4m Phương trình  
1 có nghiệm    0  m  2
x  2  m  8  4m 1  .
x  2  m  8  4m  m  2 Vậy m  2 .
Câu 33. Cho biết tập hợp tất cả các giá trị của tham số m để phương trình  1   1  a 2   2 x   3 x   5m 1  0 
có nghiệm là S   ;  , với a , b là các số 2       x   x   ba
nguyên dương và là phân số tối giản. Tính T  . a b b A. T  5  . B. T  5 . C. T 11. D. T  55 . Hướng dẫn giải Chọn B. 1
Đặt x   t , t  2 khi đó phương trình trở thành 2
2t  3t  5m  3  0 x  1   1  Phương trình 2 2 x   3 x   5m 1  0 
có nghiệm khi và chỉ khi phương trình 2     x   x
có nghiệm t thỏa mãn t  2 .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 236
Trần Đình Cư. SĐT: 0834332133
Số nghiệm của phương trình bằng số giao điểm của parabol P 2
: y  2t  3t  3 và
đường thẳng d : y  5m . Xét parabol P 2
: y  2t  3t  3 ta có bảng biến thiên như sau 3 t  2  2 4    2
y  2t  3t  3 33 11  1  8
Từ bảng biến thiên ta có phương trình có nghiệm khi và chỉ khi 5m  1  1  m   . 5  1  a 1
Vậy khi m   ;  
 thì phương trình có nghiệm    T  5 .  5  b   5
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 237
Trần Đình Cư. SĐT: 0834332133
BÀI 3. PHƯƠNG TRÌNH VÀ HỆ PHƯƠNG TRÌNH BẬC NHẤT NHIỀU ẨN
A. KIẾN THỨC CƠ BẢN CẦN NẮM
I – ÔN TẬP VỀ PHƯƠNG TRÌNH VÀ HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
1. Phương trình bậc nhất hai ẩn
Phương trình bậc nhất hai ẩn x, y có dạng tổng quát là ax +by = c ( ) 1 , trong đó , a , b c là các
hệ số, với điều kiện a và b không đồng thời bằng 0. CHÚ Ý
a) Khi a = b = 0 ta có phương trình 0x + 0y = .c Nếu c ¹ 0 thì phương trình này vô nghiệm, còn nếu
c = 0 thì mọi cặp số (x ; 0 y đều là nghiệm. 0 ) b) Khi a c
b ¹ 0, phương trình ax + by = c trở thành y = - x + (2) b b Cặp số (x ; M x ; 0 y
là một nghiệm của phương trình ( ) 1 khi và chỉ khi điểm
( 0 y thuộc đường thẳng 0 ) 0 ) (2).
Tổng quát, người ta chứng minh được rằng phương trình bậc nhất hai ẩn luôn luôn có vô số nghiệm.
Biểu diễn hình học tập nghiệm của phương trình của phương trình ( )
1 là một đường thẳng trong mặt
phẳng tọa độ Oxy.
2. Hệ hai phương trình bậc nhất hai ẩn ìï + =
Hệ phương trình bậc nhất hai ẩn có dạng tổng quát là ï 1 a x 1 b y 1 c í (3) ï + = ïî 2 a x 2 b y 2 c
Trong đó x, y là hai ẩn; các chữ số còn lại là hệ số. Nếu cặp số (x ; x ; 0 y
đồng thời là nghiệm của cả hai phương trình của hệ thì ( 0 y được gọi là một 0 ) 0 )
nghiệm của hệ phương trình (3).
Giải hệ phương trình (3) là tìm tập nghiệm của nó.
II – HỆ BA PHƯƠNG TRÌNH BẬC NHẤT BA ẨN
Phương trình bậc nhất ba ẩn có dạng tổng quát là ax +by + cz = d, trong đó x, y, z là ba ẩn; , a , b , c d là các hệ số và , a ,
b c không đồng thời bằng 0. ìï + + = 1 a x 1 b y 1 c z 1 d ï
Hệ phương trình bậc nhất ba ẩn có dạng tổng quát là ïïa
í x + b y + c z = d 4 2 2 2 2 ( ) ïïï + + = ïî 3 a x 3 b y 3 c z d3
Trong đó x, y, z là ba ẩn; các chữ còn lại là các hệ số.
Mỗi bộ ba số (x ; y ; 0 0 z
nghiệm đúng ba phương trình của hệ được gọi là một nghiệm của hệ 0 ) phương trình (4).
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 238
Trần Đình Cư. SĐT: 0834332133
Dạng 1: Giải và biện luận hệ phương trình bậc nhất hai ẩn 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
2x  4  y
Ví dụ 1. Giải hệ phương trình   4
x  2y  5  0 Lời giải
2x  4  y
2x  4  y
2x  4  y Ta có:      .
4x  2y  5  0 4x  2 
2x  45  0  1  3  0
Vậy hệ phương trình đã cho vô nghiệm. ìï6 5 ï + = 3 ïïx y
Ví dụ 2: Giải hệ phương trình ïí ï9 10 ïï - =1 ïïx y î Lời giải
Điều kiện: x  0, y  0 . ìï6 5      ï 1 1 + = 3 1 1 ï 6  5  3  ï     x y   x   y  x 3 x  3 Ta có ïí    . ï    9 10 ï      1 1 y  5 ï - =1 1 1   ï 9 10  1 ï     x y î   x   y   y 5
Vậy y x  5  3  2 .  4 1   5 x 2 y
Ví dụ 3: Giải hệ phương trình  5 2    3 x  2 y Lời giải  4 1  1   5 1 x 2 y x 2 x  3 Ta có:      . 5 2 1   y 1   3 1 x  2 y  y
mx y  2m
Ví dụ 3: Tìm m để hệ phương trình  vô nghiệm
4x my m  6 Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 239
Trần Đình Cư. SĐT: 0834332133 Cách 1.
Từ phương trình đầu ta có y mx  2m * .
Thế * vào phương trình thứ hai ta được:
x m mx m  m    2  m  2 4 2 6 4
x  2m m  6 ** .
Hệ phương trình vô nghiệm khi và chỉ khi phương trình ** vô nghiệm. 2  4  m  0
** vô nghiệm khi và chỉ khi:   m  2 . 2
2m m  6  0 Cách 2. m 1  2 D
 4  m  2  m2  m . 4 m 2m 1  2 D   2
m m  6  m   m  . x  2 2  3 m  6 m m 2m 2 D
m  2m m m  . y  2 4 m  6
Hệ phương trình vô nghiệm khi và chỉ khi: D  0 
D  0  m   . x 2 D  0  y
mx  2y 1
Ví dụ 4. Tìm m để hệ phương trình  có nghiệm
2x y  2 Lời giải
mx  2y  1(1) 
2x y  2 (2)
Từ pt  y  2  2x . Thế vào pt ta được:
mx  2(2  2x)  1  (m  4)x  5 (3)  m  4
 thì pt có nghiệm duy nhất  Hệ đã cho có nghiệm duy nhất.
mx  (m 1)y  3m
Ví dụ 5. Tìm m để hệ phương trình: x  2my m  2 có nghiệm
x  2y  4 
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 240
Trần Đình Cư. SĐT: 0834332133 Lời giải
mx  (m 1)y  3m   1 
Xét hệ x  2my m  2 2 ,
x  2y  4  3
Trừ theo vế hai phương trình 2 và 3 ta được: 2m  
1 y  2  m 4 Nếu m  1
 thì 4 vô nghiệm nên hệ vô nghiệm. 2  5m  2 Nếu m m  1
 thì 4  y
, thay vào 3 được x  . 2m   1 m 1
Thế các giá trị x, y tìm được vào  
1 ta được phương trình:
5m  2    2 . 1 . m m m    m   3m m 1 2 1
 2m5m  2 m  
1 2  m  6mm   1 m 1 2 5 
m  3m  2  0  2 m    5
mx y  3
Ví dụ 6. Tìm tất cả các giá trị của m để hệ phương trình  có nghiệm duy nhất
x my  2m 1 x ; thỏa mãn 2 2 x y 10 . 0 0 y  0 0 Lời giải
Hệ phương trình có nghiệm duy nhất khi 2
m 1  0  m  1 . Khi đó  1 y  3  
mx y  3   3 mx x ymx     m 1         .
x my  2m 1       1 3  2 1 m x m mx m x  2m  3  2  1   y m   m 1  1   0 x  
Vậy hệ phương trình có nghiệm duy nhất là: m 1  . 2m  3 y  0  m 1 m  0 Nên:  x y
10  1 2m  32 10.m  2 2 2 1 2
 6m  8m  0  4  (TM ) . 0 0 m   3
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 241
Trần Đình Cư. SĐT: 0834332133
3. Bài tập trắc nghiệm 2 3   13 x y Câu 1.
Hệ phương trình  có nghiệm là 3 2   12  x y 1 1 1 1 1 1 1 1
A. x  ; y   .
B. x   ; y  .
C. x  ; y  .
D. x  ; y  . 2 3 2 3 2 3 2 3 Hướng dẫn giải Chọn D. x  0 Điều kiện  . y  0 1 1
2a  3b 13 a  2
Đặt a  và b  thì hệ trở thành    . x y 3
a  2b 12 b   3 1 1
Vậy nghiệm của hệ là x  ; y  . 2 3 x my 1 Câu 2.
Cho hệ phương trình 
I , m là tham số. Mệnh đề nào sai?
mx y 1
A. Hệ I  có nghiệm duy nhất m  1.
B. Khi m  1 thì hệ I  có vô số nghiệm.
C. Khi m  1 thì hệ I  vô nghiệm.
D. Hệ I  có vô số nghiệm. Hướng dẫn giải Chọn D. 1 Hệ  m
I  có nghiệm duy nhất    m  1  , A đúng. m 1 1 Hệ  m
I  vô số nghiệm  
1  m 1, B đúng. Hệ I  vô nghiệm m 1 1 
m  1  m  1  , C đúng. m 1 D sai.
2x y m 1 Câu 3.
Cho hệ phương trình 
. Giá trị m thuộc khoảng nào sau đây để hệ 3
x y  4m 1
phương trình có nghiệm duy nhất  x ;
thỏa mãn 2x  3y  1? 0 0 y  0 0
A. m5; 9 . B. m 5;  1 .
C. m0; 3 . D. m 4;  1 . Hướng dẫn giải Chọn B.
2x y m 1 x m   
. Vậy phương trình có nghiệm duy nhất  ; m m   1 mà 3
x y  4m 1 y m 1
2x  3y  1  2m  3m  
1 1  m  4 . Vậy m 5;  1 . 0 0
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 242
Trần Đình Cư. SĐT: 0834332133
mx y  3 Câu 4.
Có bao nhiêu giá trị m nguyên dương để hệ phương trình  có nghiệm duy
2x my  9 nhất  ;
x y sao cho biểu thức A  3x y nhận giá trị nguyên A. 4. B. 2. C. 3. D. 1. Hướng dẫn giải Chọn B. m 1  Ta có 2 D
m  2  0 , m
  nên hệ phương trình luôn có nghiệm duy nhất. 2 m 3 1  m 3 D
 3m  9 ; D   9m  6 . x 9 m y 2 9  3m  9 x   2 
Vậy hệ luôn có nghiệm duy nhất là m  2  . 9m  6  y  2  m  2
33m  9 9m  6 33
Ta có A  3x y    . 2 2 m  2 m  2 2 m  2 Để A nguyên thì 2
m  2 là ước của 33 mà 2
m  2  2 nên ta có các trường hợp sau: + TH1: 2
m  2  3  m  1  . + TH2: 2
m  2  11  m  3  . + TH3: 2
m  2  33  m   31 .
Vậy có 2 giá trị nguyên dương của m để A nguyên.
(m 1)x y m  2 Câu 5.
Gọi S là tập hợp các giá trị của tham số m để hệ phương trình  có
mx  (m 1)y  2 
nghiệm là (2; y ) . Tổng các phần tử của tập 0 S bằng A. 0. B. 1. C. 2. D. 3. Lời giải Chọn B Ta có:
D   m  2 2
1  m  m m 1  0, m    D   m m
  m m x   1  2 2 2 3 4 D  2 m   m m
 m m y   1  2 2 4 2 2  D m  3m  4 x x    2   
Suy ra với mọi giá trị của D m m 1
m thì hệ có nghiệm duy nhất:  2 D    y m 4m 2 y   2  D m m 1 2 m  3m  4 m  1 
Để (2; y ) là nghiệm của hệ thì 2
 2  m m  2  0  0 2  m m 1 m  2
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 243
Trần Đình Cư. SĐT: 0834332133 Vậy S   1  ;  2
mx y  2m Câu 6.
Hệ phương trình 
vô nghiệm khi giá trị m bằng
4x my m  6 A. m  2 . B. m  2  . C. m 1. D. m  1  . Lời giải Chọn B m 1 2m 1 m 2m Ta có 2 D   4  m ; 2 D   2
m m  6 ; 2 D   m  2m 4  m x m  6  m y 4 m  6 Xét 2
D  0  4  m  0  m  2
Khi m  2  D D  0 hệ phương trình có vô số nghiệm x y Khi 2
m    D  4
  0 hệ phương trình vô nghiệm x
x  3y mCâu 7. Gọi
có vô số nghiệm. Khi đó: 0
m là giá trị của m để hệ phương trình  2
mx y m   9  1   1 
A. m  1;  . B. m  0; . 0      2  0  2   1   1  C. m  ; 2 . D. m   ;0 . 0      2  0  2  Lời giải Chọn B 1 3 Ta có D  1 3m . m 1
Để hệ phương trình vô số nghiệm thì D D D  0 x y 1
Ta có D  0  1 3m  0  m  3  1  1  1 x  3y x  3y x  3y  1  3  3     3
Thay m  vào hệ phương trình ta có:      3 1 1 2 1 1 1  x yx y       x  3y  3 3 9 3 9  3 1
Vậy m  hệ phương trình vô số nghiệm. 3
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 244
Trần Đình Cư. SĐT: 0834332133
2x y  2  a
Câu 8. Cho hệ phương trình:  . Gọi
là giá trị của tham số a để tổng bình phương  0 a
x  2 y a 1
hai nghiệm của hệ phương trình đạt giá trị nhỏ nhất. Chọn khẳng định đúng trong các khẳng định sau:
A. a  10;0 B. 5;8 C. a  0;5 D.8;12 0   0   Lời giải Chọn C.  5  a  2 x
x y  2  a
4x  2y  4  2a  5 Ta có :     
x  2y a 1
x  2y a 1 3ay   5 2 2 2 2  5  a  9a
10a 10a  25 1 1  1  9  9 2 2  x y        2
2a  2a  5   2a     5 25 25 5 5    2 2      10   1
Đẳng thức xảy ra khi và chỉ khi a  . 2
Dạng 2: Giải và biện luận hệ phương trình bậc nhất ba ẩn 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
2x y z  3  
Ví dụ 1. Giải hệ phương trình x y z  3
2x  2y z  2   Lời giải
2x y z  3  x  8   
x y z  3  y  1  2 
x  2 y z  2  z  12  
Vậy nghiệm duy nhất của hệ phương trình là  ;
x y; z    8  ; 1  ;12
2x  3y  4  0 
Ví dụ 2. Tìm giá trị thực của tham số m để hệ phương trình 3
x y 1  0 có duy nhất một
2mx 5y m  0  nghiệm Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 245
Trần Đình Cư. SĐT: 0834332133
2x  3y  4  0 x 1   3
x y 1  0  y  2  m 10. 2 
mx  5y m  0 2 .
m 2  5.2  m  0   Vậy m  10 .
mx ny pz  6 
Ví dụ 3. Cho  x; y; z là nghiệm của hệ phương trình 2mx  3ny pz  1 
mx  7ny 10pz  1  5 
biết hệ có nghiệm  x; y; z  1;2;3 . Tìm m, , n p Lời giải
mx ny pz  6 
Hệ phương trình 2mx  3ny pz  1 
có nghiệm  x; y; z  1;2;3 nên ta có
mx  7ny 10pz  1  5 
m  2n  3p  6 m 1  
2m  6n  3p  1   n 1  
m 14n  30 p  15   p  1 
Vậy S m n p  111  3 .
3. Bài tập trắc nghiệm
x  2my z 1 m  0   Câu 1.
Khi hệ phương trình 2x my  2z  2 có nghiệm  ;
x y; z  với  4 , giá trị  m    x  
m  4 y z 1  3
T  2017x  2018 y  2017z là A. T  20  17 . B. T  2018 . C. T  2017 . D. T  20  18 . Hướng dẫn giải Chọn C.
x  2my z 1   1 
Kí hiệu 2x my  2z  2 2. x 
m  4 y z 1 3 m  0  x z 1 Do  4 , từ   1 và 3 ta có  . m    y  0  3
Ta có T  2017x  2018y  2017z  2017 x z  2017 .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 246
Trần Đình Cư. SĐT: 0834332133
Dạng 3: Giải và biện luận hệ phương trình bậc cao 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng x y 1
Ví dụ 1. Giải hệ phương trình:  2
x  2x  2y  2  0 Lời giảix y 1   1  2
x  2x  2y  2  0  2 Ta có:  
1  y  1 x
Thế vào phương trình 2 ;ta được : 2
x x    x 2 2 2 1
 2  0  x  4x  4  0  x  2
Với x  2  y  1 Hệ có 1 nghiệm :  ;
x y  2;   1 2
x xy  2
Ví dụ 2. Giải hệ phương trình:  2 2
2x xy y  9 Lời giải Chọn D 2 x
 1 t   2 (1)
Đặt y tx thay vào hệ ta được  . 2 x   2
2  t t   9 (2) t  5 2 2  t t 9 Do 
t  1 không thỏa mãn nên suy ra 2
  2t 11t  5  0  1 . 1 t 2 t   2
+ Với t  5 thay vào ta được 2 4x  2 . 1 x  2 1
+ Với t  thay vào ta được 2 x  4  . 2  x  2  1
Vậy x  2  y 1 S x y  3 . 0 0 0 0
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 247
Trần Đình Cư. SĐT: 0834332133 2 2
ìïx + xy + y = 3
Ví dụ 3. Giải hệ phương trình ïí
ïx + xy + y = -1 ïî Lời giải (
ìï x+ y)2 -xy = ï 3 Hệ phương trình ï  í . (
ïï x+ y)+ xy =-1 ïî
Đặt S = x + y, P = . x y ( 2 S ³ 4P) 2 ìïP = S -3 2 2 ì ì ï ïS - P = 3 ïP = S -3 ï Ta được hệ mới ï ï ï í  í  íéS =1 2 ïS + P = -1 ï ïî ïS + S -2 = 0 ïê î ïïêS =-2 ïîë
Với S =1 P = -2 ìïx + y = -2 ìïx = -2- y ìïy = -1 Với ï ï ï
S = -2  P = 1  í  í  . ï í . x y = 1 ïî 2 ïx + 2x +1= 0 ïx = -1 ïî ïî
Vậy hệ phương trình có nghiệm ( ; x y) = (-1;- ) 1 .
xy  3x  2y 16
Ví dụ 4. Các nghiệm của hệ  là 2 2
x y  2x  4y  33 Hướng dẫn giải
xy  3x  2y 16 Ta có:   1 2 2
x y  2x  4y  33
xy  2x y  2  x 1 y  2  21  x  
1  y  2   x  
1   y  2  21     2 2 2    2 x  2x   1   2
y  4 y  4  38 x  
1   y  2  38 Đặt u x 1 ;
v y  2 ta được hệ phương phương uv
 u v  21 uv  
u v  21    2 2 u   v  38
u v2  2uv  38
P S  21
P S  21
Đặt S u v ; P uv ta được hệ phương phương    2
S  2P  38 2
S  2S 80  0 S  8  S 10   v  . P 13 P  31 S  8  + Khi 
thì u ; v là nghiệm của phương trình: 2
X  8X 13  0 P 13 u   4   3 u   4  3   v  v  4   3 v  4  3
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 248
Trần Đình Cư. SĐT: 0834332133 x 1 4   3
x 1 4  3   v 
y  2  4  3
y  2  4  3 x  3   3 x  3   3   v v  . y  2   3 y  2  3 S 10 + Khi 
thì u ; v là nghiệm của phương trình: 2
X 10 X  31  0 P  31 2 2
x  2xy 8x  3y 12y  9
Ví dụ 5. Giải hệ phương trình  2
x  4y 18  6 x  7  2x 3y 1  0  Hướng dẫn giảix  7   Điều kiện  1 * y    3 2 2
x  2xy  8x  3y 12y  9    1  . 2
x  4y 18  6 x  7  2x 3y 1  0  2 Có:   2
x   y   2 1 2
4 x  3y 12y  9  0 , ta coi  
1 là phương trình bậc hai ẩn x và x  3  y  9
y là tham số, giải x theo y ta được  , x y 1   2 3  x  9  7    y  Với 3
x  3y  9 thì *   1   . y    1  3  y    3
Với x y 1 thì   2 2 2
2  x  4x  6 x  7  2x 3x  2 14  0  x  3x  2  x  7 3  0
x  3x  2  
x  2  y  1 .  x  7  3
3. Bài tập trắc nghiệm 2 2
x y xy  7 Câu 1.
Hệ phương trình 
có tất cả các nghiệm là 2 2
x y xy  3 A.  ; x y   1  ; 2  ;  ; x y   2  ;  1 ;  ; x y   1  ;2;  ; x y  2;  1 . B.  ; x y   1  ; 2  ;  ; x y   2  ;  1 . C.  ;
x y  1; 2;  ; x y  2;  1 . D.  ; x y   1  ; 2  ;  ; x y   2  ;  1 ;  ;
x y  1; 2;  ; x y  2;  1 . Hướng dẫn giải Chọn D.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 249
Trần Đình Cư. SĐT: 0834332133 2 2
x y xy  7 2 2 x y  5 
 x y2  2xy  5 
 x y2  9  x y  3         2 2
x y xy  3 xy  2 xy  2 xy  2 x y  3 Với  thì  ;
x y  1; 2;  ; x y  2;  1 . xy  2 x y  3  Với  thì  ; x y   1  ; 2  ;  ; x y   2  ;  1 . xy  2 2
x  3x y Câu 2.
Hệ phương trình  có bao nhiêu nghiệm? 2
y  3y x A. 3. B. 2 . C. 1. D. 4 . Hướng dẫn giải Chọn B. 2
x  3x y    1  . 2
y  3y x  2 Lấy  1 trừ
2 theo vế ta được: y x 2 2
x y  4x  4 y   x y x y  4  0   . y  4  x 2
x  3x y 2
x  2x  0 x y  0 TH1:      . y xy xx y  2 2
x  3x y 2
x  4x  4  0 TH2:   
x y  2 . y  4  xy  4  x Vậy hệ có hai nghiệm.
 x y2   2 2
x y    2 2 2 5 4
6 4x  4xy y   0  Câu 3.
Hệ phương trình  1 có một nghiệm 2x y   3  2x yx ; . Khi đó 2 P x  0 0 y  0 y có giá trị là 0 17 A. 1. B. . C. 3. D. 2 . 16 Hướng dẫn giải Chọn A.
 x y2   2 2
x y    2 2 2 5 4
6 4x  4xy y   0   1  Ta có  1 . 2x y   3  2  2x y   x y 2 2
1  8x 12y  20xy  0   x y2x  3y  0   . 2x  3y
Với x y ta có   1 2  3x   3 2
 3x  3x 1  0 : phương trình vô nghiệm. x
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 250
Trần Đình Cư. SĐT: 0834332133  1 y   Với 2 2
x  3 y ta có   1 2  4y   3 2
 8y  6y 1  0   . 2y 1  y   4 1 3
Với y   x   P 1. 2 4 1 3 7
Với y   x   P  . 4 8 16 x y  2 Câu 4.
Cho hệ phương trình 
. Tìm tất cả các giá trị của m để hệ trên có 2 2 2
x y xy  4m  2m nghiệm.  1   1  A.  ;1  . B. 1; . C. 0;2 . D. ;    . 2    2   Hướng dẫn giải Chọn A.x y  2 x y  2     2 2 2
x y xy  4m  2mxy
  x y 2  4m  2mx y  2 x  2  y      2
2xy  4m  2m 2.  2  y 2
y  4m  2m (*)   * 2 2  2
y  4y  4m  2m  0
Hệ phương trình có nghiệm  (*) có nghiệm   '  0    2 4 2. 4
m  2m  0 1  2  8
m  4m  4  0   m  1. 2 2
x xy  3 Câu 5.
Hệ phương trình  có nghiệm khi 2 2
y xy m  4 m 1 A.  . B. m  1. C. m  1. D. m  1. m  1  Hướng dẫn giải Chọn A. 2
x xy  3  2 2 2
x y  2xy m 1  x y2 2  m 1. 2 2
y xy m  4 m 1
Phương trình này có nghiệm khi 2 m 1  0   . m  1 
 x y x y  4
Câu 6: Gọi (x; y) là nghiệm dương của hệ phương trình 
. Tổng x y 2 2
x y 128 bằng. A. 12 . B. 8 . C. 16 . D. 0 . Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 251
Trần Đình Cư. SĐT: 0834332133 Chọn C
ĐK: x y  0 x  8 Ta có : 2 2
x y x y  4  x y  8  x   2
y  16x  64 x  8 Thay 2
y  16x  64 vào PT 2 2
x y  128 ta được PT: 2
x 16x 192  0   . x  24  x  8 Suy ra PT có nghiệm 
. Vậy x y  16 y  8 3
x  2019y x Câu 7.
Hệ phương trình  có số nghiệm là: 3
y  2019x y A. 4 . B. 6 . C. 1. D. 3 . Lời giải Chọn D
Trừ hai phương trình theo vế ta được: 3 3
x  2019y y  2019x x y 2      1  3 x y 2 2
x xy y  2018  0   x y 2
x y  2018  y     0   x y 2 4      2  1  3 vì biểu thức 2 x y
 2018  y  0, x  , y   .  2  4
Với y x ta được: 3 2
x  2020x  0  x x  2020  0 x  0  y  0 
x  2020  y  2020  .
x   2020  y   2020 
Vậy hệ đã cho có 3 nghiệm.
x y xy  3
Câu 8. Giả sử  ;
x y là nghiệm của hệ  x1 y1  4  Tính x  2 y A. 2 . B. 3  . C. 1. D. 2  . Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 252
Trần Đình Cư. SĐT: 0834332133 xy  0 
. Điều kiện: x  1  . y  1  
x y xy  3
x y xy  3    .
x 1  y 1  4 
x y  2 x y xy 1 14 
a x y  a b  3  Đặt  a  2,
b  0 ta được hệ phương trình:  b   xy  2
a  2 a b 1 14 14   a  0 
a  2 a  a 32 2
1 14  2 a  5a 10 14  a  4
 a 5a 10  14  a2 2 a  14  a  14 a 2 a  6     
a  6  b  3. 2 3 
a  8a 156  0  26 a    3 a  6 x y  6  x y  6      . b  3  xy  3  xy  9 x  3
x , y là nghiệm của phương trình: 2
X  6 X  9  0  X  3   . y  3
Vậy x  2y  3 .
Câu 9: Tìm a để biểu thức F xy  2(x y) đạt giá trị nhỏ nhất, biết (x; y) là nghiệm của hệ
x y a phương trình  . 2 2 2
x y  6  a A. a  0 . B. a  3. C. a  1  . D. a  2  . Lời giải Chọn C
x y a
x y a
x y a Ta có:     
x y  6  a   x y  2 2 2 2 2 2
 2xy  6  a
xy a  3 Điều kiện tồn tại 2
x, y :  x y 2
xy a   2 a   2 4 4
3  a  4  2  a  2.
Khi đó: F a a   a  2 2 2 3 1  4  4 
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 253
Trần Đình Cư. SĐT: 0834332133
 min F  4  a  1(t / m) Do đó chọn đáp án C
Câu 10. Gọi  x ; y ; x ; 1 1   2 y
là hai nghiệm phân biệt của hệ phương trình 2  2 2
x y xy x y  8 
. Tính x x .  1 2
xy  3(x y)  1 A. 3. B. 2. C. 1. D. 0. Lời giải Chọn A
x y xy x y  
 x y2 2 2 8
 3xy x y  8 Ta có   
xy  3(x y)  1
xy  3(x y) 1
x y S Đặt 2 
; S  4P , hệ đã cho trở thành xy P S 1  (N ) 2 2
S S  3P  8
S S 31 3S  2  8
S 10S 11  0 P  2       3S P 1   
P 1 3SP  1 3SS  11   (L) P  34 t 1
Với S  1; P  2 ta có x; y là nghiệm của phương trình 2
t t  2  0   t  2 
Vậy hệ phương trình có nghiệm 1; 2  ; 2  ; 
1  x x  1 ( 2  )  2  1  3, chọn A. 1 2 3
x  2y x m
Câu 11. Tìm giá trị nguyên dương nhỏ nhất của tham số m để hệ  3 có nghiệm duy
y  2x y m nhất. A. m  2 . B. m  3 . C. m  4 . D. m  1. Lời giải Chọn B
Trừ vế với vế của hai phương trình ta được: 3 3
x  y  y  x  x  y .
Thay y bởi x vào một trong hai phương trình của hệ ta được: 3 m  x  3x . Xét hàm số   3
f x  x  3x trên R, ta có
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 254
Trần Đình Cư. SĐT: 0834332133 x  1  f 'x 2
 3x  3, f 'x  0   . x 1 Bảng biến thiên x -  -1 1 +  f'(x) + 0 - 0 + 2 +  f(x) - 2 - 
Từ bảng biến thiên suy ra: Phương trình có đúng một nghiệm  m  ;2  2; . Chọn B. 4 3 2 2
6x  (x x)y  (y 12)x  6 
Câu 12. Cho hệ phương trình  . Biết hệ có 2 nghiệm 4 2 2 2 2 5
 x  (x 1) .y 11x  5 
là: (x ; y ) ,(x ; y ). Đặt S =  . Khi đó S bằng: 1 1 2 2 1 y y2 A. 0 B. 1 C. 2 D. 3 Lời giải Chọn D 4 3 2 2 2 2 2
6x  (x x)y  (y 12)x  6 
6(x 1)  xy y(x 1)  x Ta có      4 2 2 2 2 2 2 2 2 2 2 5
 x  (x 1) .y 11x  5  5(
 x 1)  y (x 1)  x
Dễ thấy x  0 hoặc y  0 đều không là nghiệm của hệ phương trình. 2 2 2 6(x 1) x 1 1    2 2  x y x y
Với x  0; y  0 ta có: Hệ   2 2 2 2 5(x 1) (x 1) 1   2 2 2 2  x y x y 2 x 1 1 Đặt u  ; v  . x y Khi đó hệ trở thành: 2 2 2 2 2 2
6u v u v
6u v u v
6u v u v      2 2 2 2 2 2 2 2 2 4 4
5u v u v
5u v  (u v)  2uv
5u v  36u v  2uv
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 255
Trần Đình Cư. SĐT: 0834332133 2 2  3
6u v u v 2 2   6 u v
u v u v         2uv  1 2 2 2
36u v  9uv  2  0   3 3  5
 uv  36u v  2    1  uv    0; u  ,v  2     
Giải hệ được u v 1 1 ;   1; ; ;1   
  . Khi đó y  2; y  1 S =  S y y  3.   2   2   1 2 1 2 x y  2
Câu 13. Tìm các giá trị của m để hệ phương trình sau có nghiệm:  có 2 2 2
x y xy  4m  2m nghiệm:  1   1   1  A. 1;  . B.  ;1 . C. 0; . D. 1; 2     2     2   Lời giải Chọn B x y  2 x y  2    2 2 2
x y xy  4m  2m 2
xy  2m m 1
Hệ có nghiệm khi và chỉ khi 4  4 2 2m m 2
 2m m 1  0    m  1 2 3 3 2 2
x y x y xy x y  0 (1) 
Câu 14. Cho hệ phương trình  . Gọi nghiệm dương 2 2
 2x y  9  2y x 1  x  4 (2)   
của hệ phương trình là a ; c a c
 trong đó ; là các phân số tối giản. Khi đó biểu thức  b d b d
   2018    2019 P a b c d bằng A. 0 . B. 2 . C. 1. D. 1  . Lời giải Chọn B Điều kiện xác định: 2
2x y  9  0 ; 2
2y x 1  0 . Ta có 2 2
(1)  (x y)(x xy y )  xy(x y)  x y  0 2 2
 (x y)(x y 1)  0  x y .
Thế x y vào (2) ta được 2 2
2x x  9  2x x 1  x  4 (3)
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 256
Trần Đình Cư. SĐT: 0834332133 Đặt 2
2x x  9  u ; 2
2x x 1  v thì u v x  4 . Mặt khác 2 2
u v  2(x  4)  2(u v) . u v  0
Suy ra (u v)(u v  2)  0   u v  2
Với u v  0 . Suy ra x  4  0  x  4   (3) vô nghiệm. u
  v x  4
Với u v  2 ta có 
 2u x  6 u   v  2
Khi đó ta được phương trình 2
2 2x x  9  x  6 2 2
 4(2x x  9)  (x  6) x  0 2 7 
x 8x  0  x(7x 8)  0  8 . x   7 8 8
Với x  0  y  0 ; x   y  . 7 7   
Vậy hệ phương trình đã cho có 2 nghiệm là  x y     8 8 ; 0;0 , ;   .   7 7 
Do đó a  8;b  7;c  8;d  7  P  2
Dạng 4: Các bài toán thực tế phương trình, hệ phương trình 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Hiện nay tuổi của mẹ gấp 7 lần tuổi con. Sau 2 năm nữa tuổi của mẹ gấp 5 lần tuổi con.
Hỏi mẹ sinh con lúc đó mẹ bao nhiêu tuổi ? Lời giải
Gọi x x 
* là tuổi mẹ hiện nay, y y   * là tuổi con hiện nay. x  7 y
x  7 y  0 x  28 Theo đề bài ta có:      . x  2  5   y  2
x  5y  8 y  4
Vậy mẹ sinh con năm 28  4  24 tuổi.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 257
Trần Đình Cư. SĐT: 0834332133
Ví dụ 2: Một khách hàng vào cửa hàng bách hóa mua một đồng hồ treo tường, một đôi giày và
một máy tính bỏ túi. Đồng hồ và đôi giày giá 420.000 đ; máy tính bỏ túi và đồng hồ giá
570.000 đ; máy tính bỏ túi và đôi giày giá 750.000 đ. Hỏi mỗi thứ giá bao nhiêu? Lời giải
Gọi giá của đồng hồ, máy tính bỏ túi và đôi giá lần lượt là x, y, z .
x z  420.000 x 120.000  
Khi đó ta có hệ phương trình x y  570.000. Giải hệ này ta được y  450.000  
y z  750.000  z  300.000 
Ví dụ 3: Cho hai người A và B xuất phát cùng một lúc ngược chiều từ thành phố M và N. Khi họ
gặp nhau, người ta nhận thấy A đã đi nhiều hơn B là 6km. Nếu mỗi người tiếp tục đi theo
hướng cũ với cùng vận tốc ban đầu thì A sẽ đến N sau 4,5 giờ, còn B đến M sau 8 giờ
tính từ thời điểm họ gặp nhau. Gọi ,
v v lần lượt là vận tốc của người A và người B . A B
Tìm vận tốc của mỗi người Lời giải
Gọi P là điểm mà hai người A và B gặp nhau. Gọi đoạn MP x là quãng đường A đi
được, NP y là quảng đường B đi được.
Khi họ gặp nhau, người ta nhận thấy A đã đi nhiều hơn B 6km có nghĩa là đoạn MP dài
hơn NP là 6km và thời gian đi của hai người cho đến lúc gặp nhau là bằng nhau. Ta có hệ x y  6   x y (1)  v vA B
Nếu mỗi người tiếp tục đi theo hướng cũ với cùng vận tốc ban đầu thì A sẽ đến N sau 4,5 giờ,
còn B đến M sau 8 giờ tính từ thời điểm họ gặp nhau nên ta có hệ:  y  4,5 vy  4,5v A A    x x  8   8 vBvB Thế vào ta có hệ :
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 258
Trần Đình Cư. SĐT: 0834332133 8
v  4,5v  6 B A 8 
v  4,5v  6    B A v 3 8v 4,5 B v     B A    8v  4,5v v  4   A B A v vS B
3. Bài tập trắc nghiệm Câu 1.
Hai bạn Vân và Lan đi mua trái cây. Vân mua 10 quả quýt, 7 quả cam với giá tiền là
17800 . Lan mua 12quả quýt, 6 quả cam hết 18000 . Hỏi giá tiền mỗi quả quýt, quả cam là bao nhiêu?
A. Quýt 1400 , cam 800 .
B. Quýt 700 , cam 200 .
C. Quýt 800 , cam 1400 .
D. Quýt 600 , cam 800 . Hướng dẫn giải Chọn C.
Cách 1: Gọi số tiền để mua một quả quýt là x đồng ; số tiền để mua một quả cam là y đồng. 10
x  7y 17 800 x  800
Theo bài ra ta có hệ phương trình:    . 12
x  6y 18 000 y 1400
Vậy giá tiền mỗi quả quýt là 800 đồng, mỗi quả cam là 1400 đồng.
Cách 2: Thử các đáp án, Chọn C. Câu 2.
Một xe hơi khởi hành từ Krông Năng đi đến Nha Trang cách nhau 175 km. Khi về xe
tăng vận tốc trung bình hơn vận tốc trung bình lúc đi là 20 km/giờ. Biết rằng thời gian
dùng để đi và về là 6 giờ; vận tốc trung bình lúc đi là A. 60 km/giờ. B. 45 km/giờ. C. 55 km/giờ. D. 50 km/giờ. Hướng dẫn giải Chọn D.
Gọi x , y  0 lần lượt là vận tốc trung bình lúc đi và vận tốc trung bình lúc về.
Theo đề bài ta có hệ phương trình:
y x  20
y  20  x   1   175 175  175  175 .   6   6   2  x yx y Thế   1 vào 2 ta được x  50 175 175 2 6 6  
  x  230x  3500  0 
35  x  50 vì x  0 . x 20  xx    3
Vậy vận tốc lúc đi là 50 km/giờ.
Câu 3. Một đoàn xe tải chở 290 tấn xi măng cho một công trình xây đập thủy điện. Đoàn xe có 57
chiếc gồm ba loại, xe chở 3 tấn, xe chở 5 tấn và xe chở 7,5 tấn. Nếu dùng tất cả xe 7,5 tấn chở ba
chuyến thì được số xi măng bằng tổng số xi măng do xe 5 tấn chở ba chuyến và xe 3 tấn chở hai
chuyến. Hỏi số xe mỗi loại?
A. 18 xe chở 3 tấn, 19 xe chở 5 tấn và 20 xe chở 7,5 tấn.
B. 20 xe chở 3 tấn, 19 xe chở 5 tấn và 18 xe chở 7,5 tấn.
C. 19 xe chở 3 tấn, 20 xe chở 5 tấn và 18 xe chở 7,5 tấn.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 259
Trần Đình Cư. SĐT: 0834332133
D. 20 xe chở 3 tấn, 18 xe chở 5 tấn và 19 xe chở 7,5 tấn. Lời giải Chọn B
Gọi x là số xe tải chở 3 tấn, y là số xe tải chở 5 tấn và z là số xe tải chở 7,5 tấn.
Điều kiện: x, y, z nguyên dương.
ìïx + y + z = 57 ï
Theo giả thiết của bài toán ta có ï3
ïí x +5y +7,5z = 290. ï22
ïï ,5z = 6x +15y ïî
Giải hệ ta được x = 20, 19 y = , z = 18.
Câu 4: Có ba lớp học sinh 10A, 10B, 10C gồm 128 em cùng tham gia lao động trồng cây. Mỗi em
lớp 10A trồng được 3 cây bạch đàn và 4 cây bàng. Mỗi em lớp 10B trồng được 2 cây bạch đàn và
5 cây bàng. Mỗi em lớp 10C trồng được 6 cây bạch đàn. Cả ba lớp trồng được là 476 cây bạch đàn
và 375 cây bàng. Hỏi mỗi lớp có bao nhiêu học sinh?
A. 10A có 40 em, lớp 10B có 43 em, lớp 10C có 45 em.
B. 10A có 45 em, lớp 10B có 43 em, lớp 10C có 40 em.
C. 10A có 45 em, lớp 10B có 40 em, lớp 10C có 43 em.
D. 10A có 43 em, lớp 10B có 40 em, lớp 10C có 45 em. Lời giải Chọn A
Gọi số học sinh của lớp 10A, 10B, 10C lần lượt là x, y, z.
Điều kiện: x, y, z nguyên dương.
ìïx + y + z =128 ï
Theo đề bài, ta lập được hệ phương trình ï3
ïí x +2y +6z = 476.
ïïï4x +5y =375 ïî
Giải hệ ta được x = 40, y = 43, 45. z =
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 260
Trần Đình Cư. SĐT: 0834332133