Phân loại và phương pháp giải bài tập tích vô hướng hai vectơ và ứng dụng

Tài liệu gồm 79 trang, được biên soạn bởi thầy giáo Trần Đình Cư, tóm tắt lý thuyết, phân loại và phương pháp giải bài tập tích vô hướng hai vectơ và ứng dụng, giúp học sinh lớp 10 tham khảo khi học chương trình Hình học 10 chương 2 (Toán 10).

106 53 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 4: Vectơ (KNTT)

Môn: Toán 10

Thông tin:

79 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 652
N
a
0
y
0
x
-
M
O
0
x
y
x
a
0
y
0
x
M
O
1
1
1-
y
x
CHƯƠNG II. TÍCH VÔ HƯỚNG HAI VECTƠ VÀ ỨNG DỤNG
BÀI 1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC BẤT KỲ TỪ
0
0
ĐẾN
0
180
A. KIẾN THỨC CƠ BẢN CẦN NẮM
1. Định nghĩa
Với mỗi góc
()
00
0 180aa££
ta xác định một điểm
M
trên nửa đường tròn đơn vị sao cho
xOM a= và giả sử điểm
M
có tọa độ
()
00
;.
xy
Khi đó ta có định nghĩa:
· sin của góc a là
0
,y kí hiệu
0
sin ;ya =
·
cosin của góc
a
là
0
,
x
kí hiệu
0
cos ;
x
a =
· tang của góc a là
()
0
0
0
0,
y
x
x
¹
kí hiệu
0
0
tan ;
y
x
a =
· cotang của góc a là
()
0
0
0
0,
x
y
y
¹ kí hiệu
0
0
cot .
x
y
a =
2. Tính chất
Trên hình bên ta có dây cung
NM song song với trục Ox và nếu
xOM a= thì
0
180 .xON a=- Ta
có
0
,
MN
yyy==
0
.
MN
x
xx=- = Do đó
()
()
()
()
0
0
0
0
sin sin 180
cos cos 180
tan tan 180
cot cot 180 .
aa
aa
aa
aa
=-
=- -
=- -
=- -
3. Giá trị lượng giác của các góc đặc biệt
Giá trị
a
lượng giác
0
0
0
30
0
45
0
60
0
90
0
180
sin a 0
1
2
2
2
3
2
1
0
cosa
1
3
2
2
2
1
2
0
1-
tan a 0
1
3
1
3
0
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 653
cot a
3
1
1
3
0
Trong bảng kí hiệu "" để chỉ giá trị lượng giác không xác định.
Chú ý. Từ giá trị lượng giác của các góc đặc biệt đã cho trong bảng và tính chất trên, ta có thể
suy ra giá trị lượng giác của một số góc đặc biệt khác.
Chẳng hạn:
()
()
0000
000 0
3
sin120 sin 180 60 sin 60
2
2
cos135 cos 180 45 cos45 .
2
=-==
=-=-=-
4. Góc giữa hai vectơ
a) Định nghĩa
Cho hai vectơ
a
và b
đều khác vectơ 0.
Từ một điểm O bất kì ta vẽ OA a=

và .OB b=

Góc
AOB với số đo từ
0
0 đến
0
180 được gọi là góc giữa hai vectơ a
và .b
Ta kí hiệu góc giữa hai vectơ
a
và
b
là
()
,ab
. Nếu
()
0
,90ab =
thì ta nói rằng
a
và
b
vuông góc với nhau, kí hiệu là
ab^
hoặc
.ba^
b) Chú ý. Từ định nghĩa ta có
()()
,,.ab ba=

được 6)
B.CÁCDẠNGTOÁNVÀPHƯƠNGPHÁPGIẢI.
Dạng1:xácđịnhgiátrịlượnggiáccủagócđặcbiệt.
1. Phương pháp giải.
Sử dụng định nghĩa giá trị lượng giác của một góc
Sử dụng tính chất và bảng giá trị lượng giác đặc biệt
Sử dụng các hệ thức lượng giác cơ bản
2. Các ví dụ.
Ví dụ 1: Tính giá trị các biểu thức sau:
a)
Aa b c=++
202 02 0
sin 90 cos90 cos180
b)
B =- + -
20 20 20
3 sin 90 2 cos 60 3 tan 45
b
a
b
a
A
B
O
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 654
c)
C =- + - +
20 20 20 20 0 0
sin 45 2 sin 50 3 cos 45 2 sin 40 4 tan 55 .tan 35
Lời giải
a)
(
)
Aa b c a c=++-=-
222 22
.1 .0 . 1
b)
()
B
æö
æö
÷
ç
÷
ç
÷
=- + - =
ç
÷
ç
÷
÷
ç
÷
ç
÷
÷
ç
èø
èø
2
2
2
12
31 2 3 1
22
c)
(
)
C =+ - + +
20 20 20 20 0 0
sin 45 3 cos 45 2 sin 50 sin 40 4 tan 55 .cot55
()
C
æö æö
÷÷
çç
÷÷
= + - + +=+-+=
çç
÷÷
çç
÷÷
÷÷
çç
èø èø
22
20 20
22 13
3 2 sin 50 cos 40 4 2 4 4
22 22
Ví dụ 2: Tính giá trị các biểu thức sau:
a)
A =+ + +
20 2 0 2 0 2 0
sin 3 sin 15 sin 75 sin 87
b)
B =+ + ++ +
000 0 0
cos 0 cos 20 cos 40 ... cos160 cos180
c)
C =
000 00
tan 5 tan10 tan15 ...tan 80 tan 85
Lời giải
a)
(
)
(
)
A =+ + +
20 2 0 2 0 2 0
sin3 sin87 sin15 sin75
()( )
=++ +
=+=
20 20 2 0 2 0
sin 3 cos 3 sin 15 cos 15
11 2
b)
()( )( )
B =+ + + ++ +
00 00 00
cos 0 cos180 cos 20 cos160 ... cos 80 cos100
()( )( )
=-+ - ++ -
=
00 0 0 0 0
cos 0 cos 0 cos20 cos 20 ... cos 80 cos 80
0
c)
(
)
(
)
(
)
C =
00 00 00
tan 5 tan 85 tan15 tan 75 ... tan 45 tan 45
()( )( )
=
=
00 00 00
tan 5 cot5 tan15 cot5 ... tan 45 cot5
1
Dạng2:chứngminhđẳngthứclượnggiác,chứngminhbiểuthứckhông
phụthuộcx,đơngiảnbiểuthức.
1. Phương pháp giải.
Sử dụng các hệ thức lượng giác cơ bản
Sử dụng tính chất của giá trị lượng giác
Sử dụng các hằng đẳng thức đáng nhớ .
2. Các ví dụ.
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 655
Ví dụ 1: Chứng minh các đẳng thức sau(giả sử các biểu thức sau đều có nghĩa)
a)
xx xx+=-
44 22
sin cos 1 2 sin .cos
b)
xx
xx
++
=
--
1cot tan 1
1cot tan 1
c)
xx
xxx
x
+
=+++
32
3
cos sin
tan tan tan 1
cos
Lời giải
a)
x x x x xx xx+=++ -
4 4 4 4 22 22
sin cos sin cos 2 sin cos 2 sin cos
()
xx xx
xx
=+ -
=-
2
22 22
22
sin cos 2sin cos
12sincos
b)
x
xx
xx
xxx
xx
+
+
++
===
---
-
1tan1
1
1cot tan 1
tan tan
1 cot 1 tan 1 tan 1
1
tan tan
c)
xx x
xxx
+
=+
323
cos sin 1 sin
cos cos cos
(
)
xxx=++ +
22
tan 1 tan tan 1
xxx=+++
32
tan tan tan 1
Ví dụ 2: Cho tam giác
ABC . Chứng minh rằng
()
BB
AC
B
AC AC B
+
+- =
æöæö
++
÷÷
çç
÷÷
çç
÷÷
÷÷
çç
èøèø
33
sin cos
cos
22
.tan 2
sin
cos sin
22
Lời giải
Vì
ABC++=
0
180
nên
()
BB
B
VT B
B
BB
-
=+-
æöæö
--
÷÷
çç
÷÷
çç
÷÷
÷÷
çç
èøèø
33
0
00
sin cos
cos 180
22
.tan
sin
180 180
cos sin
22
BB
BBB
BVP
BBB
-
=+- =++==
33
22
sin cos
cos
22
.tan sin cos 1 2
sin 2 2
sin cos
22
Suy ra điều phải chứng minh.
Ví dụ 3: Đơn giản các biểu thức sau(giả sử các biểu thức sau đều có nghĩa)
a)
Ax xxxx=-+ -++-
00222
sin(90 ) cos(180 ) sin (1 tan ) tan
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 656
b)
B
xx x
=+-
+-
11 1
.2
sin 1 cos 1 cos
Lời giải
a)
Axx x x
x
=-+ - =
22
2
1
cos cos sin . tan 0
cos
b)
(
)
(
)
xx
B
xxx
-++
=-
-+
1 1 cos 1 cos
.2
sin 1 cos 1 cos
xx
xx
x
x
=-=-
-
æö
÷
ç
=-=
÷
ç
÷
÷
ç
èø
22
2
2
12 12
.2.2
sin sin
1cos sin
1
212cot
sin
Ví dụ 4: Chứng minh biểu thức sau không phụ thuộc vào x.
Pxxxxxx=+++++
424 424
sin 6cos 3cos cos 6sin 3sin
Lời giải
() ()
Pxxxxxx=- + + +- + +
22
224 224
1 cos 6 cos 3 cos 1 sin 6 sin 3 sin
()()
xx xx
xx
xx
=+++++
=+++
=+++
=
42 42
22
22
22
4cos 4cos 1 4sin 4sin 1
2cos 1 2sin 1
2cos 1 2sin 1
3
Vậy P không phụ thuộc vào
x .
Dạng3:xácđịnhgiátrịcủamộtbiểuthứclượnggiáccóđiềukiện.
1. Phương pháp giải.
Dựa vào các hệ thức lượng giác cơ bản
Dựa vào dấu của giá trị lượng giác
Sử dụng các hằng đẳng thức đáng nhớ
2. Các ví dụ.
Ví dụ 1: a) Cho
a =
1
sin
3
với a<<
00
90 180 . Tính
acos
và atan
b) Cho
a =-
2
cos
3
. Tính asin và acot
c) Cho
g =-tan 2 2
tính giá trị lượng giác còn lại.
Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 657
a) Vì
a<<
00
90 180 nên
a <cos 0
mặt khác aa+=
22
sin cos 1 suy ra
aa=- - =- - =-
2
122
cos 1 sin 1
93
Do đó
a
a
a
== =-
-
1
sin 1
3
tan
cos
22 22
3
b) Vì
aa+=
22
sin cos 1 nên
aa=- =-=
2
45
sin 1 cos 1
93
và
a
a
a
-
===-
2
cos 2
3
cot
sin
55
3
c) Vì
ga=- < <tan 2 2 0 cos 0 mặt khác
a
a
+=
2
2
1
tan 1
cos
nên
a =- =- =-
+
+
2
111
cos
81 3
tan 1
Ta có
a
aaaa
a
æö
÷
ç
== =--=
÷
ç
÷
÷
ç
èø
sin 1 2 2
tan sin tan .cos 2 2.
cos 3 3
a
a
a
-
= ==-
1
cos 1
3
cot
sin
22 22
3
Ví dụ 2: a) Cho
a =
3
cos
4
với a<<
00
090. Tính A
aa
aa
+
=
+
tan 3 cot
tan cot
.
b) Cho
a =tan 2 . Tính B
aa
aaa
-
=
++
33
sin cos
sin 3 cos 2 sin
Lời giải
a) Ta có
A
a
a
aa
a
a
a
a
a
+
+
+
====+
+
+
2
2
2
2
2
1
1
2
tan 3
tan 3
tan cos
12cos
11
tan 1
tan
tan
cos
Suy ra
A =+ =
917
12.
16 8
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 658
b)
()()
()
B
aa
aa a
aa
aaa
aaa
aaa
-
+- +
==
++ +
++
22
33
33
32
333
sin cos
tan tan 1 tan 1
cos cos
sin 3 cos 2 sin
tan 3 2 tan tan 1
cos cos cos
Suy ra
(
)
(
)
(
)
()
B
-
+-+
==
++ + +
321
22 1 2 1
22 3 222 1 3 82
Ví dụ 3: Biết
xxm+=sin cos
a) Tìm
xxsin cos và xx-
44
sin cos
b) Chứng minh rằng
m £ 2
Lời giải
a) Ta có
(
)
xx x xx x xx+=+ +=+
2
22
sin co s sin 2sin cos c os 1 2 sin cos
(*)
Mặt khác
xxm+=sin cos
nên
m aa=+
2
12sincos
hay
m
aa
-
=
2
1
sin cos
2
Đặt
Axx=-
44
sin cos . Ta có
()()
(
)
(
)
Axxxx xxxx=+ -=+ -
2222
sin cos sin cos sin cos sin cos
(
)
(
)
(
)
(
)
Axxxx xx xx= + - =+ -
22
2
sin cos sin cos 1 2 sin cos 1 2 sin cos
mm mm
A
æöæö
--+-
÷÷
çç
=+ - =
÷÷
çç
÷÷
çç
÷÷
èøèø
22 24
2
1132
11
22 4
Vậy
mm
A
+-
=
24
32
2
b) Ta có
xx x x£+=
22
2sin cos sin cos 1
kết hợp với (*) suy ra
(
)
xx xx+£+£
2
sin cos 2 sin cos 2
Vậy
m £ 2
C. CÂU HỎI TRẮC NGHIỆM
Câu 1: Cho hai góc
a và b với 90ab+= . Tính giá trị của biểu thức sin cos sin cosP ab ba=+.
A.
0.P = B. 1.P = C. 1.P =- D. 2.P =
Lời giải
Chọn B
Hai góc
a và b phụ nhau nên sin cos ; cos sinabab==.
Do đó,
22
sin cos sin cos sin cos 1P abbaaa=+=+=.
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 659
Câu 2: Cho hai góc
a và
b
với 90ab+= . Tính giá trị của biểu thức cos cos sin sinP ab ba=-.
A.
0.P =
B.
1.P =
C.
1.P =-
D.
2.P =
Lời giải
Chọn A
Hai góc
a
và
b
phụ nhau nên sin cos ; cos sinabab==.
Do đó,
cos cos sin sin cos sin cos sin 0P a b ba aa aa=-=-=.
Câu 3: Cho
a là góc tù. Khẳng định nào sau đây là đúng?
A.
sin 0.a < B. cos 0.a > C. tan 0.a < D. cot 0.a >
Lời giải
Chọn C
Lấy góc
0
120a =
sau đó thử ngược
Câu 4: Cho hai góc nhọn
a và b trong đó ab< . Khẳng định nào sau đây là sai?
A.
cos cos .ab< B. sin sin .ab<
C.
cot cot .ab> D. tan tan 0.ab+>
Lời giải
Chọn A
Lấy
00
30 ; 60ab==
sau đó thử ngược.
Câu 5: Khẳng định nào sau đây sai?
A.
cos75 cos50 .> B. sin 80 sin 50 .>
C.
tan 45 tan 60 .< D. cos30 sin 60 .=
Lời giải
Chọn A
Trong khoảng từ
0 đến 90 , khi giá trị của góc tăng thì giá trị cos tương ứng của góc đó
giảm.
Câu 6: Khẳng định nào sau đây đúng?
A.
sin 90 sin 100 .< B. cos95 cos100 .>
C.
tan 85 tan125 .< D. cos145 cos125 .>
Lời giải
Chọn B
Trong khoảng từ
90 đến 180 , khi giá trị của góc tăng thì:
- Giá trị sin tương ứng của góc đó giảm.
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 660
- Giá trị cos tương ứng của góc đó giảm.
Câu 7: Khẳng định nào sau đây đúng?
A.
sin 90 sin 150 .< B.
sin 90 15 sin 90 30 .
¢¢
<
C.
cos90 30 cos100 .
¢
>
D. cos150 cos120 .>
Lời giải
Chọn C
Trong khoảng từ
90 đến 180 , khi giá trị của góc tăng thì:
- Giá trị sin tương ứng của góc đó giảm.
- Giá trị cos tương ứng của góc đó giảm.
Câu 8: Chọn hệ thức đúng được suy ra từ hệ thức
22
cos sin 1?aa+=
A.
22
1
cos sin .
222
aa
+=
B.
22
1
cos sin .
333
aa
+=
C.
22
1
cos sin .
444
aa
+=
D.
22
5cos sin 5.
55
aa
æö
÷
ç
+=
÷
ç
÷
ç
èø
Lời giải
Chọn D
Từ biểu thức
22
cos sin 1aa+= ta suy ra
22
cos sin 1.
55
aa
+=
Do đó ta có
22
5cos sin 5.
55
aa
æö
÷
ç
+=
÷
ç
÷
ç
èø
Câu 9: Cho biết
3
sin .
35
a
=
Giá trị của
22
3sin 5cos
33
P
aa
=+
bằng bao nhiêu?
A.
105
.
25
P =
B.
107
.
25
P =
C.
109
.
25
P =
D.
111
.
25
P =
Lời giải
Chọn B
Ta có biểu thức
22 2 2
16
sin cos 1 cos 1 sin .
33 3 325
aa a a
+==-=
Do đó ta có
2
22
316107
3sin 5cos 3. 5. .
3352525
P
aa
æö
÷
ç
=+ =+=
÷
ç
÷
ç
èø
Câu 10: Cho biết
tan 3.a =- Giá trị của
6sin 7cos
6cos 7sin
P
aa
aa
-
=
+
bằng bao nhiêu?
A.
4
.
3
P =
B.
5
.
3
P =
C.
4
.
3
P =-
D.
5
.
3
P =-
Lời giải
Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 661
Ta có
sin
67
6sin 7cos 6tan 7 5
cos
.
sin
6cos 7sin 6 7tan 3
67
cos
P
a
aa a
a
a
aa a
a
-
--
====
++
+
Câu 11: Cho biết
2
cos .
3
a =-
Giá trị của
cot 3 tan
2cot tan
P
aa
aa
+
=
+
bằng bao nhiêu?
A.
19
.
13
P =-
B.
19
.
13
P =
C.
25
.
13
P =
D.
25
.
13
P =-
Lời giải
Chọn B
Ta có biểu thức
22 2 2
5
sin cos 1 sin 1 cos .
9
aa a a+==-=
Ta có
2
22
22 2
25
cos sin
3.
3
cot 3tan cos 3sin 19
39
sin cos
.
cos sin
2cot tan 132cos sin
25
2
2.
sin cos
39
P
aa
aa a a
aa
aa
aa a a
aa
æö
÷
ç
-+
÷
+
ç
÷
ç
èø
++
== = ==
++
æö
+
÷
ç
-+
÷
ç
÷
ç
èø
Câu 12: Cho biết
cot 5.a = Giá trị của
2
2cos 5sin cos 1P aaa=+ + bằng bao nhiêu?
A.
10
.
26
P =
B.
100
.
26
P =
C.
50
.
26
P =
D.
101
.
26
P =
Lời giải
Chọn D
Ta có
2
22
22
cos cos 1
2cos 5sin cos 1 sin 2 5
sin
sin sin
P
aa
aaa a
a
aa
æö
÷
ç
÷
=+ += ++
ç
÷
ç
÷
ç
èø
()
2
22
2 2
1 3cot 5cot 1 101
2cot 5cot 1 cot .
1cot cot 1 26
aa
aa a
aa
++
=+++= =
++
Câu 13: Cho biết
3cos sin 1aa-=,
00
090.a<< Giá trị của tan a bằng
A.
4
tan .
3
a =
B.
3
tan .
4
a =
C.
4
tan .
5
a =
D.
5
tan .
4
a =
Lời giải
Chọn A
Ta có
()
2
2
3cos sin 1 3cos sin 1 9cos sin 1aa a a a a-= =+ = +
()
22 2 2
9 cos sin 2 sin 1 9 1 sin sin 2 sin 1aa a a aa=++-=++
2
sin 1
10sin 2 sin 8 0 .
4
sin
5
a
aa
a
é
=-
ê
ê
+-=
ê
=
ê
ë
· sin 1a =- : không thỏa mãn vì
00
090.a<<
·
43 sin4
sin cos tan .
55 cos3
a
aa a
a
= =¾¾= =
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 662
Câu 14: Cho biết
2cos 2sin 2aa+=
,
00
090.a<<
Tính giá trị của
cot .a
A.
5
cot .
4
a =
B.
3
cot .
4
a =
C.
2
cot .
4
a =
D.
2
cot .
2
a =
Lời giải
Chọn C
Ta có
()
2
2
2cos 2 sin 2 2 sin 2 2cos 2sin 2 2cosaa a aa a+==-=-
()
222 2
2
2sin 4 8cos 4cos 2 1 cos 4 8cos 4 cos
cos 1
6cos 8cos 2 0 .
1
cos
3
aaa a aa
a
aa
a
=-+-=-+
é
=
ê
ê
-+=
ê
=
ê
ë
· cos 1a = : không thỏa mãn vì
00
090.a<<
·
122 cos2
cos sin cot .
33 sin4
a
aa a
a
= = ¾¾= =
Câu 15: Cho biết
sin cos .aaa+= Tính giá trị của sin cos .aa
A.
2
sin cos .aaa= B.
sin cos 2 .aaa=
C.
2
1
sin cos .
2
a
aa
-
=
D.
2
11
sin cos .
2
a
aa
-
=
Lời giải
Chọn C
Ta có
()
2
2
sincos sincosaaaa aa+= + =
2
2
1
1 2 sin cos sin cos .
2
a
a
aa aa
-
+ = =
Câu 16: Cho biết
1
cos sin .
3
aa
+=
Giá trị của
22
tan cotP aa=+ bằng bao nhiêu?
A.
5
.
4
P = B.
7
.
4
P = C.
9
.
4
P = D.
11
.
4
P =
Lời giải
Chọn B
Ta có
()
2
11
cos sin cos sin
39
aa aa+= + =
14
12sincos sincos .
99
aa aa
+ = =-
Ta có
()
2
2
22
sin cos
tan cot tan cot 2tan cot 2
cos sin
P
aa
aa aa aa
aa
æö
÷
ç
=+=+- =+-
÷
ç
÷
ç
èø
2
22
22
sin cos 1 9 7
222.
sin cos sin cos 4 4
aa
aa aa
æö
æöæö
+
÷
ç
÷÷
çç
÷
=-=-=--=
ç÷÷
çç
÷
÷÷
ç
çç
÷
ç
èøèø
èø
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 663
E
C
B
A
Câu 17: Cho biết
1
sin cos .
5
aa-=
Giá trị của
44
sin cosP aa=+
bằng bao nhiêu?
A.
15
.
5
P
= B.
17
.
5
P
= C.
19
.
5
P
= D.
21
.
5
P
=
Lời giải
Chọn B
Ta có
()
2
11
sincos sincos
5
5
aa aa-= - =
12
1 2 sin cos sin cos .
55
aa aa- = =
Ta có
()
2
44 22 22
sin cos sin cos 2 sin cosP aa aa aa=+= + -
()
2
17
12sincos .
5
aa=- =
Câu 18: Cho
O là tâm đường tròn ngoại tiếp tam giác đều .
M
NP Góc nào sau đây bằng
O
120 ?
A.
()
,
M
NNP

B.
()
,.
M
OON
 
C.
()
,.
M
NOP

D.
()
,.
M
NMP
 
Lời giải
Chọn A
Vẽ
NE MN=
 
. Khi đó
()()
,,
M
NNP NENP=
  
0000
180 180 60 120 .PNE MNP==- =-=
· Vẽ
OF MO=

. Khi đó
()()
0
,, 60.MO ON OF ON NOF===
  
· Vì
()
0
,90.MN OP MN OP^¾¾=

· Ta có
()
0
,60.MN MP NMP==

Câu 19: Cho tam giác đều
.ABC Tính
()()()
cos , cos , cos , .
P
AB BC BC CA CA AB=++
 
A.
33
.
2
P = B.
3
.
2
P = C.
3
.
2
P =- D.
33
.
2
P =-
Lời giải
Chọn C
Vẽ
BE AB=

. Khi đó
()()
0
, , 180 120AB BC BE BC CBE CBA===-=

()
0
1
cos , cos120 .
2
AB BC¾¾==-

Tương tự, ta cũng có
()()
1
cos , cos , .
2
BC CA CA AB==-
 
F
O
P
N
E
M
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 664
H
E
C
B
A
a
C
B
A
Vậy
()()()
3
cos , cos , cos ,
2
AB BC BC CA CA AB++=-
 
.
Câu 20: Cho tam giác đều
ABC có đường cao .AH Tính
()
,.AH BA
 
A.
0
30 . B.
0
60 . C.
0
120 . D.
0
150 .
Lời giải
Chọn D
Vẽ
AE BA=

.
Khi đó
()
,AH AE HAE a==
 
(hình vẽ)
0000
180 180 30 150 .BAH=- =-=
Câu 21: Tam giác
ABC vuông ở
A
và có góc
0
50 .B =
Hệ thức nào sau đây sai?
A.
()
0
, 130 .AB BC =

B.
()
0
, 40 .BC AC =
 
C.
()
0
, 50 .AB CB =

D.
()
0
, 40 .AC CB =
 
Lời giải
Chọn D
Vì
()
0000
, 180 180 40 140 .AC CB ACB=-=-=
 
Câu 22: Tam giác
ABC vuông ở
A
và có
2.
B
CAC=
Tính
()
cos , .AC CB
 
A.
()
1
cos , .
2
AC CB =
 
B.
()
1
cos , .
2
AC CB =-
 
C.
()
3
cos , .
2
AC CB =

D.
()
3
cos , .
2
AC CB =-

Lời giải
Chọn B
Xác định được
()
0
, 180 .AC CB ACB=-

Ta có
0
1
cos 60
2
AC
ACB ACB
CB
==¾¾=
()
00
, 180 120AC CB ACB¾¾=-=

Vậy
()
0
1
cos , cos120 .
2
AC CB ==-
 
Câu 23: Cho tam giác
ABC . Tính tổng
()()()
,,,.AB BC BC CA CA AB++
 
A.
180 .
B. 360 .
C. 270 .
D. 120 .
Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 665
F
I
C
B
H
A
0
100
Chọn B
Ta có
()
()
()
0
0
0
,180
, 180
,180
AB BC ABC
BC CA BCA
CA AB CAB
ì
ï
=-
ï
ï
ï
ï
ï
=-
í
ï
ï
ï
ï
=-
ï
ï
î


 
()()()
()
0000
, , , 540 540 180 360 .AB BC BC CA CA AB ABC BCA CAB¾¾++=-++=-=
 
Câu 24: Cho tam giác
ABC với
60A =
. Tính tổng
()()
,,.AB BC BC CA+

A.
120 .
B.
360 .
C.
270 .
D.
240 .
Lời giải
Chọn D
Ta có
()
()
0
0
, 180
,180
A
BBC ABC
BC CA BCA
ì
ï
=-
ï
ï
ï
í
ï
ï
=-
ï
ï
î


()()
()
0
,,360
A
BBC BCCA ABC BCA¾¾+=-+

()
00 0000
360 180 360 180 60 240 .BAC=- - =-+=
Câu 25: Tam giác
ABC có góc
A
bằng 100
và có trực tâm .
H
Tính tổng
()()()
,, ,.
H
AHB HBHC HCHA++
  
A.
360 .
B. 180 .
C. 80 .
D. 160 .
Lời giải
Chọn D
Ta có
()
()
()
,
,
,
H
AHB BHA
H
BHC BHC
H
CHA CHA
ì
ï
=
ï
ï
ï
ï
ï
=
í
ï
ï
ï
ï
=
ï
ï
î

 
 
()()()
,, ,
H
A HB HB HC HC HA BHA BHC CHA¾¾++ =++
     
()
00 0
2 2 180 100 160BHC== -=
(do tứ giác
H
IAF nội tiếp. Cho hình vuông ABCD . Tính
()
cos , .AC BA
 
Câu 26: Cho hình vuông
ABCD tâm .O Tính tổng
()()()
,,,.
A
BDC ADCB CODC++
     
A.
0
45 . B.
0
405 . C.
0
315 . D.
0
225 .
Lời giải
Chọn C
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 666
E
D
C
B
A
O
·
Ta có
,AB DC

cùng hướng nên
()
,AB DC
 
0
0= .
· Ta có ,
A
DCB
 
ngược hướng nên
()
0
,180AD CB =
 
.
· Vẽ CE DC=
 
, khi đó
()()
0
, , 135 .CO DC CO CE OCE===
  
Vậy
()()()
000 0
,,,
0 180 135 315 .
AB DC AD CB CO DC++
=+ + =
    
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 667
BÀI 2. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ
A. KIẾN THỨC CƠ BẢN CẦN NẮM
1. Định nghĩa
Cho hai vectơ
a
và
b
đều khác vectơ
0.
Tích vô hướng của
a
và
b
là một số, kí hiệu là .,ab
được
xác định bởi công thức sau:
()
..cos,.ab a b a b=

Trường hợp ít nhất một trong hai vectơ
a
và b
bằng vectơ 0
ta quy ước .0.ab=
Chú ý
·
Với a
và b
khác vectơ 0
ta có .0 .ab a b=^

· Khi ab=
tích vô hướng .aa
được kí hiệu là
2
a
và số này được gọi là bình phương vô hướng của
vectơ
.a
Ta có:
2
2
0
..cos0 .aaa a==

2. Các tính chất của tích vô hướng
Người ta chứng minh được các tính chất sau đây của tích vô hướng:
Với ba vectơ
, , abc

bất kì và mọi số
k
ta có:
·
..ab ba=

(tính chất giao hoán);
·
()
..ab c ab ac+= +
 
(tính chất phân phối);
·
() ( ) ()
...ka b k ab a kb==

;
·
22
0, 0 0.aa a³==

Nhận xét. Từ các tính chất của tích vô hướng của hai vectơ ta suy ra:
·
()
2
22
2. ;ab a abb+=+ +

·
()
2
22
2. ;ab a abb-=- +

·
()()
22
.abab a b+-=-

3. Biểu thức tọa độ của tích vô hướng
Trên mặt phẳng tọa độ
()
;; ,Oi j
cho hai vectơ
() ()
12 12
;, ;.aaabbb==

Khi đó tích vô hướng .ab
là:
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 668
11 2 2
..ab ab a b=+

Nhận xét. Hai vectơ
() ()
12 12
;, ;aaabbb==
đều khác vectơ 0
vuông góc với nhau khi và chỉ khi
11 2 2
0.ab ab+=
4. Ứng dụng
a) Độ dài của vectơ
Độ dài của vectơ
()
12
;aaa=
được tính theo công thức:
22
12
.aaa=+
b) Góc giữa hai vectơ
Từ định nghĩa tích vô hướng của hai vectơ ta suy ra nếu
()
12
;aaa=
và
()
12
;bbb=
đều khác 0
thì ta
có
()
11 2 2
2222
1212
.
cos ; .
.
.
ab abab
ab
aabb
ab
+
==
++



c) Khoảng cách giữa hai điểm
Khoảng cách giữa hai điểm
()
;
AA
A
xy và
()
;
B
B
Bx y được tính theo công thức:
()()
22
.
BA BA
AB x x y y=-+-
B. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI.
DẠNG 1 : Xác định biểu thức tích vô hướng, góc giữa hai vectơ.
1. Phương pháp giải.
Dựa vào định nghĩa
(
)
ab a b a b=..cos;

Sử dụng tính chất và các hằng đẳng thức của tích vô hướng của hai vectơ
2. Các ví dụ:
Ví dụ 1
: Cho tam giác ABC vuông tại A có ,AB a BC a==2 và G là trọng tâm.
a) Tính các tích vô hướng:
BABC.

; BC CA.
 
b) Tính giá trị của biểu thức
AB BC BC CA CAAB++...
     
c) Tính giá trị của biểu thức
GAGB GB GC GC GA++.. .
 
Lời giải (hình 2.2)
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 669
a) * Theo định nghĩa tích vô hướng ta có
() ()
BA BC BA BC BA BC a BA BC==
2
..cos,2cos,
   
.
Mặt khác
()
a
BA BC ABC
a
===
1
cos , cos
22

Nên BABC a
=
2
.

* Ta có
BC CA CB CA CB CA ACB=- =-.. .cos
   
Theo định lý Pitago ta có
(
)
CA a a a=-=
2
2
23
Suy ra
a
BC CA a a a
a
=- =-
2
3
.3.2.3
2
 
b) Cách 1: Vì tam giác
ABC
vuông tại A nên CA AB =.0
 
và từ câu a ta
có
AB BC a BC CA a=- =-
22
.,.3
   
. Suy ra AB BC BC CA CAAB a++=-
2
...4
     
Cách 2: Từ
AB BC CA++=0
  
và hằng đẳng thức
(
)
(
)
AB BC CA AB BC CA AB BC BC CA CA AB++ = + + + + +
2
222
2. . .
     
Ta có
()
AB BC BC CA CA AB AB BC CA a++=-++=-
222 2
1
... 4
2
     
c) Tương tự cách 2 của câu b) vì
GA GB GC++ =0

nên
()
GAGB GB GC GC GA GA GB GC++=-++
22 2
1
.. .
2
   
Gọi M, N, P lần lượt là trung điểm của BC, CA, AB
Dễ thấy tam giác
ABM đều nên
a
GA AM
æö
÷
ç
==
÷
ç
÷
÷
ç
èø
2
2
2
24
39
Theo định lý Pitago ta có:
G
N
M
P
C
A
B
Hình 2.2
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 670
()
aa
GB BN AB AN a
æö
÷
ç
== +=+=
÷
ç
÷
ç
÷
èø
22
22 222
44 437
99 949
()
aa
GC CP AC AP a
æö
÷
ç
== +=+=
÷
ç
÷
ç
÷
èø
22
22 22 2
44 4 13
3
99 949
Suy ra
aa a a
GAGB GB GC GC GA
æö
÷
ç
++=-++=-
÷
ç
÷
ç
÷
èø
22 2 2
14 7 13 4
.. .
29 9 9 3
   
Ví dụ 2: Cho hình vuông ABCD cạnh a. M là trung điểm của AB, G là trọng tâm tam giác ADM .
Tính giá trị các biểu thức sau:
a)
AB AD BD BC++()()
   
b)
(
)
CG CA DM+.

Lời giải (hình 2.3)
a) Theo quy tắc hình bình hành ta có
AB AD AC+=
  
Do đó
AB AD BD BC AC BD AC BC++=+()()..
     
CACB CA CB ACB==..cos
 
(
AC BD =.0
 
vì AC BD^
 
)
Mặt khác
ACB =
0
45 và theo định lý Pitago ta có :
AC a a a=+=
22
2
Suy ra
AB AD BD BC a a a++= =
02
()().2cos45
   
b) Vì G là trọng tâm tam giác
ADM nên CG CD CA CM=++

Mặt khác theo quy tắc hình bình hành và hệ thức trung điểm ta có
(
)
CA AB AD=- +
  
và
() ()()
CM CB CA CB AB AD AB AD
éù
= +=-+=-+
êú
ëû
11 1
2
22 2
     
Suy ra
()()
CG AB AB AD AB AD AB AD
æö
÷
ç
=- - + - + =- +
÷
ç
÷
÷
ç
èø
15
22
22
   
Ta lại có
(
)
CA DM A B AD AM AD AB AD
æö
÷
ç
+=-+ +-=- +
÷
ç
÷
÷
ç
èø
1
2
2
      
Nên
()
CG CA DM A B AD AB AD
æöæö
÷÷
çç
+= + +
÷÷
çç
÷÷
÷÷
çç
èøèø
51
.22
22
   
a
AB AD=+=
2
22
521
4
44
M
A
D
C
B
G
Hình 2.3
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 671
Ví dụ 3: Cho tam giác ABC có
BC a CA b AB c===,,
. M là trung điểm của BC, D là chân
đường phân giác trong góc A.
a) Tính
AB AC.
 
, rồi suy ra
cosA
.
b) Tính
AM
2

và
AD
2

Lời giải (hình 2.3)
a) Ta có
()
AB AC AB AC AB AC
éù
êú
=+--
êú
ëû
22 2
1
.
2
     
AB AC CB
éù
=+-
ëû
222
1
2
()
cba=+-
222
1
2
Mặt khác
AB AC AB AC A cb A==..coscos
 
Suy ra
()
coscba cbA+- =
222
1
2
hay
cos
cba
A
bc
+-
=
222
2
b) * Vì M là trung điểm của BC nên
(
)
AM AB AC=+
1
2

Suy ra
(
)
AM AB AC AB ABAC AC
æö
÷
ç
=+= + +
÷
ç
÷
ç
èø
222 2
11
2
44
     
Theo câu a) ta có
()
AB AC c b a=+-
222
1
.
2
 
nên
()
(
)
bc a
AM c c b a b
+-
æö
÷
ç
=+ +-+=
÷
ç
÷
÷
ç
èø
22 2
2
22222
2
11
2.
42 4

* Theo tính chất đường phân giác thì
BD AB c
DC AC b
==
Suy ra
BD b
BD DC DC
DC c
==
  
(*)
Mặt khác
BD AD AB=-
  
và
DC AC AD=-
  
thay vào (*) ta được
()
()
()
() ()
()
()
()
()()
.
b
AD AB AC AD b c AD b AB cAC
c
b c AD bAB bcABAC cAC
bcAD bc bc c b a cb
bc
AD bcabca
bc
-= - + = +
+ = + +
+ = + +- +
= +-++
+
22
2
2
2
2
22 2 2 2 22
2
2
2
1
2
2
     
   


M
A
B
C
D
Hình 2.3
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 672
Hay
(
)
()
bc
AD p p a
bc
=-
+
2
2
4

Nhận xét : Từ câu b) suy ra độ dài đường phân giác kẻ từ đỉnh A là
()
a
bc
lppa
bc
=-
+
2
Dạng 2: chứng minh các đẳng thức về tích vô hướng hoặc độ dài của đoạn thẳng.
1. Phương pháp giải.
Nếu trong đẳng thức chứa bình phương độ dài của đoạn thẳng thì ta chuyển về vectơ nhờ
đẳng thức
AB AB=
2
2

Sử dụng các tính chất của tích vô hướng, các quy tắc phép toán vectơ
Sử dụng hằng đẳng thức vectơ về tích vô hướng.
2. Các ví dụ:
Ví dụ 1
: Cho I là trung điểm của đoạn thẳng AB và M là điểm tùy ý.
Chứng minh rằng : MA MB IM IA=-
22
.
 
Lời giải:
Đẳng thức cần chứng minh được viết lại là
MA MB IM IA=-
22
.
  
Để làm xuất hiện
IM IA,

ở VP, sử dụng quy tắc ba điểm để xen điểm I vào ta được
()()()()
VT MI IA MI IB MI IA MI IA=+ +=+ -..
 
IM IA VP=-=
22

(đpcm)
Ví dụ 2: Cho bốn điểm A, B, C, D bất kì. Chứng minh rằng:
DA BC DB CA DC AB++ =...0
    
(*).
Từ đó suy ra một cách chứng minh định lí: "Ba đường cao trong tam giác đồng qui".
Lời giải:
Ta có:
DA BC DB CA DC AB++...
     
()()()
DA DC DB DB DA DC DC DB DA
DA DC DA DB DB DA DB DC DC DB DC DA
=-+-+-
=-+-+-=
...
.... ..0
     
       
(đpcm)
Gọi H là giao của hai đường cao xuất phát từ đỉnh A, B.
Khi đó ta có
HABC HC AB==.0,.0
   
(1)
Từ đẳng thức (*) ta cho điểm D trùng với điểm H ta được
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 673
HABC HB CA HC AB++ =...0
     
(2)
Từ (1) (2) ta có
HB CA =.0
 
suy ra BH vuông góc với AC
Hay ba đường cao trong tam giác đồng quy (đpcm).
Ví dụ 3: Cho nửa đường tròn đường kính AB. Có AC và BD là hai dây thuộc nửa đường tròn cắt
nhau tại E. Chứng minh rằng :
AE AC BE BD AB+=
2
..
  
Lời giải (hình 2.4)
Ta có
(
)
(
)
VT AE AB BC BE BA AD=+++..
  
AE AB AE BC BE BA BE AD=+++....
    
Vì AB là đường kính nên
,ADB ACB==
00
90 90
Suy ra
AE BC BE AD==.0,.0
  
Do đó
(
)
VT AE AB BE BA AB AE EB AB VP=+= +==
2
..
    
(đpcm).
Ví dụ 4: Cho tam giác ABC có , ,BC a CA b AB c=== và I là tâm đường tròn nội tiếp. Chứng
minh rằng
aIA bIB cIC abc++ =
22 2
Lời giải:
Ta có:
()
aIA bIB cIC aIA bIB cIC++ = ++ =
2
00
   
a IA b IB c IC abIAIB bcIB IC caIC IA+++ + + =
22 22 2 2
2. 2. 2 . 0
     
()
()()
aIA bIB cIC ab IA IB AB
bc IB IC BC ca IA IC CA
+++ +-+
++-++-=
22 22 2 2 2 2 2
22 2 222
0
()()
()( )
aabcaIA bbabcIB
c ca cb IC abc ab c a bc
++ +++ +
+++ - + + =
2222
22222
0
(
)
(
)
(
)
a b c a IA b IB c IC a b c abc++ + + =++
22 22 2 2
aIA bIB cIC abc++=
22 22 2 2
(đpcm)
Dạng 3: tìm tập hợp điểm thoả mãn đẳng thức về tích vô hướng hoặc tích độ dài.
1. Phương pháp giải.
Ta sử dụng các kết quả cơ bản sau:
Cho A, B là các điểm cố định. M là điểm di động
E
A
B
D
C
Hình 2.4
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 674
Nếu
AM k=

với k là số thực dương cho trước thì tập hợp các điểm M là đường tròn tâm
A, bán kính
Rk= .
Nếu
MA MB =.0
 
thì tập hợp các điểm M là đường tròn đường kính AB
Nếu
MAa =.0

với
a
khác
0
cho trước thì tập hợp các điểm M là đường thẳng đi qua A và
vuông góc với giá của vectơ
a
2. Các ví dụ.
Ví dụ 1.
Cho hai điểm A, B cố định có độ dài bằng a, vectơ
a
khác
0
và số thực k cho trước. Tìm
tập hợp điểm M sao cho
a)
a
MA MB =
2
3
.
4
 
b)
MA MB MA=
2
.
 
Lời giải:
a) Gọi I là trung điểm của AB ta có
(
)
(
)
aa
MA MB MI IA MI IB= + +=
22
33
.
44
  
a
MI IA-=
2
22
3
4
(Do IB I A=-
 
)
aa
MI
MI a
=+
=
22
2
3
44
Vậy tập hợp điểm M là đường tròn tâm I bán kính
Ra=
b) Ta có
MA MB MA=
2
.
 
MA MB MA=
2
.
  
()
MA MA MB-=.0
  
MA BA=.0

MA BA^
 
Vậy tập hợp điểm M là đường thẳng vuông góc với đường thẳng AB tại A.
Ví dụ 2: Cho tam giác
ABC
. Tìm tập hợp điểm M sao cho
(
)
MA MB CB BC++ =23 0
  
Lời giải (hình 2.4)
Gọi I là điểm xác định bởi
IA IB+=20

Khi đó
()
MA MB CB BC++ =23 0
  
(
)
(
)
MI IA MI IB BC BC
MI BC BC
éù
++ + =
êú
ëû
=
2
2
2.3
.


A
B
C
I
M
M'
I
'
Hình 2.4
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 675
Gọi M', I' lần lượt là hình chiếu của M, I lên đường thẳng BC
Theo công thức hình chiếu ta có
MI BC M I BC=.''.
   
do đó
MIBC BC=
2
''.

Vì
BC >
2
0
nên
MI BC'',
 
cùng hướng suy ra
M I BC BC M I BC BC M I BC= = =
22
''. ''. ''

Do I cố định nên I' cố định suy ra M' cố định.
Vậy tập hợp điểm M là đường thẳng đi qua M' và vuông góc với BC.
Ví dụ 3: Cho hình vuông ABCD cạnh a và số thực k cho trước.
Tìm tập hợp điểm M sao cho
MA MC MB MD k+=..
   
Lời giải
(hình 2.5)
Gọi I là tâm của hình vuông
ABCD
Ta có
:
()( )
MA MC MI IA MI IC=+ +.
  
()
MI MI IC IA IA IC
MI IAI C
=+ ++
=+
2
2
.
.
 

Tương tự MB MD MI IB ID=+
2
..
   
Nên MA MC MB MD k MI IB ID IA IC k+=++=
2
.. 2..
      
k
MI IB IA k MI IA
k
MI a
--==+
=+
222 2 2
22
2
2
2
kka
MI IA
+
=+=
2
2
22
Nếu
ka<-
2
: Tập hợp điểm M là tập rỗng
Nếu
ka=-
2
thì
MI M I= º0
suy ra tập hợp điểm M là điểm I
Nếu
ka>-
2
thì
ka
MI
+
=
2
2
suy ra tập hợp điểm M là đường tròn tâm I bán kính
ka
R
+
=
2
2
DẠNG 4: Biểu thức tọa độ của tích vô hướng.
1. Phương pháp giải.
Cho axybxy==
11 22
(; ), (; )

. Khi đó
I
A
D
C
B
Hình 2.5
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 676
+ Tích vô hướng hai vectơ là
ab x x y y=+
12 12
.

+ Góc của hai vectơ được xác định bởi công thức
xx yy
ab
ab
xyxy
ab
+
==
++
12 12
2222
1122
.
cos( , )



Chú ý: ab ab xx yy^ = + =
12 12
.0 0

Để xác định độ dài một vectơ đoạn thẳng ta sử dụng công thức
+ Nếu
axy= (; )
thì axy=+
22
+ Nếu
AA BB
Ax y Bx y(;), (; ) thì
BA BA
AB x x y y=-+-
22
()()
2. Các ví dụ.
Ví dụ 1:
Cho tam giác
ABC
có
(
)
(
)
(
)
;, ;, ;AB C-12 26 98
.
a) Chứng minh tam giác
ABC
vuông tại A.
b) Tính góc B của tam giác
ABC
c) Xác định hình chiếu của A lên cạnh BC
Lời giải:
a) Ta có
()()
;, ; . . .AB AC AB AC-=-+=34 86 38 46 0
  
Do đó
AB AC^
 
hay tam giác ABC vuông tại A.
b) Ta có
()( )
;, ;BC BA -11 2 3 4
 
Suy ra
(
)
(
)
(
)
..
cos cos ,
BBCBA
+-
== =
++-
2
222
11 3 2 4
1
5
11 2 3 4
 
c) Gọi
()
;Hxy
là hình chiếu của A lên BC.
Ta có
()( )()
;, ;, ;AH x y BH x y BC-- +-12 26 112
  
()()
.AH BC AH BC x y^ = -+-=011 12 2 0
 
Hay
xy+-=11 2 15 0 (1)
Mặt khác ,BH BC
 
cùng phương nên
xy
xy
+-
=-+=
26
211700
11 2
(2)
Từ (1) và (2) suy ra
,xy==
132
55
Vậy hình chiếu của A lên BC là
;H
æö
÷
ç
÷
ç
÷
ç
èø
132
55
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 677
Ví dụ 2: Cho hình thoi
ABCD
có tâm
(
)
I 1; 1 , đỉnh
(
)
A 3; 2 và đỉnh B nằm trên trục hoành. Tìm
tọa độ các đỉnh còn lại của hình thoi.
Lời giải:
Vì B nằm trên trục hoành nên giả sử
(
)
By0;
Vì I là tâm hình thoi
ABCD nên I là trung điểm của AC và BD
Suy ra
(
)
(
)
IAIA
Cxxyy=- -=-2;2 1;0,
(
)
(
)
IBIB
Dxxyy y=- -=-2;2 2;2
Do đó
AB AD AB AD= =
22
(
)
yyy+ - =+ =
2
2
921 3
Vậy
(
)
(
)
(
)
BC D--0;3, 1;0, 2; 1
Ví dụ 3: Cho ba điểm AB(3;4), (2;1) và C --(1; 2). Tìm điểm M trên đường thẳng BC để góc
AMB =
0
45
Lời giải:
Giả sử
(
)
;Mxy
suy ra
(
)
(
)
(
)
;, ;, ;MA x y MB x y BC-- -- --34 21 33
  
Vì
AMB =
0
45 suy ra
(
)
cos cos ;AMB MA BC=
 
()()
()()
.
cos
.
MABC
xy
MA BC
xy
--- -
= =
-+- +
0
22
33 34
2
45
2
3499
 
 
()()
xyxy-+-=+-
22
34 7 (*)
Mặt khác M thuộc đường thẳng BC nên hai vectơ
,MB BC
 
cùng phương
Suy ra
xy
xy
--
==+
--
21
1
33
thế vào (*) ta được
()()
yyyyy y-+-=--+==
22
2
24266802 hoặc y = 4
+ Với
yx==23, ta có
() ( )
()
;, ; cos cos ;MA MB AMB MA MB-- = =-
1
02 1 1
2
   
Khi đó
AMB =
0
135 (không thỏa mãn)
+ Với
yx==45
,
()( )
()
;, ; cos cos ;MA MB AMB MA MB---= =
1
20 3 3
2
   
Khi đó
AMB =
0
45
Vậy
()
;M 54 . là điểm cần tìm.
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 678
Ví dụ 4: Cho điểm A(2; 1). Lấy điểm B nằm trên trục hoành có hoành độ không âm sao và điểm
C
trên trục tung có tung độ dương sao cho tam giác
A
BC
vuông tại
A
. Tìm toạ độ
,
B
C
để tam giác
A
BC có diện tích lớn nhất.
Lời giải:
Gọi

;0 , 0;
B
bCc với 0b , 0c .
Suy ra

2; 1 , 2; 1AB b AC c

Theo giả thiết ta có tam giác
A
BC vuông tại
A
nên

.0 221.10 25AB AC b c c b 

Ta có
22 2
11
. ( 2) 1. 2 ( 1)
22
ABC
SABACb c

22
(2)1 45bbb
Vì
0c nên
5
2500
2
bb
Xét hàm số
2
45yx x
với
5
0
2
x
Bảng biến thiên
x
0 2
5
2
y
5
5
4
1
Suy ra giá trị lớn nhất của hàm số
2
45yx x với
5
0
2
x
là 5y
khi
0x
. Do đó diện tích
tam giác
A
BC lớn nhất khi và chỉ khi 0b
, suy ra 5c
.
Vậy

0;0B ,

0;5C là điểm cần tìm.
C. CÂU HỎI TRẮC NGHIỆM
Vấn đề 1. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ
Câu 1.
Cho a
và b
là hai vectơ cùng hướng và đều khác vectơ 0
. Mệnh đề nào sau đây đúng?
A. ..ab a b=

. B. .0ab=
. C. .1ab=-
. D. ..ab a b=-

.
Lời giải
Chọn A
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 679
Ta có
()
...cos,ab a b a b=

.
Do
a
và b
là hai vectơ cùng hướng nên
() ()
0
,0 cos,1ab ab=¾¾=

.
Vậy
..ab a b=

.
Câu 2. Cho hai vectơ
a
và
b
khác
0
. Xác định góc
a
giữa hai vectơ
a
và
b
khi
...ab a b=-

A.
0
180 .a =
B.
0
0.a =
C.
0
90 .a =
D.
0
45 .a =
Lời giải
Chọn A
Ta có
()
...cos,ab a b a b=

.
Mà theo giả thiết
..ab a b=-

, suy ra
() ()
0
cos , 1 , 180 .ab ab=- ¾¾=

Câu 3. Cho hai vectơ
a
và
b
thỏa mãn
3,a =
2b =
và
.3.ab=-
Xác định góc a giữa hai vectơ
a
và .b
A.
0
30 .a = B.
0
45 .a = C.
0
60 .a = D.
0
120 .a =
Lời giải
Ta có
() () ()
0
.31
. . .cos , cos , , 120 .
3.2 2
.
ab
ab a b ab ab ab
ab
-
=¾¾===-¾¾=

Chọn D
Câu 4.
Cho hai vectơ a
và b
thỏa mãn 1ab==
và hai vectơ
2
3
5
uab=-
và vab=+
vuông
góc với nhau. Xác định góc
a giữa hai vectơ a
và .b
A.
0
90 .a =
B.
0
180 .a =
C.
0
60 .a =
D.
0
45 .a =
Lời giải
Chọn B
Ta có
()
22
2213
.0 3 0 3 0
555
uv uv a bab a ab b
æö
÷
ç
^¾¾= - += - -=
÷
ç
÷
ç
èø


1
1.
ab
ab
==
¾¾¾¾=-

Suy ra
() ()
0
.
cos , 1 , 180 .
.
ab
ab ab
ab
==-¾¾=

Câu 5. Cho hai vectơ a
và
b
. Đẳng thức nào sau đây sai?
A.
22
2
1
..
2
ab a b a b
æö
÷
ç
=+--
÷
ç
÷
ç
èø


B.
22
2
1
..
2
ab a b a b
æö
÷
ç
=+--
÷
ç
÷
ç
èø


Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 680
C.
22
1
..
2
ab a b a b
æö
÷
ç
=+--
÷
ç
÷
ç
èø


D.
22
1
..
4
ab a b a b
æö
÷
ç
=+--
÷
ç
÷
ç
èø


Lời giải
Chọn C
Nhận thấy C và D chỉ khác nhau về hệ số
1
2
và
1
4
nên đáp án sai sẽ rơi vào C hoặc D.
Ta có
()()
22 2 2 22
1
4. .
4
ab ab ab ab ab ab ab ab
æö
÷
ç
+--=+ -- = ¾¾= +--
÷
ç
÷
ç
èø
 
· A đúng, vì
()()()
222 2
..... 2.ab abab aaabbabb a b abba +=+ +=+++= += + +


22
2
1
..
2
ab a b a b
æö
÷
ç
¾¾= +--
÷
ç
÷
ç
èø


· B đúng, vì
()()()
222 2
..... 2.ab ab ab aaabbabb a b abba -=- -=---= += +-


22
2
1
..
2
ab a b a b
æö
÷
ç
¾¾= +--
÷
ç
÷
ç
èø


Câu 6.
Cho tam giác đều ABC có cạnh bằng .a Tính tích vô hướng ..AB AC

A.
2
.2.AB AC a=
 
B.
2
3
..
2
a
AB AC =-
 
C.
2
..
2
a
AB AC =-

D.
2
..
2
a
AB AC =
 
Lời giải
Chọn D
Xác định được góc
()
,AB AC
 
là góc
A nên
()
0
,60.AB AC =

Do đó
()
2
0
. . .cos , . .cos60 .
2
a
AB AC AB AC AB AC a a===
  
Câu 7. Cho tam giác đều
ABC
có cạnh bằng
.a
Tính tích vô hướng
..AB BC

A.
2
..AB BC a=

B.
2
3
..
2
a
AB BC =

C.
2
..
2
a
AB BC
=-

D.
2
..
2
a
AB BC
=

Lời giải
Chọn C
Xác định được góc
()
,AB BC

là góc ngoài của góc
B nên
()
0
,120.AB BC =

Do đó
()
2
0
...cos,..cos120.
2
a
AB BC AB BC AB BC a a===-

Câu 8.
Gọi G là trọng tâm tam giác đều ABC có cạnh bằng a . Mệnh đề nào sau đây là sai?
A.
2
1
..
2
AB AC a=
 
B.
2
1
..
2
AC CB a=-
 
C.
2
..
6
a
GA GB =

D.
2
1
..
2
AB AG a=
 
Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 681
Chọn C
Dựa vào đáp án, ta có nhận xét sau:
· Xác định được góc
()
,AB AC
 
là góc
A nên
()
0
,60.AB AC =
 
Do đó
()
2
0
. . .cos , . .cos60
2
a
AB AC AB AC AB AC a a===¾¾
  
A đúng.
· Xác định được góc
()
,AC CB
 
là góc ngoài của góc
C
nên
()
0
, 120 .AC CB =

Do đó
()
2
0
. . .cos , . .cos120
2
a
AC CB A C CB A C CB a a
===-¾¾
   
B đúng.
· Xác định được góc
()
,GA GB

là góc
AGB
nên
()
0
, 120 .GA GB =

Do đó
()
2
0
. . .cos , . .cos120
6
33
aa a
GA GB GA GB GA GB
===-¾¾

C sai.
· Xác định được góc
()
,AB AG
 
là góc
GAB
nên
()
0
,30.AB AG =
 
Do đó
()
2
0
. . .cos , . .cos30
2
3
aa
AB AG AB AG AB AG a===¾¾
   
D đúng.
Câu 9.
Cho tam giác đều
ABC
có cạnh bằng
a
và chiều cao
AH
. Mệnh đề nào sau đây là sai?
A. .0.AH BC =
 
B.
()
0
,150.AB HA =

C.
2
..
2
a
AB AC
=
 
D.
2
..
2
a
AC CB
=

Lời giải
Chọn D
Xác định được góc
()
,
A
CCB
 
là góc ngoài của góc
A nên
()
0
, 120 .AC CB =

Do đó
()
2
0
. . .cos , . .cos120 .
2
a
AC CB A C CB AC CB a a
===-
  
Câu 10.
Cho tam giác ABC vuông cân tại
A
và có .AB AC a== Tính ..AB BC

A.
2
..AB BC a=-

B.
2
..AB BC a=

C.
2
2
..
2
a
AB BC
=-

D.
2
2
..
2
a
AB BC
=

Lời giải
Chọn A
Xác định được góc
()
,AB BC

là góc ngoài của góc
B nên
()
0
,135.AB BC =

Do đó
()
02
. . .cos , . 2.cos135 .AB BC AB BC AB BC a a a===-

Câu 11. Cho tam giác ABC vuông tại
A
và có , .
A
BcACb== Tính ..BA BC

A.
2
..BA BC b=

B.
2
..BA BC c=

Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 682
C.
22
..BA BC b c=+

D.
22
..BA BC b c=-

Lời giải
Chọn B
Ta có
()
22 2
22
...cos, ..cos.. .
c
BA BC BA BC BA BC BA BC B c b c c
bc
===+=
+

Cách khác. Tam giác
ABC
vuông tại
A
suy ra
AB AC^
.0.AB AC=
 
Ta có
()
2
22
.. . .BA BC BA BA AC BA BA AC AB c=+=+==
   
Câu 12.
Cho tam giác ABC có 2cm, 3cm, 5cm.AB BC CA=== Tính ..CA CB
 
A. . 13.CA CB =
 
B. . 15.CA CB =
 
C. . 17.CA CB =
 
D. . 19.CA CB =
 
Lời giải
Chọn B
Ta có AB BC CA+= ba điểm ,,
A
BC thẳng hàng và B nằm giữa ,.
A
C
Khi đó
()
0
. . .cos , 3.5.cos0 15.CA CB CA CB CA CB===
   
Cách khác. Ta có
()
2
2
222
2AB AB CB CA CB CBCA CA==-=- +

()()
22 2 222
11
352 15.
22
CBCA CB CA AB¾¾= +-=+-=

Câu 13. Cho tam giác ABC có , , .BC a CA b AB c=== Tính
()
..PABACBC=+
  
A.
22
.
P
bc=-
B.
22
.
2
cb
P
+
=
C.
222
.
3
cba
P
++
=
D.
222
.
2
cba
P
+-
=
Lời giải
Chọn A
Ta có
()()()
...PABACBCABACBAAC=+ =+ +
 
()()
22
2222
..AC AB AC AB AC AB AC AB b c=+ -=-=-=-
   
Câu 14.
Cho tam giác ABC có , , .BC a CA b AB c=== Gọi
M
là trung điểm cạnh .BC Tính ..AM BC

A.
22
..
2
bc
AM BC
-
=

B.
22
..
2
cb
AM BC
+
=

C.
222
..
3
cba
AM BC
++
=

D.
222
..
2
cba
AM BC
+-
=

Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 683
Chọn A
Vì
M
là trung điểm của BC suy ra 2.AB AC AM+=
  
Khi đó
()()()
11
...
22
AM BC AB AC BC AB AC BA AC=+ =+ +
   
()()
()
()
22
22
22
111
..
2222
bc
AC AB AC AB AC AB AC AB
-
= + -= -= -=
    
Câu 15.
Cho ba điểm , , OAB không thẳng hàng. Điều kiện cần và đủ để tích vô hướng
()
.0OA OB AB+=
  
là
A. tam giác OAB đều. B. tam giác OAB cân tại .O
C. tam giác
OAB
vuông tại
.O
D. tam giác
OAB
vuông cân tại
.O
Lời giải
Chọn B
Ta có
() ()()
.0 . 0OA OB AB OA OB OB OA+=+ -=
      
22
22
00.OB OA OB OA OB OA-=-==

Câu 16. Cho
, , ,
M
NPQ
là bốn điểm tùy ý. Trong các hệ thức sau, hệ thức nào sai?
A.
()
..
M
N NP PQ MNNP MNPQ+= +
  
. B. ..
M
PMN MN MP=-
   
.
C. ..
M
NPQ PQMN=
 
. D.
()()
22
M
NPQMNPQ MN PQ-+=-

.
Lời giải
Chọn B
Đáp án A đúng theo tính chất phân phối.
Đáp án B sai. Sửa lại cho đúng
..
M
PMN MN MP=
 
.
Đáp án C đúng theo tính chất giao hoán.
Đáp án D đúng theo tính chất phân phối.
Câu 17.
Cho hình vuông ABCD cạnh .a Tính ..AB AC

A.
2
..AB AC a=

B.
2
.2.AB AC a=

C.
2
2
..
2
AB AC a=
 
D.
2
1
..
2
AB AC a=
 
Lời giải
Chọn A
Ta có
()
0
,45AB AC BAC==

nên
02
2
...cos45.2..
2
AB AC AB AC a a a===
 
Câu 18.
Cho hình vuông ABCD cạnh a . Tính
()
..PACCDCA=+

Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 684
A.
1.P =-
B.
2
3.Pa=
C.
2
3.Pa=-
D.
2
2.Pa=
Lời giải
Chọn C
Từ giả thiết suy ra
2.AC a=
Ta có
()
2
....P AC CD CA ACCD ACCA CACD AC=+=+=--
      
()
()
2
202
.cos , 2..cos45 2 3.CA CD CA CD AC a a a a=- - =- - =-
 
Câu 19.
Cho hình vuông ABCD cạnh .a Tính
()( )
..PABACBCBDBA=+ ++
 
A. 22.Pa= B.
2
2.
P
a= C.
2
.
P
a= D.
2
2.
P
a=-
Lời giải
Chọn D
Ta có
()
2
.
2
BD a
BC BD BA BC BA BD BD BD BD
ì
ï
=
ï
ï
í
ï
++= + +=+=
ï
ï
î
   
Khi đó
()
.2 2 . 2 . 2 . 0PABACBD ABBDACBD BABD=+ = + =- +
      
()
2
2
2. . cos , 2. . 2. 2 .
2
BA BD BA BD a a a=- =- =-

Câu 20.
Cho hình vuông ABCD cạnh
a
. Gọi E là điểm đối xứng của
D
qua .C Tính
..AE AB

A.
2
.2.AE AB a=

B.
2
.3.AE AB a=

C.
2
.5.AE AB a=

D.
2
.5.AE AB a=

Lời giải
Chọn A
Ta có
C là trung điểm của
D
E
nên 2.DE a=
Khi đó
()
0
....AE AB AD DE AB AD AB DE AB=+ = +
  

()
02
..cos , ..cos0 2.
D
EAB DE AB DEAB a===
 
Câu 21. Cho hình vuông ABCD cạnh bằng 2. Điểm
M
nằm trên đoạn thẳng AC sao cho
4
AC
AM =
. Gọi
N
là trung điểm của đoạn thẳng .DC Tính ..
M
BMN
 
A. .4.MB MN =-
 
B. .0.MB MN =
 
C. .4.MB MN =
 
D. . 16.MB MN =
 
Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 685
Chọn B
Giả thiết không cho góc, ta phân tích các vectơ ,
M
BMN
 
theo các vectơ có giá vuông góc
với nhau.
·
()
11 31
.
44 44
M
BABAM AB ACAB ABAD AB AD=- =- =- + = -
    
·
()
111
424
M
NANAMADDN ACAD DC ABAD=- =+- =+ - +
        
()
11 3 1
.
24 4 4
AD AB AB AD AD AB=+ - + = +
    
Suy ra:
()
22
313 1 1
.3.33.
444 4 16
M
BMN AB AD AD AB ABAD AB AD ADAB
æöæö
÷÷
çç
=- += +--
÷÷
çç
÷÷
çç
èøèø
       
 
()
22
1
03 3 0 0
16
aa=+--=.
Câu 22.
Cho hình chữ nhật ABCD có 8, 5.AB AD== Tích ..AB BD
 
A. . 62.AB BD =
 
B. .64.AB BD =

C. .62.AB BD =-
 
D. .64.AB BD =-
 
Lời giải
Chọn D
Giả thiết không cho góc, ta phân tích các vectơ ,
A
BBD
 
theo các vectơ có giá vuông góc
với nhau.
Ta có
()
2
.. .. .0 64AB BD AB BA BC AB BA AB BC AB AB AB=+=+=-+=-=-
 

.
Câu 23. Cho hình thoi ABCD có
8AC =
và
6.BD =
Tính
..AB AC

A. .24.AB AC =
 
B. . 26.AB AC =

C. . 28.AB AC =

D. .32.AB AC =

Lời giải
Chọn D
Gọi OACBD=Ç, giả thiết không cho góc, ta phân tích các vectơ
,
A
BAC
 
theo các vectơ
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 686
có giá vuông góc với nhau.
Ta có
()
2
11
.....032
22
AB AC AO OB AC AO AC OB AC AC AC AC=+ = + = += =
         
.
Câu 24. Cho hình bình hành ABCD có 8cm, 12cmAB AD==, góc
ABC
nhọn và diện tích bằng
2
54 cm .
Tính
()
cos , .AB BC

A.
()
27
cos , .
16
AB BC =

B.
()
27
cos , .
16
AB BC =-

C.
()
57
cos , .
16
AB BC =

D.
()
57
cos , .
16
AB BC =-

Lời giải
Chọn D
Ta có
2
2. 54 27cm .
ABCD ABC ABC
SS S
DD
=== Diện tích tam giác ABC là:
11
...sin .. .sin .
22
ABC
S AB BC ABC AB AD ABC
D
==
2.
2.27 9
sin
.8.1216
ABC
S
ABC
AB AD
D
===

2
57
cos 1 sin
16
ABC ABC¾¾=- =(vì
ABC nhọn).
Mặt khác góc giữa hai vectơ
,AB BC

là góc ngoài của góc
ABC
Suy ra
()

0
57
cos , cos 180 cos .
16
AB BC ABC ABC
æö
÷
ç
=-=-=-
÷
ç
÷
ç
èø

Câu 25.
Cho hình chữ nhật ABCD có AB a= và 2AD a= . Gọi
K
là trung điểm của cạnh .AD
Tính
..BK AC
 
A. .0.BK AC =
 
B.
2
.2.BK AC a=-
 
C.
2
.2.BK AC a=
 
D.
2
.2.
B
KAC a=
 
Lời giải
Chọn A
Ta có
22 22
23.AC BD AB AD a a a== + = +=
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 687
Ta có
1
2
BK BA AK BA AD
AC AB AD
ì
ï
ï
=+ =+
ï
ï
í
ï
ï
ï
=+
ï
î
   

()
1
.
2
BK AC BA AD AB AD
æö
÷
ç
¾¾=+ +
÷
ç
÷
ç
èø
   
()
2
2
11 1
.. . . 0020.
22 2
BA AB BA AD AD AB AD AD a a= + + + =- +++ =
     
Câu 26. Cho tam giác ABC . Tập hợp các điểm
M
thỏa mãn
()
0MA MB MC+=
  
là:
A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Lời giải
Chọn D
Gọi
I
là trung điểm 2.BC MB MC MI¾¾+ =
  
Ta có
()
0MA MB MC+=
  
.2 0 . 0
M
AMI MAMI MA MI==^
     
.
()
*
Biểu thức
()
* chứng tỏ
M
AMI^
hay
M
nhìn đoạn
A
I
dưới một góc vuông nên tập hợp
các điểm
M
là đường tròn đường kính .AI
Câu 27. Tìm tập các hợp điểm
M
thỏa mãn
()
0MB MA MB MC++ =
   
với , , ABC là ba đỉnh của
tam giác.
A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Lời giải
Chọn D
Gọi G là trọng tâm tam giác
3.ABC MA MB MC MG¾¾++ =
   
Ta có
()
0.30.0 .
M
BMA MB MC MB MG MBMG MB MG+ + = = = ^
       
()
*
Biểu thức
()
*
chứng tỏ
M
BMG^ hay
M
nhìn đoạn BG dưới một góc vuông nên tập hợp
các điểm
M
là đường tròn đường kính .BG
Câu 28. Cho tam giác ABC . Tập hợp các điểm
M
thỏa mãn .0MA BC =
 
là:
A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Lời giải
Chọn B
Ta có .0 .
M
ABC MA BC= ^
 
Vậy tập hợp các điểm
M
là đường thẳng đi qua
A
và vuông góc với
.
B
C
Câu 29. Cho hai điểm
, AB
cố định có khoảng cách bằng a . Tập hợp các điểm N thỏa mãn
2
.2AN AB a=
 
là:
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 688
A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Lời giải
Chọn B
Gọi C là điểm đối xứng của
A
qua B . Khi đó
2.AC AB=

Suy ra
2
2
.2 2.AB AC AB a==
 
Kết hợp với giả thiết, ta có
..AN AB AB AC=
 
()
0.0AB AN AC AB CN CN AB - = = ^
   
.
Vậy tập hợp các điểm
N là đường thẳng qua C và vuông góc với .AB
Câu 30.
Cho hai điểm
, AB
cố định và
8.AB =
Tập hợp các điểm
M
thỏa mãn
.16MA MB =-
 
là:
A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn.
Lời giải
Chọn A
Gọi
I
là trung điểm của đoạn thẳng .AB IA IB¾¾=-

Ta có
()()()()
.
M
AMB MIIAMIIB MIIAMIIA=+ +=+ -
     
2
22
22 2
.
4
AB
MI IA MI IA MI=-=-=-

Theo giả thiết, ta có
222
22
8
16 16 16 0 .
444
AB AB
M
IMI MI-=-=-=-=¾¾º
Câu 31. Trong mặt phẳng tọa độ ,Oxy cho ba điểm
()()( )
3; 1 , 2;10 , 4;2 .ABC--
Tính tích vô hướng
..AB AC
 
A. . 40.AB AC =
 
B. . 40.AB AC -=
 
C. . 26.AB AC =

D. . 26.AB AC -=
 
Lời giải
Chọn A
Ta có
() ()
1;11 , 7; 3AB AC=- =-

.
Suy ra
()()
. 1 . 7 11.3 40.AB AC =- - + =
 
Câu 32. Trong mặt phẳng tọa độ ,Oxy cho hai điểm
()
3; 1A -
và
()
.2;10B
Tính tích vô hướng
..AO OB
 
A. .4.AOOB =-
 
B. .0.AOOB =
 
C. .4.AOOB =
 
D. . 16.AO OB =
 
Lời giải
Chọn C
Ta có
() ()
3;1 , 2;10 .AO OB=- =
 
Suy ra . 3.2 1.10 4.AO OB =- + =
 
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 689
Câu 33. Trong mặt phẳng tọa độ
,Oxy
cho hai vectơ
46ai j=+

và
37.bij=-

Tính tích vô hướng
..ab
A.
. 30.ab=-
B.
.3.ab=
C.
. 30.ab=
D.
. 43.ab=
Lời giải
Chọn A
Từ giả thiết suy ra
()
4;6a =
và
()
3; 7 .b =-
Suy ra
()
. 4.3 6. 7 30.ab=+-=-
Câu 34. Trong mặt phẳng tọa độ
,Oxy
cho hai vectơ
()
3;2a =-
và
()
1; 7 .b =- -
Tìm tọa độ vectơ c
biết
.9ca=
và
.20.cb=-
A.
()
1; 3 .c =- -
B.
()
1; 3 .c =-
C.
()
1; 3 .c =-
D.
()
1; 3 .c =
Lời giải
Chọn B
Gọi
()
;.cxy=
Ta có
()
.9 329 1
1; 3 .
720 3
.20
ca x y x
c
xy y
cb
ì
ï
ìì
=-+= =-
ïï
ï
ïï ï
¾¾=-
íí í
ïï ï
-- =- =
=-
ïï
ïî î
ï
î

Câu 35. Trong mặt phẳng tọa độ
,Oxy
cho ba vectơ
() ( )
1; 2 , 4; 3ab==
và
()
2;3 .c =
Tính
()
..Pabc=+

A. 0.P = B. 18.P = C. 20.P = D. 28.P =
Lời giải
Chọn B
Ta có
()
6;6 .bc+=
Suy ra
()
. 1.6 2.6 18.Pabc=+=+=

Câu 36. Trong mặt phẳng tọa độ ,Oxy cho hai vectơ
()
1;1a =-
và
()
2;0b =
. Tính cosin của góc
giữa hai vectơ
a
và
.b
A.
()
1
cos , .
2
ab =
B.
()
2
cos , .
2
ab =-
C.
()
1
cos , .
22
ab =-
D.
()
1
cos , .
2
ab =
Lời giải
Chọn B
Ta có
()
()
2
22 2
.1.21.02
cos , .
2
.
11.20
ab
ab
ab
-+
== =-
-+ +

Câu 37.
Trong mặt phẳng tọa độ
,Oxy
cho hai vectơ
()
2; 1a =- -
và
()
4; 3b =-
. Tính cosin của góc
giữa hai vectơ a
và .b
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 690
A.
()
5
cos , .
5
ab =-
B.
()
25
cos , .
5
ab =
C.
()
3
cos , .
2
ab =
D.
()
1
cos , .
2
ab =
Lời giải
Chọn A
Ta có
()
()()
2.4 1 . 3
.5
cos , .
5
41.169
.
ab
ab
ab
-+--
== =-
++

Câu 38.
Trong mặt phẳng tọa độ
,Oxy
cho hai vectơ
()
4;3a =
và
()
1;7b =
. Tính góc
a
giữa hai
vectơ
a
và .b
A.
O
90 .a =
B.
O
60 .a =
C.
O
45 .a =
D.
O
30 .a =
Lời giải
Chọn C
Ta có
() ()
0
.4.13.72
cos , , 45 .
2
16 9. 1 49
.
ab
ab ab
ab
+
== =¾¾=
++


Câu 39.
Trong mặt phẳng tọa độ ,Oxy cho hai vectơ
()
1; 2x =
và
()
3; 1y =- -
. Tính góc a giữa hai
vectơ
x
và .y
A.
O
45 .a =
B.
O
60 .a =
C.
O
90 .a =
D.
O
135 .a =
Lời giải
Chọn D
Ta có
()
() ()
()
0
1. 3 2. 1
.2
cos , , 135 .
2
14.91
.
xy
xy xy
xy
-+ -
== =-¾¾=
++



Câu 40.
Trong mặt phẳng tọa độ ,Oxy cho hai vectơ
()
2;5a =
và
()
3; 7b =-
. Tính góc a giữa hai
vectơ
a
và .b
A.
O
30 .a = B.
O
45 .a = C.
O
60 .a = D.
O
135 .a =
Lời giải
Chọn D
Ta có
()
()
()
0
2.3 5 7
.2
cos , , 135 .
2
4 25. 9 49
.
ab
ab ab
ab
+-
== =-¾¾=
++


Câu 41.
Trong mặt phẳng tọa độ
,Oxy
cho vectơ
()
9;3a =
. Vectơ nào sau đây không vuông góc
với vectơ a
?
A.
()
1
1; 3 .v =-
B.
()
2
2; 6 .v =-
C.
()
3
1; 3 .v =
D.
()
4
1; 3 .v =-
Lời giải
Chọn C
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 691
Kiểm tra tích vô hướng
.av
, nếu đáp án nào cho kết quả khác
0
thì kết luận vectơ đó
không vuông góc với
.a
Câu 42. Trong mặt phẳng tọa độ ,Oxy cho ba điểm
() ( )
1; 2 , 1;1AB-
và
()
5; 1C -
. Tính cosin của góc
giữa hai vectơ
AB

và
.AC

A.
()
1
cos , .
2
AB AC =-
 
B.
()
3
cos , .
2
AB AC =
 
C.
()
2
cos , .
5
AB AC =-
 
D.
()
5
cos , .
5
AB AC =-

Lời giải
Chọn D
Ta có
()
2; 1AB =- -

và
()
4; 3AC =-

.
Suy ra
()
()()
2.4 1 . 3
.5
cos , .
5
41.169
.
AB AC
AB AC
AB AC
-+--
== =-
++
 
 

Câu 43. Trong mặt phẳng tọa độ ,Oxy cho tam giác ABC có
()()
6;0 , 3;1AB và
()
1; 1C -- . Tính số
đo góc
B của tam giác đã cho.
A.
O
15 . B.
O
60 . C.
O
120 . D.
O
135 .
Lời giải
Chọn D
Ta có
()
3; 1BA =-

và
()
4; 2BC =- -

. Suy ra:
()
()()()
()
O
3. 4 1 . 2
.2
cos , , 135 .
2
91.164
.
BA BC
BA BC B BA BC
BA BC
-+- -
== =-¾¾= =
++



Câu 44. Trong mặt phẳng tọa độ ,Oxy cho bốn điểm
()()()
8;0 , 0;4 , 2;0ABC- và
()
3; 5 .D -- Khẳng
định nào sau đây là đúng?
A. Hai góc
BAD và
B
CD phụ nhau. B. Góc
B
CD là góc nhọn.
C.
()()
cos , cos , .AB AD CB CD=
   
D. Hai góc
BAD
và
B
CD
bù nhau.
Lời giải
Chọn D
Ta có
() () () ()
8;4, 5; 5, 2;4, 5;5.A B A D CB CD==-=-=-
  
Suy ra
()
()
()
()() ()
2222
2222
8.5 4. 5
1
cos ,
10
84.55
2. 5 4. 5
1
cos ,
10
24.55
AB AD
CB CD
ì
ï
+-
ï
==
ï
ï
ï
++
ï
í
ï
--+-
ï
ï
==-
ï
ï
++
ï
î
 
 
()()
0
cos , cos , 0 180 .AB AD CB CD BAD BCD¾¾+=+=
   
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 692
Câu 45. Trong mặt phẳng tọa độ
,Oxy
cho hai vectơ
1
5
2
uij=-

và
4vki j=-

Tìm
k
để vectơ
u
vuông góc với
.v
A.
20.k =
B.
20.k =-
C.
40.k =-
D.
40.k =
Lời giải
Chọn C
Từ giả thiết suy ra
()
1
;5, ;4.
2
uvk
æö
÷
ç
=- =-
÷
ç
÷
ç
èø
Yêu cầu bài toán:
()()
1
540 40
2
uv k k^ +- - ==-
.
Câu 46. Trong mặt phẳng tọa độ ,Oxy cho hai vectơ
1
5
2
uij=-

và 4.vki j=-

Tìm k để vectơ u
và vectơ
v
có độ dài bằng nhau.
A.
37
.
4
k =
B.
37
.
2
k =
C.
37
.
2
k =
D.
5
.
8
k =
Lời giải
Chọn C
Từ giả thiết suy ra
()
1
;5, ;4.
2
uvk
æö
÷
ç
=- =-
÷
ç
÷
ç
èø
Suy ra
11
25 101
42
u =+=
và
2
16vk=+
. Do đó để
222
1 101 37 37
16 101 16 .
2442
uv k k k k= += += = =
Câu 47. Trong mặt phẳng tọa độ ,Oxy cho ba vectơ
() ()
2;3 , 4;1ab=- =
và ckamb=+

với
, .kmÎ Biết rằng vectơ c
vuông góc với vectơ
()
ab+
. Khẳng định nào sau đây đúng?
A. 22.km= B. 32.km= C. 23 0.km+= D. 32 0.km+=
Lời giải
Chọn C
Ta có
()
()
24;3
.
2;4
ckamb k mkm
ab
ì
ï
=+ =-+ +
ï
ï
í
ï
+=
ï
ï
î


Để
()()
0cab cab^+ +=
 
()()
22 4 43 0 2 3 0.km km km-+ + + = + =
Câu 48.
Trong mặt phẳng tọa độ ,Oxy cho hai vectơ
()
2;3a =-
và
()
4;1b =
. Tìm vectơ d
biết
.4ad=
và .2bd=-
.
A.
56
;.
77
d
æö
÷
ç
=
÷
ç
÷
ç
èø
B.
56
;.
77
d
æö
÷
ç
=-
÷
ç
÷
ç
èø
C.
56
;.
77
d
æö
÷
ç
=-
÷
ç
÷
ç
èø
D.
56
;.
77
d
æö
÷
ç
=- -
÷
ç
÷
ç
èø
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 693
Lời giải
Chọn B
Gọi
()
;dxy=
. Từ giả thiết, ta có hệ
5
23 4
7
.
426
7
x
xy
xy
y
ì
ï
ï
=-
ï
ì
-+ =
ï
ï
ïï
íí
ïï
+=-
ï
îï
=
ï
ï
ï
î
Câu 49. Trong mặt phẳng tọa độ ,Oxy cho ba vectơ
() ()
4;1 , 1;4uv==
và .aumv=+

với .m Î
Tìm
m
để
a
vuông góc với trục hoành.
A. 4.m = B. 4.m =- C. 2.m =- D. 2.m =
Lời giải
Chọn B
Ta có
()
.4;14.aumv m m=+ = + +

Trục hoành có vectơ đơn vị là
()
1; 0 .i =
Vectơ a
vuông góc với trục hoành .04 0 4.ai m m=+==-
Câu 50. Trong mặt phẳng tọa độ ,Oxy cho hai vectơ
()
4;1u =
và
()
1; 4 .v =
Tìm m để vectơ
.amuv=+

tạo với vectơ bi j=+

một góc
0
45 .
A.
4.m =
B.
1
.
2
m =-
C.
1
.
4
m =-
D.
1
.
2
m =
Lời giải
Chọn C
Ta có
()
()
.41;4
.
1;1
amuv m m
bi j
ì
ï
=+= ++
ï
ï
í
ï
=+ =
ï
ï
î


Yêu cầu bài toán
()
0
2
cos , cos 45
2
ab==
()()
()()
()
22 2
41 4 5 1
22
22
217 16 17
24 1 4
mm m
mm
mm
++ + +
==
++
+++
()
2
22
10
1
5 1 17 16 17 .
25 50 25 17 16 17
4
m
mmm m
mm mm
ì
+³
ï
ï
+= ++ =-
í
ï
++= ++
ï
î
Câu 51. Trong mặt phẳng tọa độ ,Oxy tính khoảng cách giữa hai điểm
()
1; 2M - và
()
3;4 .N -
A.
4.MN =
B.
6.MN =
C. 36.MN = D. 213.MN =
Lời giải
Chọn D
Ta có
()
4;6MN =-

suy ra
()
2
2
4 6 42 2 13.MN =- + = =
Câu 52.
Trong mặt phẳng tọa độ ,Oxy cho tam giác ABC có
()() ()
1;4 , 3; 2 , 5; 4ABC
. Tính chu vi
P
của tam giác đã cho.
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 694
A.
422.P =+
B.
442.P =+
C.
882.P =+
D.
222.P =+
Lời giải
Chọn B
Ta có
()
()
()
()
()
2
2
22
2
2
2222
2; 2
2;2 2 2 2 2
4;0
404
AB
AB
BC BC
CA
CA
ì
ï
ì
ï
ï= +-=
=-
ï
ï
ï
ï
ï
ï
ï
ï
==+=
íí
ïï
ïï
ïï
=-
ïï
=- + =
ïï
î
ï
î



Vậy chu vi
P
của tam giác ABC là 442.PABBCCA=++=+
Câu 53.
Trong hệ tọa độ
()
;;Oi j
, cho vectơ
34
55
aij=- -
. Độ dài của vectơ a
bằng
A.
1
.
5
B. 1. C.
6
.
5
D.
7
.
5
Lời giải
Chọn B
Ta có
22
34 34 3 4
;1.
55 55 5 5
aij a a
æö æöæö
÷÷÷
ççç
=- - ¾¾=-- = - +- =
÷÷÷
ççç
÷÷÷
ççç
èø èøèø


Câu 54.
Trong mặt phẳng tọa độ ,Oxy cho hai vectơ
()
3;4u =
và
()
8;6v =-
. Khẳng định nào sau
đây đúng?
A. .uv=
B. u
và v
cùng phương.
C. u
vuông góc với v
. D. .uv=-
Lời giải
Chọn C
Ta có
()
.3.84.60uv=-+ =
suy ra u
vuông góc với v
.
Câu 55.
Trong mặt phẳng tọa độ ,Oxy cho các điểm
() ( ) ()
1; 2 , 2; 4 , 0;1AB C--
và
3
1;
2
D
æö
÷
ç
-
÷
ç
÷
ç
èø
. Mệnh
đề nào sau đây đúng?
A. AB

cùng phương với .CD

B.
.
A
BCD=

C.
.AB CD^

D.
.AB CD=

Lời giải
Chọn C
Ta có
()
3; 6AB =- -

và
1
1;
2
CD
æö
÷
ç
=-
÷
ç
÷
ç
èø

suy ra
()()()
1
.3.16.0.
2
AB CD =- - +- =

Vậy
AB

vuông góc với .CD

Câu 56.
Trong mặt phẳng tọa độ ,Oxy cho bốn điểm
()()()
7; 3 , 8;4 , 1;5ABC- và
()
0; 2D - . Khẳng
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 695
định nào sau đây đúng?
A. .AC CB^
 
B. Tam giác
ABC
đều.
C. Tứ giác ABCD là hình vuông.
D. Tứ giác
ABCD
không nội tiếp đường tròn.
Lời giải
Chọn C
Ta có
()
()
()
()
22
1;7 1 7 5 2
7;1 5 2
52.
1; 7 5 2
7; 1 5 2
AB AB
BC BC
AB BC CD DA
CD CD
DA DA
ì
ï
==+=
ï
ï
ï
ï
ï
=- =
ï
ï
¾¾=== =
í
ï
ï=-- =
ï
ï
ï
ï
=- =
ï
ï
î




Lại có
()
.177.10AB BC =-+ =

nên AB BC^ .
Từ đó suy ra
ABCD là hình vuông.
Câu 57.
Trong mặt phẳng tọa độ ,Oxy cho bốn điểm
()()()
1;1 , 0; 2 , 3;1ABC-
và
()
0; 2 .D -
Khẳng
định nào sau đây là đúng?
A. Tứ giác
ABCD
là hình bình hành.
B. Tứ giác ABCD là hình thoi.
C. Tứ giác ABCD là hình thang cân.
D. Tứ giác ABCD không nội tiếp được đường tròn.
Lời giải
Chọn C
Ta có
()
()
1;1
3
3;3
AB
D
CAB
DC
ì
ï
=
ï
ï
¾¾=
í
ï
=
ï
ï
î

 

.
Suy ra
D
CAB và 3.
D
CAB=
()
1
Mặt khác
22
22
13 10
.
31 10
AD
AD BC
BC
ì
ï
=+=
ï
ï
¾¾=
í
ï
ï
=+=
ï
î
()
2
Từ
()
1 và
()
2 , suy ra tứ giác ABCD là hình thang cân.
Câu 58. Trong mặt phẳng tọa độ ,Oxy cho tam giác ABC có
()()
1;1 , 1;3AB- và
()
1; 1C - . Khẳng
định nào sau đây là đúng?
A.
Tam giác ABC đều. B. Tam giác ABC có ba góc đều nhọn.
C. Tam giác ABC cân tại B . D. Tam giác ABC vuông cân tại
A
.
Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 696
Chọn D
Ta có
() ( )
2;2 , 0; 4AB BC==-

và
()
2; 2 .AC =-

Suy ra
222
22
.
AB AC
A
BAC BC
ì
ï
==
ï
í
ï
+=
ï
î
Vậy tam giác ABC vuông cân tại .A
Câu 59.
Trong mặt phẳng tọa độ
,Oxy
cho tam giác
ABC
có
()()
10;5 , 3;2AB
và
()
6; 5C -
. Khẳng
định nào sau đây là đúng?
A.
Tam giác
ABC
đều. B. Tam giác
ABC
vuông cân tại
A
.
C. Tam giác ABC vuông cân tại B . D. Tam giác ABC có góc
A
tù.
Lời giải
Chọn C
Ta có
() ()
7; 3 , 3; 7AB BC=- - = -

và
()
4; 10 .AC =- -

Suy ra
() ()()
.7.33.70AB BC =- +- - =

và
.AB BC=
Vậy tam giác
ABC vuông cân tại .B
Câu 60.
Trong mặt phẳng tọa độ ,Oxy cho tam giác ABC có
()()
2; 1 , 1; 1AB-- - và
()
2;2C - . Khẳng
định nào sau đây là đúng?
A.
Tam giác ABC đều. B. Tam giác ABC vuông cân tại
A
.
C. Tam giác ABC vuông tại
B
. D. Tam giác ABC vuông cân tại C .
Lời giải
Chọn B
Ta có
() ( )
3;0 , 3;3AB BC==-

và
()
0;3 .AC =

Do đó
222
3
.
32
AB AC
AB AC BC
BC
ì
==
ï
ï
+=
í
ï
=
ï
î
Vậy tam giác
ABC vuông cân tại .A
Câu 61.
Trong mặt phẳng tọa độ ,Oxy cho hai điểm
()
2;4A - và
()
.8;4B Tìm tọa độ điểm C thuộc
trục hoành sao cho tam giác
ABC vuông tại .C
A.
()
.6;0C B.
()
,0;0C
()
.6;0C C.
()
.0;0C D.
()
1; 0 .C -
Lời giải
Chọn B
Ta có
COxÎ nên
()
;0Cc và
()
()
2;4
.
8;4
CA c
CB c
ì
ï
=- -
ï
ï
í
ï
=-
ï
ï
î


Tam giác
ABC vuông tại C nên
()()
.0 2.8 4.40CA CB c c=-- -+ =
 
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 697
()
()
2
6;6
60 .
0
0;00
cC
cc
cC
é
=
ê
-=
ê
=
ê
ë
Câu 62. Trong mặt phẳng tọa độ
,Oxy
cho hai điểm
()
1; 2A và
()
3;1 .B - Tìm tọa độ điểm C thuộc
trục tung sao cho tam giác
ABC
vuông tại
.A
A.
()
.0;6C B.
()
.5;0C C.
()
.3;1C D.
()
0; 6 .C -
Lời giải
Chọn A
Ta có
COyÎ nên
()
0;Cc và
()
()
4; 1
.
1; 2
AB
AC c
ì
ï
=- -
ï
ï
í
ï
=- -
ï
ï
î


Tam giác
ABC vuông tại
A
nên
()()()( )
.04.1120 6.AB AC c c=- -+- - ==
 
Vậy
()
0;6C .
Câu 63. Trong mặt phẳng tọa độ
,Oxy
cho ba điểm
()()
–
4;0 , –5;0AB
và
()
.3;0C
Tìm điểm
M
thuộc trục hoành sao cho
0.MA MB MC++ =

A.
()
.
–
2;0M
B.
()
.2;0M
C.
()
.
–
4;0M
D.
()
.
–
5;0M
Lời giải
Chọn A
Ta có
M
OxÎ nên
()
;0
M
x và
()
()
()
()
4;0
5;0 63;0.
3;0
MA x
MB x MA MB MC x
MC x
ì
ï
=- -
ï
ï
ï
ï
=-- ¾¾++ =--
í
ï
ï
ï
=-
ï
ï
î

   

Do
0MA MB MC++ =
  
nên
()
63 0 2 2;0.xx M-- = =-¾¾-
Câu 64. Trong mặt phẳng tọa độ ,Oxy cho hai điểm
()
–
2;2M
và
()
.1;1N
Tìm tọa độ điểm
P
thuộc
trục hoành sao cho ba điểm
, ,
M
NP
thẳng hàng.
A.
()
.0;4P B.
()
.0;–4P C.
()
.
–
4;0P D.
()
.4;0P
Lời giải
Chọn D
Ta có
POxÎ nên
()
;0
P
x và
()
()
2; 2
.
3; 1
MP x
MN
ì
ï
=+-
ï
ï
í
ï
=-
ï
ï
î


Do
, ,
M
NP thẳng hàng nên
()
22
44;0.
31
x
xP
+-
==¾¾
-
Câu 65.
Trong mặt phẳng tọa độ ,Oxy tìm điểm
M
thuộc trục hoành để khoảng cách từ đó đến
điểm
()
1; 4N - bằng 25.
A.
()
1; 0 .M B.
() ( )
1; 0 , 3; 0 .MM-
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 698
C.
()
3;0 .M
D.
() ()
1; 0 , 3; 0 .MM
Lời giải
Chọn B
Ta có
M
OxÎ
nên
()
;0Mm
và
()
1;4.MN m=--

Theo giả thiết:
()
2
2
25 25 1 4 25MN MN m= =--+=

()
()
()
2
2
11;0
11620 230 .
33;0
mM
mmm
mM
é
=¾¾
ê
+ + = + -=
ê
=- ¾¾-
ê
ë
Câu 66.
Trong mặt phẳng tọa độ ,Oxy cho hai điểm
()
1;3A
và
()
4;2 .B
Tìm tọa độ điểm
C
thuộc
trục hoành sao cho
C
cách đều hai điểm
A
và
.B
A.
5
;0 .
3
C
æö
÷
ç
-
÷
ç
÷
ç
èø
B.
5
;0 .
3
C
æö
÷
ç
÷
ç
÷
ç
èø
C.
3
;0 .
5
C
æö
÷
ç
-
÷
ç
÷
ç
èø
D.
3
;0 .
5
C
æö
÷
ç
÷
ç
÷
ç
èø
Lời giải
Chọn B
Ta có
COxÎ
nên
()
;0Cx
và
()
()
1; 3
.
4; 2
AC x
BC x
ì
ï
=--
ï
ï
í
ï
=--
ï
ï
î


Do
()()( )()
22 22
22
55
13 42 ;0
33
CA CB CA CB x x x C
æö
÷
ç
= = -+-=-+-=¾¾
÷
ç
÷
ç
èø
.
Câu 67. Trong mặt phẳng tọa độ ,Oxy cho hai điểm
()( )
2;2 , 5; 2 .AB- Tìm điểm
M
thuộc trục
hoàng sao cho
0
90 ?AMB =
A.
()
0;1 .M B.
()
6;0 .M C.
()
1; 6 .M D.
()
0;6 .M
Lời giải
Chọn B
Ta có
M
OxÎ nên
()
;0Mm và
()
()
2; 2
.
5;2
AM m
BM m
ì
ï
=--
ï
ï
í
ï
=-
ï
ï
î


Vì
0
90AMB =
suy ra
.0AM BM =
 
nên
()()()
252.20.mm--+-=
()
()
2
1; 0
1
760 .
6
6;0
M
m
mm
m
M
é
é
=
ê
ê
-+= ¾¾
ê
ê
=
ë
ê
ë
Câu 68.
Trong mặt phẳng tọa độ ,Oxy cho hai điểm
()
1; 1A - và
()
3;2 .B Tìm
M
thuộc trục tung
sao cho
22
M
AMB+
nhỏ nhất.
A.
()
0;1 .M B.
()
0; 1 .M - C.
1
0; .
2
M
æö
÷
ç
÷
ç
÷
ç
èø
D.
1
0; .
2
M
æö
÷
ç
-
÷
ç
÷
ç
èø
Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 699
Chọn C
Ta có
M
OyÎ nên
()
0;
M
m
và
()
()
1; 1
.
3;2
M
Am
MB m
ì
ï
=--
ï
ï
í
ï
=-
ï
ï
î


Khi đó
() ()
22
22
22 2 2 2
11 32 2215.MA MB MA MB m m m m+= + =+--++-=-+
 
2
12929
2;.
222
mm
æö
÷
ç
=-+³"Î
÷
ç
÷
ç
èø
Suy ra
{}
22
min
29
.
2
MA MB+=
Dấu
'' ''=
xảy ra khi và chỉ khi
11
0; .
22
mM
æö
÷
ç
=¾¾
÷
ç
÷
ç
èø
Câu 69.
Trong mặt phẳng tọa độ ,Oxy cho hình bình hành ABCD biết
()
2;0 ,A -
()
2;5 ,B
()
6;2 .C
Tìm tọa độ điểm
.
D
A.
()
2; 3 .D -
B.
()
2;3 .D
C.
()
2; 3 .D --
D.
()
2;3 .D -
Lời giải
Chọn A
Gọi
()
;.
D
xy Ta có
()
2;AD x y=+

và
()
4; 3BC =-

. Vì ABCD là hình bình hành nên
()
24 2
2; 3 .
33
xx
AD BC D
yy
ìì
+= =
ïï
ïï
=¾¾¾¾-
íí
ïï
=- =-
ïï
îî
 
Câu 70.
Trong mặt phẳng tọa độ ,Oxy cho tam giác ABC có
() ( ) ()
1; 3 , 2; 4 , 5; 3 .AB C- Tìm tọa độ
trọng tâm
G của tam giác đã cho.
A.
10
2; .
3
G
æö
÷
ç
÷
ç
÷
ç
èø
B.
810
;.
33
G
æö
÷
ç
-
÷
ç
÷
ç
èø
C.
()
2;5 .G D.
410
;.
33
G
æö
÷
ç
÷
ç
÷
ç
èø
Lời giải
Chọn D
Tọa độ trọng tâm
()
;
GG
Gx y là
125 4
33
.
343 10
33
G
G
x
y
ì
-+
ï
ï
==
ï
ï
ï
í
ï
++
ï
==
ï
ï
ï
î
Câu 71. Trong mặt phẳng tọa độ ,Oxy cho tam giác ABC có
()()
4;1 , 2;4 ,AB-
()
2; 2 .C - Tìm tọa độ
tâm
I
của đường tròn ngoại tiếp tam giác đã cho.
A.
1
;1 .
4
I
æö
÷
ç
÷
ç
÷
ç
èø
B.
1
;1 .
4
I
æö
÷
ç
-
÷
ç
÷
ç
èø
C.
1
1; .
4
I
æö
÷
ç
÷
ç
÷
ç
èø
D.
1
1; .
4
I
æö
÷
ç
-
÷
ç
÷
ç
èø
Lời giải
Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 700
Gọi
()
;
I
xy. Ta có
()
()
()
4; 1
2; 4 .
2; 2
AI x y
BI x y
CI x y
ì
ï
=+ -
ï
ï
ï
ï
=- -
í
ï
ï
ï
=- +
ï
ï
î



Do
I
là tâm đường tròn ngoại tiếp tam giác ABC nên
22
22
IA IB
IA IB IC
IB IC
ì
ï
=
ï
==
í
ï
=
ï
î
()()()()
()()()()
()()
22 2 2
22
22 22
1
4124
429
4
1
2422
1
xyxy
x
xx
y
xyxy
y
ì
ï
ì
ï
ì
ï
ï
++-=-+-
=-
+=-+
ï
ï
ï
ï

ííí
ïïï
=
-+-=-++
ïïï
î
=
ï
î
ï
î
.
Câu 72. Trong mặt phẳng tọa độ ,Oxy cho tam giác ABC có
()()
3;0 , 3;0AB-
và
()
2;6 .C
Gọi
()
;
H
ab
là tọa độ trực tâm của tam giác đã cho. Tính
6.ab+
A. 65.ab+= B. 66.ab+= C. 67.ab+= D. 68.ab+=
Lời giải
Chọn C
Ta có
() ()
() ()
3; & 1;6
.
3; & 5;6
AH a b BC
BH a b AC
ì
ï
=+ =-
ï
ï
í
ï
=- =
ï
ï
î
 
 
Từ giả thiết, ta có:
()()
()
2
3. 1 .6 0
.0
67.
5
3.5 .6 0
.0
6
a
ab
AH BC
ab
ab
b
BH AC
ì
=
ï
ì
ï
ì
ï
ï+ -+ =
=
ï
ï
ïï
¾¾+ =
íí í
ïï ï
-+=
=
=
ïï ï
î
ï
î
ï
î
 
 
Câu 73.
Trong mặt phẳng tọa độ ,Oxy cho tam giác ABC có
()()
4;3 , 2;7AB
và
()
3; 8 .C --
Tìm toạ
độ chân đường cao
'
A
kẻ từ đỉnh
A
xuống cạnh .BC
A.
()
'1; 4.A - B.
()
'1;4.A - C.
()
'1;4.A D.
()
'4;1.A
Lời giải
Chọn C
Gọi
()
';
A
xy
. Ta có
()
()
()
'4;3
5; 15 .
'2;7
AA x y
BC
BA x y
ì
ï
=- -
ï
ï
ï
ï
=- -
í
ï
ï
ï
=- -
ï
ï
î



Từ giả thiết, ta có
()
()
'. 0 1
'
, ', thang hang
'
.
2
AA BC
AA BC
BA C
BA k BC
ì
=
^
ï
ï
í
ï
ì
ï
ï
ï
í
ï
ï
ï
î
=
ï
î

 
·
() ( ) ( )
1 5 4 15 3 0 3 13.xy xy- - - - = + =
·
()
27
231.
515
xy
xy
--
=-=-
--
Giải hệ
()
313 1
'1;4.
314
xy x
A
xy y
ìì
+= =
ïï
ïï
¾¾
íí
ïï
-=- =
ïï
îî
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 701
Câu 74. Trong mặt phẳng tọa độ ,Oxy cho tam giác
ABC
có
()( )
2;4 , 3;1 ,AB-
()
3; 1 .C -
Tìm tọa độ
chân đường cao
'
A
vẽ từ đỉnh
A
của tam giác đã cho.
A.
31
';.
55
A
æö
÷
ç
÷
ç
÷
ç
èø
B.
31
';.
55
A
æö
÷
ç
--
÷
ç
÷
ç
èø
C.
31
';.
55
A
æö
÷
ç
-
÷
ç
÷
ç
èø
D.
31
'; .
55
A
æö
÷
ç
-
÷
ç
÷
ç
èø
Lời giải
Chọn D
Gọi
()
';.
A
xy Ta có
()
()
()
'2;4
6; 2 .
'3;1
AA x y
BC
BA x y
ì
ï
=- -
ï
ï
ï
ï
=-
í
ï
ï
ï
=+ -
ï
ï
î



Vì
'
A
là chân đường cao vẽ từ đỉnh
A
của tam giác ABC nên
thaúng haøng
'
, , '
AA BC
BCA
ì
^
ï
ï
í
ï
ï
î
()()()
3
2.6 4. 2 0
'. 0 6 2 4
5
.
31
26 0 1
'
62
5
xy
x
AA BC x y
xy
xy
BA k BC
y
ì
ì
ï
ï
ìï
ï
ï- + - -=
=
ì
ï
ï
ïï
=-=
ï
ï
ï
ï
ïï ï ï

íí í í
+-
ïï ï ï
-- =
=
=
ïï ï ï
ï
î
=-
ïïï
-
ï
î
ïï
ï
î
ï
î
 
 
Câu 75. Trong mặt phẳng tọa độ Oxy , cho ba điểm
()()
3; 2 , 3; 6AB-- và
()
11;0 .C Tìm tọa độ điểm
D
để tứ giác
ABCD
là hình vuông.
A.
()
5; 8 .D - B.
()
8;5 .D C.
()
5;8 .D - D.
()
8;5 .D -
Lời giải
Chọn A
Dễ dàng kiểm tra
0
.0 90.BA BC ABC=¾¾=

Gọi
I
là tâm của hình vuông .ABCD Suy ra
I
là trung điểm của
()
4; 1 .AC I¾¾-
Gọi
()
;
D
xy, do
I
cũng là trung điểm của
()
3
4
5
2
5; 8 .
68
1
2
x
x
BD D
yy
ì
+
ï
ï
=
ï
ì
=
ï
ï
ïï
¾¾-
íí
ïï
+=-
ï
ïî
=-
ï
ï
ï
î
Câu 76. Trong mặt phẳng tọa độ ,Oxy cho hai điểm
()
2;4A
và
()
1;1 .B
Tìm tọa độ điểm C sao cho
tam giác
ABC vuông cân tại .B
A.
()
4;0 .C B.
()
2;2 .C - C.
()( )
4;0 , 2;2 .CC- D.
()
2;0 .C
Lời giải
Chọn C
Gọi
()
;Cxy
. Ta có
()
()
1; 3
.
1; 1
BA
BC x y
ì
ï
=
ï
ï
í
ï
=- -
ï
ï
î


Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 702
Tam giác
ABC
vuông cân tại
B
.0BA BC
BA BC
ì
ï
=
ï
í
ï
=
ï
î

()()
()()
22
22
1. 1 3. 1 0
13 1 1
xy
xy
ì
ï-+ -=
ï
ï
í
ï
+=-+-
ï
ï
î
2
43 0 2
hay .
10 20 0 4 2
xy y y
yy x x
ì
ìì
=- = =
ï
ïï
ïïï

ííí
ïïï
-= = =-
ïï
îïî
î
Câu 77. Trong mặt phẳng tọa độ
,Oxy
cho hình vuông ABCD có
()
1; 1A - và
()
3;0 .B Tìm tọa độ
điểm
D
, biết
D
có tung độ âm.
A.
()
0; 1 .D - B.
()
2; 3 .D - C.
()()
2; 3 , 0;1 .DD- D.
()
2; 3 .D --
Lời giải
Chọn B
Gọi C
()
;.
x
y= Ta có
()
()
2;1
.
3;
AB
BC x y
ì
ï
=
ï
ï
í
ï
=-
ï
ï
î


Vì
ABCD là hình vuông nên ta có
AB BC
AB BC
ì
ï
^
ï
í
ï
=
ï
î

()
()
()
()
()
()
222
2
231.0 23 23
4
2
3553531
xyyxyx
x
y
xy x x
ì
ìì
ï
ïï-+ = = - = -
ì
=
ï
ï
ïï
ïïïï

íííí
ïïïï
=-
-+= -= -=
ï
ïïïî
ïï
îî
ï
î
hoặc
2
2
x
y
ì
=
ï
ï
í
ï
=
ï
î
.
Với
()
1
4; 2C -
ta tính được đỉnh
()
1
2; 3D -
: thỏa mãn.
Với
()
2
2;2C ta tính được đỉnh
()
2
0;1D : không thỏa mãn.
Câu 78. Trong mặt phẳng tọa độ ,Oxy cho bốn điểm
()( )( )
1; 2 , 1; 3 , 2; 1AB C---
và
()
0; 2 .D -
Mệnh
đề nào sau đây đúng?
A. ABCD là hình vuông. B. ABCD là hình chữ nhật.
C. ABCD là hình thoi. D. ABCD là hình bình hành.
Lời giải
Chọn D
Ta có
()
()
()
2;1
1; 4
.20
2;1
AB
AB DC
BC ABCD
AB BC
DC
ì
ï
=-
ï
ï
ì
ï
ï
=
ï
ï
ï
=- - ¾¾¾¾
íí
ïï
=- ¹
ïï
ï
î
ï
=-
ï
ï
î

 



là hình hình hành.
Câu 79. Trong mặt phẳng tọa độ
,Oxy
cho tam giác OA B với
()
1; 3A và
()
4;2B . Tìm tọa độ điểm
E
là chân đường phân giác trong góc O của tam giác .OAB
A.
55
;.
22
E
æö
÷
ç
=
÷
ç
÷
ç
èø
B.
31
;.
22
E
æö
÷
ç
=-
÷
ç
÷
ç
èø
C.
()
232;4 2.E =- + + D.
()
232;4 2.E =- + -
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 703
Lời giải
Chọn D
Theo tính chất đường phân giác của tam giác ta có
2
.
2
EA OA
EB OB
==
Vì E nằm giữa hai điểm , AB nên
2
.
2
E
AEB=-

()
*
Gọi
()
;
E
xy
. Ta có
()
()
1;3
.
4;2
E
Axy
E
Bxy
ì
ï
=- -
ï
ï
í
ï
=- -
ï
ï
î


Từ
()
* , suy ra
()
()
2
14
232
2
.
242
32
2
xx
x
y
yy
ì
ï
ï
-=- -
ï
ì
ï
ï
=- +
ï
ï
ï
íí
ïï
=-
ïï
ï
î
ï
-=- -
ï
ï
î
Câu 80. Trong mặt phẳng tọa độ
,Oxy
cho ba điểm
()()
2;0 , 0;2AB
và
()
0;7 .C
Tìm tọa độ đỉnh thứ
tư
D
của hình thang cân .ABCD
A.
()
7;0 .D B.
()()
7;0 , 2;9 .DD C.
()()
0;7 , 9;2 .DD D.
()
9;2 .D
Lời giải
Chọn B
Để tứ giác
ABCD là hình thang cân, ta cần có một cặp cạnh đối song song không bằng
nhau và cặp cạnh còn lại có độ dài bằng nhau. Gọi
()
;.
D
xy
Trường hợp 1:
AB CD
CD k AB
AB CD
ì
ï
ï
=
í
ï
¹
ï
î

(với 1k ¹- )
()()
2
0; 7 2 ;2 .
27
x
k
xy kk
yk
ì
=-
ï
ï
- -=-
í
ï
=+
ï
î
()
1
Ta có
() ()
()
()
2
2
2
2
2; 2
225.
0;5 5
AD x y AD x y
AD BC x y
BC BC
ì
ï
ï
=- = - +
ï
¾¾=-+=
í
ï
ï
==
ï
î


()
2
Từ
()
1 và
()
2 , ta có
()()
()
()
22
1
22 27 25 7;0.
7
2
k
kk D
k
é
=-
ê
ê
-- + + = ¾¾
ê
=-
ê
ë
loaïi
Trường hợp 2:
AD BC
AD BC
ì
ï
ï
í
ï
¹
ï
î
. Làm tương tự ta được
()
2;9 .D =
Vậy
()
7;0D
hoặc
()
2;9D
.
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 704
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 705
c
b
a
C
B
A
I
c
b
a
C
B
A
c
b
a
C
B
A
a
m
b
m
c
m
BÀI 3. CÁC HỆ THỨC LƯỢNG TRONG TAM GIÁC VÀ GIẢI TAM GIÁC
A. KIẾN THỨC CƠ BẢN CẦN NẮM
1. Định lí côsin
Cho tam giác
ABC có ,BC a AC b== và AB c= .
Ta có
222
222
222
2.cos;
2.cos;
2.cos.
abc bc A
bca ca B
cab ab C
=+-
=+-
=+-
Hệ quả
222 222 222
cos ; cos ; cos .
222
bca cab abc
ABC
bc ca ab
+- +- +-
===
2. Định lí sin
Cho tam giác
ABC có ,BC a AC b==, AB c= và
R
là bán kính đường tròn ngoại tiếp.
Ta có
2
sin sin sin
abc
R
ABC
===
3. Độ dài đường trung tuyến
Cho tam giác
ABC có ,,
abc
mmm lần lượt là các trung tuyến kẻ từ
, , ABC
.
Ta có
22 2
2
22 2
2
222
2
;
24
;
24
.
24
a
b
c
bca
m
acb
m
abc
m
+
=-
+
=-
+
=-
4. Công thức tính diện tích tam giác
Cho tam giác
ABC có
●
,,
abc
hhh là độ dài đường cao lần lượt tương ứng với các cạnh , , BC CA AB ;
●
R là bán kính đường tròn ngoại tiếp tam giác;
●
r là bán kính đường tròn nội tiếp tam giác;
●
2
abc
p
++
=
là nửa chu vi tam giác;
●
S là diện tích tam giác.
Khi đó ta có:
111
222
abc
Sahbhch===
()()()
111
sin sin sin
222
4
.
bc A ca B ab C
abc
R
pr
pp a p b p c
===
=
=
=---
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 706
B. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI.
Dạng1:xácđịnhcácyếutốtrongtamgiác.
1. Phương pháp.
Sử dụng định lí côsin và định lí sin
Sử dụng công thức xác định độ dài đường trung tuyến và mối liên hệ của các yếu tố trong
các công thức tính diện tích trong tam giác.
2. Các ví dụ.
Ví dụ 1: Cho tam giác
ABC
có
AB AC==4, 5
và
A =
3
cos
5
.
Tính cạnh BC, và độ dài đường cao kẻ từ A.
Lời giải
Áp dụng định lí côsin ta có
BC AB AC AB AC A=+- =+- =
222 22
3
2 . .cos 4 5 2.4.5. 29
5
Suy ra
BC = 29
Vì
AA+=
22
sin cos 1
nên
AA=- =-=
2
94
sin 1 cos 1
25 5
Theo công thức tính diện tích ta có
ABC
SABACA===
114
. .sin .4.5. 8
225
(1)
Mặt khác
ABC a a
Sah h==
11
. . 29.
22
(2)
Từ (1) và (2) suy ra
aa
hh= =
11629
.29. 8
229
Vậy độ dài đường cao kẻ từ A là
a
h =
16 29
29
Ví dụ 2: Cho tam giác
ABC nội tiếp đường tròn bán kính bằng 3, biết
AB==
00
30 , 45 . Tính
độ dài trung tuyến kẻ từ A và bán kính đường tròn nội tiếp tam giác.
Lời giải
Ta có
CAB=--=--=
0 000 0
180 180 30 45 105
Theo định lí sin ta có
aRA== =
0
2 sin 2.3.sin 30 3 ,
bRB== ==
0
2
2 sin 2.3.sin 45 6. 3 2
2
cRC== »
0
2 sin 2.3.sin105 5,796
Theo công thức đường trung tuyến ta có
(
)
(
)
a
bc a
m
+- + -
=» =
22 2 2
2
2 2 18 5, 796 9
23, 547
44
Theo công thức tính diện tích tam giác ta có
ABC
bc A
SprbcAr
p
== = » »
++
0
1 sin 3 2.5,796sin 30
sin 0,943
22
3 3 2 5,796
Ví dụ 3: Cho tam giác
ABC có M là trung điểm của BC. Biết
AB BC AMB== =
513
3, 8, cos
26
.
Tính độ dài cạnh
AC
và góc lớn nhất của tam giác
ABC
.
Lời giải (hình 2.7)
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 707
BC BM= =84. Đặt AM x=
Theo định lí côsin ta có
cos
.
AM BM AB
AMB
AM AB
+-
=
222
2
Suy ra
x
x
+-
=
2
513 16 9
26 2.4.
x
xx
x
é
=
ê
ê
- +=
ê
=
ê
ë
2
13
13 20 13 91 0
713
13
Theo công thức tính đường trung tuyến ta có
(
)
.
AB AC BC
AM
AB AC
+-
=
22 2
2
2
2
TH1: Nếu
()
AC
xAC
+-
== =
222
23 8
13 13 7
4
.
Ta có
BC AC AB>>
góc A lớn nhất. Theo định lí côsin ta có
cos
...
AB AC BC
A
AB AC
+- +-
===-
222
94964 1
2 237 7
Suy ra
'A »
0
98 12
TH2: Nếu
(
)
AC
xAC
+-
== =
222
23 8
713 49 397
13 13 4 13
Ta có
BC AC AB>> góc A lớn nhất. Theo định lí côsin ta có
cos
.
..
AB AC BC
A
AB AC
+-
+-
===-
222
397
964
53
13
2
397 5161
23
13
Suy ra
'A »
0
137 32
Ví dụ 4: Cho hình chữ nhật ABCD biết AD = 1 . Giả sử E là trung điểm AB và thỏa mãn
BDE =
1
sin
3
.
Tính độ dài cạnh
AB .
Lời giải (hình 2.8)
Đặt
(
)
AB x x AE EB x=>==20
.
Vì góc
BDE nhọn nên
BDE >cos 0 suy ra

BDE BDE=- =
2
22
cos 1 sin
3
Theo định lí Pitago ta có:
DE AD AE x DE x=+=+=+
222 2 2
11
BD DC BC x BD x=+=+= +
2222 2
41 41
M
A
B
C
Hình 2.7
E
A
D
C
B
Hình 2.8
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 708
Áp dụng định lí côsin trong tam giác
BDE ta có
()( )
DE DB EB x
BDE
DE DB
xx
+- +
==
++
222 2
22
22 4 2
cos
2. 3
21 4 1
42 2
2
44102 1
2
xx x x-+===
(Do
x > 0
)
Vậy độ dài cạnh AB là 2
Dạng2:giảitamgiác.
1. Phương pháp.
Giải tam giác là tính các cạnh và các góc của tam giác dựa trên một số điều kiện cho trước.
Trong các bài toán giải tam giác người ta thường cho tam giác với ba yếu tố như sau : biết một
cạnh và hai
góc kề cạnh đó; biết một góc và hai cạnh kề góc đó; biết ba cạnh.
Để tìm các yếu tố còn lại ta sử dụng định lí côsin và định lí sin ; định lí tổng ba góc trong một
tam giác bằng
0
180
và trong một tam giác đối diện với góc lớn hơn thì có cạnh lớn hơn và ngược
lại đối diện với cạnh lớn hơn thì có góc lớn hơn.
2. Các ví dụ.
Ví dụ 1:
Giải tam giác ABC biết bc==32; 45 và
A =
0
87 .
Lời giải
Theo định lí côsin ta có
abc bcA=+- = +-
222 22 0
2 .cos 32 4 2.32.4.sin 87
Suy ra
a » 53, 8
Theo định lí sin ta có
bA
BB
a
== »
0
0
sin 32 sin 87
sin 36
53, 8
Suy ra
CAB=--»--=
00000
180 180 87 36 57
Ví dụ 2: Giải tam giác ABC biết
AB==
00
60 , 40 và c = 14 .
Lời giải
Ta có
CAB=--=--=
00000
180 180 60 40 80
Theo định lí sin ta có
cA
aa
C
== »
0
0
sin 14.sin 60
12, 3
sin
sin 80
cB
bb
C
== »
0
0
sin 14.sin 40
9, 1
sin
sin 80
Ví dụ 3: Cho tam giác
ABC
biết abc===-23, 22, 6 2. Tính góc lớn nhất của tam
giác.
Lời giải
Theo giải thiết ta có cba<< suy ra
CBA<< do đó góc A là lớn nhất.
Theo định lí côsin ta có
()
()
bca
A
bc
+- -
+- -
== ==-
--
2
2
222
86212
443 1
cos
22
2.2 2. 6 2 8 3 8
Suy ra
A =
0
120
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 709
Vậy góc lớn nhất là góc A có số đo là
0
120
.
Dạng3:ChứngMinhĐẳngThức,BấtĐẳngThứcLiênQuanĐếnCácYếuTố
CủaTamGiác,TứGiác.
1. Phương pháp giải.
Để chứng minh đẳng thức ta sử dụng các hệ thức cơ bản để biến đổi vế này thành vế kia, hai
vế cùng bằng một vế hoặc biến đổi tương đương về một đẳng thức đúng.
Để chứng minh bất đẳng thức ta sử dụng các hệ thức cơ bản, bất đẳng thức cạnh trong tam
giác và bất đẳng thức cổ điển (Cauchy, bunhiacôpxki,…)
2. Các ví dụ.
Ví dụ 1:
Cho tam giác ABC thỏa mãn ABC=
2
sin sin .sin . Chứng minh rằng
a)
abc=
2
b)
A ³
1
cos
2
Lời giải
a) Áp dụng định lí sin ta có
abc
ABC
RRR
===sin , sin , sin
222
Suy ra
abc
ABC abc
RRR
æö
÷
ç
===
÷
ç
÷
÷
ç
èø
2
22
sin sin .sin .
222
đpcm
b) Áp dụng định lí côsin và câu a) ta có
bca bcbc bcbc
A
bc bc bc
+- +- -
==³=
222 22
21
cos
2222
đpcm
Ví dụ 2: Cho tam giác ABC , chứng minh rằng:
a)
Appa
bc
-
=
()
cos
2
b)
sin sin sin cos cos cos
ABC
ABC++=4
222
Lời giải (hình 2.9)
a) Trên tia đối của tia AC lấy D thỏa
AD AB c== suy ra tam giác BDA cân tại A và
BDA A=
1
2
.
Áp dụng định lý hàm số Côsin cho
ABDD , ta có:
BD AB AD AB AD BAD
cc A
bca
cAc
bc
cc
abcbca ppa
bb
=+-
--
+-
+=+
=+++-= -
222
22 0
222
22
2..cos
=2 2 .cos(180 )
=2 (1 cos ) 2 (1 )
2
4
( )( ) ( )
Suy ra
cp p a
BD
b
-
=
()
2
Gọi I là trung điểm của BD suy ra
AI BD^
.
Trong tam giác
ADI
vuông tại I, ta có
ADIBDppa
ADI
AD c bc
-
====
()
cos cos
22
.
I
B
A
C
D
Hình 2.9
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 710
Vậy
Appa
bc
-
=
()
cos
2
.
b) Từ định lý hàm số sin, ta có:
abcp
ABC
RRRR
++=++=sin sin sin
222
(1)
Theo câu a) ta có
Appa
bc
-
=
()
cos
2
, tương tự thì
Bppb
ca
-
=
()
cos
2
và
Cppc
ab
-
=
()
cos
2
,
kết hợp với công thức
()()()
abc
S ppapbpc
R
=---=
4
Suy ra
ABC ppappbppc
bc ca ab
---
=
()()()
4 cos cos cos 4
222
ppSp
pp a p b p c
abc abc R
=---==
44
()()()
(2)
Từ (1) và (2) suy ra
ABC
ABC++=sin sin sin 4 cos cos cos
222
Nhận xét: Từ câu a) và hệ thức lượng giác cơ bản ta suy ra được các công thức
A pbpc A pbpc A ppa
bc p p a p b p c
-- -- -
===
---
()() ()() ()
sin ; tan ; cot
22()2()()
Ví dụ 3: Cho tam giác ABC , chứng minh rằng:
a)
bca
A
S
+-
=
222
cot
4
b)
cot cot cotABC++³3
Lời giải:
a) Áp dụng định lí côsin và công thức SbcA=
1
sin
2
ta có:
cos
cot
sin sin
Ab c a b c a
A
AbcA S
+- +-
== =
222 222
24
đpcm
b) Theo câu a) tương tự ta có
cab
B
S
+-
=
222
cot
4
,
abc
C
S
+-
=
222
cot
4
Suy ra
bca cababc
ABC
SSS
+- +- +-
++= + +
222 2 22 222
cot cot cot
444
abc
S
++
=
222
4
Theo bất đẳng thức Cauchy ta có
()()()
pabc p
papbpc
æöæö
---
÷÷
çç
---£ =
÷÷
çç
÷÷
÷÷
çç
èøèø
33
3
33
Mặt khác
()()()
pp
S ppapbpc S p=---£ =
32
27
33
Ta có
(
)
(
)
abc
abc
p
++
++
=£
2
222
2
3
44
suy ra
abc
S
++
£
222
43
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 711
Do đó
abc
ABC
abc
++
++³ =
++
222
222
cot cot cot 3
4.
43
đpcm.
Ví dụ 4: Cho tam giác
ABC
. Chứng minh rằng điều kiện cần và đủ để hai trung tuyến kẻ từ B và C
vuông góc với nhau là
bc a+=
22 2
5 .
Lời giải:
Gọi G là trọng tâm của tam giác
ABC
.
Khi đó hai trung tuyến kẻ từ B và C vuông góc với nhau khi và chỉ khi tam giác
GBC vuông tại G
bc
GB GC BC m m a
æöæö
÷÷
çç
+= + =
÷÷
çç
÷÷
÷÷
çç
èøèø
22
22 2 2
22
33
(*)
Mặt khác theo công thức đường trung tuyến ta có
bc
ac b ab c
mm
+- +-
==
22 2 22 2
22
2( ) 2( )
,
44
Suy ra
()
bc
mm a+=
22 2
4
(*)
9
() ()
ac b ab c
a
éù
+- +-
êú
+=
êú
êú
ëû
22 2 22 2
2
22
4
94 4
abc a++=
222 2
49bc a+=
22 2
5
(đpcm)
Ví dụ 5: Cho tứ giác ABCD có E, F là trung điểm các đường chéo. Chứng minh :
AB BC CD DA AC BD EF+++= ++
2222 22 2
4
Lời giải (hình 2.10)
Áp dụng công thức đường trung tuyến với tam giác
ABC và ADC ta có:
AC
AB BC BE+= +
2
22 2
2
2
(1)
AC
CD DA DE+= +
2
22 2
2
2
(2)
Từ (1) và (2) suy ra
()
AB BC CD DA BE DE AC+++= + +
2222 22 2
2
Mặt khác EF là đường trung tuyến tam giác
BDF nên
BD
BE DE EF+= +
2
22 2
2
2
Suy ra
AB BC CD DA AC BD EF+++= ++
2222 22 2
4
Dạng4:NhậnDạngTamGiác
1. Phương pháp giải.
Sử dụng định lí côsin; sin; công thức đường trung tuyến; công thức tính diện tích tam giác để biến
đổi giả thiết về hệ thức liên hệ cạnh(hoặc góc) từ đó suy ra dạng của tam giác.
2. Các ví dụ.
Ví dụ 1:
Cho tam giác
ABC
thoả mãn
CBA=sin 2 sin cos
. Chứng minh minh rằng tam giác
ABC
cân .
Lời giải
Áp dụng định lí côsin và sin ta có:
cbbca
CBA
RRbc
+-
==
222
sin 2 sin cos 2. .
222
cbca ab=+-=
2222
Suy ra tam giác
ABC cân tại đỉnh C.
E
F
A
D
C
B
Hình 2.10
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 712
Ví dụ 2: Cho tam giác
ABC
thoả mãn
BC
A
BC
+
=
+
sin sin
sin
cos cos
. Chứng minh rằng tam giác
ABC
vuông.
Lời giải
Ta có:
BC
AABCBC
BC
+
=+=+
+
sin sin
sin sin (cos cos ) sin sin
cos cos
ac a b a b c b c
Rca ab R
+- +- +
+=
222 222
()
22 2 2
bc a b ca b c bc cb+-++-=+
222 222 2 2
()()22
bcbcbcabac bcbc abc++ + - - =+ + - +=
332 22 2 22 2
0( )( ) ( )0
bc a ABC+= D
22 2
vuông tại A.
Ví dụ 3: Nhận dạng tam giác ABC trong các trường hợp sau:
a)
.sin sin sin
abc
aAbBcChhh++=++
b)
AB
AB
AB
+
=+
+
22
22
22
cos cos 1
(cot cot )
2
sin sin
Lời giải
a) Áp dụng công thức diện tích ta có sin
a
SbcAah==
11
22
suy ra
.sin sin sin
abc
aAbBcChhh++=++
...
S S SSSS
abc
bc ca ab a b c
++=++
2 2 2 222
()()()
abcabbcca ab bc ca++=++- +- +- =
22 2
222
0
abc==
Vậy tam giác
ABC
đều
b)
Ta có:
AB
AB
AB
+
=+
+
22
22
22
cos cos 1
(cot cot )
2
sin sin
ABAB
AB
AB
+++
=+++
+
2222
22
22
cos cos sin sin 1
(cot 1 cot 1)
2
sin sin
AB AB
AB AB
=++=
+
22222
22 2 2
2111
( ) (sin sin ) 4 sin sin
2
sin sin sin sin
ab
AB abABC
RR
æö æö
÷÷
çç
===D
÷÷
çç
÷÷
÷÷
çç
èø èø
22
22
sin sin
22
cân tại C.
C. CÂU HỎI TRẮC NGHIỆM
Câu 1:
Tam giác ABC có 5, 7, 8AB BC CA===. Số đo góc
A bằng:
A. 30 . B. 45 . C. 60 . D. 90 .
Lời giải
Chọn C
Theo định lí hàm cosin, ta có
222222
587 1
cos
2 . 2.5.8 2
AB AC BC
A
AB AC
+- +-
===
.
Do đó,
60A =.
Câu 2: Tam giác ABC có 2, 1AB AC== và
60A =. Tính độ dài cạnh BC .
A. 1.BC = B. 2.BC = C. 2.BC = D. 3.BC =
Lời giải
Chọn D
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 713
N
M
B
C
A
C
A
D
B
Theo định lí hàm cosin, ta có
222 22
2 . .cos 2 1 2.2.1.cos60 3 3BC AB AC AB AC A BC=+- =+- ==.
Câu 3: Tam giác ABC có đoạn thẳng nối trung điểm của
A
B và BC bằng 3 , cạnh 9AB = và
60ACB =
. Tính độ dài cạnh cạnh BC .
A. 336.BC =+ B. 36 3.BC =- C. 37.BC = D.
3333
.
2
BC
+
=
Lời giải
Chọn A
Gọi ,
M
N lần lượt là trung điểm của ,
A
BBC.
M
N¾¾
là đường trung bình của ABCD .
1
2
M
NAC¾¾=
. Mà
3MN =
, suy ra
6AC =
.
Theo định lí hàm cosin, ta có
222
22 2
2. . .cos
9 6 2.6. .cos60
336
AB AC BC AC BC ACB
BC BC
BC
=+-
=+ -
=+
Câu 4: Tam giác ABC có 2, 3AB AC== và
45C =. Tính độ dài cạnh BC .
A.
5.BC =
B.
62
.
2
BC
+
=
C.
62
.
2
BC
-
=
D.
6.BC =
Lời giải
Chọn B
Theo định lí hàm cosin, ta có
() ()
22
222 2
2. . .cos 2 3 2. 3. .cos45AB AC BC AC BC C BC BC=+- = +-
62
2
BC
+
=
.
Câu 5: Tam giác ABC có
60 , 45BC== và 5AB = . Tính độ dài cạnh AC .
A.
56
.
2
AC =
B. 53.AC = C. 52.AC = D. 10.AC =
Lời giải
Chọn A
Theo định lí hàm sin, ta có
556
sin 45 sin 60 2
sin sin
AB AC AC
AC
CB
= = =

.
Câu 6: Cho hình thoi ABCD cạnh bằng 1 cm và có
60BAD =. Tính độ dài cạnh AC .
A. 3.AC = B. 2.AC = C. 23.AC = D.
2.AC =
Lời giải
Chọn A
Do ABCD là hình thoi, có
60 120BAD ABC= = .
Theo định lí hàm cosin, ta có
222
22
2. . .cos
1 1 2.1.1.cos120 3 3
AC AB BC AB BC ABC
AC
=+-
=+- = =
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 714
M
B
C
A
D
B
C
A
Câu 7: Tam giác
ABC
có 4, 6, 2 7AB BC AC===. Điểm
M
thuộc đoạn
BC
sao cho
2
M
CMB=
. Tính độ dài cạnh
A
M .
A.
42.AM =
B.
3.AM =
C.
23.AM =
D.
32.AM =
Lời giải
Chọn C
Theo định lí hàm cosin, ta có :
()
2
22
222
46 27
1
cos
2. . 2.4.6 2
AB BC AC
B
AB BC
+-
+-
===
.
Do
1
22
3
MC MB BM BC=¾¾= =
.
Theo định lí hàm cosin, ta có
22 2
22
2. . .cos
1
4 2 2.4.2. 12 2 3
2
AM AB BM AB BM B
AM
=+ -
=+- = =
Câu 8: Tam giác ABC có
62
,3,2
2
AB BC CA
-
===
. Gọi
D
là chân đường phân giác trong
góc
A . Khi đó góc
ADB bằng bao nhiêu độ?
A.
45 .
B.
60 .
C.
75 .
D.
90 .
Lời giải
Chọn C
Theo định lí hàm cosin, ta có:
222
1
cos
2. . 2
120 60
AB AC BC
BAC
AB AC
BAC BAD
+-
==-
==
222
2
cos 45
2. . 2
AB BC AC
ABC ABC
AB BC
+-
===
Trong
ABDD có

60 , 45 75BAD ABD ADB= = =.
Câu 9: Tam giác ABC vuông tại
A
, đường cao 32AH cm= . Hai cạnh
A
B và AC tỉ lệ với 3 và
4 . Cạnh nhỏ nhất của tam giác này có độ dài bằng bao nhiêu?
A. 38 .cm B. 40 .cm C. 42 .cm D. 45 .cm
Lời giải
Chọn B
Do tam giác ABC vuông tại
A
, có tỉ lệ 2 cạnh góc vuông :AB AC là
3:4
nên
A
B là cạnh
nhỏ nhất trong tam giác.
Ta có
34
43
AB
AC AB
AC
= =
.
Trong
ABCD có
A
H là đường cao
2222 22 2
2
1111 1 11 9
40
4
32 16
3
AB
AH AB AC AB AB AB
AB
=+=+ =+ =
æö
÷
ç
÷
ç
÷
ç
èø
.
Câu 10: Tam giác
M
PQ
vuông tại
P
. Trên cạnh
M
Q
lấy hai điểm ,
E
F sao cho các góc
,,
M
PE EPF FPQ bằng nhau. Đặt ,,,
M
P q PQ m PE x PF y== ==. Trong các hệ thức sau, hệ
thức nào đúng?
A. .
M
EEFFQ== B.
222
.
M
Eqxxq=+-
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 715
x
y
O
B
A
x
y
O
B
A
C.
222
.
M
Fqyyq=+- D.
22 2
2.
M
Qqm qm=+ -
Lời giải
Chọn C
F
E
Q
P
M
Ta có
30 60
3
MPQ
MPE EPF FPQ MPF EPQ=== = ==.
Theo định lí hàm cosin, ta có
222
22 22
2. . .cos
2.cos30 3
ME AM AE AM AE MAE
qx qx qxqx
=+-
=+- =+-
222
22 22
2..cos
2.cos60
M
FAMAF AMAF MAF
qy qy qyqy
=+-
=+- =+-
22222
M
QMPPQqm=+=+
.
Câu 11: Cho góc
30xOy =. Gọi
A
và B là hai điểm di động lần lượt trên Ox và Oy sao cho
1AB = . Độ dài lớn nhất của đoạn OB bằng:
A.
3
.
2
B. 3. C. 22. D. 2.
Lời giải
Chọn D
Theo định lí hàm sin, ta có:
1
.sin .sin 2sin
sin 30
sin sin sin
OB AB AB
OB OAB OAB OAB
OAB AOB A OB
== = =
Do đó, độ dài
OB lớn nhất khi và chỉ khi
sin 1 90OA B OAB= =
.
Khi đó
2OB =
.
Câu 12: Cho góc
30xOy =. Gọi
A
và B là hai điểm di động lần lượt trên Ox và Oy sao cho
1AB = . Khi OB có độ dài lớn nhất thì độ dài của đoạn OA bằng:
A.
3
.
2
B. 3. C. 22. D. 2.
Lời giải
Chọn B
Theo định lí hàm sin, ta có
1
.sin .sin 2 sin
sin 30
sin sin sin
OB AB AB
OB OAB OAB OAB
OAB AOB A OB
== = =
Do đó, độ dài
OB lớn nhất khi và chỉ khi
sin 1 90OA B OAB= = .
Khi đó
2OB = .
Tam giác
OAB vuông tại
22 22
21 3AOA OB AB= - = -=.
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 716
D
A
C
B
Câu 13: Tam giác ABC có ,,AB c BC a CA b===. Các cạnh ,,abc liên hệ với nhau bởi đẳng thức
()()
22 22
bb a ca c-= -
. Khi đó góc
B
AC
bằng bao nhiêu độ?
A.
30 .
B.
45 .
C.
60 .
D.
90 .
Lời giải
Chọn C
Theo định lí hàm cosin, ta có
222222
cos
2. . 2
AB AC BC c b a
BAC
AB AC bc
+- +-
==
.
Mà
()()
()
()
22 22 32 2 3 2 33
0bb a ca c b ab ac c a b c b c-= --=-- +++=
()
()
222 222
00bcb c a bc b c a bc+ +-- =+--=
(do 0, 0bc>>)
222
bca bc+-=
Khi đó,
222
1
cos 60
22
bca
BAC BAC
bc
+-
===
.
Câu 14: Tam giác
ABC
vuông tại
A
, có ,AB c AC b==. Gọi
a
là độ dài đoạn phân giác trong
góc
B
AC
. Tính
a
theo
b
và
c
.
A.
2
.
a
bc
bc
=
+
B.
()
2
.
a
bc
bc
+
=
C.
2
.
a
bc
bc
=
+
D.
()
2
.
a
bc
bc
+
=
Lời giải
Chọn A
Ta có
2222
BC AB AC b c=+=+.
Do
A
D là phân giác trong của
BAC
22
.. .BC
AB c c c b c
BD DC DC
AC b b c b c
+
= = = =
++
.
Theo định lí hàm cosin, ta có
()
()
22 2
222 22
2
2. . .cos 2 . .cos45
cb c
BD AB AD AB AD ABD c AD c AD
bc
+
=+- =+-
+
()
() ()
22 2
3
22 2
22
2
2. 0 2. 0
cb c
bc
ADcADc ADcAD
bc bc
æö
+
÷
ç
÷
ç
÷
- +- =- + =
ç
÷
ç
÷
÷
++
ç
èø
.
2bc
AD
bc
=
+
hay
2
a
bc
bc
=
+
.
Câu 15: Hai chiếc tàu thủy cùng xuất phát từ một vị trí
A
, đi thẳng theo hai hướng tạo với nhau
góc
0
60 . Tàu
B
chạy với tốc độ 20 hải lí một giờ. Tàu C chạy với tốc độ 15 hải lí một
giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí? Kết quả gần nhất với số nào sau đây?
A. 61 hải lí. B. 36 hải lí.
C. 21 hải lí. D. 18 hải lí.
Lời giải
Chọn B
Sau 2 giờ tàu B đi được 40 hải lí, tàu C đi được 30 hải lí. Vậy tam giác ABC có
40, 30AB AC== và
0
60 .A =
Áp dụng định lí côsin vào tam giác
,ABC ta có
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 717
222
2cosabc bcA=+-
22 0
30 40 2.30.40.cos60 900 1600 1200 1300.=+- =+ - =
Vậy
1300 36BC =»
(hải lí).
Sau
2
giờ, hai tàu cách nhau khoảng
36
hải lí.
Câu 16:
Để đo khoảng cách từ một điểm
A
trên bờ sông đến gốc cây
C
trên cù lao giữa sông, người
ta chọn một điểm
B
cùng ở trên bờ với
A
sao cho từ
A
và
B
có thể nhìn thấy điểm
C
. Ta
đo được khoảng cách
40mAB = ,
0
45CAB = và
0
70CBA = .Vậy sau khi đo đạc và tính toán
được khoảng cách
AC gần nhất với giá trị nào sau đây?
A.
53 m
.
B.
30 m
.
C.
41,5 m
.
D.
41 m
.
Lời giải
Chọn C
Áp dụng định lí sin vào tam giác ,ABC ta có
sin sin
AC AB
BC
=
Vì
()
sin sinC ab=+ nên
()
0
0
.sin 40.sin 70
41,47 m.
sin
sin115
AB
AC
b
ab
==»
+
Câu 17:
Từ vị trí
A
người ta quan sát một cây cao (hình vẽ).
Biết
0
4m, 20m, 45AH HB BAC== =
.
Chiều cao của cây gần nhất với giá trị nào sau đây?
A.
17,5m
. B. 17m .
C. 16,5m . D. 16m .
Lời giải
Chọn B
Trong tam giác
A
HB , ta có
0
41
tan 11 19'
20 5
AH
ABH ABH
BH
===¾¾»
.
Suy ra
00
90 78 41'ABC ABH=- = .
Suy ra
()
00
180 56 19'ACB BAC ABC=- + = .
Áp dụng định lý sin trong tam giác
ABC , ta được
.sin
17m.
sin sin sin
AB CB AB BAC
CB
ACB BAC ACB
=¾¾= »
Câu 18: Giả sử CD h= là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm , AB trên
mặt đất sao cho ba điểm
, AB và C thẳng hàng. Ta đo được 24 mAB = ,
00
63 , 48CAD CBD==.
Chiều cao
h
của tháp gần với giá trị nào sau đây?
A. 18m . B.
18,5m
.
C. 60m . D. 60,5m .
Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 718
60°
1m
60m
O
C
D
A
B
Chọn D
Áp dụng định lí sin vào tam giác ,ABD ta có .
sin sin
A
DAB
D
b
=
Ta có
Dab=+ nên
00 0
63 48 15 .D ab=-= - =
Do đó
()
0
0
.sin 24.sin 48
68,91 m.
sin
sin15
AB
AD
b
ab
==»
-
Trong tam giác vuông
,ACD
có
.sin 61,4 m.hCD AD a== »
Câu 19:
Trên nóc một tòa nhà có một cột ăng-ten cao
5 m
. Từ vị trí quan sát
A
cao
7 m
so với
mặt đất, có thể nhìn thấy đỉnh
B
và chân
C
của cột ăng-ten dưới góc
0
50 và
0
40 so với
phương nằm ngang.
Chiều cao của tòa nhà gần nhất với giá trị nào sau đây?
A. 12m . B. 19m .
C. 24m . D. 29m .
Lời giải
Chọn B
Từ hình vẽ, suy ra
0
10BAC =
và
()
()
00000
180 180 50 90 40ABD BAD ADB=- + =-+=
.
Áp dụng định lí sin trong tam giác
ABC
, ta có
0
0
.sin 5.sin40
=18,5 m
sin10
sin sin sin
BC AC BC ABC
AC
BAC ABC BAC
=¾¾= »
.
Trong tam giác vuông
ADC , ta có
sin .sin 11, 9 m.
CD
CAD CD A C CA D
AC
=¾¾= =
Vậy
11,9 7 18,9 m.CH CD DH=+ = +=
Câu 20: Xác định chiều cao của một tháp mà không cần lên đỉnh của
tháp. Đặt kế giác thẳng đứng cách chân tháp một khoảng
60mCD = , giả sử chiều cao của giác kế là 1mOC = .Quay thanh
giác kế sao cho khi ngắm theo thanh ta nhình thấy đỉnh
A
của
tháp. Đọc trên giác kế số đo của góc
0
60AOB = . Chiều cao của
ngọn tháp gần với giá trị nào sau đây:
A. 40m . B. 114m .
C. 105m . D. 110m .
Lời giải
Chọn C
Tam giác OAB vuông tại ,
B
có
0
tan tan 60 . 60 3 m .
AB
AOB AB OB
OB
== =
Vậy chiếu cao của ngọn tháp là
()
60 3 1 m.hABOC=+= +
Câu 21:
Từ hai vị trí
A
và
B
của một tòa nhà, người ta
quan sát đỉnh
C của ngọn núi. Biết rằng độ cao
70mAB = , phương nhìn AC tạo với phương nằm
ngang góc
0
30
, phương nhìn BC tạo với phương
nằm ngang góc
0
15 30' .Ngọn núi đó có độ cao so
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 719
M
CB
A
M
A
B
C
M
CB
A
với mặt đất gần nhất với giá trị nào sau đây?
A.
135m
. B.
234m
.
C.
165m
. D.
195m
.
Lời giải
Chọn A
Từ giả thiết, ta suy ra tam giác
ABC
có
00
60 , 105 30CAB ABC
¢
==
và
70.c =
Khi đó

()
00 000
180 180 180 165 30 14 30 .ABC C AB
¢¢
++= = - + = - =
Theo định lí sin, ta có
sin sin
bc
BC
=
hay
00
70
sin105 30 sin14 30
b
=
¢¢
Do đó
0
0
70.sin105 30
269,4 m.
sin14 30
AC b
¢
== »
¢
Gọi
CH
là khoảng cách từ
C
đến mặt đất. Tam giác vuông
ACH
có cạnh
CH
đối diện
với góc
0
30 nên
269,4
134,7 m.
22
AC
CH
== =
Vậy ngọn núi cao khoảng
135 m.
Câu 22:
Tam giác ABC có 6cm, 8cmAB AC== và
10cmBC =
. Độ dài đường trung tuyến xuất
phát từ đỉnh
A
của tam giác bằng:
A. 4cm . B. 3cm . C. 7cm . D. 5cm .
Lời giải
Chọn D
Áp dụng công thức đường trung tuyến
22 2
2
24
a
bca
m
+
=-
ta được:
222222
2
8610
25
2424
a
AC AB BC
m
++
=-=-=
5.
a
m=
Câu 23: Tam giác ABC vuông tại
A
và có AB AC a==. Tính độ dài đường trung tuyến BM của
tam giác đã cho.
A. 1, 5 .BM a= B. 2.BM a= C. 3.BM a= D.
5
.
2
a
BM =
Lời giải
Chọn D
M
là trung điểm của .
22
AC a
AC AM==
Tam giác
BAMD vuông tại
A
2
222
5
.
42
aa
BM AB AM a
= + =+=
Câu 24: Tam giác ABC có 9AB = cm, 12AC = cm và 15BC = cm. Tính độ dài đường trung tuyến
A
M của tam giác đã cho.
A.
15
2
AM = cm. B. 10AM = cm. C. 9AM = cm. D.
13
2
AM = cm.
Lời giải
Chọn A
Áp dụng hệ thức đường trung tuyến
22 2
2
24
a
bca
m
+
=-
ta được:
222222
2
12 9 15 225
.
24244
a
AC AB BC
m
++
=-=-=
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 720
D
B
A
C
A
BC
M
15
.
2
a
m=
Câu 25: Tam giác ABC cân tại C , có 9cmAB = và
15
cm
2
AC =
. Gọi
D
là điểm đối xứng của B
qua
C . Tính độ dài cạnh .AD
A. 6AD = cm. B. 9AD = cm.
C. 12AD = cm. D. 12 2AD = cm.
Lời giải
Chọn C
Ta có:
D
là điểm đối xứng của B qua CC là trung điểm của .BD
AC là trung tuyến của tam giác .
D
ABD
2 2 15.BD BC AC===
Theo hệ thức trung tuyến ta có:
222
2
24
AB AD BD
AC
+
=-
2
22 2
2
2
BD
AD AC AB= +-
2
AD=
2
2
2
15 15
2. 9 144 12.
22
AD
æö
÷
ç
+-= =
÷
ç
÷
ç
èø
Câu 26: Tam giác
ABC
có 3, 8AB BC==. Gọi
M
là trung điểm của
B
C
. Biết
513
cos
26
AMB = và
3AM >
. Tính độ dài cạnh
AC
.
A. 13AC = . B. 7AC = . C.
13AC =
. D. 7AC = .
Lời giải
Chọn D
Ta có:
M
là trung điểm của
BC 4.
2
BC
BM
==
Trong tam giác
A
BM ta có:
222
cos
2.
AM BM AB
AMB
AM BM
+-
=
222
2..cos 0.AM AM BM AMB BM AB- +-=
thoaû maõn
loaïi
2
13 3 ( )
20 13
70
713
13
3( )
13
AM
AM AM
AM
é
=>
ê
ê
- +=
ê
=<
ê
ê
ë
13.AM=
Ta có:
AMB và
AMC là hai góc kề bù.
513
cos cos
26
AMC AMB=-=-
Trong tam giác
AMCD ta có:
222
2..cosAC AM CM AM CM AMC=+-
513
13 16 2. 13.4. 49 7.
26
AC
æö
÷
ç
÷
ç
=+- - = =
÷
ç
÷
÷
ç
èø
Câu 27: Tam giác ABC có trọng tâm G . Hai trung tuyến 6BM = , 9CN = và
0
120BGC = . Tính độ
dài cạnh
A
B .
A. 11AB = . B. 13AB = .
C. 211AB = . D. 213AB = .
Lời giải
Chọn D
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 721
G
N
A
BC
M
Ta có:
B
GC
và
B
GN
là hai góc kề bù mà
00
120 120 .BGC BGN= =
G là trọng tâm của tam giác ABCD
2
4.
3
1
3.
3
BG BM
GN CN
ì
ï
ï
==
ï
ï
ï
í
ï
ï
==
ï
ï
ï
î
Trong tam giác
BGND ta có:
222
2..cosBN GN BG GN BG BGN=+-
2
1
9 16 2.3.4. 13 13.
2
BN BN=+- ==
N là trung điểm của 2 2 13.AB AB BN= =
Câu 28: Tam giác
ABC
có độ dài ba trung tuyến lần lượt là
9; 12; 15
. Diện tích của tam giác
ABC
bằng:
A. 24 . B. 24 2 .
C.
72
. D. 72 2 .
Lời giải
Chọn C
Ta có:
22 2
2
2
22 2
22
2
222
2
81
24
292
144 208
24
100
225
24
a
b
c
bca
m
a
acb
mb
c
abc
m
ì
ï
+
ï
=-=
ï
ï
ì
ï
ï
=
ï
ï
ï
ï
+
ï
ï
ï
=-==
íí
ïï
ïï
ïï
=
ïï
î
+
ï
ï
=-=
ï
ï
ï
î
273
413
10
a
b
c
ì
ï
=
ï
ï
ï
ï
=
í
ï
ï
ï=
ï
ï
î
Ta có:
222
208 100 292 1
cos
2
2.4 13.10 5 13
bca
A
bc
+- + -
== =
2
2
11813
sin 1 cos 1 .
65
513
AA
æö
÷
ç
÷=- =- =
ç
÷
ç
÷
ç
èø
Diện tích tam giác
1 1 18 13
: sin .4 13.10. 72
22 65
ABC
ABC S bc A
D
D== =
Câu 29: Cho tam giác ABC có
, ,
A
BcBCaCAb===
. Nếu giữa
, , abc
có liên hệ
22 2
2bc a+= thì
độ dài đường trung tuyến xuất phát từ đỉnh
A
của tam giác tính theo
a
bằng:
A.
3
2
a
. B.
3
3
a
. C.
23a
. D.
33a
.
Lời giải
Chọn A
Hệ thức trung tuyến xuất phát từ đỉnh
A
của tam giác:
22 2
2
24
a
bca
m
+
=-
Mà:
22 2
2bc a+=
22 2
2
23 3
.
24 4 2
aa
aa a a
mm=-==
Câu 30: Cho hình bình hành ABCD có , ,
A
BaBCbBDm=== và AC n= . Trong các biểu thức
sau, biểu thức nào đúng:
A.
()
22 22
3mn ab+= + . B.
()
22 22
2mn ab+= + .
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 722
C.
()
22 22
2 mn ab+=+
. D.
()
22 22
3 mn ab+=+
.
Lời giải
Chọn B
Gọi
O
là giao điểm của
AC
và
.BD
Ta có:
1
.
22
m
BO BD
==
B
O
là trung tuyến của tam giác
ABCD
22 2
2
24
BA BC AC
BO
+
= -
()
2222
22 22
2
424
mabn
mn ab
+
= -+= + .
Câu 31: Tam giác ABC có , ,
A
BcBCaCAb===. Các cạnh , , abc liên hệ với nhau bởi đẳng thức
22 2
5ab c+= . Góc giữa hai trung tuyến
A
M và BN là góc nào?
A.
0
30
. B.
0
45
. C.
0
60
. D.
0
90
.
Lời giải
Chọn D
Gọi G là trọng tâm tam giác .ABCD
Ta có:
22 2222
2
2424
AC AB BC b c a
AM
++
=-=-
()
22
2
22
2
4
999
bc
a
AG AM
+
= = -
22 2222
2
2424
BA BC AC c a b
BN
++
=-=-
22 2
22
1
91836
ca b
GN BN
+
= = -
Trong tam giác
AGND
ta có:
()
()
22
22222
222
22
222 2
2
9 9 18 36 4
cos
2. .
2
2. .
9 9 18 36
bc
acabb
AG GN AN
AGN
AG GN
bc
acab
+
+
-+ --
+-
==
+
+
--
()
()
22
22222
22
222 2
2
9 9 18 36 4
2
2. .
9 9 18 36
bc
acabb
bc
acab
+
+
-+ --
=
+
+
--
()
()
222
22
222 2
10 2
0
2
36.2. .
9 9 18 36
cab
bc
acab
-+
==
+
+
--
0
90 .AGN=
Câu 32: Tam giác ABC có ba đường trung tuyến , ,
abc
mmm thỏa mãn
222
5
abc
mmm=+. Khi đó tam
giác này là tam giác gì?
A. Tam giác cân. B. Tam giác đều.
C. Tam giác vuông. D. Tam giác vuông cân.
Lời giải
Chọn C
Ta có:
22 2
2
22 2
2
222
2
24
24
24
a
b
c
bca
m
acb
m
abc
m
ì
ï
+
ï
=-
ï
ï
ï
ï
ï
+
ï
ï
=-
í
ï
ï
ï
ï
+
ï
ï
=-
ï
ï
ï
î
Mà:
222
5
abc
mmm=+
22 2 22 2 22 2
5
24 2424
bca acb abc
æö
+++
÷
ç
÷
-=-+-
ç
÷
ç
÷
ç
èø
222222222
10 10 5 2 2 2 2bcaacbabc+-=+-++-
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 723
22 2
bc a+=
tam giác
ABCD
vuông.
Câu 33: Tam giác
ABC
có
, ,
A
BcBCaCAb===
. Gọi
, ,
abc
mmm
là độ dài ba đường trung tuyến,
G
trọng tâm. Xét các khẳng định sau:
()
I .
()
222 222
3
4
abc
mmm abc++= ++.
()
II .
()
222 222
1
3
GA GB GC a b c++ = ++
.
Trong các khẳng định đã cho có
A.
()
I
đúng. B. Chỉ
()
II
đúng.
C. Cả hai cùng sai. D. Cả hai cùng đúng.
Lời giải
Chọn D
Ta có:
22 2
2
22 2
2
222
2
24
24
24
a
b
c
bca
m
acb
m
abc
m
ì
ï
+
ï
=-
ï
ï
ï
ï
ï
+
ï
ï
=-
í
ï
ï
ï
ï
+
ï
ï
=-
ï
ï
ï
î
()
222 222
3
4
abc
mmm abc++= ++
()()()
22 2 222 222 222
4431
.
9943
abc
GA GB GC m m m a b c a b c++ = ++= ++= ++.
Câu 34:
Tam giác ABC có 10BC = và
O
30A = . Tính bán kính R của đường tròn ngoại tiếp tam
giác
ABC .
A. 5R = . B.
10R =
. C.
10
3
R =
. D. 10 3R = .
Lời giải
Chọn B
Áp dụng định lí sin, ta có
0
10
2 10.
2.sin 30
sin 2.sin
BC BC
RR
BAC A
== = =
Câu 35: Tam giác ABC có 3, 6AB AC== và
60A =. Tính bán kính R của đường tròn ngoại tiếp
tam giác
ABC .
A. 3R = . B. 33R = . C. 3R = . D. 6R = .
Lời giải
Chọn A
Áp dụng định lí Cosin, ta có
222
2..cosBC AB AC AB AC BAC=+-
22 02222
3 6 2.3.6.cos60 27 27 .BC BC AB AC=+- = = + =
Suy ra tam giác
ABC vuông tại ,B do đó bán kính 3.
2
AC
R
==
Câu 36:
Tam giác ABC có 21cm, 17cm, 10cmBC CA AB===. Tính bán kính R của đường tròn
ngoại tiếp tam giác
ABC .
A.
85
cm
2
R =
. B.
7
cm
4
R =
.
C.
85
cm
8
R =
. D.
7
cm
2
R =
.
Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 724
Chọn C
Đặt
24.
2
AB BC CA
p
++
== Áp dụng công thức Hê – rông, ta có
()()() ()()()
2
24. 24 21 . 24 17 . 24 10 84 .
ABC
SppABpBCpCA cm
D
=---= ---=
Vậy bán kính cần tìm là
. . . . 21.17.10 85
.
44.4.848
ABC
ABC
AB BC CA AB BC CA
SR cm
RS
D
D
====
Câu 37: Tam giác đều cạnh
a
nội tiếp trong đường tròn bán kính
R
. Khi đó bán kính
R
bằng:
A.
3
2
a
R =
. B.
2
3
a
R
= .
C.
3
3
a
R
= . D.
3
4
a
R =
.
Lời giải
Chọn C
Xét tam giác
ABC đều cạnh ,a gọi
M
là trung điểm của .BC
Ta có
AM BC^
suy ra
2
22
11 3
.. . . .
22 4
ABC
a
SAMBCABBMBC
D
==-=
Vậy bán kính cần tính là
3
2
.. .. 3
.
44. 3
3
4.
4
ABC
ABC
AB BC CA A B BC CA a a
SR
RS
a
D
D
====
Câu 38: Tam giác ABC vuông tại
A
có đường cao
12
cm
5
AH = và
3
4
AB
AC
= . Tính bán kính R của
đường tròn ngoại tiếp tam giác
ABC .
A.
3.Rcm=
B.
1, 5c mR =
.
C.
2cmR =
. D. 3, 5cmR = .
Lời giải
Chọn A
Tam giác
ABC vuông tại ,A có đường cao
A
H
()
2
..AB AC AH=*
Mặt khác
33
44
AB
AB AC
AC
= = thế vào
()
,* ta được
2
2
312 83
.
45 5
AC AC
æö
÷
ç
==
÷
ç
÷
ç
èø
Suy ra
22
383 63
.23.
45 5
AB BC AB AC===+=
Vậy bán kính cần tìm là
3.
2
BC
Rcm==
Câu 39:
Cho tam giác ABC có 33, 63AB BC== và 9CA = . Gọi
D
là trung điểm
B
C . Tính bán
kính
R của đường tròn ngoại tiếp tam giác .ABD
A.
9
6
R =
. B. 3R = . C. 33R = . D.
9
2
R =
.
Lời giải
Chọn B
Vì
D
là trung điểm của BC
222
2
27
24
AB AC BC
AD
+
=-=
33.AD =
Tam giác
A
BD có 33AB BD DA=== tam giác
A
BD đều.
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 725
Nên có bán kính đường tròn ngoại tiếp là
33
.3 3 3.
33
RAB
== =
Câu 40:
Tam giác nhọn ABC có ,
A
CbBCa==, 'BB là đường cao kẻ từ B và
'CBB a= . Bán kính
đường tròn ngoại tiếp
R của tam giác ABC được tính theo , ab và a là:
A.
22
2cos
2sin
ab ab
R
a
a
+-
=
. B.
22
2cos
2sin
ab ab
R
a
a
++
=
.
C.
22
2cos
2cos
ab ab
R
a
a
++
=
. D.
22
2sin
.
2cos
ab ab
R
a
a
+-
=
Lời giải
Chọn D
Xét tam giác
BB C
¢
vuông tại
,B
¢
có
sin .sin .
BC
CBB B C a
BC
a
¢
¢¢
==
Mà
A
BBCAC
¢¢
+=
.sinAB b a a
¢
=-
và
222
.cos .BB a a
¢
=
Tam giác
ABB
¢
vuông tại ,B
¢
có
()
2
22 22
.sin .cosAB BB AB b a aaa
¢¢
=+=- +
2222222
2 .sin sin cos 2 sin .bab a a ababaa a a=- + + =+-
Bán kính đường tròn ngoại tiếp cần tính là
22
2sin
2.
2cos
sin
AB a b ab
RR
ACB
a
a
+-
==
Câu 40: Tam giác ABC có
3, 6, 60AB AC BAC== =
. Tính diện tích tam giác ABC .
A. 93
ABC
S
D
= . B.
93
2
ABC
S
D
=
.
C. 9
ABC
S
D
= . D.
9
2
ABC
S
D
= .
Lời giải
Chọn B
Ta có
0
1193
. . .sin .3.6.sin 60
222
ABC
SABACA
D
===.
Câu 41: Tam giác ABC có
4, 30 , 75AC BAC ACB===. Tính diện tích tam giác ABC .
A. 8
ABC
S
D
= . B. 43
ABC
S
D
= .
C. 4
ABC
S
D
= . D. 83
ABC
S
D
= .
Lời giải
Chọn C
Ta có
()
0
180 75 ABC BAC ACB ACB=- + == .
Suy ra tam giác
ABC
cân tại
A
nên
4AB AC==
.
Diện tích tam giác
ABC là
1
.sin 4.
2
ABC
SABACBAC
D
==
Câu 42: Tam giác ABC có 21, 17, 10abc===. Diện tích của tam giác ABC bằng:
A. 16
ABC
S
D
= . B. 48
ABC
S
D
= .
C. 24
ABC
S
D
= . D. 84
ABC
S
D
= .
Lời giải
Chọn D
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 726
Ta có
21 17 10
24
2
p
++
==
.
Do đó
()()() ()()()
24 24 21 24 17 24 10 84S ppapbpc=---= - - -=.
Câu 43: Tam giác ABC có
3, 6, 60AB AC BAC== =. Tính độ dài đường cao
a
h của tam giác.
A.
33
a
h =
. B.
3
a
h =
. C.
3
a
h =
. D.
3
2
a
h =
.
Lời giải
Chọn C
Áp dụng định lý hàm số côsin, ta có
222
2. cos 27 33BC AB AC AB AC A BC=+- =¾¾= .
Ta có
0
1193
. . .sin .3.6.sin 60
222
ABC
SABACA
D
===
.
Lại có
12
.. 3.
2
ABC a a
S
SBChh
BC
D
=¾¾= =
Câu 44: Tam giác ABC có
4, 60AC ACB==. Tính độ dài đường cao h uất phát từ đỉnh
A
của
tam giác.
A. 23h = . B. 43h = . C. 2h = . D. 4h = .
Lời giải
Chọn A
Gọi
H
là chân đường cao xuất phát từ đỉnh
A
.
Tam giác vuông
AHC , có
3
sin .sin 4. 2 3.
2
AH
ACH AH AC ACH
AC
=¾¾= = =
Câu 45: Tam giác ABC có 21, 17, 10abc===. Gọi 'B là hình chiếu vuông góc của B trên cạnh
AC . Tính 'BB .
A. '8BB = . B.
84
'
5
BB =
.
C.
168
'
17
BB =
. D.
84
'
17
BB =
.
Lời giải
Chọn C
Ta có
21 17 10
24
2
p
++
==
.
Suy ra
()()() ()()()
24 24 21 24 17 24 10 84Sppapbpc=---= ---=.
Lại có
1 1 168
. ' 84 .17. ' '
22 17
S b BB BB BB=¬¾= ¾¾=
.
Câu 46: Tam giác ABC có 8AB = cm, 18AC = cm và có diện tích bằng 64
2
cm
. Giá trị sin A ằng:
A.
3
sin
2
A =
. B.
3
sin
8
A =
.
C.
4
sin
5
A =
. D.
8
sin
9
A =
.
Lời giải
Chọn D
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 727
Ta có
118
. . .sin 64 .8.18.sin sin .
229
ABC
SABACBAC AA
D
===
Câu 47: Hình bình hành ABCD có , 2AB a BC a== và
0
45BAD = . Khi đó hình bình hành có diện
tích bằng:
A.
2
2a . B.
2
2a . C.
2
a . D.
2
3a .
Lời giải
Chọn C
Diện tích tam giác
A
BD
là
2
0
11
...sin ..2.sin45 .
222
ABD
a
SABADBADaa
D
===
Vậy diện tích hình bình hành
ABCD là
2
2
2. 2. .
2
ABCD ABD
a
SS a
D
===
Câu 48:
Tam giác
ABC
vuông tại
A
có
30AB AC==
cm. Hai đường trung tuyến BF và
CE
cắt
nhau tại
G
. Diện tích tam giác
GFC
bằng:
A.
2
50 cm
. B.
2
50 2 cm
.
C.
2
75 cm
. D.
2
15 105 cm .
Lời giải
Chọn C
Vì F là trung điểm của AC
1
15 .
2
FC A C cm==
Đường thẳng
BF cắt CE tại G suy ra G là trọng tâm tam giác .ABC
Khi đó
()
()
()
()
()
()
()
()
;
1
3; ; 10.
33
;
dB AC
BF AB
d G AC d B AC cm
GF
dG AC
== = ==
Vậy diện tích tam giác
GFC là:
()
()
2
11
.; . .10.1575.
22
GFC
SdGACFC cm
D
===
Câu 49: Tam giác đều nội tiếp đường tròn bán kính 4R = cm có diện tích bằng:
A.
2
13 cm B.
2
13 2 cm
C.
2
12 3 cm D.
2
15 cm .
Lời giải
Chọn C
Xét tam giác ABC đều, có độ dài cạnh bằng
.a
Theo định lí sin, ta có
0
0
22.48.sin6043.
sin 60
sin
BC a
Ra
BAC
= == =
Vậy diện tích cần tính là
()
2
02
11
...sin .43.sin60 123 .
22
ABC
SABACBAC cm
D
===
Câu 50: Tam giác ABC có 23, 2BC AC AB== và độ dài đường cao 2AH = . Tính độ dài cạnh
A
B .
A. 2AB = . B.
23
3
AB
=
.
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 728
C.
2AB =
hoặc
221
3
AB
= . D.
2AB =
hoặc
23
3
AB
=
Lời giải
Chọn C
Ta có
23 3
22
AB BC CA AB
p
++ +
==
.
Suy ra
3 23 3 23 23 23
2222
AB AB AB AB
S
æöæöæöæö
+--+
÷÷÷÷
çççç
÷÷÷÷
çççç
=
÷÷÷÷
çççç
÷÷÷÷
÷÷÷÷
çççç
èøèøèøèø
.
Lại có
1
.23.
2
SBCAH==
Từ đó ta có
3 23 3 23 23 23
23
2222
AB AB AB AB
æöæöæöæö
+--+
÷÷÷÷
çççç
÷÷÷÷
çççç
=
÷÷÷÷
çççç
÷÷÷÷
÷÷÷÷
çççç
èøèøèøèø
()()
22
2
91212
12 .
221
16
3
AB
AB AB
AB
é
=
--
ê
ê
¬¾= ¬¾
ê
=
ê
ë
Câu 51: Tam giác ABC có , , BC a CA b AB c=== và có diện tích S . Nếu tăng cạnh BC lên 2 lần
đồng thời tăng cạnh
AC lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích
của tam giác mới được tạo nên bằng:
A. 2S . B. 3S . C. 4S . D. 6S .
Lời giải
Chọn D
Diện tích tam giác
ABC ban đầu là
11
...sin ..sin .
22
SACBCACBabACB==
Khi tăng cạnh
BC lên 2 lần và cạnh AC lên 3 lần thì diện tích tam giác ABC lúc này là
()()
11
. 3 . 2 .sin 6. . . .sin 6 .
22
ABC
S AC BC ACB AC BC ACB S
D
===
Câu 52:
Tam giác ABC có BC a= và CA b= . Tam giác ABC có diện tích lớn nhất khi góc C
bằng:
A.
0
60 . B.
0
90 . C.
0
150 . D.
0
120 .
Lời giải
Chọn B
Diện tích tam giác ABC là
11
...sin ..sin .
22
ABC
SACBCACBabACB
D
==
Vì
,ab không đổi và
sin 1,ACB C£" nên suy ra .
2
ABC
ab
S
D
£
Dấu
""= xảy ra khi và chỉ khi
0
sin 1 90 .ACB ACB= =
Vậy giá trị lớn nhất của diện tích tam giác
ABC là .
2
ab
S =
Câu 53:
Tam giác ABC có hai đường trung tuyến
,
B
MCN
vuông góc với nhau và có 3BC = , góc
0
30BAC = . Tính diện tích tam giác ABC .
A. 33
ABC
S
D
= . B. 63
ABC
S
D
= . C. 93
ABC
S
D
= . D.
33
2
ABC
S
D
= .
Lời giải
Chọn C
Vì
222
5BM CN a b c^¾¾=+. (Áp dụng hệ quả đã có trước)
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 729
Trong tam giác
ABC
, ta có
2
222 2
2
2.cos 5 2 cos .
cos
a
abc bc Aa bcA bc
A
=+- = - ¾¾=
Khi đó
2
2
112
sin . .sin tan 3 3
22cos
a
SbcA AaA
A
== ==
.
Câu 54: Tam giác ABC có 5, 8AB AC== và
0
60BAC = . Tính bán kính r của đường tròn nội tiếp
tam giác đã cho.
A. 1r = . B. 2r = . C. 3r = . D. 23r = .
Lời giải
Chọn C
Áp dụng định lý hàm số côsin, ta có
222
2. cos 49 7BC AB AC AB AC A BC=+- =¾¾=.
Diện tích
113
. .sin .5.8. 10 3
222
SABACA===
.
Lại có
2
.3
SS
Spr r
pABBCCA
=¾¾= = =
++
.
Câu 55: Tam giác
ABC
có 21, 17, 10abc===. Tính bán kính r của đường tròn nội tiếp tam giác
đã cho.
A. 16r = . B. 7r = . C.
7
2
r =
. D. 8r = .
Lời giải
Chọn C
Ta có
21 17 10
24
2
p
++
==
.
Suy ra
()()()
=---=24 24 21 24 17 24 10 84S .
Lại có
=¾¾= = =
84 7
..
24 2
S
Spr r
p
Câu 56: Tính bán kính r của đường tròn nội tiếp tam giác đều cạnh a .
A.
3
4
a
r =
. B.
2
5
a
r =
. C.
3
6
a
r =
. D.
5
7
a
r =
.
Lời giải
Chọn C
Diện tích tam giác đều cạnh
a
bằng:
2
3
4
a
S =
.
Lại có
2
3
3
4
3
6
2
a
Sa
Spr r
a
p
=¾¾= = =
.
Câu 57: Tam giác ABC vuông tại
A
có 6AB = cm, 10BC = cm. Tính bán kính r của đường tròn
nội tiếp tam giác đã cho.
A. 1r = cm. B. 2r = cm.
C. 2r = cm. D. 3r = cm.
Lời giải
Chọn C
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 730
Dùng Pitago tính được
8AC =
, suy ra
12
2
AB BC CA
p
++
==
.
Diện tích tam giác vuông
1
.24
2
SABAC==
.Lại có .2 cm.
S
Spr r
p
=¾¾= =
Câu 58: Tam giác ABC vuông cân tại
A
, có AB a= . Tính bán kính r của đường tròn nội tiếp tam
giác đã cho.
A.
2
a
r =
. B.
2
a
r =
. C.
22
a
r =
+
. D.
3
a
r =
.
Lời giải
Chọn C
Từ giả thiết, ta có AC AB a== và 2BC a= .
Suy ra
22
22
AB BC CA
pa
æö
++ +
÷
ç
÷
ç
==
÷
ç
÷
÷
ç
èø
.
Diện tích tam giác vuông
2
1
.
22
a
SABAC
==
.
Lại có
..
22
Sa
Spr r
p
=¾¾= =
+
Câu 59: Tam giác
ABC
vuông cân tại
A
và nội tiếp trong đường tròn tâm
O
bán kính
R
. Gọi r là bán
kính đường tròn nội tiếp tam giác
ABC . Khi đó tỉ số
R
r
bằng:
A. 12+ . B.
22
2
+
. C.
21
2
-
. D.
12
2
+
.
Lời giải
Chọn A
Giả sử 2AC AB a BC a==¾¾= . Suy ra
2
22
BC a
R ==
.
Ta có
22
22
AB BC CA
pa
æö
++ +
÷
ç
÷
ç
==
÷
ç
÷
÷
ç
èø
.
Diện tích tam giác vuông
2
1
.
22
a
SABAC==
.
Lại có
..
22
Sa
Spr r
p
=¾¾= =
+
Vậy 12
R
r
=+ .
| 1/79
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CHƯƠNG II. TÍCH VÔ HƯỚNG HAI VECTƠ VÀ ỨNG DỤNG
BÀI 1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC BẤT KỲ TỪ 0 0 ĐẾN 0 180
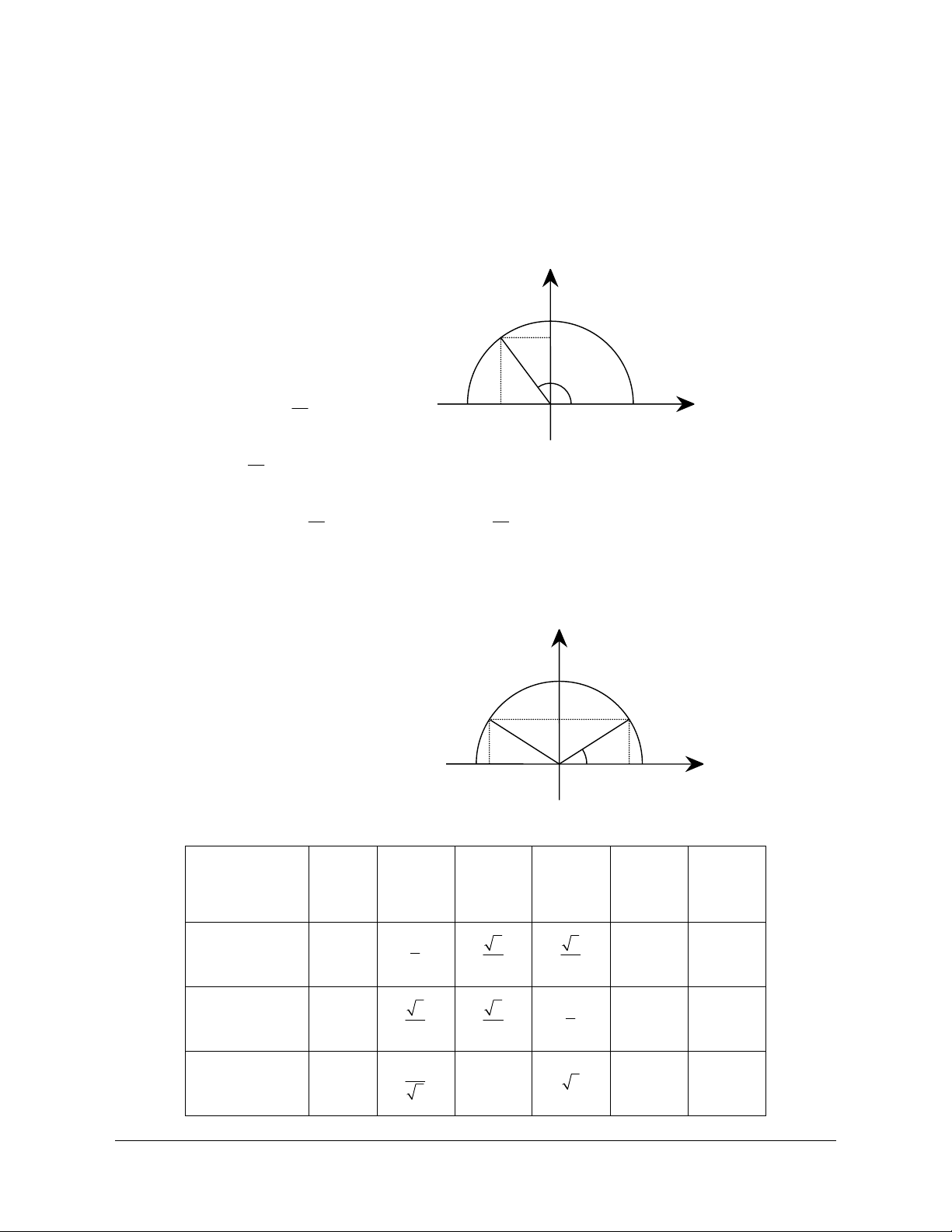
A. KIẾN THỨC CƠ BẢN CẦN NẮM 1. Định nghĩa Với mỗi góc a ( 0 0
0 £ a £180 ) ta xác định một điểm M trên nửa đường tròn đơn vị sao cho 
xOM = a và giả sử điểm M có tọa độ M (x ; y . 0 0 ) y
Khi đó ta có định nghĩa: 1
· sin của góc a là y , kí hiệu sin a = y ; 0 0 M y0
· cosin của góc a là x , kí hiệu cosa = x ; 0 0 a x
· tang của góc a là y0 (x ¹ 0 , 0 ) x x -1 0 O 1 0 kí hiệu y0 tan a = ; x0
· cotang của góc a là x0 ( x y ¹ 0 , kí hiệu 0 cot a = . 0 ) y0 y0 2. Tính chất
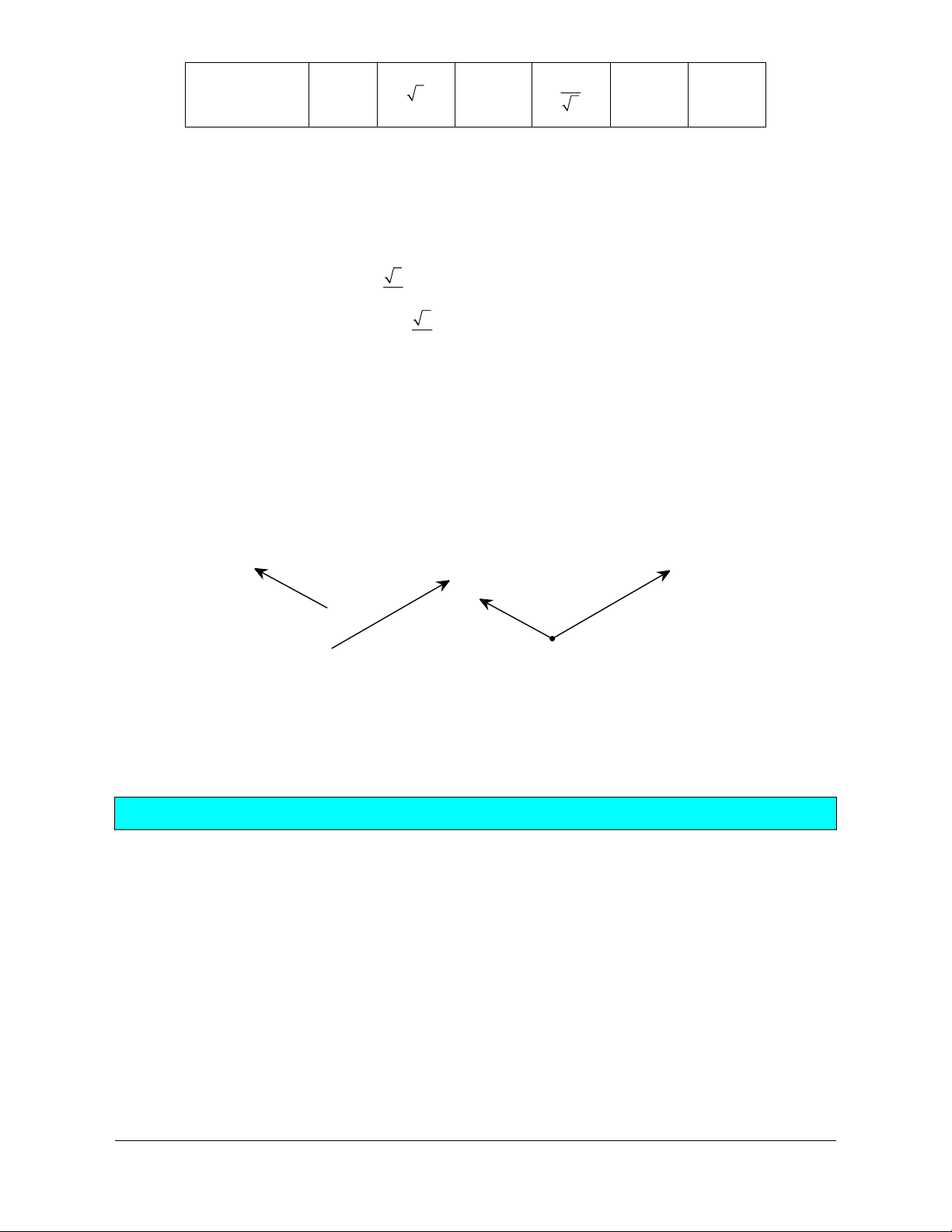
Trên hình bên ta có dây cung NM song song với trục Ox và nếu 
xOM = a thì  0 xON = 180 - . a Ta
có y = y = y , x = x - = x . Do đó M N 0 M N 0 y sin a = sin ( 0 180 -a) cos a = -cos( 0 180 -a) N y0 M tan a = -tan ( 0 180 -a) cot a = -cot ( 0 180 -a). a x -x0 O x0
3. Giá trị lượng giác của các góc đặc biệt Giá trị a 0 0 0 30 0 45 0 60 0 90 0 180 lượng giác sin a 0 1 2 3 1 0 2 2 2 1 cosa 1 3 2 0 -1 2 2 2 1 tan a 0 1 3  0 3
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 652
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 1 cot a  3 1 0  3
Trong bảng kí hiệu "" để chỉ giá trị lượng giác không xác định.
Chú ý. Từ giá trị lượng giác của các góc đặc biệt đã cho trong bảng và tính chất trên, ta có thể
suy ra giá trị lượng giác của một số góc đặc biệt khác. Chẳng hạn: 3 0 sin 120 = sin ( 0 0 180 -60 ) 0 = sin 60 = 2 2 0 cos135 = cos( 0 0 180 - 45 ) 0 = -cos 45 = - . 2
4. Góc giữa hai vectơ a) Định nghĩa       
Cho hai vectơ a và b đều khác vectơ 0. Từ một điểm O bất kì ta vẽ OA = a và OB = . b Góc   
AOB với số đo từ 0 0 đến 0
180 được gọi là góc giữa hai vectơ a và .
b Ta kí hiệu góc giữa hai vectơ          
a và b là ( ,
a b) . Nếu (a b) 0 ,
= 90 thì ta nói rằng a và b vuông góc với nhau, kí hiệu là a ^ b hoặc   b ^ . a A b    a a B b O    
b) Chú ý. Từ định nghĩa ta có ( ,ab)=( ,ba). được 6)
B. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI.
Dạng 1 : xác định giá trị lượng giác của góc đặc biệt.
1. Phương pháp giải.
 Sử dụng định nghĩa giá trị lượng giác của một góc
 Sử dụng tính chất và bảng giá trị lượng giác đặc biệt
 Sử dụng các hệ thức lượng giác cơ bản 2. Các ví dụ.
Ví dụ 1: Tính giá trị các biểu thức sau: a) A = a2 0 + b2 0 + c2 0 sin 90 cos 90 cos180 b) B = - 2 0 + 2 0 - 2 0 3 sin 90 2 cos 60 3 tan 45
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 653
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 c) C = 2 0 - 2 0 + 2 0 - 2 0 + 0 0 sin 45 2 sin 50 3 cos 45 2 sin 40 4 tan 55 . tan 35 Lời giải
a) A = a2 + b2 + c2 (- ) = a2 - c2 .1 .0 . 1 2 æ 1 ö æ ö2 2 2 b) B = 3 - (1) ç ÷ ç ÷ + 2ç ÷ - 3ç ÷ = ç ÷ ç ÷ 1 è 2 ø ç 2 ÷ è ø c) C = 2 0 + 2 0 - ( 2 0 + 2 0 ) + 0 0 sin 45 3 cos 45 2 sin 50 sin 40 4 tan 55 .cot55 æ ö2 æ ö2 2 2 1 3 C ç ÷ ç ÷ = ç ÷ + 3ç ÷ - 2 0 2 0 ç ÷ 2 sin 50 cos 40 4 2 4 4 ç 2 ÷ ç ÷ ( + ) + = + - + = ÷ è ø ç 2 ÷ è ø 2 2
Ví dụ 2: Tính giá trị các biểu thức sau: a) A = 2 0 + 2 0 + 2 0 + 2 0 sin 3 sin 15 sin 75 sin 87 b) B = 0 + 0 + 0 + + 0 + 0 cos 0 cos 20 cos 40 ... cos160 cos180 c) C = 0 0 0 0 0
tan 5 tan10 tan15 ... tan 80 tan 85 Lời giải a) A = ( 2 0 + 2 0 ) + ( 2 0 + 2 0 sin 3 sin 87 sin 15 sin 75 ) = ( 2 0 + 2 0 ) + ( 2 0 + 2 0 sin 3 cos 3 sin 15 cos 15 ) = 1 + 1 = 2 b) B = ( 0 + 0 ) +( 0 + 0 ) + +( 0 + 0 cos 0 cos180 cos20 cos160 ... cos 80 cos100 ) = ( 0 - 0 ) + ( 0 - 0 ) + + ( 0 - 0 cos 0 cos 0 cos 20 cos 20 ... cos 80 cos 80 ) = 0 c) C = ( 0 0 )( 0 0 ) ( 0 0 tan 5 tan 85
tan15 tan 75 ... tan 45 tan 45 ) = ( 0 0 )( 0 0 ) ( 0 0 tan 5 cot 5 tan15 cot 5 ... tan 45 cot 5 ) = 1
Dạng 2 : chứng minh đẳng thức lượng giác, chứng minh biểu thức không
phụ thuộc x, đơn giản biểu thức.
1. Phương pháp giải.
 Sử dụng các hệ thức lượng giác cơ bản
 Sử dụng tính chất của giá trị lượng giác
 Sử dụng các hằng đẳng thức đáng nhớ . 2. Các ví dụ.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 654
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ví dụ 1: Chứng minh các đẳng thức sau(giả sử các biểu thức sau đều có nghĩa) a) 4 x + 4 x = - 2 x 2 sin cos 1 2 sin .cos x 1 + cotx tan x + 1 b) = 1 - cotx tan x - 1 cos x + sin x c) = 3 tan x + 2
tan x + tan x + 1 3 cos x Lời giải a) 4 x + 4 x = 4 x + 4 x + 2 x 2 x - 2 x 2 sin cos sin cos 2 sin cos 2 sin cos x
= (sin x + cos x )2 2 2 - 2 2 sin x 2 cos x = 1 - 2 2 sin x 2 cos x 1 tan x + 1 1 cotx 1 + + tan x + 1 b) t anx t anx = = = 1 - cotx 1 tan x - 1 tan x - 1 1 - tanx tan x cos x + sin x 1 sin x c) = + = 2 x + + x ( 2 tan 1 tan tan x + 1) 3 cos x 2 cos x 3 cos x = 3 x + 2 tan
tan x + tan x + 1
Ví dụ 2: Cho tam giác ABC . Chứng minh rằng B B 3 3 sin cos cos(A + C ) 2 + 2 - . tan B = 2 æ A +C ö æ A +C ö sin B ç ÷ ç ÷ cosç ÷ sinç ÷ ç ÷ è 2 ø ç ÷ è 2 ø Lời giải
Vì A + B + C = 0 180 nên B B 3 3 sin cos cos( 0 180 - B ) VT = 2 + 2 - . tan B æ 0 180 - B ö æ 0 180 - B ö sin B ç ÷ ç ÷ cosç ÷ sinç ÷ ç ÷ è 2 ø ç ÷ è 2 ø B B 3 3 sin cos -cos B B B = 2 + 2 - . tan B = 2 sin + 2 cos + 1 = 2 = VP B B sin B 2 2 sin cos 2 2
Suy ra điều phải chứng minh.
Ví dụ 3: Đơn giản các biểu thức sau(giả sử các biểu thức sau đều có nghĩa) a) A = 0 - x + 0 - x + 2 x + 2 x - 2 sin(90 ) cos(180 ) sin (1 tan ) tan x
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 655
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 1 1 1 b) B = . + - 2 sin x 1 + cos x 1 - cos x Lời giải 1
a) A = cos x - cos x + 2 sin x. - 2 tan x = 0 2 cos x 1
1 - cos x + 1 + cos x b) B = . - 2 sin x
(1 - cosx )(1 + cosx ) 1 2 1 2 = . - 2 = . - 2 2 2 sin x 1 - cos x sin x sin x æ 1 ö ç ÷ = 2 ç - 1÷ = 2 2 cot x çè 2 sin x ÷ø
Ví dụ 4: Chứng minh biểu thức sau không phụ thuộc vào x. P = 4 x + 2 x + 4 x + 4 x + 2 x + 4 sin 6 cos 3 cos cos 6 sin 3 sin x Lời giải P = ( - x )2 + x + x + ( - x )2 2 2 4 2 + 2 x + 4 1 cos 6 cos 3 cos 1 sin 6 sin 3 sin x = 4 4 cos x + 2 4 cos x + 1 + 4 4 sin x + 2 4 sin x + 1
= (2 cos x + 1)2 + (2 sin x + 1)2 2 2 = 2 2 cos x + 1 + 2 2 sin x + 1 = 3
Vậy P không phụ thuộc vào x .
Dạng 3 : xác định giá trị của một biểu thức lượng giác có điều kiện.
1. Phương pháp giải.
 Dựa vào các hệ thức lượng giác cơ bản
 Dựa vào dấu của giá trị lượng giác
 Sử dụng các hằng đẳng thức đáng nhớ 2. Các ví dụ. 1
Ví dụ 1: a) Cho sin a = với 0 < a < 0 90
180 . Tính cos a và tan a 3 2
b) Cho cos a = - . Tính sin a và cota 3
c) Cho tan g = -2 2 tính giá trị lượng giác còn lại. Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 656
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 a) Vì 0 < a < 0 90
180 nên cos a < 0 mặt khác 2 a + 2 sin cos a = 1 suy ra 1 2 2 cos a = - 1 - 2 sin a = - 1 - = - 9 3 1 sin a 1 Do đó a = = 3 tan = - cos a 2 2 2 2 - 3 4 5 b) Vì 2 a + 2 sin
cos a = 1 nên sin a = 1 - 2 cos a = 1 - = và 9 3 2 cos a - 2 a = = 3 cot = - sin a 5 5 3 1
c) Vì tan g = -2 2 < 0  cos a < 0 mặt khác 2 tan a + 1 = nên 2 cos a 1 1 1 cos a = - = - = - 2 tan + 1 8 + 1 3 sin a æ 1 ö 2 2 Ta có tan a =
 sin a = tan a.cos a ç ÷ = -2 2.ç- ÷ = cos a ç ÷ è 3 ø 3 1 cos a - 1  a = = 3 cot = - sin a 2 2 2 2 3 3 tan a + 3 cot a
Ví dụ 2: a) Cho cos a = với 0 < a < 0 0 90 . Tính A = . 4 tan a + cot a sin a - cos a
b) Cho tan a = 2 . Tính B = 3 sin a + 3
3 cos a + 2 sin a Lời giải 1 1 tan a + 3 2 tan a + + 2 2 3 a) Ta có A tan a cos a = = = = 1 + 2 2 cos a 2 1 tan a + 1 1 tan a + tana 2 cos a 9 17 Suy ra A = 1 + 2. = 16 8
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 657
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 sin a cos a - tan a ( 2 tan a + 1) - ( 2 3 3 tan a + 1) b) B cos a cos a = = 3 sin a 3 3 cos a 2 sin a 3
tan a + 3 + 2 tan a ( 2 tan a + 1) + + 3 cos a 3 cos a 3 cos a 2 (2 + 1) - (2 + 1) 3( 2 - 1) Suy ra B = = 2 2 + 3 + 2 2 (2 + 1) 3 + 8 2
Ví dụ 3: Biết sin x + cos x = m
a) Tìm sin x cos x và 4 x - 4 sin cos x
b) Chứng minh rằng m £ 2 Lời giải a) Ta có ( x + x )2 = 2 x + x x + 2 sin cos sin 2sin cos
cos x = 1 + 2sinx cosx (*) m2 - 1
Mặt khác sin x + cos x = m nên m2 = 1 + 2 sin a cos a hay sin a cos a = 2 Đặt A = 4 x - 4 sin cos x . Ta có A = ( 2 x + 2 x )( 2 x - 2 sin cos sin
cos x ) = (sin x + cos x )(sin x - cosx )  A = ( x + x )2 ( x - x )2 2 sin cos sin cos
= (1 + 2 sin x cosx )(1 - 2 sin x cosx ) æ m2 - 1öæ m2 - 1ö 3 + m2 2 - m4  A2 ç ÷ç ÷ = ç1 + ÷ç1 - ÷ = ç ÷ç ÷ è 2 øè 2 ø 4 + m2 - m4 3 2 Vậy A = 2 b) Ta có x x £ 2 x + 2 2 sin cos sin
cos x = 1 kết hợp với (*) suy ra ( x + x )2 sin cos
£ 2  sin x + cos x £ 2 Vậy m £ 2
C. CÂU HỎI TRẮC NGHIỆM
Câu 1: Cho hai góc a và b với a + b = 90 . Tính giá trị của biểu thức P = sin a cosb + sin b cosa . A. P = 0. B. P =1. C. P = 1. - D. P = 2. Lời giải Chọn B
Hai góc a và b phụ nhau nên sin a = cosb; cosa = sin b . Do đó, 2 2
P = sin a cos b + sin b cos a = sin a + cos a = 1 .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 658
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 2: Cho hai góc a và b với a + b = 90 . Tính giá trị của biểu thức P = cosa cosb -sin b sin a . A. P = 0. B. P =1. C. P = 1. - D. P = 2. Lời giải Chọn A
Hai góc a và b phụ nhau nên sin a = cosb; cosa = sin b .
Do đó, P = cosa cosb -sin b sin a = cosa sin a -cosa sin a = 0 .
Câu 3: Cho a là góc tù. Khẳng định nào sau đây là đúng?
A. sin a < 0. B. cosa > 0.
C. tan a < 0.
D. cot a > 0. Lời giải Chọn C Lấy góc 0
a = 120 sau đó thử ngược
Câu 4: Cho hai góc nhọn a và b trong đó a < b . Khẳng định nào sau đây là sai?
A. cosa < cosb.
B. sin a < sin b.
C. cot a > cot b.
D. tan a + tan b > 0. Lời giải Chọn A Lấy 0 0
a = 30 ;b = 60 sau đó thử ngược.
Câu 5: Khẳng định nào sau đây sai?
A. cos75 > cos50.
B. sin 80 > sin 50.
C. tan 45 < tan 60.
D. cos30 = sin 60. Lời giải Chọn A
Trong khoảng từ 0 đến 90 , khi giá trị của góc tăng thì giá trị cos tương ứng của góc đó giảm.
Câu 6: Khẳng định nào sau đây đúng?
A. sin 90 < sin100.
B. cos95 > cos100.
C. tan 85 < tan125.
D. cos145 > cos125. Lời giải Chọn B
Trong khoảng từ 90 đến 180 , khi giá trị của góc tăng thì:
- Giá trị sin tương ứng của góc đó giảm.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 659
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
- Giá trị cos tương ứng của góc đó giảm.
Câu 7: Khẳng định nào sau đây đúng?
A. sin 90 < sin150.
B. sin 9015¢ < sin 9030¢.
C. cos9030¢ > cos100.
D. cos150 > cos120. Lời giải Chọn C
Trong khoảng từ 90 đến 180 , khi giá trị của góc tăng thì:
- Giá trị sin tương ứng của góc đó giảm.
- Giá trị cos tương ứng của góc đó giảm.
Câu 8: Chọn hệ thức đúng được suy ra từ hệ thức 2 2
cos a + sin a = 1? A. a a a a 2 2 1 cos + sin = . B. 2 2 1 cos + sin = . 2 2 2 3 3 3 æ ö C. a a a a 2 2 1 cos + sin = . D. 2 2 5ççcos + sin ÷÷= 5. 4 4 4 çè 5 5 ÷ø Lời giải Chọn D Từ biểu thức a a 2 2
cos a + sin a = 1 ta suy ra 2 2 cos + sin = 1. 5 5 æ ö Do đó ta có a a 2 2 5ççcos + sin ÷÷= 5. ç è 5 5 ÷ø Câu 9: a a a Cho biết 3 sin = . Giá trị của 2 2 P = 3 sin + 5 cos bằng bao nhiêu? 3 5 3 3 A. 105 P = . B. 107 P = . C. 109 P = . D. 111 P = . 25 25 25 25 Lời giải Chọn B Ta có biểu thức a a a a 16 2 2 2 2 sin + cos = 1  cos = 1- sin = . 3 3 3 3 25 2 Do đó ta có a a æ ö 2 2 3 16 107 P = 3 sin + 5cos = 3.ç ÷ ç ÷ + 5. = . 3 3 çè5÷ø 25 25 Câu 10: a - a
Cho biết tan a = -3. Giá trị của 6 sin 7 cos P = bằng bao nhiêu? 6 cos a +7 sin a A. 4 P = . B. 5 P = . C. 4 P = - . D. 5 P = - . 3 3 3 3 Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 660
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 sin a 6 -7 Ta có 6 sin a -7 cos a a 6 tan a -7 5 cos P = = = = . 6 cos a +7 sin a sin a 6 +7 tan a 3 6 +7 cosa Câu 11: a + a Cho biết 2
cos a = - . Giá trị của cot 3 tan P = bằng bao nhiêu? 3 2 cot a + tan a A. 19 P = - . B. 19 P = . C. 25 P = . D. 25 P = - . 13 13 13 13 Lời giải Chọn B Ta có biểu thức 2 2 2 2 5
sin a + cos a = 1  sin a = 1- cos a = . 9 2 cosa sin a æ 2ö 5 + 3 ç ÷ - ç ÷ + 3. 2 2 + + ç ÷ Ta có cot a 3 tan a a a cos a 3 sin sin cos a è 3ø 9 19 P = = = = = . 2 2 2 2 cot a + tan a cos a sin a 2 cos a + sin a æ 2ö 5 13 2 + 2.ç ÷ sin a cosa - ç ÷ + çè 3÷ø 9
Câu 12: Cho biết cot a = 5. Giá trị của 2
P = 2 cos a + 5 sin a cos a +1 bằng bao nhiêu? A. 10 P = . B. 100 P = . C. 50 P = . D. 101 P = . 26 26 26 26 Lời giải Chọn D 2 æ ö Ta có cos a cosa 1 2 2 ç ÷
P = 2 cos a + 5 sin a cos a +1 = sin aç2 + 5 + ÷ ç 2 2 çè sin a sin a sin a÷÷ø 2 1 = ( a + a + 2 2 3 cot 5 cot 1 101
2 cot a + 5 cot a +1 + cot a = = . 2 ) 2 1 + cot a cot a +1 26
Câu 13: Cho biết 3cosa -sin a = 1 , 0 0
0 < a < 90 . Giá trị của tan a bằng A. 4 tan a = . B. 3 tan a = . C. 4 tan a = . D. 5 tan a = . 3 4 5 4 Lời giải Chọn A Ta có a - a =  a = a +  a = ( a + )2 2 3 cos sin 1 3 cos sin 1 9 cos sin 1 2 2  a = a + a +  ( 2 - a) 2 9 cos sin 2 sin 1 9 1 sin
= sin a + 2 sin a +1 ésin a = -1 ê 2
 10 sin a + 2 sin a -8 = 0  ê 4 . êsin a = êë 5
· sin a = -1 : không thỏa mãn vì 0 0 0 < a < 90 . a · 4 3 sin 4 sin a =  cosa = ¾¾  tan a = = . 5 5 cosa 3
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 661
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 14: Cho biết 2 cosa + 2 sin a = 2 , 0 0
0 < a < 90 . Tính giá trị của cot . a A. 5 cot a = . B. 3 cot a = . C. 2 cot a = . D. 2 cot a = . 4 4 4 2 Lời giải Chọn C Ta có a + a =  a = - a a = ( - a)2 2 2 cos 2 sin 2 2 sin 2 2 cos 2 sin 2 2 cos 2 2
 2 sin a = 4 -8 cosa + 4 cos a  2( 2 1-cos a) 2
= 4 -8 cosa + 4 cos a écosa = 1 ê 2
 6 cos a -8 cosa + 2 = 0  ê 1 . êcosa = êë 3
· cosa = 1 : không thỏa mãn vì 0 0 0 < a < 90 . a · 1 2 2 cos 2
cos a =  sin a = ¾¾ cot a = = . 3 3 sin a 4
Câu 15: Cho biết sin a + cosa = .
a Tính giá trị của sin a cos . a A. 2
sin a cos a = a . B.
sin a cos a = 2 . a 2 2 C. a -1 a -11 sin a cos a = . D. sin a cos a = . 2 2 Lời giải Chọn C Ta có a + a = a  ( a + a)2 2 sin cos sin cos = a 2 - 2 a 1
 1+ 2 sin a cos a = a  sin a cos a = . 2 Câu 16: Cho biết 1
cos a + sin a = . Giá trị của 2 2 P =
tan a + cot a bằng bao nhiêu? 3 A. 5 P = . B. 7 P = . C. 9 P = . D. 11 P = . 4 4 4 4 Lời giải Chọn B Ta có 1 a + a =  ( a + a)2 1 cos sin cos sin = 3 9 1 4
 1+ 2 sin a cosa =  sin a cosa = - . 9 9 2 æ ö Ta có a a P =
tan a + cot a = (tan a + cot a)2 sin cos 2 2
-2 tan a cot a = ç ÷ ç + ÷ -2 ç ècosa sin a ÷ø 2 2 2 2 2
æsin a + cos aö æ ç ÷ 1 ö æ 9ö 7 = ç ÷ - 2 = ç ÷ ç ÷ ç ÷ - 2 = ç ÷ - ç ÷ - 2 = .
çè sin a cosa ÷ ç ø èsin a cosa÷ø çè 4÷ø 4
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 662
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Câu 17: Cho biết 1 sin a - cos a = . Giá trị của 4 4
P = sin a + cos a bằng bao nhiêu? 5 A. 15 P = . B. 17 P = . C. 19 P = . D. 21 P = . 5 5 5 5 Lời giải Chọn B Ta có 1 a - a =  ( a - a)2 1 sin cos sin cos = 5 5 1 2
 1-2 sin a cosa =  sin a cosa = . 5 5 Ta có P = a + a = ( a + a)2 4 4 2 2 2 2 sin cos sin cos -2 sin a cos a = - ( a a)2 17 1 2 sin cos = . 5
Câu 18: Cho O là tâm đường tròn ngoại tiếp tam giác đều MNP. Góc nào sau đây bằng O 120 ?        
A. (MN ,NP) B. (M , O ON ).
C. (MN ,OP).
D. (MN , MP). Lời giải Chọn A      
Vẽ NE = MN . Khi đó (MN ,NP)=(NE,NP) P  0  0 0 0 = F
PNE = 180 - MNP = 180 - 60 = 120 .       O
· Vẽ OF = MO . Khi đó (MO ON )= (OF ON )  0 , , = NOF = 60 .   E N M
· Vì MN ^ OP ¾¾ (MN OP) 0 , = 90 .   · Ta có (MN MP)  0 , = NMP = 60 .      
Câu 19: Cho tam giác đều ABC. Tính P = cos(AB,BC)+cos(BC,CA)+cos(CA, AB). A. 3 3 P = . B. 3 P = . C. 3 P = - . D. 3 3 P = - . 2 2 2 2 Lời giải Chọn C      
Vẽ BE = AB . Khi đó (AB BC)=(BE BC)   0 , ,
= CBE = 180 -CBA = 120   ¾¾ cos(AB, BC) 1 0 = cos120 = - . 2 C     Tương tự, ta cũng có
(BC CA)= (CA AB) 1 cos , cos , = - . 2
Giáo viên có nhu cầu sở hữu file word vui lòng A B Tra E ng 663
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133       Vậy
(AB BC)+ (BC CA)+ (CA AB) 3 cos , cos , cos , = - . 2  
Câu 20: Cho tam giác đều ABC có đường cao AH. Tính (AH,BA). A. 0 30 . B. 0 60 . C. 0 120 . D. 0 150 . Lời giải Chọn D   Vẽ AE = BA . C   Khi đó (AH AE)  ,
= HAE = a (hình vẽ) H a 0  0 0 0
= 180 - BAH = 180 -30 = 150 . B A E
Câu 21: Tam giác ABC vuông ở A và có góc  0
B = 50 . Hệ thức nào sau đây sai?     A. (AB BC) 0 , 130 = . B. (BC AC) 0 , = 40 .     C. (AB CB) 0 , = 50 . D. (AC CB) 0 , = 40 . Lời giải Chọn D   Vì (AC CB) 0  0 0 0 , 18 =
0 - ACB = 180 - 40 = 140 .  
Câu 22: Tam giác ABC vuông ở A và có BC = 2AC. Tính cos(AC,CB).     A. (AC CB) 1 cos , = . B. (AC CB) 1 cos , = - . 2 2     C. (AC CB) 3 cos , = . D. (AC CB) 3 cos , = - . 2 2 Lời giải Chọn B  
Xác định được (AC,CB) 0  = 180 - AC . B C Ta có  AC 1  0 cos ACB = = ¾¾  ACB = 60 CB 2   ¾¾ (AC CB) 0  0 , = 180 - ACB = 120 A B   Vậy cos(AC,CB) 1 0 = cos120 = - . 2      
Câu 23: Cho tam giác ABC . Tính tổng (AB,BC)+(BC,CA)+(CA, AB). A. 180 . B. 360 . C. 270 . D. 120 . Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 664
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn B (ì  ïï AB,BC ï ) 0  = 180 - ABC ïï   Ta có ( ïí BC,CA) 0  = 180 - BCA
ïï(ïï  ï CA, AB ï ) 0  = 180 -CAB î       ¾¾
(AB BC)+(BC CA)+(CA AB) 0    =
-(ABC + BCA +CAB) 0 0 0 , , , 540 = 540 -180 = 360 .    
Câu 24: Cho tam giác ABC với A = 60 . Tính tổng (AB,BC)+(BC,CA). A. 120 . B. 360 . C. 270 . D. 240 . Lời giải Chọn D (ì  ïï AB,BC ï ) 0  = 180 - ABC
Ta có ï(íï  ï BC,CA ï ) 0  = 180 - BCA ïî     ¾¾
(AB, BC)+(BC,CA) 0  
= 360 -(ABC + BCA) 0 0  = -( - BAC) 0 0 0 0 360 180
= 360 -180 + 60 = 240 .
Câu 25: Tam giác ABC có góc A bằng 100 và có trực tâm H. Tính tổng
(     
HA, HB)+(HB, HC)+(HC, HA). A. 360 . B. 180 . C. 80 . D. 160 . Lời giải Chọn D ì   ï H (ïHA,HB ï )  = BHA ïï   Ta có ( ïí HB,HC)  = BHC F ïï I ï   A (ïïHC,HA ï )  = CHA î 0 100       ¾¾
(HA HB)+(HB HC)+(HC HA)    , , ,
= BHA + BHC +CHA B C  = BHC = ( 0 0 - ) 0 2 2 180 100 = 160  
(do tứ giác HIAF nội tiếp. Cho hình vuông ABCD . Tính cos(AC,BA).      
Câu 26: Cho hình vuông ABCD tâm .
O Tính tổng (AB, DC)+(AD,CB)+(CO, DC). A. 0 45 . B. 0 405 . C. 0 315 . D. 0 225 . Lời giải Chọn C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 665
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133    
· Ta có AB, DC cùng hướng nên (AB, DC) 0 = 0 . A B     O
· Ta có AD,CB ngược hướng nên (AD CB) 0 , = 180 .      
· Vẽ CE = DC , khi đó (CO DC)= (CO CE)  0 , , = OCE = 135 . D C E      
Vậy (AB, DC)+(AD,CB)+( , CO DC ) 0 0 0 0 = 0 +180 +135 = 315 .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 666
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
BÀI 2. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ
A. KIẾN THỨC CƠ BẢN CẦN NẮM 1. Định nghĩa       
Cho hai vectơ a và b đều khác vectơ 0. Tích vô hướng của a và b là một số, kí hiệu là . a , b được
xác định bởi công thức sau:       .
a b = a . b cos( , a b).     
Trường hợp ít nhất một trong hai vectơ a và b bằng vectơ 0 ta quy ước . a b = 0. Chú ý       
· Với a và b khác vectơ 0 ta có .ab = 0  a ^ .b     
· Khi a = b tích vô hướng .aa được kí hiệu là 2
a và số này được gọi là bình phương vô hướng của  vectơ . a Ta có: 2    2 0
a = a . a . cos 0 = a .
2. Các tính chất của tích vô hướng
Người ta chứng minh được các tính chất sau đây của tích vô hướng:    Với ba vectơ , a ,
b c bất kì và mọi số k ta có:     · . a b = .
b a (tính chất giao hoán);       
· a(b+c)= .ab+ .ac (tính chất phân phối);      
· (ka).b = k( .ab)= .a(kb);    · 2 2 a ³ 0, 0 a =  a = 0.
Nhận xét. Từ các tính chất của tích vô hướng của hai vectơ ta suy ra:       · (a+b)2 2 2 = a + 2 . a b + b ;       · (a-b)2 2 2 = a -2 . a b + b ;      
· (a+b)(a-b) 2 2 = a -b .
3. Biểu thức tọa độ của tích vô hướng      
Trên mặt phẳng tọa độ (O;i; j), cho hai vectơ a =(a ;a ,
b = b ;b . Khi đó tích vô hướng . a b là: 1 2 ) ( 1 2 )
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 667
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133   .
a b = a b + a b . 1 1 2 2   
Nhận xét. Hai vectơ a = (a ;a ,
b = b ;b đều khác vectơ 0 vuông góc với nhau khi và chỉ khi 1 2 ) ( 1 2 ) a b + a b = 0. 1 1 2 2 4. Ứng dụng
a) Độ dài của vectơ
Độ dài của vectơ a = (a ;a được tính theo công thức: 1 2 )  2 2
a = a + a . 1 2
b) Góc giữa hai vectơ   
Từ định nghĩa tích vô hướng của hai vectơ ta suy ra nếu a = (a ;a và b = (b ;b đều khác 0 thì ta 1 2 ) 1 2 ) có     a b a b + a b cos( ; a b) . 1 1 2 2 =   = . 2 2 2 2 a . b
a + a . b +b 1 2 1 2
c) Khoảng cách giữa hai điểm
Khoảng cách giữa hai điểm A(x ; y và B(x ; y được tính theo công thức: B B ) A A )
AB = (x - x )2 +(y - y )2 . B A B A
B. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI.
DẠNG 1 : Xác định biểu thức tích vô hướng, góc giữa hai vectơ.
1. Phương pháp giải.      
 Dựa vào định nghĩa a b. = a . b cos(a;b)
 Sử dụng tính chất và các hằng đẳng thức của tích vô hướng của hai vectơ 2. Các ví dụ:
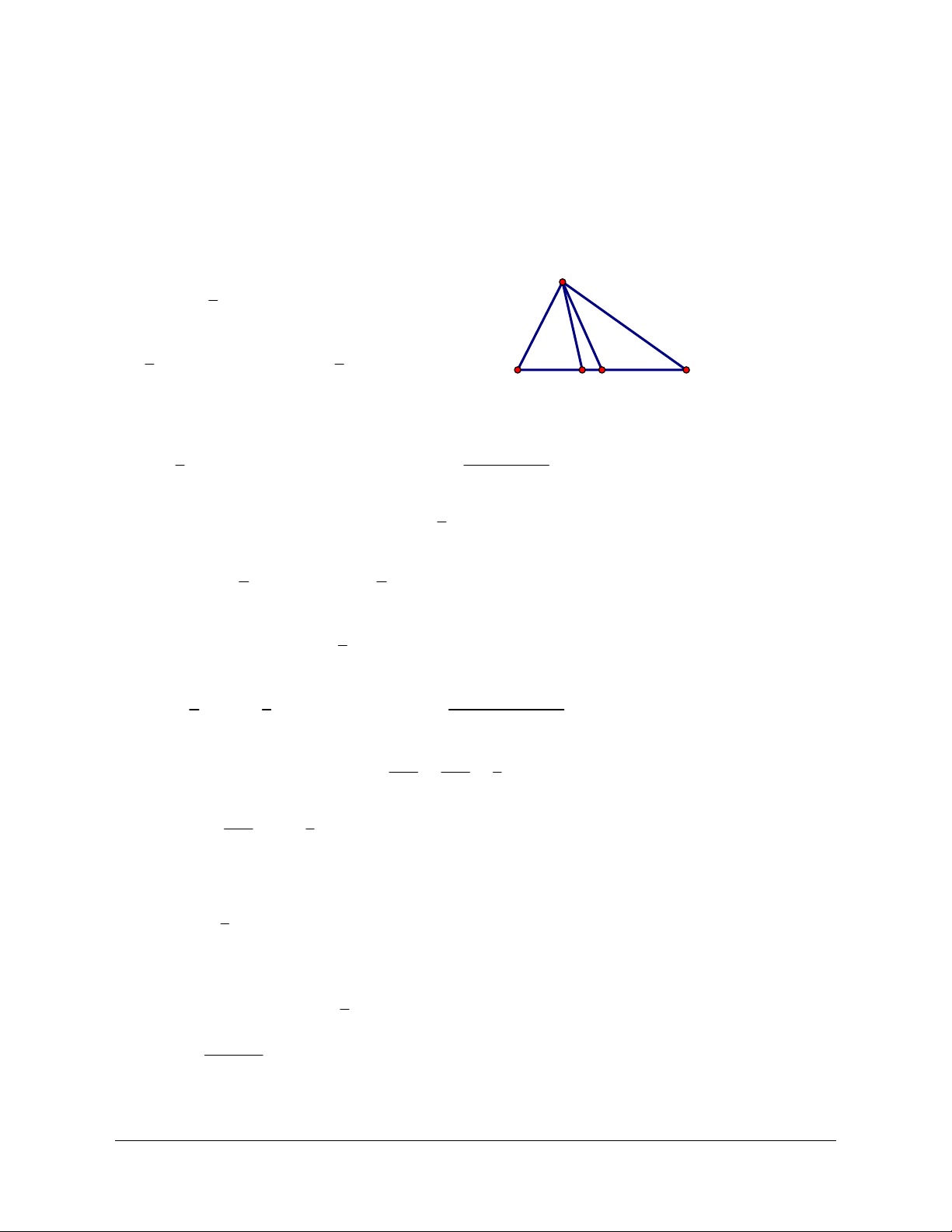
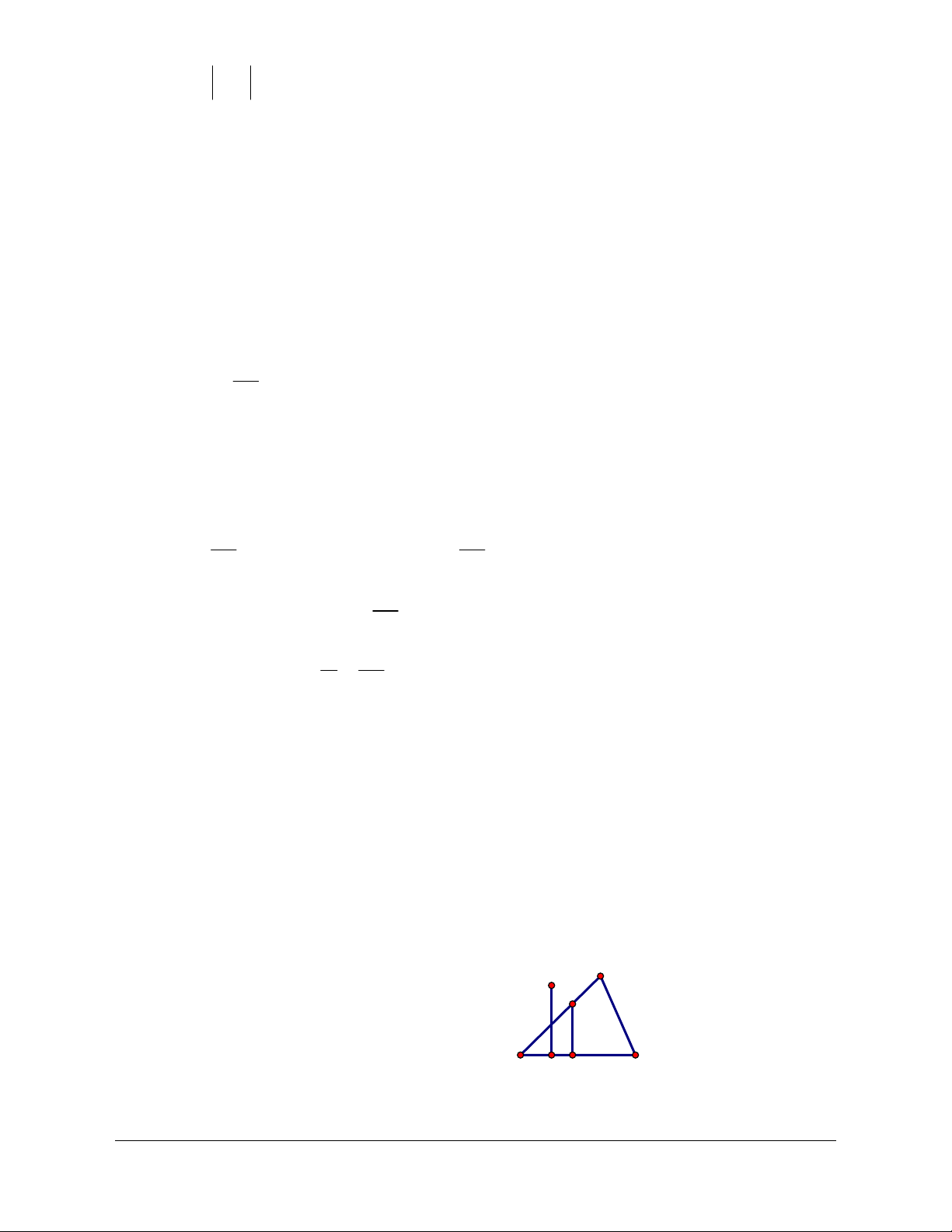
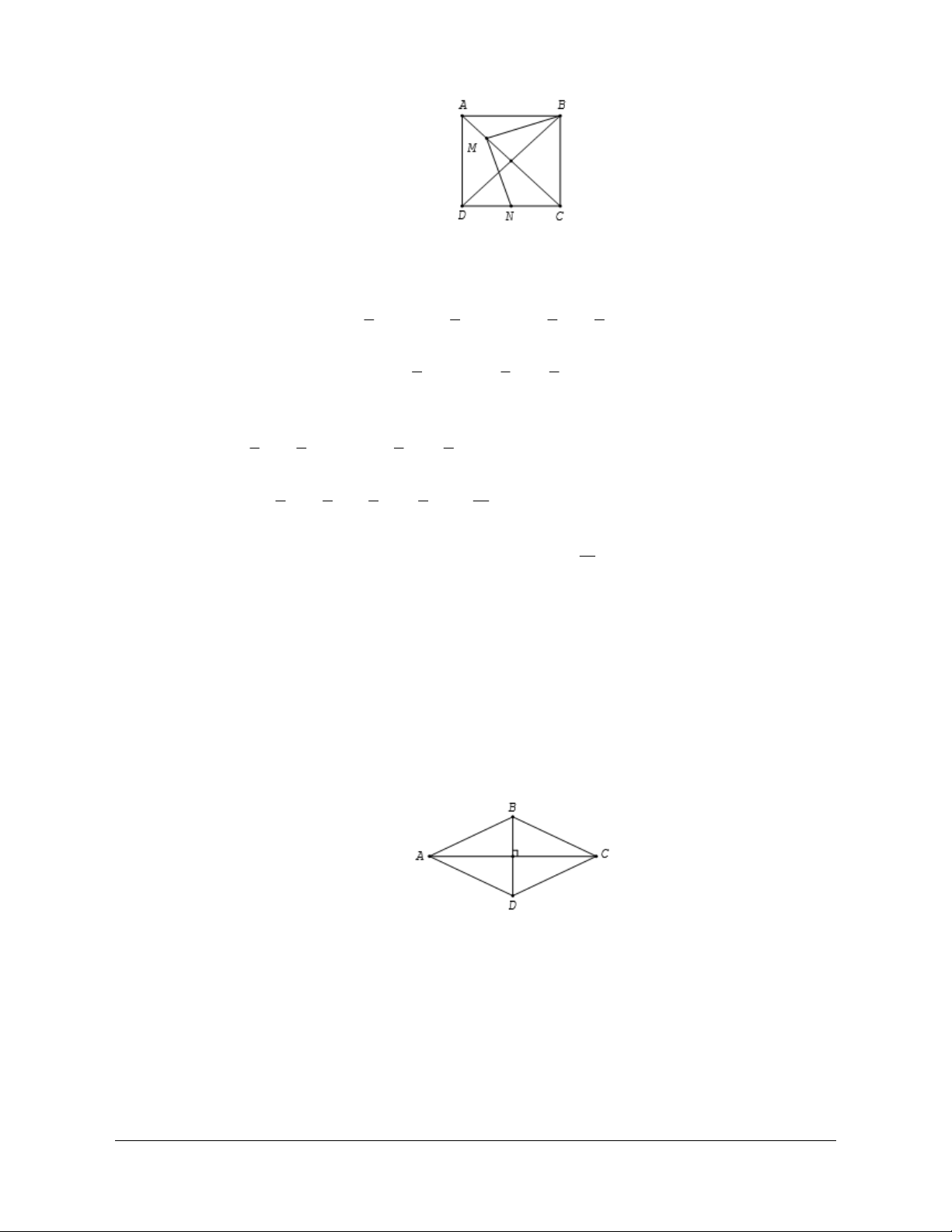
Ví dụ 1: Cho tam giác ABC vuông tại A có AB = a, BC = a 2 và G là trọng tâm.
   
a) Tính các tích vô hướng: BA BC . ; BC CA .      
b) Tính giá trị của biểu thứcAB BC . + BC CA . + CA A . B      
c) Tính giá trị của biểu thứcGAGB . + GB GC . + GC G . A
Lời giải (hình 2.2)
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 668
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 C N M G A P B Hình 2.2
a) * Theo định nghĩa tích vô hướng ta có         BA BC = BA BC (BA BC ) = a2 . . cos , 2 cos(BA,BC ).   1 Mặt khác cos( , )  a BA BC = co ABC s = = a 2 2   Nên BA BC = a2 .       * Ta có  BC CA . = C - B C
. A = - CB . CA co ACB s
Theo định lý Pitago ta có CA = ( a )2 - a2 2 = a 3   a 3 Suy ra BC C . A = a - 3. a 2 . = - a2 3 a 2  
b) Cách 1: Vì tam giác ABC vuông tại A nên CA AB . = 0 và từ câu a ta           có AB BC = a - 2 BC CA = - a2 . , .
3 . Suy ra AB BC + BC CA + CA AB = - a2 . . . 4    
Cách 2: Từ AB + BC + CA = 0 và hằng đẳng thức
(   2      
AB + BC + CA) = AB2 + BC 2 +CA2 + 2(AB BC . + BC CA . + CA AB . )Ta có       1 AB B . C + BC CA . + CA AB .
= - (AB2 + BC 2 +CA2 ) = - a2 4 2    
c) Tương tự cách 2 của câu b) vì GA + GB + GC = 0 nên       1 GAGB . + GB GC . + GC GA .
= - (GA2 +GB2 +GC 2 ) 2
Gọi M, N, P lần lượt là trung điểm của BC, CA, AB æ 2 ö2 a2 4
Dễ thấy tam giác ABM đều nên GA2 ç = ç AM ÷÷ = ç ÷ è 3 ø 9
Theo định lý Pitago ta có:
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 669
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2 4 4 4 3 7 2 2 ( 2 2 ) æ a ö a GB BN AB AN ç = = + = ça2 ÷ + ÷ = ç ÷ 9 9 9 è 4 ø 9 2 2 4 4 4 13 2 2 ( 2 2 ) æ a ö a GC CP AC AP ç = = + = ç a2 ÷ 3 + ÷ = ç ÷ 9 9 9 è 4 ø 9       æ a2 a2 a2 ö a2 1 4 7 13 4 Suy ra GAGB . + GB GC . + GC GA ç ÷ . = - ç + + ÷ = - ç ÷ 2 è 9 9 9 ø 3
Ví dụ 2: Cho hình vuông ABCD cạnh a. M là trung điểm của AB, G là trọng tâm tam giác ADM .
Tính giá trị các biểu thức sau:        a) AB ( + AD) B ( D + BC )
b) CG.(CA + DM )
Lời giải (hình 2.3)   
a) Theo quy tắc hình bình hành ta có AB + AD = AC         Do đó A
( B + AD) B
( D + BC ) = AC B . D + AC B . C A M B      = CACB .
= CA . CB co AC s B G     ( AC B
. D = 0 vì AC ^ BD ) D C Mặt khác  ACB = 0
45 và theo định lý Pitago ta có : Hình 2.3
AC = a2 + a2 = a 2    
Suy ra AB + AD BD + BC = a a 0 = a2 ( )( ) . 2 cos 45    
b) Vì G là trọng tâm tam giác ADM nên CG = CD + CA + CM   
Mặt khác theo quy tắc hình bình hành và hệ thức trung điểm ta có CA = -(AB + AD ) và  1   1    1   CM (CB CA) éCB ê (AB AD)ù = + = - + = - ú (AB + AD 2 ) 2 2 ë û 2     1   æ 5   ö Suy ra CG AB (AB AD) (AB AD 2 ) ç = - - + - + = -ç AB + AD ÷ 2 ÷ ç ÷ 2 è 2 ø       æ 1   ö Ta lại có CA DM (AB AD) AM AD ç + = - + + - = -ç AB + AD ÷ 2 ÷ ç ÷ è 2 ø    æ 5 
 öæ1   ö
Nên CG.(CA DM ) çç AB AD ÷ç + = + 2 ÷ç AB + AD ÷ 2 ÷ ç ÷ è 2 øç ÷ è 2 ø 5 2 a2 1 = AB2 + AD2 4 = 4 4
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 670
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ví dụ 3: Cho tam giác ABC có BC = a, CA = b, AB = c . M là trung điểm của BC, D là chân
đường phân giác trong góc A.   a) Tính AB AC . , rồi suy ra cosA . 2 2
b) TínhAM và AD
Lời giải (hình 2.3) a) Ta có A   é 2 2   2 1 ù AB AC .
= êAB + AC - (AB - AC ) ú 2 ê ú ë û 1 1
= éAB2 + AC 2 -CB2 ù 2 2 2 ë
û = (c +b -a ) 2 2 B M C D   Mặt khác AB AC . = AB AC .
cos A = cb cos A Hình 2.3 1
c2 +b2 -a2
Suy ra (c2 +b2 -a2 ) = cb cosA hay cosA = 2 bc 2  1  
b) * Vì M là trung điểm của BC nên AM = (AB + AC ) 2 2   2 æ 2  2 1 1 ö
Suy ra AM = (AB + AC ) = ççAB + AB 2 AC + AC ÷÷ ç ÷ 4 4 è ø   1
Theo câu a) ta có AB AC .
= (c2 + b2 - a2 ) nên 2  1 æ 1 ö 2(b2 + c2 ) 2 2 ç = ç 2 + 2. ( 2 + 2 - 2 ) - a AM c c b a + b2 ÷÷ = ç ÷ 4 è 2 ø 4 BD AB c
* Theo tính chất đường phân giác thì = = DC AC b  BD  b  Suy ra BD = DC = DC (*) DC c      
Mặt khác BD = AD - AB và DC = AC - AD thay vào (*) ta được   b     
AD - AB = (AC -AD )  (b +c )AD = bAB +cAC c 2  2   2
 (b +c )2 AD = (bAB ) + b 2 cABAC + (cAC )  2 1
 (b +c )2 AD = b c 2 2 + b
2 c. (c2 +b2 -a2 ) +c b 2 2 2 2 bcAD =
(b +c -a )(b +c +a ) (b +c )2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 671
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 bc 4 Hay AD =
p( p -a ) (b + c )2 2 bc
Nhận xét : Từ câu b) suy ra độ dài đường phân giác kẻ từ đỉnh A là l = p p -a a ( ) b +c
Dạng 2: chứng minh các đẳng thức về tích vô hướng hoặc độ dài của đoạn thẳng.
1. Phương pháp giải.
 Nếu trong đẳng thức chứa bình phương độ dài của đoạn thẳng thì ta chuyển về vectơ nhờ 2
đẳng thức AB2 = AB
 Sử dụng các tính chất của tích vô hướng, các quy tắc phép toán vectơ
 Sử dụng hằng đẳng thức vectơ về tích vô hướng. 2. Các ví dụ:
Ví dụ 1: Cho I là trung điểm của đoạn thẳng AB và M là điểm tùy ý.  
Chứng minh rằng : MA MB = IM 2 - IA2 . Lời giải:   2 2
Đẳng thức cần chứng minh được viết lại là MA MB . = IM - IA  
Để làm xuất hiện IM, IA ở VP, sử dụng quy tắc ba điểm để xen điểm I vào ta được        
VT = (MI + IA).(MI + IB ) = (MI + IA).(MI - IA) 2 2
= IM - IA = VP (đpcm)
Ví dụ 2: Cho bốn điểm A, B, C, D bất kì. Chứng minh rằng:       DA BC . + DB C . A + DC A . B = 0 (*).
Từ đó suy ra một cách chứng minh định lí: "Ba đường cao trong tam giác đồng qui". Lời giải:       Ta có: DA B . C + DB C . A + DC A . B         
= DA.(DC - DB ) + DB.(DA - DC ) + DC.(DB - DA)             = DADC . - DA DB . + DB DA . - DB DC . + DC DB . - DC DA . = 0 (đpcm)
Gọi H là giao của hai đường cao xuất phát từ đỉnh A, B.     Khi đó ta có HA B . C = 0, HC AB . = 0 (1)
Từ đẳng thức (*) ta cho điểm D trùng với điểm H ta được
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 672
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133       HA BC . + HB CA . + HC AB . = 0 (2)  
Từ (1) (2) ta có HB CA .
= 0 suy ra BH vuông góc với AC
Hay ba đường cao trong tam giác đồng quy (đpcm).
Ví dụ 3: Cho nửa đường tròn đường kính AB. Có AC và BD là hai dây thuộc nửa đường tròn cắt    
nhau tại E. Chứng minh rằng : AE AC + BE BD = AB2 . .
Lời giải (hình 2.4)      
Ta có VT = AE.(AB + BC ) + BE.(BA + AD ) D C         = AE A . B + AE BC . +BE B . A + BE A . D E
Vì AB là đường kính nên  0  ADB = , ACB = 0 90 90 A B Hình 2.4     Suy ra AE BC . = 0, BE A . D = 0        2
Do đó VT = AE AB . +BE B
. A = AB (AE + EB ) = AB = VP (đpcm).
Ví dụ 4: Cho tam giác ABC có ,
BC = a CA = b,AB = c và I là tâm đường tròn nội tiếp. Chứng
minh rằng aIA2 + bIB2 + cIC 2 = abc Lời giải:        2
Ta có: aIA + bIB + cIC = 0  (aIA + bIB + cIC ) = 0      
a2IA2 + b2IB2 + c2IC 2 + a 2 bIA I . B + b 2 cIB I . C + c 2 aIC I . A = 0
a2IA2 + b2IB2 + c2IC 2 + ab (IA2 + IB2 - AB2 ) +
+ bc (IB2 + IC 2 - BC 2 ) + ca (IA2 + IC 2 -CA2 ) = 0
 (a2 + ab + ca )IA2 + (b2 + ba + bc )IB2 +
+ (c2 + ca + cb )IC 2 - (abc2 + ab c 2 + a bc 2 ) = 0
 (a + b + c )(a2IA2 + b2IB2 + c2IC 2 ) = (a + b + c )abc
a2IA2 + b2IB2 + c2IC 2 = abc (đpcm)
Dạng 3: tìm tập hợp điểm thoả mãn đẳng thức về tích vô hướng hoặc tích độ dài.
1. Phương pháp giải.
Ta sử dụng các kết quả cơ bản sau:
Cho A, B là các điểm cố định. M là điểm di động
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 673
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 
 Nếu AM = k với k là số thực dương cho trước thì tập hợp các điểm M là đường tròn tâm
A, bán kính R = k .    Nếu MAM
. B = 0 thì tập hợp các điểm M là đường tròn đường kính AB      Nếu MAa
. = 0 với a khác 0 cho trước thì tập hợp các điểm M là đường thẳng đi qua A và 
vuông góc với giá của vectơ a 2. Các ví dụ.  
Ví dụ 1. Cho hai điểm A, B cố định có độ dài bằng a, vectơ a khác 0 và số thực k cho trước. Tìm tập hợp điểm M sao cho   a2 3 a) MA MB . = 4   b) MA MB = MA2 . Lời giải:
a) Gọi I là trung điểm của AB ta có   a2     2 3 3 . =  ( + )( + ) a MA MB MI IA MI IB = 4 4 a2 3  
MI 2 - IA2 = (Do IB = I - A ) 4 a2 a2 3 2  MI = + 4 4  MI = a
Vậy tập hợp điểm M là đường tròn tâm I bán kính R = a     2
b) Ta có MA MB = MA2 .  MA M . B = MA       
MA.(MA - MB ) = 0  MABA . = 0  MA ^ BA
Vậy tập hợp điểm M là đường thẳng vuông góc với đường thẳng AB tại A.    
Ví dụ 2: Cho tam giác ABC . Tìm tập hợp điểm M sao cho (MA + MB 2 + C 3 B )BC = 0
Lời giải (hình 2.4) A   
Gọi I là điểm xác định bởi IA + IB 2 = 0 M I    
Khi đó (MA + MB 2 + C 3 B )BC = 0 B      C M' I' é ê(MI IA) 2(MI IB )ù  + + + B . C = BC ú 2 3 ë Hình 2.4   û  MI B . C = BC 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 674
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Gọi M', I' lần lượt là hình chiếu của M, I lên đường thẳng BC  
 
 
Theo công thức hình chiếu ta có MI B
. C = M ' I ' B
. C do đó M I BC = BC 2 ' '.
 
Vì BC 2 > 0 nên M ' I ', BC cùng hướng suy ra
 
M I BC = BC 2  M I BC = BC 2 ' '. ' '.
M ' I ' = BC
Do I cố định nên I' cố định suy ra M' cố định.
Vậy tập hợp điểm M là đường thẳng đi qua M' và vuông góc với BC.
Ví dụ 3: Cho hình vuông ABCD cạnh a và số thực k cho trước.    
Tìm tập hợp điểm M sao cho MA M . C + MB MD . = k
Lời giải (hình 2.5) A B
Gọi I là tâm của hình vuông ABCD       Ta có :MA MC .
= (MI + IA)(MI + IC ) I     
= MI 2 + MI (IC + IA) + IAI.C   D C = MI 2 + IA I . C Hình 2.5    
Tương tự MB MD = MI 2 . + IB I . D        
Nên MA MC + MB MD = k MI 2 . . 2 + IB I . D + IA I . C = k kM
2 I 2 - IB2 - IA2 = k MI 2 = + IA2 2 kMI 2 = + a2 2 k k + a2  MI = + IA2 = 2 2 Nếu k < a
- 2 : Tập hợp điểm M là tập rỗng Nếu k = a
- 2 thì MI = 0  M º I suy ra tập hợp điểm M là điểm I k + a2 Nếu k > a - 2 thì MI = 2 k + a2
suy ra tập hợp điểm M là đường tròn tâm I bán kính R = 2
DẠNG 4: Biểu thức tọa độ của tích vô hướng.
1. Phương pháp giải.    Cho a = x ( ;y ), b = x
( ;y ) . Khi đó 1 1 2 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 675
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133  
+ Tích vô hướng hai vectơ là a b
. = x x + y y 1 2 1 2
+ Góc của hai vectơ được xác định bởi công thức     a b . x x + y y co a s( ,b) =   = 1 2 1 2 a b
x 2 + y2 x 2 + y2 1 1 2 2    
Chú ý: a ^ b a b
. = 0  x x + y y = 0 1 2 1 2
 Để xác định độ dài một vectơ đoạn thẳng ta sử dụng công thức   + Nếu a = x
( ;y) thì a = x 2 + y2 + Nếu A x ( ;y ), B x ( ;y ) thì AB =
x - x 2 + y - y 2 ( ) ( ) A A B B B A B A 2. Các ví dụ.
Ví dụ 1: Cho tam giác ABC có A( ; 1 2), B (- ; 2 6), C ( ; 9 8 ) .
a) Chứng minh tam giác ABC vuông tại A.
b) Tính góc B của tam giác ABC
c) Xác định hình chiếu của A lên cạnh BC Lời giải:     a) Ta có AB (- ; 3 4 ), AC ( ;
8 6)  AB.AC = - . 3 8 + . 4 6 = 0  
Do đó AB ^ AC hay tam giác ABC vuông tại A.   b) Ta có BC ( ; 11 2), BA( ; 3 -4 )   . 11 3 + . 2 -4 1
Suy ra cosB = cos(BC , BA) ( ) = = 11 + 2 3 + (-4 )2 2 2 2 5
c) Gọi H (x;y ) là hình chiếu của A lên BC.    Ta có AH (x - ;
1 y - 2), BH (x + ;
2 y - 6), BC (1 ; 1 2)  
AH ^ BC AH .BC = 0  1 (
1 x -1) + 2(y - 2) = 0 Hay x 11 + y 2 -15 = 0 (1)   x +2 y -6
Mặt khác BH ,BC cùng phương nên =  x 2 -1 y 1 +70 = 0 (2) 11 2 1 32
Từ (1) và (2) suy ra x = , y = 5 5 æ 1 32 ö
Vậy hình chiếu của A lên BC là H ç ; ÷ ç ÷ ç è 5 5 ø
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 676
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ví dụ 2: Cho hình thoi ABCD có tâm I (1;1), đỉnh A(3;2) và đỉnh B nằm trên trục hoành. Tìm
tọa độ các đỉnh còn lại của hình thoi. Lời giải:
Vì B nằm trên trục hoành nên giả sử B (0;y )
Vì I là tâm hình thoi ABCD nên I là trung điểm của AC và BD Suy ra C = ( x 2 - x ; y 2 - y = -1;0 , D = ( x 2 - x ; y 2 - y = 2;2 - y I B I B ) ( ) I A I A ) ( )
Do đó AB = AD AB2 = AD2  + (y - )2 = + y2 9 2 1  y = 3
Vậy B (0;3), C (-1;0), D (2;-1)
Ví dụ 3: Cho ba điểm A(3;4), B(2;1) và C -
( 1;-2). Tìm điểm M trên đường thẳng BC để góc  AMB = 0 45 Lời giải:   
Giả sử M (x;y ) suy ra MA(3 - x;4 - y ), MB (2 - x;1- y ), BC (- ; 3 -3)   Vì  AMB = 0 45 suy ra  cosAMB = cos(M ; A BC )   . MABC 2
-3(3 - x )- 3(4 -y )  cos 0
45 =    = MA . BC 2
(3 - x )2 + (4 -y )2 9 + 9
 ( - x )2 + ( -y )2 3 4 = x + y - 7 (*)  
Mặt khác M thuộc đường thẳng BC nên hai vectơ MB, BC cùng phương 2 - x 1- y Suy ra =
x = y + 1 thế vào (*) ta được -3 -3
( -y )2 + ( -y )2 = y -  y2 2 4 2 6 - y
6 + 8 = 0  y = 2 hoặc y = 4     1
+ Với y = 2  x = 3 , ta có MA( ; 0 2), MB (- ; 1 -1) 
 cosAMB = cos(M ; A MB ) = - 2 Khi đó  AMB = 0 135 (không thỏa mãn)     1
+ Với y = 4  x = 5 , MA(- ; 2 0), MB (- ; 3 -3) 
 cosAMB = cos(M ; A MB ) = 2 Khi đó  AMB = 0 45 Vậy M ( ;
5 4 ) . là điểm cần tìm.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 677
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ví dụ 4: Cho điểm A(2; 1). Lấy điểm B nằm trên trục hoành có hoành độ không âm sao và điểm C
trên trục tung có tung độ dương sao cho tam giác ABC vuông tại A . Tìm toạ độ B, C để tam giác
ABC có diện tích lớn nhất. Lời giải: Gọi B  ;0
b , C 0;c với b  0 , c  0 .  
Suy ra AB b  2;  1 , AC  2;  c   1
Theo giả thiết ta có tam giác ABC vuông tại A nên   .
AB AC  0  b  2 2
  1.c   1  0  c  2  b  5 1 1 Ta có 2 2 2 SA . B AC
(b  2) 1. 2  (c 1) ABC 2 2 2 2
 (b  2) 1  b  4b  5 5 Vì c  0 nên 2
b  5  0  0  b  2 5 Xét hàm số 2
y x  4x  5 với 0  x  2 Bảng biến thiên x 5 0 2 2 5 5 y 4 1 5
Suy ra giá trị lớn nhất của hàm số 2
y x  4x  5 với 0  x  là y  5 khi x  0 . Do đó diện tích 2
tam giác ABC lớn nhất khi và chỉ khi b  0 , suy ra c  5 .
Vậy B 0;0 , C 0;5 là điểm cần tìm.
C. CÂU HỎI TRẮC NGHIỆM
Vấn đề 1. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ   
Câu 1. Cho a và b là hai vectơ cùng hướng và đều khác vectơ 0 . Mệnh đề nào sau đây đúng?             A. .
a b = a . b . B. . a b = 0 . C. . a b = 1 - . D. .
a b = - a . b . Lời giải Chọn A
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 678
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133       Ta có .
a b = a . b .cos( , a b) .      
Do a và b là hai vectơ cùng hướng nên (a b) 0 , = 0 ¾¾ cos( ,ab)=1.     Vậy .
a b = a . b .         
Câu 2. Cho hai vectơ a và b khác 0 . Xác định góc a giữa hai vectơ a và b khi .
a b = - a . b . A. 0 a = 180 . B. 0 a = 0 . C. 0 a = 90 . D. 0 a = 45 . Lời giải Chọn A       Ta có .
a b = a . b .cos( , a b) .         Mà theo giả thiết .
a b = - a . b , suy ra
(a b)=- ¾¾(a b) 0 cos , 1 , = 180 .     Câu 3.  
Cho hai vectơ a và b thỏa mãn a = 3, b = 2 và a.b = 3
- . Xác định góc a giữa hai vectơ   a và . b A. 0 a = 30 . B. 0 a = 45 . C. 0 a = 60 . D. 0 a = 120 . Lời giải             Ta có - a b = a b
(a b)¾¾ (a b) a.b 3 1 . . .cos , cos , =  = = - ¾¾   ( ,ab) 0 = 120 . 3.2 2 a . b Chọn D        Câu 4.   
Cho hai vectơ a và b thỏa mãn a = b = 1 và hai vectơ 2
u = a -3b và v = a +b vuông 5  
góc với nhau. Xác định góc a giữa hai vectơ a và . b A. 0 a = 90 . B. 0 a = 180 . C. 0 a = 60 . D. 0 a = 45 . Lời giải Chọn B     æ  ö     
Ta có u ^ v ¾¾
u v =  çç a- b ç (÷÷a+b ÷ ) 2 2 2 2 13 . 0 3 = 0  a - ab-3b = 0 è5 ø 5 5    a = b 1 = ¾¾¾¾ ab = -1.       Suy ra (a b) a.b cos , =  = -1 ¾¾   ( ,ab) 0 = 180 . a . bCâu 5.
Cho hai vectơ a và b . Đẳng thức nào sau đây sai?   2  2   2  2 A.  1 æ   2 ö  1 æ   ö
a.b = ç a + b - a - b . ÷ 2 ç ÷ B.
a.b = ç a + b - a -b . ÷ ç ÷ 2 ç ÷ è ø 2 ç ÷ è ø
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 679
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133   2  2   2  2 C.  1 æ   ö  1 æ   ö
a.b = ç a + b - a -b . ÷ ç ÷ D.
a.b = ç a + b - a -b ÷ ç ÷. 2 ç ÷ è ø 4 ç ÷ è ø Lời giải Chọn C
Nhận thấy C và D chỉ khác nhau về hệ số 1 và 1 nên đáp án sai sẽ rơi vào C hoặc D. 2 4   2   2   2   2      2   2 Ta có æ ö
a + b - a -b = (a +b) -(a-b) 1 = 4ab ¾¾  .
a b = ç a + b - a-b ÷ ç ÷. 4 ç ÷ è ø   2   2               2  
· A đúng, vì a +b = (a +b) =(a +b).(a +b) 2 = . a a + . a b + . b a + .
b b = a + b + 2 . a b   2  2  1 æ   2 ö ¾¾
a.b = ç a +b - a - b . ÷ ç ÷ 2 ç ÷ è ø   2   2               2  
· B đúng, vì a-b = (a-b) =(a-b).(a-b) 2 = . a a - . a b- . b a + .
b b = a + b -2 . a b   2  2  1 æ  2  ö ¾¾
a.b = ç a + b - a -b . ÷ ç ÷ 2 ç ÷ è ø  
Câu 6. Cho tam giác đều ABC có cạnh bằng .
a Tính tích vô hướng . AB AC.   2   2   2   A. a 3 a a 2 .
AB AC = 2a . B. . AB AC = - . C. AB.AC = - . D. . AB AC = . 2 2 2 Lời giải Chọn D    
Xác định được góc (AB, AC) là góc A nên (AB AC) 0 , = 60 .    
Do đó AB AC = AB AC (AB AC) 2 a 0 . . . cos , = . a . a cos 60 = . 2  
Câu 7. Cho tam giác đều ABC có cạnh bằng .
a Tính tích vô hướng AB.BC.   2   2   2   A. a 3 a a 2 .
AB BC = a . B. . AB BC = . C. AB.BC = - . D. . AB BC = . 2 2 2 Lời giải Chọn C    
Xác định được góc (AB,BC) là góc ngoài của góc B nên (AB BC) 0 , = 120 .    
Do đó AB BC = AB BC (AB BC) 2 a 0 . . . cos , = . a . a cos120 = - . 2
Câu 8. Gọi G là trọng tâm tam giác đều ABC có cạnh bằng a . Mệnh đề nào sau đây là sai?     2     A. 1 1 a 1 2 . AB AC = a . B. 2
AC.CB = - a .
C. GA.GB = . D. 2 . AB AG = a . 2 2 6 2 Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 680
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn C
Dựa vào đáp án, ta có nhận xét sau:    
· Xác định được góc (AB, AC) là góc A nên (AB AC) 0 , = 60 .    
Do đó AB AC = AB AC (AB AC) 2 a 0 . . . cos , = . a . a cos 60 = ¾¾  A đúng. 2    
· Xác định được góc (AC,CB) là góc ngoài của góc C nên (AC CB) 0 , = 120 .    
Do đó AC CB = AC CB (AC CB) 2 a 0 . . .cos , = . a .c a os120 = - ¾¾  B đúng. 2    
· Xác định được góc (GA,GB) là góc 
AGB nên (GA GB) 0 , = 120 .    
Do đó GA GB = GA GB (GA GB) 2 a a a 0 . . .cos , = . .cos120 = - ¾¾  C sai. 3 3 6    
· Xác định được góc (AB, AG) là góc 
GAB nên (AB AG) 0 , = 30 .    
Do đó AB AG = AB AG (AB AG) 2 a a 0 . . .cos , = . a .cos 30 = ¾¾  D đúng. 3 2
Câu 9. Cho tam giác đều ABC có cạnh bằng a và chiều cao AH . Mệnh đề nào sau đây là sai?     2   2   A. a a AH .BC = 0. B. (AB HA) 0 , = 150 . C. . AB AC = .
D. AC.CB = . 2 2 Lời giải Chọn D    
Xác định được góc (AC,CB) là góc ngoài của góc A nên (AC CB) 0 , = 120 .    
Do đó AC CB = AC CB (AC CB) 2 a 0 . . .cos , = . a . a cos120 = - . 2  
Câu 10. Cho tam giác ABC vuông cân tại A và có AB = AC = .
a Tính AB.BC.     A. 2 . AB BC = a - . B. 2 .
AB BC = a . 2   2   C. a 2 a 2 . AB BC = - . D. . AB BC = . 2 2 Lời giải Chọn A    
Xác định được góc (AB,BC) là góc ngoài của góc B nên (AB BC) 0 , = 135 .    
Do đó AB BC = AB BC (AB BC) 0 2 . . .cos , = . a a 2.cos135 = a - .  
Câu 11. Cho tam giác ABC vuông tại A và có AB = ,c AC = .
b Tính BA.BC.     A. 2
BA.BC = b . B. 2
BA.BC = c .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 681
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133     C. 2 2
BA.BC = b + c . D. 2 2
BA.BC = b -c . Lời giải Chọn B     Ta có c
BA.BC = BA.BC.cos(BA, BC)  2 2 2
= BA.BC.cos B = . c b + c . = c . 2 2 b + c  
Cách khác. Tam giác ABC vuông tại A suy ra AB ^ AC  . AB AC = 0.        
Ta có BA BC = BA (BA + AC) 2 2 2 . .
= BA + BA.AC = AB = c .  
Câu 12. Cho tam giác ABC có AB = 2 cm, BC = 3 cm,
CA = 5 cm. Tính CA. . CB        
A. CA.CB = 13.
B. CA.CB = 15.
C. CA.CB = 17.
D. CA.CB = 19. Lời giải Chọn B
Ta có AB + BC = CA  ba điểm A, B, C thẳng hàng và B nằm giữa A, C.    
Khi đó CA CB = CA CB (CA CB) 0 . . .cos , = 3.5.cos 0 = 15.     Cách khác. Ta có 2 2
AB = AB = (CB -CA)2 2 2
= CB -2CBCA +CA  1 ¾¾ CBCA = ( 1 2 2 2
CB +CA - AB ) = ( 2 2 2 3 + 5 -2 ) = 15. 2 2   
Câu 13. Cho tam giác ABC có BC = , a CA = , b AB = .
c Tính P = (AB + AC).BC. 2 2 A. c + b 2 2
P = b -c . B. P = . 2 2 2 2 2 2 2 C. c + b + a c + b -a P = . D. P = . 3 2 Lời giải Chọn A       
Ta có P = (AB + AC).BC =(AB + AC).(BA + AC).      
= (AC + AB) (AC - AB) 2 2 2 2 2 2 .
= AC - AB = AC - AB = b -c .  
Câu 14. Cho tam giác ABC có BC = , a CA = , b AB = .
c Gọi M là trung điểm cạnh BC. Tính AM .BC. 2 2   2 2   A. b -c c + b AM .BC = .
B. AM .BC = . 2 2 2 2 2   2 2 2   C. c + b + a c + b -a AM .BC = .
D. AM .BC = . 3 2 Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 682
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn A   
Vì M là trung điểm của BC suy ra AB + AC = 2 AM .          Khi đó 1
AM BC = (AB + AC) 1 .
.BC = (AB + AC).(BA + AC) 2 2
1 ( ) (    - = + AC - AB) 1 = (AC - AB ) 2 2 2 2 1 b c AC AB . = ( 2 2 AC - AB ) = . 2 2 2 2
Câu 15. Cho ba điểm ,
O A, B không thẳng hàng. Điều kiện cần và đủ để tích vô hướng
(  
OA +OB).AB = 0 là
A. tam giác OAB đều.
B. tam giác OAB cân tại . O
C. tam giác OAB vuông tại . O
D. tam giác OAB vuông cân tại . O Lời giải Chọn B       
Ta có (OA +OB).AB = 0  (OA +OB).(OB-OA)= 0 2 2 2 2
OB -OA = 0  OB -OA = 0  OB = OA.
Câu 16. Cho M , N , P,
Q là bốn điểm tùy ý. Trong các hệ thức sau, hệ thức nào sai?           
A. MN (NP + PQ)= MN .NP + MN .PQ .
B. MP.MN = -MN .MP .    
   
C. MN .PQ = P . Q MN . D. ( - )( + ) 2 2 MN PQ MN
PQ = MN - PQ . Lời giải Chọn B
Đáp án A đúng theo tính chất phân phối.    
Đáp án B sai. Sửa lại cho đúng MP.MN = MN .MP .
Đáp án C đúng theo tính chất giao hoán.
Đáp án D đúng theo tính chất phân phối.  
Câu 17. Cho hình vuông ABCD cạnh . a Tính . AB AC.         A. 2 1 2
AB.AC = a . B. 2 AB.AC = a 2. C. 2 . AB AC = a . D. 2 . AB AC = a . 2 2 Lời giải Chọn A     Ta có ( 2 AB AC)  0 , = BAC = 45 nên 0 2 .
AB AC = AB.AC.cos 45 = . a a 2. = a . 2   
Câu 18. Cho hình vuông ABCD cạnh a . Tính P = AC.(CD +CA).
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 683
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. P = 1. - B. 2 P = 3a . C. 2 P = 3 - a . D. 2 P = 2a . Lời giải Chọn C
Từ giả thiết suy ra AC = a 2.       
  
Ta có P = AC (CD +CA) 2 .
= AC.CD + AC.CA = C
- A.CD - AC   = CA - CD
(CA CD)-AC = a - a -(a )2 2 0 2 . cos , 2. .cos 45 2 = -3a .     
Câu 19. Cho hình vuông ABCD cạnh .
a Tính P = (AB + AC).(BC + BD + BA). A. P = 2 2 . a B. 2 P = 2a . C. 2 P = a . D. 2 P = -2a . Lời giải Chọn D ìïBD = a 2 ï
Ta có ïí        
ïïBC + BD + BA =(BC +BA) .
+ BD = BD + BD = 2BD ïî         
Khi đó P = (AB + AC).2BD = 2AB.BD +2AC.BD = -2BA.BD +0  
= -2.BA.BD cos(BA, BD) 2 2 = -2. . a a 2. = -2a . 2  
Câu 20. Cho hình vuông ABCD cạnh a . Gọi E là điểm đối xứng của D qua C. Tính AE. . AB         A. 2
AE.AB = 2a . B. 2
AE.AB = 3a . C. 2
AE.AB = 5a . D. 2
AE.AB = 5a . Lời giải Chọn A
Ta có C là trung điểm của DE nên DE = 2 . a         
Khi đó AE.AB = (AD + DE).AB = AD.AB + DE.AB  0   = DE AB (DE AB) 0 2 . .cos ,
= DE.AB.cos 0 = 2a .
Câu 21. Cho hình vuông ABCD cạnh bằng 2. Điểm M nằm trên đoạn thẳng AC sao cho AC   AM =
. Gọi N là trung điểm của đoạn thẳng DC. Tính M . B MN . 4         A. . MB MN = -4. B. . MB MN = 0. C. . MB MN = 4. D. . MB MN = 16. Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 684
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn B  
Giả thiết không cho góc, ta phân tích các vectơ MB, MN theo các vectơ có giá vuông góc với nhau.     1   1   3  1 
· MB = AB - AM = AB - AC = AB - (AB + AD)= AB - AD. 4 4 4 4      1   1  1  
· MN = AN - AM = AD + DN - AC = AD + DC - (AB + AD) 4 2 4  1  1    
= AD + AB - (AB + AD) 3 1 = AD + A . B Suy ra: 2 4 4 4   æ  öæ  ö      
MB MN = çç AB - AD÷ç
÷ç AD + AB÷÷ = ç ÷ è øç ÷ è ø ( 2 2 3 1 3 1 1 .
3AB.AD + 3AB -3AD - AD.AB) 4 4 4 4 16 1 = ( 2 2
0 + 3a -3a -0) = 0 . 16  
Câu 22. Cho hình chữ nhật ABCD có AB = 8, 5 AD = . Tích . AB BD.         A. . AB BD = 62.
B. AB.BD = 64. C. . AB BD = -62. D. . AB BD = -64. Lời giải Chọn D  
Giả thiết không cho góc, ta phân tích các vectơ AB, BD theo các vectơ có giá vuông góc với nhau.           
Ta có AB BD = AB (BA + BC) 2 . .
= AB.BA + A .
B BC = -AB.AB + 0 = -AB = -64 .  
Câu 23. Cho hình thoi ABCD có AC = 8 và BD = 6. Tính . AB AC.         A. . AB AC = 24. B. . AB AC = 26. C. . AB AC = 28. D. . AB AC = 32. Lời giải Chọn D  
Gọi O = AC Ç BD , giả thiết không cho góc, ta phân tích các vectơ AB, AC theo các vectơ
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 685
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
có giá vuông góc với nhau. Ta có            .
AB AC = (AO +OB) 1 1 2 .AC = A . O AC +O .
B AC = AC.AC + 0 = AC = 32 . 2 2
Câu 24. Cho hình bình hành ABCD có AB = 8 cm, AD = 12 cm , góc 
ABC nhọn và diện tích bằng   2
54 cm . Tính cos(AB, BC).     A. (AB BC) 2 7 cos , = . B. (AB BC) 2 7 cos , = - . 16 16     C. (AB BC) 5 7 cos , = . D. (AB BC) 5 7 cos , = - . 16 16 Lời giải Chọn D Ta có 2 S = 2.S = 54  S
= 27 cm . Diện tích tam giác ABC là: ABCD AB D C A D BC 1  1  S
= .AB.BC.sin ABC = .AB.AD.sin ABC. AB D C 2 2  2.S 2.27 9  sin AB D C ABC = = = . AB AD 8.12 16  5 7 2  ¾¾
cos ABC = 1-sin ABC = (vì  ABC nhọn). 16  
Mặt khác góc giữa hai vectơ AB, BC là góc ngoài của góc  ABC   Suy ra æ ö cos(AB, BC) 5 7 0   = cos 1 ç 80 - ABC÷ ç ÷ = - cos ABC = - . ç ÷ è ø 16
Câu 25. Cho hình chữ nhật ABCD có AB = a và AD = a 2 . Gọi K là trung điểm của cạnh AD.   Tính BK.AC.        
A. BK.AC = 0. B. 2
BK .AC = a - 2. C. 2
BK .AC = a 2. D. 2
BK .AC = 2a . Lời giải Chọn A Ta có 2 2 2 2
AC = BD = AB + AD = 2a + a = a 3.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 686
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
ìï    1 
ïBK = BA + AK = BA + AD Ta có ïí 2
ïï  
ïAC = AB + AD ïî   æ 1 ö   ¾¾
BK .AC = ççBA + AD÷÷ ç ÷(AB + AD) è 2 ø         1 1 1
= BA.AB + BA.AD + AD.AB + AD.AD = a - + 0 + 0 + (a 2)2 2 = 0. 2 2 2   
Câu 26. Cho tam giác ABC . Tập hợp các điểm M thỏa mãn MA(MB + MC)= 0 là: A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn. Lời giải Chọn D   
Gọi I là trung điểm BC ¾¾
MB + MC = 2MI .         
Ta có MA(MB + MC)= 0  MA.2MI = 0  MA.MI = 0  MA ^ MI . ( ) * Biểu thức ( )
* chứng tỏ MA ^ MI hay M nhìn đoạn AI dưới một góc vuông nên tập hợp
các điểm M là đường tròn đường kính AI.    
Câu 27. Tìm tập các hợp điểm M thỏa mãn MB(MA + MB + MC)= 0 với A, B, C là ba đỉnh của tam giác. A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn. Lời giải Chọn D    
Gọi G là trọng tâm tam giác ABC ¾¾
MA + MB + MC = 3MG.          
Ta có MB(MA + MB + MC)= 0  MB.3MG = 0  MB.MG = 0  MB ^ MG. ( ) * Biểu thức ( )
* chứng tỏ MB ^ MG hay M nhìn đoạn BG dưới một góc vuông nên tập hợp
các điểm M là đường tròn đường kính BG.  
Câu 28. Cho tam giác ABC . Tập hợp các điểm M thỏa mãn MA.BC = 0 là: A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn. Lời giải Chọn B  
Ta có MA.BC = 0  MA ^ BC.
Vậy tập hợp các điểm M là đường thẳng đi qua A và vuông góc với BC.
Câu 29. Cho hai điểm A, B cố định có khoảng cách bằng a . Tập hợp các điểm N thỏa mãn   2
AN .AB = 2a là:
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 687
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn. Lời giải Chọn B  
Gọi C là điểm đối xứng của A qua B . Khi đó AC = 2 . AB    Suy ra 2 2 A .
B AC = 2AB = 2a .    
Kết hợp với giả thiết, ta có AN .AB = AB.AC
    
AB(AN - AC)= 0  AB.CN = 0  CN ^ AB .
Vậy tập hợp các điểm N là đường thẳng qua C và vuông góc với AB.  
Câu 30. Cho hai điểm A, B cố định và AB = 8. Tập hợp các điểm M thỏa mãn MA.MB = -16 là: A. một điểm. B. đường thẳng. C. đoạn thẳng. D. đường tròn. Lời giải Chọn A  
Gọi I là trung điểm của đoạn thẳng AB ¾¾  IA = I - . B       
  
Ta có MA.MB = (MI + IA)(MI + IB)=(MI + IA)(MI -IA) 2 2 2 AB 2 2 2
= MI - IA = MI - IA = MI - . 4 2 2 2 Theo giả thiết, ta có AB AB 8 2 2 MI - = 16 -  MI = -16 = -16 = 0 ¾¾  M º I . 4 4 4
Câu 31. Trong mặt phẳng tọa độ Oxy, cho ba điểm A(3;- ) 1 , B ( 2;10), C (
-4;2). Tính tích vô hướng   . AB AC.         A. . AB AC = 40. B. . AB AC = 40. - C. AB.AC = 26. D. . AB AC = 26. - Lời giải Chọn A   Ta có AB = ( 1; - 1 ) 1 , AC = ( 7 - ;3) .   Suy ra . AB AC = (- ) 1 .( 7 - )+11.3 = 40.
Câu 32. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(3;- )
1 và B (2;10). Tính tích vô hướng   . AO O . B         A. . AO OB = -4. B. . AO OB = 0. C. . AO OB = 4. D. . AO OB = 16. Lời giải Chọn C     Ta có AO = ( 3; - ) 1 , OB = ( 2;10). Suy ra .
AO OB = -3.2 +1.10 = 4.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 688
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133      
Câu 33. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a = 4i + 6 j và b = 3i -7 j. Tính tích vô hướng   . a . b         A. . a b = -30. B. . a b = 3. C. . a b = 30. D. . a b = 43. Lời giải Chọn A  
Từ giả thiết suy ra a = (4;6) và b = (3;-7).   Suy ra . a b = 4.3 + 6.( 7 - ) = -30.   
Câu 34. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a = ( 3; - 2) và b = ( 1; - 7
- ). Tìm tọa độ vectơ c    
biết .ca = 9 và .cb = -20.    
A. c = (-1;-3). B. c = ( 1; - 3). C. c = (1;-3). D. c = (1;3). Lời giải Chọn B
Gọi c = (x; y). ì  ïï .ca = 9 ì- ï 3x + 2 y = 9 ìïx = -1  Ta có ï ï ï í   í  í ¾¾ c = (-1;3). ï ï-x -7y = -20 ïy = 3 ï . c b = -20 ïî ïî ïî   
Câu 35. Trong mặt phẳng tọa độ Oxy, cho ba vectơ a = (1;2), b = (
4;3) và c = (2;3). Tính    P = . a (b+c).
A. P = 0. B. P = 18. C. P = 20. D. P = 28. Lời giải Chọn B     
Ta có b+c = (6;6). Suy ra P = .
a (b+c)=1.6 +2.6 =18.  
Câu 36. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a = (-1; )
1 và b = (2;0) . Tính cosin của góc 
giữa hai vectơ a và b.         A. (a b) 1 cos , = . B. (a b) 2 cos , = - . C. (a b) 1 cos , = - . D. (a b) 1 cos , = . 2 2 2 2 2 Lời giải Chọn B     Ta có ( - + a b) . a b 1.2 1.0 2 cos , =   = = - . a b (- )2 2 2 2 2 . 1 +1 . 2 + 0  
Câu 37. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a = (-2;- ) 1 và b = (4; 3 - ). Tính cosin của góc 
giữa hai vectơ a và b.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 689
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133         A. (a b) 5 cos , = - . B. (a b) 2 5 cos , = . C. (a b) 3 cos , = . D. (a b) 1 cos , = . 5 5 2 2 Lời giải Chọn A     . a b -2.4 + -1 . -3 Ta có (a b) ( ) ( ) 5 cos , =   = = - . a . b 4 +1. 16 + 9 5  
Câu 38. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a = (4;3) và b = (1;7). Tính góc a giữa hai 
vectơ a và b. A. O a = 90 . B. O a = 60 . C. O a = 45 . D. O a = 30 . Lời giải Chọn C       Ta có ( + a b) . a b 4.1 3.7 2 cos , =   = = ¾¾ ( ,ab) 0 = 45 . a . b 16 + 9. 1+ 49 2  
Câu 39. Trong mặt phẳng tọa độ Oxy, cho hai vectơ x = (1;2) và y = ( 3; - - )
1 . Tính góc a giữa hai  
vectơ x và y. A. O a = 45 . B. O a = 60 . C. O a = 90 . D. O a = 135 . Lời giải Chọn D     x.y 1. -3 + 2. -1   Ta có (x y) ( ) ( ) 2 cos , =   = = - ¾¾ (x, y) 0 = 135 . x . y 1+ 4. 9 +1 2  
Câu 40. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a = (2;5) và b = (3;-7) . Tính góc a giữa hai 
vectơ a và b. A. O a = 30 . B. O a = 45 . C. O a = 60 . D. O a = 135 . Lời giải Chọn D     . a b 2.3 + 5 -7   Ta có (a b) ( ) 2 cos , =   = = - ¾¾ ( ,ab) 0 = 135 . a . b 4 + 25. 9 + 49 2 
Câu 41. Trong mặt phẳng tọa độ Oxy, cho vectơ a = (9;3) . Vectơ nào sau đây không vuông góc  với vectơ a ?     A. v = 1;-3 . B. v = 2;-6 . C. v = 1;3 . D. v = -1;3 . 4 ( ) 3 ( ) 2 ( ) 1 ( ) Lời giải Chọn C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 690
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Kiểm tra tích vô hướng  
a.v , nếu đáp án nào cho kết quả khác 0 thì kết luận vectơ đó
không vuông góc với a.
Câu 42. Trong mặt phẳng tọa độ Oxy, cho ba điểm A(1;2), B( 1; - ) 1 và C (5;- ) 1 . Tính cosin của góc  
giữa hai vectơ AB và AC.     A. (AB AC) 1 cos , = - . B. (AB AC) 3 cos , = . 2 2     C. (AB AC) 2 cos , = - . D. (AB AC) 5 cos , = - . 5 5 Lời giải Chọn D   Ta có AB = (-2;- ) 1 và AC = (4;-3).     . AB AC -2.4 + -1 . -3 Suy ra (AB AC) ( ) ( ) 5 cos , =   = = - . AB . AC 4 +1. 16 + 9 5
Câu 43. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(6;0), B( 3; ) 1 và C (-1;- ) 1 . Tính số
đo góc B của tam giác đã cho. A. O 15 . B. O 60 . C. O 120 . D. O 135 . Lời giải Chọn D   Ta có BA = (3;- ) 1 và BC = ( 4; - 2 - ) . Suy ra:     BA BC - + - -   cos(BA, BC) . 3.( 4) ( ) 1 .( 2) 2  =   = = - ¾¾
B = (BA, BC) O = 135 . BA . BC 9 +1. 16 + 4 2
Câu 44. Trong mặt phẳng tọa độ Oxy, cho bốn điểm A(-8;0), B( 0;4), C (
2;0) và D (-3;-5). Khẳng
định nào sau đây là đúng? A. Hai góc  BAD và  BCD phụ nhau. B. Góc  BCD là góc nhọn.    
C. cos(AB, AD)= cos(CB,CD). D. Hai góc  BAD và  BCD bù nhau. Lời giải Chọn D     Ta có AB = (8;4),
AD = (5;-5), CB = ( -2;4), CD = ( 5 - ;5). ìï   ïï ( + - ï AB AD) 8.5 4.( 5) 1 cos , = = 2 2 2 2 ï 8 + 4 . 5 + 5 10 Suy ra ïí ï
(  - - + - ïï CB CD) ( 2).( 5) 4.( 5) 1 cos , = = - ï 2 2 2 2 ïïî 2 + 4 . 5 + 5 10     ¾¾  (AB AD)+ (CB CD)   0 cos , cos ,
= 0  BAD + BCD = 180 .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 691
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133       
Câu 45. Trong mặt phẳng tọa độ Oxy, cho hai vectơ 1
u = i -5 j và v = ki - 4 j Tìm k để vectơ u 2  vuông góc với . v A. k = 20. B. k = 20 - . C. k = -40. D. k = 40. Lời giải Chọn C  æ ö 
Từ giả thiết suy ra 1 u = çç ; 5÷ - ÷,v = (k;-4). ç è2 ÷ø   Yêu cầu bài toán: 1
u ^ v k +( 5 - )( 4 - ) = 0  k = -40 . 2       
Câu 46. Trong mặt phẳng tọa độ Oxy, cho hai vectơ 1
u = i -5 j và v = ki - 4 j. Tìm k để vectơ u 2 
và vectơ v có độ dài bằng nhau. A. 37 k = . B. 37 k = . C. 37 k =  . D. 5 k = . 4 2 2 8 Lời giải Chọn C  æ ö  Từ giả thiết suy ra 1 u = çç ; 5÷ - ÷,v = (k;-4). ç è2 ÷ø   Suy ra 1 1 u = + 25 = 101 và 2
v = k +16 . Do đó để 4 2   1 101 37 37 2 2 2
u = v k +16 = 101  k +16 =  k =  k =  . 2 4 4 2     
Câu 47. Trong mặt phẳng tọa độ Oxy, cho ba vectơ a = ( 2; - 3), b = ( 4; )
1 và c = ka + mb với    k, m Î .
 Biết rằng vectơ c vuông góc với vectơ (a +b) . Khẳng định nào sau đây đúng?
A. 2k = 2m.
B. 3k = 2m.
C. 2k +3m = 0.
D. 3k + 2m = 0. Lời giải Chọn C    c
ìïï = ka+mb =(-2k +4m;3k +m) Ta có ïí  . a ïï +b =(2;4) ïî      
Để c ^ (a+b)  c(a+b)= 0  2(-2k +4m)+4(3k +m)= 0  2k +3m = 0.   
Câu 48. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a = ( 2; - 3) và b = (4; )
1 . Tìm vectơ d biết     . a d = 4 và . b d = 2 - .  æ ö  æ ö  æ ö  æ ö A. 5 6 d = çç ; ÷.÷ = ç ÷ = ç ÷ = ç ÷ ç B. 5 6 d - ç ; ÷. C. 5 6 d ç ;- ÷. D. 5 6 d - ç ;- ÷. è7 7÷ø çè 7 7÷ø çè7 7÷ø çè 7 7÷ø
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 692
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn B ìï 5  ïx = - ì ï - ï + = Gọi 2x 3y 4 ï
d = (x; y). Từ giả thiết, ta có hệ ï ï 7 í  í . ï 4x + y = -2 ï 6 ïî ïïy = ïïî 7     
Câu 49. Trong mặt phẳng tọa độ Oxy, cho ba vectơ u = (4; ) 1 , v = (
1;4) và a = u + m.v với m Î .  
Tìm m để a vuông góc với trục hoành. A. m = 4. B. m = 4. - C. m = -2. D. m = 2. Lời giải Chọn B    
Ta có a = u + m.v = (4 +m;1+ 4m). Trục hoành có vectơ đơn vị là i = (1;0).   
Vectơ a vuông góc với trục hoành  .
a i = 0  4 + m = 0  m = 4 - .  
Câu 50. Trong mặt phẳng tọa độ Oxy, cho hai vectơ u = (4; )
1 và v = (1;4). Tìm m để vectơ      
a = m.u + v tạo với vectơ b = i + j một góc 0 45 . A. m = 4. B. 1 m = - . C. 1 m = - . D. 1 m = . 2 4 2 Lời giải Chọn C    a
ìïï = m.u +v =(4m +1;m +4) Ta có ïí   . b
ïï = i + j =(1; ) 1 ïî  
Yêu cầu bài toán  cos( ,ab) 2 0 = cos 45 = 2 (4m + ) 1 +(m + 4) 2 5(m + ) 1 2  =  = 2 (4m + )2 1 +(m + 4)2 2 2 + + 2 2 17m 16m 17 m ìï + ³ 5(m ) 1 0 1 2 1 17m 16m 17 ï  + = + +  í  m = - . 2 2 25
ï m +50m + 25 = 17m +16m +17 4 ïî
Câu 51. Trong mặt phẳng tọa độ Oxy, tính khoảng cách giữa hai điểm M (1;-2) và N (-3;4). A. MN = 4. B. MN = 6. C. MN = 3 6. D. MN = 2 13. Lời giải Chọn D 
Ta có MN = (-4;6) suy ra MN = (- )2 2 4 + 6 = 42 = 2 13.
Câu 52. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1;4), B( 3;2), C (
5;4) . Tính chu vi P của tam giác đã cho.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 693
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. P = 4 + 2 2. B. P = 4 + 4 2. C. P = 8 +8 2. D. P = 2 + 2 2. Lời giải Chọn B  ì ì ï
ïïAB =(2;-2) ïAB = 2 +(-2)2 2 = 2 2 ï ï ï ï ï Ta có ïíBC = (2;2) ï 2 2  íBC = 2 + 2 = 2 2 ï ï ï ï CA ïï ( 4;0) CA ï = - ï = (-4)2 2 + 0 = 4 ïî ïïî
Vậy chu vi P của tam giác ABC là P = AB + BC +CA = 4 + 4 2.     Câu 53.  
Trong hệ tọa độ (O;i ; j ) , cho vectơ 3 4
a = - i - j . Độ dài của vectơ a bằng 5 5 A. 1. B. 1. C. 6 . D. 7 . 5 5 5 Lời giải Chọn B 2 2     æ ö  æ ö æ ö Ta có 3 4 3 4 3 4
a = - i - j ¾¾  a = ç- ç ; ÷ - ÷  a = ç ÷ - ç ÷ +ç ÷ - ç ÷ = 1. 5 5 çè 5 5÷ø çè 5÷ø çè 5÷ø Câu 54.  
Trong mặt phẳng tọa độ Oxy, cho hai vectơ u = (3;4) và v = (-8;6) . Khẳng định nào sau đây đúng? A.     u = v .
B. u và v cùng phương. C.    
u vuông góc với v .
D. u = -v. Lời giải Chọn C Ta có    
u.v = 3.(-8)+ 4.6 = 0 suy ra u vuông góc với v . æ ö
Câu 55. Trong mặt phẳng tọa độ Oxy, cho các điểm A (1;2), B( 2 - ;-4), C ( 0; ) 1 và 3 D çç 1; ÷ - ÷ ç . Mệnh è 2÷ø đề nào sau đây đúng?    
A. AB cùng phương với CD.
B. AB = CD .    
C. AB ^ CD.
D. AB = CD. Lời giải Chọn C   æ ö  
Ta có AB = (-3;-6) và 1 CD = çç 1; ÷ - ÷ ç
suy ra AB CD = (- ) (- )+(- ) 1 . 3 . 1 6 . = 0. è 2÷ø 2  
Vậy AB vuông góc với CD.
Câu 56. Trong mặt phẳng tọa độ Oxy, cho bốn điểm A(7;-3), B( 8;4), C ( 1;5) và D (0; 2 - ). Khẳng
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 694
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
định nào sau đây đúng?  
A. AC ^ CB.
B. Tam giác ABC đều.
C. Tứ giác ABCD là hình vuông.
D. Tứ giác ABCD không nội tiếp đường tròn. Lời giải Chọn C ì ïïAB =( ) 2 2 1;7  AB = 1 +7 = 5 2 ïïï ïBC = (- ) 7;1  BC = 5 2 Ta có ïí ¾¾
AB = BC = CD = DA = 5 2. CD
ïï =(-1;-7)CD = 5 2 ïïï ïïDA =(7;- ) 1  DA = 5 2 ïî   Lại có . AB BC = 1( 7
- )+7.1 = 0 nên AB ^ BC .
Từ đó suy ra ABCD là hình vuông.
Câu 57. Trong mặt phẳng tọa độ Oxy, cho bốn điểm A(-1; ) 1 , B( 0;2), C ( 3; )
1 và D (0;-2). Khẳng
định nào sau đây là đúng?
A. Tứ giác ABCD là hình bình hành.
B. Tứ giác ABCD là hình thoi.
C. Tứ giác ABCD là hình thang cân.
D. Tứ giác ABCD không nội tiếp được đường tròn. Lời giải Chọn C ì ïïAB =(1; ) 1   Ta có ïí ¾¾
DC = 3AB . ïïDC =(3;3) ïî
Suy ra DC AB và DC = 3AB. ( ) 1 ì 2 2 ïïAD = 1 +3 = 10 Mặt khác ïí ¾¾
AD = BC. (2) ï 2 2 ïBC = 3 +1 = 10 ïî Từ ( )
1 và (2) , suy ra tứ giác ABCD là hình thang cân.
Câu 58. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(-1; ) 1 , B( 1;3) và C (1;- ) 1 . Khẳng
định nào sau đây là đúng?
A. Tam giác ABC đều.
B. Tam giác ABC có ba góc đều nhọn.
C. Tam giác ABC cân tại B .
D. Tam giác ABC vuông cân tại A . Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 695
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn D   
Ta có AB = (2;2), BC = (0;-4) và AC = (2;-2). ìï
Suy ra AB = AC = 2 2 ïí
. Vậy tam giác ABC vuông cân tại A. 2 2 2
ïïAB + AC = BC î
Câu 59. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(10;5), B( 3;2) và C (6; 5 - ). Khẳng
định nào sau đây là đúng?
A. Tam giác ABC đều. B.
Tam giác ABC vuông cân tại A .
C. Tam giác ABC vuông cân tại B .
D. Tam giác ABC có góc A tù. Lời giải Chọn C   
Ta có AB = (-7;-3), BC = (3;-7) và AC = (-4; 10 - ).   Suy ra .
AB BC = (-7).3 +(-3).(-7) = 0 và AB = BC.
Vậy tam giác ABC vuông cân tại B.
Câu 60. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(-2;- ) 1 , B( 1;- )
1 và C (-2;2) . Khẳng
định nào sau đây là đúng?
A. Tam giác ABC đều.
B. Tam giác ABC vuông cân tại A .
C. Tam giác ABC vuông tại B .
D. Tam giác ABC vuông cân tại C . Lời giải Chọn B   
Ta có AB = (3;0), BC = (-3;3) và AC = (0;3). ìïAB = AC = 3 Do đó ï 2 2 2 í
AB + AC = BC . ïïBC = 3 2 î
Vậy tam giác ABC vuông cân tại A.
Câu 61. Trong mặt phẳng tọa độ Oxy, cho hai điểm A( 2;
- 4) và B(8;4). Tìm tọa độ điểm C thuộc
trục hoành sao cho tam giác ABC vuông tại C. A. C(6;0).
B. C(0;0), C(6;0). C. C(0;0). D. C( 1; - 0). Lời giải Chọn B  CA ìïï =( 2 - - ; c 4)
Ta có C ÎOx nên C( ;0 c ) và ïí . CB ïï =(8- ;c4) ïî  
Tam giác ABC vuông tại C nên CA.CB = 0  ( 2
- -c).(8-c)+ 4.4 = 0
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 696
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
éc = 6  C(6;0) 2 c 6c 0 ê  - =  . ê c = 0  ê C (0;0) ë
Câu 62. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1;2) và B(-3; )
1 . Tìm tọa độ điểm C thuộc
trục tung sao cho tam giác ABC vuông tại A. A. C(0;6). B. C(5;0). C. C(3; ) 1 . D. C(0;-6). Lời giải Chọn A ì ïïAB =(-4;- ) 1
Ta có C ÎOy nên C(0;c) và ïí . ïïAC =(-1;c-2) ïî  
Tam giác ABC vuông tại A nên . AB AC = 0  (-4).(- ) 1 +(- )
1 (c-2) = 0  c = 6. Vậy C(0;6).
Câu 63. Trong mặt phẳng tọa độ Oxy, cho ba điểm A(–4;0), B(
–5;0) và C (3;0). Tìm điểm M    
thuộc trục hoành sao cho MA + MB + MC = 0.
A. M (–2;0). B. M (2;0). C. M (–4;0). D. M (–5;0). Lời giải Chọn A ì ïïMA =(-4-x;0) ïï   
Ta có M ÎOx nên M (x;0) và ïíMB = (-5- x;0) ¾¾
MA + MB + MC = (-6 -3x;0). ïïï ïMC = (3- x;0) ïî    
Do MA + MB + MC = 0 nên-6-3x = 0  x = -2 ¾¾  M (-2;0).
Câu 64. Trong mặt phẳng tọa độ Oxy, cho hai điểm M (–2;2) và N (1; )
1 . Tìm tọa độ điểm P thuộc
trục hoành sao cho ba điểm M , N , P thẳng hàng. A. P(0;4). B. P(0;–4).
C. P(–4;0). D. P (4;0). Lời giải Chọn D ì
ïïMP =(x +2;-2)
Ta có P ÎOx nên P (x;0) và ïí . ïïMN =(3;- ) 1 ïî Do x + 2 2 - M , N , P thẳng hàng nên =  x = 4 ¾¾  P (4;0). 3 -1
Câu 65. Trong mặt phẳng tọa độ Oxy, tìm điểm M thuộc trục hoành để khoảng cách từ đó đến điểm N ( 1; - 4) bằng 2 5. A. M (1;0).
B. M (1;0), M ( 3 - ;0).
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 697
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 C. M (3;0).
D. M (1;0), M ( 3;0). Lời giải Chọn B 
Ta có M ÎOx nên M (m;0) và MN = ( 1 - -m;4). 
Theo giả thiết: MN =  MN =  (- -m)2 2 2 5 2 5 1 + 4 = 2 5 ém =1 ¾¾  M 1;0 2 ( ) (1 m) 2 16 20 m 2m 3 0 ê  + + =  + - =  . ê êm = -3 ¾¾  M ( 3 - ;0) ë
Câu 66. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1;3) và B(4;2). Tìm tọa độ điểm C thuộc
trục hoành sao cho C cách đều hai điểm A và B. æ ö æ ö æ ö æ ö A. 5 C ç- ç ;0÷÷. ç ÷ ç ÷ ç ÷ ç B. 5 C ç ;0÷. C. 3 C - ç ;0÷. D. 3 C ç ;0÷. è 3 ÷ø çè3 ÷ø çè 5 ÷ø çè5 ÷ø Lời giải Chọn B ì
ïïAC =(x -1;-3)
Ta có C ÎOx nên C(x;0) và ïí .
ïïBC =(x -4;-2) ïî æ ö
Do CA = CB CA = CB  (x - )2
1 +(-3)2 = (x -4)2 +(-2)2 5 5 2 2  x = ¾¾ C çç ;0÷÷. 3 çè3 ÷ø
Câu 67. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2;2), B(5;-2). Tìm điểm M thuộc trục hoàng sao cho  0 AMB = 90 ? A. M ( ) 0;1 . B. M (6;0). C. M (1;6). D. M (0;6). Lời giải Chọn B ì
ïïAM =(m -2;-2)
Ta có M ÎOx nên M (m;0) và ïí . ïïBM =(m -5;2) ïî   Vì  0
AMB = 90 suy ra AM .BM = 0 nên (m -2)(m -5)+(-2).2 = 0. ém = 1 éM (1;0) 2
m -7m + 6 = 0  ê ê ¾¾  . êm = 6 ê ë êM (6;0) ë
Câu 68. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1;- )
1 và B(3;2). Tìm M thuộc trục tung sao cho 2 2
MA + MB nhỏ nhất. æ ö æ ö A. M ( ) 0;1 . B. M (0;- ) 1 . C. 1 M çç0; ÷÷. ç ÷ ç D. 1 M ç0;- ÷. è 2÷ø çè 2÷ø Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 698
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn C ì ïïMA =(1; 1 - -m)
Ta có M ÎOy nên M (0;m) và ïí . ïïMB =(3;2-m) ïî   Khi đó 2 2
MA + MB = MA + MB =
+(- -m)2 + +( -m)2 2 2 2 2 2 1 1 3 2 = 2m -2m +15. 2 æ 1ö 29 29 = 2ççm ÷ - ÷ + ³ ; "m Î . ç  è 2÷ø 2 2 Suy ra { 29 2 2 MA + MB } = . min 2 æ ö
Dấu '' = '' xảy ra khi và chỉ khi 1 1 m = ¾¾
M çç0; ÷÷. 2 çè 2÷ø
Câu 69. Trong mặt phẳng tọa độ Oxy, cho hình bình hành ABCD biết A(-2;0), B(2;5), C(6;2).
Tìm tọa độ điểm D. A. D(2;-3). B. D(2;3). C. D(-2;-3). D. D(-2;3). Lời giải Chọn A  
Gọi D(x; y). Ta có AD = (x +2; y) và BC = (4;-3). Vì ABCD là hình bình hành nên   ìïx + 2 = 4 ìïx = 2 AD BC ï ï = ¾¾ í  í ¾¾  D (2;-3). ïy = -3 ïy = 3 - ïî ïî
Câu 70. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1;3), B( 2 - ;4), C ( 5;3). Tìm tọa độ
trọng tâm G của tam giác đã cho. æ ö æ ö æ ö A. 10 G çç2; ÷÷. ç ÷ ç ÷ ç B. 8 10 G ç ;- ÷. C. G(2;5). D. 4 10 G ç ; ÷. è 3 ÷ø çè3 3 ÷ø çè3 3 ÷ø Lời giải Chọn D ìï 1-2 + 5 4 ïx = = ï G Tọa độ trọng tâm ï
G (x ; y là 3 3 í . G G ) ï 3 + 4 + 3 10 ïïy = = G ïïî 3 3
Câu 71. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(-4; ) 1 , B (
2;4), C (2;-2). Tìm tọa độ
tâm I của đường tròn ngoại tiếp tam giác đã cho. æ ö æ ö æ ö æ ö A. 1 I çç ;1÷÷. ç ÷ ç ÷ ç ÷ ç B. 1 I - ç ;1÷. C. 1 I 1; ç ÷. D. 1 I 1; ç - ÷. è4 ÷ø çè 4 ÷ø çè 4÷ø çè 4 ÷ø Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 699
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ì
ïïAI =(x +4; y - ) 1 ïï
Gọi I (x; y). Ta có ïíBI = (x -2; y -4). ïï CI
ïï =(x -2; y +2) ïî 2 2 ìï Do IA = IB
I là tâm đường tròn ngoại tiếp tam giác ABC nên IA IB IC ï = =  í 2 2 ïIB = IC ïî ( ì
ìïï x + )2 +(y- )2 =(x - )2 +(y - )2 ï ( ï
ìïï x + )2 =(x - )2 1 4 1 2 4 4 2 + 9 ïx = - ï  í  í  í 4 . (
ïï x -2)2 +(y -4)2 =(x -2)2 +(y +2)2 ïïy 1 ï = ïî î ïïy =1 î
Câu 72. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(-3;0), B(
3;0) và C (2;6). Gọi H ( ;
a b) là tọa độ trực tâm của tam giác đã cho. Tính a + 6 . b
A. a + 6b = 5.
B. a + 6b = 6.
C. a + 6b = 7.
D. a + 6b = 8. Lời giải Chọn C ì 
ïïAH =(a+3;b) & BC =(-1;6) Ta có ïí  . Từ giả thiết, ta có:
ïïBH =(a-3;b) & AC =(5;6) ïî ì  a ìï = ïïAH.BC = 0 ( ìï a + ) (- ) 2 3 . 1 + . b 6 = 0 ï ï ï ï í   í  í 5 ¾¾
a + 6b = 7. ï ( ï a-3).5 + . b 6 = 0 ï . 0 b BH AC ï = = ï ïî î ïïî 6
Câu 73. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(4;3), B(2;7) và C(-3;-8). Tìm toạ
độ chân đường cao A ' kẻ từ đỉnh A xuống cạnh BC. A. A '(1;-4). B. A '( 1 - ;4). C. A '(1;4). D. A '(4; ) 1 . Lời giải Chọn C ì
ïïAA ' =(x -4; y -3) ïï
Gọi A '(x; y). Ta có ïíBC = (-5; 1 - 5) . ïïï
ïBA ' = (x -2; y -7) ïî   ìïAA ' ^ BC
ìïïAA'.BC = 0 ( )1
Từ giả thiết, ta có ïí  ïí  .
ïB, A ', C thang hang ï ïî ïBA ' k BC (2) ïî = · ( )
1  -5(x - 4)-15(y -3) = 0  x + 3y = 13. x - y - · ( ) 2 7 2  =  3x - y = 1 - . -5 1 - 5 ìïx +3y = 13 ìïx = 1 Giải hệ ï ï í  í ¾¾  A '(1;4). 3 ï x - y = 1 - ïy = 4 ïî ïî
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 700
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 74. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(2;4), B( 3 - ; ) 1 , C (3;- ) 1 . Tìm tọa độ
chân đường cao A ' vẽ từ đỉnh A của tam giác đã cho. æ ö æ ö æ ö æ ö A. 3 1 A 'çç ; .÷÷ ç ÷ ç ÷ ç ÷ ç B. 3 1 A ' - ç ;- . ÷ C. 3 1 A ' - ç ; . ÷ D. 3 1 A 'ç ;- .÷ è5 5÷ø çè 5 5÷ø çè 5 5÷ø çè5 5÷ø Lời giải Chọn D ì
ïïAA ' =(x -2; y -4) ïï
Gọi A '(x; y). Ta có ïíBC = (6; 2 - ) . ïïï
ïBA ' = (x +3; y - ) 1 ïî
Vì A ' là chân đường cao vẽ từ đỉnh A của tam giác ABC nên ìïAA ' ^ BC ïí
ïB, C, A ' th aúng haøng ïî ì ì  ( ï ì
ìï x - ) +(y - ) (- ) ï 3 2 .6 4 . 2 = 0 ï ï ïï = ï ï x = AA '.BC 0 ï ï 6 ï x -2 y = 4 ï ï ï ï 5  í   í  + - í  í . x 3 y 1 ï ï ï = ï = ï 2 - x -6 y = 0 ï 1 BA ' k BC ï ï ïî ïïî 6 -2 ï ïy = - ï ï ïî ïî 5
Câu 75. Trong mặt phẳng tọa độ Oxy , cho ba điểm A(-3;-2), B(
3;6) và C (11;0). Tìm tọa độ điểm
D để tứ giác ABCD là hình vuông. A. D(5;-8). B. D(8;5). C. D(-5;8). D. D(-8;5). Lời giải Chọn A   Dễ dàng kiểm tra  0 BA.BC = 0 ¾¾  ABC = 90 .
Gọi I là tâm của hình vuông ABCD. Suy ra I là trung điểm của AC ¾¾  I (4;- ) 1 . ìïx +3 ï = 4 ï ì ï ïx = 5
Gọi D(x; y), do I cũng là trung điểm của ï 2 BD ï ¾¾ í  í  D (5;-8). ï y + 6 ïy = -8 ïï 1 ïî = - ïïî 2
Câu 76. Trong mặt phẳng tọa độ Oxy, cho hai điểm A (2;4) và B(1; )
1 . Tìm tọa độ điểm C sao cho
tam giác ABC vuông cân tại B. A. C (4;0). B. C(-2;2).
C. C (4;0), C( 2 - ;2). D. C(2;0). Lời giải Chọn C ì ïïBA =(1;3)
Gọi C(x; y) . Ta có ïí .
ïïBC =(x -1; y - ) 1 ïî
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 701
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ì  ï 1. ìï (x - ) 1 + 3.(y - ) 1 = 0 Tam giác ïBA.BC = 0
ABC vuông cân tại B  ï í  ï í 2 2 ïBA = BC 2 2 î 1 ïï +3 =(x - ) 1 +(y - ) 1 ïî ìïx = 4 -3y ìïy = 0 ìïy = 2 ï ï í í hay ï   í . 2 10 ï y -20y = 0 ïx = 4 ïx = -2 ïî ïî ïî
Câu 77. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có A(1;- )
1 và B(3;0). Tìm tọa độ
điểm D , biết D có tung độ âm. A. D(0;- ) 1 . B. D(2; 3 - ). C. D(2; 3 - ), D ( 0; ) 1 . D. D(-2;-3). Lời giải Chọn B ì ïïAB =(2; ) 1
Gọi C = (x; y). Ta có ïí .
ïïBC =(x -3; y) ïî ì  ï Vì ï ^
ABCD là hình vuông nên ta có AB BC í ïïAB = BC î 2
ìï (x -3)+1.y = 0 ìïy = 2(3- x)
ìïy = 2(3- x) ì ï ï ï ïx = 4 ï ï ìïx = 2  í  í  í  í hoặc ïí . (
ïï x -3)2 + y = 5 5 ï ï ïî ï (x -3)2 = 5 ( ïï x -3)2 2 = 1 ïy = 2 - = ï y 2 î ï ï î î ïî
Với C 4;-2 ta tính được đỉnh D 2;-3 : thỏa mãn. 1 ( ) 1 ( )
Với C 2;2 ta tính được đỉnh D 0;1 : không thỏa mãn. 2 ( ) 2 ( )
Câu 78. Trong mặt phẳng tọa độ Oxy, cho bốn điểm A(1;2), B( 1; - 3), C (-2;- ) 1 và D (0;-2). Mệnh đề nào sau đây đúng?
A. ABCD là hình vuông.
B. ABCD là hình chữ nhật.
C. ABCD là hình thoi.
D. ABCD là hình bình hành. Lời giải Chọn D ì ïïAB =(-2; ) 1 ï ì  ï ï ï ï = Ta có í ( AB DC BC 1; 4) ï = - - ¾¾ í  ¾¾
ABCD là hình hình hành. ï ï ï ïAB.BC = 2 - ¹ 0 ï ïî ïDC = (- ) 2;1 ïî
Câu 79. Trong mặt phẳng tọa độ Oxy, cho tam giác OAB với A(1;3) và B(4;2) . Tìm tọa độ điểm
E là chân đường phân giác trong góc O của tam giác OA . B æ ö æ ö A. 5 5 E = çç ; ÷÷. = ç ÷ ç B. 3 1 E ç ;- ÷. è2 2÷ø çè2 2÷ø C. E = ( 2 - + 3 2;4 + 2). D. E = (-2 +3 2;4 - 2).
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 702
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn D
Theo tính chất đường phân giác của tam giác ta có EA OA 2 = = . EB OB 2  
Vì E nằm giữa hai điểm A, B nên 2 EA = - EB. ( ) * 2 ì
ïïEA =(1-x;3- y)
Gọi E (x; y). Ta có ïí .
ïïEB =(4-x;2- y) ïî ìï 2 1
ïï -x = - (4-x) ï ìïx = -2 +3 2 Từ ( ) * , suy ra ï 2 ï í  í . ïï 2 ïï = - ï - y = - ï ( - y) y 4 2 3 2 ïî ïî 2
Câu 80. Trong mặt phẳng tọa độ Oxy, cho ba điểm A(2;0), B(
0;2) và C (0;7). Tìm tọa độ đỉnh thứ
tư D của hình thang cân ABCD. A. D(7;0).
B. D(7;0), D( 2;9).
C. D(0;7), D( 9;2). D. D(9;2). Lời giải Chọn B
Để tứ giác ABCD là hình thang cân, ta cần có một cặp cạnh đối song song không bằng
nhau và cặp cạnh còn lại có độ dài bằng nhau. Gọi D(x; y).     ìïAB CD Trường hợp 1: ïí
CD = k AB (với k ¹ -1 ) ïAB ¹ CD ïî ìï = - ( y ) ( k k) x 2k x 0; 7 2 ;2 ï  - - = -  í . ( ) 1 ïy = 2k +7 ïî ìï
ïAD = (x -2; y)  AD = (x -2)2 2 + y Ta có ïí ¾¾  AD = BC   (x -2)2 2 + y = 25. (2) ïïBC = ï (0;5) BC = 5 î ék = 1 - (loaïi) ê Từ ( ) 1 và (2) , ta có ( 2
- k -2)2 +(2k +7)2 = 25  ê ¾¾  D (7;0). 7 êk = - êë 2  ìïAD BC Trường hợp 2: ïí
. Làm tương tự ta được D = (2;9). ïAD ¹ BC ïî
Vậy D(7;0) hoặc D(2;9) .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 703
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 704
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
BÀI 3. CÁC HỆ THỨC LƯỢNG TRONG TAM GIÁC VÀ GIẢI TAM GIÁC
A. KIẾN THỨC CƠ BẢN CẦN NẮM 1. Định lí côsin
Cho tam giác ABC có BC = ,
a AC = b và AB = c . A Ta có 2 2 2 b
a = b + c -2b . c cos A; c 2 2 2
b = c + a -2c . a cos B; 2 2 2
c = a + b -2a . b cosC. B a C Hệ quả 2 2 2 2 2 2 2 2 2 b + c -a c + a -b a + b -c cos A = ; cos B = ; cosC = . 2bc 2ca 2ab 2. Định lí sin
Cho tam giác ABC có BC = ,
a AC = b , AB = c và R là bán kính đường tròn ng A oại tiếp. Ta có c b a b c = = = 2R I sin A sin B sin C B a C
3. Độ dài đường trung tuyến
Cho tam giác ABC có m , m , m lần lượt là các trung tuyến kẻ từ A, B, C . a b c Ta có A 2 2 2 b + c a 2 m = - ; a 2 4 ma b 2 2 2 c a + c b 2 m = - ; b 2 4 m m 2 2 2 b c a + b c 2 m = - . B a c C 2 4
4. Công thức tính diện tích tam giác
Cho tam giác ABC có
● h , h , h là độ dài đường cao lần lượt tương ứng với các cạnh BC, CA, AB ; a b c
● R là bán kính đường tròn ngoại tiếp tam giác;
● r là bán kính đường tròn nội tiếp tam giác; ● a + b + c p = là nửa chu vi tam giác; 2
● S là diện tích tam giác. Khi đó ta có: 1 1 1
S = ah = bh = ch 2 a 2 b 2 c 1 1 1
= bc sin A = ca sin B = absin C 2 2 2 abc = 4R = pr
= p( p-a)(p-b)(p-c).
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 705
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
B. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI.
Dạng 1: xác định các yếu tố trong tam giác. 1. Phương pháp.
 Sử dụng định lí côsin và định lí sin
 Sử dụng công thức xác định độ dài đường trung tuyến và mối liên hệ của các yếu tố trong
các công thức tính diện tích trong tam giác. 2. Các ví dụ. 3
Ví dụ 1: Cho tam giác ABC có AB = 4, AC = 5 và cos A = . 5
Tính cạnh BC, và độ dài đường cao kẻ từ A. Lời giải 3
Áp dụng định lí côsin ta có BC 2 = AB2 + AC 2 - AB 2 A . C.cos A = 2 4 + 2 5 - 2.4.5. = 29 5 Suy ra BC = 29 9 4 Vì 2 A + 2 sin
cos A = 1 nên sin A = 1 - 2 cos A = 1 - = 25 5 1 1 4
Theo công thức tính diện tích ta có S = AB A
. C.sin A = .4.5. = 8 (1) ABC 2 2 5 1 1 Mặt khác S = a h . = . 29 h . (2) ABC a a 2 2 1 16 29
Từ (1) và (2) suy ra . 29 h . = 8  h = a a 2 29 16 29
Vậy độ dài đường cao kẻ từ A là h = a 29
Ví dụ 2: Cho tam giác ABC nội tiếp đường tròn bán kính bằng 3, biết  0  A = B = 0 30 , 45 . Tính
độ dài trung tuyến kẻ từ A và bán kính đường tròn nội tiếp tam giác. Lời giải Ta có  0   C = - A - B = 0 - 0 - 0 = 0 180 180 30 45 105
Theo định lí sin ta có a = R A = 0 2 sin 2.3.sin 30 = 3 , 2 b = R 2 sin B = 0 2.3.sin 45 = 6. = 3 2 2 c = R C = 0 2 sin 2.3.sin105 » 5,796
2(b2 + c2 ) - a2 2(18 + 2 5, 796 ) - 9
Theo công thức đường trung tuyến ta có m2 = » = 23, 547 a 4 4
Theo công thức tính diện tích tam giác ta có bc A 0 1 sin 3 2.5, 796 sin 30 S
= pr = bc sin A r = » » 0,943 ABC 2 2p 3 + 3 2 + 5,796
Ví dụ 3: Cho tam giác ABC có M là trung điểm của BC. Biết  5 13
AB = 3, BC = 8, cos AMB = . 26
Tính độ dài cạnh AC và góc lớn nhất của tam giác ABC .
Lời giải (hình 2.7)
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 706
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A B M C Hình 2.7
BC = 8  BM = 4 . Đặt AM = x
Theo định lí côsin ta có 
AM 2 + BM 2 - AB2 cosAMB = AM 2 .AB x 2 5 13 + 16 - 9 Suy ra = 26 x 2.4. éx = ê 13  x2 13 - 20 x 13 + 91 = 0  êê 7 13 x = êë 13
Theo công thức tính đường trung tuyến ta có
2(AB2 + AC 2 )- BC 2 AM 2 = AB 2 .AC ( 2 + AC 2 )- 2 2 3 8
TH1: Nếu x = 13  13 =  AC = 7 . 4
Ta có BC > AC > AB  góc A lớn nhất. Theo định lí côsin ta có
AB2 + AC 2 - BC 2 9 + 49 - 64 1 cosA = = = - AB 2 .AC . 2 . 3 7 7 Suy ra A » 0 98 12 ' 7 13 49 ( 2 + AC 2 )- 2 2 3 8 397 TH2: Nếu x =  =  AC = 13 13 4 13
Ta có BC > AC > AB  góc A lớn nhất. Theo định lí côsin ta có 397 AB2 AC 2 BC 2 9 + - + - 64 53 cosA = = 13 = - AB 2 .AC 397 5161 2.3. 13 Suy ra A » 0 137 32'
Ví dụ 4: Cho hình chữ nhật ABCD biết AD = 1 . Giả sử E là trung điểm AB và thỏa mãn  1 sin BDE = . 3
Tính độ dài cạnh AB .
Lời giải (hình 2.8) Đặt AB = x
2 (x > 0)  AE = EB = x . A E B Vì góc  BDE nhọn nên  cos BDE > 0 suy ra  2 2 2 
cos BDE = 1 - sin BDE = 3
Theo định lí Pitago ta có: D C Hình 2.8
DE 2 = AD2 + AE 2 = + x2  DE = + x2 1 1
BD2 = DC 2 + BC 2 = x 2 +  BD = x 2 4 1 4 + 1
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 707
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Áp dụng định lí côsin trong tam giác BDE ta có 
DE 2 + DB2 - EB2 2 2 x 2 4 + 2 cos BDE =  = DE 2 DB . 3 2 (1 + x2 )( x2 4 + 1) 2 4 2 2
 4x - 4x + 1 = 0  2x = 1  x = (Do x > 0 ) 2
Vậy độ dài cạnh AB là 2
Dạng 2: giải tam giác. 1. Phương pháp.
 Giải tam giác là tính các cạnh và các góc của tam giác dựa trên một số điều kiện cho trước.
 Trong các bài toán giải tam giác người ta thường cho tam giác với ba yếu tố như sau : biết một cạnh và hai
góc kề cạnh đó; biết một góc và hai cạnh kề góc đó; biết ba cạnh.
Để tìm các yếu tố còn lại ta sử dụng định lí côsin và định lí sin ; định lí tổng ba góc trong một tam giác bằng 0
180 và trong một tam giác đối diện với góc lớn hơn thì có cạnh lớn hơn và ngược
lại đối diện với cạnh lớn hơn thì có góc lớn hơn. 2. Các ví dụ.
Ví dụ 1: Giải tam giác ABC biết b = 32; c = 45 và  A = 0 87 . Lời giải
Theo định lí côsin ta có
a2 = b2 + c2 - bc A = 2 + 2 - 0 2 .cos 32 4 2.32.4.sin 87 Suy ra a » 53, 8 Theo định lí sin ta có b sin A 0 32 sin 87  sin B = =  B » 0 36 a 53, 8 Suy ra  0   C = - A - B » 0 - 0 - 0 = 0 180 180 87 36 57
Ví dụ 2: Giải tam giác ABC biết  0  A = B = 0 60 , 40 và c = 14 . Lời giải Ta có  0   C = - A - B = 0 - 0 - 0 = 0 180 180 60 40 80 Theo định lí sin ta có c sin A 0 14.sin 60 a = =  a » 12, 3 sinC 0 sin 80 c sin B 0 14.sin 40 b = =  b » 9,1 sinC 0 sin 80
Ví dụ 3: Cho tam giác ABC biết a = 2 3, b = 2 2, c = 6 - 2 . Tính góc lớn nhất của tam giác. Lời giải
Theo giải thiết ta có c < b < a suy ra   
C < B < A do đó góc A là lớn nhất.
Theo định lí côsin ta có 2 2 b2 c2 a2 8 + ( 6 - 2) - + - 12 4 - 4 3 1 cos A = = = = - bc 2 2.2 2.( 6 - 2) 8 3 - 8 2 Suy ra  A = 0 120
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 708
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Vậy góc lớn nhất là góc A có số đo là 0 120 .
Dạng 3: Chứng Minh Đẳng Thức, Bất Đẳng Thức Liên Quan Đến Các Yếu Tố
Của Tam Giác, Tứ Giác.
1. Phương pháp giải.
 Để chứng minh đẳng thức ta sử dụng các hệ thức cơ bản để biến đổi vế này thành vế kia, hai
vế cùng bằng một vế hoặc biến đổi tương đương về một đẳng thức đúng.
 Để chứng minh bất đẳng thức ta sử dụng các hệ thức cơ bản, bất đẳng thức cạnh trong tam
giác và bất đẳng thức cổ điển (Cauchy, bunhiacôpxki,…) 2. Các ví dụ.
Ví dụ 1: Cho tam giác ABC thỏa mãn 2
sin A = sin B.sinC . Chứng minh rằng a) a2 = bc 1 b) cos A ³ 2 Lời giải a b c
a) Áp dụng định lí sin ta có sin A = , sin B = , sinC = R 2 R 2 R 2 æ a ö2 b c Suy ra 2 A = B C ç ÷  ç ÷ =  a2 sin sin .sin . = bc ç đpcm è R ÷ 2 ø R 2 R 2
b) Áp dụng định lí côsin và câu a) ta có
b2 + c2 - a2
b2 + c2 - bc b 2 c - bc 1 cos A = = ³ = đpcm bc 2 bc 2 bc 2 2
Ví dụ 2: Cho tam giác ABC , chứng minh rằng: A p(p - a) a) cos = 2 bc A B C
b) sin A + sin B + sinC = 4 cos cos cos 2 2 2
Lời giải (hình 2.9)
a) Trên tia đối của tia AC lấy D thỏa AD = AB = c suy ra tam giác BDA cân tại A và  1  BDA = A. 2
Áp dụng định lý hàm số Côsin cho AB D D , ta có: 2 2 2 
BD = AB + AD - AB 2 AD . .cos BAD = c2 2 - c2 0 2 .cos(180 - A) B
b2 + c2 - a2 Suy ra = c2
2 (1 + cos A) = c2 2 (1 + ) I bc 2 c c 4 = a
( + b + c) b ( + c - a) = p p ( - a) D b b A C cp(p - a) Hình 2.9 BD = 2 b
Gọi I là trung điểm của BD suy ra AI ^ BD .
Trong tam giác ADI vuông tại I, ta có ADI BD p(p - a) cos = cos ADI = = = . 2 AD c 2 bc
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 709
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A p(p - a) Vậy cos = . 2 bc a b c p
b) Từ định lý hàm số sin, ta có: sin A + sin B + sinC = + + = (1) R 2 R 2 R 2 R A p(p - a) B p(p - b) C p(p - c) Theo câu a) ta có cos = , tương tự thì cos = và cos = , 2 bc 2 ca 2 ab
kết hợp với công thức = ( - )( - )( - ) abc S p p a p b p c = R 4 A B C p p ( - a) p p
( - b) p(p - c) Suy ra 4 cos cos cos = 4 2 2 2 bc ca ab 4p 4pS p =
p(p - a) p
( - b)(p - c) = = (2) abc abc R A B C
Từ (1) và (2) suy ra sin A + sin B + sinC = 4 cos cos cos 2 2 2
Nhận xét: Từ câu a) và hệ thức lượng giác cơ bản ta suy ra được các công thức A p ( b - ) p ( -c) A p ( b - ) p ( -c) A p p ( -a) sin = ; tan = ; cot = 2 bc 2 p p ( -a) 2 p ( b - ) p ( c - )
Ví dụ 3: Cho tam giác ABC , chứng minh rằng:
b2 + c2 - a2 a) cotA = S 4
b) cot A + cot B + cotC ³ 3 Lời giải: 1
a) Áp dụng định lí côsin và công thức S = bc sin A ta có: 2 cosA
b2 +c2 -a2
b2 + c2 -a2 cot A = = = đpcm sin A b 2 c sin A S 4
c2 + a2 - b2
a2 + b2 - c2
b) Theo câu a) tương tự ta có cotB = , cotC = S 4 S 4
b2 +c2 -a2
c2 +a2 -b2
a2 +b2 -c2
Suy ra cotA + cotB + C cot = + + S 4 S 4 S 4
a2 + b2 + c2 = S 4 æ - - - ö3 æ ö3 3
Theo bất đẳng thức Cauchy ta có ( - )( - )( - ) p a b c p p a p b p c ç ÷ ç ÷ £ ç ÷ = ç ÷ ç ÷ è 3 ø ç ÷ è 3 ø 3 2 Mặt khác = ( - )( - )( - ) p p S p p a p b p
c S £ p = 27 3 3
(a + b + c)2
3(a2 + b2 + c2 )
a2 + b2 + c2 Ta có p2 = £ suy ra S £ 4 4 4 3
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 710
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
a2 + b2 + c2
Do đó cotA + cotB + cotC ³ = 3 đpcm.
a2 + b2 + c2 4. 4 3
Ví dụ 4: Cho tam giác ABC . Chứng minh rằng điều kiện cần và đủ để hai trung tuyến kẻ từ B và C
vuông góc với nhau là b2 +c2 = a2 5 . Lời giải:
Gọi G là trọng tâm của tam giác ABC .
Khi đó hai trung tuyến kẻ từ B và C vuông góc với nhau khi và chỉ khi tam giác GBC vuông tại G æ 2 ö2 æ 2 ö2 GB2 GC 2 BC 2 çç m ÷ ç  + = 
÷ + ç m ÷÷ = a2 (*) b ç ÷ c ÷ è 3 ø ç ÷ è 3 ø
Mặt khác theo công thức đường trung tuyến ta có a2 2( + c2) - b2 2 a2 ( + b2) - c2 m2 = , m2 = b c 4 4 4
Suy ra (*)  (m2 + m2 = a2 b c ) 9 é
4 2(a2 + c2 ) - b2
2(a2 + b2 ) - c2 ù ê ú  + = a2 2 2 2 2 2 2 2 ê ú  a 4
+ b + c = a 9
b + c = a 5 9 êë 4 4 úû (đpcm)
Ví dụ 5: Cho tứ giác ABCD có E, F là trung điểm các đường chéo. Chứng minh :
AB2 + BC 2 + CD2 + DA2 = AC 2 + BD2 + EF 2 4
Lời giải (hình 2.10)
Áp dụng công thức đường trung tuyến với tam giác ABC và ADC ta có: AC 2
AB2 + BC 2 = BE 2 2 + (1) B 2 A AC 2
CD2 + DA2 = DE 2 2 + (2) 2 E F Từ (1) và (2) suy ra
AB2 + BC 2 + CD2 + DA2 = (BE2 + DE2 ) + AC 2 2 D C Hình 2.10 BD2
Mặt khác EF là đường trung tuyến tam giác BDF nên BE 2 + DE 2 = EF 2 2 + 2
Suy ra AB2 + BC 2 + CD2 + DA2 = AC 2 + BD2 + EF 2 4
Dạng 4: Nhận Dạng Tam Giác 1. Phương pháp giải.
Sử dụng định lí côsin; sin; công thức đường trung tuyến; công thức tính diện tích tam giác để biến
đổi giả thiết về hệ thức liên hệ cạnh(hoặc góc) từ đó suy ra dạng của tam giác. 2. Các ví dụ.
Ví dụ 1: Cho tam giác ABC thoả mãn sinC = 2 sin B cos A. Chứng minh minh rằng tam giác ABC cân . Lời giải
Áp dụng định lí côsin và sin ta có: c
b b2 + c2 - a2
sinC = 2 sin B cos A  = 2. . R 2 R 2 b 2 c
c2 = b2 + c2 - a2  a = b
Suy ra tam giác ABC cân tại đỉnh C.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 711
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 sin B + sinC
Ví dụ 2: Cho tam giác ABC thoả mãn sin A =
. Chứng minh rằng tam giác ABC cos B + cosC vuông. Lời giải sin B + sinC Ta có: sin A =
 sin A(cos B + cosC ) = sin B + sinC cos B + cosC
a c2 + a2 - b2
a2 + b2 - c2 b + c  ( + ) = R 2 c 2 a a 2 b R 2
b c2 + a2 - b2 + c a2 + b2 - c2 = b c 2 + c b 2 ( ) ( ) 2 2
b3 + c3 + b c 2 + bc2 - a b 2 - a c 2 =
b + c b2 + c2 - a2 0 ( )( ) b ( + c) = 0
b2 + c2 = a2  A D BC vuông tại A.
Ví dụ 3: Nhận dạng tam giác ABC trong các trường hợp sau:
a) a.sin A +b sin B + c sinC = h + h + h a b c 2 cos A + 2 cos B 1 b) = 2 (cot A + 2 cot B) 2 sin A + 2 sin B 2 Lời giải 1 1
a) Áp dụng công thức diện tích ta có S = bc sin A = ah suy ra a 2 2 S 2 S 2 S 2 S 2 S 2 S 2
a.sin A +b sin B + c sinC = h + h + h a. +b. +c. = + + a b c bc ca ab a b c
a +b +c = ab +bc + ca  (a -b )2 + (b -c )2 + (c -a )2 2 2 2 = 0
a = b = c
Vậy tam giác ABC đều 2 cos A + 2 cos B 1 b) Ta có: = 2 (cot A + 2 cot B) 2 sin A + 2 sin B 2 2 cos A + 2 cos B + 2 sin A + 2 sin B 1  = 2 (cot A + 1 + 2 cot B + 1) 2 sin A + 2 sin B 2 2 1 1 1  = ( + )  2 (sin A + 2 sin B 2 ) = 2 4sin A 2 sin B 2 sin A + 2 sin B 2 2 sin A 2 sin B æ a ö2 æ b ö2  2 A = 2 sin sin B ç ÷ ç ÷  ç ÷ = ç ÷  a = b A D BC ç cân tại C. è R ÷ 2 ø çè R ÷ 2 ø
C. CÂU HỎI TRẮC NGHIỆM
Câu 1: Tam giác ABC có AB = 5, BC = 7, CA = 8 . Số đo góc A bằng: A. 30. B. 45. C. 60. D. 90. Lời giải Chọn C 2 2 2 2 2 2
Theo định lí hàm cosin, ta có 
AB + AC - BC 5 + 8 -7 1 cos A = = = . 2 . AB AC 2.5.8 2
Do đó, A = 60 .
Câu 2: Tam giác ABC có AB = 2, AC = 1 và A = 60 . Tính độ dài cạnh BC . A. BC =1. B. BC = 2. C. BC = 2. D. BC = 3. Lời giải Chọn D
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 712
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Theo định lí hàm cosin, ta có 2 2 2  2 2
BC = AB + AC -2 .
AB AC. cos A = 2 +1 -2.2.1.cos 60 = 3  BC = 3 .
Câu 3: Tam giác ABC có đoạn thẳng nối trung điểm của AB và BC bằng 3 , cạnh AB = 9 và 
ACB = 60 . Tính độ dài cạnh cạnh BC . A. BC = 3 +3 6. B. BC = 3 6 -3. C. BC = 3 7. D. 3 + 3 33 BC = . 2 Lời giải Chọn A
Gọi M , N lần lượt là trung điểm của AB, BC . A ¾¾
MN là đường trung bình của AB D C . M 1 ¾¾
MN = AC . Mà MN = 3 , suy ra AC = 6 . 2 B N C
Theo định lí hàm cosin, ta có 2 2 2 
AB = AC + BC -2.AC.BC.cos ACB 2 2 2
 9 = 6 + BC -2.6.BC.cos 60  BC = 3 +3 6
Câu 4: Tam giác ABC có AB = 2, AC = 3 và C = 45 . Tính độ dài cạnh BC . A. + - BC = 5. B. 6 2 BC = . C. 6 2 BC = . D. BC = 6. 2 2 Lời giải Chọn B
Theo định lí hàm cosin, ta có 
AB = AC + BC - AC BC C  ( )2 = ( )2 2 2 2 2 2. . . cos 2
3 + BC -2. 3.BC.cos 45 6 + 2  BC = . 2
Câu 5: Tam giác ABC có   B = 60 ,
C = 45 và AB = 5 . Tính độ dài cạnh AC . A. 5 6 AC = . B. AC = 5 3. C. AC = 5 2. D. AC = 10. 2 Lời giải Chọn A
Theo định lí hàm sin, ta có AB AC 5 AC 5 6 =  =  AC = .   sin C sin B sin 45 sin 60 2
Câu 6: Cho hình thoi ABCD cạnh bằng 1 cm và có 
BAD = 60 . Tính độ dài cạnh AC . A. AC = 3. B. AC = 2. C. AC = 2 3. D. AC = 2. Lời giải Chọn A B
Do ABCD là hình thoi, có  
BAD = 60  ABC = 120 .
Theo định lí hàm cosin, ta có A C 2 2 2 
AC = AB + BC -2.AB.BC.cos ABC 2 2
= 1 +1 -2.1.1.cos120 = 3  AC = 3 D
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 713
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 7: Tam giác ABC có AB = 4, BC = 6, AC = 2 7 . Điểm M thuộc đoạn BC sao cho
MC = 2MB . Tính độ dài cạnh AM . A. AM = 4 2. B. AM = 3. C. AM = 2 3. D. AM = 3 2. Lời giải Chọn C AB BC AC + - + - ( )2 2 2 2 2 2 4 6 2 7
Theo định lí hàm cosin, ta có : 1 cos B = = = . 2. . AB BC 2.4.6 2 A Do 1 MC = 2MB ¾¾
BM = BC = 2 . 3
Theo định lí hàm cosin, ta có 2 2 2 
AM = AB + BM -2.AB.BM . cos B 1 2 2
= 4 + 2 -2.4.2. = 12  AM = 2 3 B M C 2 Câu 8: - Tam giác ABC có 6 2 AB =
, BC = 3, CA = 2 . Gọi D là chân đường phân giác trong 2
góc A . Khi đó góc 
ADB bằng bao nhiêu độ? A. 45. B. 60. C. 75. D. 90. Lời giải Chọn C
Theo định lí hàm cosin, ta có: 2 2 2
AB + AC - BC 1 A  cos BAC = = - 2. . AB AC 2  
BAC = 120  BAD = 60 2 2 2 
AB + BC - AC 2  cos ABC = =  ABC = 45 B 2.AB.BC 2 D C Trong AB D D có    BAD = 60 ,
ABD = 45  ADB = 75 .
Câu 9: Tam giác ABC vuông tại A , đường cao AH = 32 cm . Hai cạnh AB và AC tỉ lệ với 3 và
4 . Cạnh nhỏ nhất của tam giác này có độ dài bằng bao nhiêu? A. 38 cm. B. 40 cm. C. 42 cm. D. 45 cm. Lời giải Chọn B
Do tam giác ABC vuông tại A , có tỉ lệ 2 cạnh góc vuông AB : AC là 3 : 4 nên AB là cạnh nhỏ nhất trong tam giác. Ta có AB 3 4 =  AC = AB . AC 4 3 Trong AB D
C có AH là đường cao 1 1 1 1 1 1 1 9  = + = +  = +  AB = 40 . 2 2 2 2 2 2 2 AH AB AC AB æ4 ö 2 32 AB 16AB çç AB ÷÷ çè3 ÷ø
Câu 10: Tam giác MPQ vuông tại P . Trên cạnh MQ lấy hai điểm E, F sao cho các góc   
MPE, EPF, FPQ bằng nhau. Đặt MP = ,
q PQ = m, PE = x, PF = y . Trong các hệ thức sau, hệ thức nào đúng?
A. ME = EF = F . Q B. 2 2 2
ME = q + x - x . q
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 714
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 C. 2 2 2
MF = q + y - y . q D. 2 2 2
MQ = q + m -2qm. Lời giải Chọn C P M E F Q  Ta có    MPQ  
MPE = EPF = FPQ =
= 30  MPF = EPQ = 60 . 3
Theo định lí hàm cosin, ta có 2 2 2 
ME = AM + AE -2.AM .AE.cos MAE 2 2 2 2
= q + x -2qx.cos30 = q + x -qx 3 2 2 2 
MF = AM + AF -2AM .AF.cos MAF 2 2 2 2
= q + y -2qy.cos 60 = q + y -qy 2 2 2 2 2
MQ = MP + PQ = q + m . Câu 11: Cho góc 
xOy = 30 . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho
AB = 1 . Độ dài lớn nhất của đoạn OB bằng: A. 3 . B. 3. C. 2 2. D. 2. 2 Lời giải Chọn D
Theo định lí hàm sin, ta có: y OB AB AB  1   =  OB = .sin OAB =
.sin OAB = 2 sin OAB B    sin 30 sin OAB sin AOB sin AOB
Do đó, độ dài OB lớn nhất khi và chỉ khi  
sin OAB = 1  OAB = 90 . x O A Khi đó OB = 2 . Câu 12: Cho góc 
xOy = 30 . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho
AB = 1 . Khi OB có độ dài lớn nhất thì độ dài của đoạn OA bằng: A. 3 . B. 3. C. 2 2. D. 2. 2 Lời giải Chọn B
Theo định lí hàm sin, ta có OB AB AB  1   =  OB = .sin OAB =
.sin OAB = 2 sin OAB y    sin 30 sin OAB sin AOB sin AOBB
Do đó, độ dài OB lớn nhất khi và chỉ khi  
sin OAB = 1  OAB = 90 . x O A Khi đó OB = 2 .
Tam giác OAB vuông tại 2 2 2 2
A OA = OB - AB = 2 -1 = 3 .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 715
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 13: Tam giác ABC có AB = ,c BC = ,
a CA = b . Các cạnh , a ,
b c liên hệ với nhau bởi đẳng thức ( 2 2 - )= ( 2 2 b b a
c a -c ) . Khi đó góc 
BAC bằng bao nhiêu độ? A. 30. B. 45. C. 60. D. 90. Lời giải Chọn C 2 2 2 2 2 2
Theo định lí hàm cosin, ta có 
AB + AC - BC c + b -a cos BAC = = . 2.AB.AC 2bc Mà b( 2 2
b -a ) = c( 2 2 a -c ) 3 2 2 3 2
b -a b = a c-c a - (b + c)+( 3 3 b + c ) = 0  (b + c)( 2 2 2
b + c -a -bc) 2 2 2
= 0  b + c -a -bc = 0 (do b > 0, c > 0 ) 2 2 2
b + c -a = bc 2 2 2 Khi đó,  b + c -a 1  cos BAC = =  BAC = 60 . 2bc 2
Câu 14: Tam giác ABC vuông tại A , có AB = ,c AC = b . Gọi  là độ dài đoạn phân giác trong a góc 
BAC . Tính  theo b và c . a 2(b + c) 2 (b + c) A. 2bc bc  = . B.  = . C. 2  = . D.  = . a b + c a bc a b + c a bc Lời giải Chọn A Ta có 2 2 2 2
BC = AB + AC = b + c . A
Do AD là phân giác trong của  BAC 2 2 AB c c c b + cBD = .DC = .DC = . BC = . AC b b + c b + c C B D
Theo định lí hàm cosin, ta có 2 c ( 2 2 b + c ) 2 2 2  2 2
BD = AB + AD -2.AB.AD. cos ABD  = c + AD -2 . c AD.cos 45 (b+c)2 æ 2 ç c ( 2 2 b + c )ö 3 ÷ 2bc 2 2 ç ÷ 2
AD -c 2.AD +çc -
÷ = 0  AD -c 2.AD + = 0 . ççè ( ÷ b + c)2 ÷ø (b+c)2 2bc bcAD = hay 2  = . b + c a b + c
Câu 15: Hai chiếc tàu thủy cùng xuất phát từ một vị trí A , đi thẳng theo hai hướng tạo với nhau góc 0
60 . Tàu B chạy với tốc độ 20 hải lí một giờ. Tàu C chạy với tốc độ 15 hải lí một
giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí? Kết quả gần nhất với số nào sau đây? A. 61 hải lí. B. 36 hải lí. C. 21 hải lí.
D. 18 hải lí. Lời giải Chọn B
Sau 2 giờ tàu B đi được 40 hải lí, tàu C đi được 30 hải lí. Vậy tam giác ABC có
AB = 40, AC = 30 và  0 A = 60 .
Áp dụng định lí côsin vào tam giác ABC, ta có
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 716
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2 2
a = b + c -2bc cos A 2 2 0
= 30 + 40 -2.30.40.cos 60 = 900 +1600 -1200 = 1300.
Vậy BC = 1300 » 36 (hải lí).
Sau 2 giờ, hai tàu cách nhau khoảng 36 hải lí.
Câu 16: Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông, người
ta chọn một điểm B cùng ở trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C . Ta
đo được khoảng cách AB = 40m ,  0 CAB = 45 và  0
CBA = 70 .Vậy sau khi đo đạc và tính toán
được khoảng cách AC gần nhất với giá trị nào sau đây? A. 53 m . B. 30 m . C. 41,5 m . D. 41 m . Lời giải Chọn C
Áp dụng định lí sin vào tam giác AC AB ABC, ta có = sin B sin C 0 Vì . AB sin b 40.sin 70
sin C = sin (a + b) nên AC = = » 41, 47 m. sin (a + b) 0 sin 115
Câu 17: Từ vị trí A người ta quan sát một cây cao (hình vẽ). Biết  0 AH = 4m, 20 HB = m, BAC = 45 .
Chiều cao của cây gần nhất với giá trị nào sau đây? A. 17,5m . B. 17m . C. 16,5m . D. 16m . Lời giải Chọn B Trong tam giác AH 4 1 AHB , ta có   0 tan ABH = = = ¾¾  ABH » 11 19 ' . BH 20 5 Suy ra  0  0
ABC = 90 - ABH = 78 41' . Suy ra  0   ACB = -(BAC + ABC) 0 180 = 56 19 ' .
Áp dụng định lý sin trong tam giác ABC , ta được  AB CB A .s B in BAC = ¾¾ CB = » 17m.    sin ACB sin BAC sin ACB
Câu 18: Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên
mặt đất sao cho ba điểm A, B và C thẳng hàng. Ta đo được AB = 24 m ,  0  0 CAD = 63 , 4 CBD = 8 .
Chiều cao h của tháp gần với giá trị nào sau đây? A. 18m . B. 18,5m . C. 60m . D. 60,5m . Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 717
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn D
Áp dụng định lí sin vào tam giác AD AB ABD, ta có = . sin b sin D Ta có 
a = D + b nên  0 0 0
D = a -b = 63 - 48 = 15 . 0 Do đó AB.sin b 24.sin 48 AD = = » 68, 91 m. sin (a -b) 0 sin 15
Trong tam giác vuông ACD, có h = CD = AD.sin a » 61, 4 m.
Câu 19: Trên nóc một tòa nhà có một cột ăng-ten cao 5 m . Từ vị trí quan sát A cao 7 m so với
mặt đất, có thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 0 50 và 0 40 so với phương nằm ngang.
Chiều cao của tòa nhà gần nhất với giá trị nào sau đây? A. 12m . B. 19m . C. 24m . D. 29m . Lời giải Chọn B Từ hình vẽ, suy ra  0 BAC = 10 và  0   ABD = -(BAD + ADB) 0 = -( 0 0 + ) 0 180 180 50 90 = 40 .
Áp dụng định lí sin trong tam giác ABC , ta có  0 BC AC
BC.sin ABC 5.sin 40 = ¾¾  AC = = » 18,5 m .    0 sin BAC sin ABC sin BAC sin 10 Trong tam giác vuông CD ADC , ta có   sin CAD = ¾¾
CD = AC.sin CAD = 11, 9 m. AC
Vậy CH = CD + DH =11,9 +7 = 18,9 m.
Câu 20: Xác định chiều cao của một tháp mà không cần lên đỉnh của A
tháp. Đặt kế giác thẳng đứng cách chân tháp một khoảng
CD = 60m , giả sử chiều cao của giác kế là OC = 1m .Quay thanh
giác kế sao cho khi ngắm theo thanh ta nhình thấy đỉnh A của
tháp. Đọc trên giác kế số đo của góc  0
AOB = 60 . Chiều cao của
ngọn tháp gần với giá trị nào sau đây: 60° B O A. 40m . B. 114m . 1m D 60m C C. 105m . D. 110m . Lời giải Chọn C Tam giác AB
OAB vuông tại B, có  0 tan AOB =
AB = tan 60 .OB = 60 3 m . OB
Vậy chiếu cao của ngọn tháp là h = AB +OC = (60 3 + ) 1 m.
Câu 21: Từ hai vị trí A và B của một tòa nhà, người ta
quan sát đỉnh C của ngọn núi. Biết rằng độ cao
AB = 70m , phương nhìn AC tạo với phương nằm ngang góc 0
30 , phương nhìn BC tạo với phương nằm ngang góc 0
15 30 ' .Ngọn núi đó có độ cao so
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 718
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
với mặt đất gần nhất với giá trị nào sau đây? A. 135m . B. 234m . C. 165m . D. 195m . Lời giải Chọn A
Từ giả thiết, ta suy ra tam giác ABC có  0  0
CAB = 60 , ABC = 105 30¢ và c = 70. Khi đó    0  0  
A + B +C =  C = -(A + B) 0 0 0 180 180 = 180 -165 30¢ = 14 30¢.
Theo định lí sin, ta có b c b 70 = hay = sin B sin C 0 0 sin 105 30¢ sin 14 30¢ 0 ¢ Do đó 70.sin 105 30 AC = b = » 269, 4 m. 0 sin 14 30¢
Gọi CH là khoảng cách từ C đến mặt đất. Tam giác vuông ACH có cạnh CH đối diện với góc 0 30 nên AC 269, 4 CH = =
= 134,7 m. Vậy ngọn núi cao khoảng 135 m. 2 2
Câu 22: Tam giác ABC có AB = 6cm, 8
AC = cm và BC = 10cm . Độ dài đường trung tuyến xuất
phát từ đỉnh A của tam giác bằng: A. 4cm . B. 3cm . C. 7cm . D. 5cm . Lời giải A Chọn D 2 2 2
Áp dụng công thức đường trung tuyến b + c a 2 m = - ta được: a 2 4 B C 2 2 2 2 2 2 M AC + AB BC 8 + 6 10 2 m = - = - = 25  m = 5. a 2 4 2 4 a
Câu 23: Tam giác ABC vuông tại A và có AB = AC = a . Tính độ dài đường trung tuyến BM của tam giác đã cho. A. a BM = 1,5 . a
B. BM = a 2.
C. BM = a 3. D. 5 BM = . 2 Lời giải B Chọn D AC a
M là trung điểm của AC AM = = . 2 2 Tam giác BA D
M vuông tại A C 2 A a a 5 M 2 2 2
BM = AB + AM = a + = . 4 2
Câu 24: Tam giác ABC có AB = 9 cm, AC = 12 cm và BC =15 cm. Tính độ dài đường trung tuyến
AM của tam giác đã cho. A. 15 AM = cm. B. AM =10 cm. C. AM = 9 cm. D. 13 AM = cm. 2 2 Lời giải Chọn A A 2 2 2
Áp dụng hệ thức đường trung tuyến b + c a 2 m = - ta được: a 2 4 2 2 2 2 2 2 AC + AB BC 12 + 9 15 225 2 B C m = - = - = . a M 2 4 2 4 4
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 719
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 15  m = . a 2
Câu 25: Tam giác ABC cân tại C , có AB = 9cm và 15 AC =
cm . Gọi D là điểm đối xứng của B 2
qua C . Tính độ dài cạnh AD. A. AD = 6 cm. B. AD = 9 cm. C. AD = 12 cm.
D. AD = 12 2 cm. Lời giải Chọn C
Ta có: D là điểm đối xứng của B qua C C là trung điểm của BD. D
AC là trung tuyến của tam giác D D AB.
BD = 2BC = 2AC = 15. C
Theo hệ thức trung tuyến ta có: 2 2 2 AB + AD BD 2 BD 2 AC = - 2 2 2  AD = 2AC + - AB B 2 4 2 A 2 2 æ15ö 15 2  AD = 2 2.ç ÷ ç ÷ + -9 = 144  AD = 12. ç è 2 ÷ø 2
Câu 26: Tam giác ABC có AB = 3, BC = 8 . Gọi M là trung điểm của BC . Biết  5 13 cos AMB = và 26
AM > 3 . Tính độ dài cạnh AC . A. AC = 13 .
B. AC = 7 . C. AC =13 . D. AC = 7 . Lời giải Chọn D Ta có: BC
M là trung điểm của BC BM = = 4. 2 2 2 2 Trong tam giác
AM + BM - AB ABM ta có:  cos AMB = 2AM .BM 2  2 2
AM -2AM .BM .cos AMB + BM - AB = 0. A
éAM = 13 > 3 (thoaû maõn) 20 13 ê 2 AM AM 7 0 ê  - + =  ê 7 13 13 êAM = < 3 (loaïi) êë 13  AM = 13. Ta có:  AMB và 
AMC là hai góc kề bù. B C M   5 13
 cos AMC = -cos AMB = - 26 Trong tam giác AM D C ta có: æç 5 13ö 2 2 2 
AC = AM +CM -2AM .CM .cos AMC = 13 +16 -2. 13.4. ÷ ç- ÷ ç ÷ = 49  AC = 7. çè 26 ÷ø
Câu 27: Tam giác ABC có trọng tâm G . Hai trung tuyến BM = 6 , CN = 9 và  0
BGC = 120 . Tính độ dài cạnh AB . A. AB = 11 . B. AB = 13 . C. AB = 2 11 . D. AB = 2 13 . Lời giải Chọn D
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 720
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Ta có:  BGC và 
BGN là hai góc kề bù mà  0  0
BGC = 120  BGN = 120 .
G là trọng tâm của tam giác AB D C ìï 2 ï = = A BG BM 4. ï ïï 3  í ï 1 M GN ïï = CN = 3. N ïïî 3 G Trong tam giác BGN D ta có: 2 2 2 B C
BN = GN + BG -2GN .BG.cos BGN 1 2
BN = 9 +16 -2.3.4. = 13  BN = 13. 2
N là trung điểm của AB AB = 2BN = 2 13.
Câu 28: Tam giác ABC có độ dài ba trung tuyến lần lượt là 9; 12; 15 . Diện tích của tam giác ABC bằng: A. 24 . B. 24 2 . C. 72 . D. 72 2 . Lời giải Chọn C 2 2 2 ìï b + c a 2 m ïï = - = 81 a ïï 2 4 2 ì ï a ìï = 292 ï ï a = 2 73 ï ï 2 2 2 ï + ï ï Ta có: a c b ï ï 2 ï 2 m í = - = 144  b í = 208 b ï  í = 4 13 b ï 2 4 ï ï ï ï 2 ï ï c ïï =10 2 2 2 c = 100 ïï a + b c ïî ï 2 ïî m ï = - = 225 ï c ï 2 4 ïî 2 2 2 Ta có: b + c -a 208 +100 -292 1 cos A = = = 2bc 2.4 13.10 5 13 2 æ 1 ö 18 13 2
sin A = 1-cos A = 1 ç ÷ -ç ÷ = . ç ÷ çè5 13÷ø 65 Diện tích tam giác 1 1 18 13 AB D C : S
= bcsin A = .4 13.10. = 72 AB D C 2 2 65
Câu 29: Cho tam giác ABC có AB = ,c BC = , a
CA = b . Nếu giữa , a ,
b c có liên hệ 2 2 2
b + c = 2a thì
độ dài đường trung tuyến xuất phát từ đỉnh A của tam giác tính theo a bằng: A. a 3 . B. a 3 .
C. 2a 3 . D. 3a 3 . 2 3 Lời giải Chọn A 2 2 2
Hệ thức trung tuyến xuất phát từ đỉnh b + c a A của tam giác: 2 m = - a 2 4 2 2 2 Mà: 2a a 3a a 3 2 2 2
b + c = 2a  2 m = - =  m = . a 2 4 4 a 2
Câu 30: Cho hình bình hành ABCD có AB = , a BC = , b
BD = m và AC = n . Trong các biểu thức
sau, biểu thức nào đúng: A. 2 2 m + n = ( 2 2 3 a + b ) . B. 2 2 m + n = ( 2 2 2 a + b ) .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 721
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 C. ( 2 2 + ) 2 2 2 m
n = a + b . D. ( 2 2 + ) 2 2 3 m
n = a + b . Lời giải Chọn B Gọi m
O là giao điểm của AC và BD. Ta có: 1 BO = BD = . 2 2
BO là trung tuyến của tam giác AB D C 2 2 2 BA + BC AC 2 2 2 2 m a + b n 2  BO = - 2 2  = -  m + n = ( 2 2 2 a + b ) . 2 4 4 2 4
Câu 31: Tam giác ABC có AB = ,c BC = , a
CA = b . Các cạnh , a ,
b c liên hệ với nhau bởi đẳng thức 2 2 2
a + b = 5c . Góc giữa hai trung tuyến AM và BN là góc nào? A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 . Lời giải Chọn D
Gọi G là trọng tâm tam giác AB D C. 2 2 2 2 2 2 2 4 ( 2 2 b + c ) 2 Ta có: AC + AB BC b + c a a 2 AM = - = - 2 2  AG = AM = - 2 4 2 4 9 9 9 2 2 2 2 2 2 2 2 2 BA + BC AC c + a b 1 c + a b 2 BN = - = - 2 2  GN = BN = - 2 4 2 4 9 18 36 Trong tam giác AG D N ta có: 2( 2 2 b + c ) 2 2 2 2 2 a c + a b b 2 2 2 - + - - 
AG +GN - AN 9 9 18 36 4 cos AGN = = 2.AG.GN 2( 2 2 b + c ) 2 2 2 2 a c + a b 2. - . - 9 9 18 36 2( 2 2 b + c ) 2 2 2 2 2 a c + a b b - + - - 2 2 2 9 9 18 36 4
10c -2(a +b ) = = = 0 2( 2 2 b + c ) 2 2 2 2 a c + a b 2( 2 2 b + c ) 2 2 2 2 a c + a b 2. - . - 36.2. - . - 9 9 18 36 9 9 18 36  0  AGN = 90 .
Câu 32: Tam giác ABC có ba đường trung tuyến m , m , m thỏa mãn 2 2 2
5m = m + m . Khi đó tam a b c a b c giác này là tam giác gì? A. Tam giác cân. B. Tam giác đều. C. Tam giác vuông.
D. Tam giác vuông cân. Lời giải Chọn C 2 2 2 ìï b + c a 2 m ïï = - a ïï 2 4 ïï 2 2 2 Ta có: ï a + c b ï 2 m í = - b ï 2 4 ïï 2 2 2 ïï a + b c 2 m ï = - ï c ï 2 4 ïî 2 2 2 2 2 2 2 2 2 æ + ö Mà: b c a ç ÷ a + c b a + b c 2 2 2
5m = m + m  5ç - ÷ = - + - a b c çè 2 4 ÷÷ø 2 4 2 4 2 2 2 2 2 2 2 2 2
 10b +10c -5a = 2a + 2c -b + 2a + 2b -c
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 722
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2 2
b + c = a  tam giác AB D C vuông.
Câu 33: Tam giác ABC có AB = ,c BC = , a
CA = b . Gọi m , m ,
m là độ dài ba đường trung tuyến, a b c
G trọng tâm. Xét các khẳng định sau: ( 3 1 I). 2 2 2
m + m + m =
a + b + c . (II) . 2 2 2
GA +GB +GC = ( 2 2 2
a + b + c ). a b c ( 2 2 2 ) 4 3
Trong các khẳng định đã cho có A. (I) đúng. B. Chỉ (II) đúng. C. Cả hai cùng sai.
D. Cả hai cùng đúng. Lời giải Chọn D 2 2 2 ìï b + c a 2 m ïï = - a ïï 2 4 ïï 2 2 2 Ta có: ï a + c b ï 3 2 m í = - 2 2 2
m + m + m =
a + b + c a b c ( 2 2 2 ) b ï 2 4 ï 4 ï 2 2 2 ïï a + b c 2 m ï = - ï c ï 2 4 ïî 4 4 3 1 2 2 2
GA +GB +GC = ( 2 2 2
m + m + m =
a + b + c =
a + b + c . a b c ) . ( 2 2 2 ) ( 2 2 2 ) 9 9 4 3
Câu 34: Tam giác ABC có BC =10 và  O
A = 30 . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC .
A. R = 5 . B. R =10 . C. 10 R = .
D. R =10 3 . 3 Lời giải Chọn B
Áp dụng định lí sin, ta có BC BC 10 = 2R R = = = 10.   0 sin BAC 2.sin A 2.sin 30
Câu 35: Tam giác ABC có AB = 3, 6 AC = và 
A = 60 . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC .
A. R = 3 . B. R = 3 3 . C. R = 3 . D. R = 6 . Lời giải Chọn A
Áp dụng định lí Cosin, ta có 2 2 2 
BC = AB + AC -2A . B AC.cos BAC 2 2 0 2 2 2 2
= 3 + 6 -2.3.6.cos 60 = 27  BC = 27  BC + AB = AC . Suy ra tam giác AC
ABC vuông tại B, do đó bán kính R = = 3. 2
Câu 36: Tam giác ABC có BC = 21cm, 17 CA = cm,
AB = 10cm . Tính bán kính R của đường tròn
ngoại tiếp tam giác ABC . A. 85 R = cm . B. 7 R = cm . 2 4 C. 85 R = cm . D. 7 R = cm . 8 2 Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 723
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn C Đặt
AB + BC +CA p =
= 24. Áp dụng công thức Hê – rông, ta có 2 S = p - - - = - - - = D
(p AB)(p BC)(p CA) ( ) ( ) ( ) 2 24. 24 21 . 24 17 . 24 10 84 cm . ABC
Vậy bán kính cần tìm là A . B BC.CA A . B BC.CA 21.17.10 85 S =  R = = = cm. AB D C 4R 4.S 4.84 8 AB D C
Câu 37: Tam giác đều cạnh a nội tiếp trong đường tròn bán kính R . Khi đó bán kính R bằng: A. a 3 a R = . B. 2 R = . 2 3 C. a 3 a R = . D. 3 R = . 3 4 Lời giải Chọn C
Xét tam giác ABC đều cạnh ,
a gọi M là trung điểm của BC. 2 Ta có 1 1 a 3 AM ^ BC suy ra 2 2 S
= .AM .BC = . AB - BM .BC = . AB D C 2 2 4 3
Vậy bán kính cần tính là A . B BC.CA A . B BC.CA a a 3 S =  R = = = . AB D C 2 4R 4.S AB D C a 3 3 4. 4 Câu 38: AB
Tam giác ABC vuông tại A có đường cao 12 AH = cm và 3
= . Tính bán kính R của 5 AC 4
đường tròn ngoại tiếp tam giác ABC .
A. R = 3 cm. B. R =1,5cm . C. R = 2cm . D. R = 3,5cm . Lời giải Chọn A
Tam giác ABC vuông tại A, có đường cao AH  2 A . B AC = AH ( ) * . 2 æ ö Mặt khác AB 3 3 3 12 8 3 =
AB = AC thế vào ( ) * , ta được 2 AC = ç ÷ ç ÷  AC = . AC 4 4 4 çè 5 ÷ø 5 Suy ra 3 8 3 6 3 2 2 AB = . =
BC = AB + AC = 2 3. 4 5 5
Vậy bán kính cần tìm là BC R = = 3 cm. 2
Câu 39: Cho tam giác ABC có AB = 3 3,
BC = 6 3 và CA = 9 . Gọi D là trung điểm BC . Tính bán
kính R của đường tròn ngoại tiếp tam giác ABD. A. 9 R = . B. R = 3 .
C. R = 3 3 . D. 9 R = . 6 2 Lời giải Chọn B 2 2 2 Vì AB + AC BC
D là trung điểm của BC  2 AD = - = 27  AD = 3 3. 2 4 Tam giác
ABD có AB = BD = DA = 3 3  tam giác ABD đều.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 724
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Nên có bán kính đường tròn ngoại tiếp là 3 3 R = AB = .3 3 = 3. 3 3
Câu 40: Tam giác nhọn ABC có AC = ,
b BC = a , BB ' là đường cao kẻ từ B và 
CBB ' = a . Bán kính
đường tròn ngoại tiếp R của tam giác ABC được tính theo ,
a b và a là: 2 2 2 2 A.
a + b -2abcos a
a + b + 2ab cos a R = . B. R = . 2 sin a 2 sin a 2 2 2 2 C.
a + b + 2ab cos a
a + b -2ab sin a R = . D. R = . 2 cos a 2 cosa Lời giải Chọn D ¢ Xét tam giác B C BB C
¢ vuông tại B ,¢ có  sin CBB¢ =  B C ¢ = . a sin . a BC Mà AB¢ + B C
¢ = AC AB¢ = b- . a sin a và 2 2 2 BB¢ = a .cos . a
Tam giác ABB¢ vuông tại B ,¢ có AB = BB¢ + AB¢ = (b-a a)2 2 2 2 2 .sin + a .cos a 2 2 2 2 2 2 2 = b -2a .
b sin a + a sin a + a cos a = a + b -2ab sin a.
Bán kính đường tròn ngoại tiếp cần tính là 2 2 AB
a + b -2ab sin a = 2R R = .  sin ACB 2 cosa
Câu 40: Tam giác ABC có  AB = 3, 6 AC = ,
BAC = 60 . Tính diện tích tam giác ABC . A. S = 9 3 . B. 9 3 S = . AB D C AB D C 2 C. S = 9 . D. 9 S = . AB D C AB D C 2 Lời giải Chọn B Ta có 1  1 9 3 0 S
= .AB.AC.sin A = .3.6.sin 60 = . AB D C 2 2 2
Câu 41: Tam giác ABC có   AC = 4, 30 BAC = , 
ACB = 75 . Tính diện tích tam giác ABC . A. S = 8 . B. S = 4 3 . AB D C AB D C C. S = 4 . D. S = 8 3 . AB D C AB D C Lời giải Chọn C Ta có  0  
ABC = 180 -(BAC + ACB)  75 =  = ACB .
Suy ra tam giác ABC cân tại A nên AB = AC = 4 . Diện tích tam giác 1 ABC là  S = A .
B AC sin BAC = 4. AB D C 2
Câu 42: Tam giác ABC có a = 21, 17 b = ,
c = 10 . Diện tích của tam giác ABC bằng: A. S = 16 . B. S = 48 . AB D C AB D C C. S = 24 . D. S = 84 . AB D C AB D C Lời giải Chọn D
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 725
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Ta có 21+17 +10 p = = 24 . 2
Do đó S = p(p-a)(p-b)(p-c) = 24(24 - ) 21 (24 -17)(24 -10) = 84 .
Câu 43: Tam giác ABC có  AB = 3, 6 AC = ,
BAC = 60 . Tính độ dài đường cao h của tam giác. a A. h = 3 3 . B. h = 3 . C. h = 3 . D. 3 h = . a a a a 2 Lời giải Chọn C
Áp dụng định lý hàm số côsin, ta có 2 2 2
BC = AB + AC -2 .
AB AC cos A = 27 ¾¾  BC = 3 3 . Ta có 1  1 9 3 0 S
= .AB.AC.sin A = .3.6.sin 60 = . AB D C 2 2 2 Lại có 1 2S S = .BC.h ¾¾ h = = 3. AB D C 2 a a BC
Câu 44: Tam giác ABC có  AC = 4, 6
ACB = 0 . Tính độ dài đường cao h uất phát từ đỉnh A của tam giác. A. h = 2 3 . B. h = 4 3 . C. h = 2 . D. h = 4 . Lời giải Chọn A
Gọi H là chân đường cao xuất phát từ đỉnh A . Tam giác vuông AH AHC , có   3 sin ACH = ¾¾
AH = AC.sin ACH = 4. = 2 3. AC 2
Câu 45: Tam giác ABC có a = 21, 17 b = ,
c = 10 . Gọi B ' là hình chiếu vuông góc của B trên cạnh
AC . Tính BB ' . A. BB ' = 8 . B. 84 BB ' = . 5 C. 168 BB ' = . D. 84 BB ' = . 17 17 Lời giải Chọn C Ta có 21+17 +10 p = = 24 . 2
Suy ra S = p(p-a)(p-b)(p-c) = 24(24 - ) 21 (24 -17)(24 -10) = 84 . Lại có 1 1 168 S = .
b BB '¬¾84 = .17.BB ' ¾¾  BB ' = . 2 2 17
Câu 46: Tam giác ABC có AB = 8 cm, AC = 18 cm và có diện tích bằng 64 2
cm . Giá trị sin A ằng: A. 3 sin A = . B. 3 sin A = . 2 8 C. 4 sin A = . D. 8 sin A = . 5 9 Lời giải Chọn D
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 726
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Ta có 1  1 8 S = .A .
B AC. sin BAC  64 = .8.18.sin A  sin A = . AB D C 2 2 9
Câu 47: Hình bình hành ABCD có AB = , a BC = a 2 và  0
BAD = 45 . Khi đó hình bình hành có diện tích bằng: A. 2 2a . B. 2 a 2 . C. 2 a . D. 2 a 3 . Lời giải Chọn C 2 Diện tích tam giác 1 1 a ABD là  0 S = .A .
B AD.sin BAD = . . a a 2.sin 45 = . AB D D 2 2 2 2
Vậy diện tích hình bình hành a ABCD là 2 S = 2.S = 2. = a . ABCD AB D D 2
Câu 48: Tam giác ABC vuông tại A có AB = AC = 30 cm. Hai đường trung tuyến BF và CE cắt
nhau tại G . Diện tích tam giác GFC bằng: A. 2 50 cm . B. 2 50 2 cm . C. 2 75 cm . D. 2 15 105 cm . Lời giải Chọn C Vì 1
F là trung điểm của AC FC = AC = 15 cm. 2
Đường thẳng BF cắt CE tại G suy ra G là trọng tâm tam giác ABC.
d (B;(AC)) Khi đó BF =
=  d (G (AC)) 1 AB 3 ;
= d (B;(AC)) = = d ( 10 cm.
G;(AC)) GF 3 3 Vậy diện tích tam giác 1 1 GFC là: S = .d G AC FC = = cm GF D C ( ;( )) 2 . .10.15 75 . 2 2
Câu 49: Tam giác đều nội tiếp đường tròn bán kính R = 4 cm có diện tích bằng: A. 2 13 cm B. 2 13 2 cm C. 2 12 3 cm D. 2 15 cm . Lời giải Chọn C
Xét tam giác ABC đều, có độ dài cạnh bằng . a
Theo định lí sin, ta có BC a 0 = 2R
= 2.4  a = 8.sin 60 = 4 3.  0 sin BAC sin 60
Vậy diện tích cần tính là 1  1 S
= .AB.AC.sin BAC = . = cm AB D C (4 3)2 0 2 .sin 60 12 3 . 2 2
Câu 50: Tam giác ABC có BC = 2 3,
AC = 2AB và độ dài đường cao AH = 2 . Tính độ dài cạnh AB . A. AB = 2 . B. 2 3 AB = . 3
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 727
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
C. AB = 2 hoặc 2 21 AB =
. D. AB = 2 hoặc 2 3 AB = 3 3 Lời giải Chọn C Ta có
AB + BC +CA 2 3 + 3AB p = = . 2 2 æ öæ öæ öæ ö Suy ra
ç3AB + 2 3 ÷ç3AB -2 3 ÷ç2 3 - AB ÷ç2 3 + AB S ÷ = ç ÷ç ÷ç ÷ç ÷ ç ÷ . ç ÷ç ÷ ÷ è øç ÷ç ÷ ÷ è øç ÷ç ÷ 2 2 è 2 ÷øçè 2 ÷ø Lại có 1
S = BC.AH = 2 3. 2 æ öæ öæ öæ ö Từ đó ta có
ç3AB + 2 3 ÷ç3AB -2 3 ÷ç2 3 - AB ÷ç2 3 + AB 2 3 ÷ = ç ÷ç ÷ç ÷ç ÷ ç ÷ ç ÷ç ÷ ÷ è øç ÷ç ÷ ÷ è øç ÷ç ÷ 2 2 è 2 ÷øçè 2 ÷ø ( é 2 = AB - )( 2 - AB ) AB 2 9 12 12 ê ¬¾12 = ¬¾ ê . 2 21 16 êAB = êë 3
Câu 51: Tam giác ABC có BC = , a CA = , b
AB = c và có diện tích S . Nếu tăng cạnh BC lên 2 lần
đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích
của tam giác mới được tạo nên bằng:
A. 2S . B. 3S . C. 4S . D. 6S . Lời giải Chọn D Diện tích tam giác 1 1 ABC ban đầu là  
S = .AC.BC.sin ACB = .a . b sin ACB. 2 2
Khi tăng cạnh BC lên 2 lần và cạnh AC lên 3 lần thì diện tích tam giác ABC lúc này là 1 S = . AC BC ACB = AC BC
ACB = S AB D C (3 ).(2 )  1  . sin 6. . . . sin 6 . 2 2
Câu 52: Tam giác ABC có BC = a và CA = b . Tam giác ABC có diện tích lớn nhất khi góc C bằng: A. 0 60 . B. 0 90 . C. 0 150 . D. 0 120 . Lời giải Chọn B Diện tích tam giác 1 1 ABC là   S
= .AC.BC.sin ACB = .a . b sin AC . B AB D C 2 2 Vì ab , a b không đổi và 
sin ACB £1, "C nên suy ra S £ . AB D C 2
Dấu " = " xảy ra khi và chỉ khi   0
sin ACB = 1  ACB = 90 .
Vậy giá trị lớn nhất của diện tích tam giác ab ABC là S = . 2
Câu 53: Tam giác ABC có hai đường trung tuyến BM , CN vuông góc với nhau và có BC = 3 , góc  0
BAC = 30 . Tính diện tích tam giác ABC . A. S = 3 3 . B. S = 6 3 . C. S = 9 3 . D. 3 3 S = . AB D C AB D C AB D C AB D C 2 Lời giải Chọn C Vì 2 2 2 BM ^ CN ¾¾
5a = b + c . (Áp dụng hệ quả đã có trước)
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 728
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 Trong tam giác 2a ABC , ta có 2 2 2 2
a = b + c -2b .
c cos A = 5a -2bc cos A ¾¾ bc = . cos A 2 Khi đó 1 1 2a 2
S = bc sin A = .
. sin A = a tan A = 3 3 . 2 2 cos A
Câu 54: Tam giác ABC có AB = 5, 8 AC = và  0
BAC = 60 . Tính bán kính r của đường tròn nội tiếp tam giác đã cho. A. r = 1 . B. r = 2 . C. r = 3 .
D. r = 2 3 . Lời giải Chọn C
Áp dụng định lý hàm số côsin, ta có 2 2 2
BC = AB + AC -2AB.AC cos A = 49 ¾¾  BC = 7 . Diện tích 1 1 3 S = A .
B AC. sin A = .5.8. = 10 3 . 2 2 2 Lại có S 2S S = . p r ¾¾ r = = = 3 . p
AB + BC +CA
Câu 55: Tam giác ABC có a = 21, 17 b = ,
c = 10 . Tính bán kính r của đường tròn nội tiếp tam giác đã cho. A. r =16 . B. r = 7 . C. 7 r = .
D. r = 8 . 2 Lời giải Chọn C Ta có 21+ 17 + 10 p = = 24 . 2 Suy ra S = 24(24- ) 21 (24 -17)(24 -10) = 84 . Lại có = ¾¾  = S S p r r = 84 = 7 . . p 24 2
Câu 56: Tính bán kính r của đường tròn nội tiếp tam giác đều cạnh a . A. a 3 a a a r = . B. 2 r = . C. 3 r = . D. 5 r = . 4 5 6 7 Lời giải Chọn C 2
Diện tích tam giác đều cạnh a 3 a bằng: S = . 4 2 a 3 Lại có S a 3 4 S = pr ¾¾ r = = = . p 3a 6 2
Câu 57: Tam giác ABC vuông tại A có AB = 6 cm, BC =10 cm. Tính bán kính r của đường tròn
nội tiếp tam giác đã cho. A. r = 1 cm. B. r = 2 cm. C. r = 2 cm.
D. r = 3 cm. Lời giải Chọn C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 729
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Dùng Pitago tính được
AB + BC +CA
AC = 8 , suy ra p = = 12 . 2
Diện tích tam giác vuông 1 S
S = AB.AC = 24 .Lại có S = . p r ¾¾ r = = 2 cm. 2 p
Câu 58: Tam giác ABC vuông cân tại A , có AB = a . Tính bán kính r của đường tròn nội tiếp tam giác đã cho. A. a a a a r = . B. r = . C. r =
. D. r = . 2 2 2 + 2 3 Lời giải Chọn C
Từ giả thiết, ta có AC = AB = a và BC = a 2 . æ ö Suy ra
AB + BC +CA ç2 + 2 p = = a ÷ ç ÷ ç ÷ . 2 çè 2 ÷ø 2
Diện tích tam giác vuông 1 a
S = AB.AC = . 2 2 Lại có S a S = . p r ¾¾ r = = . p 2 + 2
Câu 59: Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O bán kính R . Gọi r là bán
kính đường tròn nội tiếp tam giác ABC . Khi đó tỉ số R bằng: r A. + - + 1+ 2 . B. 2 2 . C. 2 1 . D. 1 2 . 2 2 2 Lời giải Chọn A Giả sử BC a
AC = AB = a ¾¾
BC = a 2 . Suy ra 2 R = = . 2 2 æ ö Ta có
AB + BC +CA ç2 + 2 p = = a ÷ ç ÷ ç ÷ . 2 çè 2 ÷ø 2
Diện tích tam giác vuông 1 a
S = AB.AC = . 2 2 Lại có S a R S = . p r ¾¾ r = = . Vậy = 1+ 2 . p 2 + 2 r
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 730
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133