Phân loại và phương pháp giải bài tập vectơ trong không gian, quan hệ vuông góc

Tài liệu gồm 173 trang, được biên soạn bởi thầy giáo Trần Đình Cư, tóm tắt lý thuyết, phân loại và phương pháp giải bài tập vectơ trong không gian

75 38 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 7: Quan hệ vuông góc trong không gian (KNTT)

Môn: Toán 11

Thông tin:

173 trang 9 tháng trước

Tác giả:

Profile Kim Oanh
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 695
BÀI 1. VECTO TRONG KHÔNG GIAN
A. KIẾN THỨC CƠ BẢN CẦN NẮM
I – ĐỊNH NGHĨA VÀ CÁC PHÉP TOÁN VỀ VECTƠ TRONG KHÔNG GIAN
Cho đoạn thẳng trong không gian. Nếu ta chọn điểm đầu là , điểm cuối là ta có một vectơ,
được kí hiệu là .
Định nghĩa
Vectơ trong không gian là một đoạn thẳng có hướng. Kí hiệu chỉ vectơ có điểm đầu là , điểm
cuối . Vectơ còn được kí hiệu là ,…
Các khái niệm có liên quan đế
n vectơ như giá của vectơ, độ dài của vectơ, sự cùng phương, cùng
hướng của hai vectơ, vectơ – không, sự bằng nhau của hai vectơ, … được định nghĩa tương tự như
trong mặt phẳng.
II – ĐIỀU KIỆN ĐỒNG PHẲNG CỦA BA VECTƠ
1. Khái niệm về sự đồng phẳng của ba vectơ trong không gian
Trong không gian cho ba vectơ , , đều khác vectơ – không. Nếu từ một điểm bấ
t kì ta vẽ
, , thì có thể xả ra hai trường hợp:
Trường hợp các đường thẳng , , không cùng nằm trong một mặt phẳng, khi đó ta nói
rằng vectơ , , không đồng phẳng.
Trường hợp các đường thẳng , , cùng nằm trong một mặt phẳng thi ta nói ba vectơ ,
, đồng phẳng.
Trong trường hợp này giá của các vectơ luôn luôn song song với một mặt phẳng.
a) Ba vectơ , , không đồng phẳng b) Ba vectơ , , đồng phẳng
Chú ý. Việc xác định s
ự đồng phẳng hoặc không đồng phẳng của ba vectơ nói trên không phụ
thuộc vào việc chọn điểm .
Từ đó ta có định nghĩa sau đây:
2. Định nghĩa
Trong không gian ba vectơ được gọi là đồng phẳng nếu các giá của chúng cùng song song với một
mặt phẳng.
3. Điều kiện để ba vectơ đồng phẳng
A
B
A
B
AB

AB

A
B
, , , abxy

a
b
c
O
OA a=

OB b=

OC c=

·
OA OB OC
a
b
c
·
OA OB OC
a
b
c
, , abc

a
b
c
a
b
c
O
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 696
Từ định nghĩa ba vectơ đồng phẳng và từ định lí về sự phân tích (hay biểu thị) một vectơ theo hai
vectơ hai vectơ không cùng phương trong hình học phẳng chúng ta có thể chứng minh được định lí
sau đây:
Định lí 1
Trong không gian cho hai vectơ , không cùng phương và vectơ . Khi đó ba vectơ , ,
đồng phẳng khi và chỉ khi có cặp số sao cho . Ngoài ra cặp số là duy nhất.
Định lí 2
Trong không gian cho ba vectơ không đồng phẳng , , . Khi đó với mọi vectơ ta đều tìm
được một bộ ba số sao cho . Ngoại ra bộ ba số là duy nhất.
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng1.Biểudiễnvectơ
Câu 1: Cho hình lăng trụ Đặt Gọi là trọng tâm của tam
giác Vectơ bằng:
A. B. C. D.
Lời giải
Chọn B
Gọi
I
là trung điểm của
.
B
C
¢¢
Vì
G
¢
là trọng tâm của tam giác
2
.
3
A
BC AG AI
¢¢¢ ¢ ¢ ¢
=

Ta có
()
21
.
33
A
GAAAGAA AIAA ABAC
¢¢¢¢¢¢ ¢ ¢¢¢¢
=+ =+ =+ +
       
()
()
()
11 1
33.
33 3
A
A ABAC AA ABAC abc
¢¢
=+ += ++= ++
 
   
a
b
c
a
b
c
,mn
cmanb=+

,mn
a
b
c
x
,,mnp
x
ma nb pc=++

,,mnp
..
A
BC A B C
¢¢¢
, , .aAAbABcAC
¢
===

 
G
¢
.
A
BC
¢¢¢
A
G
¢

()
1
3.
3
abc++
()
1
3.
3
abc++
()
1
3.
3
ab c++
()
1
.
3
abc++
G'
I
C
B
A
B'
C'
A'
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 697
Câu 2: Cho hình lăng trụ Đặt Hãy biểu diễn vectơ
theo các vectơ
A. B.
C. D.
Lời giải
Chọn D
Vì
B
BCC
¢¢
là hình bình hành suy ra
BC BC BB BC AA
¢¢¢¢ ¢
=+=-
   

.
A
ABAAC AAABAC abc
¢¢
=- + + =- - + =- - +
 
   
Câu 3: Cho hình lăng trụ Gọi là trung điểm của Đặt
Khẳng định nào dưới đây là đúng?
A. B.
C. D.
Lời giải
Chọn C
..
A
BC A B C
¢¢¢
, , .aAAbABcAC
¢
===

 
B
C
¢

,,.abc
.
B
Cabc
¢
=+-


.BC a b c
¢
=- + -


.
B
C abc
¢
=++


.BC a b c
¢
=- - +


C
B
A'
C'
B'
A
..
A
BC A B C
¢¢¢
M
.
B
B
¢
,, .CA a CB b AA c
¢
== =

 
1
.
2
A
Mac b=+-

1
.
2
A
Mbc a=+-

1
.
2
A
Mba c=-+

1
.
2
A
Mac b=-+

Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 698
Vì
M
là trung điểm của
1
.
2
BB BM BB
¢¢
=


Ta có
111
.
222
A
MABBM BA BB CACB BB ab c
¢¢
=+ =-+ =-++ =-++
 
 
Câu 4: Cho hình hộp tâm Gọi là tâm của hình hình hành Đặt
Khi đó
A. B.
C. D.
Lời giải
Chọn A
Gọi
,
M
N
lần lượt là trung điểm của
,.
A
BCD
Vì
I
là trung điểm của
M
N
suy ra
2OM ON OI+=
  
.
Kết hợp với
()
2
1
2.
2
2
OA OB OM
OI OA OB OC OD
OC OD ON
ì
ï
+=
ï
ï
= +++
í
ï
+=
ï
ï
î
  
 
 
M
C
B
A
B'
C'
A'
.
A
BC D A B C D
¢¢¢¢
.O
I
.
A
BC D
,, , .
A
CuCAvBDxDBy
¢¢ ¢ ¢
== = =
   

()
1
2.
4
OI u v x y=- + + +


()
1
2.
2
OI u v x y=- + + +


()
1
2.
2
OI u v x y=+++


()
1
2.
4
OI u v x y=+++


O
I
N
M
B
'
C'
D'
B
D
C
A
A
'
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 699
()
11 1 1 1 1
.
22 2 2 2 4
A
CCABDDB uvxy
æö
÷
ç
¢¢ ¢ ¢
=- - - - =- +++
÷
ç
÷
ç
èø
   

.
Câu 5: Cho hình hộp có Gọi là trung điểm của
là giao điểm của và Mệnh đều nào sau đây đúng?
A. B.
C. D.
Lời giải
Chọn A
Vì
I
là trung điểm của
2.BC AB AC AI
¢¢ ¢¢ ¢¢ ¢
+=
  
Và
K
là giao điểm của ,
A
IBD
¢¢¢
nên theo định lí Talet
2
.
3
A
KAI
¢¢
=
 
Ta có
()
21 11
.
33 33
A
KAAAKAA AIAA ABAC a bc
¢¢ ¢ ¢ ¢ ¢¢¢¢
=+ =+ =+ + =++
      

Khi đó
()
.DK DA AK CB AK AB AC AK=+=+= - +
     
11 42
.
33 33
ab a bc a bc
=-+ + += - +


Câu 6: Cho tứ diện có trọng tâm Mệnh đề nào sau đây là sai?
A. B.
C. D.
Lời giải
Chọn A
.
A
BC D A B C D
¢¢¢¢
,, .
A
BaACbAA c
¢
== =

 
I
,BC
¢¢
K
AI
¢
.
B
D
¢¢
()
1
423.
3
D
Kabc=-+

()
1
42 .
3
D
Kabc=-+

42 .
D
Kabc=-+

423.
D
Kabc=-+

K
I
C
B
A
C'
D
D
'
B
'
A
'
A
BC D
.G
()
2
.
3
A
GABACAD=++
  
()
1
.
4
A
GABACAD=++
   
()
1
.
4
OG OA OB OC OD=+++

0.GA GB GC GD+++ =

Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 700
Vì
G
là trọng tâm của tứ diện
A
BCD
suy ra 0.GA GB GC GD+++ =

Khi đó
()
11
.4
44
OG OG OA AG OB BG OC CG OD DG
==+++++++
    
() ()
11
.
44
OA OB OC OD AO OG AO OA OB OC OD=+++¾¾+=+ +++
      
()()()
111
4.
444
A
O OAABACAD AOOA ABACAD ABACAD=+ +++ =++ ++ = ++
          
 
Vậy
()
1
4
A
GABACAD=++
 
nên mệnh đề
()
2
3
A
GABACAD=++
 
sai.
Câu 7: Cho tứ diện Đặt Gọi là trọng tâm của tam giác
Trong các đẳng thức sau, đẳng thức nào sau đây đúng?
A. B.
C. D.
Lời giải
Chọn B
Gọi
M
là trung điểm của
CD
suy ra
2
.
3
BG BM
=
 
Ta có
() ()
221 1
..
332 3
A
GABBGAB BM AB BCBD AB BCBD=+=+ =+ + =+ +
    

G
B
D
C
A
.
A
BC D
,,.
A
BaACbADc===

G
.
B
CD
.
A
Gabc=++

()
1
.
3
A
Gabc=++

()
1
.
2
A
Gabc=++

()
1
.
4
A
Gabc=++

G
M
A
C
D
B
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 701
()()()
111
.
333
A
B ACABADAB ABACAD abc=+ -+- = ++ = ++
    
Câu 8: Cho tứ diện Đặt Gọi là trung điểm của đoạn thẳng
Đẳng thức nào dưới đây là đúng?
A. B.
C. D.
Lời giải
Chọn A
Vì
M
là trung điểm của
BC
suy ra
1
.
2
BM B C
=
 
Ta có
()
11
.
22
DM DA AB BM AB AD BC AB AD BA AC=++ =-+ =-+ +
      

()
11 11 1
2.
22 22 2
A
BACADabc abc=+-=+-=+-
  

Câu 9: Cho tứ diện Gọi và lần lượt là trung điểm của và Đặt
Khẳng định nào sau đây là đúng?
A. B.
C. D.
Lời giải
Chọn D
.
A
BC D
,,.
A
BaACbADc===
  
M
.BC
()
1
2.
2
DM a b c=+-

()
1
2.
2
DM a b c=-++

()
1
2.
2
DM a b c=-+

()
1
2.
2
DM a b c=+-

M
B
D
C
A
.
A
BC D
M
P
A
B
.CD
,, .
A
BbACcADd===
  
()
1
.
2
M
Pcdb=++

()
1
.
2
M
Pdbc=+-

()
1
.
2
M
Pcbd=+-

()
1
.
2
M
Pcdb=+-

Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 702
Vì
,
M
P
lần lượt là trung điểm của
,
A
BCD
2
.
2
AM AB
A
CAD AP
ì
ï
=
ï
ï
í
ï
+=
ï
ï
î

  
Ta có
()
11 111
.
22 222
M
PMAAP AMAP AB ACAD b c d=+=-+=- + + =-++
    
Dạng 2.Đẳngthứcvectơ
Câu 1: Cho hình lăng trụ tam giác Đặt . Khẳng định
nào dưới đây là đúng?
A. B.
C. D.
Lời giải
Chọn C
Ta có
0.BC AC AB d c b b c d=-=--+=

Câu 2: Cho hình lập phương Gọi là tâm của hình lập phương. Khẳng định
nào dưới đây là đúng?
A. B.
C. D.
P
M
A
C
D
B
..
A
BC A B C
¢¢¢
,,,
A
AaABbACc
¢
===

 
BC d=

.abc=+
0.
abcd+++ =
0.
bcd-+ =
.abc d++=
C
B
A
B'
C'
A'
..
A
BC D A B C D
¢¢¢¢
O
()
1
.
3
A
OABADAA
¢
=++

  
()
1
.
2
A
OABADAA
¢
=++

  
()
1
.
4
A
OABADAA
¢
=++

  
()
2
.
3
A
OABADAA
¢
=++

  
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 703
Lời giải
Chọn B
Theo quy tắc hình hộp, ta có
.
A
CABADAA
¢¢
=++


Mà
O
là trung điểm của
A
C
¢
suy ra
()
11
.
22
A
OAC ABADAA
¢¢
==++

 
Câu 3: Cho hình hộp tâm Khẳng định nào dưới đây là sai?
A. B.
C. D.
Lời giải
Chọn C
Dựa vào đáp án, ta thấy rằng:
A đúng, vì theo quy tắc hình hộp, ta có
.
A
CABADAA
¢¢
=++


B đúng, vì
0.
AB CD
AB BC CD D A
BC D A
ì
ï
=-
ï
ï
¢¢
+ ++ =
í
ï
¢¢
ï=-
ï
î

 

 
C sai, vì
AB AA AB
AD DD AD
ì
ï
¢¢
+=
ï
ï
í
ï
¢¢
ï
+=
ï
î
 



mà
.
A
BAD ABAAADDD
¢¢ ¢ ¢
¹+¹+
   
 
O
C
B
A
C'
D
D'
B'
A'
.
A
BC D A B C D
¢¢¢¢
.O
.
A
CABADAA
¢¢
=++
 
 
0.AB BC CD D A
¢¢
+++ =
 

.
A
BAA ADDD
¢¢
+=+
 

.
A
BBCCC AD DOOC
¢¢¢ ¢
++ = + +
  

O
C
B
A
C'
D
D'
B'
A'
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 704
D đúng, vì
()
()
() ( )
1:
12.
2:
AB BC CC AC CC AC
AD D O OC AO OC AC
ì
ï
¢¢¢
++ = + =
ï
ï
=
í
ï
¢¢ ¢ ¢ ¢
ï
++=+=
ï
î
  
 
    

Câu 4: Cho hình hộp Khẳng định nào dưới đây là sai?
A. B.
C. D.
Lời giải
Chọn D
Dựa vào đáp án, ta thấy rằng:
A đúng, vì
11
11
BC B C
BA B A
ì
ï
=
ï
ï
í
ï
=
ï
ï
î

 
suy ra
11 11
.
B
CBABC BA+= +
  
B đúng, vì
11 1 1
.
A
DDC DA ADDCDAACDADC+ + =++=+=
        
C đúng, vì
11
B
DBCBABB=++
  
(quy tắc hình hộp).
D sai, vì
11 1111
.
B
ADDBDBABBBDBABDBC++=++=+¹
        
Câu 5: Cho hình hộp Gọi là trung điểm của Khẳng định nào dưới đây là
đúng?
A. B.
C. D.
Lời giải
Chọn B
111 1
..ABCD A BC D
11 1 1
.
B
CBABC BA+= +
 
11 11
.
A
DDC DA DC++ =
   
11
.
B
CBABB BD++ =
  
11
.
B
ADD BD BC++=
 
C
B
A
C
1
D
D
1
B
1
A
1
111 1
..ABCD A BC D
M
.
A
D
111111
.
B
MBBBABC=+ +
   
111111
1
.
2
CM CC CD CB=+ +
   
11 1111
11
.
22
CM CC CD CB=+ +
   
11111 1
2.
B
BBABC BD++=
   
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 705
Dựa vào đáp án, ta thấy rằng:
A sai, vì
() ()
11 1 11111
11
.
22
B M B B BM BB BA BD BB B A B D
=+=+ + =+ +
        
()
1 111111 111 11
11
.
22
BB BA BA BC BB BA BC=+ + + =+ +
      
B đúng, vì
() ()
11 1 1 1111
11
.
22
C M C C CM C C CA CD C C C A C D
=+=+ +=+ +
        
()
111111111111
11
.
22
CC CB CD CD CC CD CB
=+ + + =+ +
      
C sai, vì
111111
1
2
CM CC CD CB
=+ +
   
(từ B).
D sai, vì
11111 1 111 1
.
B
BBABCBABCBAADBD++=+=+ =
       
Câu 6: Cho hình lập phương có cạnh bằng Gọi là trọng tâm của tam giác
Khẳng định nào dưới đây là đúng?
A. B. C. D.
Lời giải
Chọn D
Cách 1. Gọi
I
là tâm của hình vuông
A
BC D I
là trung điểm của
.BD
Ta có
11
3.
23
BG BI BG
BIG D B G BD BG
DG DB BD
¢¢ ¢
DD====
¢¢¢ ¢


M
C
1
B
1
A
1
C
D
1
D
B
A
.
A
BC D A B C D
¢¢¢¢
.a
G
.
A
BC
¢
3.
A
CAG
¢
=


4.
A
CAG
¢
=


4.BD BG
¢
=


3.BD B G
¢
=


G
I
D
'
C'
B'
D
A'
A
C
B
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 706
Cách 2. Theo quy tắc hình hộp, ta có
.BA B C BB BD
¢¢
++ =
 

Do
G
là trọng tâm của tam giác
A
BC
¢
suy ra
33.BA BC BB BG BD BG
¢¢
++ = =
 
 
Câu 7: Cho hình chóp có đáy là hình bình hành. Đặt
. Khẳng định nào dưới đây là đúng?
A. B. C. D.
Lời giải
Chọn A
Gọi
O
là tâm hình bình hành
.
A
BCD
Vì
O
là trung điểm của
A
C
suy ra
()
22 1.SA SC SO SO a c+= =+

Và
O
là trung điểm của BD suy ra
()
22 2.SB SD SO SO b d+= =+

Từ
()
1
và
(
)
2
, suy ra
.ac bd+=+
Câu 8: Cho hình chóp có đáy là hình bình hành tâm Gọi là điểm thỏa mãn
Khẳng định nào dưới đây là đúng?
A. không thẳng hàng. B.
C. D.
Lời giải
Chọn B
Gọi
O
là tâm hình bình hành
A
BCD
suy ra 0.OA OB OC OD+++ =
  
.SABCD
A
BC D
,,SA a SB b==
 
,SC c SD d==
 
.ac bd+= +
0.abcd+++ =
.ad bc+=+
.ab cd+=+
O
C
A
B
D
S
.SABCD
A
BC D .OG
0.GS GA GB GC GD++++ =
  
,,GSO
4.GS OG=
 
5.GS OG=
 
3.GS OG=
 
O
C
S
D
B
A
G
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 707
Ta có
40.GS GA GB GC GD GS GO OA OB O C OD++++ =+ ++++=
   
40 4GS GO GS OG+ ==
 
ba điểm
,,GSO
thẳng hàng.
Câu 9: Cho tứ diện và điểm thỏa mãn ( là trọng tâm của tứ
diện). Gọi là giao điểm của và mặt phẳng Khẳng định nào dưới đây là
đúng?
A. B. C. D.
Lời giải
Chọn C
Vì
0
G là giao điểm của đường thẳng
A
G
với mặt phẳng
()
.BCD
Suy ra
0
G là trọng tâm của tam giác
BCD
000
0.GB GC GD++ =
  
Theo bài ra, ta có
00 0 0
0
30GA GB GC GD GA GG G B G C G D+++ =+ + + + =
   

00
30 3.GA GG GA G G+ ==

Câu 10: Cho tứ diện . Gọi lần lượt là trung điểm của và là trung điểm của
Khẳng định nào dưới đây là sai?
A. B.
C. D.
Lời giải
Chọn B
A
BC D G
0GA GB GC GD+++ =

G
0
G
GA
(
)
.BCD
0
2.GA G G=-
 
0
4.GA G G=

0
3.GA G G=
 
0
2.GA G G=
 
G
G
0
M
A
C
D
B
A
BC D
,
M
N ,
A
BCD
G
.
M
N
4.
M
AMBMCMD MG+++ =
    
.GA GB GC GD++ =

0.GA GB GC GD+++ =

0.GM GN+=
 
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 708
Vì
,
M
N
lần lượt là trung điểm của
,
A
BCD
suy ra
2
.
2
GA GB GM
GC GD GN
ì
ï
+=
ï
ï
í
ï
+=
ï
ï
î

  
Mà
G
là trung điểm của
M
N
00.GM GN GA GB GC GD+=+++=
  
Khi đó
()
44.
M
AMBMCMD MG GAGBGCGD MG+++ = ++++ =
    
Câu 11: Cho hình hộp . Tìm giá trị thực của thỏa mãn đẳng thức vectơ
A. B. C. D.
Lời giải
Chọn B
Ta có
11 1 1 1 1
1.AB BC DD AB BC CC AC CC AC k+ + =++=+= =
     
Câu 12: Cho hình hộp Tìm giá trị thực của thỏa mãn đẳng thức vectơ
A. B. C. D.
Lời giải
Chọn B
G
N
M
B
D
C
A
111 1
.ABCD A BC D
k
11 1 1
.
A
BBC DD kAC++=
  
4.k = 1.k = 0.k = 2.k =
C
B
A
C
1
D
D
1
B
1
A
1
..
A
BC D A B C D
¢¢¢¢
k
()
''0.AC BA k DB C D++ + =
   
0.k = 1.k = 4.k = 2.k =
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 709
Ta có
A
CBA ACCD AD
¢¢¢
+=+=
  
 
và
.
D
BCD DBDC CB DA
¢¢¢¢
+=- ==
 
 
Suy ra
()
()
'' 0101.AC BA k DB C D AD kD A k D A k
¢¢ ¢
++ + = + =- ==
 
   
Câu 13: Gọi lần lượt là trung điểm của các cạnh và của tứ diện Gọi là
trung điểm của đoạn . Tìm giá trị thực của thỏa mãn đẳng thức vectơ
A. B. C. D.
Lời giải
Chọn C
Vì
,
M
N
lần lượt là trung điểm của
2
,.
2
I
AIC IM
AC BD
I
BID IN
ì
ï
+=
ï
ï
í
ï
+=
ï
ï
î


Mặt khác
0IM IN+=

(
I
là trung điểm của
M
N
)
0.IA IB IC ID+++ =

Ta có
() ( )()
0
21 22 1 0IA k IB kIC ID IA IB IC ID k IB k IC+- + +=++++- +- =
 

()
()
12 0kIBIC- + =

mà
20IB IC+¹

suy ra
10 1.kk-= =
Câu 14: Gọi lần lượt là trung điểm của các cạnh và của tứ diện Gọi là
trung điểm của đoạn và là một điểm bất kỳ trong không gian. Tìm giá trị thực của
thỏa mãn đẳng thức vectơ
D'
C'
B'
D
B
C
A
A'
,
M
N
A
C
B
D
.
A
BC D
I
M
N
k
()
21 0.IA k IB kIC ID+- + +=
 
2.k = 4.k = 1.k = 0.k =
I
N
M
A
B
D
C
,
M
N
A
C
B
D
.
A
BC D
I
M
N
P
k
()
.PI k PA PB PC PD=+++
  
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 710
A. B. C. D.
Lời giải
Chọn C
Vì
,
M
N
lần lượt là trung điểm của
2
,.
2
I
AIC IM
AC BD
I
BID IN
ì
ï
+=
ï
ï
í
ï
+=
ï
ï
î


Mặt khác
0IM IN+=

(
I
là trung điểm của
M
N
)
0.IA IB IC ID+++ =

Khi đó
()
44PA PB PC PD PI IA IB IC ID PI+++ = + +++ =
  
Mà
()
PI k PA PB PC PD=+++
  
nên suy ra
1
41 .
4
kk
= =
Câu 15: Cho tứ diện . Gọi lần lượt là trung điểm của và Tìm giá trị thực của
thỏa mãn đẳng thức vectơ
A. B. C. D.
Lời giải
Chọn A
Ta có
N
là trung điểm của
CD
()
21.MC MD MN+=
  
Và
M
là trung điểm của
A
B suy ra
()
02.MA MB+=
 
4.k =
1
.
2
k =
1
.
4
k =
2.k =
I
N
M
A
B
D
C
P
A
BC D
,
M
N
A
B
.CD
k
(
)
.
M
NkACBD=+

1
.
2
k =
1
.
3
k =
3.k = 2.k =
N
M
A
C
D
B
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 711
Từ
()( )
1,2
suy ra
()()()
11 1
.
22 2
M
N MCMD MAACMBBD ACBD=+=+++=+
      
Kết hợp giả thiết
()
1
.
2
MN k AC BD k
=+=

Dạng3.Đồng phẳngcủaba vectơ
Câu 1: Cho ba vectơ không đồng phẳng. Xét các vectơ , ,
Khẳng định nào dưới đây là đúng?
A. Ba vectơ đồng phẳng. B. Hai vectơ cùng phương.
C. Hai vectơ cùng phương. D. Ba vectơ đôi một cùng
phương.
Lời giải
Chọn A
Giả sử, ba vectơ
,,
x
yz
đồng phẳng, khi đó
..
x
my nz=+
.
Ta có
()()
....
.. . 3. 2..
.3.2.
my ma mb mc
my nz ma m n b m n c
nz nb nc
ì
ï
=--
ï
ï
+=-+ -+
í
ï
=- -
ï
ï
î


Khi đó
()()
2
2
2.3.2.31 .
1
20
m
m
ab ma m nb m nc m n
n
mn
ì
=
ï
ï
ì
=
ï
ï
ïï
+= - + - + + =-
íí
ïï
=-
ï
ïî
ï+ =
ï
î


Vậy ba vectơ
,,
x
yz
đồng phẳng.
Câu 2: Cho ba vectơ không đồng phẳng. Khẳng định nào dưới đây là đúng?
A. Ba vectơ đồng phẳng.
B. Ba vectơ đồng phẳng.
C. Ba vectơ đồng phẳng.
D. Ba vectơ đồng phẳng.
Lời giải
Chọn B
Ba vectơ
,,
x
yz
đồng phẳng khi và chỉ khi
,: . ..mn x my nz$=+
Với
24, 332, 233.
x
ab cy abcz abc=- + = - + = - -


Suy ra
()()
24 332 233.ab cmab cnabc-+= -+ + --

 
()()()
321
32 3 23 33 2
234
mn
mna mnb mnc mn
mn
ì
+=
ï
ï
ï
ï
=+ -++- --=-
í
ï
ï
ï-=
ï
î

hệ vô nghiệm.
,,abc
2
x
ab=+
yabc=--

32.zbc=- -
,,
x
yz
,
x
a
,
x
b
,,
x
yz
,,abc
2, 236, 36
x
ab cy a b cz a b c=++ = - - =-+ +


24, 332, 233
x
abcy abcz abc=- + = - + = - -


,23, 33
x
abcy a bcz a b c=++ = - + =-+ +


,2 3, 2
x
abcy ab cz ab c=+- = -+ =--+


Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 712
Vậy ba vectơ kể trên không đồng phẳng.
Chú ý. Bạn đọc làm tương tự với các A, C, D để thấy được các vectơ
,,
x
yz
đồng phẳng
Câu 3: Cho ba vectơ . Điều kiện nào dưới đây khẳng định ba vectơ đồng phẳng?
A. Tồn tại ba số thực thỏa mãn và
B. Tồn tại ba số thực thỏa mãn và
C. Tồn tại ba số thực sao cho
D. Giá của đồng quy.
Lời giải
Chọn B
Dựa vào đáp án, ta thấy rằng:
 Với
00mnp mn p++ = = = = suy ra
0ma nb pc++=
nên chưa kết luận được ba
vectơ
,,abc
đồng phẳng.
 Với
0mnp++ ¹
suy ra tồn tại ít nhất một số khác
0.
Giả sử
0,m ¹
ta có
0...
np
ma nb pc a b c
mm
++==- -

Suy ra tồn tại
,np
để ba vectơ
,,abc
đồng phẳng.
Câu 4: Cho hình hộp . Khẳng định nào dưới đây là đúng?
A. đồng phẳng. B. đồng phẳng.
C. đồng phẳng. D. đồng phẳng.
Lời giải
Chọn C
Ta có
11 1 1
A
DAD ACCD==+
   
suy ra
11
,,CD AD A C
  
đồng phẳng.
Câu 5: Cho hình hộp Gọi là tâm của hình bình hành và là tâm của
hình bình hành Khẳng định nào dưới đây là đúng?
A. đồng phẳng. B. đồng phẳng.
,,abc

,,abc

,,mnp
0mnp++ =
0.ma nb pc++=
,,mnp
0mnp++ ¹
0.ma nb pc++=

,,mnp
0.ma nb pc++=
,,abc

111 1
.ABCD A BC D
11
,,
B
DBD BC

111
,,CD AD A B
  
11
,,CD AD A C
  
1
,,
A
BADCA

C
B
A
C
1
D
D
1
B
1
A
1
..
A
BC D EF GH
I
A
BEF K
.BC GF
,,BD AK GF

,,BD IK GF

Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 713
C. đồng phẳng. D. đồng phẳng.
Lời giải
Chọn B
Vì
,
I
K
lần lượt là trung điểm của
A
F
và
.CF
Suy ra
I
K là đường trung bình của tam giác
A
FC IK
//
A
CIK
//
()
.
A
BCD
Mà
GF
//
()
A
BCD
và
()
BD ABCDÌ
suy ra ba vectơ
,,
B
DIKGF

đồng phẳng
Câu 6: Cho hình hộp Gọi lần lượt là tâm của hình bình hành và
Khẳng định nào dưới đây là sai?
A. B. C. D.
Lời giải
Chọn B
Dựa vào đáp án, ta thấy rằng:
A đúng, vì
,
I
KAC

cùng thuộc mặt phẳng
()
.
B
AC
¢
B đúng, vì
11
.
22
I
KIBBK AC AC
¢¢ ¢¢
=+ = =
  

C sai, vì
'
I
KIBBK
¢
=+


Ta có
11 1 1 1 1
1.AB BC DD AB BC CC AC CC AC k+ + =++=+= =
     
.
,,BD EK GF
  
,,BD IK G C

K
I
F
G
H
B
D
C
A
E
..
A
BCD A B C D
¢¢¢¢
,
I
K ABB A
¢¢
.
B
CC B
¢¢
4.k = 1.k = 0.k = 2.k =
K
I
C'
B
'
A'
C
D
'
D
B
A
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 714
Câu 7: Cho tứ diện Gọi lần lượt là trung điểm của Khẳng định nào dưới
đây là khẳng định sai?
A. Ba vectơ đồng phẳng.
B. Ba vectơ không đồng phẳng.
C. Ba vectơ đồng phẳng.
D. Ba vectơ đồng phẳng.
Lời giải
Chọn C
Vì
,
M
N
lần lượt là trung điểm của
,
A
DBC
suy ra:
()
1
2
M
NABDC=+
 
và
()
1
.
2
M
NBDAC=+
 
Khi đó, dựa vào đáp án, ta thấy rằng:
A đúng, vì
()
1
,,
2
M
NABDCABDCMN=+
  
đồng phẳng.
B đúng, vì
M
N
không nằm trong mặt phẳng
()
.
A
BC
C sai, tương tự ta thấy
A
N
không nằm trong mặt phẳng
()
.
M
NC
D đúng, vì
()
1
,,
2
M
NBDACBDACMN=+
  
đồng phẳng.
Câu 8: Cho tứ diện . Trên các cạnh và lần lượt lấy điểm sao cho
Gọi lần lượt là trung điểm của và Khẳng định nào
dưới đây là sai?
A. Ba vectơ đồng phẳng. B. Ba vectơ đồng phẳng.
C. Ba vectơ đồng phẳng. D. Ba vectơ đồng phẳng.
Lời giải
Chọn A
.
A
BC D
,
M
N ,.
A
DBC
,,
A
BDCMN

,,
A
BACMN
  
,,
A
NCMMN
  
,,
B
DACMN

M
N
B
D
C
A
A
BC D
A
D
BC
,
M
N
3, 3.AM MD BN NC==
,PQ
A
D
.BC
,,BD AC MN

,,
M
NDCPQ

,,
A
BDCPQ

,,
A
BDCMN
  
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 715
Theo bài ra, ta có
,
M
N
lần lượt là trung điểm của
,.PD QC
Khi đó, dựa vào đáp án, ta thấy rằng:
A sai, vì
3333
MN MA AC CN MN MA AC CN
M
NMDDBBN MN MD DB BN
ìì
ïï
=++ =++
ïï
ïï
íí
ïï
=++ = + +
ïï
ïï
îî
       
   
Suy ra
1
43 ,,
2
M
NAC BD BCBDACMN=- +
  
không đồng phẳng.
B đúng, vì
2
MN MP PQ QN
M
NPQDC
MN MD DC CN
ì
ï
=++
ï
ï
=+
í
ï
=++
ï
ï
î
   
 
   
Suy ra
()
1
,,
2
M
NPQDCBDACMN=+
   
đồng phẳng.
C đúng, vì với cách biểu diễn
P
Q

tương tự như trên, ta có
()
1
.
2
PQ AB DC
=+

D đúng, vì biểu diễn giống A, ta được
13
.
44
M
NABDC=+
 
Câu 9: Cho tứ diện và các điểm , xác định bởi ;
. Tìm để các đường thẳng cùng song song với một
mặt phẳng.
A. B. C. D.
Lời giải
Chọn B
Yêu cầu bài toán tương đương với tìm
x
để ba vectơ
, ,
M
NADBC

đồng phẳng.
Hệ thức
()
()
123 3
A
MABABBCAMABBC=- +=--

.
Hệ thức
()
()
2
A
NADABADxDAABBC-=-+ ++
    
()
1
A
NxABxADxBC=+ - +
   
.
Từ
()
1
và
(
)
2
, suy ra
() ()
23
M
NANAM xABxADx BC=- =+ - ++

.
N
M
P
Q
A
C
D
B
A
BC D
M
N
()
23 1AM AB AC=-

()
2DN D B xDC=+
  
x
, , AD BC MN
1.x =- 2.x =- 3.x =- 2.x =
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 716
Vậy ba vectơ
, ,
M
NADBC

đồng phẳng khi
20 2xx+= =-
.
Câu 10: Cho hình hộp Gọi là điểm trên cạnh sao cho Lấy
trên đoạn sao cho Với giá trị nào của thì
A. B. C. D.
Lời giải
Chọn A
Gọi
O
là tâm của hình hình hành
A
BCD
và
I
là trung điểm của
.DD
¢
Nối
CD
¢
cắt
CI
tại
N
N
¢¢
là trọng tâm của tam giác
.CDD
¢
Ta có
OI
là đường trung bình của tam giác
BDD
¢
suy ra
OI
//
.
B
D
¢
Mặt khác
CN CM
CI CO
¢
=
nên
M
N
¢
//
OI
suy ra
M
N
¢
//
.
B
D
¢
Theo bài ra, ta có
M
N
//
BD
¢
NN
¢
¾¾º
22
.
33
CN CD x
¢¢
= =
Câu 11: Cho hình chóp Lấy các điểm lần lượt thuộc các tia sao cho
trong đó là các số thay đổi. Để mặt phẳng đi qua
trọng tâm của tam giác thì
A. B. C. D.
Lời giải
Chọn A
..
A
BCD A B C D
¢¢¢¢
M
A
C
3.AC MC=
N
CD
¢
.CN xCD
¢¢
=
x
.
M
NBD
¢
2
.
3
x =
1
.
3
x =
1
.
4
x =
1
.
2
x =
M
N'
I
O
B
D
A
A'
C'
B'
D'
C
..SABC
,,
A
BC
¢¢¢
,,SA SB SC
,,,
SA SB SC
abc
SA SB SC
===
¢¢¢
,,abc
()
A
BC
¢¢¢
A
BC
3.abc++= 4.abc++= 2.abc++= 1.abc++=
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 717
Gọi
G
là trọng tâm của tam giác
A
BC
suy ra
0.GA GB GC++ =

Khi đó
30GS SA SB SC+++=
   
mà
., ., . .SA aSA SB b SB SC cSC
¢¢¢
===
  
 
Suy ra
3... . . ..
333
abc
SG aSA bSB cSC SG S A SB SC
¢¢¢ ¢ ¢ ¢
=++= + +
     
 
Vì
(
)
A
BC
¢¢¢
đi qua trọng tâm tam giác
A
BC
suy ra
,,GA GB GC
¢¢¢
  
đồng phẳng.
Do đó, tồn tại ba số
,,lmn
sao cho
()
222
0lmn++¹
và
...0.lGA mGB nGC
¢¢¢
++=
  
()()()
()
...0 ....
.......
333
l GS SA m GS SB n GS SB l m n SG l SA m SB nSC
lmnabc
SG SA SB SC SA SB SC
lmn lmn lmn
¢¢¢ ¢¢¢
++ +++=++=++
¢¢¢¢¢¢
= + + = + +
++ ++ ++
     
   
     

Suy ra
13.
333
abc l m n
abc
lmnlmnlmn
++= + + =++=
++ ++ ++
Dạng4.Tìmđiểmthỏamãnđẳngth ứcvectơ
Câu 1: Cho tứ diện . Gọi là trọng tâm tam giác . Điểm xác định bởi đẳng thức
vectơ Mệnh đề nào sau đây đúng?
A. trùng B. thuộc tia và
C. là trung điểm D. là trung điểm
Lời giải
Chọn B
Do
G
là trọng tâm tam giác
BCD
nên 3.
A
BACAD AG++ =
   
Kết hợp giả thiết, suy ra
3.
A
MAG=

Câu 2: Cho tứ diện . Điểm xác định bởi Mệnh đề nào sau đây
đúng?
A. là trung điểm
B. là đỉnh thứ tư của hình bình hành
G
C'
A
B
S
C
A'
B'
A
BC D G BC D
M
.
A
MABACAD=++

M
.G
M
A
G
3.AM AG=
G .
A
M
M
.
A
G
A
BC D N
.
A
NABACAD=+-
   
N .BD
N .BC DN
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 718
C. là đỉnh thứ tư của hình bình hành
C. trùng với
Lời giải
Chọn C
Ta có
.
A
NABACADANABACADBNDC=+--=-=
        
Đẳng thức chứng tỏ
N
là đỉnh thứ tư của hình bình hành
.CDBN
Câu 3: Cho tứ diện Ta định nghĩa là trọng tâm tứ diện khi và chỉ khi
Khẳng định nào sau đây sai?
A. là trung điểm của đoạn thẳng nối trung điểm của và
B. là trung điểm của đoạn thẳng nối trung điểm của và
C. là trung điểm của đoạn thẳng nối trung điểm của và
D. Cả A, B, C đều đúng.
Lời giải
Chọn D
Ta có
()( )
02 2 0 0GA GB GC GD GI GJ GI GJ+++ = + =+=
    
G
¾
¾
là trung điểm
IJ
. Do đó A đúng.
Tương tự, B và C đều đúng.
Vậy cả A, B, C đều đúng.
Câu 4: Cho hình hộp Điểm được xác định bởi đẳng thức vectơ
Mệnh đề nào sau đây đúng?
A. là tâm của mặt đáy
B. là tâm của mặt đáy
C. là trung điểm của đoạn thẳng nối hai tâm của hai mặt đáy.
N .CDBN
N .
A
.
A
BC D ''G
A
BC D
0''.GA GB GC GD+++ =

G
A
B
.CD
G
A
C .BD
G
A
D
.BC
G
N
M
A
C
D
B
..
A
BCD A B C D
¢¢¢¢
M
''''0.MA MB MC MD MA MB MC MD+++ + + + + =
       
M
.
A
BC D
M
''''.
A
BCD
M
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 719
D. Tập hợp điểm là đoạn thẳng nối hai tâm của hai mặt đáy.
Lời giải
Chọn C
Gọi
OACBD=Ç
và
'''''.OACBD=Ç
Khi đó
0OA OB OC OD+++ =
  
và '' '' '' '' 0.OA OB OC OD+++ =
   
Ta có
()()()()
M
AMBMC MD MOOA MOOB MOOC MOOD+++ = ++ ++ ++ +
        
 
4044.OA OB OC OD MO MO MO=++++ =+ =
     
Tương tự, ta cũng có
''''4'.
M
AMBMCMD MO+++ =
    
Từ đó suy ra
''''0MA MB MC MD MA MB MC MD+++ + + + + =
       
()
44'04 '0 '0MO MO MO MO MO MO+ = +=+=
     
.
Vậy điểm
M
cần tìm là trung điểm của
'.OO
Câu 5: Cho hình hộp có tâm Đặt , . Điểm xác định bởi đẳng
thức vectơ . Khẳng định nào sau đây đúng?
A. là trung điểm B. là tâm hình bình hành
C. là trung điểm D. là tâm hình bình hành
Lời giải
Chọn A
Gọi
, 'II
lần lượt là tâm các mặt đáy
, ABCD A B C D
¢¢¢¢
. Suy ra
O
là trung điểm của
'.II
Do
.
A
BCD A B C D
¢¢¢¢
là hình hộp nên .
A
BDC=

Theo giả thiết ta có
()()()
11 1 1
.
22 2 2
O M a b AB BC DC C B DB IB
=-= -= += =
    
M
.
A
BC D A B C D
¢¢¢¢
.O
A
Ba=

BC b
=

M
()
1
2
OM a b=-

M
.
B
B
¢
M
.
B
CC B
¢¢
M
.CC
¢
M
.
A
BB A
¢¢
I
I
'
O
C
B
A
C'
D
D'
B'
A'
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 720
Vì
.
A
BCD A B C D
¢¢¢¢
là hình hộp nên từ đẳng thức
OM IB=
 
suy ra
M
là trung điểm
'.BB
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 721
BÀI 2. HAI ĐƯỜNG THẲNG VUÔNG GÓC
A. KIẾN THỨC CƠ BẢN CÂN NẮM
I – TÍCH VÔ HƯỚNG CỦA HAI VECTƠ TRONG KHÔNG GIAN
1. Góc giữa hai vectơ trong không gian
Định nghĩa
Trong không gian, cho và là hai vectơ khác . Lấy một điểm bất kì, gọi và là hai
điểm sao cho . Khi đó ta gọi góc là góc giữa hai vectơ và
trong không gian, kí hiệu là .
2. Tích vô hướng của hai vectơ trong không gian
Định nghĩa
Trong không gian, cho hai vectơ và đều khác . Tích vô hướng của hai vectơ và là một
số, kí hiệu là , được xác định bở
i công thức:
.
Trong trường hợp hoặc , ta quy ước .
II – VECTƠ CHỈ PHƯƠNG CỦA ĐƯỜNG THẲNG
1. Định nghĩa
Vectơ khác được gọi là vectơ chỉ phương của đường thẳng nếu giá của vectơ song song
hoặc trùng với đường thẳng .
2. Nhận xét
a) Nếu là vectơ chỉ phương của đường thẳng thì vectơ với cũng là vectơ chỉ phương
của .
b) Mộ
t đường thẳng trong không gian hoàn toàn xác định nếu biết một điểm thuộc và một
vectơ chỉ phương của nó.
u
v
0
A
B
C
,
A
Bu=

A
Cv=

BAC
()
0180BAC£ £
u
v
()
,uv
u
v
0
u
v
.uv
(
)
...cos,uv u v uv=

=
0u =
0v =
.0uv
a
0
d
a
d
a
d
ka
¹ 0k
d
A
d
a
A
B
C
d
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 722
c) Hai đường thẳng song song với nhau khi và chỉ khi chúng là hai đường thẳng phân biệt và có hai
vectơ chỉ phương cùng phương.
III – GÓC GIỮA HAI ĐƯỜNG THẲNG TRONG KHÔNG GIAN
1. Định nghĩa
Góc giữa hai đường thẳng và trong không gian là góc giữa hai đường thẳng và cùng đi
qua một điểm và lần lượt song song với và .
2. Nhận xét
a) Để xác định góc giữa hai đường thẳng và ta có thể lấy điểm thuộc một trong hai đường
thẳng đó rồi v
ẽ một đường thẳng qua và song song với đường thẳng còn lại.
b) Nếu là vectơ chỉ phương của đường thẳng và là vectơ chỉ phương của đường thẳng và
thì góc giữa hai đường thẳng và bằng nếu và bằng nếu
. Nếu và song song hoặc trùng nhau thì góc giữa chúng bằng .
IV – HAI ĐƯỜNG THẲNG VUÔNG GÓC
1. Định nghĩa
Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng .
Người ta kí hiệu hai đường th
ẳng và vuông góc với nhau là .
2. Nhận xét
a) Nếu và lần lượt là các vectơ chỉ phương của hai đường thẳng và thì: .
b) Cho hai đường thẳng song song. Nếu một đường thẳng vuông góc với đường thẳng này thì cũng
vuông góc với đường thẳng kia.
c) Hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau.
B. PHÂN LOẠI
Dạng 1. Tính góc giữa hai đường thẳng
1. Phương pháp
Cách 1: (Theo phương pháp hình học)
Lấy điểm O tùy ý ( ta có thể lấy điểm O thuộc một trong hai đường thẳng), qua đó vẽ các
đường thẳng lần lượt song song (hoặc trùng) với hai đường thẳng đã cho.
Tính một góc trong các góc được tạo bởi giữa hai đường thẳng cắt nhau tại O.
Nếu góc đó nhọn thì đó là góc cần tìm, nếu góc đó tù thì góc cần tính là góc bù với góc
đã
tính.
a
b
¢
a
¢
b
a
b
a
b
O
O
u a
v
b
(
)
a=
,uv
a
b
a
a£ £ 090
a-180
a< £ 90 180
a
b 0
90
a
b ^ab
u
v a
b
^ =
.0
ab uv
b'
a'
O
b
a
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 723
Cách 2: (Theo phương pháp vectơ)
Tìm
12
u,u

lần lượt là các vectơ chỉ phương của hai đường thẳng
1
và
2
tính
12
u,u

Khi đó


12
12 12
12
u.u
cos , cos u ,u
|u |.|u |




2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Cho tứ diện đều ABCD. Gọi I là trung điểm của BC. Tính côsin của góc tạo bởi hai đường
thẳng DI và AB.
Hướng dẫn giải
Đặt cạnh của tứ diện có độ dài là
.a
Gọi J là trung điểm của AC.
Ta có:
()()
// , ,
I
JAB ABDI IJDI DIJ==
Kẻ
()
,HD I J H IJ^Î
Ta có:

a
IH 1 3
4
cosDIJ .
DI 6
a3 23
2
Ví dụ 2: Cho hình lập phương ABCD.A’B’C’D’. Xác định Góc tạo bởi hai đường thẳng BD và
CD’.
Hướng dẫn giải
Do
BAʹ// CDʹ
nên góc giữa BD và CD’ là góc giữa BD và BA’
Mà
AʹBD
là tam giác đều nên góc giữa BD và BA’ là
o
60 .
Vậy góc giữa BD và CD’ là
o
60 .
Ví dụ 3: Cho hình chóp S.ABC có
 SA SB SC AC AB a
và
BC a 2.
Xác định góc giữa
hai đường thẳng CS và AB.
Hướng dẫn giải
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 724
Trước hết ta tính góc giữa hai vectơ

SC
và

AB
Từ giả thiết suy ra
ABC
vuông cân tại A
Ta có:



  
 

   
SA AC .AB
SC.AB
cos SC ,AB
SC . AB SC . AB



 
2
2
a
SA.AB 0 a.a.cos120 1
2
a.a 2
a
SC . AB
Suy ra:

SC,AB 120 .
 
Vậy góc giữa hai đường thẳng SC và AB bằng
60 .
Ví dụ 4: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC và AD. Cho biết
AB CD 2a
và
MN a 3
. Xác định góc tạo bởi hai đường thẳng AB và CD
Hướng dẫn giải
Gọi I là trung điểm của AC ta có:
IM IN a
Áp dụng định lí côsin trong
IMN

222
MN IM IN 2IM.INcosMIN
222
3a a a 2a.acosMIN
1
cosM IN
2


Suy ra:
MIN 120
Vậy:


AB,CD IM,IN 180 120 60 .
Dạng 2. Chứng minh hai đường thẳng vuông góc trong không gian
1. Phương pháp
Cách 1: Dùng định nghĩa:

0
ab a,b 90
Cách 2: Dùng định lí:
b//c
ab
ac

Cách 3: Sử dụng tích vô hướng: ab a.b0

Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 725
2. .Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Cho hình chóp S.ABC có SA=SB=SC và
ASB BSC CSA
. Chứng minh rằng:
SA BC,SB AC,SC AB
Hướng dẫn

Chöùng minh: SA BC
Xeùt: SA.BC SA. SC SB SA.SC SA.SC
SA . SC cosASC SA . SB cosASB 0 SA BC


  

Ví dụ 2. Cho tứ diện ABCD đều. Gọi G là trọng tâm của tam giác BCD.
a) Chứng minh
AG CD
b) Gọi M là trung điểm của CD. Tính góc giữa AC và BM.
Hướng dẫn
a) Đặt
AB b; AC c; AD d
  
Chứng minh :
AG CD AG.CD 0
   
Với

11
AG AB AC AD b c d
33
CD AD AC d c


  
  
Từ đó:
AG.CD 0
 
b) Ta có:

AC.BM
cos AC,BM
AC . BM
 
 
Với
 
2
1a
AC.BM AC. AM AB AC.AM AC.AB AC. AC AD AC.AB
24

       
   
2
a3
AC . BM
2
 
C. BÀI TẬP TRẮC NGHIỆM
Câu 1: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Góc giữa hai đường thẳng và bằng góc giữa hai đường thẳng và khi song
song với (hoặc trùng với ).
B. Góc giữa hai đường thẳng và bằng góc giữa hai đường thẳng và thì song
song với .
C. Góc giữa hai đường thẳng là góc nhọn.
D. Góc giữa hai đường thẳng bằng góc giữa hai véctơ chỉ phương của hai đường thẳng
đó.
Lờ
i giải
a
b
ac
b
c
b
c
a
b
ac
b
c
d
c
b
G
A
B
C
D
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 726
Chọn A
A đúng theo định nghĩa.
B sai vì có thể
b
và c chéo nhau.
C sai vì có thể là góc vuông.
D sai. Nếu góc giữa hai vectơ chỉ phương là
a
với
00
090a££
thì góc giữa hai đường
thẳng bằng
a
, nếu góc giữa hai vectơ chỉ phương là
a
với
00
90 180a<£ thì góc giữa hai
đường thẳng bằng
0
180 .a-
Câu 2: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
B. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì
song song với đường thẳng còn lại.
C. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc
với đường thẳng kia.
Lời giải
Chọn D
Câu 3: Cho hai đường thẳng phân biệt và mặt phẳng , trong đó. Mệnh đề nào sau
đây là sai?
A. Nếu thì . B. Nếu thì .
C. Nếu thì . D. Nếu thì .
Lời giải
Chọn D
Vì
b
có thể nằm trong mặt phẳng
(
)
P
.
Câu 4: Cho hình lập phương . Hãy xác định góc giữa cặp vectơ và ?
A. B. C. D.
Lời giải
Chọn B
, ab
(
)
P
(
)
aP^
()
bP^
//ba
(
)
//bP
ba^
//ba
()
bP^
ba^
(
)
//bP
.
A
BC D EFGH
AB

D
H

0
45 .
0
90 .
0
120 .
0
60 .
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 727
Vì
DH AE=


(
A
DHE là hình vuông) nên
()()
0
,, 90AB DH AB AE BAE===
 
(
A
BFE là hình
vuông).
Câu 5: Cho hình lập phương . Hãy xác định góc giữa cặp vectơ và ?
A. B. C. D.
Lời giải
Chọn C
Vì
EG
A
C=


(
A
EGC
là hình chữ nhật) nên
()()
0
,, 45AB EG AB AC BAC===
  
(
A
BCD
là
hình vuông).
Câu 6: Cho hình lập phương . Góc giữa và là:
A. B. C. D.
Lời giải
Chọn C
A
B
C
D
F
H
G
E
.
A
BC D EFGH
AB

EG

0
90 .
0
60 .
0
45 .
0
120 .
E
G
H
F
D
C
B
A
.''' '
A
BC D A B C D
A
C
'D
A
0
45 .
0
90 .
0
60 .
0
120 .
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 728
Gọi
a là độ dài cạnh hình lập phương. Khi đó, tam giác
'
A
BC
đều (
'2' BCAB CA a===
) do đó
0
'60BCA=
.
Lại có,
'
D
A song song
'CB
nên
()()
0
,' ,' ' .60AC DA AC CB ACB ===
Câu 7: Cho hình hộp . Giả sử tam giác và đều có ba góc nhọn.
Góc giữa hai đường thẳng và là góc nào sau đây?
A. B. C. D.
Lời giải
Chọn B
Ta có
''AC A C
(
''
A
BCD
là hình bình hành) mà
''
D
AC nhọn nên
()( )
,,'''' ''.AC A D A C A DADC==
Câu 8: Cho hình lập phương . Chọn khẳng định sai?
A. Góc giữa và bằng B. Góc giữa và bằng
C. Góc giữa và bằng D. Góc giữa và bằng
Lời giải
Chọn B
A
B
C
D
B
'
D
'
C'
A
'
''''.ABAB CDDC '
A
BC ''
A
DC
A
C
'
A
D
'.
A
BC
''.
D
AC
'.BB D
'.BD B
D
'
C'
B
'
A
'
D
C
B
A
.''' '
A
BC D A B C D
A
C
''
B
D
0
90 . ' '
B
D '
A
A
0
60 .
A
D
'BC
0
45 .
B
D
''
A
C
0
90 .
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 729
Ta có
()()
0
', ' ' ', ' ' ' 90 .AA B BB B BB CDD ===
Khẳng định B sai.
Câu 9: Cho tứ diện đều Số đo góc giữa hai đường thẳng và bằng:
A. B. C. D.
Lời giải
Chọn C
Gọi
M
là trung điểm của
CD
.
Ta có
.0CD AM =

và .0CD MB =
 
.
Do đó
()
.. . .0CD AB CD AM MB CD AM CD MB++===
     
.
Suy ra
A
BCD^

nên số đo góc giữa hai đường thẳng
A
B và
CD
bằng
0
90 .
Câu 10: Cho tứ diện đều cạnh bằng . Gọi là tâm đường tròn ngoại tiếp tam giác .
Góc giữa và bằng bao nhiêu?
A. B. C. D.
Lời giải
Chọn C
A
'
C'
D
'
B
'
D
C
B
A
.
A
BC D
A
B
CD
0
60 .
0
30 .
0
90 .
0
45 .
C
B
D
M
A
A
BC D
a
OBCD
A
OCD
0
0.
0
30 .
0
90 .
0
60 .
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 730
Gọi
M
là trung điểm của
CD
.
Vì
A
BCD
là tứ diện đều nên
,.CD O DAMMC^^
Ta có
()
.. . .0.CD AO CD AM MO CD AM CD MO=+ +==
  
Suy ra
A
OCD^
 
nên số đo góc giữa hai đường thẳng
A
O
và
CD
bằng
0
90 .
Câu 11: Cho tứ diện đều , là trung điểm của cạnh . Khi đó bằng:
A. B. C. D.
Lời giải
Chọn B
Giả sử cạnh của tứ diện là
a .
Tam giác
BCD
đều
3
2
a
DM=
.
Tam giác
A
BC
đều
3
2
a
AM=
.
Ta có:
()
..
cos ,
3
.
.
2
AB DM AB DM
AB DM
a
AB DM
a
==
  
 
 
O
D
A
C
M
B
A
BC D
M
BC
()
cos ,
A
BDM
2
.
2
3
.
6
1
.
2
3
.
2
M
B
D
C
A
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 731
Mặt khác:
()
...
A
BDM ABAMAD ABAMABAD=-=-
      
() ()
22 2
. .cos . . .cos .
..cos30 ..cos60
33 13
.. ..
22 2 4 2 4
AB AM AB AM AB AD AB AD
AB AM AB AD
aaaa
aaa
=-
=-
=-=-=
    
 
() ()
()()
33
0,cos ,
6
os
6
,c,AB DM AB DM AB DMAB DM=> = =
  
.
Câu 12: Cho tứ diện có và . Hãy xác định góc giữa cặp
vectơ và ?
A. B. C. D.
Lời giải
Chọn D
Ta có
()
.. ..
A
BCD ABADAC ABADABAC=-=-
     
() ()
. .cos . . .cos .
..cos60 ..cos60.
AB AD AB AD AB AC AB AC
AB AD AB AC
=-
=-
       
   
Mà
.0AC AD ABCD= =

()
,90AB CD=

.
Câu 13: Cho hình chóp có và . Hãy xác định góc giữa cặp
vectơ và ?
A. B. C. D.
Lời giải
Chọn D
A
BC D
A
BACAD==
60BAC B AD==
AB

CD

60 . 45 . 120 . 90 .
C
D
B
A
.S ABC SA SB S C==
A
SB BSC CSA==
SC

AB

120 . 45 . 60 . 90 .
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 732
Ta có
()
.. ..SC AB SC SB SA SC SB SC SA=-=-
      
() ()
. .cos . . .cos .
..cos ..cos .
SC SB SC SB SC SA SC SA
SC SB BSC SC SA ASC
=-
=-
  
Mà
SA SB SC==
và
BSC ASC= .0SC A B=

.
Do đó
()
,90SC AB =

.
Câu 14: Cho hình chóp có và . Tính số đo của góc giữa hai đường thẳng
chéo nhau và
A. B. C. D.
Lời giải
Chọn D
Xét
()
.. ..SC AB CS CB CA CS CA CS CB=- - = -
     
222 222
..cos ..cos
.. ..
2. 2.
CS CA SCA CS CB SCB
SC CA SA SC CB SB
CS CA CS CB
SC CA SC CB
=-
+- +-
=-
222 222
0
22
SC CA SA SC CB SB+- +-
=-=
(do
SA SB=
và
CA CB=
)
Vậy
SC AB^
.
A
C
B
S
.S ABC SA SB= CA CB=
SC .
A
B
0
30 .
0
45 .
0
60 .
0
90 .
C
B
A
S
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 733
Câu 15: Cho hình chóp có và . Tính số đo của góc giữa hai đường
thẳng chéo nhau và
A. B. C. D.
Lời giải
Chọn D
Xét
()
.. ..SA BC SA SC SB SA SC SA SB=-=-
      
()
. .cos , . .cosSA SC SA SC SA SB SA B=-
   
..cos ..cos .SA SC ASC SA SB ASB=-
()
1
Ta có
()
chung
SA
AB AC SAB SAC c g c
SAB SAC
ì
ï
ï
ï
ï
=D=D --
í
ï
ï
ï
=
ï
î
.
Suy ra
SC SB
ASC ASB
ì
=
ï
ï
í
ï
=
ï
î
.
(
)
2
Từ
()
1
và
(
)
2
, suy ra
.0SA BC =

. Vậy
SA BC^
.
Câu 16: Cho tứ diện có , , . Gọi là góc giữa và
. Chọn khẳng định đúng?
A. B. C. D.
Lời giải
Chọn D
.SABC
A
BAC=
SAC SA B=
SA .BC
0
30 .
0
45 .
0
60 .
0
90 .
A
B
C
S
M
A
BC D
3
2
A
CAD=
60CAB DAB==
CD AD=
j
A
B
CD
4
os c
3
.j =
60 .j = 30 .j =
4
os c
1
.j =
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 734
Ta có
()
..
cos ,
.
.
A
BCD ABCD
AB CD
AB
A
CD
BCD
==


Mặt khác
()
...
A
BCD ABADAC ABADABAC=-=-
     
() ()
. .cos . . .cos .
..cos60 ..cos60
1311 1
.. . . . ..
2224 4
AB AD AB AD AB AC AB AC
AB AD AB AC
AB AD AB AD AB AD ABCD
=-
=-
=- =-=-
    
Do có
()
1
.
1
4
cos ,
.4
A
AB
BCD
AB CD
CD
-
==
.
Vậy
cos
1
4
j =
.
Câu 17: Cho tứ diện có và , . Gọi và lần
lượt là trung điểm của và . Hãy xác định góc giữa cặp vectơ và ?
A. B. C. D.
Lời giải
Chọn B
C
D
B
A
A
BC D
A
BACAD==
60BAC B AD==
90CAD =
I
J
A
B
CD
AB

I
J
120 . 90 . 60 . 45 .
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 735
Xét tam giác
ICD
có
J
là trung điểm đoạn
CD
()
1
.
2
I
JICID= +

Tam giác
A
BC
có
A
BAC=
và
0
60BA C =
A
BCD
đều
CI AB^
.
Tương tự, ta có
A
BDD
đều nên
D
IAB^ .
Ta có
()
111
....0
222
IJ AB I C ID AB IC AB ID AB=+ = + =

()
,90IJ AB AB IJ^ =
 
.
Câu 18: Cho tứ diện có . Gọi lần lượt là trung điểm của .
Góc bằng
A. B. C. D.
Lời giải
Chọn D
J
I
B
D
C
A
A
BC D
A
BCD=
,,,IJEF ,,,
A
CBCBDAD
()
,IE JF
30 . 45 . 60 . 90 .
J
E
I
F
B
D
C
A
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 736
Ta có
I
F là đường trung bình của
A
CDD
1
2
IF CD
I
FCD
ì
ï
ï
ï
í
ï
=
ï
ï
î
.
Lại có
J
E
là đường trung bình của
BCDD
1
2
JE CD
J
ECD
ì
ï
ï
ï
í
ï
=
ï
ï
î
.
IF JE
IF JE
ì
=
ï
ï
í
ï
ï
î
Tứ giác
IJEF
là hình bình hành.
Mặt khác:
1
2
1
2
IJ AB
J
ECD
ì
ï
ï
=
ï
ï
ï
í
ï
ï
=
ï
ï
ï
î
. Mà
J
BEACDIJ==
.
Do đó
IJEF
là hình thoi. Suy ra
()
90,IE JF =
.
Câu 19: Cho hình chóp có đáy là hình vuông cạnh bằng và các cạnh bên đều
bằng . Gọi và lần lượt là trung điểm của và . Số đo của góc
bằng
A. B. C. D.
Lời giải
Chọn C
Do
A
BCD
là hình vuông cạnh a 2AC a= .
22 2 2
2
A
C a SA SC==+
SACD
vuông tại
S
.
Từ giả thiết ta có
M
N
là đường trung bình của
D
SAD
1
2
NM SA=

Khi đó
1
..0
2
NM SC SA SC==
 
()
,90MN SC M N SC^ =
.
Câu 20: Cho hình chóp có tất cả các cạnh đều bằng . Gọi và lần lượt là trung
điểm của và . Số đo của góc bằng:
.SABCD
A
BC D
a
a
M
N
A
D
SD
()
,
M
NSC
45 . 30 . 90 . 60 .
M
N
D
B
C
A
S
.SABCD
a
I
J
SC BC
()
,IJ CD
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 737
A. B. C. D.
Lời giải
Chọn D
Gọi
O
là tâm của hình thoi
ABCD OJ
là đường trung bình của
.BCDD
Suy ra
1
2
OJ CD
OJ CD
ì
ï
ï
ï
í
ï
=
ï
ï
î
.
Vì
()()
,,CD OJ IJ CD IJ OJ=
.
Xét tam giác
I
OJ
, có
1
22
1
22
1
22
a
IJ SB
a
OJ CD
a
IO S A
ì
ï
ï
==
ï
ï
ï
ï
ï
ï
==
í
ï
ï
ï
ï
ï
==
ï
ï
ï
î
IOJD
đều.
Vậy
()()
,, 60IJ CD IJ OJ IJO===
.
Câu 21: Cho hình chóp có cạnh , tất cả các cạnh còn lại đều bằng . Tính số đo
của góc giữa hai đường thẳng và
A. B. C. D.
Lời giải
Chọn D
Theo giả thiết, ta có
A
BBCCDDAa====
nên
A
BCD
là hình thoi cạnh a .
Gọi
OACBD=Ç
. Ta có
()
CBD SBD c c cD=D --
.
Suy ra hai đường trung tuyến tương ứng
CO
và
SO
bằng nhau.
Xét tam giác
SAC
, ta có
1
2
SO CO AC==
.
90 . 45 . 30 . 60 .
J
I
O
C
B
D
A
S
.SABCD SA x=
a
SA .SC
0
30 .
0
45 .
0
60 .
0
90 .
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 738
Do đó tam giác
SAC
vuông tại
S
(tam giác có đường trung tuyến bằng nửa cạnh đáy).
Vậy
SA SC^
.
Câu 22: Cho hình lập phương có cạnh bằng . Tính
A. B. C. D.
Lời giải
Chọn B
Ta có
...
A
BEG ABAC=
  
Mặt khác
A
CABAD=+
 
.
Suy ra
()
2
.. .
A
BEG ABAC AB AB AD AB ABAD==+=+
  
.
Vì
A
BCD
là hình vuông .0AB AD AB AD^ =
 
2
22
.0.
A
BABADAB a+ =+=
 
Câu 23: Cho hình lập phương có cạnh . Gọi là trung điểm . Giá trị
là:
A. B. C. D.
Lời giải
Chọn A
.
A
BC D EFGH
a ..
A
BEG

2
3.a
2
.a
2
2
.
2
a
2
2.a
G
F
H
B
D
C
A
E
111 1
.ABCD A BC D
a
M
A
D
11
.
B
MBD
 
2
1
.
2
a
2
.a
2
3
.
4
a
2
2.a
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 739
Ta có
()()
111 1
.
B
MBD BBBAAMBAADDD=++ ++
    
2
1111
0
00
.. . .
B
BBA BBAD BBDD BA BAAD
=
==
=+ + ++
      

 
1
0
.BA DD
=
+

 
1
0
0
.. .
A
MBA AMAD AMDD
=
=
++ +
   


2
11
..
B
BDD BA AM AD=++
   
22
22
22
aa
aa=- + + =
.
Câu 24: Cho tứ diện có . Gọi lần lượt là trung điểm của và
. Biết vuông góc với . Tính .
A. B. C. D.
Lời giải
Chọn B
D
1
C
1
B
1
A
1
M
B
A
C
D
A
BC D
, 3
A
CaBD a==
,
M
N
A
D
BC
A
C
B
D
M
N
6
.
3
a
MN =
10
.
2
a
MN =
23
.
3
a
MN =
32
.
2
a
MN =
3a
a
P
N
M
B
D
C
A
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 740
Gọi
P
là trung điểm của
A
B
,PN PM
lần lượt là đường trung bình của tam giác
A
BCD
và
A
BDD
. Suy ra
1
22
.
13
22
a
PN AC
a
PM BD
ì
ï
ï
==
ï
ï
ï
í
ï
ï
==
ï
ï
ï
î
Ta có
A
CBD PN PM^^
hay tam giác
P
MND
vuông tại
P
Do đó
22
22
910
.
44 2
aaa
MN PN PM=+=+=
Câu 25: Cho tứ diện có vuông góc với . Mặt phẳng song song với và
lần lượt cắt tại . Tứ giác là hình gì?
A. Hình thang. B. Hình bình hành.
C. Hình chữ nhật. D. Tứ giác không phải hình thang.
Lời giải
Chọn C
Ta có
()
()()
//
// .
MNPQ AB
M
QAB
MNPQ ABC MQ
ì
ï
ï
í
ï
Ç=
ï
î
Tương tự ta có
// , // , // D
M
NCDNPABQPC
.
Do đó tứ giác
M
NPQ
là hình bình hành
Lại có
()
M
NMQdoABCD^^
.
Vậy tứ giác
M
NPQ
là hình chữ nhật.
Câu 26: Trong không gian cho hai tam giác đều và có chung cạnh và nằm trong
hai mặt phẳng khác nhau. Gọi lần lượt là trung điểm của các cạnh
và . Tứ giác là hình gì?
A. Hình bình hành. B. Hình chữ nhật. C. Hình vuông. D. Hình thang.
Lời giải
Chọn B
A
BC D
A
B
CD
(
)
P
A
B
CD
, , , BC DB AD AC , , ,
M
NPQ
M
NPQ
P
N
Q
A
C
D
B
M
A
BC
A
BC
¢
A
B
, , ,
M
NPQ
, , AC CB BC
¢
CA
¢
M
NPQ
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 741
Vì
, , ,
M
NPQ
lần lượt là trung điểm của các cạnh , , AC CB BC
¢
và
CA
¢
1
2
// //
P
QMN AB
P
QABMN
ì
ï
ï
==
ï
í
ï
ï
ï
î
M
NPQ
là hình bình hành.
Gọi
H
là trung điểm của
A
B . Vì hai tam giác
A
BC
và
A
BC
¢
đều nên
.
CH AB
CH AB
ì
^
ï
ï
í
ï
¢
^
ï
î
Suy ra
()
A
BCHC
¢
^
. Do đó
A
BCC
¢
^ .
Ta có
//
//
PQ AB
P
NCC PQPN
AB CC
ì
ï
ï
ï
ï
¢
^
í
ï
ï
¢
ï
^
ï
î
.
Vậy tứ giác
M
NPQ
là hình chữ nhật.
Câu 27: Cho tứ diện trong đó , góc giữa và là và điểm trên
sao cho . Mặt phẳng qua song song với và cắt
lần lượt tại . Diện tích bằng:
A. B. C. D.
Lời giải
Chọn C
H
N
M
Q
P
A
C
B
C'
A
BC D
6, 3AB CD==
A
B
CD
60
M
BC
2BM MC=
(
)
P
M
A
B
CD
,,BD AD AC ,,
M
NQ
M
NPQ
22. 3. 23.
3
.
2
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 742
Ta có
()
()()
//
// .
MNPQ AB
M
QAB
MNPQ ABC MQ
ì
ï
ï
í
ï
Ç=
ï
î
Tương tự ta có
// , // , // D
M
NCDNPABQPC
.
Do đó tứ giác
M
NPQ
là hình bình hành
Ta có
()
()
0
;;60AB CD QM MP==
. Suy ra
0
..sin60.
MNPQ
SQMQN=
Ta có
1
2.
3
CM MQ
CMQ CBA MQ
CB AB
DD===
∽
2
2.
3
AQ QN
AQN ACD QN
AC CD
DD===
∽
Vậy
0
3
..sin60 2.2. 23.
2
MNPQ
SQMQN===
Câu 28: Cho tứ diện có vuông góc với , . là điểm thuộc cạnh
sao cho . Mặt phẳng đi qua song song với và . Diện tích
thiết diện của với tứ diện là:
A. B. C. D.
Lời giải
Chọn D
3
6
P
N
Q
B
D
C
A
M
A
BC D
A
B
CD
4, 6AB CD==
M
BC
2
M
CBM=
(
)
P
M
A
B
CD
(
)
P
5.
6.
17
.
3
16
.
3
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 743
Ta có
()
()()
//
// .
MNPQ AB
M
NAB
MNPQ ABC MN
ì
ï
ï
í
ï
Ç=
ï
î
Tương tự ta có
// , // , //
M
QCDNPCDQPAB
. Do đó tứ giác
M
NPQ
là hình bình hành
Ta có
()
()
0
;; 90AB CD MN MQ NMQ===
tứ giác
M
NPQ
là hình chữ nhật.
Lại có
14
;
33
CM MN
CMN CBA MN
CB AB
DD===
∽
2
4.
3
AN NP
ANP ACD MP
AC CD
DD===
∽
Vậy
16
..
3
MNPQ
SMNNP==
Câu 29: Cho tứ diện có vuông góc với , . là điểm thuộc cạnh
sao cho . Mặt phẳng song song với và lần lượt cắt
tại . Diện tích lớn nhất của tứ giác bằng bao nhiêu?
A. B. C. D.
Lời giải
Chọn A
4
6
P
Q
N
A
C
D
B
M
A
BC D
A
B
CD
6AB CD==
M
BC
()
. 0 1MC x BC x=<<
(
)
P
A
B
CD
,,,
B
CDBADAC ,,,
M
NPQ
9. 11. 10. 8.
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 744
Xét tứ giác
M
NPQ
có
// //
// //
M
QNPAB
M
NPQCD
ì
ï
ï
í
ï
ï
î
M
NPQ
là hình bình hành.
Mặt khác,
A
BCD MQMN^ ^
. Do đó,
M
NPQ
là hình chữ nhật.
Vì
//
M
QAB
nên
.6
MQ CM
x
MQ x AB x
AB CB
=== =
.
Theo giả thiết
()
.1
M
C x BC BM x BC==-
.
Vì
//
M
NCD
nên
() ()
11.61
MN BM
x
MN x CD x
CD BC
==-=- =-
.
Diên tích hình chữ nhật
M
NPQ
là
() ()
2
1
. 6 1 .6 36. . 1 36 9
2
MNPQ
xx
SMNMQ xxxx
æö
+-
÷
ç
==-=-£ =
÷
ç
÷
ç
èø
.
Ta có
9
MNPQ
S =
khi
1
1
2
xxx=- =
.
Vậy diện tích tứ giác
M
NPQ
lớn nhất bằng 9 khi
M
là trung điểm của
BC
.
Câu 30: Trong không gian cho tam giác . Tìm sao cho giá trị của biểu thức
đạt giá trị nhỏ nhất.
A. là trọng tâm tam giác .
B. là tâm đường tròn ngoại tiếp tam giác .
C. là trực tâm tam giác .
D. là tâm đường tròn nội tiếp tam giác .
Lời giải
Chọn A
Gọi
G
là trọng tâm tam giác
A
BC G
cố định và 0.GA GB GC++ =

6
6
P
N
Q
B
A
C
D
M
A
BC
M
222
PMA MB MC=++
M
A
BC
M
A
BC
M
A
BC
M
A
BC
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 745
()()()
22 2
PMGGA MGGB MGGC=+++++

()
2222
32.
M
GMGGAGBGCGAGBGC=+ +++++

2222222
3.
M
GGAGBGCGAGBGC=+++³++
Dấu bằng xảy ra
.
M
Gº
Vậy
22 2
min
P
GA GB GC=++ với
M
Gº
là trọng tâm tam giác
.
A
BC
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 746
BÀI 3. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẢNG
A. KIẾN THỨC CƠ BẢN CẦN NẮM
1. Định nghĩa
Đường thẳng được gọi là vuông góc với mặt phẳng
nếu vuông góc với mọi đường thẳng nằm trong mặt
phẳng
Kí hiệu
2. Điều kiện để đường thẳng vuông góc với mặt phẳng
Định lí
Nếu một đường thẳng vuông góc với hai đường th
ẳng cắt nhau cùng thuộc một mặt
phẳng thì nó vuông góc với mặt phẳng ấy.
Hệ quả
Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì nó cũng vuông góc
với cạnh thứ ba của tam giác đó.
3. Tính chất
Tính chất 1
Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường
thẳng cho trước.
Mặt phẳng trung trực củ
a một đoạn thẳng
Người ta gọi mặt phẳng đi qua trung điểm của đoạn thẳng và vuông góc với là
mặt phẳng trung trực của đoạn thẳng
Tính chất 2
Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt
phẳng cho trước.
d
()
a
d
a
()
.a
()
.d a^
d
a
α
α
d
O
I
A
B
A
B
.
A
B
d
α
O
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 747
4. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng.
Tính chất 1
Cho hai đường thẳng song song. Mặt phẳng nào vuông góc với đường thẳng này thì cũng
vuông góc với đường thẳng kia.
Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
Tính chất 2
Cho hai mặt phẳng song song. Đường thẳng nào vuông góc với mặt phẳng này thì cũng
vuông góc với mặt phẳng kia.
Hai mặt phẳng phân biệt cùng vuông góc với m
ột đường thẳng thì song song với nhau.
Tính chất 3
Cho đường thẳng và mặt phẳng song song với nhau. Đường thẳng nào vuông góc
với thì cũng vuông góc với
Nếu một đường thẳng và một mặt phẳng (không chứa đường thẳng đó) cùng vuông góc
với một đường thẳng khác thì chúng song song với nhau.
5. Định lí ba đường vuông góc
Định nghĩa
Phép chiếu song song lên mặt phẳng theo phương vuông góc tới mặt phẳng gọi
là phép chiếu vuông góc lên mặt phẳ
ng
a
α
b
a
β
α
a
()
a
()
a
.a
a
b
α
(
)
P
(
)
P
()
.
P
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 748
Định lí (Định lí 3 đường vuông góc)
Cho đường thẳng không vuông góc với mặt phẳng và
đường thẳng nằm trong mặt phẳng Khi đó điều kiện
cần và đủ để vuông góc với là vuông góc với hình
chiếu của trên
6. Góc giữa đường thẳng và mặt phẳng
Định nghĩa
Nếu đường thẳng thì ta nói góc giữa đường thẳng và mặt phẳng bằng
Nếu đường thẳng không vuông góc với
mặt phẳng thì góc giữ
a và hình
chiếu của nó trên gọi là góc giữa
đường thẳng và mặt phẳng
Chú ý: Nếu là góc giữa đường thẳng
và mặt phẳng thì ta luôn có
B. CÂU HỎI TRẮC NGHIỆM
Dạng 1.Câuhỏilýthuyết
1.Phươngpháp
Tacầnnắmvữngcáctínhchấtsau
Tínhchất1
a)Chohaiđườngthẳngsongsong.Mặtphẳngnàovuônggócvớiđườngthẳngnày
thìcũngvuônggócvớiđườngthẳngkia.
b)Haiđườngthẳngphânbiệtcùngvuônggócvớimộtmặtphẳngthìsongsongvới
nhau.
Tínhchất2
a)Chohaimặtphẳngsongsong.Đườngthẳngnàovuônggócvớimặtphẳngnàythì
cũngvuônggócvớimặtphẳngkia.
b)Haimặtphẳngphânbiệtcùngvuônggócvớimộtđườngthẳngthìsongsongvới
nhau.
Tínhchất3
a
(
)
P
b
()
.
P
b
a
b
a
¢
a
()
.
P
b
a
b
a'
b
a'
a
P
(
)
aP^
a
(
)
P
0
90 .
a
(
)
P
a
a
¢
(
)
P
a
()
.
P
j
d
()
a
00
090.j££
φ
P
a
a'
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 749
a)Chođườngthẳngavàmặtphẳng(α)songsongvớinhau.Đườngthẳngnào
vuônggócvới(α)thìcũngvuônggócvớia.
b)Nếumộtđườngthẳngvàmộtmặtphẳng(khôngchứađườngthẳngđó)cùng
vuônggócvớimộtđườngthẳngkhácthìchúngsongsong
vớinhau.
2.Cácvídụrènluyệnkĩnăng
Vídụ1:Chohaiđườngthẳnga,bvàhaimặtphẳng(P),(Q).Mệnhđềnàosauđâyđúng?
A.



a//b
Pb.
Pa
B.



ab
Pa.
b// P
C.


ab
P//a.
bP
D.


aQ
P//Q.
bP
Hướng dẫn giải
ĐÁPÁNA



a//b
Pb
Pa
làmệnhđềđúng.Nghĩalà,chohaiđườngthẳngsongsong, mặt
phẳngnàovuônggócvớiđườngthẳngnàysẽvuônggócvớiđườngthẳngkia.
Vídụ2:Chohaiđườngthẳnga,bvàhaimặt
phẳng(P),(Q).Mệnhđềnàosauđâyđúng?
A.


aP
a//b.
bP
B.



aP
b
Pa//b.
ab
C.



P//Q
a// Q .
aP
 D.


a// P
a// Q .
PQ
Hướng dẫn giải
ĐÁPÁNB
MệnhđềAsai.Vìkhiđóhaiđườngthẳngavàbcóthểsongsonghoặctrùngnhau.
MệnhđềAchỉđúngkhiavàbphânbiệt.
MệnhđềBđúng.Thậtvậ
y,tathấy:
+NếuacắtbtạiM.Nhưvậy,quađiểmMtavẽđượchaiđườngthẳngavàbcùng
vuônggócvới(P):Vôlí.Vậyakhôngcắtb.
+Nếuachéo
b.LấyđiểmNtrêna.QuaNvẽđườngthẳng
b
ʹ// b.
Do

b
P nên

b
ʹ P.NhưvậytừđiểmNtacóhaiđườngthẳngavàb’cùng
vuônggócvới(P):Vôlí.Vậyavàbkhôngchéonhau.
+Trườnghợpatrùngbkhôngxảyravì
ab(giảthiết).
Vậy
a//b.
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 750
MệnhđềCsai.Mệnhđềđúnglà
aQ.
MệnhđềDsai.Vìlúcnàyacóthểsongsonghoặcchứatrong(Q).
Vídụ3:Chohaiđườngthẳnga,bvàhaimặtphẳng(P),(Q).Mệnhđềnàosauđâyđúng?
A.



ab
ac b//P.
cP
B.

aP
b
// P .
ab
C.



b
// P
aP
.
b
P
ab
D.


aP
P//Q.
a// Q
Hướng dẫn giải
ĐÁPÁNC
Asai:Lúcnàybcóthểchứatrong,hoặccắt,hoặcsongsongvới(P).Mệnhđềchỉđúng
khi

aP.
Bsai:Vìlúcnàybcóthểchứatrong(P).Mệnhđềchỉđúngkhi
b
P.
Dsai:Thậtvậy,nếu

P//Qhoặc
PQthìdo
aPnên
aQ:Vôlí(Tráivới
giảthiết

a// Q
).
Vídụ4:Cho



a, b,c
ca,cb
.Mệnhđềnàosauđâyđúng?
A.acắtb. B.
a//b.
 C.
ab.

 D.
a//b
.
ab
Hướng dẫn giải
ĐÁPÁND
Vìa,b,cđồngphẳngvà
ca,cb
nên
a//b
hoặc
ab.
Vídụ5:Cho




a, b
c//
ca,cb
.Mệnhđềnàosauđâyđúng?
A.acắtb. B.
a//b. C.
a//b
.
ab

D.
ab.
Hướng dẫn giải
ĐÁPÁNC
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 751
Vídụ6:Cho


a, b
c
ca,cb


caét
.Mệnhđềnàosauđâyđúng?
A.acắtb. B.
a//b. C.
a//b
ab
.
D.
ab.
Hướng dẫn giải
ĐÁPÁNC
3.Bàitậptrắcng hiệm
Câu 1: Khẳng định nào sau đây sai?
A. Nếu đường thẳng vuông góc với hai đường thẳng cắt nhau nằm trong thì
vuông góc với bất kì đường thẳng nào nằm trong
B. Nếu đường thẳng thì vuông góc với hai đường thẳng trong
C. Nếu đường thẳng vuông góc với hai đường thẳng nằm trong thì
D. Nếu và đường thẳng thì
Lời giải
Chọn C
Mệnh đề C sai vì thiếu điều ki
ện '' cắt nhau '' của hai đường thẳng nằm trong
()
.a
Ví dụ:
đường thẳng
a vuông góc với hai đường thẳng
b
và nằm trong nhưng và
song song với nhau thì khi đó chưa chắc vuông góc với
Câu 2: Trong không gian cho đường thẳng không nằm trong mặt phẳng , đường thẳng
được gọi là vuông góc với mp nếu:
A. vuông góc với hai đường thẳng phân biệt nằm trong mp
B. vuông góc với đường thẳng mà song song với mp
C. vuông góc với đường thẳng nằm trong mp
D. vuông góc với mọi đường thẳng nằm trong mp
Lời giải
d
()
a
d
()
.a
(
)
d a^
d
()
.a
d
()
a
()
.d a^
(
)
d a^
()
a a
.da^
c
()
a
b c
a
()
.a
D
(
)
P
D
(
)
P
()
.
P
aa
()
.
P
a
()
.
P
()
.
P
c
b
a
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 752
Chọn D
Đường thẳng
D
được gọi là vuông góc với mặt phẳng
()
P
nếu
D
vuông góc với mọi
đường thẳng trong mặt phẳng
()
P
.(Định nghĩa đường thẳng vuông góc với mặt phẳng).
Câu 3: Mệnh đề nào sau đây sai?
A. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song.
C. Một đường thẳng và một mặt phẳng (không chứa đường thẳng đã cho) cùng vuông
góc với một đường thẳng thì song song nhau.
D. Hai đường thẳng phân biệt cùng vuông góc với mộ
t mặt phẳng thì song song.
Lời giải
Chọn B
Mệnh đề ở câu B sai vì: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng
thì có thể cắt nhau, chéo nhau.
Câu 4: Cho hai đường thẳng phân biệt và mặt phẳng trong đó Chọn mệnh đề
sai trong các mệnh đề sau?
A. Nếu thì B. Nếu thì
C. Nếu thì D. Nếu thì
Lời giải
Chọn D
`Mệnh đề D sai vì
b
có thể nằm trong
(
)
P
.
Câu 5: Cho hai đường thẳng và mặt phẳng . Chỉ ra mệnh đề đúng trong các mệnh đề
sau:
A. Nếu và thì . B. Nếu và thì .
, ab
()
,
P
()
.aP^
()
bP^
.ab
ba
()
.bP^
()
bPÌ
.ba^ ab^
()
.bP
, ab
(
)
P
(
)
aP^
ba^
()
bP
(
)
aP
(
)
bP^
ab^
a
b
c
c
b
a
a
P
b
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 753
C. Nếu và thì . D. Nếu và thì .
Lời giải
Chọn B
Mệnh đề A sai vì
b
có thể nằm trong
()
P
.
Mệnh đề C sai vì
b
có thể cắt
(
)
P
hoặc
b
nằm trong
()
P
.
Mệnh đề D sai vì
b
có thể nằm trong
()
.
P
Câu 6: Cho là các đường thẳng trong không gian. Tìm mệnh đề sai trong các mệnh đề
sau:
A. Nếu và thì
B. Nếu vuông góc với mặt phẳng và thì
C. Nếu và thì
D. Nếu , và cắt thì vuông góc với mặt phẳng
Lời giải
Chọn D
Nếu
ab^
và
bc^
thì
ac
hoặc a cắt c hoặc a trùng c hoặc a chéo .c
()
aP
ba^
()
bP
(
)
aP
ba^
(
)
bP^
, , abc
ab^ bc^ .ac
a
()
a
()
b a
.ab^
ab
bc^
.ca^
ab^ bc^
ac
b
()
,.ac
a
P
b
a
a
b
b
P
P
a
b
P
b
b
b
a
a
c
c
P
P
P
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 754
Câu 7: Chỉ ra mệnh đề sai trong các mệnh đề sau:
A. Hai đường thẳng chéo nhau và vuông góc với nhau. Khi đó có một và chỉ một mặt
phẳng chứa đường thẳng này và vuông góc với đường thẳng kia.
B. Qua một điểm cho trước có một mặt phẳng duy nhất vuông góc với một đường
thẳng cho trước.
C. Qua một điểm cho trước có một và chỉ một đường thẳng vuông góc với mộ
t đường
thẳng cho trước.
D. Qua một điểm cho trước có một và chỉ một đường thẳng vuông góc với một mặt
phẳng cho trước.
Lời giải
Chọn C
Mệnh đề C sai vì qua một điểm
O
cho trước có vô số đường thẳng vuông góc với một
đường thẳng cho trước.
Câu 8: Trong các mệnh đề sau, mệnh đề nào sai?
A. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một đường
thẳng cho trước.
B. Có duy nhất một mặt phẳng đi qua một đường thẳng cho trước và vuông góc với một
mặt phẳng cho trước.
C. Có duy nhất một mặt ph
ẳng đi qua một điểm cho trước và vuông góc với một đường
thẳng cho trước.
D. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt
phẳng cho trước.
Lời giải
Chọn D
O
O
O
b
c
a
P
O
A
P
O
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 755
Qua một điểm cho trước có thể kẻ được vô số mặt phẳng vuông góc với mặt phẳng cho
trước.
Câu 9: Trong các mệnh đề sau đây, mệnh đề nào là đúng?
A. Nếu hai mặt phẳng vuông góc với nhau thì mọi đường thẳng thuộc mặt phẳng này sẽ
vuông góc với mặt phẳng kia.
B. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thứ ba thì song song với
nhau.
C. Vớ
i mỗi điểm và mỗi điểm thì ta có đường thẳng vuông góc với
giao tuyến của và
D. Nếu hai mặt phẳng và đều vuông góc với mặt phẳng thì giao tuyến của
và nếu có sẽ vuông góc với
Lời giải
Chọn D
Mệnh đề A sai vì nếu hai mặt phẳng vuông góc với nhau thì mọi đường thẳng thuộc mặt
phẳng này vuông góc với giao tuyến sẽ vuông góc với mặt phẳng kia.
Mệ
nh đề B sai vì còn trường hợp hai mặt phẳng cắt nhau.
Mệnh đề C sai vì đường thẳng
A
B có thể không vuông góc với giao tuyến.
Câu 10: Trong các mệnh đề sau mệnh đề nào đúng?
A. Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của
nó trên mặt phẳng đã cho.
B. Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và đường thẳng
với vuông góc với
C. Góc giữa đường thẳng và mặt phẳng bằng góc giữa đườ
ng thẳng và mặt
phẳng thì mặt phẳng song song với mặt phẳng .
(
)
A aÎ
()
B bÎ
A
B
d
()
a
()
.b
()
a
()
b
(
)
g
d
()
a
()
b
(
)
.g
b
b
()
.
P
a
(
)
P
a
(
)
Q
(
)
P
(
)
Q
Q
P
B
O C
A
A
P
R
Q
O
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 756
D. Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng và mặt
phẳng thì song song với .
Lời giải
Chọn A
Mệnh đề B sai vì hai góc này phụ nhau.
Mệnh đề C sai vì
()
P
có thể trùng
()
Q
.
Mệnh đề D sai vì
a có thể trùng
.b
Dạng2. Chứngminhđườngthẳngvuônggócvớimặtphẳng.Từđósuyrađường thẳng
vuônggóc vớiđườngthẳng
1.Phươngpháp
Đểchứngminhđườngthẳngvuônggócvớimặtphẳngtacóthểsửdụngmộtttrongcác
cáchsau
1.
ab()
ac() a()
bcA



(avuônggócvớihaiđườngthẳngcắtnhau)
2.
a//b
a()
b()


(asongsongvớimộtđườngthẳngbvuônggóc(P))
3.
a()
a()
()//()



4.
AB ( ) M | MA MB ,()
làmặtphăngtrungtrựccủaAB
5.
ABC ( )
MA MB MC MO ( )
OA OB OC



Đểchứngminhđườngthẳngvuônggócv ớiđườngthẳngngoài4cáchđãbiếtởbàihai
đườngthẳngvuônggóctacóthểmsửdụngthêmcáccáchsau
1.
a()
ab
b()



2.
a//( )
ab
b()


3.
a' hch (a)
ba ba'
b


4.
ABC,a AB
aBC
aAC


a
(
)
P
b
(
)
P
a
b
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 757
2.Cácvídụrènluyệnkĩnăng
Vídụ1:ChotứdiệnSABCcóSAvuônggócvớimặtphẳng(ABC).KẻBEvuônggócvới
AC

EAC.
Khiđó:
A.

BE SBC .

B.

BE SAB .
C.

BE SAC .

D.BElàđườngphângiáccủagóc
ABC
.
Hướng dẫn giải
ĐÁPÁNC
Do

SA BE, BE AC BE SAC .
Vídụ2:ChotamgiácABCvuôngtạiC.Kẻ

SA ABC , AE SC
và
AF SB
.Khiđó:
A.
AF// BC.
 B.

AE SBC .
C.

AF SBC .
 D

SB AEF .
Hướng dẫn giải
ĐÁPÁND
Tacó:
() ()
1
BC AC
BC SAC BC AE
BC SA
ì
ï
^
ï
^ ^
í
ï
^
ï
î
Theogiảthiết:
()
2SC AE^
Từ (1) và (2) suy ra
AE SB
mà

AF SB SB AEF .
Vídụ3:ChohìnhchópS.ABCDđáylàhìnhthoitâmOvà
SA SC
,
SB SD.

Khiđó:
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 758
A.SOlàđườngcaocủahìnhchóp.
B.TamgiácSBDvuôngcân.
C.TamgiácSACvuôngcân.
D.
1
SO BD.
2
Hướng dẫn giải
ĐÁPÁNA
Olàtâmhìnhthoi
OlàtrungđiểmcủaAC,BDmàmỗi
SAC, SBD
cân

  SO AC, SO BD SO ABCD
SOlàđườngcaohìnhchóp.
Lưuý:Tamgiác
SAC, SBD
chỉcânchứkhôngvuông
Vídụ4:ChohìnhchópS.ABCDcóđáyABCDlàhìnhthoitâmOvà
SA SC
,
SB SD.
Gọi
I,JtheothứtựlàtrungđiểmcủaABvàBCthì
A.

IJ SAD .

B.

IJ SCD .
C.

IJ SAC .

D.

IJ SBD .
Hướng dẫn giải
ĐÁPÁND
SAC , SBD
cân

SO ABCD
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 759




SO IJ
IJ// AC IJ BD
IJ SBD .
Vídụ5:ChohìnhchópS.ABCDđáyABCDlàhìnhvuôngcạnha,cạnhbên
SB b
vàtam
giácSACcântạiS.TrêncạnhABlấymộtđiểmMvới

AM x 0 x a
.Mặtphẳng

quaMsongsongvớiACvàSBcắtBC,SB,SAlầnlượttạiN,P,Q.Giátrịxđể
MNPQ
S lớn
nhấtbằng
A.
a
.
5
B.
a
.
4
C.
a
.
2
D.
a
.
3
Phântích:TrướchếttaphảixácđịnhđượcMNPQlàhìnhchữnhật
Vì

//SB
và

//AC
nênMNPQlàhìnhbìnhhành.
AC SO ( ACS )
AC BD()

caân
ñöôøng cheùo hình vuoâng

AC SBD
AC SB
,mà
MQ// SB
MN MQ
VậyMNPQlàhìnhchữnhật.
Hướng dẫn giải
ĐÁPÁNC
Tacó:MN//AC


BM a x
MN .AC .a 2 a x 2
BA a
SAB
có:MQ//SB

AM bx
MQ .SB
AB a


MNPQ
b2
SMN.MQ axx
a
Tacó:

 


2
ax x
a
axx axx
24
MNPQ
S lớnnhấtkhivàchỉkhi
axx

a
x.
2
3.Bàitậptrắcnghiệm
Câu 11: Cho hình chóp có đáy là tam giác cân tại Cạnh bên vuông góc với
đáy. Gọi lần lượt là trung điểm của và Khẳng định nào dưới đây sai?
A. B. C. D.
Lời giải
.SABC
A
BC .CSA
,
H
K
A
B
.SB
.CH AK^ .CH SB^ .CH S A^ .
A
KSB^
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 760
Chọn D
Vì
H
là trung điểm của
A
B , tam giác
A
BC
cân suy ra
.CH AB^
Ta có
()
SA ABC SA CH^^
mà
CH A B^
suy ra
()
.CH SAB^
Mặt khác
()
A
KSABÌ
CH¾¾ vuông góc với các đường thẳng
,, .SA SB AK
Và
A
KSB^
chỉ xảy ra khi và chỉ khi tam giác
SAB
cân tại
.S
.
Câu 12: Cho hình chóp có đáy là tam giác vuông tại cạnh bên vuông góc với
đáy. Gọi là chân đường cao kẻ từ của tam giác Khẳng định nào dưới đây là
sai?
A. B. C. D.
Lời giải
Chọn C
Theo bài ra, ta có
()
SA ABC^
mà
()
.BC ABC SA BCÌ^
Tam giác
A
BC
vuông tại
,B
có
A
BBC^
()
.BC SAB BC AH^^
Khi đó
()
.
AH SB
AH SBC AH SC
AH BC
ì
^
ï
ï
^ ^
í
ï
^
ï
î
K
H
A
B
C
S
.SABC
A
BC
,B
SA
H
A
.SAB
.SA BC^ .
A
HBC^ .
A
HAC^ .
A
HSC^
H
A
C
B
S
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 761
Nếu
A
HAC^
mà
SA AC^
suy ra
()
A
CSAH ACAB^^
(vô lý).
Câu 13: Cho tứ diện Gọi là trực tâm của tam giác và vuông góc với mặt
phẳng đáy. Khẳng định nào dưới đây là đúng?
A. B. C. D.
Lời giải
Chọn D
Vì
A
H vuông góc với
()
mp BCD
suy ra
.
A
HCD^
()
1
Mà
H
là trực tâm của tam giác
BCD
.
B
HCD^
(
)
2
Từ
()( )
1,2
suy ra
()
.
CD AH
CD A BH CD A B
CD BH
ì
^
ï
ï
^ ^
í
ï
^
ï
î
Câu 14: Cho hình chóp có đáy là hình thoi tâm Biết rằng
Khẳng định nào sau đây là đúng?
A. B. C. D.
Lời giải
Chọn C
Vì
SA SC=
SACD
cân tại
S
mà
O
là trung điểm
.
A
CSOAC^
.
A
BCD
H
BCD
A
H
.CD BD^ .
A
CBD= .
A
BCD= .
A
BCD^
C
D
B
A
.SABCD
A
BCD .O
,SA SC=
.SB SD=
(
)
.
A
BSAC^
.CD AC^
()
.SO ABCD^
()
.CD SBD^
C
A
B
D
S
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 762
Tương tự, ta cũng có
SO BD^
mà
()
A
CBD O ABCDÇ=Ì
()
.SO ABCD^
Câu 15: Cho hình chóp có đáy là hình thoi tâm Cạnh bên vuông góc với
đáy. Khẳng định nào sau đây là sai?
A. B. C. D.
Lời giải
Chọn D
Vì
SA
vuông góc với
()
.mp ABCD SA BD^
Mà
A
BCD
là hình thoi tâm
O
A
CBD^
nên suy ra
()
.BD SAC^
Mặt khác
()
SO SACÌ
và
()
SC SACÌ
suy ra
BD SO
BD SC
ì
^
ï
ï
í
ï
^
ï
î
.
Và
,
A
DSC
là hai đường thẳng chéo nhau.
Câu 16: Cho hình chóp có đáy là hình chữ nhật tâm Đường thẳng cuông
góc với mặt đáy . Gọi là trung điểm của Khẳng định nào dưới đây là sai?
A. B.
C. Tam giác vuông ở D. là mặt phẳng trung trực của
Lời giải
Chọn D
.SABCD
A
BCD .OSA
.SA BD^ .SC BD^ .SO BD^ .
A
DSC^
O
C
S
B
D
A
.SABCD
A
BCD .OSA
()
A
BCD
I
.SC
()
.IO ABCD^
.BC SB^
SCD .D
()
SAC
.BD
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 763
Vì
,OI
lần lượt là trung điểm của
,
A
CSC
suy ra
OI
là đường trung bình của tam giác
SAC
OI
//
SA
mà
() ()
.SA ABCD OI ABCD^^
Ta có
A
BCD
là hình chữ nhật
B
CAB^
mà
SA BC^
suy ra
.BC SB^
Tương tự, ta có được
()
()
.
CD AD
CD SD
CD SA SA ABCD
ì
^
ï
ï
^
í
ï
^^
ï
î
Nếu
()
SAC
là mặt phẳng trung trực của BD BD AC¾¾^: điều này không thể xảy ra vì
A
BCD
là hình chữ nhật.
Câu 17: Cho hình chóp với đáy là hình thang vuông tại và , có ,
. Cạnh bên vuông góc với đáy , là trung điểm của . Chỉ ra
mệnh đề sai trong các mệnh đề sau:
A. B.
C. Tam giác vuông tại . D.
Lời giải
Chọn D
Từ giả thết suy ra
A
DCE
là hình vuông .
CE AB
CE A D a
ì
^
ï
ï
í
ï
==
ï
î
I
O
C
S
B
D
A
.SABCD
A
BCD
A
D
A
DCDa==
2AB a=
SA
()
A
BCD
E
A
B
()
.CE SA B^
()
.CB SAC^
SDC
D
()
.CE S DC^
C
E
A
B
D
S
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 764
Ta có
()
()
.
do
CE A B
CE SAB
CE SA SA ABCD
ì
^
ï
ï
^
í
ï
^^
ï
î
Do đó A đúng.
Vì
1
2
CE AD a CE AB ABC=== D
vuông tại
CCBAB^
. Kết hợp với
CB SA^
(do
()
SA ABCD^
) nên suy ra
()
.CB SA C^
Do đó B đúng.
Ta có
()
()
.
do
CD AD
CD SAD CD SD
CD SA SA ABCD
ì
^
ï
ï
^ ^
í
ï
^^
ï
î
Do đó C đúng.
Dùng phương pháp loại trừ, suy ra D là đáp án sai.
Câu 18: Cho hình chóp có đáy là hình chữ nhật, cạnh bên vuông góc với mặt
phẳng đáy. Gọi lần lượt là đường cao của tam giác và tam giác Khẳng
định nào dưới đây là đúng?
A. B. C. D.
Lời giải
Chọn D
Vì
SA
vuông góc với mặt phẳng
()
A
BCD
.SA BC^
Mà
A
BBC^
nên suy ra
() ()
.BC SAB BC AE SAB^^Ì
Tam giác
SAB
có đường cao
A
E
A
ESB^
mà
()
.
A
EBC AE SBC AESC^^ ^
Tương tự, ta chứng minh được
A
FSC^
. Do đó
()
.SC AEF^
Câu 19: Cho hình chóp có Gọi lần lượt là trực tâm các tam giác và
. Mệnh đề nào sau đây sai?
A. B. C. D.
Lời giải
Chọn D
.SABCD
A
BCD SA
,
A
EAF
SAB .SAD
()
.SC AFB^
(
)
.SC AEC^
()
.SC AED^
(
)
.SC AEF^
C
A
D
B
S
F
E
SABC
()
.SA ABC^
, HK
SBC
A
BC
()
.BC SAH^
(
)
.SB CHK^
()
.
H
KSBC^
()
.BC SAB^
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 765
Ta có
()
.
BC SA
BC SAH
BC SH
ì
^
ï
ï
^
í
ï
^
ï
î
Do đó A đúng.
Ta có
()
.
CK A B
CK SA B CK SB
CK SA
ì
^
ï
ï
^ ^
í
ï
^
ï
î
Mặt khác có
.CH SB^
Từ đó suy ra
()
.SB CHK^
Do đó B đúng.
Ta có
()
()
()
.
BC SAH BC HK
H
KSBC
SB CHK SB HK
ì
ï^ ^
ï
^
í
ï
^^
ï
î
Do đó C đúng.
Dùng phương pháp lại trừ, suy ra D sai.
Câu 20: Cho hình lập phương Đường thẳng vuông góc với mặt phẳng nào
sau đây?
A. B. C. D.
Lời giải
Chọn A
Ta có
A
ADA
¢¢
là hình vuông suy ra
.
A
DAD
¢¢
^
()
1
Và
.
A
BCD A B C D
¢¢¢¢
là hình lập phương suy ra
.
A
BAD
¢
^
()
2
H
A
C
B
S
M
K
..
A
BCD A B C D
¢¢¢¢
A
C
¢
()
.
A
BD
¢
()
.
A
DC
¢¢
(
)
.
A
CD
¢¢
(
)
.
A
BCD
¢¢
C'
B
'
A
'
C
A
B
D
D
'
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 766
Từ
()( )
1,2
suy ra
()
.
A
DABCD ADAC
¢¢¢¢¢
^^
Lại có
A
BCD
là hình vuông
A
CBD^
mà
()
()
A
ABDAA ABCD
¢¢
^^
()
B
DAACC BDAC
¢¢ ¢
^ ^
. Kết hợp với
A
DAC
¢¢
^
suy ra
()
.
A
CABD
¢¢
^
Câu 21: Cho tứ diện có đôi một vuông góc với nhau. Gọi là hình chiếu của
trên mặt phẳng . Mệnh đề nào sau đây là sai?
A. B.
C. là trực tâm D.
Lời giải
Chọn D
()
.
OA OB
OA OBC OA BC
OA OC
ì
^
ï
ï
^ ^
í
ï
^
ï
î
Do đó A đúng.
()
1
Gọi
.IAHBC=Ç
Theo giả thiết ta có
()
.OH ABC OH BC^^
(
)
2
Từ
()
1
và
(
)
2
, suy ra
()
.BC AOI BC OI^^
Tam giác vuông
,BOC
ta có
222
111
.
OI OB OC
=+
Tam giác vuông
,
A
OI
ta có
222222
111111
.
OH OA OI OA OB OC
=+=++
Do đó B đúng.
Từ chứng minh trên
()
.BC AOI BC AI^^
()
3
Gọi
.
J
BH AC=Ç
Chứng mình tương tự ta có
A
CBJ^
.
(
)
4
Từ
()
3
và
()
4
, suy ra
H
là trực tâm
.
A
BCD
Do đó C đúng.
Vậy D là đáp án sai.
OABC
, , OA OB OC
H
O
()
A
BC
.OA BC^
2222
1111
.
OH OA OB OC
=++
H
.ABCD
2222
3.OH AB AC BC=++
H
B
C
O
A
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 767
Dạng3.Xácđịnhgóc–hìnhchiếu–tínhđộdài
1.
Phươngpháp
Bước1:TìmgiaođiểmOcủaavới
.
Bước2:Chọn
Aa
vàdựng
AH 
,với
H
.
Khiđó:
AOH a,
Bước 3: Tính số đo của
AOH
dựa trên
cáchệthứclượngtrongtam giác.
Cáctrườnghợpđặcbiệt
0
a() a,() 90



0
a//( )
a,( ) 0
a()




Chúý:Nếu
a,( )



thì
0
090
2.Cácvídụrènluyệnkĩnăng
Vídụ1:ChotứdiệnSABCcó

SA ABC
và
SA a, AB a 3,
tamgiácSBCcântạiS.
a)Góc
giữađườngthẳngSBvớimặtphẳng(ABC)là
A.
30 .
 B.
60 .
 C.
45 .
 D.
90 .
b)Góc
giữađườngthẳngSCvớimặtphẳng(ABC)là
A.
30 .
 B.
60 .
 C.
45 .
 D.
90 .
Hướng dẫn giải
Xácđịnhgóc
và
.Tacó:

SA ABC
AB SB(ABC)
ACSC(ABC)
laø hình chieáu cuûa treân
laø hình chieáu cuûa treân


SBA
SCA
.
a)ĐÁPÁNA

SA ABC SA AB SAB
vuôngtạiA.Dođó:
SA a 1
tan 30 .
AB
a3 3
 
a
O
H
A
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 768
b)ĐÁPÁNB


2
2222 2
SAB : SB SA AB a a 3 4a
Dođó:
 SB 2a SC SB 2a
Mặtkhác:

SA ABC S A AC SAC
vuôngtạiA
SA a 1
sin 30 .
SC 2a 2

Vídụ2:ChohìnhchópS.ABCDcóđáyABCDlàhìnhchữnhật,
AB a
,
AD a 3
.Cạnh
SAvuônggócvớiđáyvà
SA a.
a)Góc
giữađườngthẳngSBvàmặtphẳng(ABCD)là
A.
30 .
 B.
60 .
 C.
45 .
 D.
90 .
b)Góc
giữađườngthẳngSDvàmặtphẳng(ABCD)là
A.
30 .
 B.
60 .
 C.
45 .
 D.
90 .
c)Góc
giữađườngthẳngSDvàmặtphẳng(SAB)là
A.
30 .
 B.
60 .
 C.
45 .
D.
90 .
Hướng dẫn giải
Xácđịnhgóc
và
.Tacó:

SA ABCD
AB SB(ABCD)
ADSD (ABCD)
laø hình chieáu cuûa treân
laø hình chieáu cuûa treân


SBA
SDA
a)ĐÁPÁNC
Góc
giữađườngthẳngSBvàmặt
phẳng(ABCD)là
SBA

SA ABCD SAB
vuôngcântạiA
SBA 45 .
b)ĐÁPÁNA
Góc
giữađườngthẳngSDvàmặt
phẳng(ABCD)là
SDA

SA ABCD SAB
vuôngtạiA
SA 3
tan 30 .
AD 3

c)ĐÁPÁNB
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 769

DA SAB
SAlàhìnhchiếucủaSDtrên(SAB)
ASD
SAD
vuôngtạiA
AD
tan 3 60 .
SA

Vídụ3:CholăngtrụđứngABC.A’B’C’cóđáyABClàtamgiáccântạiA,
BC a
,
AAʹ a2
và
5
cosBAʹC
6
.GócgiữađườngthẳngA’Bvàmặtphẳng(AA’C’C)bằng
A.
30 .
B.
45 .
C.
60 .
 D.
90 .
Hướng dẫn giải
ĐÁPÁNA
Đặt
AB x
thì

2222
AʹBAʹCx2a
Ápdụngđịnhlícôsintrong
AʹBC
,tacó:

222
222
22
AʹBAʹCBC
cosBAʹC
2A ʹB.AʹC
2x 4a a 5
xa
6
2x 2a



Kẻ
BH AC
,khiđó

BH AAʹCʹC
SuyragócgiữađườngthẳngA’Bvàmặtphẳng
(AA’C’C)làgóc
BAʹH
.
TrongtamgiácvuôngA’BHcó
a3
BH 1
2
sin BAʹHBAʹH30.
AʹB2
a3

Vídụ4:CholăngtrụđứngABC.A’B’C’cóđáyABClàtamgiácvuôngcântạiB.Biết
AB 3cm, BCʹ 32cm
.GóchợpbởiđườngthẳngBC’vàmặtphẳng (ACC’A’)bằng
A.
90 .
B.
60 .
C.
45 .
D.
30 .
Hướng dẫn giải
ĐÁPÁND
GọiHlàtrungđiểmcủacạnhAC,suyraHC’làhình
chiếucủaBC’lênmặtphẳng(ACC’A’)
Dođó



BCʹ,ACCʹAʹ BCʹ,HCʹ
TacótamgiácBHC’vuôngtạiH,cạnh
32
BH cm
2
Tacó
BH 1
sinHCʹBHCʹB30.
BCʹ 2

Vậy


BCʹ,ACCʹAʹ 30 .
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 770
Vídụ5:ChohìnhhộpABCD.A’B’C’D’cóđáyABCDlàhìnhthoicạnha,
A60.
Chân
đườngvuônggóchạtừB’xuốngmặtphẳng(ABCD)trùngvớigiaođiểmcủahai
đườngchéocủađáyABCD.Cho
BBʹ a.
Gócgiữacạnhbênvàmặtđáybằng
A.
30 .
B.
45 .
C.
60 .
D.
90 .
Hướng dẫn giải
ĐÁPÁNC
Tínhgócgiữacạnhbênvàmặtphẳngđáy.
Gọi
OACBD
.Theogiảthiếttacó

BʹOABCD




BʹBABCDB
BʹOABCD,OABCD
HìnhchiếuB’Btrên(ABCD)làOB



BʹB, ABCD B ʹB,BO B ʹBO
TamgiácABDcó
AB AD a
,
BAD 60
ABD
là
tamgiácđều

a
OB
2
TrongtamgiácvuôngB’OB:
a
OB 1
2
cosBʹOB BʹOB 60 .
BBʹ a2

Vídụ6:ChohìnhchópS.ABCDcóđáyABCDlàhìnhvuông cócạnhbằng4a.Haimặt
phẳng(SAB)và(SAD)cùngvuônggócvớiđáy.TamgiácSABcódiệntíchbằng
2
8a 6
3
.
CôsincủagóctạobởiđườngthẳngSDvàmặtphẳng(SBC)bằng
A.
19
.
5
 B.
6
.
5
 C.
6
.
25

D.
19
.
25
Hướngdẫngiải
ĐÁPÁNA
GọiHlàhìnhchiếuvuônggóccủaDtrênmặtphẳng(SBC)



SH
SD;SBC HSD cosSD;SBC cosDSH
SD


2
ABC
118a64a6
S SA.AB SA.4a SA
22 3 3
D.SBC SBC
1
VDH.S
3
và
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 771
D.SBC S.BCD BCD
3
1
VV .SA.S
3
14a 61 32a 6
. . .4a.4a
332 9



33
SBC
SBC
132a632a6
DH.S DH
393S
Từ


BC AB
BC SAB BC SB
BC SA

SBC
11
SBC.SB.4a.SB2a.SB
22
2
2
222 2 2
SBC
4a 6 80a 80 80
SB SA AB 16a SB a S 2a
333 3





Thếvào(1)

3
2
32a 6 4a 10
DH
5
80
3.2a
3





2
2
22 2 2
4a 6 80a 80
SD SA AD 16a SD a
333





2
22
22 2
80a 4a 10 304a
SH SD HD
35 15


304
a
304 SH 19
15
SA a cos SD; SBC .
15 SD 5
80
a
3

3.Bàitậptrắcnghiệm
Câu 1: Cho hình chóp có đáy là hình vuông, cạnh bên vuông góc với mặt
phẳng đáy. Gọi lần lượt là trung điểm của Khẳng định nào dưới đây
là đúng?
A. // B. Góc giữa và bằng
C. D.
Lời giải
Chọn B
.SABCD
A
BCD SA
,,IJK ,,.
A
BBCSB
(
)
IJK
()
.SAC
SC
B
D
0
60 .
()
.BD IJK^
(
)
.BD SAC^
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 772
Xét tam giác
,SBC
có
1
2
BK BJ
BS BC
==
suy ra
J
K
song song với
()
1.SC
Tam giác
,SAB
có
1
2
BI BK
BA BS
==
suy ra
I
K
song song với
()
2.SA
Từ
()( )
1,2
suy ra
()
mp IJK
//
() ()
.mp SAC *
Vì
A
BCD
là hình vuông
B
DAC^
mà
SA BD^
suy ra
()
.BD SAC^
Kết hợp với
(
)
,*
ta được
()
BD IJK^
. Vậy góc giữa hai đường thẳng
,SC BD
bằng
0
90 .
Câu 2: Cho tứ diện có đôi một vuông góc với nhau. Khẳng định nào dưới đây
đúng?
A. Góc giữa và mặt phẳng là góc
B. Góc giữa và mặt phẳng là góc
C. Góc giữa và mặt phẳng là góc
D. Góc giữa và mặt phẳng là góc
Lời giải
Chọn B
Dựa vào đáp án, ta thấy rằng:
A sai, vì
()
CB BD
CB ABD B
CB BA
ì
^
ï
ï
^
í
ï
^
ï
î
là hình chiếu của
C
trên
()
.mp ABD
J
K
I
C
A
D
B
S
A
BCD
,,
A
BBCBD
CD
(
)
A
BD
.CBD
A
C
()
BCD
.
A
CB
A
D
()
A
BC
.
A
DB
A
C
(
)
A
BD
.CBA
B
D
C
A
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 773
Suy ra góc giữa
CD
và mặt phẳng
()
A
BD
là góc
.CDB
B đúng, vì
()
AB BC
AB BCD B
AB BD
ì
^
ï
ï
^
í
ï
^
ï
î
là hình chiếu của
A
trên
()
.mp BCD
Suy ra góc giữa đường thẳng
A
C
và mặt phẳng
()
BCD
là góc
.
A
CB
C sai, vì
()
BD BA
BD ABC B
BD BC
ì
^
ï
ï
^
í
ï
^
ï
î
là hình chiếu của
D
trên
()
.mp ABC
Suy ra góc giữa
A
D và mặt phẳng
()
A
BC
là góc
.DAB
D sai, vì
B là hình chiếu của
C
trên
()
mp ABD
suy ra góc giữa
A
C
và mặt phẳng
(
)
A
BD
là góc
.CAB
Câu 3: Cho hình chóp có đáy là tam giác vuông tại cạnh bên vuông góc với
đáy. Gọi là tâm đường tròn ngoại tiếp tam giác là hình chiếu của trên
Khẳng định nào dưới đây đúng?
A. là trung điểm của cạnh
B. là trung điểm của cạnh
C. là tâm đường tròn ngoại tiếp tam giác
D. là trọng tâm của tam giác
Lời giải
Chọn C
Ta có
SA
vuông góc với
()
mp ABC SA BC^
mà
A
BBC^
suy ra
()
BC SAB^
BC SB^
tam giác
SBC
vuông tại
B
O
là trung điểm của
.SC
Theo bài ra, ta có
()
OH ABC OH^
//
SA H
là trung điểm của
.
A
C
Mà tam giác
A
BC
vuông tại B nên
H
là tâm đường tròn ngoại tiếp tam giác
.
A
BC
Câu 4: Cho hình chóp có đáy là tam giác nhọn, cạnh bên . Gọi là
hình chiếu vuông góc của trên mặt phẳng khi đó
A. là trực tâm của tam giác
.SABC
A
BC
,
B
SA
O .SBC
H
O
(
)
.
A
BC
H
.
A
B
H
.BC
H
.
A
BC
H
.
A
BC
H
O
A
C
B
S
.SABC
A
BC SA SB SC==
H
S
(
)
,
A
BC
H
.
A
BC
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 774
B. là trọng tâm của tam giác
C. là tâm đường tròn ngoại tiếp tam giác
D. là tâm đường tròn nội tiếp tam giác
Lời giải
Chọn C
Vì
H
là hình chiếu vuông góc của
S
trên
()
mp ABC
nên ta có
 Tam giác
SAH
vuông tại
,H
có
222
.SA AH SH=+
 Tam giác
SBH
vuông tại
,H
có
222
.SB BH SH=+
 Tam giác
SCH
vuông tại
,H
có
222
.SC CH SH=+
Kết hợp điều kiện
SA SB SC==
suy ra
H
AHBHC==
nên
H
là tâm đường tròn
ngoại tiếp tam giác
.
A
BC
Câu 5: Cho hình chóp có và Gọi là hình
chiếu vuông góc của trên mặt phẳng khi đó
A. là trung điểm của
B. là trọng tâm
của tam giác
C. là trung điểm của D. là trung
điểm của
Lời giải
Chọn D
H
.
A
BC
H
.
A
BC
H
.
A
BC
H
A
B
C
S
.SABC
00 0
120 , 60 , 90BSC CSA ASB===
.SA SB SC==
I
S
(
)
,
A
BC
I
.
A
B
I
.
A
BC
I
.
A
C
I
.BC
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 775
Đặt
.SA a=
Tam giác
SAB
vuông cân tại
,S
có
22
2.AB SA SB a=+=
Tam giác
SAC
cân tại
,S
có
0
60CSA =
suy ra
.SA SC AC a== =
Áp dụng định lí Cosin cho tam giác
,SBC
ta có
222
2. . .cos
B
CSBSC SBSC BSC=+-
222 2 0 2 2 2
2.cos120 3 3 .BC a a a a BC a AB AC=+- === +
Khi đó, tam giác
A
BC
vuông tại
A
mà
I
là hình chiếu của
S
trên
()
.mp ABC
Suy ra
I
là tâm đường tròn ngoại tiếp tam giác
A
BC
hay chính là trung điểm
.BC
.
Câu 6: Cho hình hộp có đáy là hình thoi tâm , và
Hình chiếu vuông góc của trên mặt phẳng là
A. trung điểm của
B. trọng tâm của tam giác
C. tâm của hình thoi
D. trọng tâm của tam giác
Lời giải
Chọn B
Vì
A
BCD
là hình thoi
A
BAD= mà
0
60BAD =
suy ra tam giác
A
BD đều
(
)
1.
I
C
B
A
S
.
A
BCD A B C D
¢¢¢¢
A
BCD O
0
60BAD =
.
A
AABAD
¢¢¢
==
A
¢
()
A
BCD
.
A
O
.
A
BD
O .
A
BCD
.BCD
H
O
D
'
C'
B
'
D
A
'
A
C
B
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 776
Ta có
A
AABAD
¢¢¢
==
nên hình chiếu vuông góc của
A
¢
trên mặt phẳng
()
A
BCD
trùng
với tâm
I
của đường tròn ngoại tiếp tam giác
()
2.ABD
Từ
()( )
1,2
suy ra
I
là tâm đường tròn ngoại tiếp tam giác
.
A
BD
Câu 7: Cho hình chóp có các mặt bên tạo với đáy một góc bằng nhau. Hình chiếu vuông
góc của trên mặt phẳng là
A. tâm đường tròn nội tiếp tam giác
B. tâm đường tròn ngoại tiếp tam giác
C. trọng tâm của tam giác
D. giao điểm của hai đường thẳng và
Lời giải
Chọn A
Gọi
H
là hình chiếu vuông góc của
S
trên mặt phẳng
()
.
A
BCD
Gọi
,,
M
NP
lần lượt là hình chiếu của
S
trên các cạnh
,,.
A
BACBC
Ta có
()
,
SH AB
AB SHM AB HM
SM AB
ì
^
ï
ï
^ ^
í
ï
^
ï
î
tương tự ta được
,.
H
NACHPBC^^
Khi đó
()( )
()
;;,SAB ABC SM HM SMH== tương tự suy ra
.SMH SNH SPH==
SMH SNH SPH HM HN NP HD =D =D = = là tâm đường tròn nội tiếp tam giác
.
A
BC
Câu 8: Cho tứ diện có đôi một vuông góc với nhau và ,
. Độ dài đoạn thẳng bằng
A. B.
C. D.
Lời giải
Chọn A
.SABC
S
()
A
BC
.
A
BC
.
A
BC
.
A
BC
A
C .BD
N
M
A
C
B
S
H
P
A
BCD
,,
A
BBCCD
A
Ba=
,BC b CD c==
A
D
222
.abc++
222
.abc+-
222
.abc-+
222
.abc-++
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 777
Ta có
()
AB BC
AB BCD
AB CD
ì
^
ï
ï
^
í
ï
^
ï
î
tam giác
A
BD
vuông tại
.B
Lại có
()
AB CD
CD ABC
BC CD
ì
^
ï
ï
^
í
ï
^
ï
î
tam giác
BCD
vuông tại
.C
Khi đó
222
2222 222
222
.
AD AB BD
AD AB BC CD AD a b c
BD BC CD
ì
ï
=+
ï
=++=++
í
ï
=+
ï
î
Câu 9: Cho tứ diện có đôi một vuông góc với nhau. Điểm nào dưới đây các
đều bốn đỉnh của tứ diện ?
A. Trung điểm của cạnh
B. Tâm đường tròn ngoại tiếp tam giác
C. Trung điểm của cạnh
D. Trọng tâm của tam giác
Lời giải
Chọn C
.
Ta có
()
AB BC
AB BCD
AB CD
ì
^
ï
ï
^
í
ï
^
ï
î
tam giác
A
BD vuông tại
.B
Suy ra
,
2
A
D
IA IB ID== =
với
I
là trung điểm của
.
A
D
()
1
Lại có
()
AB CD
CD ABC
BC CD
ì
^
ï
ï
^
í
ï
^
ï
î
tam giác
A
CD
vuông tại
.C
C
D
B
A
A
BCD
,,
A
BBCCD
,,,
A
BC D
A
BCD
.BD
.
A
BC
.
A
D
.
A
CD
O
B
D
C
A
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 778
Suy ra
,
2
A
D
EA EC ED===
với E là trung điểm của
.
A
D
(
)
2
Từ
()( )
1,2
suy ra
I
Eº nên trung điểm của cạnh
A
D cách đều
,,,.
A
BC D
Câu 10: Cho hình chóp có đáy là tam giác đều cạnh và độ dài các cạnh bên
Gọi là trọng tâm của tam giác Độ dài đoạn thẳng bằng
A. B. C. D.
Lời giải
Chọn C
Vì
SA SB SC==
và
G
là trọng tâm tam giác
A
BC
Suy ra
G
là chân đường cao kẻ từ đỉnh
S
xuống mặt phẳng
()
.
A
BC
Gọi
M
là trung điểm của
BC
suy ra
.
22
B
Ca
BM CM===
Tam giác
A
BC
đều cạnh ,a có
31 3
..
3236
AM a a
GM == =
Tam giác
SBM
vuông tại
,
M
có
2
222
.
4
a
SM SB MB b=-=-
Tam giác
SGM
vuông tại
,G
có
22 2 2
222
93
.
412 3
aa b a
SG SM GM b
-
=-=--=
Câu 11: Cho hình vuông tâm cạnh bằng Trên đường thẳng qua và vuông góc với
mặt phẳng lấy điểm Biết góc giữa đường thẳng và mặt phẳng
bằng Độ dài cạnh bằng
A. B. C. D.
Lời giải
Chọn B
.SABC
A
BC
a
.SA SB SC b===
G .
A
BC SG
22
93
.
3
ba+
22
3
.
3
ba-
22
93
.
3
ba-
22
3
.
3
ba+
M
A
C
B
G
S
A
BCD
,O
2.a
O
()
A
BCD
.SSA
()
A
BCD
0
45 .
SO
3.SO a= 2.SO a=
3
.
2
a
SO =
2
.
2
a
SO =
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 779
Vì
O
là hình chiếu của
S
trên mặt phẳng
()
.ABCD
Suy ra
OA
là hình chiếu của
SA
trên mặt phẳng
()
ABCD
Khi đó
()
()
0
;;45SA ABCD SA OA SAO===
tam giác
SAO
vuông cân.
()
1
Tam giác
A
BC
vuông cân tại
,B
có
2
2.
22
AC AB
OA a== =
()
2
Từ
(
)
(
)
1,2 suy ra 2.SO OA a==
Câu 12: Cho hình chóp có đáy là hình chữ nhật có cạnh , . Hai mặt
bên và cùng vuông góc với mặt phẳng đáy , cạnh . Tính
góc tạo bởi đường thẳng và mặt phẳng .
A. . B. . C. . D. .
Lời giải
Chọn C
Do
()
SA ABCD^ nên
()
()
,, ,SC ABD SC ABCD SC AC SCA===
.
Xét tam giác vuông
SAC
, ta có
22
tan 3
SA SA
SCA
AC
AB BC
== =
+
.
Suy ra
0
60SCA =
.
Câu 13: Cho hình chóp có đáy là hình vuông cạnh , tâm . Cạnh bên và
vuông góc với mặt đáy . Gọi là góc giữa và mặt phẳng . Mệnh đề
nào sau đây đúng?
A. B. C. . D.
Lời giải
Chọn A
Vì
()
SA ABCD^
nên hình chiếu vuông góc của
SO
trên mặt đáy
()
ABCD
là
A
O
. Do đó
()
()
()
,,.SO ABCD SO OA SOA==
Trong tam giác vuông
SAO
, ta có
tan 2 2.
SA
SOA
OA
==
O
C
A
D
B
S
.SABCD
A
BCD
A
Ba=
2BC a=
()
SAB
()
SAD
()
A
BCD
15SA a=
SC
(
)
A
BD
0
30
0
45
0
60
0
90
.SABC
A
BCD
a
O
2SA a=
()
A
BCD
j
SO
()
A
BCD
tan 2 2.j =
0
60 .j =
tan 2.j =
0
45 .j =
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 780
Vậy
SO
hợp với mặt đáy
()
ABCD một góc nhọn
j
thỏa mãn tan 2 2j = .
Câu 14: Cho hình chóp có đáy là tam giác vuông tại , , tam giác là
tam giác đều có cạnh bằng và nằm trong mặt phẳng vuông với đáy. Tính góc giữa
đường thẳng và mặt phẳng đáy
A. . B. . C. . D. .
Lời giải
Chọn C
Gọi
H
là trung điểm của
BC
, suy ra
()
SH ABC^ .
Vì
()
SH ABC^ nên
H
A là hình chiếu của
SA
trên mặt phẳng
(
)
ABC .
Do đó
()
()
()
,,SA ABC SA AH SAH==
.
● Tam giác
SBC
đều cạnh
2a
nên 3.SH a=
● Tam giác
A
BC
vuông tại
A
nên
1
.
2
A
HBCa==
Tam giác vuông
SAH
, có
tan 3
SH
SAH
A
H
==
, suy ra
0
60SAH =
.
Câu 15: Cho hình chóp có đáy là hình vuông cạnh . Tam giác đều cạnh
và nằm trong mặt phẳng vuông góc với đáy . Gọi là góc giữa và mặt phẳng
. Mệnh đề nào sau đây đúng?
A. B. C. D.
Lời giải
Chọn A
.SABC
A
BC
A
60ABC =
SBC
2a
SA
()
A
BC
0
30
0
45
0
60
0
90
A
B
C
S
H
.SABCD
A
BCD
a
SAB
a
()
A
BCD
j
SD
()
A
BCD
5
cot .
15
j =
15
cot .
5
j =
0
30 .j =
3
cot .
2
j =
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 781
Gọi
H
là trung điểm
A
B , suy ra
()
.SH AB SH ABCD^^ Vì
(
)
SH ABCD^ nên hình
chiếu vuông góc của
SD
trên mặt đáy
()
ABCD là
H
D .
Do đó
()
()
,,.SD ABCD SD HD SDH==
● Tam giác
SAB
đều cạnh
a
nên
3
.
2
a
SH =
●
22
5
.
2
a
HD AH AB
=+=
Tam giác vuông
SHD
, có
5
cot .
15
DH
SDH
SH
==
Câu 16: Cho chóp đều có cạnh đáy bằng , cạnh bên bằng . Gọi là góc giữa giữa
cạnh bên và mặt đáy. Mệnh đề nào sau đây đúng?
A. B. C. D.
Lời giải
Chọn D
Gọi
O
là tâm mặt đáy
()
ABCD , suy ra
()
SO ABCD^ .
Vì
()
SO ABCD^
, suy ra
OA
là hình chiếu của
SA
trên mặt phẳng
()
ABCD
.
Do đó
()
()
()
,,.SA ABCD SA AO SAO==
Tam giác vuông
SOA
, có
22
14
tan .
2
SO SB BO
SAO
AO AO
-
== =
Câu 17: Cho tứ diện đều. Gọi là góc giữa và mặt phẳng . Chọn khẳng định
đúng trong các khẳng định sau?
A. . B. . C. . D. .
Lời giải
H
D
B
C
A
S
.SABCD
2
3
j
tan 7.j =
0
60 .j =
0
45 .j =
14
tan .
2
j =
A
BCD
a
A
B
()
BCD
3
cos
3
a =
3
cos
4
a =
cos 0a =
3
cos
2
a =
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 782
Chọn A
Gọi
H
là trọng tâm tam giác đều
()
.BCD AH BCD^
Gọi
a
là độ dài cạnh của tứ diện
3
.
3
a
ABCD BH=
Khi đó
3
cos .
3
BH
ABH
AB
aa===
.
Câu 18: Cho hình chóp có đáy là hình vuông tâm , cạnh bằng . Cạnh bên
. Hình chiếu vuông góc của đỉnh trên mặt phẳng là trung điểm của
của đoạn thẳng . Gọi là góc giữa và mặt phẳng . Mệnh đề nào sau đây
đúng?
A. B. C. D.
Lời giải
Chọn C
Vì
()
SH ABCD^ nên hình chiếu vuông góc của
SD
trên mặt phẳng
()
ABCD là
H
D .
Do đó
()
()
,,.SD ABCD SD HD SDH==
● Tính được
22
2.SH SA AH a=-=
● Trong tam giác
A
DH , có
22 0
2 . .cos45 10.DH AH AD AH AD a=+- =
Tam giác vuông
SHD
, có
5
tan .
5
SH
SDH
HD
==
Câu 19: Cho lăng trụ có đáy là hình thoi cạnh , . Hình chiếu vuông
góc của xuống mặt đáy trùng với giao điểm hai đường chéo của đáy và cạnh bên
. Tính góc giữa cạnh bên và mặt đáy.
A. . B. . C. . D. .
Lời giải
Chọn C
.SABCD
A
BCD O
4a
2SA a=
S
()
A
BCD
H
A
O
a
SD
()
A
BCD
tan 5.a =
tan 1.a =
5
tan .
5
a = tan 3.a =
O
H
D
B
C
A
S
.''' '
A
BCD A B C D
a
0
60BAD =
'
B
'BB a=
0
30
0
45
0
60
0
90
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 783
Gọi
OACBD=Ç
. Theo giả thiết
()
'
B
OABCD^ .
Do đó
()
', ', '
B
BABCD BBBO BBO==
.
Từ giả thiết suy ra tam giác
A
BD đều cạnh
a
, suy ra
1
22
a
BO BD==
.
Tam giác vuông
'BBO
, có
0
1
cos ' ' 60
'2
BO
BBO BBO
B
B
== =
.
Câu 20: Cho hình chóp có đáy là hình chữ nhật với . Hình chiếu
vuông góc của trên mặt đáy trùng với trọng tâm tam giác và . Gọi
lần lượt là trung điểm các cạnh và . Gọi là góc giữa đường thẳng
với mặt đáy . Mệnh đề nào sau đây đúng?
A. B. . C. . D. .
Lời giải
Chọn B
Ta có
M
NSB . Do đó
()
()
,,
M
N ABCD SB ABCD=
.
Do
()
SH ABCD^ nên
()
()
,,,
M
NABCDSBABCDSBHBSBH===
.
D
'
C'
B
'
A
'
O
D
C
B
A
.SABCD
A
BCD
,AB a=
3AD a=
H
S
A
BC
2
a
SH =
,
M
N
BC SC
a
M
N
()
A
BCD
4
tan .
3
a =
3
tan
4
a =
2
tan
3
a =
tan 1a =
H
D
C
B
A
S
M
N
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 784
Ta có
22
2
B
DABAD a=+=;
2
33
BD a
BH
==
.
Tam giác
SHB
, có
3
tan
4
SH
SBH
B
H
==
.
Câu 21: Cho hình chóp có đáy là hình vuông tâm cạnh bằng , vuông góc
với đáy. Gọi , lần lượt là trung điểm và . Tính góc giữa đường thẳng
với mặt phẳng , biết .
A. . B. . C. . D. .
Lời giải
Chọn C
Kẻ
M
KSO , do
()
SO ABCD^ , suy ra
()
M
KABCD^ .
Do đó
()
,,
M
NABCD MNNK MNK==
. Ta có
332
44
a
CK CA
== .
Tam giác
CN K
, có
22 2
0
210
cos45
22. 4
CN CK KN a
KN
CN CK
+-
== =
.
Tam giác vuông
M
NK
, có
0
1
os 60 .
2
c
NK
MNK MNK
MN
== =
Câu 22: Cho hình chóp có đáy là hình vuông cạnh . Hai mặt phẳng và
cùng vuông góc với đáy và . Gọi là góc giữa đường thẳng
và mặt phẳng . Mệnh đề nào sau đây đúng?
A. B. C. D.
Lời giải
Chọn B
.SABCD
A
BCD O
a
SO
M
NSABC
M
N
()
A
BCD
10
2
a
MN =
0
30
0
45
0
60
0
90
S
A
B
C
D
M
N
K
O
.SABCD
A
BCD
a
()
SAB
()
SAC
()
A
BCD
2SA a=
j
SB
()
SAD
5
cos .
5
j =
25
cos .
5
j =
0
60 .j =
0
30 .j =
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 785
Ta có
()
BA AD
BA SAD
BA SA
ì
^
ï
ï
^
í
ï
^
ï
î
. Suy ra hình chiếu vuông góc của
SB
trên mặt phẳng
()
SAD là
SA
. Do đó
()
()
,,.SB SAD SB SA BSA==
Tam giác vuông
SAB
, ta có
22
25
cos .
5
SB SA
BSA
SA
SA AB
== =
+
Câu 23: Cho hình chóp có đáy là hình vuông cạnh , cạnh bên và
vuông góc với đáy. Gọi là góc giữa và mặt phẳng . Chọn khẳng định đúng
trong các khẳng định sau?
A. B. C. D.
Lời giải
Chọn B
Ta có
()
BC BA
BC SAB
BC SA
ì
^
ï
ï
^
í
ï
^
ï
î
. Suy ra hình chiếu vuông góc của
SC
trên mặt phẳng
()
SAB
là
SB
. Do đó
()
()
,,.SC SAB SC SB CSB==
Tam giác vuông
SAB
, có
22
7.SB SA AB a=+=
Tam giác vuông
SBC
, có
1
tan .
7
BC
CSB
SB
==
D
C
B
A
S
.SABCD
A
BCD
a
6SA a=
a
SC
()
SAB
1
tan .
8
a =
1
tan .
7
a =
0
30 .a =
1
tan .
6
a =
S
A
B
C
D
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 786
Câu 24: Cho hình chóp có đáy là hình vuông cạnh . Cạnh bên vuông góc
với đáy, góc gữa và mặt đáy bằng . Gọi là góc giữa đường thẳng
và mặt phẳng . Mệnh đề nào sau đây đúng?
A. B. C. D.
Lời giải
Chọn A
Xác định
()
0
45 , ,SC ABCD SC AC SCA===
, suy ra 22SA AC a== .
Gọi
OACBD=Ç
, ta có
()
DO AC
D
OSAC
DO SA
ì
^
ï
ï
^
í
ï
^
ï
î
nên hình chiếu vuông góc của
SD
trên
mặt phẳng
(
)
SAC là
SO
. Do đó
()
,,SD SAC SD SO DSO==
.
Ta có
1
2
2
DO BD a==
;
22 22
10SO SA AO SA DO a=+=+=
.
Tam giác vuông
SOD
, có
5
tan
5
OD
DSO
OS
==
.
Câu 25: Cho hình hộp chữ nhật có đáy là hình vuông cạnh bằng ,
. Tính góc giữa đường thẳng với mặt phẳng .
A. . B. . C. . D. .
Lời giải
Chọn A
.SABCD
A
BCD
2a
SA
SC
()
A
BCD
0
45
j
SD
()
SAC
5
tan .
5
j =
tan 5.j =
0
60 .j =
0
45 .j =
O
S
A
B
C
D
.''' '
A
BCD A B C D
A
BCD
22
'4
A
A =
'
A
C
()
''
A
ABB
0
30
0
45
0
60
0
90
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 787
Ta có
()
''
'
BC AB
BC AA B B
BC AA
ì
^
ï
ï
^
í
ï
^
ï
î
.
Do đó
()
()
', ' ' ', ' '
A
C AABB ACAB CAB==
.
Vì
()
''BC AA B B^
'BC BA^
nên tam giác
'
A
BC
vuông tại B .
Tam giác vuông
'
A
BC
, có
22
1
tan ' .
'
3
'
BC BC
CA B
AB
AA AB
== =
+
Vậy
'
A
C
tạo với mặt phẳng
(
)
''AA B B một góc
0
30 .
Câu 26: Cho hình chóp có đáy là hình vuông cạnh . Tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Gọi lần lượt là trung điểm của các cạnh
và . Gọi là góc giữa đường thẳng và mặt phẳng . Mệnh đề nào sau đây
đúng?
A. B. C. D.
Lời giải
Chọn C
Gọi
.IHKAC=Ç
Do
,
H
K
lần lượt là trung điểm của
A
B và
A
D nên
H
KBD . Suy ra
HK AC^
. Lại có
A
CSH^
nên suy ra
()
AC SHK^ .
Do đó
()
()
()
,,.SA SHK SA SI ASI==
D
'
C'
B
'
A
'
D
C
B
A
.SABCD
A
BCD
a
SAB
, HK
A
B
A
D
j
SA
()
SHK
tan 7.j =
2
tan .
4
j =
7
tan .
7
j =
14
tan .
4
j =
I
K
H
D
B
C
A
S
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 788
Tam giác
SIA
vuông tại
I
, có
22
1
7
4
tan .
7
AC
AI
ASI
SI
SA AI
== =
-
Câu 27: Cho hình chóp có đáy là hình thang vuông tại và , ,
. Cạnh bên và vuông góc với đáy. Tính góc giữa đường thẳng với
mặt phẳng .
A. . B. . C. . D. .
Lời giải
Chọn A
Gọi
M
là trung điểm
A
D , suy ra
A
BCM
là hình vuông nên
CM A D^
.
Ta có
()
CM A D
CM SA D
CM S A
ì
^
ï
ï
^
í
ï
^
ï
î
.
Suy ra hình chiếu vuông góc của
SC
trên mặt phẳng
(
)
SAD là
SM
.
Do đó
()
,,SC SAD SC SM CSM==
.
Tam giác vuông
SMC
, có
0
22
1
tan 30
3
CM AB
CSM CSM
SM
SA AM
== = =
+
.
Câu 28: Cho hình chóp có đáy là hình vuông. Mặt bên là tam giác đều có
đường cao vuông góc với mặt phẳng . Gọi là góc giữa và mặt phẳng
. Chọn khẳng định đúng trong các khẳng định sau?
A. B. C. D.
Lời giải
Chọn D
.SABCD
A
BCD
A
B
A
BBCa==
2AD a=
2SA a=
SC
()
SAD
0
30
0
45
0
60
0
90
S
A
B
C
D
M
.SABCD
A
BCD SAB
SH
()
A
BCD
a
B
D
()
SAD
0
60 .a =
0
30 .a =
3
cos .
22
a =
3
sin .
22
a =
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 789
Gọi
I
là trung điểm
SA
. Do tam giác
SAD
đều nên
.BI SA^
()
1
Ta có
()
.
AD AB
A
D SAD AD BI
AD SH
ì
^
ï
ï
^ ^
í
ï
^
ï
î
()
2
Từ
()
1 và
(
)
2 , ta có
()
B
ISAD^ nên hình chiếu vuông góc của
BD
trên mặt phẳng
(
)
SAD
là
.ID
Do đó
()
,,.
B
DSAD BDID BDI==
Tam giác
BDI
vuông tại
I
nên
3
3
2
sin .
222
AB
BI
BDI
BD
AB
== =
Câu 29: Cho hình lập phương . Gọi là góc giữa và mặt phẳng
Chọn khẳng định đúng trong các khẳng định sau?
A. B. C. D.
Lời giải
Chọn D
Gọi
''; ''
A
CAC ICDCD HÇ= Ç=
.
Ta có
()
''
'''
'''
CD CD
CD ABCD IH
CD AD
ì
^
ï
ï
^
í
ï
^
ï
î
là hình chiếu vuông góc của
'
A
C
trên mặt
phẳng
()
''ABCD .
I
S
A
C
B
D
H
.''' '
A
BCD A B C D
a
'
A
C
()
''.
A
BCD
0
. 30a =
2
tan .
3
a =
0
.45a =
tan 2.a =
H
I
A
B
C
D
A
'
B
'
C'
D
'
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 790
Do đó
()
()
', ' ' ', ' ' ', ' .
A
C A BCD C I A BCD C I HI C IH===
Trong tam giác vuông
'CHI
, có
2
'
2
tan ' 2.
2
AB
CH
CIH
AB
IH
== =
Dạng4.ThiếtDiện
Phươngpháp
Việc xácđịnh thiết diện với một khốiđa di ện với một mặt phẳng vuông góc với một
đườngthẳngchotrước,trướchếttaphảitìmđượcđiể
mchungcủamộtmặtphẳngđãcho
vớimộtmặtcủakhốiđadiện,sauđódựavàomốiquanhệgiữatínhsongsongvàvuông
gócđểtìm ra phương của giao tuyến
giữa mặtđã cho và các mặt của khốiđa diện.
Thườngtahaydùnghệquảsauđểtìmđiểmchung
ab a()
1)
() b a//()




;
Oba
2) b ( )
O() a



Câu 1: Cho hình chóp có đáy là hình chữ nhật với , . Tam giác
đều và nằm trong mặt phẳng vuông góc với đáy. Mặt phẳng đi qua vuông góc
với . Tính diện tích của thiết diện tạo bởi với hình chóp đã cho.
A. B. C. D.
Lời giải
Chọn B
Gọi
H
là trung điểm
.
A
BSHAB^
Suy ra:
·
()
SH aÌ .
·
(
)
SH ABCD^ (do
()( )
SAB ABCD^ theo giao tuyến
A
B
).
Kẻ
() ()
.HM AB M CD HM a^ÎÌ
.SABCD
A
BCD
A
Ba=
2BC a=
SAB
()
a
S
A
B
S
()
a
2
3
.
4
a
S =
2
3
.
2
a
S =
2
3.Sa=
2
.
2
a
S =
M
H
D
C
B
A
S
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 791
Do đó thiết diện là tam giác
SHM
vuông tại
H
.
Ta có
3
2
a
SH =
,
2.
H
MBC a==
Vậy
2
13 3
..2 .
22 2
SHM
aa
Sa
D
==
Câu 2: Cho hình chóp đều có đáy là tam giác đều cạnh , tâm ; . Gọi
là điểm thuộc đoạn . Mặt phẳng đi qua và vuông góc với .
Đặt . Tính diện tích của thiết diện tạo bởi với hình chóp .
A. B. C. D.
Lời giải
Chọn B
Vì
.SABC
là hình chóp đều nên
()
SO ABC^ (
O
là tâm của tam giác
A
BC
).
Do đó
'SO AA^
mà
(
)
'AAa ^ suy ra
()
SO a
.
Tương tự ta cũng có
()
BC a
.
Qua
M
kẻ
IJ BC
với
, IABJACÎÎ
; kẻ
M
KSO
với
.
K
SAÎ
Khi đó thiết diện là tam giác
.
K
IJ
Diện tích tam giác
IJK
là
1
.
2
IJK
SIJMK
D
=
.
Trong tam giác
A
BC
, ta có
'
I
JAM
BC AA
=
suy ra
.23
'3
AM BC x
IJ
AA
==
.
Tương tự trong tam giác
SAO
, ta có
M
KAM
SO AO
=
suy ra
.
23
AM SO
M
Kx
AO
==
.
Vậy
2
12 3
.2 3 2
23
IJK
x
Sxx
D
==
.
.SABC
A
BC
a
O
2SO a=
M
()
;
A
OM AM O¹¹
()
a
M
A
O
A
Mx= S
()
a
.SABC
2
2.Sa=
2
2.Sx=
()
2
3
.
2
Sax=-
()
2
2.Sax=-
K
J
I
M
O
S
A
B
C
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 792
Câu 3: Cho hình chóp có đáy là tam giác đều cạnh , và vuông góc với đáy.
Mặt phẳng qua và vuông góc với trung tuyến của tam giác . Tính diện tích
của thiết diện tạo bởi với hình chóp đã cho.
A. B.
C. D.
Lời giải
Chọn A
Gọi
I
là trung điểm
.BC AI BC^
Kẻ
A
KSI^
()
K
SIÎ .
Từ
K
kẻ đường thẳng song song với
BC
cắt
, SB SC
lần lượt tạị
,
M
N
.
Khi đó thiết diện là tam giác
.
A
MN
Ta có
()
.
BC AI
BC SAI BC AK MN AK
BC SA
ì
^
ï
ï
^ ^ ^
í
ï
^
ï
î
Tam giác vuông
SAI
, có
22
.21
7
SA AI a
AK
SA AI
==
+
.
Tam giác
SBC
, có
22
222
44
.
77
M
NSKSA SA a
MN
BC SI SI SA AI
== = = =
+
Vậy
2
1221
..
249
AMN
a
SAKMN
D
==
Câu 4: Cho hình chóp có đáy là tam giác đều cạnh , và vuông góc với đáy.
Mặt phẳng qua trung điểm của và vuông góc với . Tính diện tích của
thiết diện tạo bởi với hình chóp đã cho.
.SABC
A
BC
a
SA a=
()
a
A
SI SBC
S
()
a
2
221
.
49
AMN
a
S
D
=
2
421
.
49
AMN
a
S
D
=
2
21
.
7
AMN
a
S
D
=
2
221
.
7
AMN
a
S
D
=
N
M
K
S
A
B
C
I
.SABC
A
BC
a
SA a=
()
a
E
SC
A
B
S
()
a
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 793
A. B.
C. D.
Lời giải
Chọn C
Gọi
F là trung điểm
A
C
, suy ra
EF SA
.
Do
()
SA ABC SA AB^^ nên
EF AB^
.
()
1
Gọi
,
J
G
lần lượt là trung điểm
,
A
BAG
.
Suy ra
CJ AB^
và
FG CJ
nên
FG AB^
.
(
)
2
Trong
SABD
kẻ
GH SA
()
H
SBÎ , suy ra
GH AB^
.
(
)
3
Từ
()
1 ,
()
2 và
(
)
3 , suy ra thiết diện cần tìm là hình thang vuông
EFGH
.
Do đó
()
1
.
2
EFGH
SEFGHFG=+
.
Ta có
1
22
a
EF SA==
;
13
24
a
FG CJ
==;
3
.
4
GH BG a
GH BG
SA BA
===
Vậy
2
13 353
.
22 4 4 32
EFGH
aaa a
S
æö
÷
ç
=+ =
÷
ç
÷
ç
èø
.
Câu 5: Cho hình chóp có đáy là tam giác đều cạnh , và vuông góc với
đáy. Gọi là mặt phẳng đi qua và vuông góc với . Tính diện tích của thiết diện
tạo bởi với hình chóp đã cho.
A. B.
2
53
.
16
EFGH
a
S
=
2
7
.
32
EFGH
a
S
=
2
53
.
32
EFGH
a
S =
2
52
.
16
EFGH
a
S =
J
H
G
E
C
B
A
S
F
.SABC
A
BC
a
2SA a=
()
a
B
SC S
()
a
2
15
.
10
BIH
a
S
D
=
2
5
.
8
BIH
a
S
D
=
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 794
C. D.
Lời giải
Chọn D
Gọi
I
là trung điểm của
A
C
, suy ra
BI AC^
.
Ta có
()
BI AC
BI SAC BI SC
BI SA
ì
^
ï
ï
^ ^
í
ï
^
ï
î
.
()
1
Kẻ
IH SC^
()
H
SCÎ .
()
2
Từ
()
1 và
()
2 , suy ra
()
SC BIH^ .
Vậy thiết diện cần tìm là tam giác
.IBH
Do
()
BI SAC BI IH^^
nên
IBHD
vuông tại
I
.
Ta có
BI
đường cao của tam giác đều cạnh
a
nên
3
2
a
BI
=
.
Tam giác
CHI
đồng dạng tam giác
CAS
, suy ra
22
.. 5
5
IH CI CI SA CI SA a
IH
SA CS CS
SA AC
== = =
+
.
Vậy
2
115
..
220
BIH
a
SBIIH
D
==
Câu 6: Cho hình chóp đều có cạnh đáy bằng , cạnh bên bằng . Mặt phẳng đi qua
và vuông góc với . Tìm hệ thức giữa và để cắt tại điểm nằm giữa
và .
A. B. C. D.
Lời giải
Chọn C
2
3
.
12
BIH
a
S
D
=
2
15
.
20
BIH
a
S
D
=
S
A
B
C
H
I
.SABC
a
b
()
a
A
SC
a
b
()
a
SC
1
C
SC
2.ab> 3.ab> 2.ab< 3.ab<
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 795
Gọi
G
là trọng tâm tam giác
A
BC
. Do
.SABC
là hình chóp đều nên
()
SG ABC^ .
Gọi
'C
là trung điểm
A
B . Suy ra
, ', CC G
thẳng hàng.
Ta có
()
'
'
AB CC
A
BSCC ABSC
SG AB
ì
^
ï
ï
^ ^
í
ï
^
ï
î
.
()
1
Trong tam giác
SAC
, kẻ
1
A
CSC^ .
()
2
Từ
()
1 và
()
2 , suy ra
()
1
SC ABC^ .
Suy ra thiết diện cần tìm là tam giác
1
A
BC thỏa mãn đi qua
A
và vuông góc với
SC
.
Tam giác
SAC
cân tại
S
nên để
1
C nằm giữa
S
và
C
khi và chỉ khi
0
90ASC <
.
Suy ra
22 2 22
cos 0 0 2 0 2.ASC SA SC AC b a a b> + - > - ><
Câu 7: Cho hình chóp có đáy là hình thang vuông tại , đáy lớn ,
, vuông góc với mặt phẳng , . Gọi là trung điểm . Gọi là
mặt phẳng qua và vuông góc với. Thiết diện của và hình chóp có diện tích
bằng:
A. . B. . C. . D. .
Lời giải
Chọn C
C'
G
C
1
S
A
B
C
.SABCD
A
BCD
A
8AD = 6BC =
SA
()
A
BCD
6SA =
M
A
B
(
)
P
M
A
B
(
)
P
10 20 15 16
K
I
N
M
D
C
B
A
S
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 796
Do
() ()
.PAB PSA^
Gọi
I
là trung điểm của
()
.SB MI SA MI PÌ
Gọi
N
là trung điểm của
()
.CD MN AB MN P^Ì
Gọi
K
là trung điểm của
SC IK BC
, mà
()
.
M
NBC MNIK IK PÌ

Vậy thiết diện của
()
P
và hình chóp là hình thang
M
NKI
vuông tại
M
.
Ta có:
M
I là đường trung bình của tam giác
SAB
1
3.
2
MI SA= =
I
K là đường trung bình của tam giác
SBC
1
3.
2
IK BC= =
M
N
là đường trung bình của hình thang
A
BCD
()
1
7.
2
MN AD BC= +=
Vậy
. 15.
2
MNKI
IK MN
SMI
+
==
Câu 8: Cho hình chóp đều có đáy là tam giác đều cạnh , tâm , đường cao ;
. Gọi là điểm thuộc đoạn . Mặt phẳng đi qua và
vuông góc với . Đặt . Tính diện tích của thiết diện tạo bởi với hình
chóp .
A. B.
C. D.
Lời giải
Chọn A
Vì
.SABC
là hình chóp đều nên
()
SO ABC^ (
O
là tâm của tam giác
A
BC
).
.SABC
A
BC
a
O
'
A
A
2SO a=
M
()
' ';OA M A M O¹¹
()
a
M
'
A
A
A
Mx= S
()
a
.SABC
(
)
22
28 6 3 3 .
IJEF
Sxaxa=- - +
()
22
28 6 3 3 .
IJEF
Sxaxa=-+
()
2
3
.
2
Sax=-
()
2
2.Sax=-
F
E
N
A
'
C
B
A
S
O
M
I
J
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 797
Do đó
'SO AA^
mà
(
)
'AAa ^ suy ra
()
SO a
.
Tương tự ta cũng có
()
BC a
.
Qua
M
kẻ
IJ BC
với
, IABJACÎÎ
; kẻ
M
NSO
với
'.NSAÎ
Qua
N
kẻ
EF BC
với
, ESBFSCÎÎ
.
Khi đó thiết diện là hình thang
.IJFE
Diện tích hình thang
()
1
2
IJEF
SIJEFMN=+
.
Tam giác
A
BC
, có
.23
.
''3
IJ AM AM BC x
IJ
BC AA AA
== =
Tam giác
SBC
, có
()
.
23 .
'' '
EF SN OM OM BC
EF x a
BC SA OA OA
== = = -
Tam giác
'SOA
, có
()
'.'
23 2 3.
''
MN MA SO MA
MN a x
SO OA OA
== =-
Vậy
()()()
22
2
4333 23 28 63 3.
3
IJEF
Sxaax xaxa=--=--+
Câu 9: Cho hình chóp có đáy là hình chữ nhật với , . Cạnh bên
và vuông góc với đáy. Mặt phẳng đi qua vuông góc với . Tính diện
tích của thiết diện tạo bởi với hình chóp đã cho.
A. B. C. D.
Lời giải
Chọn B
Trong tam giác
SAC
, kẻ
A
ISC^
()
I
SCÎ .
Trong mp
()
SBC , dựng đường thẳng đi qua
I
vuông góc với
SC
cắt
SB
tại
M
.
Trong mp
()
SCD , dựng đường thẳng qua
I
vuông góc với
SC
cắt
SD
tại
N
.
Khi đó thiết diện của hình chóp cắt bởi mp
()
a là tứ giác
A
MIN
.
.SABCD
A
BCD
A
Ba=
3AD a=
2SA a=
()
a
A
SC
S
()
a
2
6
.
7
AMIN
a
S
=
2
12 6
.
35
AMIN
a
S
=
2
66
.
35
AMIN
a
S
=
2
6
.
5
AMIN
a
S
=
N
M
I
D
C
B
A
S
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 798
Ta có
()
SC SC AMa^^ .
()
1
Lại có
()
BC AB
BC SAB BC AM
BC SA
ì
^
ï
ï
^ ^
í
ï
^
ï
î
.
()
2
Từ
()
1 và
()
2 , suy ra
()
A
MSBC AMMI^^.
Chứng minh tương tự, ta được
A
NNI^
.
Do đó
11
..
22
AMIN AMI ANI
SSS AMMIANNI
DD
=+= +
.
Vì
, ,
A
MAIAN
là các đường cao của các tam giác vuông
, , SAB SAC SAD
nên
22
.2
5
SA AB a
AM
SA AB
==
+
;
22
.
2
SA AC
A
Ia
SA AC
==
+
;
22
.221
7
SA AD a
AN
SA AD
==
+
.
Suy ra
22
30
5
a
MI AI AM=-=
và
22
14
7
a
NI AI AN=-=
.
Vậy
2
12 30 2 21 14 12 6
..
2577 35
5
AMIN
aa a a a
S
æö
÷
ç
÷
ç
=+ =
÷
ç
÷
÷
ç
èø
.
Câu 10: Cho hình lăng trụ có đáy là tam giác vuông cân tại với ;
và vuông góc với đáy. Mặt phẳng qua là trung điểm của và vuông
góc với . Thiết diện tạo bởi với hình lăng trụ là:
A. Hình thang cân. B. Hình thang vuông.
C. Tam giác. D. Hình chữ nhật.
Lời giải
Chọn B
Gọi
N
là trung điểm
A
BMNAB^
.
.'''
A
BC A B C
A
BC
A
2BC a=
'
A
Aa=
()
a
M
BC
'
A
B
()
a
.'''
A
BC A B C
R
Q
N
M
C'
B
'
A
'
C
B
A
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 799
Ta có
() ()
'' ' .
'
MN AB
MN ABB A MN AB MN
MN AA
a
ì
^
ï
ï
^ ^Ì
í
ï
^
ï
î
Từ giả thiết suy ra
'''
A
BaAA ABBA==
là hình vuông
''BA AB^
.
Trong mp
()
''
A
BB A kẻ
'NQ BA
với
'QAAÎ
.
Trong mp
(
)
''
A
CC A kẻ
QR A C
với
'
R
CCÎ
.
Vậy thiết diện là hình thang
M
NQR
vuông (do
M
N
và
QR
cùng song song với
A
C
và
M
NNQ^
).
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 800
BÀI 4. HAI MẶT PHẲNG VUÔNG GÓC
A. KIẾN THỨC CƠ BẢN CẦN NẮM
I. Góc giữa hai mặt phẳng
1. Định nghĩa: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt
phẳng đó.
Nhận xét:
Cho hai đường thẳng a và b lần lượt vuông góc với hai mặt phẳng (P) và (Q);
 
12
u,u
lần lượt
là vectơ chỉ phương của a và b. Gọi
là góc giữa (P) và (Q). Khi đó, ta có:
 
 
neáu
neáu


   
   
o
12 12
oo
12 12
u,u u,u 90
180 u ,u u,u 90
Như vậy, góc giữa hai mặt phẳng luôn nhỏ hơn hoặc bằng
o
90 .
Vectơ

n0
được gọi là vectơ pháp tuyến của mặt phẳng (P) nếu nó nằm trên đường thẳng
vuông góc với (P).
2. Cách xác định góc giữa hai mặt phẳng
Khi hai mặt phẳng (P) và (Q) cắt
nhau theo giao tuyến x, để tính góc
giữa chúng, ta chỉ việc xét một mặt
phẳng (R) vuông góc với x, lần
lượt cắt (P) và (Q) theo các giao
tuyến a và b. Lúc đó, góc giữa (P)
và (Q) bằng góc giữa hai đường
thẳng a và b.
3. Định lí 1. Gọi S là diện tích của đa
giác H trong mặ
t phẳng (P) và S’ là
diện tích hình chiếu H’ của H trên
mặt phẳng (P’) thì
Sʹ Scos ,
trong
đó
là góc giữa hai mặt phăng (P)
và (P’).

 dt AʹBC dt ABC .cos
II. Hai mặt phẳng vuông góc
1. Định nghĩa. Hai mặt phẳng gọi là vuông góc với nhau nếu góc giữa chúng bằng
o
90 .
Hai mặt phẳng (P) và (Q) vuông góc với nhau, kí hiệu:

PQ
hay

QP.


o
PQ 90
(Với
là góc giữa hai mặt phẳng (P) và (Q)).
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 801
Từ định nghĩa trên ta suy ra:


 
12
PQnn,
với
 
12
n,n
theo thứ tự là vectơ pháp tuyến của
(P) và (Q).
2. Điều kiện để hai mặt phẳng vuông góc
a) Định lí 2. Hai mặt phẳng vuông góc với nhau khi và chỉ khi mặt phẳng này chứa một đường
thẳng vuông góc với mặt phẳng kia.




Pa
PQ
aQ
Chú ý: Dùng định lí này để chứng minh hai mặt phẳng vuông góc.
b) Các hệ quả
Hệ quả 1
Nếu hai mặt phẳng (P) và (Q) vuông góc
với nhau và A là điểm nằm trong (P) thì
đường thẳng a đi qua điểm A và vuông
góc với (Q) sẽ nằm trong (P).






PQ
AP a P
Aa,a Q
Nếu hai mặt phẳng (P) và (Q) vuông góc
với nhau thì bất cứ đường thẳng a nào
thuộc (P), vuông góc với giao tuyến của
(P) và (Q) sẽ vuông góc với mặt phẳng
(Q).






PQ
PQc aQ
aP,ac
Hệ quả 2. Hai mặt phẳng cắt nhau và cùng
vuông góc với mặt phẳng thứ ba thì giao
tuyến của chúng vuông góc với mặt phẳng
thứ ba.






PQa
PR aR
QR
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 802
Hệ quả 3. Qua đường thẳng a không vuông góc với mặt phẳng (P) có duy nhất một mặt phẳng
(Q) vuông góc với mặt phẳng (P).
a không vuông góc với (P)




Qa
!Q:
QP
.
III. Hình lăng trụ đứng. Hình hộp chữ nhật. Hình lập phương
1. Hình lăng trụ đứng
a) Định nghĩa. Hình lăng trụ đứng là hình lăng trụ
có cạnh bên vuông góc với mặt đáy.
b) Nhận xét. Các mặt bên của hình lăng trụ đứng là
hình chữ nhật và vuông góc với mặt đáy.
2. Hình lăng trụ đều
a) Định nghĩa. Hình lăng trụ đều là hình lăng tr
ụ
đứng có đáy là đa giác đều.
b) Nhận xét. Các mặt bên của hình lăng trụ đều là
những hình chữ nhật bằng nhau. Ngoài ra, hình
lăng trụ đều có các tính chất của hình lăng trụ
đứng.
3. Hình hộp đứng
a) Định nghĩa. Hình hộp đứng là hình lăng trụ đứng
có đáy là hình bình hành.
b) Nhận xét. Trong hình hộp đứng bốn mặt bên đều
là hình chữ nhật.
4. Hình hộp chữ nhật
a) Định nghĩa. Hình hộp chữ nhật là hình hộp đứng
có đáy là hình chữ nhật.
b) Nhận xét. Tất cả sáu mặt của hình hộp chữ nhật
đều là hình chữ nhật.
5. Hình lập phương
Định nghĩa. Hình lập phương là hình hộp có tất cả
các mặt là hình vuông.
IV. Hình chóp đều và hình chóp cụt đều
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 803
1. Định nghĩa đều
Định nghĩa. Một hình chóp được gọi là hình chóp
đều nếu đáy của nó là đa giác đều và các cạnh
bên bằng nhau.
Đường vuông góc với mặt đáy kẻ từ đỉnh gọi là
đường cao của hình chóp.
Từ định nghĩa, suy ra:
Một hình chóp là hình chóp đều khi và chỉ khi
đáy của nó là đa giác đều và chân đường cao của
hình chóp trùng với tâm của đáy.
Một hình chóp là hình chóp đều khi và chỉ khi
đ
áy của nó là đa giác đều và các cạnh bên tạo
với mặt đáy các góc bằng nhau.
2. Hình chóp cụt đều
Khi cắt hình chóp đều bởi một mặt phẳng song
song với đáy để được một hình chóp cụt thì hình
chóp cụt đó được gọi là hình chóp cụt đều.
Đoạn thẳng nối tâm của hai đáy được gọi là đường cao của hình chóp cụt đều.
Từ định nghĩa suy ra: Các mặt bên củ
a hình chóp cụt đều là những hình thang cân bằng nhau.
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1. Câu hỏi lý thuyết
Câu 1: Cho hai mặt phẳng và song song với nhau và một điểm không thuộc và
. Qua có bao nhiêu mặt phẳng vuông góc với và ?
A. B. C. D. Vô số.
Lời giải
Chọn D
Gọi
d
là đường thẳng qua
M
và vuông góc với
()
P
. Do
()() ()
PQ dQ^
.
Giả sử
()
R
là mặt phẳng chứa
d
. Mà
()
()
() ()
() ()
dP R P
dQ R P
ìì
ïï^^
ïï
íí
ïï
^^
ïï
îî
.
Có vô số mặt phẳng
()
R
chứa
d
. Do đó có vô số mặt phẳng qua
M
, vuông góc với
()
P
và
()
Q
.
Câu 2: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Cho hai đường thẳng song song và và đường thẳng sao cho . Mọi
mặt phẳng chứa thì đều vuông góc với mặt phẳng .
(
)
P
(
)
Q
M
(
)
P
(
)
Q
M
(
)
P
(
)
Q
2. 3. 1.
a
b
c
,cacb^^
()
a
c
()
,ab
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 804
B. Cho , mọi mặt phẳng chứa thì .
C. Cho , mọi mặt phẳng chứa đều vuông góc với .
D. Cho , nếu và thì .
Lời giải
Chọn B
A sai. Trong trường hợp
a
và
b
trùng nhau, sẽ tồn tại mặt phẳng chứa
a
và
b
không
vuông góc với mặt phẳng
()
a
chứa
c
.
C sai. Trong trường hợp
a
và
b
cắt nhau, mặt phẳng
()
,ab
chứa
b
nhưng không vuông
góc với
a
.
D sai. Trong trường hợp
a
và
b
vuông góc nhau và tréo nhau, nếu
()
aa É
,
()
ba
và
()
bb É
,
()
ab
thì
()()
ab
.
Câu 3: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
B. Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một đường thẳng cho
trước.
C. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
D. Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho tr
ước.
Lời giải
Chọn C
A sai. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với
nhau hoặc cắt nhau (giao tuyến vuông góc với mặt phẳng thứ 3).
B sai. Qua một đường thẳng vô số mặt phẳng vuông góc với một đường thẳng cho trước.
D sai. Qua một điểm có vô số mặt phẳng vuông góc với một mặt phẳng cho trước.
Câu 4: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng và vuông góc với nhau và cắt nhau theo giao tuyến . Với
mỗi điểm thuộc và mỗi điểm thuộc thì ta có vuông góc với .
B. Nếu hai mặt phẳng và cùng vuông góc với mặt phẳng thì giao tuyến của
và nếu có cũng sẽ vuông góc với .
C. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thứ ba thì song song với
nhau.
D. Nếu hai mặt phẳng vuông góc với nhau thì mọi đường thẳng thuộc mặt ph
ẳng này sẽ
vuông góc với mặt phẳng kia.
Lời giải
()
a a^
()
b
a
() ()
ba^
ab^ b
a
ab^
()
a aÌ
()
b bÌ
() ()
ab^
(
)
P
(
)
Q
d
A
(
)
P
B
(
)
Q
A
B
d
(
)
P
(
)
Q
(
)
R
(
)
P
(
)
Q
(
)
R
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 805
Chọn B
A sai. Trong trường hợp
adÎ
,
bdÎ
, khi đó
A
B
trùng với
d
.
C sai. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thứ ba thì song song
với nhau hoặc cắt nhau (giao tuyến vuông góc với mặt phẳng thứ 3).
D sai. Hai mặt phẳng vuông góc với nhau, đường thẳng thuộc mặt phẳng này và vuông
góc với giao tuyến thì vuông góc với mặt phẳng kia.
Câu 5: Trong các mệnh đề sau, mệnh đề nào sau đây là đúng?
A. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ
vuông góc v
ới mặt phẳng kia.
B. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
C. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
D. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này và
vuông góc với giao tuyến của hai mặt phẳng sẽ vuông góc với mặt phẳng kia.
Lời giải
Chọn D
A sai. Hai mặt phẳng vuông góc với nhau thì đường thẳng nằ
m trong mặt phẳng này,
vuông góc với giao tuyến thì vuông góc với mặt phẳng kia.
B, C sai. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với
nhau hoặc cắt nhau (giao truyến vuông góc với mặt phẳng kia).
Câu 6: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song với nhau.
B. Qua một đường thẳng cho trước có duy nhất một mặt phẳng vuông góc với một mặt
phẳng cho trước.
C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với hai mặt
phẳng cắt nhau cho trước.
D. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau.
Lời giải
Chọn C
A sai. Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song hoặc trùng
nhau.
B sai. Nếu đường thẳng vuông góc với mặt phẳng cho trước thì có vô số mặt phẳng qua
đường thẳng và vuông góc với mặt phẳng đó. Nếu đường thẳng không vuông góc với mặt
phẳng cho trước thì không có mặt phẳng nào vuông góc với mặt phẳng đó.
D sai. Hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì song song với
nhau hoặc cắt nhau (giao truyến vuông góc với mặt phẳng kia).
Câu 7: Trong các mệnh đề sau, mệnh đề nào sai?
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 806
A. Cho đường thẳng vuông góc với đường thẳng và nằm trong mặt phẳng .
Mọi mặt phẳng chứa và vuông góc với thì vuông góc với .
B. Nếu đường thẳng vuông góc với đường thẳng và mặt phẳng chứa , mặt
phẳng chứa thì vuông góc với .
C. Cho đường thẳng vuông góc với mặt phẳng ,
mọi mặt phẳng chứa thì
vuông góc với .
D. Qua một điểm có duy nhất một mặt phẳ
ng vuông góc với một đường thẳng cho trước.
Lời giải
Chọn B
Trong trường hợp
a
và
b
vuông góc nhau và tréo nhau, nếu
(
)
PaÉ
,
(
)
Pb
và
()
QbÉ
,
()
Qa
thì
()()
PQ
.
Câu 8: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Góc giữa mặt phẳng và mặt phẳng bằng góc nhọn giữa mặt phẳng và mặt
phẳng khi mặt phẳng song song với mặt phẳng .
B. Góc giữa mặt phẳng và mặt phẳng bằng góc nhọn giữa mặt phẳng và mặt
phẳng khi mặt phẳng song song với mặt phẳng hoặc .
C. Góc giữa hai mặt phẳng luôn là góc nhọn.
D.
Cả 3 mệnh đề trên đều đúng.
Lời giải
Chọn D
Câu 9: Trong khẳng định sau về lăng trụ đều, khẳng định nào sai?
A. Đáy là đa giác đều.
B. Các mặt bên là những hình chữ nhật nằm trong mặt phẳng vuông góc với đáy.
C. Các cạnh bên là những đường cao.
D. Các mặt bên là những hình vuông.
Lời giải
Chọn D
Vì lăng trụ đều là lăng trụ đứng nên các c
ạnh bên bằng nhau và cùng vuông góc với đáy.
Do đó các mặt bên là những hình chữ nhật.
Câu 10: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu hình hộp có hai mặt là hình vuông thì nó là hình lập phương.
B. Nếu hình hộp có ba mặt chung một đỉnh là hình vuông thì nó là hình lập phương.
C. Nếu hình hộp có bốn đường chéo bằng nhau thì nó là hình lập phương.
a
bb
(
)
P
(
)
Q
a
b
(
)
P
(
)
Q
a
b
(
)
P
a
(
)
Q
b
(
)
P
(
)
Q
a
(
)
P
(
)
Q
a
(
)
P
(
)
Q
(
)
P
(
)
Q
(
)
P
(
)
R
(
)
Q
(
)
R
(
)
P
(
)
Q
(
)
P
(
)
R
(
)
Q
(
)
R
() ()
QRº
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 807
D. Nếu hình hộp có sau mặt bằng nhau thì nó là hình lập phương.
Lời giải
Chọn B
Dạng 2. Chứng minh hai mặt phẳng vuông góc
1. Phương pháp
Để chứng minh hai mặt phẳng vuông góc, ta dùng định lí: Hai mặt phẳng vuông góc với nhau
khi và chỉ khi mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
(P) a
(P) (Q).
a(Q)

Như vậy, việc chứng minh hai mặt phẳng vuông góc quy về việc chứng minh một đường thẳng
vuông góc với một mặt phẳng.
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Cho đường thẳng a và hai mặt phẳng (P) và (Q). Khẳng đinh nào sau đây đúng?
A.




aP
QP.
Qa
B.



QP
aQ.
aP
C.





PQ
aQ.
a
D. Có 2 câu đúng trong 3 câu trên.
Hướng dẫn giải
ĐÁP ÁN A
Theo định lí: “Nếu

Pa
và
aQ
thì
PQ
” thì A đúng.
Ví dụ 2: Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến
. Gọi a là đường thẳng nằm trong
(P). Khẳng định nào sau đây đúng?
A. Nếu
a thì

aQ. B.




a
aQ.
PQ
C. Nếu

aQ
thì

PQ.
D. Chỉ có 1 câu sai trong 3 câu trên.
Hướng dẫn giải
ĐÁP ÁN D




aP
aQ
a
: Sai. Vậy A sai.




a
aQ
PQ
: Đúng. Vậy B đúng.
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 808




aP
PQ
aQ
: Đúng. Vậy C đúng.
Ví dụ 3: Cho hai mặt phẳng (P) và (Q) vuông góc với nhau, giao tuyến là
.

AP
và

AQ.
Qua A, vẽ đường thẳng
ʹ
vuông góc với (Q). Khẳng đình nào sau đây sai ?
A.

ʹ P.
B.
ʹ
chéo
.
C.

ʹ .
D. Có 2 câu đúng trong 3 câu trên.
Hướng dẫn giải
ĐÁP ÁN B
Ta có:






PQ
AP ʹ P
ʹ Q
: Đúng. vậy A đúng.
Vì

ʹ P
và

 P
nên
ʹ
chéo
là sai. Vậy B sai.



 

ʹ Q
ʹ
Q
: Đúng. Vậy C đúng.
Ví dụ 4: Cho đường thẳng a và hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến
.
Khẳng đinh
nào sau đây đúng?
A.




aP
aQ.
a
B.


caét

aQ
aP.
a
C.




PQ
aP.
a
D. Cả 3 câu đều sai.
Hướng dẫn giải
ĐÁP ÁN D
Thiếu giả thiết

PQ
nên A sai (hình 1).
Thiếu giả thiết nên B sai (hình 2).
Thiếu giả thiết
cắt a nên C sai (hình 3).
Hình 1
Hình 2
Hình 3
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 809
Ví dụ 5: Cho tứ diện ABCD có tam giác ABD và tam giác ABC vuông tại B. Khẳng định nào sau
đây đúng?
A.
CB AD.
B.

AB BCD .
C.

222
AC AB BC .
D. Cả A, B, C đều đúng.
Hướng dẫn giải
ĐÁP ÁN B
Vì
ABC
vuông tại B nên
AB BC
và
ABD
vuông
tại B nên
AB BD
. Từ đó
suy ra

AB BCD
. Vậy B
đúng.
Ví dụ 6: Cho tam giác ABC đều, cạnh a. Gọi D là điểm đối xứng của A qua BC. Trên đường thẳng
vuông góc với mặt phẳng (ABC) tại D, lấy điểm S. Để cho mặt phẳng (SAB) vuông góc với mặt
phẳng (SAC), SD có độ dài tính theo a bẳng
A.
a6
.
2
B.
a3.
C.
a3
.
3
D.
a6.
Hướng dẫn giải
ĐÁP ÁN A
Vì

SD BCD
nên
SDB
và
SDC
vuông tại D.
Mà
DB DC
(ABCD là hình thoi)
nên

SDB SDC
. Suy ra,
SB SC
.
Mặt khác
AB AC
(
ABC
đều) nên
SAB SAC
. Gọi I là chân đường
vuông góc hạ từ C trong
SCA
, ta có
SA IB
và
SA IC.
Suy ra

SA BIC
.
Để cho

SAB SAC
, ta phải có
o
BIC 90
.
Suy ra

BC a
OI
22
(O là trung điểm của BC).
AIO
vuông tại I cho
a2
AI .
2
AIO ADS
∽
nên

AD a 6
SD .IO SD .
AI 2
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 810
3. Bài tập trắc nghiệm
Câu 1: Cho hình chóp có đáy là tam giác vuông cân tại , vuông góc với đáy.
Gọi là trung điểm . Khẳng định nào sau đây sai?
A. B.
C. D.
Lời giải
Chọn D
Tam giác
A
BC
cân tại
B
có
M
là trung điểm
.
A
CBMAC^
Do đó A đúng.
Ta có
()
()
()( )()
do
BM AC
B
MSAC SBM SAC
BM SA SA ABC
ì
^
ï
ï
^ ^
í
ï
^^
ï
î
. Do đó B đúng.
Ta có
()
()
()()()
do
BC BA
B
CSAB SBC SAB
BC SA SA ABC
ì
^
ï
ï
^ ^
í
ï
^^
ï
î
. Do đó C đúng.
Dùng phương pháp loại trừ thì D là đáp án sai.
Câu 2: Cho tứ diện có và nằm trong hai mặt phẳng vuông góc với nhau. Tam
giác đều, tam giác vuông tại . Gọi , lần lượt là trung điểm của và
. Khẳng định nào sau đây sai?
A. B. C. D.
Lời giải
Chọn C
.SABC
A
BC
B
SA
M
A
C
.BM AC^
()()
.SBM SAC^
()()
.SAB SBC^
()()
.SAB SAC^
S
A
B
C
M
SABC SBC
A
BC
SBC
A
BC
A
H
I
BC
A
B
.SH AB^ .
H
IAB^
()()
.SAB SAC^
()()
.SHI SAB^
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 811
Do
SBC
là tam giác đều có H là trung điểm
B
C
nên
SH BC^
.
Mà
()( )
SBC ABC^
theo giao tuyến
()
.
B
CSH ABC SHAB^ ^
Do đó A đúng.
Ta có
HI
là đường trung bình của
A
BCD
nên
.
H
IAC HIAB^
Do đó B đúng.
Ta có
()()()
.
SH AB
A
B SHI SAB SHI
HI AB
ì
^
ï
ï
^ ^
í
ï
^
ï
î
Do đó D đúng.
Dùng phương pháp loại trừ thì C là đáp án sai.
Câu 3: Cho hình chóp có đáy là tam giác vuông tại , mặt bên là tam giác
đều và mằm trong mặt phẳng vuông góc với đáy. Gọi là trung điểm của . Mệnh đề
nào sau đây sai?
A. B.
C. D.
Lời giải
Chọn B
Tam giác
SAC
đều có
I
là trung điểm của
SC
nên
A
ISC^
. Do đó A đúng.
A
B
C
S
H
I
.SABC
A
BC C SAC
I
SC
.
A
ISC^
()()
.SBC SAC^
.
A
IBC^
()()
.
A
BI SBC^
S
A
B
C
H
I
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 812
Gọi
H
là trung điểm
A
C
suy ra
SH AC^
. Mà
()( )
SAC ABC^
theo giao tuyến
A
C
nên
()
SH ABC^
do đó
SH BC^
. Hơn nữa theo giả thiết tam giác
A
BC
vuông tại
C
nên
B
CAC^
. Từ đó suy ra
()
B
CSAC BCAI^^
. Do đó C đúng.
Từ mệnh đề A và C suy ra mệnh đề D đúng.
Dùng phương pháp loại trừ thì B là đáp án sai.
Câu 4: Cho hình chóp có đáy là tam giác vuông tại , vuông góc với đáy. Gọi
lần lượt là hình chiếu của trên , và là giao điểm của với mặt
phẳng . Khẳng định nào sau đây sai?
A. B. C. D. Tam giác
đều.
Lời giải
Chọn D
Ta có
()
BC AB
BC SAB BC AH
SA BC
ì
^
ï
ï
^ ^
í
ï
^
ï
î
. Do đó A đúng.
Lại có
A
HSB^
. Từ đó suy ra
()
A
HSBC AHSC^^
.
()
1
Lại có theo giả thiết
SC AK^
.
()
2
Từ
()
1
và
(
)
2
, suy ra
()()()
SC AHK SBC AHK^^
. Do đó B đúng.
Ta có
()
()
SC AHK
SC AI
AI AHK
ì
ï
^
ï
^
í
ï
Ì
ï
î
. Do đó C đúng.
Dùng phương pháp loại trừ thì D là đáp án sai.
Câu 5: Cho tam giác đều cạnh . Gọi là điểm đối xứng với qua . Trên đường
thẳng vuông góc với mặt phẳng tại lấy điểm sao cho . Gọi là
trung điểm ; kẻ vuông góc . Khẳng định nào sau đây sai?
.SABC
A
BC
B
SA
, HK
A
SB SC
I
HK
()
A
BC
.BC AH^
(
)
(
)
.
A
HK SBC^
.SC AI^
I
AC
H
C
B
A
S
K
I
A
BC
a
D
A
BC
()
A
BC
D
S
6
2
a
SD =
I
BC
I
H
SA
()
H
SAÎ
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 813
A. B. C. D.
Lời giải
Chọn B
Từ giả thiết suy ra
A
BDC
là hình thoi nên
.
B
CAD^
Ta có
()
BC AD
BC SAD BC SA
BC SD
ì
^
ï
ï
^ ^
í
ï
^
ï
î
.
Lại có theo giả thiết
IH SA^
. Từ đó suy ra
()
SA HCB SA BH^^
. Do đó A đúng.
Tính được
3
2
a
AI =
, 23AD AI a==,
222
32
.
2
a
SA AD SD=+=
Ta có
.
22
IH AI AI SD a BC
AHI ADS IH
SD AS AS
DD====∽
tam giác
HBC
có trung tuyến
I
H
bằng nửa cạnh đáy
B
C
nên
0
90BHC =
hay
B
HHC^
. Do đó D đúng.
Từ mệnh đề A và D suy ra mệnh đề C đúng.
Dùng phương pháp loại trừ thì B là đáp án sai.
Dạng 3. Tính góc giữa hai mặt phẳng
1. Phương pháp
Khi hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến x, để xác định góc giữa chúng, ta chỉ
việc xét một mặt phẳng (K) vuông góc với x lần lượt cắt (P) và (Q) theo các giao tuyến a và b.
Lúc đó, góc giữa (P) và (Q) bằng góc giữa hai đường thẳng a và b.
Để tìm góc giữa hai mặt phẳng (P) và (Q) ta thường làm như sau:
– Xác định một điểm A trên (P), vẽ
AH Q
(tại H).
– Vẽ
HO x tại O thì AO x.
– Góc

o
OA,OH 90
là góc cần tìm.
.SA BH^
()()
.SDB SDC^
()()
.SAB SAC^
.BH HC^
S
A
B
C
D
I
H
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 814
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Cho tứ diện SABC có ABC là tam giác đều cạnh
2a,
SA vuông góc với mặt phẳng (ABC)
và
SA a.
Góc giữa hai mặt phẳng (SBC) và (ABC) bằng
A.
o
30 .
B.
o
45 .
C.
o
60 .
D.
o
90 .
Hướng dẫn giải
ĐÁP ÁN A
Gọi
là góc giữa hai mặt phẳng (SBC) và
(ABC).
Kẻ đường cao AH của
ABC ,
ta có:
BC AH
, AH là hình chiếu của SH trên
mặt phẳng (ABC) nên suy ra
BC SH
.
Vậy
SHA.
Tam giác SHA vuông tại A có:
SA a,
AH a 3
(đường cao của tam giác đều
ABC).
Suy ra:
 
o
SA a 3
tan 30 .
AH 3
a3
Ví dụ 2: Cho hình chóp đều S.ABC có ABC là tam giác đều cạnh a, cạnh bên
a21
SA .
6
Giá trị
góc
giữa hai mặt phẳng (SBC) và (ABC) bằng
A.
o
30 .
B.
o
45 .
C.
o
60 .
D.
o
90 .
Hướng dẫn giải
ĐÁP ÁN C
Xác định góc
. Gọi G là trọng tâm của
ABC
,
ta có

SG ABC .
Kẻ
AM BC
thì trọng tâm
G của
ABC
thuộc AM.
GM là hình chiếu của SM trên mặt phẳng (ABC)
nên
BC SM.
Suy ra góc cần tìm là
SMG.
Tính
. Ta có:
a3
AM
2
(đường cao của tam
giác đều ABC, cạnh a), suy ra
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 815

1a3
GM AM .
36
Tam giác SMB vuông tại M nên:








2
2
2
22 2
a21 a a a
SM SB BM SM .
623
3
Tam giác SGM vuông tại G nên:
 
o
GM a 3 3 1
cos . 60 .
SM 6 a 2
Ví dụ 3: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a và cạnh bên bằng
a3.
Gọi
là góc giữa hai mặt phẳng (ABC) và (AB’C’), thì
cos
có giá trị bằng
A.
5
.
5
B.
6
.
6
C.
3
.
3
D.
3
.
4
Hướng dẫn giải
ĐÁP ÁN A
Do ABC.A’B’C’ là hình lăng trụ đều nên B và C là hình chiếu vuông góc của B’ và C’ trên
(ABC).
Tam giác AB’C’ cân tại A. Gọi I là trung điểm của B’C’ thì
AI BʹCʹ.
Ta có

AAʹ AʹBʹCʹ AAʹ AʹIAAʹI
vuông tại A’.
Do đó:

22
2222
3a 15a
AI AAʹ AʹI3a .
44
Suy ra
a15
AI .
2
+ Diện tích

2
1a15
ABʹCʹ :S BʹCʹ.AI .
24
+ Diện tích

2
a3
ABC : Sʹ .
4
Áp dụng công thức diện tích hình chiếu của đa
giác, ta có:

2
2
Sʹ a3 4 5
cos . .
S4 5
a15
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 816
Ví dụ 4: Cho hình chóp tam giác O.ABC có OA, OB, OC vuông góc đôi một. Gọi
,,
là các
góc tạo bởi mặt phẳng (ABC) với các mặt phẳng (OAB), (OBC), (OCA). Tổng
 
222
cos cos cos
có giá trị bằng
A.
2.
B.
3
.
2
C.
1.
D.
1
.
2
Hướng dẫn giải
ĐÁP ÁN C
Gọi H là hình chiếu vuông góc của O trên
(ABC).
Đặt
OA a, OA b, OC c
và
OH h.
Kéo dài CH cắt AB tại I, ta chứng minh được

AB OCI
và

2222
1111
.
habc
Suy ra góc giữa (ABC) và (OAB) là
OIC .
Trong
OCI
ta có:
OIC COH
(góc có
cạnh tương ứng vuông góc).
Trong
OCH
ta có:

OH h
cos .
OC c
Chứng minh tương tự:

hh
cos , cos .
ab
Do đó

 


222
222 2
222 222
hhh 111
cos cos cos h 1.
abc abc
Chú ý: Có thể chứng minh bài toán bằng cách dùng công thức diện tích hình chiếu như sau:
Gọi S,
123
S,S,S
lần lượt là diện tích các tam giác ABC, OAB, OBC, OCA.
Do

OC OAB
nên
OAB
là hình chiếu vuông góc của
ABC
lên (OAB).
Ta có:

1
SScos.
Mặt khác
HAB
là hình chiếu vuông góc của
OAB
lên (ABC) nên:

2
HAB OAB 1
S S .cos S cos Scos .
Chứng minh tương tự:

22
HBC HCA
S Scos ; S Scos .
Do đó:

222
HAB HBC HCA
S S S Scos Scos Scos .
Hay


222 222
S S cos cos cos cos cos cos 1.
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 817
Ví dụ 5: Cho hình lăng trụ đứng tam giác ABC.A’B’C’ có tam giác ABC vuông cân tại B,
AB a.
Để góc tạo bởi (AB’C’) và (ABC) bằng
o
60
thì độ dài cạnh bên của lăng trụ bằng bao nhiêu?
A.
a.
B.
a3.
C.
2a.
D.
a5.
Hướng dẫn giải
ĐÁP ÁN B
Ta có
BC AB
và
BC BBʹ
nên

BC ABBʹAʹ .
Mà
BʹCʹ// BC
nên

BʹCʹ ABBʹAʹ .
Suy ra:
BʹCʹ ABʹ ABʹCʹ
vuông tại B’.
Gọi S là diện tích của
ABʹCʹ
và S’ là diện
tích
ABC.
Từ giả thiết ta có:

2
o
a1
Sʹ Scos60 S.
22
. Do đó
2
Sa.
Mà

1
SBʹCʹ.ABʹ ABʹ 2a.
2
Từ tam giác ABB’ vuông tại B ta có:

222222
BBʹ ABʹ AB 4a a 3a BBʹ a3.
3. Bài tập trắc nghiệm
Câu 1: Cho hình chóp có đáy là tam giác vuông tại , , tam giác là
tam giác đều có bằng cạnh và nằm trong mặt phẳng vuông với đáy. Gọi là góc giữa
hai mặt phẳng và . Mệnh đề nào sau đây đúng?
A. B. C. D.
Lời giải
Chọn B
.SABC
A
BC
A
60ABC =
SBC
2a
j
()
SAC
()
A
BC
0
60 .j =
tan 2 3.j =
3
tan .
6
j =
1
tan .
2
j =
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 818
Gọi
H
là trung điểm của
B
C
, suy ra
()
SH BC SH ABC^^
.
Gọi
K
là trung điểm
A
C
, suy ra
H
KAB nên
H
KAC^
.
Ta có
()
.
AC HK
A
CSHK ACSK
AC SH
ì
^
ï
ï
^ ^
í
ï
^
ï
î
Do đó
()( )
()
,,.SAC ABC SK HK SKH==
Tam giác vuông
A
BC
, có
1
.cos .
22
a
AB BC ABC a HK AB====
Tam giác vuông
SHK
, có
tan 2 3
SH
SKH
HK
==
.
Câu 2: Cho hình chóp có đáy là tam giác đều cạnh . Cạnh bên và vuông
góc với mặt đáy . Gọi là góc giữa hai mặt phẳng và . Mệnh đề nào
sau đây đúng?
A. B. C. D.
Lời giải
Chọn D
Gọi
M
là trung điểm của
B
C
, suy ra
A
MBC^
.
Ta có
()
AM BC
BC SAM BC SM
BC SA
ì
^
ï
ï
^ ^
í
ï
^
ï
î
.
A
B
C
S
H
K
.SABC
A
BC
a
3SA a=
()
A
BC
j
()
SBC
()
A
BC
0
30 .j =
5
sin .
5
j =
0
60 .j =
25
sin .
5
j =
S
A
B
C
M
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 819
Do đó
()( )
()
,,.SBC ABC SM AM SMA==
Tam giác
A
BC
đều cạnh
a
, suy ra trung tuyến
3
.
2
a
AM =
Tam giác vuông
SAM
, có
22
25
sin .
5
SA SA
SMA
SM
SA AM
== =
+
Câu 3: Cho hình chóp có đáy là hình vuông tâm , cạnh . Đường thẳng
vuông góc với mặt phẳng đáy và . Tính góc giữa hai mặt phẳng
và .
A. . B. . C. . D. .
Lời giải
Chọn C
Gọi
Q
là trung điểm
B
C
, suy ra
OQ BC^
.
Ta có
()
.
BC OQ
BC SOQ BC SQ
BC SO
ì
^
ï
ï
^ ^
í
ï
^
ï
î
Do đó
()( )
,,.SBC ABCD SQ OQ SQO==
Tam giác vuông
SOQ
, có
tan 3.
SO
SQO
OQ
==
Vậy mặt phẳng
()
SBC
hợp với mặt đáy
()
A
BCD
một góc
0
60 .
Câu 4: Cho hình chóp có đáy là hình thoi tâm , cạnh , góc ,
. Gọi là góc giữa hai mặt phẳng và Mệnh đề nào
sau đây đúng?
A. B. C. D.
Lời giải
Chọn A
.SABCD
A
BCD O
a
SO
()
A
BCD
3
2
a
SO =
()
SBC
()
A
BCD
0
30
0
45
0
60
0
90
.SABCD
A
BCD
I
a
0
60BAD =
3
2
a
SA SB SD== =
j
()
SBD
(
)
.
A
BCD
tan 5.j =
5
tan .
5
j =
3
tan .
2
j =
0
45 .j =
H
I
S
D
C
B
A
QO
S
D
C
B
A
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 820
Từ giả thiết suy ra tam giác
A
BD đều cạnh
a
.
Gọi
H là hình chiếu của
S
trên mặt phẳng
()
A
BCD
. Do
SA SB SD==
nên suy ra H cách
đều các đỉnh của tam giác
A
BD
hay
H
là tâm của tam gác đều
A
BD
.
Suy ra
13
36
a
HI AI
== và
22
15
.
6
a
SH SA AH
=-=
Vì
A
BCD
là hình thoi nên HI BD^ . Tam giác
SBD
cân tại
S
nên
SI BD^
.
Do đó
()( )
,,SBD ABCD SI AI SIH==
.
Trong tam vuông
SHI
, có
tan 5.
SH
SIH
HI
==
Câu 5: Cho hình chóp có đáy là hình thang vuông vuông tại và ,
. Cạnh bên và vuông góc với mặt phẳng Gọi là góc giữa
hai mặt phẳng và . Mệnh đề nào sau đây đúng?
A. B. C. D.
Lời giải
Chọn A
Gọi
M
là trung điểm
A
BADCM
là hình vuông
2
A
B
CM AD a===
.
Suy ra tam giác
A
CB
có trung tuyến bằng nửa cạnh đáy nên vuông tại
C
.
Ta có
()
.
BC SA
BC SAC BC SC
BC AC
ì
^
ï
ï
^ ^
í
ï
^
ï
î
Do đó
()( )
,,.SBC ABCD SC AC SCA==
Tam giác
SAC
vuông tại
A
2
tan .
2
SA
AC
j==
Câu 6: Cho hình chóp đều có tất cả các cạnh bằng . Gọi là trung điểm . Tính
góc giữa hai mặt phẳng và .
.SABCD
A
BCD
A
D
2,
A
Ba=
A
DCDa== SA a=
(
)
.
A
BCD
j
()
SBC
()
A
BCD
2
tan .
2
j =
0
45 .j =
0
60 .j =
0
30 .j =
M
D
C
B
A
S
.SABCD
a
M
SC
j
(
)
M
BD
()
A
BCD
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 821
A. B. C. D.
Lời giải
Chọn C
Gọi
'
M
là trung điểm
()
''.OC MM SO MM ABCD^
Theo công thức diện tích hình chiếu, ta có
'
cos .
M
BD MBD
SSj
DD
=
0
'
.2
cos 45 .
.' ' 2
MBD
MBD
S
BD MO MO
SBDMOMO
jj
D
D
= = = ==
Câu 7: Trong không gian cho tam giác đều và hình vuông cạnh nằm trên hai mặt
phẳng vuông góc. Gọi lần lượt là trung điểm của , . Gọi là góc giữa hai
mặt phẳng và . Mệnh đề nào sau đây đúng?
A. B. C. D.
Lời giải
Chọn B
Dễ dàng xác định giao tuyến của hai mặt phẳng
()
SAB
và
()
SCD
là đường thẳng d đi qua
S
và song song với
A
B
.
Trong mặt phẳng
()
SAB
có
.SH AB SH d^^
90 .j = 60 .j = 45 .j = 30 .j =
M
'
M
A
B
C
D
S
O
SAB
A
BCD
a
,H
K
A
B
CD
j
()
SAB
()
SCD
2
tan .
3
j =
23
tan .
3
j =
3
tan .
3
j =
3
tan .
2
j =
K
H
D
C
B
A
S
d
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 822
Ta có
()
.
CD HK
CD SHK CD SK d SK
CD SH
ì
^
ï
ï
^ ^^
í
ï
^
ï
î
Từ đó suy ra
()()
,,.SAB SCD SH SK HSK==
Trong tam giác vuông
SHK
, có
23
tan .
3
HK
HSK
SH
==
Câu 8: Cho hình chóp đều có tất cả các cạnh đều bằng . Gọi là góc giữa hai mặt
phẳng và . Mệnh đề nào sau đây đúng?
A. B. C. D.
Lời giải
Chọn D
Gọi
OACBD=Ç
. Do hình chóp
.SABCD
đều nên
()
SO ABCD^
.
Gọi
M
là trung điểm của
SD
. Tam giác
SCD
đều nên
CM SD^
.
Tam giác
SBD
có
SB SD a==
, 2BD a= nên vuông tại
.SSBSDOMSD^ ^
Do đó
()()
,,SBD SCD OM CM=
.
Ta có
()
OC BD
OC SBD OC OM
OC SO
ì
^
ï
ï
^ ^
í
ï
^
ï
î
.
Tam giác vuông
M
OC
, có
tan 2
OC
CMO
OM
==
.
Câu 9: Cho hình chóp có đáy là tam giác vuông tại , . Hình chiếu
vuông góc của trên mặt đáy trùng với tâm đường tròn ngoại tiếp tam giác
và . Gọi là góc giữa hai đường thẳng và . Mệnh đề nào sau đây đúng?
A. B. C. D.
Lời giải
Chọn C
.SABCD
a
j
()
SBD
()
SCD
tan 6.j =
2
tan .
2
j =
3
tan .
2
j =
tan 2.j =
O
M
B
D
C
A
S
.SABC
A
BC
A
A
BACa==
H
S
()
A
BC
A
BC
6
2
a
SH =
j
SB
A
C
2
cot .
4
j =
cot 7.j =
7
cot .
7
j =
14
cot .
4
j =
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 823
Gọi
H là trung điểm
B
C
. Tam giác
A
BC
vuông tại
A
nên H là tâm đường tròn ngoại
tiếp tam giác
A
BC
. Theo giả thiết, ta có
()
SH ABC^
.
Qua
B
kẻ Bx AC . Khi đó
,,SB AC SB Bx=
.
Kẻ
HE Bx^
tại
E
, cắt
A
C
tại
M
.
Suy ra
A
MEB là hình chữ nhật nên
1
22
1
22
a
BE AM AC
a
HE HM AB
ì
ï
ï
== =
ï
ï
ï
í
ï
ï
== =
ï
ï
ï
î
.
Ta có
()
Bx HE
Bx SHE Bx SE
Bx SH
ì
^
ï
ï
^ ^
í
ï
^
ï
î
.
Tam giác vuông
SEB
, có
22
7
cot
7
BE AM
SBE
SE
SH HE
== =
+
.
Câu 10: Cho hình chóp có đáy là tam giác vuông cân tại . Gọi là trung điểm
. Biết rằng vuông góc với mặt phẳng và Tính cosin của góc
tọa bởi hai mặt phẳng và .
A. B. C. D.
Lời giải
Chọn D
E
M
H
S
C
B
A
.SABC
A
BC C
H
A
B
SH
()
A
BC
.
A
BSH a==
a
()
SAB
()
SAC
1
cos .
3
a =
2
cos .
3
a =
3
cos .
3
a =
2
cos .
3
a =
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 824
Ta có
()
SH ABC SH CH^^
.
()
1
Tam giác
A
BC
cân tại
C
nên
CH AB^
.
(
)
2
Từ
()
1
và
(
)
2
, suy ra
()
CH SAB^
.
Gọi
I
là trung điểm
A
C
BC AC
H
IBC HI AC
^
¾¾¾¾¾¾^
.
()
3
Mặt khác
A
CSH^
(do
()
SH ABC^
).
(
)
4
Từ
()
3
và
(
)
4
, suy ra
()
A
CSHI^
.
Kẻ
()
H
KSIKSI^Î
.
()
5
Từ
()
A
CSHI ACHK^^
.
(
)
6
Từ
()
5
và
(
)
6
, suy ra
()
H
KSAC^
.
Vì
()
()
H
KSAC
H
CSAB
ì
ï
^
ï
í
ï
^
ï
î
nên góc giữa hai mặt phẳng
()
SAC
và
()
SAB
bằng góc giữa hai đường
thẳng
H
K
và
H
C
.
Xét tam giác
CHK
vuông tại
K
, có
1
22
a
CH AB==
;
222
111
3
a
HK
HK SH HI
=+=
.
Do đó
2
cos .
3
HK
CHK
CH
==
Nhận xét. Bài làm sử dụng lý thuyết
''
()
()
()()
1
12
2
,,
d
dd
d
a
ab
b
ì
ï
^
ï
=
í
ï
^
ï
î
''
. Nếu ta sử dụng lý
thuyết quen thuộc
''
góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng lần lượt nằm
trong hai mặt phẳng và cùng vuông góc với giao tuyến
''
thì rất khó.
Câu 11: Cho hình chóp có đáy là tam giác vuông tại cạnh bên vuông góc với
đáy. Gọi lần lượt là trung điểm của các cạnh và Góc giữa hai mặt phẳng
và là
S
K
I
H
C
B
A
.SABC
A
BC
,B
SA
,
E
F
A
B
.
A
C
()
SEF
()
SBC
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 825
A. B. C. D.
Lời giải
Chọn C
Gọi
(
)
d
là đường thẳng đi qua
S
và song song với
.
E
F
Vì
E
F
là đường trung bình tam giác
A
BC
suy ra
E
F
//
B
C
.
Khi đó
(
)
d
//
E
F //
B
C
()()() ()
1.SEF SBC dÇ=
Ta có
()
()
SA BC SA ABC
AB BC
ì
ï
^^
ï
í
ï
^
ï
î
suy ra
() ()
2.
BC SE
BC SAB
BC SB
ì
^
ï
ï
^
í
ï
^
ï
î
Từ
(
)
(
)
1,2
suy ra
()
()
()()
()
;;.
dSE
SEF SBC SE SB BSE
dSB
ì
ï
^
ï
==
í
ï
^
ï
î
Câu 12: Cho hai tam giác và nằm trên hai mặt phẳng vuông góc với nhau và
Với giá trị nào của thì hai mặt phẳng và
vuông góc.
A. B. C. D.
Lời giải
Chọn A
.CSF
.BSF
.BSE
.CSE
E
F
B
C
A
S
A
CD BCD
,2.AC AD BC BD a CD x==== =
x
()
A
BC
(
)
A
BD
3
.
3
a
.
2
a
2
.
2
a
.
3
a
M
N
B
C
D
A
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 826
Gọi
,
M
N
lần lượt là trung điểm của
,.
A
BCD
Ta có
A
NCD^
mà
()()
A
CD BCD^
suy ra
()
.
A
NBCDANBN^^
Tam giác
A
BC
cân tại
,C
có
M
là trung điểm của
A
B
suy ra
.CM AB^
Giả sử
()()
A
BC BCD^
mà
CM AB^
suy ra
()
.CM ABD CM DM^^
Khi đó, tam giác
M
CD
vuông cân tại
M
2.
22
AB CD
M
NABCDx====
Lại có
2222
,AN BN AC AN a x== - =- mà
222
.
A
BANBN=+
Suy ra
()
22 2 2 2
3
243 .
3
a
ax x a x x-= = =
Câu 13: Cho hình chóp có đáy là hình vuông cạnh Cạnh bên và vuông
góc với mặt phẳng Xác định để hai mặt phẳng và tạo với nhau
một góc
A. B. C. D.
Lời giải
Chọn C
Từ
A
kẻ
A
H
vuông góc với
()
.SB H SBÎ
Ta có
()
SA BC
BC SAB BC AH
AB BC
ì
^
ï
ï
^ ^
í
ï
^
ï
î
mà
A
HSB^
suy ra
()
.
A
HSBC^
Từ
A
kẻ
A
K
vuông góc với
(
)
,SD K SDÎ
tương tự, chứng minh được
()
.SK SCD^
Khi đó
()
SC AHK^
suy ra
()()
()
0
;; 60.SBC SCD AH AK HAK===
Lại có
SAB SAD AH AKD=D =
mà
0
60HAK =
suy ra tam giác
A
HK
đều.
Tam giác
SAB
vuông tại
,S
có
222
22
111
.
xa
AH
AH SA AB
x
a
=+ =
+
Suy ra
22
22
22
22
.
xSHx
SH SA AH
SB
x
a
xa
=-= =
+
+
.SABCD
A
BCD
.a
SA x=
(
)
.
A
BCD
x
()
SBC
()
SCD
0
60 .
3
.
2
a
x =
.
2
a
x =
.
x
a=
2.
x
a=
H
K
C
A
D
B
S
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 827
Vì
HK //
B
D suy ra
2
22
22 22
1
.
2
.2
SH HK x xa x
x
a
SB BD
xa
xaa xa
= = ==
+
++
Câu 14: Cho hình lăng trụ tứ giác đều có đáy cạnh bằng góc giữa hai mặt
phẳng và có số đo bằng Độ dài cạnh bên của hình lăng trụ bằng
A. B. C. D.
Lời giải
Chọn C
Vì
.
A
BCD A B C D
¢¢¢¢
là lăng trụ tứ giác đều
()
AB BB
AB BB C B
AB BC
ì
¢
^
ï
ï
¢¢
^
í
ï
^
ï
î
.
Khi đó
()( )
()
()
()
()
A
BC BB C B BC
A
BCD BB C B BC
A
BC ABCD AB
ì
¢¢¢ ¢
ï
Ç=
ï
ï
ï
ï
¢¢
Ç=
í
ï
ï
ï
¢
Ç=
ï
ï
î
suy ra
()
()
()
0
;;60.ABC ABCD BC BC C BC
¢¢¢
===
Đặt
,AA x
¢
= tam giác
B
CC
¢
vuông tại ,C có
0
tan tan 60 . 3.
CC
CBC x a a
BC
¢
¢
== =
Câu 15: Cho hình chóp đều có cạnh đáy bằng góc giữa mặt bên và mặt đáy bằng
Tính độ dài đường cao của khối chóp.
A. B. C. D.
Lời giải
Chọn C
.
A
BCD A B C D
¢¢¢¢
,a
()
A
BCD
()
A
BC
¢
0
60 .
2.a 3.a
3.a 2.a
B
'
C'
D
'
C
D
B
A
A
'
.SABC
,a
0
60 .
SH
3
.
2
a
SH =
2
.
3
a
SH =
.
2
a
SH =
3
.
2
a
SH =
M
A
C
B
H
S
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 828
Gọi
H
là chân đường cao kẻ từ đỉnh
S
xuống mặt phẳng
(
)
.
A
BCD
Vì
.SABC
là hình chóp đều có
SA SB SC==
nên suy ra H chính là tâm đường tròn ngoại
tiếp tam giác
.
A
BC
Gọi
M
là trung điểm của
,BC
ta có
()
BC AM
BC SAM
BC SH
ì
^
ï
ï
^
í
ï
^
ï
î
.
Khi đó
()( )
()
0
;; 60SBC ABC SM AM SMA===
.
Tam giác
A
BC
đều có
22
33
.
236
aAMa
AM AB MB HM=-===
Tam giác
A
HM
vuông tại
,
H
có
0
3
tan tan 60 . .
62
SH a a
SMA SH
HM
== =
Vậy độ dài đường cao
.
2
a
SH =
Dạng 4. Thiết diện
Câu 1: Cho hình chóp có đáy là hình thang vuông tại và , đáy lớn ; cạnh
bên vuông góc với đáy. Gọi là điểm trên cạnh và ; là điểm
trên đoạn và . Mặt phẳng qua và vuông góc với mặt phẳng .
Thiết diện tạo bởi với hình chóp đã cho là:
A. tam giác. B. hình thang cân.
C. hình thang vuông. D. hình bình hành.
Lời giải
Chọn C
Ta có
()
AB AD
A
BSAD
AB SA
ì
^
ï
ï
^
í
ï
^
ï
î
. Mà
() ( )
SADa ^
suy ra
()
AB a
.
Qua
M
kẻ đường thẳng song song với
A
B
cắt
B
C
tại
N
.
Qua
E
kẻ đường thẳng song song với
A
B
cắt
SB
tại
P
.
Khi đó thiết diện là hình thang
M
NPQ
(do
M
NPQ
).
.SABCD
A
BCD
A
D
A
B
SA
Q
SA
,QA¹ QS¹
M
A
D
M
A¹
()
a
QM
()
SAD
()
a
A
B
C
D
S
P
N
M
Q
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 829
Vì
()
A
BSAD^
suy ra
()
M
NSAD^
nên
M
NEM^
.
Do đó thiết diện
NPE
là hình thang vuông tại
E
và
M
.
Câu 2: Cho hình chóp đều . Mặt phẳng qua , song song với và vuông góc với
mặt phẳng . Thiết diện tạo bởi với hình chóp đã cho là:
A. tam giác đều. B. tam giác cân. C. tam giác vuông. D. tứ giác.
Lời giải
Chọn B
Gọi
I
là trung điểm
B
C
.
Trong tam giác
SAI
kẻ
A
HSI^
()
H
SIÎ
.
Trong tam giác
SBC
, qua
H
kẻ đường song song với
B
C
, cắt
SC
ở
M
, cắt
SB
ở
N
.
Qua cách dựng ta có
()
.
B
CAMN
()
1
Ta có
()
()()()
.
do
SI AH
SI AMN SBC AMN
SI MN SI BC
ì
^
ï
ï
^ ^
í
ï
^^
ï
î
()
2
Từ
()
1
và
(
)
2
, suy ra thiết diện cần tìm là tam giác
A
MN
.
Dễ thấy
H
là trung điểm của
M
N
mà
()
A
HSBC^
suy ra
A
HMN^
. Tam giác
A
MN
có
đường cao
A
H vừa là trung tuyến nên nó là tam giác cân đỉnh
A
.
Câu 3: Cho hình chóp đều . Mặt phẳng qua và vuông góc với mặt phẳng .
Thiết diện tạo bởi với hình chóp đã cho là:
A. tam giác cân. B. hình hình hành. C. hình thang vuông. D. hình thang
cân.
Lời giải
Chọn D
SABC
()
a
A
BC
()
SBC
()
a
N
M
H
I
C
B
A
S
.SABCD
()
a
A
B
()
SCD
()
a
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 830
Gọi
,
I
J
lần lượt là trung điểm của
CD
và
A
B
.
Trong tam giac
SIJ
kẻ
J
KSI^
.
Trong tam giac
SIJ
, qua
K
kẻ đường thẳng song song với
CD
cắt
SC
tại
M
, cắt
SD
tại
N
.
Ta dễ dàng chứng minh được
()()
A
BMN SCD^
.
Khi đó thiết diện cần tìm là hình thang
A
BMN
.
Vì hình chóp đã cho là hình chóp đều nên suy ra
A
NBM=
.
Vậy thiết diện là hình thang cân.
Câu 4: Cho hình chóp có đáy là hình thang vuông tại và ,
; cạnh bên và vuông góc với đáy. Mặt phẳng qua và
vuông góc với mặt phẳng . Tính diện tích của thiết diện tạo bởi với hình
chóp đã cho.
A. B. C. D.
Lời giải
Chọn C
Gọi
E
là trung điểm
A
B
, suy ra
A
ECD
là hình vuông nên
DE AC^
.
()
1
J
I
D
C
B
A
S
O
M
N
K
.SABCD
A
BCD
A
D
2,
A
BaADDCa===
SA a=
()
a
SD
()
SAC
S
()
a
2
.
2
a
S
=
2
2
.
2
a
S =
2
3
.
2
a
S =
2
.
4
a
S
=
S
E
D
C
B
A
Giáo viên có nhu cầu sở hữu file word vui lòng
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Trang 831
Mặt khác
()
SA ABCD SA DE^^
.
(
)
2
Từ
()
1
và
(
)
2
, suy ra
()()()
D
E SAC SDE SAC^^
.
Ta có
()
()()
() ( )
.
SDE SD
SDE
SDE SAC
a
ü
ï
É
ï
º
ý
ï
^
ï
þ
Vậy thiết diện là tam giác
SDE
.
Ta có
22 22
2; 2SD SA DA a SE SA AE a=+= =+=; 22
D
EACDC a== = .
Do đó tam giác
SDE
đều có cạnh
2a
nên
22
33
42
SDE
SD a
S
D
==.
Câu 5: Cho hình chóp có đáy là hình chữ nhật tâm với Cạnh
bên và vuông góc với đáy. Gọi là mặt phẳng qua và vuông góc với
Tính diện tích của thiết diện tạo bởi và hình chóp đã cho.
A. B. C. D.
Lời giải
Chọn B
Gọi
,
M
N
lần lượt là trung điểm
,
A
DBC
. Khi đó:
·
M
N
đi qua
.O
·
()
.
MN AD
M
NSAD
MN SA
ì
^
ï
ï
^
í
ï
^
ï
î
Từ đó suy ra
() ( )
SMNa º
và thiết diện cần tìm là tam giác
SMN
.
Tam giác
SMN
vuông tại
M
nên
2
2
2
11 2
...
2222
SMN
AD a
SSMMNSA AB
D
æö
÷
ç
==+=
÷
ç
÷
ç
èø
.SABCD
A
BCD O
,AB a=
2.AD a=
SA a=
()
a
SO
()
.SAD
S
()
a
2
3
.
2
a
S =
2
2
.
2
a
S =
2
.
2
a
S =
2
.Sa=
N
M
O
S
A
B
C
D
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 832
BÀI5.KHOẢNGCÁCH
A.KIẾNTHỨCSÁCHGIÁOKHOACẦNNẮM
1.Khoảngcáchtừmộtđiểmđếnmộtđườngthẳng
a)Địnhnghĩa:
KhoảngcáchtừmộtđiểmMđếnđường
thẳng
làkhoảngcáchgiữahaiđiểmM
vàHtrongđóHlàhìnhchiếuvuônggóc
củaMtrênđườngthẳng
.
Kýhiệu:

dM, MH.
b)Chúý:Nếu
M
thì

dM, 0.
M
Δ
P
H
2.Khoảngcáchtừmộtđiểmđếnmặtphẳng
a)Địnhnghĩa:
Khoảng cách từ mộtđiểm Mđến mặt
phẳng(P)làkhoảngcáchgiữahaiđiểm
MvàH,trongđóHlàhìnhchiếuvuông
góccủađiểmMtrênmặtphẳng(P).
Kíhiệu:


dM,P MH.
P
M
H
b)Chúý:
Nếu

MPthì


dM,P 0.
3.Khẳngcáchgiữađườngthẳngvàmặtphẳngsongsong
a)Địnhnghĩa:
Khoảng cách từ mộtđường thẳng ađến
một mặt phẳng (P) song song với abằng
khoảngcáchtừmộtđiểmtùyýcủaađến
(P).
Tứclà:



da,P dM,P , M a.
b)Chúý:Khi





aP
da,P 0.
aP
a
P
N
M
H
K
4.Khoảngcáchgiữahaimặtphẳngsongsong
a)Địnhnghĩa:
Khoảng cách giữa hai mặt phẳng song
songbằngkhoảngcáchtừmộtđiểmtùyý
củamặtnàyđếnmặtkia.
Tứclà:




d P,Q dM,Q , M Q.
b)Chúý:Khi





PQ
dP,Q 0.
PQ
Q
P
N
M
H
K
5.Khoảngcáchgiữahaiđườngthẳngchéonhau
a)Địnhnghĩa:
Đườngthẳngagọilàđườngvuônggócchungcủahaiđườngthẳngchéonhau và
ʹ nếua
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 833
c
a
b
B'
C'
A'
A
D
C
B
D'
H
cắt ởMvàcắt ʹởNđồngthờivuônggócvớicả
và
ʹ.
Đoạn MNđược gọi làđoạn vuông góc
chungcủahaiđườngthẳngchéonhau
và
ʹ.
Khoảng cách giữa haiđường thẳng chéo
nhaulàđộdàiđoạnvuônggócchungcủa
haiđườngthẳngđó.
b)Chúý:
Khi




ʹ
d,ʹ 0.
ʹ
Khi

 // ʹ d,ʹ dM, ʹ

với
M.
a
Δ'
Δ
N
M
B.PHÂNLOẠIVÀPHƯƠNGPHÁPGIẢITOÁNTRẮCNGHIỆM
DAÏNG 1: KHOAÛNG CAÙCH TÖØ 1 ÑIEÅM ÑEÁN ÑÖÔØNG THAÚNG
1.PhươngPháp
Cáchxácđịnh:
Việcdựnghìnhchiếucủamộtđiểmtrênđườngthẳngtrongkhônggian,tacóthểlàmtheo2
cáchsau:
Dựngmặtphẳngđiquađiểmvàđườngthẳngđãcho.Rồitrênmặtph
ẳngđóquađiểmđãcho
dựngđoạnvuônggóctừđiểmtớiđườngthẳng.
Dựngmộtmặtphẳngđiquađiểmđãchovàvuônggócvớiđườngthẳng,lúcđógiaođiểm
củ
ađườngthẳngvớimặtphẳngvừadựngchínhlàhìnhchiếucủađiểmtrênđườngthẳng.
Tínhtoán:Saukhiđãxácđịnhđượckhoảngcáchcầntính,tadùngcáchệthứclượngtrongtam
giác,đagiác,đườngtròn,…đểtínhtoán.
2.Vídụ
Vídụ1:
ChohìnhhộpchữnhậtABCD.A’B’C’D’có
AB a, AD b, AAʹ c.
Khoảngcáchtừđiểm
AđếnđườngthẳngBD’bằng
A.

22
222
ab c
.
abc

B.

22
222
bb c
.
abc
C.

22
222
cb c
.
abc

D.

22
222
abc b c
.
abc
Hướngdẫngiải
ĐÁPÁNA
Do AB ADʹnên tam giác ABD’ vuông tại A. Trong tam giác ABD’ kẻ đườngcao AH thì

AH d A,BDʹ .
Trong
ADDʹ
,tacó:


2222
22222
ADʹ AD DDʹ bc
BDʹ AB ADʹ abc
Xét ABDʹ ,tađược:
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 834
a
a
a
60°
J
O
I
B'
C'
A
C
B
A'
K
H
22
222
AH.BDʹ AB.ADʹ
AB.ADʹ ab c
AH
BDʹ
abc


Vậy



22
222
ab c
dA,BDʹ AH .
abc
Vídụ2:ChohìnhlăngtrụABC.A’B’C’cóđáyABClàtamgiácđềutâmO,cạnha,hìnhchiếucủa
C’trên(ABC)trùngvớitâmcủađáy.CạnhbênCC’hợpvới(ABC)góc
o
60 .GọiIlàtrungđiểm
củaAB.Khoảngcách
Câu2.1.từđiểmOđếnđườngthẳngCC’bằng
A.
a
.
2
B.
3a
.
2
C.
a
.
4
D.
a
.
3
Hướngdẫngiải
ĐÁPÁNA
Theogiảthiết,suyra:

CʹOABC,suyra:



ABC
OC hch CCʹ CCʹ,ABC CʹCO
Theogiảthiết,tacó:
o
CʹCO 60
Trong(C’CO)dựng OH CCʹtạiHtađược:

dO,CCʹ OH .
Xét
COH

o
2a 3 3 a
OH OC.sin30 . .
32 2 2
Suyra:

a
dO,CCʹ .
2

Câu2.2.KhoảngcáchtừđiểmCđếnđườngthẳngIC’bằng
A.
2a 13
.
3
B.
3a 13
.
13
C.
a3
.
3
D.
a13
.
3
Hướngdẫngiải
ĐÁPÁNB
Tính

dC,ICʹ
Trong(C’IC)dựng CK ICʹtạiKtađược:
dC,ICʹ CK
Xét

OCʹ.CI
CICʹ OCʹ.CI CK.ICʹ CK
ICʹ
Mà

o
a3 a3
OCʹ OC.tan60 . 3 a;CI
32

22
22 2 2
a13a
ICʹ IO OCʹ a
12 12
Nên


a3
a.
3a 3a 13
2
dC,ICʹ CK .
13
a13 13
23

Câu2.3.KhoảngcáchtừđiểmOđếnđườngthẳngA’B’bằng
A.
2a 7
.
3
B.
a7
.
3
C.
a7
.
2
D.
a7
.
4
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 835
a
a
a
F
E
C
A
D
B
S
H
Hướngdẫngiải
ĐÁPÁNC
Tính

dO,AʹBʹ
Vì

CʹOABC//AʹBʹCʹ OCʹ AʹBʹCʹ
. Gọi J là trungđiểm của

 AʹBʹ CʹJAʹBʹ AʹBʹCʹ OJ AʹBʹ(địnhlí3đườngvuônggóc)
Tứclà:

dO,AʹBʹ OJ
Xét

2
222
3a a 7
OCʹJOJ OCʹ CʹJa
42
Tứclà:

a7
dO,AʹBʹ .
2

Vídụ3:ChohìnhchópS.ABCDcóđáyABCDlàhìnhvuôngcạnha,SAvuônggócvớimặtphẳng
(ABCD)và SA a. GọiElàtrungđiểmcủacạnhCD.KhoảngcáchtừđiểmSđếnđườngthẳng
BEbằ
ng
A.
2a 5
.
5
B.
a5
.
3
C.
a5
.
5
D.
3a 5
.
5
Hướngdẫngiải
ĐÁPÁND
Vì

SA ABCD
,trongmặtphẳng(ABCD)nếudựng
AH BE
tạiHthì SH BE (địnhlí3đườngvuônggóc).Tứclàkhoảng
cáchtừđiểmSđếnđườngthẳngBEbằngđoạnSH.
Tacó:

2
ABE
11a1
SAB.EFa.a AH.BE
2222
Mà

2
222
aa5
BE BC CE a
42
Nên

2
a2a
AH
BE
5
,mà
SAH
vuôngtạiA,nên:

2
222
4a 3a 3a 5
SH SA AH a
55
5
Ví dụ 4: Cho hình chóp S.ABCD cóđáy ABCD là hình vuông cạnh a, tâm O, SA (ABCD) ,
SA a. GọiIlàtrungđiểmcủaSCvàM làtrungđiểmcủaAB.KhoảngcáchtừđiểmIđến
đườngthẳngCMbằng
A.
a2
.
5
B.
a3
.
17
C.
a30
.
10
D.
a3
.
7
Hướngdẫngiải
ĐÁPÁNC
Do IO (ABCD) nênnếudựng OK CM (K CM)
thì
IK CM .
Tứclà:d(I,CM) IK .
Mà

2
22 2
a
IK OI OK OK
4
Do
OMC
1
SOK.MC
2
I
O
M
C
A
D
B
S
K
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 836
a
a
a
a3
3
O
I
H
A
C
B
S
K





222
OMC
2
2
aaa
2
284
2S
a
OK
MC
25
a
a
4
Suyra

22
aaa6a30
IK .
420 10
25
Vídụ5:ChohìnhchópđềuS.ABCcócạnhđáybằnga,gọiOlàtâmcủađáyvà
a3
SO
3
.GọiIlà
trungđiểmcủaBCvàKlàhìnhchiếucủaOlênSI.KhoảngcáchtừOđếnSAbằng
A.
a5
.
5
B.
a3
.
3
C.
a2
.
3
D.
a6
.
6
Hướngdẫngiải
ĐÁPÁND
Dựng
OH SA
tạiH d(O,SA) OH
Tacó:
 
22a3a3
OA AI . SO
3323
,
suyra:

11a3 a6
OH SA . . 2
223 6
Vậy

a6
dO,SA
6
.
DAÏNG 2: KHOAÛNG CAÙCH TÖØ MOÄT ÑIEÅM
ÑEÁN MAËT PHAÚNG
1.Phươngpháp
Đểtínhkhoảngcáchtừmộtđiểmđếnmộtmặtphẳng,trướchếttaphảitìmhìnhchiếuvuông
góccủađiểmđótrênmặtphẳng.Việcdựnghìnhchiếucủađiểm
trênmặtphẳng,tahaydùng
mộttrongcáccáchsau:
Cách1:
Tìm một mặt phẳng (Q)chứa Mvà vuông góc
với(P).
Xácđịnh

mP Q.
Dựng

 Mx m P Q ,
suy ra
HMx m
làđiểmcầntìm.
Cách2:
m
Q
P
M
H
Giả sử đã biếtđường thẳng
d, dựng
Mx //d , lúcđó

HMx P là hình chiếu
vuônggóccủađiểmMtrênmặtphẳng(P).
Cách3:
Dựavàotínhchấttrụccủatamgiác:Cho
ABC
nằmtrên(P),hìnhchiếuvuônggóccủađiểm
Mtrên(P)làtâmđườngtrònngoạitiếp
ABC ,tứclànếu
MA MB MC khiđóhìnhchiếu
củađiểmMtrên(P)làtâmOcủađườngtrònngoạitiếp
ABC.
Chúý.Khitínhkhoảngcáchtừmộtđiểmđếnmộtmặtphẳngtacầnbiếtvậndụngchúýsaumột
cáchkhéoléođểtừviệcphảitínhkhoảngcáchtừmộtđiểmnàyđến
mặtphẳng(khóxácđịnh)
đếnviệctínhkhoảngcáchtừđiểmkhácđếnmặtphẳng(dễxácđịnhhơn).
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 837
Nếu
 


 MA// d M, d A, .
Nếu






dM,
IM
MA I .
IA
dA,
P
H
M
I
A
K
2.Vídụ
Vídụ1:
ChohìnhchópS.ABCDcóđáylàhìnhvuông,SAvuônggócvớiđáy,
SA a.
Gócgiữa
đườngthẳngSDvàmặtphẳng(SAC)bằng
o
30 .KhoảngcáchtừđiểmDđếnmặtphẳng(SBM)
vớiMlàtrungđiểmCDbằng
A.
a
.
3

B.
2a
.
3
C.
4a
.
3
D.
5a
.
3
Hướngdẫngiải
ĐÁPÁNA
Dễdàngchứngminhđược
DB SAC HìnhchiếuvuônggóccủaDSlên(SAC)làSO,góc
giữaSDvà(SAC)là
o
DSO 30 .Đặt
DO x ,tacó SO x 3 (OlàgiaocủaACvàBD)
Từ

222
a
SO AO SA x
2
GọiNlàtrungđiểmcủaAB DN// BM
Suyra







1
dD;SBM dN;SBM dA;SBM
2
Kẻ AI BM, AH SM .
Từđóchứngminhđược
 

 AH SBM d A; SBM AH
Trong(ABCD):

2
ABM ABCD BCM
a
SS 2S
2
Mà

ABM
12a
SAI.BMAI
2
5
Khiđó:



22 2
111 a
AH a d D; SBM .
33
AH AI SA
Vídụ2:ChohìnhchópS.ABCDcóđáyABCDlàhìnhchữnhậtvới AB a 2 và BC a. Cạnh
bênSAvuônggócvớiđáyvàgócgiữacạnhbênSCvớiđáylà
0
60
.KhoảngcáchtừđiểmCđến
mặtphẳng(SBD)bằng
A.
a38
.
29

B.
3a 58
.
29
C.
3a 38
.
29
D.
3a
.
29
Hướngdẫngiải
ĐÁPÁNB
Gọi H là hình chiếu vuông góc
củaAtrênBDvàKlàhìnhchiếu
vuônggóccủaAtrênSH.
Tacó SA BD và AH BD nên
O
M
D
N
B
C
A
S
I
H
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 838
60°
B
D
C
A
S
H
K
O
F
E
Q
P
D
C
A
B
S
I
H

BD SAH .
Suy ra
AK BD
. Mà
AK SH
nên

AK SBD
Tacó:




dC;SBD dA;SBD AK
Tacó:
 
22 222 2 2
11111129
AK SA AH SA AB AD 18a
Vậy



3a 58
dC;SBD AK .
29

Vídụ3:ChohìnhchópS.ABCDcóđáyABCDlàhìnhvuôngcạnha,
SA ABCD và SA a 3 .
GọiIlàhìnhchiếucủaAlênSC.TừIlầnlượtvẽcácđườngthẳngsongsongvớiSB,SDcắtBC,
CDtạiP,Q.GọiE,FlầnlượtlàgiaođiểmcủaPQvớiAB,AD.KhoảngcáchtừEđếnmặtphẳng
(SBD)bằng
A.
3a 21
.
11
B.
a21
9
.
C.
3a 21
.
7
D.
a21
.
7
Hướngdẫngiải
ĐÁPÁNC
Gọi O là tâm của hình vuông
ABCD.
Qua A dựng AH SO . Dễ dàng
chứngminhđược AH BD
Khiđó


AH d A, SBD
TrongtamgiácvuôngSAC,tacó:
2
CI.SC AC
22
222
IC AC AC
SC
SC SA AC


22 2
22
222
AB BC 2a 2
5
2a 3a
SA AB BC


CBS có

IP CP CI CP 2
IP// SP
SB CB CS CB 5
ÁpdụngđịnhlýTalet:

BE BP 3 BE BC CP 3
CQ PC 2 CQ PC 2
Mà

5
AB CD CQ QP CQ BE BE
3
Do AEF vuôngtạiAnên:


2
2
22
AEF
111 3232a
S AE.AF AE AB BE AB
222 2525
(đvdt)





DA 5 3
dE,SBD dA,SBD
DE 3 5
TamgiácSAOvuôngtạiA,khiđó

2
2
22 2
111 3a
AH
7
AH SA AO
Vậy


3a 21
dE,SBD .
7
Ví dụ 4: Cho khối chóp S.ABC cóđáy là tam giác vuông tại B,
BA a, BC 2a ,
SA 2a ,
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 839
A
C
B
S
H
K
I
A
D
B
C
S
H

SA ABC . GọiH,KlầnlượtlàhìnhchiếucủaAtrênSB,SC.KhoảngcáchtừđiểmKđếnmặt
phẳng(SAB)bằng
A.
8a
.
9
B.
a
.
9
C.
2a
.
9
D.
5a
.
9
Hướngdẫngiải
ĐÁPÁN
Vì

BC SA B nên:
AH BC, AH SBC
 AH HK, AH SC
mà
AK SC

SC AHK
Tacó:

AB.SA 2a
AH
SB
5
,

AC.SA 2 5a
AK
SC 3
,

22
8a
HK AK AH
35
,
4a
SK
3

3
S.AHK
14a2a 8a 32
V... a
63 135
535
Mặtkhác

22
4
SH SA AH a
5
nên
2
AHS
4
Sa
5
Vậykhoảngcáchcầntìmlà:



KSAH
AHS
3V
8a
dK,SAB .
S9
Ví dụ 5: Cho hình chóp S.ABCDđáy là hình thang,

o
ABC BAD 90 , BA BC a ,
AD 2a.
CạnhbênSAvuônggócvớiđáyvà
SA a 2. GọiHlàhìnhchiếucủaAlênSB.Khoảngcách
từHđếnmặtphẳng(SCD)bằng
A.
5a
.
3
B.
4a
.
3
C.
2a
.
3
D.
a
.
3
Hướngdẫngiải
ĐÁPÁND
GọiIlàtrungđiểmAD.
Tacó

AD
CI IA ID
2
,suyra
ACDvuôngtạiCCD AC .
Mà

SA ABCD SA CD 
nêntacó
CD SD
hay
SCD
vuông.Gọi
12
d,dlần
lượtlàkhoảngcáchtừB,Hđến(SCD)
Tacó:

SA SB
SAB SHA
SH SA
∽

2
2
SH SA 2
SB 3
SB
mà

2
21
1
d
SH 2 2
dd
SB d 3 3
ThểtíchkhốitứdiệnS.BCD:

3
SBCD
11 2a
VSA.AB.BC
32 6
Tacó:

22
SC SA AC 2a ,
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 840
60°
K
H
C
B
A
S
M
H
A
C
B
S
K
M
D

22 2
SCD
1
CD CI ID 2a S SC.CD 2a
2
Tacó:

3
S.BCD 1 SCD 1
2
2a
3.
1a
6
Vd.Sd
32
2a
VậykhoảngcáchtừHđến(SCD)là
21
2a
dd
33
.
Vídụ6:ChohìnhchópS.ABCcótamgiácABCvuôngtạiA,
AB AC a
,IlàtrungđiểmcủaSC,
hìnhchiếuvuônggóccủaSlênmặtphẳng
ABC
làtrungđiểmHcủaBC,mặtphẳng
SAB
tạovớiđáymộtgócbằng
o
60
.KhoảngcáchtừđiểmIđếnmặtphẳng
SAB
theoabằng
A.
a3
.
2
B.
a3
.
8
C.
a3
.
4
D.
a
.
4
Hướngdẫngiải
ĐÁPÁNC
GọiKlàtrungđiểmcủaAB
HK AB 1
Vì

SH ABC nên SH AB  
2
Từ(1)và(2)AB SK
Dođógócgiữa

SAB
vớiđáybằnggócgiữaSKvàHKvà
bằng
o
SKH 60
Tacó

a3
SH HK.tanSKH
2
Vì IH//SB nên

IH// SAB .
Dođó




dI,SAB dH,SAB
TừHkẻ
HM SK tạiM
 

 HM SAB d H, SAB HM
Tacó

2222
11116 a3
HM
4
HM HK SH 3a
.
Vídụ7:ChohìnhchópS.ABCcóđáylàtamgiácvuôngtạiAvà
AB 2a , AC 2a 3. Hìnhchiếu
vuônggóccủaStrênmặtphẳng(ABC)làtrungđiểmHcủacạnhAB.Gócgiữahaimặtphẳng
(SBC)và(ABC)bằng
o
30 .KhoảngcáchtừtrungđiểmMcủacạnhBCđếnmặtphẳng(SAC)
bằng
A.
a3
.
5
B.
a5
.
3
C.
a5
.
5
D.
3a
.
5
Hướngdẫngiải
ĐÁPÁNC
Trongmặtphẳng(ABC)kẻ HK BC tạiK

BC SHK
Từgiảthiếttacó:
o
SHK 30


22
BC AB AC 4a


AC HK 3 a 3
sinABC HK
BC HB 2 2
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 841
K
H
C
B
A
S
M
TrongtamgiácSHKcó

a
SH HKtanSKH
2
DoMlàtrungđiểmcủacạnhBCnênMH//AC,dođóMH//(SAC).
Suyra:




dM,SAC dH,SAC
Trongmặtphẳng(SAB)kẻ
HD SA tạiD.Tacó:

AC SAB AC DH DH SAC

222
111 a5
HD
5
DH HA HS
Vậy





a5
dM,SAC dH,SAC HD .
5
Vídụ8:
ChohìnhchópS.ABCcótamgiácABCvuôngtạiA,
AB AC a ,IlàtrungđiểmcủaSC,
hìnhchiếuvuônggóccủaSlênmặtphẳng(ABC)làtrungđiểmHcủaBC,mặtphẳng(SAB)tạo
vớiđáy1gócbằng
o
60 .KhoảngcáchtừđiểmIđếnmặtphẳng(SAB)theoabằng
A.
a3
.
5
B.
a5
.
4
C.
a3
.
4
D.
a3
.
2
Hướngdẫngiải
ĐÁPÁNC
GọiKlàtrungđiểmcủaAB
HK AB 1
Vì

SH ABC
nên

SH AB 2
Từ(1)và(2)
AB SK
Dođógócgiữa(SAB)vớiđáybằnggócgiữa
SKvàHKbằng
o
SKH 60
.
Tacó:

a3
SH HKtanSKH
2
Vậy

3
S.ABC ABC
111 a3
VS.SH.AB.AC.SH
332 12
Vì
IH//SB
nên

IH// SAB
.Dođó
dI,SAB dH,SAB 
TừHkẻ HM SK tạiM
 HM SAB d H, SAB HM
Tacó:

2222
11116 a3
HM
4
HM HK SH 3a
.
Vậy


a3
dI,SAB
4
.
Vídụ9:ChohìnhchópS.ABCcóđáyABClàtamgiácđềucạnha.GọiIlàtrungđiểmcạnhAB.
HìnhchiếuvuônggóccủađỉnhStrênmặtphẳngđáylàtrungđiểmHcủaCI,gócgiữađường
thẳngSAvàmặtđáybằng
o
60 . KhoảngcáchtừđiểmHđếnmặtphẳng
SBC bằng
A.
a7
.
29
B.
a21
.
429
C.
a21
.
329
D.
a21
.
29
Hướngdẫngiải
ĐÁPÁNB
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 842
H'
K
H
I
A
B
C
S
E
I'
H
'
K
H
I
A
B
C
A
'
Tacó:

22
a3
CI AC AI
2
Dođó

22
a7
AH AI IH
4
,suyra 
o
a21
SH AH.tan60
4
.
GọiA’, H’, I’lần lượt làhình chiếu của A, H, I trên BC, E là hình chiếu của H trênSH’ thì
 

 HE SBC d H; SBC HE .
Tacó:

11 a3
HHʹ IIʹ AAʹ
24 8
.Từ 
22 2
11 1 a21
HE
HE HS HHʹ
429
Vậy


a21
dH;SBC .
429

Vídụ10:ChohìnhchópS.ABCDcóđáyABCDlàhìnhthoicạnha.Góc
o
BAC 60 ,hìnhchiếu
củaStrênmặtphẳng

ABCD trùngvớitrọngtâmcủatamgiácABC.Mặtphẳng

SAC hợp
vớimặtphẳng

ABCD góc
o
60 . KhoảngcáchtừBđếnmặtphẳng
SCD bằng
A.
a
.
112
B.
2a
.
111
C.
6a
.
112
D.
3a
.
112
Hướngdẫngiải
ĐÁPÁNC
Trong

SBD kẻ
OE//SH
khiđó ta có
OC, OD, OEđôi một vuông góc.
Và:

aa33a
OC , OD , OE
228
Ápdụngcôngthức:



222
2
1111
OC OD OE
dO,SCD
3a
d
112


Mà





6a
dB,SCD 2dO,SCD .
112
DAÏNG 3: KHOAÛNG CAÙCH GIÖÕA HAI MAËT PHAÚNG SONG SONG. KHOAÛNG CAÙCH TÖØ ÑÖÔØNG
THAÚNG ÑEÁN MAËT PHAÚNG
1.Phươngpháp
Việctínhkhoảngcáchgiữamột đườngthẳngvàmộtmặtphẳngsongsongvớinó,hoặctính
khoảngcáchgiữahaimặtphẳngsongsongđềuquyvềviệctínhkhoảngcáchtừđi
ểmđếnmặt
E
O
H
A
B
C
D
S
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 843
a
a
a
a
a
I
B
C
A'
C'
B'
A
J
phẳng.Cầnlưuýviệcchọnđiểmtrênđườnghoặctrênmặtsaochoviệcxácđịnhkhoảngcách
đơngiảnnhất.
2.Vídụ
Vídụ1:
ChohìnhlăngtrụABC.A’B’C’cótấtcảcáccạnhbênvàcạnhđáyđềubằnga.Hìnhchiếu
vuônggóccủaAtrên(A’B’C’)trùngvớitrungđiểmcủaB’C’.
Câu1.1.KhoảngcáchtừAA’đếnmặtbên
BCC ’B’
bằng
A.
a3
.
4
B.
a3
.
3
C.
3a 2
.
4
D.
a3
.
2
Hướngdẫngiải
ĐÁPÁNA
Tacó:

AAʹ// BBʹ BCCʹBʹ

AAʹ// BCCʹBʹ
Gọi

AAʹ
J
hch I IJ AAʹ// BBʹ IJ BBʹ
Mặtkhác,theogiảthiếtsuyra:






BʹCʹ AʹIAAʹI
BʹCʹ AAʹI
BʹCʹ AI AAʹI
Suyra:
IJ BʹCʹ ,tứclà

IJ BCCʹBʹ ,
mà
J
AAʹnên


dAAʹ,BCCʹBʹ IJ
Trong

AI.AʹI
AAʹIIJ.AAʹ AI.AʹIIJ
AAʹ
.
Dễthấy
a3
AʹI
2
,

2
22 2
3a a
AI AAʹ AI a
42
.
Suyra:

aa 3
.
a3
22
IJ
a4
.Vậy


a3
dAAʹ,BCCʹBʹ .
4
Câu1.2.Khoảngcáchgiữahaimặtđáycủalăngtrụbằng
A.
a
.
4
B.
a
.
2
C.
a2
.
4
D.
a5
.
2
Hướngdẫngiải
ĐÁPÁNB
Haiđáy của lăng trụ song song nên
dABC,AʹBʹCʹ dA,AʹBʹCʹ mà

AABC và



a
AI AʹBʹCʹ dABC,AʹBʹCʹ AI .
2
Vídụ2:ChohìnhhộpchữnhậtABCD.A’B’C’D’có
AB a, BC b,
CCʹ c.
2.1.KhoảngcáchtừAA’đến(BDD’B’)bằng
A.

222
abc
.
abc

B.
22
abc
.
ab

C.
22
ab
.
ab

D.
22
ac
.
ac
Hướngdẫngiải
ĐÁPÁNC
Tacó:

AAʹ// BBʹ BDDʹBʹ
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 844

AAʹ// BDDʹBʹ
.Dođó:




dAAʹ,BDDʹBʹ dA,BDDʹBʹ
Gọi

BD
HhchA AHBD
mà

BDDʹBʹ ABCD
suyra:

AH BDDʹBʹ
.Tứclà:


dA,BDDʹBʹ AH
Xét

22 2
111
ABD
AH AB AD


22
22 22
11ab
ab ab
nên

22
2
22
22
ab ab
AH AH
ab
ab
Vậy:


22
ab
dAAʹ,BDDʹBʹ .
ab

2.2.GọiM,NlầnlượtlàtrungđiểmcủaAA’,BB’.KhoảngcáchtừMNđến(ABC’D’)bằng
A.

222
2abc
.
abc
B.
22
abc
.
2a b
C.
22
bc
.
2a b
D.
22
2ac
.
ac
Hướngdẫngiải
ĐÁPÁNC
N
M
C
B
D
C'
D'
A'
B'
A
K
Tacó:

MN// AB ABCʹDʹ MN// ABCʹDʹ .Suyra:




dMN,ABCʹDʹ dM,ABCʹDʹ ,nhưngA’Mcắtmặtphẳng(ABC’D’)tạiAvàMlàtrung
điểmcủaAA’.Nên:




1
dM,ABCʹDʹ dAʹ,ABCʹDʹ
2
Gọi

ADʹ
KhchAʹ AʹKADʹmà
ABCʹDʹ AAʹDʹD,suyra:

AʹKABCʹDʹ .Tứclà:


dAʹ,ABCʹDʹ AʹK.
Xét

22
22 22222
11111cb
AʹADʹ
AʹKAʹAAʹDʹ cb cb
,nên:

22
2
22
22
cb bc
AʹKAʹK
cb
b
c
.Vậy


22
bc
dM,ABCʹDʹ .
2a b
2.3.Khoảngcáchgiữahaimặtphẳng
ADʹBʹvà
CʹBD bằng
C
B
D
C'
D'
A'
B'
A
H
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 845
a
a
K
H
N
M
P
B
C
A
S
A.

222
abc
.
abc
B.

abc
.
ab bc ca
C.

222
abc
.
2a c c
D.

22 22 22
abc
.
ab bc ca
Hướngdẫngiải
ĐÁPÁND
G
1
O'
O
C
B
D
C'
D'
A'
B'
A
Tacó:

BʹDʹ// BD CʹBD BʹDʹ// CʹBD
Gọi
 OACBD,Oʹ AʹCʹ BʹDʹ
Suyra:

AOʹ// CʹOCʹBD AOʹ // CʹBD
Mà

AOʹ,BʹDʹ ABʹDʹ ,AOʹ BʹDʹ Oʹ ADʹBʹ // CʹBD
TađãchứngminhđượcA’Cbịcácmặt(AD’B’),(C’BD)chiathànhbađoạnbằngnhau.
Dođó:




1
dADʹBʹ ,CʹBD d G , Cʹ BD d Aʹ,ADʹBʹ
VìA’A,A’B’,A’D’đôimộtvuônggóc,nếu:



22 2222
2
1111111
AʹAAʹBʹ AʹDʹ abc
dAʹ,ADʹBʹ
Vậy:






22 22 22
abc
dAʹ,ADʹBʹ dADʹBʹ ,CʹBD
ab bc ca
Tacầnchúýkếtquảsau:NếutứdiệnOABCcócáccạnhOA,OB,OCđôimộtvuônggócthì:



22 2
111
dO,ABC .
OA OB OC
Vídụ3:ChohìnhchópS.ABCcóđáy làtamgiácđềucạnha,mặtbênSBCvuônggócvớiđáy
ABC.GọiM,N,PlầnlượtlàtrungđiểmcủaAB,SA,AC.Khoảngcáchgiữahai(MNP)và(SBC)
b
ằng
A.
a3
.
3
B.
a3
.
2
C.
a3
.
4
D.
3a 3
.
2
Hướngdẫngiải
ĐÁPÁNC
Theogiảthiết,suyra:
 
 


MN//SB SAB MN// SAB
NP//SC SAC NP// SAC
Mà

MN,NP MNP ,MN NP N nên
MNP // SBC .
GọiHlàtrungđiểmcủaBC AH BC 
(do ABCđều)
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 846
H
B
C
A
'
C'
B
'
A
K
Mà

ABC SBC và

AH ABC
 
BC ABC SBC AH SBC
Gọi

 K AH MP KH SBC d K, SBC KH
Vì

MNP // SBC
và

KMNP
Dođó:





1a3
d MNP,SBC dK,SBC KH AH .
24
Vídụ4:ChohìnhlăngtrụABC.A’B’C’cótấtcảcáccạnhđềubằnga.Góctạobởicạnhbênvàmặtphẳng
đáybằng
o
30 .
HìnhchiếuHcủađiểmAtrênmặtphẳng(A’B’C’)thuộcđườngthẳngB’C’.Khoảng
cáchgiữahaimặtphẳngđáybằng
A.
a
.
3
B.
a
.
2

C.
a2
.
2
 D.
a3
.
2
Hướngdẫngiải
ĐÁPÁNB
KhoảngcáchgiữahaimặtphẳngđáychínhbằngAH.
Trong HAAʹ ,tacó:
o
Aʹ 30 .


o
a
AH AAʹ.sin Aʹ a.sin30 .
2
DAÏNG 4. KHOAÛNG CAÙCH GIÖÕA HAI ÑÖÔØNG THAÚNG CHEÙO NHAU
1.Phươngpháp
Đểtínhkhoảngcáchgiữahaiđườngthẳngchéonhau,tacóthểsửdụngmộttrongcáccáchsau:
Cách1:Dựngmặtphẳng(P)chứađườngthẳngavàsongsongvớib.Khoảngcáchtừbđến(P)
làkhoảngcáchcầntìm.
Cách2:Dựnghaimặtphẳngsongsong vàlầnlượtchứahaiđườngthẳng.Khoảngcáchgiữa
haimặtphẳngđólàkhoảngcáchcầntìm.
Cách3:Dựngđoạnvuônggócchungvàtínhđộdàiđoạnđó.
Cáchdựngđoạnvuônggócchungcủahaiđườngthẳngchéonhau:
Cách1:Khi ab
+Dựngmột(P) b , (P) atạiH.
+Trong(P)dựng
HK b tạiK.
+ĐoạnHKlàđoạnvuônggócchungcủa
avàb.
Cách2:
+Dựng
(P) b , (P)//a
.
+Dựng

P
aʹ hch a ,bằngcáchlấy
Ma
dựngđoạn MN ( ), lúcđó a’ là
đườngthẳngđiquaNvàsongsonga.
+Gọi
Haʹ b
,dựng
HK //MN
HKlà
đoạnvuônggócchung.
Cách3:
+Dựngmặtphẳng(P)vuônggócvớiatại
điểmM.
+Dựnghìnhchiếub’củabtrên(P).
+ Dựng hình chiếu vuông góc H của M
trênb’.
b
a
P
H
K
a'
a
b
P
M
K
H
N
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 847
+TừHdựngđườngthẳngsongsongvới
a,cắtbtạiđiểmB.
a
b'
P
B
A
M
H
+QuaBdựngđườngthẳngsongsongvớiMH,cắtat ạiđiểmA.Khiđó,ABlàđoạnvuônggóc
chungcủaavàb.
2.Vídụ
Ví dụ 1:
Cho hình chóp S.ABCD cóđáy là hình chữ nhật ABCD có
AD 2AB ,

SA ABCD , SC 2a 5
vàgócgiữa SCvà
ABCD
bằng
o
60
,MlàtrungđiểmcủacạnhBC.
KhoảngcáchgiữahaiđườngthẳngAMvàSDbằng
A.
a510
.
17
B.
a51
.
17
C.
2a 510
.
17
D.
3a 510
.
17
Hướngdẫngiải
ĐÁPÁNA
Tacó

SA ABCD SC cóhìnhchiếutrên
ABCD làAC


o
SC ,ABCD SC,AC SCA 60
TagiácSACvuôngtạiA


o
AC SC.cos60 a 5
và

o
SA SC.sin60 a 15
Tacó
222
AB AD AC
22
5AB 5a AB a
Dựng hình bình hành AMDN và dựng
AH SN
tạiH.
Tacó:


 AM// DN AM// SDN d AM, SDN d A, SDN
AM MD nênAMDNlàhìnhchữnhật.
ND AN
mà
 DN SA DN SAN
DN AH mà
 AH SN AH SDN d A, SDN AH
Tacó

22 2 22 2
1111117
AH AS AN 15a 2a 30a

a510
AH
17
.Vậy

a510
dAM,SD .
17
Vídụ2:ChohìnhchópS.ABCcóđáyABClàtamgiácvuôngtạiB,
AB 2a ,
o
BAC 60 ,cạnhbên
SAvuônggócvớiđáyvà
SA a 3 .GọiMlàtrungđiểmcủacạnhAB.Khoảngcáchgiữahai
đườngthẳngSBvàCMbằng
N
M
C
B
A
D
S
H
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 848
M
N
A
C
B
S
E
H
A.
a10
.
17
B.
2a 3
.
29
C.
2a 3
.
19
D.
a3
.
13
Hướngdẫngiải
ĐÁPÁNB
GọiNlàtrungđiểmcạnhSA.
Do

SB// CMN nên



dSB,CM dSB,CMN



dB,CMN dA,CMN
Kẻ
AE MC, E MC
vàkẻ
 AH NE, H NE
Chứngminhđược

 

 AH CMN d A, CMN AH
Tính
AMC
2S
AE
MC
trongđó:
2
AMC
113
SAM.AC.sinCAMa.4a.a3
2a 3
AE
222
13
MC a 13


Tínhđược



 
2a 3 2a 3 2a 3
AH d A, CMN d SB ,CM .
29 29 29
Ví dụ 3: Cho hình chóp S.ABCD cóđáy là hình thang vuông tại A, D, SA vuô ng góc vớiđáy,
 SA AD a, AB 2a .KhoảngcáchgiữaABvàSCbằng
A.
a
.
2
B.
a
.
2
C.
a2. D. 2a 2.
Hướngdẫngiải
ĐÁPÁNB
Tacó:AB//DCnên



dAB,SC dAB,SDC .
Trong mặt phẳng (SAD) t ừ A kẻ

AH SD, H SD 1
Tacó:





DC AD
DC SAD
DC SA
DC AH 2
E
A
D
C
S
B
H
Từ(1)và(2)suyra

AH SCD



AH d AB, SCD d AB,SC
TrongtamgiácvuôngSADcó:

2222
1112 a
AH .
AH AD SA a
2
Vídụ4:ChohìnhchópS.ABCDcóđáyABCDlàhìnhthoicạnha,
o
ABC 60 ,cạnhbênSAvuông
gócvớiđáy,SCtạovớiđáymộtgóc
o
60
.KhoảngcáchgiữahaiđườngthẳngAB,SDbằng
A.
3a
.
5
B.
2a
.
5
C.
a
.
15
D.
3a
.
15
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 849
60°
60°
H
A
B
C
D
S
60°
E
A
C
B
S
D
I
K
H
O
H
B
D
C
A
S
I
Hướngdẫngiải
ĐÁPÁND



S.ACD
SCD
3V
dAB,SD dA,SCD
S
Gọi H là trungđiểm CD. Ta có:
CD SH
.
Dođó

2
SCD
1a15
SCD.SH
24
Vậy


S.ACD
SCD
3V
3a
dAB,SD dA,SCD .
S
15

Lưuý:
Ởtrêntađãsửdụngcôngthức
S.ABCD ABCD
1
VSA.S
3
.Đâylàcôngthứcthểtíchcủakhối
đadiệnhọcởchươngtrình12
1
VB.h
3



Ví dụ 5:
Cho hình chóp S.ABCD cóđáy ABCD là hình chữ nhật, AB a,
AD a 3,

SA ABCD ,gócgiữamặtphẳng(SBD)vàm ặtphẳng(ABCD)bằng
o
60
.Khoảng
cáchgiữahaiđườngthẳngACvàSDbằng
A.
3a
.
2
B.
a
.
4
C.
3a
.
4
D.
2a
.
3
Hướngdẫngiải
ĐÁPÁNA
Trong mặt phẳng (ABCD)đường thẳng
qua D song song với AC, cắtđường
thẳngABtạiE.
Trong tam giác ADE kẻ đường cao AK

 KDE SAK SDE.Dựng

AH SK
tạiH,suyra

AH SDE .
Do

AC// SDE 


dAC;SD dA;SDE AH
Tacó:


a3 3a 3a
AK AH d AC;SD .
24 4
Vídụ6:
ChohìnhchópS.ABCDcóđáyABCDlà hìnhthoi cócạnhbằng a3,
O
BAD 120 và
cạnhbênSAvuônggócvớimặtphẳngđáy.Biếtrằngsốđocủagócgiữahaimặtphẳng(SBC)
và(ABCD)bằng
O
60 . KhoảngcáchgiữahaiđườngthẳngBDvàSCbằng
A.
a7
.
14
B.
3a 7
.
4
C.
3a 7
.
14
D.
a7
.
8
Hướngdẫngiải
ĐÁPÁNC
Gọi OACBD.
Vì
DB AC, BD SC nên

BD SAC tạiO.
Kẻ
OI SC OI làđườngvuônggócchungcủaBDvàSC.
Sử dụng hai tam giácđồng dạng ICO và ACS hoặc
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 850
đườngcaocủatamgiácSAC,suyrađược
3a 7
OI .
14

Vậy

3a 7
dBD,SC .
14
Vídụ7:ChohìnhchópS.ABCDcóđáylàhìnhvuôngABCDcạnha,cạnhbênSAvuônggócvới
mặtphẳngđáy.GócgiữaSCvàmặtphẳngđáybằng
o
45 .
GọiElàtrungđiểmBC.Khoảngcách
giữahaiđườngthẳngDEvàSCtheoabằng
A.
a
.
19
B.
2a 38
.
9
C.
a38
.
19
D.
a38
.
9
Hướngdẫngiải
ĐÁPÁNC
TừCdựng

CI // DE DE // SCI .
TừAdựng AK CI ,cắtEDtạiHvàCItạiK.
Trong(SAK)dựng
HT SK .
Do

CI SAK
nên

HT SCI






CD.AI 3a
AK ,
CI
5
1a
HK AK
3
5
dDE;SC dH;SCI
SA.HK a 38
HT .
SK 19
Vídụ8:ChohìnhchópS.ABCDcóđáylàhìnhchữnhậtABCD,đườngthẳngSAvuônggócvới
mặtphẳng(ABCD)và
SA AD a.
KhoảngcáchgiữahaiđườngthẳngABvàSCbằng
A.
a2
.
10
B.
a2
.
6
C.
a2
.
4
D.
a2
.
2
Hướngdẫngiải
ĐÁPÁND
Trongmặtphẳng(SAD),
vẽ
AH SD, H SD
Mặt khác ABCD là hình chữ nhật nên

CD SAD AH SCD
VậykhoảngcáchgiữaABvàSCchínhlàAH.
TrongtamgiácvuôngSADcóAHlàđường
caonên

22 2
111 a2
AH
2
AH AS AD
VậykhoảngcáchgiữahaiđườngthẳngABvàSCbằng
a2
.
2
Vídụ9:ChohìnhchópS.ABCcótamgiácSABđềucạnha,tamgiácABCcânt ạiC.Hìnhchiếu
củaStrênmặtphẳng
ABC làtrungđiểmcủacạnhAB,góchợpbởicạnhSCvàmặtđáylà
o
30 .TínhkhoảngcáchcủahaiđườngthẳngSAvàBC.
H
E
D
A
B
C
S
I
K
T
H
B
A
D
C
S
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 851
A.
3a
.
13
B.
3a
.
13
C.
a
.
13
D.
2a
.
13
Hướngdẫngiải
ĐÁPÁNA
GọiHlàtrungđiểmcạnhAB,tacóSHlà
đườngcaocủahìnhchópS.ABCvàCHlà
đườngcaocủatamgiácABC.Từgiảthiết
tađược
o
SCH 30 . Tam giácSHCvuông
tạiHnên


o
SH 3a
tan30 CH SH. 3
CH 2
DựnghìnhbìnhhànhABCD,khiđó



d BC, SA d BC, SAD


dB,SAD 2dH,SAD
GọiG,KlầnlượtlàhìnhchiếucủaHtrên cácđườngthẳngADvàSG.Tacó:


AD HG
AD SHG HK AD
AD SH
Mà HK SG nên

HK SAD hay
dH,SAD HK
TamgiácSHGvuôngtạiHnên:

2222222
11111152 3a
HK
HK HG HS HB HC HS 9a
213
Vậy

3a
dBC,SA
13
.
Vídụ 10:ChohìnhchópS.ABCD, tứgiác ABCDlàhìnhthang cân,haiđáy là BCvà AD.Biết
SA a 2, AD 2a, AB BC CD a . Hìnhchiếu vuông góc của S trên mặt phẳng
ABCD
trùngvớitrungđiểmcạnhAD.KhoảngcáchgiữahaiđườngthẳngSBvàADbằng
A.
a21
.
3
B.
a21
.
7
C.
a
.
7
D.
3a
.
7
Hướngdẫngiải
ĐÁPÁNB
Tacó:

2
ABCD ABI
3a 3
S3S
4
Xét SBI vuôngtạiIcó:


2222
SI SB BI a SI a









SIBC
SBC
AD// BC
AD// SBC
BC SBC
dAD,BC dAD,SBC
3V
dI,SBC
S
D
H
A
C
B
S
G
K
I
A
D
B
C
S
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 852

33
SIBC S.ABCD
2
SBC
1 1a3a3
VV . ;
33412
a7
Sppapbpc
4


Vậy

a21
dAD,SB .
7

C.BÀITẬPRÈNLUYỆNTỐCĐỘ
Câu1:ChohìnhlậpphươngABCD.A’B’C’D’cạnha.KhoảngcáchtừCđếnACbằng
A.
a6
.
7
B.
a3
.
2
C.
a6
.
3
D.
a6
.
2
Câu2:
ChohìnhchóptứgiácS.ABCDcótấtcảcáccạnhđềubằnga.KhoảngcáchtừDđếnđường
thẳngSBbằng
A.a.B.
a
.
2

C.
a
.
3

D.
a3
.
2
Câu 3:
Cho tam giác ABC có  AB 14,BC 10,AC 16 . Trênđường thẳng vuông góc với mặt
phẳng(ABC)tạiAlấyđiểmOsaocho
OA 8
.KhoảngcáchtừđiểmOđếncạnhBCbằng
A.
83.
B.
16.
C.
82.
D.
24.
Câu4:
HìnhchópS.ABCcóđáyABClàtamgiácvuôngtạiA,
BC 2a ,
o
ABC 60 .GọiMlàtrung
điểmcạnhBCvà
 SA SC SM a 5 .KhoảngcáchtừSđếncạnhABbằng
A.
a17
.
4
B.
a19
.
2
 C.
a19
.
4
 D.
a17
.
2
Câu5:
ChohìnhchópS.ABCDcóđáyABCDlàhìnhthoicạnha,gócBACbằng
o
60
.Hìnhchiếu
vuônggóccủaStrênmặtphẳng

ABCD
làđiểmHthuộcđoạnBDsaocho
HD 2HB.
Đường
thẳngSOtạovớimặtphẳng

ABCD
góc
o
60 vớiOlàgiaođiểmcủaACvàBD.Khoảngcách
từBđếnmặtphẳng

SCD bằng
A.
3a 7
.
15
 B.
3a 7
.
14
 C.
a7
.
11
 D.
2a 7
.
15
Câu6:
ChohìnhchópS.ABCcócácmặtABC,SBClà nhữngtamgiácđềucạnha.Gócgiữahaimặt
phẳng(SBC)và(ABC)bằng
o
60 . Hìnhchiếuvuông góccủaSxuống(ABC)nằmtrongtamgiác
ABC.KhoảngcáchtừBđếnmặtphẳng(SAC)theoabằng
A.
2a 13
.
13
 B.
3a 13
.
13
 C.
3a 13
.
11
 D.
a13
.
13
Câu7:
ChohìnhchópS.ABCD,đáylàhìnhchữnhậttâmI,có AB a, BC a 3. GọiHlàtrung
điểmAI.BiếtSHvuônggócvớimặtphẳngđáyvàtamgiácSACvuôngtạiS.KhoảngcáchtừC
đếnmặtphẳng(SBD)bằng
A.
3a
.
11
B.
a
.
13
 C.
3a
.
15
 D.
5a
.
17
Câu8:
ChohìnhchópS.ABCDcóđáyABCDlàhìnhvuông,
BD 2a
;tamgiácSACvuôngtạiSvà
nằmtrongmặtphẳngvuônggócvớiđáy,
SC a 3. KhoảngcáchtừđiểmBđếnmặtphẳng
(SAD)bằng
A.
3a 21
.
7
 B.
a21
.
7
 C.
4a 21
.
7
 D.
2a 21
.
7
Câu9:
ChohìnhchópS.ABCDcóđáyABCDlàhìnhchữnhậtcó
AB a
, BC 2a 2 .Hìnhchiếu
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 853
củaSlên mặt phẳngđáy làtrọng tâmcủatamgiác ABC.Góc giữađường thẳng SB và mặt
phẳng(ABCD)bằng
o
60 .KhoảngcáchtừđiểmAđếnmặtphẳng(SBC)bằng
A.
3a 21
.
7
 B.
a21
.
7
 C.
4a 21
.
7
 D.
2a 21
.
7
Câu10:
ChohìnhchópS.ABCcó

o
AB AC, BC a 3, BAC 120 .
GọiIlàtrungđiểmcạnhAB.
HìnhchiếuvuônggóccủađỉnhStrênmặtphẳngđáylàtrungđiểmHcủaCI,gócgiữađường
thẳngSAvàmặtđáybằng
o
60 . KhoảngcáchtừđiểmAđếnmặtphẳng(SBC)bằng
A.
4a 37
.
37
 B.
a
.
37
 C.
3a 37
.
37
 D.
2a 37
.
37
Câu11:
ChohìnhchópS.ABCDcóđáyABCDlàhìnhthangvuôngtạiAvàB.HìnhchiếucủaSlên
mặtphẳng(ABCD)trùngvớigiaođiểmIcủaACvàBC.Mặtbên(SAB)hợpvớiđáymột
góc
o
60 .
Biếtrằng
 AB BC a, AD 3a.
KhoảngcáchtừDđếnmặtphẳng(SAB)theoabằng
A.
4a 3
.
5
 B.
3a
.
4
 C.
3a 3
.
7
 D.
3a 3
.
2
Câu12:
ChohìnhchópS.ABCDcóđáyABCDlàhìnhthoitâmOcạnhbằnga,góc
o
DAB 120 .
Haimặtphẳng(SAC)và(SBD)cùngvuônggócvớiđáy.Gócgiữa(SBC)vàmặtđáybằng
o
60
.
KhoảngcáchtừAđến(SBC)bằng
A.
a3
.
5
B.
3a
.
4
 C.
3a
.
7
 D.
3a 3
.
2
Câu13:
Trongmặtphẳng(P),chohìnhthoiABCDcóđộdàicáccạnhbằnga,
o
ABC 120 .GọiGlà
trọng tâm tam giác ABD. Trênđường thẳng vuông góc với (P) tại G, lấyđi ểm S sao cho
o
ASC 90 .
KhoảngcáchtừđiểmGđếnmặtphẳng(SBD)theoabằng
A.
a
.
17
B.
a2
.
27
 C.
a2
.
17
 D.
a
.
37
Câu14:
ChohìnhchópS.ABCDcóđáyABCDlàhìnhvuông,
BD 2a
;tamgiácSACvuôngtạiS
vànằmtrongmặtphẳngvuônggócvớiđáy,
SC a 3
.KhoảngcáchtừđiểmBđếnmặtphẳng
(SAD)bằng
A.
2a 13
.
7
 B.
2a
.
7
 C.
2a 21
.
7
 D.
a13
.
7
Câu15:
ChohìnhhộpthoiABCD.A’B’C’D’cócáccạnhđềubằngavà

o
BAD BAAʹ DAAʹ 60 .
Khoảngcáchgiữahaimặtphẳngđáy(ABCD)và(A’B’C’D’)bằng
A.
a5
.
5
B.
a10
.
5
 C.
a6
.
3
D.
a3
.
3
Câu16:
ChotứdiệnABCDcó
AB BCD ,AB 5a,BC 3a,CD 4a .GọiM,Nlầnlượtlàtrung
điểmcủaACvàAD.
Câu16.1.KhoảngcáchgiữađườngthẳngMNvàmặtphẳng(BCD)bằng
A.
2a
.
3
B.
a
.
2
C.
a
.
4
D.
5a
.
2
Câu16.2.Gọi(P)làmặtphẳngchứaMNvàđiquatrungđiểmKcủaAB.Khoảngcáchgiữahai
mặtphẳng(P)và(BCD)bằng
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 854
A.
a
.
3
B.
3a
.
2
 C.
5a
.
4
 D.
5a
.
2
Câu17:ChohìnhchópcụttứgiácđềuABCD.A’B’C’D’.ĐáylớnABCDcócạnhbằnga,đáynhỏ
A’B’C’D’cócạnh bằngb.Gócgiữamặtbênvàđáylớnbằng
o
60 . Khoảngcáchgiữahaimặtđáy
củahìnhchópcụtđềubằng
A.
ab 3
.
2
B.

ab 3
.
2
 C.
ab 3
.
2

D.
b
a3
.
2
Câu18:
ChohìnhlậpphươngABCD.A’B’C’D’cạnha.Khoảngcáchgiữahaimặtphẳng(BA’C’)và
(ACD’)bằng
A.
a3
.
2
B.
a3
.
3
 C.
a3
.
2
D.
a3
.
5
Câu19:
ChohìnhchópS.ABCDcóđáyABCDlàhìnhchữnhậtvới
AB 3a, AD 2a
.Hìnhchiếu
vuônggóccủaSlênmặtphẳng
(ABCD) làđiểmHthuộccạnhABsaocho
AH 2HB.
Gócgiữa
mặtphẳng
(SCD)
vàmặtphẳng
(ABCD)
bằng
o
60 .
KhoảngcáchgiữahaiđườngthẳngSCvà
ADbằng
A.
a39
.
15
 B.
6a 39
.
13
 C.
a39
.
3
 D.
a39
.
11
Câu20:ChohìnhchópS.ABCDcóđáyABCDlàhìnhvuôngcạnha,
a17
SD
2
,hìnhchiếuvuông
gócHcủaStrênmặtphẳng(ABCD)làtrungđiểmcủađoạnAB.GọiKlàtrungđiểmcủađoạn
AD.KhoảngcáchgiữahaiđườngthẳngHKvàSD
theoabằng
A.
a3
.
25
B.
a3
.
45
 C.
a3
.
15
 D.
a3
.
5
Câu21:
ChohìnhchópS.ABCcó
a70
SC
5
,đáyABClàtamgiácvuôngtạiA,
AB 2a, AC a
vàhìnhchiếucủaSlênmặtphẳng(ABC)làtrungđiểmcạnhAB.Khoảngcáchgiữahaiđường
thẳngBCvàSAbằng
A.
3a
.
5
B.
4a
.
5

 C.
a
.
5
 D.
2a
.
5
Câu22:
ChohìnhchópS.ABCcóđáylàtamgiácABCđềucạnhbằng3a.Chânđườngcaohạtừ
đỉnhSlênmặtphẳng(ABC)làđiểmHthuộccạnhABsaocho
AB 3AH ,góctạobởiđường
thẳngSCvàmặtphẳng(ABC)bằng
o
60 .
KhoảngcáchgiữahaiđườngthẳngSAvàBCbằng
A.
3a 21
.
29
 B.
3a 21
.
19
 C.
a21
.
39
 D.
3a 21
.
7
Câu23:
ChohìnhchópS.ABCDcóđáyABCDlàhìnhchữnhậtvới
AB a , AD 2a .Hìnhchiếu
vuônggóccủaStrênmặtphẳngđáylàtrungđiểmcủaHvàAD,gócgiữaSBvàmặtphẳngđáy
(ABCD)là
o
45 .KhoảngcáchgiữahaiđườngthẳngSDvàBHtheoabằng
A.
2a
.
3
B.
2
a.
5
.
C.
2
a.
3
D.
a
.
3
Câu24:
ChohìnhchópS.ABCDcóđáyABCDlàhìnhvuôngtâmO,cạnha.CạnhbênSDhợpvới
mặtđáymộtgóc
o
60 vàhìnhchiếuvuônggócHcủađỉnhSlênmặtđáylàtrungđiểmcủacạnh
AB.KhoảngcáchgiữahaiđườngthẳngSAvàBDbằng
A.
a 345
.
31
B.
a 546
.
31

C.
a645
.
31
 D.
a 465
.
31
Câu 25:
Cho hình chóp S.ABCD cóđáy ABCD là hình thang vuông tại A và B, với
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 855
H
A
C
B
D
S
C
B
D
A
C'
A'
B
'
D
'
H

 AB BC a, AD 2a a 0 .Cácmặtbên
SAC và
SBD cùngvuônggócvớimặtđáy.Biết
gócgiữahaimặtphẳng

SAB
và
ABCD
bằng
o
60 . KhoảngcáchgiữahaiđườngthẳngCDvà
SBbằng
A.
2a 3
.
5
 B.
2a 3
.
15
 C.
a3
.
15
 D.
3a 3
.
5
Câu26:
ChohìnhchópS.ABCDcóđáyABCDlàhìnhthoicạnha,góc
o
ABC 60 cạnhbên SD a 2 .
Hình chiếu vuông góc của S trên mặt phẳng (ABCD) làđiểm H thuộcđoạn BD sao cho
HD 3HB
.GọiMlàtrungđiểmcủacạnhSD.KhoảngcáchgiữahaiđườngthẳngCM
vàSB
bằng
A.
a3
.
40
B.
a30
.
8
 C.
a3
.
8
 D.
a3
.
4
Câu 27:
Cho hình chóp S.ABCD cóđáy ABCD là hình thang vuông tại B và C,
AB 2BC 4CD 2a ,giảsửMvàNlầnlượtlàtrungđiểmABvàBC.Haimặtphẳng(SMN)
và(SBD)cùngvuông gócvớimặtph ẳngđ
áyvàcạnh bênSB hợpvới(ABCD)mộtgóc
o
60 .
KhoảngcáchgiữaSNvàBDbằng
A.
3
a.
15

B.
3
a.
65

C.
3
a.
55

D.
3
a.
35
Câu 28: Cho hình chóp S.ABCD cóđáy ABCD là hình thang vuông tại A, B. Biết
 AD 2AB 2BC 2a, SA SD SC 3a .KhoảngcáchgiữahaiđườngthẳngSBvàCDbằng
A.
a5
.
3
B.
a3
.
3
 C.
a3
.
2
D.
a2
.
2
D.HƯỚNGDẪNGIẢICHITIẾT
Câu1.ĐÁPÁNC
Nhậnxétrằng:
 BACʹ CAʹADACʹ AʹAC
 BʹCʹADʹCʹA

nênkhoảngcáchtừcácđiểmB,C,D,A’,B’,D’đếnđường
chéoAC’đềubằngnhau.
Hạ CH vuônggócvớiAC’,tađược:

22 2
111 a6
CH .
3
CH AC CCʹ

Câu2.ĐÁPÁNA
GọiHlàgiaođiểmcủaACvàBD.
 AB BC CD DA a ABCDlàhìnhthoi.
Dođó
AC BD
đồngthờiHlàtrungđiểmcủaACvàBD.
SAC cântạiS SH AC(1)
SBD cântạiS SH BD (2)
Từ(1)và(2)suyra:

SH ABCD (3)
Vì SA SB SC SD 
nên HA HB HC HD
SuyraABCDlàhìnhvuông(tứgiácđều) (4)
Từ(3)và(4)tađượcS.ABCDlàhìnhchóptứgiácđều.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 856
A
C
B
O
H
60°
I
K
M
A
C
B
S
H
Xét
SBD
tacó:

22 2
SA SB a,BD a 2 BD SB SD
.
Thếnên
SBD vuôngtạiS.
Suyra DS SB .Vậy

dD,SB DS a.
Câu3.ĐÁPÁNB
NửachuvitamgiácABC:


14 16 10
p20
2


ABC
S 20. 20 14 20 16 20 10 40 3

ABC
2S
80 3
AH 8 3
BC 10
NốiOHthì
OH BC
.KhoảngcáchtừOđếnBClàOH:

22
OH OA AH 16
Câu4.ĐÁPÁNB
ChânđườngcaohìnhchóplàtâmHcủađườngtrònngoại
tiếptamgiácAMC(Do SA SC SM ).
Góc
o
AMC 120 ,nênHởngoàitam giácAMCvàHAMlà
tamgiácđềunên:
HM AM a

2222
SH SM HM 5a a 2a
TừHkẻ HK ABthì
SK AB
:SKlàkhoảngcáchtừSđếncạnhAB.

a3
HK MI
2
(doABMlàtamgiácđềucạnhbằnga)

22
22 2
3a 19a a 19
SK SH HK 4a
442
.
Câu5.Phântích:
Tacó





H.SCD H.SCD S .HCD
SCD SCD SCD
3VVV
3399
dB,SCD dH,SCD . . .
22S2S2S
ĐÁPÁNB
TrongtamgiácSHOcó:


o
SH HO.tan60
1a 3 a
..3
32 2
Tacó:

HCD
2
11a
S CO.HD . . OD OH
222
aa 31a 3 a
...
4232 16



23
S.HDC HDC
11aaa
V.SH.S.. 1
3321696

Mặtkhác:
 
22 22
a57 a21
SD SH HD ;SC SH HC
66
60°
60°
H
O
C
B
A
D
S
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 857
H
I
A
B
C
D
S
N
K
60°
M
A
C
B
S
H
K
C
B
A
D
S
H
J
 



2
SCD
a57 a21 SC SD CD
SD ; SC ; CD a, p
66 2
a21
SppSCpSDpCD 3
12
Từ(1),(2)tacó


3a 7
dB,SCD .
14
Câu6.ĐÁPÁNB
GọiMlàtrungđiểmcủaBC.
Lậpluậnđượcgócgiữa(SBC)và(ABC)là
o
SMA 60
SAM
đềucạnhbằng
a3
2

2
SAM
33a
S
16





3
S.ABC SAM
2
SAC
3
B.SAC
2
SAC
1a3
VBC.S
316
1a 13 a 3 a 39
S.
24 2 16
3V
3a 3 3a 13
dB,SAC .
S13
a39
16.
16
Câu7.ĐÁPÁND

SH ABCD SH AC
SAC vuôngtạiS 
2
SH HA.HC

22
AC AB BC 2a ,suyra:






a3a a3
HA , HC SH
22 2
CI 2HI d C, SBD 2d I, SBD
Hạ
HN BD, N BD
và
HK SN, KN
.
Suyra:

HK SBD nên


dH,SBD HK
Tacó:

ABD
AB.AD a 3
AB.AD 2 S 2HN.BD HN
2BD 4
Tacó:

222
111 3a
HK
HK HN SH
215
.Vậy



3a
dC,SBD 2HK .
15
Câu8.ĐÁPÁND
Kẻ SH AC, H AC
Do
 
SAC ABCD SH ABCD

22
SA.SC a 3
SA AC SC a, SH
AC 2
Tacó:




22
a
AH SA SH CA 4 HA
2
dC,SAD 4dH,SAD


Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 858
120°
K
H
I
A
B
C
S
H'
E
Do
 

BC// SAD d B, SAD d C, SAD 4d H, SAD
Kẻ

 HK AD K AD , HJ SK J SK
Chứngminhđược

SHK SAD mà
HJ SK HJ SAD


dH,SAD HJ;
AHK
vuôngtại 
o
a2
KHKAHsin45
4

22
SH.HK a 3
HJ
27
SH HK
.Vậy



2a 3 2a 21
dB,SAD .
7
7
Câu9.ĐÁPÁND
GọiHlàtrọngtâmcủatamgiácABCvàO
là tâm của hình chữ nhật, ta
có:

2
2
221
BH BO . AC
332
1
a22aa
3


Ta có

SH ABCD
nên góc giữa SB và
mặtphẳng(ABCD)làgóc
o
SBH 60
TrongtamgiácvuôngSHBtacó:

o
SH BHtanSBH a.tan60 a 3
Tacó:









3
dA;SBC2dO;SBC2.dH;SBC3dH;SBC
2
Kẻ

 HK BC K BC , HI SK I SK 1
Tacó:

SH ABCD SH BC
Dođó

BC SHK BC HI 2
Từ(1)và(2)suyra

HI SBC nên
dH;SBC HI
Tacó

11
HK DC a
33
.TrongtamgiácvuôngSHKtacó:

22 2
2
a
a3.
SH.HK a 3 a 21
3
HI
14
28
SH HK a
3a
9
.
Vậy





3a 21
dA;SBC 3dH;SBC 3HI
14
.
Câu10.ĐÁPÁNC

H
I
A'
B
C
A
I'
K
H'
O
K
H
C
B
A
D
S
I
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 859
TheođịnhlýCôsintrongtamgiácABCtađược
AB AC a
Tacó

2
22 2 o
7a
CI AI AC 2AI.AC.cos120
4

a7
CI
2
Dođó:



222
2
2
2AI AC CI
3a a 3
AH AH
4164
Suyra

o
3a
SH AH.tan60
4
AHcắtBCtạiK.GọiA’,H’,I’lầnlượtlàhìnhchiếucủaA,H,ItrênBC.
Tacó:





dA;SBC
AK AAʹ
4
HK HHʹ
dH;SBC
dA;SBC 4dH;SBC
GọiElàhìnhchiếucủaHtrênSH’thì
 HE SBC d H; SBC HE

1a
HHʹ AAʹ
48
vàtừ

22 2
11 1 3a
HE
HE HS HHʹ
437
Vậy



3a 37
dA;SBC 4HE .
37

Câu11.ĐÁPÁND
GọiKlàhìnhchiếucủaIlênAB.
Suyra
o
SKI 60 .
Do

KI BI
IK //AD
AD BD
.
Mà
BI BC a 1
ID AD 3a 3
BI 1 BI 1
BI ID 4 BD 4


Suyra

KI 1 3a 3a 3
KI SI
AD 4 4 4
GọiHlàhìnhchiếucủaIlênSK.Tacó

AB IK
AB IH
AB SI
Từđósuyra
 

 IH SAB d I; SAB IH
Màdo


 DB 4IB d D; SAB 4d I ; SAB 4IH
Lạicó

22 2 22
1111616 3a3
IH
8
IH IS IK 27a 9a
.Vậy


3a 3
dD;SAB
2
.
Câu12.ĐÁPÁNB
60°
I
B
C
D
A
S
K
H
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 860
K
C
B
A
D
S
H
J
G
D
O
A
B
C
S
H





SAC ABCD
SBD ABCD
SAC SBD SO
SO ABCD SO BC

 

Kẻ

OK BC BC SOK




o
SBC , ABCD SKO 60






AO SBC C
dA;SBC 2dO;SBC



  





222
SBC SOK
SBC SOK SK OH SBC d O; SBC OH
OH SK
111 3a 3a
OH d A; SBC .
84
OH OK OS
Câu13.ĐÁPÁNB

oo
ABC 120 BAD 60 ABD đềucạnha.
GọiOlàgiaođiểmcủaACvàBD.

a3 2 a3
AO ; AG AO ; AC a 3
233

a6
SG GA.GC
3

(
SAC
vuôngtạiS,đườngcaoSG).
Kẻ

 GH SO GH SBD vì


 BD GH SAO d G; SBD GH
SGO vuôngtạiG,đườngcaoGH

22 22
11127 a2
GH .
GH GS GO 2a
27
Câu14.ĐÁPÁNC
Kẻ
SH AC, H AC
Do
 
SAC ABCD SH ABCD
22
SA AC SC a,
SA.S C a 3
SH
AC 2



Tacó:





22
a
AH SA SH CA 4HA d C, SAD 4d H, SAD
2
Do
 

BC// SAD d B, SAD d C, SAD 4d H, SAD
120°
60°
O
A
D
C
B
S
K
H
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 861
O
A
'
B
'
D
'
A
C
B
C'
D
H
Kẻ

 HK AD K AD , HJ SK J SK
Chứngminhđược

SHK SAD mà
HJ SK HJ SAD


dH,SAD HJ
AHK
vuôngtại

o
a2
KHKAHsin45
4

22
SH.HK a 3
HJ
27
SH HK
.Vậy



2a 3 2a 21
dB,SAD .
7
7
Câu15.ĐÁPÁNC
Hạ AʹHAC,tacónhậnxét:


BD AC
BD OAAʹ
BD AʹO
BD AʹHAʹHABCD


Vàvì

ABCD // AʹBʹCʹDʹnên
AʹH
chínhlàkhoảngcáchgiữahaimặtphẳngđáy.
NhậnxétrằnghìnhchópA’.ABDlàhìnhchópđều,nêntalầnlượtcó:

2 2a3 a3
AH AO .
3323

22
2222
a2a a6
AʹHAʹAAHa AʹH.
33 3
Câu16.1.ĐÁPÁND


MN// CD
MN// BCD
CD BCD


Töø keû

MMH//AB
MH BCD
AB BCD
Vậy:


MH d MN , BCD
ABC
cho: 
AB 5a
MH .
22
Câu16.2.ĐÁPÁND
Tính


dP,BCD:

MN// CD
P//BCD
MK // BC





MP
5a
MH d P , BCD .
2
MH BCD

Câu17.ĐÁPÁNC
Lưuý: Cầnchúýrằng,tronghìnhchópcụtđềuthìcácmặtbênlànhữnghìnhthangcânbằngnhau,các
gócgiữamặtbênvàmặtđáybằngnhau.
GọiO,O’lầnlượtlàtâmcủahaihìnhvuôngABCDvàA’B’C’D’;KvàJlầnlượtlàtrungđiểm
củaA’D’vàAD.
GọiHlàhìnhchiếucủaKtrên(ABCD)thì
KH OJ tạiHvàKHlàkhoảngcáchcầntìm.
Gọi làgócgiữamặtbênvàmặtđáycủahìnhchópcụtthì
K
H
M
N
A
B
C
D
H
M
N
A
B
C
D
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 862
60°
K
H
I
A
B
C
D
S
K
H
O'
O
C'
B
'
D
'
A
'
C
A
B
D
φ
H
J
K
O'
B'
A'
C'
O
B
D
C
A
D
'

o
KJH 60 .
Tacó:

b
a
OʹK;OJ
22
.
KHOO’làhìnhchữnhậtnên:

ab
JH OJ OʹK
2

ab 3
KH 2.KH
HJK : tan KH .
HJ a b 2

Câu18.Phântích:
Chứngminh
BʹDBCʹ
:



 

BCʹ CBʹ
BCʹ CDAʹBʹ BCʹ BʹD1
BCʹ DC DC BBʹCʹC
Chứngminh AʹCʹ BʹD:



 

AʹCʹ BʹDʹ
AʹCʹ BDDʹBʹ AʹCʹ BʹD2
AʹCʹ BBʹ BBʹ AʹBʹCʹDʹ
XácđịnhgiaođiểmKvàH:

 

 




BBʹDʹDBʹD
BCʹAʹ BBʹDʹDBOʹ Oʹ AʹCʹ BʹDʹ BʹDBCʹAʹ K
BʹDBOʹ K
BBʹDʹDBʹD
ACDʹ BBʹDʹDDʹOO AC BD BʹDACDʹ H
BʹDDʹOH
ĐÁPÁNB
Từ(1)và(2)suyra BʹD(BCʹAʹ)  (3)
Mặtkhác:

BCʹ// ADʹ
BCʹAʹ // ACDʹ 4
BAʹ// CDʹ
Từ(3)và(4)suyra:

BʹDACDʹ 5
Tacó:

BʹDBAʹCʹ K,BʹDBCʹAʹ
,

BʹDDʹAC H,BʹDACDʹ
DođóKHlàkhoảngcáchcầntìm.


2
22 2 22
BDBʹ :BʹDBDBʹBa2a3aBʹDa3
DễthấytronghìnhchữnhậtBB’D’Dtacó:

1a3
KH BʹD.
33
Câu19.ĐÁPÁNA
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 863
D
I
H
B
C
A
K
S
J
K
H
D
A
B
C
S
E
F
Kẻ

HK CD K CD .Khiđó:

 
CD HK
CD SHK CD SK
CD SH
Vậy góc giữa (SCD) và (ABCD) là góc
o
SKH 60
TrongtamgiácvuôngSHK:


o
SH HKtan60 2a 3
Vì


SBC // AD d AD,SC d A, SBC
.
Trong(SAB)kẻ AI SB ,khiđó:

 
BC AB
BC SAB BC AI
BC SH
.Mà
SB AI AI SBC
Vậy



22
SH.AB 2a 3.3a 6a 39
dAD,SC dA,SBC AI .
SB 13
12a a
Câu20.ĐÁPÁND

SH ABCD SH HD
.Tacó:

22
222
SH SD HD
SD AH HD
SH a 3





HK // BD HK// SBD


dHK,SD dH,SBD
GọiElàhìnhchiếuvuônggóccủaHtrênBDvàFlàhìnhchiếuvuônggóccủaHtrênSE.
Tacó: BD HE và BD SH nên
BD SHE BD HF mà
HF SE dođó

HF SBD .Suy
ra


dH,SBD HF
Tacó:

a2
HE HBsinEBH
4

22
HS.HE a 3
HF
5
HS HE
.
Vậy

a3
dHK,SD .
5
Câu21.ĐÁPÁNB
TamgiácAHCvuôngcâncạnhanên
CH a 2
TamgiácSHCvuôngtạiHnên


22
2a
SH SC CH
5
Dựng
AK BC, HI BC .Đường
thẳngquaA songsong với BC cắt IH
tạiD

BC// SAD



 d BC,SA s BC, SAD d B, SAD 2d H , SAD

AD SDH SAD SDH .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 864
60°
H
C
A
D
B
S
E
F
Kẻ

 HJ SD HJ SAD d H, SAD HJ
Tacó

222
111 2a a
AK HD
AK AB AC
55

222
111 2a
HJ
5
HJ HD HS
.Vậy

4a
dBC,SA .
5
Câu22.ĐÁPÁNA
Nhậnthấy

SH ABC HC
làhìnhchiếucủaSCtrênmặtphẳng(ABC)

o
SCH 60 làgócgiữaSCvàmặtphẳng(ABC)
Tacó

222 o
HC AC AH 2AC.AH.cos60

22 2
1
9a a 2.3a.a. 7a
2

o
HC a 7 SH HC.tan60 a 21
Dựng

 
AD CB AD// CB BC// SAD



d SA;BC d BC; SAD d B; SAD 3d H; S AD
Dựng
HE AD
tạiE

AD SHE


SAD SHE(theogiaotuyếnSE)
Dựng

HF SE tạiF

HF SAD
HF d H; SAD
Tacó:

o
a3
HE AH.sin60
2


222222
1114129
HF HE SH 3a 21a 21a
a21 3a21
HF d B; SAD
29 29


Vậy

3a 21
dSA;BC .
29

Câu23.ĐÁPÁNB
45°
K
H
B
A
D
C
S
Do SH (ABCD) nêngócgiữaSBvàmặtph ẳngđáy(ABCD)làgóc
o
SBH 45 .Tacó
SBH
vuôngcântạiHnên
SH BH a 2
GọiKlàtrungđiểmcủaBC,tacó
BH// DK BH// SDK .
Suyra:


d BH;SD d BH; SDK d H; SDK
TứdiệnSHDKvuôngtạiHnên



2222
2
11115
HS HK HD 2a
dH;SDK
Vậy



2
dBH;SD dH;SDK a
5
.
Câu24.ĐÁPÁND
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 865
60°
M
E
O
H
C
B
A
D
S
K
M
H
O
C
B
A
D
S
I
H
D
O
A
B
C
S
E
K
Tacó SH (ABCD) .
Tính

a5 a15
HD ; SH
22
DựngEsaochoAEBOlàhìnhbìnhhành.GọiMlàtrung
điểmcủaAE.HạHKvuônggócvớiSM.
Chứngminh

HK SAE
vàtínhđược
a465
HK
62
Tínhđược


a 465
dBD;SA 2HK .
31

Câu25.ĐÁPÁNA
Gọi

HACBD SH ABCDvà
1
BH BD
3
Kẻ

HE AB AB SHE ,hay




o
SAB ; ABCD SEH 60
Mà

12a 2a3
HE AD SH
33 3
Gọi O là trungđiểm AD, ta có ABCD là hình vuông cạnh a ACD có trung tuyến
1
CO AD
2
CD AC CD (SAC) VÀ
BO// CD hay CD//(SBO) và BO (SAC)



d CD;SB d CD; SBO d C; SBO
TínhchấttrọngtâmtamgiácBCO

1a2
IH IC
36

22
5a 2
IS IH HS
6
Kẻ
CK SI mà CK BO CK (SBO) d(C,(SBO)) CK
TrongtamgiácSICcó:

SIC
11 SH.IC2a3
SSH.ICSI.CKCK
22 SI5
Vậy

2a 3
dCD,SB
5
.
Câu26.ĐÁPÁNB
TừgiảthiếtcótamgiácABCđềucạnha.
Gọi

a3
OACBD BO BDa3
2

33
HD BD a 3
44
22
22 22
27a 5a a 5
SH SD HD 2a SH
16 16 4




 
22
222
5a 3a a 2
SB SH HB SB
16 16 2
BD AC
AC SBD AC OM
AC SH
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 866
DiệntíchtamgiácMAClà

2
MAC
111a2a2
SOM.ACSB.AC .a
24428








SB//OM SB// MAC
d SB;CM d SB; MAC d S; MAC d D; MAC





M.ACD ACD ABCD
1111
V d M; ABCD .S . d S; ABCD . S
3322

3
S.ABCD
1a15
V
496
Mặtkhác


M.ACD MAC
1
VdD;MAC.S
3



3
M.ACD
2
MAC
a15
3V
a30
32
dD;MAC .
S8
a2
8
Câu27.ĐÁPÁNB
H
N
M
A
B
C
D
S
K
Gọi

 HMN BI SMN SBI SH
Dohaimặtphẳng(SMN)và(SBI)cùngvuônggócvới
ABCD
SH ABCD
DễthấyBHlàhìnhchiếuvuônggóccủaSBlênmặtphẳngđáy,suyra
o
SBH 60 .
GọiMvàNlầnlượtlàtrungđiểmABvàBC,mà
AB 4CD
nênsuyra
MN BD
tạiH.
XéttamgiácBMNtacó:

2222
1115 a
BH
BH BM BN a
5
XéttamgiácSBHlạicó:

o
SH a 15
tanSBH SH HB.tan60
HB 5
TínhkhoảngcáchgiữaSNvàBD.
Do


BD SH
BD SMN
BD MN
DựngHKvuônggócSN,suyraHKlàđoạnvuônggócchungcủa
SNvàBD

dBD,SN HK.
Xét
BHN có: 
22
22
aaa5
HN BN BH
45 10
Xét
SHN tacó: 
22 2222
11120565 3
HK a
65
HK SH HN a 3a 3a
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ.
Face: Trần Đình Cư. SĐT: 0834332133
Trang 867
H
A
D
B
C
S
Vậy

3
dBD,SN a
65
.
Câu28.ĐÁPÁND
Theogiảthiếttacó BC AB a
GọiHlàtrungđiểmcủaAD
HA HD a
Từgiảthiết
ABCHlàhìnhvuôngcạnhatâmO


CH a
1a2
CO AC
22
Trong tam giác ACD có CH là trung tuyến và
1
CH AD
2
ACD vuôngtạiC HlàtâmđườngtrònngoạitiếptamgiácACD.
GọiKlàhìnhchiếuvuônggóccủaStrênmặtphẳng(ABCD)
SK ABCD
,SKlàđườngcao
củahìnhchópS.ABC.
Hơn nữa các tam g iác vuông SKA, SKC và SKD bằng nhau vì SK chung và
 SA SD SC 3a KA KC KD
KlàtâmđườngtrònngoạitiếptamgiácACD KtrùngvớiH.
TrongtamgiácvuôngSHDtacó: 
22222
SH SD HD 9a a 2 2a
TứgiácBCDHlàhìnhbìnhhành(vì
HD// BC, HD BC
)
CD// BH
Tacó:



CD// BH SBH
CD// SBH
CD SBH
TacóSBvàCDlàhaiđườngthẳngchéonhau.
Mặtkhác


CD// SBH
SB SBH


d CD,SB d CD , SBH d C, SBH
Tacó
 

 
CO HB
a2
CO SBH d C, SBH CO .
CO SH
2
| 1/173
| | Tải xuống

Có thể bạn quan tâm:

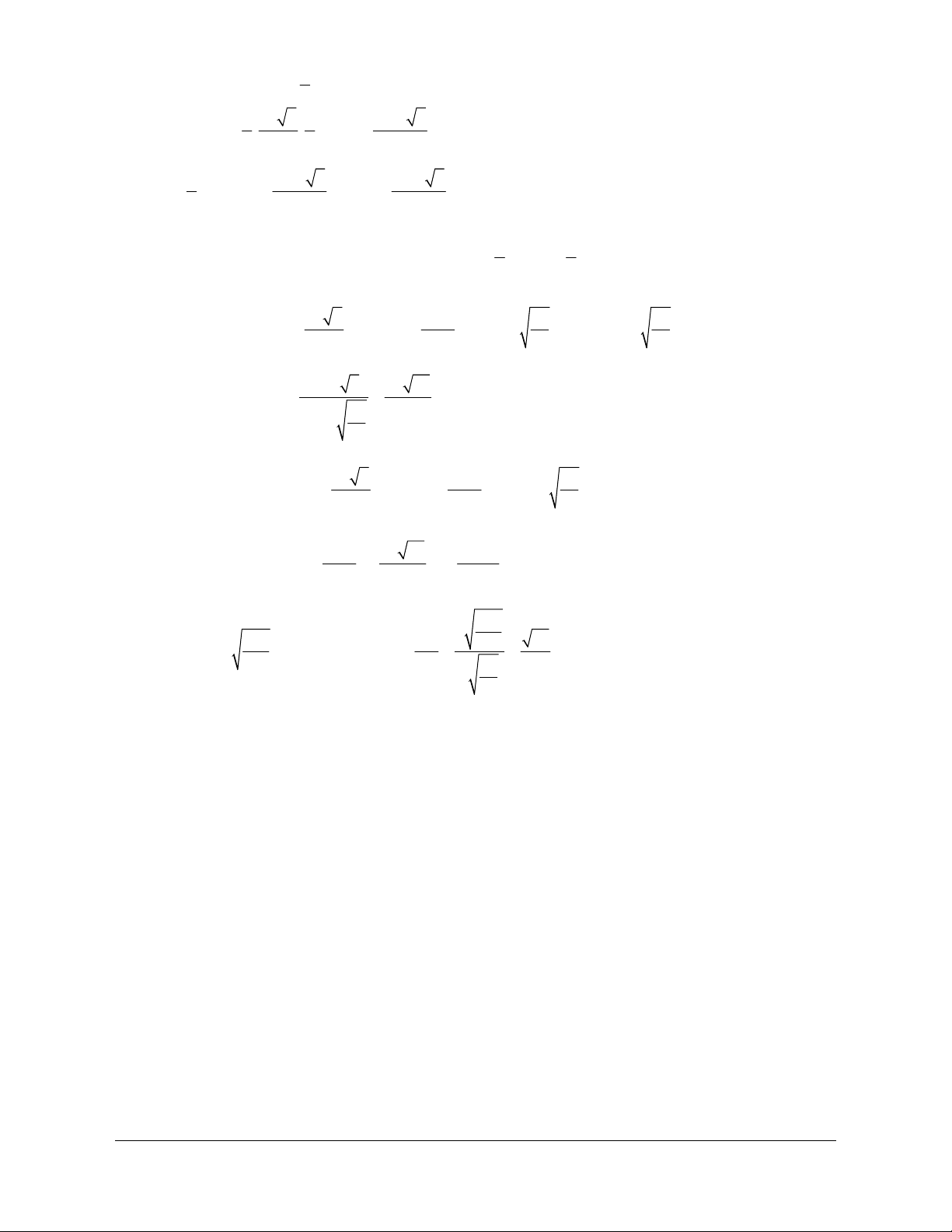
Preview text:

BÀI 1. VECTO TRONG KHÔNG GIAN
A. KIẾN THỨC CƠ BẢN CẦN NẮM
I – ĐỊNH NGHĨA VÀ CÁC PHÉP TOÁN VỀ VECTƠ TRONG KHÔNG GIAN
Cho đoạn thẳng AB trong không gian. Nếu ta chọn điểm đầu là A , điểm cuối là B ta có một vectơ, 
được kí hiệu là AB . Định nghĩa 
Vectơ trong không gian là một đoạn thẳng có hướng. Kí hiệu
AB chỉ vectơ có điểm đầu là A , điểm     cuối .
B Vectơ còn được kí hiệu là , a ,
b x, y ,…
Các khái niệm có liên quan đến vectơ như giá của vectơ, độ dài của vectơ, sự cùng phương, cùng
hướng của hai vectơ, vectơ – không, sự bằng nhau của hai vectơ, … được định nghĩa tương tự như trong mặt phẳng.
II – ĐIỀU KIỆN ĐỒNG PHẲNG CỦA BA VECTƠ
1. Khái niệm về sự đồng phẳng của ba vectơ trong không gian   
Trong không gian cho ba vectơ , a b , c
đều khác vectơ – không. Nếu từ một điểm O bất kì ta vẽ      
OA = a , OB = b , OC = c thì có thể xả ra hai trường hợp:
· Trường hợp các đường thẳng OA , , OB OC không cùng
nằm trong một mặt phẳng, khi đó ta nói    rằng vectơ , a b , c không đồng phẳng. 
· Trường hợp các đường thẳng , , OA OB OC cùng
nằm trong một mặt phẳng thi ta nói ba vectơ , a   b , c đồng phẳng.   
Trong trường hợp này giá của các vectơ , a ,
b c luôn luôn song song với một mặt phẳng.       a) Ba vectơ , a b , c không
đồng phẳng b) Ba vectơ , a b , c đồng phẳng
Chú ý. Việc xác định sự đồng phẳng hoặc không đồng phẳng của ba vectơ nói trên không phụ
thuộc vào việc chọn điểm . O
Từ đó ta có định nghĩa sau đây: 2. Định nghĩa
Trong không gian ba vectơ được gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng.
3. Điều kiện để ba vectơ đồng phẳng
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 695
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Từ định nghĩa ba vectơ đồng phẳng và từ định lí về sự phân tích (hay biểu thị) một vectơ theo hai
vectơ hai vectơ không cùng phương trong hình học phẳng chúng ta có thể chứng minh được định lí sau đây: Định lí 1      
Trong không gian cho hai vectơ a , b không cùng phương và vectơ . c Khi đó ba vectơ a , , b c   
đồng phẳng khi và chỉ khi có cặp số m,n sao cho c = ma + nb . Ngoài ra cặp số m,n là duy nhất. Định lí 2    
Trong không gian cho ba vectơ không đồng phẳng , , . a b c Khi đó với mọi vectơ x ta đều tìm    
được một bộ ba số m, ,
n p sao cho x = ma + nb + pc . Ngoại ra bộ ba số m, n, p là duy nhất.
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1. Biểu diễn vectơ      
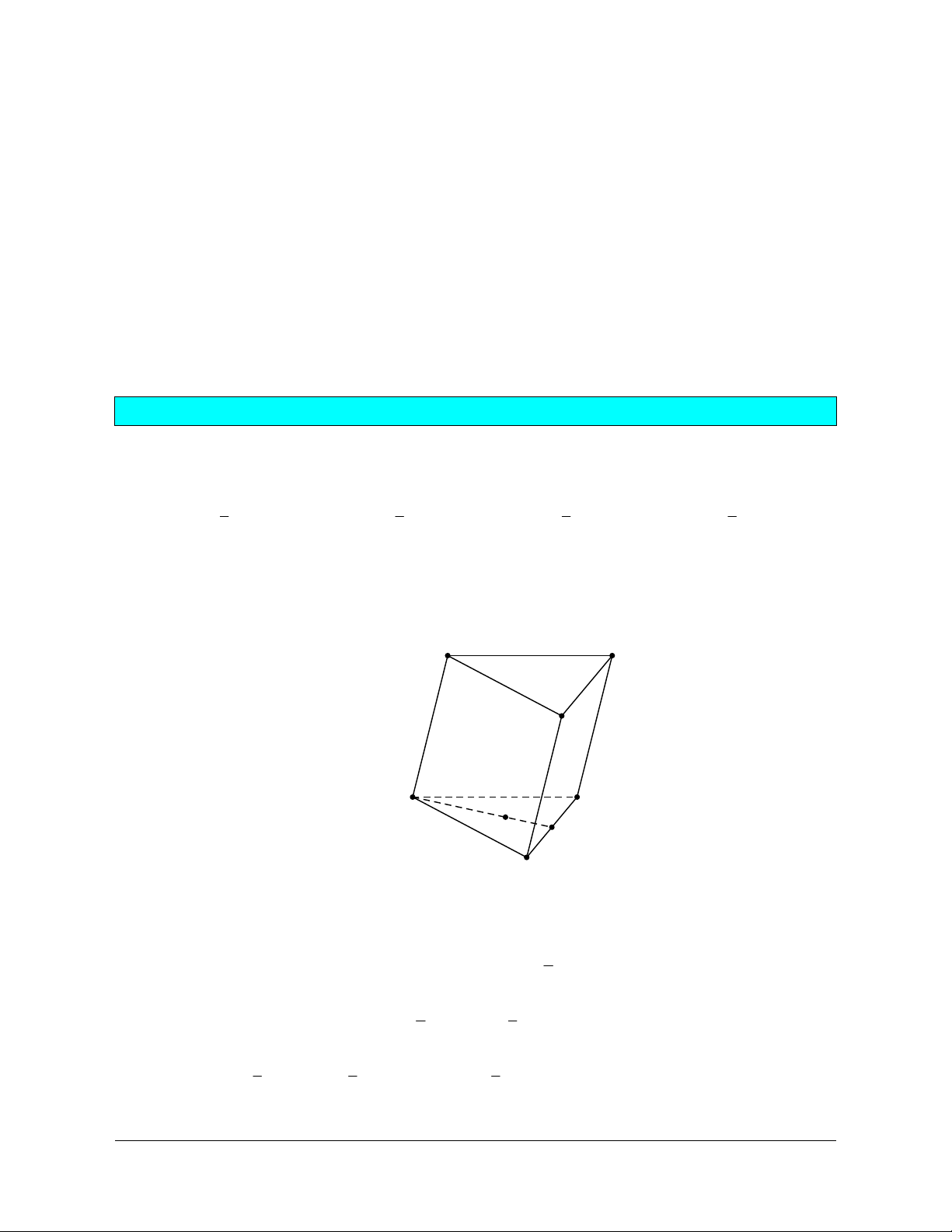
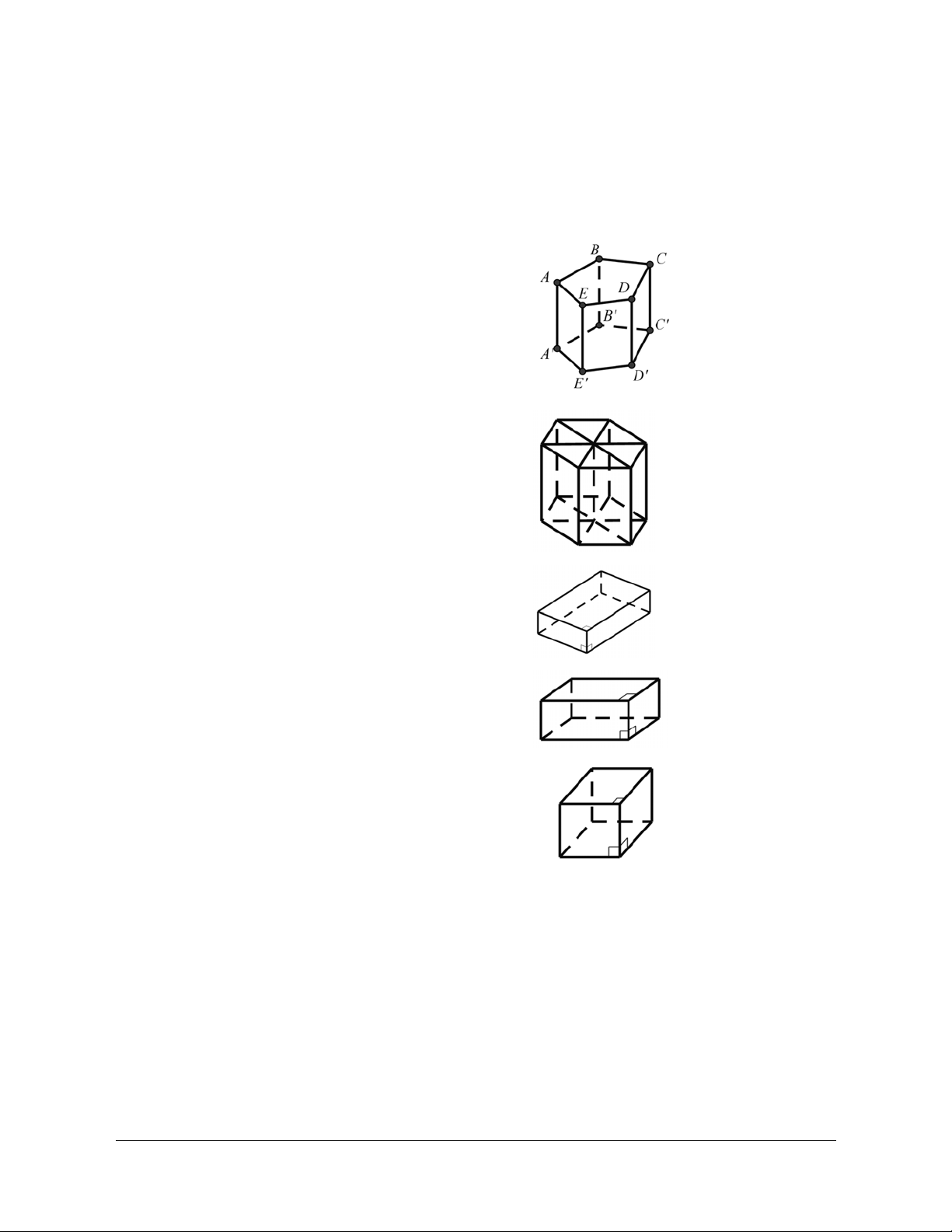
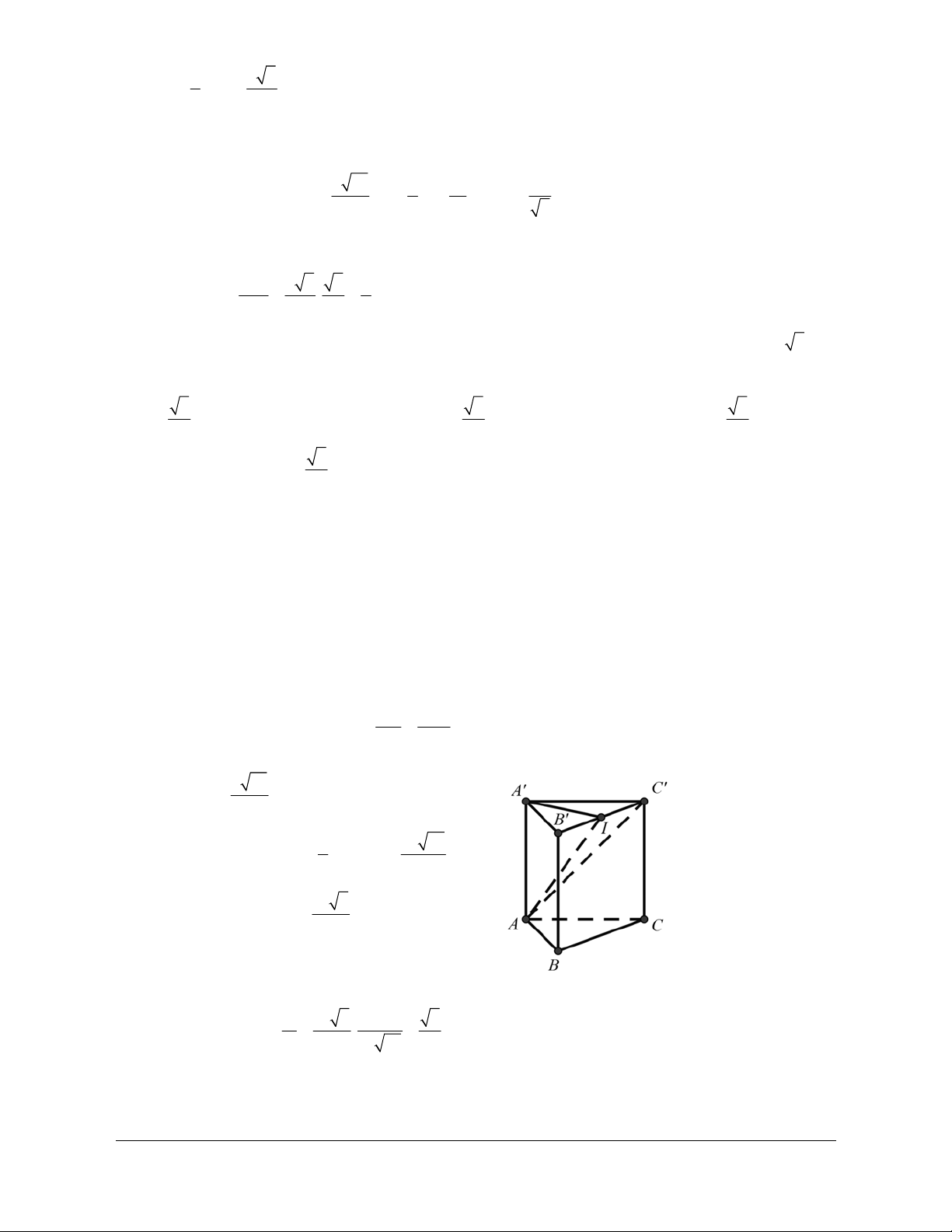
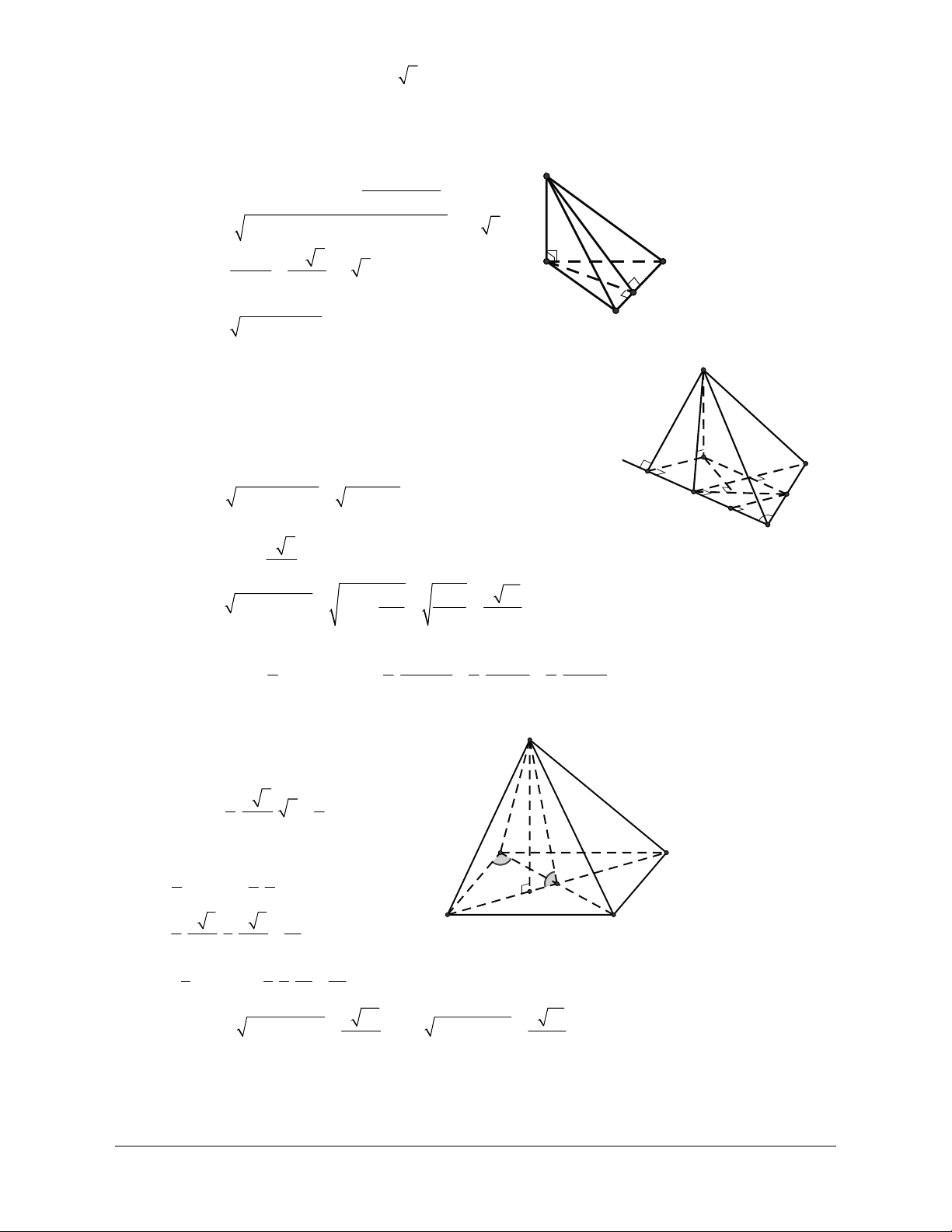
Câu 1: Cho hình lăng trụ ABC.A B ¢ C ¢ .¢ Đặt a = AA , ¢ b = A , B c = A .
C Gọi G ¢ là trọng tâm của tam  giác A ¢B C
¢ .¢ Vectơ AG¢ bằng:     A. 1 (  1   1   1  
a + 3b + c ).
B. (3a +b +c).
C. (a +b +3c).
D. (a +b +c). 3 3 3 3 Lời giải Chọn B A C B A' C' G' I B'
Gọi I là trung điểm của B C ¢ .¢  
Vì G¢ là trọng tâm của tam giác 2 A ¢B C
¢ ¢  A¢G ¢ = A¢I . 3         Ta có 2 1
AG ¢ = AA ¢ + A ¢G ¢ = AA ¢ +
A ¢I = AA ¢ + (A¢B¢ + A¢C¢). 3 3  1        
= AA¢ + (AB + AC) 1
= ( AA¢+ AB + AC) 1 3
= (3a +b +c). 3 3 3
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 696
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133       
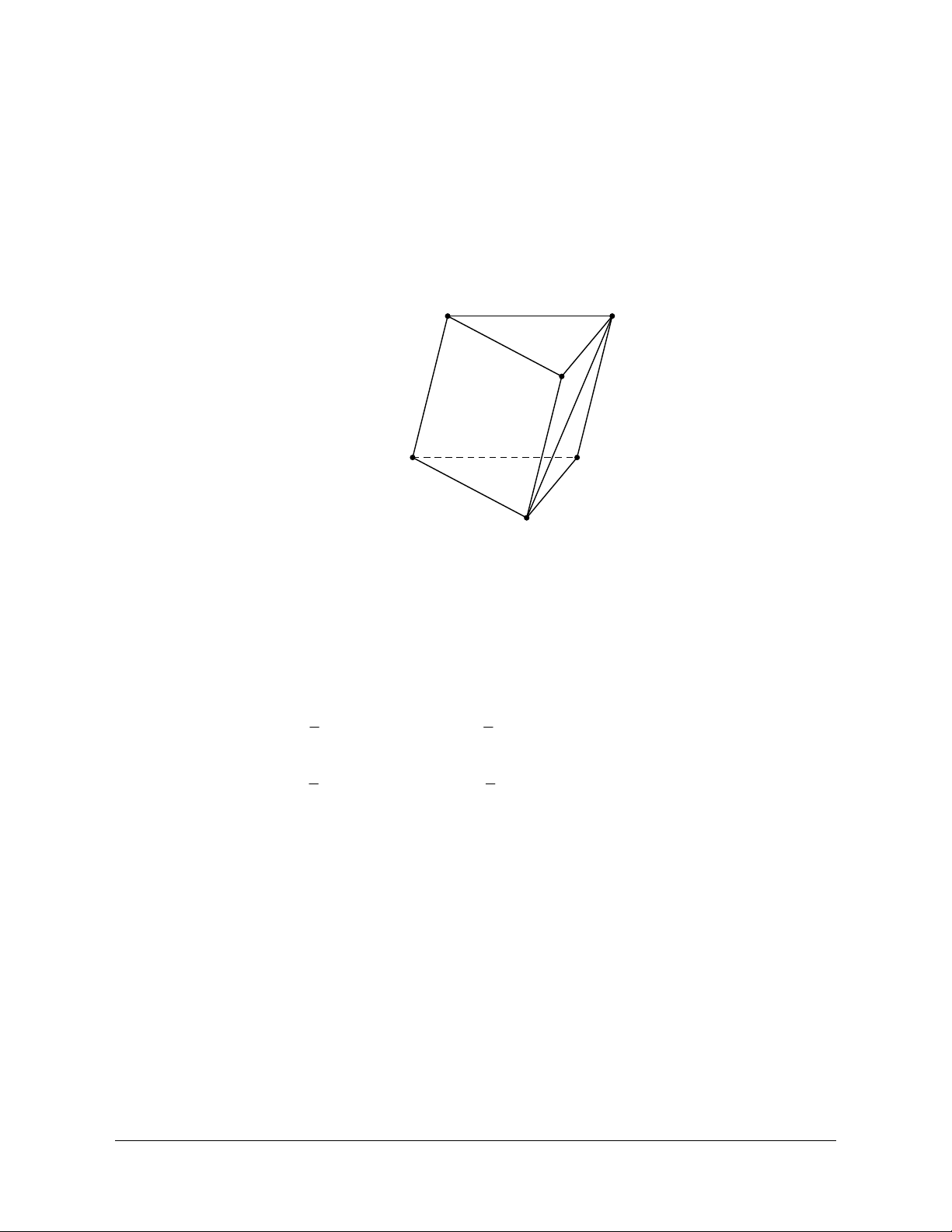
Câu 2: Cho hình lăng trụ ABC.A B ¢ C
¢ .¢ Đặt a = AA ,¢ b = A , B c = A .
C Hãy biểu diễn vectơ B C ¢  theo các vectơ   a, b, c.         A. B C ¢ = a +b- . c B. B C ¢ = -a + b- . c         C. B C ¢ = a +b+ . c D. B C ¢ = -a-b + . c Lời giải Chọn D A C B A' C' B'      Vì BB C ¢ C
¢ là hình bình hành suy ra B C ¢ = B C ¢ ¢ + B B ¢ = BC - AA¢         
= - AA ¢ + BA + AC = - AA ¢ - AB + AC = -a -b + c .     Câu 3:  
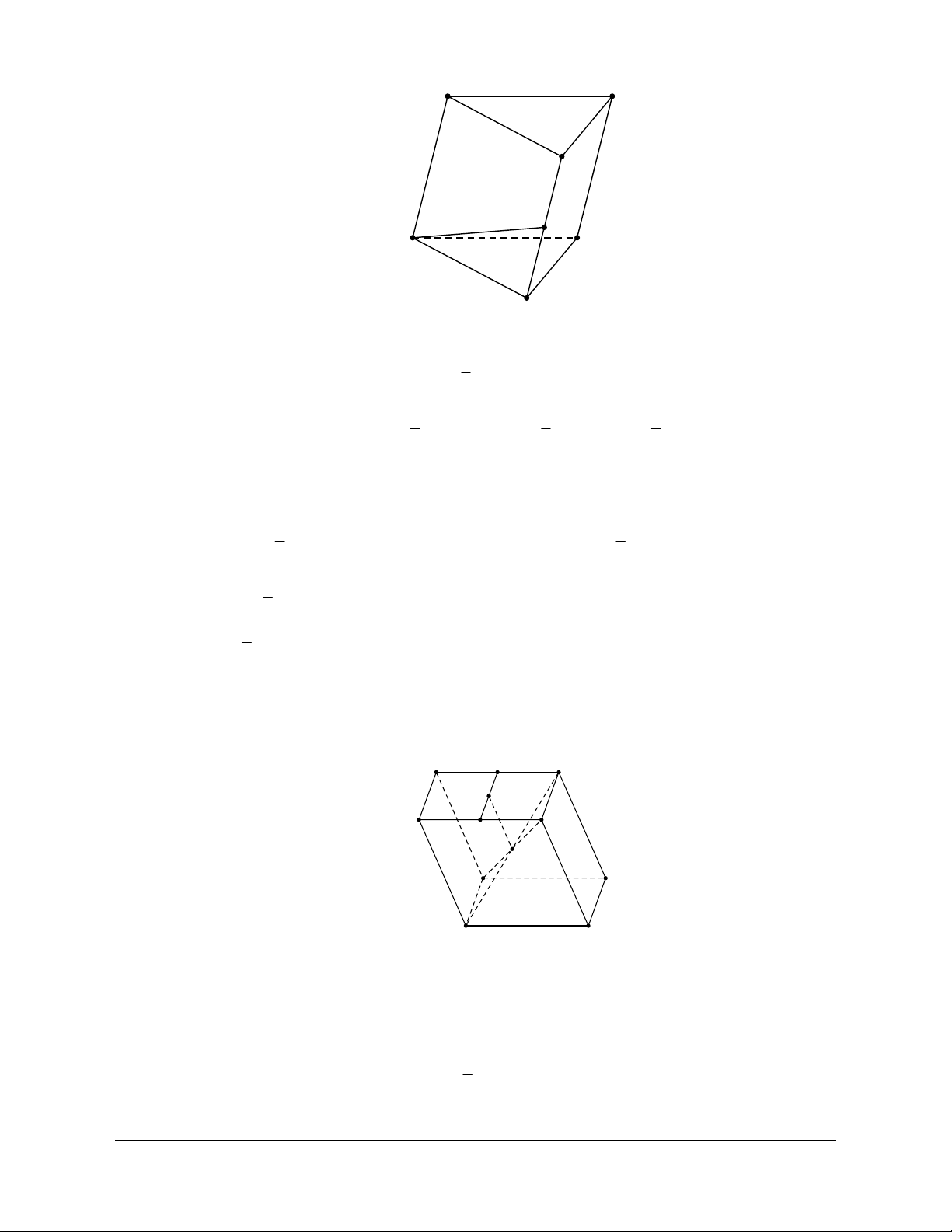
Cho hình lăng trụ ABC.A B ¢ C
¢ .¢ Gọi M là trung điểm của BB .¢ Đặt
CA = a, CB = b, AA ¢ = c.
Khẳng định nào dưới đây là đúng?  1       1 
A. AM = a +c - . b
B. AM = b+c - . a 2 2    1   1   
C. AM = b-a + c.
D. AM = a -c + . b 2 2 Lời giải Chọn C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 697
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A C B M A' C' B'  1 
Vì M là trung điểm của BB¢  BM = BB¢. 2     1    1    1 
Ta có AM = AB +BM =-BA + BB¢ = C
- A +CB + BB¢ =-a +b+ c. 2 2 2
Câu 4: Cho hình hộp ABC . D A B ¢ C ¢ D ¢ ¢ tâm .
O Gọi I là tâm của hình hình hành ABC . D Đặt        
AC ¢ = u, CA ¢ = v, BD ¢ = x, DB ¢ = y. Khi đó  1      1    
A. 2OI = - (u +v + x + y).
B. 2OI = - (u +v + x + y). 4 2  1    
C. 2OI = (u +v + x + y). D. 2  1    
2OI = (u +v + x + y). 4 Lời giải Chọn A D N C I A B M O D' C' A' B'
Gọi M , N lần lượt là trung điểm của AB, CD.   
Vì I là trung điểm của MN suy ra OM +ON = 2OI . ì   ïï + =     
Kết hợp với OA OB 2OM 1 ïí 
  2OI = (OA +OB +OC +OD). ï 2 OC ï +OD = 2ON ïî
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 698
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
1 æ 1  1  1  1 ö 1     = ç- ç AC ¢ - CA ¢ - BD ¢ -
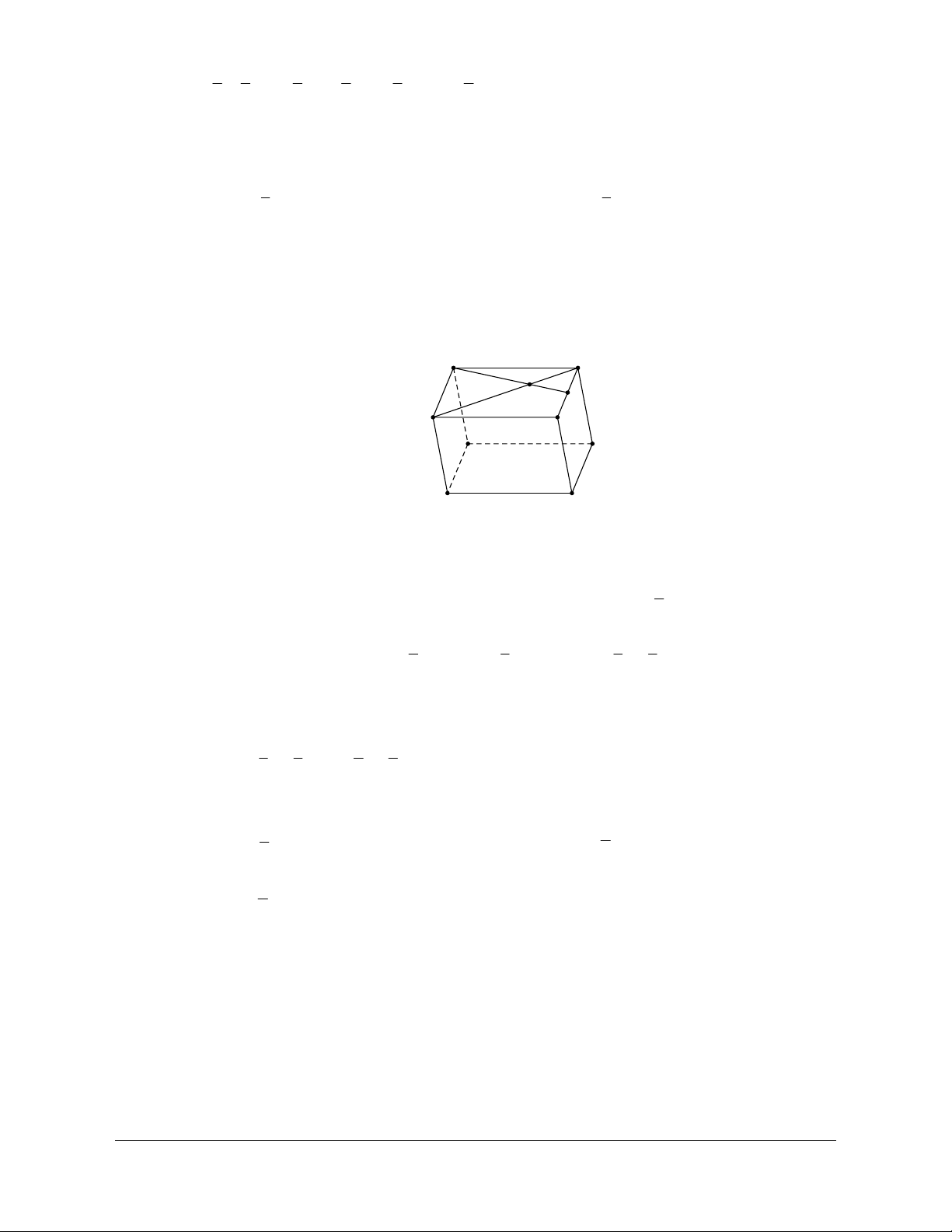
DB¢÷÷ = - (u + v + x + y). . 2 çè 2 2 2 2 ÷ø 4     Câu 5:   Cho hình hộp ABC . D A B ¢ C ¢ D
¢ ¢ có AB = a, AC = b, AA¢ = c . Gọi I là trung điểm của B C ¢ ,¢
K là giao điểm của A I ¢ và B D
¢ .¢ Mệnh đều nào sau đây đúng?     A. 1   1  
DK = (4a -2b +3c). B.
DK = (4a -2b +c). 3 3     C.    
DK = 4a - 2b + c.
D. DK = 4a -2b +3c. Lời giải Chọn A A' B' K I D' C' A B D C   
Vì I là trung điểm của B C
¢ ¢  A ¢B¢ + A ¢C ¢ = 2 A ¢I .   Và 2
K là giao điểm của A ¢I , B D
¢ ¢ nên theo định lí Talet  A¢K = A¢I. 3          Ta có 2 1  
AK = AA ¢ + A ¢K = AA ¢ +
A ¢I = AA ¢ + (A¢B¢ + A¢C¢) 1 1
= a + b + c . 3 3 3 3        
Khi đó DK = DA + AK =CB + AK =(AB-AC)+ AK .  1 1  4 2      
= a -b + a + b + c = a - b + c . 3 3 3 3
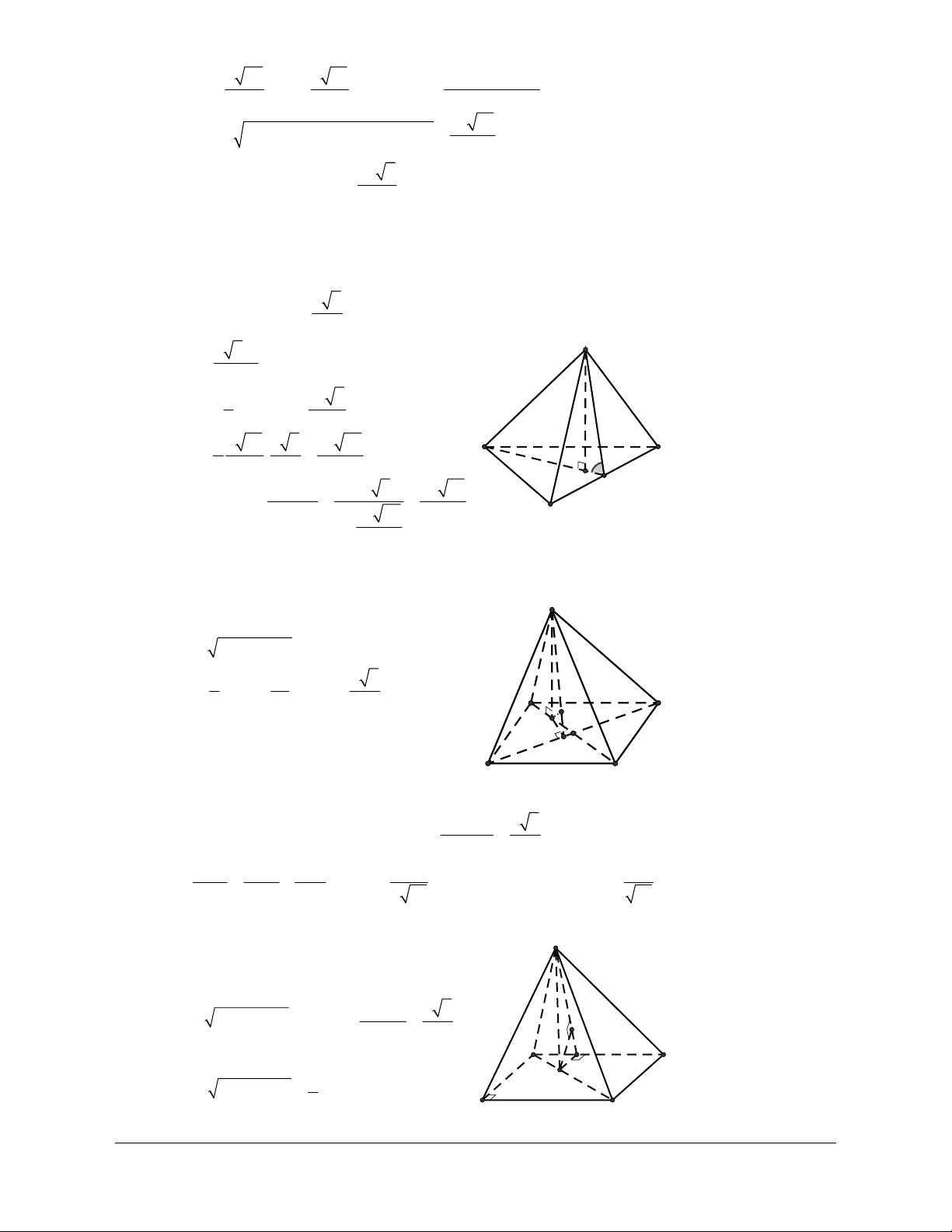
Câu 6: Cho tứ diện ABCD có trọng tâm G. Mệnh đề nào sau đây là sai?      1    A. 2 AG =
(AB+AC +AD).
B. AG = (AB + AC + AD). 3 4 
1         
C. OG = (OA +OB +OC +OD).
D. GA +GB +GC +GD = 0. 4 Lời giải Chọn A
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 699
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A G B D C     
Vì G là trọng tâm của tứ diện ABCD suy ra GA +GB +GC +GD = 0.  1 
1        
Khi đó OG = .4OG = (OA +AG +OB+BG +OC +CG +OD +DG) 4 4
1       
   
= (OA +OB +OC +OD) 1 ¾¾
AO +OG = AO + (OA +OB +OC +OD). 4 4  1
     
  
  
= AO + ( OA +AB +AC +AD) 1
= AO +OA + (AB + AC +AD) 1 4
= (AB+AC + AD). 4 4 4 
1        Vậy 2
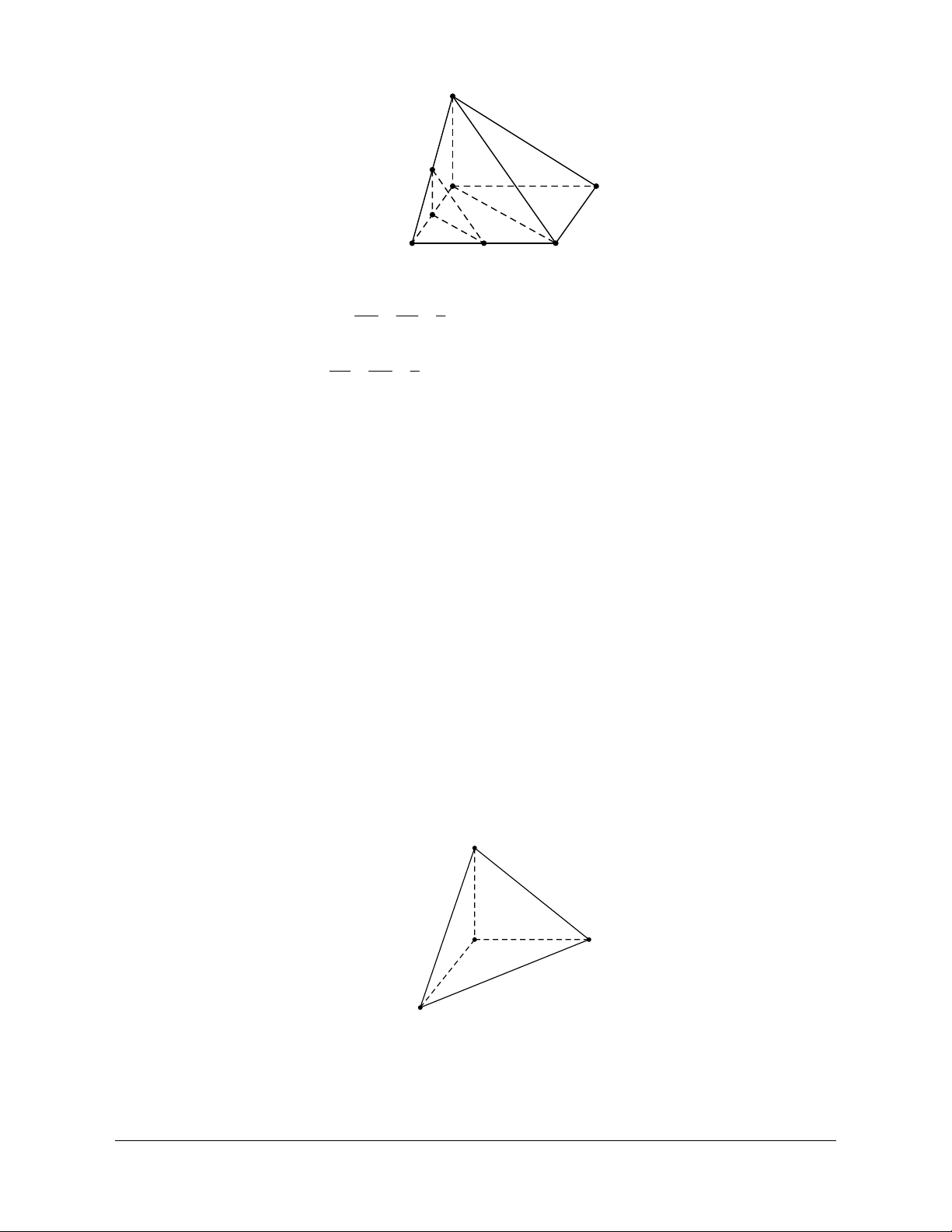
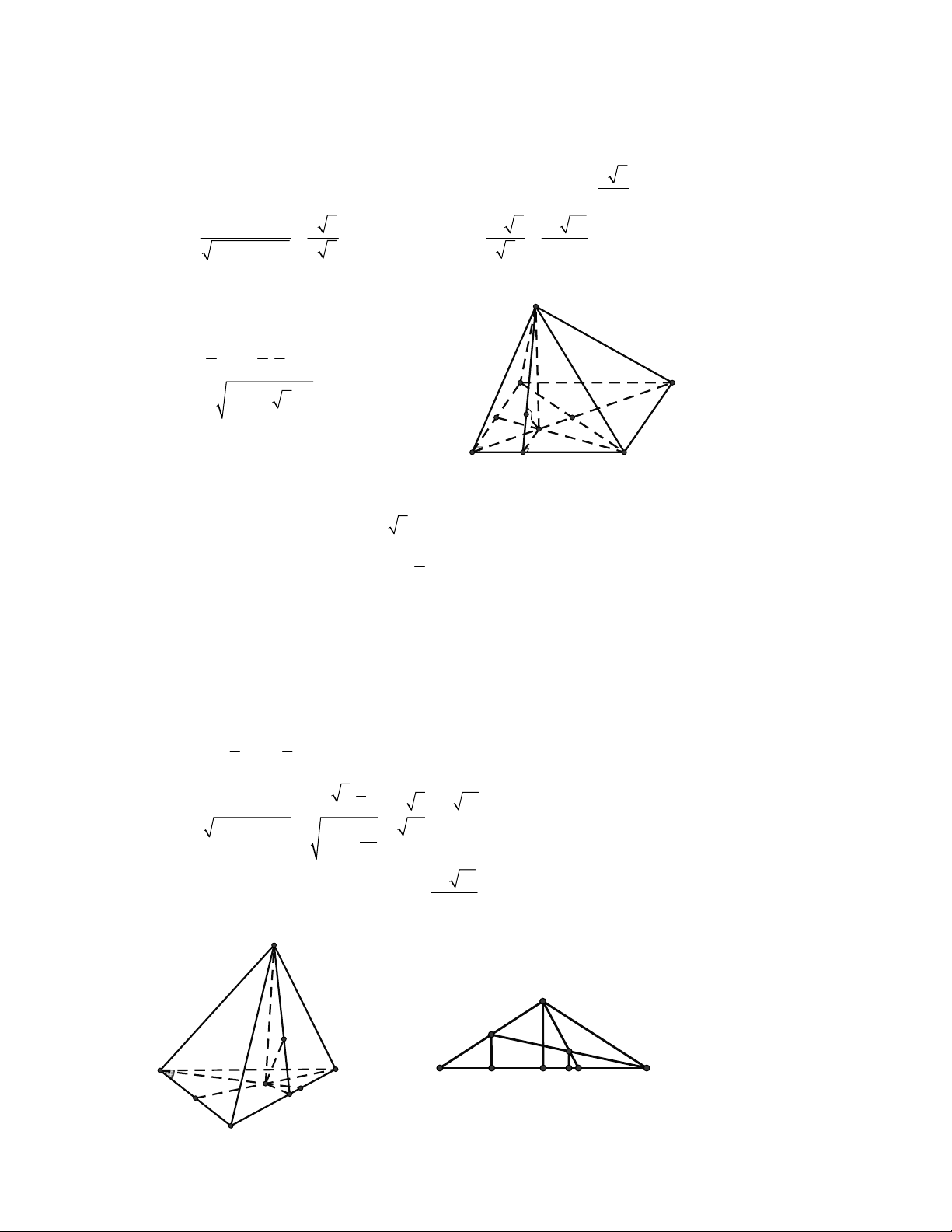
AG = (AB + AC + AD) nên mệnh đề AG = (AB + AC + AD) sai. 4 3     Câu 7:   Cho tứ diện ABC . D Đặt
A B = a, AC = b, AD = c . Gọi G là
trọng tâm của tam giác BCD.
Trong các đẳng thức sau, đẳng thức nào sau đây đúng?     A.   1  
AG = a + b + c.
B. AG = (a +b +c). 3  1     1   
C. AG = (a +b +c).
D. AG = (a +b +c). 2 4 Lời giải Chọn B A B D G M C  
Gọi M là trung điểm của CD suy ra 2 BG = BM . 3            Ta có 2 2 1
AG = AB + BG = AB + BM = AB + (BC +BD) 1 .
= AB + (BC + BD). 3 3 2 3
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 700
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133  1          
= AB + (AC - AB + AD - AB) 1
= (AB + AC + AD) 1
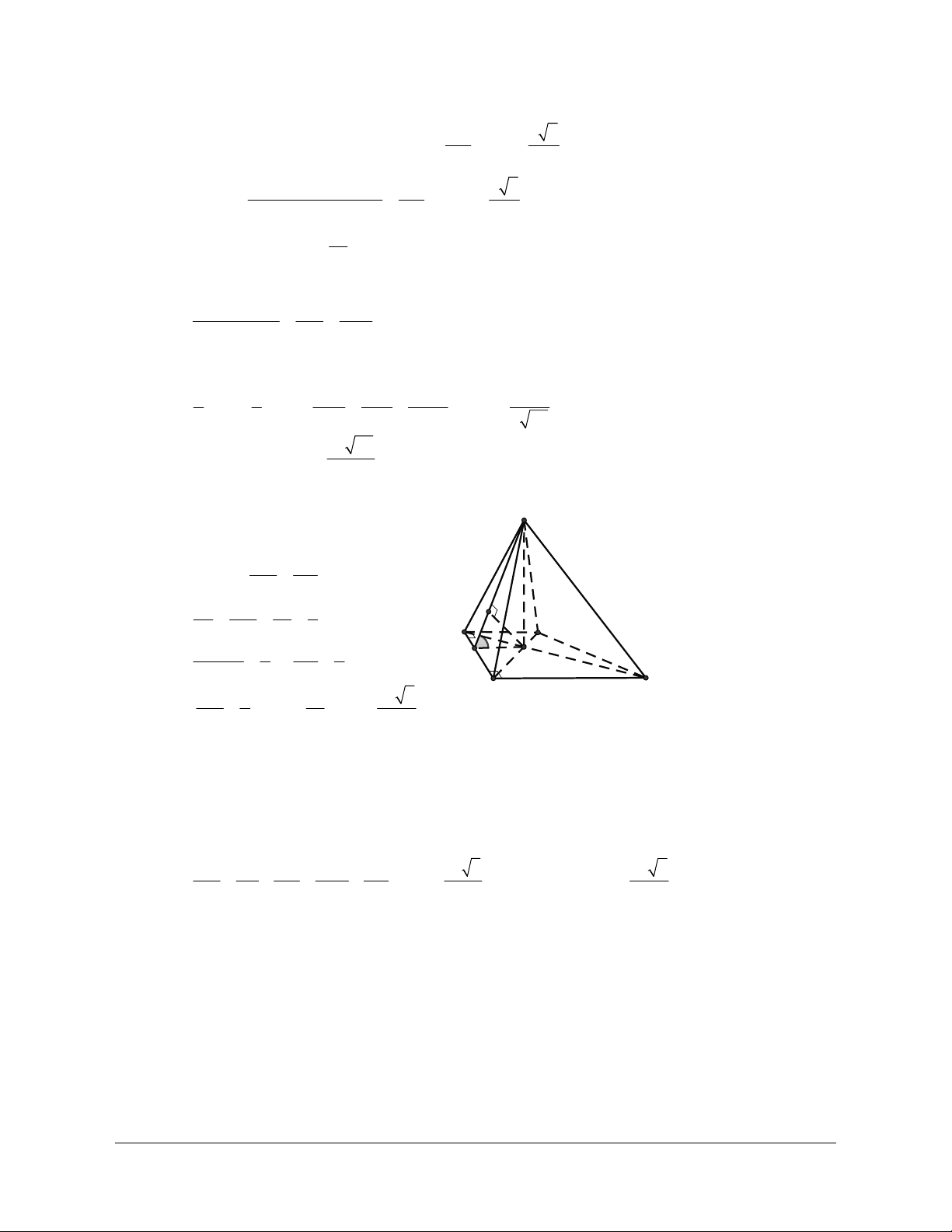
= (a +b+c). 3 3 3     Câu 8:   Cho tứ diện ABC . D Đặt
A B = a, A C = b, A D = c . Gọi M là trung điểm của đoạn thẳng .
BC Đẳng thức nào dưới đây là đúng?  1     1   
A. DM = (a +b -2c).
B. DM = (-2a +b +c). 2 2  1     1   
C. DM = (a -2b +c).
D. DM = (a +2b -c). 2 2 Lời giải Chọn A A B D M C  1 
Vì M là trung điểm của BC suy ra BM = B . C 2 
     1    1  
Ta có DM = DA + AB +BM = AB-AD + BC = AB-AD + (BA +AC). 2 2
1  1   1 1  1     
= AB + AC - AD = a + b -c = (a +b -2c). 2 2 2 2 2
Câu 9: Cho tứ diện ABC . D
Gọi M và P lần lượt là trung điểm của AB và . CD Đặt      
A B = b, A C = c, A D = d . Khẳng định nào sau đây là đúng?  1     1   
A. MP = (c +d +b).
B. MP = (d +b -c). 2 2  1     1   
C. MP = (c +b -d).
D. MP = (c +d -b). 2 2 Lời giải Chọn D
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 701
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A M B D P C ì   ïï = Vì 2 AM AB ï
M , P lần lượt là trung điểm của A , B CD  í   .
ïïAC + AD = 2 AP ïî     
1  1   1  1 1  
Ta có MP = MA + AP =-AM + AP =- AB + (AC +AD)=- b + c + d. 2 2 2 2 2
Dạng 2. Đẳng thức vectơ       Câu 1:  
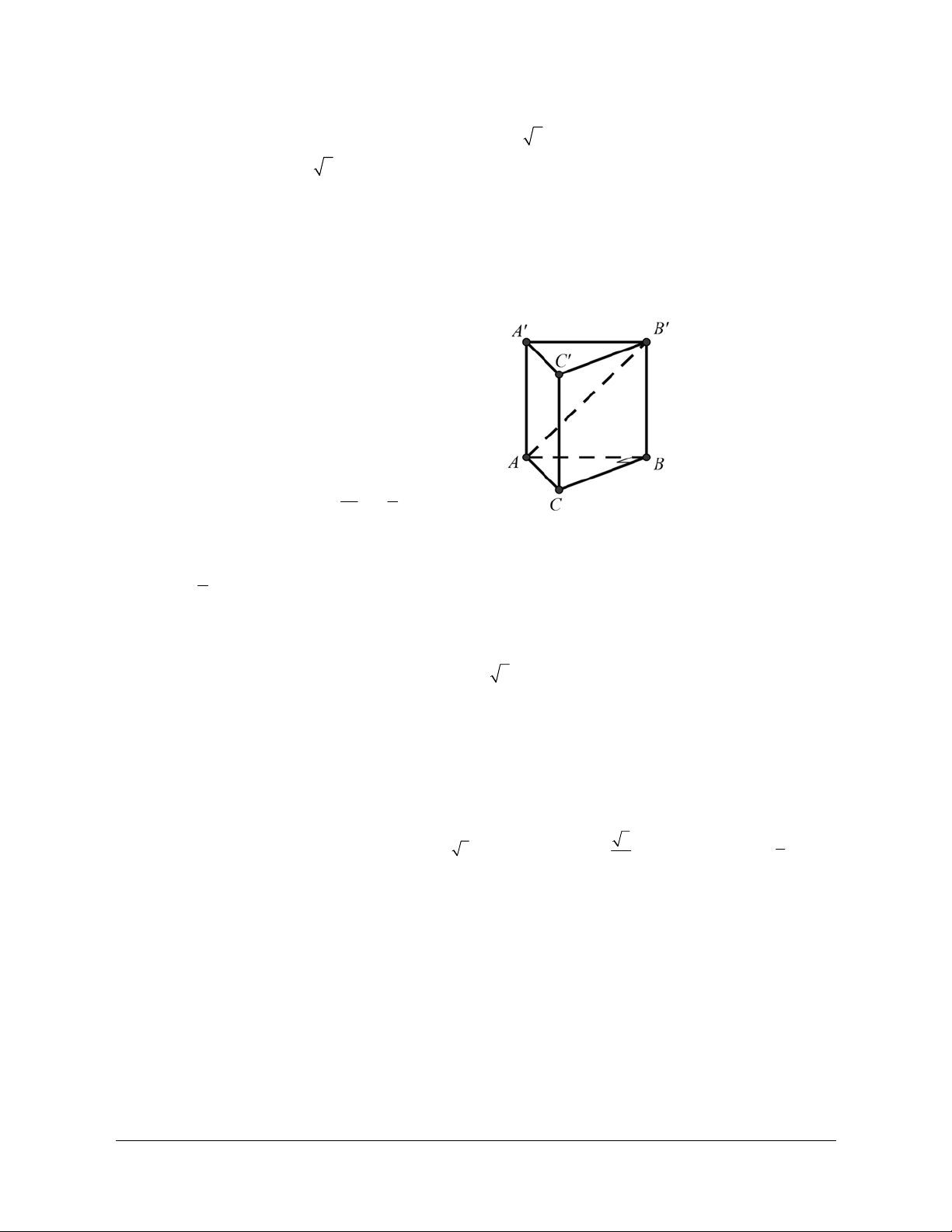
Cho hình lăng trụ tam giác A . BC A B ¢ C ¢ .¢ Đặt
AA ¢ = a, AB = b, AC = c, BC = d . Khẳng định
nào dưới đây là đúng?     A.    
a = b + c.
B. a +b + c + d = 0.      C.   
b - c + d = 0.
D. a + b + c = d. Lời giải Chọn C A C B A' C' B'         Ta có  
BC = AC - AB d = c - b b - c + d = 0.
Câu 2: Cho hình lập phương ABC . D A B ¢ C ¢ D
¢ .¢ Gọi O là tâm của hình lập phương. Khẳng định
nào dưới đây là đúng?     
1    A. 1
AO = (AB + AD + AA¢).
B. AO = (AB + AD + AA¢). 3 2 
1        C. 2 AO =
(AB+AD+AA¢).
D. AO = (AB + AD + AA¢). 4 3
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 702
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn B A' B' D' C' O A B D C    
Theo quy tắc hình hộp, ta có AC¢ = AB + AD + AA .¢  1 
1   
Mà O là trung điểm của AC¢ suy ra AO = AC¢ = (AB+AD +AA¢). 2 2
Câu 3: Cho hình hộp ABC . D A B ¢ C ¢ D ¢ ¢ tâm .
O Khẳng định nào dưới đây là sai?         
A. AC ¢ = AB + AD + AA .¢
B. AB + BC ¢ +CD + D A ¢ = 0.          
C. AB + AA¢ = AD + DD .¢
D. AB + BC +CC ¢ = AD¢ + D O ¢ +OC .¢ Lời giải Chọn C A' B' D' C' O A B D C
Dựa vào đáp án, ta thấy rằng:    
A đúng, vì theo quy tắc hình hộp, ta có AC¢ = AB + AD + AA .¢ ì  ïï = -     
B đúng, vì AB CD ïí
  AB + BC ¢ +CD + D A ¢ = 0. ïïBC¢ = -D A ¢ ïî ì   ïï + ¢ = ¢      
C sai, vì AB AA AB ïí
mà AB¢ ¹ AD¢  AB + AA¢ ¹ AD + DD .¢ ï  
ïAD + DD¢ = AD¢ ïî
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 703
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133       (
ìïï )1: AB +BC +CC¢ = AC +CC¢ = AC¢ D đúng, vì ïí        ( ) 1 = (2). (
ïï 2): AD¢+ D O
¢ +OC¢ = AO +OC¢ = AC¢ ïî
Câu 4: Cho hình hộp ABCD.A B C D . 1 1 1 1
Khẳng định nào dưới đây là sai?        
A. BC + BA = B C + B A .
A D + D C + D A = DC. 1 1 1 1 B. 1 1 1 1        
C. BC + BA + BB = BD .
BA + DD + BD = BC. 1 1 D. 1 1 Lời giải Chọn D A1 B1 D1 C1 A B D C
Dựa vào đáp án, ta thấy rằng: ì  ïï =    
A đúng, vì BC ï 1 B 1 C í
BC + BA = B C + B A . ï  suy ra 1 1 1 1 ïBA = ïî 1 B 1 A         
B đúng, vì AD + D C + D A = AD + DC + DA = AC + DA = D . 1 1 1 1 C    
C đúng, vì B = + + (quy tắc hình hộp). 1 D BC BA B 1 B         
D sai, vì BA + DD + BD = BA + BB + BD = BA + BD ¹ BC. 1 1 1 1 1 1
Câu 5: Cho hình hộp ABCD.A B C D . M A . D 1 1 1 1 Gọi là trung điểm của
Khẳng định nào dưới đây là đúng?        1 
A. B M = B B + B A + B C .
C M = C C +C D + C B . 1 1 1 1 1 1 B. 1 1 1 1 1 1 2   1  1     
C. C M =C C + C D + C B .
BB + B A + B C = 2B D. 1 1 1 1 1 1 D. 2 2 1 1 1 1 1 1 Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 704
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A B M D C A1 B1 D C 1 1
Dựa vào đáp án, ta thấy rằng:     1   
1  
A sai, vì B M = B B +BM = BB + BA +BD = BB + B A +B D . 1 1 1 ( ) 1 ( 1 1 1 1) 2 2
 1      1  = BB +
B A + B A + B C = BB + B A + B C . 1 ( 1 1 1 1 1 1) 1 1 1 1 1 2 2     1   
1  
B đúng, vì C M =C C +CM =C C + CA +CD =C C + C A +C D . 1 1 1 ( ) 1 ( 1 1 1 1) 2 2 
1      1 
=C C + C B +C D +C D =C C +C D + C B . 1 ( 1 1 1 1 1 1) 1 1 1 1 1 2 2    1  C sai, vì = + + (từ B). 1 C M 1 C C 1 C 1 D 1 C 1 B 2        
D sai, vì BB + B A + B C = BA + BC = BA + A D = BD . 1 1 1 1 1 1 1 1 1 1
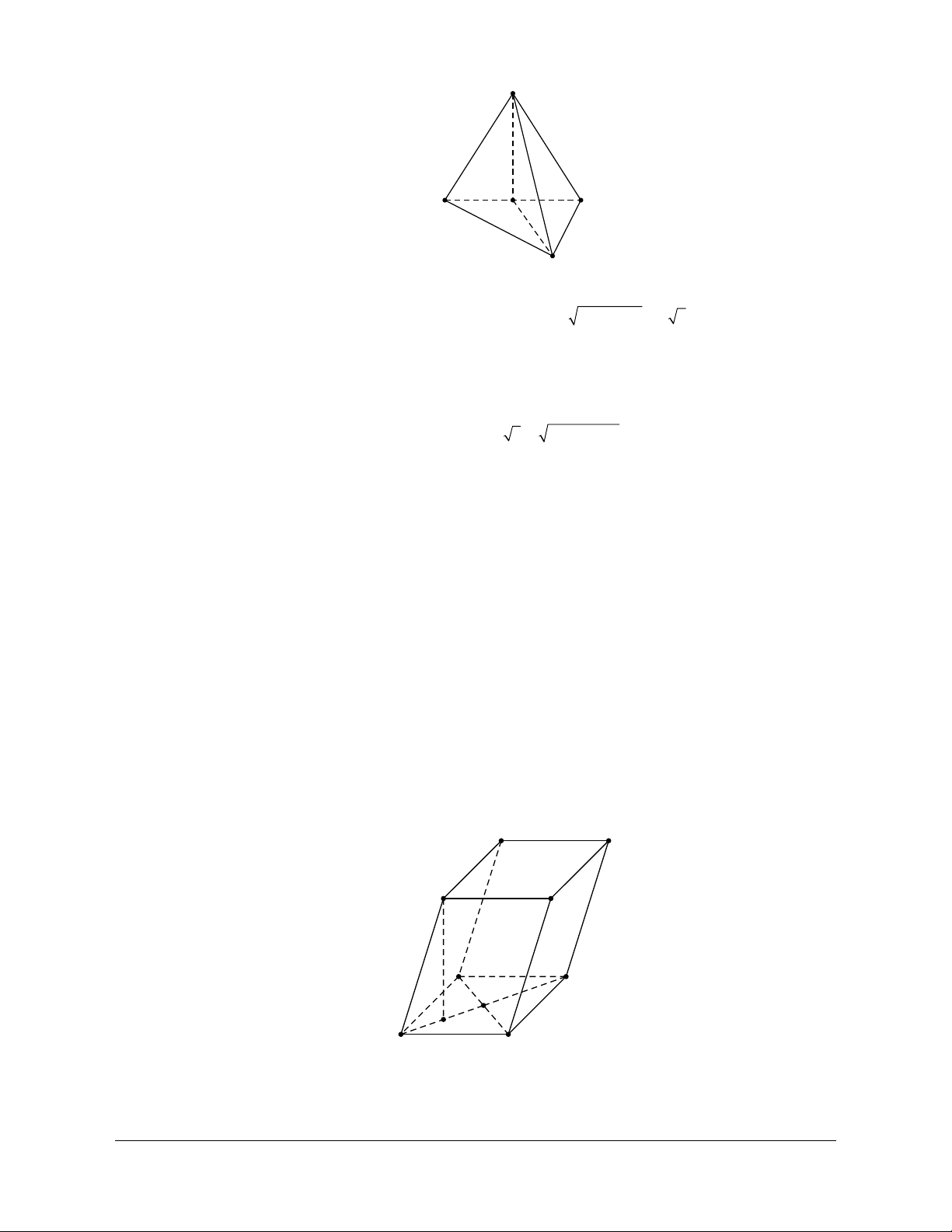
Câu 6: Cho hình lập phương ABC . D A B ¢ C ¢ D ¢ ¢ có cạnh bằng . a Gọi G là trọng tâm của tam giác AB C
¢ . Khẳng định nào dưới đây là đúng?        
A. AC¢ = 3 AG.
B. AC¢ = 4 AG.
C. BD¢ = 4 BG.
D. BD¢ = 3 BG. Lời giải Chọn D C B I D A G C' B' D' A'
Cách 1. Gọi I là tâm của hình vuông ABCD I là trung điểm của BD.   Ta có BG BI 1 BG 1 DBIG  DD B ¢ G ¢  = = 
=  BD¢ = 3 BG. D G ¢ D B ¢ ¢ 2 BD ¢ 3
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 705
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133    
Cách 2. Theo quy tắc hình hộp, ta có BA + BC + BB¢ = BD¢.      
Do G là trọng tâm của tam giác AB C
¢ suy ra BA + BC + BB¢ = 3BG BD¢ = 3 BG.    Câu 7:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Đặt
SA = a, SB = b ,    
SC = c, SD = d . Khẳng định nào dưới đây là đúng?          A.        
a + c = b + d .
B. a +b + c + d = 0.
C. a + d = b + c.
D. a + b = c + d. Lời giải Chọn A S B A O D C
Gọi O là tâm hình bình hành ABCD.     Vì  
O là trung điểm của AC suy ra SA + SC = 2 SO  2 SO = a + c ( ) 1 .      
Và O là trung điểm của BD suy ra SB +SD = 2SO  2SO = b + d (2).   Từ ( )  
1 và (2) , suy ra a +c = b +d.
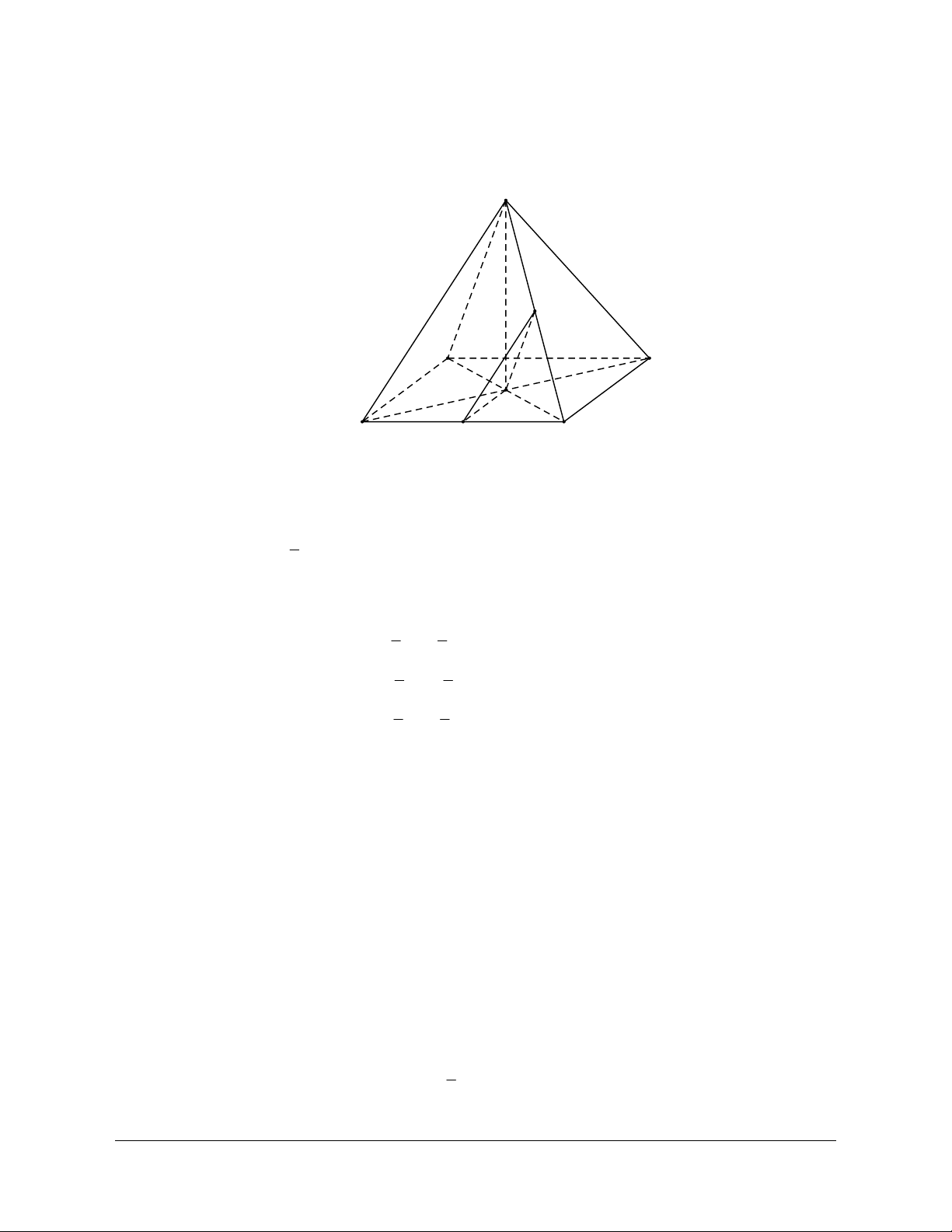
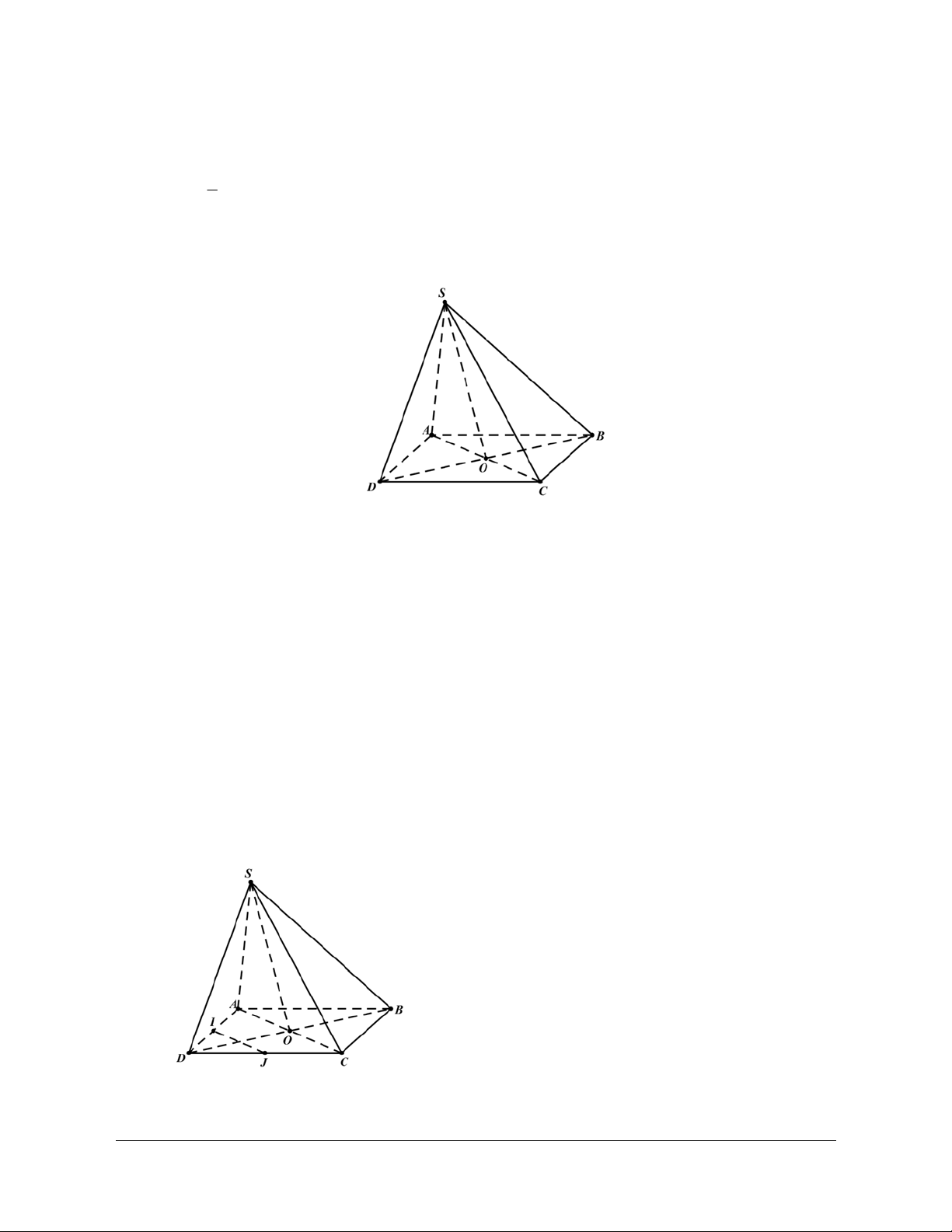
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm . O Gọi G là điểm thỏa mãn      
GS + GA + GB + GC + GD = 0. Khẳng định nào dưới đây là đúng?   A.
G, S, O không thẳng hàng.
B. GS = 4 OG.    
C. GS = 5 OG.
D. GS = 3 OG. Lời giải Chọn B S B A G O D C     
Gọi O là tâm hình bình hành ABCD suy ra OA +OB +OC +OD = 0.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 706
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133            
Ta có GS +GA +GB +GC +GD = GS +4GO +OA +OB +OC +OD = 0.     
GS + 4GO = 0  GS = 4 OG  ba điểm G, S, O thẳng hàng.     
Câu 9: Cho tứ diện ABCD và điểm
G thỏa mãn GA +GB +GC +GD = 0 ( G là trọng tâm của tứ diện). Gọi G GA (BCD). 0 là giao điểm của và mặt phẳng
Khẳng định nào dưới đây là đúng?        
A. GA = -2G G. GA = 4 G G. GA = 3 G G. GA = 2 G G. 0 B. 0 C. 0 D. 0 Lời giải Chọn C A G B D G0 M C
Vì G là giao điểm của đường thẳng 0
AG với mặt phẳng (BCD).    
Suy ra G là trọng tâm của tam giác
G B +G C +G D = 0. 0 BCD 0 0 0          
Theo bài ra, ta có GA +GB +GC +GD = GA +3GG +G B +G C +G D = 0 0 0 0 0
  0     
GA +3GG = 0  GA = 3G G. 0 0
Câu 10: Cho tứ diện . ABCD Gọi
M , N lần lượt là trung điểm của AB, CD và G là trung điểm của
MN . Khẳng định nào dưới đây là sai?         
A. MA + MB + MC + MD = 4MG.
B. GA +GB +GC = GD.        
C. GA +GB +GC +GD = 0.
D. GM +GN = 0. Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 707
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A M G B D N C ì   ïï + = Vì GA GB GM ï
M , N lần lượt là trung điểm của A , B CD suy ra 2 í   . ïGC ï +GD = 2GN ïî        
Mà G là trung điểm của MN GM +GN = 0  GA +GB +GC +GD = 0.          
Khi đó MA + MB + MC + MD = 4 MG +(GA +GB +GC +GD)= 4 M . G
Câu 11: Cho hình hộp ABCD. 1 A 1 B 1 C 1
D . Tìm giá trị thực của k
thỏa mãn đẳng thức vectơ    
A B + B C + DD = k AC . 1 1 1 1 A. k = 4. B. k =1. C. k = 0. D. k = 2. Lời giải Chọn B A1 B1 D1 C1 A B D C         
Ta có AB + B C + DD = AB + BC +CC = AC +CC = AC k =1. 1 1 1 1 1 1
Câu 12: Cho hình hộp ABC . D A B ¢ C ¢ D
¢ .¢ Tìm giá trị thực của k
thỏa mãn đẳng thức vectơ     
AC + BA ' + k (DB +C ' D) = 0. A. k = 0. B. k =1. C. k = 4. D. k = 2. Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 708
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 B C A D C' B' A' D'           
Ta có AC + BA¢ = AC +CD¢ = AD¢ và DB +C D
¢ = DB - DC ¢ = C B ¢ = D A ¢ .         
Suy ra AC + BA ' + k(DB +C' D)= AD¢+k D A ¢ = 0  (k - ) 1 D A ¢ = 0  k =1. Câu 13: Gọi
M , N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABC . D Gọi I là
trung điểm của đoạn MN . Tìm giá trị thực của k
thỏa mãn đẳng thức vectơ      IA +(2k - )
1 IB + k IC + ID = 0. A. k = 2. B. k = 4. C. k =1. D. k = 0. Lời giải Chọn C A M I C D N B ì   ïï + = Vì IA IC IM ï
M , N lần lượt là trung điểm của 2
AC, BD  í   .
ïïIB + ID = 2 IN ïî   
    
Mặt khác IM + IN = 0 ( I là trung điểm của MN )  IA +IB +IC +ID = 0.    
      
Ta có IA +(2k - )
1 IB +kIC + ID = IA + IB + IC + ID +(2k -2)IB +(k - ) 1 IC = 0
 0        (k - )
1 (2 IB + IC)= 0 mà 2 IB + IC ¹ 0 suy ra k -1 = 0  k = 1. Câu 14: Gọi
M , N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABC . D Gọi I là trung điểm của đoạn MN và P là
một điểm bất kỳ trong không gian. Tìm giá trị thực của     
k thỏa mãn đẳng thức vectơ PI = k (PA + PB + PC + PD).
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 709
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 1 1 A. k = 4. B. k = . C. k = . D. k = 2. 2 4 Lời giải Chọn C A M P I C D N B ì   ïï + = Vì IA IC IM ï
M , N lần lượt là trung điểm của 2
AC, BD  í   .
ïïIB + ID = 2 IN ïî        
Mặt khác IM + IN = 0 ( I là trung điểm của MN )  IA + IB + IC + ID = 0.          
Khi đó PA + PB + PC + PD = 4 PI +(IA +IB +IC +ID)= 4 PI      1
Mà PI = k(PA +PB +PC +PD) nên suy ra 4k =1 k = . 4
Câu 15: Cho tứ diện . ABCD Gọi
M , N lần lượt là trung điểm của AB và .
CD Tìm giá trị thực của   
k thỏa mãn đẳng thức vectơ MN = k (AC + BD). 1 A. 1 k = . B. k = . C. k = 3. D. k = 2. 2 3 Lời giải Chọn A A M B D N C   
Ta có N là trung điểm của CD MC + MD = 2 MN ( ) 1 .   
Và M là trung điểm của AB suy ra MA + MB = 0 (2).
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 710
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133  1  
1     1   Từ ( )
1 ,(2) suy ra MN = (MC + MD)= (MA + AC + MB +BD)= (AC +BD). 2 2 2   
Kết hợp giả thiết MN = k(AC +BD) 1  k = . 2
Dạng 3. Đồng phẳng của ba vectơ    Câu 1:        Cho ba vectơ a, b, c không
đồng phẳng. Xét các vectơ ,
x = 2a + b
y = a - b - c ,   
z = -3b - 2c. Khẳng định nào dưới đây là đúng?
A. Ba vectơ     
x, y, z đồng phẳng.
B. Hai vectơ x, a cùng phương.  C. Hai vectơ    
x , b cùng phương.
D. Ba vectơ x, y, z đôi một cùng phương. Lời giải Chọn A
Giả sử, ba vectơ      
x, y, z đồng phẳng, khi đó x = m.y + . n z . ì  ï    ï = - - 
Ta có m.y m.a m.b m.c ï     í   m.y + .
n z = m.a -(m + 3n).b -(m + 2n).c. ï   ï . n z = -3 . n b -2 . n c ïî m ìï = 2   ï    ì ï ï = Khi đó ï ï
a + b = m a -(m + n) b -(m + n) m 2 2 . 3 . 2 .c m í + 3n = 1 -  í . ï n ï = 1 - ï ïî m ï + 2n = 0 ïî Vậy ba vectơ   
x, y, z đồng phẳng.  Câu 2:   Cho ba vectơ
a, b, c không
đồng phẳng. Khẳng định nào dưới đây là đúng?    A. Ba vectơ         
x = a + b + 2c, y = 2a - 3b - 6c, z = - a + 3b + 6c đồng phẳng.    B. Ba vectơ         
x = a - 2b + 4c, y = 3a - 3b + 2c, z = 2a - 3b - 3c đồng phẳng.    C. Ba vectơ         
x = a + b + c, y = 2a - 3b + c, z = - a + 3b + 3c đồng phẳng.    D. Ba vectơ         
x = a + b - c, y = 2a - b + 3c, z = - a - b + 2c đồng phẳng. Lời giải Chọn B Ba vectơ      
x, y, z đồng phẳng khi và chỉ khi $ m, n : x = m.y + . n z.    Với         
x = a -2b + 4c, y = 3a -3b + 2c, z = 2a -3b -3c.    Suy ra      
a -2b + 4c = m (3a -3b +2c)+n(2a -3b -3c). 3 ìï m + 2n =1  ï (   ï 3
= m + 2n)a -3(m + n)b +(2m -3n)c  -
í 3m -3n = -2  hệ vô nghiệm. ï2ïïm-3n = 4 ïî
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 711
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Vậy ba vectơ kể trên không đồng phẳng.
Chú ý. Bạn đọc làm tương tự với các A, C, D để thấy được các vectơ   
x, y, z đồng phẳng   Câu 3:     Cho ba vectơ . a, b, c
Điều kiện nào dưới đây khẳng định ba vectơ a, b, c đồng phẳng?  
A. Tồn tại ba số thực ,   m ,
n p thỏa mãn m + n + p = 0 và ma + nb + pc = 0.  
B. Tồn tại ba số thực ,   m ,
n p thỏa mãn m + n + p ¹ 0 và ma + nb + pc = 0.  
C. Tồn tại ba số thực ,   m ,
n p sao cho ma + nb + pc = 0.  D. Giá của  
a, b, c đồng quy. Lời giải Chọn B
Dựa vào đáp án, ta thấy rằng:   Với  
m + n + p = 0  m = n = p = 0 suy ra ma + nb + pc = 0 nên chưa kết luận được ba  vectơ  
a, b, c đồng phẳng.
Với m + n + p ¹ 0 suy ra tồn tại ít nhất một số khác 0.    Giả sử    n p
m ¹ 0, ta có ma + nb + pc = 0  a = - .b - .c. m m  Suy ra tồn tại  
n, p để ba vectơ a, b, c đồng phẳng.
Câu 4: Cho hình hộp . ABCD. 1 A 1 B 1 C 1 D
Khẳng định nào dưới đây là đúng?
  
   A. BD, BD , CD , A D, 1 B 1 C đồng phẳng. B. 1 1 A 1 B đồng phẳng.
  
   C. CD , A D, AB, AD, 1 1 A C đồng phẳng. D. 1 C A đồng phẳng. Lời giải Chọn C A1 B1 D1 C1 A B D C    
   Ta có AD = = + suy ra CD , AD, đồng phẳng. 1 A 1 D 1 A C C 1 D 1 1 A C
Câu 5: Cho hình hộp ABC .
D EFGH. Gọi I là tâm của hình bình hành ABEF và K là tâm của
hình bình hành BCGF. Khẳng định nào dưới đây là đúng?
  
  
A. BD, AK , GF đồng phẳng. B.
BD, IK , GF đồng phẳng.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 712
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
  
  
C. BD, EK , GF đồng phẳng.
D. BD, IK , GC đồng phẳng. Lời giải Chọn B D C B A K I H G E F
Vì I , K lần lượt là trung điểm của AF và CF.
Suy ra IK là đường trung bình của tam giác AFC IK // AC IK //(ABCD).
  
Mà GF //(ABCD) và BD Ì(ABCD) suy ra ba vectơ BD, IK, GF đồng phẳng
Câu 6: Cho hình hộp ABC . D A B ¢ C ¢ D ¢ .¢ Gọi
I , K lần lượt là tâm của hình bình hành ABB A ¢ ¢ và BCC B
¢ .¢ Khẳng định nào dưới đây là sai? A. k = 4. B. k =1. C. k = 0. D. k = 2. Lời giải Chọn B B A C D K I A' B' C' D'
Dựa vào đáp án, ta thấy rằng:  
A đúng, vì IK , AC cùng thuộc mặt phẳng (B AC ¢ ).    1  1 
B đúng, vì IK = IB¢ +B K ¢ = AC = A C ¢ .¢ 2 2   
C sai, vì IK = IB¢ + B ' K         
Ta có AB + B C + DD = AB + BC +CC = AC +CC = AC k =1. . 1 1 1 1 1 1
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 713
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 7: Cho tứ diện ABC . D Gọi
M , N lần lượt là trung điểm của
AD, BC. Khẳng định nào dưới
đây là khẳng định sai?
  
A. Ba vectơ AB, DC, MN đồng phẳng.
   B. Ba vectơ
AB, AC, M N không đồng phẳng.
  
C. Ba vectơ AN , CM , MN đồng phẳng.
  
D. Ba vectơ BD, AC, MN đồng phẳng. Lời giải Chọn C A M B D N C  1  
Vì M , N lần lượt là trung điểm của AD, BC suy ra: MN = (AB+DC) và 2  1  
MN = (BD + AC). 2
Khi đó, dựa vào đáp án, ta thấy rằng:  1  
  
A đúng, vì MN = (AB+DC) A , B D , C MN đồng phẳng. 2
B đúng, vì MN không nằm trong mặt phẳng (ABC).
C sai, tương tự ta thấy AN không nằm trong mặt phẳng (MNC).  1  
  
D đúng, vì MN = (BD +AC) B ,
D AC, MN đồng phẳng. 2
Câu 8: Cho tứ diện ABCD . Trên các cạnh AD và BC lần lượt lấy điểm M , N sao cho
AM = 3 MD, BN = 3 NC. Gọi
P, Q lần lượt là trung điểm của AD và .
BC Khẳng định nào dưới đây là sai?
  
  
A. Ba vectơ BD, AC, MN đồng phẳng.
B. Ba vectơ MN , DC, PQ đồng phẳng.
  
  
C. Ba vectơ AB, DC, PQ đồng phẳng.
D. Ba vectơ AB, DC, MN đồng phẳng. Lời giải Chọn A
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 714
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A P M B D Q N C
Theo bài ra, ta có M , N lần lượt là trung điểm của PD, QC.
Khi đó, dựa vào đáp án, ta thấy rằng: ì        ï ì ï = + + ï ï ï = + + A sai, vì MN MA AC CN MN MA AC CN ï í     í ï ï    
ïMN = MD + DB + BN 3
ï MN = 3MD + 3DB + 3BN ïî ïî    1 
  
Suy ra 4 MN = AC -3BD + BC B , D A ,
C MN không đồng phẳng. 2 ì    ïï = + +   
B đúng, vì MN MP PQ QN
ïí     2MN = PQ + DC
ïïMN = MD + DC +CN ïî  1  
  
Suy ra MN = (PQ+DC) B , D A , C MN đồng phẳng. 2   1  
C đúng, vì với cách biểu diễn PQ tương tự như trên, ta có PQ = (AB+DC). 2  1  3 
D đúng, vì biểu diễn giống A, ta được MN = AB + D . C 4 4   
Câu 9: Cho tứ diện ABCD và các điểm , M N xác định bởi ;
AM = 2 AB - AC 3 ( ) 1   
DN = DB + x DC (2) . Tìm x để các đường thẳng AD, BC,
MN cùng song song với một mặt phẳng. A. x = 1. - B. x = 2. - C. x = 3. - D. x = 2. Lời giải Chọn B
  
Yêu cầu bài toán tương đương với tìm x để ba vectơ MN , AD,
BC đồng phẳng.        Hệ thức ( )
1  AM = 2AB -3(AB + BC)  AM = A - B -3BC .       
Hệ thức (2)  AN - AD = AB - AD + x (DA + AB +BC)    
AN = (1+ x )AB - x AD + x BC .       Từ ( )
1 và (2) , suy ra MN = AN - AM = (2 + x) AB - x AD +(x + 3)BC .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 715
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
   Vậy ba vectơ MN , AD,
BC đồng phẳng khi 2 + x = 0  x = -2 .
Câu 10: Cho hình hộp ABC . D A B ¢ C ¢ D ¢ .¢ Gọi M là
điểm trên cạnh AC sao cho AC = 3MC. Lấy N trên đoạn C D ¢ sao cho C N ¢ = x C D
¢ . Với giá trị nào của x thì MN BD . ¢ 1 1 A. 2 1 x = . B. x = . C. x = . D. x = . 3 3 4 2 Lời giải Chọn A C B M O D A N' C' B' I D' A'
Gọi O là tâm của hình hình hành ABCD và I là trung điểm của DD .¢ Nối C D
¢ cắt CI tại N ¢  N ¢ là trọng tâm của tam giác CDD .¢
Ta có OI là đường trung bình của tam giác BDD¢ suy ra OI // BD .¢ ¢ Mặt khác CN CM =
nên MN ¢ //OI suy ra MN ¢ // BD .¢ CI CO Theo bài ra, ta có 2 2 MN // BD ¢ ¾¾
N º N ¢  C N ¢ = C D ¢  x = . 3 3
Câu 11: Cho hình chóp S.AB . C Lấy các điểm A ,
¢ B ,¢ C¢ lần lượt thuộc các tia SA, SB, SC sao cho
SA = , SB = , SC a b = , c trong đó , a ,
b c là các số thay đổi. Để mặt phẳng (A¢B C ¢ ¢) đi qua SA ¢ SB¢ SC ¢
trọng tâm của tam giác ABC thì
A. a+b+c = 3.
B. a+b+c = 4.
C. a+b+c = 2.
D. a+b+c =1. Lời giải Chọn A
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 716
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 S C' A C G B A' B'    
Gọi G là trọng tâm của tam giác ABC suy ra GA +GB +GC = 0.           
Khi đó 3GS +SA +SB +SC = 0 mà SA = . a SA , ¢ SB = . b SB , ¢ SC = . c SC ¢.         Suy ra 3 = . ¢ + . ¢ + . a ¢  = . b ¢ + . c SG a SA b SB c SC SG SA SB ¢ + .SC .¢ 3 3 3
   Vì (A B ¢ C
¢ ¢) đi qua trọng tâm tam giác ABC suy ra GA ,¢ GB ,¢ GC¢ đồng phẳng.    
Do đó, tồn tại ba số l, m, n sao cho ( 2 2 2
l + m + n ¹ 0) và l.GA ¢ + m.GB ¢ + . n GC ¢ = 0.           
l.(GS +SA¢)+m.(GS +SB¢)+ .n(GS +SB¢)= 0  (l +m +n)SG = l.SA¢+m.SB¢+ .nSC .¢        l  = . m ¢ + . n ¢ + . a ¢ = . b ¢ + . c SG SA SB SC SA SB ¢ + .SC . ¢ l + m + n l + m + n l + m + n 3 3 3 Suy ra a b c l m n + + = + +
= 1  a + b + c = 3. 3 3 3 l + m + n l + m + n l + m + n
Dạng 4. Tìm điểm thỏa mãn đẳng thức vectơ
Câu 1: Cho tứ diện . ABCD Gọi G là
trọng tâm tam giác BCD . Điểm M xác định bởi đẳng thức    
vectơ AM = AB + AC + AD. Mệnh đề nào sau đây đúng?
A. M trùng G.
B. M thuộc tia AG và AM = 3 . AG
C. G là trung điểm AM .
D. M là trung điểm A . G Lời giải Chọn B    
Do G là trọng tâm tam giác BCD nên AB + AC + AD = 3AG.  
Kết hợp giả thiết, suy ra AM = 3AG.    
Câu 2: Cho tứ diện . ABCD Điểm N xác định bởi
AN = AB + AC - AD. Mệnh đề nào sau đây đúng?
A. N là trung điểm . BD
B. N là đỉnh thứ tư của hình bình hành BCDN.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 717
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
C. N là đỉnh thứ tư của hình bình hành CDBN.
C. N trùng với A. Lời giải Chọn C          
Ta có AN = AB + AC - AD AN - AB = AC - AD BN = DC.
Đẳng thức chứng tỏ N là đỉnh thứ tư của hình bình hành CDBN .
Câu 3: Cho tứ diện ABC . D
Ta định nghĩa ''G là trọng tâm tứ diện ABCD khi và chỉ khi     
GA + GB + GC + GD = 0 ' . Khẳng định nào sau đây sai?
A. G là trung điểm của đoạn thẳng nối trung điểm của AB và . CD
B. G là trung điểm của đoạn thẳng nối trung điểm của AC và . BD
C. G là trung điểm của đoạn thẳng nối trung điểm của AD và . BC
D. Cả A, B, C đều đúng. Lời giải Chọn D A M G B D N C           
Ta có (GA +GB)+(GC +GD)= 0  2GI +2GJ = 0  GI +GJ = 0 ¾¾
G là trung điểm IJ . Do đó A đúng.
Tương tự, B và C đều đúng.
Vậy cả A, B, C đều đúng.
Câu 4: Cho hình hộp ABC . D A B ¢ C ¢ D ¢ .¢ Điểm M
được xác định bởi đẳng thức vectơ         
MA + MB + MC + MD + MA ' + MB ' + MC ' + MD ' = 0. Mệnh đề nào sau đây đúng?
A. M là tâm của mặt đáy ABC . D
B. M là tâm của mặt đáy
A ' B 'C ' D '.
C. M là trung điểm của đoạn thẳng nối hai tâm của hai mặt đáy.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 718
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 D. Tập hợp điểm M là
đoạn thẳng nối hai tâm của hai mặt đáy. Lời giải Chọn C
Gọi O = AC Ç BD và O ' = A 'C 'Ç B ' D '.          
Khi đó OA +OB +OC +OD = 0 và O ' A ' +O ' B ' +O 'C ' +O ' D ' = 0.            
Ta có MA + MB + MC + MD =(MO+OA)+(MO +OB)+(MO+OC)+(MO +OD)        
= OA +OB +OC +OD + 4MO = 0 + 4MO = 4M . O     
Tương tự, ta cũng có MA ' + MB ' + MC ' + MD ' = 4MO '.         
Từ đó suy ra MA + MB + MC + MD + MA ' + MB ' + MC ' + MD ' = 0         
 4MO + 4MO ' = 0  4(MO + MO')= 0  MO + MO' = 0 .
Vậy điểm M cần tìm là trung điểm của OO '.    
Câu 5: Cho hình hộp ABC . D A B ¢ C ¢ D ¢ ¢ có tâm . O Đặt , AB = a BC = b . Điểm M xác định bởi đẳng  1   thức vectơ . OM = (a- ) b
Khẳng định nào sau đây đúng? 2
A. M là trung điểm BB . ¢
B. M là tâm hình bình hành BCC B ¢ .¢
C. M là trung điểm CC . ¢
D. M là tâm hình bình hành ABB A ¢ .¢ Lời giải Chọn A A' B' I' D' C' O B A I D C
Gọi I , I ' lần lượt là tâm các mặt đáy ABCD, A¢B C ¢ D
¢ ¢ . Suy ra O là trung điểm của II '.   Do ABC . D A B ¢ C ¢ D
¢ ¢ là hình hộp nên AB = DC.  1   1   1   1  
Theo giả thiết ta có OM = (a- )
b = (AB-BC) = (DC +CB) = DB = I . B 2 2 2 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 719
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133   Vì ABC . D A B ¢ C ¢ D
¢ ¢ là hình hộp nên từ đẳng thức OM = IB suy ra M là trung điểm BB '.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 720
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
BÀI 2. HAI ĐƯỜNG THẲNG VUÔNG GÓC
A. KIẾN THỨC CƠ BẢN CÂN NẮM
I – TÍCH VÔ HƯỚNG CỦA HAI VECTƠ TRONG KHÔNG GIAN
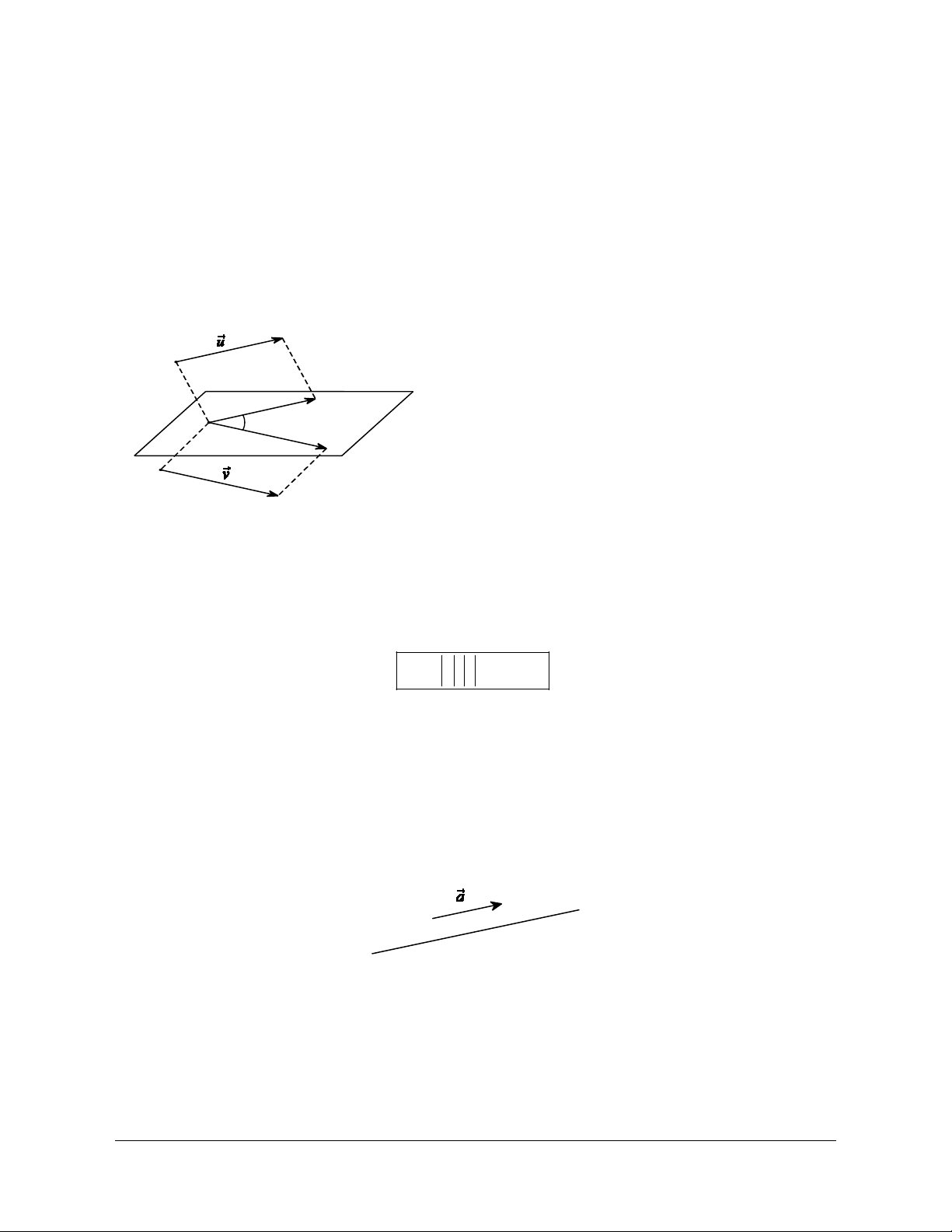
1. Góc giữa hai vectơ trong không gian Định nghĩa   
Trong không gian, cho u và v là hai vectơ khác 0 . Lấy một điểm
A bất kì, gọi B và C là hai      điểm sao cho  
A B = u, AC = v . Khi đó ta gọi góc BAC (0 £ BAC £180 )
 là góc giữa hai vectơ u và   
v trong không gian, kí hiệu là ( , u v) . B A C
2. Tích vô hướng của hai vectơ trong không gian Định nghĩa     
Trong không gian, cho hai vectơ u và
v đều khác 0 . Tích vô hướng của hai vectơ u và v là một   số, kí hiệu là .
u v , được xác định bởi công thức:       .
u v = u . v . cos(u,v) .       Trong trường hợp
u = 0 hoặc v = 0 , ta quy ước . . u v = 0
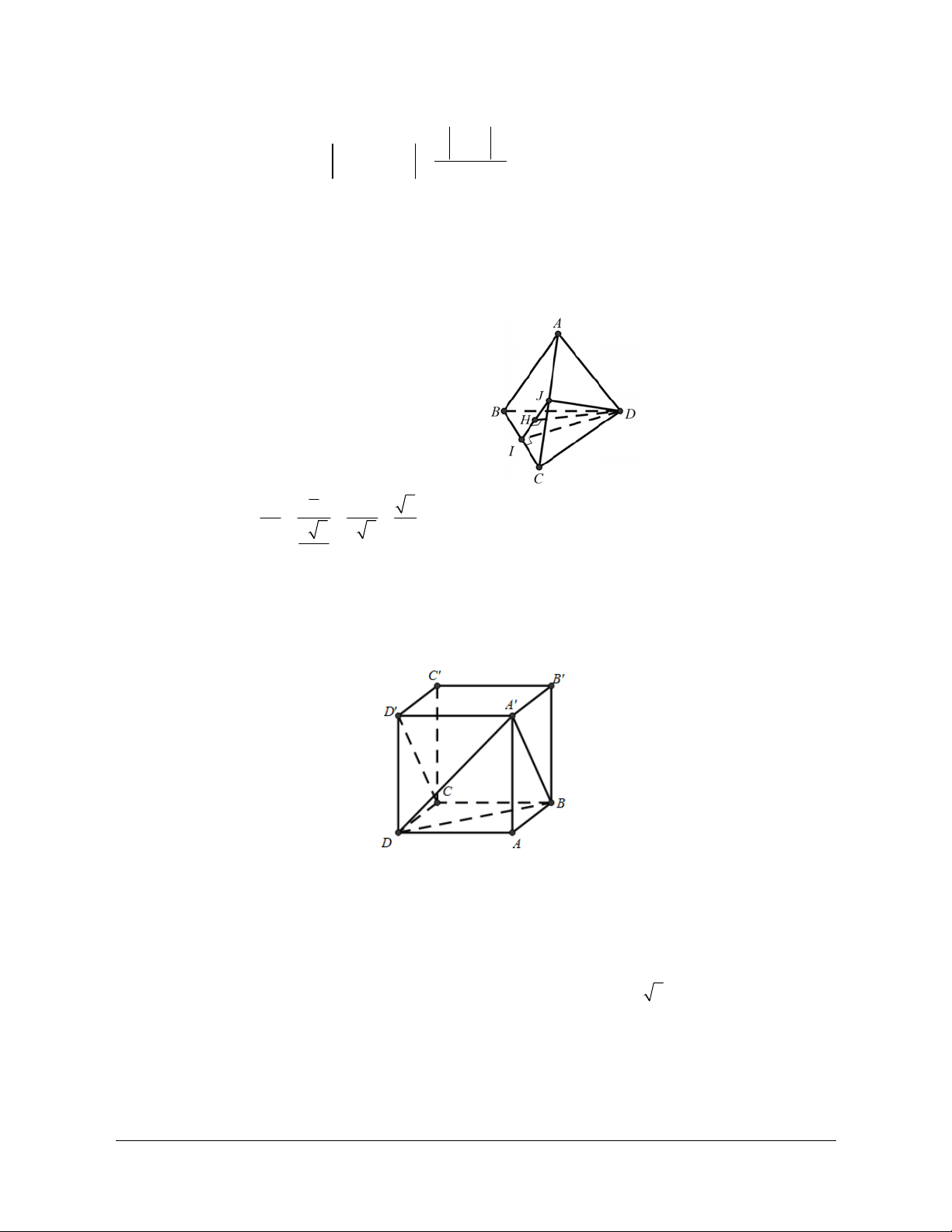
II – VECTƠ CHỈ PHƯƠNG CỦA ĐƯỜNG THẲNG 1. Định nghĩa    Vectơ a khác 0
được gọi là vectơ chỉ phương của đường thẳng
d nếu giá của vectơ a song song
hoặc trùng với đường thẳng . d d 2. Nhận xét   a) Nếu a là
vectơ chỉ phương của đường thẳng d thì vectơ ka với
k ¹ 0 cũng là vectơ chỉ phương của . d
b) Một đường thẳng trong không gian hoàn toàn xác định nếu biết một điểm A thuộc d và một  vectơ chỉ phương a của nó.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 721
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
c) Hai đường thẳng song song với nhau khi và chỉ khi chúng là hai đường thẳng phân biệt và có hai
vectơ chỉ phương cùng phương.
III – GÓC GIỮA HAI ĐƯỜNG THẲNG TRONG KHÔNG GIAN 1. Định nghĩa
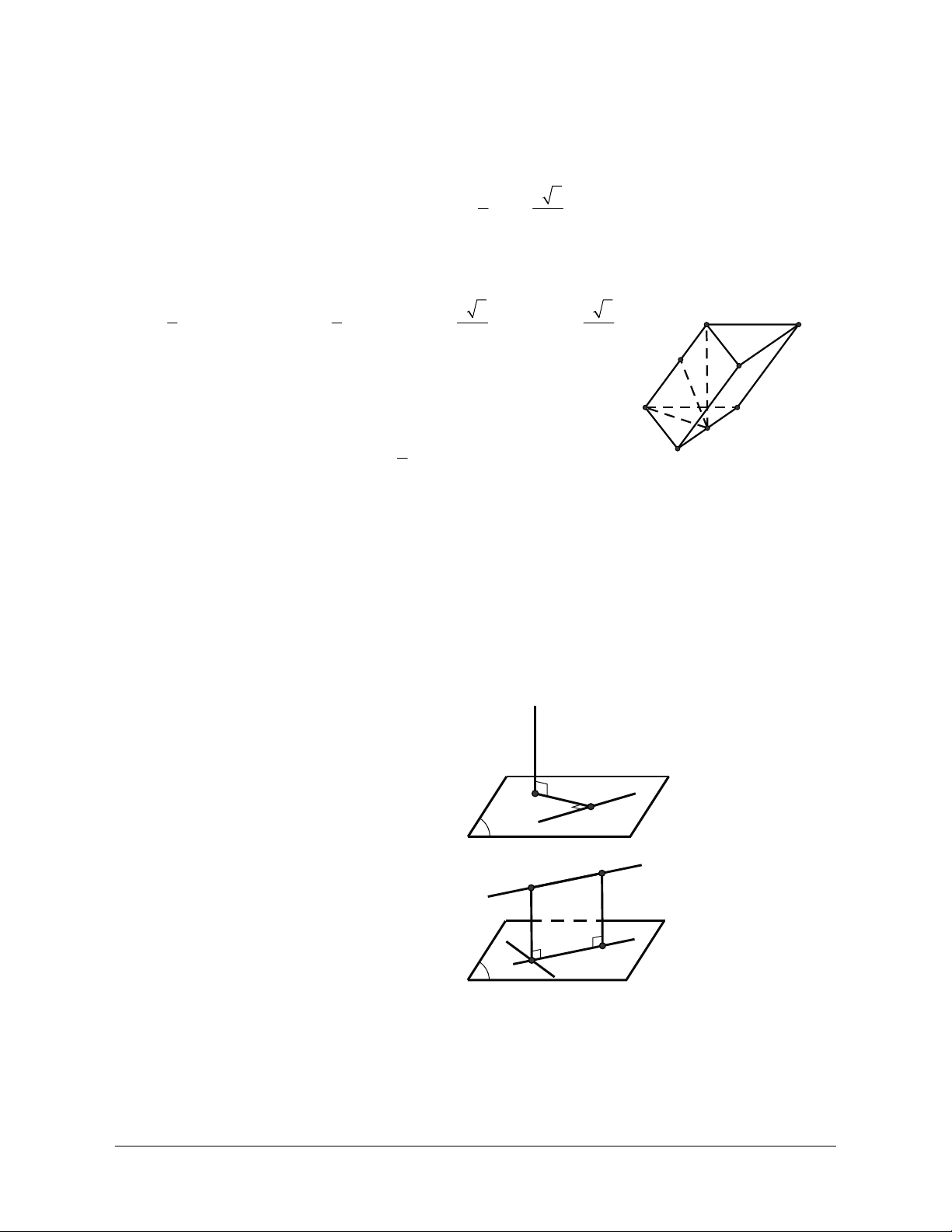
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a¢ và b¢ cùng đi
qua một điểm và lần lượt song song với a và b . a b a' O b' 2. Nhận xét
a) Để xác định góc giữa hai đường thẳng a và b ta có thể lấy điểm
O thuộc một trong hai đường
thẳng đó rồi vẽ một đường thẳng qua O và song song với đường thẳng còn lại.  
b) Nếu u là vectơ chỉ phương của đường thẳng a và v là vectơ chỉ phương của đường thẳng b và ( ,
u v) = a thì góc giữa hai đường thẳng a và b bằng
a nếu 0 £ a £ 90 và bằng - 180 a nếu
90 < a £180 . Nếu a và b song song hoặc trùng nhau thì góc giữa chúng bằng . 0
IV – HAI ĐƯỜNG THẲNG VUÔNG GÓC 1. Định nghĩa
Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng .  90
Người ta kí hiệu hai đường thẳng a và b vuông góc với nhau là a ^ b . 2. Nhận xét    
a) Nếu u và v lần lượt là các vectơ chỉ phương của hai đường thẳng a và b thì: a ^ b  . u v = 0 .
b) Cho hai đường thẳng song song. Nếu một đường thẳng vuông góc với đường thẳng này thì cũng
vuông góc với đường thẳng kia.
c) Hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau. B. PHÂN LOẠI
Dạng 1. Tính góc giữa hai đường thẳng 1. Phương pháp
Cách 1: (Theo phương pháp hình học)
 Lấy điểm O tùy ý ( ta có thể lấy điểm O thuộc một trong hai đường thẳng), qua đó vẽ các
đường thẳng lần lượt song song (hoặc trùng) với hai đường thẳng đã cho.
 Tính một góc trong các góc được tạo bởi giữa hai đường thẳng cắt nhau tại O.
 Nếu góc đó nhọn thì đó là góc cần tìm, nếu góc đó tù thì góc cần tính là góc bù với góc đã tính.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 722
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Cách 2: (Theo phương pháp vectơ)      Tìm 1
u ,u2 lần lượt là các vectơ chỉ phương của hai đường thẳng 1  và 2 tính 1 u ,u2     u .u
 Khi đó cos ,   cosu ,u  1 2 1 2 1 2    | 1 u | . | u2 |
2. Các ví dụ rèn luyện kĩ năng
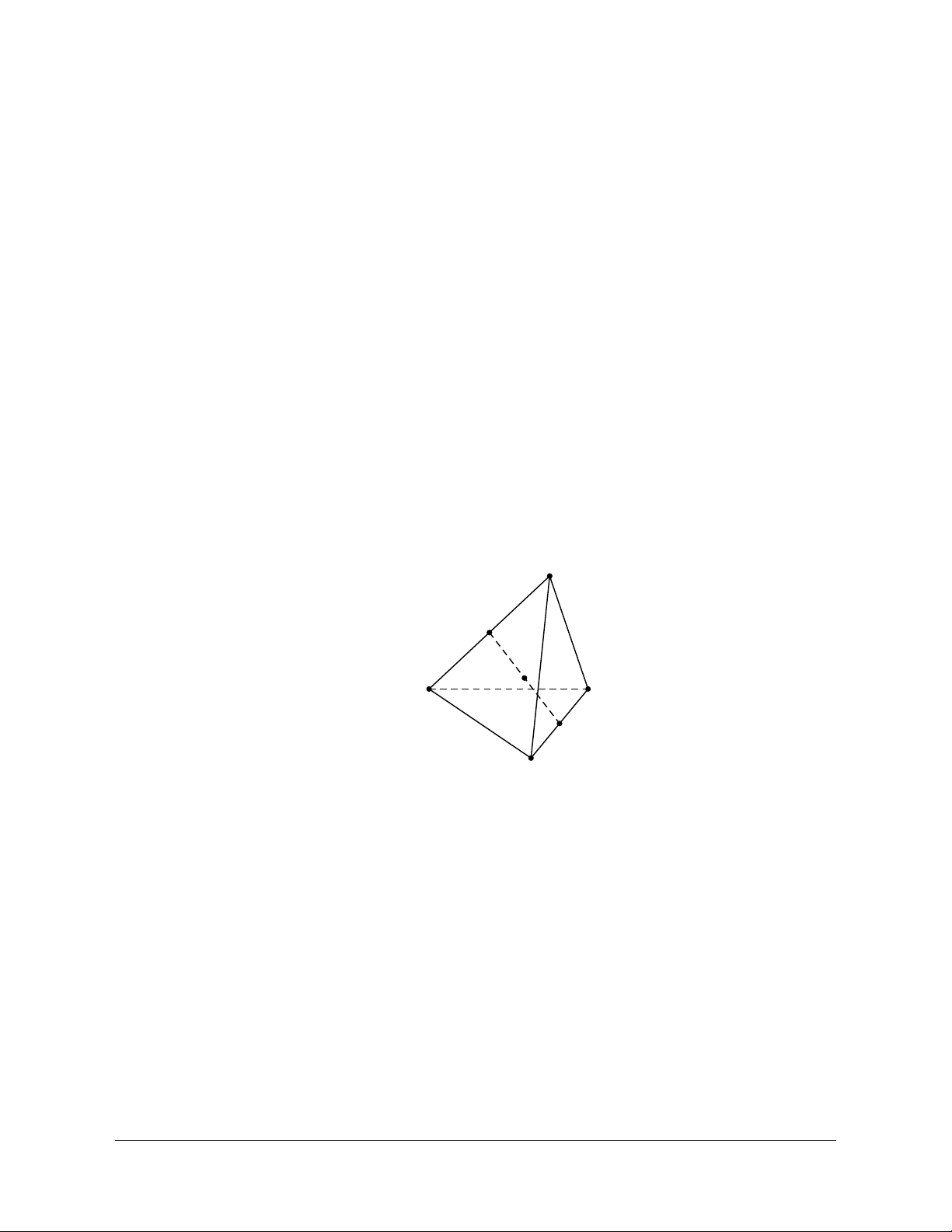
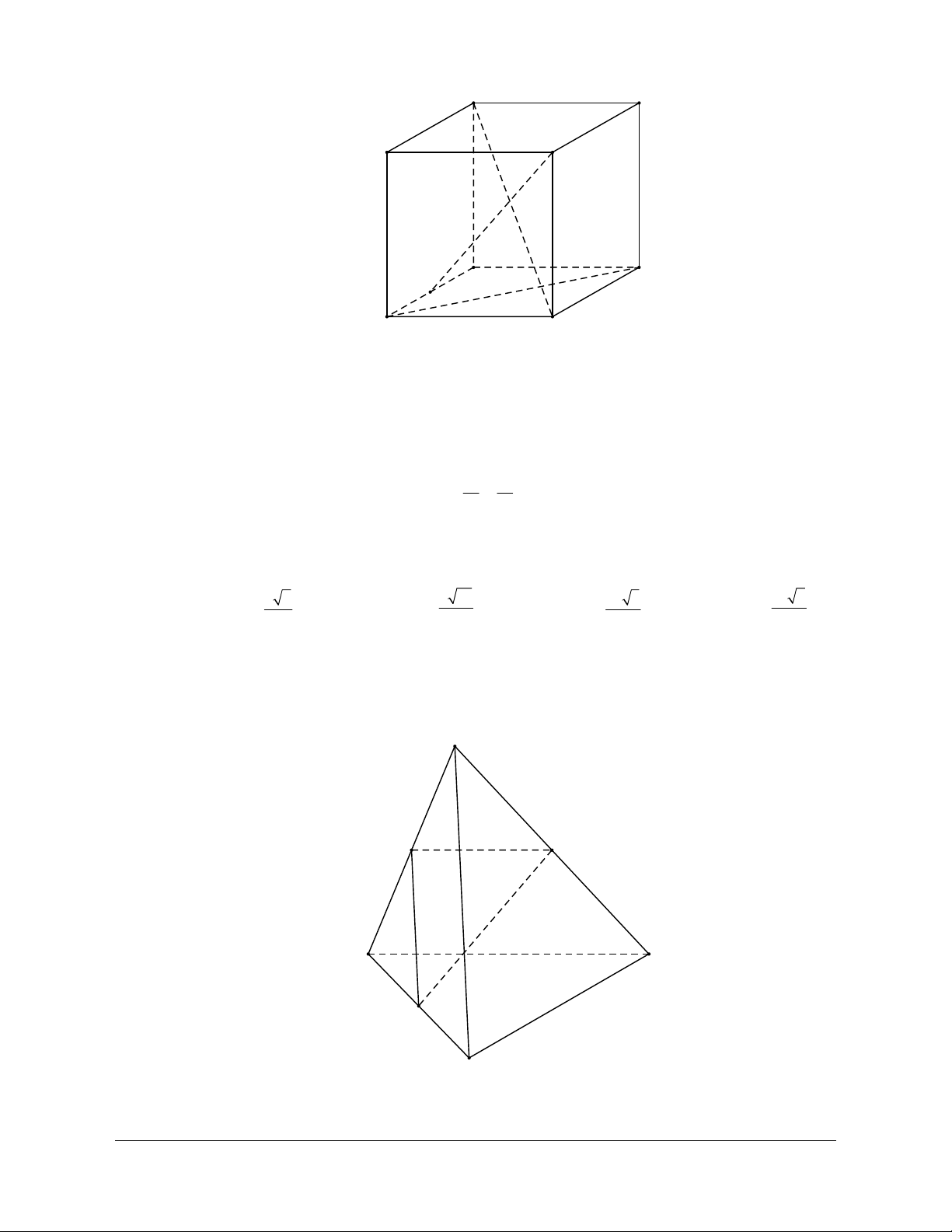
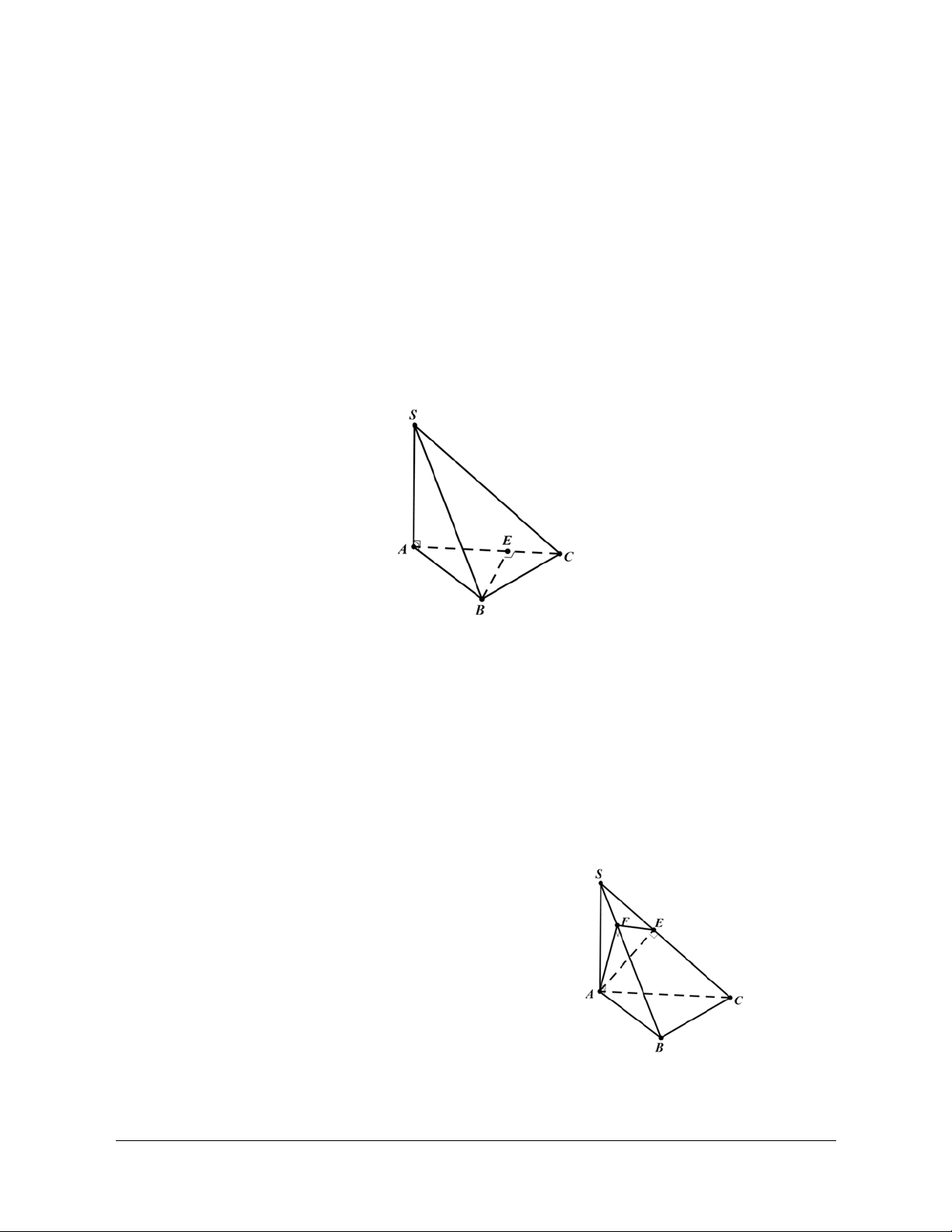
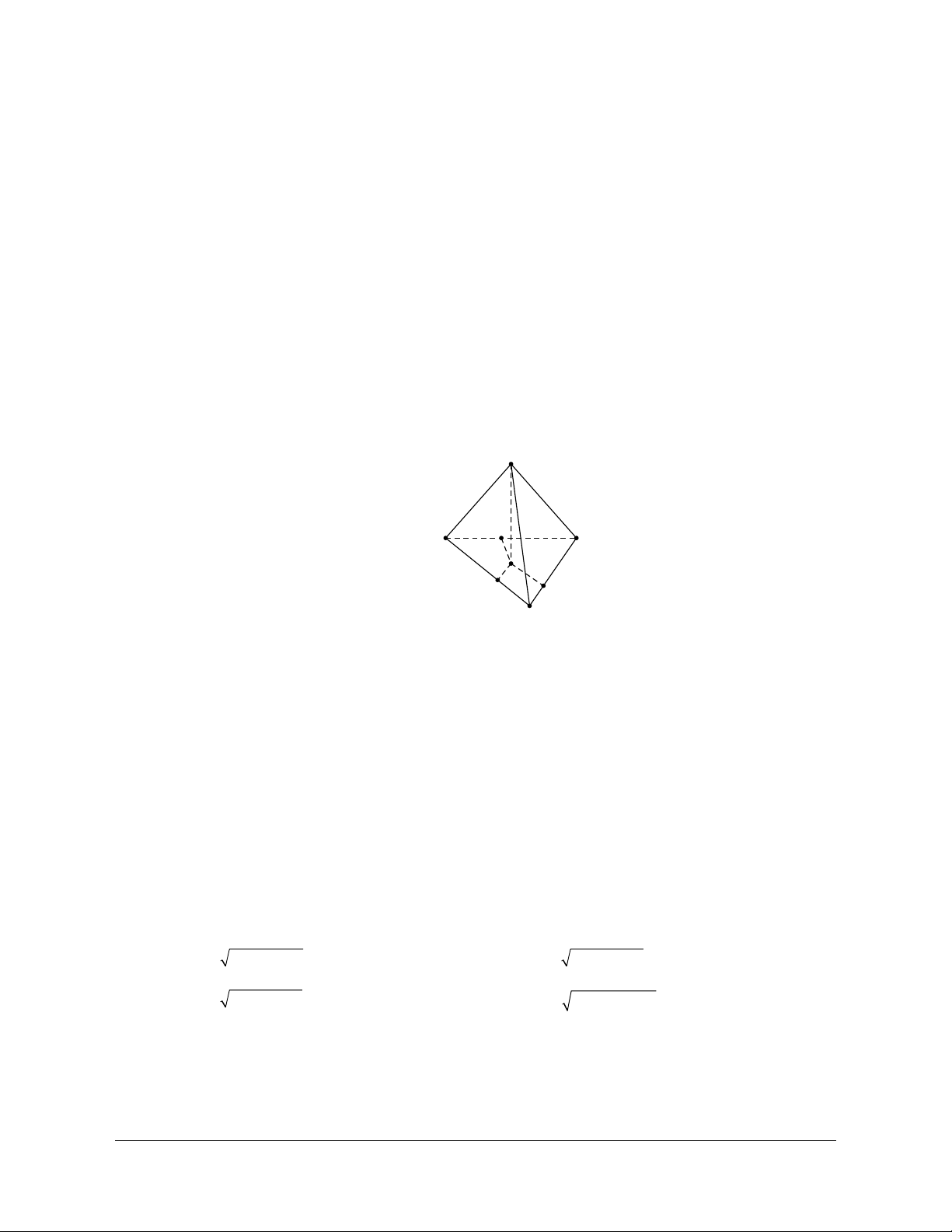
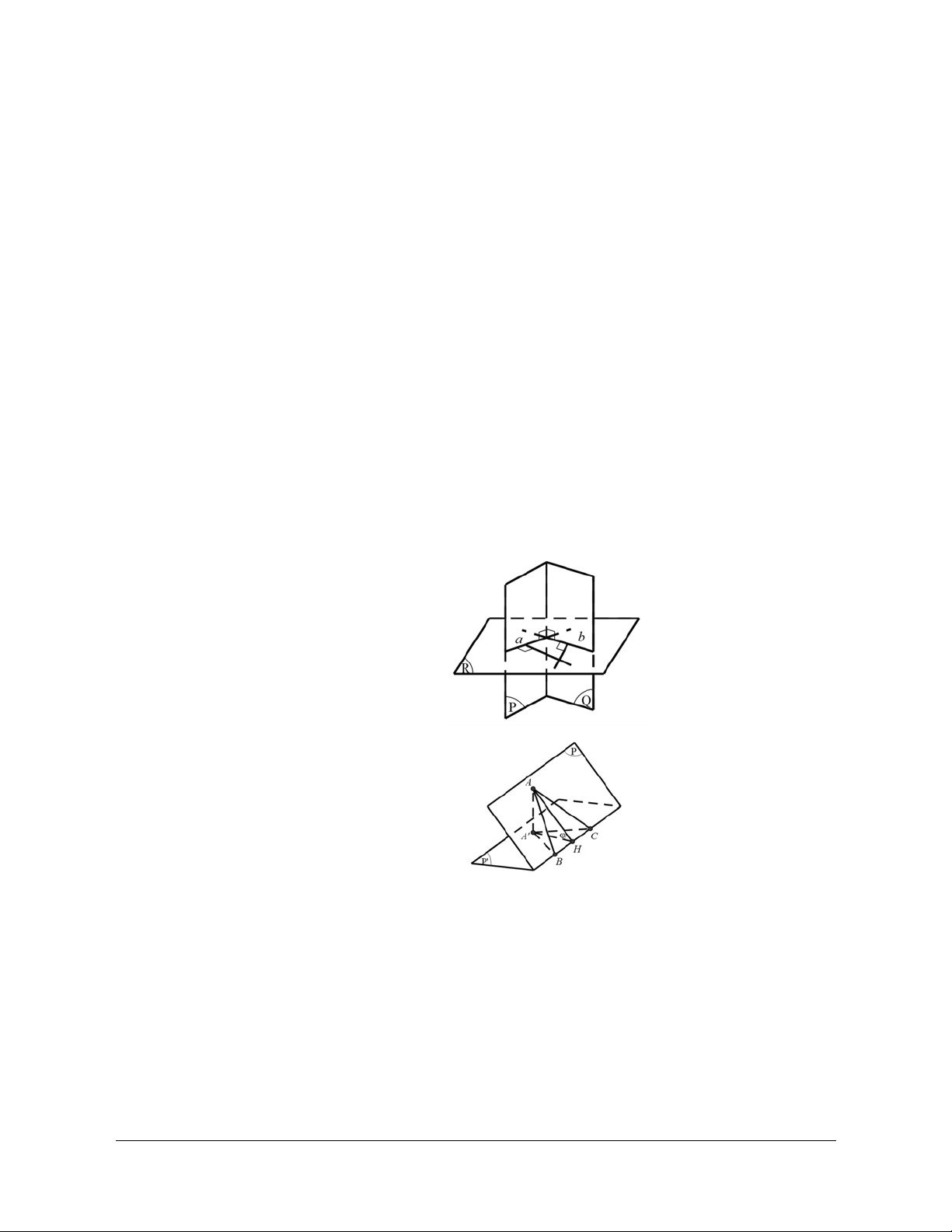
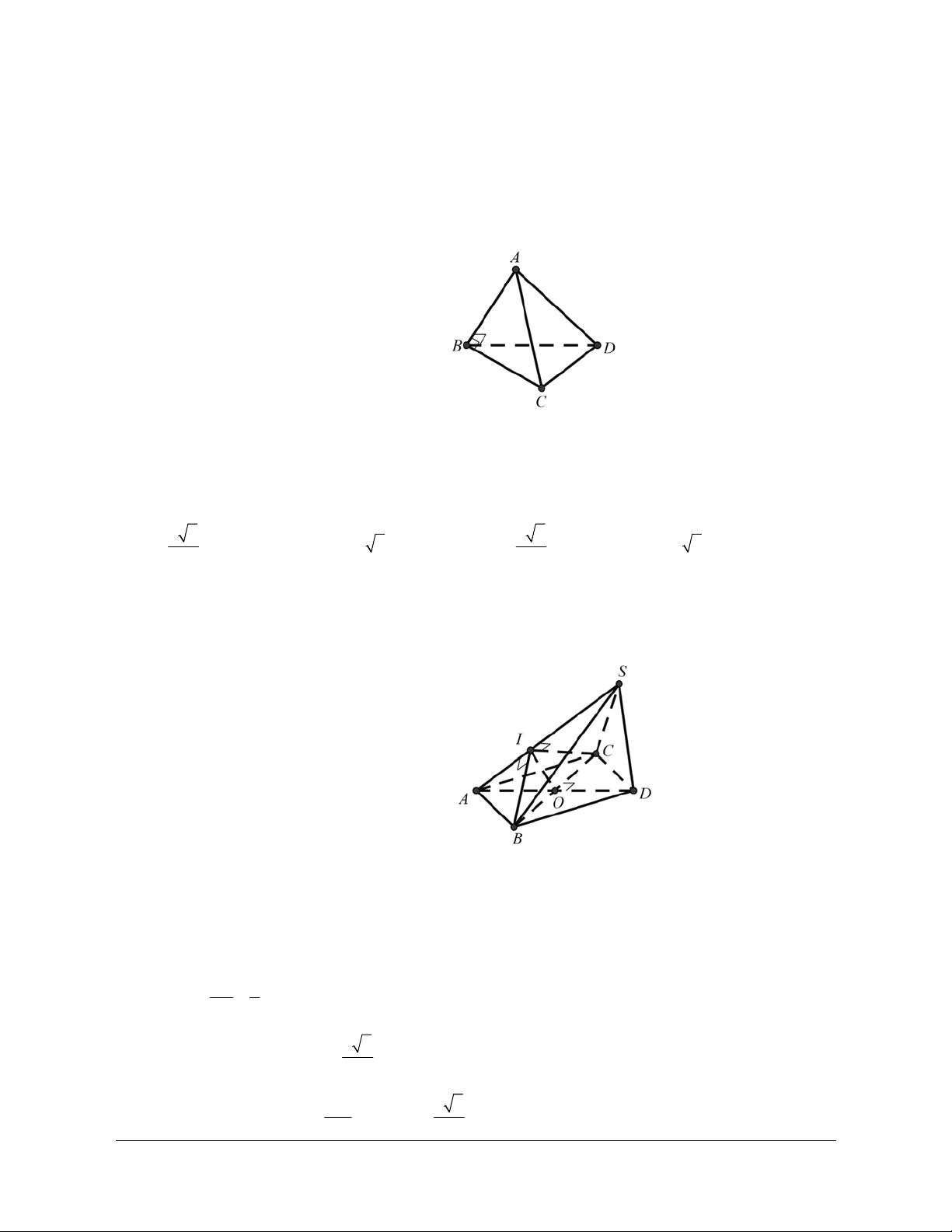
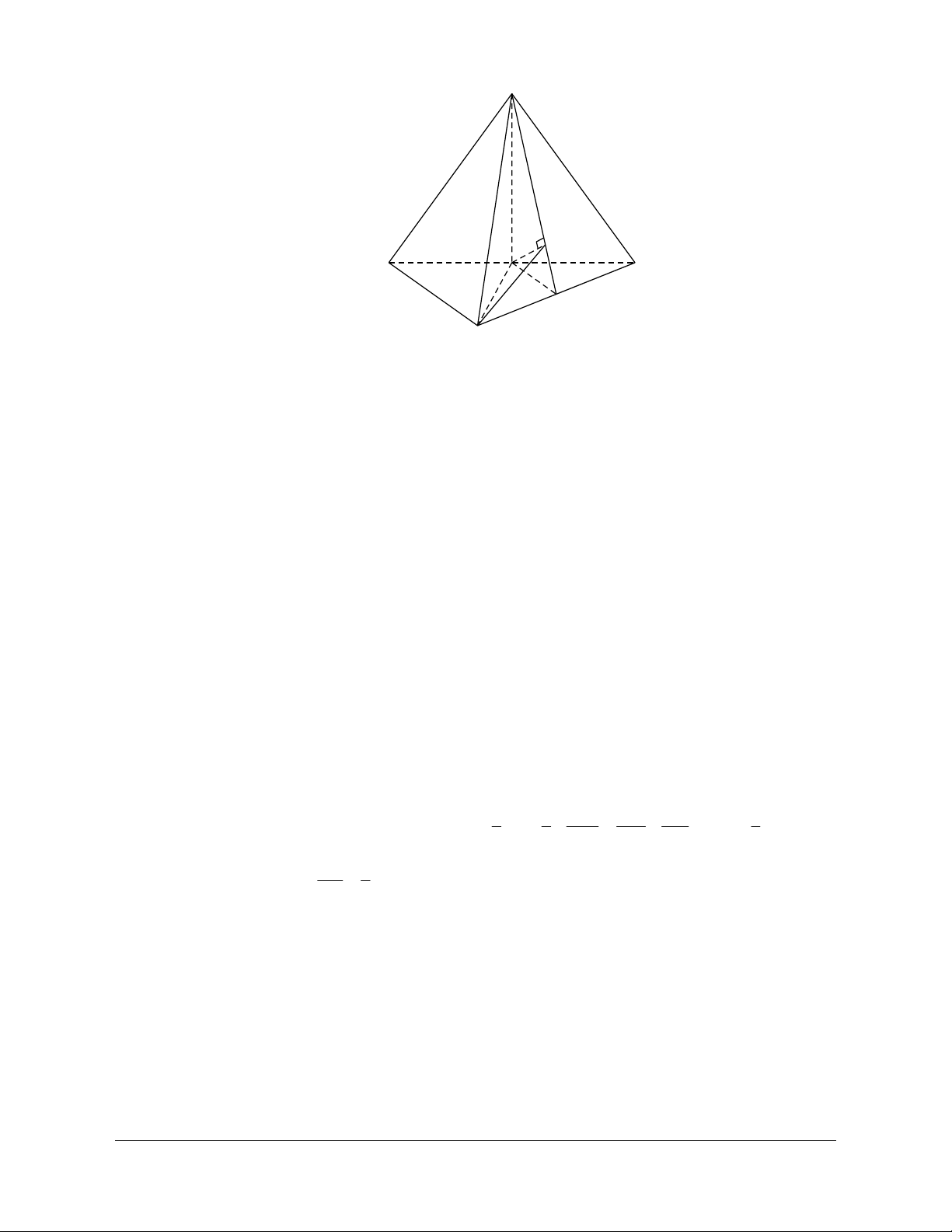
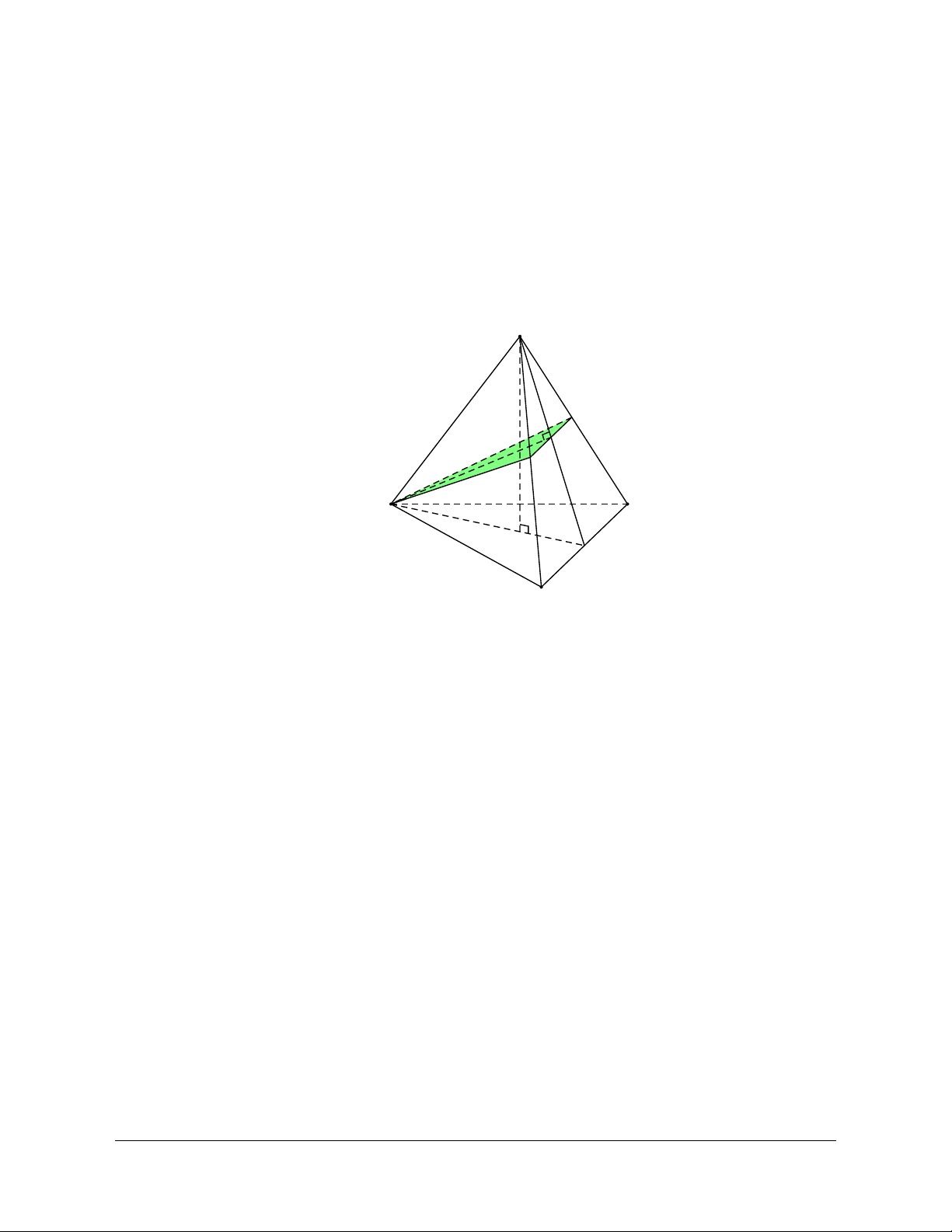
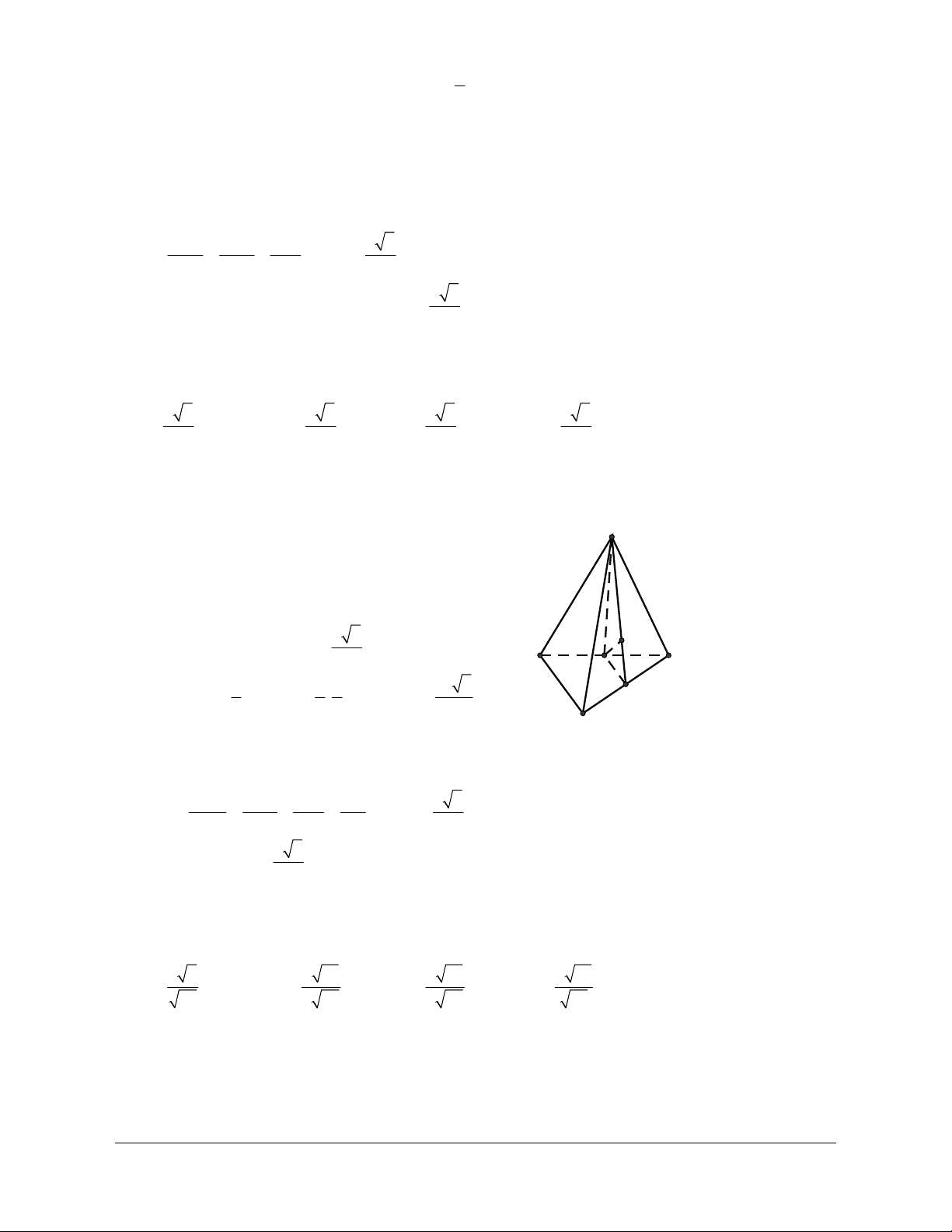
Ví dụ 1: Cho tứ diện đều ABCD. Gọi I là trung điểm của BC. Tính côsin của góc tạo bởi hai đường thẳng DI và AB. Hướng dẫn giải
Đặt cạnh của tứ diện có độ dài là . a
Gọi J là trung điểm của AC.
Ta có: IJ AB  (AB DI) = (IJ DI)  // , , = DIJ
Kẻ HD ^ IJ,(H Î IJ) a Ta có:   IH   1  3 4 cos DIJ . DI a 3 2 3 6 2
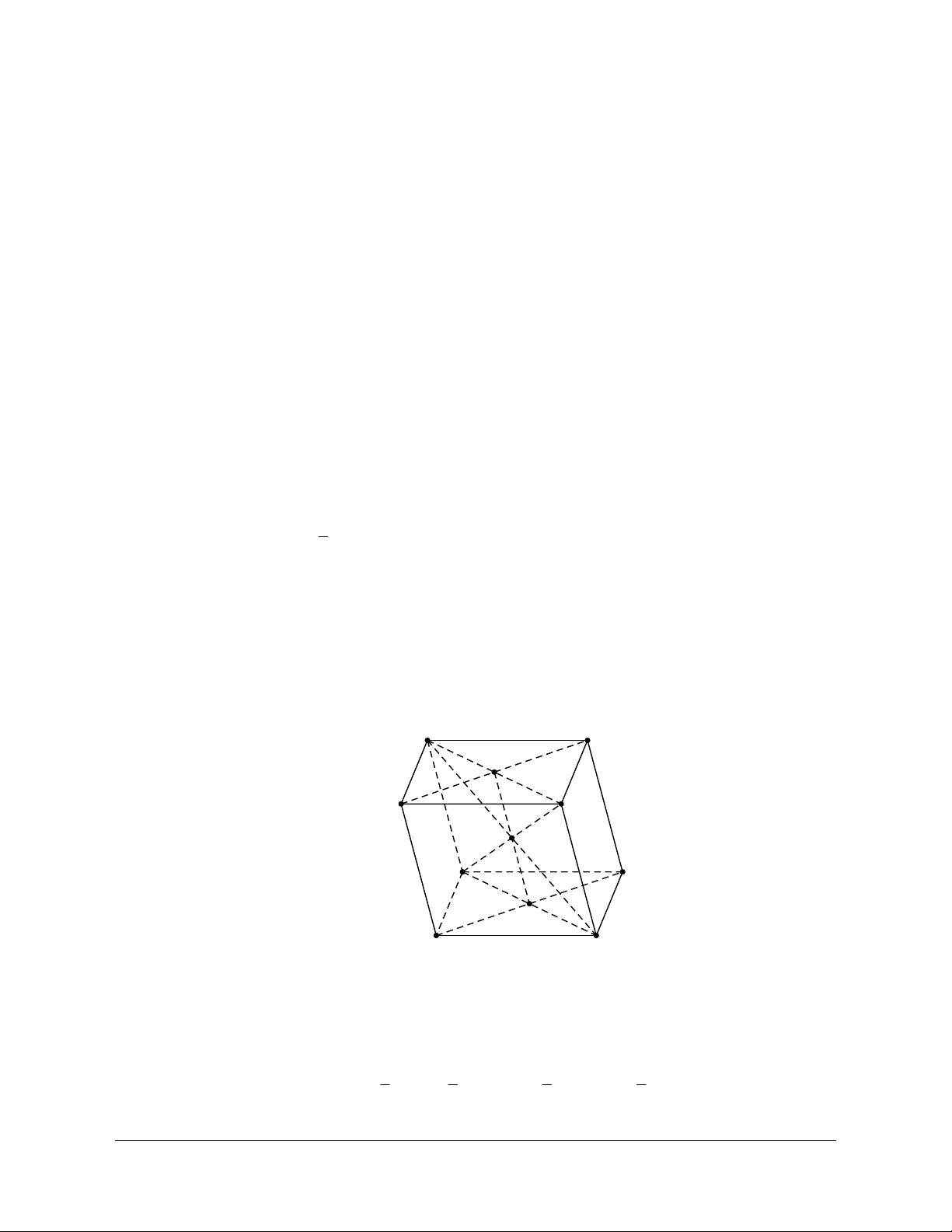
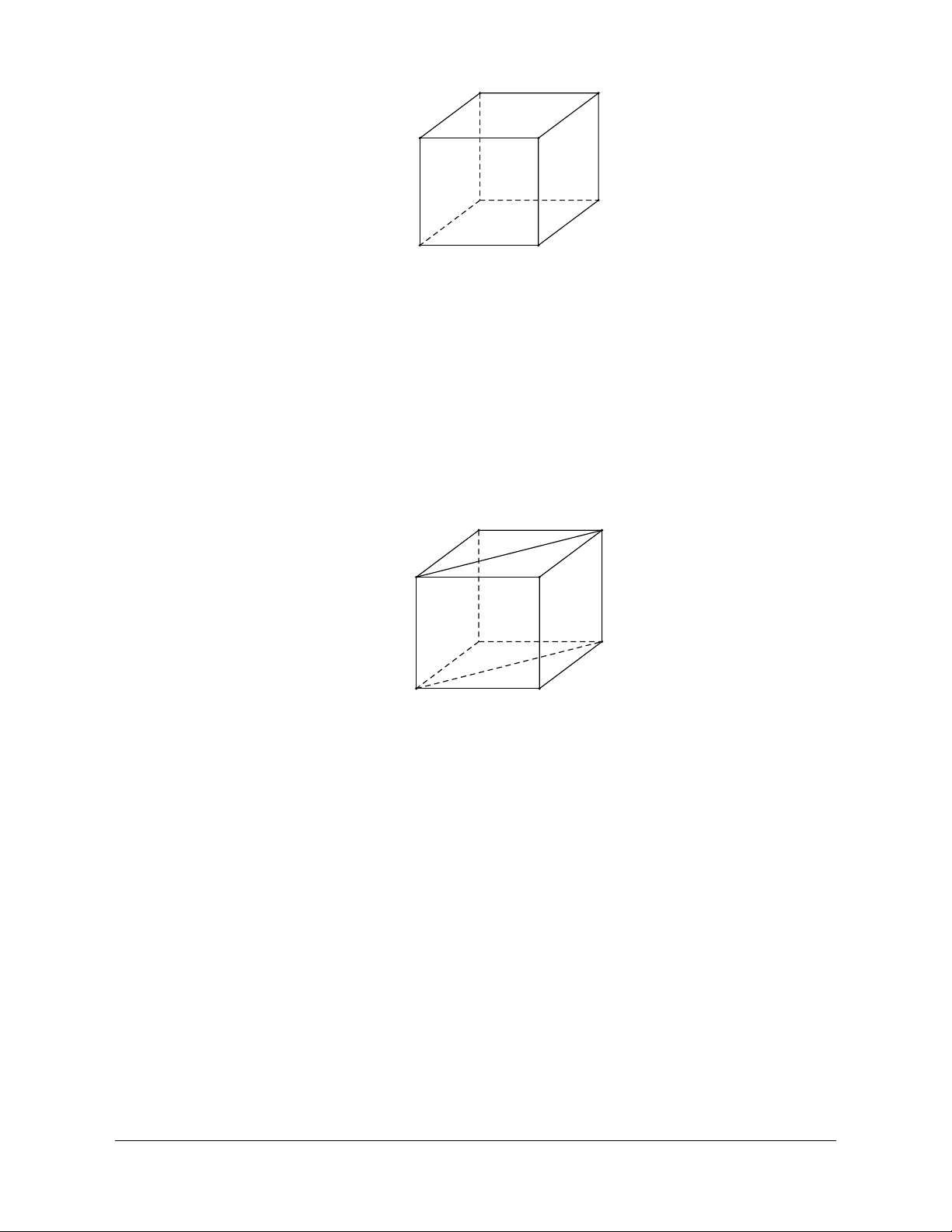
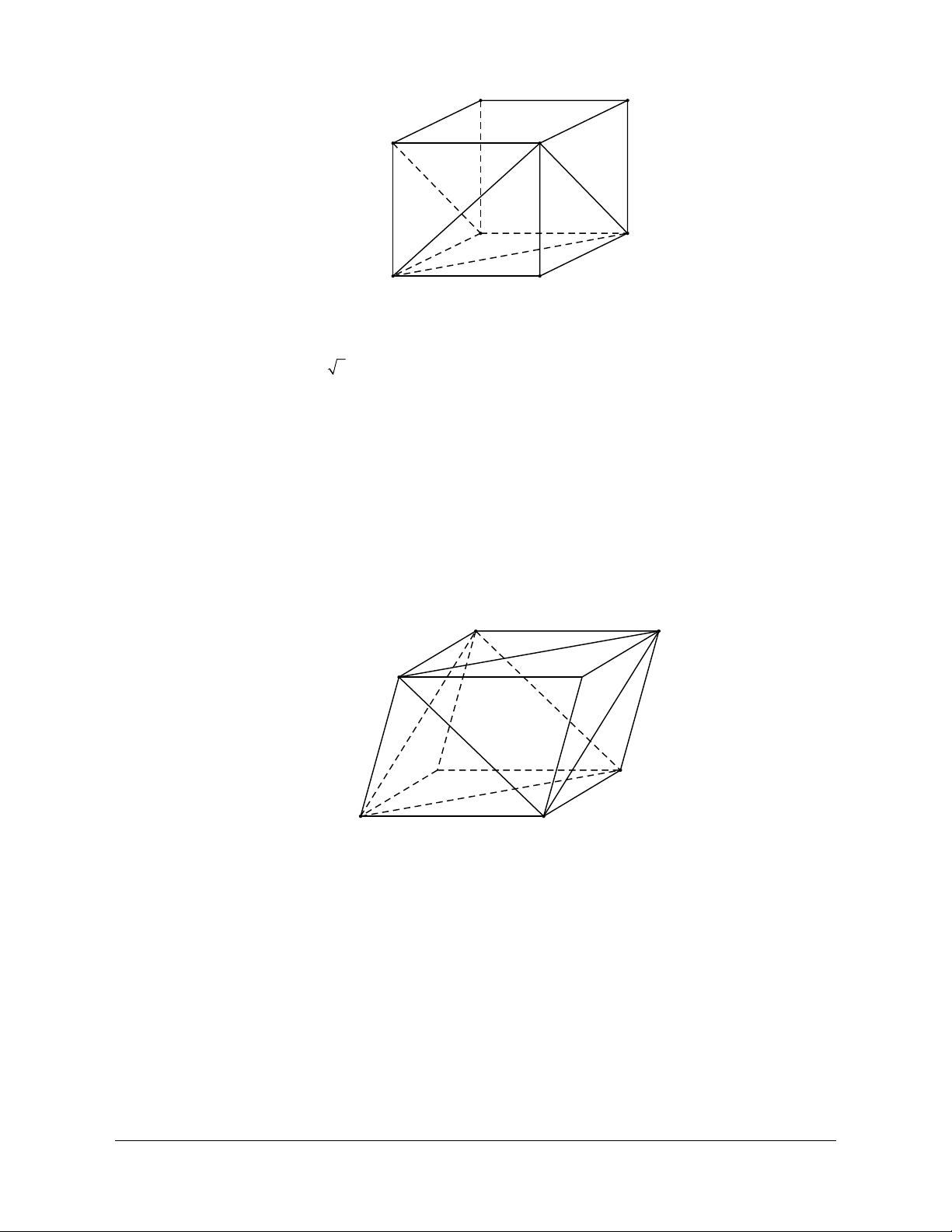
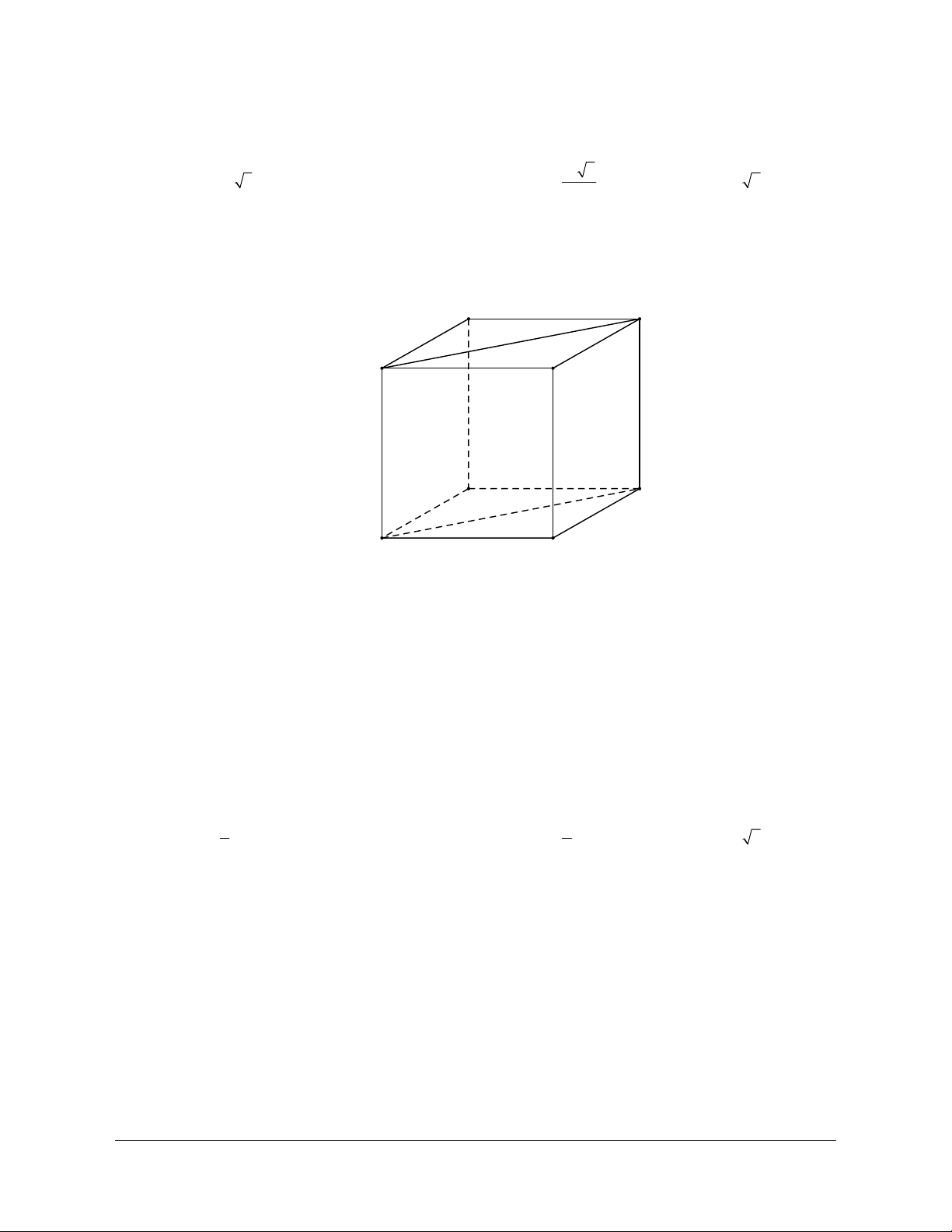
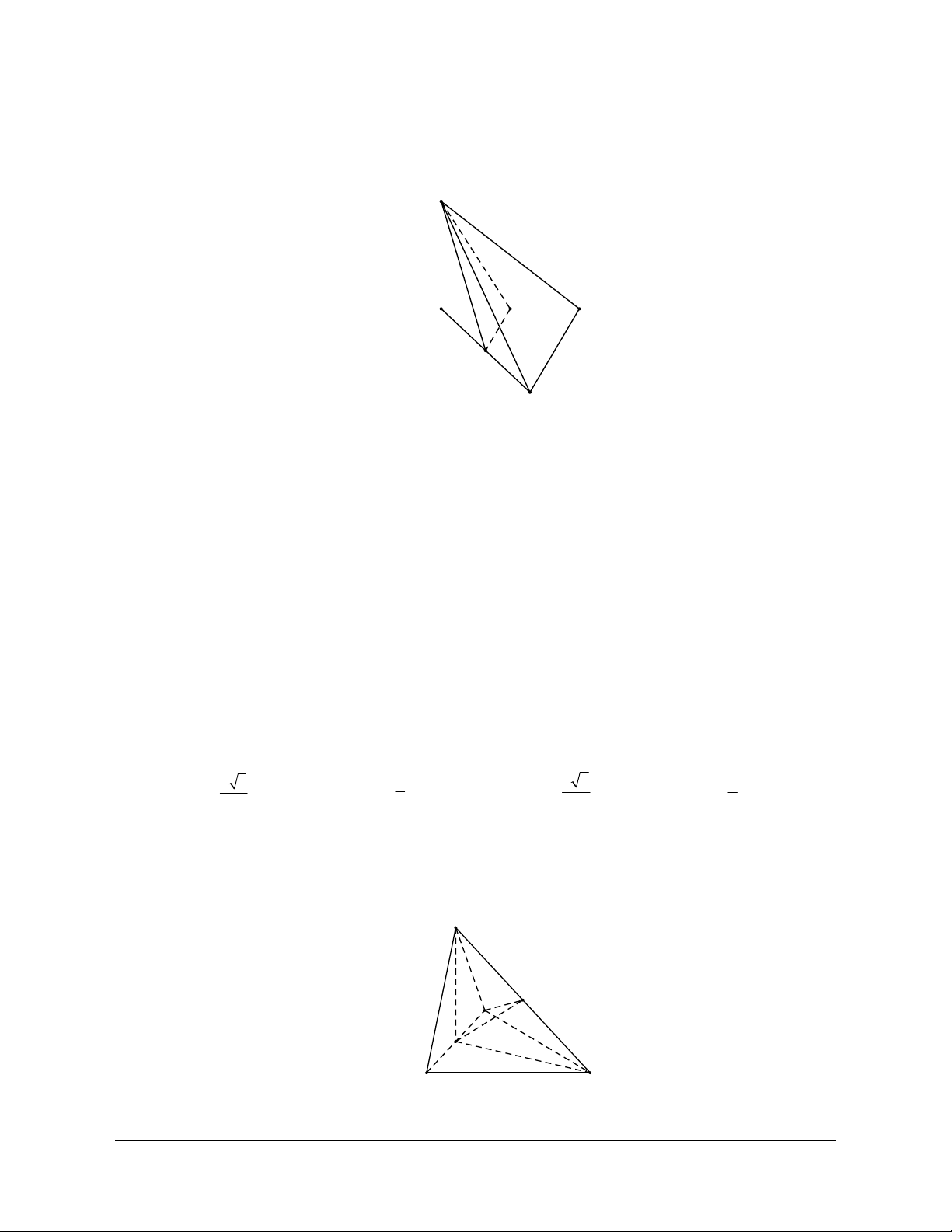
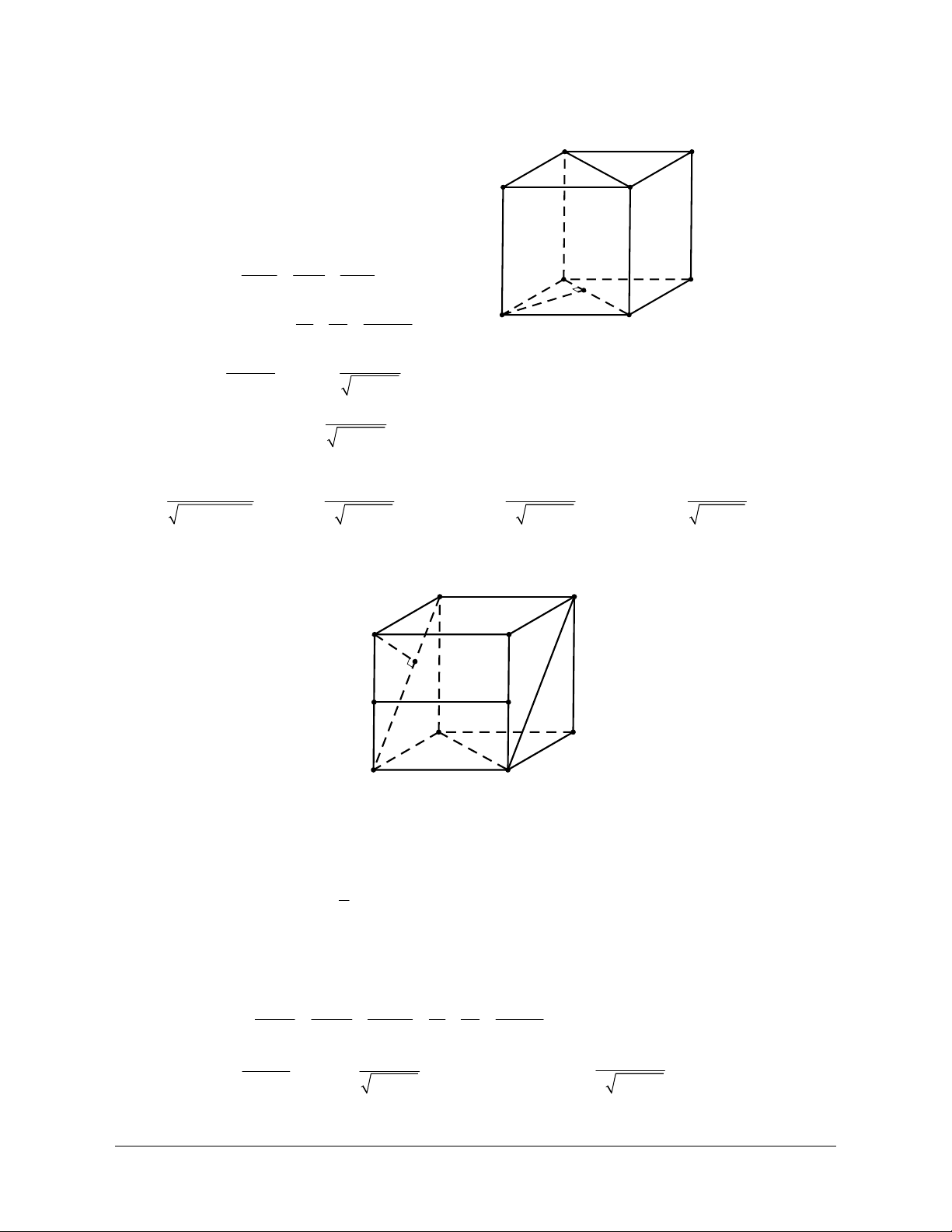
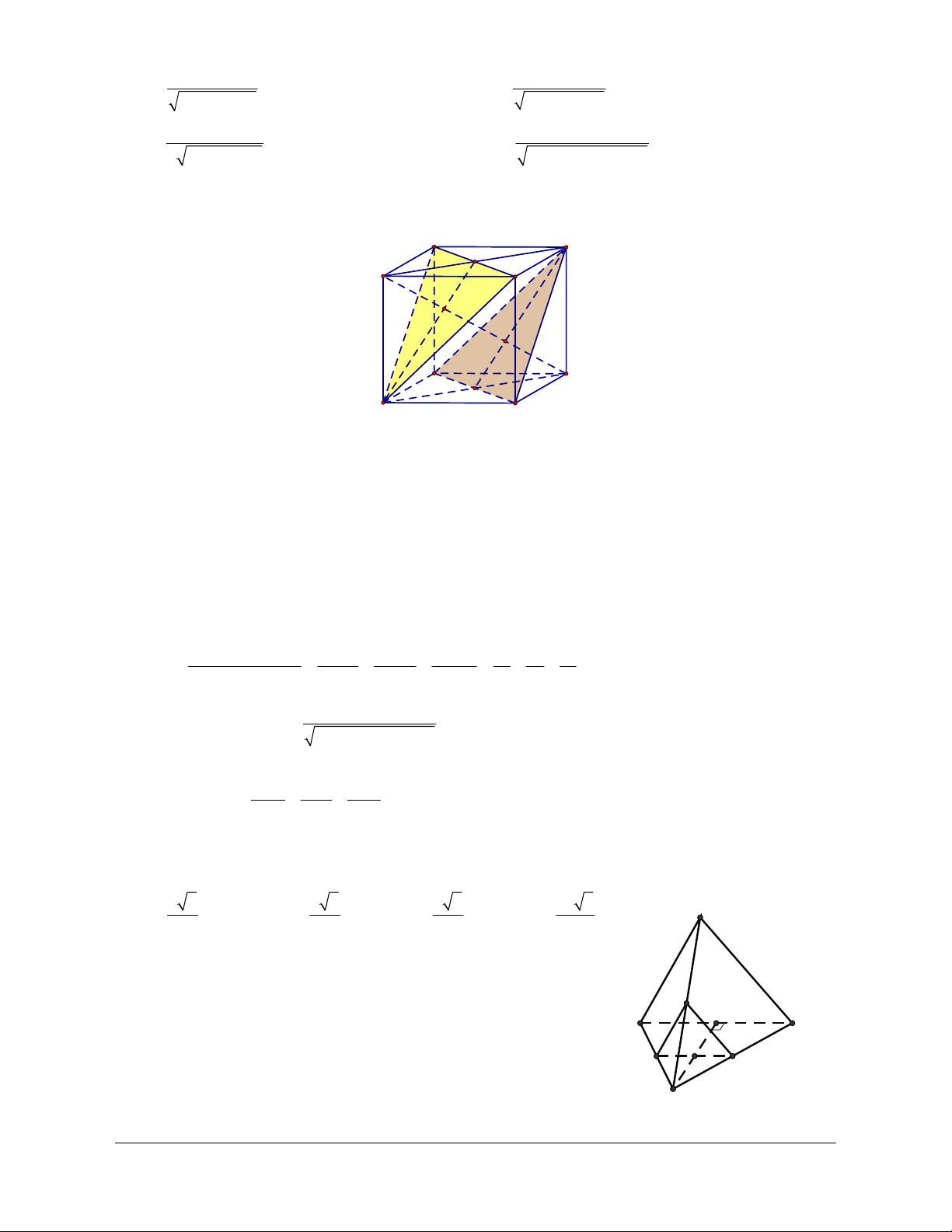
Ví dụ 2: Cho hình lập phương ABCD.A’B’C’D’. Xác định Góc tạo bởi hai đường thẳng BD và CD’. Hướng dẫn giải
Do BAʹ// CDʹ nên góc giữa BD và CD’ là góc giữa BD và BA’
Mà AʹBD là tam giác đều nên góc giữa BD và BA’ là o 60 .
Vậy góc giữa BD và CD’ là o 60 .
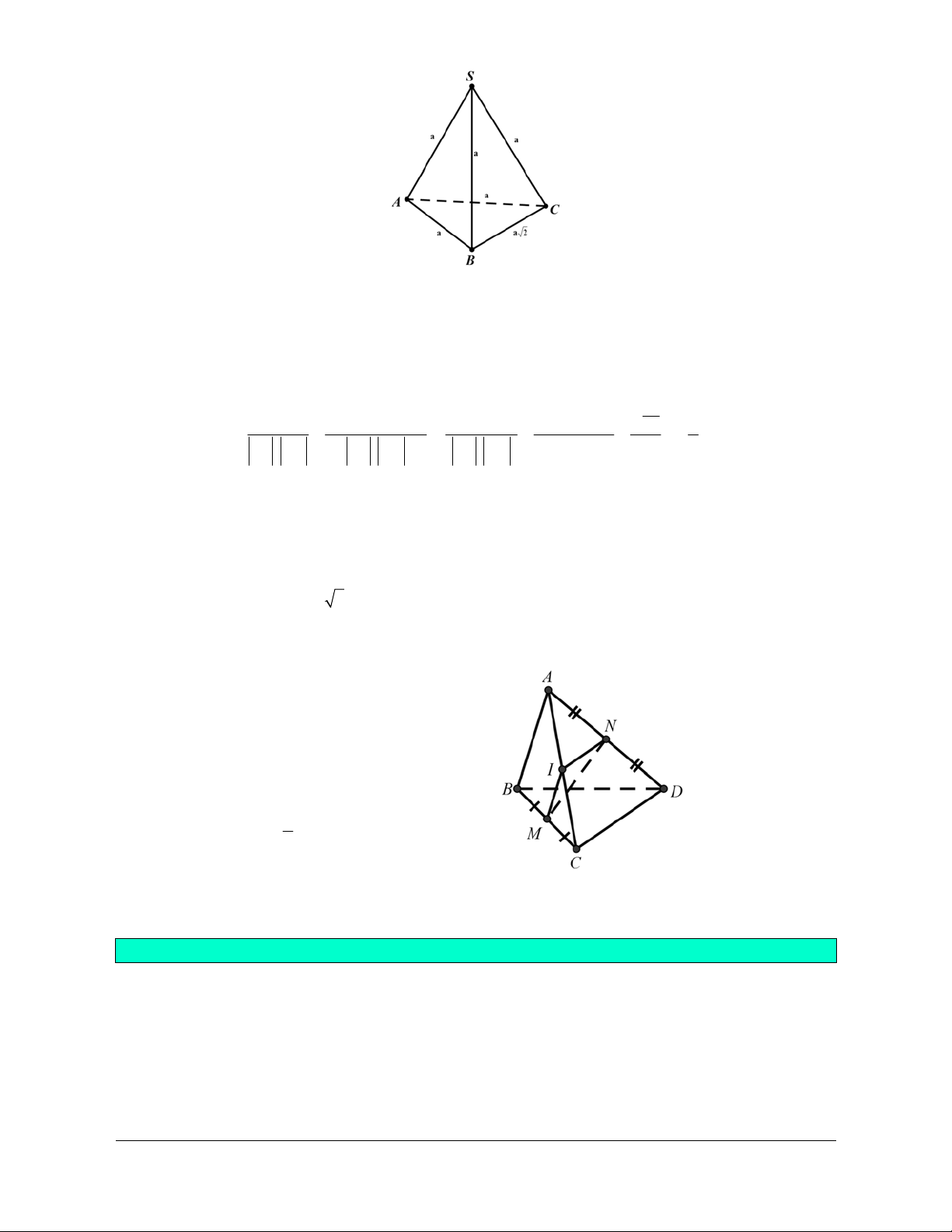
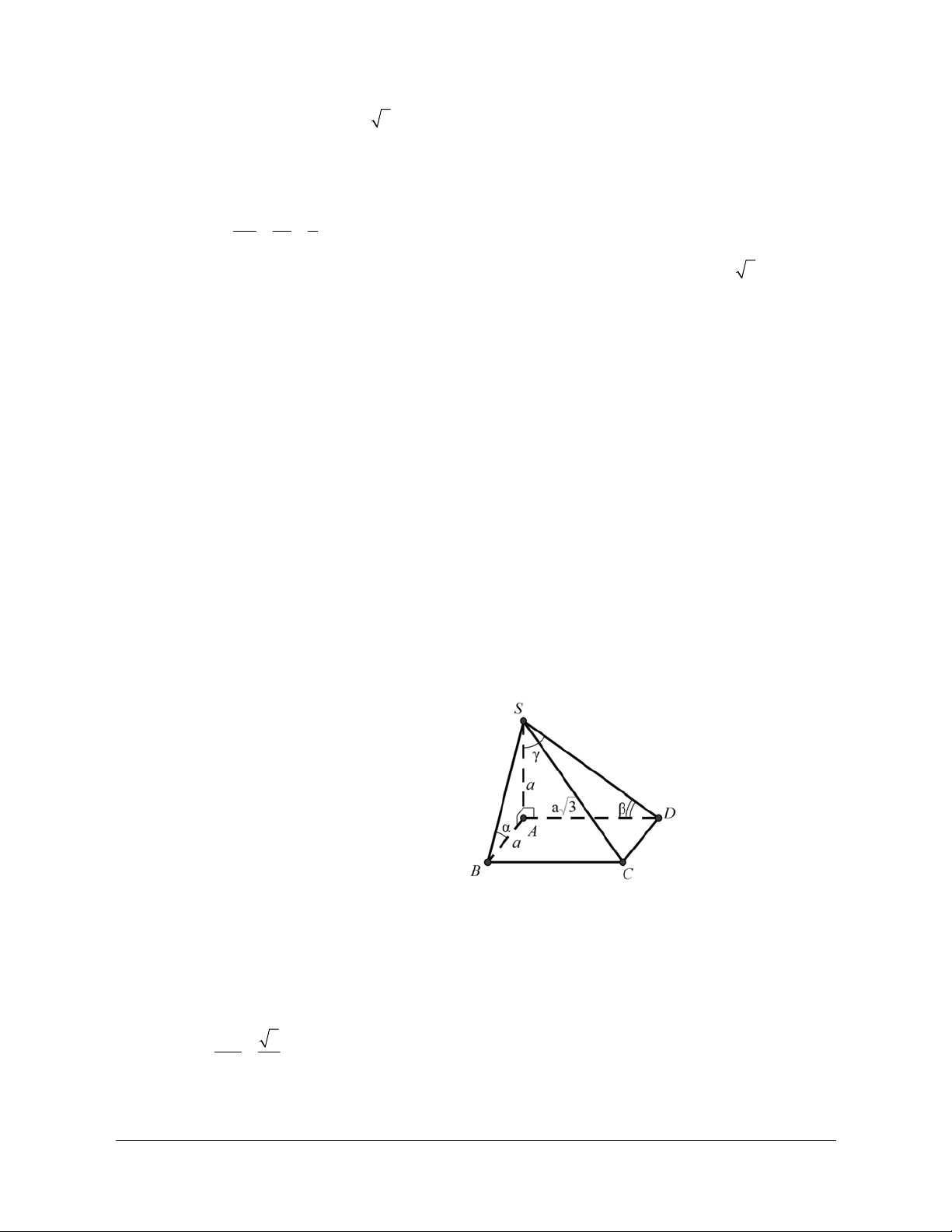
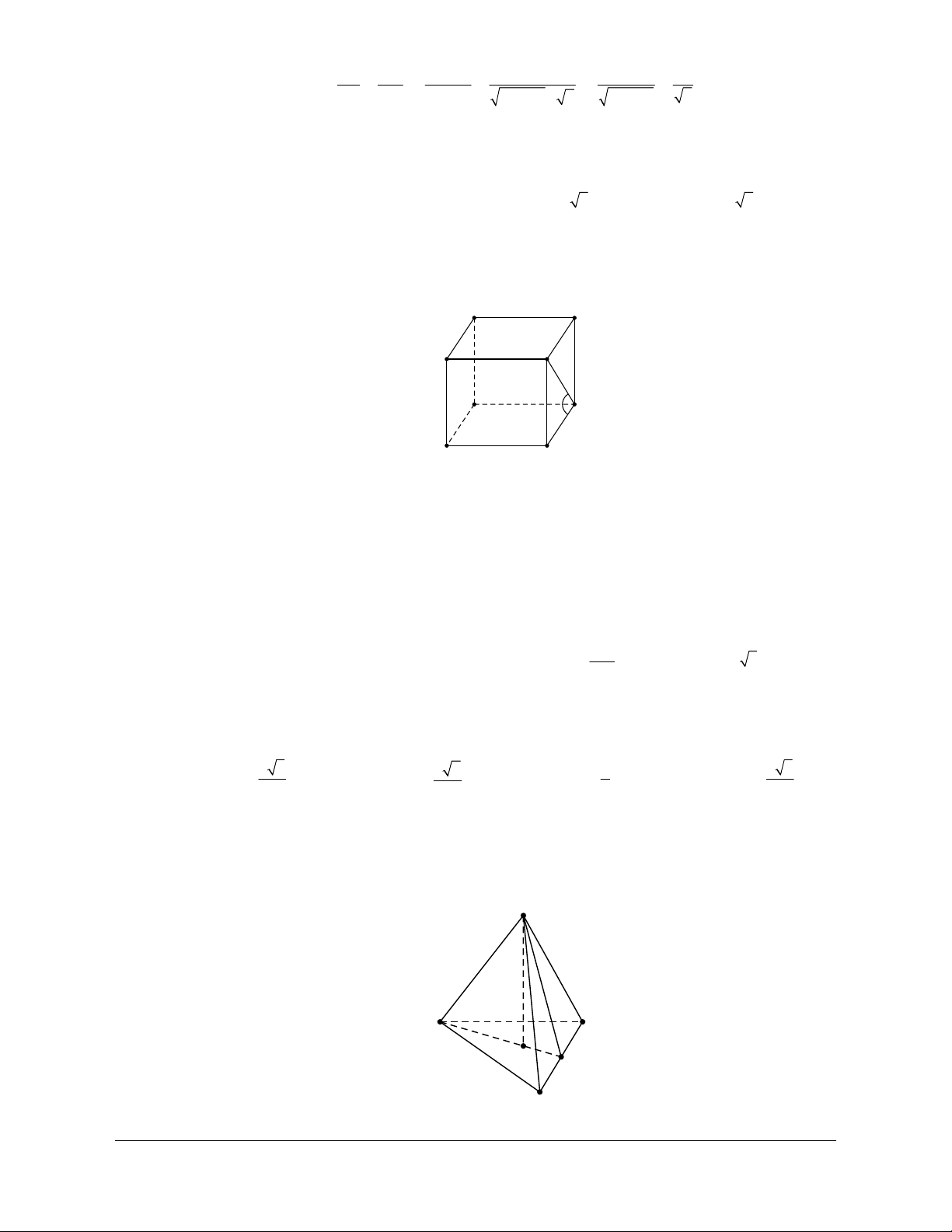
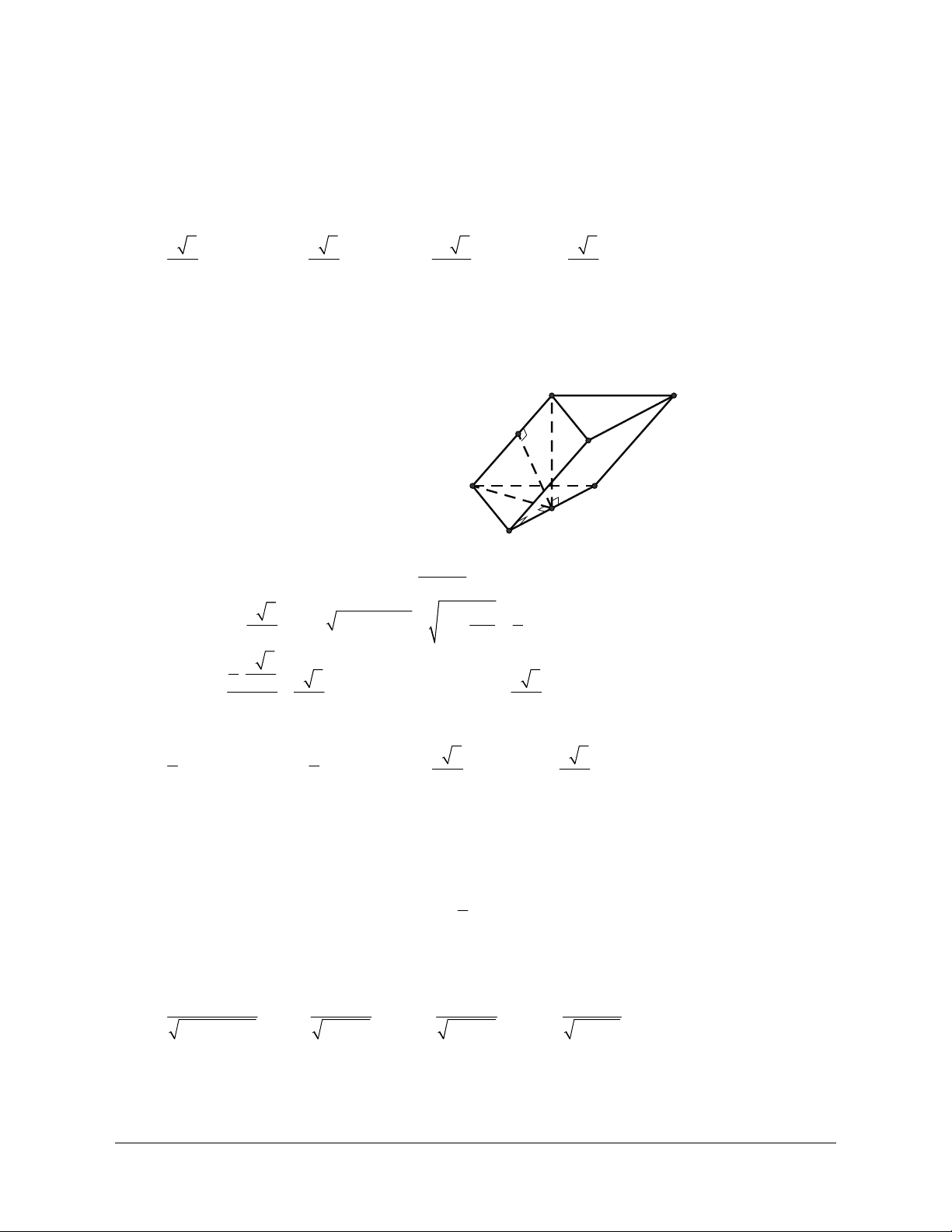
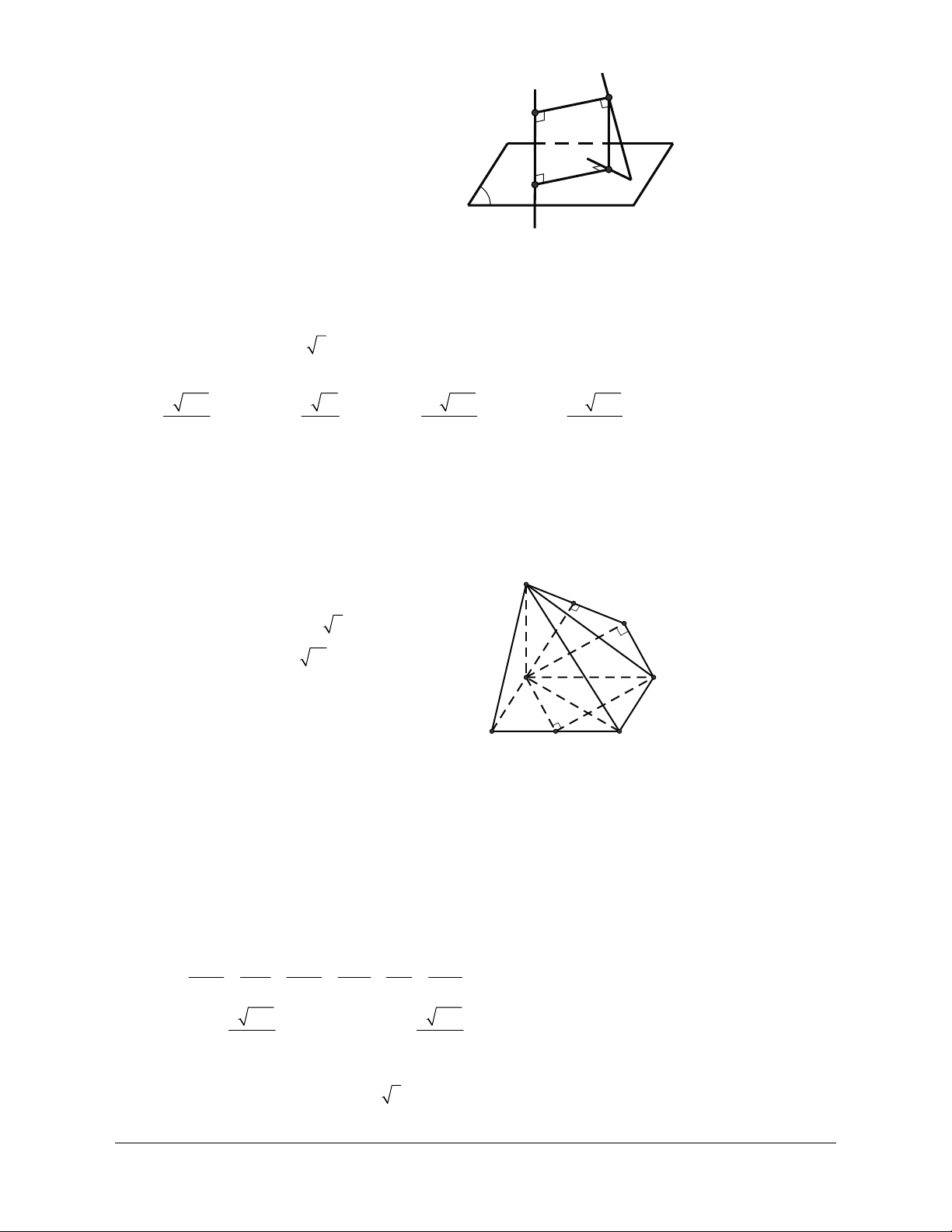
Ví dụ 3: Cho hình chóp S.ABC có SA  SB  SC  AC  AB  a và BC  a 2. Xác định góc giữa
hai đường thẳng CS và AB. Hướng dẫn giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 723
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133  
Trước hết ta tính góc giữa hai vectơ SC và AB
Từ giả thiết suy ra ABC vuông cân tại A Ta có:
       2  a SA.AB  0 a.a.cos120 1
cos  SC,AB SC.AB SAAC.AB
     
     2   2 SC . AB SC . AB a.a SC . AB a 2  
Suy ra: SC,AB  120 .
Vậy góc giữa hai đường thẳng SC và AB bằng 60.
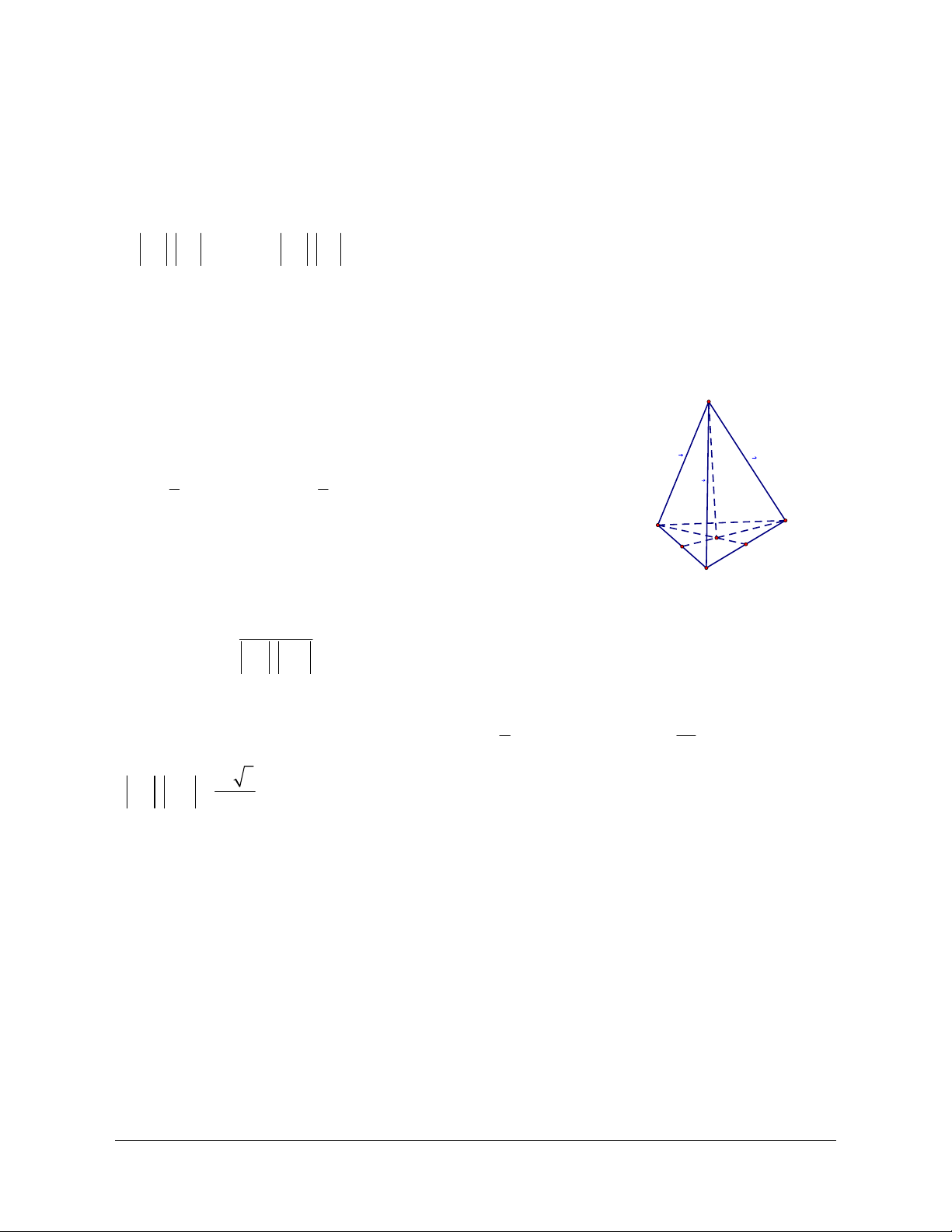
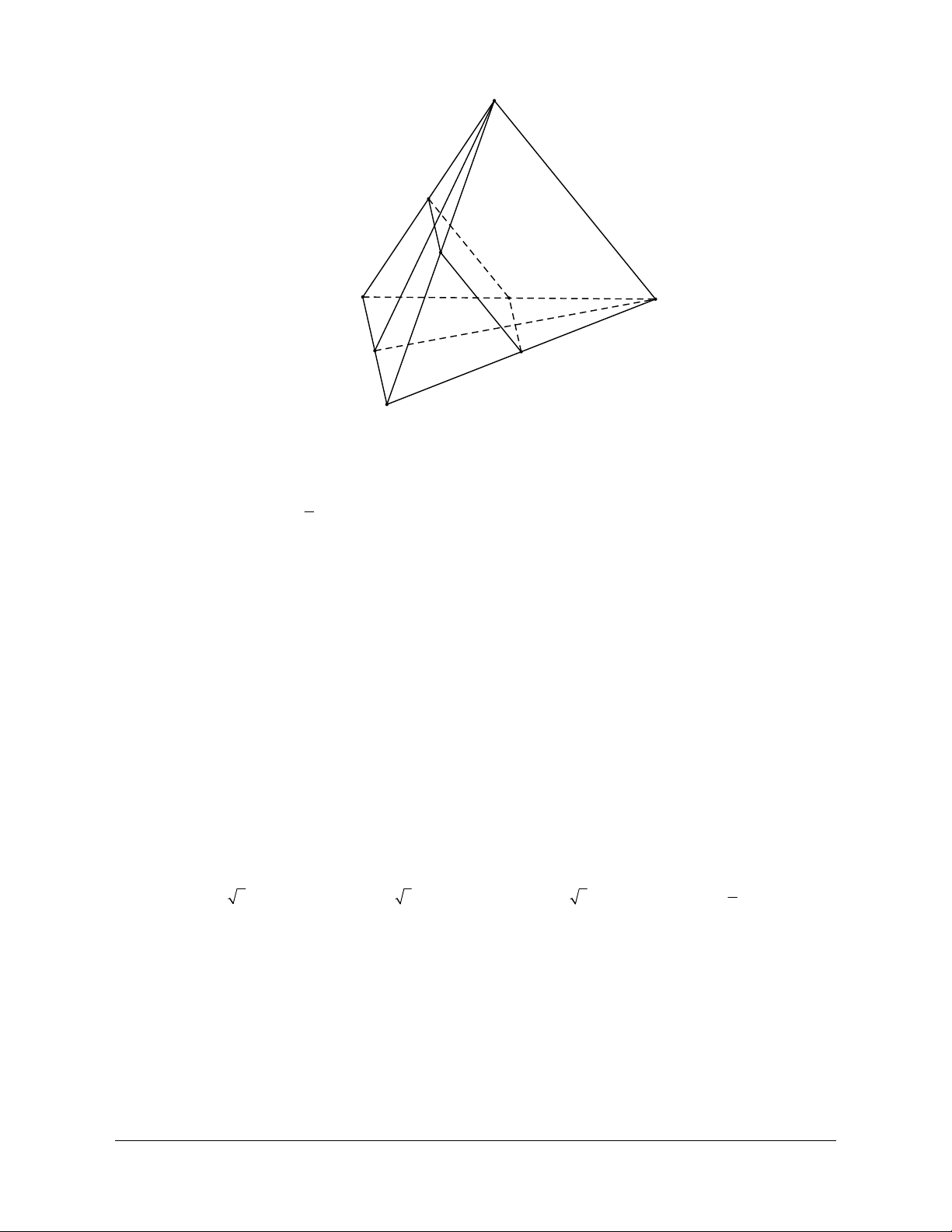
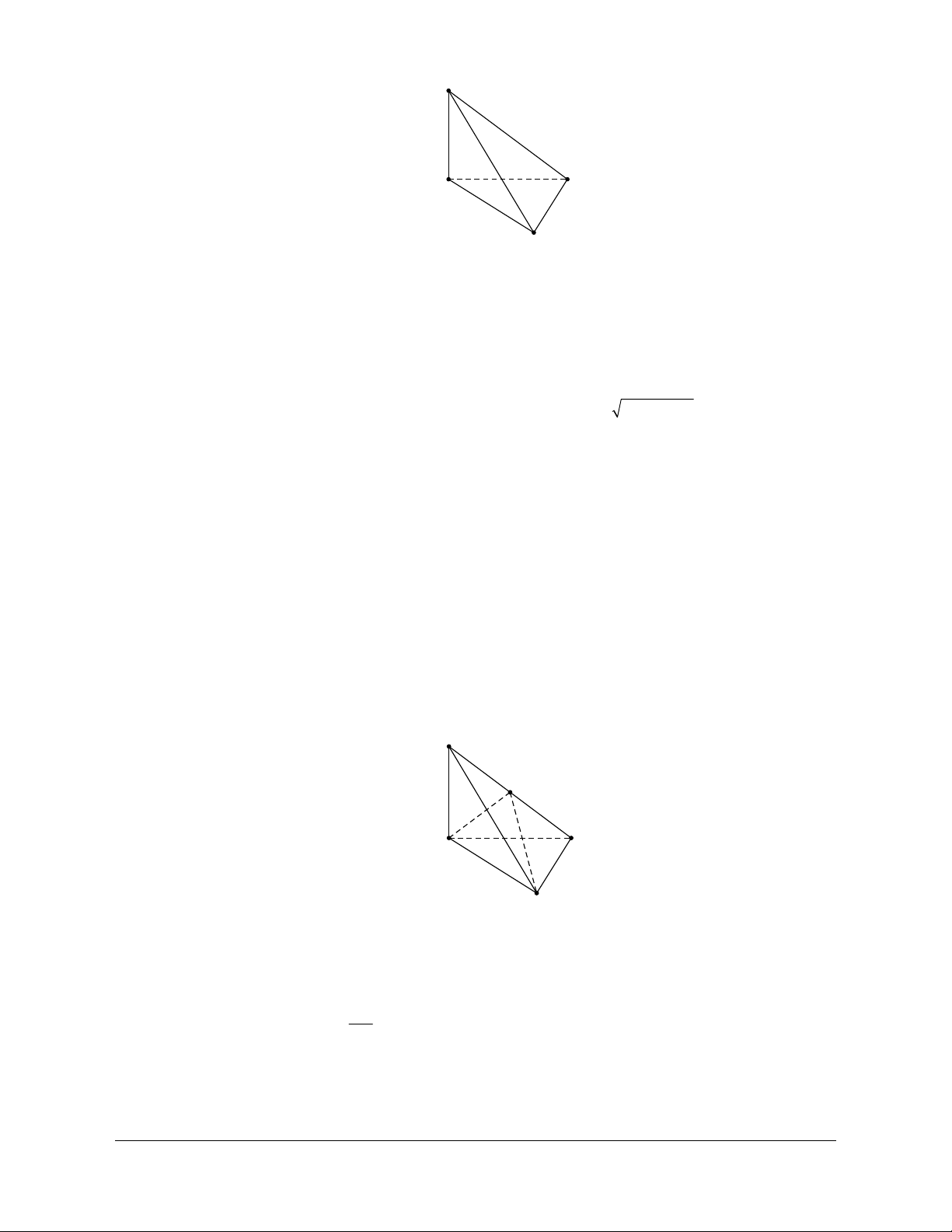
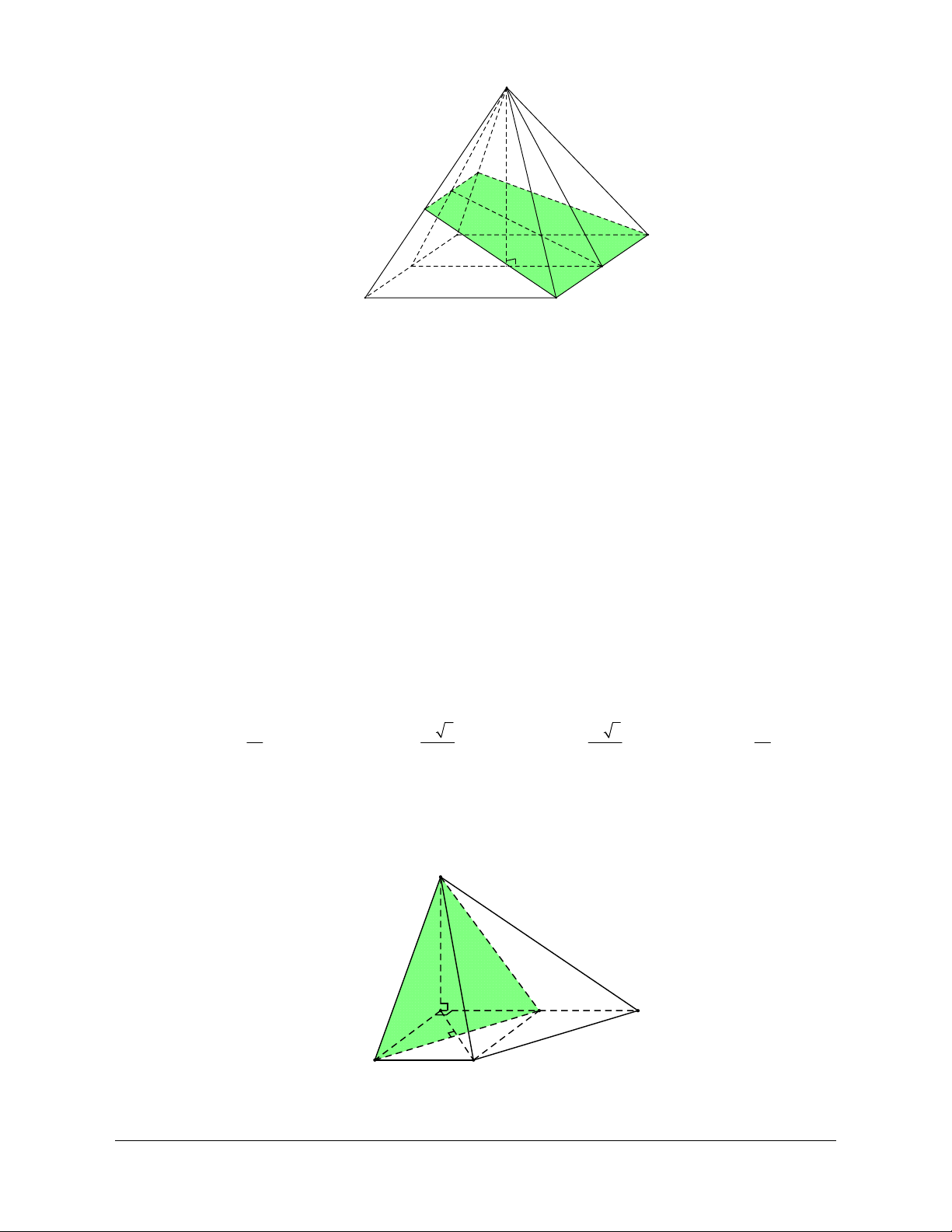
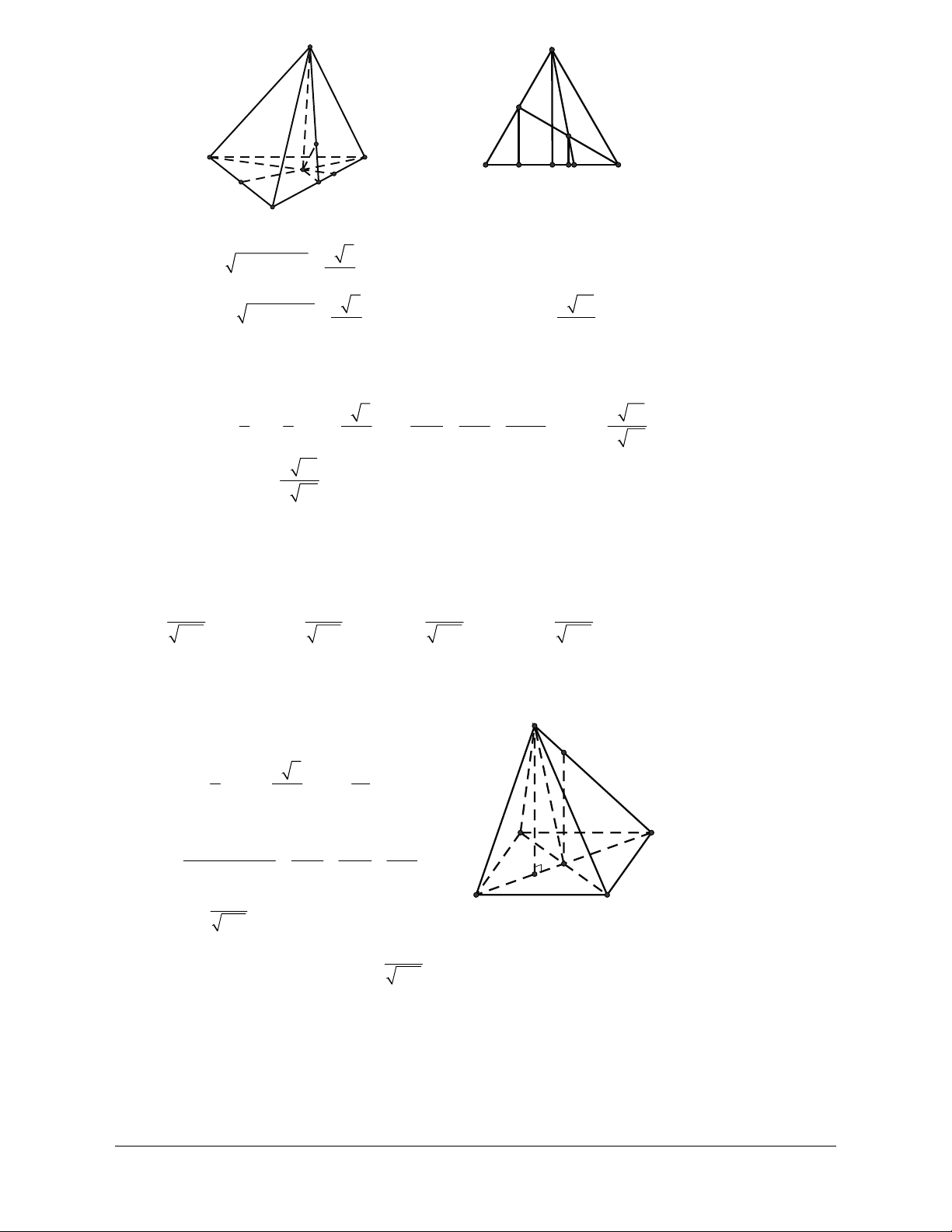
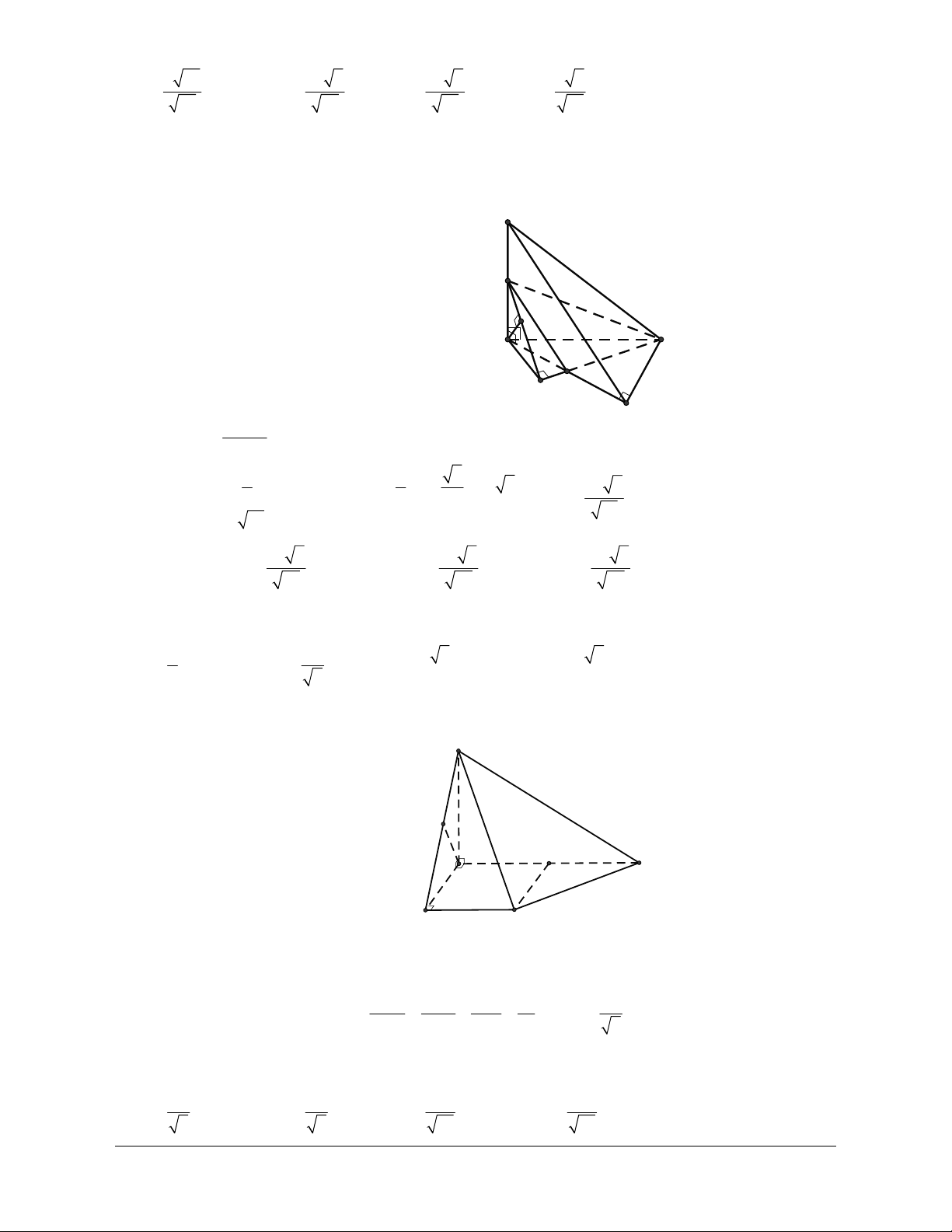
Ví dụ 4: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC và AD. Cho biết
AB  CD  2a và MN  a 3 . Xác định góc tạo bởi hai đường thẳng AB và CD Hướng dẫn giải
Gọi I là trung điểm của AC ta có: IM  IN  a Áp
dụng định lí côsin trong IMN 2 2 2 
MN  IM  IN  2IM.IN cos MIN 2 2 2 
3a  a  a  2a.a cos MIN  1  cosMIN   2 Suy ra:  MIN  120 Vậy:        AB,CD
IM,IN  180  120  60 . 
Dạng 2. Chứng minh hai đường thẳng vuông góc trong không gian 1. Phương pháp
Cách 1: Dùng định nghĩa:      0 a b a,b  90 b / /c
Cách 2: Dùng định lí:   a  b a  c  
Cách 3: Sử dụng tích vô hướng: a  b  a.b  0
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 724
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
2. .Các ví dụ rèn luyện kĩ năng
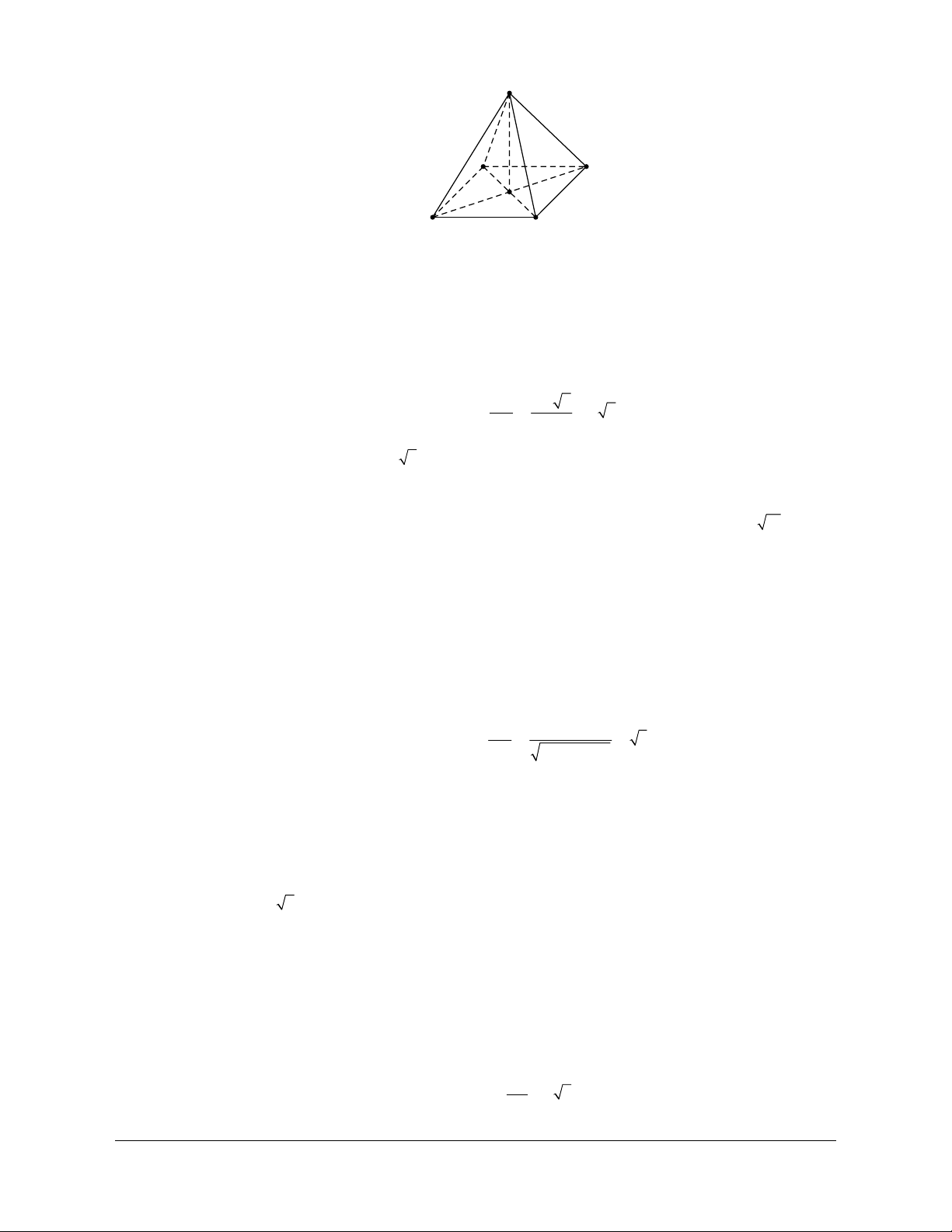
Ví dụ 1. Cho hình chóp S.ABC có SA=SB=SC và   
ASB  BSC  CSA . Chứng minh rằng: SA  BC,SB  AC,SC  AB Hướng dẫn Chöùng minh: SA  BC
    
   
Xeùt: SA.BC  SA.SCSB  SA.SCSA.SC      
 SA . SC cosASC  SA . SB cosASB  0  SA  BC
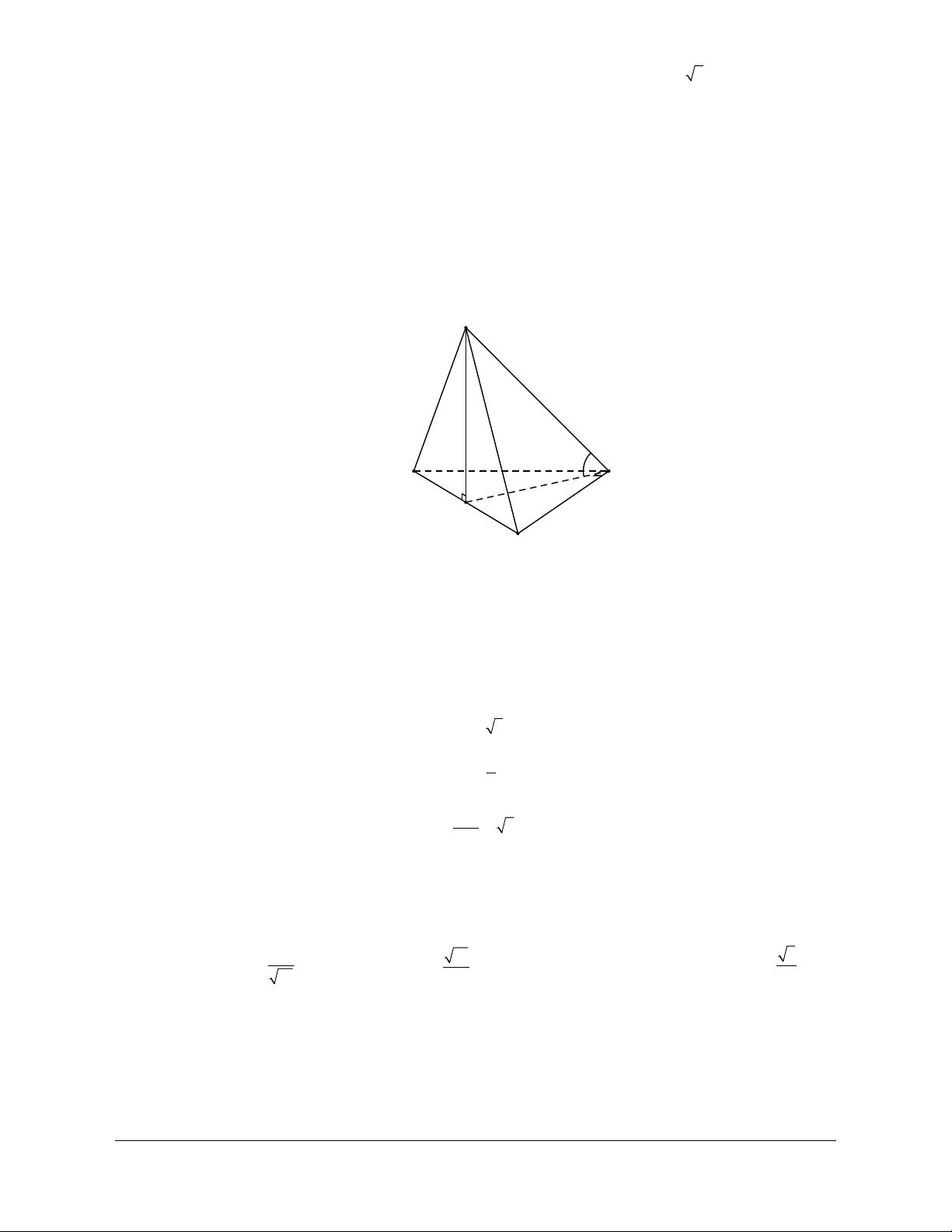
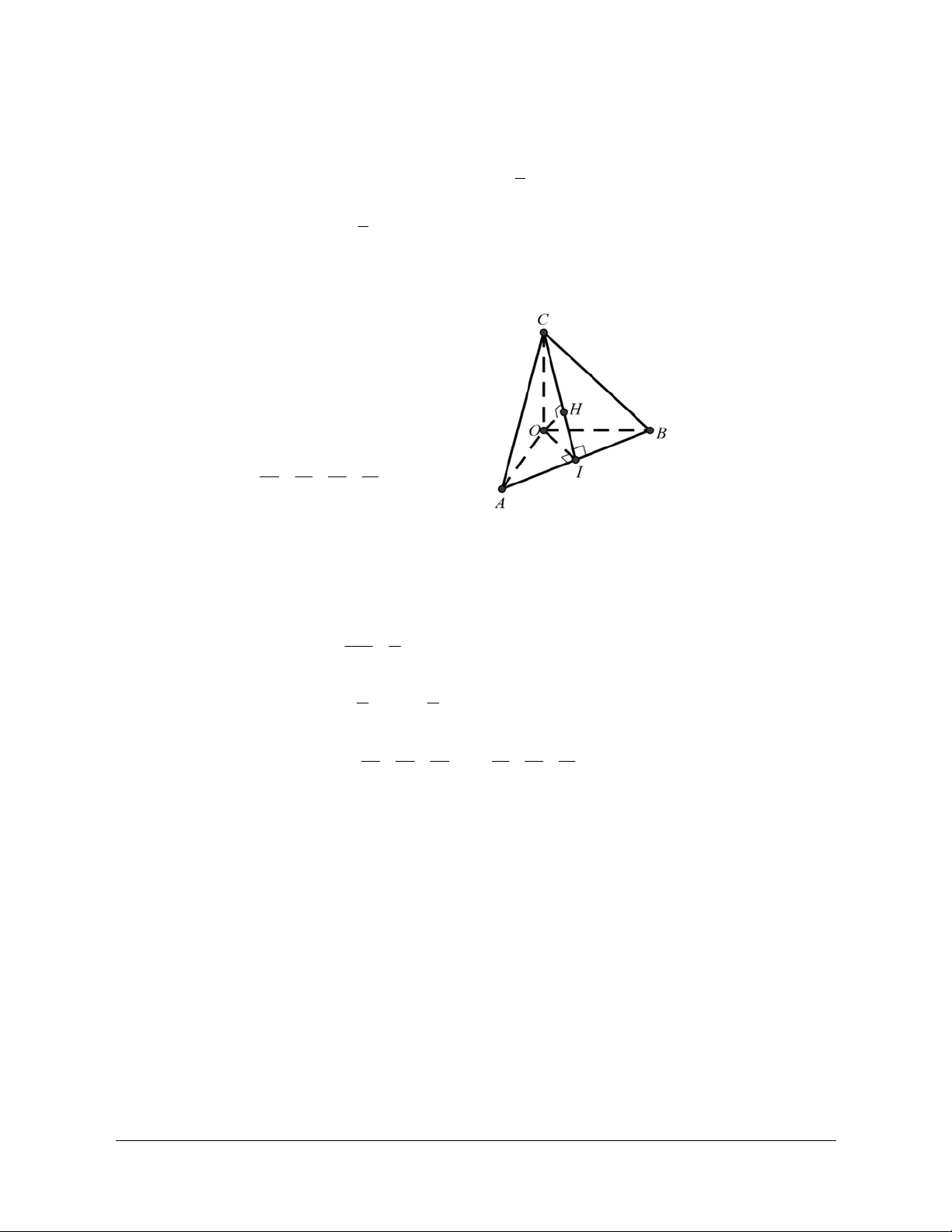
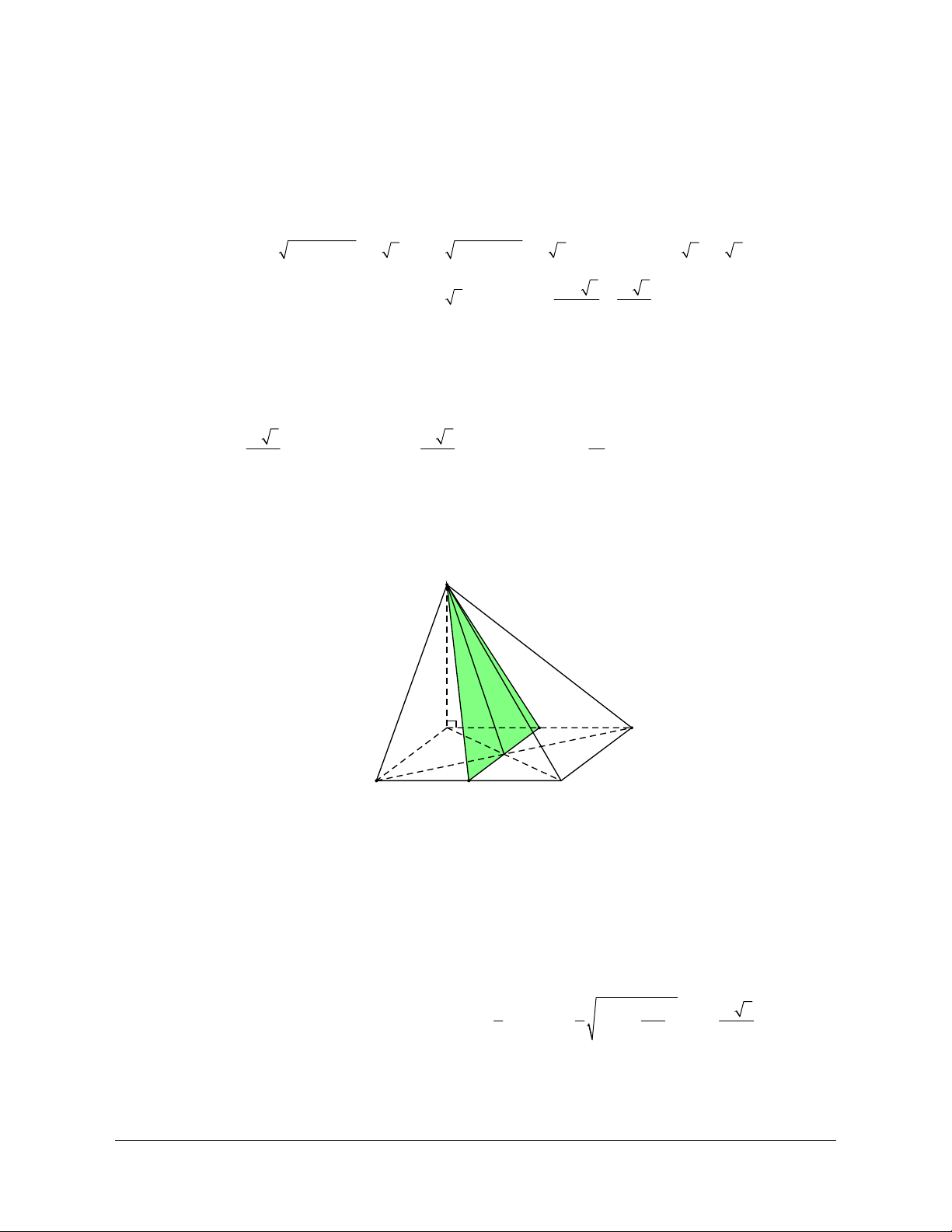
Ví dụ 2. Cho tứ diện ABCD đều. Gọi G là trọng tâm của tam giác BCD. a) Chứng minh AG  CD
b) Gọi M là trung điểm của CD. Tính góc giữa AC và BM. Hướng dẫn
     
a) Đặt AB  b; AC  c; AD  d A    
Chứng minh : AG  CD  AG.CD  0 Với  b d
1            1 AG AB AC AD  b cd c 3 3     
CD  AD AC  d c D B   G Từ đó: AG.CD  0 C b) Ta có:      AC.BM
cos AC,BM    AC . BM Với
    
                  2 1 a AC.BM AC. AM AB
AC.AM AC.AB AC. AC AD  AC.AB  2 4   2 a 3 AC . BM  2
C. BÀI TẬP TRẮC NGHIỆM
Câu 1: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Góc giữa hai đường thẳng a và b bằng góc giữa hai đường thẳng a và c khi b song song với
c (hoặc b trùng với ) c .
B. Góc giữa hai đường thẳng a và b
bằng góc giữa hai đường thẳng a và c thì b song song với . c
C. Góc giữa hai đường thẳng là góc nhọn.
D. Góc giữa hai đường thẳng bằng góc giữa hai véctơ chỉ phương của hai đường thẳng đó. Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 725
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn A A đúng theo định nghĩa.
B sai vì có thể b và c chéo nhau.
C sai vì có thể là góc vuông.
D sai. Nếu góc giữa hai vectơ chỉ phương là a với 0 0
0 £ a £ 90 thì góc giữa hai đường
thẳng bằng a , nếu góc giữa hai vectơ chỉ phương là a với 0 0
90 < a £180 thì góc giữa hai đường thẳng bằng 0 180 - . a
Câu 2: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
B. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì
song song với đường thẳng còn lại.
C. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia. Lời giải Chọn D
Câu 3: Cho hai đường thẳng phân biệt ,
a b và mặt phẳng , (P) trong
đó a ^ (P) . Mệnh đề nào sau đây là sai? A. Nếu b ^ (P ) thì / b / a . B. Nếu /
b / (P ) thì b ^ a . C. Nếu /
b / a thì b ^ (P) . D. Nếu b ^ a thì / b / (P ) . Lời giải Chọn D
Vì b có thể nằm trong mặt phẳng (P) .  
Câu 4: Cho hình lập phương ABC .
D EFGH . Hãy xác định góc giữa cặp vectơ AB và DH ? A. 0 45 . B. 0 90 . C. 0 120 . D. 0 60 . Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 726
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 H G E F D C A B      
Vì DH = AE ( ADHE là hình vuông) nên (AB DH )=(AB AE)  0 , ,
= BAE = 90 ( ABFE là hình vuông).  
Câu 5: Cho hình lập phương ABC .
D EFGH . Hãy xác định góc giữa cặp vectơ AB và EG ? A. 0 90 . B. 0 60 . C. 0 45 . D. 0 120 . Lời giải Chọn C H G E F D C A B      
Vì EG = AC ( AEGC là hình chữ nhật) nên (AB EG)=(AB AC)  0 , ,
= BAC = 45 ( ABCD là hình vuông).
Câu 6: Cho hình lập phương ABC .
D A ' B 'C ' D ' . Góc giữa AC và DA ' là: A. 0 45 . B. 0 90 . C. 0 60 . D. 0 120 . Lời giải Chọn C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 727
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 D' C' A' B' D C A B
Gọi a là độ dài cạnh hình lập phương. Khi đó, tam giác AB 'C đều (
AB ' = B 'C = CA = a 2 ) do đó  0 B 'CA = 60 .
Lại có, DA ' song song CB ' nên (AC DA ) = (AC CB )  0 , ' , ' = ACB ' = 60 .
Câu 7: Cho hình hộp . ABC .
D A ' B 'C ' D '
Giả sử tam giác AB'C và A ' DC ' đều có ba góc nhọn.
Góc giữa hai đường thẳng AC và A ' D là góc nào sau đây? A.     AB 'C.
B. DA 'C '.
C. BB ' D.
D. BDB '. Lời giải Chọn B B' C' A' D' B C A D
Ta có AC A 'C ' ( A ' B 'CD là hình bình hành) mà 
DA 'C ' nhọn nên
(AC A ' D) = (A 'C ' A ' D)  , , = DA 'C '.
Câu 8: Cho hình lập phương . ABC .
D A ' B 'C ' D ' Chọn khẳng định sai?
A. Góc giữa AC và B ' D ' bằng 0 90 .
B. Góc giữa B ' D ' và AA ' bằng 0 60 .
C. Góc giữa AD và B'C bằng 0 45 .
D. Góc giữa BD và A'C' bằng 0 90 . Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 728
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 D' C' A' B' D C A B
Ta có (AA B D )= (BB B D )  0 ', ' '
', ' ' = BB 'C = 90 . Khẳng định B sai.
Câu 9: Cho tứ diện đều ABC .
D Số đo góc giữa hai đường thẳng AB và CD bằng: A. 0 60 . B. 0 30 . C. 0 90 . D. 0 45 . Lời giải Chọn C A C B M D
Gọi M là trung điểm của CD .      
Ta có CD.AM = 0 và CD.MB = 0 .           Do đó C . D AB = C .
D (AM + MB) = C . D AM +C . D MB = 0 .  
Suy ra AB ^ CD nên số đo góc giữa hai đường thẳng AB và CD bằng 0 90 .
Câu 10: Cho tứ diện
ABCD đều cạnh bằng . a Gọi O là tâm
đường tròn ngoại tiếp tam giác BCD .
Góc giữa AO và CD bằng bao nhiêu? A. 0 0 . B. 0 30 . C. 0 90 . D. 0 60 . Lời giải Chọn C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 729
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A B D O M C
Gọi M là trung điểm của CD .
Vì ABCD là tứ diện đều nên AM ^CD, OM ^C . D          
Ta có CD.AO =C .
D (AM + MO) = CD.AM +C . D MO = 0.  
Suy ra AO ^ CD nên số đo góc giữa hai đường thẳng AO và CD bằng 0 90 .
Câu 11: Cho tứ diện đều , ABCD M là trung điểm của cạnh . BC Khi đó
cos(AB, DM ) bằng: 1 A. 2 3 . B. 3 . C. . D. . 2 6 2 2 Lời giải Chọn B A B D M C
Giả sử cạnh của tứ diện là a . Tam giác a BCD đều 3  DM = . 2 Tam giác a ABC đều 3  AM = . 2       Ta có: ( ) . AB DM . cos , AB DM
AB DM =   = AB . DM a 3 . a 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 730
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133  
  
    Mặt khác: A .
B DM = AB (AM - AD) = A . B AM - A . B AD        
= AB . AM .cos( .
AB AM )- AB . AD .cos( . AB AD)    
= AB . AM .cos30- AB . AD .cos 60 2 2 2 a 3 3 1 3 = . . - . . a a a a a a = - = 2 2 2 4 2 4      cos(AB, DM ) 3 =
>  (AB, DM )=(AB DM ) cos(AB, DM ) 3 0 , = . 6 6
Câu 12: Cho tứ diện ABCD có AB = AC = AD và  
BAC = BAD = 60 . Hãy xác định góc giữa cặp   vectơ AB và CD ? A. 60 .  B. 45 .  C. 120 . D. 90 . Lời giải Chọn D A C D B  
  
    Ta có A . B CD = A .
B (AD - AC) = A . B AD - A . B AC        
= AB . AD .cos( .
AB AD)- AB . AC .cos( . AB AC)    
= AB . AD .cos 60- AB . AC .cos 60.     Mà AC = AD  . AB CD = 0  ( , AB CD) = 90 .
Câu 13: Cho hình chóp S.ABC có SA =SB =SC và   
ASB = BSC = CSA . Hãy xác định góc giữa cặp   vectơ SC và AB ? A. 120 . B. 45 .  C. 60 . D. 90 . Lời giải Chọn D
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 731
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 S A C B     
   
Ta có SC.AB = SC.(SB-SA)= SC.SB-SC.SA        
= SC . SB .cos(SC.SB)- SC . SA .cos(SC.SA)  
= SC.SB.cos BSC -SC.SA.cos ASC.  
Mà SA = SB = SC và  
BSC = ASC SC.AB = 0 .  
Do đó (SC, AB)= 90.
Câu 14: Cho hình chóp S.ABC có SA =SB và CA =CB . Tính số đo của góc giữa hai đường thẳng
chéo nhau SC và A . B A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 . Lời giải Chọn D S A C B     
   
Xét SC.AB = CS
- .(CB-CA)=CS.CA -CS.CB  
= CS.CA.cosSCA -CS.C . B cos SCB 2 2 2 2 2 2 + - + - = . . SC CA SA - . .SC CB SB CS CA CS CB 2SC.CA 2SC.CB 2 2 2 2 2 2
SC +CA -SA
SC +CB -SB = -
= 0 (do SA = SB và CA = CB ) 2 2 Vậy SC ^ AB .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 732
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 15: Cho hình chóp S.ABC có AB = AC và  
SAC = SAB . Tính số đo của góc giữa hai đường
thẳng chéo nhau SA và . BC A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 . Lời giải Chọn D S A B M C     
    Xét . SA BC = .
SA (SC -SB) = . SA SC - . SA SB       = SA SC (SA SC)  . .cos ,
- SA . SB .cosSAB  
= SA.SC.cos ASC -SA.SB.cos ASB. ( ) 1 ìSA ï chung ïï
Ta có ïíAB = AC S D AB = S
D AC (c- g-c). ïïï  SA ï B = SAC î SC ìï = SB Suy ra ïí . (2) ï  ïASC = ASB î   Từ ( )
1 và (2) , suy ra SA.BC = 0 . Vậy SA ^ BC . 3
Câu 16: Cho tứ diện ABCD có AC = AD ,  
CAB = DAB = 60 , CD = AD . Gọi j là góc giữa AB và 2
CD . Chọn khẳng định đúng? 3 1 A. os c j = . B. j = 60. C. j = 30. D. os c j = . 4 4 Lời giải Chọn D
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 733
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A C D B     A . B CD A . B CD
Ta có cos(AB,CD)=   = AB . A . CD B CD  
  
    Mặt khác A .
B CD = AB(AD - AC) = A . B AD - A . B AC        
= AB . AD .cos( .
AB AD)- AB . AC .cos( . AB AC) = . AB AD. cos 60- . AB AC. cos 60 1 3 1 1 1 = . AB AD. - A . B AD. = - A . B AD = - . AB CD. 2 2 2 4 4 1 - A . B CD
Do có cos(AB,CD) 4 1 = = . AB.CD 4 1 Vậy cosj = . 4
Câu 17: Cho tứ diện ABCD có AB = AC = AD và   
BAC = BAD = 60 , CAD = 90 . Gọi I và J lần  
lượt là trung điểm của AB và CD . Hãy xác định góc giữa cặp vectơ AB và IJ ? A. 120 . B. 90 .  C. 60 . D. 45 .  Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 734
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A I B D J C  1  
Xét tam giác ICD có J là trung điểm đoạn CD IJ = (IC +ID). 2
Tam giác ABC có AB = AC và  0
BAC = 60  DABC đều  CI ^ AB .
Tương tự, ta có DABD đều nên DI ^ AB .  
1   
1   1  
Ta có IJ.AB = (IC +ID).AB = . IC AB + . ID AB = 0 2 2 2    
I J ^ AB  ( , AB IJ ) = 90 .
Câu 18: Cho tứ diện ABCD có AB =CD . Gọi
I , J , E, F lần lượt là trung điểm của .
AC, BC, BD, AD Góc
(IE, JF ) bằng A. 30 . B. 45 .  C. 60 . D. 90 . Lời giải Chọn D A F I B D E J C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 735
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìïIF CD ï Ta có ï
IF là đường trung bình của DACD  í 1 . ïIF = CD ïïî 2 ìïJE CD ï Lại có ï
JE là đường trung bình của DBCD  í 1 . ïJE = CD ïïî 2 ìïIF = JE ï  í  Tứ giác ï
IJEF là hình bình hành. IF JE ïî  ìï 1 ïIJ = AB ï Mặt khác: ï 2 í . Mà =  = . ï AB CD IJ JE 1 ïïJE = CD ïïî 2
Do đó IJEF là hình thoi. Suy ra (IE, JF )= 90 .
Câu 19: Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng . a
Gọi M và N lần lượt là trung điểm của AD và SD .
Số đo của góc (MN ,SC) bằng A. 45 .  B. 30 . C. 90 . D. 60 . Lời giải Chọn C S N B C A M D
Do ABCD là hình vuông cạnh a AC = a 2 . 2 2 2 2
AC = 2a = SA +SC  DSAC vuông tại S .  1 
Từ giả thiết ta có MN là đường trung bình của DDSA NM = SA 2   1   Khi đó NM.SC = .
SA SC = 0  MN ^ SC  (MN ,SC) = 90 . 2
Câu 20: Cho hình chóp S.ABCD có tất cả các cạnh đều bằng . a Gọi I và
J lần lượt là trung
điểm của SC và BC . Số đo của góc (IJ, CD) bằng:
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 736
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. 90 .  B. 45 .  C. 30 . D. 60 . Lời giải Chọn D S I A D O B J C
Gọi O là tâm của hình thoi ABCD OJ là đường trung bình của DBCD. OJ ìï  CD ï Suy ra ïí 1 . OJ ï = CD ïïî 2
Vì CD OJ  (IJ,CD)= (IJ,OJ ) . ìï 1 a ïIJ = SB = ïï 2 2 ïïï Xét tam giác 1 a ï IOJ , có OJ í = CD =  D đều. ï IOJ 2 2 ïïï 1 a ïïIO = SA = ïïî 2 2
Vậy (IJ CD)= (IJ OJ )  , , = IJO = 60 .
Câu 21: Cho hình chóp S.ABCD có cạnh ,
SA = x tất cả các cạnh còn lại đều bằng a . Tính số đo
của góc giữa hai đường thẳng SA và . SC A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 . Lời giải Chọn D
Theo giả thiết, ta có AB = BC = CD = DA = a nên ABCD là hình thoi cạnh a .
Gọi O = AC Ç BD . Ta có DCBD = DSBD (c-c-c) .
Suy ra hai đường trung tuyến tương ứng CO và SO bằng nhau. 1
Xét tam giác SAC , ta có SO =CO = AC . 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 737
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Do đó tam giác SAC vuông tại S (tam giác có đường trung tuyến bằng nửa cạnh đáy).
Vậy SA ^ SC .  
Câu 22: Cho hình lập phương ABC .
D EFGH có cạnh bằng . a Tính AB.EG. 2 A. a 2 2 2 a 3. B. a . C. . D. 2 a 2. 2 Lời giải Chọn B H G E F D C A B        Ta có A . B EG = A .
B AC. Mặt khác AC = AB + AD .          
Suy ra AB EG = AB AC = AB(AB + AD) 2 . . = AB + A . B AD .  
Vì ABCD là hình vuông  AB ^ AD AB.AD = 0 2   2 2  AB + A .
B AD = AB + 0 = a .
Câu 23: Cho hình lập phương ABCD. a M AD 1 A 1 B 1 C 1 D có cạnh . Gọi là trung điểm . Giá trị   B M . 1 B 1 D là: 1 3 A. 2 a . B. 2 a . C. 2 a . D. 2 a 2. 2 4 Lời giải Chọn A
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 738
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 D1 C1 B1 A1 D C M A B         Ta có B M . = + + + + 1 B 1 D
( 1BB BA AM )(BA AD D 1D)         
      2  
= BB .BA + BB .AD + B .
B DD + BA + BA. + .
BA DD + AM .BA + AM .AD + AM .DD 1 1 1 1 AD    1   1
 =0 =0 =0 0 = 0 = 0 =   2   2 2 = a a B .
B DD + BA + AM . 2 2 = - + + = . 1 1 AD a a 2 2
Câu 24: Cho tứ diện ABCD có AC = , a BD = 3a . Gọi
M , N lần lượt là trung điểm của AD và BC
. Biết AC vuông góc với . BD Tính MN . A. a 6 a 10 2a 3 3a 2 MN = . B. MN = . C. MN = . D. MN = . 3 2 3 2 Lời giải Chọn B A P M a B 3a D N C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 739
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Gọi P là trung điểm của AB PN , PM lần lượt là đường trung bình của tam giác DABC ìï 1 a ïPN = AC = ï và ï D 2 2 ABD . Suy ra í . ï 1 3a ïïPM = BD = ïïî 2 2
Ta có AC ^ BD PN ^ PM hay tam giác DPMN vuông tại P 2 2 Do đó a 9a a 10 2 2 MN = PN + PM = + = . 4 4 2
Câu 25: Cho tứ diện ABCD có AB vuông góc với .
CD Mặt phẳng (P) song song với AB và CD lần lượt cắt BC, D , B , AD AC tại . M , N , P, Q
Tứ giác MNPQ là hình gì? A. Hình thang. B. Hình bình hành. C. Hình chữ nhật.
D. Tứ giác không phải hình thang. Lời giải Chọn C A P Q B D N M C ( ìï MNPQ)/ / AB Ta có ïí  MQ/ / AB. ( ï MNPQ)Ç(ABC)= ï MQ î
Tương tự ta có MN / / CD, NP/ / AB, QP/ / D C .
Do đó tứ giác MNPQ là hình bình hành
Lại có MN ^ MQ(do AB ^ CD ) .
Vậy tứ giác MNPQ là hình chữ nhật.
Câu 26: Trong không gian cho hai tam giác đều ABC và ABC¢ có chung cạnh AB và nằm trong
hai mặt phẳng khác nhau. Gọi M , N , P, Q
lần lượt là trung điểm của các cạnh AC, CB, BC ¢ và C A
¢ . Tứ giác MNPQ là hình gì? A. Hình bình hành. B. Hình chữ nhật. C. Hình vuông. D. Hình thang. Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 740
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 C' Q P A M C H N B Vì M , N , P,
Q lần lượt là trung điểm của các cạnh AC, CB, BC ¢ và C A ¢ ìï 1
ïPQ = MN = AB ï  í 2  ï
MNPQ là hình bình hành.
ïïPQ / / AB / / MN î ìï ^ Gọi CH AB ï
H là trung điểm của AB . Vì hai tam giác ABC và ABC¢ đều nên í . C ï H ¢ ^ AB ïî
Suy ra AB ^(CHC¢) . Do đó AB ^CC¢ . ìïPQ/ / AB ï
Ta có ïïíPN / / CC¢  PQ ^ PN . ïïïAB ^CC¢ ïî
Vậy tứ giác MNPQ là hình chữ nhật.
Câu 27: Cho tứ diện ABCD trong
đó AB = 6, CD = 3 , góc giữa AB và CD là 60 và điểm M trên
BC sao cho BM = 2MC . Mặt phẳng (P) qua M song song với AB và CD cắt
BD, AD, AC lần lượt tại .
M , N , Q
Diện tích MNPQ bằng: 3 A. 2 2. B. 3. C. 2 3. D. . 2 Lời giải Chọn C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 741
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A 6 P Q B D N 3 M C ( ìï MNPQ)/ / AB Ta có ïí  MQ/ / AB. ( ï MNPQ)Ç(ABC)= ï MQ î
Tương tự ta có MN / / CD, NP/ / AB, QP/ / D C .
Do đó tứ giác MNPQ là hình bình hành Ta có  (AB CD)  = (QM MP) 0 ; ; = 60 . Suy ra 0 S
= QM .QN . sin 60 . MNPQ Ta có CM MQ 1
DCMQ ∽ DCBA  = =  MQ = 2. CB AB 3 AQ QN 2
DAQN ∽ DACD  = =  QN = 2. AC CD 3 Vậy 3 0 S
= QM .QN .sin 60 = 2.2. = 2 3. MNPQ 2
Câu 28: Cho tứ diện ABCD có AB vuông góc với , CD
AB = 4, CD = 6 . M là điểm thuộc cạnh
BC sao cho MC = 2BM . Mặt phẳng
(P) đi qua M song song với AB và CD . Diện tích thiết diện của
(P) với tứ diện là: A. 5. B. 17 16 6. C. . D. . 3 3 Lời giải Chọn D
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 742
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A 4 P N B D Q M 6 C ( ìï MNPQ)/ / AB Ta có ïí  MN / / A . ( ï )Ç( ) B MNPQ ABC = ï MN î Tương tự ta có M /
Q / CD, NP/ / CD, QP/ / AB . Do đó tứ giác MNPQ là hình bình hành Ta có  (AB CD)  = (MN MQ)  0 ; ;
= NMQ = 90  tứ giác MNPQ là hình chữ nhật. Lại có CM MN 1 4
DCMN ∽ DCBA  = =  MN = ; CB AB 3 3 AN NP 2
DANP ∽ DACD  = =  MP = 4. AC CD 3 Vậy 16 S = MN .NP = . MNPQ 3
Câu 29: Cho tứ diện ABCD có AB vuông góc với , CD AB = CD = 6 . M là điểm thuộc cạnh BC
sao cho MC = x.BC (0 < x < )
1 . Mặt phẳng(P) song song với AB và CD lần lượt cắt BC, D ,
B AD, AC tại .
M , N , P,Q
Diện tích lớn nhất của tứ giác bằng bao nhiêu? A. 9. B. 11. C. 10. D. 8. Lời giải Chọn A
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 743
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A 6 P Q B D N 6 M C ìïMQ/ / NP/ / Xét tứ giác AB ï MNPQ có í  là hình bình hành. ï MNPQ
MN / / PQ/ / CD ïî
Mặt khác, AB ^ CD MQ ^ MN . Do đó, MNPQ là hình chữ nhật. Vì MQ CM
M Q/ / A B nên =
= x MQ = x.AB = 6x . AB CB
Theo giả thiết MC = x.BC BM = (1- x)BC . Vì MN BM MN / / CD nên =
= 1- x MN = (1- x).CD = 6(1- x). CD BC
Diên tích hình chữ nhật MNPQ là 2 æ x + - x ö S = MN MQ = - x x = x - x £ ç ÷ ç ÷ = . MNPQ ( ) ( ) 1 . 6 1 .6 36. . 1 36 9 çè 2 ÷ø 1 Ta có S
= 9 khi x =1-x x = . MNPQ 2
Vậy diện tích tứ giác MNPQ lớn nhất bằng 9 khi M là trung điểm của BC .
Câu 30: Trong không gian cho tam giác ABC . Tìm M sao cho giá trị của biểu thức 2 2 2
P = MA + MB + MC đạt giá trị nhỏ nhất.
A. M là trọng tâm tam giác ABC .
B. M là tâm đường tròn ngoại tiếp tam giác ABC .
C. M là trực tâm tam giác ABC .
D. M là tâm đường tròn nội tiếp tam giác ABC . Lời giải Chọn A    
Gọi G là trọng tâm tam giác ABC G cố định và GA +GB +GC = 0.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 744
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133       = ( + )2 +( + )2 +( + )2 P MG GA MG GB MG GC     2
= MG + MG (GA +GB +GC) 2 2 2 3 2 .
+GA +GB +GC 2 2 2 2 2 2 2
= 3MG +GA +GB +GC ³ GA +GB +GC .
Dấu bằng xảy ra  M º G. Vậy 2 2 2 = + + với º
là trọng tâm tam giác ABC. mi P n GA GB GC M G
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 745
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
BÀI 3. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẢNG
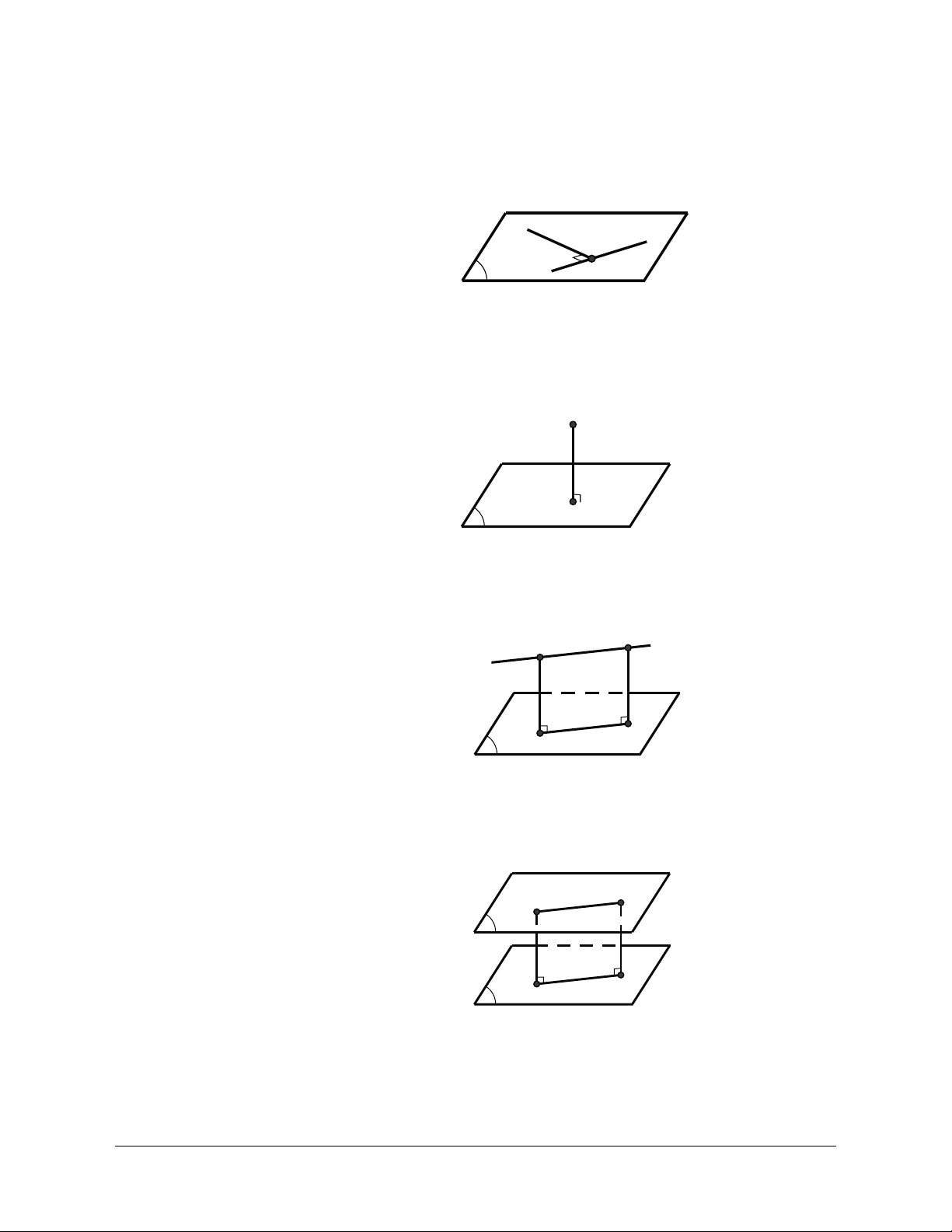
A. KIẾN THỨC CƠ BẢN CẦN NẮM 1. Định nghĩa Đường thẳng
d được gọi là vuông góc với mặt phẳng (a) d
nếu d vuông góc với mọi đường thẳng a nằm trong mặt phẳng (a). a Kí hiệu d ^ (a). α
2. Điều kiện để đường thẳng vuông góc với mặt phẳng Định lí
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt
phẳng thì nó vuông góc với mặt phẳng ấy. Hệ quả
Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì nó cũng vuông góc
với cạnh thứ ba của tam giác đó. 3. Tính chất Tính chất 1
Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước. d O α
Mặt phẳng trung trực của một đoạn thẳng
Người ta gọi mặt phẳng đi qua trung điểm
I của đoạn thẳng AB và vuông góc với AB là
mặt phẳng trung trực của đoạn thẳng A . B Tính chất 2
Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước. d O α
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 746
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
4. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng. Tính chất 1
Cho hai đường thẳng song song. Mặt phẳng nào vuông góc với đường thẳng này thì cũng
vuông góc với đường thẳng kia.
Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau. a b α Tính chất 2
Cho hai mặt phẳng song song. Đường thẳng nào vuông góc với mặt phẳng này thì cũng
vuông góc với mặt phẳng kia.
Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau. a α β Tính chất 3 Cho đường thẳng a và
mặt phẳng (a) song song với nhau. Đường thẳng nào vuông góc với (a) thì cũng vuông góc với . a
Nếu một đường thẳng và một mặt phẳng (không chứa đường thẳng đó) cùng vuông góc
với một đường thẳng khác thì chúng song song với nhau. b a α
5. Định lí ba đường vuông góc Định nghĩa
Phép chiếu song song lên mặt phẳng (P) theo
phương vuông góc tới mặt phẳng (P) gọi
là phép chiếu vuông góc lên mặt phẳng (P).
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 747
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Định lí (Định lí 3 đường vuông góc)
Cho đường thẳng a không vuông góc với mặt phẳng (P) và a đường thẳng
b nằm trong mặt phẳng (P). Khi đó điều kiện
cần và đủ để b vuông góc với a là b vuông góc với hình a' chiếu
a¢ của a trên (P). P b
b a b a'
6. Góc giữa đường thẳng và mặt phẳng Định nghĩa
Nếu đường thẳng a ^ (P) thì ta nói góc giữa đường thẳng a và mặt phẳng (P) bằng 0 90 .
Nếu đường thẳng a không vuông góc với a
mặt phẳng (P) thì góc giữa a và hình chiếu
a¢ của nó trên (P) gọi là góc giữa đường thẳng φ a' a và mặt phẳng (P). P
Chú ý: Nếu j là góc giữa đường thẳng
d và mặt phẳng (a) thì ta luôn có 0 0 0 £ j £ 90 .
B. CÂU HỎI TRẮC NGHIỆM
Dạng 1. Câu hỏi lý thuyết 1. Phương pháp
Ta cần nắm vững các tính chất sau Tính chất 1
a) Cho hai đường thẳng song song. Mặt phẳng nào vuông góc với đường thẳng này
thì cũng vuông góc với đường thẳng kia.
b) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau. Tính chất 2
a) Cho hai mặt phẳng song song. Đường thẳng nào vuông góc với mặt phẳng này thì
cũng vuông góc với mặt phẳng kia.
b) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau. Tính chất 3
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 748
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
a) Cho đường thẳng a và mặt phẳng (α) song song với nhau. Đường thẳng nào
vuông góc với (α) thì cũng vuông góc với a.
b) Nếu một đường thẳng và một mặt phẳng (không chứa đường thẳng đó) cùng
vuông góc với một đường thẳng khác thì chúng song song với nhau.
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Cho hai đường thẳng a, b và hai mặt phẳng (P), (Q). Mệnh đề nào sau đây đúng? a // b  a  b 
A.   P    P   b. B. a. P a b // P    a  b  a  Q C.  
    P//a. D. P // Q . b P  b  P      Hướng dẫn giải ĐÁP ÁN A a // b     P  
b là mệnh đề đúng. Nghĩa là, cho hai đường thẳng song song, mặt P a
phẳng nào vuông góc với đường thẳng này sẽ vuông góc với đường thẳng kia.
Ví dụ 2: Cho hai đường thẳng a, b và hai mặt phẳng (P), (Q). Mệnh đề nào sau đây đúng? a  P  a  P   A. a // b.
B. b  P  a// b. b  P    a  b  P//Q a // P  C. a // Q . D.   a // Q . a  P      P  Q    Hướng dẫn giải ĐÁP ÁN B
 Mệnh đề A sai. Vì khi đó hai đường thẳng a và b có thể song song hoặc trùng nhau.
Mệnh đề A chỉ đúng khi a và b phân biệt.
 Mệnh đề B đúng. Thật vậy, ta thấy:
+ Nếu a cắt b tại M. Như vậy, qua điểm M ta vẽ được hai đường thẳng a và b cùng
vuông góc với (P): Vô lí. Vậy a không cắt b.
+ Nếu a chéo b. Lấy điểm N trên a. Qua N vẽ đường thẳng bʹ // b.
Do b  P nên bʹ  P. Như vậy từ điểm N ta có hai đường thẳng a và b’ cùng
vuông góc với (P): Vô lí. Vậy a và b không chéo nhau.
+ Trường hợp a trùng b không xảy ra vì a  b (giả thiết). Vậy a // b.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 749
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
 Mệnh đề C sai. Mệnh đề đúng là a  Q.
 Mệnh đề D sai. Vì lúc này a có thể song song hoặc chứa trong (Q).
Ví dụ 3: Cho hai đường thẳng a, b và hai mặt phẳng (P), (Q). Mệnh đề nào sau đây đúng? a   b  a  P
A. a  c   b // P. B.   b // P. a  b  c P   a  P   b // P a  P C.    . D.   P // Q . a  b  b   P a // Q      Hướng dẫn giải ĐÁP ÁN C
A sai: Lúc này b có thể chứa trong, hoặc cắt, hoặc song song với (P). Mệnh đề chỉ đúng khi a  P .
B sai: Vì lúc này b có thể chứa trong (P). Mệnh đề chỉ đúng khi b  P.
D sai: Thật vậy, nếu P // Q hoặc P  Q thì do a  P nên a  Q : Vô lí (Trái với giả thiết a // Q ). a,b,c   Ví dụ 4: Cho 
. Mệnh đề nào sau đây đúng? c  a, c   b A. a cắt b. B. a // b. C. a  b. a // b D.  a  .  b Hướng dẫn giải ĐÁP ÁN D
Vì a, b, c đồng phẳng và c  a, c  b nên a // b hoặc a  b. a,b   
Ví dụ 5: Cho c // 
. Mệnh đề nào sau đây đúng? c  a, c   b a // b A. a cắt b. B. a // b. C.  a  .  b D. a  b. Hướng dẫn giải ĐÁP ÁN C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 750
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 a,  b   
Ví dụ 6: Cho c caét  . Mệnh đề nào sau đây đúng? c  a, c  b  a // b A. a cắt b. B. a // b. C.  . a   b D. a  b. Hướng dẫn giải ĐÁP ÁN C 3. Bài tập trắc nghiệm
Câu 1: Khẳng định nào sau đây sai?
A. Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong (a) thì d
vuông góc với bất kì đường thẳng nào nằm trong (a).
B. Nếu đường thẳng d ^ (a) thì d vuông góc với hai đường thẳng trong (a).
C. Nếu đường thẳng d vuông góc với hai đường thẳng nằm trong (a) thì d ^ (a). D. Nếu d ^ (a) và đường thẳng a  (a) thì d ^ . a Lời giải Chọn C ac b
Mệnh đề C sai vì thiếu điều kiện '' cắt nhau '' của hai đường thẳng nằm trong (a). Ví dụ:
đường thẳng a vuông góc với hai đường thẳng b và c nằm trong (a) nhưng b và c
song song với nhau thì khi đó
a chưa chắc vuông góc với (a).
Câu 2: Trong không gian cho đường thẳng D không nằm trong mặt phẳng , (P) đường thẳng D
được gọi là vuông góc với mp (P) nếu:
A. vuông góc với hai đường thẳng phân biệt nằm trong mp (P).
B. vuông góc với đường thẳng a mà a song song với mp (P).
C. vuông góc với đường thẳng
a nằm trong mp (P).
D. vuông góc với mọi đường thẳng nằm trong mp (P). Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 751
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn D
Đường thẳng D được gọi là vuông góc với mặt phẳng (P) nếu D vuông góc với mọi
đường thẳng trong mặt phẳng (P) .(Định nghĩa đường thẳng vuông góc với mặt phẳng).
Câu 3: Mệnh đề nào sau đây sai?
A. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song.
C. Một đường thẳng và một mặt phẳng (không chứa đường thẳng đã cho) cùng vuông
góc với một đường thẳng thì song song nhau.
D. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song. Lời giải Chọn B c c a a   b b
Mệnh đề ở câu B sai vì: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng
thì có thể cắt nhau, chéo nhau.
Câu 4: Cho hai đường thẳng phân biệt ,
a b và mặt phẳng (P), trong đó
a ^ (P). Chọn mệnh đề
sai trong các mệnh đề sau? A. Nếu thì b ^ (P) a  . b B. Nếu b a thì b ^ (P). C. Nếu b Ì (P) thì b ^ . a D. Nếu a ^ b thì b  (P ). Lời giải Chọn D a P b
`Mệnh đề D sai vì b có thể nằm trong (P) .
Câu 5: Cho hai đường thẳng , a b và mặt phẳng . (P)
Chỉ ra mệnh đề đúng trong các mệnh đề sau:
A. Nếu a ^ (P) và b ^ a thì b  (P).
B. Nếu a  (P) và b ^ (P) thì a ^ b .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 752
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
C. Nếu a  (P) và b ^ a thì b  (P).
D. Nếu a  (P) và b ^ a thì b ^ (P) . Lời giải Chọn B
Mệnh đề A sai vì b có thể nằm trong (P) . a P b
Mệnh đề C sai vì b có thể cắt (P) hoặc b nằm trong (P) . a a b P P b
Mệnh đề D sai vì b có thể nằm trong (P). a P b Câu 6: Cho , a ,
b c là các đường thẳng trong không gian. Tìm mệnh đề sai trong các mệnh đề sau:
A. Nếu a ^ b và b ^ c thì a  .c
B. Nếu a vuông góc với mặt phẳng (a) và b  (a) thì a ^ . b C. Nếu a b và b ^ c thì c ^ . a
D. Nếu a ^ b , b ^ c và a cắt c thì b vuông góc với mặt phẳng ( , a c). Lời giải Chọn D
Nếu a ^ b và b ^ c thì a c hoặc a cắt c hoặc a trùng c hoặc a chéo .c b b b a P P P a c c
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 753
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 7: Chỉ ra mệnh đề sai trong các mệnh đề sau:
A. Hai đường thẳng chéo nhau và vuông góc với nhau. Khi đó có một và chỉ một mặt
phẳng chứa đường thẳng này và vuông góc với đường thẳng kia. B. Qua một điểm O cho
trước có một mặt phẳng duy nhất vuông góc với một đường thẳng  cho trước. C. Qua một điểm O cho
trước có một và chỉ một đường thẳng vuông góc với một đường thẳng cho trước.
D. Qua một điểm O cho trước có một và chỉ một đường thẳng vuông góc với một mặt phẳng cho trước. Lời giải Chọn C b P O a c
Mệnh đề C sai vì qua một điểm O cho trước có vô số đường thẳng vuông góc với một
đường thẳng cho trước.
Câu 8: Trong các mệnh đề sau, mệnh đề nào sai?
A. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
B. Có duy nhất một mặt phẳng đi qua một đường thẳng cho trước và vuông góc với một mặt phẳng cho trước.
C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
D. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước. Lời giải Chọn D A P O
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 754
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Qua một điểm cho trước có thể kẻ được vô số mặt phẳng vuông góc với mặt phẳng cho trước.
Câu 9: Trong các mệnh đề sau đây, mệnh đề nào là đúng?
A. Nếu hai mặt phẳng vuông góc với nhau thì mọi đường thẳng thuộc mặt phẳng này sẽ
vuông góc với mặt phẳng kia.
B. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thứ ba thì song song với nhau. C. Với mỗi điểm A Î (a) và
mỗi điểm B Î (b) thì ta có đường thẳng AB vuông góc với giao tuyến d của (a) và (b).
D. Nếu hai mặt phẳng (a) và
(b) đều vuông góc với mặt phẳng (g) thì giao tuyến d của
(a) và (b) nếu có sẽ vuông góc với (g). Lời giải Chọn D
Mệnh đề A sai vì nếu hai mặt phẳng vuông góc với nhau thì mọi đường thẳng thuộc mặt
phẳng này vuông góc với giao tuyến sẽ vuông góc với mặt phẳng kia. A Q B P O C
Mệnh đề B sai vì còn trường hợp hai mặt phẳng cắt nhau. A P R Q O
Mệnh đề C sai vì đường thẳng AB có thể không vuông góc với giao tuyến.
Câu 10: Trong các mệnh đề sau mệnh đề nào đúng?
A. Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của
nó trên mặt phẳng đã cho.
B. Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và đường thẳng b
với b vuông góc với (P).
C. Góc giữa đường thẳng a và mặt phẳng
(P) bằng góc giữa đường thẳng a và mặt phẳng (Q) thì
mặt phẳng (P) song song với mặt phẳng . (Q)
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 755
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
D. Góc giữa đường thẳng a và mặt phẳng
(P) bằng góc giữa đường thẳng b và mặt
phẳng (P) thì a song song với . b Lời giải Chọn A
Mệnh đề B sai vì hai góc này phụ nhau.
Mệnh đề C sai vì (P) có thể trùng (Q) .
Mệnh đề D sai vì a có thể trùng . b
Dạng 2. Chứng minh đường thẳng vuông góc với mặt phẳng. Từ đó suy ra đường thẳng
vuông góc với đường thẳng 1. Phương pháp
Để chứng minh đường thẳng vuông góc với mặt phẳng ta có thể sử dụng một ttrong các cách sau a  b  () 
1. a  c  ()  a  () (a vuông góc với hai đường thẳng cắt nhau) bc  A  a / /b 2. 
 a  () ( a song song với một đường thẳng b vuông góc (P) ) b  () a  ( )  3.   a  () () / /( ) 
4. AB  ()  M | MA  
MB , () là mặt phăng trung trực của AB  ABC   () 
5. MA  MB  MC  MO  () OA  OB  OC 
Để chứng minh đường thẳng vuông góc với đường thẳng ngoài 4 cách đã biết ở bài hai
đường thẳng vuông góc ta có thểm sử dụng thêm các cách sau a  () 1.   a  b b  () a / /() 2.   a  b b  () a'  hch (a) 3.    b  a  b  a' b   ABC,a  AB 4.   a  BC  a  AC
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 756
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Cho tứ diện SABC có SA vuông góc với mặt phẳng (ABC). Kẻ BE vuông góc với AC E AC. Khi đó: A. BE  SBC. B. BE  SAB. C. BE  SAC.
D. BE là đường phân giác của góc  ABC . Hướng dẫn giải ĐÁP ÁN C
Do SA  BE, BE  AC  BE  SAC.
Ví dụ 2: Cho tam giác ABC vuông tại C. Kẻ SA  ABC , AE  SC và AF  SB . Khi đó: A. AF // BC. B. AE  SBC. C. AF  SBC. D SB  AEF. Hướng dẫn giải ĐÁP ÁN D Ta có: ìïBC ^ AC ïí
BC ^ (SAC) BC ^ AE ( ) 1 ïBC ^ SA ïî
Theo giả thiết: SC ^ AE ( ) 2
Từ (1) và (2) suy ra AE  SB mà AF  SB  SB  AEF.
Ví dụ 3: Cho hình chóp S.ABCD đáy là hình thoi tâm O và SA  SC , SB  SD. Khi đó:
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 757
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
A. SO là đường cao của hình chóp.
B. Tam giác SBD vuông cân.
C. Tam giác SAC vuông cân. D.  1 SO BD. 2 Hướng dẫn giải ĐÁP ÁN A
O là tâm hình thoi  O là trung điểm của AC, BD mà mỗi SAC, SBD cân
 SO  AC, SO  BD  SO  ABCD  SO là đường cao hình chóp.
Lưu ý: Tam giác SAC, SBD chỉ cân chứ không vuông
Ví dụ 4: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SA  SC , SB  SD. Gọi
I, J theo thứ tự là trung điểm của AB và BC thì A. IJ  SAD. B. IJ  SCD. C. IJ  SAC. D. IJ  SBD. Hướng dẫn giải ĐÁP ÁN D
SAC, SBD cân  SO  ABCD
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 758
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133  SO  IJ IJ // AC  IJ  BD  IJ  SBD.
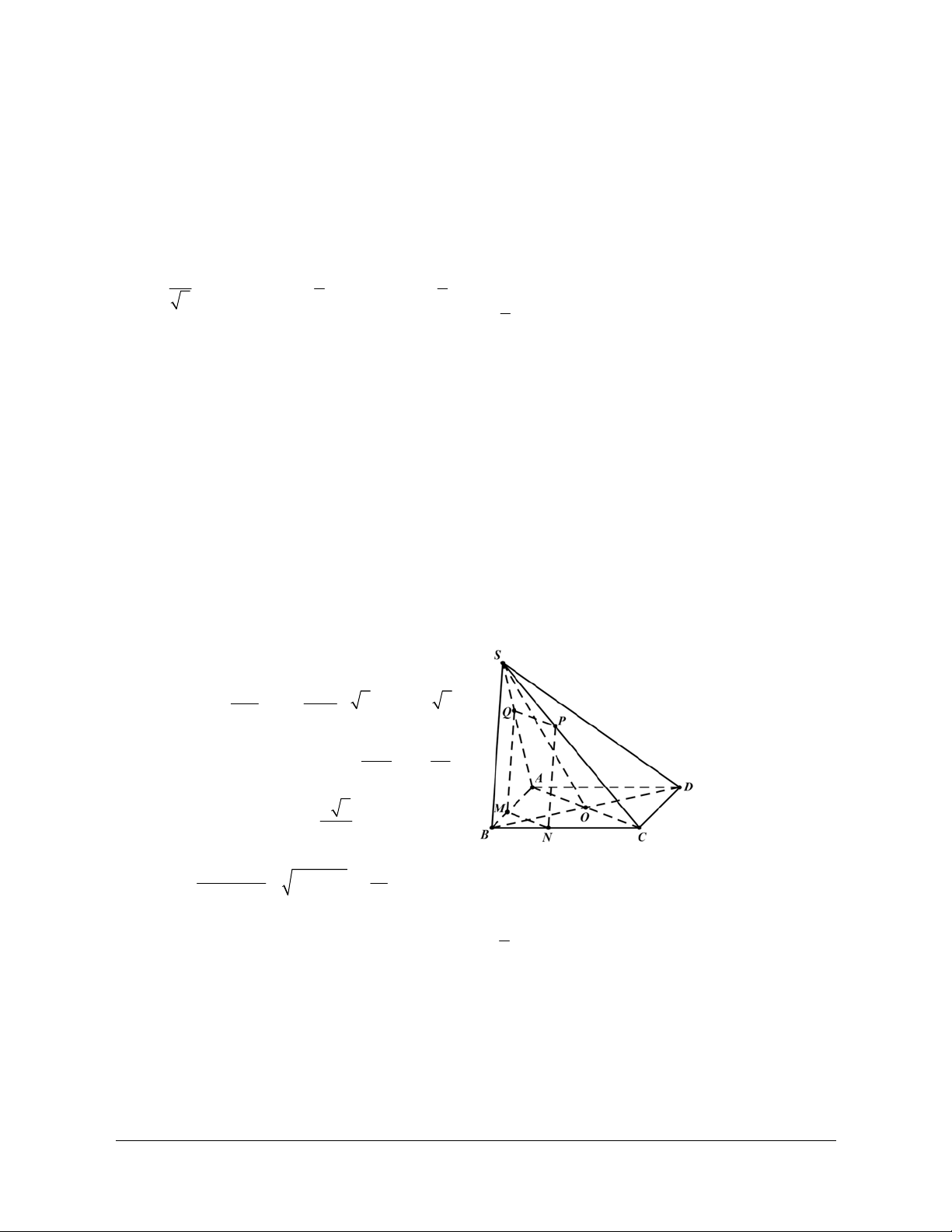
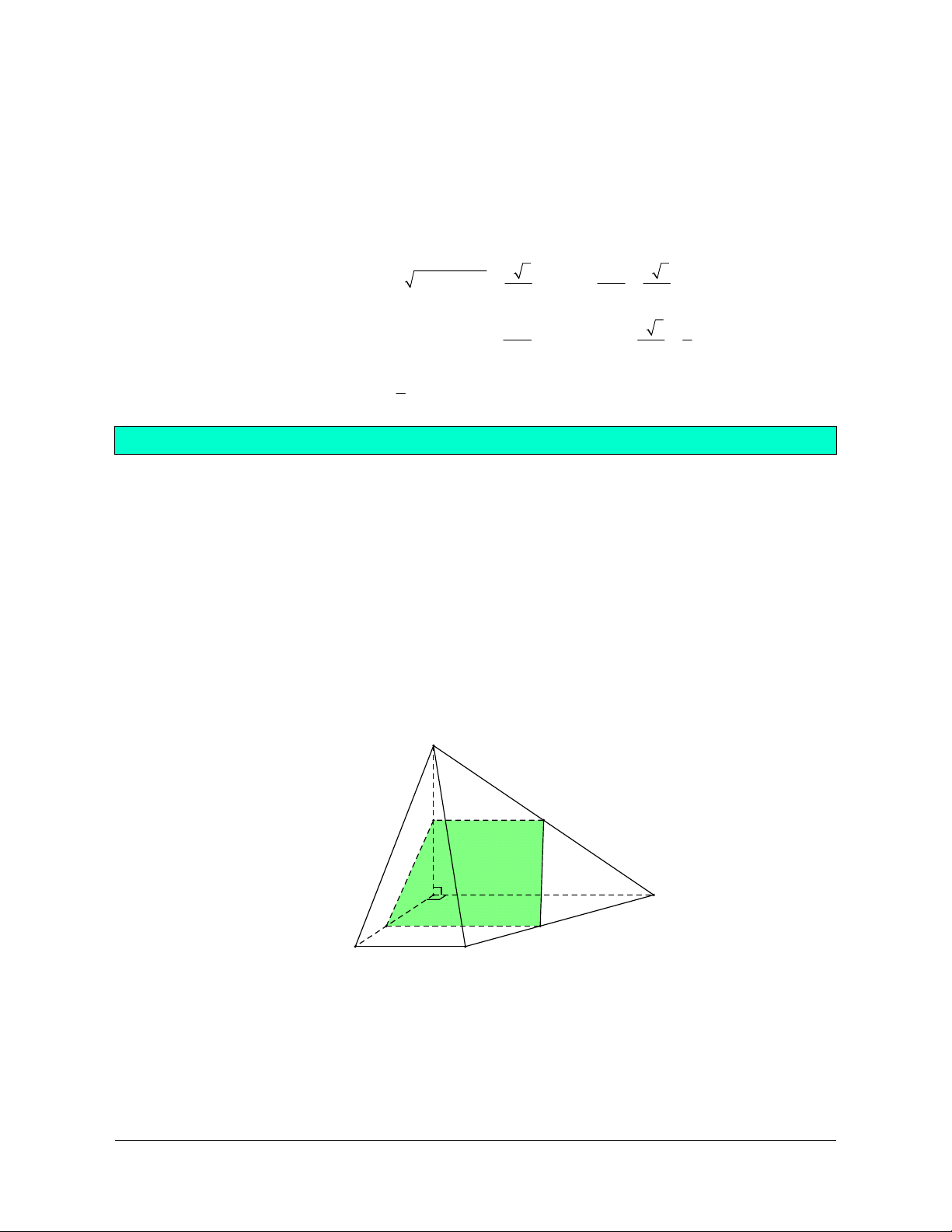
Ví dụ 5: Cho hình chóp S.ABCD đáy ABCD là hình vuông cạnh a, cạnh bên SB  b và tam
giác SAC cân tại S. Trên cạnh AB lấy một điểm M với AM  x0  x  a . Mặt phẳng 
qua M song song với AC và SB cắt BC, SB, SA lần lượt tại N, P, Q. Giá trị x để S lớn MNPQ nhất bằng a a a D. A. . B. . C. . 5 4 2 a . 3
Phân tích: Trước hết ta phải xác định được MNPQ là hình chữ nhật
Vì  // SB và  // AC nên MNPQ là hình bình hành. AC  SO ( A  CS caân)    AC  SBD
AC  BD (ñöôøng cheùo hình vuoâng)
 AC  SB , mà MQ // SB  MN  MQ
Vậy MNPQ là hình chữ nhật. Hướng dẫn giải ĐÁP ÁN C Ta có: MN // AC BM a     x MN .AC .a 2  a  x 2 BA a  AM bx SAB có: MQ // SB  MQ  .SB  AB a   b 2 S MN.MQ a  x x MNPQ  a    2 a x x a Ta có:  a  xx   a  xx 2 4  S
lớn nhất khi và chỉ khi a  x  x   a x . MNPQ 2
3. Bài tập trắc nghiệm
Câu 11: Cho hình chóp S.ABC có đáy ABC là tam giác cân tại
C. Cạnh bên SA vuông góc với đáy. Gọi
H , K lần lượt là trung điểm của AB và .
SB Khẳng định nào dưới đây sai?
A. CH ^ AK.
B. CH ^S . B
C. CH ^S . A
D. AK ^ S . B Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 759
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn D S K B C H A
Vì H là trung điểm của AB , tam giác ABC cân suy ra CH ^ AB.
Ta có SA ^ (ABC) SA ^ CH mà CH ^ AB suy ra CH ^ (SAB).
Mặt khác AK Ì (SAB) ¾¾
CH vuông góc với các đường thẳng SA, SB, AK.
Và AK ^ SB chỉ xảy ra khi và chỉ khi tam giác SAB cân tại S. .
Câu 12: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại
B, cạnh bên SA vuông góc với
đáy. Gọi H là chân đường cao kẻ từ A của tam giác SA .
B Khẳng định nào dưới đây là sai?
A. SA ^ B . C
B. AH ^ B . C
C. AH ^ A . C
D. AH ^ S . C Lời giải Chọn C S H A C B
Theo bài ra, ta có SA ^ (ABC) mà BC Ì(ABC) SA ^ BC.
Tam giác ABC vuông tại B, có AB ^ BC BC ^ (SAB) BC ^ AH. ìï ^ Khi đó AH SB ïí
AH ^ (SBC)  AH ^ SC. ïAH ^ BC ïî
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 760
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Nếu AH ^ AC mà SA ^ AC suy ra AC ^ (SAH )  AC ^ AB (vô lý).
Câu 13: Cho tứ diện ABC . D Gọi H là
trực tâm của tam giác BCD và AH vuông góc với mặt
phẳng đáy. Khẳng định nào dưới đây là đúng?
A. CD ^ B . D
B. AC = B . D
C. AB =C . D
D. AB ^C . D Lời giải Chọn D A B D C
Vì AH vuông góc với mp (BCD) suy ra AH ^ CD. ( ) 1
Mà H là trực tâm của tam giác BCD BH ^ CD. (2) CD ìï ^ AH Từ ( ) 1 ,(2) suy ra ïí
CD ^ (ABH )  CD ^ A . B CD ï ^ BH ïî
Câu 14: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm . O Biết rằng
SA = SC, SB = S . D
Khẳng định nào sau đây là đúng?
A. AB ^ (SAC).
B. CD ^ A . C
C. SO ^ (ABCD).
D. CD ^ (SBD). Lời giải Chọn C S A B D C
Vì SA = SC  DSAC cân tại S mà O là trung điểm AC SO ^ AC.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 761
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Tương tự, ta cũng có SO ^ BD mà AC Ç BD = O Ì(ABCD)  SO ^ (ABCD).
Câu 15: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm .
O Cạnh bên SA vuông góc với
đáy. Khẳng định nào sau đây là sai?
A. SA ^ B . D
B. SC ^ B . D
C. SO ^ B . D
D. AD ^ S . C Lời giải Chọn D S A D O B C
Vì SA vuông góc với mp (ABCD)  SA ^ BD.
Mà ABCD là hình thoi tâm O AC ^ BD nên suy ra BD ^ (SAC). ìïBD ^ SO
Mặt khác SO Ì(SAC) và SC Ì(SAC) suy ra ïí . ïBD ^ SC ïî
Và AD, SC là hai đường thẳng chéo nhau.
Câu 16: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm . O Đường thẳng SA cuông góc với mặt đáy .
(ABCD) Gọi I là trung điểm của .
SC Khẳng định nào dưới đây là sai?
A. IO ^ (ABCD).
B. BC ^S . B
C. Tam giác SCD vuông ở . D
D. (SAC) là mặt phẳng trung trực của . BD Lời giải Chọn D
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 762
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 S I A D O B C Vì ,
O I lần lượt là trung điểm của AC, SC suy ra OI là đường trung bình của tam giác
SAC OI // SA mà SA ^ (ABCD)  OI ^ (ABCD).
Ta có ABCD là hình chữ nhật  BC ^ AB mà SA ^ BC suy ra BC ^ SB. CD ìï ^ AD
Tương tự, ta có được ïí ï ^ ï (  CD ^ SD CD SA SA ^ (ABCD)) . î
Nếu (SAC) là mặt phẳng trung trực của BD ¾¾
BD ^ AC : điều này không thể xảy ra vì
ABCD là hình chữ nhật.
Câu 17: Cho hình chóp S.ABCD với đáy ABCD là hình thang vuông tại A và D , có
AD =CD = a ,
AB = 2a . Cạnh bên SA vuông góc với đáy (ABCD) , E là trung điểm của . AB Chỉ ra
mệnh đề sai trong các mệnh đề sau:
A. CE ^ (SAB).
B. CB ^ (SAC).
C. Tam giác SDC vuông tại . D
D. CE ^ (SDC). Lời giải Chọn D S E A B D C CE ìï ^ AB
Từ giả thết suy ra ADCE là hình vuông ï  í . CE ï = AD = a ïî
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 763
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 CE ìï ^ AB Ta có ïí
CE ^ (SAB). Do đó A đúng. C ï E ^ SA ( do SA ^ ABCD) ïî 1
Vì CE = AD = a CE = AB A
D BC vuông tại C CB ^ AB . Kết hợp với CB ^ SA (do 2
SA ^ (ABCD) ) nên suy ra CB ^ (SAC). Do đó B đúng. CD ìï ^ AD Ta có ïí
CD ^ (SAD)  CD ^ SD. Do đó C đúng. C ï D ^ SA ( do SA ^ ABCD) ïî
Dùng phương pháp loại trừ, suy ra D là đáp án sai.
Câu 18: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi
AE, AF lần lượt là đường cao của tam giác SAB và tam giác . SAD Khẳng
định nào dưới đây là đúng?
A. SC ^ (AFB).
B. SC ^ (AEC).
C. SC ^ (AED).
D. SC ^ (AEF ). Lời giải Chọn D S F E D A B C
Vì SA vuông góc với mặt phẳng (ABCD)  SA ^ BC.
Mà AB ^ BC nên suy ra BC ^ (SAB) BC ^ AE Ì(SAB).
Tam giác SAB có đường cao AE AE ^ SB mà AE ^ BC AE ^ (SBC) AE ^ SC.
Tương tự, ta chứng minh được AF ^ SC . Do đó SC ^ (AEF ).
Câu 19: Cho hình chóp SABC có SA ^ (ABC). Gọi
H , K lần lượt là trực tâm các tam giác SBC và
ABC . Mệnh đề nào sau đây sai? A. BC ^ (SAH ). B.
SB ^ (CHK ). C. HK ^ (SBC). D.
BC ^ (SAB). Lời giải Chọn D
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 764
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 S A C H K M B ìïBC ^ SA  Ta có ïí
BC ^ (SAH ). Do đó A đúng. ïBC ^ SH ïî CK ìï ^ AB  Ta có ïí
CK ^ (SAB) CK ^ S . B CK ï ^ SA ïî
Mặt khác có CH ^ SB. Từ đó suy ra SB ^ (CHK ). Do đó B đúng.
ìïBC ^ (SAH ) BC ^ HK  Ta có ïí
HK ^ (SBC). Do đó C đúng. SB ï
^ (CHK )  SB ^ ï HK î
Dùng phương pháp lại trừ, suy ra D sai.
Câu 20: Cho hình lập phương ABC . D A B ¢ C ¢ D
¢ .¢ Đường thẳng AC¢ vuông góc với mặt phẳng nào sau đây?
A. (A ¢BD).
B. (A ¢DC ¢).
C. (A ¢CD ¢).
D. (A¢B C ¢ D). Lời giải Chọn A A' B' D' C' A B D C Ta có AA ¢D A
¢ là hình vuông suy ra AD¢ ^ A¢ . D ( ) 1 Và ABC . D A B ¢ C ¢ D
¢ ¢ là hình lập phương suy ra AB ^ A¢D. (2)
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 765
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Từ ( ) 1 ,(2) suy ra A D ¢ ^(ABC D ¢ ¢)  A D ¢ ^ AC .¢
Lại có ABCD là hình vuông  AC ^ BD mà AA¢ ^ BD (AA¢ ^ (ABCD))  BD ^ (AA C ¢ C
¢ )  BD ^ AC¢ . Kết hợp với A D
¢ ^ AC¢ suy ra AC¢ ^(A¢BD).
Câu 21: Cho tứ diện OABC có OA, , OB OC
đôi một vuông góc với nhau. Gọi H là hình chiếu của
O trên mặt phẳng .
(ABC) Mệnh đề nào sau đây là sai?
A. OA ^ B . C B. 1 1 1 1 = + + . 2 2 2 2 OH OA OB OC
C. H là trực tâm AB D . C D. 2 2 2 2
3OH = AB + AC + BC . Lời giải Chọn D A H C O B OA ìï ^ OB  ïí
OA ^ (OBC)  OA ^ BC. Do đó A đúng. ( ) 1 OA ï ^ OC ïî
 Gọi I = AH Ç BC.
Theo giả thiết ta có OH ^ (ABC) OH ^ BC. (2) Từ ( )
1 và (2) , suy ra BC ^ (AOI )  BC ^ OI . Tam giác vuông 1 1 1 BOC, ta có = + . 2 2 2 OI OB OC Tam giác vuông 1 1 1 1 1 1 AOI , ta có = + = + + . Do đó B đúng. 2 2 2 2 2 2 OH OA OI OA OB OC
 Từ chứng minh trên BC ^ (AOI )  BC ^ AI . (3)
Gọi J = BH Ç AC. Chứng mình tương tự ta có AC ^ BJ . (4)
Từ (3) và (4), suy ra H là trực tâm DABC. Do đó C đúng. Vậy D là đáp án sai.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 766
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Dạng 3. Xác định góc – hình chiếu – tính độ dài 1. Phương pháp
 Bước 1: Tìm giao điểm O của a với  .  a
Bước 2: Chọn A  a và dựng AH   , với A H .   Khi đó: AOH  a, O H  
Bước 3: Tính số đo của AOH dựa trên 
các hệ thức lượng trong tam giác.
Các trường hợp đặc biệt   0
a  ()  a,()  90   a / /()   0  a,()   0 a ( )      0
Chú ý: Nếu a,()     thì 0    90
2. Các ví dụ rèn luyện kĩ năng
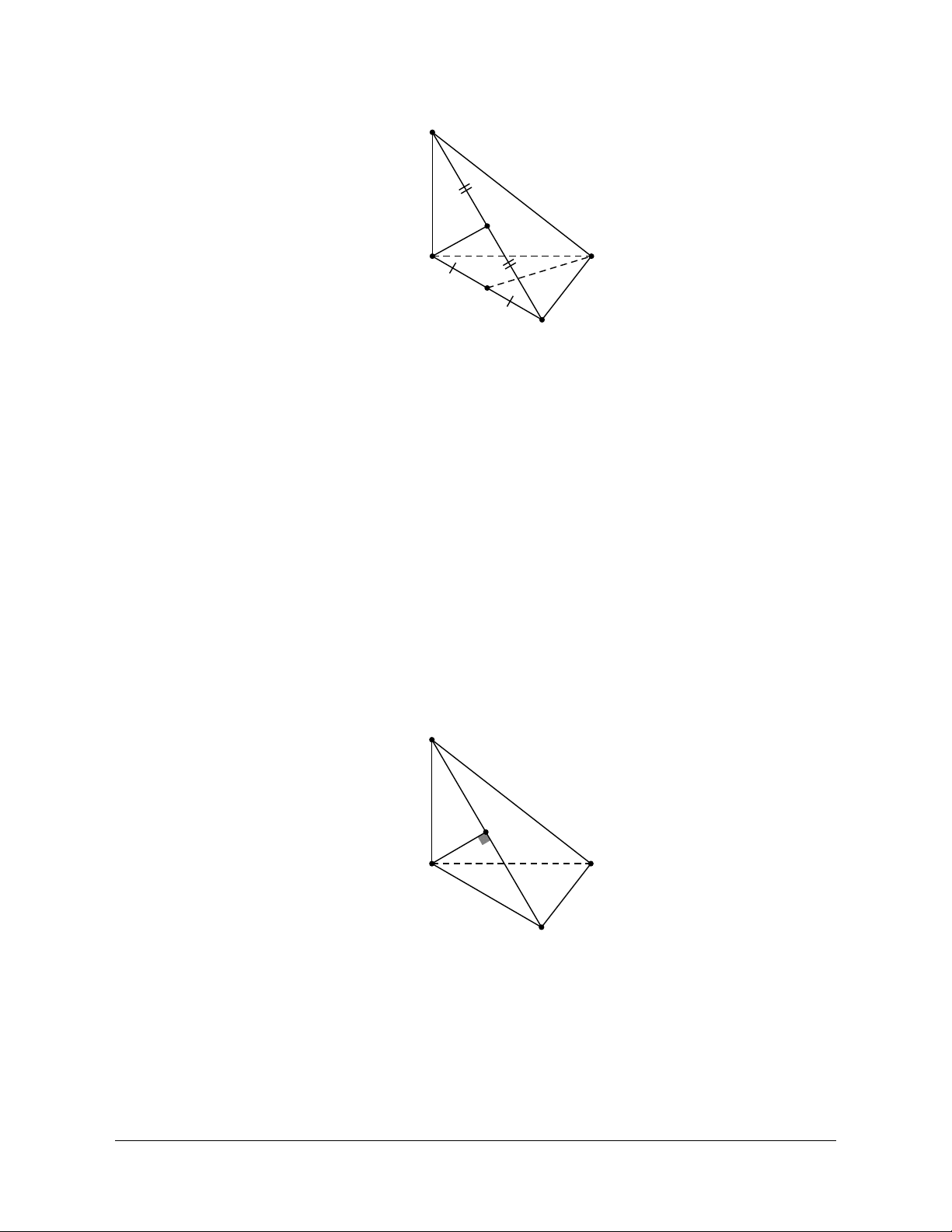
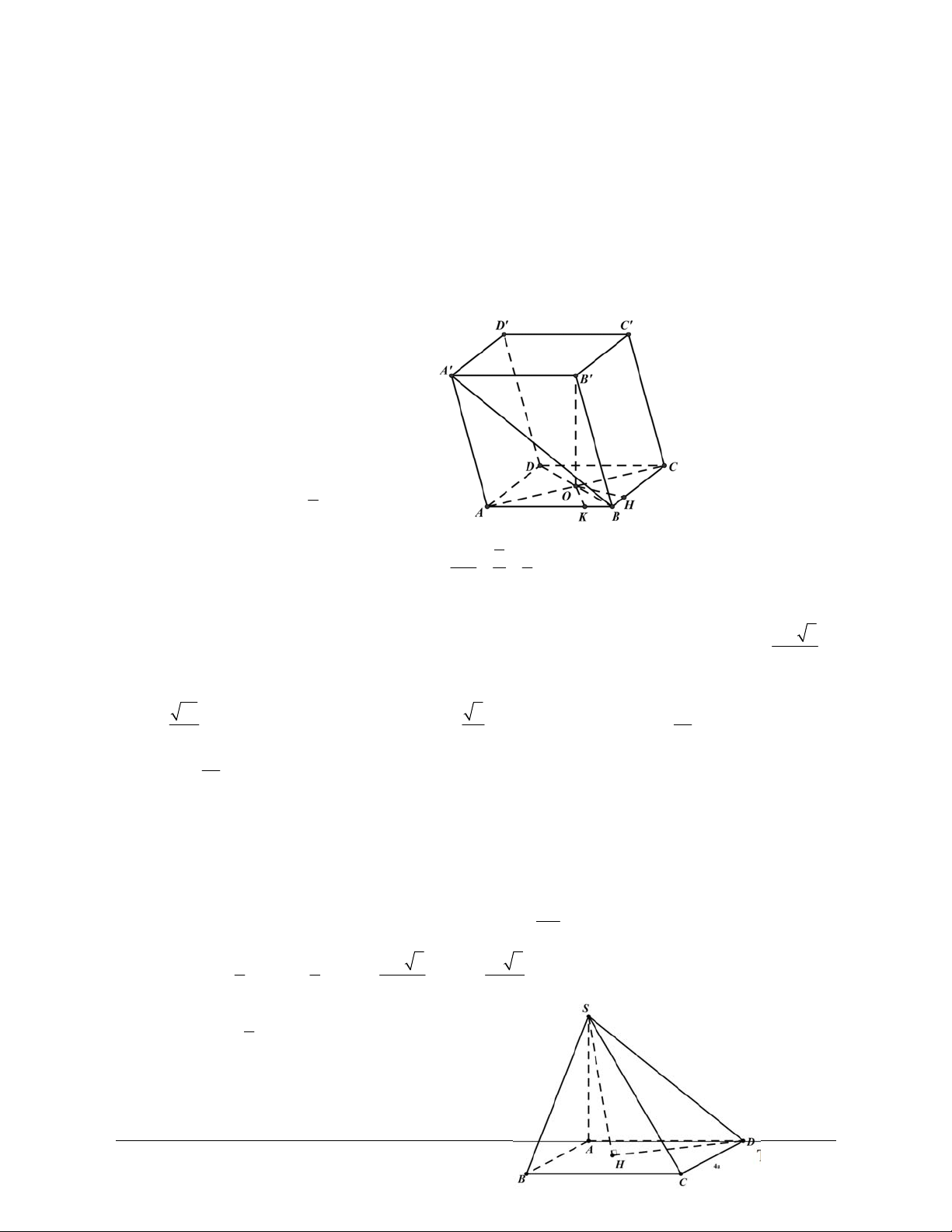
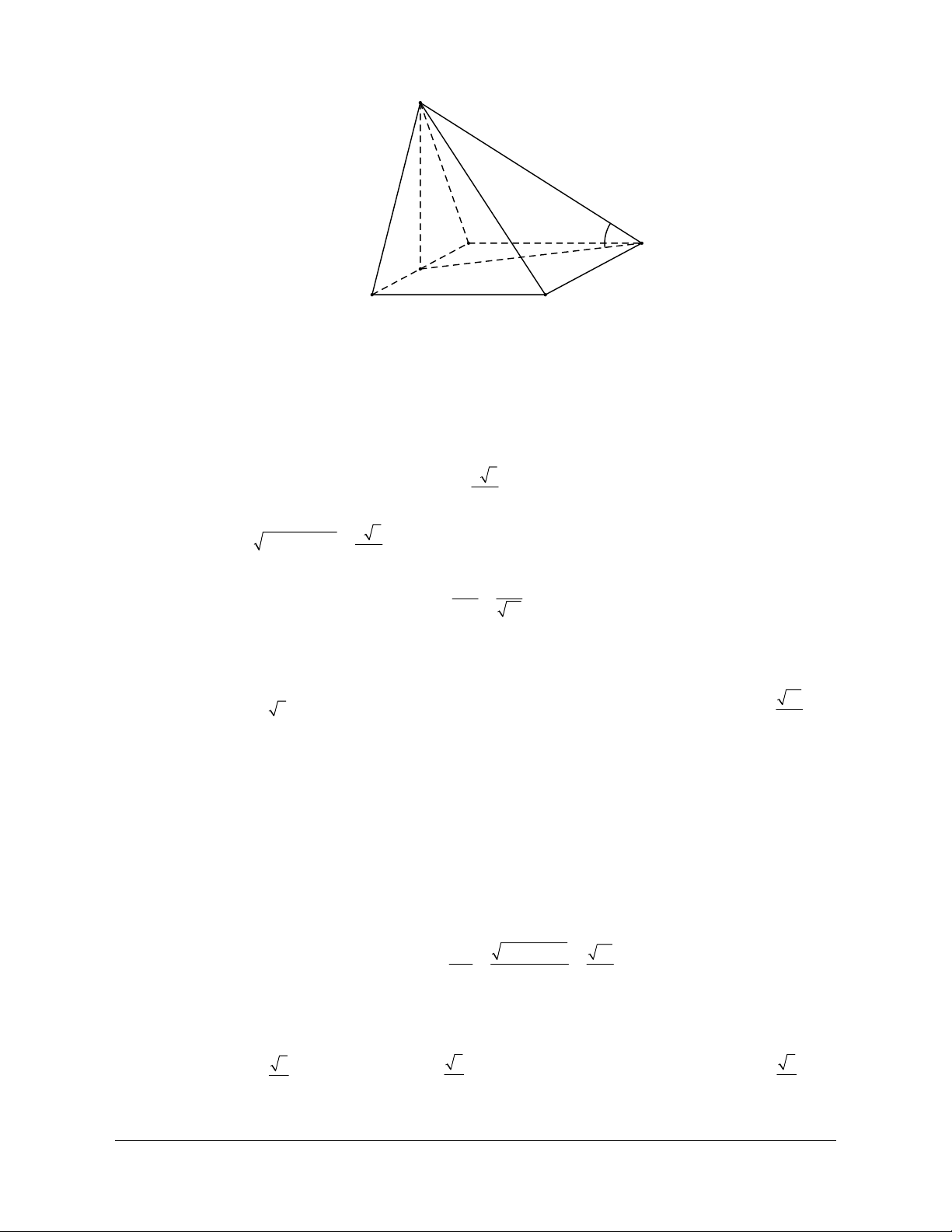
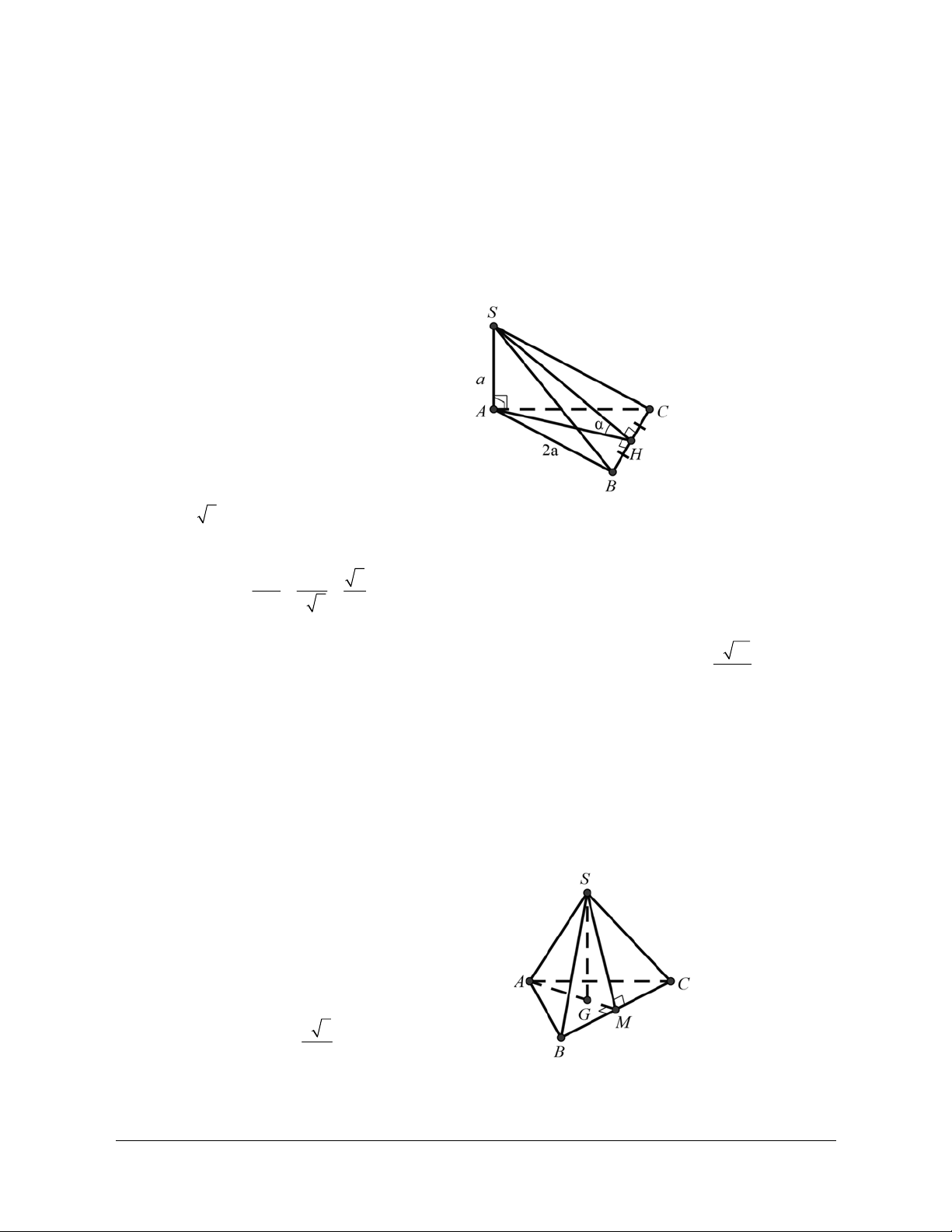
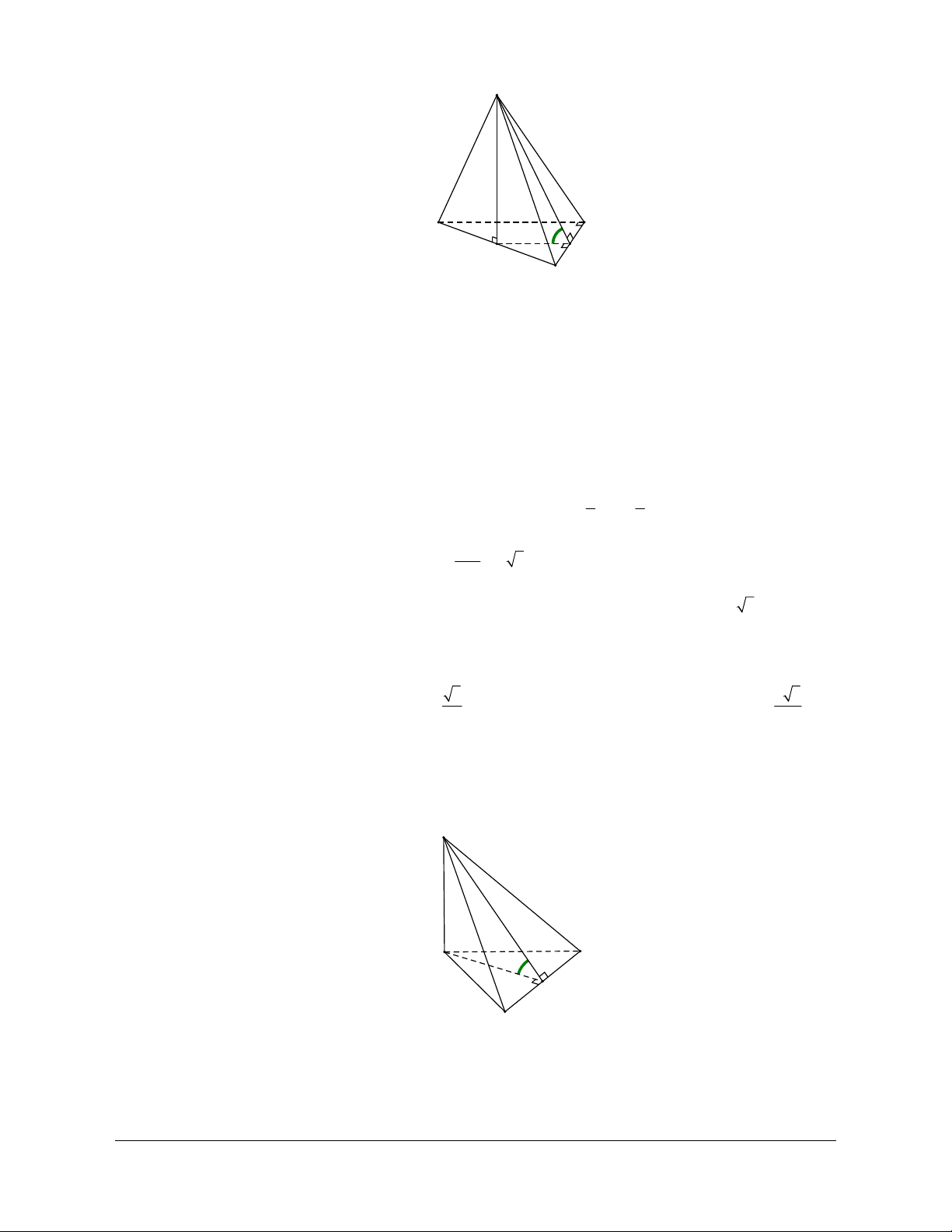
Ví dụ 1: Cho tứ diện SABC có SA  ABC và SA  a, AB  a 3, tam giác SBC cân tại S.
a) Góc  giữa đường thẳng SB với mặt phẳng (ABC) là A. 30 .  B. 60 .  C. 45 .  D. 90 . 
b) Góc  giữa đường thẳng SC với mặt phẳng (ABC) là A. 30 .  B. 60 .  C. 45 .  D. 90 .  Hướng dẫn giải
Xác định góc  và  . Ta có: SA  ABC
AB laø hình chieáu cuûa SB treân (ABC)
 AC laø hình chieáu cuûa SC treân (ABC)     SBA    .     SCA a) ĐÁP ÁN A
SA  ABC  SA  AB  SAB vuông tại A. Do đó: SA a 1 tan        30 . AB a 3 3
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 767
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 b) ĐÁP ÁN B 2  2  2  2  2     2 SAB : SB SA AB a a 3 4a
Do đó: SB  2a  SC  SB  2a
Mặt khác: SA  ABC  SA  AC  SAC vuông tại A SA a 1  sin       30 . SC 2a 2
Ví dụ 2: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  a , AD  a 3 . Cạnh
SA vuông góc với đáy và SA  a.
a) Góc  giữa đường thẳng SB và mặt phẳng (ABCD) là A. 30 .  B. 60 .  C. 45 .  D. 90 . 
b) Góc  giữa đường thẳng SD và mặt phẳng (ABCD) là A. 30 .  B. 60 .  C. 45 .  D. 90 . 
c) Góc  giữa đường thẳng SD và mặt phẳng (SAB) là A. 30 .  B. 60 .  C.   45 . D. 90 .  Hướng dẫn giải
Xác định góc  và  . Ta có:   
AB laø hình chieáu cuûa SB treân (ABCD)   SBA SA  ABCD    
AD laø hình chieáu cuûa SD treân (ABCD)      SDA a) ĐÁP ÁN C
Góc  giữa đường thẳng SB và mặt phẳng (ABCD) là  SBA
SA  ABCD  SAB vuông cân tại A   SBA    4  5 . b) ĐÁP ÁN A
Góc  giữa đường thẳng SD và mặt phẳng (ABCD) là  SDA
SA  ABCD  SAB vuông tại A SA 3  tan      30 . AD 3 c) ĐÁP ÁN B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 768
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
DA  SAB  SA là hình chiếu của SD trên (SAB)     ASD  AD
SAD vuông tại A  tan    3    60 . SA
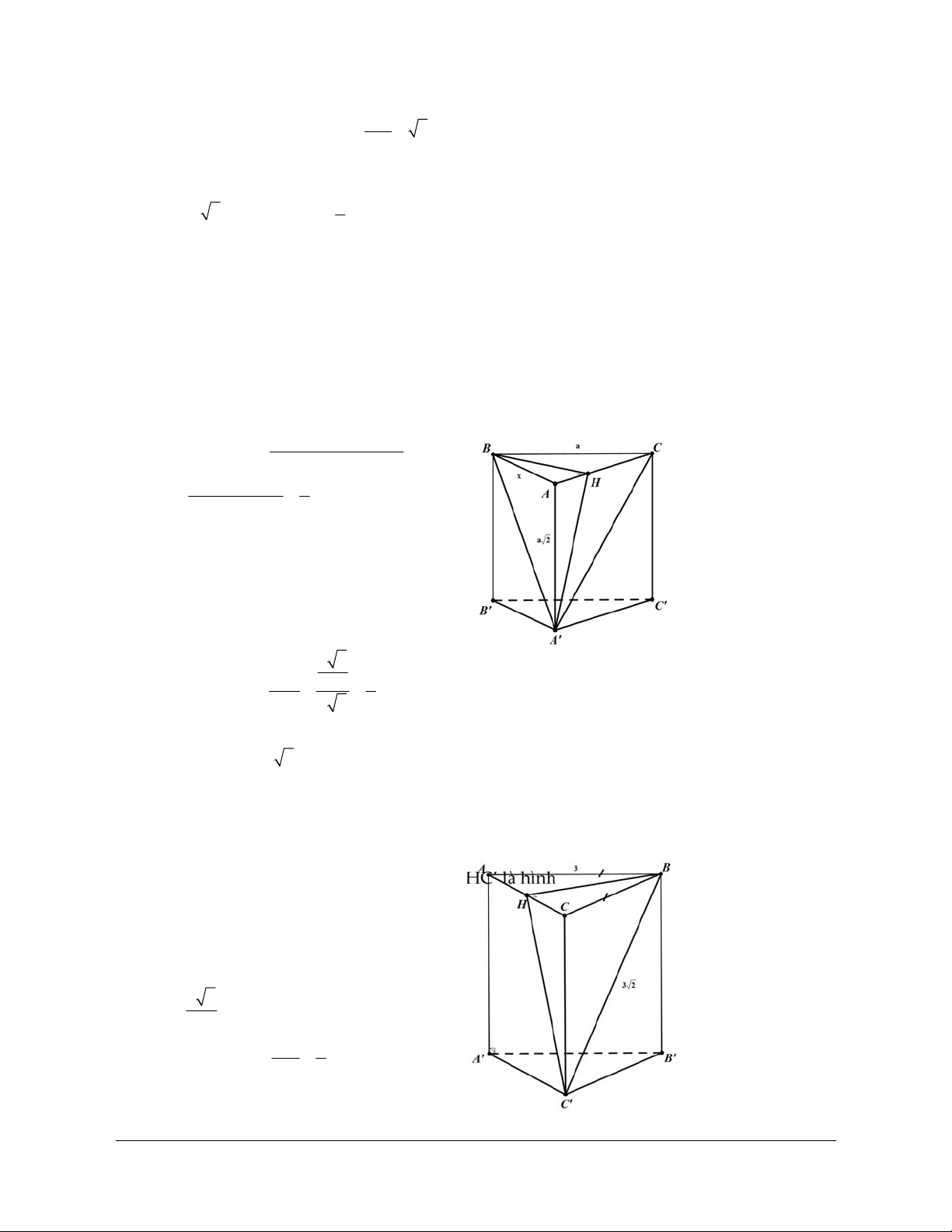
Ví dụ 3: Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân tại A, BC  a , AAʹ  a 2 và   5 cos BAʹC
. Góc giữa đường thẳng A’B và mặt phẳng (A A’C’C) bằng 6 A. 30 .  B. 45 .  C. 60 .  D. 90 .  Hướng dẫn giải ĐÁP ÁN A Đặt AB  x thì 2  2  2  2 Aʹ B AʹC x 2a
Áp dụng định lí côsin trong Aʹ BC , ta có:  2 2 2 Aʹ B  AʹC  BC cos BAʹC  2Aʹ B.AʹC 2 2 2 2x  4a  a 5     2 x a 2 2 x  2a  6
Kẻ BH  AC , khi đó BH  AAʹCʹC
Suy ra góc giữa đường thẳng A’B và mặt phẳng (AA’C’C) là góc  BAʹH .
Trong tam giác vuông A’BH có a 3  BH 1 2  sin BAʹH     BAʹH  30 . Aʹ B a 3 2
Ví dụ 4: Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B. Biết
AB  3cm, BCʹ  3 2cm . Góc hợp bởi đường thẳng BC’ và mặt phẳng (ACC’A’) bằng A. 90 .  B. 60 .  C. 45 .  D. 30 .  Hướng dẫn giải ĐÁP ÁN D
Gọi H là trung điểm của cạnh AC, suy ra HC’ là hình
chiếu của BC’ lên mặt phẳng (ACC’A’) Do đó         BCʹ, ACCʹ Aʹ BCʹ,HCʹ
Ta có tam giác BHC’ vuông tại H, cạnh  3 2 BH cm 2 BH 1 Ta có   sin HCʹ B    HCʹB  30 . BCʹ 2 Vậy     BCʹ, ACCʹ Aʹ  30 . 
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 769
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ví dụ 5: Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a,  A  60 .  Chân
đường vuông góc hạ từ B’ xuống mặt phẳng (ABCD) trùng với giao điểm của hai
đường chéo của đáy ABCD. Cho BBʹ  a. Góc giữa cạnh bên và mặt đáy bằng A. 30 .  B. 45 .  C. 60 .  D. 90 .  Hướng dẫn giải ĐÁP ÁN C
Tính góc giữa cạnh bên và mặt phẳng đáy.
Gọi O  AC  BD . Theo giả thiết ta có BʹO  ABCD BʹB  ABCD   B  BʹO  ABCD , O  ABCD
 Hình chiếu B’B trên (ABCD) là OB
BʹB,ABCD BʹB,BO     BʹBO
Tam giác ABD có AB  AD  a ,  BAD  60  ABD là tam giác đều   a OB 2 a OB 1
Trong tam giác vuông B’OB:  2  cos BʹOB     BʹOB  60 . BBʹ a 2
Ví dụ 6: Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng 4a. Hai mặt 2 8a 6
phẳng (SAB) và (SAD) cùng vuông góc với đáy. Tam giác SAB có diện tích bằng . 3
Côsin của góc tạo bởi đường thẳng SD và mặt phẳng (SBC) bằng 19 6 6 A. . B. . C. . 5 5 25 19 D. . 25 Hướng dẫn giải ĐÁP ÁN A
Gọi H là hình chiếu vuông góc của D trên mặt phẳng (SBC)               SH SD; SBC HSD cos SD; SBC  cos DSH  SD 2  1  1  8a 6   4a 6 S SA.AB SA.4a SA ABC 2 2 3 3  1 V DH.S và D.SBC SBC 3
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 770
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 1 V  V  .SA.S D.SBC S.BCD BCD 3 3 1 4a 6 1 32a 6  . . .4a.4a  3 3 2 9 3 3  1  32a 6   32a 6 DH.S DH SBC 3 9 3SSBC BC  AB 1 1 Từ 
 BC  SAB  BC   S
 BC.SB  .4a.SB  2a.SB BC  SB  SA SBC 2 2 2 2   2 2 2 4a 6 2 80a 80 2 80 SB  SA  AB     16a   SB  a  S  2a SBC  3  3 3 3   3 32a 6 4a 10 Thế vào (1)  DH   80 5 2 3.2a 3  2 2 2  2  2   4a 6   2 16a  80a  SD  80 SD SA AD   a  3  3 3  2 2 2  2  2 
2  80a   4a 10   304a SH SD HD   3  5  15 304 a   304       SH  15 SA a cos SD; SBC  19 . 15 SD 80 5 a 3
3. Bài tập trắc nghiệm
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với mặt phẳng đáy. Gọi
I , J, K lần lượt là trung điểm của
AB, BC, S .
B Khẳng định nào dưới đây là đúng?
A. (IJK ) //(SAC).
B. Góc giữa SC và BD bằng 0 60 .
C. BD ^ (IJK ).
D. BD ^ (SAC). Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 771
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 S K A D I B J C Xét tam giác BK BJ SBC, có 1 =
= suy ra JK song song với SC ( ) 1 . BS BC 2 Tam giác BI BK SAB, có 1 = =
suy ra IK song song với SA (2). BA BS 2 Từ ( )
1 ,(2) suy ra mp (IJK ) // mp (SAC) ( ) * .
Vì ABCD là hình vuông  BD ^ AC mà SA ^ BD suy ra BD ^ (SAC).
Kết hợp với (*), ta được BD ^ (IJK ). Vậy góc giữa hai đường thẳng SC, BD bằng 0 90 .
Câu 2: Cho tứ diện ABCD có
AB, BC, BD
đôi một vuông góc với nhau. Khẳng định nào dưới đây đúng? A. Góc giữa CD và
mặt phẳng (ABD) là góc  CBD.
B. Góc giữa AC và mặt phẳng (BCD) là góc  ACB. C. Góc giữa AD và
mặt phẳng (ABC) là góc  ADB. D. Góc giữa AC và
mặt phẳng (ABD) là góc  CBA. Lời giải Chọn B A B D C
Dựa vào đáp án, ta thấy rằng: CB ìï ^ BD A sai, vì ïí
CB ^ (ABD)  B là hình chiếu của C trên mp (ABD). CB ï ^ BA ïî
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 772
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Suy ra góc giữa CD và mặt phẳng (ABD) là góc  CDB. ìïAB ^ BC B đúng, vì ïí
AB ^ (BCD)  B là hình chiếu của A trên mp (BCD). ïAB ^ BD ïî
Suy ra góc giữa đường thẳng AC và mặt phẳng (BCD) là góc  A CB. ìï ^
C sai, vì BD BA ïí
BD ^ (ABC)  B là hình chiếu của D trên mp (ABC). ïBD ^ BC ïî
Suy ra góc giữa AD và mặt phẳng (ABC) là góc  DA B.
D sai, vì B là hình chiếu của C trên mp (ABD) suy ra góc giữa AC và mặt phẳng (ABD) là góc  CAB.
Câu 3: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại
B, cạnh bên SA vuông góc với
đáy. Gọi O là tâm đường tròn ngoại tiếp tam giác SB .
C H là hình chiếu của O trên
(ABC). Khẳng định nào dưới đây đúng?
A. H là trung điểm của cạnh A . B
B. H là trung điểm của cạnh . BC
C. H là tâm đường tròn ngoại tiếp tam giác A . BC
D. H là trọng tâm của tam giác A . BC Lời giải Chọn C S O A H C B
Ta có SA vuông góc với mp (ABC) SA ^ BC mà AB ^ BC suy ra BC ^ (SAB)
BC ^ SB  tam giác SBC vuông tại B O là trung điểm của SC.
Theo bài ra, ta có OH ^ (ABC)  OH // SA H là trung điểm của AC.
Mà tam giác ABC vuông tại B nên H là tâm đường tròn ngoại tiếp tam giác ABC.
Câu 4: Cho hình chóp S.ABC có đáy ABC là tam giác nhọn, cạnh bên SA =SB =SC . Gọi H là
hình chiếu vuông góc của S trên mặt phẳng (ABC), khi đó
A. H là trực tâm của tam giác A . BC
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 773
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
B. H là trọng tâm của tam giác A . BC
C. H là tâm đường tròn ngoại tiếp tam giác A . BC
D. H là tâm đường tròn nội tiếp tam giác ABC. Lời giải Chọn C S A B H C
Vì H là hình chiếu vuông góc của S trên mp (ABC) nên ta có Tam giác
SAH vuông tại H , có 2 2 2
SA = AH +SH . Tam giác
SBH vuông tại H , có 2 2 2
SB = BH +SH . Tam giác
SCH vuông tại H , có 2 2 2
SC = CH +SH .
Kết hợp điều kiện SA = SB = SC suy ra HA = HB = HC nên H là tâm đường tròn
ngoại tiếp tam giác ABC.
Câu 5: Cho hình chóp S.ABC có  0  0  0
BSC = 120 ,CSA = 60 , ASB = 90 và SA = SB = . SC Gọi I là hình chiếu vuông góc của S trên mặt phẳng (ABC), khi đó
A. I là trung điểm của A . B
B. I là trọng tâm của tam giác A . BC
C. I là trung điểm của A . C D. I là trung điểm của . BC Lời giải Chọn D
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 774
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 S C B I A Đặt SA = .
a Tam giác SAB vuông cân tại S, có 2 2
AB = SA +SB = a 2.
Tam giác SAC cân tại S, có  0
CSA = 60 suy ra SA = SC = AC = . a
Áp dụng định lí Cosin cho tam giác SBC, ta có 2 2 2 
BC = SB + SC - 2.SB.SC. cos BSC 2 2 2 2 0 2 2 2
BC = a + a - 2a . cos120 = 3a BC = a 3 = AB + AC .
Khi đó, tam giác ABC vuông tại A mà I là hình chiếu của S trên mp (ABC).
Suy ra I là tâm đường tròn ngoại tiếp tam giác ABC hay chính là trung điểm BC. .
Câu 6: Cho hình hộp ABC . D A B ¢ C ¢ D ¢ ¢ có
đáy ABCD là hình thoi tâm O ,  0 BAD = 60 và A A ¢ = A B ¢ = A¢ .
D Hình chiếu vuông góc của A¢ trên mặt phẳng (ABCD) là A. trung điểm của A . O
B. trọng tâm của tam giác A . BD C. tâm
O của hình thoi ABC . D
D. trọng tâm của tam giác BC . D Lời giải Chọn B B' C' A' D' B C O H A D
Vì ABCD là hình thoi  AB = AD mà  0
BA D = 60 suy ra tam giác ABD đều ( ) 1 .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 775
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ta có A ¢A = A ¢B = A ¢D nên hình chiếu vuông góc của A ¢ trên mặt phẳng (ABCD) trùng
với tâm I của đường tròn ngoại tiếp tam giác ABD (2). Từ ( )
1 ,(2) suy ra I là tâm đường tròn ngoại tiếp tam giác ABD.
Câu 7: Cho hình chóp S.ABC có các mặt bên tạo với đáy một góc bằng nhau. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là
A. tâm đường tròn nội tiếp tam giác ABC.
B. tâm đường tròn ngoại tiếp tam giác A . BC
C. trọng tâm của tam giác ABC.
D. giao điểm của hai đường thẳng AC và . BD Lời giải Chọn A S P A C H M N B
Gọi H là hình chiếu vuông góc của S trên mặt phẳng (ABCD).
Gọi M , N , P lần lượt là hình chiếu của S trên các cạnh A , B AC, BC. SH ìï ^ AB Ta có ïí
AB ^ (SHM )  AB ^ HM , tương tự ta được HN ^ AC, HP ^ B . C SM ï ^ AB ïî
Khi đó (SAB) (ABC)  =(SM HM )   ; ;
= SMH , tương tự suy ra   
SMH = SNH = SPH.  SM D H = S D NH = SP
D H HM = HN = NP H là tâm đường tròn nội tiếp tam giác ABC.
Câu 8: Cho tứ diện ABCD có
AB, BC, CD
đôi một vuông góc với nhau và AB = a , BC = , b CD = c . Độ dài đoạn thẳng AD bằng A. 2 2 2
a + b + c . B. 2 2 2
a + b - c . C. 2 2 2
a - b + c . D. 2 2 2
-a + b + c . Lời giải Chọn A
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 776
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A B D C ìïAB ^ BC Ta có ïí
AB ^ (BCD)  tam giác ABD vuông tại . B ïAB ^ CD ïî ìïAB ^ CD Lại có ïí
CD ^ (ABC)  tam giác BCD vuông tại C. ïBC ^ CD ïî 2 2 2
ìïAD = AB + BD Khi đó ï 2 2 2 2 2 2 2 í
AD = AB + BC +CD AD = a +b + c . 2 2 2
ïïBD = BC +CD î
Câu 9: Cho tứ diện ABCD có
AB, BC, CD
đôi một vuông góc với nhau. Điểm nào dưới đây các đều bốn đỉnh A, ,
B C, D của tứ diện ? ABCD
A. Trung điểm của cạnh . BD
B. Tâm đường tròn ngoại tiếp tam giác ABC.
C. Trung điểm của cạnh A . D
D. Trọng tâm của tam giác A . CD Lời giải Chọn C A O B D C . ìïAB ^ BC Ta có ïí
AB ^ (BCD)  tam giác ABD vuông tại . B ïAB ^ CD ïî Suy ra AD
IA = IB = ID =
, với I là trung điểm của AD. ( ) 1 2 ìïAB ^ CD Lại có ïí
CD ^ (ABC)  tam giác ACD vuông tại C. ïBC ^ CD ïî
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 777
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Suy ra AD
EA = EC = ED =
, với E là trung điểm của AD. (2) 2 Từ ( )
1 ,(2) suy ra I º E nên trung điểm của cạnh AD cách đều A, , B C, . D
Câu 10: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và độ dài các cạnh bên
SA = SB = SC = . b Gọi G là
trọng tâm của tam giác A .
BC Độ dài đoạn thẳng SG bằng 2 2 2 2 2 2 2 2
A. 9b + 3a b -3a 9b - 3a b + 3a . B. . C. . D. . 3 3 3 3 Lời giải Chọn C S C A G M B
Vì SA = SB = SC và G là trọng tâm tam giác ABC
Suy ra G là chân đường cao kẻ từ đỉnh S xuống mặt phẳng (ABC). Gọi BC a
M là trung điểm của BC suy ra BM = CM = = . 2 2 Tam giác AM a a ABC đều cạnh , a có 3 1 3 GM = = . = . 3 2 3 6 2 Tam giác a
SBM vuông tại M , có 2 2 2
SM = SB - MB = b - . 4 2 2 2 2 Tam giác a a 9b -3a
SGM vuông tại G, có 2 2 2
SG = SM -GM = b - - = . 4 12 3
Câu 11: Cho hình vuông ABCD tâm O, cạnh bằng 2 . a Trên
đường thẳng qua O và vuông góc với mặt phẳng (ABCD) lấy điểm
S. Biết góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng 0 45 . Độ dài cạnh SO bằng A. a 3 a 2 SO = a 3.
B. SO = a 2. C. SO = . D. SO = . 2 2 Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 778
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 S A D O B C
Vì O là hình chiếu của S trên mặt phẳng (ABCD).
Suy ra OA là hình chiếu của SA trên mặt phẳng (ABCD)
Khi đó SA (ABCD)  =(SA OA)   0 ; ;
= SAO = 45  tam giác SAO vuông cân. ( ) 1 Tam giác AC AB
ABC vuông cân tại B, có 2 OA = = = a 2. (2) 2 2 Từ ( )
1 ,(2) suy ra SO = OA = a 2.
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh ,
AB = a BC = 2a . Hai mặt
bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy , (ABCD) cạnh .
SA = a 15 Tính
góc tạo bởi đường thẳng SC và mặt phẳng . (ABD) A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 . Lời giải Chọn C
Do SA ^ (ABCD) nên SC (ABD)  = SC (ABCD)    , ,
= SC, AC = SCA . Xét tam giác vuông SA SA SAC , ta có  tan SCA = = = 3 . 2 2 AC AB + BC Suy ra  0 SCA = 60 .
Câu 13: Cho hình chóp S.ABC có đáy ABCD là hình vuông cạnh , a tâm O .
Cạnh bên SA = 2a và
vuông góc với mặt đáy .
(ABCD) Gọi j là góc giữa SO và mặt phẳng . (ABCD) Mệnh đề nào sau đây đúng? A. tan j = 2 2. B. 0 j = 60 . C. tan j = 2. . D. 0 j = 45 . Lời giải Chọn A
Vì SA ^ (ABCD) nên hình chiếu vuông góc của SO trên mặt đáy (ABCD) là AO . Do đó (SO (ABCD))  =(SO OA)   , , = SOA. Trong tam giác vuông SA SAO , ta có  tan SOA = = 2 2. OA
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 779
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Vậy SO hợp với mặt đáy (ABCD) một góc nhọn j thỏa mãn tan j = 2 2 .
Câu 14: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , 
ABC = 60 , tam giác SBC là
tam giác đều có cạnh bằng 2a và
nằm trong mặt phẳng vuông với đáy. Tính góc giữa đường thẳng SA và mặt phẳng đáy (ABC) A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 . Lời giải Chọn C S A B H C
Gọi H là trung điểm của BC , suy ra SH ^ (ABC).
Vì SH ^ (ABC) nên HA là hình chiếu của SA trên mặt phẳng (ABC).
Do đó (SA (ABC))  =(SA AH )   , , = SAH .
● Tam giác SBC đều cạnh 2a nên SH = a 3.
● Tam giác ABC vuông tại A nên 1 AH = BC = . a 2 Tam giác vuông SH SAH , có  tan SAH = = 3 , suy ra  0 SAH = 60 . AH
Câu 15: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh . a Tam giác SAB đều cạnh a
và nằm trong mặt phẳng vuông góc với đáy .
(ABCD) Gọi j là góc giữa SD và mặt phẳng
(ABCD) . Mệnh đề nào sau đây đúng? A. 5 3 cot j = . B. 15 cot j = . C. 0 j = 30 . D. cot j = . 15 5 2 Lời giải Chọn A
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 780
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 S A D H B C
Gọi H là trung điểm AB , suy ra SH ^ AB SH ^ (ABCD). Vì SH ^(ABCD) nên hình
chiếu vuông góc của SD trên mặt đáy (ABCD) là HD .
Do đó SD (ABCD)  =(SD HD)   , , = SDH. ● Tam giác a
SAB đều cạnh a nên 3 SH = . 2 ● a 5 2 2
HD = AH + AB = . 2 Tam giác vuông DH SHD , có  5 cot SDH = = . SH 15
Câu 16: Cho chóp đều S.ABCD có cạnh đáy bằng , 2 cạnh bên bằng .
3 Gọi j là góc giữa giữa
cạnh bên và mặt đáy. Mệnh đề nào sau đây đúng? A. 14 tan j = 7. B. 0 j = 60 . C. 0 j = 45 . D. tan j = . 2 Lời giải Chọn D
Gọi O là tâm mặt đáy (ABCD) , suy ra SO ^ (ABCD) .
Vì SO ^ (ABCD) , suy ra OA là hình chiếu của SA trên mặt phẳng (ABCD).
Do đó (SA (ABCD))  =(SA AO)   , , = SA . O 2 2 Tam giác vuông SO SB - BO 14 SOA , có  tan SAO = = = . AO AO 2
Câu 17: Cho tứ diện
ABCD đều. Gọi a là góc giữa AB và mặt phẳng .
(BCD) Chọn khẳng định
đúng trong các khẳng định sau? 3 3 A. 3 cos a = . B. cosa = . C. cosa = 0 . D. cosa = . 3 4 2 Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 781
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn A
Gọi H là trọng tâm tam giác đều BCD AH ^ (BCD). Gọi a
a là độ dài cạnh của tứ diện 3 ABCD BH = . 3 Khi đó  BH 3
a = ABH  cosa = = . . AB 3
Câu 18: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , cạnh bằng . 4a Cạnh bên
SA = 2a . Hình chiếu vuông góc của đỉnh S trên
mặt phẳng (ABCD) là trung điểm của H của đoạn thẳng .
AO Gọi a là góc giữa SD và mặt phẳng .
(ABCD) Mệnh đề nào sau đây đúng? A. tan a = 5. B. tan a = 5 1. C. tan a = . D. tan a = 3. 5 Lời giải Chọn C S A D H O B C
Vì SH ^(ABCD) nên hình chiếu vuông góc của SD trên mặt phẳng (ABCD) là HD .
Do đó SD (ABCD)  =(SD HD)   , , = SDH. ● Tính được 2 2
SH = SA - AH = a 2.
● Trong tam giác ADH , có 2 2 0
DH = AH + AD -2AH .AD. cos 45 = a 10. Tam giác vuông SH SHD , có  5 tan SDH = = . HD 5
Câu 19: Cho lăng trụ ABC .
D A ' B'C ' D ' có
đáy là hình thoi cạnh a ,  0
BAD = 60 . Hình chiếu vuông góc của
B ' xuống mặt đáy trùng với giao điểm hai đường chéo của đáy và cạnh bên
BB ' = a . Tính góc giữa cạnh bên và mặt đáy. A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 . Lời giải Chọn C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 782
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 D' C' B' A' D C O A B
Gọi O = AC Ç BD . Theo giả thiết B 'O ^ (ABCD) .
Do đó BB (ABCD)    ',
= BB ', BO = B ' BO .
Từ giả thiết suy ra tam giác a
ABD đều cạnh a , suy ra 1 BO = BD = . 2 2 Tam giác vuông BO 1 B ' BO , có   0 cos B ' BO =
=  B ' BO = 60 . BB ' 2
Câu 20: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = ,
a AD = a 3 . Hình chiếu a vuông góc H của S trên
mặt đáy trùng với trọng tâm tam giác ABC và SH = . Gọi 2
M , N lần lượt là trung điểm các cạnh BC và SC . Gọi a là góc giữa đường thẳng MN với mặt đáy .
(ABCD) Mệnh đề nào sau đây đúng? 3 A. 4 2 tan a = . B. tan a = . C. tan a = . D. tan a =1 . 3 4 3 Lời giải Chọn B S N A D H B M C
Ta có MN SB . Do đó MN (ABCD)  = SB (ABCD)  , , .
Do SH ^(ABCD) nên MN (ABCD)  = SB (ABCD)    , ,
= SB, HB = SBH .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 783
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Ta có 2 2 BD a
BD = AB + AD = 2a ; 2 BH = = . 3 3 Tam giác SH SHB , có  3 tan SBH = = . BH 4
Câu 21: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a , SO vuông góc với đáy. Gọi , M N
lần lượt là trung điểm SA và BC . Tính góc giữa đường thẳng MN với mặt phẳng , a 10 (ABCD) biết . MN = 2 A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 . Lời giải Chọn C S M A B K O N D C
Kẻ MK SO , do SO ^ (ABCD) , suy ra MK ^ (ABCD) . Do đó a MN (ABCD)    ,
= MN , NK = MNK . Ta có 3 3 2 CK = CA = . 4 4 2 2 2 Tam giác 2
CN +CK - KN a 10 CNK , có 0 = cos 45 =  KN = . 2 2CN .CK 4 Tam giác vuông NK 1 MNK , có   0 cos MNK = =  MNK = 60 . MN 2
Câu 22: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh . a Hai mặt phẳng (SAB) và
(SAC) cùng vuông góc với đáy (ABCD) và SA = 2a .
Gọi j là góc giữa đường thẳng SB và mặt phẳng . (SAD)
Mệnh đề nào sau đây đúng? A. 5 2 5 cosj = . B. cosj = . C. 0 j = 60 . D. 0 j = 30 . 5 5 Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 784
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 S A D B C ìï ^ Ta có BA AD ïí
BA ^ (SAD). Suy ra hình chiếu vuông góc của SB trên mặt phẳng ïBA ^ SA ïî
(SAD) là SA . Do đó SB (SAD)  =(SB SA)   , , = BSA. Tam giác vuông SB SA 2 5 SAB , ta có  cos BSA = = = . 2 2 SA + 5 SA AB
Câu 23: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh , a
cạnh bên SA = a 6 và
vuông góc với đáy. Gọi a là góc giữa SC và mặt phẳng .
(SAB) Chọn khẳng định đúng
trong các khẳng định sau? A. 1 1 1 tan a = . B. tan a = . C. 0 a = 30 . D. tan a = . 8 7 6 Lời giải Chọn B S A D B C ìï ^ Ta có BC BA ïí
BC ^ (SAB). Suy ra hình chiếu vuông góc của SC trên mặt phẳng (SAB) ïBC ^ SA ïî
là SB . Do đó SC (SAB)  =(SC SB)   , , = C . SB
Tam giác vuông SAB , có 2 2
SB = SA + AB = a 7. Tam giác vuông BC SBC , có  1 tan CSB = = . SB 7
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 785
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 24: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh .
2a Cạnh bên SA vuông góc với đáy, góc gữa SC và mặt đáy (ABCD) bằng . 0
45 Gọi j là góc giữa đường thẳng SD và mặt phẳng . (SAC)
Mệnh đề nào sau đây đúng? A. 5 tan j = . B. tan j = 5. C. 0 j = 60 . D. 0 j = 45 . 5 Lời giải Chọn A S A D O B C Xác định 0 45 = SC,(ABCD)   
= SC, AC = SCA , suy ra SA = AC = 2a 2 . ìï ^ Gọi DO AC
O = AC Ç BD , ta có ïí
DO ^ (SAC) nên hình chiếu vuông góc của SD trên ïDO ^ SA ïî
mặt phẳng (SAC) là SO . Do đó SD (SAC)    ,
= SD,SO = DSO . Ta có 1
DO = BD = a 2 ; 2 2 2 2
SO = SA + AO = SA + DO = a 10 . 2 Tam giác vuông OD SOD , có  5 tan DSO = = . OS 5
Câu 25: Cho hình hộp chữ nhật ABC .
D A ' B'C ' D ' có
đáy ABCD là hình vuông cạnh bằng , 2 2
AA ' = 4 . Tính góc giữa đường thẳng
A 'C với mặt phẳng .
(AA ' B ' B) A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 . Lời giải Chọn A
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 786
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A' D' B' C' A D B C ìï ^ Ta có BC AB ïí
BC ^ (AA ' B ' B) . ïBC ^ AA ' ïî
Do đó A C (AA B B)  =(A C A B)   ' , ' ' ' , ' = CA ' B .
Vì BC ^ (AA ' B ' B)  BC ^ BA ' nên tam giác A ' BC vuông tại B . Tam giác vuông BC BC 1 A ' BC , có  tan CA ' B = = = . 2 2 A ' B AA ' + AB 3
Vậy A 'C tạo với mặt phẳng (AA ' B ' B) một góc 0 30 .
Câu 26: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh . a Tam giác SAB đều và nằm
trong mặt phẳng vuông góc với đáy. Gọi
H, K lần lượt là trung điểm của các cạnh AB và .
AD Gọi j là góc giữa đường thẳng SA và mặt phẳng . (SHK ) Mệnh đề nào sau đây đúng? 2 14 A. 7 tan j = 7. B. tan j = . C. tan j = . D. tan j = . 4 7 4 Lời giải Chọn C S K D A H I B C
Gọi I = HK Ç AC. Do H , K lần lượt là trung điểm của AB và AD nên HK BD . Suy ra
HK ^ AC . Lại có AC ^ SH nên suy ra AC ^ (SHK ) .
Do đó (SA (SHK ))  =(SA SI )   , , = ASI .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 787
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 1 AC Tam giác AI 7
SIA vuông tại I , có  4 tan ASI = = = . 2 2 SI SA - AI 7
Câu 27: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B ,
AB = BC = a ,
AD = 2a . Cạnh bên SA = a 2 và vuông góc với đáy. Tính góc giữa đường thẳng SC với mặt phẳng . (SAD) A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 . Lời giải Chọn A S A M D B C
Gọi M là trung điểm AD , suy ra ABCM là hình vuông nên CM ^ AD . ìï ^ Ta có CM AD ïí  CM ^ (SAD). CM ï ^ SA ïî
Suy ra hình chiếu vuông góc của SC trên mặt phẳng (SAD) là SM . Do đó SC (SAD)    ,
= SC,SM = CSM . Tam giác vuông CM AB 1 SMC , có   0 tan CSM = = =  CSM = 30 . 2 2 SM SA + AM 3
Câu 28: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều có
đường cao SH vuông góc với mặt phẳng . (ABCD)
Gọi a là góc giữa BD và mặt phẳng
(SAD). Chọn khẳng định đúng trong các khẳng định sau? A. 0 a = 60 . B. 0 a = 30 . C. 3 3 cos a = . D. sin a = . 2 2 2 2 Lời giải Chọn D
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 788
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 S I A D H B C
Gọi I là trung điểm SA . Do tam giác SAD đều nên BI ^ SA. ( ) 1 ìï ^ Ta có AD AB ïí
AD ^ (SAD)  AD ^ BI. (2) ïAD ^ SH ïî Từ ( )
1 và (2) , ta có BI ^ (SAD) nên hình chiếu vuông góc của BD trên mặt phẳng (SAD)
là ID. Do đó BD (SAD)    ,
= BD, ID = BDI. AB 3 Tam giác BI 3
BDI vuông tại I nên  2 sin BDI = = = . BD AB 2 2 2
Câu 29: Cho hình lập phương . ABC .
D A ' B'C ' D ' Gọi a là góc giữa AC ' và mặt phẳng (A ' BCD ').
Chọn khẳng định đúng trong các khẳng định sau? A. 2 0 a = 30 . B. tan a = . C. 0 a = 45 .
D. tan a = 2. 3 Lời giải Chọn D A' D' B' C' I H A D B C
Gọi A 'C Ç AC ' = I ; C ' D ÇCD ' = H . ìï ^
Ta có C ' D CD ' ïí
C ' D ^ (A ' BCD ')  IH là hình chiếu vuông góc của AC ' trên mặt C
ï ' D ^ A ' D ' ïî
phẳng (A ' BCD ').
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 789
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Do đó AC (A BCD )
 =C I (A BCD )    ', ' ' ' , '
' = C ' I , HI = C ' IH . AB 2 Trong tam giác vuông C ' H C ' HI , có  2 tan C ' IH = = = 2. IH AB 2
Dạng 4. Thiết Diện Phương pháp
Việc xác định thiết diện với một khối đa diện với một mặt phẳng vuông góc với một
đường thẳng cho trước, trước hết ta phải tìm được điểm chung của một mặt phẳng đã cho
với một mặt của khối đa diện, sau đó dựa vào mối quan hệ giữa tính song song và vuông
góc để tìm ra phương của giao tuyến giữa mặt đã cho và các mặt của khối đa diện.
Thường ta hay dùng hệ quả sau để tìm điểm chung a  b a  () O b  a 1)   2)  b  () ( ;  ) b    a / /() O()  a
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với ,
AB = a BC = 2a . Tam giác
SAB đều và nằm trong mặt phẳng vuông góc với đáy. Mặt phẳng
(a) đi qua S vuông góc
với AB . Tính diện tích S của thiết diện tạo bởi
(a) với hình chóp đã cho. 2 2 2 A. a 3 a 3 a S = . B. S = . C. 2 S = a 3. D. S = . 4 2 2 Lời giải Chọn B S A D H M B C
Gọi H là trung điểm AB SH ^ AB. Suy ra: · SH Ì(a).
· SH ^ (ABCD) (do (SAB) ^ (ABCD) theo giao tuyến AB ).
Kẻ HM ^ AB (M ÎCD) HM Ì(a).
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 790
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Do đó thiết diện là tam giác SHM vuông tại H . 2 Ta có a 3 1 a 3 a 3 SH = , HM = BC = 2 . a Vậy S = . .2a = . 2 SH D M 2 2 2
Câu 2: Cho hình chóp đều S.ABC có
đáy ABC là tam giác đều cạnh , a tâm O ; SO = 2a . Gọi M là điểm thuộc đoạn .
AO (M ¹ A; M ¹ O) Mặt phẳng
(a) đi qua M và vuông góc với . AO
Đặt AM = x . Tính diện tích S của thiết diện tạo bởi
(a) với hình chóp S.ABC . A. 3 2 S = 2a . B. 2 S = 2x . C. S = (a- x)2 .
D. S = (a- x)2 2 . 2 Lời giải Chọn B S K J A C M O I B
Vì S.ABC là hình chóp đều nên SO ^ (ABC) (O là tâm của tam giác ABC ).
Do đó SO ^ AA ' mà (a) ^ AA ' suy ra SO  (a) .
Tương tự ta cũng có BC  (a) .
Qua M kẻ IJ BC với I Î AB, J Î AC ; kẻ MK SO với K Î SA.
Khi đó thiết diện là tam giác KIJ .
Diện tích tam giác IJK là 1 S = IJ.MK . IJ D K 2 Trong tam giác IJ AM AM BC x ABC , ta có = suy ra . 2 3 IJ = = . BC AA ' AA ' 3 Tương tự trong tam giác AM SO SA O , ta có MK AM = suy ra . MK = = 2x 3 . SO AO AO Vậy 1 2x 3 2 S = .2x 3 = 2x . DIJK 2 3
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 791
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 3: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA = a và vuông góc với đáy.
Mặt phẳng (a) qua A và vuông góc với trung tuyến
SI của tam giác SBC . Tính diện tích
S của thiết diện tạo bởi
(a) với hình chóp đã cho. 2 2 A. 2a 21 4a 21 S = . S = . AM D N B. AM D N 49 49 2 2 C. a 21 2a 21 S = . S = . AM D N D. AM D N 7 7 Lời giải Chọn A S N K M A C I B
Gọi I là trung điểm BC AI ^ BC. Kẻ AK ^ SI (K Î SI ) .
Từ K kẻ đường thẳng song song với BC cắt SB, SC lần lượt tạị M , N .
Khi đó thiết diện là tam giác AMN . ìï ^ Ta có BC AI ïí
BC ^ (SAI )  BC ^ AK MN ^ AK . ïBC ^ SA ïî Tam giác vuông SA.AI a 21 SAI , có AK = = . 2 2 + 7 SA AI 2 2 Tam giác MN SK SA SA 4 4a SBC , có = = = =  MN = . 2 2 2 BC SI SI SA + AI 7 7 2 Vậy 1 2a 21 S = AK .MN = . DAMN 2 49
Câu 4: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA = a và vuông góc với đáy.
Mặt phẳng (a) qua trung điểm
E của SC và vuông góc với AB . Tính diện tích S của thiết diện tạo bởi
(a) với hình chóp đã cho.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 792
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2 A. 5a 3 a 7 S = . S = . EFGH B. EFGH 16 32 2 2 C. 5a 3 5a 2 S = . S = . EFGH D. EFGH 32 16 Lời giải Chọn C S H E F A C G J B
Gọi F là trung điểm AC , suy ra EF SA .
Do SA ^ (ABC)  SA ^ AB nên EF ^ AB . ( ) 1
Gọi J, G lần lượt là trung điểm AB, AG .
Suy ra CJ ^ AB và FG CJ nên FG ^ AB . (2)
Trong DSAB kẻ GH SA (H Î SB) , suy ra GH ^ AB . ( ) 3 Từ ( ) 1 , (2) và ( )
3 , suy ra thiết diện cần tìm là hình thang vuông EFGH . Do đó 1 S = EF +GH FG . EFGH ( ). 2 Ta có 1 a a GH BG a EF = SA = ; 1 3 FG = CJ = ; 3 =  GH = BG = . 2 2 2 4 SA BA 4 2 æ ö Vậy 1 a 3a a 3 5a 3 S = ç ÷ ç + ÷. = . EFGH 2 çè2 4 ÷ø 4 32
Câu 5: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , SA = 2a và vuông góc với đáy. Gọi (a) là
mặt phẳng đi qua B và vuông góc với SC . Tính diện tích S của thiết diện tạo bởi
(a) với hình chóp đã cho. 2 2 A. a 15 a 5 S = . S = . BI D H B. BI D H 10 8
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 793
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2 C. a 3 S = . a 15 S = . BI D H D. BI D H 12 20 Lời giải Chọn D S H A I C B
Gọi I là trung điểm của AC , suy ra BI ^ AC . ìï ^ Ta có BI AC ïí
BI ^ (SAC)  BI ^ SC . ( ) 1 ïBI ^ SA ïî
Kẻ IH ^ SC (H Î SC) . (2) Từ ( )
1 và (2) , suy ra SC ^ (BIH ) .
Vậy thiết diện cần tìm là tam giác IBH .
Do BI ^ (SAC) BI ^ IH nên DIBH vuông tại I . Ta có a
BI đường cao của tam giác đều cạnh a nên 3 BI = . 2
Tam giác CHI đồng dạng tam giác CAS , suy ra IH CI CI .SA CI .SA a 5 =  IH = = = . 2 2 SA CS CS + 5 SA AC 2 Vậy 1 a 15 S = BI .IH = . DBIH 2 20
Câu 6: Cho hình chóp đều S.ABC có cạnh đáy bằng , a cạnh bên bằng . b Mặt phẳng (a) đi qua
A và vuông góc với . SC Tìm hệ thức giữa a và
b để (a) cắt SC tại điểm C1 nằm giữa S và C .
A. a > b 2.
B. a > b 3.
C. a < b 2.
D. a < b 3. Lời giải Chọn C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 794
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 S C1 A C G C' B
Gọi G là trọng tâm tam giác ABC . Do S.ABC là hình chóp đều nên SG ^ (ABC).
Gọi C ' là trung điểm AB . Suy ra C, C ', G thẳng hàng. ìï ^ Ta có AB CC ' ïí
AB ^ (SCC ')  AB ^ SC . ( ) 1 SG ï ^ AB ïî
Trong tam giác SAC , kẻ AC ^ SC . (2) 1 Từ ( )
1 và (2) , suy ra SC ^ (ABC . 1 )
Suy ra thiết diện cần tìm là tam giác ABC thỏa mãn đi qua A và vuông góc với SC . 1
Tam giác SAC cân tại S nên để C nằm giữa S và C khi và chỉ khi  0 ASC < 90 . 1 Suy ra  2 2 2 2 2
cos ASC > 0  SA + SC - AC > 0  2b - a > 0  a < b 2.
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại , A đáy lớn , AD = 8 BC = 6
, SA vuông góc với mặt phẳng , (ABCD) SA = 6 . Gọi M là trung điểm . AB Gọi (P) là
mặt phẳng qua M và vuông góc với AB . Thiết diện của (P) và hình chóp có diện tích bằng: A. 10 . B. 20 . C. 15 . D. 16 . Lời giải Chọn C S I K A D M N B C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 795
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Do (P) ^ AB  (P)  SA.
Gọi I là trung điểm của SB MI SA MI Ì(P).
Gọi N là trung điểm của CD MN ^ AB MN Ì(P).
Gọi K là trung điểm của SC IK BC , mà MN BC MN IK IK Ì(P).
Vậy thiết diện của (P) và hình chóp là hình thang MNKI vuông tại M . Ta có:
MI là đường trung bình của tam giác SAB 1
MI = SA = 3. 2
IK là đường trung bình của tam giác SBC 1
IK = BC = 3. 2 1
MN là đường trung bình của hình thang ABCD MN = (AD + BC) = 7. 2 Vậy IK + MN S = .MI = 15. MNKI 2
Câu 8: Cho hình chóp đều S.ABC có
đáy ABC là tam giác đều cạnh , a tâm O , đường cao AA ' ; SO = 2a . Gọi M là điểm thuộc đoạn . OA ' (
M ¹ A '; M ¹ O) Mặt phẳng
(a) đi qua M và vuông góc với . AA ' Đặt . AM = x Tính
diện tích S của thiết diện tạo bởi (a) với hình chóp . S.ABC A. S = - ( 2 2
2 8x -6 3ax +3a ). S = x - ax + a IJEF ( 2 2 2 8 6 3 3 ). IJEF B. C. 3 S = (a- x)2 .
D. S = (a- x)2 2 . 2 Lời giải Chọn A S F N E A J C O M A' I B
Vì S.ABC là hình chóp đều nên SO ^ (ABC) (O là tâm của tam giác ABC ).
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 796
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Do đó SO ^ AA ' mà (a) ^ AA ' suy ra SO  (a) .
Tương tự ta cũng có BC  (a) .
Qua M kẻ IJ BC với I Î AB, J Î AC ; kẻ MN SO với N Î SA '.
Qua N kẻ EF BC với E Î SB, F Î SC .
Khi đó thiết diện là hình thang IJFE. Diện tích hình thang 1 S = IJ + EF MN . IJEF ( ) 2 Tam giác IJ AM AM BC x ABC , có . 2 3 =  IJ = = . BC AA ' AA ' 3 Tam giác EF SN OM OM .BC SBC , có = =  EF = = 2(x 3 -a). BC SA ' OA ' OA ' Tam giác MN MA ' S . O MA ' SOA ' , có =  MN = = 2(3a-2x 3). SO OA ' OA ' Vậy 2 S = x - a a - x = - x - ax + a IJEF (4 3 3 )(3 2 3) 2( 2 2 8 6 3 3 ). 3
Câu 9: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với ,
AB = a AD = a 3 . Cạnh bên
SA = 2a và vuông góc với đáy. Mặt phẳng
(a) đi qua A vuông góc với SC . Tính diện tích
S của thiết diện tạo bởi
(a) với hình chóp đã cho. 2 2 2 2 A. a 6 12a 6 6a 6 a 6 S = . S = . S = . S = . AMIN B. AMIN C. AMIN D. 7 35 35 AMIN 5 Lời giải Chọn B S N I M D A B C
Trong tam giác SAC , kẻ AI ^ SC ( I Î SC) .
Trong mp(SBC), dựng đường thẳng đi qua I vuông góc với SC cắt SB tại M .
Trong mp(SCD) , dựng đường thẳng qua I vuông góc với SC cắt SD tại N .
Khi đó thiết diện của hình chóp cắt bởi mp (a) là tứ giác AMIN .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 797
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ta có SC ^ (a) SC ^ AM . ( ) 1 ìï ^ Lại có BC AB ïí
BC ^ (SAB)  BC ^ AM . (2) ïBC ^ SA ïî Từ ( )
1 và (2) , suy ra AM ^ (SBC)  AM ^ MI .
Chứng minh tương tự, ta được AN ^ NI . Do đó 1 1 S = S +S
= AM .MI + AN .NI . AMIN AMI D A D NI 2 2 Vì AM , AI ,
AN là các đường cao của các tam giác vuông SAB, SAC, SAD nên SA.AB 2a SA.AC SA.AD 2a 21 AM = = ; AI = = a 2 ; AN = = . 2 2 SA + AB 5 2 2 SA + AC 2 2 + 7 SA AD Suy ra a 30 a 14 2 2
MI = AI - AM = và 2 2
NI = AI - AN = . 5 7 æ ö 2 Vậy 1 ç 2a a 30
2a 21 a 14 ÷ 12a 6 S = ç . + . ÷ ç ÷ = . AMIN 2 çè 5 5 7 7 ÷ø 35
Câu 10: Cho hình lăng trụ A .
BC A ' B'C ' có
đáy ABC là tam giác vuông cân tại A với ; BC = a 2
AA ' = a và vuông góc với đáy. Mặt phẳng (a) qua M là trung điểm của BC và vuông góc với .
AB ' Thiết diện tạo bởi
(a) với hình lăng trụ A .
BC A ' B'C ' là: A. Hình thang cân. B. Hình thang vuông. C. Tam giác. D. Hình chữ nhật. Lời giải Chọn B B' C' A' R Q C B M N A
Gọi N là trung điểm AB MN ^ AB .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 798
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìï ^ Ta có MN AB ïí
MN ^ (ABB ' A ')  MN ^ AB '  MN Ì(a). ïMN ^ AA ' ïî
Từ giả thiết suy ra AB = a = AA '  ABB ' A ' là hình vuông  BA ' ^ AB ' .
Trong mp (ABB ' A ') kẻ NQ BA ' với Q Î AA ' .
Trong mp (ACC ' A ') kẻ QR AC với R Î CC ' .
Vậy thiết diện là hình thang MNQR vuông (do MN và QR cùng song song với AC và MN ^ NQ ).
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 799
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
BÀI 4. HAI MẶT PHẲNG VUÔNG GÓC
A. KIẾN THỨC CƠ BẢN CẦN NẮM
I. Góc giữa hai mặt phẳng
1. Định nghĩa: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó. Nhận xét:  
 Cho hai đường thẳng a và b lần lượt vuông góc với hai mặt phẳng (P) và (Q); u , u lần lượt 1 2
là vectơ chỉ phương của a và b. Gọi  là góc giữa (P) và (Q). Khi đó, ta có:       u ,u u ,u 90 1 2  neáu  1 2   o         o 180  o  u ,u u ,u 90 1 2  neáu  1 2  
Như vậy, góc giữa hai mặt phẳng luôn nhỏ hơn hoặc bằng o 90 .  
 Vectơ n  0 được gọi là vectơ pháp tuyến của mặt phẳng (P) nếu nó nằm trên đường thẳng vuông góc với (P).
2. Cách xác định góc giữa hai mặt phẳng
Khi hai mặt phẳng (P) và (Q) cắt
nhau theo giao tuyến x, để tính góc
giữa chúng, ta chỉ việc xét một mặt
phẳng (R) vuông góc với x, lần
lượt cắt (P) và (Q) theo các giao
tuyến a và b. Lúc đó, góc giữa (P)
và (Q) bằng góc giữa hai đường thẳng a và b.
3. Định lí 1. Gọi S là diện tích của đa
giác H trong mặt phẳng (P) và S’ là
diện tích hình chiếu H’ của H trên
mặt phẳng (P’) thì Sʹ  Scos, trong
đó  là góc giữa hai mặt phăng (P) và (P’).
dt Aʹ BC  dt ABC.cos
II. Hai mặt phẳng vuông góc
1. Định nghĩa. Hai mặt phẳng gọi là vuông góc với nhau nếu góc giữa chúng bằng o 90 .
Hai mặt phẳng (P) và (Q) vuông góc với nhau, kí hiệu: P  Q hay Q  P.
        o P Q
90 (Với  là góc giữa hai mặt phẳng (P) và (Q)).
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 800
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133    
Từ định nghĩa trên ta suy ra: P  Q  n  n , với n , n theo thứ tự là vectơ pháp tuyến của 1 2 1 2 (P) và (Q).
2. Điều kiện để hai mặt phẳng vuông góc
a) Định lí 2. Hai mặt phẳng vuông góc với nhau khi và chỉ khi mặt phẳng này chứa một đường
thẳng vuông góc với mặt phẳng kia. P  a P Q
a  Q       
Chú ý: Dùng định lí này để chứng minh hai mặt phẳng vuông góc. b) Các hệ quả Hệ quả 1
 Nếu hai mặt phẳng (P) và (Q) vuông góc
với nhau và A là điểm nằm trong (P) thì
đường thẳng a đi qua điểm A và vuông
góc với (Q) sẽ nằm trong (P). P  Q   A P     a  P A a, a Q    
 Nếu hai mặt phẳng (P) và (Q) vuông góc
với nhau thì bất cứ đường thẳng a nào
thuộc (P), vuông góc với giao tuyến của
(P) và (Q) sẽ vuông góc với mặt phẳng (Q).  P  Q   P Q    c   a  Q a P   , a  c
Hệ quả 2. Hai mặt phẳng cắt nhau và cùng
vuông góc với mặt phẳng thứ ba thì giao
tuyến của chúng vuông góc với mặt phẳng thứ ba.
PQ  a
P  R  a  R Q R   
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 801
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Hệ quả 3. Qua đường thẳng a không vuông góc với mặt phẳng (P) có duy nhất một mặt phẳng
(Q) vuông góc với mặt phẳng (P).  Q   a
a không vuông góc với (P)  !Q   :  . Q   P
III. Hình lăng trụ đứng. Hình hộp chữ nhật. Hình lập phương
1. Hình lăng trụ đứng
a) Định nghĩa. Hình lăng trụ đứng là hình lăng trụ
có cạnh bên vuông góc với mặt đáy.
b) Nhận xét. Các mặt bên của hình lăng trụ đứng là
hình chữ nhật và vuông góc với mặt đáy.
2. Hình lăng trụ đều
a) Định nghĩa. Hình lăng trụ đều là hình lăng trụ
đứng có đáy là đa giác đều.
b) Nhận xét. Các mặt bên của hình lăng trụ đều là
những hình chữ nhật bằng nhau. Ngoài ra, hình
lăng trụ đều có các tính chất của hình lăng trụ đứng. 3. Hình hộp đứng
a) Định nghĩa. Hình hộp đứng là hình lăng trụ đứng
có đáy là hình bình hành.
b) Nhận xét. Trong hình hộp đứng bốn mặt bên đều
là hình chữ nhật.
4. Hình hộp chữ nhật
a) Định nghĩa. Hình hộp chữ nhật là hình hộp đứng
có đáy là hình chữ nhật.
b) Nhận xét. Tất cả sáu mặt của hình hộp chữ nhật
đều là hình chữ nhật.
5. Hình lập phương
Định nghĩa. Hình lập phương là hình hộp có tất cả các mặt là hình vuông.
IV. Hình chóp đều và hình chóp cụt đều
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 802
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
1. Định nghĩa đều
Định nghĩa. Một hình chóp được gọi là hình chóp
đều nếu đáy của nó là đa giác đều và các cạnh bên bằng nhau.
 Đường vuông góc với mặt đáy kẻ từ đỉnh gọi là
đường cao của hình chóp. Từ định nghĩa, suy ra:
 Một hình chóp là hình chóp đều khi và chỉ khi
đáy của nó là đa giác đều và chân đường cao của
hình chóp trùng với tâm của đáy.
Một hình chóp là hình chóp đều khi và chỉ khi
đáy của nó là đa giác đều và các cạnh bên tạo
với mặt đáy các góc bằng nhau.
2. Hình chóp cụt đều Khi
cắt hình chóp đều bởi một mặt phẳng song
song với đáy để được một hình chóp cụt thì hình
chóp cụt đó được gọi là hình chóp cụt đều.
Đoạn thẳng nối tâm của hai đáy được gọi là đường cao của hình chóp cụt đều.
Từ định nghĩa suy ra: Các mặt bên của hình chóp cụt đều là những hình thang cân bằng nhau.
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1. Câu hỏi lý thuyết
Câu 1: Cho hai mặt phẳng (P) và (Q) song song với nhau và một điểm M không thuộc (P) và
(Q) . Qua M có bao nhiêu mặt phẳng vuông góc với (P) và (Q) ? A. 2. B. 3. C. 1. D. Vô số. Lời giải Chọn D
Gọi d là đường thẳng qua M và vuông góc với (P) . Do (P) (Q)  d ^ (Q). d ìï ^ (P) ( ìï R) ^ (P) Giả sử ( ï ï
R ) là mặt phẳng chứa d . Mà í  í . d ï ^ (Q) ( ï R) ^ ïî ï (P) î
Có vô số mặt phẳng (R) chứa d . Do đó có vô số mặt phẳng qua M , vuông góc với (P) và (Q) .
Câu 2: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Cho hai đường thẳng song song a và b và đường thẳng c sao cho c ^ , a c ^ b . Mọi mặt phẳng (a) chứa c thì
đều vuông góc với mặt phẳng . ( , a b)
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 803
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 B. Cho ,
a ^ (a) mọi mặt phẳng (b) chứa a thì (b) ^ (a) . C. Cho ,
a ^ b mọi mặt phẳng chứa
b đều vuông góc với . a D. Cho , a ^ b nếu a Ì (a) và b Ì (b ) thì (a) ^ (b) . Lời giải Chọn B
A sai. Trong trường hợp a và b trùng nhau, sẽ tồn tại mặt phẳng chứa a và b không
vuông góc với mặt phẳng (a) chứa c .
C sai. Trong trường hợp a và b cắt nhau, mặt phẳng ( ,
a b) chứa b nhưng không vuông góc với a .
D sai. Trong trường hợp a và b vuông góc nhau và tréo nhau, nếu (a)É a , (a) b và
(b)É b , (b) a thì (a) (b) .
Câu 3: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
B. Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước.
C. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
D. Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước. Lời giải Chọn C
A sai. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với
nhau hoặc cắt nhau (giao tuyến vuông góc với mặt phẳng thứ 3).
B sai. Qua một đường thẳng vô số mặt phẳng vuông góc với một đường thẳng cho trước.
D sai. Qua một điểm có vô số mặt phẳng vuông góc với một mặt phẳng cho trước.
Câu 4: Trong các mệnh đề sau, mệnh đề nào đúng? A. Hai mặt phẳng (P) và (Q) vuông góc
với nhau và cắt nhau theo giao tuyến . d Với mỗi điểm A thuộc (P) và mỗi điểm
B thuộc (Q) thì ta có AB vuông góc với . d
B. Nếu hai mặt phẳng (P) và (Q) cùng vuông góc với mặt phẳng (R) thì giao tuyến của
(P) và (Q) nếu có cũng sẽ vuông góc với . (R)
C. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thứ ba thì song song với nhau.
D. Nếu hai mặt phẳng vuông góc với nhau thì mọi đường thẳng thuộc mặt phẳng này sẽ
vuông góc với mặt phẳng kia. Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 804
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn B
A sai. Trong trường hợp a Î d , b Î d , khi đó AB trùng với d .
C sai. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thứ ba thì song song
với nhau hoặc cắt nhau (giao tuyến vuông góc với mặt phẳng thứ 3).
D sai. Hai mặt phẳng vuông góc với nhau, đường thẳng thuộc mặt phẳng này và vuông
góc với giao tuyến thì vuông góc với mặt phẳng kia.
Câu 5: Trong các mệnh đề sau, mệnh đề nào sau đây là đúng?
A. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ
vuông góc với mặt phẳng kia.
B. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
C. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
D. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này và
vuông góc với giao tuyến của hai mặt phẳng sẽ vuông góc với mặt phẳng kia. Lời giải Chọn D
A sai. Hai mặt phẳng vuông góc với nhau thì đường thẳng nằm trong mặt phẳng này,
vuông góc với giao tuyến thì vuông góc với mặt phẳng kia.
B, C sai. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với
nhau hoặc cắt nhau (giao truyến vuông góc với mặt phẳng kia).
Câu 6: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song với nhau.
B. Qua một đường thẳng cho trước có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với hai mặt
phẳng cắt nhau cho trước.
D. Hai mặt phẳng cùng vuông góc với một mặt phẳng thứ ba thì vuông góc với nhau. Lời giải Chọn C
A sai. Hai mặt phẳng cùng song song với một mặt phẳng thứ ba thì song song hoặc trùng nhau.
B sai. Nếu đường thẳng vuông góc với mặt phẳng cho trước thì có vô số mặt phẳng qua
đường thẳng và vuông góc với mặt phẳng đó. Nếu đường thẳng không vuông góc với mặt
phẳng cho trước thì không có mặt phẳng nào vuông góc với mặt phẳng đó.
D sai. Hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì song song với
nhau hoặc cắt nhau (giao truyến vuông góc với mặt phẳng kia).
Câu 7: Trong các mệnh đề sau, mệnh đề nào sai?
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 805
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
A. Cho đường thẳng a vuông góc với đường thẳng b và
b nằm trong mặt phẳng . (P) Mọi mặt phẳng
(Q) chứa a và vuông góc với b thì (P) vuông góc với . (Q)
B. Nếu đường thẳng a vuông góc với đường thẳng b và mặt phẳng (P) chứa , a mặt phẳng
(Q) chứa b thì (P) vuông góc với . (Q)
C. Cho đường thẳng a vuông góc với mặt phẳng ,
(P) mọi mặt phẳng (Q) chứa a thì (P) vuông góc với . (Q)
D. Qua một điểm có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước. Lời giải Chọn B
Trong trường hợp a và b vuông góc nhau và tréo nhau, nếu (P)É a , (P) b và (Q)É b ,
(Q) a thì (P) (Q).
Câu 8: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Góc giữa mặt phẳng (P) và mặt phẳng
(Q) bằng góc nhọn giữa mặt phẳng (P) và mặt
phẳng (R) khi mặt phẳng (Q) song song với mặt phẳng . (R)
B. Góc giữa mặt phẳng (P) và mặt phẳng
(Q) bằng góc nhọn giữa mặt phẳng (P) và mặt
phẳng (R) khi mặt phẳng (Q) song song với mặt phẳng (R) hoặc . (Q) º (R )
C. Góc giữa hai mặt phẳng luôn là góc nhọn.
D. Cả 3 mệnh đề trên đều đúng. Lời giải Chọn D
Câu 9: Trong khẳng định sau về lăng trụ đều, khẳng định nào sai?
A. Đáy là đa giác đều.
B. Các mặt bên là những hình chữ nhật nằm trong mặt phẳng vuông góc với đáy.
C. Các cạnh bên là những đường cao.
D. Các mặt bên là những hình vuông. Lời giải Chọn D
Vì lăng trụ đều là lăng trụ đứng nên các cạnh bên bằng nhau và cùng vuông góc với đáy.
Do đó các mặt bên là những hình chữ nhật.
Câu 10: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu hình hộp có hai mặt là hình vuông thì nó là hình lập phương.
B. Nếu hình hộp có ba mặt chung một đỉnh là hình vuông thì nó là hình lập phương.
C. Nếu hình hộp có bốn đường chéo bằng nhau thì nó là hình lập phương.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 806
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
D. Nếu hình hộp có sau mặt bằng nhau thì nó là hình lập phương. Lời giải Chọn B
Dạng 2. Chứng minh hai mặt phẳng vuông góc 1. Phương pháp
Để chứng minh hai mặt phẳng vuông góc, ta dùng định lí: Hai mặt phẳng vuông góc với nhau
khi và chỉ khi mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
(P)  a (P) (Q). a  (Q)
Như vậy, việc chứng minh hai mặt phẳng vuông góc quy về việc chứng minh một đường thẳng
vuông góc với một mặt phẳng.
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Cho đường thẳng a và hai mặt phẳng (P) và (Q). Khẳng đinh nào sau đây đúng? a  P  Q  P A.  
   Q  P. B.   a  Q . Q  a a  P      P  Q C.    a  Q.
D. Có 2 câu đúng trong 3 câu trên. a    Hướng dẫn giải ĐÁP ÁN A
Theo định lí: “Nếu P  a và a  Q thì P  Q ” thì A đúng.
Ví dụ 2: Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến . Gọi a là đường thẳng nằm trong
(P). Khẳng định nào sau đây đúng? a    A. Nếu  a   thì a  Q. B.  
    a  Q. P Q 
C. Nếu a  Q thì P  Q.
D. Chỉ có 1 câu sai trong 3 câu trên. Hướng dẫn giải ĐÁP ÁN D
a  P a  Q: Sai. Vậy A sai. a    a     : Đúng. Vậy B đúng.
P  Q  a  Q 
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 807
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 a  P  P Q : Đúng. Vậy C đúng.
a  Q       
Ví dụ 3: Cho hai mặt phẳng (P) và (Q) vuông góc với nhau, giao tuyến là . AP và AQ.
Qua A, vẽ đường thẳng ʹ vuông góc với (Q). Khẳng đình nào sau đây sai ? A. ʹ  P. B. ʹ chéo . C. ʹ  .
D. Có 2 câu đúng trong 3 câu trên. Hướng dẫn giải ĐÁP ÁN B P  Q
Ta có: AP   ʹ  P: Đúng. vậy A đúng. ʹ Q    
Vì ʹ  P và   P nên ʹ chéo  là sai. Vậy B sai. ʹ  Q ʹ : Đúng. Vậy C đúng.
  Q       
Ví dụ 4: Cho đường thẳng a và hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến . Khẳng đinh nào sau đây đúng? a  P a  Q A.     a  Q. B.   a  P. a    a ca ét   P  Q C.    a  P.
D. Cả 3 câu đều sai. a    Hướng dẫn giải ĐÁP ÁN D
Thiếu giả thiết P  Q nên A sai (hình 1).
Thiếu giả thiết nên B sai (hình 2).
Thiếu giả thiết  cắt a nên C sai (hình 3). Hình 1 Hình 2 Hình 3
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 808
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ví dụ 5: Cho tứ diện ABCD có tam giác ABD và tam giác ABC vuông tại B. Khẳng định nào sau đây đúng? A. CB  AD. B. AB  BCD. C. 2  2  2 AC AB BC .
D. Cả A, B, C đều đúng. Hướng dẫn giải ĐÁP ÁN B Vì ABC vuông tại B nên AB  BC và ABD vuông
tại B nên AB  BD . Từ đó
suy ra AB  BCD . Vậy B đúng.
Ví dụ 6: Cho tam giác ABC đều, cạnh a. Gọi D là điểm đối xứng của A qua BC. Trên đường thẳng
vuông góc với mặt phẳng (ABC) tại D, lấy điểm S. Để cho mặt phẳng (SAB) vuông góc với mặt
phẳng (SAC), SD có độ dài tính theo a bẳng A. a 6 . B. a 3. C. a 3 . D. a 6. 2 3 Hướng dẫn giải ĐÁP ÁN A Vì
SD  BCD nên SDB và SDC vuông tại D.
Mà DB  DC (ABCD là hình thoi)
nên SDB  SDC . Suy ra, SB  SC .
Mặt khác AB  AC ( ABC đều) nên
SAB  SAC . Gọi I là chân đường
vuông góc hạ từ C trong SCA , ta có
SA  IB và SA  IC. Suy ra SA  BIC .
Để cho SAB  SAC , ta phải có   o BIC 90 . Suy ra  BC  a OI
(O là trung điểm của BC). 2 2 AIO vuông tại I cho  a 2 AI . 2  AD a 6 AIO ∽ ADS nên SD  .IO  SD  . AI 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 809
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
3. Bài tập trắc nghiệm
Câu 1: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , SA vuông góc với đáy. Gọi M là trung điểm . AC
Khẳng định nào sau đây sai?
A. BM ^ A . C
B. (SBM ) ^ (SAC).
C. (SAB) ^ (SBC).
D. (SAB) ^ (SAC). Lời giải Chọn D S A M C B
Tam giác ABC cân tại B có M là trung điểm AC BM ^ AC. Do đó A đúng. ìïBM ^ AC Ta có ïí  ^  ^ . Do đó B đúng. ïBM ^ SA ï
( SA ^(ABC)) BM (SAC) (SBM ) (SAC) do î ìïBC ^ BA Ta có ïí  ^  ^ . Do đó C đúng. ïBC ^ SA ï
( SA ^(ABC)) BC (SAB) (SBC) (SAB) do î
Dùng phương pháp loại trừ thì D là đáp án sai.
Câu 2: Cho tứ diện SABC có SBC và ABC nằm trong hai mặt phẳng vuông góc với nhau. Tam giác
SBC đều, tam giác ABC vuông tại . A Gọi , H I
lần lượt là trung điểm của BC và
AB . Khẳng định nào sau đây sai? A. SH ^ . AB
B. HI ^ A . B
C. (SAB) ^ (SAC).
D. (SHI ) ^ (SAB). Lời giải Chọn C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 810
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 S B H C I A
Do SBC là tam giác đều có H là trung điểm BC nên SH ^ BC .
Mà (SBC) ^(ABC) theo giao tuyến BC SH ^(ABC)  SH ^ A . B Do đó A đúng.
Ta có HI là đường trung bình của DABC nên HI AC HI ^ AB. Do đó B đúng. ìï ^ Ta có SH AB ïí
AB ^ (SHI )  (SAB) ^ (SHI ). Do đó D đúng. ïHI ^ AB ïî
Dùng phương pháp loại trừ thì C là đáp án sai.
Câu 3: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại , C
mặt bên SAC là tam giác
đều và mằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của . SC Mệnh đề nào sau đây sai? A. AI ^ S . C B. (SBC) ^ (SAC).
C. AI ^ B . C
D. (ABI ) ^ (SBC). Lời giải Chọn B S I A B H C
Tam giác SAC đều có I là trung điểm của SC nên AI ^ SC . Do đó A đúng.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 811
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Gọi H là trung điểm AC suy ra SH ^ AC . Mà (SAC) ^(ABC) theo giao tuyến AC nên
SH ^ (ABC) do đó SH ^ BC . Hơn nữa theo giả thiết tam giác A BC vuông tại C nên
BC ^ A C . Từ đó suy ra BC ^ (SAC)  BC ^ AI . Do đó C đúng.
Từ mệnh đề A và C suy ra mệnh đề D đúng.
Dùng phương pháp loại trừ thì B là đáp án sai.
Câu 4: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , SA vuông góc với đáy. Gọi
H , K lần lượt là hình chiếu của A trên SB , SC và I là giao điểm của HK với mặt phẳng .
(ABC) Khẳng định nào sau đây sai?
A. BC ^ AH.
B. (AHK ) ^ (SBC).
C. SC ^ AI. D. Tam giác IAC đều. Lời giải Chọn D S K H A C B I ìï ^ Ta có BC AB ïí
BC ^ (SAB)  BC ^ AH . Do đó A đúng. SA ï ^ BC ïî
Lại có AH ^ SB . Từ đó suy ra AH ^ (SBC)  AH ^ SC . ( ) 1
Lại có theo giả thiết SC ^ AK . (2) Từ ( )
1 và (2) , suy ra SC ^ (AHK )  (SBC) ^ (AHK ) . Do đó B đúng. SC ìï ^ (AHK ) Ta có ïí  ^ . Do đó C đúng. ï Ì ï ( ) SC AI AI AHK î
Dùng phương pháp loại trừ thì D là đáp án sai.
Câu 5: Cho tam giác đều ABC cạnh . a Gọi D là
điểm đối xứng với A qua BC . Trên đường
thẳng vuông góc với mặt phẳng a 6 (ABC) tại
D lấy điểm S sao cho SD = . Gọi I là 2 trung điểm ; BC
kẻ IH vuông góc SA (H Î SA) . Khẳng định nào sau đây sai?
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 812
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
A. SA ^ BH.
B. (SDB) ^ (SDC).
C. (SAB) ^ (SAC).
D. BH ^ H . C Lời giải Chọn B S H A B I D C
Từ giả thiết suy ra ABDC là hình thoi nên BC ^ AD. ìï ^ Ta có BC AD ïí
BC ^ (SAD)  BC ^ SA . ïBC ^ SD ïî
Lại có theo giả thiết IH ^ SA . Từ đó suy ra SA ^ (HCB) SA ^ BH . Do đó A đúng. Tính được a 3 3a 2 AI =
, AD = 2AI = a 3 , 2 2 2 SA = AD + SD = . 2 2 Ta có IH AI AI .SD a BC
DAHI ∽ DADS  =  IH = = =
 tam giác HBC có trung tuyến SD AS AS 2 2
IH bằng nửa cạnh đáy BC nên  0
BHC = 90 hay BH ^ HC . Do đó D đúng.
Từ mệnh đề A và D suy ra mệnh đề C đúng.
Dùng phương pháp loại trừ thì B là đáp án sai.
Dạng 3. Tính góc giữa hai mặt phẳng 1. Phương pháp
 Khi hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến x, để xác định góc giữa chúng, ta chỉ
việc xét một mặt phẳng (K) vuông góc với x lần lượt cắt (P) và (Q) theo các giao tuyến a và b.
Lúc đó, góc giữa (P) và (Q) bằng góc giữa hai đường thẳng a và b.
 Để tìm góc giữa hai mặt phẳng (P) và (Q) ta thường làm như sau:
– Xác định một điểm A trên (P), vẽ AH  Q (tại H).
– Vẽ HO  x tại O thì AO  x. – Góc    o OA,OH 90 là góc cần tìm.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 813
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Cho tứ diện SABC có ABC là tam giác đều cạnh 2a, SA vuông góc với mặt phẳng (ABC)
và SA  a. Góc giữa hai mặt phẳng (SBC) và (ABC) bằng A. o 30 . B. o 45 . C. o 60 . D. o 90 . Hướng dẫn giải ĐÁP ÁN A
Gọi  là góc giữa hai mặt phẳng (SBC) và (ABC).
Kẻ đường cao AH của ABC, ta có:
BC  AH , AH là hình chiếu của SH trên
mặt phẳng (ABC) nên suy ra BC  SH . Vậy    SHA.
Tam giác SHA vuông tại A có: SA  a,
AH  a 3 (đường cao của tam giác đều ABC). Suy ra:   SA  a  3 tan    o 30 . AH a 3 3
Ví dụ 2: Cho hình chóp đều S.ABC có ABC là tam giác đều cạnh a, cạnh bên  a 21 SA . Giá trị 6
góc  giữa hai mặt phẳng (SBC) và (ABC) bằng A. o 30 . B. o 45 . C. o 60 . D. o 90 . Hướng dẫn giải ĐÁP ÁN C Xác
định góc  . Gọi G là trọng tâm của ABC ,
ta có SG  ABC. Kẻ AM  BC thì trọng tâm G của ABC thuộc AM.
GM là hình chiếu của SM trên mặt phẳng (ABC)
nên BC  SM. Suy ra góc cần tìm là    SMG. Tính  . Ta có:  a 3 AM (đường cao của tam 2
giác đều ABC, cạnh a), suy ra
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 814
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133  1  a 3 GM AM . 3 6
Tam giác SMB vuông tại M nên:  2 a 21  a 2 2 2  2  2      a  SM  a SM SB BM     .  6   2  3 3
Tam giác SGM vuông tại G nên:   GM  a 3 3  1 cos .    o 60 . SM 6 a 2
Ví dụ 3: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a và cạnh bên bằng a 3.
Gọi  là góc giữa hai mặt phẳng (ABC) và (AB’C’), thì cos có giá trị bằng A. 5 . B. 6 . C. 3 . 5 6 3 D. 3 . 4 Hướng dẫn giải ĐÁP ÁN A
Do ABC.A’B’C’ là hình lăng trụ đều nên B và C là hình chiếu vuông góc của B’ và C’ trên (ABC).
Tam giác AB’C’ cân tại A. Gọi I là trung điểm của B’C’ thì AI  BʹCʹ.
Ta có AAʹ  AʹBʹCʹ  AAʹ  AʹI  AAʹI vuông tại A’. 2 2 Do đó: 2  2  2  2  3a  15a AI AAʹ AʹI 3a . 4 4 Suy ra  a 15 AI . 2 2 + Diện tích   1  a 15 ABʹCʹ : S BʹCʹ.AI . 2 4 2 + Diện tích   a 3 ABC : Sʹ . 4 Áp
dụng công thức diện tích hình chiếu của đa giác, ta có: 2   Sʹ  a 3 4  5 cos . . 2 S 4 a 15 5
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 815
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ví dụ 4: Cho hình chóp tam giác O.ABC có OA, OB, OC vuông góc đôi một. Gọi , ,  là các
góc tạo bởi mặt phẳng (ABC) với các mặt phẳng (OAB), (OBC), (OCA). Tổng 2   2   2 cos cos cos  có giá trị bằng A. 2. B. 3 . C. 1. 2 D. 1 . 2 Hướng dẫn giải ĐÁP ÁN C
Gọi H là hình chiếu vuông góc của O trên (ABC).
Đặt OA  a, OA  b, OC  c và OH  h.
Kéo dài CH cắt AB tại I, ta chứng minh được 1 1 1 1 AB  OCI và    . 2 2 2 2 h a b c
Suy ra góc giữa (ABC) và (OAB) là  OIC  . Trong OCI ta có:   OIC  COH   (góc có
cạnh tương ứng vuông góc). Trong  OH h OCH ta có: cos    . OC c Chứng minh tương tự:   h   h cos , cos . a b 2 2 2 h h h  1 1 1  Do đó 2 cos   2 cos   2 cos      2 h    1. 2 2 2  2 2 2  a b c  a b c 
Chú ý: Có thể chứng minh bài toán bằng cách dùng công thức diện tích hình chiếu như sau:
Gọi S, S , S , S lần lượt là diện tích các tam giác ABC, OAB, OBC, OCA. 1 2 3
Do OC  OAB nên OAB là hình chiếu vuông góc của ABC lên (OAB). Ta có: S  Scos. 1
Mặt khác HAB là hình chiếu vuông góc của OAB lên (ABC) nên: S  S .cos   S cos   2 S cos . HAB OAB 1 Chứng minh tương tự: S  2 S cos ; S  2 S cos . HBC HCA Do đó: S  S  S  2 S cos   2 S cos   2 S cos . HAB HBC HCA Hay   2   2   2   2   2   2 S S cos cos cos cos cos cos   1.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 816
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ví dụ 5: Cho hình lăng trụ đứng tam giác ABC.A’B’C’ có tam giác ABC vuông cân tại B, AB  a.
Để góc tạo bởi (AB’C’) và (ABC) bằng o
60 thì độ dài cạnh bên của lăng trụ bằng bao nhiêu? A. a. B. a 3. C. 2a. D. a 5. Hướng dẫn giải ĐÁP ÁN B
Ta có BC  AB và BC  BBʹ nên BC  ABBʹAʹ.
Mà BʹCʹ// BC nên BʹCʹ  ABBʹAʹ. Suy ra:
BʹCʹ  ABʹ  ABʹCʹ vuông tại B’.
Gọi S là diện tích của ABʹCʹ và S’ là diện tích ABC. Từ giả thiết ta có: 2  o  a  1 Sʹ S cos 60 S. . Do đó 2 2  2 S a . Mà  1 S BʹCʹ.ABʹ  ABʹ  2a. 2
Từ tam giác ABB’ vuông tại B ta có: 2  2  2  2  2  2 BBʹ ABʹ AB 4a a 3a  BBʹ  a 3.
3. Bài tập trắc nghiệm
Câu 1: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , 
ABC = 60 , tam giác SBC là
tam giác đều có bằng cạnh 2a và nằm trong mặt phẳng vuông với đáy. Gọi j là góc giữa
hai mặt phẳng (SAC) và (ABC). Mệnh đề nào sau đây đúng? 1 A. 0 j = 3 60 . B. tan j = 2 3. C. tan j = . D. tan j = . 6 2 Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 817
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 S B A H K C
Gọi H là trung điểm của BC , suy ra SH ^ BC SH ^ (ABC) .
Gọi K là trung điểm AC , suy ra HK AB nên HK ^ AC . ìï ^ Ta có AC HK ïí
AC ^ (SHK )  AC ^ SK . ïAC ^ SH ïî
Do đó (SAC) (ABC)  =(SK HK )   , , = SKH. Tam giác vuông a A BC , có  1
AB = BC.cos ABC = a HK = AB = . 2 2 Tam giác vuông SH SHK , có  tan SKH = = 2 3 . HK
Câu 2: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh . a
Cạnh bên SA = a 3 và vuông góc với mặt đáy . (ABC)
Gọi j là góc giữa hai mặt phẳng (SBC) và (ABC). Mệnh đề nào sau đây đúng? A. 0 j = 5 30 . B. sin j = . C. 0 j = 2 5 60 . D. sin j = . 5 5 Lời giải Chọn D S A C M B
Gọi M là trung điểm của BC , suy ra AM ^ BC . ìï ^ Ta có AM BC ïí
BC ^ (SAM )  BC ^ SM . ïBC ^ SA ïî
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 818
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Do đó (SBC) (ABC)  =(SM AM )   , , = SMA. Tam giác a
A BC đều cạnh a , suy ra trung tuyến 3 AM = . 2 Tam giác vuông SA SA 2 5 SA M , có  sin SMA = = = . 2 2 SM + 5 SA AM
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , cạnh . a Đường thẳng SO
vuông góc với mặt phẳng đáy a 3 (ABCD) và SO =
. Tính góc giữa hai mặt phẳng (SBC) 2 và . (ABCD) A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 . Lời giải Chọn C
Gọi Q là trung điểm BC , suy ra OQ ^ BC . ìï ^ Ta có BC OQ ïí
BC ^ (SOQ)  BC ^ S . Q ïBC ^ SO ïî
Do đó (SBC) (ABCD)    , = S , Q OQ = SQ . O Tam giác vuông SO SOQ , có  tan SQO = = 3. OQ
Vậy mặt phẳng (SBC) hợp với mặt đáy (ABCD) một góc 0 60 .
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I , cạnh ,  0 a góc BAD = 60 , a 3
SA = SB = SD =
. Gọi j là góc giữa hai mặt phẳng (SBD) và (ABCD). Mệnh đề nào 2 sau đây đúng? A. 5 3 tan j = 5. B. tan j = . C. tan j = . D. 0 j = 45 . 2 5 Lời giải Chọn A S S C B H I A B A D O Q D C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 819
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Từ giả thiết suy ra tam giác ABD đều cạnh a .
Gọi H là hình chiếu của S trên mặt phẳng (ABCD) . Do SA = SB = SD nên suy ra H cách
đều các đỉnh của tam giác ABD hay H là tâm của tam gác đều ABD . Suy ra 1 a 3 a 15 HI = AI = và 2 2
SH = SA - AH = . 3 6 6
Vì ABCD là hình thoi nên HI ^ BD . Tam giác SBD cân tại S nên SI ^ BD .
Do đó (SBD) (ABCD)    ,
= SI , AI = SIH . Trong tam vuông SH SHI , có  tan SIH = = 5. HI
Câu 5: Cho hình chóp S.ABCD có đáy là hình thang vuông ABCD vuông tại A và D , AB = 2 , a
AD =CD = a . Cạnh bên SA = a và vuông góc với mặt phẳng
(ABCD). Gọi j là góc giữa
hai mặt phẳng (SBC) và (ABCD) . Mệnh đề nào sau đây đúng? A. 2 tan j = . B. 0 j = 45 . C. 0 j = 60 . D. 0 j = 30 . 2 Lời giải Chọn A S A M B D C Gọi AB
M là trung điểm A B ADCM là hình vuông CM = AD = a = . 2
Suy ra tam giác ACB có trung tuyến bằng nửa cạnh đáy nên vuông tại C . ìï ^ Ta có BC SA ïí
BC ^ (SAC)  BC ^ SC. ïBC ^ AC ïî
Do đó (SBC) (ABCD)    ,
= SC, AC = SCA. Tam giác SA
S A C vuông tại A 2  tan j = = . AC 2
Câu 6: Cho hình chóp đều S.ABCD có tất cả các cạnh bằng . a Gọi M là trung điểm . SC Tính góc
j giữa hai mặt phẳng (MBD) và (ABCD) .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 820
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. j = 90. B. j = 60. C. j = 45.
D. j = 30. Lời giải Chọn C S M B C M' O A D
Gọi M ' là trung điểm OC MM '  SO MM ' ^ (ABCD).
Theo công thức diện tích hình chiếu, ta có S = cos . j S M D ' BD M D BD SD BD.MO MO 2 M ' BD 0  cosj = = = =  j = 45 . S BD.M 'O M 'O 2 MB D D
Câu 7: Trong không gian cho tam giác đều SAB và hình vuông ABCD cạnh
a nằm trên hai mặt phẳng vuông góc. Gọi H , K
lần lượt là trung điểm của , AB CD .
Gọi j là góc giữa hai mặt phẳng (SAB) và .
(SCD) Mệnh đề nào sau đây đúng? A. 2 2 3 3 3 tan j = . B. tan j = . C. tan j = . D. tan j = . 3 3 3 2 Lời giải Chọn B S d A D H K B C
Dễ dàng xác định giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng d đi qua
S và song song với AB .
Trong mặt phẳng (SAB) có SH ^ AB SH ^ d.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 821
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìï ^ Ta có CD HK ïí
CD ^ (SHK )  CD ^ SK d ^ SK . CD ï ^ SH ïî
Từ đó suy ra (SAB) (SCD)    ,
= SH ,SK = HSK. Trong tam giác vuông HK S HK , có  2 3 tan HSK = = . SH 3
Câu 8: Cho hình chóp đều S.ABCD có tất cả các cạnh đều bằng . a
Gọi j là góc giữa hai mặt
phẳng (SBD) và (SCD) . Mệnh đề nào sau đây đúng? A. 2 3 tan j = 6. B. tan j = . C. tan j = . D. tan j = 2. 2 2 Lời giải Chọn D S M A D O B C
Gọi O = AC Ç BD . Do hình chóp S.ABCD đều nên SO ^ (ABCD) .
Gọi M là trung điểm của SD . Tam giác SCD đều nên CM ^ SD .
Tam giác SBD có SB = SD = a , BD = a 2 nên vuông tại S SB ^ SD OM ^ SD.
Do đó (SBD) (SCD)   , = OM ,CM . ìï ^ Ta có OC BD ïí
OC ^ (SBD)  OC ^ OM . OC ï ^ SO ïî Tam giác vuông OC M OC , có  tan CMO = = 2 . OM
Câu 9: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại , A
AB = AC = a . Hình chiếu vuông góc H của S trên mặt đáy (ABC) trùng
với tâm đường tròn ngoại tiếp tam giác ABC và . a 6 SH =
Gọi j là góc giữa hai đường thẳng SB và AC . Mệnh đề nào sau đây đúng? 2 A. 2 14 cot j = . B. 7 cot j = 7. C. cot j = . D. cot j = . 4 7 4 Lời giải Chọn C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 822
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 S E B C H M A
Gọi H là trung điểm BC . Tam giác ABC vuông tại A nên H là tâm đường tròn ngoại
tiếp tam giác ABC . Theo giả thiết, ta có SH ^ (ABC).
Qua B kẻ Bx AC . Khi đó  
SB, AC = S , B Bx .
Kẻ HE ^ Bx tại E , cắt AC tại M . ìï 1 a
ïBE = AM = AC = ï Suy ra ï 2 2
AMEB là hình chữ nhật nên í . ï 1 a
ïïHE = HM = AB = ïïî 2 2 ìï ^ Ta có Bx HE ïí
Bx ^ (SHE )  Bx ^ SE . ïBx ^ SH ïî Tam giác vuông BE AM 7 SEB , có  cot SBE = = = . 2 2 SE + 7 SH HE
Câu 10: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại . C Gọi H là trung điểm
AB . Biết rằng SH vuông góc với mặt phẳng (ABC) và AB = SH = .
a Tính cosin của góc
a tọa bởi hai mặt phẳng (SAB) và . (SAC) A. 1 3 2 cos a = 2 . B. cosa = . C. cosa = . D. cosa = . 3 3 3 3 Lời giải Chọn D
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 823
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 S K B H A I C
Ta có SH ^ (ABC) SH ^CH . ( ) 1
Tam giác ABC cân tại C nên CH ^ AB . (2) Từ ( )
1 và (2) , suy ra CH ^ (SAB) .
Gọi I là trung điểm ^ AC BC AC ¾¾
HI BC ¾¾¾¾
HI ^ AC . (3)
Mặt khác AC ^ SH (do SH ^ (ABC)). (4)
Từ (3) và (4) , suy ra AC ^(SHI ) .
Kẻ HK ^ SI (K Î SI ) . (5)
Từ AC ^ (SHI ) AC ^ HK . (6)
Từ (5) và (6) , suy ra HK ^(SAC) . ìïHK ^ (SAC) Vì ïí
nên góc giữa hai mặt phẳng (SAC) và (SAB) bằng góc giữa hai đường ïHC ^ ï (SAB) î
thẳng HK và HC . Xét tam giác a 1 1 1 a
CHK vuông tại K , có 1 CH = AB = ; = +  HK = . 2 2 2 2 2 HK SH HI 3 Do đó  HK 2 cosCHK = = . CH 3 ìï ^ a ï 1 d ( )
Nhận xét. Bài làm sử dụng lý thuyết '' í  (a),(b)   = d , '' . Nếu ta sử dụng lý d ï ^ ï (b) 1 d2 2 î
thuyết quen thuộc '' góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng lần lượt nằm
trong hai mặt phẳng và cùng vuông góc với giao tuyến '' thì rất khó.
Câu 11: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại
B, cạnh bên SA vuông góc với đáy. Gọi
E, F lần lượt là trung điểm của các cạnh AB và A .
C Góc giữa hai mặt phẳng
(SEF ) và (SBC) là
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 824
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A.     CSF. B. BSF. C. BSE. D. CSE. Lời giải Chọn C S F C A E B
Gọi (d) là đường thẳng đi qua S và song song với EF.
Vì EF là đường trung bình tam giác ABC suy ra EF // BC .
Khi đó (d)// EF // BC  (SEF )Ç(SBC)=(d) ( ) 1 . SA ìï ^ BC ï (SA ^(ABC)) ìï ^ Ta có BC SE í suy ra ï
BC ^ (SAB)  í (2). ïïAB ^ BC ï î BC ^ SB ïî ( ìï d) ^ SE Từ ( ) 1 ,(2) suy ra ïí  (SEF ) (SBC)  =(SE SB)   ; ; = BSE. ( ï d) ^ ï SB î
Câu 12: Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và
AC = AD = BC = BD = ,
a CD = 2x. Với giá trị nào của x thì hai mặt phẳng (ABC) và (ABD) vuông góc. A. a 3 a a 2 a . B. . C. . D. . 3 2 2 3 Lời giải Chọn A A M C N D B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 825
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Gọi M , N lần lượt là trung điểm của A , B C . D
Ta có AN ^ CD mà (ACD) ^ (BCD) suy ra AN ^(BCD) AN ^ BN .
Tam giác ABC cân tại C, có M là trung điểm của AB suy ra CM ^ AB.
Giả sử (ABC) ^(BCD) mà CM ^ AB suy ra CM ^ (ABD) CM ^ DM . Khi đó, tam giác AB CD
M CD vuông cân tại M MN = =
AB = CD = 2x. 2 2 Lại có 2 2 2 2 AN = BN = AC - AN = a - x , mà 2 2 2
AB = AN + BN . Suy ra 2( a 3 2 2 a - x ) 2 2 2
= 4x a = 3x x = . 3
Câu 13: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh
a. Cạnh bên SA = x và vuông góc với mặt phẳng (ABCD). Xác định
x để hai mặt phẳng (SBC) và (SCD) tạo với nhau một góc 0 60 . 3 A. a a x = . B. x = . C. x = . a D. x = 2 . a 2 2 Lời giải Chọn C S K H D A B C
Từ A kẻ AH vuông góc với SB (H Î SB). ìï ^ Ta có SA BC ïí
BC ^ (SAB)  BC ^ AH mà ^
suy ra AH ^ (SBC). ï A H SB AB ^ BC ïî
Từ A kẻ AK vuông góc với SD (K ÎSD), tương tự, chứng minh được SK ^(SCD).
Khi đó SC ^ (AHK ) suy ra (SBC) (SCD)  =(AH AK )   0 ; ; = HAK = 60 .
Lại có DSAB = DSAD AH = AK mà  0
HAK = 60 suy ra tam giác AHK đều. Tam giác 1 1 1 xa
SAB vuông tại S, có = +  AH = . 2 2 2 2 2 AH SA AB x + a 2 2 Suy ra 2 2 x SH x
SH = SA - AH =  = . 2 2 2 2 + SB x + a x a
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 826
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 Vì SH HK x xa x 1
HK // BD suy ra =  =  =  x = . a 2 2 2 2 2 2 SB BD x + a
x + a .a 2 x + a 2
Câu 14: Cho hình lăng trụ tứ giác đều ABC . D A B ¢ C ¢ D ¢ ¢ có đáy cạnh bằng ,
a góc giữa hai mặt phẳng ( 0
ABCD ) và (ABC ¢) có số đo bằng
60 . Độ dài cạnh bên của hình lăng trụ bằng A. 2 . a B. 3 . a C. a 3. D. a 2. Lời giải Chọn C A' B' C' D' A B D C ìï ^ ¢ Vì AB BB ï ABC . D A B ¢ C ¢ D
¢ ¢ là lăng trụ tứ giác đều  í  AB ^ (BB C ¢ B ¢ ) . ïAB ^ BC ïî ( ìï ABC¢ ï )Ç(BB C ¢ B ¢ ) = BC¢ ï Khi đó (
ïïí ABCD)Ç(BB C¢ B¢)= BC suy ra (ABC¢) (ABCD)  =(BC¢ BC)   0 ; ; = C BC ¢ = 60 .
ï(ïïïABC¢)Ç(ABCD)= AB ïî ¢ Đặt CC
AA ¢ = x, tam giác BCC ¢ vuông tại C, có  0 tan C B ¢ C =
x = tan 60 .a = a 3. BC
Câu 15: Cho hình chóp đều S.ABC có cạnh đáy bằng , a góc
giữa mặt bên và mặt đáy bằng 0 60 .
Tính độ dài đường cao SH của khối chóp. A. a 3 a 2 a a SH = . B. SH = . C. SH = 3 . D. SH = . 2 3 2 2 Lời giải Chọn C S A C H M B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 827
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Gọi H là chân đường cao kẻ từ đỉnh S xuống mặt phẳng (ABCD).
Vì S.ABC là hình chóp đều có SA = SB = SC nên suy ra H chính là tâm đường tròn ngoại tiếp tam giác ABC. ìï ^ Gọi BC AM ï
M là trung điểm của BC, ta có í
BC ^ (SAM ) . ïBC ^ SH ïî
Khi đó (SBC) (ABC)  =(SM AM )   0 ; ; = SMA = 60 . Tam giác a 3 AM a 3 A BC đều có 2 2 AM = AB - MB =  HM = = . 2 3 6 Tam giác SH a 3 a
AHM vuông tại H , có  0 tan SMA =  SH = tan 60 . = . HM 6 2
Vậy độ dài đường cao a SH = . 2
Dạng 4. Thiết diện
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D , đáy lớn ; AB cạnh
bên SA vuông góc với đáy. Gọi Q là điểm trên cạnh SA và Q ¹ A, Q ¹ S ; M là điểm
trên đoạn AD và M ¹ A . Mặt phẳng (a) qua QM và vuông góc với mặt phẳng . (SAD) Thiết diện tạo bởi
(a) với hình chóp đã cho là: A. tam giác. B. hình thang cân. C. hình thang vuông. D. hình bình hành. Lời giải Chọn C S Q P A B M N D C ìï ^ Ta có AB AD ïí
AB ^ (SAD) . Mà (a) ^ (SAD) suy ra AB  (a) . ïAB ^ SA ïî
Qua M kẻ đường thẳng song song với AB cắt BC tại N .
Qua E kẻ đường thẳng song song với AB cắt SB tại P .
Khi đó thiết diện là hình thang MNPQ (do MN PQ ).
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 828
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Vì AB ^ (SAD) suy ra MN ^ (SAD) nên MN ^ EM .
Do đó thiết diện MNPE là hình thang vuông tại E và M .
Câu 2: Cho hình chóp đều . SABC
Mặt phẳng (a) qua A , song song với BC và vuông góc với mặt phẳng . (SBC) Thiết diện tạo bởi
(a) với hình chóp đã cho là: A. tam giác đều. B. tam giác cân. C. tam giác vuông. D. tứ giác. Lời giải Chọn B S M H N A B I C
Gọi I là trung điểm BC .
Trong tam giác SAI kẻ AH ^ SI (H ÎSI ).
Trong tam giác SBC , qua H kẻ đường song song với BC , cắt SC ở M , cắt SB ở N .
Qua cách dựng ta có BC  (AMN ). ( ) 1 ìï ^ Ta có SI AH ïí
SI ^ (AMN )  (SBC) ^ (AMN ). (2) SI ï ^ MN ( do SI ^ BC) ïî Từ ( )
1 và (2) , suy ra thiết diện cần tìm là tam giác AMN .
Dễ thấy H là trung điểm của MN mà AH ^ (SBC) suy ra AH ^ MN . Tam giác AMN có
đường cao AH vừa là trung tuyến nên nó là tam giác cân đỉnh A .
Câu 3: Cho hình chóp đều . S.ABCD
Mặt phẳng (a) qua AB và vuông góc với mặt phẳng . (SCD) Thiết diện tạo bởi
(a) với hình chóp đã cho là: A. tam giác cân. B. hình hình hành.
C. hình thang vuông. D. hình thang cân. Lời giải Chọn D
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 829
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 S N K M D A I J O C B
Gọi I , J lần lượt là trung điểm của CD và AB .
Trong tam giac SIJ kẻ JK ^ SI .
Trong tam giac SIJ , qua K kẻ đường thẳng song song với CD cắt SC tại M , cắt SD tại N .
Ta dễ dàng chứng minh được (ABMN ) ^ (SCD) .
Khi đó thiết diện cần tìm là hình thang ABMN .
Vì hình chóp đã cho là hình chóp đều nên suy ra AN = BM .
Vậy thiết diện là hình thang cân.
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D , AB = 2 ,
a AD = DC = a ; cạnh bên SA = a và vuông góc với đáy. Mặt phẳng (a) qua SD và
vuông góc với mặt phẳng . (SAC) Tính
diện tích S của thiết diện tạo bởi (a) với hình chóp đã cho. 2 2 2 2 A. a a 2 a 3 a S = . B. S = . C. S = . D. S = . 2 2 2 4 Lời giải Chọn C S A E B D C
Gọi E là trung điểm AB , suy ra AECD là hình vuông nên DE ^ AC . ( ) 1
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 830
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Mặt khác SA ^ (ABCD) SA ^ DE . (2) Từ ( )
1 và (2) , suy ra DE ^ (SAC)  (SDE) ^ (SAC). (SDE)É SD üï Ta có
ïý(a)º(SDE).
(SDE) ^ (SAC)ïïþ
Vậy thiết diện là tam giác SDE . Ta có 2 2 2 2
SD = SA + DA = a 2; 2
SE = SA + AE = a
; DE = AC = DC 2 = a 2 . 2 2 Do đó tam giác SD 3 a 3
SDE đều có cạnh a 2 nên S = = . SD D E 4 2
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O với AB = , a AD = 2 . a Cạnh
bên SA = a và vuông góc với đáy. Gọi (a) là mặt phẳng qua SO và vuông góc với (SAD).
Tính diện tích S của thiết diện tạo bởi (a) và hình chóp đã cho. 2 2 2 A. a 3 a 2 a S = . B. S = . C. S = . D. 2 S = a . 2 2 2 Lời giải Chọn B S A M D O B N C
Gọi M , N lần lượt là trung điểm AD, BC . Khi đó:
· MN đi qua O. ìï ^ · MN AD ïí  MN ^ (SAD). ïMN ^ SA ïî
Từ đó suy ra (a)º(SMN ) và thiết diện cần tìm là tam giác SMN . 2 2 æ ö Tam giác 1 1 AD a 2 2 = = +ç ÷
S M N vuông tại M nên S SM .MN SA ç ÷ .AB = . DSMN 2 2 çè 2 ÷ø 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 831
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 BÀI 5. KHOẢNG CÁCH
A. KIẾN THỨC SÁCH GIÁO KHOA CẦN NẮM
1. Khoảng cách từ một điểm đến một đường thẳng a) Định nghĩa:
Khoảng cách từ một điểm M đến đường
thẳng  là khoảng cách giữa hai điểm M M Δ
và H trong đó H là hình chiếu vuông góc P H
của M trên đường thẳng .
Ký hiệu: dM,  MH.
b) Chú ý: Nếu M  thì dM,  0.
2. Khoảng cách từ một điểm đến mặt phẳng a) Định nghĩa: M
Khoảng cách từ một điểm M đến mặt
phẳng (P) là khoảng cách giữa hai điểm
M và H, trong đó H là hình chiếu vuông
góc của điểm M trên mặt phẳng (P). P H
Kí hiệu: dM,P  MH.
b) Chú ý: Nếu M P thì dM,P  0.
3. Khẳng cách giữa đường thẳng và mặt phẳng song song a) Định nghĩa: N a M
Khoảng cách từ một đường thẳng a đến
một mặt phẳng (P) song song với a bằng
khoảng cách từ một điểm tùy ý của a đến (P). K
Tức là: da,P  dM,P, Ma. P H a  P b) Chú ý: Khi  d a, P 0. a   P     
4. Khoảng cách giữa hai mặt phẳng song song a) Định nghĩa: N
Khoảng cách giữa hai mặt phẳng song M
song bằng khoảng cách từ một điểm tùy ý Q
của mặt này đến mặt kia.
Tức là: d P ,Q  dM,Q , MQ. K  P H P  Q b) Chú ý: Khi  d P , Q 0.
P  Q      
5. Khoảng cách giữa hai đường thẳng chéo nhau a) Định nghĩa:
 Đường thẳng a gọi là đường vuông góc chung của hai đường thẳng chéo nhau  và ʹ nếu a
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 832
Face: Trần Đình Cư. SĐT: 0834332133
cắt  ở M và cắt ʹ ở N đồng thời vuông góc với cả  và ʹ.
 Đoạn MN được gọi là đoạn vuông góc a
chung của hai đường thẳng chéo nhau  Δ và ʹ. M
 Khoảng cách giữa hai đường thẳng chéo
nhau là độ dài đoạn vuông góc chung của hai đường thẳng đó. b) Chú ý:    Δ'  ʹ Khi   d,ʹ  N    0.  ʹ
 Khi  // ʹ  d,ʹ  dM,ʹ với M  .
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI TOÁN TRẮC NGHIỆM
DAÏNG 1: KHOAÛNG CAÙCH TÖØ 1 ÑIEÅM ÑEÁN ÑÖÔØNG THAÚNG 1. Phương Pháp Cách xác định:
Việc dựng hình chiếu của một điểm trên đường thẳng trong không gian, ta có thể làm theo 2 cách sau:
 Dựng mặt phẳng đi qua điểm và đường thẳng đã cho. Rồi trên mặt phẳng đó qua điểm đã cho
dựng đoạn vuông góc từ điểm tới đường thẳng.
 Dựng một mặt phẳng đi qua điểm đã cho và vuông góc với đường thẳng, lúc đó giao điểm
của đường thẳng với mặt phẳng vừa dựng chính là hình chiếu của điểm trên đường thẳng.
Tính toán: Sau khi đã xác định được khoảng cách cần tính, ta dùng các hệ thức lượng trong tam
giác, đa giác, đường tròn, … để tính toán. 2. Ví dụ
Ví dụ 1: Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB  a, AD  b, AAʹ  c. Khoảng cách từ điểm
A đến đường thẳng BD’ bằng 2 a b  2 c 2 b b  2 c A. . B. . 2 a  2 b  2 c 2 a  2 b  2 c 2 c b  2 c 2 abc b  2 c C. . D. . 2 a  2 b  2 c 2 a  2 b  2 c
Hướng dẫn giải ĐÁP ÁN A
Do AB  ADʹ nên tam giác ABD’ vuông tại A. Trong tam giác ABD’ kẻ đường cao AH thì AH  dA,BDʹ. D' C' Trong ADDʹ , ta có: ADʹ  2 AD  2 DDʹ  2 b  2 c B' A' 2 2 2 2 2 c
BDʹ  AB  ADʹ  a  b  c H D Xét ABDʹ , ta được: b C A a B
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 833
Face: Trần Đình Cư. SĐT: 0834332133 AH.BDʹ  AB.ADʹ 2 2 AB.ADʹ a b  c  AH   2 2 2 BDʹ a  b  c 2 2 a b c Vậy dA,BDʹ   AH  . 2 a  2 b  2 c
Ví dụ 2: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều tâm O, cạnh a, hình chiếu của
C’ trên (ABC) trùng với tâm của đáy. Cạnh bên CC’ hợp với (ABC) góc o
60 . Gọi I là trung điểm của AB. Khoảng cách
Câu 2.1. từ điểm O đến đường thẳng CC’ bằng a 3a a a A. . B. . C. . D. . 2 2 4 3
Hướng dẫn giải ĐÁP ÁN A C' A'
Theo giả thiết, suy ra: CʹO  ABC , suy ra: J B' OC hch CCʹ  CCʹ,ABC         CʹCO ABC K H  Theo giả thiết, ta có:  o CʹCO 60 a 60° A
Trong (C’CO) dựng OH  CCʹ tại H ta được: a C O I dO,CCʹ  OH . a B 2 a 3 3 a Xét COH  OH  o OC.sin 30  . .  3 2 2 2 Suy ra:    a d O,CCʹ . 2
Câu 2.2. Khoảng cách từ điểm C đến đường thẳng IC’ bằng 2a 13 3a 13 a 3 a 13 A. . B. . C. . D. . 3 13 3 3
Hướng dẫn giải ĐÁP ÁN B Tính dC,ICʹ
Trong (C’IC) dựng CK  ICʹ tại K ta được: dC,ICʹ  CK Xét      OCʹ.CI CICʹ OCʹ.CI CK.ICʹ CK ICʹ a 3 a 3 Mà OCʹ  o OC.tan 60  . 3  a; CI  3 2 2 2 2  2  2  a  2  13a ICʹ IO OCʹ a 12 12 a 3 a. 3a 3a 13 Nên     2 d C,ICʹ CK   . a 13 13 13 2 3
Câu 2.3. Khoảng cách từ điểm O đến đường thẳng A’B’ bằng 2a 7 a 7 a 7 a 7 A. . B. . C. . D. . 3 3 2 4
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 834
Face: Trần Đình Cư. SĐT: 0834332133
Hướng dẫn giải ĐÁP ÁN C Tính dO,Aʹ Bʹ Vì
CʹO  ABC // AʹBʹCʹ  OCʹ  Aʹ BʹCʹ . Gọi J là trung điểm của
Aʹ Bʹ  Cʹ J  Aʹ Bʹ  Aʹ BʹCʹ  OJ  Aʹ Bʹ (định lí 3 đường vuông góc)
Tức là: dO,Aʹ Bʹ  OJ 2 3a a 7 Xét OCʹ J  OJ  2 OCʹ  2 Cʹ J  2 a   4 2 Tức là:    a 7 d O,Aʹ Bʹ . 2
Ví dụ 3: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng
(ABCD) và SA  a. Gọi E là trung điểm của cạnh CD. Khoảng cách từ điểm S đến đường thẳng BE bằng 2a 5 a 5 a 5 3a 5 A. . B. . C. . D. . 5 3 5 5
Hướng dẫn giải ĐÁP ÁN D
Vì SA  ABCD , trong mặt phẳng (ABCD) nếu dựng AH  BE
tại H thì SH  BE (định lí 3 đường vuông góc). Tức là khoảng S
cách từ điểm S đến đường thẳng BE bằng đoạn SH. 2 1 1 a 1 Ta có: S  AB.EF  a.a   AH.BE ABE 2 2 2 2 a 2 a a 5 Mà BE  2 BC  2 CE  2 a   A D 4 2 2 a F a 2a E Nên AH  
, mà SAH vuông tại A, nên: BE H 5 B a C 2  2  2  2  4a  3a  3a 5 SH SA AH a 5 5 5
Ví dụ 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tâm O, SA  (ABCD) ,
SA  a. Gọi I là trung điểm của SC và M là trung điểm của AB. Khoảng cách từ điểm I đến đường thẳng CM bằng a 2 a 3 a 30 a 3 A. . B. . C. . D. . 5 17 10 7
Hướng dẫn giải ĐÁP ÁN C
Do IO  (ABCD) nên nếu dựng OK  CM (K  CM) thì IK  CM . S Tức là: d(I,CM)  IK . 2 a Mà IK  2 OI  2 OK   2 OK 4 1 Do S  OK.MC I OMC 2 A D M O K B C
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 835
Face: Trần Đình Cư. SĐT: 0834332133  2 2 2 a a a  2    2S 2 8 4 a OMC    OK    2 MC a 2 5 2 a  4 2 2 a a a 6 a 30 Suy ra IK     . 4 20 2 5 10
Ví dụ 5: Cho hình chóp đều S.ABC có cạnh đáy bằng a, gọi O là tâm của đáy và  a 3 SO . Gọi I là 3
trung điểm của BC và K là hình chiếu của O lên SI. Khoảng cách từ O đến SA bằng a 5 a 3 a 2 a 6 A. . B. . C. . D. . 5 3 3 6
Hướng dẫn giải S ĐÁP ÁN D
Dựng OH  SA tại H  d(O,SA)  OH a 3 H 2 2 a 3 a 3 3 Ta có: OA  AI  .   SO , 3 3 2 3 K a 1 1 a 3 a 6 A C suy ra: OH  SA  . . 2  2 2 3 6 a a O I Vậy    a 6 d O,SA . 6 B
DAÏNG 2: KHOAÛNG CAÙCH TÖØ MOÄT ÑIEÅM ÑEÁN MAËT PHAÚNG 1. Phương pháp
Để tính khoảng cách từ một điểm đến một mặt phẳng, trước hết ta phải tìm hình chiếu vuông
góc của điểm đó trên mặt phẳng. Việc dựng hình chiếu của điểm trên mặt phẳng, ta hay dùng một trong các cách sau: Cách 1: Q
 Tìm một mặt phẳng (Q) chứa M và vuông góc M với (P).
 Xác định m  P  Q. m
 Dựng Mx  m  P Q, suy ra H  Mx  m P H là điểm cần tìm. Cách 2:
Giả sử đã biết đường thẳng d   , dựng Mx // d   , lúc đó H  Mx  P là hình chiếu
vuông góc của điểm M trên mặt phẳng (P). Cách 3:
Dựa vào tính chất trục của tam giác: Cho ABC nằm trên (P), hình chiếu vuông góc của điểm
M trên (P) là tâm đường tròn ngoại tiếp ABC , tức là nếu MA  MB  MC khi đó hình chiếu
của điểm M trên (P) là tâm O của đường tròn ngoại tiếp ABC.
Chú ý. Khi tính khoảng cách từ một điểm đến một mặt phẳng ta cần biết vận dụng chú ý sau một
cách khéo léo để từ việc phải tính khoảng cách từ một điểm này đến mặt phẳng (khó xác định)
đến việc tính khoảng cách từ điểm khác đến mặt phẳng (dễ xác định hơn).
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 836
Face: Trần Đình Cư. SĐT: 0834332133
 Nếu MA //   dM,  dA,. M dM,   IM A  Nếu MA      I  dA,   .  IA I P H K 2. Ví dụ
Ví dụ 1: Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy, SA  a. Góc giữa
đường thẳng SD và mặt phẳng (SAC) bằng o
30 . Khoảng cách từ điểm D đến mặt phẳng (SBM)
với M là trung điểm CD bằng a 2a 4a 5a A. . B. . C. . D. . 3 3 3 3
Hướng dẫn giải ĐÁP ÁN A
Dễ dàng chứng minh được DB  SAC  Hình chiếu vuông góc của DS lên (SAC) là SO, góc  giữa SD và (SAC) là  o
DSO 30 . Đặt DO  x , ta có SO  x 3 (O là giao của AC và BD) a S Từ 2 SO  2 AO  2 SA  x  2
Gọi N là trung điểm của AB  DN // BM Suy ra H         1 d D; SBM d N; SBM dA;SBM A D 2 N Kẻ AI  BM, AH  SM . O M I
Từ đó chứng minh được B C
AH  SBM  dA;SBM  AH 2 a Trong (ABCD): S  S  2S  ABM ABCD BCM 2 1 2a Mà S  AI.BM  AI  ABM 2 5 1 1 1  a Khi đó:  
 AH  a  dD;SBM  . 2 2 2 AH AI SA 3 3
Ví dụ 2: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  a 2 và BC  a. Cạnh
bên SA vuông góc với đáy và góc giữa cạnh bên SC với đáy là 0
60 . Khoảng cách từ điểm C đến mặt phẳng (SBD) bằng a 38 3a 58 3a 38 3a A. . B. . C. . D. . 29 29 29 29
Hướng dẫn giải ĐÁP ÁN B
Gọi H là hình chiếu vuông góc
của A trên BD và K là hình chiếu vuông góc của A trên SH.
Ta có SA  BD và AH  BD nên
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 837
Face: Trần Đình Cư. SĐT: 0834332133 S BD  SAH .
Suy ra AK  BD . Mà AK  SH nên AK  SBD K A B
Ta có: dC;SBD  dA;SBD  AK 60° H 1 1 1 1 1 1 29 Ta có:       D 2 2 2 2 2 2 2 C AK SA AH SA AB AD 18a Vậy      3a 58 d C; SBD AK . 29
Ví dụ 3: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA  ABCD và SA  a 3.
Gọi I là hình chiếu của A lên SC. Từ I lần lượt vẽ các đường thẳng song song với SB, SD cắt BC,
CD tại P, Q. Gọi E, F lần lượt là giao điểm của PQ với AB, AD. Khoảng cách từ E đến mặt phẳng (SBD) bằng 3a 21 a 21 3a 21 a 21 A. . B. . C. . D. . 11 9 7 7
Hướng dẫn giải ĐÁP ÁN C
Gọi O là tâm của hình vuông S ABCD.
Qua A dựng AH  SO . Dễ dàng
chứng minh được AH  BD I
Khi đó AH  dA,SBD H
Trong tam giác vuông SAC, ta có: D A F 2  O CI.SC AC Q 2 2 IC AC AC B    P C 2 2 2 SC SC SA  AC E 2 2 2 AB  BC 2a 2    2 SA   2 2 AB  BC  2 2 2a  3a 5  IP CP CI CP 2 CBS có IP // SP      SB CB CS CB 5 BE BP 3 BE BC  CP 3 Áp dụng định lý Talet:      CQ PC 2 CQ PC 2 Mà       5 AB CD CQ QP CQ BE BE 3
Do AEF vuông tại A nên: 2  1  1  1 32 32a S AE.AF AE AB BE AB (đvdt) AEF   2 2  2  2 2 2 25 25 DA  5      3 d E, SBD dA,SBD DE 3 5 2 1 1 1 3a
Tam giác SAO vuông tại A, khi đó    2 AH  2 2 2 AH SA AO 7 Vậy     3a 21 d E, SBD . 7
Ví dụ 4: Cho khối chóp S.ABC có đáy là tam giác vuông tại B, BA  a, BC  2a , SA  2a ,
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 838
Face: Trần Đình Cư. SĐT: 0834332133
SA  ABC. Gọi H, K lần lượt là hình chiếu của A trên SB, SC. Khoảng cách từ điểm K đến mặt phẳng (SAB) bằng 8a a 2a 5a A. . B. . C. . D. . 9 9 9 9
Hướng dẫn giải ĐÁP ÁN
Vì BC  SAB nên: AH  BC, AH  SBC S
 AH  HK, AH  SC mà AK  SC  SC  AHK K AB.SA 2a Ta có: AH   , SB 5 H  AC.SA  2 5a AK , SC 3 A C  2  2  8a HK AK AH ,  4a SK 3 5 3  V  1 4a 2a 8a . . .  32 3 a S.AHK B 6 3 5 3 5 135 4 4 Mặt khác SH  2 SA  2 AH  a nên S  2 a AHS 5 5 3V 8a
Vậy khoảng cách cần tìm là: dK,SAB  KSAH  . S 9 AHS  
Ví dụ 5: Cho hình chóp S.ABCD đáy là hình thang,   o
ABC BAD 90 , BA  BC  a , AD  2a.
Cạnh bên SA vuông góc với đáy và SA  a 2. Gọi H là hình chiếu của A lên SB. Khoảng cách
từ H đến mặt phẳng (SCD) bằng 5a 4a 2a a A. . B. . C. . D. . 3 3 3 3
Hướng dẫn giải ĐÁP ÁN D Gọi I là trung điểm AD. Ta có    AD CI IA ID
, suy ra ACD vuông tại C  CD  AC . 2 S
Mà SA  ABCD  SA  CD
nên ta có CD  SD hay SCD vuông. Gọi d , d lần 1 2
lượt là khoảng cách từ B, H đến (SCD) SA SB Ta có: SAB ∽ SHA   SH SA H 2 A I D  SH  SA  2 2 SB SB 3 SH d 2 2 mà  2   d  d 2 1 SB d 3 3 B C 1 3 1 1 2a
Thể tích khối tứ diện S.BCD: V  SA. AB.BC  SBCD 3 2 6 Ta có:  2  2 SC SA AC  2a ,
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 839
Face: Trần Đình Cư. SĐT: 0834332133  2  2    1 CD CI ID 2a S SC.CD  2 2a SCD 2 3 2a 3. 1 a Ta có:    6 V d .S d  S.BCD 1 SCD 1 2 3 2a 2 2 a
Vậy khoảng cách từ H đến (SCD) là d  d  . 2 1 3 3
Ví dụ 6: Cho hình chóp S.ABC có tam giác ABC vuông tại A, AB  AC  a , I là trung điểm của SC,
hình chiếu vuông góc của S lên mặt phẳng ABC là trung điểm H của BC, mặt phẳng SAB
tạo với đáy một góc bằng o
60 . Khoảng cách từ điểm I đến mặt phẳng SAB theo a bằng a 3 a 3 a 3 a A. . B. . C. . D. . 2 8 4 4
Hướng dẫn giải ĐÁP ÁN C
Gọi K là trung điểm của AB  HK  AB 1 S
Vì SH  ABC nên SH  AB 2
Từ (1) và (2)  AB  SK
Do đó góc giữa SAB với đáy bằng góc giữa SK và HK và  bằng  o SKH 60 M  Ta có   a 3 SH HK.tan SKH 2 C B H 60°
Vì IH // SB nên IH // SAB . K
Do đó dI,SAB  dH,SAB A Từ H kẻ HM  SK tại M
 HM  SAB  dH,SAB  HM 1 1 1 16 a 3 Ta có     HM  . 2 2 2 2 HM HK SH 3a 4
Ví dụ 7: Cho hình chóp S.ABC có đáy là tam giác vuông tại A và AB  2a , AC  2a 3. Hình chiếu
vuông góc của S trên mặt phẳng (ABC) là trung điểm H của cạnh AB. Góc giữa hai mặt phẳng (SBC) và (ABC) bằng o
30 . Khoảng cách từ trung điểm M của cạnh BC đến mặt phẳng (SAC) bằng a 3 a 5 a 5 3a A. . B. . C. . D. . 5 3 5 5 S
Hướng dẫn giải ĐÁP ÁN C
Trong mặt phẳng (ABC) kẻ HK  BC tại K D  BC  SHK  A C Từ giả thiết ta có:  o SHK 30  2  2 BC AB AC  4a H M K  AC HK 3 a 3 B sin ABC     HK  BC HB 2 2
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 840
Face: Trần Đình Cư. SĐT: 0834332133  Trong tam giác SHK có   a SH HK tan SKH 2
Do M là trung điểm của cạnh BC nên MH // AC, do đó MH // (SAC).
Suy ra: dM,SAC  dH,SAC
Trong mặt phẳng (SAB) kẻ HD  SA tại D. Ta có:
AC  SAB  AC  DH  DH  SAC 1  1  1   a 5 HD 2 2 2 DH HA HS 5 Vậy          a 5 d M, SAC d H, SAC HD . 5
Ví dụ 8: Cho hình chóp S.ABC có tam giác ABC vuông tại A, AB  AC  a , I là trung điểm của SC,
hình chiếu vuông góc của S lên mặt phẳng (ABC) là trung điểm H của BC, mặt phẳng (SAB) tạo với đáy 1 góc bằng o
60 . Khoảng cách từ điểm I đến mặt phẳng (SAB) theo a bằng a 3 a 5 a 3 a 3 A. . B. . C. . D. . 5 4 4 2
Hướng dẫn giải ĐÁP ÁN C
Gọi K là trung điểm của AB  HK  AB 1 S
Vì SH  ABC nên SH  AB 2
Từ (1) và (2)  AB  SK
Do đó góc giữa (SAB) với đáy bằng góc giữa  SK và HK bằng  o SKH 60 .  M Ta có:   a 3 SH HK tan SKH C 2 H B 3 1 1 1 a 3 K Vậy V  S .SH  . AB.AC.SH  S.ABC ABC 3 3 2 12 A
Vì IH // SB nên IH // SAB . Do đó dI,SAB  dH,SAB
Từ H kẻ HM  SK tại M  HM  SAB  dH,SAB  HM 1 1 1 16 a 3 Ta có:     HM  . 2 2 2 2 HM HK SH 3a 4 Vậy     a 3 d I, SAB . 4
Ví dụ 9: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Gọi I là trung điểm cạnh AB.
Hình chiếu vuông góc của đỉnh S trên mặt phẳng đáy là trung điểm H của CI, góc giữa đường
thẳng SA và mặt đáy bằng o
60 . Khoảng cách từ điểm H đến mặt phẳng SBC bằng a 7 a 21 a 21 a 21 A. . B. . C. . D. . 29 4 29 3 29 29
Hướng dẫn giải ĐÁP ÁN B
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 841
Face: Trần Đình Cư. SĐT: 0834332133 S A I H E A C B C H A' K I' H' K I H' B a 3 Ta có: CI  2 AC  2 AI  2 a 7 a 21 Do đó AH  2 AI  2 IH  , suy ra SH  o AH.tan 60  . 4 4
Gọi A’, H’, I’ lần lượt là hình chiếu của A, H, I trên BC, E là hình chiếu của H trên SH’ thì
HE  SBC  dH;SBC  HE . 1 1 a 3 1 1 1 a 21
Ta có: HHʹ  IIʹ  AAʹ  . Từ    HE  2 4 8 2 2 2 HE HS HHʹ 4 29 Vậy     a 21 d H; SBC . 4 29 
Ví dụ 10: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Góc  o BAC 60 , hình chiếu
của S trên mặt phẳng ABCD trùng với trọng tâm của tam giác ABC. Mặt phẳng SAC hợp
với mặt phẳng ABCD góc o
60 . Khoảng cách từ B đến mặt phẳng SCD bằng a 2a 6a 3a A. . B. . C. . D. . 112 111 112 112
Hướng dẫn giải ĐÁP ÁN C
Trong SBD kẻ OE // SH khi đó ta có S
OC, OD, OE đôi một vuông góc. E a a 3 3a Và: OC  , OD  , OE  2 2 8 Áp dụng công thức: A D 1 1 1 1    2 d O,SCD 2 2 2 OC OD OE O H 3a  B d  C 112 Mà         6a d B, SCD 2d O, SCD . 112
DAÏNG 3: KHOAÛNG CAÙCH GIÖÕA HAI MAËT PHAÚNG SONG SONG. KHOAÛNG CAÙCH TÖØ ÑÖÔØNG THAÚNG ÑEÁN MAËT PHAÚNG 1. Phương pháp
Việc tính khoảng cách giữa một đường thẳng và một mặt phẳng song song với nó, hoặc tính
khoảng cách giữa hai mặt phẳng song song đều quy về việc tính khoảng cách từ điểm đến mặt
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 842
Face: Trần Đình Cư. SĐT: 0834332133
phẳng. Cần lưu ý việc chọn điểm trên đường hoặc trên mặt sao cho việc xác định khoảng cách đơn giản nhất. 2. Ví dụ
Ví dụ 1: Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh bên và cạnh đáy đều bằng a. Hình chiếu
vuông góc của A trên (A’B’C’) trùng với trung điểm của B’C’.
Câu 1.1. Khoảng cách từ AA’ đến mặt bên BCC’B  ’ bằng a 3 a 3 3a 2 a 3 A. . B. . C. . D. . 4 3 4 2
Hướng dẫn giải ĐÁP ÁN A
Ta có: AAʹ // BBʹ  BCCʹ Bʹ  AAʹ// BCCʹBʹ C A Gọi J  hch
I  IJ  AAʹ // BBʹ  IJ  BBʹ AAʹ
Mặt khác, theo giả thiết suy ra: J B a BʹCʹ  AʹI   AAʹI a  BʹCʹ AAʹI BʹCʹ  AI   AAʹI     a A' C'
Suy ra: IJ  BʹCʹ , tức là IJ  BCCʹ Bʹ , a I a
mà J  AAʹ nên dAAʹ,BCCʹBʹ  IJ B' Trong      AI.AʹI AAʹI IJ.AAʹ AI.AʹI IJ . AAʹ 2 3a a Dễ thấy  a 3 AʹI , AI  2 AAʹ  2 AI  2 a   . 2 4 2 a a 3 . a 3 Suy ra:  2 2 IJ  . Vậy     a 3 d AAʹ, BCCʹ Bʹ . a 4 4
Câu 1.2. Khoảng cách giữa hai mặt đáy của lăng trụ bằng a a A. . B. . a 2 a 5 C. . D. . 4 2 4 2
Hướng dẫn giải ĐÁP ÁN B
Hai đáy của lăng trụ song song nên d ABC ,AʹBʹCʹ  dA,AʹBʹCʹ mà AABC và          a AI Aʹ BʹCʹ d ABC , Aʹ BʹCʹ AI . 2
Ví dụ 2: Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB  a, BC  b , CCʹ  c.
2.1. Khoảng cách từ AA’ đến (BDD’B’) bằng abc abc ab ac A. . B. . C. . D. . 2 a  2 b  2 c 2 a  2 b 2 a  2 b 2 a  2 c
Hướng dẫn giải ĐÁP ÁN C
Ta có: AAʹ // BBʹ  BDDʹ Bʹ
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 843
Face: Trần Đình Cư. SĐT: 0834332133
 AAʹ// BDDʹBʹ . Do đó:
dAAʹ,BDDʹBʹ  dA,BDDʹBʹ
Gọi H  hch A  AH  BD mà D' BD C'
BDDʹBʹ  ABCD suy ra: A' B'
AH  BDDʹBʹ . Tức là:
dA,BDDʹBʹ  AH 1 1 1 Xét ABD    D 2 2 2 AH AB AD C H 2 1 1 a  2    b A B 2 2 2 2 a b a b 2 2 a b ab nên 2 AH   AH  2 a  2 2 b a  2 b ab
Vậy: dAAʹ,BDDʹBʹ  . 2 a  2 b
2.2. Gọi M, N lần lượt là trung điểm của AA’, BB’. Khoảng cách từ MN đến (ABC’D’) bằng 2abc abc bc 2ac A. . B. . C. . D. . 2 a  2 b  2 c 2 2 a  2 b 2 2 a  2 b 2 a  2 c
Hướng dẫn giải ĐÁP ÁN C D' C' A' B' K N M D C A B
Ta có: MN// AB  ABCʹ Dʹ  MN // ABCʹDʹ . Suy ra:
dMN,ABCʹDʹ  dM,ABCʹDʹ , nhưng A’M cắt mặt phẳng (ABC’D’) tại A và M là trung điểm của AA’. Nên:     1 d M, ABCʹ Dʹ dAʹ,ABCʹDʹ 2 Gọi K  hch
Aʹ  AʹK  ADʹ mà ABCʹDʹ  AAʹDʹ D , suy ra: ADʹ
AʹK  ABCʹDʹ . Tức là: dAʹ,ABCʹDʹ  AʹK . 2 1 1 1 1 1 c  2 b Xét Aʹ ADʹ       , nên: 2 2 2 2 2 2 2 AʹK Aʹ A Aʹ Dʹ c b c b 2 2 2  c b   bc bc AʹK AʹK
. Vậy dM,ABCʹDʹ  . 2 c  2 2 b b  2 c 2 2 a  2 b
2.3. Khoảng cách giữa hai mặt phẳng ADʹ Bʹ và Cʹ BD bằng
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 844
Face: Trần Đình Cư. SĐT: 0834332133 abc abc A. . B. . 2 a  2 b  2 c ab  bc  ca abc abc C. . D. . 2 2 a  2 c  2 c 2 2 a b  2 2 b c  2 2 c a
Hướng dẫn giải ĐÁP ÁN D D' C' O' A' B' G1 C D O A B
Ta có: Bʹ Dʹ // BD  CʹBD  Bʹ Dʹ// CʹBD
Gọi O  AC  BD,Oʹ  AʹC  ʹ Bʹ Dʹ
Suy ra: AOʹ // CʹO  CʹBD  AOʹ // CʹBD
Mà AOʹ,BʹDʹ  ABʹDʹ,AOʹ BʹDʹ  Oʹ  ADʹBʹ// CʹBD
Ta đã chứng minh được A’C bị các mặt (AD’B’), (C’BD) chia thành ba đoạn bằng nhau.
Do đó: d ADʹBʹ ,CʹBD  dG ,CʹBD  d Aʹ, ADʹBʹ 1   
Vì A’A, A’B’, A’D’ đôi một vuông góc, nếu: 1 1 1 1 1 1 1 2 d Aʹ,ADʹBʹ       2 2 2 2 2 2 Aʹ A Aʹ Bʹ Aʹ Dʹ a b c abc
Vậy: dAʹ,ADʹBʹ 
 d ADʹBʹ,CʹBD 2 2 a b  2 2 b c  2 2 c a
Ta cần chú ý kết quả sau: Nếu tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc thì:     1  1  1 d O, ABC . 2 2 2 OA OB OC
Ví dụ 3: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, mặt bên SBC vuông góc với đáy
ABC. Gọi M, N, P lần lượt là trung điểm của AB, SA, AC. Khoảng cách giữa hai (MNP) và (SBC) bằng a 3 a 3 a 3 3a 3 S A. . B. . C. . D. . 3 2 4 2
Hướng dẫn giải ĐÁP ÁN C Theo giả thiết, suy ra: N H a
MN // SB  SAB  MN // SAB B C
NP // SC  SAC  NP // SAC M K P
Mà MN,NP  MNP ,MN  NP  N nên MNP // SBC . a
Gọi H là trung điểm của BC  AH  BC A (do ABC đều)
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 845
Face: Trần Đình Cư. SĐT: 0834332133
Mà ABC  SBC và AH  ABC
BC  ABC  SBC  AH  SBC
Gọi K  AH  MP  KH  SBC  dK,SBC  KH
Vì MNP // SBC và K MNP 1 a 3
Do đó: d MNP ,SBC  dK,SBC  KH  AH  . 2 4
Ví dụ 4: Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh đều bằng a. Góc tạo bởi cạnh bên và mặt phẳng đáy bằng o
30 . Hình chiếu H của điểm A trên mặt phẳng (A’B’C’) thuộc đường thẳng B’C’. Khoảng
cách giữa hai mặt phẳng đáy bằng a a a 2 a 3 C A. . B. . C. . D. . A 3 2 2 2 K
Hướng dẫn giải B ĐÁP ÁN B
Khoảng cách giữa hai mặt phẳng đáy chính bằng AH. A'C' Trong HAAʹ , ta có:  o Aʹ 30 . H  a AH  AAʹ.sin Aʹ  o a.sin 30  . B' 2
DAÏNG 4. KHOAÛNG CAÙCH GIÖÕA HAI ÑÖÔØNG THAÚNG CHEÙO NHAU 1. Phương pháp
Để tính khoảng cách giữa hai đường thẳng chéo nhau, ta có thể sử dụng một trong các cách sau:
Cách 1: Dựng mặt phẳng (P) chứa đường thẳng a và song song với b. Khoảng cách từ b đến (P)
là khoảng cách cần tìm.
Cách 2: Dựng hai mặt phẳng song song và lần lượt chứa hai đường thẳng. Khoảng cách giữa
hai mặt phẳng đó là khoảng cách cần tìm.
Cách 3: Dựng đoạn vuông góc chung và tính độ dài đoạn đó.
Cách dựng đoạn vuông góc chung của hai đường thẳng chéo nhau:
Cách 1: Khi a  b
+ Dựng một (P)  b, (P)  a tại H. a
+ Trong (P) dựng HK  b tại K.
+ Đoạn HK là đoạn vuông góc chung của b a và b. HCách 2: K P
+ Dựng (P)  b, (P) // a . + Dựng aʹ  hch M
 a , bằng cách lấy M a P K a
dựng đoạn MN  () , lúc đó a’ là
đường thẳng đi qua N và song song a. a' + Gọi H  a 
ʹ b , dựng HK // MN  HK là N đoạn vuông góc chung. b P HCách 3:
+ Dựng mặt phẳng (P) vuông góc với a tại điểm M.
+ Dựng hình chiếu b’ của b trên (P).
+ Dựng hình chiếu vuông góc H của M trên b’.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 846
Face: Trần Đình Cư. SĐT: 0834332133
+ Từ H dựng đường thẳng song song với a a, cắt b tại điểm B. B A b' H P M
+ Qua B dựng đường thẳng song song với MH, cắt a tại điểm A. Khi đó, AB là đoạn vuông góc chung của a và b. 2. Ví dụ
Ví dụ 1: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD có AD  2AB ,
SA  ABCD , SC  2a 5 và góc giữa SC và ABCD bằng o
60 , M là trung điểm của cạnh BC.
Khoảng cách giữa hai đường thẳng AM và SD bằng a 510 a 51 2a 510 3a 510 A. . B. . C. . D. . 17 17 17 17
Hướng dẫn giải ĐÁP ÁN A
Ta có SA  ABCD  SC có hình chiếu trên ABCD là AC            o SC,ABCD SC,AC SCA 60 S Ta giác SAC vuông tại A H N   o AC SC.cos 60  a 5 và  o SA SC.sin 60  a 15 A D Ta có 2 2 2 AB  AD  AC 2 2  5AB  5a  AB  a B M C
Dựng hình bình hành AMDN và dựng AH  SN tại H. Ta có:
 AM // DN  AM // SDN  dAM,SDN  dA,SDN
 AM  MD nên AMDN là hình chữ nhật.
 ND  AN mà DN  SA  DN  SAN
 DN  AH mà AH  SN  AH  SDN  dA,SDN  AH 1 1 1 1 1 17 Ta có      2 2 2 2 2 2 AH AS AN 15a 2a 30a   a 510 AH . Vậy    a 510 d AM,SD . 17 17 
Ví dụ 2: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB  2a ,  o BAC 60 , cạnh bên
SA vuông góc với đáy và SA  a 3 . Gọi M là trung điểm của cạnh AB. Khoảng cách giữa hai
đường thẳng SB và CM bằng
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 847
Face: Trần Đình Cư. SĐT: 0834332133 a 10 2a 3 2a 3 a 3 A. . B. . C. . D. . 17 29 19 13
Hướng dẫn giải ĐÁP ÁN B
Gọi N là trung điểm cạnh SA. S Do SB // CMN nên
dSB,CM  dSB,CMN N
 dB,CMN  dA,CMN
Kẻ AE  MC, E  MC và kẻ H AH  NE, H  NE A C Chứng minh được M E
AH  CMN  dA,CMN  AH B 2S Tính AE  AMC trong đó: MC 1  1 3  2 S  AM.AC.sinCAM  a.4a.  a 3  2a 3 AMC 2 2 2   AE   13 MC  a 13  2a 3 2a 3 2a 3 Tính được AH   dA,CMN   dSB,CM  . 29 29 29
Ví dụ 3: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A, D, SA vuông góc với đáy,
SA  AD  a, AB  2a . Khoảng cách giữa AB và SC bằng a a A. . B. . C. a 2. D. 2a 2. 2 2
Hướng dẫn giải ĐÁP ÁN B Ta có: AB // DC nên S
dAB,SC  dAB,SDC .
Trong mặt phẳng (SAD) từ A kẻ AH  SD, H  SD 1 H Ta có: E B DC  AD A   DC  SAD DC  SA   DC  AH 2 D C
Từ (1) và (2) suy ra AH  SCD
AH  dAB,SCD  dAB,SC 1 1 1 2 a
Trong tam giác vuông SAD có:     AH  . 2 2 2 2 AH AD SA a 2 
Ví dụ 4: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,  o
ABC 60 , cạnh bên SA vuông
góc với đáy, SC tạo với đáy một góc o
60 . Khoảng cách giữa hai đường thẳng AB, SD bằng 3a 2a a 3a A. . B. . C. . D. . 5 5 15 15
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 848
Face: Trần Đình Cư. SĐT: 0834332133
Hướng dẫn giả S i ĐÁP ÁN D 3V
dAB,SD  dA,SCD  S.ACD SSCD
Gọi H là trung điểm CD. Ta có: CD  SH . A D 2 1 a 15 60° Do đó S  CD.SH  SCD 60° H 2 4 B C 3V 3a
Vậy dAB,SD  dA,SCD S.ACD   . SSCD 15 1
Lưu ý: Ở trên ta đã sử dụng công thức S V .ABCD  SA. ABCD S 3
. Đây là công thức thể tích của khối  1 
đa diện học ở chương trình 12  V  B.h 3   
Ví dụ 5: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  a,
AD  a 3 , SA  ABCD , góc giữa mặt phẳng (SBD) và mặt phẳng (ABCD) bằng o 60 . Khoảng
cách giữa hai đường thẳng AC và SD bằng 3a a 3a 2a A. . B. . C. . D. . 2 4 4 3
Hướng dẫn giải ĐÁP ÁN A S
Trong mặt phẳng (ABCD) đường thẳng
qua D song song với AC, cắt đường thẳng AB tại E.
Trong tam giác ADE kẻ đường cao AK H
KDE  SAK  SDE. Dựng A 60° B E
AH  SK tại H, suy ra AH  SDE . I K Do AC// SDE D C
 dAC;SD  dA;SDE  AH a 3 3a 3a Ta có: AK   AH   dAC;SD  . 2 4 4 
Ví dụ 6: Cho hình chóp S.ABCD có đáy ABCD là hình thoi có cạnh bằng a 3 ,  O BAD 120 và
cạnh bên SA vuông góc với mặt phẳng đáy. Biết rằng số đo của góc giữa hai mặt phẳng (SBC) và (ABCD) bằng O
60 . Khoảng cách giữa hai đường thẳng BD và SC bằng a 7 3a 7 3a 7 a 7 A. . B. . C. . D. . 14 4 14 8 S
Hướng dẫn giải ĐÁP ÁN C Gọi O  AC  BD. I A B
Vì DB  AC, BD  SC nên BD  SAC tại O. O H
Kẻ OI  SC  OI là đường vuông góc chung của BD và SC. D C
Sử dụng hai tam giác đồng dạng ICO và ACS hoặc
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 849
Face: Trần Đình Cư. SĐT: 0834332133
đường cao của tam giác SAC, suy ra được  3a 7 OI . 14 Vậy    3a 7 d BD,SC . 14
Ví dụ 7: Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, cạnh bên SA vuông góc với
mặt phẳng đáy. Góc giữa SC và mặt phẳng đáy bằng o
45 . Gọi E là trung điểm BC. Khoảng cách
giữa hai đường thẳng DE và SC theo a bằng a A. . 2a 38 a 38 a 38 B. . C. . D. . 19 9 19 9
Hướng dẫn giải ĐÁP ÁN C
Từ C dựng CI // DE  DE // SCI.
Từ A dựng AK  CI , cắt ED tại H và CI tại K. S
Trong (SAK) dựng HT  SK .
Do CI  SAK nên HT  SCI  CD.AI  3a AK , D CI 5 A I T  1  a HK AK H K 3 5 B E C
dDE;SC  dH;SCI   SA.HK  a 38 HT . SK 19
Ví dụ 8: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD, đường thẳng SA vuông góc với
mặt phẳng (ABCD) và SA  AD  a. Khoảng cách giữa hai đường thẳng AB và SC bằng a 2 a 2 a 2 a 2 A. . B. . C. . D. . 10 6 4 2
Hướng dẫn giải ĐÁP ÁN D S Trong mặt phẳng (SAD), vẽ AH  SD, H SD
Mặt khác ABCD là hình chữ nhật nên H B
CD  SAD  AH  SCD A
Vậy khoảng cách giữa AB và SC chính là AH.
Trong tam giác vuông SAD có AH là đường D C cao nên 1  1  1   a 2 AH 2 2 2 AH AS AD 2 a 2
Vậy khoảng cách giữa hai đường thẳng AB và SC bằng . 2
Ví dụ 9: Cho hình chóp S.ABC có tam giác SAB đều cạnh a, tam giác ABC cân tại C. Hình chiếu
của S trên mặt phẳng ABC là trung điểm của cạnh AB, góc hợp bởi cạnh SC và mặt đáy là o
30 . Tính khoảng cách của hai đường thẳng SA và BC.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 850
Face: Trần Đình Cư. SĐT: 0834332133 3a 3a a 2a A. . B. . C. . D. . 13 13 13 13
Hướng dẫn giải ĐÁP ÁN A
Gọi H là trung điểm cạnh AB, ta có SH là S
đường cao của hình chóp S.ABC và CH là
đường cao của tam giác ABC. Từ giả thiết  ta được  o SCH 30 . Tam giác SHC vuông tại H nên K D SH 3a  o tan 30  CH  SH. 3  G CH 2 A C
Dựng hình bình hành ABCD, khi đó H
dBC,SA  dBC,SAD B
 dB,SAD  2dH,SAD
Gọi G, K lần lượt là hình chiếu của H trên các đường thẳng AD và SG. Ta có:
AD  HG AD  SHG HK   AD AD SH 
Mà HK  SG nên HK  SAD hay dH,SAD  HK
Tam giác SHG vuông tại H nên: 1
 1  1  1  1  1  52   3a HK 2 2 2 2 2 2 2 HK HG HS HB HC HS 9a 2 13 Vậy    3a d BC,SA . 13
Ví dụ 10: Cho hình chóp S.ABCD, tứ giác ABCD là hình thang cân, hai đáy là BC và AD. Biết
SA  a 2 , AD  2a, AB  BC  CD  a . Hình chiếu vuông góc của S trên mặt phẳng ABCD
trùng với trung điểm cạnh AD. Khoảng cách giữa hai đường thẳng SB và AD bằng a 21 a 21 a 3a A. . B. . C. . D. . 3 7 7 7
Hướng dẫn giải ĐÁP ÁN B S 2 3a 3 Ta có: S  3S  ABCD ABI 4
Xét SBI vuông tại I có: 2  2  2  2 SI SB BI a  SI  a AD // BC  A D
BC  SBC  AD // SBC  I
 dAD,BC  dAD,SBC B C
 dI,SBC  3VSIBC S SBC
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 851
Face: Trần Đình Cư. SĐT: 0834332133 3 3 1 1 a 3 a 3 V  V  .  ; SIBC S.ABCD 3 3 4 12 
       2a 7 S p p a p b p c  SBC 4 Vậy    a 21 d AD,SB . 7
C. BÀI TẬP RÈN LUYỆN TỐC ĐỘ
Câu 1: Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Khoảng cách từ C đến AC bằng a 6 a 3 a 6 a 6 A. . B. . C. . D. . 7 2 3 2
Câu 2: Cho hình chóp tứ giác S.ABCD có tất cả các cạnh đều bằng a. Khoảng cách từ D đến đường thẳng SB bằng a a a 3 A. a. B. . C. . D. . 2 3 2
Câu 3: Cho tam giác ABC có AB  14, BC  10,AC  16 . Trên đường thẳng vuông góc với mặt
phẳng (ABC) tại A lấy điểm O sao cho OA  8 . Khoảng cách từ điểm O đến cạnh BC bằng A. 8 3. B. 16. C. 8 2. D. 24.
Câu 4: Hình chóp S.ABC có đáy ABC là tam giác vuông tại A, BC  2a ,  o ABC 60 . Gọi M là trung
điểm cạnh BC và SA  SC  SM  a 5 . Khoảng cách từ S đến cạnh AB bằng a 17 a 19 a 19 a 17 A. . B. . C. . D. . 4 2 4 2
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc BAC bằng o 60 . Hình chiếu
vuông góc của S trên mặt phẳng ABCD là điểm H thuộc đoạn BD sao cho HD  2HB. Đường
thẳng SO tạo với mặt phẳng ABCD góc o
60 với O là giao điểm của AC và BD. Khoảng cách
từ B đến mặt phẳng SCD bằng 3a 7 3a 7 a 7 2a 7 A. . B. . C. . D. . 15 14 11 15
Câu 6: Cho hình chóp S.ABC có các mặt ABC, SBC là
những tam giác đều cạnh a. Góc giữa hai mặt
phẳng (SBC) và (ABC) bằng o
60 . Hình chiếu vuông góc của S xuống (ABC) nằm trong tam giác
ABC. Khoảng cách từ B đến mặt phẳng (SAC) theo a bằng 2a 13 3a 13 3a 13 a 13 A. . B. . C. . D. . 13 13 11 13
Câu 7: Cho hình chóp S.ABCD, đáy là hình chữ
nhật tâm I, có AB  a, BC  a 3. Gọi H là trung
điểm AI. Biết SH vuông góc với mặt phẳng đáy và tam giác SAC vuông tại S. Khoảng cách từ C
đến mặt phẳng (SBD) bằng 3a a 3a 5a A. . B. . C. . D. . 11 13 15 17
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, BD  2a ; tam giác SAC vuông tại S và
nằm trong mặt phẳng vuông góc với đáy, SC  a 3. Khoảng cách từ điểm B đến mặt phẳng (SAD) bằng 3a 21 a 21 4a 21 2a 21 A. . B. . C. . D. . 7 7 7 7
Câu 9: Cho hình chóp S.ABCD có đáy ABCD là hì nh chữ nhật có AB  a , BC  2a 2 . Hình chiếu
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 852
Face: Trần Đình Cư. SĐT: 0834332133
của S lên mặt phẳng đáy là trọng tâm của tam giác ABC. Góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng o
60 . Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng 3a 21 a 21 4a 21 2a 21 A. . B. . C. . D. . 7 7 7 7 
Câu 10: Cho hình chóp S.ABC có    o
AB AC, BC a 3 , BAC 120 . Gọi I là trung điểm cạnh AB.
Hình chiếu vuông góc của đỉnh S trên mặt phẳng đáy là trung điểm H của CI, góc giữa đường
thẳng SA và mặt đáy bằng o
60 . Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng 4a 37 a 3a 37 2a 37 A. . B. . C. . D. . 37 37 37 37
Câu 11: Cho hình chóp S.ABC
D có đáy ABCD là hì nh thang vuông tại A và B. Hình chiếu của S lên
mặt phẳng (ABCD) trùng với giao điểm I của AC và BC. Mặt bên (SAB) hợp với đáy một góc o
60 . Biết rằng AB  BC  a, AD  3a. Khoảng cách từ D đến mặt phẳng (SAB) theo a bằng 4a 3 3a 3a 3 3a 3 A. . B. . C. . D. . 5 4 7 2 
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh bằng a, góc  o DAB 120 .
Hai mặt phẳng (SAC) và (SBD) cùng vuông góc với đáy. Góc giữa (SBC) và mặt đáy bằng o 60 .
Khoảng cách từ A đến (SBC) bằng a 3 3a 3a 3a 3 A. . B. . C. . D. . 5 4 7 2 
Câu 13: Trong mặt phẳng (P), cho hình thoi ABCD có độ dài các cạnh bằng a,  o ABC 120 . Gọi G là
trọng tâm tam giác ABD. Trên đường thẳng vuông góc với (P) tại G, lấy điểm S sao cho   o
ASC 90 . Khoảng cách từ điểm G đến mặt phẳng (SBD) theo a bằng a a 2 a 2 a A. . B. . C. . D. . 17 27 17 37
Câu 14: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, BD  2a ; tam giác SAC vuông tại S
và nằm trong mặt phẳng vuông góc với đáy, SC  a 3 . Khoảng cách từ điểm B đến mặt phẳng (SAD) bằng 2a 13 2a 2a 21 a 13 A. . B. . C. . D. . 7 7 7 7   
Câu 15: Cho hình hộp thoi ABCD.A’B’C’D’ có các cạnh đều bằng a và    o BAD BAAʹ DAAʹ 60 .
Khoảng cách giữa hai mặt phẳng đáy (ABCD) và (A’B’C’D’) bằng a 5 a 10 a 6 a 3 A. . B. . C. . D. . 5 5 3 3
Câu 16: Cho tứ diện ABCD có AB  BCD ,AB  5a,BC  3a,CD  4a . Gọi M, N lần lượt là trung điểm của AC và AD.
Câu 16.1. Khoảng cách giữa đường thẳng MN và mặt phẳng (BCD) bằng 2a a a 5a A. . B. . C. . D. . 3 2 4 2
Câu 16.2. Gọi (P) là mặt phẳng chứa MN và đi qua trung điểm K của AB. Khoảng cách giữa hai
mặt phẳng (P) và (BCD) bằng
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 853
Face: Trần Đình Cư. SĐT: 0834332133 a 3a 5a 5a A. . B. . C. . D. . 3 2 4 2
Câu 17: Cho hình chóp cụt tứ giác đều ABCD.A’B’C’D’. Đáy lớn ABCD có cạnh bằng a, đáy nhỏ
A’B’C’D’ có cạnh bằng b. Góc giữa mặt bên và đáy lớn bằng o
60 . Khoảng cách giữa hai mặt đáy
của hình chóp cụt đều bằng ab 3 a  b 3 a  b 3 b a 3 A. . B. . C. . D. . 2 2 2 2
Câu 18: Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Khoảng cách giữa hai mặt phẳng (BA’C’) và (ACD’) bằng a 3 a 3 a 3 a 3 A. . B. . C. . D. . 2 3 2 5
Câu 19: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  3a, AD  2a . Hình chiếu
vuông góc của S lên mặt phẳng (ABCD) là điểm H thuộc cạnh AB sao cho AH  2HB. Góc giữa
mặt phẳng (SCD) và mặt phẳng (ABCD) bằng o
60 . Khoảng cách giữa hai đường thẳng SC và AD bằng a 39 6a 39 a 39 a 39 A. . B. . C. . D. . 15 13 3 11
Câu 20: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,  a 17 SD , hình chiếu vuông 2
góc H của S trên mặt phẳng (ABCD) là trung điểm của đoạn AB. Gọi K là trung điểm của đoạn
AD. Khoảng cách giữa hai đường thẳng HK và SD theo a bằng a 3 a 3 a 3 a 3 A. . B. . C. . D. . 25 45 15 5
Câu 21: Cho hình chóp S.ABC có  a 70 SC
, đáy ABC là tam giác vuông tại A, AB  2a, AC  a 5
và hình chiếu của S lên mặt phẳng (ABC) là trung điểm cạnh AB. Khoảng cách giữa hai đường thẳng BC và SA bằng 3a 4a a 2a A. . B. . C. . D. . 5 5 5 5
Câu 22: Cho hình chóp S.ABC có đ áy là tam giác
ABC đều cạnh bằng 3a. Chân đường cao hạ từ
đỉnh S lên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho AB  3AH , góc tạo bởi đường
thẳng SC và mặt phẳng (ABC) bằng o
60 . Khoảng cách giữa hai đường thẳng SA và BC bằng 3a 21 3a 21 a 21 3a 21 A. . B. . C. . D. . 29 19 39 7
Câu 23: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  a , AD  2a . Hình chiếu
vuông góc của S trên mặt phẳng đáy là trung điểm của H và AD, góc giữa SB và mặt phẳng đáy (ABCD) là o
45 . Khoảng cách giữa hai đường thẳng SD và BH theo a bằng A. 2a . B. 2 a . C. 2 a . D. a . 3 5 3 3 .
Câu 24: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Cạnh bên SD hợp với mặt đáy một góc o
60 và hình chiếu vuông góc H của đỉnh S lên mặt đáy là trung điểm của cạnh
AB. Khoảng cách giữa hai đường thẳng SA và BD bằng a 345 a 546 a 645 a 465 A. . B. . C. . D. . 31 31 31 31
Câu 25: Cho hình chóp S.ABCD có đáy
ABCD là hình thang vuông tại A và B, với
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 854
Face: Trần Đình Cư. SĐT: 0834332133
AB  BC  a, AD  2a a  0 . Các mặt bên SAC và SBD cùng vuông góc với mặt đáy. Biết
góc giữa hai mặt phẳng SAB và ABCD bằng o
60 . Khoảng cách giữa hai đường thẳng CD và SB bằng 2a 3 2a 3 a 3 3a 3 A. . B. . C. . D. . 5 15 15 5 
Câu 26: Cho hình chóp S.ABCD có đ áy ABCD là hình th oi cạnh a, góc  o
ABC 60 cạnh bên SD  a 2 .
Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là điểm H thuộc đoạn BD sao cho
HD  3HB . Gọi M là trung điểm của cạnh SD. Khoảng cách giữa hai đường thẳng CM và SB bằng a 3 a 30 a 3 a 3 A. . B. . C. . D. . 40 8 8 4
Câu 27: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại B và C,
AB  2BC  4CD  2a , giả sử M và N lần lượt là trung điểm AB và BC. Hai mặt phẳng (SMN)
và (SBD) cùng vuông góc với mặt phẳng đáy và cạnh bên SB hợp với (ABCD) một góc o 60 .
Khoảng cách giữa SN và BD bằng 3 3 3 3 A. a . B. a . C. a . D. a . 15 65 55 35
Câu 28: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B. Biết
AD  2AB  2BC  2a, SA  SD  SC  3a . Khoảng cách giữa hai đường thẳng SB và CD bằng a 5 a 3 a 3 a 2 A. . B. . C. . D. . 3 3 2 2
D. HƯỚNG DẪN GIẢI CHI TIẾT Câu 1. ĐÁP ÁN C Nhận xét rằng: D C
BACʹ  CAʹA  DACʹ  AʹAC  BʹCʹA   B DʹCʹ A A
nên khoảng cách từ các điểm B, C, D, A’, B’, D’ đến đường
chéo AC’ đều bằng nhau. H
Hạ CH vuông góc với AC’, ta được: C' D' 1  1  1   a 6 CH . 2 2 2 CH AC CCʹ 3 A' B' Câu 2. ĐÁP ÁN A
Gọi H là giao điểm của AC và BD.
AB  BC  CD  DA  a  ABCD là hình thoi. S
Do đó AC  BD đồng thời H là trung điểm của AC và BD.
SAC cân tại S  SH  AC (1)
SBD cân tại S  SH  BD (2)
Từ (1) và (2) suy ra: SH  ABCD (3) C B Vì SA  SB  SC  SD nên HA  HB  HC  HD H D
Suy ra ABCD là hình vuông (tứ giác đều) (4) A
Từ (3) và (4) ta được S.ABCD là hình chóp tứ giác đều.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 855
Face: Trần Đình Cư. SĐT: 0834332133 Xét SBD ta có:     2  2  2 SA SB a, BD a 2 BD SB SD .
Thế nên SBD vuông tại S.
Suy ra DS  SB . Vậy dD,SB  DS  a. Câu 3. ĐÁP ÁN B O 14  16  10
Nửa chu vi tam giác ABC: p   20 2 S
 20.20 1420 1620  10  40 3 ABC AH  2S 80 3 ABC   8 3 A C BC 10
Nối OH thì OH  BC . Khoảng cách từ O đến BC là OH: H 2 2 B OH  OA  AH  16 Câu 4. ĐÁP ÁN B S
Chân đường cao hình chóp là tâm H của đường tròn ngoại
tiếp tam giác AMC (Do SA  SC  SM ).  Góc  o
AMC 120 , nên H ở ngoài tam giác AMC và HAM là tam giác đều nên: H C HM  AM  a K 2 2 2 2 A
SH  SM  HM  5a  a  2a M 60° I
Từ H kẻ HK  AB thì SK  AB : SK là khoảng cách từ S đến cạnh AB. B   a 3 HK MI
(do ABM là tam giác đều cạnh bằng a) 2 2 2  2  2  2  3a  19a  a 19 SK SH HK 4a . 4 4 2 Câu 5. Phân tích: 3 3 3V 9 V 9 V
Ta có dB,SCD  dH,SCD  H.SCD .  H.SCD .  S.HCD . 2 2 S 2 S 2 S SCD SCD SCD ĐÁP ÁN B S Trong tam giác SHO có:  o SH HO.tan 60  1 a 3  a . . 3 3 2 2 Ta có: A D 1 1 a 60° S  CO.HD  . . OD  OH 60° HCD   2 2 2 O H 2 a a 3 1 a 3 a BC . . .  4 2 3 2 16 2 3 1 1 a a a V  .SH.S  . .  1 S.HDC HDC   3 3 2 16 96 a 57 a 21 Mặt khác: SD  2 SH  2 HD  ; SC  2 SH  2 HC  6 6
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 856
Face: Trần Đình Cư. SĐT: 0834332133 a 57 a 21 SC  SD      CD SD ; SC ; CD a, p 6 6 2 2  a 21 S p p SC p SD p CD 3 SCD
          12 Từ (1), (2) ta có     3a 7 d B, SCD . 14 Câu 6. ĐÁP ÁN B
Gọi M là trung điểm của BC. 
Lập luận được góc giữa (SBC) và (ABC) là  o SMA 60  a 3 SAM đều cạnh bằng 2 S 2   3 3a S SAM 16 3  1  a 3 V BC.S S.ABC SAM 3 16 2 1 a 13 a 3 a 39 A C S  .  SAC 60° 2 4 2 16 H 3 M dB,SAC  3V 3a 3 3a 13 B.SAC   . 2 S a 39 13 B SAC 16. 16 Câu 7. ĐÁP ÁN D
SH  ABCD  SH  AC S SAC vuông tại S  2 SH  HA.HC  2  2 AC AB BC  2a , suy ra:  a  3a   a 3 HA , HC SH 2 2 2 A D K
CI  2HI  dC,SBD  2dI,SBD H I N
Hạ HN  BD, N  BD và HK  SN, KN . B C
Suy ra: HK  SBD nên dH,SBD  HK AB.AD a 3 Ta có: AB.AD  2S  2HN.BD  HN   ABD 2BD 4 1 1 1 3a Ta có:    HK  . Vậy      3a d C, SBD 2HK . 2 2 2 HK HN SH 2 15 15 Câu 8. ĐÁP ÁN D S Kẻ SH  AC, H AC
Do SAC  ABCD  SH  ABCD  2  2   SA.SC  a 3 SA AC SC a, SH J AC 2 A D Ta có: K H 2 2 a AH  SA  SH   CA  4HA 2 B C
 dC,SAD  4dH,SAD
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 857
Face: Trần Đình Cư. SĐT: 0834332133
Do BC // SAD  dB,SAD  dC,SAD  4dH,SAD
Kẻ HK  AD K  AD , HJ  SK J SK
Chứng minh được SHK  SAD mà HJ  SK  HJ  SAD  a 2
dH,SAD  HJ ; AHK vuông tại K  HK  o AHsin 45  4   SH.HK  a 3 2a 3 2a 21 HJ . Vậy dB,SAD   . 2 SH  2 HK 2 7 7 7 Câu 9. ĐÁP ÁN D S
Gọi H là trọng tâm của tam giác ABC và O là tâm của hình chữ nhật, ta 2 2 1 có: BH  BO  . AC 3 3 2 A D 1  a  2 2a2 2  a 3 I O
Ta có SH  ABCD nên góc giữa SB và HB K C mặt phẳng (ABCD) là góc  o SBH 60
Trong tam giác vuông SHB ta có:    o
SH BH tan SBH a.tan 60  a 3 3
Ta có: dA;SBC  2dO;SBC  2. dH;SBC  3dH;SBC 2
Kẻ HK  BC K  BC , HI  SK I SK 1
Ta có: SH  ABCD  SH  BC
Do đó BC  SHK  BC  HI 2
Từ (1) và (2) suy ra HI  SBC nên dH;SBC  HI 1 1
Ta có HK  DC  a . Trong tam giác vuông SHK ta có: 3 3 a a 3.  SH.HK   a 3  a 21 3 HI . 2 SH  2 2 HK a 28 14 2 3a  9 Vậy          3a 21 d A; SBC 3d H; SBC 3HI . 14 Câu 10. ĐÁP ÁN C S A I E H A C B C 120° I' A'H' K H K I H' B
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 858
Face: Trần Đình Cư. SĐT: 0834332133
Theo định lý Côsin trong tam giác ABC ta được AB  AC  a 2 7a Ta có 2 CI  2 AI  2 AC  o 2AI.AC.cos120    a 7 CI 4 2 2 AI AC CI 2  2  2 2 2 3a a 3 Do đó: AH    AH  4 16 4 3a Suy ra SH  o AH.tan 60  4
AH cắt BC tại K. Gọi A’, H’, I’ lần lượt là hình chiếu của A, H, I trên BC. dA;SBC AK AAʹ Ta có:
 dA;SBC  4dH;SBC dH;SBC    4 HK HHʹ
Gọi E là hình chiếu của H trên SH’ thì HE  SBC  dH;SBC  HE  1  a 1 1 1 3a HHʹ AAʹ và từ    HE  4 8 2 2 2 HE HS HHʹ 4 37 Vậy      3a 37 d A; SBC 4HE . 37 Câu 11. ĐÁP ÁN D
Gọi K là hình chiếu của I lên AB. S  Suy ra  o SKI 60 . KI BI Do IK //AD   . AD BD BI BC a 1 Mà    H ID AD 3a 3 B C 60° BI 1 BI 1     K I BI  ID 4 BD 4 D A KI 1 3a 3a 3 Suy ra   KI   SI  AD 4 4 4 AB  IK
Gọi H là hình chiếu của I lên SK. Ta có   AB   IH AB SI 
Từ đó suy ra IH  SAB  dI;SAB  IH
Mà do DB  4IB  dD;SAB  4dI;SAB  4IH 1 1 1 16 16 3a 3 Lại có      IH  . Vậy     3a 3 d D; SAB . 2 2 2 2 2 IH IS IK 27a 9a 8 2 Câu 12. ĐÁP ÁN B
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 859
Face: Trần Đình Cư. SĐT: 0834332133 SAC  ABCD  S   SBD  ABCD   
SAC  SBD  SO
 SO  ABCD  SO  BC H
Kẻ OK  BC  BC  SOK A B 120° 60°         o SBC , ABCD SKO 60 O K D C AO  SBC  C
 dA;SBC  2dO;SBC SBC  SOK   SBC SOK   
 SK   OH  SBC   d O;SBC   OH  O H  SK   1  1  1   3a      3a O H d A ; SBC . 2 2 2 O H O K O S 8 4 Câu 13. ĐÁP ÁN B  o     o ABC 120
BAD 60  ABD đều cạnh a.
Gọi O là giao điểm của AC và BD.   a 3  2  a 3 AO ; AG AO ; AC  a 3 2 3 3 S    a 6 SG GA.GC 3
( SAC vuông tại S, đường cao SG). H B GH  SO  GH  C Kẻ SBD vì O
BD  GH  SAO  dG;SBD  GH G A D
SGO vuông tại G, đường cao GH  1  1  1  27   a 2 GH . 2 2 2 2 GH GS GO 2a 27 Câu 14. ĐÁP ÁN C S
Kẻ SH  AC, H AC
Do SAC  ABCD  SH  ABCD 2 2 SA  AC  SC  a, J SA.SC a 3 A D SH   K AC 2 H Ta có: B C  2  2  a AH SA SH
 CA  4HA  dC,SAD  4dH,SAD 2
Do BC // SAD  dB,SAD  dC,SAD  4dH,SAD
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 860
Face: Trần Đình Cư. SĐT: 0834332133
Kẻ HK  AD K  AD , HJ  SK J SK
Chứng minh được SHK  SAD mà HJ  SK  HJ  SAD  dH,SAD  HJ  a 2 AHK vuông tại K  HK  o AH sin 45  4   SH.HK  a 3 2a 3 2a 21 HJ . Vậy dB,SAD   . 2 SH  2 HK 2 7 7 7 Câu 15. ĐÁP ÁN C D' A'
Hạ AʹH  AC , ta có nhận xét: B' C' BD  AC   BD  OAAʹ BD   AʹO D A
 BD  AʹH  AʹH  ABCD H O C B
Và vì ABCD // AʹBʹCʹ Dʹ nên AʹH chính là khoảng cách giữa hai mặt phẳng đáy.
Nhận xét rằng hình chóp A’.ABD là hình chóp đều, nên ta lần lượt có:  2  2 a 3  a 3 AH AO . 3 3 2 3 2 2 2  2  2  2  a  2a   a 6 AʹH Aʹ A AH a AʹH . 3 3 3 Câu 16.1. ĐÁP ÁN D MN // CD  A
CD  BCD  MN // BCD  Töø M k eû MH //AB
AB  BCD  MH  BCD  N
Vậy: MH  dMN,BCD M  AB 5a ABC cho: MH   . B D 2 2 H Câu 16.2. ĐÁP ÁN D A C
Tính d P,BCD :
MN // CD P//BCD N K MK // BC  M M P  5a MH d P , BCD . MH  BCD         2 B D H Câu 17. ĐÁP ÁN C C
Lưu ý: Cần chú ý rằng, trong hình chóp cụt đều thì các mặt bên là những hình thang cân bằng nhau, các
góc giữa mặt bên và mặt đáy bằng nhau.
Gọi O, O’ lần lượt là tâm của hai hình vuông ABCD và A’B’C’D’; K và J lần lượt là trung điểm của A’D’ và AD.
Gọi H là hình chiếu của K trên (ABCD) thì KH  OJ tại H và KH là khoảng cách cần tìm.
Gọi  là góc giữa mặt bên và mặt đáy của hình chóp cụt thì
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 861
Face: Trần Đình Cư. SĐT: 0834332133 D' C'     o KJH 60 . K O' A' B' b a Ta có: OʹK  ; OJ  . 2 2 
KHOO’ là hình chữ nhật nên:    a b JH OJ OʹK D C 2 KH 2.KH a  J φ  b 3 H HJK : tan    KH  O . HJ a  b 2 A B
Câu 18. Phân tích: Chứng minh Bʹ D  BCʹ : BCʹ   CBʹ  BCʹ  BCʹ CDAʹ Bʹ BCʹ Bʹ D 1  DCDC   BBʹCʹC       
Chứng minh AʹCʹ  Bʹ D : AʹCʹ   Bʹ Dʹ  AʹCʹ  AʹCʹ BDDʹ Bʹ AʹCʹ Bʹ D 2  BBʹBBʹ   AʹBʹCʹDʹ       
Xác định giao điểm K và H: BBʹDʹD  BʹD
BCʹAʹ BBʹDʹD BOʹOʹ AʹCʹ BʹDʹ    
  BʹD  BCʹAʹ  K  Bʹ D  BOʹ  K  BBʹ Dʹ D  Bʹ D
ACDʹ BBʹDʹD DʹOO AC BD    
  Bʹ D  ACDʹ  H  Bʹ D  DʹO  H ĐÁP ÁN B D' C'
Từ (1) và (2) suy ra Bʹ D  (BCʹ Aʹ) (3) O' Mặt khác: A' BCʹ // ADʹ B'
  BCʹAʹ// ACDʹ 4 K BAʹ // CDʹ
Từ (3) và (4) suy ra: Bʹ D  ACDʹ 5 H D C
Ta có: Bʹ D  BAʹCʹ  K,BʹD  BCʹAʹ , O
Bʹ D  DʹAC  H,Bʹ D  ACDʹ A B
Do đó KH là khoảng cách cần tìm. 2  2  2  2     2  2 BDBʹ : Bʹ D BD Bʹ B a 2 a 3a  Bʹ D  a 3 1 a 3
Dễ thấy trong hình chữ nhật BB’D’D ta có: KH  Bʹ D  . 3 3 S Câu 19. ĐÁP ÁN A A D I 60° H K B C
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 862
Face: Trần Đình Cư. SĐT: 0834332133
Kẻ HK  CD K CD . Khi đó: CD  HK
  CD  SHK  CD   SK CD SH 
Vậy góc giữa (SCD) và (ABCD) là góc   o SKH 60 Trong tam giác vuông SHK:  o SH HK tan 60  2a 3
Vì SBC // AD  dAD,SC  dA,SBC .
Trong (SAB) kẻ AI  SB , khi đó:
BC  AB BC  SAB BC  . Mà SB  AI  AI  SBC  AI BC SH SH.AB 2a 3.3a 6a 39
Vậy dAD,SC  dA,SBC  AI    . 2 SB  2 13 12a a Câu 20. ĐÁP ÁN D S
SH  ABCD  SH  HD . Ta có: 2 2 SH  SD  HD 2  SD   2 2 AH  HD  F  SH  a 3 B C E HK// BD  HK // SBD H A
 dHK,SD  dH,SBD K D
Gọi E là hình chiếu vuông góc của H trên BD và F là hình chiếu vuông góc của H trên SE.
Ta có: BD  HE và BD  SH nên BD  SHE  BD  HF mà HF  SE do đó HF  SBD . Suy ra dH,SBD  HF  HS.HE a 3 Ta có:   a 2 HE HBsin EBH  HF   . 4 2  2 5 HS HE Vậy    a 3 d HK,SD . 5 Câu 21. ĐÁP ÁN B S
Tam giác AHC vuông cân cạnh a nên CH  a 2
Tam giác SHC vuông tại H nên 2a SH  2 SC  2 CH  5 I K B C J Dựng AK  BC, HI  BC . Đường
thẳng qua A song song với BC cắt IH H tại D  BC // SAD D A
 dBC,SA  sBC,SAD  dB,SAD  2dH,SAD
AD  SDH  SAD  SDH .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 863
Face: Trần Đình Cư. SĐT: 0834332133
Kẻ HJ  SD  HJ  SAD  dH,SAD  HJ 1 1 1 2a a Ta có    AK   HD  2 2 2 AK AB AC 5 5 1  1  1   2a HJ . Vậy    4a d BC,SA . 2 2 2 HJ HD HS 5 5 Câu 22. ĐÁP ÁN A
Nhận thấy SH  ABC  HC là hình chiếu của SC trên mặt phẳng (ABC)    o
SCH 60 là góc giữa SC và mặt phẳng (ABC) 1 Ta có 2  2  2  o HC AC AH 2AC.AH.cos60  2 9a  2 a  2.3a.a.  2 7a 2     o HC a 7 SH HC.tan 60  a 21  
Dựng AD  CB  AD // CB  BC // SAD
 dSA; BC  dBC;SAD  dB;SAD  3dH;SAD
Dựng HE  AD tại E  AD  SHE
 SAD  SHE (theo giao tuyến SE)
Dựng HF  SE tại F  HF  SAD  HF  dH;SAD S a 3 Ta có: HE  o AH.sin 60  2 1 1 1 4 1 29      2 2 2 2 2 2 HF HE SH 3a 21a 21a F a 21       3a 21 HF d B; SAD  60° C 29 29 E A H Vậy    3a 21 d SA; BC . D B 29 Câu 23. ĐÁP ÁN B S D C H 45° K A B
Do SH  (ABCD) nên góc giữa SB và mặt phẳng đáy (ABCD) là góc  o SBH 45 . Ta có SBH
vuông cân tại H nên SH  BH  a 2
Gọi K là trung điểm của BC, ta có BH // DK  BH // SDK .
Suy ra: dBH;SD  dBH;SDK  dH;SDK 1 1 1 1 5
Tứ diện SHDK vuông tại H nên 2 d H;SDK     2 2 2 2 HS HK HD 2a Vậy        2 d BH; SD d H; SDK a . 5 Câu 24. ĐÁP ÁN D
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 864
Face: Trần Đình Cư. SĐT: 0834332133 S Ta có SH  (ABCD) . a 5 a 15 Tính HD  ; SH  K 2 2 A 60° D
Dựng E sao cho AEBO là hình bình hành. Gọi M là trung M E
điểm của AE. Hạ HK vuông góc với SM. H O B C
Chứng minh HK  SAE và tính được  a 465 HK 62 Tính được     a 465 d BD; SA 2HK . 31 Câu 25. ĐÁP ÁN A
Gọi H  AC  BD  SH  ABCD và S  1 BH BD 3
Kẻ HE  AB  AB  SHE , hay A D O K        o SAB ; ABCD SEH 60 I 1 2a 2a 3 E Mà HE  AD   SH  H 3 3 3 B C
Gọi O là trung điểm AD, ta có ABCD là hình vuông cạnh a  ACD có trung tuyến  1 CO AD 2
CD  AC  CD  (SAC) VÀ BO // CD hay CD // (SBO) và BO  (SAC)
d CD; SB  d CD;SBO  dC;SBO 1 a 2
Tính chất trọng tâm tam giác BCO  IH  IC  3 6   2  2  5a 2 IS IH HS 6
Kẻ CK  SI mà CK  BO  CK  (SBO)  d(C,(SBO))  CK 1 1 SH.IC 2a 3 Trong tam giác SIC có: S  SH.IC  SI.CK  CK   SIC 2 2 SI 5 Vậy    2a 3 d CD,SB . 5 Câu 26. ĐÁP ÁN B
Từ giả thiết có tam giác ABC đều cạnh a. a 3
Gọi O  AC  BD  BO   BD  a 3 2 3 3 S  HD  BD  a 3 4 4 2 2 M 2 2 2 2 27a 5a a 5 SH  SD  HD  2a    SH  16 16 4 A 2 2 D 2  2  2  5a  3a   a 2 SB SH HB SB 16 16 2 O BD  AC H
 AC  SBD  AC  OM B AC  C  SH
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 865
Face: Trần Đình Cư. SĐT: 0834332133 2 1 1 1 a 2 a 2
Diện tích tam giác MAC là S  OM.AC  SB.AC  .a  MAC 2 4 4 2 8 SB // OM  SB // MAC
 dSB;CM  dSB;MAC  dS;MAC  dD;MAC  1     1 1 1 V d M; ABCD .S . d S; ABCD . S M.ACD ACD    ABCD 3 3 2 2 3  1  a 15 V S.ABCD 4 96 Mặt khác  1 V d D; MAC .S M.ACD    MAC 3 3 a 15      3V a 30 M.ACD  32 d D; MAC  . 2 S a 2 8 MAC 8 Câu 27. ĐÁP ÁN B S M A B K H N D C
Gọi H  MN  BI  SMN  SBI  SH
Do hai mặt phẳng (SMN) và (SBI) cùng vuông góc với ABCD  SH  ABCD 
Dễ thấy BH là hình chiếu vuông góc của SB lên mặt phẳng đáy, suy ra  o SBH 60 .
Gọi M và N lần lượt là trung điểm AB và BC, mà AB  4CD nên suy ra MN  BD tại H. 1 1 1 5 a Xét tam giác BMN ta có:     BH  2 2 2 2 BH BM BN a 5 Xét tam giác SBH lại có:   SH   o  a 15 tan SBH SH HB.tan 60 HB 5
Tính khoảng cách giữa SN và BD. BD  SH Do   BD  SMN BD   MN
Dựng HK vuông góc SN, suy ra HK là đoạn vuông góc chung của
SN và BD  dBD,SN  HK . 2 2 a a a 5 Xét BHN có: HN  2 BN  2 BH    4 5 10 1 1 1 20 5 65 3 Xét SHN ta có:       HK  a 2 2 2 2 2 2 HK SH HN a 3a 3a 65
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 866
Face: Trần Đình Cư. SĐT: 0834332133 Vậy    3 d BD,SN a . 65 Câu 28. ĐÁP ÁN D
Theo giả thiết ta có BC  AB  a S
Gọi H là trung điểm của AD  HA  HD  a
Từ giả thiết  ABCH là hình vuông cạnh a tâm O CH  a    1 a 2 CO  AC   2 2 A H D
Trong tam giác ACD có CH là trung tuyến và  1 CH AD 2 B C
 ACD vuông tại C  H là tâm đường tròn ngoại tiếp tam giác ACD.
Gọi K là hình chiếu vuông góc của S trên mặt phẳng (ABCD)  SK  ABCD , SK là đường cao của hình chóp S.ABC.
Hơn nữa các tam giác vuông SKA, SKC và SKD bằng nhau vì SK chung và
SA  SD  SC  3a  KA  KC  KD
 K là tâm đường tròn ngoại tiếp tam giác ACD  K trùng với H.
Trong tam giác vuông SHD ta có: 2  2  2  2  2 SH SD HD 9a a  2 2a
Tứ giác BCDH là hình bình hành (vì HD // BC, HD  BC )  CD // BH CD// BH   SBH Ta có:  CD // SBH CD   SBH   
Ta có SB và CD là hai đường thẳng chéo nhau. CD//SBH Mặt khác  SB   SBH
 dCD,SB  dCD,SBH  dC,SBH CO  HB a 2 Ta có 
 CO  SBH  dC,SBH  CO  CO  .  SH 2
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Trang 867
Face: Trần Đình Cư. SĐT: 0834332133