Phân tích Lý thuyết trò chơi và Mô hình hóa tâm lý xã hội môn Kinh tế vi mô | Trường Đại học Kinh Tế Quốc Dân

theo những bước hợp lý. Loại hành vi “ như thế ” này có thể phát triển dưới áp lực
của chọn lọc tự nhiên, như chúng ta đã lưu ý trước đó trong cuộc thảo luận liên
quan đến sự lặp lại và học hỏi; nhớ lại sự phức tạp toán học rõ ràng của chim gõ
kiến. Như chúng ta cũng đã lưu ý nhiều lần, từ chương đầu tiên, cách biện minh “
như thế ” này sử dụng rất phổ biến trong kinh tế học, đặc biệt là bởi những người
ủng hộ mô hình chuẩn. Tuy nhiên, nếu lý thuyết trò chơi tiêu chuẩn không dự đoán
chính xác, chúng ta có thể kết luận rằng suy luận “ như thế ” là không chính xác và
mô hình cần phải được xác định lại. Điểm này được xây dựng thêm theo tính năng thứ hai dưới đây.
Mặc dù không có tư duy chiến lược áp dụng cho một số tình huống trò chơi
mà mô hình chuẩn dự đoán xấu, nhưng chúng ta sẽ thấy trong phần còn lại của
chương này rằng chính sự tồn tại của tư duy chiến lược phức tạp hơn mới là
nguyên nhân gây ra nhiều điều bất thường. Trong những tình huống này, việc mô
hình hóa các tình huống được cải thiện có thể dẫn đến những dự đoán chính xác
của nhiều phát hiện thực nghiệm, chỉ ra rằng lý thuyết trò chơi vẫn hữu ích như
một công cụ dự đoán và giải thích.
Trong bối cảnh mô hình hóa, thách thức được đặt ra là một mô hình tốt phải
có hai đặc điểm chính, để phù hợp với các mô hình hành vi khác nói chung:
1. Giải thích và dự đoán – Nó phải có khả năng giải thích kết quả của nhiều trò
chơi khác nhau về các thông số nội sinh. Như chúng ta đã thấy trước đó
trong phần này, những thay đổi trong cấu trúc của trò chơi có thể dẫn đến
những kết quả thực nghiệm rất khác nhau. Ví dụ, việc giới thiệu sự cạnh
tranh của người đề xuất và sự cạnh tranh của người trả lời trong các trò chơi
thương lượng tối hậu thư có ảnh hưởng mạnh mẽ đến các phản hồi. Một mô
hình tốt phải có khả năng giải thích cho những khác biệt như vậy một cách
tiết kiệm, mà không cần đến các biến chứng đặc biệt. Một đặc điểm liên
quan khác của mô hình như vậy là nó có thể đưa ra các dự đoán mới thú vị.
2. Cơ sở tâm lí – Điều này có nghĩa là các mô hình phải dựa trêm các cơ chế
tâm lý đã biết. Điều đó không nhất thiết có nghĩa là mô hình thực sự kết hợp
rõ ràng các quá trình tâm lý hoặc thần kinh trong công thức toán học của nó,
nhưng ít nhất nó phải tương thích với quá trình đó, và cũng tương thích với
kết quả của các nghiên cứu khác. Vấn đề này sẽ trở nên rõ ràng hơn khi
chúng ta chuyển sang thảo luận các mô hình cụ thể.
Nhìn chung, chúng ta sẽ thấy rằng tất cả các mô hình đều có những ưu điểm và
nhược điểm nhất định; các mô hình có những đặc điểm thực tế hơn có sự phong
phú hơn về mặt tâm lý và sức mạnh dự đoán lớn hơn, nhưng độ phức tạp được bổ
sung thêm vào của chúng khiến chúng trửo nên khó xử lý hơn. Do đó, sự lựa chọn
mô hình của một nhà nghiên cứu cuối cùng sẽ được xác định bởi mục đích tring
tâm trí (Falk và Fischbacher, 2005 ).
Các vấn đề trong mô hình hóa
Falk và Fischbacher ( 2005 ) mô tả bốn câu hỏi chính mà các mô hình kết hợp các
sở thích xã hội cần giải quyết:
1. Về những giao dịch công bằng, tiêu chuẩn tham khảo là gì?
Một tiêu chuẩn chung ở đây là phân phối đồng đều các khoản thanh toán.
2. Những ý định quan trọng như thế nào?
Trong các mô hình chống bất bình đẳng ( IA ), những mô hình này hoàn toàn
không quan trọng, nhưng trong các mô hình tương hỗ, chúng lại là một
thành phần thiết yếu. Điều này có nghĩa là, không chỉ có sự kết hợp các hành
động của người chơi quan trọng mà còn là niềm tin của họ, và các khả năng
hành động thay thế được mở ra cho họ.
3. Mục đích của hình phạt là gì?
Trong mô hình IA, mục đích duy nhất của một người chơi giảm bớt lợi ích
của người chơi khác là giảm sự bất bình đẳng, nhưng trong các mô hình có
đi có lại, động cơ là để trả thù cho một hành động không tử tế. Do đó, với
mô hình sau, người ta cần phải tuân thủ cả hình phạt và phần thưởng ngay cả
khi sự bất bình đẳng không giảm.
4. Ai là đại lí tham khảo có liên quan?
Vấn đề này phát sinh trong các trò chơi nhiều người chơi. Trong một số mô
hình người chơi đánh giá sự công bằng đối với các cá nhân một cách riêng
biệt, trong khi ở các mô hình khác, tác nhân tham chiếu là toàn bộ nhóm.
Các kết quả thực nghiệm liên quan đến những câu hỏi này được thảo luận trong phần 10.7.
Lý thuyết trò chơi tâm lý
Chúng ta đã thấy rằng sở thích xã hội liên quan đến những hậu quả phân phối hành
động của mọi người và niềm tin của mọi người về động cơ và ý định cơ bản. Đã có
nhiều nghiên cứu trong 20 năm qua cho thấy rằng mọi người thường quan tâm đến
khía cạnh này và nhánh của lý thuyết trò chơi hành vi kiểm tra những điều này hiện
được gọi là “ Lý thuyết trò chơi tâm lý ” ( PGT ). PGT mô hình hóa các lợi ích dựa
trên niềm tin cũng như hành động ( Dufwenberg, 2006 ) và được sử dụng để khái
niệm hóa những cảm xúc phụ thuộc vào niềm tin như có đi có lại, ác cảm tội lỗi,
hối tiếc và xấu hổ. Sự phát triển ban đầu của PGT đã được đề xuất trong một bài
báo của Geanakoplos, Pearce and Stacchetti (1989). Một vài ví dụ ở giai đoạn này
sẽ giúp người đọc hiểu được bản chất của ưu đãi xã hội, sự công bằng, tương hỗ và PGT.
Ann đi taxi và boa cho người lái xe ( Bill ) nhiều như cô ấy tin rằng anh ta
mong dợi nhận được. Cô ấy phải chịu cảm giác tội lỗi nếu cô ấy boa ít hơn.
Carol được một người lạ ( Dave ) ngồi cạnh trên máy bay mời một viên kẹo;
cô ấy thích kẹo nhưng từ chối nhận nó vì cô ấy tin rằng khi nhận nó, cô ấy sẽ
có nghĩa vụ với người lạ theo một cách nào đó, ngay cả khi điều đó có nghĩa
là cố gắng bắt đầu cuộc trò chuyện trong chuyến bay. Cô ấy thà từ bỏ kẹo
còn hơn là cảm thấy buộc phải đáp lại. Nếu cô ấy nhận kẹo nhưng không
đáp lại, cô ấy sẽ lại cảm thấy tội lỗi, bởi vì cô ấy tin rằng người lạ sẽ tin việc
nhận kẹo cho thấy cô ấy là người thân thiện và cô ấy sẽ làm anh ta thất vọng
nếu không đáp ứng mong đợi của anh ta. Dave sau đó sẽ có đánh giá thấp về cô ấy.
Ellen lo lắng cho sức khỏe của bản thân và hỏi ý kiến của bác sĩ gia đình.
Frank, một người bạn của cô ấy. Frank chẩn đoán một căn bệnh nghiêm
trọng. Frank nhận ra Ellen đau khổ vì sự lo lắng của cô ấy, đồng thời cũng
nhận thấy rằng nếu anh kê cho cô loại thuốc thích hợp nhất cho căn bệnh của
mình, điều này cũng sẽ tiết lộ cho Ellen biết được mức độ nghiêm trọng của
căn bệnh và làm tăng thêm sự lo lắng của cô ấy. Vì Frank quan tâm đến
Ellen nên anh ấy miễn cưỡng kê cho cô loại thuốc tốt nhất; làm như vậy
khiến anh ấy cảm thấy tội lỗi vì đã khiến cô ấy thêm đau khổ.
Gene nộp đơn xin thăng chức trong công ty của mình. Ông chủ của anh,
Henry, viết cho anh ta một bản báo cáo không thuận lợi, và đơn của anh ta bị
từ chối. Gene tin rằng điều này là một là một phần do sự thiếu hiểu biết của
Henry về chất lượng và số lượng công việc của mình, nhưng cũng do sự
ghen tị nghề nghiệp, Gene tin rằng Henry tin Gene là một công nhân vượt
trội và bị anh ta đe dọa. Do đó, Gene phàn nàn về hành vi cùa Henry với ông
chủ của Henry, mặc dù điều này liên quan đến việc anh ta phải làm nhiều
việc hơn và nguy cơ bị trà thù khi Henry phát hiện ra việc không trung thành của mình.
Irene chia sẻ chiếc bánh cô ấy đã mua với Jim và Kayla. Kayla nhận thấy
rằng phần của Jim lớn hơn phần của cô ấy. Cô ấy nghi ngờ rằng Irene cố tình
cho cô ấy một phần nhỏ hơn, nhưng cô ấy tin rằng điều này có thể là vì Irene
tin Jim thích ăn bánh hơn cô ấy, vì vậy cô ấy không cảm thấy khó chịu. Tuy
nhiên, Jim lại nghĩ rằng phần không bằng nhau là do ngẫu nhiên và đề nghị
chia cho Kayla một phần của anh ấy, vì anh ấy cảm thấy có lỗi nếu được
chia phần lớn hơn và chấp nhận nó mà không nói bất cứ điều gì.
Một số yếu tố xuất hiện từ những tình huống khác nhau này. Đầu tiên, kết quả hoặc
tiện ích phần lớn là phi tiền tệ, ngoại trừ tiền boa, mà thay vào đó phụ thuộc vào
niềm tin. Thứ hai, tiện ích của mọi người không chỉ phụ thuộc vào niềm tin của
chính họ mà còn phụ thuộc vào niềm tin của người khác và niềm tin của người
khác về niềm tin của chính họ; do đó, các mô hình PGT có thể được coi là liên
quan đến một hệ thống phân cấp niềm tin. Thứ ba, những cảm xúc như tức giận,
ghen tị, thất vọng, đổ lỗi, tự hào, xấu hổ, biết ơn và cảm giác tội lỗi, hoặc muốn
trốn tránh tội lỗi, có liên quan đến các lợiu ích của con người (Geanakoplos, Pearce
and Stacchetti, 1989; Battigalli and Dufwenberg, 2007). Những cảm xúc này chủ
yếu phụ thuộc vào kỳ vọng và niềm tin trước đó của chúng ta, những điều này rõ
ràng thay đổi theo tùy tình huống. Ví dụ, chúng ta thường quan tâm liệu mình có
khiến người khác buồn phiền hay không, hoặc liệu họ có đánh giá thấp về chúng ta
hay không. Tuy nhiên, trong những tình huống khác, chúng ta có thể muốn gây đau
khổ cho người khác, hoặc có thể không quan tâm đến ý kiến của họ về chúng ta.
Tất cả những yếu tố này có nghĩa là PGT phức tạp hơn lý thuyết trò chơi tiêu chuẩn.
Gần đây, đã có những nỗ lực mở rộng phạm vi và mức độ phức tạp của PGT
hơn nữa để xử lí nhiều dạng động cơ phụ thuộc vào niềm tin hợp lý được
minh họa trong các ví dụ trên. Đặc biệt, Battigalli và Dufwenberg (2009) đề
xuất thêm bốn khía cạnh của sự phát triển:
1. Niềm tin được cập nhật – PGT ban đầu chỉ cho phếp niềm tin ban đầu
ảnh hưởng đến lợi ích của người chơi.
2. Niềm tin của người khác – PGT ban đầu chỉ cho phép niềm tin của chính
người chơi ảnh hưởng đến lợi ích của anh ta, nhưng chúng ta có thể thấy
rằng đôi khi lợi ích của người khác, chẳng hạn như sự tôn trọng của họ
dành cho anh ta, ảnh hưởng đến lợi ích của anh ta.
3. Sự phụ thuộc vào kế hoạch – PGT, và các trò chơi truyền thống khác, giả
định rằng các tiện ích chỉ bị ảnh hưởng bởi kết quả thực tế, nhưng ý định
chưa thực hiện được cũng có thể ảnh hưởng đến tiện ích. Ví dụ: nếu
chúng ta tin rằng một người chơi khác có ý định làm hại chúng ta ngay cả
khi kế hoạch của họ bị cản trở và những thiệt hãi đã bị ngăn chặn, điều
này vẫn sẽ ảnh hưởng đến niềm tin của chúng ta đối với người chơi khác
và lợi ích của chúng ta.
4. Phân tích không cân bằng – PGT, giống như các lý thuyết trò chơi khác,
chỉ xem xét các tình huống cân bằng, nhưng trên thực tế, người chơi có
thể không phối hợp để đạt được trạng thái cân bằng.
Một số khía cạnh sẽ được xem xét kỹ hơn trong phần tiếp theo.
Bản chất và tính năng của các mô hình
Nhìn chung, các mô hình sở thích xã hội hiện tại thuộc hai loại chính được đề cập
ở trên: mô hình IA và mô hình tương hỗ. Cả hai mô hình này đều duy trì giả định
cơ bản trong mô hình tiêu chuẩn rằng người chơi nhắm đến việc tối đa hóa tiện ích
và người chơi cũng cho rằng những người chơi khác cũng làm như vậy. Cả hai mô
hình này đều khác với mô hình chuẩn ở chỗ chúng làm phong phú thêm hoặc sửa
đổi hàm thỏa dụng để tính đến các sở thích xã hội. Các mô hình IA đơn giản hơn,
bởi vì chúng chỉ kết hợp niềm tin bậc nhất của người chơi về sự bất bình đẳng
trong phân phối. Chúng không phải là mô hình PGT vì chúng không kết hợp hệ
thống phân cấp niềm tin như đã thảo luận trước đó và chúng không tính đến cảm
xúc của người chơi ngoài mong muốn giảm bất bình đẳng. Các mô hình tương hỗ
phức tạp hơn và đa dạng hơn về bản chất, đồng thời có thể tính đến nhiều loại cảm
xúc như tức giận, ghen tị, thất vọng, đổ lỗi, tự hào, xấu hổ, biết ơn và cảm giác tội lỗi.
Ở giai đoạn này, một vài ví dụ đơn giản sẽ mang đến cho người đọc những
hương vị khác của các mô hình PGT và một số hàm ý:
1. Trò chơi “ Món quà bất ngờ ”
Đây là một trò chơi hai người chơi trong đó chỉ có người chơi 1 di chuyển.
Người chơi 1 có hai lựa chọn: anh ấy có thể gửi hoa cho người chơi 2 hoặc
anh ấy có thể gửi sôcôla. Anh ấy biết rằng người chơi 2 thích một trong hai
món quà, nhưng anh ấy thích làm cô ấy ngạc nhiên. Vì vậy, nếu anh ấy nghĩ
rằng người chơi 2 đang mong đợi hoa nhiều hơn sôcôla, thì anh ấy sẽ nhận
được nhiều lợi ích hơn từ việc gửi sôcôla và ngược lại (phỏng theo
Geanakoplos, Pearce và Stacchetti, 1989). Trong lý thuyết trò chơi tiêu
chuẩn, luôn có sự cân bằng trong các chiến lược thuần túy nếu chỉ có một
người chơi di chuyển; trong trò chơi này, nếu chúng ta bỏ qua sự thích thú từ
yếu tố bất ngờ, thì trạng thái cân bằng chiến lược thuần túy sẽ liên quan đến
việc đưa ra món quà mà người chơi 1 tin rằng sẽ mang lại cho người chơi 2
nhiều tiện ích nhất. Tuy nhiên, với yếu tố bất ngờ, có một trạng thái cân
bằng chiến lược hỗn hợp duy nhất, trong đó người chơi 1 gửi từng món quà với xác suất bằng nhau.
2. Trò chơi thất vọng / trả đũa
Đây là một trò chơi tuần tự, một lần nữa được chuyển thể từ Geanakoplos,
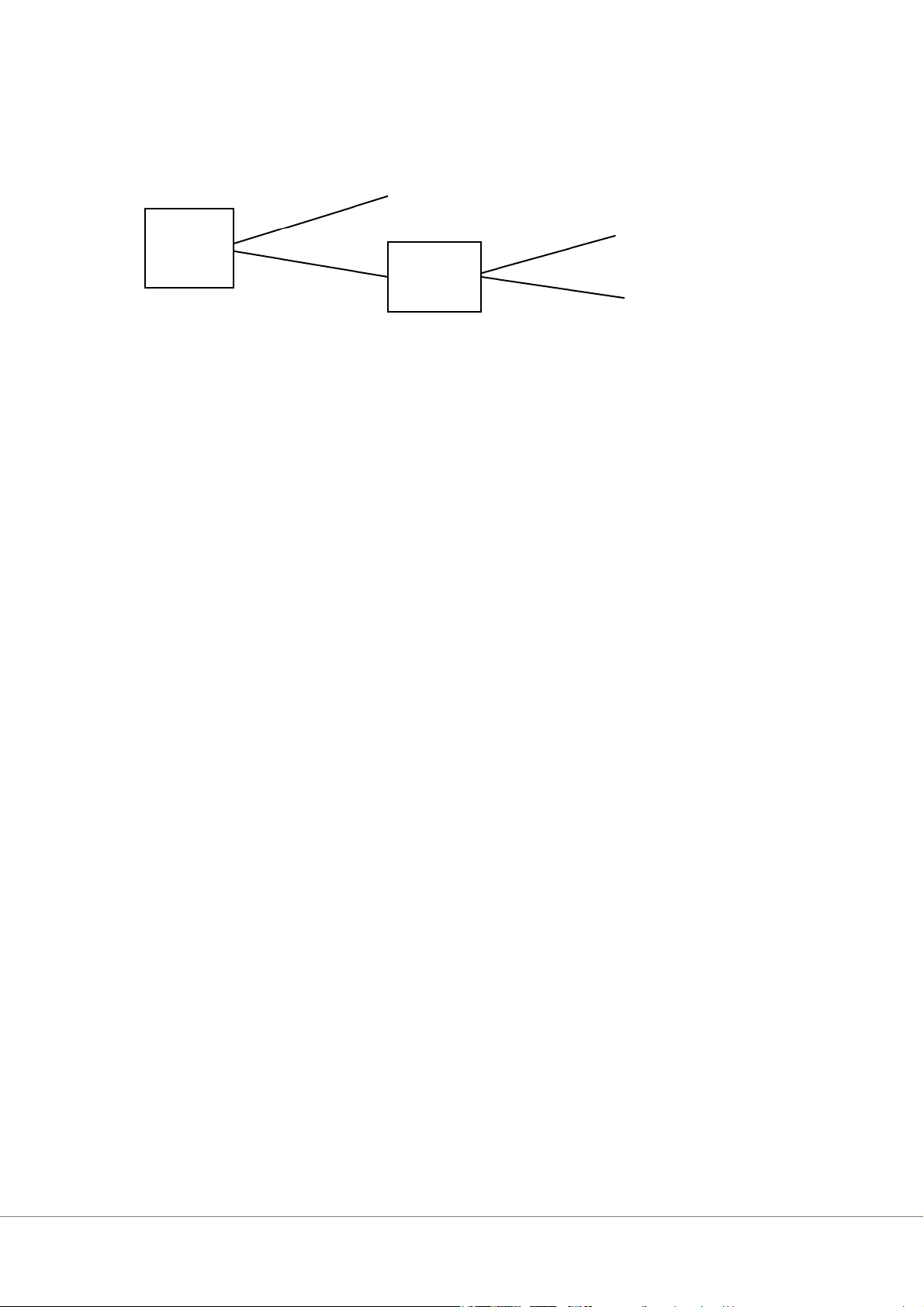
Pearce và Stacchetti. Nó được thể hiện ở dạng mở rộng trong Hình 10.1
Hình 10.1 Trò chơi thất vọng / trả đũa lên 10,10 0, A 1 lên 2 xuống xuống 11, B
Người chơi 1 chỉ quan tâm đến kết quả vật lý,nhưng phần thưởng của người
chơi 2 tại hai trong số các điểm nút cuối phụ thuộc vào kỳ vọng ban đầu của
anh ta. Nếu anh ta cam chịu khi bắt đầu trò chơi với ý tưởng rằng 1 sẽ chọn
xuống, thì A = 1 và B = 5 ( đây có thể được coi là phần thưởng bằng tiền );
do đó 2 chọn xuống nếu 1 chọn xuống, vì vậy (xuống, xuống) là một trạng
thái cân bằng đáng tin cậy. Mặt khác, nếu 2 tự tin rằng 1 sẽ chơi lên, 2 sẽ
thấy thất vọng nếu 1 chơi xuống, và điều này làm thay đổi giá trị của phần
thưởng A và B, khi đó A = 2 và B = 0. Trong tình huống này, chơi lên nhận
được lợi ích từ việc làm hại 1, trong khi chơi xuống sẽ mất đi lợi ích từ sự
thất vọng trước sự phản bội của 1. Do đó, theo niềm tin này bằng 2, trạng
thái cân bằng là (tăng, không di chuyển). Một hàm ý quan trọng ở đây là
phương pháp quy nạp ngược, được sử dụng để giải các trò chơi tuần tự trong
SGT, không hoạt động với các trò chơi tâm lý. Phát hiện này được thảo luận trong các phần sau
Các khía cạnh và khái niệm cụ thể hơn liên quan đến mô hình hóa sẽ được xem xét
trong hai phần tiếp theo, trong đó nền tảng tâm lý và sự khác biệt dẫn đến cấu trúc
của các mô hình khác nhau sẽ được thảo luận chi tiết hơn. Sau đó, khả năng của
các mô hình trong việc giải thích các kết quả thực nghiệm sẽ được thảo luận trong Phần 10.7.
10.5 Các mô hình chống bất bình đẳng
Những mô hình này giả định rằng mọi người quan tâm đến phần thưởng của chính
họ và quy mô tương đối của những phần thưởng này so với phần thưởng của
những người khác. Cần lưu ý rằng đôi khi những mô hình như vậy được gọi là mô
hình “không thích bất bình đẳng”. Thuật ngữ sau cùng ít phù hợp hơn. Sự khác biệt
giữa bất bình đẳng và bất công đã được đề cập trước đó, trong các cuộc thảo luận
về cả ý định và yếu tố tuổi tác. Điểm quan trọng nhất ở đây là bất bình đẳng là một
thuật ngữ trung lập và không ngụ ý đánh giá giá trị, trong khi bất bình đẳng là một
thuật ngữ mang tính quy tắc hoặc giá trị liên quan đến khái niệm chủ quan về sự
công bằng. Do đó, nếu một người đề xuất ít hơn 50% chiếc bánh trong một tối hậu
thư, điều này có thể bị từ chối vì ác cảm với sự bất bình đẳng. Như chúng ta đã
thấy, sự mơ hồ này có thể được loại bỏ bằng cách sử dụng một công cụ đề xuất
ngẫu nhiên, chẳng hạn như máy tính. Nếu sự từ chối xảy ra trong tình huống này,
nguyên nhân chắc hẳn là do ác cảm với sự bất bình đẳng.
Trước khi xem xét chi tiết các mô hình IA, sẽ rất hữu ích nếu xem xét kỹ
hơn bản chất của lòng vị tha, vì lòng vị tha đôi khi được coi là cơ sở của các sở
thích xã hội. Điều này cũng sẽ giúp hiểu được mức độ liên quan của các thuật ngữ
“nội sinh”, “tiết kiệm” và “đặc biệt”, được sử dụng trong phần trước khi mô tả các
đặc điểm của mô hình tốt.
Như chúng ta đã thấy, một số tác giả phân biệt giữa lòng vị tha thuần túy,
trong đó lợi ích của một người chơi tăng lên khi lợi ích của một người chơi khác
tăng lên, và lòng vị tha không thuần túy, trong đó tiện ích của người chơi tăng
lên từ hành động đóng góp cho người khác ( Margolis, ).
1982 Vì vậy, nếu tôi cảm
thấy hạnh phúc hơn khi cho bạn mượn ô tô của tôi (và do đó làm cho bạn hạnh
phúc hơn), nhưng không phải nếu người hàng xóm của tôi cho bạn mượn ô tô của
anh ấy, thì đây là lòng vị tha không thuần túy.
Hai điểm cơ bản cần được thực hiện ở giai đoạn này. Thứ nhất, cả hai loại
lòng vị tha ở trên đều không cấu thành lòng vị tha thuần túy theo nghĩa mà đôi khi
nó được sử dụng trong tâm lý học (Batson, ).
1991 Tâm lý vị tha đề cập đến mục
tiêu làm tăng phúc lợi của người khác mà
làm tăng phúc lợi của chính mình, không
dù là vật chất hay tâm lý. Một hiện tượng như vậy là xa lạ với kinh tế học, vì nó
không thể được đưa vào bất kỳ mô hình tối đa hóa tiện ích nào, dù là tiêu chuẩn
hay hành vi. Trong bất kỳ loại mô hình kinh tế nào, không yếu tố nào có thể ảnh
hưởng đến hành vi của một cá nhân trừ khi nó có thể được kết hợp theo một cách
nào đó vào chức năng tiện ích của người đó, mặc dù Amartya Sen ( ) dường 1977
như đã hình dung ra thực tế của tâm lý vị tha. Tuy nhiên, nghiên cứu thần kinh học
hiện nay có xu hướng hỗ trợ mô hình kinh tế, như được minh họa trong nghiên cứu
trường hợp cuối cùng ở chương đầu tiên.
Điểm thứ hai là lòng vị tha, như đã định nghĩa ở trên, chỉ có thể giải thích
cho sự tương hỗ tích cực; nó không thể giải thích sự tương hỗ tiêu cực phổ biến
được quan sát thấy trong các phát hiện thực nghiệm được báo cáo trước đó. Bất kỳ
mô hình nào chỉ giải thích các phát hiện thực nghiệm dưới dạng lòng vị tha sẽ phải
kết hợp các biến chứng đặc biệt như thay đổi các dấu hiệu liên quan đến lợi ích của
người khác. Những biến chứng này không được giải thích trong chính cấu trúc của
mô hình, nghĩa là chúng là ngoại sinh chứ không phải nội sinh. Điều này cũng sẽ
làm cho mô hình thiếu tính phân tích, vì mô hình sẽ phải được điều chỉnh để giải
thích các tình huống khác nhau.
Do đó, bất kỳ mô hình sở thích xã hội thành công nào cũng phải vượt ra
ngoài lòng vị tha, vì nó cũng phải có khả năng giải thích hành vi ác ý, giống như
các hình thức trừng phạt khác nhau mà chúng ta đã quan sát thấy trong các loại trò chơi khác nhau. Mô hình Fehr–Schmidt
Fehr và Schmidt (1999) đã đề xuất một mô hình (mô hình FS), đôi khi được gọi là
mô hình “tội lỗi/ ghen tị”, nhưng thực ra các tác giả gọi là mô hình ác cảm bất bình
đẳng. Họ sử dụng thuật ngữ bất bình đẳng dựa trên cơ sở rằng các đánh giá về sự
công bằng dựa trên một số điểm tham chiếu “trung lập”. Họ tham khảo các tài liệu
về tâm lý học xã hội liên quan đến so sánh xã hội (Stouffer et al., 1949; Festinger,
1954; Homans, 1961; Adams, 1963), lưu ý rằng điểm mấu chốt trong nghiên cứu
này là các khoản hoàn trả vật chất tương đối ảnh hưởng đến hạnh phúc của con
người. và hành vi. Họ cũng ghi nhận một số phát hiện thực nghiệm hỗ trợ trực tiếp
cho giả thuyết của họ (Loewenstein, Thompson và Bazerman, 1989; Agell và
Lundborg, 1995; Clark và Oswald, 1996; Bewley, 1998). Trong các tình huống
thực tế, việc xác định nhóm tham chiếu có liên quan và kết quả có xu hướng đặt ra
các vấn đề về mô hình hóa, nhưng trong các tình huống thử nghiệm, có vẻ hợp lý
hơn khi giả định rằng nhóm tham chiếu có liên quan là các đối tượng khác trong
nghiên cứu và kết quả tham chiếu là thu nhập trung bình của các đối tượng này.
Do đó, trong mô hình FS, người ta giả định rằng, ngoài các đối tượng hoàn
toàn ích kỷ, một số đối tượng cũng sẽ không thích các kết quả không công bằng.
Sự bất bình đẳng như vậy có thể phát sinh từ việc kém hơn hoặc tốt hơn so với
những người khác. Do đó, chức năng tiện ích của một cá nhân không chỉ phụ thuộc
vào sự hoàn trả bằng tiền của chính họ, mà còn phụ thuộc vào sự khác biệt giữa sự
hoàn trả này và của những người khác.
Tình huống này có thể được mô hình hóa bằng toán học như sau:
Trong một tập hợp n người chơi, phân bổ xã hội được đưa ra bởi vectơ tiền chi trả: x = (, , ..., xn)
Hàm tiện ích của người chơi i là một hàm vectơ này và được cho ra bởi: (10.1)
Trong đó là thước đo mức độ ác cảm của người chơi i đối với sự bất bình đẳng bất
lợi, và là thước đo mức độ ác cảm của anh ta đối với sự bất bình đẳng có lợi. Do
đó, thuật ngữ thứ hai trong phương trình (10.1) đo lường tổn thất tiện ích từ bất
bình đẳng bất lợi và thuật ngữ thứ ba đo lường tổn thất tiện ích do bất bình đẳng có
lợi. Ba giả định khác có liên quan:
1. , có nghĩa là người chơi ít bị ảnh hưởng bởi bất bình đẳng có lợi hơn bất lợi.
Điều này chắc chắn có vẻ là một giả định hợp lý dưới ánh sáng của bằng
chứng thực nghiệm trực tiếp (Loewenstein, Thompson và Bazerman, 1989).
2. , ranh giới thấp hơn có nghĩa là người chơi thực sự phải chịu đựng sự bất
bình đẳng có lợi, thay vì cảm thấy được hưởng lợi từ nó. Giả định này chắc
chắn là đáng nghi ngờ (Frank, 1985; Wilkinson, 2004), và Fehr và Schmidt
thừa nhận khả năng của những người tham gia tìm kiếm địa vị với giá trị
âm, nhưng họ biện minh cho giả định trên với lí do rằng những người tham
gia đó 'hầu như không có tác động đến hành vi cân bằng'. Ranh giới trên = 1
có thể được hiểu là một người chơi sẵn sàng vứt bỏ một đô la để giảm lợi thế
tương đối của mình so với người chơi j có cùng số tiền, điều này dường như không thể xảy ra.
3. Số lượng người chơi không đồng nhất, nghĩa là những người chơi khác nhau
có giá trị và khác nhau. Do đó, và có các phân phối chứ không phải các
giá trị đơn lẻ cho toàn bộ dân số.
Sử dụng hàm tiện ích trong phương trình (10.1), Fehr và Schmidt sau đó áp dụng
phân tích lý thuyết trò chơi ( tương tự như phân tích được sử dụng trong chương
trước liên quan đến các chiến lược liên tục ) để lấy các giá trị trung bình của và ,
đôi khi được gọi là 'sự ghen tị' và 'cảm giác tội lỗi', cần thiết để giải thích các kết
quả thực nghiệm khác nhau.
Mô hình FS đưa ra một số kết luận liên quan đến các biến thể khác nhau của
trò chơi tối hậu thư và hàng hóa công cộng. Trong khi thuyết tân cổ điển dự đoán
hoàn toàn tự do trong trò chơi hàng hóa công cộng (không đóng góp) và không sẵn
sàng tham gia vào hình phạt tốn kém, thì mô hình FS dự đoán rằng cả đóng góp và
hình phạt sẽ xảy ra nếu người chơi đủ ghen tị và phạm tội. Mô hình đưa ra các kết
luận cụ thể liên quan đến (1) các điều kiện mà mọi người sẽ đi xe miễn phí ( trong
đó m là lợi nhuận cận biên cho lợi ích công cộng), (2) cần bao nhiêu người đi xe
miễn phí ( ) để khiến mọi người đi xe miễn phí (), và (3) mức độ tội lỗi và đố kỵ k
cần thiết để cân bằng xuất hiện khi có một số đóng góp và trừng phạt tích cực (một
lần nữa được xác định theo các thông số nội sinh , , m và c, chi phí trừng phạt.)
Điểm mạnh kép của mô hình FS là: 1. Sự đơn giản
Mô hình đơn giản về hình thức, về số lượng tham số liên quan và tuyến tính
của hàm (mặc dù tính năng thứ hai có thể dễ dàng sửa đổi). 2. Độ bền
Đặc điểm này đề cập đến khả năng giải thích sự khác biệt lớn trong kết quả
quan sát được từ các trò chơi khác nhau. Ví dụ, nó phù hợp với trò chơi tối
hậu thư thông thường và các biến thể với sự cạnh tranh của cả người đề xuất
và người phản hồi. Về khía cạnh cạnh tranh, mô hình đưa ra một dự đoán thú
vị: trong cạnh tranh người đề xuất, số lượng người đề xuất không ảnh hưởng
đến đề nghị cân bằng gần như bằng không, trong khi trong cạnh tranh đáp
ứng, số lượng người phản hồi nhiều hơn sẽ làm giảm đề nghị cân bằng cao
nhất. Những dự đoán tương phản này vẫn chưa được xác nhận bằng thực
nghiệm. Bản chất của bằng chứng thực nghiệm và điều này liên quan như
thế nào đến các mô hình khác nhau được thảo luận trong Phần 10.7, cùng
với những lời chỉ trích về phương pháp luận liên quan. Mô hình Bolton–Ockenfels
Mô hình này (BO), do Bolton và Ockenfels (2000) đề xuất, thường được gọi là mô
hình ERC, vì nó liên quan đến công bằng, tương hỗ và cạnh tranh. Nó tương tự
như mô hình FS ở nhiều khía cạnh, vì người chơi quan tâm đến phần thưởng của
chính họ và phần chia sẻ tương đối của họ. Giả định rằng người chơi thích phần
thưởng tương đối bằng với phần thưởng trung bình, nghĩa là họ sẽ hy sinh để
chuyển phần của mình đến gần mức trung bình hơn nếu họ ở trên hoặc dưới mức đó.
Tình huống này có thể được mô hình hóa bằng toán học như sau: ) (10.2)
Mô hình BO, giống như mô hình FS, sử dụng phân tích lý thuyết trò chơi để rút ra
những kết luận cụ thể về trạng thái cân bằng trong nhiều trò chơi khác nhau. Ví dụ:
nó dự đoán rằng trong các trò chơi tối hậu thư, những người phản hồi sẽ luôn từ
chối các đề nghị bằng 0 và tỷ lệ từ chối sẽ giảm khi tỷ lệ phần trăm đề nghị tăng
lên. Nó cũng dự đoán rằng các ưu đãi tối hậu thư sẽ lớn hơn các ưu đãi của nhà độc
tài và trong các trò chơi ba người, việc phân bổ cho những người nhận không hoạt
động sẽ bị bỏ qua. Những dự đoán này phần lớn được xác nhận bởi những phát hiện thực nghiệm.
Có ba điểm khác biệt chính giữa mô hình BO và mô hình FS:
1. Mô hình BO quan tâm đến cổ phần tương đối, trong khi mô hình FS quan
tâm đến chênh lệch tuyệt đối.
2. Mô hình BO chỉ so sánh giữa phần thưởng của một cá nhân với phần thưởng
trung bình của tất cả những người chơi khác. Nó không so sánh số tiền chi
trả của mỗi người chơi với số tiền chi trả tối đa và tối thiểu của những người
khác, giống như mô hình FS.
3. Mô hình BO đề xuất một thái độ đối xứng đối với sự bất bình đẳng, trong đó
cảm giác tội lỗi và đố kỵ có sức mạnh ngang nhau (= ), trong khi mô hình FS
đề xuất rằng đố kỵ mạnh hơn cảm giác tội lỗi.
Trong cả ba khía cạnh, mô hình FS dường như vượt trội hơn, cả về những phát
hiện thực nghiệm phù hợp và nền tảng tâm lý. Có thể đưa ra một minh họa đơn
giản bằng cách sử dụng trò chơi ba người trong đó phân bổ tiền chi trả được
đưa ra bởi (). Theo mô hình BO, sở thích của người chơi đầu tiên phải độc lập
với , vì tổng số tiền chi trả sẽ không đổi và do đó, tỷ lệ tương đối của người
chơi đầu tiên không bị ảnh hưởng. Tuy nhiên, theo mô hình FS, khi tăng lên, sự
ghen tị với phần thưởng của người chơi thứ ba và cảm giác tội lỗi liên quan đến
phần thưởng của người chơi thứ hai đều tăng lên, khiến cho độ thỏa dụng của
người chơi thứ nhất giảm xuống. Một nghiên cứu của Charness và Rabin (2000)
đã xác nhận dự đoán này, và những phát hiện thực nghiệm tương tự được xem
xét trong Phần 10.7. Tuy nhiên, kết luận này không có nghĩa là mô hình FS có
thể giải thích tất cả các kết quả thực nghiệm trong các trò chơi như vậy, hoặc nó
hoàn thành trong việc nắm bắt tất cả các yếu tố tâm lý có liên quan, như chúng ta sẽ thấy bây giờ. 10.6 Mô hình đối ứng
Tính tương hỗ dựa trên ý tưởng rằng quan niệm của mọi người về sự công bằng
không chỉ phụ thuộc vào sự bình đẳng hay bất bình đẳng mà còn phụ thuộc vào ý
định của con người. Như đã giải thích trong phần trước, lòng vị tha chỉ giải thích
được tính tương hỗ tích cực, nhưng bất kỳ mô hình thực tế nào cũng phải có khả
năng giải thích và dự đoán tính tương hỗ tiêu cực được quan sát rộng rãi theo kinh
nghiệm. Nói chung, mọi người có thể có ý định 'tử tế' hoặc 'không tử tế' đối với
người khác, tùy thuộc vào những gì chúng ta tin là ý định của họ đối với chúng ta.
Do đó, ý định phụ thuộc vào niềm tin và khả năng có thể xảy ra. Ví dụ: nếu chúng
ta không có lựa chọn nào khác ngoài việc đưa ra đề nghị bất bình đẳng cho ai đó
thì điều này không bị đánh giá là không công bằng như khi chúng ta có lựa chọn
giữa việc đưa ra đề nghị công bằng và đề nghị không công bằng. Bằng chứng thực
nghiệm liên quan đến điều này được trình bày trong phần tiếp theo.
Một điểm khởi đầu tốt cho việc thảo luận về các mô hình tương hỗ là mô
hình do Rabin (1993) đề xuất, vì đây là mô hình chính thức đầu tiên thuộc loại này
và là mô hình đơn giản nhất. Mô hình Rabin
Cơ sở trung tâm của mô hình Rabin được thể hiện bằng tuyên bố:
Nếu ai đó đối xử tốt với bạn, thì sự công bằng buộc bạn phải đối xử tốt với
anh ta. Nếu ai đó ác ý với bạn, thì sự công bằng cho phép - và tính thù hận ra
lệnh - rằng bạn ác ý với anh ta. (tr. 1281)
Mô hình này là mô hình hai người chơi, trong đó các tiện ích phụ thuộc vào niềm
tin. Chiến lược của người chơi 1, , phụ thuộc vào niềm tin của anh ta về chiến lược
của người chơi kia, , và niềm tin của anh ta về niềm tin của người chơi 2, liên quan
đến chiến lược của người chơi 1, . Một mô tả tương tự có thể được áp dụng cho
chiến lược của người chơi 2. Trên cơ sở những niềm tin này, hai cấu trúc quan
trọng có thể được xác định: (1) 'lòng tốt' của người chơi 1 đối với người chơi 2 và
(2) nhận thức của người chơi 1 về 'lòng tốt' của người chơi 2 đối với anh ta. Việc
xác định và giải thích các cấu trúc này đòi hỏi một lượng nỗ lực trí tuệ nhất định và
sau đây là phần trình bày khá chi tiết về phân tích có liên quan, sử dụng tình huống PD làm minh họa.
1. Lòng tốt của người chơi 1 đối với người chơi 2
Cho rằng người chơi 1 có niềm tin liên quan đến chiến lược của người chơi
2, chiến lược của chính anh ta bao gồm phân bổ phần thưởng cho người chơi
2 trong số các phần thưởng có thể có. Đặt phần thưởng cao nhất và thấp nhất
cho người chơi 2 là () và (). Sau đó, chúng ta cần định nghĩa một khoản
hoàn trả công bằng, (), mà Rabin thực hiện bằng cách lấy trung bình các
khoản hoàn trả cao nhất và thấp nhất (mặc dù định nghĩa cụ thể này không
ảnh hưởng đến phân tích cơ bản). Lòng tốt của người chơi 1 đối với người
chơi 2 bây giờ có thể được thể hiện như sau:
Điều này có thể được giải thích bằng cách nói rằng sự công bằng của người
chơi 1 đối với người chơi 2 là một chức năng của chiến lược của chính anh
ta () và niềm tin của anh ta đối với chiến lược của người chơi 2 (), và được
xác định bởi tỷ lệ của cách trên hoặc dưới công bằng. Chỉ ra rằng phần
thưởng thực tế của người chơi 2 nằm ở (tử số), được chia tỷ lệ theo phạm vi
phần thưởng mà người chơi 1 có thể đã chỉ ra (mẫu số). Do đó, nếu người
chơi 2 nhận được phần thưởng cao hơn phần thưởng công bằng, thì tử số là
dương và người chơi 1 đang tử tế. Mặt khác, nếu người chơi 2 nhận được
phần thưởng thấp hơn phần thưởng công bằng, thì tử số là âm và người chơi
1 là người không tử tế.
2. Nhận thức của người chơi 1 về sự tử tế của người chơi 2
Nhận thức này phụ thuộc vào điều mà người chơi 1 tin rằng người chơi 2 tin
người chơi 1 sẽ làm (). Do đó, nó có thể được viết như sau: (10.4)
Sau đó, Rabin giả định rằng sở thích xã hội của người chơi 1 được cung cấp
bởi hàm tiện ích ba thành phần: (10.5)
Thành phần đầu tiên của hàm, , biểu thị khoản hoàn trả bằng tiền trực tiếp
của người chơi 1. Thành phần thứ hai, , biểu thị độ thỏa dụng trong nhận
thức của người chơi 1 về lòng tốt của người chơi 2, trong đó là trọng số cho
thấy công bằng chuyển đổi thành tiện ích tiền tệ như thế nào (người chơi
không có sở thích xã hội nào có = 0). Thành phần thứ ba, biểu thị lợi ích
của tính tương hỗ; nó là một chức năng của sản phẩm của lòng tốt mà họ
mong đợi và lòng tốt của chính họ. Cần lưu ý rằng thuật ngữ này là tích cực
nếu sự hào phóng của người chơi 1 được người chơi 2 đáp lại, hoặc nếu sự
ác ý của họ được người chơi 2 đáp lại. Do đó, cả sự tương hỗ tích cực và tiêu
cực đều mang lại lợi ích tích cực, không giống như mô hình lòng vị tha.
Khi đó, trạng thái cân bằng cho mô hình có thể được rút ra trên cơ sở người
chơi tối đa hóa tiện ích xã hội, giả sử kỳ vọng hợp lý,. Điều này có nghĩa là niềm
tin về chiến lược của người chơi khác là đúng và niềm tin về niềm tin của người
chơi khác cũng đúng. Một minh họa về hoạt động của mô hình có thể được đưa ra
dưới dạng tình huống PD, giả sử các khoản hoàn trả bằng tiền như trong Bảng 10.3.
Bảng 10.3 Thế tiến thoái lưỡng nan của người tù – sự hoàn trả bằng tiền Người chơi 2 Hợp tác Khuyết điểm Người chơi 1 Hợp tác 4,4 0,6 Khuyết điểm 6,0 1,1
Có thể thấy rằng các khoản hoàn trả bằng tiền tương ứng với các điều kiện được
mô tả trong Bảng 10.2, do đó, chiến lược ưu thế của mỗi người chơi là đào ngũ,
nếu các lợi ích xã hội bị bỏ qua. Bây giờ chúng ta phải tính toán tiện ích xã hội
bằng cách điều chỉnh các khoản hoàn trả bằng tiền để kết hợp các yếu tố công bằng
hoặc 'lòng tốt', theo hàm tiện ích trong phương trình (10.5). Những phép tính này
được thể hiện cho từng cặp trong số bốn cặp chiến lược có thể xảy ra đối đầu với
người chơi 1 (các chiến lược của người chơi 2 giống hệt nhau vì các khoản hoàn
trả bằng tiền trong Bảng 10.3 là đối xứng). 1. Hợp tác/ hợp tác
Số hạng thứ hai ở trên () là dương vì người ta cho rằng người chơi kia là tử
tế, và số hạng thứ ba () cũng tích cực vì có sự tương hỗ tích cực.
2. Hợp tác/ Khuyết điểm
Trong trường hợp này cả số hạng thứ hai và thứ ba đều âm. Không chỉ là
người chơi khác có ý nghĩa, nhưng họ không đáp lại lòng tốt của người chơi 1.
3. Khuyết điểm/ hợp tác
Thuật ngữ thứ hai là tích cực vì người chơi khác được coi là tốt bụng,
nhưng thuật ngữ thứ ba là tiêu cực vì sự xấu tính của người chơi 1 không được đáp lại.
4. Khuyết điểm/ khuyết điểm
Thuật ngữ thứ hai là tiêu cực vì người chơi khác được coi là xấu tính, nhưng
thuật ngữ thứ ba là tích cực vì người chơi 1 đang đáp lại sự ác ý của người chơi kia.
Bây giờ chúng ta có thể xây dựng một bảng hoàn trả mới với các tiện ích xã hội
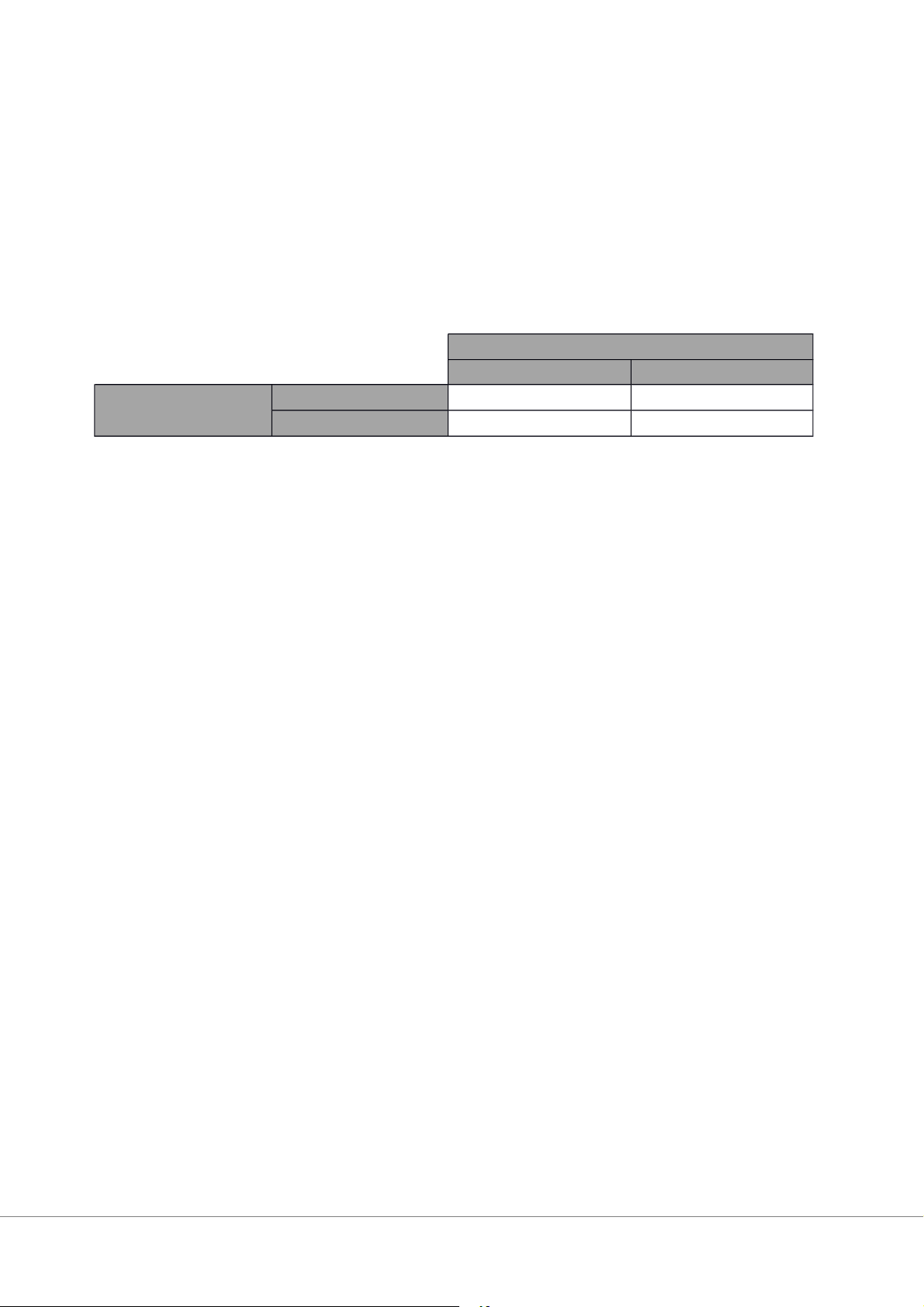
cho từng cặp chiến lược. Điều này được thể hiện trong Bảng 10.4
Bảng 10.4 Thế tiến thoái lưỡng nan của người tù – tiện ích xã hội Người chơi 2 Hợp tác Khuyết điểm Người chơi 1 Hợp tác Khuyết điểm
Trong tình huống được sửa đổi, chiến lược vượt trội cho mỗi người chơi không
nhất thiết phải là đào ngũ. Phần thưởng cho sự hợp tác nếu người chơi kia hợp tác
sẽ lớn hơn phần thưởng cho sự phản bội nếu a, nghĩa là, nếu . Hàm ý ở đây là nếu
mọi người có sở thích xã hội đủ mạnh liên quan đến công bằng sẽ có một tình
huống cân bằng Nash với hai trạng thái cân bằng trong các chiến lược thuần túy:
hợp tác/hợp tác và khuyết điểm/ khuyết điểm. Ngoài ra, tình hình có thể được xem
xét dưới dạng cân bằng chiến lược hỗn hợp. Mô hình Falk-Fischbacher
Falk và Fischbacher (2006) đã xây dựng một mô hình tương hỗ khác, mô hình này
đề xuất một hàm tiện ích xã hội kết hợp bốn yếu tố trái ngược với ba yếu tố trong
mô hình của Rabin. Ngoài việc bao gồm các khoản hoàn trả bằng tiền hoặc 'vật
chất', lòng tốt và tính tương hỗ, nó cũng tính đến mức độ cố ý của người chơi. Mô
hình FF có hai biến thể quan trọng so với mô hình Rabin: (1) lòng tốt được đo
lường theo sự khác biệt giữa các khoản hoàn trả của những người chơi khác nhau,
thay vì theo các khoản hoàn trả có thể có cho một người chơi và (2) ý định được
coi là phụ thuộc vào các phân bổ có sẵn, cả được chọn và không được chọn. Hai
biến thể này hiện được giải thích chi tiết hơn. 1. Đo lường lòng tốt
Trong mô hình Rabin, lòng tốt được đánh giá dựa trên số tiền người chơi
nhận được so với một số phần thưởng 'công bằng' cho chính họ, điều này lại
phụ thuộc vào phạm vi phần thưởng có thể có của chính họ. Ngược lại, mô
hình FF đề xuất rằng người chơi đánh giá sự công bằng dựa trên sự khác biệt
giữa phần thưởng kỳ vọng của chính họ và phần thưởng của người chơi khác 2. Đo lường ý định
Trong mô hình FF có một hàm ý định so sánh một tập hợp các khoản hoàn
trả khả dĩ với các khoản hoàn trả thay thế. Trong trường hợp này, chi phí cơ
hội đối với người ra quyết định có liên quan đến việc đánh giá tính công
bằng trong phân bổ của họ. Ví dụ, trong một trò chơi tối hậu thư, việc đưa ra
mức 80%/20% có thể bị coi là không công bằng trong một số trường hợp,
nhưng lại công bằng ở những trường hợp khác, tùy thuộc vào những lựa
chọn thay thế nào dành cho người ra quyết định. Nếu phương án thay thế
duy nhất là 90%/10%, thì tỷ lệ chia 80%/20% có thể được đánh giá là công bằng
Các chi tiết khác của mô hình FF không được đưa ra ở đây, vì nó được phát triển
để phân tích các trò chơi dạng tuần tự hoặc dạng mở rộng, thay vì các trò chơi dạng
bình thường đồng thời được minh họa trong các bảng mà chúng ta đã sử dụng cho
đến nay. Chúng ta đã thấy trong chương trước rằng việc phân tích các trò chơi dạng
mở rộng phức tạp hơn so với việc phân tích các trò chơi đồng thời. Trong lý thuyết
trò chơi tiêu chuẩn, điều này liên quan đến việc sử dụng phương pháp quay lui,
nhưng như chúng ta đã thấy trong phần về PGT, điều này không thể áp dụng được
trong các trò chơi tâm lý.
Mô hình Dufwenberg–Kirchsteiger
Dufwenberg và Kirchsteiger (2004) đề xuất một biến thể của mô hình FF. Giống
như mô hình FF và không giống như mô hình Rabin, mô hình DK liên quan đến
tính tương hỗ tuần tự và cũng đo lường sự công bằng về sự khác biệt giữa phần
thưởng kỳ vọng của chính người chơi và phần thưởng của người chơi khác. Mô
hình DK cũng dựa trên PGT, nhưng mở rộng phân tích đến các tình huống mà
niềm tin và kỳ vọng của người chơi có thể thay đổi trong suốt trò chơi, trong khi
trong bài báo gốc của Geanakoplos, Pearce và Stacchetti (1989) các điều kiện hoặc
niềm tin ban đầu vẫn được giữ nguyên. liên tục trong suốt trò chơi. Một hệ quả của
việc mở rộng phân tích này là sự đảo ngược sở thích có thể xảy ra do sự thay đổi
trong niềm tin của người chơi. Phân tích DK của trò chơi PD tuần tự đưa ra kết
luận tương tự như mô hình Rabin: nếu người chơi có độ nhạy cảm tương hỗ cao thì
có thể dẫn đến giải pháp cân bằng Nash kép. Cả hai người chơi có thể hợp tác vì cả
lý do vật chất và có đi có lại; hoặc cả hai đều có thể phản bội vì những kỳ vọng
thỏa mãn bản thân, với việc mỗi người chơi tin rằng người kia không tử tế và đáp lại cũng không tử tế.
Mô hình DK cũng đưa ra một số dự đoán thú vị liên quan đến trò chơi con
rết, một trò chơi lòng tin đã thảo luận ở chương trước. Trong phiên bản DK của trò
chơi, tại mọi nút, người chơi ra quyết định có thể lấy (khuyết tật) hoặc bỏ qua,
trong trường hợp đó, phần thưởng vật chất của họ bị giảm đi một trong khi phần
thưởng vật chất của người chơi khác tăng lên hai phần. Một trò chơi bốn giai đoạn
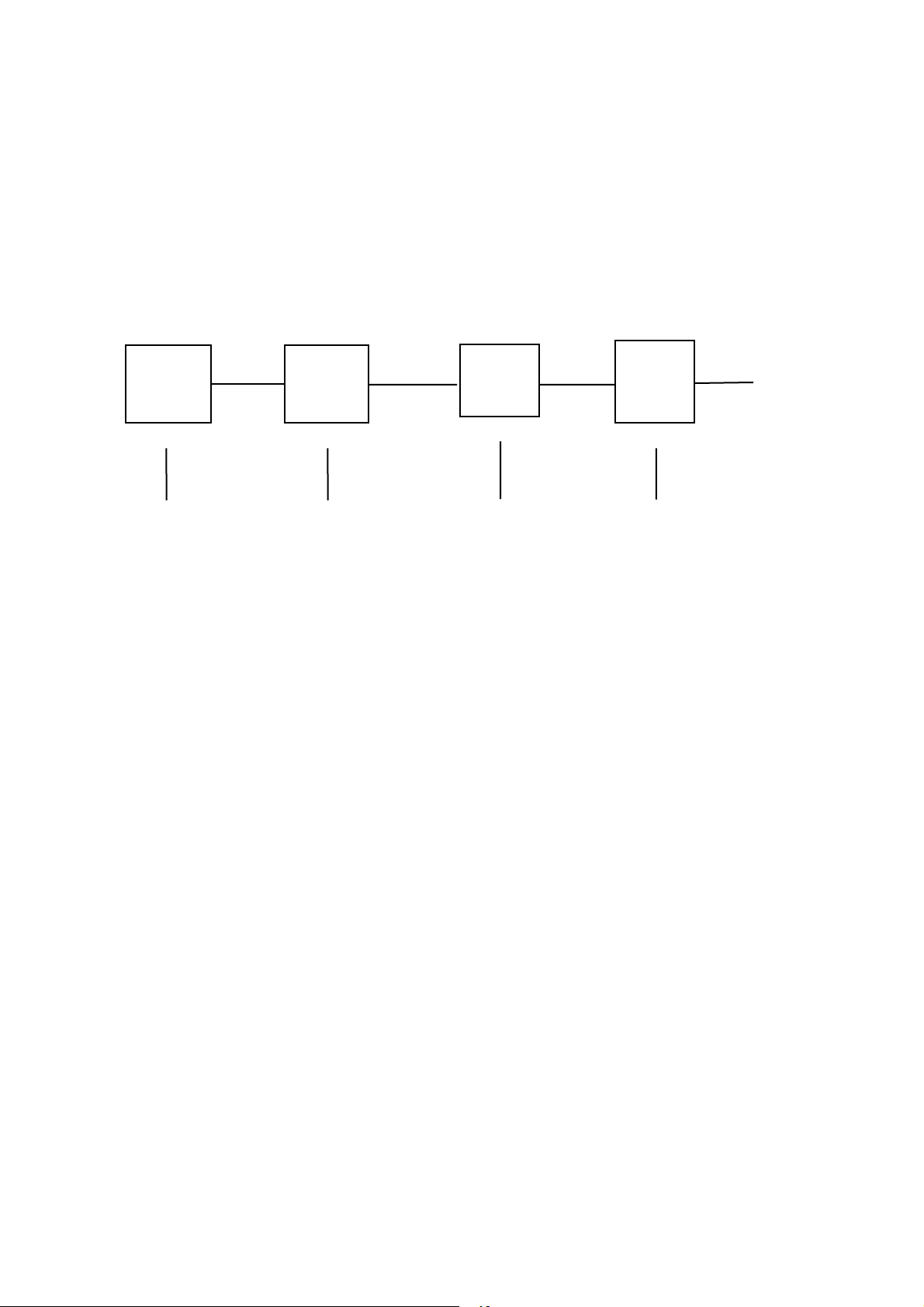
được biểu diễn trong Hình 10.2
Hình 10.2 Trò chơi con rết tương hỗ qua qua qua qua 3,2 A AB B lấy lấy lấy lấy 1,0 0,2 2,1 1,3
Dự đoán thú vị nhất ở đây là chỉ cần một trong số những người chơi được thúc đẩy
bởi sự tương hỗ là đủ để cả hai người chơi ở lại chế độ cuối cùng hoặc cuối cùng
trừ một chế độ. Ví dụ: ngay cả khi A nghi ngờ rằng B sẽ thực hiện ở chế độ cuối
cùng, A vẫn có thể chuyển cho anh ta ở nút trước đó nếu B đã hợp tác cho đến thời
điểm đó và do đó đã thiết lập một khuôn mẫu tử tế thông thường. Hậu quả của việc
này là B có thể hợp tác cho đến phương thức cuối cùng ngay cả khi anh ta hoàn
toàn ích kỷ. Một dự đoán khác rút ra từ điều này là số lượng màn chơi trong trò
chơi càng nhiều thì người chơi càng có khả năng hợp tác, vì điều đó cho phép xây
dựng lòng tốt giữa họ nhiều hơn. Dufwenberg (2002) đã đề cập đến quá trình này
trong một trò chơi tâm lý dựa trên động cơ thúc đẩy bởi sự ác cảm tội lỗi là “cảm
ứng chuyển tiếp tâm lý”
Bây giờ chúng ta có thể thấy rằng có một số khác biệt giữa các mô hình
Rabin và DK, trong đó quan trọng nhất có thể được tóm tắt dưới đây:
1. Mô hình DK áp dụng cho các trò chơi tuần tự cũng như các trò chơi đồng thời.
2. Mô hình DK áp dụng cho các trò chơi có nhiều hơn hai người chơi.