Phân tích một số câu vận dụng trong đề minh họa THPTQG 2020 môn Toán

Tài liệu gồm có 39 trang được biên soạn bởi thầy giáo Nguyễn Minh Nhiên, trình bày lời giải chi tiết và đi sâu phân tích một số bài toán vận dụng – vận dụng cao trong đề minh họa THPT Quốc gia môn Toán năm học 2019 – 2020

17 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu ôn thi THPTQG môn Toán

Môn: Toán

Thông tin:

39 trang 6 tháng trước

Tác giả:

Profile Nguyễn Vân
Trang 1
NGUYỄN MINH NHIÊN
LỜI GIẢI VÀ PHÂN TÍCH MỘT SỐ CÂU VẬN DỤNG TRONG ĐỀ THAM KHẢO
KỲ THI THPT QUỐC GIA NĂM 2020
Nguyễn Minh Nhiên
Đề thi tham khảo kỳ thi THPT quốc gia năm 2020 giúp giáo viên, học sinh đánh giá mức độ đề
thi qua đó có những định hướng quá trình ôn tập. Bài viết này, xin phân tích một số bài toán được khai
thác theo nhiều hướng giúp chúng ta có những cách tiếp cận khác nhau đối với những dạng toán vận
dụng trong các đề thi THPT quốc gia.
Câu 38: Cho hàm số
f x
có
3 3
f
và
'
1 1
f x
x x
với
0
. Khi đó
8
3
f x dx
bằng
A.
7
. B.
197
6
. C.
29
2
. D.
181
6
.
Lời giải 1:
8 8
3 3
8 3 d d 7 8 10
1 1
x
f f f x x x f
x x
.
8 8 8
2
8
3
3 3 3
229 197
d d 8 8 3 3 d 80 9
6 6
1 1
x
f x x xf x xf x x f f x
x x
.
Lời giải 2:
Ta có
1 1 1 1
1
1
1 1 1
1 1 1
x x
x
f x
x x x
x x
Suy ra
2 1
f x x x C
Mà
3 3 4
f C
. Do đó
2 1 4
f x x x
.
Vì vậy
8
3
197
2 1 4 d
6
x x x
Nhận xét:
Với giả thiết như vậy ta có thể xử lý theo hai hướng:
Hướng 1: Tìm
f x
từ đó suy ra
8
3
d
f x x
. Nếu để ý kỹ hơn thì thấy
1 1 1 1
1
1
1 1 1
1 1 1
x x
x
x x x
x x
Khi đó, có thể dễ dàng tìm
f x
.
Hướng 2: Sử dụng tích phân từng phần
8 8 8
2
8
3
3 3 3
d d 8 8 3 3 d
1 1
x
f x x xf x xf x x f f x
x x
Như thế, chỉ cần tính
8
f
là xong.
Trang 2
NGUYỄN MINH NHIÊN
BÀI TẬP TƯƠNG TỰ CÂU 38
Câu 38.1: Cho hàm số
f x
liên tục trên
0;
. Biết
ln
x
f x
x
và
1 0
f
. Giá trị của
1
d
e
f x x
bằng
A.
2
. B.
1
2
. C.
1
6
. D.
2
2
.
Câu 38.2: Biết rằng
sin
x x
là một nguyên hàm của hàm số
f x
trên R. Gọi
( )
F x
là một nguyên hàm
của hàm số
'( ) '( ) cos
f x f x x
thỏa mãn
0 0
F
. Giá trị của
4
F
bằng
A.
. B.
4
. C.
0
. D.
2
.
Câu 38.3: Cho hàm số
f x
liên tục trên
thỏa mãn các điều kiện:
0 2 2,
f
0,
f x
x
và
2
. 2 1 1 ,
f x f x x f x
x
.
Khi đó giá trị
1
f
bằng
A.
26
. B.
24
. C.
15
. D.
23
.
Trang 3
NGUYỄN MINH NHIÊN
LỜI GIẢI BÀI TẬP TƯƠNG TỰ CÂU 38
Câu 38.1: Cho hàm số
f x
liên tục trên
0;
. Biết
ln
x
f x
x
và
1 0
f
. Giá trị của
1
d
e
f x x
bằng
A.
2
. B.
1
2
. C.
1
6
. D.
2
2
.
Lời giải
Chọn D
Ta có
2
ln ln
d d ln d ln
x x
f x x x x x C
. Nên
2
ln
x
f x C
, với
C
là hằng số.
Mà
2
ln
1 0 0
2
x
f C f x .
Do đó,
2
1 1
ln 2
d d
2 2
e e
x e
f x x x
.
Câu 38.2: Biết rằng
sin
x x
là một nguyên hàm của hàm số
f x
trên R. Gọi
( )
F x
là một nguyên hàm
của hàm số
'( ) '( ) cos
f x f x x
thỏa mãn
0 0
F
. Giá trị của
4
F
bằng
A.
. B.
4
. C.
0
. D.
2
.
Lời giải
Chọn D
sin
x x
là một nguyên hàm của hàm số
f x
sin ' sin cos
f x x x x x x
( ) sin cos
f x x x x
'( ) 2 cos sin
f x x x x
' 2 cos sin
f x x x x
' ' 2 sin
f x f x x
Khi đó
( ) '( ) '( ) cos d 2 sin .cos d sin2 d cos 2
F x f x f x x x x x x x x x C
Từ (0) 0 C ( ) cos 2
2 2 2 4 2
F F x x F
.
Câu 38.3: Cho hàm số
f x
liên tục trên
thỏa mãn các điều kiện:
0 2 2,
f
0,
f x
x
và
2
. 2 1 1 ,
f x f x x f x
x
.
Khi đó giá trị
1
f
bằng
A.
26
. B.
24
. C.
15
. D.
23
.
Trang 4
NGUYỄN MINH NHIÊN
Lời giải
Chọn B
Ta có
2
. 2 1 1
f x f x x f x
2
.
2 1
1
f x f x
x
f x
.
Suy ra
2
.
d 2 1 d
1
f x f x
x x x
f x
2
2
d 1
2 1 d
2 1
f x
x x
f x
2 2
1
f x x x C
.
Theo giả thiết
0 2 2
f , suy ra
2
1 2 2 3
C C
.
Với
3
thì
2
2 2 2
1 3 3 1
f x x x f x x x
. Vậy
1 24
f .
Trang 5
NGUYỄN MINH NHIÊN
Câu 43: Có bao nhiêu cặp số nguyên
( ; )
x y
thỏa mãn
0 2020
và
3
log (3 3) 2 9
y
x x y
?
A.
2019
. B.
6
. C.
2020
. D.
4
.
Lời giải
Điều kiện:
0
nên
3
log (3 3)
x
xác định.
Ta có
3 3 3
log (3 3) 2 9 log ( 1) ( 1) 2 log 3 9
y y y
x x y x x
3 3
log ( 1) ( 1) log 9 9
y y
x x
1
Xét hàm số
3
( ) log , 0;f t t t t

có
( ) 1 0, 0;
ln 3
f t t

.
Do đó hàm số luôn đồng biến trên
0;

.
Khi đó
1 9 1
y
x
Vì
0 2020
x
nên
9
0 9 1 2020 0 log 2021
y
y
.
Do
y
nguyên nên
0;1;2;3
y
.
; 0;0 ; 8;1 ; 80;2 ; 728; 3
x y .
Vậy có 4 cặp số nguyên
( ; )
x y
thỏa mãn.
Nhận xét:
Với dạng toán này việc quan trọng nhất là xác định được hàm đặc trưng
3
( ) log , 0;f t t t t

.
Ngoài ra, nếu để ý hàm số
3
log (3 3)
y x x
đồng biến trên
1;

, hàm số
2 9
x
cũng đồng
biến trên
;
 
nên
3
0 2020 1 2 9 log 6063 2020 1 4
y
x y y
.
Trang 6
NGUYỄN MINH NHIÊN
BÀI TẬP TƯƠNG TỰ CÂU 43
Câu 43.1: Có bao nhiêu cặp số
( ; )
nguyên thỏa mãn các điều kiện
0 2020
và
2
log (2 2) 3 8
y
x x y
?
A. 2019. B. 2018. C. 1. D. 4.
Câu 43.2: Có bao nhiêu giá trị nguyên của tham số
m
để tồn tại cặp số
;
x y
thỏa mãn đồng thời các
điều kiện
3 5 3 1
e e 1 2 2
x y x y
x y
và
2 2
3 3
log 3 2 1 6 log 9 0
x y m x m
?
A.
6
. B.
5
. C.
8
. D.
7
.
Câu 43.3: Cho phương trình
7
7 log
x
m x m
với
m
là tham số. Có bao nhiêu giá trị nguyên của
25;25
m
để phương trình đã cho có nghiệm?
A.
9
. B.
25
. C.
24
. D.
26
.
Câu 43.4: Cho phương trình
2
2 2
1 2 1 1
log 2 3 log 1 2 2
2
x
x x x
x x
, gọi
S
là tổng tất
cả các nghiệm của nó. Khi đó, giá trị của
S
là
A.
2
. B.
1 13
S
. C.
2
. D.
1 13
S
.
Trang 7
NGUYỄN MINH NHIÊN
LỜI GIẢI BÀI TẬP TƯƠNG TỰ CÂU 43
Câu 43.1: Có bao nhiêu cặp số
( ; )
nguyên thỏa mãn các điều kiện
0 2020
và
2
log (2 2) 3 8
y
x x y
?
A. 2019. B. 2018. C. 1. D. 4.
Lời giải
Chọn D
Do
0 2020
nên
2
log (2 2)
luôn có nghĩa.
Ta có
2
log (2 2) 3 8
y
x x y
2 2
log ( 1) 1 3 log 2 8
y y
x x
2 2
log ( 1) 1 log 8 8
y y
x x
(1)
Xét hàm số
2
( ) log , 0;f t t t t

có
( ) 1 0, 0;
ln 2
f t t

.
Do đó hàm số luôn đồng biến trên
0;

.
Khi đó
1 8 1
y
x
Ta có
0 2020
nên
8
0 8 1 2020 0 log 2021 3,66
y
y
.
Mà
nên
0;1;2;3
y .
Vậy có 4 cặp số
( ; )
nguyên thỏa yêu cầu bài toán.
Câu 43.2: Có bao nhiêu giá trị nguyên của tham số
m
để tồn tại cặp số
;
x y
thỏa mãn đồng thời các
điều kiện
3 5 3 1
e e 1 2 2
x y x y
x y
và
2 2
3 3
log 3 2 1 6 log 9 0
x y m x m
?
A.
6
. B.
5
. C.
8
. D.
7
.
Lời giải
Chọn B
Ta có
3 5 3 1
e e 1 2 2
x y x y
x y
3 5 3 1
e 3 5 e 3 1
x y x y
x y x y
.
Xét hàm số
e
t
f t t
trên
. Ta có
e 1 0
t
f t
nên hàm số đồng biến trên
.
Do đó phương trình có dạng
3 5 3 1
f x y f x y
3 5 3 1
x y x y
2 1 2
y x
.
Thế vào phương trình còn lại ta được
2 2
3 3
log 6 log 9 0
x m x m
.
Đặt
3
log
t x
, phương trình có dạng
2 2
6 9 0
t m t m
.
Để phương trình có nghiệm thì
0
2
3 12 0
m m
0 4
.
Do đó có
5
số nguyên
m
thỏa mãn.
Câu 43.3: Cho phương trình
7
7 log
x
m x m
với
m
là tham số. Có bao nhiêu giá trị nguyên của
25;25
m
để phương trình đã cho có nghiệm?
A.
9
. B.
25
. C.
24
. D.
26
.
Trang 8
NGUYỄN MINH NHIÊN
Lời giải
Chọn C
ĐK:
x m
Đặt
7
log
t x m
ta có
7
7
x
t
m t
m x
7 7
x t
x t
1
Do hàm số
7
u
f u u
đồng biến trên
, nên ta có
1
t x
. Khi đó:
7 7
x x
m x m x
.
Xét hàm số
7
x
g x x
1 7 ln 7 0
x
g x
7
log ln 7
x
.
Bảng biến thiên
x
7
log ln 7
g x
0
7
log ln 7
g
g x
Từ đó phương trình đã cho có nghiệm khi và chỉ khi
7
log ln 7 0,856
m g (các nghiệm này đều
thỏa mãn điều kiện vì
7 0
x
x m
)
Do
m
nguyên thuộc khoảng
25;25
, nên
24; 16;...; 1
m
.
Câu 43.4: Cho phương trình
2
2 2
1 2 1 1
log 2 3 log 1 2 2
2
x
x x x
x x
, gọi
S
là tổng tất
cả các nghiệm của nó. Khi đó, giá trị của
S
là
A.
2
. B.
1 13
S
. C.
2
. D.
1 13
S
.
Lời giải
Chọn D
Điều kiện
1
2
2
0
x
x
.
Ta có
2
2 2
1 2 1 1
log 2 3 log 1 2 2
2
x
x x x
x x
2
2
2 2
1 1
log 2 2 1 log 2 2 1
x x
x x
1
2 2 1
f x f
x
Xét hàm số
2
2
log 1
f t t t ,
0
t
.
Trang 9
NGUYỄN MINH NHIÊN
Ta có
2 1
ln 2
f t t
2
2 ln 2. 2 ln 2. 1
0
.ln 2
t t
,
0
.
Do đó hàm số
f t
đồng biến trên khoảng
0;

.
Nên
1
1 2 2x
x
3 2
2 4 1 0
x x x
1
3 13
2
3 13
2
x
x
x
Kết hợp với điều kiện ta được
1
3 13
x
x
. Vậy
1 13
S
.
Trang 10
NGUYỄN MINH NHIÊN
Câu 46: Cho hàm số bậc bốn
y f x
có đồ thị như hình dưới đây
x
y
4
O
Số điểm cực trị của hàm số
3 2
3
g x f x x
là
A.
5.
B.
3.
C.
7.
D.
11.
Lời giải
Từ đồ thị suy ra hàm số
y f x
có
3
điểm cực trị
1 2 3
0 4
x x x
Xét hàm số
3 2
3
g x f x x
, ta có
2 3 2
3 6 3
g x x x f x x
2
3 2
3 2
0
3 6 0
0 2
3 0
3 , 1;2; 3
i
x
x x
g x x
f x x
x x x i
Ta có đồ thị hàm số
3 2
3
y x x
x
y
x=x
2
x=x
3
x=x
1
-3
4
1
-2
O
Ta có nhận xét rằng phương trình
3 2
1
3
x x x
có
1
nghiệm; phương trình
3 2
2
3
x x x
có
3
nghiệm;
phương trình
3 2
3
3
x x x
có
1
nghiệm cả
5
nghiệm này đôi một phân biệt, đều khác
0; 2
.
Như vậy,
0
g x
có
7
nghiệm đơn phân biệt
Do đó hàm số
g x
có
7
điểm cực trị.
Nhận xét:
Để xác định số cực trị của hàm
g x f u x
ta thường hướng đến việc xét dấu
g x u x f u x
.
Nếu
g x
đổi dấu
0
x
TXĐ của
g x
thì
0
x
là điểm cực trị. Những trường hợp đơn giản khi
g x
là
hàm đa thức thì đơn giản hơn bằng việc đi tìm số nghiệm đơn và nghiệm bội lẻ.
Trang 11
NGUYỄN MINH NHIÊN
BÀI TẬP TƯƠNG TỰ CÂU 46
Câu 46.1: Cho hàm số
3 2
y f x ax bx cx d
có các điểm cực trị là
0;
a
2 3
a
và có đồ thị
là đường cong như hình vẽ.
x
y
a2
3
y=f(x)
3
1
O
Đặt
2019 2020
g x f f x
. Số điểm cực trị của hàm số là
A.
2
. B.
8
. C.
10
. D.
6
.
Câu 46.2: Cho hàm số
4 3 2
y f x ax bx cx dx e
. Biết rằng hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ bên. Hỏi hàm số
2
2
g x f x x
có bao nhiêu điểm cực đại?
x
y
y=f'(x)
1
-4
4
O
A.
5
. B.
3
. C.
1
. D.
2
.
Câu 46.3: Cho
f x
là đa thức bậc
4
và hàm số
y f x
có đồ thị là đường cong như hình vẽ.
x
y
1
-2
-4
y=f'(x)
-3
O
Số điểm cực đại của hàm số
3
3
g x f x x
là
A.
5.
B.
2.
C.
3.
D.
4.
Trang 12
NGUYỄN MINH NHIÊN
Câu 46.4: Cho
4 3 2
f x x ax bx cx d
và hàm số
y f x
có đồ thị là đường cong như hình vẽ.
x
y
1
-1
O
Số điểm cực trị của hàm số
y f f x
là
A.
7
. B.
11
. C.
9
. D.
8
.
Câu 46.5: Cho hàm số
y f x
có đạo hàm đến cấp hai trên
và
0 0; ,
f f x x
. Biết
hàm số
y f x
có đồ thị như hình vẽ. Hàm số
2
g x f x mx
, với
m
là tham số dương, có nhiều
nhất bao nhiêu điểm cực trị?
x
y
y=f'(x)
1
5
3
4
2
O
1
A.
1
B.
2
C.
5
D.
3
Trang 13
NGUYỄN MINH NHIÊN
LỜI GIẢI BÀI TẬP TƯƠNG TỰ CÂU 46
Câu 46.1: Cho hàm số
3 2
y f x ax bx cx d
có các điểm cực trị là
0;
a
2 3
a
và có đồ thị
là đường cong như hình vẽ.
x
y
a2
3
y=f(x)
3
1
O
Đặt
2019 2020
g x f f x
. Số điểm cực trị của hàm số là
A.
2
. B.
8
. C.
10
. D.
6
.
Lời giải
Chọn B
x
y
y=a
a2
3
y=f(x)
3
1
O
3 .
g x f f x f x
.
0 3 . 0
g x f f x f x
0
0
f f x
f x
0
0
f x
f x a
x
x a
,
2 3
a
.
0
f x
có 3 nghiệm đơn phân biệt
1
x
,
2
x
,
3
x
khác
0
và
a
.
Vì
2 3
a
nên
f x a
có 3 nghiệm đơn phân biệt
4
x
,
5
x
,
6
x
khác
1
x
,
2
x
,
3
x
,
0
,
a
.
Suy ra
0
g x
có 8 nghiệm đơn phân biệt.
Do đó hàm số
2019 2020
g x f f x
có 8 điểm cực trị.
Câu 46.2: Cho hàm số
4 3 2
y f x ax bx cx dx e
. Biết rằng hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ bên. Hỏi hàm số
2
2
g x f x x
có bao nhiêu điểm cực đại?
Trang 14
NGUYỄN MINH NHIÊN
x
y
y=f'(x)
1
-4
4
O
A.
5
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn C
Ta có:
2
2 2 . 2 0
y x f x x
2
2
2
1
2 4
2 1
2 4
x
x x
x x
x x
1
1 5
x
x
.
x

1 5
1
1 5
2 2
x
|
0
2 2
f x
0
|
0
g x
0
0
0
Suy ra hàm số có 1 cực đại.
Câu 46.3: Cho
f x
là đa thức bậc
4
và hàm số
y f x
có đồ thị là đường cong như hình vẽ.
x
y
1
-2
-4
y=f'(x)
-3
O
Số điểm cực đại của hàm số
3
3
g x f x x
là
A.
5.
B.
2.
C.
3.
D.
4.
Lời giải
Chọn B
Ta có
2 3
3 3 3
g x x f x x
,
3
3
3 3 0 (1)
0
' 3 0 (2)
x
g x
f x x
(1) 1
.
Dựa vào đồ thị đã cho thì
3
3
3 2
(2)
3 1
x x
x x
Trang 15
NGUYỄN MINH NHIÊN
Trong đó phương trình
3
1
3 2
2
x
x x
x
.
Còn phương trình:
3
3 1
x x
có 3 nghiệm phân biệt:
1
2 1
x
,
2
1 0
x
và
3
1 2
x
Ta có bảng biến thiên của hàm số
g x
Vậy hàm số
g x
có 2 điểm cực đại.
Câu 46.4: Cho
4 3 2
f x x ax bx cx d
và hàm số
y f x
có đồ thị là đường cong như hình vẽ.
x
y
1
-1
O
Số điểm cực trị của hàm số
y f f x
là
A.
7
. B.
11
. C.
9
. D.
8
.
Lời giải
Chọn A
Từ đồ thị và giả thiết suy ra
2 3 2
1 3 1
f x x x x x f x x
Ta có
3
3 3 2
. 3 1
g x f f x f f x f x x x x x x
3 3 2
1 1 1 1 3 1
x x x x x x x x
3
3
2
0
0
1
1
1
1
0
( 0, 76)
1 0
1, 32
1 0
1
3 1 0
3
x
x
x
x
x
x
g x
x a
x x
x b b
x x
x
x
Do đó, hàm số
g x
có
7
điểm cực trị.
Trang 16
NGUYỄN MINH NHIÊN
Câu 46.5: Cho hàm số
y f x
có đạo hàm đến cấp hai trên
và
0 0; ,
f f x x
. Biết
hàm số
y f x
có đồ thị như hình vẽ. Hàm số
2
g x f x mx
, với
m
là tham số dương, có nhiều
nhất bao nhiêu điểm cực trị?
x
y
y=f'(x)
1
5
3
4
2
O
1
A.
1
B.
2
C.
5
D.
3
Lời giải
Chọn D
Từ đồ thị hàm số
y f x
suy ra
0, 0;f x x

.
Do đó,
2
0, 0;f x x
.
Xét hàm số
2
h x f x mx
;
2
2 .
h x x f x m
.
Với
0
x
,
0
h x
Phương trình
0
h x
vô nghiệm.
Với
0
x
ta có
2
2 2 2 2
2
2 4 2
3
x
h x f x x f x f x
.
Từ đồ thị hàm số
y f x
ta thấy với
0
x
, đồ thị hàm số
y f x
luôn nằm trên đường thẳng
3
x
y
.
x
y
y=f'(x)
1
5
3
4
2
O
1
Trang 17
NGUYỄN MINH NHIÊN
Do đó,
2
2
2
2 0, 0 0, 0
x
f x x h x x
hay hàm số
y h x
đồng biến trên
0;
.
Mà
0 0
h m
và
lim
x
h x

nên phương trình
0
h x
có một nghiệm duy nhất
0
0;x
Bảng biến thiên
x
0
0
x

y
0


y
0
0
h x
Khi đó phương trình
0
h x
có
2
nghiệm phân biệt.
Đồng thời hàm số
y h x
đạt cực tiểu tại
0
x x
, giá trị cực tiểu
0
0
h x
.
Vậy hàm số
y h x
có
3
điểm cực trị.
Trang 18
NGUYỄN MINH NHIÊN
Câu 48: Cho hàm số
( )
f x
liên tục trên
thỏa mãn
3 2 10 6
( ) (1 ) 2 ,
xf x f x x x x x
.
Khi đó
0
1
( )d
f x x
bằng
A.
17
20
. B.
13
4
. C.
17
4
. D.
1
.
Lời giải 1:
Gọi
F x
là một nguyên hàm của hàm
f x
trên
.
Với
x
ta có
3 2 10 6
( ) (1 ) 2
xf x f x x x x
2 3 2 11 7 2
( ) (1 ) 2 (*)
x f x xf x x x x
2 3 2 11 7 2
( )d (1 )d 2 d
x f x x xf x x x x x x
12 8 3
3 3 2 2
1 1 2
( )d( ) (1 )d(1 )
3 2 12 8 3
x x x
f x x f x x C
12 8 3
3 2
1 1 2
1
3 2 12 8 3
x x x
F x F x C
.
Thay
0
ta được
1 1
0 1
3 2
F F C
1
.
Thay
1
ta được
1 1 5
1 0
3 2 8
F F C
2
.
Thay
1
ta được
1 1 17
1 0
3 2 24
F F C
3
.
Từ
1 , 2
suy ra
5 5 3
1 0 1 0
6 8 4
F F F F
.
Từ
2 , 3
suy ra
1 32
1 1 1 1 4
3 24
F F F F
.
Vậy
0
1
3 13
d 0 1 4
4 4
f x x F F
.
Lời giải 2:
Từ
3 2 10 6
( ) (1 ) 2
xf x f x x x x
2 3 2 2 11 7
( ) (1 ) 2
x f x xf x x x x
,
.
Suy ra, hàm số
2 3 2 2
( ) (1 ) 2
x f x xf x x
là hàm lẻ. Ta có
1
11 7
0
1
d
24
x x x
Do đó
0 1
2 3 2 2 2 3 2 2
1 0
1
( ) (1 ) 2 d ( ) (1 ) 2
24
x f x xf x x x x f x xf x x
.
Trang 19
NGUYỄN MINH NHIÊN
0 0
3 3 2 2
1 1
1 1
3 3 2 2
0 0
1 1 2
d 1 d 1
3 2 3
1 1 2 1
d 1 d 1
3 2 3 24
f x x f x x
f x x f x x
0 1 1 1
1 0 0 0
1 1 4 1 1 15
d d d d
3 2 3 3 2 24
f x x f x x f x x f x x
0 1 1
1 0 0
15
2 d 3 d 8 5 d
4
f x x f x x f x x
0 1
1 0
13
d 4 d
4
f x x f x x
Lời giải 3:
Ta có
3 2 10 6
( ) (1 ) 2
xf x f x x x x
,
1
Thay
x
bởi
x
ta được
3 2 10 6
( ) (1 ) 2
xf x f x x x x
,
x
2
Từ
1 , 2
suy ra
3 3 3 3
4 , 4,xf x xf x x x f x f x x
.
Thay
3
x
bởi
x
ta được
4
f x f x
.
Do đó,
0 0 1 0 1
1 1 0 1 1
d d d 4 d 4 d 4
f x f x x f x x f x x x f x x
Từ
1
2 3 2 11 7 2
( ) (1 ) 2
x f x xf x x x x
1 1 1
3 3 2 2 11 7 2
0 0 0
1 1 5
( )d( ) (1 )d(1 ) 2 d
3 2 8
f x x f x x x x x x
1 1 1
0 0 0
1 1 5 3
( )d ( )d ( )d
3 2 8 4
f x x f x x f x x
Do đó,
0
1
3 13
( )d 4
4 4
f x x
.
Lời giải 4:
Với
ta có
3 2 10 6
( ) (1 ) 2
xf x f x x x x
2 3 2 11 7 2
( ) (1 ) 2 (*)
x f x xf x x x x
1 1 1
2 3 2 11 7 2
0 0 0
( )d (1 )d 2 d
x f x x xf x x x x x x
1 1
3 3 2 2
0 0
1 1 5
( )d( ) (1 )d(1 )
3 2 8
f x x f x x
1 1 1
0 0 0
1 1 5 3
( )d ( )d ( )d
3 2 8 4
f x x f x x f x x
Trang 20
NGUYỄN MINH NHIÊN
Mặt khác
0 0 0
2 3 2 11 7 2
1 1 1
(*) ( )d (1 )d 2 d
x f x x xf x x x x x x
0 0
2
3 3 2
1 1
1 1 17
(*) ( )d (1 )d 1
3 2 24
f x x f x x
0 1 0
1 0 1
1 1 17 1 3 17 13
( )d ( )d ( )d 3 .
3 2 24 2 4 24 4
f x x f x x f x x
.
Lời giải 5: Đi tìm hàm
Ban đầu ta sẽ nghĩ đến có
3 2
, 1
f x f x
thì bên vế phải có thể đưa liên quan gì đến
3 2
,1
x x
không?
Ta có
3
3 10 3 3
2 2
xf x x x x f x x
Vậy thì nghĩ thêm việc cũng tạo tiếp cái
3
2 2 4 6
1 2 3 3 3
x x x x
Hay
3
2 2 2 4 6
1 1 2 3 3 3
f x x x x x
.
Như thế ta sẽ có
3 3
3 3 2 2 2 4 6 6
2 1 1 2 3 3 3
x f x x f x x x x x x
3 3
3 3 2 2 2 4
2 1 1 2 3 3 3
x f x x f x x x x
3 3
3 3 4 2 2 2
2 3 1 1 2 3 1 0
x f x x x f x x x
3 3
3 3 3 2 2 2
3 2 1 1 3 1 2 0
x f x x x f x x x
Đặt
3
3 2
g x f x x x
ta được
3 2
1 0
xg x g x
.
Thay
x
bởi
x
ta được
3 2
1 0
xg x g x
hay
3 3
,xg x xg x x
.
Do đó
g x
là hàm lẻ.
Như vậy
3 2 3 2
1 0 1 ,xg x g x xg x g x x
.
Từ giả thiết ta có
0 1 0
g g
.
Vì
liên tục trên
1; 0
nên
g x
liên tục trên
1; 0
.
Đặt
1;0
max 0, 1; 0
M g x x
.
Giả sử
0
M
khi đó
1;0 :
a g a M
.
Chọn
1 1;0
x b a
Ta được
3 3
g a
M
bg b g a g b M
b b
do
0;1
b
.
Trang 21
NGUYỄN MINH NHIÊN
Điều này mẫu thuẫn do
1;0
max
M g x
.
Do vậy
1;0
max 0, 1;0
g x x
.
Hay
3
0, 1; 0 3 2, 1;0
g x x f x x x x
.
Vậy
0 0
3
1 1
13
( )d ( 3 2)d
4
f x x x x x
.
Nhận xét chung:
Ở
5
cách trên, khi giải quyết bài toán dạng này ta thường hướng tới:
Biến đổi giả thiết đi đến tính chất
d d
u f u x f u u
.
Dựa theo tính chất hàm chẵn, hàm lẻ.
Sử dụng các phép thế xác định hàm số
.
* Với lời giải 1, 2, 3, 4: Ta đều sử dụng đến tính chất
d d
u f u x f u u
hay
d d
u b
b
a
u a
u x f u x x f x x
Vì thế ta mới nghĩ đến việc tạo ra đạo hàm của
3 2
;1
x x
bằng việc nhân hai vế của giả thiết với
x
để tạo
ra
0 0
2 3
1 1
1
d d
3
x f x x f x x
;
1 1
2 3
0 0
1
d d
3
x f x x f x x
;
0 1
2
1 0
1
1 d d
2
xf x x f x x
và
1 1
2
0 0
1
1 d d
2
xf x x f x x
.
Trong các đổi biến này xuất hiện
1
0
d
f x x
buộc ta phải đi tính thêm
1
0
d
f x x
. Ở đây, nếu cận không
phải là
1;0;1
thì các cách làm này sẽ bị phá sản, ví dụ yêu cầu tính
3
0
d
f x x
, lúc này chắc chỉ còn
cách đi tìm
. Vì thế, các cận
1;0;1
phải được liên hệ mật thiết với
3 2
,1
x x
.
Ngoài ra, với hai tính chất:
Hàm số
2 3 2 2
( ) (1 ) 2
x f x xf x x
là hàm lẻ;
Hàm số
4
f x f x
là hàm chẵn
cũng hữu ích cho việc tính toán nhanh hơn.
* Lỗi sai có thể mắc dẫn đến các phương án nhiễu
17
20
,
17
4
đều sai dấu khi tính
0 1
2
1 0
1
1 d d
2
xf x x f x x
và
1 1
2
0 0
1
1 d d
2
xf x x f x x
.
* Với lời giải 5: Việc tìm
khá khó khăn, không nói là mò. Nếu
f x
là những hàm quen thuộc thì
rất có thể đoán bằng việc thử các giá trị và cân bằng hệ số.
Khi đó, mục đích khai thác tính chất
d d
u f u x f u u
coi như phá sản.
Trang 22
NGUYỄN MINH NHIÊN
BÀI TẬP TƯƠNG TỰ CÂU 48
Câu 48.1: Cho hàm
f x
liên tục trên
\ 0
thỏa mãn
2 3
2 2, \ 0
xf x f x x x
.
Giá trị
2
1
d
f x x
nằm trong khoảng nào?
A.
5;6
. B.
3; 4
. C.
1;2
. D.
2; 3
.
Câu 48.2: Cho hàm số
y f x
liên tục trên đoạn
0;4
và thỏa mãn điều kiện
2 2
4 6 2 4 , 0;2
xf x f x x x
.
Giá trị
4
0
d
f x x
bằng
A.
5
. B.
2
. C.
20
. D.
10
.
Câu 48.3: Cho hàm
( )
y f x
liên tục trên đoạn
0;1
và thỏa mãn
2
1 2 2 1, 0;1
f x f x x x x
.
Giá trị của
1
0
( )
f x dx
bằng
A.
4
3
B.
2
3
C.
1
2
. D.
1
3
Câu 48.4: Cho hàm số
y f x
liên tục và có đạo hàm trên
thỏa mãn
2
5 7 1 3 2
f x f x x x
,
x
.
Biết rằng
1
0
. ' d
a
x f x x
b
, với
a
b
là phân số tối giản. Giá trị của
8 3
a b
là
A.
1
.
B.
0
.
C.
16
. D.
16
.
Câu 48.5: Cho hàm số
f x
liên tục trên đoạn
2
;1
3
và thỏa mãn
2
2 ( ) 3 5
3
f x f x
x
2
;1 .
3
x
Tích phân
1
2
3
ln d
f x x x
bằng
A.
5 2 1
ln
3 3 3
. B.
5 2 1
ln
3 3 3
. C.
5 2 1
ln
3 3 3
. D.
5 2 1
ln
3 3 3
.
Trang 23
NGUYỄN MINH NHIÊN
LỜI GIẢI BÀI TẬP TƯƠNG TỰ CÂU 48
Câu 48.1: Cho hàm
f x
liên tục trên
\ 0
thỏa mãn
2 3
2 2, \ 0
xf x f x x x
.
Giá trị
2
1
d
f x x
nằm trong khoảng nào?
A.
5;6
. B.
3; 4
. C.
1;2
. D.
2; 3
.
Lời giải
Chọn D
Ta có
2 3
2 2, \ 0
2
xf x f x x x
x
2 2
2 3
1 1
1
2 d 2 d
2
xf x f x x x x
x
2
2 2
4
2 2
1 1
1
1 1 1
d 2 d 2 ln 2
2 2 4 2
x
f x x f x x x x
4 4
1 2
1 1 7 1
d d ln 2
2 2 4 2
f x x f x x
2
1
1 7 1
d ln 2
2 4 2
f x x
2
1
7
d ln 2 2;3
2
f x x
Câu 48.2: Cho hàm số
y f x
liên tục trên đoạn
0;4
và thỏa mãn điều kiện
2 2
4 6 2 4 , 0;2
xf x f x x x
.
Giá trị
4
0
d
f x x
bằng
A.
5
. B.
2
. C.
20
. D.
10
.
Lời giải
Chọn A
Ta có
2 2
4 6 2 4
xf x f x x
.
2 2
2 2
0 0
4 6 2 d 4 d
xf x f x x x x
2 2
2 2
0 0
2 d 3 2 d 2f x x f x x
4 4 4
0 0 0
2 d 3 d d
5
f x x f x x f x x
Trang 24
NGUYỄN MINH NHIÊN
Câu 48.3: Cho hàm
( )
y f x
liên tục trên đoạn
0;1
và thỏa mãn
2
1 2 2 1, 0;1
f x f x x x x
.
Giá trị của
1
0
( )
f x dx
bằng
A.
4
3
B.
2
3
C.
1
2
. D.
1
3
Lời giải
Chọn D
Ta có
2
1 2 2 1
f x f x x x
1 1
2
0 0
(1 ) (2 2 1)
I f x dx x x dx
1
3 2
0
1
2
(1 )
0
3
I f x dx x x x
1
0
2
(1 ) 1
3
I f x dx
Xét
1
0
(1 )
f x dx
, đặt
t x dt dx
. Đổi cận
0 1; 1 0
x t x t
Ta có
1 0 1
0 1 0
(1 ) ( )( ) ( ) 2
f x dx f t dt f t dt I
Từ
1 ; 2
1
0
2
2 ( )
3
f x dx
1
0
1
( )
3
f x dx
.
Câu 48.4: Cho hàm số
y f x
liên tục và có đạo hàm trên
thỏa mãn
2
5 7 1 3 2
f x f x x x
,
x
.
Biết rằng
1
0
. ' d
a
x f x x
b
, với
a
b
là phân số tối giản. Giá trị của
8 3
a b
là
A.
1
.
B.
0
.
C.
16
. D.
16
.
Lời giải
Chọn B
Từ
2
5 7 1 3 2
f x f x x x
thay
x
bởi
1
x
ta được
2
5 1 7 3 1
f x f x x
.
Do đó ta có hệ
2
2
5 7 1 3 2
7 5 1 3 1
f x f x x x
f x f x x
Suy ra
2 2 2
25 49 15 2 21 1 24 36 30 21
f x f x x x x f x x x
Hay
2
1 1
12 10 7 12 5
8 4
f x x x f x x
Do đó
1 1
0 0
1 3
. ' d 12 5 d
4 8
a
x f x x x x x
b
3
8
a
b
Trang 25
NGUYỄN MINH NHIÊN
Vậy
8 3 0
a b
Câu 48.5: Cho hàm số
f x
liên tục trên đoạn
2
;1
3
và thỏa mãn
2
2 ( ) 3 5
3
f x f x
x
2
;1 .
3
x
Tích phân
1
2
3
ln d
f x x x
bằng
A.
5 2 1
ln
3 3 3
. B.
5 2 1
ln
3 3 3
. C.
5 2 1
ln
3 3 3
. D.
5 2 1
ln
3 3 3
.
Lời giải
Chọn D
Cách 1:
Từ
2
2 ( ) 3 5
3
f x f x
x
thay
x
bởi
2
3
x
ta được
2 10
2 3
3 3
f f x
x x
.
Do đó
2
10 2 2
4 9 10 2 2
f x f x x f x x f x
x x
x
1 1
2
2 2
3 3
2
l
3
l
5 2 1
ln
3
n d 2 n d
3
xf x x x x
x
Cách 2:
Ta có
1 1
1
2
3
2 2
3 3
d
ln d ln
f x x
xf x x f x x
x
. Từ
2 2
2 ( ) 3 5 , ;1
3 3
f x f x x
x
.
Thay
1
và
2
3
x
vào (1) ta được hệ
2
(1) 0
2 (1) 3 5
3
2 5
2 10
2 3 (1)
3 3
3 3
f
f f
f
f f
.
Xét
1
2
3
d
f x
I x
x
Đặt
2
2 2
d d ,
3
x x t
, đổi cận
2
1
3
2
1
3
x t
x t
.
Khi đó
2
1 1
3
2
1 2 2
3 3
2 1 2 2
. d d d
3 3 3
2
3 2
f t f t f x
t t x
t
I
t x
.
Trang 26
NGUYỄN MINH NHIÊN
Ta có
1 1
2 2
3 3
2
d
d
3
2 3 2 3
f x
f x x
x
I I
x x
1 1
2 2
3 3
5 1
5 d 5d
3 3
2
2 ( ) 3
3
f x f
I
x
x x I
x
Vậy
1 1
1
2
3
2 2
3 3
d
2 2 1 5 2 1
ln d ln ln1. 1 ln ln
3 3 3 3 3 3
f x x
f x x x f x x f f
x
.
Trang 27
NGUYỄN MINH NHIÊN
Câu 49: Cho khối chóp
.
S ABC
có đáy
ABC
là tam giác vuông cân tại
, , 90 ,
A AB a SBA SCA
góc giữa hai mặt phẳng
SAB
và
SAC
bằng
60
. Thể tích khối chóp đã cho bằng
A.
3
a
. B.
3
3
a
. C.
3
2
a
. D.
3
6
a
.
Lời giải
Từ giả thiết ta dựng hình chóp
S ABDC
với
ABDC
là hình
vuông và
SD ABDC
.
Vì
SAB SAC
nên nếu
BH
là đường cao của
SAB
thì
tương ứng
CH
cũng là đường cao của
SAC
.
Mà
SA SAB SAC
nên
, , 60
SAB SAC BH CH
hay
60
BHC
hoặc
120
BHC
.
Vì
BH CH
nên
HI
là phân giác góc
BHC
hay
30
IHC
hoặc
60
IHC
.
Nếu
30
IHC
thì
2
sin 30
CI
CH a
, không thỏa mãn.
Do đó
2
3
sin 60
CI
CH a
.
Mà
2 2
2 2 2 2 2 2
1 1 1 3 1 1
2
SC a SD SC CD a
CH CA CS a a SC
.
Do vậy,
3
.
1
.
3 6
S ABC ABC
a
V S SD
.
Chú ý:
Ta có thể chỉ ra tồn tại hình chóp
S ABDC
như sau:
Gọi
D
là hình chiếu vuông góc của
S
lên mặt phẳng
ABC
. Ta có
AB SB
AB SBD AB BD
AB SD
.
Tương tự
AC CD
ABDC
là hình vuông cạnh
a
.
Nhận xét:
Trong bài toán trên ta đã sử dụng phương pháp tạo hình ẩn, tức là từ hình đa diện ban đầu, tạo
thêm những điểm mới để tạo ra hình đa diện mới ở đó tính chất dễ khai thác hơn. Một số hình quen
thuộc mà tính chất dễ khai thác là: Hình lập phương, hình hộp chữ nhật, lăng trụ đứng, hình chóp đều,
hình chóp đáy là hình chữ nhật và cạnh bên vuông góc với đáy,…
I
a
H
a
D
C
B
A
S
Trang 28
NGUYỄN MINH NHIÊN
BÀI TẬP TƯƠNG TỰ CÂU 49
Câu 49.1: Cho tứ diện
ABCD
có
10
AB CD
,
5
AD BC
,
13
AC BD
. Gọi
là góc
giữa
AB
và
ACD
, giá trị
cos
bằng
A.
6 10
35
. B.
865
35
. C.
10
10
. D.
3 10
10
.
Câu 49.2: Cho tứ diện
ABCD
có
4; 5; 6
AB CD AC BD AD BC
. Thể tích của khối tứ
diện
ABCD
bằng
A.
15 6
4
. B.
15 6
2
. C.
45 6
4
. D.
45 6
2
.
Câu 49.3: Cho tứ diện
ACFG
có số đo các cạnh lần lượt là
2,
AC AF FC a
3,
AG a
GF GC a
. Thể tích của khối tứ diện
ACFG
bằng
A.
3
6
a
. B.
3
3
a
. C.
3
12
a
. D.
3
15
3
a
.
Câu 49.4: Cho tứ diện
ABCD
có
2 , 7 , 3
AB BD AD a AC a BC a
. Biết khoảng cách giữa
hai đường thẳng
AB CD
bằng
a
, tính thể tích của khối tứ diện
ABCD
.
A.
3
2 6
3
a
. B.
3
2 2
3
a
. C.
3
2 6
a
. D.
3
2 2
a
.
Trang 29
NGUYỄN MINH NHIÊN
LỜI GIẢI BÀI TẬP TƯƠNG TỰ CÂU 49
Câu 49.1: Cho tứ diện
ABCD
có
10
AB CD
,
5
AD BC
,
13
AC BD
. Gọi
là góc
giữa
AB
và
ACD
, giá trị
cos
bằng
A.
6 10
35
. B.
865
35
. C.
10
10
. D.
3 10
10
.
Lời giải
Chọn B
I
H
G
E
F
D
C
B
A
Dựng hình hộp
AEDF GBHC
.
Do các cạnh đối của tứ diện
ABCD
bằng nhau nên các đường chéo của mỗi mặt của hình hộp bằng nhau
suy ra
AEDF GBHC
là hình hộp chữ nhật.
Đặt
, , , , 0
AE x AF y AG z x y z .
Ta có hệ
2 2
2 2
2 2
5
1
13 2
3
10
x y
x
y z y
z
z x
Ta thấy
AB
//
HF
; ;
AB ACD HF ACD
Gọi
I HF CD
;
sin
d F ACD
IF
.
Tứ diện
FACD
vuông tại
F
nên:
2 2 2
2
1 1 1 1 49
36
;
FA FD FC
d F ACD
6
;
7
d F ACD
.
Mà
2 2
1 1 10
2 2 2
FI FH FC FD .
6 10 865
sin cos
35 35
.
Trang 30
NGUYỄN MINH NHIÊN
Câu 49.2: Cho tứ diện
ABCD
có
4; 5; 6
AB CD AC BD AD BC
. Thể tích của khối tứ
diện
ABCD
bằng
A.
15 6
4
. B.
15 6
2
. C.
45 6
4
. D.
45 6
2
.
Lời giải
Chọn A
D
K
N
M
C
B
A
Dựng tứ diện
AMNK
, sao cho
, ,
B C D
là trung điểm của các cạnh
, ,
MN NK KM
. Tứ diện
AMNK
vuông tại
.
A
2 2 2
2 2 2
2 2 2
3 6
64 54
100 10 10
144 90
3 10
AM
AM AN AM
AN AK AN AN
AK AM AK
AK
.
1 1 15 6
. . .3 6 10.3 10 15 6
6 6 4
AMNK ABCD
V AM AN AK V
.
Câu 49.3: Cho tứ diện
ACFG
có số đo các cạnh lần lượt là
2,
AC AF FC a
3,
AG a
GF GC a
. Thể tích của khối tứ diện
ACFG
bằng
A.
3
6
a
. B.
3
3
a
. C.
3
12
a
. D.
3
15
3
a
.
Lời giải
Chọn A
Dựng hình lập phương như hình vẽ
Khi đó
.
ABCD EFGH
là hình lập phương cạnh
a
nên thể tích
của hình lập phương là
3
V a
.
Thể tích tứ diện
ACGF
có được là do ta chia hình lập phương
theo các mặt phẳng
ACGE
,
ACF
và
AGF
. Khi đó ta có
3
. .
1 1 1
.
3 2 3 6
ACGF ABC EFG ABCD EFGH
a
V V V
.
H
G
E
F
D
C
B
A
Trang 31
NGUYỄN MINH NHIÊN
Câu 49.4: Cho tứ diện
ABCD
có
2 , 7 , 3
AB BD AD a AC a BC a
. Biết khoảng cách giữa
hai đường thẳng
AB CD
bằng
a
, tính thể tích của khối tứ diện
ABCD
.
A.
3
2 6
3
a
. B.
3
2 2
3
a
. C.
3
2 6
a
. D.
3
2 2
a
.
Lời giải
Chọn B
F
G
E
H
D
C
B
A
Từ giả thiết
AB AC
Dựng lăng trụ đứng
.
AGF BCE
với
D
là trung điểm
EF
.
3.
AGF BCE ABCD
V V
Khi đó, vì
/ / , ,
AB CEFG d AB CD d B CE BH a
với
H CE BH CE
Ta tính được
2 3
1 2 2
3 2 2 2 . .
3 3
BCE ABCD BCE
BE a BC CE a S a V AB S a
.
Trang 32
NGUYỄN MINH NHIÊN
Câu 50: Cho hàm số
f x
. Hàm số
y f x
có đồ thị như hình sau.
x
y
4
1
-2
-2
O
Hàm số
2
1 2
g x f x x x
nghịch biến trên khoảng nào dưới đây?
A.
3
1;
2
. B.
1
0;
2
. C.
2; 1
. D.
2; 3
.
Lời giải
Ta có
2 1 2 2 1
g x f x x
1 2
0 1 2 1
g x f x
.
Đặt
1 2
t x
khi đó
1
trở thành
2
t
f t
. Từ đồ thị các hàm
số
y f t
và
2
t
y
.
Ta có
1 3
2 0 2 1 2 0
2 2
4 1 2 4 3
2
2
x
t x
t
f t
t x
x
.
Hàm số
y g x
nghịch biến trên các khoảng
1 3
;
2 2
và
3
;
2

.
Vậy phương án A đúng.
Nhận xét:
Đây là bài toán gặp khá nhiều trong các đề thi THPT quốc gia những năm gần đây, ý tưởng là
xét tính đơn điệu của hàm số
y f u x v x
dựa trên so sánh giá trị các hàm
,
u x f x v x
trên khoảng nào đó để xét dấu
u x f u x v x
bằng cách sử dụng đồ thị hoặc đánh giá.
t
y
2
-t
y=
y=f'(t)
4
1
-2
-2
O
Trang 33
NGUYỄN MINH NHIÊN
BÀI TẬP TƯƠNG TỰ CÂU 50
Câu 50.1: Cho hàm số
f x
liên tục trên
, hàm số
y f x
có đồ thị như hình vẽ. Xét hàm số
2
2 3 1 9 6 4
h x f x x x
. Hãy chọn khẳng định đúng.
x
y
4
4
2
2
-2
-2
O
A. Hàm số
h x
nghịch biến trên
. B. Hàm số
h x
nghịch biến trên
1
1;
3
.
C. Hàm số
h x
đồng biến trên
1
1;
3
. D. Hàm số
h x
đồng biến trên
.
Câu 50.2: Cho hàm số
f x
có bảng xét dấu của đạo hàm như sau
x

1 2 3 4

f x
0
0
0
0
Hàm số
3
3 2 3
y f x x x
đồng biến trên khoảng nào dưới đây?
A.
1; .

B.
; 1 .

C.
1; 0 .
D.
0;2 .
Câu 50.3: Cho hàm số
f x
có đồ thị của hàm số
'
y f x
như hình vẽ
x
y
2
-2
1
3-3
O
Hàm số
3
2
2 1 2
x
y f x x x
nghịch biến trên khoảng nào sau đây?
A.
6; 3
. B.
3;6
. C.
6;

. D.
1; 0
.
Trang 34
NGUYỄN MINH NHIÊN
Câu 50.4: Cho hàm số
y f x
liên tục và có đạo hàm trên
. Biết hàm số
f x
có đồ thị được cho
trong hình vẽ. Có bao nhiêu giá trị nguyên của
m
thuộc
2019;2019
để hàm số
2019 2
x
g x f mx
đồng biến trên
0;1
?
x
y
O 1
A.
2028
. B.
2019
. C.
2011
. D.
2020
.
Câu 50.5: Cho hàm số
y f x
có đồ thị của hàm số
y f x
được cho như hình bên. Hàm số
2
2 2
y f x x
nghịch biến trên khoảng
3
1
5
4
2
3
2
1
-1
-2
x
y
O
A.
3; 2
. B.
2; 1
. C.
1; 0
. D.
0;2
.
Câu 50.6: Cho hàm số
y f x
có đạo hàm trên
. Biết đồ thị hàm
y f x
như hình vẽ. Hàm số
3
3 1 3
g x f x x x
đồng
biến trên khoảng nào?
A.
1 1
;
4 3
. B.
2;0
.
C.
1
;1
3
. D.
4;

.
x
y
432O 1
Trang 35
NGUYỄN MINH NHIÊN
BÀI TẬP TƯƠNG TỰ CÂU 50
Câu 50.1: Cho hàm số
f x
liên tục trên
, hàm số
y f x
có đồ thị như hình vẽ. Xét hàm số
2
2 3 1 9 6 4
h x f x x x
. Hãy chọn khẳng định đúng.
x
y
4
4
2
2
-2
-2
O
A. Hàm số
h x
nghịch biến trên
. B. Hàm số
h x
nghịch biến trên
1
1;
3
.
C. Hàm số
h x
đồng biến trên
1
1;
3
. D. Hàm số
h x
đồng biến trên
.
Lời giải
Chọn C
2
2 3 1 9 6 4
h x f x x x
6 3 1 6 3 1
h x f x x
.
Xét bất phương trình
0
h x
6 3 1 6 3 1 0
f x x
3 1 3 1
f x x
(*)
t
y
y=f'(t)
y=t
4
4
2
2
-2
-2
O
Quan sát hình vẽ
ta thấy: Xét trên khoảng
2; 4
thì
2 2
f x x x
.
1
* 2 3 1 2 1
3
x x
.
Hàm số
h x
đồng biến trên
1
1;
3
.
Trang 36
NGUYỄN MINH NHIÊN
Câu 50.2: Cho hàm số
f x
có bảng xét dấu của đạo hàm như sau
x

1 2 3 4

f x
0
0
0
0
Hàm số
3
3 2 3
y f x x x
đồng biến trên khoảng nào dưới đây?
A.
1; .

B.
; 1 .

C.
1; 0 .
D.
0;2 .
Lời giải
Chọn C
Ta có
2
3 2 3
y f x x
Với
1; 0 2 1;2 2 0
x x f x
, lại có
2
3 0 0; 1;0
x y x
Vậy hàm số
3
3 2 3
y f x x x
đồng biến trên khoảng
1; 0 .
Chú ý:
+) Ta xét
2
1;2 1; 2 3; 4 2 0; 3 0
x x f x x

Suy ra hàm số nghịch biến trên khoảng
1;2
nên loại hai phương án
A,D.
+) Tương tự ta xét
2
; 2 2 ;0 2 0; 3 0 0; ; 2
x x f x x y x
  
Suy ra hàm số nghịch biến trên khoảng
; 2

nên loại hai phương án
B.
Câu 50.3: Cho hàm số
f x
có đồ thị của hàm số
'
y f x
như hình vẽ
x
y
2
-2
1
3-3
O
Hàm số
3
2
2 1 2
x
y f x x x
nghịch biến trên khoảng nào sau đây?
A.
6; 3
. B.
3;6
. C.
6;

. D.
1; 0
.
Lời giải
Chọn D
Ta có
2
2
' 2 ' 2 1 2 2 2 ' 2 1 1 3
y f x x x f x x
Nhận xét: Hàm số
y f x
có
' 1 3 3
f x x
và
3
' 1
3
x
f x
x
Do đó ta xét các trường hợp
Với
6 3 13 2 1 7
x x
suy ra
' 0
y
hàm số đồng biến (loại)
Với
3 6 5 2 1 11
x x
suy ra
' 0
y
hàm số đồng biến (loại)
Với
6 11 2 1
x x
suy ra
' 0
y
hàm số đồng biến (loại)
Trang 37
NGUYỄN MINH NHIÊN
Với
1 0 3 2 1 1
x x
nên
2 ' 2 1 2
f x
và
2
0 1 3 2
x
suy ra
' 0
y
hàm
số đồng biến (nhận)
Câu 50.4: Cho hàm số
y f x
liên tục và có đạo hàm trên
.
Biết hàm số
f x
có đồ thị được cho trong hình vẽ. Có bao nhiêu
giá trị nguyên của
m
thuộc
2019;2019
để hàm số
2019 2
x
g x f mx
đồng biến trên
0;1
?
A.
2028
. B.
2019
.
C.
2011
. D.
2020
.
Lời giải
Chọn D
Ta có
2019 ln 2019. 2019
x x
g x f m
.
Ta lại có hàm số
2019
x
y
đồng biến trên
0;1
.
Với
0;1
x
thì
2019 1;2019
x
mà hàm
y f x
đồng biến trên
1;
nên hàm
2019
x
y f
đồng
biến trên
0;1
.
Mà
2019 0; 2019 0, 0;1
x x
f x
nên hàm
2019 ln 2019. 2019
x x
h x f
đồng biến trên
0;1
.
Hay
0 0, 0;1
h x h x
.
Do vậy, hàm số
g x
đồng biến trên
0;1
0
g x
với mọi
0;1
x
2019 .ln 2019. 2019 , 0;1
x x
m f x
0
m
.
Vậy
0
m
.
Câu 50.5: Cho hàm số
y f x
có đồ thị của hàm số
y f x
được cho như hình bên. Hàm số
2
2 2
y f x x
nghịch biến trên khoảng
3
1
5
4
2
3
2
1
-1
-2
x
y
O
A.
3; 2
. B.
2; 1
. C.
1; 0
. D.
0;2
.
Lời giải
Chọn C
x
y
O
1
Trang 38
NGUYỄN MINH NHIÊN
3
1
5
4
2
3
2
1
-1
-2
x
y
O
Ta có
2
2 (2 ) (2 ) 2 (2 ) 2 2 (2 ) 2
y f x x y x f x x f x x
0 (2 ) 0 (2 ) (2 ) 2
y f x x f x x
Đặt
2
t x
suy ra
2
f t t
.
Dựa vào đồ thị ta thấy đường thẳng
2
y t
cắt đồ thị
y f t
tại ba điểm có hoành độ liên tiếp là
1 2;3; 4 5
a b
Do đó cùng từ đồ thị ta có
3 2 3 1 2
( ) 2
2 2
a t a x x a
f t t
t b x b x b
Vì
1 2 0 2 1
a a
nên
( 1;0) ( 1;2 )
a
. Do đó, hàm số nghịch biến trên khoảng
1;2
a
nên cũng nghịch biến trên
1; 0
.
Vì
4 5 3 2 2
b b
nên
( 3; 2) ( ;2 )
b

. Do đó, hàm số nghịch biến trên khoảng
;2
b

thì không nghịch biến trên
3; 2
.
Vậy hàm số nghịch biến trên khoảng
1; 0
.
Câu 50.6: Cho hàm số
y f x
có đạo hàm trên
. Biết đồ thị hàm
y f x
như hình vẽ.
x
y
432
O 1
Hàm số
3
3 1 3
g x f x x x
đồng biến trên khoảng nào?
A.
1 1
;
4 3
. B.
2;0
. C.
1
;1
3
. D.
4;

.
Lời giải
Chọn A
Ta có
2
3 3 1 1
g x f x x
Trang 39
NGUYỄN MINH NHIÊN
0
3 1 1
3 1 0
2
3 3 1 4
1
x
x
f x
x
x
.
2
0
3 1 0
3
1
x
f x
x
Bảng xét dấu của
g x
x
1
0
2
3
1
2

3 1
f x
0
0
0
0
2
1
x
0
0
g x
Vậy hàm số đồng biến trên khoảng
2
0;
3
.
| 1/39
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

LỜI GIẢI VÀ PHÂN TÍCH MỘT SỐ CÂU VẬN DỤNG TRONG ĐỀ THAM KHẢO
KỲ THI THPT QUỐC GIA NĂM 2020 Nguyễn Minh Nhiên
Đề thi tham khảo kỳ thi THPT quốc gia năm 2020 giúp giáo viên, học sinh đánh giá mức độ đề
thi qua đó có những định hướng quá trình ôn tập. Bài viết này, xin phân tích một số bài toán được khai
thác theo nhiều hướng giúp chúng ta có những cách tiếp cận khác nhau đối với những dạng toán vận
dụng trong các đề thi THPT quốc gia. x 8
Câu 38: Cho hàm số f x có f 3  3 và f 'x 
với x  0. Khi đó f xdx  bằng x  1 x  1 3 197 29 181 A. 7 . B. . C. . D. . 6 2 6 Lời giải 1: 8 3 8      8 d x f f f x x  dx  7  f  8 10. 3 3 x  1  x  1 N 8 8 8 2 8 x 229 197 G
f x dx  xf x  xf  x dx  8f 8  3f 3  dx  80  9   U        . 3       x  1 x  1 6 6 Y 3 3 3 Ễ Lời giải 2: N M x  1  1 x  1 1 I x    1 N Ta có f x    1  H x  1 x  1 x  1 x  1 1 x  1 N   H IÊ
Suy ra f x  x  2 x  1 C N
Mà f 3  3  C  4. Do đó f x  x  2 x  1  4 . 8 197
Vì vậy x  2 x 1  4dx   6 3 Nhận xét:
Với giả thiết như vậy ta có thể xử lý theo hai hướng: 8
Hướng 1: Tìm f x từ đó suy ra f xdx 
. Nếu để ý kỹ hơn thì thấy 3 x
 x 1 1 x 1 1 1    x   x  x  1 x 1   1 1 1 1 x  1
Khi đó, có thể dễ dàng tìm f x.
Hướng 2: Sử dụng tích phân từng phần 8   d    8  
  d  8 83 3 8 2 8 x f x x xf x xf x x f f  dx  3 3 3 3 x  1  x  1
Như thế, chỉ cần tính f 8 là xong. Trang 1
BÀI TẬP TƯƠNG TỰ CÂU 38 e
Câu 38.1: Cho hàm số f x liên tục trên 0;   . Biết   lnx f x  và f   1  0. Giá trị của f  xdx x 1 bằng 1 1 e  2 A. e  2 . B. . C. . D. . 2 6 2
Câu 38.2: Biết rằng x sin x là một nguyên hàm của hàm số f  x
  trên R. Gọi F(x) là một nguyên hàm  
của hàm số f '(x)  f '(  x) cosx    
thỏa mãn F 0  0. Giá trị của F     bằng 4   A.  . B. . C. 0 . D. . 4 2 N G U
Câu 38.3: Cho hàm số f x liên tục trên  thỏa mãn các điều kiện: Y Ễ N 2 
f 0  2 2, f x 0, x   và f x.f x  2x  1 1  f x, x   . M IN H Khi đó giá trị f   1 bằng N H I A. Ê 26 . B. 24 . C. 15 . D. 23 . N Trang 2
LỜI GIẢI BÀI TẬP TƯƠNG TỰ CÂU 38 e
Câu 38.1: Cho hàm số f x liên tục trên 0;   . Biết   lnx f x  và f   1  0. Giá trị của f  xdx x 1 bằng 1 1 e  2 A. e  2 . B. . C. . D. . 2 6 2 Lời giải Chọn D x x x Ta có f   x x  x  x    x 2 ln ln d d ln d ln  C . Nên f x 2 ln 
C , với C là hằng số. x 2 2 x
Mà f     C   f x 2 ln 1 0 0  . 2 e e ln x e 2 Do đó, f x 2 dx dx      . N 2 2 1 1 G U
Câu 38.2: Biết rằng x sin x là một nguyên hàm của hàm số f  x
  trên R. Gọi F(x) là một nguyên h Yàm Ễ   N
của hàm số f '(x)  f '(  x) cosx
F 0  0. Giá trị của F     bằng     M  thỏa mãn   4 IN H   A.  . B. . C. 0 . D. . N 4 2 H Lời giải IÊN Chọn D
x sinx là một nguyên hàm của hàm số f  x    f  x
   x sinx'  sinx  x cosx
 f(x)  sinx  x cosx
 f '(x)  2cosx  x sinx
 f ' x  2cosx  xsinx
 f 'x f ' x  2sinx Khi đó
F(x)  f '(x)  f '(  x) cosx dx  2 sinx.cosx dx  sin2x dx       cos2x C      2        Từ F(0)  0  C 
 F(x)   cos2x   F    . 2 2 2 4 2
Câu 38.3: Cho hàm số f x liên tục trên  thỏa mãn các điều kiện:
f 0  2 2, f x 0, x   và f x f x   x   2 . 2
1 1  f x, x   . Khi đó giá trị f   1 bằng A. 26 . B. 24 . C. 15 . D. 23 . Trang 3 Lời giải Chọn B f x.f x
Ta có f x f x   x   2 . 2 1 1  f x   2x  1 . 2   1  f x f x.f x d 2 1  f x Suy ra dx  2x  1 dx     2x  1 dx   2     2 1 f x  x  x C . 2   2   1  f x 2 1  f x
Theo giả thiết f 0  2 2 , suy ra   2 1 2 2  C  C  3. Với C  3 thì
 f x  x  x   f x  x  x  2 2 2 2 1 3
3 1 . Vậy f  1  24 . N G U Y Ễ N M IN H N H IÊ N Trang 4
Câu 43: Có bao nhiêu cặp số nguyên (x;y) thỏa mãn 0  x  2020 và log (3  3)   2  9y x x y ? 3 A. 2019 . B. 6 . C. 2020 . D. 4 . Lời giải
Điều kiện: x  0 nên log (3x  3) xác định. 3 Ta có
log (3  3)   2  9y  log (  1)  (  1)  2 log 3y  9y x x y x x 3 3 3
 log (  1)  (  1)  log 9y  9y x x   1 3 3 1
Xét hàm số f (t)  log t  t,t  0; có f (t) 
 1  0, t  0;. 3   t ln 3
Do đó hàm số luôn đồng biến trên 0;. Khi đó   1   9y x 1 y N
Vì 0  x  2020 nên 0  9  1  2020  0  y  log 2021 . 9 G U
Do y nguyên nên y  0;1;2;3 . Y   Ễ N
 x;y  0;0 ; 8;1 ; 80;2 ; 728;3 .
          M IN
Vậy có 4 cặp số nguyên (x;y) thỏa mãn. H Nhận xét: N H
Với dạng toán này việc quan trọng nhất là xác định được hàm đặc trưng I
f(t)  log t  t,t  0; . 3  Ê N
Ngoài ra, nếu để ý hàm số y  log (3x  3)  x đồng biến trên 1;, hàm số 2 9x x  cũng đồng 3 biến trên  ;
  nên 0   2020  1  2  9y x y  log 6063  2020  1   y  4 . 3 Trang 5
BÀI TẬP TƯƠNG TỰ CÂU 43
Câu 43.1: Có bao nhiêu cặp số (x ;y) nguyên thỏa mãn các điều kiện 0  x  2020 và log (2  2)   3  8y x x y ? 2 A. 2019. B. 2018. C. 1. D. 4.
Câu 43.2: Có bao nhiêu giá trị nguyên của tham số m để tồn tại cặp số x;y thỏa mãn đồng thời các điều kiện 3x5y x3y 1 e e    1  2x  2y và 2
log 3x  2y  1m  6 2 log x  m  9  0 ? 3 3 A. 6 . B. 5 . C. 8 . D. 7 .
Câu 43.3: Cho phương trình 7x  m  log x  m với m là tham số. Có bao nhiêu giá trị nguyên của 7   m  25;2 
5 để phương trình đã cho có nghiệm? A. 9 . B. 25 . C. 24 . D. 26 . 2 1 2x  1  1
Câu 43.4: Cho phương trình log x  2  x  3  log  1  
    2 x  2 , gọi S là tổng tất 2   2   N 2 x  x  G U
cả các nghiệm của nó. Khi đó, giá trị của S là Y Ễ N 1 13 1 13 A. S  2 . B. S   . C. S  2 . D. S   . M 2 2 IN H N H I Ê N Trang 6
LỜI GIẢI BÀI TẬP TƯƠNG TỰ CÂU 43
Câu 43.1: Có bao nhiêu cặp số (x ;y) nguyên thỏa mãn các điều kiện 0  x  2020 và log (2  2)   3  8y x x y ? 2 A. 2019. B. 2018. C. 1. D. 4. Lời giải Chọn D
Do 0  x  2020 nên log (2x  2) luôn có nghĩa. 2 Ta có log (2  2)   3  8y x x y
 log (  1)   1  3log 2y  8y x x 2 2 2
 log (  1)   1  log 8y  8y x x (1) 2   2 1
Xét hàm số f (t)  log t  t,t  0; có f (t) 
 1  0, t  0;. 2   t ln2 N G
Do đó hàm số luôn đồng biến trên 0;. U Y Khi đó y  x   Ễ  1 8 1 N y M
Ta có 0  x  2020 nên 0  8  1  2020  0  y  log 2021  3,66 . 8 IN H
Mà y   nên y  0;1;2;  3 . N H
Vậy có 4 cặp số (x ;y)nguyên thỏa yêu cầu bài toán. IÊN
Câu 43.2: Có bao nhiêu giá trị nguyên của tham số m để tồn tại cặp số x;y thỏa mãn đồng thời các điều kiện 3x5y x3y 1 e e    1  2x  2y và 2
log 3x  2y  1m  6 2 log x  m  9  0 ? 3 3 A. 6 . B. 5 . C. 8 . D. 7 . Lời giải Chọn B Ta có 3x5y x3y 1 e e    1  2x  2y 3x5y  x y x3y 1 e 3 5 e       x  3y  1. Xét hàm số    et f t
 t trên  . Ta có    et f t
 1  0 nên hàm số đồng biến trên  .
Do đó phương trình có dạng f 3x  5y  f x  3y  
1  3x  5y  x  3y  1  2y  1 2x .
Thế vào phương trình còn lại ta được 2 log x m  6 2 log x  m  9  0. 3 3
Đặt t  log x , phương trình có dạng 2 t m   2 6 t  m  9  0 . 3
Để phương trình có nghiệm thì   0  2
3m  12m  0  0  m  4 .
Do đó có 5 số nguyên m thỏa mãn.
Câu 43.3: Cho phương trình 7x  m  log x  m với m là tham số. Có bao nhiêu giá trị nguyên của 7   m  25;2 
5 để phương trình đã cho có nghiệm? A. 9 . B. 25 . C. 24 . D. 26 . Trang 7 Lời giải Chọn C ĐK: x  m 7x  m  t
Đặt t  log x  m ta có   7x   7t x  t  1 7   7  t   m  x  Do hàm số    7u f u
 u đồng biến trên  , nên ta có  1  t  x . Khi đó: 7x      7x m x m x .
Xét hàm số     7x g x x     1 7x g x
ln 7  0  x  log ln7 . 7   Bảng biến thiên x  log ln 7 7    gx  0  g log ln 7 N  7  G U g x Y   Ễ N M I N   H N
Từ đó phương trình đã cho có nghiệm khi và chỉ khi m  g log ln7  0
 ,856 (các nghiệm này đều 7   H I x Ê
thỏa mãn điều kiện vì x  m  7  0 ) N
Do m nguyên thuộc khoảng 25;25, nên m  24;16;.. ;  1 . 2 1 2x  1  1
Câu 43.4: Cho phương trình log x  2  x  3  log  1  
    2 x  2 , gọi S là tổng tất 2   2 2 x  x
cả các nghiệm của nó. Khi đó, giá trị của S là 1 13 1 13 A. S  2 . B. S   . C. S  2 . D. S   . 2 2 Lời giải Chọn D  1 2  x   Điều kiện  2 . x  0  2 1 2x  1  1
Ta có log x  2  x  3  log  1       2 x  2 2   2 2 x  x         x    x    2 2 1   1 log 2 2 1  log 2     2   1   
    1  f  x  2  f 2        1 2 2  x     x       x 
Xét hàm số f t  log t  t  2 1 , t  0. 2 Trang 8 1 2 2ln2.t  2ln2.t  1 Ta có f  t   2t  1   0, t  0 . t ln2 t.ln 2
Do đó hàm số f t đồng biến trên khoảng 0;. x 1  3 13 Nên   1 1  x  2  2   3 2
x  2x  4x 1  0  x  x  2  3  13 x   2 x  1  1 13
Kết hợp với điều kiện ta được  3  13 . Vậy S   . x  2  2 N G U Y Ễ N M I N H N H IÊ N Trang 9
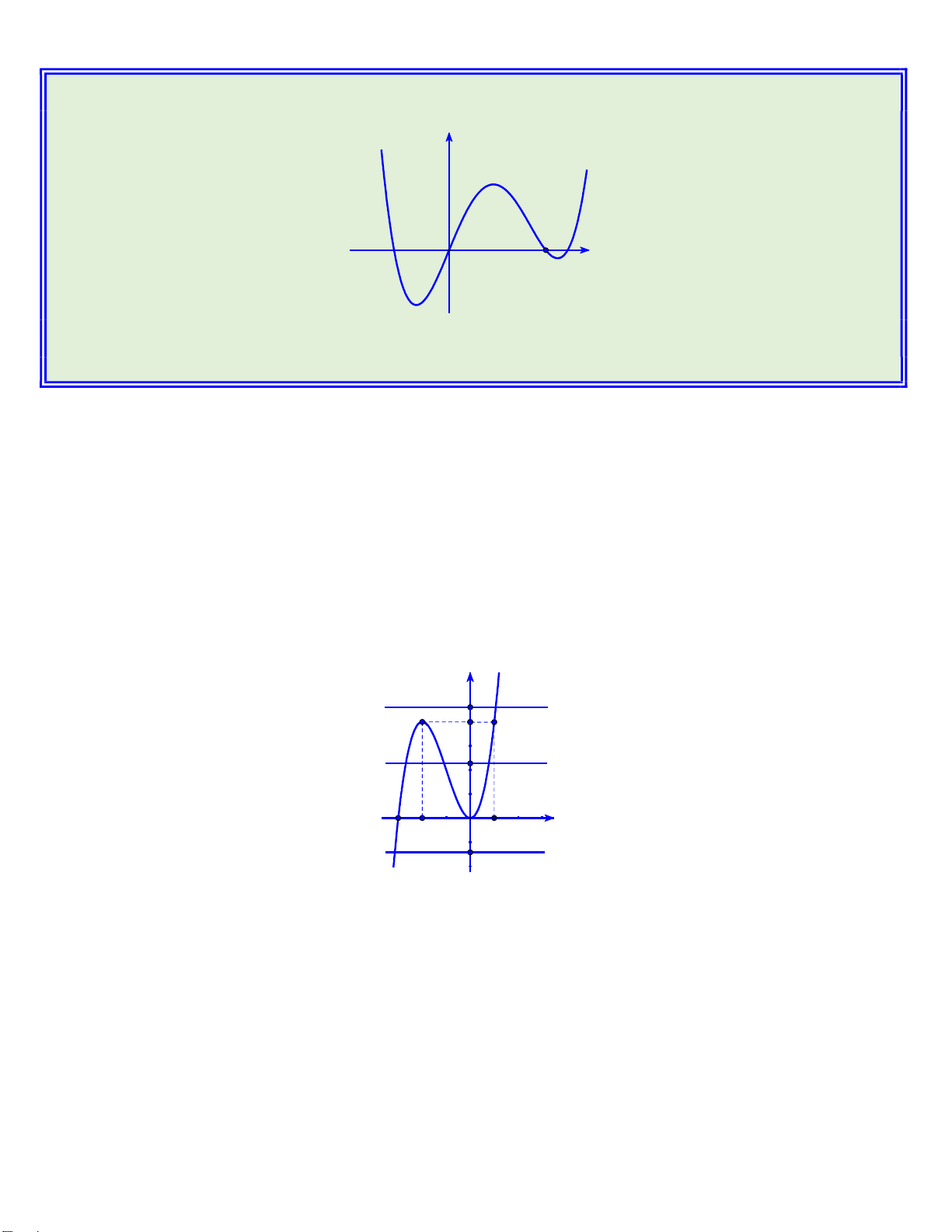
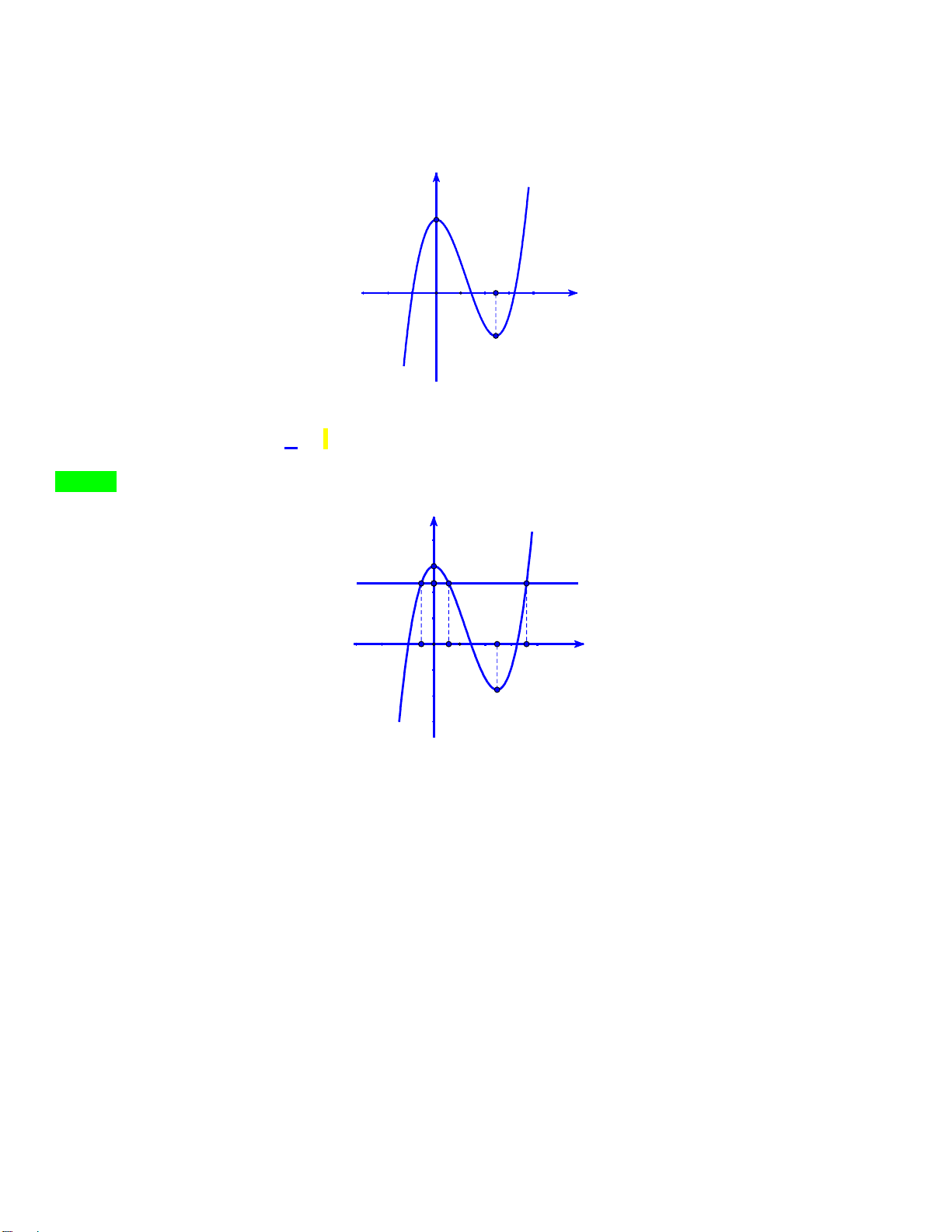
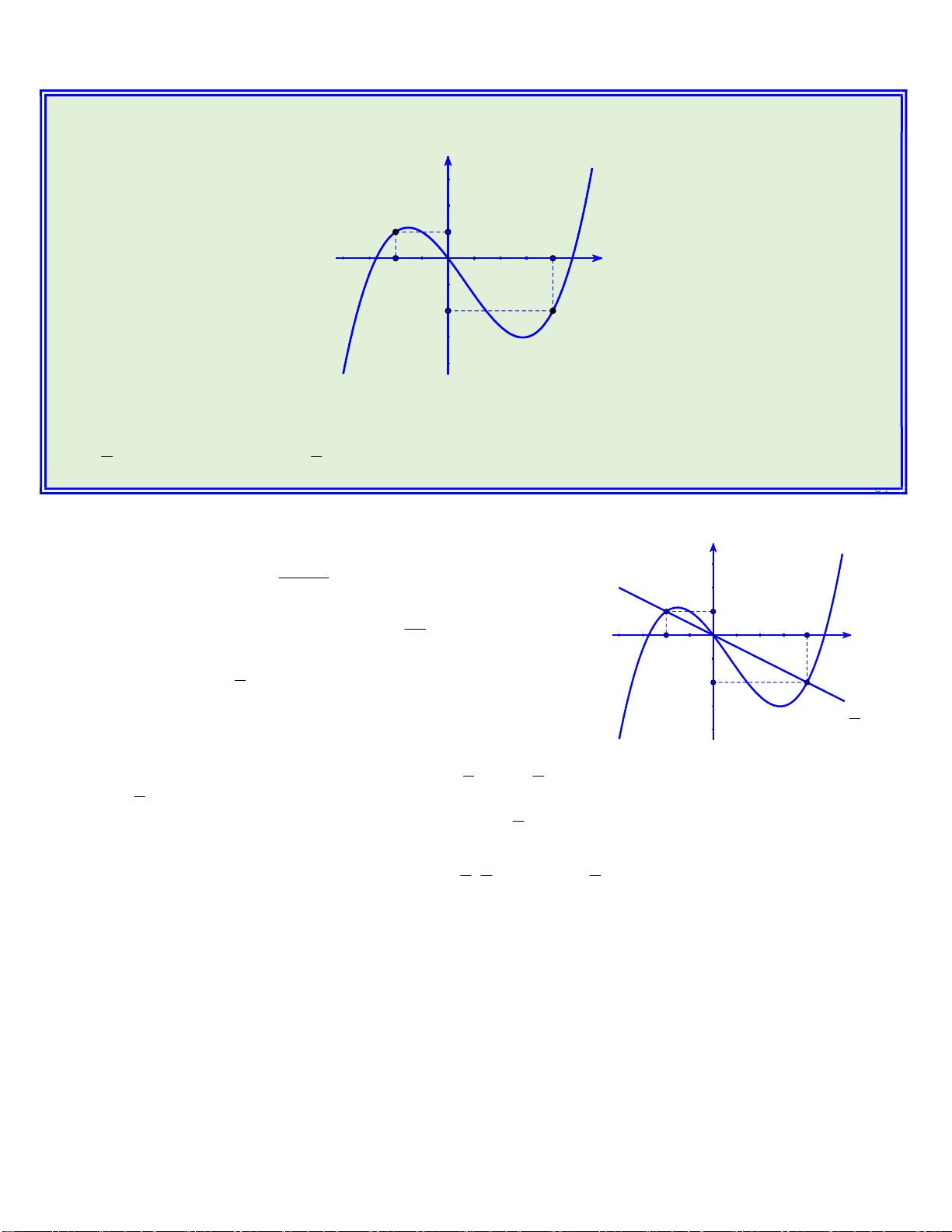
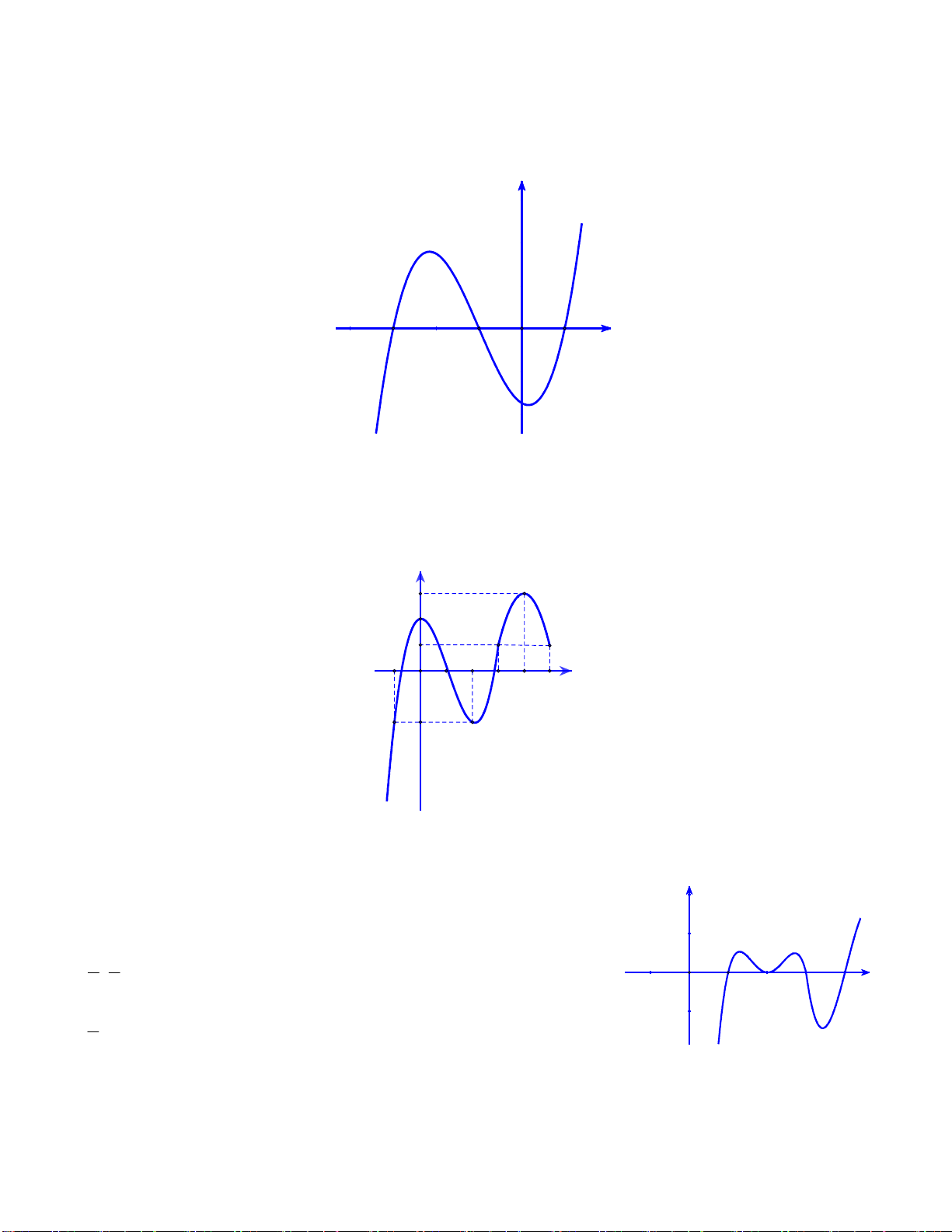
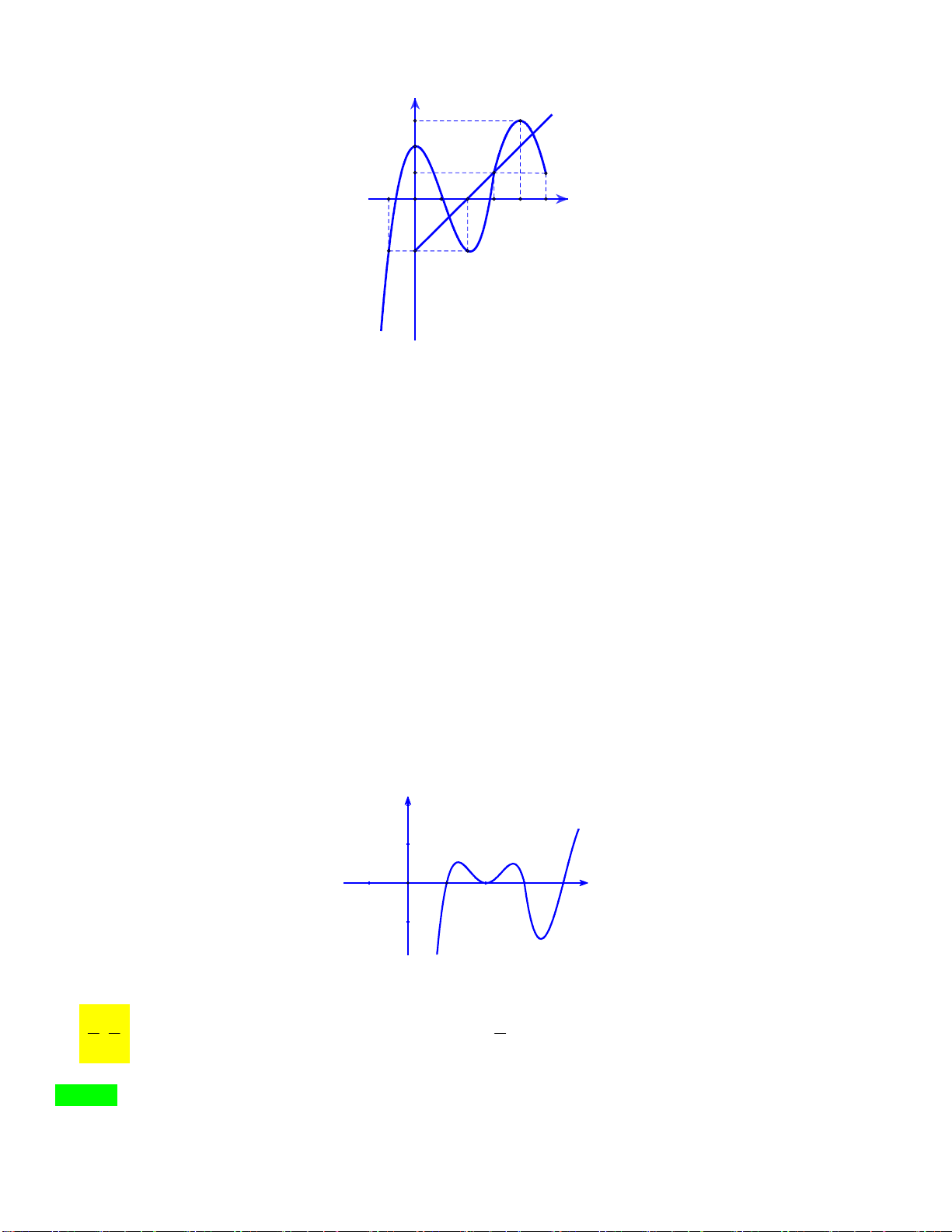
Câu 46: Cho hàm số bậc bốn y  f x có đồ thị như hình dưới đây y O 4 x
Số điểm cực trị của hàm số g x  f  3 2 x  3x  là A. 5. B. 3. C. 7. D. 11. Lời giải
Từ đồ thị suy ra hàm số y  f x có 3 điểm cực trị x  0  x  4  x 1 2 3 N G U Xét hàm số 3 2 g x  f x  3x , ta có 2 3 2
g x  3x  6x f  x  3x Y           Ễ N  2 x  0   M 3x  6x  0   I gx  0    x  2 N 3 2 f  x  3x  0  H    3 2 x  3x  x ,i  1;2;3 i N  H Ta có đồ thị hàm số 3 2 I y  x  3x Ê N y x=x3 4 x=x2 -3 -2 O 1 x x=x1
Ta có nhận xét rằng phương trình 3 2
x  3x  x có 1 nghiệm; phương trình 3 2
x  3x  x có 3 nghiệm; 1 2 phương trình 3 2
x  3x  x có 1 nghiệm cả 5 nghiệm này đôi một phân biệt, đều khác 0;2. 3
Như vậy, gx  0 có 7 nghiệm đơn phân biệt
Do đó hàm số g x có 7 điểm cực trị. Nhận xét:
Để xác định số cực trị của hàm g x  f ux ta thường hướng đến việc xét dấu
gx  uxf ux .
Nếu gx đổi dấu x TXĐ của g x thì x là điểm cực trị. Những trường hợp đơn giản khi g x là 0 0
hàm đa thức thì đơn giản hơn bằng việc đi tìm số nghiệm đơn và nghiệm bội lẻ. Trang 10
BÀI TẬP TƯƠNG TỰ CÂU 46
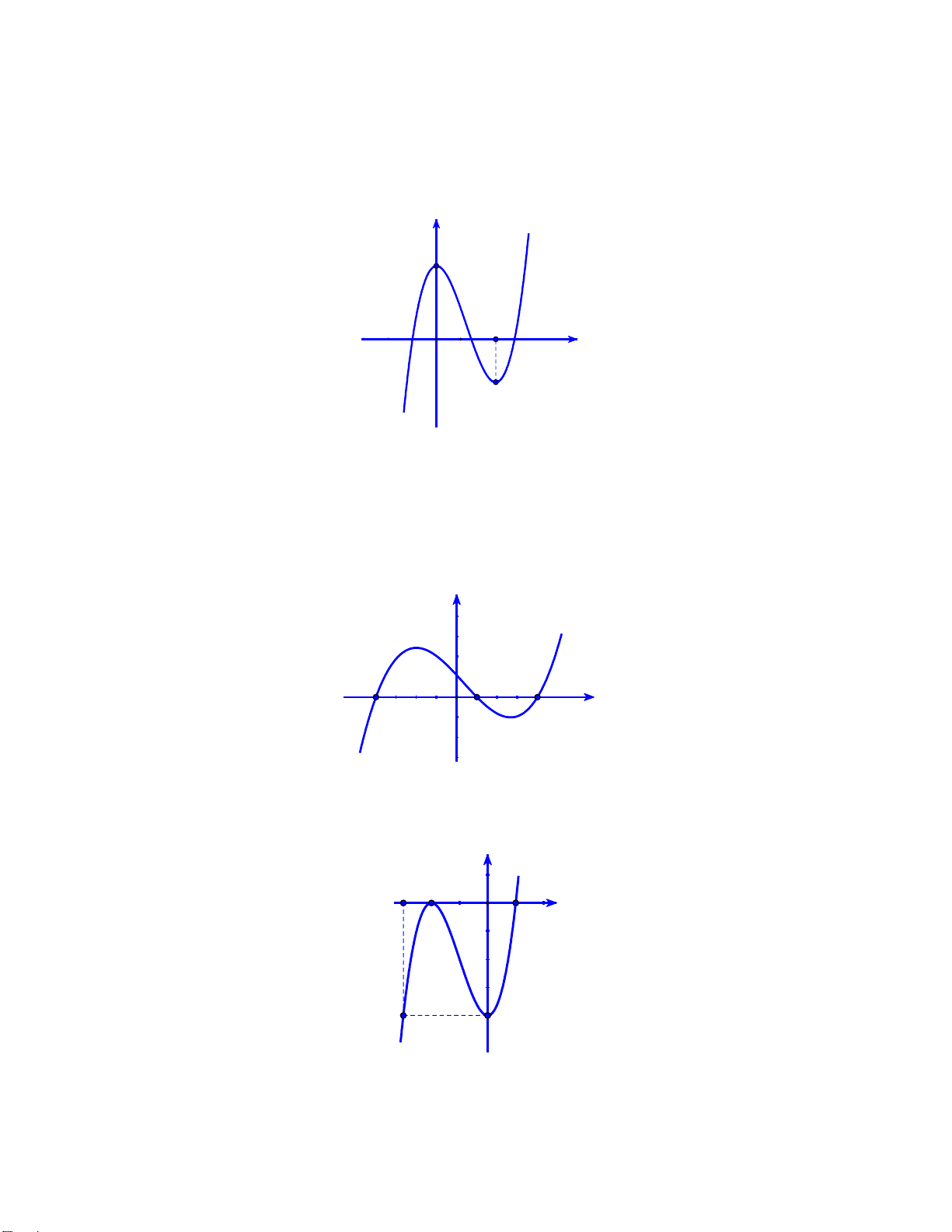
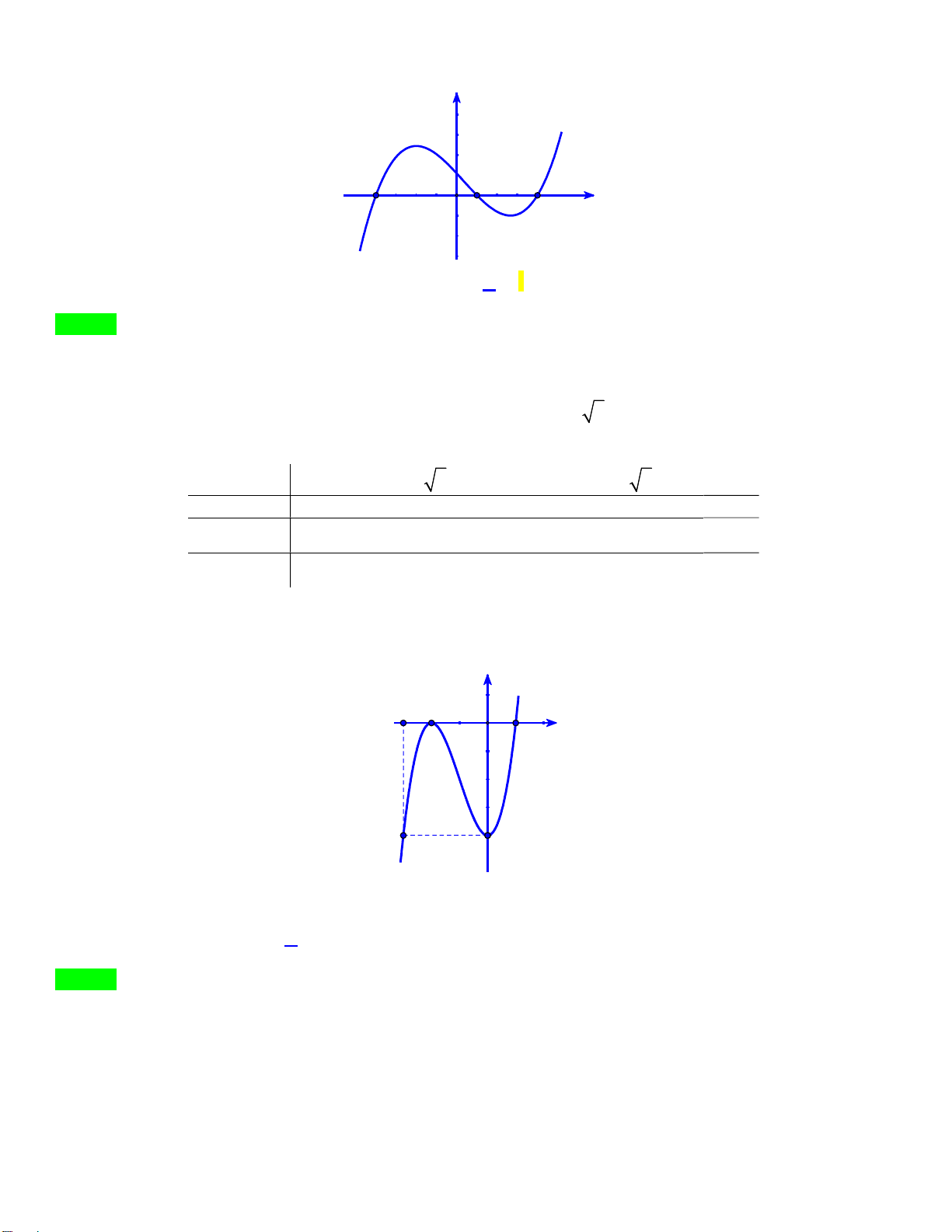
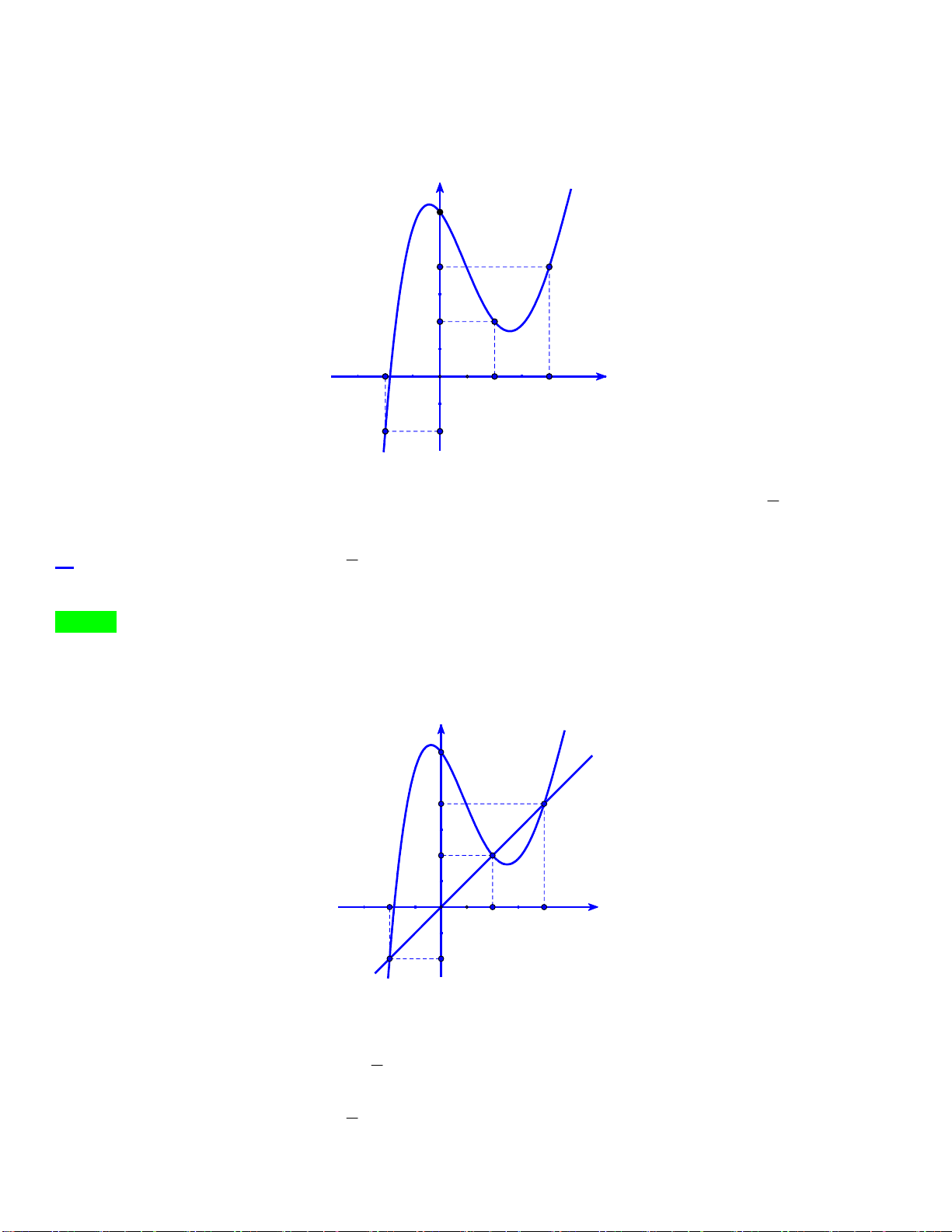
Câu 46.1: Cho hàm số    3 2 y
f x  ax bx  cx  d có các điểm cực trị là 0;a 2  a  3 và có đồ thị
là đường cong như hình vẽ. y y=f(x) 3 2 a 3 O x 1
Đặt g x  2019f f x  2020 . Số điểm cực trị của hàm số là N G A. 2 . B. 8 . C. 10 . D. 6. U Y
Câu 46.2: Cho hàm số    4 3 2 y
f x  ax bx  cx  dx e . Biết rằng hàm số y  f x liên tục trên Ễ N 2
và có đồ thị như hình vẽ bên. Hỏi hàm số g x  f 2x  x có bao nhiêu điểm cực đại? M     IN H y N H y=f'(x) IÊN -4 O 1 4 x A. 5. B. 3 . C. 1. D. 2 .
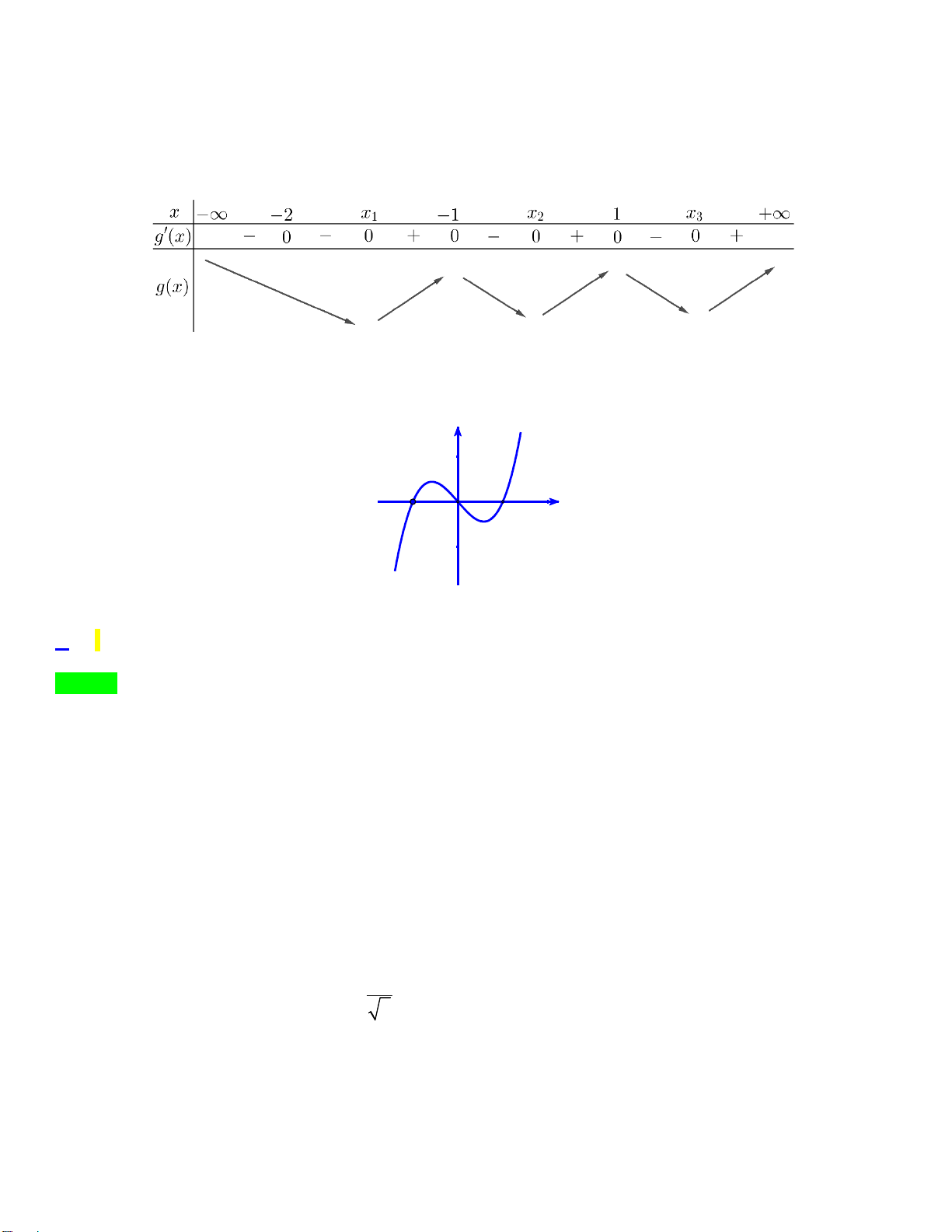
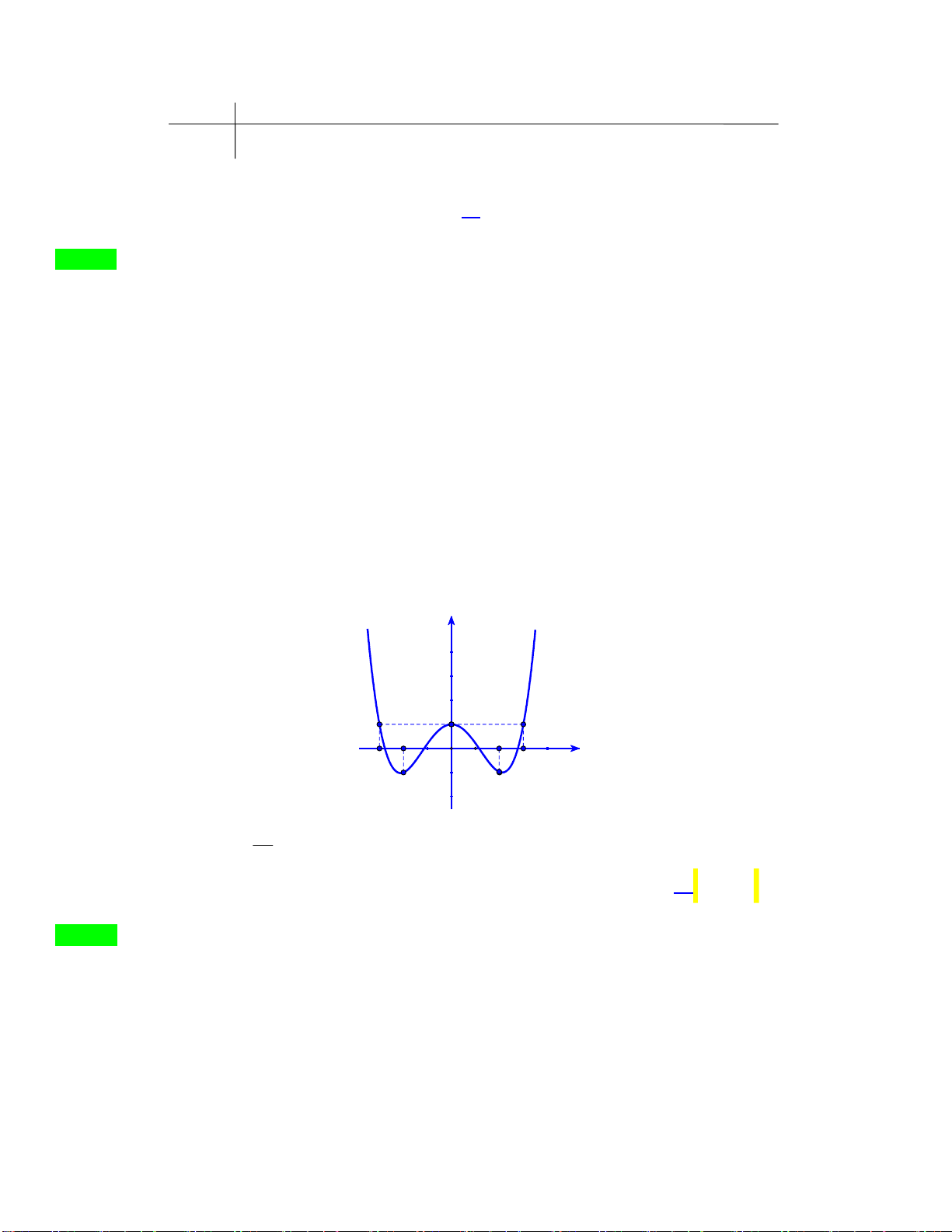
Câu 46.3: Cho f x là đa thức bậc 4 và hàm số y  f x có đồ thị là đường cong như hình vẽ. y -3 -2 O 1 x -4 y=f'(x)
Số điểm cực đại của hàm số g x  f  3 x  3x là A. 5. B. 2. C. 3. D. 4. Trang 11 Câu 46.4: Cho   4 3 2
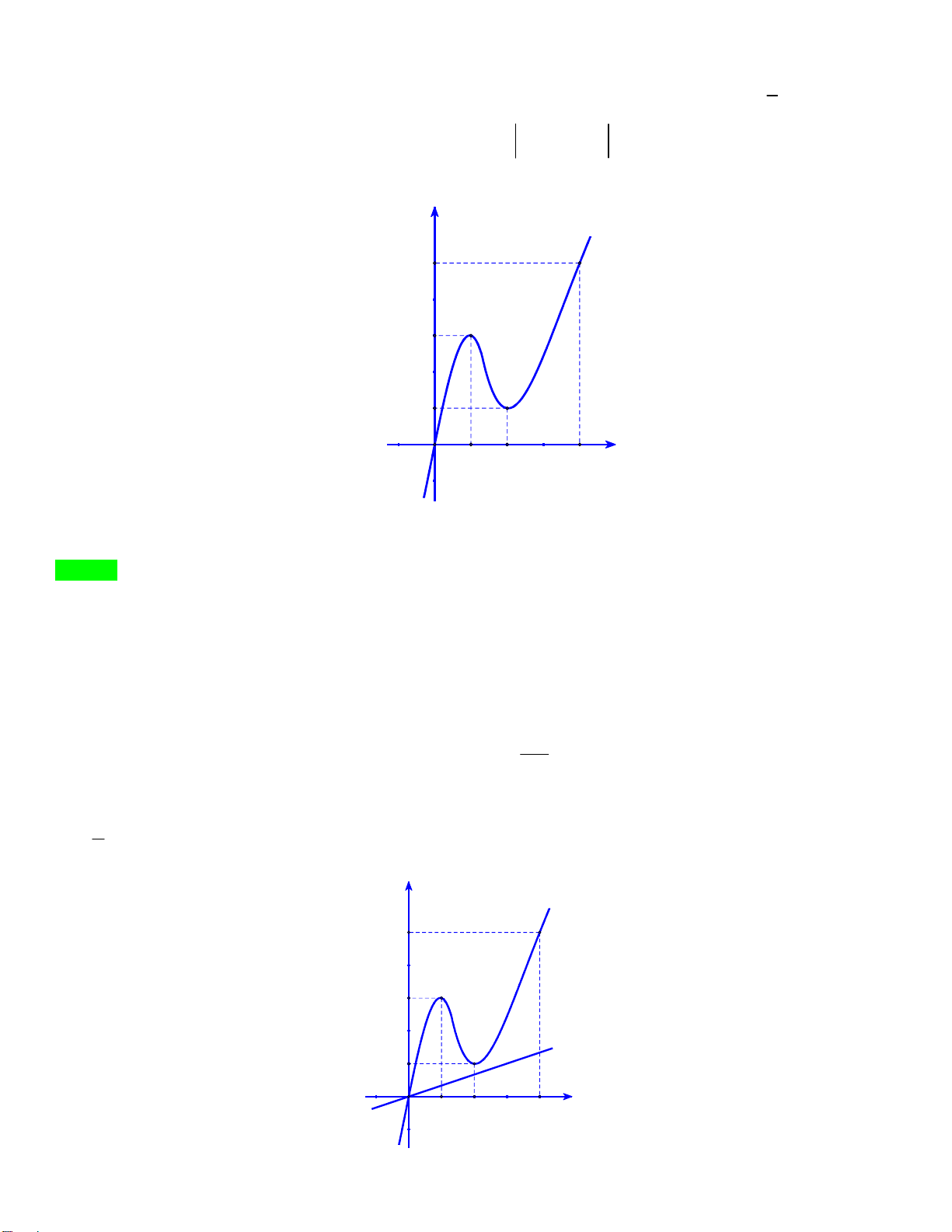
f x  x  ax bx cx  d và hàm số y  f x có đồ thị là đường cong như hình vẽ. y -1 O 1 x
Số điểm cực trị của hàm số y  f f   x là A. 7 . B. 11. C. 9. D. 8 .
Câu 46.5: Cho hàm số y  f x có đạo hàm đến cấp hai trên  và f    f  x 1 0 0;
  , x   . Biết 6
hàm số y  f x có đồ thị như hình vẽ. Hàm số     2 g x
f x mx , với m là tham số dương, có nhiều N G
nhất bao nhiêu điểm cực trị? U Y y Ễ N y=f'(x) M I 5 N H N H IÊ 3 N 1 O 1 2 4 x A. 1 B. 2 C. 5 D. 3 Trang 12
LỜI GIẢI BÀI TẬP TƯƠNG TỰ CÂU 46
Câu 46.1: Cho hàm số    3 2 y
f x  ax bx  cx  d có các điểm cực trị là 0;a 2  a  3 và có đồ thị
là đường cong như hình vẽ. y y=f(x) 3 2 a 3 O x 1
Đặt g x  2019f f x  2020 . Số điểm cực trị của hàm số là A. 2 . B. 8 . C. 10 . D. 6. Lời giải N G Chọn B U Y y Ễ N y=f(x) M 3 IN H y=a N H 2 a 3 IÊN O x 1
gx  3f f x .f x. f x 0 f    f x  0 f x  a
gx  0  3f f x .f x  0     , 2  a  3. f   x  0 x  0 x  a 
f x  0 có 3 nghiệm đơn phân biệt x , x , x khác 0 và a . 1 2 3
Vì 2  a  3 nên f x  a có 3 nghiệm đơn phân biệt x , x , x khác x , x , x , 0 , a . 4 5 6 1 2 3
Suy ra gx  0 có 8 nghiệm đơn phân biệt.
Do đó hàm số g x  2019f f x  2020 có 8 điểm cực trị.
Câu 46.2: Cho hàm số    4 3 2 y
f x  ax bx  cx  dx e . Biết rằng hàm số y  f x liên tục trên 
và có đồ thị như hình vẽ bên. Hỏi hàm số g x  f  2
2x  x  có bao nhiêu điểm cực đại? Trang 13 y y=f'(x) -4 O 1 4 x A. 5. B. 3 . C. 1. D. 2 . Lời giải Chọn C  x  1  2 2x  x  4  x  1
Ta có: y    x f  2 2 2 . 2x  x   0      . 2  2x  x  1 x  1  5   2  2x  x  4  N G x  1 5 1 1  5  U Y 2  2x  |  0   Ễ N f 2 2x  0  |  0  M  I g x  0  0  0  N H
Suy ra hàm số có 1 cực đại. N H
Câu 46.3: Cho f x là đa thức bậc 4 và hàm số y  f x có đồ thị là đường cong như hình vẽ. IÊN y -3 -2 O 1 x -4 y=f'(x)
Số điểm cực đại của hàm số g x  f  3 x  3x là A. 5. B. 2. C. 3. D. 4. Lời giải Chọn B 3 3x  3  0 (1) Ta có gx   2 x  f  3 3 3 x  3x, g x 0      f '   3 x  3x  0 (2) (1)  x  1  . 3 x  3x  2
Dựa vào đồ thị đã cho thì (2)    3 x  3x  1  Trang 14 x  1 Trong đó phương trình 3 x 3x 2      x  2.  Còn phương trình: 3
x  3x  1 có 3 nghiệm phân biệt: 2  x  1 , 1  x  0 và 1  x  2 1 2 3
Ta có bảng biến thiên của hàm số g x
Vậy hàm số g x có 2 điểm cực đại. Câu 46.4: Cho   4 3 2
f x  x  ax bx cx  d và hàm số y  f x có đồ thị là đường cong như hình vẽ. y N G U Y -1 O 1 x Ễ N M IN H     N
Số điểm cực trị của hàm số y f f x là H I A. 7 . B. 11. C. 9. D. 8 . Ê N Lời giải Chọn A
Từ đồ thị và giả thiết suy ra f x  x  2 x   3
 x  x  f x 2 1  3x 1 3   
Ta có gx  f f 
 x  f  f   x f   x  3
 x  x  3x x      2 . 3x  1  
 x x  x   3
x  x   3x x   2 1 1 1 1 3x  1 x  0 x  0     x  1 x  1     x  1    g x x 1 0       3  x  a( 0,76) x  x 1  0   3 x  b x  x   b  1,32 1 0    2  1 3x 1  0 x     3
Do đó, hàm số g x có 7 điểm cực trị. Trang 15
Câu 46.5: Cho hàm số y  f x có đạo hàm đến cấp hai trên  và f    f  x 1 0 0;
  , x   . Biết 6
hàm số y  f x có đồ thị như hình vẽ. Hàm số     2 g x
f x mx , với m là tham số dương, có nhiều
nhất bao nhiêu điểm cực trị? y y=f'(x) 5 3 1 N O 1 2 4 x G U Y Ễ A. 1 B. 2 C. 5 D. 3 N Lời giải M I Chọn D N H
Từ đồ thị hàm số y  f x suy ra f x  0,x  0;. N H Do đó, 2
f  x  0, x  0; . I     Ê N 2 2
Xét hàm số h x  f x mx ; hx  2x.f x m .
Với x  0, hx  0  Phương trình hx  0 vô nghiệm. x
Với x  0 ta có h x  f x  x f x   f x  2 2 2 2 2 2 2 4 2  . 3
Từ đồ thị hàm số y  f xta thấy với x  0, đồ thị hàm số y  f xluôn nằm trên đường thẳng x y  . 3 y y=f'(x) 5 3 1 O 1 2 4 x Trang 16 2 2x Do đó, 2f  2 x 
 0, x  0  h x  0,x  0 hay hàm số y  hxđồng biến trên 0;. 3 Mà h0  m
  0 và lim h x   nên phương trình hx  0 có một nghiệm duy nhất x   x  0; 0   Bảng biến thiên x  0 x 0  y   0    y 0 h x 0 
Khi đó phương trình h x  0 có 2 nghiệm phân biệt.
Đồng thời hàm số y  h x đạt cực tiểu tại x  x , giá trị cực tiểu hx  0. 0  N 0 G U
Vậy hàm số y  h x có 3 điểm cực trị. Y Ễ N M IN H N H IÊ N Trang 17
Câu 48: Cho hàm số f (x) liên tục trên  thỏa mãn 3 2 10 6 xf(x )  f(1  x )  x
  x  2x, x   . 0 Khi đó f(x)dx  bằng 1 17 13 17 A.  . B.  . C. . D. 1 . 20 4 4 Lời giải 1:
Gọi F x là một nguyên hàm của hàm f x trên  . Với x   ta có 3 2 10 6 xf(x )  f(1  x )  x   x  2x 2 3 2 11 7 2
 x f(x )  xf(1 x )  x   x  2x (*) 2 3 2  x f x x  xf  x x      11 7 2 ( )d (1 )d x   x  2x dx 12 8 3 N 1 3 3 1 2 2 x x 2x G  f(x )d(x ) f(1  x )d(1  x )     C   U 3 2 12 8 3 Y Ễ 1 1 x x 2   1 x F x F  x     C . N     12 8 3 3 2 3 2 12 8 3 M I 1 1 N
Thay x  0 ta được F 0 F   1  C  1. H 3 2 N H 1 1 5
Thay x  1 ta được F 1  F 0   C 2 . I       Ê 3 2 8 N 1 1 17
Thay x  1 ta được F  
1  F 0  C 3. 3 2 24 5 5 3 Từ   1 ,  2 suy ra F    1 F 0     F   1F0  . 6 8 4 1 32
Từ 2,3 suy ra F    1 F  1      F 
 1F 1 4. 3 24 0 3 13 Vậy
f xdx  F 0F  1  4    . 4 4 1 Lời giải 2: Từ 3 2 10 6 xf(x )  f(1  x )  x   x  2x 2 3 2 2 11 7
 x f(x )  xf(1  x )  2x  x   x , x   . 1 1 Suy ra, hàm số 2 3 2 2
x f(x )  xf(1 x )  2x là hàm lẻ. Ta có  11 7 x   x dx   24 0 Do đó 0 1 2 3 2 2 2 3 2 2 1 x f(x ) xf(1 x ) 2x  dx x f(x ) xf(1 x ) 2x                 . 24 1 0 Trang 18 0 1  f  x  x  0 3 3 1  f   2  x   2  x  2 d 1 d 1  3 2 3 1 1 1 1   f  x  x  1 3 3 1  f   2  x   2  x  2 1 d 1 d 1   3 2 3 24 0 0 0 1  f  x 1 1 x  f  x 1 4 1 x    f  x 1 1 x  f  x 15 d d d dx  3 2 3 3 2 24 1 0 0 0 0  f x 1 x  f x 1 x    f x 15 2 d 3 d 8 5 dx     4 1 0 0 0  f x 1 x    f x 13 d 4 dx     4 1 0 Lời giải 3: Ta có 3 2 10 6 xf(x )  f(1  x )  x
  x  2x , x    1 Thay x bởi x  ta được 3 2 10 6 x  f( x  )  f(1 x )  x
  x  2x , x   2 N 3 3 3 3 G Từ  
1 ,2 suy ra xf x  xf x   4x,x    f x  f  x    4  , x   . U Y Thay 3 . Ễ
x bởi x ta được f x f  x    4 N Do đó, M I 0 0 1 0 1 N   H f   x f  x   dx  f   xdx  f
 xdx   4dx  4  f  xdx  4 N 1 1 0 1 1 H I Từ  x f x  xf  x  x   x  x Ê  1 2 3 2 11 7 2 ( ) (1 ) 2 N 1 1 1 1 3 3 1 2 2  f x x  f  x  x      11 7 2 x   x  x  5 ( )d( ) (1 )d(1 ) 2 dx   3 2 8 0 0 0 1 1 1 1 1 5 3  f(x)dx 
f(x)dx    f(x)dx   3  2  8  4 0 0 0 0 3 13 Do đó, f(x)dx  4     . 4 4 1 Lời giải 4: Với x   ta có 3 2 10 6 xf(x )  f(1  x )  x   x  2x 2 3 2 11 7 2
 x f(x )  xf(1 x )  x   x  2x (*) 1 1 1 2 3 2
 x f(x )dx  xf(1  x )dx      11 7 2 x   x  2x dx 0 0 0 1 1 1 3 3 1 2 2 5  f(x )d(x )  f(1  x )d(1  x )   3  2  8 0 0 1 1 1 1 1 5 3  f(x)dx 
f(x)dx    f(x)dx   3  2  8  4 0 0 0 Trang 19 0 0 0 Mặt khác 2 3 2
(*)  x f(x )dx  xf(1  x )dx      11 7 2 x   x  2x dx 1 1 1 0 1  f x  x  0 1  f  x   x  2 3 3 2  17 (*) ( )d (1 )d 1    3 2   24 1 1 0 1 0 1 1 17 1 3 17   13  f(x)dx  f(x)dx    f(x)dx  3 .     . 3  2  24  2 4 24 4 1 0 1
Lời giải 5: Đi tìm hàm f x
Ban đầu ta sẽ nghĩ đến có f  3 x  f  2
, 1 x  thì bên vế phải có thể đưa liên quan gì đến 3 2 x ,1 x không?  
Ta có xf x   x  x  x f x  x 3 3 10 3 3 2  2  
Vậy thì nghĩ thêm việc cũng tạo tiếp cái  x 3 2 2 4 6 1
 2  3  3x  3x  x N
Hay f  x   x 3 2 2 2 4 6 1 1
 2  3  3x  3x x . G U Như thế ta sẽ có Y Ễ 3 3  3 3   2 2  2 4 6 6 N
x f x  x   2  f 1x 1x   2  3  3x  3x x  x M     IN 3 3  3 3   2 2  2 4 H
 x f x x   2  f 1x  1x   2  3 3x  3x     N  H 3 3     I 3 3 4 2 2 2 Ê
 x f x x   2  3x  f 1x 1x   2  31x   0 N     x f x  x 3 x    f  x   x 3 3 3 3 2 2  2 3 2 1 1 3 1 x  2              0     Đặt g x  f x 3
 x  3x  2 ta được xg  3x  g 2 1 x   0. Thay x  bởi x ta được x  g  3x   g 2
1 x   0 hay xg 3x  x  g  3x  ,x  .
Do đó g x là hàm lẻ. Như vậy xg  3 x  g 2
 x    xg 3x  g 2 1 0 x  1, x    .
Từ giả thiết ta có g 0  g   1  0.
Vì f x liên tục trên 1;0    
 nên gx liên tục trên 1;0   .
Đặt M  max g x  0, x  1;0    1;0    .   Giả sử M  0 khi đó a    1  ; 0 : ga  M .
Chọn x  b   1  a   1  ; 0 g a M
Ta được bg  3b  ga  g  3b      M do b  0; 1. b b Trang 20
Điều này mẫu thuẫn do M  max g x . 1;0    
Do vậy max g x  0, x  1;0    1;0    .  
Hay g x  x     f   x 3 0, 1;0  x
  3x  2, x  1;0   . 0 0 13 Vậy 3 f(x)dx  ( x   3x  2)dx     . 4 1 1 Nhận xét chung:
Ở 5 cách trên, khi giải quyết bài toán dạng này ta thường hướng tới:
 Biến đổi giả thiết đi đến tính chất u f  udx  f  udu.
 Dựa theo tính chất hàm chẵn, hàm lẻ.
 Sử dụng các phép thế xác định hàm số f x.
* Với lời giải 1, 2, 3, 4: Ta đều sử dụng đến tính chất ub b  u f  udx  f  udu hay u
 xf ux dx  f  xdx N a ua G U
Vì thế ta mới nghĩ đến việc tạo ra đạo hàm của 3 2
x ;1 x bằng việc nhân hai vế của giả thiết với x để tYạo Ễ ra N 0 0 1 1 M 2 3 1 2 3 1 I x f x dx  f x dx ; x f x dx  f x dx ; N             3 3 H 1 1 0 0 N 0 1 1 1 H 2 1 xf 1 x dx   f x dx 1 và 2 xf 1 x dx  f x dx . I             Ê 2 2 N 1 0 0 0 1 1
Trong các đổi biến này xuất hiện f xdx 
buộc ta phải đi tính thêm f xdx 
. Ở đây, nếu cận không 0 0 3
phải là 1;0;1 thì các cách làm này sẽ bị phá sản, ví dụ yêu cầu tính f xdx  , lúc này chắc chỉ còn 0
cách đi tìm f x. Vì thế, các cận 1;0;1 phải được liên hệ mật thiết với 3 2 x ,1 x .
Ngoài ra, với hai tính chất:  Hàm số 2 3 2 2
x f(x )  xf(1 x )  2x là hàm lẻ;
 Hàm số f x f  x
   4 là hàm chẵn
cũng hữu ích cho việc tính toán nhanh hơn. 17 17
* Lỗi sai có thể mắc dẫn đến các phương án nhiễu  , đều sai dấu khi tính 20 4 0 1 1 xf   x  1 2 1 1 dx   f  xdx 1 và xf   2 1 x dx  f  xdx . 2 2 1 0 0 0
* Với lời giải 5: Việc tìm f x khá khó khăn, không nói là mò. Nếu f x là những hàm quen thuộc thì
rất có thể đoán bằng việc thử các giá trị và cân bằng hệ số.
Khi đó, mục đích khai thác tính chất u f  udx  f
 udu coi như phá sản. Trang 21
BÀI TẬP TƯƠNG TỰ CÂU 48
Câu 48.1: Cho hàm f x liên tục trên  \   0 thỏa mãn xf  2x f  x 3 1 2  x   2, x   \   0 . 2x 2 Giá trị f xdx  nằm trong khoảng nào? 1 A. 5;6. B. 3;4. C. 1;2. D. 2;3.
Câu 48.2: Cho hàm số y  f x liên tục trên đoạn 0;4
  và thỏa mãn điều kiện xf  2x f  x 2 4
6 2  4  x , x  0;2   . 4 Giá trị f xdx  bằng 0     A. . B. . C. . D. . 5 2 20 10 N G
Câu 48.3: Cho hàm y  f (x) liên tục trên đoạn 0;1 U   và thỏa mãn Y         Ễ f x f  x 2 1 2x 2x 1, x 0;1   . N 1 M Giá trị của I f(x)dx N  bằng H 0 N 4 2 1 1 H A. B. C. . D. IÊ 3 3 2 3 N
Câu 48.4: Cho hàm số y  f x liên tục và có đạo hàm trên  thỏa mãn  
f x f  x   2 5 7 1 3 x  2x,x   . 1 a Biết rằng . ' d a x f x x   
, với là phân số tối giản. Giá trị của 8a  3b là b b 0 A. 1. B. 0 . C. 16 . D. 16 . 2 
Câu 48.5: Cho hàm số f x liên tục trên đoạn  ;1  và thỏa mãn 3     2    2f(x)  3f      5x 2       x ;1 . 3x  3    1 Tích phân f   xlnxdx bằng 2 3 5 2 1 5 2 1 5 2 1 5 2 1 A. ln  . B. ln  . C.  ln  . D.  ln  . 3 3 3 3 3 3 3 3 3 3 3 3 Trang 22
LỜI GIẢI BÀI TẬP TƯƠNG TỰ CÂU 48
Câu 48.1: Cho hàm f x liên tục trên  \   0 thỏa mãn xf  2x f  x 3 1 2  x   2, x   \   0 . 2x 2 Giá trị f xdx  nằm trong khoảng nào? 1 A. 5;6. B. 3;4. C. 1;2. D. 2;3. Lời giải Chọn D Ta có xf  2 x  f  x 3 1 2  x   2, x   \   0 2x 2 2    xf
   2x f  x  3 1 2 dx  x     2dx     2x  1 1 2 N 2 2 4   G 1 2 2 1 x 1  f x d x 
f 2x d 2x    ln x  2x U
          2 2  4 2  Y 1 1 1 Ễ 4 4 2 N 1 1 7 1 1 7 1 M  f  xdx  f
 xdx   ln2  f  xdx   ln2 I 2 2 4 2 2 4 2 N 1 2 1 H 2 7 N
 f xdx   ln2   2;3 H 2 I 1 Ê N Câu 48.2: Cho hàm số liên tục trên đoạn   y  f x 0;4
  và thỏa mãn điều kiện xf  2x f  x 2 4
6 2  4  x , x  0;2   . 4 Giá trị f xdx  bằng 0     A. . B. . C. . D. . 5 2 20 10 Lời giải Chọn A Ta có xf  2 x  f  x 2 4 6 2  4  x . 2
  4xf x  6f 2x 2 2 2 dx  4  x dx  0 0 2  2 f  x dx  2 2 2  3 f  2xd2x  0 0 4  2 f x 4 dx  3 f x 4 dx   f xdx       5 0 0 0 Trang 23
Câu 48.3: Cho hàm y  f (x) liên tục trên đoạn 0;1   và thỏa mãn f x f  x 2 1
 2x  2x  1, x  0;1   . 1 Giá trị của f(x)dx  bằng 0 4 2 1 1 A. B. C. . D. 3 3 2 3 Lời giải Chọn D Ta có f x f  x 2 1  2x  2x  1 1 1 1 2  1 2
 I  f(1 x)dx  (2x  2x  1)dx    3 2
 I  f(1 x)dx   x  x  x   3  0 0 0 0 1 2  I  f(1 x)dx    1 3 N 0 G 1 U Y Xét f(1 x)dx 
, đặt t  1  x  dt  d
 x . Đổi cận x  0  t  1;x  1  t  0 Ễ 0 N 1 0 1 M I Ta có f(1 x)dx  f(t)( d  t)  f(t)dt  I    2 N H 0 1 0 N 1 1 H 2 1
Từ 1 ; 2  2 f (x)dx   f(x)dx  I     Ê  3  . 3 N 0 0
Câu 48.4: Cho hàm số y  f x liên tục và có đạo hàm trên  thỏa mãn
f x f  x   2 5 7 1 3 x  2x,x   . 1 a Biết rằng . ' d a x f x x   
, với là phân số tối giản. Giá trị của 8a  3b là b b 0 A. 1. B. 0 . C. 16 . D. 16 . Lời giải Chọn B
Từ f x f  x   2 5 7 1
3 x  2x thay x bởi 1x ta được f  x f x   2 5 1 7 3 x  1. 5  f
 x 7f 1  x  3 2 x  2x Do đó ta có hệ  
 7f x  5f 1 x  3   2x  1 Suy ra
f x f x   2x  x  2x     f x 2 25 49 15 2 21 1 24  36x  30x  21 1 1 Hay f x    2
12x 10x  7  f x   12x 5 8 4 1 1 a 1 3 a   3 Do đó   x.f '  xdx   x  12x 5dx     b 4 8 b   8 0 0  Trang 24 Vậy 8a  3b  0 2 
Câu 48.5: Cho hàm số f x liên tục trên đoạn  ;1  và thỏa mãn 3     2    2f(x)  3f      5x 2       x ;1 . 3x  3    1 Tích phân f   xlnxdx bằng 2 3 5 2 1 5 2 1 5 2 1 5 2 1 A. ln  . B. ln  . C.  ln  . D.  ln  . 3 3 3 3 3 3 3 3 3 3 3 3 Lời giải Chọn D Cách 1:  2  2  2    10 Từ 2f (x)  3f      5x  thay x bởi ta được 2f    3f   x . 3x  3x 3x  3x N 10 2 2 G
Do đó 4f x 9f x  10x   f x   2x  f x    2 U 2 x x x Y Ễ N 1 1   M 2 lnxf  x dx      2l 5 2 1 nxdx  ln  I      2  N  x    3 3 3 2 2 H 3 3 N H Cách 2: IÊ 1 1 1 f x dx     N 2   2 Ta có lnxf  x dx  f x lnx 
2f(x)  3f    5x, x   ;1 .        2  . Từ x 3x    3  2 3 2   3 3    2 2  f(1)  3f      5 f(1)  0 2    3   
Thay x  1 và x  vào (1) ta được hệ       . 3 2       5 2    10 2     3 (1) f f f          3 3   3 3   1 f x Xét I  dx  x 2 3  2 2 2 x    t  1 Đặt x   dx   dt,, đổi cận  3 . 2 3t  3t  2 x   1  t   3       2 2   1 2   2 f  . dt f    dt f        dx 3 2 1 1 2 3t  t 3t   3x  Khi đó I     3  2  t  . x 1 2 2 3 3 3t Trang 25  2        2      1   1 f d d x f x x  2f(x) 3f 3x  1   1 3  5 1 Ta có 2I  3I  2  3   5I x  dx  5dx   I  x  x  x  3 3 2 2 2 2 3 3 3 3 1 1 1 f x dx 2 2      1 5 2 1 Vậy f
 xln dxx  f x   lnx           2 ln1.f  1 ln f    ln  . x 3   3 3 3 3 3 2 3 2 3 3 N G U Y Ễ N M IN H N H IÊ N Trang 26
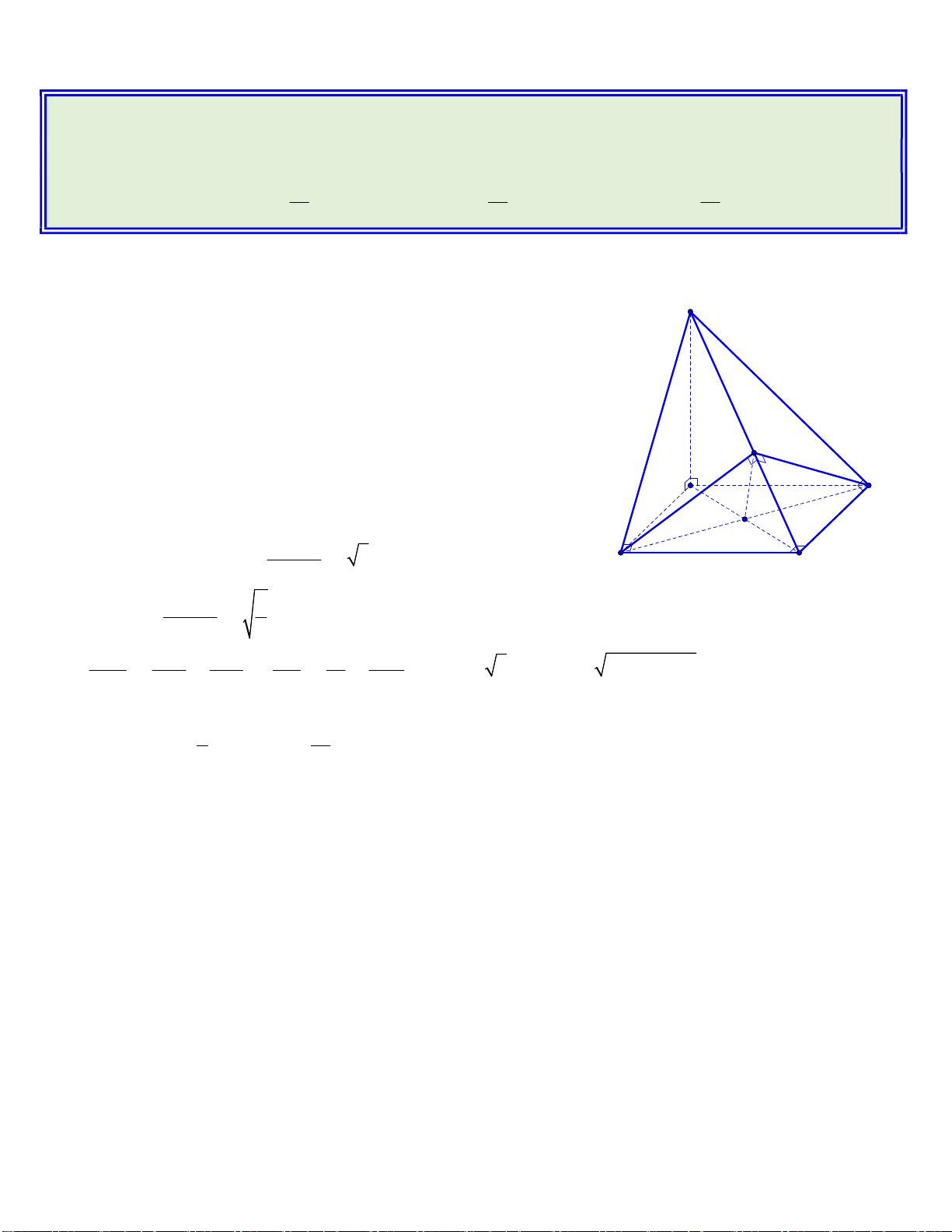
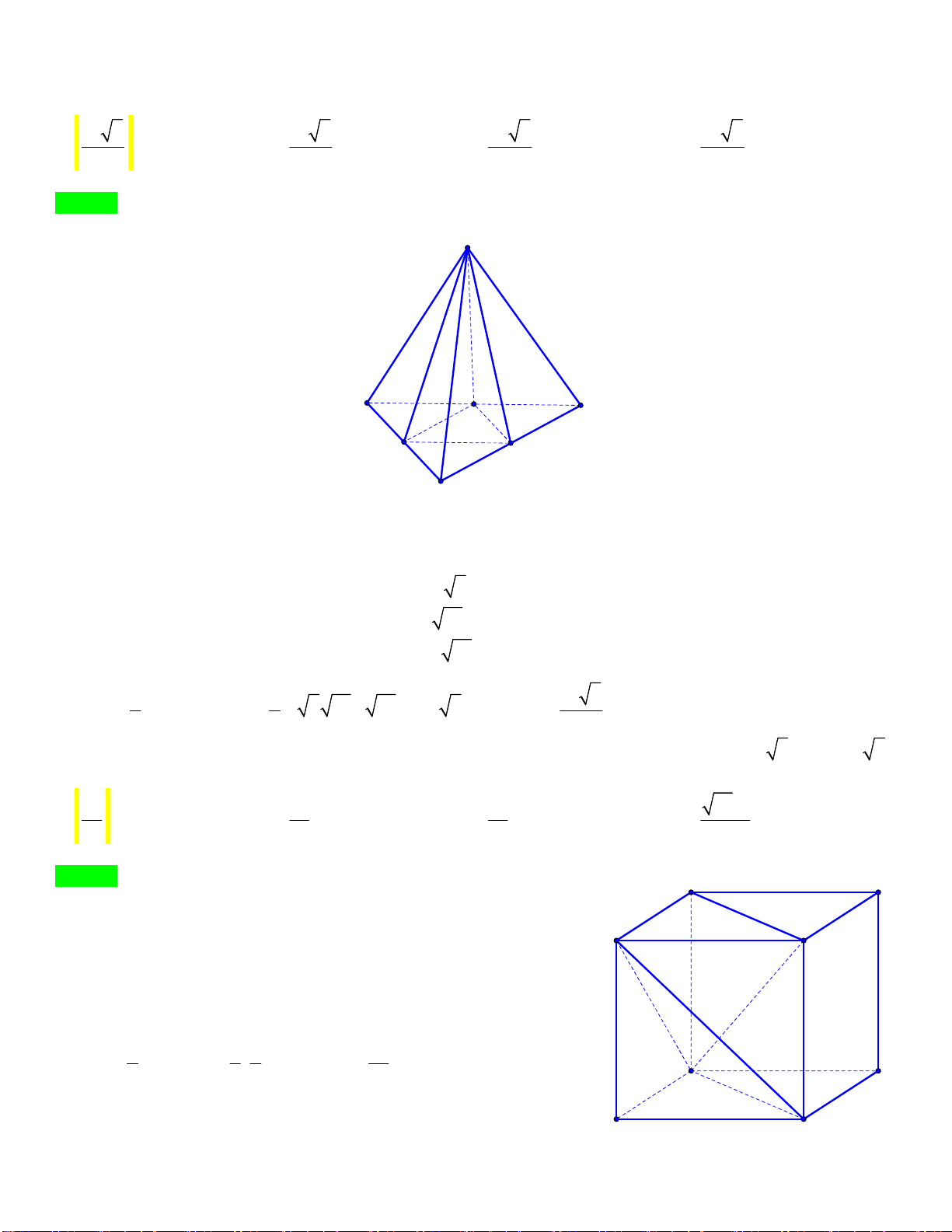
Câu 49: Cho khối chóp S.ABC có đáy ABC là tam giác vuông cân tại   ,
A AB  a,SBA  SCA  90 ,
góc giữa hai mặt phẳng SAB và SAC  bằng 60. Thể tích khối chóp đã cho bằng 3 a 3 a 3 a A. 3 a . B. . C. . D. . 3 2 6 Lời giải S
Từ giả thiết ta dựng hình chóp S.ABDC với ABDC là hình
vuông và SD  ABDC .
Vì SAB  SAC nên nếu BH là đường cao của SAB thì
tương ứng CH cũng là đường cao của SAC .
Mà SA  SAB SAC  nên SAB SAC    BH CH  , ,  60 H hay  BHC  60 hoặc  BHC  120 . N D G Vì nên U BH  CH HI là phân giác góc  BHC hay BY    Ễ IHC  30 hoặc  IHC  60 . a N I  CI M Nếu  IHC  30 thì CH   2a , không thỏa mãn.  C a I A N sin 30 H CI 2 N Do đó CH   a . H sin 60 3 IÊN 1 1 1 3 1 1 Mà 2 2 .     
 SC  2a  SD  SC CD  a 2 2 2 2 2 2 CH CA CS 2a a SC 3 1 a Do vậy, V  S .SD  . S.ABC 3 A  BC 6 Chú ý:
Ta có thể chỉ ra tồn tại hình chóp S.ABDC như sau:
Gọi D là hình chiếu vuông góc của S lên mặt phẳng ABC . Ta có A  B  SB 
 AB  SBD  AB  BD A  B  SD .
Tương tự AC CD ABDC là hình vuông cạnh a. Nhận xét:
Trong bài toán trên ta đã sử dụng phương pháp tạo hình ẩn, tức là từ hình đa diện ban đầu, tạo
thêm những điểm mới để tạo ra hình đa diện mới ở đó tính chất dễ khai thác hơn. Một số hình quen
thuộc mà tính chất dễ khai thác là: Hình lập phương, hình hộp chữ nhật, lăng trụ đứng, hình chóp đều,
hình chóp đáy là hình chữ nhật và cạnh bên vuông góc với đáy,… Trang 27
BÀI TẬP TƯƠNG TỰ CÂU 49
Câu 49.1: Cho tứ diện ABCD có AB  CD  10 , AD  BC  5 , AC  BD  13 . Gọi  là góc
giữa AB và ACD, giá trị cos bằng 6 10 865 10 3 10 A. . B. . C. . D. . 35 35 10 10
Câu 49.2: Cho tứ diện ABCD có AB  CD  4;AC  BD  5;AD  BC  6 . Thể tích của khối tứ diện ABCD bằng 15 6 15 6 45 6 45 6 A. . B. . C. . D. . 4 2 4 2
Câu 49.3: Cho tứ diện ACFG có số đo các cạnh lần lượt là AC  AF  FC  a 2, AG  a 3,
GF  GC  a . Thể tích của khối tứ diện ACFG bằng 3 3 3 3 N a a a 15a A. . B. . C. . D. . G U 6 3 12 3 Y Ễ
Câu 49.4: Cho tứ diện ABCD có AB  BD  AD  2a,AC  7a,BC  3a . Biết khoảng cách gi Nữa M
hai đường thẳng AB,CD bằng a , tính thể tích của khối tứ diện ABCD . IN H 3 2a 6 3 2a 2 N A. . B. . C. 3 2a 6 . D. 3 2a 2 . H 3 3 IÊ N Trang 28
LỜI GIẢI BÀI TẬP TƯƠNG TỰ CÂU 49
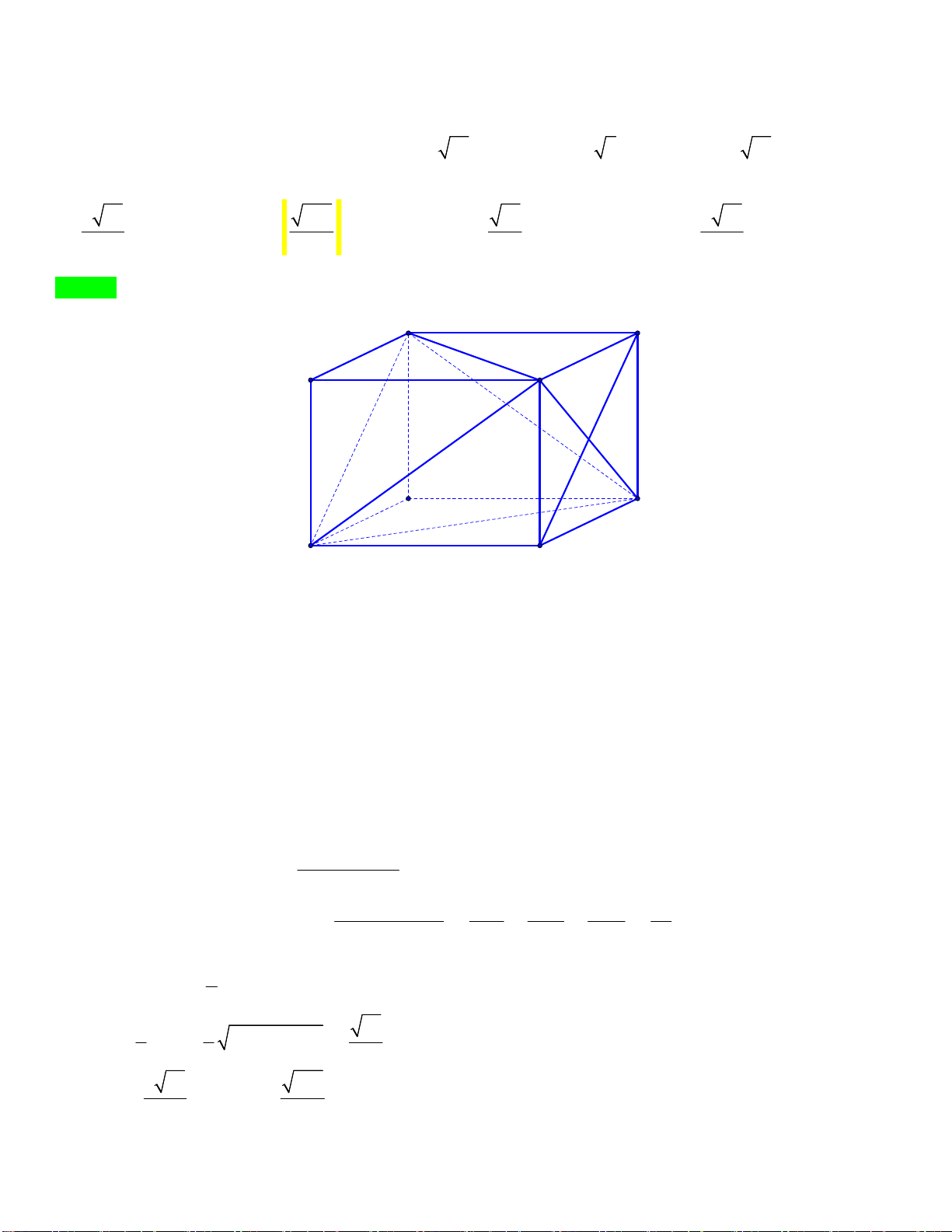
Câu 49.1: Cho tứ diện ABCD có AB  CD  10 , AD  BC  5 , AC  BD  13 . Gọi  là góc
giữa AB và ACD, giá trị cos bằng 6 10 865 10 3 10 A. . B. . C. . D. . 35 35 10 10 Lời giải Chọn B A F E D I N G G U C Y Ễ N M B H I N H
Dựng hình hộp AEDF.GBHC . N
Do các cạnh đối của tứ diện ABCD bằng nhau nên các đường chéo của mỗi mặt của hình hộp bằng nh Hau suy ra I
AEDF.GBHC là hình hộp chữ nhật. Ê N Đặt AE  x,AF  , y AG  z x,y, z  0 .    2 2 x y  5 x   1   Ta có hệ  2 2 y  z 13 y      2    2 2 z   x  10 z   3  
Ta thấy AB //HF  AB;ACD    HF;ACD    d F;ACD
Gọi I  HF CD  sin  . IF 1 1 1 1 49
Tứ diện FACD vuông tại F nên:     2 d F;ACD 2 2 2 FA FD FC 36  d F ACD 6 ;  . 7 1 1 10 Mà 2 2 FI  FH  FC  FD  . 2 2 2 6 10 865  sin   cos  . 35 35 Trang 29
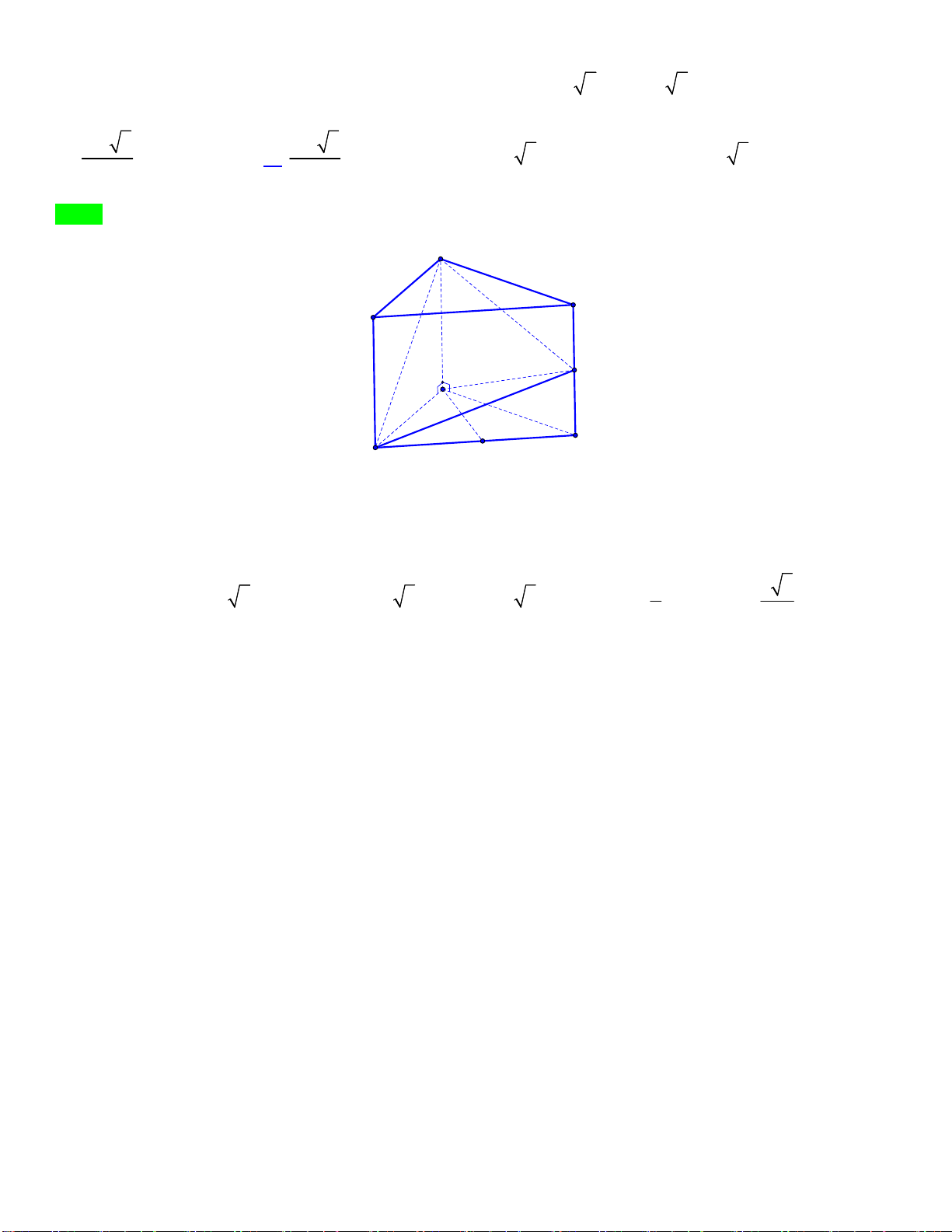
Câu 49.2: Cho tứ diện ABCD có AB  CD  4;AC  BD  5;AD  BC  6 . Thể tích của khối tứ diện ABCD bằng 15 6 15 6 45 6 45 6 A. . B. . C. . D. . 4 2 4 2 Lời giải Chọn A A M D K B C N G U N Y Ễ
Dựng tứ diện AMNK , sao cho B,C,D là trung điểm của các cạnh N M
MN,NK,KM . Tứ diện AMNK vuông tại . A IN  2 2   2       H AM AN 64 A  M  54 A  M  3 6    N  2 2  2  . H A  N  AK  100  A  N  10  A  N  10    IÊ  2 2  2 AK  AM  144 AK  90   A       K  3 10 N  1 1 15 6 V
 AM.AN.AK  .3 6 10.3 10  15 6 V  . AMNK 6 6 ABCD 4
Câu 49.3: Cho tứ diện ACFG có số đo các cạnh lần lượt là AC  AF  FC  a 2, AG  a 3,
GF  GC  a . Thể tích của khối tứ diện ACFG bằng 3 a 3 a 3 a 3 15a A. . B. . C. . D. . 6 3 12 3 Lời giải Chọn A E H
Dựng hình lập phương như hình vẽ
Khi đó ABCD.EFGH là hình lập phương cạnh a nên thể tích F G
của hình lập phương là 3 V  a .
Thể tích tứ diện ACGF có được là do ta chia hình lập phương
theo các mặt phẳng ACGE,ACF và AGF. Khi đó ta có 3 1 1 1   . a V V V  . ACGF ABC .EFG ABCD. 3 2 3 EFGH 6 D A B C Trang 30
Câu 49.4: Cho tứ diện ABCD có AB  BD  AD  2a,AC  7a,BC  3a . Biết khoảng cách giữa
hai đường thẳng AB,CD bằng a , tính thể tích của khối tứ diện ABCD . 3 2a 6 3 2a 2 A. . B. . C. 3 2a 6 . D. 3 2a 2 . 3 3 Lời giải Chọn B A F G D B E C H N G Từ giả thiết U  AB  AC Y
Dựng lăng trụ đứng AGF.BCE với D là trung điểm EF V  3.V Ễ AGF.BCE ABCD N
Khi đó, vì AB / / CEFG  d A , B CD  d ,
B CE  BH  a với H CE,BH  CE M       IN 1 2 2 H Ta tính được 2 3
BE  a 3  BC  CE  2 2a  S  2a V  .AB.S  a . BCE ABCD BCE N 3 3 H IÊN Trang 31
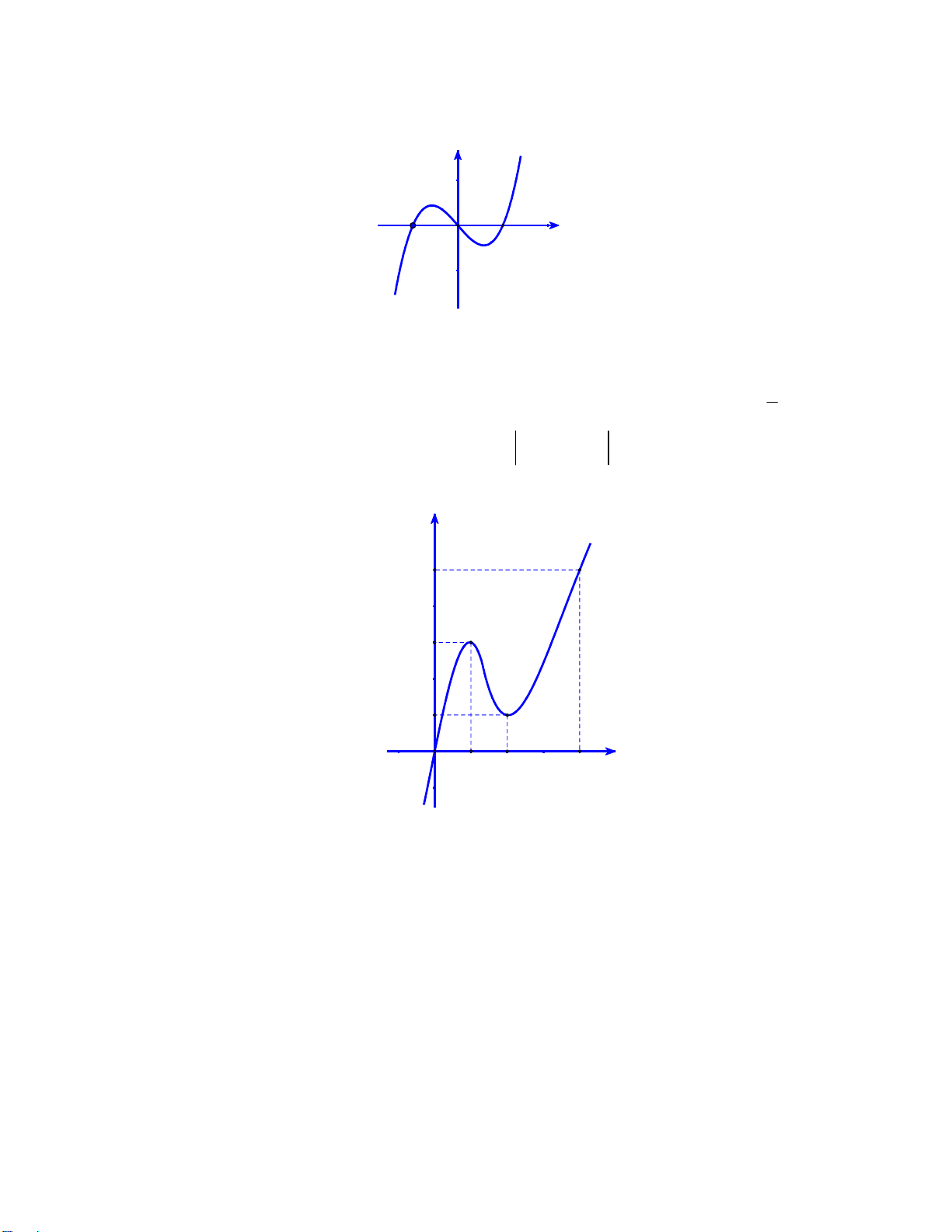
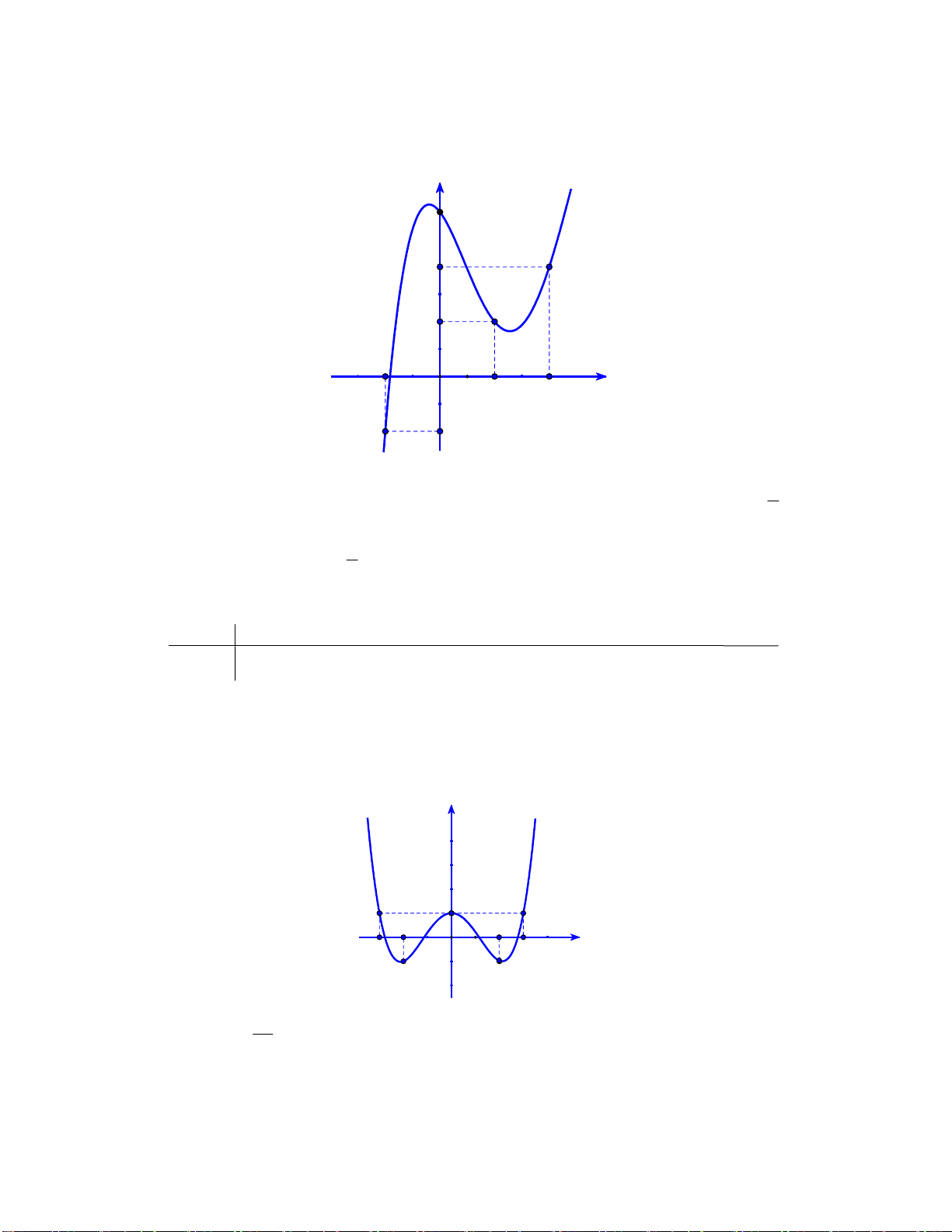
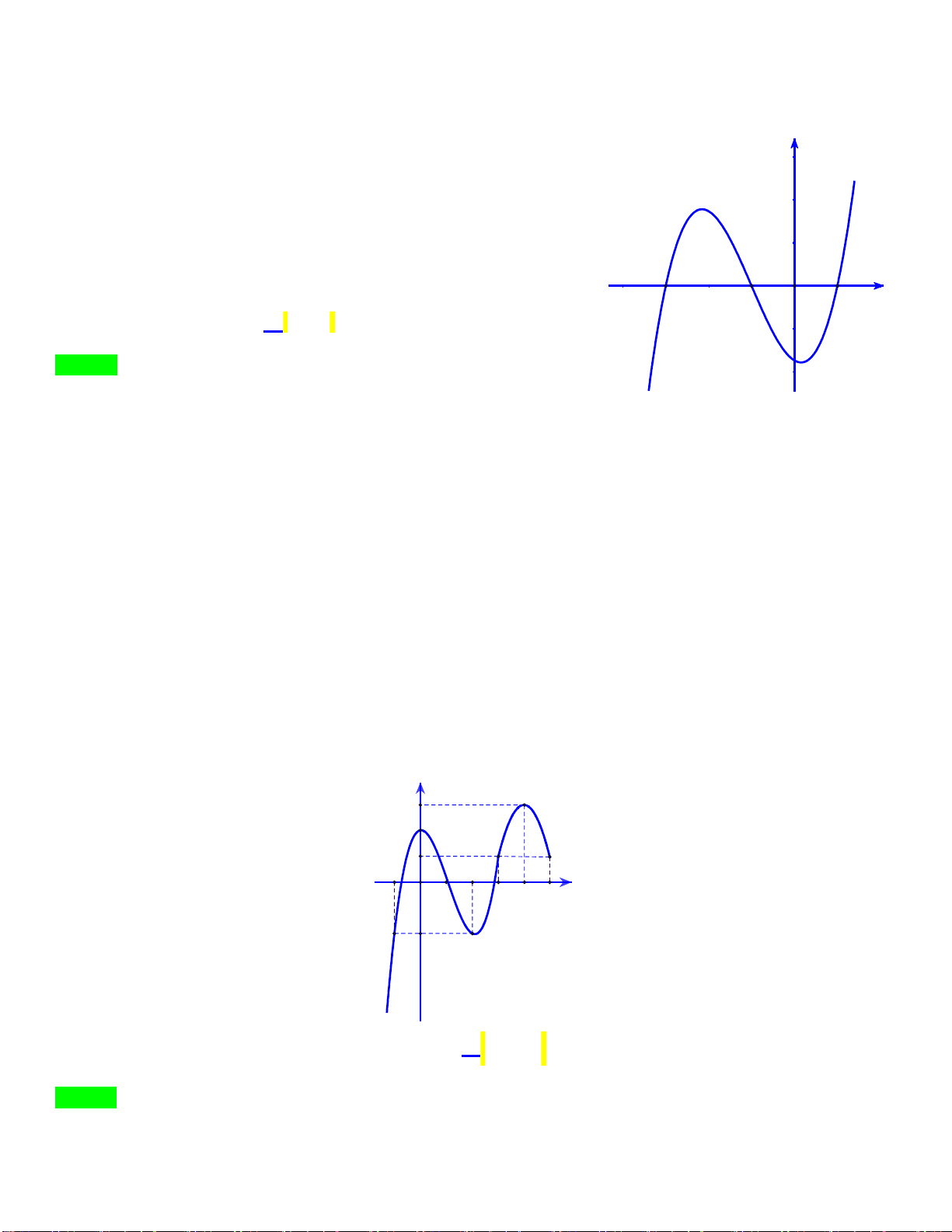
Câu 50: Cho hàm số f x. Hàm số y  f x có đồ thị như hình sau. y 1 4 -2 O x -2
Hàm số g x  f   x 2
1 2  x  x nghịch biến trên khoảng nào dưới đây?  3  1 A. 1  ;     . B. 0;   . C. 2; 1. D. 2;  3 . N  2  2 G U Lời giải Y Ễ
Ta có g x  2f  1  2x  2x  1 N     y M 1 2x y=f'(t) IN
gx  0  f 12x   1. H 2 N t  1 H
Đặt t  1  2x khi đó  
1 trở thành f t . Từ đồ thị các hàm 4 IÊ 2 -2 O t N t
số y  f t và y   . 2 -2 -t y= Ta có 2 1 3            f t t 2 t 0 2 1 2x 0 x   2 2      . 2 t 4 1   2x  4     3  x    2      1 3 3
Hàm số y  g x nghịch biến trên các khoảng  ;     và   ;   . 2 2  2 Vậy phương án A đúng. Nhận xét:
Đây là bài toán gặp khá nhiều trong các đề thi THPT quốc gia những năm gần đây, ý tưởng là
xét tính đơn điệu của hàm số y  f ux vxdựa trên so sánh giá trị các hàm uxf x, v  x
trên khoảng nào đó để xét dấu uxf ux vx bằng cách sử dụng đồ thị hoặc đánh giá. Trang 32
BÀI TẬP TƯƠNG TỰ CÂU 50
Câu 50.1: Cho hàm số f x liên tục trên  , hàm số y  f x có đồ thị như hình vẽ. Xét hàm số h x  f  x   2 2 3
1  9x  6x  4 . Hãy chọn khẳng định đúng. y 4 2 -2 O 2 4 x -2 N G  1 U
A. Hàm số h x nghịch biến trên  .
B. Hàm số h x nghịch biến trên   1;  . Y  3 Ễ N   1 M
C. Hàm số h x đồng biến trên   1;    .
D. Hàm số h x đồng biến trên  . I  3 N  H
Câu 50.2: Cho hàm số f x có bảng xét dấu của đạo hàm như sau N   H I x  1 2 3 4  Ê N f x  0  0  0  0  Hàm số y  f x   3 3
2  x  3x đồng biến trên khoảng nào dưới đây? A. 1;. B.  ;   1. C. 1;0. D. 0;2.
Câu 50.3: Cho hàm số f x có đồ thị của hàm số y  f 'x như hình vẽ y 1 -3 -2 2 3 O x x
Hàm số y  f  x   3 2 2 1 
 x  2x nghịch biến trên khoảng nào sau đây? 3 A. 6;  3 . B. 3;6. C. 6;. D. 1;0. Trang 33
Câu 50.4: Cho hàm số y  f x liên tục và có đạo hàm trên  . Biết hàm số f x có đồ thị được cho
trong hình vẽ. Có bao nhiêu giá trị nguyên của m thuộc 2019;2019   để hàm số   2019x g x f
mx 2 đồng biến trên 0;1   ? y O 1 x A. N 2028. B. 2019 . C. 2011 . D. 2020 . G
Câu 50.5: Cho hàm số y  f x có đồ thị của hàm số y  f  x được cho như hình bên. Hàm U     số Y Ễ y   f  x 2 2 2
 x nghịch biến trên khoảng N M y IN H 3 N 2 H IÊ 1 N -1 O 1 2 3 4 5 x -2 A. 3;  2 . B. 2;  1 . C. 1;0. D. 0;2.
Câu 50.6: Cho hàm số y  f x có đạo hàm trên  . Biết đồ thị hàm y
y  f x như hình vẽ. Hàm số g x  f  x   3 3 1  x  3x đồng biến trên khoảng nào? 1 1 A.  ;   . B. 2;0. 4 3 O 1 2 3 4 x 1  C.  ;1  . D. 4;. 3  Trang 34
BÀI TẬP TƯƠNG TỰ CÂU 50
Câu 50.1: Cho hàm số f x liên tục trên  , hàm số y  f x có đồ thị như hình vẽ. Xét hàm số h x  f  x   2 2 3
1  9x  6x  4 . Hãy chọn khẳng định đúng. y 4 2 -2 O 2 4 x -2 N G  1 U
A. Hàm số h x nghịch biến trên  .
B. Hàm số h x nghịch biến trên   1;  . Y  3 Ễ N   1 M
C. Hàm số h x đồng biến trên   1;    .
D. Hàm số h x đồng biến trên  . I  3 N  H Lời giải N Chọn C H IÊ h x  f  x   2 2 3
1  9x  6x  4  hx  6f 3x  1 63x  1. N
Xét bất phương trình hx  0  6f 3x  
1  63x  1 0  f 3x  1 3x 1(*) y y=f'(t) y=t 4 2 -2 O 2 4 t -2
Quan sát hình vẽ ta thấy: Xét trên khoảng 2; 4 thì f x x  2  x  2 .    1
*  2  3x  1  2  1   x  . 3    1
Hàm số h x đồng biến trên   1;   .  3 Trang 35
Câu 50.2: Cho hàm số f x có bảng xét dấu của đạo hàm như sau x  1 2 3 4  f x  0  0  0  0  Hàm số y  f x   3 3
2  x  3x đồng biến trên khoảng nào dưới đây? A. 1;. B.  ;   1. C. 1;0. D. 0;2. Lời giải Chọn C Ta có y   f x   2 3 2 x   3     
Với x  1;0  x  2  1;2  f x  2  0, lại có 2
x  3  0  y  0; x  1;0
Vậy hàm số y  f x   3 3
2  x  3x đồng biến trên khoảng 1;0. Chú ý:
+) Ta xét x        x      f x   2 1;2 1; 2 3;4 2  0;x  3  0
Suy ra hàm số nghịch biến trên khoảng 1;2 nên loại hai phương án A,D. N G +) Tương tự ta xét U 2 Y x   ;
 2  x  2   ;
 0  f x  2  0;x  3  0  y  0;x   ;  2 Ễ N
Suy ra hàm số nghịch biến trên khoảng  ;
 2 nên loại hai phương án B. M I Câu 50.3: Cho hàm số
có đồ thị của hàm số như hình vẽ N f x y  f 'x H N y H IÊN 1 -3 -2 2 3 O x x
Hàm số y  f  x   3 2 2 1 
 x  2x nghịch biến trên khoảng nào sau đây? 3 A. 6;  3 . B. 3;6. C. 6;. D. 1;0. Lời giải Chọn D
Ta có y  f  x    x  x   f  x   x  2 2 ' 2 ' 2 1 2 2 2 ' 2 1 1  3 x 
Nhận xét: Hàm số y  f x có f 'x  1  3  x  3 và f x 3 ' 1    x 3 
Do đó ta xét các trường hợp
Với 6  x  3  13  2x 1  7 suy ra y '  0 hàm số đồng biến (loại)
Với 3  x  6  5  2x 1  11 suy ra y '  0 hàm số đồng biến (loại)
Với 6  x  11  2x  1 suy ra y '  0 hàm số đồng biến (loại) Trang 36
Với 1  x  0  3  2x  1  1 nên 2f '2x   1  2 và  x  2 0
1  3  2 suy ra y '  0 hàm số đồng biến (nhận)
Câu 50.4: Cho hàm số y  f x liên tục và có đạo hàm trên  . y
Biết hàm số f x có đồ thị được cho trong hình vẽ. Có bao nhiêu
giá trị nguyên của m thuộc 2019;2019   để hàm số   2019x g x f
mx 2 đồng biến trên 0;1   ? A. 2028 . B. 2019 . O 1 x C. 2011 . D. 2020 . Lời giải Chọn D
Ta có    2019x ln2019. 2019x g x f m. Ta lại có hàm số 2019x y  đồng biến trên 0;1   .   x    N Với x 0;1   thì 2019 1;2019 
 mà hàm y  f xđồng biến trên 1; nên hàm  2019x y f  đồ Gng U biến trên 0;1 Y   . Ễ x x x x   N
Mà 2019  0; f 2019   0, x
  0; 1 nên hàm hx  2019 ln2019.f 2019  đồng biến trên 0;1   . M      I Hay h x h 0 0, x 0;1 N       . H    
Do vậy, hàm số g x đồng biến trên 0;1  g x  với mọi x 0;1 N       0   H x x I
 m  2019 .ln2019.f  2019 , x   0;1  m  . Ê     0 N Vậy m  0 .
Câu 50.5: Cho hàm số y  f x có đồ thị của hàm số y  f x được cho như hình bên. Hàm số y   f  x 2 2 2
 x nghịch biến trên khoảng y 32 1 -1 O 1 2 3 4 5 x -2 A. 3;  2 . B. 2;  1 . C. 1;0. D. 0;2. Lời giải Chọn C Trang 37 y 32 1 -1 O 1 2 3 4 5 x -2 Ta có 2
y  2f(2  x)  x  y  (  2  x) 2
 f (2  x)  2x  2f (2  x)  2x
y  0  f (2  x)  x  0  f (2  x)  (2  x) 2
Đặt t  2  x suy ra f t  t 2 .
Dựa vào đồ thị ta thấy đường thẳng y  t  2 cắt đồ thị y  f t tại ba điểm có hoành độ liên tiếp là NG 1  a  2;3;4  b  5 U Y
Do đó cùng từ đồ thị ta có Ễ N a  t  3 a  2  x  3 1  x  2 a     M f (t)  t  2  t b  2 x b    x     2 b I    N  H
 Vì 1  a  2  0  2 a  1 nên (1;0)  (1;2 a). Do đó, hàm số nghịch biến trên khoảng N H
1;2a nên cũng nghịch biến trên 1;0. IÊN
 Vì 4  b  5  3  2 b  2 nên (3;2)  ( ;
 2 b). Do đó, hàm số nghịch biến trên khoản g  ;
 2 b thì không nghịch biến trên 3;  2 .
Vậy hàm số nghịch biến trên khoảng 1;0.
Câu 50.6: Cho hàm số y  f x có đạo hàm trên  . Biết đồ thị hàm y  f x như hình vẽ. y O 1 2 3 4 x
Hàm số g x  f  x   3 3
1  x  3x đồng biến trên khoảng nào? 1 1 1  A.  ;     . B. 2;0. C.  ;1 . D. 4;. 4 3 3  Lời giải Chọn A Ta có gx   f    x   2 3 3 1 1x  Trang 38   x  0    f  x   3x 1 1 3 1  0      2 . 3  3x  1  4    x  1  3  2    0 3 1  0  x f x     3 x  1 
Bảng xét dấu của gx x 2  1  0 1 2  3 f 3x  1   0  0  0  0  2 1  x  0    0   gx    2
Vậy hàm số đồng biến trên khoảng 0;   .  3 N G U Y Ễ N M IN H N H IÊN Trang 39