Phân tích tín hiệu trên miền tần số - Xử lý số tín hiệu | Môn: Khoa học | Trường đại học sư phạm kỹ thuật TP. Hồ Chí Minh

06/10/2016 Xử lý số tín hiệu 1
PHÂN TÍCH TÍN HIỆU
TRÊN MIỀN TẦN SỐ
Biến đổi Fourier (Fourier transform-FT) 2
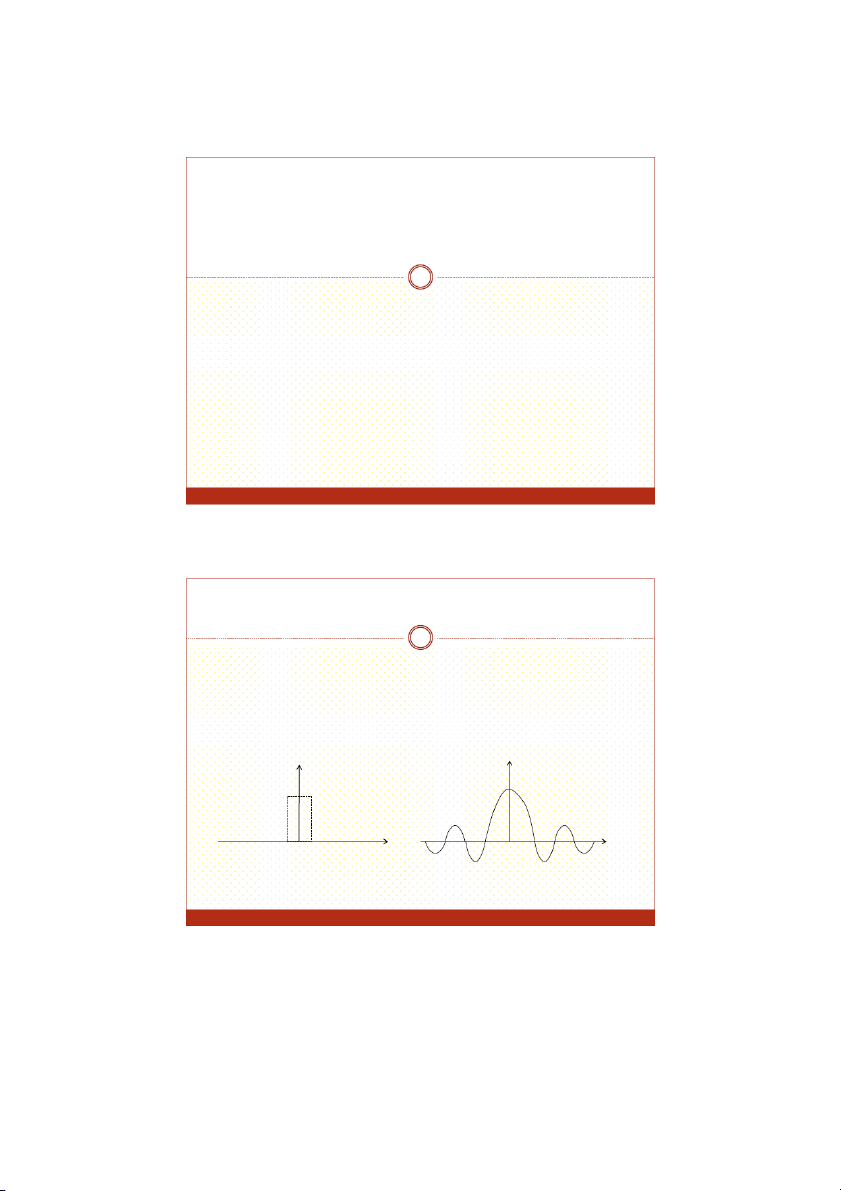
 Tín hiệu x(t) không tuần hoàn   X   xt     e j t dt  X(ω) x(t) ω -τ/2 t τ/2 -2π/τ 2π/τ 1 06/10/2016
Chuỗi Fourier (Fourier series-FS) 3
 Tín hiệu x(t) tuần hoàn, chu kỳ T , tần số F 1 0 = /T    x(t   jk t a e  0 )   j 2 k F t a e 0 k k k  k  1  a x(t)e 2 0 dt k    j k F t T T X(f) x(t ) τ f t -F F -T 0 T 0 0 p p
Chuỗi Fourier rời rạc của tín hiệu tuần
hoàn (Discrete Fourier series-DFS) 4
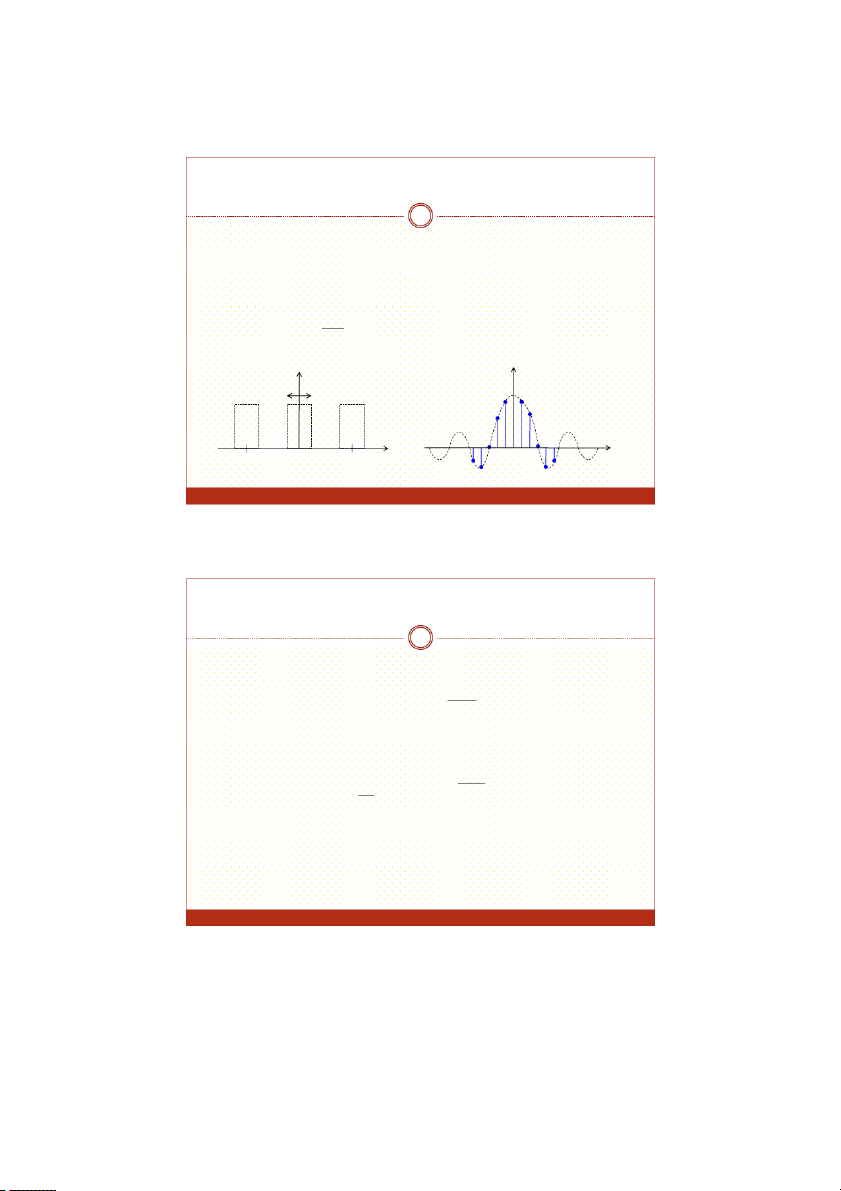
Cho tín hiệu x(n)rời rạc t ầ u n hoàn với chu kỳ N  N 1 π 2 k n x( ~ n  a~ )  j N e k k0 Với N1 π 2 k n a  1 ~ ~ x(n) e k    j N N n0 2 06/10/2016
Các phép biến đổi Fourier 5 Miền thời gian Miền tần số 2.5 2 1.5 1 0.5 0 1 T 0 1 2 3 4 5 6 7 8 Periodic time, t FS Discrete X   x(t) e ω jk t dt    k (period T) T 0 2.5 Continuous  2 j t   1.5 Aperiodic FT Continuous X( )   x(t) e dt 1    0.5 0 0 2 4 6 8 10 12 time, t 2.5 N 1 π 2 k n j 2 1.5  1 ~ a x(n) e k 1    N Periodic DFS Discrete 0.5 N n0 0 0 1 2 3 4 5 6 7 8 (period T) time, tk  Discrete  j n X( )   x(n)e 2.5 DTFT Continuous n 2 1.5 Aperiodic 1 N 1 π 2 k n 0.5 j 1 0 a ~  x(n)  N 0 2 4 6 8 10 12 DFT time, t e k  k Discrete N n 0
Biến đổi Fourier thời gian rời rạc
Discrete – Time Fourier Transform (DTFT) 6 DTFT 
 Định nghĩa: x(n)     X  j e    X  j e  xn     j n e  n  1 x( n)  X  j e   e j  d  2 2   Với e j  cos  j sin tuần hoàn chu kỳ 2π,  j 
thể hiện từ 0-2π hoặc từ -π đến π rồi lấy tuần X e  hoàn 3 06/10/2016
Biến đổi Fourier thời gian rời rạc
Discrete – Time Fourier Transform (DTFT) 7
 Biểu diễn theo Modul và Argument j j j ( ) X (e
)  X (e ) e Phoå biên Phoå pha độ
 Biểu diễn theo phần thực phần ảo Re, Im  Re X ( j
e )  j Im X ( j e ) phoå thöïc phoå aûo
Biến đổi Fourier thời gian rời rạc
Discrete – Time Fourier Transform (DTFT) 8
 Biểu diễn theo độ lớn và pha j j j ( )
Gỉa sử: X (e )  ( A e )e  X( j e )  (  j A e )    j
( )   ( ) khiA(e )0  ( ) khiA (  j e )0 4 06/10/2016
Biến đổi Fourier thời gian rời rạc
Discrete – Time Fourier Transform (DTFT) 
 Ví dụ: Cho phổ tín hiệu   2
X (e )  sin 3 i j .e Hãy xác định:
- Các thành phần phần thực, ảo - X (  j e
)  () A( j e )  ()
Biến đổi Fourier thời gian rời rạc
Discrete – Time Fourier Transform (DTFT)
 Sự tồn tại của biến đổi fourier:
 Điều kiện để FT[x(n)] hội tụ l : à 
 xn   n  n  3  x(n)    u( ) n  Ví dụ: Cho
 4 . Hãy tính và vẽ m t ậ 
độ phổ năng lượng của x(n) 5 06/10/2016
Biến đổi Fourier thời gian rời rạc
Discrete – Time Fourier Transform (DTFT) 11
 Ví dụ :Tìm biến đổi fourier của các tín hiệu sau: a) x(n)= (n) b) x(n)= (n-1) c) x(n)= u(n) d) x(n) = 2nu(n) n e)  1 
x(n)    u (n )  2  f) x( )
n  rect (n) N
Biến đổi Fourier thời gian rời rạc
Discrete – Time Fourier Transform (DTFT) 12
 Sự tồn tại của biến đổi fourier:
 Điều kiện để FT[x(n)] hội tụ l : à 
 xn   n 6 06/10/2016
Biến đổi nghịch Fourier thời gian rời rạc
Invert Discrete – Time Fourier Transform (IDTFT)
Biến đổi Fourier thời gian rời rạc nghịch (IDTFT) 1 x(n)   j   j  X (e )e n  d 2  2 
 Ví dụ: Xác định x(n) và vẽ x(n) với   c 2 1       i
X (e )   c c 0 
Định lý của biến đổi fourier  Tuyến tính Nếu x ( ) FT n    X ( j e ), x ( ) FT n    X ( j e ) 1 1 2 2 Thì
ax (n)  bx (n) FT   aX ( j
e )  bX ( j e ) 1 2 1 2
Ví dụ: Xác định biến đổi fourier x(n)  2x (n)  3x (n) 1 2 n n  1   1
x (n)    u (n )
x (n)    u( ) n 1 2  2   3 7 06/10/2016
Định lý của biến đổi fourier
 Dịch chuyển thời gian x(n) FT    X ( j e ) FT j j 0
x(n  n )    X (e ) n e 0 1
 Ví dụ: Tìm X (  j e ) với x( )
n  rect (n  n ) N 0
Định lý của biến đổi fourier
 Dịch chuyển tần số: x (n) FT    X ( j e )
x(n) jn FT j   0 e   X ( ( ) 0 e ) 8 06/10/2016
Định lý của biến đổi fourier
 Đảo thời gian: x (n) FT    X ( j e ) x( n  ) FT 
  X (  j e )
Định lý của biến đổi fourier
 Vi phân thời gian: x(n) FT    X ( j e ) x( )
n  x(n  ) 1 FT    X ( j e  ) 1 ( j n  0  e ) 9 06/10/2016
Định lý của biến đổi fourier
 Tích chập thời gian: x ( ) FT n    X ( j e ), x ( ) FT n    X ( j e ) 1 1 2 2 x ( ) n * x ( ) FT n    X ( j e ).X (  j e ) 1 2 1 2
Định lý của biến đổi fourier
 Tích chập miền tần số x ( ) FT n    X ( j e ) 1 1 FT 1
x (n).x (n) j j    X e X e 1 2  ( )* ( ) 1 2  2 10 06/10/2016
Định lý của biến đổi fourier
 Định lý Parseval  2  1  E  2 x(n)  X (e j )  d   x 2 n   
 Mật độ phổ năng lượng: 2 s  X ( j e ) xx
Đáp ứng tần số của hệ thống LTI
 Miền thời gian x(n) y(n) =x(n)*h(n) h(n)
 Miền tần số X ( j e ) Y ( j e )  H ( j e ).X ( j e ) H ( j e ) Y ( j  e j  ) H (e )  X ( j e ) 11