Phát triển bài toán vận dụng cao đề minh họa THPT 2020 môn Toán lần 2

Tài liệu gồm có 51 trang, được biên soạn bởi thầy giáo Lê Văn Đoàn, hướng dẫn giải và phát triển các bài toán vận dụng cao (VDC) trong đề minh họa kỳ thi tốt nghiệp THPT năm 2020 môn Toán lần 2 (câu 46, 47, 48, 49 và 50).

22 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu ôn thi THPTQG môn Toán

Môn: Toán

Thông tin:

51 trang 6 tháng trước

Tác giả:

Profile Nguyễn Vân
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 125 -
Câu 46. Cho hàm số
( )f x
có bảng biến thiên bên dưới. Số nghiệm thuộc đoạn
5
0;
2
của phương
trình
(sin ) 1f x
là
A.
7.
B.
4.
C.
5.
D.
6.
Lôøi giaûi tham khaûo
Đặt
0; 1; 2..
5
0;
2
3 5
sin cos , 0 cos 0 ; ;
2 2 2 2
k
x
t x t x t x x k x
x

0
2
3
2
5
2
t
0
0
t
1
1
0
1
Phương trình
( ) 1f t
và nhìn lên bảng biến thiên đề:
Bieän luaän nghieäm döïa vaøo baûng bieán thieân hoaëc ñoà thò haøm f(x)
1) Cho hàm số
( )y f x
có bảng biến thiên như hình vẽ bên dưới. Có bao nhiêu số nguyên
m
để
phương trình
(2 sin 1) ( )f x f m
có nghiệm thực ?
A.
5.
B.
4.
C.
3.
D.
2.
Lời giải tham khảo
Đặt
2 sin 1.t x
Ta có
1 sin 1 1 2 sin 1 3 1 3 [ 1;3].x x t t
Phương trình
(2 sin 1) ( )f x f m
có nghiệm
( ) ( )f t f m
có nghiệm thuộc đoạn
[ 1;3].
[ 1;3] [ 1;3]
min ( ) ( ) max ( ).f t f m f t
Từ bảng biến thiên, suy ra
[ 1;3]
min ( ) 2f t
và
[ 1;3]
max ( ) 2.f t
Do đó
2 ( ) 2f m
1 3.m
Do
{ 1;0;1;2;3} :m m
có
5
giá trị nguyên của
m
thỏa bài toán.
Chọn đáp án A.
1
:
1
t
t
cho
0
nghiệm
.x
1 :t
cho
1
nghiệm
.x
1
:
( 1;0)
t
t
cho
2
nghiệm
.x
[0;1) :t
cho
3
nghiệm
.x
1y
1 : 0x a
nghiệm
.x
( 1;0) :x b
2
nghiệm
.
x
(0;1) :x c
3
nghiệm
.x
0 : 0x d
nghiệm
.x
Vậy có
5
nghiệm
.x
Chọn đáp án C.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 126 -
2)
Cho hàm số
( )y f x
có đồ thị như hình vẽ bên dưới. Có bao nhiêu giá trị nguyên của
m
để
phương trình
2 ( )f f x m
có đúng
4
nghiệm phân biệt
[ 4; 0].x
A.
1.
B.
2.
C.
7.
D.
5.
Lời giải tham khảo
Đặt
( )t f x
và do
[ 4; 0]x
nên từ đồ thị, suy ra giá trị của
( ) [0;3].t f x
( ) (0;2] :t f x
có
2
nghiệm
.x
( ) (2;3] {0} :t f x
có
1
nghiệm
.x
Yêu cầu bài toán
phương trình
( )
2
m
f t
cần có
2
nghiệm
(0;2].t
Dựa vào đồ thị, suy ra
3 4 6 8.
2
m
m
Do
7.m m
Chọn đáp án A.
3) Cho hàm số
( )y f x
liên tục trên
và có đồ thị như hình vẽ. Gọi
S
là tập hợp tất cả các giá trị
nguyên của tham số
m
để phương trình
(sin ) 3 sinf x x m
có nghiệm thuộc khoảng
(0; ).
Tổng các phần tử của
S
bằng
A.
9.
B.
10.
C.
6.
D.
5.
Lời giải tham khảo
Đặt
sint x
và do
(0; ) (0;1].x t
(vẽ đường tròn lượng giác).
Khi đó phương trình trở thành
( ) 3 ( )m f t t g t
với
(0;1].t
Phương trình có nghiệm
(0;1] (0;1]
min ( ) max ( ).g t m g t
Ta có:
( ) ( ) 3.g t f t
Mà từ
(0;1]
thì đồ thị đi xuống nên
( ) 0 ( ) 3 0 ( ) 0.
f t f t g t
Do đó hàm số
( )g t
nghịch biến trên
(0;1].
Suy ra:
(0;1]
min ( ) (1) (1) 3 1 3 4g t g f
và
(0;1]
max ( ) (0) (0) 1.g t g f
Vậy
4 1 { 4; 3; 2; 1;0}.
m
m m
Nên tổng giá trị của
m
bằng
10.
Chọn đáp án B.
Lưu ý. Tại vị trí max (x=0) không có dấu
" "
vì
(0;1].t
Nếu không để ý sẽ dễ nhầm chọn đáp án A.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 127 -
Baøi toaùn keát hôïp giöõa haøm soá vaø tích phaân
Cho hàm số
4 3 2
( )f x ax bx cx dx m
với
, , , , a b c d m
và
0.a
Hàm số
( )y f x
có
đồ thị như hình vẽ. Phương trình
( )f x m
có bao nhiêu nghiệm ?
A.
(0) 0
(1) 0
g
g
B.
(0) 0
(1) 0
g
g
C.
(0) 0
( 2) 0
g
g
D.
(1) 0
( 2) 0
g
g
Lời giải tham khảo
Ta có:
( ) ( ) .g x f x x
Cho
( ) 0g x
( ) 2 0 1.f x x x x x
Mà
1 0 1
2 2 0
( )d ( )d ( )dg x x g x x g x x
0 1
1 2
2 0
( ) d ( ) df x x x f x x x S S
(1) ( 2) 0 (1) ( 2).g g g g
Vẽ lại bảng biến thiên bên phải.
Điều kiện cần và đủ để phương trình
( ) 0g x
có
4
nghiệm
khi
(0) 0g
và
(1) 0.g
Chọn đáp án A.
Baøi toaùn chöùa tham soá m trong baøi toaùn chöùa haøm cuï theå
Có bao nhiêu giá trị nguyên
m
( 10)m
để phương trình
1
4
2 log ( 2 )
x
x m m
có nghiệm ?
Lời giải tham khảo
Điều kiện:
2 0.x m
Ta có
1
4 2
2 log ( 2 ) 2 log ( 2 ) 2
x x
x m m x m m
2 2
log 2 2 log ( 2 ) ( 2 ) (2 ) ( 2 ).
x x x
x m x m f f x m
Do hàm số
2
( ) logf t t t
đồng biến nên
2 2
x
x m
2 2 ( )
x
m x g x
có
2
( ) 2 ln 2 1 0 log (ln 2).
x
g x x
Phương trình có nghiệm khi
2 2
1
2 ( log (ln 2)) ( log (ln 2))
2
m g m g
0,457.
Do
m
nguyên và
10,m
nên
{1;2; 3;4;5;6;7;8;9}.m
Các giá trị này đều thỏa điều kiện.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 128 -
Baøi taäp töông töï vaø môû roäng
46.1. Cho hàm số
( )y f x
có bảng biến thiên bên dưới. Số nghiệm thuộc đoạn
[0;2 ]
của phương
trình
(cos ) 2 0f x
là
A.
3.
B.
0.
C.
2.
D.
1.
46.2. Cho hàm số
( )y f x
có bảng biến thiên bên dưới. Số nghiệm thuộc đoạn
[ ;2 ]
của phương
trình
2 (sin ) 3 0f x
là
A.
4.
B.
6.
C.
3.
D.
8.
46.3. Cho hàm số
( )y f x
có bảng biến thiên như hình vẽ bên dưới. Số nghiệm thuộc đoạn
7
0;
2
của phương trình
2 (2 cos ) 1 0f x
là
A.
7.
B.
4.
C.
5.
D.
6.
46.4. Cho hàm số
( )y f x
có bảng biến thiên như hình vẽ bên dưới. Số nghiệm thuộc đoạn
[ ];
của phương trình
3 (2 sin ) 1 0f x
là
A.
4.
B.
5.
C.
2.
D.
6.
46.5. Cho hàm số
( )y f x
có bảng biến thiên bên như hình vẽ bên dưới. Số nghiệm đoạn
[ 2 ;2 ]
của phương trình
4 (cos ) 5 0f x
là
A.
4.
B.
6.
C.
3.
D.
8.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 129 -
46.6. Cho hàm số
( )y f x
có bảng biến thiên bên dưới. Số nghiệm thuộc đoạn
9
0;
2
của phương
trình
(2 sin 1) 1f x
là
A.
7.
B.
4.
C.
5.
D.
6.
46.7. Cho hàm số
( )y f x
có bảng biến thiên bên dưới. Số nghiệm thuộc đoạn
2 ;
2
của phương
trình
3 (sin cos ) 4 0f x x
là
A.
4.
B.
5.
C.
3.
D.
8.
46.8. Cho hàm số
( )y f x
có bảng biến thiên dưới và
(2) 0f
. Số nghiệm thuộc
[0;2 ]
của phương
trình
2
2 (cos cos 1) 1 0f x x
bằng
A.
3.
B.
0.
C.
2.
D.
1.
46.9. Cho đồ thị hàm số
( )y f x
như hình. Số nghiệm của phương trình
(2 sin ) 1f x
trên
[0;2 ]
là
A.
1.
B.
2.
C.
3.
D.
4.
46.10. Cho hàm số
( )y f x
có đồ thị như hình vẽ bên dưới. Số nghiệm thuộc đoạn
3
;2
2
của
phương trình
3 (cos ) 5 0f x
là
A.
4.
B.
7.
C.
6.
D.
8.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 130 -
46.11. Cho hàm số
3 2
( )f x ax bx bx c
có đồ thị như hình vẽ. Số nghiệm nằm trong
5
;
2 2
của phương trình
(cos 1) cos 1f x x
là
A.
2.
B.
3.
C.
4.
D. 5.`
46.12. Cho hàm số
( )y f x
có bảng biến thiên bên dưới. Số nghiệm thuộc đoạn
5
0;
2
của phương
trình
sin 2f x
là
A.
7.
B.
4.
C.
5.
D.
6.
46.13. Cho hàm số
( )y f x
có bảng biến thiên bên dưới. Số nghiệm thuộc đoạn
[0;3 ]
của phương
trình
(sin ) 1f x
là
A.
2.
B.
4.
C.
6.
D.
8.
46.14. Cho hàm số
( )y f x
có bảng biến thiên bên dưới. Số nghiệm của phương trình
2
( )
e 4
f x
là
A.
3.
B.
5.
C.
4.
D.
6.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 131 -
46.15. Cho hàm số
( )y f x
liên tục trên
R
và có đồ thị như hình vẽ. Số nghiệm thực của phương trình
( ) 1 0f f x
là
A.
4.
B.
7.
C.
6.
D.
9.
46.16. Cho hàm số
( )y f x
xác định và liên tục trên
,
có đồ thị như hình vẽ. Hỏi có bao nhiêu giá trị
nguyên của tham số
m
để phương trình
( 408 392 34)f x x m
có đúng
6
nghiệm
thực phân biệt ?
A.
1.
B.
2.
C.
3.
D.
4.
46.17. Cho hàm số
( )y f x
xác định và liên tục trên
,
có bảng biến thiên như hình vẽ bên dưới. Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
sao cho phương trình
(sin ) 6 3f x m
có
8
nghiệm phân biệt thuộc đoạn
[0; 3 ].
Tổng các phần tử của
S
bằng
A.
1.
B.
18.
C.
6.
D.
3.
46.18. Cho hàm số
( )y f x
có đồ thị như hình vẽ. Số giá trị nguyên của tham số
m
để phương trình
(sin )f x m
có đúng
5
nghiệm thuộc
3
;
2
là
A.
7.
B.
6.
C.
4.
D.
5.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 132 -
46.19. Cho hàm số
( )y f x
liên tục trên
có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của
tham số
m
để phương trình
2 (cos )f f x m
có nghiệm
; .
2
x
A.
5.
B.
3.
C.
2.
D.
4.
46.20. Cho hàm số
4 2
( ) ,f x ax bx c
0a
và có đồ thị như hình vẽ. Tổng các giá trị nguyên của
tham số
m
để phương trình
2 (sin ) 3f f x m
có nghiệm
0;
2
x
bằng
A.
1.
B.
2.
C.
3.
D.
4.
46.21. Cho hàm số
( )f x
có bảng biến thiên bên dưới. Có bao nhiêu giá trị nguyên của tham số
m
để
phương trình
(2 sin ) 2 0f x m
có đúng
6
nghiệm phân biệt thuộc
[0;3 ] ?
A.
0.
B.
2.
C.
3.
D.
1.
46.22. Cho hàm số
( )y f x
có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số
m
để
phương trình
( (sin ))f f x m
có đúng hai nghiệm thuộc khoảng
(0; )
?
A.
1.
B.
2.
C.
3.
D. 4.
46.23. Cho hàm số bậc ba
3 2
( ) ( , , ,f x ax bx cx d a b c d
và
0)a
có đồ thị như hình vẽ.
Phương trình
2 2 2
[ ( 1)] ( 1) 2 0f x f x
có bao nhiêu nghiệm ?
A.
1.
B.
3.
C.
4.
D.
5.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 133 -
46.24. Cho hàm số
4 2
, ( 0)y ax bx c a
như hình vẽ bên dưới. Có bao nhiêu điểm trên đường
tròn lượng giác biểu diễn nghiệm của phương trình
( (cos2 )) 0.f f x
A.
1.
B.
3.
C.
4.
D. Vô số.
46.25. Cho hàm số
( )y f x
liên tục trên đoạn
[ 2;6]
và có đồ thị như hình vẽ bên dưới. Có bao nhiêu
số nguyên
m
để phương trình
(sin )f x m
có nghiệm.
A.
10.
B.
6.
C.
9.
D.
5.
46.26. Cho hàm số
( )y f x
liên tục trên đoạn
[ 2;6]
có đồ thị như hình bên dưới. Có bao nhiêu số
nguyên
m
để phương trình
(cos )f x m
có nghiệm
;
2 2
x
A.
10.
B.
6.
C.
2.
D.
5.
46.27. Cho hàm số
( )y f x
xác định trên
và có đồ thị như hình bên. Có bao nhiêu giá trị nguyên
của tham số
m
để phương trình
4 sin 1
3
3
x
f m
có nghiệm ?
A.
2.
B.
3.
C.
4.
D.
5.
46.28. Cho hàm số
( )y f x
xác định trên
và có đồ thị như hình bên. Có bao nhiêu giá trị nguyên
của tham số
m
để phương trình
4 4
4(sin cos )f x x m
có nghiệm ?
A.
2.
B.
4.
C.
3.
D.
5.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 134 -
O
y
1
1
1
3
5
46.29. Cho hàm số
( )y f x
liên tục trên
và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của
m
để phương trình
( (sin ))f f x m
có nghiệm thuộc khoảng
(0; )
?
A.
1.
B.
2.
C.
3.
D.
4.
46.30. Cho hàm số
( )y f x
xác định, liên tục trên
và có đồ thị như hình vẽ. Tập hợp tất cả các giá
trị của tham số
m
để phương trình
2
( 2 2) 3 1f x x m
có nghiệm thuộc đoạn
[0;1]
là
A.
[0;4].
B.
[ 1;0].
C.
[0;1].
D.
1
;1
3
46.31. Cho hàm số
( )y f x
liên tục trên
và có đồ thị như hình vẽ. Tập hợp các giá trị thực của tham
số
m
để phương trình
2
( 4 1)f x x m
có nghiệm là
A.
[ 2;0].
B.
[ 4; 2].
C.
[ 4; 0].
D.
[ 1;1].
46.32. Cho hàm số
( )y f x
xác định, liên tục trên
và có đồ thị như hình vẽ. Có bao nhiêu giá trị
nguyên của
m
để phương trình
2
(2 2 )f x x m
có nghiệm.
A.
6.
B.
7.
C.
3.
D.
2.
46.33. Cho hàm số
( )y f x
xác định trên
và có đồ thị như hình. Có bao nhiêu giá trị nguyên của
m
để phương trình
2
2 (3 4 6 9 ) 3f x x m
có nghiệm ?
A.
13.
B.
12.
C.
8.
D.
10.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 135 -
46.34. Cho hàm số
( )y f x
liên tục trên
và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của
m
để phương trình
2
( 2 )f x x m
có đúng
4
nghiệm thực phân biệt thuộc đoạn
3 7
;
2 2
?
A.
1.
B.
2.
C.
3.
D.
4.
46.35. Cho hàm số
( )y f x
liên tục trên
có đồ thị như hình. Có bao nhiêu giá trị nguyên của tham
số
m
để phương trình
( ) 1 ( )f f x m f x m
có đúng
3
nghiệm phân biệt trên
[ 1;1].
A.
1.
B.
2.
C.
3.
D.
4.
46.36.
Cho hàm số
( )y f x
liên tục trên
và có đồ thị như hình vẽ dưới đây. Số giá trị nguyên
của tham số
m
để phương trình
e
2
1
( )
8
x
m
f
có hai nghiệm thực phân biệt là
A.
4.
B.
5.
C.
6.
D.
7.
46.37.
Cho hàm số
( )y f x
liên tục
trên
và có đồ thị như hình vẽ dưới đây. Có bao nhiêu giá trị
nguyên của
m
để
2
(2 log )f x m
có nghiệm duy nhất trên
1
;2 .
2
A.
4.
B.
5.
C.
6.
D.
9.
46.38. Cho hàm số
( )y f x
có đồ thị như hình vẽ. Hỏi có tất cả bao nhiêu số nguyên dương
100m
phương trình
2 2
( ) 2020f x m
có đúng hai nghiệm phân biệt.
A.
55.
B.
56.
C.
54.
D.
99.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 136 -
x
y
O
4
2
2
6
2
4
46.39. Cho hàm số
( )y f x
có đồ thị như hình bên dưới. Có bao nhiêu số nguyên của tham số
m
để
phương trình
1
1
3 2
x
f x m
có nghiệm thuộc đoạn
[ 2;2].
A.
8.
B.
9.
C.
10.
D.
11.
46.40. Cho hàm số
( )y f x
liên tục trên
và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của
m
để phương trình
( ) ( )f x f m
có đúng hai nghiệm phân biệt ?
A.
4.
B.
1.
C.
2.
D.
3.
46.41. Cho hàm số
( )y f x
liên tục trên
và có đồ thị như hình vẽ. Tìm tất cả các giá trị nguyên của
m
để phương trình
(1 sin ) ( )f x f m
có nghiệm.
A.
{ 1; 0;1;2}.m
B.
{0;1;2}.m
C.
.m
D.
{1;2}.m
46.42. Phương trình
3 3
2
log ( 1) 27 8 1
y
x y x
có
bao
nhiêu cặp nghiệm nguyên
( ; )x y
với
1992 2020
[8 ;8 ] ?x
A.
26.
B.
28.
C.
24.
D.
30.
46.43. Cho phương trình
2
3 3
) ( 2)log 5 0
log (3x m x m
(m
là tham số thực). Tìm tập hợp tất cả
các giá trị của
m
để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn
[1;9].
A. (2;4).
B.
[2;4].
C.
(4; ).
D.
[2;4).
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 137 -
46.44. Cho hàm số
( )f x
có đạo hàm trên
,
đồ thị hàm số
( )y f x
như trong hình vẽ bên. Hỏi phương
trình
( ) 0f x
có tất cả bao nhiêu nghiệm biết
( ) 0.f a
A.
3.
B.
2.
C.
1.
D.
0.
46.45. Cho
( )y f x
có đồ thị của
( )y f x
như hình vẽ bên dưới. Đặt
2
( ) ( ).g x f x
Mệnh đề nào dưới
đây đúng ?
A.
(0) (1) ( 1).g g g
B.
( 1) (0) (1).g g g
C.
(1) ( 1) (0).g g g
D.
( 1) (1) (0).g g g
46.46. Cho hàm số
( )f x
liên tục trên
và có đồ thị hàm số
( )f x
như hình vẽ bên dưới. Đặt
2
1
( ) ( ) 3.
2
g x f x x
Điều kiện để phương trình
( ) 0g x
có
4
nghiệm phân biệt là
A.
(0) 0
( 2) 0
g
g
B.
(0) 0
( 2) 0
g
g
C.
(0) 0
(1) 0
g
g
D.
(1) 0
( 2) 0
g
g
46.47. Cho hàm số
( )f x
liên tục trên
và có đồ thị hàm số
( )f x
như hình vẽ bên dưới. Đặt
3
1
( ) ( ) 1
3
g x f x x x
Điều kiện để
( ) 0g x
có
4
nghiệm phân biệt là
A.
(1) 0
( 1) 0
g
g
B.
(1) 0
( 1) 0
g
g
C.
(1) 0
(2) 0
g
g
D.
(1) 0
(2) 0
g
g
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 138 -
46.48. Cho phương trình
2
2 2
log (2 ) ( 2)log 2 0
x m x m
(m
tham số). Tập hợp các giá trị của
m
để phương trình có hai nghiệm phân biệt thuộc đoạn
[1;2].
A.
(1;2).
B.
[1;2].
C.
[1;2).
D.
[2; ).
46.49. Có bao nhiêu giá trị nguyên của
m
để phương trình
2
9 3 3
log log (3 1) log
x x m
có nghiệm
A.
2.
B.
3.
C.
[1;2).
D.
[2; ).
46.50. Cho phương trình
2
2 2
2 log (3 2 )log (4 ) 8 5 0
x m x m
(với
m
là tham số). Tập hợp tất cả
các giá trị của
m
để phương trình đã cho có
2
nghiệm phân biệt thuộc đoạn
[ 2;2]
là
A.
5
;3
2
B.
5
;3
2
C.
5
;3
2
D.
[3; ).
46.51. Giá trị thực của tham số
m
để phương trình
9 2(2 1).3 3(4 1) 0
x x
m m
có hai nghiệm
thực
1
,x
2
x
thỏa mãn
1 2
( 2)( 2) 12x x
thuộc khoảng nào sau đây ?
A.
(3;9).
B.
(9; ).
C.
1
;3
4
D.
1
;2
2
46.52. Cho phương trình
2 2 2
2 3 2 2
3 9 3 3 .
x x m x x x x m
Có bao nhiêu giá trị nguyên của tham số
[ 2018;2018]m
để phương trình đã cho có
4
nghiệm phân biệt ?
A.
2018.
B.
2019.
C.
2020.
D.
2021.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 139 -
Câu 47. Xét các số thực dương
, , , a b x y
thỏa mãn
1, 1a b
và
.
x y
a b ab
Giá trị nhỏ nhất
của biểu thức
2P x y
thuộc tập hợp nào dưới đây ?
A.
(1;2).
B.
5
2;
2
C.
[3;4).
D.
5
;3
2
Lôøi giaûi tham khaûo
Theo đề thì
, 1 log 0
a
a b b
và
log 0.
b
a
Ta có
2 2
1 1
2 log ( ) 1 log log
.
2 2
2 log ( ) log 1
x y x y
a a a
b b
x ab b x b
a b ab a b ab
y ab a
Khi đó:
Cauchy
3 1 3 1 3 5
2 log log 2 log .log 2 ;3 .
2 2 2 2 2 2
a b a b
P x y b a b a
Chọn đáp án D.
Baøi toaùn doàn bieán, roài söû duïng baát ñaúng thöùc Cauchy hoaëc khaûo saùt haøm moät bieán
1) Cho
,x
y
là các số thực thỏa mãn
4 4
log ( ) log ( ) 1.x y x y
Tìm giá trị nhỏ nhất của
2 .x y
Lời giải tham khảo
Điều kiện:
0, 0.x y x y
Ta có:
4 4 4
log ( ) log ( ) 1 log ( )( ) 1 ( ).( ) 4x y x y x y x y x y x y
( )
Suy luận. Đề yêu cầu tìm min của tổng
2 ( ),x y
mà từ đề có dạng tích
( ),
nên nghĩ đến việc sử dụng bất
đẳng thức trung bình cộng – trung bình nhân
( : )AM GM Cauchy
bằng cách sử dụng đồng nhất:
2
1 3
2 .( ) .( ) ( ). ( ). ,
1
2 2
a b
x y a x y b x y a b x a b y a b
a b
và có lời giải:
Ta có:
Cauchy
4
1 3 1 3 3
2 ( ) ( ) 2 . ( ).( ) 2 4 2 3.
2 2 2 2 4
x y x y x y x y x y

Suy ra
min(2 ) 2 3.x y
2) Đặt
3
log ( )
a
m ab
với
, 1a b
và
2
log 16 log .
a b
P b a
Tìm
m
để
P
đạt giá trị nhỏ nhất ?
Lời giải tham khảo
Vì
1, 1 log 0
a
a b b
và
log 0.
b
a
Ta có:
1
3
3
1 1 1
log ( ) log ( ) log ( ) (log log ) (1 log ).
3 3 3
a a a a a a
m ab ab ab a b b
Khi đó:
Cauchy
2 2 2
3
16 8 8 8 8
(log ) (log ) 3. (log ) 12.
log log log log log
a a a
a a a a a
P b b b
b b b b b
Suy ra
min 12P
khi
2
8 1
(log ) log 2 (1 log ) 1.
log 3
a a a
a
b b m b
b
3) Xét các số thực dương
, , x y z
thay đổi sao cho tồn tại các số thực
, , 1a b c
và thỏa mãn
.
x y z
a b c abc
Tìm giá trị lớn nhất của biểu thức
2
16 16
.P x
y z
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 140 -
Lời giải tham khảo
Từ đề bài có:
2 2 2
2 log ( ) 0
2 log ( ) 0
2 log ( ) 0
a
x y z x y z
b
c
x abc
a b c abc a b c abc y abc
z abc
1 1
log ( ) 2 log
2
1 1 1 1 1 1 1 1 16 16 16
log ( ) 2 log 2 2 32
2
1
1
log ( )
2 log
2
a abc
b abc
c
abc
x abc a
x
y abc b
y x y z y z x y z x
z abc
c
z
Khi đó
Cauchy
2 2 2
3
16 8 8 8 8
32 32 32 3 20.
P x x x
x x x x x
Suy ra
max 20.P
4) Cho
, 0x y
thỏa
2
ln ln ln( ).x y x y
Giá trị nhỏ nhất của
x y
bằng bao nhiêu ?
Lời giải tham khảo
Ta có:
2 2 2 2
ln ln ln( ) ln( ) ln( ) ( 1)x y x y xy x y xy x y y x x
( )
Vì
0, 0x y
nên
( )
xảy ra khi
1 0 1.x x
Với
2
1 0
1
x
x y
x
Khi đó:
Cauchy2
1
2( 1) 3 2 2 3.
1 1
x
x y x x
x x
Suy ra
min( ) 2 2 3.x y
5) Cho
, 0x y
thỏa
log( 2 ) log log .x y x y
Tìm giá trị nhỏ nhất của
2 2
4
1 2 1
x y
P
y x
Lời giải tham khảo
Ta có:
log( 2 ) log log log( 2 ) log( )x y x y x y xy
Cauchy
2
1 ( 2 )
2 . .(2 )
2 8
x y
x y xy x y
2 0
2 8.
x y
x y

Khi đó:
Cauchy-Schwarz
2 2 2
(2 ) ( 2 ) 2 2 4 24
( 2 2) 4
1 2 1 ( 2 ) 2 25 2 2 25
x y x y x y
P x y
y x x y x y
Cauchy
4 24 32
10 4
5 25 5
Do đó
32
min
5
P
6) Xét các số thực
,a b
thỏa
1
1.
3
b a
Tìm giá trị nhỏ nhất của
2
3 1
log 12 log 3.
4
a b
a
b
P a
Lời giải tham khảo
Ta có:
2
2
3 1 3 1 12
log 12 log 3 log 3.
4 4
(log 1)
a b a
a
a
b b
P a
b
Mà
3 3 2
3 1
3 1 4 ( 1)(2 1) 0 :
4
b
b b b b b
luôn đúng với
1
3
b
(xem lại pp S.O.S).
Suy ra:
1
1
3 3
3
3 1 3 1
log log .
4 4
a
a a
b b
b b
Do đó:
2 2
12 12
3log 3 3(log 1)
(log 1) (log 1)
a a
a a
P b b
b b
Cauchy
3
2
3 3 12 3 3
(log 1) (log 1) 3. 12 9.
2 2 2 2
(log 1)
a a
a
b b
b
Vậy
min 9.P
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 141 -
7) Cho
, 0x y
thỏa
4 1.xy y
Tìm giá trị nhỏ nhất của
6(2 ) 2
ln
x y x y
P
x y
Lời giải tham khảo
Ta có:
2
2
chia 0
2
1 4 1
4 1 4 2 4 0 4.
y
x x
xy y
y y y y
y
Khi đó:
6(2 ) 2
ln 12 6. ln 2 .
x y x y y x
P
x y x y
Đặt
, (0;4].
x
t t
y
Suy ra
6
( ) 12 ln( 2)
P f t t
t
có
2
6 1
( ) 0 3 21 (0; 4].
2
f t t
t
t
Lập bảng biến thiên, suy ra
27
min min ( ) (4) ln 6.
2
P f t f
8) Cho
, 0a b
thỏa mãn
2 2
3 4b ab a
và
32
[4;2 ].a
Tìm giá trị lớn nhất và giá trị nhỏ nhất của
biểu thức
2
8
3
log 4 log
4 4
b
b
P a
Lời giải tham khảo
Ta có
2 2
3 4b ab a
(đẳng cấp)
2
2
hia 0
1
1 3 4 (do : . 0) 4 .
4
c b
a a a
a b b a
b b b
Do đó:
2 2 2
2 2
2
2
2
log 4 log 2 3 log
3 3
log 4 log log
4 4 log 1 4
log
2
a
a a a
P a a a
a a
Đặt
2
log a x
và do
32
[4;2 ] [2; 32].a x
Khi đó
2 3
( ), [2;32].
1 4
x
P x f x x
x
Ta có:
2
3 3
( ) 0 3 [2;32].
4
( 1)
f x x
x
Tính
11 19 778
(2) , (3) , (32)
2 4 31
f f f
Suy ra
778
max
32
P
và
19
min
4
P
9) Cho hai số thực dương
1, 1a b
và biết phương trình
2
1
. 1
x x
a b
có nghiệm thực. Tìm giá trị
nhỏ nhất của biểu thức
4
log ( )
log
a
a
P ab
b
Lời giải tham khảo
Ta có:
1, 1 log 0.
a
a b b
Lấy lôga cơ số
1a
hai vế của phương trình
2 2
1 1
. 1 log ( . ) log 1
x x x x
a a
a b a b
2
1 2
log log 0 (log ). log 0.
x x
a a a a
a b x b x b
Theo đề, phương trình có nghiệm
log 0
2
(log ) 4 log 0 log 4.
a
b
a a a
b b b
Khi đó:
log
4 4 4 3
log ( ) 1 log log 1
log log 4 log 4
a
a a a
a a a
b
P ab b b
b b b
Cauchy
3
2 4 1 6.
4
Vậy giá trị nhỏ nhất của
P
bằng
6.
Dấu
4
" " log 4 .
a
b b a
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 142 -
Söû duïng f(u) = f(v) hoaëc f(u) > f(v) hoaëc f(u) < f(v) khi hai gaëp hai haøm khaùc loaïi
1) Xét
0, 0x y
thỏa
1
3
log ( 1)( 1) 9 ( 1)( 1).
y
x y x y
Tìm giá trị nhỏ nhất của
2 .x y
Lời giải tham khảo
Ta có
1
3 3
log ( 1)( 1) 9 ( 1)( 1) ( 1)log ( 1)( 1) ( 1)( 1) 9
y
x y x y y x y x y
: ( 1) 0
3 3 3
9 9
log ( 1).( 1) 1 log ( 1) 1 log ( 1)
1 1
y
x y x x x y
y y
3 3 3 3
9 9 9
log ( 1) 1 log 9 log ( 1) log
1 1 1
x x y
y y y
9
( 1)
1
f x f
y
Xét hàm số
3
( ) log , (0; )f t t t t 
có
1
( ) 1 0, 0
ln 3
f t t
t
( ) :f t
đồng biến.
Nên
9 9 8
( 1) 1
1 1 1
y
f x f x x
y y y
Suy ra
Cauchy
8 9 9
2 2 2 1 2( 1) 3 6 2 3.
1 1 1
y
x y y y y
y y y
Vậy
min( 2 ) 6 2 3.x y
2) Cho
, 0x y
thỏa
2
2 log ( ) 8.
x
xy xy x
Tìm giá trị nhỏ nhất của
2
.P x y
Lời giải tham khảo
Ta có:
2 2
2 log ( ) 8 2 log [ ( 1)] 8
x
xy xy x xy x x y
: 2
2 2 2 2
1 4 1 4 1
log log ( 1) log ( 1) log
2 2 2
x
y x y y y x
x x
2 2 2 2 2
1 4 1 1 1 4 1 4
( 1) log ( 1) log 4 log ( 1) log ( 1) log
2 2 2 2 2
y y x y y
x x x
4 4 4
( 1) 1 1.
f y f y y
x x x
Do đó:
Cauchy
3
2 2 2 2
3
4 2 2 2 2
1 1 3 1 3 4 1.
P x y x x x
x x x x x
Vậy giá trị nhỏ nhất của
P
bằng
3
3 4 1.
3) Cho
, 0x y
thỏa
2 2
2 2
2 2
2 log ( 1) log (2 ) 2 2.
y x
x y
Tìm GTLN của
2( ) 1 .
P x y
Lời giải tham khảo
Ta có:
2
2 2 2
22 2 2 2 1
2 2 2 2
2 log ( 1) log (2 ) 2 2 log ( 1) log (2 ) 2 2
y
y x x y
x y x y
2 2
2 1 2 2 2
2 2
2 log ( 1) 2 log [(1 ) 1] ( ) (1 ).
x y
x y f x f y
Do hàm số
2
( ) 2 log ( 1)
t
f t t
luôn đồng biến với
0t
nên
2 2 2 2
( ) 1 1.x y x y
Cauchy-Schwarz
2 2 2 2
2( ) 1 2(1. 1. ) 1 2 (1 1 )( ) 1 2 2.1 1 2 2 1.
P x y x y x y
Vậy giá trị lớn nhất của biểu thức thức
P
là
2 2 1.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 143 -
4) Có bao nhiêu cặp số nguyên
( ; )x y
thỏa mãn
0 2020x
và
2
log (4 4) 1 2 ?
y
x x y
Lời giải tham khảo
Ta có:
2 2 2
log (4 4) 1 2 log 4 log ( 1) 1 2
y y
x x y x x y
2 2
( 1) log ( 1) 2 log 2 ( 1) (2 ) 1 2 2 1
y y y y y
x x f x f x x
0 2020 0
2
0 2 1 2020 2 2 2021 0 log 2021 10,98
x y y
y
Mà
{0;1;2;3;4;5;6;7;8;9;10}y y x
nên có
10
cặp nguyên
( ; )x y
thỏa bài toán.
5) Có bao nhiêu số nguyên
m
để phương trình
2
2
2
2
3 3 1
log 5 2
2 1
x x m
x x m
x x
có hai
nghiệm phân biệt lớn hơn
1.
Lời giải tham khảo
Phương trình đã cho
2
2
log 2
2
2
2
3 3 1
log 5 3
4 2 2
x x m
x x m
x x
2 2 2 2
2 2
log (3 3 1) (3 3 1) log (4 2 2) (4 2 2)x x m x x m x x x x
2 2 2 2
(3 3 1) (4 2 2) 3 3 1 4 2 2f x x m f x x x x m x x
2 2
5 1 0 5
1 ( )
x x m m x
x g x
có
( ) 2 5 0 5/2.g x x x
6) Cho phương trình
2
2
3
2
2
log 4 .
1
x x m
x x m
x
Có bao nhiêu giá trị nguyên của tham số
[ 2018;2018]m
để phương trình có hai nghiệm trái dấu ?
Lời giải tham khảo
PT
2 2
2 2
3 3 3
2 2
2 2
log 3 3 log 3
1 3 3
log
x x m x x m
x x m x x m
x x
2 2 2 2
3 3
log (2 ) (2 ) log (3 3) (3 3)x m x m
x x x x
2 2 2 2 2
) (3 3) 2 3 3 3 0.
(2
x m f x m x x m
f x x x x

Phương trình có hai nghiệm trái dấu
. 0 1.(3 ) 0 3.a c m m
Do
{4;5;6;...;2018}
[ 2018;2018
m
m
có
2018 4
1 2015
1
giá trị nguyên
.m
7) Tính tổng
S
các nghiệm nguyên dương của
2
3 2
2
2
2 6 8
log 9 8 2 0.
4 6
x x
x x x
x x
Bất phương trình
2
2 2
2
2
( 1)(2 6 8)
( 1) (2 6 8) ( 4 6) 0
( 1)( 4 6)
log
x x x
x x x x x
x x x
3 2 3 2 3 2 3 2
2 2
log (2 4 2 (2 4 2 ( 5 ( 5
8) 8) log 10 6) 10 6)
x x
x x x x x x x x x x
Do hàm đặc trưng
2
( ) log
t t
f t
đồng biến nên
3 2 3 2
2 4 2 5
8 10 6
x
x x x x x
3 2
9 8 2 0x x
x
Từ bảng biến thiên, phương trình có hai nghiệm phân biệt lớn
hơn
1
khi
21
3.
4
m
Do
{ 5; 4}.m m
Có
2
giá trị thỏa bài toán.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 144 -
Baøi taäp töông töï vaø môû roäng
47.1 Xét các số thực dương
, , , a b x y
thỏa mãn
1, 1a b
và
.
x y
a b a b
Giá trị nhỏ nhất của
2x y
bằng
A.
4.
B.
2 5.
C.
2 3.
D.
3 2.
47.2 Xét các số thực dương
, , x y z
thay đổi sao cho tồn tại các số thực
, , 1a b c
và thỏa mãn
.
x y z
a b c abc
Giá trị nhỏ nhất của biểu thức
2
2x y z
bằng
A.
6.
B.
1
2
C.
8.
D.
17
2
47.3 Cho các số thực
,x
y
thỏa
4 4
log ( ) log ( ) 1.x y x y
Giá trị nhỏ nhất của
(3 2 ) ex y
bằng
A.
2e 3.
B.
2e.
C.
e 5.
D.
2
e 5
2
47.4 Cho
, 0x y
thỏa mãn
log log(2 ).y xy
Giá trị nhỏ nhất của
1
y
x
thuộc khoảng nào ?
A.
(1;2).
B.
[2;3).
C.
9
3;
2
D.
11
;6
2
47.5 Xét các số thực dương
,x
y
thỏa mãn
2
0,5 0,5 0,5
log log log ( ).x y x y
Giá trị nhỏ nhất của biểu
thức
3P x y
bằng
A.
9.
B.
8.
C.
25 2
4
D.
17
2
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 145 -
47.6 Cho
,x y
là các số thực dương thỏa mãn
2019 2019 201
2
9
l
.
og log log (
)
x
x y
y
Giá trị nhỏ nhất của
biểu thức
2T x y
thuộc khoảng nào sau đây ?
A.
(7; 8).
B.
(6;7).
C.
(5;6).
D.
(8;9).
47.7 Xét các số thực
, x y
thỏa
0 2,x
0y
và
1 1 2
2 2
log (4 2 ) log log 9 0.x y
Giá trị lớn nhất
của
32
31
P y
x
thuộc khoảng nào sau đây ?
A.
1
1;
8
B.
1
;1
8
C.
[1;2).
D.
4
2;
3
47.8 Xét
1, 1a b
và đặt
3
2
log ( ).
a
m a b
Khi biểu thức
2
log ( ) 54 log 2020
a ab
P ab a
đạt giá
trị nhỏ nhất thì
m
thuộc khoảng nào sau đây ?
A.
(1;2).
B.
5
2;
2
C.
[3;4).
D.
5
;3
2
47.9 Cho
, 0x y
thỏa mãn
2
4 6 1.y xy y
Giá trị nhỏ nhất của
3( 2 ) 2
ln
x y x y
P
x y
thuộc khoảng nào sau đây ?
A.
(1;3].
B.
11 13
;
2 2
C.
13
;7 .
2
D.
11
3;
2
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 146 -
47.10 Cho
, 0x y
thỏa
ln(2 ) ln(3 ) ln .x y x y
Giá trị nhỏ nhất của
2 2
4
1 1 2
x y
P
y x
thuộc
khoảng nào sau đây ?
A.
3
0;
2
B.
3
;4 .
2
C.
(4;5].
D.
11
5;
2
47.11 Xét
, 0a b
thỏa mãn
2 2
2 3 .a ab b
Biết giá trị nhỏ nhất của
3
9
1
log (2 ) log
2 27
b
b
P a
có
dạng
min 6
m
P
n
với
m
n
là phân số tối giản. Giá trị của
m n
thuộc khoảng nào ?
A.
(1;4].
B.
(4;8].
C.
(8;10].
D.
(10;20).
47.12 Cho
0 1.b a
Giá trị nhỏ nhất của biểu thức
2
4(3 1)
log 8 log 1
9
a b
a
b
P a
bằng
A.
6.
B.
3
3 2.
C.
8.
D.
7.
47.13 Cho
, a b
thỏa mãn
4
3
a b
và biểu thức
3
2
16 log 3 log
12 16
a a
b
a
P a
b
có giá trị nhỏ nhất.
Khi đó giá trị của
a b
bằng
A.
7
2
B.
4.
C.
11
2
D.
6.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 147 -
47.14 Cho hai số thực
1, 1.a b
Biết phương trình
2
1
. 1
x x
a b
có hai nghiệm phân biệt
1 2
, .x x
Giá
trị nhỏ nhất của biểu thức
2
1 2
1 2
1 2
4( )
x x
P x x
x x
bằng
A.
4.
B.
3
3 2.
C.
3
3 4.
D.
3
4.
47.15 Cho
, , 1.a b c
Biết rằng biểu thức
log ( ) log ( ) 4 log ( )
a b c
P bc ac ab
đạt giá trị nhỏ nhất
bằng
m
khi
log .
b
c n
Tính giá trị
.m n
A.
12.m n
B.
25
2
m n
C.
14.m n
D.
10.m n
47.16 Cho
1, 1.a b
Giá trị nhỏ nhất của biểu thức
4
1 1
log log
ab
ab
S
a b
bằng
A.
4
9
B.
9
4
C.
9
2
D.
1
4
47.17 Xét các số thực
, a b
thỏa
1.a b
Giá trị nhỏ nhất của
2 2
log ( ) 3 log
ba
b
a
P a
b
bằng
A.
19.
B.
13.
C.
14.
D.
15.
47.18 Cho
1 0.a b
Giá trị nhỏ nhất của biểu thức
2 36
log log
a ab
P b a
bằng
A.
19.
B.
16.
C.
13.
D.
11.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 148 -
47.19 Cho hai số thực
, a b
thỏa mãn
2 2
4 1
log (2 8 ) 1.
a b
a b
Khi
4 6 5P a b
đạt giá trị lớn nhất
thì giá trị của
a
b
bằng
A.
8
5
B.
13
2
C.
13
4
D.
17
44
47.20 Cho
0, 1a b
và
.a b a
Giá trị nhỏ nhất của
log 2 log
a
b
b
a
P a
b
bằng
A.
9
2
B.
7.
C.
5.
D.
4.
47.21 Cho
1
, 1.
3
a b
Khi biểu thức
4 2
3
log log ( 9 81)
a b
P b a a
đạt giá trị nhỏ nhất thì tổng
a b
bằng
A.
2
3 9 .
B.
3
9 2 .
C.
2 9 2.
D.
3 3 2.
47.22 Cho
, 0a b
thỏa
5
4 2 5
log 3 4.
a b
a b
a b
Giá trị nhỏ nhất của
2 2
a b
bằng
A.
1
2
B.
1.
C.
3
2
D.
5
2
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 149 -
47.23 Cho
, 0x y
thỏa
3
log 3 .
x y
xy x y
xy
Giá trị nhỏ nhất của
2 2
9
1 3 1
x y
P
y x
bằng
A.
10.
B.
71
7
C.
72
7
D.
73
7
47.24 Cho
, 0x y
là thỏa mãn
2
2
2 1
2 1 log
1
y
x x y
x
Giá trị nhỏ nhất của biểu thức
2 1 2
e 4 2 1
x
P x y
bằng
A.
1
2
B.
1.
C.
1
2
D.
1.
47.25 Xét
, 0x y
thỏa mãn
3
1
log 3 3 4.
3
y
xy x y
x xy
Giá trị nhỏ nhất của
x y
bằng
A.
4 3 4
3
B.
4 3 4
3
C.
4 3 4
9
D.
4 3 4
9
47.26 Cho
, 0x y
thỏa mãn
2
2( 1)
2
2
2018
( 1)
x y
x y
x
Giá trị nhỏ nhất của
2 3y x
bằng
A.
1
2
B.
7
8
C.
3
4
D.
5
6
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 150 -
47.27 Cho
, 0x y
thỏa mãn
2
2 1 2
( 1).2 ( ).2 .
xy x y
xy x y
Giá trị nhỏ nhất của
y
bằng
A.
3
7
B.
2.
C.
9
4
D.
4 3
1.
3
47.28 Cho
,x
0y
thỏa mãn
2 1
2
3
1
xy x y
x y
xy
Giá trị nhỏ nhất của
4x y
bằng
A.
4 3 9.
B.
6 4 3.
C.
2 3 2.
D.
4 3 6.
47.29
Cho
, 0x y
thỏa mãn
3
1
log 3 2 4.
2
xy
xy x y
x y
Giá trị nhỏ nhất của
x y
bằng
A.
9 11 19
9
B.
9 11 19
9
C.
18 11 29
21
D.
2 11 3
3
47.30 Cho
, x y
thỏa mãn điều kiện
1
2 .(3 1) 3 3 1.
x y x y
x y
Giá trị nhỏ nhất của
2 2
P x xy y
bằng
A.
0.
B.
2.
C.
2.
D.
3.
47.31 Cho các số thực
, x y
thỏa mãn đẳng thức
2
3
2 3 log 5
( 4)
3 5 .
x x
y
Giá trị nhỏ nhất của biểu thức
2
4 1 ( 3)
P y y y
bằng
A.
89
4
B.
16.
C.
41
4
D.
8.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 151 -
47.32 Cho
, [1;2]x y
và số thực
m
thỏa mãn
2 2
(9 ) 6 .x m y xy
Tổng giá trị lớn nhất và giá trị
nhỏ nhất của biểu thức
2
2 1 2
4
log log log ( 1)
P x y m
bằng
A.
0.
B.
2.
C.
2
log 7.
D.
2
2 log 3.
47.33 Cho dãy số
( )
n
u
thỏa mãn
1
6,
n n
u u
2n
và
2 5 9
2
log log 8 11.
u u
Đặt
1 2
.
n n
S u u u
Tìm số tự nhiên
n
nhỏ nhất thỏa mãn
20172018.
n
S
A.
2587.
B.
2590.
C.
2593.
D.
2584.
47.34 Cho dãy số
( )
n
u
có số hạng đầu
1
1u
thỏa
2 2 2 2
2 1 2 1 2 2
log (5 ) log (7 ) log 5 log 7
u u
và
1
7
n n
u u
với mọi
1.n
Giá trị nhỏ nhất của
n
để
1111111
n
u
bằng
A.
11.
B.
8.
C.
9.
D.
10.
47.35 Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2 2 sin sinm m x x
có
nghiệm thực ?
A.
0.
B.
1.
C.
2.
D.
3.
47.36 Hỏi có bao nhiêu giá trị nguyên của tham số thực
m
nhỏ hơn
10
sao cho phương trình
e e
x x
m m
có nghiệm thực ?
A.
9.
B.
8.
C.
10.
D.
7.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 152 -
47.37 Có bao nhiêu giá trị nguyên của
m
để
3
3
3 3 sin sinm m x x
có nghiệm ?
A.
7.
B.
3.
C.
5.
D.
2.
47.38 Tìm các giá trị của tham số
m
để phương trình
ln ln( )
m m x x
có nhiều nghiệm nhất.
A.
0.m
B.
1.m
C.
e.m
D.
1.m
47.39 Tìm giá trị lớn nhất của
m
để phương trình
ln[ ln( cos )] cosm m x x
có nghiệm thực ?
A.
e 1
2
B.
e 1.
C.
e.
D.
1.
47.40 Cho hàm số
3
( ) 2 .
m
f x x x
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
( ( ))f f x x
có nghiệm trên
[1;2].
A.
0.
B.
4.
C.
2.
D.
3.
47.41 Cho hàm số
2
2
( ) 5 log .f x x x m
Có bao nhiêu giá trị nguyên của tham số
m
để phương
trình
( ( ))f f x x
có nghiệm không bé hơn
1.
A.
9.
B.
8.
C.
7.
D.
16.
47.42 Cho hàm số
2
( ) e .
x
f x x m m
Có bao nhiêu giá trị nguyên của tham số
m
để phương
trình
2 2
( ( ) )f f x m x m
có nghiệm trên
[0;ln10].
A.
0.
B.
2.
C.
4.
D. Vô số.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 153 -
47.43 Cho hàm số
2
( ) 1 ln .f x x x m
Có bao nhiêu giá trị nguyên của tham số
m
để phương
trình
( ( ))f f x x
có nghiệm trên
[ 3; 3].
A.
0.
B.
5.
C. Vô số.
D.
3.
47.44 Cho hàm số
2
( ) e .
x
f x x m m
Có bao nhiêu giá trị nguyên của tham số
m
để phương
trình
2 2
( ( ) )f f x m x m
có nghiệm trên
[0;ln10].
A.
0.
B.
2.
C.
4.
D. Vô số.
47.45 Có bao nhiêu giá trị nguyên của tham số thực
m
để phương trình
3
3
( )
f f x m x m
có
nghiệm
[1;2],x
biết
5 3
( ) 3 4 .f x x x m
A.
16.
B.
15.
C.
17.
D.
18.
47.46 Tìm các giá trị thực của
m
để phương trình
3
2 3 3 2 2 1
2 ( 6 9 )2 2 1
x m x x x
x x x m
có
một nghiệm duy nhất.
A.
( ;4].m 
B.
[8; ).m 
C.
(4; 8).m
D.
( ;4) (8; ).m  
47.47 Có bao nhiêu số nguyên
m
để phương trình
2
2
2
2
3 3 1
log 5 2
2 1
x x m
x x m
x x
có hai
nghiệm phân biệt lớn hơn
1.
A.
3.
B. Vô số.
C.
2.
D.
4.
47.48 Có tất cả bao nhiêu giá trị nguyên của tham số thực
m
sao cho phương trình
3
log ( ) 2 3 3 1
x
m x m x
có nghiệm thuộc đoạn
[0;2]
?
A.
9.
B.
7.
C.
6.
D.
5.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 154 -
Câu 48. Cho hàm số
( )
1
x m
f x
x
(m
là tham số thực). Gọi
S
là tập hợp tất cả các giá trị của
m
sao
cho
[0;1] [0;1]
max ( ) min ( ) 2.
f x f x
Số phần tử của
S
là
A.
6.
B.
2.
C.
1.
D.
4.
Lôøi giaûi tham khaûo
Khi
1m
hàm số là hàm hằng
( ) 1f x
nên
[0;1] [0;1]
max ( ) min ( ) 1f x f x
thỏa nên nhận
1.m
Khi
1m
hàm số đơn điệu trên đoạn
[0;1]
nên:
Khi
(0); (1)f f
cùng dấu thì
[0;1] [0;1]
1
max ( ) min ( ) (0) (1)
2
m
f x f x f f m
Khi
(0); (1)f f
trái dấu thì
[0;1]
min ( ) 0,
f x
[0;1]
1
max ( ) max (0) ; (1) max ;
2
m
f x f f m
TH1. Cùng dấu, tức
(0). (1) 0 ( 1) 0 1f f m m m
hoặc
0.m
Do đó
[0;1] [0;1]
1
1
max ( ) min ( ) 2 2
5
2
3
m
m
f x f x m
m
(thỏa
1m
hoặc
0).m
TH2. Trái dấu
(0). (1) 0 ( 1) 0 1 0.f f m m m
Do đó
[0;1] [0;1]
2
2
max ( ) min ( ) 2 5
1
2
3
2
m
m
f x f x m
m
m
(không thỏa
1 0).m
Kết luận: Có
2
giá trị
m
thỏa mãn bài toán. Chọn đáp án B.
Baøi toaùn chöùa tham soá trong haøm cuï theå
1) Cho hàm số
3 2
( 1) 1.y x m x m
Tìm tham số
m
sao cho
[0;1]
min 5.y
Lời giải tham khảo
Ta có:
2 2
3 1 0.y x m
Do đó hàm số đã cho luôn đồng biến
[0;1].
[0;1]
min (0)y y
5 1 4.m m
Cần nhớ: Cho hàm số
( )y f x
xác định và liên tục trên đoạn
[ ; ].a b
( )y f x
đồng biến
[ ; ]
[ ; ]
min ( )
.
max ( )
a b
a b
y y a
y y b
( )y f x
nghịch biến
[ ; ]
[ ; ]
min ( )
.
max ( )
a b
a b
y y b
y y a
2) Tìm tham số
m
để hàm số
1mx
y
x m
có
[ 1;2]
min 2.y m
Lời giải tham khảo
Điều kiện:
.x m
Ta có:
2
2
1
0,
( )
m
y x m
x m
Hàm số luôn nghịch biến trên
[ 1;2].
[ 1;2]
2 1
min (2)
2
2
1
[ 1;2]
2
m
y y
m
m
x m
m
x
m
2 2
4 2 1 2 3 0
1 1
2 2
m m m m
m m
m m
3.m
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 155 -
3) Tìm tham số
m
để hàm số
1
x m
y
x
thỏa mãn
[2;4]
min 3.y
Lời giải tham khảo
Điều kiện:
1.x
Ta có:
2
1
( 1)
m
y
x
TH 1. Nếu
0y
1m
[2;4]
1 min 1 3y y
loại.
TH 2. Nếu
0 1y m
Hàm số đồng biến trên đoạn
[2;4].
[2;4]
min (2)y y
3 2 1 :m m
không thỏa.
TH 3. Nếu
0y
1m
Hàm số nghịch biến trên đoạn
[2;4].
[2;4]
min (4)y y
4
3 5 :
3
m
m
thỏa
1.m
Kết luận:
5m
là giá trị cần tìm.
4) Tìm tham số
m
sao cho
2
4
1
m x
y
x
thỏa mãn
[1;3] [1;3]
2 max min 12.y y
Lời giải tham khảo
Điều kiện:
1.x
Ta có
2
2
4
( 1)
m
y
x
TH 1. Nếu
2
4 0 2m m
thì
[1;3] [1;3]
4 min max 4 :y y y
không thỏa.
Do đó
2m
không thỏa mãn.
TH 2. Nếu
2
2
4 0
2
m
m
m
thì hàm số đồng biến trên
[1; 3].
2
[1;3]
4
min (1)
2
m
y y
và
2
[1;3]
3 4
max (3)
4
m
y y
Khi đó theo đề, ta có:
2 2
2
[1;3] [1;3]
3 4 4
2 max min 12 2. 12 12 2 3 :
4 2
m m
y y m m
nhận.
TH 3. Nếu
2
4 0 2 2
m m
thì hàm số nghịch biến trên
[1; 3].
2
[1;3]
3 4
min (3)
4
m
y y
và
2
[1;3]
4
max (1)
2
m
y y
Khi đó theo đề, ta có:
2 2
2
[1;3] [1;3]
4 3 4
2 max min 12 2. 12 36 6 :
2 4
m m
y y m m
loại.
Kết luận:
2 3.m
Baøi toaùn max – min khi ñeà cho ñoà thò hoaëc baûng bieán thieân
1) Cho hàm số
( )y f x
có đồ thị trên
[ 2;3]
như hình vẽ. Gọi
,M m
là giá trị lớn nhất và giá trị
nhỏ nhất của hàm số
2
(3 sin 2).y f x
Tổng
M m
bằng bao nhiêu ?
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 156 -
Lời giải tham khảo
Đặt
2
3sin 2.t x
Với
min max
[ ; ].t t t
Ta có:
2
0 sin 1x
2
0 3 sin 3x
2
2 3 sin 2 5x 2 5.t
Suy ra
[2;5].t
Khi đó
2
(3 sin 2) ( )y f x f t
với
[2;5].t
Dựa vào đồ thị
[2;5]
[2;5]
max 5 khi 3
.
min 2 khi 5
M y t
m y t
Suy ra:
7.M m
2) Cho hàm số
( )f x
liên tục trên
và có đồ thị
( )f x
như hình vẽ. Đặt
2
( ) 2 ( ) ( 1) .g x f x x
Khi
đó giá trị nhỏ nhất của hàm số
( )y g x
trên đoạn
[ 3;3]
bằng
A.
(0).g
B.
(1).g
C.
( 3).g
D.
(3).g
Lời giải tham khảo
Ta có:
( ) 2 ( ) 3( 1) 2 ( ) ( 1)g x f x x f x x
Suy ra
3
( ) 0 ( ) 1 .
1
x
g x f x x
x
Từ bảng biến thiên
[ 3;3]
min ( ) ( 3); (3) .g x g g
Hình vẽ, ta có:
1 2 1 2
2 2S S S S
1 3
3 1
2 ( ) ( 1) d 2 ( 1) ( ) df x x x x f x x
1 3
3 1
( )d ( )dg x x g x x
(1) ( 3) (1) (3)g g g g ( 3) (3)g g
[ 3;3]
min ( ) ( 3).g x g
Giaù trò lôùn nhaát vaø nhoû nhaát cuûa haøm trò tuyeät ñoái
Tìm tất cả các giá trị thực của tham số thực
m
sao cho giá trị lớn nhất của hàm số
3
3
y x x m
trên đoạn
[0;3]
bằng
16.
Lời giải tham khảo
Xét hàm số
3
( ) 3x mf x x
có
2
( ) 3 3 0 1 [0; 3]f x x x
hoặc
1 [0; 3].x
Tính
(0) , (1) 2, (3) 18.f m f m f m
Từ đó có bảng biến thiên như sau:
Suy ra:
[0;3] [0;3]
max max ( ) max 2 ; 18 16y f x m m
2 16
2 16
14
18 16 16 18 16
.
18 16
18 16
2
16 2 16
2 16
m
m
m
m m
m
m
m
m
m
Hình vẽ thêm
khi giải
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 157 -
Baøi taäp töông töï vaø môû roäng
48.1. Tìm tham số
m
để hàm số
1mx
y
x m
đạt giá trị lớn nhất bằng
1
3
trên đoạn
[0;2].
A.
1.m
B.
1.m
C.
3.m
D.
3.m
48.2. Tìm tham số thực
m
để hàm số
5
( )
mx
f x
x m
đạt giá trị nhỏ nhất trên đoạn
[0;1]
bằng
7.
A.
2.m
B.
0.m
C.
1.m
D.
5.m
48.3. Tìm các giá trị của
m
để giá trị nhỏ nhất của hàm số
3 2
3y x x m
trên
[ 1;1]
bằng
0.
A.
4.m
B.
2.m
C.
6.m
D.
0.m
48.4. Cho hàm số
3 2
3 6.y x m x
Tìm tất cả các giá trị thực của tham số
m
sao cho giá trị lớn nhất
của hàm số trên đoạn
[0;3]
bằng
42.
A.
1.m
B.
1.m
C.
1.m
D.
{ 2;1}.m
48.5. Cho hàm số
3 2 2
( 1) .y x mx m m x
Tìm tất cả các giá trị thực của tham số
m
sao cho
giá trị nhỏ nhất của hàm số trên đoạn
[ 1;1]
bằng
6.
A.
2.m
B.
2.m
C.
6.m
D.
1 5.m
48.6. Tìm tất cả các giá trị của tham số thực
m
để giá trị nhỏ nhất của hàm số
3 2
3 6y x mx
trên
đoạn
[0;3]
bằng
2.
A.
2.m
B.
31
27
m
C.
3
2
m
D.
1.m
48.7. Cho hàm số
1
x m
y
x
(m
là tham số thực) thỏa mãn
[1;2]
min 2.y
Mệnh đề nào đúng ?
A.
1.m
B.
1 2.m
C.
2 3.m
D.
3.m
48.8. Cho hàm số
1
x m
y
x
(m
là tham số thực) thỏa mãn
[2;4]
max 3.y
Mệnh đề nào đúng ?
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 158 -
A.
1.m
B.
3 4.m
C.
1 3.m
D.
4.m
48.9. Cho hàm số
2
4
x m
y
x
(m
là tham số thực). Gọi
S
là tập hợp các giá trị
m
thỏa mãn
[ 2;0]
max 4.y
Số phần tử của
S
là
A.
0.
B.
1.
C.
2.
D. Vô số.
48.10. Cho hàm số
2
1
x m
y
x
(m
là tham số thực). Gọi
S
là tập hợp tất cả các giá trị
m
thỏa mãn
[2;4] [2;4]
max min 8.y y
Số phần tử của
S
là
A.
0.
B.
1.
C.
2.
D. Vô số.
48.11. Cho hàm số
2
4
1
m x
y
x
(m
là tham số thực). Gọi
S
là tập hợp tất cả các số nguyên
m
thỏa
mãn
[1;3] [1;3]
2 max min 12.y y
Số phần tử của
S
là
A.
0.
B.
1.
C.
2.
D.
4.
48.12. Cho hàm số
2
4
1
m x
y
x
(m
là tham số thực). Gọi
S
là tập hợp số nguyên
m
thỏa mãn
[1;3] [1;3]
3 max 2 min 4.y y
Số phần tử của
S
là
A.
0.
B.
3.
C.
4.
D.
5.
48.13. Cho hàm số
2
1
x m
y
x
(m
là tham số thực). Gọi
S
là tập hợp tất cả các số thực
m
thỏa mãn
2 2
[ 1;0] [ 1;0]
2(max ) 3(min ) 3.
y y
Số phần tử của
S
là
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 159 -
A.
0.
B.
1.
C.
2.
D.
3.
48.14. Cho hàm số
3
3 1
x m
y
x
(m
là tham số thực) thỏa
[1;6]
min 2.y
Mệnh đề nào đúng ?
A.
3.m
B.
3 2.m
C.
2 3.m
D.
1.m
48.15. Cho hàm số
2
tan 2
tan 1
m x
y
x
với
m
là tham số thực. Số các giá trị
m
thỏa mãn
0;
4
max 3y
là
A.
0.
B.
1.
C.
2.
D.
3.
48.16. Cho hàm số
ln 2
ln 2
x m
y
x
(m
là tham số thực). Gọi
S
là tập hợp các giá trị
m
thỏa
2
[1;e ]
max 1.y
Số phần tử của
S
là
A.
0.
B.
1.
C.
2.
D. Vô số.
48.17. Cho hàm số
( )y f x
xác định và liên tục trên đoạn
[ 3;3].
Gọi
,M m
lần lượt là giá trị lớn nhất
và giá trị nhỏ nhất của hàm số
( ( ))y f f x
trên đoạn
[ 1;0].
Giá trị của
M m
bằng
A.
1.
B.
3.
C.
4.
D.
6.
48.18. Cho hàm số
( )y f x
liên tục trên đoạn
[ 1;3]
và có đồ thị như hình bên. Gọi
M
và
m
lần lượt
là giá trị lớn nhất và nhỏ nhất của hàm số
( ( ))y f f x
trên đoạn
[ 1;0].
Giá trị
M m
bằng
A.
2.
B.
3.
C.
4.
D.
5.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 160 -
48.19. Cho hàm số
( )y f x
xác định, liên tục trên đoạn
[ 2;2]
và có đồ thị là đường cong trong hình
vẽ bên dưới. Gọi
, M m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số
( ( ))y f f x
trên đoạn
[ 1;1].
Giá trị của
M m
bằng
A.
2.
B.
4.
C.
6.
D.
8.
48.20. Cho hàm số
( )y f x
xác định, liên tục trên đoạn
[ 5;3]
và có đồ thị như hình vẽ bên dưới. Gọi
, M m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số
( ( ))y f f x
trên đoạn
[ 4;0].
Giá trị
của
M m
bằng
A.
3.
B.
7.
C.
4.
D.
6.
48.21. Cho hàm số
( )y f x
liên tục trên
và có đồ thị như hình. Gọi
,M m
lần lượt là giá trị lớn nhất
và giá trị nhỏ nhất của hàm số
( (sin ))y f f x
trên đoạn
[0; ].
Giá trị của
M m
bằng
A.
1.
B.
3.
C.
4.
D.
2.
48.22. Cho hàm số
( )y f x
liên tục trên
và có đồ thị như hình. Gọi
,M m
lần lượt là giá trị lớn nhất
và giá trị nhỏ nhất của hàm số
2
( (log ))y f f x
trên đoạn
[2;4].
Giá trị của
M m
bằng
A.
1.
B.
3.
C.
5.
D.
8.
48.23. Cho hàm số
( ).y f x
Đồ thị
( )y f x
như hình bên dưới. Giá trị nhỏ nhất và giá trị lớn nhất
của hàm số trên đoạn
[0;3]
lần lượt là
A.
(1), (0).f f
B.
(2), (0).f f
C.
(1), (3).f f
D.
(0), (3).f f
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 161 -
48.24. Cho
( )y f x
có đồ thị của
( )y f x
như hình vẽ dưới. Đặt
[ 2;6] [ 2;6]
max ( ), min ( ).M f x m f x
Giá
trị của biểu thức
P M m
bằng
A.
(0) (2).f f
B.
(5) ( 2).f f
C.
(5) (6).f f
D.
(0) ( 2).f f
48.25. Cho hàm số
4 3 2
( ) ,f x ax bx cx dx e
biết hàm số
( )y f x
có đồ thị
( )C
như hình vẽ
và diện tích của hình phẳng giới hạn bởi
( )C
và trục hoành bằng
27.
Gọi
, M m
lần lượt là giá
trị lớn nhất và giá trị nhỏ nhất của hàm số
( )y f x
trên đoạn
[ 3;3].
Giá trị của
M m
bằng
A.
27.
B.
36.
C.
48.
D.
75.
48.26. Cho hàm số
5 4 3 2
( )f x x bx cx dx ex
với
, , , .b c d e
Hàm số
( )y f x
có đồ thị
như hình vẽ. Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )y f x
trên đoạn
[ 1;3].
Giá trị của tổng
M m
bằng
A.
63.
B.
21.
C.
196
3
D.
272
3
48.27. Cho hàm số
( )y f x
xác định, liên tục trên
và
(2) 0.f
Hàm số
( )y f x
có đồ thị như hình
vẽ bên dưới. Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( ) ( )g x f x
trên trên đoạn
[ 1;3].
Giá trị của
M
và
m
lần lượt là
A.
( 1), (3).M f m f
B.
(3) , ( 1) .M f m f
C.
( 1) , (2) .M f m f
D.
( 1) , (3) .M f m f
48.28. Cho hàm số
3 2
( )f x ax bx cx d
có đồ thị
( ).C
Biết đồ thị
( )C
tiếp xúc với đường thẳng
4y
tại điểm có hoành độ âm và đồ thị của hàm số
( )y f x
như hình vẽ bên dưới. Giá trị lớn
nhất của hàm số
( )y f x
trên
[0;3]
bằng
A.
20.
B.
60.
C.
22.
D.
3.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 162 -
48.29. Cho hàm số
3 2
( ) 3 .f x x x
Gọi
, M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm
số
( ) (1 2 sin ) 1 .
g x f x
Giá trị của biểu thức
M m
bằng
A.
3.
B.
1.
C.
2.
D.
4.
48.30. Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho giá trị nhỏ nhất của hàm số
3 2
3
y x x m
trên đoạn
[1; 3]
bằng
3.
Tổng tất cả các phần tử của
S
bằng
A.
3.
B.
2.
C.
4.
D.
7.
48.31. Có bao nhiêu giá trị của
m
để giá trị lớn nhất của hàm số
4 2
8
y x x m
trên đoạn
[ 1;3]
bằng
2018
?
A.
0.
B.
2.
C.
4.
D.
6.
48.32. Gọi
S
là tập hợp tất cả các giá trị của tham số thực
m
sao cho giá trị lớn nhất của hàm số
2
sin 2 sin
y x x m
bằng
1.
Số phần tử của
S
là
A.
0.
B.
1.
C.
4.
D.
3.
48.33. Gọi
S
là tập hợp tất cả các giá trị của tham số thực
m
sao cho giá trị lớn nhất của hàm số
2
ln ln
y x x m
trên đoạn
[1;e]
bằng
2.
Số phần tử của
S
là
A.
1.
B.
2.
C.
4.
D.
6.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 163 -
48.34. Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho giá trị lớn nhất của hàm số
2
( )
1
x mx m
f x
x
trên đoạn
[1;2]
bằng
2.
Tổng tất cả các phần tử của
S
bằng
A.
11
3
B.
13
6
C.
11
6
D.
1
3
48.35. Có bao nhiêu giá trị của tham số
m
để giá trị lớn nhất của hàm số
( 1) 1
1
m x m
y
x
trên
đoạn
[ 3; 2]
bằng
1
2
A.
1.
B.
2.
C.
0.
D.
6.
48.36. Cho hàm số
2
( )
2
x m
f x
x
(m
là tham số thực). Gọi
S
là tập hợp tất cả các giá trị của
m
sao
cho
[0;2] [0;2]
max ( ) min ( ) 4.
f x f x
Số phần tử của
S
là
A.
0.
B.
2.
C.
3.
D.
4.
48.37. Cho hàm số
( )
2
x m
f x
x
(m
là tham số thực). Gọi
S
là tập hợp tất cả các giá trị của
m
nguyên
thuộc
[ 10;10]
sao cho
[0;1] [0;1]
max ( ) min ( ) 2.
f x f x
Số phần tử của
S
là
A.
18.
B.
8.
C.
10.
D.
19.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 164 -
48.38. Cho hàm số
3 2
( ) 3 .f x x x m
Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho
[1;3] [1;3]
max ( ) 2 min ( ) .f x f x
Số phần tử của
S
là
A.
2.
B.
3.
C.
4.
D.
1.
48.39. Cho hàm số
4 2
( ) 2f x x x m
với
m
là tham số. Gọi
S
là tập hợp tất cả các giá trị của
m
nguyên thuộc đoạn
[ 10;10]
sao cho
[0;2] [0;2]
max ( ) 3 min ( ) .f x f x
Số phần tử của
S
là
A.
5.
B.
4.
C.
6.
D.
3.
48.40. Cho hàm số
3 2
( ) 3 2 1f x x x m
(m
là tham số thực). Gọi
S
là tập hợp tất cả các giá trị
của
m
sao cho
[1;3] [1;3]
max ( ) min ( ) 10.
f x f x
Số các giá trị nguyên của
S
thuộc đoạn
[ 30;30]
là
A.
56.
B.
61.
C.
55.
D.
57.
48.41. Cho hàm số
2
( ) 2( 1) 2 1.f x x m x m
Gọi
S
là tập hợp tất cả các giá trị của tham số
m
sao cho
[0;4] [0;4]
max ( ) min ( ) 8.
f x f x
Số phần tử của
S
là
A.
0.
B.
2.
C.
3.
D.
1.
48.42. Cho hàm số
4
( ) .
1
x mx m
f x
x
Số giá trị nguyên của
m
để
[1;2] [1;2]
max ( ) 2 min ( ) 0
f x f x
là
A.
15.
B.
14.
C.
13.
D.
12.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 165 -
Câu 49. Cho hình hộp
.ABCD A B C D
có chiều cao bằng
8
và diện tích đáy bằng
9.
Gọi
, , M N P
và
Q
lần lượt là tâm của các mặt bên
, , ABB A BCC B CDD C
và
.DAA D
Thể tích của
khối đa diện lồi có các đỉnh là các điểm
, , , , , , A B C D M N P
và
Q
bằng
A.
27.
B.
30.
C.
18.
D.
36.
Lôøi giaûi tham khaûo
Ta có
.
9.8 72.
ABCD A B C D
V
Gọi
, , , I J K L
là trung điểm các cạnh
, , , .AA BB CC DD
Suy ra
.
36.
ABCD IJKL
V
Do hình chóp
.AMIQ
đồng dạng với hình chóp
.A B A D
theo tỉ số
1
2
nên
. .
1 1 1 9 3
. .8.
8 8 3 2 2
A MQI A B A D
V V
Do đó
. . .
3
4 36 4. 30.
2
ABCD MNPQ ABCD IJKL A MIQ
V V V
Chọn đáp án D.
1. Cho hình chóp
.S ABC
có thể tích bằng
.V
Gọi
G
là trọng tâm tam giác
.SBC
Mặt phẳng
( )
đi qua hai điểm
, A G
và song song với
.BC
Mặt phẳng
( )
cắt các cạnh
, SB SC
lần lượt tại
các điểm
M
và
.N
Thể tích khối chóp
.S AMN
bằng
A.
9
V
B.
2
V
C.
4
9
V
D.
4
V
Vì
2
3
SM SN SG
MM BC
SB SC SE
Nên
2 2 4
3 3 9
SAMN
SABC
V
SA SM SN
V SA SB SC
Suy ra
.
4
9
S AMN
V
V
Chọn đáp án D.
2. Cho hình chóp tứ giác
.S ABCD
có thể tích bằng
.V
Lấy điểm
A
trên cạnh
SA
sao cho
3 .SA SA
Mặt phẳng qua
A
và song song với đáy của hình chóp cắt các cạnh
,SB
,SC
SD
lần lượt tại
, , .B C D
Thể tích khối chóp
.S A B C D
bằng
A.
3
V
B.
81
V
C.
9
V
D.
27
V
Ta có:
3
.
.
1 1
3 27
S A B C
S ABC
V
SA SB SC
V SA SB SC
Tương tự:
.
.
1
27
S A D C
S ADC
V
SA SD SC
V SA SD SC
Mà
. . .S A B C D S A B C S A C D
V V V
. . .
1 1
( )
27 27 27
S ABC S ACD S ABCD
V
V V V
Chọn D.
D'
C'
B'
A
D
B
C
S
A'
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 166 -
3. Cho khối hộp
.ABCD A B C D
có thể tích bằng
2018.
Gọi
M
là trung điểm của cạnh
.AB
Mặt
phẳng
( )MB D
chia khối chóp
.ABCD A B C D
thành hai khối đa diện. Thể tích phần khối đa
diện chứa đỉnh
A
bằng
A.
5045
6
B.
7063
6
C.
10090
17
D.
7063
12
Gọi
, .BM AA E ED AD N
Ta có
M
trung điểm
AB M
trung điểm
.EB
N
là trung điểm của
ED
và
.AD
Khi đó:
.
.
1
8
E AMN
E A B D
V
EA EM EN
V EA EB ED
. . .
7 7 1
.2. .
8 8 2
AMN A B D E A B D A A B D
V V V
.
7 7063
24 12
ABCD A B C D
V
Chọn đáp án D.
Baøi taäp töông töï vaø môû roäng
49. 1 Cho hình lập phương
ABCDA B C D
có cạnh bằng
.a
Gọi
M
là trung điểm của
,CD
N
là
trung điểm của
.A D
Thể tích của tứ diện
MNB C
bằng
A.
3
3
a
B.
3
6
a
C.
3
4
a
D.
3
2
5
a
49. 2 Cho khối tứ diện đều
ABCD
có thể tích là
.V
Gọi
,M
,N
,P
Q
lần lượt là trung điểm của
,AC
,AD
,BD
.BC
Thể tích khối chóp
BMNPQ
bằng
A.
6
V
B.
3
V
C.
4
V
D.
2
3
V
49. 3 Cho hình lăng trụ
. .ABC A B C
Gọi
,M
,N
P
lần lượt là các điểm thuộc các cạnh
,AA
,BB
CC
sao cho
2 ,AM MA
2 ,NB NB
.PC PC
Gọi
1
,V
2
V
lần lượt là thể tích của hai khối
đa diện
ABCMNP
và
.A B C MNP
Tính tỉ số
1
2
V
V
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 167 -
C
C
B
B
A
A
Q
P
N
M
I
A.
1
2
2.
V
V
B.
1
2
1
2
V
V
C.
1
2
1.
V
V
D.
1
2
2
3
V
V
49. 4 Cho khối chóp
.S ABCD
có đáy là hình bình hành
.ABCD
Gọi
,M
,N
,P
Q
lần lượt là trọng
tâm các tam giác
,SAB
,SBC
,SCD
.SDA
Biết thể tích khối chóp
.S MNPQ
là
,V
khi đó thể tích
của khối chóp
.S ABCD
bằng
A.
27
4
V
B.
2
9
.
2
V
C.
9
4
V
D.
81
8
V
49. 5 Cho hình tứ diện
ABCD
có
12, 10.AB CD AD
Gọi
, M N
lần lượt là trung điểm của
, .AB CD
Biết rằng
MN
vuông góc với
AB
và
CD
đồng thời
8.MN
Thể tích khối tứ diện
ABCD
bằng
A.
96 3.
B.
96.
C.
96 2.
D.
192.
49. 6 Cho khối lăng trụ
.ABC A B C
có thể tích bằng
1.
Gọi
,M
N
lần lượt là trung điểm của các
đoạn thẳng
AA
và
.BB
Đường thẳng
CM
cắt đường thẳng
C A
tại
,P
đường thẳng
CN
cắt
đường thẳng
C B
tại
.Q
Thể tích khối đa diện lồi
A MPB NQ
bằng
A.
1.
B.
1
3
C.
1
2
D.
2
3
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 168 -
C'
49. 7 Cho khối lăng trụ
.ABC A B C
có thể tích bằng
2.
Gọi
M
là trung điểm của
AA
và
N
là điểm
nằm trên cạnh
BB
sao cho
2 .BN B N
Đường thẳng
CM
cắt đường thẳng
C A
tại
,P
đường
thẳng
CN
cắt đường thẳng
C B
tại
.Q
Thể tích của khối đa diện
A MPB NQ
bằng
A.
7
9
B.
5
9
C.
2
3
D.
13
9
49. 8 Cho hình lăng trụ
.ABC A B C
có thể tích bằng
.V
Gọi
M
là trung điểm cạnh
,BB
điểm
N
thuộc cạnh
CC
sao cho
2 .CN C N
Thể tích khối chóp
.ABCNM
bằng
A.
7
12
V
B.
7
18
V
C.
5
18
V
D.
3
V
49. 9 Cho khối hộp
.ABCD A B C D
có thể tích
.V
Điểm
E
thỏa
3 .AE AB
 
Thể tích của khối đa
diện gồm các điểm chung của khối hộp và khối chóp
.E ADD
bằng
A.
4
27
V
B.
2
V
C.
19
54
V
D.
25
54
V
49. 10 Cho khối lập phương
.ABCD A B C D
cạnh
.a
Các điểm
, E F
lần lượt là trung điểm của
C B
và
.C D
Mặt phẳng
( )AEF
cắt khối lập phương đã cho thành hai phần, gọi
1
V
là thể tích khối
chứa điểm
A
và
2
V
là thể tích khối chứa điểm
.C
Khi đó
1
2
V
V
bằng
A.
25
47
B.
1.
C.
8
17
D.
17
25
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 169 -
S
N
M
A
C
B
A'
B'
C'
49. 11 Cho lăng trụ đều
.ABC A B C
có độ dài tất cả các cạnh bằng
3.
Gọi
, M N
là trung điểm của
hai cạnh
AB
và
.AC
Thể tích của khối đa diện
AMNA B C
bằng
A.
34 3
12
B.
21 3
5
C.
63 3
16
D.
45 3
16
49. 12 Cho lăng trụ
.ABC A B C
có thể tích bằng
2.
Gọi
, M N
lần lượt là hai điểm nằm trên hai cạnh
AA
và
BB
sao cho
M
là trung điểm của
AA
và
3 2 .B N BB
Đường thẳng
CM
cắt đường
thẳng
A C
tại
P
và đướng thẳng
CN
cắt đường thẳng
B C
tại
.Q
Thể tích khối đa diện lồi
A MPB NQ
bằng
A.
13
18
B.
23
9
C.
5
9
D.
7
18
49. 13 Cho khối hộp
.ABCD A B C D
có thể tích bằng
2018.
Gọi
M
là trung điểm của cạnh
.AB
Mặt
phẳng
( )MB D
chia khối chóp
ABCDA B C D
thành hai khối đa diện. Thể tích phần khối đa
diện chứa đỉnh
A
bằng
A.
5045
6
B.
7063
6
C.
10090
17
D.
7063
12
49. 14 Cho hình lập phương
.ABCD A B C D
cạnh
.a
Gọi
M
là trung điểm của
, BC N
thuộc cạnh
CD
thỏa
1
3
CN
CD
Mặt phẳng
( )A MN
chia khối lập phương thành hai khối, gọi
( )H
là khối
chứa điểm
.A
Thể tích của khối ( )H bằng
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 170 -
C'
B
S
I
M
P
N
C'
B'
D'
C
A
D
B
A'
Q
P
N
M
A
B
D
C
S
A.
3
53
137
a
B.
3
55
144
a
C.
3
47
154
a
D.
3
65
113
a
49. 15 Cho hình hộp chữ nhật
. .ABCD A B C D
Gọi
, , M N P
lần lượt là trung điểm của
,BC
, .C D DD
Biết thể tích của khối hộp chữ nhật đó bằng
226,
thể tích của khối đa diện
AMNP
bằng
A.
113
3
B.
117
4
C.
113
4
D.
117
3
49. 16 Cho khối lăng trụ
.ABC A B C
có góc giữa hai mặt phẳng
( )ABB A
và
( )ACC A
là
60
và
14
2
AA
Tính
.
,
ABC A B C
V
biết
( , ) 1d A BB
và
( , ) 2.d A CC
A.
43
6
B.
43
3
C.
42
6
D.
42
3
49. 17 Cho khối chóp tứ giác
.S ABCD
có thể tích
,V
đáy
ABCD
là một hình bình hành. Gọi
, , , M N P Q
lần lượt là trung điểm các cạnh
, , , .SB BC CD DA
Tính thể tích khối chóp
.M CNQP
theo
.V
A.
3
8
V
B.
3
4
V
C.
16
V
D.
3
16
V
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 171 -
I
O
D'
C'
B'
C
D
B
A
S
49. 18 Cho khối chóp
.S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
, 2 .a SA a
Hai mặt phẳng
( )SAB
và
( )SAD
cùng vuông góc với
( ).ABCD
Một mặt phẳng
( )P
qua
A
và vuông góc
,SC
cắt các cạnh
, , SB SC SD
lần lượt tại
, , .B C D
Gọi
1
V
và
2
V
lần lượt là thể tích của khối chóp
.S AB C D
và khối đa diện
. .ABCD D C B
Tỉ số
1
2
V
V
bằng
A.
8
15
B.
8
7
C.
32
13
D.
1
2
49. 19 Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành và có thể tích
.V
Điểm
P
là trung
điểm của
,SC
một mặt phẳng qua
AP
cắt hai cạnh
SD
và
SB
lần lượt tại
M
và
.N
Gọi
1
V
là
thể tích khối chóp
. .S AMPN
Giá trị lớn nhất của
1
V
V
thuộc khoảng
A.
1
0;
5
B.
1 1
;
5 3
C.
1 1
;
3 2
D.
1
;1
2
49. 20 Cho khối chóp
.S ABCD
có đáy là hình bình hành thể tích bằng
1.
Gọi
M
là điểm đối xứng của
C
qua
, B N
là trung điểm cạnh
.SC
Mặt phẳng
( )MDN
chia khối chóp
.S ABCD
thành hai
khối đa diện, thể tích của khối đa diện chứa đỉnh
S
bằng
A.
5
6
B.
7
12
C.
5
8
D.
12
19
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 172 -
49. 21 Cho khối chóp
.S ABCD
có đáy là hình bình hành, thể tích bằng
1.
Gọi
M
là trung điểm cạnh
,SA
các điểm
, E F
lần lượt là điểm đối xứng của
A
qua
B
và
.D
Mặt phẳng
( )MEF
cắt các
cạnh
, SB SD
lần lượt tại các điểm
, .N P
Thể tích của khối đa diện
ABCDMNP
bằng
A.
2
3
B.
1
3
C.
3
4
D.
1
4
49. 22 Cho tứ diện
,ABCD
trên các cạnh
,BC
,BD
AC
lần lượt lấy các điểm
,M
,N
P
sao cho
3 ,BC BM
2 3BD BN
và
2 .AC AP
Mặt phẳng
( )MNP
chia khối tứ diện
ABCD
thành
hai phần có thể tích là
1
,V
2
.V
Tỉ số
1
2
V
V
bằng
A.
26
19
B.
3
19
C.
15
19
D.
26
13
49. 23 Cho hình chóp
.S ABCD
có đáy là hình bình hành. Gọi
, , , M N P Q
lần lượt là trọng tâm của
các tam giác
, , , .SAB SBC SCD SDA
Gọi
O
là điểm bất kỳ trên mặt phẳng đáy
.ABCD
Biết thể
tích khối chóp
OMNPQ
bằng
.V
Tính thể tích khối chóp
. .S ABCD
A.
27
.
8
V
B.
27
.
2
V
C.
9
.
4
V
D.
27
.
4
V
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 173 -
Câu 50. Có bao nhiêu số nguyên
x
sao cho tồn tại số thực
y
thỏa mãn
2 2
3 4
?
l o (og (
l g
)
)x y x y
A.
3.
B.
2.
C.
1.
D. Vô số.
Lôøi giaûi tham khaûo
Đặt
2 2
2 2
3 4
3
log ( ) log .
( )
4
t
t
x y
x y x y t
x y
Áp dụng bất đẳng thức Cauchy Schwarz
2 2 2 2
( )( )ax by a b x y
và dấu
" "
khi
,
x y
a b
được:
2
2 2 2 2
3
2
3 1
3 1. 1. (1 1 )( ) 2.4 9 2.4 2 log 2.
2 2
t
t t t t
x y x y t
Do đó
3
2
1
log 2
2
2 2 2
4 4 4 1, 89 1 ., {, }37 1 37 1;0;1
xt t
x y x x x
Thử lại:
Với
2
3 0
0
1
4
t
t
y t
x
y
y
(thỏa).
Với
2
3 1 0
1
0
4 1
t
t
y t
x
y
y
(thỏa).
Với
2 2
2
0
3 1
1 5
3 1 2
1 4 1
t
t
t
t
y
x x y
y
y
mâu thuẫn
3
2
o
2 2
l g 2
4x y
(loại)
Vậy có hai giá trị
{ }.0;1x
Chọn đáp án D.
Baøi taäp töông töï vaø môû roäng
50. 1 Có bao nhiêu số nguyên
y
để tồn tại số thực
x
thỏa mãn
2 2
3 2
log ( 2 ) log ( )x y x y
?
A.
3.
B.
2.
C.
1.
D. Vô số.
50. 2 Cho
, x y
là các số thực thỏa mãn
2
log (2 2) 3 8 .
y
x x y
Biết
0 2018,x
số cặp
( ; )x y
nguyên thỏa mãn đẳng thức là
A.
2.
B.
3.
C.
4.
D.
5.
50. 3 Có bao nhiêu cặp số nguyên
( ; )x y
thỏa mãn các điều kiện
0 2020,x
1 2020y
và
1
2 2
4 log ( 3) 16.2 log (2 1)
x y
y x
?
A.
2019.
B.
2020.
C.
1010.
D.
1011.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 174 -
50. 4 Có bao nhiêu cặp số nguyên dương
( ; )x y
thỏa
2020x
và
3 3
2
log 8 2 1
x
x x y y
y
?
A.
1010.
B.
2020.
C.
2019.
D.
1011.
50. 5 Có bao nhiêu cặp số nguyên
( ; )x y
thỏa
2020x
và
2
2
log 3( 1)
2 1
y
y x y x
x
?
A.
1010.
B.
44.
C.
2020.
D.
1011.
50. 6 Cho phương trình
2
2 2 2
2
log (2 4 4) 2 2 1.
y
x x y x x
Hỏi có bao nhiêu cặp số nguyên
dương
( ; )x y
và
0 100x
thỏa mãn phương trình đã cho ?
A.
4.
B.
3.
C.
1.
D.
2.
50. 7 Có bao nhiêu cặp số nguyên
( ; )x y
thoả mãn
0 2020y
và
3
3
3 3 6 9 log
x
x y y
?
A.
9.
B.
7.
C.
8.
D.
2019.
50. 8 Có bao nhiêu cặp số nguyên dương
( ; )x y
thoả mãn
0 2020x
và
( 1).3 .27
x y
x y
?
A.
2020.
B.
673.
C.
672.
D.
2019.
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 175 -
50. 9 Xét các số thực dương
, x y
thỏa mãn
3
3
3(3 ) log 3.
y
y x x
Giá trị nhỏ nhất của biểu thức
2
9
logy x
bằng
A.
7
16
B.
7
16
C.
9
16
D.
9
16
50. 10 Xét các số thực dương
, x y
thỏa mãn
2
log (4 16) 3 8 2
y
x x y
. Gọi
o o
( ; )x y
là cặp
( ; )x y
khi biểu thức
2
3 1 8
y
P x x
đạt giá trị nhỏ nhất. Giá trị của
3
o o
3x y
bằng
A.
9.
B.
7.
C.
7.
D.
9.
50. 11 Có bao nhiêu giá trị nguyên của tham số thực
m
để tồn tại cặp số
( ; )x y
thỏa mãn đồng thời
3 5 3 1
e e 1 2 2
x y x y
x y
và
2 2
3 3
log (3 2 1) ( 6)log 9 0 ?
x y m x m
A.
6.
B.
5.
C.
7.
D.
8.
50. 12 Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
để tồn tại duy nhất cặp
( ; )x y
thỏa mãn
đồng thời các điều kiện
2 2
2
log (4 4 4) 1
x y
x y
và
2 2
2 2 2 0.x y x y m
Tổng các
phần tử của
S
bằng
A.
33.
B.
24.
C.
15.
D.
5.
50. 13 Biết trong tất cả các cặp
( ; )x y
thỏa mãn
2 2
2 2
log ( 2) 2 log ( 1)
x y x y
chỉ có duy nhất
một cặp
( ; )x y
thỏa mãn
3 4 0.x y m
Tổng các giá trị của tham số
m
bằng
A.
20.
B.
46.
C.
28.
D.
14.
| 1/51
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789  5
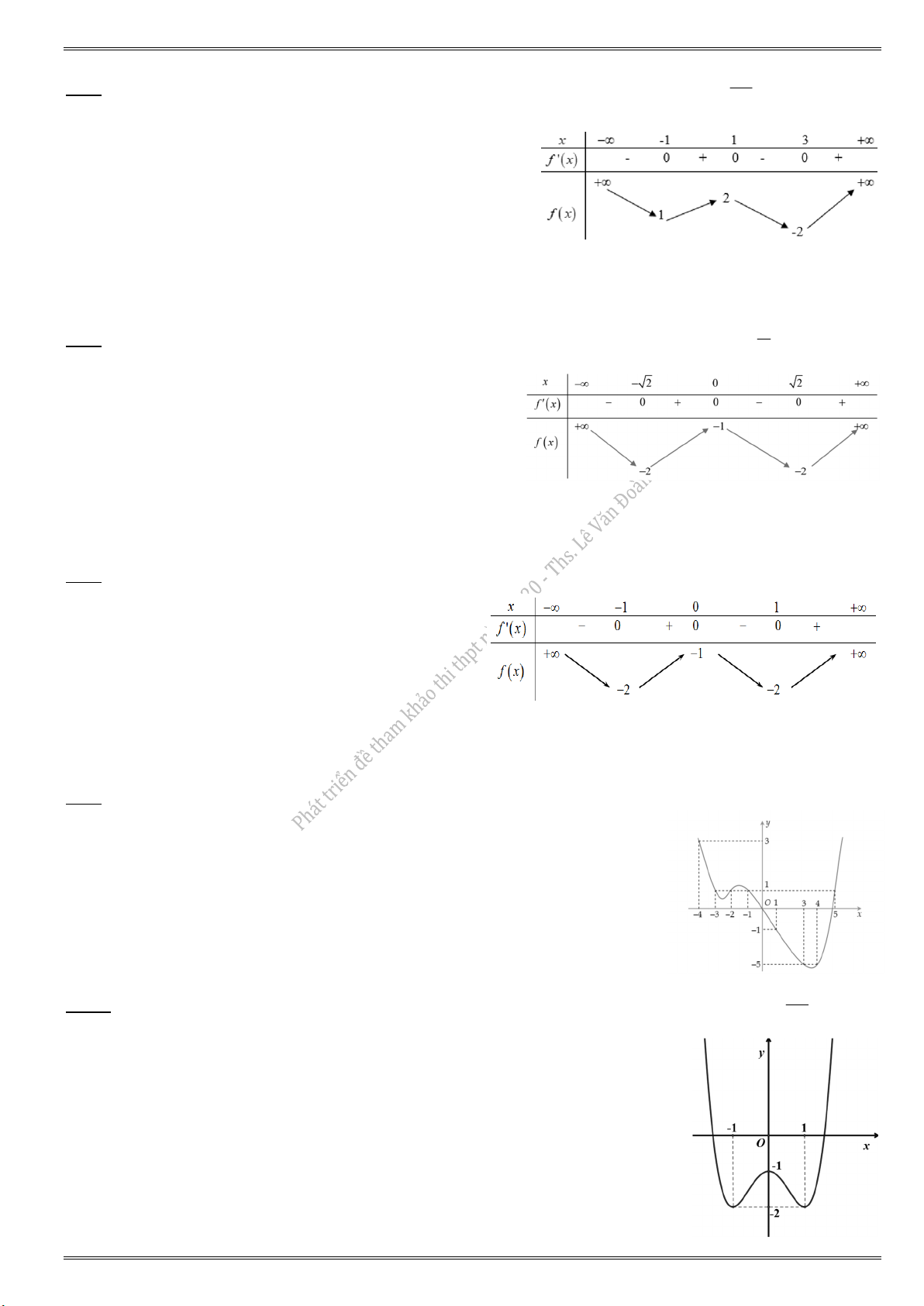
Câu 46. Cho hàm số f (x) có bảng biến thiên bên dưới. Số nghiệm thuộc đoạn 0;   của phương 2   
trình f (sin x)  1 là A. 7. B. 4. C. 5. D. 6.
Lôøi giaûi tham khaûo    k 3 5   Đặt 0; 1; 2..
t  sin x t  cos x, t  0  cos x  0  x   k        x   ; ;    5 2 x 0;   2 2 2   2      x 3 5   0  t  1   2 2 2  : cho 0 nghiệm x. t  1  t   0  0 
t  1 : cho 1 nghiệm x. 1 1 t  1  t  : x cho 2 nghiệm . 0  t  (1; 0)  1
t  [0;1) : cho 3 nghiệm x.
Phương trình f (t)  1 và nhìn lên bảng biến thiên đề:
x a  1 : 0 nghiệm x.
x b  ( 1
 ;0) : 2 nghiệm x.
x c  (0;1) : 3 nghiệm x. y  1
x d  0 : 0 nghiệm x.
Vậy có 5 nghiệm x. Chọn đáp án C.
Bieän luaän nghieäm döïa vaøo baûng bieán thieân hoaëc ñoà thò haøm f(x)
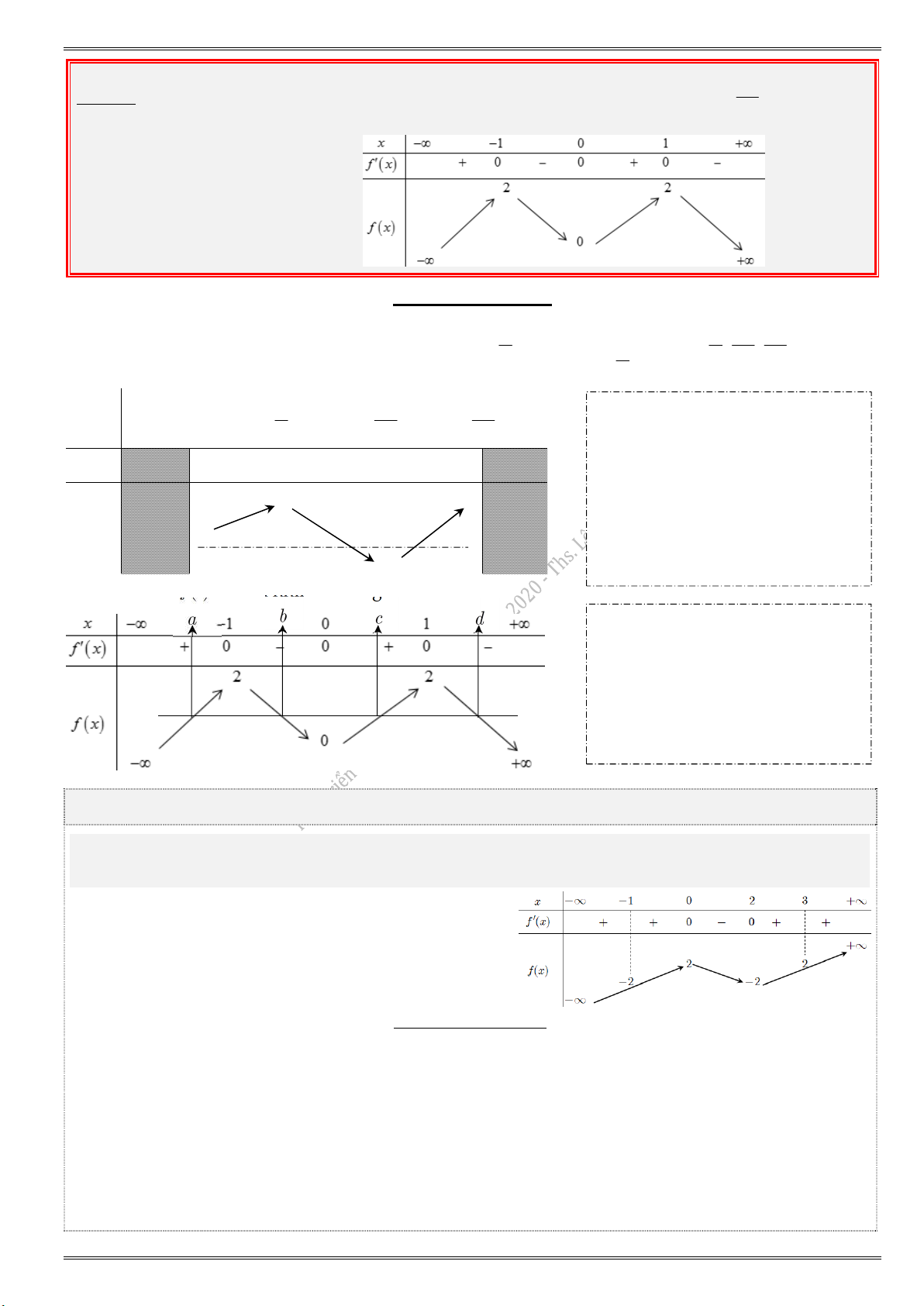
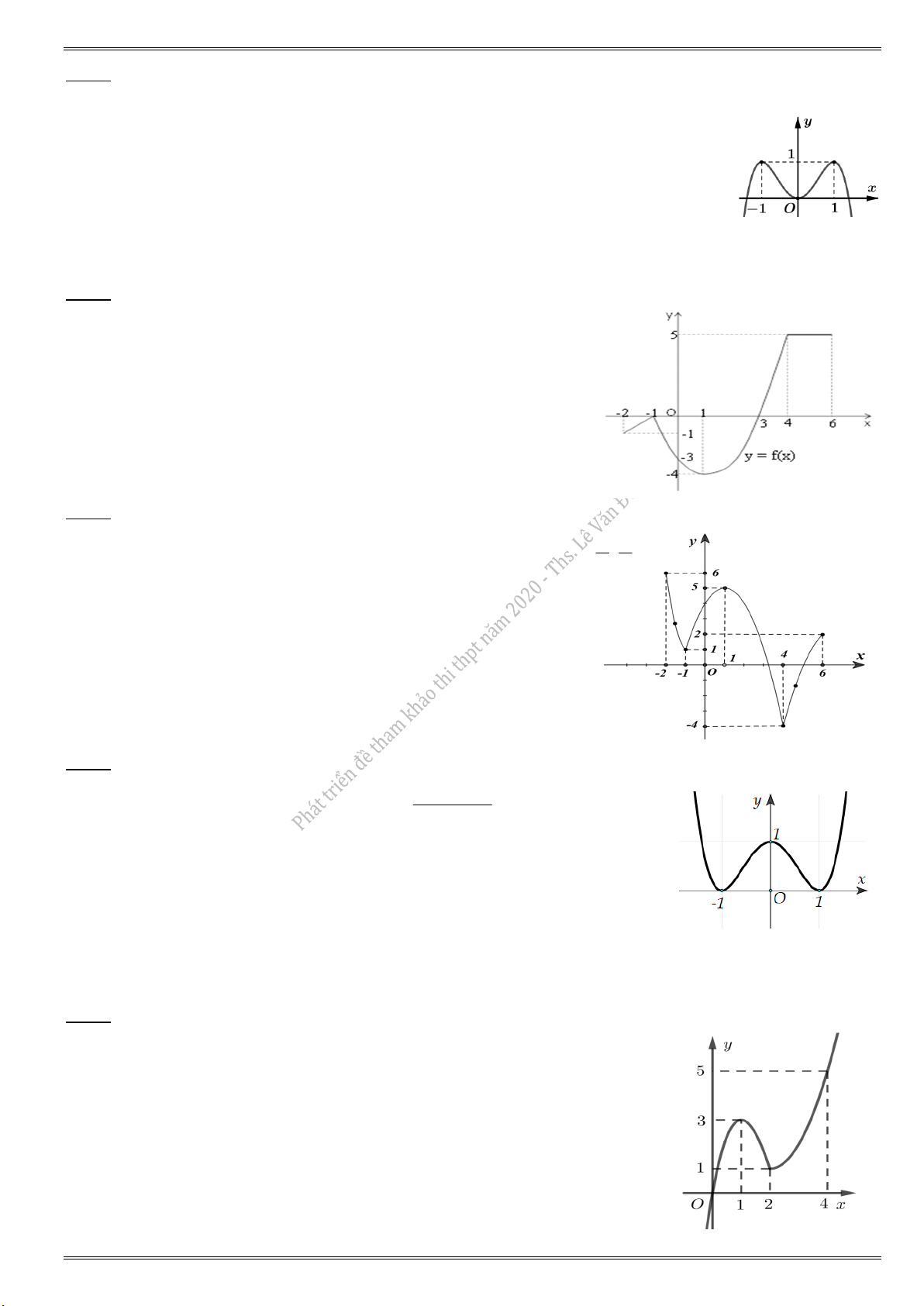
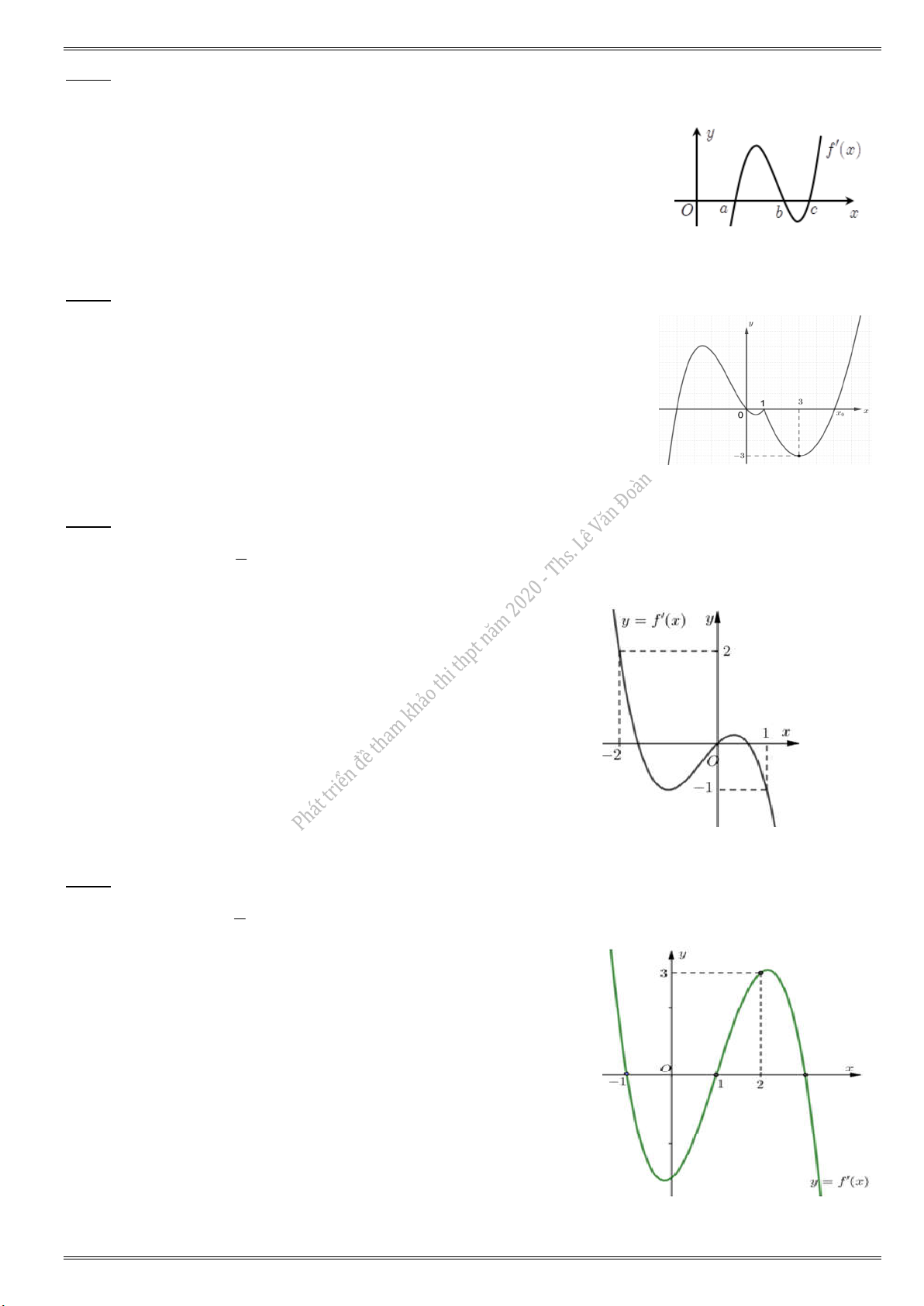
1) Cho hàm số y f (x) có bảng biến thiên như hình vẽ bên dưới. Có bao nhiêu số nguyên m để
phương trình f (2 sin x  1)  f (m) có nghiệm thực ? A. 5. B. 4. C. 3. D. 2.
Lời giải tham khảo
Đặt t  2 sin x  1. Ta có 1  sin x  1  1  2 sin x  1  3  1  t  3  t  [1; 3].
Phương trình f (2 sin x  1)  f (m) có nghiệm  f (t)  f (m) có nghiệm thuộc đoạn [1; 3].
 min f (t)  f (m)  max f (t). Từ bảng biến thiên, suy ra min f (t)  2
 và max f (t)  2. [1;3] [1;3] [1;3] [1;3]
Do đó 2  f (m)  2  1   m  3.
Do m    m  {1; 0;1;2; 3} : có 5 giá trị nguyên của m thỏa bài toán. Chọn đáp án A.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 125 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
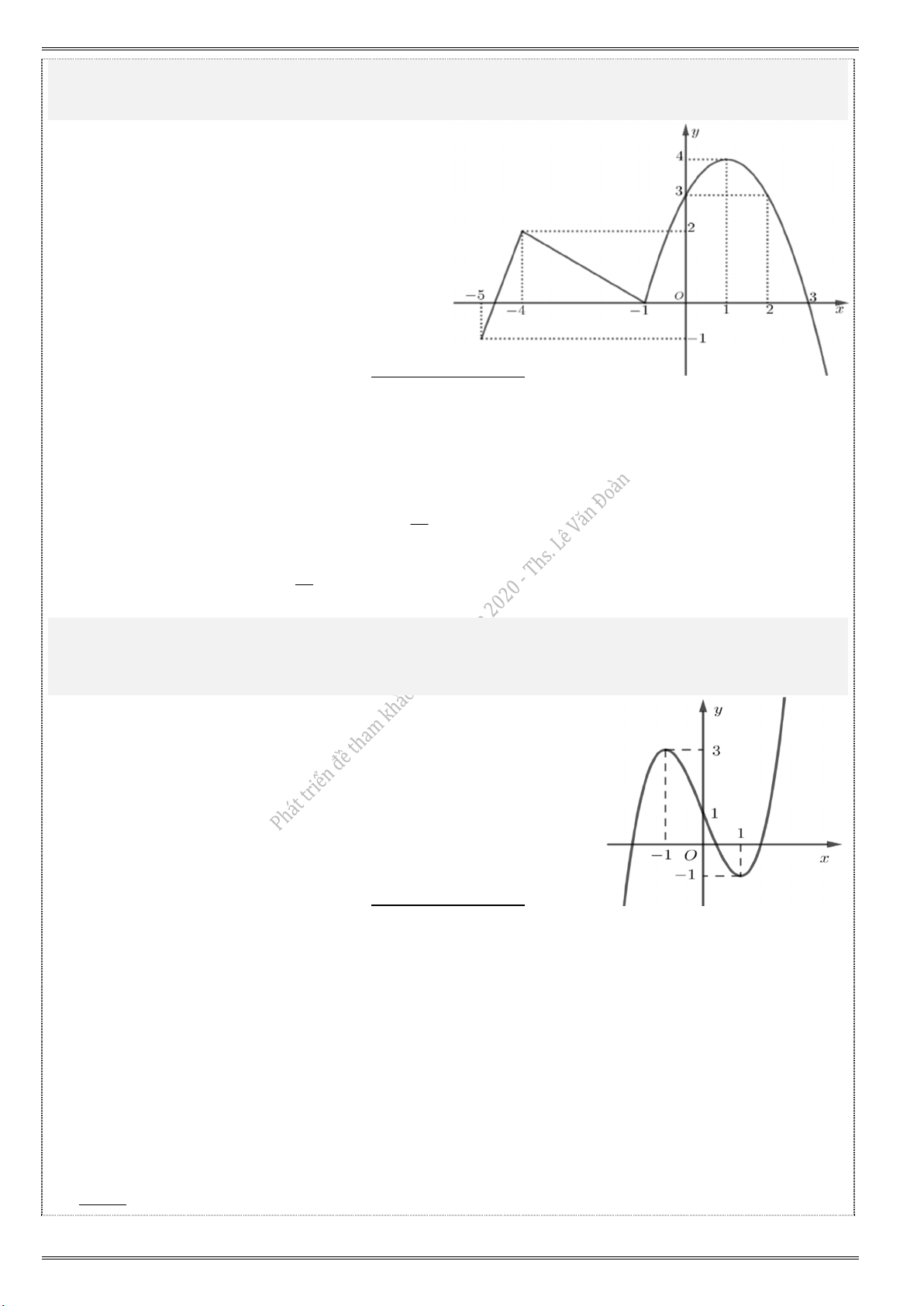
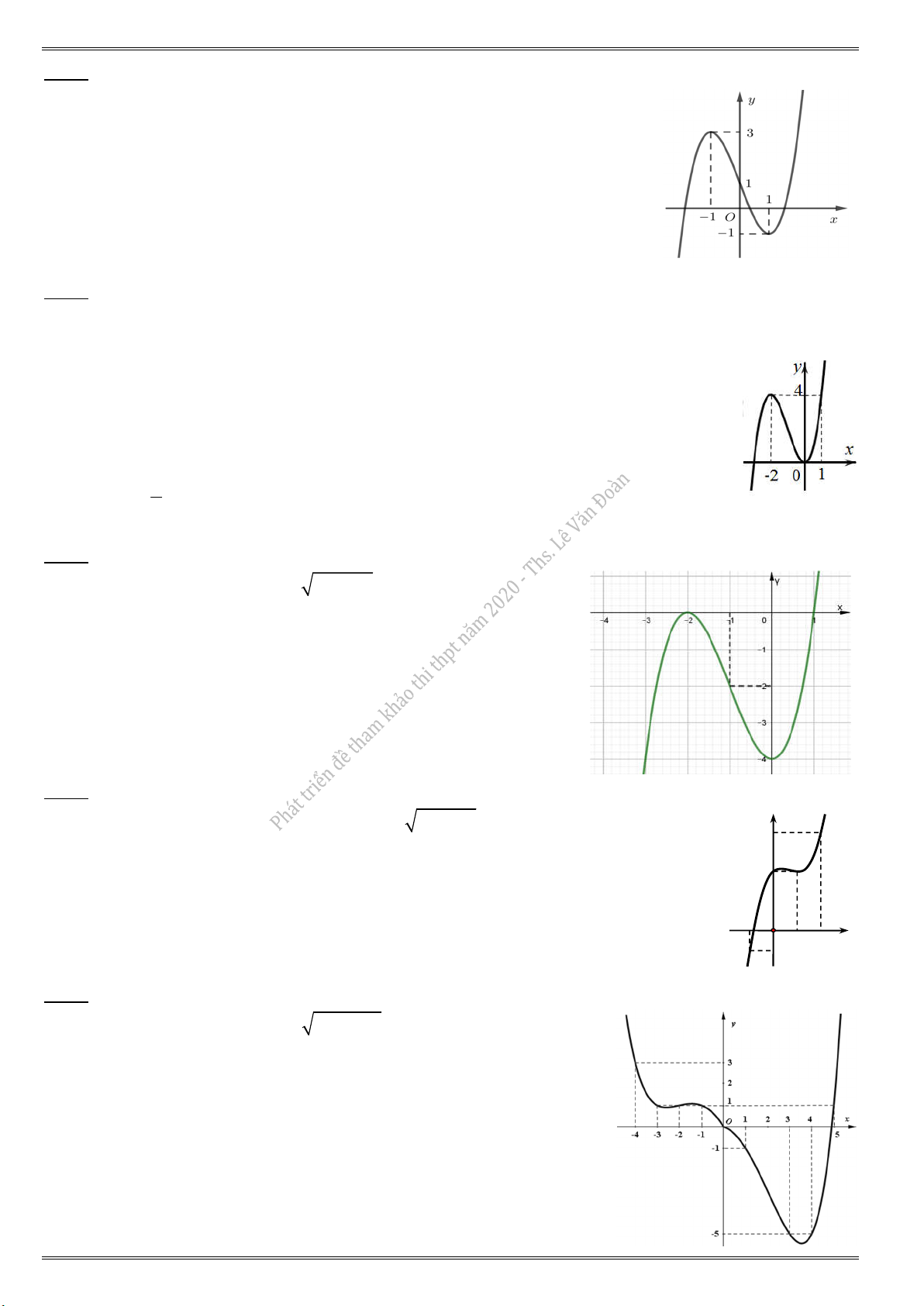
2) Cho hàm số y f (x) có đồ thị như hình vẽ bên dưới. Có bao nhiêu giá trị nguyên của m để
phương trình 2f f (x
)  m có đúng 4 nghiệm phân biệt x  [4;0]. A. 1. B. 2. C. 7. D. 5.
Lời giải tham khảo
Đặt t f (x) và do x  [4; 0] nên từ đồ thị, suy ra giá trị của t f (x)  [0; 3].
t f (x)  (0;2] : có 2 nghiệm x.
t f (x)  (2; 3]  {0} : có 1 nghiệm x. m
Yêu cầu bài toán  phương trình f (t) 
cần có 2 nghiệm t  (0;2]. 2 m
Dựa vào đồ thị, suy ra 3 
 4  6  m  8. Do m    m  7. Chọn đáp án A. 2
3) Cho hàm số y f (x) liên tục trên  và có đồ thị như hình vẽ. Gọi S là tập hợp tất cả các giá trị
nguyên của tham số m để phương trình f (sin x)  3 sin x m có nghiệm thuộc khoảng (0; ).
Tổng các phần tử của S bằng A. 9. B. 1  0. C. 6. D. 5  .
Lời giải tham khảo
Đặt t  sin x và do x  (0; )  t  (0;1]. (vẽ đường tròn lượng giác).
Khi đó phương trình trở thành m f (t)  3t g(t) với t  (0;1].
Phương trình có nghiệm  min g(t)  m  max g(t). (0;1] (0;1] Ta có: g (
t)  f (t)  3. Mà từ (0;1] thì đồ thị đi xuống nên f (t)  0  f (t)  3  0  g (t)  0.
Do đó hàm số g(t) nghịch biến trên (0;1].
Suy ra: min g(t)  g(1)  f (1)  3  1  3  4 và max g(t)  g(0)  f (0)  1. (0;1] (0;1] Vậy 4 1 m m       m  { 4  ; 3  ; 2  ; 1
 ;0}. Nên tổng giá trị của m bằng 1  0. Chọn đáp án B.
Lưu ý. Tại vị trí max (x=0) không có dấu "  " vì t  (0;1]. Nếu không để ý sẽ dễ nhầm chọn đáp án A.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 126 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
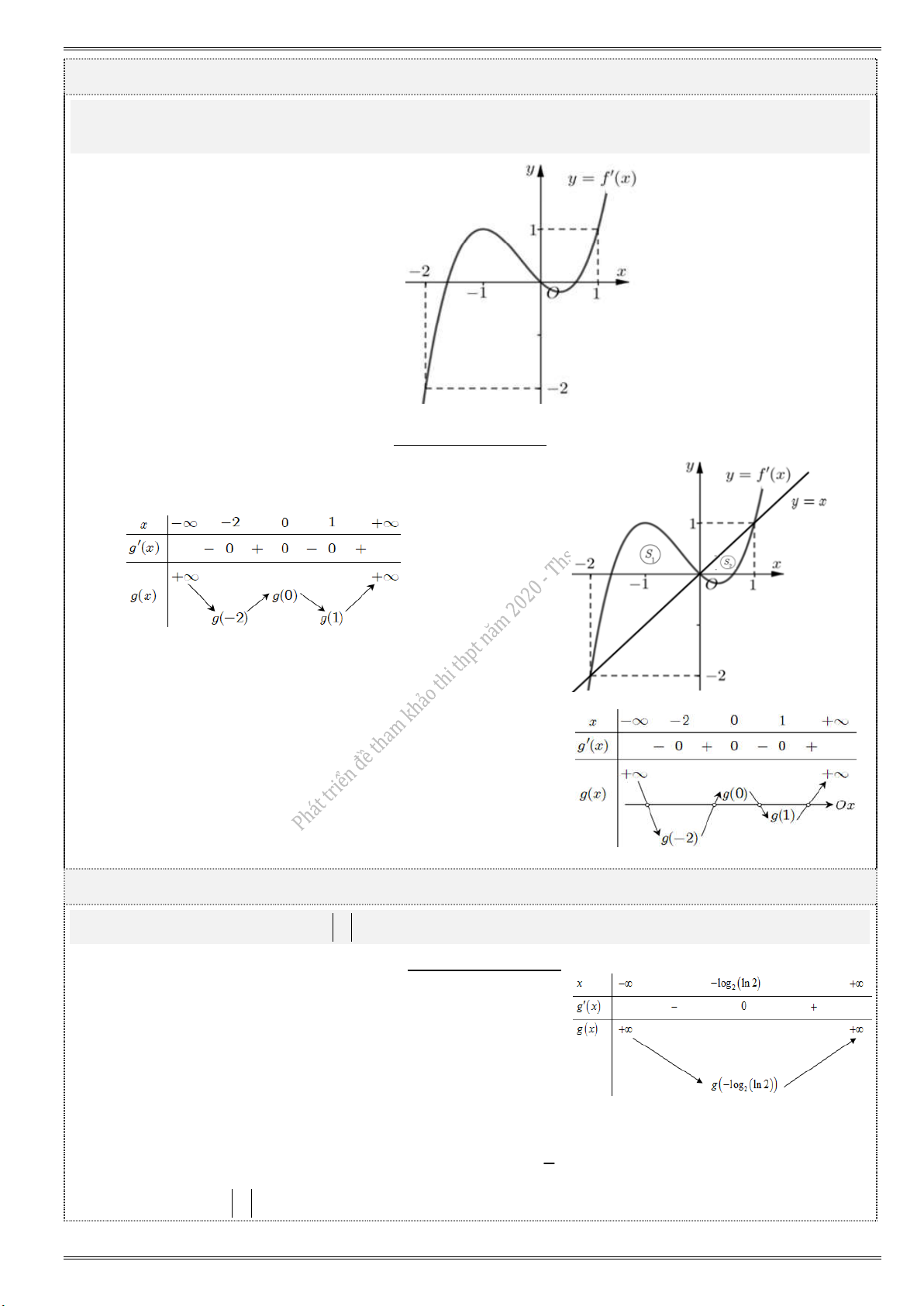
Baøi toaùn keát hôïp giöõa haøm soá vaø tích phaân Cho hàm số 4 3 2
f (x )  ax bx cx dx m với a, , b ,
c d, m   và a  0. Hàm số y f (  x) có
đồ thị như hình vẽ. Phương trình f (x)  m có bao nhiêu nghiệm ? g  (0)  0  A.   g  (1)  0  g  (0)  0  B.   g  (1)  0  g  (0)  0  C.   g  ( 2  )  0  g  (1)  0  D.   g  ( 2  )  0 
Lời giải tham khảo Ta có: g (
x)  f (x)  x. Cho g (x)  0  f (
x)  x x  2
  x  0  x  1. 1 0 1 Mà g (  x)dx g (  x)dx g (  x)dx    2  2 0 0 1   f (
x)  x dx   f (
x)  x dx S S       1 2  2 0
g(1)  g(2)  0  g(1)  g(2).
Vẽ lại bảng biến thiên bên phải.
Điều kiện cần và đủ để phương trình g(x)  0 có 4 nghiệm
khi g(0)  0 và g(1)  0. Chọn đáp án A.
Baøi toaùn chöùa tham soá m trong baøi toaùn chöùa haøm cuï theå
Có bao nhiêu giá trị nguyên m ( m  10) để phương trình x 1
2   log (x  2m)  m có nghiệm ? 4
Lời giải tham khảo
Điều kiện: x  2m  0. Ta có x 1 2   log (  2 )   2x x m m
 log (x  2m)  2m 4 2
 log 2x  2x  log (  2 )  (  2 )  (2x x m x m f
)  f (x  2m). 2 2
Do hàm số f (t)  log t t đồng biến nên 2x x  2m 2  2  2x m
x g(x) có ( )  2x g x
ln 2  1  0  x   log (ln 2). 2 1
Phương trình có nghiệm khi 2m g( log (ln 2))  m
g(log (ln 2))  0, 457. 2 2 2
Do m nguyên và m  10, nên m  {1;2; 3; 4; 5; 6; 7; 8; 9}. Các giá trị này đều thỏa điều kiện.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 127 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Baøi taäp töông töï vaø môû roäng
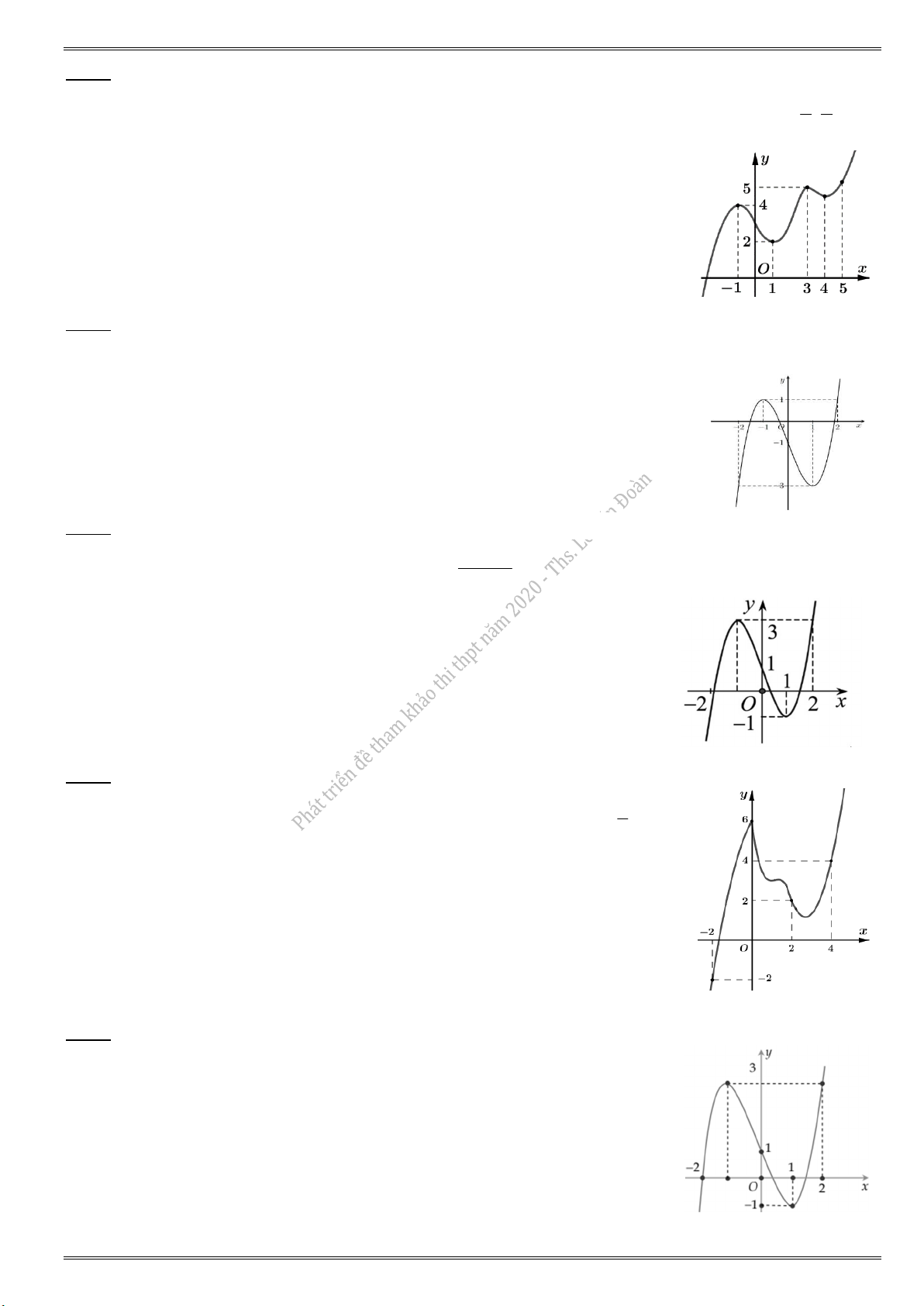
46.1. Cho hàm số y f (x) có bảng biến thiên bên dưới. Số nghiệm thuộc đoạn [0;2] của phương
trình f (cos x)  2  0 là A. 3. B. 0. C. 2. D. 1.
46.2. Cho hàm số y f (x) có bảng biến thiên bên dưới. Số nghiệm thuộc đoạn [ ;
2] của phương
trình 2f (sin x)  3  0 là A. 4. B. 6. C. 3. D. 8.  7
46.3. Cho hàm số y f (x) có bảng biến thiên như hình vẽ bên dưới. Số nghiệm thuộc đoạn 0;   2   
của phương trình 2f (2 cos x)  1  0 là A. 7. B. 4. C. 5. D. 6.
46.4. Cho hàm số y f (x ) có bảng biến thiên như hình vẽ bên dưới. Số nghiệm thuộc đoạn [ ;  ]
của phương trình 3f (2 sin x)  1  0 là A. 4. B. 5. C. 2. D. 6.
46.5. Cho hàm số y f (x ) có bảng biến thiên bên như hình vẽ bên dưới. Số nghiệm đoạn [2 ; 2]
của phương trình 4f (cos x)  5  0 là A. 4. B. 6. C. 3. D. 8.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 128 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789  9
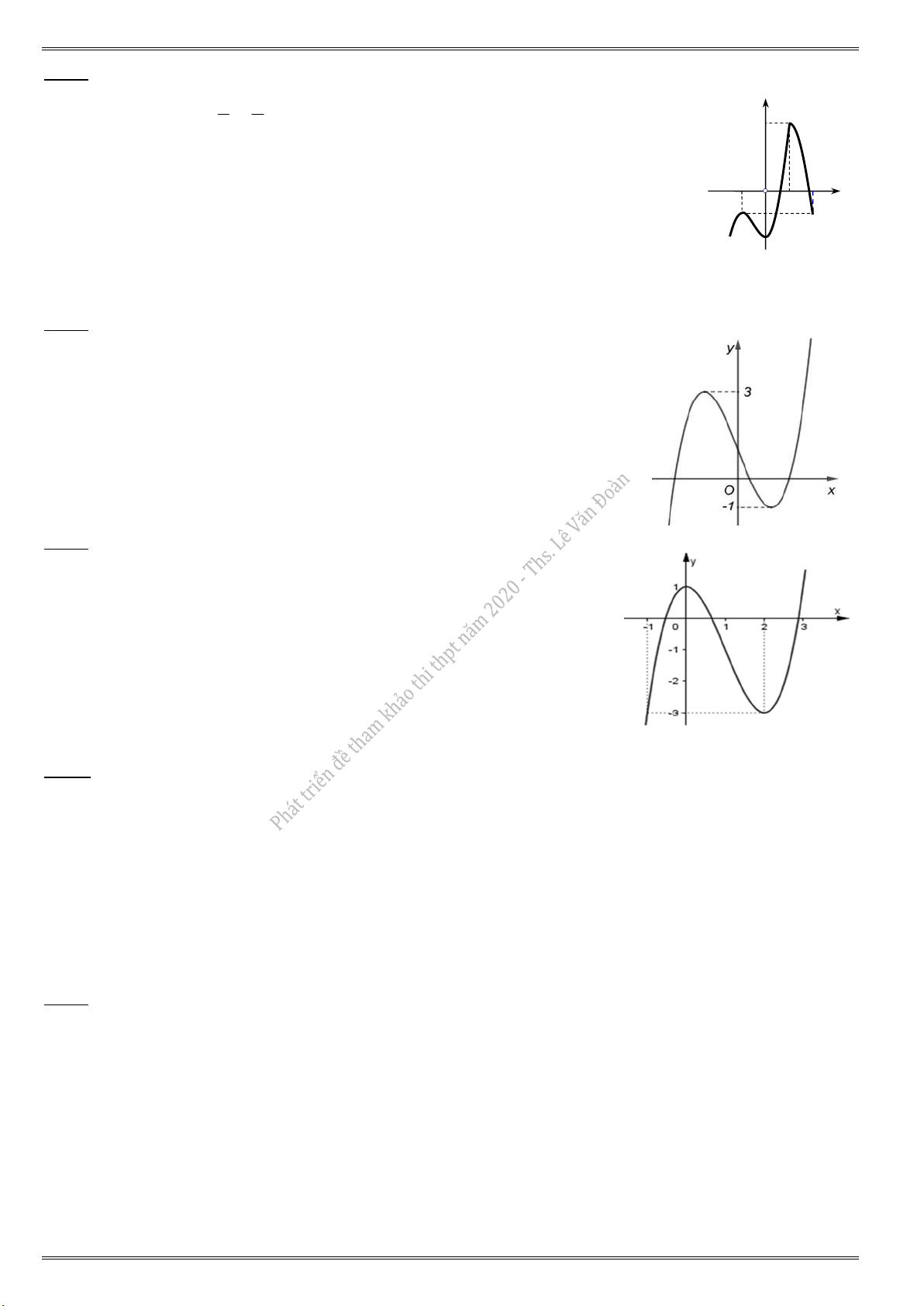
46.6. Cho hàm số y f (x) có bảng biến thiên bên dưới. Số nghiệm thuộc đoạn 0;   của phương 2   
trình f (2 sin x  1)  1 là A. 7. B. 4. C. 5. D. 6. 
46.7. Cho hàm số y f (x) có bảng biến thiên bên dưới. Số nghiệm thuộc đoạn 2 ;   của phương 2   
trình 3f (sin x  cos x)  4  0 là A. 4. B. 5. C. 3. D. 8.
46.8. Cho hàm số y f (x) có bảng biến thiên dưới và f (2)  0 . Số nghiệm thuộc [0;2] của phương trình 2
2f (cos x  cos x  1)  1  0 bằng A. 3. B. 0. C. 2. D. 1.
46.9. Cho đồ thị hàm số y f (x) như hình. Số nghiệm của phương trình f (2 sin x)  1 trên [0;2] là A. 1. B. 2. C. 3. D. 4.  3
46.10. Cho hàm số y f (x) có đồ thị như hình vẽ bên dưới. Số nghiệm thuộc đoạn  ;2  của 2   
phương trình 3f (cos x)  5  0 là A. 4. B. 7. C. 6. D. 8.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 129 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 5   46.11. Cho hàm số 3 2
f (x)  ax bx bx c có đồ thị như hình vẽ. Số nghiệm nằm trong   ;    2 2 
của phương trình f (cos x  1)  cos x  1 là A. 2. B. 3. C. 4. D. 5. `  5
46.12. Cho hàm số y f (x) có bảng biến thiên bên dưới. Số nghiệm thuộc đoạn 0;   của phương 2   
trình f  sin x   2 là A. 7. B. 4. C. 5. D. 6.
46.13. Cho hàm số y f (x) có bảng biến thiên bên dưới. Số nghiệm thuộc đoạn [0; 3] của phương
trình f (sin x)  1 là A. 2. B. 4. C. 6. D. 8. 2 f (x )
46.14. Cho hàm số y f (x) có bảng biến thiên bên dưới. Số nghiệm của phương trình e  4 là A. 3. B. 5. C. 4. D. 6.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 130 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
46.15. Cho hàm số y f (x) liên tục trên R và có đồ thị như hình vẽ. Số nghiệm thực của phương trình
f f(x  )  1  0 là A. 4. B. 7. C. 6. D. 9.
46.16. Cho hàm số y f (x) xác định và liên tục trên ,
 có đồ thị như hình vẽ. Hỏi có bao nhiêu giá trị
nguyên của tham số m để phương trình f ( 408  x  392  x  34)  m có đúng 6 nghiệm thực phân biệt ? A. 1. B. 2. C. 3. D. 4.
46.17. Cho hàm số y f (x) xác định và liên tục trên ,
 có bảng biến thiên như hình vẽ bên dưới. Gọi
S là tập hợp tất cả các giá trị nguyên của tham số m sao cho phương trình f (sin x)  6  3m có
8 nghiệm phân biệt thuộc đoạn [0; 3]. Tổng các phần tử của S bằng A. 1. B. 18. C. 6. D. 3.
46.18. Cho hàm số y f (x) có đồ thị như hình vẽ. Số giá trị nguyên của tham số m để phương trình  3
f (sin x)  m
có đúng 5 nghiệm thuộc   ;   là  2  A. 7. B. 6. C. 4. D. 5.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 131 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
46.19. Cho hàm số y f (x) liên tục trên  có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của 
tham số m để phương trình f  2f (cosx)  m có nghiệm x   ;. 2     A. 5. B. 3. C. 2. D. 4. 46.20. Cho hàm số 4 2
f (x)  ax bx  ,
c a  0 và có đồ thị như hình vẽ. Tổng các giá trị nguyên của 
tham số m để phương trình f 2f (sin x)  3  m có nghiệm x  0;   bằng 2    A. 1. B. 2. C. 3. D. 4.
46.21. Cho hàm số f (x) có bảng biến thiên bên dưới. Có bao nhiêu giá trị nguyên của tham số m để
phương trình f (2 sin x m)  2  0 có đúng 6 nghiệm phân biệt thuộc [0; 3] ? A. 0. B. 2. C. 3. D. 1.
46.22. Cho hàm số y f (x) có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m để
phương trình f (f (sin x))  m có đúng hai nghiệm thuộc khoảng (0; ) ? A. 1. B. 2. C. 3. D. 4.
46.23. Cho hàm số bậc ba 3 2
f (x )  ax bx cx d (a, b, c, d   và a  0) có đồ thị như hình vẽ. Phương trình 2 2 2
[f (x  1)]  f (x  1)  2  0 có bao nhiêu nghiệm ? A. 1. B. 3. C. 4. D. 5.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 132 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 46.24. Cho hàm số 4 2
y ax bx c, (a  0) như hình vẽ bên dưới. Có bao nhiêu điểm trên đường
tròn lượng giác biểu diễn nghiệm của phương trình f (f (cos 2x))  0. A. 1. B. 3. C. 4. D. Vô số.
46.25. Cho hàm số y f (x) liên tục trên đoạn [ 2
 ;6] và có đồ thị như hình vẽ bên dưới. Có bao nhiêu
số nguyên m để phương trình f (sin x)  m có nghiệm. A. 10. B. 6. C. 9. D. 5.
46.26. Cho hàm số y f (x) liên tục trên đoạn [ 2
 ;6] có đồ thị như hình bên dưới. Có bao nhiêu số   
nguyên m để phương trình f (cos x)  m có nghiệm x   ;    2 2    A. 10. B. 6. C. 2. D. 5.
46.27. Cho hàm số y f (x ) xác định trên  và có đồ thị như hình bên. Có bao nhiêu giá trị nguyên 4 sinx 1   
của tham số m để phương trình 3f    m  có nghiệm ?  3  A. 2. B. 3. C. 4. D. 5.
46.28. Cho hàm số y f (x ) xác định trên  và có đồ thị như hình bên. Có bao nhiêu giá trị nguyên
của tham số m để phương trình 4 4 f 4(sin x cos x)   m   có nghiệm ? A. 2. B. 4. C. 3. D. 5.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 133 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
46.29. Cho hàm số y f (x) liên tục trên  và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của
m để phương trình f (f (sin x))  m có nghiệm thuộc khoảng (0; ) ? A. 1. B. 2. C. 3. D. 4.
46.30. Cho hàm số y f (x) xác định, liên tục trên  và có đồ thị như hình vẽ. Tập hợp tất cả các giá
trị của tham số m để phương trình 2
f (x  2x  2)  3m  1 có nghiệm thuộc đoạn [0;1] là A. [0; 4]. B. [1; 0]. C. [0;1].  1  D.  ;1   3   
46.31. Cho hàm số y f (x) liên tục trên  và có đồ thị như hình vẽ. Tập hợp các giá trị thực của tham
số m để phương trình 2
f ( 4x x  1)  m có nghiệm là A. [2; 0]. B. [4;2]. C. [4; 0]. D. [1;1].
46.32. Cho hàm số y f (x) xác định, liên tục trên  và có đồ thị như hình vẽ. Có bao nhiêu giá trị y
nguyên của m để phương trình 2
f (2  2x x )  m có nghiệm. 5 A. 6. 3 B. 7.  1 C. 3. O x 1 2  1 D. 2.
46.33. Cho hàm số y f (x) xác định trên  và có đồ thị như hình. Có bao nhiêu giá trị nguyên của m để phương trình 2
2f (3  4 6x  9x )  m  3 có nghiệm ? A. 13. B. 12. C. 8. D. 10.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 134 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
46.34. Cho hàm số y f (x) liên tục trên  và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của  3 7
m để phương trình 2
f (x  2x)  m có đúng 4 nghiệm thực phân biệt thuộc đoạn  ;   ? 2 2   A. 1. B. 2. C. 3. D. 4.
46.35. Cho hàm số y f (x) liên tục trên  có đồ thị như hình. Có bao nhiêu giá trị nguyên của tham
số m để phương trình f f (x)  m  1  f (x)  m có đúng 3 nghiệm phân biệt trên [1;1]. A. 1. B. 2. C. 3. D. 4.
46.36. Cho hàm số y f (x) liên tục trên  và có đồ thị như hình vẽ dưới đây. Số giá trị nguyên 2 m x 1
của tham số m để phương trình f (e ) 
có hai nghiệm thực phân biệt là 8 A. 4. B. 5. C. 6. D. 7.
46.37. Cho hàm số y f (x) liên tục trên  và có đồ thị như hình vẽ dưới đây. Có bao nhiêu giá trị 1 
nguyên của m để f (2 log x)  m có nghiệm duy nhất trên  ;2. 2 2   A. 4. B. 5. C. 6. D. 9.
46.38. Cho hàm số y f (x) có đồ thị như hình vẽ. Hỏi có tất cả bao nhiêu số nguyên dương m  100 phương trình 2 2
f (x )  m  2020 có đúng hai nghiệm phân biệt. A. 55. B. 56. C. 54. D. 99.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 135 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
46.39. Cho hàm số y f (x) có đồ thị như hình bên dưới. Có bao nhiêu số nguyên của tham số m để 1 xy  
phương trình f   1  x m     
có nghiệm thuộc đoạn [ 2;2]. 6 3 2  A. 8. 2 O 4 x 2 2 B. 9. C. 10. 4 D. 11.
46.40. Cho hàm số y f (x) liên tục trên  và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của
m để phương trình f (x)  f (m) có đúng hai nghiệm phân biệt ? A. 4. B. 1. C. 2. D. 3.
46.41. Cho hàm số y f (x) liên tục trên  và có đồ thị như hình vẽ. Tìm tất cả các giá trị nguyên của
m để phương trình f (1  sin x)  f (m) có nghiệm.
A. m  {1; 0;1;2}.
B. m  {0;1;2}. C. m  .  D. m  {1;2}. 46.42. Phương trình 3 3 log (  1)  27  8y x y
 1  x có bao nhiêu cặp nghiệm nguyên (x;y) với 2 1992 2020 x  [8 ; 8 ] ? A. 26. B. 28. C. 24. D. 30.
46.43. Cho phương trình 2
log (3x)  (m  2)log x m  5  0 (m là tham số thực). Tìm tập hợp tất cả 3 3
các giá trị của m để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn [1; 9]. A. (2; 4). B. [2; 4]. C. (4;  )  . D. [2; 4).
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 136 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
46.44. Cho hàm số f (x) có đạo hàm trên ,
 đồ thị hàm số y f (x) như trong hình vẽ bên. Hỏi phương
trình f (x)  0 có tất cả bao nhiêu nghiệm biết f (a)  0. A. 3. B. 2. C. 1. D. 0.
46.45. Cho y f (x) có đồ thị của y f (
x) như hình vẽ bên dưới. Đặt 2
g(x )  f (x ). Mệnh đề nào dưới đây đúng ?
A. g(0)  g(1)  g(1).
B. g(1)  g(0)  g(1).
C. g(1)  g(1)  g(0).
D. g(1)  g(1)  g(0).
46.46. Cho hàm số f (x) liên tục trên  và có đồ thị hàm số f (
x) như hình vẽ bên dưới. Đặt 1 2
g(x)  f (x)  x  3. Điều kiện để phương trình g(x)  0 có 4 nghiệm phân biệt là 2 g  (0)  0  A.   g  ( 2  )  0  g  (0)  0  B.   g  ( 2  )  0  g  (0)  0  C.   g  (1)  0  g  (1)  0  D.   g  ( 2  )  0 
46.47. Cho hàm số f (x) liên tục trên  và có đồ thị hàm số f (
x) như hình vẽ bên dưới. Đặt 1 3
g(x)  f (x)  x x  1 Điều kiện để g(x)  0 có 4 nghiệm phân biệt là 3 g  (1)  0  A.   g  ( 1  )  0  g  (1)  0  B.   g  ( 1  )  0  g  (1)  0  C.   g  (2)  0  g  (1)  0  D.   g  (2)  0 
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 137 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
46.48. Cho phương trình 2
log (2x)  (m  2)log x m  2  0 (m tham số). Tập hợp các giá trị của m 2 2
để phương trình có hai nghiệm phân biệt thuộc đoạn [1;2]. A. (1;2). B. [1;2]. C. [1;2). D. [2; ).
46.49. Có bao nhiêu giá trị nguyên của m để phương trình 2
log x  log (3x  1)  log m có nghiệm 9 3 3 A. 2. B. 3. C. [1;2). D. [2; ).
46.50. Cho phương trình 2
2 log x  (3  2m)log (4x)  8  5m  0 (với m là tham số). Tập hợp tất cả 2 2
các giá trị của m để phương trình đã cho có 2 nghiệm phân biệt thuộc đoạn [ 2;2] là 5    A.  ; 3   2  5  B.  ; 3   2    5   C.  ; 3   2  D. [3; ). 
46.51. Giá trị thực của tham số m để phương trình 9x  2(2  1).3x m
 3(4m 1)  0 có hai nghiệm
thực x , x thỏa mãn (x  2)(x  2)  12 thuộc khoảng nào sau đây ? 1 2 1 2 A. (3; 9). B. (9; ). 1    C.  ; 3   4   1    D.   ;2    2  2 2 2
46.52. Cho phương trình 2x 3  x mx x  2  x 2 3 9 3 3  x m    
. Có bao nhiêu giá trị nguyên của tham số
m  [2018;2018] để phương trình đã cho có 4 nghiệm phân biệt ? A. 2018. B. 2019. C. 2020. D. 2021.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 138 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Câu 47. Xét các số thực dương , a ,
b x, y thỏa mãn a  1, b  1 và x y
a b ab . Giá trị nhỏ nhất
của biểu thức P x  2y thuộc tập hợp nào dưới đây ?  5 5  A. (1;2). B. 2  ;     C. [3;4). D. ;3  2    2  
Lôøi giaûi tham khaûo Theo đề thì ,
a b  1  log b  0 và log a  0. a b  1 1  x ab   b x   b x y x y 2 log ( ) 1 log log  Ta có 2 2 a a
a b ab a
b ab   2 2 a . 2
 y  log (ab)  log a 1  b b  Cauchy 3 1  3 1 3 5    
Khi đó: P x  2y
  log b  log a   2 log b.log a   2   ;3. 2 2 a b  2 2 a b 2 2   Chọn đáp án D.
Baøi toaùn doàn bieán, roài söû duïng baát ñaúng thöùc Cauchy hoaëc khaûo saùt haøm moät bieán
1) Cho x, y là các số thực thỏa mãn log (x y)  log (x y)  1. Tìm giá trị nhỏ nhất của 2x y. 4 4
Lời giải tham khảo
Điều kiện: x y  0, x y  0.
Ta có: log (x y)  log (x y)  1  log (x y)(x y)  1  (x y).(x y)  4 ( )  4 4 4
Suy luận. Đề yêu cầu tìm min của tổng 2x  ( y
 ), mà từ đề có dạng tích ( )
 , nên nghĩ đến việc sử dụng bất
đẳng thức trung bình cộng – trung bình nhân (AM GM : Cauchy) bằng cách sử dụng đồng nhất: a  b  2  1 3
2x y a.(x y)  .(
b x y)  (a b).x  (a b).y  
a  , b và có lời giải: a  b  1 2 2  Cauchy 1 3 1 3 3
Ta có: 2x y
(x y)  (x y)  2
. (x y).(x y)  2  4  2 3. 2 2
2 2  4 4 
Suy ra min(2x y)  2 3. 2) Đặt 3
m  log ( ab) với a, b  1 và 2
P  log b  16 log a. Tìm m để P đạt giá trị nhỏ nhất ? a a b
Lời giải tham khảo
Vì a  1, b  1  log b  0 và log a  0. a b 1 1 1 1 Ta có: 3 3
m  log ( ab )  log (ab) 
log (ab)  (log a  log b)  (1  log b). a a 3 a 3 a a 3 a Cauchy 16 8 8 8 8 Khi đó: 2 2 2
P  (log b)   (log b)    3.3 (log b)    12. a log a b log b log a b log b log b a a a a a 8 1
Suy ra min P  12 khi 2 (log b) 
 log b  2  m  (1  log b)  1. a log a b 3 a a
3) Xét các số thực dương x, ,
y z thay đổi sao cho tồn tại các số thực a, ,
b c  1 và thỏa mãn 16 16 x y z
a b c abc . Tìm giá trị lớn nhất của biểu thức 2 P    x . y z
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 139 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Lời giải tham khảo 2
 x  log (abc)  0  a  Từ đề bài có: x y z 2x 2y 2z
a b c abc a b c abc  2
y  log (abc)  0 b
2z  log (abc) 0  c   1 1 x  log (abc)     2 log a  2 a abc   x  1   1 1 1 1 1 1 1 16 16 16 y  log (abc)   
   2 log b     2    2     32    2 b abcy x y z y z x y z x    1   1 z   log (abc)     c 2 log c  2 abc   z Cauchy 16 8 8    8 8 Khi đó 2 2 2 3 P  32 
x  32     x   32  3
  x  20. Suy ra max P  20. x x x  x x
4) Cho x, y  0 thỏa 2
ln x  ln y  ln(x y). Giá trị nhỏ nhất của x y bằng bao nhiêu ?
Lời giải tham khảo Ta có: 2 2 2 2
ln x  ln y  ln(x y)  ln(xy)  ln(x y)  xy x y y(x  1)  x ( )  2 x
Vì x  0, y  0 nên ( )
 xảy ra khi x 1  0  x  1. Với x  1  0  y   x  1 2 Cauchy x 1
Khi đó: x y x   2(x  1) 
 3  2 2  3. Suy ra min(x y)  2 2  3. x  1 x  1 2 2 x 4y
5) Cho x, y  0 thỏa log(x  2y)  log x  log y. Tìm giá trị nhỏ nhất của P    1  2y 1  x
Lời giải tham khảo
Ta có: log(x  2y)  log x  log y  log(x  2y)  log(xy) Cauchy 2 1 (x  2y)
x  2y xy  .x.(2y)  x 2y  0
    x  2y  8. Khi đó: 2 8 2 2 Cauchy-Schwarz 2 x (2y) (x 2y) x 2y 2 4     24 P        
(x  2y  2)  4 1 2y 1 x (x 2y) 2  25 x 2y 2       25   Cauchy 4 24 32 32    10  4   Do đó min P   5 25 5 5 1 3b 1   
6) Xét các số thực ,
a b thỏa  b a  1. Tìm giá trị nhỏ nhất của 2 P  log 
  12 log a  3. 3 a  4  b  a
Lời giải tham khảo 3b 1    3b 1     12 Ta có: 2 P  log 
  12 log a  3  log     3. a   b a     2  4 
 4  (log b 1) a a 3b  1 1 Mà 3 3 2
b  3b  1  4b  (b  1)(2b  1)  0 : luôn đúng với b (xem lại pp S.O.S). 4 3 1  a  1 3b 1 3b 1   3   3 Suy ra: 3  b  log    log b . 4 a  4  a  12 12
Do đó: P  3 log b
 3  3(log b 1)  a 2 a 2 (log b 1) (log b 1) a a Cauchy 3 3 12 3 3 3
 (log b  1)  (log b  1)   3.
  12  9. Vậy min P  9. a a 2 2 2 (log b  1) 2 2 a
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 140 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 6(2x y) x  2y
7) Cho x, y  0 thỏa xy  4y  1. Tìm giá trị nhỏ nhất của P   ln  x y
Lời giải tham khảo 2   2  x   x y 1 4 1 Ta có: chia 0
xy  4y  1        
 4    2  4  0   4. 2 y   y y y  y 6(2x y) x 2y yx      x Khi đó: P   ln
 12  6.  ln  2. Đặt t  , t  (0;4]. x y x y  y 6 6 1
Suy ra P f (t)  12 
 ln(t  2) có f (t)   
 0  t  3  21  (0; 4]. t 2 t t  2 27
Lập bảng biến thiên, suy ra min P  min f (t)  f (4)   ln 6. 2
8) Cho a, b  0 thỏa mãn 2 2
b  3ab  4a và 32
a  [4;2 ]. Tìm giá trị lớn nhất và giá trị nhỏ nhất của 3 b
biểu thức P  log 4a  log  b 2 4 4 8
Lời giải tham khảo 2     2  a   a   a c b 1 Ta có 2 2
b  3ab  4a (đẳng cấp) hia 0 
1  3   4   
(do : a.b  0)  b  4a.  b    b  b 4 3 log 4a 3 log a  2 3 log a Do đó: 2 2 2
P  log 4a  log a   log a    a 2 2 4 a 4 log a  1 4 2 2 log2 2 x  2 3
Đặt log a x và do 32
a  [4;2 ]  x  [2; 32]. Khi đó P
x f (x), x  [2; 32]. 2 x  1 4 3 3 Ta có: f (  x)  
 0  x  3  [2;32]. 2 (x  1) 4 11 19 778 778 19 Tính f (2)  , f (3)  , f (32)   Suy ra max P  và min P   2 4 31 32 4 2
9) Cho hai số thực dương a  1, b  1 x x 1 a .b   1 và biết phương trình
có nghiệm thực. Tìm giá trị 4
nhỏ nhất của biểu thức P  log (ab)   a log b a
Lời giải tham khảo
Ta có: a  1, b  1  log b  0. a 2 2
Lấy lôga cơ số a  1 hai vế của phương trình x x 1  x x 1 a .b 1 log (a .b    )  log 1 a a 2 x x 1  2
 log a  log b
 0  x  (log b).x  log b  0. a a a a 2 log b  0
Theo đề, phương trình có nghiệm    (log b)  4 log b  0 a
 log b  4. a a a 4 4 log b  4  3
Khi đó: P  log (ab)   1  log a b         log b  1 a log a b log b  4 log b  4 a a a a Cauchy 3
 2   4  1  6. Vậy giá trị nhỏ nhất của P bằng 6. Dấu 4
"  "  log b  4  b a . 4 a
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 141 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Söû duïng f(u) = f(v) hoaëc f(u) > f(v) hoaëc f(u) < f(v) khi hai gaëp hai haøm khaùc loaïi y 1 
1) Xét x  0, y  0 thỏa log (  x 1)(y 1)  
 9  (x  1)(y  1). x y 3  
Tìm giá trị nhỏ nhất của 2 .
Lời giải tham khảo y 1  Ta có log (  x 1)(y 1) 9 (x 1)(y 1) (y 1)log (x 1)(y 1)          
 (x  1)(y  1)  9 3   3   y  9 9 : ( 1) 0 log (x 1).(y 1)      x  1 
 log (x  1)  x  1   log (y  1) 3   3 3 y  1 y  1 9 9 9  9 
 log (x  1)  x  1 
 log 9  log (y  1)   log
f (x  1)  f     3 3 3 3 y  1 y  1 y  1 y  1 1
Xét hàm số f (t)  log t  ,
t t  (0; )
 có f (t) 
 1  0, t  0  f (t) : đồng biến. 3 t ln 3  9    9 8  y
Nên f (x  1)  f    x  1   x    y  1 y  1 y  1 Cauchy 8  y 9 9
Suy ra x  2y
 2y  2y  1   2(y  1)   3  6 2  3. y  1 y  1 y  1
Vậy min(x  2y)  6 2  3.
2) Cho x, y  0 thỏa 2  log (  )x xy xy x
 8. Tìm giá trị nhỏ nhất của 2
P x y. 2
Lời giải tham khảo Ta có: 2  log (  )x xy xy x
 8  2xy x log [x(y  1)]  8 2 2 x 1 4 1 4 1 : 2 y
log x log (y 1)       
y  log (y  1)   log x  2 2  2 2 2 x 2 x 2 1 4 1 1 1 4 1 4
 (y  1)  log (y  1) 
 log 4  log x  (y  1)  log (y  1)   log 2 2 2 2 2 2 x 2 2 2 x 2 x 4    4 4
f (y  1)  f    y  1   y   1.  x  x x Cauchy 4  2 2   2 2 Do đó: 2 2 2 2 3 3
P x y x   1  x
    1  3 x    1  3 4  1. x  x x  x x
Vậy giá trị nhỏ nhất của P bằng 3 3 4  1. 2 2  
3) Cho x, y  0 thỏa y 2 2 2 log (
 1)  log (2  )  2x x y  2.  P x y  2 2    Tìm GTLN của 2( ) 1 .
Lời giải tham khảo 2 2 2 y 2   Ta có: y 2 2 x 2 2 2 x 1 2 log (  1)  log (2  )  2  2 log (
 1)  log (2  )  2  2 y x y x y   2 2  2 2   2 2 x 2 1 y  2 2 2
 2  log (x  1)  2
 log [(1  y )  1]  f (x )  f (1  y ). 2 2 Do hàm số ( )  2t f t
 log (t  1) luôn đồng biến với t  0 nên 2 2 2 2 ( )
  x  1  y x y  1. 2 Cauchy-Schwarz 2 2 2 2
P  2(x y)  1  2(1.x  1.y)  1 
2 (1  1 )(x y )  1  2 2.1  1  2 2  1.
Vậy giá trị lớn nhất của biểu thức thức P là 2 2  1.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 142 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
4) Có bao nhiêu cặp số nguyên (x;y) thỏa mãn 0  x  2020 và log (4  4)    1  2y x x y ? 2
Lời giải tham khảo Ta có: log (4  4) 
  1  2y  log 4  log (  1)    1  2y x x y x x y 2 2 2
 (  1)  log (  1)  2y  log 2y  (  1)  (2y )      1  2y   2y x x f x f x x  1 2 2 0  x  2020 y 0
    0  2  1  2020  2  2y  2021  0  y  log 2021  10, 98 2
Mà y    y  {0;1;2; 3; 4; 5; 6;7; 8; 9;10}  x   nên có 10 cặp nguyên (x;y) thỏa bài toán. 2
3x  3x m  1
5) Có bao nhiêu số nguyên m để phương trình 2 log
x  5x  2  m có hai 2 2 2x x  1
nghiệm phân biệt lớn hơn 1.
Lời giải tham khảo 2 log 2
3x  3x m  1 Phương trình đã cho 2 2   log
x  5x  3  m 2 2 4x  2x  2 2 2 2 2
 log (3x  3x m  1)  (3x  3x m  1)  log (4x  2x  2)  (4x  2x  2) 2 2 2 2 2 2
f (3x  3x m  1)  f (4x  2x  2)  3x  3x m  1  4x  2x  2 2 2
x  5x m  1  0  m x  5x  1  g(x) có g (
x)  2x  5  0  x  5/2.
Từ bảng biến thiên, phương trình có hai nghiệm phân biệt lớn 21 hơn 1 khi   m  3. 4
m    m    Do
{ 5; 4}. Có 2 giá trị thỏa bài toán. 2
2x x m 6) Cho phương trình 2 log
x x  4  .
m Có bao nhiêu giá trị nguyên của tham số 3 2 x  1
m  [2018;2018] để phương trình có hai nghiệm trái dấu ?
Lời giải tham khảo 2 2
2x x m
2x x m PT 2 2  log
 log 3  x x  3  m  log
x x  3  m 3 2 3 3 2 x  1 3x  3 2 2 2 2
 log (2x x m)  (2x x m)  log (3x  3)  (3x  3) 3 3 2 2 2 2 2
f (2x x m)  f (3x  3)  2x x m  3x  3  x x  3  m  0.
Phương trình có hai nghiệm trái dấu a.c  0  1.(3  m)  0  m  3. 2018  4 Do m  [ 2
 018;2018  m  {4;5;6;...;2018} có
 1  2015 giá trị nguyên m. 1 2 2x  6x  8
7) Tính tổng S các nghiệm nguyên dương của 3 2 log
x  9x  8x  2  0. 2 2 x  4x  6 2
(x  1)(2x  6x  8) Bất phương trình  2 2  log (x 1) (2x 6x 8) (x 4x 6)         0 2 2 (x 1)(x 4x 6)      3 2 3 2 3 2 3 2
 log (2x  4x  2x  8)(2x  4x  2x  8)  log (x  5x 10x  6) (x  5x 10x  6) 2 2
Do hàm đặc trưng f (t)  log t t đồng biến nên 3 2 3 2
2x  4x  2x  8  x  5x  10x  6 2 3 2
x  9x  8x  2  0  
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 143 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Baøi taäp töông töï vaø môû roäng 47.1
Xét các số thực dương , a ,
b x, y thỏa mãn a  1, b  1 và x y
a b a b. Giá trị nhỏ nhất của
x  2y bằng A. 4. B. 2 5. C. 2 3. D. 3 2. 47.2
Xét các số thực dương x, ,
y z thay đổi sao cho tồn tại các số thực a, ,
b c  1 và thỏa mãn x y z
a b c abc. Giá trị nhỏ nhất của biểu thức 2
x y  2z bằng A. 6. 1 B.  2 C. 8. 17 D. 2 47.3
Cho các số thực x, y thỏa log (x y)  log (x y)  1. Giá trị nhỏ nhất của (3x  2y) e bằng 4 4 A. 2e 3. B. 2e. C. e 5. 2 e 5 D.  2 1 47.4
Cho x, y  0 thỏa mãn log y  log(2  xy). Giá trị nhỏ nhất của
y thuộc khoảng nào ? x A. (1;2). B. [2; 3).  9 C. 3;   2  11  D.  ;6  2   47.5
Xét các số thực dương x, y thỏa mãn 2
log x  log y  log (x y ). Giá trị nhỏ nhất của biểu 0,5 0,5 0,5
thức P x  3y bằng A. 9. B. 8. 25 2 C.  4 17 D.  2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 144 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 47.6
Cho x,y là các số thực dương thỏa mãn 2 log x  log y  log
(x y). Giá trị nhỏ nhất của 2019 2019 2019
biểu thức T  2x y thuộc khoảng nào sau đây ? A. (7; 8). B. (6; 7). C. (5; 6). D. (8; 9). 47.7
Xét các số thực x, y thỏa 0  x  2, y  0 và log (4  2x)  log y  log 9  0. Giá trị lớn nhất 1 1 2 2 2 32 của P  31 
y thuộc khoảng nào sau đây ? x  1   A.  1  ;    8  1  B.  ;1   8   C. [1;2).  4 D. 2  ;   3  3 47.8
Xét a  1, b  1 và đặt 2
m  log ( a b). Khi biểu thức 2
P  log (ab)  54 log a  2020 đạt giá a a ab
trị nhỏ nhất thì m thuộc khoảng nào sau đây ? A. (1;2).  5 B. 2  ;   2  C. [3; 4). 5  D.  ;3  2   3(x 2y) 2x y     47.9
Cho x, y  0 thỏa mãn 2
4y xy  6y  1. Giá trị nhỏ nhất của P   ln  x  y 
thuộc khoảng nào sau đây ? A. (1; 3]. 11 13 B.  ;   2 2   13  C.  ;7.  2    11   D. 3;    2 
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 145 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 2 2 4x y
47.10 Cho x, y  0 thỏa ln(2x y)  ln(3x)  ln y. Giá trị nhỏ nhất của P   thuộc 1  y 1  2x khoảng nào sau đây ?  3  A. 0  ;     2 3   B. ;4  .  2  C. (4; 5].  11  D. 5  ;     2  1 b
47.11 Xét a, b  0 thỏa mãn 2 2
2a ab  3b . Biết giá trị nhỏ nhất của P  log (2a)  log có b 3 2 27 9 m m dạng min P   6 với
là phân số tối giản. Giá trị của m n thuộc khoảng nào ? n n A. (1; 4]. B. (4; 8]. C. (8;10]. D. (10;20). 4(3b 1)
47.12 Cho 0  b a  1. Giá trị nhỏ nhất của biểu thức 2 P  log
 8 log a  1 bằng a 9 b a A. 6. B. 3 3 2. C. 8. D. 7. 4  3 a   
47.13 Cho a, b thỏa mãn a b  và biểu thức 2 P  16 log    3 log a   có giá trị nhỏ nhất. 3
a 12b  16 a  b
Khi đó giá trị của a b bằng 7 A.  2 B. 4. 11 C.  2 D. 6.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 146 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 2
47.14 Cho hai số thực a  1, b  1. Biết phương trình x x 1
a .b   1 có hai nghiệm phân biệt x , x . Giá 1 2 2  x x   
trị nhỏ nhất của biểu thức 1 2 P    
  4(x x ) bằng 1 2
x x  1 2 A. 4. B. 3 3 2. C. 3 3 4. D. 3 4. 47.15 Cho , a ,
b c  1. Biết rằng biểu thức P  log (bc)  log (ac)  4 log (ab) đạt giá trị nhỏ nhất a b c
bằng m khi log c n. Tính giá trị m n. b
A. m n  12. 25
B. m n   2
C. m n  14.
D. m n  10. 1 1
47.16 Cho a  1, b  1. Giá trị nhỏ nhất của biểu thức S   bằng log a log b 4 ab ab 4 A. 9 9 B.  4 9 C. 2 1 D. 4 a    
47.17 Xét các số thực a, b thỏa a b  1. Giá trị nhỏ nhất của 2 2
P  log (a )  3 log   a
b b  bằng b A. 19. B. 13. C. 14. D. 15.
47.18 Cho 1  a b  0. Giá trị nhỏ nhất của biểu thức 2 36
P  log b  log a bằng a ab A. 19. B. 16. C. 13. D. 11.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 147 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
47.19 Cho hai số thực a, b thỏa mãn log
(2a  8b)  1. Khi P  4a  6b  5 đạt giá trị lớn nhất 2 2 a 4b 1  a thì giá trị của bằng b 8 A.  5 13 B.   2 13 C.   4 17 D. 44 a   
47.20 Cho a  0, b  1 và a b a. Giá trị nhỏ nhất của P  log a  2 log   bằng a   b b  b 9 A.  2 B. 7. C. 5. D. 4. 1 47.21 Cho a
, b  1. Khi biểu thức 4 2
P  log b  log (a  9a  81) đạt giá trị nhỏ nhất thì tổng 3 3a b a b bằng A. 2 3  9 . B. 3 9  2 . C. 2  9 2. D. 3  3 2. 4a 2b 5     47.22 Cho ,
a b  0 thỏa log 
  a  3b  4. Giá trị nhỏ nhất của 2 2 a b bằng 5  a b  1 A.  2 B. 1. 3 C.  2 5 D.  2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 148 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 x 3y     2 2 x 9y
47.23 Cho x, y  0 thỏa log 
  xy x  3y.  P   
Giá trị nhỏ nhất của bằng  xy  1  3y 1  x A. 10. 71 B.  7 72 C.  7 73 D.  7 2y  1
47.24 Cho x, y  0 là thỏa mãn 2
x  2x y  1  log
 Giá trị nhỏ nhất của biểu thức 2 x  1 2x 1  2 P  e
 4x  2y  1 bằng 1 A.  2 B. 1. 1 C.   2 D. 1. 1  y
47.25 Xét x, y  0 thỏa mãn log
 3xy x  3y  4. Giá trị nhỏ nhất của x y bằng 3 x  3xy 4 3  4 A.  3 4 3  4 B.  3 4 3  4 C.  9 4 3  4 D.  9 2    x y x y 2
47.26 Cho x, y  0 thỏa mãn 2( 1) 2018 
 Giá trị nhỏ nhất của 2y  3x bằng 2 (x  1) 1 A. 2 7 B.  8 3 C. 4 5 D. 6
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 149 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 2
47.27 Cho x, y  0 thỏa mãn 2xy 1  2 ( 1).2 ( ).2x y xy x y    
. Giá trị nhỏ nhất của y bằng 3 A. 7 B. 2. 9 C. 4 4 3 D. 1. 3     x y xy x y 2 47.28 Cho ,
x y  0 thỏa mãn 2 1 3 
 Giá trị nhỏ nhất của x  4y bằng xy  1 A. 4 3  9. B. 6  4 3. C. 2 3  2. D. 4 3  6. 1  xy
47.29 Cho x, y  0 thỏa mãn log
 3xy x  2y  4. Giá trị nhỏ nhất của x y bằng 3 x  2y 9 11  19 A. 9 9 11  19 B.  9 18 11  29 C. 21 2 11  3 D. 3
47.30 Cho x, y   thỏa mãn điều kiện x y  1 2  .(3x y
  1)  3x  3y  1. Giá trị nhỏ nhất của 2 2
P x xy y bằng A. 0. B. 2. C. 2. D. 3. 2 x 2  x3 log 5
47.31 Cho các số thực x, y thỏa mãn đẳng thức 3 (  y4) 3  5
. Giá trị nhỏ nhất của biểu thức 2
P  4 y y  1  (y  3) bằng 89 A.   4 B. 16. 41 C.   4 D. 8.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 150 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
47.32 Cho x, y  [1;2] và số thực m thỏa mãn 2 2
x  (9  m)y  6xy. Tổng giá trị lớn nhất và giá trị 2
nhỏ nhất của biểu thức P  log x  log y  log ( m  1) 2 1 2 bằng 4 A. 0. B. 2. C. log 7. 2 D. 2 log 3. 2
47.33 Cho dãy số (u ) thỏa mãn u u
 6, n  2 và log u  log u  8  11. Đặt n n n 1  2 5 2 9
S u u   u . Tìm số tự nhiên n nhỏ nhất thỏa mãn S  20172018. n 1 2 n n A. 2587. B. 2590. C. 2593. D. 2584.
47.34 Cho dãy số (u ) có số hạng đầu u  1 thỏa 2 2 2 2
log (5u )  log (7u )  log 5  log 7 và u  7u n 1 2 1 2 1 2 2 n 1  n
với mọi n  1. Giá trị nhỏ nhất của n để u  1111111 bằng n A. 11. B. 8. C. 9. D. 10.
47.35 Có bao nhiêu giá trị nguyên của tham số m để phương trình m  2 m  2 sin x  sin x có nghiệm thực ? A. 0. B. 1. C. 2. D. 3.
47.36 Hỏi có bao nhiêu giá trị nguyên của tham số thực m nhỏ hơn 10 sao cho phương trình   ex  ex m m có nghiệm thực ? A. 9. B. 8. C. 10. D. 7.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 151 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
47.37 Có bao nhiêu giá trị nguyên của m để 3 3
m  3 m  3 sinx  sin x có nghiệm ? A. 7. B. 3. C. 5. D. 2.
47.38 Tìm các giá trị của tham số m để phương trình ln m  ln(m x)    x   có nhiều nghiệm nhất.
A. m  0.
B. m  1.
C. m  e.
D. m  1.
47.39 Tìm giá trị lớn nhất của m để phương trình ln[m  ln(m  cos x )]  cos x có nghiệm thực ? e  1 A. 2 B. e  1. C. e. D. 1. 47.40 Cho hàm số 3 ( )    2m f x x x
. Có bao nhiêu giá trị nguyên của tham số m để phương trình
f (f (x))  x có nghiệm trên [1;2]. A. 0. B. 4. C. 2. D. 3. 47.41 Cho hàm số 2
f (x)  x  5x  log .
m Có bao nhiêu giá trị nguyên của tham số m để phương 2
trình f (f (x))  x có nghiệm không bé hơn 1  . A. 9. B. 8. C. 7. D. 16. 47.42 Cho hàm số x 2
f (x)  e  x m m. Có bao nhiêu giá trị nguyên của tham số m để phương trình 2 2
f (f (x)  m )  x m có nghiệm trên [0;ln10]. A. 0. B. 2. C. 4. D. Vô số.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 152 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 47.43 Cho hàm số 2
f (x)  x x  1  ln m. Có bao nhiêu giá trị nguyên của tham số m để phương
trình f (f (x))  x có nghiệm trên [ 3; 3]. A. 0. B. 5. C. Vô số. D. 3. 47.44 Cho hàm số x 2
f (x)  e  x m m. Có bao nhiêu giá trị nguyên của tham số m để phương trình 2 2
f (f (x)  m )  x m có nghiệm trên [0;ln10]. A. 0. B. 2. C. 4. D. Vô số.
47.45 Có bao nhiêu giá trị nguyên của tham số thực m để phương trình f f x m  3 3 ( )
x m có
nghiệm x  [1;2], biết 5 3
f (x)  x  3x  4m. A. 16. B. 15. C. 17. D. 18. 3
47.46 Tìm các giá trị thực của m để phương trình x 2   m3x 3 2 x 2  x 1 2 (x 6x 9x m)2 2        1 có
một nghiệm duy nhất. A. m  ( ;  4].
B. m  [8; ). 
C. m  (4; 8). D. m  ( ;  4)  (8; )  . 2
3x  3x m  1
47.47 Có bao nhiêu số nguyên m để phương trình 2 log
x  5x  2  m có hai 2 2 2x x  1
nghiệm phân biệt lớn hơn 1. A. 3. B. Vô số. C. 2. D. 4.
47.48 Có tất cả bao nhiêu giá trị nguyên của tham số thực m sao cho phương trình log (  )  2  3x m x m
 3x  1 có nghiệm thuộc đoạn [0;2] ? 3 A. 9. B. 7. C. 6. D. 5.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 153 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 x m
Câu 48. Cho hàm số f (x ) 
(m là tham số thực). Gọi S là tập hợp tất cả các giá trị của m sao x  1
cho max f (x)  min f (x)  2. Số phần tử của S là [0;1] [0;1] A. 6. B. 2. C. 1. D. 4.
Lôøi giaûi tham khaûo
 Khi m  1 hàm số là hàm hằng f(x)  1 nên max f (x)  min f (x)  1 thỏa nên nhận m  1. [0;1] [0;1]
 Khi m  1 hàm số đơn điệu trên đoạn [0;1] nên: m  1
 Khi f (0); f(1) cùng dấu thì max f(x)  min f(x)  f (0)  f (1)  m   [0;1] [0;1] 2  m  1    
Khi f (0); f (1) trái dấu thì min f (x)  0, max f (x)  max  f (0) ; f (1)  max m ;   [0;1] [0;1]  2   
TH1. Cùng dấu, tức f (0).f (1)  0  m(m  1)  0  m  1 hoặc m  0. m   1 m  1 
Do đó max f (x)  min f (x)  2  m   2   5
 (thỏa m  1 hoặc m  0). [0;1] [0;1] 2 m    3
TH2. Trái dấu f (0).f (1)  0  m(m  1)  0  1  m  0.  m  2 m   2     
Do đó max f (x)  min f (x)  2   m  1  m  5   (không thỏa 1   m  0). [0;1] [0;1]  2    2 m   3  
Kết luận: Có 2 giá trị m thỏa mãn bài toán. Chọn đáp án B.
Baøi toaùn chöùa tham soá trong haøm cuï theå 1) Cho hàm số 3 2
y x  (m  1)x m  1. Tìm tham số m sao cho miny  5. [0;1]
Lời giải tham khảo Ta có: 2 2
y  3x m  1  0. Do đó hàm số đã cho luôn đồng biến [0;1].
 miny y(0)  5  m  1  m  4. [0;1]
Cần nhớ: Cho hàm số y f (x) xác định và liên tục trên đoạn [a;b]. m
 iny y(a)   m
 in y y(b) 
y f (x)   đồng biến [a;b ]   .
y f (x) nghịch biến [a;b ]   . m
 ax y y(b)  m
 ax y y(a)  [a;b ]  [a;b ]  mx  1
2) Tìm tham số m để hàm số y
có min y m  2. x m [ 1  ;2]
Lời giải tham khảo 2 m   1
Điều kiện: x m. Ta có: y 
 0, x m  Hàm số luôn nghịch biến trên [1;2]. 2 (x m)    2m  1 min  y y(2)    m  2 2   2 
4 m  2m 1 m   2m  3  0   [1;2]     2  m    x     m    m   1   m  1    m  1   m  3.         x  [ 1;2]         m   2  m  2  m  2          
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 154 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 x m
3) Tìm tham số m để hàm số y
thỏa mãn min y  3. x  1 [2;4]
Lời giải tham khảo 1  m
Điều kiện: x  1. Ta có: y   2 (x  1)
TH 1. Nếu y  0  m  1
  y  1  miny  1  3  loại. [2;4]
TH 2. Nếu y  0  m  1
  Hàm số đồng biến trên đoạn [2;4].
 min y y(2)  3  m  2  m  1 : không thỏa. [2;4]
TH 3. Nếu y  0  m  1
  Hàm số nghịch biến trên đoạn [2;4]. m  4
 min y y(4)  3 
m  5 : thỏa m  1.  [2;4] 3
Kết luận: m  5 là giá trị cần tìm. 2 m x  4
4) Tìm tham số m sao cho y
thỏa mãn 2 max y  min y  12. x  1 [1;3] [1;3]
Lời giải tham khảo 2 m  4
Điều kiện: x  1. Ta có y   2 (x  1)  TH 1. Nếu 2
m  4  0  m  2
 thì y  4  miny  max y  4 : không thỏa. [1;3] [1;3]
Do đó m  2 không thỏa mãn. m   2   TH 2. Nếu 2 m  4  0 
thì hàm số đồng biến trên [1; 3]. m   2  2 m  4 2 3m  4
 min y y(1) 
và max y y(3) 
 Khi đó theo đề, ta có: [1;3] 2 [1;3] 4 2 2 3m  4 m  4 2
2 max y  min y  12  2. 
 12  m  12  m  2 3 : nhận. [1;3] [1;3] 4 2  TH 3. Nếu 2 m  4  0  2
  m  2 thì hàm số nghịch biến trên [1; 3]. 2 3m  4 2 m  4
 min y y(3) 
và max y y(1) 
 Khi đó theo đề, ta có: [1;3] 4 [1;3] 2 2 2 m  4 3m  4 2
2 max y  min y  12  2. 
 12  m  36  m  6 : loại. [1;3] [1;3] 2 4
Kết luận: m  2 3.
Baøi toaùn max – min khi ñeà cho ñoà thò hoaëc baûng bieán thieân
1) Cho hàm số y f (x) có đồ thị trên [2; 3] như hình vẽ. Gọi M, m là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y f (3 sin x  2). Tổng M m bằng bao nhiêu ?
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 155 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Lời giải tham khảo Đặt 2
t  3 sin x  2. Với t  [t ;t ]. min max Ta có: 2 0  sin x  1 2
 0  3 sin x  3 2
 2  3 sin x  2  5  2  t  5. Suy ra t  [2;5]. Khi đó 2
y f (3 sin x  2)  f (t) với t  [2;5]. M
  maxy  5 khi t  3  Dựa vào đồ thị [2;5]  
. Suy ra: M m  7. m
  min y  2 khi t  5  [2;5] 
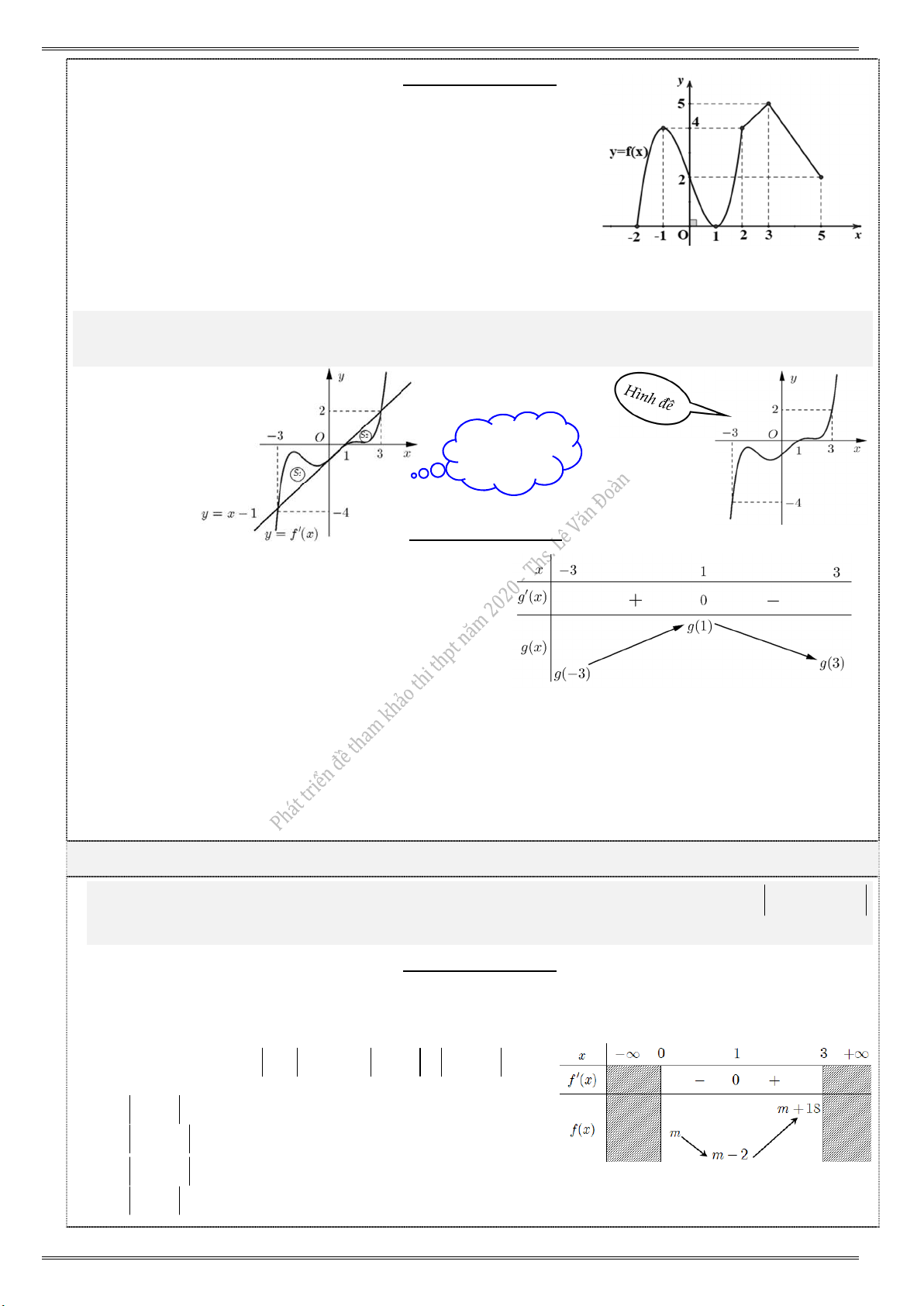
2) Cho hàm số f (x) liên tục trên  và có đồ thị f (
x) như hình vẽ. Đặt 2
g(x)  2f (x)  (x  1) . Khi
đó giá trị nhỏ nhất của hàm số y g(x) trên đoạn [3; 3] bằng
A. g(0). B. g(1). Hình vẽ thêm C. g(3). khi giải
D. g(3).
Lời giải tham khảo Ta có: g (
x)  2f (x)  3(x  1)  2 f (x)  (x  1)   x   3  Suy ra g (
x)  0  f (x)  x 1  . x   1 
Từ bảng biến thiên  min g(x)  g(3); g(3  ) . [3;3] 1 3
Hình vẽ, ta có: S S  2S  2S  2
f (x)(x 1) dx  2 (x 1) f (x) dx   1 2 1 2     3  1 1 3  g (  x)dx g  (  x)dx  
g(1)  g(3)  g(1)  g(3)  g(3)  g(3)  min g(x)  g(3). [3;3] 3 1
Giaù trò lôùn nhaát vaø nhoû nhaát cuûa haøm trò tuyeät ñoái
Tìm tất cả các giá trị thực của tham số thực m sao cho giá trị lớn nhất của hàm số 3
y x  3x m
trên đoạn [0; 3] bằng 16.
Lời giải tham khảo Xét hàm số 3
f (x)  x  3x m có 2 f (
x)  3x  3  0  x  1  [0;3] hoặc x  1  [0;3]. Tính f (0)  ,
m f (1)  m  2, f (3)  m  18. Từ đó có bảng biến thiên như sau:
Suy ra: max y  max f (x)  max m  2 ; m  18   16 [0;3] [0;3] m  2  16   m   2  16        m  14  m  18  16  
16  m  18  16         .   m  18  16  m   18  16      m  2 m  2  16 
 16  m  2  16       
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 156 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Baøi taäp töông töï vaø môû roäng mx  1 1
48.1. Tìm tham số m để hàm số y
đạt giá trị lớn nhất bằng trên đoạn [0;2]. x m 3 A. m  1. B. m  1. C. m  3. D. m  3. mx  5
48.2. Tìm tham số thực m để hàm số f (x) 
đạt giá trị nhỏ nhất trên đoạn [0;1] bằng 7. x m A. m  2.
B. m  0. C. m  1.
D. m  5.
48.3. Tìm các giá trị của m để giá trị nhỏ nhất của hàm số 3 2 y x
  3x m trên [1;1] bằng 0. A. m  4. B. m  2. C. m  6. D. m  0. 48.4. Cho hàm số 3 2
y x  3m x  6. Tìm tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất
của hàm số trên đoạn [0; 3] bằng 42. A. m  1.
B. m  1. C. m  1.
D. m  {2;1}. 48.5. Cho hàm số 3 2 2 y x
  mx  (m m  1)x. Tìm tất cả các giá trị thực của tham số m sao cho
giá trị nhỏ nhất của hàm số trên đoạn [1;1] bằng 6. A. m  2. B. m  2  . C. m   6.
D. m  1  5.
48.6. Tìm tất cả các giá trị của tham số thực m để giá trị nhỏ nhất của hàm số 3 2
y x  3mx  6 trên đoạn [0; 3] bằng 2. A. m  2. 31 B. m   27 3 C. m   2 D. m  1. x m
48.7. Cho hàm số y
(m là tham số thực) thỏa mãn min y  2. Mệnh đề nào đúng ? x  1 [1;2] A. m  1.
B. 1  m  2.
C. 2  m  3. D. m  3. x m
48.8. Cho hàm số y
(m là tham số thực) thỏa mãn max y  3. Mệnh đề nào đúng ? x  1 [2;4]
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 157 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 A. m  1.
B. 3  m  4.
C. 1  m  3. D. m  4. 2 x m
48.9. Cho hàm số y
(m là tham số thực). Gọi S là tập hợp các giá trị m thỏa mãn x  4
max y  4. Số phần tử của S là [ 2;0  ] A. 0. B. 1. C. 2. D. Vô số. 2x m
48.10. Cho hàm số y
(m là tham số thực). Gọi S là tập hợp tất cả các giá trị m thỏa mãn x  1
max y  min y  8. Số phần tử của S là [2;4] [2;4] A. 0. B. 1. C. 2. D. Vô số. 2 m x  4
48.11. Cho hàm số y
(m là tham số thực). Gọi S là tập hợp tất cả các số nguyên m thỏa x  1
mãn 2 max y  min y  12. Số phần tử của S là [1;3] [1;3] A. 0. B. 1. C. 2. D. 4. 2 m x  4
48.12. Cho hàm số y
(m là tham số thực). Gọi S là tập hợp số nguyên m thỏa mãn x  1
3 max y  2 min y  4. Số phần tử của S là [1;3] [1;3] A. 0. B. 3. C. 4. D. 5. 2x m
48.13. Cho hàm số y
(m là tham số thực). Gọi S là tập hợp tất cả các số thực m thỏa mãn x  1 2 2
2(max y)  3(min y)  3. Số phần tử của S là [ 1  ;0] [ 1  ;0]
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 158 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 A. 0. B. 1. C. 2. D. 3. x  3  m
48.14. Cho hàm số y
(m là tham số thực) thỏa min y  2. Mệnh đề nào đúng ? x  3  1 [1;6] A. m  3.
B. 3  m  2.
C. 2  m  3. D. m  1. 2 m tan x  2
48.15. Cho hàm số y
với m là tham số thực. Số các giá trị m thỏa mãn max y  3 là tan x  1   0;   4   A. 0. B. 1. C. 2. D. 3. ln x  2m
48.16. Cho hàm số y
(m là tham số thực). Gọi S là tập hợp các giá trị m thỏa max y  1. ln x  2 2 [1;e ]
Số phần tử của S là A. 0. B. 1. C. 2. D. Vô số.
48.17. Cho hàm số y f (x) xác định và liên tục trên đoạn [ 3
 ;3]. Gọi M, m lần lượt là giá trị lớn nhất
và giá trị nhỏ nhất của hàm số y f (f (x)) trên đoạn [ 1
 ;0]. Giá trị của M m bằng A. 1. B. 3. C. 4. D. 6.
48.18. Cho hàm số y f (x) liên tục trên đoạn [1; 3] và có đồ thị như hình bên. Gọi M và m lần lượt
là giá trị lớn nhất và nhỏ nhất của hàm số y f (f (x)) trên đoạn [ 1
 ;0]. Giá trị M m bằng A. 2. B. 3. C. 4. D. 5.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 159 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
48.19. Cho hàm số y f (x ) xác định, liên tục trên đoạn [ 2
 ;2] và có đồ thị là đường cong trong hình
vẽ bên dưới. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y f (f (x)) trên đoạn [ 1
 ;1]. Giá trị của M m bằng A. 2. B. 4. C. 6. D. 8.
48.20. Cho hàm số y f (x ) xác định, liên tục trên đoạn [ 5
 ; 3] và có đồ thị như hình vẽ bên dưới. Gọi
M, m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y f (f (x)) trên đoạn [ 4  ;0]. Giá trị
của M m bằng A. 3. B. 7. C. 4. D. 6.
48.21. Cho hàm số y f (x ) liên tục trên  và có đồ thị như hình. Gọi M, m lần lượt là giá trị lớn nhất
và giá trị nhỏ nhất của hàm số y f (f (sin x)) trên đoạn [0; ]. Giá trị của M m bằng A. 1. B. 3. C. 4. D. 2.
48.22. Cho hàm số y f (x ) liên tục trên  và có đồ thị như hình. Gọi M, m lần lượt là giá trị lớn nhất
và giá trị nhỏ nhất của hàm số y f (f (log x)) trên đoạn [2; 4]. Giá trị của M m bằng 2 A. 1. B. 3. C. 5. D. 8.
48.23. Cho hàm số y f (x). Đồ thị y f (
x) như hình bên dưới. Giá trị nhỏ nhất và giá trị lớn nhất
của hàm số trên đoạn [0; 3] lần lượt là
A. f (1), f (0).
B. f (2), f (0).
C. f (1), f (3).
D. f (0), f (3).
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 160 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
48.24. Cho y f (x) có đồ thị của y f (
x) như hình vẽ dưới. Đặt M  max f(x), m  min f(x). Giá [ 2;  6] [ 2;  6]
trị của biểu thức P M m bằng
A. f (0)  f (2).
B. f (5)  f (2).
C. f (5)  f (6).
D. f (0)  f (2). 48.25. Cho hàm số 4 3 2
f (x)  ax bx cx dx  ,
e biết hàm số y f (
x) có đồ thị (C ) như hình vẽ
và diện tích của hình phẳng giới hạn bởi (C ) và trục hoành bằng 27. Gọi M, m lần lượt là giá
trị lớn nhất và giá trị nhỏ nhất của hàm số y f (x) trên đoạn [3; 3]. Giá trị của M m bằng A. 27. B. 36. C. 48. D. 75. 48.26. Cho hàm số 5 4 3 2
f (x)  x bx cx dx ex với , b ,
c d, e  .
 Hàm số y f (  x) có đồ thị
như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y f (x)
trên đoạn [1; 3]. Giá trị của tổng M m bằng A. 63. B. 21. 196 C. 3 272 D. 3
48.27. Cho hàm số y f (x) xác định, liên tục trên  và f (2)  0. Hàm số y f (
x) có đồ thị như hình
vẽ bên dưới. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số g(x)  f (x)
trên trên đoạn [1; 3]. Giá trị của M và m lần lượt là
A. M f (1), m f (3).
B. M f (3) , m f (1) .
C. M f (1) , m f (2) .
D. M f (1) , m f (3) . 48.28. Cho hàm số 3 2
f (x)  ax bx cx d có đồ thị (C ). Biết đồ thị (C ) tiếp xúc với đường thẳng
y  4 tại điểm có hoành độ âm và đồ thị của hàm số y f (
x) như hình vẽ bên dưới. Giá trị lớn
nhất của hàm số y f (x) trên [0; 3] bằng A. 20. B. 60. C. 22. D. 3.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 161 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 48.29. Cho hàm số 3 2
f (x)  x  3x . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm
số g(x)  f (1  2 sin x)  1 . Giá trị của biểu thức M m bằng A. 3. B. 1. C. 2. D. 4.
48.30. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị nhỏ nhất của hàm số 3 2
y x  3x m trên đoạn [1; 3] bằng 3. Tổng tất cả các phần tử của S bằng A. 3  . B. 2. C. 4. D. 7.
48.31. Có bao nhiêu giá trị của m để giá trị lớn nhất của hàm số 4 2 y x
 8x m trên đoạn [1;3] bằng 2018 ? A. 0. B. 2. C. 4. D. 6.
48.32. Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị lớn nhất của hàm số 2
y  sin x  2 sin x m bằng 1. Số phần tử của S là A. 0. B. 1. C. 4. D. 3.
48.33. Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị lớn nhất của hàm số 2
y  ln x  ln x m trên đoạn [1; e] bằng 2. Số phần tử của S là A. 1. B. 2. C. 4. D. 6.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 162 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
48.34. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số 2
x mx m f (x) 
trên đoạn [1;2] bằng 2. Tổng tất cả các phần tử của S bằng x  1 11 A.   3 13 B.  6 11 C.   6 1 D.  3
(m  1)x m  1
48.35. Có bao nhiêu giá trị của tham số m để giá trị lớn nhất của hàm số y  trên x  1 1
đoạn [3;2] bằng  2 A. 1. B. 2. C. 0. D. 6. 2x m
48.36. Cho hàm số f (x) 
(m là tham số thực). Gọi S là tập hợp tất cả các giá trị của m sao x  2
cho max f (x)  min f (x)  4. Số phần tử của S là [0;2] [0;2] A. 0. B. 2. C. 3. D. 4. x m
48.37. Cho hàm số f (x) 
(m là tham số thực). Gọi S là tập hợp tất cả các giá trị của m nguyên x  2
thuộc [10;10] sao cho max f (x)  min f (x)  2. Số phần tử của S là [0;1] [0;1] A. 18. B. 8. C. 10. D. 19.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 163 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 48.38. Cho hàm số 3 2
f (x)  x  3x m. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho
max f (x)  2 min f (x) . Số phần tử của S là [1;3] [1;3] A. 2. B. 3. C. 4. D. 1. 48.39. Cho hàm số 4 2
f (x)  x  2x m với m là tham số. Gọi S là tập hợp tất cả các giá trị của m
nguyên thuộc đoạn [10;10] sao cho max f (x)  3 min f (x) . Số phần tử của S là [0;2] [0;2] A. 5. B. 4. C. 6. D. 3. 48.40. Cho hàm số 3 2
f (x)  x  3x  2m  1 (m là tham số thực). Gọi S là tập hợp tất cả các giá trị
của m sao cho max f (x)  min f (x)  10. Số các giá trị nguyên của S thuộc đoạn [30; 30] là [1;3] [1;3] A. 56. B. 61. C. 55. D. 57. 48.41. Cho hàm số 2
f (x)  x
  2(m  1)x  2m  1. Gọi S là tập hợp tất cả các giá trị của tham số m
sao cho max f (x)  min f (x)  8. Số phần tử của S là [0;4] [0;4] A. 0. B. 2. C. 3. D. 1. 4
x mx m
48.42. Cho hàm số f (x) 
. Số giá trị nguyên của m để max f (x)  2 min f (x)  0 là x  1 [1;2] [1;2] A. 15. B. 14. C. 13. D. 12.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 164 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Câu 49. Cho hình hộp ABCD.AB CD
  có chiều cao bằng 8 và diện tích đáy bằng 9. Gọi M, N, P
và Q lần lượt là tâm của các mặt bên ABB A  , BCC B  , CDD C
  và DAAD . Thể tích của
khối đa diện lồi có các đỉnh là các điểm ,
A B, C, D, M, N , P và Q bằng A. 27. B. 30. C. 18. D. 36.
Lôøi giaûi tham khaûo Ta có V  9.8  72.
ABCD.AB CD  
Gọi I , J , K, L là trung điểm các cạnh AA , BB , CC , DD . Suy ra V  36. ABCD.IJKL Do hình chóp .
AMIQ đồng dạng với hình chóp . A B A  D 1 1 1 1 9 3 theo tỉ số nên VV  . .8.   2 . A MQI A. 8 B A  D  8 3 2 2 3 Do đó VV  4V  36  4.  30. ABCD.MNPQ ABCD.IJKL . A MIQ 2 Chọn đáp án D.
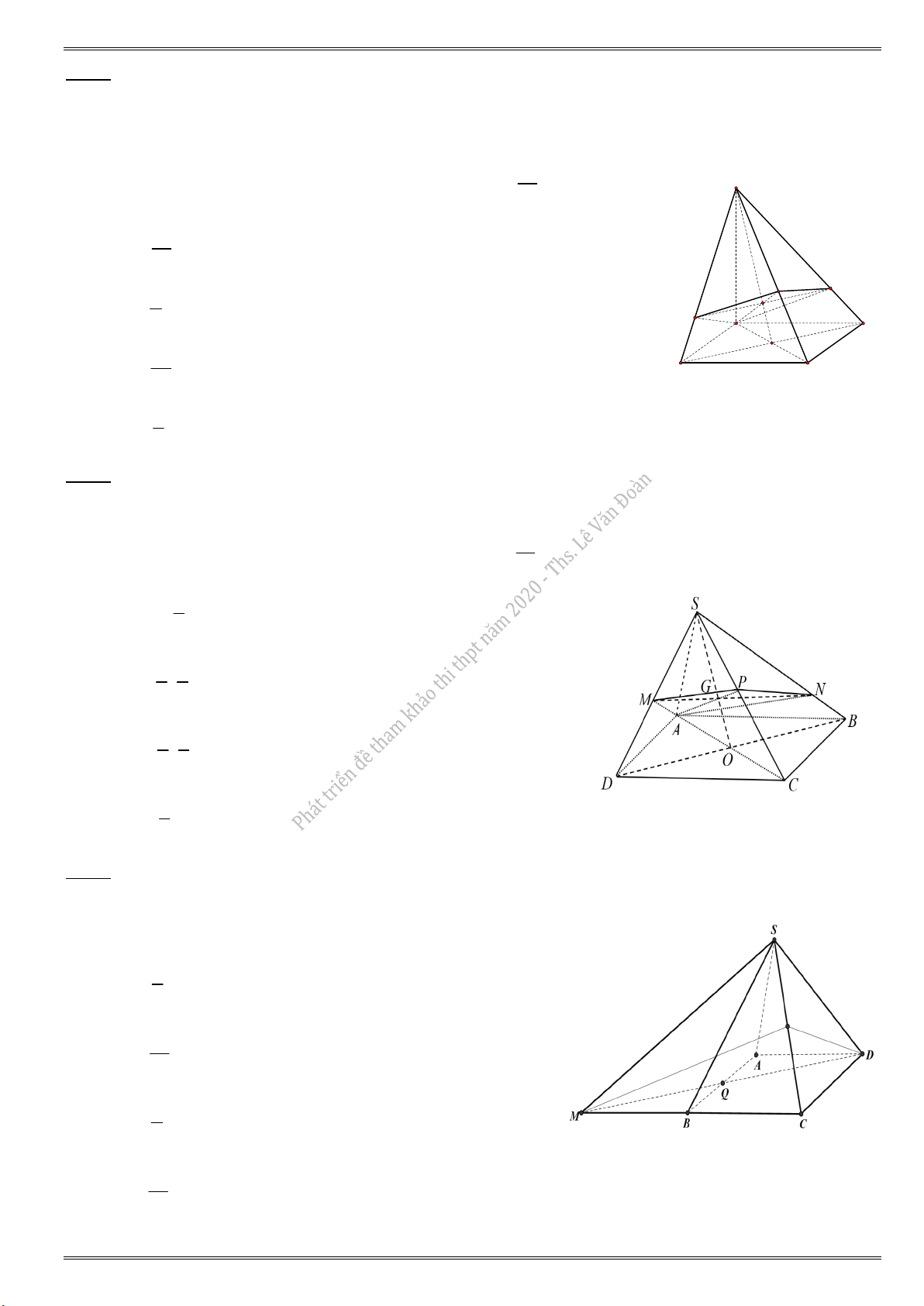
1. Cho hình chóp S.ABC có thể tích bằng V . Gọi G là trọng tâm tam giác SBC . Mặt phẳng ( ) đi qua hai điểm ,
A G và song song với BC . Mặt phẳng ( )
cắt các cạnh S ,
B SC lần lượt tại
các điểm M và N . Thể tích khối chóp S.AMN bằng V SM SN SG 2 A.
Vì MM BC      9 SB SC SE 3 V V SA SM SN 2 2 4 B. SAMN        2 Nên V SA SB SC 3 3 9 SABC 4V C. 4V 9 Suy ra V   S .AMN 9 V D. Chọn đáp án D. 4
2. Cho hình chóp tứ giác S.ABCD có thể tích bằng V . Lấy điểm A trên cạnh SA sao cho
SA  3SA . Mặt phẳng qua A và song song với đáy của hình chóp cắt các cạnh S ,
B SC, SD
lần lượt tại B , C , D .
 Thể tích khối chóp S.AB CD   bằng V S 3 V      A.    SA SB SC 1   1 S .A B C 3 Ta có:         D' V SA SB SCA' 3 27 S .ABC V C' B. B' V       SA SD SC 1 81
Tương tự: S.A D C      V SA SD SC 27 V S .ADC C. 9 A D Mà VVV
S .AB CD  
S .AB C  
S .AC D   V 1 1 V D. C  (VV )  V   27 Chọn D. S .ABC S .ACD S . 27 27 ABCD 27 B
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 165 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
3. Cho khối hộp ABCD.AB CD
  có thể tích bằng 2018. Gọi M là trung điểm của cạnh AB. Mặt phẳng (MB D
 ) chia khối chóp ABCD.AB CD
  thành hai khối đa diện. Thể tích phần khối đa
diện chứa đỉnh A bằng
BM AA  E ED  AD N 5045 Gọi , . A. 6
Ta có M trung điểm AB M trung điểm EB .  N 7063
là trung điểm của ED  và AD. B. 6 V EA EM EN 1
Khi đó: E.AMN      V EAEBED 8 10090
E .AB D   C. 17 7 7 1  VV  .2. .V
AMN .AB D  
E .AB D   . 8 8 2 A AB D   7063 D. 7 7063 12  V
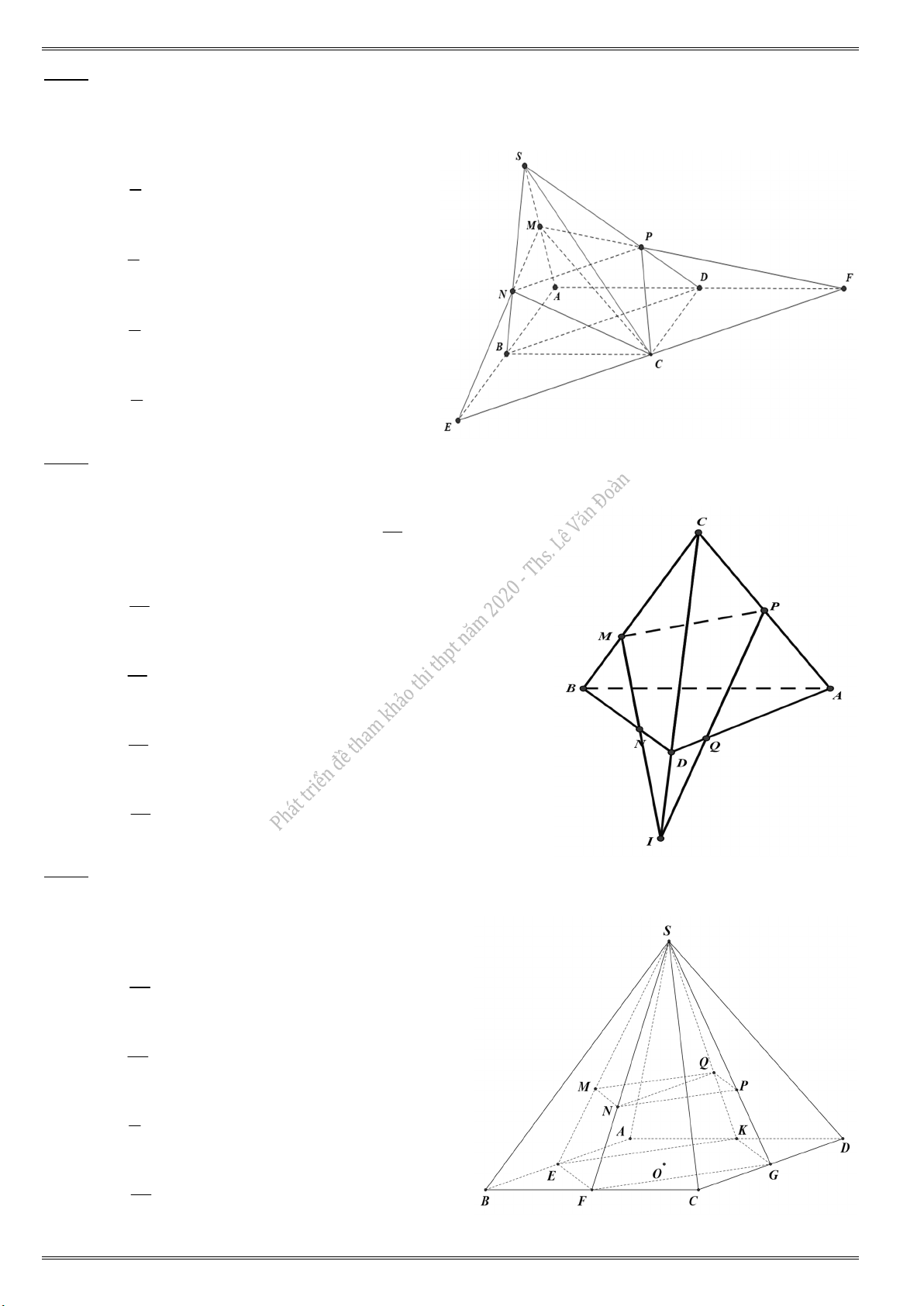
Chọn đáp án D. ABCD. 24 AB CD   12
Baøi taäp töông töï vaø môû roäng
49. 1 Cho hình lập phương ABCDAB CD
  có cạnh bằng a. Gọi M là trung điểm của C , D N là
trung điểm của AD . Thể tích của tứ diện MNB C   bằng 3 a A.  3 3 a B.  6 3 a C.  4 3 2a D.  5
49. 2 Cho khối tứ diện đều ABCD có thể tích là V . Gọi M, N, P, Q lần lượt là trung điểm của AC, A , D B ,
D BC. Thể tích khối chóp BMNPQ bằng V A. 6 V B.  3 V C.  4 V 2 D.  3
49. 3 Cho hình lăng trụ ABC .AB C
 . Gọi M, N, P lần lượt là các điểm thuộc các cạnh AA , BB ,
CC  sao cho AM  2MA , NB  2N ,
B PC PC . Gọi V , V lần lượt là thể tích của hai khối 1 2 V
đa diện ABCMNP và AB CMN
P. Tính tỉ số 1  V2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 166 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 V A. 1  2. V 2 V 1 B. 1   V 2 2 V C. 1  1. V2 V 2 D. 1   V 3 2
49. 4 Cho khối chóp S.ABCD có đáy là hình bình hành ABCD. Gọi M, N, P, Q lần lượt là trọng
tâm các tam giác SA ,
B SBC, SC , D .
SDA Biết thể tích khối chóp S.MNPQ là V, khi đó thể tích
của khối chóp S.ABCD bằng 27V A. 4 2 9   B.   V .  2 9V C.  4 81V D.  8
49. 5 Cho hình tứ diện ABCD có AB CD  12, AD  10. Gọi M, N lần lượt là trung điểm của
AB, CD. Biết rằng MN vuông góc với AB và CD đồng thời MN  8. Thể tích khối tứ diện ABCD bằng A. 96 3. B. 96. C. 96 2. D. 192.
49. 6 Cho khối lăng trụ ABC .AB C
  có thể tích bằng 1. Gọi M, N lần lượt là trung điểm của các
đoạn thẳng AA và BB . Đường thẳng CM cắt đường thẳng C A
  tại P, đường thẳng CN cắt đường thẳng C B
  tại Q. Thể tích khối đa diện lồi AMPB NQ bằng A. 1. A C 1  M B. B 3 I N 1 P C. AC 2 B 2 D. Q 3
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 167 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
49. 7 Cho khối lăng trụ ABC.AB C
  có thể tích bằng 2. Gọi M là trung điểm của AA và N là điểm
nằm trên cạnh BB sao cho BN  2B N
 . Đường thẳng CM cắt đường thẳng C A   tại , P đường
thẳng CN cắt đường thẳng C B   tại .
Q Thể tích của khối đa diện AMPB NQ bằng 7 A. 9 5 B. 9 2 C. 3 13 D. 9
49. 8 Cho hình lăng trụ ABC.AB C
  có thể tích bằng V. Gọi M là trung điểm cạnh BB , điểm N
thuộc cạnh CC  sao cho CN  2C N
 . Thể tích khối chóp . ABCNM bằng 7V A. 12 7V B. 18 5V C. 18 V D. 3  
49. 9 Cho khối hộp ABC . D AB CD
  có thể tích V. Điểm E thỏa AE  3AB. Thể tích của khối đa
diện gồm các điểm chung của khối hộp và khối chóp E.ADD bằng 4V A. 27 V B. 2 19V C. 54 25V D. 54
49. 10 Cho khối lập phương ABC . D AB CD
  cạnh a. Các điểm E, F lần lượt là trung điểm của C B   và C D
 . Mặt phẳng (AEF) cắt khối lập phương đã cho thành hai phần, gọi V là thể tích khối 1 V
chứa điểm A và V là thể tích khối chứa điểm C . Khi đó 1 bằng 2 V2 C' 25 A. 47 B. 1. 8 C. 17 17 D. 25
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 168 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
49. 11 Cho lăng trụ đều ABC.AB C
  có độ dài tất cả các cạnh bằng 3. Gọi M, N là trung điểm của S
hai cạnh AB và AC. Thể tích của khối đa diện AMNAB C   bằng 34 3 A. 12 N A C 21 3 B. 5 M B 63 3 C. 16 C' A' 45 3 D. 16 B'
49. 12 Cho lăng trụ ABC.AB C
  có thể tích bằng 2. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh
AA và BB sao cho M là trung điểm của AA và 3B N
  2BB . Đường thẳng CM cắt đường
thẳng AC  tại P và đướng thẳng CN cắt đường thẳng B C
  tại Q. Thể tích khối đa diện lồi AMPB NQ bằng 13 A. 18 23 B. 9 5 C. 9 7 D. 18
49. 13 Cho khối hộp ABC . D AB CD
  có thể tích bằng 2018. Gọi M là trung điểm của cạnh A . B Mặt phẳng (MB D
 ) chia khối chóp ABCDAB CD
  thành hai khối đa diện. Thể tích phần khối đa
diện chứa đỉnh A bằng 5045 A. 6 7063 B. 6 10090 C. 17 7063 D. 12
49. 14 Cho hình lập phương ABC . D AB CD
  cạnh a. Gọi M là trung điểm của BC, N thuộc cạnh CN 1 CD thỏa
  Mặt phẳng (AMN ) chia khối lập phương thành hai khối, gọi (H) là khối CD 3 chứa điểm .
A Thể tích của khối (H) bằng
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 169 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 3 53a C' A. 137 3 B 55a B. 144 3 47a C. 154 3 65a D. 113
49. 15 Cho hình hộp chữ nhật ABC . D AB CD
 . Gọi M, N, P lần lượt là trung điểm của BC, C D
 , DD . Biết thể tích của khối hộp chữ nhật đó bằng 226, thể tích của khối đa diện AMNP bằng I 113 A. A' B' 3 117 N D' B. C' 4 113 C. P 4 117 A B D. 3 S M D C
49. 16 Cho khối lăng trụ ABC.AB C
  có góc giữa hai mặt phẳng (ABB A  )  và (ACC A  )  là 60 và 14 AA   Tính V ,
d ABB  và d(A ,CC )   2. 2
ABC .AB C   biết ( , ) 1 43 A. 6 43 B. 3 42 C. 6 42 D. 3
49. 17 Cho khối chóp tứ giác S.ABCD có thể tích V, đáy ABCD là một hình bình hành. Gọi
M, N, P, Q lần lượt là trung điểm các cạnh S ,
B BC, C , D D .
A Tính thể tích khối chóp
M.CNQP theo V. S 3V A. 8 3V B. M 4 V Q C. A 16 D 3V B P D. N 16 C
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 170 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
49. 18 Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng ,
a SA  2a. Hai mặt phẳng
(SAB) và (SAD) cùng vuông góc với (ABCD). Một mặt phẳng (P) qua A và vuông góc SC, cắt các cạnh ,
SB SC, SD lần lượt tại B , C , D . Gọi V và V lần lượt là thể tích của khối chóp 1 2 V S.AB CD   ABCD D CB   S và khối đa diện . . Tỉ số 1 bằng V2 8 A. 15 D' C' 8  I B. B' A D 7 O 32 C. B C 13 1 D. 2
49. 19 Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích V. Điểm P là trung
điểm của SC, một mặt phẳng qua AP cắt hai cạnh SD và SB lần lượt tại M và N. Gọi V là 1 V
thể tích khối chóp S.AMPN. Giá trị lớn nhất của 1 thuộc khoảng V  1   A. 0;     5 1 1   B.  ;    5 3 1 1   C.  ;    3 2 1    D.  ;1   2 
49. 20 Cho khối chóp S.ABCD có đáy là hình bình hành thể tích bằng 1. Gọi M là điểm đối xứng của C qua ,
B N là trung điểm cạnh SC. Mặt phẳng (MDN) chia khối chópS.ABCD thành hai
khối đa diện, thể tích của khối đa diện chứa đỉnh S bằng 5 A. 6 7 B. 12 5 C. 8 12 D. 19
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 171 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
49. 21 Cho khối chóp S.ABCD có đáy là hình bình hành, thể tích bằng 1. Gọi M là trung điểm cạnh S ,
A các điểm E, F lần lượt là điểm đối xứng của A qua B và D. Mặt phẳng (MEF) cắt các cạnh S ,
B SD lần lượt tại các điểm N, P. Thể tích của khối đa diện ABCDMNP bằng 2 A. 3 1 B. 3 3 C. 4 1 D. 4
49. 22 Cho tứ diện ABC ,
D trên các cạnh BC, B ,
D AC lần lượt lấy các điểm M, N, P sao cho
BC  3BM, 2BD  3BN và AC  2AP. Mặt phẳng (MNP) chia khối tứ diện ABCD thành V
hai phần có thể tích là V , V . Tỉ số 1 bằng 1 2 V2 26 A. 19 3 B. 19 15 C. 19 26 D. 13
49. 23 Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N, P, Q lần lượt là trọng tâm của các tam giác SA ,
B SBC, SC , D SD .
A Gọi O là điểm bất kỳ trên mặt phẳng đáy ABC . D Biết thể
tích khối chóp OMNPQ bằng V. Tính thể tích khối chóp S.ABC . D 27 A. V . 8 27 B. V . 2 9 C. V . 4 27 D. V . 4
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 172 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Câu 50. Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn 2 2
log (x y)  log (x y ) ? 3 4 A. 3. B. 2. C. 1. D. Vô số.
Lôøi giaûi tham khaûo x
  y  3t  Đặt 2 2
log (x y)  log (x y )  t   . 3 4 2 2 x   y  4t  x y
Áp dụng bất đẳng thức Cauchy Schwarz 2 2 2 2
ax by  (a b )(x y ) và dấu "  " khi  , được: a b 2t   t t t t 3   1 2 2 2 2
3  1.x  1.y  (1  1 )(x y )  2.4  9  2.4     2  t  log 2.   3 2 2 2 1 log 2 3 2 Do đó 2 2 t 2 t 2 x
x y  4  x  4  4
 1, 89  1, 37  x  , 1 37 
 x  {1;0;1 . } Thử lại: y   3t t   0 y   3t 1 t   0      Với x  0     (thỏa).
 Với x  1     (thỏa). 2 y   4t y   1 2 t   y   4  1 y   0       y   3t  1 t   0 log 2 3    Với 2 2 x  1    
x y  5 mâu thuẫn 2 2 2 x y  4 (loại) 2 y   1  4t  1 y   3t  1  2    
Vậy có hai giá trị x  {0; }
1 . Chọn đáp án D.
Baøi taäp töông töï vaø môû roäng
50. 1 Có bao nhiêu số nguyên y để tồn tại số thực x thỏa mãn 2 2
log (x  2y)  log (x y ) ? 3 2 A. 3. B. 2. C. 1. D. Vô số.
50. 2 Cho x, y là các số thực thỏa mãn log (2  2)   3  8y x x y
. Biết 0  x  2018, số cặp (x;y) 2
nguyên thỏa mãn đẳng thức là A. 2. B. 3. C. 4. D. 5.
50. 3 Có bao nhiêu cặp số nguyên (x;y) thỏa mãn các điều kiện 0  x  2020, 1  y  2020 và x 1
4   log (  3)  16.2y y
 log (2x  1) ? 2 2 A. 2019. B. 2020. C. 1010. D. 1011.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 173 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 x
50. 4 Có bao nhiêu cặp số nguyên dương (x;y) thỏa x  2020 và 3 3 x x  log
 8y  2y  1 ? 2 y A. 1010. B. 2020. C. 2019. D. 1011.  y 
50. 5 Có bao nhiêu cặp số nguyên (x;y) thỏa x  2020 và 2 log   
  3(y x  1)  y x ?
2 2 1  x  A. 1010. B. 44. C. 2020. D. 1011. 2
50. 6 Cho phương trình 2 y 2 2
log (2x  4x  4)  2  y x  2x  1. Hỏi có bao nhiêu cặp số nguyên 2
dương (x;y) và 0  x  100 thỏa mãn phương trình đã cho ? A. 4. B. 3. C. 1. D. 2.
50. 7 Có bao nhiêu cặp số nguyên (x;y) thoả mãn 0  y  2020 và x 3
3  3x  6  9y  log y ? 3 A. 9. B. 7. C. 8. D. 2019.
50. 8 Có bao nhiêu cặp số nguyên dương (x;y) thoả mãn 0  x  2020 và (  1).3x  .27y x y ? A. 2020. B. 673. C. 672. D. 2019.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 174 -
Phaùt trieån ñeà tham khaûo thpt quoác gia naêm 2020 laàn 2
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
50. 9 Xét các số thực dương x, y thỏa mãn 3(3y y)  x  log x  3. Giá trị nhỏ nhất của biểu thức 3 3 2
y  log x bằng 9 7 A.   16 7 B.  16 9 C.  16 9 D.   16
50. 10 Xét các số thực dương x, y thỏa mãn log (4  16)   3  8y x x y
 2 . Gọi (x ;y ) là cặp (x;y) 2 o o khi biểu thức 2   3  1  8y P x x
đạt giá trị nhỏ nhất. Giá trị của 3
x  3y bằng o o A. 9. B. 7. C. 7.  D. 9.
50. 11 Có bao nhiêu giá trị nguyên của tham số thực m để tồn tại cặp số (x;y) thỏa mãn đồng thời 3x 5y x 3y 1 e e  
 1  2x  2y và 2 2
log (3x  2y  1)  (m  6)log x m  9  0 ? 3 3 A. 6. B. 5. C. 7. D. 8.
50. 12 Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất cặp (x;y) thỏa mãn
đồng thời các điều kiện log
(4x  4y  4)  1 và 2 2
x y  2x  2y  2  m  0. Tổng các 2 2 x y  2
phần tử của S bằng A. 33. B. 24. C. 15. D. 5.
50. 13 Biết trong tất cả các cặp (x;y) thỏa mãn 2 2
log (x y  2)  2  log (x y  1) chỉ có duy nhất 2 2
một cặp (x;y) thỏa mãn 3x  4y m  0. Tổng các giá trị của tham số m bằng A. 20. B. 46. C. 28. D. 14.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 175 -