



























Preview text:
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
PBM-PHÂN TÍCH, BÌNH LUẬN VÀ PHÁT TRIỂN MỘT SỐ CÂU VDC
ĐỀ THI TỐT NGHIỆP THPT NĂM 2020
Môn: Toán – MÃ ĐỀ 101 (Câu: 43 – 50)
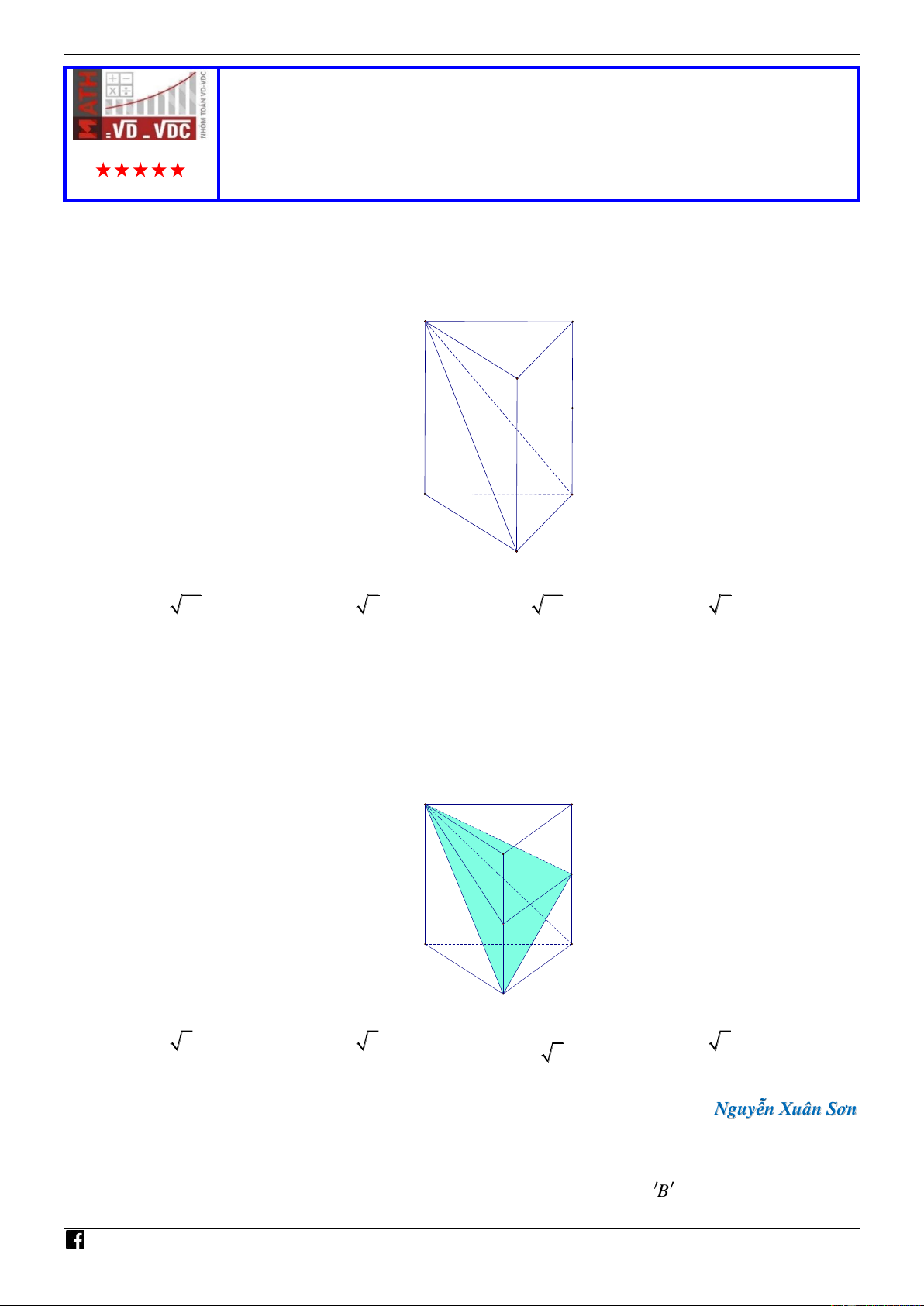
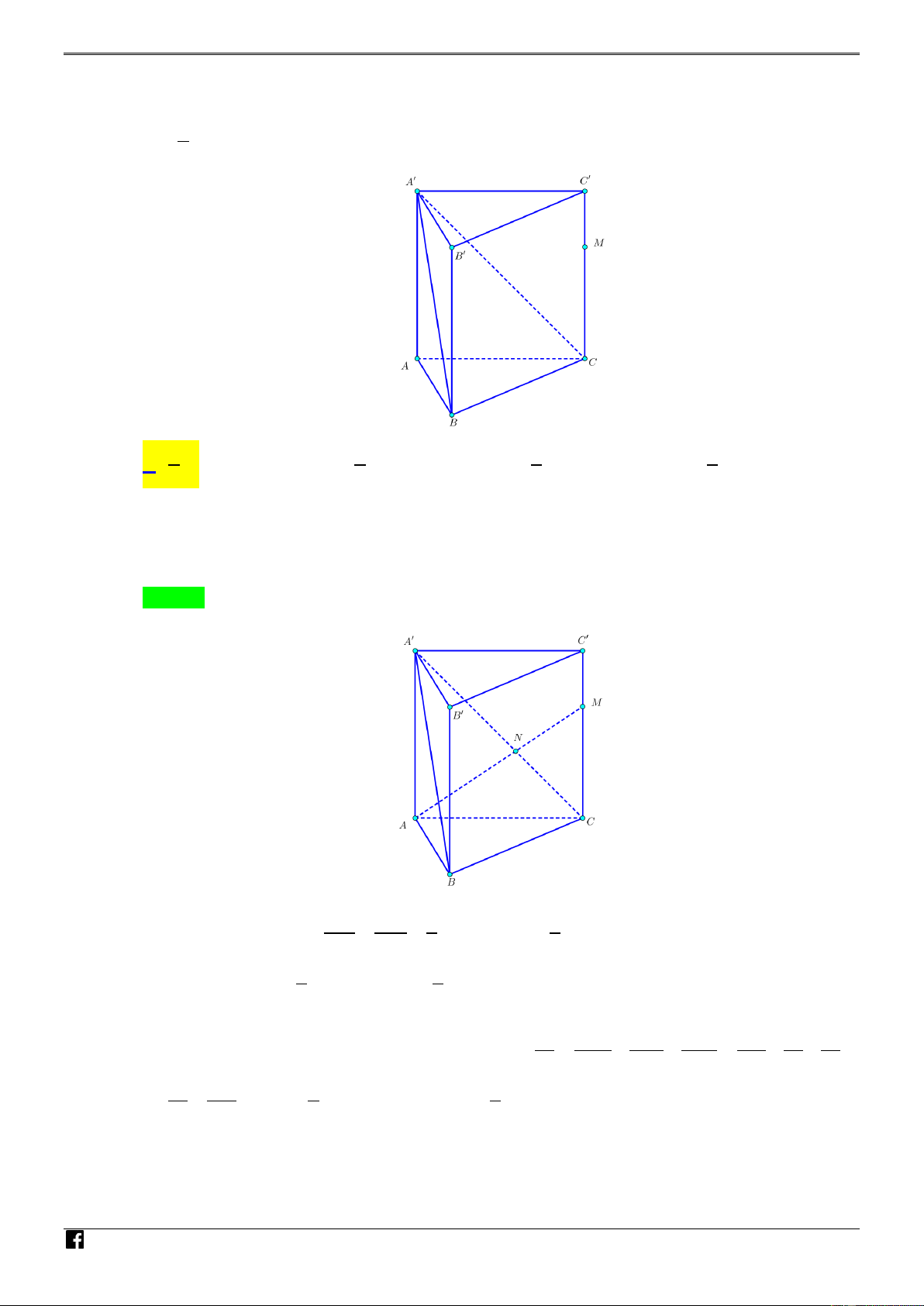
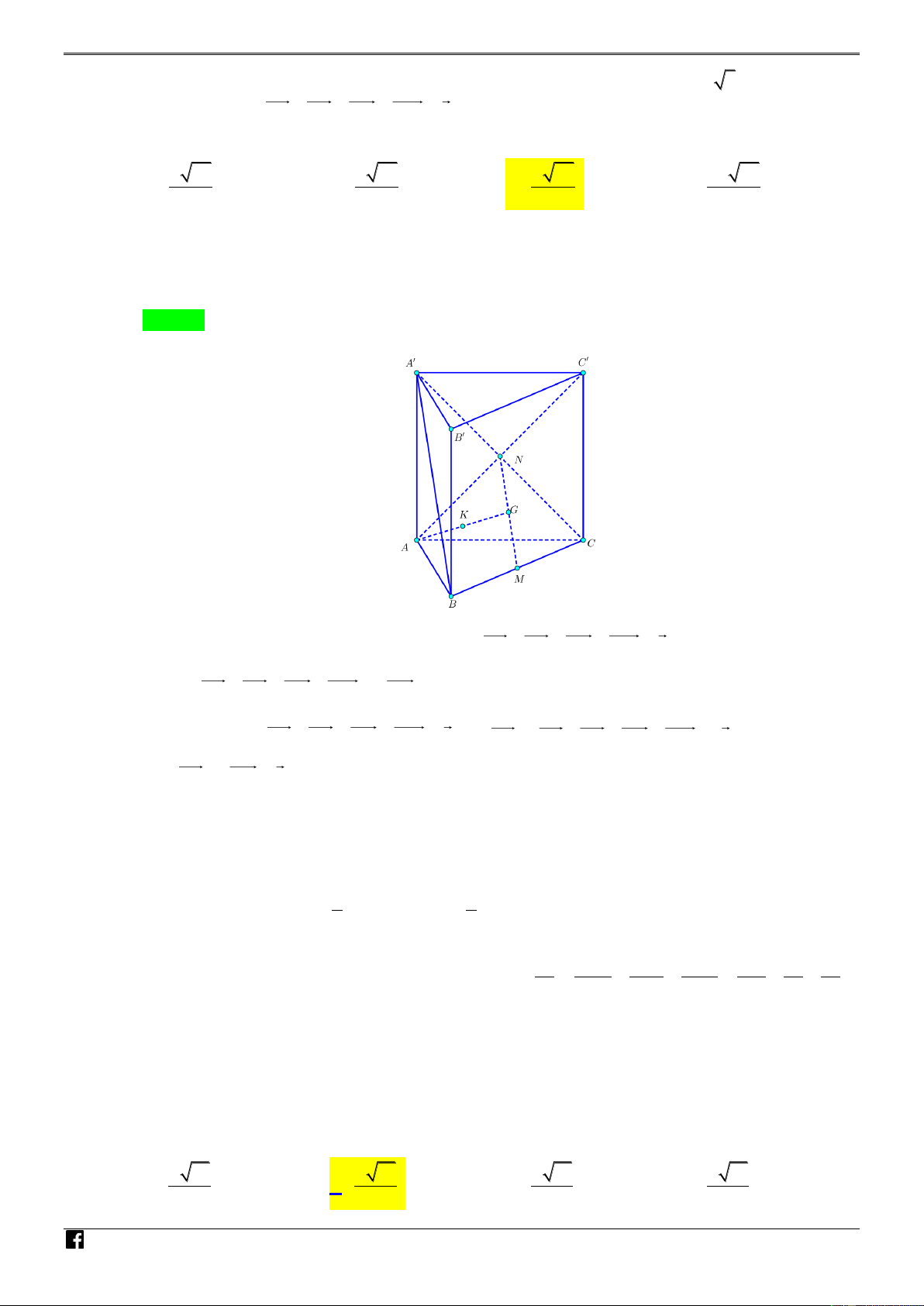
Câu 43. [MÃ 101 - TN 2020] Cho hình lăng trụ đứng AB . C A B C
có tất cả các cạnh bằng a . Gọi M là
trung điểm của CC (tham khảo hình bên). Khoảng cách từ M đến mặt phẳng A B C bằng A' C' NHÓ M TO B' M ÁN VD – V A C D C B 21a 2a 21a 2a A. . B. . C. . D. . 14 2 7 4
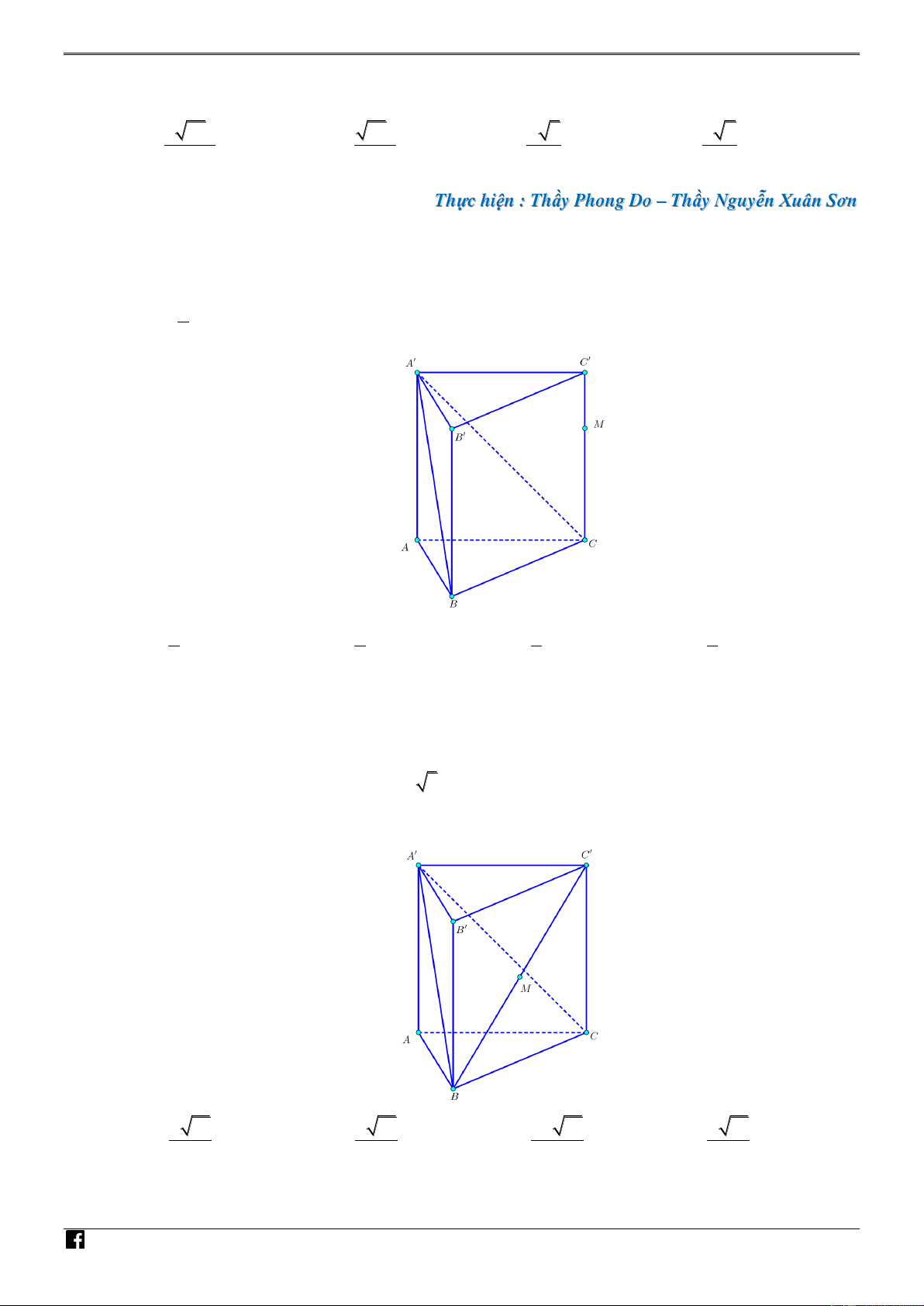
Câu 1. [PHÁT TRIẾN CÂU 43 – MÃ 101 – TN 2020] Cho hình lăng trụ đứng AB . C A B C có tất
cả các cạnh bằng a . Gọi M là trung điểm của CC , N là trung điểm của BB (tham khảo
hình bên). Khoảng cách từ N đến mặt phẳng A B M bằng A' C' NHÓ B' M M TO ÁN N A C VD – B V D C 2a 2a 2a A. . B. . C. a 2 . D. . 2 4 8
Thực hiện Thầy Nguyễn Xuân Sơn
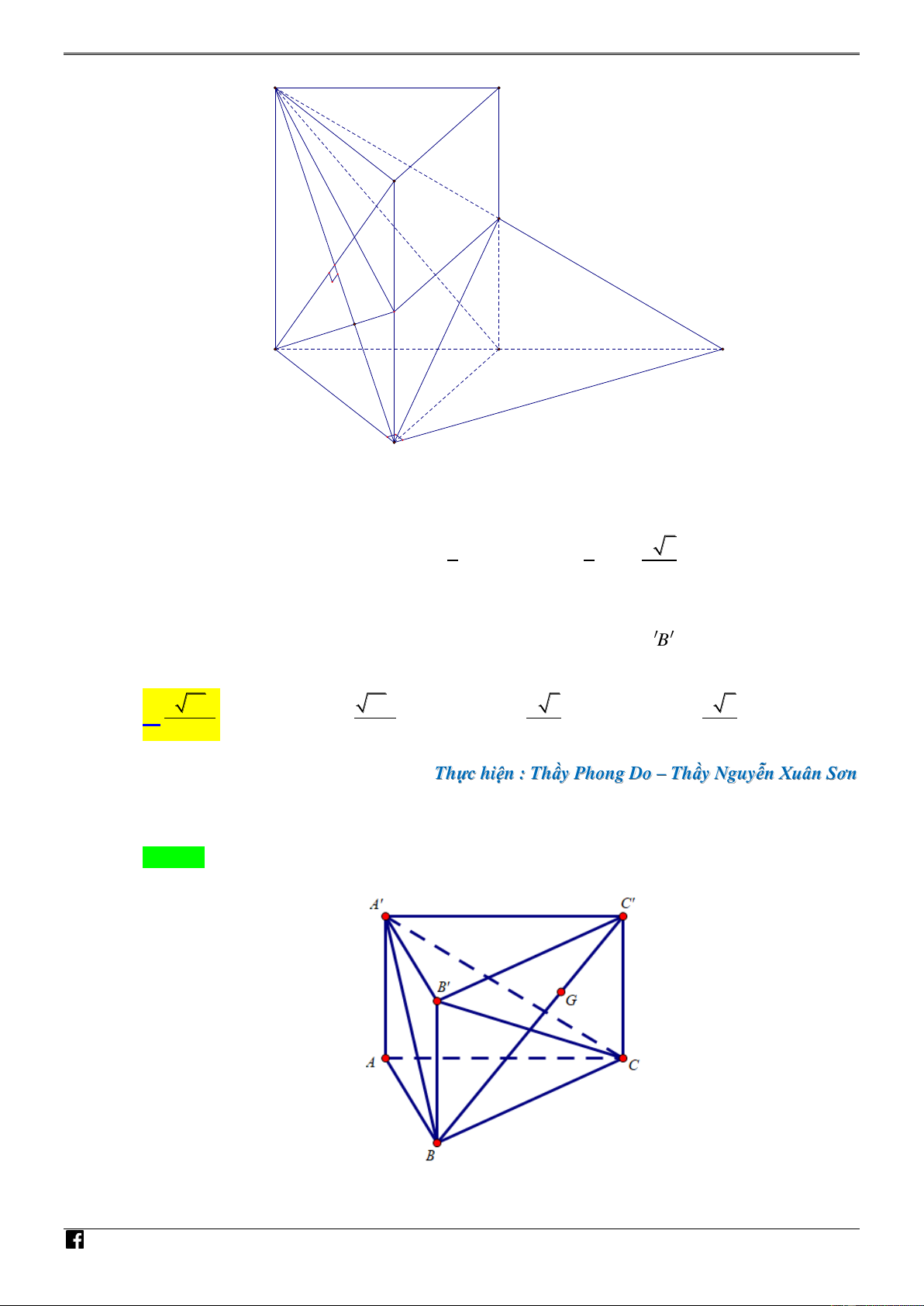
Câu 2. [PHÁT TRIẾN CÂU 43 – MÃ 101 – TN 2020] Cho hình lăng trụ đều AB . C A B C có cạnh
bên bằng cạnh đáy và bằng a . Gọi G là trọng tâm của tam giác CC B .
https://www.facebook.com/groups/toanvd.vdc Trang 1
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
Khoảng cách từ G đến mặt phẳng A B C bằng : 2 21a 21a a 3 2 2 A. B.. C. D. 21 7 3 3
Thực hiện : Thầy Phong Do – Thầy Nguyễn Xuân Sơn
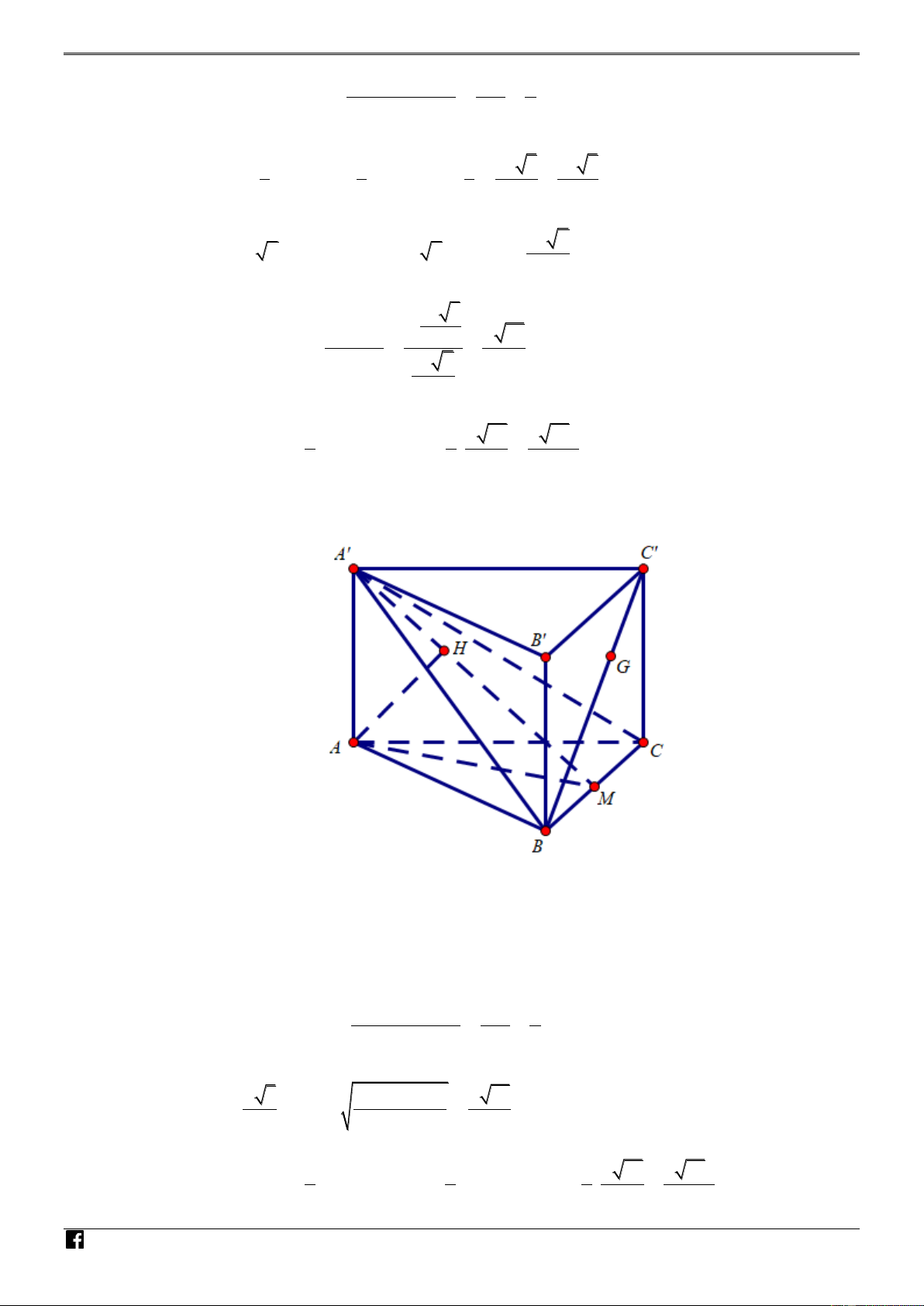
Câu 3. [PHÁT TRIẾN CÂU 43 – MÃ 101 – TN 2020] Cho hình lăng trụ đứng AB . C A B C có đáy
là tam giác vuông cân tại A với AB a và AA 2a . Trên cạnh CC lấy điểm M sao cho 1 NHÓ C M
CM (tham khảo hình bên). Khoảng cách từ M đến mặt phẳng A B C bằng 2 M TO ÁN VD – V D C 4 2 3 9 A. a . B. a . C. a . D. a . 9 3 2 4
Thực hiện : Thầy Hoàng Xuân Bính -PB : Thầy Nguyễn Xuân Sơn
Câu 4. [PHÁT TRIẾN CÂU 43 – MÃ 101 – TN 2020] Cho hình lăng trụ tam giác đều AB .
C A B C có AB a và AA a 3 . Gọi M là trung điểm của BC (tham khảo hình bên).
Khoảng cách từ M đến mặt phẳng A B C bằng? NHÓ M TO ÁN VD – V D C a 15 a 15 2a 15 a 15 A. . B. . C. . D. . 5 10 5 20
Thực hiện : Hoàng Xuân Bính-PB : Nguyễn Xuân Sơn
https://www.facebook.com/groups/toanvd.vdc Trang 2
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
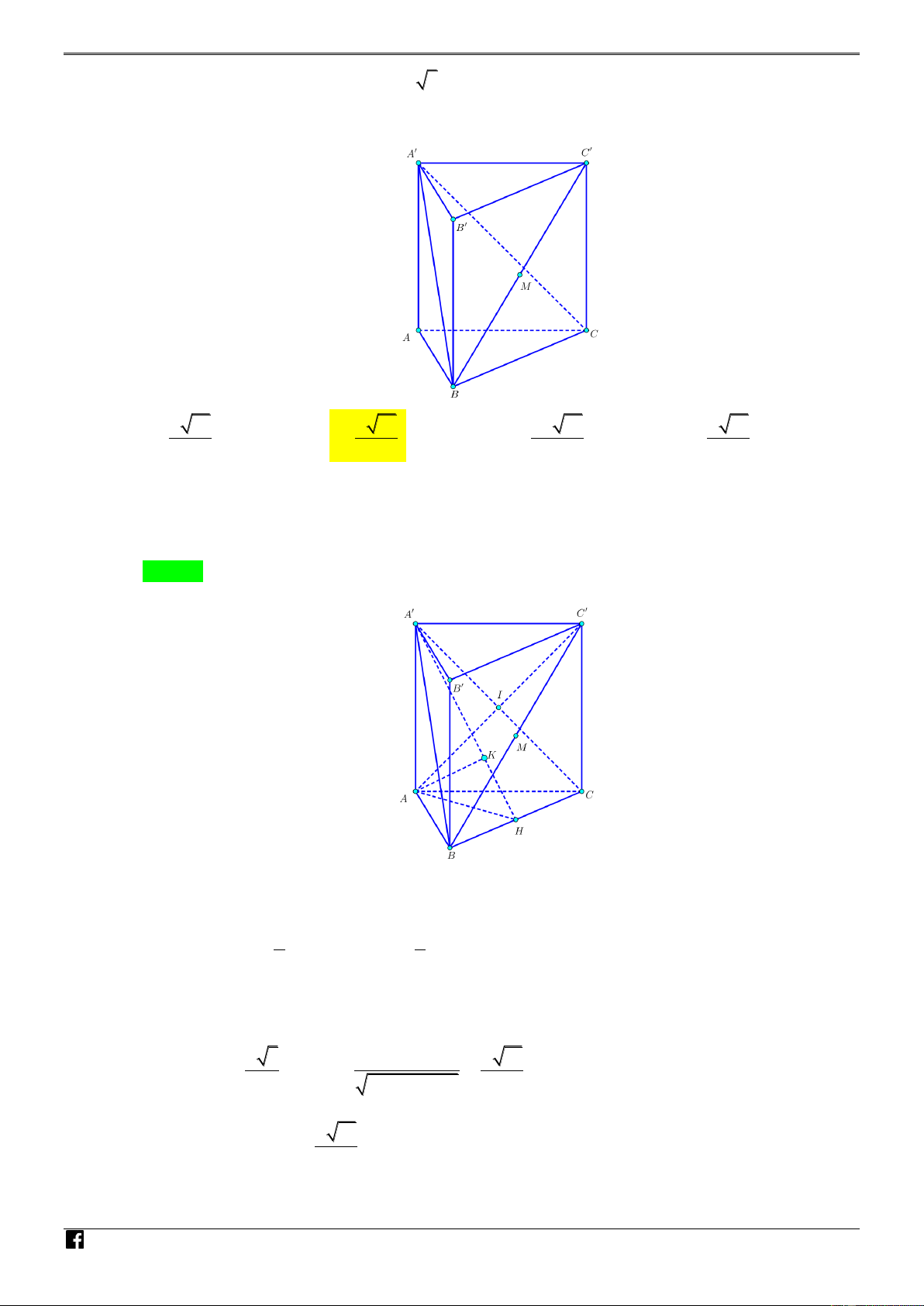
Câu 5. [PHÁT TRIẾN CÂU 43 – MÃ 101 – TN 2020] Cho hình lăng trụ đứng tam giác AB . C A B C
, đáy ABC là tam giác vuông cân tại A có AB a và AA a 5 .Goi K là điểm
thỏa mãn hệ thức 5KA KB KC KC 0 . Tính khoảng cách từ K đến mặt phẳng A B C . a 55 a 55 a 55 2a 55 A. . B. . C. . D. . 44 11 22 11
Thực hiện : Hoàng Xuân Bính-Phản biện : Nguyễn Xuân Sơn
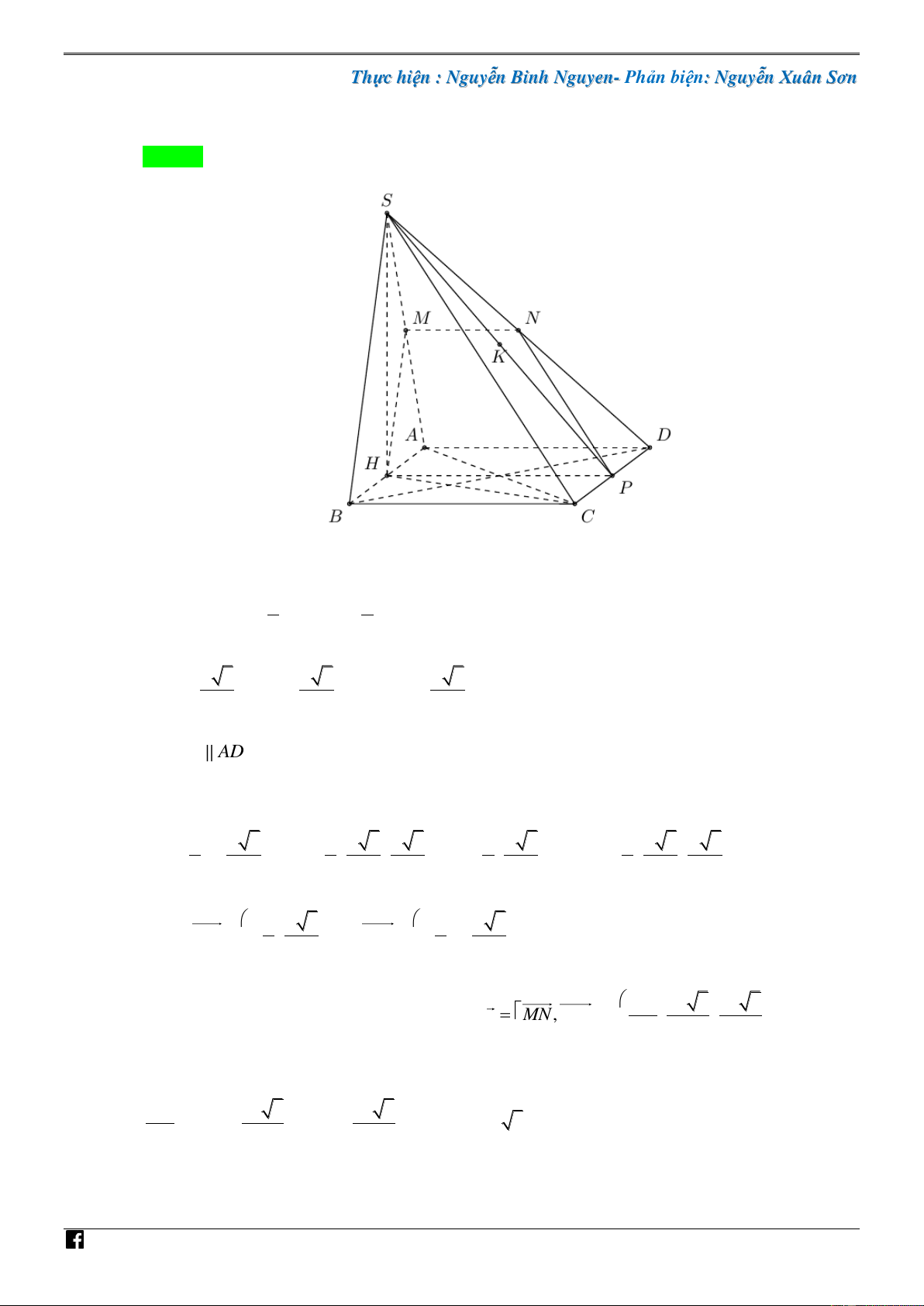
Câu 6. [PHÁT TRIẾN CÂU 43 – MÃ 101 – TN 2020] Cho hình chóp S.ABCD có đáy là hình thoi NHÓ cạnh a , ABC 60
, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. M
Gọi H , M , N lần lượt là trung điểm các cạnh AB , SA , SD và P là giao điểm của (HMN) với TO
CD . Khoảng cách từ trung điểm K của đoạn thẳng SP đến mặt phẳng (HMN) bằng ÁN a 15 a 15 a 15 a 15 VD A. . B. . C. . D. . 30 20 15 10 – V n D
Thực hiện : Nguyễn Binh Nguyen- Ph
ản biện: Nguyễn Xuân Sơ C
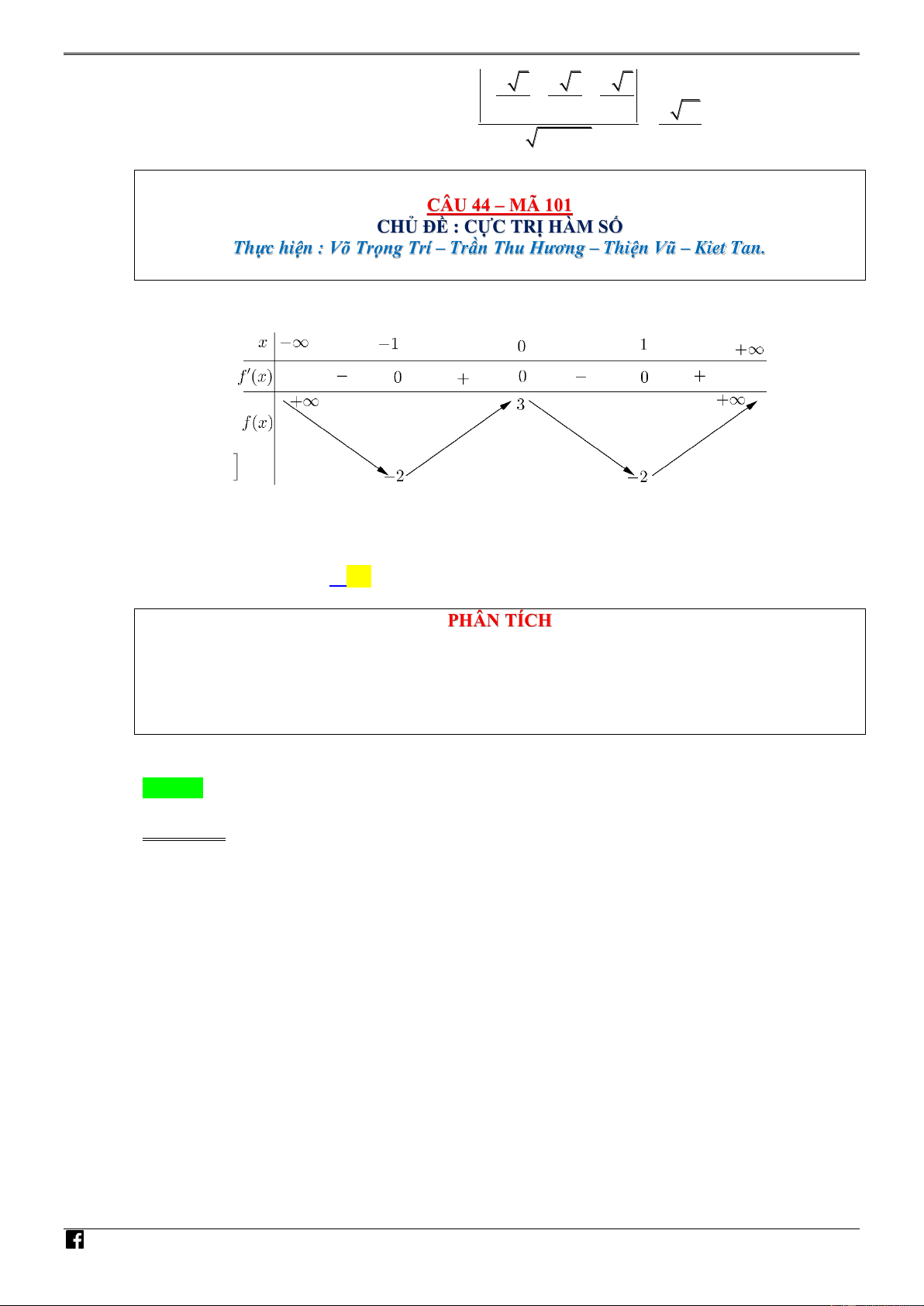
Câu 44. [ ĐỀ GỐC-MÃ 101- TN 2020 ] Cho hàm số bậc bốn f x có bảng biến thiên như sau:
Số điểm cực trị của hàm số g x x f x 2 4 1 là NHÓ A. 11. B. 9 . C. 7 . D. 5 . M
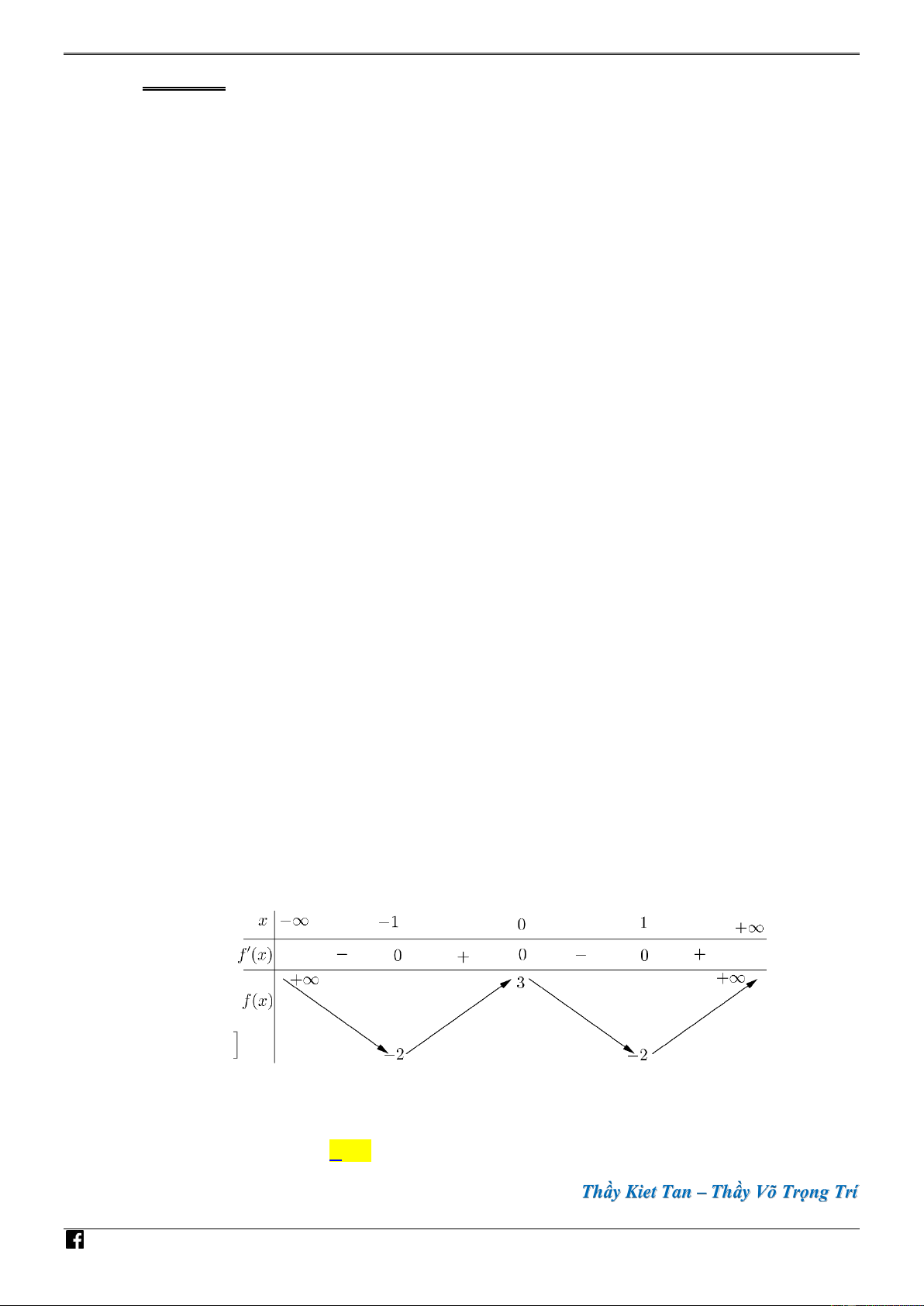
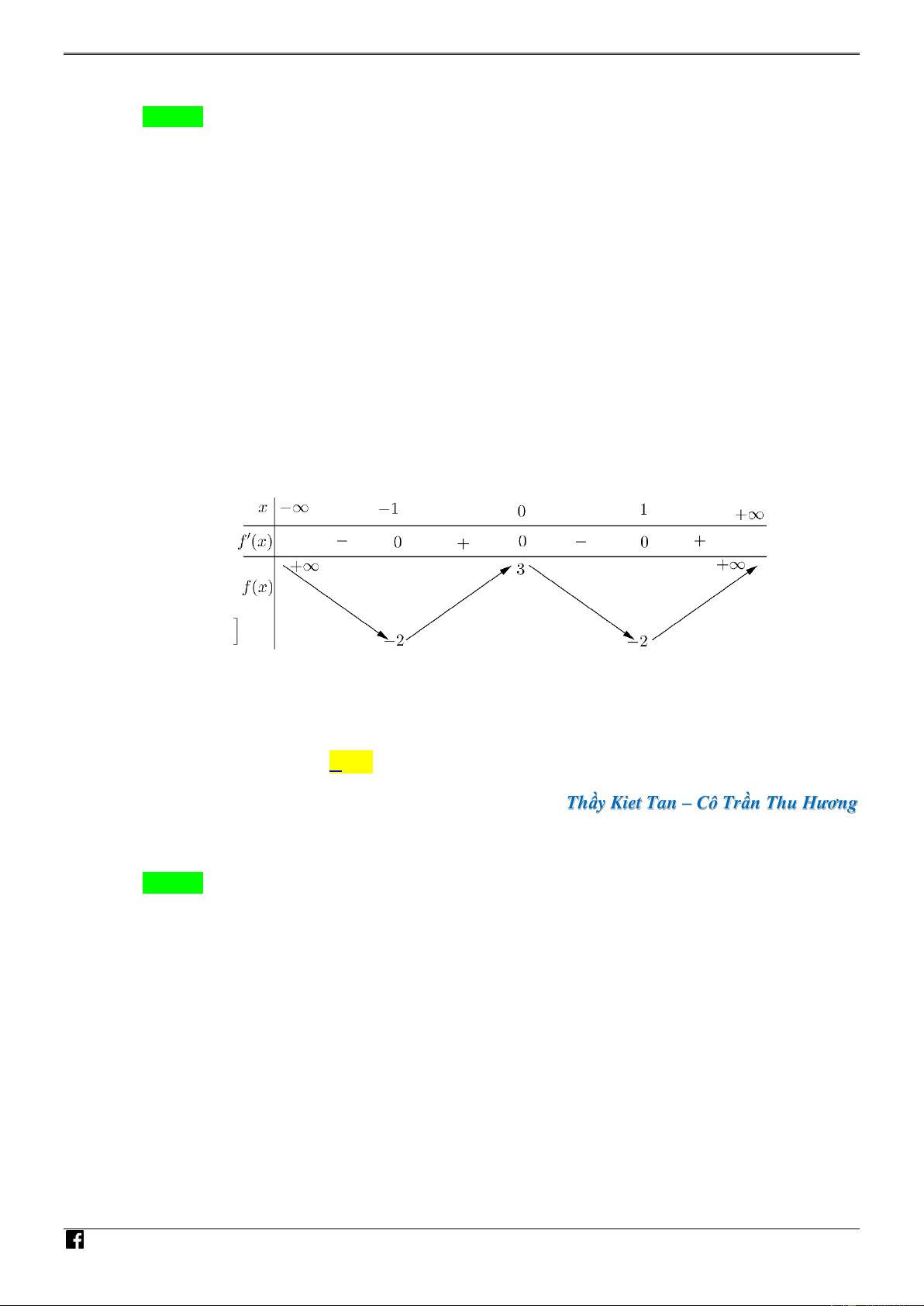
Câu 7. [PHÁT TRIẾN CÂU 44 – MÃ 101 – TN 2020] Cho hàm số bậc bốn f x có bảng biến TO ÁN thiên như sau: VD – V D C 4
Số điểm cực trị của hàm số g x x
1 f x 3 1 3 là A. 2 . B. 3 . C. 1. D. 5 .
https://www.facebook.com/groups/toanvd.vdc Trang 3
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
Thầy Kiet Tan – Thầy Võ Trọn g Trí
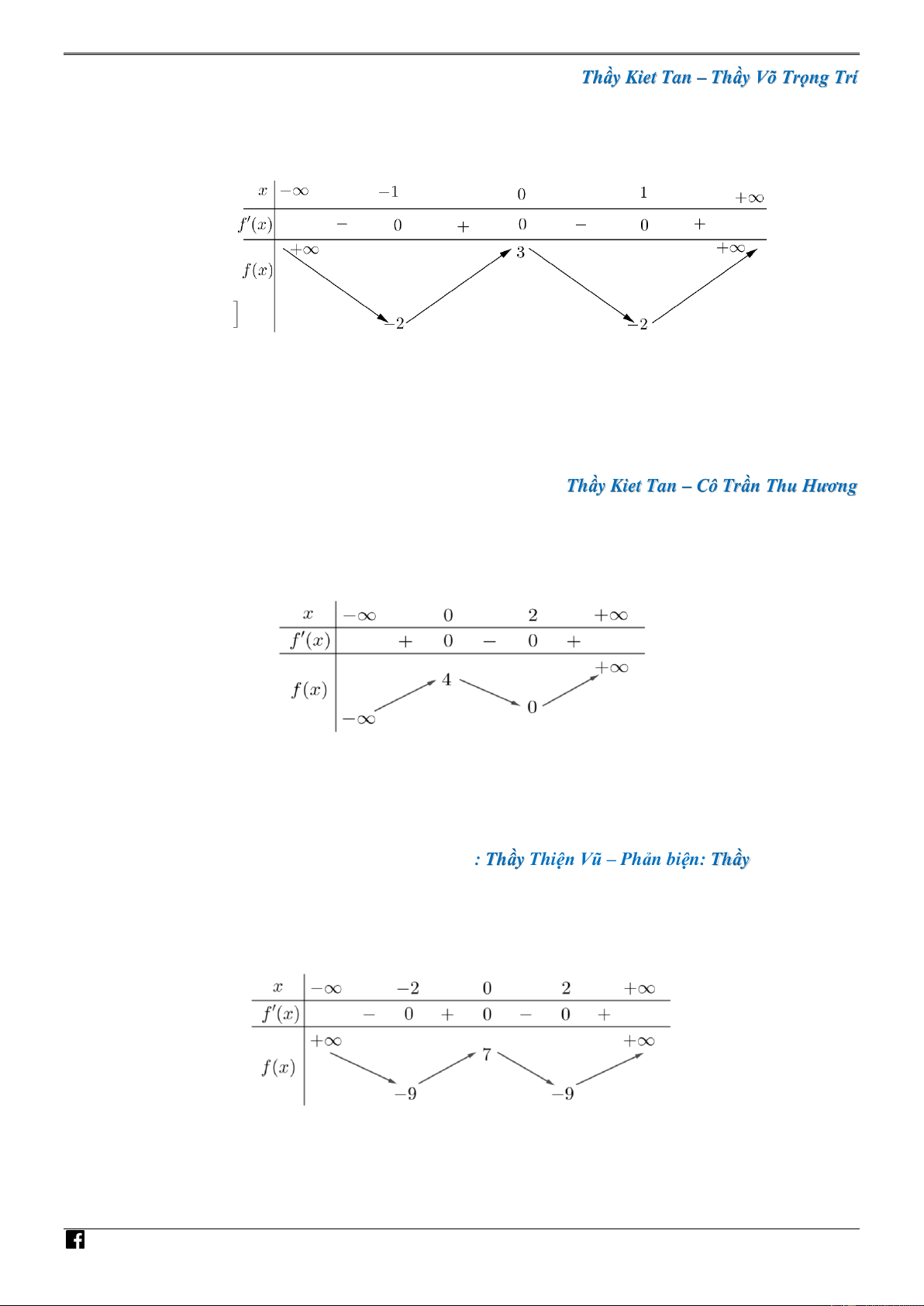
Câu 8. [PHÁT TRIẾN CÂU 44 – MÃ 101 – TN 2020] Cho hàm số bậc bốn f x có bảng biến thiên như sau: NHÓ 4 M
Tính tổng tất cả các giá trị m để số điểm cực trị của hàm số g x x m f x 3 2 bằng TO 3. ÁN VD A. 2 . B. 0 . C. 1. D. 6 . –
Thầy Kiet Tan – Cô Trần Thu Hươn g V D C
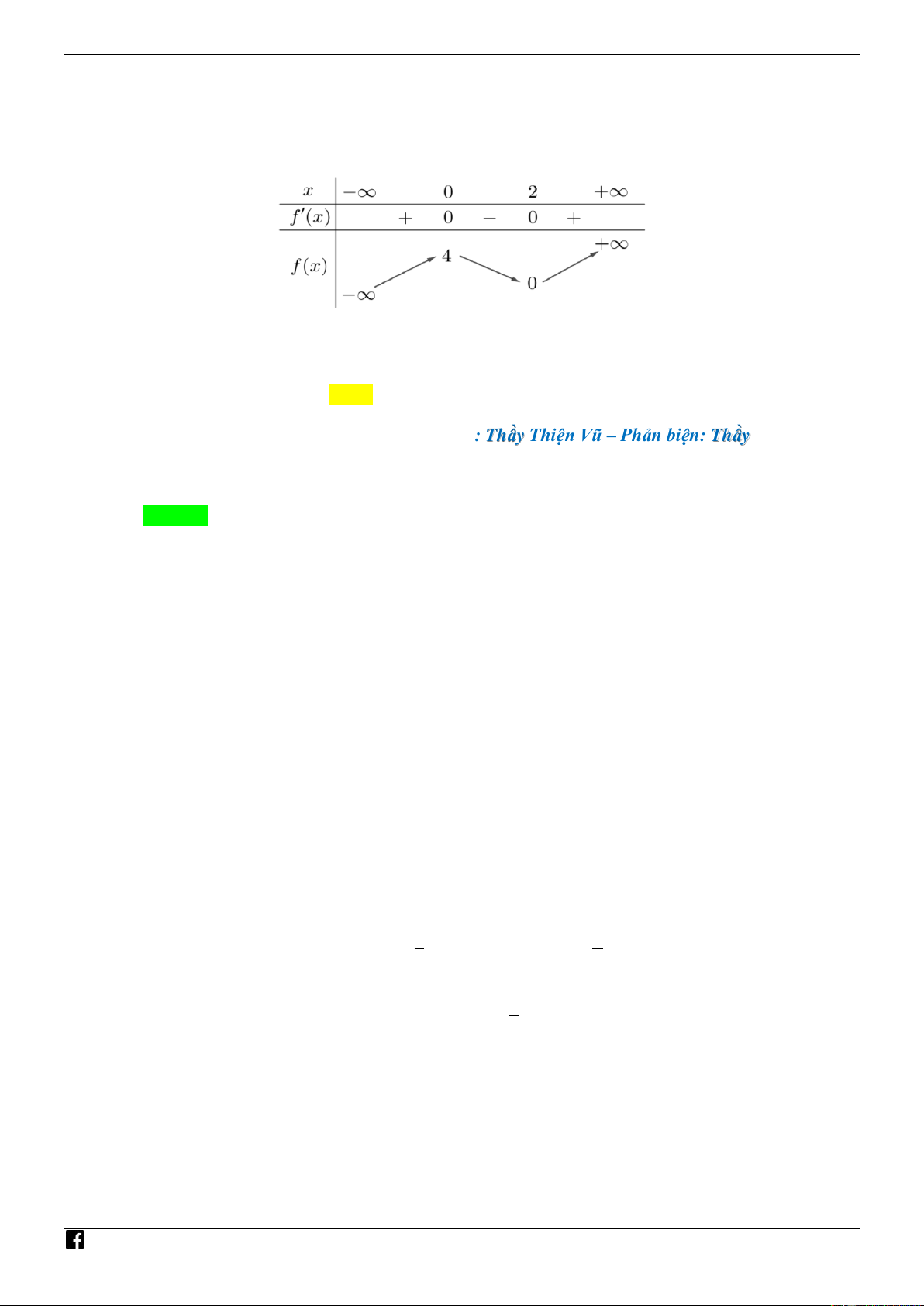
Câu 9. [PHÁT TRIẾN CÂU 44 – MÃ 101 – TN 2020] Cho hàm số bậc ba f x có bảng biến thiên như sau:
Số điểm cực trị của hàm số g x x f x 2 3 3 1 là A. 6 . B. 4 . C. 7 . D. 3 . NHÓ
Thực hiện: Thầ
y Thiện Vũ – Phản biện: Thầ
y Võ Trọng Trí M TO
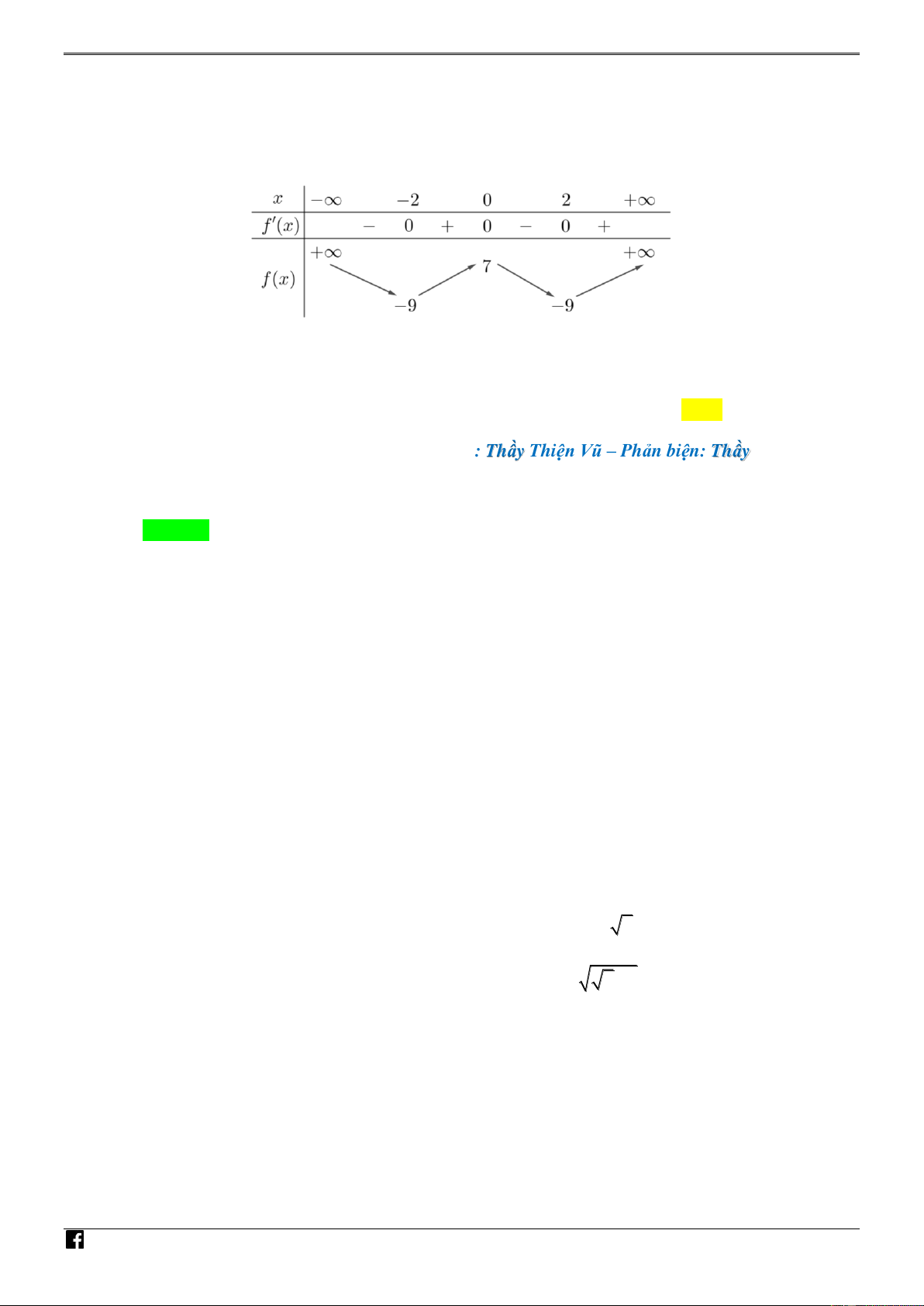
Câu 10. [PHÁT TRIẾN CÂU 44 – MÃ 101 – TN 2020] Cho hàm số bậc bốn f x có bảng biến ÁN thiên như sau: VD – V D C
Số điểm cực trị của hàm số g x 4
x f x 2 2 1 là A. 9 . B. 4 . C. 7 . D. 5 .
https://www.facebook.com/groups/toanvd.vdc Trang 4
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
Thực hiện: Thầ
y Thiện Vũ – Phản biện: Thầ
y Võ Trọng Trí
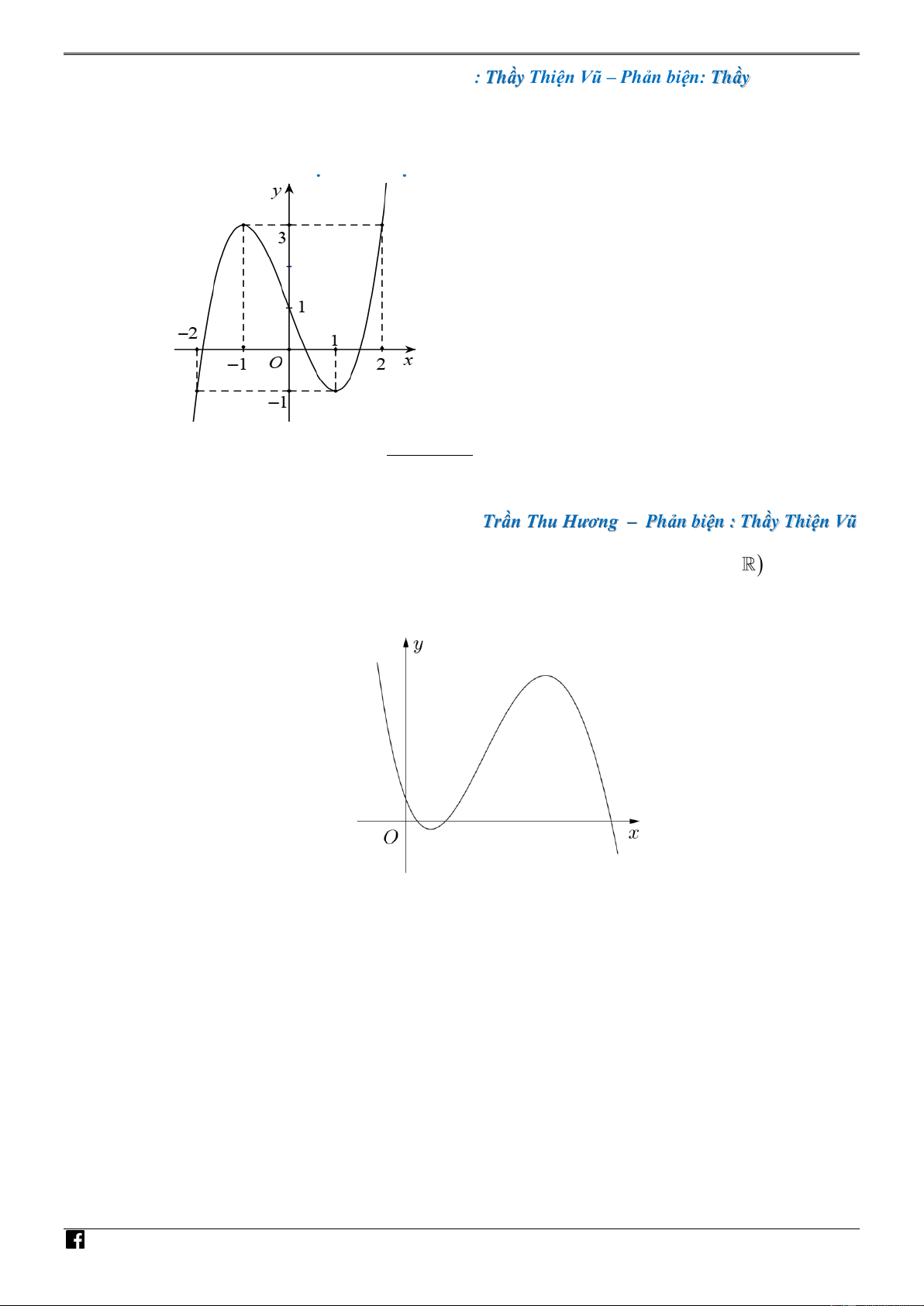
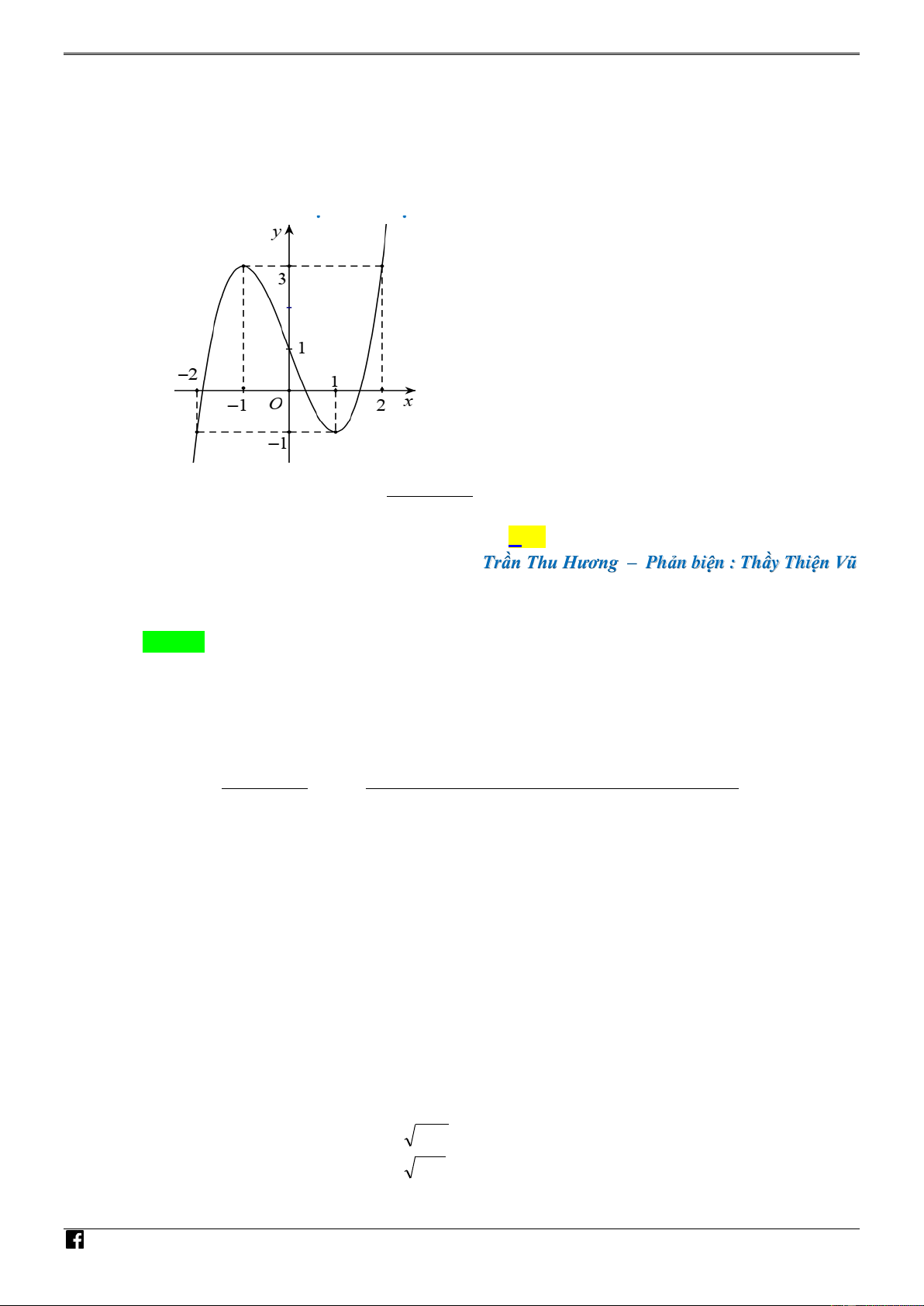
Câu 11. [PHÁT TRIẾN CÂU 44 – MÃ 101 – TN 2020] Cho hàm số bậc ba y f (x) có đồ thị như hình vẽ sau NHÓ M TO ÁN f (x 4 2 ) 1 VD
Số điểm cực trị của hàm số y là 2 x e – V
A. 8 . B. 5 . C. 9 . D. 7 . D C
Thực hiện: Cô Trần Thu Hương – Phản biện : Thầy Thiện Vũ
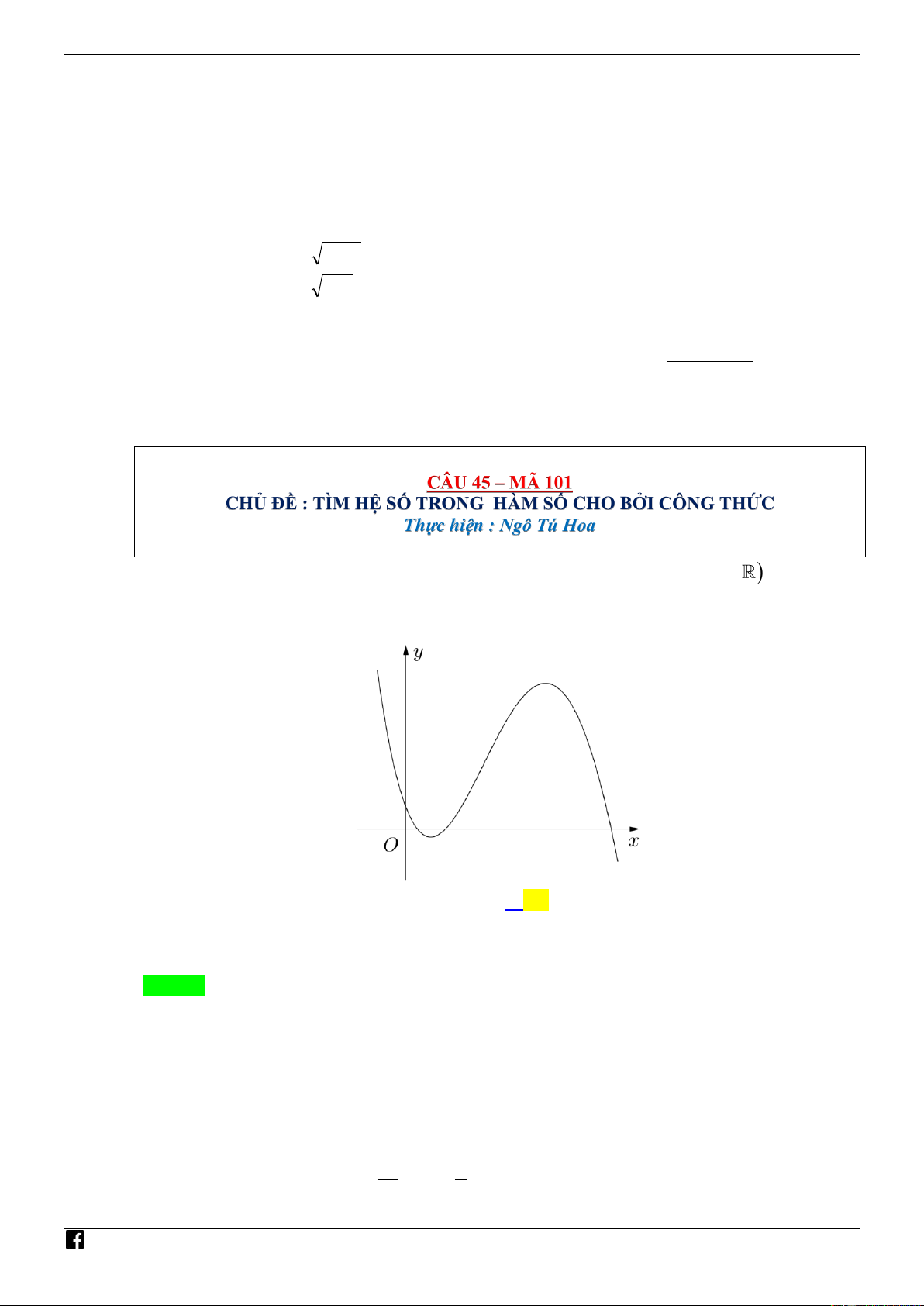
Câu 45. [ ĐỀ GỐC-MÃ 101- TN 2020 ] Cho hàm số 3 2
y ax bx cx d , a , b ,
c d có đồ thị là
đường cong trong hình bên. Có bao nhiêu số dương trong các số a , b , c , d ? NHÓ M TO A. 4 . B. 1. C. 2 . D. 3 . ÁN
Câu 12. [PHÁT TRIẾN CÂU 45 – MÃ 101 – TN 2020] Cho hàm số 3 2
y ax bx cx d có đồ thị VD
như hình vẽ dưới đây: – V D C
https://www.facebook.com/groups/toanvd.vdc Trang 5
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 NHÓ
Số lớn nhất trong các số , a , b , c d là M TO A. . b B. d. C. . a D. . c ÁN Câu 13 ax 1
. [PHÁT TRIẾN CÂU 45 – MÃ 101 – TN 2020] Cho hàm số f x có BBT như VD bx c –
hình vẽ. Trong các số a, ,
b c có bao nhiêu giá trị dương? V D C A.1 . B. 0 . C. 2 . D. 3 . Câu 14 ax 1
. [PHÁT TRIẾN CÂU 45 – MÃ 101 – TN 2020] Cho hàm số f x a, , b c có bx c
BBT như hình vẽ. Giá trị của a b c thuộc khoảng nào sau đây? NHÓ M TO ÁN VD – V D C A. 1 ;0 . B. 2 ; 1 . C. 1; 2 . D. 0 ;1 . Câu 15 ax b
. [PHÁT TRIẾN CÂU 45 – MÃ 101 – TN 2020] Hàm số y
. Có đồ thị như cx d hình vẽ:
https://www.facebook.com/groups/toanvd.vdc Trang 6
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 NHÓ
Trong các số sau: a ;
b bd ;bc; ad; ad
bc có bao nhiêu số dương M
A. 3 . B. 2 .C. 4 .D. 5 . TO ax b ÁN
Câu 16. [PHÁT TRIẾN CÂU 45 – MÃ 101 – TN 2020] Cho hàm số y cx có đồ thị như d VD hình vẽ dưới – y V D C O x
Hỏi có bao nhiêu số dương trong các số a ; b b ;
c ad; ad bc ? A. 1. B. 2 . C. 3 . D. 4 . NHÓ
Câu 46. [ MÃ 101- TN 2020] Gọi S là tập hợp tất cả các số tự nhiên có 4 chữ số đôi một khác nhau và M
các chữ số thuộc tập 1, 2,3, 4,5,6,7,8,
9 . Chọn ngẫu nhiên một số thuộc S , xác suất để số đó TO
không có hai chữ số liên tiếp nào cùng chẵn bằng ÁN VD 25 5 65 55 A. . B. . C. . D. . 42 21 126 126 – V D
Câu 17. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020] Một tổ có 4 bạn nam và 5 bạn nữ. C
Cần chọn ra 4 bạn để xếp thành một hàng dài tham gia diễu hành. Tính xác suất để trong hàng
không có 3 bạn nữ nào đứng liên tiếp nhau. 41 49 85 89 A. . B. . C. . D. . 54 54 108 108
Thực hiện : Thầy Nguyễn Ngọc Hoá –Phản biện: Thầy Nguyễn Thanh Hải
https://www.facebook.com/groups/toanvd.vdc Trang 7
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
Câu 18. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020]Gọi S là tập hợp tất cả các số tự
nhiên có 4 chữ số đôi một khác nhau và các chữ số thuộc tập 2,3, 4,5,6,7,8, 9 . Chọn ngẫu
nhiên một số thuộc S , xác suất để số đó không có hai chữ số liên tiếp nào cùng chia hết cho 3 bằng 9 19 5 16 A. . B. . C. . D. . 14 28 7 21
Thực hiện : Thầy Nguyễn Ngọc Hoá –Phản biện: Thầy Nguyễn Thanh Hải
Câu 19. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020] Xếp ngẫu nhiên 10 học sinh gồm 2 NHÓ
học sinh lớp 11A và 3 học sinh lớp 11B và 5 học sinh của lớp 11C thành một hàng ngang. Tính M
xác suất để không có học sinh nào của cùng một lớp đứng cạnh nhau. TO 3 11 1 2 A. . B. . C. . D. . ÁN 126 630 126 63 VD
Thực hiện : Thầy Nguyễn Thanh Hải – Phản biện: Thầy Nguyễn Khắc Thành – V
Câu 20. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020] Gọi E là tập các số tự nhiên có 5 D C
chữ số được lập từ các chữ số 0;1;2;3;4;5. Chọn ngẫu nhiên một số thuộc tập E . Tính xác suất
để số được chọn là số chẵn, có đúng hai chữ số 0 và không đứng cạnh nhau, các chữ số còn lại có
mặt không quá một lần. 2 2 1 4 A. . B. . C. . D. . 15 45 45 15
Thực hiện : Thầy Nguyễn Thanh Hải – Phản biện: Thầy Nguyễn Khắc Thành
Câu 21. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020] Cho tập E 1,2,3,4, 5 .
Viết ngẫu nhiên lên bảng hai số tự nhiên, mỗi số gồm 3 chữ số đôi một khác nhau thuộc tập E.
Tính xác suất để trong hai số đó có đúng một số có chữ số 1 . 12 13 144 151 NHÓ A. . B. . C. . D. . 25 25 295 295 M TO
Thực hiện : Thầy Nguyễn Khắc Thành–Phản biện: Thầy Nguyễn Ngọc Hoá ÁN
Câu 22. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020] Cho hai hộp đựng bi: hộp A đựng 7 VD
viên bi xanh, 7 viên bi đỏ; hộp B đựng 5 viên bi xanh, 9 viên bi đỏ. Bốc ngẫu nhiên 3 viên bi –
trong hộp A bỏ vào hộp B, sau đó bốc ngẫu nhiên 3 viên bi trong hộp B bỏ lại hộp A. Tính xác V D
suất để sau khi đổi bi xong số bi xanh trong hai hộp bằng nhau. C 567 343 49 49 A. . B. . C. . D. . 1768 352 96 264
Thực hiện : Thầy Nguyễn Khắc Thành–Phản biện: Thầy Nguyễn Ngọc Hoá
Câu 23. Viết lên bảng năm số tự nhiên có hai chữ số khác nhau theo thứ tự tăng dần được tạo thành từ
https://www.facebook.com/groups/toanvd.vdc Trang 8
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
các chữ số 0,1, 2,3, 4,5, 6, 7,8,9 và mỗi chữ số chỉ xuất hiện 1 lần. Xác suất để 5 số đều chia hết cho 3 là 1 1 2 2 A. . B. . C. . D. . 21 35 105 189
Thực hiện Cô Đoàn Thị Lan Oanh – Phản Biện Thầy Nguyễn Khắc Thành
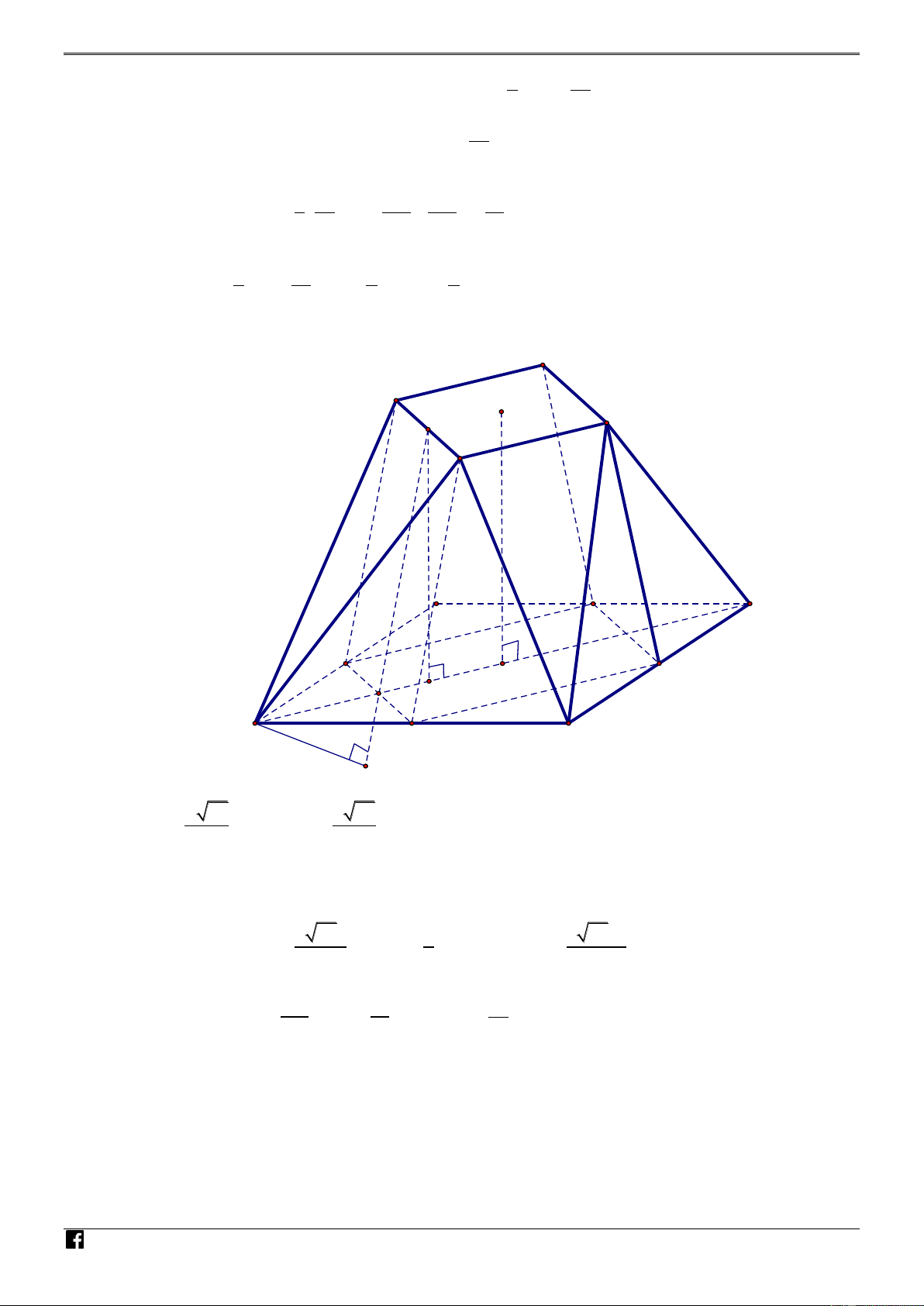
Câu 47. [ ĐỀ GỐC MÃ 101 – TN 2020] Cho hình chóp đều S.ABCD có cạnh đáy bằng a , cạnh bên
bằng 2a và O là tâm của đáy. Gọi M , N , P , Q lần lượt là các điểm đối xứng với O qua
trọng tâm của các tam giác SAB , SBC , SCD , SDA và S ' là điểm đối xứng với S qua O . NHÓ
Thể tích của khối chóp S '.MNPQ bằng M 3 20 14a 3 40 14a 3 10 14a 3 2 14a TO A. . B. . C. . D. . 81 81 81 9 ÁN VD
Câu 24. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020] Cho hình chóp tứ giác đều S.ABCD có đáy –
ABCD là hình vuông cạnh a có tâm là O , mặt bên tạo với đáy một góc 60 . Gọi M , N, , P Q V D
lần lượt là ảnh của O qua các phép đối xứng qua mặt phẳng SAB , SBC , SCD , SDA . Biết C
S là điểm đối xứng với S qua mặt phẳng ABCD . Tính thể tích khối chóp S .MNPQ . 9 3 9 3 27 3 27 3 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 16 32 32 16
Thực hiện : Ngô Dung – Phản biện : Cô Thoa Nguyễn
Câu 25. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020] Cho khối bát diện đều ABCDEF có thể tích
V . Gọi O là tâm của hình vuông ABCD . Lấy A đối xứng với A qua ED , B đối xứng với 1 1
B qua EA ; C đối xứng với C qua EB và D đối xứng với D qua EC . Tính theo V thể tích 1 1
khối chóp F.A B C D . 1 1 1 1 NHÓ 3V 4V A. V . B. . C. 2V . D. . M 2 3 TO ÁN
Thực hiện : Ngô Dung – Phản biện : Cô Thoa Nguyễn VD
Câu 26. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020] Chóp S.ABC có SA vuông góc với đáy và –
đáy là tam giác ABC vuông tại A . Gọi ,
D E, F lần lượt là ảnh của , A ,
B C qua phép vị tự V D 1 C
tâm S tỉ số k
. Biết thể tích khối S.ABCD bằng V và thể tích khối đa diện DEFABC 2 V
bằng V . Tính tỉ số . V 8 2 13 4 A. . B. . C. . D. . 27 3 27 9
Thực hiện : Ngô Dung – Phản biện : Cô Thoa Nguyễn
https://www.facebook.com/groups/toanvd.vdc Trang 9
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
Câu 27. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020] Cho hình lập phương ABC .
D A B C D cạnh a . Gọi ,
O O , M , N, ,
P Q lần lượt là tâm của đáy ABCD , A B C D và của bốn mặt bên. Gọi
S, I, J , H, K lần lượt là ảnh của k . Tính thể tích
O , M , N, ,
P Q qua phép vị tự tâm O tỉ số 3
V của khối đa diện được tạo bởi các đỉnh S, I, J , H, K, A , B ,C , D . 3 49a 3 11a 3 49a 3 11a A. . B. . C. . D. . 2 3 6 6
Tác giả: Ngô Tú Hoa – Phản biện : Nguyễn Thị Hồng Gấm và Thoa Nguyễ n. NHÓ
Câu 28. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020] Cho hình lập phương ABC . D A B C D M
cạnh a . Gọi ,
O O , M , N, ,
P Q lần lượt là tâm của đáy ABC ,
D A B C D và của bốn mặt TO
bên.Gọi S, I, J, H, K lần lượt là ảnh của O , M , N, ,
P Q qua phép vị tự tâm O tỉ số k 3 . Tính ÁN
thể tích khối đa diện được tạo bởi các đỉnh S, I, J, H, K, , A , B C, D . VD A. . B. . C. .D. . –
Ngô Tú Hoa – Nguyễn Thị Hồng Gấm V D C
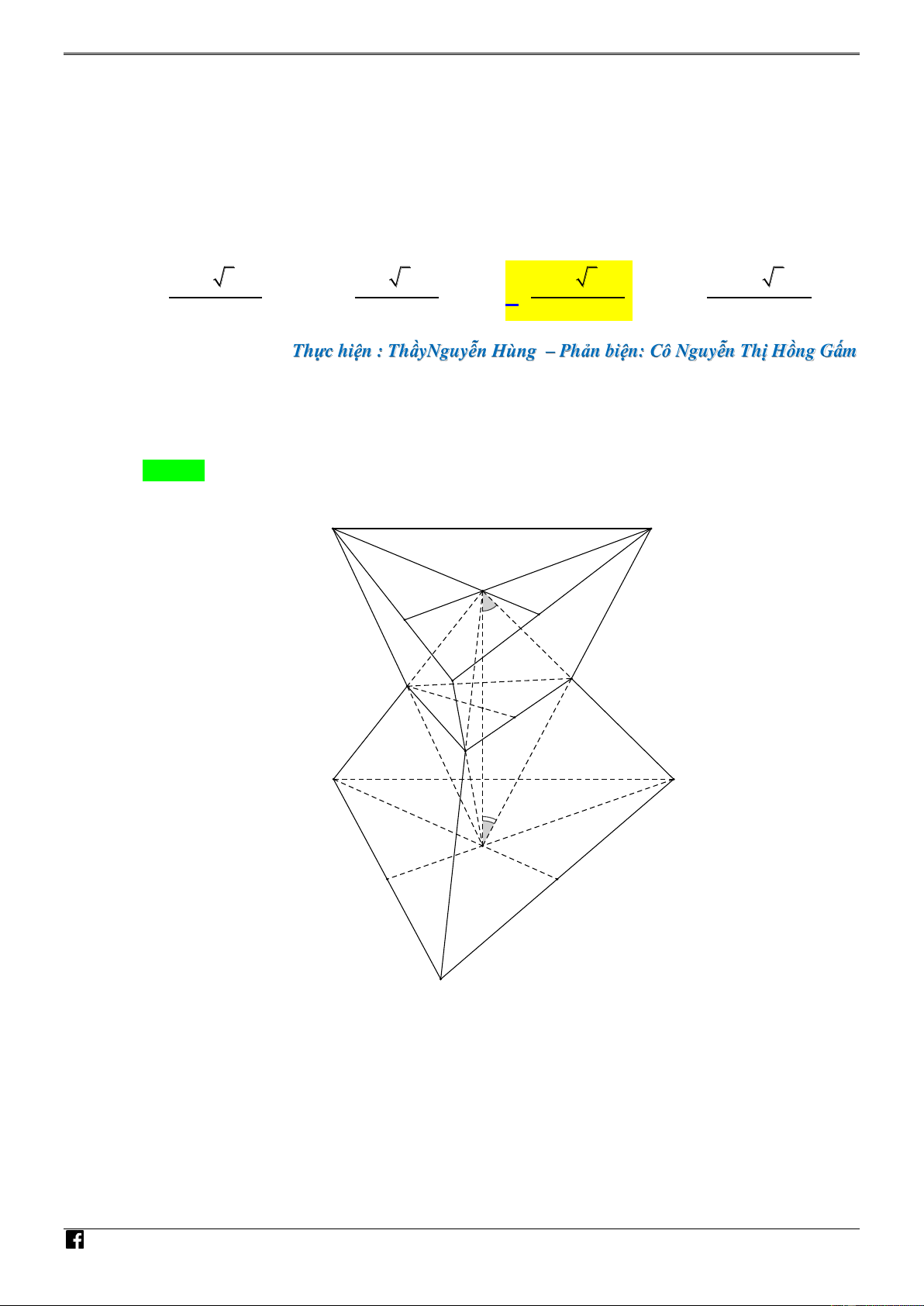
Câu 29. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020] Cho hai hình chóp tam giác đều có cùng
chiều cao. Biết đỉnh của hình chóp này trùng với tâm của đáy hình chóp kia, mỗi cạnh bên của
hình chóp này đều cắt một cạnh bên của hình chóp kia. Cạnh bên có độ dài bằng a của hình chóp
thứ nhất tạo với đường cao một góc 0
30 , cạnh bên của hình chóp thứ hai tạo với đường cao một góc 0
45 . Tính thể tích phần chung của hai hình chóp đã cho ? 3 3 2 3 a 3 2 3 a 3 9 2 3 a 3 27 2 3 a A. . B. . C. . D. . 64 32 64 64
Thực hiện : ThầyNguyễn Hùng – Phản biện: Cô Nguyễn Thị Hồng Gấm
Câu 48. [ ĐỀ GỐC-MÃ 101- TN 2020 ] Xét các số thực không âm
x và y thỏa mãn x y 1 2x . y 4 3 NHÓ
.Giá trị nhỏ nhất của biểu thức 2 2
P x y 4x 6y bằng M 33 65 49 57 TO A. . B. . C. . D. . 4 8 8 8 ÁN
Câu 30. [PHÁT TRIẾN CÂU 48 – MÃ 101 – TN 2020] Xét các số thực không âm x và y thỏa mãn VD – 1 9 9 2x y 1 V
. Giá trị nhỏ nhất của biểu thức 2 2 x y . x 2 1 P x 5y x y bằng D 2 2 8 C 3 5 5 13 A. . B. . C. . D. . 16 16 8 8
Trương Đức Thịnh – Phạm Ninh – Đạt Lâm Huy – Thơm Chu.
Câu 31. [PHÁT TRIẾN CÂU 48 – MÃ 101 – TN 2020] Cho các số thực dương ;
x y thỏa mãn
https://www.facebook.com/groups/toanvd.vdc Trang 10
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 5x 7 2 5x x x
xlog 4xy x 4xy . Giá trị nhỏ nhất của 2 P y là 5 4xy y 133 113 117 A. . B. . C. 28 . D. . 4 4 8
Trương Đức Thịnh – Phạm Ninh – Đạt Lâm Huy – Thơm Chu.
Câu 32. [PHÁT TRIẾN CÂU 48 – MÃ 101 – TN 2020] Cho hai số thực dương ,
x y thoả mãn 2 2 3 3log 32 3 1 2 y x x y
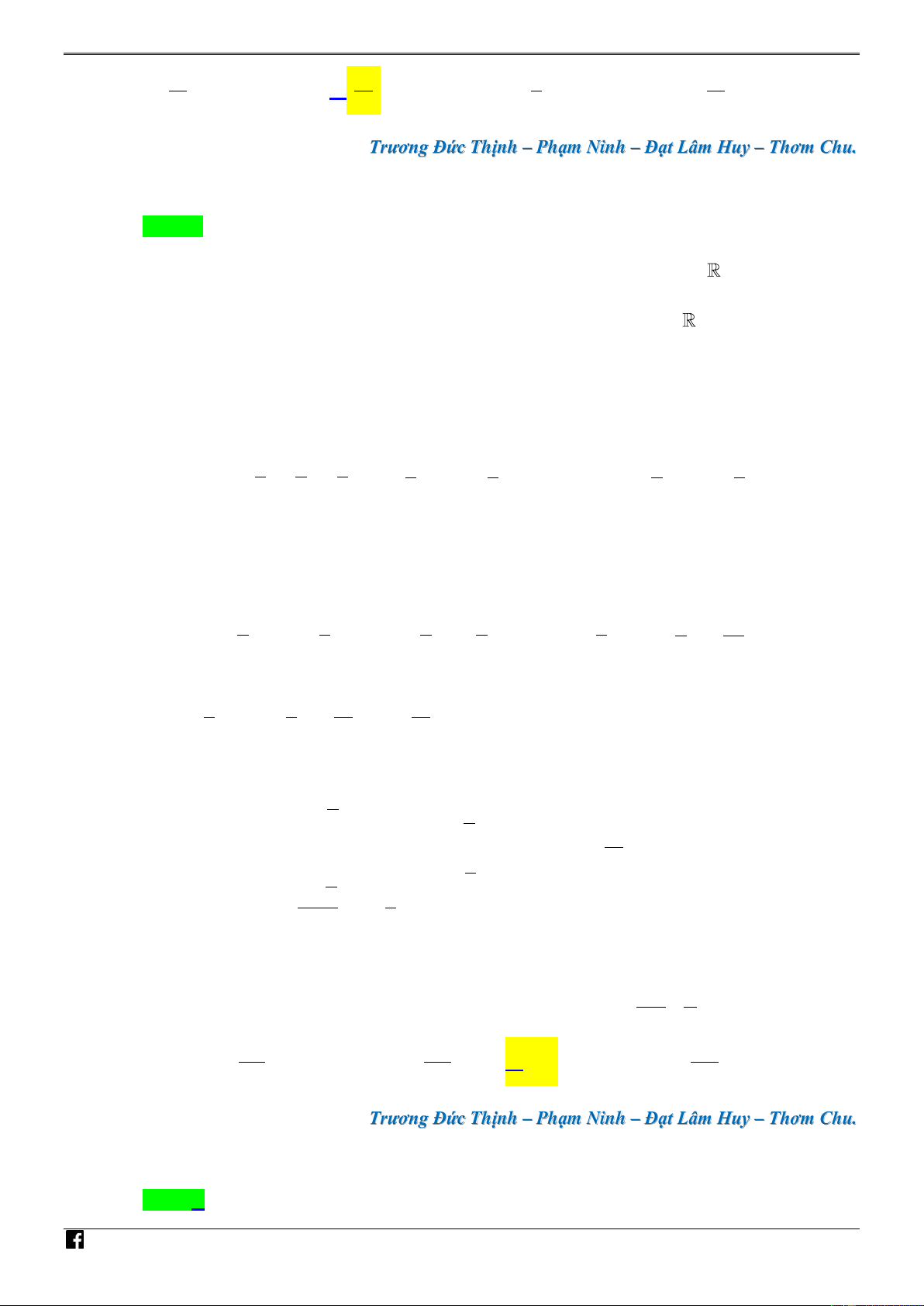
. Giá trị nhỏ nhất của biểu thức x P bằng 2 y NHÓ e ln 2 e ln 2 e ln 2 e A. . B. . C. . D. . M 2 2 2 2 ln 2 TO
Trương Đức Thịnh – Phạm Ninh – Đạt Lâm Huy – Thơm Chu. ÁN VD
Câu 33. [PHÁT TRIẾN CÂU 48 – MÃ 101 – TN 2020] Cho ;
x y là hai số thực dương thỏa mãn – y x 2 2 V x 3y x y D và 1 1
. Giá trị nhỏ nhất của biểu thức P x y 2 2 x y 2 C 2 2 xy bằng y 13 9 A. . B. . C. 2 . D. 6 . 2 2
Trương Đức Thịnh – Phạm Ninh – Đạt Lâm Huy – Thơm Chu.
Câu 34. [PHÁT TRIẾN CÂU 48 – MÃ 101 – TN 2020] Xét các số thực x và y thỏa mãn 2 2 2 2 x y 2
. Biết rằng giá trị nhỏ nhất của biểu thức 2 2 2x y .4 5 P x y 4x 6y là a b với , a b
. Giá trị của a b bằng 130 265 265 130 A. . B. . C. . D. . 4 2 4 2 NHÓ
Trương Đức Thịnh – Phạm Ninh – Đạt Lâm Huy – Thơm Chu. M
Câu 49. [ ĐỀ GỐC-MÃ 101- TN 2020 ] Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không TO
quá 728 số nguyên y thỏa mãn log 2
x y log (x y) ? 4 ÁN 3 VD A. 59 . B. 58 . C. 116 . D. 115 . – V
Câu 35. [PHÁT TRIẾN CÂU 49 – MÃ 101 – TN 2020] Có bao nhiêu số nguyên y sao cho ứng với D C
mỗi y có không quá 100 số nguyên x thỏa mãn log 2 y 2 3 x x y 0. 5 A. 19 . B. 18 . C. 20 . D. 17 .
Thực hiện : Thầy Nguyễn Sỹ – Phản Biện : Thầy Nguyễn Tất Thành.
Câu 36. [PHÁT TRIẾN CÂU 49 – MÃ 101 – TN 2020] Có bao nhiêu giá trị nguyên của tham số m
https://www.facebook.com/groups/toanvd.vdc Trang 11
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 1 để bất phương trình log 2 x m
0 có tối đa 50 nghiệm nguyên. x m 2 e A. 15 . B. 16 . C. 14 . D. 17 .
Thực hiện : Thầy Nguyễn Sỹ – Phản Biện : Thầy Nguyễn Tất Thành.
Câu 37. [PHÁT TRIẾN CÂU 49 – MÃ 101 – TN 2020] Có bao nhiêu số nguyên y sao cho ứng với 1
mỗi y có không quá 10 số nguyên x thỏa mãn log 2 x y log x y 0 . 5 2 2x y A. 30 . B. 18 . C. 32 . D. 17 . NHÓ
Thực hiện : Thầy Nguyễn Sỹ – Phản Biện : Thầy Nguyễn Tất Thành. M TO
Câu 38. [PHÁT TRIẾN CÂU 49 – MÃ 101 – TN 2020] Có bao nhiêu số nguyên x sao cho ứng với ÁN
mỗi x có không quá 26 số nguyên y thỏa mãn log 2
x y log 2
x x 27 log (x y) ? 5 4 3 VD A. 211. B. 423. C. 424 . D. 212 . – V D
Thực hiện : Thầy Nguyễn Tất Thành– Phản Biện : Thầy Nguyễn Sỹ. C
Câu 39. [PHÁT TRIẾN CÂU 49 – MÃ 101 – TN 2020] Có bao nhiêu số nguyên x sao cho ứng với mỗi
x có không quá 10 số nguyên y thỏa mãn 2 x 7 y 26 4
2 x y 8192 và x y 0 ? A. 16 . B. 15 . C. 17 . D. 7 .
Thực hiện : Thầy Nguyễn Tất Thành– Phản Biện : Thầy Nguyễn Sỹ.
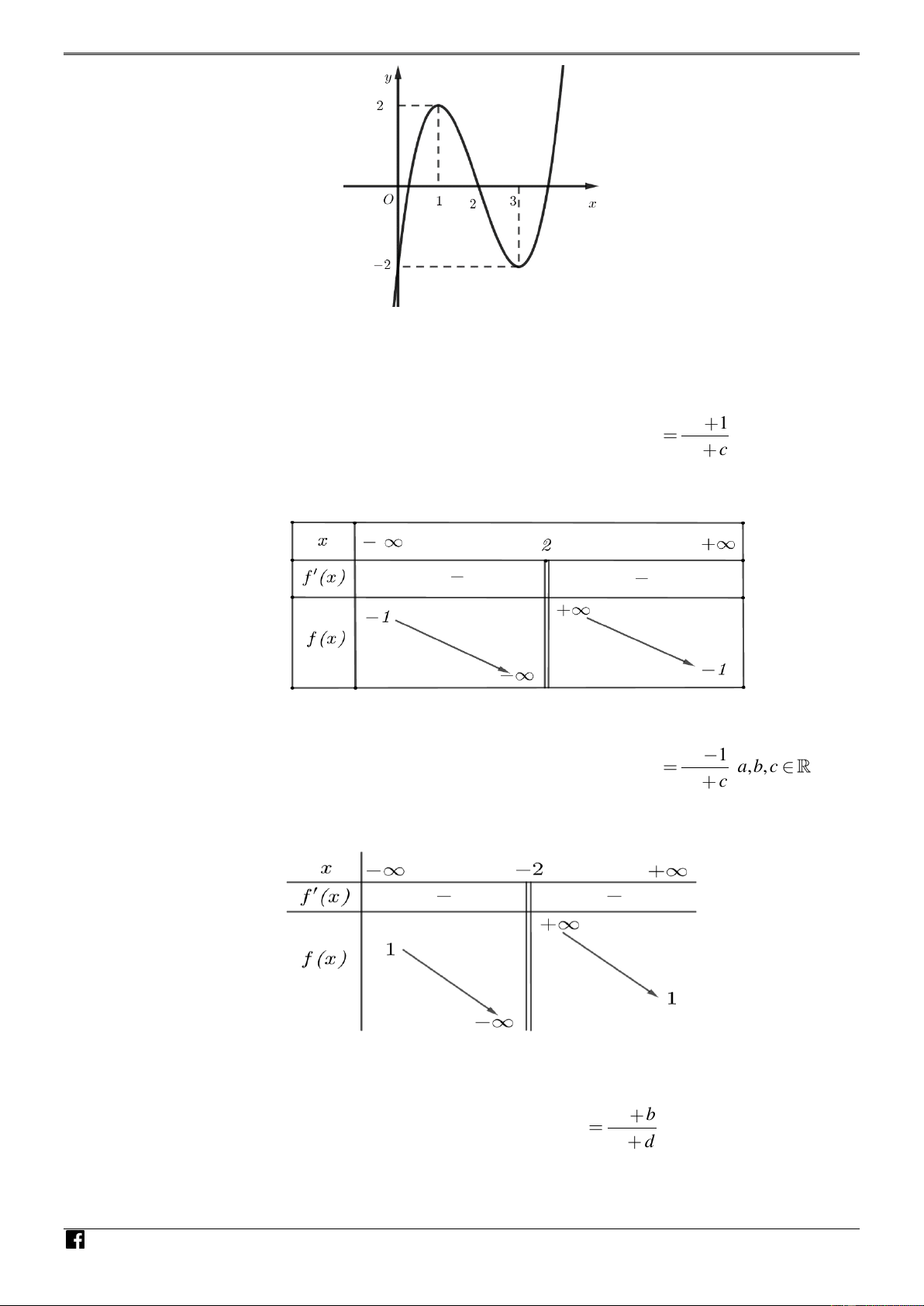
Câu 50. [ ĐỀ GỐC-MÃ 101- TN 2020 ] Cho hàm số bậc ba y f (x) có đồ thị là đường cong trong hình sau: NHÓ M TO ÁN
Số nghiệm thực phân biệt của phương trình f 3
x f (x) 1 0 là VD A. 8 . B. 5 . C. 6 . D. 4 . – V D
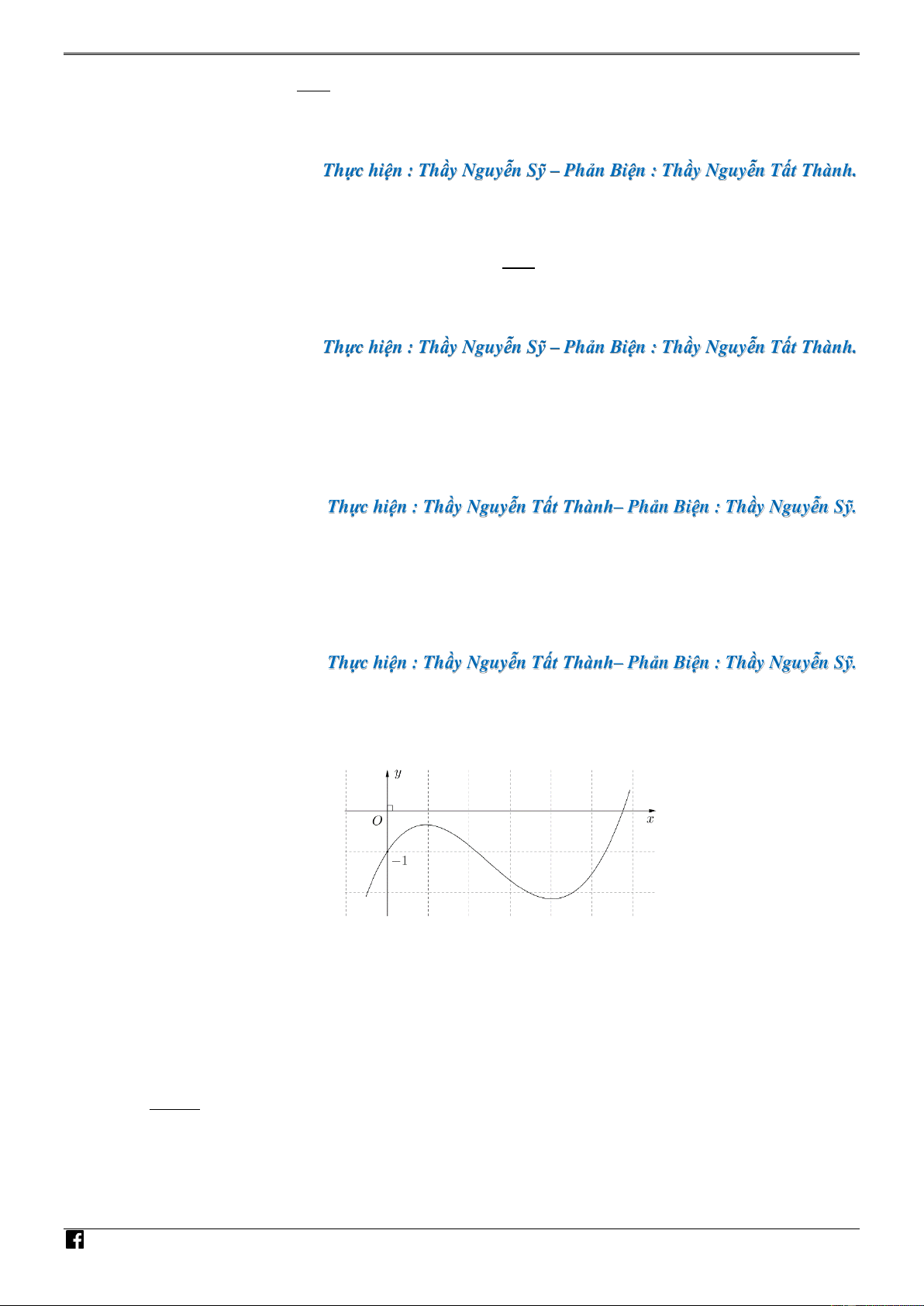
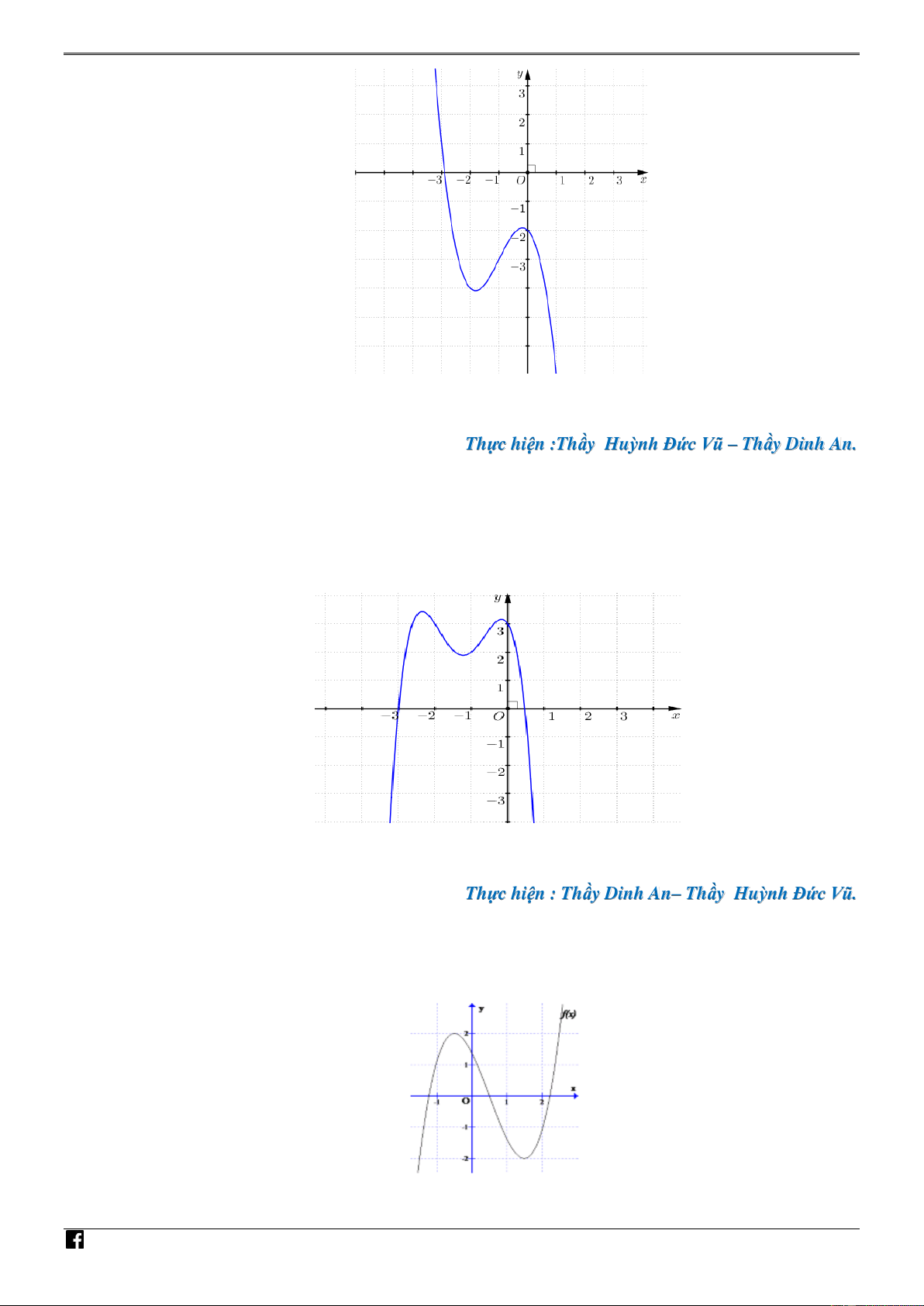
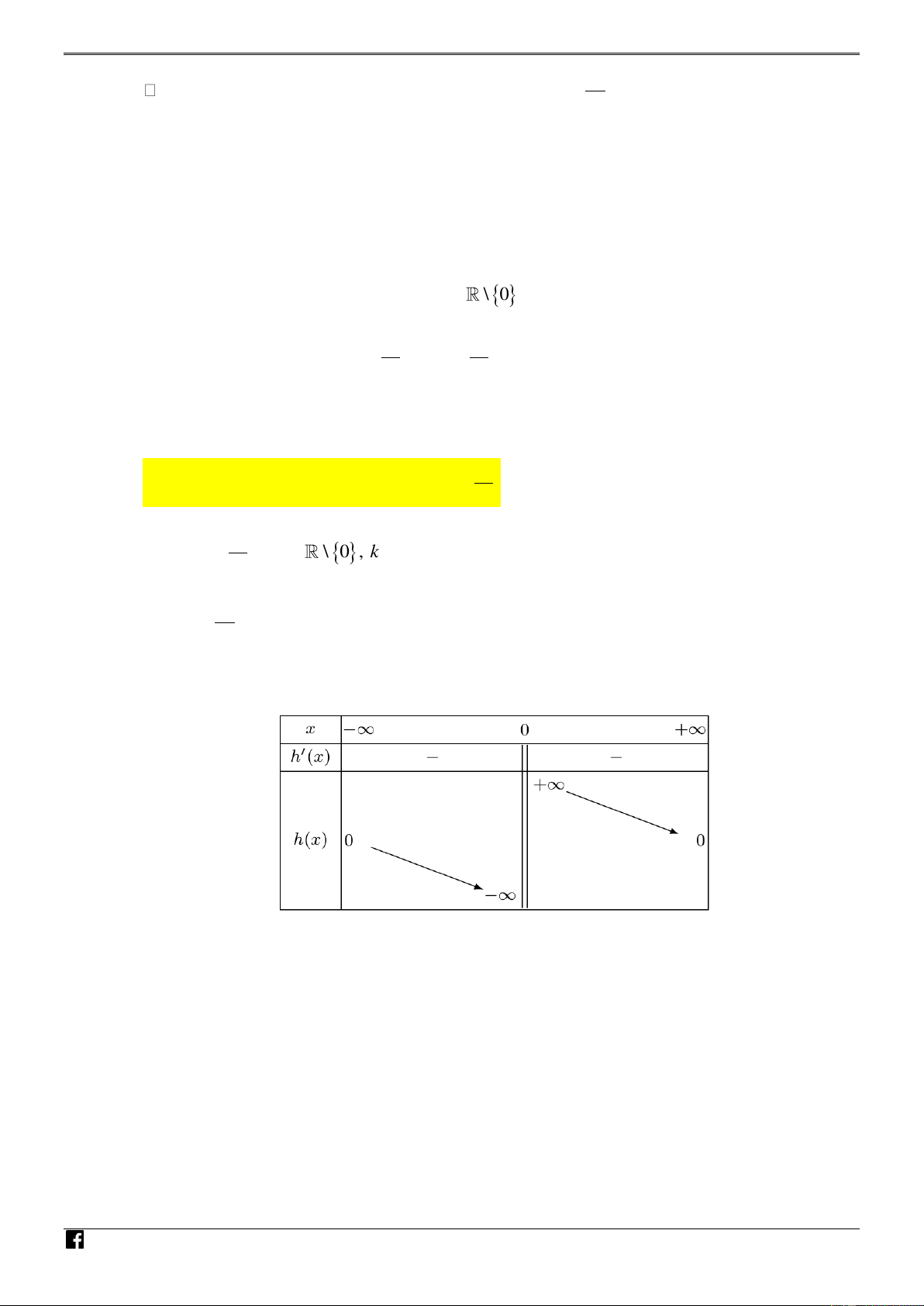
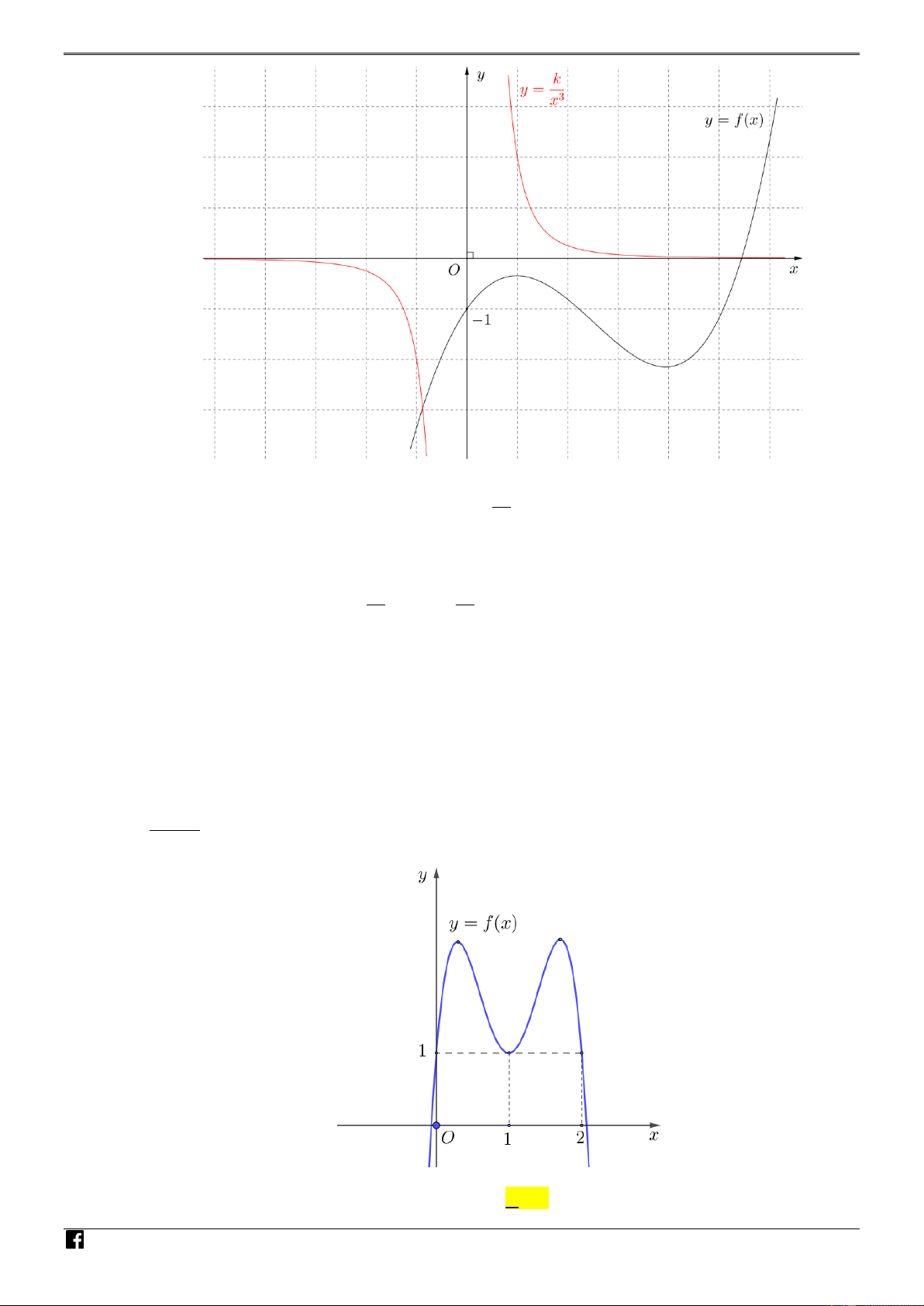
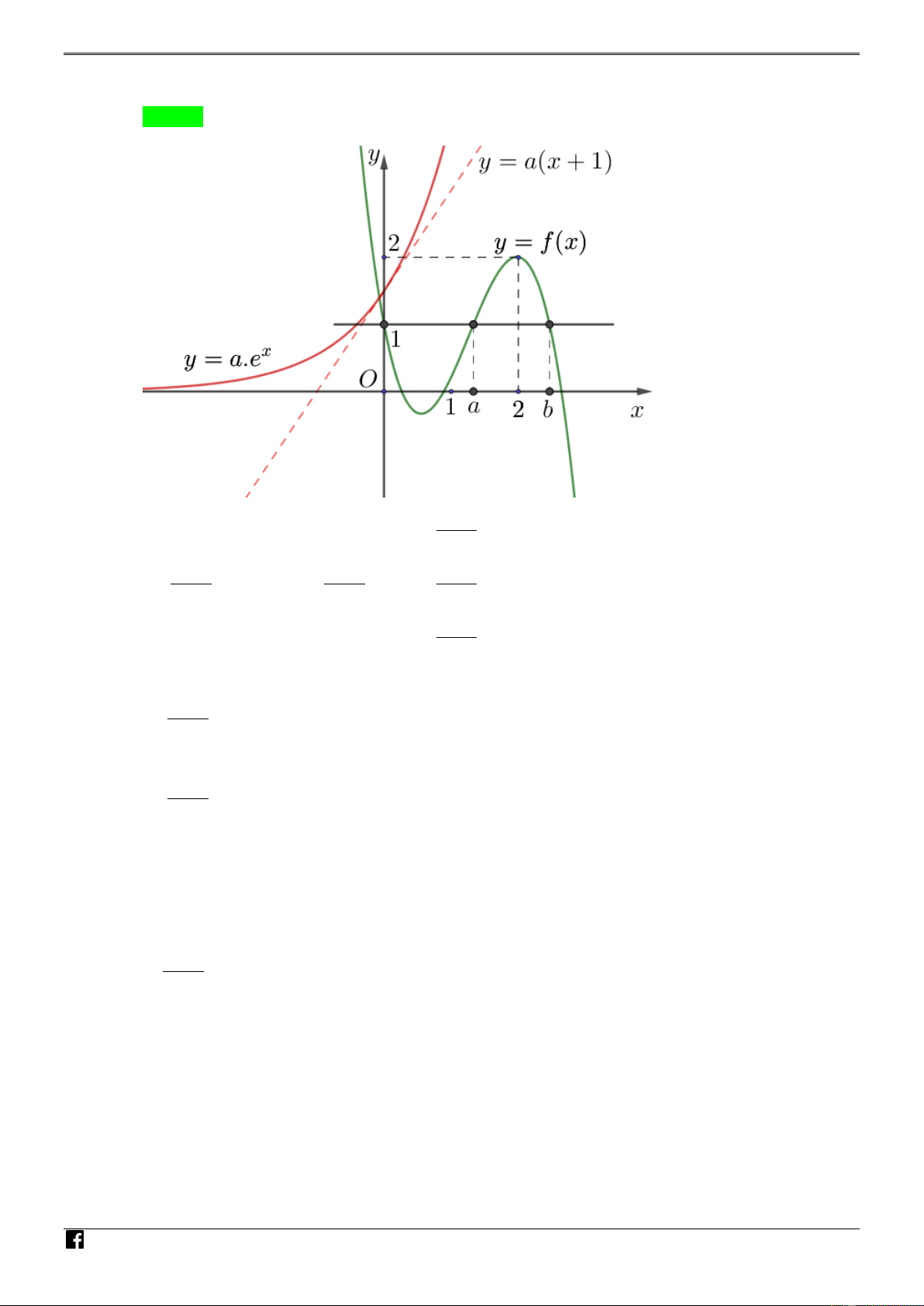
Câu 40. [PHÁT TRIẾN CÂU 50 – MÃ 101 – TN 2020] Cho hàm số đa thức bậc bốn y f (x) có C
đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình
4 f x f 1 0 là 2 ln x
https://www.facebook.com/groups/toanvd.vdc Trang 12
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 NHÓ M TO A. 8 . B. 5 . C. 6 . D. 4 . ÁN
Thực hiện :Thầy Huỳnh Đức Vũ – Thầy Dinh An. VD –
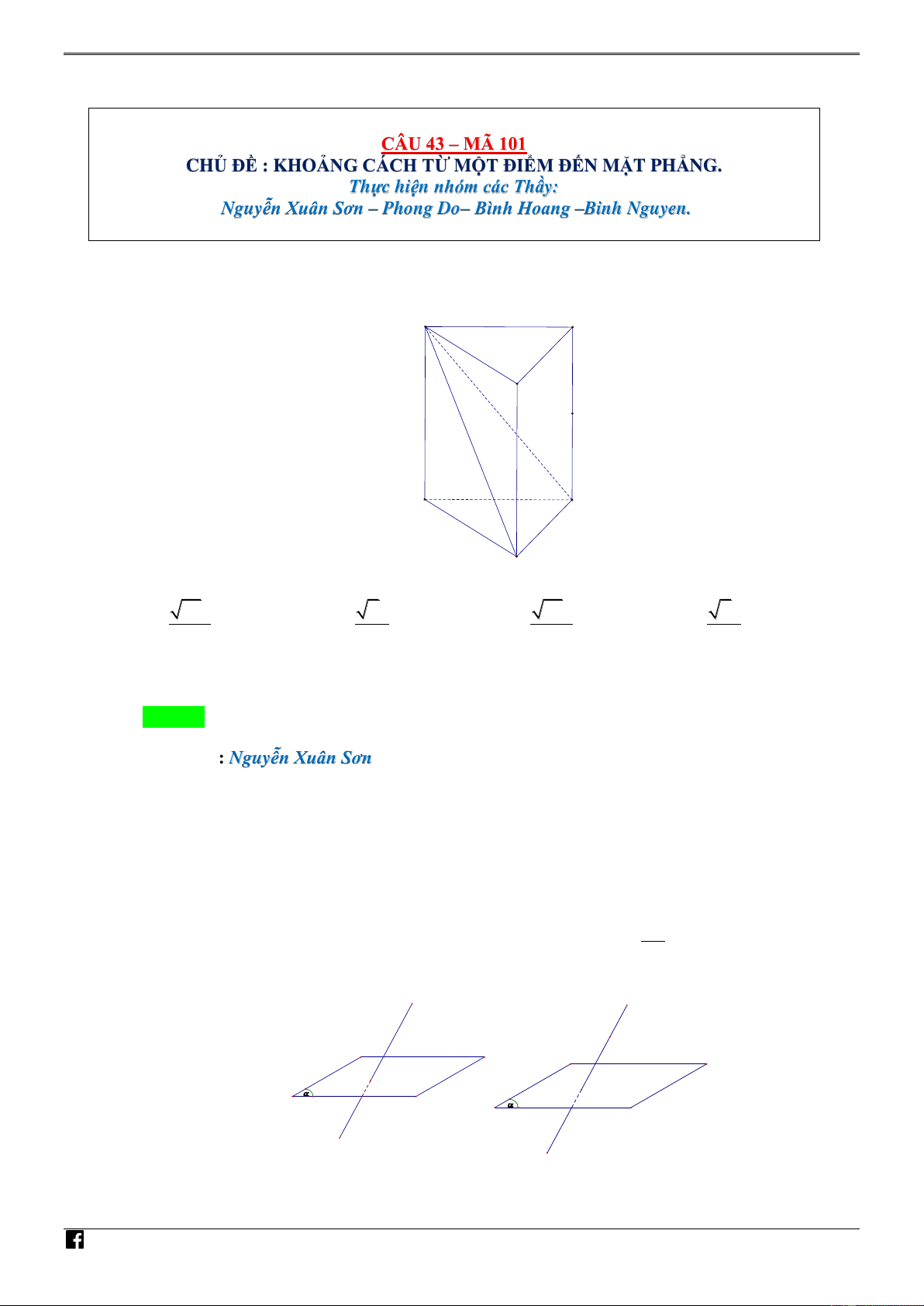
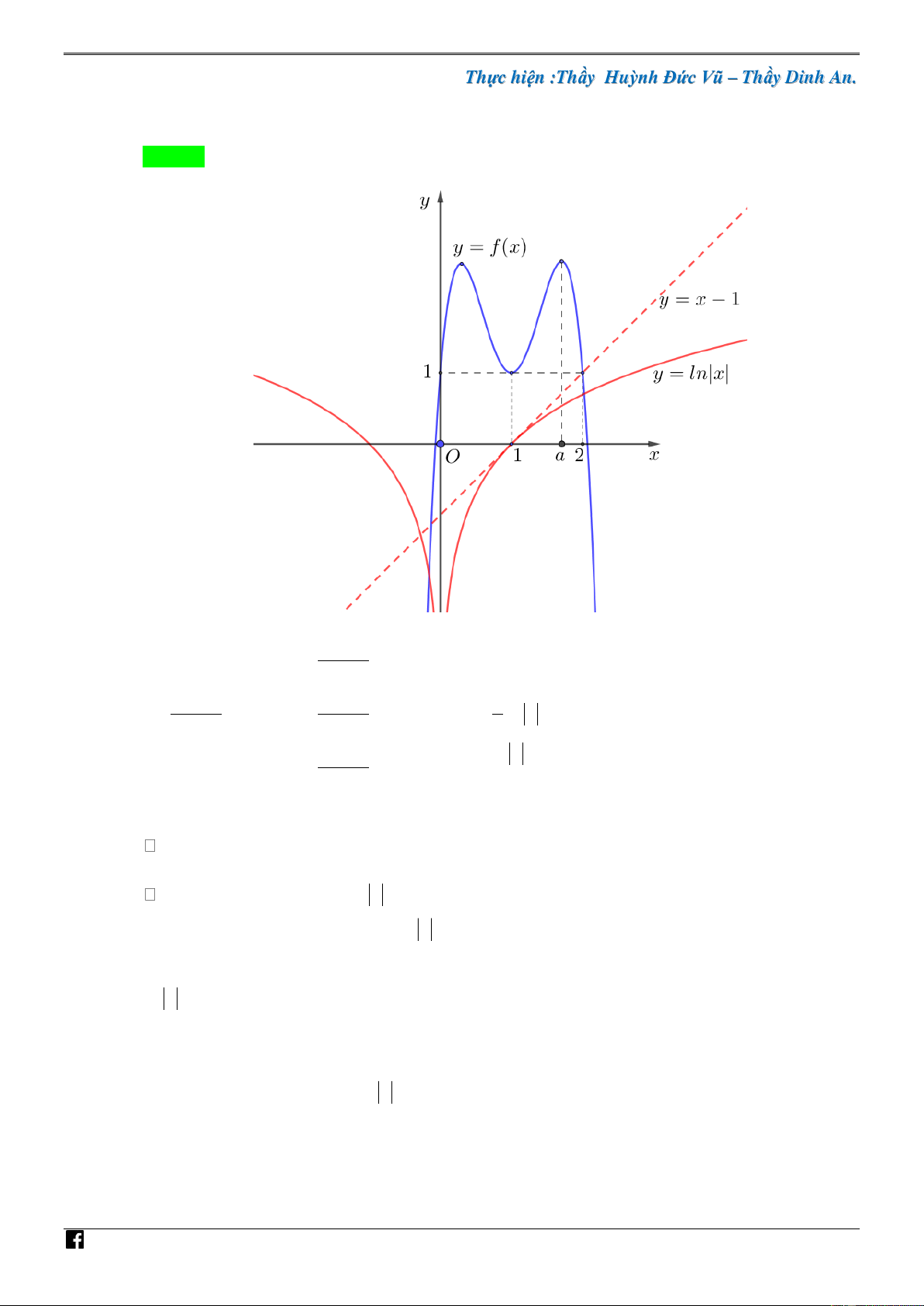
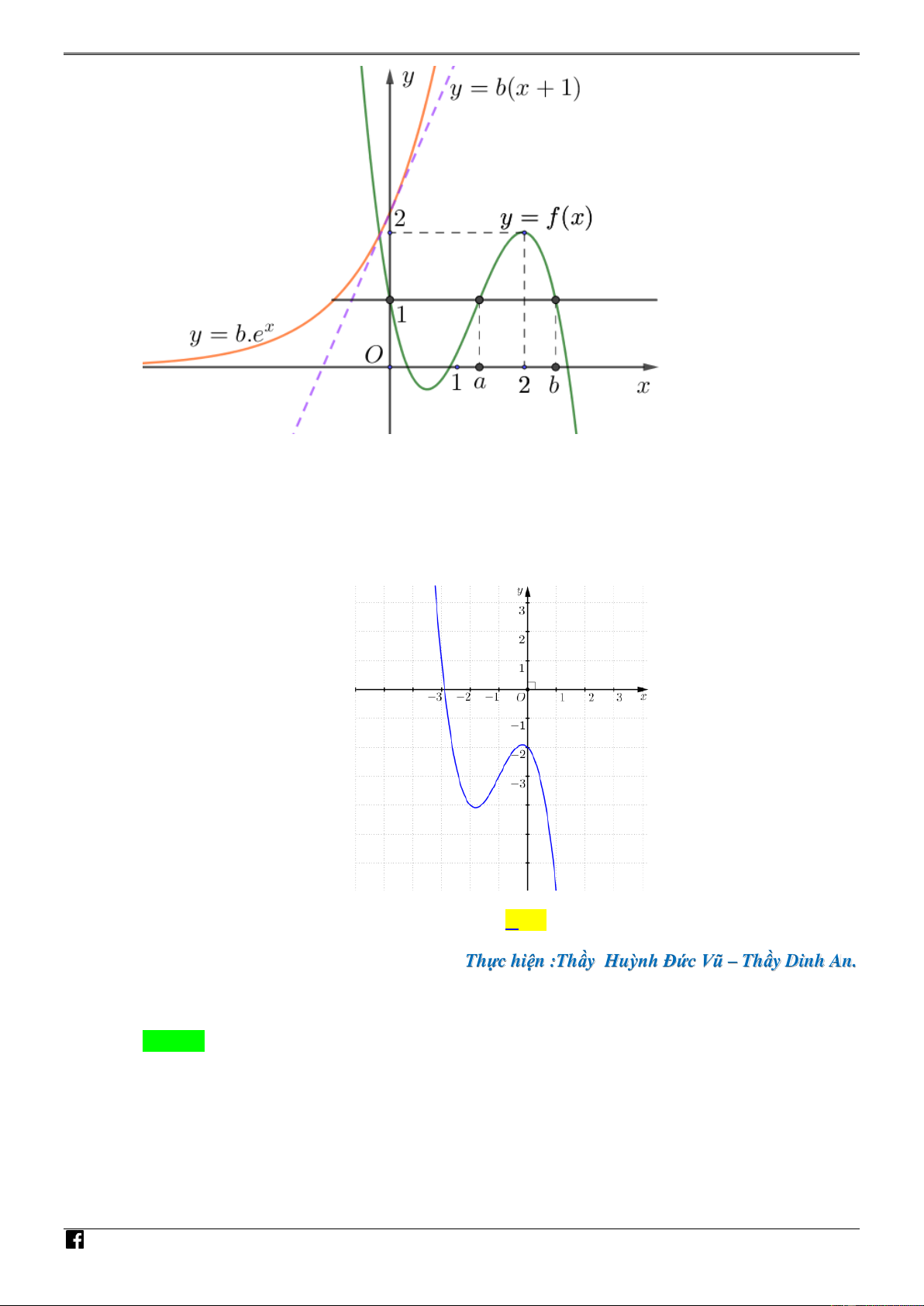
Câu 41. [PHÁT TRIẾN CÂU 50 – MÃ 101 – TN 2020] Cho hàm số đa thức bậc ba y f (x) có đồ V D C
f x
thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình f 1 0 x e là NHÓ M A. 8 . B. 5 . C. 6 . D. 4 . TO ÁN
Thực hiện :Thầy Huỳnh Đức Vũ – Thầy Dinh An. VD
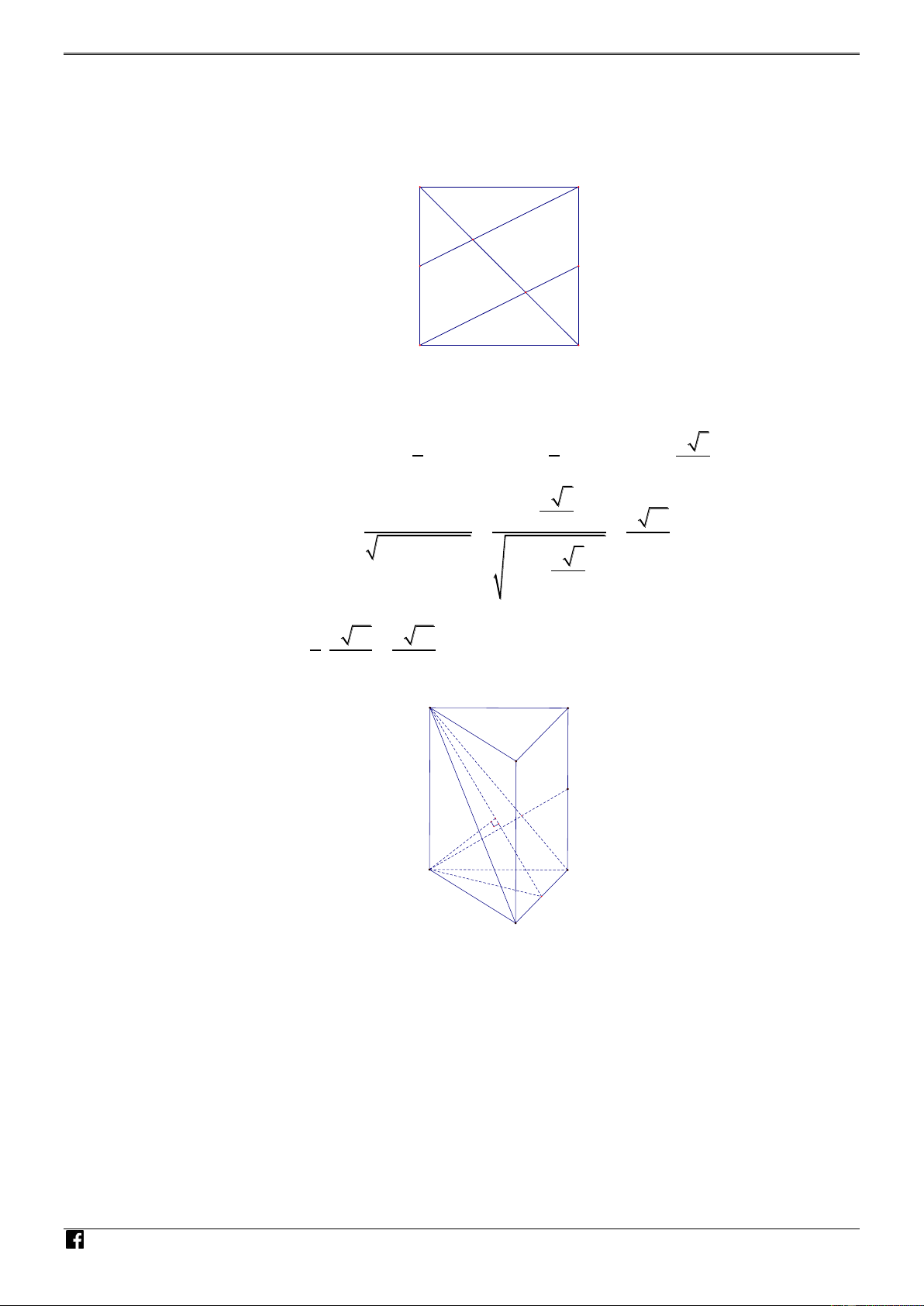
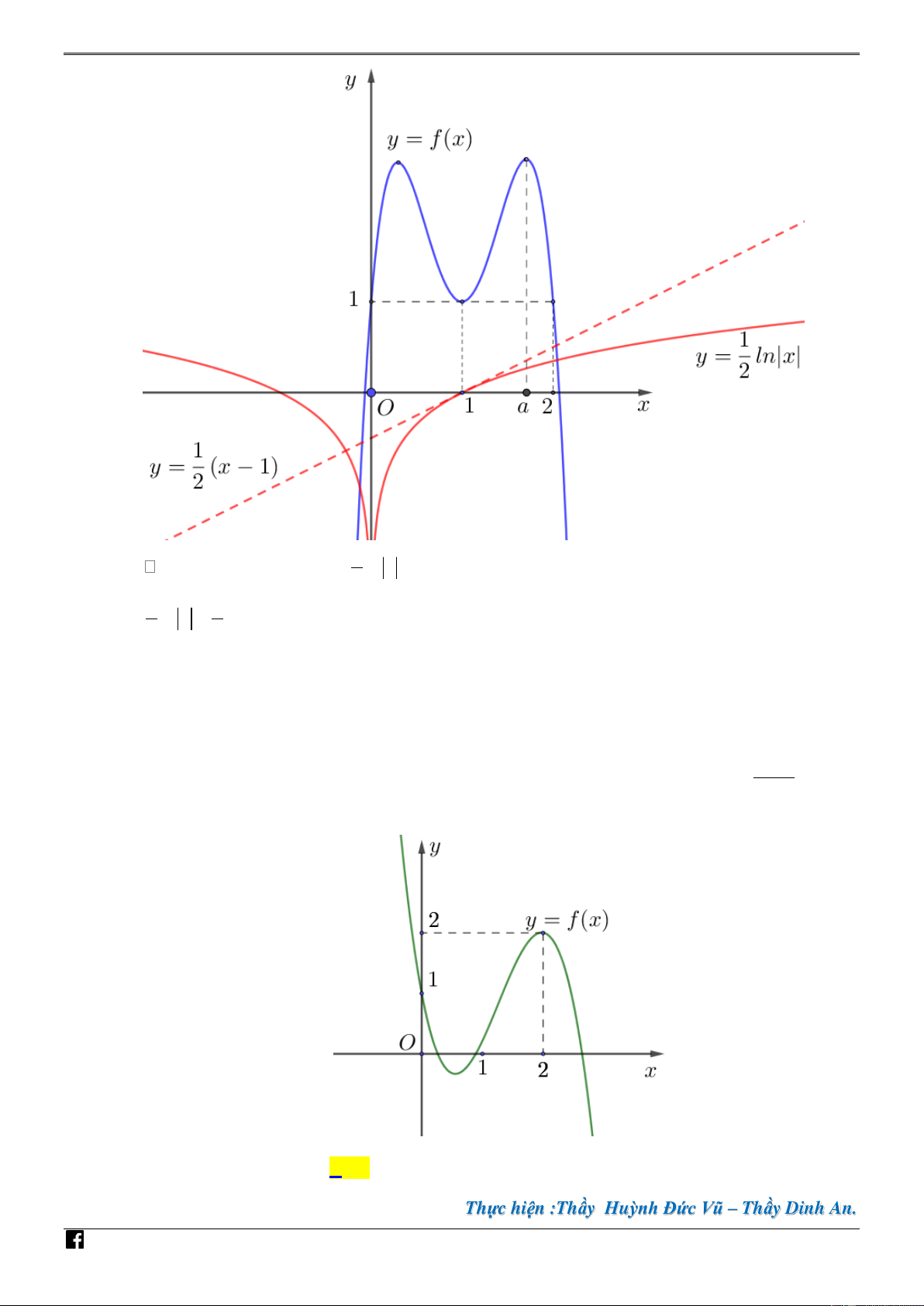
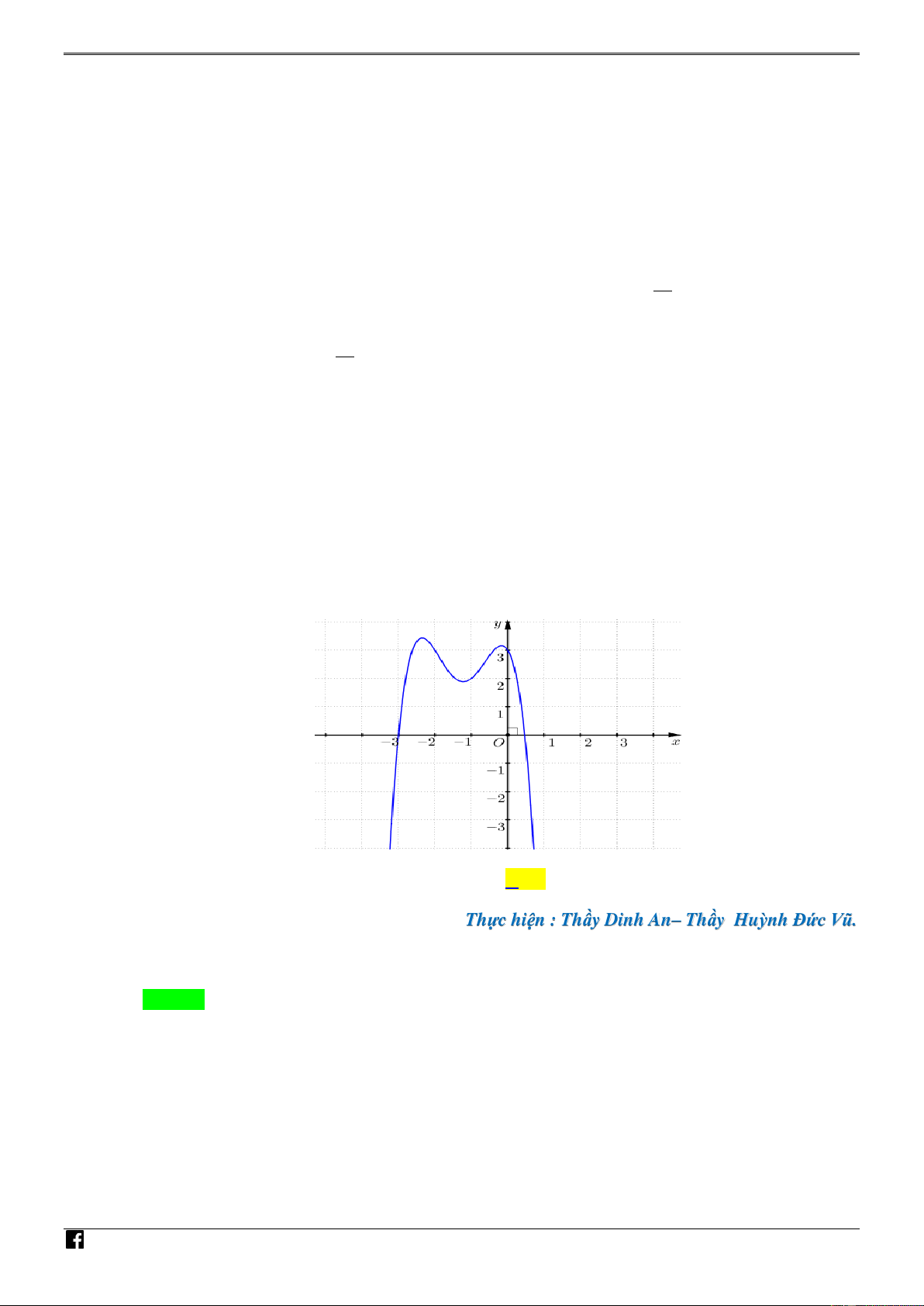
Câu 42. [PHÁT TRIẾN CÂU 50 – MÃ 101 – TN 2020] Cho hàm số bậc ba y f x có đồ thị là – V 5 D
đường cong trong hình vẽ. Số nghiệm thực phân biệt của phương trình f x f x 2 0 là C
https://www.facebook.com/groups/toanvd.vdc Trang 13
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 NHÓ M TO A. 8 . B. 5 . C. 6 . D. 4 . ÁN
Thực hiện :Thầy Huỳnh Đức Vũ – Thầy Dinh An. VD –
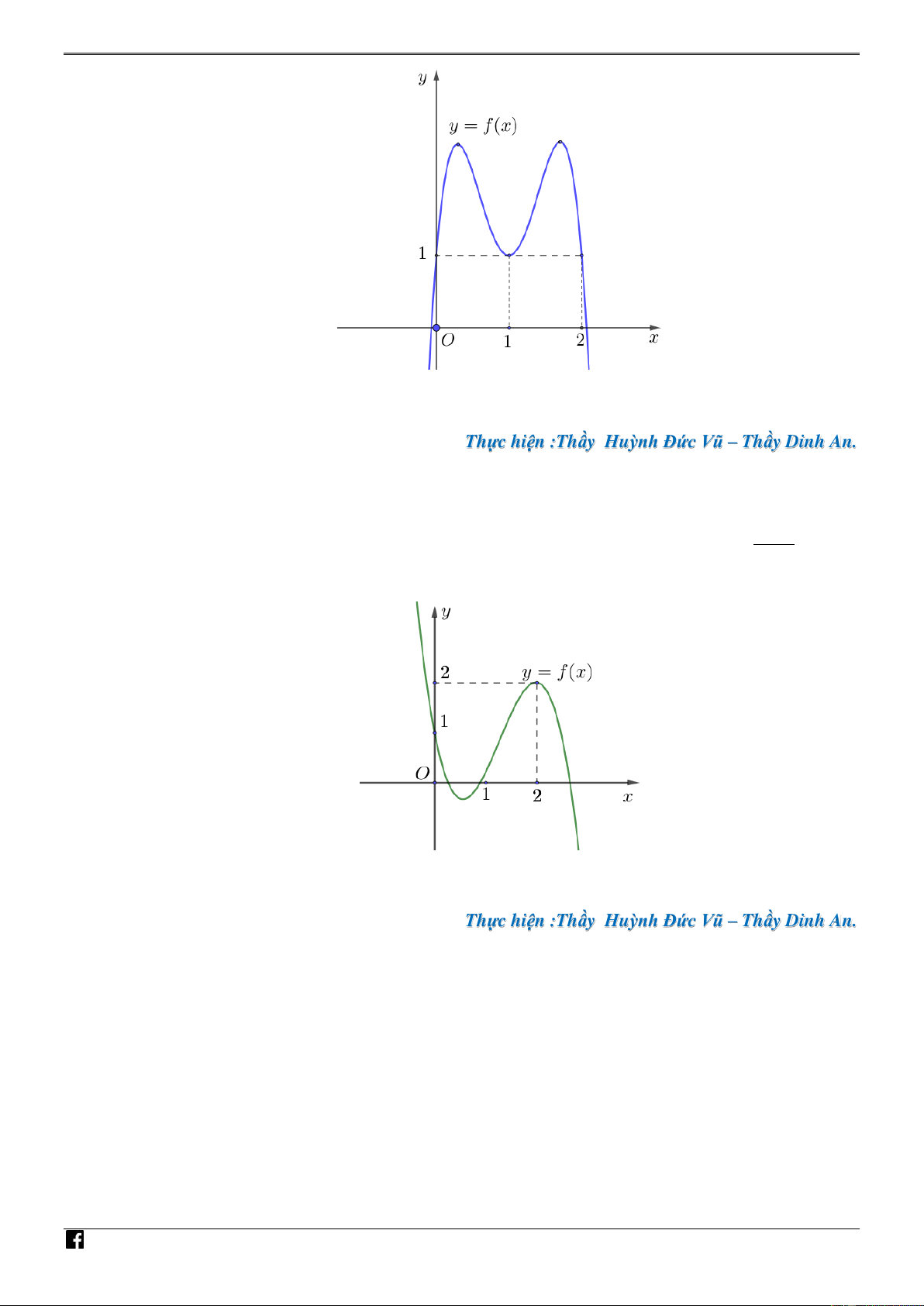
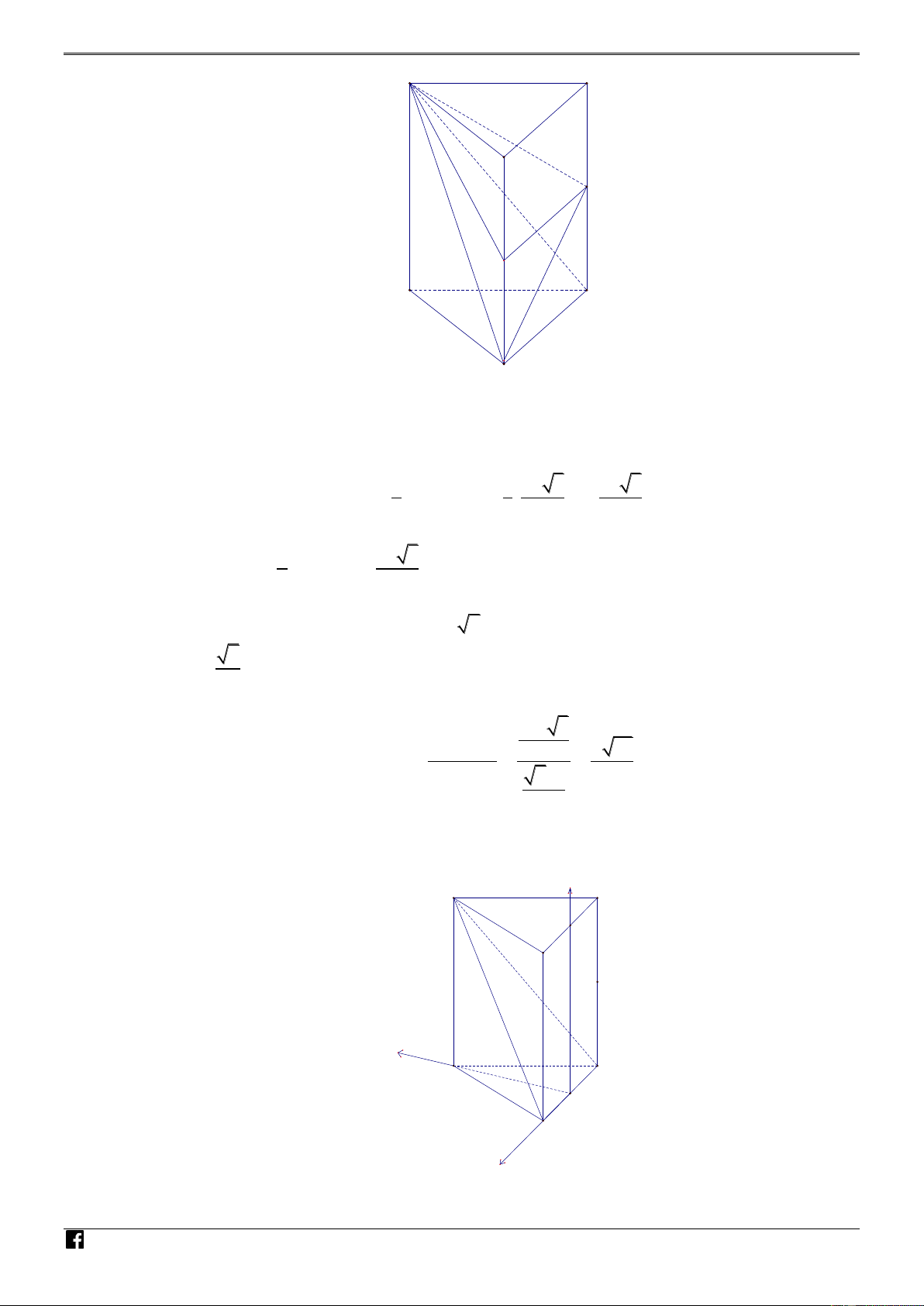
Câu 43. [PHÁT TRIẾN CÂU 50 – MÃ 101 – TN 2020] Cho hàm số bậc bốn y f x có đồ thị là V D C
đường cong trong hình vẽ. Số nghiệm thực phân biệt của phương trình f x 2 2
f x 3 0 là NHÓ A. 8 . B. 6 . C. 9 . D. 12 . M TO
Thực hiện : Thầy Dinh An– Thầy Huỳnh Đức Vũ. ÁN
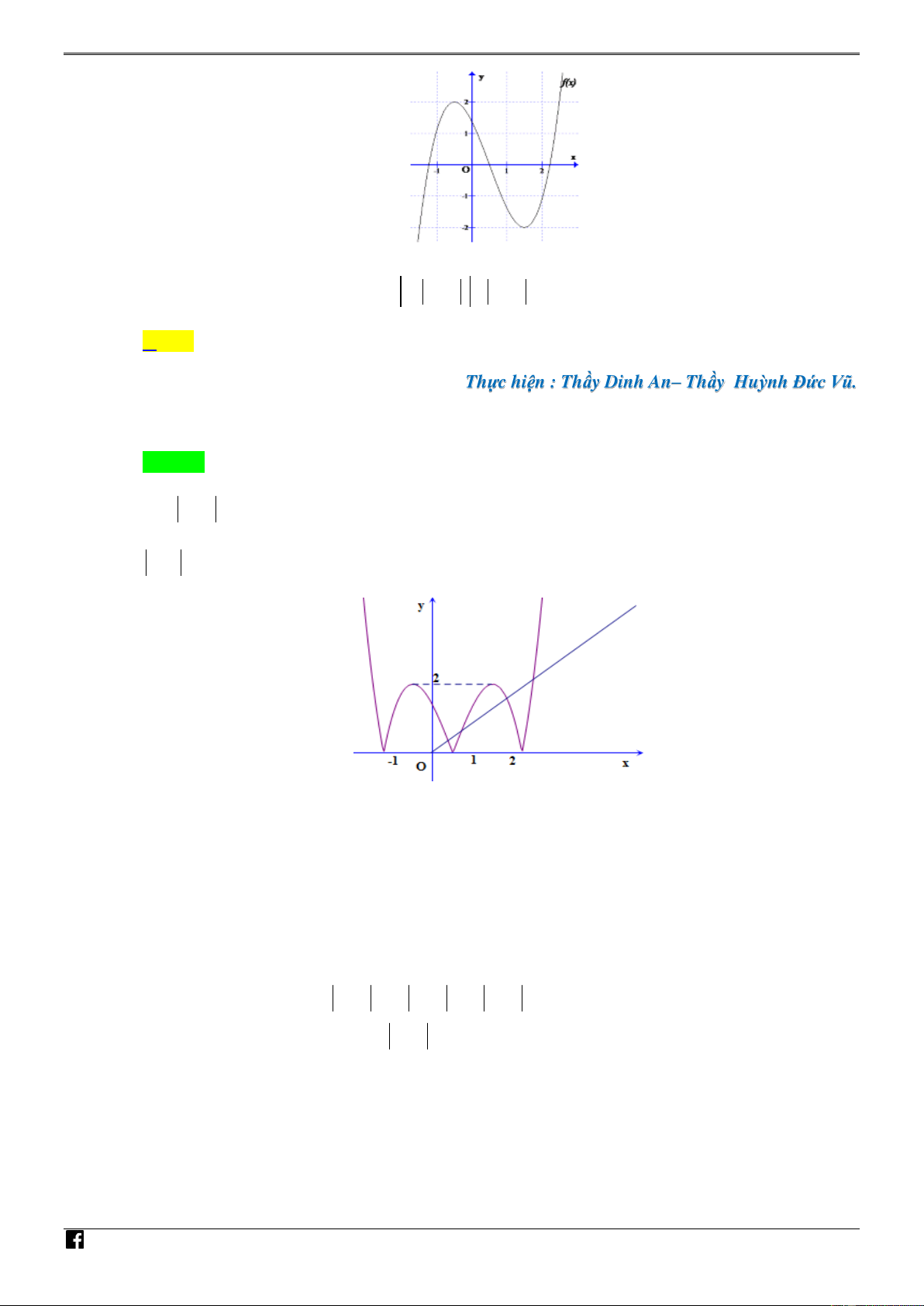
Câu 44. [PHÁT TRIẾN CÂU 50 – MÃ 101 – TN 2020] Cho hàm số y f x có đồ thị như hình VD vẽ. – V D C
https://www.facebook.com/groups/toanvd.vdc Trang 14
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
Số nghiệm thực của phương trình f f x f x 0 là A. 20 . B. 24 . C. 10 . D. 4 .
Thực hiện : Thầy Dinh An– Thầy Huỳnh Đức Vũ. NHÓ M TO ÁN VD – V D C NHÓ M TO ÁN VD – V D C
https://www.facebook.com/groups/toanvd.vdc Trang 15
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
HƢỚNG DẪN GIẢI CHI TIẾT CÂU 43 – MÃ 101
CHỦ ĐỀ : KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MẶT PHẲNG.
Thực hiện nhóm các Thầy:
Nguyễn Xuân Sơn – Phong Do– Bình Hoang –Binh Nguyen.
Câu 43. [MÃ 101 - TN 2020] Cho hình lăng trụ đứng AB . C A B C
có tất cả các cạnh bằng a . Gọi M là
trung điểm của CC (tham khảo hình bên). Khoảng cách từ M đến mặt phẳng A B C bằng NHÓ A' C' M TO B' M ÁN VD – V A D C C B 21a 2a 21a 2a A. . B. . C. . D. . 14 2 7 4 Lời giải Chọn A
Phân tích: Nguyễn Xuân Sơn
Bài toán tính khoảng cách là bài toán đặc trưng của khối 11, tuy nhiên với dạng bài toán này
chúng ta có thể dùng cả ba phương pháp để giải quyết: tính toán đơn thuần theo cách lớp 11, NHÓ
tính theo tọa độ và tính dựa vào thể tích và tỉ lệ thể tích. M
*) Tính toán theo cách lớp 11: Học sinh cần nắm được 2 đơn vị kiến thức chính TO ÁN HI
+) Cho đường thẳng HJ cắt tại I . Khi đó ta có d H,
.d J, VD JI – H V D H C J I I J
https://www.facebook.com/groups/toanvd.vdc Trang 16
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
+) Cho hình vuông ABCD với M , N lần lượt là trung điểm của BC và AD . Gọi
BM AC P , ND AC Q . Ta luôn có tính chất sau: BP 2PM , DQ 2QN ,
AP PQ QC . B A P M N Q NHÓ D C M TO
Vận dụng các tính chất trên ta có cách giải Câu 43 như sau: ÁN 1 1 a VD
d M , A B
C d , A A B
C AI . Mà 3 AH , 2 2 2 – V a 3 D . a C AA .AH a 21 2 AI . 2 2 2 7 AA AH 2 a 3 a 2 a a
Vậy d M A B C 1 21 21 , . . 2 7 14 A' C' B' M I NHÓ M A C TO H ÁN B VD
*) Tính theo thể tích và tỉ lệ thể tích: – V D C
https://www.facebook.com/groups/toanvd.vdc Trang 17
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 A' C' B' M N A C NHÓ M B TO ÁN
Gọi N là trung điểm của BB , khi đó lăng trụ AB . C A B C
bị chia thành 3 phần có thể tích bằng nhau VD – 2 3 1 1 a 3 a 3 V V A . ACB VA B CMN VA .MNB C VABC. . . A B C a D 3 3 4 12 C 3 1 a 3 Suy ra M V .A B C VA .MNBC . 2 24 Mà tam giác A B C có A B A C
a 2 , BC a . Vậy diện tích tam giác A B C là: 7 2 S A B C a . 4 3 3a 3 3V a 21
Vậy khoảng cách từ d M A B C M .A BC 24 , 2 S A B C 7a 14 4 NHÓ
*) Tính theo tọa độ: M z TO A' C' ÁN B' VD M – V D C x A C O B y
https://www.facebook.com/groups/toanvd.vdc Trang 18
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 1
Chọn hệ tọa độ như hình vẽ, cho a 1. Ta có tọa độ các điểm O 0;0;0 , B 0; ;0 , 2 3 1 1 1 3 1 1 A ; 0; 0 , C 0; ;0 , B 0; ;1 , C 0; ;1 , A ; 0;1 , M 0; ; , 2 2 2 2 2 2 2 3 1 3 1
AB ; ; 1
, AC ; ; 1
. Một vectơ pháp tuyến của mặt phẳng A B C là: 2 2 2 2 3 n A B , A C 1 ;0; 2 NHÓ 3 M
Phương trình mặt phẳng A BC : 1
x 0 0 y 0
z 0 0 2
x 3z 0. 2 TO ÁN 1 3 2 21 VD
Vậy d M , A B C . 4 3 14 – V D
Câu 1. [PHÁT TRIẾN CÂU 43 – MÃ 101 – TN 2020] Cho hình lăng trụ đứng AB . C A B C có tất C
cả các cạnh bằng a . Gọi M là trung điểm của CC , N là trung điểm của BB (tham khảo
hình bên). Khoảng cách từ N đến mặt phẳng A B M bằng A' C' B' M N A C B NHÓ 2a 2a 2a A. . B. . C. a 2 . D. . 2 4 8 M TO
Thực hiện Thầy Nguyễn Xuân Sơn ÁN Lời giải VD Chọn B – V D C
https://www.facebook.com/groups/toanvd.vdc Trang 19
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 A' C' B' M R N NHÓ Q A C M TO ÁN VD B – V Gọi A M
AC Q , suy ra AC CQ a . Mà BC a , vậy tam giác ABQ vuông tại B . D C
Ta có d N A B
M d N A B Q 1
d A A B Q 1 a 2 , , , AR 2 2 4
Câu 2. [PHÁT TRIẾN CÂU 43 – MÃ 101 – TN 2020] Cho hình lăng trụ đều AB . C A B C có cạnh
bên bằng cạnh đáy và bằng a . Gọi G là trọng tâm của tam giác CC B .
Khoảng cách từ G đến mặt phẳng A B C bằng : 2 21a 21a a 3 2 2 A. B.. C. D. 21 7 3 3
Thực hiện : Thầy Phong Do – Thầy Nguyễn Xuân Sơn Lời giải NHÓ Chọn A M TO ÁN VD – V D C
https://www.facebook.com/groups/toanvd.vdc Trang 20
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
d G, A B C GB 2 C G A B
C B , suy ra
d C , A B . C C B 3 2 3 Ta có 1 1 1 a 3 a 3 V V .C C.S . . a . C .A BC ABC. 3 A B C 3 ABC 3 4 12 2 a 7 Lại có A B
a 2 , CB a, A C
a 2 S . A B C 4 3 a 3 NHÓ 3. 3V a 21
Suy ra d C A B C C . A BC 12 , . 2 M S a A BC 7 7 TO 4 ÁN 2 2 a 21 2 21a VD
Vậy d G, A B
C d C ,A B C . . 3 3 7 21 – V Cách 2: D C NHÓ M
Gọi M là trung điểm BC , H là hình chiếu của A lên A M TO ÁN BC AM
BC AH , mà AH A M
nên AH A B
C hay AH d , A A B C VD BC AA – V
d G, A B C GB 2 D C G A B
C B , suy ra
d C , A B
C d , A A B C C
d C , A B ; C C B 3 2 2 Ta có a 3 AA .AM a 21 AM , AH . 2 2 2 AA AM 7 2 2 2 a 21 2 21a
Vậy d G, A B
C d C , A B
C d , A A B C . 3 3 3 7 21
https://www.facebook.com/groups/toanvd.vdc Trang 21
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
Câu 3. [PHÁT TRIẾN CÂU 43 – MÃ 101 – TN 2020] Cho hình lăng trụ đứng AB . C A B C có đáy
là tam giác vuông cân tại A với AB a và AA 2a . Trên cạnh CC lấy điểm M sao cho 1 C M
CM (tham khảo hình bên). Khoảng cách từ M đến mặt phẳng A B C bằng 2 NHÓ M TO ÁN VD 4 2 3 9 A. a . B. a . C. a . D. a . – 9 3 2 4 V D
Thực hiện : Thầy Hoàng Xuân Bính -PB : Thầy Nguyễn Xuân Sơn C Lời giải Chọn A NHÓ M TO ÁN MC MN Gọi MA A C N thì 2 MN NA AA do đó: 2 NA 3 3 VD
d M A B C 2
d A A B C 2 ; ;
h với d ; A A B
C h. – 3 3 V D C 1 1 1 1 1 1 1 Vì AA , A ,
B AC đôi một vuông góc tại A nên ta có: 2 2 2 2 2 2 2 h AA AB AC 4a a a 1 9 2 hay h
a d M A B C 4 ; a . 2 2 h 4a 3 9
Câu 4. [PHÁT TRIẾN CÂU 43 – MÃ 101 – TN 2020] Cho hình lăng trụ tam giác đều
https://www.facebook.com/groups/toanvd.vdc Trang 22
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 AB .
C A B C có AB a và AA a 3 . Gọi M là trung điểm của BC (tham khảo hình bên).
Khoảng cách từ M đến mặt phẳng A B C bằng? NHÓ M TO ÁN a 15 a 15 2a 15 a 15 A. . B. . C. . D. . VD 5 10 5 20 –
Thực hiện : Hoàng Xuân Bính-PB : Nguyễn Xuân Sơn V D C Lời giải Chọn B NHÓ M TO
Gọi I là tâm của mặt bên ACC A
. Khi đó ta có M là trung điểm của BC nên ÁN
d M A B C 1
d C A B C 1 ; ; d ; A A B C. VD 2 2 – V
Gọi H là trung điểm BC , hạ AK A H thì A H d ; A A B C. D C Ta có: a 3 AA .AH a 15 AH AK . 2 2 2 AA AH 5 a
Vậy: d M A B C 15 ; . 10
Câu 5. [PHÁT TRIẾN CÂU 43 – MÃ 101 – TN 2020] Cho hình lăng trụ đứng tam giác
https://www.facebook.com/groups/toanvd.vdc Trang 23
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 AB .
C A B C , đáy ABC là tam giác vuông cân tại A có AB a và AA a 5 .Goi K là điểm
thỏa mãn hệ thức 5KA KB KC KC 0 . Tính khoảng cách từ K đến mặt phẳng A B C . a 55 a 55 a 55 2a 55 A. . B. . C. . D. . 44 11 22 11
Thực hiện : Hoàng Xuân Bính-Phản biện : Nguyễn Xuân Sơn Lời giải NHÓ Chọn C M TO ÁN VD – V D C
Gọi G là trọng tâm tứ diện ABCC thì ta có: GA GB GC GC 0
Do đó: KA KB KC KC 4KG .
Theo giả thiết: 5KA KB KC KC 0 4KA KA KB KC KC 0
4KA 4KG 0 K là trung điểm AG .
Mặt khác: gọi M , N là trung điểm của BC và AC thì G là trọng tâm tứ diện ABCC nên sẽ là NHÓ
trung điểm MN G A B C. M TO
Khi đó: d K A B C 1 ; 1 d ;
A ABC h với h d ; A A B C. ÁN 2 2 VD Vì 1 1 1 1 1 1 1 AA , A ,
B AC đôi một vuông góc tại A nên ta có: 2 2 2 2 2 2 2 – h AA AB AC 5a a a V D C
Câu 6. [PHÁT TRIẾN CÂU 43 – MÃ 101 – TN 2020] Cho hình chóp S.ABCD có đáy là hình thoi cạnh a , ABC 60
, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy.
Gọi H , M , N lần lượt là trung điểm các cạnh AB , SA , SD và P là giao điểm của (HMN) với
CD . Khoảng cách từ trung điểm K của đoạn thẳng SP đến mặt phẳng (HMN) bằng a 15 a 15 a 15 a 15 A. . B. . C. . D. . 30 20 15 10
https://www.facebook.com/groups/toanvd.vdc Trang 24
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
Thực hiện : Nguyễn Binh Nguyen- Ph
ản biện: Nguyễn Xuân Sơ n Lời giải Chọn B NHÓ M TO ÁN VD – V D C
Xét hình chóp S.ABCD trong hệ tọa độ Oxyz như hình vẽ. Khi đó ta có a a
H (0;0;0) , A ;0;0 , B ; 0; 0 , 2 2 a 3 a 3 a 3 S 0;0; , C 0; ; 0 , D ; a ; 0 . 2 2 2
Có MN AD nên suy ra P là trung điểm của CD .
Theo công thức trung điểm, ta suy ra NHÓ a a 3
a a 3 a 3 a a 3
a a 3 a 3 M ;0; , N ; ; , P ; ; 0 , K ; ; 4 4 2 4 4 2 2 4 4 4 M TO ÁN Ta có a a 3 a a 3 MN ; ; 0
, HM ;0; . 4 4 4 4 VD – 2 2 2 V Véc 3a a 3 a 3 D
-tơ pháp tuyến của mặt phẳng (HMN) là n MN, HM ; ; . C 16 16 16
Phương trình mặt phẳng (HMN) là 2 2 2 3a a 3 a 3 (x 0) ( y 0)
(z 0) 0 3x y z 0. 16 16 16
https://www.facebook.com/groups/toanvd.vdc Trang 25
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 a 3 a 3 a 3 4 4 4 a 15
Vậy khoảng cách cần tìm là dK,(HMN) 3 11 20 CÂU 44 – MÃ 101
CHỦ ĐỀ : CỰC TRỊ HÀM SỐ
Thực hiện : Võ Trọng Trí – Trần Thu Hương – Thiện Vũ – Kiet Tan.
Câu 44. [ ĐỀ GỐC-MÃ 101- TN 2020 ] Cho hàm số bậc bốn f x có bảng biến thiên như sau: NHÓ M TO ÁN VD – V D C
Số điểm cực trị của hàm số g x x f x 2 4 1 là A. 11. B. 9 . C. 7 . D. 5 . PHÂN TÍCH
Bài này dựa vào tính chất sau của đa thức:
Cho đa thức f x bậc k có k nghiệm (nghiệm có thể trùng nhau) trong đó có m nghiệm bội
chẵn và n nghiệm bội lẻ. Khi đó số cực trị của hàm số f x bằng 2m n 1. Lời giải Chọn B NHÓ Cách 1: M
Xét đa thức g x x f x 2 4 1 là đa thức bậc 12. TO ÁN Ta có VD x 0 x 0 –
x 1 aa 1
x a 1a 1 4 V x 0 4 2 D
g x x f x 1 0
x 1 b 1
b 0 x b 1 1 b 0 2 C f x 1 0
x 1 c0 c 1
x c 10 c 1
x 1 d d 1
x d 1d 1
Như vậy đa thức có nghiệm bội 4 là x 0 , và các nghiêm kép x a 1,b 1,c 1,d 1 ( tất cả là 12 nghiệm)
Vậy số cực trị hàm số là 5.2 1 9 .
https://www.facebook.com/groups/toanvd.vdc Trang 26
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
Cách 2: Ta chọn hàm f x 4 2
5x 10x 3 . Đạo hàm
g x x f x 2 3 4
x f x f x 3 4 1 2 1
1 2x f x
1 2 f x
1 xf x 1 . x 0 3
2x f x 1 0
Ta có g x 0
f x . f
x xf x 1 0 2 1 1 0 2 f x
1 xf x 1 0 NHÓ x 1 1, 278 M 4 x 1 0, 606 TO
+) f x
1 0 * 5 x 1 10 x 1 3 0 x 1 0 ,606 ÁN x 1 1 , 278 VD –
Phương trình có bốn nghiệm phân biệt khác 0 . V D t x 1 C 4 2 3 +) 2 f x 1 xf x
1 0 25t 10t 3 t
1 20t 20t 0 t 1,199 t 0,731 4 3 2
30t 20t 40t 20t 6 0 t 0 , 218 t 1 ,045
Phương trình có bốn nghiệm phân biệt khác 0 và khác các nghiệm của phương trình * .
Vậy số điểm cực trị của hàm số g x là 9 .
CÂU HỎI TƢƠNG TỰ, PHÁT TRIỂN NHÓ
Câu 7. [PHÁT TRIẾN CÂU 44 – MÃ 101 – TN 2020] Cho hàm số bậc bốn f x có bảng biến M TO thiên như sau: ÁN VD – V D C 4
Số điểm cực trị của hàm số g x x
1 f x 3 1 3 là A. 2 . B. 3 . C. 1. D. 5 .
Thầy Kiet Tan – Thầy Võ Trọn g Trí
https://www.facebook.com/groups/toanvd.vdc Trang 27
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 Lời giải Chọn B Xét đa thứ 4
c g x x
1 f x 3 1 3 là đa thức bậc 17. x 1 4 x a 1 0 x 1 0 x 1 0 Ta có
g x x 4 1 f x 3 1 3 0 f x x 1 1 3
x 1 a 1
x b 1 2
x 1 b 1 NHÓ
Như vậy đa thức có 17 nghiệm, trong đó nghiệm x a 1 và x b 1 bội 3, nghiệm x 1 bội M 10. TO
Vậy số cực trị hàm số là 1.2 2 1 3 . ÁN VD
Câu 8. [PHÁT TRIẾN CÂU 44 – MÃ 101 – TN 2020] Cho hàm số bậc bốn f x có bảng biến – thiên như sau: V D C Tính tổ 4
ng tất cả các giá trị m để số điểm cực trị của hàm số g x x m f x 3 2 bằng 3. A. 2 . B. 0 . C. 1. D. 6 .
Thầy Kiet Tan – Cô Trần Thu Hươn g NHÓ Lời giải M Chọn B TO 4 ÁN
Xét đa thức g x x m f x 3 2 là đa thức bậc 12. VD x m – 4 V
Ta có g x x m f x 3
2 0 x 1 D C x 1
Như vậy đa thức có 12 nghiệm, trong đó nghiệm x m là nghiệm bội 4 và x 1 , x 1 là các nghiệm bội 6. Nếu m 1 hoặc m 1
thì số cực trị hàm số đã cho là 2.2 1 3. Nếu m 1
thì số cực trị hàm số đã cho là 3.2 1 5.
https://www.facebook.com/groups/toanvd.vdc Trang 28
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
Vậy tổng các giá trị m để hàm số đã cho có 3 cực trị là 0
Câu 9. [PHÁT TRIẾN CÂU 44 – MÃ 101 – TN 2020] Cho hàm số bậc ba f x có bảng biến thiên như sau: NHÓ
Số điểm cực trị của hàm số g x x f x 2 3 3 1 là M TO A. 6 . B. 4 . C. 7 . D. 3 . ÁN
Thực hiện: Thầ
y Thiện Vũ – Phản biện: Thầ
y Võ Trọng Trí VD Lời giải – V D Chọn B. C
Ta chọn hàm f x 3 2
x 3x 4 . Đạo hàm
g x x f x 2 2 3
x f x f x 2 3 3 1 6 3 1 3
1 3x f 3x
1 f 3x
1 2xf 3x 1 . 2 3x 0
Ta có gx 0 f 3x 1 0 . f 3x
1 2xf 3x 1 0 +) 2
3x 0 : Phương trình có nghiệm kép x 0 . NHÓ 3 2 x M
+) f 3x
1 0 3x 1 33x 1 4 0 3 1 2 TO 3x 1 1 ÁN
Phương trình có nghiệm kép 1 x và nghiệm đơn 2 x . VD 3 3 – t 3x 1 V 2 3 2 2 D +) f 3x 1 2xf 3x 1 0 t 3t 4 t 1 3t 6t 0 C 3 t 0 , 457 3x 1 0 , 457 3 2
3t 9t 4t 4 0 t 1, 457 3x 1 1,457 . t 2 3x 1 2
Phương trình có ba nghiệm phân biệ 1 t x 0
,486 ; x 0,152 ; x . 3
https://www.facebook.com/groups/toanvd.vdc Trang 29
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
Vậy số điểm cực trị của hàm số g x là 4 .
Câu 10. [PHÁT TRIẾN CÂU 44 – MÃ 101 – TN 2020] Cho hàm số bậc bốn f x có bảng biến thiên như sau: NHÓ
Số điểm cực trị của hàm số g x 4
x f x 2 2 1 M là TO A. 9 . B. 4 . C. 7 . D. 5 . ÁN VD
Thực hiện: Thầ
y Thiện Vũ – Phản biện: Thầ
y Võ Trọng Trí – Lời giải V D C Chọn D.
Ta chọn hàm f x 4 2
x 8x 7 . Đạo hàm
g x x f x 2 3 2 5 x f 2
x f 2 x 3 x f 2
x f 2 x 2 x f 2 4 1 4 1 1 4 1 1 x 1 . 3 4x 0
Ta có gx 0 f 2 x 1 0 . f 2 x 2 1 x f 2 x 1 0 NHÓ +) 3
4x 0 : Phương trình có nghiệm bội lẻ x 0 . M 2 TO 4 2 x 1 1 +) f 2 x 1 0 2 x 2 1 8 x 1 7 0 . 2 ÁN x 1 7 VD Do 2
x 1 1 nên phương trình có ba nghiệm x 0 ; x 7 1 . – V D 2 t x 1 C +) 2 2 2
f x 1 x f x 1 0 4 2
t t t 3 8 7
1 4t 16t 0 t 2,191 t 1 4 3 2
5t 4t 24t 16t 7 0 . t 0 ,307 t 2 ,085
https://www.facebook.com/groups/toanvd.vdc Trang 30
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 Do 2
t x 1 1 nên phương trình có ba nghiệm x 0 ; x 1 ,091.
Vậy số điểm cực trị của hàm số g x là 5 .
Câu 11. [PHÁT TRIẾN CÂU 44 – MÃ 101 – TN 2020] Cho hàm số bậc ba y f (x) có đồ thị như hình vẽ sau NHÓ M TO ÁN VD 4 2 –
f (x )1 V
Số điểm cực trị của hàm số y là 2 x D e C
A. 8 . B. 5 . C. 9 . D. 7 .
Thực hiện: Cô Trần Thu Hương – Phản biện : Thầy Thiện Vũ Lời giải Chọn C
Dựa vào đồ thị tìm được hàm số f (x) 3
x 3x 1
f (x )14 2 . 4 f (x ) 1 3 2 2 2 . f '(x 2 ). 1 . x x e
f (x ) 1 4 2 2 x Ta có .e 2 . x y y' 2 x e 2xe2 NHÓ 3 2 4 2 y' 0 . 4 f ( 2 x ) 1 . f '( 2 x 2 ). 1 .
x ex f ( 2 x ) 1 .ex 2 . x 0 M TO 3 f ( 2 2 x ) 1 2 . . x ex . 4 f '( 2 x ) 1 f ( 2 x ) 1 0 ÁN 2 x VD 2 .xe 0 ) 1 ( 2 –
f (x ) 1 0 ( ) 2 V 2 2 D 4 f '(x ) 1 f (x ) 1 0 ) 3 ( C +) ) 1 ( x 0 . 2 x 1 88 , 1 x 53 , 2 +) 2 2 x 1 53 , 1 x 2 35 , 1 x 1 35 , 0
https://www.facebook.com/groups/toanvd.vdc Trang 31
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
+) Giải (3): Đặt x2 1 t ( )
2 4 f '(t) f (t) 0 4 3 2 t 3 ( 3 t 3t ) 1 0 3 t 12 2
t 3t 13 0 t 12 , 12 x t 96 , 0 12 , 13 x 96 , 1 t 17 , 1 NHÓ f (x 4 2 ) 1
Vậy phương trình y' 0 có 9 nghiệm đơn phân biệt do đó hàm số y có 9 M 2 x e TO ÁN điểm cực trị. VD – CÂU 45 – MÃ 101 V
CHỦ ĐỀ : TÌM HỆ SỐ TRONG HÀM SỐ CHO BỞI CÔNG THỨC D C
Thực hiện : Ngô Tú Hoa
Câu 45. [ ĐỀ GỐC-MÃ 101- TN 2020 ] Cho hàm số 3 2
y ax bx cx d , a , b ,
c d có đồ thị là
đường cong trong hình bên. Có bao nhiêu số dương trong các số a , b , c , d ? NHÓ M TO A. 4 . B. 1. C. 2 . D. 3 . ÁN Lời giải VD – Chọn C V D C
Ta có lim y a 0 . x
Gọi x , x là hoành độ hai điểm cực trị của hàm số suy ra x , x nghiệm phương trình 1 2 1 2 2
y 3ax 2bx c 0 nên theo định lý Viet: 2b b
+) Tổng hai nghiệm x x
0 0 b 0. 1 2 3a a
https://www.facebook.com/groups/toanvd.vdc Trang 32
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 +) Tích hai nghiệ c m x x 0 c 0 . 1 2 3a
Lại có đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên d 0 .
Vậy có 2 số dương trong các số a , b , c , d .
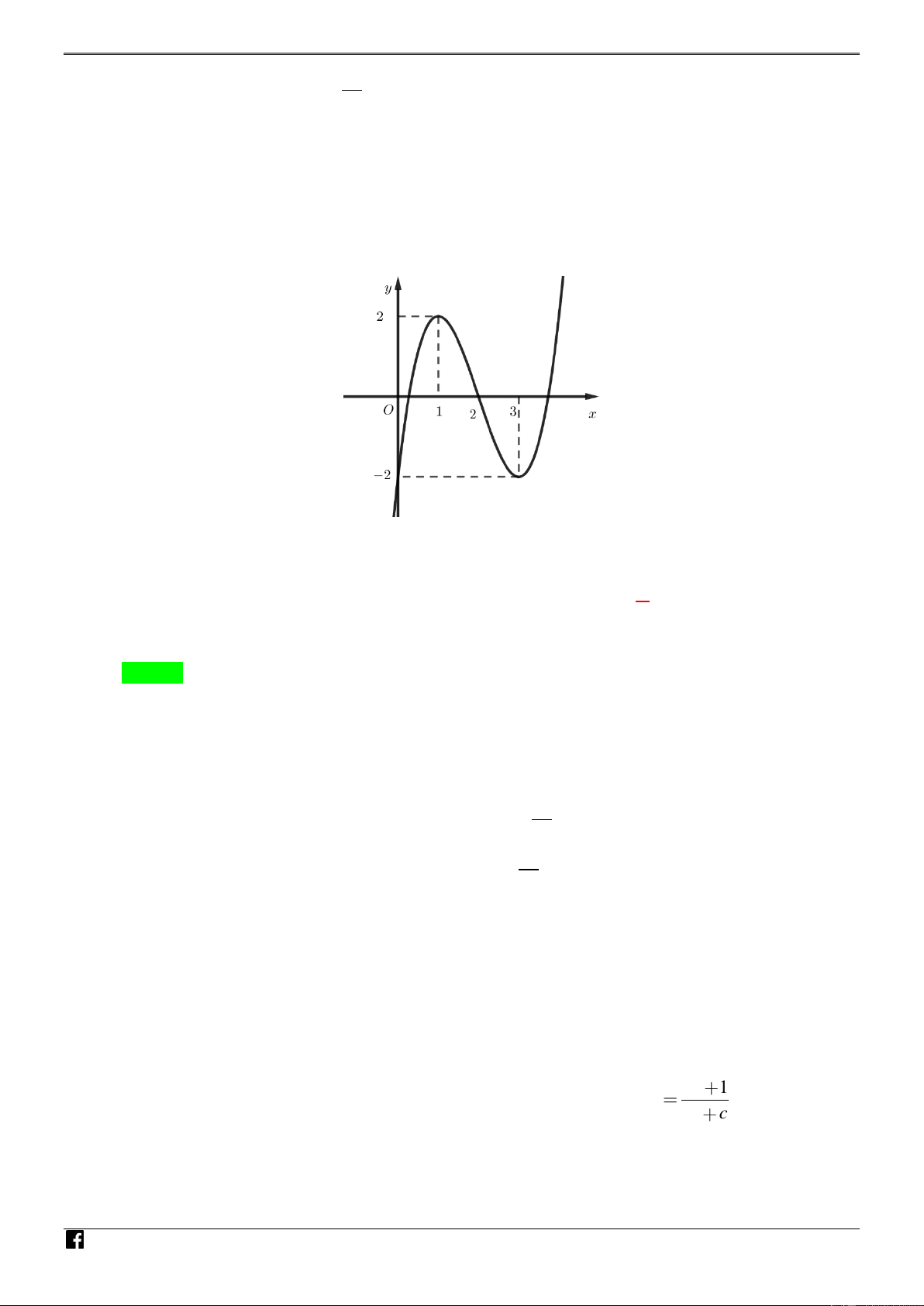
Câu 12. [PHÁT TRIẾN CÂU 45 – MÃ 101 – TN 2020] Cho hàm số 3 2
y ax bx cx d có đồ thị
như hình vẽ dưới đây: NHÓ M TO ÁN VD – V D C
Số lớn nhất trong các số , a , b , c d là A. . b B. d. C. . a D. . c Lời giải Chọn D Ta có 2
y 3ax 2bx c
+) Đồ thị cắt trục Oy tại điểm có tung độ bằng 2 d 2 0 . 2b
x x 4 1 2 NHÓ b 6 a +) Hàm số 3a
có hai điểm cực trị x 1 và x 3 nên . 1 2 c c 9a x .x 3 M 1 2 3a TO ÁN Suy ra 3 2
y ax 6ax 9ax 2 . VD b – +) Lại có y 6
1 2 4a 2 2 a 1 . V c 9 D C
Vậy b d a c . Câu 13. ax
[PHÁT TRIẾN CÂU 45 – MÃ 101 – TN 2020] Cho hàm số 1 f x có BBT như bx c
hình vẽ. Trong các số a, ,
b c có bao nhiêu giá trị dương?
https://www.facebook.com/groups/toanvd.vdc Trang 33
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 A.1 . B. 0 . C. 2 . D. 3 . Lời giải NHÓ Chọn A M TO a c TCN: y 1 0 ; TCĐ: x 2 0 ; Hàm Số nghịch biến ÁN b b VD a b 2 a 0 – ac 2b 2 c 2b 2b b b 0 V c 0 D ac b ac b 0 C Câu 14. ax
[PHÁT TRIẾN CÂU 45 – MÃ 101 – TN 2020] Cho hàm số 1 f x a, , b c có bx c
BBT như hình vẽ. Giá trị của a b c thuộc khoảng nào sau đây? NHÓ A. 1 ;0 . B. 2 ; 1 . C. 1; 2 . D. 0 ;1 . M TO Lời giải ÁN Chọn D VD – c V
Từ BBT ta có tiệm cận đứng x 2
2b c D b C a
Tiệm cận ngang y
1 a b b ac b
Hàm số nghịch biến trên từng khoảng xác định nên f x bx c 0 ac b 0 2 1 2
2b b 0 b 0 P a b c 2
b thì 0 P 1 2
https://www.facebook.com/groups/toanvd.vdc Trang 34
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 Câu 15. ax b
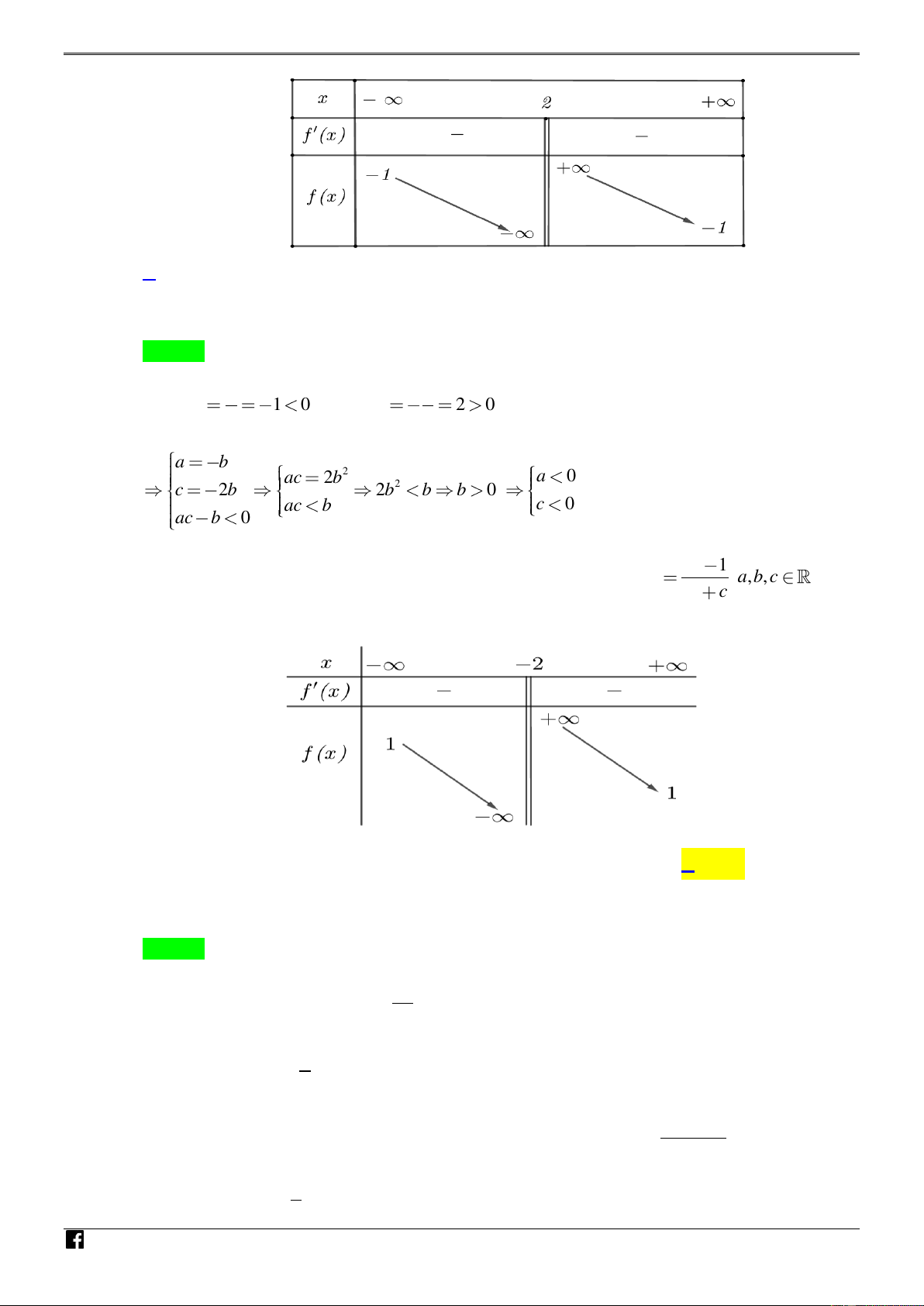
[PHÁT TRIẾN CÂU 45 – MÃ 101 – TN 2020] Hàm số y
. Có đồ thị như cx d hình vẽ: NHÓ M TO ÁN VD
Trong các số sau: a ;
b bd ;bc; ad; ad
bc có bao nhiêu số dương
A. 3 . B. 2 .C. 4 .D. 5 . – V Lời giải D C Chọn A
Hàm số nghịc biến nên ad bc 0 . Đồ b
thị giao trục hoành tại hoành độ x 0 ab 0 . a Đồ b
thị giao trục tung tại tung độ y 0 bd 0 d ab 0 Ta có : 2 b ad 0 ad 0 . bd 0 TCĐ : d a x 1 0 cd 0 ; TCN : y 1 0 ac 0 c c ab 0 NHÓ Và có 2 a bc 0 bc 0 . ac 0 M
Vậy có 3 số dương thuộc a , b ad,bc TO ÁN
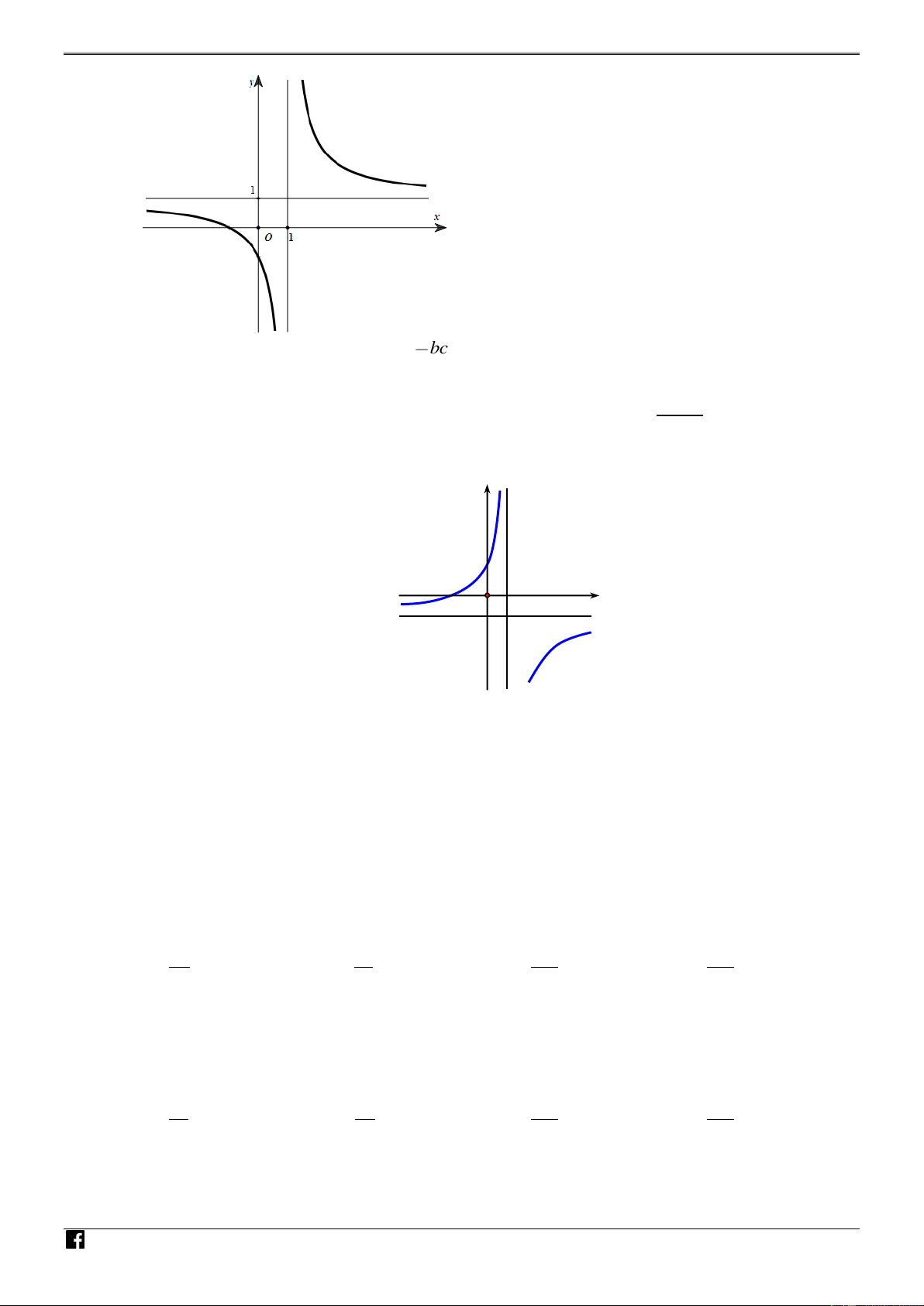
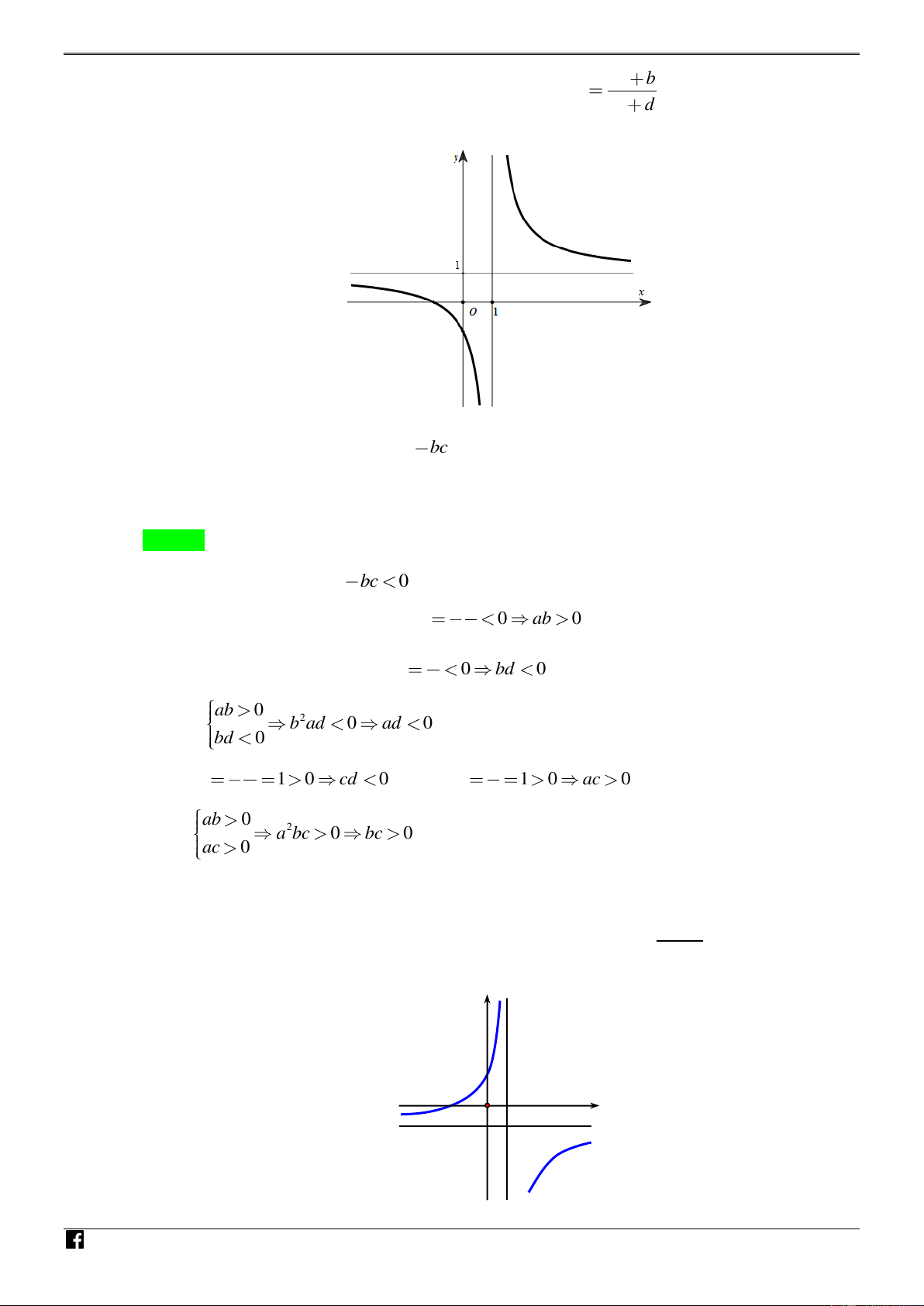
Câu 16. [PHÁT TRIẾN CÂU 45 – MÃ 101 – TN 2020] Cho hàm số ax b y VD cx có đồ thị như d hình vẽ dưới – y V D C O x
https://www.facebook.com/groups/toanvd.vdc Trang 35
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
Hỏi có bao nhiêu số dương trong các số a ; b b ;
c ad; ad bc ? A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn C.
HS đồng biến nên ad bc 0 . NHÓ b
Giao với trục hoành Ox tại x 0 ab 0 . a M TO TCĐ : d a x 0 cd 0 và TCN : y 0 ac 0 . ÁN c c VD cd 0 Ta có 2 c ad 0 ad 0 . – ac 0 V D C ab 0 Và có 2 a bc 0 bc 0 ac 0
Vậy có 3 số dương . CÂU 46 – MÃ 101
CHỦ ĐỀ : BÀI TOÁN XÁC SUẤT CHỌN SỐ TN THOẢ MÃN ĐK
Thực hiện :Nhóm các thầy
Nguyễn Khắc Thành – Nguyễn Ngọc Hoá – Nguyễn Thanh Hải.
Câu 46. [ MÃ 101- TN 2020] Gọi S là tập hợp tất cả các số tự nhiên có 4 chữ số đôi một khác nhau và
các chữ số thuộc tập 1, 2,3, 4,5,6,7,8,
9 . Chọn ngẫu nhiên một số thuộc S , xác suất để số đó NHÓ
không có hai chữ số liên tiếp nào cùng chẵn bằng M 25 5 65 55 TO A. . B. . C. . D. . 42 21 126 126 ÁN VD Lời giải – Chọn A V D C Cách 1: Có 4
A cách tạo ra số có 4 chữ số phân biệt từ X 1, 2,3, 4,5,6,7,8, 9 . 9 4 S A 3024. 9 3024.
https://www.facebook.com/groups/toanvd.vdc Trang 36
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
Gọi biến cố A:”chọn ngẫu nhiên một số thuộc S , xác suất để số đó không có hai chữ số liên tiếp nào cùng chẵn”.
Nhận thấy không thể có 3 chữ số chẵn hoặc 4 chữ số chẵn vì lúc đó luôn tồn tại hai chữ số
chẵn nằm cạnh nhau.
Trƣờng hợp 1: Cả 4 chữ số đều lẻ.
Chọn 4 số lẻ từ X và xếp thứ tự có 4 A số. 5
Trƣờng hợp 2: Có 3 chữ số lẻ, 1 chữ số chẵn. NHÓ
Chọn 3 chữ số lẻ, 1 chữ số chẵn từ X và xếp thứ tự có 3 1 C .C .4! số. 5 4 M
Trƣờng hợp 3: Có 2 chữ số chẵn, 2 chữ số lẻ. TO ÁN
Chọn 2 chữ số lẻ, 2 chữ số chẵn từ X có 2 2 C .C cách. 5 4 VD
Xếp thứ tự 2 chữ số lẻ có 2! cách.
Hai chữ số lẻ tạo thành 3 khoảng trống, xếp hai chữ số chẵn vào 3 khoảng trống và sắp thứ tự – V có 3! cách. D C
trường hợp này có 2 2 C .C .2!.3! số. 5 4 A A C .C .4! C .C .2!.3! 25 Vậy P A 4 3 1 2 2 5 5 4 5 4 . 3024 42 Cách 2:
Số phần tử của không gian mẫu là n 4 A 3024 . 9
Gọi A : “Lấy được số không có hai chữ số liên tiếp nào cùng chẵn”
A : “Lấy được số có hai chữ số chẵn liên tiếp”
Ta có các trường hợp sau: NHÓ
TH1: Có đúng hai chữ số liên tiếp cùng chẵn. M TO
- Chọn 2 chữ số chẵn và sắp xếp có 2 A cách 4 ÁN VD
- Xếp 2 chữ số chẵn trên vào 2 trong 4 vị trí có 3 cách – V
- Chọn 2 chữ số lẻ và xếp vào 2 vị trí còn lại có 2 A cách 5 D C
Trường hợp này có: 2 2
A .3.A 720 số 4 5
TH2: Có 3 chữ số chẵn trong đó có ít nhất 2 chữ số chẵn liên tiếp
- Chọn 3 chữ số chẵn và sắp xếp có 3 A cách 4
- Chọn một chữ số lẻ có 5 cách
https://www.facebook.com/groups/toanvd.vdc Trang 37
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
- Xếp chữ số lẻ này vào một trong 4 vị trí đầu, giữa, cuối trong dãy 3 chữ số chẵn có 4 cách. Trường hợp này có 3 A .5.4 480 4
TH3: Có 4 chữ số chẵn. Trường hợp này có 4! 24 cách
n A 720 480 24 1224
P A P A 1224 25 1 1 . 3024 42 NHÓ PHÂN TÍCH M
Đây là bài toán xác suất liên quan đến các số tự nhiên. TO
Bài toán hỏi về tính chất một số tự nhiên có 4 chữ số khác nhau trong đó không có hai chữ số ÁN
liên tiếp nào cùng chẵn.
Ta có hai cách giải quyết trực tiếp và gián tiếp thông qua biến cố đối. Cách giải quyết nào cũng VD
cần sự phân tích xem có những trường hợp thuận lợi nào để xảy ra biến cố và sử dụng các kiến –
thức về hai quy tắc đếm cũng như các khái niệm hoán vị, chỉnh hợp, tổ hợp. V D C
Ta có thể phát triển bài toán theo một số hướng sau đây:
Hƣớng 1: Thay vì hỏi về số chẵn ta hỏi số lẻ. Hƣ
ớng 2: Tăng số lượng các chữ số liên tiếp cùng chẵn. Hƣ
ớng 3: Hỏi sang biến cố đối. Hƣ
ớng 4: Thay đối tượng các chữ số chẵn và lẻ thành đối tượng là các bạn nam và nữ. Hƣ
ớng 5: Thay đổi sang một tính chất tương tự khác của các số tự nhiên.
Câu 17. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020] Một tổ có 4 bạn nam và 5 bạn nữ.
Cần chọn ra 4 bạn để xếp thành một hàng dài tham gia diễu hành. Tính xác suất để trong hàng
không có 3 bạn nữ nào đứng liên tiếp nhau. 41 49 85 89 A. . B. . C. . D. . 54 54 108 108 NHÓ
Thực hiện : Thầy Nguyễn Ngọc Hoá –Phản biện: Thầy Nguyễn Thanh Hải M Lời giải TO ÁN Chọn B VD
Số phần tử của không gian mẫu là n 4 A 3024 . 9 – V
Gọi A : “Trong hàng không có 3 bạn nữ nào đứng liên tiếp nhau” D C
A : “Trong hàng có ít nhất 3 bạn nữ đứng liên tiếp nhau”
Ta có các trường hợp sau:
TH1: Có 3 bạn nữ liên tiếp nhau
- Chọn 3 bạn nữ và sắp xếp có 3 A cách. 5
https://www.facebook.com/groups/toanvd.vdc Trang 38
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
- Chọn 1 bạn nam có 4 cách
- Xếp bạn nam vào hàng có 2 cách. TH này có 3 A .4.2 160 . 5
TH2: Có 4 bạn nữ liên tiếp nhau. TH này có 4 A 120 cách 5
n A 160120 280 NHÓ
P A P A 280 49 1 1 . M 3024 54 TO ÁN
Câu 18. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020]Gọi S là tập hợp tất cả các số tự VD
nhiên có 4 chữ số đôi một khác nhau và các chữ số thuộc tập 2,3, 4,5,6,7,8, 9 . Chọn ngẫu –
nhiên một số thuộc S , xác suất để số đó không có hai chữ số liên tiếp nào cùng chia hết cho 3 V D bằng C 9 19 5 16 A. . B. . C. . D. . 14 28 7 21
Thực hiện : Thầy Nguyễn Ngọc Hoá –Phản biện: Thầy Nguyễn Thanh Hải Lời giải Chọn C
Số phần tử của không gian mẫu bằng 4 A 1680 . 8
Gọi A: “chọn được số không có hai chữ số liên tiếp nào cùng chia hết cho 3”.
A : “Chọn được số có ít nhất hai chữ số liên tiếp cùng chia hết cho 3” NHÓ
Ta có các trường hợp sau: M TO
TH1: Có hai chữ số liên tiếp chia hết cho 3 ÁN VD
- Chọn 2 chữ số chia hết cho 3 và sắp xếp có 2 A cách 3 –
- Xếp 2 chữ số này vào 2 vị trí liên tiếp trong 4 vị trí có 3 cách V D C
- Chọn 2 chữ số trong 5 chữ số không chia hết cho 3 và xếp vào 2 vị trí còn lại có 2 A cách 5 TH này có: 2 2
A .3.A 360 số. 3 5
TH2: Có 3 chữ số trong đó ít nhất 2 chữ số liên tiếp chia hết cho 3
- Chọn 3 chữ số cùng chia hết cho 3 và sắp xếp có 3! cách
https://www.facebook.com/groups/toanvd.vdc Trang 39
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
- Chọn 1 chữ số không chia hết cho 3 có 5 cách
- Điền chữ số này vào 1 trong 4 vị trí đầu, giữa, cuối 3 chữ số trên có 4 cách
TH này có 3!.5.4 120 .
n A 360120 480 P A P A 480 5 1 1 . 1680 7
Câu 19. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020] Xếp ngẫu nhiên 10 học sinh gồm 2
học sinh lớp 11A và 3 học sinh lớp 11B và 5 học sinh của lớp 11C thành một hàng ngang. Tính NHÓ
xác suất để không có học sinh nào của cùng một lớp đứng cạnh nhau. 3 11 1 2 M A. . B. . C. . D. . TO 126 630 126 63 ÁN
Thực hiện : Thầy Nguyễn Thanh Hải – Phản biện: Thầy Nguyễn Khắc Thành VD Lời giải – V D Chọn B C
Số phần tử của không gian mẫu là n 10!
Gọi A là biến cố thỏa yêu cầu bài toán.
- Xếp 5 học sinh lớp 11C vào hàng có 5! cách
(Sau khi xếp sẽ có 6 vị trí trống (4 giữa và 2 ở hai đầu), chẳng hạn 1C2C3C4C5C6
- Nếu xếp xen kẽ 5 học sinh lớp A và B từ phía tận cùng bên trái (12345) có 5! cách xếp, tương
tự xếp từ phía bên phải (23456) cũng sẽ có 5! Cách xếp
- Nếu xếp 5 học lớp A và B vào các vị trí 2345 trong đó có 1 vị trí xếp 2 học sinh có 3 A .2!.2.3 4 cách NHÓ
Suy ra n A 5!. 2
2.5! A .2!.2.3 63360 3 M
Vậy P A 63360 11 . TO 10! 630 ÁN
Câu 20. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020] Gọi E là tập các số tự nhiên có 5 VD
chữ số được lập từ các chữ số 0;1;2;3;4;5. Chọn ngẫu nhiên một số thuộc tập E . Tính xác suất –
để số được chọn là số chẵn, có đúng hai chữ số 0 và không đứng cạnh nhau, các chữ số còn lại có V D
mặt không quá một lần. C 2 2 1 4 A. . B. . C. . D. . 15 45 45 15
Thực hiện : Thầy Nguyễn Thanh Hải – Phản biện: Thầy Nguyễn Khắc Thành Lời giải Chọn C
https://www.facebook.com/groups/toanvd.vdc Trang 40
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
Ta có: A 0;1;2;3;4;
5 a a ...a ( a chẵn; đúng 2 chữ số 0, không cạnh nhau). 1 2 5 5 TH1: a 0 5
+ Chọn vị trí xếp số 0 còn lại có 2 cách (loại a , a ). 1 4
+ Còn 3 vị trí xếp bởi 5 chữ số có 3 A cách. 5 Trường hợp này có 3 2.A số. 5 NHÓ
TH2: a 0 suy ra a có 2 cách chọn 5 5 M
+ Chọn ra 2 vị trí không cạnh nhau từ a a a để xếp số 0 có 1 cách (vào a và a ). 2 3 4 2 4 TO ÁN
+ Còn 4 chữ số xếp vào 2 vị trí có 2 A cách. 4 VD Trường hợp này có: 2 2.A số. 4 – V 3 2 D 2.A 2.A 144 1 5 4 C
Do đó xác suất cần tìm là: P . 4 5.6 6480 45
Câu 21. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020] Cho tập E 1,2,3,4, 5 .
Viết ngẫu nhiên lên bảng hai số tự nhiên, mỗi số gồm 3 chữ số đôi một khác nhau thuộc tập E.
Tính xác suất để trong hai số đó có đúng một số có chữ số 1 . 12 13 144 151 A. . B. . C. . D. . 25 25 295 295
Thực hiện : Thầy Nguyễn Khắc Thành–Phản biện: Thầy Nguyễn Ngọc Hoá Lời giải NHÓ Chọn C M TO
Từ tập E 1,2,3,4, 5 có thể lập được 3
A 60 số tự nhiên gồm ba chữ số đôi một khác nhau. 5 ÁN Trong 60 số đó có: 3
A 24 số không có mặt chữ số 1 và có 60 24 36 số có mặt chữ số 1. 4 VD –
Gọi A là tập các số không có mặt chữ số 1 n A 3 A 24 4 V D C
Gọi B là tập các số luôn có mặt chữ số 1 nB 60 24 36
Để trong hai số được viết lên bảng có đúng một số có mặt chữ số 1 thì ta lấy 1 số thuộc tập A và lấy
một số thuộc tập B để viết lên bảng.
https://www.facebook.com/groups/toanvd.vdc Trang 41
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 1 1 C .C 144
Vậy xác suất cần tính là: 24 36 p . 2 C 295 60
Câu 22. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020] Cho hai hộp đựng bi: hộp A đựng 7
viên bi xanh, 7 viên bi đỏ; hộp B đựng 5 viên bi xanh, 9 viên bi đỏ. Bốc ngẫu nhiên 3 viên bi
trong hộp A bỏ vào hộp B, sau đó bốc ngẫu nhiên 3 viên bi trong hộp B bỏ lại hộp A. Tính xác
suất để sau khi đổi bi xong số bi xanh trong hai hộp bằng nhau. 567 343 49 49 A. . B. . C. . D. . 1768 352 96 264 NHÓ
Thực hiện : Thầy Nguyễn Khắc Thành–Phản biện: Thầy Nguyễn Ngọc Hoá M TO Lời giải ÁN Chọn A VD – Không gian mẫu: n 3 3 C C V 14 17 D C
Trƣờng hợp 1: Lần thứ nhất lấy được cả 3 viên bi xanh, sau đó trả lại phải bốc 2 viên bi xanh
và 1 viên bi đỏ, số cách bốc là: 3 0 2 1
C .C .C .C 7 7 8 9
Trƣờng hợp 2: Lần thứ nhất lấy được cả 2 viên bi xanh và 1 viên bi đỏ, sau đó trả lại phải bốc
1 viên bi xanh và 2 viên bi đỏ, số cách bốc là: 2 1 1 2
C .C .C .C 7 7 7 10
Trƣờng hợp 3: Lần thứ nhất lấy được cả 1 viên bi xanh và 2 viên bi đỏ, sau đó trả lại 3 viên bi đỏ, số cách bốc là: 1 2 0 3
C .C .C .C 7 7 6 11
Gọi X là biến cố sau khi đổi bi xong số bi xanh trong hai hộp bằng nhau NHÓ n A 3 0 2 1 2 1 1 2 1 2 0 3
C .C .C .C C .C .C .C C .C .C .C 7 7 8 9 7 7 7 10 7 7 6 11 M TO
Vậy xác suất cần tính là ÁN VD 3 0 2 1 2 1 1 2 1 2 0 3 n X
C .C .C .C C .C .C .C C .C .C .C 8820 46305 24255 567 p X 7 7 8 9 7 7 7 10 7 7 6 11 . – n 3 3 3 3 C C C C 1768 14 17 14 17 V D C
Câu 23. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020] Viết lên bảng năm số tự nhiên có hai chữ số
khác nhau theo thứ tự tăng dần được tạo thành từ các chữ số 0,1, 2,3, 4,5,6,7,8,9 và mỗi chữ số
chỉ xuất hiện 1 lần. Xác suất để 5 số đều chia hết cho 3 là 1 1 2 2 A. . B. . C. . D. . 21 35 105 189
Thực hiện Cô Đoàn Thị Lan Oanh – Phản Biện Thầy Nguyễn Khắc Thành
https://www.facebook.com/groups/toanvd.vdc Trang 42
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 Lời giải Chọn C Không gian mẫu:
5 chữ số đứng đầu của 5 số có hai chữ số có 5
C cách chọn (chọn 5 chữ số trong 9 chữ số khác 9 0).
5 chữ số còn lại thay phiên đứng cùng 5 chữ số đứng đầu vừa chọn, có 5! cách.
Mỗi cách chọn 5 số cho duy nhất một cách viết theo thứ tự tăng dần, nên số phần tử của không NHÓ
gian mẫu là n 5 5!.C 15120 . 9 M TO
Đếm số phần tử của biến cố A “5 số đó đều chia hết cho 3”. ÁN
Một số có hai chữ số mà chia hết cho 3 thì có 2 trường hợp: cả hai chữ số đều chia hết cho 3 VD
hoặc một chữ số chia 3 dư 1, 1 chữ số chia 3 dư 2. –
Ta chia 10 chữ số thành 3 nhóm như sau: V D C
Nhóm 1 (chia hết cho 3): 0;3;6;9 .
Nhóm 2 (chia 3 dư 1): 1;4;7 .
Nhóm 3 (chia 3 dư 2): 2;5;8 .
Xét nhóm 1: Ta cần chọn ra 2 số dạng a0;bc . Các chữ số a, ,
b c là hoán vị của 3 chữ số 3;6;9 ,
do đó có 3! 6 số được lập.
Xét nhóm 2 và 3: Để lập được số có hai chữ số chia hết cho 3, ta cần chọn 1 chữ số trong nhóm
2 và 1 chữ số trong nhóm 3. Ta xét các cặp số 1,d ,4,e,7, f với d, ,
e f được chọn từ
nhóm 3. Số cách chọn d, ,
e f là 3! 6 , do đó có 6 cách chọn 3 cặp số 1, d ,4, e,7, f . Mỗi NHÓ
cặp số sẽ tạo thành 2 số có hai chữ số khác nhau chia hết cho 3, nên có 6.2.2.2 48 cách chọn
3 số có hai chữ số từ nhóm 2 và 3. M TO
Vậy số phần tử của biến cố A là n A 6.48 228 . ÁN n A 288 2 VD
Xác suất của biến cố A là P . A n 15120 105 – V D C
https://www.facebook.com/groups/toanvd.vdc Trang 43
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 CÂU 47 – MÃ 101
CHỦ ĐỀ : THỂ TÍCH KHỐI ĐA DIỆN
Thực hiện :Nhóm các Thầy Cô giáo
Ngô Dung – Thoa Nguyễn – Ngô Tú Hoa – Nguyễn Thị Hồng Gấm – Nguyễn Hùng. I. BÀI TOÁN GỐC:
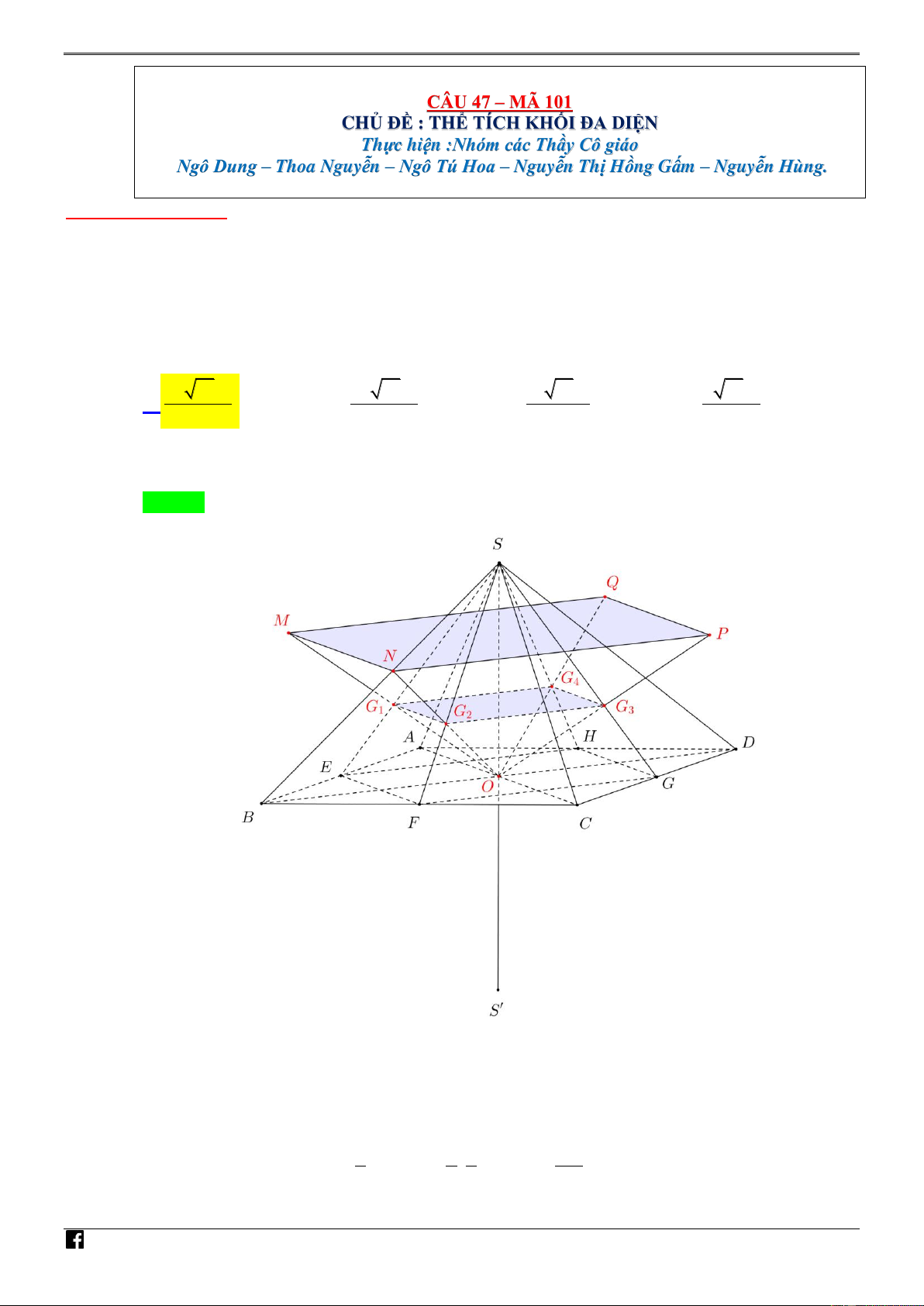
Câu 47. [ ĐỀ GỐC MÃ 101 – TN 2020] Cho hình chóp đều S.ABCD có cạnh đáy bằng a , cạnh bên
bằng 2a và O là tâm của đáy. Gọi M , N , P , Q lần lượt là các điểm đối xứng với O qua
trọng tâm của các tam giác SAB , SBC , SCD , SDA và S ' là điểm đối xứng với S qua O . NHÓ
Thể tích của khối chóp S '.MNPQ bằng M TO 3 20 14a 3 40 14a 3 10 14a 3 2 14a A. . B. . C. . D. . ÁN 81 81 81 9 VD Lời giải – V Chọn A. D C NHÓ M TO ÁN VD – V D C
Gọi G ,G ,G ,G lần lượt là trọng tâm S A , B S BC, S C , D S DA. 1 2 3 4 E, F, ,
G H lần lượt là trung điểm của các cạnh A , B BC,C , D DA . 2 Ta có 4 4 1 8a S 4S 4. S 4. . E . G HF . MNPQ 1 G 2 G 3 G 4 G 9 EFGH 9 2 9
https://www.facebook.com/groups/toanvd.vdc Trang 44
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
d S ,MNPQ d S , ABCD d O,MNPQ
d S, ABCD 2d O,G G G G 1 2 3 4
d S ABCD 2 ,
d S, ABCD 3 5
d S ABCD 5a 14 , 3 6 2 3 1 5a 14 8a 20a 14 Vậy V . S . MNPQ 3 6 9 81 NHÓ
II. PHÂN TÍCH Ý TƢỞNG : M TO ÁN VD Ngô Dung –
Ta đã biết : Bài toán thể tích khối đa diện chương trình HÌNH HỌC KHÔNG GIAN của THPT V D
thường đưa về tính thể tích các khối quen biết có công thức tính : Đó là khối lăng trụ và khối C
chóp. Thì hai khối quen biết này để tính được cần 2 yếu tố : ĐƯỜNG CAO VÀ DIỆN TÍCH
ĐÁY. Cả 2 yếu tố này trong câu 47 – Mã 101 đều đưa về : cách tìm tỷ số đoạn thẳng qua phép
biến hình . Và bài toán được thực hiện qua khối chóp tứ giác đều đã cho cạnh đáy và cạnh bên.
Chính vì vậy các tỷ lệ trong bài toán dễ dàng thực hiện vì tính đối xứng của khối chóp dạng này.
TỶ SỐ ĐOẠN THẲNG TRONG TÍNH ĐƢỜNG CAO CỦA BÀI TOÁN THỂ TÍCH :
Độ dài đường cao là khoảng cách từ S đến mặt phẳng MNPQ : Được tính nhờ đường cao của
khối chóp đã biết qua tỉ lệ của phép đối xứng tâm.
TỶ SỐ ĐOẠN THẲNG TRONG TÍNH DIỆN TÍCH ĐÁY CỦA BÀI TOÁN THỂ TÍCH :
Đáy MNPQ của chóp cần tìm được tạo từ các điểm M , N, ,
P Q là ảnh của tâm O qua phép đối
xứng tâm mà tâm là trọng tâm các mặt bên. Do tính đều của chóp nên rõ ràng tỷ số các cạnh này
dễ ràng tìm được bằng cách lần lượt sử dụng tính chất trọng tâm và giả thiết ảnh qua phép đối xứng tâm. NHÓ
Như vậy sử dụng phép biến hình ta có thể mở rộng nhiều bài toán tính thể tích khối đa diện
mà thực tế chỉ cần đưa về là BÀI TOÁN THỂ TÍCH CƠ BẢN. M TO
III. CÁC VÍ DỤ PHÁT TRIỂN . ÁN PHÁT TRIỂN 1: VD
Theo ý tƣởng đỉnh và đáy là ảnh qua phép đối xứng qua mặt phẳng. – V D
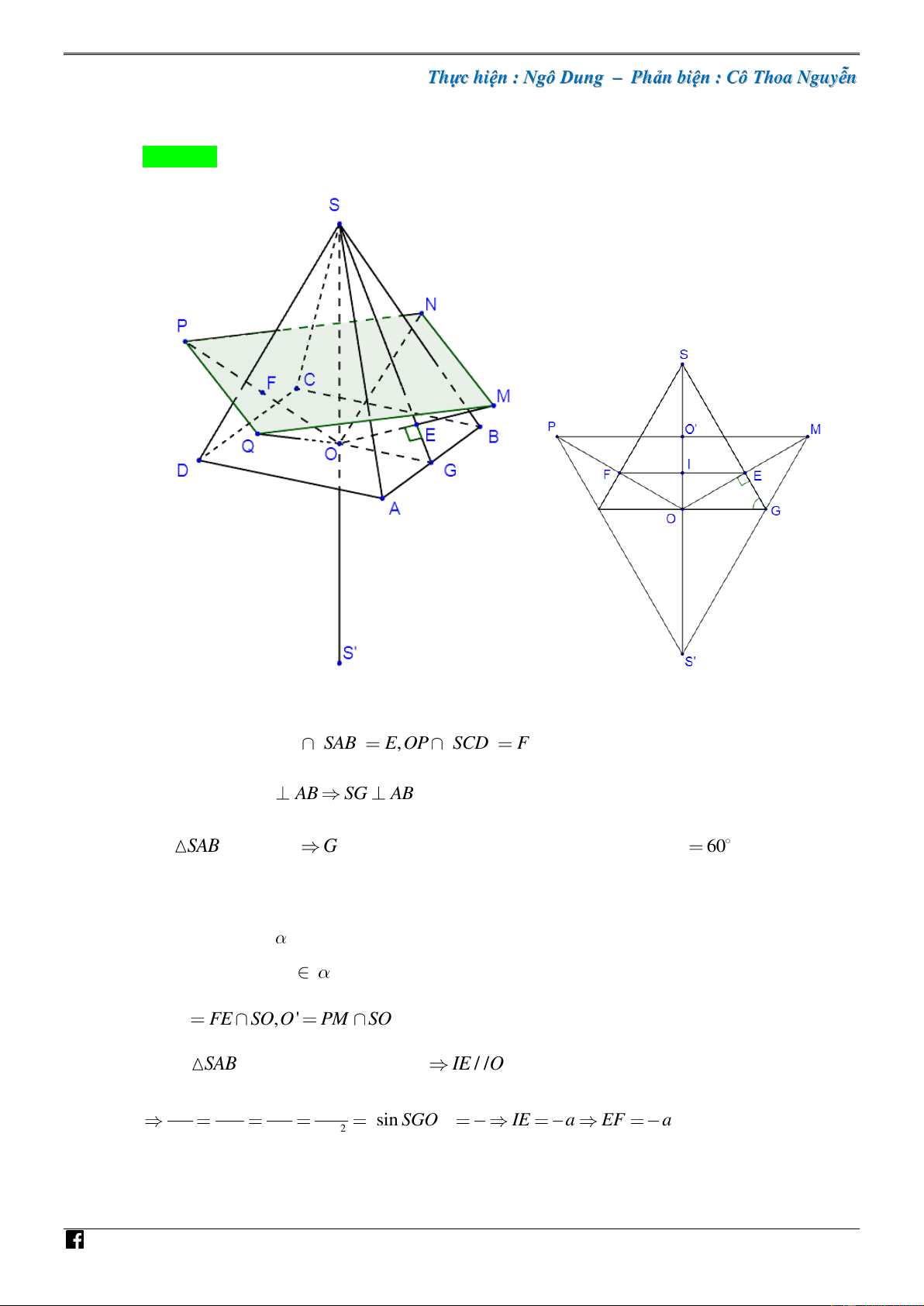
Câu 24. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020] Cho hình chóp tứ giác đều S.ABCD có đáy C
ABCD là hình vuông cạnh a có tâm là O , mặt bên tạo với đáy một góc 60 . Gọi M , N, , P Q
lần lượt là ảnh của O qua các phép đối xứng qua mặt phẳng SAB , SBC , SCD , SDA . Biết
S là điểm đối xứng với S qua mặt phẳng ABCD . Tính thể tích khối chóp S .MNPQ . 9 3 9 3 27 3 27 3 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 16 32 32 16
https://www.facebook.com/groups/toanvd.vdc Trang 45
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
Thực hiện : Ngô Dung – Phản biện : Cô Thoa Nguyễn Lời giải Chọn B . NHÓ M TO ÁN VD – V D C
Ta lấy các điểm OM SAB E, OP SCD
F và kéo dài SE cắt AB tại G Khi đó do SOE AB SG AB NHÓ
Mà SAB cân tại S
G là trung điểm AB và đồng thời cũng có SGO 60 M * Tính S : TO MNPQ ÁN - Xét mặt phẳng
đi qua trục SS ' chứa các điểm G và trung điểm của đoạn DC , khi đó VD
các điểm E, F, M , P – V D Gọi I FE S , O O ' PM SO . C
Ta có SAB cân tại S nên FE / /OG IE / /OG 2 2 SI IE SE SO 3 3 3 sin SGO IE a EF a 2 SO OG SG SG 4 8 4
https://www.facebook.com/groups/toanvd.vdc Trang 46
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 Do ,
P M là ảnh của O qua phép đối xứng qua mặt SAB , SCD hay ,
P M là ảnh của O qua OE EM phép đố 3
i xứng qua tâm E, F
FE / /PM , PM 2EF a OF FN 2 Hay có 3 PM / / A , D PM a 2 Cũng tương tự 3
vậy ta sẽ chứng minh được NQ / / AB, NQ a 2 NHÓ Khi đó 1 9 2 S M . P NQ a MNPQ M 2 8 TO
* Tính đường cao hình chóp S .MNPQ ÁN VD S O M , P S O NQ
S O chính là đường cao cần tìm, – V 1 3 3 3 D S O S O OO SO 2.OI SO 2. SO SO a C 4 2 4 9 3
* Tính thể tích khối chóp 3
S .MNPQ :V a S .MNPQ 32 PHÁT TRIỂN 2:
Theo ý tƣởng đáy là ảnh qua phép đối xứng trục.
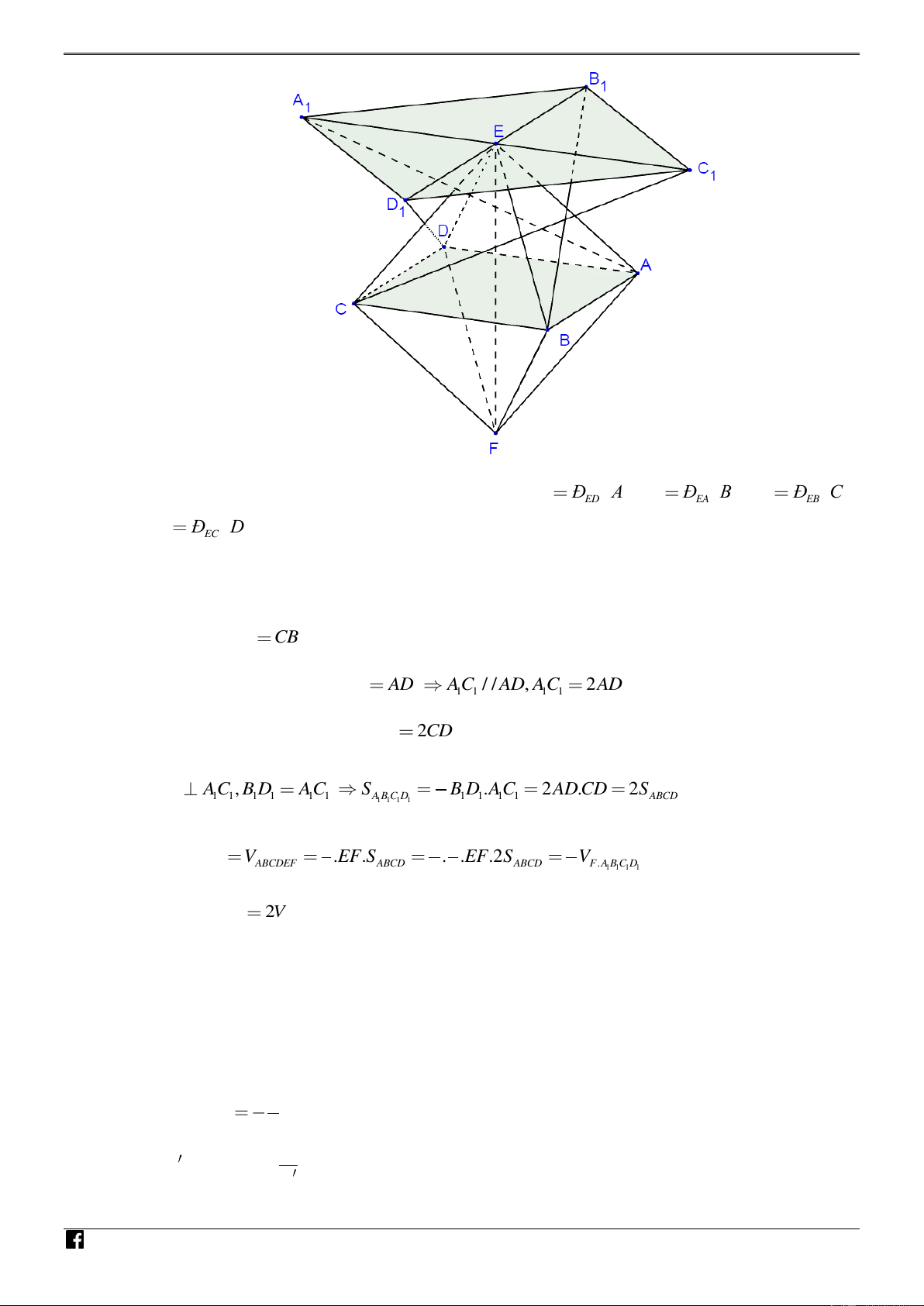
Câu 25. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020] Cho khối bát diện đều ABCDEF có thể tích
V . Gọi O là tâm của hình vuông ABCD . Lấy A đối xứng với A qua ED , B đối xứng với 1 1
B qua EA ; C đối xứng với C qua EB và D đối xứng với D qua EC . Tính theo V thể tích 1 1
khối chóp F.A B C D . 1 1 1 1 NHÓ 3V 4V A. V . B. . C. 2V . D. . M 2 3 TO
Thực hiện : Ngô Dung – Phản biện : Cô Thoa Nguyễn ÁN VD Lời giải – Chọn C. V D C
https://www.facebook.com/groups/toanvd.vdc Trang 47
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 NHÓ M TO ÁN VD – Ta có các tam giác đề V
u ABE, BCE,CDE, DAE nên A Đ A , B Đ B , C Đ C 1 ED 1 EA 1 EB D C , D Đ D 1 EC
Có tam giác EBC là tam giác đều nên phép đối xứng qua trục EB biến C thành C sẽ là 1
phép đối xứng tâm với tâm đối xứng là trung điểm EB , do đó CBC E là hình bình hành. Hay 1 EC / /C , B EC CB . 1 1
Tương tự ta có EA / / A , D EA AD A C / / A , D A C 2AD . 1 1 1 1 1 1
Tương tự ta được B D / /C , D B D 2CD . 1 1 1 1 1 B D A C , B D A C S B D .A C 2A . D CD 2S 1 1 1 1 1 1 1 1 A B C D 1 1 1 1 ABCD 1 1 1 1 2 NHÓ 1 1 1 1 Lại có : V V .EF.S . .EF.2S V ABCDEF ABCD ABCD F . A B C D 1 1 1 1 M 3 2 3 2 TO Nên V 2V . F . 1 A 1 B 1 C 1 D ÁN VD PHÁT TRIỂN 3,4,5 : –
Theo ý tƣởng đỉnh và đáy là ảnh qua phép Vị Tự của một số điểm đặc biệt. V D C
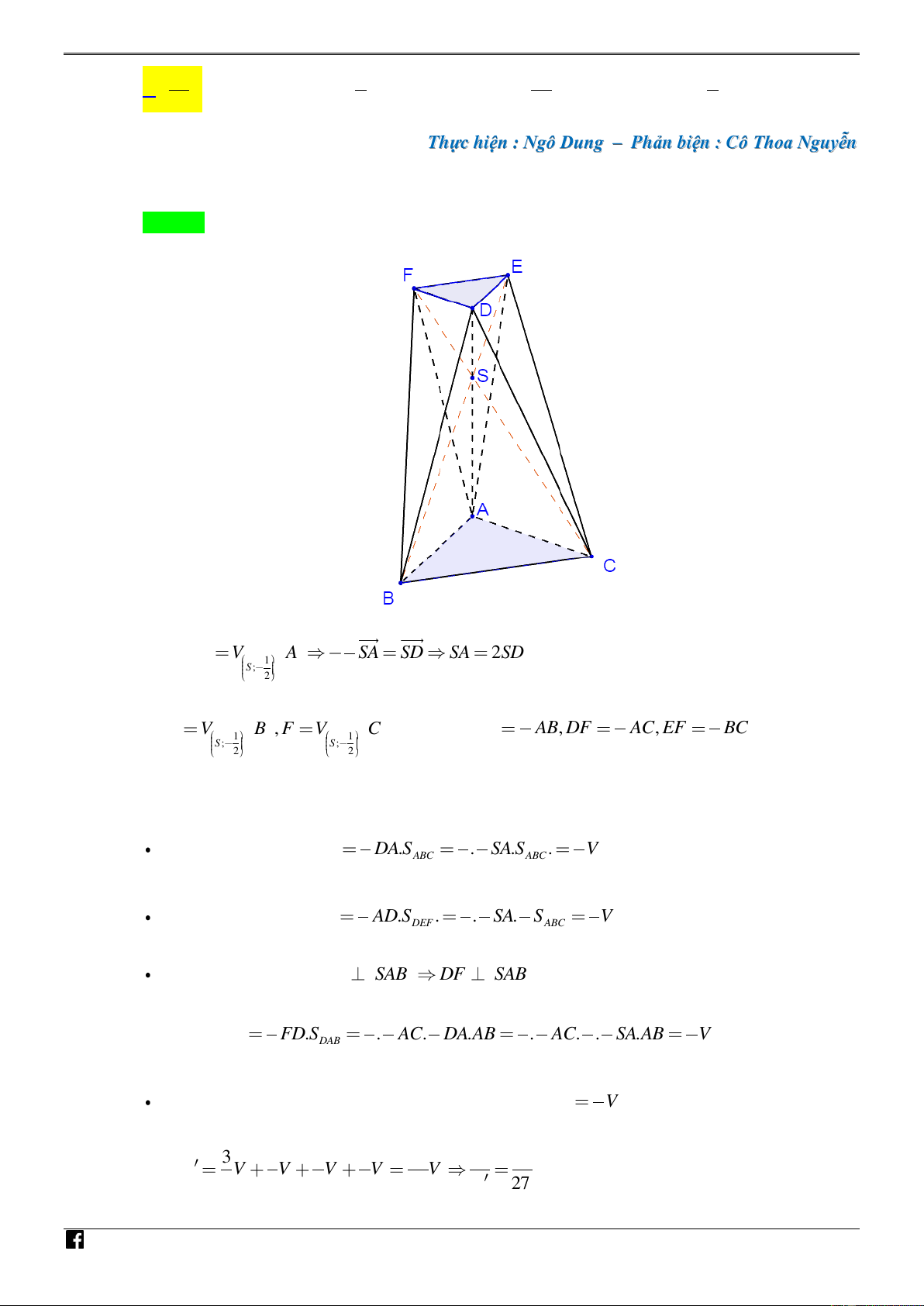
Câu 26. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020] Chóp S.ABC có SA vuông góc với đáy và
đáy là tam giác ABC vuông tại A . Gọi ,
D E, F lần lượt là ảnh của , A ,
B C qua phép vị tự 1
tâm S tỉ số k
. Biết thể tích khối S.ABCD bằng V và thể tích khối đa diện DEFABC 2 V
bằng V . Tính tỉ số . V
https://www.facebook.com/groups/toanvd.vdc Trang 48
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 8 2 13 4 A. . B. . C. . D. . 27 3 27 9
Thực hiện : Ngô Dung – Phản biện : Cô Thoa Nguyễn Lời giải Chọn A NHÓ M TO ÁN VD – V D C 1 Ta có: D V A SA SD SA 2SD 1 S ; 2 2 Và E V B , F V C nên ta có 1 1 1 DF A , B DF AC, EF BC 1 1 S ; S ; 2 2 2 2 2
Khối DEF.ABC được chia thành 4 khối: . D ABC, .
A DEF, F.DAB và . E DAC . NHÓ 1 1 3 3 Thể tích . D ABC :V D . A S . S . A S . V D.ABC 3 ABC 3 2 ABC 2 M TO 1 1 3 1 3 Thể tích . A DEF :V A . D S . . S . A S V ÁN . A DEF 3 DEF 3 2 4 ABC 8 VD
Thể tích F.DAB :Do AC SAB DF SAB – V D 1 1 1 1 1 1 1 3 3 C Khi đó V F . D S . A . C D . A AB . A . C . S . A AB V F .DAB DAB 3 3 2 2 3 2 2 2 4 3 Thể tích .
D ABC tương tự tính thể tích F.DAB : V V E.DAC 4 3 3 3 3 27 V 8 Vậy V V V V V V . 2 8 4 4 8 V 27
https://www.facebook.com/groups/toanvd.vdc Trang 49
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
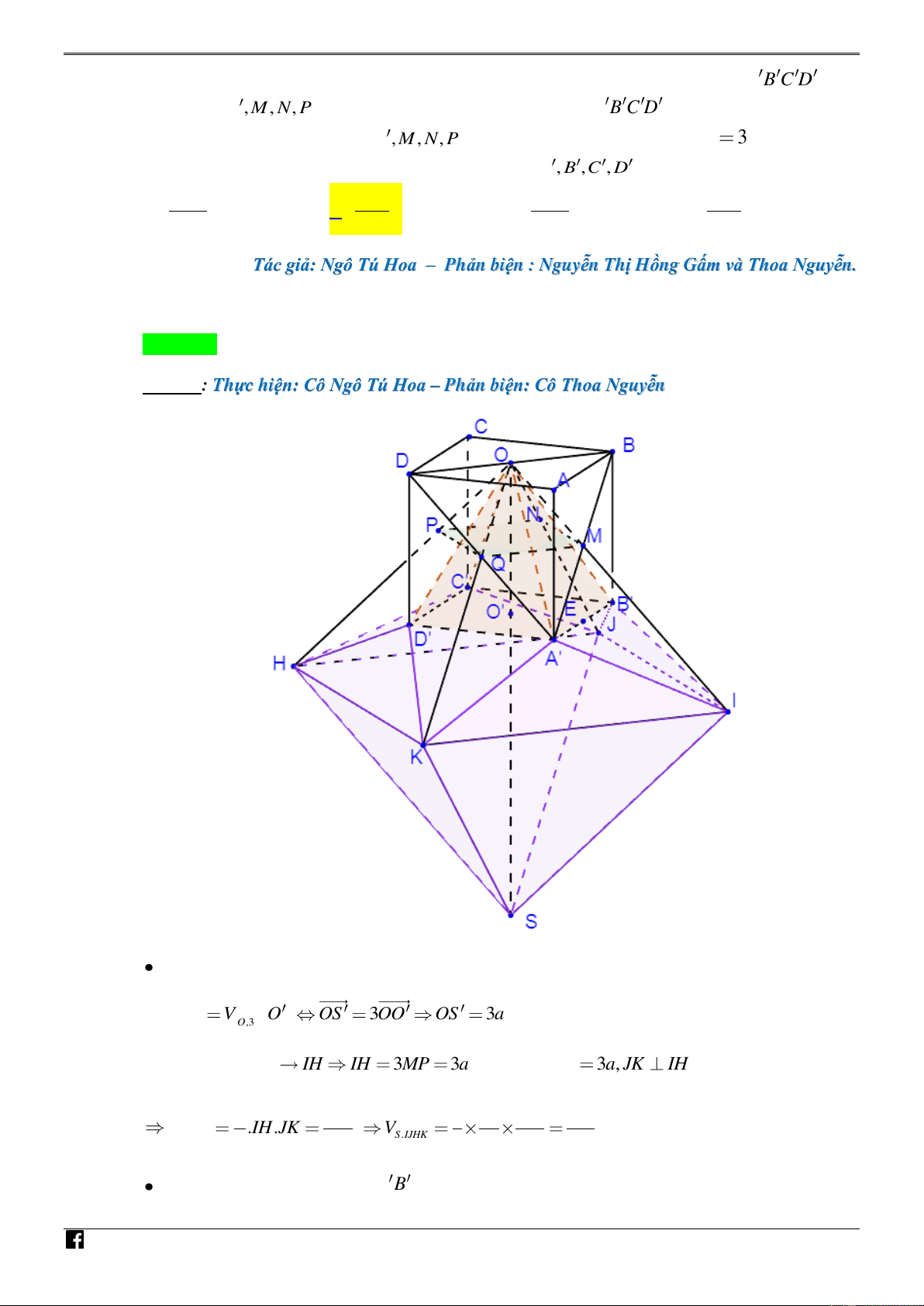
Câu 27. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020] Cho hình lập phương ABC .
D A B C D cạnh a . Gọi ,
O O , M , N, ,
P Q lần lượt là tâm của đáy ABCD , A B C D và của bốn mặt bên. Gọi
S, I, J , H, K lần lượt là ảnh của k . Tính thể tích
O , M , N, ,
P Q qua phép vị tự tâm O tỉ số 3
V của khối đa diện được tạo bởi các đỉnh S, I, J , H, K, A , B ,C , D . 3 49a 3 11a 3 49a 3 11a A. . B. . C. . D. . 2 3 6 6
Tác giả: Ngô Tú Hoa – Phản biện : Nguyễn Thị Hồng Gấm và Thoa Nguyễ n. Lời giải NHÓ Chọn B . M TO
Cách 1: Thực hiện: Cô Ngô Tú Hoa – Phản biện: Cô Thoa Nguyễn ÁN VD – V D C NHÓ M TO ÁN VD
Tính thể tích khối chóp S.IJHK : – V Ta có D S V O OS 3OO OS 3a O,3 C Và có : V : MP IH IH 3MP
3a , tương tự JK 3 , a JK IH O,3 2 1 9a 2 3 1 3a 9a 9a S .IH.JK V . IJHK 2 2 S .IJHK 3 2 2 4
Tính thể tích khối tứ diện OIA B
https://www.facebook.com/groups/toanvd.vdc Trang 50
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 a a 3a I V M OI 3OM , ta có OM 2 OI O,3 2 2 2 2 5a a 5
Gọi E là trung điểm A B thì 2 2 2 OE OO O E OE . 4 2 1 5 1 2 2 2 OM OE ME 3 2 4 4 9 1 cos MOE sin MOE 1 2OM .OE 1 5 10 10 10 2 2 2 NHÓ 2 1 1 5 3 1 3a 2 S
OE.OM .sin MOE a OEI M 2 2 2 2 10 8 TO 2 3 ÁN Và có 1 1 3a a A B OEI nên V S .A B a OIA B 3 OEI 3 8 8 VD 3 – a V
Tính thể tích khối chóp tứ giác đều . O A B C D : V . O. A B C D D 3 C
Tính thể tích V cần tìm.
Để ý có M ,Q lần lượt là trung điểm A ,
B A D , nên các điểm M , , Q A , ,
B D đều nằm trong
mặt phẳng A BD , tương tự như vậy với các điểm còn lại.
Nên do tính chất đối xứng của hình ta có : V V V V 4V 2V V 4V S.IJHK O.IJHK O.A B C D OIA B S.IJHK O.A B C D OIA B 3 9 1 1 11a 3 V 2 4 a . 4 3 8 3 NHÓ
Cách 2: Cô Nguyễn Thị Hồng Gấm – Phản biện: Cô Thoa Nguyễn M TO ÁN VD – V D C
https://www.facebook.com/groups/toanvd.vdc Trang 51
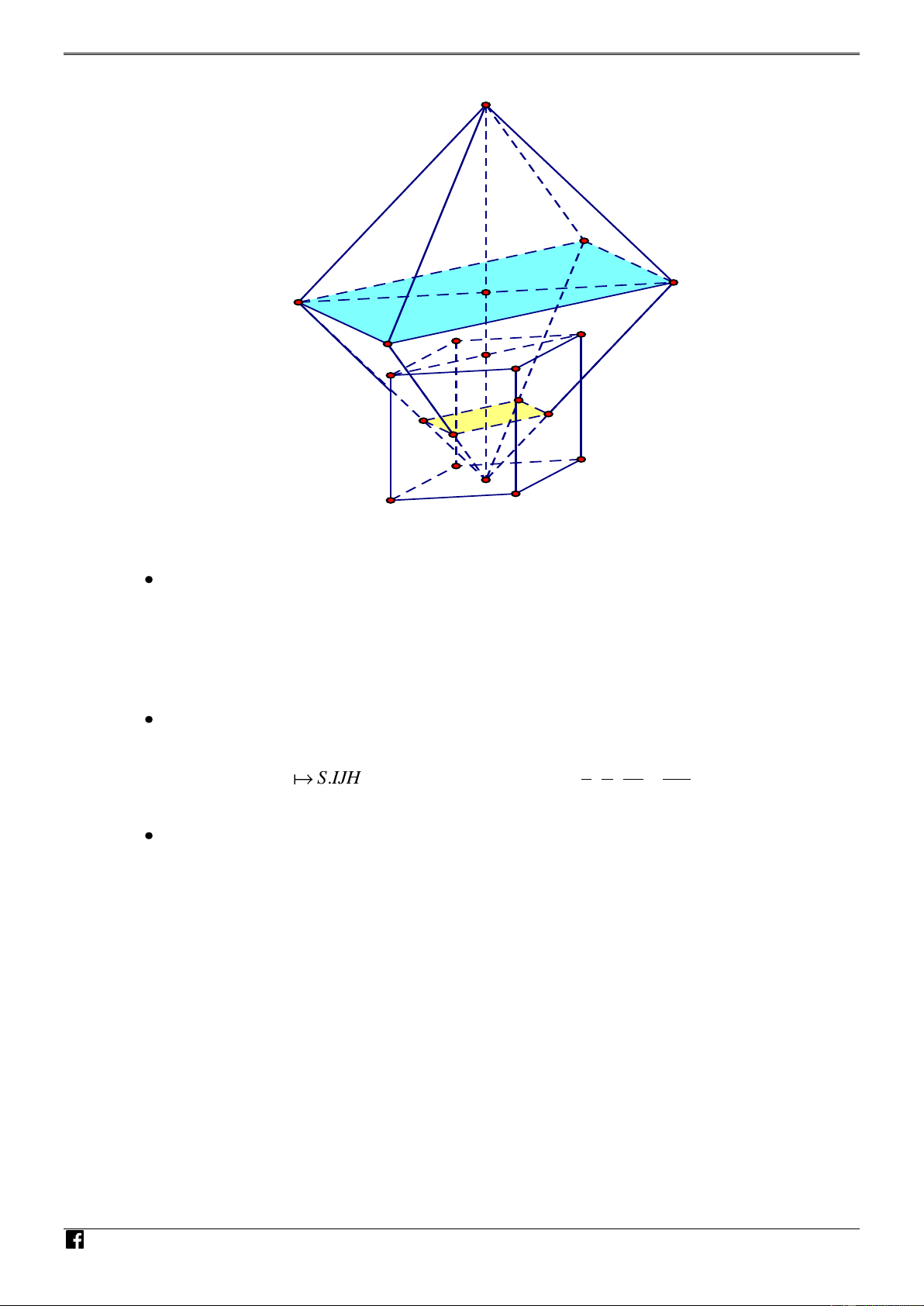
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 S H G K I NHÓ O' J M TO Q ÁN M P VD N C D – O V D A B C
Ta có thể tích cần tìm là V V V 1 2
V : thể tích khối chóp đều S.IJHK 1
V : Khối đa diện tạo bởi A ,
B ,C , D , I, J, H, K . 2 Tính V : 1 2 3 Vì 1 a a 9a V : O .MNPQ
S.IJHK nên V 27 V 27 . O,3 1 O '.MNPQ 3 2 2 4 NHÓ
Tính V : Khối đa diện tạo bởi A ,
B ,C , D , I, J, H, K . 2 M TO ÁN VD – V D C
https://www.facebook.com/groups/toanvd.vdc Trang 52
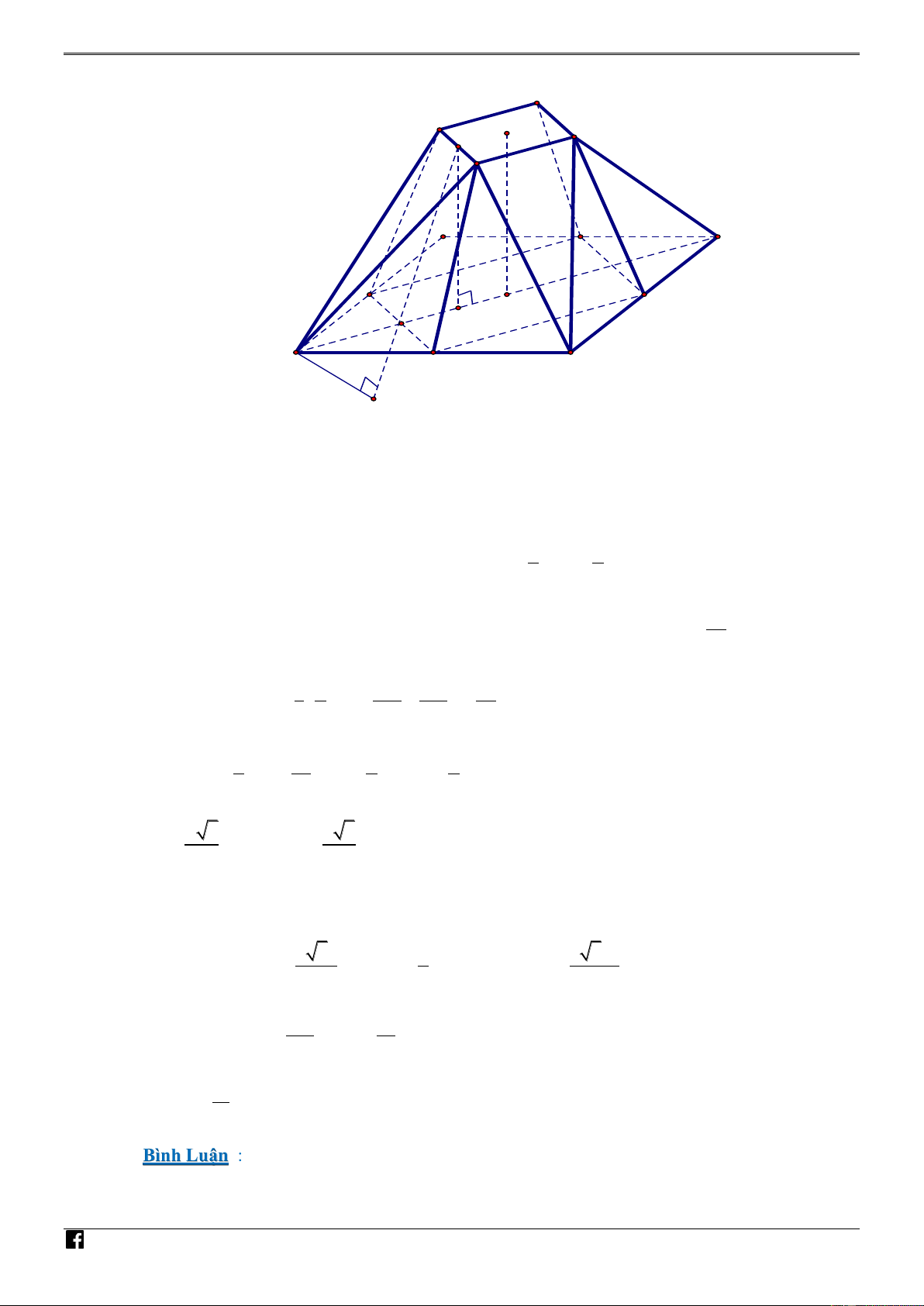
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 D' A' O' C' TB' D1 J K A1 G C1 L NHÓ F H M B I 1 TO E ÁN VD V V 4V . 2 1 A 1 B 1 C 1 D .A B C D H . 1 A 1 B A B – V D
Theo tính chất của phép vị tự ta có IJHK là hình vuông có đường chéo IK 3MP 3a . C 1 a A B C D .A B C D
là chóp cụt có chiều cao O G O O . 1 1 1 1 2 2 3a
( A , B ,C , D là các trung điểm các cạnh của hình vuông I JHK ,có A B ). 1 1 1 1 1 1 2 2 2 1 a 9a 3a 19 Vậy 2 3 V a a . 1 A 1 B 1 C 1 D .A B C D 3 2 4 2 24 1 3a a a HL LG HJ , FG LF . 4 4 2 4 NHÓ a 5 2 5 TL sinTLF . 4 5 M TO
Vì A B HJ, A B O G A B A B
HTL HE A B A B . 1 1 1 1 1 1 1 1 ÁN 2 VD 6 5a 1 5 5a
HE HL sin TLF , S TL A B A B . A B A B 1 1 20 1 1 2 16 – V D 3 5a 17 3 C Do vậy V V a . H . A B A B 2 1 1 32 12 11 Vậy 3 V a . 3 Bình Luận :
Ta có thể mở rộng bài toán tương tự tính :
Tính thể tích V của khối đa diện được tạo bởi các đỉnh S, I, J, H, K, , A , B C, D .
https://www.facebook.com/groups/toanvd.vdc Trang 53
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
Câu 28. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020] Cho hình lập phương ABC . D A B C D
cạnh a . Gọi ,
O O , M , N, ,
P Q lần lượt là tâm của đáy ABC ,
D A B C D và của bốn mặt
bên.Gọi S, I, J, H, K lần lượt là ảnh của O , M , N, ,
P Q qua phép vị tự tâm O tỉ số k 3 . Tính
thể tích khối đa diện được tạo bởi các đỉnh S, I, J, H, K, , A , B C, D . A. . B. . C. .D. .
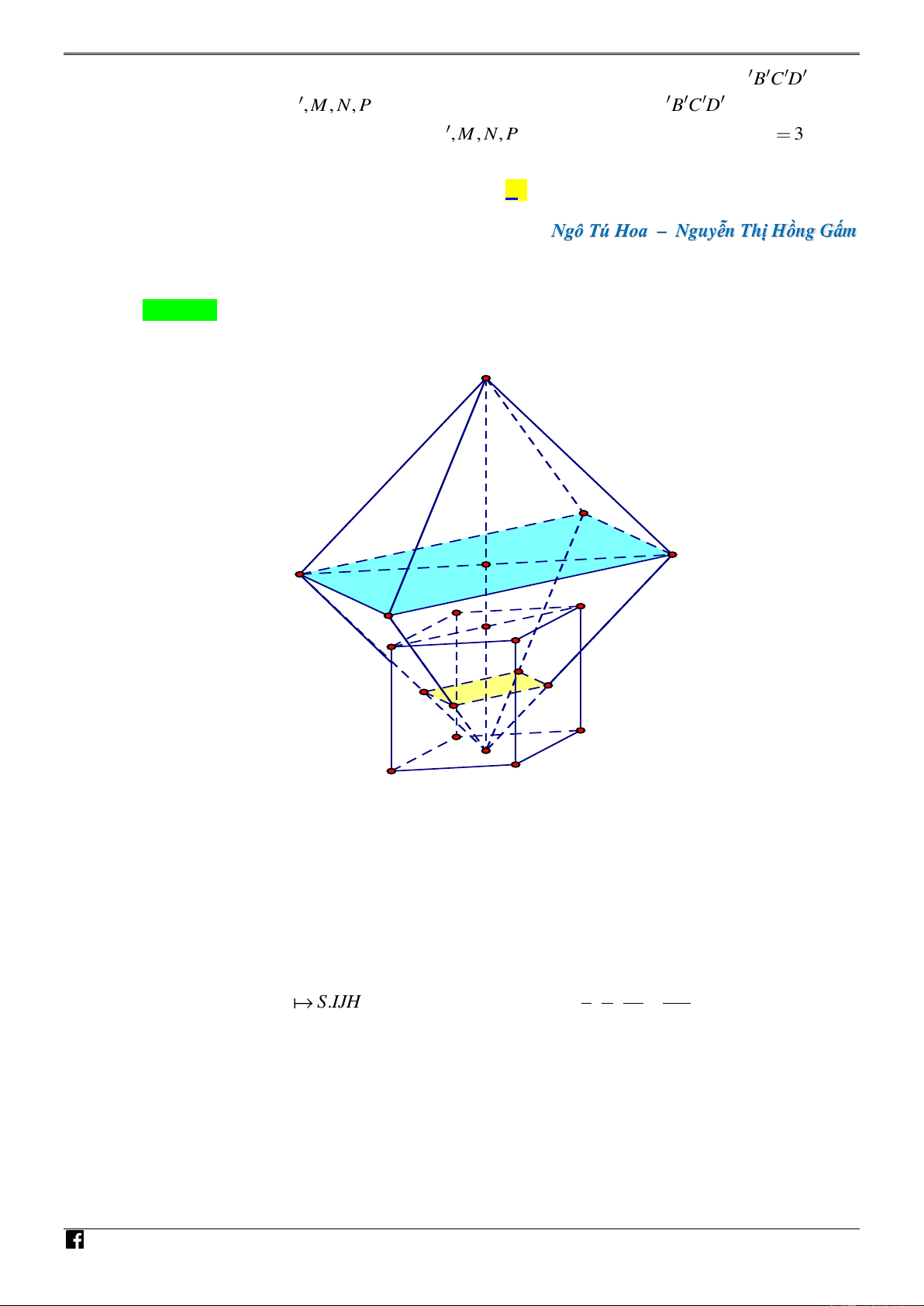
Ngô Tú Hoa – Nguyễn Thị Hồng Gấm Lời giải Chọn B . NHÓ M S TO ÁN VD – V D H C G K I O' J Q M P N C D O A B NHÓ
Ta có thể tích cần tìm là V V V 1 2 M TO
V : thể tích khối chóp đều S.IJHK 1 ÁN
V : Khối đa diện tạo bởi , A , B C, ,
D I, J , H, K . 2 VD 2 3 – 1 a a 9a V Vì V : O .MNPQ
S.IJHK nên V 27 V 27 . O,3 1 O '.MNPQ D 3 2 2 4 C V V 4V . 2 1 A 1 B 1 C 1 D .AB D C H . 1 A 1 B AB
Theo tính chất của phép vị tự ta có IJHK là hình vuông có đường chéo IK 3MP 3a .
https://www.facebook.com/groups/toanvd.vdc Trang 54
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 3 3a A B C D .AB D
C là chóp cụt có chiều cao OG O O
. ( A , B ,C , D là các trung điểm 1 1 1 1 2 2 1 1 1 1 các cạ 3a
nh của hình vuông IJHK , có A B ). 1 1 2 2 2 1 3a 9a 3a 19 Vậy 2 3 V a a . 1 A 1 B 1 C 1 D .A B C D 3 2 4 2 8 1 3a a a HL LG HJ , FG LF . 4 4 2 4 NHÓ D M TO A O C ÁN T VD B – V D C D K 1 J A1 C1 G L F H B1 I E a 37 6 37 TL sinTLF . NHÓ 4 37 M
Vì A B HJ, A B OG A B AB HTL HE A B AB . 1 1 1 1 1 1 1 1 TO ÁN 9 37a 2 1 5 37a
HE HL sin TLF , S
TL A B AB . A B AB 1 1 VD 74 1 1 2 16 – 3 V 5a 31 29 3 D Do vậy V V a . Vậy 3 V a H . 1 A 1 B AB 2 C 96 12 6
https://www.facebook.com/groups/toanvd.vdc Trang 55
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 PHÁT TRIỂN 6 :
Theo ý tƣởng Thể Tích khối đa diện có kết hợp góc
Câu 29. [PHÁT TRIẾN CÂU 46 – MÃ 101 – TN 2020] Cho hai hình chóp tam giác đều có cùng
chiều cao. Biết đỉnh của hình chóp này trùng với tâm của đáy hình chóp kia, mỗi cạnh bên của
hình chóp này đều cắt một cạnh bên của hình chóp kia. Cạnh bên có độ dài bằng a của hình chóp
thứ nhất tạo với đường cao một góc 0
30 , cạnh bên của hình chóp thứ hai tạo với đường cao một góc 0
45 . Tính thể tích phần chung của hai hình chóp đã cho ? 3 3 2 3 a 3 2 3 a 3 9 2 3 a 3 27 2 3 a A. . B. . C. . D. . 64 32 64 64 NHÓ
Thực hiện : ThầyNguyễn Hùng – Phản biện: Cô Nguyễn Thị Hồng Gấm M TO ÁN Lời giải VD Chọn C – V D C B' D' A α C' P M H N B β D NHÓ A' M TO ÁN VD – C V D C Hai hình chóp . A BCD và A . B C D
là hai hình chóp đều, có chung đường cao AA , A là tâm của tam giác B C D
và A là tâm của tam giác BCD.
Ta có: BCD// B C D
; AB AC AD a; BAA ; AAB . Do AB cắt A B
tại M nên AB// A B .
Gọi N là giao điểm của AC và A C
; P là giao điểm của AD và A D .
https://www.facebook.com/groups/toanvd.vdc Trang 56
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
Tương tự ta có: AC// A C
, AD// A D .
Từ đó suy ra các cạnh của B CD và B C D
song song với nhau từng đôi một. MB AB MA AB Ta có: NC A C MB NC MN // BC . NA AC MA NA
AB AC; AB A C NHÓ
Tương tự ta có: NP // CD và MP // BD . M TO Suy ra: M
NP là tam giác đều. Gọi H là giao điểm của OO và MNP , H là tâm của tam giác ÁN MNP . VD Trong tam giác AA D
có: AA A . D cos . a cos 1 . – V
Đặt x MH . Hai tam giác AHM và tam giác A H
M vuông tại H cho: D C
AH MH.cot . x cot
AA xcot cot 2 . A H
MH.cot . x cot a Từ 1 và 2 suy ra: a x .cos .cos cot cot x . cot cot
Tam giác MNP đều có cạnh MN x 3 nên: 2 2 2 2 MN 3 3 3x 3 3 a cos S . M NP 4 4 4 cot cot 2
Phần chung của hai hình chóp . A BCD và A . B C D
là hai hình chóp đỉnh A và A có chung NHÓ
nhau mặt đáy là tam giác MNP . Do đó thể tích của nó là: M 3 3 1 1 a . 3.cos TO V .S . AH A H S AA M NP . . 3 3 MNP 4cot cot 2 ÁN VD 92 3 9 3 3 a a –
Với 30 và 45 thì V . 2 V 64 32 3 1 D C
https://www.facebook.com/groups/toanvd.vdc Trang 57
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 CÂU 48 – MÃ 101
CHỦ ĐỀ : GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT
Thực hiện : Nhóm các Thầy Cô
Trương Đức Thịnh – Phạm Ninh – Đạt Lâm Huy – Thơm Chu.
Câu 48. [ ĐỀ GỐC-MÃ 101- TN 2020 ] Xét các số thực không âm
x và y thỏa mãn x y 1 2x . y 4 3.
Giá trị nhỏ nhất của biểu thức 2 2
P x y 4x 6y bằng 33 65 49 57 A. . B. . C. . D. . 4 8 8 8 NHÓ M TO
PHÂN TÍCH VÀ BÌNH LUẬN ÁN
Dạng toán: Đây là dạng toán tìm giá trị lớn nhất, nhỏ nhất của hàm số nhiều biến số với giả
thiết các biến rằng buộc bởi một đẳng thức hay bất đẳng thức liên qua tới mũ hay logarit. VD
Hướng giải: – V
Bước 1: Tìm mối liện hệ giữa các biến ta có 2 hướng như sau: D C
Hướng 1: Từ giả thiết của bài toán ta sử dụng biến đổi phù hợp để đưa về dạng
f u f v sử dụng tính đơn điệu của hàm f x để đưa ra mối liên hệ giữa các biến.
Hướng 2: Từ giả thiết ta đưa về k. f
u f v l g
u g v 0
từ đó dựa vào tính
đơn điệu của hàm f x, g x sử dụng các đánh giá phù hợp để đưa ra mối liên hệ giữa các biến.
Bước 2: Từ mối liên hệ giữa các biến ta thay vào biểu thức cần tìm giá trị lớn nhất, nhỉ nhất
để đánh giá. Đến đay ta có các hướng để giải quyết bài toán như sau:
Hướng 1: Đưa về hàm 1 biến để khảo sát
Hướng 2: Sử sụng các bất đẳng thức cơ bản để đánh giá.
Hướng 3: Sử dụng vị trí tương đối của các đối tượng hình học cơ bản để đánh giá. NHÓ Lời giải M TO Chọn B ÁN
Cách 1: Biến đổi giả thiết VD 2x2 y2 2 y 1 32x 2 y 32 .2 3 2 .2 3 2 2 2 .2 3 2 2 x y x y x y x * – V D 3 C
Nếu 3 2x 0 x
khi đó do y 0 nên * luôn đúng. 2 2 Ta có 3 3 33 2 P 0 4. 6.0 (1). 2 2 4
Nếu 3 2x 0 khi đó * có dạng f 2y f 3 2x với .2t f t t
https://www.facebook.com/groups/toanvd.vdc Trang 58
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
Xét hàm số .2t f t t
xác định và liên tục trên 0; . Có ' 2t .2t f t t .ln 2 0, t 0
f t đồng biến trên 0; . Từ đó suy ra 3
2 y 3 2x y
x mà 3 x 0 nên 2 2 2 2 3 3 45 5 65 65 2 P x
x 4x 6 x 2
P 2x 5x 2 x (2), đẳng thức 2 2 4 4 8 8 5 x 4 xảy ra khi
. Từ (1) và (2) chọn B. 1 NHÓ y 4 M TO Cách 2: ÁN Với mọi , x y không âm ta có VD 3 3 x y xy – x y 3 3 1 2 2 2x . y 4 3 x . y 4
x y . y 4 1 0 (1) V 2 2 D C 3 3 3 xy
Nếu x y
0 thì x y . y 4
1 0 .y 0 2 4 1 0 (vô lí) 2 2 3 3 3 xy
Nếu x y
0 thì x y . y 4
1 0 .y 0 2 4 1 0 (luôn đúng) 2 2 Vậy 3
1 x y 0 3 x y . 2 2
Ta có P x y x y x 2 y 2 2 2 4 6 2 3 13. NHÓ 2 Áp 1 2 1 3 65
dụng bất đẳng thức Bunhyakovski ta được P
x y 5 13 5 13 . 2 2 2 8 M TO 5 5 ÁN 3 x x x y Đẳ 4 65 4 ng thức xảy ra khi 2 . Vậy min P . VD 1 8 1
x 3 y 2 y y – 4 4 V D C Cách 3: Ta có 2x2 y2 2 y 1 32x 2 y 32 .2 3 2 .2 3 2 2 2 .2 3 2 2 x y x y x y x *
Nếu 3 2x 0 khi đó * có dạng f 2y f 3 2x với .2t f t t
https://www.facebook.com/groups/toanvd.vdc Trang 59
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
Xét hàm số .2t f t t
xác định và liên tục trên 0; . Có
' 2t .2t f t t .ln 2 0, t 0
f t đồng biến trên 0; . Từ đó suy ra
* 2 y 3 2x 2x 2 y 3 0 . 3
Nếu 3 2x 0 x
khi đó do y 0 nên * luôn đúng. Suy ra 2y 3 2x . 2 Tóm lại ta được
* 2x 2 y 3 0 1 . Ta có 2 2
P x y x y x 2 y 2 2 2 4 6 2 3
13 hay x 2 y 3 P 13 2. NHÓ
Ta thấy tập hợp các giá trị ,
x y thỏa mãn giả thiết
1 là các điểm M ,
x y nửa mặt phẳng M TO
Oxy bờ là đường thẳng : 2x 2y 3 0 không chứa I 2 ; 3
và cả các điểm nằm trên . ÁN
Đẳng thức 2 là đường tròn tâm I 2 ; 3
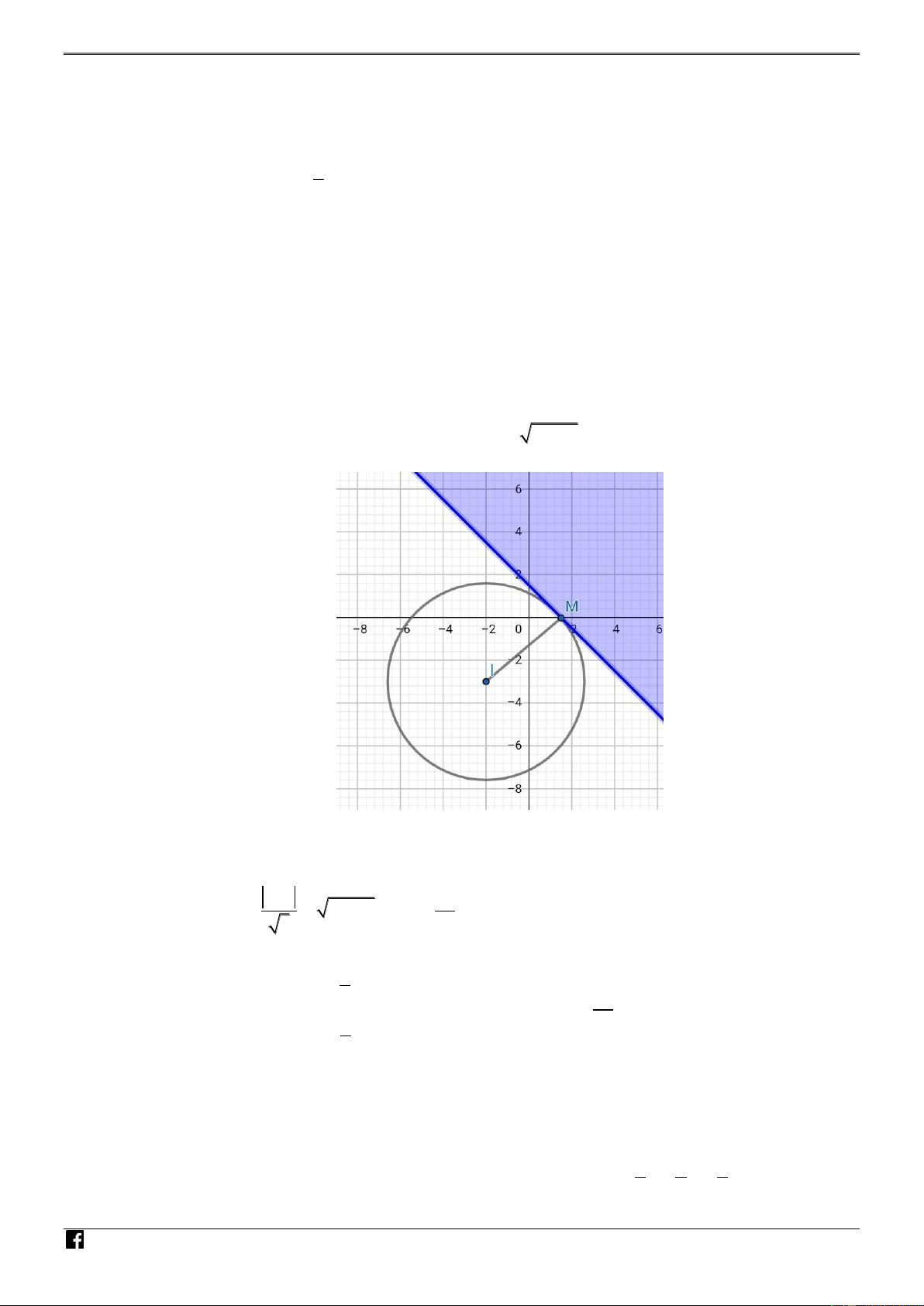
, R P 13 . VD – V D C NHÓ
Dễ thấy P nhỏ nhất khi đương thẳng và đường tròn C tiếp xúc nhau do đó M TO d I 13 65 ; R
P 13 P . ÁN 8 8 VD 5 x – 4 V Dấu bằng xảy ra khi
. Vậy giá trị nhỏ nhất của P là 65 . D 1 8 C y 4
CÂU HỎI TƢƠNG TỰ, PHÁT TRIỂN
Câu 30. [PHÁT TRIẾN CÂU 48 – MÃ 101 – TN 2020] Xét các số thực không âm x và y thỏa mãn 1 9 9 2x y 1
. Giá trị nhỏ nhất của biểu thức 2 2 x y . x 2 1 P x 5y x y bằng 2 2 8
https://www.facebook.com/groups/toanvd.vdc Trang 60
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 3 5 5 13 A. . B. . C. . D. . 16 16 8 8
Trương Đức Thịnh – Phạm Ninh – Đạt Lâm Huy – Thơm Chu. Lời giải Chọn B Xét hàm số 2 1 .2 x y f y x y x là hàm số
đối với biến y , liên tục trên . x y NHÓ
Ta có f y 2 1 1 . x 2 ln 2 0, x
0 . Do đó, f y đồng biến trên . M Mặt khác, 2x y 1 x y . x 2
1 f y f 1 2x y 12x 2x y 1. TO ÁN Ta có: VD 2 2 2 2 1 9 9 2 2 1 1 2 1 1
P x 5y x y – x y 2y 1 x y 2 2 8 4 4 4 4 V D C
Theo bất đẳng thức Bunhyakovski, ta có: 2 2 2 2 2 1 1 1 1 1 1 25 4 1 x y
2x y 2x y 1 4 4 2 4 4 4 16 2 2 1 1 5 5 x y P 4 4 16 16 . 1 y 1 2 x NHÓ 4 5 Dấu “=” xảy ra 2x y 1 min P . 1 . Vậy 16 M 1 y x 2 TO 1 4 y ÁN 2 4 VD
Câu 31. [PHÁT TRIẾN CÂU 48 – MÃ 101 – TN 2020] Cho các số thực dương ;
x y thỏa mãn – 5x 7 2 x V
x x 5 x log
4xy x 4xy . Giá trị nhỏ nhất của 2 P y là 5 D 4xy y C 133 113 117 A. . B. . C. 28 . D. . 4 4 8
Trương Đức Thịnh – Phạm Ninh – Đạt Lâm Huy – Thơm Chu. Lời giải Chọn C
https://www.facebook.com/groups/toanvd.vdc Trang 61
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 x 0 ;
x y là các số thực dương thỏa mãn 2 10x x x
xlogxy x xy nên suy ra 1 . y 4 x 5x 2
x x 5 x log
4xy x 4xy x 1
log x log 4y 1 4y 5 5 5 x 5x 5x 5x x
log x log 4y 1 4y 1 log
log 4y 1 4y 1 . 5 5 5 5 x x x
Xét hàm số f t log t t xác định và liên tục trên 0;. Có f t 1 ' 1 0, t 0 5 NHÓ t M x TO
f t đồng biến trên 0;. Từ đó suy ra 5 4y 1 nên x ÁN x VD 5 7 4 y 1 7 27 27 27 2 2 2 2 27 27 P y y y 1 y 1 2 33 y . . 1 P 28 4xy y 4 y y 4 y 8y 8y y y – V . D C x 1 Khi
3 thì đẳng thức xảy ra . y 2
Câu 32. [PHÁT TRIẾN CÂU 48 – MÃ 101 – TN 2020] Cho hai số thực dương ,
x y thoả mãn 2 2 3 3log 32 3 1 2 y x x y
. Giá trị nhỏ nhất của biểu thức x P bằng 2 y e ln 2 e ln 2 e ln 2 e A. . B. . C. . D. . 2 2 2 2 ln 2
Trương Đức Thịnh – Phạm Ninh – Đạt Lâm Huy – Thơm Chu. NHÓ Lời giải Chọn B M TO Ta có : 2 2 y 3 2 2 3log 32 3 1 2 3 log 1 32 3 8.2 y x x y x x y 2 2 ÁN 2 2 y VD 3log 2x 32x 3y 8.2 2 2 – V 2t D Đặt t log 2x x
. Thay vào phương trình 2 ta được phương trình: 2 C 2 2 2t y 2t 2 3 32 3 8.2 3 8.2 3 8.2 y t y t y 3 2 Xét hàm số 2 3 8.2 x f x x , x . Có 2 3 16.2 . x f x ln 2 0, x .
https://www.facebook.com/groups/toanvd.vdc Trang 62
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 2y 2 2 y Từ đó ta có: 3 t
y , nên ta có : log 2x y x . Vậy P 2 2 2 y x 2x ln 2 x 2x 2x x ln 2 1 Xét hàm số 2 g x , x 0 . Ta có g x 2x 2 2 2x 2x 2 suy ra : g x 0 x ln 2 1 0 x . ln 2
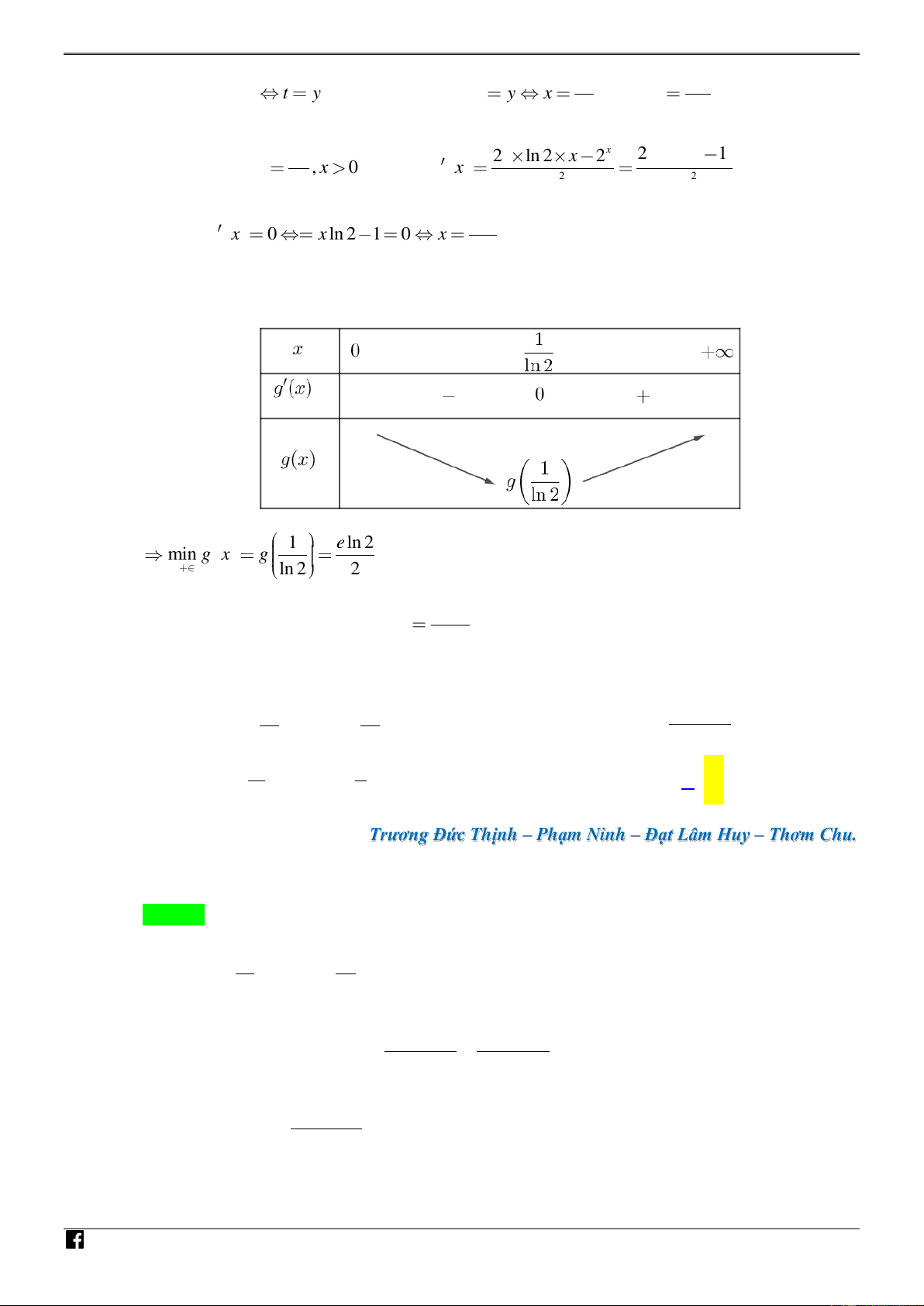
Ta có bảng biến thiên của hàm g x như sau: NHÓ M TO ÁN VD – V D C 1 e ln 2 min g x g 0; ln 2 2 e ln 2
Vậy giá trị nhỏ nhất của P là : P min 2
Câu 33. [PHÁT TRIẾN CÂU 48 – MÃ 101 – TN 2020] Cho ;
x y là hai số thực dương thỏa mãn y x 2 2 x 3y và x 1 y 1
. Giá trị nhỏ nhất của biểu thức P x y 2 2 2x 2y 2 xy bằng y 13 9 A. . B. . C. 2 . D. 6 . 2 2 NHÓ
Trương Đức Thịnh – Phạm Ninh – Đạt Lâm Huy – Thơm Chu. M Lời giải TO Chọn D ÁN y x VD Ta có x 1 y 1 y x 2 2 4x 1 4y x y 1 – 2 2 V D x y C ln 4 1 ln 4 1 ln 4x 1 ln 4y y x 1 (vì , x y 0 ). x y ln 4t 1
Xét hàm số f t
trên khoảng 0; . t
https://www.facebook.com/groups/toanvd.vdc Trang 63
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
4t.ln 4 .t ln4t 1 4t ln4t
4t 1ln4t t 1
Ta có f t 4 1 0, t 0 2 t 4t 2 1 t
f t luôn nghịch biến trên khoảng 0; .
Lại có f x f y x y . 2 Đặt x t 3 t
, khi đó t 1; P . y t 1 NHÓ 2 t 3 2 t 2t 3 t 1 M
Cách 1: Xét P
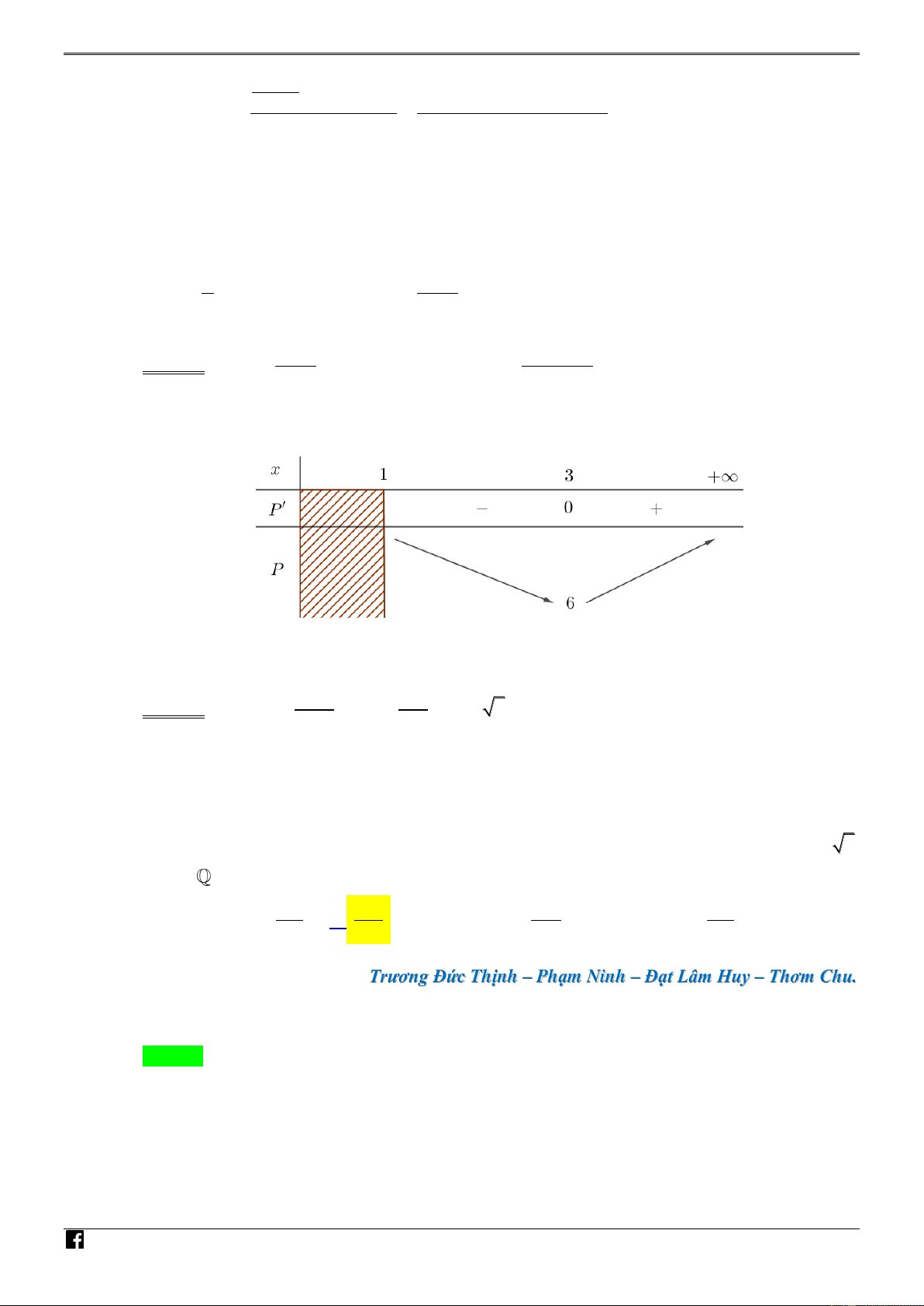
với t 1; , ta có P ; P 0 2 TO t 1 t 1 t 3 ÁN Bảng biến thiên VD – V D C
Từ bảng biến thiên, suy ra giá trị nhỏ nhất của P bằng 6 khi t 3 hay x 3y . 2 Cách 2: t 3 4 Ta có P t 1
2 2 4 2 6 (AM – GM). t 1 t 1
Suy ra, giá trị nhỏ nhất của P bằng 6 khi t 3 hay x 3y .
Câu 34. [PHÁT TRIẾN CÂU 48 – MÃ 101 – TN 2020] Xét các số thực x và y thỏa mãn NHÓ 2 2 2 2 x y 2
. Biết rằng giá trị nhỏ nhất của biểu thức 2 2 2x y .4 5 P x y 4x 6y là a b M với , a b
. Giá trị của a b bằng TO 130 265 265 130 A. . B. . C. . D. . ÁN 4 2 4 2 VD
Trương Đức Thịnh – Phạm Ninh – Đạt Lâm Huy – Thơm Chu. –V D Lời giải C Chọn B Ta có 2 2 2 2 2 2
2 2x 2y 4 2 2 2 y 1 2 5 2x 2 2 y 2 5 2 .2 5 2 .2 5 2 2 2 .2 5 2 2 x y x y x y x *. Nếu 2
5 2x 0 khi đó do VT 0;VP 0 nên * không xảy ra.
https://www.facebook.com/groups/toanvd.vdc Trang 64
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 Nếu 2
5 2x 0 khi đó * có dạng f 2 y f 2 2
5 2x với .2t f t t .
Xét hàm số .2t f t t
xác định và liên tục trên 0; . Có ' 2t .2t f t t .ln 2 0, t 0 5
f t đồng biến trên 0; . Từ đó suy ra 2 2 2 2
* 2 y 5 2x x y 1 . 2 Ta có 2 2
P x y x y x 2 y 2 2 2 4 6 2 3
13 hay x 2 y 3 P 13 2.
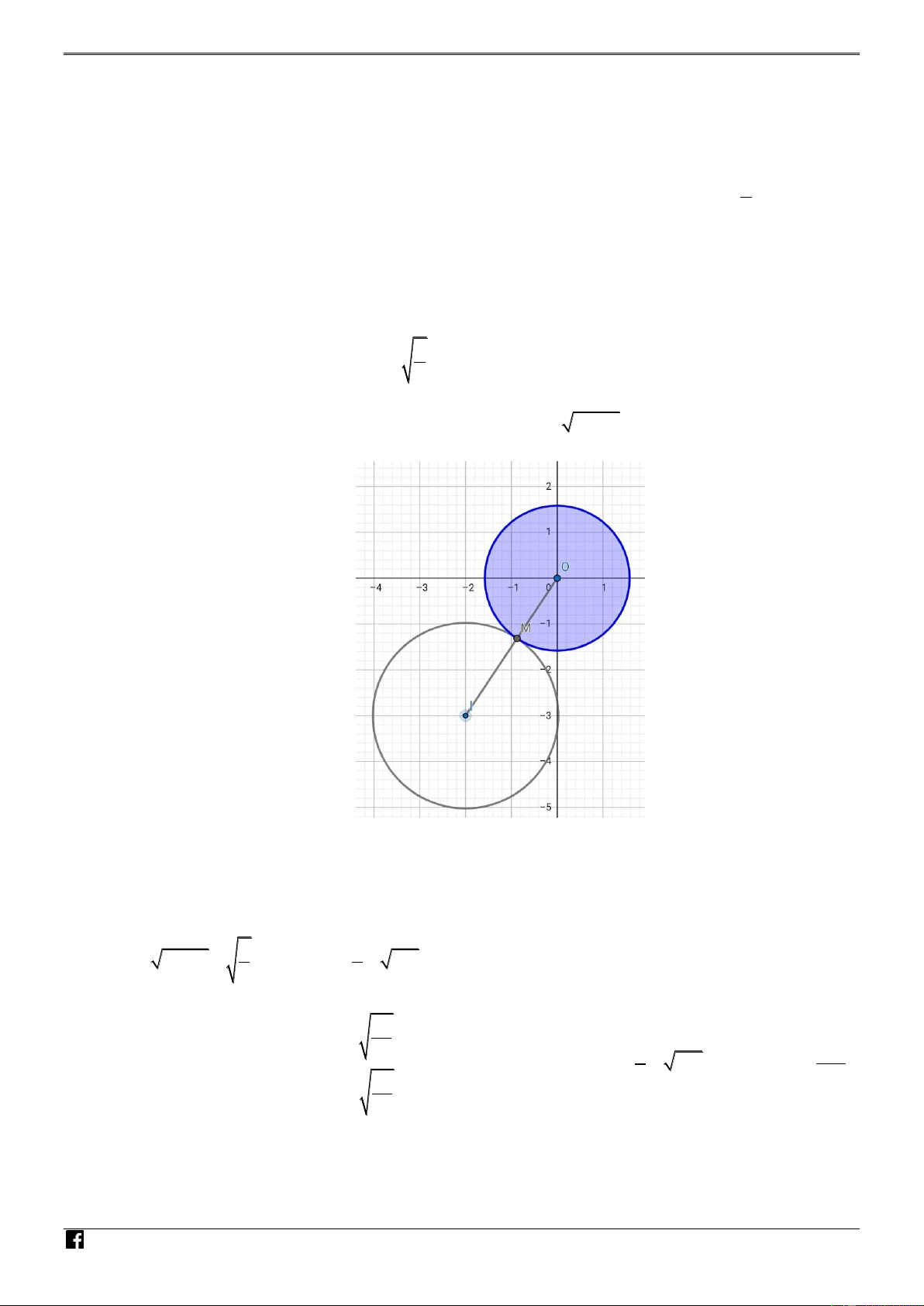
Ta thấy tập hợp các giá trị ,
x y thỏa mãn giả thiết
1 là các điểm M ,
x y trên mặt phẳng NHÓ C tâm 5 O, R M
Oxy là hình tròn 2 TO ÁN
Đẳng thức 2 là đường tròn C tâm I 2 ; 3
, R P 13 . VD – V D C NHÓ M TO
Dễ thấy P nhỏ nhất khi đó đường tròn C và đường tròn C tiếp xúc ngoài với nhau ÁN 5 5 VD P 13
OI P 130 . 2 2 – V D 5 C x 2 26 265 Dấu bằng xảy ra khi
. Vậy giá trị nhỏ nhất của P là 5 130 suy ra a b . 5 2 2 y 3 26
https://www.facebook.com/groups/toanvd.vdc Trang 65
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 CÂU 49 – MÃ 101
CHỦ ĐỀ : TÌM NGHIỆM NGUYÊN CỦA PT
Thực hiện : Thầy Nguyễn Sỹ – Thầy Nguyễn Tất Thành.
Câu 49. [ ĐỀ GỐC-MÃ 101- TN 2020 ] Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không
quá 728 số nguyên y thỏa mãn log 2
x y log (x y) ? 4 3 A. 59 . B. 58 . C. 116 . D. 115 . NHÓ
PHÂN TÍCH VÀ BÌNH LUẬN M
Thầy Nguyễn S ỹ TO
Đây là bài toán khó đòi hỏi khả năng tư duy cao. ÁN
*) Ta có thể phát biểu lại bài toán thành quen thuộc: Có bao nhiêu giá trị nguyên của tham số 2 VD m để BPT log
m x log (m x) có không quá 728 nghiệm nguyên. 4 3 –
*) Coi x như tham số ta xét BPT theo ẩn y . V D
Ứng với mỗi giá trị của x ta xét hàm số theo biến y . Trên miền xác định D ( ; x ) , hàm C
số f ( y) log (x y) log 2
x y là hàm số đồng biến và ta thấy BPT f y 0 luôn có ít 3 4
nhất một nghiệm là y x 1. Do đó để BPT có tối đa 728 nghiệm nguyên thì chỉ cần
f (x 729) 0 . Lời giải Chọn C
Với mọi x ta có 2 x x .
Xét hàm số f (y) log (x y) log 2 x y . 3 4 NHÓ
Tập xác định D ( ; x ) (do 2
y x y x ). M TO 1 1 ÁN f '( y) x D (do 2
x y x y 0 , ln 4 ln 3 ) (x y) ln 3 0, 2 x yln 4 VD –
f tăng trên D . V D C
Ta có f (x 1) log (x x 1) log 2
x x 1 0 . 3 4
Có không quá 728 số nguyên y thỏa mãn f y 0
f (x 729) 0 log 729 log 2
x x 729 0 3 4 2 6
x x 729 4 0 2
x x 3367 0
https://www.facebook.com/groups/toanvd.vdc Trang 66
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 5 7,5 x 58,5
Mà x nên x 5 7, 56,...,5 8 . Vậy có 58 ( 5
7) 1116 số nguyên x thỏa.
CÂU HỎI TƢƠNG TỰ, PHÁT TRIỂN
Câu 35. [PHÁT TRIẾN CÂU 49 – MÃ 101 – TN 2020] Có bao nhiêu số nguyên y sao cho ứng với
mỗi y có không quá 100 số nguyên x thỏa mãn log 2 y 2 3 x x y 0. 5 NHÓ A. 19 . B. 18 . C. 20 . D. 17 . M
Thực hiện : Thầy Nguyễn Sỹ – Phản Biện : Thầy Nguyễn Tất Thành. TO Lời giải ÁN VD Chọn C – 2 2 2 V Xét hàm số log 3 x y f x x y
với x y ; . 5 D C Ta có f x 1 ' . x y 2 x y 2 2.3 ln 3 0, x y 2 ln 5
Suy ra hàm số f x đồng biến trên khoảng 2 y ; .
lim f x 2 Ta có xy f y 2 2 2 y y2 1 3 0
Do đó để BPT f x 0 có không quá 100 số nguyên x thỏa mãn f 2 y 10 1 0 2 2 y 1 01 2 2 y NHÓ
log y 101 y 3 0 5 2 2 y y202 3 log 101 M 5 TO 2
2y y 202 log log 101 0 3 5 ÁN 1 0,33 y 9,83 VD
Mà y y 1 0; 9 ;...;
9 . Vậy có 20 giá trị nguyên của . y – V D
Câu 36. [PHÁT TRIẾN CÂU 49 – MÃ 101 – TN 2020] Có bao nhiêu giá trị nguyên của tham số m C 1 để bất phương trình log 2 x m
0 có tối đa 50 nghiệm nguyên. x m 2 e A. 15 . B. 16 . C. 14 . D. 17 .
Thực hiện : Thầy Nguyễn Sỹ – Phản Biện : Thầy Nguyễn Tất Thành. Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 67
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 Chọn C ĐKXĐ 2 x m . Xét hàm số 1 f x
log x m với 2 x m . x m 2 2 e Ta có f x xm 1 ' e x m 2 0, x m 2 ln 2
Suy ra, hàm số f x nghịch biến trên khoảng 2 m ; . NHÓ
lim f x M 2 xm TO Ta thấy f 1 2 m 1 0 ÁN 2 m m 1 e VD
Do đó để BPT f x 0 có không quá 50 nghiệm nguyên f 2 m 5 1 0 – V D C 1 2 2 log m 51 m 0 2 2 m 51 m e 2 m m51 e log 51 2 2
m m 51 ln log 51 0 2 6 ,78 m 7,78
Mà m m 6 ; 5 ;...,
7 . Vậy có 14 giá trị nguyên của tham số m .
Câu 37. [PHÁT TRIẾN CÂU 49 – MÃ 101 – TN 2020] Có bao nhiêu số nguyên y sao cho ứng với 1
mỗi y có không quá 10 số nguyên x thỏa mãn log 2 x y log x y 0 . 5 2 2x y NHÓ A. 30 . B. 18 . C. 32 . D. 17 .
Thực hiện : Thầy Nguyễn Sỹ – Phản Biện : Thầy Nguyễn Tất Thành. M TO Lời giải ÁN Chọn C VD – Với mỗi 2 2 y
y y y y V D C 1 2
Xét hàm số f x
log x y log x y với x ;y . 5 2 2x y Ta có f x x y 1 1 ' 2 .ln 2 ; x y x y ln 5 x y 0, : 2 ln 2
https://www.facebook.com/groups/toanvd.vdc Trang 68
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 2 vì x y x y 0 ln 5 ln 2 0
Suy ra hàm số f x nghịch biến trên khoảng ; y .
lim f x x y Ta có
f y 1 1 log 2 y y 1 0; 2 y y 5 2
Do đó để BPT f x 0 có không quá 10 số nguyên x thỏa mãn f y 1 1 0 NHÓ M 1
log y y 11 log 11 0 11 2 5 TO 2 2 11 log 112 ÁN 2 2
y y 11 5 11 VD log 2 11 2 2
y y 11 5 0 – 1 5,35 y 16,35 V D C
Mà y y 1 5; 1 4;...;1
6 . Vậy có 32 giá trị nguyên của . y
Câu 38. [PHÁT TRIẾN CÂU 49 – MÃ 101 – TN 2020] Có bao nhiêu số nguyên x sao cho ứng với
mỗi x có không quá 26 số nguyên y thỏa mãn log 2
x y log 2
x x 27 log (x y) ? 5 4 3 A. 211. B. 423. C. 424 . D. 212 .
Thực hiện : Thầy Nguyễn Tất Thành– Phản Biện : Thầy Nguyễn Sỹ. Lời giải Chọn C Với mọi x ta có 2 2
x x x x . NHÓ
Xét hàm số f (y) log (x y) log 2
x y log 2
x x 27 . 3 5 4 M TO
Tập xác định D ( ; x ) . Ta có ÁN 1 1 VD f '( y) x D (do 2
x y x y 0 , ln 5 ln 3 ) (x y) ln 3 0, 2 x yln 5 – V D
f đồng biến trên D . C
Ta có f (x 1) log (x x 1) log 2 x x 1 log 2
x x 27 0 . 3 5 4
y x 1 là một nghiệm của bất phương trình đã cho.
Suy ra, để có không quá 26 số nguyên y thỏa mãn f y 0
https://www.facebook.com/groups/toanvd.vdc Trang 69
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
f (x 27) 0 log 27 log 2
x x 27 log 2
x x 27 0 3 5 4 log 2
x x 27 log 2
x x 27 3 5 4 log 4.log 2
x x 27 log 2
x x 27 3 5 4 4
(log 4 1) log x x 27 log 20 5 2 2 3
3 x x 27 4 . 5 4 2
11,5 x 212,5 . NHÓ Mà x nên 2 11 x 212 . M Vậy có 212 ( 2
11) 1 424. số nguyên x thỏa mãn yêu cầu. TO ÁN
Câu 39. [PHÁT TRIẾN CÂU 49 – MÃ 101 – TN 2020] Có bao nhiêu số nguyên x sao cho ứng với x y x y VD
mỗi x có không quá 10 số nguyên y thỏa mãn 2 7 26 4 2
8192 và x y 0 ? – A. 16 . B. 15 . C. 17 . D. 7 . V D
Thực hiện : Thầy Nguyễn Tất Thành– Phản Biện : Thầy Nguyễn Sỹ. C Lời giải Chọn A Xét hàm số 2 x 7 y 26 ( ) 4 2 x y f y 8192 .
Tập xác định D ( ; x )
vì x y 0 y x và x Ta có : 2 x 7 y26 '( ) 7.4 ln 4 2x . y f y ln 2 0, x
D f nghịch biến trên D . Ta có 2 x 7 x 19 x x 1 13
f (x 1) 4 2 2 0 NHÓ 2 vì 49 27 7 27 27 2 2
x 7x 19 x 7x x 4 4 2 4 4 M TO 27 27 2 2 x x x x 1 7 19 13 7 19 13 4 2 ÁN 4 4 2 2 4 2 0 2 VD
y x 1 là một nghiệm của bất phương trình f y 0. – V D C
Suy ra, để có không quá 10 số nguyên y thỏa mãn f y 0 2 x 7 x51 xx 1 1 13
f (x 11) 0 4 2 2 0 2 x x 1 1 7 51 13 2 13 4 2
x 7x 51 log 2 11 4 11 2 2
https://www.facebook.com/groups/toanvd.vdc Trang 70
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 1 2 13
x 7x 51 log 2 0 . 4 11 2 1
1,8 x 4,8 . Mà x nên 1 1 x 4 . Vậy có 4 ( 1
1) 116. số nguyên x thỏa mãn yêu cầu. CÂU 50 – MÃ 101 NHÓ
CHỦ ĐỀ : GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT
Thực hiện :Thầy Dinh An – Thầy Huỳnh Đức Vũ . M TO
Câu 50. [ ĐỀ GỐC-MÃ 101- TN 2020 ] Cho hàm số bậc ba y f (x) có đồ thị là đường cong trong ÁN hình sau: VD – V D C
Số nghiệm thực phân biệt của phương trình f 3
x f (x) 1 0 là A. 8 . B. 5 . C. 6 . D. 4 .
PHÂN TÍCH VÀ BÌNH LUẬN.
- Bài toán cho đồ thị hàm số bậc ba y f x và hỏi số nghiệm của phương trình f 3
x f x 1 0. Đây là dạng toán tương giao hàm ẩn, hàm hợp. NHÓ
Tuy nhiên bài toán tƣơng giao này có hai bƣớc:
Bƣớc 1: Tương giao giữa đồ thị hàm số y f t và đường thẳng y 1 . Bước này M
khá đơn giản vì trong bài toán có cho sẵn dữ kiện để có thể tìm ra số nghiệm t của phương TO
trình, thậm chí có thể cho thấy được các nghiệm thuộc khoảng nào. ÁN Bƣớ a
c 2: Tương giao giữa đồ thị hàm số y f x và đổ thị y . Với đồ thị 3 x VD
y f x cho trước thì học sinh cần nắm chắc các dạng đồ thị hàm y x với là các số –
nguyên. Đến bước này thì rõ ràng các em họ V
c sinh chỉ cần tìm được số giao điểm mà không cần D
quan tâm các hoành độ giao điểm thuộc khoảng nào nữa. C
Các hƣớng phát triển của bài toán:
Hƣớng 1: Thay đổi đồ thị hàm bậc ba thành đồ thị một hàm số khác; thay đổi tương giao bước
hai từ hàm lũy thừa mũ nguyên lẻ thành hàm số lũy thừa số nguyên chẵn, mũ không nguyên;
hoặc thay hàm lũy thừa thành các hàm số khác như hàm mũ, logarit, đưa dấu giá trị tuyệt đối
vào để nhân đôi đồ thị (vì nếu chỉ có hàm mũ hoặc logarit thông thường thì đồ thị chỉ có một nhánh).
Hƣớng 2: Thay vì hỏi số nghiệm của phương trình thuần túy thì có thể lồng ghép vào
bài toán: Tìm số tiệm cận ngang, có thể là số tiệm cận của đồ thị hàm số. Ví dụ như: Tìm số
https://www.facebook.com/groups/toanvd.vdc Trang 71
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 1
tiệm cận ngang của đồ thị hàm số: y
. Hoặc có thể đổi câu hỏi thành tìm số f 3
x f x 1
cực trị, hoặc khoảng đồng biến nghịch biến của hàm số, cũng dựa trên cách xử lí bài toán tương
giao của các đồ thị. Tuy nhiên với cách hỏi này, hàm số phải cho khéo để có thể tạo ra đạo hàm như mong muốn. Lời giải Chọn C NHÓ x 0 3 M f (x) 0 x f (x) 0 TO 3
( ) 1 0 3 ( ) 3 1 ( ) 0 a f x f x f x f x x f x a f (x) (do x 0) 3 ÁN x 3
x f (x) b 0 b VD f (x) (do x 0) 3 x – V D C
f (x) 0 có một nghiệm dương x c . k f (x)
với x 0, k 0 . 3 NHÓ x k M
Đặt g(x) f (x) . 3 TO x ÁN 3k g (
x) f '(x) . 4 x VD 3k –
Với x c , nhìn hình ta ta thấy f ( ) x 0 g (
x) f (x) 0 4 V x D C
g(x) 0 có tối đa một nghiệm. g(c) 0 Mặt khác
và g(x) liên tục trên ; c
lim g(x) x
g(x) 0 có duy nhất nghiệm trên ; c . k
Với 0 x c thì f (x) 0
g(x) 0 vô nghiệm. 3 x
https://www.facebook.com/groups/toanvd.vdc Trang 72
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 3k
Với x 0 , nhìn hình ta thấy f ( ) x 0 g (
x) f (x) 0 4 x
g(x) 0 có tối đa một nghiệm.
lim g(x) 0 Mặt khác x 0
và g(x) liên tục trên ;0 .
lim g(x) x
g(x) 0 có duy nhất nghiệm trên ;0 .
Tóm lại g(x) 0 có đúng hai nghiệm trên \ 0 . NHÓ a b
Suy ra hai phương trình f (x) , f (x)
có 4 nghiệm phân biệt khác 0 và khác c . M 3 x 3 x TO 3 ÁN
Vậy phương trình f x f (x) 1 0 có đúng 6 nghiệm. VD k –
Cách xử lí khác cho phƣơng trình f (x) . 3 V x D C Xé k t h(x) , D \ k . h 0 , 0 3 x 3k h ( x) 0, x
D h(x) nghịch biến trên từng khoảng xác định. 4 x Bảng biến thiên NHÓ M TO ÁN
Từ đó vẽ đồ thị các hàm số y f (x) và y (
h x) trên cùng hệ trục tọa độ, ta được hình vẽ. VD –
(Lƣu ý: do f (x) là hàm bậc ba nên ta chắc chắn được hình dáng đồ thị của nó khi x và V D x ). C
https://www.facebook.com/groups/toanvd.vdc Trang 73
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 NHÓ M TO ÁN VD – V k D
Nhìn vào đồ thị, ta thấy phương trình f (x)
có đúng 2 nghiệm, 2 nghiệm này khác 0 và 3 C x khác c . a b
Mỗi phương trình f (x) , f (x)
đều có 2 nghiệm phân biệt khác 0 và khác c . 3 x 3 x
Vậy phương trình f 3
x f (x) 1 0 có đúng 6 nghiệm.
CÂU HỎI TƢƠNG TỰ, PHÁT TRIỂN
Câu 40. [PHÁT TRIẾN CÂU 50 – MÃ 101 – TN 2020] Cho hàm số đa thức bậc bốn y f (x) có
đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình
4 f x NHÓ f 1 0 là 2 ln x M TO ÁN VD – V D C A. 8 . B. 5 . C. 6 . D. 4 .
https://www.facebook.com/groups/toanvd.vdc Trang 74
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
Thực hiện :Thầy Huỳnh Đức Vũ – Thầy Dinh An. Lời giải Chọn C NHÓ M TO ÁN VD – V D C 4 f x 0 2 ln x
f x 0 1
4 f x 4 f x 1 f 1 0
1 f x ln x 2 2 2 ln x ln x 2 4 f x f
x ln x 3 2 2 ln x NHÓ x x 0 1 f (x) 0 . x x 2 2 M TO
Xét phương trình f x ln x , vì y f x là hàm số đa thức bậc bốn nên ta có ÁN +)Trên ;
0 đồ thị hàm số y ln x cắt đồ thị hàm số y f x tại duy nhất một điểm. VD
+) Trên 0;a, với x a1;2 là một điểm cực đại của hàm số y f x –
ln x ln x x 1 f (x), x ;
0 a nên trên khoảng ;
0 a phương trình vô nghiệm. V D C +) Trên ;
a , ta thấy đồ thị hàm số y ln x cắt đồ thị hàm số y f x tại duy nhất một điểm.
Do đó, phương trình f x ln x có đúng 2 nghiệm phân biệt và hai nghiệm này khác với hai
nghiệm của phương trình (1).
https://www.facebook.com/groups/toanvd.vdc Trang 75
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 NHÓ M TO ÁN VD – V D C
Xét phương trình f x 1
ln x . Tương tự như phương trình (2) và với đánh giá 2 1 1 ln x x
1 f (x), x ;
0 a ta cũng chứng minh được phương trình này có đúng 2 2 2
nghiệm phân biệt và 2 nghiệm này không trùng với các nghiệm của hai phương trình (1) và (2).
Vậy phương trình đã cho có 6 nghiệm phân biệt.
Câu 41. [PHÁT TRIẾN CÂU 50 – MÃ 101 – TN 2020] Cho hàm số đa thức bậc ba y f (x) có đồ
f x
thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình f 1 0 x e là NHÓ M TO ÁN VD – V D C A. 8 . B. 5 . C. 6 . D. 4 .
Thực hiện :Thầy Huỳnh Đức Vũ – Thầy Dinh An.
https://www.facebook.com/groups/toanvd.vdc Trang 76
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 Lời giải Chọn B NHÓ M TO ÁN VD – V D f x C 0 (1) x e
f x
f x f x f
1 0 f 1 a (2) x x x 1;2 e e e f x b 2. (3) x e
x x 0;1 1 f x +)
0 f x 0 x x x ;1 x 2 1 e
x x b 3 f x +) a f x ae x 1;2 x . e NHÓ
Trên 0; , ta có x 1 x e x
ae ax
1 f (x). Suy ra trên khoảng này phương trình (2) vô nghiệm. M TO Trên ;
0, vì hàm số y f (x) là hàm số đa thức bậc ba nên kết hợp với đồ thị ta thấy ÁN
phương trình (2) có nghiệm duy nhất trên khoảng này. VD f x +)
b f (x) x
be . Ta có x
be b x
1 f (x), x
>0 và lập luận tương tự như phương trình x e – V
(2) ta chứng minh được phương trình này có nghiệm duy nhất trên ; 0. D C
https://www.facebook.com/groups/toanvd.vdc Trang 77
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 NHÓ M TO ÁN VD
Các nghiệm của ba phương trình (1), (2), (3) không trùng nhau. – V
Vậy phương trình đã cho có 5 nghiệm phân biệt. D C
Câu 42. [PHÁT TRIẾN CÂU 50 – MÃ 101 – TN 2020] Cho hàm số bậc ba y f x có đồ thị là
đường cong trong hình vẽ. Số nghiệm thực phân biệt của phương trình f 5
x f x 2 0 là NHÓ M TO ÁN A. 8 . B. 5 . C. 6 . D. 4 . VD
Thực hiện :Thầy Huỳnh Đức Vũ – Thầy Dinh An. – V Lời giải D C Chọn C f 5
x f x 2 0 f 5
x f x 2 * Dựa vào đồ thị
https://www.facebook.com/groups/toanvd.vdc Trang 78
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101 5
x f x 0 1 5
* x f x a 2 1 a 0 . 5
x f x b 3 3 b 2 x 0 x 0 1 . f x 0 x x 3 x 2 1 1 Xét a
2 : dễ thấy x 0 không là nghiệm. Với x 0 , 2 f x . 5 x NHÓ a
Vẽ đồ thị hàm số f x 1
a 0 và hàm số y f x trên cùng hệ trục tọa độ suy ra 5 M x TO
phương trình có 2 nghiệm. ÁN
Tương tự xét phương trình 3 phương trình có 2 nghiệm. VD –
Vậy phương trình đã cho có 6 nghiệm. V D C
Câu 43. [PHÁT TRIẾN CÂU 50 – MÃ 101 – TN 2020] Cho hàm số bậc bốn y f x có đồ thị là
đường cong trong hình vẽ. Số nghiệm thực phân biệt của phương trình f x 2 2
f x 3 0 là NHÓ M A. 8 . B. 6 . C. 9 . D. 12 . TO ÁN
Thực hiện : Thầy Dinh An– Thầy Huỳnh Đức Vũ. VD Lời giải – Chọn C V D C 2 2
f x 2 f x 3 0 f x 2 f x 3 *
https://www.facebook.com/groups/toanvd.vdc Trang 79
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
x 22 f x 0
x 22 f x a 1 ;0
Ta có: f x 2 2
f x 3 .
x 22 f x b 2
x 22 f x c 3 ; 2 x 2
Xét phương trình: x 2 2
f x 0
mà f x 0 có hai nghiệm f x 0 x 2
2 . f x 0 có ba nghiệm. NHÓ
Xét phương trình: x 2 2
f x a 0 M a Do x 2 2 0 ; x 2
không là nghiệm của phương trình f x 0 TO x 22 ÁN Xét a 2a g x g x 2 3 VD x 2 x 2 – V Bảng biến thiên: D C
Từ bảng biến thiên với a
f x 0 f x có 2 nghiệm. NHÓ x 2 2 M Tương tự: 2 x 2 2
f x b và x 2 f x c ,
b c 0 mỗi phương trình cũng có hai TO nghiệm. ÁN VD
Vậy số nghiệm của phương trình f x 2 2
f x 3 là 9 nghiệm. – V D
Câu 44. [PHÁT TRIẾN CÂU 50 – MÃ 101 – TN 2020] Cho hàm số y f x có đồ thị như hình C vẽ.
https://www.facebook.com/groups/toanvd.vdc Trang 80
NHÓM TOÁN VD – VDC PBM - Phát triển đề thi tốt nghiệp THPT năm 2020 - Môn Toán - Mã đề 101
Số nghiệm thực của phương trình f f x f x 0 là NHÓ A. 20 . B. 24 . C. 10 . D. 4 . M TO
Thực hiện : Thầy Dinh An– Thầy Huỳnh Đức Vũ. ÁN Lời giải VD Chọn A – V D
Đặt f x t 0. Khi đó phương trình trở thành C
f t t , 1 .
Từ đồ thị hàm số ta có NHÓ
t a,0 a 1 M
t b ,a b 1 TO
Phương trình 1 có 4 nghiệm
t c ,1 c 2 ÁN
t d,2 d VD –
Khi đó các phương trình f x a , f x b , f x c mỗi phương trình có 6 nghiệm phân biệt V DC
không trùng nhau. Phương trình f x d có 2 nghiệm phân biệt không trùng với nghiệm của 3 phương trình trên.
Vậy phương trình đã cho có 20 nghiệm phân biêt. ----HẾT----
https://www.facebook.com/groups/toanvd.vdc Trang 81




