Phát triển các bài toán VD – VDC trong đề thi TN THPT 2021 môn Toán (đợt 1)

Tài liệu gồm 43 trang, được biên soạn bởi tập thể quý thầy, cô giáo nhóm Strong Team Toán VD – VDC, phát triển các bài toán mức độ vận dụng – vận dụng cao (câu 36 – 37 – 38 – 39 – 40 – 41 – 42 – 43 – 44 – 45 – 46 – 47 – 48 – 49 – 50) trong đề thi chính thức tốt nghiệp Trung học Phổ thông năm 2021 môn Toán

21 11 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 1

PHÁT TRIỂN ĐỀ THI TN-THPT-QG BGD 2021

MÔN: TOÁN

THỜI GIAN: 90 PHÚT

SP ĐƯỢC THỰC HIỆN BỞI TỔ 27-STRONG TEAM

ĐỀ BÀI

Câu 1. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 36) Cho hình lăng trụ đứng

.ABC A B C

  

có

đáy

là tam giác đều cạnh

, cạnh bên

2AA a





(tham khảo hình bên). Góc giữa



và



bằng

30

60

45

120

Câu 2. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 36) Cho hình lăng trụ tam giác đều

.ABC A B C

  

có

AB a

và

3AA a





(tham khảo hình bên).

Góc giữa hai đường thẳng



và



bằng

30

. B.

90

. C.

45

. D.

60

Câu 3. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 36) Cho hình lập phương

.ABCD A B C D

   

(hình vẽ bên dưới). Góc giữa hai đường thẳng

và



bằng

45

. B.

90

. C.

30

. D.

60

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 2

Câu 4. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 37) Với mọi số thực

thỏa mãn

 

3 3 27

log 2log 3log 1 1a b c   

, khẳng định đúng là

20a b c  

. B.

 

2 1 3a b c   

 

13a c b

. D.

 

19a c b

Câu 5. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 37) Với mọi số thực

thỏa mãn

3log 2log 3ab

, khẳng định nào dưới đây đúng?

8ab 

. B.

6ab 

. C.

3 2 8ab

. D.

3 2 6ab

Câu 6. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 37) Cho các số thực dương

,,a b x

thỏa mãn

1 1 1

2 2 2

log log log

x a b

. Mệnh đề nào dưới đây đúng?

x a b

. B.

x a b

. C.

x a b





. D.

x a b





Câu 7. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 38) Nếu

 

d2f x x







thì

 

2dx f x x









bằng

. B.

. C.

. D.

Câu 8. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 38) Nếu

 

d2f x x 



thì

 

2 3 1 df x x x









bằng

30

. B.

28

. C.

26

. D.

27

Câu 9. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 38) Cho

 

d5f x x







. Khi đó

 

2sin dI f x x x









bằng

7I 

. B.





. C.

3I 

. D.





Câu 10. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 38) Cho

 

d2f x x







và

 

d1g x x







. Khi

đó

   

2 3 dI x f x g x x





  



bằng

I 

. B.

I 

. C.

I 

. D.

I 

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 3

Câu 11. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 39) Cho hàm số

 

3 2 1khi 2

2 3 khi 2

x x x



  









Gọi

là nguyên hàm của

trên thỏa mãn

 

14F 

. Giá trị của

   

2 0 3 3FF

bằng

. B.

. C.

61

. D.

69

Câu 12. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 39) Cho hàm số

 

2 3 1khi 0

1 khi 0

x x x



  













Biết

 

là một nguyên hàm của hàm số

 

thỏa mãn

 

F 

. Giá trị của

   

4 4 3FF

nằm trong khoảng nào?

 

52;53

. B.

 

53;54

. C.

 

54;55

. D.

 

55;56

Câu 13. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 39) Cho hàm số

 

3 2 1khi 3

4 32 khi 3

x x x



  





  



Giả sử

là nguyên hàm của

trên thỏa mãn

 

14F 

. Giá trị của

   

3 2 4FF

bằng

69

. B.

25

. C.

45

. D.

53

Câu 14. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 40) Có bao nhiêu số nguyên

thỏa mãn

 

8 2 . log 2 21 4 0?





   



. B.

. C.

. D.

Câu 15. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 40) Có bao nhiêu số nguyên

thỏa mãn

 

9 3 .9 log 2 18 5 0

x x x



   

A. 1 B. Vô số. C. 17. D. 16.

Câu 16. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 40) Có bao nhiêu số nguyên

thỏa mãn

 

log 25 2. 2 2 .4 0

x x x



   

A. 1 B. 18. C. 16. D. 17.

Câu 17. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 40) Có bao nhiêu số nguyên

thỏa mãn

 

9 27 log 2022 1 0



   





2020

. B.

2022

. C.

. D.

Câu 18. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 41) Cho hàm số bậc bốn

 

y f x

có đồ thị là

đường cong trong hình bên

Số nghiệm thực phân biệt của phương trình

 

2 1 0f f x 

là

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 4

. B.

. C.

. D.

Câu 19. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 41) Cho hàm số

 

có bảng biến thiên như

Số nghiệm thực phân biệt của phương trình

 

4 2 1f x x

là

. B.

. C.

. D.

Câu 20. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 41) Cho hàm số

 

y f x

có bảng biến thiên

như sau

Số nghiệm thuộc đoạn









của phương trình

 

cos 2f f x 

là

. B.

. C.

. D.

Câu 21. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 42) Một hình nón đỉnh

, đáy là hình tròn tâm

và

SO a

. Một mặt phẳng

 

qua đỉnh

cắt đường tròn

 

theo dây cung

sao cho

góc

90AOB 

và cách

một khoảng

. Diện tích xung quanh hình nón bằng



. B.



. C.



. D.

2 10



Câu 22. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 42) Cắt hình nón

 

bởi mặt phẳng

 



đi

qua đỉnh và có khoảng cách đến tâm

của đường tròn đáy là

ta được thiết diện là tam giác

đều cạnh

. Thể tích của

 

bằng



. B.

4 13



. C.

8 13



. D.

7 a



Câu 23. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 42) Cho hình trụ đứng có hai đáy là hai đường

tròn tâm

và tâm



, bán kính bằng

, chiều cao hình trụ bằng

. Mặt phẳng đi qua trung

điểm



và tạo với



một góc

30

, cắt đường tròn đáy tâm

theo dây cung

. Độ dài

đoạn

là

. B.

. C.

. D.

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 5

Câu 24. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 42) Hình nón

 

có đỉnh

, tâm đường tròn

đáy là

, góc ở đỉnh bằng

120

. Một mặt phẳng qua

cắt hình nón

 

theo thiết diện là tam

giác vuông

SAB

. Biết rằng khoảng cách giữa hai đường thẳng

và

bằng

. Tính diện tích

xung quanh

của hình nón

 

36 3





. B.

27 3





. C.

18 3





. D.





Câu 25. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 43) Trên tập hợp các số phức, xét phương trình

 

2 1 5 0z m z m m    

(

là tham số thực). Gọi

là tập hợp các giá trị nguyên

để

phương trình đó có nghiệm

thỏa mãn

32zz

. Tổng các phần tử của tập

là

. B.

. C.

. D.

Câu 26. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 43) Trong tập số phức, cho phương trình

 

2 2 1 3 2 0,z m z m m m      

. Có bao nhiêu giá trị nguyên của

trong đoạn

 

0;2021

để phương trình có 2 nghiệm phân biệt

;zz

thỏa mãn

zz

A. 2016. B. 202 C. 202 D. 2017.

Câu 27. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 44) Cho hai số phức

thỏa

11iz 

và

2zi

. Khi biểu thức

23P z z

đạt giá trị nhỏ nhất thì

2zz

bằng

. B.

. C.

. D.

Câu 28. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 44) Xét các số phức

thỏa mãn

2z 

2 5 1iw i  

. Khi

4z wz

đạt giá trị nhỏ nhất thì

zw

bằng

25

. B.

 

2 1 5

. C.

15

. D.

2 5 2

Câu 29. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 44) Cho hai số phức

,zz

thỏa mãn

3 5 2zi  

và

26i z i  

. Khi

2T i z z

đạt giá trị nhỏ nhất thì

zz

bằng

5629

. B.

. C.

. D.

2259

Câu 30. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 44) Cho hai số phức

,zz

thỏa mãn

35zi  

và

15z i z i    

. Khi

T z i z

đạt giá trị nhỏ nhất thì phần thực

của

5zz

bằng

. B.

. C.

18

. D.

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 6

Câu 31. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 45) Trong không gian

Oxyz

, cho đường thẳng

2 3 1

x y z







. Hình chiếu vuông góc của

trên mặt phẳng

 

: 5 0P x y z   

là đường

thẳng có phương trình

1 1 1

x y z



. B.

2 5 2

1 1 1

x y z  



2 5 2

4 3 1

x y z  





. D.

2 5 2

2 5 7

x y z  





Câu 32. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 45) Trong không gian

Oxyz

cho đường thẳng

d y t













  



. Hình chiếu vuông góc của

trên mặt phẳng

 

Oxz

là đường thẳng có phương

trình

















. B.













  



. C.

















. D.













  



Câu 33. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 45) Trong không gian

Oxyz

, cho đường thẳng

1 1 3

1 2 2

x y z

  





. Hình chiếu vuông góc của

trên mặt phẳng

 

:2 2 3 0P x y z   

là

đường thẳng có phương trình

2 1 5

17 10 14

x y z  



. B.

2 1 5

17 10 14

x y z  





2 1 5

17 10 14

x y z  





. D.

2 1 5

17 10 14

x y z  





Câu 34. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 45) Trong không gian

Oxyz

, cho đường thẳng

1 2 3

2 4 1

x y z

  



. Hình chiếu vuông góc của

trên mặt phẳng

 

: 2 1 0P x y z   

là

đường thẳng có phương trình

2 4 1

x y z



. B.

2 1 5

2 4 1

x y z  



2 4 3

x y z





. D.

2 1 5

2 4 3

x y z  





Câu 35. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 46) Cho hàm số

 

y f x x ax bx c    

có

đồ thị

 

, đường thẳng

y mx n

là tiếp tuyến của

 

tại điểm có hoành độ

1x 

và cắt

 

tại điểm có hoành độ bằng

(với

và

là các số thực). Diện tích hình phẳng

giới hạn bởi đồ thị hàm số

 

f x mx n





và trục hoành bằng

16.ln2

. B.

. C.

ln2

. D.

16.ln2

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 7

Câu 36. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 46) Cho hàm số

 

y f x ax bx c   

với

,,abc

. Biết rằng hàm số

   

g x f x





có hai giá trị cực trị là

và

3

. Diện tích hình

phẳng giới hạn bởi đồ thị hàm số

 

và

   

2 .e

h x ax b





bằng

. B.

. C.



. D.

ee

Câu 37. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 46) Cho hàm số

 

4 3 2

f x x ax bx cx d    

với

, , ,a b c d 

. Biết hàm số

         

g x f x f x f x f x

  

   

có ba giá trị cực trị là

14

;

4; 6. Diện tích hình phẳng giới hạn bởi các đường

 





và

1y 

bằng

2ln3

. B.

ln10

. C.

ln3

. D.

ln5

Câu 38. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 46) Cho hàm số

 

3f x x bx cx d   

với

,,b c d 

. Biết hàm số

       

g x f x f x f x

 

  

có hai giá trị cực trị là

12; 6

. Diện tích

hình phẳng giới hạn bởi các đường

 





và

1y 

bằng

2ln3

. B.

ln6

. C.

2ln 2

. D.

ln5

Câu 39. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 46) Cho hai hàm số

 

1f x x ax bx   

và

 

3g x cx dx  

 

, , ,a b c d 

. Biết rằng đồ thị của hàm số

 

y f x

và

 

y g x

cắt nhau

tại hai điểm có hoành độ lần lượt là

2

; 1. Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích

bằng

. B.

. C.

. D.

Câu 40. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 47) Có bao nhiêu cặp số nguyên

 

;xy

thỏa

mãn

2 2021x

và

 

2 log 2 2

x x y



   

A. 2020. B. 10. C. 9. D. 2019.

Câu 41. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 47) Có bao nhiêu số nguyên

sao cho tồn tại









thỏa mãn

 

8 1 .8

x xy x





A. 7. B. C. 6. D. 5.

Câu 42. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 47) Có bao nhiêu số nguyên

5y 

để tồn tại số

thực

thỏa mãn

 

15 6

log 4 3 1 log 2x y x x y    

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 8

Câu 43. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 48) Cho khối hộp chữ nhật

.ABCD A B C D

   

có

AB a

23AD a

. Gọi

là trung điểm cạnh

, góc giữa hai mặt phẳng

 

A BI



và

 

ABCD

bằng

60

. Thể tích của khối hộp chữ nhật đã cho bằng

. B.

. C.

23a

. D.

33a

Câu 44. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 48) Cho hình hộp chữ nhật

.ABCD A B C D

   

có

đáy là hình vuông cạnh

, góc giữa hai mặt phẳng

 

A BM



và

 

ABCD

bằng

với

là

trung điểm

. Thể tích khối hộp chữ nhật đã cho bằng

2 15

. B.

. C.

. D.

2 15

Câu 45. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 48) Cho khối lăng trụ đứng

.ABC A B C

  

có đáy

là tam giác đều. Mặt phẳng

 

A BC



tạo với đáy góc

30

và tam giác

A BC



có diện tích bằng

Thể tích

của khối lăng trụ đã cho là

64 3

. B.

. C.

16 3

. D.

Câu 46. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 49) Trong không gian

Oxyz

, cho ba điểm

   

2;3;9 , 2;3;4AB

và

 

2;15;9 .C

Một mặt cầu

 

luôn đi qua

, AB

và tiếp xúc với mặt

phẳng

 

Oxy

tại

Biết rằng khi

đạt giá trị nhỏ nhất thì tọa độ tâm của mặt cầu

 

là

 

;;I a b c

. Khi đó

2a b c

bằng

13

. B. 9. C. 2 D. 6.

Câu 47. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 49) Trong không gian

Oxyz

, cho hai điểm

 

5;1;1A

và điểm

 

5;0;5B

. Xét hai điểm

và

thay đổi thuộc mặt phẳng

 

: 2 0P x z  

sao cho

2MN 

. Giá trị lớn nhất của

AM BN

bằng

3 11

. B.

. C.

. D.

Câu 48. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 49) Trong không gian với hệ tọa độ

Oxyz

, cho

mặt phẳng

 

:2 2 15 0P x y z   

. Gọi

là điểm di động trên

 

là điểm thuộc tia

sao cho

. 10OM ON 

. Khoảng cách nhỏ nhất từ

đến mặt phẳng

 

bằng bao nhiêu?

. B.

. C.

. D.

Câu 49. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 50) Cho hàm số

 

y f x

có đạo hàm

   

 

7 9 ,f x x x x



    

. Có bao nhiêu giá trị nguyên dương của tham số

để hàm số

 

23g x f ax bx m   

với

.0ab

có ít nhất 3 điểm cực trị?

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 9

Câu 50. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 50) Cho hàm số

 

liên tục trên , có bảng

biến thiên dưới đây

Có bao nhiêu giá trị nguyên của tham số

để hàm số

 

6 5 2021y f x m   

có 3 điểm cực

đại?

. B.

. C.

. D.

HẾT

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 10

BẢNG ĐÁP ÁN

LỜI GIẢI CHI TIẾT

Câu 1. [1H3-4.6-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 36) Cho hình lăng trụ đứng

.ABC A B C

  

có đáy là tam giác đều cạnh

, cạnh bên

2AA a





(tham khảo hình bên). Góc giữa



và



bằng

30

60

45

120

Lời giải

FB tác giả: Nguyễn Hường

Ta có:

3AB BC a





   

..AB BC BB A B BB B C

       

  

2 2 2 2

B B A B B C a a a

    

    

 

cos ,

. 3 2

AB BC

AB BC a



   



Vậy góc giữa



và



bằng

60

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 11

Câu 2. [1H3-4.6-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 36) Cho hình lăng trụ tam giác đều

.ABC A B C

  

có

AB a

và

3AA a





(tham khảo hình bên).

Góc giữa hai đường thẳng



và



bằng

30

. B.

90

. C.

45

. D.

60

Lời giải

FB tác giả: Liễu Hoàng

Ta có:

//AA CC



nên góc giữa hai đường thẳng



và



là góc giữa hai đường thẳng



và



và bằng góc

A AB



(do

A AB



nhọn).

Tam giác

AA B



vuông tại



nên

tan 30

A AB A AB

   

    

Vậy góc giữa hai đường thẳng



và



bằng

30

Câu 3. [1H3-4.6-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 36) Cho hình lập phương

.ABCD A B C D

   

(hình vẽ bên dưới). Góc giữa hai đường thẳng

và



bằng

45

. B.

90

. C.

30

. D.

60

Lời giải

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 12

FB tác giả: Đinh Ngọc

Ta có:

   

, , 60AC A D A C A D DA C 

     

  

Vì

A D A C C D

   



Câu 4. [2D2-3.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 37) Với mọi số thực

thỏa

mãn

 

3 3 27

log 2log 3log 1 1a b c   

, khẳng định đúng là

20a b c  

. B.

 

2 1 3a b c   

 

13a c b

. D.

 

19a c b

Lời giải

FB tác giả: Hiếu Lưu

Ta có:

 

3 3 27

log 2log 3log 1 1a b c   

 

log log 3log 1 1a b c    

 

3 3 3 3

log log 1 log 3 loga c b    

 

log 1 log 3a c b  





 

13a c b  

Câu 5. [2D2-3.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 37) Với mọi số thực

thỏa

mãn

3log 2log 3ab

, khẳng định nào dưới đây đúng?

8ab 

. B.

6ab 

. C.

3 2 8ab

. D.

3 2 6ab

Lời giải

FB tác giả: Trần Minh Hưng

Ta có:

3log 2log 3ab

log log 3ab  

log 3ab

3 2 3

2ab

8ab

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 13

Câu 6. [2D2-3.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 37) Cho các số thực dương

,,a b x

thỏa mãn

1 1 1

2 2 2

log log log

x a b

. Mệnh đề nào dưới đây đúng?

x a b

. B.

x a b

. C.

x a b





. D.

x a b





Lời giải

FB tác giả: Quang Trí

Ta có:

1 1 1

2 2 2

log log log

x a b

1 1 1

2 2 2

log log logx a b



  

log log .x a b





.x a b





Câu 7. [2D3-2.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 38) Nếu

 

d2f x x







thì

 

2dx f x x









bằng

. B.

. C.

. D.

Lời giải

FB tác giả: Nguyễn Thị Quỳnh Nga

Ta có:

   

3 3 3

1 1 1

2 d 2 d d 8 2 6.x f x x x x f x x

  

     





  

Câu 8. [2D3-2.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 38) Nếu

 

d2f x x 



thì

 

2 3 1 df x x x









bằng

30

. B.

28

. C.

26

. D.

27

Lời giải

FB tác giả: Quang Thoại

Ta có

   

 

3 3 3

1 1 1

2 3 1 d 2 d 3 1 df x x x f x x x x



     



  

+ Ta có

 

2 d 4f x x 



+ Mặt khác

   

3 1 d 24x x x x      



Vậy

 

2 3 1 d 4 24 28f x x x



      





SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 14

Câu 9. [2D3-2.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 38) Cho

 

d5f x x







. Khi đó

 

2sin dI f x x x









bằng

7I 

. B.





. C.

3I 

. D.





Lời giải

FB tác giả: Duyên Nguyễn

Ta có:

   

2 2 2

0 0 0

2sin d d +2 sin dI f x x x f x x x x

  

  





  

   

d 2cos 5 2 0 1 7f x x x



     



Vậy:

7I 

Câu 10. [2D3-2.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 38) Cho

 

d2f x x







và

 

d1g x x







. Khi đó

   

2 3 dI x f x g x x





  



bằng

I 

. B.

I 

. C.

I 

. D.

I 

Lời giải

FB tác giả: Duyên Nguyễn

Ta có:

   

2 3 dI x f x g x x



  







   

2 d 3 d

f x x g x x





  





 

2.2 3 1

  



Vậy

I 

Câu 11. [2D3-2.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 39) Cho hàm số

 

3 2 1khi 2

2 3 khi 2

x x x



  









. Gọi

là nguyên hàm của

trên thỏa mãn

 

14F 

. Giá trị

của

   

2 0 3 3FF

bằng

. B.

. C.

61

. D.

69

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 15

Lời giải

FB tác giả: Son Que Nguyen.

Ta có:

   

2 d 3 dI f x x f x x



       

2 0 2 1 3 3 3 1F F F F   





     

2 0 3 3 1F F F  

Do đó

   

2 0 3 3 4F F I  

Mà

   

2 d 2 2 3 d 8f x x x x    



và

   

 

3 2 3

1 1 2

3 d 3 2 3 d 3 3 2 1 df x x x x x x x    

  

57

Do đó

65I 

. Vậy

   

2 0 3 3 4 69F F I    

Câu 12. [2D3-2.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 39) Cho hàm số

 

2 3 1khi 0

1 khi 0

x x x



  













. Biết

 

là một nguyên hàm của hàm số

 

thỏa mãn

 

F 

. Giá trị của

   

4 4 3FF

nằm trong khoảng nào?

 

52;53

. B.

 

53;54

. C.

 

54;55

. D.

 

55;56

Lời giải

FB tác giả: Trịnh Trung Hiếu

Ta có

     

 

d 0 2 1- d

f x x F F x x





    



⇒

   

2 2 5

0 2 1

3 3 3



     

. Hàm số

 

liên tục tại

0x 

Mặt khác

 

d 1 d

f x x x x x x C    



khi 0x 

 

F 

⇒

 

C    

⇒

1C 

Vậy

 

F x x x  

khi 0x 

. Từ đó ta tính được

 

F 

Xét

 

2 3 2

d 2 3 1 d

f x x x x x x x x C      



khi 0x 

Ta có

 

0 1 1FC  

Vậy

 

F x x x x   

khi 0x 

. Từ đó ta tính được

 

4 3 4. 34

F 

Vậy

   

55 157

4 4 3 34 52,(3)

FF     

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 16

Câu 13. [2D3-2.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 39) Cho hàm số

 

3 2 1khi 3

4 32 khi 3

x x x



  





  



. Giả sử

là nguyên hàm của

trên thỏa mãn

 

14F 

. Giá

trị của

   

3 2 4FF

bằng

69

. B.

25

. C.

45

. D.

53

Lời giải

FB tác giả: Hiếu Lê

Ta có

           

3 d d 3 1 3 2 4 1I f x x f x x F F F F



        



Do đó

             

3 2 4 2 1 3 2 4 8 3 2 4 8I F F F F F F F I            

Mà

 

3 d 3 3 2 1 d 27f x x x x x



      



và

 

4 3 4

1 1 3

d 3 2 1 d 4 32 d 34f x x x x x x x      

  

Suy ra

27 34 61I     

Vậy

   

3 2 4 61 8 53FF      

Câu 14. [2D2-6.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 40) Có bao nhiêu số nguyên

thỏa mãn

 

8 2 . log 2 21 4 0?





   



. B.

. C.

. D.

Lời giải

FB tác giả: Quang Thoại

Điều kiện:

x 

 

Trường hợp 1:

   

2 3 2

8 2 0 2 2

3 2 0

2 21 9

log 2 21 4 0 log 2 21 4

x x x x











  

   



   



  



   



   









    





  







Kết hợp với điều kiện

 

ta được

 

 

6; 2 1x   

Trường hợp này ta được

giá trị nguyên của

thỏa yêu cầu.

Trường hợp 2:

   

2 3 2

8 2 0 2 2

3 2 0

2 21 9

log 2 21 4 0 log 2 21 4

x x x x





  





   





  

   





    







Trường hợp này không có giá trị nào của

thỏa mãn.

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 17

Vậy có

giá trị nguyên của

thỏa ycbt gồm

 

6; 5; 4; 3; 2;1    

Câu 15. [2D2-6.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 40) Có bao nhiêu số nguyên

thỏa mãn

 

9 3 .9 log 2 18 5 0

x x x



   

A. 1 B. Vô số. C. 17. D. 16.

Lời giải

FB tác giả: Nguyễn Thanh Bằng

Điều kiện:

 

9*x 

Trường hợp 1:

 

2 3 2

9 3 .9 0

2 3 2

2 50

log 2 18 5 0

2 18 2

2 25

x x x



























  



   

   









  





















Kết hợp với điều kiện

 

ta được





9;25x 

Mà

 

10;11;...;25xx  



có 16 giá trị nguyên của

thỏa mãn.

Trường hợp 2:

 

2 3 2

9 3 .9 0

2 3 2

2 50

log 2 18 5 0

2 18 2

x x x







  





  

  

   



  















Trường hợp này không có giá trị nào của

thỏa mãn.

Kết hợp các trường hợp, ta có tất cả 16 giá trị nguyên của

thỏa mãn đề.

Câu 16. [2D2-6.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 40) Có bao nhiêu số nguyên

thỏa mãn

 

log 25 2. 2 2 .4 0

x x x



   

A. 1 B. 18. C. 16. D. 17.

Lời giải

FB tác giả: Nguyễn Thanh Bằng

Điều kiện:

 

25 *x 

Ta có:

 

log 25 2. 2 2 .4 0

x x x



   

 

log 25 2 0

25 3

16 1

2 2 .4 0

x x x





  











       

   



















Kết hợp với điều kiện

 

ta được

 

16;1x

Mà

 

15; 14;...;0xx    



có 16 giá trị nguyên của

thỏa mãn.

Vậy có 16 giá trị nguyên của

thỏa mãn yêu cầu của bài toán.

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 18

Câu 17. [2D2-6.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 40) Có bao nhiêu số nguyên

thỏa mãn

 

9 27 log 2022 1 0



   





2020

. B.

2022

. C.

. D.

Lời giải

Tác giả: Hồ Hữu Tình

Điều kiện

 

2022 * .x 

Ta có

 

9 27 0

log 2022 1 0

9 27 log 2022 1 0

9 27 0

log 2022 1 0













  











    



















  









Khi đó

 

2 3 0

1 2020

log 2022 1

2022 2

2022

2020





























      

   



  











  















 

2 3 0

log 2022 1

2022 2

2022

2020





















      

   



  





  











Kết hợp điều kiện

 

ta có tất cả

giá trị nguyên của

là

2021; 2020; 0; 1

Câu 18. [2D1-5.3-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 41) Cho hàm số bậc bốn

 

y f x

có đồ thị là đường cong trong hình bên

Số nghiệm thực phân biệt của phương trình

 

2 1 0f f x 

là

. B.

. C.

. D.

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 19

Lời giải

Tác giả: Tăng Văn Vũ

Ta biến đổi:

 

2 1 0

f f x f f x    

Căn cứ vào đồ thị hàm số đã cho ta thấy:

 

   

f x a a

f x b b

f f x

f x c c

f x d d



  



   



  



  







Căn cứ vào đồ thị hàm số

 

y f x

ta có:

+ Với

1a 

, phương trình

 

f x a

vô nghiệm.

+ Với

10b  

, phương trình

 

f x b

có 4 nghiệm thực phân biệt.

+ Với

01c

, phương trình

 

f x c

có 2 nghiệm thực phân biệt.

+ Với

1d 

, phương trình

 

f x d

có 2 nghiệm thực phân biệt.

Các nghiệm của các phương trình

 

f x a

 

f x b

 

f x c

và

 

f x d

là các nghiệm

thực phân biệt.

Vậy phương trình đã cho có

nghiệm thực phân biệt.

Câu 19. [2D1-5.3-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 41) Cho hàm số

 

có bảng

biến thiên như sau

Số nghiệm thực phân biệt của phương trình

 

4 2 1f x x

là

. B.

. C.

. D.

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 20

Lời giải

Tác giả: Tăng Văn Vũ

Dựa vào bảng biến thiên ta thấy:

 

2 4 2 4

4 2 0

4 2 1 4 2 0 2

4 2 2

x x a a

f x x x x b b

x x c c



  



      



  





Vẽ đồ thị (hoặc bảng biến thiên) của hàm số

42y x x

Căn cứ vào đồ thị hàm số

42y x x

, ta có:

+ Với

0a 

, phương trình

 

4 2 1x x a

có 2 nghiệm thực phân biệt.

+ Với

02b

, phương trình

 

4 2 2x x b

có 4 nghiệm thực phân biệt.

+ Với

2c 

, phương trình

 

4 2 3x x c

vô nghiệm.

Các nghiệm của các phương trình

 

và

 

là các nghiệm thực phân biệt.

Vậy phương trình đã cho có

nghiệm thực phân biệt.

Câu 20. [2D1-5.3-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 41) Cho hàm số

 

y f x

có bảng

biến thiên như sau

Số nghiệm thuộc đoạn









của phương trình

 

cos 2f f x 

là

. B.

. C.

. D.

Lời giải

FB tác giả: Phạm Hùng

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 21

Từ bảng biến thiên ta suy ra:

 

cos 1

cos 2

cos 1

f f x















TH1:

 

cos 1fx

Đặt

costx

 

1;1t 

Khi đó phương trình

 

cos 1fx

trở thành

 

1ft

, với

 

1;1t 

Đây là phương trình có hoành độ giao điểm của đồ thị hàm số

 

y f t

và đường thẳng

1y 

Dựa vào bảng biến thiên, ta có

 

  



   







phương trình vô nghiệm.

TH2:

 

cos 1fx

Tương tự TH1: Đặt

costx

 

1;1t 

 

   

 

   

; 1 L

1;0

0;1

1; L

   





  











  



+ Với

 

1;0tn  

Ứng với mỗi giá trị

 

1;0t 

thì phương trình

cos xt

có

nghiệm phân biệt thuộc









+ Với

 

0;1tp

Ứng với mỗi giá trị

 

0;1t 

thì phương trình

cos xt

có

nghiệm phân biệt thuộc









Hiển nhiên,

nghiệm trong những trường hợp trên đều khác nhau.

Vậy phương trình đã cho có

nghiệm thuộc đoạn









Câu 21. [2H2-1.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 42) Một hình nón đỉnh

, đáy là

hình tròn tâm

và

SO a

. Một mặt phẳng

 

qua đỉnh

cắt đường tròn

 

theo dây cung

sao cho góc

90AOB 

và cách

một khoảng

. Diện tích xung quanh hình nón bằng



. B.



. C.



. D.

2 10



Lời giải

FB tác giả: Minh Trí

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 22

Gọi

là trung điểm của

. Kẻ

OH SI

2 2 2

1 1 1

OH SO OI



2 2 2 2

1 4 1 3

OI a a a

   

OI

Tam giác

OAB

vuông cân tại

nên:

AB OI

R OA OB  

Suy ra:

2 2 2

6 15

SB SO OB a



    





Diện tích xung quanh của hình nón:

6 15 10

3 3 3

a a a

S Rl





  

Câu 22. [2H2-1.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 42) Cắt hình nón

 

bởi mặt

phẳng

 



đi qua đỉnh và có khoảng cách đến tâm

của đường tròn đáy là

ta được thiết

diện là tam giác đều cạnh

. Thể tích của

 

bằng



. B.

4 13



. C.

8 13



. D.

7 a



Lời giải

FB tác giả: Shangri La

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 23

Gọi

là tâm đường tròn đáy và thiết diện là tam giác

SAB

đều cạnh

Gọi

là trung điểm của

Kẻ

OK SH

, khi đó

 

d , 1

a SO OH

O SK

SO OH



  



Mặt khác

SAB

đều có cạnh

suy ra

4 . 2 3

SH a a

Lại có

2 2 2 2 2

12 .OH SH SO a SO   

Thay vào

 

ta được

2 2 2 2

2 2 2

3 . 12 . 12

a SO a SO SO a SO

SO a

SO a SO



   



Ta có

   

4 3 7OA a a a  

Vậy

 

.7 .3 7

V a a a





Câu 23. [2H2-1.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 42) Cho hình trụ đứng có hai đáy

là hai đường tròn tâm

và tâm



, bán kính bằng

, chiều cao hình trụ bằng

. Mặt phẳng đi

qua trung điểm



và tạo với



một góc

30

, cắt đường tròn đáy tâm

theo dây cung

. Độ dài đoạn

là

. B.

. C.

. D.

Lời giải

FB tác giả: Hoàng Yến

Gọi

lần lượt là trung điểm của



và

Ta có

 

; ; 30OO ABM OO MN OMN



   

Tam giác

OMN

vuông tại

có

tan .ON OMN OM

tan30 .

ON a   

2 2 2

AB NB OB ON a     

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 24

Câu 24. [2H2-1.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 42) Hình nón

 

có đỉnh

, tâm

đường tròn đáy là

, góc ở đỉnh bằng

120

. Một mặt phẳng qua

cắt hình nón

 

theo thiết

diện là tam giác vuông

SAB

. Biết rằng khoảng cách giữa hai đường thẳng

và

bằng

Tính diện tích xung quanh

của hình nón

 

36 3





. B.

27 3





. C.

18 3





. D.





Lời giải

FB tác giả: Hoàng Yến

Theo giả thiết ta có tam giác

SAB

vuông tại

và

3OH 

và

60BSO 

Gọi

là bán kính đường tròn đáy của hình nón thì đường sinh

sin60

l SB l   



SAB

vuông tại S nên:

AB l r

. Suy ra

BH AB

Xét tam giác

OBH

vuông tại

, ta có

9 3 3

rr   

Vậy

18 3

S rl





Câu 25. [2D4-4.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 43) Trên tập hợp các số phức, xét

phương trình

 

2 1 5 0z m z m m    

(

là tham số thực). Gọi

là tập hợp các giá trị

nguyên

để phương trình đó có nghiệm

thỏa mãn

32zz

. Tổng các phần tử của tập

là

. B.

. C.

. D.

Lời giải

FB tác giả: Nam Hồng Lê

zz

nên

0 0 0 0 0

3 2 3 2 0 2       z z z z z

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 25

( 1) 5 3 1



      m m m m

TH1: Nếu

0 3 1 0



       mm

, phương trình có 2 nghiệm thực

Khi đó

22   zz

Thay

2z

vào phương trình ta được:

 

9 8 0 TM





   







Thay

2z

vào phương trình ta được:

 

0 TM





  







TH2: Nếu

0 3 1 0



       mm

, phương trình có 2 nghiệm phức

,zz

thỏa mãn

2 1 1 2

,2z z z z  

. Khi đó

1 2 1

5 41

. 5 4

z z z m m m



     

(Không thỏa mãn).

Vậy

 

0;1;8S

Suy ra tổng là

Câu 26. [2D4-4.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 43) Trong tập số phức, cho phương

trình

 

2 2 1 3 2 0,z m z m m m      

. Có bao nhiêu giá trị nguyên của

trong đoạn

 

0;2021

để phương trình có 2 nghiệm phân biệt

;zz

thỏa mãn

zz

A. 2016. B. 202 C. 202 D. 2017.

Lời giải

FB tác giả: Nhật Lê

Phương trình có 2 nghiệm phân biệt

TH1:

0 4 5 0





       







Phương trình đã cho có 2 nghiệm thực phân biệt

,zz

Theo định lí Vi-ét ta có:

 

z z m

z z m m

   







  





Theo đề bài ta có:

1 2 1 2

z z z z   

(vì

zz

)

0zz  

 

10m   

1m

(nhận)

TH2:





  







Phương trình luôn có 2 nghiệm phức

,zz

luôn thỏa mãn

zz

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 26

Vậy có 2017 giá trị

thỏa mãn.

Câu 27. [2D4-5.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 44) Cho hai số phức

thỏa

11iz 

và

2zi

. Khi biểu thức

23P z z

đạt giá trị nhỏ nhất thì

2zz

bằng

. B.

. C.

. D.

Lời giải

FB tác giả: Tho Nguyen

Ta có:

1 1 1

1 1 1 1iz i z z i

       

2 2 2zi  

Gọi

là điểm biểu diễn số phức



Tập hợp

thuộc đường tròn tâm

 

0 ; 2I 

2R 

Ta có:

2 2 2

2 2 3 3 6z i z i z i        

Gọi

là điểm biểu diễn số phức

3z



Tập hợp

thuộc đường tròn tâm

 

0; 3I









Suy ra:

23P z z MN  

min min

P MN

, , ,M N I I





thẳng hàng (

nằm giữa

và

)

3MN 

và

2IM II





là trung điểm của



. Từ đó ta tính được

   

0;0 , 0;3MN

2 0, 3 3z z i   

. Khi đó,

22z z i

. Vậy

22zz

Câu 28. [2D4-5.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 44) Xét các số phức

thỏa

mãn

2z 

2 5 1iw i  

. Khi

4z wz

đạt giá trị nhỏ nhất thì

zw

bằng

25

. B.

 

2 1 5

. C.

15

. D.

2 5 2

Lời giải

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 27

FB tác giả: Ngọ Thị Hằng

Ta có:

2 5 1 . 1 5 2 1

iw i i w w i



         

Ta có:

2 2 2

4 . . 2T z wz z wz z z wz z z z z w z z w z              

Đặt

 

,,z a bi a b  

, suy ra

2z z bi

. Vì

2 2 2zb    

Gọi

,AB

lần lượt là điểm biểu diễn của

,2w bi

nên:

thuộc đường tròn tâm

 

5; 2 ; 1IR  

thuộc trục

và

x  

2 2 2.4 8T AB MN    

Dấu

""

xảy ra khi và chỉ khi

 

4; 2 4 2 2 5A M w i w        

và

 

0; 2 2 2 1B N bi i b z a i          

2 1 4 3 3 3 2z a a a z i z               

Vậy

2 2 5zw  

Câu 29. [2D4-5.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 44) Cho hai số phức

,zz

thỏa

mãn

3 5 2zi  

và

26i z i  

. Khi

2T i z z

đạt giá trị nhỏ nhất thì

zz

bằng

5629

. B.

. C.

. D.

2259

Lời giải

FB tác giả: Dương Thị Lý

Giả sử

,MN

lần lượt là điểm biểu diễn cho số phức

2iz

và

z

Ta có

3 5 2 2 . 3 5 2 .2z i i z i i      

2 6 10 4iz i   

Suy ra tập hợp điểm

là đường tròn

 

tâm

 

6; 10I 

và bán kính

4R 

2 6 . 2 .6i z i i i z i i      

1 2 6zi    

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 28

Suy ra tập hợp điểm

là đường tròn

 

tâm

 

1;2J 

và bán kính

6R 

Ta có

2T i z z MN  

13 4 6 3minT IJ R R      

Đạt được khi

58 82

4 58 82 41 29

;

13 13

13 13 13 13 13

7 43 46 43 46

43 46

;

13 13 13 13 13

13 13

IM IJ iz i z i

IN IJ z i z i





  



      





  

     

  

   



   

      





  



  





Vậy

2 75 5629

13 13 13

z z i   

Câu 30. [2D4-5.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 44) Cho hai số phức

,zz

thỏa

mãn

35zi  

và

15z i z i    

. Khi

T z i z

đạt giá trị nhỏ nhất thì phần

thực của

5zz

bằng

. B.

. C.

18

. D.

Lời giải

FB tác giả: Dương Thị Lý

Giả sử

   

; , ;M x y N x y



lần lượt là điểm biểu diễn cho số phức

và

Ta có

       

3 5 3 1 5 3 1 5z i x y i x y            

Suy ra tập hợp điểm

là đường tròn

 

tâm

 

3;1I

và bán kính

5R 

2 2 2 2

1 5 1 5 1z i z i i z i i z i          

       

1 1 1 5x y i x y i

   

        

2 6 0xy



   

Suy ra tập hợp điểm

là đường thẳng

 

: 2 6 0d x y  

Ta có

T z i z MN  

 

minT d I d R  

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 29

Đạt được khi

là hình chiếu của

trên

và

IM IN

Suy ra

8 19

;







và

 

2;3M

23zi  

;

2 2 1 2

8 19 19 8

5 21 5

5 5 5 5

iz i z i z z i        

Vậy phần thực của

5zz

là

Câu 31. [2H3-3.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 45) Trong không gian

Oxyz

, cho

đường thẳng

2 3 1

x y z







. Hình chiếu vuông góc của

trên mặt phẳng

 

: 5 0P x y z   

là đường thẳng có phương trình

1 1 1

x y z



. B.

2 5 2

1 1 1

x y z  



2 5 2

4 3 1

x y z  





. D.

2 5 2

2 5 7

x y z  





Lời giải

FB tác giả: Bùi Tuấn Anh

Phương trình tham số của

: 2 3

d y t













  



Gọi

 

M d P

 

2 ;2 3 ; 1M t t t   

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 30

   

:2 2 3 1 5 0 1 2;5; 2M P t t t t M          

Gọi



là hình chiếu vuông góc của

lên mặt phẳng

 

là mặt phẳng chứa



và

   

 

, 4; 3; 1

Q d P

Q P n n

n u n

d Q n u



  





    





  





 

, 2; 5;7

d Q P

d P u n

u n n

d Q u n







  





    







  





Đường thẳng



qua điểm

 

2;5; 2M 

và nhận

 

2; 5;7

u   

là vectơ chỉ phương có

phương trình chính tắc là

2 5 2

2 5 7

x y z

  







Câu 32. [2H3-3.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 45) Trong không gian

Oxyz

cho

đường thẳng

d y t













  



. Hình chiếu vuông góc của

trên mặt phẳng

 

Oxz

là đường thẳng

có phương trình

















. B.













  



. C.

















. D.













  



Lời giải

FB tác giả: Phuong Tran

Mặt phẳng

 

:0Oxz y 

có véctơ chỉ phương là

 

1;1;2u 

   

1;0; 1d Oxz A  

. Gọi



là hình chiếu vuông góc của

trên

 

Oxz

A 

và



có véctơ chỉ phương là

 

1;0;2v 















  



Câu 33. [2H3-3.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 45) Trong không gian

Oxyz

, cho

đường thẳng

1 1 3

1 2 2

x y z

  





. Hình chiếu vuông góc của

trên mặt phẳng

 

:2 2 3 0P x y z   

là đường thẳng có phương trình

2 1 5

17 10 14

x y z  



. B.

2 1 5

17 10 14

x y z  





2 1 5

17 10 14

x y z  





. D.

2 1 5

17 10 14

x y z  





Lời giải

FB tác giả: Phuong Tran

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 31

có véctơ chỉ phương là

 

1;2; 2u 

Mặt phẳng

 

có véctơ pháp tuyến là

 

2; 2;1n 

Gọi đường thẳng

là hình chiếu vuông góc của

trên mặt phẳng

 

là mặt phẳng chứa

và



 

có véctơ pháp tuyến là

,un





và

   

a P Q

a

có véctơ chỉ phương là

 

, , 17; 10;14u n n



  



   

2; 1;5d P I   

Ia

2 1 5

17 10 14

x y z

  

  



Câu 34. [2H3-3.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 45) Trong không gian

Oxyz

, cho

đường thẳng

1 2 3

2 4 1

x y z

  



. Hình chiếu vuông góc của

trên mặt phẳng

 

: 2 1 0P x y z   

là đường thẳng có phương trình

2 4 1

x y z



. B.

2 1 5

2 4 1

x y z  



2 4 3

x y z





. D.

2 1 5

2 4 3

x y z  





Lời giải

FB tác giả: Phuong Tran

Gọi đường thẳng

là hình chiếu vuông góc của

trên

 

có véctơ chỉ phương là

 

2;4;1u 

và

đi qua

 

1;2;3M

Mặt phẳng

 

có véctơ pháp tuyến là

 

1; 1;2n 

Có

 

d P a

















nhận

 

2;4;1u 

làm véctơ chỉ phương

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 32

Gọi

là hình chiếu vuông góc của

trên

 

MH y t







  









mà

   

0;3;1H P H

a

đi qua

 

0;3;1H

2 4 1

x y z



  

Câu 35. [2D3-3.1-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 46) Cho hàm số

 

y f x x ax bx c    

có đồ thị

 

, đường thẳng

y mx n

là tiếp tuyến của

 

tại

điểm có hoành độ

1x 

và cắt

 

tại điểm có hoành độ bằng

(với

và

là các

số thực). Diện tích hình phẳng giới hạn bởi đồ thị hàm số

 

f x mx n





và trục hoành

bằng

16.ln2

. B.

. C.

ln2

. D.

16.ln2

Lời giải

FB tác giả: Dương Thái Bảo

Vì

   

f x mx n x ax b m x c n       

là hàm số bậc ba có hai nghiệm

1x 

(nghiệm

kép) và

2x 

nên

     

12f x mx n x x    

Đặt

       

12g x f x mx n x x     

, suy ra

 

33g x x





Phương trình hoành độ giao điểm

 

1 2 0





  







Diện tích hình phẳng cần tìm là

 

1 .2 d .2 d

3 16.ln 2

g x g x

S x x g x x





   



Câu 36. [2D3-3.1-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 46) Cho hàm số

 

y f x ax bx c   

với

,,abc

. Biết rằng hàm số

   

g x f x





có hai giá trị cực trị là

và

3

. Diện tích hình phẳng giới hạn bởi đồ thị hàm số

 

và

   

2 .e

h x ax b





bằng

. B.

. C.



. D.

ee

Lời giải

FB tác giả: Dương Thái Bảo

Ta có

       

' .e 2 .e

g x f x f x ax a b x b c







       





SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 33

Gọi

là hai nghiệm của

 



, khi đó

 



















và

 















Ta có phương trình hoành độ giao điểm

     

.e 2 .e 2 .e 0

x x x

f x ax b ax a b x b c

  







         









Vậy diện tích hình phẳng được giới hạn bằng

       

2 .e d d 8

S ax a b x b c x g x x g x g x







         





Câu 37. [2D3-3.1-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 46) Cho hàm số

 

4 3 2

f x x ax bx cx d    

với

, , ,a b c d 

. Biết hàm số

         

g x f x f x f x f x

  

   

có ba giá trị cực trị là

14

; 4; 6. Diện tích hình phẳng

giới hạn bởi các đường

 





và

1y 

bằng

2ln3

. B.

ln10

. C.

ln3

. D.

ln5

Lời giải

FB tác giả: Luu Le Van

Xét hàm số:

         

g x f x f x f x f x

  

   

Ta có

           

( ) ( ) 24g x f x f x f x f x f x f x f x

       

       

Vì

 

24fx





. Gọi

1 2 3

;;x x x

là các điểm cực trị của hàm số thì ta có

     

1 2 3

0g x g x g x

  

  

và có thể giả sử

 

















Xét phương trình:

 

         

1 24 24 0

f x g x f x f x f x x x







  

          











Diện tích hình phẳng cần tính là

 

1 1 2

1 d 1 d 1 d

24 24 24

x x x

f x f x f x

S x x x

g x g x g x



     

     

     

  

     

  

 

24 24

g x g x

   





   



   



   

ln 24 ln 24

g x g x   

       

2 1 3 2

ln 24 ln 24 ln 24 ln 24g x g x g x g x       

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 34

ln 4 24 ln 14 24 ln 6 24 ln 4 24 ln3         

Câu 38. [2D3-3.1-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 46) Cho hàm số

 

3f x x bx cx d   

với

,,b c d 

. Biết hàm số

       

g x f x f x f x

 

  

có hai giá

trị cực trị là

12; 6

. Diện tích hình phẳng giới hạn bởi các đường

 





và

1y 

bằng

2ln3

. B.

ln6

. C.

2ln 2

. D.

ln5

Lời giải

FB tác giả: Luu Le Van

Xét hàm số:

       

g x f x f x f x

 

  

Ta có

         

( ) 18g x f x f x f x f x f x

     

     

Vì

 

18fx





. Gọi

;xx

là các điểm cực trị của hàm số thì ta có

   

0g x g x





và có thể

giả sử

 















Xét phương trình:

 

       

1 18 18 0

f x g x f x f x





 

        









Diện tích hình phẳng cần tính là

 

   

 

2 2 2 2

1 1 1 1

18 ( 18)

1 d d d d

18 18 18 18

x x x x

f x f x g x g x g x

S x x x x

g x g x g x g x

       



  

    

       

   

       

   

 

ln 18

gx

   

ln 18 ln 18g x g x   

ln 6 18 ln 12 18 ln4 2ln2      

Câu 39. [2D3-3.1-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 46) Cho hai hàm số

 

1f x x ax bx   

và

 

3g x cx dx  

 

, , ,a b c d 

. Biết rằng đồ thị của hàm số

 

y f x

và

 

y g x

cắt nhau tại hai điểm có hoành độ lần lượt là

2

; 1. Hình phẳng giới hạn

bởi hai đồ thị đã cho có diện tích bằng

. B.

. C.

. D.

Lời giải

FB tác giả: Luu Le Van

Theo bài ra ta có:

 

   

( 2) 2

16 4 2 1 4 2 3

1 1 3

a b c d

  



     









     









   

4 2 14

a c b d

    



  











   







Ta có

       

2f x g x x a c x b d x      

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 35

Diện tích hình phẳng cần tính là

   

 

   

 

d 2 dS f x g x x x a c x b d x x



       



   

5 3 2

x x x

a c b d x





     





Thay

  









ta có

     

 

5 3 2

1 2 1 2 1 2

2. 3. 2 1 2

5 3 2 10

     

      

Câu 40. [2D2-5.5-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 47) Có bao nhiêu cặp số nguyên

 

;xy

thỏa mãn

2 2021x

và

 

2 log 2 2

x x y



   

A. 2020. B. 10. C. 9. D. 2019.

Lời giải

FB tác giả: Nguyễn Thị Vân

Đặt

 

1 1 1

log 2 2 2 2 2 .

y y t t y

x t x x

  

       

Phương trình đã cho trở thành:

 

2 2 2 2 2.2 2.2

y t y y t

t y y t



       

Xét hàm số

 

2.2

f x x

đồng biến trên

.yt

Suy ra phương trình

 

1 1 1

log 2 2 2 2 .

y y y y

x y x x

  

      

2 2021 2 2 2021 1 1 log 2021



        

2 log 2021 1.y   

y

nên

 

2;3;4;...;11y 

có 10 giá trị nguyên của

Mà





nên với mỗi số nguyên

 

2;3;4;...;11y 

xác định duy nhất một giá trị nguyên của

Vậy có 10 cặp số nguyên

 

;xy

thỏa mãn bài toán.

Câu 41. [2D2-5.5-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 47) Có bao nhiêu số nguyên

sao

cho tồn tại









thỏa mãn

 

8 1 .8

x xy x





A. 7. B. C. 6. D. 5.

Lời giải

FB tác giả: Thao nguyen

   

2 4 2 4

8 1 .8 8 1 0

x xy x x xy x

xy xy

  

     

Xét

hàm số

   

x xy x

f x xy



  

Áp dụng BĐT

 

a x a  

ta có

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 36

   

 

2 4 2

8 1 7 2 4 1 1

x xy x

f x xy x xy x xy



        

 

14 3 14 0, 5x x y y    

Do đó

4y 

Với

 

2 1 0y xy f x      

(loại)

Với

 

1 8 1

y f x x



    

Ta có

 

5 0; 0









 

0fx

có nghiệm









1y

thỏa

mãn

Với

 

0 8 8

2 TM





   







0y

thỏa

mãn

Với

0y 

có

   

5 30

5 8 1 5 0 , 0

f y y



     

 

8 1 0, 1; 2;



   

     

   

   

 

0fx

có nghiệm









Vậy

 

1 ; 0 ; 1 ;y 

Câu 42. [2D2-5.5-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 47) Có bao nhiêu số nguyên

5y 

để tồn tại số thực

thỏa mãn

 

15 6

log 4 3 1 log 2x y x x y    

Lời giải

FB tác giả: Nguyễn Huỳnh Tấn Trung

Đặt

 

15 6

4 3 1 15 0

log 4 3 1 log 2

1 6 1

x y x x y t



   



      



   





(*).

Hệ có nghiệm



đường thẳng

:4 3 1 15 0

xy    

và đường tròn

   

: 1 6 1

C x y   

có điểm chung, với tâm

 

1;0I

 

5 15

, 6 1 225 10.15 25.6 0

15 6. 10 0

t t t t

d I R



         



   





Xét hàm số

 

15 6. 10



  





Đạo hàm

 

15.ln15 6. ln 0,

f t t





   





Do vậy: hàm số

 

đồng biến trên

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 37

Khi đó

 

0 0,9341f t t  

 

1 6 1

xy   

nên

y 

, dẫn đến

6y 

Kết hợp giả thiết ta suy ra

6.y 

Thử lại:

Với

6y 

, hệ (*) trở thành

 

4 19 15 0

15 23

6 35 225 1089 46.15 16.6

1 6 35

t t t t



  







      





  







(**)

Nếu

0t 

thì

15 1,6 1 225 1089 46.15 16.6

t t t t t

     

Nếu

1 15 6

t   

, ta sẽ chứng minh

225 1089 62.15 .



Thật vậy, ta có

 

225 1089 62.15 15 31 128 0

t t t

     

Dẫn đến

225 1089 62.15 46.15 16.6

t t t t

   

Nếu

01t

thì

15 15,6 6 225 1089 46.15 16.6

t t t t t

     

Vậy (**) vô nghiệm.

Câu 43. [2H1-3.2-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 48) Cho khối hộp chữ nhật

.ABCD A B C D

   

có

AB a

23AD a

. Gọi

là trung điểm cạnh

, góc giữa hai mặt

phẳng

 

A BI



và

 

ABCD

bằng

60

. Thể tích của khối hộp chữ nhật đã cho bằng

. B.

. C.

23a

. D.

33a

Lời giải

FB tác giả: Huong Nguyen

Gọi



là góc giữa hai mặt phẳng

 

A BI



và

 

ABCD

Trong

 

ABCD

: Kẻ

AH BI

tại

;

AA BI





( do

 

AA ABCD





suy ra

A H BI





Vậy

 

, 60A H AH AHA





   

Tam giác

ABI

vuông tại

là đường cao nên có:

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 38

2 2 2 2 2 2

1 1 1 1 1 4 3

3 3 2

AH AB AI a a a

      

Tam giác

A AH



vuông tại

có:

.tan60

AA AH



  

. .2 3 3 3

ABCD A B C D ABCD

V AA S a a

   



  

Câu 44. [2H1-3.2-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 48) Cho hình hộp chữ nhật

.ABCD A B C D

   

có đáy là hình vuông cạnh

, góc giữa hai mặt phẳng

 

A BM



và

 

ABCD

bằng

với

là trung điểm

. Thể tích khối hộp chữ nhật đã cho bằng

2 15

. B.

. C.

. D.

2 15

Lời giải

FB tác giả: Dương Thái Bảo

Gọi

là trung điểm của

là giao điểm của

và

Vì

ABCD

là hình vuông nên ta có

AN BM

, suy ra

A H MB





Do đó

60A HA





Ta có

AH a



, suy ra

2 15

.tan60

AA AH a





Thể tích khối hộp chữ nhật đã cho bằng

2 15

ABCD

V AA S a





Câu 45. [2H1-3.2-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 48) Cho khối lăng trụ đứng

.ABC A B C

  

có đáy là tam giác đều. Mặt phẳng

 

A BC



tạo với đáy góc

30

và tam giác

A BC



có diện tích bằng

. Thể tích

của khối lăng trụ đã cho là

64 3

. B.

. C.

16 3

. D.

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 39

Lời giải

FB tác giả: Sơn Trường

Gọi

là trung điểm cạnh

Vì

.ABC A B C

  

là lăng trụ đứng có đáy là tam giác đều nên

.ABC A B C

  

là khối lăng trụ đều.

Do đó ta có:

A B A C





. Suy ra tam giác

A BC



cân tại



A I BC





Mặt khác: tam giác

ABC

đều

AI BC

Suy ra

 

BC A IA





Vậy góc giữa mặt phẳng

 

A BC



và mặt đáy bằng góc

30A IA





Ta có: tam giác

ABC

là hình chiếu của tam giác

A BC



trên mặt đáy

Nên

.cos 8.cos30 4 3

ABC A BC





   

Đặt

AB x

4 3 4

ABC

Sx    

Ta có:

2 3 .tan 2

AI AA AI AIA



    

Suy ra:

. 2.4 3 8 3

ABC A B C ABC

V AA S

  



  

Câu 46. [2H3-2.8-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 49) Trong không gian

Oxyz

, cho

ba điểm

   

2;3;9 , 2;3;4AB

và

 

2;15;9 .C

Một mặt cầu

 

luôn đi qua

, AB

và tiếp xúc với

mặt phẳng

 

Oxy

tại

Biết rằng khi

đạt giá trị nhỏ nhất thì tọa độ tâm của mặt cầu

 

là

 

;;I a b c

. Khi đó

2a b c

bằng

13

. B. 9. C. 2 D. 6.

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 40

Lời giải

FB tác giả: Lê Văn Đoàn

Ta có:

   

0;0; 5AB AB Oxy   

Và

 

2;3;0 , HD

là hình chiếu của

, AI

lên mặt

 

Oxy

9, 4HA HB  

Ta có

. . 6HD HA HB KD HA HB   

D

thuộc đường tròn

()C

tâm

6r 

Gọi

là hình chiếu của

lên

 

Oxy

 

2;15;0K

12HK r   

nằm ngoài

 

Ta có

   

2 2 2 2

9 81 81 12 6 3 3CD CK DK DK HK r          

min

33CD

. Dấu

""

xảy ra khi

, , H K D

và

nằm giữa

Ta có:

6,r HD

12HK 

2HK HD

là trung điểm

HK 

 

2;9;0D

Gọi

 

;;I a b c

là tâm của

 

, vì

là hình chiếu của

lên mặt phẳng

   

2;9;Oxy I c

I

nằm trên

 

Pz

là mặt phẳng trung trực của

,AB

   

P Oxy c

2, 9,

a b c   

26a b c   

Câu 47. [2H3-2.8-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 49) Trong không gian

Oxyz

, cho

hai điểm

 

5;1;1A

và điểm

 

5;0;5B

. Xét hai điểm

và

thay đổi thuộc mặt phẳng

 

: 2 0P x z  

sao cho

2MN 

. Giá trị lớn nhất của

AM BN

bằng

3 11

. B.

. C.

. D.

Oxy

(2;3;9)

(2;3;0)

(2;15;9)

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 41

Lời giải

FB tác giả: Tân Ngọc

Ta có

cùng phía so với

 

. Gọi

lần lượt là hình chiếu của

lên mặt phẳng

 

. Khi đó

 

3;1; 1H 

 

1;0;1K

Ta có

 

d d , 2 2,

AP

 

d d , 4 2

BP

Đặt

()

A T A





, khi đó ta có

||AM BN A N BN A B



   

Rõ ràng



nằm trên đường tròn có tâm

và có bán kính bằng

, đường tròn này cắt mặt

phẳng tạo bởi

 

,AH BK

tại hai điểm, giả sử

là điểm cách

một khoảng lớn hơn.

Khi đó ta có

max max

AM BN A B A I



   

Vậy

   

 

2 2 2

2 2 3 2 33

max B A

A B d d H MNIB K



       

Câu 48. [2H3-2.8-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 49) Trong không gian với hệ tọa

độ

Oxyz

, cho mặt phẳng

 

:2 2 15 0P x y z   

. Gọi

là điểm di động trên

 

là điểm

thuộc tia

sao cho

. 10OM ON 

. Khoảng cách nhỏ nhất từ

đến mặt phẳng

 

bằng bao

nhiêu?

. B.

. C.

. D.

Lời giải

FB tác giả: Tân Ngọc

Gọi

là hình chiếu vuông góc của

trên

 

và

thuộc tia

thỏa mãn

. 10OK OH 

 

d ; 5OH O P

nên

2OK 

Lại có:

..OK OH OM ON

ONK

đồng dạng tam giác

OHM

. Suy ra

90ONK  

. Do đó

thuộc đường tròn đường kính

. Suy ra

 

d , d ,N P K P

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 42

Vậy khi

NK

thì khoảng cách từ

đến

 

nhỏ nhất và bằng

3KH 

Câu 49. [2D1-2.6-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 50) Cho hàm số

 

y f x

có đạo

hàm

   

 

7 9 ,f x x x x



    

. Có bao nhiêu giá trị nguyên dương của tham số

để hàm

số

 

23g x f ax bx m   

với

.0ab

có ít nhất 3 điểm cực trị?

Lời giải

FB tác giả: Văn Nguyễn

Ta có BBT của hàm

 

y h x ax bx  

như sau

Ta có

 

  

 

3 3 3

. 2 3 . 2 3

x ax b ax b

g x ax bx f ax bx m f ax bx m

ax bx





  

        



Rõ ràng

 



không xác định tại

0x 

và đổi dấu khi

đi qua 0 nên

0x 

là 1 điểm cực trị

của hàm số

 

23g x f ax bx m   

Ta có:

 

3 3 3

2 3 7 4 2

2 3 0 2 3 3 2

2 3 3 6 2

ax bx m ax bx m

f ax bx m ax bx m ax bx m

ax bx m ax bx m



      





            



        



Để hàm số

 

có ít nhất

điểm cực trị thì phương trình

 

0gx





có ít nhất

nghiệm phân

biệt khác

và

 



đổi dấu khi đi qua ít nhất

trong số các nghiệm đó.

Từ BBT ta có

4 2 0 2mm   

Vì

nguyên dương nên

1m 

Vậy có 1 giá trị của

thỏa mãn yêu cầu đề bài.

Câu 50. [2D1-2.6-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 50) Cho hàm số

 

liên tục trên

, có bảng biến thiên dưới đây

SP TỔ 27-STRONG TEAM PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021

STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 43

Có bao nhiêu giá trị nguyên của tham số

để hàm số

 

6 5 2021y f x m   

có 3 điểm cực

đại?

. B.

. C.

. D.

Lời giải

FB tác giả: Nam du

Xét hàm số

 

6 5 2021y f x m   

Đặt

6(6 5)

6 5 (6 5) '

(6 5)

u x x u



     



Hàm

đạt cực trị tại

x 

Bảng biến thiên

Suy ra hàm số

( ) 2021y f u m  

có 3 điểm cực đại

2017 0

2024 2017

2024 0





     







 

2023, 2022, 2021, 2020, 2019, 2018 .mm        

HẾT

Bấm Tải xuống để xem toàn bộ.

| 1/43

| | Tải xuống

Preview text:

SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
PHÁT TRIỂN ĐỀ THI TN-THPT-QG BGD 2021 MÔN: TOÁN THỜI GIAN: 90 PHÚT
SP ĐƯỢC THỰC HIỆN BỞI TỔ 27-STRONG TEAM ĐỀ BÀI Câu 1.
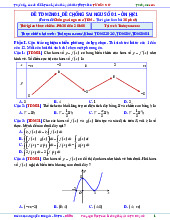
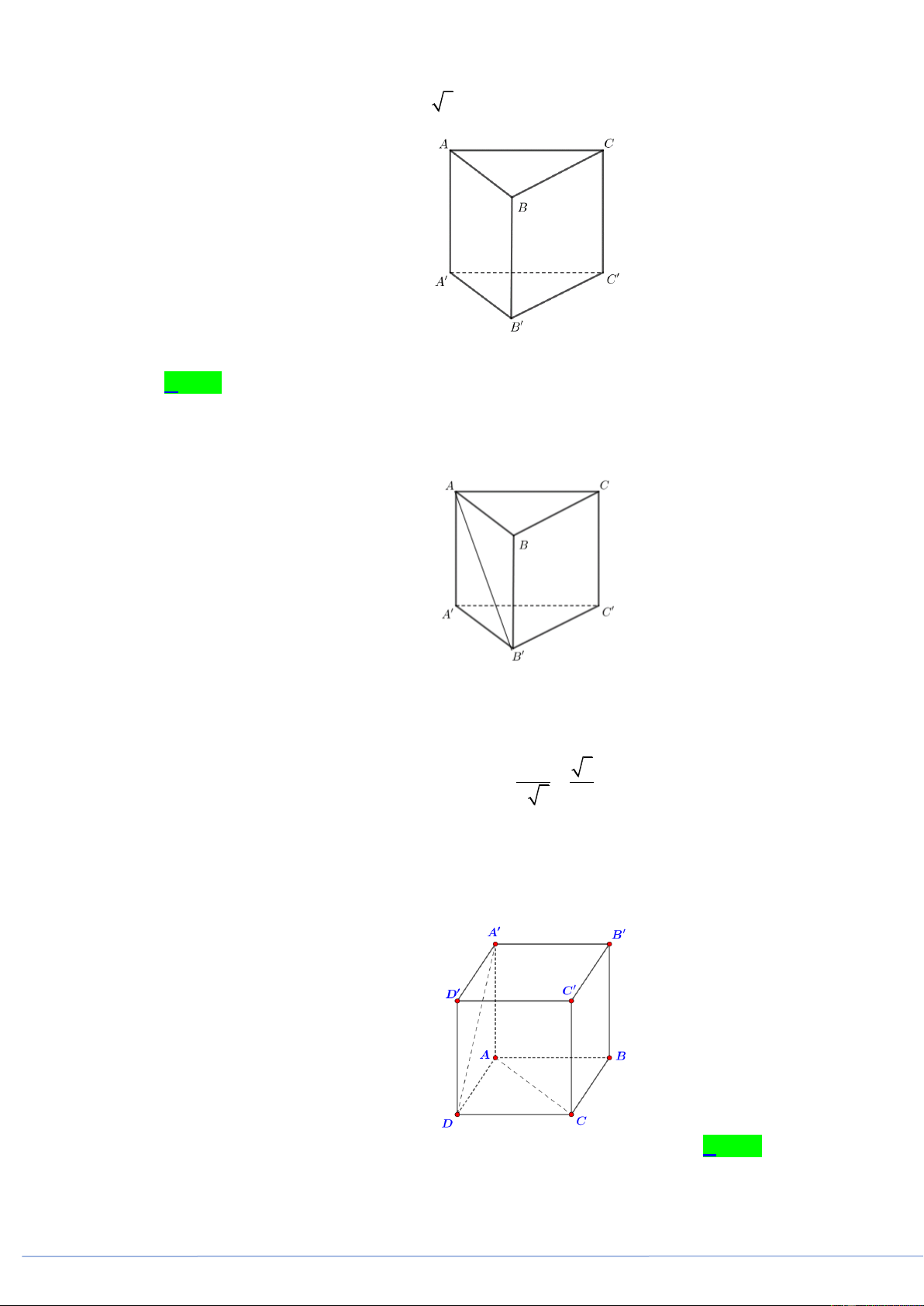
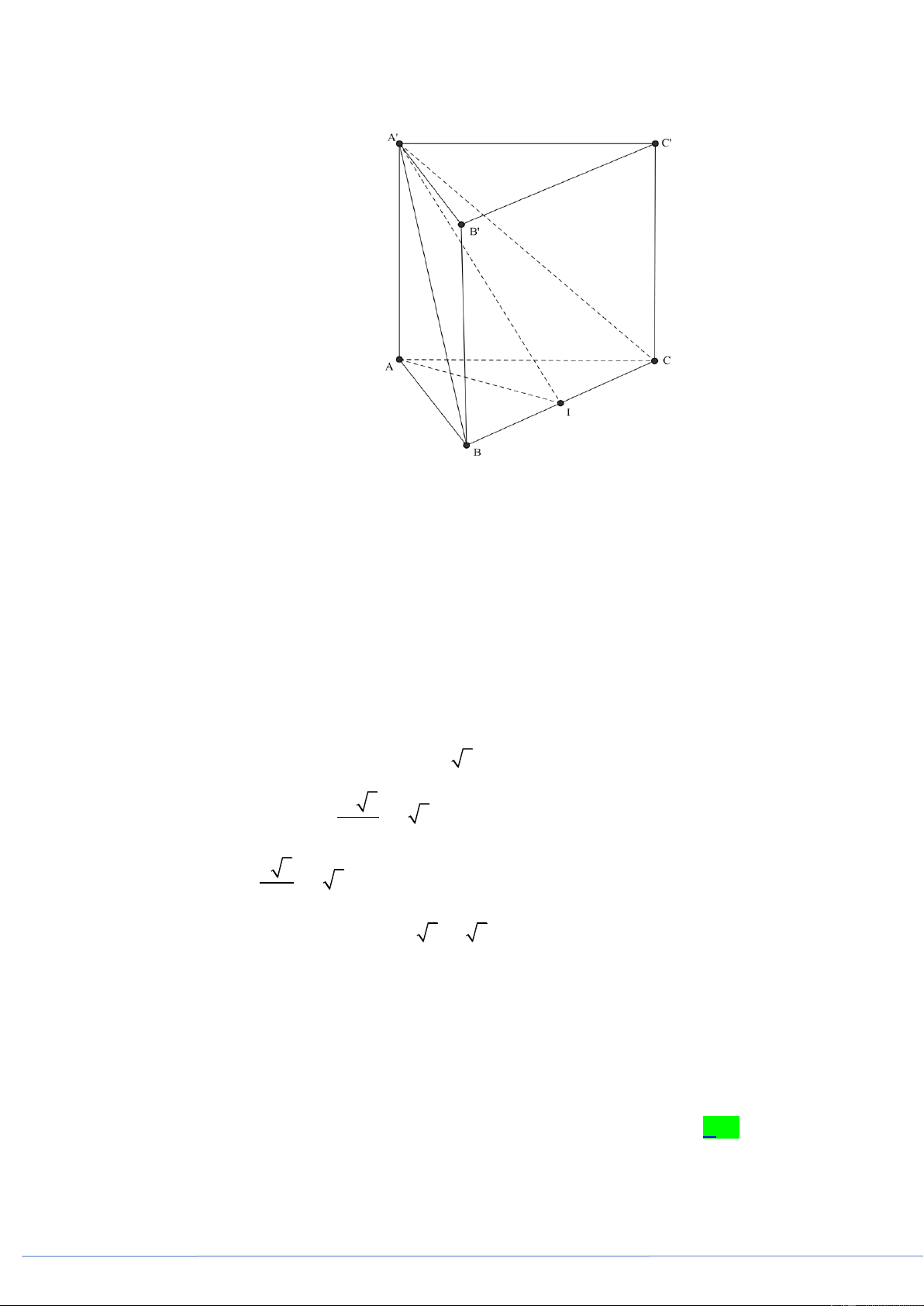
(PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 36) Cho hình lăng trụ đứng AB . C A B  C   có đáy
là tam giác đều cạnh a , cạnh bên AA  a 2 (tham khảo hình bên). Góc giữa AB và BC bằng A. 30 B. 60 C. 45 D. 120 Câu 2.
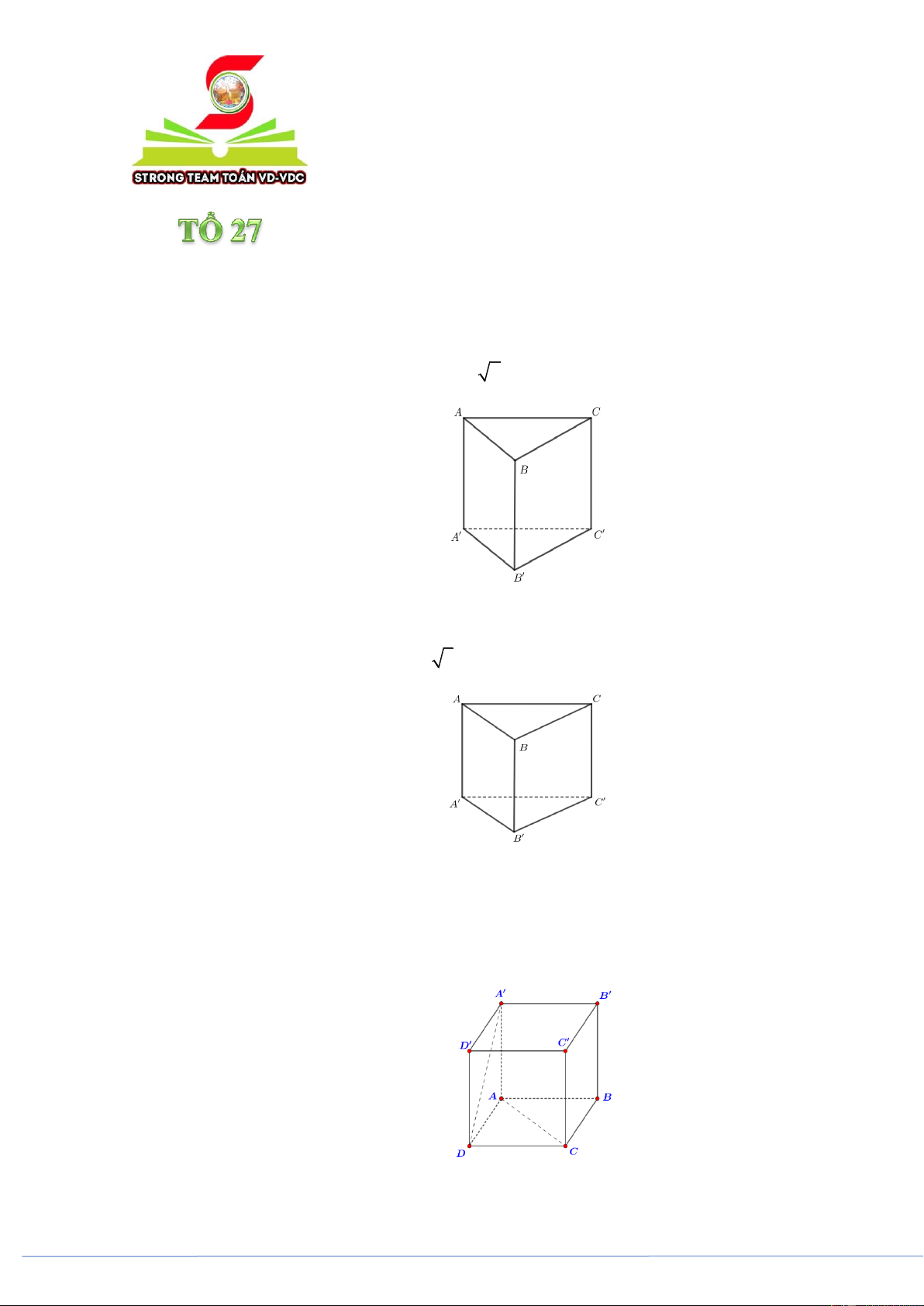
(PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 36) Cho hình lăng trụ tam giác đều AB . C AB C
  có AB  a và AA  a 3 (tham khảo hình bên).
Góc giữa hai đường thẳng AB và CC bằng A. 30 . B. 90 . C. 45 . D. 60 . Câu 3.
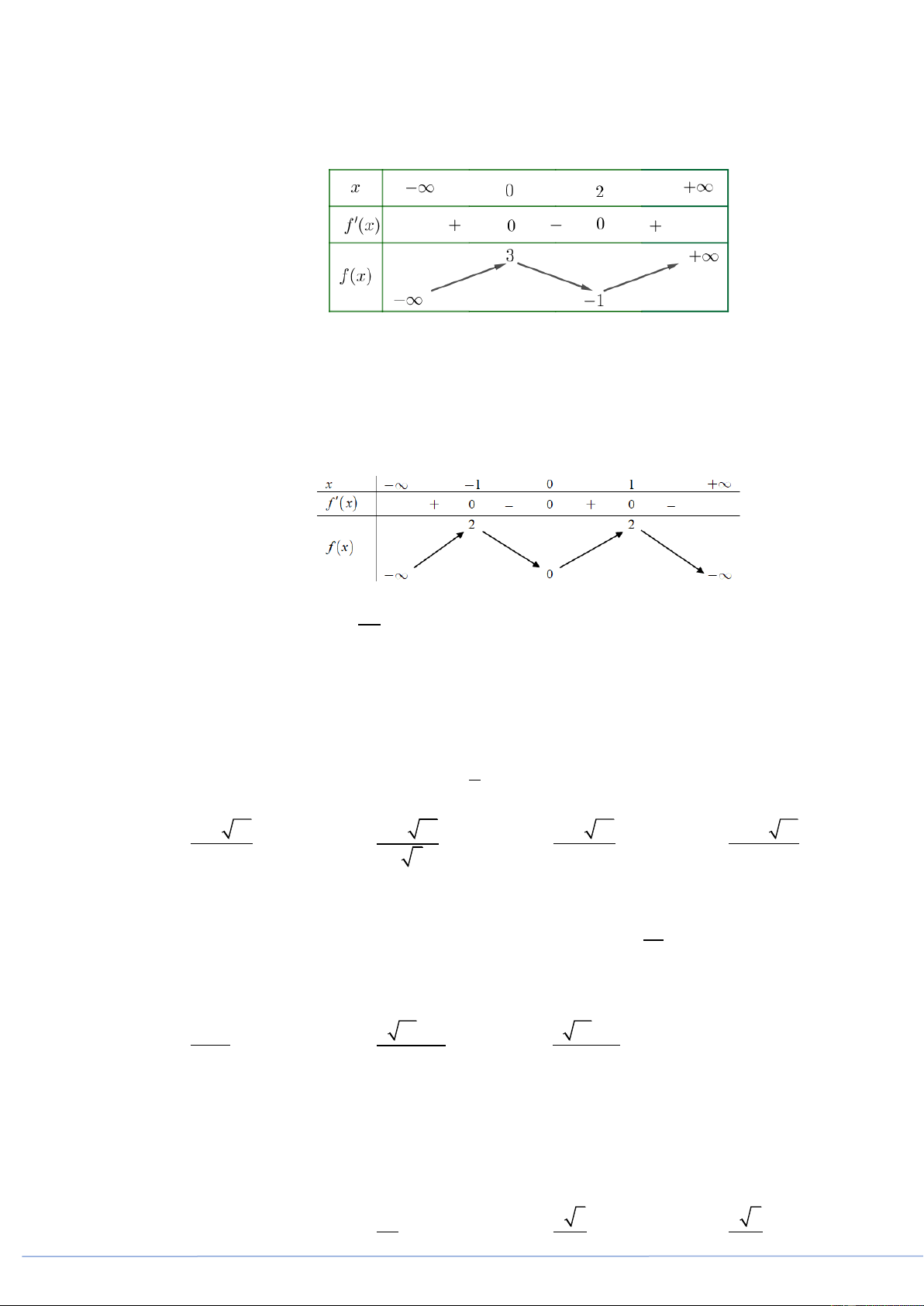
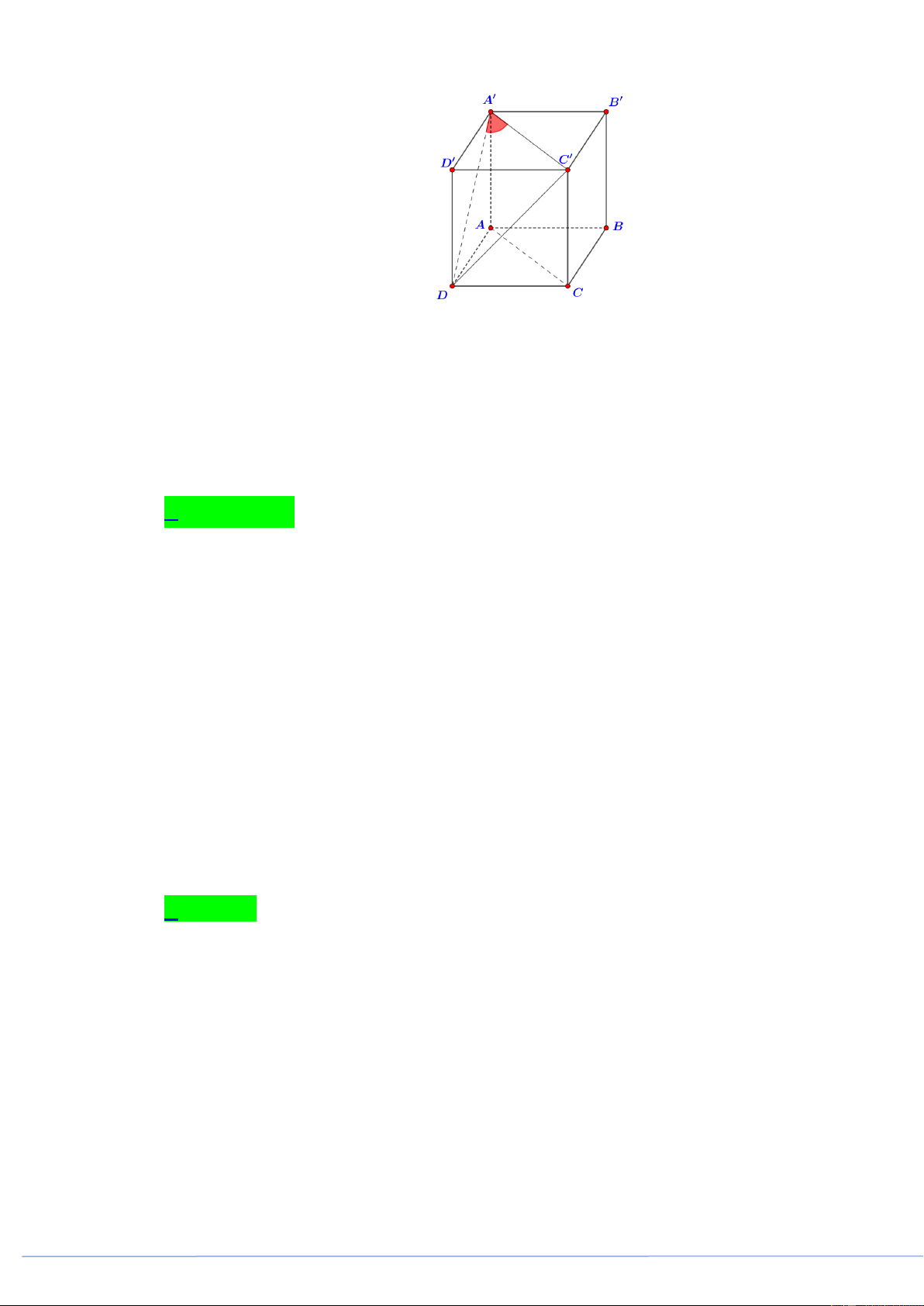
(PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 36) Cho hình lập phương ABC . D A B  C  D  
(hình vẽ bên dưới). Góc giữa hai đường thẳng AC và AD bằng A. 45 . B. 90 . C. 30 . D. 60 .
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 1
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021 Câu 4.
(PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 37) Với mọi số thực a , b , c thỏa mãn
log a  2 log b  3log
c 1  1 , khẳng định đúng là 3 3 27  
A. a  2b  c  0 .
B. a  b  c  3 2 1  3.
C. a c   2 1  3b .
D. a c   2 1  9b . Câu 5.
(PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 37) Với mọi số thực a , b thỏa mãn
3log a  2log b  3 , khẳng định nào dưới đây đúng? 2 2 A. 3 2 a b  8 . B. 3 2 a b  6 .
C. 3a  2b  8.
D. 3a  2b  6 . Câu 6.
(PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 37) Cho các số thực dương a, b, x thỏa mãn 2 1 log x 
log a  log b . Mệnh đề nào dưới đây đúng? 1 1 1 3 5 2 2 2 2 1  2 1 2 1 3 A. 3 5
x  a b . B. x 
a  b . C. 3 5 x  a b . D. 5 2 x a b  . 3 5 3 3 Câu 7.
(PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 38) Nếu f
 xdx  2 thì 2x f   xdx  1  1  bằng A. 6 . B. 8 . C. 10 . D. 12 . 3 Câu 8.
(PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 38) Nếu
f  x dx  2   thì 1 3 2 f  x 2
 3x 1 dx   bằng 1 A. 30  . B. 28  . C. 26  . D. 27  .  2 Câu 9.
(PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 38) Cho f
 xdx  5. Khi đó 0  2 I   f
 x2sin xdx  bằng 0 
A. I  7 . B. I  5  .
C. I  3 .
D. I  5   . 2 2 2
Câu 10. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 38) Cho f
 xdx  2 và gxdx  1   . Khi 1  1  2
đó I  x  2 f  
x3g xdx  bằng 1  17 7 5 11 A. I  . B. I  . C. I  . D. I  . 2 2 2 2
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 2
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021 2 3
 x  2x 1khi x  2
Câu 11. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 39) Cho hàm số f  x   . 2x  3 khi x  2
Gọi F là nguyên hàm của f trên thỏa mãn F  
1  4 . Giá trị của 2F 0  3F 3 bằng A. 65 . B. 57 . C. 61  . D. 69  . 2
2x 3x 1khi x  0
Câu 12. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 39) Cho hàm số f  x   . 2 1   x khi x  0
Biết F  x là một nguyên hàm của hàm số f  x thỏa mãn F   5 2  . Giá trị của 3 F  4
   4F 3 nằm trong khoảng nào?
A. 52;53 .
B. 53;54 .
C. 54;55 . D. 55;56 . 2 3
 x  2x 1khi x  3
Câu 13. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 39) Cho hàm số f  x   .
4x  32 khi x  3
Giả sử F là nguyên hàm của f trên thỏa mãn F  
1  4 . Giá trị của 3F  2
   F 4 bằng A. 69  . B. 25  . C. 45  . D. 53  .
Câu 14. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 40) Có bao nhiêu số nguyên x thỏa mãn  3 x x 2 8  2
.log 2x2 140?  3  A. 10 . B. 8 . C. 6 . D. 7 .
Câu 15. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 40) Có bao nhiêu số nguyên x thỏa mãn  2x x x 1 9 3 .9  
log 2x18 5 0? 2    A. 1 B. Vô số. C. 17. D. 16.
Câu 16. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 40) Có bao nhiêu số nguyên x thỏa mãn log  25 2. 3x x 3 2 2 2 .4 x x       0 ? 3  A. 1 B. 18. C. 16. D. 17.
Câu 17. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 40) Có bao nhiêu số nguyên x thỏa mãn    2
9x  27x  log x  2022 1  0 ? 1    2  A. 2020 . B. 2022 . C. 5 . D. 4 .
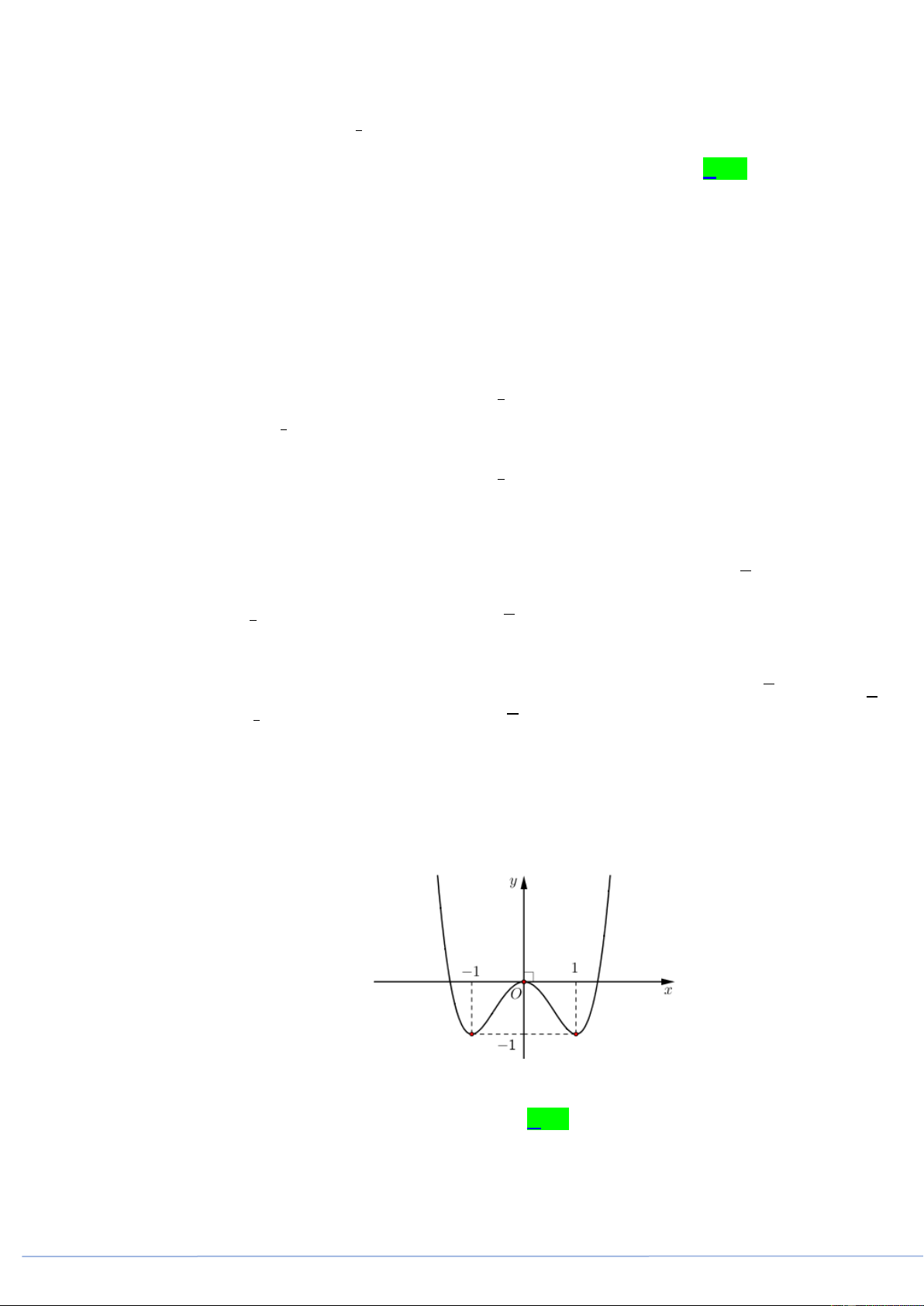
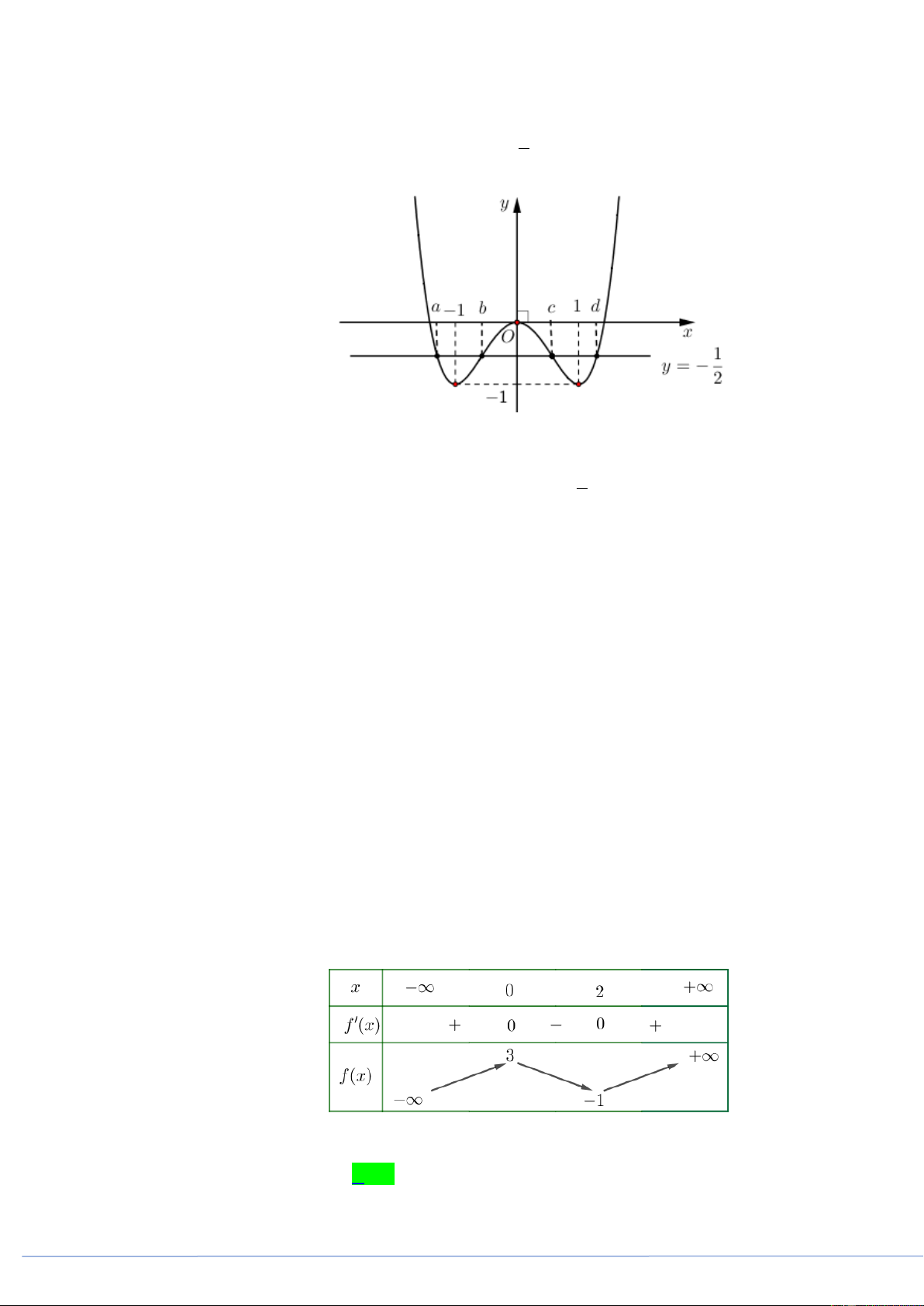
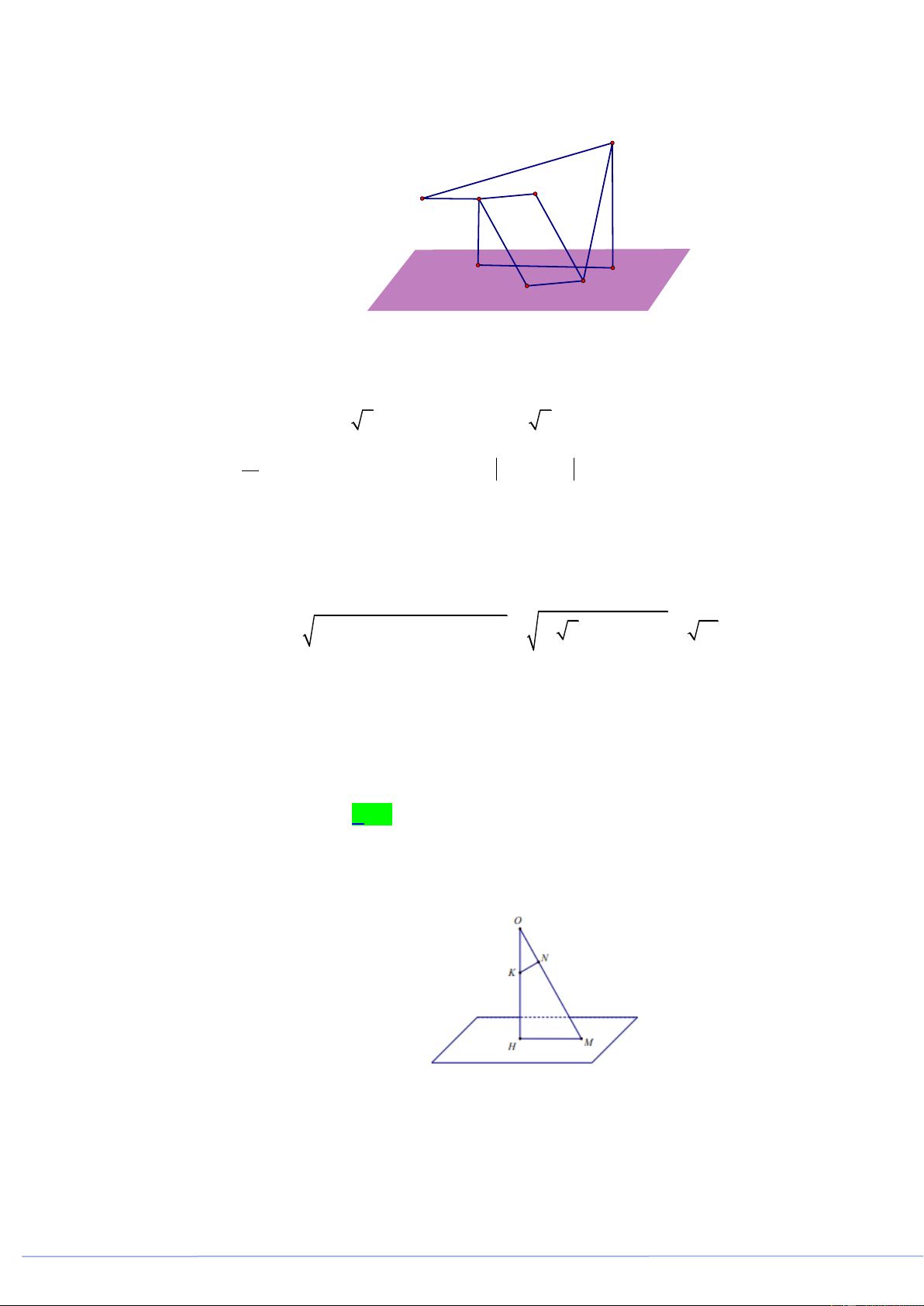
Câu 18. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 41) Cho hàm số bậc bốn y  f  x có đồ thị là
đường cong trong hình bên
Số nghiệm thực phân biệt của phương trình 2 f  f  x 1  0 là
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 3
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021 A. 9 . B. 4 . C. 8 . D. 7 .
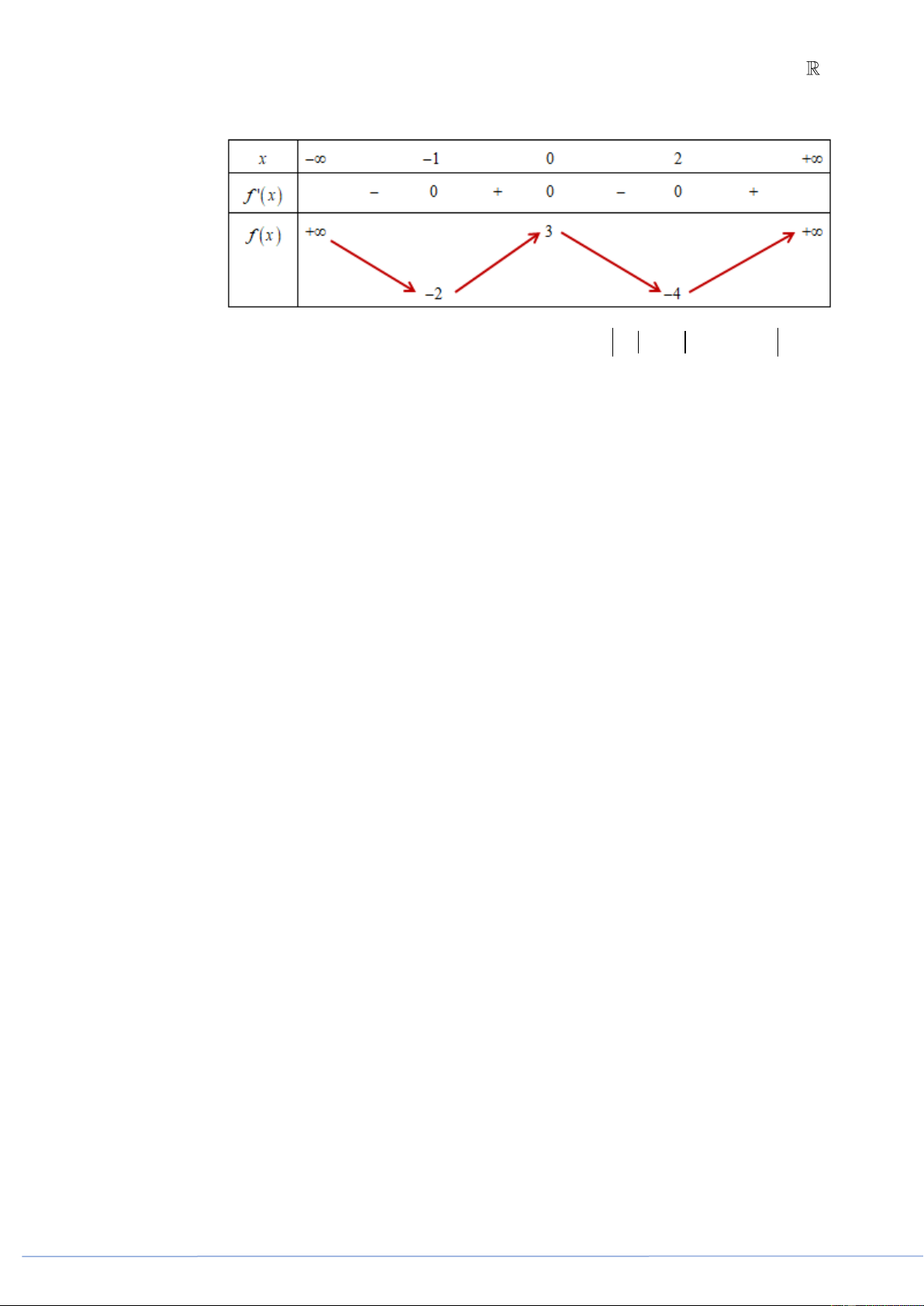
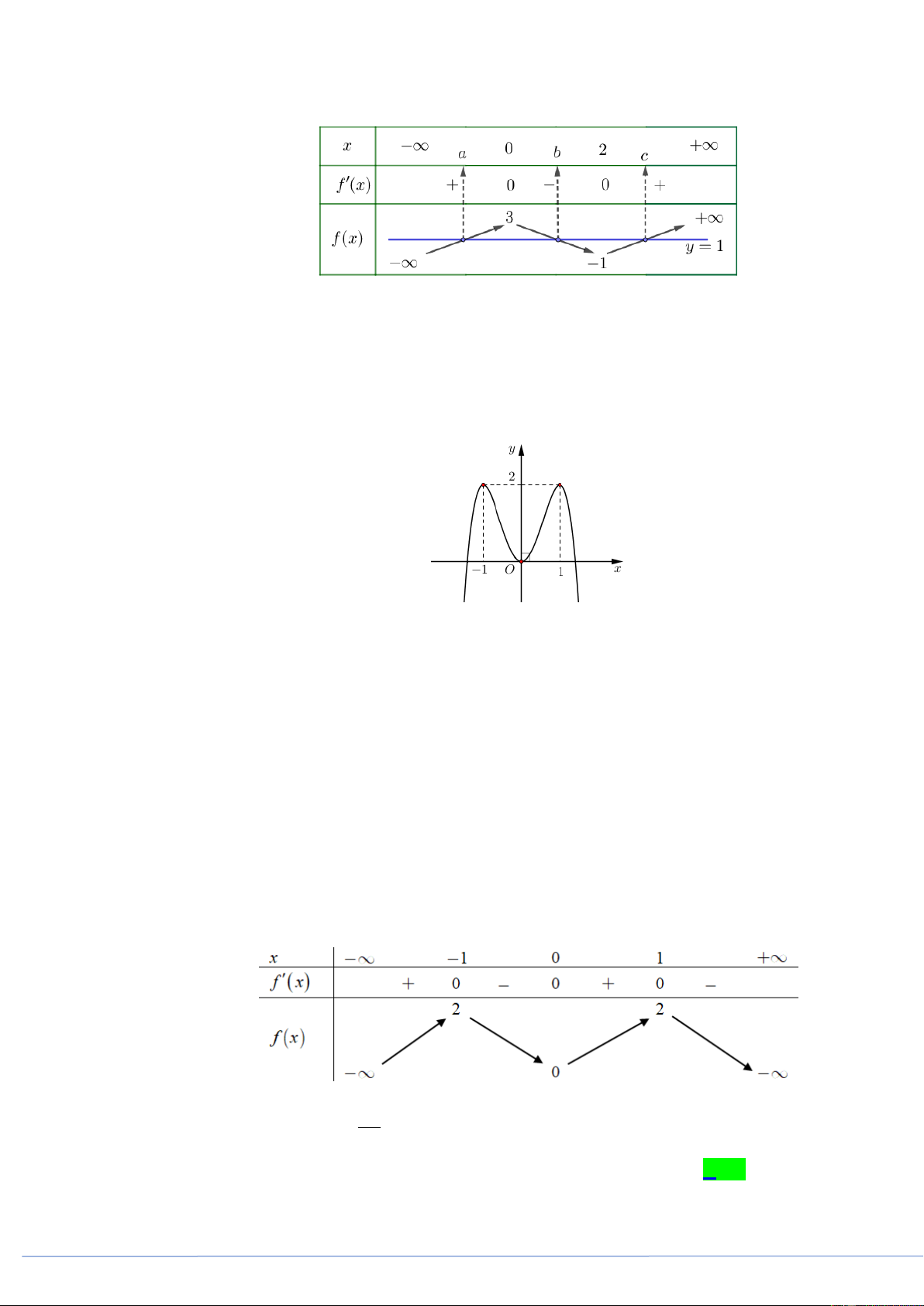
Câu 19. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 41) Cho hàm số f  x có bảng biến thiên như sau
Số nghiệm thực phân biệt của phương trình f  2 4
4x  2x  1 là A. 9 . B. 6 . C. 8 . D. 12 .
Câu 20. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 41) Cho hàm số y  f  x có bảng biến thiên như sau  9 
Số nghiệm thuộc đoạn 0; 
 của phương trình f  f cos x  2 là  2  A. 3 . B. 5 . C. 7 . D. 9 .
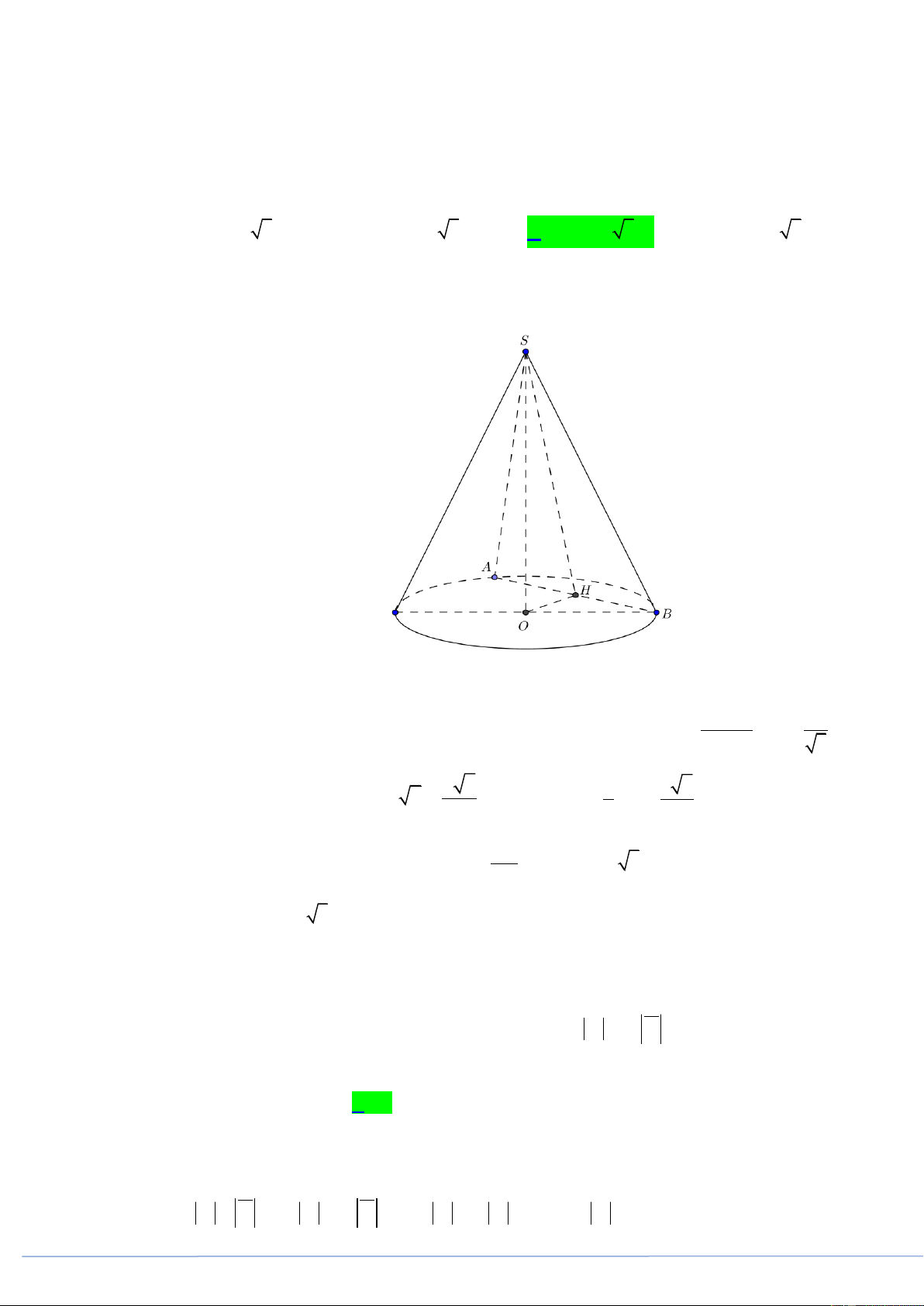
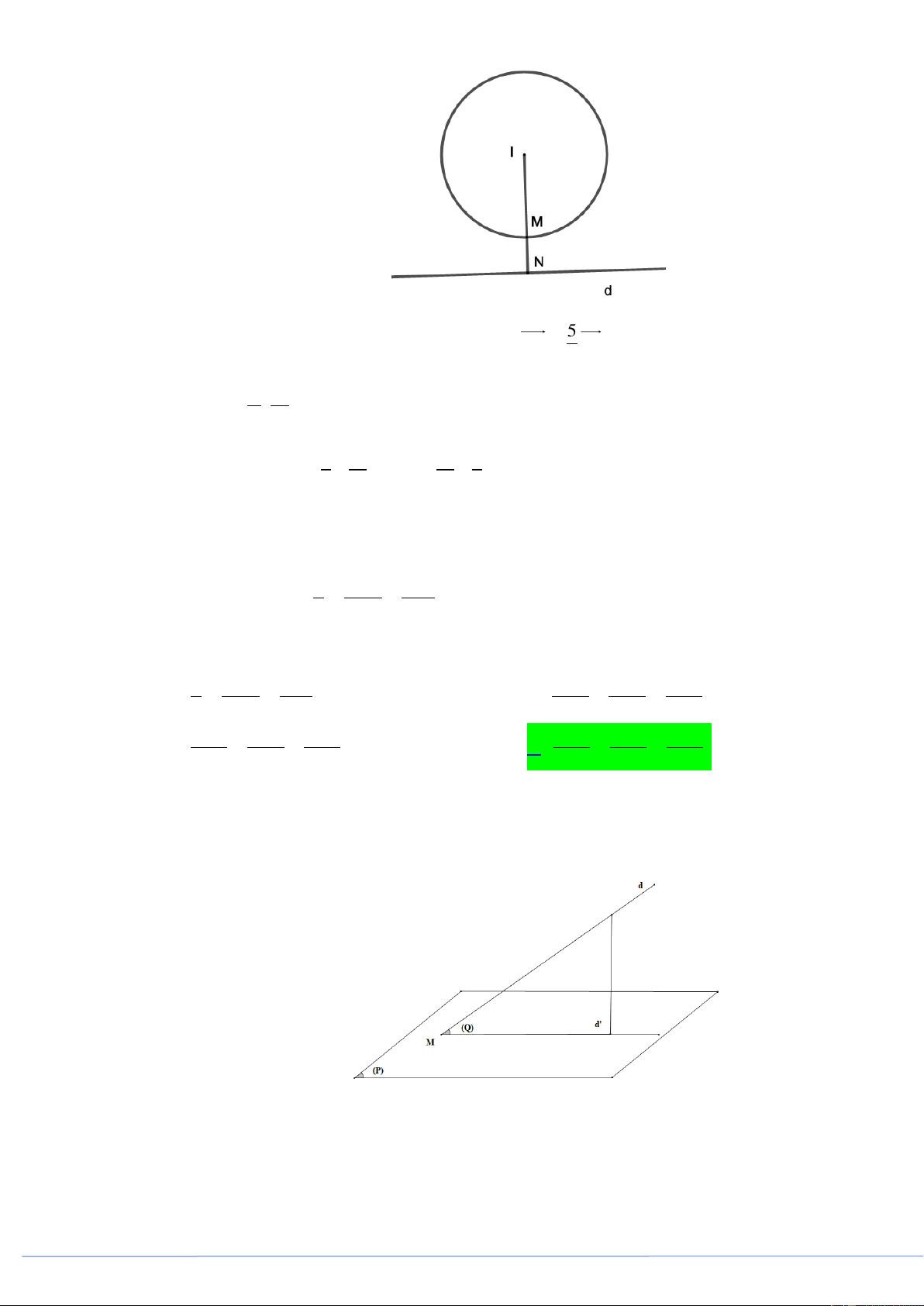
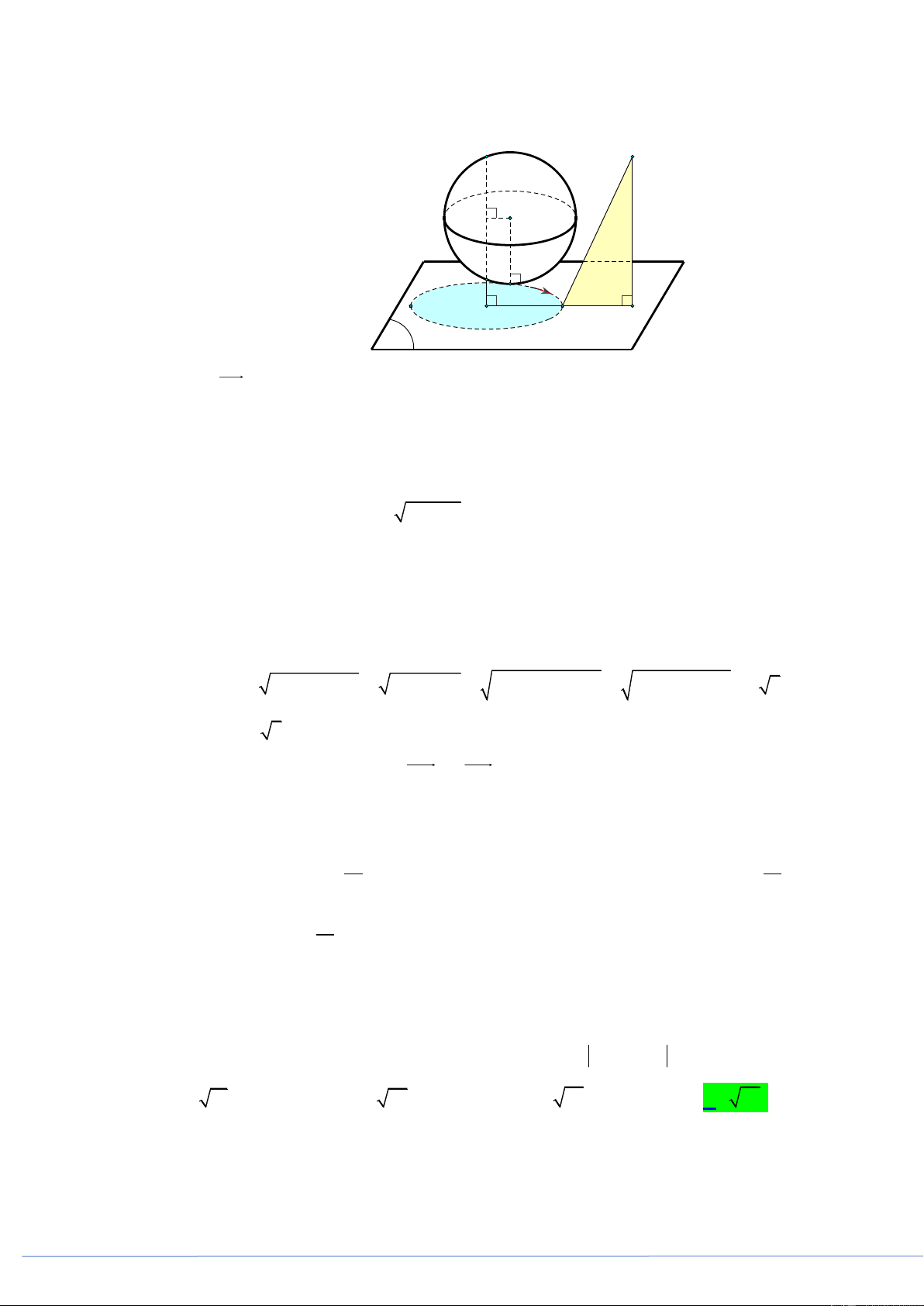
Câu 21. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 42) Một hình nón đỉnh S , đáy là hình tròn tâm
O và SO  a . Một mặt phẳng  P qua đỉnh S cắt đường tròn O theo dây cung AB sao cho a
góc AOB  90 và cách O một khoảng
. Diện tích xung quanh hình nón bằng 2 2  a 10 2  a 10 2  a 10 2 2 a 10 A. . B. . C. . D. . 6 3 3 3 3
Câu 22. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 42) Cắt hình nón  N  bởi mặt phẳng   đi qua đỉ a
nh và có khoảng cách đến tâm O của đường tròn đáy là 3 ta được thiết diện là tam giác 2
đều cạnh 4a . Thể tích của  N  bằng 3 7 a 3 4 13 a 3 8 13 a A. . B. . C. . D. 3 7 a . 3 3 3
Câu 23. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 42) Cho hình trụ đứng có hai đáy là hai đường
tròn tâm O và tâm O , bán kính bằng a , chiều cao hình trụ bằng 2a . Mặt phẳng đi qua trung
điểm OO và tạo với OO một góc 30 , cắt đường tròn đáy tâm O theo dây cung AB . Độ dài đoạn AB là 2a 4 3 2 6 A. a . B. . C. a . D. a . 3 9 3
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 4
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
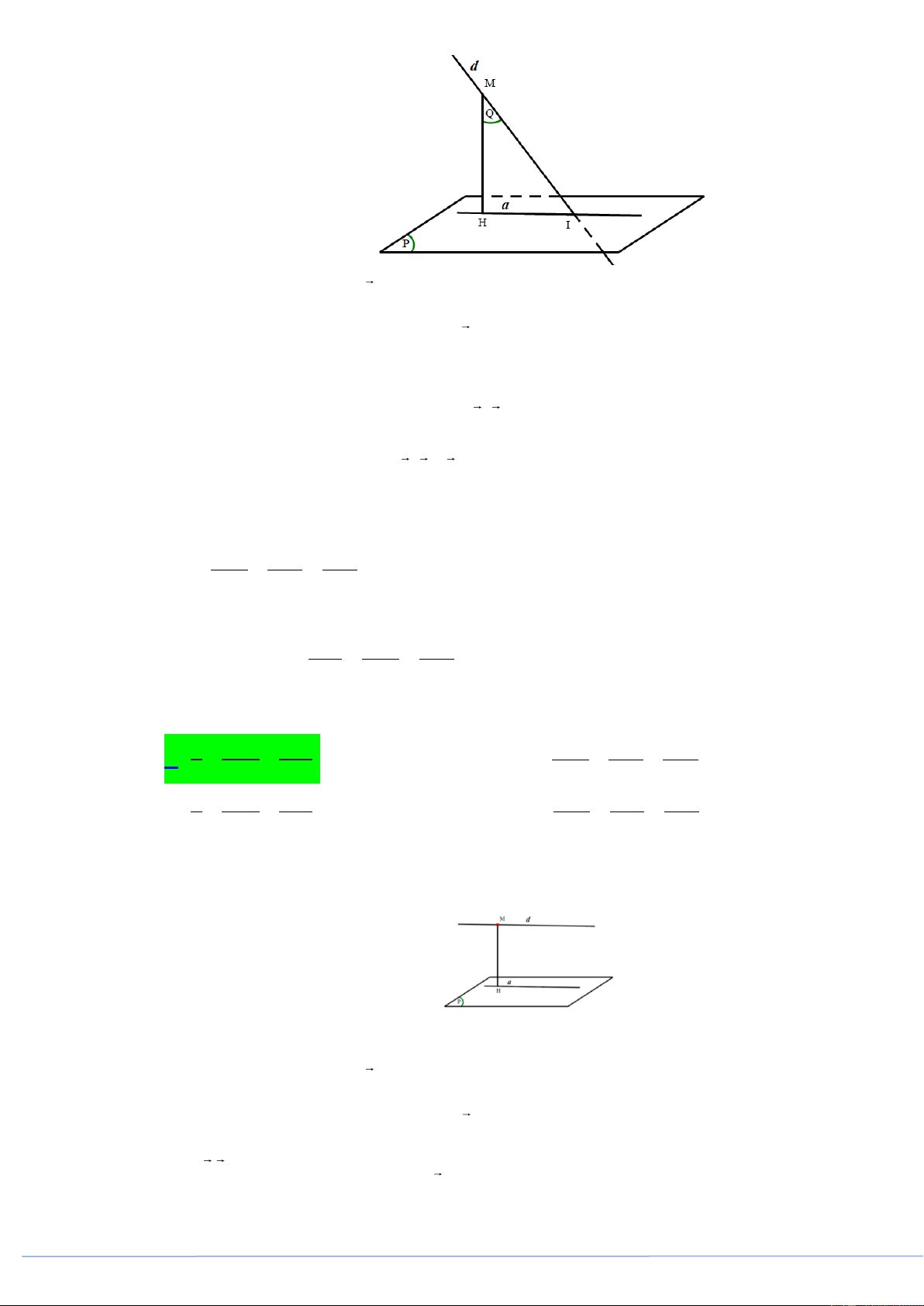
Câu 24. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 42) Hình nón  N  có đỉnh S , tâm đường tròn
đáy là O , góc ở đỉnh bằng 120 . Một mặt phẳng qua S cắt hình nón  N  theo thiết diện là tam
giác vuông SAB . Biết rằng khoảng cách giữa hai đường thẳng AB và SO bằng 3 . Tính diện tích
xung quanh S của hình nón  N  xq A. S  36 3 . B. S  27 3 . C. S  18 3 . D. S  9 3 . xq xq xq xq
Câu 25. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 43) Trên tập hợp các số phức, xét phương trình 2
z  m   2 2
1 z  m  5m  0 ( m là tham số thực). Gọi S là tập hợp các giá trị nguyên m để
phương trình đó có nghiệ 3
m z thỏa mãn z
 3 z  2 . Tổng các phần tử của tập S là 0 0 0 A. 8 . B. 9 . C. 4 . D. 7 .
Câu 26. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 43) Trong tập số phức, cho phương trình 2
z  m   2 2 2
1 z  m  3m  2  0, m 
. Có bao nhiêu giá trị nguyên của m trong đoạn
0;202 1 để phương trình có 2 nghiệm phân biệt z ;z thỏa mãn z  z ? 1 2 1 2 A. 2016. B. 202 C. 202 D. 2017.
Câu 27. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 44) Cho hai số phức z , z thỏa iz 1  1 và 1 2 1
z  i  2 . Khi biểu thức P  2z  3z
đạt giá trị nhỏ nhất thì z  2z bằng 2 1 2 1 2 A. 4 . B. 1. C. 3 . D. 2 .
Câu 28. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 44) Xét các số phức z , w thỏa mãn z  2 ,
iw  2  5i  1. Khi 2
z  wz  4 đạt giá trị nhỏ nhất thì z  w bằng A. 2  5 .
B. 21 5. C. 1 5 . D. 2 5  2 .
Câu 29. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 44) Cho hai số phức z , z thỏa mãn 1 2
z  3i  5  2 và i z  2  i  6 . Khi T  2i z  z
đạt giá trị nhỏ nhất thì z  z bằng 1 2 1 2 1 2 5629 2259 A. . B. 13 . C. 26 . D. . 13 13
Câu 30. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 44) Cho hai số phức z , z thỏa mãn 1 2
z  3  i 
5 và z 1 i  z  5  i . Khi T  z  i z đạt giá trị nhỏ nhất thì phần thực 1 2 2 1 2
của z  5z bằng 1 2 A. 19 . B. 21 . C. 18  . D. 5 .
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 5
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
Câu 31. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 45) Trong không gian Oxyz , cho đường thẳng x y  2 z 1 d :  
. Hình chiếu vuông góc của d trên mặt phẳng  P : x  y  z  5  0 là đường 2 3 1 
thẳng có phương trình x y  2 z 1 x  2 y  5 z  2 A.   . B.   . 1 1 1 1 1 1 x  2 y  5 z  2 x  2 y  5 z  2 C.   . D.   . 4 3  1  2  5  7
Câu 32. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 45) Trong không gian Oxyz cho đường thẳng x  1 t 
d :  y  t
. Hình chiếu vuông góc của d trên mặt phẳng Oxz  là đường thẳng có phương z  1   2t  trình x  0 x  0 x  1 t x 1 t    
A.  y  t .
B.  y  t .
C.  y  t . D.  y  0 .     z  0  z  1   2t  z  0  z  1   2t 
Câu 33. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 45) Trong không gian Oxyz , cho đường thẳng x 1 y 1 z  3 d :   P
x  y  z   là 1 2 2
 . Hình chiếu vuông góc của d trên mặt phẳng   : 2 2 3 0
đường thẳng có phương trình x  2 y 1 z  5 x  2 y 1 z  5 A.   . B.   17 10 14 1  7 10 1  . 4 x  2 y 1 z  5 x  2 y 1 z  5 C.     17 10 1  . D. 4 1  7 1  . 0 14
Câu 34. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 45) Trong không gian Oxyz , cho đường thẳng x 1 y  2 z  3 d :  
. Hình chiếu vuông góc của d trên mặt phẳng  P : x  y  2z 1  0 là 2 4 1
đường thẳng có phương trình x y  3 z 1 x  2 y 1 z  5 A.   . B.   . 2 4 1 2 4 1 x y  3 z 1 x  2 y 1 z  5 C.     2 4  3  . D. 2 4  3  .
Câu 35. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 46) Cho hàm số    3 2 y
f x  x  ax  bx  c có
đồ thị C  , đường thẳng y  mx  n là tiếp tuyến của C  tại điểm có hoành độ x  1  và cắt
C tại điểm có hoành độ bằng 2 (với a , b , c , m và n là các số thực). Diện tích hình phẳng  
giới hạn bởi đồ thị hàm số   2     1 2 f x mx n y x và trục hoành bằng 15 15 5 5 A. . B. . C. ln 2 . D. . 16.ln 2 16 16 16.ln 2
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 6
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
Câu 36. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 46) Cho hàm số    2 y
f x  ax  bx  c với
a, b, c  . Biết rằng hàm số    .e x g x f x  
có hai giá trị cực trị là 5 và 3  . Diện tích hình
phẳng giới hạn bởi đồ thị hàm số g  x và   2 .e x h x ax b    bằng A. 2 . B. 8 . C. 5 3 e e  . D. 5 3 e  e .
Câu 37. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 46) Cho hàm số   4 3 2
f x  x  ax  bx  cx  d
với a, b, c, d 
. Biết hàm số g  x  f  x  f  x  f   x  f   x có ba giá trị cực trị là 14  ; f  x
4; 6. Diện tích hình phẳng giới hạn bởi các đường y  y  bằng g  x  và 1 24 A. 2 ln 3 . B. ln10 . C. ln 3 . D. ln 5 .
Câu 38. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 46) Cho hàm số f  x 3 2
 3x  bx  cx  d với
b, c, d 
. Biết hàm số g  x  f  x  f  x  f   x có hai giá trị cực trị là 12  ; 6 . Diện tích f  x
hình phẳng giới hạn bởi các đường y  y  bằng g  x  và 1 18 A. 2 ln 3 . B. ln 6 . C. 2 ln 2 . D. ln 5 .
Câu 39. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 46) Cho hai hàm số f  x 4 2
 x  ax  bx 1 và g  x 2
 cx  dx  3 a, b, c, d   . Biết rằng đồ thị của hàm số y  f x và y  g x cắt nhau
tại hai điểm có hoành độ lần lượt là 2
 ; 1. Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng 45 99 3 A. . B. 2 . C. . D. . 5 10 2
Câu 40. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 47) Có bao nhiêu cặp số nguyên  x ; y  thỏa 
mãn 2  x  2021 và 2y  log  y 1 x  2  2x  y ? 2  A. 2020. B. 10. C. 9. D. 2019.
Câu 41. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 47) Có bao nhiêu số nguyên y sao cho tồn tại  1  2  x  ; 5 
 thỏa mãn 2x xy     4 8 1 .8 x xy ?  2  A. 7. B. C. 6. D. 5.
Câu 42. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 47) Có bao nhiêu số nguyên y  5 để tồn tại số
thực x thỏa mãn log 4x  3y   1  log  2 2
x  2x  y ? 15 6  A. 3. B. 0. C. 1. D. 2.
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 7
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
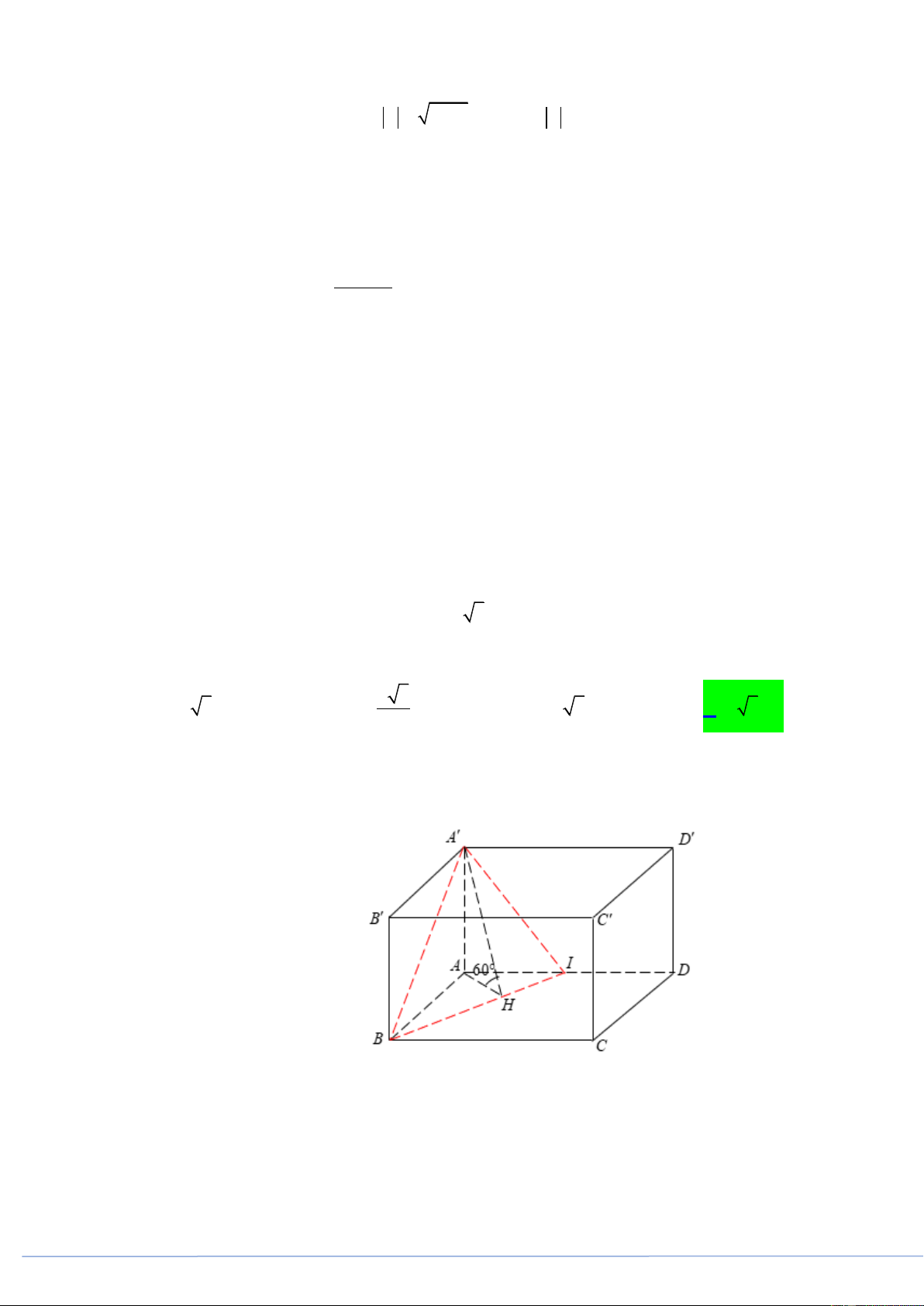
Câu 43. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 48) Cho khối hộp chữ nhật ABC . D A B  C  D   có
AB  a , AD  2a 3 . Gọi I là trung điểm cạnh AD , góc giữa hai mặt phẳng  ABI  và
 ABCD bằng 60. Thể tích của khối hộp chữ nhật đã cho bằng 2 3 A. 3 3 a . B. 3 a . C. 3 2 3 a . D. 3 3 3 a . 3
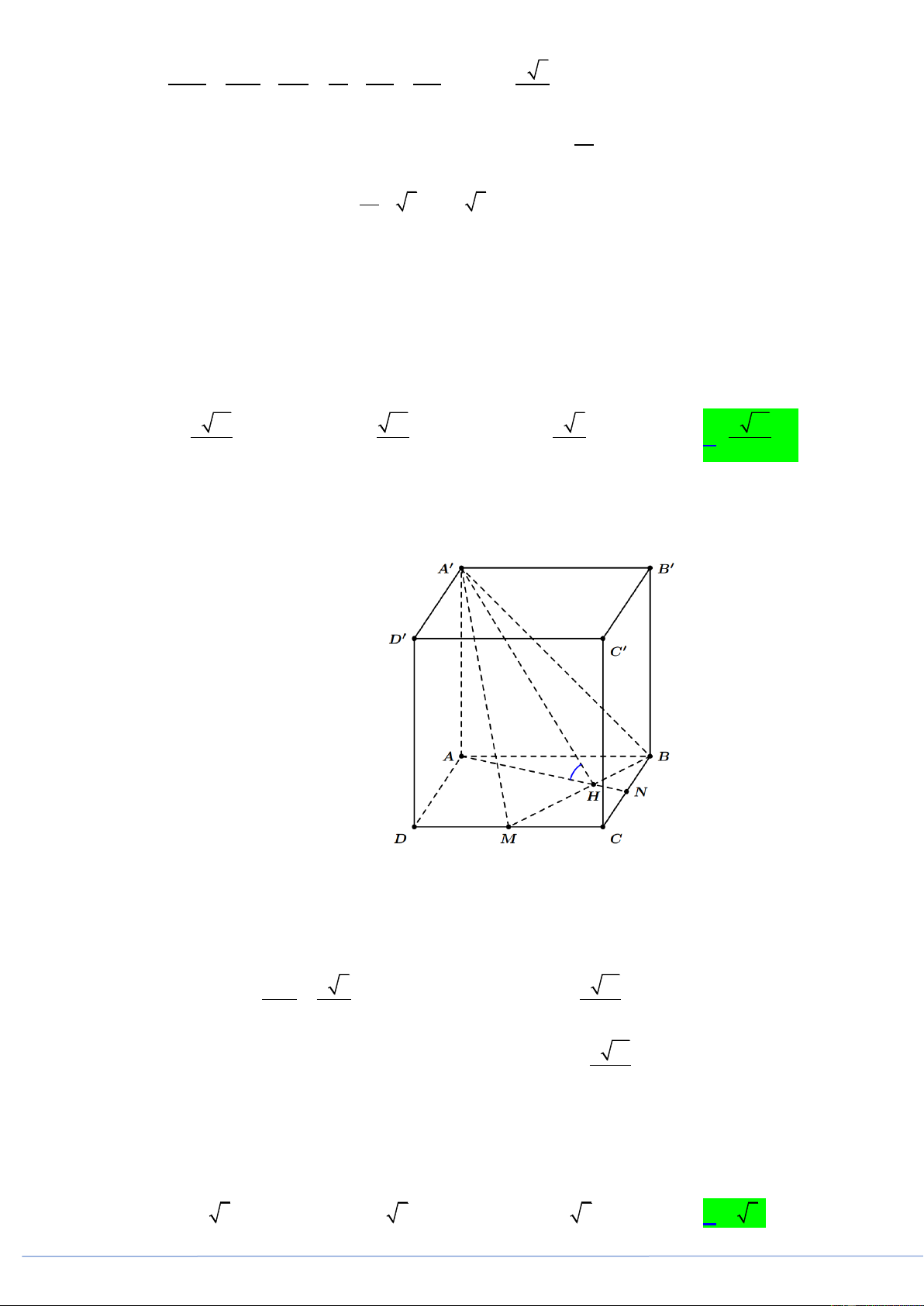
Câu 44. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 48) Cho hình hộp chữ nhật ABC . D A B  C  D   có
đáy là hình vuông cạnh a , góc giữa hai mặt phẳng  ABM  và  ABCD bằng o 60 với M là
trung điểm CD . Thể tích khối hộp chữ nhật đã cho bằng 2 15 15 2 5 2 15 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 15 5 5 5
Câu 45. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 48) Cho khối lăng trụ đứng AB . C A B  C   có đáy
là tam giác đều. Mặt phẳng  ABC  tạo với đáy góc 30 và tam giác A B
 C có diện tích bằng 8 .
Thể tích V của khối lăng trụ đã cho là A. 64 3 . B. 2 3 . C. 16 3 . D. 8 3 .
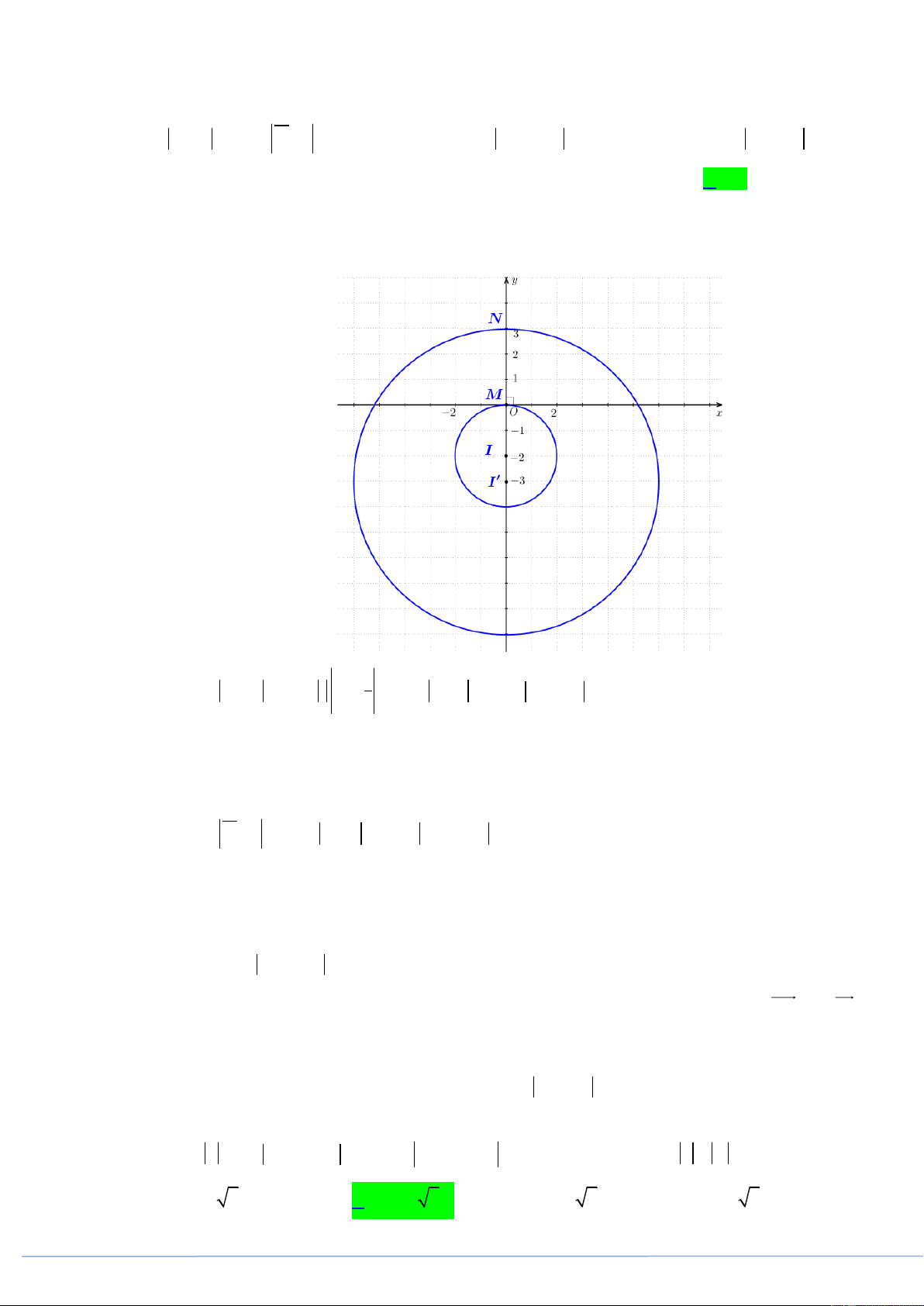
Câu 46. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 49) Trong không gian Oxyz , cho ba điểm
A2;3;9, B 2;3;4  và C 2;15;9. Một mặt cầu S  luôn đi qua ,
A B và tiếp xúc với mặt
phẳng Oxy  tại .
D Biết rằng khi CD đạt giá trị nhỏ nhất thì tọa độ tâm của mặt cầu S  là
I a ;b;c . Khi đó a  b  2c bằng A. 13  . B. 9. C. 2 D. 6.
Câu 47. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 49) Trong không gian Oxyz , cho hai điểm A5; 
1;1 và điểm B 5;0;5 . Xét hai điểm M và N thay đổi thuộc mặt phẳng
P: x  z  2  0 sao cho MN  2. Giá trị lớn nhất của AM  BN bằng A. 3 11 . B. 21 . C. 17 . D. 33 .
Câu 48. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 49) Trong không gian với hệ tọa độ Oxyz , cho
mặt phẳng  P : 2x  2 y  z 15  0 . Gọi M là điểm di động trên  P , N là điểm thuộc tia
OM sao cho OM.ON  10 . Khoảng cách nhỏ nhất từ N đến mặt phẳng  P bằng bao nhiêu? A. 5 . B. 3 . C. 2 . D. 4 .
Câu 49. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 50) Cho hàm số y  f  x có đạo hàm
f  x   x   2 7 x  9, x
  . Có bao nhiêu giá trị nguyên dương của tham số m để hàm số
g  x  f  3
ax  bx  2m  3 với .
a b  0 có ít nhất 3 điểm cực trị? A. 1. B. 2. C. 3. D. 4.
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 8
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
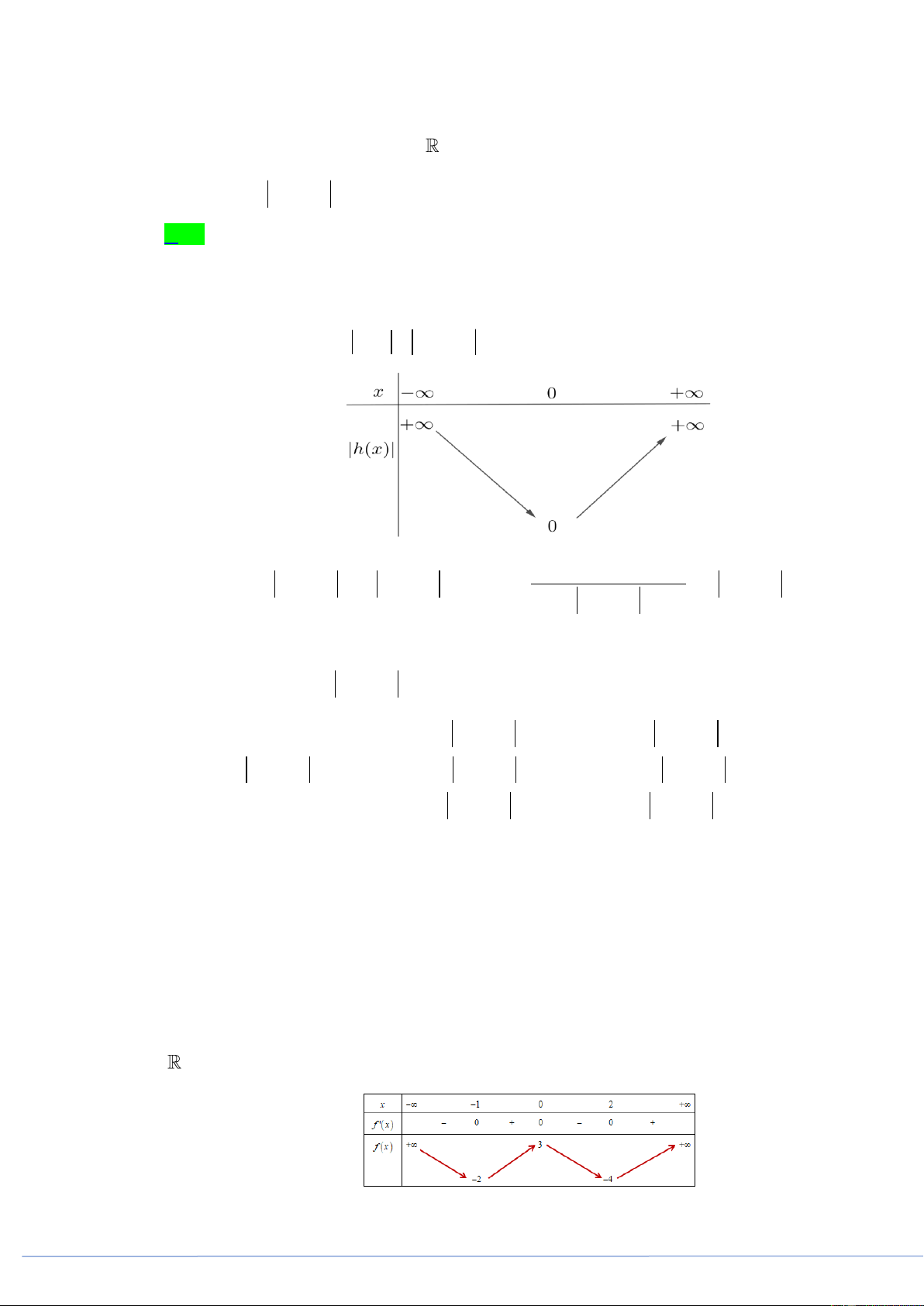
Câu 50. (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 50) Cho hàm số f  x liên tục trên , có bảng biến thiên dưới đây
Có bao nhiêu giá trị nguyên của tham số m để hàm số y  f  6x  5   2021 m có 3 điểm cực đại? A. 5 . B. 6 . C. 7 . D. 8 . HẾT
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 9
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021 BẢNG ĐÁP ÁN 1 2 3 4 5 6 7 8 9 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 B A D C A C A B A A D A D C D C D C B D C D D C B 26 27 28 29 30 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 5 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 D D B A B D D D A D B C C C B C B D D D D D B A B
LỜI GIẢI CHI TIẾT Câu 1.
[1H3-4.6-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 36) Cho hình lăng trụ đứng AB . C A B  C
  có đáy là tam giác đều cạnh a , cạnh bên AA  a 2 (tham khảo hình bên). Góc giữa AB và BC bằng A. 30 B. 60 C. 45 D. 120 Lời giải
FB tác giả: Nguyễn Hường
Ta có: AB  BC  a 3 1 3
AB .BC  BB  A B
 .BB B C   2 2 2 2  B B   A B  .B C
   2a  a  a . 2 2 3 2     AB BC a AB .BC 1 2 cos ,    2 AB .BC 3a 2
Vậy góc giữa AB và BC bằng 60 .
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 10
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021 Câu 2.
[1H3-4.6-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 36) Cho hình lăng trụ tam giác đều AB . C AB C
  có AB  a và AA  a 3 (tham khảo hình bên).
Góc giữa hai đường thẳng AB và CC bằng A. 30 . B. 90 . C. 45 . D. 60 . Lời giải
FB tác giả: Liễu Hoàng
Ta có: AA // CC nên góc giữa hai đường thẳng AB và CC là góc giữa hai đường thẳng AB
và AA và bằng góc AAB (do AAB nhọn). a 3 Tam giác AA B
  vuông tại A nên tan A A  B    A A  B  30 . a 3 3
Vậy góc giữa hai đường thẳng AA và BC bằng 30 . Câu 3.
[1H3-4.6-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 36) Cho hình lập phương ABC . D A B  C  D
  (hình vẽ bên dưới). Góc giữa hai đường thẳng AC và AD bằng A. 45 . B. 90 . C. 30 . D. 60 . Lời giải
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 11
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
FB tác giả: Đinh Ngọc
Ta có:  AC, A D     A C  , A D    DA C    60 . Vì A D   A C    C D  . Câu 4.
[2D2-3.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 37) Với mọi số thực a , b , c thỏa
mãn log a  2 log b  3log
c 1  1 , khẳng định đúng là 3 3 27  
A. a  2b  c  0 .
B. a  b  c  3 2 1  3.
C. a c   2 1  3b .
D. a c   2 1  9b . Lời giải
FB tác giả: Hiếu Lưu
Ta có: log a  2 log b  3log c 1  1 3 3 27   2
 log a  log b  3log c 1  1 3 3 3   3
 log a  log c   2 1  log 3  log b 3 3 3 3  log a  c   1   log   2 3b 3 3 
 a c   2 1  3b . Câu 5.
[2D2-3.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 37) Với mọi số thực a , b thỏa
mãn 3log a  2 log b  3 , khẳng định nào dưới đây đúng? 2 2 A. 3 2 a b  8 . B. 3 2 a b  6 .
C. 3a  2b  8.
D. 3a  2b  6 . Lời giải
FB tác giả: Trần Minh Hưng
Ta có: 3log a  2 log b  3 2 2 3 2
 log a  log b  3 2 2 3 2  log a b  3 2 3 2 3  a b  2 3 2  a b  8 .
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 12
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021 Câu 6.
[2D2-3.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 37) Cho các số thực dương a, b, x 2 1 thỏa mãn log x 
log a  log b . Mệnh đề nào dưới đây đúng? 1 1 1 3 5 2 2 2 2 1  2 1 2 1 3 A. 3 5
x  a b . B. x 
a  b . C. 3 5 x  a b . D. 5 2 x a b  . 3 5 Lời giải
FB tác giả: Quang Trí  2 1 2 1 Ta có: log x  log a  log b 3 5
 log x  log a  log b 1 1 1 3 5 1 1 1 2 2 2 2 2 2 2 1  3 5
 log x  log a .b 1 1 2 2 2 1  3 5
 x  a .b . 3 Câu 7.
[2D3-2.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 38) Nếu f
 xdx  2 thì 1  3 2x  f   xdx  bằng 1  A. 6 . B. 8 . C. 10 . D. 12 . Lời giải
FB tác giả: Nguyễn Thị Quỳnh Nga 3 3 3
Ta có: 2x  f  
xdx  2 d x x  f  
 xdx 82  6. 1  1  1  3 Câu 8.
[2D3-2.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 38) Nếu
f  x dx  2   thì 1 3 2 f  x 2
 3x 1 dx   bằng 1 A. 30  . B. 28  . C. 26  . D. 27  . Lời giải
FB tác giả: Quang Thoại 3 3 3 Ta có 2 f  x 2
 3x 1 dx  2 f
 xdx  2 3  x    1dx . 1 1 1 3
+ Ta có 2 f  x dx  4   . 1 3 3 + Mặt khác  2 3  x   1 dx   3
x  x  2  4 . 1 1 3 Vậy 2 f  x 2
3x 1dx  4  24  2  8   . 1
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 13
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021  2 Câu 9.
[2D3-2.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 38) Cho f
 xdx  5. Khi đó 0  2 I   f
 x2sin xdx  bằng 0 
A. I  7 . B. I  5  .
C. I  3 .
D. I  5   . 2 Lời giải
FB tác giả: Duyên Nguyễn    2 2 2
Ta có: I   f
 x2sin xdx  f 
 xdx+2 sin xdx  0 0 0  2   f  x  2 dx 2 cos x  5  20   1  7 0 0 Vậy: I  7 . 2
Câu 10. [2D3-2.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 38) Cho f
 xdx  2 và 1  2 2
g  x dx  1  
. Khi đó I  x  2 f  
x3g xdx  bằng 1  1  17 7 5 11 A. I  . B. I  . C. I  . D. I  . 2 2 2 2 Lời giải
FB tác giả: Duyên Nguyễn 2 Ta có: I  x  2 f  
x3g xdx  1  2 2 2 2 x   2 f
 xdx3 g  xdx 2 1  1  1   3  2.2  3  1 2  17 2 17 Vậy I  . 2
Câu 11. [2D3-2.1-3] (PHÁT TRIỂN ĐỀ
101 BGD NĂM 2021 CÂU 39) Cho hàm số 2     f  x 3x 2x 1khi x 2  
. Gọi F là nguyên hàm của f trên thỏa mãn F   1  4 . Giá trị 2x  3 khi x  2
của 2F 0  3F 3 bằng A. 65 . B. 57 . C. 61  . D. 69  .
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 14
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021 Lời giải
FB tác giả: Son Que Nguyen. Ta có: 0 3 I  2 f
 xdx3 f
 xdx  2F 02F  13F 33F  1 
  2F 0  3F 3  F   1 . 1 1
Do đó 2F 0  3F 3  I  4 . 0 1
Mà 2 f  xd x  2
 2x  3d x  8    1 0 3 2 3
và 3 f  x dx  3 2x  3dx  3  2 3x  2x     1dx 57. 1 1 2 Do đó I  65
 . Vậy 2F 0 3F 3  I 4  69  .
Câu 12. [2D3-2.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 39) Cho hàm số 2     f  x 2x 3x 1khi x 0  
. Biết F  x là một nguyên hàm của hàm số f  x thỏa mãn 2 1   x khi x  0 F   5 2 
. Giá trị của F  4
   4F 3 nằm trong khoảng nào? 3
A. 52;53 .
B. 53;54 .
C. 54;55 . D. 55;56 . Lời giải
FB tác giả: Trịnh Trung Hiếu 0 0 2  Ta có
f  x dx  F 0  F  2     2 1- x dx    . 3 2  2  2  2  5 ⇒F 0   F  2   
 1. Hàm số f x liên tục tại x  0 3 3 3 1 Mặt khác f
 xdx   2 1 x  3 dx  x 
x  C khi x  0 . 1 3 1 5 F   5 2  ⇒ 2    2
 3  C  ⇒C 1. 3 1 3 3 1 1 Vậy F  x 3
 x  x 1, khi x  0. Từ đó ta tính được F   55 4  . 3 3 2 3 Xét f
 xdx   2
2x  3x   3 2 1 dx  x 
x  x  C khi x  0 . 2 3 2
Ta có F 0  1  C  1 2 2 3 Vậy F  x 3 2
 x  x  x 1, khi x  0 . Từ đó ta tính được F   17 4 3  4.  34 . 3 2 2
Vậy F    F   55 157 4 4 3  34  52,(3) . 3 3
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 15
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
Câu 13. [2D3-2.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 39) Cho hàm số 2     f  x 3x 2x 1khi x 3  
. Giả sử F là nguyên hàm của f trên thỏa mãn F   1  4 . Giá
4x  32 khi x  3 trị của 3F  2
   F 4 bằng A. 69  . B. 25  . C. 45  . D. 53  . Lời giải
FB tác giả: Hiếu Lê 1 4 Ta có I  3  f
 xdx f
 xdx  3  F   1  3F  2
   F 4  F   1 . 2  1
Do đó I  3F  2
   F 4  2F   1  3F  2
   F 4 8  3F  2
   F 4  I 8 . 1 1 Mà 3  f
 xdx  3    2
3x  2x   1 dx  2  7 2  2  4 3 4 và f
 xdx   2
3x  2x   1 dx   4
 x  32dx  34 . 1 1 3 Suy ra I  2  7 34  6  1. Vậy 3F  2
   F 4  61  8  53  .
Câu 14. [2D2-6.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 40) Có bao nhiêu số nguyên x 3  thỏa mãn  x x 2 8  2
.log 2x2 140?  3  A. 10 . B. 8 . C. 6 . D. 7 . Lời giải
FB tác giả: Quang Thoại Điề 21 u kiện: x   * . 2 Trường hợp 1:    3 3 x 2 x x 2 3x x 2 3 8   2  0 2  2
x  3x  2  0   6   x  2       x    log  2x   21  4  0 log   2x   1 21  4  2x  21  9  x 1 3 3 x  6 
Kết hợp với điều kiện * ta được x 6; 2  1 .
Trường hợp này ta được 6 giá trị nguyên của x thỏa yêu cầu. Trường hợp 2: 3 3 x x 2 3x x 2 3 8   2  0 2  2
x  3x  2  0 x  2         . log  2x  2  1  4  0 log   2x  2  1  4  2x  21  9 x  6  3 3
Trường hợp này không có giá trị nào của x thỏa mãn.
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 16
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
Vậy có 6 giá trị nguyên của x thỏa ycbt gồm  6  ; 5  ; 4  ;3;2;  1 .
Câu 15. [2D2-6.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 40) Có bao nhiêu số nguyên x 2 thỏa mãn  x x x 1 9 3 .9  
log 2x18 5 0? 2    A. 1 B. Vô số. C. 17. D. 16. Lời giải
FB tác giả: Nguyễn Thanh Bằng
Điều kiện: x  9 * . Trường hợp 1:  1            2 x 2 x x x  1 1 2 x 3x 2 2 9 3 .9 0 3   3
2x  3x  2  2 x            log  2x 18 2 5        x  2 5 0 2x 18 2 2x 50   2 2  x  25 x  25
Kết hợp với điều kiện * ta được x  9;25 Mà x 
 x 10;11;...;2 
5  có 16 giá trị nguyên của x thỏa mãn. Trường hợp 2: 2 2 x x x   1 1 2 x 3x 2 2 9  3 .9  0 3   3
2x  3x  2   x  2        log  2x 18 2 5  5  0 2x 18  2 2x  50  2 x  25
Trường hợp này không có giá trị nào của x thỏa mãn.
Kết hợp các trường hợp, ta có tất cả 16 giá trị nguyên của x thỏa mãn đề.
Câu 16. [2D2-6.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 40) Có bao nhiêu số nguyên x 3 thỏa mãn log  25 2. x x 3 2 2 2 .4 x x       0 ? 3  A. 1 B. 18. C. 16. D. 17. Lời giải
FB tác giả: Nguyễn Thanh Bằng
Điều kiện: x  25 * . 3 Ta có: log  25 2. x x 3 2 2 2 .4 x x       0 3  log  x  25 2  2  0 x  25  3 x  16     3 x 16          16  x  1 3 3    3 x x 3 2 x x 6 5 2  2 .4  0 2  2 x
x  6  5x x  1
Kết hợp với điều kiện * ta được x  1  6;  1 Mà x   x  15  ; 14  ;...; 
0  có 16 giá trị nguyên của x thỏa mãn.
Vậy có 16 giá trị nguyên của x thỏa mãn yêu cầu của bài toán.
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 17
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
Câu 17. [2D2-6.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 40) Có bao nhiêu số nguyên x   2
thỏa mãn 9x  27x  log x  2022 1  0 ? 1    2  A. 2020 . B. 2022 . C. 5 . D. 4 . Lời giải
Tác giả: Hồ Hữu Tình
Điều kiện x  2022*. Ta có 2  9x   27x  0  1
 log x  2022 1  0 1          2 
9x  27x log  x  2022 2 1  0  1  2 x x    2  9  27  0   2 log x  2022 1  0 1       2 Khi đó  2 3 2  2 x 3x 2x  3   3  3 x x 2     
2x  3x  0  2 1                    x  1 x 2020 1 log 2022 1          x  0 1 x 2022 x 2022 2   2   2  x  2020  2 2  2 x 3x 2x  3x    3 3 3 2    
2x  3x  0 0  x  3 2                   x  1 2 0 1 x log 2022 1 1 
x  2022    x  2022  2 2      x  2020  2 2
Kết hợp điều kiện * ta có tất cả 4 giá trị nguyên của x là 2021  ;  2020; 0; 1.
Câu 18. [2D1-5.3-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 41) Cho hàm số bậc bốn y  f  x
có đồ thị là đường cong trong hình bên
Số nghiệm thực phân biệt của phương trình 2 f  f  x 1  0 là A. 9 . B. 4 . C. 8 . D. 7 .
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 18
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021 Lời giải
Tác giả: Tăng Văn Vũ
Ta biến đổi: f  f  x    f  f  x 1 2 1 0   . 2
 f x  a a    1 
 f  x  b1 b  0 1 
Căn cứ vào đồ thị hàm số đã cho ta thấy: f  f x     . 2
f  x  c 0  c   1 
 f x  d d   1
Căn cứ vào đồ thị hàm số y  f  x ta có: + Với a  1
 , phương trình f  x  a vô nghiệm. + Với 1
  b  0 , phương trình f x  b có 4 nghiệm thực phân biệt.
+ Với 0  c  1, phương trình f  x  c có 2 nghiệm thực phân biệt.
+ Với d  1, phương trình f  x  d có 2 nghiệm thực phân biệt.
Các nghiệm của các phương trình f  x  a , f  x  b , f  x  c và f  x  d là các nghiệm thực phân biệt.
Vậy phương trình đã cho có 8 nghiệm thực phân biệt.
Câu 19. [2D1-5.3-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 41) Cho hàm số f  x có bảng biến thiên như sau
Số nghiệm thực phân biệt của phương trình f  2 4
4x  2x  1 là A. 9 . B. 6 . C. 8 . D. 12 .
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 19
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021 Lời giải
Tác giả: Tăng Văn Vũ 2 4
4x  2x  a a  0 
Dựa vào bảng biến thiên ta thấy: f  2 4 4x  2x  2 4
 1  4x  2x  b0  b  2 .  2 4
4x  2x  c c  2 
Vẽ đồ thị (hoặc bảng biến thiên) của hàm số 2 4
y  4x  2x :
Căn cứ vào đồ thị hàm số 2 4
y  4x  2x , ta có:
+ Với a  0 , phương trình 2 4
4x  2x  a  
1 có 2 nghiệm thực phân biệt.
+ Với 0  b  2 , phương trình 2 4
4x  2x  b 2 có 4 nghiệm thực phân biệt.
+ Với c  2 , phương trình 2 4
4x  2x  c 3 vô nghiệm.
Các nghiệm của các phương trình  
1 , 2 và 3 là các nghiệm thực phân biệt.
Vậy phương trình đã cho có 6 nghiệm thực phân biệt.
Câu 20. [2D1-5.3-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 41) Cho hàm số y  f  x có bảng biến thiên như sau  9 
Số nghiệm thuộc đoạn 0; 
 của phương trình f  f cos x  2 là  2  A. 3 . B. 5 . C. 7 . D. 9 . Lời giải
FB tác giả: Phạm Hùng
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 20
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
 f cos x  1 
Từ bảng biến thiên ta suy ra: f  f cos x  
 2   f cosx1
TH1: f cos x  1 
Đặt t  cos x , t 1;  1
Khi đó phương trình f cos x  1
 trở thành f t  1, với t 1;  1 .
Đây là phương trình có hoành độ giao điểm của đồ thị hàm số y  f t  và đường thẳng y  1  .
t  a  
Dựa vào bảng biến thiên, ta có f t  1  1     phương trình vô nghiệm. t  b 1
TH2: f cos x  1
Tương tự TH1: Đặt t  cos x , t 1;  1
t  m ;    1  L 
t  n1;0
f t   1  t  p0; 1 
t  q1;    L
+ Với t  n  1; 0    Ứ 9
ng với mỗi giá trị t  1; 0 thì phương trình cos x  t có 4 nghiệm phân biệt thuộc 0;    2 
+ Với t  p  0;  1    Ứ 9
ng với mỗi giá trị t  0; 
1 thì phương trình cos x  t có 5 nghiệm phân biệt thuộc 0;   .  2 
Hiển nhiên, 9 nghiệm trong những trường hợp trên đều khác nhau.  9 
Vậy phương trình đã cho có 9 nghiệm thuộc đoạn 0;   .  2 
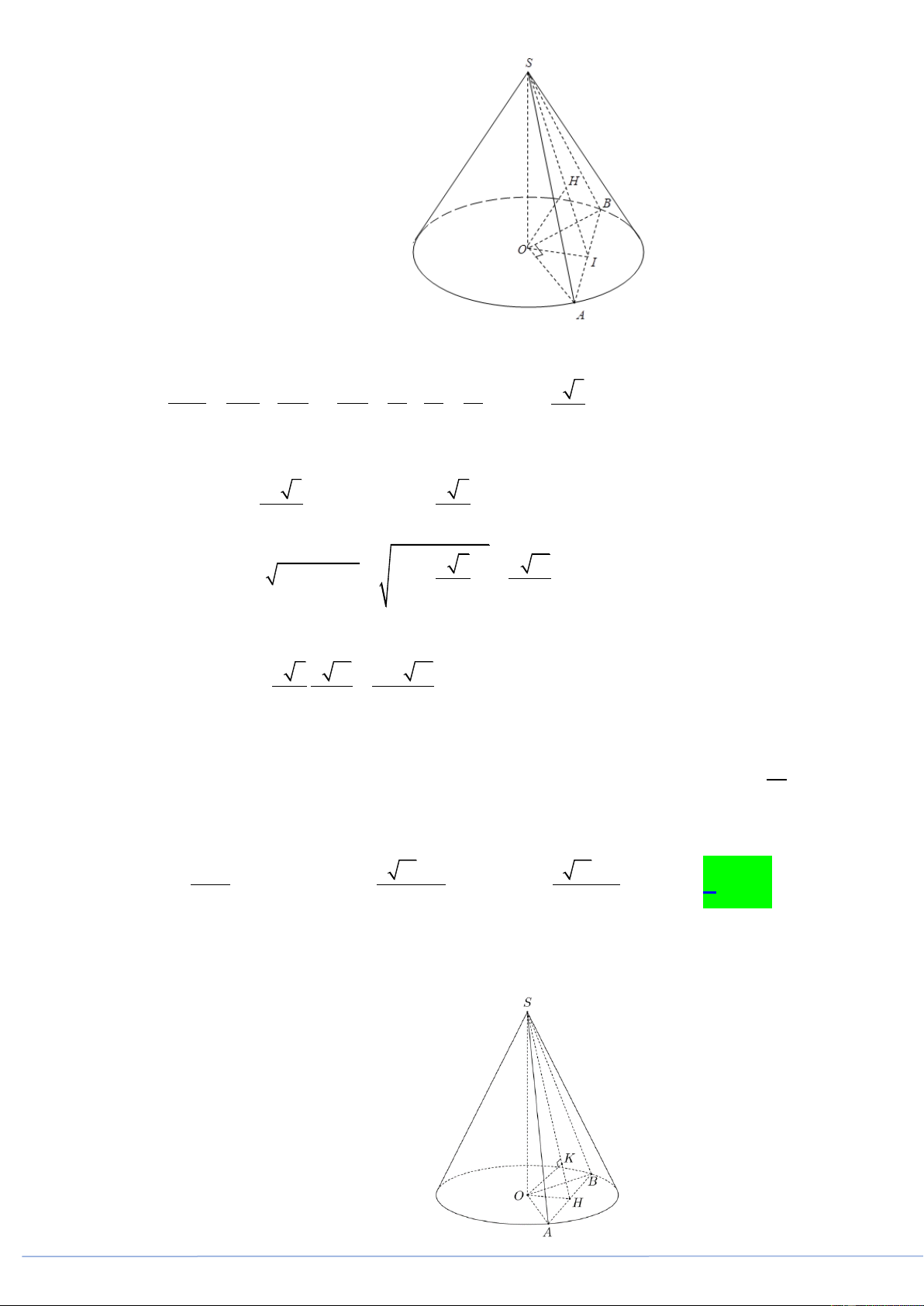
Câu 21. [2H2-1.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 42) Một hình nón đỉnh S , đáy là
hình tròn tâm O và SO  a . Một mặt phẳng  P qua đỉnh S cắt đường tròn O theo dây cung a
AB sao cho góc AOB  90 và cách O một khoảng
. Diện tích xung quanh hình nón bằng 2 2  a 10 2  a 10 2  a 10 2 2 a 10 A. . B. . C. . D. . 6 3 3 3 3 Lời giải
FB tác giả: Minh Trí
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 21
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
Gọi I là trung điểm của AB . Kẻ OH  SI 1 1 1   1 4 1 3     a 3  OI  . 2 2 2 OH SO OI 2 2 2 2 OI a a a 3
Tam giác OAB vuông cân tại O nên: 2a 3 a 6 AB  2OI 
, R  OA  OB  . 3 3 2  a 6  a 15 Suy ra: 2 2 2 SB  SO  OB  a       . 3 3  
Diện tích xung quanh của hình nón: 2 a 6 a 15  a 10 S   Rl    . xq 3 3 3
Câu 22. [2H2-1.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 42) Cắt hình nón  N  bởi mặt a
phẳng   đi qua đỉnh và có khoảng cách đến tâm O của đường tròn đáy là 3 ta được thiết 2
diện là tam giác đều cạnh 4a . Thể tích của  N  bằng 3 7 a 3 4 13 a 3 8 13 a A. . B. . C. . D. 3 7 a . 3 3 3 Lời giải
FB tác giả: Shangri La
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 22
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
Gọi O là tâm đường tròn đáy và thiết diện là tam giác SAB đều cạnh 4a .
Gọi H là trung điểm của AB . 3a . SO OH
Kẻ OK  SH , khi đó d O,   SK     1 2 2 2 SO  OH 3 Mặt khác S
 AB đều có cạnh 4a suy ra SH  4 . a  2 3a . 2 Lại có 2 2 2 2 2
OH  SH  SO  12a  SO . 2 2 2 2 3a .
SO 12a  SO .
SO 12a  SO Thay vào   1 ta được    SO  3a . 2 2 2 2
SO 12a  SO 2 3a 2 2
Ta có OA  4a  3a  a 7 . 1 Vậy 2 3      V a a a . N  .7 .3 7 3
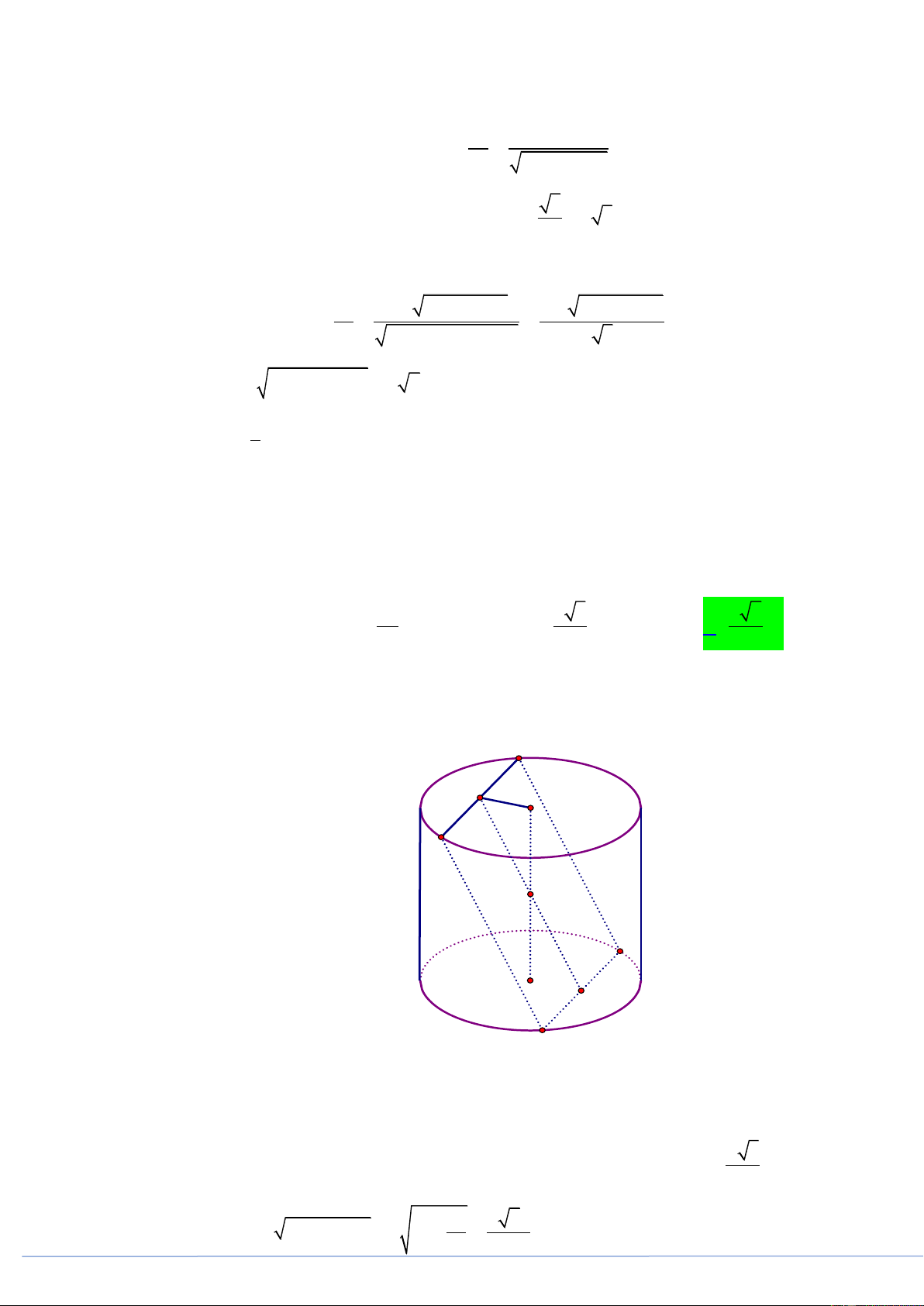
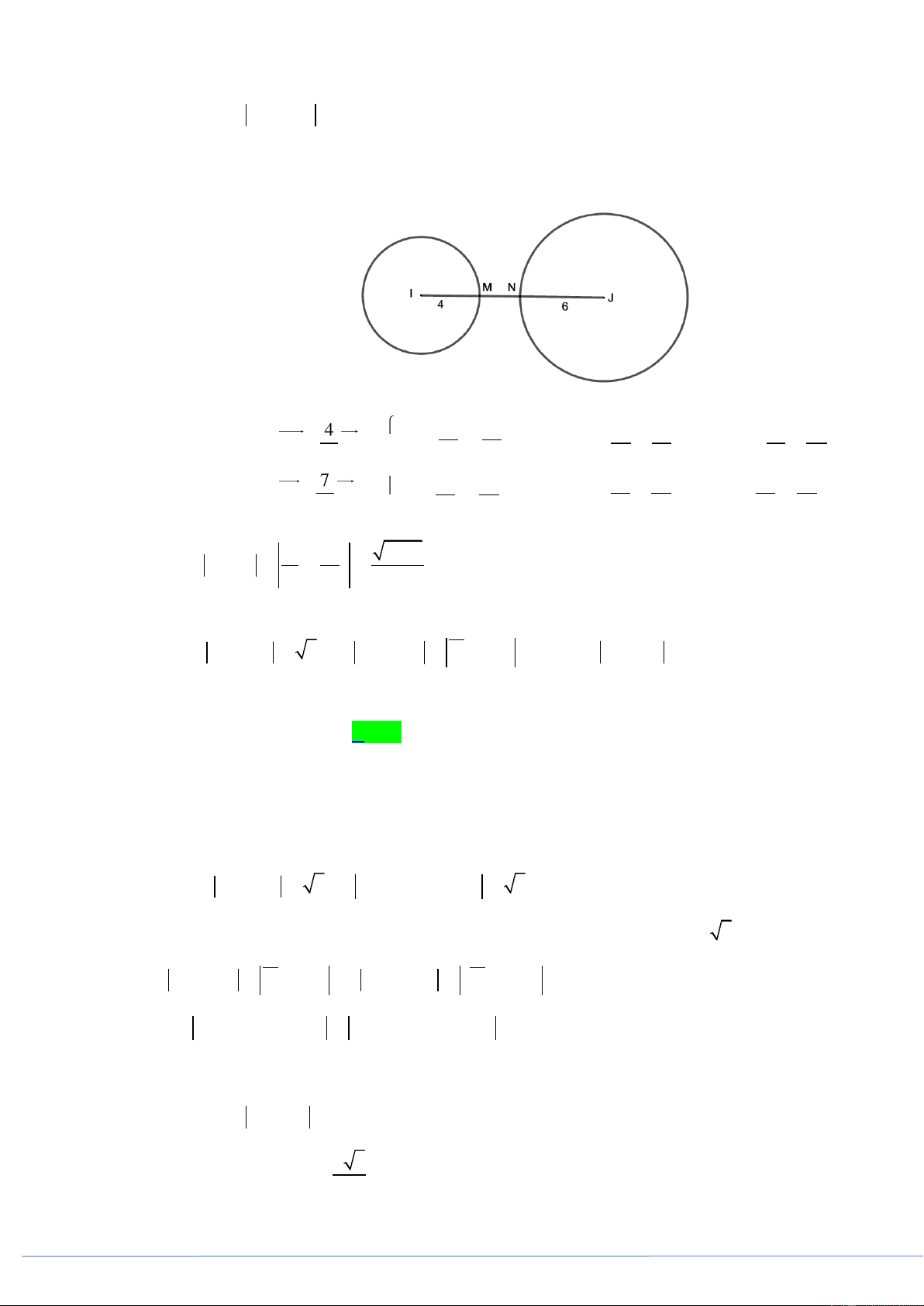
Câu 23. [2H2-1.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 42) Cho hình trụ đứng có hai đáy
là hai đường tròn tâm O và tâm O , bán kính bằng a , chiều cao hình trụ bằng 2a . Mặt phẳng đi
qua trung điểm OO và tạo với OO một góc 30 , cắt đường tròn đáy tâm O theo dây cung AB
. Độ dài đoạn AB là 2a 4 3 2 6 A. a . B. . C. a . D. a . 3 9 3 Lời giải
FB tác giả: Hoàng Yến B N O A M O'
Gọi M , N lần lượt là trung điểm của OO và AB .
Ta có OO ; ABM   OO ; MN   OMN  30 . a
Tam giác OMN vuông tại O có ON  3
tan OMN.OM  ON  tan 30 .  a  . 3 2 a 2 6a 2 2 2
AB  2NB  2 OB  ON  2 a   . 3 3
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 23
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
Câu 24. [2H2-1.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 42) Hình nón  N  có đỉnh S , tâm
đường tròn đáy là O , góc ở đỉnh bằng 120 . Một mặt phẳng qua S cắt hình nón  N  theo thiết
diện là tam giác vuông SAB . Biết rằng khoảng cách giữa hai đường thẳng AB và SO bằng 3 .
Tính diện tích xung quanh S của hình nón  N  xq A. S  36 3 . B. S  27 3 . C. S  18 3 . D. S  9 3 . xq xq xq xq Lời giải
FB tác giả: Hoàng Yến
Theo giả thiết ta có tam giác SAB vuông tại S và OH  3 và BSO  60 . r 2r
Gọi r là bán kính đường tròn đáy của hình nón thì đường sinh l  SB   l  . sin 60 3 2 6 1 r 6 S
 AB vuông tại S nên: AB  l 2 
r . Suy ra BH  AB  . 3 2 3 2 6r
Xét tam giác OBH vuông tại H , ta có 2 9 
 r  r  3 3 . 9 Vậy S   rl 18 3 xq
Câu 25. [2D4-4.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 43) Trên tập hợp các số phức, xét phương trình 2
z  m   2 2
1 z  m  5m  0 ( m là tham số thực). Gọi S là tập hợp các giá trị 3
nguyên m để phương trình đó có nghiệm z thỏa mãn z
 3 z  2 . Tổng các phần tử của tập 0 0 0 S là A. 8 . B. 9 . C. 4 . D. 7 . Lời giải
FB tác giả: Nam Hồng Lê 3 3
Do z  z nên z
 3 z  2  z 3 z  2  0  z  2 0 0 0 0 0 0 0
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 24
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021 2 2 
  (m 1)  m  5m  3m 1. 1
TH1: Nếu   0  3m 1  0  m   , phương trình có 2 nghiệm thực 3
Khi đó z  2  z  2 . 0 0 m 1
Thay z  2 vào phương trình ta được: 2
m  9m  8  0   TM. 0 m  8 m  0 Thay z  2
 vào phương trình ta được: 2
m  m  0   TM. 0 m 1 1
TH2: Nếu   0  3m 1  0  m   , phương trình có 2 nghiệm phức z , z thỏa mãn 3 1 2 5  41
z  z , z  z  2 . Khi đó 2 2
z .z  z
 m  5m  4  m  (Không thỏa mãn). 2 1 1 2 1 2 1 2 Vậy S  0;1;  8 . Suy ra tổng là 9 .
Câu 26. [2D4-4.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 43) Trong tập số phức, cho phương trình 2
z  m   2 2 2
1 z  m  3m  2  0, m 
. Có bao nhiêu giá trị nguyên của m trong đoạn
0;202 1 để phương trình có 2 nghiệm phân biệt z ;z thỏa mãn z  z ? 1 2 1 2 A. 2016. B. 202 C. 202 D. 2017. Lời giải
FB tác giả: Nhật Lê
Phương trình có 2 nghiệm phân biệt m  5 TH1: 2
  0  m  4m  5  0  m 1
Phương trình đã cho có 2 nghiệm thực phân biệt z , z . 1 2
z  z   m 1  1 2  
Theo định lí Vi-ét ta có:  2
z z  m  3m  2  1 2
Theo đề bài ta có: z  z  z  z (vì z  z ) 1 2 1 2 1 2
 z  z  0 1 2  m   1  0  m 1 (nhận) m  5
TH2:   0  m  1 
Phương trình luôn có 2 nghiệm phức z , z luôn thỏa mãn z  z . 1 2 1 2
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 25
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
Vậy có 2017 giá trị m thỏa mãn.
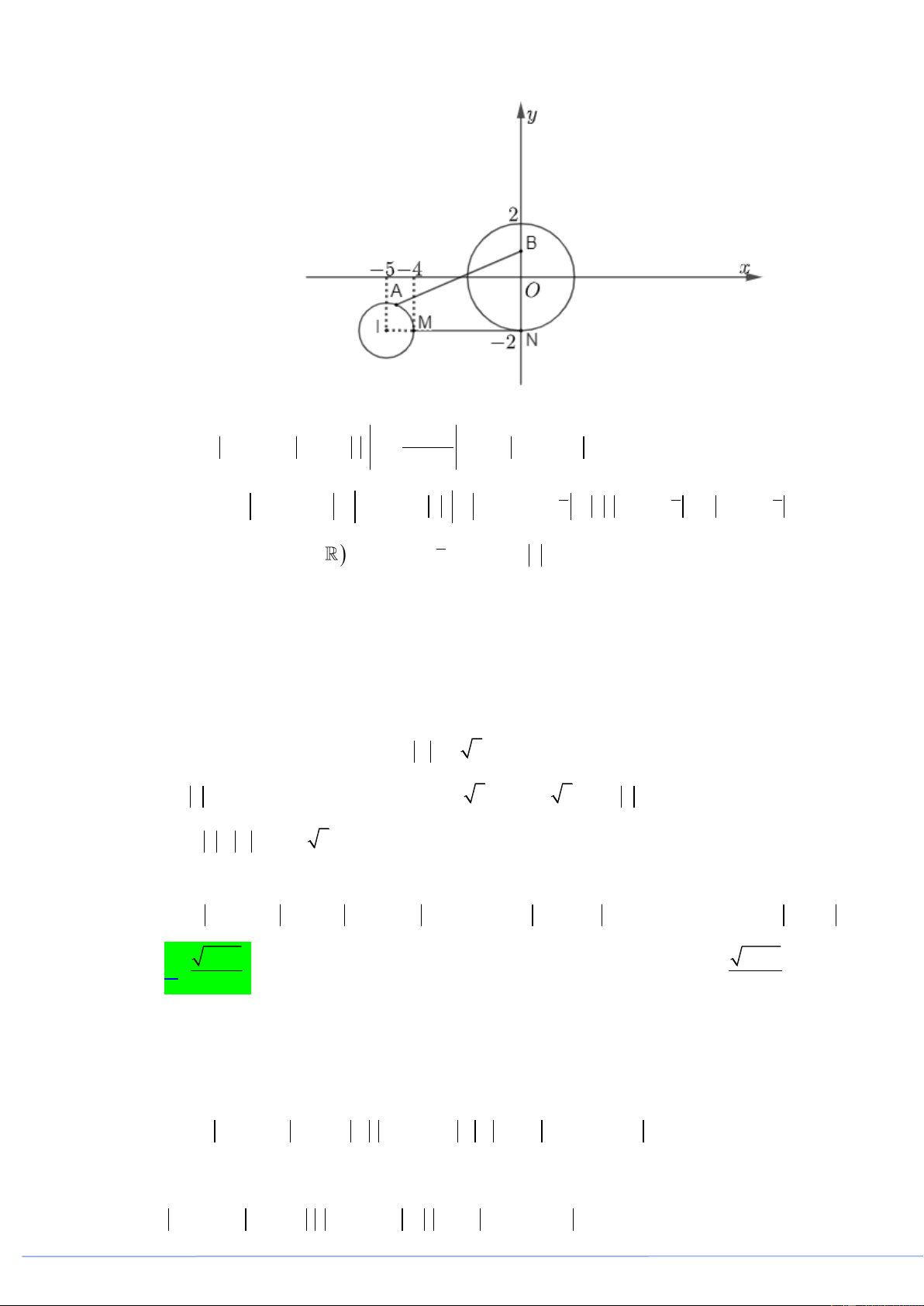
Câu 27. [2D4-5.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 44) Cho hai số phức z , z thỏa 1 2
iz 1  1 và z  i  2 . Khi biểu thức P  2z  3z đạt giá trị nhỏ nhất thì z  2z bằng 1 2 1 2 1 2 A. 4 . B. 1. C. 3 . D. 2 . Lời giải
FB tác giả: Tho Nguyen 1
Ta có: iz 1  1  i z 
1  z  i  1  2z  2i  2 1 1 1 i 1
Gọi M là điểm biểu diễn số phức 2z . 1
 Tập hợp M thuộc đường tròn tâm I 0 ; 2 , R  2 .
Ta có: z  i  2  z  i  2  3
 z  3i  6 2 2 2
Gọi N là điểm biểu diễn số phức 3  z . 2
 Tập hợp N thuộc đường tròn tâm I0; 3 , R  6.
Suy ra: P  2z  3z  MN 1 2  P  MN
 M , N, I, I thẳng hàng ( M nằm giữa N và I ) MN  3 và IM  2  II , M min min
là trung điểm của NI . Từ đó ta tính được M 0;0, N 0;3 .
 2z  0, 3z  3i . Khi đó, z  2z  2i . Vậy z  2z  2 . 1 2 1 2 1 2
Câu 28. [2D4-5.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 44) Xét các số phức z , w thỏa
mãn z  2 , iw  2  5i  1. Khi 2
z  wz  4 đạt giá trị nhỏ nhất thì z  w bằng A. 2  5 .
B. 21 5. C. 1 5 . D. 2 5  2 . Lời giải
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 26
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
FB tác giả: Ngọ Thị Hằng 2   5i
Ta có: iw  2  5i  1  i . w 
1  w  5  2i  1. i 2 Ta có: 2 2 2
T  z  wz  4  z  wz  z
 z  wz  z.z  z . z  w  z  2 z  w  z .
Đặt z  a  bi,a,b   , suy ra z  z  2bi . Vì z  2  2   b  2 . Gọi ,
A B lần lượt là điểm biểu diễn của , w 2bi nên:
A thuộc đường tròn tâm I 5; 2; R  1, B thuộc trục Oy và 4   x  4 B
T  2AB  2MN  2.4  8
Dấu "  " xảy ra khi và chỉ khi A  M  4  ; 2    w  4
  2i  w  2 5 và B  N 0; 2    2bi  2
 i  b  1 z  a  i 2 2
 z  2  a 1  4  a  3  a   3  z   3  i  z  2
Vậy z  w  2  2 5 .
Câu 29. [2D4-5.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 44) Cho hai số phức z , z thỏa 1 2
mãn z  3i  5  2 và i z  2  i  6 . Khi T  2i z  z đạt giá trị nhỏ nhất thì z  z bằng 1 2 1 2 1 2 5629 2259 A. . B. 13 . C. 26 . D. . 13 13 Lời giải
FB tác giả: Dương Thị Lý
Giả sử M , N lần lượt là điểm biểu diễn cho số phức 2iz và z . 1 2
Ta có z  3i  5  2  2i . z  3i  5  2i .2  2iz  6  10i  4 . 1 1 1
Suy ra tập hợp điểm M là đường tròn C
tâm I 6; 10 và bán kính R  4 . 1  1
i z  2  i  6  i . i z  2  i  i .6   z  1  2i  6 . 2 2 2
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 27
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
Suy ra tập hợp điểm N là đường tròn C
tâm J 1; 2 và bán kính R  6 . 2  2
Ta có T  2i z  z  MN . 1 2
minT  IJ  R  R  13  4  6  3 . 1 2  4   58 82   58 82  41 29 IM  IJ M  ;     2iz    i z    i   1  1  13   13 13    Đạt đượ 13 13 13 13 c khi        7    43 46  43 46 43 46 IN IJ    N  ;  z    i z   i   2 2  13   13 13    13 13  13 13 2 75 5629
Vậy z  z   i  . 1 2 13 13 13
Câu 30. [2D4-5.1-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 44) Cho hai số phức z , z thỏa 1 2
mãn z  3  i 
5 và z 1 i  z  5  i . Khi T  z  i z đạt giá trị nhỏ nhất thì phần 1 2 2 1 2
thực của z  5z bằng 1 2 A. 19 . B. 21 . C. 18  . D. 5 . Lời giải
FB tác giả: Dương Thị Lý
Giả sử M  x ; y, N  x; y lần lượt là điểm biểu diễn cho số phức z và iz 1 2 2 2
Ta có z  3  i  5  x  3  y 1 i  5  x  3  y 1  5. 1        
Suy ra tập hợp điểm M là đường tròn C  tâm I 3; 
1 và bán kính R  5 .
z 1 i  z  5  i  i z  i 1  i z  5i 1 2 2 2 2  x   1   y  
1 i  x  
1   y  5i  x  2 y  6  0 .
Suy ra tập hợp điểm N là đường thẳng d  : x  2 y  6  0 .
Ta có T  z  i z  MN . 1 2
minT  d  I d  2 5 ,  R  . 5
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 28
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021 Đạt đượ 5
c khi N là hình chiếu của I trên d và IM  IN . 7  8 19  Suy ra N ;   và M 2;3  5 5   8 19 19 8
z  2  3i ; iz   i  z 
 i  z  5z  21 5i 1 2 2 1 2 5 5 5 5
Vậy phần thực của z  5z là 21 . 1 2
Câu 31. [2H3-3.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 45) Trong không gian Oxyz , cho   đườ x y 2 z 1 ng thẳng d :  
. Hình chiếu vuông góc của d trên mặt phẳng 2 3 1 
P: x  y  z 5  0 là đường thẳng có phương trình x y  2 z 1 x  2 y  5 z  2 A.   . B.   . 1 1 1 1 1 1 x  2 y  5 z  2 x  2 y  5 z  2 C.   . D.   . 4 3  1  2  5  7 Lời giải
FB tác giả: Bùi Tuấn Anh  x  2t 
Phương trình tham số của d : y  2  3t .
 z  1t 
Gọi M  d   P  M 2t ; 2  3t ; 1 t  .
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 29
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
Do M   P : 2t  2  3t 1 t  5  0  t  1  M 2;5;  2 .
Gọi d  là hình chiếu vuông góc của d lên mặt phẳng  P . Q là mặt phẳng chứa d và d .
Q  P  n  n  Q
P   n  u ,n     Q d P 4; 3;    d  Q 1  n  u  Q d 
d   P  u    n  d
P   u        n , n d Q P  2; 5;7  
d  Q  u   n  d Q 
Đường thẳng d qua điểm M 2;5; 2 và nhận u  2
 ; 5;7 là vectơ chỉ phương có d '      phương trình chính tắ x 2 y 5 z 2 c là d :   . 2  5  7
Câu 32. [2H3-3.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 45) Trong không gian Oxyz cho x  1 t 
đường thẳng d : y  t
. Hình chiếu vuông góc của d trên mặt phẳng Oxz  là đường thẳng z  1   2t  có phương trình x  0 x  0 x  1 t x 1 t    
A.  y  t .
B.  y  t .
C.  y  t . D.  y  0 .     z  0  z  1   2t  z  0  z  1   2t  Lời giải
FB tác giả: Phuong Tran
Mặt phẳng Oxz  : y  0 , d có véctơ chỉ phương là u  1;1; 2
d  Oxz   A1;0;  
1 . Gọi  là hình chiếu vuông góc của d trên Oxz  x  1 t  
A  và  có véctơ chỉ phương là v  1;0; 2   :  y  0 . z  1   2t 
Câu 33. [2H3-3.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 45) Trong không gian Oxyz , cho x 1 y 1 z  3 đường thẳng d :   1 2 2
 . Hình chiếu vuông góc của d trên mặt phẳng
P: 2x  2y  z 3  0 là đường thẳng có phương trình x  2 y 1 z  5 x  2 y 1 z  5 A.   . B.   17 10 14 1  7 10 1  . 4 x  2 y 1 z  5 x  2 y 1 z  5 C.     17 10 1  . D. 4 1  7 1  . 0 14 Lời giải
FB tác giả: Phuong Tran
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 30
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
d có véctơ chỉ phương là u  1; 2;  2
Mặt phẳng  P có véctơ pháp tuyến là n  2;  2  ;1
Gọi đường thẳng a là hình chiếu vuông góc của d trên mặt phẳng  P , Q là mặt phẳng chứa
a và d  Q có véctơ pháp tuyến là u , n 
 và a  P  Q
 a có véctơ chỉ phương là u , n , n   1  7;10;14   
d   P  I 2; 1;5  I  a x  2 y 1 z  5  a :   1  7 1  . 0 14
Câu 34. [2H3-3.2-3] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 45) Trong không gian Oxyz , cho x 1 y  2 z  3 đường thẳng d :  
. Hình chiếu vuông góc của d trên mặt phẳng 2 4 1
P: x  y  2z 1 0 là đường thẳng có phương trình x y  3 z 1 x  2 y 1 z  5 A.   . B.   . 2 4 1 2 4 1 x y  3 z 1 x  2 y 1 z  5 C.     2 4  3  . D. 2 4  3  . Lời giải
FB tác giả: Phuong Tran
Gọi đường thẳng a là hình chiếu vuông góc của d trên  P
d có véctơ chỉ phương là u  2; 4 
;1 và d đi qua M 1; 2;3
Mặt phẳng  P có véctơ pháp tuyến là n  1; 1; 2 u  .n  0 Có 
 d // P  nhận u  2;4  ;1 làm véctơ chỉ phương      a M P
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 31
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
Gọi H là hình chiếu vuông góc của M trên  P x  1 t 
 MH : y  2  t mà H P  H 0;3;  1 z  3 2t 
 a đi qua H 0;3;  1 x y  3 z 1  a :   . 2 4 1
Câu 35. [2D3-3.1-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 46) Cho hàm số    3 2 y
f x  x  ax  bx  c có đồ thị C  , đường thẳng y  mx  n là tiếp tuyến của C  tại
điểm có hoành độ x  1
 và cắt C tại điểm có hoành độ bằng 2 (với a , b , c , m và n là các  
số thực). Diện tích hình phẳng giới hạn bởi đồ thị hàm số   2     1 2 f x mx n y x và trục hoành bằng 15 15 5 5 A. . B. . C. ln 2 . D. . 16.ln 2 16 16 16.ln 2 Lời giải
FB tác giả: Dương Thái Bảo Vì   3 2
f x  mx  n  x  ax  b  m x  c  n là hàm số bậc ba có hai nghiệm x  1  (nghiệm 2
kép) và x  2 nên f  x  mx  n   x   1  x  2 . Đặ 2
t g  x  f  x  mx  n   x  
1  x  2 , suy ra g x 2  3x  3 . x  1 
Phương trình hoành độ giao điểm  2
x   gx 1 2  0   . x 1
Diện tích hình phẳng cần tìm là 1 S  x   1 g x 1 g x 5 2   1 .2 dx  g x   .2 dx    . 3 16.ln 2 1  1 
Câu 36. [2D3-3.1-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 46) Cho hàm số    2 y
f x  ax  bx  c với a, b, c 
. Biết rằng hàm số    .e x g x f x  
có hai giá trị cực trị là 5 và 3
 . Diện tích hình phẳng giới hạn bởi đồ thị hàm số g  x và   2 .e x h x ax b    bằng A. 2 . B. 8 . C. 5 3 e e  . D. 5 3 e  e . Lời giải
FB tác giả: Dương Thái Bảo  
Ta có          x 2 ' .e    
2     .e x g x f x f x ax a b x b c   .
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 32
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021 g   x  0 g   x  5 1  1 
Gọi x , x là hai nghiệm của g x , khi đó  và  . 1 2 g   x  0 g   x  3 2  2 
Ta có phương trình hoành độ giao điểm   x  x
f x .ex  2ax  b x 2 .e
 ax  2a  b  x 1
x  b  c .e  0    x  x  2
Vậy diện tích hình phẳng được giới hạn bằng x x 2 2 S  ax   2a b 2
x  b  c .exdx  g
 xdx  g x  g x  8   . 2   1 x x 1 1
Câu 37. [2D3-3.1-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 46) Cho hàm số   4 3 2
f x  x  ax  bx  cx  d
với a, b, c, d  . Biết hàm số
g  x  f  x  f  x  f   x  f   x có ba giá trị cực trị là 14
 ; 4; 6. Diện tích hình phẳng f  x
giới hạn bởi các đường y  y  bằng g  x  và 1 24 A. 2 ln 3 . B. ln10 . C. ln 3 . D. ln 5 . Lời giải
FB tác giả: Luu Le Van
Xét hàm số: g  x  f  x  f  x  f   x  f   x .
Ta có g x  f  x  f   x  f  (
 x)  f   (x)  f x  f  x  f  x  24 Vì
f  x  24 . Gọi x ; x ; x
là các điểm cực trị của hàm số thì ta có 1 2 3
g  x  14  1  
g x  g x
 g x  0 và có thể giả sử g x  4 2  1   2   3 g   x  6 3  Xét phương trình:   f  x x x1                  g  x 1 f  x g  x 24 f  x f  x f x 24 0 x x2  24 x  x  3
Diện tích hình phẳng cần tính là x x x 3 f  x 2 f  x 3      f x  S      x     x      x  g x   g x   g x     x    1 d  x    1 d  x    1 d 24 24 24  1 1 2 x x 2  g x 3 
 gx      x     x x   ln g x 2  24  ln g x  x   3 24 x g x   g x    x 1 2 x    d  x    d 24 24  1 2
 ln g x  24  ln g x  24  ln g x  24  ln g x  24 2   1  3  2 
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 33
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021  ln 4  24  ln 1
 4  24  ln 6  24  ln 4  24  ln 3 .
Câu 38. [2D3-3.1-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 46) Cho hàm số f  x 3 2
 3x  bx  cx  d với b,c, d  . Biết hàm số g  x  f  x  f x  f  x có hai giá f  x trị cực trị là 12
 ; 6 . Diện tích hình phẳng giới hạn bởi các đường y  y  bằng g  x  và 1 18 A. 2 ln 3 . B. ln 6 . C. 2 ln 2 . D. ln 5 . Lời giải
FB tác giả: Luu Le Van
Xét hàm số: g  x  f  x  f  x  f   x
Ta có g x  f  x  f   x  f  (
 x)  f x  f  x 18
Vì f  x  18 . Gọi x ; x là các điểm cực trị của hàm số thì ta có g x  g x  0 và có thể 1   2  1 2 g   x  12 1  giả sử g   x  6 2  Xét phương trình: f  x x  x             g  x 1 f  x g  x 18 f  x f  x 1 18 0 18 x  x  2
Diện tích hình phẳng cần tính là x x x x 2  f  x 2 
 f x  g x 2 18   gx 2 
 (g x 18)  S      x     x     x     x  g x   g x   g x   g x      x    1 d  x    d  x    d  x    d 18 18 18 18  1 1 1 1  ln g x 2
18 x  ln g x 18  ln g x 18  ln 6 18  ln 1
 2 18  ln 4  2ln 2 . 2   1 x1
Câu 39. [2D3-3.1-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 46) Cho hai hàm số f  x 4 2
 x  ax  bx 1 và g x 2
 cx  dx  3 a, b, c, d   . Biết rằng đồ thị của hàm số
y  f  x và y  g  x cắt nhau tại hai điểm có hoành độ lần lượt là 2
 ; 1. Hình phẳng giới hạn
bởi hai đồ thị đã cho có diện tích bằng 45 99 3 A. . B. 2 . C. . D. . 5 10 2 Lời giải
FB tác giả: Luu Le Van  f ( 2)   g  2 16
  4a  2b 1  4c  2d  3 Theo bài ra ta có:     f    1  g   1 1
  a  b 1  c  d  3 4
 a  c  2b  d   14  a  c  2       a  c 
b  d  1 b   d  3
Ta có f  x  g  x 4
 x  a  c 2
x  b  d  x  2
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 34
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
Diện tích hình phẳng cần tính là 1 S    1
f  x  g  xdx    4
x  a  c 2
x  b  d  x  2dx 2  2  1 5  x 
   3x    2x    a c b d  2x  5 3 2  2 a  c  2    5   3   2 5 3 2 1 2 1 2 1 2 99 Thay  ta có S   2.  3.  21  2    . b   d  3 5 3 2 10
Câu 40. [2D2-5.5-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 47) Có bao nhiêu cặp số nguyên  
x ; y  thỏa mãn 2  x  2021 và 2y  log  y 1 x  2  2x  y ? 2  A. 2020. B. 10. C. 9. D. 2019. Lời giải
FB tác giả: Nguyễn Thị Vân Đặt log  y 1 x 2   y 1  t t y 1 t x 2 2 x 2 2          . 2
Phương trình đã cho trở thành: y  t y 1 2 2 2 2    
  2.2y   2.2t t y y  t Xét hàm số    2.2x f x
 x đồng biến trên  y  t. Suy ra phương trình log  y 1 x 2   y 1  y y 1 y x 2 2 x 2         . 2 y 1 2 x 2021 2 2     
 20211 y 1 log 2021  2  y  log 20211. 2 2 Do y 
nên y 2;3; 4;...;1 
1 có 10 giá trị nguyên của y . Mà 1 2y x  
nên với mỗi số nguyên y 2;3; 4;...;1 
1 xác định duy nhất một giá trị nguyên của x .
Vậy có 10 cặp số nguyên  ;
x y  thỏa mãn bài toán.
Câu 41. [2D2-5.5-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 47) Có bao nhiêu số nguyên y sao  1  2  cho tồn tại x  ; 5 
 thỏa mãn 2x xy     4 8 1 .8 x xy ?  2  A. 7. B. C. 6. D. 5. Lời giải
FB tác giả: Thao nguyen 2
x  xy     2 2 4 x 2 x  xy4 8 1 .8  8 x xy  1 xy  0 2   Xét 2 x xy 4 x   
hàm số f  x  8 1 xy Áp dụng BĐT x
a  x a   1 1 ta có
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 35
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021   2
2 x  xy4 x f x 
   xy   2 8 1
7 2x  xy  4x 1 1 xy 2
 14x  x 3y 14 0 ,  y  5 Do đó y  4 Với y  2   xy  1
  f  x  0 (loại)  Với      2 2 x 5 1  8 x y f x x 1    1  Ta có f   1 5  0 ; f  0  
 f  x  0 có nghiệm x  ;5  y 1 thỏa    mãn 2   2  x  0 2 Với 2 x 4 y  0  8  8 x  
 y  0 thỏa mãn x  2  TM
Với y  0 có f   5 y 30 5  8
 1 5y  0 ,  y  0 y 3 1     y  2 2 f  8  1  0 ,  y      1; 2;   2   2     1
f  x  0 có nghiệm x  ; 5    2 
Vậy y   1 ; 0 ; 1 ;  .
Câu 42. [2D2-5.5-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 47) Có bao nhiêu số nguyên y  5
để tồn tại số thực x thỏa mãn log 4x  3y   1  log  2 2
x  2x  y ? 15 6  A. 3. B. 0. C. 1. D. 2. Lời giải
FB tác giả: Nguyễn Huỳnh Tấn Trung
4x  3y 115t  0 
Đặt log 4x  3y   1  log  2 2
x  2x  y  t   (*). 15 6    x   2 2
1  y  6t 1
Hệ có nghiệm  đường thẳng  : 4  3 115t x y
 0 và đường tròn     2 2 : 1   6t C x y 1
có điểm chung, với tâm I 1;0 t 
 d I  5 15 ,  R 
 6t 1  225t 10.15t  25.6t  0 5 t   t 2  15  6. 10  0    5  t  
Xét hàm số f t  t 2 15  6. 10    5  t  
Đạo hàm f t t 2 2 15 .ln15  6. ln  0, t     5  5
Do vậy: hàm số f t  đồng biến trên .
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 36
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
Khi đó f t  0  t  0,9341 Do   2 2 1   6t x y 1 nên 6t y 
1, dẫn đến y  6
Kết hợp giả thiết ta suy ra y  6. Thử lại:
Với y  6 , hệ (*) trở thành t 2 4x 19 15  0  15t  23  t t t t            (**)  x    6 35 225 1089 46.15 16.6 2 1  6t  35  4 
Nếu t  0 thì 15t 1, 6t 1 225t 1089 46.15t 16.6t       . Nếu 1 15t 6t t  
 , ta sẽ chứng minh 225t 1089 62.15t   . Thật vậy, ta có t t  t     2 225 1089 62.15 15 31 128  0 Dẫn đến 225t 1089 62.15t 46.15t 16.6t     .
Nếu 0  t  1 thì 15t 15, 6t 6 225t 1089 46.15t 16.6t       Vậy (**) vô nghiệm.
Câu 43. [2H1-3.2-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 48) Cho khối hộp chữ nhật ABC . D A B  C  D
  có AB  a , AD  2a 3 . Gọi I là trung điểm cạnh AD , góc giữa hai mặt
phẳng  ABI  và  ABCD bằng 60 . Thể tích của khối hộp chữ nhật đã cho bằng 2 3 A. 3 3 a . B. 3 a . C. 3 2 3 a . D. 3 3 3 a . 3 Lời giải
FB tác giả: Huong Nguyen
Gọi  là góc giữa hai mặt phẳng  ABI  và  ABCD .
Trong  ABCD : Kẻ AH  BI tại H ; AA  BI ( do AA   ABCD suy ra A H   BI Vậy    A H
 , AH   AHA  60.
Tam giác ABI vuông tại A , AH là đường cao nên có:
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 37
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021 1 1 1 1 1 4 a 3       AH  . 2 2 2 2 2 2 AH AB AI a 3a 3a 2 3a Tam giác A A
 H vuông tại A có: AA  AH.tan 60  2 3a 2 3 V         AA .S .2 3 a 3 3 a . ABCD. A B C D ABCD 2
Câu 44. [2H1-3.2-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 48) Cho hình hộp chữ nhật ABC . D A B  C  D
  có đáy là hình vuông cạnh a , góc giữa hai mặt phẳng  ABM  và  ABCD bằng o
60 với M là trung điểm CD . Thể tích khối hộp chữ nhật đã cho bằng 2 15 15 2 5 2 15 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 15 5 5 5 Lời giải
FB tác giả: Dương Thái Bảo
Gọi N là trung điểm của BC , H là giao điểm của MB và AN .
Vì ABCD là hình vuông nên ta có AN  BM , suy ra A H   MB . Do đó o A H  A  60 . 2 AB 2 5 2 15 Ta có AH   a , suy ra o
AA  AH . tan 60  a . AN 5 5 2 15
Thể tích khối hộp chữ nhật đã cho bằng 3
V  AA .S  a . ABCD 5
Câu 45. [2H1-3.2-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 48) Cho khối lăng trụ đứng AB . C A B  C
  có đáy là tam giác đều. Mặt phẳng  ABC tạo với đáy góc 30 và tam giác A B  C
có diện tích bằng 8 . Thể tích V của khối lăng trụ đã cho là A. 64 3 . B. 2 3 . C. 16 3 . D. 8 3 .
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 38
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021 Lời giải
FB tác giả: Sơn Trường
Gọi I là trung điểm cạnh BC . Vì AB . C A B  C
  là lăng trụ đứng có đáy là tam giác đều nên AB . C A B  C
  là khối lăng trụ đều. Do đó ta có: A B   A C
 . Suy ra tam giác A B
 C cân tại A  A I  BC .
Mặt khác: tam giác ABC đều  AI  BC .
Suy ra BC   A I  A .
Vậy góc giữa mặt phẳng  ABC  và mặt đáy bằng góc A I  A  30 .
Ta có: tam giác ABC là hình chiếu của tam giác A B
 C trên mặt đáy Nên S  S     .cos 8.cos 30 4 3 . ABC A BC 2 x 3
Đặt AB  x  S   4 3  x  4 . ABC 4 x 3 Ta có: AI 
 2 3  AA  AI.tan AIA  2 . 2 Suy ra: V        AA .S 2.4 3 8 3 . ABC. A B C ABC
Câu 46. [2H3-2.8-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 49) Trong không gian Oxyz , cho
ba điểm A2;3;9, B 2;3;4  và C 2;15;9. Một mặt cầu S  luôn đi qua ,
A B và tiếp xúc với
mặt phẳng Oxy  tại .
D Biết rằng khi CD đạt giá trị nhỏ nhất thì tọa độ tâm của mặt cầu S  là
I a ;b;c . Khi đó a  b  2c bằng A. 13  . B. 9. C. 2 D. 6.
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 39
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021 Lời giải
FB tác giả: Lê Văn Đoàn A(2;3;9) C(2;15;9) I B D H(2;3;0) D K Oxy
Ta có: AB  0;0;  5  AB  Oxy .
Và H 2;3;0, D là hình chiếu của ,
A I lên mặt Oxy .
 HA  9, HB  4 . Ta có 2 HD  H . A HB  KD  H . A HB  6 .
 D thuộc đường tròn (C) tâm H , r  6 .
Gọi K là hình chiếu của C lên Oxy   K 2;15;0 .
 HK 12  r  K nằm ngoài C . 2 2 Ta có 2 2 2 2
CD  CK  DK  9  DK  81  HK  r   81 12  6  3 3 .  CD
 3 3 . Dấu "  " xảy ra khi H , K, D và D nằm giữa HK . min
Ta có: r  HD  6, HK  12  HK  2HD  D là trung điểm HK  D 2;9;0 .
Gọi I a ;b ;c là tâm của S  , vì D là hình chiếu của I lên mặt phẳng Oxy  I 2;9; c .
 I nằm trên P 13 : z 
là mặt phẳng trung trực của AB,  P Oxy 13 //  c  . 2 2 13
 a  2, b  9, c 
 a b  2c  6 . 2
Câu 47. [2H3-2.8-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 49) Trong không gian Oxyz , cho hai điểm A5; 
1;1 và điểm B 5;0;5 . Xét hai điểm M và N thay đổi thuộc mặt phẳng
P: x  z  2  0 sao cho MN  2. Giá trị lớn nhất của AM  BN bằng A. 3 11 . B. 21 . C. 17 . D. 33 .
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 40
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021 Lời giải
FB tác giả: Tân Ngọc B A' I A H K M N P
Ta có A , B cùng phía so với  P . Gọi H , K lần lượt là hình chiếu của A , B lên mặt phẳng
P . Khi đó H 3;1;  1 , K 1;0;  1 . Ta có d  d  ,
A P  2 2, d  d B P  . B  ,  4 2 A
Đặt A  T ( )
A , khi đó ta có | AM  BN | AN  BN  AB . MN
Rõ ràng A nằm trên đường tròn có tâm A và có bán kính bằng MN , đường tròn này cắt mặt
phẳng tạo bởi  AH , BK  tại hai điểm, giả sử I là điểm cách B một khoảng lớn hơn.
Khi đó ta có | AM  BN |  A B 
 A  I . max max 2 2 2 2 Vậy A B 
 IB  d  d   HK  MN   2 2 3 2  33 . max B A
Câu 48. [2H3-2.8-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 49) Trong không gian với hệ tọa
độ Oxyz , cho mặt phẳng P : 2x  2y  z 15  0 . Gọi M là điểm di động trên P , N là điểm
thuộc tia OM sao cho OM.ON  10 . Khoảng cách nhỏ nhất từ N đến mặt phẳng  P bằng bao nhiêu? A. 5 . B. 3 . C. 2 . D. 4 . Lời giải
FB tác giả: Tân Ngọc
Gọi H là hình chiếu vuông góc của O trên  P và K thuộc tia OH thỏa mãn OK.OH 10 . Do OH  d  ;
O  P  5 nên OK  2 .
Lại có: OK.OH  OM.ON  O
 NK đồng dạng tam giác OHM . Suy ra ONK  90 . Do đó N
thuộc đường tròn đường kính OK . Suy ra d  N,P  d K,P .
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 41
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
Vậy khi N  K thì khoảng cách từ N đến  P nhỏ nhất và bằng KH  3 .
Câu 49. [2D1-2.6-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 50) Cho hàm số y  f  x có đạo
hàm f  x   x   2 7 x  9, x
  . Có bao nhiêu giá trị nguyên dương của tham số m để hàm
số g  x  f  3
ax  bx  2m  3 với .
a b  0 có ít nhất 3 điểm cực trị? A. 1. B. 2. C. 3. D. 4. Lời giải
FB tác giả: Văn Nguyễn Ta có BBT của hàm    3 y
h x  ax  bx như sau 2 2
x 3ax  b ax  b 
Ta có g x 3
 ax  bx . f  3
ax  bx  2m  3     . f  3
ax  bx  2m  3 . 3  ax  bx
Rõ ràng g x không xác định tại x  0 và đổi dấu khi x đi qua 0 nên x  0 là 1 điểm cực trị
của hàm số g  x  f  3
ax  bx  2m  3 . 3 3
 ax  bx  2m  3  7
 ax  bx  4  2m   Ta có: f  3
ax  bx  2m  3 3 3
 0   ax  bx  2m  3  3   ax  bx  2m .   3 3
 ax  bx  2m  3  3
 ax  bx  6  2m  
Để hàm số g  x có ít nhất 3 điểm cực trị thì phương trình g x  0 có ít nhất 2 nghiệm phân
biệt khác 0 và g x đổi dấu khi đi qua ít nhất 2 trong số các nghiệm đó.
Từ BBT ta có 4  2m  0  m  2
Vì m nguyên dương nên m  1
Vậy có 1 giá trị của m thỏa mãn yêu cầu đề bài.
Câu 50. [2D1-2.6-4] (PHÁT TRIỂN ĐỀ 101 BGD NĂM 2021 CÂU 50) Cho hàm số f  x liên tục trên
, có bảng biến thiên dưới đây
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 42
SP TỔ 27-STRONG TEAM
PHÁT TRIỂN ĐỀ THI TN-THPT-QG-BGD NĂM 2021
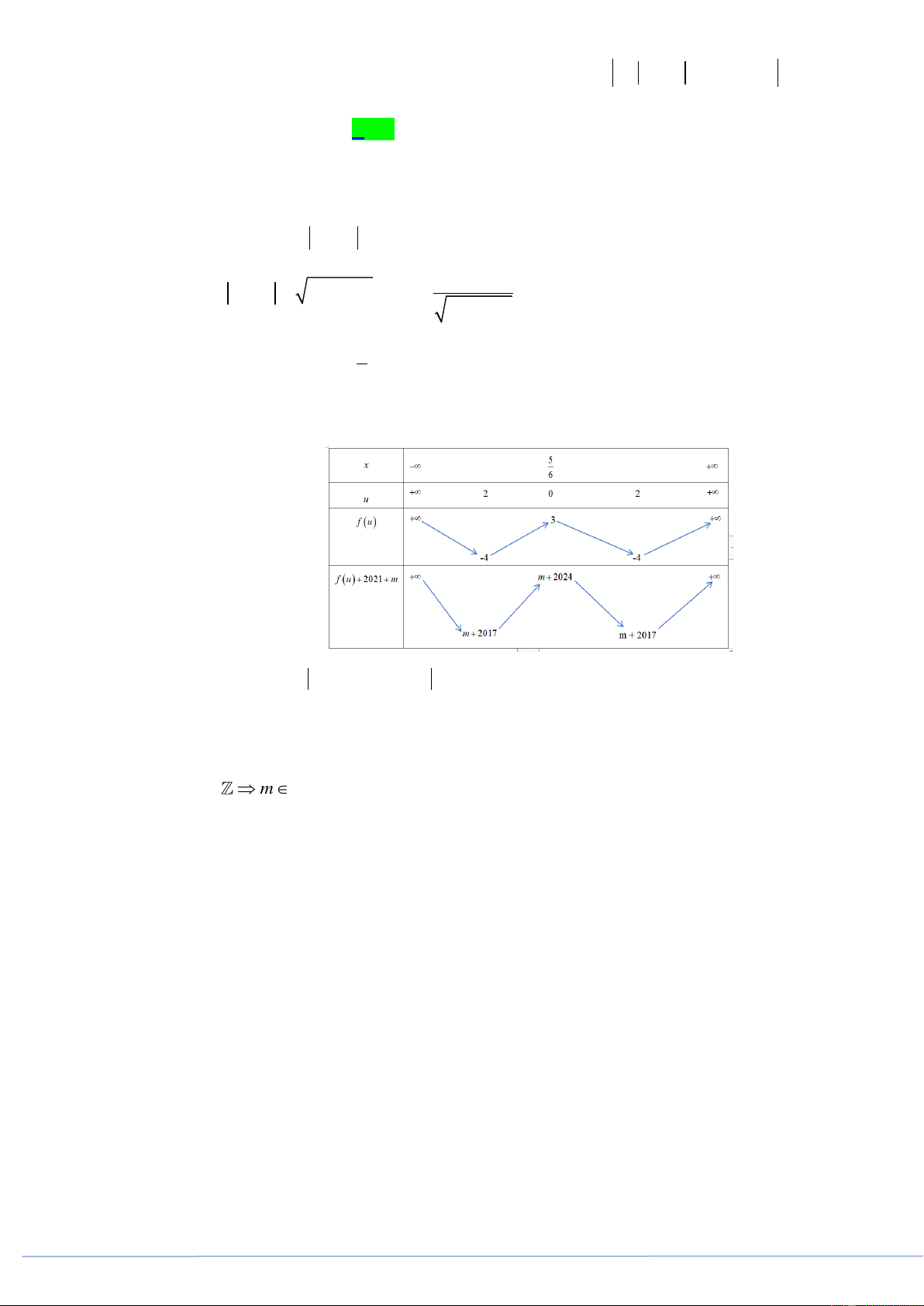
Có bao nhiêu giá trị nguyên của tham số m để hàm số y  f  6x  5   2021 m có 3 điểm cực đại? A. 5 . B. 6 . C. 7 . D. 8 . Lời giải
FB tác giả: Nam du
Xét hàm số y  f  6x  5   2021 m 6(6x  5) Đặt 2
u  6x  5  (6x  5)  u '  2 (6x  5) 5
Hàm u đạt cực trị tại x  6 Bảng biến thiên
Suy ra hàm số y  f (u)  2021 m có 3 điểm cực đại m  2017  0    2  024  m  2  017 m  2024  0 Do m   m  202  3, 202  2, 202  1, 202  0, 201  9, 201  8. HẾT
STRONG TEAM TOÁN VD-VDC- Nơi hội tụ của những đam mê toán THPT Trang 43

Phát triển các bài toán VD – VDC trong đề thi TN THPT 2021 môn Toán (đợt 1)

Thông tin :

Tài liệu liên quan:

TOP 20 câu trắc nghiệm phát triển câu 39 từ đề minh họa THPTQG môn Toán năm 2024 (có đáp án)

TOP 20 câu trắc nghiệm phát triển câu 40 từ đề minh họa THPTQG môn Toán năm 2024 (có đáp án)

Phát triển các bài toán VD – VDC trong đề tham khảo TN THPT 2024 môn Toán

Tài liệu ôn tập lý thuyết thi tốt nghiệp Trung học Phổ thông môn Toán

Chuyên đề khảo sát hàm số: Tính đơn điệu của hàm số | Tài liệu ôn thi THPTQG môn Toán