




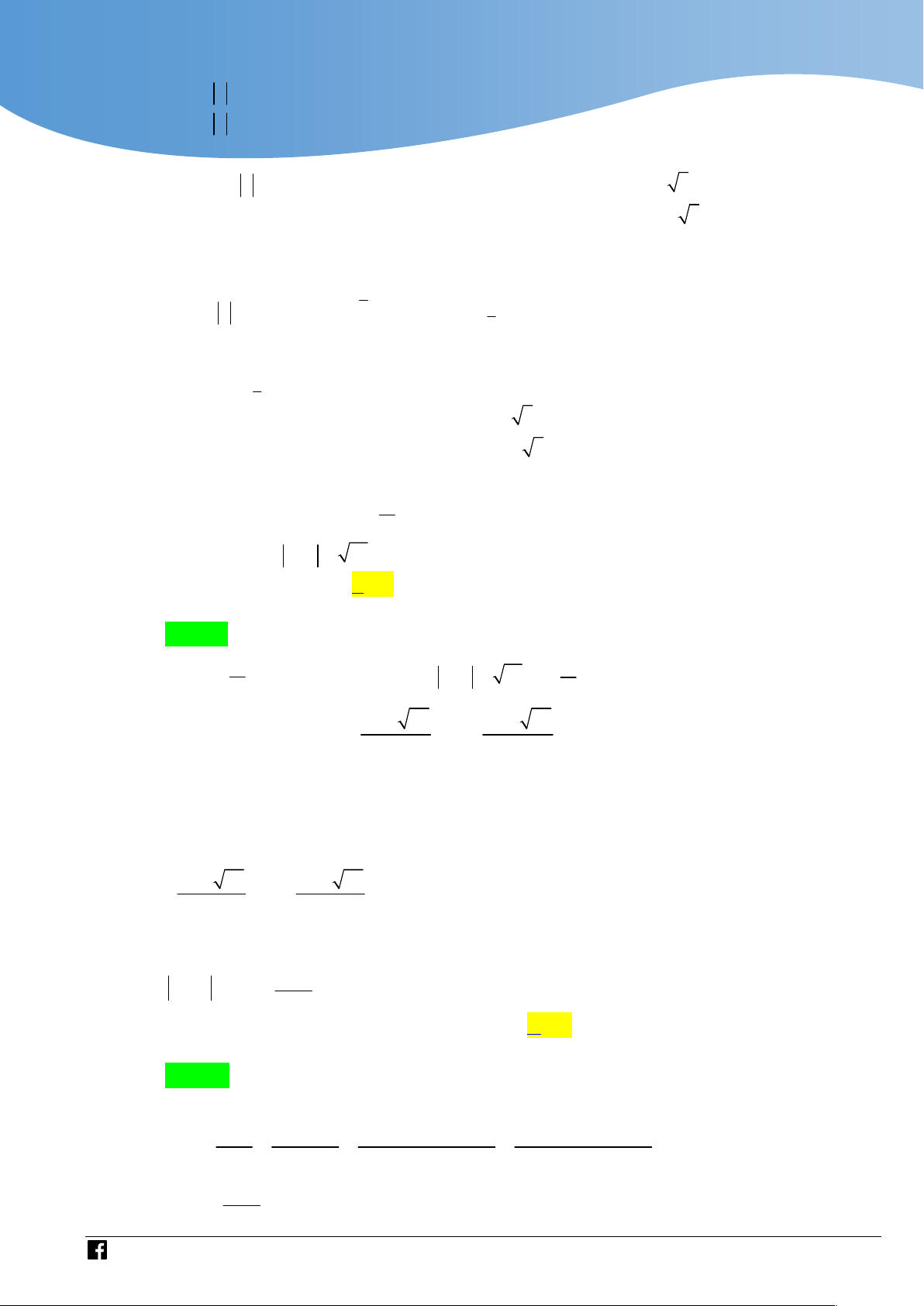


















Preview text:
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Định hướng ôn thi tốt nghiệp THPT
Phân tích, định hướng tìm lời giải, xây dựng các bài tương tự các câu VD – VDC
ĐỀ THI THAM KHẢO TỐT NGHIỆP THPT NĂM 2021
Ngày 31/3/2021 Bộ GD&ĐT chính thức công bố đề thi tham khảo, tạo điều
kiện thuận lợi cho giáo viên và các em học sinh ôn tập. Trên cơ sở đó, các trường
THPT, các Sở GD &ĐT cũng tổ chức ra các đề thi thử tốt nghiệp THPT nhằm
đánh giá năng lực của các em học sinh và cũng là dịp để các em được làm quen với các dạng toán trắc nghiệm.
Kỳ thi tốt nghiệp THPT năm 2021 đã đến gần, để tạo điều kiện cho quý thầy
cô cùng các em có tài liệu ôn tập trong thời gian gấp rút này Nhóm Giáo viên Toán
Việt Nam xin gửi tới quý thầy cô và các em bài viết “Phân tích, định hướng tìm lời giải,
xây dựng các bài tương tự các câu VD – VDC Đề thi tham khảo tốt nghiệp THPT Năm 2021”
Hy vọng bài viết sẽ giúp quý thầy cô có thêm tài liệu tham khảo; các em học sinh
nắm chắc các kiến thức trong chương trình THPT; tiếp cận được với các bài toán mới,
hay và lạ. Đặc biệt, rèn luyện tốt kỹ năng thi trắc nghiệm môn Toán.
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Câu 41 2 x 1 khix 2 2
Cho hàm số f x
. Tích phân f 2 sin x 1cos d x x bằng: 2
x 2x 3 khix 2 0 23 23 17 17 A. . B. . C. . D. . 3 6 6 3
Facebook: Nam Phương – Thủy Dao – Trần Chinh
Phân tích định hướng tìm lời giải:
- Đây là bài toán tính tích phân của hàm hợp.
- Để tính được tích phân trên ta phải thực hiện phép đổi biến để đưa về hàm đã cho.
- Cụ thể các bước thực hiện như sau:
+ B1: Đặt 2sin x 1 t . + B2: Biểu thị cos d
x x theo tdt . b
+ B3: Đổi cận, và tính tích phân f t dt . a Lời giải Chọn B 2 Xét I
f 2sin x 1 cos d x x 0 1
Đặt 2sin x 1 t 2cos d
x x dt cos d x x dt 2
Đổi cận: x 0 t 1; x t 3 . 2 3 3 2 3 1 1 1 1 I
f t dt
f t dt
2t 2t 3dt 2t 1 dt 2 2 2 2 1 1 1 2 3 3 1 t 2 1 t 3 23 2 t 3t t . 2 3 1 2 3 2 6 Bình luận:
+ Đây là dạng toán thuộc mức độ vận dụng, việc nhận ra hướng giải đòi hỏi học sinh phải
nắm chắc các khái niệm và tính chất của tích phân cũng như các phương pháp tính tích phân.
+ Học sinh thường lúng túng, và dễ mắc sai lầm khi tách cận hoặc quên nhân thêm phân 3 1 1 số để tính I
f t dt
dẫn đến có thể chọn các đáp án nhiễu 2 2 1 3 2 2 20 I
f t dt 2
t 2t 3dt 2 t 1 dt 3 1 1 1 3 2 3 1 1 1 17 hoặc I
f t dt
2t 2t 3dt 2t 1 dt 2 2 2 6 1 1 2 3 2 3 17
hoặc I f t dt 2
t 2t 3dt 2 t 1 dt . 3 1 1 2
Hướng phát triển:
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Hướng phát triển 1: Biểu thức có chứa tham số. Sử dụng tính liên tục để tìm tham số.
Hướng phát triển 2: Sử dụng diện tích hình phẳng để tính tích phân.
Hướng phát triển 3: Tích phân có chứa dấu giá trị tuyệt đối.
Hướng phát triển 4: Sử dụng quy tắc tính tích phân.
Bài tập tương tự 2 3
x 2x 1 khi x 0 Câu 1:
Cho hàm số f (x)
liên tục trên thỏa mãn 2 ax b khi x 0 2
2cosx sinxf( c
osx 2 sin x)dx 2 . Giá trị của biểu thức P 2a b bằng 0 A. 8 . B. 33 . C. 25 . D. 11 . Lời giải Chọn B 2 3
x 2x 1 khi x 0
Ta có: f (x)
liên tục trên khi hàm số liên tục tại x 0 2 ax b khi x 0 hay b 1. 2
Xét: 2 cosx s inxf( c
osx 2 sin x)dx 2 . 0 Đặt c
osx 2 sin x t sin x 2 cosxdx dt . Ta có: 2 2 0 2
2cosx sinxf( c
osx 2 sin x)dx
f (t)dt
f (t)dt f (t)dt 0 1 1 0 0 2ax 2 1 dt 2
3x 2x
1 dt 2 a 17. 1 0 Câu 2:
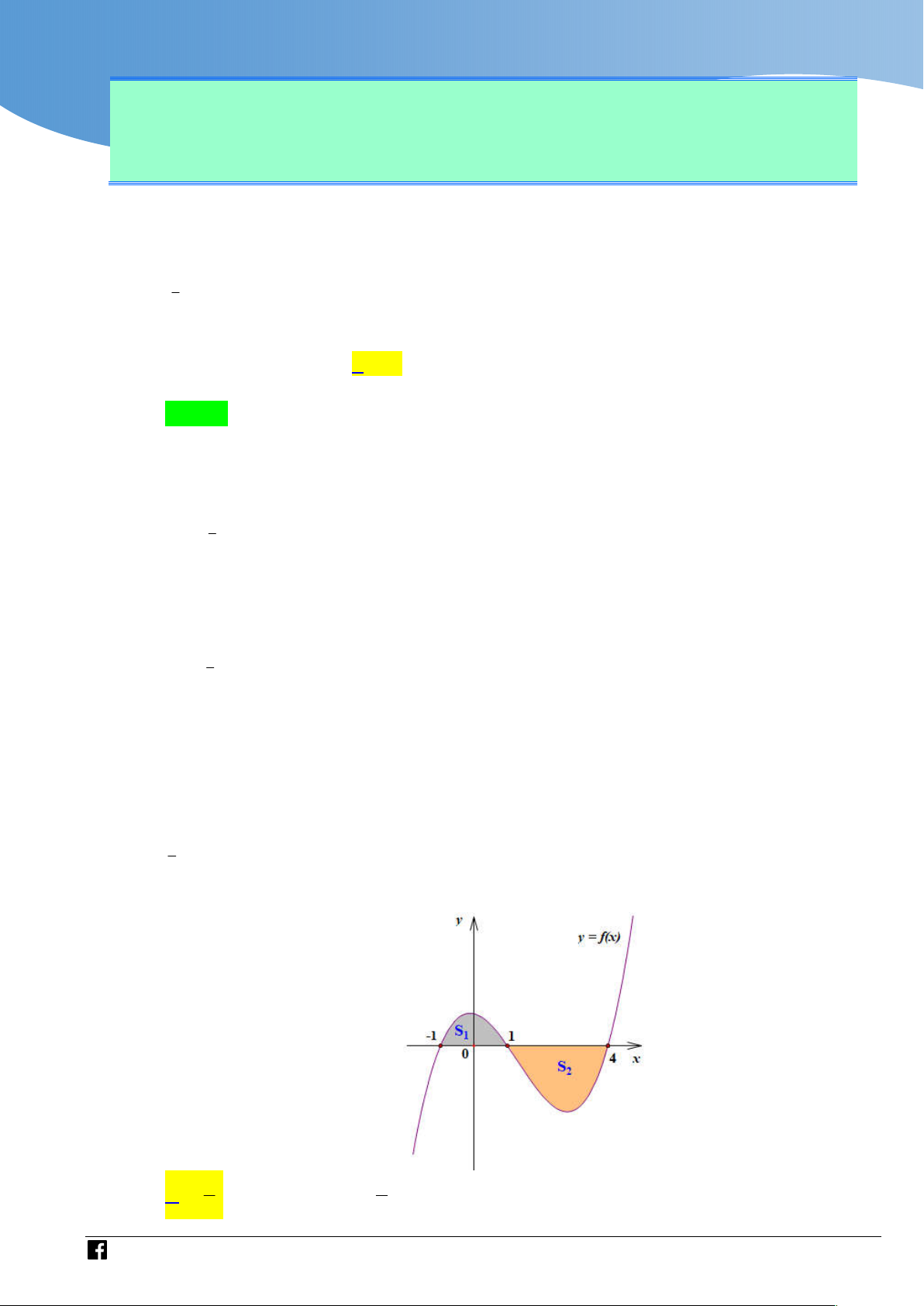
Cho hàm số f x liên tục trên và có đồ thị như hình vẽ bên dưới. Gọi S và S lần 1 2
lượt là diện tích của hai hình phẳng trong hình, biết S 3 và S 7 . Tích phân 1 2 2 cos .
x f 5sin x 1 dx bằng 0 4 4 A. . B. C. 2 . D. 2. 5 5
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Lời giải Chọn A 2
Xét I cos xf 5sin x 1 d x . 0 1
Đặt 5sin x 1 t cos d x x dt . 5
Với x 0 t 1 x t 4 2 4 4 1 4 1 1 1 1 1 1 4 I
f t dt
f x dx
f x dx
f x dx S S 1 2 . 5 5 5 5 5 5 5 1 1 1 1 2 x m , x 0 Câu 3: Cho hàm số
y f x liên tục trên . Giá trị 2 cos x 3 , x 0 2 I f
2cos x 1sin xdx bằng 0 1 2 1 A. 0. B. . C. . D. . 3 3 3 Lời giải Chọn C
Hàm số liên tục trên nên ta có: lim f x lim f x f 0 m 1 m 1. x 0 x 0
x 0 t 1 1
Đặt t 2 cos x 1
dt sin xdx . Đổi cận: . 2 x t 1 2 2 1 1 0 1 1 1 1 Khi đó: I f
2cos x 1 sin xdx f
t dt f
x dx f
x dx f x dx 2 2 2 0 1 1 1 0 0 x 1 u 1 Xét
f x dx
. Đặt u x du dx . Đổi cận: .
x 0 u 0 1 0 0 1 Suy ra
f x dx f u du f x dx . 1 1 0 0 1 1 1 1 1 2 Vậy I
f x dx f x dx .2 f x dx 2 x 1 dx . 2 2 3 1 0 0 0 1 2
x 2 khi 0 x 2 e f ln x 2 6 Câu 4:
Cho hàm số f x 2 2 . Khi đó dx xf
x 1dx bằng x
x 5 khi 2 x 5 1 3 19 37 27 A. . B. . C. . D. 5. 2 2 2 Lời giải Chọn B 2 e f ln x 1 Xét I d . x
t ln x dt dx 1 Đặt x x 1
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
x 1 t 0 Đổi cận 2
x e t 2 2 e f ln x 2 2 2 2 1 x 2 Suy ra I dx
f t dt= f x dx x 2 dx 2x 5. 1 x 2 4 0 1 0 0 0 2 6 Xét I xf
2x 1 dx Đặt 2 2 2 t
x 1 t x 1 tdt d x . x 2 3
x 3 t 2
Đổi cận x 2 6 t 5 2 6 5 5 5 27
Suy ra I xf 2 x 1 dx f t tdt f x d x x x 5 d x x . 2 2 3 2 2 2 2 e f ln x 2 6 27 37 Vậy dx xf 2
x 1dx 5 . x 2 2 1 3 Câu 42
Có bao nhiêu số phức z thỏa mãn z 2 và z 2iz 2 là số thuần ảo? A. 1 . B. 0 . C. 2 . D. 4 .
Faceboock: Phong Do – Huong Duong
Phân tích định hướng tìm lời giải:
- Đây là dạng toán tìm số phức thỏa mãn điều kiện cho trước, một bài toán ở mức độ vận dụng
- Từ điều kiện cho trước thiết lập hệ phương trình liên quan đến x, y của số phức
z x yi x; y
- Xác định x; y từ hệ đã cho hoặc chuyển về phương pháp hình học để giải quyết bài toán. Lời giải
Cách 1: Giả sử z x yi x; y z x yi Ta có:
z 2iz 2 x y 2ix 2 yi xx 2 y y 2 xy x 2 y 2i 2 2 2 2
x y 2 x y 2
Do đó yêu cầu bài toán 2 2
x y 2 x y 2 0
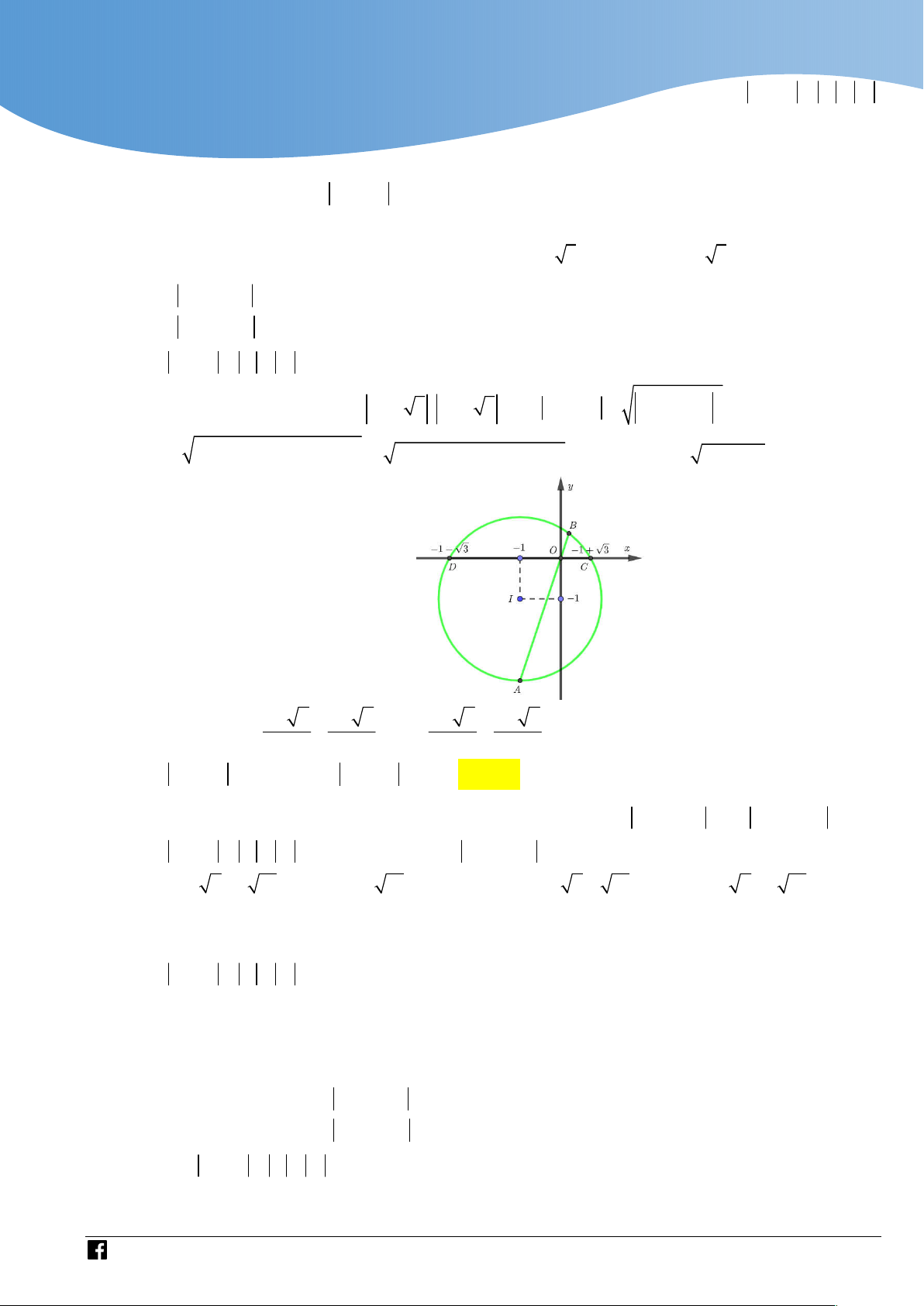
x y 2x 2 y 0 1 3 x 2 1 3 y 2 2 x y 2 2 x 2 2 1 y 2
2 y 2 y 1 0 2
2 2x 2 y 0 x y 1 x y 1 1 3 x 2 1 3 y 2
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Vậy có 2 số phức z thỏa mãn yêu cầu bài toán. Bình luận:
- Vì bài toán hỏi có bao nhiêu số phức thỏa mãn điều kiện nên có thể dùng phương pháp
hình học dựa vào vị trí tương đối để tìm số giao điểm.
- HS phải nhận ra điểm mấu chốt của bài toán này là số điểm biểu diễn của số phức z
chính là số điểm chung của đường tròn và đường thẳng (hoặc đường tròn); và được xác
định dựa vào xét vị trí tương đối giữa đường thẳng và đường tròn hoặc vị trí tương đối
của hai đường tròn. Đây là câu hỏi kiểm tra kiến thức ở mức độ VD.
- Từ đó ta có cách giải khác như sau:
Cách 2: Đưa về tương giao của hai đường tròn
Giả sử z x yi x; y z x yi Ta có:
z 2iz 2 x y 2ix 2 yi xx 2 y y 2 xy x 2 y 2i 2 2 2 2
x y 2
x y 2 (1)
Do đó yêu cầu bài toán 2 2
x y 2 x y 2 0
x y 2x 2 y 0 (2) Nhận xét:
1 là phương trình của đường tròn tâm O bán kính R 2 1
2 là phương trình của đường tròn tâm I 1; 1 bán kính R 2 2
Ta có: 0 R R OI 2 R R 2 2 nên hai đường tròn cắt nhau. 1 2 1 2
Vậy có 2 số phức z thỏa mãn yêu cầu bài toán.
Cách 3: Đưa về tương giao giữa đường thẳng và đường tròn 2 2 2 2
x y 2
x y 2 (3)
Biến đổi đưa về hệ 2 2
x y 2x 2 y 0
x y 1 0 (4)
Nhận xét: 3 là phương trình của đường tròn tâm O bán kính R 2
4 là phương trình của đường thẳng d : x y 1 0 . 1 1
Ta có: d O, d
R 2 , suy ra đường thẳng cắt đường tròn tại hai điểm 2 2
Vậy có 2 số phức z thỏa mãn yêu cầu bài toán. Hướng phát triển: Hướng phát triển 1:
Xét các số phức thỏa mãn điều kiện (cho một giả thiết về modun, một giả thiết về số thuần
ảo/ số thực) đưa về phương trình hoặc hệ phương trình.
Nếu cho giả thiết số thuần ảo thì chỉ cần xác định phần thực và cho bằng 0.
Nếu cho giả thiết là số thực thì chỉ cần xác định phần ảo và cho bằng 0.
Hướng phát triển 2:
Tìm các số phức thỏa mãn điều kiện bằng phương pháp modun hai vế
Hướng phát triển 3:
Xét các số phức thỏa mãn điều kiện đưa về phương trình hoặc hệ phương trình chứa tham số
Hướng phát triển 4:
Tìm số các số phức z x yi, x, y thỏa mãn điều kiện đưa về được hệ bất phương
trình. Ta tìm quỹ tích các điểm biểu diễn số phức là miền hình phẳng giới hạn nào. Từ đó
đếm số điểm có tọa độ nguyên thỏa mãn.
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Bài tập tương tự
Câu 1. Cho số phức z thỏa mãn z 3i z 1 và z
1 z 2i là số thực. Tính z . 10 2 10 A. z 10 . B. z 2 10 . C. z . D. z . 5 5 Lời giải
Giả sử z x yi x, y . 2 2
z 3i z 1 x y 3i x 1 yi 2
x y x 2 3 1 y
x 3y 4 0 1
z z i 2 2 1
2 (x y x 2 y) 2x y 2i là số thực 2x y 2 0 2 2 x
x 3y 4 0 5 2 6 2 10 Từ 1 ,2 ta có z i có z .
2x y 2 0 6 5 5 5 y 5
Câu 2. Có bao nhiêu số phức z thỏa mãn z 3 2i 2 2 và 2 z i
là số thuần ảo? A. 0 . B. 4 . C. 3 . D. 2 . Lời giải Chọn C
Giả sử z x yi, (x, y ) z i
x 2 y 2 3 2 2 2 3 2 8 1
x y 1 2 2
z i2 x y 2 2
1 2x( y 1)i là số thuần ảo 2
x y 1
0 x 1 y 3 x y 1 TH1: Từ
1 ,2 ta có: x3
2 y 22 8
y 2 y 2 2 2
8 y 0 x 1 x 1 y TH2: Từ
1 ,3 ta có: x3
2 y 22 8 y 3 3
y 42 y 22 2
8 y 6 y 6 0 y 3 3
Vậy có 3 số phức thỏa mãn. 5
Câu 3. Có bao nhiêu số phức z thỏa mãn z 3i 1 iz và z i
là số thuần ảo? z i A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn C
Điều kiện: z i
Đặt z x yi, x, y 1 iz 1 i x yi 1 y xi
z i iz x y i y xi x y 2 y2 2 2 3 1 3 1 3 1 x
y 2 y2 3 1 y 2 .
Do đó z x 2i z i x i .
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Ta có 5 5 5 x i 5x 5 z i x i x i x 1 i 2 2 2 z i x i x 1 x 1 x 1
(Chú ý: Ta tìm phần thực, cho bằng 0 nên phần ảo không cần tính) 5 5x x 0 x 0 z i
là số thuần ảo x 0 z i 2 2 x 1 x 4 x 2
Vậy tìm được 3 số phức thỏa mãn. i i
Câu 4. Có bao nhiêu số phức z x yi, x, y thỏa mãn 1 0 và z z . z z 4 ? z z A. 2. B. 1. C. 0 . D. 4 . Lời giải Chọn D
Điều kiện: z 0 i i - 2 2 1 0 .
z z i(z z) 0 x y 2 y 0 1 z z
- z z . z z 4 . x y 1 2 1 2 2 2 x .y 1 x Từ 1 ,2 ta có: 2 y 2 2
x y 2 y 0 4 3
y 2 y 1 0 Nhận xét: Vì 4 3 y y y 3 2 2 1 0 1
y y y
1 0 có 2 nghiệm y khác 0 nên
có 4 giá trị của x . Vậy có 4 số phức thỏa mãn yêu cầu bài toán. z
Câu 5. Có bao nhiêu số phức z x yi, ( ,
x y ) thỏa mãn z 1 i 10 và là một số z 2 thuần ảo? A. 2. B. 1. C. 0 . D. 4 . Lời giải Chọn B
z x yi, ( ,
x y ) . Điều kiện z 2 z i
x 2 y 2 1 10 1 1 10 1 2 2 z
x y 2x 2 yi là số thuần ảo khi 2 2
x y 2x 0 2 z 2 x 22 2 y
x 2; y 0 x 2 1 y 2 1 10 y 2 x 4 Từ 1 , 2 ta có hệ: 8 4 2 2 2
5x 18x 16 0 x ;
x y 2x 0 y 5 5
Vì z 2 nên có 1 số phức thỏa mãn
Câu 6. Có bao nhiêu số phức z x yi, ( ,
x y ) thỏa mãn 2 3
z 2i z 0 ? A. 1. B. 2 . C. 0 . D. 4 . Lời giải Chọn D
Cách 1: Lấy modun hai vế z 0 2 3 2 Ta có: 3
z 2i z 0 z 2 z z 2
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM TH1: z 0 3
z 0 z 0 . TH2: z 2 z 2i 2 3 3
z i z z i
z i 2 2 0 8 0 2
z 2iz 4 0 z 3 i
z 3 i
Vậy có 4 số phức thỏa mãn yêu cầu bài toán
Cách 2: Sử dụng hai số phức bằng nhau z 0 2 3 3
z 2i z 0 z 2 .
i z.x 0 2 z 2i z 0
x 0; y 0 2 2
x y 2 y 0 x 0; y 2 Xét: 2
z 2i z 0 2x y 1 0 x 3; y 1
x 3; y 1
Vậy có 4 số phức thỏa mãn yêu cầu bài toán. m
Câu 7. Có bao nhiêu số phức z
1 3 mi,(m ) có phần thực, phần ảo là những giá 2
trị nguyên và z i 10 ? A. 1. B. 2 . C. 5 . D. 4 . Lời giải Chọn B m 2 m Với 2 z
1 3 mi,(m ) z i 10 1 2 m 10 2 2 6 2 34 6 2 34 2
5m 12m 20 0 m 5 5
Vì số phức z có phần thực, phần ảo là những giá trị nguyên nên m m 0 m2 m 2 6 2 34 6 2 34 m 5 5
Vậy có 2 số phức z thỏa mãn yêu cầu bài toán.
Câu 8. Gọi S là tập hợp các số thực m sao cho với mỗi mS có đúng một số phức thỏa mãn
z m 9 và z
là số thuần ảo. Tính tổng của các phần tử của tập S. z 6 A. 6 . B. 12. C. 0 . D. 2 4 . Lời giải Chọn C
Gọi z x iy với x, y . Điều kiện z 6 . z x iy
x iy x 6iy x x 6 2 y 6iy Ta có . z 6 x 6 iy
x 62 y x 62 2 2 y Do đó z
là số thuần ảo khi x x y x 2 2 2 6 0 3 y 9. z 6
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Mặt khác z m x m2 2 9 y 81
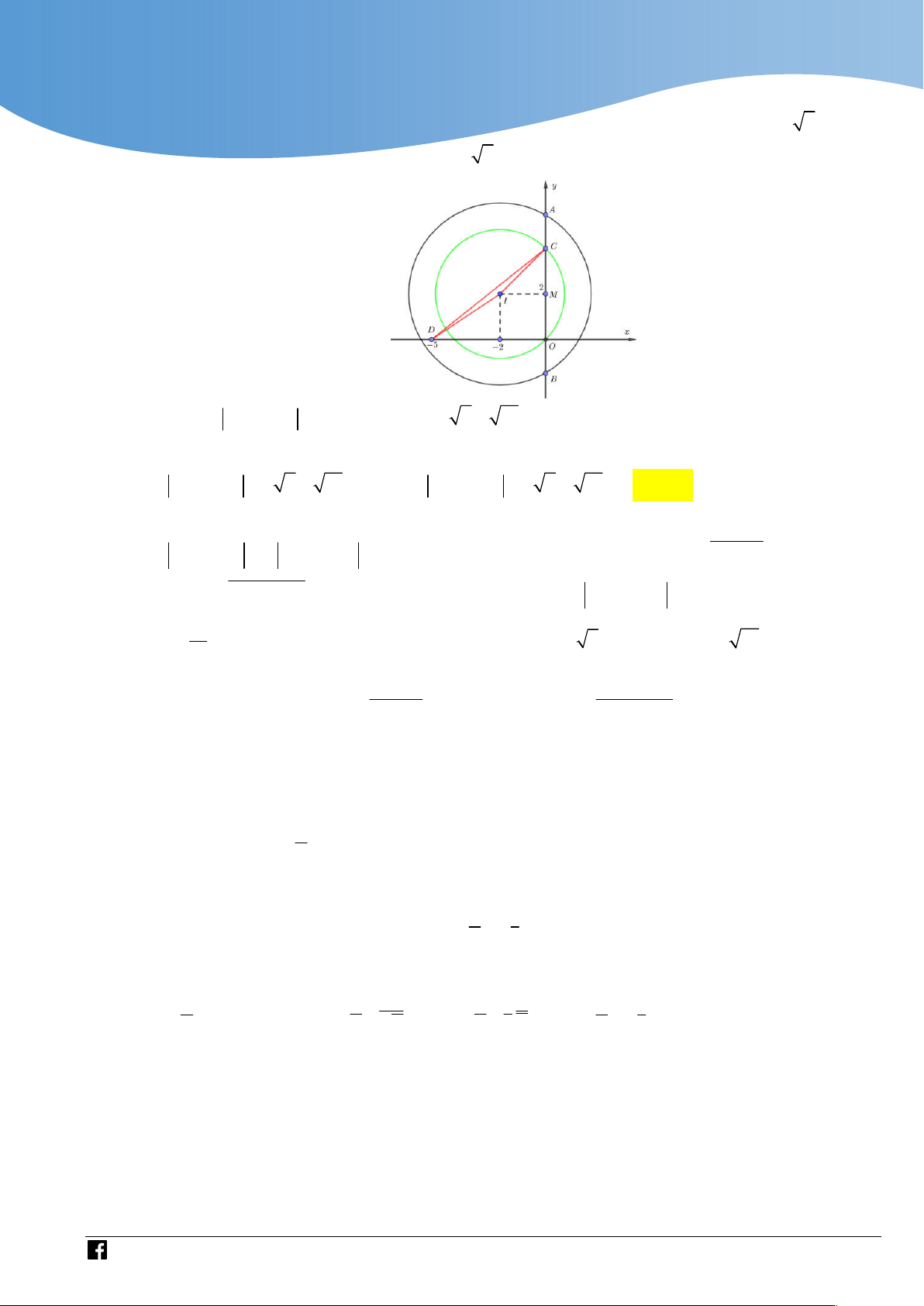
Để có đúng một số phức thỏa mãn yêu cầu bài toán thì hệ phương trình x 32 2 y 9
có đúng một nghiệm hoặc hai nghiệm trong đó có một nghiệm 6; 0
x m 2 2 y 81
Xét trường hợp hệ có nghiệm 6; 0 m Ta có: m2 3 6 81
không thỏa mãn vì hai đường tròn trên tiếp xúc nhau tại m 15 6; 0 m 3 Xét TH m 15
Nghĩa là hai đường tròn C : x 32 2
y 9 và C : x m y 81 tiếp xúc nhau. 2 2 2 1
Xét C có tâm I 3;0 bán kính R 3 và C có tâm I ;
m 0 bán kính R 9. 2 2 1 1 1 2
I I R R m 3 6 Cần có 1 2 1 2 m 9; 9 .
I I R R m 3 12 1 2 1 2
Vậy tổng là 9 (9) 0 .
Câu 9. Có bao nhiêu giá trị nguyên của tham số m10;10
0 để tồn tại số phức z đồng thời 2 2
thỏa mãn z 2 4i z 2i và z 2 i z 3i m ? A. 68. B. 78. C. 86 . D. 87 . Lời giải Chọn D
Gọi z x yi , x y .
Ta có: z 2 4i z 2i x 2 y 4i x 2 y i
x 2 y 2 x y2 2 2 4 2
x y 4 . 2 2 2 2
Mặt khác z 2 i z 3i m x 2 y
1 i x 3 yi m
x 2 y 2 x y2 2 2 1 3 m 2 2 2 2
x 4x 4 y 2 y 1 x 9 6 y y m 2 2 2
x y 2x 2y 7 m 2 2
2 x y m 2 do x y 4 x y 4
Để tồn tại số phức z thỏa mãn yêu cầu có nghiệm thực 2 2 2
x y m 2
x y m x y2 2 2 2 2 16 m 14 .
Vì m&m10;10 0 m 14;15;...;10 0 .
Vậy có 87 giá trị m nguyên thỏa mãn.
Câu 10. Có bao nhiêu số phức z x yi, x, y thỏa mãn: z 2 3i z i 2 3 A. 11. B. 5 . C. 10 . D. 9 . Lời giải
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Chọn A
z 2 3i z i 2 y 2 0
z 2 3i z i 2 3 2 2
z i 2 3 x 2 y 1 9
Dựa vào miền phẳng giới hạn bởi hệ có 11 số phức thỏa mãn
Câu 11. Có bao nhiêu số phức z x yi, ( x, y ) thỏa mãn 2 z i z z 3i và z z có phần ảo không âm? A. 1. B. 2. C. 3. D. 4. Lời giải Chọn D 2 2 Ta có: 2
2 z i z z 3i 2 x y 1 2y 3 2 2 2 4 x y 1 2y 3 2 2 2
4 x 4 y 8 y 4 4 y 12 y 9 . 5 2 2
4 y 4 x 5 y x 1 4
Số phức z z 2yi có phần ảo không âm y 0 2 . 5 2
y x Từ 1 , 2 ta có hệ 4 y 0
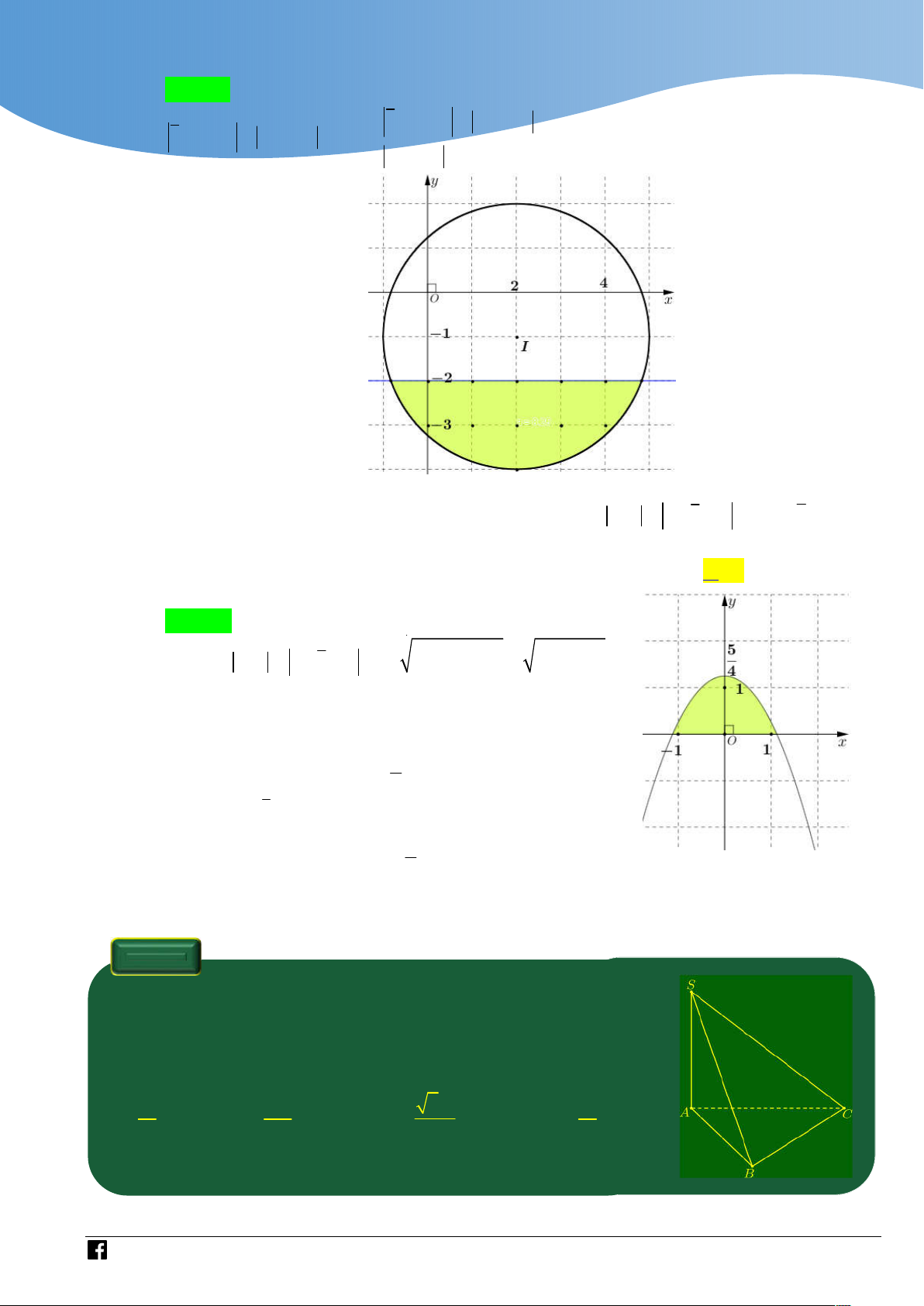
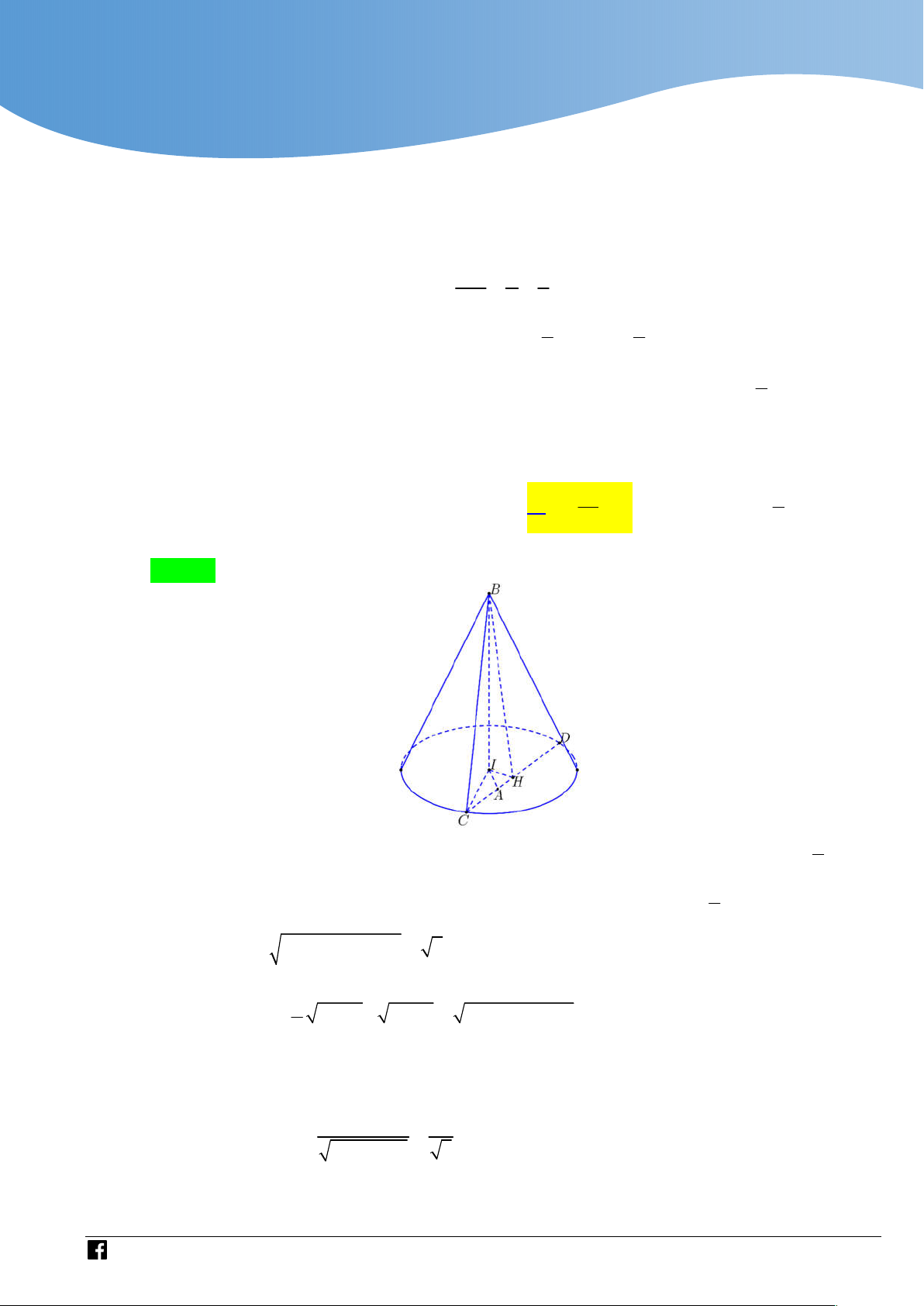
Dựa vào miền phẳng giới hạn bởi hệ có 4 số phức thỏa mãn. Câu 43 Cho hình chóp .
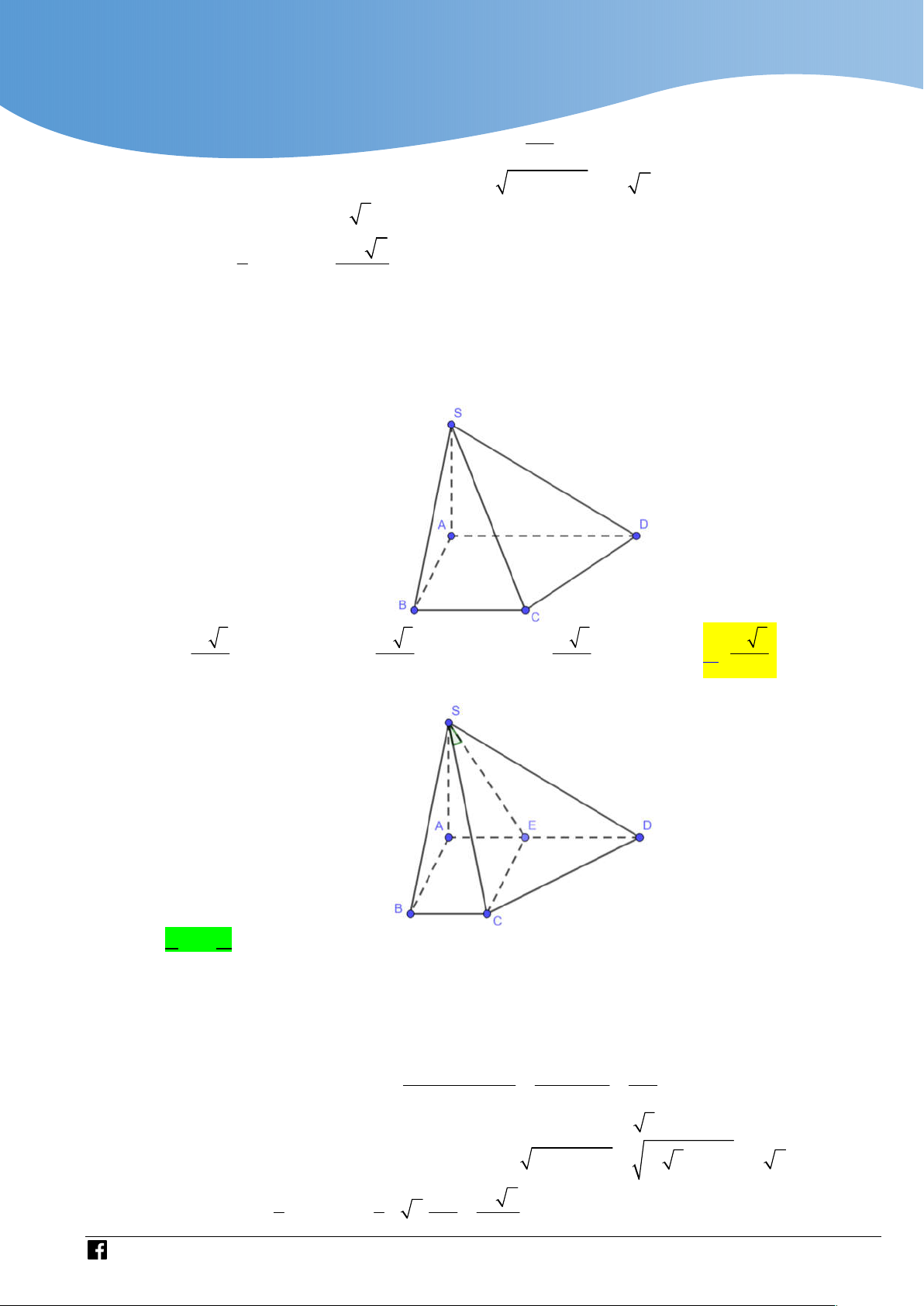
S ABC có đáy ABC là tam giác đều cạnh a,
cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa SA và
mặt phẳng SBC bằng
45 (tham khảo hình vẽ). Thể tích của khối chóp . S ABC bằng 3 a 3 3a 3 3a 3 a A. . B. . C. . D. . 8 8 12 4
Faceboock: Nguyễn Ngọc Chi – Bình Hoàng – Nguyen Trong Chanh – Nguyễn Ngọc Hóa
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Phân tích định hướng tìm lời giải:
Bài toán trên là bài toán về tính thể tích khối chóp liên quan góc giữa một đường thẳng
và mặt phẳng. Thông thường đề bài hay cho góc giữa một cạnh bên và mặt đáy của hình
chóp liên quan đến chân đường cao của hình chóp, tức hình chiếu của đường thẳng lên
mặt phẳng tương đối dễ xác định, thì dạng bài này đề lại cho góc giữa một đường thẳng
và mặt phẳng mà tương đối khó xác định hình chiếu của đường lên mặt hơn. Khi xác định
được góc giữa đường thẳng và mặt phẳng suy ra độ dài đường cao, từ đó tính thể tích
khối chóp. Để làm tốt được bài tập dạng này các em cần nắm chắc phương pháp xác định
góc giữa đường thẳng và mặt phẳng sau đây.
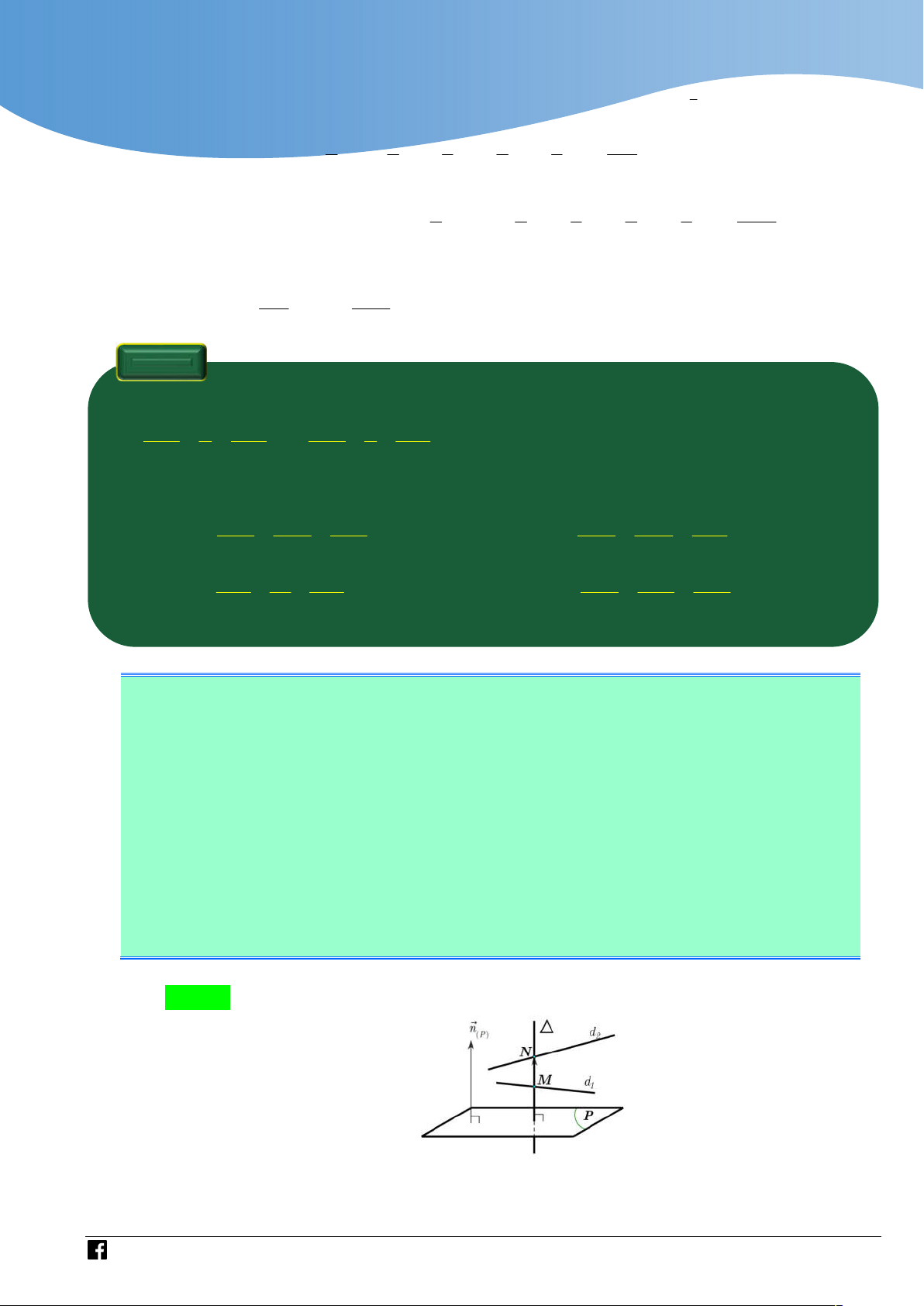
Phương pháp xác định góc giữa đường thẳng và mặt phẳng:
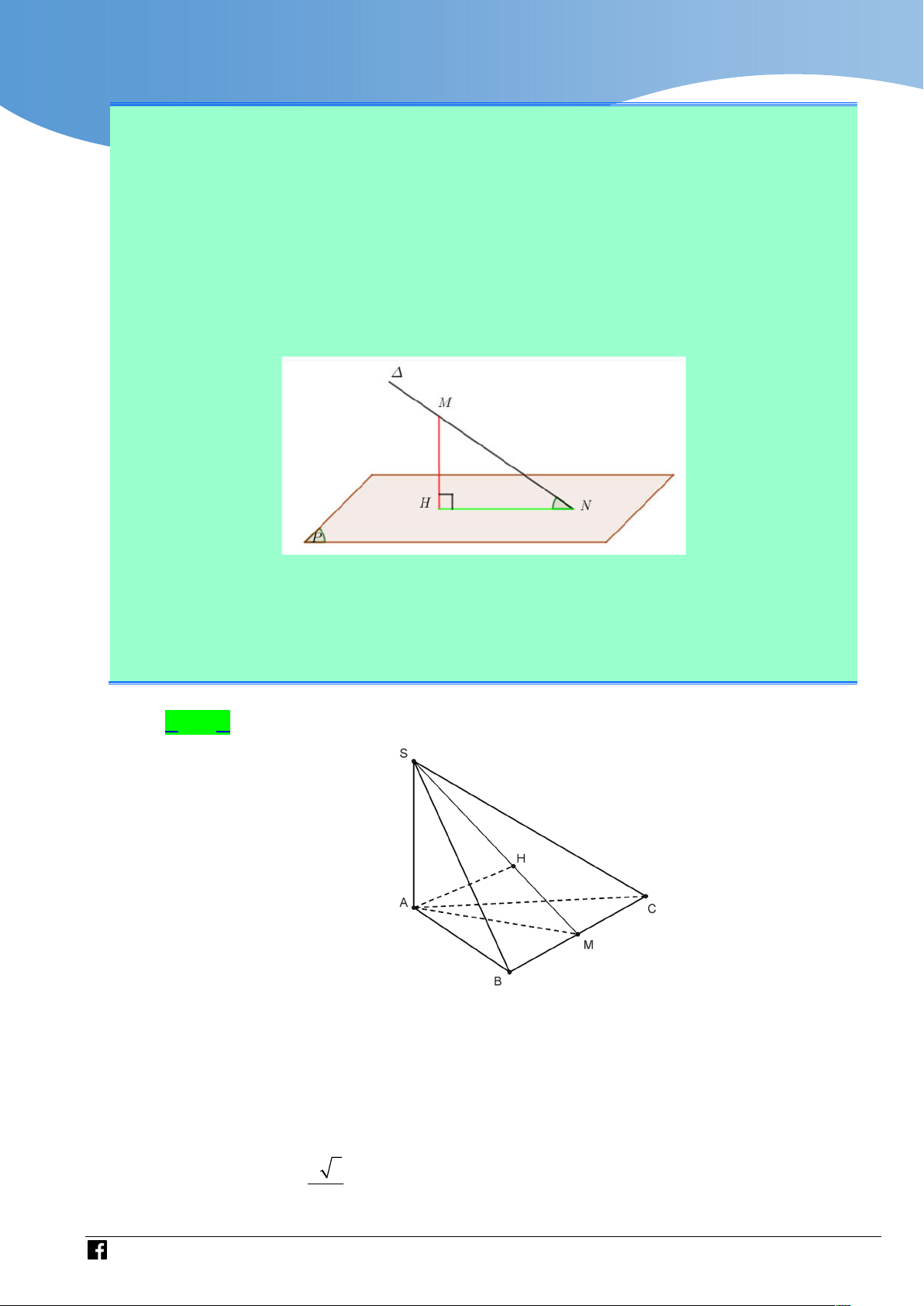
Bước 1: Xác định giao điểm N P Giao điểm tại đâu đỉnh của góc tại đó.
Bước 2: Lấy điểm M sao cho M N , sau đó hạ MH vuông góc mặt phẳng P
tại H . (Bước này là bước khó xác định nhất khi làm bài).
Bước 3: Nối H với N suy ra ; P MNH . Lời giải Chọn A BC AM
Gọi M là trung điểm của BC . Ta có
BC SAM SBC SAM BC SA
Dựng AH vuông góc với SM . Do SBC SAM AH SBC .
Góc giữa SA và mặt phẳng SBC là góc ASH hay ASM
Theo giả thiết ta có ASM 45 vì vậy tam giác SAM vuông cân tại A . a 3
Ta có SA AM . 2
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 2 3 1 1 a 3 a 3 a
Thể tích khối chóp S.ABC bằng V .S . A S . . . 3 A BC 3 2 4 8 Bình luận:
- Bài toán trên ở mức vận dụng (mức 3), kết hợp hai đơn vị kiến thức là xác định góc giữa
đường với mặt (yếu tố then chốt) và tính thể tích khối chóp. Học sinh cần nắm rõ và vận
dụng được chương góc – khoảng cách trong chương trình lớp 11 để có thể giải quyết được dạng toán này. Hướng phát triển:
Hướng 1: Xây dựng bài toán tính góc giữa một cạnh bên với một mặt bên chứa đường cao.
Hướng 2: Xây dựng các bài toán tính góc giữa một cạnh đáy và một mặt bên không chứa đường cao. Bài tập tương tự Câu 1:
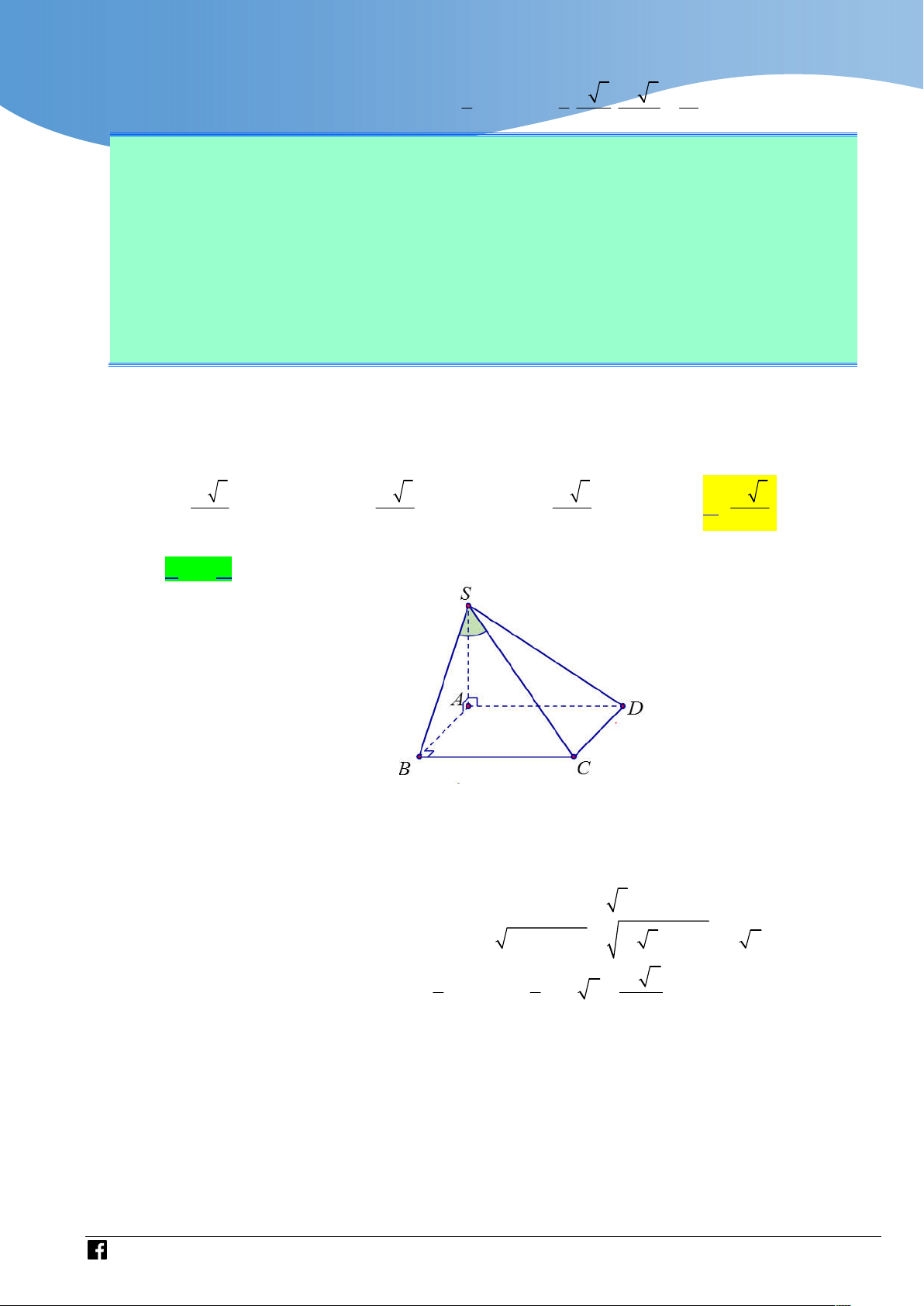
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a . Cạnh bên SA vuông góc với
mặt phẳng đáy, cạnh bên SC tạo với mặt phẳng SAB một góc 30 . Thể tích của khối chóp đó bằng 3 a 3 3 a 2 3 a 2 3 a 2 A. . B. . C. . D. . 3 4 2 3 Lời giải Chọn D BC SA Ta có:
BC SAB SB là hình chiếu của SC lên mặt phẳng SAB . BC AB
SC SA B SC S ,
, B CSB 30. 0
Xét tam giác SBC vuông tại B có SB B .
C cot30 a 3 .
Xét tam giác SAB vuông tại A có SA SB AB a 2 2 2 2 3 a a 2 . 3 2 1 1 a 2 Mà S A . B BC a 2 V S
.SA .a .a 2 ABCD . Vậy . 3 ABCD 3 3
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Câu 2:
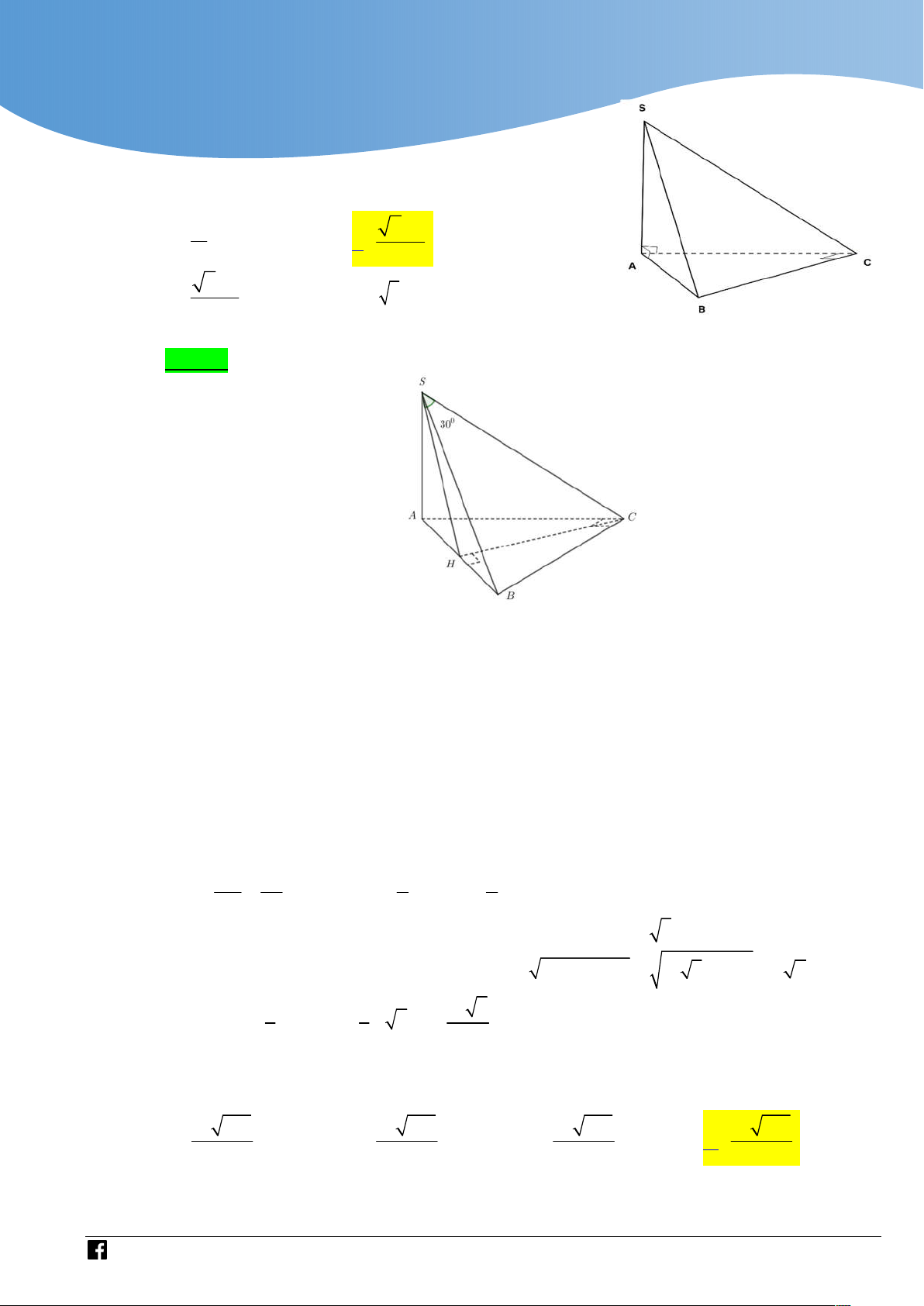
Cho hình chóp S.ABC có đáy là tam giác vuông cân
đỉnh C , AB 2a , cạnh bên SA vuông góc với mặt
phẳng đáy. Góc giữa SC và mặt phẳng SAB bằng
30 ( tham khảo hình vẽ). Thể tích của khối chóp S.ABC bằng 3 a 3 2.a A. . B. . 3 3 3 6.a 3 C. . D. 6.a . 3 Lời giải Chọn B
Gọi H là trung điểm AB AH BH a . Khi đó CH AB (do ABC cân tại C ) Ta có: C H AB CH SA
CH SAB
AB SA A A ,
B SA SAB
hay SH là hình chiếu vuông góc của SC lên mặt phẳng SAB .
Suy ra SC SAB 0 , C SH 30 .
Tam giác ABC vuông tại C nên ta có: AB 2a 1 1 2 CH a S CH .AB
.a, 2a a 2 2 ABC 2 2 0
Tam giác SHC vuông tại H nên ta có: SH C .
H cot30 a 3 .
Tam giác SAH vuông tại A nên ta có: SA SH AH a 2 2 2 2 3 a a 2 . 3 1 1 a 2 Vậy 2 V S . A S .a 2.a . S.ABC 3 A BC 3 3 Câu 3:
Cho hình chóp S.ABC có AC a , BC 2a , 0
ACB 120 , cạnh bên SA vuông góc với đáy.
Đường thẳng SC tạo với mặt phẳng SAB góc 0
3 0 . Tính thể tích của khối chóp S.ABC 3 a 105 3 a 105 3 a 105 3 a 105 A. . B. . C. . D. . 7 28 21 42
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Lời giải Chọn D 2 1 1 3 a 3 Ta S A . C B .
C sin ACB . . a 2 . a A BC 2 2 2 2 2 2 2 2
Xét tam giác ABC ta có AB AC BC 2A . C B .
C cos ACB 7a
Gọi H là hình chiếu vuông góc của C lên AB khi đó do đường thẳng SC tạo với mặt 0 phẳng SAB góc 0 3 0 nên CSH 30 . 2 1 a 3 a 21
Xét ABC ta có .CH.AB CH . 2 2 7 CH 2a 21
Xét SCH vuông tại H ta có SC . 0 sin 30 7 a 35
Xét SAC vuông tại A ta có 2 2
SA SC AC . 7 2 3 1 1 a 35 a 3 a 105 Vậy V .S . A S . . . SABC 3 A BC 3 7 2 42 Câu 4:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a , BC a 3 . Cạnh bên
SA vuông góc với đáy và đường thẳng SC tạo với mặt phẳng SAB một góc 30 . Tính
thể tích V của khối chóp S.ABCD theo a . 3 2 6a 3 2a 3 3 3a A. V . B. V .
C. V 3a . D. V . 3 3 3 Lời giải Chọn A BC SA Ta có:
BC SAB SB là hình chiếu của SC lên mặt phẳng SAB . BC AB
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
SC SA B SC S ,
, B CSB 30. Xét tam giác BC
SBC vuông tại B có tan 30 SB 3a . SB
Xét tam giác SAB vuông tại A có 2 2
SA SB AB 2a 2 . Mà 2 S A . B BC a 3 . ABCD 3 1 2a 6 Vậy V S .SA . 3 ABCD 3 Câu 5:
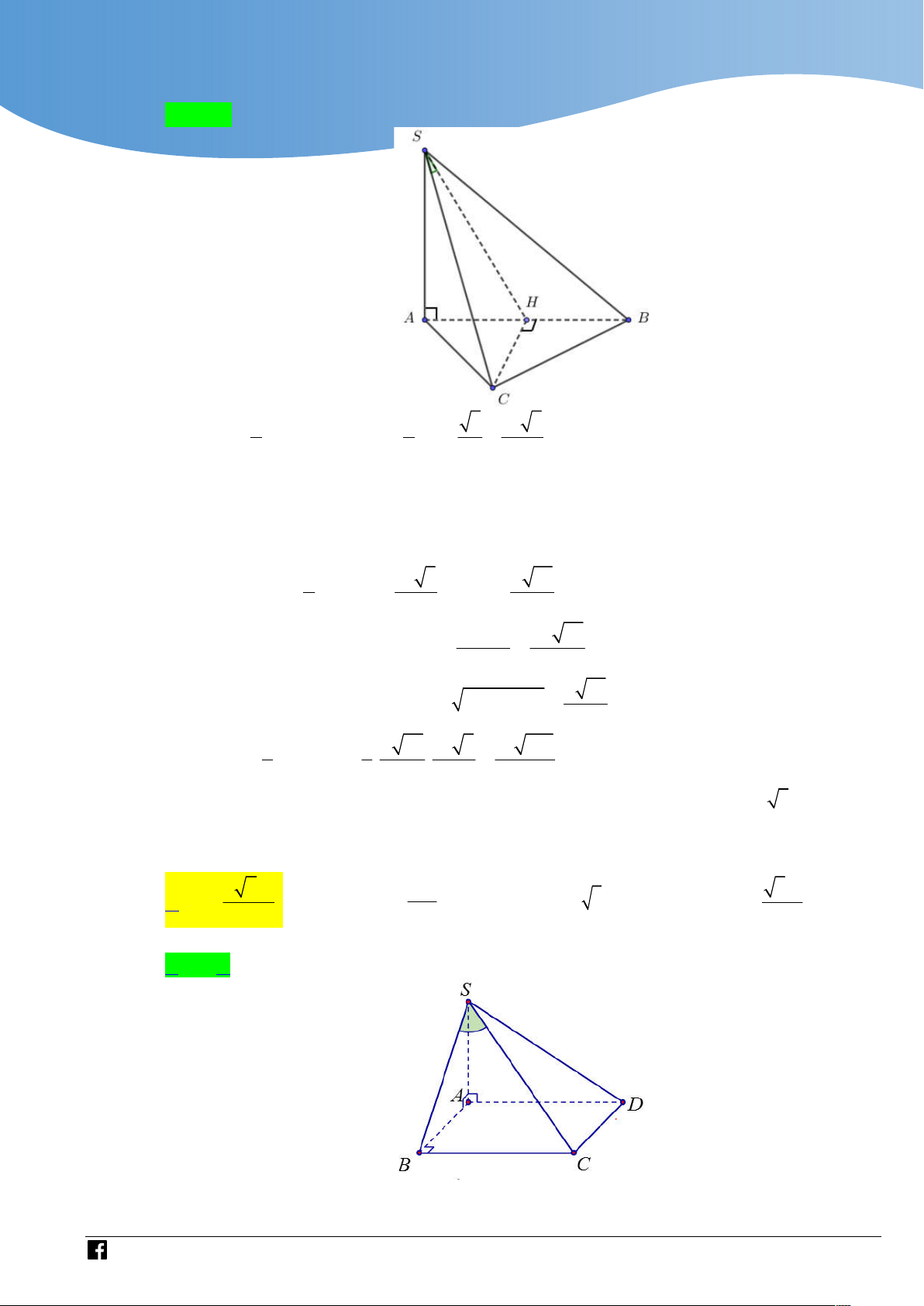
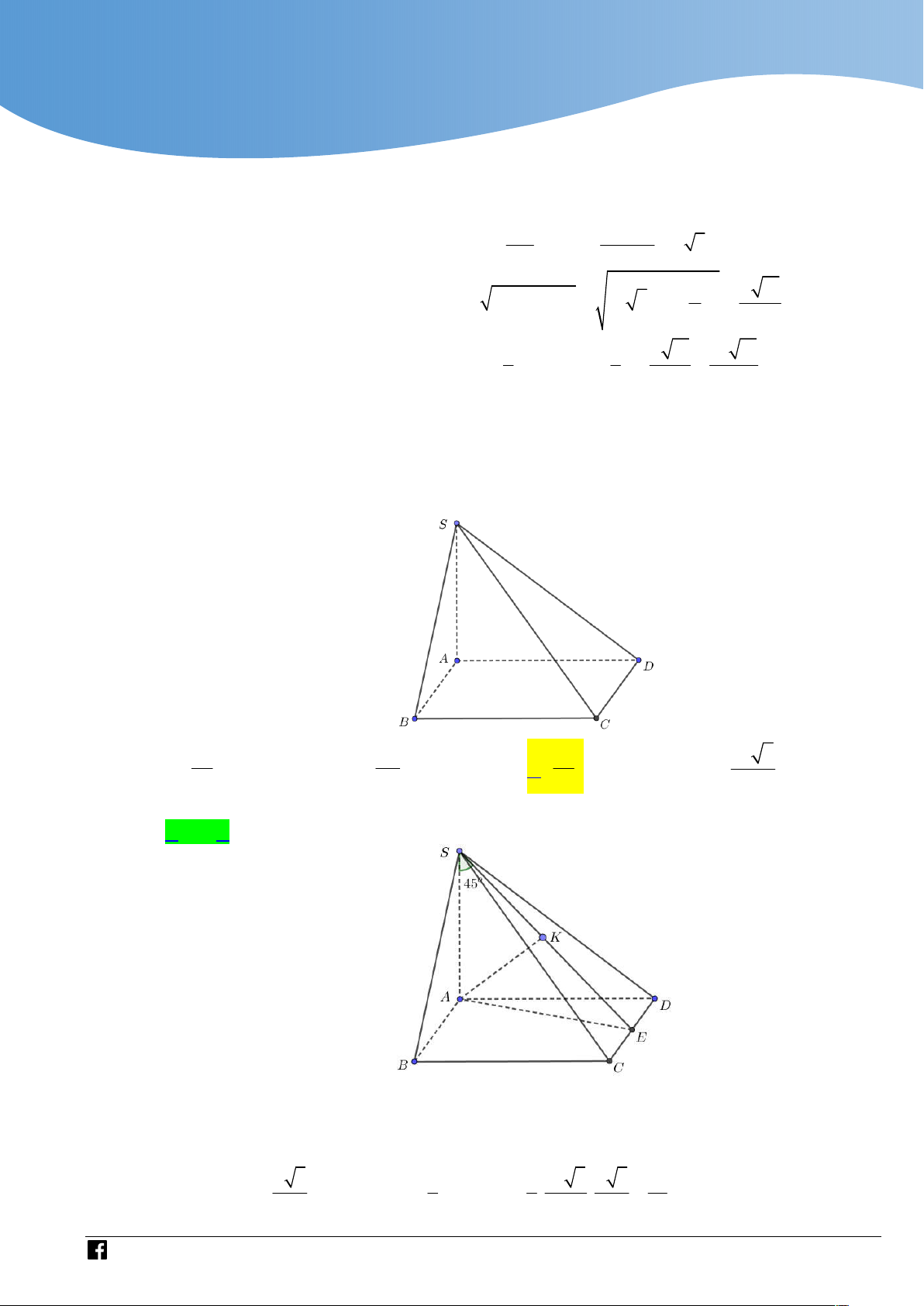
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B . AB BC a ,
AD 2a ; cạnh bên SA vuông góc với mặt phẳng ABC
D (tham khảo hình vẽ bên). Góc
giữa đường thẳng SC và mặt phẳng SAD bằng 0
3 0 . Tính thể tích khối chóp S.ABCD . 3 a 3 3 a 3 3 a 2 3 a 2 A. . B. . C. . D. . 6 2 3 2 . Lời giải Chọn D
Gọi E là trung điểm của AD thì ta dễ dàng chứng minh ABCE là hình vuông
CE AB a C E AD Ta có:
CE SAD SC SAD 0 , CSE 30 . CE SA
AD BC AB a a 2 2 a 3a
Diện tích mặt đáy là: S . ABCD 2 2 2
Tam giác SCE vuông tại E nên ta có: 0
SE CE.cot 30 a 3 .
Tam giác SAE vuông tại A nên ta có: SA SE AE a 2 2 2 2 3 a a 2 . 2 3 1 1 3a a 2 Vậy V .S . A S .a 2. . S . ABCD 3 ABCD 3 2 2
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Câu 6:
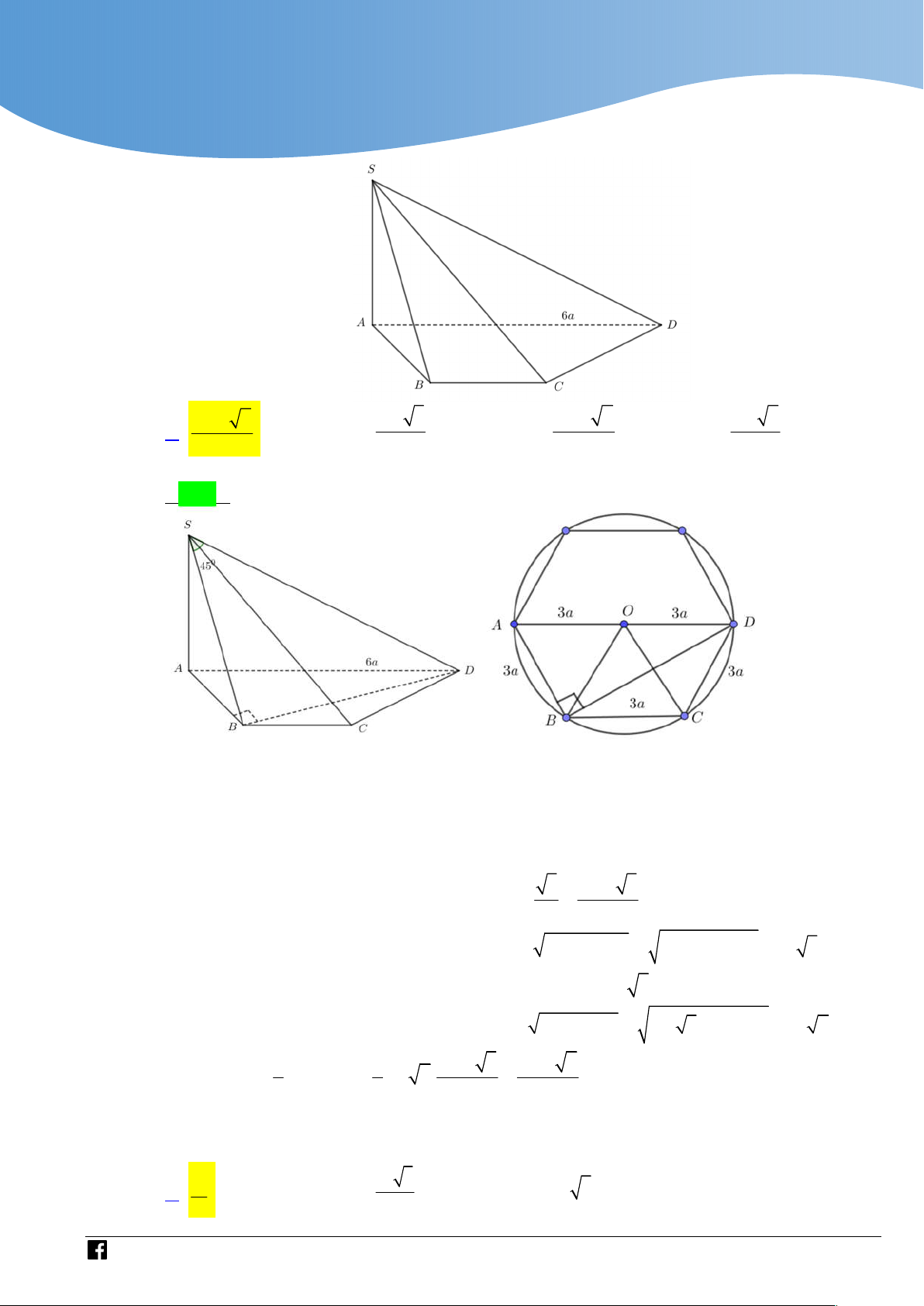
Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều với đáy lớn AD 6a . SA
vuông góc với mặt phẳng đáy. Biết góc giữa SD và mặt phẳng SAB bằng 0 45 . Thể
tích khối chóp S.ABCD bằng 3 3 3 3 27a 6 9a 3 27a 2 9a 2 A. . B. . C. . D. . 4 4 4 4 Lời giải Chọn A 0
Do đáy ABCD là nửa lục giác đều nên ABD 90 (góc chắn nửa đường tròn). BD SA Ta có:
BD SAB . Suy ra SB là hình chiếu vuông góc của SD lên mặt BD AB
phẳng SAB nên SD SAB 0 , DSB 45 . 2 2 3 27a 3
Diện tích mặt đáy là: S 3.S 3. a . ABCD O AB 3 . 4 4 2 2
Tam giác ABD vuông tại B nên ta có: 2 2
BD AD AB 6a 3a 3a 3 .
Tam giác SBD vuông cân tại B nên ta có: SB BD 3a 3 . 2
Tam giác SAB vuông tại A nên ta có: SA SB AB a a2 2 2 3 3 3 3a 2 . 2 3 1 1 27a 3 27a 6 Vậy V .S . A S .3a 2. S.ABCD 3 ABCD 3 4 4 Câu 7:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SAvuông góc với mặt phẳng đáy.
Biết góc giữa AC và mặt phẳng SCD bằng 0
3 0 . Thể tích khối chóp S.ABCD bằng 3 3 a 3 3 A. a . B. . C. a 3. D. 3 a . 3 12
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Lời giải Chọn A
Gọi H là hình chiếu của A trên cạnh SD . C
D AD (ABCDlµ . h v « u ng) Ta có
CD SAD CD AH . C D SA
SAABC D AH CD Do đó
AH SCD . Vậy hình chiếu vuông góc của AC trên mặt phẳng AH SD SCD 0
là HC . Suy ra góc giữa AC và SCD là ACH. Theo giả thiết ta có ACH 30 .
Vì ABCD là hình vuông cạnh a nên A C a 2 .
Xét tam giác AHC vuông tại H (vì AH SC D ) có: AH a 2 0 sin ACH AH A .
C sin ACH a 2.sin 30 . AC 2
Xét tam giác SAD vuông tại A có chiều cao AH nên 1 1 1 1 1 1 2 1 1 SA a . 2 2 2 2 2 2 2 2 2 AH AS AD SA AH AD a a a 3 Vậy 1 1 a 2 V .SA.S .a.a . S . ABC D 3 ABC D 3 3 Câu 8:
[THI-THU-SỞ HÒA BÌNH-2020-2021] Cho hình chóp S.ABCD có đáy là hình vuông
cạnh a . Hình chiếu vuông góc của S lên mặt phẳng ABC
D trùng với trung điểm của
cạnh AB . Góc giữa SC và SAB bằng 0
3 0 .Thể tích của khối chóp S.ABCD bằng 3 a 11 3 a 11 3 a 11 3 a 11 A. . B. . C. . D. . 2 4 3 6 Lời giải Chọn D
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Gọi H là trung điểm của AB . Từ giả thiết suy ra SH ABC D . CB BA Ta có :
CB SAB SB là hình chiếu của SC trên
CB SAdo SA ABCD
SAB . Suy ra SC SA B SC S 0 ,
, B BSC 30 . Trong tam giác vuông BC BC SBC có : 0 tan 30 SB a 3. 0 SB tan 30 2 2 2 2 a a 11
Trong tam giác vuông SBH có : SH SB BH a 3 . 2 2 3 1 1 2 a 11 a 11
Thể tích của khối chóp S.ABCD : V .S .SH .a . . S.ABCD 3 ABCD 3 2 6 Câu 9:
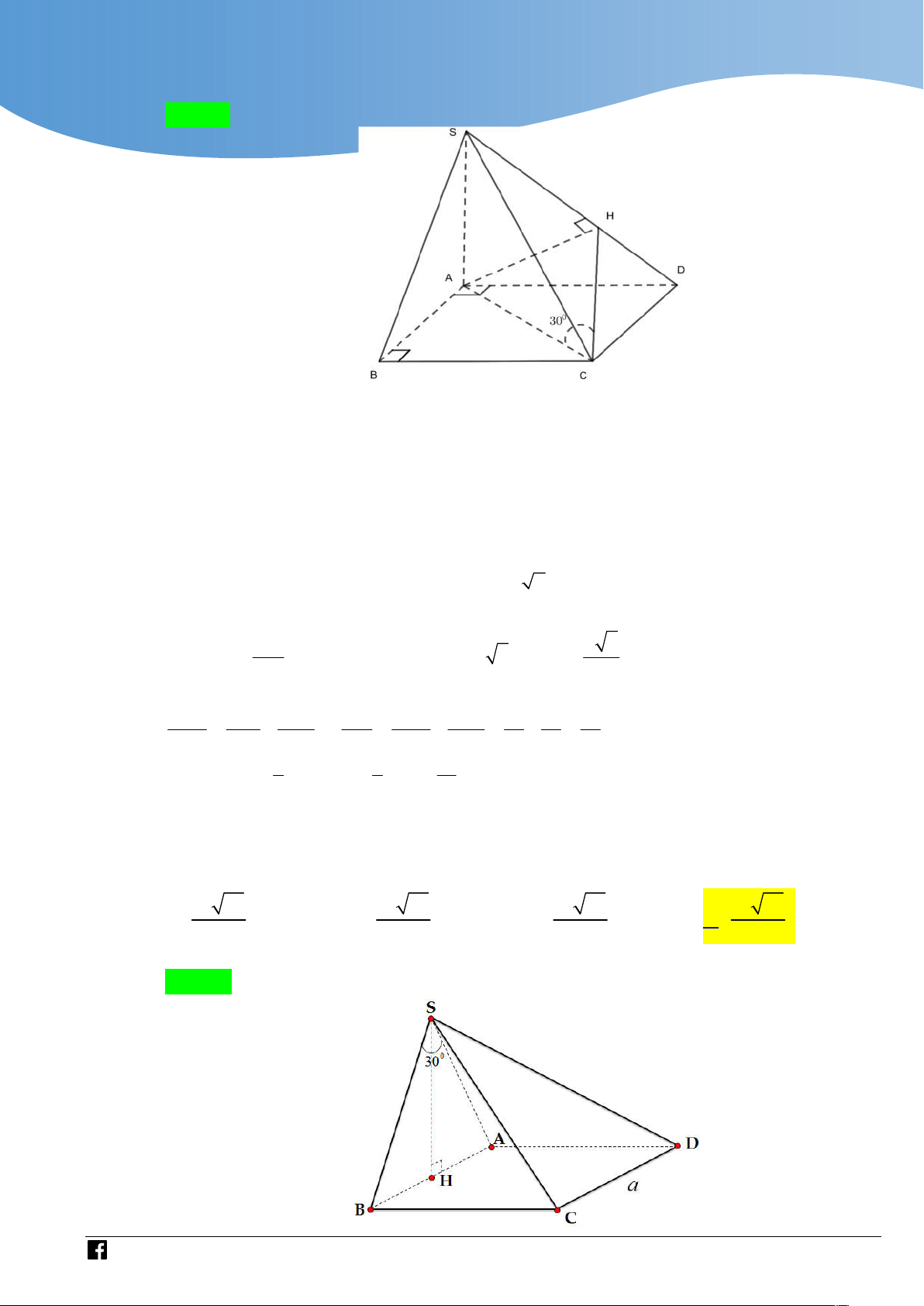
[Sở-GDĐT-Thái-Nguyên-L2-NH-2020-2021]Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh , 60o a ABC
, cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa SA
và mặt phẳng SCD bằng 45o (tham khảo hình vẽ). Thể tích của khối chóp S.ABCD bằng 3 a 3 3a 3 a 3 a 3 A. . B. . C. . D. . 8 4 4 4 Lời giải Chọn C
Ta có tam giác ACD đều cạnh a . Gọi E là trung điểm C . D C D SA AK CD Kẻ AK S . E Do
CD SAE
AK SCD o 45 ASK. CD AE AK SE a 3 2 3 1 1 a 3 a 3 a
SA AE . Vậy V .S .SA . . . 2 S.ABCD 3 ABCD 3 2 2 4
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Câu 44
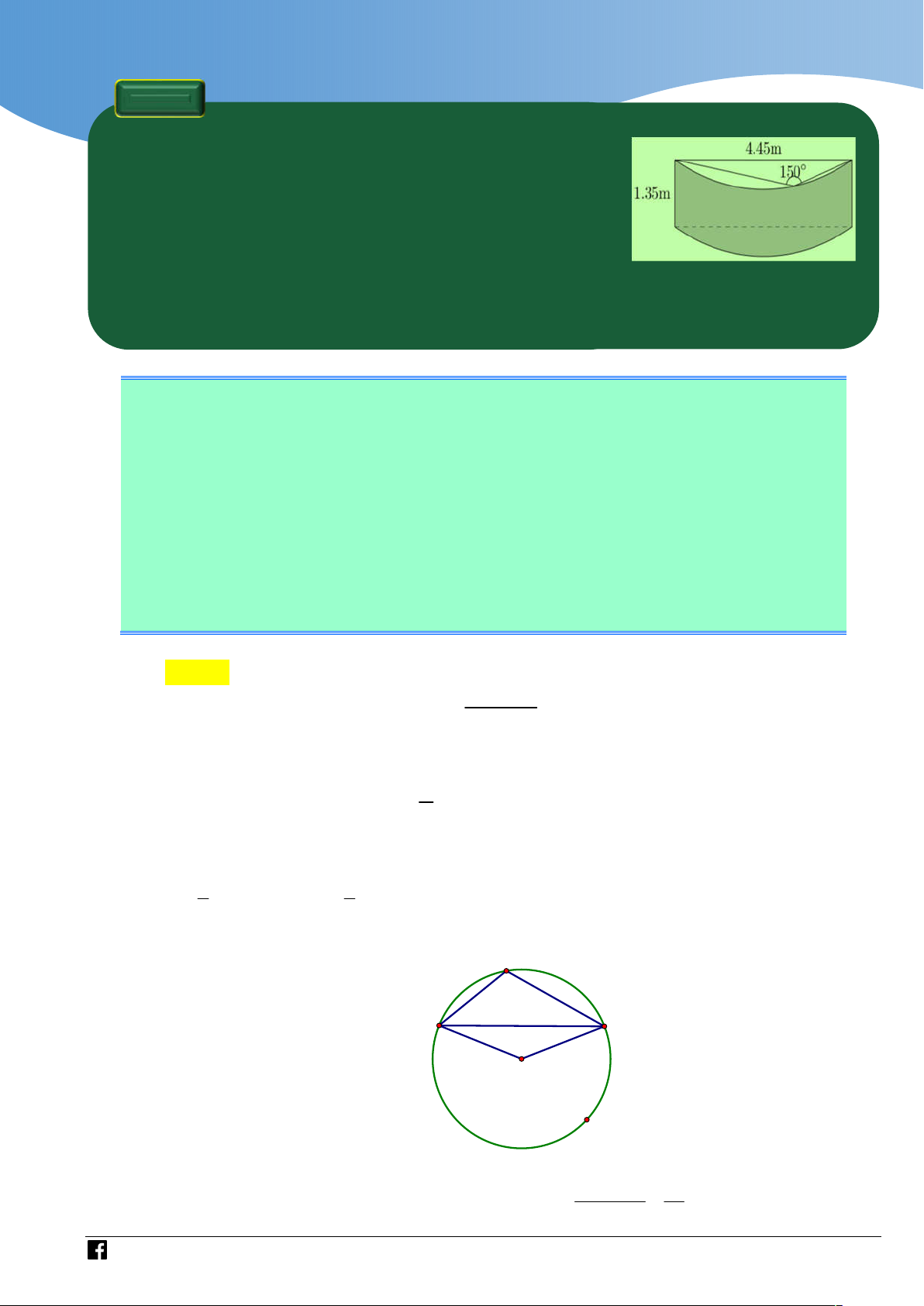
Ông Bình làm lan can ban công ngôi nhà của mình bằng một
tấm kính cường lực. Tấm kính đó là một phần của mặt xung
quanh của một hình trụ như hình bên. Biết giá tiền của 2 1m
kính như trên là 1.500.000 đồng. Hỏi số tiền (làm tròn đến
hàng nghìn) mà ông Bình mua tấm kính trên là bao nhiêu? A. 23.591.000 đồng. B. 36.173.000 đồng. C. 9.437.000 đồng. D. 4.718.000 đồng.
Faceboock: Huỳnh Văn Ánh – Phong Do
Phân tích và định hướng tìm lời giải:
- Đây là tình thực tiễn liên qua đến các kiến thức mà các em đã được học về vấn đề diện tích của mặt tròn xoay;
- Để giải quyết được tình huống trên các em phải thực hiện thông qua các bước sau:
Bước 1. Xác định yêu cầu của bài toán thực tiễn;
Bước 2. Tổ chức cho học sinh phân tích và làm rõ các “cụm từ” có nghĩa trong bài toán
thực tiễn trong mô hình Toán học;
Bước 3. Đề xuất giải pháp giải quyết bài toán thực tiễn(trong mô hình Toán học);
Bước 4. Thực hiện giải pháp(trong mô hình Toán học);
Bước 5. Chuyển kết quả trong mô hình toán học sang lời giải của bài toán thực tiễn. Lời giải Chọn C
Bán kính của đường tròn đáy là 4, 45 R 4, 45m . 2 sin 150
Vì dây cung bằng bán kính nên mép trên của tấm kính là cung tròn có số đo 60 của đường tròn đáy.
Do đó diện tích tấm kính bằng 1 diện tích xung quang của hình trụ có chiều cao 1, 35m 6
và bán kính đáy R 4, 45m .
Số tiền mà ông Bình mua tấm kính trên là 1 1 T .2 Rh.1500000
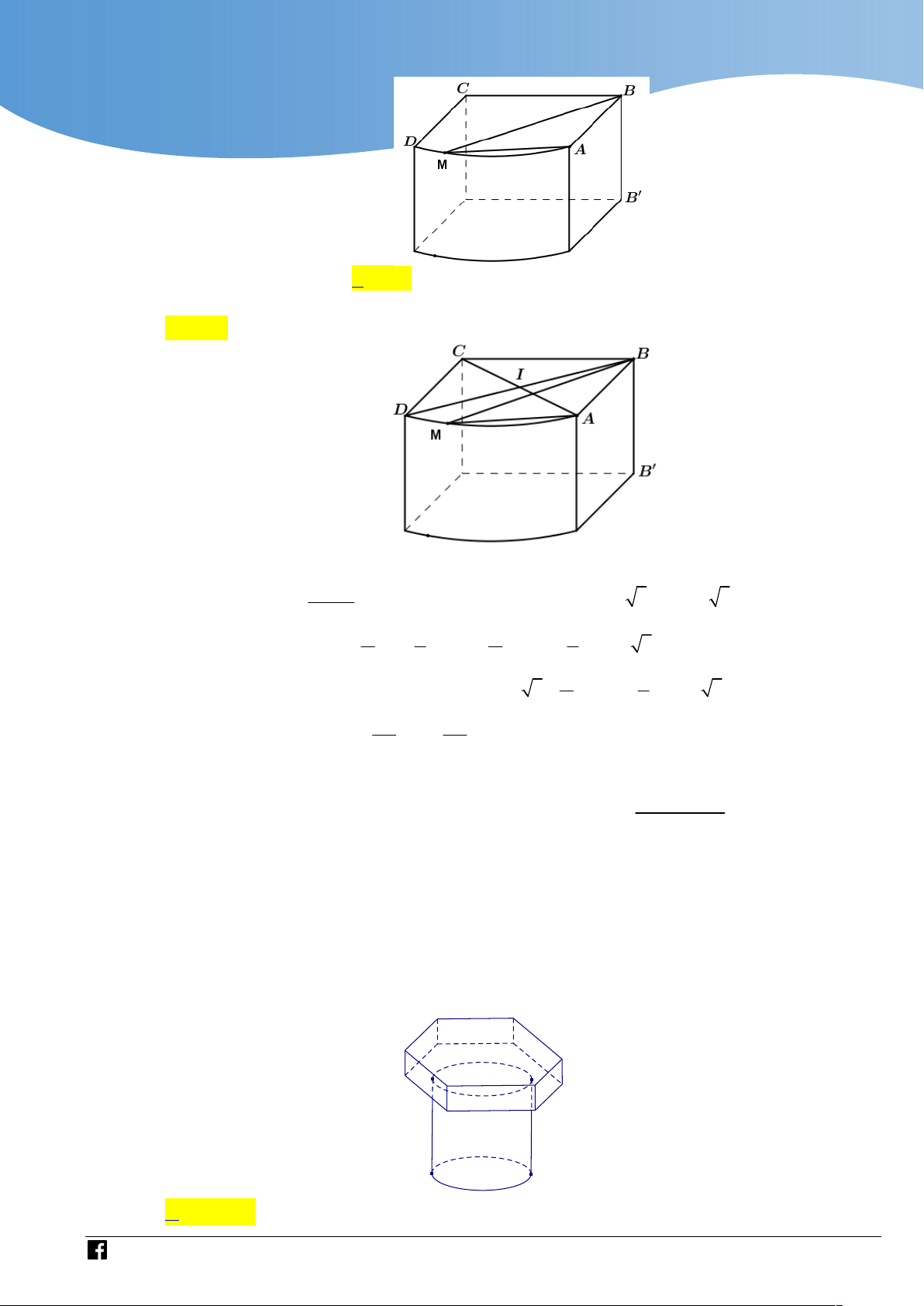
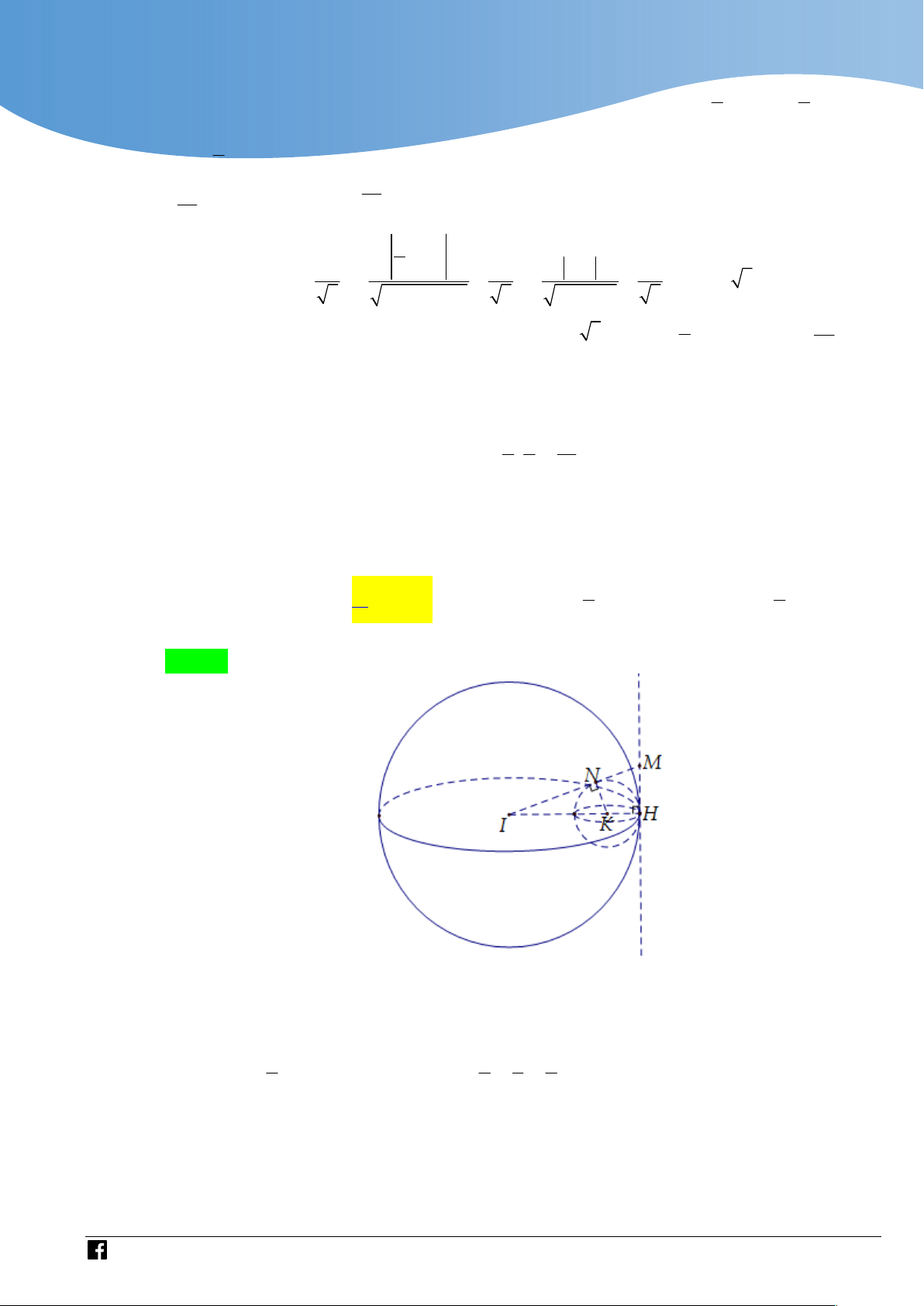
.2 .4, 45.1, 35.1500000 9437000 đồng. 6 6 Cách 2: A 150 B 4,45 m C I
Gọi đường tròn tâm I bán kính R (như hình vẽ). Ta sẽ tính độ dài cung nhỏ BC.
Áp dụng đính lí sin trong tam giác ABC ta có BC 89 R . 0 2 sin 150 20
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 2 2 2 2 2 2
IB IC BC
R R BC 1
Trong tam giác IBC có cos I I . 2 2I . B I C 2R 2 3 Độ dài cung nhỏ BC là 89 l .R (m). 3 60 Diện tích phần kính là 801 l.1, 35 . 400
Số tiền mua tấm kính là 801 .1.500.000 9436558, 933 . 400 Bình luận:
- Đây là là một tình huống xảy ra trong thực tiễn, để giải quyết tình huống này đòi hỏi các
em phải có năng lực mô hình hóa toán học. Nghĩa là, các em phải lựa chọn mô hình toán
đã học phù hợp với tình huống thực tiễn để phát biểu tình huống xảy ra thành bài toán
trong mô hình toán học; giải quyết bài toán toán học. Từ đó, chuyển kết quả trong mô
hình toán học sang lời giải bài toán thực tiễn. Đây là bài toán kiểm tra mức độ VDC
Hướng phát triển bài toán
Hướng 1. Sử dụng mô hình toán học các kiến thức liên quan đến mặt trụ, mặt cầu;
Hướng 2. Sử dụng mô hình toán học các kiến thức liên quan đến khối trụ, khối chóp; Bài tập tương tự Câu 1:
Ông A được nhà nước cho thuê 100 ha đất trồng rừng Thông với thời gian 10 năm thu
hoạch. Biết sau 10 năm cây trưởng thành với chiều cao khoảng 15 m và khi thu hoạch
thì với mỗi cây Thông đạt chuẩn thu hoạch được 1 khối gỗ loại I hình trụ có chiều cao
5 m chu vi vòng tròn thân 2 m và được 1 khối gỗ loại II hình trụ có chiều cao 4 mchu
vi vòng tròn thân 1,4 m .Với mỗi 3
1 m gỗ thu hoạch loại I , loại II lãi tương ứng được
150 và 100 ngàn đồng. Biết 1 ha trung bình có 100 cây thu hoạch. Hỏi sau khi thu hoạch
ông A lãi với số tiền gần bằng: A. 2.500.000.000 . B. 3.000.000.000 . C. 3.500.000.000 . D. 4.000.000.000 Lời giải Chọn B Gọi R,R 1
2 lần lược là bán bính khối gỗ loại I và loại II 1 R 1 2 R 2 Ta có: 1 2 R 1, 4 0.7 2 R 2 Vậy mỗi cây thu hoạch được 5 2
V R .5 3 m gỗ loại I và 1 1 0,72 .4 2
V R .4 3 m gỗ loại II 2 2 Vậy: tổng số tiền thu sau thu hoạch là:
T V.100.100.150000 V
.100.100.100000 3011211600 1 2 . Câu 2:
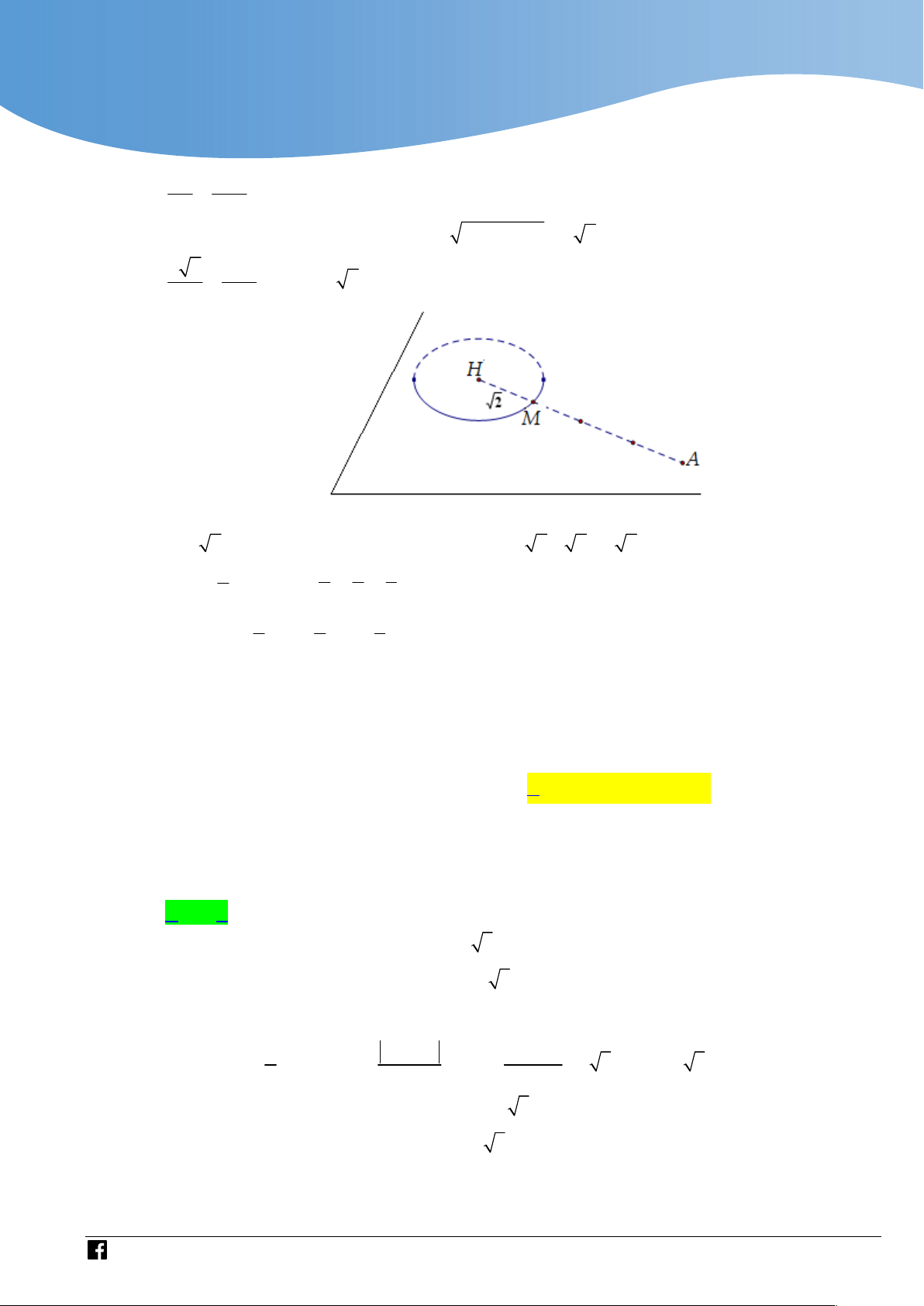
Một cơ sở sản xuất bể cá không nắp với chiều cao BB bằng cạnh bên BA bằng 0, 7 m
như hình vẽ. Biết 3 mặt xung quanh và mặt đáy được được đúc bằng nhựa cao cấp với chi phí 2
100000 / m , mặt cong phía trước dùng chất liệu kính dẽo cao cấp với giá 2
200000 / m . Với thiết kế sao cho cung DM là một phần của đường tròn ngoại tiếp hình
chữ nhật ABCD và M thuộc cung AD , AMB 30. Hỏi cơ sở sản xuất được tối đa bao
nhiêu bể cá với số tiền 200000000 đồng
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM A. 620 . B. 624 . C. 628 . D. 608 Lời giải Chọn B
Ta có: AMB 30 ACB DCA 60 DIA120 Xét B
AM ta có: AB 2R R AB 0, 7 BC AB 3 0,7. 3 sin M Diện tích mặt đáy: 3 3 S R S (0, 7) d ABCD 0, 72 2 2 3 3 4 3 4 Diện tích phần nhưa là 3
S 2.0, 7 2 0, 7 2 3 (0, 7) 0, 72 2 3 1 3 4 Diện tích phần kính 2 2 S R.h .0, 7 2 2 3 3
Vậy tổng số tiền cho một sản phẩm là T S .100000S .200000 320216 1 2
Vậy với số tiền 200000000 thì cơ sở sản xuất tối đa được 200000000 624 cái. 320216 Câu 3:
[THPT-THỊ-XÃ-QUẢNG-TRỊ-2021] Để chế tạo ra một cái đinh ốc, người ta đúc một
vật bằng thép có dạng như hình vẽ bên. Trong đó, phần phía trên có dạng là một hình
lăng trụ lục giác đều có chiều cao bằng 3cm và độ dài cạnh đáy bằng 4cm; phần phía
dưới có dạng một hình trụ có trục trùng với trục của lăng trụ đều phái trên, chiều cao
bằng 12cm và chu vi đường tròn đáy bằng một nữa chu vi đáy của lăng trụ. Biết mỗi 3 m
thép có giá là m triệu đồng. Khi đó, giá nguyên liệu để làm một vật như trên gần nhất
với kết quả nào dưới đây?
A. 262, 2 m đồng.
B. 537, 2m đồng.
C. 26, 22 m đồng.
D. 53, 72 m đồng.
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Lời giải Chọn A Gọi , V V,V 1
2 lần lượt là thể tích của vật thể, thể tích của hình lăng trụ phía trên và thể tích 2 4 3
hình trụ phía dưới. Ta có: V h .S 3.6. 72 3 cm . LT 3 1 4
Chu vi lục giác đều là: 6.4 24cm .
Suy ra chu vi của đường tròn đáy là 6
C 12cm 2 R R
( R bán kính đường tròn đáy). 2 6 432 Do đó: 2
V R .h .12 cm . T 3 2 Khi đó: 432
V V V 72 3 3 cm . 1 2 432
Giá nguyên liệu để làm vật thể là: T V.m 72 3 m 262, 2m đồng. Câu 4:
[ĐỀ-THI-CHINH-PHỤC-MÔN-TOÁN-VTV7-LẦN-1-2021] Để chuẩn bị cổ vũ cho đội
tuyển Việt Nam tham dự vòng loại thứ ba World Cup 2022. Một hội cổ động viên dự
định trang trí 1000 chiếc nón là với cách sơn như sau: Tính theo độ dài đường sinh của
chiếc nón lá là 40cm, kể từ đỉnh nón cứ 8cm thì sơn màu đỏ, màu vàng xen kẽ nhau
như hình minh họa, sau đó dán 20 ngôi sao vàng vào mỗi chiếc nón.
Biết rằng đường kính của đường tròn đáy nón 40 cm, mỗi ngôi sao vàng giá 200 đồng,
sơn màu vàng giá 5000 đồng/ 2
m , sơn màu đỏ giá 4000 đồng/ 2
m . Hỏi giá thành để trang
trí 1000 chiếc nón lá đó gần với số tiền nào sau đây?
A. 5105840 đồng.
B. 5105841 đồng.
C. 5156106 đồng. D. 5156107 đồng. Lời giải Chọn B
Hình nón đã cho có độ dài đường sinh là 0, 4 m và bán kính đường tròn đáy là r 0, 2
m. Khi đó cắt hình nón theo một đường sinh rồi trải phẳng, ta được một hình quạt có
bán kính và độ dài cung tròn tương ứng là 2 r , hay ta được một nửa hình tròn tròn bán kính .
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Khi đó, trên bán kính của nửa hình tròn, mỗi dải màu có độ dài . Suy ra tổng diện tích 5 2 2 2 2 2 1 4 3 2 1 phần màu vàng là: 2 . 2 5 5 5 5 5 2 2 2 2 2 1 4 3 2 1 3
Tổng diện tích phần màu đỏ là: 2 1 . 2 5 5 5 5 10
Vậy tổng số tiền trang trí 1000 chiếc nón là 2 2 3 1000 5000 4000 20 200 5105841 đồng. 5 10 Câu 45
Trong không gian Oxyz , cho mặt phẳng P : 2x 2y z 3 0 và hai đường thẳng x 1 y z 1 x 2 y z 1 d : , d :
. Đường thẳng vuông góc với P , đồng thời cắt cả 1 2 1 2 2 1 2 1
d và d có phương trình là 1 2 A. x 3 y 2 z 2 x 2 y 2 z 1 . B. . 2 2 1 3 2 2 C. x 1 y z 1 x 2 y 1 z 2 . D. . 2 2 1 2 2 1
Faceboock: Nguyễn Khắc Thành – Nguyễn Văn Viễn – Uyen Hoang
Phân tích và định hướng tìm lời giải:
- Đây là bài toán lập phương trình đường thẳng thỏa mãn điều kiện cho trước.
- Để lập phương trình đường thẳng chúng ta cần xác định một điểm nó đi qua và một
véctơ chỉ phương. Để xác định hai yếu tố trên chúng ta thực hiện thông qua các bước sau:
Bước 1: Giả sử cắt d d 1 ,
2 lần lượt tại M và N . Khi đó tọa độ của các điểm M và N
theo thứ tự thỏa mãn phương trình tham số của d d 1 và 2 .
Bước 2: Đường thẳng P dẫn đến VTCP của và VTPT của P cùng phương.
Dựa vào điều kiện cùng phương của hai véc tơ ta tìm được tọa độ các điểm M , N .
Bước 3: Đường thẳng đi qua hai điểm M và N . Lời giải Chọn A
Gọi M và N lần lượt là giao điểm của với d d 1 và 2 .
Vì M d M 2m 1; ;
m 2m 1 và N d N n 2; 2 ; n n 1 . 2 1
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Ta có MN n 2m 1; 2n ;
m n 2m .
Vì P nên MN cùng phương với n . P 2; 2; 1 n 2m 1 2n m n 2m m n 1 m 0 Do đó . 2 2 1 2m n 1 n 1
Đường thẳng đi qua M 1;0; 1 , N 3;2; 2
và có véctơ chỉ phương là MN 2;2; 1 nên
có phương trình là x 3 y 2 z 2 . 2 2 1 Bình luận:
- Đây là câu hỏi ở mức độ vận dụng nội dung xoay quanh các kiến thức về điểm, đường thẳng, mặt phẳng.
- Để giải tốt được các câu hỏi về dạng này người học cần nắm vững được các kiến thức
liên quan đến hệ tọa độ trong không gian như : Tọa độ của điểm, tọa độ của véc tơ, các
véc tơ cùng phương, vị trí tương đối giữa đường thẳng và mặt phẳng, vị trí tương đối
giữa hai đường thẳng. Ngoài ra người học cần có được các kỹ năng như : Kỹ năng tham
số hóa tọa độ của một điểm khi biết điểm đó thuộc đường thẳng có phương trình tham số
(hoặc chính tắc) cho trước ; kỹ năng sử dụng các phép toán cơ bản của véc tơ ; kỹ năng sử
dụng các công thức liên quan đến khoảng cách ; …
- Người học cần nắm vững được cách giải các dạng toán cơ bản như : Viết phương trình
đường thẳng đi qua một điểm đồng thời cắt hai đường thẳng phân biệt cho trước ; viết
phương trình đường thẳng song song với một đường thẳng cho trước đồng thời cắt hai
đường thẳng phân biệt cho trước ; viết phương trình đường thẳng đi qua một điểm
đồng thời vuông góc với hai đường thẳng phân biệt cho trước ;… Hướng phát triển:
Hướng 1: Viết phương trình đường thẳng song song với một đường thẳng cho trước
đồng thời cắt hai đường thẳng phân biệt cho trước.
Hướng 2: Viết phương trình đường thẳng vuông góc với một đường thẳng cho trước
đồng thời cắt hai đường thẳng phân biệt cho trước
Hướng 3: Viết phương trình đường thẳng đi qua 1 điểm đồng thời cắt hai đường thẳng
phân biệt cho trước
Hướng 4: Viết phương trình đường thẳng đi qua điểm A đồng thời cắt d1 và vuông góc
với đường thẳng d2 .
Bài tập tương tự x 1 3t x 3 y 1 z 2 Câu 1:
Trong không gian Oxyz , cho các đường thẳng d : , d : y 2 t , 1 2 2 1 2 z 4 t x 3 y 2 z d :
. Đường thẳng song song với d và cắt đồng thời d ,d có phương 3 3 1 2 4 1 6 trình là A. x 1 y z 4 x y z . B. 1 4 . 4 1 6 4 1 6
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM C. x 3 y 1 z 2 x y z . D. 3 1 2 . 4 1 6 4 1 6 Lời giải Chọn D
Gọi Δ là đường thẳng cần tìm. Δ cắt d d 1 và
2 lần lượt tại A , B A3 2 ; a 1 ;
a 2 2a, B 1 3 ; b 2 ; b 4
b, AB 4 2a 3 ; b 1 a 2 ; b 6
2a b d u 4; 1 ;6 3 có VTCP là 4
2a 3b 1 a 2b 6 2a b a 0 Δ / /d 3 4 1 6 b 0
Vậy Δ đi qua A3; 1
; 2 và có VTCP AB 4 ;1; 6
Phương trình Δ : x 3 y 1 z 2 . 4 1 6 x y z 1 Câu 2:
Trong không gian với hệ trục tọa độ Oxyz , cho các đường thẳng d : , 1 1 2 x 3 y z 1 x 1 y 2 z : , :
. Đường thẳng vuông góc với d đồng thời cắt 1 2 1 1 2 1 2 1
, tương ứng tại ,
A B sao cho độ dài đoạn thẳng AB nhỏ nhất. Biết rằng có một 1 2
vectơ chỉ phương là u ; a ;
b 3. Giá trị 2a 3b bằng A. 15 . B. 15 C. 0 . D. 9 . Lời giải Chọn A A3 2 ; a ;
a 1 a, B 1 ; b 2 2 ;
b b, AB 2 2a ;
b 2 a 2 ; b 1
a b
d có VTCP là u 1;1; 2 d
Δ d u . AB 0 a b 2 d
AB b b AB b b b 2 2 2 6 ; ; 3 2 12 45 2 3 27 27 a 1 Vậy AB 3 3 xảy ra khi AB 3; 3 ; 3 min b 3
Δ có một VTCP là u 3;3;3. Vậy a b 3 2a 3b 15 . Câu 3:
Trong không gian với hệ trục tọa độ x 1 y 3 z 2
O xyz , cho các đường thẳng : , 1 3 2 1 x 2 y 1 z 1 :
. Gọi là đường thẳng đi qua điểm A 4 ; 5 ; 3 và đồng thời cắt 2 2 3 5 , 1
2. Đường thẳng có một vectơ chỉ phương là
A. u 3;2; 1 . B. u 3; 2 ; 1 C. u 3 ; 2; 1 .
D. u 3; 2; 1 . Lời giải Chọn A Giả sử cắt , 1
2 lần lượt tại M , N . M 1 3 ; a 3 2 ;
a 2 a, N 2 2 ; b 1 3 ; b 1 5b
MN 3 3a 2 ;
b 2 2a 3 ; b 1
a 5b AM 3 3 ; a 2 2 ; a 1 a
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 3
3a 2b k 3 3a k 1
A, M , N thẳng hàng MN k AM 2 2a 3b k 2 2a a 0
a b k a b 0 1 5 1
Vậy ta được: M 1 ; 3 ; 2, N 2; 1 ;
1 , MN 3;2; 1 Câu 4:
Trong không gian với hệ tọa độ Oxyz, cho điểm A 1;2; 3 và hai đường thẳng x 2 y 2 z 3 x 1 y 1 z 1 d : , d :
. Phương trình đường thẳng qua A , 1 2 1 1 2 1 2 1 vuông góc với d d 1 và cắt 2 là A. x 2 y 1 z 2 x y z . B. 1 2 3 . 1 3 5 1 3 5 C. x 1 y 3 z 5 x y z . D. 1 2 3 . 1 2 3 1 3 5 Lời giải Chọn A
Gọi M là giao điểm của với d M d M 1 ; t 1 2 ; t 1 t 2 . Vì 2 nên .
Ta có AM t;1 2t; 4 t là véc tơ chỉ phương của và u 2;1;1 là véc tơ chỉ 1 phương của d . 1
Vì d nên AM.u 0 2. t 1. 1
2t 1. 4
t 0 t 1 . 1 1
Khi đó, đi qua A1;2;3 và có véc tơ chỉ phương u AM 1; 3; 5 nên có phương x 1 y 2 z 3 trình là . 1 3 5
Để ý rằng, điểm B2;1; 2 và u 1
;3;5 cũng là một véc tơ chỉ phương của x 2 y 1 z 2 nên phương trình là . 1 3 5
Một số hướng phát triển khác: Câu 5:
Trong không gian với hệ tọa độ Oxyz , cho hai điểm (
A 1;1;1) , B(2; 0;1) và mặt phẳng
(P) :x y 2z 2 0. Viết phương trình chính tắc của đường thẳng d đi qua A , song
song với mặt phẳng (P) sao cho khoảng cách từ B đến d lớn nhất. x 1 y 1 z 1 x y z 2 A. d : . B. d : . 3 1 2 2 2 2 x 2 y 2 z x 1 y 1 z 1 C. d : . D. d : . 1 1 1 3 1 1 Lời giải Chọn C Ta có: AB 1; 1 ; 0
P có một VTPT là n 1;1;2
Gọi VTCP của d là u
Kẻ BH d A
BH vuông tại H BH AB d B, d AB d B, d AB max
Xảy ra khi H A d AB u AB 1
Lại có d / / P u n .Suy ra u .n; AB 1;1; 1 2
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM x 1 y 1 z 1 Phương trình d : . Suy ra, chọn C. 1 1 1 Câu 6:
Trong không gian với hệ tọa độ Oxyz , cho hai điểm A1; 2; 3 , B 2 ; 2 ;1 và mặt phẳng
: 2x 2y z 9 0 . Gọi M là điểm thay đổi trên mặt phẳng sao cho M luôn
nhìn đoạn AB dưới một góc vuông. Xác định phương trình đường thẳng MB khi MB
đạt giá trị lớn nhất. x 2 t x 2 2t
x 2 t x 2 t A. y 2 2t B. y 2 t
C. y 2 D. y 2 t z 1 2t z 1 2t z 1 2t z 1 Lời giải Chọn C
Nhận thấy B
Ta có: AB 3; 4
; 4 AB 41
Gọi d là đường thẳng qua A và d x 1 y 2 z 3 Phương trình d : 2 2 1
Gọi K d K 3 ; 2 ; 1
M luôn nhìn đoạn AB dưới một góc vuông M thuộc mặt cầu S đường kính AB
Lại có M M chạy trên đường tròn C S
Lại có B C có đường kính là BK BM BK
MB đạt giá trị lớn nhất khi M K BK 1 ; 0; 2
x 2 t
Vậy phương trình BM là: y 2 . z 1 2t Câu 46
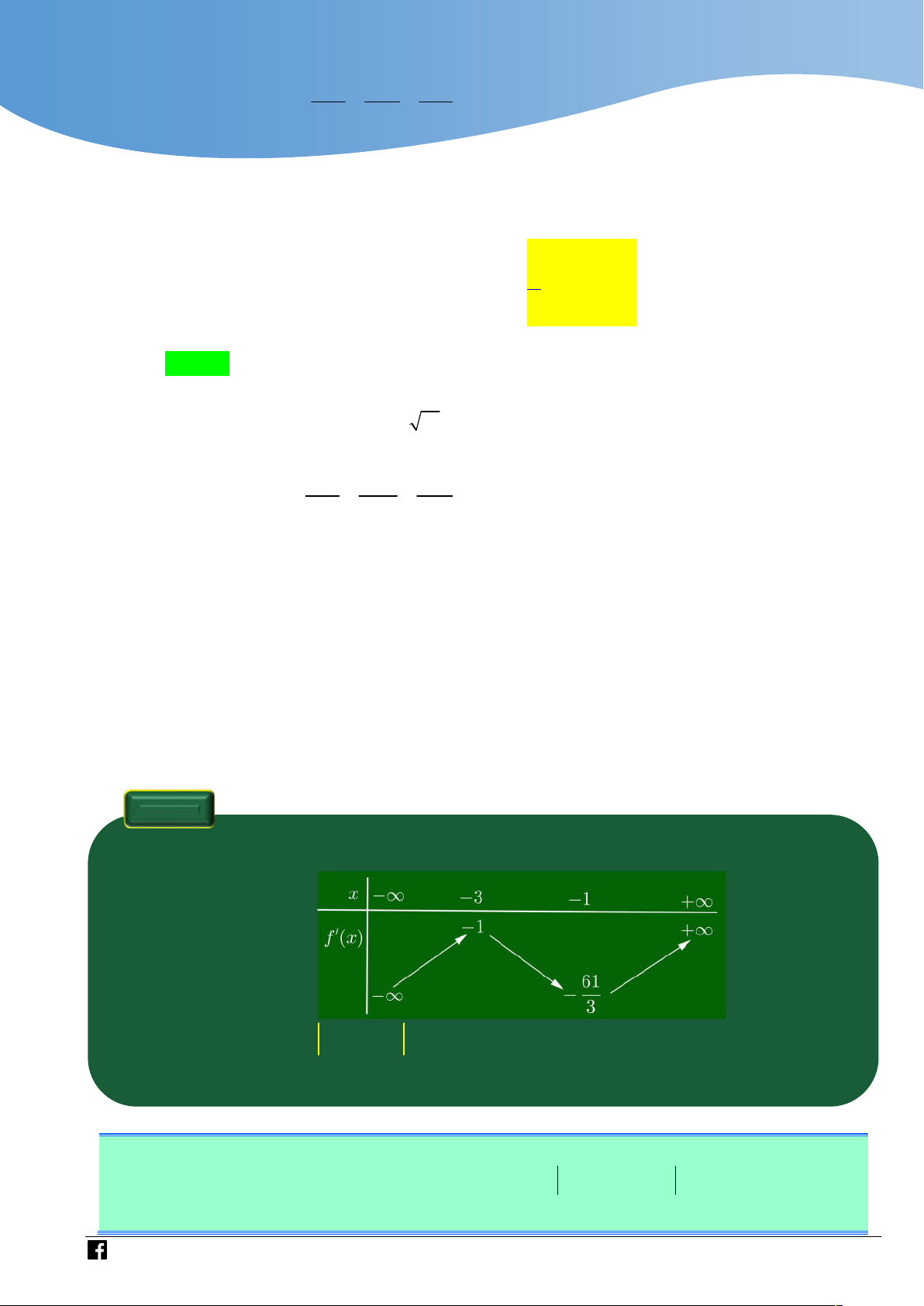
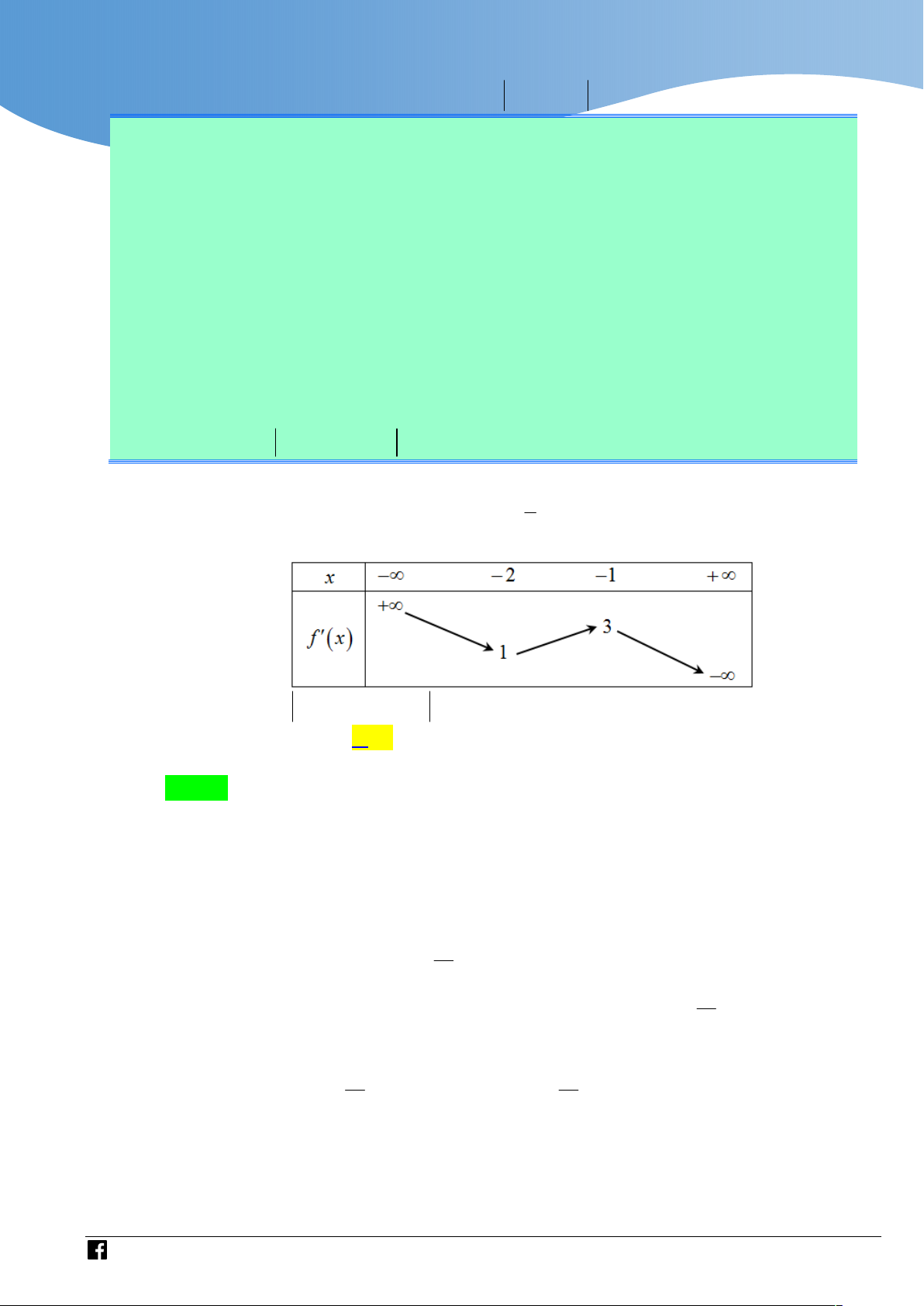
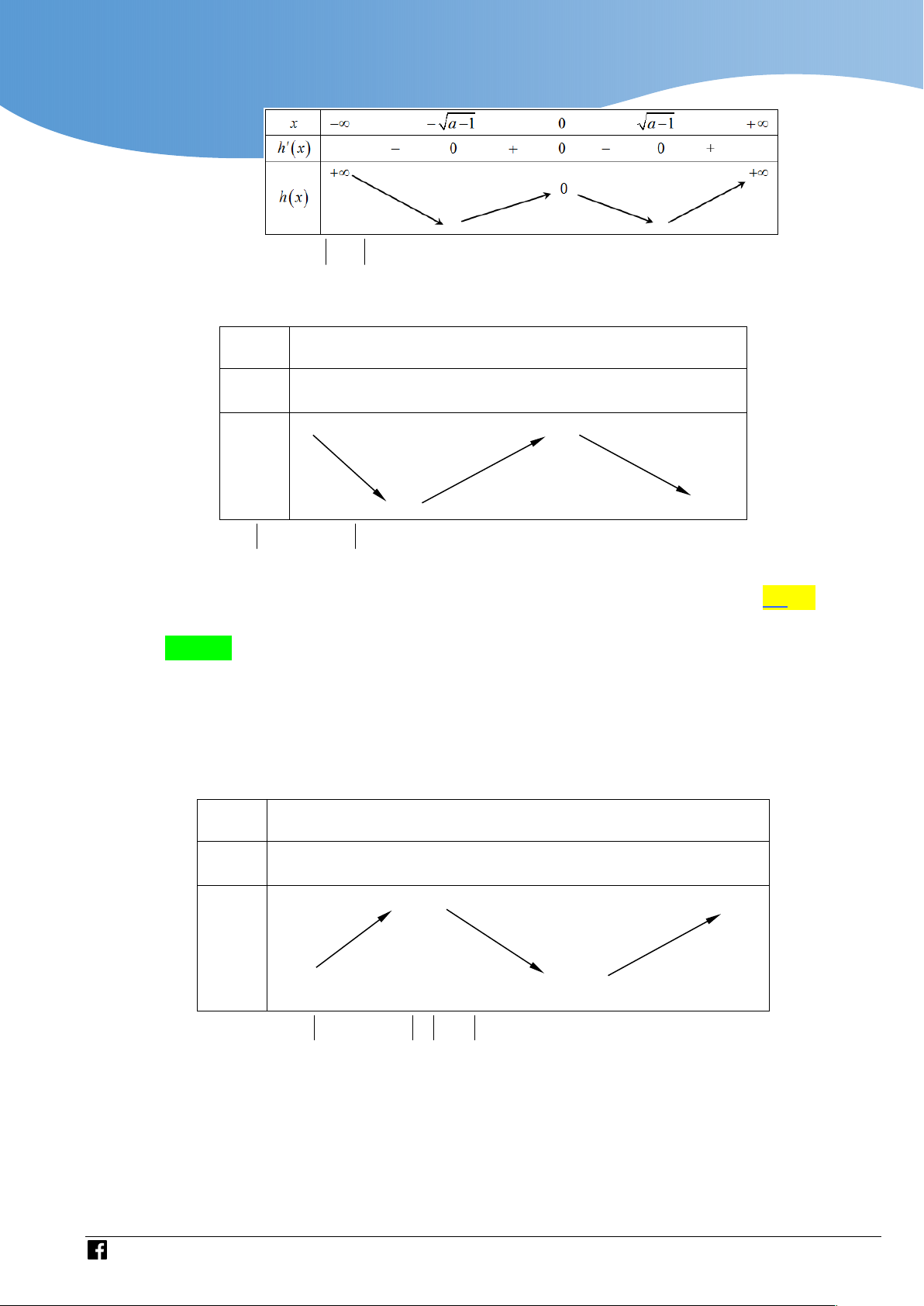
Cho f x là hàm số bậc bốn thỏa mãn f 0 0 . Hàm số f x có bảng biến thiên như sau:
Hàm số g x f 3
x 3x có bao nhiêu điểm cực trị? A. 3 . B. 5 . C. 4 . D. 2 .
Faceboock: An Dinh – Hà Hoàng – Nguyễn Tất Thành
Phân tích và định hướng tìm lời giải:
- Đây là bài toán tìm cực trị của hàm số có dạng g x f u x v x khi biết bảng biến
thiên hoặc đồ thị của hàm y f x .
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
- Để xác định số cực trị của hàm g x h x với h x f u x v x ta cần lập bảng biến
thiên của hàm số h x f u x v x nhờ giả thiết bài toán.
- Từ bảng biến thiên của hàm số h x f u x v x suy ra bảng biến thiên hàm số
g x h x . Từ đó, suy ra số điểm cực trị của hàm số g x h x .
- Để lập bảng biến thiên của hàm số h x f u x v x ta thực hiện các bước như sau:
Bước 1. Tìm tập xác định.
Bước 2. Tính đạo hàm h x . Tìm các điểm x i 1, 2,..., n mà tại đó đạo hàm bằng 0 hoặc i không xác định.
Bước 3. Sắp xếp các điểm x theo thứ tự tăng dần và lập bảng biến thiên của hàm số h x . i
Bước 4. Từ bảng biến thiên của hàm số h x , suy ra bảng biến thiên của hàm số
g x h x . Từ đó, kết luận bài toán Lời giải Chọn A 3 x
Ta có: f x a x
1 x 3 f x f x 2 dx a
2x 3x b . 3 f 3 1 29 a 3 29 x Do 2 61
2 f x
2x 3x 1 . f 1 2 3 3 b 1
Xét hàm số h x f 3
x 3x có h x 2 x f 3 3
x 3 , h x 2 x f 3 0 3 x 3 0 .
Nhận xét rằng, x 0 không phải là nghiệm của phương trình 2 x f 3 3 x 3 0 nên 1 2 3x f 3
x 3 0 f 3 x * 2 x 1 Nếu x ;
0 thì f x f 3 0 x 0 mà 0 nên * vô nghiệm trên ; 0 . 2 x 1
Nếu x 0; thì f x đồng biến nên 3 f
x đồng biến, mà hàm số nghịch biến 2 x nên phương trình
* không có quá 1 nghiệm. 1 1 1
Mặt khác lim y lim f
và lim y lim f 3 x nên 3 x 2 2 x0 x0 x x x x phương trình
* có ít nhất một nghiệm dương. (2) 1 Từ
1 và (2) suy ra f 3 x x x x 0 2 0 0 x
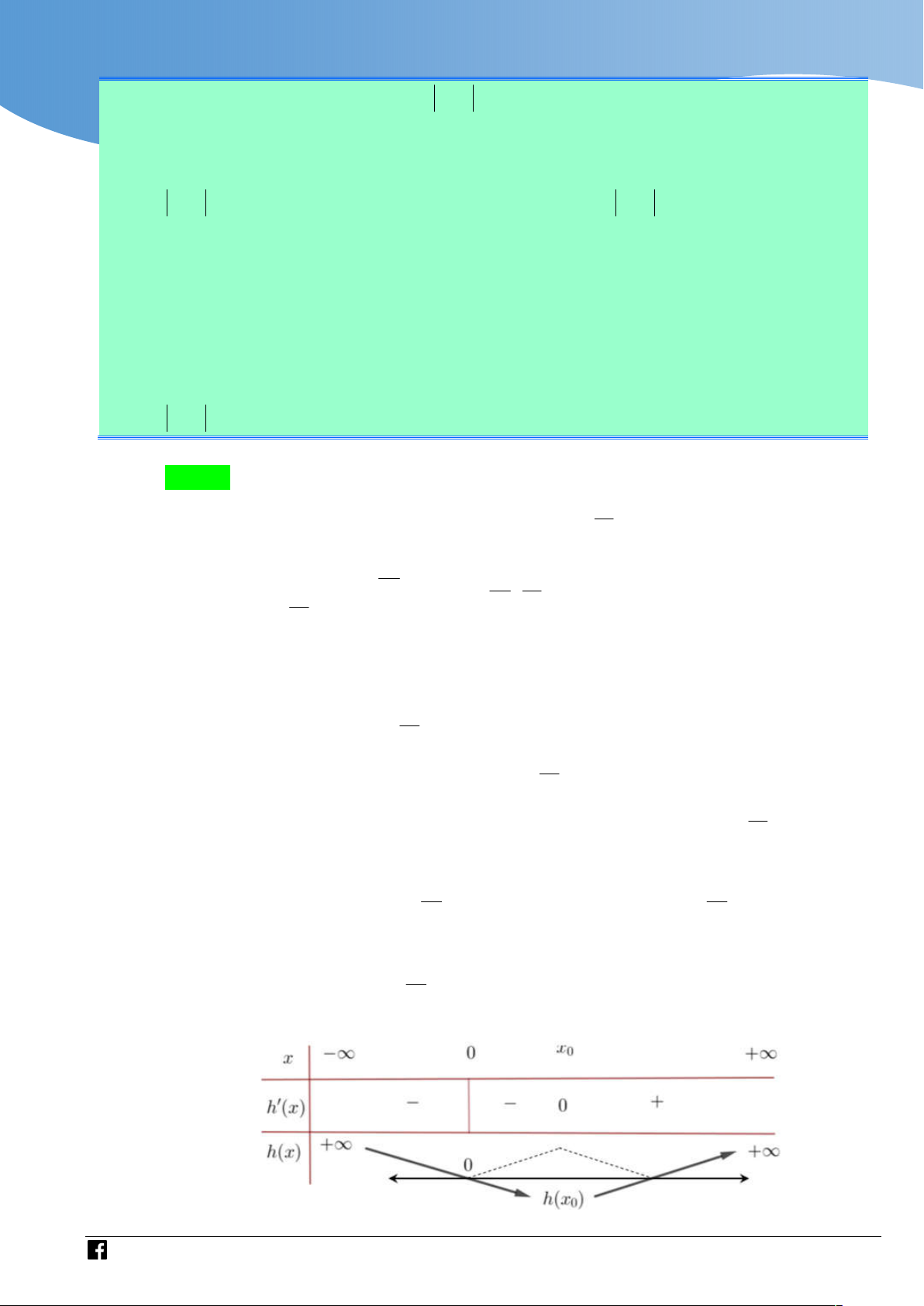
Ta có bảng biên thiên của hàm số h x
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Từ bảng biến thiên suy ra hàm số g x f 3
x 3x có ba điểm cực trị. Bình luận:
- Đây là bài toán lập tìm cực trị của hàm trị tuyệt đối của hàm hợp. Để làm được bài
toán này đòi hỏi các em phải nắm vững và sử dụng thành thạo bài toán tìm điểm cực trị
của hàm số, hàm hợp; áp dụng vào hàm trị tuyệt đối của hàm hợp. Đây là câu hỏi kiểm
tra kiến thức tổng hợp ở mức độ VDC. Hướng phát triển:
Hướng phát triển 1: Cho hàm số y f x có bảng bảng biến thiên hàm số f x . Tìm số
điểm cực trị của hàm số g x f u x h x
Hướng phát triển 2: Cho hàm số y f x có đồ thị hàm số f x . Tìm số điểm cực trị
của hàm số g x f u x h x .
Hướng phát triển 3: Cho hàm số y f x có đồ thị hàm số f x . Tìm số điểm cực trị
của hàm số g x f u x h x .
Bài tập tương tự 1 Câu 1:
Cho f x là hàm bậc bốn thỏa mãn f 0 . Hàm số f x có bảng biến thiên như 2 sau:
Hàm số g x f 5
x 5x 2021 có bao nhiêu điểm cực trị? A. 3 . B. 2 . C.1. D. 4 . Lời giải Chọn B
Đặt h x f 5
x 5x 2021, ta có h x 4 x f 5 5 x 5.
Xét h x 4 x f 5 0 5
x 5 0 * .
Nhận xét rằng, x 0 không phải là nghiệm của phương trình * .
Với x 0 , từ bảng biến thiên ta thấy f x 0 nên f 5
x 0 nên * vô nghiệm. 1
Với x 0 , ta có * f 5 x . 4 x 1
Khi đó, vì f x nghịch biến nên 5 f
x cũng nghịch biến, mà đồng biến trên 4 x
khoảng 0; nên phương trình * có tối đa 1 nghiệm trên khoảng 0; . 1 1 Ta lại có lim f
và lim f 5 x
nên * có đúng 1 nghiệm 5 x 4 4 x 0 x x x
x x 0; . 0
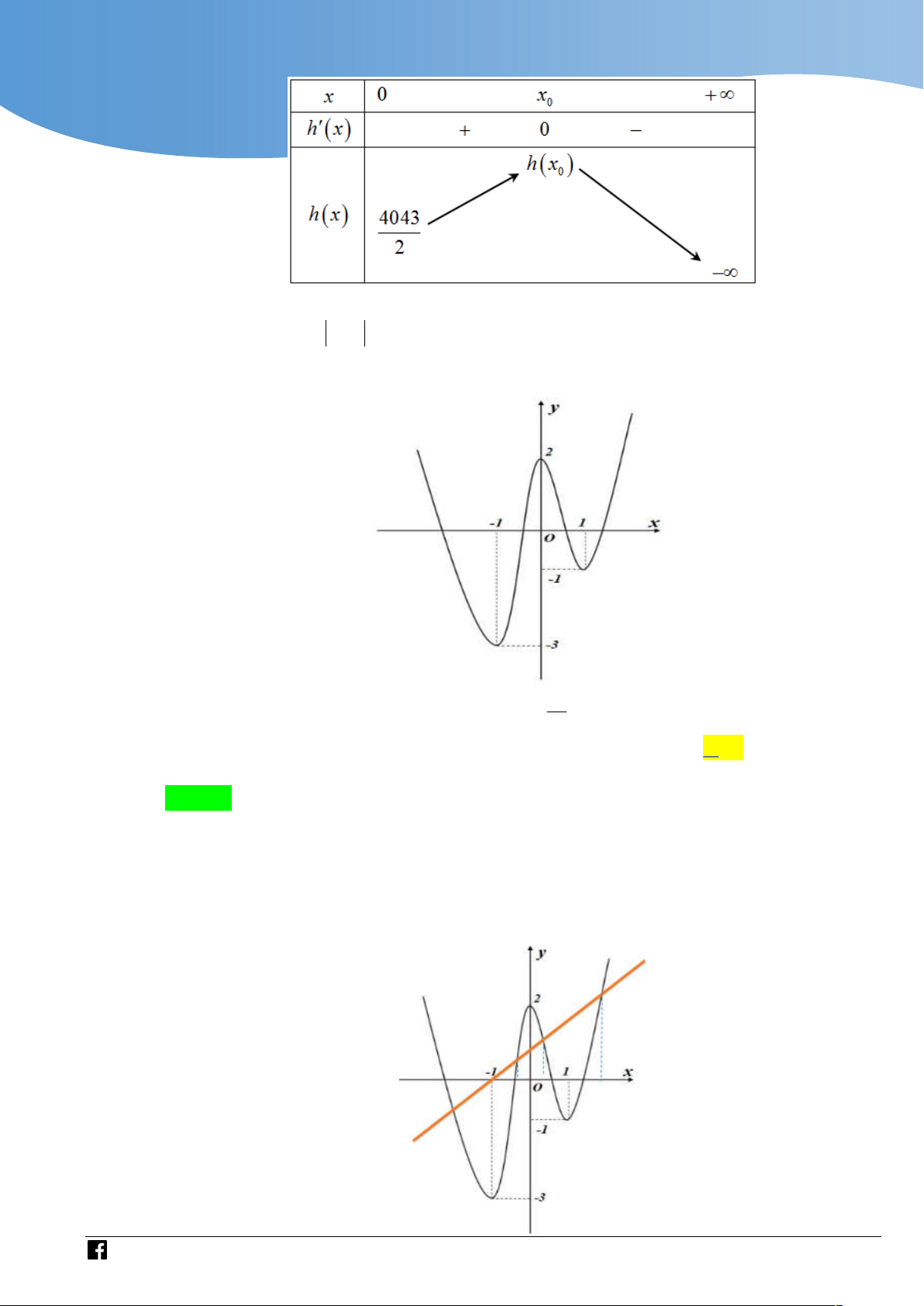
Xét bảng biến thiên của h x :
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Dựa vào bảng biến thiên ta thấy phương trình h x 0 có nghiệm duy nhất x x . 1 0
Vậy hàm số g x h x có 2 điểm cực trị. Câu 2.
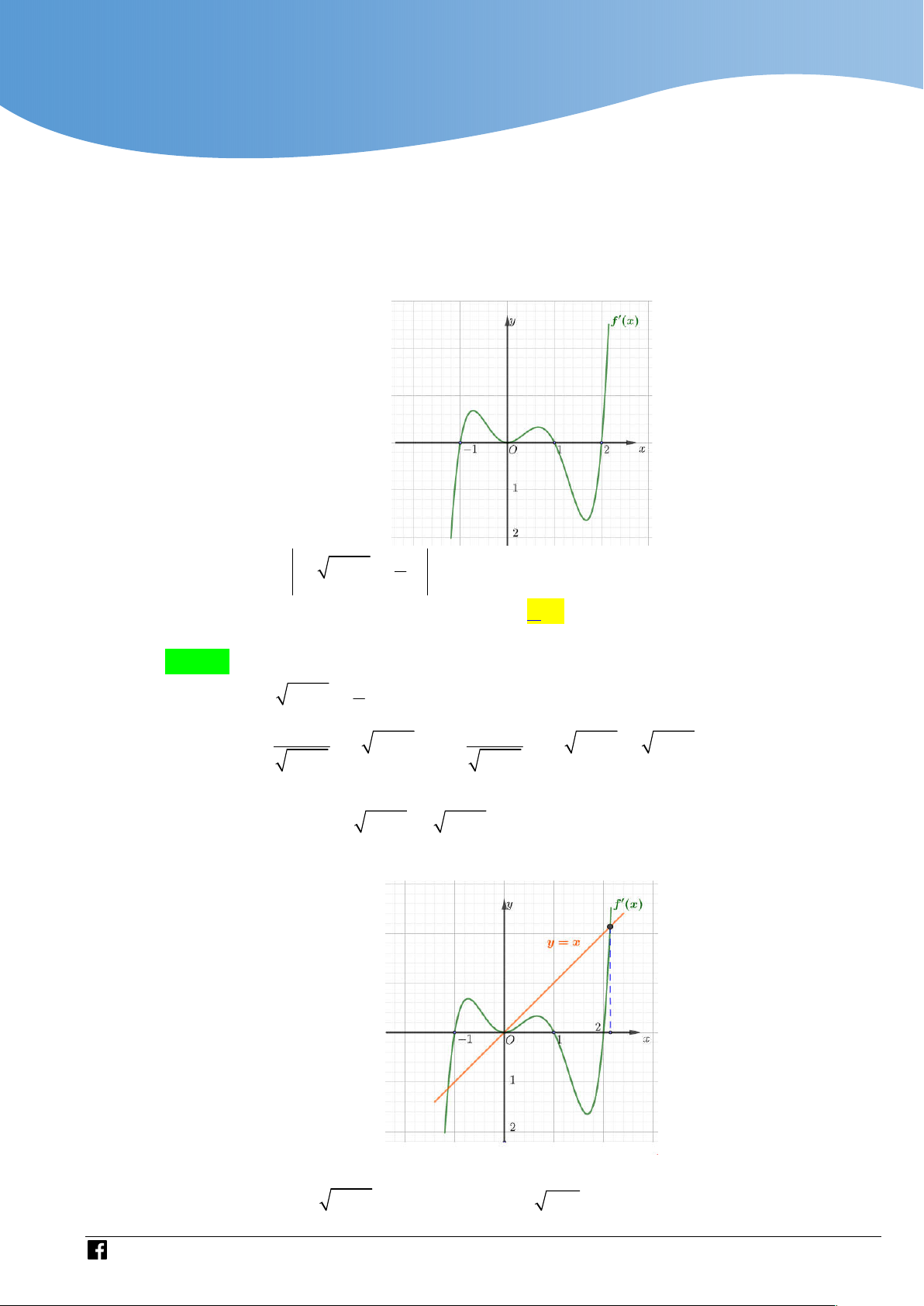
Cho hàm số y f x . Biết đồ thị của y f x như hình vẽ dưới đây. 4 x
Số điểm cực trị của hàm số g x f 2 x x 3 2 2
2x 3x 2x 2 là 2 A. 6 . B. 8 . C. 9 . D. 7 . Lời giải Chọn D Ta có:
g x x f 2
x x 3 2
x x x x f 2
x x 2 2 1 2 2 6 6 2 2 1 2 x 2x 1
Với u x x x 2 2 2 1 1 1,x
Dựa vào đồ thị của y f x và đường thẳng y x 1 ta có
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM x 1 x 1 2 x
u a 1 ;0 x 1 a 1 0; 1 1
g x 0
f u u 1
u b 0; 1 x 2 1 b 1 1;2
u c 1;2 x 2 1 c 1 2;3
Như vậy g x 0 có 7 nghiệm đơn phân biệt, nên hàm số g x có 7 điểm cực trị. Câu 3.
Cho f x là hàm đa thức thỏa mãn f 0 0 . Hàm số y f x có đồ thị như hình bên dưới. 1
Hàm số g x f 2 x 1 2
x có bao nhiêu điểm cực trị? 2 A. 3 . B. 2 . C. 5 . D. 4 . Lời giải Chọn C 1
Xét h x f 2 x 1 2 x . 2 x x
Ta có h x . f 2
x 1 x . f 2x 1 2 x 1 2 2 x 1 x 1 x 0
Suy ra h x 0 . f 2 x 1 2 x 1 *
Dựa vào đồ thị hàm số f x : x 0 x 0
Ta có h x 0 2
x 1 a a 2 x a 1
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Và h0 f
1 0 nên ta có bảng biến thiên
Vậy hàm số g x h x có 5 cực trị.
Câu 4: Cho hàm số y f x liên tục trên , có bẳng biến thiên như sau: x - a b + y' 0 0 6 y 5
Đặt h x m f x 2 ( m là tham số ). Có bao nhiêu giá trị nguyên của m sao cho
hàm số y h x có đúng 5 cực trị ? A. Vô sô '. B. 12. C. 0. D. 10. Lời giải Chọn D
Đặt g x m f x 2 g ' x f ' x 2 x 2 a x 2 a
g ' x 0 f ' x 2 0 . x 2 b x 2 b Ta có bảng biến thiên x - a 2 b 2 + g ' x 0 0 m 5 g x m 6
Để hàm số h x m f x 2 g x có đúng 5 cực trị điều kiện là m 5 0 5
m 6 m 4 , 3 , 2 , 1 , 0,1, 2, 3, 4, 5 . m 6 0
Do m nguyên nên m 4 , 3 , 2 , 1 , 0,1, 2,3, 4,
5 . Vậy có 10 giá trị của m .
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Câu 47 log a
Có bao nhiêu số nguyên aa 2 sao cho tồn tại số thực x thoả mãn: logx a 2 x 2 ? A. 8 . B. 9 . C. 1 . D. Vô số.
Faceboock: Lê Thanh Bình – Chanh Muối – Nguyễn Tất Thành
Phân tích định hướng tìm lời giải:
+ Đây là bài toán tìm tham số a để phương trình mũ có nghiệm;
+ Để giải bài toán này thông thường chúng ta sử dụng một trong các phương pháp sau đây:
Cách 1: Đặt ẩn phụ đưa về giải hệ phương trình đối xứng loại 2. f
x, y a f
y, x a
Cách 2: Sử dụng phương pháp hàm số
+ Cho phương trình f x c ( với c là hằng số). Nếu hàm số f x luôn đồng biến hoặc
luôn nghịch biến trên khoảng K và tồn tại x K , sao cho f x c thì phương trình 0 0
f x c có nghiệm duy nhất x x trên khoảng K . 0
+ Cho phương trình f x g x . Nếu hàm số f x luôn đồng biến (hoặc luôn nghịch biến)
trên khoảng K còn g x luôn nghịch biến (hoặc luôn đồng biến) trên khoảng K và tồn tại
x K , sao cho f x g x thì phương trình f x g x có nghiệm duy nhất x x trên 0 0 0 0 khoảng K .
+ Cho phương trình f u f v . Nếu hàm số f t luôn đồng biến (hoặc luôn nghịch biến)
trên khoảng K thì từ phương trình f u f v ta có u v trên khoảng K . Ở đây ta nói
f t là hàm số đặc trưng của PT.
+ f u f v mà f t luôn đồng biến (hoặc luôn nghịch biến) trên khoảng K thì bất
phương trình tương đương với u v ( hoặc u v ) trên khoảng K . Ở đây ta nói f t là
hàm số đặc trưng của bpt. Chú ý:
+ Nhận dạng f u f v hay f u f v thường sử dụng cách này khi phương trình,
bất phương trình chứa các ẩn vừa nằm trong dấu loga ( trên mũ) và ẩn nằm ngoài dấu loga
( không trên mũ), hoặc PT, BPT vừa chứa loga vừa chứa mũ.
+ Để đưa về dạng f u f v hay f u f v ta thường biến đổi bằng cách thêm bớt dựa
vào những biểu thức trong loga, biểu thức trên số mũ sao cho biểu thức trong loga, biểu
thức trên mũ cùng xuất hiện ở một vế của phương trình hay bất phương trình. 2
3x 3x m 1
Ví dụ: Phương trình cho ở dạng 2 log
x 5x 1 m 2 2 4x 2x 2 Vì 2
4x 2x 2 0 , x nên điều kiện là 2
3x 3x m 1 0 * Với điều kiện
* phương trình đã cho tương đương với phương trình log 2
3x 3x m 1 log 2
4x 2x 2 2
x 5x 1 m 2 2
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Để đưa về dạng f u f v , thì ta phải biến đổi 2
x 5x 1 m sao cho xuất hiện 2
x x 2 4 2
2 , 3x 3x m
1 vì hai biểu thức này nằm trong dấu loga. Nên ta được: log 2
3x 3x m 1 log 2
4x 2x 2 2
4x 2x 2 2
3x 3x m 1 2 2 log 2
3x 3x m 1 2
3x 3x m 1 log 2
4x 2x 2 2 4x 2x 2 2 2
+ Việc chứng minh hàm số f t luôn đồng biến, nghịch biến trên K khi làm bài trắc nghiệm
có thể sử dụng máy tính cầm tay: MODE 7- với 570, MODE 8- với 580. Lời giải Chọn A
Điều kiện: x 2. Đặt m log a 0 m
Khi đó phương trình trở thành: m
x 2 x 2. Đặt m
y x 2 , y 2 thì ta có hệ phương trình m
y x 2 1 m x y 2 2
Lấy (1) – (2) vế theo vế ta được m m
y y x x 3 Xét hàm m
f t t t với m 0;t 0 có f t m 1 ' . m t 1 0, t 0 m
f t t t đồng biến 0; . log x 2
Do đó 3 y x m
x x 2 .
m log x log x 2 m 1 log x
log a 1 a 10. Do đó, mọi số a 2;3;4;...; 9 đều thỏa mãn. Bình luận:
- Việc cho hàm số f u; f v như nào rất quan trọng. Vì khi thi trắc nghiệm với công cụ
hỗ trợ của máy tính cầm tay học sinh có thể dễ dàng bấm máy để tìm ra mối liên hệ giữa u
và v . Tất nhiên việc bấm máy tính dựa trên nền tảng kiến thức tốt của học sinh. Khi hướng
đi làm tự luận gây khó khăn cho học sinh thì hướng giải bằng công cụ hỗ trợ máy tính cầm
tay cũng là 1 phương án tốt.
- Ví dụ giải câu 47 dựa trên hướng tự luận và sự hỗ trợ của máy tính cầm tay
Câu 47. Có bao nhiêu số nguyên a a 2 sao cho tồn tại số thực x thoả mãn: x a loga log 2 x 2 ? Lời giải
Để tìm mối liên hệ giữa a và x ở bài này chưa có thể tìm ra ngay bằng máy tính .
Dựa vào nhận xét log c log b b a a c ta có log x log a a x
. Công việc này nhằm mục đích để đưa về t
cùng log a . Khi đó đặt log a t phương trình trở thành t
x 2 x 2 ( điều kiện x 2 )
Cho t 100 bấm máy tính ta có x 0,9956130378 . Tuy nhiên chưa thấy được mối liên hệ
giữa x và t . Vì đề bài có t x nên bấm máy log x t t 2
x 98 x x 2 t log x a . x 2 log log x
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM log x 2
Đến đây có thể khảo sát hàm số y
bằng phương pháp đạo hàm hay dùng máy log x
tính CASIO MODE 7- với 570, MODE 8- với 580. Hướng phát triển:
Hướng phát triển 1: Thay đổi yêu cầu như tìm điều kiện liên quan đến tương giao đồ thị…
Hướng phát triển 2: Thay đổi phương trình thành bất phương trình.
Hướng phát triển 3: Thay đổi hàm số f u; f v kết hợp với hàm số chẵn , hàm số lẻ.
Câu 1. Có bao nhiêu giá trị nguyên của m với m 1 sao cho tồn tại số thực x thỏa mãn: m log x m 3log5 5 x 3 1 . A. 4 . B. 3 . C. 5 . D. 8 . Lời giải Chọn B
Điều kiện: x 0 Đặt log5 x m
3 u thay vào phương trình 1 ta được: log5 m log5 3 m u x x u 3 . log5 x u m 3 Vì log5 m log5 u u m
. Từ đó ta có hệ Phương trình . log5 m x u 3
Xét hàm đặc trưng t
f t m 3 trên .
Do m 1. Suy ra hàm số f t đồng biến trên .
Do đó, f log x f log u x u . 5 5
Vì thế, ta đưa về xét phương trình: log5 x log5 m log5 3 3 3 m x m x x x x log x 3 log m 5 log x 3 log x log x 3 log .
x log m log m 5 5 5 5 5 5 5 log x 5 log x 3 5
Do x 0 nên x 3 x nên log m 1 m 5 . 5 log x 5 m Suy ra m 2,3,
4 . Vậy có 3 giá trị tham số m thỏa mãn. 1 m 5 Câu 2. Có bao nhiêu m nguyên m 2 021; 202 1 để phương trình
6x 2m log
18 x 1 12m có nghiệm? 3 6 A. 211. B. 2020 . C. 2023. D. 212 . Lời giải Chọn C
Phương trình 6x 2 log 18 1 12 6x m x m
2m 3log 6 3x 2m 3 3 6 6 6x 2 3 1 log 3 2 3 6x m x m 3log
3x 2m 3 2m 3, * 6 6
Đặt log 3 2 3 6y y x m
3x 2m 3 6
Mặt khác, PT(*) trở thành: 6x 3y 2m 3
6y 3x 2m 3, 1
Ta có hệ: 6x 3y 2m3, 2
Lấy (1) trừ vế với vế cho (2), ta được
6y 6x 3 3 6x 3 6y x y x 3y 3
Xét hàm số 6t f t 3t, t .
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Ta có ' 6t f t ln 6 3 0, t .
Suy ra hàm số f t đồng biến trên
Mà PT (3) f x f y x . y
Thay y x vào PT (1), ta được 6x 3 2 3 6x x m
3x 2m 3 .
Xét hàm số 6x g x
3x , với x . Ta có x 3
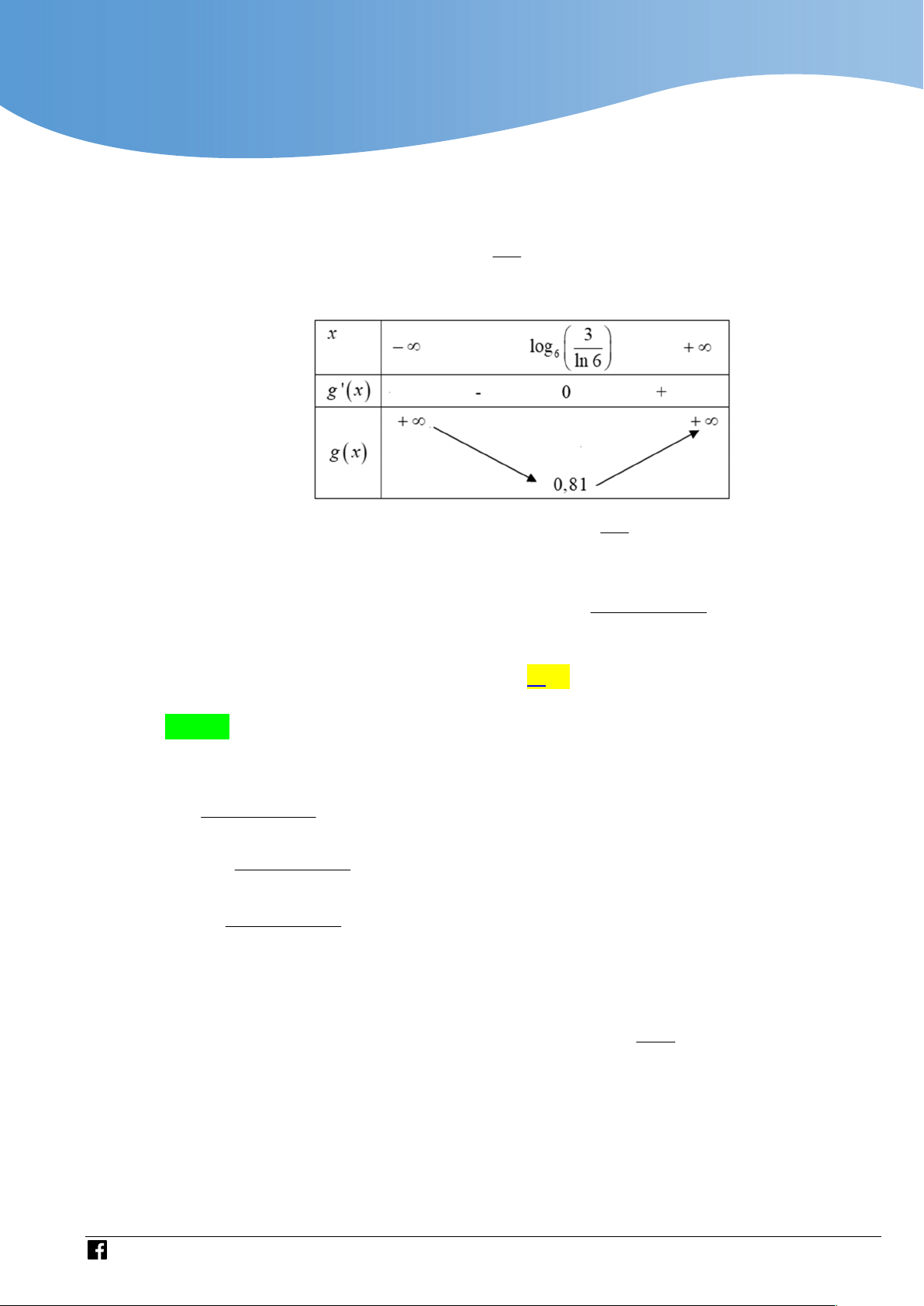
g ' x 6 ln 6 3 g ' x 0 x log6 ln 6 BBT: 3
Từ đó suy ra PT đã cho có nghiệm 2m 3 g log 0,81 m 1 ,095 6 ln 6
Vậy có 2023 số nguyên m thỏa mãn yêu cầu. 2
3x 3x m 1
Câu 3. Có bao nhiêu số nguyên m để đồ thị hàm số y log cắt đồ thị hàm số 2 2 2x x 1 2
y x 5x 2 m tại hai điểm có hoành độ lớn hơn 1? A. 3 . B. Vô số. C. 2 . D. 4 . Lời giải Chọn C Điều kiện: 2
3x 3x m 1 0 .
- Ta có phương trình hoành độ giao điểm : 2
3x 3x m 1 2 log
x 5x 2 m * 2 2 2x x 1 2
3x 3x m 1 2 log
1 x 5x 1 m 2 2 2x x 1 2
3x 3x m 1 2 log
x 5x 1 m 2 2 4x 2x 2 log 2
3x 3x m 1 log 2
4x 2x 2 2
4x 2x 2 2
3x 3x m 1 2 2 log 2
3x 3x m 1 2
3x 3x m 1 log 2
4x 2x 2 2
4x 2x 2 1 2 2 1
Xét hàm số: f t t log t trên D 0; , có f t 1 0 , t D , 2 t.ln 2
Do đó hàm số f t đồng biến trên D f 2
x x f 2 1 4 2 2
3x 3x m 1 2 2
4x 2x 2 3x 3x m 1 . Vì 2
4x 2x 2 0 , x nên 2
3x 3x m 1 0 2
x 5x m 1 2 .
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 5
- Xét hàm số: g x 2
x 5x trên , có g x 2x 5 g x 0 x . 2 - Bảng biến thiên:
Để hai đồ thị hàm số cắt nhau tại 2 điểm có hoành độ lớn hơn 1 thì phương trình * có
hai nghiệm phân biệt lớn hơn 1 thì phương trình 2 có hai nghiệm phân biệt lớn hơn 25 21 1 khi và chỉ khi
m 1 4
m 3 , do m nên m 5 ; 4 , hay có 2 4 4
giá trị nguyên của m thỏa mãn yêu cầu bài toán. 3
Câu 4. Tổng các giá trị nguyên của m để phương trình x2 m 3 x 3 2 x x x m x2 x 1 2 6 9 2 2 1 chỉ có 2 nghiệm là: A. T 32 . B. T 12 . C. T 4 . D. T 4 . Lời giải Chọn B Ta có : 3 3 3 x2 m 3 x 3 2 x x x m x2 x 1 2 6 9 2 2 1 m3x 3 2 2 2 8 3 2 2 x x m x 3 m x x m x x3 3 2 2 3 2 2 . Xét hàm 3 2t h t t trên . có h t t 2 '
2 .ln 2 3t 0, t
nên hàm số liên tục và đồng biến trên .
Do đó từ (1) suy ra m x x3 3 2 2 3
m 8 9x 6x x .
Xét hàm số f x 3 2
x 6x 9x 8 trên . x 3
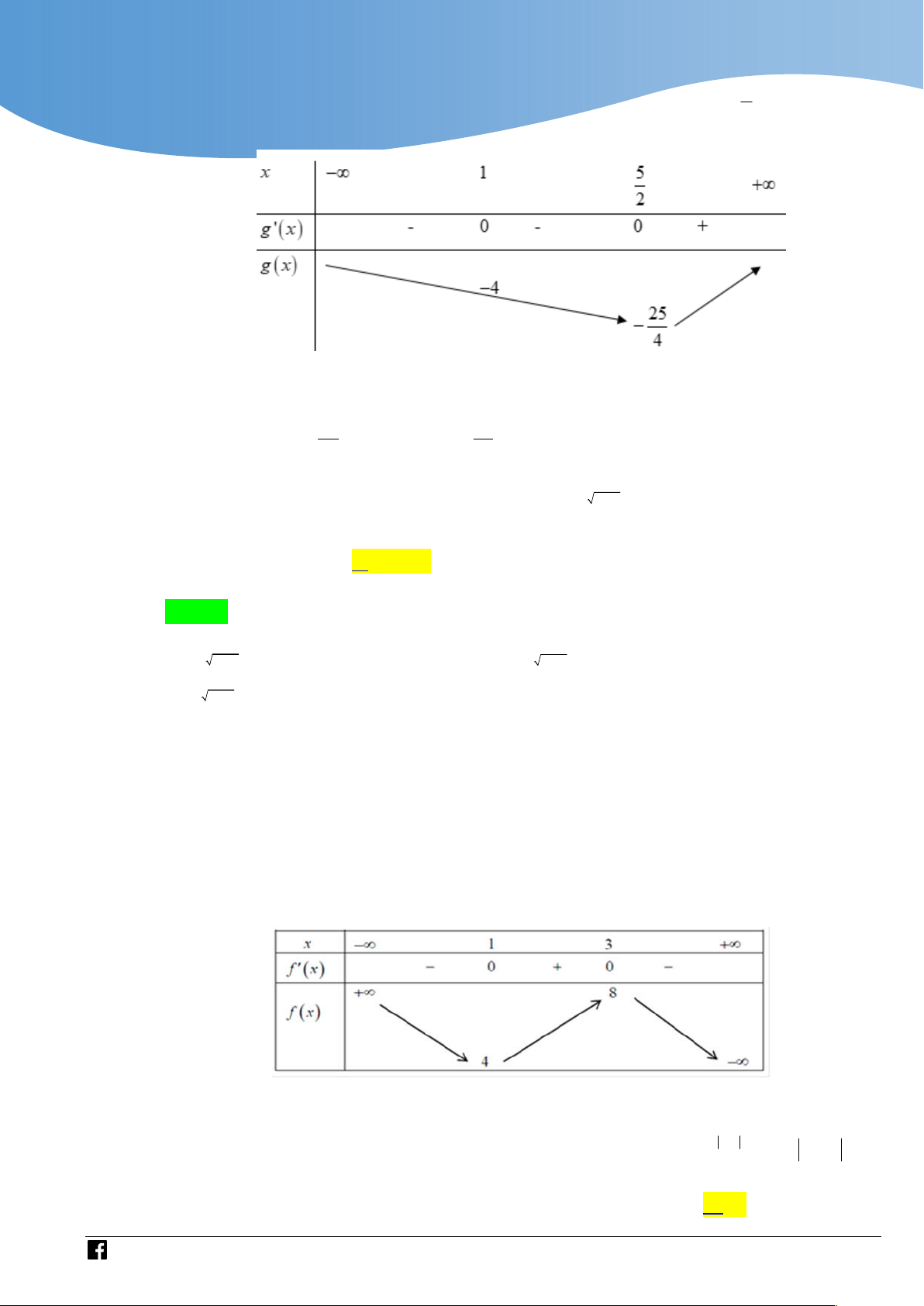
có f x 2 3
x 12x 9 ; f x 0 . x 1 Bảng biến thiên
Dựa vào bảng biến thiên ta có, phương trình có 2 nghiệm phân biệt khi m 4;m 8 T 12 2
Câu 5. Tổng tất cả các giá trị của m để phương trình x 1 2
.log 2 2 3 4 xm x x .log 2 x m 2 2 2
có đúng ba nghiệm phân biệt là A. 1. B. 2 . C. 0 . D. 3 .
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Lời giải Chọn D 2 Ta có x 1 2
.log 2 2 3 4 xm x x .log
2 x m 2 1 2 2 x 2 1 2 .log 2 2 1 2 2 xm x .log
2 x m 2 2 2 2
Xét hàm số 2t f t
.log t 2 ,t 0. 2
Vì f t 0, t
0 hàm số đồng biến trên 0; 2 2 Khi đó 2 f x 1
f 2 x m x 1 2 x m 2
x 4x 1 2m 03 2
x 2m 14
Phương trình
1 có đúng ba nghiệm phân biệt nếu xảy ra các trường hợp sau: 3
+) PT 3 có nghiệm kép khác hai nghiệm phân biệt của PT 4 m , thay vào PT 2 4 thỏa mãn 1
+) PT 4 có nghiệm kép khác hai nghiệm phân biệt của PT 3 m , thay vào PT 2 3 thỏa mãn
+) PT 4 có hai nghiệm phân biệt và PT 3 có hai nghiệm phân biệt, trong đó có một
nghiệm của hai PT trùng nhau 1 3
4 x 2m 1 ,với m . Thay vào PT 3 tìm được m 1. 2 2 1 3
m ;1; . T 3. 2 2
Chú ý: Cách tìm điều kiện để có đúng ba nghiệm có thể sử dụng đồ thị như sau: 2 2
x 4x 1 2m 0
2m x 4x 103 2 2 x 2m 1
2m x 1 4
Câu 6. Có bao nhiêu giá trị nguyên của tham số m để bất phương trình: 3 2 x 2x 2 3 2 ln
x 3x 2 m 0 nghiệm đúng với x 0; 3 ? 2 x m A. 3 . B. 0 . C. 2 . D. 4 . Lời giải Chọn B
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 3 2 x 2x 2 Điều kiện: 0 . 2 x m Do 3 2
x 2x 2 0 với x 0;
3 nên bài toán này ta chỉ xét với điều kiện 2
x m 0 * Với điều kiện * ta có bất phương trình 3 2
x x 2 x m 3 2 ln 2 2 ln
x 3x 2 m 0 3 2 x x 3 2
x x 2 x m 2 ln 2 2 2 2 ln
x m 1
Xét hàm: f t ln t t trên 0; . 1
f 't 1 0 với t
0; f t là hàm đồng biến trên 0; . t Do đó: 3 2 2
1 x 2x 2 x m 3 2
m x 3x 2 .
Đặt g x 3 2
x 3x 2 .
Bất phương trình đã cho nghiệm đúng với x 0; 3 khi: 2
x m 0 x 0; 3 m 0
. Vậy không tồn tại giá trị của m thỏa mãn bài toán.
m min g x m 2 x 0; 3
Câu 7. Cho hàm số 2 ln 1 x x f x x x e e
. Tập nghiệm của bất phương trình 3x f
f 2x 1 0 là?
A. S ; 0 B. S 2 021;202
1 . C. S 2
021; . D. S 0; . Lời giải Chọn D Ta có: 2
x 1 0 , x ; 2 2 2 x 1
x x x
x 1 x 0 ,x Suy ra TXĐ: x x 1
Ta có: ln 2 1 ln x x f x x x e e e e 2 x 1 x 2 ln 1 x x x
x e e f x . 1
3x 2 1 3x f f x f
f 1 2x (2) 1 Ta có: ' x x f x e e 0, x
nên hàm số đã cho đồng biến trên . 2 x 1
Vậy 2 3x 1 2x
Khi x 0 ta có 3x 1 ; 1 2 1 3x x 1 2x, x 0
Khi x 0 ta có 3x 1 ; 1 2 1 3x x 1 2x
Vậy tập nghiệm: S 0;
Câu 8. Cho hàm số 2 2 x 1 x x 1 x f x e e
. Có bao nhiêu số nguyên m 2 021; 202 1 thỏa mãn 12
f m 7 f 0 ? m 1 A. 4038 B. 2025 C. 5 D. 4036 Lời giải Chọn B 2 2 Ta có x 1 x x 1 x f x e e
f x
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 12 12
f m 7 f 0 f f
m 7 f 7 m m 1 m 1 2 x x x x x 1
Mặt khác ta có f x 2 2 1 x 1 1 .e . x e
0 suy ra hàm số đồng 2 2 x 1 x 1 2 12 12 m 6m 5 1 m 5
biến. Do đó ta có f
f 7 m 7 m 0 m 1 m 1 m 1 m 1 Mà m 2 021; 202 1 m 2 021; 2 1; 5
Suy ra có 2025 giá trị nguyên dương m thỏa mãn. Câu 48
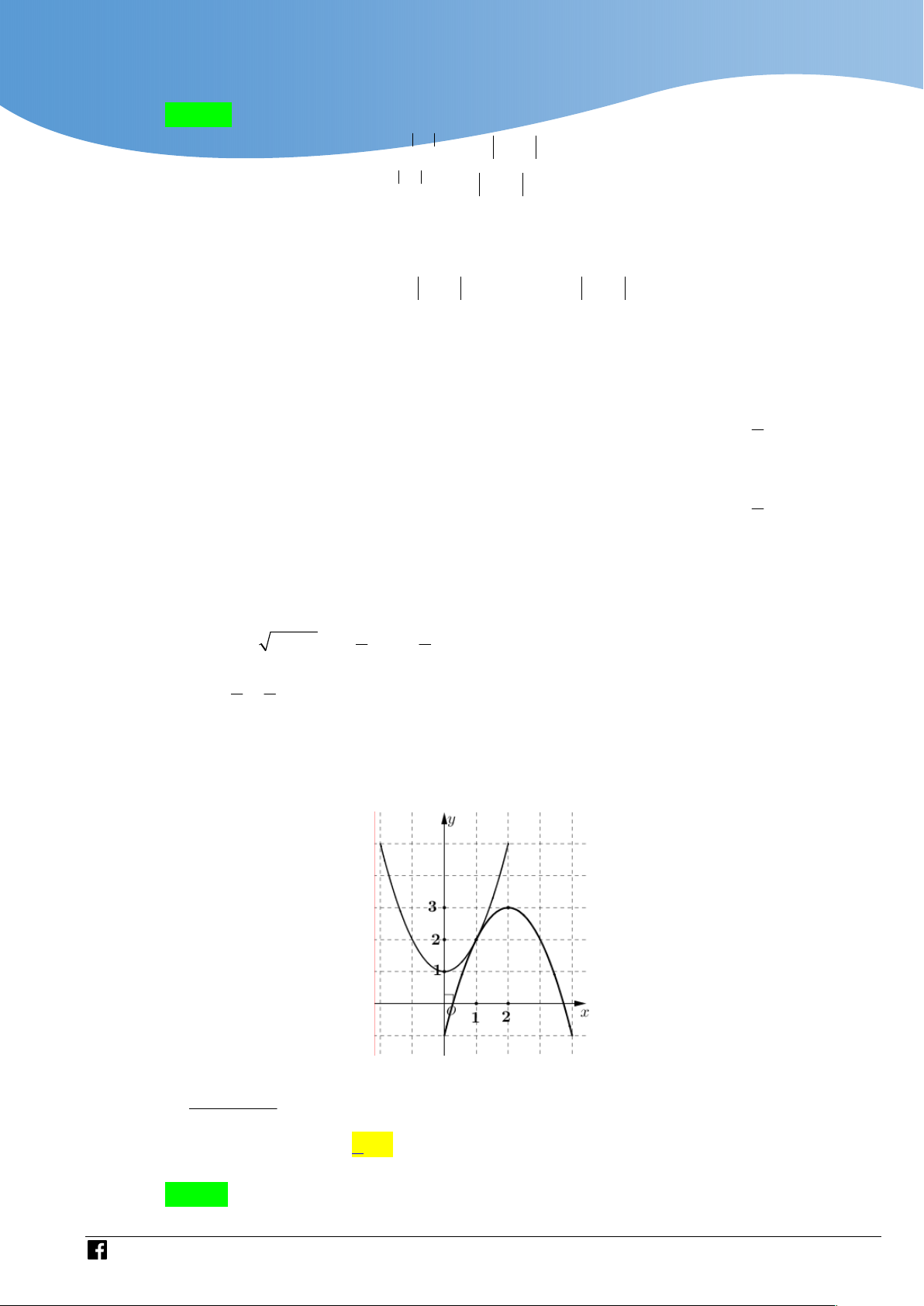
Cho hàm số bậc ba y f x có đồ thị là đường cong trong
hình bên. Biết hàm số f x đạt cực trị tại hai điểm x ,x 1 2
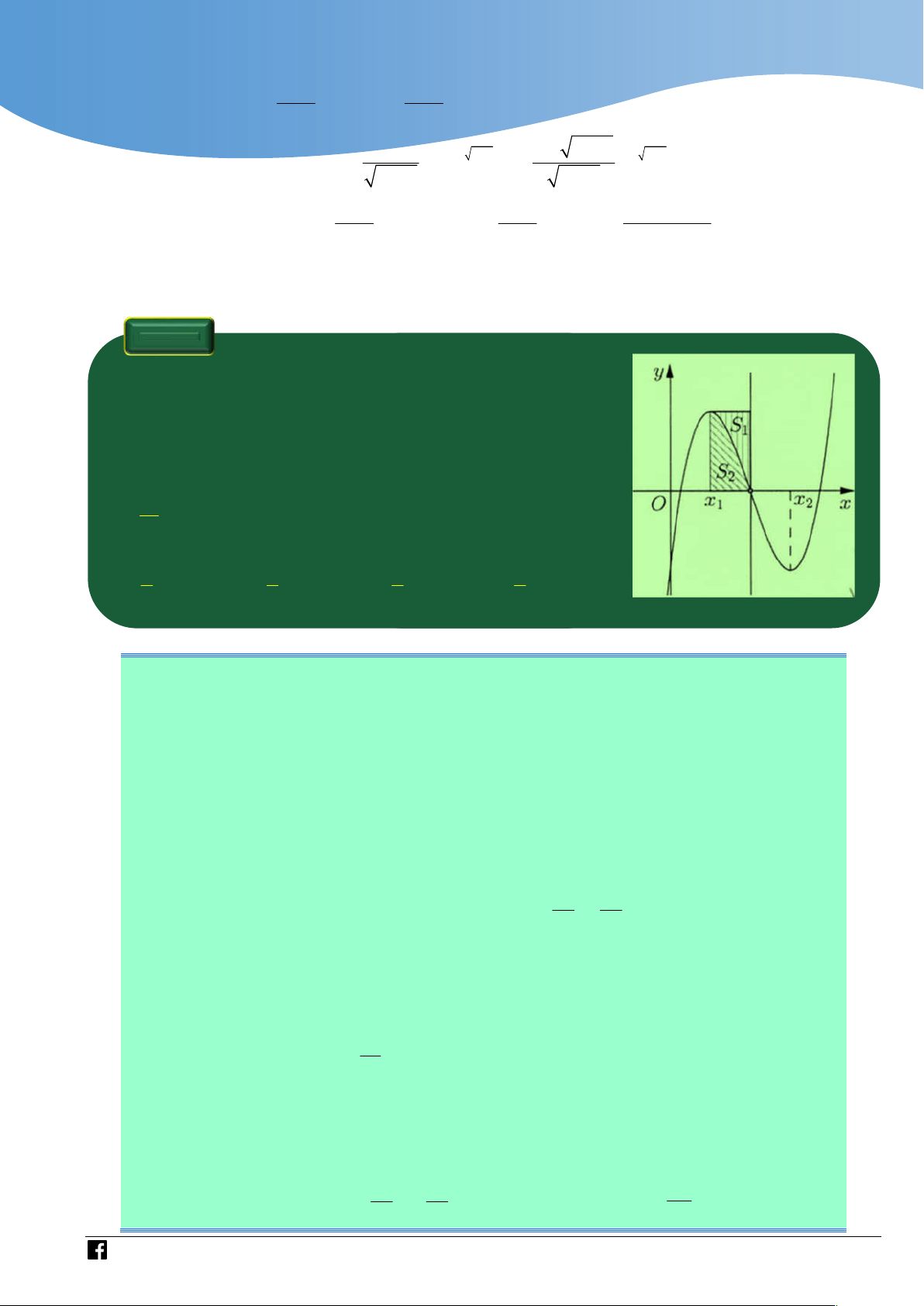
thoả mãn x x 2 và f x f x
0 . Gọi S và S là 1 2 2 1 1 2
diện tích của hai hình phẳng được gạch trong hình bên. Tỉ S số 1 bằng S2 3 5 3 3 A. . B. . C. . D. . 4 8 8 5
Faceboock: Lại Nhật Hoan – Nguyễn Bá Nam
Phân tích định hướng tìm lời giải:
Bài toán ứng dụng tích phân để tính diện tích hình phẳng rất phong phú và đa dạng.
Trong phần này xin đề cập đến một số VD và bài tập sử dụng các đồ thị đã được khảo
sát trong chương trình THPT để tính diện tích hình phẳng, tính tỷ số diện tích các hình
phẳng, tập trung và việc quy các đồ thị hàm tổng quát về các đồ thị dạng “ chuẩn tắc
“. Những bài toán này yêu cầu học sinh biết thiết lập, đặt vị trí đồ thị dạng tổng quát
về dạng dễ tính toán cũng có thể đặc biệt hóa nếu làm bài trắc nghiệm. Thầy cô khi dạy
cần nhắc lại một số tính chất của các đồ thị và các phép biến đổi đưa dạng tổng quảt
của hàm về dạng chuẩn tắc b 1) Hàm số bậc 2: 2
y ax bx c a 0 có đỉnh I ;
, đồ thi P 2a 4a
Dùng phép tịnh tiến theo IO biến đồ thị P thành đồ thị P 2
: y ax ( đưa về dạng 1 chuẩn tắc) 2) Hàm số bậc 3: 3 2
y ax bx cx d a 0 , có tâm đối xứng là điểm uốn. Ta có thể 3 b viết 3 2
ax bx cx d a x mx n
với y mx n là phương trình tiếp tuyến của 3a
đồ thị tại điểm uốn. Như vậy phép tịnh tiến theo IO ( với I là điểm uốn) sẽ biến đồ thị
C thành đồ thị C có phương trình 3 y
a x px (đưa về dạng chuẩn tắc) 1 3) Hàm trùng phương 4 2
y ax bx c có thể có 3 cực trị hoặc 1 cực trị. Sử dụng phép 2 b biến đổi 4 2 2
ax bx c a x
, phép tịnh tiến theo u 0;
biến đồ thị C 2a 4a 4a
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM thành đồ thị 2 2 2 y a x m
nếu C có 1 cực trị, hoặc thành 2 2 2 y a x m nếu C
vó 3 cực trị ( đưa về dạng chuẩn tắc) ax b ax b a k
4) Hàm số b1/b1: y
có đồ thị C có thể biến đổi , đồ thị hàm cx d cx d c d x c d a số nhận I ;
làm giao điểm hai tiệm cận và là tâm đối xứng. c c k
Dùng phép tịnh tiến theo IO biến đồ thị C thành đồ thị C có phương trình y 1 x
( đưa về dạng chuẩn tắc)
5) Các hàm số lượng giác cơ bản y asin mx n b . y a cosmx n b có chu kì tuần 2 hoàn là T
, Maxy a b , Miny a b . m
Ta sẽ dùng dạng chuẩn tắc để chuẩn hóa các hàm cho các bài toán tính toán định lượng
và không phụ thuộc vào vị trí đồ thị đặt ở đâu trong hệ trục. Lời giải Chọn D
Tịnh tiến điểm uốn về gốc tọa độ, ta được hình vẽ bên dưới.
Khi đó, do f x là hàm bậc ba, nhận gốc tọa độ là tâm đối xứng nên x 1 ; x 1. 1 2
Chọn f x 2
x f x 3 3 3 x 3x . 0 5 3 S 3 Nên S 3 x 3x 1 dx
; S S 2 S . 2 1 2 1 4 4 S 5 1 2
Các câu phát triển
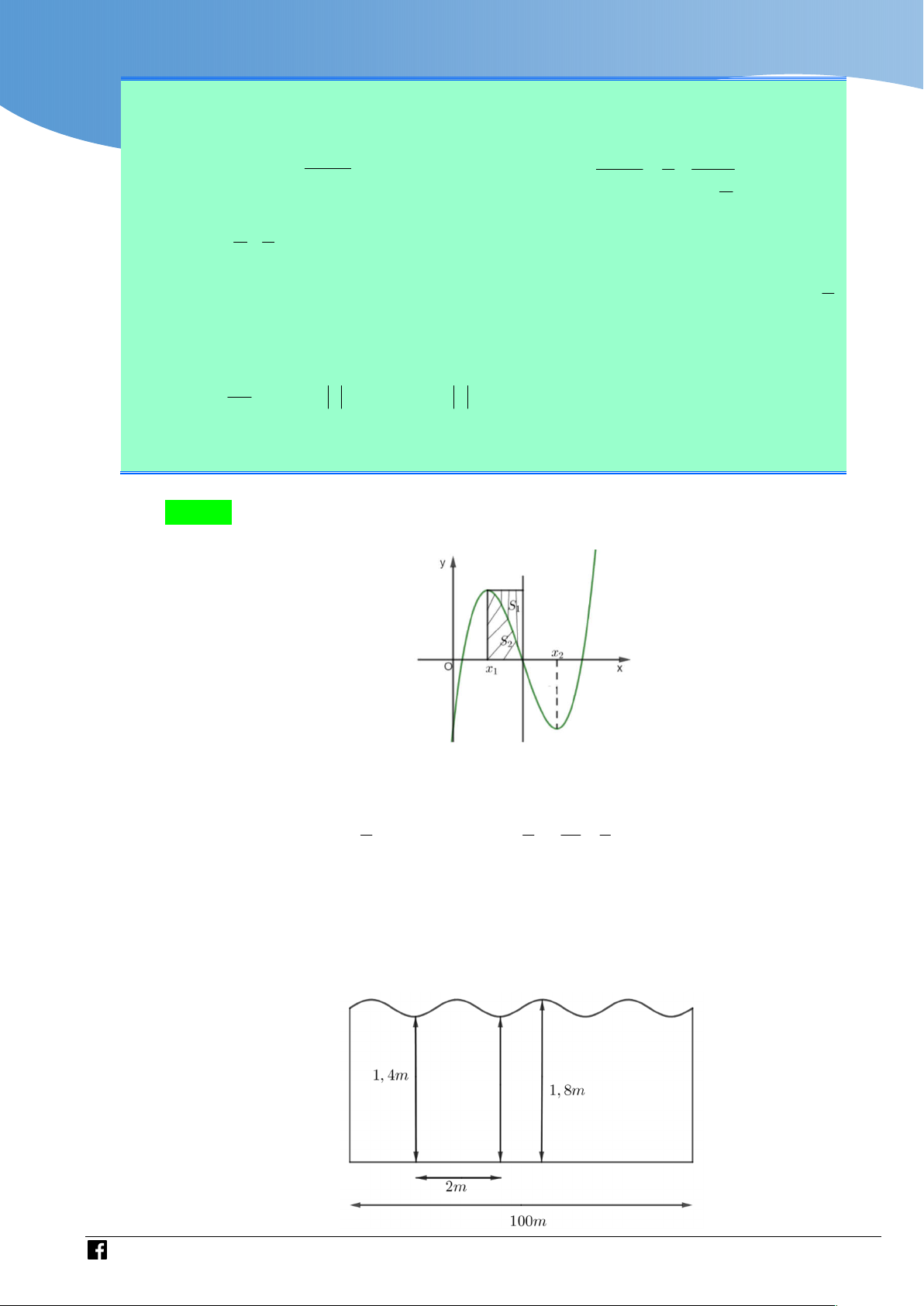
Câu 1. Người ta xây một tường rào dài 100m , tập hợp các điểm phía trên của hàng rào tạo
thành một đường hình sin ( như hình vẽ). Điểm cao nhất trên tường rào cách móng 1,8m
, điểm thấp nhất nằm phía trên tường rào cách móng 1, 4m , hai điểm thấp nhất liền kề
nhau cách nhau 2m . Tính diện tích tường rào ?
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM A. 2 54,5 m B. 2 55 m C. 2 160 m D. 2 165 m Lời giải Chọn C Cách 1:
Đặt hệ trục tọa độ Oxy sao cho Ox là móng của tường, với đơn vị trên trục là (mét),
như vậy phần tường xây là phần diện tích hình phẳng giới hạn bởi đường cong y .
a sin mx b ,
Do chu kì tuần hoàn bằng 2 nên m , và số chu kì bằng 50 .
max y 1,8 a b 1,8 a 0, 2
vậy y 0, 2sin x 1,6
min y 1, 4 a b 1, 4 b 1, 6 100
S 0,2sin x 1,6dx 160 2 m . 0
Cách 2: Kẻ đường thẳng y 1,6 Ox ta thấy phần diện tích bị “hụt” bằng phần diện
tích “dư ra “, nên diện tích tường cần tính bằng diện tích hình chữ nhật có chiều dài
bằng 100m và chiều rộng bằng 1,6m . Vậy diện tích tường rào bằng 2 160 m .
Câu 2. Cho Parabol P , 2
y mx và hình vuông OACB có A O
x , B Oy , trọng tâm G của tam
giác OAC thuộc Parabol P . Gọi S , S là diện tích hai phần của hình vuông bị chia bởi 1 2 S
parabol P.Biết S S , tính 1 . 1 2 S2 2 2 1 1 A. . B. . C. . D. . 3 5 4 3 Lời giải Chọn D
Gọi A3a,0 , B0;3a suy ra C 3a; 3a G 2a; a 1 9a G
P 4am 1 m
, AC P K 3a;
nên K thuộc đoạn AC . 4a 4 3a 2 2 9a 27a Vậy 2 3 2 S mx dx 9ma , S 9a S 1 ABCD 2 4 4 0 S 1 Vậy 1 S 3 2 ax b
Câu 3. Cho đồ thị C của hàm số y
, gọi A là giao điểm hai tiệm cận của đồ thị C . cx d
Một hình vuông ABCD có các đỉnh B, D lần lượt thuộc hai tiệm cận, và tâm I của hình
vuông thuộc C . Biết diện tích hình vuông bằng 4 , đồ thị C chia hình vuông thành
2 phần có diện tích S , S S S . Tính S . 1 2 1 2 1 A. 3 2 ln 2 B. 2 ln 2 C. 4 2 ln 3 D. 2 ln 3 Lời giải Chọn A
Không làm mất tính tổng quát, xét phương trình đường cong C ở dạng chuẩn tắc k y k 0 x
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Như vậy C nhận 2 trục Ox , Oy làm hai tiệm cận khi đó A O . hình vuông ABCD có
diện tích bằng 4 nên B2; 0 , D0;2 , C 2;2 đường thẳng BC có phương trình y 2 1
, Tâm của hình vuông là I 1; 1 , I
C suy ra k 1.Phương trình C : y , x 1
C BC M ; 2 . 2 2 1 Ta được S 2 dx 3 2 ln 2 . 1 x 1 2
Câu 4. Cho đồ thị C của hàm số 4 2
f x ax bx c , có ba điểm cực trị ,
A B ,C biết tam giác
ABC cân tại A và diện tích miền phẳng giới hạn bởi đồ thị C và đường thẳng BC bằng
16 . Tính độ dài đoạn BC . 64 A. 12. B.13 . C. . D.15 . 5 Lời giải Chọn D
Do f x có 3 điểm cực trị nên có thể chuẩn hóa 2 2 2 f x a x m khi đó A 4
0; am , Bm;0 , C m;0 m 0 khi đó B, C Ox
Vậy diện tích hình phẳng giới hạn bởi đồ thị C và đường thẳng BC là m 5 S
a x m 2 16 a m 2 2 dx 15 m 16
Cũng có diện tích tam giác ABC là 5 S
am Vậy ta luôn có S S ABC 15 ABC
Theo bài ra S 16 suy ra S 15 . ABC
Câu 5. Cho đồ thị C của hàm số bậc 3: 3 2
y ax bx cx d có hai điểm cực trị là M , P và
hình chữ nhật MNPQ có MN Ox . Biết diện tích của phần hình phẳng giới hạn bởi đồ
thị và đường thẳng MN bằng 10 . Tính diện tích hình chữ nhật MNPQ . 80 320 125 A. . B. . C. . D. 12. 9 27 12 Lời giải Chọn B
Do hàm số có hai cực trị, nên ta có thể chuẩn hóa y a 3 2
x 3m x m 0
suy ra y a 2 2 ' 3
x m khi đó M 3 m am P 3 ; 2 ,
m; 2am suy ra N 3 m; 2am
Đường thẳng MN có phương trình 3
y 2am , MN cắt C tại M và K với x 2m ( MN k
chính là tiếp tuyến của C tại điểm cực trị M)
Diện tích hình phẳng giới hạn bởi đồ thị và đường thẳng MN là 2m 4 S 27 a m 3 2am a 3 2
x 3m xdx 4 m S 27
Diện tích hình chữ nhật MNPQ là 4 S 8 a m suy ra MNPQ S 32 MNPQ
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 320
Theo bài ra S 10 suy ra S . MNPQ 27 Câu 49
Xét hai số phức z , z thỏa mãn z 1, z 2 và z z 3 . Giá trị lón nhất 3z z 5i 1 2 1 2 1 2 1 2 bằng A. 5 19 . B. 5 19 .
C. 5 2 19 . D. 5 2 19 .
Faceboock: Nguyễn Khải Định hướng:
+ Đây là bài toán tìm max z z , min z z với z là số phức thay đổi thỏa mãn 0 0
z z r 0 . Để giải bài toán này chúng ta có hai cách cơ bản: 1
-Cách 1: Áp dụng BĐT mô đun:
z z z z z z z z
z z z z hay r z z z z r z z . 1 1 0 1 1 0 1 1 0 1 0 0 1 0
-Cách 2: Biểu diễn hình hộc số phức:
Trong mặt phẳng phức, gọi M z , A z , khi đó: M thuộc đường tròn tâm I z , bán kính 1 0
r và z z MA . Ta có MI IA MA MI IA r z z z z r z z . 0 1 0 0 1 0 2
+Tất cả giả thiết của đề bài đều cho ở dạng mz nz r , chính vì thế ta xét: mz nz bởi vì 1 2 1 2 2 z . z z . 2 2 2
+Bằng tính toán ta có kết quả: 2 2 mz nz m z n z
mn z .z z .z . Trong đó , m n 1 2 1 2 1 2 1 2
là các số thực và z , z là các số phức. Như vậy từ giả thiết ta sẽ tính được 3z z và đưa bài 1 2 1 2
toán đã cho về bài toán quen thuộc. Lời giải 1 2 2 2 + 3 z z z z
z .z z .z
5 z .z z .z z .z z .z 2; 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 2 2
3z z 9 z z
3 z .z z .z 19 . 1 2 1 2 1 2 1 2
+Có: 3z z 5
i 3z z 5
i 3z z 5i 5 19 . 1 2 1 2 1 2 57 4 19 z i 1 19 19 +Khi
và thỏa mãn điều kiện đề bài thì 3z z 5i 5 19 . Vậy 1 2 3 57 7 19 z i 2 19 19
max 3z z 5i 5 19 Chọn B. 1 2 Lời giải 2
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM z 1 1
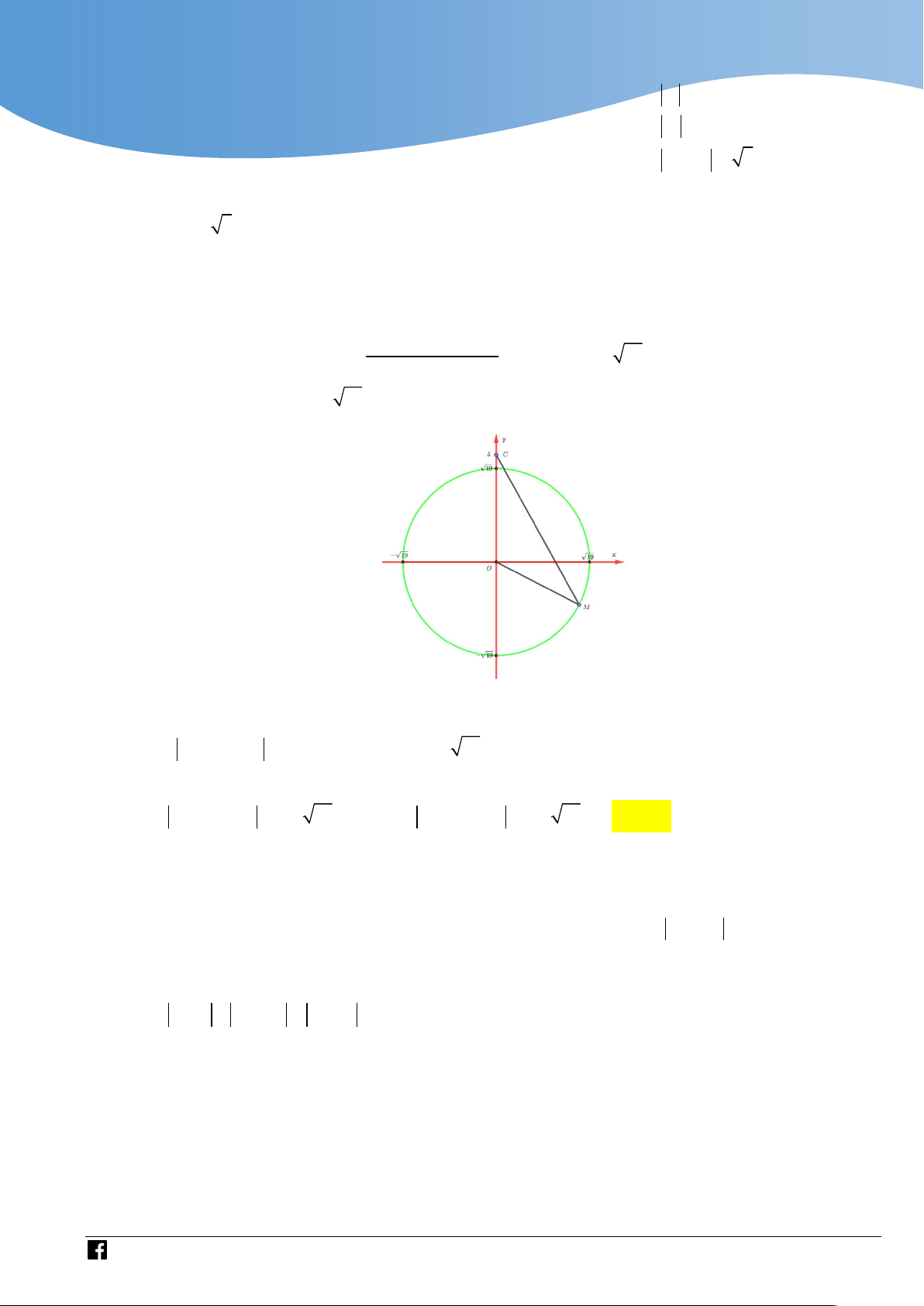
+Trong mặt phẳng phức, gọi (
A z ), B(z ), C(5i), M (3z z ) ; Vì z 2 nên A thuộc 1 2 1 2 2 z z 3 1 2
đường tròn tâm O(0; 0) bán kính R 1, B thuộc đường tròn tâm O(0; 0) bán kính R 2 , và 1 2 AB 3 . 2 2 2 O
M 3OA OB O
M 9OA OB 6OAOB
+Ta có 2 2 2
AB OB OA
AB OA OB 2OAOB 2 2 2
OA OB AB 2 2 2
OM 9OA OB 6
19 OM 19 M thuộc đường tròn tâm 2
O(0;0) bán kính R 19 . 3
+ 3z z 5i MC MO OC 5 19 . Đẳng thức xảy ra khi và chỉ khi O thuộc đoạn thẳng 1 2
MC . Như vậy, rõ ràng tồn tại các số phức z , z thỏa mãn điều kiện bài toán và 1 2
3z z 5i 5 19 . Vậy max 3z z 5i 5 19 Chọn B. 1 2 1 2 Bình luận:
1.Đây là câu hỏi VDC, câu hỏi này đã xuất hiện trong đề thi thử của trường chuyên Đại học
Vinh năm 2018. Điểm then chốt của câu hỏi này là phải tính được 3z z . 1 2
2.Những BĐT mô đun hay dùng:
z z z z z z 1 . Đẳng thức ở 1 xảy ra khi và chỉ khi 1 2 1 2
z z 0 2
z z 0 2 . k
, k 0 : z z k z z 1 2 k
, 0 k 1: z z k z z 1 1 2
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM z z 1 2
z z z z z z z z z z 2 z
2 . Vậy đẳng thức ở 2 xảy ra 1 2 1 2 1 2 2
z z 0 2
z z 0 2 khi và chỉ khi . k
, k 0 : z z k z z 1 2 k
, k ;
0 1; : z z k z z 1 1 2
3.Tập hợp điểm biểu diễn số phức
+Trong mặt phẳng phức, số phức z x yi x, y được biểu diễn bằng -Điểm M ( ;
x y) , kí hiệu M (z) .
-Véc tơ OM (x; y) .
-Véc tơ u (x; y) .
+Biểu diễn hình học của z z , z z , kz (k ) . 1 2 1 2 1
Gọi M , u lần lượt biểu diễn số phức z ; Gọi N , v lần lượt biểu diễn số phức z . Ta có 1 2
OM ON và u v biểu diễn số phức z z ; OM ON và u v biểu diễn số phức z z ; 1 2 1 2
kOM và ku biểu diễn số phức kz . 1 +Với M , ,
A B lần lượt biểu diễn số phức z, z , z thì OM z ; AB z z . 1 2 2 1
4.Tìm được min 3z z 5i bằng BĐT 3z z 5
i 3z z 5 i 5 19 . 1 2 1 2 1 2
Hướng Phát Triển: z z
Hướng 1: Khai thác BĐT 1 2
z z z z 2 z . 1 2 2 Câu 1:
[Sở GD & ĐT Phú Thọ-2021] Có bao nhiêu số phức z có phần thực, phần ảo là các số nguyên
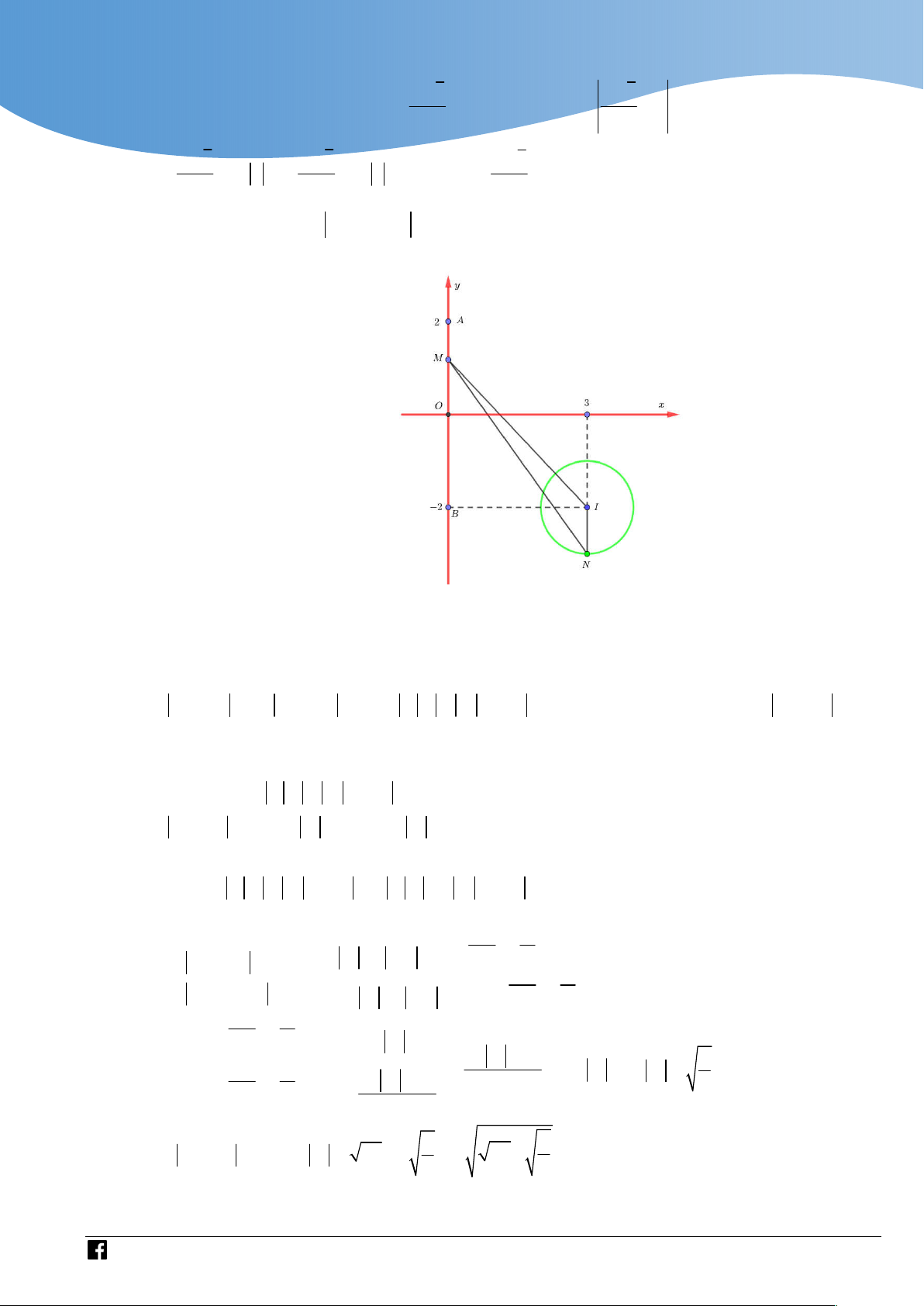
đồng thời thỏa mãn z 7 và z z 1 i z 1 i z 2 2i ? A. 6 . B. 7 . C. 8 . D. 9 . Định hướng:
+Khai thác giả thiết z z 1 i z 1 i z 2 2i . Nghĩ đến BĐT z z 1 2
z z z z 2 z . 1 2 2
+Đẳng thức xảy ra khi và chỉ khi z z k z z ; k , k ; 0 1; . 1 1 2 Lời giải z z +Áp dụng BĐT 1 2
z z z z 2 z ta có: 1 2 2
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
z 1 i z 1 i 2 z
z 1 i z 2 2i z z 1 i
z 2 2i z 2 z 1 i
z 1 i k z 1 i z 1 i ; k , k ; 0 1;
z mz
z 2 2i; m , m ; 0 1;
z 2k
1 1 i; k , k ; 0 1;
z x 1 i; x , x ; 1 2; .
z 2m 1 i; m , m ; 0 1;
+Vì z 7 x 2 7 x 4 ; 3 ; 2 ; 1 ; 2;3; 4 Chọn B.
Hướng 2: Khai thác BĐT z z z z
z z z z
z z z z . 1 2 1 2 1 2 Câu 2:
[Sở GD & ĐT Hòa Bình-2021] Xét các số phức z, w thỏa mãn z 2 , w 3 2i 1. Giá trị lớn nhất của biểu thức 2
H z 2zw 4 bằng A. 16 2 . B. 18 2 . C. 8 . D. 24 .
Định hướng: z z z z + Biến đổi kết luận : 2
H z 2zw z.z 2z w 4 w . 2 2 z z
+ Để tìm max H , biến đổi H 4
3 2i w 3 2i . 2 Lời giải 2 2 2 z z 2 z z 2 z z z z + Vì z
z 4 nên 0 2 4 16 . 2i 2 2i 2i z z z z z z + Ta có 2
H z 2zw z.z 2z w 4 w 4
3 2i w 3 2i 2 2 2 2 z z z z z z 4
3 2i 4 w 3 2i 4 4 3
2 i 4 4 9 2 24 . 2 2i 2i z 2i + Khi
18 14 (thỏa mãn điều kiện đề bài) thì H 24 . Vậy max H 24 Chọn D. w i 5 5 Nhận xét: 1.Tìm min H : z z z z z z + H 4
3 2i w 3 2i 4
3 2i 4 w 3 2i 4 3 2 i 4 2 2 2i 2 z z 4 9 2 4 8 . 2i z 2 i + Khi
(thỏa mãn điều kiện đề bài) thì H 8 . Vậy min H 8 . w 2 2i
2.Biểu diễn hình học số phức
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM z z z z
Trong mặt phẳng phức, gọi M
, N w thì NM w ; Vì 2 2 2 2 z z 2 z z 2 z z z z 4 2
2 nên điểm M thuộc đoạn thẳng AB với 2i 2 2i (0 A ; 2), B(0; 2
) ; Vì w 3 2i 1 N là điểm thuộc đường tròn C có tâm I (3; 2 ) , bán kính r 1.
+ Ta có NM IN MI NM MI 1 IB 1 2 H 8 (Chú ý IB AB ).
+ NM NI IM 1 MI 1 maxI ; A I
B 6 H 24 . Câu 3:
[Sưu Tầm Trên Nhóm Giáo Viên Toán Việt Nam] Xét hai số phức z , z thay đổi thỏa mãn 1 2
z 1 i 2 , z 1 i 2 và z z z z . Giá trị nhỏ nhất của biểu thức z 2z bằng 1 2 1 2 1 2 1 2 A. 0 . B. 1. C. 2 . D. 4 . Định hướng:
Thấy ngay từ z z z z z k z với k ,
k 0 . Từ đây sẽ có 1 2 1 2 1 2
z 2z k 2 z . Sẽ đi tính z theo k . 1 2 2 2 Lời giải
+Ta có z z z z z z z z z k z với k ,
k 0 . Chú ý rằng 1 2 1 2 1 2 1 2 1 2
z , z đều khác 0 . 1 2 2 2
z 1 i 2 z
1 i z 1 i z 1 i 4 2 2 2 2 +
kz 1 i 2 2 2 2 2 k z
1 i k z 1 i z 1 i 4 2 2 2
z 1 i z 1 i 2 2 z 2 2 2 2 2 k z 2 2 2 2 2 2 2 z z . 2 2 k k z i k z 2 1
z 1 i 2 2 2 k 2 2
+ z 2z k 2 z 2k 2 2 2k .2 4 . 1 2 2 k k
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 1 7 1 7 1 7 1 7 +Khi z i , z i
và thỏa mãn điều kiện đề bài thì 1 2 2 2 4 4
z 2z 4 . Vậy min z 2z 4 Chọn D. 1 2 1 2 Câu 4:
[Sở GD & ĐT Hải Phòng-2021] Xét hai số phức z , z thỏa mãn z z 3 và 1 2 1 2
z 6 8i 7 z . Gọi M , m lần lượt là giá trị lớn nhất và nhỏ nhất của biểu thức 1 2
P z 2z 21 3i . Khi đó giá trị của 2 2 M m bằng 1 2 A. 220 . B. 223. C. 224 . D. 225 . Định hướng:
+Khai thác giả thiết. Từ giả thiết, không thể tính được z 2z . Nhận thấy xuất hiện số 1 2 3; 7;10 6 8i .
+ 7 z 6 8i z z z
6 8i z z 6 8i 7 . 1 2 1 2 1 2 Lời giải
+Ta có 7 z 6 8i z z z
6 8i z z 6 8i 7 . Suy ra 1 2 1 2 1 2
z z k 6 8i ; k , k 0 1 2 3
. Vì z z 3 z z 3 4i . 1 2 1 2
z m z z 6 8i ; m , 0 m 1 5 2 1 2 7m 3 z 3 4i 3 4i 1 5 5 3 +
z 2z 21 3i
21m 32 28m 1 i 1 2 7m 5 z 3 4i 2 5 3 P
21m 322 28m 2 1 2
3 49m 56m 41 . 5
+Vì 0 m 1 nên P 3 7m 7m 8 41 3 41 ; P m 2 3 7 4 25 15 . Khi 7 3 z 3 4i 1 z 3 4i 1 5 5
và thỏa mãn điều kiện đề bài thì P 3 41 ; Khi và thỏa 4 z 0 z 3 4i 2 2 5
mãn điều kiện đề bài thì P 15 .
+Kết luận: M 3 41; m 15 2 2
M m 144 Chọn E.
Hướng 3: Biểu diễn hình học các số phức Câu 5:
[Sưu Tầm Trên Nhóm Giáo Viên Toán Việt Nam] Xét hai số phức z , z thay đổi thỏa mãn 1 2
z 1 i 2 , z 1 i 2 và z z z z . Giá trị nhỏ nhất của biểu thức z 2z bằng 1 2 1 2 1 2 1 2 A. 0 . B. 1. C. 2 . D. 4 .
Định hướng:
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM + (
A z ), B(z ) thuộc đường tròn T có tâm I ( 1 ; 1
) bán kính R 2 ; Vì z z z z 1 2 1 2 1 2
AB OA OB nên O thuộc đoạn thẳng AB . Vì O T nên O .
A OB OC.OD với C, D là
giao điểm của T và đường thẳng d qua O .
+Bằng tính toán thấy z 2z OA 2OB . 1 2 Lời giải
+ Trong mặt phẳng phức, gọi (
A z ), B(z ) , C 1 3 0i và D 1 3 0i ; Vì 1 2
z 2 2i 2 1 nên ,
A B thuộc đường tròn T có tâm I( 1 ; 1
) bán kính R 2 ; Vì
z 2 2i 2 2
z z z z AB OA OB nên O thuộc đoạn thẳng AB . Rõ ràng C, D T . 1 2 1 2 2 +Ta có O .
A OB OC.OD 1 3 . 1 3 2 ; z 2z OA 2OB 1 2 2 2
OA 4OB 4OAOB 2 2
OA 4OB 4O .
A OB OA 2OB 2 O . A 2OB 4 . 1 7 1 7 1 7 1 7 +Khi z i , z i
và thỏa mãn điều kiện đề bài thì 1 2 2 2 4 4
z 2z 4 . Vậy min z 2z 4 Chọn D. 1 2 1 2 Câu 6:
[Đông Hà Quảng Trị -2021] Xét các số phức z , z thỏa mãn z 2 2i 4 , z 2 2i 4 và 1 2 1 2
z z z z . Giá trị lớn nhất của z z 5 bằng 1 2 1 2 1 2 A. 2 2 5 13 . B. 13 . C. 2 2 13 . D. 2 3 13 . Định hướng:
+Từ giả thiết thấy ngay (
A z ), B(z ) thuộc đường tròn tâm I ( 2
; 2) bán kính R 4 ; Vì 1 2 1
z z z z AB OA OB nên O thuộc đoạn thẳng AB . 1 2 1 2
+Từ kết luận, ta phải tìm tập hợp điểm C(z z ) . 1 2 Lời giải
+Trong mặt phẳng phức, gọi (
A z ), B(z ), C(z z ) . Gọi M là trung điểm của đoạn thẳng 1 2 1 2
z 2 2i 4 1 AB và D( 5 ;0) ; Vì nên ,
A B thuộc đường tròn tâm I ( 2
; 2) bán kính R 4 1
z 2 2i 4 2
; Vì z z z z AB OA OB nên O thuộc đoạn thẳng AB . 1 2 1 2
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
+Vì OC OA OB 2OM OM MC 2OM OM MC M là trung điểm của đoạn
thẳng OC nên O,C đối xứng với nhau qua đường thẳng IM . Do vậy IC IO 2 2 C
thuộc đường tròn tâm I bán kính R 2 2 . 2
+Ta có z z 5 CD CI ID 2 2 13 . Đẳng thức xảy ra khi và chỉ khi I thuộc đoạn 1 2
thẳng CD . Như vậy, rõ ràng tồn tại các số phức z , z thỏa mãn điều kiện bài toán và 1 2
z z 5 2 2 13 . Vậy max z z 5 2 2 13 Chọn C. 1 2 1 2 Câu 7:
[Chuyên Lê Khiết Quảng Ngãi-L1/N2021] Xét các số phức z , z thỏa mãn điều kiện 1 2
z 1 i 1, z 2 i 2 . Số phức z thay đổi sao cho z z . 1 i z và 1 1 1 2
z z . z 2 i là số thuần ảo. Giá trị nhỏ nhất của z 3 2i bằng 2 2 11 A. . B. 3 . C. 2 2 . D. 13 1. 5 Định hướng:
+Khai thác được giả thiết: z z . 1 i z và z z . z 2 i là số thuần ảo. Trong mặt 2 2 1 1 phẳng phức, gọi (
A z ), B(z ), M (z), I (1 i), K (2 i) thì MA I , A MB KB . 1 2 Lời giải
+Bài toán phụ: Trong mặt phẳng phức, gọi véc tơ u, v theo thứ tự biểu diễn số phức z, w . Khi
đó, uv 0 z.w là số thuần ảo. Chứng minh
z a bi, w c di , a , b ,
c d thì zw wz a bic di a bic di
2ac bd 2uv .
z.w là số thuần ảo z.w z.w 0 z.w z.w 0 zw wz 0 uv 0 .
+Trong mặt phẳng phức, gọi (
A z ), B(z ), I 1 i , K 2 i , M (z) thì từ giả thiêt suy ra: 1 2 M . A IA 0, M .
B KB 0 ; Điểm A thuộc đường tròn C tâm I bán kính r 1 và điểm B 1 1
thuộc đường đường tròn C tâm K bán kính r 2 . 2 2
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
+ MA 0 thì M A z 1 i 1 z 3 2i z 1 i 2 3i
z 1 i 2 3i 13 1 .
+ MB 0 thì M B z 2 i 2 . Từ đây có z 3 2i z 2 i 1 i
z 2 i 1 i 2 2 . Khi z 2 2 1 2 i (thỏa mãn điều kiện đề bài) thì
z 3 2i 2 2 .
+ MA và MB đều khác 0 thì M nằm ngoài C đồng thời nằm ngoài C . Trong trường hợp 2 1 này, luôn có
z 3 2i min 2 2; 13
1 . So sánh ba trường hợp ta có
min z 3 2i 2 2 Chọn C. Câu 50
Trong không gian Oxyz , cho hai điểm A 2;1; 3 và B6; 5; 5 . Xét khối nón N có đỉnh A
, đường tròn đáy nằm trên mặt cầu đường kính AB . Khi N có thể tích lớn nhất thì mặt
phẳng chứa đường tròn đáy của N có phương trình dạng 2x by cz d 0 . Giá trị của
b c d bằng A. 21 . B. 12 . C. 18 . D. 15 .
Faceboock: Trương Quốc Toản – Tạ Minh Đức – Trương Đức Thịnh – DucThanh Phạm
Phân tích định hướng tìm lời giải:
- Đây là bài toán lập phương trình mặt phẳng chứa đường tròn đáy của một hình nón,
ứng với trường hợp thể tích của khối nón đạt giá trị lớn nhất;
- Để lập phương trình mặt phẳng chúng ta cần xác định hai yếu tố: một điểm thuộc mặt
phẳng và một véctơ pháp tuyến;
- Trong bài toán này, hai yếu tố trên chỉ xác định được khi thể tích khối nón đạt giá trị
lớn nhất. Từ đó, chúng ta quy về bài toán tìm giá trị lớn nhất của khối nón N ;
+ Xác định chiều cao h và bán kính đáy r của khối nón N .
+ Tìm giá trị lớn nhất của biểu thức 1 2 V r h 3 Lời giải
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
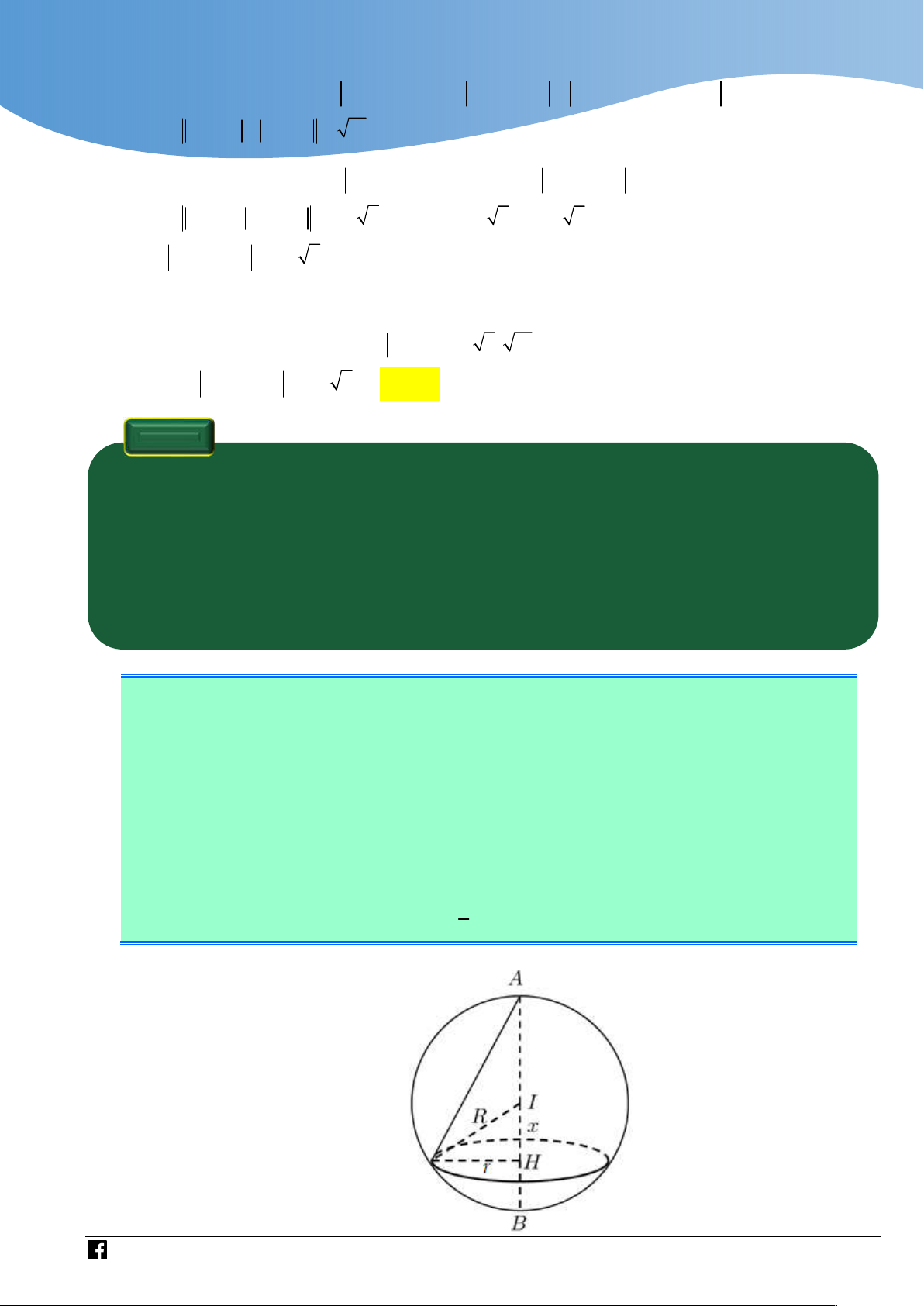
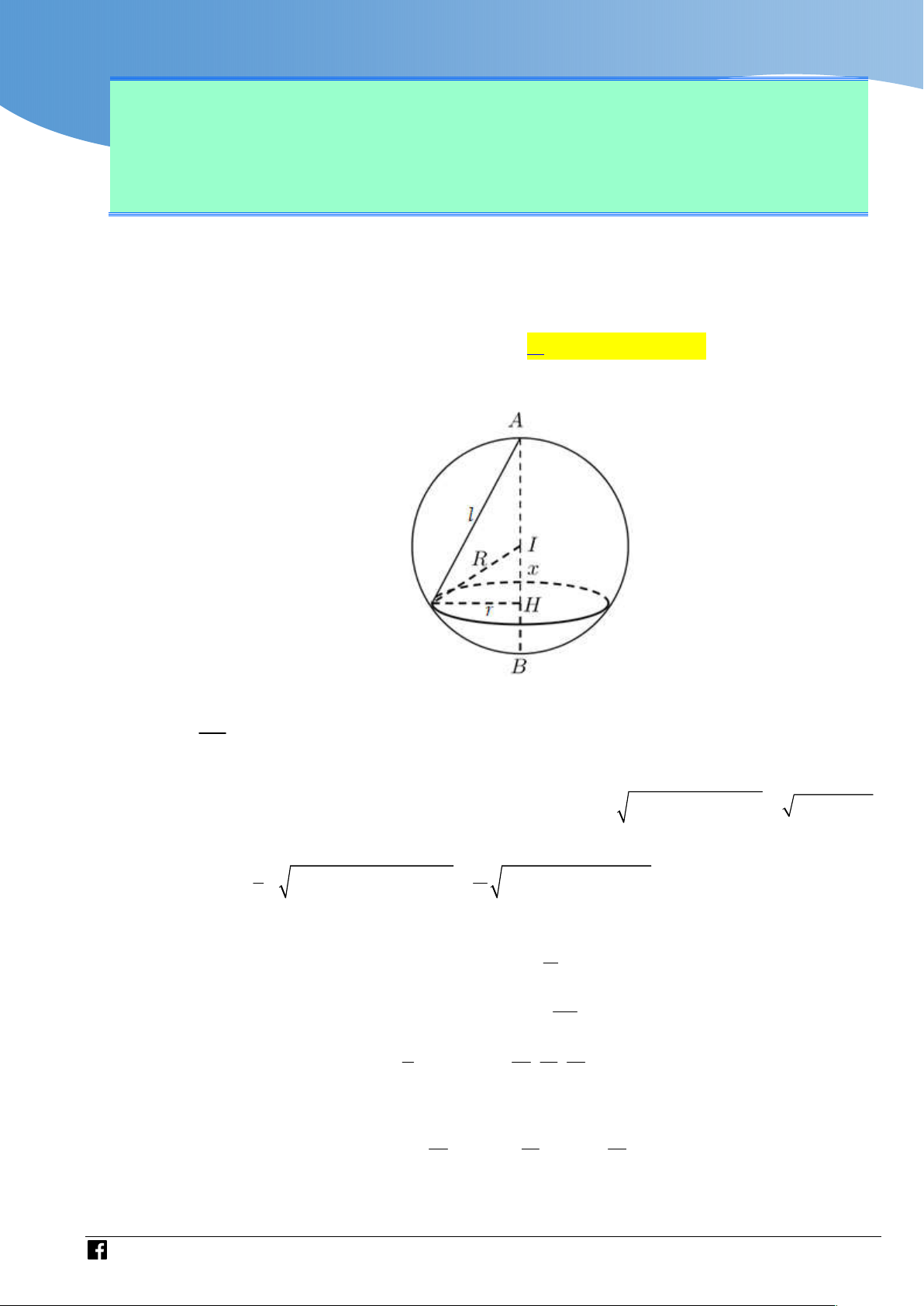
Mặt cầu đường kính AB có tâm I 4;3;
4 là trung điểm của AB và có bán kính AB R
3 . Gọi h , r là chiều cao và bán kính đáy khối nón N ; H là tâm đường tròn 2 đáy của N .
Đặt IH x0 x R . Ta có: 2 2 2 2 2
r R IH
R x ; h x R
Thể tích khối nón N : 1 1 2 V r h 2 2
R x R x 3 3 Xét hàm số 3 2 2 3
f x x Rx R x R với 0 x R
Ta có: f x 2 2 3
x 2Rx R ; R
f x 0 x 3
Từ đó, ta tìm được V R max khi 4 h
AH 4, BH 2 . 3 2 14 11 13 Gọi H ;
x y; z , khi đó: AH AB H ; ; . 3 3 3 3
Do đó, mặt phẳng chứa đường tròn đáy của N đi qua H và nhận AB làm vecto pháp 14 11 13
tuyến có phương trình là: 2 x 2 y 1 z
0 2x 2 y z 21 0 . 3 3 3
Vậy b c d 18 . Suy ra Chọn C. Bình luận:
- Đây là bài toán lập phương trình mặt phẳng, để xác định các yếu tố lập được phương
trình của mặt phẳng nói trên học sinh phải có kiến thức tổng hợp liên quan đến thể tích
khối nón, giá trị lớn nhất của hàm số trên một khoảng. Đặc biệt, học sinh phải nhận ra mẫu
chốt của bài toán là các yếu tố chỉ được xác định khi khối nón đạt thể tích lớn nhất. Đây là
câu hỏi kiểm tra kiến thức ở mức độ VDC. 1
- Có thể tìm giá trị lớn nhất của V 2 2
R x R x bằng cách sử dụng bất đẳng thức 3
Côsi cho ba số dương như sau: 1
R x R x R x 3 3 2 2 32 R V
2R 2x R x R x 6 6 3 81 R
Dấu bằng xảy ra khi và chỉ khi x . 3 Hướng phát triển:
Hướng phát triển 1: Dữ nguyên giả thiết bài toán, thay đổi kết luận. Tính giá trị biểu thức
liên quan đến các hệ số phương trình mặt phẳng chứa đáy của khối nón khi khối nón có
diện tích xung quanh lớn nhất
Hướng phát triển 2: Thay đổi giả thiết khối nón bằng khối trụ có trục nằm trên đường thẳng
AB , đường tròn đáy nằm trên mặt cầu đường kính AB . Tính giá trị biểu thức liên quan
đến các hệ số của phương trình hai mặt phẳng song song đồng thời chứa hai đáy của khối
trụ khi khối trụ có thể tích lớn nhất.
Hướng phát triển 3: Thay đổi giả thiết bài toán cho điểm A , mặt cầu S và một mặt phẳng
(P) cố định. Viết phương trình đường thẳng đi qua A tiếp xúc với mặt cầu S và cắt
P tại B sao cho AB nhỏ nhất.
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Hướng phát triển 4: Thay đổi giả thiết khối nón N có đỉnh A, đường tròn đáy là giao của
mặt phẳng qua B với mặt cầu S O;OA . Mặt phẳng P đi qua hai điểm A , B. Thay
đổi kết luận khi diện tích thiết diện của hình nón cắt bởi mặt phẳng P có giá trị lớn nhất
thì mặt phẳng P có phương trình là? Bài tập tương tự Câu 1.
Trong không gian Oxyz , cho hai điểm A2;1;3 và B 6;5;5 . Xét khối nón N có đỉnh
A , đường tròn đáy nằm trên mặt cầu đường kính AB . Khi N có diện tích xung quanh
lớn nhất thì mặt phẳng chứa đường tròn đáy của N có phương trình là
A. 8x 8y 2z 21 0 .
B. 2x 2 y z 21 0 .
C. 8x 8y 4z 21 0 .
D. 2x 2 y z 21 0 . Lời giải
Mặt cầu đường kính AB có tâm I 4;3;4 là trung điểm của AB và có bán kính AB R 3 . Gọi ,
h r là chiều cao và bán kính đáy khối nón N ; H là tâm đường tròn 2
đáy của N .
Đặt IH x 0 x R . Ta có: 2 2 2 2 2
r R IH R x ; l R x2 2 2 2
R x 2xR 2R
Diện tích xung quanh của khối nón N : 1 S rl R x xR R R R x x R xq 2 2 2 2 2 2 2 2 3 3 Xét hàm số 3 2 2 3
f x x Rx R x R với 0 x R R
Ta có: f x 2 2 3
x 2Rx R ; f x 0 x 3 4R
Từ đó, ta suy ra S đạt giá trị lớn nhất khi h
AH 4, BH 2 . xq 3 2 14 11 13 Gọi H ;
x y; z , khi đó: AH AB H ; ; . 3 3 3 3
Do đó, mặt phẳng chứa đường tròn đáy của N đi qua H và nhận AB làm vecto pháp 14 11 13
tuyến có phương trình là: 2 x 2 y 1 z
0 2x 2 y z 21 0 . 3 3 3
Suy ra Chọn B.
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Câu 2. Trong không gian Oxyz , cho hai điểm A1;0;0, B 3; 4; 4
. Xét khối trụ T có trục là
đường thẳng AB và có hai đường tròn đáy nằm trên mặt cầu đường kính AB . Khi T
có thể tích lớn nhất, hai đáy của T nằm trên hai mặt phẳng song song lần lượt có
phương trình là x by cz d 0 và x by cz d 0 . Khi đó giá trị của biểu thức 1 2
b c d d thuộc khoảng nào sau đây? 1 2 A. 0;2 1 . B. 1 1; 0 . C. 2 9; 1 8 . D. 2 0; 1 1 . Lời giải
Mặt cầu đường kính AB có tâm I 2; 2; 2
và bán kính bằng 3.
Gọi x 0 x 3 là bán kính đáy của T , khi đó T có chiều cao bằng 2
h 2 9 x , do
đó thể tích của T bằng 3 2 2 x x 2 2 2 9 x x x 2 2 V x x 2 x 2 2 2 9 4 . . . 9 4 12 3 . 2 2 3
T có thể tích lớn nhất bằng V
12 3 khi x 6 . max
Khi đó gọi P là mặt phẳng chứa đường tròn đáy của T , P có phương trình tổng
quát dạng x 2 y 2z d 0 . Khoảng cách từ tâm I 2; 2; 2
đến P bằng 3 nên
2 2.2 2.2 d d 3 3 10 3 . 3 d 3 3 10
Vậy b c d d 2 2 3 3 10 3 3 10 2
0 . Suy ra Chọn C. 1 2 Câu 3:
Trong không gian Oxyz , cho mặt cầu x 2 y 2 z 2 1 2 2 9 và mặt phẳng
P : 2x y 2z 1 0 . Đường thẳng đi qua O tiếp xúc với mặt cầu S và cắt P tại
A sao cho OA nhỏ nhất có phương trình là x y z x y z x y z x y z A. : . B. : . C. : . D. : . 10 7 2 1 0 7 2 10 7 2 10 7 2 Lời giải
Ta thấy O 0;0;0 thuộc mặt cầu S .
Mặt phẳng Q đi qua O và tiếp xúc mặt cầu S có phương trình Q : x 2 y 2z 0 .
Khi đó Q .
Gọi d P Q và H là hình chiếu vuông góc của O lên đường thẳng d .
Vì A là giao điểm của và P , Q, d P Q
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
A d . Do đó OA OH . OA
OH , dấu bằng xảy ra H A min
Khi đó đường thẳng đi qua O và H, tức là đi qua điểm O , cắt và vuông góc với d
Mặt phẳng P,Q lần lượt có vectơ pháp tuyến là u 2;1; 2 và u 1; 2; 2 . 2 1
Đường thẳng d có vectơ chỉ phương u u ,u 2; 2;3 d 1 2
Mặt khác Q , đường thẳng có một vectơ chỉ phương u u , n 10 ; 7; 2 . d (Q ) x y z
Vậy phương trình đường thẳng :
. Suy ra Chọn B. 1 0 7 2 1 5
Câu 4. Trong không gian
Oxyz , cho hai điểm A 0; 2; , B 0; 0;
. Xét khối nón N có đỉnh 2 2 5
B , đường tròn đáy là giao của mặt phẳng qua A với mặt cầu S O; . Mặt phẳng 2
P đi qua hai điểm A , B. Khi diện tích thiết diện của hình nón cắt bởi mặt phẳng P
có giá trị lớn nhất thì mặt phẳng P đi qua điểm nào sau đây? 1 1 A. 0;1;3 B. 0;1; 3 . C. 0; ; 3 . D. 0;3; . 2 2 Lời giải Chọn C 1
Dễ thấy mp nhận OB làm véc tơ pháp tuyến nên phương trình là z 0 . 2 1
Khi đó chiều cao của khối nón h d ;
B 2, tâm đáy là I 0;0; bán kính đường 2 tròn đáy 2 2
r R d ;
O 6 .
Gọi thiết diện là tam giác BCD , H là trung điểm CD . Đặt IH x,0 x IA 2 Khi đó 1 S 2 x 4 .2 6 2 x 4 x 2 2 x 24 BCD 2 Ta có 2 4 2 S
x 2x 24 f x dễ thấy Maxf x 25 do đó MaxS 5 đạt được SAB BCD 0;2 khi IH 1. BI.IH 2
Khi đó d I; P . 2 2 BI IH 5
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 1 5
Gọi phương trình của P là
ax by cz d 0 do P qua A 0; 2; , B 0; 0; nên 2 2 c 2b d 0 b c 2 5c . 5c d d 0 2 2 1 c d 2 2 2 2 c 2
Lại có d I; P
a 3c . 2 2 2 2 2 5
a b c 5 a 2c 5 5 1
Từ đó ta tìm được 2 phương trình mặt phẳng là
3x y z 0 . Do đó 0; ; 3 2 2 thuộc P . Câu 5. 2 2
Trong không gian tọa độ Oxyz , cho hai mặt cầu S 2
: x y 1 z 2 16 , 1 4 7 14
S : x 2 1 y 2 2
1 z 1 và điểm A ; ;
. Gọi I là tâm của mặt cầu S và 1 2 3 3 3
P là mặt phẳng tiếp xúc với cả hai mặt cầu S và S . Xét các điểm M thay đổi và 2 1
thuộc mặt phẳng P sao cho đường thẳng IM tiếp xúc với mặt cầu S . Khi đoạn 2
thẳng AM ngắn nhất thì M ; a ;
b c . Tính giá trị của T a b c . 7 7 A. T 1. B. T 1 . C. T . D. T . 3 3 Lời giải Chọn B
Mặt cầu S có tâm I 0;1; 2 bán kính R 4 và mặt cầu S có tâm K 1; 1;0 bán 2 1 1 kính R 1. 2
Có IK 3 , suy ra IK R R nên hai mặt cầu S và S tiếp xúc trong tại H . 2 1 1 2 4 4 5 2 Suy ra IH
IK , IK 1; 2; 2 H ; ; . 3 3 3 3
Vì P là mặt phẳng tiếp xúc với cả hai mặt cầu S và S nên P qua H và nhận 2 1
vectơ IK 1; 2; 2 là một vectơ pháp tuyến. Suy ra ra phương trình mặt phẳng P
là x 2 y 2z 6 0 .
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Giả sử điểm M thay đổi trên P thỏa mãn đường thẳng IM tiếp xúc với mặt cầu
S , tiếp điểm tương ứng là N . 2 Ta có I KN và I
MH đồng dạng (vì 0
IHM INK 90 , MIH chung) suy ra IN NK * . IH HM Với 2 2
NK R 1; IH 4; IK 3; IN
IK NK 2 2 nên * 2 2 2 1 HM 2 . 4 HM
Mặt khác ta lại có A P và M thay đổi thuộc đường tròn C tâm H bán kính R
2 nên AM ngắn nhất bằng HA R 4 2 2 3 2 khi điểm M thoả mãn 3 4 2 5 AM AH M ; ; 4 3 3 3 4 2 5
Suy ra a ;b ;c
T a b c 1 . Chọn B. 3 3 3 2 2 Câu 6.
Trong không gian Oxyz , cho hai mặt cầu: S 2
: x y 1 z 2 3 và 1
S : x 62 y 72 z 82 27 . Hai điểm E, F lần lượt thuộc S và S , M là 2 1 2
trung điểm của EF . Khi OM đạt giá trị nhỏ nhất thì M thuộc mặt phẳng nào sau đây?
A. P : x y z 2 0 .
B. Q : x y z 1 0 .
C. R : x y z 4 0 .
D. T : x y z 5 0 . Lời giải Chọn B
S có tâm I 0;1; 2 , bán kính R 3 . 1 1 1
S có tâm I 6; 7
;8 , bán kính R 3 3 . 2 2 2
Gọi I là trung điểm của I I I 3; 3 ;3 . 1 2 1 IE IF IE IF
Ta có: IM IE IF IM 3 IM 2 3 . 2 2 2
Gọi S là mặt cầu tâm I , bán kính R 3 . 3 3
S là mặt cầu tâm I , bán kính R 2 3 . 4 4
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Ta có: OI 3 3 . OM
OI R 3 khi và chỉ khi M là giao của đoạn thẳng OI và S . 4 min 4 Suy ra M 1; 1 ;
1 . Do đó M thuộc mặt phẳng Q .
https://www.facebook.com/groups/toanvd.vdc