Phát triển đề tham khảo tốt nghiệp THPT 2021 môn Toán – Lê Văn Đoàn

Tài liệu gồm 146 trang, được biên soạn bởi thầy giáo Lê Văn Đoàn, phát triển đề tham khảo tốt nghiệp THPT 2021 môn Toán, với những câu hỏi và bài tập trắc nghiệm tương tự, có đáp án; tài liệu giúp học sinh lớp 12 rèn luyện để chuẩn bị cho kỳ thi tốt nghiệp THPT môn Toán 

27 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu ôn thi THPTQG môn Toán

Môn: Toán

Thông tin:

146 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
20
21
–
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 1 -
========  =========
Câu 1. Có bao nhiêu cách chọn 3 học sinh từ một nhóm có 5 học sinh ?
A. 5!. B.
3
5
.A
C.
3
5
.C
D.
3
5 .
Lôøi giaûi tham khaûo
Số cách chọn 3 học sinh từ một nhóm gồm
5
học sinh là tổ hợp chập 3 của 5 phần tử có
3
5
C
cách.
Chọn đáp án C.
Hoaùn vò – Toå hôïp – Chænh hôïp
Sắp xếp vị trí
n
phần tử
Sử dụng hoán vị !.
n
P n
1
( : SHIFT ).
casio n x
Chọn k trong
n
tùy ý Sử dụng tổ hợp
!
( )!. !
k
n
n
C
n k k
( : SHIFT ).
casio n k
Chọn k trong
n
và sắp xếp Sử dụng chỉnh hợp
!
. ! .
( )!
k k
n n
n
C k A
n k
( SHIFT ).n k
Baøi taäp töông töï vaø môû roäng
1.1. Cần chọn 3 người đi công tác từ một tổ có 30 người, khi đó số cách chọn là
A.
3
30
.A
B.
30
3 .
C. 10. D.
3
30
.C
1.2. Cho 8 điểm trong đó không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác mà ba đỉnh của
nó được chọn từ 8 điểm trên ?
A. 336. B. 56.
C. 168. D. 84.
1.3. Có
( 0)n n
phần tử lấy ra
(0 )k k n
phần tử đem đi sắp xếp theo một thứ tự nào đó, mà khi
thay đổi thứ tự ta được cách sắp xếp mới. Khi đó số cách sắp xếp là
A.
.
k
n
C
B.
.
n
k
A
C.
.
k
n
A
D. .
n
P
1.4. Một tổ có 10 học sinh. Hỏi có bao nhiêu cách chọn ra 2 học sinh từ tổ đó để giữ hai chức vụ tổ
trưởng và tổ phó.
A.
2
10
.A
B.
2
10
.C
C.
8
10
.A
D.
2
10 .
1.5. Cho A là tập hợp gồm 20 điểm phân biệt. Số đoạn thẳng có hai đầu mút phân biệt thuộc tập A
là
A. 170. B. 160.
C. 190. D. 360.
1.6. Số véctơ khác 0
có điểm đầu, điểm cuối là hai trong 6 đỉnh của lục giác ABCDEF là
A.
6
.P B.
2
6
.C
C.
2
6
.A
D. 36.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 2 -
1.7. Có bao nhiêu cách sắp xếp
5
học sinh thành một hàng dọc ?
A.
5
5
.
B.
5!.
C.
4 !.
D.
5.
1.8. Từ tập
{2; 3; 4; 5; 6}
X
có thể lập được bao nhiêu số tự nhiên có ba chữ số mà các chữ số đôi
một khác nhau ?
A.
60.
B.
125.
C.
10.
D.
6.
1.9. Trong một buổi khiêu vũ có
20
nam và
18
nữ. Hỏi có bao nhiêu cách chọn ra một đôi nam nữ để
khiêu vũ ?
A.
2
38
.
C
B.
2
38
.
A
C.
2 1
20 18
.
C C
D.
1 1
20 18
.
C C
1.10. Một tổ có
6
học sinh nam và
9
học sinh nữ. Hỏi có bao nhiêu cách chọn
5
học sinh đi lao động
trong đó có
2
học sinh nam ?
A.
2 3
9 6
. .
C C
B.
2 3
6 9
.
C C
C.
2 3
6 9
. .
A A
D.
2 3
6 9
. .
C C
Câu 2. Cho cấp số cộng
( )
n
u
với
1
1
u
và
2
3.
u
Giá trị của
3
u
bằng
A.
6.
B.
9.
C.
4.
D.
5.
Lôøi giaûi tham khaûo
Ta có:
2 1
3 1 2.
d u u
Suy ra
3 1
2 1 2.2 5.
u u d
Chọn đáp án D.
Caáp soá coäng Caáp soá nhaân
1
:
k k
u u d
công sai.
1
:
k
k
u
q
u
công bội.
, ,
a b c
là cấp số cộng
2
a c
b
, ,
a b c
là cấp số nhân
2
.
b ac
1
( 1) .
n
u u n d
1
1
. .
n
n
u u q
1 1
( ) 2 ( 1) .
2 2
n n
n n
S u u u n d
1 2 1
1
1
n
n n
q
S u u u u
q
Baøi taäp töông töï vaø môû roäng
2.1. Cho cấp số cộng
( )
n
u
có
1
3,
u
6
27.
u
Công sai của cấp số cộng đã cho bằng
A.
7.
B.
5.
C.
8.
D.
6.
2.2. Cho cấp số cộng
( )
n
u
có
1
2
u
và công sai
3.
d
Tìm số hạng
10
.
u
A.
9
10
2.3 .
u
B.
10
25.
u
C.
10
28.
u
D.
10
29.
u
2.3. Cho cấp số cộng
( )
n
u
có
1
11
u
và công sai
4.
d
Hãy tính
99
.
u
A.
401.
B.
403.
C.
402.
D.
404.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 3 -
2.4. Biết bốn số
5, , 15, x y
theo thứ tự lập thành cấp số cộng. Giá trị của biểu thức
3 2x y
bằng
A. 50. B. 70.
C. 30. D. 80.
2.5. Cho cấp số cộng ( )
n
u có
5
15u và
20
60.u Tổng
20
S của 20 số hạng đầu tiên của cấp số cộng
bằng
A. 600. B. 60.
C. 250. D. 500.
2.6. Cho dãy số ( )
n
u là một cấp số cộng có
1
3u và công sai 4.d Biết tổng
n
số hạng đầu của dãy
số ( )
n
u là 253.
n
S Giá trị của
n
bằng
A. 9. B. 11.
C. 12. D. 10.
2.7. Cho cấp số nhân ( ),
n
u biết
1
1u và
4
64.u Công bội của cấp số nhân bằng
A. 21. B. 4.
C. 4. D. 2 2.
2.8. Cho cấp số nhân ( )
n
u có
1
2u và công bội
3.q
Số hạng
2
u bằng
A. 6. B. 6.
C. 1. D. 18.
2.9. Xác định số hạng đầu và công bội của cấp số nhân ( )
n
u có
4 2
54u u và
5 3
108.u u
A.
1
3u và
2.q
B.
1
9u và
2.q
C.
1
9u và
–2.q
D.
1
3u và
–2.q
2.10. Một cấp số nhân có số hạng đầu
1
3,u công bội
2.q
Biết 765.
n
S Giá trị của
n
bằng
A. 7. B. 6.
C. 8. D. 9.
Câu 3. Cho hàm số
( )f x
có bảng biến thiên sau:
Hàm số đã cho đồng biến trên khoảng nào, trong các khoảng sau đây ?
A.
( 2;2).
B.
(0;2).
C.
( 2;0).
D.
(2; ).
Lôøi giaûi tham khaûo
Từ bảng biến thiên, suy ra 0y
khi
( ; 2), (0;2).x x
Chọn đáp án B.
Ñôn ñieäu (ñoàng bieán vaø nghòch bieán)
Định lí (thừa nhận): Giả sử hàm số
( )y f x
có đạo hàm trên khoảng .K
Nếu
( ) 0, f x x K
thì hàm số đồng biến trên khoảng .K
Nếu
( ) 0, f x x K
thì hàm số nghịch biến trên khoảng .K
Nếu
( ) 0, f x x K
thì hàm số không đổi trên khoảng .K
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 4 -
O
x
y
1
2
2
3
Baøi taäp töông töï vaø môû roäng
3.1. Cho hàm số
( )y f x
có bảng biến thiên bên dưới. Hàm số đã cho nghịch biến trên khoảng nào
dưới đây ?
A.
(0;1).
B.
( ;0).
C.
(1; ).
D.
( 1; 0).
3.2. Cho hàm số
( )y f x
có bảng biến thiên dưới. Hàm số đã cho đồng biến trên khoảng nào ?
A.
( 2; ).
B.
( 2;3).
C.
(3; ).
D.
( ; 2).
3.3. Cho hàm số
( )y f x
có đồ thị như hình vẽ dưới. Hàm số đã cho đồng biến trên khoảng
A.
( 1; 3).
B.
( ; 2).
C.
( ;3).
D.
( 2;2).
3.4. Cho hàm số
( )y f x
có đồ thị như hình vẽ dưới. Hàm số đã cho đồng biến trên khoảng nào ?
A.
( ; 3).
B.
( 3; 1).
C.
( 2;2).
D.
( 2; 1).
3.5. Cho hàm số
( )y f x
có đạo hàm
2
( ) 1,f x x
.x Mệnh đề nào dưới đây đúng ?
A. Hàm số nghịch biến trên khoảng
( ;0).
B. Hàm số nghịch biến trên khoảng
(1; ).
C. Hàm số nghịch biến trên khoảng
( 1;1).
D. Hàm số đồng biến trên khoảng
( ; ).
3.6. Cho hàm số
( )y f x
có bảng xét dấu đạo hàm như sau
Mệnh đề nào dưới đây đúng ?
A. Hàm số đồng biến trên khoảng
( 2;0).
B. Hàm số đồng biến trên khoảng
( ;0).
C. Hàm số nghịch biến trên khoảng
(0;2).
D. Hàm số nghịch biến trên khoảng
( ; 2).
3.7. Cho hàm số
3 2
.3y x x Mệnh đề nào dưới đây đúng ?
A. Hàm số nghịch biến trên khoảng
(2; ).
B. Hàm số đồng biến trên khoảng
(0;2).
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 5 -
C. Hàm số nghịch biến trên khoảng
(0;2).
D. Hàm số nghịch biến trên khoảng
( ;0).
3.8. Cho hàm số
4 2
2 .y x x Mệnh đề nào dưới đây đúng ?
A. Hàm số nghịch biến trên khoảng
( 1;1).
B. Hàm số đồng biến trên khoảng
( ; 2).
C. Hàm số nghịch biến trên khoảng
( ; 2).
D. Hàm số đồng biến trên khoảng
( 1;1).
3.9. Cho hàm số
2
1
x
y
x
. Mệnh đề nào dưới đây đúng ?
A. Hàm số nghịch biến trên khoảng
( ; 1).
B. Hàm số đồng biến trên khoảng
( ; 1).
C. Hàm số nghịch biến trên khoảng
( ; ).
D. Hàm số nghịch biến trên khoảng
( 1; ).
3.10. Cho hàm số
2
2 1.y x Mệnh đề nào dưới đây đúng ?
A. Hàm số nghịch biến trên khoảng
( 1;1).
B. Hàm số đồng biến trên khoảng
(0; ).
C. Hàm số đồng biến trên khoảng
( ;0).
D. Hàm số nghịch biến trên khoảng
(0; ).
Câu 4. Cho hàm số
( )f x
có bảng biến thiên sau:
Điểm cực trị đại của hàm số đã cho là
A. 3.x B. 1.x C. 2.x D. 2.x
Lôøi giaûi tham khaûo
Từ bảng biến thiên, thấy y
đổi dấu từ
sang khi qua 2x nên 2x là điểm cực đại.
Chọn đáp án D.
Cöïc trò
Điều kiện cần (định lí 1): Nếu hàm số
( )y f x
có đạo hàm trên khoảng
( ; )a b
và đạt cực đại (hoặc
cực tiểu) tại
x
thì
( ) 0.f x
Điều kiện đủ (định lí 2):
Nếu
( )f x
đổi dấu từ âm sang dương khi
x
đi qua điểm
x
(theo chiều tăng) thì hàm số
( )
y f x
đạt cực tiểu tại điểm
.x
Nếu
( )f x
đổi dấu từ dương sang âm khi
x
đi qua điểm
x
(theo chiều tăng) thì hàm số
( )
y f x
đạt cực đại tại điểm
.x
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 6 -
Định lí 3: Giả sử
( )
y f x
có đạo hàm cấp
2
trong
( ; ),
x h x h
với
0.
h
Khi đó:
Nếu
( ) 0, ( ) 0
y x y x
thì
x
là điểm cực tiểu.
Nếu
( ) 0, ( ) 0
o o
y x y x
thì
x
là điểm cực đại.
Cần nhớ: Điểm cực đại (cực tiểu) của hàm số là
,
x
giá trị cực đại (cực tiểu) của hàm số là
( )
f x
(hay
y
C
Đ
hoặc
CT
).
y
Điểm cực đại của đồ thị hàm số là
( ; ( )).
M x f x
Baøi taäp töông töï vaø môû roäng
4.1. Cho hàm số
( )
y f x
có bảng biến thiên sau:
Khẳng định nào sau đây là đúng ?
A. Hàm số đạt cực đại tại
2.
x
B. Hàm số đạt cực đại tại
3.
x
C. Hàm số đạt cực đại tại
2.
x
D. Hàm số đạt cực đại tại
4.
x
4.2. Cho hàm số
( )
y f x
liên tục trên
và có bảng biến thiên:
Khẳng định nào sau đây là đúng ?
A. Hàm số có đúng hai điểm cực trị.
B. Hàm số có giá trị cực tiểu bằng
1
và
1.
C. Hàm số có giá trị lớn nhất bằng
0
và giá trị nhỏ nhất bằng
3.
D. Hàm số đạt cực đại tại
0.
x
4.3. Cho hàm số
( )
y f x
xác định, liên tục trên
và có bảng biến thiên:
Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số có giá trị lớn nhất bằng
2
và giá trị nhỏ nhất bằng
3.
B. Hàm số có đúng một cực trị.
C. Hàm số đạt cực đại tại
0
x
và đạt cực tiểu tại
1.
x
D. Hàm số có giá trị cực tiểu bằng
2.
4.4. Cho hàm số
( )
f x
có đồ thị như hình vẽ. Giá trị cực đại của hàm số là
A.
2.
x
B.
1.
y
CĐ
C.
3.
y
CĐ
D.
(2; 3).
M
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 7 -
4.5. Cho hàm số
( )y f x
có đồ thị như hình bên. Mệnh đề nào dưới đây đúng ?
A. Hàm số có giá trị cực tiểu bằng 2.
B. Hàm số đạt cực đại tại 0x và đạt cực tiểu tại 2.x
C. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng 2.
D. Hàm số có ba điểm cực trị.
4.6. Gọi
1
x là điểm cực đại,
2
x là điểm cực tiểu của hàm số
3
3 2.y x x Giá trị
1 2
2x x bằng
A. 2. B. 1.
C. 1. D. 0.
4.7. Diểm cực đại của đồ thị hàm số
4 2
2 2y x x có tọa độ là
A.
( 1;1).
B.
(2;0).
C.
(1;1).
D.
(0;2).
4.8. Hàm số
3 2
3 2y x x mx đạt cực tiểu tại 2x khi
A.
0.m
B. 0.m
C.
0.m
D. 0.m
4.9. Cho hàm số
4 2
.y x ax b Biết rằng đồ thị hàm số nhận điểm
( 1; 4)A
là điểm cực tiểu. Tổng
2a b bằng
A. 1. B. 0.
C. 1. D. 2.
4.10. Cho hàm số
3 2
( ) 3 1.f x x x mx Tìm giá trị của tham số
m
để hàm số có hai điểm cực trị
1
,x
2
x thỏa mãn
2 2
1 2
3.x x
A.
3
2
m
B.
1
2
m
C. 2.m D. 1.m
Câu 5. Cho hàm số
( )
f x
có bảng xét dấu của
( )
f x
như sau:
Hàm số
( )f x
có bao nhiêu điểm cực trị ?
A.
4.
B.
1.
C.
2.
D.
3
Lôøi giaûi tham khaûo
Từ bảng xét dấu, ta có ( )f x
đổi dấu 4 lần có 4 điểm cực trị. Chọn đáp án A.
Baøi taäp töông töï vaø môû roäng
5.1. Cho hàm số
( )f x
có bảng xét dấu của
( )f x
như sau:
Số điểm cực trị của hàm số đã cho là
A. 3. B. 0.
C. 2. D. 1.
5.2. Cho hàm số
( )f x
có bảng biến thiên như hình dưới. Tìm giá trị cực đại y
CĐ
và giá trị cực tiểu
CT
y
của hàm số đã cho.
A.
CT
3, 2.y y
CĐ
B.
CT
2, 0.y y
CĐ
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 8 -
C.
CT
2, 2.y y
CĐ
D.
CT
3, 0.y y
CĐ
5.3. Cho hàm số
( )f x
có đạo hàm
3
( ) ( 1)( 2) ,f x x x x
.x Số điểm cực trị của hàm số đã cho
là
A. 3. B. 2.
C. 5. D. 1.
5.4. Hàm số
( )f x
xác định và liên tục trên và có đạo hàm
2
( ) 2( 1) ( 1).f x x x
Hỏi khẳng định
nào sau đây đúng về hàm số
( ).f x
A. Hàm số
( )f x
đạt cực đại tại điểm 1.x
B. Hàm số
( )f x
đạt cực tiểu tại điểm 1.x
C. Hàm số
( )f x
đạt cực đại tại điểm 1.x
D. Hàm số
( )f x
đạt cực tiểu tại điểm 1.x
5.5. Cho hàm số
( )f x
có đạo hàm là
2
( ) (e 1)( 2)
x
f x x x
với mọi .x Số điểm cực tiểu của
hàm số đã cho là
A. 0. B. 1.
C. 2. D. 3.
5.6. Cho hàm số
( )f x
có đồ thị
( )f x
của nó trên khoảng K như hình vẽ. Khi đó trên
,K
hàm số
( )y f x
có bao nhiêu điểm cực trị ?
A. 1.
B. 4.
C. 3.
D. 2.
5.7. Hàm số
( )y f x
có đồ thị như hình vẽ dưới đây. Hàm số
( ) 3 2019y f x x
có bao nhiêu
điểm cực trị ?
A. 1.
B. 2.
C. 3.
D. 4.
5.8. Hàm số
( )y f x
có đồ thị như hình vẽ dưới đây. Hàm số
( ) e 2019y f x x
có bao nhiêu
điểm cực trị ?
A. 0.
B. 1.
C. 2.
D. 3.
5.9. Cho hàm số
( )y f x
có đồ thị như hình vẽ bên dưới. Hỏi đồ thị hàm số
( )y f x
có bao nhiêu
điểm cực trị ?
A. 2.
B. 3.
C. 4.
D. 5.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 9 -
5.10. Cho hàm số
( )y f x
có đồ thị như hình vẽ bên dưới. Hỏi đồ thị hàm số
( )y f x
có bao nhiêu
điểm cực trị ?
A. 2.
B. 3.
C. 4.
D. 5.
Câu 6. Tiệm cận đứng của đồ thị hàm số
2 4
1
x
y
x
là đường thẳng
A. 1.x B. 1.x C. 2.x D. 2.x
Lôøi giaûi tham khaûo
Ta có:
1
1
2 4
lim
1
x
x
x

và
1
2 4
lim
1
x
x
x
nên 1x là tiệm cận đứng. Chọn đáp án A.
Ñöôøng tieäm caän
Tìm đường tiệm cận ngang
TÝnh
lim
x
y

một số cụ thể y là tiệm cận ngang.
Tìm đường tiệm cận đứng
o
TÝnh
lim
x x
y
o
x x
là tiệm cận đứng.
Đối với hàm số
ax b
y
cx d
Tiệm cận đứng cho mẫu 0cx d và tiệm cận ngang
a
y
c
Baøi taäp töông töï vaø môû roäng
6.1. Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số
1 4
?
2 1
x
y
x
A.
2.y
B.
4.y
C.
1
2
y
D.
2.y
6.2. Tiệm cận ngang của đồ thị hàm số
5
1
y
x
là đường thẳng có phương trình ?
A. 5.y B. 0.x
C. 1.x D. 0.y
6.3. Cho hàm số
2 1
2
x
y
x
có đồ thị
( ).C
Tìm tọa độ giao điểm I
của hai đường tiệm cận của đồ thị
( ).C
A.
( 2;2).I
B.
(2;2).I
C.
(2; 2).I
D.
( 2; 2).I
6.4. Khoảng cách từ gốc tọa độ đến giao điểm của hai đường tiệm cận của đồ thị hàm số
2 1
1
x
y
x
bằng
A.
5.
B. 5.
C.
3.
D.
2.
6.5. Tìm số tiệm cận đứng của đồ thị hàm số
2
2
3 2
?
4
x x
y
x
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 10 -
A. 1. B. 2.
C. 3. D. 4.
6.6. Tiệm cận đứng của đồ thị hàm số
3
2
3 2
3 2
x x
y
x x
là đường thẳng
A. 2.x B.
2.y
C.
1,x
2.x D. 1.x
6.7. Số đường tiệm cận của đồ thị hàm số
2
2
1
x x
y
x
là
A. 1. B. 2.
C. 0. D. 3.
6.8. Đồ thị hàm số
2
2
9
2 8
x
y
x x
có bao nhiêu đường tiệm cận ?
A. 1. B. 0.
C. 3. D. 2.
6.9. Cho hàm số
( )y f x
xác định trên
\ {1},
liên tục trên mỗi khoảng xác định và có bảng biến
thiên như hình bên. Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận ?
A. 3. B. 1.
C. 2. D. 4.
6.10. Cho hàm số
( )y f x
có bảng biến thiên như hình dưới. Hỏi đồ thị hàm số
( )y f x
có bao nhiêu
đường tiệm cận ?
A. 3. B. 4.
C. 2. D. 1.
Câu 7. Đồ thị của hàm số nào dưới đây có dạng như đường cong hình bên ?
A.
4 2
2 1.y x x
B.
4 2
2 1.y x x
C.
3 2
3 1.y x x
D.
3 2
3 1.y x x
Lôøi giaûi tham khaûo
Đồ thị có dáng chữ W đồ thị bậc bốn trùng phương và
0.a
Chọn đáp án B.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 11 -
Nhận dạng đồ thị hàm số bậc ba
3 2
, ( 0).
y ax bx cx d a
Hình dáng: (nhận dạng được dấu của
) :
a
: 0.
N a
: 0.
a
И
Nhận dạng dấu của
:
c
Nếu
2
cực trị nằm hai bên trục
0.
Oy ac
Còn nếu có 1 cực trị
0.
Oy c
Nếu
2
cực trị nằm cùng bên so
0.
Oy ac
Nhận dạng dấu của hệ số
:
d
Đồ thị
( ) : 0
C Oy x y d
xem dương hay âm.
Điểm đặc biệt trên đồ thị.
Nhận dạng đồ thị hàm số bậc bốn trùng phương
4 2
, ( 0).
y ax bx c a
Hình dáng: (nhận dạng được dấu của
a
và
) :
b
0
M :
0
a
b
0
W :
0
a
b
0
:
0
ab
a
0
:
0
ab
a
Tương giao (nhận dạng được dấu của
)
c
Cắt
: 0
Oy x y c
xem dương hay âm ?
Nhận dạng đồ thị hàm số nhất biến
ax b
y
cx d
Tiệm cận:
Tiệm cận đứng
0
d
cx d x
c
xem dương hay âm ?
Tiệm cận ngang
a
y
c
dương hay âm ?
Đơn điệu:
2
( )
ad bc
y
cx d
Xem đồ thị
( )
C
từ trái sang phải:
Nếu đi lên
HS đồng biến
0 0.
y ad bc
Nếu đi xuống
HS nghịch biến
0 0.
y ad bc
Tương giao với hai trục tọa độ:
Cắt trục
: 0
b
Ox y x
a
xem dương hay âm ?
cắt trục
: 0
b
Oy x y
d
xem dương hay âm ?
Điểm đặc biệt trên đồ thị.
Nhận dạng đồ thị hàm số mũ
.
x
y a
Đồ thị nằm trên trục
.
Ox
Từ trái sang phải nếu đồ thị
( ) :
C
Đi lên
Đồng biến
1.
a
Đi xuống
Nghịch biến
0 1.
a
Nhận dạng đồ thị hàm số lôgarit
log .
a
y x
Đồ thị hàm số nằm bên trái
.
Oy
Từ trái sang phải nếu đồ thị
( )
C
Đi lên
ĐB
1.
a
Đi xuống
0 1.
a
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 12 -
Baøi taäp töông töï vaø môû roäng
7.1. Đường cong ở hình bên là đồ thị của hàm số nào ?
A.
3 2
1.y x x
B.
4 2
1.y x x
C.
3 2
1.y x x
D.
4 2
1.y x x
7.2. Đường cong ở hình bên là đồ thị của hàm số nào ?
A.
3
4.y x
B.
3 2
3 4.y x x
C.
3 2
3 4.y x x
D.
3 2
3 2.y x x
7.3. Đường cong ở hình bên là đồ thị của hàm số nào ?
A.
1
2 1
x
y
x
B.
2 1
x
y
x
C.
1
2 1
x
y
x
D.
3
2 1
x
y
x
7.4. Đường cong ở hình bên là đồ thị của hàm số nào ?
A.
4 2
2 .y x x
B.
4 2
2 .y x x
C.
4 2
2 1.y x x
D.
4 2
2 .y x x
7.5. Đường cong ở hình bên là đồ thị của hàm số nào ?
A.
2
1.y x x
B.
3
3 1.y x x
C.
4 2
1.y x x
D.
3
3 1.y x x
7.6. Đường cong ở hình bên là đồ thị của hàm số nào ?
A.
2 1
1
x
y
x
B.
2 1
1
x
y
x
C.
2 1
1
x
y
x
D.
1 2
1
x
y
x
7.7. Đường cong ở hình bên là đồ thị của hàm số nào ?
A.
2 .
x
y
B.
2
log .y x
C.
1
2
x
y
D.
1
2
log .y x
7.8. Đường cong ở hình bên là đồ thị của hàm số nào ?
A.
1
2
log .y x B.
2
log .y x
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 13 -
C.
1
2
x
y
D.
2 .
x
y
7.9. Đường cong ở hình bên là đồ thị của hàm số nào ?
A.
1
2
x
y
B.
2
5
log .
y x
C.
3
log .
y x
D.
2 .
x
y
7.10. Đường cong ở hình bên là đồ thị của hàm số nào ?
A.
e .
x
y
B.
7
log .
y x
C.
1
2
log .
y x
D.
1
e
x
y
Câu 8. Đồ thị hàm số
3
3 2
y x x
cắt trục tung tại điểm có tung độ bằng
A.
0.
B.
1.
C.
2.
D.
2.
Lôøi giaûi tham khaûo
Ta có:
3
3 2
2.
: 0
y x x
y
Oy x
Chọn đáp án C.
Töông giao cuûa hai ñoà thò
Cho hàm số
( )
y f x
có đồ thị
1
( )
C
và hàm số
( )
y g x
có đồ thị
2
( ).
C
Số nghiệm của phương trình
( ) ( )
f x g x
là số điểm chung của hai đồ thị
1
( )
C
và
2
( ).
C
Phương trình
( ) ( )
f x g x
được gọi là phương trình hoành độ giao điểm của hai đồ thị hàm số.
Baøi taäp töông töï vaø môû roäng
8.1. Đồ thị của hàm số
4 2
2
y x x
cắt trục hoành tại bao nhiêu điểm ?
A.
0.
B.
2.
C.
4.
D.
3.
8.2. Số giao điểm của đồ thị hàm số
4 2
2 2
y x x
và
2
4
y x
là
A.
0.
B.
4.
C.
1.
D.
2.
8.3. Biết đường thẳng
2 2
y x
cắt đồ thị hàm số
3
2
y x x
tại một điểm duy nhất, kí hiệu
( ; ).
x y
Tìm
.
y
A.
4.
y
B.
0.
y
C.
2.
y
D.
1.
y
8.4. Tìm tọa độ giao điểm của đường thẳng
1
y x
với đồ thị hàm số
1
2
x
y
x
A.
(4; 3), (0; 1).
A B
B.
( 1; 3).
C
C.
(3; 1).
D
D.
( 1;0), (3;4).
I J
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 14 -
8.5. Tìm tập hợp
m
để đồ thị hàm số
2
1
x m
y
x
cắt đường thẳng
1
y x
tại
2
điểm phân biệt ?
A.
( ;2].
B.
( ;2).
C.
( ; 2).
D.
(2; ).
8.6. Tìm tất cả các giá trị của tham số
m
để đường thẳng
2 1
y x
cắt đồ thị hàm số
1
x m
y
x
A.
3
1.
2
m
B.
3
2
m
C.
3
1.
2
m
D.
3
2
m
8.7. Với giá trị nào của
m
thì đồ thị hàm số
3
( 1) 5
y x m x
cắt trục hoành tại điểm có hoành
độ bằng
2 ?
A.
1
2
m
B.
1
2
m
C.
15
2
m
D.
15
2
m
8.8. Tìm tất cả các giá trị của tham số
m
để đồ thị hàm số
3 2
3 1
y x x
cắt đường thẳng
2 3
y m
tại ba điểm phân biệt ?
A.
0 4.
m
B.
0 2.
m
C.
3 1.
m
D.
0 2.
m
8.9. Tìm tập hợp
m
để đồ thị hàm số
3 2 2
3 2 2
y x x m m
cắt trục hoành tại ba điểm phân biệt.
A.
( 2; 2) ( 1;1).
B.
(1; ).
C.
( 2;0).
D.
( 1;0) (1;2).
8.10. Tìm tập hợp
m
để đường thẳng
1
y mx
và đồ thị hàm số
3
3 1
y x x
có
3
điểm chung.
A.
3.
m
B.
3.
m
C.
3.
m
D.
3.
m
8.11. Tìm tất cả các giá trị của tham số
m
sao cho đồ thị của hai hàm số
3 2
2 2
y x x mx
và
2
y x m
có một điểm chung duy nhất.
A.
3.
m
B.
3.
m
C.
3.
m
D.
3.
m
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 15 -
8.12. Tìm số giao điểm của đồ thị hàm số
4 2 2
2 1
y x x m
với trục hoành (với
m
là tham số).
A.
1.
B.
2.
C.
3.
D.
4.
8.13. Tìm tập hợp
m
để đồ thị hàm số
4 2
2 2
y x mx m
cắt trục
Ox
tại
4
điểm phân biệt.
A.
(2; ).
B.
( ;1).
C.
( ; 1) (2; ).
D.
(0; ).

8.14. Tìm các giá trị của
m
để dường thẳng
1
y
cắt đồ thị hàm số
4 2
(3 2) 3
y x m x m
tại
bốn điểm phân biệt.
A.
1
3
1
m
m
B.
1 0.
m
C.
1
3
0
m
m
D.
1
3
0
m
m
8.15. Tìm tất cả các giá trị thực của tham số
m
sao cho đồ thị hàm số
4 2 2
2(2 1) 4
y x m x m
cắt
trục hoành tại bốn điểm phân biệt
1 2 3 4
, , ,
x x x x
thỏa mãn
2 2 2 2
1 2 3 4
6.
x x x x
A.
1
4
m
B.
1
2
m
C.
1
4
m
D.
1
4
m
Câu 9. Với
a
là số thực tùy ý,
3
log (9 )
a
bằng
A.
3
1
log .
2
a
B.
3
2 log .
a
C.
2
3
(log ) .
a
D.
3
2 log .
a
Lôøi giaûi tham khaûo
Ta có:
3 3 3 3
log (9 ) log 9 log 2 log .
a a a
Chọn đáp án D.
Coâng thöùc muõ & loâgarít
Cho
a
và
b
là các số thực dương
x
và
y
là những số thực tùy ý.
. . ...
n
a a a a a

x
x
x
a a
b
b
n số a
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 16 -
.
x y x y
a a a
( )
m
n
n
m m
n
a a a
1
x
x y n
y n
a
a a
a a
0
( ) 1, ( ) 0
u x u x
.
( ) ( )
x y x y y x
a a a
. ( . )
x x x
a b a b
Cho
0 1
a
và
, 0.
b c
log ( ) ( )
b
a
f x b f x a
log .log .
n
a a
b n b
1
log log
n
a
a
b b
n
log log log
a a a
b
b c
c
log
log
log
c
a
c
b
b
a
1 ln
log log
log ln
a a
b
b
b b
a a
log 1 0, log 1
a a
a
log log log
b b a
c a b
a c b a
log ( ) log log
a a a
b c b c
e
log ln
b b
và
10
log log .
b b
Baøi taäp töông töï vaø môû roäng
9.1. Cho
b
là số thực dương khác
1.
Giá trị của
1
2
2
log ( . )
b
b b
bằng
A.
3
2
B.
1.
C.
5
2
D.
1
4
9.2. Cho
0 1.
a
Giá trị của biểu thức
3
2
log ( . )
a
P a a
bằng
A.
4
3
B.
3.
C.
5
3
D.
5
2
9.3. Cho
a
là số thực dương khác
4.
Giá trị của
3
4
log
64
a
a
bằng
A.
3.
B.
1
3
C.
3.
D.
1
3
9.4. Cho
log 1
a
x
và
log 4.
a
y
Giá trị của
2 3
log ( )
a
x y
bằng
A.
3.
B.
10.
C.
14.
D.
65.
9.5. Cho
, 0
a b
và
, 1,
a b
giá trị của
3 4
log .log
b
a
P b a
bằng
A.
18.
B.
24.
C.
12.
D.
6.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 17 -
9.6. Cho
a
là số thực dương thỏa mãn
10,
a
mệnh đề nào dưới đây sai ?
A.
log(10. ) 1 log .
a a
B.
10
log log 1.
a
a
C.
log(10 ) .
a
a
D.
10
log( ) .
a a
9.7. Với các số thực
,
x
y
dương bất kì. Mệnh đề nào dưới đây đúng ?
A.
2 2 2
log ( ) log log .
x y x y
B.
2 2 2
log ( ) log . log .
xy x y
C.
2
2 2 2
log 2 log log .
x
x y
y
D.
2
2
2
log
log
log
x
x
y y
9.8. Cho
a
là một số thực dương. Khi đó
3
3
2
5
.
a a
bằng
A.
1
15
.
a
B.
2
5
.
a
C.
1
15
.
a
D.
19
15
.
a
9.9. Cho các số thực
,
x
y
thỏa mãn
2 3
x
và
3 4.
y
Giá trị biểu thức
8 9
x y
bằng
A.
43.
B.
17.
C.
24.
.
3 2
2 3
log 3 log 4.
9.10. Cho hai số thực dương
a
và
.
b
Rút gọn biểu thức
1 1
3 3
6 6
a b b a
A
a b
ta được
A.
6
.
A ab
B.
3
.
A ab
C.
3
1
A
ab
D.
6
1
A
ab
Câu 10. Đạo hàm của hàm số
2
x
y
là
A.
2 ln 2.
x
y
B.
2 .
x
y
C.
2
ln 2
x
y
D.
1
.2 .
x
y x
Lôøi giaûi tham khaûo
Theo công thức
( ) . .ln
u u
a u a a
thì
2
x
y
có đạo hàm
2 ln 2.
x
y
Chọn đáp án A.
Ñaïo haøm cuûa haøm soá muõ vaø loâgarít
( ) . .ln .
u u
a u a a
(ln )
u
u
u
(log )
ln
a
u
u
u a
Baøi taäp töông töï vaø môû roäng
10.1. Hàm số
2
2
2
x x
y
có đạo hàm là
A.
2
2
2 .ln2.
x x
y
B.
2
2
(4 1).2 .ln2.
x x
y x
C.
2
2 2
(2 ).2 .ln2.
x x
y x x
D.
2
(4 1).ln(2 ).
y x x x
10.2. Hàm số
1 2
e
x
y
có đạo hàm là
A.
1 2
2e .
x
y
B.
1 2
e .
x
y
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 18 -
C.
1 2
2e .
x
y
D.
1 2
2e .
x
y
10.3. Hàm số
2 3
2
x
y
có đạo hàm là
A.
2 2
2 ln 4.
x
B.
2
4 ln 4.
x
C.
2 2
2 ln16.
x
D.
2 3
2 ln 2.
x
10.4. Hàm số
2
1
8
x
y
có đạo hàm là
A.
2
2 .8 .
x
x
B.
2
2 .8 ln 4.
x
x
C.
2
2
( 1).8 .
x
x
D.
2
1
6 .8 .ln2.
x
x
10.5. Đạo hàm của hàm số
2
log (2 1)
y x
là
A.
2
(2 1)ln
x x
B.
2
(2 1)ln2
x
C.
2ln2
1
x
D.
2
( 1)ln 2
x
10.6. Hàm số
2
2
( ) log ( 2 )
f x x x
có đạo hàm là
A.
2
ln2
2
x x
B.
2
1
( 2 )ln 2
x x
C.
2
(2 2)ln 2
2
x
x x
D.
2
2 2
( 2 )ln 2
x
x x
10.7. Đạo hàm của hàm số
2
log( )
y x x
là
A.
2
1
( )ln10
x x
B.
2
2 1
x
x x
C.
2
2 1
( )log e
x
x x
D.
2
2 1
.log e.
x
x x
10.8. Cho hàm số
.
y x
Giá trị của
(1)
y
bằng
A.
2
ln .
B.
ln .
C.
0.
D.
( 1).
10.9. Hãy tính đạo hàm của hàm số
3
2 3
.
y x x
trên khoảng
(0; ).

A.
6
7
. .
6
x
B.
9
.
x
C.
3
4
. .
3
x
D.
7
6
7
x
10.10. Đạo hàm của hàm số
2
2
log (2 1)
y x
là
A.
2
2 log (2 1)
(2 1)ln2
x
x
B.
2
4 log (2 1)
(2 1)ln2
x
x
C.
2
4 log (2 1)
2 1
x
x
D.
2
(2 1)ln2
x
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 19 -
Câu 11. Với
a
là hai số thực dương tùy ý,
3
a
bằng
A.
6
.
a
B.
3
2
.
a
C.
2
3
.
a
D.
1
6
.
a
Lôøi giaûi tham khaûo
Theo công thức
,
n
m
n
m
a a
ta có
3
3
2
.
a a
Chọn đáp án B.
Baøi taäp töông töï vaø môû roäng
11.1. Rút gọn biểu thức
1
6
3
.
P x x
với
0.
x
A.
1
8
.
P x
B.
2
9
.
P x
C.
.
P x
D.
2
.
P x
11.2. Rút gọn biểu thức
5
3
3
:
Q b b
với
0
b
A.
2
.
Q b
B.
5
9
.
Q b
C.
4
3
.
Q b
D.
4
3
.
Q b
11.3. Cho biểu thức
4
3
2 3
. . ,
P x x x
với
0.
x
Mệnh đề nào dưới đây đúng ?
A.
1
2
.
P x
B.
13
24
.
P x
C.
1
4
.
P x
D.
2
3
.
P x
11.4. Tính giá trị của biểu thức
2017 2016
(7 4 3) (4 3 7) .
P
A.
1.
P
B.
7 4 3.
P
C.
7 4 3.
P
D.
2016
(7 4 3) .
P
11.5. Giá trị của biểu thức
(1 3) (3 3)
bằng
A.
1008
12 .
B.
1008
4 .
C.
1008
(1 3) .
D.
1008
(3 3) .
11.6. Với
a
và
b
là hai số thực dương tùy ý và
1,
a
log ( )
a
a b
bằng
A.
1
log .
2
a
b
B.
1
2 log .
2
a
b
C.
2 log .
a
b
D.
1 2 log .
a
b
11.7. Với
, 0
a b
và
1,
a
thì
3
2
)
(log
a
a b
bằng
A.
1
log .
6
a
b
B.
3
log .
2
a
b
C.
3
6 log .
2
a
b
D.
2 1
log .
3 6
a
b
11.8. Cho
a
và
b
là hai số thực dương thỏa mãn
3
. 10.
a b
Giá trị của
1 1
log log
2 3
a b
bằng
A.
0.
B.
1.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 20 -
C.
10.
D.
1.
11.9. Cho
a
và
b
là hai số thực dương thỏa mãn
3
27.
ab
Giá trị của
3 3
log 6 log
a b
bằng
A.
3.
B.
6.
C.
9.
D.
1.
11.10. Xét các số thực
a
và
b
thỏa mãn
1
3
3
27
9
log log 3.
3
b
a
Mệnh đề nào đúng ?
A.
1
2
18
a b
B.
1
2
18
a b
C.
1
2
18
b a
D.
1
2
18
a b
Câu 12. Nghiệm của phương trình
2 4
5 25
x
là
A.
3.
x
B.
2.
x
C.
1.
x
D.
1.
x
Lôøi giaûi tham khaûo
Ta có:
2 4
5
5 25 2 4 log 25 2 3.
x
x x
Chọn đáp án A.
Phöông trình muõ cô baûn (vôùi ñieàu kieän xaùc ñònh)
0 log .
x
a
a b x b
( ) ( )
( ) ( ).
f x g x
a a f x g x
Baøi taäp töông töï vaø môû roäng
12.1. Nghiệm phương trình
2 1
3 27
x
là
A.
5.
x
B.
1.
x
C.
2.
x
D.
4.
x
12.2. Phương trình
2 1
5 125
x
có nghiệm là
A.
3
2
x
B.
5
2
x
C.
1.
x
D.
3.
x
12.3. Số nghiệm của phương trình
2
2 1
x x
là
A.
0.
B.
3.
C.
1.
D.
2.
12.4. Phương trình
2
2 5 4
2 4
x x
có tổng tất cả các nghiệm bằng
A.
1.
B.
1.
C.
5
2
D.
5
2
12.5. Tích số của tất cả các nghiệm thực của phương trình
2
3
2
7 49 7
x x
bằng
A.
1.
B.
1.
C.
1
2
D.
1
2
12.6. Tích tất cả các nghiệm của phương trình
2
ln 2 1
3 4
x x
bằng
A.
3
1 2 log 2.
B.
3
1 2 log 2.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 21 -
C.
1 2 ln 2.
D.
1 2ln2.
12.7. Nghiệm của phương trình
1
3 .5 7
x x
là
A.
15
log 35.
x
B.
21
log 5.
x
C.
21
log 35.
x
D.
15
log 21.
x
12.8. Nghiệm của phương trình
5
3 3 121
x x
là
A.
2
log 3.
x
B.
3
log 2.
x
C.
3
log 2.
x
D.
2
log 3.
x
12.9. Gọi
1 2 1 2
, ( )
x x x x
là hai nghiệm của phương trình
2
1 2
9 3 .
x x
Giá trị
1 2
2 3
x x
bằng
A.
5.
B.
10.
C.
11.
D.
28.
12.10. Tích các nghiệm của phương trình
2 3
2 2
(3 2 2) (3 2 2)
x x x
bằng
A.
0.
B.
2.
C.
1.
D.
1.
Câu 13. Nghiệm của phương trình
2
log (3 ) 3
x
là
A.
2.
x
B.
2.
x
C.
8
3
x
D.
1
2
x
Lôøi giaûi tham khaûo
3
2
8
log (3 ) 3 3 2
3
x x x
Chọn đáp án C.
Phöông trình muõ & loâgarít cô baûn (vôùi ñieàu kieän xaùc ñònh)
log
.
b
a
x b x a
log ( ) log ( ) ( ) ( ).
a a
f x g x f x g x
Baøi taäp töông töï vaø môû roäng
13.1. Nghiệm của phương trình
2
log ( 5) 4
x
là
A.
3.
x
B.
13.
x
C.
21.
x
D.
11.
x
13.2. Phương trình
2
3
log ( 10 9) 2
x x
có nghiệm là
A.
10
.
0
x
x
B.
2
.
0
x
x
C.
2
.
9
x
x
D.
10
.
9
x
x
13.3. Nghiệm của phương trình
ln(4 ) 100
x
là
A.
100
e 4.
x
B.
100
4 10 .
x
C.
100
4 e .
x
D.
100
10 4.
x
13.4. Nghiệm của phương trình
log( 1) 2
x
là
A.
101.
x
B.
2
e 1.
x
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 22 -
C.
2
e 1.
x
D.
2
1.
x
13.5. Nghiệm của phương trình
100
log10 250
x
thuộc khoảng
A.
(0;2).
B.
(2; ).

C.
( ; 2).

D.
( 2; 0).
13.6. Nghiệm của phương trình
3 2
log (log ) 1
x
là
A.
8.
x
B.
6.
x
C.
9.
x
D.
2.
x
13.7. Nghiệm của phương trình
3 1
2
log (3 1) 3
x
là
A.
2.
x
B.
1.
x
C.
3.
x
D.
8.
x
13.8. Nghiệm của phương trình
3 3
log 2 1) l 1
( (
og 1)
x x
là
A.
4.
x
B.
3.
x
C.
2.
x
D.
1.
x
13.9. Tìm tập nghiệm
S
của phương trình
2 2
log 1) lo 1
(
g ) 3
(
.
x x
A.
.
3
{
3
}
;
S
B.
{4}.
S
C.
{ }.
3
S
D.
.
10 0
{ }
; 1
S
13.10. Tập nghiệm của phương trình
2 4 3
log ( 3) 2 log 3.log 2
x x
là
A.
{5}.
B.
{4;5}.
C.
{4}.
D.
{2;4}.
Câu 14. Cho hàm số
2
( ) 3 1.
f x x
Trong các khẳng định sau, khẳng định nào đúng ?
A.
2
( )d 3 .
f x x x x C
B.
3
( )d .
f x x x x C
C.
3
1
( )d .
3
f x x x x C
D.
3
( )d .
f x x x C
Lôøi giaûi tham khaûo
Áp dụng công thức nguyên hàm cơ bản thì
2 3
( )d (3 1)d .
f x x x x x x C
Chọn đáp án B.
Baûng nguyeân haøm cuûa moät soá haøm thöôøng gaëp
0d .
x C
d .
k x kx C
1
d .
1
n
n
x
x x C
n
1
1 ( )
( ) d .
1
n
n
ax b
ax b x C
a n
1
d ln .
x x C
x
1 1
d ln .
x ax b C
ax b a
2
1 1
d .
x C
x
x
2
1 1 1
d .
( )
x C
a ax b
ax b
sin d cos .
x x x C
1
sin( )d cos( ) .
ax b x ax b C
a
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 23 -
cos d sin .
x x x C
1
cos( )d sin( ) .
ax b x ax b C
a
2
1
d cot .
sin
x x C
x
2
d 1
cot( ) .
sin ( )
x
ax b C
a
ax b
2
1
d tan .
cos
x x C
x
2
d 1
tan( ) .
cos ( )
x
ax b C
a
ax b
e d e .
x x
x C
1
e d e .
ax b ax b
x C
a
d .
ln
x
x
a
a x C
a
1
d .
ln
x
x
a
a x C
a
♦ Nhận xét. Khi thay
x
bằng
( )
ax b
thì khi lấy nguyên hàm nhân kết quả thêm
1
a
Một số công thức cần nhớ
Bậc chẵn của sin và cosin
Hạ bậc:
2 2
1 1 1 1
sin cos2 , cos cos 2 .
2 2 2 2
a a a a
tan d ln cos .
x x x C
cot d ln sin .
x x x C
1 2
d .
x ax b C
a
ax b
3
2
d ( ) .
3
ax b x ax b C
a
Baøi taäp töông töï vaø môû roäng
14.1. Họ nguyên hàm của hàm số
3
( )
f x x x
là
A.
4 2
.
x x C
B.
2
3 1 .
x C
C.
3
.
x x C
D.
4 2
1 1
.
4 2
x x C
14.2. Họ tất cả các nguyên hàm của hàm số
6
2
1 1
( ) 7 2
f x x
x
x
là
A.
7
1
ln 2 .
x x x
x
B.
7
1
ln 2 .
x x x C
x
C.
7
1
ln 2 .
x x x C
x
D.
7
1
ln 2 .
x x x C
x
14.3. Họ tất cả các nguyên hàm của hàm số
( ) 5
x
f x
là
A.
5 .
x
C
B.
5 ln 5 .
x
C
C.
5
.
ln 5
x
C
D.
1
5
.
1
x
C
x
14.4. Họ tất cả các nguyên hàm của hàm số
5
( ) e
x
f x
là
A.
5
e ln 5 + .
x
C
B.
5
1
e + .
5
x
C
C.
5
5e + .
x
C
D.
5
e .
x
C
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 24 -
14.5. Họ tất cả các nguyên hàm của hàm số
2
( )
4 3
f x
x
là
A.
3
2 ln 2 .
2
x C
B.
1 3
ln 2 .
2 2
x C
C.
1 3
ln 2 .
2 2
x C
D.
1
ln 4 3 .
4
x C
14.6. Một nguyên hàm
( )
F x
của hàm số
2
( ) 3 2 5
f x x x
thỏa mãn
(1) 4
F
là
A.
3 2
5 3.
x x x
B.
3 2
5 3.
x x x
C.
3 2
5 3.
x x x
D.
3 2
5 3.
x x x
14.7. Họ tất cả các nguyên hàm của hàm số
8
( ) (2 1)
f x x
là
A.
9
(2 1)
.
9
x
C
B.
9
(1 2 )
.
18
x
C
C.
9
(2 1)
.
18
x
C
D.
9
(1 2 )
.
9
x
C
14.8. Họ nguyên hàm của hàm số
2
( ) 2 .3 .7
x x x
f x
là
A.
84
.
ln 84
x
C
B.
2
2 .3 .7
.
ln 4.ln 3.ln 7
x x x
C
C.
84 .
x
C
D.
84 .ln 84 .
x
C
14.9. Họ tất cả các nguyên hàm của hàm số
( ) 2 3
là
A.
2
(2 3) 2 3 .
3
x x C
B.
1
(2 3) 2 3 .
3
x x C
C.
1
(2 3) 2 3 .
3
x x C
D.
1
2 3 .
2
x C
14.10. Họ tất cả các nguyên hàm của hàm số
1
( )
2 2 1
f x
x
là
A.
1
2 1 .
2
x C
B.
2 1 .
x C
C.
2 2 1 .
x C
D.
1
.
(2 1) 2 1
C
x x
Câu 15. Cho hàm số
( ) cos2 .
f x x
Trong các khẳng định sau, khẳng định nào đúng ?
A.
1
( )d sin2 .
2
f x x x C
B.
1
( )d sin 2 .
2
f x x x C
C.
( )d 2 sin 2 .
f x x x C
D.
( )d 2 sin 2 .
f x x x C
Lôøi giaûi tham khaûo
Áp dụng công thức nguyên hàm cơ bản:
1
cos(2 )d sin(2 ) .
2
x x x C
Chọn A.
Baøi taäp töông töï vaø môû roäng
15.1. Họ nguyên hàm của hàm số
( ) sin 2 cos 3
f x x x
là
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 25 -
A.
1 1
cos 2 sin 3 .
2 3
x x C
B.
1 1
cos 2 sin 3 .
2 3
x x C
C.
cos2 sin 3 .
x x C
D.
cos2 sin 3 .
x x C
15.2. Một nguyên hàm
( )
F x
của hàm số
( ) cos 2
f x x
thỏa mãn
2
2
F
là
A.
1
sin 2 2 .
2
x
B.
3
sin 2
2
x x
C.
sin 2 .
x
D.
2 2 .
x
15.3. Họ nguyên hàm của hàm số
( ) sin cos
f x x x
là
A.
1
cos 2 .
4
x C
B.
1
cos2 .
4
x C
C.
sin2 .
x C
D.
sin cos .
x x C
15.4. Cho
( )
F x
là một nguyên hàm của
2
( ) 4 cos 5
f x x
thỏa
( ) 0.
F
Hàm số
( )
F x
là
A.
3 sin2 3 .
x x
B.
3
4 4
cos 5 5 .
3 3
x x
C.
3 sin 2 3 .
x x
D.
3
4
sin 5 5 .
3
x x
15.5. Họ nguyên hàm của hàm số
( ) sin 5 sin 2
f x x x
là
A.
cos 3 cos 7
.
6 14
x x
C
B.
sin 3 sin 7
.
6 14
x x
C
C.
cos 3 cos 7
.
6 14
x x
C
D.
sin 3 cos7
.
6 14
x x
C
15.6. Họ nguyên hàm hàm số
( ) sin 5 cos
f x x x
là
A.
1
cos 5 .
5
x C
B.
1
cos 5 .
5
x C
C.
cos 4 cos 6
.
8 12
x x
C
D.
1 1
cos 4 cos 6 .
8 12
x x C
15.7. Họ nguyên hàm của hàm số
2
( ) tan
f x x
là
A.
tan .
x C
B.
tan .
x x C
C.
tan .
x x C
D.
tan .
x x C
15.8. Một nguyên hàm
( )
F x
của hàm số
2
1
( ) sin
cos
f x x
x
thỏa mãn
2
4 2
F
là
A.
cos tan .
x x C
B.
cos tan 2 1.
x x
C.
cos tan 2 1.
x x
D.
cos tan 2 1.
x x
15.9. Cho hàm số
( )
f x
thỏa mãn
( ) sin
f x x x
và
(0) 1.
f
Khi đó hàm số
( )
f x
là
A.
2
cos 2.
2
x
x
B.
2
cos 2.
2
x
x
C.
2
1
cos
2 2
x
x
D.
2
cos .
2
x
x
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 26 -
15.10. Cho hàm số
( )
f x
thỏa mãn
( ) 2 cos2
f x x
và
2 .
2
f
Mệnh đề nào sau đây sai ?
A.
(0) .
f
B.
sin 2
( ) 2 .
2
x
f x x
C.
sin 2
( ) 2 .
2
x
f x x
D.
0.
2
f
Câu 16. Nếu
2
1
( )d 5
f x x
và
3
2
( )d 2
f x x
thì
3
1
( )d
f x x
bằng
A.
3.
B.
7.
C.
10.
D.
7.
Lôøi giaûi tham khaûo
Ta có
3 2 3
1 1 2
( )d ( )d ( )d 5 2 3.
f x x f x x f x x
Chọn đáp án A.
Tính chaát cuûa nguyeân haøm vaø tích phaân
( ) ( ), ( )d ( ) ( ) ( ).
b
b
a
a
F x f x f x x F x F b F a
. ( )d . ( )d , ( )d ( )d .
b b b a
a a a b
k f x x k f x x f x x f x x
( ) ( ) d ( )d ( )d .
b b b
a a a
f x g x x f x x g x x
( )d ( )d ( )d ...
b b b
a a a
f t t f u u f x x
( )d ( ) , ( )d ( ) .....
b b
b b
a a
a a
f x x f x f x x f x
( )d ( )d ( )d .
b c b
a a c
f x x f x x f x x
Baøi taäp töông töï vaø môû roäng
16.1. Cho
3
1
( )d 2016
f x x
và
3
4
( )d 2017,
f x x
khi đó
4
1
( )d
f x x
bằng
A.
4023.
B.
1.
C.
1.
D.
0.
16.2. Nếu
2
0
( )d 3
f x x
thì
2
0
4 ( ) 3 d
f x x
bằng
A.
2.
B.
6.
C.
8.
D.
4.
16.3. Nếu
9
0
( )d 37
f x x
và
0
9
( )d 16
g x x
thì
9
0
2 ( ) 3 ( ) d
f x g x x
bằng
A.
26.
B.
58.
C.
143.
D.
122.
16.4. Nếu
2
0
( )d 3
f x x
và
2
0
( )d 2
g x x
thì
2
0
2 ( ) 2 ( ) d
x f x g x x
bằng
A.
18.
B.
5.
C.
11.
D.
3.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 27 -
16.5. Cho hàm số
( )
f x
có đạo hàm liên tục trên đoạn
[2;3],
đồng thời
(2) 2
f
và
(3) 5.
f
Khi đó giá
trị của tích phân
3
2
d
( )
f x
x
bằng
A.
3.
B.
7.
C.
10.
D.
3.
16.6. Cho hàm
( )
f x
có
( )
f x
liên tục trên
[1;3],
( 1) 3
f
và
3
1
( )d 10.
f x x
Giá trị của
(3)
f
bằng
A.
13.
B.
7.
C.
13.
D.
7.
16.7. Cho hàm số
( )
f x
liên tục trên
,
có
1
0
( )d 2
f x x
và
3
1
( )d 6.
f x x
Khi đó
3
0
( )d
f x x
bằng
A.
8.
B.
12.
C.
36.
D.
4.
16.8. Cho hàm số
2
3 khi 0 1
( ) .
4 khi 1 2
x x
f x
x x
Tích phân
2
0
( )d
f x x
bằng
A.
7
2
B.
5
2
C.
1.
D.
2.
16.9. Cho hàm số
( )
y f x
liên tục trên
[ ; ],
a b
nếu
( )d 5
d
a
f t t
và
( )d 2
d
b
f u u
thì
( )d
b
a
f x x
bằng
A.
3.
B.
7.
C.
5.
D.
10.
16.10. Nếu
3
1
( ) 3 ( ) d 10
f x g x x
và
3
1
2 ( ) ( ) d 6
f x g x x
thì
3
1
( ) ( ) d
f x g x x
bằng
A.
8.
B.
9.
C.
6.
D.
7.
Câu 17. Tích phân
2
3
1
d
x x
bằng
A.
15
3
B.
17
4
C.
7
4
D.
15
4
Lôøi giaûi tham khaûo
Ta có:
2
2
4 4 4
3
1
1
2 1 15
d
4 4 4
x
x x
Chọn đáp án D.
Baøi taäp töông töï vaø môû roäng
17.1. Với
m
là tham số thực, ta có
2
1
(2 1)d 4.
mx x
Khi đó
m
thuộc tập hợp nào sau đây ?
A.
( 3; 1).
B.
[ 1; 0).
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 28 -
C.
[0;2).
D.
[2;6).
17.2. Tích phân
2
3 1
1
e d
x
x
bằng
A.
5 2
1
(e e ).
3
B.
5 2
1
e e .
3
C.
5 2
e e .
D.
5 2
e e .
17.3. Tích phân
2018
0
2 d
x
x
bằng
A.
2018
2
ln 2
B.
2018
2 1
ln 2
C.
2018
2 1.
D.
2018
2 .
17.4. Tích phân
2
1
d
2 3
x
x
bằng
A.
7
2 ln
5
B.
1
ln 35.
2
C.
7
ln
5
D.
1 7
ln
2 5
17.5. Giả sử
4
0
2
sin 3 d
2
x x a b
với với
, .
a b
Khi đó giá trị của
a b
bằng
A.
1
6
B.
1
6
C.
3
10
D.
1
5
17.6. Biết
1
0
1d
3
a b
x x
c
với
0
a
và
b
c
là phân số tối giản. Khi đó
2 3
a b c
bằng
A.
32.
B.
45.
C.
96.
D.
134.
17.7. Nếu
2
4
3
d 13 7
1 3
x a b
x
với
,
a b
thì
2 3
2
a b
bằng
A.
13.
B.
29.
C.
5.
D.
13.
17.8. Cho hàm số
( )
f x
có
(0) 2
f
và
( ) (e 1)e ,
x x
f x
.
x
Khi đó
1
0
( )d
f x x
bằng
A.
1
1 ln 2.
2
B.
1
ln 2
2 4
C.
1
e
2
D.
1
e
2
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 29 -
17.9. Cho hàm số
( )
f x
có
(0) 1
f
và
2
1
( ) ,
cos
f x
x
; .
2 2
x
Khi đó
4
0
( )d
f x x
bằng
A.
1
1 ln 2.
2
B.
1
ln 2
2 4
C.
1
ln 3.
2
D.
1
2
17.10. Cho hàm số
2
khi 0 1
( ) .
1
2 1 khi 1 3
x
f x
x
x x
Khi đó
3
0
( )d
f x x
bằng
A.
6 ln 4.
B.
4 ln 4.
C.
6 ln 2.
D.
2 2 ln2.
Câu 18. Số phức liên hợp của số phức
3 2
z i
là
A.
3 2 .
z i
B.
2 3 .
z i
C.
3 2 .
z i
D.
3 2 .
z i
Lôøi giaûi tham khaûo
Ta có
( )
z a bi a bi
nên
3 2 .
z i
Chọn đáp án A.
Kieán thöùc cô baûn cuûa soá phöùc
Số phức
z a bi
với
,
a b
và
2
1.
i
Gọi
a
là phần thực và
b
là phần ảo của số phức
.
z
Ta gọi
z a bi
là số phức liên hợp của
.
z
Điểm
( ; )
M a b
trong mặt phẳng được gọi là điểm biểu diễn của số phức
.
z a bi
Môđun của số phức
z a bi
là
2 2
.
z OM a b

Hai số phức là bằng nhau nếu phần thực và phần ảo của chúng tương ứng bằng nhau.
Số phức là thuần ảo
phần thực bằng
0
và số thực
phần ảo bằng
0.
Baøi taäp töông töï vaø môû roäng
18.1. Số phức liên hợp của số phức
2
z i
là
A.
2 .
z i
B.
2 .
z i
C.
2 .
z i
D.
2 .
z i
18.2. Tìm số phức liên hợp của
(3 1).
z i i
A.
3 .
i
B.
3 .
i
C.
3 .
i
D.
3 .
i
18.3. Số phức liên hợp của
(1 )(3 2 )
z i i
là
A.
1 .
i
B.
5 .
i
C.
5 .
i
D.
1 .
i
18.4. Cho số phức
z
thỏa mãn
1 .
3 2
z
i
i
Tìm số phức liên hợp
.
z
A.
5 .
i
B.
1 5 .
i
C.
5 .
i
D.
1 5 .
i
18.5. Cho số phức
z
thỏa
( 1) 2
2 3 .
1 2
i z
i
i
Đặt
,
z a bi
khi đó
a b
bằng
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 30 -
A.
1.
B.
1.
C.
6.
D.
6.
18.6. Cho số phức
z
thoả
(1 ) 14 2 .
i z i
Biết
.
z a bi
Giá trị của
a b
bằng
A.
4.
B.
14.
C.
4.
D.
14.
18.7. Cho số phức
2 .
z i
Tìm
.
z
A.
3.
z
B.
5.
z
C.
2.
z
D.
5.
z
18.8. Tính môđun của số phức
z
thỏa mãn
(2 ) 13 1.
z i i
A.
34.
z
B.
34.
z
C.
5 34
3
z
D.
34
3
z
18.9. Cho số phức
2 3 .
z i
Tìm môđun của số phức
(1 ) .
w i z z
A.
3.
w
B.
5.
w
C.
4.
w
D.
7.
w
18.10. Tìm tất cả các cặp số thực
( ; )
x y
thỏa điều kiện
3 2 1 (2 ) .
x yi y x i
A.
(1;1).
B.
(1;1), (0; 1).
C.
(1;0), ( 1; 1).
D.
( 1; 1).
Câu 19. Cho hai số phức
3
z i
và
2 3 .
w i
Số phức
z w
bằng
A.
1 4 .
i
B.
1 2 .
i
C.
5 4 .
i
D.
5 2 .
i
Lôøi giaûi tham khaûo
Ta có
(3 ) (2 3 ) 1 2 .
z w i i i
Chọn đáp án B.
Baøi taäp töông töï vaø môû roäng
19.1. Cho hai số phức
1
2
z i
và
2
1 3 .
z i
Phần thực của số phức
1 2
z z
bằng
A.
1.
B.
3.
C.
4.
D.
2.
19.2. Cho các số phức
1 2
z i
và
2 .
w i
Hỏi số phức
.
u z w
có đặc điểm nào ?
A. Phần thực là
4
và phần ảo là
3.
B. Phần thực là
0
và phần ảo là
3.
C. Phần thực là
0
và phần ảo là
3 .
i
D. Phần thực là
4
và phần ảo là
3 .
i
19.3. Cho hai số phức
1
1 3
z
i
và
2
2 5 .
z i
Phần ảo của số phức
1 2
z z z
bằng
A.
2.
B.
2.
C.
3.
D.
3.
19.4. Cho hai số phức
1
5 7
z i
và
2
2 3 .
z i
Tính số phức
1 2
.
z z z
A.
7 4 .
z i
B.
2 5 .
z i
C.
2 5 .
z i
D.
3 10 .
z i
19.5. Cho hai số phức
1 3 , 2 .
z i w i
Tìm phần ảo của số phức
. .
u z w
A.
7.
B.
5 .
i
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 31 -
C.
5.
D.
7 .
i
19.6. Cho số phức
3 2 .
z i
Tìm phần thực của số phức
2
.
z
A.
9.
B.
12.
C.
5.
D.
13.
19.7. Cho số phức
1 2 .
z i
Phần thực của số phức
3
2
.
w z z z
z
là
A.
33
5
B.
31
5
C.
32
5
D.
32
5
19.8. Cho số phức
z
thỏa
(1 ) 1 3 0.
i z i
Tìm phần ảo của số phức
w 1 .
iz z
A. Phần ảo là
1.
B. Phần ảo là
3.
C. Phần ảo là
2.
D. Phần ảo là
1.
19.9. Tìm phần thực
a
và phần ảo
b
của số phức
10
(1 ) .
z i
A.
0, 32.
a b
B.
0, 32 .
a b i
C.
0, 32.
a b
D.
32, 0.
a b
19.10. Cho số phức
( , )
z a bi a b
thỏa mãn
(1 ) 2 3 2 .
i z z i
Giá trị của
a b
bằng
A.
1
2
B.
1
2
C.
1.
D.
1.
Câu 20. Trên mặt phẳng tọa độ, điểm biểu diễn của số phức
3 2
i
có tọa độ là
A.
(2;3).
B.
( 2;3).
C.
(3;2).
D.
(3; 2).
Lôøi giaûi tham khaûo
Điểm biểu diễn của
z a bi
có tọa độ là
( ; )
a b
nên
3 2
i
biểu diễn bởi
(3; 2).
Chọn đáp án D.
Baøi taäp töông töï vaø môû roäng
20.1. Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức
3 2
z i
?
A.
( 3;2).
P
B.
(2; 3).
Q
C.
(3; 2).
N
D.
)
(
2; 3 .
M
20.2. Trên mặt phẳng tọa độ, biết
( 1;2)
M
là điểm biểu diễn của số phức
.
z
Phần thực của
z
bằng
A.
1.
B.
2.
C.
2.
D.
1.
20.3. Trên mặt phẳng tọa độ, biết
( 3;1)
M
là điểm biểu diễn số phức
.
z
Phần thực của
z
bằng
A.
1.
B.
3.
C.
1.
D.
3.
20.4. Cho hai số phức
1 2
2 , 1 .
z i z i
Trên mặt phẳng tọa độ
,
Oxy
điểm biểu diễn số phức
1 2
2
z z
có tọa độ là
A.
(5; 1).
B.
( 1;5).
C.
(5;0).
D.
(0;5).
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 32 -
20.5. Cho hai số phức
1
1
z i
và
2
2 .
z i
Trên mặt phẳng
,
Oxy
điểm biểu diễn số phức
1 2
2
z z
có tọa độ là
A.
(2;5).
B.
(3;5).
C.
(5;2).
D.
(5;3).
20.6. Cho hai số phức
1
1
z i
và
2
1 2 .
z i
Trên mặt phẳng toạ độ
,
Oxy
điểm biểu diễn số phức
1 2
3
z z
có toạ độ là
A.
(4; 1).
B.
( 1; 4).
C.
(4;1).
D.
(1; 4).
20.7. Trên mặt phẳng tọa độ, điểm biểu diễn số phức
2
(1 2 )
z i
là điểm nào dưới đây ?
A.
( 3; 4).
P
B.
(5; 4).
Q
C.
(4; 3).
N
D.
(5; 4).
M
20.8. Điểm
M
trong hình vẽ bên là điểm biểu diễn số phức
A.
2 .
z i
B.
1 2 .
z i
C.
2 .
z i
D.
1 2 .
z i
20.9. Điểm nào trong hình vẽ bên là điểm biểu diễn số phức
1 2
z i
?
A.
.
N
B.
.
P
C.
.
M
D.
.
Q
20.10. Cho số phức
z
thỏa
(1 ) 3 .
i z i
Hỏi điểm biểu diễn của
z
là điểm nào trong các điểm sau ?
A. Điểm
.
P
B. Điểm
.
Q
C. Điểm
.
M
D. Điểm
.
N
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 33 -
Câu 21. Một khối chóp có diện tích đáy bằng 6 và chiều cao bằng 6. Thể tích của khối chóp đó
bằng
A. 10. B. 30. C. 90. D. 15.
Lôøi giaûi tham khaûo
Thể tích khối chóp là
1
.
3
V S h với S là diện tích đáy, h là chiều cao nên
6 5
10.
3
V
Chọn đáp án A.
Thể tích khối chóp
1
3
V S
đchãp ¸ y
. chiÒu cao .
Đặc biệt:
3
2
12
Tø diÖn ®Òu
(c¹nh)
V
Xác định diện tích đáy
1 1
sin ( )( )( ),
2 2
ABC a
S ah ab C p p a p b b c
với
:
2
a b c
p
nửa chu vi.
1
2
S
tam gi¸c vu«ng
(tÝch hai c¹nh gãc vu«ng).
2
3
4
S
tam gi¸c ®Òu
(c¹nh)
2
4
S
tam gi¸c vu«ng c©n
(c¹nh huyÒn)
2
S
H×nh thang
(®¸y lín ®¸y bÐ) chiÒu cao
S
H×nh ch÷ nhËt
dµi réng.
2
g
S
H×nh vu«n
(c¹nh) .
Xác định chiều cao
Hình chóp có 1 mặt bên vuông góc với mặt đáy: Chiều cao của hình chóp là chiều cao của tam
giác chứa trong mặt bên vuông góc với đáy.
Hình chóp có 2 mặt bên vuông góc với mặt đáy: Chiều cao của hình chóp là giao tuyến của hai
mặt bên cùng vuông góc với mặt phẳng đáy.
Hình chóp có các cạnh bên bằng nhau: Chân đường cao của hình chóp là tâm đường tròn ngoại
tiếp đa giác đáy.
Khối chóp đều
Đáy là đa giác đều và mặt bên là những tam giác cân bằng nhau.
Chân đường cao trùng với tâm đường tròn ngoại tiếp đa giác đáy.
Góc giữa các cạnh bên và mặt đáy bằng nhau, góc giữa các mặt bên và mặt đáy bằng nhau.
Baøi taäp töông töï vaø môû roäng
21.1. Cho tứ diện .O ABC có các cạnh ,OA ,OB OC đôi một vuông góc với nhau. Biết 2cm,OA
3cm,OB 6cm.OC Thể tích của khối tứ diện .O ABC bằng
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 34 -
A.
3
6cm .
B.
3
36cm .
C.
3
12cm .
D.
3
18cm .
21.2. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
.
a
Biết
( )
SA ABCD
và
3.
SA a
Thể tích của khối chóp
.
S ABCD
bằng
A.
3
3.
a
B.
3
3
12
a
C.
3
3
3
a
D.
3
4
a
21.3. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
,
a
( )
SA ABC
và
3.
SA a
Thể tích
khối chóp
.
S ABC
bằng
A.
3
3
4
a
B.
3
2
a
C.
3
3
8
a
D.
3
4
a
21.4. Cho
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
.
a
Biết
( )
SA ABCD
và
3.
SC a
Thể tích
của khối chóp
.
S ABCD
bằng
A.
3
3
2
a
B.
3
3
a
C.
3
2
3
a
D.
3
3
3
a
21.5. Cho khối chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
và hai mặt bên
( ),
SAB
( )
SAC
cùng
vuông góc với đáy. Biết
3.
SC a
Thể tích khối chóp
.
S ABC
bằng
A.
3
2 6
9
a
B.
3
6
12
a
C.
3
3
4
a
D.
3
3
2
a
21.6. Thể tích của khối tứ diện đều có cạnh là
3
bằng
A.
4 2
9
B.
2 2.
C.
2.
D.
9 2
4
21.7. Cho khối chóp tứ giác đều có cạnh đáy bằng
,
a
cạnh bên bằng
2 .
a
Thể tích của khối chóp đã cho
bằng
A.
3
2
6
a
B.
3
11
12
a
C.
3
14
2
a
D.
3
14
6
a
21.8. Cho khối chóp tam giác đều
.
S ABC
có cạnh đáy bằng
a
và cạnh bên
3.
SA a
Thể tích của
khối chóp
.
S ABC
bằng
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 35 -
A.
3
35
24
a
B.
3
3
6
a
C.
3
2
6
a
D.
3
2
2
a
21.9. Cho hình chóp
.
S ABC
có đáy là tam giác đều cạnh
,
a
mặt phẳng
( )
SAB
vuông góc với mặt phẳng
( )
ABC
và tam giác
SAB
vuông cân tại
.
S
Thể tích khối chóp
.
S ABC
bằng
A.
3
3
12
a
B.
3
3
24
a
C.
3
3
3
a
D.
3
3
4
a
21.10. Cho khối chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
3 .
a
Tam giác
SAB
vuông cân
tại
S
và nằm trong mặt phẳng vuông với đáy. Thể tích hình chóp đã cho bằng
A.
3
9 3.
a
B.
3
9 3
2
a
C.
3
9 .
a
D.
3
9
2
a
Câu 22. Thể tích khối hộp chữ nhật có ba kích thước
2; 3; 7
bằng
A.
14.
B.
42.
C.
126.
D.
12.
Lôøi giaûi tham khaûo
Thể tích cần tìm là
2 3 7 42.
V
Chọn đáp án B.
Theå tích khoái laêng truï, hoäp chöõ nhaät vaø laäp phöông
Thể tích của khối lăng trụ
.
V B h
với
B
là diện tích đáy và
h
là chiều cao. Đặc biệt:
Thể tích khối hộp chữ nhật
V abc
với
a
là chiều dài,
b
là chiều rộng và
c
là chiều cao.
Thể tích khối lập phương
3
V a
với
a
là cạnh.
Baøi taäp töông töï vaø môû roäng
22.1. Thể tích khối lập phương có cạnh
3
a
là
A.
3
2 .
a
B.
3
27 .
a
C.
3
8 .
a
D.
3
3 .
a
22.2. Diện tích toàn phần của một khối lập phương là
150
2
cm .
Thể tích của khối lập phương bằng
A.
125
3
cm .
B.
100
3
cm .
C.
25
3
cm .
D.
75
3
cm .
c
b
a
a
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 36 -
22.3. Cho khối hộp chữ nhật
.
ABCD A B C D
có thể tích
.
V
Mệnh đề nào sau đây đúng ?
A.
. . .
V AB BC AA
B.
1
. . .
3
V AB BC AA
C.
. . .
V AB AC AA
D.
. . .
V AB AC AD
22.4. Tính thể tích của khối chữ nhật
.
ABCD A B C D
biết rằng
,
AB a
2 ,
AD a
14.
AC a
A.
3
14
3
a
B.
3
2 .
a
C.
3
6 .
a
D.
3
5.
a
22.5. Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng
3.
Thể tích khối lăng trụ đã cho bằng
A.
9 3
4
B.
27 3
4
C.
27 3
2
D.
9 3
2
22.6. Thể tích của khối lăng trụ tứ giác đều
.
ABCD A B C D
có tất cả các cạnh là
a
bằng
A.
3
3 .
a
B.
3
3
2
a
C.
3
.
a
D.
3
3
4
a
22.7. Cho khối lăng trụ đứng
.
ABC A B C
có
,
BB a
đáy
ABC
là tam giác vuông cân tại
B
và
.
AB a
Thể tích của khối lăng trụ đã cho bằng
A.
3
2
a
B.
3
6
a
C.
3
3
a
D.
3
.
a
22.8. Cho hình lăng trụ tam giác đều
.
ABC A B C
có
2
AB a
và
3.
AA a
Thể tích khối lăng trụ
.
ABC A B C
bằng
A.
3
.
a
B.
3
4
a
C.
3
3 .
a
D.
3
3
4
a
22.9. Tính thể tích của một khối lăng trụ tam giác đều
.
ABC A B C
có
5
AC a
và đáy là tam giác
đều cạnh
4 .
a
A.
3
12 .
a
B.
3
20
3
a
C.
3
20 3.
a
D.
3
12 3.
a
22.10. Cho khối lập phương
.
ABCD A B C D
có thể tích
1.
Thể tích khối lăng trụ
.
ABC A B C
bằng
A.
1
3
B.
1
2
C.
1
6
D.
2
3
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 37 -
Câu 23. Công thức tính thể tích V của khối nón có bán kính đáy r và chiều cao h là
A. .V rh B.
2
.V r h C.
1
.
3
V rh D.
2
1
.
3
V r h
Lôøi giaûi tham khaûo
Theo công thức SGK thì
2
1
.
3
V r h Chọn đáp án D.
Xaùc ñònh caùc yeáu toá cô baûn cuûa khoái noùn
Các yếu tố cơ bản cần nắm vững của khối nón
xq nón
.S r
2
tp xq áy
.S S S r r
đ
2
nón áy
1 1
. .
3 3
V S h r h
đ
Baøi taäp töông töï vaø môû roäng
23.1. Cho khối nón có chiều cao 3h và bán kính đáy 4.r Thể tích của khối nón đã cho bằng
A. 16 . B. 48 .
C. 36 . D. 4 .
23.2. Thể tích khối nón có bán kính đáy là 3
cm
và độ dài đường sinh là 5
cm
bằng
A. 12
3
cm . B. 15
3
cm .
C. 36
3
cm . D. 45
3
cm .
23.3. Cho khối nón có đường sinh là 5 và diện tích đáy là 9 . Thể tích của khối nón đã cho bằng
A. 12 . B. 24 .
C. 36 . D. 45 .
23.4. Cho hình nón có bán kính đáy bằng 2 và góc ở đỉnh bằng 60 . Diện tích xung quanh của hình
nón đã cho bằng
A. 8 . B. 16 .
C.
8 3
3
D.
16 3
3
23.5. Cho hình nón bán kính đáy bằng
a
và thể tích khối nón bằng
3
3
.
3
a
Diện tích toàn phần của
hình nón đó bằng
A.
2
3 .a B.
2
4 .a
C.
2
2 .a D.
2
.a
23.6. Cho hình nón có bán kính bằng 5 và góc ở đỉnh bằng 60 . Diện tích xung quanh của hình nón đã
cho bằng
A. 50 . B. 100 .
C.
50 3
3
D.
100 3
3
: đường sinh.
:h chiều cao.
:r
bán kính đáy.
: góc ở đỉnh.
Mối liên hệ:
2 2 2
.
h r
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 38 -
23.7. Trong không gian, cho tam giác
OAB
vuông tại
O
có
3,
OA
4.
OB
Diện tích toàn phần của
hình nón tạo thành khi quay tam giác
OAB
quanh
OA
bằng
A.
36 .
B.
20 .
C.
26 .
D.
52 .
23.8. Trong không gian, cho tam giác
ABC
vuông tại
,
A AB a
và
30 .
ACB
Thể tích của khối
nón nhận được khi quay tam giác
ABC
quanh cạnh
AC
bằng
A.
3
3
3
a
B.
3
3
9
a
C.
3
3 .
a
D.
3
.
a
23.9. Cắt hình nón bởi một mặt phẳng đi qua trục ta được một tam giác vuông cân có cạnh huyền bằng
2.
a
Thể tích của khối nón bằng
A.
3
2
4
a
B.
3
7
3
a
C.
3
12
a
D.
3
2
12
a
23.10. Cắt một khối nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác đều
cạnh bằng
2 .
a
Thể tích của khối nón bằng
A.
3
3 .
a
B.
3
.
a
C.
3
2 3 .
a
D.
3
3
3
a
Câu 24. Một hình trụ có bán kính đáy
4cm
r
và độ dài đường sinh
3cm.
Diện tích xung
quanh của hình trụ đó bằng
A.
2
12 cm .
B.
2
48 cm .
C.
2
24 cm .
D.
2
36 cm .
Lôøi giaûi tham khaûo
Ta có
2
xq
2 2 4 3 24 cm .
S rl
Chọn đáp án C.
Maët truï
xq
2 .
S rh
2
tp xq áy
2 2 2 .
S S S rh r
đ
2
tru áy
. .
V S h r h
đ
Baøi taäp töông töï vaø môû roäng
24.1. Cho khối trụ có độ dài đường sinh bằng
a
và bán kính đáy bằng
.
R
Thể tích khối trụ đã cho bằng
A.
2
.
aR
B.
2
2 .
aR
C.
2
1
.
3
aR
D.
2
.
aR
24.2. Một hình trụ có chiều cao bằng
6cm
và diện tích đáy bằng
2
4cm .
Thể tích của khối trụ bằng
A.
3
8cm .
B.
3
12cm .
C.
3
24cm .
D.
3
72cm .
:
h
chiều cao
đường sinh.
:
r
bán kính đáy.
O'
O
h
h
r
r
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 39 -
24.3. Cho hình trụ có bán kính đáy bằng
3cm,
độ dài đường cao bằng
4cm.
Diện tích xung quanh
của hình trụ này bằng
A.
2
24 cm .
B.
2
22 cm .
C.
2
26 cm .
D.
2
20 cm .
24.4. Diện tích toàn phần của hình trụ có bán kính đáy
a
và đường cao
3
a
bằng
A.
2
2 ( 3 1).
a
B.
2
3.
a
C.
2
( 3 1).
a
D.
2
2 ( 3 1).
a
24.5. Cho hình trụ
( )
T
có chiều cao là
5
và diện tích xung quanh là
30 .
Thể tích khối trụ
( )
T
bằng
A.
30 .
B.
75 .
C.
15 .
D.
45 .
24.6. Cho khối trụ có chu vi đáy bằng
4
a
và độ dài đường cao bằng
.
a
Thể tích của khối trụ bằng
A.
2
.
a
B.
3
4
3
.
a
C.
3
4
.
a
D.
3
16
.
a
24.7. Cho hình nón có diện tích xung quanh bằng
2
3
a
và bán kính đáy bằng
.
a
Độ dài đường sinh
của hình nón đã cho bằng
A.
2 2 .
a
B.
3 .
a
C.
2
3
a
D.
3
2
a
24.8. Cho một hình trụ có bán kính đáy bằng
a
và chiều cao bằng
2 .
a
Một hình nón có đáy trùng với
một đáy của hình trụ và đỉnh trùng với tâm của đường tròn đáy thứ hai của hình trụ. Độ dài
đường sinh của hình nón bằng
A.
5.
a
B.
2 .
a
C.
.
a
D.
3 .
a
24.9. Cho hình trụ có bán kính đáy bằng
2 .
a
Một mặt phẳng đi qua trục của hình trụ và cắt hình trụ
theo thiết diện là hình vuông. Thể tích khối trụ đã cho bằng
A.
3
18 .
a
B.
3
4 .
a
C.
3
8 .
a
D.
3
16 .
a
24.10. Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật
ABCD
có
AB
và
CD
thuộc hai đáy của hình trụ với
4
AB a
và
5 .
AC a
Thể tích khối trụ đã cho bằng
A.
3
16 .
a
B.
3
12 .
a
C.
3
4 .
a
D.
3
8 .
a
Câu 25. Trong không gian
,
Oxyz
cho hai điểm
(1;1;2)
A
và
(3;1;0).
B
Trung điểm của đoạn thẳng
AB
có tọa độ là
A.
(4;2;2).
B.
(2;1;1).
C.
(2;0; 2).
D.
(1; 0; 1).
Lôøi giaûi tham khaûo
Trung điểm
I
của
AB
có tọa độ là
3 1 1 1 2 0
2, 1, 1.
2 2 2
I I I
x y z
Chọn đáp án B.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 40 -
Heä truï toïa ñoä Oxyz vaø baøi toaùn lieân quan
Định nghĩa:
( ; ; ) . . . ( ; ; ).
M a b c OM a i b j c k a b c

Cần nhớ:
( ) 0, ( ) 0, ( ) 0
0, 0, 0
M Oxy z M Oyz x M Oxz y
M Ox y z M Oy x z M Oz x y
Tính chất: cho hai điểm
( ; ; ), ( ; ; ).
A A A B B B
A x y z B x y z
( ; ; )
B A B A B A
AB x x y y z z

2 2 2
( ) ( ) ( ) .
B A B A B A
AB x x y y z z
Gọi
M
là trung điểm
AB
; ;
2 2 2
A B A B A B
x x y y z z
M
Gọi
G
là trọng tâm tam giác
ABC
; ;
3 3 3
A B C A B C A B C
x x x y y y z z z
G
Baøi taäp töông töï vaø môû roäng
25.1. Trong không gian
,
Oxyz
cho các điểm
(1;2;3)
M
và
(3;4;7).
N
Tọa độ của véctơ
MN

là
A.
(4;6;10).
B.
(2; 3;5).
C.
(2;2; 4).
D.
( 2; 2; 4).
25.2. Trong không gian
,
Oxyz
cho hai điểm
(1; 1;2)
A
và
(2;1;1).
B
Độ dài đoạn
AB
bằng
A.
2.
B.
6.
C.
2.
D.
6.
25.3. Trong không gian
,
Oxyz
cho
(1; 2;3)
u
và
( 1;2; 3).
v
Môđun của
2
u v
bằng
A.
26.
B.
126.
C.
85.
D.
185.
25.4. Trong không gian
,
Oxyz
cho hai điểm
(3; 2;3)
A
và
( 1;2;5).
B
Tìm tọa độ trung điểm
I
của
đoạn thẳng
.
AB
A.
( 2;2;1).
I
B.
(1; 0;4).
I
C.
(2;0;8).
I
D.
(2; 2; 1).
I
25.5. Trong không gian
,
Oxyz
cho hai điểm
(1;2;4)
A
và
(2;4; 1).
B
Tìm tọa độ trọng tâm
G
của tam
giác
.
OAB
A.
(6;3;3).
G
B.
(2;1;1).
G
C.
(2;1;1).
G
D.
(1;2;1).
G
25.6. Trong không gian
,
Oxyz
cho điểm
(3; 1;1).
A
Hình chiếu vuông góc của điểm
A
trên mặt phẳng
( )
Oyz
là điểm
A.
(3;0;0).
M
B.
(0; 1;1).
N
C.
(0; 1; 0).
P
D.
(0;0;1).
Q
25.7. Trong không gian
,
Oxyz
cho điểm
(2; 3;5).
A
Điểm
A
đối xứng với
A
qua trục
Oy
là
A.
(2;3;5).
A
B.
(2; 3; 5).
A
C.
( 2; 3;5).
A
D.
( 2; 3; 5).
A
25.8. Trong không gian
,
Oxyz
cho ba điểm
(2; 1;5), (5; 5;7), ( ; ;1).
A B M x y
Nếu
, ,
A B M
thẳng
hàng thì tổng
x y
bằng
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 41 -
A.
11.
B.
11.
C.
3.
D.
3.
25.9. Trong không gian
,
Oxyz
cho hai điểm
(0;1; 2)
A
và
(3; 1;1).
B
Tìm tọa độ điểm
M
sao cho
3 .
AM AB
 
A.
(9; 5;7).
M
B.
(9;5;7).
M
C.
( 9;5; 7).
M
D.
(9; 5; 5).
M
25.10. Trong không gian
,
Oxyz
cho ba điểm
(1;2;3),
M
(2; 3;1),
N
(3;1;2).
P
Tìm tọa độ điểm
Q
sao cho
MNPQ
là hình bình hành.
A.
(2; 6;4).
Q
B.
(4; 4; 0).
Q
C.
(2;6; 4).
Q
D.
( 4; 4; 0).
Q
Câu 26. Trong không gian
,
Oxyz
mặt cầu
2 2 2
( ) : ( 1) 9
S x y z
có bán kính bằng
A.
9.
B.
3.
C.
81.
D.
6.
Lôøi giaûi tham khaûo
Phương trình mặt cầu là:
2 2 2 2
( ) ( ) ( )
x a y b z c R
nên
2
9 3.
R R
Chọn đáp án B.
Xaùc ñònh caùc yeáu toá cô baûn cuûa maët caàu
Để viết phương trình mặt cầu
( ),
S
ta cần tìm tâm
( ; ; )
I a b c
và bán kính
.
R
Khi đó:
2 2 2 2
( ) : ( ) ( ) ( ) .
S x a y b z c R
(Tìm tâm lấy ngược dấu và
R
lấy căn)
Ví dụ:
2 2 2
( ) : ( 1) ( 2) 5
S x y z
Tâm
(1; 2; 0)
I
và
5.
R
2 2 2
( ) : 2 2 2 0
S x y z ax by cz d
với
2 2 2
0
R a b c d
(hệ số
, ,
x y z
chia
2).
Ví dụ:
2 2 2
( ) : 4 6 2 11 0
S x y z x y z
(2; 3;1)
I
và
2 2 2
2 ( 3) 1 11 5.
R
26.1. Trong không gian
,
Oxyz
cho mặt cầu
2 2 2
( ) : ( 1) ( 2) ( 1) 9.
S x y z
Tìm tọa độ tâm
I
và
bán kính
R
của mặt cầu
( ) ?
S
A.
( 1;2;1)
I
và
3.
R
B.
(1; 2; 1)
I
và
3.
R
C.
( 1;2;1)
I
và
9.
R
D.
(1; 2; 1)
I
và
9.
R
26.2. Trong không gian
,
Oxyz
cho mặt cầu
2 2 2
( ) : ( 2) ( 2) 8.
S x y z
Tìm tọa độ tâm
I
và bán
kính
R
của mặt cầu
( ) ?
S
A.
(0; 2;2), 64.
I R
B.
(0;2; 2), 4.
I R
C.
(0; 2; 2), 2 2.
I R
D.
(0;2; 2), 2 2.
I R
26.3. Trong không gian
,
Oxyz
cho mặt cầu
2 2 2
( ) : 2 4 6 10 0.
S x y z x y z
Xác định tâm
I
và bán kính
R
của mặt cầu
( )
S
?
A.
(1; 2;3) 2.
I R
B.
( 1;2; 3), 2.
I R
C.
( 1;2; 3), 4.
I R
D.
(1; 2;3), 4.
I R
26.4. Trong không gian
,
Oxyz
cho mặt cầu
2 2 2
( ) : 4 2 4 16 0.
S x y z x y z
Xác định tâm
I
và bán kính
R
của mặt cầu
( )
S
?
A.
( 2; 1;2),
I
5.
R
B.
( 2; 1;2),
I
5.
R
C.
(2;1; 2),
I
5.
R
D.
(4;2; 4),
I
13.
R
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 42 -
26.5. Trong không gian
,
Oxyz
cho mặt cầu
2 2 2
( ) : 2 4 4 0
S x y z x y z m
có bán kính
5.
R
Tìm tham số thực
?
m
A.
16.
m
B.
16.
m
C.
4.
m
D.
4.
m
26.6. Trong không gian
,
Oxyz
tìm tất cả các giá trị thực của tham số
m
sao cho phương trình
2 2 2
2 2 4 0
x y z x y z m
là phương trình của một mặt cầu.
A.
6.
m
B.
6.
m
C.
6.
m
D.
6.
m
26.7. Trong không gian
,
Oxyz
phương trình nào sau đây là phương trình mặt cầu có tâm
( 1;2;1)
I
và
đi qua điểm
(0;4; 1) ?
A
A.
2 2 2
( 1) ( 2) ( 1) 9.
x y z
B.
2 2 2
( 1) ( 2) ( 1) 3.
x y z
C.
2 2 2
( 1) ( 2) ( 1) 3.
x y z
D.
2 2 2
( 1) ( 2) ( 1) 9.
x y z
26.8. Trong không gian với hệ tọa độ
,
Oxyz
cho hai điểm
(1;2;3)
A
và
( 1;4;1).
B
Phương trình mặt cầu
( )
S
có đường kính
AB
là
A.
2 2 2
( 1) ( 2) ( 3) 12.
x y z
B.
2 2 2
( 3) ( 2) 3.
x y z
C.
2 2 2
( 1) ( 4) ( 1) 12.
x y z
D.
2 2 2
( 3) ( 2) 12.
x y z
26.9. Trong không gian
,
Oxyz
cho mặt cầu
2 2 2
( ) : ( 1) ( 2) ( 3) 25
S x y z
và điểm
(1;1;1).
M
Tìm khẳng định đúng ?
A. Điểm
M
nằm bên ngoài
( ).
S
B. Điểm
M
nằm bên trong
( ).
S
C. Điểm
M
thuộc mặt cầu
( ).
S
D. Đường kính mặt cầu bằng
5.
26.10. Trong không gian
,
Oxyz
cho mặt cầu
2 2 2
( ) : ( 1) ( 1) ( 2) 6
S x y z
và điểm
(2;2;4).
M
Tìm khẳng định đúng ?
A. Điểm
M
nằm bên ngoài
( ).
S
B. Điểm
M
nằm bên trong
( ).
S
C. Điểm
M
thuộc mặt cầu
( ).
S
D. Đường kính mặt cầu bằng
6.
Câu 27. Trong không gian
,
Oxyz
mặt phẳng nào dưới đây đi qua điểm
(1; 2;1) ?
M
A.
1
( ) : 0.
P x y z
B.
2
( ) : 1 0.
P x y z
C.
3
( ) : 2 0.
P x y z
D.
4
( ) : 2 1 0.
P x y z
Lôøi giaûi tham khaûo
Thay tọa độ của điểm
(1; 2;1)
M
trực tiếp vào các phương trình để kiểm tra. Chọn đáp án A.
Xaùc ñònh caùc yeáu toá cô baûn cuûa maët phaúng
Véctơ pháp tuyến
n
của mặt phẳng
( )
P
là véctơ có giá vuông góc với
( ).
P
Nếu
n
là một véctơ
pháp tuyến của
( )
P
thì
.
k n
cũng là một véctơ pháp tuyến của
( ).
P
Nếu mặt phẳng
( )
P
có cặp véctơ chỉ phương là
1 2
,
u u
thì
( )
P
có véctơ pháp tuyến là
1 2
[ , ].
n u u
Mặt phẳng
( ) : 0
P ax by cz d
có một véctơ pháp tuyến là
( ; ; ).
n a b c
Nếu
( ; ; ) ( ) : 0 0.
M M M M M M
M x y z P ax by cz d ax by cz d
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 43 -
Để viết phương trình mặt phẳng ( ),P ta cần xác định 1 điểm đi qua và 1 VTPT:
( )
( ; ; )
( ) : ( ) : ( ) ( ) ( ) 0 .
Qua
VTPT ( ; ; )
P
M x y z
P P a x x b y y
n c
c z
b
z
a
Baøi taäp töông töï vaø môû roäng
27.1. Trong không gian ,Oxyz cho mặt phẳng ( ) : 3 2 0.P x z Véctơ nào dưới đây là một véctơ
pháp tuyến của ( ) ?P
A.
4
(1;0 1).n
B.
1
(3; 1;2).n
C.
3
(3; 1;0).n
D.
2
(3; 0; 1).n
27.2. Trong không gian ,Oxyz tọa độ vectơ pháp tuyến của mặt phẳng ( )Oxy là
A.
1
(0;1; 0).n
B.
2
(1;1; 0).n
C.
3
(0; 0;1).n
D.
4
(1;0;0).n
27.3. Trong không gian ,Oxyz cho ba điểm (2; 1; 3),A (4; 0;1)B và ( 10;5; 3).C Véctơ nào dưới đây là
một véctơ pháp tuyến của mặt phẳng ( ) ?ABC
A.
1
(1;8;2).n
B.
2
(1;2;0).n
C.
3
(1;2;2).n
D.
4
(1; 2;2).n
27.4. Trong không gian ,Oxyz cho mặt phẳng ( ) : 2 5.P x y z Điểm nào dưới đây thuộc ( ) ?P
A. (2; 1;5).Q B. (0;0; 5).P
C. ( 5;0; 0).N D. (1;1;6).M
27.5. Trong không gian ,Oxyz cho điểm ( ;1;6)M m và mặt phẳng ( ) : 2 5 0.P x y z Điểm M
thuộc mặt phẳng( )P khi giá trị của tham số
m
bằng
A. 1.m B. 1.m
C. 3.m D. 2.m
27.6. Trong không gian ,Oxyz cho điểm (1; 1;2017)A và mặt phẳng ( ) : 2 2016 0.P mx y mz
Tìm tham số
m
để điểm A thuộc mặt phẳng ( ) ?P
A. 1007.m B. 1.m
C. 1.m D. 1009.m
27.7. Trong không gian ,Oxyz cho mặt phẳng ( ) : 2 2 4 0.P x y z Khoảng cách từ điểm (1;2;1)M
đến ( )P bằng
A. 3. B. 4.
C. 1. D.
1
3
27.8. Trong không gian
,Oxyz
cho hai mặt phẳng ( ) : 2 0P x y z và ( ) : 2 7 0.Q x y z
Khoảng cách giữa ( )P và ( )Q bằng
A.
7.
B. 7 6.
C. 6 7. D.
7 6
6
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 44 -
27.9. Trong không gian
,Oxyz
cho mặt phẳng
( ) : 8 4 8 11 0P x y z
và
( ) : 2 2 7 0.
Q x y
Góc giữa ( )P và ( )Q bằng
A. 45 . B. 90 .
C. 30 . D. 60 .
27.10. Trong không gian
,Oxyz
cho đường thẳng :
1 2 1
x y z
d
và mặt
( ) : 5 11 2 4 0.P x y z
Góc giữa d và ( )P bằng
A. 90 . B. 30 .
C. 60 . D. 45 .
Câu 28. Trong không gian ,Oxyz véctơ nào dưới đây là một véctơ chỉ phương của đường thẳng đi
qua gốc tọa độ O và điểm (1; 2;1) ?M
A.
1
(1;1;1).u
B.
2
(1;2;1).u
C.
3
(0;1;0).u
D.
4
(1; 2;1).u
Lôøi giaûi tham khaûo
Ta có (1; 2;1)OM

là một véctơ chỉ phương của đường thẳng .OM Chọn đáp án D.
Xaùc ñònh caùc yeáu toá cô baûn cuûa ñöôøng thaúng
Véctơ chỉ phương u
của đường thẳng
d
là véctơ có giá song song hoặc trùng với đường thẳng
.d
Nếu
d
có một véctơ chỉ phương là u
thì .k u
cũng là một véctơ chỉ phương của
.d
Nếu có hai véctơ
1
n
và
2
n
cùng vuông góc với
d
thì
d
có một véctơ chỉ phương là
1 2
[ , ].
u n n
Để viết phương trình đường thẳng ,d ta cần tìm điểm đi qua và một véctơ chỉ phương.
Nếu đường thẳng
1 2 3
Qua ( ; ; )
:
VTCP : ( ; ; )
d
M x y z
d
u a a a
thì ta có hai dạng phương trình đường thẳng:
Phương trình đường thẳng
d
dạng tham số
1
2
3
, ( ).
x x a t
y y a t t
z z a t
Phương trình đường thẳng
d
dạng chính tắc
1 2 3
1 2 3
, ( 0).
x x y y z z
a a a
a a a
Điểm
1 1
2 2
3 3
( ; ; ) : :
M
M M M M
M
x x a t x x a t
M x y z d y y a t y y a t
z z a t z z a t
luôn đúng (các giá trị t giống nhau).
Điểm
1 2 3 1 2 3
( ; ; ) : :
M M M
M M M
x x y y z z x x y y z z
M x y z d
a a a a a a
đúng.
Baøi taäp töông töï vaø môû roäng
28.1. Trong không gian ,Oxyz cho đường thẳng
1 2
:
1 1 3
x y z
d
Điểm nào sau đây thuộc ?d
A. (1;0;2).Q B. (1; 2;0).N
C. (1; 1;3).P D. ( 1;2;0).M
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 45 -
28.2. Trong không gian
,
Oxyz
đường thẳng
1 2 3
:
1 1 1
x y z
d
đi qua điểm nào dưới đây ?
A.
( 1;2; 3).
M
B.
(3;2;1).
N
C.
(1;2;3).
P
D.
(0;0;0).
Q
28.3. Trong không gian
,
Oxyz
cho đường thẳng
2 1
:
1 1 3
x y z
đi qua điểm
(2; ; ).
M m n
Giá trị
m n
bằng
A.
1.
B.
7.
C.
3.
D.
1.
28.4. Trong không gian
,
Oxyz
cho đường thẳng
1 2
: 3 ( ).
2
x t
d y t t
z t
Biết
( ; 2;1) .
A m m d
Tìm
khẳng đúng trong các khẳng định sau ?
A.
( ; 4).
m

B.
[ 4;2).
m
C.
(6; ).
m
D.
[2;6].
m
28.5. Trong không gian
,
Oxyz
một véctơ chỉ phương của đường thẳng
2 1
:
1 2 1
x y z
d
là
A.
( 1;2;1).
u
B.
(2;1; 0).
u
C.
( 1;2; 0).
u
D.
(2;1;1).
u
28.6. Trong không gian
,
Oxyz
cho hai điểm
(2; 3; 4)
A
và
(4; 1; 2).
B
Véctơ nào dưới đây là 1 véctơ
chỉ phương của đường thẳng
?
AB
A.
(6;2; 3).
u
B.
(3;1; 3).
u
C.
(1; 2;1).
u
D.
( 1;2;1).
u
28.7. Trong không gian
,
Oxyz
cho một véctơ chỉ phương của đường thẳng : 2
1 2
x t
d y
z t
là
A.
(1; 0; 2).
u
B.
(1;2; 0).
u
C.
( 1;2;0).
u
D.
(1;2; 2).
u
28.8. Trong không gian
,
Oxyz
gọi
1
,
M
2
M
lần lượt là hình chiếu vuông góc của
(2;5;4)
M
lên trục
Ox
và mặt phẳng
( ).
Oyz
Véctơ nào dưới đây là một véctơ chỉ phương của đường thẳng
1 2
.
M M
A.
3
(2; 0;4).
u
B.
2
( 2;5;4).
u
C.
4
(0; 3;4).
u
D.
1
( 2;0;4).
u
28.9. Trong không gian
,
Oxyz
cho đường thẳng
d
là giao tuyến của hai mặt phẳng
( ) : 1 0
P x y
và mặt phẳng
( ) : 2 3 0.
Q x y z
Đường thẳng
d
có một véctơ chỉ phương là
A.
(1;1;0).
u
B.
(1; 2;1).
u
C.
(1;1; 3).
u
D.
(1; 1; 3).
u
28.10. Trong không gian
,
Oxyz
cho đường thẳng
d
vuông góc với mặt phẳng
( ) : 4 3 0.
P x z
Véctơ
nào dưới đây là một véctơ chỉ phương của đường thẳng
?
d
A.
(4;1; 3).
u
B.
(4;0; 1).
u
C.
(4;1; 1).
u
D.
(4; 1;3).
u
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 46 -
Câu 29. Chọn ngẫu nhiên một số trong
15
số nguyên dương đầu tiên. Xác suất để chọn được số chẵn
bằng
A.
7
8
B.
8
15
C.
7
15
D.
1
2
Lôøi giaûi tham khaûo
Trong
15
số nguyên dương đầu tiên
1,2,3, ,15,
đếm được có
7
số chẵn nên xác suất cần tìm là
7
15
Chọn đáp án C.
Baøi taäp töông töï vaø môû roäng
29.1. Chọn ngẫu nhiên hai số khác nhau từ
27
số nguyên dương đầu tiên. Xác suất để chọn được hai
số có tổng là một số chẵn bằng
A.
13
27
B.
14
27
C.
1
2
D.
365
729
29.2. Gọi
S
là tập các số tự nhiên có bốn chữ số khác nhau được tạo từ tập
{1; 2; 3; 4; 5}.
E
Chọn
ngẫu nhiên một số từ tập
.
S
Tính xác suất để số được chọn là một số chẵn ?
A.
3
4
B.
2
5
C.
3
5
D.
1
2
29.3. Một hộp đựng
11
viên bi được đánh số từ
1
đến
11.
Lấy ngẫu nhiên
4
viên bi, rồi cộng các số
trên các bi lại với nhau. Xác suất để kết quả thu được là
1
số lẻ bằng
A.
31
32
B.
11
32
C.
16
33
D.
21
32
29.4. Cho
14
tấm thẻ đánh số từ
1
đến
14.
Chọn ngẫu nhiên
3
thẻ. Xác suất để tích
3
số ghi trên
3
tấm
thẻ này chia hết cho
3
bằng
A.
30
91
B.
61
91
C.
31
91
D.
12
17
29.5. Gọi
S
là tất cả các số tự nhiên gồm hai chữ số khác nhau lập từ
0, 1, 2, 3, 4, 5, 6.
Chọn ngẫu
nhiên hai số từ tập
.
S
Tích xác suất để tích hai số được chọn là số chẵn ?
A.
1
6
B.
2
5
C.
5
6
D.
3
4
29.6. Gọi
A
là tập hợp các số có ba chữ số khác nhau được lập từ các chữ số
1, 2, 3, 4, 5.
Chọn ngẫu
nhiên ba số từ tập hợp
,
A
xác suất để trong ba số được chọn có đúng một số có mặt chữ số
4
bằng
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 47 -
A.
2484
8555
B.
5
17
C.
2518
8555
D.
4
17
29.7. Chọn ngẫu nhiên một số từ tập các số tự nhiên có ba chữ số đôi một khác nhau. Xác suất để số
được chọn có tổng các chữ số là chẵn bằng
A.
61
81
B.
4
9
C.
41
81
D.
16
81
29.8. Cho tập hợp
{0; 1; 2; 3; 4; 5; 6}.
A
Gọi
S
là tập hợp các số tự nhiên có
5
chữ số đôi một khác
nhau và luôn có mặt chữ số
5
được lập từ các chữ số thuộc tập
.
A
Chọn ngẫu nhiên một số từ
,
S
xác suất để số được chọn chia hết cho
5
bằng
A.
1
4
B.
2
9
C.
9
26
D.
11
26
29.9. Cho tập
{1;2;3;4;....;19;20}
S
gồm
20
số tự nhiên từ
1
đến
20.
Lấy ngẫu nhiên ba số thuộc
.
S
Xác suất để ba số lấy được lập thành một cấp số cộng bằng
A.
7
38
B.
3
38
C.
5
38
D.
1
114
29.10. Có
11
cái ghế (mỗi ghế chỉ ngồi được một người) được sắp xếp trên một hàng ngang. Xếp ngẫu
nhiên
6
học sinh ngồi vào, mỗi học sinh ngồi đúng một ghế. Xác suất sao cho không có hai ghế
trống nào kề nhau bằng
A.
4
85
B.
1
22
C.
1
3
D.
1
11
Câu 30. Hàm số nào sau đây đồng biến trên
?
A.
1
2
x
y
x
B.
2
2 .
y x x
C.
3 2
.
y x x x
D.
4 2
3 2.
y x x
Lôøi giaûi tham khaûo
Hàm số đồng biến trên
trước hết phải có tập xác định
,
D
loại câu A, xét các câu khác. Chỉ có
3 2 2
( ) 3 2 1 0,
x x x x x x
nên
3 2
y x x x
đồng biến trên
.
Chọn đáp án C.
Baøi taäp töông töï vaø môû roäng
30.1. Hàm số nào sau đây nghịch biến trên
?
A.
3 2
3 .
y x x
B.
3 2
3 3 2.
y x x x
C.
3
3 1.
y x x
D.
3
2018.
y x
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 48 -
30.2. Hàm số nào dưới đây đồng biến trên khoảng
( ; )
 
?
A.
3
3 3 2.
y x x
B.
3
2 5 1.
y x x
C.
4 2
3 .
y x x
D.
2
1
x
y
x
30.3. Hàm số nào trong các hàm số sau đồng biến trên
( ; ) ?
 
A.
3 2
2 1.
y x x
B.
7 2 sin 3 .
y x x
C.
4 1
.
2
x
y
x
D.
tan .
y x
30.4. Hàm số nào sau đây thỏa mãn với mọi
1 2 1 2
, ,
x x x x
thì
1 2
( ) ( ) ?
A.
4 2
( ) 2 1.
f x x x
B.
2
(
3
)
1
x
f
x
x
C.
3 2
( ) 1.
f x x x
D.
3 2
( ) 3 1.
f x x x x
30.5. Hàm số nào sau đây đồng biến trên tập xác định của chúng ?
A.
ln .
y x
B.
e .
x
y
C.
1
3
x
y
D.
1
5
log .
y x
30.6. Trong các hàm số sau, hàm số nào nghịch biến trên
?
A.
e
3
x
y
B.
2
3
x
y
C.
0,5
log .
y x
D.
5
log .
y x
30.7. Điều kiện của
a
để hàm số
( ) (1 ln )
x
f x a
đồng biến trên
là
A.
1
e 1.
a
B.
1.
a
C.
0.
a
D.
e.
a
30.8. Hỏi với giá trị nào của
a
thì hàm số
(3 )
x
y a
nghịch biến trên
?
A.
2 3.
a
B.
0 1.
a
C.
2.
a
D.
0.
a
30.9. Cho hàm số
3 2
.
y ax bx cx d
Hỏi hàm số luôn đồng biến trên
khi nào ?
A.
2
0, 0
0, 3 0
a b c
a b ac
B.
2
0, 0
0, 3 0
a b c
a b ac
C.
2
0, 0
0, 3 0
a b c
a b ac
D.
2
0
0, 3 0
a b c
a b ac
30.10. Hàm số
2
1
1
mx m
y
x
với
m
là tham số. Mệnh đề nào dưới đây là đúng ?
A. Hàm số đồng biến trên
\ { 1}.
B. Hàm số đồng biến trên
.
C. Hàm số nghịch biến trên các khoảng xác định.
D. Hàm số đồng biến trên các khoảng xác định.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 49 -
Câu 31. Gọi
,
M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
4 2
( ) 2 3
f x x x
trên đoạn
[0;2].
Tổng
M m
bằng
A.
11.
B.
14.
C.
5.
D.
13.
Lôøi giaûi tham khaûo
Ta có
3
( ) 4 4
f x x x
và
( ) 0 0 1 1.
f x x x x
Trên đoạn
[0;2],
xét các giá trị
(0) 3, (1) 2, (2) 11.
f f f
Do đó
11, 2
M m
và
13.
M m
Chọn đáp án D.
Giaù trò lôùn nhaát vaø giaù trò nhoû nhaát cuûa haøm soá
Bài toán 1. Tìm GTLN & GTNN trên đoạn
[ ; ].
a b
Tính
,
y
cho
0
y
tìm nghiệm
[ ; ].
i
x a b
Tính
[ ; ] [ ; ]
( ), ( ), ( ) max , min .
i
a b a b
y a y b y x y y
Bài toán 2. Tìm GTLN, GTNN trên khoảng
( ; ).
a b
Tính
,
y
cho
0
y
tìm nghiệm
.
i
x
Lập bảng biến thiên
( ; ) ( ; )
max , min .
a b a b
y y
Định lí. Nếu
( )
y f x
đồng biến trên
[ ; ]
[ ; ]
min ( )
[ ; ]
max ( )
a b
a b
y f a
a b
y f b
và nghịch biến
[ ; ]
[ ; ]
min ( )
[ ; ] .
max ( )
a b
a b
y f b
a b
y f a
BĐT Côsi: Với
1 2
, ,.., 0
n
a a a
có
1 2 1 2
... .
n
n n
x x x n x x x
Dấu
1 2
" " .
n
a a a
Baøi taäp töông töï vaø môû roäng
31.1. Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
2
2 3 4
3
x
y x x
trên đoạn
[ 4; 0]
lần
lượt là
M
và
.
m
Tổng
M m
bằng
A.
28
3
B.
17
3
C.
5.
D.
5.
31.2. Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
1
x
y
x
trên đoạn
[ 1;0]
lần lượt là
M
và
.
m
Tổng
M m
bằng
A.
2.
B.
4.
C.
3.
D.
1.
31.3. Giá trị lớn nhất của hàm số
2
5
y x x
bằng
A.
0.
B.
5
2
C.
6.
D.
2.
31.4. Giá trị lớn nhất của hàm số
3 2
cos 2 sin cos
y x x x
bằng
A.
58
max
27
y
B.
1
max
3
y
C.
max 2.
y
D.
max 2.
y
31.5. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2cos 2
cos 2
x
y
x
bằng
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 50 -
O
2
2
3
1
1
2
3
y
x
A.
4
max 0,min
3
y y
B.
4
max ; min 0.
3
y y
C.
max 1; min 0.
y y
D.
max 0; min 1.
y y
31.6. Tìm giá trị nhỏ nhất của hàm số
2
2
y x
x
trên khoảng
(0; ).

A.
(0; )
min 1.
y

B.
(0; )
min 2.
y

C.
(0; )
min 3.
y

D.
(0; )
min 4.
y

31.7. Trên khoảng
(0;1)
hàm số
3
1
y x
x
đạt giá trị nhỏ nhất tại
x
bằng
A.
3
1
3
B.
4
1
3
C.
1
2
D.
1
3
31.8. Cho hàm số
3 2
3 6.
y x m x
Tìm tất cả các giá trị thực của tham số
m
sao cho giá trị lớn nhất
của hàm số trên đoạn
[0;3]
bằng
42.
A.
1.
m
B.
1.
m
C.
1.
m
D.
2.
m
31.9. Cho hàm số
( )
f x
có đạo hàm
2
( ) ( 2) ( 3),
f x x x x
.
x
Giá trị lớn nhất của hàm số đã
cho trên đoạn
[0;4]
bằng
A.
(0).
f
B.
(2).
f
C.
(3).
f
D.
(4).
f
31.10. Cho hàm số
( )
f x
có đạo hàm trên
và có đồ thị
( )
y f x
như hình vẽ. Biết rằng
(0) (3) (2) (5).
f f f f
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
f x
trên đoạn
[0;5]
lần
lượt là
A.
(0),
f
(5).
f
B.
(2),
f
(0).
f
C.
(1),
f
(3).
f
D.
(5),
f
(2).
f
31.11. Cho hàm số
( )
y f x
liên tục trên đoạn
[ 1; 3]
và có đồ thị như hình. Gọi
M
và
m
lần lượt là
giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
[0;2].
Giá trị của
M m
bằng
A.
0.
B.
1.
C.
4.
D.
5.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 51 -
31.12. Cho hàm số ( )y f x xác định và liên tục trên đoạn [ 3; 3]. Gọi ,M m lần lượt là giá trị lớn nhất
và giá trị nhỏ nhất của hàm số ( ( ))y f f x trên đoạn [ 1;0].
Khi đó
M m
bằng
A.
1.
B.
3.
C.
4.
D.
6.
31.13. Cho hàm số
( )f x
liên tục trên
và có đồ thị như hình. Gọi ,M m lần lượt là giá trị lớn nhất và
giá trị nhỏ nhất của hàm số ( (sin ))y f f x trên đoạn [0; ]. Giá trị
M m
bằng
A.
1.
B.
3.
C.
4.
D.
2.
31.14. Cho hàm số ( )y f x xác định, liên tục trên
và có đồ thị như hình vẽ. Tập hợp các giá trị của
tham số m để phương trình
2
( 2 2) 3 1f x x m
có nghiệm thuộc đoạn [0;1] là
A. [0;4].
B. [ 1;0].
C. [0;1].
D.
1
;1
3
31.15. Cho hàm số ( )y f x liên tục trên đoạn [ 3;3]. Tìm tất cả các giá trị của tham số m để phương
trình
2 ( ) 1f f x m có nghiệm trên đoạn [ 1;0] ?
A. 3 1.m
B. 3 3.m
C. 0 1.m
D. 3 0.m
31.16. Cho hàm số
3 2
y ax bx cx d
có hình dạng như hình bên dưới. Giá trị lớn nhất của biểu
thức
2
2 2020P a cd a c bằng
A. 2019.
B. 2020.
C. 2021.
D. 2022.
31.17. Cho hàm số
( ) , ( , , )
ax b
f x a b c
x c
có bảng biến thiên như hình vẽ bên dưới. Giá trị lớn
nhất của biểu thức
3 2
3 3P ab ab c c bằng
A.
3.
B.
3.
C.
11.
D.
11.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 52 -
31.18. Cho hàm số ( )y f x liên tục trên và có đồ thị hàm số ( )y f x
như hình vẽ. Bất phương
trình
2
( ) 3f x x m
nghiệm đúng với mọi ( 1;1)x khi và chỉ khi:
A. (0) 3.m f
B. (1) 3.m f
C. (1) 3.m f
D. (0) 3.m f
31.19. Cho hàm số ( ).y f x Hàm số ( )y f x
có bảng biến thiên như hình dưới. Tìm tất cả các giá trị
của tham số
m
để bất phương trình
2 3
3 3 3 ( )m x f x x
nghiệm đúng (0;3) ?x
A.
(0).m f
B.
(0).m f
C.
(3).m f
D.
(1) 1.m f
31.20. Cho hàm số ( ),f x hàm số ( )y f x
liên tục trên
và có đồ thị như hình. Bất phương trình
( ) 2f x x m
(m
là tham số thực) có nghiệm trên (0;2) khi và chỉ khi
A. (0).m f
B. (2) 4.m f
C. (0).m f
D. (2) 4.m f
Câu 32. Tập nghiệm của bất phương trình
2
4
3 27
x
là
A. [ 1;1]. B. ( ;1]. C. [ 7; 7]. D. [1; ).
Lôøi giaûi tham khaûo
Ta có:
2
4 2 2
3
3 27 4 log 27 3 1 1 1.
x
x x x
Chọn đáp án A.
Baát phöông trình muõ vaø loâgarít
Đặt điều kiện.
Cơ số (0;1)a bất phương trình đổi chiều. Nếu 1a bất phương trình không đổi chiều.
Giao tập nghiệm với điều kiện và chọn đáp án.
Baát phöông trình muõ vaø loâgarit giaûi baèng phöông phaùp ñaët aån phuï
Dạng cơ bản:
2 ( ) ( ) ( )
2
. . 0 0.
.(log ) .(log ) 0 log .
PPf x f x f x
PP
a a a
a a t a
x x t x
( ) ( ) ( )
( )
1
PPf x f x f x
f x
a a b a b
a
đặt
( )
0.
f x
t a
2 ( ) ( ) 2 ( ) 2 ( )
. .( ) . 0 chia
PPf x f x f x f x
a ab b b
đặt
( )
0.
f x
a
t
b
( ) ( )
f x f x
a b c với . 1a b
PP
đặt
( ) ( )
1
f x f x
t a b
t
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 53 -
Baøi taäp töông töï vaø môû roäng
32.1. Tập nghiệm của bất phương trình
2
13
3 27
x
là
A.
(4; ).
B.
( 4; 4).
C.
( ; 4).
D.
(0; 4).
32.2. Tập nghiệm của bất phương trình
2
23
3 9
x
là
A.
( 5;5).
B.
( ;5).
C.
(5; ).
D.
(0;5).
32.3. Tập nghiệm của bất phương trình
2 2
x
là
A.
[0;1).
B.
( ;1).
C.
(0;1).
D.
(1; ).
32.4. Tập nghiệm của bất phương trình
2
4
1
2
2
x x
x
là
A.
( 2; ).
S
B.
(2; ).
S
C.
( 2;2).
S
D.
( ; 2) (2; ).
S
32.5. Hỏi bất phương trình
2
2 10
3 4
1
2
2
x
x x
có bao nhiêu nghiệm nguyên dương ?
A.
2.
B.
4.
C.
6.
D.
3.
32.6. Tập nghiệm của bất phương trình
2
1 9
5 5
x x x
là
A.
[ 2; 4].
B.
[ 4;2].
C.
( ;2] [4; ).
D.
( ; 4] [2; ).
32.7. Tập nghiệm của bất phương trình
2
3
log (36 ) 3
x
là
A.
( ; 3] [3; ).
B.
( ;3].

C.
[ 3; 3].
D.
(0;3].
32.8. Tập nghiệm của bất phương trình
2
3
log (31 ) 3
x
là
A.
( ;2].

B.
[ 2;2].
C.
( ; 2] [2; ).
D.
(0;2].
32.9. Tìm tập nghiệm
S
của bất phương trình
3 1
2
log (log ) 1.
x
A.
(0;1).
S
B.
1
;1
8
S
C.
(1; 8).
S
D.
(1; 3).
S
32.10. Tập nghiệm
S
của bất phương trình
3
6
log log ( 2) 0
x
là khoảng
( ; ).
a b
Giá trị
b a
bằng
A.
2.
B.
4.
C.
3.
D.
5.
32.11. Tập nghiệm của bất phương trình
4 3.2 2 0
x x
là
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 54 -
A.
( ; 0) (1; ).

B.
[0;1).
C.
(1;2).
D.
(0;1).
32.12. Tập nghiệm của bất phương trình
2 1
3 10.3 3 0
x x
là
A.
[ 1;0).
B.
( 1;1).
C.
(0;1].
D.
[ 1;1].
32.13. Số nghiệm nguyên của bất phương trình
3 9.3 10
x x
là
A.
7.
B.
1.
C.
5.
D. Vô số.
32.14. Tập nghiệm của bất phương trình
9 2.6 4 0
x x x
là
A.
(0; ).
B.
.
C.
\ {0}.
D.
[0; ).

32.15. Số nghiệm nguyên của bất phương trình
2
(17 12 2) (3 8)
x x
là
A.
1.
B.
2.
C.
4.
D.
3.
32.16. Tập nghiệm của bất phương trình
2
2 2
log 5 log 4 0
x x
là
A.
( ;2] [16; ).
 
B.
[2;16].
C.
(0;2] [16; ).

D.
( ;1] [4; ).
 
32.17. Tập nghiệm của bất phương trình
2
log 2019 log 2018 0
x x
là
A.
2018
[10;10 ].
B.
2018
[10;10 ).
C.
[1;2018].
D.
2018
(10;10 ).
32.18. Cho hàm số
3
( ) .e .
x
f x x
Tập nghiệm của bất phương trình
( ) 0
f x
là
A.
1
0; .
3
B.
(0;1).
C.
1
; .
3
D.
1
; .
3

32.19. Tập nghiệm của của bất phương trình
1
3
1 2
log 0
x
x
là
A.
1
; .
3

B.
1
0; .
3
C.
1 1
; .
3 2
D.
1
; .
3

32.20. Bất phương trình
1 1 1
4 5.2 16 0
x x x x
có tập nghiệm là
[ ; ].
a b
Khi đó
2 2
a b
bằng
A.
5.
B.
10.
C.
12.
D.
17.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 55 -
Câu 33. Nếu
3
1
2 ( ) 1 d 5
f x x
thì
3
1
( )d
f x x
bằng
A.
3.
B.
2.
C.
3
4
D.
3
2
Lôøi giaûi tham khaûo
Áp dụng tính chất tích phân
3 3 3
1 1 1
3
5 2 ( ) 1 d 2 ( )d 2 ( )d
2
f x x f x x f x x
Chọn đáp án D.
Baøi taäp töông töï vaø môû roäng
33.1. Biết
1
0
( ) 2 d 2.
f x x x
Khi đó
1
0
( )d
f x x
bằng
A.
1.
B.
4.
C.
2.
D.
0.
33.2. Cho hàm số
f x
liên tục trên
và
2
2
0
( ) 3 d 10.
f x x x
Khi đó
2
0
( )d
f x x
bằng
A.
2.
B.
2.
C.
18.
D.
18.
33.3. Cho
( ), ( )
f x g x
là hai hàm số liên tục trên đoạn
[1;3]
thỏa mãn
3
1
( ) 3 ( ) d 10
f x g x x
và
3
1
2 ( ) ( ) d 6.
f x g x x
Khi đó
3
1
( ) ( ) d
f x g x x
bằng
A.
7.
B.
6.
C.
8.
D.
9.
33.4. Biết
3
( )
F x x
là một nguyên hàm của hàm số
( )
f x
trên
.
Giá trị của
3
1
d
1 ( )f x
x
bằng
A.
20.
B.
22.
C.
26.
D.
28.
33.5. Nếu
1
0
( ) 2 d (1)
xf x x x f
thì
1
0
( )d
f x x
bằng
A.
2.
B.
2.
C.
1.
D.
1.
33.6. Cho hai hàm số
( ), ( )
f x g x
xác định và liên tục trên
thỏa mãn
2
( )d
f x x x x C
và
4 3
( )d .
g x x x x C
Khi đó
1
0
( ) ( ) d
f x g x x
bằng
A.
51
10
B.
71
105
C.
4.
D.
77
60
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 56 -
33.7. Nếu
2
2
1
( 1)d 2
xf x x
thì
5
2
( )d
f x x
bằng
A.
2.
B.
1.
C.
4.
D.
1.
33.8. Nếu
2
1
(3 1)d 20
f x x
thì
5
2
( )d
f x x
bằng
A.
20.
B.
40.
C.
10.
D.
60.
33.9. Cho hàm số
( )
f x
liên tục và có đạo hàm trên
,
thỏa mãn
2
( 2 )d 3 .
f x x x x C
Khi đó
3
0
( ) 1d
f x x x
bằng
A.
94
15
B.
442
15
C.
22
15
D.
326
15
33.10. Biết hàm số
( ) 2 1 2021
F x x x
là một nguyên hàm của hàm số
( )
f x
trên
và tích phân
2
1
5
(2 1)d
a
f x x
b b
với
a
b
là phân số tối giản. Khi đó
2
a b b
bằng
A.
8.
B.
8.
C.
48.
D.
48.
33.11. Nếu
( )
f x
có đạo hàm trên
thỏa
(1) 1,
f
(2) 4
f
thì
2
2
1
( ) 2 ( ) 1
d
f x f x
x
x
x
bằng
A.
1 ln 4.
B.
4 ln2.
C.
1
ln 4.
2
D.
1
ln 2
2
33.12. Cho hàm số
( )
f x
xác định và liên tục trên
.
Gọi
( )
g x
là một nguyên hàm của hàm số
2
( )
x
y
x f x
Biết
4
3
( )d 1
g x x
và
4 (4) 3 (3) 4.
g g
Khi đó
4
2
2
3
d
( )
x
x
x f x
bằng
A.
2.
B.
4.
C.
3.
D.
1.
33.13. Cho hàm số
( )
f x
thỏa
1
2
0
( )d 12
x f x x
và
2 (1) (1) 2.
f f
Khi đó
1
0
( )d
f x x
bằng
A.
6.
B.
5.
C.
7.
D.
8.
33.14. Cho hàm số
2
2 khi 0
( )
3 2 khi 0
ax x
f x
x bx x
(với
,
a b
là các tham số thực) thỏa
1
1
( )d 2.
f x x
Giá
trị nhỏ nhất của biểu thức
2 2
( 1) (1)
P f f
bằng
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 57 -
A. 5. B.
25
4
C. 2. D.
25
2
33.15. Cho hàm số
2
1 khi 1
( )
khi 1
ax x
f x
x b x
có đạo hàm trên
( , a b
là các tham số thực). Khi đó
2
1
( )df x x
bằng
A.
1
3
B.
19
3
C.
26
3
D.
25
3
33.16. Cho hàm số ( )y f x có đồ thị như hình vẽ, biết
3
3
( ) d 2.f x x
Giá trị của
m
bằng
A.
3
4
B. 5.
C.
3.
D.
1
2
33.17. Cho
( )f x
có đạo hàm trên thỏa
1
2
0
( ) 3 2 ( ) ( )d .f x x x f x f x x
Khi đó
2
0
( )df x x
bằng
A.
10
3
B.
10
3
C.
26
15
D.
26
15
33.18. Cho
( )f x
là hàm số lẻ thỏa mãn
0
2
( )d 2.f x x
Khi đó
2
0
( )df x x
bằng
A.
2.
B.
2.
C.
1.
D.
1.
33.19. Cho
( )f x
là hàm số chẵn và liên tục trên
thỏa
1
1
( )d 2.f x x
Khi đó
1
0
( )df x x
bằng
A. 1. B. 2.
C.
1
2
D.
1
4
33.20. Xét tích phân
1
1
( )
d 4,
1 2
x
f x
x
với ( )f x là hàm số chẵn trên
[ 1;1],
khi đó
1
1
( )df x x
bằng
A. 2. B. 16.
C. 4. D. 8.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 58 -
Câu 34. Cho số phức
3 4 .
z i
Môđun của số phức
(1 )
i z
bằng
A.
50.
B.
10.
C.
10.
D.
5 2.
Lôøi giaûi tham khaûo
Dùng tính chất môđun của tích:
(1 ) 1 . 3 4 2 5 5 2.
i z i i
Chọn đáp án D.
Baøi taäp töông töï vaø môû roäng
34.1. Cho hai số phức
1
2 3
z i
và
2
1 2 .
z i
Môđun của số phức
1 2
( 2)
z z
bằng
A.
15.
B.
5 5.
C.
65.
D.
137.
34.2. Cho hai số phức
1
3 4
z
i
và
2
4 3 .
z
i
Môđun của số phức
1
2
2
3
z
z
bằng
A.
5
2
B.
2
3
C.
1.
D.
2.
34.3. Cho số phức
3 4 .
z i
Tính môđun của số phức
25
w iz
z
A.
2.
B.
2.
C.
5.
D.
5.
34.4. Tìm môđun của số phức
(1 ) ,
w z z
biết
z
thỏa mãn
2
(3 2 ) (2 ) 4 .
i z i i
A.
2.
B.
10.
C.
8.
D.
2.
34.5. Cho hai số phức
1
2 3
z i
và
2
1 2 .
z i
Tính môđun của số phức
1 2
( 2) .
z z z
A.
15.
B.
5 5.
C.
65.
D.
137.
34.6. Cho số phức
2 3 .
z i
Tìm môđun của số phức
(1 ) .
w i z z
A.
3.
B.
5.
C.
4.
D.
7.
34.7. Cho hai số phức
1
1
z i
và
2
2 3 .
z i
Tính môđun của số phức
1 2
.
z z
A.
13.
B.
5.
C.
1.
D.
5.
34.8. Cho hai số phức
1 3
z i
và
1 .
w i
Môđun của số phức
.
z w
bằng
A.
2 5.
B.
2 2.
C.
20.
D.
8.
34.9. Tìm môđun của số phức
2 4 2 2016
1 , .
n
z i i i i n
A.
2.
z
B.
1.
z
C.
1008.
z
D.
2006.
z
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 59 -
34.10. Cho số phức
z
thỏa
1
(2 ) 5 .
1
i
i z i
i
Tìm môđun của số phức
2
1 2 .
w z z
A.
4.
w
B.
2 7.
w
C.
10.
w
D.
100.
w
34.11. Cho số phức
z
thỏa mãn điều kiện
(1 ) 4 7 7 .
i z z i
Tìm môđun của số phức
.
z
A.
3.
z B.
5.
z
C.
5.
z D.
3.
z
34.12. Cho
z
số phức thỏa mãn
(1 2 ) 2 4 .
z i z i
Tìm môđun của số phức
.
z
A.
3.
z
B.
5.
z
C.
5.
z
D.
3.
z
34.13. Cho số phức
z a bi
thỏa mãn
2
3 (2 ) 7 17 .
z
z i i
z
Trên mặt phẳng tọa độ, điểm biểu
diễn của số phức
z
là
A.
(2; 3).
M
B.
( 2;3).
N
C.
(2; 3).
P
D.
( 2; 3).
Q
34.14. Cho số phức
z
thỏa mãn
2
5 (2 ) 17 19 9
z
z i i
z
Trên mặt phẳng tọa độ, điểm biểu diễn
của số phức
z a bi
là
A.
(4; 3).
Q
B.
(3; 4).
N
C.
( 4;3).
M
D.
( 3;4).
P
34.15. Cho số phức
z a bi
thỏa mãn
2
2 . (5 7 ) (17 ) .
z z i z i z
Trên mặt phẳng tọa độ, điểm
biểu diễn của số phức
z
khác gốc tọa độ là
A.
( 1;2).
N
B.
(2; 1).
P
C.
( 2;1).
Q
D.
(1; 2).
M
34.16. Cho số phức
z
thỏa mãn
2
(3 ) 24 12 (5 )
z
i z i i
z
Tỉ số giữa phần thực và phần ảo là
A.
3
B.
3.
C.
2
7
D.
5
3
34.17. Cho số phức
z
thỏa mãn
2
. (6 8 ) (5 ) (23 73 ) .
z z i i z i z
Tỉ số giữa phần thực và phần
ảo bằng
A.
2
5
B.
2
7
C.
2.
D.
3.
34.18. Cho các số phức
z
thỏa
( 2 )( 2 ) 16.
z i z i
Biết rằng tập hợp các điểm biểu diễn các số
phức
(1 ) 2
w i z i
là một đường tròn. Tìm bán kính
R
của đường tròn đó.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 60 -
D'
B'
C'
D
A
C
B
A'
A.
2r
B. 5.r
C.
4 2.r
D. 3.r
34.19. Cho các số phức
z
thỏa ( )( ) 9.z i z i Biết trong mặt phẳng tọa độ các điểm biểu diễn của
số phức
(3 4 ) 2w i z i
cùng thuộc một đường tròn cố định có bán kính là
A. 5.r B. 14.r
C. 23.r D. 15.r
34.20. Cho các số phức
z
thỏa . (3 ) (3 ) 9 0.z z z i z i Biết rằng tập hợp các điểm biểu diễn
các số phức 2 . 5w i z i là một đường tròn. Tìm bán kính R của đường tròn đó.
A. 5. B. 1.
C. 2. D. 7.
Câu 35. Cho hình hộp chữ nhật .ABCD A B C D
có 2AB AD và
2 2AA
(tham khảo hình
vẽ bên). Góc giữa đường thẳng CA
và mặt phẳng ( )ABCD bằng
A. 30 .
B. 45 .
C. 60 .
D. 90 .
Lôøi giaûi tham khaûo
Góc cần tìm là
.A CA
Vì đáy hình vuông nên
2 2 2AC AB
và
tan 1 45 .
AA
AC
Chọn đáp án B.
Xaùc ñònh goùc giöõa ñöôøng thaúng vaø maët phaúng
Cần nhớ: “Góc giữa đường thẳng và mặt phẳng là góc tạo bởi nó và hình chiếu của nó lên mặt phẳng”.
B.1. Tìm giao điểm
( )AB P A
(1)
B.2. Tìm hình chiếu H của B lên mặt phẳng
( ).P
Đặt câu hỏi: “Đường nào qua B và vuông góc với
( )P
?
Trả lời:
( )BH P
tại H
(2)
(nếu chưa có thì dựng)
Từ
(1),(2),
suy ra AH là hình chiếu của AB lên mặt phẳng
( ).P
Do đó góc giữa đường thẳng AB và
( )P
là góc giữa AB và
,AH
chính là góc
.BAH
B.3. Sử dụng hệ thức lượng trong tam giác để tìm góc (thường sử dụng tan).
Baøi taäp töông töï vaø môû roäng
35.1. Cho hình lập phương .ABCD A B C D
có cạnh bằng
a
(minh họa như hình bên). Góc giữa
đường thẳng AB
và mặt phẳng
( )BDD B
bằng
A. 60 .
B. 90 .
C. 45 .
D. 30 .
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 61 -
35.2. Cho hình lập phương .ABCD A B C D
(tham khảo hình vẽ bên). Tang góc giữa đường
thẳng BD
và mặt phẳng ( )ADD A
bằng
A.
3
3
B.
6
3
C.
2
2
D.
2
6
35.3. Cho hình hộp chữ nhật .ABCD A B C D
có , 2 .AB AA a AD a
Gọi góc giữa đường chéo
A C
và mặt phẳng đáy( )ABCD là . Khi đó tan bằng
A.
5
5
B.
5.
C.
3
3
D.
3.
35.4. Cho hình lăng trụ đứng .ABC A B C
có đáy ABC là tam giác vuông cân tại ,A AB AA a
(tham khảo hình vẽ bên). Tính tang của góc giữa đường thẳng BC
và mặt phẳng
A.
2
2
B.
6
3
C.
2.
D.
3
3
35.5. Cho hình lăng trụ đứng .ABC A B C
có đáy
ABC
là một tam giác vuông cân tại ,B ,AB a
3.BB a
Góc giữa đường thẳng A B
và mặt phẳng ( )BCC B
bằng
A.
30 .
B.
90 .
C.
60 .
D.
45 .
35.6. Cho hình lập phương . .ABCD A B C D
Gọi O
là trung điểm của của .A C
Tính tan với
là góc tạo bởi BO
và mặt phẳng ( ).ABCD
A.
3.
B.
2.
C. 1.
D.
2
2
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 62 -
35.7. Cho hình lập phương .ABCD A B C D
cạnh bằng
.a
Gọi ,M N lần lượt là trung điểm của cạnh
AC và ,B C
là góc giữa đường thẳng MN và mặt phẳng ( ).A B C D
Giá trị sin bằng
A.
1
2
B.
2 5
5
C.
2
2
D.
5
2
35.8. Cho hình hộp chữ nhật .ABCD A B C D
có cạnh 2,AB a
6AD a
và
2 2.AA a
Tính
côsin của góc giữa đường thẳng B D
và mặt phẳng ( ).B D C
A.
35
38
B.
1
3
C.
1
6
D.
3
11
35.9. Cho hình lập phương .ABCD A B C D
có cạnh bằng ,a gọi
là góc giữa đường thẳng A B
và
mặt phẳng ( ).BB D D
Khi đó sin bằng
A.
3
4
B.
3
2
C.
3
5
D.
1
2
35.10. Cho hình chóp .S ABC có SA vuông góc với mặt phẳng ( ),ABC
2,SA a
tam giác ABC vuông
cân tại B và 2AC a (minh họa như hình). Góc giữa đường thẳng SB và mặt phẳng ( )ABC bằng
A. 30 .
B. 45 .
C. 60 .
D. 90 .
35.11. Cho hình chóp .S ABCD có đáy ABCD là hình chữ nhật,
2,AB a
,AD a SA vuông góc
với đáy và SA a (minh họa như hình bên dưới). Góc giữa đường thẳng SC và mặt phẳng
( )SAB bằng
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 63 -
A
B
C
D
S
B D
C
A
A
C
S
B
D
A
B
C
S
H
A
S
D
CB
A.
90 .
B.
60 .
C.
45 .
D.
30 .
35.12. Cho tứ diện đều
ABCD
có cạnh bằng
a
(minh họa như hình bên). Côsin góc giữa đường thẳng
AB
và mặt phẳng
( )
BCD
bằng
A.
3
2
B.
3
3
C.
1.
D.
2
3
35.13. Cho hình chóp
.
S ABC
có các mặt
ABC
và
SBC
là các tam giác đều và nằm trong hai mặt
phẳng vuông góc với nhau (minh họa như hình bên). Góc giữa đường thẳng
SA
và mặt phẳng
( )
ABC
bằng
A.
45 .
B.
75 .
C.
60 .
D.
30 .
35.14. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
,
a SD a
và
SD
vuông góc với
mặt phẳng đáy (minh họa như hình bên). Góc giữa đường thẳng
SA
và mặt phẳng
( )
SBD
bằng
A.
45 .
B.
1
arcsin
4
C.
30 .
D.
60 .
35.15. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông. Mặt bên
SAB
là tam giác đều có đường
cao
SH
vuông góc với
( )
ABCD
(minh họa như hình bên). Gọi
là góc giữa đường thẳng
BD
và mặt phẳng
( ).
SAD
Giá trị của
sin
bằng
A.
6
4
B.
1
2
C.
3
2
D.
10
4
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 64 -
M
A
C
S
B
M
B
D
A
C
M
A
B C
D
S
A
C
S
B
35.16. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
,
a
cạnh bên
SA
vuông góc với mặt
đáy và
2 .
SA a
Gọi
M
là trung điểm của
SC
(minh họa như hình bên). Gọi
là góc giữa
đường thẳng
BM
và mặt phẳng
(
).
ABC
Giá trị của
cos
bằng
A.
7
14
B.
1.
C.
5
7
D.
21
7
35.17. Cho tứ diện
ABCD
có tam giác
BCD
đều cạnh
,
a AB
vuông góc với
( ), 2
BCD AB a
và
M
là trung điểm đoạn
AD
(minh họa như hình bên). Gọi
là góc giữa đường thẳng
CM
với mặt
phẳng
( ).
BCD
Khi đó giá trị của
tan
bằng
A.
1.
B.
2 3
3
C.
2.
D.
6
3
35.18. Cho hình chóp tứ giác đều
.
S ABCD
có tất cả các cạnh bằng
.
a
Gọi
M
là trung điểm
SD
(minh
họa như hình bên). Gọi
là góc giữa đường thẳng
BM
và
( ).
ABCD
Khi đó
tan
bằng
A.
2
2
B.
2.
C.
0,5.
D.
1
3
35.19. Cho chóp
.
S ABC
có
SA
vuông góc với đáy, tam giác
ABC
vuông tại
.
B
Biết
SA AB
BC
(xem hình vẽ). Góc giữa đường thẳng
SB
và mặt phẳng
( )
SAC
bằng
A.
30 .
B.
45 .
C.
60 .
D.
90 .
35.20. Cho hình chóp
.
S ABC
có đáy là tam giác vuông cân tại
,
B
,
AB a
,
SA AB
,
SC BC
2 .
SB a
Gọi
,
M
N
là trung điểm
,
SA
.
BC
Gọi
là góc giữa
MN
với
( ).
ABC
Tính
cos .
A.
cos 1.
B.
6
cos
3
C.
cos 0,5.
D.
10
cos
5
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 65 -
Câu 36. Cho hình chóp tứ giác đều .S ABCD có độ dài cạnh đáy bằng 2 và độ dài cạnh bên bằng
3
(tham khảo hình vẽ). Khoảng cách từ S đến mặt phẳng
( )ABCD
bằng
A. 7. B. 1. C.
7.
D. 11.
Lôøi giaûi tham khaûo
Gọi O là tâm của đáy thì
[ ,( )] .d S ABCD SO
Ta có
2 2
2
2 2
AC
OA
và 3SA nên
2 2 2
3 2 7.SO SA OA Chọn đáp án B.
Khoaûng caùch töø moät ñieåm ñeán ñöôøng thaúng
Khoaûng caùch töø chaân ñöôøng cao ñeán maët beân Tæ soá khoaûng caùch (töø ñieåm ñeán maët)
Baøi toaùn 1. Cho tứ diện SABC có
( ).
SA ABC
Tính khoảng cách từ điểm chân A đến mặt
( ).
SBC
B1. Tìm giao tuyến của mặt bên và mặt đáy.
( ) ( ) .SBC ABC BC
B2. Dựng hình
( ).
AH BC
AI SBC
AI SH
Suy ra
( ;( )) .d A SBC AI
Baøi toaùn 2. Tính khoảng cách từ điểm M (không
phải là chân đường cao) đến mặt phẳng
( ).P
Có d qua M và
( ) .d P I
Dựng
( ).
MH P
Suy ra:
( ,( ))d M P MH
(khó tìm).
Do đó ( ;( )) ( ,( ))
IM
d M P d A P
IA
(bài toán 1)
Khoaûng caùch giöõa hai ñöôøng thaúng cheùo nhau
Khoaûng caùch giöõa hai ñöôøng cheùo nhau vaø
vuoâng goùc nhau laø ñoä daøi ñoaïn vuoâng chung
Khoaûng caùch giöõa hai ñöôøng thaúng cheùo nhau
vaø khoâng vuoâng goùc nhau
Cho hình chóp .S ABC có đáy là tam giác vuông cân
tại
,A
mặt bên
( )SBC
là tam giác đều và nằm trong
mặt phẳng vuông góc với mặt phẳng đáy. Xác định
khoảng cách giữa hai đường thẳng SA và .BC
Dễ dàng chứng minh được
( ).BC SHA
.BC SA
Từ chân
,H
dựng HK SA và có
.HK BC Suy ra:
( , ) .d SA BC KH
Cho hình chóp .S ABCD có
( ).SA ABCD
Tính
khoảng cách giữa cạnh bên SB và cạnh thuộc mặt
phẳng đáy .AC
B1. Tìm giao điểm:
( ) .SB ABCD B
B2. Qua
,B
dựng
d AC
và .
AH d
AK SH
( , ) ( ,( )) ( ,( ))
d AC SB d AC SHB d A SHB
B3. Sử dụng bài toán 1
( ,( )) .
d A SHB AK
(điểm cắt)
(điểm cũ)
chân đường cao
(điểm mới)
d
P
I
M
H
A
K
K
H
B
C
A
S
điểm cũ
điểm mới
điểm cắt
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 66 -
A
B
C
D
S
A
B
C
D
S
A
C
B
S
A
C
B
D
Baøi taäp töông töï vaø môû roäng
36.1. Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
.
a
Biết
SA
vuông góc với đáy và
SA a
(tham khảo hình vẽ). Khoảng cách từ điểm
A
đến mặt phẳng
( )
SBD
bằng
A.
2
3
a
B.
3
a
C.
2 3
a
D.
2
6
a
36.2. Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh bằng
,
a
SA
vuông góc với mặt phẳng
( ).
ABCD
Biết góc giữa
SC
và mặt phẳng
( )
ABCD
bằng
60
(tham khảo hình vẽ). Khoảng cách
từ điểm
B
đến mặt phẳng
( )
SCD
bằng
A.
10
5
a
B.
2
2
a
C.
2
a
D.
42
7
a
36.3. Cho hình chóp
.
S ABC
có đáy là tam giác vuông ở
,
A
biết
( )
SA ABC
và
2 ,
AB a
3 ,
AC a
4
SA a
(tham khảo hình vẽ). Khoảng cách từ điểm
A
đến mặt phẳng
( )
SBC
bằng
A.
12 61
61
a
B.
2 .
a
C.
43
12
a
D.
6 29
29
a
36.4. Cho tứ diện
ABCD
có cạnh
AD
vuông góc với mặt phẳng
( ),
ABC
4,
AC AD
3,
AB
5
BC
(tham khảo hình vẽ). Khoảng cách từ điểm
A
đến mặt phẳng
( )
BCD
bằng
A.
12
34
B.
60
769
C.
769
60
D.
34
12
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 67 -
A
S
D
CB
A
S
D
CB
A
S
D
CB
M
S
B
C
A
36.5. Hình chóp
.
S ABCD
có đáy là hình thoi cạnh
,
a
góc
60 ,
BAC SA
vuông góc với mặt phẳng
( ),
ABCD
góc giữa hai mặt phẳng
( )
SBC
và
( )
ABCD
bằng
60
(tham khảo hình vẽ). Khoảng
cách từ điểm
A
đến mặt phẳng
( )
SBC
bằng
A.
2
3
a
B.
2 .
a
C.
3
4
a
D.
.
a
36.6. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh bằng
1.
Tam giác
SAB
đều và nằm
trong mặt phẳng vuông góc với mặt đáy
( )
ABCD
(tham khảo hình vẽ). Khoảng cách từ điểm
B
đến mặt phẳng
(
)
SCD
bằng
A.
1.
B.
21
3
C.
2.
D.
21
7
36.7.
Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông tâm
O
cạnh
,
a
mặt bên
SAB
là tam giác
đều và nằm trong mặt phẳng vuông góc với đáy (tham khảo hình vẽ). Khoảng cách từ trọng tâm
G
của tam giác
SAB
đến mặt phẳng
( )
SBC
bằng
A.
3
6
a
B.
5
3
a
C.
2 2
9
a
D.
21
21
a
36.8. Cho hình chóp tam giác đều
.
S ABC
có
2
SA a
và
3 .
AB a
Gọi
M
là trung điểm
SC
(tham
khảo hình vẽ). Khoảng cách từ điểm
M
đến mặt phẳng
( )
SAB
bằng
A.
3 21
.
14
a
B.
3 3
.
2
a
C.
3 3
.
4
a
D.
3 21
.
7
a
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 68 -
A
B
C
D
S
G
D'
A'
B'
D
C
B
A
C'
O
B
A
C
M
B'
C'
A
C
B
A'
36.9. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật
,
AB a
3.
AD a
Cạnh bên
SA
vuông góc với đáy và
2
SA a
(tham khảo hình vẽ). Khoảng cách từ điểm
C
đến mặt phẳng
( )
SBD
bằng
A.
2 57
19
a
B.
2
5
a
C.
5
2
a
D.
57
19
a
36.10. Cho hình phương
.
ABCD A B C D
có tất cả các cạnh bằng
a
(tham khảo hình vẽ). Khoảng cách
từ trọng tâm
G
của tam giác
A BD
đến mặt phẳng
( )
CB D
bằng
A.
2
81
a
B.
2 3
3
a
C.
2 3
9
a
D.
6
18
a
36.11. Cho tứ diện
OABC
có
,
OA
,
OB
OC
đôi một vuông góc với nhau và
OA OB OC a
(tham
khảo hình vẽ). Khoảng cách giữa hai đường thẳng
OA
và
BC
bằng
A.
3
.
2
a
B.
1
.
2
a
C.
2
.
2
a
D.
3
.
2
a
36.12. Cho hình lăng trụ đều
.
ABC A B C
có tất cả các cạnh bằng
.
a
Gọi
M
là trung điểm của cạnh
BC
(tham khảo hình bên). Khoảng cách giữa hai đường thẳng
AM
và
B C
là
A.
2.
a
B.
2
2
a
C.
1
.
2
a
D.
2
4
a
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 69 -
A
D
C
B
S
A
S
D
CB
A
C
B
S
M
A
D
C
B
36.13. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
,
a
cạnh
SA a
và vuông góc với
mặt đáy
( )
ABCD
(tham khảo hình bên). Khoảng cách giữa hai đường thẳng
SC
và
BD
bằng
A.
3
4
a
B.
6
3
a
C.
2
a
D.
6
6
a
36.14. Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
,
a
SA a
và
SA
vuông góc với đáy (tham
khảo hình bên). Khoảng cách giữa hai đường thẳng
AB
và
SC
bằng
A.
2.
a
B.
2
2
a
C.
2
3
a
D.
2
4
a
36.15. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
, 3 , 4 .
B AB a BC a
Cạnh bên
SA
vuông góc với đáy. Góc tạo bởi giữa
SC
và đáy bằng
60 .
Gọi
M
là trung điểm của
AC
(tham khảo hình bên). Khoảng cách giữa hai đường thẳng
AB
và
SM
bằng
A.
13
2
a
B.
10 3
79
a
C.
5
2
a
D.
5 3.
a
36.16. Cho tứ diện đều
ABCD
cạnh bằng
.
a
Gọi
M
là trung điểm của
CD
(tham khảo hình bên).
Khoảng cách giữa hai đường thẳng
AC
và
BM
bằng
A.
22
11
a
B.
2
3
a
C.
3
3
a
D.
5
2
a
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 70 -
A
S
D
CB
M
A
C
B
S
A
S
D
CB
M
A
S
D
CB
36.17. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông cạnh
2 ,
a
cạnh bên
5,
SA a
mặt bên
SAB
là tam giác cân đỉnh
S
và thuộc mặt phẳng vuông góc với mặt phẳng đáy (tham khảo hình
bên). Khoảng cách gữa hai đường thẳng
AD
và
SC
bằng
A.
2 5
5
a
B.
4 5
5
a
C.
15
5
a
D.
2 15
5
a
36.18. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông tại
,
B
,
AB a
cạnh bên
SA
vuông góc
với mặt đáy và
2.
SA a
Gọi
M
là trung điểm của
AB
(tham khảo hình bên). Khoảng cách
giữa hai đường thẳng
SM
và
BC
bằng
A.
2
a
B.
2
3
a
C.
3
3
a
D.
2
2
a
36.19. Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh
a
và hai điểm
,
M N
lần lượt là trung điểm
, .
AB AD
Tam giác
SAB
đều và nằm trong mặt phẳng vuông góc với đáy (tham khảo hình vẽ).
Khoảng cách giữa hai đường thẳng
SM
và
NC
bằng
A.
3
4
a
B.
.
a
C.
5
10
a
D.
3 5
10
a
36.20. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
, 2 ,
AB a AD a
SA
vuông góc với
mặt phẳng đáy và
SA a
(tham khảo hình vẽ). Gọi
M
là trung điểm của
.
CD
Khoảng cách
giữa hai đường thẳng
SD
và
BM
bằng
A.
21
21
a
B.
2 21
21
a
C.
2 7
7
a
D.
7
7
a
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 71 -
Câu 37. Trong không gian ,Oxyz mặt cầu có tâm là gốc tọa độ O và đi qua điểm (0;0;2)M có phương
trình là
A.
2 2 2
2.x y z
B.
2 2 2
4.x y z
C.
2 2 2
( 2) 4.x y z
D.
2 2 2
( 2) 2.x y z
Lôøi giaûi tham khaûo
Bán kính của mặt cầu là 2,MO và do có tâm ở (0;0;0)O nên có phương trình là
2 2 2
4.x y z
Chọn đáp án C.
Vieát phöông trình maët caàu
Dạng 1. Cơ bản
2 2 2 2
( ) : ( ) : ( ) ( ) ( ) .
; )
:
( ;T
S S x a y b z c R
BK
â
R
m I a b c
Dạng 2. Viết phương trình mặt cầu ( )S có tâm I và đi qua điểm .A
Phương pháp:
( ) : .
:
T
S
BK R A
âm I
I
Dạng 3. Viết phương trình mặt cầu ( )S có đường kính ,AB với , A B cho trước.
Phương pháp:
( ) :
1
:
2
T
S
BK R A
âm I
B
Dạng 4. Viết phương trình mặt cầu ( )S có tâm I và tiếp xúc với ( ).P
Phương pháp:
( ) : .
: ;(
)
T
S
BK R d d
âm
I P
I
Cần nhớ: ( ) : 0, ( ) : 0, ( ) : 0.Oxy z Oyz y Oxz x
Dạng 5. Viết phương trình mặt cầu ( )S có tâm I và cắt mặt phẳng ( )P theo giao tuyến là một
đường tròn có bán kính
.r
Phương pháp:
2 2
( ) : .
(
: ;( ))
T
S
BK R d I r
â
P
m I
Cần nhớ: Chu vi đường tròn 2C r và diện tích
2
t
.S r
đ
Dạng 6. Viết phương trình mặt cầu ( )S tâm I và tiếp xúc với đường .d
Phương pháp:
( ) : .
: ( ; )
T
S
BK R d d
â I
I
m
Nếu
2 2 2 2 2 2
( ; ; ) ( ; ) , ( ; ) , ( ; ) .I a b c d I Ox b c d I Oy a c d I Oz a b
Dạng 7. Viết phương trình mặt cầu ( )S có tâm I và cắt đường thẳng d tại hai điểm , .A B
Phương pháp:
2
2
( ) : .
: ( )
2
;( )
â
A
T
S
B
BK R d I P
m I
là trung điểm của
.
AB
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 72 -
Baøi taäp töông töï vaø môû roäng
37.1. Trong không gian
,
Oxyz
mặt cầu có tâm
(1;1;1)
I
và diện tích bằng
4
có phương trình là
A.
2 2 2
( 1) ( 1) ( 1) 4.
x y z
B.
2 2 2
( 1) ( 1) ( 1) 1.
x y z
C.
2 2 2
( 1) ( 1) ( 1) 4.
x y z
D.
2 2 2
( 1) ( 1) ( 1) 1.
x y z
37.2. Trong không gian
,
Oxyz
mặt cầu
( )
S
có tâm có tâm
(1; 3;2)
I
và đi qua điểm
(5; 1; 4)
A
là
A.
2 2 2
( ( 24.
( 1) 3) 2)
x y z
B.
2 2 2
( ( 24.
( 1) 3) 2)
x y z
C.
2 2 2
( ( 24.
( 1) 3) 2)
x y z
D.
2 2 2
( ( 24.
( 1) 3) 2)
x y z
37.3. Trong không gian
,
Oxyz
cho hai điểm
(1;1;1)
I
và
(1;2; 3).
A
Phương trình của mặt cầu có tâm
I
và đi qua điểm
A
là
A.
2 2 2
( 1) ( 1) ( 1) 29.
x y z
B.
2 2 2
( 1) ( 1) ( 1) 5.
x y z
C.
2 2 2
( 1) ( 1) ( 1) 25.
x y z
D.
2 2 2
( 1) ( 1) ( 1) 5.
x y z
37.4. Trong không gian
,
Oxyz
cho điểm
(1; 2; 3).
M
Gọi
I
là hình chiếu vuông góc của
M
trên trục
.
Ox
Phương trình nào dưới đây là phương trình mặt cầu tâm
I
bán kính
IM
?
A.
2 2 2
( 1) 13.
x y z
B.
2 2 2
( 1) 13.
x y z
C.
2 2 2
( 1) 17.
x y z
D.
2 2 2
( 1) 13.
x y z
37.5. Trong không gian
,
Oxyz
cho hai điểm
(2;1;1), (0; 3; 1).
A B
Mặt cầu
( )
S
đường kính
AB
có
phương trình là
A.
2 2 2
( 2) 3.
x y z
B.
2 2 2
( 1) ( 2) 3.
x y z
C.
2 2 2
( 1) ( 2) ( 1) 9.
x y z
D.
2 2 2
( 1) ( 2) 9.
x y z
37.6. Trong không gian
,
Oxyz
cho điểm
(1; 2; 3).
I
Hỏi phương trình nào sau đây là phương trình mặt
cầu
( )
S
có tâm
I
và tiếp xúc với trục tung
.
Oy
A.
2 2 2
( 1) ( 2) ( 3) 10.
x y z
B.
2 2 2
( 1) ( 2) ( 3) 10.
x y z
C.
2 2 2
( 1) ( 2) ( 3) 10.
x y z
D.
2 2 2
( 1) ( 2) ( 3) 9.
x y z
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 73 -
37.7. Trong không gian
,
Oxyz
phương trình mặt cầu
( )
S
có tâm
(1;2; 3)
I
và tiếp xúc với mặt phẳng
( )
Oxy
là
A.
2 2 2
( 1) ( 2) ( 3) 9.
x y z
B.
2 2 2
( 1) ( 2) ( 3) 14.
x y z
C.
2 2 2
( 1) ( 2) ( 3) 14.
x y z
D.
2 2 2
( 1) ( 2) ( 3) 9.
x y z
37.8. Trong không gian
,
Oxyz
cho điểm
(2;1;1)
A
và mặt phẳng
( ) : 2 2 1 0.
P x y z
Phương
trình của mặt cầu tâm
A
và tiếp xúc với
( )
P
là
A.
2 2 2
2) ( 1) ( 1) 9.
(
x y z
B.
2 2 2
2) ( 1) ( 1) 2.
(
x y z
C.
2 2 2
2) ( 1) 1) 4.
( (
x y z
D.
2 2 2
2) ( 1) ( 1) 36.
(
x y z
37.9. Trong không gian
,
Oxyz
biết mặt phẳng
( ) : 2 6 0
P x y z
cắt trục
Oy
tại
A
và
( )
P
cắt
đường thẳng
1 4 2
:
2 2 1
x y z
d
tại
.
B
Phương trình mặt cầu có tâm
A
và bán kính
AB
là
A.
2 2 2
( 3) 9.
x y z
B.
2 2 2
( 3) 3.
x y z
C.
2 2 2
( 3) 3.
x y z
D.
2 2 2
( 3) 3.
x y z
37.10. Trong không gian
,
Oxyz
cho tam giác
ABC
với
(2;2;0), (1; 0;2), (0;4;4).
A B C
Phương trình mặt
cầu có tâm
A
và đi qua trọng tâm
G
của tam giác
ABC
là
A.
2 2 2
( 2) ( 2) 4.
x y z
B.
2 2 2
( 2) ( 2) 25.
x y z
C.
2 2 2
( 2) ( 2) 16.
x y z
D.
2 2 2
( 2) ( 2) 5.
x y z
37.11. Trong không gian
,
Oxyz
cho hình bình hành
ABCD
có
(1;2; 1),
A
(2; 1; 3),
B
( 3;5;1).
C
Phương trình mặt cầu tâm
D
và đi qua điểm
A
là
A.
2 2 2
( 4) ( 8) ( 5) 64.
x y z
B.
2 2 2
( 4) ( 8) ( 3) 65.
x y z
C.
2 2 2
( 4) ( 8) ( 3) 64.
x y z
D.
2 2 2
( 4) ( 8) ( 5) 65.
x y z
37.12. Gọi
I
là hình chiếu của
(3; 1; 2)
M
lên mặt phẳng
( ).
Oxy
Phương trình nào sau đây là phương
trình mặt cầu tâm
I
bán kính
.
IM
A.
2 2 2
( 3) ( 1) ( 2) 4.
x y z
B.
2 2 2
( 3) ( 1) 4.
x y z
C.
2 2 2
( 3) ( 1) ( 2) 2.
x y z
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 74 -
D.
2 2 2
( 3) 4.
x y z
37.13. Trong không gian
,
Oxyz
cho điểm
(1;1;1)
I
và mặt phẳng
( ) : 2 2 4 0.
P x y z
Mặt cầu
( )
S
tâm
I
cắt
( )
P
theo một đường tròn bán kính
4.
r
Phương trình của
( )
S
là
A.
2 2 2
( 1) ( 1) ( 1) 16.
x y z
B.
2 2 2
( 1) ( 1) ( 1) 9.
x y z
C.
2 2 2
( 1) ( 1) ( 1) 5.
x y z
D.
2 2 2
( 1) ( 1) ( 1) 25.
x y z
37.14. Trong không gian
,
Oxyz
viết phương trình mặt cầu
( )
S
có tâm
( 2; 3; 4)
I
biết mặt cầu
( )
S
cắt
mặt phẳng tọa độ
( )
Oxz
theo một hình tròn giao tuyến có diện tích bằng
16 .
A.
2 2 2
2) ( 3) ( 4) 25.
(
x y z
B.
2 2 2
( 2) ( 3) ( 4) 5.
x y z
C.
2 2 2
( 2) ( 3) ( 4) 16.
x y z
D.
2 2 2
( 2) ( 3) ( 4) 9.
x y z
37.15. Trong không gian
,
Oxyz
cho mặt cầu
2 2 2
( ) : ( 1) ( 1) ( 1) 25
S x y z
có tâm
I
và mặt
phẳng
( ) : 2 2 7 0.
P x y z
Thể tích của khối nón đỉnh
I
và đường tròn đáy là giao tuyến
của mặt cầu
( )
S
và mặt phẳng
( )
P
bằng
A.
12 .
B.
48 .
C.
36 .
D.
24 .
37.16. Trong không gian
,
Oxyz
cho mặt cầu
( )
S
có tâm
( 2; 3; 4)
I
và biết
( )
S
cắt mặt phẳng
( )
Oxz
theo
một đường tròn giao tuyến có diện tích bằng
16 .
Diện tích xung quanh của khối nón có đỉnh là
I
và đường tròn đáy là giao tuyến của mặt cầu
( )
S
và mặt phẳng
( )
P
bằng
A.
12 .
B.
20 .
C.
24 .
D.
36 .
37.17. Trong không gian
,
Oxyz
phương trình mặt cầu đi qua hai điểm
(3; 1;2),
A
(1;1; 2)
B
và có tâm
thuộc trục
Oz
là
A.
2 2 2
2 10 0.
x y z z
B.
2 2 2
( 1) 11.
x y z
C.
2 2 2
( 1) 11.
x y z
D.
2 2 2
2 11 0.
x y z y
37.18. Trong không gian
,
Oxyz
phương trình mặt cầu
( )
S
đi qua hai điểm
(2;1;0), ( 2; 3;2)
A B
và có
tâm
I
nằm trên đường thẳng
1
:
2 1 2
x y z
d
là
A.
2 2 2
( 1) ( 1) ( 2) 17.
x y z
B.
2 2 2
( 1) ( 1) ( 2) 9.
x y z
C.
2 2 2
( 1) ( 1) ( 2) 5.
x y z
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 75 -
D.
2 2 2
( 1) ( 1) ( 2) 16.x y z
37.19. Trong không gian
,Oxyz
mặt cầu ( )S có tâm (5;6; 8),I cắt trục Ox tại , A B sao cho tam giác
IAB vuông tại I có phương trình là
A.
2 2 2
( 5) ( 6) ( 8) 200.x y z
B.
2 2 2
( 5) ( 6) ( 8) 20.x y z
C.
2 2 2
( 5) ( 6) ( 8) 100.x y z
D.
2 2 2
( 5) ( 6) ( 8) 10.x y z
37.20. Trong không gian
,Oxyz
mặt cầu
( )S
đi qua điểm O và cắt các tia
,Ox
,Oy
Oz lần lượt tại các
điểm
,A
,B
C khác O thỏa mãn tam giác ABC có trọng tâm là điểm
(2; 4; 8).G
Tọa độ tâm của
mặt cầu
( )S
là
A.
4 8 16
; ; .
3 3 3
B.
(1;2;3).
C.
2 4 8
; ; .
3 3 3
D.
(3; 6;12).
Câu 38. Trong không gian
,Oxyz
đường thẳng đi qua hai điểm
(1;2; 1)A
và
(2; 1;1)B
có phương
trình tham số là
A.
1 2
2 3 .
1 2
x t
y t
z t
B.
1
2 3 .
1 2
x t
y t
z t
C.
1
3 2 .
2
x t
y t
z t
D.
1
1 2 .
x t
y t
z t
Lôøi giaûi tham khaûo
Ta có (1; 3;2)AB

là vector chỉ phương của đường thẳng, nó đi qua điểm
(1;2; 1)A
nên có phương
trình tham số là
1
2 3 , .
1 2
x t
y t t
z t
Chọn đáp án A.
Vieát phöông trình ñöôøng thaúng
Để viết phương trình đường thẳng, ta cần tìm một điểm đi qua và một véctơ chỉ phương.
1
2
3
1 2 3
1 2 3
1 2 3
: , ( ).
Qua ( ; ; )
:
VTCP : ( ; ; )
: , ( 0).
d
x x a t
d y y a t t
M x y z
d
z z a t
u a a a
x x y y z z
d a a a
a a a
Một số dạng viết phương trình mặt phẳng thường gặp (tham khảo):
Dạng 1. Viết phương trình tham số và chính tắc (nếu có) của đường thẳng d đi qua A và .B
Phương pháp. Đường thẳng
Qua (hay )
: .
VTCP :
d
A B
d
u AB

A
B
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 76 -
Dạng 2. Viết phương trình đường thẳng
d
dạng tham số và chính tắc (nếu có), biết
d
đi qua điểm
M và song song với đường thẳng .
Phương pháp. Ta có
Qua ( ; ; )
: .
VTCP :
d
M x y z
d
u u
Dạng 3. Viết phương trình đường thẳng d dạng tham số và chính tắc (nếu có), biết d đi qua điểm
M và vuông góc với mặt phẳng
( ) : 0.P ax by cz d
Phương pháp. Ta có
( )
Qua
: .
VTCP : ( ; ; )
d P
M
d
u n a b c
Dạng 4. Viết phương trình tham số và chính tắc của đường thẳng d là giao tuyến của hai mặt
phẳng
( )P
và
( )Q
cho trước.
Phương pháp. Ta có
( ) ( )
: .
VTCP :
Qua ( ) (
, ]
)
[
d P Q
d
A P
n
Q
u n
Dạng 5. Viết phương trình tham số và chính tắc (nếu có) của đường thẳng d đi qua điểm M và
vuông góc với hai đường thẳng
1 2
, d d cho trước.
Phương pháp. Ta có
1 2
: .
P
Qua
VTC : [ , ]
d d d
d
u u u
M
Dạng 6. Viết phương trình đường thẳng d qua M và song song với hai mặt phẳng
( ), ( ).P Q
Phương pháp. Ta có
: .
VTCP : [
Qu
]
a
,
d P Q
d
u
M
n n
Dạng 7. Viết phương trình đường thẳng d qua
,M
vuông góc d
và song song mặt
( ).P
Phương pháp. Ta có
: .
VTCP : [
Qua
, ]
d d P
d
u u n
M
Dạng 8. Phương trình đường thẳng d nằm trong mặt
( ),P
song song mặt
( )Q
và qua .M
Phương pháp. Ta có
: .
VTCP : [
Qu
]
a
,
d P Q
d
u
M
n n
Baøi taäp töông töï vaø môû roäng
38.1. Trong không gian
,Oxyz
phương trình đường thẳng d đi qua hai điểm
(1;2; 3),A
(3; 6;1)B
là
A.
2 2 1
1 4 2
x y z
B.
1 2 3
3 1 1
x y z
C.
3 6 1
1 4 2
x y z
D.
3 1 1
1 4 2
x y z
38.2. Trong không gian
,Oxyz
phương trình trung tuyến AM của tam giác ABC với
(3;1;2),A
( 3;2;5),B
(1;6; 3)C
là
A.
1
1 3 .
8 4
x t
y t
z t
B.
1 4
3 3 .
4 1
x t
y t
z t
P
d
M
A
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 77 -
C.
3 4
1 3 .
2
x t
y t
z t
D.
1 3
3 4 .
4
x t
y t
z t
38.3. Trong không gian
,
Oxyz
cho tam giác
ABC
có
( 1;3;2),
A
(2; 0;5)
B
và
(0; 2;1).
C
Phương trình
trung tuyến
AM
của tam giác
ABC
là
A.
1 3 2
2 2 4
x y z
B.
1 3 2
2 4 1
x y z
C.
2 4 1
1 3 2
x y z
D.
1 3 2
2 4 1
x y z
38.4. Trong không gian
,
Oxyz
phương trình đường thẳng
d
đi qua điểm
(1;3; 4)
M
và song song với
trục hoành là
A.
1
3 .
4
x t
y
z
B.
1
3 .
4
x
y t
z
C.
1
3 .
4
x
y
y t
D.
1
3 .
4
x
y
y t
38.5. Trong không gian
,
Oxyz
cho ba điểm
(0; 1; 3),
A
(1;0;1),
B
( 1;1;2).
C
Phương trình đường
thẳng
d
đi qua điểm
A
và song song với
BC
là
A.
1 3
2 1 1
x y z
B.
1 1
2 1 1
x y z
C.
1 3
2 1 1
x y z
D.
1 1
2 1 1
x y z
38.6. Trong không gian
,
Oxyz
phương trình đường thẳng đi qua điểm
(2; 1;0)
M
và song song với
đường thẳng
2 1
:
1 2 3
x y z
d
có dạng
A.
2 1
1 2 3
x y z
B.
2 1
5 1 1
x y z
C.
2 1
1 2 3
x y z
D.
2 1
5 1 1
x y z
38.7. Trong không gian
,
Oxyz
phương trình đường thẳng đi qua
(1;2; 3)
A
và vuông góc với mặt
phẳng
( )
Oyz
là
A.
1
2 2 .
3 3
x t
y t
z t
B.
1
2 2 .
3 3
x t
y t
z t
C.
1
2 .
3
x t
y
z
D.
1
2 2 .
3 3
x t
y t
z t
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 78 -
38.8. Trong không gian
,
Oxyz
đường thẳng đi qua điểm
(2;1; 4)
M
và vuông góc với mặt phẳng
( ) : 2 2 3 8 0
P x y z
có phương trình là
A.
2 2 3
2 1 4
x y z
B.
2 1 4
2 2 3
x y z
C.
2 1 4
2 2 3
x y z
D.
2 2 3
2 1 4
x y z
38.9. Trong không gian
,
Oxyz
đường thẳng đi qua điểm
(2; 3; 4)
A
và vuông góc với mặt phẳng
( ) : 3 5 0
P x y
có phương trình là
A.
2
3 3 .
4 5
x t
y t
z t
B.
2
3 3 .
4
x t
y t
z
C.
1 2
3 3 .
4
x t
y t
z t
D.
2 1
3 3 .
4
x t
y t
z
38.10. Trong không gian
,
Oxyz
viết phương trình đường thẳng
d
đi qua điểm
(2;1; 5),
M
đồng thời
vuông góc với hai véctơ
(1;0;1)
a
và
(4;1; 1).
b
A.
2 1 5
1 5 1
x y z
B.
2 1 5
1 5 1
x y z
C.
2 1 5
1 5 1
x y z
D.
1 5 1
2 1 5
x y z
38.11. Cho
( 1;1;3)
M
và hai đường thẳng
1
1 3 1
: ;
3 2 1
x y z
d
2
1
:
1 3 2
x y z
d
Phương
trình đường thẳng đi qua
,
M
đồng thời vuông góc với
1
d
và
2
d
là
A.
1
1 .
1 3
x t
y t
z t
B.
1 .
3
x t
y t
z t
C.
1
1 .
3
x t
y t
z t
D.
1
1 .
3
x t
y t
z t
38.12. Viết phương trình đường thẳng đi qua
(2; 1;5),
A
đồng thời song song với mặt phẳng
( ) : 2 2 1 0
P x y z
và vuông góc với đường
1 3
:
2 1 3
x y z
A.
2 1 5
5 2 4
x y z
B.
2 1 5
5 2 4
x y z
C.
2 1 5
5 2 4
x y z
D.
5 2 4
2 1 5
x y z
38.13. Trong không gian
,
Oxyz
đường thẳng đi qua
(1; 1;2),
M
song song đồng thời với hai mặt phẳng
( ) : 2 1 0
P x y z
và
( ) : 2 3 3 0
Q x y z
có phương trình
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 79 -
A.
1 1 2
1 5 3
x y z
B.
1 1 2
1 5 3
x y z
C.
1 1 2
1 5 3
x y z
D.
1 5 3
1 1 2
x y z
38.14. Trong không gian
,
Oxyz
cho
(1;2;3), ( 3;5;7), ( 1; 4; 1).
A B C
Viết phương trình đường
thẳng vuông góc với mặt phẳng
( )
ABC
tại trọng tâm
G
của tam giác
.
ABC
A.
1 1 3
2 4 5
x y z
B.
1 1 3
2 4 5
x y z
C.
1 1 3
2 4 5
x y z
D.
1 1 3
2 4 5
x y z
38.15. Trong không gian
,
Oxyz
viết đường thẳng
nằm trong mặt phẳng
( ) : 2 4 0
P x y z
và
vuông góc với đường thẳng
1 2
:
1 2 3
x y z
d
Biết
đi qua điểm
(0;1;3).
M
A.
1 3
1 1 1
x y z
B.
1 3
1 1 1
x y z
C.
1 3
1 1 1
x y z
D.
1 3
1 1 1
x y z
38.16. Trong không gian
,
Oxyz
phương trình đường thẳng
d
qua
(1;2;3),
A
đồng thời
d
cắt và vuông
góc với trục hoành
Ox
là
A.
1
2 .
3 3
x
y
z t
B.
1
2 2 .
3 3
x
y t
z t
C.
1
2 .
3 3
x t
y
z t
D.
1
2 .
3 3
x
y
z t
38.17. Trong không gian
,
Oxyz
cho đường
2 1 1
:
1 1 1
x y z
d
và mặt
( ) : 2 2 0.
P x y z
Đường thẳng
nằm trong
( ),
P
cắt
d
và vuông góc với
d
có phương trình là
A.
1
2 .
x t
y
z t
B.
1
2 .
x t
y
z t
C.
1
2 .
x t
y t
z t
D.
1
2 .
x t
y
z t
38.18. Trong không gian
,
Oxyz
cho ba điểm
(2; 0;0), (0; 3; 0), (0;0; 4).
A B C
Gọi
H
là trực tâm tam giác
.
ABC
Tìm phương trình chính tắc của đường thẳng
.
OH
A.
4 3 2
x y z
B.
3 4 2
x y z
C.
6 4 3
x y z
D.
4 3 2
x y z
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 80 -
Câu 39. Cho hàm số ( ),f x đồ thị của hàm số
( )y f x
là đường cong như hình bên. Giá trị lớn nhất
của hàm số ( ) (2 ) 4g x f x x trên đoạn
3
;2
2
bằng
A. (0).f
B. ( 3) 6.f
C. (2) 4.f
D. (4) 8.f
Lôøi giaûi tham khaûo
Đặt
3
;2
2
2 [ 3; 4].
x
t x t
Hàm số trở thành ( ) ( ) 2 , [ 3;4].h t f t t t
Ta có:
0
( ) ( ) 2, ( ) 0 ( ) 2 , [ 3; 4].
2
t
h t f t h t f t t
t
Từ bảng biến thiên, suy ra:
max ( ) (2) (2) 4.h t h f
Chọn đáp án C.
Baøi taäp töông töï vaø môû roäng
39.1. Cho hàm số ( )y f x liên tục trên
có đồ thị
( )y f x
cho như hình vẽ dưới đây. Đặt
2
( ) 2 ( ) ( 1) .g x f x x Mệnh đề nào dưới đây đúng ?
A.
[ 3;3]
min ( ) (1).g x g
B.
[ 3;3]
max ( ) (1).g x g
C.
[ 3;3]
max ( ) (3).g x g
D.
[ 3;3]
max ( ).g x
39.2. Cho hàm số ( )y f x liên tục trên
có đồ thị
( )y f x
cho như hình vẽ dưới đây. Giá trị nhỏ
nhất của hàm số
3
1
( )
3
y f x x x
bằng
A.
2
(2)
3
f
B.
2
( 1)
3
f
C.
2
3
D.
2
(1)
3
f
39.3. Cho đồ thị
( )y f x
như hình vẽ. Xét hàm số
3 2
3 3
( ) ( ) 20.
3 4 2
x x x
g x f x Giá trị nhỏ
nhất của hàm số ( )g x trên đoạn [ 3;1] bằng
A.
( 1).g
B.
(1).g
C.
( 3).g
D. ( 3) (1).g g
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 81 -
x
y
O
4
2
2
6
2
4
39.4. Cho hàm số ( ).y f x Có bảng xét dấu đạo hàm như sau:
Bất phương trình
2
2
( ) e
x x
f x m
đúng (0;2)x khi
A. (0) 1.m f B.
1
(1)
e
m f
C. (0) 1.m f D.
1
(1)
e
m f
39.5. Cho hàm số ( ).y f x Hàm số
( )y f x
có đồ thị như hình vẽ bên dưới. Tìm các giá trị của m
để
2
2 ( 2) 4 3m f x x x
nghiệm đúng ( 3; ).x 
A. 2 (0) 1.m f
B. 2 (0) 1.m f
C. 2 ( 1).m f
D. 2 ( 1).m f
39.6. Cho hàm số ( ).y f x Hàm số
( )y f x
có đồ thị như hình vẽ bên. Tìm m để bất phương trình
2
2 ( 1) 2 4m f x x x
nghiệm đúng [ 4;2].x
A. 2 (0) 1.m f
B. 2 ( 3) 4.m f
C. 2 (3) 16.m f
D. 2 (1) 4.m f
39.7. Cho hàm số ( )y f x liên tục trên
và có đồ thị như hình vẽ. Gọi
S
là tập hợp tất cả các giá trị
nguyên của tham số m để phương trình (sin ) 3 sinf x x m có nghiệm thuộc khoảng (0; ).
Tổng các phần tử của
S
bằng
A.
9.
B.
10.
C.
6.
D. 5.
39.8. Cho hàm số ( )y f x có đồ thị như hình bên dưới. Có bao nhiêu số nguyên của tham số m để
phương trình
1
1
3 2
x
f x m
có nghiệm thuộc đoạn [ 2;2] ?
A.
8.
B.
9.
C.
10.
D.
11.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 82 -
39.9. Cho hàm số ( ).y f x Hàm số
( )y f x
có bảng biến thiên như hình bên dưới. Bất phương trình
2
( ) 3e
x
f x m
có nghiệm ( 2;2)x khi
A. ( 2) 3.m f
B.
3
(2) 3e .m f
C.
3
(2) 3e .m f
D. ( 2) 3.m f
39.10. Cho hàm số
( )y f x
có đồ thị như hình vẽ. Hàm số (2 sin ) 4 siny f x x có giá trị lớn nhất
trên khoảng
(0; )
bằng
A.
7.
B. 5.
C. 6.
D. 4.
39.11. Cho hàm số
( )y f x
có đồ thị hàm số như hình vẽ. Hàm số (cos ) cos 6y f x x có giá trị
nhỏ nhất trên khoảng ;
2 2
bằng
A. 3.
B. 0.
C. 1.
D. 2.
39.12. Cho hàm số ( ).y f x Đồ thị
( )y f x
như hình bên dưới. Giá trị nhỏ nhất và giá trị lớn nhất
của hàm số trên đoạn [0;3] lần lượt là
A. (1), (0).f f
B. (2), (0).f f
C. (1), (3).f f
D. (0), (3).f f
39.13. Cho ( )y f x có đồ thị của
( )y f x
như hình vẽ dưới. Đặt
[ 2;6] [ 2;6]
max ( ), min ( ).M f x m f x
Giá
trị của biểu thức
P M m
bằng
A. (0) (2).f f
B. (5) ( 2).f f
C. (5) (6).f f
D. (0) ( 2).f f
39.14. Cho hàm số ( )y f x có đạo hàm
( )f x
xác định và liên tục trên . Hàm số
( )y f x
có đồ thị
như hình vẽ dưới. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y f x trên đoạn [ 2;1]. Giá trị của
M m
bằng
A. (1) (0).f f
B. (1) ( 2).f f
C. ( 2) ( 1).f f
D. ( 1) (0).f f
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 83 -
39.15. Cho hàm số
5 4 3 2
( ) .f x ax bx cx dx ex n
Đồ thị hàm số
( )y f x
như hình vẽ. Đặt
[ 3;2] [ 3;2]
max , min .M f x m f x
Giá trị của
M m
bằng
A.
1
(2).
2
f f
B. (0,5) (0).f f
C. ( 3) (2).f f
D. ( 3) (0).f f
39.16. Cho hàm số ( )y f x xác định, liên tục trên và (2) 0.f Hàm số
( )y f x
có đồ thị như hình
vẽ bên dưới. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số ( ) ( )g x f x
trên trên đoạn [ 1;3]. Giá trị của M và m lần lượt là
A. ( 1), (3).M f m f
B. (3) , ( 1) .M f m f
C. ( 1) , (2) .M f m f
D.
( 1) , (3) .
M f m f
39.17. Cho hàm số
3 2
( )f x ax bx cx d
có đồ thị ( ).C Biết đồ thị ( )C tiếp xúc với đường thẳng
4y tại điểm có hoành độ âm và đồ thị của hàm số
( )y f x
như hình vẽ bên dưới. Giá trị lớn
nhất của hàm số ( )y f x trên [0;3] bằng
A. 20.
B. 60.
C. 22.
D. 3.
39.18. Cho hàm số ( )f x liên tục trên và có đồ thị
( )f x
như hình vẽ. Đặt
2
( ) 2 ( ) ( 1) .g x f x x
Khi
đó giá trị nhỏ nhất của hàm số ( )y g x trên đoạn [ 3;3] bằng
A. (0).g
B. (1).g
C. ( 3).g
D. (3).g
39.19. Cho hàm số
4 3 2
1
y x ax bx
( , a b các tham số) đạt giá trị nhỏ nhất tại 0.x Khi a b
đạt giá trị lớn nhất thì
4 3 3
1b ab b
bằng
A. 9.
B.
7.
C. 5.
D. 6.
39.20. Cho hàm số
( )y f x
có đồ thị như hình bên. Tổng tất cả các giá trị của tham số m sao cho giá
trị nhỏ nhất của hàm số
2
( )y f x m
trên đoạn
[ 1;1]
bằng 9 là
A. 3.
B. 1.
C. 2.
D. 4.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 84 -
Câu 40. Có bao nhiêu số nguyên dương
y
sao cho ứng với mỗi
y
có không quá
10
số nguyên
x
thỏa mãn
1
(2 2)(2 ) 0 ?
x x
y
A.
1024.
B.
2047.
C.
1022.
D.
1023.
Lôøi giaûi tham khaûo
Ta có:
1
(2 2)(2 ) 0
x x
y
với
x
và
.
y
TH 1. Nếu
1
2 2
1 1
2 2 0
1
.
2 2
2 0
log log
x
x
x x
y
x y x y
Theo yêu cầu bài toán, một
y
có không quá 10 số nguyên
,
x
mà
1
2
x
2
10 log 1
y
10 1
2 2 .
y
Mà
y
nguyên dương
Không tồn tại
y
thỏa mãn yêu cầu bài toán.
TH 2. Nếu
1
2 2
1 1
2 2 0
1
.
2 2
2 0
log log
x
x
x x
y
x y x y
Theo yêu cầu bài toán, một
y
có không quá 10 số nguyên
,
x
mà
1
2
x
2
0 log 10
y
10
0 2 1024
y
{1; 2; 3...;1023; 1024}
y
y
có
1024
giá trị.
Chọn đáp án A.
Baøi taäp töông töï vaø môû roäng
40.1. Có bao nhiêu giá trị nguyên dương của
y
sao cho mỗi giá trị của
y
có ít nhất
1
số nguyên
,
x
nhưng không quá
6
số nguyên ?
A.
2048.
B.
2016.
C.
1012.
D.
2023.
40.2. Số giá trị nguyên dương của tham số
m
để bất phương trình
2
(2 2)(2 ) 0
x x
m
có không
quá
6
nghiệm nguyên là
A.
29.
B.
33.
C.
32.
D.
31.
40.3. Số giá trị nguyên của tham số
m
để bất phương trình
2
2 2
2 log ( 1)log 1 0
x m x m
chứa
không quá
10
số nguyên dương là
A.
6.
B.
8.
C.
7.
D.
9.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 85 -
40.4. Số giá trị nguyên dương của tham số
m
để bất phương trình
2 2 2
3 3 .(3 1) 3 0
x x m m
có
không quá
30
nghiệm nguyên là
A.
28.
B.
29.
C.
30.
D.
31.
40.5. Số giá trị nguyên của tham số
m
để bất phương trình
2
ln( 2 ) 2 ln(2 1)
x x m x
chứa đúng
2
số nguyên là
A.
4.
B.
8.
C.
3.
D.
9.
40.6. Gọi
S
là tập hợp nghiệm nguyên của bất phương trình
2
2
log
2 2 2
2 2
log ( ) 2 log .
x
mx mx x
Có bao
nhiêu giá trị nguyên của tham số
m
để tập hợp
S
có đúng
8
phần tử ?
A.
5.
B.
6.
C.
10.
D.
11.
40.7. Gọi
S
là tập hợp các giá trị nguyên của
[ 2021;2021]
y
sao cho ứng với mỗi
y
thì có đúng
2
giá trị của
x
thỏa mãn
4
2
4 . . e e 3 ?
x y x y
x x x
A.
2020.
B.
4040.
C.
2022.
D.
2021.
40.8. Xét các số thực
,
x y
thỏa mãn
2
2 2
.
log ( 4 ).log ( 4 )
y y
x x x x y
y
Có bao nhiêu
số nguyên không âm
y
sao cho tồn tại số thực
x
thỏa mãn đẳng thức trên ?
A.
0.
B.
1.
C.
7.
D. Vô số.
40.9. Xét các số thực
,
x y
thỏa mãn
2
2
2
1
log ( ) 1.
log ( )
x y y
x y
Có bao nhiêu số nguyên
;1
[ ]
3
y
để tồn tại số thực
; )
[
1
x

thỏa mãn đẳng thức trên ?
A.
1.
B.
2.
C.
3.
D.
0.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 86 -
40.10. Có bao nhiêu số nguyên
y
để tồn tại số thực
x
thỏa mãn
2 2
3 2
log ( 2 ) log ( )
x y x y
?
A.
3.
B.
2.
C.
1.
D. Vô số.
40.11. Có bao nhiêu số nguyên
x
sao cho tồn tại số thực
y
thỏa mãn
2 2
3 4
?
l o (og (
l g
)
)x y x y
A.
3.
B.
2.
C.
1.
D. Vô số.
40.12. Có tất cả bao nhiêu giá trị nguyên của
m
để phương trình
2
log ( ) 2 2 3 1
x
m x m x
có
nghiệm thuộc đoạn
[0;2] ?
A.
6.
B.
5.
C.
4.
D.
3.
40.13. Có bao nhiêu giá trị nguyên
( ; )
a b
thỏa mãn
1 2020
a
và
1
3
2.3 log ( 3 ) 3
b b
a a b
?
A.
7.
B.
2020.
C.
2021.
D.
6.
40.14. Có tất cả bao nhiêu bộ số nguyên
( ; ; )
x y z
thỏa mãn đồng thời
2 3
e 2 2
x y z
x y z
và
2
0
z yz x
?
A.
5.
B.
2.
C.
4.
D.
7.
40.15. Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
để tồn tại duy nhất cặp
( ; )
x y
thỏa mãn
đồng thời các điều kiện
2 2
2
log (4 4 4) 1
x y
x y
và
2 2
2 2 2 0.
x y x y m
Tổng các
phần tử của
S
bằng
A.
33.
B.
24.
C.
15.
D.
5.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 87 -
40.16. Có bao nhiêu giá trị nguyên của tham số thực
m
để tồn tại cặp số
( ; )
x y
thỏa mãn đồng thời
2 1 3 2
e e 1
x y x y
x y
và
2 2
2 2
log (2 1) ( 4)log 4 0 ?
x y m x m
A.
3.
B.
4.
C.
5.
D.
6.
40.17. Có bao nhiêu giá trị nguyên của tham
m
để
3 3 3
3log 2 log log
( 3). (18 2 ). 32 0
x y x
x m y m x
có
6
cặp số thực dương
( ; )
x y
sao cho
1 ?
xy
A.
6.
B.
7.
C.
8.
D.
10.
40.18. Có bao nhiêu cặp số thực
( , )
x y
thỏa mãn
2 2
2 2
2 2
log log
log log ?
log ( ) 1 log ( ) 1
x y
x y
xy xy
A.
4.
B.
1.
C.
2.
D.
3.
40.19. Tìm tập hợp tất cả các giá trị của tham số thực
m
để tồn tại cặp số thực
( ; )
x y
thỏa mãn đồng thời
.
x y m
và
4
log ( 12).log 2 1 ?
x y
x y
A.
( ; 4].

B.
{4}.
C.
[0;4].
D.
[4; ).

40.20. Có bao nhiêu giá trị nguyên của tham số
m
sao cho phương trình
2 2
3 4
x m x m
có nghiệm ?
A.
0.
B.
3.
C.
2.
D. Vô số.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 88 -
Câu 41. Cho hàm số
2
2
1 khi 2
( ) .
2 3 khi 2
x x
f x
x x x
Tích phân
2
0
(2 sin 1)cos df x x x
bằng
A.
23
3
B.
23
6
C.
17
6
D.
17
3
Lôøi giaûi tham khaûo
Đặt
2sin 1 d 2 cos dt x t x x
3 3
2
0 1 1
1 1
(2 sin 1)cos d ( )d ( )d
2 2
f x x x f t t f x x
2 3
2 2
1 2
1 1 23
( 2 3)d ( 1)d
2 2 6
x x x x x
Chọn đáp án B.
Baøi taäp töông töï vaø môû roäng
41.1. Cho hàm số
2
( 1)e khi 0
( ) .
1 khi 0
x
x x
f x
x x x
Biết
1
1
( )d e,
a
f x x c
b
với
a
b
là phân số tối giản.
Giá trị của tổng a b c bằng
A. 9. B. 11.
C. 12. D. 14.
41.2. Cho hàm số
2
3 2 khi 1
( ) .
5 khi 1
x x x
f x
x x
Khi đó
1
2
0 0
d2 cos (sin ) 3 2 d(3 )x f x x f x x
bằng
A. 32. B. 31.
C.
32
3
D.
71
6
41.3. Cho hàm số
2
2 khi 0
( )
3 2 khi 0
ax x
f x
x bx x
(với
, a b
là các tham số thực) thỏa
1
1
( )d 2.f x x
Giá
trị nhỏ nhất của biểu thức
2 2
( 1) (1)P f f
bằng
A. 5. B. 2.
C.
25
4
D.
25
2
41.4. Cho ( )y f x là hàm bậc ba như hình vẽ. Nếu
4
1
( 1)d 7
x f x x
và
2
2
1
2 ( 1)d 3
x f x x
thì phương trình tiếp tuyến của hàm số trên tại điểm có hoành độ bằng 3 là
A. 4.y x
B. 2 7.y x
C.
1 5
2 2
y x
D. 3 10.y x
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 89 -
41.5. Cho hàm số
2
khi 0
( )
2 khi 0
x x a x
f x
bx x
có đạo hàm trên
(với
,
a b
là các tham số thực).
Nếu
1
1
( )d
m
f x x
n
với
,
m n
thì
2
m n
bằng
A.
19.
B.
20.
C.
59
2
D.
13
3
41.6. Biết hàm số
( )
F x
liên tục trên
,
là một nguyên hàm của hàm số
3
1
khi 0
( ) .
2 1
(2 1) khi 0
x
f x
x
x x
Biết
(4) ( 1) 8.
F F
Khi đó
( 2) 2 (12)
F F
bằng
A.
121
8
B.
281
16
C.
27.
D.
20.
41.7. Cho hàm số
( )
f x
liên tục trên
và thỏa mãn
16
2
2
1
4
( )
cot (sin )d d 1.
f x
x f x x x
x
Khi đó
1
1/8
(4 )
d
f x
x
x
bằng
A.
3.
B.
2.
C.
3
2
D.
5
2
41.8. Hàm số
( )
f x
xác định trên
,
thỏa
3 8
2
3 2
( 16 )d ( )d 8.
f x x x f x x
Khi đó
8
2
2
( )
d
f x
x
x
bằng
A.
2.
B.
4.
C.
1
2
D.
1
4
41.9. Nếu
ln 6
ln 3
d
3ln ln
e 2e 3
x x
x
a b
với
,
a b
là các số nguyên dương thì
ab
bằng
A.
20.
B.
10.
C.
15.
D.
10.
41.10. Biết
2
0
sin
d ln 3 ln2
cos2 3 cos 2
x
x a b
x x
với
, .
a b
Khi đó
3 2
2 3
a ab b
bằng
A.
26.
B.
6.
C.
3.
D.
4.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 90 -
41.11. Cho
( )
f x
có đạo hàm trên
thỏa
1
2
0
( ) 3 2 ( ) ( )d .
f x x x f x f x x
Khi đó
2
0
( )d
f x x
bằng
A.
10
3
B.
10
3
C.
26
15
D.
26
15
41.12. Cho hàm số
( )
f x
xác định và có đạo hàm tại mọi điểm
0.
x
Biết rằng
(2) 4, ( 2) 0
và
3
( ) ( )
xf x f x x
với mọi
0.
x
Giá trị của
(2) ( 1)
f f
bằng
A.
8.
B.
9
2
C.
11
2
D.
15
2
41.13. Cho hàm số
( )
f x
xác định trên
*
thỏa mãn
2
1
( ) ,
f x
x
( 1) 1,
f
(1) 0
f
và
(2) 0.
f
Giá
trị của
( 2)
f
bằng
A.
1 2 ln2.
B.
2 ln 2.
C.
3 ln2.
D.
ln 2.
41.14. Cho hàm số
( )
f x
liên tục trên
(0; )

và thỏa mãn
2
( ) 2 1
( 1) .ln( 1).
2
4
f x x
f x x
x
x x
Biết
17
1
( )d ln 5 2 ln
f x x a b c
với
, , .
a b c
Giá trị của
2
a b c
bằng
A.
29
2
B.
5.
C.
7.
D.
37.
41.15. Cho hàm số
( )
f x
có đạo hàm liên tục trên
thỏa
2
3 2
( ) ( 1) e , .
x
xf x f x x
Khi đó
0
1
( )d
f x x
bằng
A.
1
2
B.
3e.
C.
3(1 e).
D.
3(e 1).
41.16. Cho hàm số
( )
f x
có đạo hàm liên tục trên
thỏa mãn
(e 1) ( ) ( ) ,
x
f f x f x x x
và
(0) 2 (ln 2) 1.
f f
Khi đó
3
2
( )d
f x x
bằng
A.
1
ln 2 1.
2
B.
2 ln 2.
C.
2
3
D.
2 ln 2 2.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 91 -
41.17. Cho hàm số
( )
f x
có đạo hàm liên tục trên
thỏa mãn
3 2
( 2) 1,
f x x x x
.
x
Giá
trị của
4
2
8
( )d
x f x x
thuộc khoảng nào dưới đây ?
A.
( 20; 10).
B.
(20;25).
C.
(10;20).
D.
( 25; 20).
41.18. Cho hàm số
( )
f x
thỏa mãn
(0) (1) 1
f f
và
1
( ) , ;
3
3 1 1
x
f x x
x

Khi đó
1
0
( )d
f x x
bằng
A.
3509
3402
B.
3295
6804
C.
3295
3402
D.
3509
6804
41.19. Biết rằng
(2 )d ln 2 , (0; ).
f x x x x C x

Họ các nguyên hàm của
(2 1) ( )
x f x
trên
khoảng
(0; )

là
A.
4 ln .
2
x C
x
B.
4 ln .
2
x C
x
C.
1
2 ln .
x C
x
D.
2 ln .
4
x C
x
41.20. Biết
2
( ) e
x
F x x
là một nguyên hàm của hàm số
( )
f x
trên
.
Khi đó
( )e d
x
f x x
bằng
A.
2e ( 1) .
x
x x C
B.
2e ( 1) .
x
x x C
C.
2 1
.
e
x
x
x C
D.
2 1
.
e
x
x
x C
Câu 42. Có bao nhiêu số phức
z
thỏa mãn
2
z và
( 2 )( 2)
z i z
là số thuần ảo ?
A.
1.
B.
0.
C.
2.
D.
4.
Lôøi giaûi tham khaûo
Giả sử
, ( , )
z x yi x y
.
z x yi
Ta có:
2 2
( 2 )( 2) 2 2 4 2 2 2 ( )
z i z zz z iz i x y x yi i x yi
2 2 2 2
2 2 2 2 ( 2 2 ) (2 2 )
x y x yi xi y x y x y x y i
là số thuần ảo
2 2
2 2 0
x y x y
có dạng là đường tròn
1
( )
C
có tâm
1
(1; 1),
I
bán kính
1
2.
R
Ta lại có:
2 2
2 2
z x y
là đường tròn
2
( )
C
có tâm là
(0;0),
O
bán kính
2
2.
R
Vẽ hai đường tròn
1
( )
C
và
2
( )
C
lên cùng hệ trục.
có hai điểm chung nên tồn tại
2
số phức.
Chọn đáp án C.
Lưu ý. Ta có thể giải hệ phương trình sẽ tìm được hai cặp
( ; ),
x y
tức có
2
số phức thỏa bài toán.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 92 -
Baøi taäp töông töï vaø môû roäng
42.1. Cho các số phức
1
,
z
2
z
thỏa mãn
1 2
1 8
z z i
và
1
2
z
z
là số thuần ảo. Khi đó
1 2
z z
bằng
A.
65.
B.
65.
C.
65
2
D.
65
2
42.2. Có bao nhiêu số phức
z
thỏa mãn
2 2 2
z i và
2
( 1)
z
là số thuần ảo ?
A.
0.
B.
4.
C.
3.
D.
2.
42.3. Có bao nhiêu số phức
z
thỏa mãn
2
z i và
( 1)( )
z z i
là số thực ?
A.
1.
B.
2.
C.
3.
D.
4.
42.4. Có bao nhiêu số phức
z
thỏa mãn
1 2
1
3 4
z i
z i
và số phức
2
z i
z i
là số thuần ảo ?
A.
0.
B.
1.
C.
2.
D.
4.
42.5. Biết rằng có hai số phức thỏa mãn
2 2
z i z z i
và
(2 )( )
z i z
là số thực. Tổng các
phần ảo của hai số phức đó bằng
A.
9.
B.
7.
C.
5.
D.
3.
42.6. Có bao nhiêu số phức
z
thỏa mãn điều kiện
. 2
z z z
và
2 ?
z
A.
1.
B.
2.
C.
3.
D.
4.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 93 -
42.7. Cho số phức
( , )
z a bi a b
thỏa
2 (1 ) 0
z i z i
và
1.
z
Khi đó
a b
bằng
A.
1.
B.
5.
C.
3.
D.
7.
42.8. Cho số phức
( , )
z a bi a b
thỏa
2 2
2
2 1 2
iz z i
z
i i
và
1.
z
Tính
22
.
b b
a
a
A.
5.
B.
1.
C.
5.
D.
1.
42.9. Cho số phức
( , )
z a bi a b
thỏa mãn
3
18 26 .
Tính
2 2
( 2) (4 ) .
T z z
A.
2.
B.
4.
C. 0.
D. 1.
42.10. Cho số phức
z
thỏa mãn
(3 4 ) 4 3 5 2 0.
z i z i
Môđun của số phức
z
bằng
A.
2.
B.
2.
C.
2 2.
D.
1.
42.11. Cho số phức
z
thỏa
2
1 (2 3 )
2.
i i z
i
z
z
Khi đó môđun của
z
thuộc khoảng nào sau đây
?
A.
3
;2 .
2
B.
(2; ).

C.
(0;1).
D.
1 3
;
2 2
42.12. Cho hai số phức
1 2
,
z z
thỏa mãn
1 2
2, 2.
z z
Gọi
,
M N
lần lượt là điểm biểu diễn số
phức
1
z
và
2
.
iz
Biết rằng
45
MON
với
O
là gốc tọa độ. Khi đó
2 2
1 2
4
z z
bằng
A.
4 2.
B.
4.
C.
6.
D.
4 5.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 94 -
42.13. Cho các số phức
z
thỏa
( 2 )( 2 ) 16.
z i z i
Biết rằng tập hợp các điểm biểu diễn các số
phức
(1 ) 2
w i z i
là một đường tròn. Bán kính của đường tròn đó bằng
A.
2.
B.
5.
C.
4 2.
D.
3.
42.14. Cho các số phức
z
thỏa
. (4 5 ) (4 5 ) 16 0.
z z z i z i
Trong mặt phẳng tọa độ các điểm
biểu diễn của số phức
3
4
2
z i
w i
i
cùng thuộc một đường tròn cố định có tọa độ tâm là
A.
(4;5).
I
B.
(1;3).
I
C.
( 4 5).
I
D.
(8; 3).
I
42.15. Cho số phức
z a bi
thỏa mãn
2
2 . (5 7 ) (17 ) .
z z i z i z
Trên mặt phẳng tọa độ, điểm
biểu diễn của số phức
z
khác gốc tọa độ là
A.
( 1;2).
N
B.
(2; 1).
P
C.
( 2;1).
Q
D.
(1; 2).
M
42.16. Cho số phức
z
thỏa mãn
2
. (6 8 ) (5 ) (23 73 ) .
z z i i z i z
Tỉ số giữa phần thực và phần
ảo là
A.
2
5
B.
2
7
C.
2.
D.
3.
42.17. Cho số phức
2
3 ( 4)
z m m i
với
.
m
Gọi
( )
C
là tập hợp các điểm biểu diễn số phức
z
trong mặt phẳng tọa độ. Diện tích hình phẳng giới hạn bởi
( )
C
và trục hoành bằng
A.
4
3
B.
32
3
C.
8
3
D.
1.
42.18. Gọi
S
là tập hợp tất cả các số nguyên
m
sao cho tồn tại hai số phức phân biệt
1
,
z
2
z
thỏa
1
z z i
và
2 1.
z m m
Tổng các phần tử của
S
bằng
A.
1.
B.
2.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 95 -
45°
H
M
A
C
B
S
C.
3.
D.
4.
42.19. Có bao nhiêu giá trị của tham số
m
để tồn tại duy nhất số phức
z
thỏa mãn đồng thời
z m
và
2
4 3 ?
z m mi m
A.
0.
B.
1.
C.
2.
D.
3.
42.20. Cho phương trình
2
2 0
z z c
(với
c
là số thực và
1
c
) có hai nghiệm phức
1
z
và
2
.
z
Gọi
,
M N
lần lượt là điểm biểu diễn cho
1
z
và
2
z
trong mặt phẳng tọa độ
.
Oxy
Biết
2 2
1 2
4 6.
z z
Chu vi tam giác
OMN
(với
O
là gốc tọa độ) bằng
A.
2( 5 6).
B.
2( 6 7).
C.
2(3 6).
D.
2(2 6).
Câu 43. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
,
a
cạnh bên
SA
vuông góc với
mặt phẳng đáy, góc giữa
SA
và mặt phẳng
( )
SBC
là
45
(tham khảo hình bên dưới). Thể
tích khối chóp
.
S ABC
bằng
A.
3
8
a
B.
3
3
8
a
C.
3
3
12
a
D.
3
4
a
Lôøi giaûi tham khaûo
Gọi
M
là trung điểm của
BC
và
H
là hình chiếu của
A
lên
.
SM
( ,( )) 45
SA SBC ASH ASM
SAM
vuông cân tại
.
A
Suy ra:
3
2
a
SA AM
Do đó
2 3
.
1 1 3 3
.
3 3 2 4 8
S ABC ABC
a a a
V SAS
Chọn đáp án A.
Baøi taäp töông töï vaø môû roäng
43.1. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông,
SA
vuông góc với mặt phẳng đáy và
3 .
SA a
Biết góc giữa
SD
và
( )
SAC
là
30 ,
thể tích của khối chóp
.
S ABC
bằng
A.
3
9 .
a
B.
3
6 .
a
A
C
B
S
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 96 -
C.
3
9
2
a
D.
3
3 .
a
43.2. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật với
, 2 .
AB a B a
Mặt bên
( )
SAB
nằm trong mặt phẳng vuông góc với mặt phẳng đáy
( ),
ABCD
gọi
H
là trung điểm của cạnh
,
AB
góc giữa đường thẳng
SH
và mặt phẳng
( )
SCD
bằng
30 .
Thể tích khối chóp
.
S ACD
bằng
A.
3
4 3
3
a
B.
3
2 3.
a
C.
3
2 .
a
D.
3
2 3
3
a
43.3. Cho khối lăng trụ đứng
.
ABC A B C
có đáy là tam giác đều. Mặt phẳng
( )
A BC
tạo với đáy
góc
30
và tam giác
A BC
có diện tích bằng
8.
Thể tích của khối lăng trụ đã cho bằng
A.
8 3.
B.
16 3.
C.
64 3.
D.
2 3.
43.4. Cho lăng trụ tam giác đều
.
ABC A B C
có cạnh đáy bằng
a
và
.
AB BC
Thể tích của khối
lăng trụ đã cho bằng
A.
3
.
a
B.
3
6.
a
C.
3
6
8
a
D.
3
6
4
a
43.5. Cho khối chóp
.
S ABC
có
,
AB a
2 ,
AC a
120 ,
BAC
,
SA ABC
góc giữa
( )
SBC
và
( )
ABC
là
60 .
Thể tích khối chóp
.
S ABC
bằng
A.
3
21
14
a
B.
3
7
14
a
C.
3
3 21
14
a
D.
3
7
7
a
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 97 -
43.6. Cho hình lăng trụ đứng
. ,
ABC A B C
đáy
ABC
là tam giác vuông tại
,
A
cạnh
AA
hợp với
B C
một góc
60
và khoảng cách giữa chúng bằng
,
a
2 .
B C a
Thể tích của khối lăng trụ
.
ABC A B C
bằng
A.
3
2
a
B.
3
3
2
a
C.
3
3
4
a
D.
3
4
a
43.7. Cho hình chóp
.
S ABC
có
SA
vuông góc với đáy, mặt phẳng
( )
SAB
vuông góc với mặt phẳng
( ),
SBC
góc giữa hai mặt phẳng
( )
SAC
và
( )
SBC
bằng
60 ,
2,
SB a
45 .
BSC
Thể tích
khối chóp
.
S ABC
bằng
A.
3
2
15
a
B.
3
2 3 .
a
C.
3
2 2 .
a
D.
3
2 3
15
a
43.8. Cho lăng trụ
.
ABC A B C
có đáy là tam giác vuông cân tại
B
và
3.
AB a
Hình chiếu vuông
góc của
A
lên mặt phẳng
( )
ABC
là điểm
H
thuộc cạnh
AC
sao cho
2 .
HC HA
Mặt bên
( )
ABB A
tạo với đáy một góc
60 .
Thể tích khối lăng trụ đã cho bằng
A.
3
6
a
B.
3
3
a
C.
3
3
5
a
D.
3
3
2
a
43.9. Cho hình lăng trụ đứng
.
ABC A B C
có đáy là tam giác
ABC
vuông cân tại
A
và
6.
BC a
Góc giữa mặt phẳng
( )
AB C
và mặt phẳng
( )
BCC B
bằng
60 .
Thể tích của khối đa diện
AB CA C
bằng
A.
3
3
a
B.
3
3 3
2
a
C.
3
3
2
a
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 98 -
D.
3
3
3
a
43.10. Cho lăng trụ tam giác đều
.
ABC A B C
có cạnh đáy bằng
2 ,
a
khoảng cách từ
A
đến mặt phẳng
( )
A BC
bằng
6
2
a
Khi đó thể tích khối lăng trụ
.
ABC A B C
bằng
A.
3
.
a
B.
3
3 .
a
C.
3
4
.
3
a
D.
3
4 3
.
3
a
43.11. Cho hình chóp tứ giác
.
S ABCD
có đáy là vuông; mặt bên
( )
SAB
là tam giác đều và nằm trong
mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm
A
đến mặt phẳng
( )
SCD
bằng
3 7
7
a
Thể tích của khối chóp
.
S ABCD
bằng
A.
3
1
.
3
a
B.
3
.
a
C.
3
2
.
3
a
D.
3
3
2
a
43.12. Cho hình lăng trụ đứng
. ,
ABC A B C
biết đáy
ABC
là tam giác đều cạnh
.
a
Khoảng cách từ
trọng tâm
G
của tam giác
ABC
đến mặt phẳng
( )
A BC
bằng
/6.
a
Thể tích khối lăng trụ
.
ABC A B C
bằng
A.
3
3 2
8
a
B.
3
0,5 .
a
C.
3
3 2
4
a
D.
3
3 2
16
a
43.13. Cho lăng trụ
.
ABC A B C
có đáy là tam giác đều cạnh
.
a
Hình chiếu vuông góc của điểm
A
lên mặt phẳng
( )
ABC
trùng với trọng tâm của tam giác
ABC
. Biết khoảng cách giữa hai đường
thẳng
AA
và
BC
bằng
3
4
a
Khi đó thể tích của khối lăng trụ
.
ABC A B C
bằng
A.
3
3
6
a
B.
3
3
24
a
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 99 -
C.
3
3
12
a
D.
3
3
36
a
43.14. Cho tứ diện
OABC
biết
,
OA
,
OB
OC
đôi một vuông góc với nhau, biết
3,
OA
4
OB
và
thể tích khối tứ diện
OABC
bằng
6.
Khi đó khoảng cách từ
O
đến mặt phẳng
( )
ABC
bằng
A.
3.
B.
41
12
C.
144
41
D.
12
41
43.15. Cho hình chóp
.
S ABC
có đáy là tam giác
ABC
đều cạnh
,
a
tam giác
SBA
vuông tại
,
B
tam
giác
SAC
vuông tại
.
C
Biết góc giữa hai mặt phẳng
( )
SAB
và
( )
ABC
bằng
60 .
Thể tích khối
chóp
.
S ABC
bằng
A.
3
3
8
a
B.
3
3
12
a
C.
3
3
6
a
D.
3
3
4
a
43.16. Cho hình chóp
.
S ABC
có đáy là tam giác vuông cân tại
,
B
2 ,
AB a
90 ,
SAB SCB
góc
giữa đường thẳng
AB
và
( )
SBC
bằng
30 .
Thể tích của khối chóp
.
S ABC
bằng
A.
3
4 3
9
a
B.
3
4 3
3
a
C.
3
2 3
9
a
D.
3
2 3
3
a
43.17. Cho khối chóp
.
S ABC
có
,
AB BC
,
BC SC
,
SC SA
,
BC a
15
SC a
và góc giữa
,
AB
SC
bằng
30 .
Thể tích khối chóp
.
S ABC
bằng
A.
3
5
2
a
B.
3
5 3
2
a
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 100 -
C.
3
5
.
6
a
D.
3
5 3
6
a
43.18. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông cân tại
, 90 ,
A SBA SCA
,
AB a
góc giữa mặt phẳng
( )
SAB
và
( )
SAC
bằng
60 .
Thể tích khối chóp đã cho bằng
A.
3
.
a
B.
3
3
a
C.
3
2
a
D.
3
6
a
43.19. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
,
a
cạnh bên
SA
vuông góc với mặt
phẳng đáy. Gọi
I
là tâm mặt cầu ngoại tiếp hình chóp
. .
S ABC
Biết rằng khoảng cách từ
I
đến
mặt phẳng
( )
SBC
bằng
3
,
18
a
thể tích khối chóp
.
S ABC
bằng
A.
3
3 3
20
a
B.
3
.
a
C.
3
3.
a
D.
3
5
20
a
43.20. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
4 .
a
Biết
SA
vuông góc với mặt đáy
( )
ABC
và
6 3.
SA a
Gọi
, ,
M N P
lần lượt là trung điểm của các cạnh
, , .
SB BC SC
Gọi
điểm
K
sao cho
AK
là đường kính của mặt cầu ngoại tiếp hình chóp
. .
S ABC
Thể tích khối tứ
diện
KMNP
bằng
A.
3
13
2
a
B.
3
8 .
a
C.
3
7 .
a
D.
3
6 .
a
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 101 -
Câu 44. Ông Bình làm lan can ban công ngôi nhà của mình bằng tấm kính cường lực. Tấm kính đó là
một phần của mặt xung quanh của một hình trụ như hình bên. Biết giá tiền của
2
1m kính
như trên là 1.500.000 đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông Bình mua tấm
kính trên là bao nhiêu ?
A. 23.591.000 đồng. B. 36.173.000đồng. C. 9.437.000 đồng. D. 4.718.000đồng.
Lôøi giaûi tham khaûo
Bán kính của đường tròn đáy là
4,45
4,45m.
2 sin150
R
Do đó, mép trên của tấm kính bằng
1
6
diện tích xung quanh của hình trụ có chiều cao 1, 35m
và bán kính đáy 4, 45m.R
Số tiền mà ông Bình mua tấm kính trên là
1
.2
6
T Rh
1
2 .4, 45.1,35.1500000
6
9.437.000 đồng. Chọn đáp án C.
Baøi taäp töông töï vaø môû roäng
44.1. Ông An làm lan can ban công của ngôi nhà bằng một miếng kính cường lực. Miếng kính này là
một phần của mặt xung quanh của một hình trụ như hình bên. Biết
4m, 150AB AEB (E
là điểm chính giữa cung )AB và 1, 4m.DA Giá tiền của
2
1m kính này là
2.000.000
đồng. Số
tiền (làm tròn) mà ông An phải trả bằng
A.
11.820.000
đồng.
C.
10.840.000
đồng.
B.
10.250.000
đồng.
D. 11.730.000 đồng.
44.2. Một thùng hình trụ có chiều cao 3m,h bán kính đường tròn đáy 1mR chứa một lượng
nước. Biết rằng nếu đặt thùng nằm ngang ta được chiều cao mực nước trong thùng là 0, 5m.d
Hỏi thể tích lượng nước có trong thùng gần nhất với kết quả nào sau đây ?
A.
3
1, 75m .
B.
3
1,8m .
C.
3
1, 85m .
D.
3
1, 9m .
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 102 -
44.3. Một ống thủy tinh hình trụ có chiều cao 14,2cm và bán kính đáy 1,45cm đang chứa dung dịch
2 4
.H SO
Khi đặt ổng thủy tinh nằm ngang thì diện tích bề mặt dung dịch trên thành ống chiếm
41, 67% diện tích xung quanh ống. Thể tích dung dịch
2 4
H SO
trong ống bằng
A.
3
32, 47cm .
B.
3
33, 86cm .
C.
3
31, 62cm .
D.
3
30,12cm .
44.4. Người thợ gia công của một cơ sở chất lượng cao X cắt một miếng tôn hình tròn với bán kính
60cm
thành ba miếng hình quạt bằng nhau. Sau đó người thợ ấy quấn và hàn ba miếng tôn đó
để được ba cái phễu hình nón. Thể tích của mỗi cái phễu đó bằng
A.
16 2
3
lít.
B.
16 2
3
lít.
C. 8 2 lít.
D.
160 2
lít.
44.5. Người ta bỏ ba quả bóng bàn cùng kích thước vào trong một chiếc hộp hình trụ có đáy bằng hình
tròn lớn của quả bóng bàn và chiều cao bằng ba lần đường kính bóng bàn. Gọi
1
S
là tổng diện
tích của ba quả bóng bàn,
2
S
là diện tích xung quanh của hình trụ. Khẳng định nào đúng ?
A.
1 2
6
.
5
S S
B.
1 2
.S S
C.
1 2
3
.
2
S S
D.
1
2
2.
S
S
44.6. Một ly nước hình trụ có chiều cao
20cm
và bán kính đáy bằng
4cm.
Bạn An đổ nước vào ly cho
đến khi mực nước cách đáy ly 17cm thì dừng lại. Sau đó bạn An lấy các viên đá lạnh hình cầu
có cùng bán kính
2cm
thả vào ly nước. Bạn An cần dùng ít nhất bao nhiêu viên đá để nước tràn
ra khỏi ly ?
A. 5.
B.
4.
C.
6.
D. 7.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 103 -
44.7. Một ly nước rỗng hình trụ có chiều cao
20cm
và bán kính đáy
4cm.
An bỏ vào ly
5
viên đá hình
cầu có bán kính
2cm
sau đó đổ trà sữa vào cho đến khi đầy ly. Tính lượng trà sữa mà An đã
dùng để đổ đầy ly ?
A.
200
3
B.
800
.
3
C.
800 .
D.
150 .
44.8. Một khối pha lê gồm một hình cầu
1
( )
H
bán kính
R
và một hình nón
2
( )
H
có bán kính đáy và
đường sinh lần lượt là
,
r
thỏa mãn
1
2
r
và
3
2
R
xếp chồng lên nhau (tham khảo hình
vẽ bên dưới). Biết tổng diện tích mặt cầu
1
( )
H
và diện tích toàn phần của hình nón
2
( )
H
là
2
91cm .
Tính diện tích của khối cầu
1
( ).
H
A.
2
104
cm .
5
B.
2
16cm .
C.
2
64cm .
D.
2
26
cm .
5
44.9. Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng
3
lần đường kính của đáy;
một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng
của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón đó (như hình vẽ ) thì thấy nước
trong cốc tràn ra ngoài. Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban
đầu (bỏ qua bề dày của lớp vỏ thủy tinh).
A.
5
9
B.
2
3
C.
1
2
D.
4
9
44.10. Một bình đựng nước dạng hình nón (không có đáy), đựng đầy nước. Người ta thả vào đó một
khối cầu có đường kính bằng một nửa chiều cao của bình nước và đo được thể tích tràn ra là
3
32
(dm ).
3
Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của hình nón và toàn bộ khối
cầu chìm trong nước, trong đó mặt nước là tiết diện của khối cầu (hình vẽ bên). Thể tích nước
còn lại trong bình bằng
A.
3
16
(dm ).
3
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 104 -
B.
3
32
(dm ).
3
C.
3
40
(dm ).
3
D.
3
64
(dm ).
3
44.11. Một cái ly nước dạng hình nón, đựng đầy nước. Người ta thả vào đó một khối cầu không thấm
nước, có đường kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là
.V
Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa khối cầu
chìm trong nước như hình vẽ. Thể tích nước còn lại trong ly bằng
A.
2
V
B.
1
.V
C.
1
.
3
V
D.
1
.
6
V
44.12. Nguời ta đặt được vào trong một hình nón hai khối cầu có bán kính lần lượt là a và
2a
sao cho
các khối cầu đều tiếp xúc với mặt xung quanh của hình nón, hai khối cầu tiếp xúc với nhau và
khối cầu lớn tiếp xúc với đáy của hình nón (tham khảo hình vẽ). Bán kính đáy của hình nón đã
cho bằng
A.
13
2
a
B.
2 2 .a
C.
3 .a
D.
2 3.a
44.13. Một quả cầu có thể tích
3
256
(cm )
3
được đặt vào một chiếc cốc có dạng hình trụ với đường kính
đáy là
6cm
như hình vẽ. Phần nhô ra khỏi chiếc cốc của quả cầu bằng (kết quả làm tròn đến hàng
phần trăm).
A. 2, 00cm.
B. 4, 00cm.
C. 4,65cm.
D. 6, 65cm.
44.14. Một cái phễu có dạng hình nón, chiều cao của phễu là
20cm
(hình 1). Người ta đổ một lượng
nước vào phễu sao cho chiều cao của cột nước trong phễu là
10cm.
Nếu bịt kín miệng phễu rồi
lật ngược lên (hình 2). Khi đó chiều cao cột nước trong phễu bằng giá trị nào sau đây ?
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 105 -
A. 0,87cm.
B. 1, 07cm.
C. 5cm.
D.
10cm.
44.15. Cho một đồng hồ cát gồm
2
hình nón chung đỉnh ghép lại, trong đó đường sinh bất kỳ của hình
nón tạo với đáy một góc
60
như hình bên dưới. Biết rằng chiều cao của đồng hồ là
30cm
và
tổng thể tích của đồng hồ là
3
1000 cm . Hỏi nếu cho đầy lượng cát vào phần trên thì khi chảy hết
xuống dưới, khi đó tỉ lệ thể tích lượng cát chiếm chỗ và thể tích phần dưới là bao nhiêu ?
A.
1
3 3
B.
1
8
C.
1
27
D.
1
64
44.16. Một bình đựng nước dạng hình nón không nắp đựng đầy nước. Biết rằng chiều cao của bình gấp
3
lần bán kính đáy của nó. Người ta thả vào bình đó một khối trụ và đo được thể tích nước trào
ra ngoài là
3
16
dm .
9
Biết một mặt của khối trụ nằm trên mặt đáy của hình nón và khối trụ có
chiều cao bằng đường kính đáy của hình nón (như hình vẽ). Tính bán kính đáy R của bình nước.
A.
2 dm.R
B.
3 dm.R
C.
4 dm.R
D.
5 dm.R
44.17. Ông A dự định sử dụng hết
2
6,7m
kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật
không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có
dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm).
A.
3
1,23m .
B.
3
1,11m .
C.
3
1,57m .
D.
3
2, 48m .
44.18. Một bác thợ gò hàn làm một chiếc thùng hình hộp chữ nhật (không nắp) bằng tôn thể tích
3
665,5dm .
Chiếc thùng này có đáy là hình vuông cạnh (dm),x chiều cao (dm).h Để làm chiếc
thùng, bác thợ phải cắt một miếng tôn như hình. Tìm
x
để bác thợ sử dụng ít nguyên liệu nhất ?
A. 10,5 dm.x
B.
12 dm.x
C.
11 dm.x
D.
9 dm.x
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 106 -
h
x
O
44.19. Cho hình nón đỉnh ,O chiều cao là
.h
Một khối nón khác có đỉnh là tâm
I
của đáy và đáy là một
thiết diện song song với đáy của hình nón đã cho. Để thể tích của khối nón đỉnh
I
lớn nhất thì
chiều cao của khối nón này bằng bao nhiêu ?
A.
2
h
B.
3
h
C.
2
3
h
D.
3
3
h
44.20. Có tấm bìa hình tam giác vuông cân
ABC
có cạnh huyền
BC
bằng .a Người ta muốn cắt tấm
bìa đó thành hình chữ nhật MNPQ rồi cuộn lại thành một hình trụ không đáy như hình vẽ. Diện
tích hình chữ nhật đó bằng bao nhiêu để diện tích xung quanh của hình trụ là lớn nhất ?
A.
2
2
a
B.
2
4
a
C.
2
12
a
D.
2
8
a
Câu 45. Trong không gian ,Oxyz cho mặt phẳng ( ) : 2 2 3 0P x y z và phương trình hai
đường thẳng
1
1 1
: ,
2 1 2
x y z
d
2
2 1
:
1 2 1
x y z
d
Đường thẳng vuông góc với
( ),P đồng thời cắt cả
1
d
và
2
d
có phương trình là
A.
3 2 2
.
2 2 1
x y z
B.
2 2 1
.
3 2 2
x y z
C.
1 1
.
2 2 1
x y z
D.
2 1 2
.
2 2 1
x y z
Lôøi giaûi tham khaûo
Gọi
1 2
, .M d d N d d
Khi đó (1 2 ; ; 1 2 ), (2 ;2 ; 1 ).M t t t N s s s
( 2 1;2 ; 2 ).MN s t s t s t

Từ hình vẽ có
( )
(2;2; 1)
P
MN n

Suy ra:
2 1 2 2
2 2 1
s t s t s t
2 1 2s 1
2 2s 4 0
s t t s
s t t t
(1; 0; 1)
.
(3;2; 2)
M
N
Đường thẳng
cần tìm đi qua (3;2; 2)N và một có véctơ chỉ phương
( )
(2;2; 1)
P
u n
là
3 2 2
2 2 1
x y z
Chọn đáp án A.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 107 -
Baøi taäp töông töï vaø môû roäng
45.1. Trong không gian
,
Oxyz
cho mặt phẳng
( ) : 3 3 5 1 0
P x y z
và phương trình hai đường
thẳng
1
1 3
: ,
2 4 3
x y z
d
2
2 4
:
1 1 3
x y z
d
Đường thẳng vuông góc với
( )
P
đồng
thời cắt
1
d
và
2
d
tại
A
và
,
B
độ dài
AB
bằng
A.
2 43.
B.
43.
C.
2 13.
D.
13.
45.2. Trong không gian
,
Oxyz
cho điểm
(1;0;2)
A
và đường thẳng
1 1
:
1 1 2
x y z
d
Phương
trình đường thẳng
đi qua
,
A
vuông góc và cắt
d
là
A.
1 2
1 1 1
x y z
B.
1 2
1 1 1
x y z
C.
1 2
2 2 1
x y z
D.
1 2
1 3 1
x y z
45.3. Trong không gian
,
Oxyz
viết phương trình đường thẳng
d
đi qua điểm
(2; 1;3),
A
vuông góc
với đường thẳng
1
5 2
:
4 1 1
x y z
d
và cắt đường thẳng
2
1 1 1
:
2 3 4
x y z
d
A.
2 1 3
1 2 2
x y z
B.
2 1 3
1 2 2
x y z
C.
2 1 3
1 2 2
x y z
D.
2 1 3
1 2 2
x y z
45.4. Trong không gian
,
Oxyz
viết phương trình đường thẳng
d
đi qua
(1; 1;4),
M
đồng thời
d
song
song với mặt phẳng
( ) : 2 2 15 0
P x y z
và
d
cắt đường thẳng
1 1
:
3 4 5
x y z
A.
1 1 4
2 3 7
x y z
B.
1 1 4
4 1 1
x y z
C.
1 1 4
4 1 1
x y z
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 108 -
D.
1 1 4
2 3 7
x y z
45.5. Trong không gian
,
Oxyz
viết phương trình đường thẳng
d
nằm trong
( ) : 3 0,
P x y z
đồng thời
d
cắt
1
6 10 5
:
2 7 3
x y z
d
và vuông góc với
2
1 2 3
:
1 3 9
x y z
d
A.
4 3 2
3 4 1
x y z
B.
4 3 2
62 22 25
x y z
C.
4 3 2
3 4 1
x y z
D.
4 3 2
3 4 1
x y z
45.6. Trong không gian
,
Oxyz
cho điểm
(1; 1;2),
A
mặt phẳng
( ) : 2 5 0
P x y z
và đường
thẳng
1 2
:
2 1 1
x y z
d
Viết phương trình đường thẳng
cắt
d
và
( )
P
lần lượt tại
M
và
N
sao cho
A
là trung điểm của đoạn thẳng
.
MN
A.
1 1 2
1 3 2
x y z
B.
1 1 2
2 3 2
x y z
C.
1 1 2
2 3 2
x y z
D.
1 1 2
2 3 1
x y z
45.7. Trong không gian
,
Oxyz
cho đường
1 1 2
:
2 1 2
x y z
d
và
( ) : 3 2 5 0.
P x y z
Phương trình đường thẳng
qua
(2; 1;1)
A
và cắt
d
tại
,
M
cắt
( )
P
tại
N
để
A
là trung điểm
MN
là
A.
3 2
1 1 1
x y z
B.
2 2 1
1 1 1
x y z
C.
3 2
1 1 1
x y z
D.
2 1 1
8 2 7
x y z
45.8. Trong không gian
,
Oxyz
cho đường thẳng
1 1 1
: ,
1 2 1
x y z
d
mặt phẳng
( ) : 4 0
x y z
và
4
;0;1
3
G
Phương trình đường thẳng
cắt
d
và
( )
lần lượt tại
,
M N
sao cho tam giác
OMN
nhận
G
làm trọng tâm là
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 109 -
A.
1
1 3 .
3 2
x t
y t
z t
B.
2 1
2 2 1
x y z
C.
0
1 .
3 4
x
y t
z t
D.
1 1 1
.
2 2 1
x y z
45.9. Trong không gian
,
Oxyz
cho đường thẳng
2
: 3 ,
3
x t
d y t
z
mặt phẳng
( ) : 1 0
x y z
và
điểm
2 2
;1;
3 3
G
Phương trình đường thẳng
cắt
d
và
( )
lần lượt tại
,
M N
sao cho tam giác
OMN
nhận
G
làm trọng tâm là
A.
1
2 .
3 4
x
y t
z t
B.
1
1 3 .
3 2
x t
y t
z t
C.
0
1 .
3 4
x
y t
z t
D.
2
3 3 .
3 2
x t
y t
z t
45.10. Trong không gian
,
Oxyz
cho đường thẳng
2
: 1 ,
4
x t
d y t
z t
mặt phẳng
( ) : 5 0
x y z
và
hai điểm
( 1;0;3),
C
( 2; 1;2).
D
Phương trình đường thẳng
cắt
d
và
( )
lần lượt tại
,
A B
sao cho tứ giác
ABCD
là hình bình hành là
A.
1
1 .
3 4
x
y t
z t
B.
1 2 1
1 1 1
x y z
C.
1
.
3 4
x t
y t
z t
D.
3 2 5
1 1 1
x y z
45.11. Trong không gian
,
Oxyz
cho hai đường thẳng chéo nhau
1
1 2 1
:
2 1 1
x y z
và
2
2 1 2
:
4 1 1
x y z
Đường thẳng chứa đoạn vuông góc chung của
1
và
2
đi qua
điểm nào sau đây ?
A.
(0; 2; 5).
M
B.
(1; 1; 4).
N
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 110 -
C.
(2;0;1).
P
D.
(3;1; 4).
Q
45.12. Trong không gian
,
Oxyz
cho
1
1 1 1
:
2 1 2
x y z
và
2
1 1 1
:
2 2 1
x y z
. Diện
tích mặt cầu có bán kính nhỏ nhất, đồng thời tiếp xúc với
1
và
2
bằng
A.
16
17
B.
4 17
17
C.
16 17
17
D.
4
17
45.13. Trong không gian
,
Oxyz
mặt phẳng
( ) : 2 6 3 0
P x y z
cắt trục
Oz
và đường thẳng
5 6
:
1 2 1
x y z
d
lần lượt tại
A
và
.
B
Phương trình mặt cầu đường kính
AB
là
A.
2 2 2
( 2) ( 1) ( 5) 36.
x y z
B.
2 2 2
( 2) ( 1) ( 5) 9.
x y z
C.
2 2 2
( 2) ( 1) ( 5) 9.
x y z
D.
2 2 2
( 2) ( 1) ( 5) 36.
x y z
45.14. Trong không gian
,
Oxyz
cho hai đường thẳng
1
1 3
: 2 ,
2
x t
d y t
z
2
1 2
:
2 1 2
x y z
d
và mặt
phẳng
( ) : 2 2 3 0.
P x y z
Phương trình mặt phẳng đi qua giao điểm của
1
d
và
( ),
P
đồng
thời vuông góc với
2
d
là
A.
2 2 22 0.
x y z
B.
2 2 13 0.
x y z
C.
2 2 13 0.
x y z
D.
2 2 22 0.
x y z
45.15. Trong không gian
,
Oxyz
cho đường thẳng
d
đi qua
(2;0;0),
A
cắt chiều âm trục
Oy
tại điểm
B
sao cho diện tích tam giác
OAB
bằng
1.
Phương trình tham số đường thẳng
d
là
A.
1 2
.
0
x t
y t
z
B.
2 2
.
0
x t
y t
z
C.
2 2
.
0
x t
y t
z
D.
2 2
.
1
x t
y t
z
45.16. Trong không gian
,
Oxyz
cho ba điểm
(1;2; 1), (2;1;1), (0;1;2)
A B C
và phương trình đường
thẳng
1 1 2
:
2 1 2
x y z
d
Lập phương trình đường thẳng
đi qua trực tâm của tam
giác
,
ABC
biết
nằm trong
( )
ABC
và vuông góc với đường thẳng
.
d
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 111 -
A.
1 1 1
:
12 2 11
x y x
B.
2 1 1
:
12 2 11
x y z
C.
2 1 1
:
12 2 11
x y z
D.
2 1 1
:
12 2 11
x y z
45.17. Trong không gian
,
Oxyz
cho mặt phẳng
( ) : 2 3 4 0
P x y z
và hai đường thẳng
1
1 1
: ,
1 1 2
x y z
d
2
1 3 1
:
2 1 1
x y z
d
Mặt phẳng
( )
song song với
( )
P
và cắt
1
,
d
2
d
theo thứ tự tại
,
M
N
sao cho
3.
MN
Điểm nào sau đây thuộc
( )
?
A.
(1;2;3).
A
B.
(0;1; 3).
B
C.
(0; 1; 3).
C
D.
(0;1;3).
D
45.18. Trong không gian với hệ tọa độ
,
Oxyz
cho bốn đường thẳng
1
1 2
: ,
1 2 2
x y z
d
2
2 2
: ,
2 4 4
x y z
d
3
1
: ,
2 1 1
x y z
d
4
2 1
: .
2 2 1
x y z
d
Gọi
là đường thẳng
cắt cả bốn đường thẳng đã cho. Một véctơ chỉ phương của đường thẳng
là
A.
3
(2;0; 1).
u
B.
2
(2;1; 1).
u
C.
1
(2;1;1).
u
D.
4
(1;2; 2).
u
45.19. Trong không gian
,
Oxyz
cho tam giác
ABC
có
(2;3;3),
A
phương trình đường trung tuyến
1
d
kẻ từ
B
là
3 3 2
,
1 2 1
x y z
phương trình đường phân giác trong
2
d
của góc
C
là
2 4 2
.
2 1 1
x y z
Đường thẳng
BC
có một véctơ chỉ phương là
A.
(2;1; 1).
u
B.
(1;1;0).
u
C.
(1; 1;0).
u
D.
(1;2;1).
u
45.20. Trong không gian
,
Oxyz
cho hình thoi
ABCD
có tâm
(2;1; 3),
I
phương trình đường thẳng
2 1
: ,
1 2 1
x y z
BC
đỉnh
D
thuộc mặt phẳng
( ) : 2 15 0.
P x y z
Đường thẳng
AC
cắt mặt phẳng
( )
Oyz
tại điểm có cao độ bằng
A.
5.
B.
23.
C.
17.
D.
3.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 112 -
Câu 46. Cho ( )f x là hàm bậc bốn thỏa mãn (0) 0.f Hàm số ( )f x
có bảng biến thiên như sau:
Hàm số
3
( ) ( ) 3g x f x x có bao nhiêu điểm cực trị ?
A. 3. B. 2. C. 1. D. 4.
Lôøi giaûi tham khaûo
Ta có:
3
2
( ) ( 1)( 3) ( ) ( )d 2 3 .
3
x
f x a x x f x f x x f x a x x b
Do
( 3) 1
61
( 1)
3
f
f
29
2
1
a
b
3
2
29
( ) 2 3 1.
2 3
x
f x x x
Xét hàm số
3
( ) ( ) 3h x f x x
có
2 3
( ) 3 ( ) 3 0h x x f x
3
2
1
( )f x
x
(1)
Dựa vào bảng biến thiên đề bài, ta có:
Nếu ( ;0)x  thì
3
( ) 0 ( ) 0f x f x
mà
2
1
0
x
nên (1) vô nghiệm trên ( ;0).
Nếu (0; )x  thì
3
( ) 1 ( ) 1f x f x
đồng biến nên
3
( )f x
đồng biến, mà hàm số
2
1
y
x
nghịch biến nên phương trình (1) không quá 1 nghiệm.
Ta có:
3
2
0
1
lim ( )
x
f x
x

và
3
2
1
lim ( )
x
f x
x


nên có bảng biến thiên sau:
Từ bảng biến thiên, suy ra hàm số
3
( ) ( ) 3g x f x x có 3 điểm cực trị. Chọn đáp án A.
Baøi taäp töông töï vaø môû roäng
46.1. Cho ( )f x là hàm bậc bốn và có (0) 0.f Hàm số
( )f x
có bảng biến thiên sau:
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 113 -
Hàm số
3
2
2) )( (
3
g xx f x
có bao nhiêu điểm cực trị ?
A. 1.
B. 2.
C. 3.
D. 4.
46.2. Cho ( )f x là hàm bậc bốn và có (0) 0.f Hàm số
( )f x
có bảng biến thiên sau:
Hàm số
3
1
2) )( (
3
g xx f x
có bao nhiêu điểm cực trị ?
A. 1.
B. 2.
C. 3.
D. 4.
46.3. Cho hàm số
( )y f x
có đạo hàm trên và hàm ( )y f x
có đồ thị như hình vẽ. Trên đoạn
[ 3;4],
hàm số
2
( ) 1 ln( 8 16)
2
x
g x f x x
có bao nhiêu điểm cực trị ?
A. 1.
B. 2.
C.
0.
D. 3.
46.4. Cho hàm số ( )y f x có đạo hàm liên tục trên và (0) 0, (4) 4.f f Biết đồ thị hàm số
( )y f x
có đồ thị như hình vẽ bên dưới.
Số điểm cực trị của hàm số
2
( ) ( ) 2g x f x x
là
A. 1.
B. 2.
C. 3.
D. 5.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 114 -
46.5. Cho hàm số đa thức
( )f x
có đạo hàm trên . Biết
( 2) 0f
và đồ thị của hàm số ( )y f x
như
hình vẽ bên dưới.
Hàm số
2
4 ( ) 4y f x x có bao nhiêu điểm cực tiểu ?
A. 1.
B. 3.
C. 4.
D. 2.
46.6. Cho hàm số
4 3 2
( ) , ( 0).f x ax bx cx dx e ae Đồ thị hàm số ( )y f x
như hình vẽ bên
dưới. Hàm số
2
4 ( )y f x x có bao nhiêu điểm cực tiểu ?
A. 3.
B. 4.
C. 2.
D.
5.
46.7. Cho hàm số
( )f x
có bảng biến thiên của hàm số ( )f x
bên dưới. Số điểm cực trị của hàm số
2
( 2 )y f x x là
A. 9.
B. 3.
C.
7.
D. 5.
46.8. Cho hàm số bậc bốn
( )y f x
có đồ thị như hình vẽ bên dưới. Số điểm cực tiểu của hàm số
3 2
( ) ( 3 )g x f x x là
A. 3.
B.
7.
C. 4.
D. 5.
46.9. Biết rằng hàm số
( )f x
xác định, liên tục trên có đồ thị được cho như hình vẽ bên dưới. Số
điểm cực đại của hàm số
( ( )) 2021y f f x
là
A. 1.
B. 3.
C. 2.
D. 4.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 115 -
46.10. Cho hàm số ( )f x có đạo hàm liên tục trên
có (5) 12.f Đồ thị hàm số ( )f x
được cho như
hình. Số điểm cực trị của hàm số
2
(1 2 ) 2 2y f x x x
là
A.
3.
B.
5.
C.
7.
D.
6.
46.11. Cho hàm số bậc bốn ( )f x có
3
(0) .
2
f Hàm số
( )y f x
có đồ thị trong hình vẽ bên. Số điểm
cực trị của hàm số
2
4 ( 1) 2y f x x x là
A.
3.
B.
5.
C.
4.
D.
6.
46.12. Cho hàm số ( )y f x có đạo hàm
3
( ) 4 2f x x x
và (0) 1.f Số điểm cực tiểu của hàm số
3 2
( ) ( 2 3)g x f x x
là
A. 0.
B.
1.
C.
2.
D.
3.
46.13. Cho hàm số ( )y f x có đạo hàm
2
( ) 3 3f x x
và (2) 4.f Hàm số
2
( ) (1 2 )g x f x
có
bao nhiêu điểm cực trị ?
A.
3.
B.
4.
C. 5.
D.
6.
46.14. Cho ( )f x là hàm số bậc ba. Đồ thị các hàm số ( )y f x và ( )y f x
lần lượt là các đường cong
trong hình vẽ bên. Xét hàm số
2
( ) ( ( )), .g x f x f x x
Biết rằng đồ thị hàm số ( )y g x
không
tiếp xúc với trục hoành. Số điểm cực trị của ( )g x là
A. 4.
B. 5.
C.
7.
D. 8.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 116 -
46.15. Hàm số ( )y f x có bảng xét dấu đạo hàm
( )f x
bên dưới. Có bao nhiêu số nguyên [ 5;5]m
để hàm số
2 2
( 2 1)y f x mx m
đồng biến trên khoảng (0;1) ?
A. 5.
B. 8.
C.
7.
D. 6.
46.16. Cho hàm số ( )y f x có đạo hàm liên tục trên
.
Đồ thị của
( )y f x
như hình vẽ. Có tất cả
bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
2
4 ( ) 2y f x m x mx
đồng biến
trên khoảng (1;2) ?
A. 2.
B. 3.
C. 0.
D. 1.
46.17. Cho hàm số ( )y f x có đạo hàm liên tục trên
.
Biết (0) 0f và đồ thị hàm số ( )y f x
như
hình vẽ bên dưới. Hàm số
2
4 ( )y f x x
đồng biến trên khoảng nào dưới đây ?
A. (0;4).
B. ( 2; 0).
C. (4; ).
D. ( ; 2).
46.18. Cho hàm số ( )f x liên tục trên có ( 1) 0f và có đồ thị hàm số
( )y f x
như hình vẽ. Hàm
số
2
2 ( 1)y f x x
đồng biến trên khoảng nào sau đây ?
A. (3; ).
B. ( 1;2).
C. (0; ).
D. (0;3).
46.19. Cho hàm số ( )y f x liên tục trên
thỏa mãn
2
(3 15 ) ( ) (10 5 ) ( ) 0,x x f x x f x
0,x
(1) 4f và
2 2
( ) ( ) 0.f x f x
Tổng giá trị cực đại và cực tiểu của hàm số ( )y f x bằng
A.
3
3 4.
B.
3
2 4.
C.
3
3 4.
D.
4
3 2.
46.20. Cho hàm số ( )y f x liên tục trên
và có đồ thị hàm số
( )
y f x
như hình bên dưới. Hàm số
2 4 6 2
15 (2 ) 10 30 20y f x x x x
có bao nhiêu điểm cực trị ?
A.
1.
B.
2.
C.
3.
D. 5.
x
y
– 2
4
1
– 2
O
x
y
– 2
4
1
– 2
O
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 117 -
Câu 47. Có bao nhiêu số nguyên
( 2)
a a
sao cho tồn tại số thực
x
thỏa
log log
( 2) 2 ?
x a
a x
A.
8.
B.
9.
C.
1.
D. Vô số.
Lôøi giaûi tham khaûo
Điều kiện:
2.
x
Đặt
log 0.
m a
Phương trình trở thành
( 2) 2.
m m
x x
Đặt
2
m
y x
và
2
y
thì ta có hệ phương trình
2
2
m
m
y x
x y
( ) (0; )
( ) ( )
m
f t t tm m m m
x y x y x x y y f x f y x y

2
m
x x
log( 2)
log log( 2) 1
log
x
m x x m
x
log 1
a
10.
a
2,
{2;3; 4;...;9} :
a a
a
có
8
thỏa mãn bài toán. Chọn đáp án A.
Baøi taäp töông töï vaø môû roäng
47.1 Có bao nhiêu số nguyên
a
( 2)
a
sao cho tồn tại số thực
x
thỏa
2 2
log log
2 ( 1) 2 ?
a a
a x x
A.
1.
B.
2.
C.
3.
D.
0.
47.2 Có bao nhiêu số nguyên
a
( 2)
a
sao cho tồn tại số thực
x
thỏa
ln ln
( 3) 3 ?
x x
a x
A.
1.
B.
2.
C.
3.
D.
0.
47.3 Có tất cả bao nhiêu giá trị nguyên của số thực
y
nhỏ hơn
10
sao cho tồn tại số thực
x
thỏa mãn
e e
x x
y y ?
A.
9.
B.
8.
C.
10.
D.
7.
47.4 Có bao nhiêu số nguyên
y
để tồn tại số thực
x
thỏa
ln 3 sin ln( 4 sin ) sin
y x y x x
?
A.
6.
B.
10.
C.
5.
D.
9.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 118 -
47.5 Có tất cả bao nhiêu số nguyên
y
sao cho có đúng
2
số thực
(0;10)
x
thỏa mãn:
2 3 3
8 3 .4 (3 1).2 ( 1) ( 1)
x x x
x x y x y x
?
A.
101.
B.
100.
C.
102.
D.
103.
47.6 Gọi
1
a
là số thực sao cho tồn tại duy nhất số thực
x
thỏa
log .
x
a
a x
Mệnh đề nào đúng ?
A.
(1,2; 1, 3).
a
B.
(1, 3; 1, 4).
a
C.
(1, 4; 1,5).
a
D.
(1, 5; 1,6).
a
47.7 Phương trình
3
3 2
2 ( 3) .2 (8 ).2 4
x m x x x
x x m
có ba nghiệm phân biệt khi và chỉ khi
( ; ).
m a b
Khi đó giá trị
2 2
b a
bằng
A.
48.
B.
36.
C.
64.
D.
72.
47.8 Giả sử
,
a
b
là các số thực sao cho
3 3 3 2
.10 .10
x x
x y a b
đúng với mọi các số thực dương
, ,
x y z
thỏa mãn
log( )
x y z
và
2 2
log( ) 1.
x y z
Giá trị của
a b
bằng
A.
31
2
B.
29
2
C.
31
2
D.
25
2
47.9 Xét các số thực dương
,
x y
thỏa mãn
2
log (4 16) 3 8 2
y
x x y
. Gọi
o o
( ; )
x y
là cặp
( ; )
x y
khi biểu thức
2
3 1 8
y
P x x
đạt giá trị nhỏ nhất. Giá trị của
3
o o
3
x y
bằng
A.
9.
B.
7.
C.
7.
D.
9.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 119 -
47.10 Có bao nhiêu giá trị nguyên của tham số thực
m
để tồn tại cặp số
( ; )
x y
thỏa mãn đồng thời
2 1 3 2
e e 1
x y x y
x y
và
2 2
2 2
log (2 1) ( 4)log 4 0 ?
x y m x m
A.
3.
B.
4.
C.
5.
D.
6.
47.11 Cho phương trình
2
2 2 2
2
log (2 4 4) 2 2 1.
y
x x y x x
Hỏi có bao nhiêu cặp số nguyên
dương
( ; )
x y
và
0 100
x
thỏa mãn phương trình đã cho ?
A.
4.
B.
3.
C.
1.
D.
2.
47.12 Có bao nhiêu cặp số nguyên dương
( ; )
x y
thỏa mãn
0 2020
x
và
( 1).3 .27 ?
x y
x y
A.
2020.
B.
673.
C.
672.
D.
2019.
47.13 Có bao nhiêu cặp số nguyên
( ; )
x y
thỏa mãn đồng thời các điều kiện
0 2020,
x
1 2020
y
và
1
2 2
4 log ( 3) 16.2 log (2 1)
x y
y x
?
A.
2019.
B.
2020.
C.
1010.
D.
1011.
47.14 Có tất cả bao nhiêu bộ ba số thực
( , , )
x y z
thỏa mãn đồng thời các điều kiện
3 3
2
2 23
2 .4 .16 128
yx z
và
2 4 2 2 4 2
( ) 4 ( )
xy z xy z
?
A.
3.
B.
4.
C.
1.
D.
2.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 120 -
47.15 Cho hàm số bậc ba ( )y f x có đồ thị như hình vẽ bên. Số nghiệm thực phân biệt của phương
trình ( ( )) 1f xf x là
A. 3.
B. 6.
C.
7.
D. 8.
47.16 Có tất cả bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn [ 2020;2020] để phương trình
2 2
2020
2021
log ( 3 ) log ( )x x x m có đúng hai nghiệm phân biệt ?
A.
4035.
B. 2023.
C.
2022.
D. 4036.
47.17 Gọi S là tập hợp tất cả các giá trị nguyên của tham số
m
thuộc đoạn [ 20;20] để phương trình
2 2
2021
2021
log ( 3 ) log ( )x x x m có đúng hai nghiệm phân biệt. Tổng tất cả các phần tử của tập
S bằng
A.
203.
B. 206.
C.
3.
D. 6.
47.18 Có tất cả bao nhiêu giá trị nguyên của ( 10;10)y để tồn tại 2 số thực x thỏa mãn:
2 2
3 5
log ( 2 4) log ( 2 )x x x x y
A. 4.
B. 3.
C. 6.
D. 9.
47.19 Có bao nhiêu giá trị của (0;2020)y để tồn tại số thực
x
thỏa mãn
2
4 4 2 .cos( )
x x
x y
?
A. 324.
B. 322.
C. 320.
D. 321.
47.20 Với giá trị nào của y thì tồn tại đúng 1 số thực
x
thỏa mãn
9 9 3 cos( )
x x
y x
?
A. 3.y
B. 6.y
C. 3.y
D. 6.y
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 121 -
Câu 48. Cho hàm số bậc ba ( )y f x có đồ thị là đường cong trong hình bên. Biết hàm số ( )f x đạt
cực trị tại hai điểm
1 2
, x x thỏa mãn
2 1
2x x và
1 2
( ) ( ) 0.f x f x Gọi
1
S và
2
S là diện
tích của hai hình phẳng được gạch trong hình bên. Tỉ số
1
2
S
S
bằng
A.
3
4
B.
5
8
C.
3
8
D.
3
5
Lôøi giaûi tham khaûo
Tịnh tiến điểm uốn về gốc tọa độ, ta được hình vẽ bên.
Khi đó, do ( )f x là hàm bậc ba, nhận gốc tọa độ là tâm đối xứng
nên
1 2
1, 1x x
Chọn
2 3
( ) 3 3 ( ) 3 .f x x f x x x
Do đó
0
3
2
1
5
( 3 )d
4
S x x x
Mà
1 2
2S S
Suy ra:
1
1
2
3 3
4 5
S
S
S
Chọn đáp án D.
Baøi taäp töông töï vaø môû roäng
48.1. Cho hàm số bậc ba ( )y f x có đồ thị là đường cong trong hình bên. Biết hàm số ( )f x đạt cực trị
tại hai điểm
1 2
,
x x
thỏa mãn
2 1
4
x x
và
1 2
( ) ( ) 0.
f x f x
Gọi
1
S
và
2
S
là diện tích của hai
hình phẳng được gạch trong hình bên. Tỉ số
1
2
S
S
bằng
A. 5/3.
B.
3
5
C. 1.
D. 3/4.
48.2. Cho hàm số bậc ba
3 2
( )f x ax bx cx d
và đường thẳng : ( )d g x mx n có đồ thị như
hình vẽ. Nếu diện tích phần tô bằng bằng
1
2
thì diện tích phần gạch bằng
A.
5
2
B. 2.
C. 1.
D.
3
2
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 122 -
48.3. Cho đường cong
3
( ) : 8 27C y x x
và đường thẳng
y m
cắt
( )C
tại hai điểm phân biệt nằm
trong gốc phần tư thứ nhất của hệ trục tọa độ
Oxy
và chia thành 2 miền phẳng (gạch sọc và kẻ
caro) có diện tích bằng nhau (tham khảo hình vẽ bên). Mệnh đề nào sau đây là đúng ?
A.
1
0
2
m
B.
1
1.
2
m
C.
3
1
2
m
D.
3
2.
2
m
48.4. Cho
( )y f x
xác định trên
[ 3; 3]
có đồ thị như hình vẽ. Biết
1 2 3
, , S S S có diện tích lần lượt là
3, 1
và 3. Khi đó
1
1
(1 ) (3 )dx f x x
bằng
A.
1
2
B. 7.
C.
5
9
D. 4.
48.5. Hình phẳng
( )H
được giới hạn bởi đồ thị
( )C
của hàm đa thức bậc ba và parabol
( )P
có trục đối
xứng vuông góc với trục hoành. Phần tô đậm của hình vẽ có diện tích bằng
A.
37
12
B.
7
12
C.
11
12
D.
5
12
48.6. Cho hai hàm số
2 2
2( )f x ax bx cx
và
2
2( )g d xx x e
( , , , , ).a b c d e
Biết rằng
đồ thị của hàm số
( )y f x
và
( )y g x
cắt nhau tại ba điểm có hoành độ lần lượt là
2;
1;
1
(tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
A.
37
6
B.
13
2
C.
9
2
D.
37
12
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 123 -
48.7. Cho hàm số
4 3 2
, ( 0)y ax bx cx dx e a
có đồ thị
( )C
và đường
:d y mx n
cắt
đồ thị
( )C
tại các điểm có hoành độ lần lượt là
2; 1; 0; 1.
Biết rằng hình phẳng giới hạn bởi
( ), C d
và đường thẳng
2, 0x x
có diện tích bằng 1. Diện tích hình phẳng giới hạn bởi
đồ thị
( ),C
đường thẳng
,d
trục tung và đường 1x bằng
A.
11
30
B.
19
30
C.
49
30
D.
19
15
48.8. Cho hàm số
4 2
, ( 0)y ax bx c a
có đồ thị
( )C
và tiếp tuyến d của đồ thị
( )C
tại điểm có
hoành độ
1,x
cắt
( )C
tại hai giao điểm còn lại có hoành bằng
0, 2x x
(tham khảo hình
vẽ). Biết rằng hình phẳng giới hạn bởi
( ), C d
và đường thẳng
0, 2x x
có diện tích bằng
28/5.
Tính diện tích hình phẳng giới hạn bởi đồ thị
( ),C
đường thẳng d và
0, 1.x x
A.
27
5
B.
29
5
C.
1
5
D.
5
12
48.9. Cho hàm số ( )y f x và ( )y g x là hai hàm số liên tục trên có đồ thị hàm số là ( ),y f x
( ).y g x
Gọi , , a b c là các hoành độ giao điểm của đồ thị hàm số ( )f x
và ( ).g x
Hàm số
( ) ( )y f x g x m
có nhiều điểm cực trị nhất khi và chỉ khi
A. ( ) ( ) ( ) ( ).f a g a x f b g b
B. ( ) ( ) ( ) ( ).f c g c m f b g b
C. ( ) ( ) ( ) ( ).f b g b m f a g a
D. ( ) ( ) ( ) ( ).f c g c m f b g b
48.10. Cho hàm số
( )y f x
có đạo hàm liên tục trên . Đồ thị hàm số ( )f x
được cho như hình vẽ bên.
Tìm tất cả các giá trị thật của tham số m để bất phương trình
2
(1 2 ) 2 2f x x x m
có nghiệm
trên ( 0,5; 1) ?
A.
1 2
(2)
2 3
m f
B.
1 3
(2)
2 2
m f
C.
( 1) 2
2 3
f
m
D.
21
(0)
4
m f
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 124 -
48.11. Cho hàm số bậc bốn ( )f x có ( 1) 7.f Hàm số ( )y f x
có đồ thị trong hình vẽ bên. Số điểm
cực trị của hàm số
2
64( 1)y f x x x
là
A. 3.
B. 5.
C. 7.
D. 6.
48.12. Cho hai hàm số
4 3 2
( )f x ax bx cx dx e
và
3 2
( ) .g x mx nx px q
Đồ thị của hai
hàm số ( ),y f x
( )y g x
như hình vẽ bên dưới. Tổng các nghiệm của phương trình
( ) ( )f x q g x e bằng
A.
13
3
B.
13
3
C.
4
3
D.
4
3
48.13. Cho đường cong
3 2
( ) : ( )C f x x ax bx c
và đường thẳng : ( )d y g x là tiếp tuyến của
( )C tại điểm có hoành độ 1.x Biết rằng diện tích hình phẳng giới hạn bởi ( )C và d bằng
108 . Giao điểm thứ hai của d và ( )C có hoành độ 0,m khi đó m thuộc khoảng nào ?
A. (0;2).
B. (2;4).
C.
(4;6).
D. (6; ).
48.14. Cho đường cong
3
( ) : .C y x
Xét điểm A có hoành độ dương thuộc đồ thị ( ).C Tiếp tuyến của
( )C tại A tạo với ( )C một hình phẳng có diện tích bằng 27. Hoành độ của điểm A thuộc khoảng
nào dưới đây ?
A.
1
0;
2
B.
1
;1
2
C.
3
1;
2
D.
3
;2
2
48.15. Gọi
1
S và
2
S lần lượt là diện tích các hình phẳng giới hạn bởi
2
( ) :P y x k
( 0)k và đường
thẳng : 2d y x như hình vẽ. Nếu
1 2
S S thì k bằng
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 125 -
A.
2
5
B.
7
9
C.
3
2
D.
3
4
48.16. Cho parabol
2
( ) : ,P y x
điểm
(0;1).A
Một đường thẳng đi qua
A
cắt
( )P
tại hai điểm
, B C
sao cho
2AC AB
như hình vẽ bên. Thể tích của khối tròn xoay được tạo thành khi quay phần
gạch chéo quanh trục hoành gần với giá trị nào nhất sau đây ?
A.
13, 3.
B.
8.
C.
7,3.
D.
11.
48.17. Cho parabol
2
( ) : ,P y x
điểm
(0;2).A
Một đường thẳng đi qua
A
cắt
( )P
tại hai điểm
, B C
sao cho
3 2AC AB
như hình vẽ bên. Thể tích của khối tròn xoay được tạo thành khi quay phần
gạch chéo quanh trục hoành gần với giá trị nào nhất sau đây ?
A.
34.
B.
11.
C. 7.
D.
21.
48.18. Cho parabol
2
( ) : ,P y x
điểm
(0;1).A
Một đường thẳng
d
đi qua
A
cắt
( )P
tại hai điểm
2 2
( ; ), ( ; )B b b C c c
sao cho
4AC AB
như hình vẽ bên. Gọi
1
S là diện tích hình phẳng giới hạn
bởi
{( ); ; ; 0}P d x b x
và
2
S là diện tích hình phẳng giới hạn bởi
{( ); ; ; 0}.P d x b x
Tỉ số diện tích
1 2
/S S bằng
A.
181
2944
B.
17
608
C.
13
112
D.
2763
2944
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 126 -
48.19. Cho parabol
2
y x
có đồ thị như hình vẽ, diện tích
2 1
2 .S S Gọi
1 2
, V V là thể tích hình phẳng
1 2
, S S quay quanh trục hoành. Tính
2
1
V
V
A.
4
2 3.
B.
4
3 2.
C.
2.
D.
4.
48.20. Cho hàm số
2
y x
có đồ thị
( )C
như hình vẽ. Kí hiệu
1
( )H là hình phẳng được giới hạn bởi
( ),C
, ( 0)x a a
và trục hoành;
2
( )H là hình phẳng được giới hạn bởi
( ),C
, ( 0)x b b
và
trục hoành lần lượt có diện tích
1 2
, .S S Đồng thời
1 2
, V V là thể tích khối tròn xoay tạo thành khi
quay
1 2
( ), ( )H H xung quanh trục hoành. Biết rằng
1 2
243 32 .V V Tỉ số
1
2
S
S
bằng
A.
4
9
B.
8
27
C.
2
3
D.
16
81
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 127 -
Câu 49. Xét hai số phức
1 2
, z z thỏa mãn
1
1,z
2
2z và
1 2
3.z z Giá trị lớn nhất của
1 2
3z 5z i bằng
A.
5 19.
B.
5 19.
C.
5 2 19.
D.
5 2 19.
Lôøi giaûi tham khaûo
Cách giải 1. Phương pháp hình học.
Gọi A là điểm biểu diễn số phức
1
,z B là điểm biểu diễn số phức
2
z và C là điểm biểu diễn
số phức
1 2
3 ,w z z điểm (0;5).M
Ta có:
2 2 2 2
3 (3 ) 9 6 .OC OA OB OC OA OB OA OB OAOB
     
2 2 2
2 2 2 2
9 6. . .cos( , ) 9 6 19
2
OA OB AB
OA OB OAOB OA OB OA OB
 
19.w Mà MC OM OC nên
1 2
max
3z 5z i
max
MC , , O M C thẳng hàng
Suy ra
1 2
max
3z 5 5 19.z i OM R
Chọn đáp án B.
Cách giải 2. Phương pháp đại số.
Đặt
1
z a bi và
2
.z c di Suy ra:
2 2 2 2 2 2
1, 4, ( ) ( ) 3.a b c d a c b d
Do đó
2 2 2 2
2 2 3 1.a ac c b bd d ac bd
Ta có:
1 2
3 3( ) (3 )z z a c b d i nên
2 2
1 2
3 (3 ) (3 )z z a c b d
2 2 2 2
9( ) ( ) 6( ) 19.a b c d ac bd
Áp dụng bất đẳng thức ,z z z z
ta có
1 2 1 2
3 5 3 5 19 5.z z i z z i
Chọn đáp án B.
Baøi taäp töông töï vaø môû roäng
Dạng 1. ĐIỂM VÀ ĐƯỜNG THẲNG
Cho đường thẳng ( ) : 0Ax By C và điểm ( ).M Điểm ( )N sao cho NM nhỏ nhất
K
là hình chiếu của N lên ( ), nghĩa là
min [ ,( )]
.
N
NM NK d M K
,( )
min
2 2
O
C
z OH d
A B
Khi đó M H và tọa độ ( ) ( ).H OH
[ ;( )]
min
2 2
( )
N
Ax By C
z x y i NK d
A B
Khi đó M K và tọa độ ( ) ( ).K MK
49. 1 Xét các số phức z x yi thỏa mãn 2 4 2z i z i và z đạt giá trị nhỏ nhất. Khi đó giá
trị của 3 2x y bằng
A. 2.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 128 -
B.
3.
C.
4.
D.
5.
49. 2 Xét các số phức
z
thỏa mãn
( 2 ) 4 1
z z i i
là một số thực. Giá trị nhỏ nhất của
z
bằng
A.
8
5
B.
16
5
C.
9
6
D.
7
5
49. 3 Xét các số phức
z
thỏa mãn
2 2 4 .
z i z i
Giá trị nhỏ nhất của
1
iz
bằng
A.
2 2.
B.
2.
C.
2
2
D.
3 2
2
49. 4 Xét các số phức
z
thỏa
1 1 2 .
z i z i
Giá trị nhỏ nhất của
(3 4 ) 5 10
i z i
bằng
A.
7 3
26
B.
15
2
C.
17
2
D.
5 13
26
49. 5 Xét các số phức
z
thỏa mãn
1 2 .
z z i
Giá trị nhỏ nhất của
(1 2 ) 11 2
i z i
bằng
A.
5
2
B.
2
5
C.
2
5
D.
5
2
Dạng 2. ĐIỂM VÀ ĐƯỜNG TRÒN
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 129 -
Cho tập hợp điểm ( ; )M x y biểu diễn các số phức z x yi là một đường tròn ( )C có tâm ( ; )I a b và
bán kính .R Gọi N là điểm biểu diễn số phức .z
Phương pháp 1. Hình học
min 1 1
min
max 2 2
max
khi
khi
z OM OM OI R M M
z OM OM OI R M M
Khi đó
1 2
( ) ( ) { ; }.OI C M M
min 1 1
min
max 2 2
max
khi
khi
z z MN NN NI R M N
z z MN NN NI R M N
Khi đó
1 2
( ) ( ) { ; }.NI C N N
Lưu ý. Nếu đề bài yêu cầu tìm tổng phần thực, phần ảo tương ứng với
min max
, z z thì từ nhận xét
I là trung điểm của
1 2
M M suy ra: tổng phần thực 2 ,a tổng phần ảo 2 .b
Phương pháp 2. Bất đẳng thức Cauchy – Schwarz
Giả sử tập hợp điểm là đường tròn
2 2 2
( ) : ( ) ( )C x a y b R và viết lại:
2 2 2 2
( ) : 2 2 0 2 2C x y ax by c x y ax by c
2
2 2 2 2 2 2
2 2 2 ( ) 2 ( ) 2 2z x y z x y ax by c a x a b y b a b c
nhằm lợi dụng
2 2 2
( ) ( )x a y b R trong bất đẳng thức Cauchy – Schwarz (điểm rơi):
2 2
2 2 2 2 2 2 2 2
(4 4 ) ( ) ( ) 2 .( ) 2 .( ) (4 4 ) ( ) ( )
R R
a b x a y b a x a b y b a b x a y b
 
Suy ra:
2
2 2 2 2 2 2 2 2
2 2 2 ( ) 2 2 2 ( )a b c R a b z a b c R a b
2 2 2 2 2 2 2 2
2 2 2 ( ) 2 2 2 ( ).a b c R a b z a b c R a b
Phương pháp 3. Lượng giác
Giả sử tập hợp điểm là đường tròn
2 2
2 2 2
( ) : ( ) ( ) 1,
x a y b
C x a y b R
R R
gợi ta đến
công thức
2 2
sin cos 1t t
nên đặt
sin
sin
cos
cos
x a
t
x a R t
R
y b y b R t
t
R
Do đó:
2
2 2 2 2 2 2
( sin ) ( cos )z x y z x y a R t b R t
2
2 2 2 2 2
(sin cos ) 2 .sin 2 .cosz a b R t t aR t bR t
2
2 2 2 2 2
2 .sin( )z a b R R a b t
và luôn có 1 sin( ) 1t nên suy ra:
2 2 2 2 2 2 2 2
2 2 .a b R a b z a b R a b
Phương pháp 4. Sử dụng bất đẳng thức trị tuyệt đối
1 2 1 2 1 2
.z z z z z z
49. 6 Cho các số phức thỏa mãn 2 2 1.z i Giá trị lớn nhất của z bằng
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 130 -
A.
4 2 2.
B.
2 2.
C.
2 2 1.
D.
3 2 1.
49. 7 Xét các số phức
z
thỏa
2 4 2.
z i
Gọi
1 2
,
z z
là hai số phức có môđun lớn nhất và nhỏ nhất.
Tổng phần ảo của
1 2
,
z z
bằng
A.
8.
B.
4.
C.
8.
D.
4.
49. 8 Xét các số phức
z
thỏa mãn điều kiện
(1 ) 1 7 2.
i z i
Gọi
,
m M
lần lượt là giá trị nhỏ
nhất và giá trị lớn nhất của biểu thức
.
P z
Giá trị của
M m
bằng
A.
4.
B.
10.
C.
2.
D.
24.
49. 9 Xét các số phức
,
z w
thỏa mãn
w iz
và
(1 ) 2 2 2.
i z i Giá trị lớn nhất của
z w
bằng
A.
3.
B.
2 3.
C.
3 2.
D.
3 3.
49. 10 Xét các số phức
z
thỏa mãn
2 2
4 2 .
z z iz
Giá trị nhỏ nhất của
z i
bằng
A.
1.
B.
2.
C.
3.
D.
4.
49. 11 Xét các số phức
z
thỏa mãn điều kiện
2
2 5 ( 1 2 )( 3 1) .
z z z i z i
Giá trị nhỏ nhất của
2 2
z i
bằng
A.
0,5.
B.
1.
C.
3
2
D.
2.
Dạng 3. ĐƯỜNG TRÒN VÀ ĐƯỜNG TRÒN
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 131 -
49. 12 Xét các số phức
1 2
,
z z
thỏa mãn
1
4 1
z
và
2
2 1.
iz
Giá trị nhỏ nhất của
1 2
2
z z
bằng
A.
2 5 2.
B.
4 2.
C.
4 2 3.
D.
4 2 3.
49. 13 Xét các số phức
1 2
,
z z
thỏa mãn
1
3 5 2
z i
và
2
1 2 4.
iz i
Giá trị lớn nhất của biểu
thức
1 2
2 3
P iz z
bằng
A.
313 16.
B.
313.
C.
313 8.
D.
313 2 5.
49. 14 Xét các số phức
,
z w
thỏa
3 2 2
z và
4 2 2 2.
w i Biết
z w
đạt giá trị nhỏ nhất
khi
0
z z
và
0
.
w w
Giá trị của
0 0
3
z w
bằng
A.
2 2.
B.
6 2.
C.
4 2.
D.
1.
49. 15 Cho các số phức
,
z w
thỏa mãn
5 3 3
z i
và
4 2 2.
iw i
Giá trị lớn nhất của biểu
thức
3 2
iz w
bằng
A.
554 5.
B.
578 13.
C.
578 5.
D.
554 13.
49. 16 Cho hai số phức
1 2
,
z z
thỏa mãn
1
2 3 2
z i
và
2
1 2 1.
z i
Giá trị lớn nhất của biểu
thức
1 2
z z
bằng
A.
3 34.
B.
3 10.
C.
3.
D.
6.
Dạng 4. ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 132 -
49. 17 Biết rằng số phức
( , )
z x yi x y
thỏa mãn đồng thời
3 4 5
z i và biểu thức
2 2
2
P z z i
đạt giá trị lớn nhất. Giá trị của
z
bằng
A.
33.
B.
50.
C.
10.
D.
5 2.
49. 18 Xét các số phức
z
thỏa mãn
1 3 13.
z i Gọi
,
m M
lần lượt là giá trị nhỏ nhất và lớn nhất
của biểu thức
2 2
2 3 .
P z z i
Tổng
m M
bằng
A.
10.
B.
25.
C.
34.
D.
40.
49. 19 Xét các số phức
( , )
z x yi x y
thỏa mãn
(1 ) 2 4.
i z i
Giá trị lớn nhất của biểu
thức
3
P x y
bằng
A.
4.
B.
4 2.
C.
4 2 2.
D.
8.
49. 20 Xét các số phức
1
z
thỏa mãn
2 2
1 1
2 1
z z i
và các số phức
2
z
thỏa
2
4 5.
z i Giá
trị nhỏ nhất của
1 2
z z
bằng
A.
5.
B.
2 5.
C.
2 5
5
D.
3 5
5
Dạng 5. MỘT SỐ LOẠI KHÁC (ĐOẠN THẲNG VÀ TIA, PARABOL, ELIP,…)
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 133 -
49. 21 Xét các số phức
z
thỏa mãn
2 4 7 6 2.
z i z i Gọi
,
m M
lần lượt là giá trị nhỏ nhất
và giá trị lớn nhất của
1 .
T z i
Giá trị của
m M
bằng
A.
5 2 73
2
B.
5 2 2 73.
C.
13 73.
D.
5 2 2 73
2
49. 22 Xét các số phức
z
thỏa mãn
1 8 3 53.
z i z i Giá trị lớn nhất của biểu thức
1 2
P z i
bằng
A.
53.
B.
53.
C.
185
.
2
D.
106.
49. 23 Xét các số phức
z
thỏa
2 3 6 2 17.
z i z i Gọi
,
M m
lần lượt là giá trị lớn nhất và
giá trị nhỏ nhất của
1 2 2 .
P z i z i
Giá trị
m M
bằng
A.
3 2.
B.
3 2 2
2
C.
8 2 2 5.
D.
6 2 2 5
3
49. 24 Xét các số phức
z
thỏa mãn
2 2 1 3 34.
iz i z i Giá trị nhỏ nhất của biểu thức
(1 ) 2
P i z i
bằng
A.
9
.
17
B.
3 2.
C.
4 2.
D.
26.
49. 25 Xét các số phức
z
đồng thời thỏa mãn
4 3 4 3 10
z i z i
và
3 4
z i
nhỏ nhất.
Môđun của số phức
z
bằng
A.
5.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 134 -
B.
5 2.
C.
6 2.
D.
10.
49. 26 Xét hai số phức
1 2
,
z z
thỏa mãn
1 1 1
2 2
z i z z i
và
2
10 1.
z i
Giá trị nhỏ nhất của
biểu thức
1 2
z z
bằng
A.
10 1.
B.
101 1.
C.
101 1.
D.
3 5 1.
49. 27 Xét các số phức
( , )
z a bi a b
thỏa mãn điều kiện
2
4( ) 15 ( 1) .
z z i i z z
Tính
4
P a b
khi
1
3
2
z i
đạt giá trị nhỏ nhất.
A.
4.
P
B.
5.
P
C.
6.
P
D.
7.
P
49. 28 Xét số phức
z a bi
thỏa
2 3 2 .
z i z z i
Tính
8 7
a b
khi biểu thức
6
7
P z i
đạt
giá trị nhỏ nhất.
A.
8 7 8.
a b
B.
8 7 5.
a b
C.
8 7 6.
a b
D.
8 7 7.
a b
49. 29 Xét các số phức
z
thỏa mãn
1.
z
Giá trị lớn nhất của
1 2 1
T z z
bằng
A.
2 5.
B.
2 10.
C.
3 2.
D.
3 5.
49. 30 Xét các số phức
z
thỏa
4 4 10.
z z
Giá trị lớn nhất và nhỏ nhất của
z
lần lượt là
A.
10
và
4.
B.
5
và
4.
C.
4
và
3.
D.
5
và
3.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 135 -
Câu 50. Trong không gian ,Oxyz cho hai điểm (2;1; 3)A và (6;5;5).B Xét khối nón ( )N có đỉnh
,
A
đường tròn đáy nằm trên mặt cầu đường kính .AB Khi ( )N có thể tích lớn nhất thì mặt
phẳng chứa đường tròn đáy của ( )N có phương trình dạng 2 0.x by cz d Giá trị của
b c d bằng
A. 21. B. 12. C. 18. D. 15.
Lôøi giaûi tham khaûo
Ta có 6.AB
Gọi , h r là chiều cao và bán kính đáy hình nón ( ).N
R là bán kính mặt cầu ( )S đường kính .AB
Gọi I là trung điểm AB và H là tâm
đường tròn đáy của ( ).N
Để thể tích hình nón ( )N lớn nhất thì .h R
Ta có:
2 2 2 2 2
( )r R IH R h R
Thể tích khối nón
Cauchy
3
2 2 2
1 1 (4 )
. . . ( ) . . .(4 2 )
3 3 6 6 27
R
V h r h R h R h h R h
Dấu " " xảy ra khi
4
4 2 4, 2.
3
h R h h R AH BH
Gọi ( ; ; ),H x y z khi đó:
2 14 11 13
; ;
3 3 3 3
AH AB H
 
Phương trình mặt phẳng chứa đường tròn đáy của ( )N đi qua H và nhận AB

làm vécto pháp
tuyến là
14 11 13
2 2 1 0
3 3 3
x y z
2 2 21 0x y z 18.b c d
Chọn đáp án D.
Baøi taäp töông töï vaø môû roäng
50. 1 Trong không gian ,Oxyz cho mặt cầu
2 2 2
( ) : ( 1) ( 2) ( 3) 27.S x y z
Gọi ( )P là mặt
phẳng đi qua hai điểm (0; 0; 4),A (2;0;0)B và cắt ( )S theo giao tuyến là đường tròn ( )C sao
cho khối nón đỉnh là tâm của ( )S và đáy là là đường tròn ( )C có thể tích lớn nhất. Biết rằng
( ) : 0,P ax by z c khi đó a b c bằng
A. 4.
B. 8.
C. 0.
D. 2.
50. 2 Trong không gian ,Oxyz cho mặt cầu
2 2 2
( ) : ( 1) ( 2) ( 3) 48.S x y z
Gọi ( )P là mặt
phẳng đi qua hai điểm (0;0; 4), (2;0; 0)A B và cắt mặt cầu ( )S theo giao tuyến là đường tròn
( ).C Khối nón ( )N có đỉnh là tâm của ( ),S đường tròn đáy là ( )C có thể tích lớn nhất bằng
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 136 -
A.
128
3
B.
39 .
C.
88
3
C.
215
3
50. 3 Trong không gian
,
Oxyz
cho mặt cầu
2 2 2
( ) : ( 1) ( 2) 1.
S x y z
Xét điểm
M
di động trên
đường thẳng
1 1 2
: ,
2 1 2
x y z
d
từ
M
kẻ ba tiếp tuyến
, ,
MA MB MC
đến
( )
S
với
, ,
A B C
là các tiếp điểm. Khi đường tròn ngoại tiếp tam giác
ABC
có bán kính nhỏ nhất bằng
thì phương trình mặt phẳng qua 3 điểm
, ,
A B C
là
( ) : 0.
ABC ax by z d
Khi đó
2 2
a b d
bằng
A.
3.
B.
1.
C.
2.
D.
3.
50. 4 Trong không gian
Oxyz
Cho
1 2 1
:
2 1 2
x y z
d
và
( ) : 2 2 16 0.
P x y z
Mặt cầu
( )
S
cắt
d
tại
,
A B
sao cho
8
AB
và cắt
( )
P
theo giao tuyến là đường tròn có bán kính
3.
r
Bán kính của mặt cầu
( )
S
nhỏ nhất có thể là
A.
3.
B.
1.
C.
2.
D.
3.
50. 5 Trong không gian với hệ toạ độ
,
Oxyz
cho đường thẳng
1 3
: 2 .
2 3 (1 )
x a at
y t
z a a t
Biết khi
a
thay đổi luôn tồn tại một mặt cầu cố định đi qua điểm
(1;1;1)
M
và tiếp xúc với đường thẳng
.
Tìm bán kính của mặt cầu đó.
A.
5 3.
B.
4 3.
C.
7 3.
D.
3 5.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 137 -
50. 6 Trong không gian
,
Oxyz
cho hai điểm
(1;2;3), (2;3;4).
A B
Một mặt cầu
( )
S
bán kính
R
luôn
tiếp xúc với ba mặt phẳng tọa độ và đoạn thẳng
AB
luôn nằm trong
( )
S
(mọi điểm thuộc đoạn
thẳng
AB
đều nằm trong
( )
S
). Giá trị nguyên lớn nhất của
R
đạt được là
A.
4.
B.
6.
C.
5.
D.
3.
50. 7 Trong không gian với hệ trục tọa độ
,
Oxyz
Cho ba mặt phẳng
( ) : 5 0,
P x y z
( ) : 1 0
Q x y z
và
( ) : 2 0.
R x y z
Ứng với mỗi cặp
,
A B
lần lượt thuộc hai mặt
phẳng
( ), ( )
P Q
thì mặt cầu đường kính
AB
luôn cắt mặt phẳng
( )
R
theo một đường tròn. Tìm
bán kính nhỏ nhất của đường tròn đó.
A.
1
3
B.
2
3
C.
1
2
D.
1.
50. 8 Trong không gian
Oxyz
cho điểm
( 2;0;0)
A
và ba mặt phẳng
1
( ) : 2 2 5 0,
P x y z
2
( ) : 2 2 13 0,
P x y z
3
( ) : 2 2 5 0.
P x y z
Mặt cầu
( )
S
có tâm
( ; ; )
I a b c
và đi qua
A
đồng thời tiếp xúc với hai mặt phẳng
1 2
( ),( ).
P P
Khi khối cầu
( )
S
cắt mặt phẳng
3
( )
P
theo thiết
diện là hình tròn có diện tích lớn nhất thì
2
a b c
bằng
A.
3.
B.
0.
C.
3.
D.
2.
50. 9 Trong không gian
,
Oxyz
cho hai điểm
(1;2; 1), (3;0;3).
A B
Biết mặt phẳng
( )
P
đi qua điểm
A
và cách
B
một khoảng lớn nhất. Phương trình mặt phẳng
( )
P
là
A.
2 2 5 0.
x y z
B.
2 3 0.
x y z
C.
2 2 4 3 0.
x y z
D.
2 2 0.
x y z
50. 10 Trong không gian
,
Oxyz
cho ba điểm
(1; 0; 2), ( 3;2;4), (0;2; 3).
A B C
Mặt phẳng
( )
P
thay đổi
đi qua
C
và không cắt đoạn thẳng
.
AB
Gọi
1 2
,
d d
lần lượt là khoảng cách từ
,
A B
đến
( ).
P
Phương trình mặt cầu
( )
S
có tâm
,
O
tiếp xúc với
( ),
P
ứng với
1 2
d d
lớn nhất là
A.
2 2 2
6.
x y z
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 138 -
B.
2 2 2
9
2
x y z
C.
2 2 2
12.
x y z
D.
2 2 2
32
3
x y z
50. 11 Trong không gian
,
Oxyz
phương trình mặt
( )
P
chứa đường thẳng
2 2
:
1 1 1
x y z
d
và
( )
P
cách điểm
(2;1;1)
M
một khoảng lớn nhất là
A.
3 5 0.
x y z
B.
2 5 7 10 0.
x y z
C.
2 5 3 0.
x y z
D.
5 3 0.
x y z
50. 12 Trong không gian
,
Oxyz
gọi
( )
P
là mặt phẳng đi qua hai điểm
(1; 7; 8),
A
(2; 5; 9)
B
sao
cho khoảng cách từ điểm
(7; 1; 2)
M
đến
( )
P
đạt giá trị lớn nhất. Biết
( )
P
có một véctơ pháp
tuyến là
( ; ; 4),
n a b
khi đó giá trị của tổng
a b
bằng
A.
1.
B.
3.
C.
6.
D.
2.
50. 13 Trong không gian
,
Oxyz
phương trình đường thẳng đi qua điểm
(1;1; 1),
A
nằm trong mặt
phẳng
( ) : 2 0
P x y z
và cách điểm
(0;2;1)
B
một khoảng lớn nhất là
A.
1 1 1
1 3 1
x y z
B.
1 1 1
2 3 1
x y z
C.
1 1 1
1 3 1
x y z
D.
1 1 1
2 3 2
x y z
50. 14 Trong không gian
,
Oxyz
phương trình đường thẳng
d
đi qua gốc tọa độ
,
O
vuông góc với đường
thẳng
1
1
:
2 1 2
x y z
d
và cách điểm
(2;1;1)
M
khoảng lớn nhất là
A.
1 3 2
x y z
B.
1 3 2
x y z
C.
1 6 4
x y z
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 139 -
D.
1 6 4
x y z
50. 15 Trong không gian
,
Oxyz
phương trình đường thẳng
d
đi qua gốc tọa độ
,
O
nằm trong mặt phẳng
( ) : 2 0
P x y z
và cách điểm
(1;2;1)
M
một khoảng nhỏ nhất là
A.
4 13 5
x y z
B.
4 13 5
x y z
C.
4 12 5
x y z
D.
4 12 5
x y z
50. 16 Trong không gian
,
Oxyz
cho hai điểm
( 3;0;1),
A
(1; 1; 3)
B
và phương trình mặt phẳng
( ) : 2 2 5 0.
P x y z
Phương trình chính tắc của đường thẳng
d
đi qua
,
A
song song với
( )
P
sao cho khoảng cách từ
B
đến
d
nhỏ nhất là
A.
3 1
26 11 2
x y z
B.
3 1
26 11 2
x y z
C.
3 1
26 11 2
x y z
D.
3 1
26 11 2
x y z
50. 17 Trong không gian
,
Oxyz
cho mặt cầu
2 2 2
( ) : 2 4 4 0
S x y z x y z
và
(1;1; 1).
M
Viết
phương trình mặt phẳng
( )
P
đi qua
M
và cắt
( )
S
theo giao tuyến là đường tròn có bán kính
nhỏ nhất ?
A.
2 3 0.
x y z
B.
3 2 0.
x y z
C.
0.
x y
D.
2 0.
x y z
50. 18 Trong không gian
,
Oxyz
cho điểm
( 3;3; 3),
M
mặt phẳng
( ) : 2 2 15 0
P x y z
và mặt
cầu
2 2 2
( ) : ( 2) ( 3) ( 5) 100.
S x y z
Đường thẳng
qua
,
M
nằm trên mặt phẳng
( )
P
cắt
( )
S
tại
,
A B
sao cho độ dài
AB
lớn nhất. Phương trình đường thẳng
là
A.
3 3 3
1 1 3
x y z
B.
3 3 3
1 4 6
x y z
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 140 -
C.
3 3 3
16 11 10
x y z
D.
3 3 3
5 1 8
x y z
50. 19 Trong không gian
,
Oxyz
cho điểm
(0;1;2),
E
mặt phẳng
( ) : 3 0
P x y z
và mặt cầu
2 2 2
( ) : ( 1) ( 3) ( 4) 25.
S x y z
Phương trình đường thẳng
d
đi qua điểm
E
nằm trong
( )
P
và cắt mặt cầu
( )
S
tại hai điểm có khoảng cách lớn nhất là
A.
1 2
3 .
4
x t
y t
z t
B.
2
1 .
2
x t
y t
z t
C.
1
3 .
4 2
x
y t
z t
D.
0
1 .
2
x
y t
z t
50. 20 Trong không gian
,
Oxyz
cho điểm
(3;3;2 6).
A
Đường thẳng
( )
qua
A
tạo với trục
Oz
một góc
30 , ( )
cắt mặt phẳng
Oxy
tại điểm
.
B
Khi
OB
nhỏ nhất, đường thẳng
( )
có phương trình
là
A.
1 1
1 1
6
x y z
B.
5 5
1 1
6
x y z
C.
3 3 2 6
1 1
6
x y z
D.
1 1
1 1
6
x y z
50. 21 Trong không gian
,
Oxyz
cho phương trình mặt cầu
2 2 2
( ) : 4 0
S x y z
và đường thẳng
3 3
:
1 1 1
x y z
d
Hai mặt phẳng
( ), ( )
P P
chứa
d
và tiếp xúc với
( )
S
tại
A
và
.
B
Đường
thẳng
AB
đi qua điểm có tọa độ là
A.
1 1 4
; ;
3 3 3
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 141 -
B.
4
1;1;
3
C.
1 4
1; ;
3 3
D.
1 1 4
; ;
3 3 3
50. 22 Trong không gian
,
Oxyz
cho mặt cầu
2 2 2
( ) : 2 4 6 67 0
S x y z x y z
và đường thẳng
13 1
:
1 1 4
x y z
d
Qua
d
dựng các tiếp diện tới
( ),
S
tiếp xúc với
( )
S
tại
, .
A B
Đường
thẳng
AB
đi qua điểm nào sau đây ?
A.
23 1
; ;6
2 2
B.
(8;1;4).
C.
(6; 9;6).
D.
17 7 9
; ;
2 2 2
50. 23 Trong không gian
,
Oxyz
hãy viết phương trình của mặt phẳng
( )
P
chứa đường thẳng
1 1 2
:
2 1 2
x y z
d
và tạo với đường
1 1
:
1 2 1
x y z
d
góc lớn nhất.
A.
4 7 0.
x y z
B.
4 7 0.
x y z
C.
3 4 0.
x y z
D.
3 4 0.
x y z
50. 24 Trong không gian
,
Oxyz
viết phương trình mặt phẳng
( )
P
đi qua gốc tọa độ
,
O
vuông góc với
mặt phẳng
( ) : 2 1 0,
Q x y z
đồng thời tạo với trục
Oy
góc lớn nhất.
A.
2 5 0.
x y z
B.
2 2 0.
x y z
C.
3 2 4 0.
x y z
D.
3 2 0.
x y z
50. 25 Trong không gian
,
Oxyz
cho mặt phẳng
( ) : 3 0
P x y z
và
1 2
:
1 2 1
x y z
d
Phương trình đường thẳng nằm trong
( ),
P
cắt
d
và tạo với
d
một góc nhỏ nhất là
A.
1 1 1
1 4 5
x y z
B.
1 1 1
3 2 1
x y z
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 142 -
C.
1 1 1
1 4 5
x y z
D.
1 4 5
1 1 1
x y z
50. 26 Trong không gian
,
Oxyz
phương trình đường thẳng
d
đi qua
(1; 1;2),
A
song song với
( ) : 2 3 0
P x y z
và tạo với đường thẳng
1 1
:
1 2 2
x y z
d
một góc nhỏ nhất là
A.
1 1 2
1 5 7
x y z
B.
1 1 2
1 5 7
x y z
C.
1 1 2
1 3 5
x y z
D.
1 1 2
2 3 5
x y z
50. 27 Trong không gian
,
Oxyz
cho đường thẳng
2 1 2
:
4 4 3
x y z
d
và mặt phẳng
( ) : 2 2 1 0
P x y z
. Đường thẳng
đi qua
( 2;1; 2),
E
song song với
( ),
P
đồng thời tạo
với
d
góc bé nhất. Biết
có một véctơ chỉ phương
( ; ;1).
u m n
Khi đó
2 2
m n
bằng
A.
5.
B.
4.
C.
3.
D.
4.
50. 28 Trong không gian
,
Oxyz
viết phương trình mặt phẳng
( )
P
đi qua điểm
(9;1;1),
M
cắt các tia
,
Ox
,
Oy
Oz
tại
, ,
A B C
sao cho thể tích tứ diện
OABC
có giá trị nhỏ nhất.
A.
9 9 27 0.
x y z
B.
9 9 9 0.
x y z
C.
9 9 27 0.
x y z
D.
9 9 0.
x y z
50. 29 Trong không gian
,
Oxyz
cho điểm
(1; 4;9).
M
Gọi
( )
P
là mặt phẳng đi qua
M
và cắt ba tia
, ,
Ox Oy Oz
lần lượt tại các điểm
, ,
A B C
(khác
)
O
sao cho
( )
OA OB OC
đạt giá trị nhỏ
nhất. Mặt phẳng
( )
P
đi qua điểm nào dưới đây ?
A.
(12;0; 0).
B.
(0;0;12).
C.
(6;0;0).
D.
(0;6;0).
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 143 -
50. 30 Trong không gian
,
Oxyz
cho ba điểm
( ;0; 0),
A a
(0; ;0),
B b
(0;0; )
C c
với
, ,
a b c
là những số
dương thay đổi thỏa mãn
2 2 2
4 16 49.
a b c
Khi khoảng cách từ gốc tọa độ
O
đến mặt phẳng
( )
ABC
đạt giá trị lớn nhất thì
2 2 2
a b c
bằng
A.
49
4
B.
11.
C.
51
5
D.
49
5
50. 31 Trong không gian
,
Oxyz
cho mặt phẳng
( )
P
đi qua
(1;2;1), ( 1; 0; 1),
M N
đồng thời cắt
,
Ox Oy
theo thứ tự tại
,
A B
(khác
)
O
sao cho
3 .
AM BN
Khi đó
( )
P
có một véctơ pháp
tuyến
(1; ; )
n m n
thì tổng
m n
bằng
A.
2.
B.
1.
C.
1.
D.
0.
50. 32 Trong không gian
,
Oxyz
cho
(1; 2;3),
A
(2;1;1)
B
và mặt phẳng
( ) : 2 2 0.
P x y z
Tìm
hoành độ của
C
thuộc
( )
P
sao cho tam giác
ABC
cân tại
C
và có chu vi nhỏ nhất ?
A.
4
3
B.
2
3
C.
1.
D.
1
3
50. 33 Trong không gian
,
Oxyz
cho mặt phẳng
( ) : 2 0
P x y z
và hai điểm
(3;4;1),
A
(7; 4; 3).
B
Điểm
( ; ; ), ( 2)
M a b c a
thuộc
( )
P
sao cho tam giác
ABM
vuông tại
M
và có diện
tích nhỏ nhất. Khi đó giá trị biểu thức
a b c
bằng
A.
6.
B.
8.
C.
4.
D.
0.
50. 34 Trong không gian
,
Oxyz
cho hai đường thẳng
1
1 2
: ,
1 2 1
x y z
d
2
2 2
: 1
1
x t
d y t
z t
và mặt
phẳng
( ) : 2 5 0.
P x y z
Lập phương trình đường thẳng song song với mặt phẳng
( )
P
và
cắt
1 2
,
d d
lần lượt tại
,
A B
sao cho độ dài đoạn
AB
nhỏ nhất ?
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 144 -
A.
1 2 2
1 1 1
x y z
B.
1 2 2
1 1 2
x y z
C.
1 2
1 1 3
x y z
D.
2 1 1
1 1 3
x y z
50. 35 Trong không gian
,
Oxyz
cho đường thẳng
1
1 1
: ;
2 1 1
x y z
d
2
1 2
:
1 2 1
x y z
d
Viết
phương trình mặt phẳng
( )
P
song song với
( ) : 2 3 0
Q x y z
và cắt
1 2
,
d d
theo đoạn
thẳng có độ dài nhỏ nhất ?
A.
2 10 0.
x y z
B.
2 0.
x y z
C.
2 1 0.
x y z
D.
2 7 0.
x y z
50. 36 Trong không gian
,
Oxyz
cho hai điểm
5
1; 2;
2
A
và
5
4;2; .
2
B
Tìm hoành độ điểm
M
trên mặt
phẳng
( )
Oxy
sao cho
45
ABM
và tam giác
MAB
có diện tích nhỏ nhất ?
A.
5
2
B.
1.
C.
3
2
D.
2.
50. 37 Trong không gian
,
Oxyz
cho ba điểm
(1; 2;1),
A
(5;0; 1),
B
(3;1;2)
C
và mặt phẳng
( ) : 3 3 0.
Q x y z
Gọi
( ; ; ) ( )
M a b c Q
thỏa mãn
2 2 2
2
MA MB MC
nhỏ nhất. Tổng
5
a b c
bằng
A.
11.
B.
9.
C.
15.
D.
14.
50. 38 Trong không gian
,
Oxyz
cho các điểm
(5;8; 11),
A
(3;5; 4),
B
(2;1; 6)
C
và mặt cầu
2 2 2
( ) : ( 4) ( 2) ( 1) 9.
S x y z
Gọi
( ; ; )
M M M
M x y z
là điểm trên
( )
S
sao cho biểu thức
MA MB MC
  
đạt giá trị nhỏ nhất. Giá trị của tổng
M M
x y
bằng
A.
4.
B.
0.
Phaùt trieån ñeà tham khaûo thpt naêm 2021 Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !” Trang - 145 -
C.
2.
D.
2.
50. 39 Trong không gian
,
Oxyz
cho hai điểm
(13;3; 2), (1;0;1)
A B
và phương trình hai mặt cầu
2 2 2
1
( ) : 25,
S x y z
2 2 2
2
( ) : ( 5) 10.
S x y z
Gọi
M
nằm trên đường tròn giao tuyến
của
1 2
( ), ( )
S S
thỏa mãn
2 2 2
2 3
P MA MB MC
đạt giá trị nhỏ nhất. Giá trị của biểu thức
bằng
A.
186 36 2.
B.
36.
C.
18 6 2.
D.
16.
50. 40 Trong không gian
,
Oxyz
cho mặt phẳng
( ) : 2 1 0
P x y z
và hai điểm
(0; 2; 3),
A
(2;0;1).
B
Điểm
( ; ; ) ( )
M a b c P
sao cho
MA MB
nhỏ nhất. Giá trị
2 2 2
a b c
bằng
A.
41
4
B.
9
4
C.
7
4
D.
3.
| 1/146
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

– 2021   
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
========  =========
Câu 1. Có bao nhiêu cách chọn 3 học sinh từ một nhóm có 5 học sinh ? 3 A. 5 !. B. A . C. 3 C . D. 3 5 . 5 5
Lôøi giaûi tham khaûo
Số cách chọn 3 học sinh từ một nhóm gồm 5 học sinh là tổ hợp chập 3 của 5 phần tử có 3 C cách. 5 Chọn đáp án C.
Hoaùn vò – Toå hôïp – Chænh hôïp
Sắp xếp vị trí n phần tử  Sử dụng hoán vị P n !. 1
(casio : n SHIFT x  ). n n k !
Chọn k trong n tùy ý  Sử dụng tổ hợp C   casio nk n ( : SHIFT ).
(n k)!.k ! n k !
Chọn k trong n và sắp xếp  Sử dụng chỉnh hợp C .k ! k
A . (n SHIFT  k). n (n k)! n
Baøi taäp töông töï vaø môû roäng
1.1. Cần chọn 3 người đi công tác từ một tổ có 30 người, khi đó số cách chọn là 3 A. A . B. 30 3 . 30 3 C. 10. D. C . 30
1.2. Cho 8 điểm trong đó không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác mà ba đỉnh của
nó được chọn từ 8 điểm trên ? A. 336. B. 56. C. 168. D. 84.
1.3. Có n (n  0) phần tử lấy ra k (0  k n) phần tử đem đi sắp xếp theo một thứ tự nào đó, mà khi
thay đổi thứ tự ta được cách sắp xếp mới. Khi đó số cách sắp xếp là A. k C . B. n A . n k C. k A . D. P . n n
1.4. Một tổ có 10 học sinh. Hỏi có bao nhiêu cách chọn ra 2 học sinh từ tổ đó để giữ hai chức vụ tổ trưởng và tổ phó. 2 2 A. A . B. C . 10 10 8 C. A . D. 2 10 . 10
1.5. Cho A là tập hợp gồm 20 điểm phân biệt. Số đoạn thẳng có hai đầu mút phân biệt thuộc tập A là A. 170. B. 160. C. 190. D. 360. 
1.6. Số véctơ khác 0 có điểm đầu, điểm cuối là hai trong 6 đỉnh của lục giác ABCDEF là 2 A. P . B. C . 6 6 2 C. A . D. 36. 6
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 1 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
1.7. Có bao nhiêu cách sắp xếp 5 học sinh thành một hàng dọc ? A. 5 5 . B. 5!. C. 4 ! . D. 5.
1.8. Từ tập X  {2; 3; 4; 5; 6} có thể lập được bao nhiêu số tự nhiên có ba chữ số mà các chữ số đôi một khác nhau ? A. 60. B. 125. C. 10. D. 6.
1.9. Trong một buổi khiêu vũ có 20 nam và 18 nữ. Hỏi có bao nhiêu cách chọn ra một đôi nam nữ để khiêu vũ ? 2 2 A. C . B. A . 38 38 2 1 1 1 C. C C . D. C C . 20 18 20 18
1.10. Một tổ có 6 học sinh nam và 9 học sinh nữ. Hỏi có bao nhiêu cách chọn 5 học sinh đi lao động
trong đó có 2 học sinh nam ? 2 3 2 3
A. C .C .
B. C C . 9 6 6 9 2 3 2 3
C. A .A .
D. C .C . 6 9 6 9
Câu 2. Cho cấp số cộng (u ) với u  1 và u  3. Giá trị của u bằng n 1 2 3 A. 6. B. 9. C. 4. D. 5.
Lôøi giaûi tham khaûo
Ta có: d u u  3  1  2. Suy ra u u  2d  1  2.2  5. Chọn đáp án D. 2 1 3 1 Caáp soá coäng Caáp soá nhaân ukuu d :
q công bội. k 1  k công sai. 1 : uk a c a, ,
b c là cấp số cộng  b   a, ,
b c là cấp số nhân 2
b ac. 2
u u  (n  1)d. n 1 u u .q   . n 1 n 1 n n 1 nq S (u u ) 2u (n 1)d      .
S u u    u u   n 1 n  1 2 2  n 1 2 n 1 1 q
Baøi taäp töông töï vaø môû roäng
2.1. Cho cấp số cộng (u ) có u  3, u  27. Công sai của cấp số cộng đã cho bằng n 1 6 A. 7. B. 5. C. 8. D. 6.
2.2. Cho cấp số cộng (u ) có u  2 và công sai d  3. Tìm số hạng u . n 1 10 9 A. u  2  .3 . B. u  25. 10 10 C. u  28. D. u  29. 10 10
2.3. Cho cấp số cộng (u ) có u  11 và công sai d  4. Hãy tính u . n 1 99 A. 401. B. 403. C. 402. D. 404.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 2 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
2.4. Biết bốn số 5, x, 15, y theo thứ tự lập thành cấp số cộng. Giá trị của biểu thức 3x  2y bằng A. 50. B. 70. C. 30. D. 80.
2.5. Cho cấp số cộng (u ) có u  1
 5 và u  60. Tổng S của 20 số hạng đầu tiên của cấp số cộng n 5 20 20 bằng A. 600. B. 60. C. 250. D. 500.
2.6. Cho dãy số (u ) là một cấp số cộng có u  3 và công sai d  4. Biết tổng n số hạng đầu của dãy n 1
số (u ) là S  253. Giá trị của n bằng n n A. 9. B. 11. C. 12. D. 10.
2.7. Cho cấp số nhân (u ), biết u  1 và u  64. Công bội của cấp số nhân bằng n 1 4 A. 21. B. 4. C. 4. D. 2 2.
2.8. Cho cấp số nhân (u ) có u  2 và công bội q  3. Số hạng u bằng n 1 2 A. 6  . B. 6. C. 1. D. 18.
2.9. Xác định số hạng đầu và công bội của cấp số nhân (u ) có u u  54 và u u  108. n 4 2 5 3
A. u  3 và q  2.
B. u  9 và q  2. 1 1
C. u  9 và q  –2.
D. u  3 và q  –2. 1 1
2.10. Một cấp số nhân có số hạng đầu u  3, công bội q  2. Biết S  765. Giá trị của n bằng 1 n A. 7. B. 6. C. 8. D. 9.
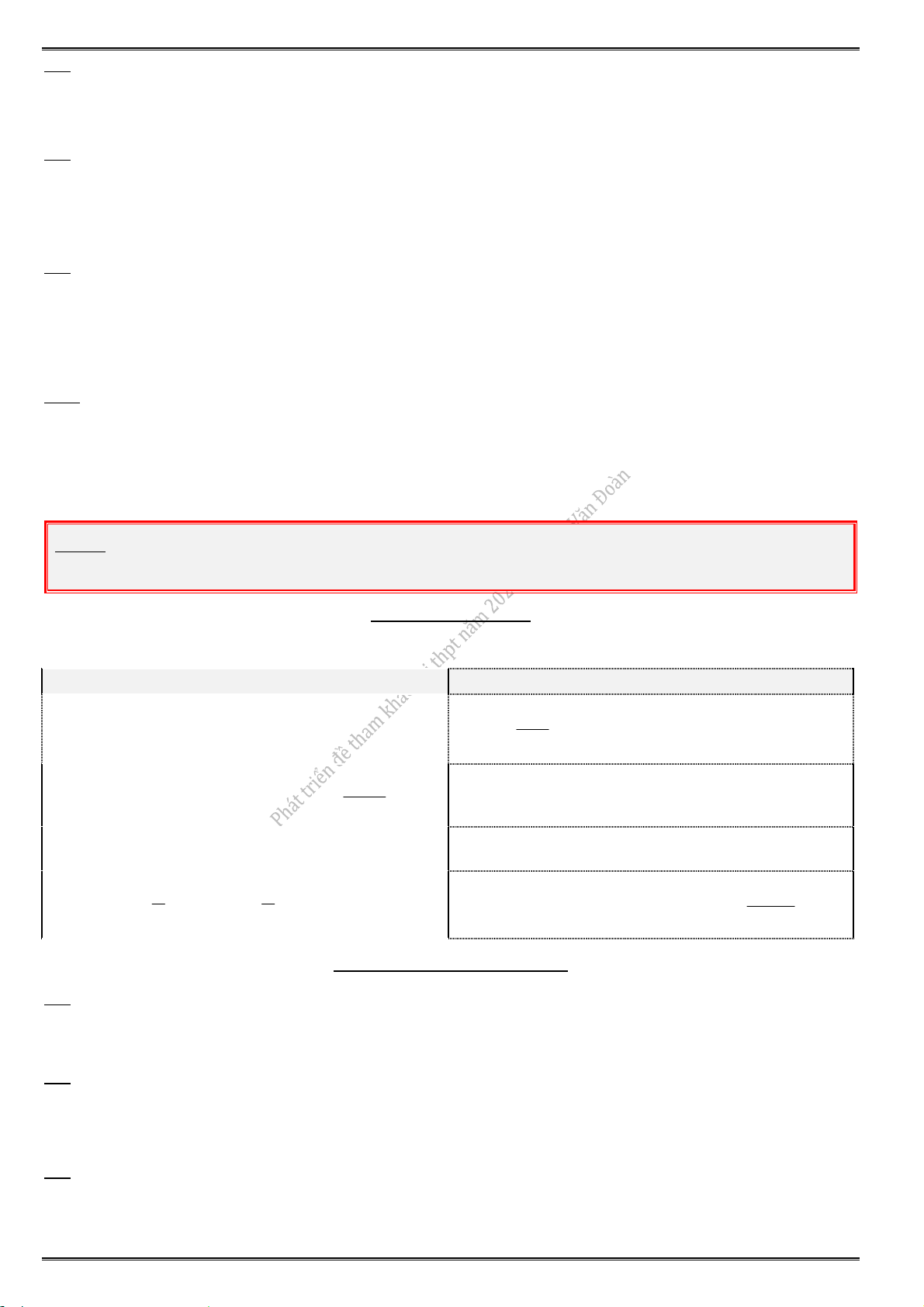
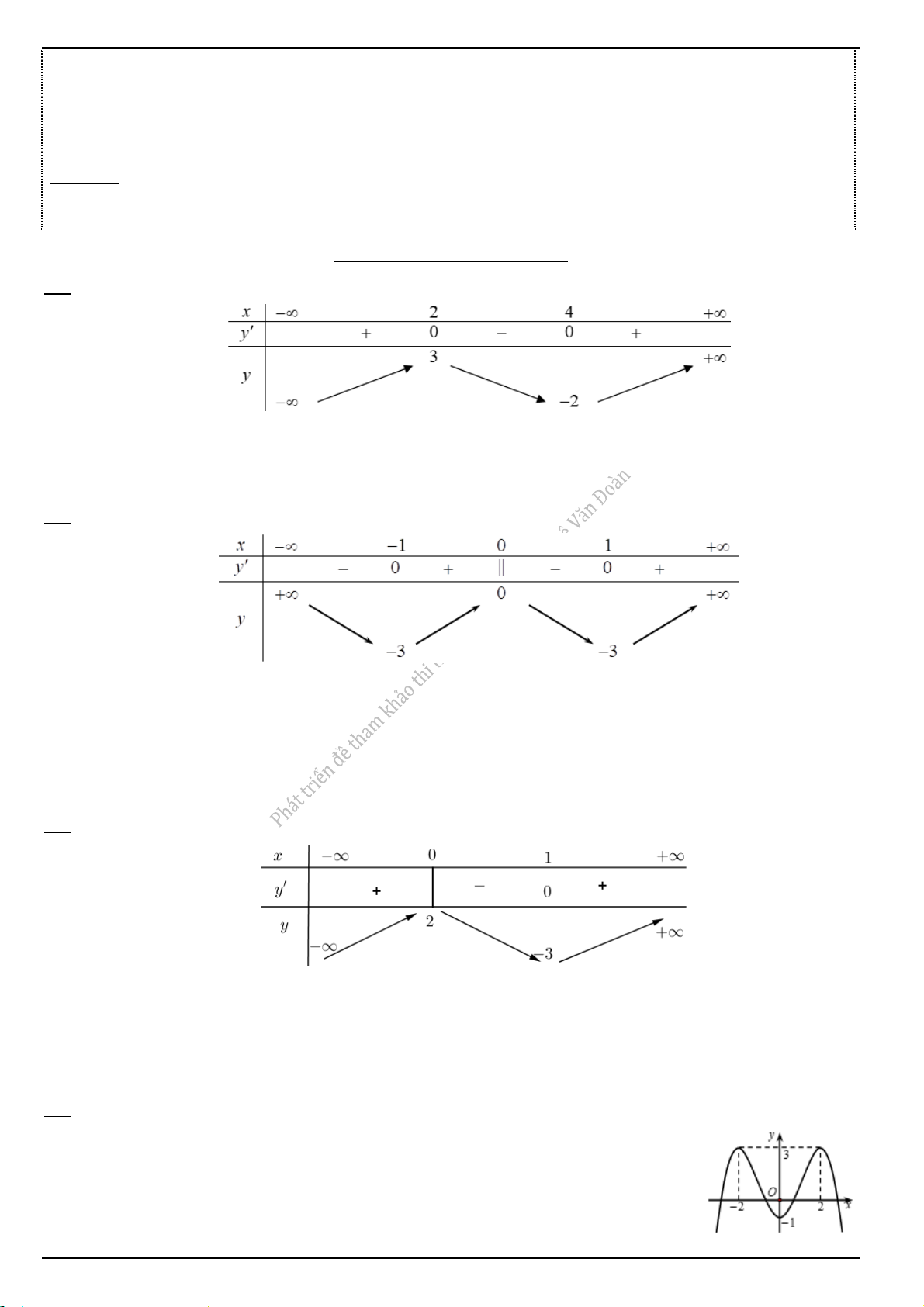
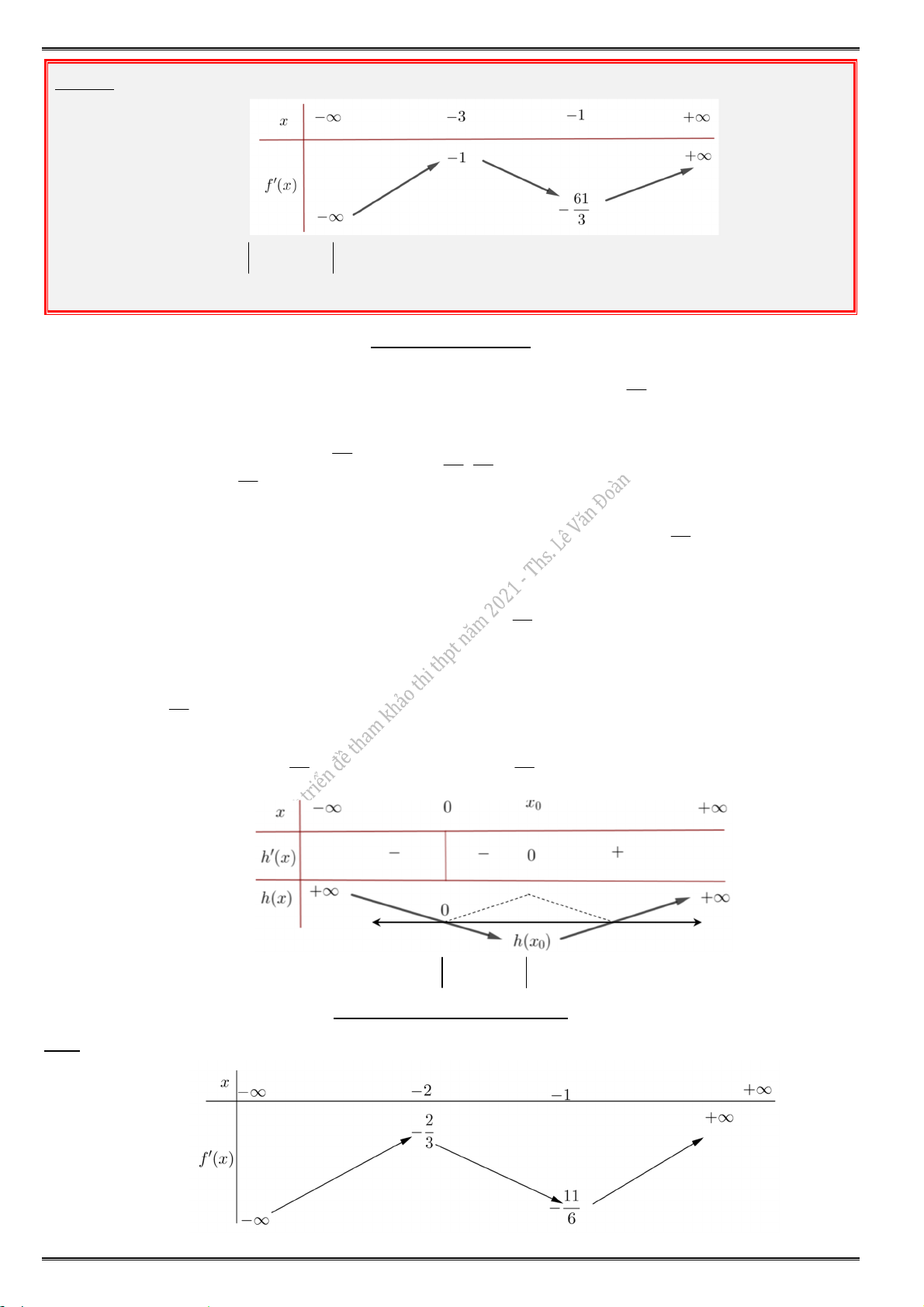
Câu 3. Cho hàm số f (x ) có bảng biến thiên sau:
Hàm số đã cho đồng biến trên khoảng nào, trong các khoảng sau đây ? A. (2;2). B. (0;2). C. (2; 0). D. (2;).
Lôøi giaûi tham khaûo
Từ bảng biến thiên, suy ra y  0 khi x  ( ;
 2), x  (0;2). Chọn đáp án B.
Ñôn ñieäu (ñoàng bieán vaø nghòch bieán)
Định lí (thừa nhận): Giả sử hàm số y f (x) có đạo hàm trên khoảng K . Nếu f (  x)  0, x
  K thì hàm số đồng biến trên khoảng K . Nếu f (  x)  0, x
  K thì hàm số nghịch biến trên khoảng K . Nếu f (  x)  0, x
  K thì hàm số không đổi trên khoảng K .
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 3 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Baøi taäp töông töï vaø môû roäng
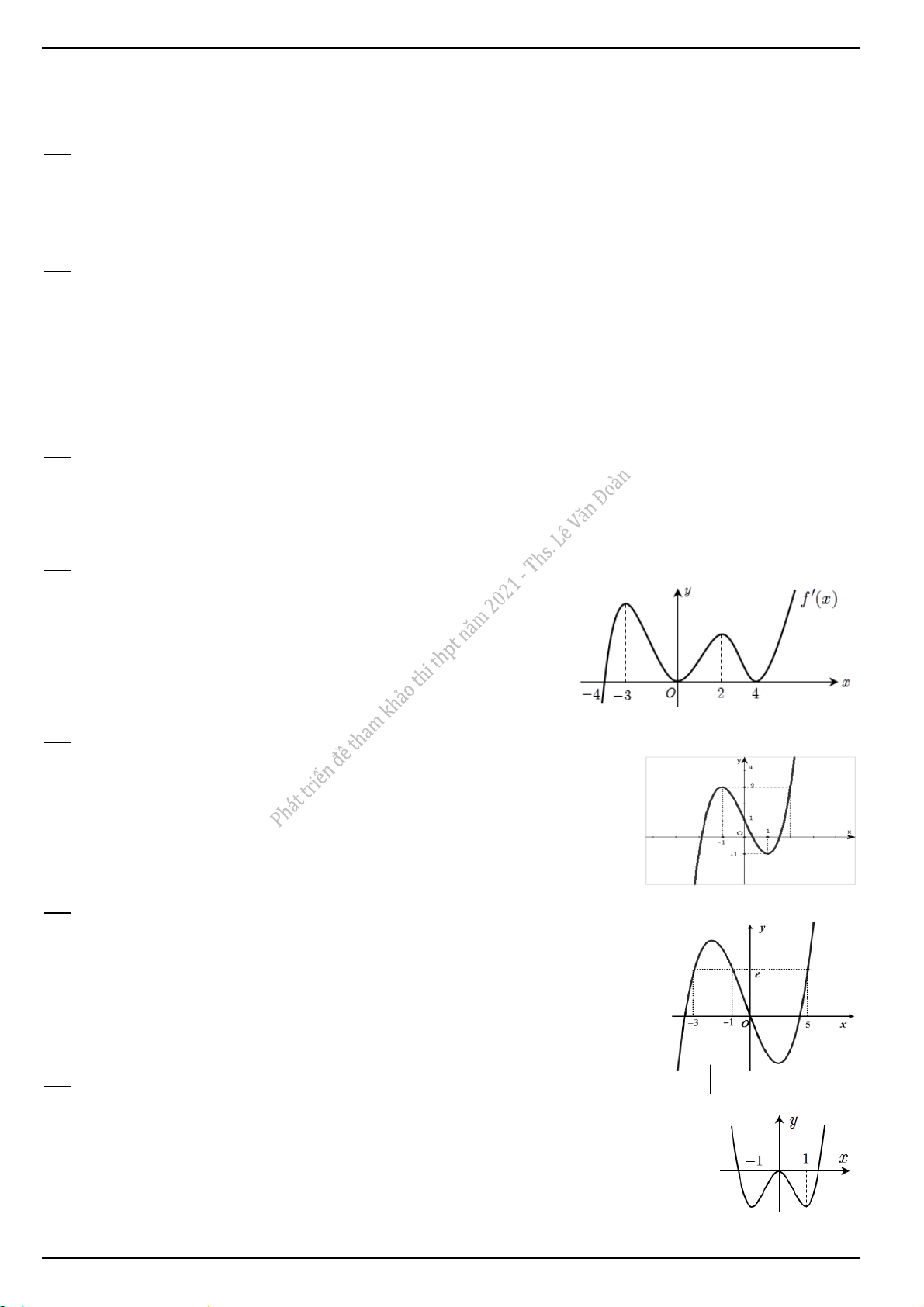
3.1. Cho hàm sốy f (x) có bảng biến thiên bên dưới. Hàm số đã cho nghịch biến trên khoảng nào dưới đây ? A. (0;1). B. ( ;  0). C. (1; ). D. (1; 0).
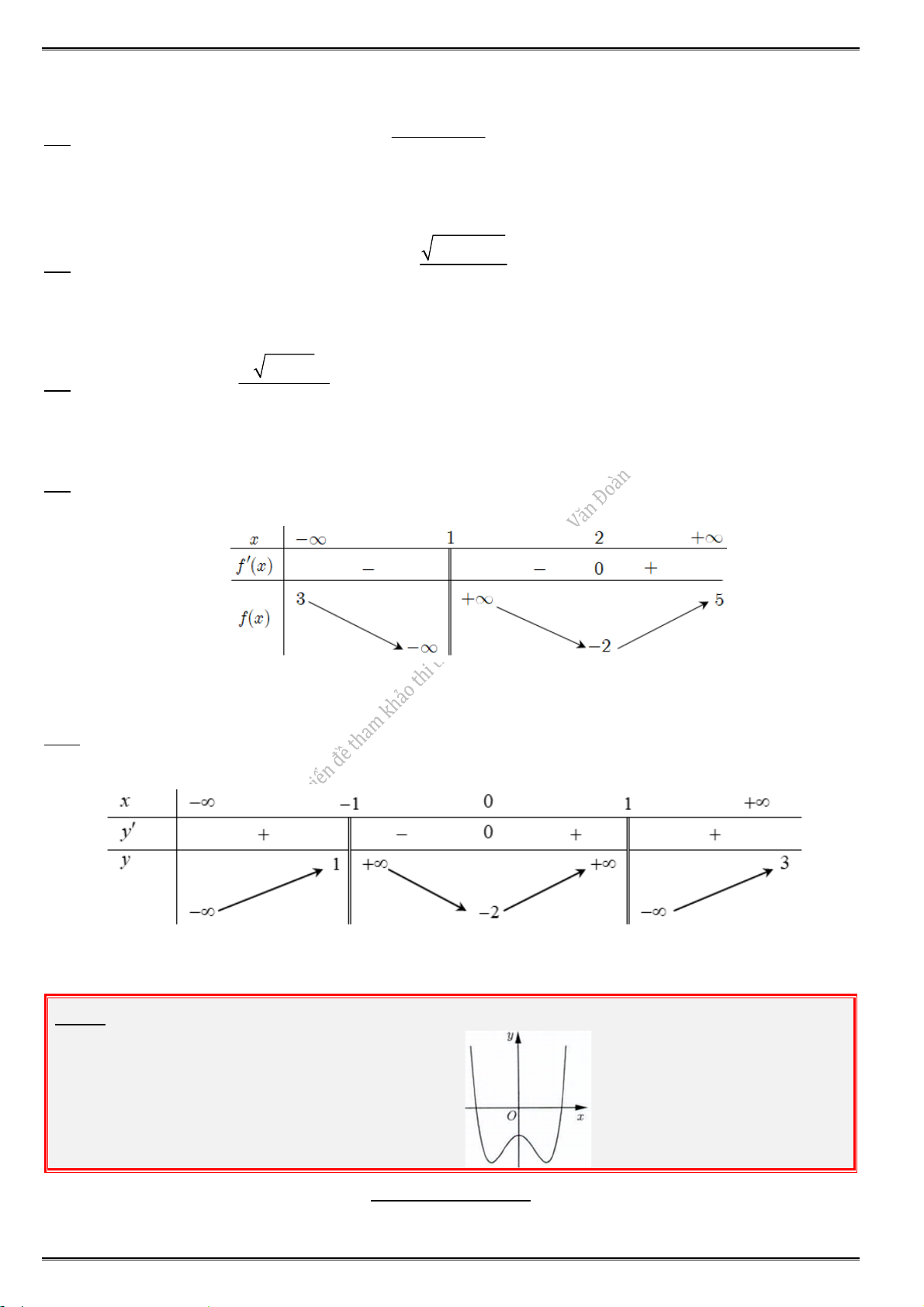
3.2. Cho hàm số y f (x) có bảng biến thiên dưới. Hàm số đã cho đồng biến trên khoảng nào ? A. (2; ). B. (2; 3). C. (3;  )  . D. ( ;  2).
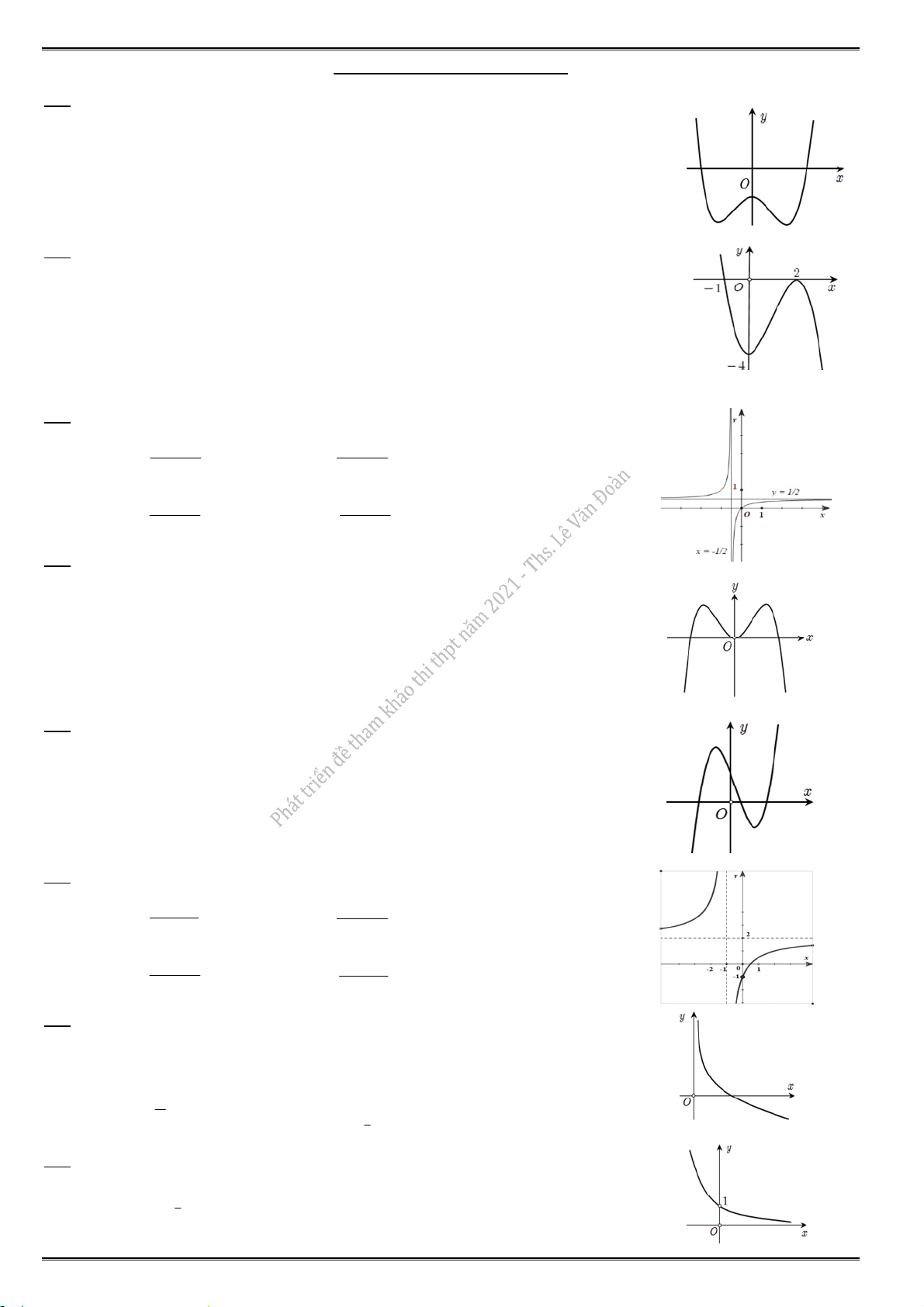
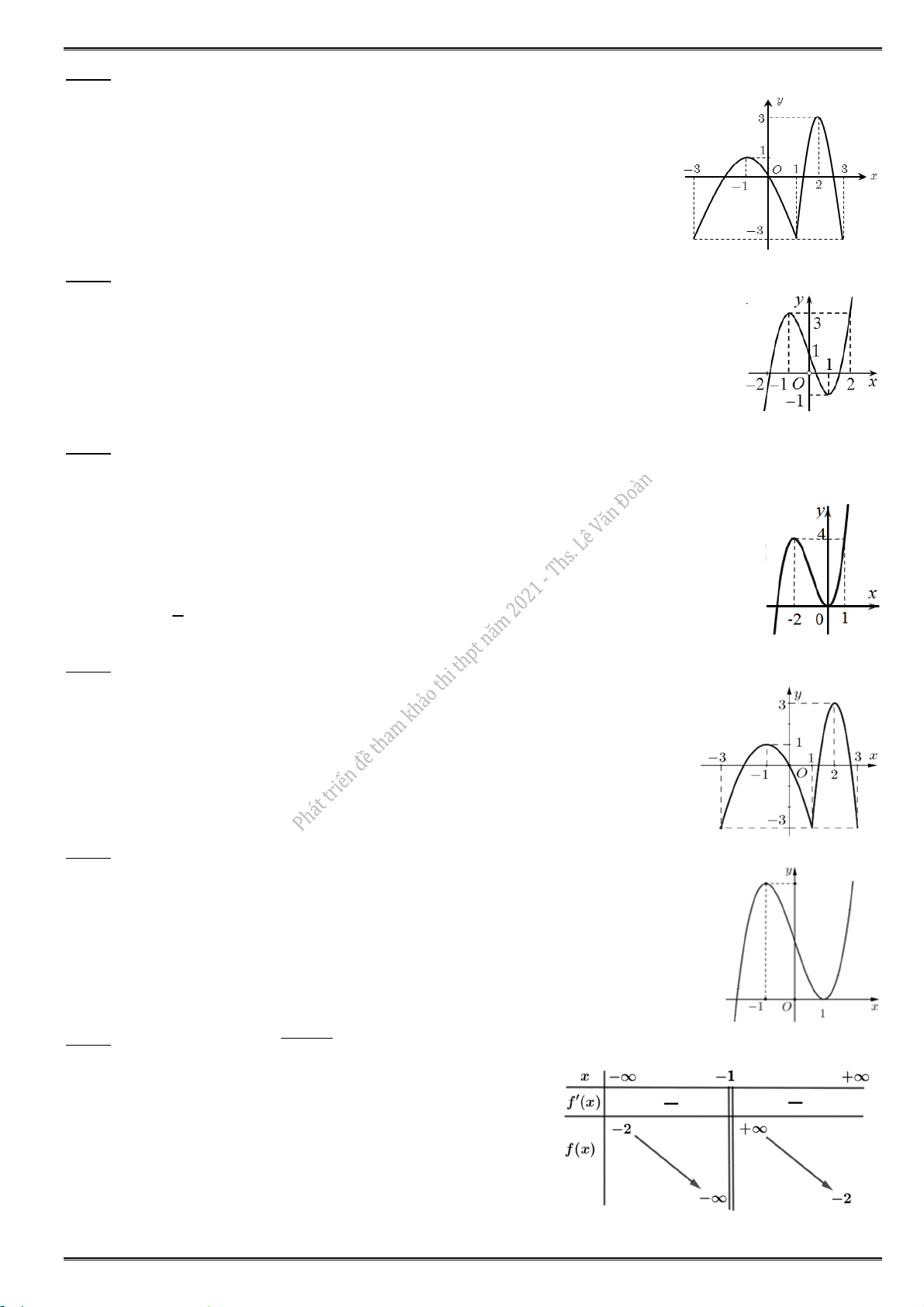
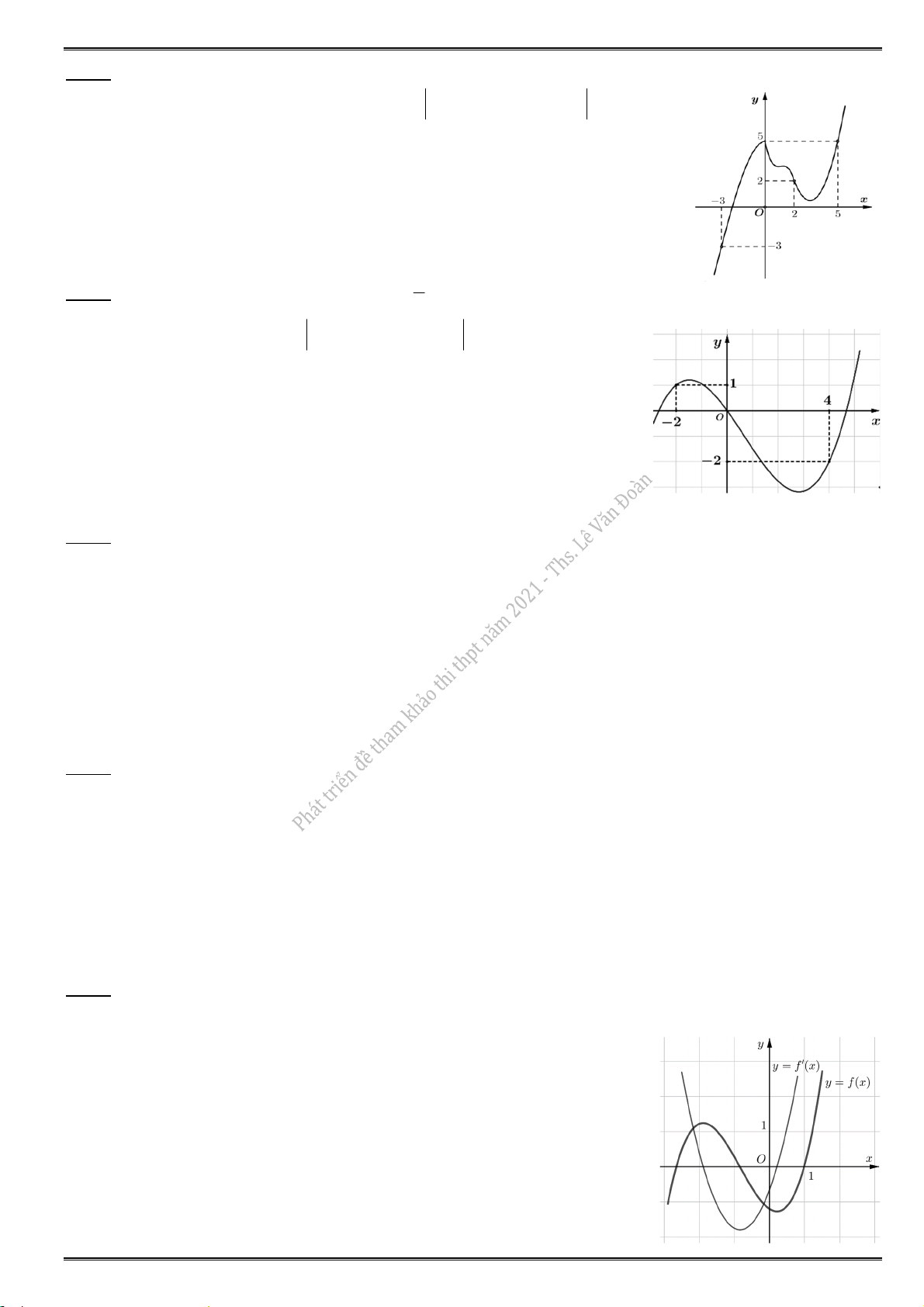
3.3. Cho hàm số y f (x) có đồ thị như hình vẽ dưới. Hàm số đã cho đồng biến trên khoảng y A. (1; 3). 3 B. ( ;  2). O C. ( ;  3). 2  2 x 1  D. (2;2).
3.4. Cho hàm số y f (x) có đồ thị như hình vẽ dưới. Hàm số đã cho đồng biến trên khoảng nào ? A. ( ;  3  ). B. ( 3  ; 1  ). C. ( 2  ;2). D. ( 2  ; 1  ).
3.5. Cho hàm số y f (x) có đạo hàm 2 f (
x)  x  1, x   .
 Mệnh đề nào dưới đây đúng ?
A. Hàm số nghịch biến trên khoảng ( ;  0).
B. Hàm số nghịch biến trên khoảng (1; ).
C. Hàm số nghịch biến trên khoảng (1;1).
D. Hàm số đồng biến trên khoảng ( ;   )  .
3.6. Cho hàm số y f (x) có bảng xét dấu đạo hàm như sau
Mệnh đề nào dưới đây đúng ?
A. Hàm số đồng biến trên khoảng (2; 0).
B. Hàm số đồng biến trên khoảng ( ;  0).
C. Hàm số nghịch biến trên khoảng (0;2).
D. Hàm số nghịch biến trên khoảng ( ;  2). 3.7. Cho hàm số 3 2
y x  3x . Mệnh đề nào dưới đây đúng ?
A. Hàm số nghịch biến trên khoảng (2;).
B. Hàm số đồng biến trên khoảng (0;2).
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 4 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
C. Hàm số nghịch biến trên khoảng (0;2).
D. Hàm số nghịch biến trên khoảng ( ;  0). 3.8. Cho hàm số 4 2
y x  2x . Mệnh đề nào dưới đây đúng ?
A. Hàm số nghịch biến trên khoảng (1;1).
B. Hàm số đồng biến trên khoảng ( ;  2).
C. Hàm số nghịch biến trên khoảng ( ;  2).
D. Hàm số đồng biến trên khoảng (1;1). x  2
3.9. Cho hàm số y
. Mệnh đề nào dưới đây đúng ? x  1
A. Hàm số nghịch biến trên khoảng ( ;  1).
B. Hàm số đồng biến trên khoảng ( ;  1).
C. Hàm số nghịch biến trên khoảng ( ;   )  .
D. Hàm số nghịch biến trên khoảng (1; ). 3.10. Cho hàm số 2
y  2x  1. Mệnh đề nào dưới đây đúng ?
A. Hàm số nghịch biến trên khoảng (1;1).
B. Hàm số đồng biến trên khoảng (0; ).
C. Hàm số đồng biến trên khoảng ( ;  0).
D. Hàm số nghịch biến trên khoảng (0; ).
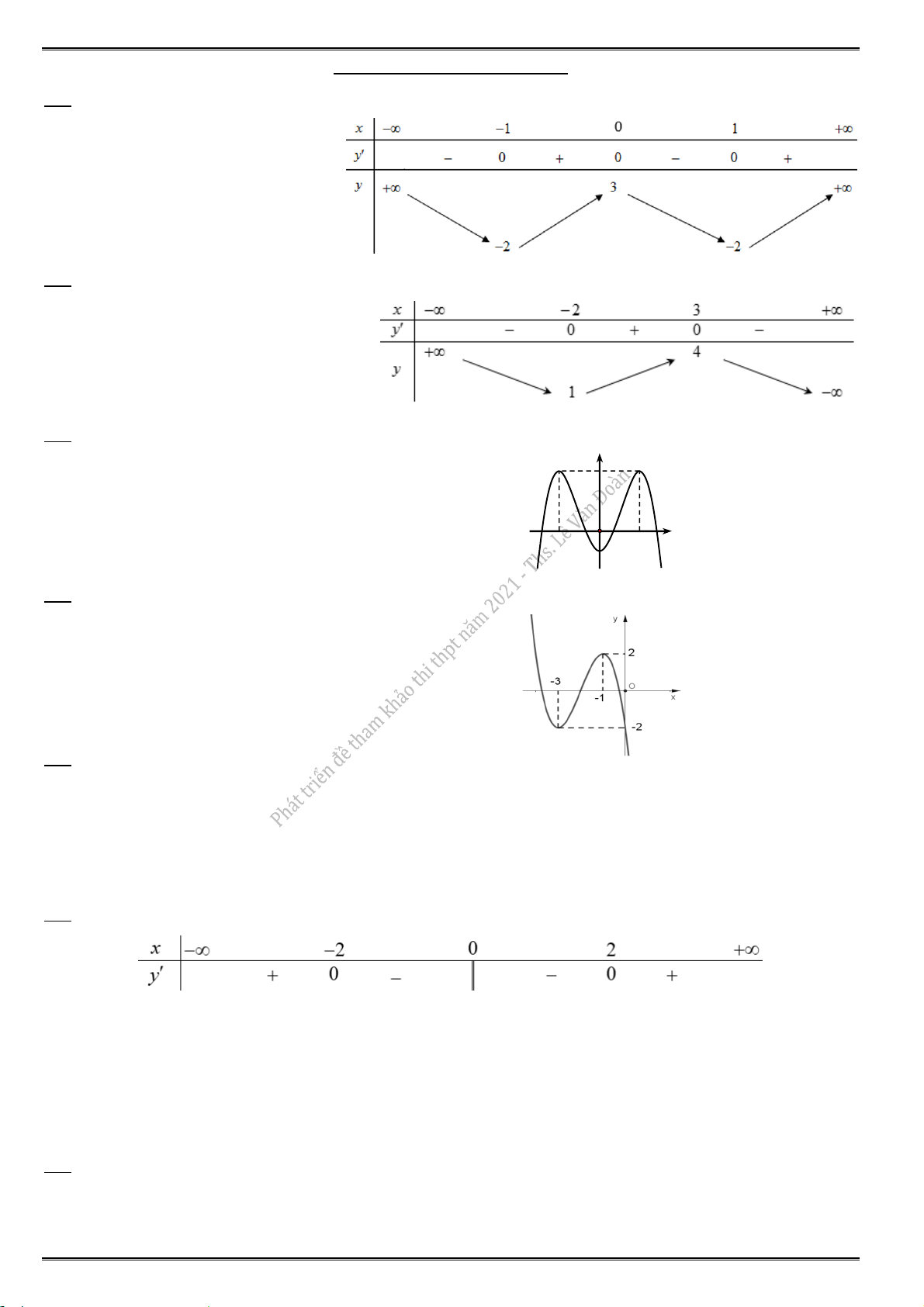
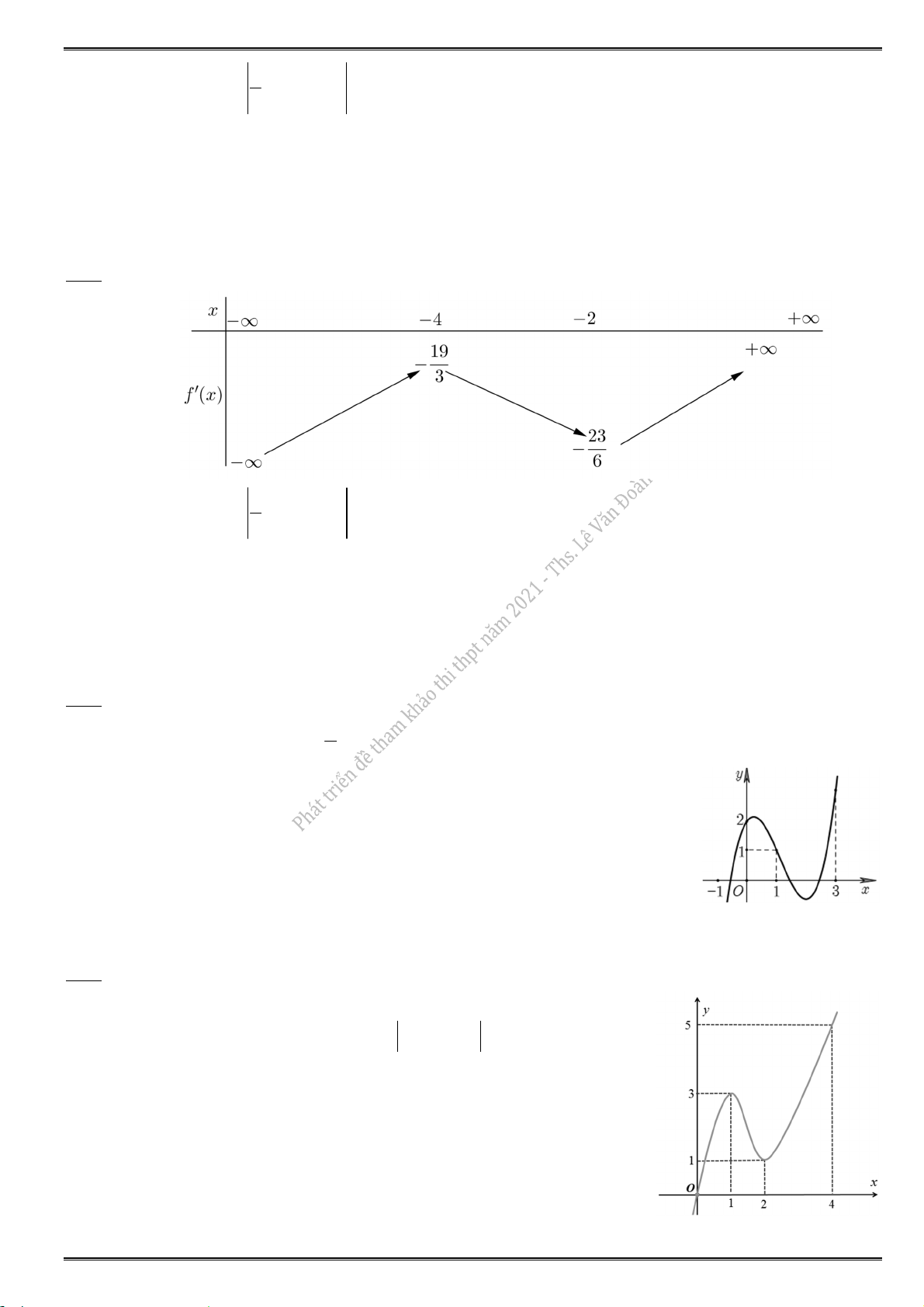
Câu 4. Cho hàm số f (x ) có bảng biến thiên sau:
Điểm cực trị đại của hàm số đã cho là
A. x  3.
B. x  1.
C. x  2. D. x  2.
Lôøi giaûi tham khaûo
Từ bảng biến thiên, thấy y đổi dấu từ  sang  khi qua x  2 nên x  2 là điểm cực đại. Chọn đáp án D. Cöïc trò
Điều kiện cần (định lí 1): Nếu hàm số y f(x) có đạo hàm trên khoảng ( ; a )
b và đạt cực đại (hoặc
cực tiểu) tại x thì f (  x )  0.  
Điều kiện đủ (định lí 2): Nếu f (
x) đổi dấu từ âm sang dương khi x đi qua điểm x (theo chiều tăng) thì hàm số y f(x) 
đạt cực tiểu tại điểm x .  Nếu f (
x) đổi dấu từ dương sang âm khi x đi qua điểm x (theo chiều tăng) thì hàm số y f(x) 
đạt cực đại tại điểm x . 
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 5 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Định lí 3: Giả sử y f(x) có đạo hàm cấp 2 trong (x  ;
h x h), với h  0. Khi đó:   Nếu y (
x )  0, y (x )  0 thì x là điểm cực tiểu.    Nếu y (
x )  0, y (x )  0 thì x là điểm cực đại. o o
Cần nhớ: Điểm cực đại (cực tiểu) của hàm số là x , giá trị cực đại (cực tiểu) của hàm số là f (x ) (hay  
y hoặc y ). Điểm cực đại của đồ thị hàm số là M(x ; f (x )). CĐ CT  
Baøi taäp töông töï vaø môû roäng
4.1. Cho hàm số y f (x) có bảng biến thiên sau:
Khẳng định nào sau đây là đúng ?
A. Hàm số đạt cực đại tại x  2.
B. Hàm số đạt cực đại tại x  3.
C. Hàm số đạt cực đại tại x  2.
D. Hàm số đạt cực đại tại x  4.
4.2. Cho hàm số y f (x) liên tục trên  và có bảng biến thiên:
Khẳng định nào sau đây là đúng ?
A. Hàm số có đúng hai điểm cực trị.
B. Hàm số có giá trị cực tiểu bằng 1 và 1.
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng 3  .
D. Hàm số đạt cực đại tại x  0.
4.3. Cho hàm số y f (x) xác định, liên tục trên  và có bảng biến thiên:
Khẳng định nào sau đây là khẳng định đúng ?
A. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng 3  .
B. Hàm số có đúng một cực trị.
C. Hàm số đạt cực đại tại x  0 và đạt cực tiểu tại x  1.
D. Hàm số có giá trị cực tiểu bằng 2.
4.4. Cho hàm số f (x ) có đồ thị như hình vẽ. Giá trị cực đại của hàm số là
A. x  2. B. y  1. CĐ C. y  3. CĐ D. M (2; 3).
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 6 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
4.5. Cho hàm số y f (x) có đồ thị như hình bên. Mệnh đề nào dưới đây đúng ?
A. Hàm số có giá trị cực tiểu bằng 2.
B. Hàm số đạt cực đại tại x  0 và đạt cực tiểu tại x  2.
C. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng 2.
D. Hàm số có ba điểm cực trị.
4.6. Gọi x là điểm cực đại, x là điểm cực tiểu của hàm số 3 y x
  3x  2. Giá trị x  2x bằng 1 2 1 2 A. 2. B. 1. C. 1  . D. 0.
4.7. Diểm cực đại của đồ thị hàm số 4 2
y x  2x  2 có tọa độ là A. (1;1). B. (2; 0). C. (1;1). D. (0;2). 4.8. Hàm số 3 2
y x  3x mx  2 đạt cực tiểu tại x  2 khi A. m  0. B. m  0. C. m  0. D. m  0. 4.9. Cho hàm số 4 2
y x ax b. Biết rằng đồ thị hàm số nhận điểm (
A 1; 4) là điểm cực tiểu. Tổng
2a b bằng A. 1  . B. 0. C. 1. D. 2. 4.10. Cho hàm số 3 2
f (x)  x  3x mx  1. Tìm giá trị của tham số m để hàm số có hai điểm cực trị
x , x thỏa mãn 2 2 x x  3. 1 2 1 2 3 1 A. m   B. m   2 2 C. m  2  . D. m  1.
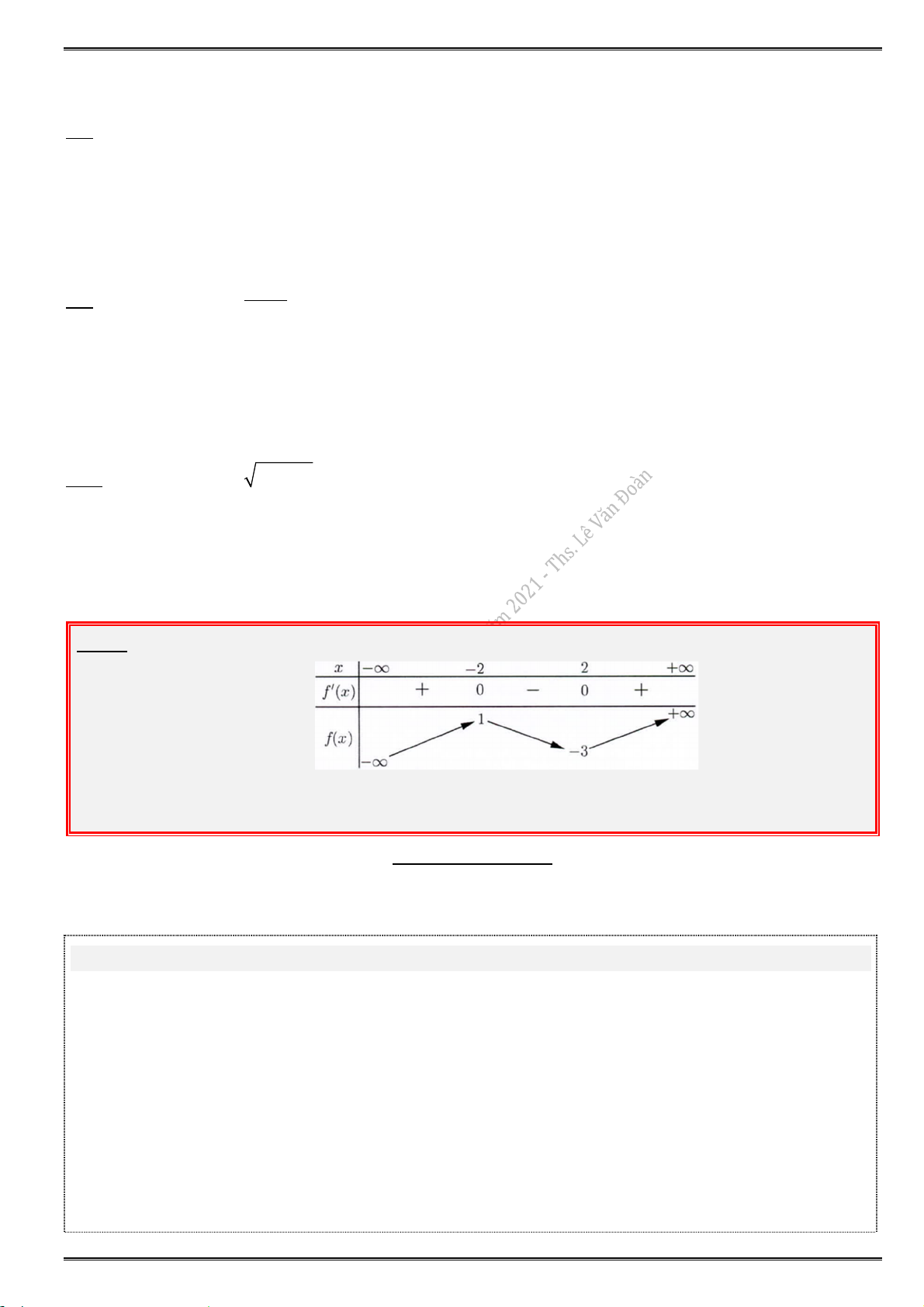
Câu 5. Cho hàm số f (x) có bảng xét dấu của f (  x) như sau:
Hàm số f (x) có bao nhiêu điểm cực trị ? A. 4. B. 1. C. 2. D. 3
Lôøi giaûi tham khaûo
Từ bảng xét dấu, ta có f (
x) đổi dấu 4 lần  có 4 điểm cực trị. Chọn đáp án A.
Baøi taäp töông töï vaø môû roäng
5.1. Cho hàm số f (x) có bảng xét dấu của f (  x) như sau:
Số điểm cực trị của hàm số đã cho là A. 3. B. 0. C. 2. D. 1.
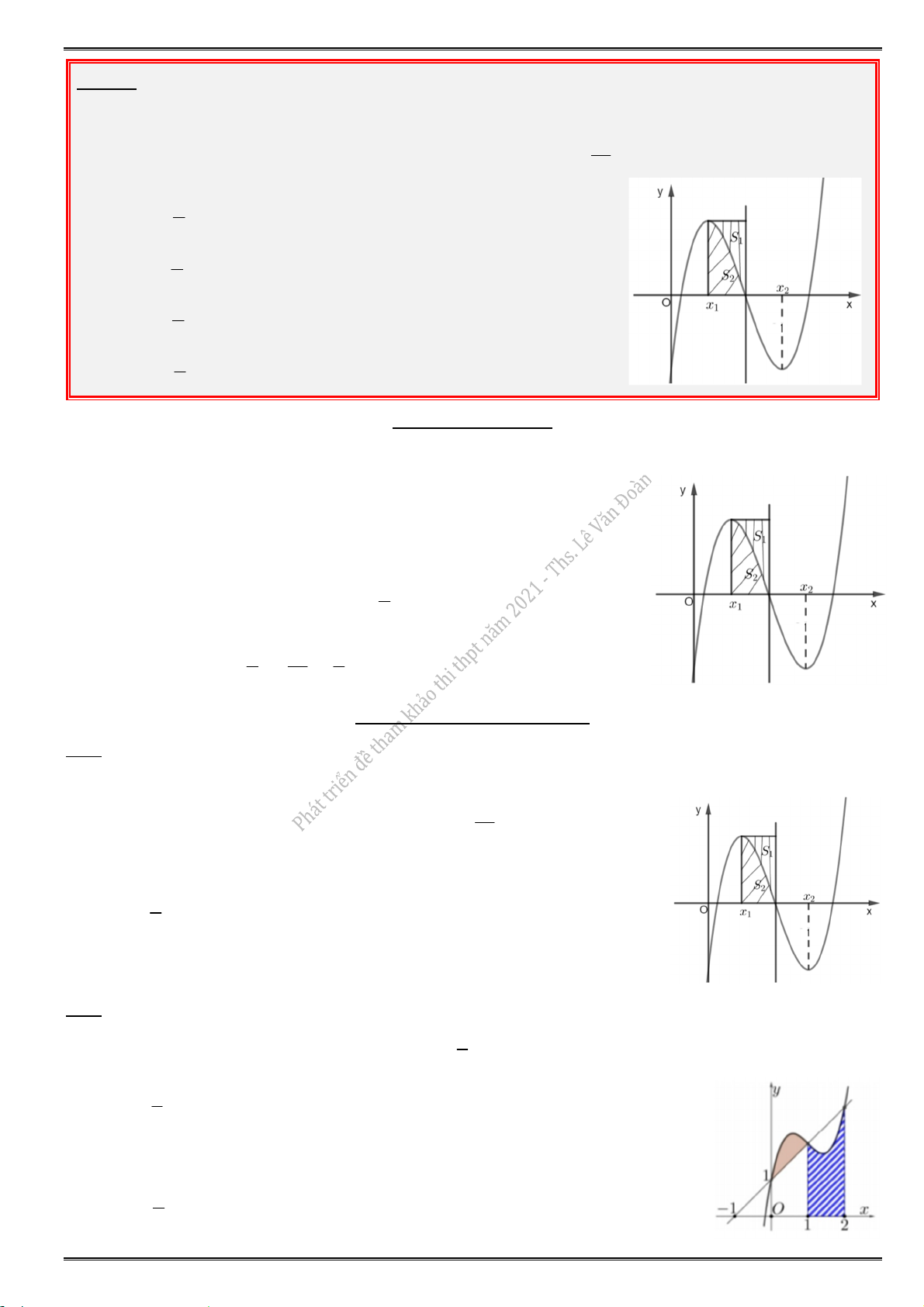
5.2. Cho hàm số f (x) có bảng biến thiên như hình dưới. Tìm giá trị cực đại y
và giá trị cực tiểu y CĐ CT của hàm số đã cho. A. y  3, y  2  . CĐ CT B. y  2, y  0. CĐ CT
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 7 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 C. y  2  , y  2. CĐ CT D. y  3, y  0. CĐ CT
5.3. Cho hàm số f (x) có đạo hàm 3 f (
x)  x(x 1)(x  2) , x   .
 Số điểm cực trị của hàm số đã cho là A. 3. B. 2. C. 5. D. 1.
5.4. Hàm số f (x) xác định và liên tục trên  và có đạo hàm 2 f (  x)  2
 (x 1) (x  1). Hỏi khẳng định
nào sau đây đúng về hàm số f (x).
A. Hàm số f (x) đạt cực đại tại điểm x  1.
B. Hàm số f (x) đạt cực tiểu tại điểm x  1.
C. Hàm số f (x) đạt cực đại tại điểm x  1.
D. Hàm số f (x) đạt cực tiểu tại điểm x  1.
5.5. Cho hàm số f (x) có đạo hàm là x 2 f (
x)  (e 1)(x x 2) với mọi x  .
 Số điểm cực tiểu của hàm số đã cho là A. 0. B. 1. C. 2. D. 3.
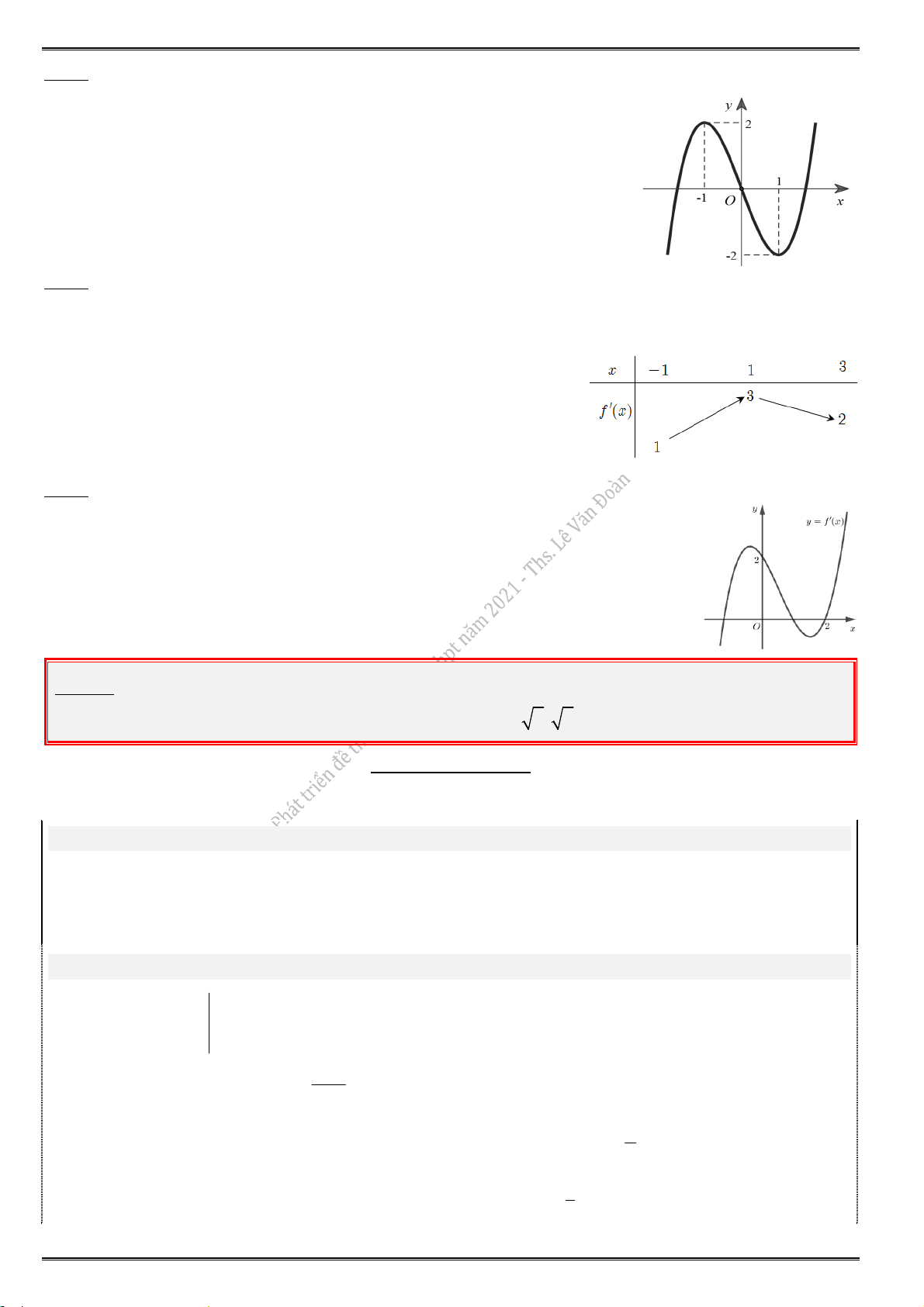
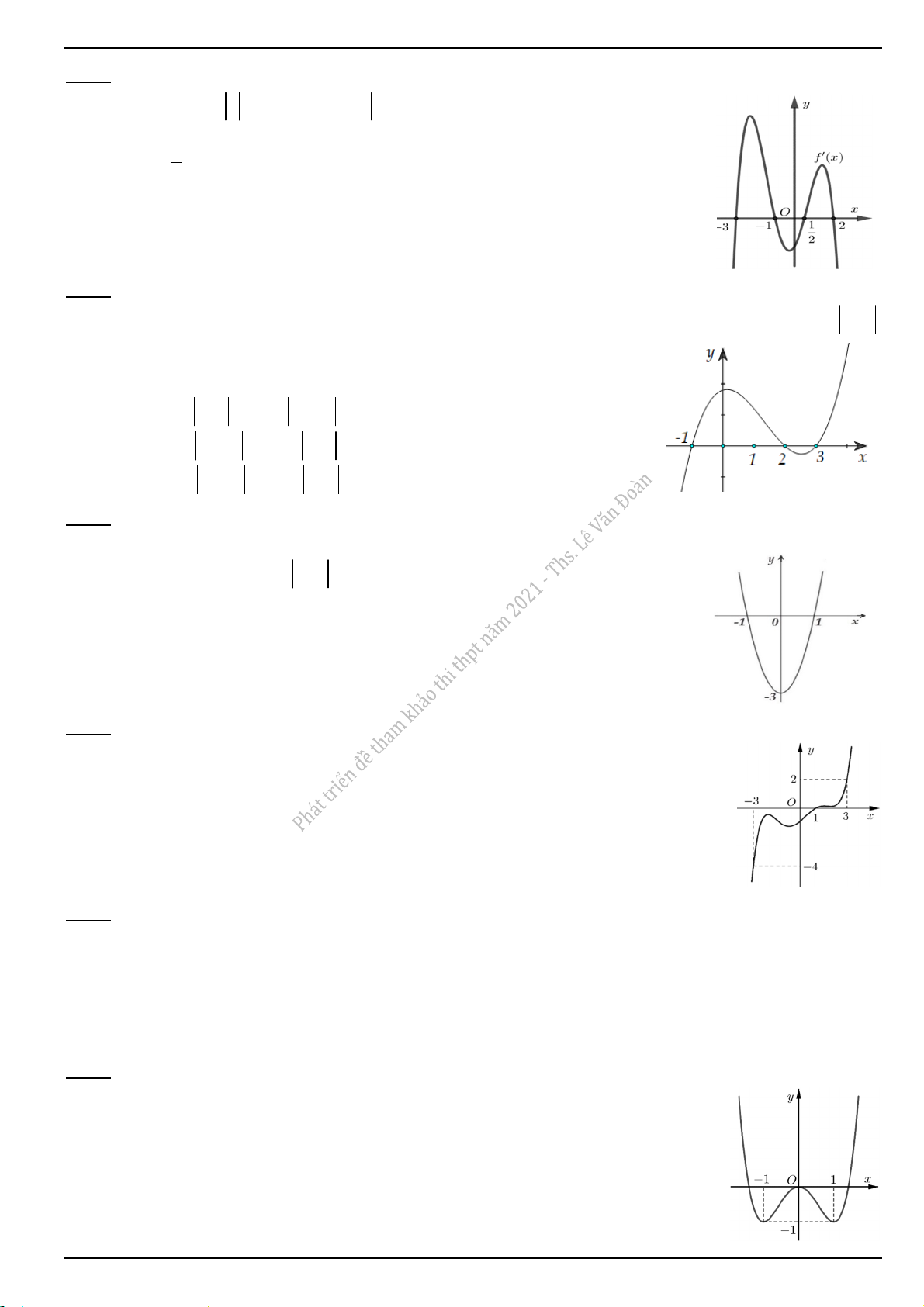
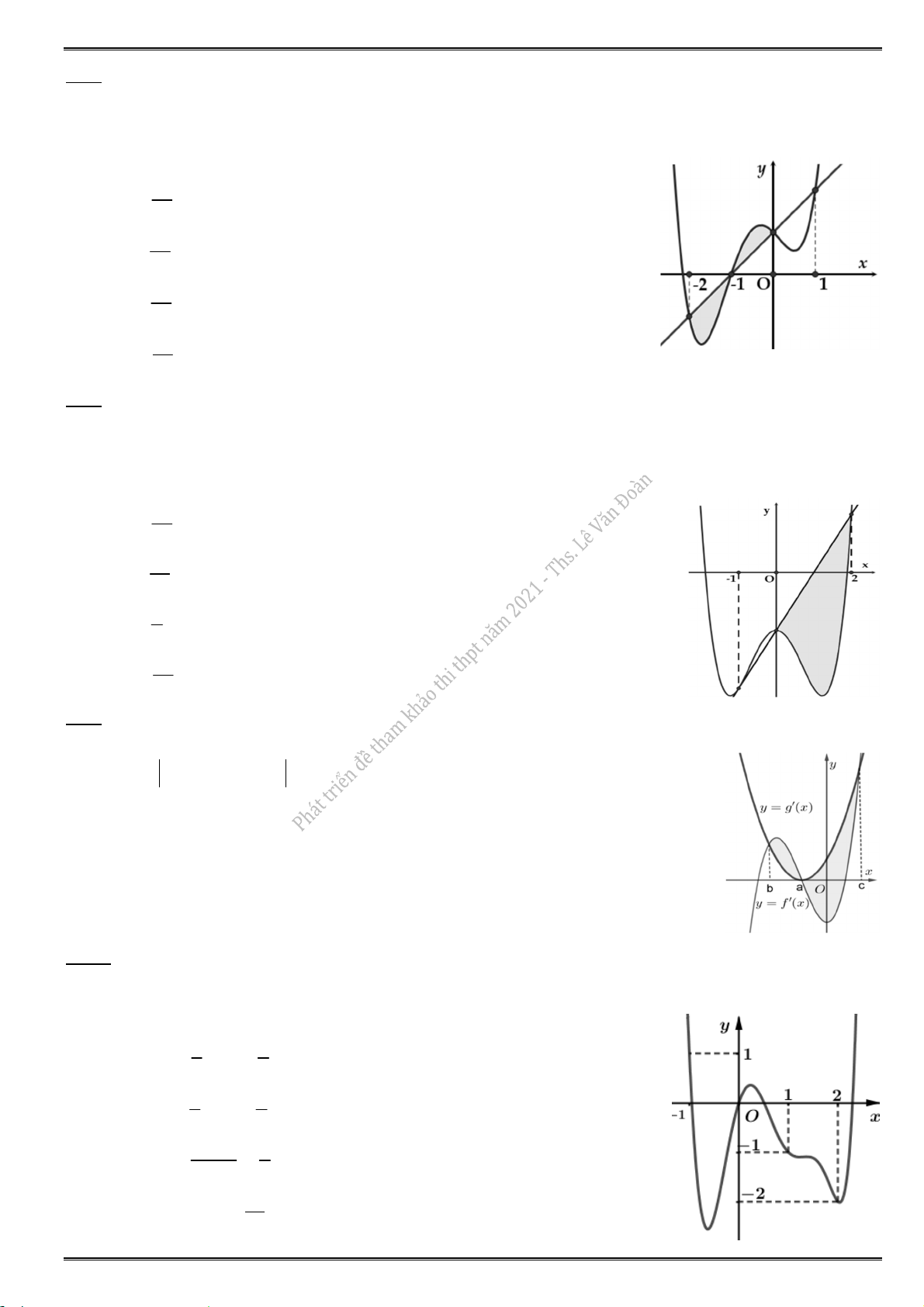
5.6. Cho hàm số f (x) có đồ thị f (
x ) của nó trên khoảng K như hình vẽ. Khi đó trên K, hàm số
y f (x) có bao nhiêu điểm cực trị ? A. 1. B. 4. C. 3. D. 2.
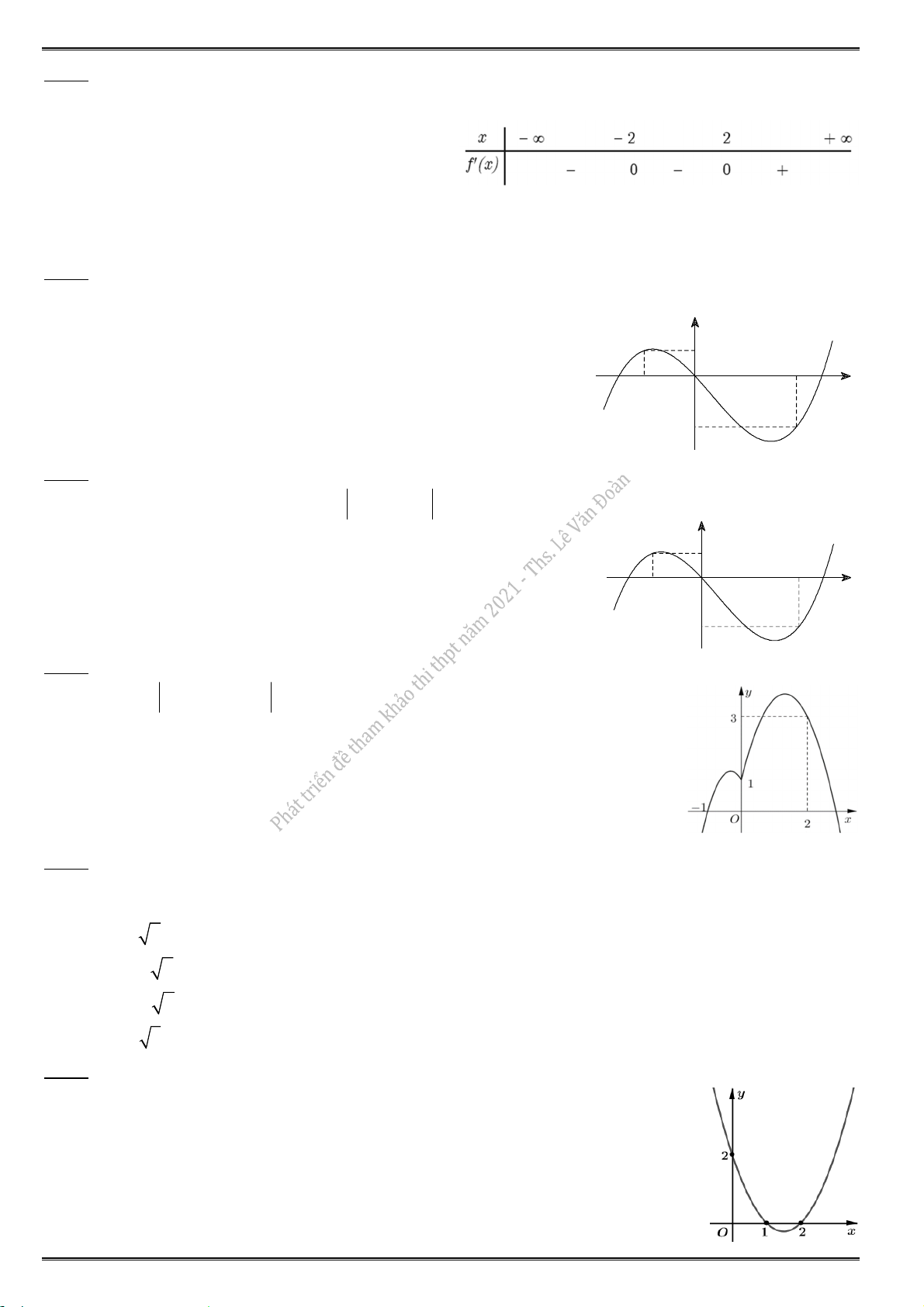
5.7. Hàm số y f (
x ) có đồ thị như hình vẽ dưới đây. Hàm số y f (x)  3x  2019 có bao nhiêu điểm cực trị ? A. 1. B. 2. C. 3. D. 4.
5.8. Hàm số y f (
x ) có đồ thị như hình vẽ dưới đây. Hàm số y f (x)  ex  2019 có bao nhiêu điểm cực trị ? A. 0. B. 1. C. 2. D. 3.
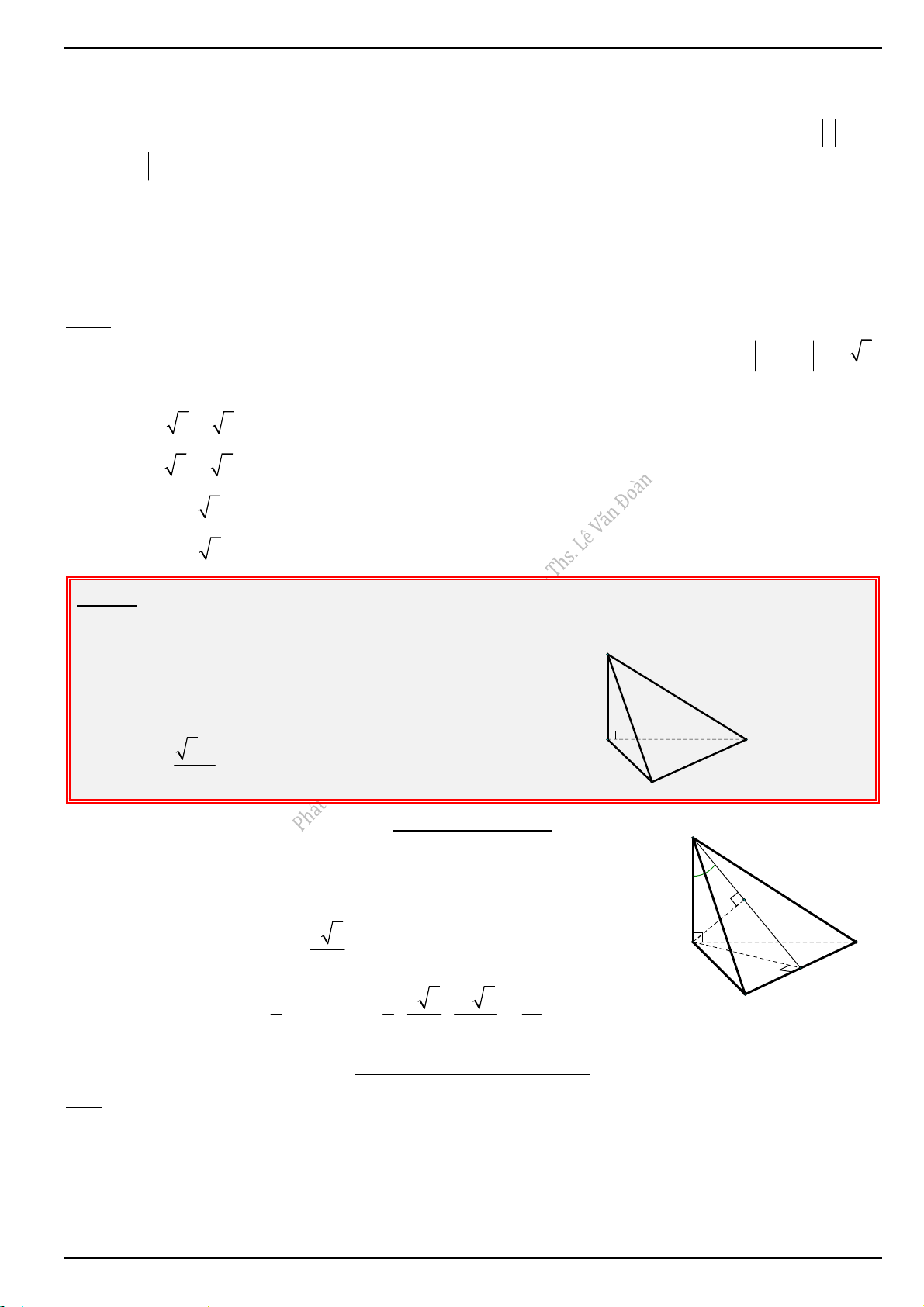
5.9. Cho hàm số y f (x) có đồ thị như hình vẽ bên dưới. Hỏi đồ thị hàm số y f (x) có bao nhiêu điểm cực trị ? A. 2. B. 3. C. 4. D. 5.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 8 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
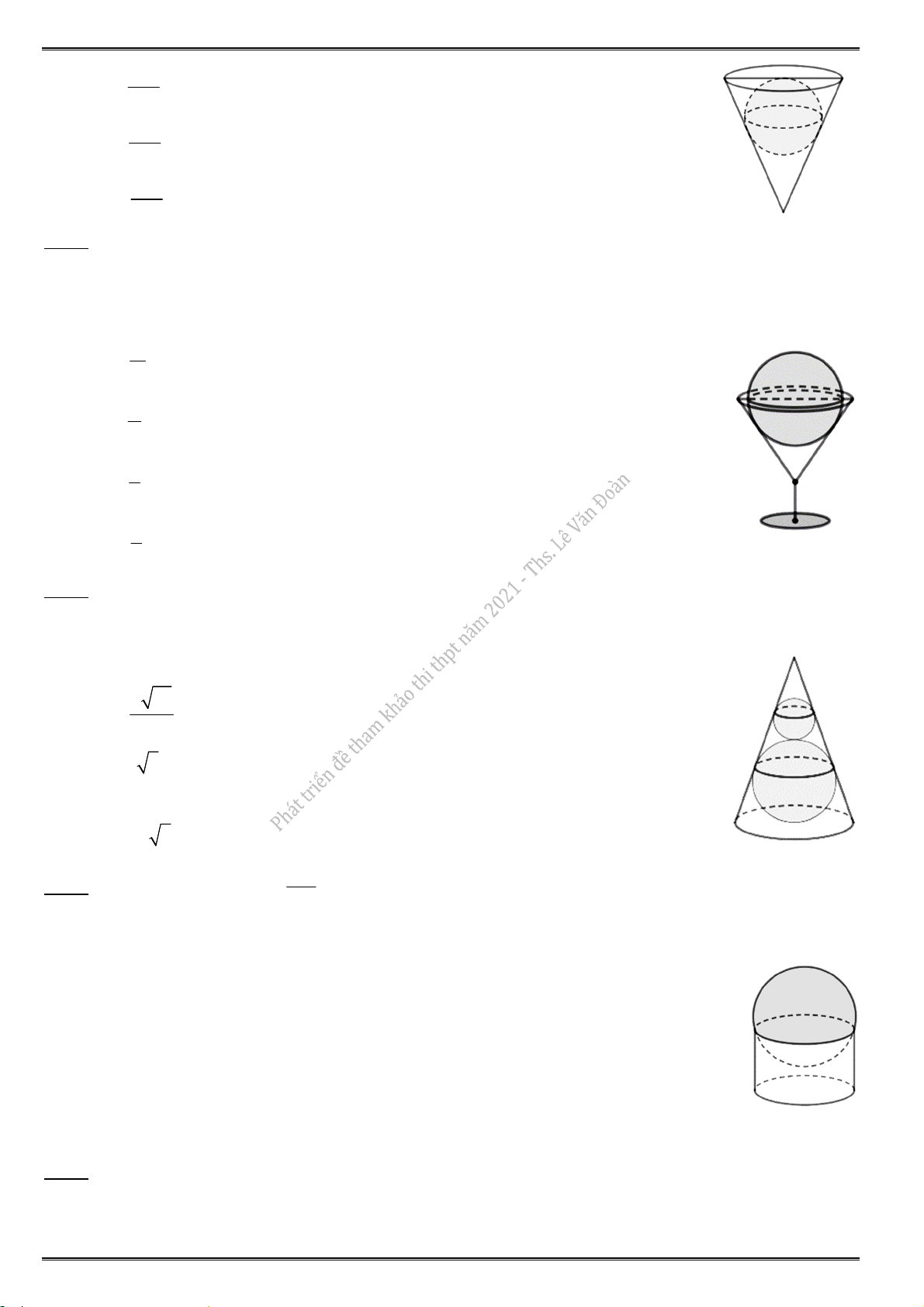
5.10. Cho hàm số y f (x) có đồ thị như hình vẽ bên dưới. Hỏi đồ thị hàm số y f ( x ) có bao nhiêu điểm cực trị ? A. 2. B. 3. C. 4. D. 5. 2x  4
Câu 6. Tiệm cận đứng của đồ thị hàm số y  là đường thẳng x  1
A. x  1. B. x  1.
C. x  2. D. x  2.
Lôøi giaûi tham khaûo 2x  4 2x  4 Ta có: lim   và lim
  nên x  1 là tiệm cận đứng. Chọn đáp án A. 1 x 1  x  1 x 1  x  1
Ñöôøng tieäm caän
Tìm đường tiệm cận ngang TÝnh
 lim y  một số cụ thể y là tiệm cận ngang. x 
Tìm đường tiệm cận đứng TÝnh
  lim y    x x là tiệm cận đứng. x x  o o ax ba
Đối với hàm số y
 Tiệm cận đứng cho mẫu cx d  0 và tiệm cận ngang y   cx d c
Baøi taäp töông töï vaø môû roäng 1  4x
6.1. Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số y  ? 2x  1 A. y  2. B. y  4. 1 C. y  
D. y  2. 2 5
6.2. Tiệm cận ngang của đồ thị hàm số y
là đường thẳng có phương trình ? x  1 A. y  5. B. x  0. C. x  1. D. y  0. 2x  1
6.3. Cho hàm số y
có đồ thị (C ). Tìm tọa độ giao điểm I C x  2
của hai đường tiệm cận của đồ thị ( ). A. I (2;2). B. I (2;2). C. I (2;2).
D. I (2;2). 2x  1
6.4. Khoảng cách từ gốc tọa độ đến giao điểm của hai đường tiệm cận của đồ thị hàm số y x  1 bằng A. 5. B. 5. C. 3. D. 2. 2 x  3x  2
6.5. Tìm số tiệm cận đứng của đồ thị hàm số y  ? 2 x  4
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 9 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 A. 1. B. 2. C. 3. D. 4. 3 x  3x  2
6.6. Tiệm cận đứng của đồ thị hàm số y  là đường thẳng 2 x  3x  2 A. x  2. B. y  2.
C. x  1, x  2. D. x  1. 2 x   2x
6.7. Số đường tiệm cận của đồ thị hàm số y  là x 1 A. 1. B. 2. C. 0. D. 3. 2 9  x
6.8. Đồ thị hàm số y
có bao nhiêu đường tiệm cận ? 2 x  2x  8 A. 1. B. 0. C. 3. D. 2.
6.9. Cho hàm số y f (x) xác định trên  \ {1}, liên tục trên mỗi khoảng xác định và có bảng biến
thiên như hình bên. Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận ? A. 3. B. 1. C. 2. D. 4.
6.10. Cho hàm số y f (x) có bảng biến thiên như hình dưới. Hỏi đồ thị hàm số y f (x) có bao nhiêu đường tiệm cận ? A. 3. B. 4. C. 2. D. 1.
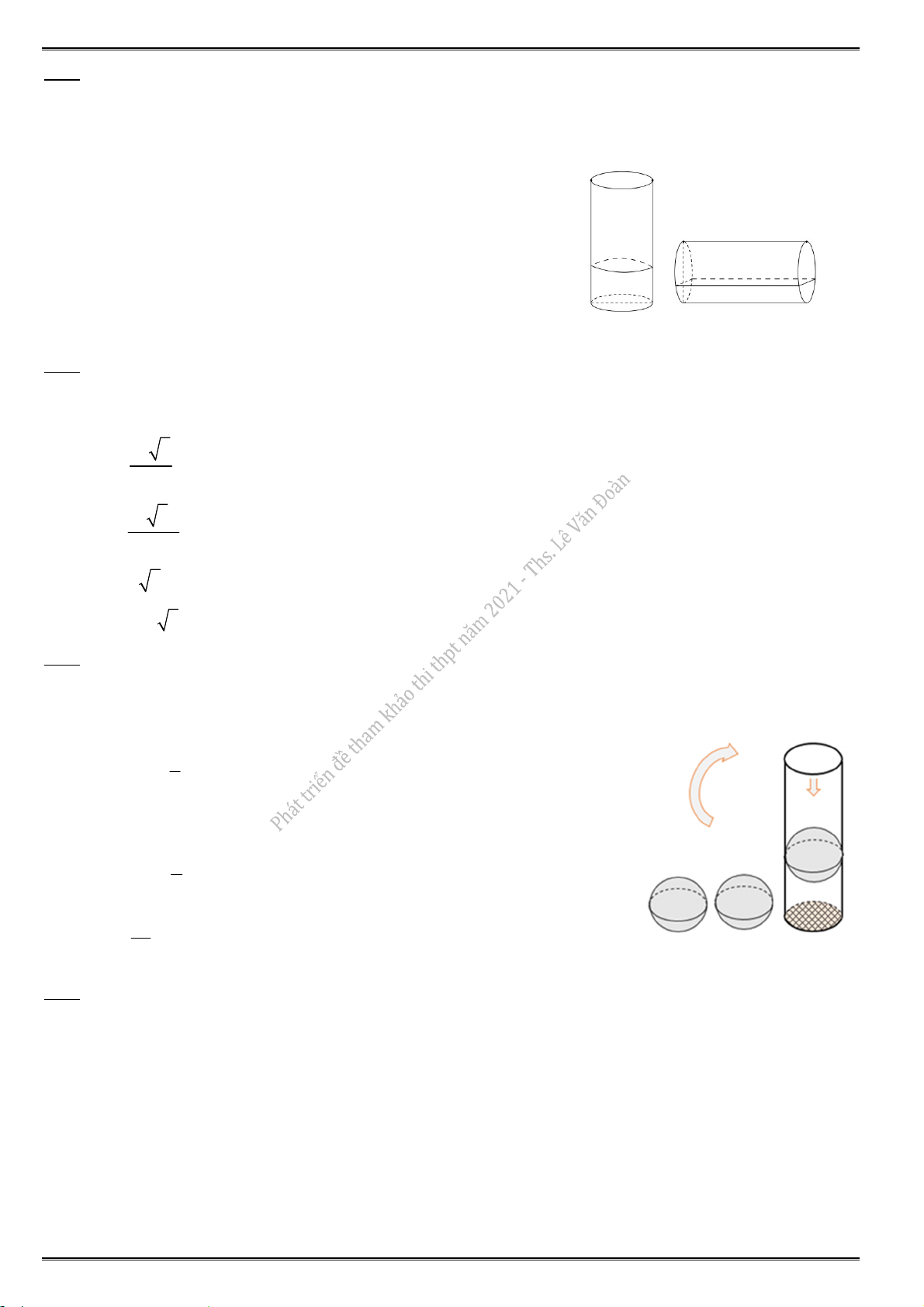
Câu 7. Đồ thị của hàm số nào dưới đây có dạng như đường cong hình bên ? A. 4 2 y x   2x  1. B. 4 2
y x  2x  1. C. 3 2
y x  3x  1. D. 3 2 y x   3x  1.
Lôøi giaûi tham khaûo
Đồ thị có dáng chữ W  đồ thị bậc bốn trùng phương và a  0. Chọn đáp án B.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 10 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
 Nhận dạng đồ thị hàm số bậc ba 3 2
y ax bx cx d, (a  0).
 Hình dáng: (nhận dạng được dấu của a) : N : a  0. И : a  0.
 Nhận dạng dấu của c :
 Nếu 2 cực trị nằm hai bên trục Oy ac  0. Còn nếu có 1 cực trị  Oy c  0.
 Nếu 2 cực trị nằm cùng bên so Oy ac  0.
 Nhận dạng dấu của hệ số d : Đồ thị (C )  Oy : x  0  y d xem dương hay âm.
 Điểm đặc biệt trên đồ thị.
 Nhận dạng đồ thị hàm số bậc bốn trùng phương 4 2
y ax bx  , c (a  0).
 Hình dáng: (nhận dạng được dấu của a và b) : a   0     a   0  ab  0  ab  0   M :    W :     :     :   b   0         b 0  a 0  a 0 
 Tương giao (nhận dạng được dấu của c ) Cắt Oy : x  0  y c xem dương hay âm ? ax b
 Nhận dạng đồ thị hàm số nhất biến y   cx d  Tiệm cận: d
 Tiệm cận đứng cx d  0  x   xem dương hay âm ? c a
 Tiệm cận ngang y  dương hay âm ? c ad bc
 Đơn điệu: y 
 Xem đồ thị (C ) từ trái sang phải: 2 (cx d)
 Nếu đi lên  HS đồng biến  y  0  ad bc  0.
 Nếu đi xuống  HS nghịch biến  y  0  ad bc  0.
 Tương giao với hai trục tọa độ: b
 Cắt trục Ox : y  0  x   xem dương hay âm ? a b
 cắt trục Oy : x  0  y  xem dương hay âm ? d
 Điểm đặc biệt trên đồ thị.
 Nhận dạng đồ thị hàm số mũ x y a .
 Đồ thị nằm trên trục Ox.
 Từ trái sang phải nếu đồ thị (C ) :
Đi lên  Đồng biến  a  1.
Đi xuống  Nghịch biến  0  a  1.
 Nhận dạng đồ thị hàm số lôgarit y  log x. a
 Đồ thị hàm số nằm bên trái Oy.
 Từ trái sang phải nếu đồ thị (C )
Đi lên  ĐB a  1.
Đi xuống  0  a  1.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 11 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Baøi taäp töông töï vaø môû roäng
7.1. Đường cong ở hình bên là đồ thị của hàm số nào ? A. 3 2 y x
  x  1. B. 4 2
y x x  1. C. 3 2
y x x  1. D. 4 2 y x
  x  1.
7.2. Đường cong ở hình bên là đồ thị của hàm số nào ? A. 3 y x   4. B. 3 2
y x  3x  4. C. 3 2 y x   3x  4. D. 3 2 y x   3x  2.
7.3. Đường cong ở hình bên là đồ thị của hàm số nào ? x  1 x A. y   B. y   2x  1 2x  1 x  1 x  3 C. y   D. y   2x  1 2x  1
7.4. Đường cong ở hình bên là đồ thị của hàm số nào ? A. 4 2
y x  2x . B. 4 2
y x  2x . C. 4 2 y x
  2x  1. D. 4 2 y x   2x .
7.5. Đường cong ở hình bên là đồ thị của hàm số nào ? A. 2 y x
  x  1. B. 3 y x
  3x  1. C. 4 2
y x x  1. D. 3
y x  3x  1.
7.6. Đường cong ở hình bên là đồ thị của hàm số nào ? 2x  1 2x  1 A. y   B. y   x  1 x  1 2x  1 1  2x C. y   D. y   x  1 x  1
7.7. Đường cong ở hình bên là đồ thị của hàm số nào ? A. 2 .x y
B. y  log x. 2 x 1  
C. y      y  log x.  D. 2 1 2
7.8. Đường cong ở hình bên là đồ thị của hàm số nào ?
A. y  log x.
B. y  log x. 1 2 2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 12 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 1 C. y   D. 2 .x y 2x
7.9. Đường cong ở hình bên là đồ thị của hàm số nào ? x 1  
A. y      y  log x.  B. 2 2 5 C. y  log . x x y  3 D. 2 .
7.10. Đường cong ở hình bên là đồ thị của hàm số nào ? x
A. y  e . B. y  log x. 7 1
C. y  log x. D. y   1 ex 2
Câu 8. Đồ thị hàm số 3
y x  3x  2 cắt trục tung tại điểm có tung độ bằng A. 0. B. 1. C. 2. D. 2  .
Lôøi giaûi tham khaûo  3 y
  x  3x  2  Ta có: 
y  2. Chọn đáp án C. Oy : x  0 
Töông giao cuûa hai ñoà thò
Cho hàm số y f (x) có đồ thị (C ) và hàm số y g(x) có đồ thị (C ). 1 2
 Số nghiệm của phương trình f (x)  g(x) là số điểm chung của hai đồ thị (C ) và (C ). 1 2
 Phương trình f (x)  g(x) được gọi là phương trình hoành độ giao điểm của hai đồ thị hàm số.
Baøi taäp töông töï vaø môû roäng
8.1. Đồ thị của hàm số y  4 x  2
2x cắt trục hoành tại bao nhiêu điểm ? A. 0. B. 2. C. 4. D. 3.
8.2. Số giao điểm của đồ thị hàm số 4 2
y x  2x  2 và 2 y x   4 là A. 0. B. 4. C. 1. D. 2.
8.3. Biết đường thẳng y  2x  2 cắt đồ thị hàm số 3
y x x  2 tại một điểm duy nhất, kí hiệu
(x ;y ). Tìm y .   
A. y  4.
B. y  0.  
C. y  2. D. y  1  .   x  1
8.4. Tìm tọa độ giao điểm của đường thẳng y x  1 với đồ thị hàm số y   x  2 A. (4
A ; 3), B(0;1).
B. C (1; 3).
C. D(3;1).
D. I (1; 0), J (3; 4).
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 13 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 2x m
8.5. Tìm tập hợp m để đồ thị hàm số y
cắt đường thẳng y  1  x tại 2 điểm phân biệt ? x  1 A. ( ;  2]. B. ( ;  2).
C. (;2). D. (2;). x m
8.6. Tìm tất cả các giá trị của tham số m để đường thẳng y  2x  1 cắt đồ thị hàm số y   x 1 3 3 A.   m  1  .
B. m    2 2 3 3 C.   m  1  .
D. m    2 2
8.7. Với giá trị nào của m thì đồ thị hàm số 3
y x  (m 1)x  5 cắt trục hoành tại điểm có hoành độ bằng 2 ? 1 1 A. m  
B. m    2 2 15 15 C. m   D. m    2 2
8.8. Tìm tất cả các giá trị của tham số m để đồ thị hàm số y  3 x  2
3x  1 cắt đường thẳng
y  2m  3 tại ba điểm phân biệt ?
A. 0  m  4.
B. 0  m  2. C. 3   m  1.
D. 0  m  2.
8.9. Tìm tập hợp m để đồ thị hàm số 3 2 2
y x  3x  2m  2m cắt trục hoành tại ba điểm phân biệt. A. ( 2  ; 2  ) ( 1  ;1).
B. (1; ). C. (2; 0).
D. (1; 0)  (1;2).
8.10. Tìm tập hợp m để đường thẳng y mx  1 và đồ thị hàm số 3
y x  3x  1 có 3 điểm chung. A. m  3  .
B. m  3. C. m  3  .
D. m  3.
8.11. Tìm tất cả các giá trị của tham số m sao cho đồ thị của hai hàm số 3 2
y x  2x mx  2 và 2
y x m có một điểm chung duy nhất.
A. m  3. B. m  3  .
C. m  3.
D. m  3.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 14 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
8.12. Tìm số giao điểm của đồ thị hàm số 4 2 2
y x  2x m  1 với trục hoành (với m là tham số). A. 1. B. 2. C. 3. D. 4.
8.13. Tìm tập hợp m để đồ thị hàm số y  4 x  2
2mx m  2 cắt trục Ox tại 4 điểm phân biệt. A. (2;). B. ( ;  1). C. ( ;  1)  (2; )  . D. (0;  ). 
8.14. Tìm các giá trị của m để dường thẳng y  1 cắt đồ thị hàm số 4 2
y x  (3m  2)x  3m tại bốn điểm phân biệt.  1 m    A.  3 
B. 1  m  0. m   1   1  1 m     m     C.  3  D.  3  m   0     m  0  
8.15. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số 4 2 2
y x  2(2m  1)x  4m cắt
trục hoành tại bốn điểm phân biệt x , x , x , x thỏa mãn 2 2 2 2
x x x x  6. 1 2 3 4 1 2 3 4 1 A. m   4 1
B. m    2 1
C. m    4 1
D. m    4
Câu 9. Với a là số thực tùy ý, log (9a) bằng 3 1 A.  log a.
B. 2 log a. C. 2 (log a) . D. 2  log a. 3 2 3 3 3
Lôøi giaûi tham khaûo
Ta có: log (9a)  log 9  log a  2  log a. Chọn đáp án D. 3 3 3 3
Coâng thöùc muõ & loâgarít
Cho a và b là các số thực dương x và y là những số thực tùy ý. xx n
a a.a.a...a    a a       x   n số a b b 
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 15 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 m x yx yaa .a
n m  (n )m n a aa xa x y n  1 0  a   a   u  (x)  1,  ( u x)  0 y n a a  
x.y  ( x )y  ( y )x a a a
x . x  ( . )x a b a b Cho 0  a  1 và , b c  0. n
 log f (x)  b f (x) ba
 log b n. log b. a a a 1 b  log b b  log
 log b  log c n log a a n a a a c log b 1 lnb  log c b   log b   log b a log a a log a a lna c b
 log 1  0, log a  1 log c log a log b b b a a aacb a
 log (b c)  log b  log c
 log b  lnb và log b  log . b a a a e 10
Baøi taäp töông töï vaø môû roäng 1
9.1. Cho b là số thực dương khác 1. Giá trị của 2 2
log (b .b ) bằng b 3 A.B. 1. 2 5 1 C.D.  2 4 3
9.2. Cho 0  a  1. Giá trị của biểu thức 2
P  log (a. a ) bằng a 4 A. B. 3. 3 5 5 C. D.  3 2  3 a   
9.3. Cho a là số thực dương khác 4. Giá trị của log   bằng a   64 4 1 A. 3. B.  3 1 C. 3  . D.   3
9.4. Cho log x  1
 và log y  4. Giá trị của 2 3 log (x y ) bằng a a a A. 3. B. 10. C. 14. D. 65.
9.5. Cho a, b  0 và a, b  1, giá trị của 3 4
P  log b .log a bằng a b A. 18. B. 24. C. 12. D. 6.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 16 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
9.6. Cho a là số thực dương thỏa mãn a  10, mệnh đề nào dưới đây sai ? 10  
A. log(10.a)  1  log a. B.  log   loga  1.   a 
C. log(10a )  a. D. 10 log(a )  a.
9.7. Với các số thực x, y dương bất kì. Mệnh đề nào dưới đây đúng ?
A. log (x y)  log x  log y.
B. log (xy)  log x. log y. 2 2 2 2 2 2  2 x    x  log x   C. log 
  2 log x  log y. D. 2 log     2   2 2     y  2 y  log y 2 3
9.8. Cho a là một số thực dương. Khi đó 3 2 5 a . a bằng 1 2 A. 15 a . B. 5 a . 1 19  C. 15 a . D. 15 a .
9.9. Cho các số thực x, y thỏa mãn 2x  3 và 3y  4. Giá trị biểu thức 8x 9y  bằng A. 43. B. 17. C. 24. . 3 2 log 3  log 4. 2 3 1 1 3 3 a b b a
9.10. Cho hai số thực dương a và .
b Rút gọn biểu thức A  ta được 6 6 a b A. 6 A ab. B. 3 A ab. 1 1 C. A   D. A   3 ab 6 ab
Câu 10. Đạo hàm của hàm số 2x y  là 2x A. 2x y  ln 2. B. 2x y  . C. y   D. x 1 y x.2    . ln 2
Lôøi giaûi tham khaûo
Theo công thức ( u )  . u a
ua .lna thì 2x y  có đạo hàm 2x y 
ln 2. Chọn đáp án A.
Ñaïo haøm cuûa haøm soá muõ vaø loâgarít uu
 ( u)  . u a
ua .lna.  (ln u)    (log u)   u a u lna
Baøi taäp töông töï vaø môû roäng 2 10.1. Hàm số 2 2 x x y   có đạo hàm là 2 2 A. 2 2 x x y    .ln2. B. 2 (4 1).2 x x y x     .ln2. 2 C. 2 2 (2 ).2 x x y x x     .ln2. D. 2
y  (4x  1).ln(2x x). 10.2. Hàm số 1 2 e x y   có đạo hàm là A. 1 2 2e x y    . B. 1 2 e x y    .
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 17 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 C. 1 2 2e x y     . D. 1 2 2e x y     . 10.3. Hàm số 2 3 2 x y   có đạo hàm là A. 2x2 2 ln 4. B. x2 4 ln 4. C. 2x 2 2  ln16. D. 2x3 2 ln 2. 2 10.4. Hàm số 1 8x y   có đạo hàm là 2 2 A. 2 .8x x . B. 2 .8x x ln 4. 2 2  C. 2 ( 1).8x x  . D. x 1 6x.8 .ln2.
10.5. Đạo hàm của hàm số y  log (2x  1) là 2 2 2 2 ln 2 2 A. B. C. D. (2x  1)ln x (2x  1)ln 2 x  1 (x  1)ln 2 10.6. Hàm số 2
f (x)  log (x  2x) có đạo hàm là 2 ln 2 1 (2x  2)ln 2 2x  2 A. B. C. D.  2 x  2x 2 (x  2x)ln 2 2 x  2x 2 (x  2x)ln 2
10.7. Đạo hàm của hàm số 2
y  log(x x) là 1 2x  1 2x  1 2x  1 A. B. C. D. .log e. 2 (x x)ln10 2 x x 2 (x x)log e 2 x x
10.8. Cho hàm số y x
. Giá trị của y (1) bằng A. 2 ln . B. ln . C. 0. D. (
   1).
10.9. Hãy tính đạo hàm của hàm số y  3 2 3
x . x trên khoảng (0; )  . 7 6 4 6
A. . x . B. 9 x . C. 3 . x . D.  6 3 7 7 x
10.10. Đạo hàm của hàm số 2
y  log (2x  1) là 2 2 log (2x  1) 4 log (2x  1) 4 log (2x  1) 2 A. 2  B. 2  C. 2  D. (2x  1)ln 2 (2x  1)ln 2 2x  1 (2x  1)ln 2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 18 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Câu 11. Với a là hai số thực dương tùy ý, 3 a bằng 3 2 1 A. 6 a . B. 2 a . C. 3 a . D. 6 a .
Lôøi giaûi tham khaûo n 3 Theo công thức m n m
a a , ta có 3 2
a a . Chọn đáp án B.
Baøi taäp töông töï vaø môû roäng 1
11.1. Rút gọn biểu thức 6 3
P x . x với x  0. 1 2 A. 8
P x . B. 9 P x . 2 C. P x .
D. P x . 5
11.2. Rút gọn biểu thức 3 3
Q b : b với b  0 5 A. 2 Q b . B. 9 Q b . 4  4 C. 3 Q b . D. 3 Q b . 4
11.3. Cho biểu thức 3 2 3
P x. x . x , với x  0. Mệnh đề nào dưới đây đúng ? 1 13 A. 2 P x . B. 24 P x . 1 2 C. 4 P x . D. 3 P x .
11.4. Tính giá trị của biểu thức 2017 2016 P  (7  4 3) (4 3  7) . A. P  1.
B. P  7  4 3.
C. P  7  4 3. D. 2016 P  (7  4 3) .
11.5. Giá trị của biểu thức 2016 2016 (1  3) (3  3) bằng 1008 1008 A. 12 . B. 4 . C. 1008 (1  3) . D. 1008 (3  3) .
11.6. Với a và b là hai số thực dương tùy ý và a  1, log (a b ) bằng a 1 1 A.  log . b B. 2  log . b 2 a 2 a C. 2  log . b D. 1  2 log . b a a 11.7. Với ,
a b  0 và a 1, thì 2
log (a b) bằng 3 a 1 3
A. log b.
B. log b. 6 a 2 a 3 2 1 C. 6  log b. D.  log b. 2 a 3 6 a 1 1
11.8. Cho a và b là hai số thực dương thỏa mãn 3
a . b  10. Giá trị của loga  logb bằng 2 3 A. 0. B. 1.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 19 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 C. 10. D. 1.
11.9. Cho a và b là hai số thực dương thỏa mãn 3
ab  27. Giá trị của log a  6 log b bằng 3 3 A. 3. B. 6. C. 9. D. 1. 9b   
11.10. Xét các số thực a và b thỏa mãn 3 log    log 3.  
Mệnh đề nào đúng ? 3 a 1 3  27 1 1
A. a  2b  
B. a  2b   18 18 1 1
C. 2b a  
D. 2a b   18 18
Câu 12. Nghiệm của phương trình 2x 4 5   25 là
A. x  3.
B. x  2.
C. x  1. D. x  1.
Lôøi giaûi tham khaûo Ta có: 2x 4
5   25  2x  4  log 25  2  x  3. Chọn đáp án A. 5
Phöông trình muõ cô baûn (vôùi ñieàu kieän xaùc ñònh) x
a b  0  x  log . b f x g x aaf x g x a  ( ) ( ) ( ) ( ).
Baøi taäp töông töï vaø môû roäng
12.1. Nghiệm phương trình 2x 1 3   27 là A. x  5. B. x  1. C. x  2. D. x  4. 2x 1  12.2. Phương trình 5  125 có nghiệm là 3 5 A. x   B. x   2 2
C. x  1. D. x  3. 2
12.3. Số nghiệm của phương trình 2x x   1 là A. 0. B. 3. C. 1. D. 2. 2
12.4. Phương trình 2x 5  x 4 2
 4 có tổng tất cả các nghiệm bằng A. 1. B. 1. 5 5 C. D.   2 2 2 3 x x  
12.5. Tích số của tất cả các nghiệm thực của phương trình 2 7  49 7 bằng A. 1. B. 1. 1 1 C.   D.  2 2 2
12.6. Tích tất cả các nghiệm của phương trình x x  ln 2 1 3   4 bằng A. 1  2 log 2.
B. 1  2 log 2. 3 3
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 20 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 C. 1  2 ln 2.
D. 1  2ln 2.
12.7. Nghiệm của phương trình x x 1 3 .5   7 là
A. x  log 35. B. x  log 5. 15 21
C. x  log 35.
D. x  log 21. 21 15 
12.8. Nghiệm của phương trình x 5 3  3x  121 là A. x  log 3.
B. x   log 2. 2 3 C. x  log 2.
D. x   log 3. 3 2 2 12.9. x x
Gọi x , x (x x ) là hai nghiệm của phương trình x 1  x 2 9 3   . Giá trị 1 2 2  3 bằng 1 2 1 2 A. 5. B. 10. C. 11. D. 28. 2 3
12.10. Tích các nghiệm của phương trình x x  2  x 2 (3 2 2) (3 2 2)     bằng A. 0. B. 2. C. 1. D. 1.
Câu 13. Nghiệm của phương trình log (3x)  3 là 2 8 1
A. x  2.
B. x  2. C. x   D. x   3 2
Lôøi giaûi tham khaûo 8 3
log (3x)  3  3x  2  x
Chọn đáp án C. 2 3
Phöông trình muõ & loâgarít cô baûn (vôùi ñieàu kieän xaùc ñònh) b
 log x b x a . f x
g x f x g x a  log ( ) log ( ) ( ) ( ). a a
Baøi taäp töông töï vaø môû roäng
13.1. Nghiệm của phương trình log (x  5)  4 là 2 A. x  3. B. x  13. C. x  21. D. x  11. 13.2. Phương trình 2
log (x  10x  9)  2 có nghiệm là 3 x  10   x  2  A. .  B. . x  0     x 0  x  2   x  10  C. .  D. . x  9     x 9 
13.3. Nghiệm của phương trình ln(4  x)  100 là A. 100 x  e  4. B. 100 x  4 10 . C. 100 x  4  e . D. 100 x  10  4.
13.4. Nghiệm của phương trình log(x  1)  2 là A. x  101. B. 2 x  e  1.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 21 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 C. 2 x  e  1. D. 2
x  1.
13.5. Nghiệm của phương trình 100
log10 x  250 thuộc khoảng A. (0;2). B. (2;  )  . C. ( ;  2  ). D. (2; 0).
13.6. Nghiệm của phương trình log (log x)  1 là 3 2
A. x  8.
B. x  6.
C. x  9.
D. x  2.
13.7. Nghiệm của phương trình 3x 1 log (3   1)  3 là 2
A. x  2.
B. x  1.
C. x  3.
D. x  8.
13.8. Nghiệm của phương trình log 2
( x  1)  log (x  1)  1 là 3 3 A. x  4. B. x  3. C. x  2. D. x  1.
13.9. Tìm tập nghiệm S của phương trình log (x  1)  log (x  1)  3. 2 2 A. S  { 3  ;3 . }
B. S  {4}. C. S  { } 3 .
D. S  { 10; 0 1 . }
13.10. Tập nghiệm của phương trình log (x  3)  2 log 3. log x  2 là 2 4 3 A. {5}. B. {4;5}. C. {4}. D. {2;4}. Câu 14. Cho hàm số 2
f (x)  3x  1. Trong các khẳng định sau, khẳng định nào đúng ? A. 2
f (x)dx  3x x C.  B. 3
f (x)dx x x C.  1 C. 3
f (x)dx x x C.  D. 3
f (x)dx x C.  3
Lôøi giaûi tham khaûo
Áp dụng công thức nguyên hàm cơ bản thì 2 3
f (x)dx
(3x  1)dx x x C.   Chọn đáp án B.
Baûng nguyeân haøm cuûa moät soá haøm thöôøng gaëp 0dx C. 
 kdx kx C.  n 1 x n 1 ax b   n 1 ( ) n x dx  C. 
 (ax b) dx  C.  n  1 a n  1 1 1 1
dx  ln x C.  
dx  ln ax b C.  x ax b a 1 1 1 1 1  dx   C.  dx    C.  2 2 x x (ax b) a ax b 1
sin x dx  cos x C. 
 sin(ax b)dx   cos(ax b) C.  a
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 22 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 1
cosx dx  sin x C . 
 cos(ax b)dx  sin(ax b) C.  a 1 dx 1
dx  cotx C.  
  cot(ax b) C.  2 sin x 2 sin (ax b) a 1 dx 1
dx  tan x C.  
 tan(ax b) C.  2 cos x 2 cos (ax b) a ax b  1 exd  ex xC .   e d eax b x   C.  a x a a  x 1 x x a dx  C.   a dx  C.  lna lna 1
♦ Nhận xét. Khi thay x bằng (ax  )
b thì khi lấy nguyên hàm nhân kết quả thêm  a
Một số công thức cần nhớ 1 1 1 1
 Bậc chẵn của sin và cosin  Hạ bậc: 2 2
sin a   cos2a, cos a   cos 2a. 2 2 2 2 
tanx dx  ln cosx C.  
cotx dx  ln sinx C.  1 2 2  dx
ax b C.   3
ax bdx
(ax b)  C.  ax b a 3a
Baøi taäp töông töï vaø môû roäng
14.1. Họ nguyên hàm của hàm số 3
f (x)  x x là A. 4 2
x x C. B. 2 3x  1 C. 1 1 C. 3
x x C. D. 4 2
x x C. 4 2 1 1
14.2. Họ tất cả các nguyên hàm của hàm số 6
f (x)  7x    2 là 2 x x 1 1 A. 7
x  ln x   2x. B. 7 x  ln x   2x C. x x 1 1 C. 7
x  ln x   2x C. D. 7
x  ln x   2x C. x x
14.3. Họ tất cả các nguyên hàm của hàm số ( ) 5x f x  là
A. 5x C .
B. 5x ln 5  C . 5x x 1 5  C. C. D. C. ln 5 x  1
14.4. Họ tất cả các nguyên hàm của hàm số 5 ( ) e x f x  là 1 A. 5 e x ln 5 +C . B. 5 e x +C. 5 C. 5 5e x +C . D. 5 e x C  .
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 23 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 2
14.5. Họ tất cả các nguyên hàm của hàm số f (x)  là 4x  3  3   1 3 A. 2 ln 2
x   C.  ln 2x  C.  B.  2 2 2 1  3   1 C. ln 2
x   C.
D. ln 4x  3  C. 2  2 4
14.6. Một nguyên hàm F(x) của hàm số 2
f (x)  3x  2x  5 thỏa mãn F(1)  4 là A. 3 2
x x  5x  3. B. 3 2
x x  5x  3. C. 3 2
x x  5x  3. D. 3 2
x x  5x  3.
14.7. Họ tất cả các nguyên hàm của hàm số 8
f (x)  (2x  1) là 9 (2x  1) 9 (1  2x) A. C. B. C. 9 18 9 (2x  1) 9 (1  2x) C. C. D. C. 18 9
14.8. Họ nguyên hàm của hàm số 2 ( ) 2 x.3x.7x f x  là 84x 2 2 x.3x.7x A. C. B. C . ln 84 ln 4. ln 3.ln 7
C. 84x C.
D. 84x.ln 84 C.
14.9. Họ tất cả các nguyên hàm của hàm số f (x )  2x  3 là 2 1
A. (2x  3) 2x  3  C.
B. (2x  3) 2x  3  C. 3 3 1 1
C.  (2x  3) 2x  3  C . D.
2x  3  C . 3 2 1
14.10. Họ tất cả các nguyên hàm của hàm số f (x)  là 2 2x  1 1 A.
2x  1 C.
B. 2x  1 C. 2 1
C. 2 2x  1 C. D. C.
(2x  1) 2x  1
Câu 15. Cho hàm số f (x )  cos 2x. Trong các khẳng định sau, khẳng định nào đúng ? 1 1 A.
f (x)dx  sin 2x C.  B.
f (x)dx   sin 2x C.  2 2 C.
f (x)dx  2 sin 2x C.  D.
f (x)dx  2  sin 2x C. 
Lôøi giaûi tham khaûo 1
Áp dụng công thức nguyên hàm cơ bản:
cos(2x)dx  sin(2x)  C .  Chọn A. 2
Baøi taäp töông töï vaø môû roäng
15.1. Họ nguyên hàm của hàm số f (x)  sin 2x  cos 3x là
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 24 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 1 1 1 1
A.  cos 2x
sin 3x C . B. cos 2x
sin 3x C . 2 3 2 3
C. cos 2x  sin 3x C.
D. cos 2x  sin 3x C.   
15.2. Một nguyên hàm F(x) của hàm số f (x )  cos 2x thỏa mãn F    2  là  2  1 3
A. sin 2x  2 .
B. x  sin 2x   2 2 C. sin x  2 . D. 2x  2 .
15.3. Họ nguyên hàm của hàm số f (x )  sin x cos x là 1 1
A. cos 2x C .
B.  cos 2x C . 4 4
C. sin 2x C.
D. sin x cosx C.
15.4. Cho F(x) là một nguyên hàm của 2
f (x)  4 cos x  5 thỏa F()  0. Hàm số F(x) là 4 4 A. 3
x  sin 2x  3 . B. 3 cos x  5x   5 . 3 3 4 C. 3
x  sin 2x  3 . D. 3
sin x  5x  5 . 3
15.5. Họ nguyên hàm của hàm số f (x)  sin 5x sin 2x là cos 3x cos 7x sin 3x sin 7x A.  C. B.  C. 6 14 6 14 cos 3x cos 7x sin 3x cos 7x C.  C. D.  C. 6 14 6 14
15.6. Họ nguyên hàm hàm số f (x)  sin 5x cos x là 1 1
A.  cos 5x C.
B. cos 5x C . 5 5 cos 4x cos 6x 1 1 C.   C. D. cos 4x  cos 6x C. 8 12 8 12
15.7. Họ nguyên hàm của hàm số 2
f (x)  tan x là
A. tan x C.
B. tan x x C .
C. x  tan x C .
D. tan x x C . 1    2
15.8. Một nguyên hàm F(x) của hàm số f (x)  sin x
thỏa mãn F    là 2 cos x      4  2
A. cos x  tan x C.
B.  cos x  tan x  2  1.
C. cos x  tan x  2  1.
D.  cos x  tan x  2  1.
15.9. Cho hàm số f (x ) thỏa mãn f (
x)  x  sinx và f (0)  1. Khi đó hàm số f (x) là 2 x 2 x A.
 cos x  2. B.
 cos x  2. 2 2 2 x 1 2 x C.
 cos x   D.  cos x. 2 2 2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 25 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789   
15.10. Cho hàm số f (x ) thỏa mãn f (
x)  2  cos2x và f    2 .
Mệnh đề nào sau đây sai ?  2  sin 2x A. f (0)  .
B. f (x )  2x   . 2 sin 2x  
C. f (x )  2x   . D. f     0. 2  2 2 3 3 Câu 16. Nếu
f (x)dx  5  và
f (x)dx  2  thì f (x)dx  bằng 1 2 1 A. 3. B. 7. C. 10. D. 7  .
Lôøi giaûi tham khaûo 3 2 3 Ta có
f (x)dx
f (x)dx
f (x)dx  5  2  3.    Chọn đáp án A. 1 1 2
Tính chaát cuûa nguyeân haøm vaø tích phaân b b b b a bF (
x)  f (x), f (x)dx F(x)  F(b)  F(a).   .
k f(x)dx  . k f(x)d ,
x f(x)dx   f(x)dx.     a a a a a b b b b b b b
f(x) g(x)  dx
f (x)dx g(x)dx.      
f (t)dt
f (u)du
f (x)dx  ...    a a a a a a b b b c b b bf (
x)dx f (x) , f  (x)dx f (x) .....   
f (x)dx
f (x)dx f (x)dx.    a a a a a a c
Baøi taäp töông töï vaø môû roäng 3 3 4 16.1. Cho
f (x)dx  2016  và
f (x)dx  2017,  khi đó f (x)dx  bằng 1 4 1 A. 4023. B. 1. C. 1. D. 0. 2 2 16.2. Nếu
f (x)dx  3  thì 4f(x) 3  dx    bằng 0 0 A. 2. B. 6. C. 8. D. 4. 9 0 9 16.3. Nếu
f (x)dx  37  và
g(x)dx  16  thì
2f(x) 3g(x)  dx    bằng 0 9 0 A. 26. B. 58. C. 143. D. 122. 2 2 2 16.4. Nếu
f (x)dx  3  và
g(x)dx  2  thì 2x f (x) 2g(x)   dx    bằng 0 0 0 A. 18. B. 5. C. 11. D. 3.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 26 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
16.5. Cho hàm số f (x) có đạo hàm liên tục trên đoạn [2; 3], đồng thời f (2)  2 và f (3)  5. Khi đó giá 3 trị của tích phân f (  x d ) x  bằng 2 A. 3  . B. 7. C. 10. D. 3. 3
16.6. Cho hàm f (x) có f (
x) liên tục trên [1;3], f(1)  3 và f (x)dx  10. 
Giá trị của f (3) bằng 1  A. 13. B. 7  . C. 13. D. 7. 1 3 3
16.7. Cho hàm số f (x) liên tục trên ,  có
f (x)dx  2  và
f (x)dx  6.  Khi đó f (x)dx  bằng 0 1 0 A. 8. B. 12. C. 36. D. 4.  2 3
x khi 0  x  1  2 
16.8. Cho hàm số f (x)   . Tích phân f (x)dx  bằng 4
  x khi 1  x  2  0 7 5 A.B.  2 2 C. 1. D. 2. d d b
16.9. Cho hàm số y f (x ) liên tục trên [a;b], nếu
f (t)dt  5  và
f (u)du  2  thì f (x)dx  bằng a b a A. 3. B. 7. C. 5. D. 10. 3 3 3 16.10. Nếu
f(x) 3g(x)  dx  10         và
2f (x)  g(x) dx  6    thì
f (x)  g(x) dx    bằng 1 1 1 A. 8. B. 9. C. 6. D. 7. 2 Câu 17. Tích phân 3 x dx  bằng 1 15 17 7 15 A. B. C. D. 3 4 4 4
Lôøi giaûi tham khaûo 2 2 4 4 4 x 2  1 15 Ta có: 3 x dx      Chọn đáp án D. 4 4 4 1 1
Baøi taäp töông töï vaø môû roäng 2
17.1. Với m là tham số thực, ta có
(2mx  1)dx  4. 
Khi đó m thuộc tập hợp nào sau đây ? 1 A. (3;1). B. [1; 0).
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 27 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 C. [0;2). D. [2; 6). 2 17.2. Tích phân 3x 1 e  dx  bằng 1 1 1 A. 5 2 (e  e ). B. 5 2 e  e . 3 3 C. 5 2 e  e . D. 5 2 e  e . 2018 17.3. Tích phân 2x dx  bằng 0 2018 2 2018 2  1 A. B.  ln 2 ln 2 C. 2018 2  1. D. 2018 2 . 2 dx 17.4. Tích phân  bằng 2x  3 1 7 1 A. 2 ln  B. ln 35. 5 2 7 1 7 C. ln  D. ln  5 2 5 4 2 17.5. Giả sử
sin 3x dx a b
với với a, b  .
 Khi đó giá trị của a b bằng 2 0 1 1 A.   B.   6 6 3 1 C.   D.  10 5 1 a b b 17.6. Biết x  1dx   
với a  0 và là phân số tối giản. Khi đó 2 3
a b c bằng 3 c c 0 A. 32. B. 45. C. 96. D. 134. 2  3 17.7. Nếu
dx a 13  b 7 
với a, b   thì 2 3
2a b bằng  4  1 3x A. 13. B. 29. C. 5. D. 13. 1
17.8. Cho hàm số f (x ) có f (0)  2 và ( ) (e x 1)ex f x     , x   .  Khi đó f (x)dx  bằng 0 1 1 A. 1  ln 2. B. ln 2   2 2 4 1 1 C. e   D. e   2 2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 28 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 1      4
17.9. Cho hàm số f (x ) có f (0)  1 và f (  x)  , x    ; . Khi đó f (x )dx  bằng 2   cos x  2 2 0 1 1 A. 1  ln 2. B. ln 2   2 2 4 1 1 C. ln 3. D.  2 2  2  khi 0  x  1 3 
17.10. Cho hàm số f (x )  x  1 . Khi đó f (x)dx  bằng 2
 x 1 khi 1  x  3  0 A. 6  ln 4. B. 4  ln 4. C. 6  ln 2. D. 2  2 ln 2.
Câu 18. Số phức liên hợp của số phức z  3  2i là
A. z  3  2 . i
B. z  2  3 . i C. z  3   2i.
D. z  3  2i.
Lôøi giaûi tham khaûo
Ta có z  (a bi)  a bi nên z  3  2 .
i Chọn đáp án A.
Kieán thöùc cô baûn cuûa soá phöùc
 Số phức z a bi với a, b   và 2
i  1. Gọi a là phần thực và b là phần ảo của số phức . z
 Ta gọi z a bi là số phức liên hợp của z.
 Điểm M (a;b) trong mặt phẳng được gọi là điểm biểu diễn của số phức z a b .i 
 Môđun của số phức z a bi là 2 2
z OM a b .
 Hai số phức là bằng nhau nếu phần thực và phần ảo của chúng tương ứng bằng nhau.
 Số phức là thuần ảo  phần thực bằng 0 và số thực  phần ảo bằng 0.
Baøi taäp töông töï vaø môû roäng
18.1. Số phức liên hợp của số phức z  2  i là A. z  2   .i
B. z  2  i. C. z  2  . i
D. z  2  . i
18.2. Tìm số phức liên hợp của z i(3i  1).
A. 3  i.
B. 3  i.
C. 3  i. D. 3  . i
18.3. Số phức liên hợp của z  (1  i)(3  2i) là
A. 1  i. B. 5  . i C. 5  . i D. 1  i. z
18.4. Cho số phức z thỏa mãn
 1  i. Tìm số phức liên hợp z . 3  2i A. 5  . i
B. 1  5i. C. 5  . i D. 1  5 . i (i  1)z  2
18.5. Cho số phức z thỏa
 2  3i. Đặt z a b ,i khi đó a b bằng 1  2i
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 29 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 A. 1. B. 1. C. 6. D. 6.
18.6. Cho số phức z thoả (1  i)z  14  2 .
i Biết z a b .
i Giá trị của a b bằng A. 4. B. 14. C. 4. D. 14.
18.7. Cho số phức z  2  . i Tìm z .
A. z  3.
B. z  5.
C. z  2.
D. z  5.
18.8. Tính môđun của số phức z thỏa mãn z(2  i)  13i  1.
A. z  34.
B. z  34. 5 34 34 C. z   D. z   3 3
18.9. Cho số phức z  2  3 .
i Tìm môđun của số phức w  (1  i)z z . A. w  3. B. w  5. C. w  4  . D. w  7.
18.10. Tìm tất cả các cặp số thực (x;y) thỏa điều kiện 3x yi  2y  1  (2  x ) . i A. (1;1). B. (1;1), (0;1).
C. (1; 0), (1;1).
D. (1;1).
Câu 19. Cho hai số phức z  3  i và w  2  3i. Số phức z w bằng
A. 1  4i.
B. 1  2i.
C. 5  4i. D. 5  2i.
Lôøi giaûi tham khaûo
Ta có z w  (3  i)  (2  3i)  1  2i. Chọn đáp án B.
Baøi taäp töông töï vaø môû roäng
19.1. Cho hai số phức z  2  i và z  1  3i. Phần thực của số phức z z bằng 1 2 1 2 A. 1. B. 3. C. 4. D. 2.
19.2. Cho các số phức z  1  2i và w  2  i. Hỏi số phức u z.w có đặc điểm nào ?
A. Phần thực là 4 và phần ảo là 3.
B. Phần thực là 0 và phần ảo là 3.
C. Phần thực là 0 và phần ảo là 3i.
D. Phần thực là 4 và phần ảo là 3i.
19.3. Cho hai số phức z  1  3i và z  2  5i. Phần ảo của số phức z z z bằng 1 2 1 2 A. 2. B. 2. C. 3. D. 3.
19.4. Cho hai số phức z  5  7i và z  2  3i. Tính số phức z z z . 1 2 1 2
A. z  7  4i.
B. z  2  5i.
C. z  2  5 . i
D. z  3  10i.
19.5. Cho hai số phức z  1  3 , i w  2  .
i Tìm phần ảo của số phức u z .w. A. 7  . B. 5i.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 30 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 C. 5. D. 7i.
19.6. Cho số phức z  3  2 .
i Tìm phần thực của số phức 2 z . A. 9. B. 12. C. 5. D. 13. 2
19.7. Cho số phức z  1  2 .
i Phần thực của số phức 3
w z   z.z là z 33 31 A.   B.   5 5 32 32 C.   D. 5 5
19.8. Cho số phức z thỏa (1  i)z  1  3i  0. Tìm phần ảo của số phức w  1  iz z. A. Phần ảo là 1.
B. Phần ảo là 3.
C. Phần ảo là 2.
D. Phần ảo là 1.
19.9. Tìm phần thực a và phần ảo b của số phức 10
z  (1  i) .
A. a  0, b  32.
B. a  0, b  32i.
C. a  0, b  32.
D. a  32, b  0.
19.10. Cho số phức z a bi (a, b  ) thỏa mãn (1  i)z  2z  3  2 .
i Giá trị của a b bằng 1 1 A. B.   2 2 C. 1. D. 1.
Câu 20. Trên mặt phẳng tọa độ, điểm biểu diễn của số phức 3  2i có tọa độ là A. (2; 3). B. (2; 3). C. (3;2). D. (3;2).
Lôøi giaûi tham khaûo
Điểm biểu diễn của z a bi có tọa độ là (a;b) nên 3  2i biểu diễn bởi (3;2). Chọn đáp án D.
Baøi taäp töông töï vaø môû roäng
20.1. Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức z  3  2i ?
A. P(3;2).
B. Q(2;3).
C. N (3;2). D. M (2; 3).
20.2. Trên mặt phẳng tọa độ, biết M (1;2) là điểm biểu diễn của số phức z. Phần thực của z bằng A. 1. B. 2. C. 2. D. 1.
20.3. Trên mặt phẳng tọa độ, biết M (3;1) là điểm biểu diễn số phức z. Phần thực của z bằng A. 1. B. 3. C. 1. D. 3.
20.4. Cho hai số phức z  2  ,
i z  1  i. Trên mặt phẳng tọa độ Oxy, điểm biểu diễn số phức 1 2
2z z có tọa độ là 1 2 A. (5;1). B. (1; 5). C. (5; 0). D. (0; 5).
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 31 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
20.5. Cho hai số phức z  1  i và z  2  i. Trên mặt phẳng Oxy, điểm biểu diễn số phức z  2z 1 2 1 2 có tọa độ là A. (2;5). B. (3; 5). C. (5;2). D. (5; 3).
20.6. Cho hai số phức z  1  i và z  1  2i. Trên mặt phẳng toạ độ Oxy, điểm biểu diễn số phức 1 2
3z z có toạ độ là 1 2 A. (4;1). B. (1; 4). C. (4;1). D. (1; 4).
20.7. Trên mặt phẳng tọa độ, điểm biểu diễn số phức 2
z  (1  2i) là điểm nào dưới đây ? A. P(3; 4). B. Q(5; 4). C. N (4;3). D. M (5; 4).
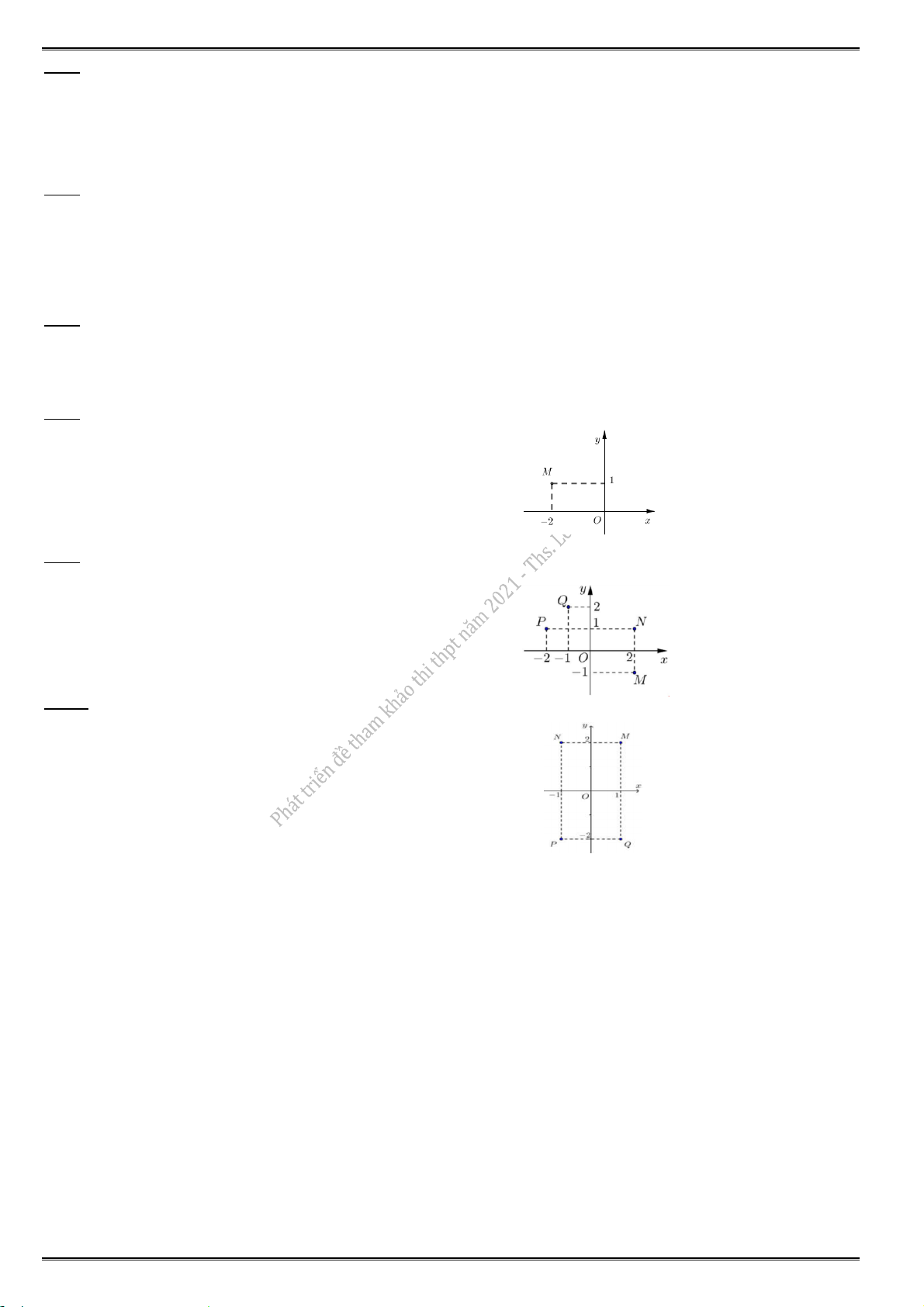
20.8. Điểm M trong hình vẽ bên là điểm biểu diễn số phức A. z  2   .i
B. z  1  2i. C. z  2  . i
D. z  1  2 . i
20.9. Điểm nào trong hình vẽ bên là điểm biểu diễn số phức z  1   2i ? A. N . B. P . C. M . D. Q.
20.10. Cho số phức z thỏa (1  i)z  3  i. Hỏi điểm biểu diễn của z là điểm nào trong các điểm sau ? A. Điểm P . B. Điểm Q. C. Điểm M . D. Điểm N .
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 32 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Câu 21. Một khối chóp có diện tích đáy bằng 6 và chiều cao bằng 6. Thể tích của khối chóp đó bằng A. 10. B. 30. C. 90. D. 15.
Lôøi giaûi tham khaûo 1 6 5
Thể tích khối chóp là V
S.h với S là diện tích đáy, h là chiều cao nên V   10. 3 3 Chọn đáp án A. 1 3 (c¹nh)  2
 Thể tích khối chóp V
 S . chiÒu cao . Đặc biệt: V   chãp 3 đ¸y Tø diÖn ®Òu 12
Xác định diện tích đáy 1 1
a b c S
ah ab sinC  (
p p a)(p b)(b c), với p  : nửa chu vi. ABC 2 a 2 2 1 2 (c¹nh)  3 S
 (tÝch hai c¹nh gãc vu«ng).  S   tam gi¸c vu«ng 2 tam gi¸c ®Òu 4 2 (c¹nh huyÒn) (®¸y lín  ®¸y bÐ  ) chiÒu cao  S    S   tam gi¸c vu«ng c©n 4 H×nh thang 2  S  dµiréng. 2  S  (c¹nh) . H×nh ch÷ nhËt H×nh vu« g n
Xác định chiều cao
Hình chóp có 1 mặt bên vuông góc với mặt đáy: Chiều cao của hình chóp là chiều cao của tam
giác chứa trong mặt bên vuông góc với đáy.
Hình chóp có 2 mặt bên vuông góc với mặt đáy: Chiều cao của hình chóp là giao tuyến của hai
mặt bên cùng vuông góc với mặt phẳng đáy.
Hình chóp có các cạnh bên bằng nhau: Chân đường cao của hình chóp là tâm đường tròn ngoại tiếp đa giác đáy. Khối chóp đều
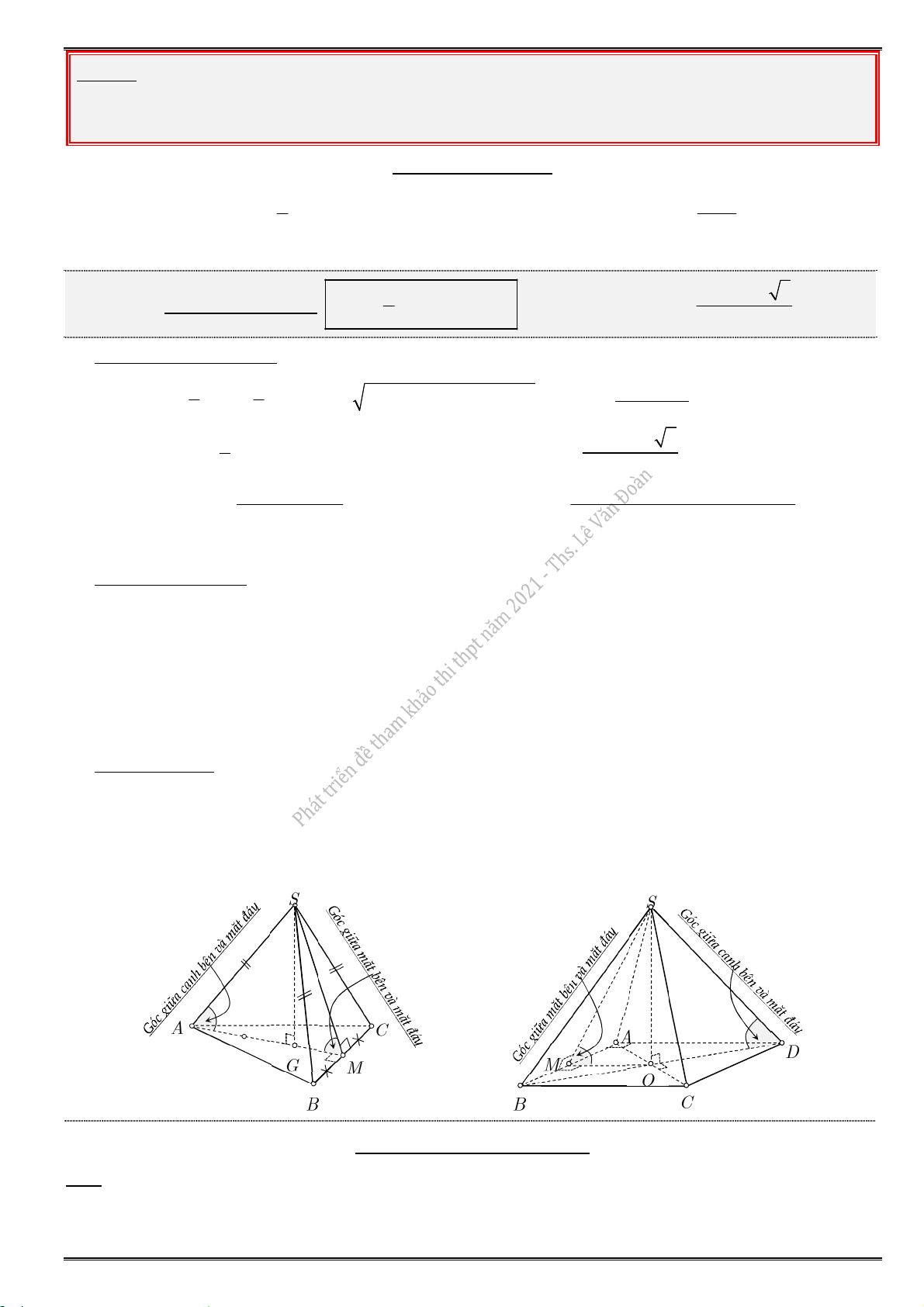
 Đáy là đa giác đều và mặt bên là những tam giác cân bằng nhau.
 Chân đường cao trùng với tâm đường tròn ngoại tiếp đa giác đáy.
 Góc giữa các cạnh bên và mặt đáy bằng nhau, góc giữa các mặt bên và mặt đáy bằng nhau.
Baøi taäp töông töï vaø môû roäng
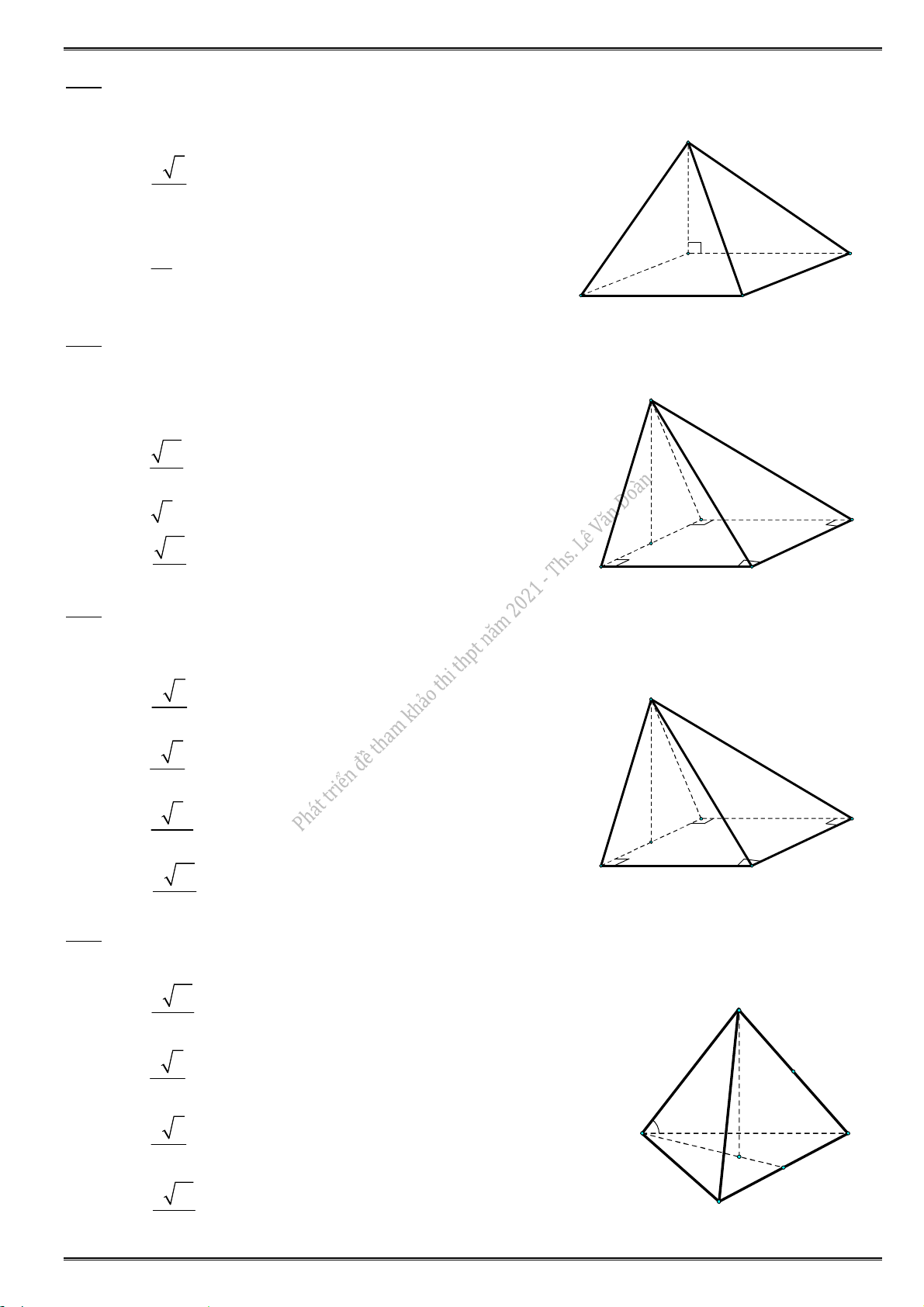
21.1. Cho tứ diện O.ABC có các cạnh O ,
A OB, OC đôi một vuông góc với nhau. Biết OA  2cm,
OB  3cm, OC  6cm. Thể tích của khối tứ diện O.ABC bằng
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 33 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 A. 3 6cm . B. 3 36cm . C. 3 12cm . D. 3 18cm .
21.2. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Biết SA  (ABCD) và SA a 3.
Thể tích của khối chóp S.ABCD bằng 3 a 3 A. 3 a 3. B.  12 3 a 3 3 a C.D.  3 4
21.3. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh ,
a SA  (ABC ) và SA a 3. Thể tích
khối chóp S.ABC bằng 3 3a 3 a A. B.  4 2 3 3a 3 a C. D.  8 4
21.4. Cho S.ABCD có đáy ABCD là hình vuông cạnh a. Biết SA  (ABCD) và SC a 3. Thể tích
của khối chóp S.ABCD bằng 3 3a 3 a A. B.  2 3 3 a 2 3 a 3 C. D.  3 3
21.5. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a và hai mặt bên (SAB), (SAC ) cùng
vuông góc với đáy. Biết SC a 3. Thể tích khối chóp S.ABC bằng 3 2a 6 3 a 6 A. B.  9 12 3 a 3 3 a 3 C. D.  4 2
21.6. Thể tích của khối tứ diện đều có cạnh là 3 bằng 4 2 A.B. 2 2. 9 9 2 C. 2. D.  4
21.7. Cho khối chóp tứ giác đều có cạnh đáy bằng a, cạnh bên bằng 2a. Thể tích của khối chóp đã cho bằng 3 2a 3 11a A. B.  6 12 3 14a 3 14a C. D.  2 6
21.8. Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên SA a 3. Thể tích của
khối chóp S.ABC bằng
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 34 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 3 35a 3 3a A. B. 24 6 3 2a 3 2a C. D. 6 2
21.9. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, mặt phẳng (SAB ) vuông góc với mặt phẳng
(ABC ) và tam giác SAB vuông cân tại S. Thể tích khối chóp S.ABC bằng 3 a 3 3 a 3 A. B. 12 24 3 a 3 3 a 3 C. D. 3 4
21.10. Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 3a. Tam giác SAB vuông cân
tại S và nằm trong mặt phẳng vuông với đáy. Thể tích hình chóp đã cho bằng 3 9a 3 A. 3 9a 3. B. 2 3 9a C. 3 9a . D. 2
Câu 22. Thể tích khối hộp chữ nhật có ba kích thước 2; 3; 7 bằng A. 14. B. 42. C. 126. D. 12.
Lôøi giaûi tham khaûo
Thể tích cần tìm là V  2  3 7  42. Chọn đáp án B.
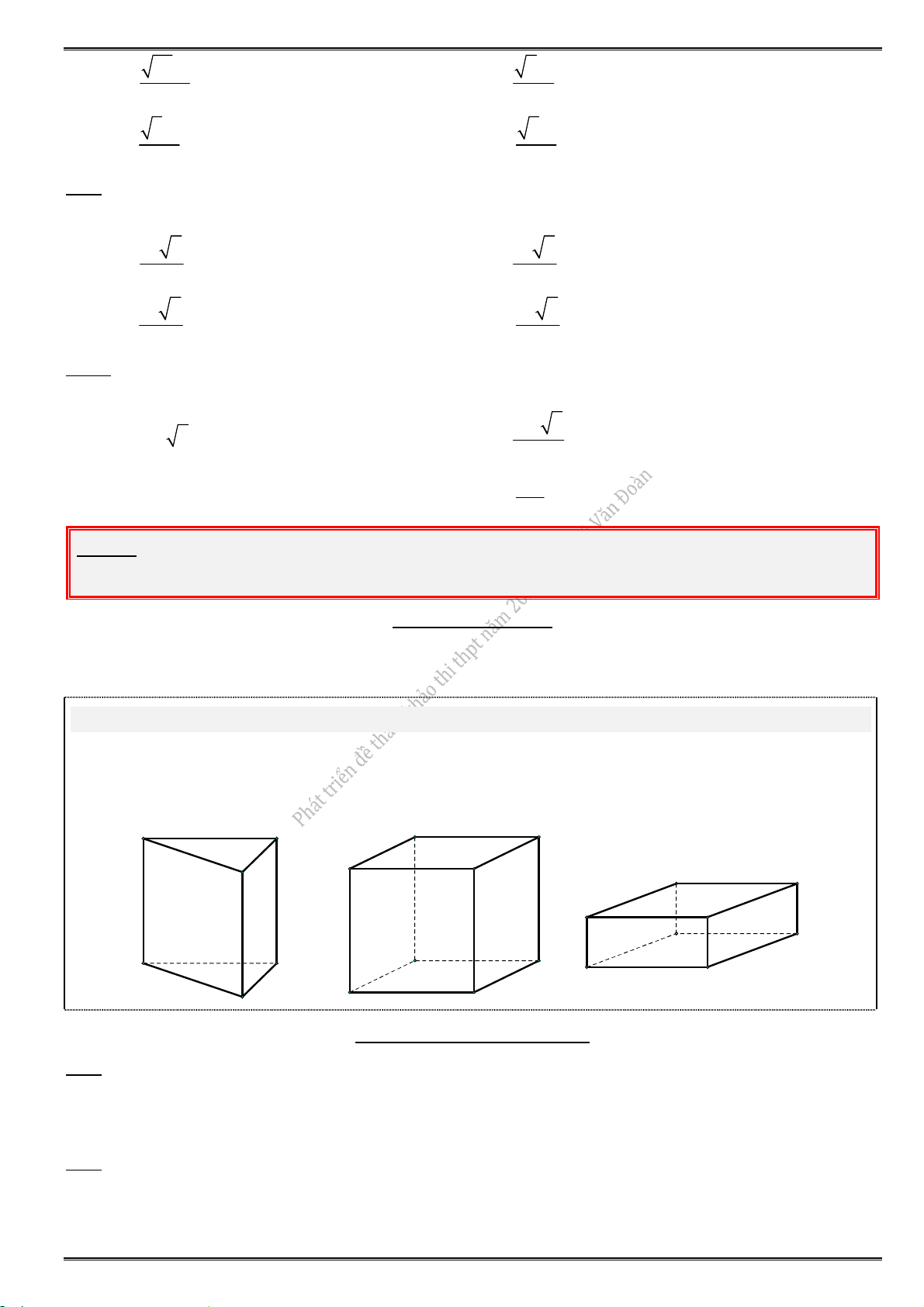
Theå tích khoái laêng truï, hoäp chöõ nhaät vaø laäp phöông
Thể tích của khối lăng trụ V B.h với B là diện tích đáy và h là chiều cao. Đặc biệt:
 Thể tích khối hộp chữ nhật V abc với a là chiều dài, b là chiều rộng và c là chiều cao.
 Thể tích khối lập phương 3
V a với a là cạnh. c b a a
Baøi taäp töông töï vaø môû roäng
22.1. Thể tích khối lập phương có cạnh 3a là A. 3 2a . B. 3 27a . C. 3 8a . D. 3 3a .
22.2. Diện tích toàn phần của một khối lập phương là 150 2
cm . Thể tích của khối lập phương bằng A. 125 3 cm . B. 100 3 cm . C. 25 3 cm . D. 75 3 cm .
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 35 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
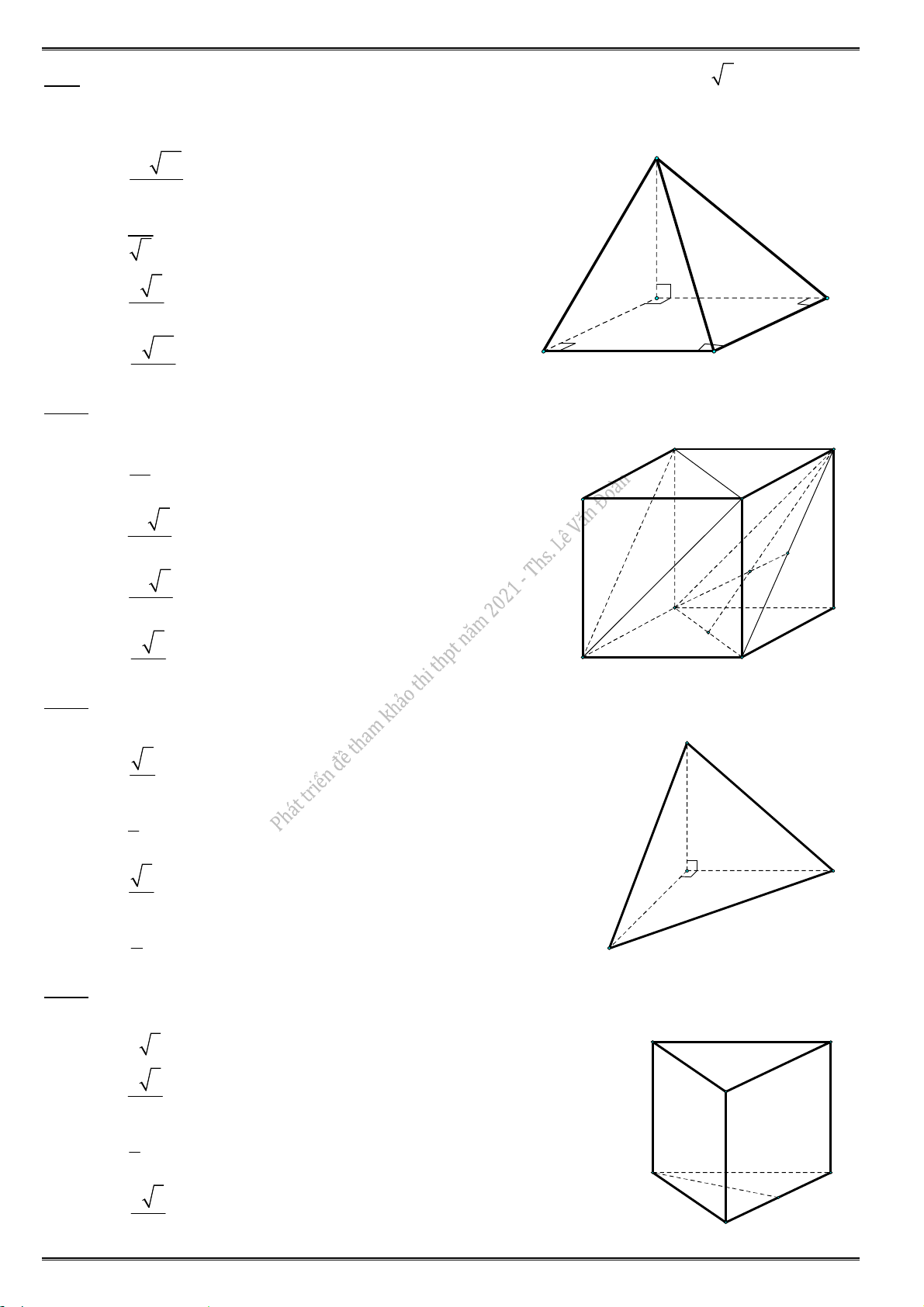
22.3. Cho khối hộp chữ nhật ABC . D AB CD
  có thể tích V. Mệnh đề nào sau đây đúng ? 1
A. V AB.BC.AA . B. V
AB.BC.AA . 3
C. V AB.AC .AA .
D. V AB.AC .AD.
22.4. Tính thể tích của khối chữ nhật ABC . D AB CD
  biết rằng AB  , a AD  2 ,
a AC   a 14. 3 a 14 A. B. 3 2a . 3 C. 3 6a . D. 3 a 5.
22.5. Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3. Thể tích khối lăng trụ đã cho bằng 9 3 27 3 A. B.  4 4 27 3 9 3 C. D.  2 2
22.6. Thể tích của khối lăng trụ tứ giác đều ABC . D AB CD
  có tất cả các cạnh là a bằng 3 a 3 A. 3 3a . B.  2 3 a 3 C. 3 a . D.  4
22.7. Cho khối lăng trụ đứng ABC.AB C
  có BB  a, đáy ABC là tam giác vuông cân tại B và
AB a. Thể tích của khối lăng trụ đã cho bằng 3 a 3 a A. B.  2 6 3 a C. D. 3 a . 3
22.8. Cho hình lăng trụ tam giác đều ABC.AB C
  có AB  2a vàAA  a 3. Thể tích khối lăng trụ
ABC.AB C   bằng 3 a A. 3 a . B.  4 3 3a C. 3 3a . D.  4
22.9. Tính thể tích của một khối lăng trụ tam giác đều ABC.AB C
  có AC   5a và đáy là tam giác đều cạnh 4a. 3 20a A. 3 12a . B.  3 C. 3 20a 3. D. 3 12a 3.
22.10. Cho khối lập phương ABC . D AB CD
  có thể tích 1. Thể tích khối lăng trụ ABC.AB C   bằng 1 1 A. B.  3 2 1 2 C.D.  6 3
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 36 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Câu 23. Công thức tính thể tích V của khối nón có bán kính đáy r và chiều cao h là 1 1
A. V r  h. B. 2 V r  h. C. V r  h. D. 2 V r  h. 3 3
Lôøi giaûi tham khaûo 1 Theo công thức SGK thì 2 V r
 h. Chọn đáp án D. 3
Xaùc ñònh caùc yeáu toá cô baûn cuûa khoái noùn
Các yếu tố cơ bản cần nắm vững của khối nón   : đường sinh. Sr  . xq nón  h : chiều cao. 2
S S Sr   r .
r : bán kính đáy. tp xq á đ y
: góc ở đỉnh. 1 1 2 VS .h r  h . Mối liên hệ: 2 2 2
  h r . nón á đ y 3 3
Baøi taäp töông töï vaø môû roäng
23.1. Cho khối nón có chiều cao h  3 và bán kính đáy r  4. Thể tích của khối nón đã cho bằng A. 16 . B. 48. C. 36. D. 4.
23.2. Thể tích khối nón có bán kính đáy là 3 cm và độ dài đường sinh là 5 cm bằng A. 12 3 cm . B. 15 3 cm . C. 36 3 cm . D. 45 3 cm .
23.3. Cho khối nón có đường sinh là 5 và diện tích đáy là 9. Thể tích của khối nón đã cho bằng A. 12 .
B. 24.
C. 36.
D. 45.
23.4. Cho hình nón có bán kính đáy bằng 2 và góc ở đỉnh bằng 60. Diện tích xung quanh của hình nón đã cho bằng A. 8. B. 16 . 8 3 16 3 C.D.  3 3 3
23.5. Cho hình nón bán kính đáy bằng a và thể tích khối nón bằng 3 a
. Diện tích toàn phần của 3 hình nón đó bằng A. 2 3 a . B. 2 4 a . C. 2 2 a . D. 2 a .
23.6. Cho hình nón có bán kính bằng 5 và góc ở đỉnh bằng 60. Diện tích xung quanh của hình nón đã cho bằng A. 50 . B. 100 . 503 1003 C. D.  3 3
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 37 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
23.7. Trong không gian, cho tam giác OAB vuông tại O có OA  3, OB  4. Diện tích toàn phần của
hình nón tạo thành khi quay tam giác OAB quanh OA bằng A. 36 .
B. 20.
C. 26.
D. 52.
23.8. Trong không gian, cho tam giác ABC vuông tại ,
A AB a và ACB  30 .  Thể tích của khối
nón nhận được khi quay tam giác ABC quanh cạnh AC bằng 3 3 a 3 3 a A.B.  3 9 C. 3 3 a . D. 3 a .
23.9. Cắt hình nón bởi một mặt phẳng đi qua trục ta được một tam giác vuông cân có cạnh huyền bằng
a 2. Thể tích của khối nón bằng 3 a 2 3 a 7 A.B.  4 3 3 a 3 a 2 C.D.  12 12
23.10. Cắt một khối nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác đều
cạnh bằng 2a. Thể tích của khối nón bằng A. 3 3a . B. 3 a . 3 3a C. 3
23a . D. 3
Câu 24. Một hình trụ có bán kính đáy r  4cm và độ dài đường sinh   3cm. Diện tích xung
quanh của hình trụ đó bằng A. 2 12cm . B. 2 48cm . C. 2 24cm . D. 2 36cm .
Lôøi giaûi tham khaûo Ta có 2 S  2 r
 l  2 4  3  24cm . Chọn đáp án C. xq Maët truï S  2 r  h. r xq O'
   h :chiều cao  đường sinh. 2
S S  2S  2 r  h  2 r . h h tp xq á đ y
r :bán kính đáy. 2 V
S .h r  h. r tru á đ y O
Baøi taäp töông töï vaø môû roäng
24.1. Cho khối trụ có độ dài đường sinh bằng a và bán kính đáy bằng .
R Thể tích khối trụ đã cho bằng A. 2 a  R . B. 2 2 a  R . 1 C. 2 a  R . D. 2 aR . 3
24.2. Một hình trụ có chiều cao bằng 6cm và diện tích đáy bằng 2
4cm . Thể tích của khối trụ bằng A. 3 8cm . B. 3 12cm . C. 3 24cm . D. 3 72cm .
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 38 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
24.3. Cho hình trụ có bán kính đáy bằng 3cm, độ dài đường cao bằng 4cm. Diện tích xung quanh của hình trụ này bằng A. 2 24cm . B. 2 22cm . C. 2 26cm . D. 2 20cm .
24.4. Diện tích toàn phần của hình trụ có bán kính đáy a và đường cao a 3 bằng A. 2 2 a ( 3 1). B. 2 a 3. C. 2 a ( 3  1). D. 2 2 a ( 3  1).
24.5. Cho hình trụ (T ) có chiều cao là 5 và diện tích xung quanh là 30. Thể tích khối trụ (T ) bằng A. 30. B. 75 . C. 15 . D. 45.
24.6. Cho khối trụ có chu vi đáy bằng 4 a
và độ dài đường cao bằng .
a Thể tích của khối trụ bằng 4 A. 2 a . B. 3 a . 3 C. 3 4 a . D. 3 16 a .
24.7. Cho hình nón có diện tích xung quanh bằng 2 3 a
và bán kính đáy bằng a. Độ dài đường sinh
của hình nón đã cho bằng A. 2 2a. B. 3a. 2a 3a C.D.  3 2
24.8. Cho một hình trụ có bán kính đáy bằng a và chiều cao bằng 2a. Một hình nón có đáy trùng với
một đáy của hình trụ và đỉnh trùng với tâm của đường tròn đáy thứ hai của hình trụ. Độ dài
đường sinh của hình nón bằng A. a 5. B. 2a. C. . a D. 3a.
24.9. Cho hình trụ có bán kính đáy bằng 2a. Một mặt phẳng đi qua trục của hình trụ và cắt hình trụ
theo thiết diện là hình vuông. Thể tích khối trụ đã cho bằng A. 3 18 a . B. 3 4 a . C. 3 8 a . D. 3 16 a .
24.10. Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB và
CD thuộc hai đáy của hình trụ với AB  4a và AC  5a. Thể tích khối trụ đã cho bằng A. 3 16 a . B. 3 12 a . C. 3 4 a . D. 3 8 a .
Câu 25. Trong không gian Oxyz, cho hai điểm (
A 1;1;2) và B(3;1; 0). Trung điểm của đoạn thẳng AB có tọa độ là A. (4; 2;2). B. (2;1;1).
C. (2; 0;2). D. (1; 0;1).
Lôøi giaûi tham khaûo 3  1 1  1 2  0
Trung điểm I của AB có tọa độ là x   2, y   1, z   1. I 2 I 2 I 2 Chọn đáp án B.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 39 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Heä truï toïa ñoä Oxyz vaø baøi toaùn lieân quan    
Định nghĩa: M (a;b;c)  OM a.i  .
b j c.k  (a;b;c). M
  (Oxy)  z  0, M  (Oyz)  x  0, M  (Oxz)  y  0  Cần nhớ:   M
Ox y z  0, M Oy x z  0, M Oz x y  0 
Tính chất: cho hai điểm (
A x ;y ;z ), B(x ;y ;z ). A A A B B B 
AB  (x x ; y y ; z z ) 2 2 2
AB  (x x )  (y y )  (z z ) . B A B A B A B A B A B Ax x y y z z      
Gọi M là trung điểm AB A B M  ; A B ; A B     2 2 2  x x x y y y z z z         
Gọi G là trọng tâm tam giác ABC A B CG  ; A B C ; A B C     3 3 3 
Baøi taäp töông töï vaø môû roäng 
25.1. Trong không gian Oxyz, cho các điểm M(1;2; 3) và N (3; 4; 7). Tọa độ của véctơ MN là A. (4; 6;10). B. (2; 3; 5). C. (2;2; 4). D. (2;2;4).
25.2. Trong không gian Oxyz, cho hai điểm (
A 1;1;2) và B(2;1;1). Độ dài đoạn AB bằng A. 2. B. 6. C. 2. D. 6.    
25.3. Trong không gian Oxyz, cho u  (1; 2  ;3) và v  ( 1  ;2; 3
 ). Môđun của u  2v bằng A. 26. B. 126. C. 85. D. 185.
25.4. Trong không gian Oxyz, cho hai điểm (
A 3;2; 3) và B(1;2;5). Tìm tọa độ trung điểm I của đoạn thẳng AB.
A. I (2;2;1). B. I (1; 0; 4). C. I (2; 0; 8).
D. I (2;2;1).
25.5. Trong không gian Oxyz, cho hai điểm (
A 1;2;4) và B(2; 4;1). Tìm tọa độ trọng tâm G của tam giác OAB. A. G(6; 3; 3). B. G(2;1;1). C. G(2;1;1). D. G(1;2;1).
25.6. Trong không gian Oxyz, cho điểm (
A 3;1;1). Hình chiếu vuông góc của điểm A trên mặt phẳng (Oyz) là điểm A. M(3; 0; 0).
B. N (0;1;1).
C. P(0;1; 0). D. Q(0; 0;1).
25.7. Trong không gian Oxyz, cho điểm (
A 2;3;5). Điểm A đối xứng với A qua trục Oy là A. A (  2;3;5). B. A (  2; 3  ; 5  ). C. A (  2  ; 3  ;5). D. A (  2  ; 3  ; 5  ).
25.8. Trong không gian Oxyz, cho ba điểm (
A 2;1;5), B(5;5;7), M(x;y;1). Nếu ,
A B, M thẳng
hàng thì tổng x y bằng
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 40 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 A. 11. B. 11. C. 3  . D. 3.
25.9. Trong không gian Oxyz, cho hai điểm (
A 0;1;2) và B(3;1;1). Tìm tọa độ điểm M sao cho   AM  3A . B
A. M(9;5; 7). B. M(9; 5; 7).
C. M (9; 5;7).
D. M (9;5;5).
25.10. Trong không gian Oxyz, cho ba điểm M (1;2; 3), N (2;3;1), P(3;1;2). Tìm tọa độ điểm Q sao cho
MNPQ là hình bình hành.
A. Q(2;6; 4).
B. Q(4;4; 0). C. Q(2; 6; 4).
D. Q(4;4; 0).
Câu 26. Trong không gian Oxyz, mặt cầu 2 2 2
(S) : x  (y  1)  z  9 có bán kính bằng A. 9. B. 3. C. 81. D. 6.
Lôøi giaûi tham khaûo
Phương trình mặt cầu là: 2 2 2 2
(x a)  (y b)  (z c)  R nên 2
R  9  R  3. Chọn đáp án B.
Xaùc ñònh caùc yeáu toá cô baûn cuûa maët caàu
Để viết phương trình mặt cầu (S ), ta cần tìm tâm I (a; ; b c) và bán kính . R Khi đó: 2 2 2 2
 (S) : (x a)  (y b)  (z c)  R .
(Tìm tâm lấy ngược dấu và R lấy căn) Ví dụ: 2 2 2
(S) : (x  1)  (y  2)  z  5  Tâm I (1;2; 0) và R  5.  2 2 2
(S) : x y z  2ax  2by  2cz d  0 với 2 2 2
R a b c d  0 (hệ số x,y, z chia 2). Ví dụ: 2 2 2
(S) : x y z  4x  6y  2z  11  0  I(2;3;1) và 2 2 2
R  2  (3)  1  11  5.
26.1. Trong không gian Oxyz, cho mặt cầu 2 2 2
(S) : (x  1)  (y  2)  (z  1)  9. Tìm tọa độ tâm I và
bán kính R của mặt cầu (S ) ?
A. I (1;2;1) và R  3.
B. I (1;2;1) và R  3.
C. I (1;2;1) và R  9.
D. I (1;2;1) và R  9.
26.2. Trong không gian Oxyz, cho mặt cầu 2 2 2
(S) : x  (y  2)  (z  2)  8. Tìm tọa độ tâm I và bán
kính R của mặt cầu (S ) ?
A. I (0;2;2), R  64.
B. I (0;2;2), R  4.
C. I (0;2; 2), R  2 2. D. I(0;2; 2
 ), R  2 2.
26.3. Trong không gian Oxyz, cho mặt cầu 2 2 2
(S) : x y z  2x  4y  6z  10  0. Xác định tâm I
và bán kính R của mặt cầu (S ) ?
A. I (1;2; 3) R  2.
B. I (1;2;3), R  2.
C. I (1;2;3), R  4.
D. I (1;2; 3), R  4.
26.4. Trong không gian Oxyz, cho mặt cầu 2 2 2
(S) : x y z  4x  2y  4z  16  0. Xác định tâm I
và bán kính R của mặt cầu (S ) ?
A. I (2;1;2), R  5.
B. I (2;1;2), R  5.
C. I (2;1;2), R  5.
D. I (4;2;4), R  13.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 41 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
26.5. Trong không gian Oxyz, cho mặt cầu 2 2 2
(S) : x y z  2x  4y  4z m  0 có bán kính
R  5. Tìm tham số thực m ? A. m  16. B. m  16. C. m  4. D. m  4.
26.6. Trong không gian Oxyz, tìm tất cả các giá trị thực của tham số m sao cho phương trình 2 2 2
x y z  2x  2y  4z m  0 là phương trình của một mặt cầu. A. m  6. B. m  6. C. m  6. D. m  6.
26.7. Trong không gian Oxyz, phương trình nào sau đây là phương trình mặt cầu có tâm I (1;2;1) và đi qua điểm ( A 0;4;1) ? A. 2 2 2
(x  1)  (y  2)  (z  1)  9. B. 2 2 2
(x  1)  (y  2)  (z  1)  3. C. 2 2 2
(x  1)  (y  2)  (z  1)  3. D. 2 2 2
(x  1)  (y  2)  (z  1)  9.
26.8. Trong không gian với hệ tọa độ Oxyz, cho hai điểm (
A 1;2;3) và B(1; 4;1). Phương trình mặt cầu
(S) có đường kính AB là A. 2 2 2
(x 1) (y 2) (z  3)  12. B. 2 2 2
x  (y  3)  (z  2)  3. C. 2 2 2
(x 1) (y  4) (z 1)  12. D. 2 2 2
x  (y  3)  (z  2)  12.
26.9. Trong không gian Oxyz, cho mặt cầu 2 2 2
(S) : (x  1)  (y  2)  (z  3)  25 và điểm M(1;1;1).
Tìm khẳng định đúng ?
A. Điểm M nằm bên ngoài (S ).
B. Điểm M nằm bên trong (S ).
C. Điểm M thuộc mặt cầu (S ).
D. Đường kính mặt cầu bằng 5.
26.10. Trong không gian Oxyz, cho mặt cầu 2 2 2
(S) : (x  1)  (y  1)  (z  2)  6 và điểm M(2;2;4).
Tìm khẳng định đúng ?
A. Điểm M nằm bên ngoài (S ).
B. Điểm M nằm bên trong (S ).
C. Điểm M thuộc mặt cầu (S ).
D. Đường kính mặt cầu bằng 6.
Câu 27. Trong không gian Oxyz, mặt phẳng nào dưới đây đi qua điểm M(1;2;1) ?
A. (P ) : x y z  0.
B. (P ) : x y z  1  0. 1 2
C. (P ) : x  2y z  0.
D. (P ) : x  2y z  1  0. 3 4
Lôøi giaûi tham khaûo
Thay tọa độ của điểm M (1;2;1) trực tiếp vào các phương trình để kiểm tra. Chọn đáp án A.
Xaùc ñònh caùc yeáu toá cô baûn cuûa maët phaúng  
 Véctơ pháp tuyến n của mặt phẳng (P) là véctơ có giá vuông góc với (P). Nếu n là một véctơ 
pháp tuyến của (P) thì k.n cũng là một véctơ pháp tuyến của (P).     
 Nếu mặt phẳng (P) có cặp véctơ chỉ phương là u , u thì (P) có véctơ pháp tuyến là n  [u ,u ]. 1 2 1 2 
 Mặt phẳng (P) : ax by cz d  0 có một véctơ pháp tuyến là n  (a; ; b c).
 Nếu M(x ;y ;z )  (P) : ax by cz d  0  ax by cz d  0. M M M M M M
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 42 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Để viết phương trình mặt phẳng (P), ta cần xác định 1 điểm đi qua và 1 VTPT: Q
 ua M(x ;y ;z )  (P) :     
 (P) : a(x x )  ( b y y )  (
c z z )  0 . V  TPT n  (a; ; b c)     (P ) 
Baøi taäp töông töï vaø môû roäng
27.1. Trong không gian Oxyz, cho mặt phẳng (P) : 3x z  2  0. Véctơ nào dưới đây là một véctơ
pháp tuyến của (P) ?  
A. n  (1; 0  1). B. n  (3; 1  ;2). 4 1  
C. n  (3;1; 0).
D. n  (3; 0; 1  ). 3 2
27.2. Trong không gian Oxyz, tọa độ vectơ pháp tuyến của mặt phẳng (Oxy) là  
A. n  (0;1; 0).
B. n  (1;1; 0). 1 2  
C. n  (0; 0;1).
D. n  (1; 0; 0). 3 4
27.3. Trong không gian Oxyz, cho ba điểm (
A 2;1; 3), B(4; 0;1) và C(10;5; 3). Véctơ nào dưới đây là
một véctơ pháp tuyến của mặt phẳng (ABC ) ?  
A. n  (1; 8;2).
B. n  (1; 2; 0). 1 2  
C. n  (1;2;2). D. n  (1; 2  ;2). 3 4
27.4. Trong không gian Oxyz, cho mặt phẳng (P) : x  2y z  5. Điểm nào dưới đây thuộc (P) ?
A. Q(2;1; 5).
B. P(0; 0;5).
C. N (5; 0; 0).
D. M (1;1; 6).
27.5. Trong không gian Oxyz, cho điểm M(m;1;6) và mặt phẳng (P) : x  2y z  5  0. Điểm M
thuộc mặt phẳng(P) khi giá trị của tham số m bằng
A. m  1. B. m  1.
C. m  3.
D. m  2.
27.6. Trong không gian Oxyz, cho điểm (
A 1;1;2017) và mặt phẳng (P) : mx  2y mz  2016  0.
Tìm tham số m để điểm A thuộc mặt phẳng (P) ? A. m  1  007. B. m  1.
C. m  1.
D. m  1009.
27.7. Trong không gian Oxyz, cho mặt phẳng (P) : 2x  2y z  4  0. Khoảng cách từ điểm M(1;2;1) đến (P) bằng A. 3. B. 4. 1 C. 1. D.  3
27.8. Trong không gian Oxyz, cho hai mặt phẳng (P) : 2x y z  0 và (Q) : 2x y z  7  0.
Khoảng cách giữa (P) và (Q) bằng A. 7. B. 7 6. 7 6 C. 6 7. D. 6
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 43 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
27.9. Trong không gian Oxyz, cho mặt phẳng (P) : 8x  4y  8z  11  0 và (Q) : 2x  2y  7  0.
Góc giữa (P) và (Q) bằng A. 45 .  B. 90 .  C. 30 .  D. 60 .  x y z
27.10. Trong không gian Oxyz, cho đường thẳng d : 
 và mặt (P) : 5x  11y  2z  4  0. 1 2  1
Góc giữa d và (P) bằng A. 90. B. 30. C. 60. D. 45.
Câu 28. Trong không gian Oxyz, véctơ nào dưới đây là một véctơ chỉ phương của đường thẳng đi
qua gốc tọa độ O và điểm M(1;2;1) ?    
A. u  (1;1;1).
B. u  (1;2;1).
C. u  (0;1; 0). D. u  (1; 2  ;1). 1 2 3 4
Lôøi giaûi tham khaûo 
Ta có OM  (1;2;1) là một véctơ chỉ phương của đường thẳng OM. Chọn đáp án D.
Xaùc ñònh caùc yeáu toá cô baûn cuûa ñöôøng thaúng
 Véctơ chỉ phương u của đường thẳng d là véctơ có giá song song hoặc trùng với đường thẳng  
d. Nếu d có một véctơ chỉ phương là u thì k.u cũng là một véctơ chỉ phương của d.     
 Nếu có hai véctơ n và n cùng vuông góc với d thì d có một véctơ chỉ phương là u  [n ,n ]. 1 2 1 2
 Để viết phương trình đường thẳng d, ta cần tìm điểm đi qua và một véctơ chỉ phương. Q
 ua M(x ;y ;z ) 
Nếu đường thẳng d :     
thì ta có hai dạng phương trình đường thẳng: V
 TCP : u  (a ;a ;a )  d 1 2 3  x
  x a t   1 
Phương trình đường thẳng d dạng tham số y
  y a t , (t  ).  2
z  z a t   3  x x y y z z
Phương trình đường thẳng d dạng chính tắc      , (a a a  0). 1 2 3 a a a 1 2 3 x
  x a t x   x a t   1  M  1    
 Điểm M(x ;y ;z )  d : y
  y a t y
y a t : luôn đúng (các giá trị t giống nhau). M M M  2 M  2   z  z a t z      z a t   3   M  3  x x y y z z x x y y z z
Điểm M(x ;y ;z )  d :    MMM       : đúng. M M M a a a a a a 1 2 3 1 2 3
Baøi taäp töông töï vaø môû roäng x  1 y  2 z
28.1. Trong không gian Oxyz, cho đường thẳng d : 
  Điểm nào sau đây thuộc d ? 1 1  3
A. Q(1; 0;2).
B. N (1;2; 0).
C. P(1;1; 3).
D. M(1;2; 0).
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 44 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 x  1 y  2 z  3
28.2. Trong không gian Oxyz, đường thẳng d :  
đi qua điểm nào dưới đây ? 1 1 1
A. M(1;2; 3). B. N (3;2;1).
C. P(1;2; 3).
D. Q(0; 0; 0). x y  2 z  1
28.3. Trong không gian Oxyz, cho đường thẳng  :  
đi qua điểm M (2;m;n). Giá trị 1 1  3 m n bằng A. 1. B. 7. C. 3. D. 1. x   1  2t 
28.4. Trong không gian Oxyz, cho đường thẳng d : y   3t (t  ). Biết (
A m;m  2;1)  d. Tìm
z  2 t 
khẳng đúng trong các khẳng định sau ? A. m  ( ;  4). B. m  [ 4  ;2).
C. m  (6;  )  .
D. m  [2; 6]. x  2 y 1 z
28.5. Trong không gian Oxyz, một véctơ chỉ phương của đường thẳng d :   là 1  2 1  
A. u  (1; 2;1).
B. u  (2;1; 0).  
C. u  (1; 2; 0).
D. u  (2;1;1).
28.6. Trong không gian Oxyz, cho hai điểm ( A 2; 3; 4
 ) và B(4;1;2). Véctơ nào dưới đây là 1 véctơ
chỉ phương của đường thẳng AB ?  
A. u  (6; 2; 3).
B. u  (3;1; 3).  
C. u  (1;2;1).
D. u  (1; 2;1). x   t 
28.7. Trong không gian Oxyz, cho một véctơ chỉ phương của đường thẳng d : y   2  là z   1 2t   
A. u  (1; 0; 2  ).
B. u  (1;2; 0).   C. u  ( 1  ;2;0). D. u  (1;2; 2  ).
28.8. Trong không gian Oxyz, gọi M , M lần lượt là hình chiếu vuông góc của M (2; 5; 4) lên trục Ox 1 2
và mặt phẳng (Oyz). Véctơ nào dưới đây là một véctơ chỉ phương của đường thẳng M M . 1 2  
A. u  (2; 0; 4).
B. u  (2; 5; 4). 3 2  
C. u  (0;3; 4). D. u  ( 2  ;0; 4). 4 1
28.9. Trong không gian Oxyz, cho đường thẳng d là giao tuyến của hai mặt phẳng (P) : x y  1  0
và mặt phẳng (Q) : x  2y z  3  0. Đường thẳng d có một véctơ chỉ phương là  
A. u  (1;1; 0).
B. u  (1;2;1).   C. u  (1;1; 3  ). D. u  (1; 1  ; 3  ).
28.10. Trong không gian Oxyz, cho đường thẳng d vuông góc với mặt phẳng (P) : 4x z  3  0. Véctơ
nào dưới đây là một véctơ chỉ phương của đường thẳng d ?  
A. u  (4;1; 3).
B. u  (4; 0; 1  ).   C. u  (4;1; 1  ). D. u  (4; 1  ;3).
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 45 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Câu 29. Chọn ngẫu nhiên một số trong 15 số nguyên dương đầu tiên. Xác suất để chọn được số chẵn bằng 7 8 7 1 A. B. C. D.  8 15 15 2
Lôøi giaûi tham khaûo 7
Trong 15 số nguyên dương đầu tiên 1, 2, 3, ,
 15, đếm được có 7 số chẵn nên xác suất cần tìm là  15 Chọn đáp án C.
Baøi taäp töông töï vaø môû roäng
29.1. Chọn ngẫu nhiên hai số khác nhau từ 27 số nguyên dương đầu tiên. Xác suất để chọn được hai
số có tổng là một số chẵn bằng 13 14 A. B.  27 27 1 365 C. D.  2 729
29.2. Gọi S là tập các số tự nhiên có bốn chữ số khác nhau được tạo từ tập E  {1; 2; 3; 4; 5}. Chọn
ngẫu nhiên một số từ tập S. Tính xác suất để số được chọn là một số chẵn ? 3 2 A. B.  4 5 3 1 C. D.  5 2
29.3. Một hộp đựng 11 viên bi được đánh số từ 1 đến 11. Lấy ngẫu nhiên 4 viên bi, rồi cộng các số
trên các bi lại với nhau. Xác suất để kết quả thu được là 1 số lẻ bằng 31 11 A. B.  32 32 16 21 C. D. 33 32
29.4. Cho 14 tấm thẻ đánh số từ 1 đến 14. Chọn ngẫu nhiên 3 thẻ. Xác suất để tích 3 số ghi trên 3 tấm
thẻ này chia hết cho 3 bằng 30 61 A. B. 91 91 31 12 C. D. 91 17
29.5. Gọi S là tất cả các số tự nhiên gồm hai chữ số khác nhau lập từ 0, 1, 2, 3, 4, 5, 6. Chọn ngẫu
nhiên hai số từ tập S. Tích xác suất để tích hai số được chọn là số chẵn ? 1 2 A. B. 6 5 5 3 C. D. 6 4
29.6. Gọi A là tập hợp các số có ba chữ số khác nhau được lập từ các chữ số 1, 2, 3, 4, 5. Chọn ngẫu
nhiên ba số từ tập hợp ,
A xác suất để trong ba số được chọn có đúng một số có mặt chữ số 4 bằng
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 46 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 2484 5 A. B. 8555 17 2518 4 C. D. 8555 17
29.7. Chọn ngẫu nhiên một số từ tập các số tự nhiên có ba chữ số đôi một khác nhau. Xác suất để số
được chọn có tổng các chữ số là chẵn bằng 61 4 A. B.  81 9 41 16 C. D. 81 81
29.8. Cho tập hợp A  {0; 1; 2; 3; 4; 5; 6}. Gọi S là tập hợp các số tự nhiên có 5 chữ số đôi một khác
nhau và luôn có mặt chữ số 5 được lập từ các chữ số thuộc tập .
A Chọn ngẫu nhiên một số từ S,
xác suất để số được chọn chia hết cho 5 bằng 1 2 A. B. 4 9 9 11 C. D. 26 26
29.9. Cho tập S  {1;2; 3; 4;....;19;20} gồm 20 số tự nhiên từ 1 đến 20. Lấy ngẫu nhiên ba số thuộc S.
Xác suất để ba số lấy được lập thành một cấp số cộng bằng 7 3 A. B.  38 38 5 1 C. D.  38 114
29.10. Có 11 cái ghế (mỗi ghế chỉ ngồi được một người) được sắp xếp trên một hàng ngang. Xếp ngẫu
nhiên 6 học sinh ngồi vào, mỗi học sinh ngồi đúng một ghế. Xác suất sao cho không có hai ghế trống nào kề nhau bằng 4 1 A. B. 85 22 1 1 C. D.  3 11
Câu 30. Hàm số nào sau đây đồng biến trên  ? x  1 A. y   B. 2
y x  2x. C. 3 2
y x x x. D. 4 2
y x  3x  2. x  2
Lôøi giaûi tham khaûo
Hàm số đồng biến trên  trước hết phải có tập xác định D  ,
 loại câu A, xét các câu khác. Chỉ có 3 2 2
(x x x)  3x  2x  1  0, x    nên 3 2
y x x x đồng biến trên .  Chọn đáp án C.
Baøi taäp töông töï vaø môû roäng
30.1. Hàm số nào sau đây nghịch biến trên  ? A. 3 2
y x  3x . B. 3 2 y x
  3x  3x  2. C. 3 y x   3x  1. D. 3
y x  2018.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 47 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
30.2. Hàm số nào dưới đây đồng biến trên khoảng ( ;   )  ? A. 3
y  3x  3x  2. B. 3
y  2x  5x  1. x  2 C. 4 2
y x  3x . D. y   x  1
30.3. Hàm số nào trong các hàm số sau đồng biến trên ( ;   )  ? A. y  3 x  2 2x  1.
B. y  7x  2 sin 3x. 4x  1 C. y  .
D. y  tan x. x  2
30.4. Hàm số nào sau đây thỏa mãn với mọi x , x  ,
x x thì f (x )  f (x ) ? 1 2 1 2 1 2 2x  1 A. 4 2
f (x)  x  2x  1.
B. f (x)   x  3 C. 3 2
f (x)  x x  1. D. 3 2
f (x)  x x  3x  1.
30.5. Hàm số nào sau đây đồng biến trên tập xác định của chúng ?
A. y  ln x. B. e x y   . x 1  
C. y      y  log x.  D. 3 1 5
30.6. Trong các hàm số sau, hàm số nào nghịch biến trên  ? xx  e   2  
A. y      y      B. 3 3 C. y  log x.
D. y  log x. 0,5 5
30.7. Điều kiện của a để hàm số ( )  (1  ln )x f x
a đồng biến trên  là A. 1 e  a  1. B. a  1. C. a  0. D. a  e.
30.8. Hỏi với giá trị nào của a thì hàm số  (3  )x y
a nghịch biến trên  ?
A. 2  a  3.
B. 0  a  1.
C. a  2. D. a  0. 30.9. Cho hàm số 3 2
y ax bx cx d. Hỏi hàm số luôn đồng biến trên  khi nào ? a
  b  0, c  0  
a b  0, c  0  A.    2 B.
a  0, b  3ac  0  2      a 0, b 3ac 0  a
  b  0, c  0  
a b c  0  C.    2 D.
a  0, b  3ac  0  2      a 0, b 3ac 0  2 mx  1  m
30.10. Hàm số y
với m là tham số. Mệnh đề nào dưới đây là đúng ? x  1
A. Hàm số đồng biến trên  \ { 1  }.
B. Hàm số đồng biến trên . 
C. Hàm số nghịch biến trên các khoảng xác định.
D. Hàm số đồng biến trên các khoảng xác định.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 48 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Câu 31. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 4 2
f (x)  x  2x  3
trên đoạn [0;2]. Tổng M m bằng A. 11. B. 14. C. 5. D. 13.
Lôøi giaûi tham khaûo Ta có 3 f (
x)  4x  4x và f (x)  0  x  0  x  1   x  1.
Trên đoạn [0;2], xét các giá trị f (0)  3, f (1)  2, f (2)  11.
Do đó M  11, m  2 và M m  13. Chọn đáp án D.
Giaù trò lôùn nhaát vaø giaù trò nhoû nhaát cuûa haøm soá
Bài toán 1. Tìm GTLN & GTNN trên đoạn [a;b ]. Bài toán 2. Tìm GTLN, GTNN trên khoảng (a;b).
 Tính y , cho y  0 tìm nghiệm x  [a;b].
 Tính y , cho y  0 tìm nghiệm x . i i
 Tính y(a), y(b), y(x )  max , y miny.
 Lập bảng biến thiên  max y, miny. i [a;b ] [a;b ] (a;b) (a;b)
miny f(a)  
miny f (b)  
Định lí. Nếu y f (x ) đồng biến trên [a;b ] [a;b]   [a;b] a b   .  và nghịch biến [ ; ]
max y f (b) 
maxy f (a)  [a;b ]  [a;b ] 
BĐT Côsi: Với a ,a ,..,a  0 có n
x x    x n x x ...x . Dấu "  "  a a    a . 1 2 n 1 2 n 1 2 n 1 2 n
Baøi taäp töông töï vaø môû roäng 3 x
31.1. Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số y   2
2x  3x  4 trên đoạn [4; 0] lần 3 lượt là M và .
m Tổng M m bằng 28 17 A.   B.   3 3 C. 5  . D. 5. x  3
31.2. Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  trên đoạn [ 1
 ;0] lần lượt là M và 1  x .
m Tổng M m bằng A. 2. B. 4. C. 3. D. 1.
31.3. Giá trị lớn nhất của hàm số 2 y x
  5x bằng 5 A. 0. B.  2 C. 6. D. 2.
31.4. Giá trị lớn nhất của hàm số 3 2
y  cos x  2 sin x  cos x bằng 58 1 A. max y   B. max y   27 3 C. max y  2.
D. max y  2. 2  cosx  2
31.5. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  bằng cos x  2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 49 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 4 4
A. max y  0, min y    B. max y  ; min y  0. 3 3
C. max y  1; min y  0.
D. max y  0; min y  1. 2
31.6. Tìm giá trị nhỏ nhất của hàm số 2
y x  trên khoảng (0; )  . x
A. min y  1.
B. min y  2. (0;) (0;)
C. min y  3.
D. min y  4. (0;) (0;) 1
31.7. Trên khoảng (0;1) hàm số 3
y x  đạt giá trị nhỏ nhất tại x bằng x  1 1 A. B.  3 3 4 3 1 1 C. D. 2 3 31.8. Cho hàm số 3 2
y x  3m x  6. Tìm tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất
của hàm số trên đoạn [0; 3] bằng 42.
A. m  1. B. m  1. C. m  1. D. m  2.
31.9. Cho hàm số f (x) có đạo hàm 2 f (  x)  x
 (x  2) (x  3), x   .
 Giá trị lớn nhất của hàm số đã
cho trên đoạn [0; 4] bằng A. f (0). B. f (2). C. f (3). D. f (4).
31.10. Cho hàm số f (x) có đạo hàm trên  và có đồ thị y f (
x) như hình vẽ. Biết rằng
f (0)  f (3)  f (2)  f (5). Giá trị lớn nhất và giá trị nhỏ nhất của hàm số f (x) trên đoạn [0;5] lần lượt là
A. f (0), f (5).
B. f (2), f (0).
C. f (1), f (3).
D. f (5), f (2).
31.11. Cho hàm số y f (x) liên tục trên đoạn [1; 3] và có đồ thị như hình. Gọi M và m lần lượt là
giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn [0;2]. Giá trị của M m bằng y A. 0. 3 2 B. 1. 1 2 x  1 O 3 C. 4.  2 D. 5.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 50 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
31.12. Cho hàm số y f (x ) xác định và liên tục trên đoạn [3; 3]. Gọi M , m lần lượt là giá trị lớn nhất
và giá trị nhỏ nhất của hàm số y f (f (x)) trên đoạn [1; 0].
Khi đó M m bằng A. 1. B. 3. C. 4. D. 6.
31.13. Cho hàm số f (x ) liên tục trên  và có đồ thị như hình. Gọi M , m lần lượt là giá trị lớn nhất và
giá trị nhỏ nhất của hàm số y f (f (sin x)) trên đoạn [0; ]. Giá trị M m bằng A. 1. B. 3. C. 4. D. 2.
31.14. Cho hàm số y f (x) xác định, liên tục trên  và có đồ thị như hình vẽ. Tập hợp các giá trị của
tham số m để phương trình 2
f (x  2x  2)  3m  1 có nghiệm thuộc đoạn [0;1] là A. [0; 4]. B. [1; 0]. C. [0;1].  1  D.  ;1   3   
31.15. Cho hàm số y f (x) liên tục trên đoạn [3; 3]. Tìm tất cả các giá trị của tham số m để phương
trình f 2f (x)  
1  m có nghiệm trên đoạn [1;0] ?
A. 3  m  1.
B. 3  m  3.
C. 0  m  1.
D. 3  m  0. 31.16. Cho hàm số 3 2
y ax bx cx d có hình dạng như hình bên dưới. Giá trị lớn nhất của biểu thức 2
P  2a cd a c  2020 bằng A. 2019. B. 2020. C. 2021. D. 2022. ax b
31.17. Cho hàm số f (x )  , (a, ,
b c  ) có bảng biến thiên như hình vẽ bên dưới. Giá trị lớn x c nhất của biểu thức 3 2
P ab  3ab c  3c bằng A. 3. B. 3  . C. 11. D. 1  1.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 51 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
31.18. Cho hàm số y f (x ) liên tục trên  và có đồ thị hàm số y f (
x) như hình vẽ. Bất phương trình 2
f (x)  x  3  m nghiệm đúng với mọi x  (1;1) khi và chỉ khi:
A. m f (0)  3.
B. m f (1)  3.
C. m f (1)  3.
D. m f (0)  3.
31.19. Cho hàm số y f (x). Hàm số y f (
x) có bảng biến thiên như hình dưới. Tìm tất cả các giá trị
của tham số m để bất phương trình 2 3
3m  3x  3f (x)  x nghiệm đúng x  (0; 3) ?
A. m f (0).
B. m f (0).
C. m f (3).
D. m f (1)  1.
31.20. Cho hàm số f (x ), hàm số y f (
x) liên tục trên  và có đồ thị như hình. Bất phương trình
f (x)  2x m (m là tham số thực) có nghiệm trên (0;2) khi và chỉ khi
A. m f (0).
B. m f (2)  4.
C. m f (0).
D. m f (2)  4. 2
Câu 32. Tập nghiệm của bất phương trình 4 3 x   27 là A. [1;1]. B. ( ;  1].
C. [ 7; 7 ]. D. [1;  )  .
Lôøi giaûi tham khaûo 2 Ta có: 4 x  2 2 3
 27  4  x  log 27  3  x  1  1  x  1. Chọn đáp án A. 3
Baát phöông trình muõ vaø loâgarít
Đặt điều kiện.
Cơ số a  (0;1)  bất phương trình đổi chiều. Nếu a  1  bất phương trình không đổi chiều.
Giao tập nghiệm với điều kiện và chọn đáp án.
Baát phöông trình muõ vaø loâgarit giaûi baèng phöông phaùp ñaët aån phuï 2 f (x ) f (x ) PP f (x )  .  a  .  a 0  t a  0.  Dạng cơ bản: 2  .
(log x)  .(log x)   0 PP  t  log x. a a a f xf x f x 1 ( ) ( ) ( )  PP aab a   b   đặt f (x ) t a  0. f (x ) a f (x ) a    2 f (x ) f (x ) 2f (x ) PP 2 f (x )  .  a.(ab)  .  b  0   chia b
 đặt t     0.  b  f x f x 1 ( ) ( )  f x f x ab
c với a.b  1 PP   đặt ( ) ( ) t ab   t
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 52 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Baøi taäp töông töï vaø môû roäng 2
32.1. Tập nghiệm của bất phương trình x 1  3 3  27 là A. (4;  )  . B. (4; 4). C. ( ;  4). D. (0; 4). 2
32.2. Tập nghiệm của bất phương trình x 2  3 3  9 là A. (5; 5). B. ( ;  5). C. (5; ). D. (0; 5).
32.3. Tập nghiệm của bất phương trình 2 x  2 là A. [0;1). B. ( ;  1). C. (0;1). D. (1; ). 2 x x  1  
32.4. Tập nghiệm của bất phương trình x 4    2   là 2
A. S  (2;  )  .
B. S  (2; ).
C. S  (2;2). D. S  ( ;
 2)  (2; ). 2x 1  0   2  
32.5. Hỏi bất phương trình x 3x 4 1 2    
có bao nhiêu nghiệm nguyên dương ? 2 A. 2. B. 4. C. 6. D. 3. 2   
32.6. Tập nghiệm của bất phương trình x 1 x x 9 5  5 là A. [ 2  ; 4]. B. [ 4  ;2]. C. ( ;  2]  [4; ). D. ( ;  4]  [2; ). 2
32.7. Tập nghiệm của bất phương trình log (36  x )  3 là 3 A. ( ;  3]  [3;  )  . B. ( ;  3]. C. [ 3  ; 3]. D. (0; 3]. 2
32.8. Tập nghiệm của bất phương trình log (31  x )  3 là 3 A. ( ;  2]. B. [ 2  ;2]. C. ( ;  2]  [2; ). D. (0;2].
32.9. Tìm tập nghiệm S của bất phương trình log (log x)  1. 3 1 2 1   
A. S  (0;1).
B. S   ;1   8 
C. S  (1; 8).
D. S  (1; 3).
32.10. Tập nghiệm S của bất phương trình log log (x 2)   0 a b Giá trị b a bằng 3   là khoảng ( ; ). 6 A. 2. B. 4. C. 3. D. 5.
32.11. Tập nghiệm của bất phương trình 4x 3.2x   2  0 là
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 53 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 A. ( ;  0)  (1; )  . B. [0;1). C. (1;2). D. (0;1).
32.12. Tập nghiệm của bất phương trình 2x 1
3   10.3x  3  0 là A. [1; 0). B. (1;1). C. (0;1]. D. [1;1].
32.13. Số nghiệm nguyên của bất phương trình 3x 9.3 x    10 là A. 7. B. 1. C. 5. D. Vô số.
32.14. Tập nghiệm của bất phương trình 9x 2.6x 4x    0 là A. (0; )  . B. .  C.  \ {0}. D. [0; )  . 2
32.15. Số nghiệm nguyên của bất phương trình (17 12 2)x (3 8)x    là A. 1. B. 2. C. 4. D. 3.
32.16. Tập nghiệm của bất phương trình 2
log x  5 log x  4  0 là 2 2 A. ( ;  2]  [16; )  . B. [2;16]. C. (0;2]  [16;  )  . D. ( ;  1]  [4; )  .
32.17. Tập nghiệm của bất phương trình 2
log x  2019 log x  2018  0 là A. 2018 [10;10 ]. B. 2018 [10;10 ). C. [1; 2018]. D. 2018 (10;10 ). 32.18. Cho hàm số 3 ( ) .e x f x x  
. Tập nghiệm của bất phương trình f (  x)  0 là  1   A. 0  ; .  B. (0;1).  3 1     1   C.  ;    .    ;  .  D. 3   3 1  2x
32.19. Tập nghiệm của của bất phương trình log  0 là 1 x 3 1     1   A.  ;    .  0  ; .  B. 3   3 1 1    1   C.  ; .    ;  .  D. 3 2  3
32.20. Bất phương trình xx 1  x x 1  1 4 5.2  
 16  0 có tập nghiệm là [a;b]. Khi đó 2 2
a b bằng A. 5. B. 10. C. 12. D. 17.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 54 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 3 3 Câu 33. Nếu 2f(x) 1  dx  5    thì f (x)dx  bằng 1 1 3 3 A. 3. B. 2. C. D. 4 2
Lôøi giaûi tham khaûo 3 3 3 3
Áp dụng tính chất tích phân 5 2f(x) 1 
 dx  2 f (x)dx  2 
f (x)dx        Chọn đáp án D. 2 1 1 1
Baøi taäp töông töï vaø môû roäng 1 1 33.1. Biết
f(x) 2x  dx  2.    Khi đó f (x)dx  bằng 0 0 A. 1. B. 4. C. 2. D. 0. 2 2
33.2. Cho hàm số f x liên tục trên  và  2 f (x) 3x   dx  10.    Khi đó f (x)dx  bằng 0 0 A. 2  . B. 2. C. 18. D. 1  8. 3
33.3. Cho f (x ), g(x ) là hai hàm số liên tục trên đoạn [1; 3] thỏa mãn
f(x) 3g(x)  dx  10    và 1 3 3
2f(x) g(x)  dx  6.      Khi đó
f (x)  g(x) dx    bằng 1 1 A. 7. B. 6. C. 8. D. 9. 3 33.4. Biết 3
F(x)  x là một nguyên hàm của hàm số f (x ) trên .  Giá trị của 1  f (x)  dx    bằng 1 A. 20. B. 22. C. 26. D. 28. 1 1 33.5. Nếu
xf (x)  2x dx f(1)    thì f (x)dx  bằng 0 0 A. 2. B. 2. C. 1. D. 1.
33.6. Cho hai hàm số f (x), g(x) xác định và liên tục trên  thỏa mãn 2
f (x)dx x x C  và 1 4 3
g(x)dx x x C.  Khi đó
f(x)g(x) dx    bằng 0 51 71 A. B.  10 105 77 C. 4. D.  60
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 55 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 2 5 33.7. Nếu 2
xf (x  1)dx  2  thì f (x)dx  bằng 1 2 A. 2. B. 1. C. 4. D. 1. 2 5 33.8. Nếu
f (3x  1)dx  20  thì f (x)dx  bằng 1 2 A. 20. B. 40. C. 10. D. 60.
33.9. Cho hàm số f (x) liên tục và có đạo hàm trên ,  thỏa mãn 2
f (2x)dx x  3x C .  Khi đó 3
f (x) x  1dx  bằng 0 94 442 A. B.  15 15 22 326 C.   D.  15 15
33.10. Biết hàm số F(x)  2x  1  x  2021 là một nguyên hàm của hàm số f (x) trên  và tích phân 2 a 5 a
f (2x  1)dx   
với là phân số tối giản. Khi đó 2
a b b bằng b b b 1 A. 8. B. 8. C. 48. D. 4  8.
2  f (x)  2 f (x)  1  
33.11. Nếu f (x) có đạo hàm trên  thỏa f (1)  1, f (2)  4 thì   dx   bằng 2  xx  1 A. 1  ln 4. B. 4  ln 2. 1 1 C.  ln 4. D. ln 2   2 2
33.12. Cho hàm số f (x) xác định và liên tục trên .
 Gọi g(x) là một nguyên hàm của hàm số x 4 4 2 x y
 Biết g(x)dx  1 
và 4g(4)  3g(3)  4. Khi đó dx  bằng 2
x f (x) 2
x f (x) 3 3 A. 2. B. 4. C. 3. D. 1. 1 1
33.13. Cho hàm số f (x) thỏa 2 x f  (  x)dx  12 
và 2f (1)  f (  1)  2  . Khi đó f (x)dx  bằng 0 0 A. 6. B. 5. C. 7. D. 8. 2  ax khi x  0  1 
33.14. Cho hàm số f (x)   a b
f (x)dx  2. 2 
(với , là các tham số thực) thỏa  Giá
3x  2bx khi x  0  1 2 2
trị nhỏ nhất của biểu thức Pf ( 1) f (1)        bằng
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 56 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 25 A. 5. B. 4 25 C. 2. D. 2 a
 x  1 khi x  1 
33.15. Cho hàm số f (x)   a b 2
có đạo hàm trên  ( , là các tham số thực). Khi đó x
b khi x  1  2 f (x )dx  bằng 1 1 19 A. B. 3 3 26 25 C. D. 3 3 3
33.16. Cho hàm số y f (x ) có đồ thị như hình vẽ, biết f (  x) dx  2. 
Giá trị của m bằng 3 3 A.   4 B. 5. C. 3  . 1 D.   2 1 2
33.17. Cho f (x) có đạo hàm trên  thỏa 2
f (x)  x  3x  2 f (x)f (  x)dx.  Khi đó f (x)dx  bằng 0 0 10 10 A. B.   3 3 26 26 C. D.   15 15 0 2
33.18. Cho f (x) là hàm số lẻ thỏa mãn
f (x)dx  2.  Khi đó f (x)dx  bằng 2 0 A. 2. B. 2  . C. 1. D. 1  . 1 1
33.19. Cho f (x ) là hàm số chẵn và liên tục trên  thỏa
f (x)dx  2.  Khi đó f (x)dx  bằng 1 0 A. 1. B. 2. 1 1 C.D.  2 4 1 f (x) 1
33.20. Xét tích phân dx  4, 
với f (x) là hàm số chẵn trên [ 1
 ;1], khi đó f (x)dx  bằng 1  2x 1 1 A. 2. B. 16. C. 4. D. 8.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 57 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Câu 34. Cho số phức z  3  4i. Môđun của số phức (1  i)z bằng A. 50. B. 10. C. 10. D. 5 2.
Lôøi giaûi tham khaûo
Dùng tính chất môđun của tích: (1  i)z  1  i . 3  4i  2  5  5 2. Chọn đáp án D.
Baøi taäp töông töï vaø môû roäng
34.1. Cho hai số phức z  2  3i và z  1  2i. Môđun của số phức (z  2)z bằng 1 2 1 2 A. 15. B. 5 5. C. 65. D. 137. 2z
34.2. Cho hai số phức z  3  4i và z  4  3 .
i Môđun của số phức 1 bằng 1 2 3z2 5 2 A. B.  2 3 C. 1. D. 2. 25
34.3. Cho số phức z  3
 4 .i Tính môđun của số phức w iz   z A. 2. B. 2. C. 5. D. 5.
34.4. Tìm môđun của số phức w  (1  z)z , biết z thỏa mãn 2
(3  2i)z  (2  i)  4  i. A. 2. B. 10. C. 8. D. 2.
34.5. Cho hai số phức z  2  3i và z  1  2i. Tính môđun của số phức z  (z  2)z . 1 2 1 2 A. 15. B. 5 5. C. 65. D. 137.
34.6. Cho số phức z  2  3 .
i Tìm môđun của số phức w  (1  i)z z . A. 3. B. 5. C. 4. D. 7.
34.7. Cho hai số phức z  1  i và z  2  3 .
i Tính môđun của số phức z z . 1 2 1 2 A. 13. B. 5. C. 1. D. 5.
34.8. Cho hai số phức z  1  3i và w  1  .
i Môđun của số phức z.w bằng A. 2 5. B. 2 2. C. 20. D. 8.
34.9. Tìm môđun của số phức 2 4 2n 2016
z  1  i i      i      i , n  .
A. z  2.
B. z  1.
C. z  1008.
D. z  2006.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 58 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 1  i
34.10. Cho số phức z thỏa (2  i)z
 5  i. Tìm môđun của số phức 2
w  1  2z z . 1  i A. w  4. B. w  2 7. C. w  10. D. w  100.
34.11. Cho số phức z thỏa mãn điều kiện (1  i)z  4z  7  7i. Tìm môđun của số phức . z A. z  3. B. z  5. C. z  5. D. z  3.
34.12. Cho z số phức thỏa mãn z  (1  2i)z  2  4 .
i Tìm môđun của số phức . z A. z  3. B. z  5. C. z  5. D. z  3. 2 z
34.13. Cho số phức z a bi thỏa mãn 3z  (2  i)
 7 17i. Trên mặt phẳng tọa độ, điểm biểu z
diễn của số phức z là
A. M(2;3).
B. N (2; 3).
C. P(2; 3).
D. Q(2;3). 2 z
34.14. Cho số phức z thỏa mãn 5z(2  i)  17  19i  9
 Trên mặt phẳng tọa độ, điểm biểu diễn z
của số phức z a bi là
A. Q(4; 3).
B. N (3;4).
C. M (4; 3). D. P(3; 4). 2
34.15. Cho số phức z a bi thỏa mãn 2z.z  (5  7i) z  (17  i)z . Trên mặt phẳng tọa độ, điểm
biểu diễn của số phức z khác gốc tọa độ là A. N (1;2). B. P(2;1). C. Q(2;1). D. M (1;2). 2 z
34.16. Cho số phức z thỏa mãn (3  i)z  24  12i  (5  i)
 Tỉ số giữa phần thực và phần ảo là z A. 3  B. 3. 2 5 C. D.   7 3 2
34.17. Cho số phức z thỏa mãn z.z (6  8i)  (5  i) z  (
 23  73i)z. Tỉ số giữa phần thực và phần ảo bằng 2 2 A. B.  5 7 C. 2. D. 3.
34.18. Cho các số phức z thỏa (z  2  i)(z  2  i)  16. Biết rằng tập hợp các điểm biểu diễn các số
phức w  (1  i)z  2i là một đường tròn. Tìm bán kính R của đường tròn đó.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 59 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 A. r  2 B. r  5. C. r  4 2. D. r  3.
34.19. Cho các số phức z thỏa (z i)(z i)  9. Biết trong mặt phẳng tọa độ các điểm biểu diễn của
số phức w  (3  4i)z  2  i cùng thuộc một đường tròn cố định có bán kính là A. r  5. B. r  14. C. r  23. D. r  15.
34.20. Cho các số phức z thỏa z.z z(3  i)  z (3  i)  9  0. Biết rằng tập hợp các điểm biểu diễn
các số phức w  2i.z  5i là một đường tròn. Tìm bán kính R của đường tròn đó. A. 5. B. 1. C. 2. D. 7.
Câu 35. Cho hình hộp chữ nhật ABCD.AB CD
  có AB AD  2 và AA  2 2 (tham khảo hình
vẽ bên). Góc giữa đường thẳng CA và mặt phẳng (ABCD) bằng A. 30 .  B. 45 .  C. 60 .  D. 90 . 
Lôøi giaûi tham khaûo
Góc cần tìm là ACA  . AA
Vì đáy hình vuông nên AC AB 2  2 2 và tan
 1   45. Chọn đáp án B. AC
Xaùc ñònh goùc giöõa ñöôøng thaúng vaø maët phaúng
Cần nhớ: “Góc giữa đường thẳng và mặt phẳng là góc tạo bởi nó và hình chiếu của nó lên mặt phẳng”.
B.1. Tìm giao điểmAB  (P )  A (1)
B.2. Tìm hình chiếu H của B lên mặt phẳng (P).
Đặt câu hỏi: “Đường nào qua B và vuông góc với (P ) ?
Trả lời: BH  (P ) tại H (2) (nếu chưa có thì dựng)
Từ (1),(2), suy ra AH là hình chiếu của AB lên mặt phẳng (P). 
Do đó góc giữa đường thẳng AB và (P ) là góc giữa AB và AH, chính là góc BAH .
B.3. Sử dụng hệ thức lượng trong tam giác để tìm góc (thường sử dụng tan).
Baøi taäp töông töï vaø môû roäng
35.1. Cho hình lập phương ABCD.AB CD
  có cạnh bằng a (minh họa như hình bên). Góc giữa
đường thẳng AB và mặt phẳng (BDD B  )  bằng D' C' A. 60. A' B' B. 90. C. 45. D C D. 30. A B
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 60 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
35.2. Cho hình lập phương ABCD.AB CD
  (tham khảo hình vẽ bên). Tang góc giữa đường
thẳng BD và mặt phẳng (ADD A  )  bằng 3 A.  3 6 B.  3 2 C.  2 2 D.  6
35.3. Cho hình hộp chữ nhật ABCD.AB CD
  có AB AA  a, AD  2a. Gọi góc giữa đường chéo
AC và mặt phẳng đáy(ABCD) là . Khi đó tan bằng 5 A.  5 B. 5. 3 C.  3 D. 3.
35.4. Cho hình lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác vuông cân tại ,
A AB AA  a
(tham khảo hình vẽ bên). Tính tang của góc giữa đường thẳng BC  và mặt phẳng 2 A.  2 6 B.  3 C. 2. 3 D.  3
35.5. Cho hình lăng trụ đứng ABC.AB C
  có đáy ABC là một tam giác vuông cân tại B, AB a,
BB  a 3. Góc giữa đường thẳng AB và mặt phẳng (BCC B  ) bằng A. 30 .  B. 90 .  C. 60 .  D. 45 . 
35.6. Cho hình lập phương ABC . D AB CD
 . Gọi O là trung điểm của của AC . Tính tan với
là góc tạo bởi BO và mặt phẳng (ABCD). A. 3. B. 2. C. 1. 2 D. 2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 61 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
35.7. Cho hình lập phương ABCD.AB CD   cạnh bằng .
a Gọi M, N lần lượt là trung điểm của cạnh AC và B C
 , là góc giữa đường thẳng MN và mặt phẳng (AB CD  )
 . Giá trị sin bằng 1 A.  2 2 5 B.  5 2 C.  2 5 D.  2
35.8. Cho hình hộp chữ nhật ABCD.AB CD
  có cạnh AB a 2, AD a 6 và AA  2a 2. Tính
côsin của góc giữa đường thẳng B D
 và mặt phẳng (B DC  ). 35 A.  38 1 B.  3 1 C.  6 3 D.  11
35.9. Cho hình lập phương ABCD.AB CD   có cạnh bằng ,
a gọi là góc giữa đường thẳng AB và mặt phẳng (BB DD
 ). Khi đó sin bằng 3 A.  4 3 B.  2 3 C.  5 1 D.  2
35.10. Cho hình chóp S .ABC có SA vuông góc với mặt phẳng (ABC ), SA a 2, tam giác ABC vuông
cân tại B và AC  2a (minh họa như hình). Góc giữa đường thẳng SB và mặt phẳng (ABC ) bằng A. 30. B. 45. C. 60. D. 90.
35.11. Cho hình chóp S .ABCD có đáy ABCD là hình chữ nhật, AB a 2, AD a, SA vuông góc
với đáy và SA a (minh họa như hình bên dưới). Góc giữa đường thẳng SC và mặt phẳng (SAB) bằng
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 62 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 S A. 90. B. 60. C. 45. A D D. 30. B C
35.12. Cho tứ diện đều ABCD có cạnh bằng a (minh họa như hình bên). Côsin góc giữa đường thẳng
AB và mặt phẳng (BCD) bằng A 3 A.  2 3 B.  3 B D C. 1. 2 C D.  3
35.13. Cho hình chóp S .ABC có các mặt ABC và SBC là các tam giác đều và nằm trong hai mặt
phẳng vuông góc với nhau (minh họa như hình bên). Góc giữa đường thẳng SA và mặt phẳng (ABC ) S bằng A. 45. B. 75 .  A C C. 60. D. 30. B
35.14. Cho hình chóp S .ABCD có đáy ABCD là hình vuông cạnh a, SD a và SD vuông góc với
mặt phẳng đáy (minh họa như hình bên). Góc giữa đường thẳng SA và mặt phẳng (SBD) bằng S A. 45. 1 B. arcsin  4 C. 30. D C D. 60. A B
35.15. Cho hình chóp S .ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều có đường
cao SH vuông góc với (ABCD) (minh họa như hình bên). Gọi là góc giữa đường thẳng BD
và mặt phẳng (SAD). Giá trị của sin bằng S 6 A.  4 1 B.  2 3 C. A D 2 H 10 D. B C 4
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 63 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
35.16. Cho hình chóp S .ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt
đáy và SA  2a. Gọi M là trung điểm của SC (minh họa như hình bên). Gọi là góc giữa
đường thẳng BM và mặt phẳng (ABC ). Giá trị của cos bằng S 7 A.  14 M B. 1. 5 C. A C 7 21 D.  7 B
35.17. Cho tứ diện ABCD có tam giác BCD đều cạnh a, AB vuông góc với (BCD), AB  2a và M
là trung điểm đoạn AD (minh họa như hình bên). Gọi là góc giữa đường thẳng CM với mặt BCD A phẳng (
). Khi đó giá trị của tan bằng A. 1. M 2 3 B.  3 B D C. 2. 6 D.  3 C
35.18. Cho hình chóp tứ giác đều S .ABCD có tất cả các cạnh bằng a. Gọi M là trung điểm SD (minh
họa như hình bên). Gọi là góc giữa đường thẳng BM và (ABCD). Khi đó tan bằng S 2 A.  2 M B. 2. C. 0, 5. A D 1 D.  3 B C
35.19. Cho chóp S .ABC có SA vuông góc với đáy, tam giác ABC vuông tại B. Biết SA AB BC S
(xem hình vẽ). Góc giữa đường thẳng SB và mặt phẳng (SAC ) bằng A. 30. B. 45. A C C. 60. D. 90 .  B
35.20. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, AB a, SA AB, SC BC,
SB  2a. Gọi M, N là trung điểm S ,
A BC. Gọi là góc giữa MN với (ABC ). Tính cos .
A. cos  1. 6 B. cos   3
C. cos  0, 5. 10 D. cos   5
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 64 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Câu 36. Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 2 và độ dài cạnh bên bằng 3
(tham khảo hình vẽ). Khoảng cách từ S đến mặt phẳng (ABCD) bằng A. 7. B. 1. C. 7. D. 11.
Lôøi giaûi tham khaûo
Gọi O là tâm của đáy thì d[S,(ABCD)]  SO. AC 2 2 Ta có OA  
 2 và SA  3 nên 2 2 2
SO SA OA  3  2  7. Chọn đáp án B. 2 2
Khoaûng caùch töø moät ñieåm ñeán ñöôøng thaúng
Khoaûng caùch töø chaân ñöôøng cao ñeán maët beân
Tæ soá khoaûng caùch (töø ñieåm ñeán maët)
Baøi toaùn 1. Cho tứ diện SABC có SA  (ABC ). Baøi toaùn 2. Tính khoảng cách từ điểm M (không
Tính khoảng cách từ điểm chân A đến mặt (SBC ). phải là chân đường cao) đến mặt phẳng (P). d M (điểm cũ)
A chân đường cao (điểm mới) I H K (điểm cắt) P
B1. Tìm giao tuyến của mặt bên và mặt đáy.
Có d qua M và d  (P)  I . Dựng MH  (P ).
(SBC )  (ABC )  BC .
Suy ra: d(M,(P))  MH (khó tìm). điểm cũ A  H BC   B2. Dựng hình 
AI  (SBC ). IM AI SH d M P   d A P  Do đó ( ;( ))
( ,( )) (bài toán 1) IA Suy ra d( ;
A (SBC ))  AI . điểm mới điểm cắt
Khoaûng caùch giöõa hai ñöôøng thaúng cheùo nhau
Khoaûng caùch giöõa hai ñöôøng cheùo nhau vaø
Khoaûng caùch giöõa hai ñöôøng thaúng cheùo nhau
vuoâng goùc nhau laø ñoä daøi ñoaïn vuoâng chung
vaø khoâng vuoâng goùc nhau
Cho hình chóp S.ABC có đáy là tam giác vuông cân Cho hình chóp S.ABCD có SA  (ABCD). Tính tại ,
A mặt bên (SBC ) là tam giác đều và nằm trong khoảng cách giữa cạnh bên SB và cạnh thuộc mặt
mặt phẳng vuông góc với mặt phẳng đáy. Xác định phẳng đáy AC .
khoảng cách giữa hai đường thẳng SA và BC . S K A B
B1. Tìm giao điểm: SB  (ABCD)  B. H CAH d  
B2. Qua B, dựng d AC và  .
Dễ dàng chứng minh được BC  (SH ). A AK SH   BC S .
A Từ chân H, dựng HK SA và có
d(AC,SB)  d(AC,(SHB))  d( , A (SHB))
HK BC. Suy ra: d(S , A BC )  KH .
B3. Sử dụng bài toán 1 d( ,
A (SHB))  AK.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 65 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Baøi taäp töông töï vaø môû roäng
36.1. Cho hình chóp S.ABCD có đáy là hình vuông cạnh .
a Biết SA vuông góc với đáy và SA a
(tham khảo hình vẽ). Khoảng cách từ điểm A đến mặt phẳng (SBD) bằng 2a S A.  3 a B.  3 a C. A 2 3 D a 2 D.  6 B C
36.2. Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng ,
a SA vuông góc với mặt phẳng
(ABCD). Biết góc giữa SC và mặt phẳng (ABCD) bằng 60 (tham khảo hình vẽ). Khoảng cách
từ điểm B đến mặt phẳng (SCD) bằng S a 10 A.  5 a 2 B.  2 a A C. D 2 a 42 D. B C 7
36.3. Cho hình chóp S.ABC có đáy là tam giác vuông ở ,
A biết SA  (ABC ) và AB  2a, AC  3a,
SA  4a (tham khảo hình vẽ). Khoảng cách từ điểm A đến mặt phẳng (SBC ) bằng S 12a 61 A.  61 B. 2a. a 43 C. A C 12 6a 29 D.  29 B
36.4. Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC ), AC AD  4, AB  3,
BC  5 (tham khảo hình vẽ). Khoảng cách từ điểm A đến mặt phẳng (BCD) bằng 12 D A.  34 60 B.  769 769 C. A C 60 34 D.  12 B
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 66 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
36.5. Hình chóp S.ABCD có đáy là hình thoi cạnh ,
a góc BAC  60 , SA vuông góc với mặt phẳng
(ABCD), góc giữa hai mặt phẳng (SBC ) và (ABCD) bằng 60 (tham khảo hình vẽ). Khoảng
cách từ điểm A đến mặt phẳng (SBC ) bằng S a 2 A.  3 B. 2a. A 3a D C.  4 D. . a B C
36.6. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 1. Tam giác SAB đều và nằm
trong mặt phẳng vuông góc với mặt đáy (ABCD) (tham khảo hình vẽ). Khoảng cách từ điểm B
đến mặt phẳng (SCD) bằng S A. 1. 21 B.  3 C. 2. A D 21 D.  7 B C
36.7. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh ,
a mặt bên SAB là tam giác
đều và nằm trong mặt phẳng vuông góc với đáy (tham khảo hình vẽ). Khoảng cách từ trọng tâm
G của tam giác SAB đến mặt phẳng (SBC ) bằng S a 3 A. 6 a 5 B. 3 2 2a A D C. 9 a 21 B C D. 21
36.8. Cho hình chóp tam giác đều S.ABC có SA  2a và AB  3a. Gọi M là trung điểm SC (tham
khảo hình vẽ). Khoảng cách từ điểm M đến mặt phẳng (SAB) bằng 3 21 S A. a. 14 3 3 M B. a. 2 3 3 A C C. a. 4 3 21 D. a. 7 B
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 67 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
36.9. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB a, AD a 3. Cạnh bên SA
vuông góc với đáy và SA  2a (tham khảo hình vẽ). Khoảng cách từ điểm C đến mặt phẳng (SBD) bằng S 2a 57 A.  19 2a B.  5 a 5 A C.D 2 a 57 D.B C 19
36.10. Cho hình phương ABCD.AB CD
  có tất cả các cạnh bằng a (tham khảo hình vẽ). Khoảng cách
từ trọng tâm G của tam giác ABD đến mặt phẳng (CB D  )  bằng D' A' 2a A.  81 C' B' 2a 3 B.  3 2a 3 G C. D 9 A a 6 D.  18 C B
36.11. Cho tứ diện OABC có O ,
A OB, OC đôi một vuông góc với nhau và OA OB OC a (tham
khảo hình vẽ). Khoảng cách giữa hai đường thẳng OA và BC bằng C 3 A. a. 2 1 B. a. 2 O B 2 C. a. 2 3 D. a. 2 A
36.12. Cho hình lăng trụ đều ABC .AB C
  có tất cả các cạnh bằng .
a Gọi M là trung điểm của cạnh
BC (tham khảo hình bên). Khoảng cách giữa hai đường thẳng AM và B C  là A' C' A. a 2. a 2 B' B.  2 1 C. a. 2 A C a 2 M D.  4 B
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 68 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
36.13. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh ,
a cạnh SA a và vuông góc với
mặt đáy (ABCD) (tham khảo hình bên). Khoảng cách giữa hai đường thẳng SC và BD bằng a 3 S A.  4 a 6 B.  3 a C. A 2 B a 6 D. D C 6
36.14. Cho hình chóp S.ABCD có đáy là hình vuông cạnh ,
a SA a và SA vuông góc với đáy (tham
khảo hình bên). Khoảng cách giữa hai đường thẳng AB và SC bằng S A. a 2. a 2 B.  2 a 2 C. A 3 D a 2 D.  4 B C
36.15. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB  3a, BC  4a. Cạnh bên
SA vuông góc với đáy. Góc tạo bởi giữa SC và đáy bằng 60. Gọi M là trung điểm của AC
(tham khảo hình bên). Khoảng cách giữa hai đường thẳng AB và SM bằng a 13 S A.  2 10a 3 B.  79 A 5a C C.  2 D. 5a 3. B
36.16. Cho tứ diện đều ABCD cạnh bằng .
a Gọi M là trung điểm của CD (tham khảo hình bên).
Khoảng cách giữa hai đường thẳng AC và BM bằng A a 22 A.  11 a 2 B.  3 B a 3 C C.  3 M 5a D.  2 D
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 69 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
36.17. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, cạnh bên SA a 5, mặt bên
SAB là tam giác cân đỉnh S và thuộc mặt phẳng vuông góc với mặt phẳng đáy (tham khảo hình
bên). Khoảng cách gữa hai đường thẳng AD và SC bằng S 2a 5 A.  5 4a 5 B.  5 a 15 AD C. 5 2a 15 D. B C 5
36.18. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB a, cạnh bên SA vuông góc
với mặt đáy và SA a 2. Gọi M là trung điểm của AB (tham khảo hình bên). Khoảng cách
giữa hai đường thẳng SM và BC bằng S a A.  2 a 2 B.  3 a 3  A C. C 3 M a 2 D.  2 B
36.19. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và hai điểm M, N lần lượt là trung điểm
AB, AD. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy (tham khảo hình vẽ).
Khoảng cách giữa hai đường thẳng SM và NC bằng S 3a A. 4 B. . a 5a C. A 10 D 3 5a D.  10 B C
36.20. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a, AD  2a, SA vuông góc với
mặt phẳng đáy và SA a (tham khảo hình vẽ). Gọi M là trung điểm của CD. Khoảng cách
giữa hai đường thẳng SD và BM bằng S a 21 A.  21 2a 21 B.  21 2a 7 A D C.  7 M a 7 D. B C 7
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 70 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Câu 37. Trong không gian Oxyz, mặt cầu có tâm là gốc tọa độ O và đi qua điểm M(0; 0;2) có phương trình là A. 2 2 2
x y z  2. B. 2 2 2
x y z  4. C. 2 2 2
x y  (z  2)  4. D. 2 2 2
x y  (z  2)  2.
Lôøi giaûi tham khaûo
Bán kính của mặt cầu là MO  2, và do có tâm ở (
O 0;0;0) nên có phương trình là 2 2 2
x y z  4. Chọn đáp án C.
Vieát phöông trình maët caàu
 Tâm I(a;b;c) 
Dạng 1. Cơ bản 2 2 2 2 (S) : 
 (S) : (x a)  (y b)  (z c)  R .  BK : R 
Dạng 2. Viết phương trình mặt cầu (S) có tâm I và đi qua điểm . A  Tâm I
Phương pháp: (S ) :  . 
BK : R IA 
Dạng 3. Viết phương trình mặt cầu (S) có đường kính AB, với ,
A B cho trước.  Tâm I 
là trung điểm của AB .
Phương pháp: (S) :  1 
 BK : R AB  2
Dạng 4. Viết phương trình mặt cầu (S) có tâm I và tiếp xúc với (P).  Tâm I
Phương pháp: (S ) :  . 
BK : R d d I ;(P)     
Cần nhớ: (Oxy) : z  0, (Oyz) : y  0, (Oxz) : x  0.
Dạng 5. Viết phương trình mặt cầu (S) có tâm I và cắt mặt phẳng (P) theo giao tuyến là một
đường tròn có bán kính r.  Tâm I
Phương pháp: (S) :  . 2 2
 BK : R d (I;(P))  r  
Cần nhớ: Chu vi đường tròn C  2r và diện tích 2 S r . đt
Dạng 6. Viết phương trình mặt cầu (S) tâm I và tiếp xúc với đường d.  Tâm I
Phương pháp: (S ) :  . 
BK : R d(I;d)  Nếu 2 2 2 2 2 2 I(a; ;
b c)  d(I ;Ox)  b c , d(I;Oy)  a c , d(I;Oz)  a b .
Dạng 7. Viết phương trình mặt cầu (S) có tâm I và cắt đường thẳng d tại hai điểm ,
A B.  Tâm I  Phương pháp: 2 (S) :    . AB 2 
 BK : R d (I;(P ) )          2  
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 71 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Baøi taäp töông töï vaø môû roäng
37.1. Trong không gian Oxyz, mặt cầu có tâm I (1;1;1) và diện tích bằng 4 có phương trình là A. 2 2 2
(x  1)  (y 1)  (z 1)  4. B. 2 2 2
(x  1)  (y  1)  (z  1)  1. C. 2 2 2
(x  1)  (y  1)  (z  1)  4. D. 2 2 2
(x 1)  (y 1)  (z  1)  1.
37.2. Trong không gian Oxyz, mặt cầu (S ) có tâm có tâm I (1;3;2) và đi qua điểm ( A 5;1; 4) là A. 2 2 2
(x  1)  (y  3)  (z  2)  24. B. 2 2 2
(x  1)  (y  3)  (z  2)  24. C. 2 2 2
(x  1)  (y  3)  (z  2)  24. D. 2 2 2
(x  1)  (y  3)  (z  2)  24.
37.3. Trong không gian Oxyz, cho hai điểm I (1;1;1) và (
A 1;2; 3). Phương trình của mặt cầu có tâm I
và đi qua điểm A là A. 2 2 2
(x  1)  (y  1)  (z  1)  29. B. 2 2 2
(x  1)  (y  1)  (z  1)  5. C. 2 2 2
(x  1)  (y  1)  (z  1)  25. D. 2 2 2
(x  1)  (y  1)  (z  1)  5.
37.4. Trong không gian Oxyz, cho điểm M (1;2; 3). Gọi I là hình chiếu vuông góc của M trên trục
Ox. Phương trình nào dưới đây là phương trình mặt cầu tâm I bán kính IM ? A. 2 2 2
(x 1)  y z  13. B. 2 2 2
(x 1)  y z  13. C. 2 2 2
(x  1)  y z  17. D. 2 2 2
(x  1)  y z  13.
37.5. Trong không gian Oxyz, cho hai điểm (
A 2;1;1), B(0; 3;1). Mặt cầu (S) đường kính AB có phương trình là A. 2 2 2
x  (y  2)  z  3. B. 2 2 2
(x 1)  (y  2)  z  3. C. 2 2 2
(x  1)  (y  2)  (z  1)  9. D. 2 2 2
(x 1)  (y  2)  z  9.
37.6. Trong không gian Oxyz, cho điểm I (1;2; 3). Hỏi phương trình nào sau đây là phương trình mặt
cầu (S ) có tâm I và tiếp xúc với trục tung Oy. A. 2 2 2
(x  1)  (y  2)  (z  3)  10. B. 2 2 2
(x  1)  (y  2)  (z  3)  10. C. 2 2 2
(x  1)  (y  2)  (z  3)  10. D. 2 2 2
(x 1)  (y  2)  (z  3)  9.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 72 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
37.7. Trong không gian Oxyz, phương trình mặt cầu (S ) có tâm I (1;2; 3) và tiếp xúc với mặt phẳng (Oxy) là A. 2 2 2
(x  1)  (y  2)  (z  3)  9. B. 2 2 2
(x 1)  (y  2)  (z  3)  14. C. 2 2 2
(x  1)  (y  2)  (z  3)  14. D. 2 2 2
(x 1)  (y  2)  (z  3)  9.
37.8. Trong không gian Oxyz, cho điểm (
A 2;1;1) và mặt phẳng (P) : 2x y  2z  1  0. Phương
trình của mặt cầu tâm A và tiếp xúc với (P) là A. 2 2 2
(x  2)  (y 1)  (z 1)  9. B. 2 2 2
(x  2)  (y 1)  (z 1)  2. C. 2 2 2
(x  2)  (y 1)  (z  1)  4. D. 2 2 2
(x  2)  (y 1)  (z 1)  36.
37.9. Trong không gian Oxyz, biết mặt phẳng (P) : x  2y z  6  0 cắt trục Oy tại A và (P) cắt x  1 y  4 z  2 đường thẳng d :  
tại B. Phương trình mặt cầu có tâm A và bán kính AB 2 2 1 là A. 2 2 2
x  (y  3)  z  9. B. 2 2 2
x  (y  3)  z  3. C. 2 2 2
x  (y  3)  z  3. D. 2 2 2
x  (y  3)  z  3.
37.10. Trong không gian Oxyz, cho tam giác ABC với (
A 2;2; 0), B(1; 0;2), C(0;4; 4). Phương trình mặt
cầu có tâm A và đi qua trọng tâm G của tam giác ABC là A. 2 2 2
(x  2)  (y  2)  z  4. B. 2 2 2
(x  2)  (y  2)  z  25. C. 2 2 2
(x  2)  (y  2)  z  16. D. 2 2 2
(x  2)  (y  2)  z  5.
37.11. Trong không gian Oxyz, cho hình bình hành ABCD có (
A 1;2;1), B(2; 1  ; 3), C( 3  ;5;1).
Phương trình mặt cầu tâm D và đi qua điểm A là A. 2 2 2
(x  4)  (y  8)  (z  5)  64. B. 2 2 2
(x  4)  (y  8)  (z  3)  65. C. 2 2 2
(x  4)  (y  8)  (z  3)  64. D. 2 2 2
(x  4)  (y  8)  (z  5)  65.
37.12. Gọi I là hình chiếu của M (3;1;2) lên mặt phẳng (Oxy). Phương trình nào sau đây là phương
trình mặt cầu tâm I bán kính IM . A. 2 2 2
(x  3)  (y  1)  (z  2)  4. B. 2 2 2
(x  3)  (y  1)  z  4. C. 2 2 2
(x  3)  (y  1)  (z  2)  2.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 73 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 D. 2 2 2
(x  3)  y z  4.
37.13. Trong không gian Oxyz, cho điểm I (1;1;1) và mặt phẳng (P) : 2x y  2z  4  0. Mặt cầu (S )
tâm I cắt (P) theo một đường tròn bán kính r  4. Phương trình của (S ) là A. 2 2 2
(x  1)  (y 1)  (z 1)  16. B. 2 2 2
(x 1)  (y 1)  (z  1)  9. C. 2 2 2
(x 1)  (y 1)  (z  1)  5. D. 2 2 2
(x  1)  (y 1)  (z 1)  25.
37.14. Trong không gian Oxyz, viết phương trình mặt cầu (S ) có tâm I (2; 3; 4) biết mặt cầu (S ) cắt
mặt phẳng tọa độ (Oxz) theo một hình tròn giao tuyến có diện tích bằng 16. A. 2 2 2
(x  2)  (y  3)  (z  4)  25. B. 2 2 2
(x  2)  (y  3)  (z  4)  5. C. 2 2 2
(x  2)  (y  3)  (z  4)  16. D. 2 2 2
(x  2)  (y  3)  (z  4)  9.
37.15. Trong không gian Oxyz, cho mặt cầu 2 2 2
(S) : (x  1)  (y 1)  (z  1)  25 có tâm I và mặt
phẳng (P ) : x  2y  2z  7  0. Thể tích của khối nón đỉnh I và đường tròn đáy là giao tuyến
của mặt cầu (S ) và mặt phẳng (P) bằng
A. 12. B. 48. C. 36. D. 24.
37.16. Trong không gian Oxyz, cho mặt cầu (S ) có tâm I (2; 3; 4) và biết (S ) cắt mặt phẳng (Oxz) theo
một đường tròn giao tuyến có diện tích bằng 16 .
Diện tích xung quanh của khối nón có đỉnh là
I và đường tròn đáy là giao tuyến của mặt cầu (S) và mặt phẳng (P) bằng
A. 12. B. 20 .
C. 24.
D. 36.
37.17. Trong không gian Oxyz, phương trình mặt cầu đi qua hai điểm (3
A ;1;2), B(1;1;2) và có tâm thuộc trục Oz là A. 2 2 2
x y z  2z  10  0. B. 2 2 2
(x 1)  y z  11. C. 2 2 2
x  (y 1)  z  11. D. 2 2 2
x y z  2y 11  0.
37.18. Trong không gian Oxyz, phương trình mặt cầu (S) đi qua hai điểm ( A 2;1;0), B( 2  ; 3;2) và có x  1 y z
tâm I nằm trên đường thẳng d :   là 2 1 2 A. 2 2 2
(x  1)  (y  1)  (z  2)  17. B. 2 2 2
(x  1)  (y  1)  (z  2)  9. C. 2 2 2
(x  1)  (y  1)  (z  2)  5.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 74 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 D. 2 2 2
(x  1)  (y  1)  (z  2)  16.
37.19. Trong không gian Oxyz, mặt cầu (S) có tâm I(5; 6; 8), cắt trục Ox tại ,
A B sao cho tam giác
IAB vuông tại I có phương trình là A. 2 2 2
(x  5)  (y  6)  (z  8)  200. B. 2 2 2
(x  5)  (y  6)  (z  8)  20. C. 2 2 2
(x  5)  (y  6)  (z  8)  100. D. 2 2 2
(x  5)  (y  6)  (z  8)  10.
37.20. Trong không gian Oxyz, mặt cầu (S ) đi qua điểm O và cắt các tia Ox, Oy, Oz lần lượt tại các điểm ,
A B, C khác O thỏa mãn tam giác ABC có trọng tâm là điểm G(2; 4; 8). Tọa độ tâm của mặt cầu (S ) là 4 8 16   A.  ; ; .  3 3 3  B. (1;2; 3). 2 4 8   C.  ; ; .  3 3 3 D. (3; 6;12).
Câu 38. Trong không gian Oxyz, đường thẳng đi qua hai điểm (
A 1;2;1) và B(2;1;1) có phương trình tham số là x   1  2t     x   1  t x   1  t x   1  t         A. y   2  3t . y   2  3t . y   3  2t . y   1  2t .  B. C. D. z   1  2t               z 1 2t  z 2 t  z t 
Lôøi giaûi tham khaûo 
Ta có AB  (1;3; 2) là vector chỉ phương của đường thẳng, nó đi qua điểm (
A 1;2;1) nên có phương x   1  t 
trình tham số là y
  2  3t , t  .   Chọn đáp án A. z   1  2t 
Vieát phöông trình ñöôøng thaúng
Để viết phương trình đường thẳng, ta cần tìm một điểm đi qua và một véctơ chỉ phương. x
  x a t   1  d : y
  y a t , (t  ).   2
 Qua M(x ;y ;z )   d :      z  
  z a t      3 VTCP : u
(a ;a ;a )   d 1 2 3  x x y y z z d :      , (a a a  0). 1 2 3 a a a 1 2 3
Một số dạng viết phương trình mặt phẳng thường gặp (tham khảo):
Dạng 1. Viết phương trình tham số và chính tắc (nếu có) của đường thẳng d đi qua A và B.
 Qua A (hay B)  B
Phương pháp. Đường thẳng d :    . 
 VTCP : u AB A d 
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 75 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Dạng 2. Viết phương trình đường thẳng d dạng tham số và chính tắc (nếu có), biết d đi qua điểm
M và song song với đường thẳng . 
 Qua M(x ;y ;z ) 
Phương pháp. Ta có d :       . 
 VTCP : u ud  
Dạng 3. Viết phương trình đường thẳng d dạng tham số và chính tắc (nếu có), biết d đi qua điểm
M và vuông góc với mặt phẳng (P) : ax by cz d  0. d  Qua MM
Phương pháp. Ta có d :    . 
 VTCP : u n  (a; ; b c)  d (P )  P
Dạng 4. Viết phương trình tham số và chính tắc của đường thẳng d là giao tuyến của hai mặt
phẳng (P) và (Q) cho trước.
 Qua A  (P)  (Q) A
Phương pháp. Ta có d :     . 
 VTCP : u  [n ,n ]  d (P ) (Q) 
Dạng 5. Viết phương trình tham số và chính tắc (nếu có) của đường thẳng d đi qua điểm M và
vuông góc với hai đường thẳng d , d cho trước. 1 2  Qua M
Phương pháp. Ta có d :     .  VT P
C : u  [u ,u ] d d d  1 2
Dạng 6. Viết phương trình đường thẳng d qua M và song song với hai mặt phẳng (P), (Q).  Qua M
Phương pháp. Ta có d :     . 
 VTCP : u  [n ,n ]  d P Q
Dạng 7. Viết phương trình đường thẳng d qua M , vuông góc d  và song song mặt (P).  Qua M
Phương pháp. Ta có d :     . 
 VTCP : u  [u ,n ]  d d P
Dạng 8. Phương trình đường thẳng d nằm trong mặt (P ), song song mặt (Q) và qua M .  Qua M
Phương pháp. Ta có d :     . 
 VTCP : u  [n ,n ]  d P Q
Baøi taäp töông töï vaø môû roäng
38.1. Trong không gian Oxyz, phương trình đường thẳng d đi qua hai điểm (
A 1;2;3), B(3;6;1) là x  2 y  2 z  1 x  1 y  2 z  3 A.    B.    1 4 2 3 1 1 x  3 y  6 z  1 x  3 y  1 z  1 C.    D.    1 4 2 1 4 2
38.2. Trong không gian Oxyz, phương trình trung tuyến AM của tam giác ABC với (3 A ;1;2),
B(3;2;5), C(1;6;3) là x   1  t   x   1  4t     A. y   1  3t . y   3  3t .  B. z   8  4t       z 4 1t 
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 76 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 x   3  4t   x   1  3t     C. y   1  3t . y   3  4t .  D. z   2 t       z 4 t 
38.3. Trong không gian Oxyz, cho tam giác ABC có (
A 1; 3;2), B(2; 0;5) và C(0;2;1). Phương trình
trung tuyến AM của tam giác ABC là x  1 y  3 z  2 x  1 y  3 z  2 A.    B.    2 2 4 2 4 1 x  2 y  4 z  1 x  1 y  3 z  2 C.    D.    1 3 2 2 4 1
38.4. Trong không gian Oxyz, phương trình đường thẳng d đi qua điểm M (1; 3; 4) và song song với trục hoành là x   1  t   x   1     A. y   3 . y   3  t .  B. z   4      z 4  x   1   x   1     C. y   3 . y   3 .  D. y   4 t       y 4 t 
38.5. Trong không gian Oxyz, cho ba điểm (0
A ;1; 3), B(1;0;1), C(1;1;2). Phương trình đường
thẳng d đi qua điểm A và song song với BC là x y  1 z  3 x  1 y z  1 A.    B.    2 1 1 2 1 1 x y  1 z  3 x  1 y z  1 C.    D.    2 1 1 2 1 1
38.6. Trong không gian Oxyz, phương trình đường thẳng đi qua điểm M (2;1; 0) và song song với x y  2 z  1 đường thẳng d :   có dạng 1 2 3 x  2 y  1 z x  2 y  1 z A.    B.    1 2 3 5 1 1 x  2 y  1 z x  2 y  1 z C.    D.    1 2 3 5 1 1
38.7. Trong không gian Oxyz, phương trình đường thẳng đi qua (
A 1;2;3) và vuông góc với mặt phẳng (Oyz ) là x   1  t   x   1  t     A. y   2  2t . y   2  2t .  B. z   3  3t        z 3 3t  x   1  t   x   1 t     C. y   2 . y   2  2t .  D. z   3        z 3 3t 
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 77 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
38.8. Trong không gian Oxyz, đường thẳng đi qua điểm M (2;1;4) và vuông góc với mặt phẳng
(P) : 2x  2y  3z  8  0 có phương trình là x  2 y  2 z  3 x  2 y  1 z  4 A.    B.    2 1 4 2 2 3 x  2 y  1 z  4 x  2 y  2 z  3 C.    D.    2 2 3 2 1 4
38.9. Trong không gian Oxyz, đường thẳng đi qua điểm (
A 2;3; 4) và vuông góc với mặt phẳng
(P) : x  3y  5  0 có phương trình là x   2  t   x   2  t     A. y   3  3t . y   3  3t .  B. z   4  5t      z 4  x   1  2t   x   2  1t     C. y   3  3t . y   3  3t .  D. z   4t       z 4 
38.10. Trong không gian Oxyz, viết phương trình đường thẳng d đi qua điểm M (2;1;5), đồng thời  
vuông góc với hai véctơ a  (1; 0;1) và b  (4;1; 1  ). x  2 y  1 z  5 x  2 y  1 z  5 A.    B.    1 5 1 1 5 1 x  2 y  1 z  5 x  1 y  5 z  1 C.    D.    1 5 1 2 1 5 x  1 y  3 z  1 x  1 y z
38.11. Cho M (1;1; 3) và hai đường thẳng d :   ; d :    Phương 1 3 2 1 2 1 3 2
trình đường thẳng đi qua M , đồng thời vuông góc với d và d là 1 2 x   1t   x   t      A. y   1  t . y    t B. 1 .  z   1  3t       z 3 t  x   1t   x   1 t     C. y   1  t . y   1  t .  D. z   3  t       z 3 t 
38.12. Viết phương trình đường thẳng đi qua (
A 2;1;5), đồng thời song song với mặt phẳng x  1 y z  3
(P) : 2x y  2z  1  0 và vuông góc với đường :    2 1 3 x  2 y  1 z  5 x  2 y  1 z  5 A.    B.    5 2 4 5 2 4 x  2 y  1 z  5 x  5 y  2 z  4 C.    D.    5 2 4 2 1 5
38.13. Trong không gian Oxyz, đường thẳng đi qua M (1;1;2), song song đồng thời với hai mặt phẳng
(P) : x y  2z  1  0 và (Q) : x  2y  3z  3  0 có phương trình
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 78 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 x  1 y  1 z  2 x  1 y  1 z  2 A.    B.    1 5 3 1 5 3 x  1 y  1 z  2 x  1 y  5 z  3 C.    D.    1 5 3 1 1  2
38.14. Trong không gian Oxyz, cho (
A 1;2; 3), B(3; 5;7), C (1;4;1). Viết phương trình đường
thẳng vuông góc với mặt phẳng (ABC ) tại trọng tâm G của tam giác ABC. x  1 y  1 z  3 x  1 y  1 z  3 A.    B.    2 4 5 2 4 5 x  1 y  1 z  3 x  1 y  1 z  3 C.    D.    2 4 5 2 4 5
38.15. Trong không gian Oxyz, viết đường thẳng  nằm trong mặt phẳng (P) : 2x y z  4  0 và x y  1 z  2
vuông góc với đường thẳng d :  
 Biết  đi qua điểm M(0;1;3). 1 2 3 x y  1 z  3 x y  1 z  3 A.    B.    1 1 1 1 1 1 x y  1 z  3 x y  1 z  3 C.    D.    1 1 1 1 1 1
38.16. Trong không gian Oxyz, phương trình đường thẳng d qua (
A 1;2; 3), đồng thời d cắt và vuông
góc với trục hoành Ox là x   1   x   1     A. y   2 . y   2  2t .  B. z   3  3t       z 3 3t  x   1  t   x   1     C. y   2 . y   2 .  D. z   3  3t        z 3 3t  x  2 y  1 z  1
38.17. Trong không gian Oxyz, cho đường d :  
và mặt (P) : 2x y  2z  0. 1 1 1
Đường thẳng  nằm trong (P ), cắt d và vuông góc với d có phương trình là x   1  t   x   1 t     A. y   2 . y   2 .  B. z   t        z t  x   1t   x   1  t     C. y   2  t . y   2 .  D. z   t       z t 
38.18. Trong không gian Oxyz, cho ba điểm (
A 2; 0; 0), B(0; 3; 0), C (0; 0; 4). Gọi H là trực tâm tam giác
ABC. Tìm phương trình chính tắc của đường thẳng OH . x y z x y z A.    B.    4 3 2 3 4 2 x y z x y z C.    D.    6 4 3 4 3 2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 79 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Câu 39. Cho hàm số f (x), đồ thị của hàm số y f (
x) là đường cong như hình bên. Giá trị lớn nhất  3 
của hàm số g(x)  f (2x)  4x trên đoạn  ;2  bằng 2   
A. f (0). B. f ( 3  )  6.
C. f (2)  4. D. f (4)  8.
Lôøi giaûi tham khaûo  3  x ;2   Đặt 2 t 2x   
t  [3; 4].
Hàm số trở thành h(t)  f (t)  2t, t   [ 3  ;4]. t  0  Ta có: h (
t)  f (t)  2, h (t)  0  f (t)  2  , t  [3; 4]. t  2 
Từ bảng biến thiên, suy ra:
max h(t)  h(2)  f (2)  4. Chọn đáp án C.
Baøi taäp töông töï vaø môû roäng
39.1. Cho hàm số y f (x) liên tục trên  có đồ thị y f (
x) cho như hình vẽ dưới đây. Đặt 2
g(x)  2f (x)  (x  1) . Mệnh đề nào dưới đây đúng ?
A. min g(x )  g(1). [3;3 ]
B. max g(x)  g(1). [3;3]
C. max g(x )  g(3). [3;3] D.   max g(x). [3;3]
39.2. Cho hàm số y f (x) liên tục trên  có đồ thị y f (
x) cho như hình vẽ dưới đây. Giá trị nhỏ 1 nhất của hàm số 3
y f (x)  x x bằng 3 2 2 A. f (2)   B. f ( 1  )   3 3 2 2 C. D. f (1)   3 3 3 2 x 3x 3x
39.3. Cho đồ thị y f (
x) như hình vẽ. Xét hàm số g(x)  f (x)     20. Giá trị nhỏ 3 4 2
nhất của hàm số g(x) trên đoạn [ 3  ;1] bằng A. g(1).
B. g(1).
C. g(3). D. g( 3  )  g(1).
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 80 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
39.4. Cho hàm số y f (x). Có bảng xét dấu đạo hàm như sau: 2 Bất phương trình 2 ( )  ex x f x
m đúng x  (0;2) khi 1
A. m f (0)  1.
B. m f (1)   e 1
C. m f (0)  1.
D. m f (1)   e
39.5. Cho hàm số y f (x). Hàm số y f (
x) có đồ thị như hình vẽ bên dưới. Tìm các giá trị của m để 2
m  2f (x  2)  x  4x  3 nghiệm đúng x  ( 3  ; )  .
A. m  2f (0)  1.
B. m  2f (0)  1.
C. m  2f ( 1  ).
D. m  2f ( 1  ).
39.6. Cho hàm số y f (x). Hàm số y f (
x) có đồ thị như hình vẽ bên. Tìm m để bất phương trình 2 m 2 f (x 1) 2x      x  4  
nghiệm đúng x  [ 4  ;2].
A. m  2f (0)  1.
B. m  2f ( 3  )  4.
C. m  2f (3)  16.
D. m  2f (1)  4.
39.7. Cho hàm số y f (x) liên tục trên  và có đồ thị như hình vẽ. Gọi S là tập hợp tất cả các giá trị
nguyên của tham số m để phương trình f (sin x)  3 sin x m có nghiệm thuộc khoảng (0; ) .
Tổng các phần tử của S bằng A. 9  . B. 1  0. C. 6  . D. 5.
39.8. Cho hàm số y f (x) có đồ thị như hình bên dưới. Có bao nhiêu số nguyên của tham số m để 1 x   
phương trình f   1  x m có nghiệm thuộc đoạn [2;2] ? y 3 2  6 A. 8. 2 O 4 x B. 9. 2 2 C. 10. 4 D. 11.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 81 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
39.9. Cho hàm số y f (x). Hàm số y f (
x) có bảng biến thiên như hình bên dưới. Bất phương trình 2 ( ) 3ex f x  
m có nghiệm x  ( 2  ;2) khi
A. m f ( 2  )  3. B. 3
m f (2)  3e . C. 3
m f (2)  3e .
D. m f ( 2  )  3.
39.10. Cho hàm số y f (x) có đồ thị như hình vẽ. Hàm số y f (2 sin x)  4 sin x có giá trị lớn nhất
trên khoảng (0; ) bằng A. 7. B. 5. C. 6. D. 4.
39.11. Cho hàm số y f (x) có đồ thị hàm số như hình vẽ. Hàm số y f (cos x)  cos x  6 có giá trị     
nhỏ nhất trên khoảng   ;   2 2 bằng A. 3. B. 0. C. 1. D. 2.
39.12. Cho hàm số y f (x). Đồ thị y f (
x) như hình bên dưới. Giá trị nhỏ nhất và giá trị lớn nhất
của hàm số trên đoạn [0; 3] lần lượt là
A. f (1), f (0).
B. f (2), f (0).
C. f (1), f (3).
D. f (0), f (3).
39.13. Cho y f (x) có đồ thị của y f (
x) như hình vẽ dưới. Đặt M  max f (x), m  min f (x). Giá [2;6] [2;6]
trị của biểu thức P M m bằng
A. f (0)  f (2).
B. f (5)  f ( 2  ).
C. f (5)  f (6).
D. f (0)  f ( 2  ).
39.14. Cho hàm số y f (x) có đạo hàm f (
x) xác định và liên tục trên . Hàm số y f (x) có đồ thị
như hình vẽ dưới. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y f x  trên đoạn [ 2
 ;1]. Giá trị của M m bằng
A. f (1)  f (0).
B. f (1)  f (2). C. f ( 2  )  f ( 1  ). D. f ( 1
 )  f(0).
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 82 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 39.15. Cho hàm số 5 4 3 2
f (x)  ax bx cx dx ex n. Đồ thị hàm số y f (
x) như hình vẽ. Đặt
M  max f x , m  min f x . Giá trị của M m bằng [ 3  ;2] [ 3  ;2] 1  
A. f    f (2).  2
B. f (0, 5)  f (0). C. f ( 3
 )  f (2). D. f ( 3
 )  f (0).
39.16. Cho hàm số y f (x) xác định, liên tục trên  và f (2)  0. Hàm số y f (
x) có đồ thị như hình
vẽ bên dưới. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số g(x)  f (x) trên trên đoạn [ 1
 ;3]. Giá trị của M và m lần lượt là
A. M f ( 1
 ), m f (3).
B. M f (3) , m f ( 1  ) .
C. M f (1) , m f (2) .
D. M f (1) , m f (3) . 39.17. Cho hàm số 3 2
f (x)  ax bx cx d có đồ thị (C ). Biết đồ thị (C ) tiếp xúc với đường thẳng
y  4 tại điểm có hoành độ âm và đồ thị của hàm số y f (x) như hình vẽ bên dưới. Giá trị lớn
nhất của hàm số y f (x) trên [0; 3] bằng A. 20. B. 60. C. 22. D. 3.
39.18. Cho hàm số f (x) liên tục trên  và có đồ thị f (
x) như hình vẽ. Đặt 2
g(x)  2f (x)  (x  1) . Khi
đó giá trị nhỏ nhất của hàm số y g(x) trên đoạn [ 3  ;3] bằng
A. g(0). B. g(1). C. g( 3  ).
D. g(3). 39.19. Cho hàm số 4 3 2
y x ax bx  1 (a, b các tham số) đạt giá trị nhỏ nhất tại x  0. Khi a b
đạt giá trị lớn nhất thì 4 3 3
b ab b  1 bằng A. 9. B. 7. C. 5. D. 6.
39.20. Cho hàm số y f (x) có đồ thị như hình bên. Tổng tất cả các giá trị của tham số m sao cho giá 2
trị nhỏ nhất của hàm số y
f(x) m   
 trên đoạn [1;1] bằng 9 là A. 3. B. 1. C. 2. D. 4.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 83 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Câu 40. Có bao nhiêu số nguyên dương y sao cho ứng với mỗi y có không quá 10 số nguyên x thỏa mãn x 1
(2   2)(2x y)  0 ? A. 1024. B. 2047. C. 1022. D. 1023.
Lôøi giaûi tham khaûo Ta có: x 1
(2   2)(2x y)  0 với x   và y    .     x 1  1 1 2   2  0 x     1  x       TH 1. Nếu    2   2 . 2x   y  0  x   log y x   log y   2   2   1
Theo yêu cầu bài toán, một y có không quá 10 số nguyên x, mà x    10  log y  1 2 2 10 1 2 y 2   
. Mà y nguyên dương  Không tồn tại y thỏa mãn yêu cầu bài toán.     x 1  1 1 2   2  0 x     1  x       TH 2. Nếu    2   2 . 2x   y  0  x   log y x   log y   2   2   1
Theo yêu cầu bài toán, một y có không quá 10 số nguyên x, mà x    0  log y  10 2 2 10   0  y  2  1024 y  
y  {1; 2; 3...;1023; 1024} có 1024 giá trị. Chọn đáp án A.
Baøi taäp töông töï vaø môû roäng
40.1. Có bao nhiêu giá trị nguyên dương của y sao cho mỗi giá trị của y có ít nhất 1 số nguyên x,
nhưng không quá 6 số nguyên ? A. 2048. B. 2016. C. 1012. D. 2023.
40.2. Số giá trị nguyên dương của tham số m để bất phương trình x2 (2
 2)(2x m)  0 có không
quá 6 nghiệm nguyên là A. 29. B. 33. C. 32. D. 31.
40.3. Số giá trị nguyên của tham số m để bất phương trình 2
2 log x  (m  1) log x m  1  0 chứa 2 2
không quá 10 số nguyên dương là A. 6. B. 8. C. 7. D. 9.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 84 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
40.4. Số giá trị nguyên dương của tham số m để bất phương trình 2x 2  x m 2 3 3 .(3  
 1)  3m  0 có
không quá 30 nghiệm nguyên là A. 28. B. 29. C. 30. D. 31.
40.5. Số giá trị nguyên của tham số m để bất phương trình 2
ln(x  2x m)  2 ln(2x 1) chứa đúng 2 số nguyên là A. 4. B. 8. C. 3. D. 9. 2 2 2 log x
40.6. Gọi S là tập hợp nghiệm nguyên của bất phương trình 2 2
mx  log (mx )  2  log x. Có bao 2 2
nhiêu giá trị nguyên của tham số m để tập hợp S có đúng 8 phần tử ? A. 5. B. 6. C. 10. D. 11.
40.7. Gọi S là tập hợp các giá trị nguyên của y  [ 2
 021;2021] sao cho ứng với mỗi y thì có đúng 2
giá trị của x thỏa mãn 4 x yx y  2 4x. x . e  e  3x ? A. 2020. B. 4040. C. 2022. D. 2021.
40.8. Xét các số thực x, y thỏa mãn y y 2
log ( x x  4 ).log ( x x  4 )  y y. Có bao nhiêu 2 2
số nguyên không âm y sao cho tồn tại số thực x thỏa mãn đẳng thức trên ? A. 0. B. 1. C. 7. D. Vô số. 1
40.9. Xét các số thực x, y thỏa mãn 2
log (x y) 
y  1. Có bao nhiêu số nguyên 2 log (x y) 2 y  [ ;
3 1] để tồn tại số thực x  [ ; 1  )
 thỏa mãn đẳng thức trên ? A. 1. B. 2. C. 3. D. 0.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 85 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
40.10. Có bao nhiêu số nguyên y để tồn tại số thực x thỏa mãn 2 2
log (x  2y)  log (x y ) ? 3 2 A. 3. B. 2. C. 1. D. Vô số.
40.11. Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn 2 2
log (x y)  log (x y ) ? 3 4 A. 3. B. 2. C. 1. D. Vô số.
40.12. Có tất cả bao nhiêu giá trị nguyên của m để phương trình log (  )  2  2x m x m  3x 1 có 2
nghiệm thuộc đoạn [0;2] ? A. 6. B. 5. C. 4. D. 3.
40.13. Có bao nhiêu giá trị nguyên (a;b) thỏa mãn 1  a  2020 và b b 1 2.3 log (a 3   
)  3a b ? 3 A. 7. B. 2020. C. 2021. D. 6.
40.14. Có tất cả bao nhiêu bộ số nguyên (x;y;z) thỏa mãn đồng thời 2x yz  3 e 
 2x y z  2 và 2
z yz x  0 ? A. 5. B. 2. C. 4. D. 7.
40.15. Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất cặp (x;y) thỏa mãn
đồng thời các điều kiện log
(4x  4y  4)  1 và 2 2
x y  2x  2y  2  m  0. Tổng các 2 2 x y  2 
phần tử của S bằng A. 33. B. 24. C. 15. D. 5.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 86 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
40.16. Có bao nhiêu giá trị nguyên của tham số thực m để tồn tại cặp số (x;y) thỏa mãn đồng thời 2x y  1  3x 2 e
 e  y x y  1 và 2 2
log (2x y  1)  (m  4)log x m  4  0 ? 2 2 A. 3. B. 4. C. 5. D. 6. 3 log x 2 log y log x
40.17. Có bao nhiêu giá trị nguyên của tham m để 3 3 3 x  (m  3).y
 (18  2m).x  32  0
có 6 cặp số thực dương (x;y) sao cho xy  1 ? A. 6. B. 7. C. 8. D. 10. log x log y
40.18. Có bao nhiêu cặp số thực (x,y) thỏa mãn 2 2 
 log x  log y ? 2 2 log (xy)  1 log (xy)  1 2 2 A. 4. B. 1. C. 2. D. 3.
40.19. Tìm tập hợp tất cả các giá trị của tham số thực m để tồn tại cặp số thực (x;y) thỏa mãn đồng thời
x.y m và log (x y  12).log 2  1 ? 4 x yA. ( ;  4]. B. {4}. C. [0; 4]. D. [4; )  . 2 2
40.20. Có bao nhiêu giá trị nguyên của tham số m sao cho phương trình 3x m  4x m   có nghiệm ? A. 0. B. 3. C. 2. D. Vô số.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 87 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789  2 x   1 khix  2  2 
Câu 41. Cho hàm số f (x )   . Tích phân
f (2 sin x  1)cos x dx  bằng 2 x
  2x  3 khix  2  0 23 23 17 17 A. B. C. D. 3 6 6 3
Lôøi giaûi tham khaûo 2 3 3 1 1
Đặt t  2 sin x  1  dt  2 cos x dx
f (2 sin x  1)cos x dx
f (t)dt f (x)dx    2 2 0 1 1 2 3 1 1 23 2 2 
(x  2x  3)dx  (x  1)dx     Chọn đáp án B. 2 2 6 1 2
Baøi taäp töông töï vaø môû roäng (   1)ex x khi x  0 1  a a
41.1. Cho hàm số f (x)   . Biết
f (x)dx   ce,  với là phân số tối giản. 2 x
x  1 khi x  0  b b 1 
Giá trị của tổng a b c bằng A. 9. B. 11. C. 12. D. 14.  2 3
x  2x khi x  1 2 1 
41.2. Cho hàm số f (x)  
. Khi đó 2 cos x f (sin x d
) x  3 f (3  2x d ) x   bằng 5
  x khi x  1  0 0 A. 32. B. 31. 32 71 C. D.  3 6 2  ax khi x  0  1 
41.3. Cho hàm số f (x)   a b
f (x)dx  2. 2
(với , là các tham số thực) thỏa  Giá 3
x  2bx khi x  0  1 2 2
trị nhỏ nhất của biểu thức Pf( 1) f (1)        bằng A. 5. B. 2. 25 25 C. D. 4 2 4 2
41.4. Cho y f (x ) là hàm bậc ba như hình vẽ. Nếu x f  (
x  1)dx  7  và 2 2x f (
x  1)dx  3  1 1
thì phương trình tiếp tuyến của hàm số trên tại điểm có hoành độ bằng 3 là
A. y x  4.
B. y  2x  7. 1 5 C. y x   2 2
D. y  3x  10.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 88 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789  2 x
  x a khi x  0 
41.5. Cho hàm số f (x)  
có đạo hàm trên  (với a, b là các tham số thực). 2  bx khi x  0  1 m Nếu
f (x)dx   với m, n
  thì m  2n bằng n 1  A. 19. B. 20. 59 13 C. D.  2 3  1  khi x  0 
41.6. Biết hàm số F(x) liên tục trên , là một nguyên hàm của hàm số f (x)   2x  1 .  3 (
 2x 1) khi x  0 
Biết F(4)  F( 1
 )  8. Khi đó F(2)  2F(12) bằng 121 281 A. B. 8 16 C. 27. D. 20. 2 16 f ( x )
41.7. Cho hàm số f (x) liên tục trên  và thỏa mãn 2
cotx f (sin x)dx  dx  1.   Khi đó x 1 4
1 f (4x) dx  bằng x 1/8 A. 3. B. 2. 3 5 C. D.  2 2 3 8 8 f(x)
41.8. Hàm số f (x) xác định trên ,  thỏa 2
f ( x  16  x)dx
f (x)dx  8.   Khi đó dx  2 x 3  2 2 bằng A. 2. B. 4. 1 1 C. D.  2 4 ln 6 dx 41.9. Nếu  3lna  lnb  với ,
a b là các số nguyên dương thì ab bằng ex  2e x   3 ln 3 A. 20. B.  10. C. 15. D. 10. 2 sin x 41.10. Biết
dx a ln 3  b ln 2  với , a b  .  Khi đó 3 2
a  2ab  3b bằng
cos2x  3 cos x  2 0 A. 26. B. 6. C. 3. D. 4.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 89 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 1 2
41.11. Cho f (x) có đạo hàm trên  thỏa 2
f (x)  x  3x  2 f (x)f (  x)dx.  Khi đó f (x)dx  bằng 0 0 10 10 A. B.   3 3 26 26 C. D.   15 15
41.12. Cho hàm số f (x) xác định và có đạo hàm tại mọi điểm x  0. Biết rằng f (2)  4, f (2)  0 và 3 xf (
x)  f (x)  x với mọi x  0. Giá trị của f (2)  f(1) bằng 9 A. 8. B.  2 11 15 C. D.  2 2 1
41.13. Cho hàm số f (x) xác định trên *  thỏa mãn f  (  x) 
, f (1)  1, f (1)  0 và f (2)  0. Giá 2 x
trị của f (2) bằng A. 1  2 ln 2. B. 2  ln 2. C. 3  ln 2. D. ln 2. f ( x ) 2x  1
41.14. Cho hàm số f (x) liên tục trên (0;  )  và thỏa mãn 2 f (x  1)   .ln(x  1). Biết 2 4 x x x 17
f (x)dx a ln 5  2 lnb c  với a, ,
b c  . Giá trị của a b  2c bằng 1 29 A. B. 5. 2 C. 7. D. 37. 2
41.15. Cho hàm số f (x) có đạo hàm liên tục trên  thỏa 3 2 ( )  (  1)  ex xf x f x , x  .  Khi đó 0 f (x)dx  bằng 1  1 A. B. 3e. 2 C. 3(1  e). D. 3(e  1).
41.16. Cho hàm số f (x) có đạo hàm liên tục trên  thỏa mãn (ex f
 1)  f (x)  f (
x)  x, x    và 3
f (0)  2f (ln 2)  1. Khi đó f (x)dx  bằng 2 1 A. ln 2  1. B. 2 ln 2. 2 2 C.  
D. 2 ln 2  2. 3
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 90 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
41.17. Cho hàm số f (x) có đạo hàm liên tục trên  thỏa mãn 3 2
f (x x  2)  x x  1, x   .  Giá 4 trị của 2 x f (  x)dx
thuộc khoảng nào dưới đây ? 8  A. (20;10). B. (20;25). C. (10;20). D. (25;20). x  1 
41.18. Cho hàm số f (x) thỏa mãn f (0)  f (1)  1 và f  (  x)  , x    ;      Khi đó 3x  1  1 3   1 f (x)dx  bằng 0 3509 3295 A.   B.   3402 6804 3295 3509 C.   D.   3402 6804 41.19. Biết rằng
f (2x)dx  ln x  2x C, x  (0; )  . 
Họ các nguyên hàm của (2x  1)f (  x) trên khoảng (0;  )  là 2 2 A.
 4 ln x C. B.
 4 ln x C. x x 1 4 C.
 2 ln x C. D.
 2 ln x C. x x 41.20. Biết 2 ( ) e x F x x   
là một nguyên hàm của hàm số f ( x  ) trên .  Khi đó ( )e x f x  dx  bằng A. 2e x
 (x 1)  x C. B. 2e x
 (x  1)  x C. 2x  1 2x  1 C. x C. D.
x C. ex ex
Câu 42. Có bao nhiêu số phức z thỏa mãn z  2 và (z  2i)(z  2) là số thuần ảo ? A. 1. B. 0. C. 2. D. 4.
Lôøi giaûi tham khaûo
Giả sử z x  ,
yi (x, y  )  z x y . i Ta có: 2 2
(z  2i)(z  2)  zz  2z  2iz  4i x y  2x  2yi  2i(x yi) 2 2 2 2
x y  2x  2yi  2xi  2y  (x y  2x  2y)  (2x  2y)i là số thuần ảo  2 2
x y  2x  2y  0 có dạng là đường tròn (C ) có tâm I (1; 1
 ), bán kính R  2. 1 1 1 Ta lại có: 2 2
z  2  x y  2 là đường tròn (C ) có tâm là O(0;0), bán kính R  2. 2 2
Vẽ hai đường tròn (C ) và (C ) lên cùng hệ trục. 1 2
 có hai điểm chung nên tồn tại 2 số phức. Chọn đáp án C.
 Lưu ý. Ta có thể giải hệ phương trình sẽ tìm được hai cặp (x;y), tức có 2 số phức thỏa bài toán.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 91 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Baøi taäp töông töï vaø môû roäng z
42.1. Cho các số phức z , z
z z  1  8i và 1 là số thuần ảo. Khi đó z z bằng 1 2 thỏa mãn 1 2 z 1 2 2 A. 65. B. 65. 65 C.  2 65 D.  2
42.2. Có bao nhiêu số phức z thỏa mãn z  2  i  2 2 và 2
(z  1) là số thuần ảo ? A. 0. B. 4. C. 3. D. 2.
42.3. Có bao nhiêu số phức z thỏa mãn z i  2 và (z  1)(z i) là số thực ? A. 1. B. 2. C. 3. D. 4. z  1  2i z  2i
42.4. Có bao nhiêu số phức z thỏa mãn  1 và số phức là số thuần ảo ? z  3  4i z i A. 0. B. 1. C. 2. D. 4.
42.5. Biết rằng có hai số phức thỏa mãn 2 z i z z  2i và (2  z)(i z ) là số thực. Tổng các
phần ảo của hai số phức đó bằng A. 9. B. 7. C. 5. D. 3.
42.6. Có bao nhiêu số phức z thỏa mãn điều kiện z.z z  2 và z  2 ? A. 1. B. 2. C. 3. D. 4.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 92 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
42.7. Cho số phức z a bi ( ,
a b  ) thỏa z  2  i z (1  i)  0 và z  1. Khi đó a b bằng A. 1. B. 5. C. 3. D. 7. 2  iz z  2i
42.8. Cho số phức z a bi (a, b  ) thỏa 
 2z và z  1. Tính 2 2
a b a . b 2  i 1  2i A. 5. B. 1. C. 5. D. 1.
42.9. Cho số phức z a bi ( ,
a b  ) thỏa mãn 3 z  18  26 . i Tính 2 2
T  (z  2)  (4  z) . A. 2. B. 4. C. 0. D. 1.
42.10. Cho số phức z thỏa mãn z (
 3 4i) z 4 3i     5 2  0.  
Môđun của số phức z bằng A. 2. B. 2. C. 2 2. D. 1. 1  i (2  3i)z
42.11. Cho số phức z thỏa  i
 2. Khi đó môđun của z thuộc khoảng nào sau đây 2 z z ? 3   A. ;2  .  2  B. (2;  )  . C. (0;1). 1 3 D.  ;    2 2  
42.12. Cho hai số phức z , z thỏa mãn z  2, z  2. Gọi M, N lần lượt là điểm biểu diễn số 1 2 1 2 
phức z và iz . Biết rằng MON  45 với O là gốc tọa độ. Khi đó 2 2
z  4z bằng 1 2 1 2 A. 4 2. B. 4. C. 6. D. 4 5.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 93 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
42.13. Cho các số phức z thỏa (z  2  i)(z  2  i)  16. Biết rằng tập hợp các điểm biểu diễn các số
phức w  (1  i)z  2i là một đường tròn. Bán kính của đường tròn đó bằng A. 2. B. 5. C. 4 2. D. 3.
42.14. Cho các số phức z thỏa z.z z(4  5i)  z (4  5i)  16  0. Trong mặt phẳng tọa độ các điểm z  3i
biểu diễn của số phức w
 4  i cùng thuộc một đường tròn cố định có tọa độ tâm là 2  i A. I (4;5). B. I (1; 3). C. I ( 4   5). D. I (8;3). 2
42.15. Cho số phức z a bi thỏa mãn 2z.z  (5  7i) z  (17  i)z . Trên mặt phẳng tọa độ, điểm
biểu diễn của số phức z khác gốc tọa độ là A. N (1;2). B. P(2;1). C. Q(2;1). D. M (1;2). 2
42.16. Cho số phức z thỏa mãn z.z (6  8i)  (5  i) z  (
 23  73i)z. Tỉ số giữa phần thực và phần ảo là 2 A. 5 2 B.  7 C. 2. D. 3. 42.17. Cho số phức 2
z m  3  (m  4)i với m  .
 Gọi (C ) là tập hợp các điểm biểu diễn số phức
z trong mặt phẳng tọa độ. Diện tích hình phẳng giới hạn bởi (C ) và trục hoành bằng 4 A.  3 32 B.  3 8 C.  3 D. 1.
42.18. Gọi S là tập hợp tất cả các số nguyên m sao cho tồn tại hai số phức phân biệt z , z thỏa 1 2
z  1  z i và z  2m m  1. Tổng các phần tử của S bằng A. 1. B. 2.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 94 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 C. 3. D. 4.
42.19. Có bao nhiêu giá trị của tham số m để tồn tại duy nhất số phức z thỏa mãn đồng thời z m và 2
z  4m  3mi m ? A. 0. B. 1. C. 2. D. 3.
42.20. Cho phương trình 2
z  2z c  0 (với c là số thực và c  1) có hai nghiệm phức z và z . Gọi 1 2
M, N lần lượt là điểm biểu diễn cho z và z trong mặt phẳng tọa độ Oxy. Biết 2 2 z z  4 6. 1 2 1 2
Chu vi tam giác OMN (với O là gốc tọa độ) bằng A. 2( 5  6).
B. 2( 6  7). C. 2(3  6). D. 2(2  6).
Câu 43. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh ,
a cạnh bên SA vuông góc với
mặt phẳng đáy, góc giữa SA và mặt phẳng (SBC ) là 45 (tham khảo hình bên dưới). Thể
tích khối chóp S.ABC bằng S 3 a 3 3a A. B.  8 8 A C 3 3a 3 a C. D.  12 4 B
Lôøi giaûi tham khaûo S
Gọi M là trung điểm của BC và H là hình chiếu của A lên SM. 45°     (S ,
A (SBC ))  ASH ASM  45  S
AM vuông cân tại . A H a 3 A C
Suy ra: SA AM   2 M 2 3 1 1 a 3 a 3 a B Do đó VS . AS    
Chọn đáp án A. S .ABC 3 ABC 3 2 4 8
Baøi taäp töông töï vaø môû roäng
43.1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt phẳng đáy và SA  3 .
a Biết góc giữa SD và (SAC ) là 30 , thể tích của khối chóp S.ABC bằng A. 3 9a . B. 3 6a .
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 95 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 3 9a C. 2 D. 3 3a .
43.2. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a, B  2a. Mặt bên (SAB)
nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABCD), gọi H là trung điểm của cạnh
AB, góc giữa đường thẳng SH và mặt phẳng (SCD) bằng 30 .
 Thể tích khối chóp S.ACD bằng 3 4a 3 A.  3 B. 3 2a 3. C. 3 2a . 3 2a 3 D.  3
43.3. Cho khối lăng trụ đứng ABC.AB C
  có đáy là tam giác đều. Mặt phẳng (ABC) tạo với đáy
góc 30 và tam giác ABC có diện tích bằng 8. Thể tích của khối lăng trụ đã cho bằng A. 8 3. B. 16 3. C. 64 3. D. 2 3.
43.4. Cho lăng trụ tam giác đều ABC.AB C
  có cạnh đáy bằng a và AB  BC . Thể tích của khối lăng trụ đã cho bằng A. 3 a . B. 3 a 6. 3 a 6 C. 8 3 a 6 D. 4 
43.5. Cho khối chóp S.ABC có AB a, AC  2a, BAC  120 ,
SA  ABC , góc giữa (SBC ) và (ABC ) là 60 .
 Thể tích khối chóp S.ABC bằng 3 21a A.  14 3 7a B.  14 3 3 21a C.  14 3 7a D.  7
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 96 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
43.6. Cho hình lăng trụ đứng ABC.AB C
 , đáy ABC là tam giác vuông tại ,
A cạnh AA hợp với B C
 một góc 60 và khoảng cách giữa chúng bằng , a B C
  2a. Thể tích của khối lăng trụ
ABC.AB C   bằng 3 a A.  2 3 3a B.  2 3 3a C.  4 3 a D.  4
43.7. Cho hình chóp S.ABC có SA vuông góc với đáy, mặt phẳng (SAB) vuông góc với mặt phẳng (SBC ), 
góc giữa hai mặt phẳng (SAC ) và (SBC ) bằng 60 ,
SB a 2, BSC  45. Thể tích
khối chóp S.ABC bằng 3 a 2 A.  15 B. 3 2 3a . C. 3 2 2a . 3 2a 3 D.  15
43.8. Cho lăng trụ ABC.AB C
  có đáy là tam giác vuông cân tại B và AB a 3. Hình chiếu vuông
góc của A lên mặt phẳng (ABC ) là điểm H thuộc cạnh AC sao cho HC  2H . A Mặt bên (ABB A  )
 tạo với đáy một góc 60 .
 Thể tích khối lăng trụ đã cho bằng 3 a A.  6 3 a B.  3 3 3a C.  5 3 3a D.  2
43.9. Cho hình lăng trụ đứng ABC.AB C
  có đáy là tam giác ABC vuông cân tại A và BC a 6.
Góc giữa mặt phẳng (AB C
 ) và mặt phẳng (BCC B  ) bằng 60 .
 Thể tích của khối đa diện AB C
AC  bằng A. 3 a 3 3 3a 3 B. 2 3 a 3 C. 2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 97 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 3 a 3 D. 3
43.10. Cho lăng trụ tam giác đều ABC.AB C
  có cạnh đáy bằng 2 ,
a khoảng cách từ A đến mặt phẳng a 6
(ABC ) bằng
 Khi đó thể tích khối lăng trụ ABC.AB C   bằng 2 A. 3 a . B. 3 3a . 4 C. 3 a . 3 4 3 D. 3 a . 3
43.11. Cho hình chóp tứ giác S.ABCD có đáy là vuông; mặt bên (SAB) là tam giác đều và nằm trong 3 7a
mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm A đến mặt phẳng (SCD) bằng  7
Thể tích của khối chóp S.ABCD bằng 1 A. 3 a . 3 B. 3 a . 2 C. 3 a . 3 3 3a D.  2
43.12. Cho hình lăng trụ đứng ABC.AB C
 , biết đáy ABC là tam giác đều cạnh a. Khoảng cách từ
trọng tâm G của tam giác ABC đến mặt phẳng (ABC ) bằng a/6. Thể tích khối lăng trụ
ABC.AB C   bằng 3 3a 2 A.  8 B. 3 0,5a . 3 3a 2 C.  4 3 3a 2 D.  16
43.13. Cho lăng trụ ABC.AB C
  có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A
lên mặt phẳng (ABC ) trùng với trọng tâm của tam giác ABC . Biết khoảng cách giữa hai đường a 3
thẳng AA và BC bằng
 Khi đó thể tích của khối lăng trụ ABC.AB C   bằng 4 3 a 3 A.  6 3 a 3 B.  24
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 98 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 3 a 3 C.  12 3 a 3 D.  36
43.14. Cho tứ diện OABC biết O ,
A OB, OC đôi một vuông góc với nhau, biết OA  3, OB  4 và
thể tích khối tứ diện OABC bằng 6. Khi đó khoảng cách từ O đến mặt phẳng (ABC ) bằng A. 3. 41 B.  12 144 C.  41 12 D.  41
43.15. Cho hình chóp S.ABC có đáy là tam giácABC đều cạnh ,
a tam giác SBA vuông tại B, tam
giác SAC vuông tại C. Biết góc giữa hai mặt phẳng (SAB) và (ABC ) bằng 60 .  Thể tích khối
chóp S.ABC bằng 3 3a A.  8 3 3a B.  12 3 3a C.  6 3 3a D.  4  
43.16. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, AB  2 ,
a SAB SCB  90 , góc
giữa đường thẳng AB và (SBC ) bằng 30 .
 Thể tích của khối chóp S.ABC bằng 3 4a 3 A.  9 3 4a 3 B. 3 3 2a 3 C.  9 3 2a 3 D.  3
43.17. Cho khối chóp S.ABC có AB BC, BC SC, SC S ,
A BC a, SC  15a và góc giữa
AB, SC bằng 30 .
 Thể tích khối chóp S.ABC bằng 3 5a A.  2 3 5 3a B.  2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 99 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 5 C. 3 a . 6 3 5 3a D.  6  
43.18. Cho hình chóp S .ABC có đáy ABC là tam giác vuông cân tại ,
A SBA SCA  90 ,  AB a,
góc giữa mặt phẳng (SAB ) và (SAC ) bằng 60. Thể tích khối chóp đã cho bằng A. 3 a . 3 a B.  3 3 a C.  2 3 a D.  6
43.19. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh ,
a cạnh bên SA vuông góc với mặt
phẳng đáy. Gọi I là tâm mặt cầu ngoại tiếp hình chóp S.ABC. Biết rằng khoảng cách từ I đến a 3
mặt phẳng (SBC ) bằng
, thể tích khối chóp S.ABC bằng 18 3 3a 3 A. 20 B. 3 a . C. 3 a 3. 3 a 5 D.  20
43.20. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 4a. Biết SA vuông góc với mặt đáy
(ABC ) và SA  6a 3. Gọi M, N, P lần lượt là trung điểm của các cạnh SB, BC, SC. Gọi
điểm K sao cho AK là đường kính của mặt cầu ngoại tiếp hình chóp S.ABC. Thể tích khối tứ diện KMNP bằng 3 13a A.  2 B. 3 8a . C. 3 7a . D. 3 6a .
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 100 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Câu 44. Ông Bình làm lan can ban công ngôi nhà của mình bằng tấm kính cường lực. Tấm kính đó là
một phần của mặt xung quanh của một hình trụ như hình bên. Biết giá tiền của 2 1m kính
như trên là 1.500.000 đồng. Hỏi số tiền (làm tròn đến hàng nghìn) mà ông Bình mua tấm kính trên là bao nhiêu ?
A. 23.591.000 đồng. B. 36.173.000 đồng.
C. 9.437.000 đồng.
D. 4.718.000 đồng.
Lôøi giaûi tham khaûo 4, 45
Bán kính của đường tròn đáy là R   4, 45m. 2 sin150 1
Do đó, mép trên của tấm kính bằng diện tích xung quanh của hình trụ có chiều cao 1, 35m 6
và bán kính đáy R  4, 45m.
Số tiền mà ông Bình mua tấm kính trên là 1 1 T  .2 R  h  2 .
4, 45.1, 35.1500000  9.437.000 đồng. Chọn đáp án C. 6 6
Baøi taäp töông töï vaø môû roäng
44.1. Ông An làm lan can ban công của ngôi nhà bằng một miếng kính cường lực. Miếng kính này là 
một phần của mặt xung quanh của một hình trụ như hình bên. Biết AB  4m, AEB  150 (E
là điểm chính giữa cung AB) và DA  1, 4m. Giá tiền của 2
1m kính này là 2.000.000 đồng. Số
tiền (làm tròn) mà ông An phải trả bằng A. 11.820.000 đồng. C. 10.840.000 đồng. B. 10.250.000 đồng. D. 11.730.000 đồng.
44.2. Một thùng hình trụ có chiều cao h  3m, bán kính đường tròn đáy R  1m chứa một lượng
nước. Biết rằng nếu đặt thùng nằm ngang ta được chiều cao mực nước trong thùng là d  0, 5m.
Hỏi thể tích lượng nước có trong thùng gần nhất với kết quả nào sau đây ? A. 3 1, 75m . B. 3 1, 8m . C. 3 1, 85m . D. 3 1, 9m .
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 101 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
44.3. Một ống thủy tinh hình trụ có chiều cao 14, 2cm và bán kính đáy 1, 45cm đang chứa dung dịch
H SO . Khi đặt ổng thủy tinh nằm ngang thì diện tích bề mặt dung dịch trên thành ống chiếm 2 4
41, 67% diện tích xung quanh ống. Thể tích dung dịch H SO trong ống bằng 2 4 A. 3 32, 47cm . B. 3 33, 86cm . C. 3 31, 62cm . D. 3 30,12cm .
44.4. Người thợ gia công của một cơ sở chất lượng cao X cắt một miếng tôn hình tròn với bán kính
60cm thành ba miếng hình quạt bằng nhau. Sau đó người thợ ấy quấn và hàn ba miếng tôn đó
để được ba cái phễu hình nón. Thể tích của mỗi cái phễu đó bằng 16 2 A. lít. 3 16 2 B. lít. 3
C. 8 2 lít.
D. 160 2 lít.
44.5. Người ta bỏ ba quả bóng bàn cùng kích thước vào trong một chiếc hộp hình trụ có đáy bằng hình
tròn lớn của quả bóng bàn và chiều cao bằng ba lần đường kính bóng bàn. Gọi S là tổng diện 1
tích của ba quả bóng bàn, S là diện tích xung quanh của hình trụ. Khẳng định nào đúng ? 2 6
A. S S . 1 2 5
B. S S . 1 2 3 C. S S . 1 2 2 S D. 1  2. S2
44.6. Một ly nước hình trụ có chiều cao 20cm và bán kính đáy bằng 4cm. Bạn An đổ nước vào ly cho
đến khi mực nước cách đáy ly 17cm thì dừng lại. Sau đó bạn An lấy các viên đá lạnh hình cầu
có cùng bán kính 2cm thả vào ly nước. Bạn An cần dùng ít nhất bao nhiêu viên đá để nước tràn ra khỏi ly ? A. 5. B. 4. C. 6. D. 7.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 102 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
44.7. Một ly nước rỗng hình trụ có chiều cao 20cm và bán kính đáy 4cm. An bỏ vào ly 5 viên đá hình
cầu có bán kính 2cm sau đó đổ trà sữa vào cho đến khi đầy ly. Tính lượng trà sữa mà An đã dùng để đổ đầy ly ? 200 A. 3 800 B. . 3 C. 800 . D. 150 .
44.8. Một khối pha lê gồm một hình cầu (H ) bán kính R và một hình nón (H ) có bán kính đáy và 1 2 1 3
đường sinh lần lượt là r,  thỏa mãn r
 và   R xếp chồng lên nhau (tham khảo hình 2 2
vẽ bên dưới). Biết tổng diện tích mặt cầu (H ) và diện tích toàn phần của hình nón (H ) là 2 91cm . 1 2
Tính diện tích của khối cầu (H ). 1 104 A. 2 cm . 5 B. 2 16cm . C. 2 64cm . 26 D. 2 cm . 5
44.9. Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng 3 lần đường kính của đáy;
một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng
của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón đó (như hình vẽ ) thì thấy nước
trong cốc tràn ra ngoài. Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban
đầu (bỏ qua bề dày của lớp vỏ thủy tinh). 5 A. 9 2 B. 3 1 C. 2 4 D. 9
44.10. Một bình đựng nước dạng hình nón (không có đáy), đựng đầy nước. Người ta thả vào đó một
khối cầu có đường kính bằng một nửa chiều cao của bình nước và đo được thể tích tràn ra là 32 3
(dm ). Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của hình nón và toàn bộ khối 3
cầu chìm trong nước, trong đó mặt nước là tiết diện của khối cầu (hình vẽ bên). Thể tích nước còn lại trong bình bằng 16 A. 3 (dm ). 3
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 103 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 32 B. 3 (dm ). 3 40 C. 3 (dm ). 3 64 D. 3 (dm ). 3
44.11. Một cái ly nước dạng hình nón, đựng đầy nước. Người ta thả vào đó một khối cầu không thấm
nước, có đường kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là V .
Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa khối cầu
chìm trong nước như hình vẽ. Thể tích nước còn lại trong ly bằng V A. 2 1 B. V . 1 C. V. 3 1 D. V . 6
44.12. Nguời ta đặt được vào trong một hình nón hai khối cầu có bán kính lần lượt là a và 2a sao cho
các khối cầu đều tiếp xúc với mặt xung quanh của hình nón, hai khối cầu tiếp xúc với nhau và
khối cầu lớn tiếp xúc với đáy của hình nón (tham khảo hình vẽ). Bán kính đáy của hình nón đã cho bằng a 13 A. 2
B. 2 2a. C. 3 . a D. 2a 3. 256
44.13. Một quả cầu có thể tích 3
(cm ) được đặt vào một chiếc cốc có dạng hình trụ với đường kính 3
đáy là 6cm như hình vẽ. Phần nhô ra khỏi chiếc cốc của quả cầu bằng (kết quả làm tròn đến hàng phần trăm). A. 2, 00cm. B. 4, 00cm. C. 4, 65cm. D. 6, 65cm.
44.14. Một cái phễu có dạng hình nón, chiều cao của phễu là 20cm (hình 1). Người ta đổ một lượng
nước vào phễu sao cho chiều cao của cột nước trong phễu là 10cm. Nếu bịt kín miệng phễu rồi
lật ngược lên (hình 2). Khi đó chiều cao cột nước trong phễu bằng giá trị nào sau đây ?
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 104 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 A. 0, 87cm. B. 1, 07cm. C. 5cm. D. 10cm.
44.15. Cho một đồng hồ cát gồm 2 hình nón chung đỉnh ghép lại, trong đó đường sinh bất kỳ của hình
nón tạo với đáy một góc 60 như hình bên dưới. Biết rằng chiều cao của đồng hồ là 30cm và
tổng thể tích của đồng hồ là 3
1000cm . Hỏi nếu cho đầy lượng cát vào phần trên thì khi chảy hết
xuống dưới, khi đó tỉ lệ thể tích lượng cát chiếm chỗ và thể tích phần dưới là bao nhiêu ? 1 A. 3 3 1 B. 8 1 C. 27 1 D. 64
44.16. Một bình đựng nước dạng hình nón không nắp đựng đầy nước. Biết rằng chiều cao của bình gấp
3 lần bán kính đáy của nó. Người ta thả vào bình đó một khối trụ và đo được thể tích nước trào 16 ra ngoài là 3
dm . Biết một mặt của khối trụ nằm trên mặt đáy của hình nón và khối trụ có 9
chiều cao bằng đường kính đáy của hình nón (như hình vẽ). Tính bán kính đáy R của bình nước. A. R  2 dm.
B. R  3 dm.
C. R  4 dm. D. R  5 dm.
44.17. Ông A dự định sử dụng hết 2
6,7m kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật
không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có
dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm). A. 3 1,23m . B. 3 1,11m . C. 3 1,57m . D. 3 2, 48m .
44.18. Một bác thợ gò hàn làm một chiếc thùng hình hộp chữ nhật (không nắp) bằng tôn thể tích 3
665,5dm . Chiếc thùng này có đáy là hình vuông cạnh x (dm), chiều cao h (dm). Để làm chiếc
thùng, bác thợ phải cắt một miếng tôn như hình. Tìm x để bác thợ sử dụng ít nguyên liệu nhất ?
A. x  10, 5 dm.
B. x  12 dm.
C. x  11 dm.
D. x  9 dm.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 105 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
44.19. Cho hình nón đỉnh ,
O chiều cao là h. Một khối nón khác có đỉnh là tâm I của đáy và đáy là một
thiết diện song song với đáy của hình nón đã cho. Để thể tích của khối nón đỉnh I lớn nhất thì
chiều cao của khối nón này bằng bao nhiêu ? O h A. 2 h B. h 3 2h C. x 3 h 3 D. 3
44.20. Có tấm bìa hình tam giác vuông cân ABC có cạnh huyền BC bằng a. Người ta muốn cắt tấm
bìa đó thành hình chữ nhật MNPQ rồi cuộn lại thành một hình trụ không đáy như hình vẽ. Diện
tích hình chữ nhật đó bằng bao nhiêu để diện tích xung quanh của hình trụ là lớn nhất ? 2 a A. 2 2 a B. 4 2 a C. 12 2 a D. 8
Câu 45. Trong không gian Oxyz, cho mặt phẳng (P) : 2x  2y z  3  0 và phương trình hai x  1 y z  1 x  2 y z  1 đường thẳng d :   , d :  
 Đường thẳng vuông góc với 1 2 1 2 2 1 2 1
(P), đồng thời cắt cả d và d có phương trình là 1 2 x  3 y  2 z  2 x  2 y  2 z  1 A.   . B.   . 2 2 1 3 2 2 x  1 y z  1 x  2 y  1 z  2 C.   . D.   . 2 2 1 2 2 1
Lôøi giaûi tham khaûo
Gọi M d d , N d d . 1 2
Khi đó M(1  2t;t;1  2t), N (2  s;2s;1  s). 
MN  (s  2t  1;2s t; s   2t).  
Từ hình vẽ có MN  n  (2;2;1) (P ) s  2t  1 2s t s   2t s
  2t  1  2s t s   1    M  (1; 0;1)  Suy ra:         . 2 2 1
2s t  2s  4t t   0      N(3;2; 2)   
Đường thẳng  cần tìm đi qua N (3;2;2) và một có véctơ chỉ phương u n  (2;2; 1  ) (P ) x  3 y  2 z  2 là  
Chọn đáp án A. 2 2 1
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 106 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Baøi taäp töông töï vaø môû roäng
45.1. Trong không gian Oxyz, cho mặt phẳng (P) : 3x  3y  5z  1  0 và phương trình hai đường x  1 y  3 z x y  2 z  4 thẳng d :   , d :  
 Đường thẳng vuông góc với (P) đồng 1 2 4 3 2 1 1 3
thời cắt d và d tại A và B, độ dài AB bằng 1 2 A. 2 43. B. 43. C. 2 13. D. 13. x  1 y z  1
45.2. Trong không gian Oxyz, cho điểm (
A 1;0;2) và đường thẳng d :    Phương 1 1 2
trình đường thẳng  đi qua ,
A vuông góc và cắt d là x  1 y z  2 A.    1 1 1 x  1 y z  2 B.    1 1 1  x  1 y z  2 C.    2 2 1 x  1 y z  2 D.    1 3  1
45.3. Trong không gian Oxyz, viết phương trình đường thẳng d đi qua điểm ( A 2; 1  ;3), vuông góc x y  5 z  2 x  1 y  1 z  1
với đường thẳng d :  
và cắt đường thẳng d :    1 4 1  1  2 2 3 4 x  2 y  1 z  3 A.    1 2 2 x  2 y  1 z  3 B.    1 2  2  x  2 y  1 z  3 C.    1 2 2 x  2 y  1 z  3 D.    1 2 2
45.4. Trong không gian Oxyz, viết phương trình đường thẳng d đi qua M(1; 1
 ;4), đồng thời d song x  1 y  1 z
song với mặt phẳng (P) : x  2y  2z 15  0 và d cắt đường thẳng  :    3  4 5 x  1 y  1 z  4 A.    2 3  7  x  1 y  1 z  4 B.    4 1 1  x  1 y  1 z  4 C.    4 1  1
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 107 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 x  1 y  1 z  4 D.    2 3 7 
45.5. Trong không gian Oxyz, viết phương trình đường thẳng d nằm trong (P) : x y z  3  0, x  6 y  10 z  5 x  1 y  2 z  3
đồng thời d cắt d :  
và vuông góc với d :    1 2 7  3 2 1 3 9 x  4 y  3 z  2 A.    3 4 1 x  4 y  3 z  2 B.    62 2  2 25 x  4 y  3 z  2 C.    3 4  1 x  4 y  3 z  2 D.    3 4 1
45.6. Trong không gian Oxyz, cho điểm ( A 1; 1
 ;2), mặt phẳng (P) : x y 2z  5  0 và đường x  1 y z  2 thẳng d :  
 Viết phương trình đường thẳng  cắt d và (P) lần lượt tại M 2 1 1
và N sao cho A là trung điểm của đoạn thẳng MN. x  1 y  1 z  2 A.    1  3 2 x  1 y  1 z  2 B.    2 3  2 x  1 y  1 z  2 C.    2 3 2 x  1 y  1 z  2 D.    2 3 1  x  1 y  1 z  2
45.7. Trong không gian Oxyz, cho đường d :  
và (P) : x  3y  2z  5  0. 2 1  2
Phương trình đường thẳng  qua ( A 2; 1
 ;1) và cắt d tại M, cắt (P) tại N để A là trung điểm MN là x  3 y  2 z A.    1 1 1 x  2 y  2 z  1 B.    1 1  1  x  3 y z  2 C.    1 1 1 x  2 y  1 z  1 D.    8  2  7 x  1 y  1 z  1
45.8. Trong không gian Oxyz, cho đường thẳng d :   , mặt phẳng 1 2 1  4  ( )
: x y z  4  0   và G  ; 0;1  
Phương trình đường thẳng  cắt d và ( )
lần lượt tại 3 
M, N sao cho tam giác OMN nhận G làm trọng tâm là
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 108 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 x   1  t  A. y   1  3t .  z   3  2t  x  2 y  1 z B.    2 2 1 x   0  C. y   1  t .  z   3  4t  x  1 y  1 z  1 D.   . 2 2 1 x   2 t 
45.9. Trong không gian Oxyz, cho đường thẳng d : y   3  t ,
 x y z    mặt phẳng ( ) : 1 0 và z   3  2 2  
điểm G  ;1;    M N
Phương trình đường thẳng  cắt d và ( )
lần lượt tại , sao cho tam giác 3 3
OMN nhận G làm trọng tâm là x   1   x   1  t     A. y   2  t . y   1  3t .  B. z   3  4t       z 3 2t  x   0   x   2  t     C. y   1  t . y   3  3t .  D.z   3  4t       z 3 2t  x   2 t 
45.10. Trong không gian Oxyz, cho đường thẳng d : y   1  t ,
 x y z    mặt phẳng ( ) : 5 0 và z   4  t  hai điểm C( 1  ;0;3), ( D 2  ; 1
 ;2). Phương trình đường thẳng  cắt d và ( )
lần lượt tại , A B
sao cho tứ giác ABCD là hình bình hành là x   1  x  1 y  2 z  1 A. y   1  t .     B. 1 1 1 z   3  4t  x   1  t  x  3 y  2 z  5 C. y   t .     D. 1 1 1 z   3  4t  x  1 y  2 z  1
45.11. Trong không gian Oxyz, cho hai đường thẳng chéo nhau  :   và 1 2 1 1 x  2 y  1 z  2  :  
 Đường thẳng chứa đoạn vuông góc chung của  và  đi qua 2 4 1 1 1 2 điểm nào sau đây ?
A. M (0;2;5).
B. N (1;1;4).
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 109 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 C. P(2; 0;1). D. Q(3;1;4). x  1 y  1 z  1 x  1 y  1 z  1
45.12. Trong không gian Oxyz, cho  :   và  :   . Diện 1 2 1 2 2 2 2 1
tích mặt cầu có bán kính nhỏ nhất, đồng thời tiếp xúc với  và  bằng 1 2 16 A. 17 417 B. 17 1617 C. 17 4 D. 17
45.13. Trong không gian Oxyz, mặt phẳng (P) : 2x  6y z  3  0 cắt trục Oz và đường thẳng x  5 y z  6 d :  
lần lượt tại A và .
B Phương trình mặt cầu đường kính AB là 1 2 1  A. 2 2 2
(x  2)  (y  1)  (z  5)  36. B. 2 2 2
(x  2)  (y  1)  (z  5)  9. C. 2 2 2
(x  2)  (y  1)  (z  5)  9. D. 2 2 2
(x  2)  (y  1)  (z  5)  36. x   1  3t  x  1 y  2 z
45.14. Trong không gian Oxyz, cho hai đường thẳng d : y
  2  t , d :   và mặt 1  2 2 1 2 z   2 
phẳng (P) : 2x  2y  3z  0. Phương trình mặt phẳng đi qua giao điểm của d và (P), đồng 1
thời vuông góc với d là 2
A. 2x y  2z  22  0.
B. 2x y  2z  13  0.
C. 2x y  2z  13  0.
D. 2x y  2z  22  0.
45.15. Trong không gian Oxyz, cho đường thẳng d đi qua (
A 2; 0; 0), cắt chiều âm trục Oy tại điểm B
sao cho diện tích tam giác OAB bằng 1. Phương trình tham số đường thẳng d là x   1 2t   x   2  2t     A. y   t . y   t  .  B. z   0      z 0  x   2  2t   x   2  2t     C. y   t  . y   t .  D. z   0      z 1 
45.16. Trong không gian Oxyz, cho ba điểm (
A 1;2;1), B(2;1;1), C (0;1;2) và phương trình đường x  1 y  1 z  2 thẳng d :  
 Lập phương trình đường thẳng  đi qua trực tâm của tam 2 1 2
giác ABC, biết  nằm trong (ABC ) và vuông góc với đường thẳng d.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 110 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 x  1 y  1 x  1 A.  :    12 2 11 x  2 y  1 z  1 B.  :    12 2 11 x  2 y  1 z  1 C.  :    12 2 11 x  2 y  1 z  1 D.  :    12 2 11
45.17. Trong không gian Oxyz, cho mặt phẳng (P) : x  2y  3z  4  0 và hai đường thẳng x  1 y z  1 x  1 y  3 z  1 d :   , d :  
 Mặt phẳng () song song với (P) và cắt 1 1 1 2 2 2 1 1
d , d theo thứ tự tại M, N sao cho MN  3. Điểm nào sau đây thuộc () ? 1 2 A. ( A 1;2;3).
B. B(0;1;3).
C. C(0;1; 3). D. D(0;1; 3). x  1 y  2 z
45.18. Trong không gian với hệ tọa độ Oxyz, cho bốn đường thẳng d :   , 1 1 2 2 x  2 y  2 z x y z  1 x  2 y z  1 d :   , d :   , d :  
. Gọi  là đường thẳng 2 2 4 4 3 2 1 1 4 2 2 1
cắt cả bốn đường thẳng đã cho. Một véctơ chỉ phương của đường thẳng  là 
A. u  (2; 0; 1  ). 3  B. u  (2;1; 1  ). 2 
C. u  (2;1;1). 1 
D. u  (1;2; 2  ). 4
45.19. Trong không gian Oxyz, cho tam giác ABC có (
A 2; 3; 3), phương trình đường trung tuyến d 1 x  3 y  3 z  2 kẻ từ B là  
, phương trình đường phân giác trong d của góc C là 1 2 1 2 x  2 y  4 z  2  
. Đường thẳng BC có một véctơ chỉ phương là 2 1 1 
A. u  (2;1;1). 
B. u  (1;1; 0). 
C. u  (1;1; 0). 
D. u  (1;2;1).
45.20. Trong không gian Oxyz, cho hình thoi ABCD có tâm I (2;1;3), phương trình đường thẳng x  2 y  1 z BC :  
, đỉnh D thuộc mặt phẳng (P) : x y  2z  15  0. Đường thẳng 1 2 1
AC cắt mặt phẳng (Oyz) tại điểm có cao độ bằng A. 5. B. 2  3. C. 1  7. D. 3  .
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 111 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Câu 46. Cho f (x) là hàm bậc bốn thỏa mãn f (0)  0. Hàm số f (
x) có bảng biến thiên như sau: Hàm số 3
g(x)  f (x )  3x có bao nhiêu điểm cực trị ? A. 3. B. 2. C. 1. D. 4.
Lôøi giaûi tham khaûo x   
Ta có: f x a x x   f x
f x x f   x 3 2 ( ) ( 1)( 3) ( ) ( )d  a
 2x  3x   b.    3 
f (3)  1    29  a     3 29 x    Do  61  2  f (  x)  
 2x  3x  1.   2   f (  1)    2  3        3 b 1  1 Xét hàm số 3
h(x)  f (x )  3x có 2 3 h (
x)  3x f (x )  3  0 3  f (  x )  (1) 2 x
Dựa vào bảng biến thiên đề bài, ta có: 1  Nếu x  ( ;  0) thì 3 f (
x)  0 f (x )  0 mà
 0 nên (1) vô nghiệm trên ( ;  0). 2 x
 Nếu x  (0; )  thì 3 f (
x)  1  f (x )  1 đồng biến nên 3 f (
x ) đồng biến, mà hàm số 1 y
nghịch biến nên phương trình (1) không quá 1 nghiệm. 2 x  1   1  Ta có: 3 lim f (  x )     và 3 lim f (  x ) 
   nên có bảng biến thiên sau:   2    x0 x   2 x x  
Từ bảng biến thiên, suy ra hàm số 3
g(x)  f (x )  3x có 3 điểm cực trị. Chọn đáp án A.
Baøi taäp töông töï vaø môû roäng
46.1. Cho f (x) là hàm bậc bốn và có f (0)  0. Hàm số f (
x) có bảng biến thiên sau:
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 112 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 2 Hàm số 3 g(x) 
f (x )  2x có bao nhiêu điểm cực trị ? 3 A. 1. B. 2. C. 3. D. 4.
46.2. Cho f (x) là hàm bậc bốn và có f (0)  0. Hàm số f (
x) có bảng biến thiên sau: 1 Hàm số 3 g(x) 
f (x )  2x có bao nhiêu điểm cực trị ? 3 A. 1. B. 2. C. 3. D. 4.
46.3. Cho hàm số y f (x) có đạo hàm trên  và hàm y f (
x) có đồ thị như hình vẽ. Trên đoạn x  [ 3  ;4],   hàm số 2
g(x)  f   1  ln(x  8x  16) 
có bao nhiêu điểm cực trị ? 2  A. 1. B. 2. C. 0. D. 3.
46.4. Cho hàm số y f (x) có đạo hàm liên tục trên  và f (0)  0, f (4)  4. Biết đồ thị hàm số y f (
x) có đồ thị như hình vẽ bên dưới.
Số điểm cực trị của hàm số 2
g(x)  f (x )  2x là A. 1. B. 2. C. 3. D. 5.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 113 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
46.5. Cho hàm số đa thức f (x ) có đạo hàm trên . Biết f (2)  0 và đồ thị của hàm số y f (  x) như hình vẽ bên dưới. Hàm số 2
y  4f (x)  x  4 có bao nhiêu điểm cực tiểu ? A. 1. B. 3. C. 4. D. 2. 46.6. Cho hàm số 4 3 2
f (x)  ax bx cx dx  ,
e (ae  0). Đồ thị hàm số y f (
x) như hình vẽ bên dưới. Hàm số 2
y  4f (x)  x có bao nhiêu điểm cực tiểu ? A. 3. B. 4. C. 2. D. 5.
46.7. Cho hàm số f (x ) có bảng biến thiên của hàm số f (
x) bên dưới. Số điểm cực trị của hàm số 2
y f (x  2x) là A. 9. B. 3. C. 7. D. 5.
46.8. Cho hàm số bậc bốn y f (x) có đồ thị như hình vẽ bên dưới. Số điểm cực tiểu của hàm số 3 2
g(x)  f (x  3x ) là A. 3. B. 7. C. 4. D. 5.
46.9. Biết rằng hàm số f (x ) xác định, liên tục trên  có đồ thị được cho như hình vẽ bên dưới. Số
điểm cực đại của hàm số y f (f (x))  2021 là A. 1. B. 3. C. 2. D. 4.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 114 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
46.10. Cho hàm số f (x) có đạo hàm liên tục trên  có f (5)  12. Đồ thị hàm số f (
x) được cho như
hình. Số điểm cực trị của hàm số 2
y f (1  2x)  2x  2x là A. 3. B. 5. C. 7. D. 6. 3
46.11. Cho hàm số bậc bốn f (x) có f (0) 
. Hàm số y f (x) có đồ thị trong hình vẽ bên. Số điểm 2 cực trị của hàm số 2
y  4f (x  1)  x  2x là A. 3. B. 5. C. 4. D. 6.
46.12. Cho hàm số y f (x) có đạo hàm 3 f (
x)  4x  2x và f (0)  1. Số điểm cực tiểu của hàm số 3 2
g(x)  f (x  2x  3) là A. 0. B. 1. C. 2. D. 3. 2
46.13. Cho hàm số y f (x) có đạo hàm 2 f (
x)  3x  3 và f (2)  4. Hàm số g(x) f(1 2x)     có
bao nhiêu điểm cực trị ? A. 3. B. 4. C. 5. D. 6.
46.14. Cho f (x) là hàm số bậc ba. Đồ thị các hàm số y f (x) và y f (
x) lần lượt là các đường cong
trong hình vẽ bên. Xét hàm số 2
g(x)  f (x f (x)), x  .
 Biết rằng đồ thị hàm số y g (  x) không
tiếp xúc với trục hoành. Số điểm cực trị của g(x) là A. 4. B. 5. C. 7. D. 8.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 115 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
46.15. Hàm số y f (x) có bảng xét dấu đạo hàm f (
x) bên dưới. Có bao nhiêu số nguyên m  [ 5  ;5] để hàm số 2 2
y f (x  2mx m  1) đồng biến trên khoảng (0;1) ? A. 5. B. 8. C. 7. D. 6.
46.16. Cho hàm số y f (x) có đạo hàm liên tục trên .
 Đồ thị của y f (x) như hình vẽ. Có tất cả
bao nhiêu giá trị nguyên dương của tham số m để hàm số 2
y  4f (x m)  x  2mx đồng biến trên khoảng (1;2) ? y A. 2. 1 4 B. 3. – 2 O x C. 0. – 2 D. 1.
46.17. Cho hàm số y f (x) có đạo hàm liên tục trên .
 Biết f (0)  0 và đồ thị hàm số y f (x) như
hình vẽ bên dưới. Hàm số 2
y  4f (x)  x đồng biến trên khoảng nào dưới đây ? y A. (0; 4). 1 B. ( 2  ; 0). 4 – 2 O x C. (4;  )  . D. ( ;  2  ). – 2
46.18. Cho hàm số f (x) liên tục trên  có f ( 1
 )  0 và có đồ thị hàm số y f (x) như hình vẽ. Hàm số 2
y  2f (x  1)  x đồng biến trên khoảng nào sau đây ? A. (3;  )  . B. ( 1  ;2). C. (0;  )  . D. (0; 3).
46.19. Cho hàm số y f (x) liên tục trên  thỏa mãn 2
(3x  15x)f (
x)  (10  5x)f(x)  0, x  0, 2 2 f (1)  4
 và f (x) 
f (x)  0.    
Tổng giá trị cực đại và cực tiểu của hàm số y f (x) bằng A. 3 3 4. B. 3 2 4. C. 3 3 4. D. 4 3 2.
46.20. Cho hàm số y f (x) liên tục trên  và có đồ thị hàm số y f (
x) như hình bên dưới. Hàm số 2 4 6 2
y  15f (2x x )  10x  30x  20 có bao nhiêu điểm cực trị ? A. 1. B. 2. C. 3. D. 5.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 116 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Câu 47. Có bao nhiêu số nguyên a (a  2) sao cho tồn tại số thực x thỏa log x log (  2) a ax  2 ? A. 8. B. 9. C. 1. D. Vô số.
Lôøi giaûi tham khaûo
Điều kiện: x  2. Đặt m  loga  0. Phương trình trở thành ( m  2)m xx  2.  m y   x  2  Đặt m
y x  2 và y  2 thì ta có hệ phương trình  m x   y  2   m m m m ( )   (0;)
 x y x y x x y y f (x)  f (y) m f t t t
x y log(x  2) m
x x  2  m log x  log(x  2)  m
 1  loga  1  a  10. log x a 2  , a   
 a  {2; 3; 4;...;9} : có 8 thỏa mãn bài toán. Chọn đáp án A.
Baøi taäp töông töï vaø môû roäng log a log a 47.1
Có bao nhiêu số nguyên a (a  2) sao cho tồn tại số thực x thỏa 2 2 2a(x  1)  x  2 ? A. 1. B. 2. C. 3. D. 0. 47.2
Có bao nhiêu số nguyên a (a  2) sao cho tồn tại số thực x thỏa ln x ln (  3) x ax  3 ? A. 1. B. 2. C. 3. D. 0. 47.3
Có tất cả bao nhiêu giá trị nguyên của số thực y nhỏ hơn 10 sao cho tồn tại số thực x thỏa mãn   ex  ex y y ? A. 9. B. 8. C. 10. D. 7. 47.4
Có bao nhiêu số nguyên y để tồn tại số thực x thỏa ln y  3 sin x ln(y 4 sin x)     sin x   ? A. 6. B. 10. C. 5. D. 9.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 117 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 47.5
Có tất cả bao nhiêu số nguyên y sao cho có đúng 2 số thực x  (0;10) thỏa mãn: x x 2 x 3 3
8  3x.4  (3x  1).2  (y  1)x  (y  1)x ? A. 101. B. 100. C. 102. D. 103. 47.6
Gọi a  1 là số thực sao cho tồn tại duy nhất số thực x thỏa x
a  log x. Mệnh đề nào đúng ? a
A. a  (1, 2; 1, 3).
B. a  (1, 3; 1, 4).
C. a  (1, 4; 1, 5).
D. a  (1, 5; 1, 6). 3 47.7
Phương trình xm 3  x 2 2
 (  3) .2x  (8  ).2x x x m
 4 có ba nghiệm phân biệt khi và chỉ khi
m  (a;b). Khi đó giá trị 2 2 b a bằng A. 48. B. 36. C. 64. D. 72. 47.8 Giả sử ,
a b là các số thực sao cho 3 3 3x 2   .10  .10 x x y a b
đúng với mọi các số thực dương x, ,
y z thỏa mãn log(x y)  z và 2 2
log(x y )  z  1. Giá trị của a b bằng 31 A.  2 29 B.  2 31 C.   2 25 D.   2 47.9
Xét các số thực dương x, y thỏa mãn log (4  16)   3  8y x x y
 2 . Gọi (x ;y ) là cặp (x;y) 2 o o khi biểu thức 2   3  1  8y P x x
đạt giá trị nhỏ nhất. Giá trị của 3
x  3y bằng o o A. 9. B. 7. C. 7. D. 9.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 118 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
47.10 Có bao nhiêu giá trị nguyên của tham số thực m để tồn tại cặp số (x;y) thỏa mãn đồng thời 2x y  1  3x 2 e
 e  y x y  1 và 2 2
log (2x y  1)  (m  4)log x m  4  0 ? 2 2 A. 3. B. 4. C. 5. D. 6. 2
47.11 Cho phương trình 2 y 2 2
log (2x  4x  4)  2  y x  2x  1. Hỏi có bao nhiêu cặp số nguyên 2
dương (x;y) và 0  x  100 thỏa mãn phương trình đã cho ? A. 4. B. 3. C. 1. D. 2.
47.12 Có bao nhiêu cặp số nguyên dương (x;y) thỏa mãn 0  x  2020 và (  1).3x  .27y x y ? A. 2020. B. 673. C. 672. D. 2019.
47.13 Có bao nhiêu cặp số nguyên (x;y) thỏa mãn đồng thời các điều kiện 0  x  2020, 1  y  2020 và x 1
4   log (  3)  16.2y y
 log (2x  1) ? 2 2 A. 2019. B. 2020. C. 1010. D. 1011. 3 2 3 2 3 2
47.14 Có tất cả bao nhiêu bộ ba số thực (x, ,
y z) thỏa mãn đồng thời các điều kiện 2 x .4 y .16 z  128 và 2 4 2 2 4 2
(xy z )  4  (xy z ) ? A. 3. B. 4. C. 1. D. 2.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 119 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
47.15 Cho hàm số bậc ba y f (x) có đồ thị như hình vẽ bên. Số nghiệm thực phân biệt của phương
trình f (xf (x))  1  là A. 3. B. 6. C. 7. D. 8.
47.16 Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 2
 020;2020] để phương trình 2 2 log
(x  3x)  log
(x m) có đúng hai nghiệm phân biệt ? 2020 2021 A. 4035. B. 2023. C. 2022. D. 4036.
47.17 Gọi S là tập hợp tất cả các giá trị nguyên của tham số m thuộc đoạn [20;20] để phương trình 2 2 log
(x  3x)  log
(x m) có đúng hai nghiệm phân biệt. Tổng tất cả các phần tử của tập 2021 2021 S bằng A. 203. B. 206. C. 3. D. 6.
47.18 Có tất cả bao nhiêu giá trị nguyên của y  ( 1
 0;10) để tồn tại 2 số thực x thỏa mãn: 2 2
log (x  2x  4)  log (x  2x y) 3 5 A. 4. B. 3. C. 6. D. 9.
47.19 Có bao nhiêu giá trị của y  (0;2020) để tồn tại số thực x thỏa mãn x x 2 4 4 2    .cos(x y) ? A. 324. B. 322. C. 320. D. 321.
47.20 Với giá trị nào của y thì tồn tại đúng 1 số thực x thỏa mãn 9x  9  3x y cos(x) ? A. y  3. B. y  6  . C. y  3  .
D. y  6.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 120 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Câu 48. Cho hàm số bậc ba y f (x) có đồ thị là đường cong trong hình bên. Biết hàm số f (x) đạt
cực trị tại hai điểm x , x thỏa mãn x x  2 và f (x )  f (x )  0. Gọi S và S là diện 1 2 2 1 1 2 1 2 S
tích của hai hình phẳng được gạch trong hình bên. Tỉ số 1 bằng S2 3 A. 4 5 B.  8 3 C.  8 3 D. 5
Lôøi giaûi tham khaûo
Tịnh tiến điểm uốn về gốc tọa độ, ta được hình vẽ bên.
Khi đó, do f (x) là hàm bậc ba, nhận gốc tọa độ là tâm đối xứng nên x  1  , x  1 1 2 Chọn 2 3 f (
x)  3x  3  f (x)  x  3x. 0 5 Do đó 3 S
(x  3x)dx   
Mà S S  2 2 4 1 2 1  3 S 3 Suy ra: 1 S  
  Chọn đáp án D. 1 4 S 5 2
Baøi taäp töông töï vaø môû roäng
48.1. Cho hàm số bậc ba y f (x) có đồ thị là đường cong trong hình bên. Biết hàm số f (x) đạt cực trị
tại hai điểm x , x thỏa mãn x x  4 và f (x )  f (x )  0. Gọi S và S là diện tích của hai 1 2 2 1 1 2 1 2 S
hình phẳng được gạch trong hình bên. Tỉ số 1 bằng S2 A. 5/3. 3 B.  5 C. 1. D. 3/4.
48.2. Cho hàm số bậc ba 3 2
f (x)  ax bx cx d và đường thẳng d : g(x)  mx n có đồ thị như 1
hình vẽ. Nếu diện tích phần tô bằng bằng thì diện tích phần gạch bằng 2 5 A.  2 B. 2. C. 1. 3 D.  2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 121 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
48.3. Cho đường cong 3
(C ) : y  8x  27x và đường thẳng y m cắt (C ) tại hai điểm phân biệt nằm
trong gốc phần tư thứ nhất của hệ trục tọa độ Oxy và chia thành 2 miền phẳng (gạch sọc và kẻ
caro) có diện tích bằng nhau (tham khảo hình vẽ bên). Mệnh đề nào sau đây là đúng ? 1 A. 0  m   2 1 B.m  1. 2 3 C. 1  m   2 3 D. m  2. 2
48.4. Cho y f (x) xác định trên [3; 3] có đồ thị như hình vẽ. Biết S , S , S có diện tích lần lượt là 1 2 3 1 3, 1 và 3. Khi đó (1  x)f (  3x)dx  bằng 1  1 A.  2 B. 7. 5 C.   9 D. 4.
48.5. Hình phẳng (H ) được giới hạn bởi đồ thị (C ) của hàm đa thức bậc ba và parabol (P ) có trục đối
xứng vuông góc với trục hoành. Phần tô đậm của hình vẽ có diện tích bằng 37 A.  12 7 B.  12 11 C.  12 5 D.  12
48.6. Cho hai hàm số 2 2
f (x)  ax bx cx  2 và 2
g(x)  dx x e  2 (a, , b ,
c d, e  ). Biết rằng
đồ thị của hàm số y f (x) và y g(x) cắt nhau tại ba điểm có hoành độ lần lượt là 2; 1; 1
(tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng 37 A.  6 13 B.  2 9 C.  2 37 D.  12
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 122 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 48.7. Cho hàm số 4 3 2
y ax bx cx dx  ,
e (a  0) có đồ thị (C ) và đường d : y mx n cắt
đồ thị (C ) tại các điểm có hoành độ lần lượt là 2;  1; 0; 1. Biết rằng hình phẳng giới hạn bởi
(C ), d và đường thẳng x  2, x  0 có diện tích bằng 1. Diện tích hình phẳng giới hạn bởi
đồ thị (C ), đường thẳng d, trục tung và đường x  1 bằng 11 A.  30 19 B.  30 49 C.  30 19 D.  15 48.8. Cho hàm số 4 2
y ax bx  ,
c (a  0) có đồ thị (C) và tiếp tuyến d của đồ thị (C) tại điểm có hoành độ x  1
 , cắt (C) tại hai giao điểm còn lại có hoành bằng x  0, x  2 (tham khảo hình
vẽ). Biết rằng hình phẳng giới hạn bởi (C), d và đường thẳng x  0, x  2 có diện tích bằng
28/5. Tính diện tích hình phẳng giới hạn bởi đồ thị (C ), đường thẳng d và x  0, x  1  . 27 A.  5 29 B.  5 1 C.  5 5 D.  12
48.9. Cho hàm số y f (x) và y g(x) là hai hàm số liên tục trên  có đồ thị hàm số là y f (  x), y g (  x). Gọi , a ,
b c là các hoành độ giao điểm của đồ thị hàm số f (
x) và g (x). Hàm số
y f (x)  g(x )  m có nhiều điểm cực trị nhất khi và chỉ khi
A. f (a)  g(a)  x f (b)  g(b).
B. f (c)  g(c)  m f (b)  g(b).
C. f (b)  g(b)  m f (a)  g(a).
D. f (c)  g(c)  m f (b)  g(b).
48.10. Cho hàm số y f (x) có đạo hàm liên tục trên . Đồ thị hàm số f (
x) được cho như hình vẽ bên.
Tìm tất cả các giá trị thật của tham số m để bất phương trình 2
f (1  2x)  2x  2x m có nghiệm trên (0, 5; 1) ? 1 2 A. m f (2)   2 3 1 3 B. m f (2)   2 2 f ( 1  ) 2 C. m    2 3 21
D. m f (0)   4
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 123 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
48.11. Cho hàm số bậc bốn f (x ) có f (1)  7. Hàm số y f (
x) có đồ thị trong hình vẽ bên. Số điểm cực trị của hàm số 2
y f (x  1)  x  4x  6 là A. 3. B. 5. C. 7. D. 6.
48.12. Cho hai hàm số 4 3 2
f (x)  ax bx cx dx e và 3 2
g(x)  mx nx px q. Đồ thị của hai
hàm số y f (
x), y g (x) như hình vẽ bên dưới. Tổng các nghiệm của phương trình
f (x)  q g(x)  e bằng 13 A.  3 13 B.   3 4 C.  3 4 D.   3
48.13. Cho đường cong 3 2
(C ) : f (x)  x ax bx c và đường thẳng d : y g(x) là tiếp tuyến của
(C ) tại điểm có hoành độ x  1. Biết rằng diện tích hình phẳng giới hạn bởi (C ) và d bằng
108 . Giao điểm thứ hai của d và (C ) có hoành độ m  0, khi đó m thuộc khoảng nào ? A. (0;2). B. (2; 4). C. (4; 6). D. (6; )  .
48.14. Cho đường cong 3
(C ) : y x . Xét điểm A có hoành độ dương thuộc đồ thị (C ). Tiếp tuyến của
(C ) tại A tạo với (C ) một hình phẳng có diện tích bằng 27. Hoành độ của điểm A thuộc khoảng nào dưới đây ?  1   A. 0;     2 1    B.  ;1   2   3   C. 1  ;    2 3    D.  ;2   2 
48.15. Gọi S và S lần lượt là diện tích các hình phẳng giới hạn bởi 2
(P) : y x k (k  0) và đường 1 2
thẳng d : y  2x như hình vẽ. Nếu S S thì k bằng 1 2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 124 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 2 A.  5 7 B. 9 3 C. 2 3 D.  4 48.16. Cho parabol 2
(P) : y x , điểm (
A 0;1). Một đường thẳng đi qua A cắt (P) tại hai điểm , B C
sao cho AC  2AB như hình vẽ bên. Thể tích của khối tròn xoay được tạo thành khi quay phần
gạch chéo quanh trục hoành gần với giá trị nào nhất sau đây ? A. 13, 3. B. 8. C. 7,3. D. 11. 48.17. Cho parabol 2
(P) : y x , điểm (
A 0;2). Một đường thẳng đi qua A cắt (P) tại hai điểm , B C
sao cho 3AC  2AB như hình vẽ bên. Thể tích của khối tròn xoay được tạo thành khi quay phần
gạch chéo quanh trục hoành gần với giá trị nào nhất sau đây ? A. 34. B. 11. C. 7. D. 21. 48.18. Cho parabol 2
(P) : y x , điểm (
A 0;1). Một đường thẳng d đi qua A cắt (P) tại hai điểm 2 2 B( ; b b ), C ( ;
c c ) sao cho AC  4AB như hình vẽ bên. Gọi S là diện tích hình phẳng giới hạn 1
bởi {(P); d; x  ;
b x  0} và S là diện tích hình phẳng giới hạn bởi {(P); d; x  ; b x  0}. 2
Tỉ số diện tích S / S bằng 1 2 181 A.  2944 17 B.  608 13 C.  112 2763 D.  2944
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 125 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 48.19. Cho parabol 2
y x có đồ thị như hình vẽ, diện tích S  2S . Gọi V , V là thể tích hình phẳng 2 1 1 2 V
S , S quay quanh trục hoành. Tính 2  1 2 V1 A. 4 2 3. B. 4 3 2. C. 2. D. 4. 48.20. Cho hàm số 2
y x có đồ thị (C ) như hình vẽ. Kí hiệu (H ) là hình phẳng được giới hạn bởi 1 (C), x  ,
a (a  0) và trục hoành; (H ) là hình phẳng được giới hạn bởi (C), x  ,
b (b  0) và 2
trục hoành lần lượt có diện tích S , S . Đồng thời V , V là thể tích khối tròn xoay tạo thành khi 1 2 1 2 S
quay (H ), (H ) xung quanh trục hoành. Biết rằng 243V  32V . Tỉ số 1 bằng 1 2 1 2 S2 4 A. 9 8 B.  27 2 C.  3 16 D.  81
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 126 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Câu 49. Xét hai số phức z , z thỏa mãn z  1, z  2 và z z  3. Giá trị lớn nhất của 1 2 1 2 1 2
3z  z  5i bằng 1 2 A. 5  19. B. 5  19.
C. 5  2 19. D. 5  2 19.
Lôøi giaûi tham khaûo
Cách giải 1. Phương pháp hình học.
Gọi A là điểm biểu diễn số phức z , B là điểm biểu diễn số phức z và C là điểm biểu diễn 1 2
số phức w  3z z , điểm M(0; 5). 1 2        Ta có: 2 2 2 2
OC  3OA OB OC  (3OA OB)  9OA OB  6O . AOB   2 2 2
OA OB AB 2 2 2 2
 9OA OB  6.O . AOB.cos(O ,
A OB)  9OA OB  6  19 2
w  19. Mà MC OM OC nên 3z  z  5iMC
O, M, C thẳng hàng 1 2 max max
Suy ra 3z  z  5i
OM R  5  19. Chọn đáp án B. 1 2 max
Cách giải 2. Phương pháp đại số.
Đặt z a bi và z c di. Suy ra: 2 2 2 2 2 2
a b  1, c d  4, (a c)  (b d)  3. 1 2 Do đó 2 2 2 2
a  2ac c b  2bd d  3  ac bd  1.
Ta có: 3z z  3(a c)  (3b d)i nên 1 2 2 2
3z z  (3a c)  (3b d) 2 2 2 2
 9(a b )  (c d )  6(ac bd)  19. 1 2
Áp dụng bất đẳng thức z z   z z  , ta có 3z z  5i  3z z  5i  19  5. 1 2 1 2 Chọn đáp án B.
Baøi taäp töông töï vaø môû roäng
Dạng 1. ĐIỂM VÀ ĐƯỜNG THẲNG Cho đường thẳng ( )
 : Ax By C  0 và điểm M  ( )  . Điểm N  ( )
 sao cho NM nhỏ nhất  K
là hình chiếu của N lên ( )  , nghĩa là NMNK dM K. min [N ,()] CzOH d   O  ,( ) min     2 2 A B
Khi đó M H và tọa độ H  ( )   (OH ).
Ax By C
z  (x y i)  NK d       [N ;()] min 2 2 A B
Khi đó M K và tọa độ K  ( )   (MK ).
49. 1 Xét các số phức z x yi thỏa mãn z  2  4i z  2i và z đạt giá trị nhỏ nhất. Khi đó giá
trị của 3x  2y bằng A. 2.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 127 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 B. 3. C. 4. D. 5.
49. 2 Xét các số phức z thỏa mãn z(z  2  i)  4i  1 là một số thực. Giá trị nhỏ nhất của z bằng 8 A.  5 16 B.  5 9 C.  6 7 D. 5
49. 3 Xét các số phức z thỏa mãn z  2  2i z  4i . Giá trị nhỏ nhất của iz  1 bằng A. 2 2. B. 2. 2 C. 2 3 2 D. 2
49. 4 Xét các số phức z thỏa z  1  i z  1  2i . Giá trị nhỏ nhất của (3  4i)z  5  10i bằng 7 3 A.  26 15 B.  2 17 C.  2 5 13 D. 26
49. 5 Xét các số phức z thỏa mãn z z  1  2i . Giá trị nhỏ nhất của (1  2i)z  11  2i bằng 5 A.  2 2 B.  5 2 C.  5 5 D. 2
Dạng 2. ĐIỂM VÀ ĐƯỜNG TRÒN
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 128 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Cho tập hợp điểm M (x;y) biểu diễn các số phức z x yi là một đường tròn (C ) có tâm I (a;b) và bán kính .
R Gọi N là điểm biểu diễn số phức z .
Phương pháp 1. Hình học zOM
OM OI R khi M M   min 1 1 min    zOM
OM OI R khi M M  max 2 2  max
Khi đó (OI )  (C )  {M ;M }. 1 2  z z   MN
NN NI R khi M N    min 1 1 min    z z   MN
NN NI R khi M N  max 2 2  max
Khi đó (NI )  (C )  {N ;N }. 1 2
Lưu ý. Nếu đề bài yêu cầu tìm tổng phần thực, phần ảo tương ứng với z , z thì từ nhận xét min max
I là trung điểm của M M suy ra: tổng phần thực 2a, tổng phần ảo 2b. 1 2
Phương pháp 2. Bất đẳng thức Cauchy – Schwarz
Giả sử tập hợp điểm là đường tròn 2 2 2
(C) : (x a)  (y b)  R và viết lại: 2 2 2 2
(C) : x y  2ax  2by c  0  x y  2ax  2by c 2 2 2 2 2 2 2
z x y z x y  2ax  2by c  2 (
a x a)  2 (
b y b)  2a  2b c nhằm lợi dụng 2 2 2
(x a)  (y b)  R trong bất đẳng thức Cauchy – Schwarz (điểm rơi): 2 2  2 2  2 2  2 2 (4a 4b ) (x a) (y b) 2a.(x a) 2 . b (y b) (4a 4b ) (x a) (y b)                   

 2 2 R R 2 2 2 2 2 2 2 2 2
Suy ra: 2a  2b c  2R (a b )  z  2a  2b c  2R (a b ) 2 2 2 2 2 2 2 2
 2a  2b c  2R (a b )  z  2a  2b c  2R (a b ).
Phương pháp 3. Lượng giác 2 2 x a     y b     
Giả sử tập hợp điểm là đường tròn 2 2 2
(C ) : (x a)  (y b)  R        1,  gợi ta đến  R     R  x a   sint x
  a R sint   công thức 2 2
sin t  cos t  1 nên đặt R      y b y
  b R cost   cost   R 2 2 2 2 2 2 2
Do đó: z x y z x y  (a R sint)  (b R cost) 2 2 2 2 2 2
z a b R (sin t  cos t)  2a .
R sint  2b . R cost 2 2 2 2 2 2
z a b R  2R a b .sin(t  )
và luôn có 1  sin(t )  1 nên suy ra: 2 2 2 2 2 2 2 2
a b  2R a b z a b  2R a b .
Phương pháp 4. Sử dụng bất đẳng thức trị tuyệt đối z z
z z z z . 1 2 1 2 1 2
49. 6 Cho các số phức thỏa mãn z  2  2i  1. Giá trị lớn nhất của z bằng
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 129 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 A. 4 2  2. B. 2  2. C. 2 2  1. D. 3 2  1.
49. 7 Xét các số phức z thỏa z  2  4i  2. Gọi z , z là hai số phức có môđun lớn nhất và nhỏ nhất. 1 2
Tổng phần ảo của z , z bằng 1 2 A. 8  . B. 4. C. 8. D. 4.
49. 8 Xét các số phức z thỏa mãn điều kiện (1  i)z  1  7i  2. Gọi m, M lần lượt là giá trị nhỏ
nhất và giá trị lớn nhất của biểu thức P z . Giá trị của M m bằng A. 4. B. 10. C. 2. D. 24.
49. 9 Xét các số phức z, w thỏa mãn w iz và (1  i)z  2  2i  2. Giá trị lớn nhất của z w bằng A. 3. B. 2 3. C. 3 2. D. 3 3.
49. 10 Xét các số phức z thỏa mãn 2 2
z  4  z  2iz . Giá trị nhỏ nhất của z i bằng A. 1. B. 2. C. 3. D. 4.
49. 11 Xét các số phức z thỏa mãn điều kiện 2
z  2z  5  (z 1  2i)(z  3i 1) . Giá trị nhỏ nhất của
z  2  2i bằng A. 0, 5. B. 1. 3 C.  2 D. 2.
Dạng 3. ĐƯỜNG TRÒN VÀ ĐƯỜNG TRÒN
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 130 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
49. 12 Xét các số phức z , z thỏa mãn z  4  1 và iz  2  1. Giá trị nhỏ nhất của z  2z bằng 1 2 1 2 1 2 A. 2 5  2. B. 4  2. C. 4 2  3. D. 4 2  3.
49. 13 Xét các số phức z , z thỏa mãn z  3i  5  2 và iz  1  2i  4. Giá trị lớn nhất của biểu 1 2 1 2
thức P  2iz  3z bằng 1 2 A. 313  16. B. 313. C. 313  8.
D. 313  2 5.
49. 14 Xét các số phức z, w thỏa z  3 2  2 và w  4 2i  2 2. Biết z w đạt giá trị nhỏ nhất
khi z z và w w . Giá trị của 3z w bằng 0 0 0 0 A. 2 2. B. 6 2. C. 4 2. D. 1.
49. 15 Cho các số phức z, w thỏa mãn z  5  3i  3 và iw  4  2i  2. Giá trị lớn nhất của biểu
thức 3iz  2w bằng A. 554  5. B. 578  13. C. 578  5. D. 554  13.
49. 16 Cho hai số phức z , z thỏa mãn z  2  3i  2 và z  1  2i  1. Giá trị lớn nhất của biểu 1 2 1 2
thức z z bằng 1 2 A. 3  34. B. 3  10. C. 3. D. 6.
Dạng 4. ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 131 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
49. 17 Biết rằng số phức z x yi (x, y  ) thỏa mãn đồng thời z  3  4i  5 và biểu thức 2 2
P z  2  z i đạt giá trị lớn nhất. Giá trị của z bằng A. 33. B. 50. C. 10. D. 5 2.
49. 18 Xét các số phức z thỏa mãn z  1  3i  13. Gọi m, M lần lượt là giá trị nhỏ nhất và lớn nhất 2 2
của biểu thức P z  2  z  3i . Tổng m M bằng A. 10. B. 25. C. 34. D. 40.
49. 19 Xét các số phức z x yi (x, y  ) thỏa mãn (1  i)z  2  i  4. Giá trị lớn nhất của biểu
thức P x y  3 bằng A. 4. B. 4 2. C. 4  2 2. D. 8. 2 2
49. 20 Xét các số phức z thỏa mãn z  2  z i  1 và các số phức z thỏa z  4  i  5. Giá 1 1 1 2 2
trị nhỏ nhất của z z bằng 1 2 A. 5. B. 2 5. 2 5 C.  5 3 5 D.  5
Dạng 5. MỘT SỐ LOẠI KHÁC (ĐOẠN THẲNG VÀ TIA, PARABOL, ELIP,…)
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 132 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
49. 21 Xét các số phức z thỏa mãn z  2  i z  4  7i  6 2. Gọi m, M lần lượt là giá trị nhỏ nhất
và giá trị lớn nhất của T z  1  i . Giá trị của m M bằng 5 2  73 A.  2
B. 5 2  2 73. C. 13  73. 5 2  2 73 D.  2
49. 22 Xét các số phức z thỏa mãn z  1  i z  8  3i  53. Giá trị lớn nhất của biểu thức
P z  1  2i bằng A. 53. B. 53. 185 C. . 2 D. 106.
49. 23 Xét các số phức z thỏa z  2  3i z  6  i  2 17. Gọi M, m lần lượt là giá trị lớn nhất và
giá trị nhỏ nhất của P z  1  2i z  2  i . Giá trị m M bằng A. 3 2. 3 2  2 B.  2
C. 8 2  2 5. 6 2  2 5 D.  3
49. 24 Xét các số phức z thỏa mãn iz  2i  2  z  1  3i  34. Giá trị nhỏ nhất của biểu thức
P  (1  i)z  2i bằng 9 A. . 17 B. 3 2. C. 4 2. D. 26.
49. 25 Xét các số phức z đồng thời thỏa mãn z  4  3i z  4  3i  10 và z  3  4i nhỏ nhất.
Môđun của số phức z bằng A. 5.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 133 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 B. 5 2. C. 6 2. D. 10.
49. 26 Xét hai số phức z , z thỏa mãn 2 z i z z  2i và z i  10  1. Giá trị nhỏ nhất của 1 2 1 1 1 2
biểu thức z z bằng 1 2 A. 10  1. B. 101  1. C. 101  1. D. 3 5  1.
49. 27 Xét các số phức z a bi ( ,
a b  ) thỏa mãn điều kiện 2
4(z z ) 15i i(z z  1) . Tính 1 P a
  4b khi z   3i đạt giá trị nhỏ nhất. 2
A. P  4. B. P  5.
C. P  6.
D. P  7. 6
49. 28 Xét số phức z a bi thỏa 2 z  3i z z  2i . Tính 8a  7b khi biểu thức P z i đạt 7 giá trị nhỏ nhất.
A. 8a  7b  8.
B. 8a  7b  5.
C. 8a  7b  6.
D. 8a  7b  7.
49. 29 Xét các số phức z thỏa mãn z  1. Giá trị lớn nhất của T z  1  2 z  1 bằng A. 2 5. B. 2 10. C. 3 2. D. 3 5.
49. 30 Xét các số phức z thỏa z  4  z  4  10. Giá trị lớn nhất và nhỏ nhất của z lần lượt là A. 10 và 4. B. 5 và 4. C. 4 và 3. D. 5 và 3.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 134 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
Câu 50. Trong không gian Oxyz, cho hai điểm (
A 2;1; 3) và B(6;5;5). Xét khối nón (N ) có đỉnh , A
đường tròn đáy nằm trên mặt cầu đường kính AB. Khi (N ) có thể tích lớn nhất thì mặt
phẳng chứa đường tròn đáy của (N ) có phương trình dạng 2x by cz d  0. Giá trị của
b c d bằng A. 21. B. 12. C. 18. D. 15.
Lôøi giaûi tham khaûo Ta có AB  6.
Gọi h, r là chiều cao và bán kính đáy hình nón (N ).
R là bán kính mặt cầu (S) đường kính AB.
Gọi I là trung điểm AB và H là tâm
đường tròn đáy của (N ).
Để thể tích hình nón (N ) lớn nhất thì h  . R Ta có: 2 2 2 2 2
r R IH R  (h R) Cauchy 3 1 1 (4R) Thể tích khối nón 2  2 2 V h. r h. .  R (h ) R     
 .h.h.(4R  2h)    3 3   6 6 27 4
Dấu "  " xảy ra khi h  4R  2h h
R AH  4, BH  2. 3  2  14 11 13  
Gọi H (x;y;z), khi đó: AH AB H   ; ;  3  3 3 3  
Phương trình mặt phẳng chứa đường tròn đáy của (N ) đi qua H và nhận AB làm vécto pháp  14  11  13       tuyến là 2 x     2 y     1 z     0   3     3     3 
 2x  2y z  21  0  b c d  1  8. Chọn đáp án D.
Baøi taäp töông töï vaø môû roäng
50. 1 Trong không gian Oxyz, cho mặt cầu 2 2 2
(S) : (x  1)  (y  2)  (z  3)  27. Gọi (P) là mặt phẳng đi qua hai điểm (
A 0; 0;4), B(2; 0; 0) và cắt (S) theo giao tuyến là đường tròn (C ) sao
cho khối nón đỉnh là tâm của (S) và đáy là là đường tròn (C ) có thể tích lớn nhất. Biết rằng
(P) : ax by z c  0, khi đó a b c bằng A. 4. B. 8. C. 0. D. 2.
50. 2 Trong không gian Oxyz, cho mặt cầu 2 2 2
(S) : (x  1)  (y  2)  (z  3)  48. Gọi (P) là mặt phẳng đi qua hai điểm (
A 0;0;4), B(2;0; 0) và cắt mặt cầu (S) theo giao tuyến là đường tròn
(C ). Khối nón (N ) có đỉnh là tâm của (S), đường tròn đáy là (C ) có thể tích lớn nhất bằng
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 135 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 128 A.  3 B. 39 . 88 C.  3 215 C.  3
50. 3 Trong không gian Oxyz, cho mặt cầu 2 2 2
(S) : (x 1)  y  (z  2)  1. Xét điểm M di động trên x 1 y 1 z  2 đường thẳng d :  
, từ M kẻ ba tiếp tuyến M ,
A MB, MC đến (S) với 2 1 2  ,
A B ,C là các tiếp điểm. Khi đường tròn ngoại tiếp tam giác ABC có bán kính nhỏ nhất bằng
thì phương trình mặt phẳng qua 3 điểm ,
A B, C là (ABC ) : ax by z d  0. Khi đó
2a b  2d bằng A. 3. B. 1. C. 2. D. 3. x 1 y  2 z  1
50. 4 Trong không gian Oxyz Cho d :  
và (P) : 2x  2y z  16  0. Mặt cầu 2 1  2 
(S) cắt d tại ,
A B sao cho AB  8 và cắt (P) theo giao tuyến là đường tròn có bán kính r  3.
Bán kính của mặt cầu (S ) nhỏ nhất có thể là A. 3. B. 1. C. 2. D. 3. x
  1  3a at 
50. 5 Trong không gian với hệ toạ độ Oxyz, cho đường thẳng  : y   2  t .  Biết khi a z
  2  3a (1 a)t 
thay đổi luôn tồn tại một mặt cầu cố định đi qua điểm M (1;1;1) và tiếp xúc với đường thẳng . 
Tìm bán kính của mặt cầu đó. A. 5 3. B. 4 3. C. 7 3. D. 3 5.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 136 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
50. 6 Trong không gian Oxyz, cho hai điểm (
A 1;2;3), B(2;3;4). Một mặt cầu (S) bán kính R luôn
tiếp xúc với ba mặt phẳng tọa độ và đoạn thẳng AB luôn nằm trong (S ) (mọi điểm thuộc đoạn
thẳng AB đều nằm trong (S ) ). Giá trị nguyên lớn nhất của R đạt được là A. 4. B. 6. C. 5. D. 3.
50. 7 Trong không gian với hệ trục tọa độ Oxyz, Cho ba mặt phẳng (P) : x y z  5  0,
(Q) : x y z  1  0 và (R) : x y z  2  0. Ứng với mỗi cặp ,
A B lần lượt thuộc hai mặt
phẳng (P), (Q) thì mặt cầu đường kính AB luôn cắt mặt phẳng (R) theo một đường tròn. Tìm
bán kính nhỏ nhất của đường tròn đó. 1 A. 3 2 B. 3 1 C. 2 D. 1.
50. 8 Trong không gian Oxyz cho điểm (
A 2;0;0) và ba mặt phẳng (P ) : 2x y  2z  5  0, 1
(P ) : 2x y  2z  13  0, (P ) : 2x  2y z  5  0. Mặt cầu (S) có tâm I (a;b;c) và đi qua A 2 3
đồng thời tiếp xúc với hai mặt phẳng (P ),(P ). Khi khối cầu (S ) cắt mặt phẳng (P ) theo thiết 1 2 3
diện là hình tròn có diện tích lớn nhất thì a b  2c bằng A. 3. B. 0. C. 3. D. 2.
50. 9 Trong không gian Oxyz, cho hai điểm (
A 1;2;1), B(3; 0;3). Biết mặt phẳng (P) đi qua điểm A
và cách B một khoảng lớn nhất. Phương trình mặt phẳng (P) là
A. x  2y  2z  5  0.
B. x y  2z  3  0.
C. 2x  2y  4z  3  0.
D. 2x y  2z  0.
50. 10 Trong không gian Oxyz, cho ba điểm (
A 1; 0;2), B(3;2;4), C (0;2; 3). Mặt phẳng (P) thay đổi
đi qua C và không cắt đoạn thẳng A .
B Gọi d , d lần lượt là khoảng cách từ ,
A B đến (P). 1 2
Phương trình mặt cầu (S ) có tâm ,
O tiếp xúc với (P), ứng với d d lớn nhất là 1 2 A. 2 2 2
x y z  6.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 137 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 9 B. 2 2 2
x y z   2 C. 2 2 2
x y z  12. 32 D. 2 2 2
x y z   3 x  2 y z  2
50. 11 Trong không gian Oxyz, phương trình mặt (P) chứa đường thẳng d :   và (P) 1 1 1 
cách điểm M(2;1;1) một khoảng lớn nhất là
A. x y  3z  5  0.
B. 2x  5y  7z  10  0.
C. 2x y  5z  3  0.
D. x y  5z  3  0.
50. 12 Trong không gian Oxyz, gọi (P) là mặt phẳng đi qua hai điểm (
A 1;7;8), B(2;5;9) sao
cho khoảng cách từ điểm M(7; 1  ; 2
 ) đến (P) đạt giá trị lớn nhất. Biết (P) có một véctơ pháp 
tuyến là n  (a;b; 4), khi đó giá trị của tổng a b bằng A. 1  . B. 3. C. 6. D. 2.
50. 13 Trong không gian Oxyz, phương trình đường thẳng đi qua điểm (
A 1;1;1), nằm trong mặt
phẳng (P) : 2x y z  0 và cách điểm B(0;2;1) một khoảng lớn nhất là x  1 y  1 z  1 A.    1 3 1 x  1 y  1 z  1 B.    2 3 1 x  1 y  1 z  1 C.    1 3 1  x  1 y  1 z  1 D.    2 3 2 
50. 14 Trong không gian Oxyz, phương trình đường thẳng d đi qua gốc tọa độ ,
O vuông góc với đường x  1 y z thẳng d :  
và cách điểm M(2;1;1) khoảng lớn nhất là 1 2 1  2  x y z A.    1 3 2 x y z B.    1 3  2 x y z C.    1 6 4
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 138 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 x y z D.    1 6  4
50. 15 Trong không gian Oxyz, phương trình đường thẳng d đi qua gốc tọa độ O, nằm trong mặt phẳng
(P) : 2x y z  0 và cách điểm M(1;2;1) một khoảng nhỏ nhất là x y z A.    4 13 5 x y z B.    4 13 5  x y z C.    4 1  2 5 x y z D.    4 1  2 5 
50. 16 Trong không gian Oxyz, cho hai điểm (
A 3;0;1), B(1;1; 3) và phương trình mặt phẳng
(P) : x  2y  2z  5  0. Phương trình chính tắc của đường thẳng d đi qua , A song song với
(P) sao cho khoảng cách từ B đến d nhỏ nhất là x  3 y z  1 A.    26 11 2  x  3 y z  1 B.    26 1  1 2 x  3 y z  1 C.    26 11 2 x  3 y z  1 D.    2  6 11 2 
50. 17 Trong không gian Oxyz, cho mặt cầu 2 2 2
(S ) : x y z  2x  4y  4z  0 và M(1;1;1). Viết
phương trình mặt phẳng (P) đi qua M và cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất ?
A. 2x y  3z  0.
B. x  3y  2z  0.
C. x y  0.
D. 2x y z  0.
50. 18 Trong không gian Oxyz, cho điểm M(3; 3;3), mặt phẳng (P) : 2x  2y z  15  0 và mặt cầu 2 2 2
(S) : (x  2)  (y  3)  (z  5)  100. Đường thẳng  qua M, nằm trên mặt phẳng (P) cắt (S) tại ,
A B sao cho độ dài AB lớn nhất. Phương trình đường thẳng  là x  3 y  3 z  3 A.    1 1 3 x  3 y  3 z  3 B.    1 4 6
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 139 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 x  3 y  3 z  3 C.    16 11 1  0 x  3 y  3 z  3 D.    5 1 8
50. 19 Trong không gian Oxyz, cho điểm E(0;1;2), mặt phẳng (P) : x y z  3  0 và mặt cầu 2 2 2
(S) : (x  1)  (y  3)  (z  4)  25. Phương trình đường thẳng d đi qua điểm E nằm trong
(P) và cắt mặt cầu (S) tại hai điểm có khoảng cách lớn nhất là x   1  2t  A. y   3  t .  z   4 t  x   2t  B. y   1  t .  z   2 t  x   1  C. y   3  t .  z   4  2t  x   0  D. y   1  t .  z   2 t 
50. 20 Trong không gian Oxyz, cho điểm (
A 3;3;2 6). Đường thẳng( )
 qua A tạo với trục Oz một góc 30 ,  ( )
 cắt mặt phẳng Oxy tại điểm B. Khi OB nhỏ nhất, đường thẳng ( )  có phương trình là x  1 y  1 z A.    1 1 6 x  5 y  5 z B.    1 1  6 x  3 y  3 z  2 6 C.    1 1 6 x  1 y  1 z D.    1 1 6
50. 21 Trong không gian Oxyz, cho phương trình mặt cầu 2 2 2
(S) : x y z  4  0 và đường thẳng x  3 y  3 z d : 
  Hai mặt phẳng (P), (P )
 chứa d và tiếp xúc với (S) tại A và B. Đường 1 1 1
thẳng AB đi qua điểm có tọa độ là 1 1 4  
A.  ; ;    3 3 3
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 140 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789  4   B. 1  ;1;    3  1 4   C. 1  ; ;    3 3 1 1 4   D.  ; ;    3 3 3
50. 22 Trong không gian Oxyz, cho mặt cầu 2 2 2
(S) : x y z  2x  4y  6z  67  0 và đường thẳng x  13 y  1 z d : 
  Qua d dựng các tiếp diện tới (S), tiếp xúc với (S) tại , A . B Đường 1 1 4
thẳng AB đi qua điểm nào sau đây ? 23 1    A.  ; ;6   2 2  B. (8;1; 4). C. (6; 9  ;6). 17 7 9   D.  ; ;    2 2 2
50. 23 Trong không gian Oxyz, hãy viết phương trình của mặt phẳng (P) chứa đường thẳng x  1 y  1 z  2 x  1 y z  1 d :  
và tạo với đường d  :   góc lớn nhất. 2 1 2 1 2 1
A. x  4y z  7  0.
B. x  4y z  7  0.
C. x  3y z  4  0.
D. x  3y z  4  0.
50. 24 Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua gốc tọa độ , O vuông góc với
mặt phẳng (Q) : 2x y z 1  0, đồng thời tạo với trục Oy góc lớn nhất.
A. 2x  5y z  0.
B. 2x  2y z  0.
C. 3x  2y  4z  0.
D. 3x  2y z  0. x y  1 z  2
50. 25 Trong không gian Oxyz, cho mặt phẳng (P) : x y z  3  0 và d :    1 2 1
Phương trình đường thẳng nằm trong (P), cắt d và tạo với d một góc nhỏ nhất là x  1 y  1 z  1 A.    1 4 5 x  1 y  1 z  1 B.    3 2 1
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 141 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 x  1 y  1 z  1 C.    1 4 5 x  1 y  4 z  5 D.    1 1 1
50. 26 Trong không gian Oxyz, phương trình đường thẳng d đi qua (
A 1;1;2), song song với x  1 y  1 z
(P) : 2x y z  3  0 và tạo với đường thẳng d : 
 một góc nhỏ nhất là 1 2  2 x  1 y  1 z  2 A.    1 5  7 x  1 y  1 z  2 B.    1 5  7  x  1 y  1 z  2 C.    1 3 5 x  1 y  1 z  2 D.    2 3  5 x  2 y  1 z  2
50. 27 Trong không gian Oxyz, cho đường thẳng d :   và mặt phẳng 4 4  3
(P) : 2x y  2z  1  0 . Đường thẳng  đi qua E(2;1;2), song song với (P), đồng thời tạo 
với d góc bé nhất. Biết  có một véctơ chỉ phương u  (m;n;1). Khi đó 2 2 m n bằng A. 5. B. 4. C. 3. D. 4.
50. 28 Trong không gian Oxyz, viết phương trình mặt phẳng (P ) đi qua điểm M (9;1;1), cắt các tia Ox, Oy, Oz tại ,
A B, C sao cho thể tích tứ diện OABC có giá trị nhỏ nhất.
A. x  9y  9z  27  0.
B. x  9y  9z  9  0.
C. x  9y  9z  27  0.
D. x  9y  9z  0.
50. 29 Trong không gian Oxyz, cho điểm M (1; 4; 9). Gọi (P ) là mặt phẳng đi qua M và cắt ba tia
Ox, Oy, Oz lần lượt tại các điểm ,
A B, C (khác O) sao cho (OA OB OC ) đạt giá trị nhỏ
nhất. Mặt phẳng (P ) đi qua điểm nào dưới đây ? A. (12; 0; 0). B. (0; 0;12). C. (6; 0; 0). D. (0; 6; 0).
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 142 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789
50. 30 Trong không gian Oxyz, cho ba điểm (
A a;0; 0), B(0;b;0), C(0; 0;c) với a, ,
b c là những số
dương thay đổi thỏa mãn 2 2 2
a  4b  16c  49. Khi khoảng cách từ gốc tọa độ O đến mặt phẳng
(ABC ) đạt giá trị lớn nhất thì 2 2 2
a b c bằng 49 A.  4 B. 11. 51 C.  5 49 D.  5
50. 31 Trong không gian Oxyz, cho mặt phẳng (P ) đi qua M(1;2;1), N (1; 0;1), đồng thời cắt
Ox, Oy theo thứ tự tại ,
A B (khác O) sao cho AM  3BN. Khi đó (P ) có một véctơ pháp 
tuyến n  (1; m;n) thì tổng m n bằng A. 2. B. 1  . C. 1. D. 0.
50. 32 Trong không gian Oxyz, cho (
A 1;2;3), B(2;1;1) và mặt phẳng (P) : x y  2z  2  0. Tìm
hoành độ của C thuộc (P) sao cho tam giác ABC cân tại C và có chu vi nhỏ nhất ? 4 A. 3 2 B. 3 C. 1. 1 D.  3
50. 33 Trong không gian Oxyz, cho mặt phẳng (P) : x y z  2  0 và hai điểm ( A 3;4;1),
B(7;4;3). Điểm M(a;b;c), (a  2) thuộc (P) sao cho tam giác ABM vuông tại M và có diện
tích nhỏ nhất. Khi đó giá trị biểu thức a b c bằng A. 6. B. 8. C. 4. D. 0. x   2  2tx  1 y  2 z 
50. 34 Trong không gian Oxyz, cho hai đường thẳng d :   , d : y
  1  t và mặt 1 1 2 1 2
z  1t 
phẳng (P) : x y  2z  5  0. Lập phương trình đường thẳng song song với mặt phẳng (P) và
cắt d , d lần lượt tại ,
A B sao cho độ dài đoạn AB nhỏ nhất ? 1 2
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 143 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 x  1 y  2 z  2 A.    1 1 1 x  1 y  2 z  2 B.    1 1 2  x  1 y  2 z C.    1 1 3  x  2 y  1 z  1 D.    1 1 3  x  1 y  1 z x  1 y  2 z
50. 35 Trong không gian Oxyz, cho đường thẳng d :   ; d :    Viết 1 2 1 1 2 1 2 1
phương trình mặt phẳng (P) song song với (Q) : x y  2z  3  0 và cắt d , d theo đoạn 1 2
thẳng có độ dài nhỏ nhất ?
A. x y  2z  10  0.
B. x y  2z  0.
C. x y  2z  1  0.
D. x y  2z  7  0.  5    5  
50. 36 Trong không gian Oxyz, cho hai điểm A 1  ; 2  ;   B 4;2; .  và
Tìm hoành độ điểm M trên mặt  2  2 
phẳng (Oxy) sao cho ABM  45 và tam giác MAB có diện tích nhỏ nhất ? 5 A. 2 B. 1. 3 C. 2 D. 2.
50. 37 Trong không gian Oxyz, cho ba điểm (
A 1;2;1), B(5;0;1), C(3;1;2) và mặt phẳng
(Q) : 3x y z  3  0. Gọi M(a; ;
b c)  (Q) thỏa mãn 2 2 2
MA MB  2MC nhỏ nhất. Tổng
a b  5c bằng A. 11. B. 9. C. 15. D. 14.
50. 38 Trong không gian Oxyz, cho các điểm (
A 5; 8;11), B(3;5;4), C(2;1;6) và mặt cầu 2 2 2
(S) : (x  4)  (y  2)  (z  1)  9. Gọi M(x ;y ;z ) là điểm trên (S) sao cho biểu thức M M M   
MA MB MC đạt giá trị nhỏ nhất. Giá trị của tổng x y bằng M M A. 4. B. 0.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 144 -
Phaùt trieån ñeà tham khaûo thpt naêm 2021
Bieân soaïn: Ths. Leâ Vaên Ñoaøn – 0933.755.607 – 0929.031.789 C. 2. D. 2.
50. 39 Trong không gian Oxyz, cho hai điểm (
A 13; 3;2), B(1;0;1) và phương trình hai mặt cầu 2 2 2
(S ) : x y z  25, 2 2 2
(S ) : (x  5)  y z  10. Gọi M nằm trên đường tròn giao tuyến 1 2
của (S ), (S ) thỏa mãn 2 2 2
P MA  2MB  3MC đạt giá trị nhỏ nhất. Giá trị của biểu thức 1 2 bằng
A. 186  36 2. B. 36. C. 18  6 2. D. 16.
50. 40 Trong không gian Oxyz, cho mặt phẳng (P) : x  2y z  1  0 và hai điểm ( A 0;2; 3),
B(2; 0;1). Điểm M(a; ;
b c)  (P) sao cho MA MB nhỏ nhất. Giá trị 2 2 2
a b c bằng 41 A. 4 9 B.  4 7 C. 4 D. 3.
“Thaønh coâng laø noùi khoâng vôùi löôøi bieáng !”
Trang - 145 -
Document Outline

  • BÌA PHÁT TRIỂN ĐỀ THAM KHẢO 2021
  • Phát triển đề tham khảo 2021 - Ths. Lê Văn Đoàn