Phép dời hình và phép đồng dạng trong mặt phẳng – Lê Minh Tâm

Tài liệu gồm 59 trang, được biên soạn bởi thầy giáo Lê Minh Tâm, tóm tắt lý thuyết SGK và tuyển chọn bài tập trắc nghiệm + tự luận chuyên đề phép dời hình và phép đồng dạng trong mặt phẳng, giúp học sinh lớp 11

27 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 11

Môn: Toán 11

Thông tin:

59 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
TÀI LIỆU LƯU HÀNH NỘI BỘ
LÊ MINH TÂM
CHƯƠNG 01
PHÉP DỜI HÌNH
& PHÉP ĐỒNG DẠNG
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
LÊ MINH TÂM
Trang 2
MỤC LỤC
§1. PHÉP BIẾN HÌNH ......................................................................................................................... 4
I. ĐỊNH NGHĨA: ............................................................................................................................................ 4
II. KÝ HIỆU: ..................................................................................................................................................... 4
III. TÍNH CHẤT: ............................................................................................................................................ 4
§2. PHÉP TỊNH TIẾN .......................................................................................................................... 5
I. ĐỊNH NGHĨA: ............................................................................................................................................ 5
II. TÍNH CHẤT: .............................................................................................................................................. 5
III. BIỂU THỨC TỌA ĐỘ: ........................................................................................................................... 6
IV. BÀI TẬP: .................................................................................................................................................... 8
4.1. Tự Luận. ................................................................................................................................................. 8
4.2. Trắc nghiệm. ........................................................................................................................................ 11
§3. PHÉP ĐỐI XỨNG TRỤC ........................................................................................................................... 17
I. ĐỊNH NGHĨA: .......................................................................................................................................... 17
II. TÍNH CHẤT: ............................................................................................................................................ 17
III. BIỂU THỨC TỌA ĐỘ: ......................................................................................................................... 17
IV. BÀI TẬP: .................................................................................................................................................. 18
4.1. Tự Luận. ............................................................................................................................................... 18
4.2. Trắc nghiệm. ........................................................................................................................................ 21
§4. PHÉP ĐỐI XỨNG TÂM ................................................................................................................ 25
I. ĐỊNH NGHĨA: .......................................................................................................................................... 25
II. TÍNH CHẤT: ............................................................................................................................................ 25
III. BIỂU THỨC TỌA ĐỘ: ......................................................................................................................... 25
IV. BÀI TẬP: .................................................................................................................................................. 26
4.1. Tự Luận. ............................................................................................................................................... 26
4.2. Trắc nghiệm. ........................................................................................................................................ 28
§4. PHÉP QUAY ............................................................................................................................... 31
I. ĐỊNH NGHĨA: .......................................................................................................................................... 31
II. TÍNH CHẤT: ............................................................................................................................................ 31
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 3
LÊ MINH TÂM
III. BIỂU THỨC TỌA ĐỘ: ......................................................................................................................... 32
IV. BÀI TẬP: .................................................................................................................................................. 32
4.1. Tự Luận. ............................................................................................................................................... 32
4.2. Trắc nghiệm. ........................................................................................................................................ 34
§5. PHÉP DỜI HÌNH ......................................................................................................................... 38
I. ĐỊNH NGHĨA: .......................................................................................................................................... 38
II. TÍNH CHẤT: ............................................................................................................................................ 38
III. KHÁI NIỆM HAI HÌNH BẰNG NHAU: .......................................................................................... 38
IV. BÀI TẬP: .................................................................................................................................................. 38
4.1. Tự Luận. ............................................................................................................................................... 38
4.2. Trắc nghiệm. ........................................................................................................................................ 40
§6. PHÉP VỊ TỰ .......................................................................................................................................... 44
I. ĐỊNH NGHĨA: .......................................................................................................................................... 44
II. TÍNH CHẤT: ............................................................................................................................................ 44
III. CÁCH TÌM TÂM VỊ TỰ CỦA HAI ĐƯỜNG TRÒN: ................................................................... 45
IV. BIỂU THỨC TỌA ĐỘ: ......................................................................................................................... 46
IV. BÀI TẬP: .................................................................................................................................................. 46
4.1. Tự Luận. ............................................................................................................................................... 46
4.2. Trắc nghiệm. ........................................................................................................................................ 48
§7. PHÉP ĐỒNG DẠNG .............................................................................................................................. 53
I. ĐỊNH NGHĨA: .......................................................................................................................................... 53
II. TÍNH CHẤT: ............................................................................................................................................ 53
III. KHÁI NIỆM HAI HÌNH ĐỒNG DẠNG: ......................................................................................... 53
IV. BÀI TẬP: .................................................................................................................................................. 53
4.1. Tự Luận. ............................................................................................................................................... 53
4.2. Trắc nghiệm. ........................................................................................................................................ 56
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 4
LÊ MINH TÂM
§1. PHÉP BIẾN HÌNH
I. ĐỊNH NGHĨA:
ĐN: Phép biến hình là một quy tắc để với mỗi điểm
M
của mặt phẳng, xác định được một
điểm duy nhất điểm
M
của mặt phẳng. Điểm
M
gọi là ảnh của
M
qua phép biến hình đó.
II. KÝ HIỆU:
Kí hiệu:
f
là một phép biến hình nào đó, và
M
là ảnh của
M
qua phép
f
. Ta viết:
M f M
hay
hay
:f M M
hay
f
MM
.
Lưu ý:
+ Điểm
M
gọi là tạo ảnh,
M
là ảnh.
+
f
là phép biến hình đồng nhất
,f M M M H
. Điểm
M
gọi là điểm bất động, điểm
kép, bất biến.
+
12
,ff
là các phép biến hình thì
21
ff
là phép biến hình.
Nếu H là một hình nào đó thì tập hợp các điểm
M f M
, với
MH
, tạo thành hình
H
được gọi là ảnh của H qua phép biến hình
f
, và ta viết:
H f H
.
III. TÍNH CHẤT:
Phép dời hình là phép biến hình không làm thay đổi khoảng cách giữa hai điểm bất kỳ.
Phép dời hình biến:
+ Ba điểm thẳng hàng thành ba điểm thẳng hàng.
+ Đường thẳng thành đường thẳng.
+ Tịa thành tia.
+ Tam giác thành tam giác và bằng tam giác đã cho.
+ Đường tròn thành đường tròn có cùng bán kính với đường tròn đã cho.
+ Góc thành góc và bằng góc đã cho.
------------------HẾT------------------
CHƯƠNG
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 5
LÊ MINH TÂM
§2. PHÉP TỊNH TIẾN
I. ĐỊNH NGHĨA:
– Trong mặt phẳng cho vectơ
u
, phép tịnh tiến theo vectơ
u
là phép biến hình biến mỗi điểm
M
thành điểm
M
sao cho
MM u
.
– Ký hiệu:
v
T
. Như vậy
u
T M M MM u

.
Nhận xét: Phép tịnh tiến là phép đồng nhất
0v
.
II. TÍNH CHẤT:
Tính chất 1:
Cho
v
v
T M M
T N N
thì
M N MN

.
Tính chất 2:
Qua phép tịnh tiến
v
T
,
– Đường thẳng biến thành đường thẳng song song song hoặc trùng với nó.
– Đoạn thẳng biến thành đoạn thẳng bằng nó.
– Tam giác biến thành tam giác bằng nó.
– Đường tròn biến thành đường tròn có cùng bán kính.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 6
LÊ MINH TÂM
Ví dụ 01.
Cho hình vẽ như hình bên dưới. Xác định
,,
EA AD AE
T BF T AEB T ADF
.
Lời giải
* Xác định
EA
T BF
.
Ta có
EA
EA
EA
T B F
T BF FD
T F D

.
* Xác định
AD
T AEB
.
Ta có
AD
AD AD
AD
T A D
T E F T AEB DFC
T B C
.
* Xác định
AE
T ADF
.
Ta có
AE
AE AE
AE
T A E
T D F T ADF EFB
T F B
.
III. BIỂU THỨC TỌA ĐỘ:
– Trong mặt phẳng
Oxy
, cho điểm
;M x y
và vectơ
;v a b
. Gọi
M
là ảnh của
M
qua phép
tịnh tiến theo vectơ
v
. Khi đó:
;
v
x x a x x a
T M M x y MM v
y y b y y b



.
– Biểu thức trên được gọi là biểu thức tọa độ của phép tịnh tiến theo
v
.
– Phép tịnh tiến bảo toàn thứ tự các điểm của đa giác.
– Hai đường thẳng song song có vô số phép tịnh tiến biến đường này thành đường kia.
CHÚ Ý
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 7
LÊ MINH TÂM
Ví dụ 02.
Trong mặt phẳng tọa độ
Oxy
, cho vectơ
12;v 
.
a. Tìm tọa độ của điểm
M
là ảnh của
32;M
qua phép
v
T
.
b. Tìm tọa độ của điểm
N
biết
v
T N N
và
41;N
Lời giải
a. Tìm tọa độ của điểm
M
là ảnh của
32;M
qua phép
v
T
.
3 1 1 3 2
2 2 2 2 0
;
v
xx
T M M x y MM v
yy



.
Vậy
20;M
.
b. Tìm tọa độ của điểm
N
biết
v
T N N
và
41;N
4 1 4 1 5
1 2 1 2 1
;
v
xx
T N N x y NN v
yy


.
Vậy
51;N
.
Ví dụ 03.
Trong mặt phẳng tọa độ
Oxy
, cho vectơ
21;v
.
a. Tìm ảnh của đường thẳng
3 5 0:d x y
qua phép
v
T
.
b. Tìm ảnh của đường tròn
22
4 2 4 0:C x y x y
qua phép
v
T
.
Lời giải
a. Tìm ảnh của đường thẳng
3 5 0:d x y
qua phép
v
T
.
Gọi
3 5 0;:M x y d y x
(1).
22
11
;
v
x x x x
T M M x y MM v
y y y y




(2)
Thay (2) vào (1) ta được:
2 3 1 5 0 3 4 0x y x y
Vậy
3 4 0:d x y
.
b. Tìm ảnh của đường tròn
22
4 2 4 0:C x y x y
qua phép
v
T
.
Gọi
22
4 2 4 0;:N x y C x y x y
(3)
22
11
;
v
x x x x
T N N x y NN v
y y y y




(4)
Thay (4) vào (3) ta được:
22
22
2 1 4 2 2 1 4 0 9 0x y x y x y
Vậy
22
90:C x y
.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 8
LÊ MINH TÂM
IV. BÀI TẬP:
4.1. Tự Luận.
Bài toán xác định ảnh trong hệ tọa độ qua Phép Tịnh Tiến
Phương pháp:
Sử dụng biểu thức tọa độ của phép tịnh tiến.
Trong mặt phẳng tọa độ
Oxy
cho vec tơ
;v a b
. Với mỗi điểm
;M x y
ta có
;M x y
là
ảnh của
M
qua phép tịnh tiến theo
v
. Khi đó
x x a x x a
MM v
y y b y y b


.
Bài 01.
Trong mặt phẳng
Oxy
, cho điểm
25;A
. Tìm tọa độ điểm
A
là ảnh của điểm
A
qua
phép tịnh tiến theo vec-tơ
12;v
Lời giải:
Gọi
2 1 3
33
5 2 3
;;
x
A x y A
y
.
Bài 02.
Trong mặt phẳng với hệ tọa độ
Oxy
, cho điểm
23;M
là ảnh của điểm
35;N
qua phép
tịnh tiến theo vec-tơ
v
. Tìm
v
.
Lời giải:
Ta có
2 3 3 5 1 8;;v NM
.
Bài 03.
Trong mặt phẳng tọa độ
Oxy
cho vec tơ
12;v 
, hai điểm
35;A
,
11;B
và đường
thẳng
d
có phương trình
2 3 0xy
.
1. Tìm tọa độ của
A
,
B
theo thứ tự là ảnh của
A
,
B
qua phép tịnh tiến theo vec tơ
v
.
2. Tìm tọa độ của điểm
C
sao cho
A
là ảnh của
C
qua phép tịnh tiến theo vec tơ
v
.
3. Tìm phương trình của đường thẳng
d
là ảnh của
d
qua phép tịnh tiến theo vec tơ
v
.
Lời giải:
1. Tìm tọa độ của
A
,
B
theo thứ tự là ảnh của
A
,
B
qua phép tịnh tiến theo vec tơ
v
.
Tọa độ của
A
là
3 1 2
5 2 7
A
A
x
y
27;A
.
Tọa độ của
B
là
1 1 2
1 2 3
B
B
x
y
23;B

.
2. Tìm tọa độ của điểm
C
sao cho
A
là ảnh của
C
qua phép tịnh tiến theo vec tơ
v
.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 9
LÊ MINH TÂM
Giả sử
;
CC
xy
là tọa độ của điểm
C
31
52
C
C
x
y

4
3
C
C
x
y
43;C
.
3. Tìm phương trình của đường thẳng
d
là ảnh của
d
qua phép tịnh tiến theo vec tơ
v
.
Giả sử
;M x y d
và
;M x y
là ảnh của
M
qua phép tịnh tiến theo vec tơ
v
.
11
12
22
;
x x x x
M x y
y y y y



.
Vì
;M x y d
1 2 3 02xy


208xy

.
Vậy
208: xyd


.
Bài 04.
Trong mặt phẳng tọa độ
Oxy
, ảnh của đường thẳng
2 4 0:d x y
qua phép vị tự theo vec
tơ
35;v
có phương trình là:
Lời giải:
Phương trình ảnh của đường thẳng
d
là
20':d x y c
.
Ảnh của điểm
04;Ad
qua phép tịnh tiến theo vecto
35;v
là
39;Ad

.
Suy ra
2 3 9 0 3cc
. Vậy
2 3 0':d x y
Bài 05.
Trong mặt phẳng tọa độ
Oxy
cho đường thẳng có phương trình
4 3 0xy
. Ảnh của
đường thẳng qua phép tịnh tiến
T
theo véc-tơ
21;v 
có phương trình là
Lời giải:
Cách 1: Gọi
là ảnh của qua phép
T
v
. Khi đó
song song hoặc trùng với nên
có
phương trình dạng
40x y c
.
Chọn điểm
03;A
. Gọi
;A x y
là ảnh của
A
qua phép tịnh tiến theo véc-tơ
21;v 
3;AA x y
.
Ta có
T
v
A A AA v

2
31
x
y
2
2
x
y
22;A
Mặt khác điểm
A

, suy ra tọa độ điểm
A
thỏa mãn phương trình
40x y c
6c
hay
4 6 0: xy
.
Ta có
0 2 2
22
3 1 2
;;
v
xx
T A A x y AA v A
yy


.
Vì
A

nên
4 2 2 0 6 4 6 0.:c c x y
.
Cách 2: Gọi
;M x y
là điểm bất kỳ thuộc đường thẳng .
Gọi
22
11
;
v
x x x x
M x y T M MM v
y y y y




.
Thay
2xx

và
1yy

vào phương trình ta được
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 10
LÊ MINH TÂM
4 2 1 3 0 4 6 0x y x y
.
Bài 06.
Trong mặt phẳng tọa độ
Oxy
, ảnh của đường tròn
22
1 3 4:C x y
qua phép tịnh
tiến theo vectơ
32;v
là đường tròn có phương trình
Lời giải:
Đường tròn
C
có tâm
13;I
, bán kính
2R
.
Gọi
;I x y
là ảnh của
13;I
qua phép tịnh tiến vectơ
32;v
.
Ta có
13
2
32
5
32
;
x
x
II v I
y
y



.
Vì phép tịnh tiếp bảo toàn khoảng cách nên
2RR

.
Vậy ảnh của đường tròn
C
qua
v
T
là đường tròn
C
có tâm
25;I
, bán kính
2R
nên có phương trình
22
2 5 4xy
.
Bài 07.
Trong mặt phẳng tọa độ
Oxy
cho đường tròn
C
có phương trình
22
2 4 4 0x y x y
.
Tìm ảnh của
C
qua phép tịnh tiến theo vec tơ
23;v 
.
Lời giải:
Đường tròn
C
có tâm
12;I
, bán kính
2
2
1 2 4 3R
.
Giả sử
v
C T C
. Gọi
I
là tâm đường tròn
C
1 2 2 3 1 1;;
v
IIT
.
Do đó
C
có phương trình
22
1 1 9xy
.
Bài 08.
Trong mặt phẳng tọa độ
Oxy
cho vectơ
. Phép tịnh tiến theo vectơ
v
biến đường
tròn
2
2
11:C x y
thành đường tròn
C
. Mệnh đề nào sau đây đúng?
Lời giải:
Đường tròn
C
có tâm
01;I
, bán kính
1R
.
Gọi
;I x y
là ảnh của
01;I
qua phép tịnh tiến vectơ
32;v
.
Ta có
0 3 3
31
1 2 1
;
xx
II v I
yy



.
Vì phép tịnh tiến bảo toàn khoảng cách nên
1RR

.
Vậy ảnh của đường tròn
C
qua phép
v
T
là đường tròn
C
có tâm
31;I

, bán
kính
R
nên có phương trình
22
3 1 1:C x y
.
Bài 09.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 11
LÊ MINH TÂM
Trong mặt phẳng tọa độ
Oxy
cho đường tròn
C
có phương trình
22
4 6 5 0x y x y
.
Thực hiện liên tiếp hai phép tịnh tiến theo các vectơ
12;u 
và
11;v 
thì đường tròn
C
biến thành đường tròn
C
có phương trình là
Lời giải:
Từ giả thiết suy ra
C
là ảnh của
C
qua phép tịnh tiến theo
a u v
.
Ta có
23;a u v
.
Biểu thức tọa độ của
a
T
là
2
3
xx
yy


thay vào
C
ta được
22
2 3 4 2 6 3 5 0x y x y
22
18 0xy

.
Bài 10.
Trong mặt phẳng tọa độ
Oxy
, cho vectơ
21;v
. Phép tịnh tiên theo vectơ
v
biến
parabol
2
:Pyx
thành parabol
P
. Khi đó phương trình của
P
là
Lời giải:
Biểu thức tọa độ của
v
T
là
2
1
xx
yy


thay vào
P
ta được
2
2
1 2 4 3y x y x x
.
4.2. Trắc nghiệm.
Câu 1. Mệnh đề nào sau đây là sai ? Trong mặt phẳng, phép tịnh tiến
à
vv
T M M v T N N


(
với
0v
). Khi đó
A.
''MM NN
. B.
''MN M N
.
C.
''MN NM
. D.
''MM NN
Lời giải:
Chọn C
Câu 2. Có bao nhiêu phép tịnh tiến biến một đường thẳng cho trước thành chính nó?
A. Không có. B. Chỉ có một. C. Chỉ có hai. D. Vô số.
Lời giải:
Chọn D
Phép tịnh tiến theo vectơ
v
, với
v
là vectơ chỉ phương đường thẳng
d
biến một đường
thẳng cho trước thành chính nó. Khi đó sẽ có vô số vectơ
v
thõa mãn.
Câu 3. Có bao nhiêu phép tịnh tiến biến một đường tròn cho trước thành chính nó?
A. Không có. B. Một. C. Hai. D. Vô số.
Lời giải:
Chọn B
Chỉ có duy nhất phép tịnh tiến theo vectơ
0
.
Câu 4. Có bao nhiêu phép tịnh tiến biến một hình vuông thành chính nó?
A. Không có. B. Một. C. Bốn. D. Vô số.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 12
LÊ MINH TÂM
Lời giải:
Chọn B
Chỉ có duy nhất phép tịnh tiến theo vectơ
0
.
Câu 5. Giả sử qua phép tịnh tiến theo vectơ
0v
, đường thẳng d biến thành đường thẳng
’d
. Câu
nào sau đây sai?
A.
d
trùng
’d
khi
v
là vectơ chỉ phương của d.
B.
d
song song với
’d
khi
v
là vectơ chỉ phương của d.
C.
d
song song với d’ khi
v
không phải là vectơ chỉ phương của
d
.
D.
d
không bao giờ cắt
’d
.
Lời giải:
Chọn B
Xét B:
d
song song với
’d
khi
v
là vectơ có điểm đầu bất kỳ trên
d
và điểm cuối bất kỳ
trên
’d
.
Câu 6. Cho
P
,
Q
cố định. Phép tịnh tiến
T
biến điểm
M
bất kỳ thành
2
M
sao cho
2
2MM PQ
.
A.
T
là phép tịnh tiến theo vectơ
PQ
. B.
T
là phép tịnh tiến theo vectơ
2
MM
.
C.
T
là phép tịnh tiến theo vectơ
2PQ
. D.
T
là phép tịnh tiến theo vectơ
1
2
PQ
.
Lời giải:
Chọn C
Gọi
22
v
T M M MM v
Từ
2
22MM PQ PQ v
.
Câu 7. Cho phép tịnh tiến
u
T
biến điểm
M
thành
1
M
và phép tịnh tiến
v
T
biến
1
M
thành
2
M
.
A. Phép tịnh tiến
uv
T
biến
1
M
thành
2
M
.
B. Một phép đối xứng trục biến
M
thành
2
M
.
C. Không thể khẳng định được có hay không một phép dời hình biến M thành M2.
D. Phép tịnh tiến
uv
T
biến
M
thành
2
M
.
Lời giải:
Chọn D
1
1
1 1 2 2 2
12
12
u
uv
v
T M M
u MM
u v MM M M MM T M M
T M M
v M M



.
Câu 8. Cho phép tịnh tiến vectơ
v
biến
A
thành
’A
và
M
thành
’M
. Khi đó:
A.
''AM A M
. B.
2 ''AM A M
. C.
''AM A M
. D.
32''AM A M
.
Lời giải:
Chọn C
Theo tính chất trong SGK
v
v
T A A
AM A M
T M M


.
Câu 9. Tìm mệnh đề sai trong các mệnh đề sau:
A. Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 13
LÊ MINH TÂM
B. Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng.
C. Phép tịnh tiến biến tam giác thành tam giác bằng tam giác đã cho.
D. Phép tịnh tiến biến đường thẳng thành đường thẳng song song với đường thẳng đã cho.
Lời giải:
Chọn B
Theo tính chất SGK, Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc
trùng với nó.
Câu 10. Cho phép tịnh tiến vectơ
v
biến
A
thành
’A
và
M
thành
’M
. Khi đó
A.
' '.AM A M
B.
2 ' '.AM A M
C.
' '.AM A M
D.
2 ' '.AM A M
Lời giải:
Chọn C
Câu 11. Trong mặt phẳng
Oxy
cho điểm
25;A
. Phép tịnh tiến theo vectơ
12;v
biến
A
thành
điểm có tọa độ là:
A.
31;
. B.
16;
. C.
37;
. D.
47;
.
Lời giải:
Chọn C
2 1 3
37
5 2 7
;
BA
v
B
v
B A B
v
x x x
x
T A B AB v B
y y y y


.
Câu 12. Trong mặt phẳng
Oxy
cho điểm
25;A
. Hỏi
A
là ảnh của điểm nào trong các điểm sau
qua phép tịnh tiến theo vectơ
12;v
?
A.
31;
. B.
13;
. C.
47;
. D.
24;
.
Lời giải:
Chọn B
2 1 1
13
5 2 3
;
MA
v
M
v
MA
B
v
x x x
x
T M A MA v M
y y y
y



.
Câu 13. Trong mặt phẳng tọa độ
Oxy
, cho phép biến hình
f
xác định như sau: Với mỗi
; ,M x y
ta
có
'M f M
sao cho
' ’; ’M x y
thỏa
2';xx
3'yy
A.
f
là phép tịnh tiến theo vectơ
23;v
.
B.
f
là phép tịnh tiến theo vectơ
23;v 
.
C.
f
là phép tịnh tiến theo vectơ
23;v 
.
D.
f
là phép tịnh tiến theo vectơ
23;v
.
Lời giải:
Chọn C
Câu 14. Trong mặt phẳng Oxy, phép tịnh tiến theo vectơ
13;v
biến điểm
21;A
thành điểm nào
trong các điểm sau:
A.
1
21.;A
B.
2
13.;A
C.
3
34.;A
D.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 14
LÊ MINH TÂM
Lời giải:
Chọn C
Câu 15. Trong mặt phẳng
Oxy
, cho
;v a b
. Giả sử phép tịnh tiến theo
v
biến điểm
;M x y
thành
’ ’; ’M x y
. Ta có biểu thức tọa độ của phép tịnh tiến theo vectơ
v
là:
A.
'
'
x x a
y y b


B.
'
'
x x a
y y b


C.
'
'
x b x a
y a y b
D.
'
'
x b x a
y a y b
.
Lời giải:
Chọn A
Câu 16. Trong mặt phẳng
Oxy
cho
2
điểm
16;A
,
14– ;–B
. Gọi
C
,
D
lần lượt là ảnh của
A
và
B
qua phép tịnh tiến theo vectơ
15;v
.Tìm khẳng định đúng trong các khẳng định sau:
A.
ABCD
là hình thang. B.
ABCD
là hình bình hành.
C.
ABDC
là hình bình hành. D. Bốn điểm
A
,
B
,
C
,
D
thẳng hàng.
Lời giải:
Chọn D
2
2 11
11
;
CA
vC
v
C A C
v
x x x
x
C T A C
y y y y



.
0
01
1
;
DB
v
D
v
D B D
v
x x x
x
D T B D
y y y y


.
2 10 3 15 2 10; , ; , ;AB BC CD
.
Xét cặp
,AB BC
: Ta có
2 10
3 15
,,A B C


thẳng hàng.
Xét cặp
,BC CD
: Ta có
3 15
2 10
,,B C D

thẳng hàng.
Vậy
, , ,A B C D
thẳng hàng.
Câu 17. Trong mặt phẳng tọa độ
Oxy
, cho
13;v 
và đường thẳng
d
có phương trình
2 3 5 0xy
. Viết phương trình đường thẳng
'd
là ảnh của
d
qua phép tịnh tiến
v
T
.
A.
2 6 0':d x y
B.
60':dxy
C.
2 6 0':d x y
D.
2 3 6 0':d x y
Lời giải:
Chọn D
Cách 1. Sử dụng biểu thức tọa độ của phép tịnh tiến.
Lấy điểm
;M x y
tùy ý thuộc
d
, ta có
2 3 5 0 *xy
Gọi
11
33
''
' '; '
''
v
x x x x
M x y T M
y y y y



Thay vào (*) ta được phương trình
2 1 3 3 5 0 2 3 6 0' ' ' 'x y x y
.
Vậy ảnh của
d
là đường thẳng
2 3 6 0':d x y
.
Cách 2. Sử dụng tính chất của phép tịnh tiến
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 15
LÊ MINH TÂM
Do
'
v
d T d
nên
'd
song song hoặc trùng với
d
, vì vậy phương trình đường thẳng
'd
có
dạng
2 3 0x y c
.(**)
Lấy điểm
11;Md
. Khi đó
1 1 1 3 0 2' ; ;
v
M T M
.
Do
2 0 3 2 0 6' ' . .M d c c
Vậy ảnh của
d
là đường thẳng
2 3 6 0':d x y
.
Cách 3. Để viết phương trình
'd
ta lấy hai điểm phân biệt
,MN
thuộc
d
, tìm tọa độ các
ảnh
', 'MN
tương ứng của chúng qua
v
T
. Khi đó
'd
đi qua hai điểm
'M
và
'N
.
Cụ thể: Lấy
1 1 2 3; , ;MN
thuộc
d
, khi đó tọa độ các ảnh tương ứng là
0 2 3 0' ; , ' ;MN
. Do
'd
đi qua hai điểm
', 'MN
nên có phương trình
2
0
2 3 6 0
32
y
x
xy
.
Câu 18. Trong mặt phẳng tọa độ
Oxy
, cho đường tròn
C
có phương trình
22
2 4 4 0x y x y
.
Tìm ảnh của
C
qua phép tịnh tiến theo vectơ
23;v 
.
A.
22
2 7 0':C x y x y
B.
22
70':C x y x y
C.
22
2 2 7 0':C x y x y
D.
22
80':C x y x y
Lời giải:
Chọn C
Cách 1. Sử dụng biểu thức tọa độ.
Lấy điểm
;M x y
tùy ý thuộc đường tròn
C
, ta có
22
2 4 4 0 *x y x y
Gọi
22
33
''
' '; '
''
v
x x x x
M x y T M
y y y y



Thay vào phương trình (*) ta được
22
22
2 3 2 2 4 3 4 0
2 2 7 0
' ' ' '
' ' ' '
x y x y
x y x y
.
Vậy ảnh của
C
là đường tròn
22
2 2 7 0':C x y x y
.
Cách 2. Sử dụng tính chất của phép tịnh tiến
Dễ thấy
C
có tâm
12;I
và bán kính
3r
. Gọi
'
v
C T C
và
' '; ' ; 'I x y r
là tâm và
bán kính của
( ')C
.
Ta có
1 2 1
11
2 3 1
'
';
'
x
I
y

và
3'rr
nên phương trình của đường tròn
'C
là
22
1 1 9xy
Câu 19. Trong mặt phẳng
Oxy
, ảnh của đường tròn:
22
1 3 4–xy
qua phép tịnh tiến theo
vectơ
32;v
là đường tròn có phương trình:
A.
22
2 5 4.xy
B.
22
2 5 4––xy
.
C.
22
1 3 4–xy
. D.
22
4 1 4–xy
.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 16
LÊ MINH TÂM
Lời giải:
Chọn B
Đường tròn đề đã cho có tâm
13;I
, bán kính
2R
.
Đường tròn cần tìm có tâm
I
, bán kính
2RR

.
Khi đó
1 3 2
25
3 2 5
;
II
v
I
v
I I I
v
x x x
x
I T I I
y y y y




Vậy phương trình đường tròn cần tìm
22
2 5 4––xy
.
Câu 20. Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho phép tịnh tiến theo
21– ;–v
, phép tịnh tiến
theo
v
biến parabol
2
:Pyx
thành parabol
P
. Khi đó phương trình của
P
là:
A.
2
45y x x
. B.
2
45–y x x
. C.
2
43y x x
. D.
2
45–y x x
Lời giải:
Chọn C
Chọn
;M x y
tùy ý trên
P
. Gọi
;
v
M x y T M
.
Vì
v
T P P
nên
MP

.
Ta có
22
11
;
v
x x x x
T M M x y
y y y y





. Suy ra
21;M x y


Vì
21;M x y P

nên
2
2
1 2 4 3'y x y x x
.
Suy ra
2
43;:M x y P y x x
.
Vậy:
2
43:P y x x
.
------------------HẾT------------------
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 17
LÊ MINH TÂM
§3. PHÉP ĐỐI XỨNG TRỤC
I. ĐỊNH NGHĨA:
Cho đường thẳng
.d
– Phép biến hình
+ biến mỗi điểm
Md
thành chính nó,
+ biến mỗi điểm
Md
thành
M
,
sao cho
d
là đường trung trực của
MM
được gọi là phép đối xứng
qua đường thẳng
d
hay phép đối xứng trục
.d
– Đường thẳng
d
được gọi là trục của phép đối xứng hoặc đơn giản
gọi là trục đối xứng.
– Phép đối xứng trục
d
thường được kí hiệu là:
.
d
Ñ
– Nếu hình
H
là ảnh của hình
H
qua phép đối xứng trục
d
thì ta còn nói
H
đối xứng với
H
qua
d
, hay
H
và
H
đối xứng với nhau qua
.d
Nhận xét.
– Cho đường thẳng
.d
Với mối điểm
M
gọi
0
M
là hình chiếu vuông góc của
M
trên đường
thẳng
.d
Khi đó:

00
.
d
M Ñ M M M M M

dd
M Ñ M M Ñ M
– Đường thẳng
d
được gọi là trục đối xứng của hình
H
nếu phép đối xứng qua
d
biến hình
H
thành chính nó. Khi đó ta nói hình
H
có trục đối xứng.
II. TÍNH CHẤT:
Tính chất 1:
Phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kì.
Tính chất 2:
Phép đối xứng trục biến đường thẳng thành đường thẳng, biến đoạn
thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó,
biến đường tròn thành đường tròn có cùng bán kính.
III. BIỂU THỨC TỌA ĐỘ:
– Trong mặt phẳng
Oxy
, với mỗi điểm
;M x y
, gọi
;
d
M x y Ð M
.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 18
LÊ MINH TÂM
Nếu chọn
d
là trục
Ox
, thì
'
'
xx
yy

. Nếu chọn
d
là trục
Oy
, thì
'
'
xx
yy

.
IV. BÀI TẬP:
4.1. Tự Luận.
Bài toán xác định ảnh trong hệ tọa độ qua Phép Đối Xứng Trục
Phương pháp:
Sử dụng biểu thức tọa độ của phép đối xứng trục.
– Trong mặt phẳng
Oxy
, với mỗi điểm
;M x y
, gọi
;
d
M x y Ð M
.
Nếu chọn
d
là trục
Ox
, thì
'
'
xx
yy

. Nếu chọn
d
là trục
Oy
, thì
'
'
xx
yy

.
Bài 01.
Cho tứ giác
.ABCD
Hai đường thẳng
AC
và
BD
cắt nhau tại
.E
Xác định ảnh của tam giác
ABE
qua phép đối xứng qua đường thẳng
.CD
Lời giải
Chỉ cần xác định ảnh của các đỉnh của tam giác
,,A B E
qua phép đối xứng trục đó.
Ảnh phải tìm là tam giác
'''
.A BE
Bài 02.
Trong mặt phẳng
Ox ,y
cho điểm
15;,M
đường thẳng
d
có phương trình
2 4 0xy
và
đường tròn
22
2 4 4 0:.C x y x y
a. Tìm ảnh của
;;M d C
qua phép đối xứng trục
Ox
.
b. Tìm ảnh của
M
qua phép đối xứng qua đường thẳng
.d
Lời giải
a. Tìm ảnh của
;;M d C
qua phép đối xứng trục
Ox
.
Gọi
;Md

và
C
theo thứ tự là ảnh của
;Md
và
C
qua phép đối xứng trục
Ox
.
Khi đó
Để tìm ảnh của
d
ta sử dụng biểu thức tọa độ của phép đối xứng trục
Ox
.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 19
LÊ MINH TÂM
Gọi
;N x y
là ảnh của điểm
;N x y
qua phép đối xứng trục
Ox
.
Khi đó
x x x x
y y y y






Ta có
2 4 0 2 4 0 2 4 0:.N d x y x y d x y
Để tìm
C
, ta thấy rằng
C
có tâm
12;J
bán kính
3.R
Gọi
J
là ảnh của
J
qua phép đối xứng trục
Ox
.
Khi đó
12;.J
Do đó
C
là đường tròn tâm
12;,J
bán kính bằng
3.
Từ đó suy ra
C
có phương trình:
22
1 2 9.xy
b. Tìm ảnh của
M
qua phép đối xứng qua đường thẳng
.d
Đường thẳng
1
d
đi qua
M
vuông góc với
d
có phương trình
5
1
2 7 0
12
.
y
x
xy
Giao của
d
và
1
d
là
0
M
có tọa độ thỏa mãn hệ:
2 4 0 2
2 7 0 3.
x y x
x y y



Vậy
0
23;.M
Từ đó suy ra ảnh của
M
qua phép đối xứng qua đường thẳng
d
là
M

sao cho
0
M
là trung điểm của
MM

do đó
31;.M

Bài 03.
Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
với
1;5A
,
1;2B
,
6; 4C
. Gọi
G
là
trọng tâm của tam giác
ABC
. Phép đối xứng trục
Oy
Ñ
biến điểm
G
thành điểm
G
có tọa
độ là
Lời giải
Tọa độ trọng tâm
2
3
1
3
A B C
G
G
A B C G
G
xxx
x
x
y y y y
y


2;1G
.
Gọi
;;
Oy
G x y G x y


Ñ
thì
2
1
x x x
y y y






.
Bài 04.
Trong mặt phẳng tọa độ
Oxy
, cho điểm
2;3M
. Tọa độ điểm là ảnh của
M
qua phép đối
xứng qua đường thẳng
:0d x y
là ?
Lời giải
Nhận xét:
Đường thẳng
: 0 :d x y d y x
là đường phân giác của góc phần tư thứ nhất.
Biểu thức tọa độ của phép đối xứng qua đường phân giác
yx
là
Gọi
;;
d
M x y M x y


Ñ
thì
3
2
x y x
y x y







.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 20
LÊ MINH TÂM
Bài 05.
Trong mặt phẳng tọa độ
Oxy
, cho đường thẳng
: 2 0d x y
. Ảnh của đường thẳng
d
qua
phép đối xứng trục
Ox
có phương trình là
Lời giải
Cách 1: Trục
Ox
có phương trình
0y
.
Tọa độ giao điểm
A
của
d
và
Ox
thỏa mãn hệ
2 0 2
2;0
00
x y x
A
yy





.
Vì
A Ox
nên qua phép đối xứng trục
Ox
biến thành chính nó, tức
2;0AA
.
Chọn điểm
1;1 1; 1
Ox
B d B
Ñ
.
Vậy đường thẳng
d
là ảnh của
d
qua phép đối xứng trục
Ox
đi qua hai điểm
2;0A
và
1; 1B
nên có phương trình
20xy
.
Cách 2: Biểu thức tọa độ qua phép đối xứng trục
Ox
là
x x x x
y y y y






, thay vào
d
ta
được
20xy

.
Bài 06.
Trong mặt phẳng tọa độ
Oxy
cho đường tròn
22
: 1 2 4C x y
. Phép đối xứng trục
Ox
biến đường tròn
C
thành đường tròn
C
có phương trình là
Lời giải
Cách 1: Đường tròn
C
có tâm
1; 2I
và bán kính
2R
.
Ta có
Ñ
1; 2 1;2
Ox
II
và
Ñ
22
Ox
R R R
.
Do đó
C
có phương trình
22
1 2 4xy
.
Cách 2: Biểu thức tọa độ qua phép đối xứng trục
Ox
là
x x x x
y y y y
.
Thay vào
C
, ta được
22
1 2 4xy
hay
22
1 2 4xy
.
Bài 07.
Trong mặt phẳng tọa độ
Oxy
cho đường tròn
22
: 1 4 1C x y
và đường thẳng
d
có
phương trình
0yx
. Phép đối xứng trục
d
biến đường tròn
C
thành đường tròn
C
có phương trình là
Lời giải
Biểu thức tọa độ của phép đối xứng qua trục
:0d y x
là
xy
yx
.
Thay vào
C
, ta đươc
22
1 4 1yx
hay
22
4 1 1xy
.
Bài 08.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 21
LÊ MINH TÂM
Trong mặt phẳng tọa độ
Oxy
cho hai đường tròn
22
: 1 2 4C x y
và
2
2
: 3 4C x y
. Viết phương trình trục đối xứng của
C
và
C
.
Lời giải
Trục đối xứng của hai đường tròn là trung trực của đoạn nối hai tâm đường tròn. Viết
ra được phương trình trục đối xứng là
1xy
hay
1yx
.
Bài 09.
Trong mặt phẳng tọa độ
Oxy
cho parabol
P
có phương trình
2
yx
. Hỏi parabol nào là
ảnh của
P
qua phép đối xứng trục tung?
Lời giải
Biểu thức tọa độ qua phép đối xứng trục tung là
xx
yy
.
Thay vào
P
, ta được
2
yx
.
Bài 10.
Trong mặt phẳng tọa độ
Oxy
cho parabol
2
: 2 3P y x x
. Phép đối xứng trục
Ox
biến
parabol
P
thành parabol
P
có phương trình là
Lời giải
Biểu thức tọa độ qua phép đối xứng trục
Ox
là
xx
yy
.
Thay vào
P
, ta được
2
23y x x
hay
2
23y x x
.
4.2. Trắc nghiệm.
Câu 1. Hình gồm hai đường tròn có tâm và bán kính khác nhau có bao nhiêu trục đối xứng?
A. Không có. B. Một. C. Hai. D. Vô số
Lời giải:
Chọn B
Một đường tròn có vô số trục đối xứng đi qua tâm của đường tròn đó.
Vậy: Trục đối xứng thỏa yêu cầu của bài toán là đường thẳng nối hai tâm của đường tròn đã
cho.
Câu 2. Hình gồm hai đường thẳng
d
và
d
vuông góc với nhau đó có mấy trục đối xứng?
A.
0
. B.
2
. C.
4
. D. Vô số
Lời giải:
Chọn C
Có bốn trục đối xứng gồm
,dd
và hai đường phân giác của hai góc tạo bởi
,dd
.
Câu 3. Hình nào sau đây là có trục đối xứng:
A. Tam giác bất kì. B. Tam giác cân.
C. Tứ giác bất kì. D. Hình bình hành.
Lời giải:
Chọn B
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 22
LÊ MINH TÂM
Câu 4. Cho tam giác
ABC
đều. Hỏi hình là tam giác
ABC
đều có bao nhiêu trục đối xứng:
A. Không có trục đối xứng. B. Có 1 trục đối xứng.
C. Có 2 trục đối xứng. D. Có 3 trục đối xứng.
Lời giải:
Chọn D
3 trục đối xứng của tam giác đều là 3 đường trung trực của 3 cạnh.
Câu 5. Trong mặt phẳng
Oxy
, cho điểm
2;3M
. Hỏi trong bốn điểm sau điểm nào là ảnh của
M
qua phép đối xứng trục
Ox
?
A.
3;2
. B.
2; –3
. C.
3; –2
. D.
–2;3
Lời giải:
Chọn B
'
'


Đ
Ox
xx
MM
yy
. Suy ra
2; 3
M
.
Câu 6. Trong mặt phẳng
Oxy
, cho điểm
2;3M
. Hỏi
M
là ảnh của điểm nào trong các điểm sau
qua phép đối xứng trục
Oy
?
A.
3;2
. B.
2; –3
. C.
3; –2
. D.
–2;3
Lời giải:
Chọn D
'
'


Đ
Oy
xx
MM
yy
. Suy ra
2;3
M
.
Câu 7. Trong mặt phẳng
Oxy
, cho điểm
2;3M
. Hỏi trong bốn điểm sau điểm nào là ảnh của
M
qua phép đối xứng qua đường thẳng
: – 0d x y
?
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 23
LÊ MINH TÂM
A.
3;2
. B.
2; –3
. C.
3; –2
. D.
–2;3
Lời giải:
Chọn A
Gọi
H
là hình chiếu vuông góc của
M
trên
d
. Suy ra
: 5 0 MH x y
.
H d MH
. Ta có hệ phương trình
0
5
50
2

xy
xy
xy
. Vậy:
55
;
22



H
.
Đ
d
MM
. Suy ra
H
là trung điểm của
MM
.
Vậy:
3;2
M
.
Câu 8. Trong mặt phẳng
Oxy
, cho Parapol
P
có phương trình
2
24xy
. Hỏi Parabol nào trong
các Parabol sau là ảnh của
P
qua phép đối xứng trục
Oy
?
A.
2
24xy
. B.
2
–24xy
. C.
2
24yx
. D.
2
–24yx
Lời giải:
Chọn A
Gọi
; M x y P
tùy ý.
'
'; '


Đ
Oy
xx
M M x y
yy
.
Suy ra
;

M x y
.
Vì
MP
nên
2
2
' 24 ' 24

x y x y
.
Vậy
2
' : 24
M P x y
.
Câu 9. Trong mặt phẳng
Oxy
, cho đường thẳng
2 4 0:d x y
. Tìm ảnh của
d
qua phép đối
xứng trục
Ox
.
A.
2 2 4 0':dxy
B.
2 2 0':d x y
C.
3 2 4 0':d x y
D.
2 4 0':d x y
Lời giải:
Chọn D
Lấy
;M x y d
2 4 0xy
(1)
Gọi
'; 'N x y
là ảnh của
M
qua phép đối xứng
ox
Ð
.
Ta có
''
''
x x x x
y y y y




.
Thay vào
1
ta được
2 4 0''xy
.
Vậy
2 4 0':d x y
.
Câu 10. Trong mặt phẳng
Oxy
, cho đường thẳng đường tròn
22
: 2 4 4 0 C x y x y
. Tìm ảnh
của
C
qua phép đối xứng trục
Ox
.
A.
22
' : 2 2 9 C x y
B.
22
' : 1 1 9 C x y
C.
22
' : 3 2 9 C x y
D.
22
' : 1 2 9 C x y
Lời giải:
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 24
LÊ MINH TÂM
Chọn D
Cách 1: Ta thấy
C
có tâm
1;2I
và bán kính
3R
.
Gọi
', 'IR
là tâm và bán kính của
'C
thì
' 1; 2I
và
'3RR
, do đó
22
' : 1 2 9 C x y
.
Cách 2: Lấy
22
; 2 4 4 0 2 P x y C x y x y
.
Gọi
'; 'Q x y
là ảnh của
P
qua phép đối xứng
ox
Ð
. Ta có
''
''




x x x x
y y y y
thay vào
2
ta được
22
' ' 2 ' 4 ' 4 0 x y x y
, hay
22
' : 2 4 4 0 C x y x y
.
------------------HẾT------------------
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 25
LÊ MINH TÂM
§4. PHÉP ĐỐI XỨNG TÂM
I. ĐỊNH NGHĨA:
Cho điểm
I
.
– Phép biến hình
+ biến điểm
I
thành chính nó,
+ biến mỗi điểm
M
khác
I
thành
M
sao cho
I
là trung điểm của
MM
được gọi là phép đối xứng tâm
I
.
– Điểm
I
được gọi là tâm đối xứng.
– Phép đối xứng tâm
I
thường được kí hiệu là
I
§
Nhận xét.
– Nếu hình
H
là ảnh của hình
H
qua
I
§
thì ta còn nói
H
đối xứng với
H
qua tâm
I
, hay
H
và
H
đối xứng với nhau qua
.I
Từ đinh nghĩa suy ra
.
I
M M IM IM

§
– Điểm
I
được gọi là tâm đối xứng của hình
H
nếu phép đối xứng tâm
I
biến hình
H
thành
chính nó. Khi đó ta nói
H
là hình có tâm đối xứng;
II. TÍNH CHẤT:
Tính chất 1:
Nếu
I
Ð M M
và
I
Ð N N
thì
M N MN


, từ đó suy ra
.MN MN

Tính chất 2:
Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc
trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác
thành tam giác bằng nó, biến đường tròn thành đường tròn cùng bán kính.
III. BIỂU THỨC TỌA ĐỘ:
– Trong mặt phẳng
Oxy
, với mỗi điểm
;M x y
, gọi
;
I
M x y Ð M
.
Với
00;IO
, ta có
;;
O
M x y M x y


§
thì
.
xx
yy


PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 26
LÊ MINH TÂM
Với
;I a b
, ta có
;;
I
M x y M x y


§
thì
2
2
.
x a x
y b y


IV. BÀI TẬP:
4.1. Tự Luận.
Bài toán xác định ảnh trong hệ tọa độ qua Phép Đối Xứng Tâm
Phương pháp:
Sử dụng biểu thức tọa độ của phép đối xứng trục.
– Trong mặt phẳng
Oxy
, với mỗi điểm
;M x y
, gọi
;
I
M x y Ð M
.
Với
00;IO
, ta có
;;
O
M x y M x y


§
thì
.
xx
yy


Với
;I a b
, ta có
;;
I
M x y M x y


§
thì
2
2
.
x a x
y b y


– Để tìm tâm đối xứng của một hình ta có nhận xét như sau:
Nếu hình đã cho là một đa giác thì sử dụng tính chất:
Một đa giác có tâm đối xứng
I
thì qua phép đối xứng tâm
I
+ mỗi đỉnh của nó phải biến thành một đỉnh của đa giác,
+ mỗi cạnh của nó phải biến thành một cạnh của đa giác song song và bằng cạnh ấy.
Nếu hình đã cho không phải một đa giác thì sử dụng định nghĩa.
Bài 01.
Trong mặt phẳng tọa độ
Oxy
cho phép đối xứng tâm
00;O
biến điểm
23;M
thành
điểm
M
có tọa độ là
Lời giải
Biểu thức tọa độ của phép đối xứng tâm
00;O
là
xx
yy


23;M

.
Bài 02.
Phép đối xứng tâm
;I a b
biến điểm
13;A
thành điểm
17;A
. Tính tổng
T a b
.
Lời giải
Từ giả thiết suy ra
I
là trung điểm của
AA
11
1
2
37
5
2
a
b


6T
.
Bài 03.
Trong mặt phẳng toạ độ
Oxy
cho điểm
23;I
và đường thẳng
d
có phương trình
3 2 1 0.xy
Tìm toạ độ điểm
'I
và phương trình đường thẳng
'd
lần lượt là ảnh của
I
và
d
qua phép đối xứng tâm
O
.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 27
LÊ MINH TÂM
Lời giải
Ta có
23';I
.
Từ biểu thức toạ độ của phép đối xứng tâm qua gốc toạ độ ta có
.
xx
yy


Thay biểu thức của
x
và
y
vào phương trình của
d
ta được
3 2 1 0'xy
hay
3 2 1 0xy

.
Do đó phương trình của
3 2 1 0:d x y
.
Bài 04.
Trong các mặt phẳng tọa độ
0xy
cho đường thẳng
20:d x y
. Tìm phương trình đường
thẳng
d
là ảnh của
d
qua phép đối xứng tâm
12;I
Lời giải
Qua phép đối xứng tâm , đường thẳng biến thành đường thẳng song song hoặc
trùng với nó nên
0:d x y c
.
Chọn
11;Ad
.
Ta có
13;;
I
IA IA
D A A x y A
Ad


.
Thay vào
d
ta được
1 3 0 4 4 0:c c d x y
.
Cách 2 . Biểu thức tọa độ của phép đối xứng tâm
;I a b
là
22
24
x a x x x
y b y y y





.
Thay vào phương trình đường thẳng
d
ta được
2 4 2 0 4 0x y x y
.
Bài 05.
Trong mặt phẳng tọa độ
Oxy
, tìm phương trình đường tròn
C
là ảnh của đường tròn
22
3 1 9:C x y
qua phép đối xứng tâm
00;O
.
Lời giải
Cách 1. Đường tròn
C
có tâm
31;I
, bán kính
3R
.
Gọi
I
là điểm đối xứng của
31;I
qua phép đối xứng tâm
0 0 3 1;;OI

.
Phép đối xứng tâm bảo toàn khoảng cách nên
3RR

.
Vậy phương trình đường tròn
22
3 1 9:C x y
.
Cách 2. Biểu thức tọa độ của phép đối xứng tâm
00;O
là
xx
yy


.
Thay vào
C
ta được
2 2 2 2
3 1 9 3 1 9x y x y
.
Bài 06.
Chứng minh rằng nếu một tứ giác có tâm đối xứng thì nó phải là hình bình hành.
Lời giải
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 28
LÊ MINH TÂM
Giả sử tứ giác
ABCD
có tâm đối xứng là
I
.
Qua phép đối xứng tâm
I
, tứ giác
ABCD
biến thành chính nó nên đỉnh
A
chỉ có
thể biến thành
,,A B C
và
D
.
Nếu đỉnh
A
biến thành chính nó thì theo ví dụ trên
A
trùng với
I
.
Khi đó tứ giác có hai đỉnh đối xứng qua
A
điều đó vô lí.
Nếu đỉnh
A
biến thành
B
hoặc
D
thì tâm đối xứng thuộc các cạnh
AB
hoặc
AD
của tứ giác nên cũng suy ra điều vô lí.
Do đó
A
chỉ có thể biến thành
.C
Lí luận tương tự
B
chỉ có thể biến thành
D
.
Khi đó tâm đối xứng
I
là trung điểm của hai đường chéo
AC
và
BD
nên tứ giác
ABCD
phải là hình bình hành.
4.2. Trắc nghiệm.
Câu 1. Hình nào sau đây có tâm đối xứng?
A. Hình thang. B. Hình tròn. C. Parabol. D. Tam giác bất kì.
Lời giải:
Chọn B
Tâm đối xứng của hình tròn là tâm của hình tròn đó.
Câu 2. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Tam giác đều có tâm đối xứng. B. Tứ giác có tâm đối xứng.
C. Hình thang cân có tâm đối xứng. D. Hình bình hành có tâm đối xứng.
Lời giải:
Chọn D
Tâm đối xứng của hình bình hành là giao điểm của hai đường chéo.
Câu 3. Hình nào sau đây không có tâm đối xứng?
A. Hình vuông. B. Hình tròn. C. Hình tam giác đều. D. Hình thoi.
Lời giải:
Chọn C
Hình vuông và hình thoi có tâm đối xứng là giao điểm của hai đường chéo.
Câu 4. Trong các hình sau đấy, hình nào không có tâm đối xứng?
A. Hình gồm một đường tròn và một hình chữ nhật nội tiếp.
B. Hình gồm một đường tròn và một tam giác đều nội tiếp.
C. Hình lục giác đều.
D. Hình gồm một hình vuông và đường tròn nội tiếp.
Lời giải:
Chọn B
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 29
LÊ MINH TÂM
Tam giác đều không có tâm đối xứng.
Câu 5. Trong các hình dưới đây, hình nào không có tâm đối xứng?
A. Đường elip. B. Đường hypebol.
C. Đường parabol. D. Đồ thị hàm số
sinyx
.
Lời giải:
Chọn C
Đường parabol không có tâm đối xứng.
Câu 6. Trong mặt phẳng tọa độ
Oxy
cho phép đối xứng tâm
12;I
biến điểm
;M x y
thành
;M x y
. Mệnh đề nào sau đây là đúng?
A.
2
2
xx
yy
. B.
2
4
xx
yy
. C.
2
4
xx
yy
. D.
2
2
xx
yy


.
Lời giải:
Chọn B
Ta có
12;IM x y
,
12;IM x y
.
Vì
I
Ñ M M
nên
IM IM

11
22
xx
yy
2
4
xx
yy
.
Câu 7. Phép đối xứng tâm
00;O
biến điểm
;A m m
thành điểm
A
nằm trên đường thẳng
60xy
. Tìm
m
.
A.
3m
. B.
4m
. C.
3m 
. D.
4m
.
Lời giải:
Chọn A
Ta có
: ; ;
O
D A m m A m m
.
Do
A
nằm trên đường thẳng
60xy
nên
60mm
3m
.
Câu 8. Trong mặt phẳng tọa độ
Oxy
cho điểm
21;M
. Thực hiện liên tiếp phép đối xứng qua tâm
O
và phép tịnh tiếp theo vectơ
12;v
biến điểm
M
thành điểm nào trong các điểm sau?
A.
13;A
. B.
20;B
. C.
02;C
. D.
11;D
.
Lời giải:
Chọn A
Phép đối xứng tâm
00;O
biến điểm
21;M
thành điểm
21;M

.
Phép tịnh tiến theo vectơ
12;v
biến điểm
M
thành điểm
M

M M v

11;MD

.
Câu 9. Trong mặt phẳng tọa độ
0xy
, tìm phương trình đường tròn
C
là ảnh của đường tròn
22
1:C x y
qua phép đối xứng tâm
10;I
A.
2
2
21:C x y
. B.
2
2
21:C x y
.
C.
2
2
21:C x y
. D.
2
2
21:C x y
.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 30
LÊ MINH TÂM
Lời giải:
Chọn A
Biểu thức tọa độ của phép đối xứng tâm
10;I
là
2
0
xx
y y y


.
Thay vào
C
ta được
2 2 2
2
2 1 2 1x y x y
.
Câu 10. Trong mặt phẳng tọa độ
Oxy
cho đường tròn
22
1 3 16:C x y
. Giả sử phép đối
xứng tâm
I
biến điểm
13;A
thành điểm
;B a b
. Tìm phương trình của đường tròn
C
là
ảnh của đường tròn
C
qua phép đối xứng tâm
I
.
A.
22
1:C x a y b
. B.
22
4:C x a y b
.
C.
22
9:C x a y b
. D.
22
16:C x a y b
.
Lời giải:
Chọn D
Theo giả thiết điểm
13;A
biến thành điểm
;B a b
qua phép đối xứng tâm
I
.
Nên ta có
21
23
I A B
I A B
x x x a
y y y b
.
Biểu thức tọa độ của phép đối xứng tâm
I
là
21
1
2 3 3
I
I
x x x a x
x a x
y y y b y y b y


.
Thay vào
C
ta được
2 2 2 2
16 16a x b y x a y b
.
------------------HẾT------------------
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 31
LÊ MINH TÂM
§4. PHÉP QUAY
I. ĐỊNH NGHĨA:
Cho điểm
O
và góc lượng giác .
– Phép biến hình biến điểm
O
thành chính nó, biến mỗi điểm
M
khác
O
thành điểm
M
sao
cho
OM OM
và góc lượng giác
;OM OM
bằng được gọi là phép quay tâm
O
góc .
– Điểm
O
được gọi là tâm quay, được gọi là góc quay của phép quay đó.
– Phép quay tâm
O
góc thường được kí hiệu là
,O
Q
.
– Chiều dương của phép quay là chiều dương của đường tròn lượng giác nghĩa là chiều
ngược với chiều quay của kim đồng hồ.
– Với
k
là số nguyên ta luôn có:
+ Phép quay
2,Ok
Q
là phép đồng nhất.
+ Phép quay
21,Ok
Q
là phép đối xứng tâm
O
.
II. TÍNH CHẤT:
Tính chất 1:
Cho
,O
Q M M
và
,O
Q N N
thì
MN MN

.
Tính chất 2:
– Phép quay tâm
O
góc biến đoạn thẳng thành đoạn thẳng cùng độ dài.
– Phép quay tâm
O
góc biến đường thẳng thành đường thẳng.
– Phép quay tâm
O
góc biến tam giác thành tam giác bằng nó.
– Phép quay tâm
O
góc biến đường tròn thành đường tròn có cùng bán
kính.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 32
LÊ MINH TÂM
III. BIỂU THỨC TỌA ĐỘ:
– Trong mặt phẳng
Oxy
, cho điểm
;M x y
và điểm
;I a b
. Gọi
M
là ảnh của
M
qua phép
quay tâm
I
góc . Khi đó
,
cos sin
;
sin cos
I
x x a y b a
M x y Q M
y x a y b b

IV. BÀI TẬP:
4.1. Tự Luận.
Bài toán xác định ảnh trong hệ tọa độ qua Phép Quay
Phương pháp:
Sử dụng biểu thức tọa độ của phép quay.
– Trong mặt phẳng
Oxy
, cho điểm
;M x y
và điểm
;I a b
. Gọi
M
là ảnh của
M
qua phép
quay tâm
I
góc . Khi đó
,
cos sin
;
sin cos
I
x x a y b a
M x y Q M
y x a y b b

Bài 01.
Cho 3 điểm
,,A B C
thẳng hàng theo thứ tự trên. Cùng thuộc nửa mặt phẳng có bờ là
,AB
vẽ các tam giác đều
,.ABD BCE
Chứng minh
60 .,,DC AE DC AE
Lời giải
Xét
60;
:;
B
Q C E D A
CD EA
.
Khi đó
CD EA
và
60 .,CD EA
Xét :
– Nếu thì ta quay theo chiều dương là ngược chiều kim đồng hồ.
– Nếu thì ta quay theo chiều âm là cùng chiều kim đồng hồ.
– Nếu thì .
– Nếu thì là trung điểm của .
Xét và cho thì góc .
CHÚ Ý
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 33
LÊ MINH TÂM
Bài 02.
Trong mặt phẳng tọa độ
Oxy
, cho
3 0 0 2 3 2 0 3; , ; , ; , ;A B C D
tìm tọa độ ảnh của các
đối tượng sau biết
90;
,
O
Q B B
90 90 90; ; ;
, , .
O O O
Q A A Q C C Q D D
Lời giải
3 0 0 2 3 2 0 3; , ; , ; , ;A B C D
.
90
90
03
;
'
;
';
O
OA
Q
A
OA OA
A
O
AA
.
90
90
20
;
;
;
O
Q
OB
OB OB
B B B
OB

90 90
23
;;
;
OO
Q C C Q OBCA OB C A C

90
90
03
;
;
;
O
OD OD
Q D D D A
ODOD

.
Bài 03.
Trong mặt phẳng tọa độ
,Oxy
tìm ảnh của đường thẳng
3 4 2 0:d x y
qua
2
;O
Q



Lời giải
Gọi
2
4 3 0
;
:
O
d Q d d d d x y c



.
Lấy
2
22
;
;
O
d A Q A dA




.
Ta có
2 2 4 2 3 2 0 2; . .A d c c

.
Vậy
4 3 2 0:.d x y
Bài 04.
Trong mặt phẳng
Oxy
, cho đường thẳng
2 11 0: xy
. Viết phương trình đường thẳng
là ảnh của đường thẳng
qua phép quay tâm
O
góc
90
.
Lời giải
Gọi điểm
;M x y
bất kì thuộc đường thẳng
,
;M x y
là ảnh của điểm
M
qua
phép quay tâm
O
góc
90
.
Khi đó
M
sẽ thuộc đường thẳng
.
Theo biểu thức tọa độ của phép quay tâm
O
, góc quay
90
ta có:
90 90
90 90
.cos .sin
.sin .cos
x x y x y x y
y x y y x y x

.
Thay vào phương trình
ta có
2 11 0 2 11 0'y x x y
Vậy phương trình
là
2 11 0xy
.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 34
LÊ MINH TÂM
Bài 05.
Trong mặt phẳng toạ độ
Oxy
, cho điểm
30;A
. Tìm toạ độ điểm
A
là ảnh của điểm
A
qua phép quay tâm
00;O
góc quay
2
.
Lời giải
Gọi
;A x y
. Ta có
2
2
,
,
O
OA OA
Q A A
OA OA





.
Vì
2
3 0 0
,
;;
OA OA
A Ox A Oy A y



. Mà
3OA OA y
.
Do góc quay
0
2
y
. Vậy
03;A
.
Bài 06.
Trong mặt phẳng toạ độ
Oxy
, cho hai đường thẳng
a
và
b
có phương trình lần lượt là
2 5 0xy
và
2 3 0xy
. Nếu có phép quay biến đường thẳng này thành đường thẳng
kia thì số đo của góc quay
0 180()
là
Lời giải
Ta thấy hai đường thẳng
a
và
b
có phương trình
2 5 0xy
và
2 3 0xy
là
vuông góc với nhau. Suy ra
90
.
Bài 07.
Trong hệ tọa độ
Oxy
, cho đường tròn
C
có phương trình:
22
1 2 25.xy
Ảnh của
đường tròn
C
qua phép quay tâm
O
góc quay
0
90
là
Lời giải
C
có tâm
12;I
.
Gọi
0
00
00
90
90 2 90 2
1
2 90 90
,
cos sin cos sin
cos sin .
cos sin
O
x x y x x
I Q I
y y x y
y



Suy ra
21;I
.
Vậy phương trình
( ')C
:
22
1 2 25.xy
4.2. Trắc nghiệm.
Câu 1. Có bao nhiêu điểm biến thành chính nó qua phép quay tâm
O
góc với
2k
(
k
là
một số nguyên)?
A.
0
. B.
1
. C.
2
. D. Vô số.
Lời giải:
Chọn B
Điểm đó chính là tâm quay
O
.
Câu 2. Cho tam giác đều tâm
O
. Với giá trị nào dưới đây của thì phép quay
,O
Q
biến tam giác
đều thành chính nó?
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 35
LÊ MINH TÂM
A.
3
. B.
2
3
. C.
3
2
. D.
2
.
Lời giải:
Chọn B
Các góc quay để biến tam giác đều thành chính nó là:
0
;
2
3
;
4
3
;
4
.
Câu 3. Cho tam giác đều
ABC
. Hãy xác định góc quay của phép quay tâm
A
biến
B
thành
C
.
A.
30
. B.
90
.
C.
120
. D.
60
hoặc
60
.
Lời giải:
Chọn D
Tam giác
ABC
đều, nên
60BAC 
. Khi đó
60
,A
Q B C
.
Câu 4. Cho tam giác đều tâm
O
. Hỏi có bao nhiêu phép quay tâm
O
góc với
02
, biến
tam giác trên thành chính nó?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải:
Chọn C
Do
02
nên ta có góc quay là
0
;
2
3
;
4
3
.
Câu 5. Cho hình vuông tâm
O
. Xét phép quay
Q
có tâm quay
O
và góc quay . Với giá trị nào
sau đây của , phép quay
Q
biến hình vuông thành chính nó?
A.
6
. B.
4
. C.
3
. D.
2
.
Lời giải:
Chọn D
Các góc quay để biến hình vuông thành chính nó là:
0
;
2
; ;
3
2
;
2
.
Câu 6. Trong mặt phẳng toạ độ
Oxy
, cho điểm
30;A
. Tìm toạ độ điểm
A
là ảnh của điểm
A
qua
phép quay tâm
00;O
góc quay
2
.
A.
03;A
. B.
03;A
. C.
30;A
. D.
2 3 2 3;A
.
Lời giải:
Chọn B
Gọi
;A x y
. Ta có
2
2
,
,
O
OA OA
Q A A
OA OA




.
Vì
2
3 0 0
,
;;
OA OA
A Ox A Oy A y


. Mà
3OA OA y
.
Do góc quay
0
2
y
. Vậy
03;A
.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 36
LÊ MINH TÂM
Câu 7. Trong mặt phẳng toạ độ
Oxy
, cho hai đường thẳng
a
và
b
có phương trình lần lượt là
4 3 5 0xy
và
7 4 0xy
. Nếu có phép quay biến đường thẳng này thành đường thẳng
kia thì số đo của góc quay
0 180()
là
A.
45
. B.
60
. C.
90
. D.
120
.
Lời giải:
Chọn B
Đường thẳng
4 3 5 0:a x y
có vectơ pháp tuyến
43;
a
n
. Đường thẳng
7 4 0:b x y
có vectơ pháp tuyến
17;
b
n
. Góc là góc tạo bởi
a
và
b
.
Ta có
2 2 2 2
4 1 3 7
2
45
2
4 3 1 7
..
cos cos ,
.
ab
nn

.
Vậy
45
.
Câu 8. Trong mặt phẳng với hệ toạ độ
Oxy
, cho đường thẳng
2 6 0: xy
. Viết phương trình
đường thẳng
là ảnh của đường thẳng
qua phép quay tâm
O
góc
90
.
A.
2 6 0xy
. B.
2 6 0xy
. C.
2 6 0xy
. D.
2 6 0xy
.
Lời giải:
Chọn A
Đường thẳng
có vectơ pháp tuyến
1
12;n
, vì đường thẳng
vuông góc với đường
thẳng
nên đường thẳng
có vectơ pháp tuyến
2
21;n 
.
Đường thẳng
cắt trục
Oy
tại
03;A
nên ảnh của
A
qua phép quay tâm
O
góc
90
là
điểm
30;B
thuộc đường thẳng
nên phương trình đường thẳng
là
2 6 0xy
.
Câu 9. Ảnh của điểm
23;M
qua phép quay tâm
12;I
góc quay
120
là
A.
5 3 5 3 3 9
22
;M




. B.
5 3 1 3 3 1
22
;M




.
C.
5 3 5 3 3 9
22
;M





. D.
5 3 1 3 3 9
22
;M




.
Lời giải:
Chọn C
Chú ý: Trong mặt phẳng
Oxy
, giả sử
; , ;M x y I a b
và
;
;
I
M x y Q
thì
.cos .sin
.sin .cos
x a x a y b
y b x a y b
Vậy ảnh của điểm
23;M
qua phép quay tâm
12;I
góc quay
120
là
;M x y
:
1 3 120 5 120
2 3 120 5 120
cos sin
sin cos
x
y
5 3 5
2
3 3 9
2
x
y
.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 37
LÊ MINH TÂM
Vậy
5 3 5 3 3 9
22
;M





.
Câu 10. Trong mặt phẳng
Oxy
, cho điểm
21;M
. Xác định tọa độ điểm
M
là ảnh của điểm
M
qua phép quay tâm
O
góc
90
.
A.
12;M
. B.
12;M
. C.
12;M

. D.
12;M
.
Lời giải:
Chọn C
Theo biểu thức tọa độ của phép quay tâm
O
, góc quay
90
ta có:
90 90 1
12
90 90 2
.cos .sin
';
.sin .cos
x x y x y x
M
y x y y x y
.
------------------HẾT------------------
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 38
LÊ MINH TÂM
§5. PHÉP DỜI HÌNH
I. ĐỊNH NGHĨA:
– Phép dời hình là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì.
Nhận xét.
– Các phép đồng nhất, tịnh tiến, đối xứng trục, đối xứng tâm và phép quay đều là những phép
dời hình.
– Phép biến hình có được bằng cách thực hiện liên tiếp hai phép dời hình là một phép dời hình.
II. TÍNH CHẤT:
Tính chất:
Phép dời hình:
+ Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự
giữa các điểm.
+ Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng
thành đoạn thẳng bằng nó.
+ Biến tam giác thành tam giác bằng nó, biến góc thành góc bằng nó.
+ Biến đường tròn thành đường tròn có cùng bán kính.
III. KHÁI NIỆM HAI HÌNH BẰNG NHAU:
– Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
IV. BÀI TẬP:
4.1. Tự Luận.
Bài toán xác định ảnh trong hệ tọa độ qua Phép Dời Hình
Phương pháp:
Sử dụng định nghĩa, tính chất và biểu thức tọa độ của phép dời hình (tịnh tiến, đối xứng
trục/ tâm, quay).
– Xét phép dời hình biến thành thì nó biến trọng tâm, trực tâm, tâm đường
tròn ngoại tiếp, nội tiếp của tương ứng với trọng tâm, trực tâm, tâm đường tròn
ngoại tiếp, nội tiếp của
– Phép dời hình biến đa giác cạnh thành đa giác cạnh, biến đỉnh thành đỉnh tương
ứng, biến cạnh thành cạnh.
– Hai hình được gọi là bằng nhau khi và chỉ khi có một phép dời hình biến hình này
thành hình kia.
CHÚ Ý
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 39
LÊ MINH TÂM
Bài 01.
Cho tam giác đều
ABC
và
G
là trọng tâm tam, giác
ABC
. Tìm ảnh của tam giác
ABC
lần
lượt qua
AG
T
và
0
60,B
Q
a. Qua
AG
T
. b.Qua
0
60,B
Q
Lời giải
a. Qua
AG
T
:
Ta có
1
AG
T A A G
;
11
AG
T B B BB AG
;
11
AG
T C C CC AG
Vậy
1 1 1
AG
T ABC A B C
b.Qua
0
60,B
Q
0
60,B
Q B B
;
0
11
60,
,
B
Q A A A C

;
0
1
60,B
Q C C
,
1
C
đối xứng với
A
qua
BC
Vậy
0
11
60,B
Q ABC A BC
Bài 02.
Trong mặt phẳng tọa độ
Oxy
, cho đường thẳng
3 3 0:d x y
. Hỏi phép dời hình có
được bằng cách thực hiện liên tiếp phép đối xứng tâm
12;I
và phép tịnh tiến
21;v 
biến đường thẳng
d
thành đường thẳng nào trong các đường thẳng sau?
Lời giải
Gọi
'd
là ảnh cần tìm của
d
.
Khi đó
'd
song song hoặc trùng
d
nên phương trình
'd
có dạng:
30x y c
.
Gọi
10;Ad
Suy ra
'AA
là đường cao của lăng trụ:
4'h AA a
.
Phép đối xứng tâm
12;I
biến
10;A
thành
14;B
.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 40
LÊ MINH TÂM
Phép tịnh tiến theo vectơ
21;v 
biến
14;B
thành
15;C
.
Mà
1 5 3 0; ' :C d x y c
nên
3 1 5 0 8. cc
.
Vậy
3 8 0':d x y
.
Bài 03.
Cho đường tròn
22
4 2 4 0:C x y x y
. Tìm ảnh của
C
khi thực hiện liên tiếp
phé
p
tịnh tiến theo vectơ
21;u 
và
phé
p tịnh tiến theo vectơ
13;v
.
Lời giải
Theo giả thiết
22
4 2 4 0:C x y x y
có tâm
21;I
, bán kính
1R
.
Phép tịnh tiến theo vectơ
21;u 
biến
21;I
thành
00;O
.
Phép tịnh tiến theo vectơ
13;v
biến
00;O
thành
13';I
.
Do đó, ảnh của
C
khi thực hiện liên tiếp
phé
p tịnh tiến theo vectơ
21;u 
và
phé
p tịnh tiến theo vectơ
13;v
là đường tròn
'C
có tâm
13';I
và bán kính
1R
Vậy
22
1 3 1':C x y
.
4.2. Trắc nghiệm.
Câu 1. Hợp thành của hai phép tịnh tiến là phép nào trong các phép dưới đây?
A. Phép đối xứng trục. B. Phép đối xứng tâm.
C. Phép tịnh tiến. D. Phép quay.
Lời giải:
Chọn C
Hợp thành của hai phép tịnh tiến là phép tịnh tiến với vectơ tịnh tiến là vectơ tổng của hai
vectơ tịnh tiến của hai phép tịnh tiến đã cho.
Câu 2. Phép dời hình có được bằng cách thực hiện liên tiếp phép tịnh tiến
v
và phép đối xứng tâm
I
là phép nào trong các phép dưới đây?
A. Phép đối xứng trục. B. Phép đối xứng tâm.
C. Phép đồng nhất. D. Phép tịnh tiến.
Lời giải:
Chọn B
Tâm đối xứng là
J
thỏa mãn
1
2
IJ v
.
Câu 3. Phép dời hình có được bằng cách thực hiện liên tiếp hai phép đối xứng qua hai đường thẳng
song song là phép nào trong các phép dưới đây?
A. Phép đối xứng trục. B. Phép đối xứng tâm.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 41
LÊ MINH TÂM
C. Phép tịnh tiến. D. Phép quay, góc quay khác .
Lời giải:
Chọn C
Vectơ tịnh tiến là
2u HK
, với
,HK
lần lượt là hai điểm nằm trên hai đường thẳng song
song đã cho, đồng thời
HK
sẽ vuông góc với hai đường thẳng đó.
Câu 4. Phép dời hình có được bằng cách thực hiện liên tiếp hai phép đối xứng qua hai đường thẳng
vuông góc với nhau là phép nào trong các phép dưới đây?
A. Phép đối xứng trục. B. Phép đối xứng tâm.
C. Phép tịnh tiến. D. Phép quay, góc quay khác .
Lời giải:
Chọn B
Tâm đối xứng là giao điểm của hai đường thẳng đã cho.
Câu 5. Phép dời hình có được bằng cách thực hiện liên tiếp hai phép đối xứng qua hai đường thẳng
căt nhau ( không vuông góc) là phép nào trong các phép dưới đây?
A. Phép đối xứng trục. B. Phép đối xứng tâm.
C. Phép tịnh tiến. D. Phép quay, góc quay khác .
Lời giải:
Chọn D
Tâm quay là giao điểm của hai đường thẳng đã cho, góc quay là góc giữa hai đường thẳng
đó.
Câu 6. Phép dời hình có được bằng cách thực hiện liên tiếp hai phép đối xứng tâm là phép nào trong
các phép dưới đây?
A. Phép đối xứng trục. B. Phép đối xứng tâm.
C. Phép tịnh tiến. D. Phép quay.
Lời giải:
Chọn C
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 42
LÊ MINH TÂM
Vectơ tịnh tiến là
2 'u II
, với
,'II
lần lượt là tâm đối xứng của hai phép đối xứng tâm đã
cho.
Câu 7. Trong mặt phẳng tọa độ
Oxy
, cho đường tròn
C
có phương trình
22
2 1 9xy
.
Phương trình đường tròn
C
là ảnh của
C
qua phép dời hình có được bằng cách thực
hiện liên tiếp một phép tịnh tiến theo
14;v 
và phép đối xứng trục
Oy
là
A.
22
1 5 9:C x y
. B.
22
3 3 9:C x y
.
C.
22
3 3 9:C x y
. D.
22
1 5 9:C x y
.
Lời giải:
Chọn D
Ta có:
C
là đường tròn tâm
21;I
và bán kính
3R
.
Gọi
15;;
v
I a b T I I

tâm của
C
là
15;
Oy
I D I


.
Qua phép dời hình bán kính đường tròn không đổi nên phương trình
C
là:
22
1 5 9xy
.
Câu 8. Cho hàm số
3
32y x x
có đồ thị
C
. Tịnh tiến
C
qua phải 2 đơn vị rồi tịnh tiến
xuống dưới 1 đơn vị. Ảnh của
C
là đồ thị của hàm số
A.
32
6 9 1y x x x
. B.
32
6 9 1y x x x
.
C.
32
6 9 1y x x x
. D.
32
6 9 1y x x x
.
Lời giải:
Chọn D
Mỗi điểm
3
; 3 2 1M x y C y x x
.
Gọi
1 1 1
;M x y
là ảnh của
M
qua phép tịnh tiến qua phải 2 đơn vị, tức là tịnh tiến theo véc
tơ
2;0u
, khi đó ta có:
1
1
2xx
yy

.
Gọi
2 2 2
;M x y
là ảnh khi tịnh tiến
1 1 1
;M x y
xuống dưới 1 đơn vị, tức là tịnh tiến theo véc
tơ
0; 1v
, khi đó ta có:
2 1 2
2 1 2
22
1 1 1
x x x x x
y y y y y



.
Thay vào phương trình
1
ta được:
3
32
2 2 2 2 2 2 2
1 2 3 2 2 6 9 1y x x y x x x
. Suy ra
2
M
thuộc đồ thị hàm số có
phương trình
32
6 9 1y x x x
.
Vậy ảnh của
C
qua phép biến hình trên là đồ thị của hàm số có phương trình
32
6 9 1y x x x
.
Câu 9. Trong mặt phẳng
Oxy
, cho đường thẳng
d
có phương trình
20xy
. Xác định phương
trình đường thẳng
d
là ảnh của đường thẳng
d
qua phép dời hình có được bằng cách
thực hiện liên tiếp phép tịnh tiến theo véc tơ
1;1v
và phép quay tâm
O
, góc quay
2
.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 43
LÊ MINH TÂM
A.
: 2 0d x y

. B.
: 2 0d x y
.
C.
:0d x y

. D.
: 1 0d x y
.
Lời giải:
Chọn A
Cách 1: Gọi
11
//
vd
d T d d
hoặc
1
dd
phương trình
1
d
có dạng
0x y c
.
Gọi
11
;
2
O
d Q d d d




phương trình
d
có dạng
0x y c
.
Lấy
1
1;1 0;2
v
M d M T M
và
11
Md
.
Gọi
1
;
2
2;0 2
O
M Q M M c



.
Vậy phương trình
d
là
20xy
.
Cách 2: Ta có
v
là véc tơ chỉ phương của đường thẳng
d
nên ảnh của đường thẳng
d
qua phép tịnh
tiến theo
v
là đường thẳng
d
.
Gọi
;
2
O
d Q d d d




phương trình
d
có dạng
0x y c
.
Lấy
0;2Md
. Gọi
1
;
2
2;0 2
O
M Q M M c



.
Vậy phương trình
d
là
20xy
.
Câu 10. Trong mặt phẳng
Oxy
, cho đường thẳng
:3 4 1 0d x y
. Thực hiện liên tiếp phép vị tự
tâm
O
tỉ số
3k 
và phép tịnh tiến theo véc tơ
1;2u
thì đường thẳng
d
biến thành
đường thẳng
d
có phương trình là
A.
3 4 2 0xy
. B.
3 4 2 0xy
. C.
3 4 5 0xy
. D.
3 4 5 0xy
.
Lời giải:
Chọn A
Theo công thức tọa độ phép vị tự ta có
3
3
3
3
x
x
xx
y y y
y






.
Thay vào phương trình của
d
ta có:
3. 4. 1 0 3 4 3 0
33
xy
x y d


.
Theo công thức tọa độ phép tịnh tiến ta có
11
22
x x x x
y y y y
 




.
Thay vào phương trình của
d

ta có
3 1 4 2 3 0 3 4 2 0x y x y
.
Vậy đường thẳng
d
có phương trình
3 4 2 0xy
.
------------------HẾT------------------
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 44
LÊ MINH TÂM
§6. PHÉP VỊ TỰ
I. ĐỊNH NGHĨA:
– Cho một điểm
O
cố định và một số
k
không đổi,
0k
. Khi đó
phép vị tự tâm
O
tỷ số
0k
là phép biến hình biến mỗi điểm
M
thành
M
sao cho
OM kOM
.
– Ký hiệu:
,Ok
V M M OM kOM

.
Nhận xét:
– Phép vị tự biên tâm vị tự thành chính nó.
– Khi
0k
thì
M
và
M
cùng phía với điểm
O
.
– Khi
0k
thì
M
và
M
khác phía với điểm
O
.
– Khi
1k 
thì
M
và
M
đối xứng nhau qua
O
.
– Khi
1k
thì
M
và
M
có vị trí trùng nhau nên phép vị tự tỷ số
1k
là phép đồng nhất.
–
1
;
;
Ok
O
k
V M M V M M




II. TÍNH CHẤT:
Tính chất
1:
Nếu phép vị tự tỷ số
k
biến hai điểm
,MN
tuỳ
ý thành hai điểm
,MN

thì
M N kMN

và
M N k MN

.
Tính chất
2:
Phép vị tự tỷ số
k
biến:
– Ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các
điểm.
– Đường thẳng thành đường thẳng song song hoặc trùng, tia thành tia, đoạn
thẳng thành đoạn thẳng.
– Tam giác thành tam giác đồng dạng với nó, góc thành góc bằng nó.
– Đường tròn bán kính
R
thành đường tròn có bán kính
kR
.
O'
O
R'
A'
R
A
I
A
B
C
A'
B'
C'
C'
B'
A'
C
B
A
I
I
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 45
LÊ MINH TÂM
III. CÁCH TÌM TÂM VỊ TỰ CỦA HAI ĐƯỜNG TRÒN:
Cho hai đường tròn
,IR
và
,IR

.
Trường
hợp 1:
Trường hợp
I
trùng với
I
.
Phép vị tự tâm
I
, tỉ số
R
R
và phép vị tự tâm
I
,
tỉ số
R
R
biến đường tròn
,IR
thành đường
tròn
,IR

.
Trường
hợp 2:
Trường hợp
I
khác
I
và
RR
.
+ Lấy
M
bất kì thuộc
,IR
, đường thẳng qua
I
song song với
IM
cắt
,IR

tại
M
và
M

.
+ Giả sử
,MM
nằm cùng phía đối với đường thẳng
II
, còn
,MM

nằm
khác phía với đường thẳng
II
.
+ Giả sử đường thẳng
MM
cắt
II
tại
O
nằm ngoài đoạn thẳng
II
, còn
đường thẳng
MM

cắt
II
tại
1
O
nằm ngoài đoạn thẳng
II
.
+ Khi đó phép vị tự tâm
O
, tỉ số
R
R
và phép vị tự tâm
1
O
, tỉ số
R
R
biến
đường tròn
,IR
thành đường tròn
,IR

.
+ Ta gọi
O
là tâm vị tự ngoài, còn
1
O
là tâm vị tự trong của 2 đường tròn.
Trường
hợp 3:
Trường hợp
I
khác
I
và
RR
.
+ Khi đó
MM
song song với
II
nên chỉ có phép vị tự tâm
1
O
, tỉ số
1
R
k
R
biến đường tròn
,IR
thành đường tròn
,IR

.
+ Nó chính là phép đối xứng tâm
1
O
.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 46
LÊ MINH TÂM
IV. BIỂU THỨC TỌA ĐỘ:
– Trong mặt phẳng
Oxy
, cho điểm
;M x y
và điểm
;I a b
. Gọi
M
là ảnh của
M
qua phép
vị tự tâm
I
. Khi đó
;
;;
Ik
x a k x a x a k x a
V M M IM kIM x a y b k x a y b
y b k y b y b k y b







IV. BÀI TẬP:
4.1. Tự Luận.
Bài toán xác định ảnh trong hệ tọa độ qua Phép Quay
Phương pháp:
Sử dụng biểu thức tọa độ của phép vị tự.
– Trong mặt phẳng
Oxy
, cho điểm
;M x y
và điểm
;I a b
. Gọi
M
là ảnh của
M
qua phép
vị tự tâm
I
. Khi đó
;
;;
Ik
x a k x a x a k x a
V M M IM kIM x a y b k x a y b
y b k y b y b k y b







Bài 01.
Trong mặt phẳng tọa độ
Oxy
cho hai điểm
4;6M
và
' 3;5M
. Phép vị tự tâm
I
, tỉ số
1
2
k
biến điểm
M
thành điểm
'M
. Tìm tọa độ tâm vị tự
I
.
Lời giải
Gọi
;I x y
. Suy ra
4 ;6IM x y
,
' 3 ;5IM x y
.
Ta có
1
;
2
1
34
10
1
2
' ' 10;4 .
14
2
56
2
I
xx
x
V M M IM IM I
y
yy





Bài 02.
Trong mặt phẳng
Oxy
, cho điểm
35;A
và đường thẳng
2 4 0:d x y
. Hãy tìm ảnh của
điểm
A
và ảnh của
d
qua phép vị tự
12;I
và tỷ số
2k 
.
Lời giải
Gọi
;A x y
là ảnh của
A
qua phép vị tự
;Ik
V
Theo biểu thức toạ độ, ta có:
1 2 3 1 9
2 2 5 2 16
x
y
Vậy ảnh của điểm
A
là
9 16;A
.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 47
LÊ MINH TÂM
Gọi
d
là ảnh của
d
qua phép vị tự
;Ik
V
.
Vì
//dd
nên phương trình đường thẳng
d
có dạng:
20x y c
.
Gọi
;
;
,
Ik
V M M x y
Theo biểu thức toạ độ, ta có:
1 2 2 1 7
2 2 0 2 6
x
y
Khi đó
Md

nên
2 7 6 0 8. cc
Vậy pt đường thẳng
2 8 0:d x y
Bài 03.
Trong mặt phẳng tọa độ
Oxy
cho đường thẳng
: 3 0d x y
. Phép vị tự tâm
O
, tỉ số
2k
biến
d
thành đường thẳng nào ?
Lời giải
Cách 1: Ta có
;2
: //
O
V d d d d
nên
:2 0
d x y c
(
3c
do
1k
).
Chọn
0;3 Ad
. Ta có
;2
2


O
OA OA
V A A
Ad
.
Từ
2 (0;6)OA OA A


. Thay vào
d
ta được
:2 6 0d x y
.
Cách 2: Giả sử phép vị tự
;2O
V
biến điểm
;M x y
thành điểm
;
M x y
.
Ta có
1
2
2
2
21
2
xx
xx
OM OM
yy
yy

.
Thay vào ta được
2 3 0 2 6 0
22
xy
xy


.
Bài 04.
Trong mặt phẳng tọa độ
Oxy
cho đường tròn
22
: 1 5 4 C x y
và điểm
2; 3I
. Gọi
C
là ảnh của
C
qua phép vị tự tâm
I
tỉ số
2k 
. Khi đó
C
có phương trình là
Lời giải
⬥ Đường tròn
C
có tâm
1;5K
và bán kính
2
R
⬥ Gọi
;2
2 2 1 2
4
;2
19
3 2 5 3



I
x
x
V K K x y IK IK
y
y
4; 19
K
là tâm
của đường tròn
C
.
⬥ Bán kính
R
của
C
là
||k = 2 2 = 4
RR
⬥ Vậy
22
: 4 19 16
C x y
Bài 05.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 48
LÊ MINH TÂM
Cho phép vị tự
13;I
và tỷ số
2k 
. Tìm ảnh của đường tròn
22
2 1 3:C x y
qua
;Ik
V
.
Lời giải
Đường tròn
C
có tâm
21;J
và bán kính
3R
.
Gọi
;
;
Ik
V J J x y
Theo biểu thức toạ độ, ta có:
1 2 2 1 1
3 2 1 3 11
x
y
Toạ độ
1 11;J
,
2 3 2 3R
.
Ảnh của đường tròn
C
qua
;Ik
V
có phương trình:
22
1 11 12xy
.
4.2. Trắc nghiệm.
Câu 1. Cho hai đường thẳng cắt nhau
d
và
d
. Có bao nhiêu phép vị tự biến đường thẳng
d
thành đường thẳng
d
?
A.
0
. B.
1
. C.
2
. D. Vô số.
Lời giải:
Chọn A
Vì qua phép vị tự, đường thẳng biến thành đường thẳng song song hoặc trùng với nó.
Câu 2. Cho hai đường thẳng song song
d
và
d
. Có bao nhiêu phép vị tự với tỉ số
20k
biến
đường thẳng
d
thành đường thẳng
d
?
A.
0
. B.
1
. C.
2
. D. Vô số.
Lời giải:
Chọn D
Lấy hai điểm
A
và
A
tùy ý trên
d
và
d
.
Chọn điểm
O
thỏa mãn
20OA OA
.
Khi đó phép vị tự tâm
O
tỉ số
20k
sẽ biến đường thẳng
d
thành đường thẳng
d
. Do
A
và
A
tùy ý trên
d
và
d
nên suy ra có vô số phép vị tự.
Câu 3. Cho hai đường thẳng song song
d
và
'd
và một điểm
O
không nằm trên chúng. Có bao
nhiêu phép vị tự tâm
O
biến đường thẳng
d
thành đường thẳng
'd
?
A. 0. B. 1. C. 3. D. Vô số.
Lời giải:
Chọn B
Kẻ đường thẳng
qua
O
cắt
d
tại
A
và cắt
'd
tại
'A
.
Gọi
k
là số thỏa mãn
'OA kOA
. Khi đó phép vị tự tâm
O
tỉ số
k
sẽ biến
d
thành
'd
.
Do
k
xác định duy nhất (không phụ thuộc vào
) nên có duy nhất một phép vị tự.
Câu 4. Cho hai đường thẳng cắt nhau
d
và
'd
. Có bao nhiêu phép vị tự biến mỗi đường thẳng
thành chính nó.
A. 0. B. 1. C. 2. D. Vô số.
Lời giải:
Chọn D
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 49
LÊ MINH TÂM
Tâm vị tự là giao điểm của
d
và
'd
.
Tỉ số vị tự là số
k
khác
0
(hoặc tâm vị tự tùy ý, tỉ số
1k
đây là phép đồng nhất.)
Câu 5. Cho hai đường tròn bằng nhau
;OR
và
'; 'OR
với tâm
O
và
'O
phân biệt. Có bao nhiêu
phép vị tự biến
;OR
thành
'; 'OR
?
A. 0. B. 1. C. 2. D. Vô số.
Lời giải:
Chọn B
Phép vị tự có tâm là trung điểm
OO'
, tỉ số vị tự là
1
.
Câu 6. Cho đường tròn
;3O
và điểm
I
nằm ngoài
O
sao cho
9OI
. Gọi
'; 'OR
là ảnh của
;3O
qua phép vị tự
;5I
V
. Tính
'R
.
A.
'9R
B.
5
'
3
R
C.
' 27R
D.
' 15R
.
Lời giải:
Chọn D
Ta có
' . 5. 5.3 15R k R R
.
Câu 7. Trong mặt phẳng tọa độ
Oxy
cho phép vị tự tâm
2;3I
tỉ số
2k 
biến điểm
7;2M
thành điểm
'M
có tọa độ là:
A.
10;2
B.
20;5
C.
18;2
D.
10;5
Lời giải:
Chọn B
Gọi
';M x y
. Suy ra
9; 1 , ' 2; 3IM IM x y
.
Ta có
;2
2 2. 9
20
' ' 2 ' 20;5
5
3 2. 1
I
x
x
V M M IM IM M
y
y

.
Câu 8. Trong mặt phẳng tọa độ
Oxy
cho phép vị tự
V
, tỉ số
2k
biến điểm
1; 2A
thành điểm
' 5;1A
. Hỏi phép vị tự
V
biến điểm
0;1B
thành điểm có tọa độ nào sau đây?
A.
0;2
B.
12; 5
C.
7;7
D.
11;6
Lời giải:
Chọn C
Gọi
';B x y
là ảnh của
B
qua phép vị tự
V
.
Suy ra
' ' 5; 1A B x y
và
1;3AB 
.
Theo giả thiết, ta có
5 2. 1
7
' ' 2
7
1 2.3
x
x
A B AB
y
y



.
Câu 9. Trong mặt phẳng tọa độ
Oxy
cho đường thẳng
: 2 1 0xyd
. Lập phương trình đường
thẳng
d
là ảnh của
d
qua phép
( , 2)O
V
là:
A.
3 3 0xy
. B.
3 6 0xy
. C.
3 6 0xy
. D.
3 3 0xy
.
Lời giải:
Chọn B
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 50
LÊ MINH TÂM
⬥ Ta có
( , 2)
2
2
( , ) ( ; ) 2
2
2
O
x
x
xx
V M x y M x y OM OM
y y y
y






Thay vào phương trình đường thẳng
d
31
3 0 3 6 0.
22
x y x y
⬥ Vậy phương trình đường thẳng
d
:
3 6 0xy
Câu 10. Trong mặt phẳng tọa độ
Oxy
Phép vị tự tâm
3; 1I
, tỉ số
2
biến parabol
2
: 2 2 1 P y x x
. Thành parabol có phương trình là:
A.
2
83y x x
. B.
2
8 14y x x
. C.
2
2 4 5y x x
. D.
2
21y x x
.
Lời giải:
Chọn B
⬥ Gọi
P
là ảnh của qua phép vị tự tâm
3; 1I
, tỉ số
2
.
Đỉnh của parabol
()P
có tọa độ
13
;
22




A
.
Khi đó đỉnh của
P
là
;2
I
V A A
.
Ta có
2IA IA
.
Suy ra
4; 2
A
.
Trong bốn đáp án thì chỉ có parabol
2
8 14y x x
có đỉnh
4; 2
A
.
Câu 11. Trong mặt phẳng tọa độ
Oxy
cho đường tròn
2
2
: 3 4 C x y
. Gọi
C
là ảnh của
C
qua phép vị tự tâm
O
tỉ số
2k 
. Khi đó
C
có phương trình là
A.
2
2
6 16 xy
. B.
2
2
6 16 xy
.
C.
2
2
6 64 xy
. D.
2
2
6 64 xy
.
Lời giải:
Chọn A
⬥ Đường tròn
C
có tâm
0;3I
và bán kính
2
R
⬥ Gọi
,2
O
C V C
có tâm
;2
0; 6

O
I V I I
và bán kính
R
của
C
là
||k = 2 2 = 4
RR
⬥ Vậy
2
2
: 6 16
C x y
Câu 12. Trong mặt phẳng tọa độ
Oxy
cho đường tròn
22
: 1 3 9 C x y
. Gọi
C
là ảnh của
C
qua phép vị tự tâm
2; 4A
tỉ số
2k 
. Khi đó
C
có phương trình là
A.
22
2 6 36 xy
. B.
22
4 6 36 xy
.
C.
22
8 12 16 0x y x y
. D.
22
2 6 36 xy
.
Lời giải:
Chọn B
⬥ Đường tròn
C
có tâm
1; 3I
và bán kính
3
R
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 51
LÊ MINH TÂM
⬥
;2
2 1 1 2 2
4
;
6
2 3 1 2 4


A
x
x
V I I x y
y
y
và bán kính
R
của
()C
là
| | 3k = 2 = 6
RR
⬥ Vậy
22
4 6 36 xy
Câu 13. Trong mặt phẳng tọa độ , cho đường tròn phép vị tự tâm tỉ
số biến đường tròn thành đường tròn có phương trình là
A. B.
C. D.
Lời giải:
Chọn B
Gọi Qua phép vi tự tâm tỉ số biến đường tròn thành đường
tròn thì điềm bicn thành Khi đó, ta có
Và nên
Vậy phương trình đường tròn cần tìm là .
Câu 14. Cho tam giác có trọng tâm . Gọi , , lần lượt là trung điểm các cạnh ,
, . Khi đó phép vị tự nào sau đây biến tam giác thành tam giác ?
A. Phép vị tự tâm , tỉ số . B. Phép vị tự tâm , tỉ số .
C. Phép vị tự tâm , tỉ số . D. Phép vị tự tâm , tỉ số .
Lời giải:
Chọn D
Ta có ; ; .
Từ đó suy ra .
Oxy
( ) :C
22
1 1 4xy
O
2k
C
22
2 2 8xy
22
2 2 16xy
22
2 2 16xy
22
1 1 8xy
;.M x y C
O
2k
C
C
;M x y
;M x y
2
.
2
x
x
x kx
OM k OM
y ky y
y



;x y C
22
2 2 2 2
1 1 4 1 1 4 2 2 16
22
xy
x y x y


22
2 2 16xy
ABC
G
A
B
C
BC
CA
AB
ABC
ABC
G
2
G
1
2
G
1
2
A
2
2GA GA

2GB GB

2GC GC

,2G
V A B C ABC
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 52
LÊ MINH TÂM
Câu 15. Cho tam giác có cố định, đỉnh chạy trên một đường tròn cố định không
có điểm chung với đường thẳng và là trọng tâm tam giác . Khi đó, quỹ tích trọng
tâm là ảnh của đường tròn qua phép biến hình nào sau đây?
A. Phép tịnh tiến theo vectơ .
B. Phép vị tự tâm tỉ số trong đó là trung điểm của .
C. Phép vì tự tâm tỉ số trong đó là trung điểm của .
D. Phép tịnh tiến theo
Lời giải:
Chọn C
Gọi I là trung điểm của , khi đó cố định. Ta có suy ra là ảnh của qua
phép vị tự tâm tỉ số . Mà thuộc đường tròn nên thuộc đường tròn
là ảnh của đường tròn qua phép vị tự tâm tỉ số .
------------------HẾT------------------
ABC
,BC
A
( ; )OR
BC
G
ABC
G
;OR
BC
I
3,k
I
BC
I
1
,
3
k
I
BC
1
3
v IA
BC
I
1
3
IG IA
G
A
I
1
3
k
A
;OR
G
;OR

;OR
I
1
3
k
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 53
LÊ MINH TÂM
§7. PHÉP ĐỒNG DẠNG
I. ĐỊNH NGHĨA:
– Phép biến hình
F
được gọi là phép đồng dạng tỉ số
k
0k
nếu với hai điểm
, MN
bất kì
và ảnh
', 'MN
tương ứng của chúng ta luôn có
' ' .M N kMN
Nhận xét
Phép dời hình là phép đồng dạng tỉ số 1.
Phép vị tự tỉ số
k
là phép đồng dạng tỉ số
k
.
Nếu thưc hiện liên tiếp các phép đồng dạng ta được một phép đồng dạng.
II. TÍNH CHẤT:
Tính chất:
Phép đồng dạng tỉ số
:k
– Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa
các điểm ấy;
– Biến đường thẳng thành đường thẳng.
– Biến tia thành tia, biến đoạn thẳng thành đọan thẳng.
– Biến tam giác thành tam giác đồng dạng với nó.
– Biến góc thành góc bằng nó;
– Biến đường tròn bán kính
R
thành đường tròn bán kính
.kR
III. KHÁI NIỆM HAI HÌNH ĐỒNG DẠNG:
– Hai hình được gọi là đồng dạng với nhau nếu có một phép đồng dạng biến hình này thành
hình kia.
IV. BÀI TẬP:
4.1. Tự Luận.
Bài toán xác định ảnh trong hệ tọa độ qua Phép Đồng Dạng
Phương pháp:
Sử dụng định nghĩa, tính chất của phép đồng dạng.
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 54
LÊ MINH TÂM
Bài 01.
Trong mặt phẳng , cho đường thẳng có phương trình . Viết phương trình
đường thẳng là ảnh của qua phép đồng dạng có được bằng cách thực hiện liên tiếp
phép vị tự tâm tỉ số và phép quay tâm góc
Lời giải
Gọi là ảnh của qua phép vị tự tâm tỉ số .
Vì song song hoặc trùng với nên phương trình có dạng .
Lấy .
Gọi thuộc .
Vậy phương trình là .
Ảnh của (đường phân giác góc phần tư thứ hai) qua phép quay tâm góc
là đường thẳng .
Vậy phương trình của là .
Bài 02.
Trong mặt phẳng tọa độ , cho đường tròn . Ảnh của đường tròn
qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm , tỉ
số và phép tịnh tiến theo véc-tơ có phương trình là
Lời giải
Gọi ; là tâm và bán kính đường tròn .
.
Phép vị tự biến đường tròn tâm thành đường tròn tâm bán kính .
.
Phép tịnh tiến theo véc-tơ biến đường tròn tâm bán kính thành đường tròn
tâm bán kính .
Vậy phương trình đường tròn ảnh: .
Bài 03.
Trong mặt phẳng tọa độ , cho đường tròn . Gọi là ảnh của
đường tròn qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm
Oxy
d
20xy
d
d
1; 1I 
1
2
k
O
45
1
d
d
1; 1I 
1
2
k
1
d
d
0x y c
1;1Md
1
;
2
1
;
2
I
M x y V M IM IM



1
1 1 1
2
0;0
1
1 1 1
2
x
M
y

1
d
1
d
0xy
1
d
O
45
Oy
d
0x
Oxy
22
: 1 2 9C x y
C
1; 1I
1
3
k
3; 4v
1; 2M
3R
C
;
1
3
Ik
V M O IO IM

1; 0O
M
O
1
1
3
RR

4; 4
v
T O O O

v
O
R
O

1RR

22
4 4 1xy
Oxy
22
: 2 1 9C x y
C
C
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 55
LÊ MINH TÂM
, tỉ số và phép tịnh tiến theo véc-tơ . Tìm bán kính của đường tròn
.
Lời giải
Đường tròn có bán kính .
Gọi là ảnh của đường tròn qua phép vị tự tâm , tỉ số , ta có là
ảnh của qua phép tịnh tiến theo véc-tơ .
Khi đó đường tròn có bán kính và đường tròn có bán kính
.
Bài 04.
Trong mặt phẳng với hệ trục tọa độ cho đường tròn và
. Phép đồng dạng tỉ số biến thành . Tìm .
Lời giải
Ta có
Suy ra có bán kính .
Suy ra có bán kính . Do đó .
Bài 05.
Trong mặt phẳng tọa độ cho đường thẳng có phương trình . Viết
phương trình đường thẳng là ảnh của qua phép đồng dạng có được bằng cách thực
hiện liên tiếp phép vị tự tâm tỉ số và phép quay tâm góc .
Lời giải
Xét điểm và nằm trên đường thẳng .
Qua phép vị tự tâm điêm biến thành điểm với tọa độ thỏa mãn
. Vậy .
Qua phép quay tâm góc , điểm biến thành điểm .
Qua phép vị tự tâm điểm biến thành điểm với tọa độ thỏa mãn
. Vậy .
O
1
3
k 
1; 3v 
R
C
C
3R
1
C
C
O
1
3
k 
C
1
C
1; 3v 
1
C
1
1
.3 1
3
R k R
C
1RR

Oxy
22
1
: 2 2 2 0C x y x y
22
2
: 12 16 0C x y x y
F
k
1
C
2
C
k
22
1
: 2 2 2 0C x y x y
22
2
1 1 2xy
1
C
1
2R
22
2
: 12 16 0C x y x y
22
2
6 8 10xy
2
C
2
10R
2
1
5
R
k
R

Oxy
d
20 xy
d
d
1; 1I
1
2
k
O
45
1;1A
2;0B
d
1; 1I
A
A
1
11
2
1
11
2
AA
AA
xx
yy
0;0
A
O
45
A
0;0

A
1; 1I
B
B
1
11
2
1
11
2
BB
BB
xx
yy
11
;
22



B
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 56
LÊ MINH TÂM
Qua phép quay tâm góc , biến điểm thanh điểm với tọa độ thỏa mãn
. Vậy .
Do đó đường thẳng biến thành đường thẳng có phương trình .
4.2. Trắc nghiệm.
Câu 1. Mệnh đề nào sau đây là sai?
A. Phép dời hình là phép đồng dạng. B. Phép vị tự là phép đồng dạng.
C. Phép đồng dạng là phép dời hình. D. Phép vị tự không phải là phép dời hình.
Lời giải:
Chọn C
Khi thì phép đồng dạng không là phép dời hình.
Câu 2. Mệnh đề nào sau đây là sai?
A. Hai đường thẳng bất kì luôn đồng dạng. B. Hai đường tròn bất kì luôn đồng dạng.
C. Hai hình vuông bất kì luôn đồng dạng. D. Hai hình chữ nhật bất kì luôn đồng dạng.
Lời giải:
Chọn D
Ví dụ hình chữ nhật có và hình chữ nhật có
khi đó không tồn tại số thực để thỏa mãn .
Câu 3. Cho tam giác và đồng dạng với nhau theo tỉ số . Mệnh để nào sau đây là sai?
A. là tỉ số hai trung tuyến tương ứng.
B. là tỉ số hai đường cao tương ứng.
C. là tỉ số hai góc tương ứng.
D. là tỉ số hai bán kính đường tròn ngoại tiếp tương ứng.
Lời giải:
Chọn C
Vì hai tam giác đồng dạng thì các góc tương ứng bằng nhau.
Câu 4. Mọi phép dời hình cũng là phép đồng dạng với tỉ số bằng
A. . B. . C. . D. .
Lời giải:
Chọn A
Tính chất: Phép dời hình là phép đồng dạng tỉ số .
Câu 5. Mệnh đề nào sau dây là sai?
A. Phép dời hình là phép đồng dạng tỉ số .
B. Phép đồng dạng biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
O
45
B

B
cos 45 . sin 45 .
sin 45 . cos 45 .


B B B
B B B
x x y
y x y
2
0;
2





B
d

AB
0x
1k
ABCD
2, 4AB AD
MNPQ
3, 5MN MQ
k
MN kAB
MQ kAD
ABC
ABC
k
k
k
k
k
k
1k
1k 
0k
2k
1k
1k
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 57
LÊ MINH TÂM
C. Phép vị tự tỉ số là phép đồng dạng tỉ số .
D. Phép đồng dạng bảo toàn độ lớn góc.
Lời giải:
Chọn B
Phép đồng dạng biến đường thẳng thành đường thẳng song song hoặc trùng với nó hoặc
cắt nó.
Câu 6. Trong mặt phẳng , cho điểm . Phép đồng dạng có được bằng cách thực hiện liên
tiếp phép vị tự tâm tỉ số và phép đối xứng qua trục sẽ biến điểm thành điểm
nào sau đây.
A. . B. . C. . D. .
Lời giải:
Chọn C
Gọi
Gọi
.
Câu 7. Trong mặt phẳng , cho đường thẳng có phương trình . Viết phương trình
đường thẳng là ảnh của qua phép đồng dạng có được bằng cách thực hiện liên tiếp
phép vị tự tâm tỉ số và phép quay tâm góc
A. . B. . C. . D. .
Lời giải:
Chọn B
Gọi là ảnh của qua phép vị tự tâm tỉ số .
Vì song song hoặc trùng với nên phương trình có dạng .
Lấy .
Gọi thuộc .
Vậy phương trình là .
Ảnh của (đường phân giác góc phần tư thứ hai) qua phép quay tâm góc là
đường thẳng .
Vậy phương trình của là .
k
k
Oxy
2;4M
O
1
2
k
Oy
M
1;2
2;4
1;2
1; 2
1
;
2
1
;;
2
O
x
M x y V M x y
y




1;2M
;D
Oy
M x y M
1;2M

Oxy
d
20xy
d
d
1; 1I 
1
2
k
O
45
0y
0x
yx
yx
1
d
d
1; 1I 
1
2
k
1
d
d
0x y c
1;1Md
1
;
2
1
;
2
I
M x y V M IM IM



1
1 1 1
2
0;0
1
1 1 1
2
x
M
y

1
d
1
d
0xy
1
d
O
45
Oy
d
0x
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 58
LÊ MINH TÂM
Câu 8. Trong mặt phẳng , cho đường tròn có phương trình . Phép đồng
dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm tỉ số và phép quay tâm
góc sẽ biến thành đường tròn nào sau đây?
A. . B. .
C. . D. .
Lời giải:
Chọn D
Đường tròn có tâm và bán kính .
Suy ra phép vị tự tâm tỉ số biến thành đường tròn có tâm , bán
kính .
Phép quay biến thành có tâm , bán kính .
Vậy phương trình đường tròn là: .
Câu 9. Trong mặt phẳng , cho hai điểm . Phép đồng dạng tỉ số biến điểm
thành , biến thành . Tính độ dài
A. . B. . C. . D. .
Lời giải:
Chọn A
Phép đồng dạng tỉ số biến điểm thành , biến thành thì
.
Câu 10. Trong mặt phẳng , cho hai đường tròn và có phương trình
và . Gọi là ảnh của qua phép đồng dạng tỉ số , khi đó giá
trị của là
A. . B. . C. . D. .
Lời giải:
Chọn A
Đường tròn có bán kính , đường tròn có bán kính .
Suy ra tỉ số đồng dạng .
Oxy
C
22
2 2 4xy
O
1
2
k
O
90
C
22
2 2 1xy
22
1 1 1xy
22
2 1 1xy
22
1 1 1xy
C
2;2I
2R
O
1
2
k
C
C
1;1I
1R
;90O
Q
C
C

1;1I

1RR

C

22
1 1 1xy
Oxy
2; 3 , 4;1AB
1
2
k
A
A
B
B
AB

13AB

2 13AB

52
2
AB

52AB

1
2
k
A
A
B
B
22
11
4 2 1 3 13
22
A B AB

Oxy
C
C
22
4 5 0x y y
22
2 2 14 0x y x y
'C
C
k
k
4
3
3
4
9
16
16
9
C
3R
C
4R
4
3
R
k
R

PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trang 59
LÊ MINH TÂM
------------------HẾT------------------
| 1/59
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

LÊ MINH TÂM CHƯƠNG 01 PHÉP DỜI HÌNH
& PHÉP ĐỒNG DẠNG
TÀI LIỆU LƯU HÀNH NỘI BỘ
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG MỤC LỤC
§1. PHÉP BIẾN HÌNH ......................................................................................................................... 4
I. ĐỊNH NGHĨA: ............................................................................................................................................ 4
II. KÝ HIỆU: ..................................................................................................................................................... 4
III. TÍNH CHẤT: ............................................................................................................................................ 4
§2. PHÉP TỊNH TIẾN .......................................................................................................................... 5
I. ĐỊNH NGHĨA: ............................................................................................................................................ 5
II. TÍNH CHẤT: .............................................................................................................................................. 5
III. BIỂU THỨC TỌA ĐỘ: ........................................................................................................................... 6
IV. BÀI TẬP: .................................................................................................................................................... 8
4.1. Tự Luận. ................................................................................................................................................. 8
4.2. Trắc nghiệm. ........................................................................................................................................ 11
§3. PHÉP ĐỐI XỨNG TRỤC ........................................................................................................................... 17
I. ĐỊNH NGHĨA: .......................................................................................................................................... 17
II. TÍNH CHẤT: ............................................................................................................................................ 17
III. BIỂU THỨC TỌA ĐỘ: ......................................................................................................................... 17
IV. BÀI TẬP: .................................................................................................................................................. 18
4.1. Tự Luận. ............................................................................................................................................... 18
4.2. Trắc nghiệm. ........................................................................................................................................ 21
§4. PHÉP ĐỐI XỨNG TÂM ................................................................................................................ 25
I. ĐỊNH NGHĨA: .......................................................................................................................................... 25
II. TÍNH CHẤT: ............................................................................................................................................ 25
III. BIỂU THỨC TỌA ĐỘ: ......................................................................................................................... 25
IV. BÀI TẬP: .................................................................................................................................................. 26
4.1. Tự Luận. ............................................................................................................................................... 26
4.2. Trắc nghiệm. ........................................................................................................................................ 28
§4. PHÉP QUAY ............................................................................................................................... 31
I. ĐỊNH NGHĨA: .......................................................................................................................................... 31
II. TÍNH CHẤT: ............................................................................................................................................ 31 LÊ MINH TÂM Trang 2
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
III. BIỂU THỨC TỌA ĐỘ: ......................................................................................................................... 32
IV. BÀI TẬP: .................................................................................................................................................. 32
4.1. Tự Luận. ............................................................................................................................................... 32
4.2. Trắc nghiệm. ........................................................................................................................................ 34
§5. PHÉP DỜI HÌNH ......................................................................................................................... 38
I. ĐỊNH NGHĨA: .......................................................................................................................................... 38
II. TÍNH CHẤT: ............................................................................................................................................ 38
III. KHÁI NIỆM HAI HÌNH BẰNG NHAU: .......................................................................................... 38
IV. BÀI TẬP: .................................................................................................................................................. 38
4.1. Tự Luận. ............................................................................................................................................... 38
4.2. Trắc nghiệm. ........................................................................................................................................ 40
§6. PHÉP VỊ TỰ .......................................................................................................................................... 44
I. ĐỊNH NGHĨA: .......................................................................................................................................... 44
II. TÍNH CHẤT: ............................................................................................................................................ 44
III. CÁCH TÌM TÂM VỊ TỰ CỦA HAI ĐƯỜNG TRÒN: ................................................................... 45
IV. BIỂU THỨC TỌA ĐỘ: ......................................................................................................................... 46
IV. BÀI TẬP: .................................................................................................................................................. 46
4.1. Tự Luận. ............................................................................................................................................... 46
4.2. Trắc nghiệm. ........................................................................................................................................ 48
§7. PHÉP ĐỒNG DẠNG .............................................................................................................................. 53
I. ĐỊNH NGHĨA: .......................................................................................................................................... 53
II. TÍNH CHẤT: ............................................................................................................................................ 53
III. KHÁI NIỆM HAI HÌNH ĐỒNG DẠNG: ......................................................................................... 53
IV. BÀI TẬP: .................................................................................................................................................. 53
4.1. Tự Luận. ............................................................................................................................................... 53
4.2. Trắc nghiệm. ........................................................................................................................................ 56 Trang 3 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG CHƯƠNG
§1. PHÉP BIẾN HÌNH I. ĐỊNH NGHĨA:
 ĐN: Phép biến hình là một quy tắc để với mỗi điểm M của mặt phẳng, xác định được một
điểm duy nhất điểm M của mặt phẳng. Điểm M gọi là ảnh của M qua phép biến hình đó. II. KÝ HIỆU:
 Kí hiệu: f là một phép biến hình nào đó, và M là ảnh của M qua phép f . Ta viết:
M  f M hay f M  M hay f : M M hay f M  M . Lưu ý:
+ Điểm M gọi là tạo ảnh, M là ảnh.
+ f là phép biến hình đồng nhất  f M  M , M
 H . Điểm M gọi là điểm bất động, điểm kép, bất biến.
+ f , f là các phép biến hình thì f
f là phép biến hình. 1 2 2 1
 Nếu H là một hình nào đó thì tập hợp các điểm M  f M , với MH , tạo thành hình H
được gọi là ảnh của H qua phép biến hình f , và ta viết: H  f H . III. TÍNH CHẤT:
Phép dời hình là phép biến hình không làm thay đổi khoảng cách giữa hai điểm bất kỳ. Phép dời hình biến:
+ Ba điểm thẳng hàng thành ba điểm thẳng hàng.
+ Đường thẳng thành đường thẳng. + Tịa thành tia.
+ Tam giác thành tam giác và bằng tam giác đã cho.
+ Đường tròn thành đường tròn có cùng bán kính với đường tròn đã cho.
+ Góc thành góc và bằng góc đã cho.
------------------HẾT------------------ Trang 4 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
§2. PHÉP TỊNH TIẾN I. ĐỊNH NGHĨA:
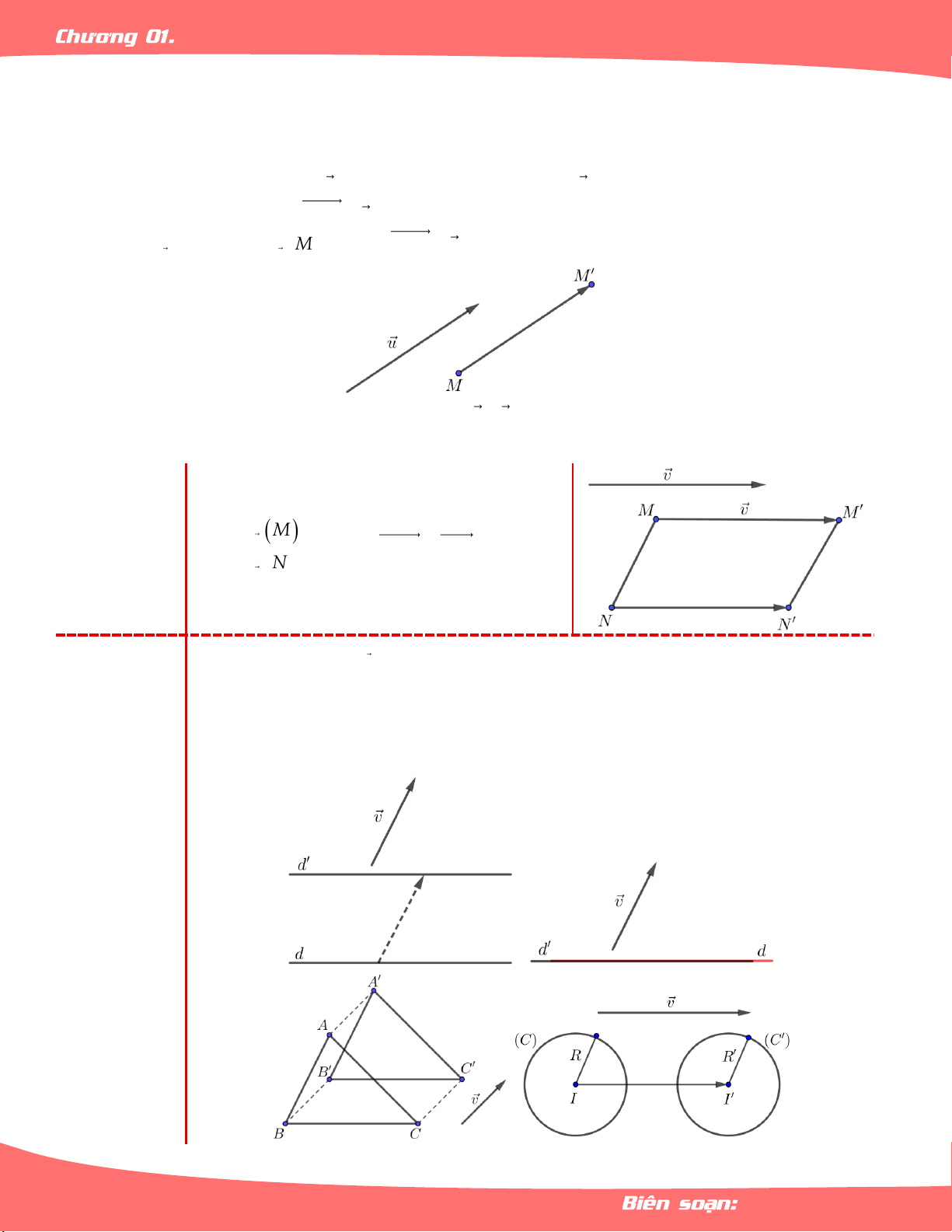
– Trong mặt phẳng cho vectơ u , phép tịnh tiến theo vectơ u là phép biến hình biến mỗi điểm
M thành điểm M sao cho MM  u .
– Ký hiệu: T . Như vậy T M M  MM  u . u   v
Nhận xét: Phép tịnh tiến là phép đồng nhất  v  0 . II. TÍNH CHẤT: T
 M  M
Tính chất 1: Cho v  thì M N
   MN . T N    N  v
Qua phép tịnh tiến T , v
– Đường thẳng biến thành đường thẳng song song song hoặc trùng với nó.
– Đoạn thẳng biến thành đoạn thẳng bằng nó.
– Tam giác biến thành tam giác bằng nó.
– Đường tròn biến thành đường tròn có cùng bán kính. Tính chất 2: Trang 5 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG  CHÚ Ý
– Phép tịnh tiến bảo toàn thứ tự các điểm của đa giác.
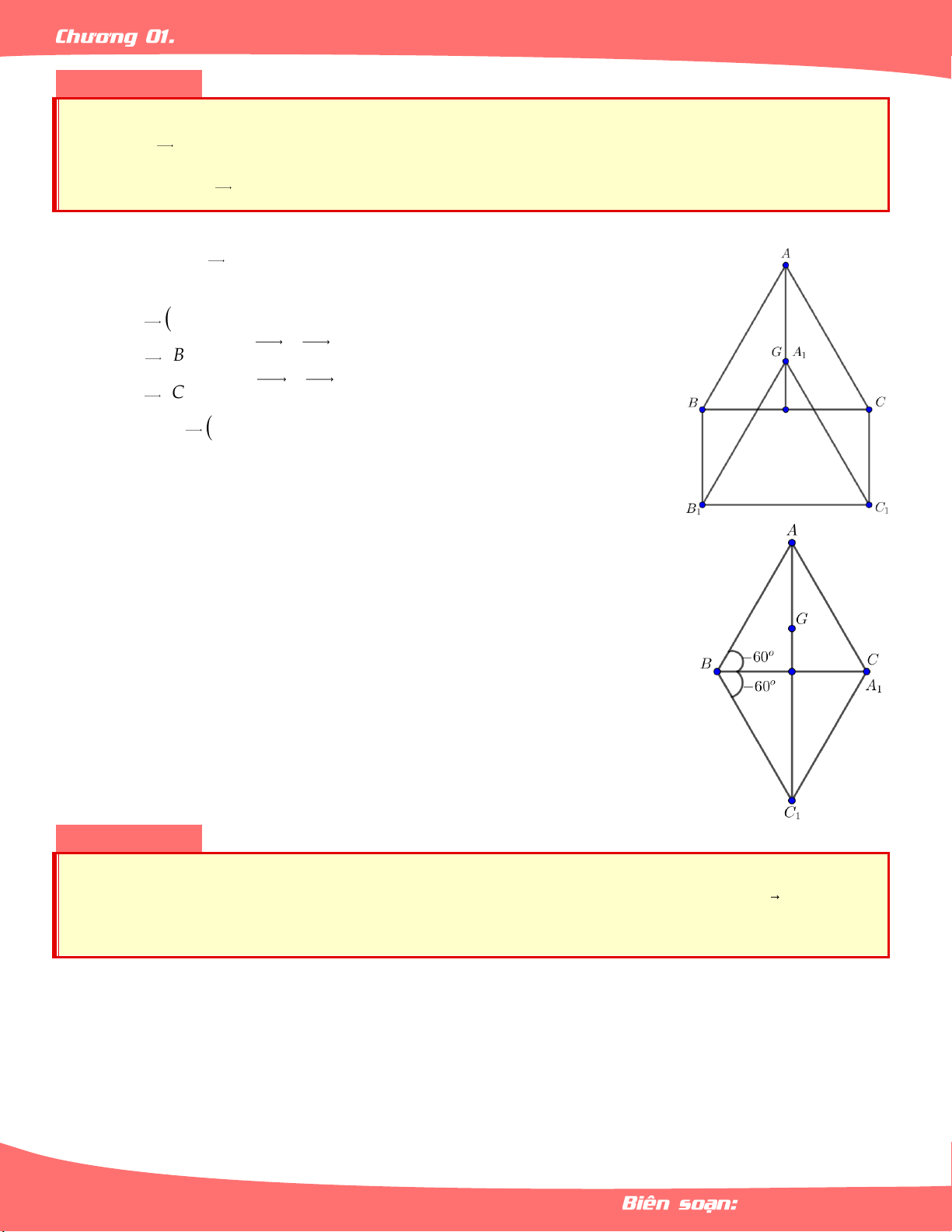
– Hai đường thẳng song song có vô số phép tịnh tiến biến đường này thành đường kia. Ví dụ 01.
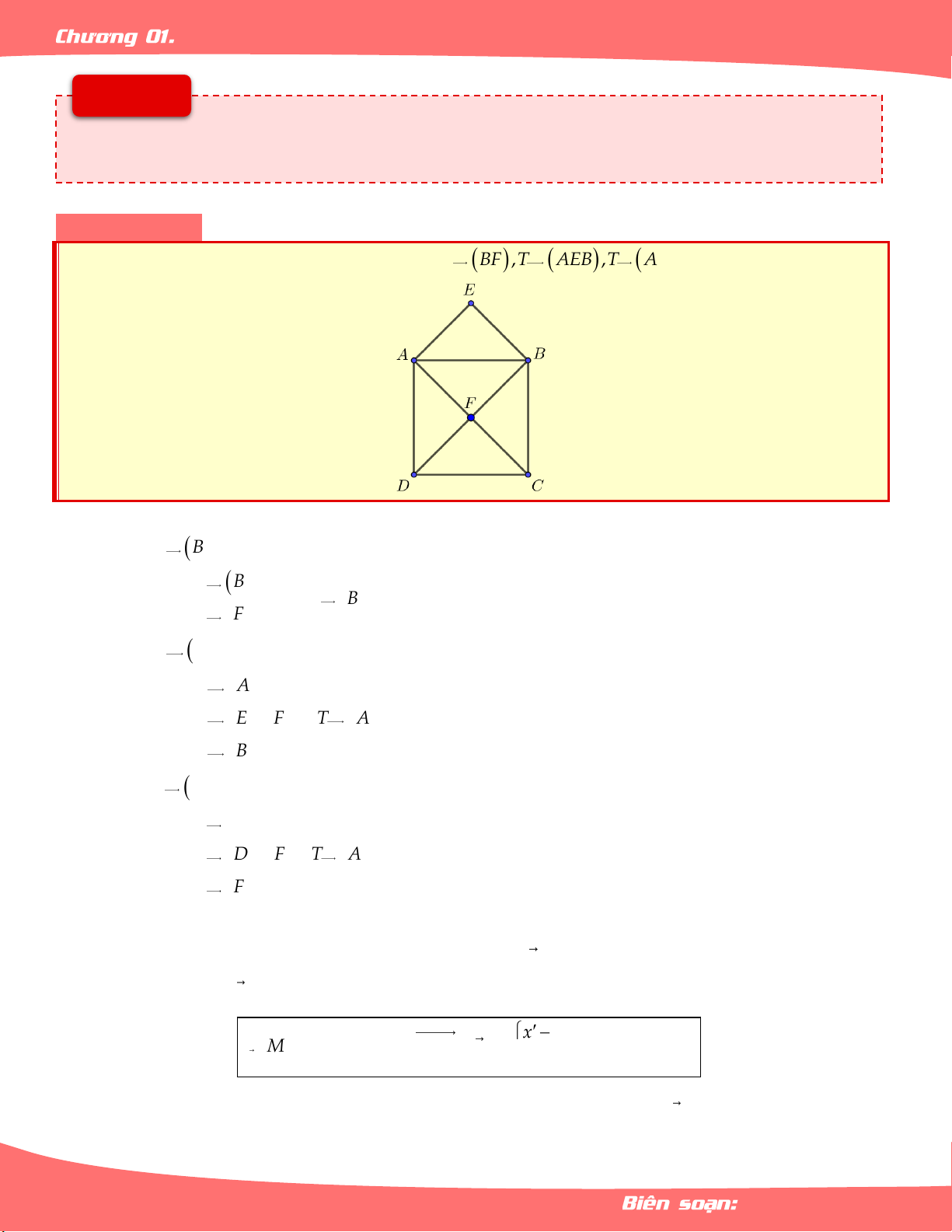
Cho hình vẽ như hình bên dưới. Xác định T BF ,T AEB,T ADF . EA AD AE Lời giải
* Xác định T BF . EA T
 B  F Ta có EA    . T F
T BF FD EA   DEA
* Xác định T AEB . AD T  A  D AD  Ta có T
E  F T AEB  DFC . AD ADT  B  CAD
* Xác định T ADF . AE T  A  E AE  Ta có T
D  F T ADF  EFB . AE AET  F  BAE
III. BIỂU THỨC TỌA ĐỘ:
– Trong mặt phẳng Oxy , cho điểm M x; y và vectơ v   ;
a b . Gọi M là ảnh của M qua phép
tịnh tiến theo vectơ v . Khi đó:    
x  x a
x  x a T M
M x ; y  MM  v     . v
y  y b y  y    b
– Biểu thức trên được gọi là biểu thức tọa độ của phép tịnh tiến theo v . Trang 6 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG Ví dụ 02.
Trong mặt phẳng tọa độ Oxy , cho vectơ v   1  ; 2 .
a. Tìm tọa độ của điểm M là ảnh của M 3; 2   qua phép T . v
b. Tìm tọa độ của điểm N biết T N N và N4;  1 v   Lời giải
a. Tìm tọa độ của điểm M là ảnh của M 3; 2   qua phép T . v     x    x     T M
M x ; y  MM  v     . v  3 1 1 3 2 y  2  2
y  2  2  0 Vậy M2;0 .
b. Tìm tọa độ của điểm N biết T N N và N4;  1 v         x   x    T N
N x ; y  NN  v     . v  4 1 4 1 5 1 y  2 y  1 2  1    Vậy N 5;   1 . Ví dụ 03.
Trong mặt phẳng tọa độ Oxy , cho vectơ v   2  ;   1 .
a. Tìm ảnh của đường thẳng d : x 3y  5  0 qua phép T . v
b. Tìm ảnh của đường tròn C 2 2
: x y  4x  2y  4  0 qua phép T . v Lời giải
a. Tìm ảnh của đường thẳng d : x 3y  5  0 qua phép T . v Gọi M  ;
x yd : x 3y  5  0 (1).    
x  x  
x x  T M M x ; y 2 2
MM  v     (2) v
y  y  1 
y y 1
Thay (2) vào (1) ta được: x  2  3y  
1  5  0  x  3y  4  0
Vậy d : x 3y  4  0 .
b. Tìm ảnh của đường tròn C 2 2
: x y  4x  2y  4  0 qua phép T . v Gọi N  ;
x yC 2 2
: x y  4x  2y  4  0 (3)    
x  x  
x x  T N N x ; y 2 2
NN  v     (4) v
y  y  1 
y y 1
Thay (4) vào (3) ta được:
x 2 y 2  x  y  2 2 2 1 4 2 2
1  4  0  x  y  9  0 Vậy C 2 2
: x y  9  0 . Trang 7 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG IV. BÀI TẬP:
4.1. Tự Luận.
Bài toán xác định ảnh trong hệ tọa độ qua Phép Tịnh Tiến Phương pháp:
Sử dụng biểu thức tọa độ của phép tịnh tiến.
Trong mặt phẳng tọa độ Oxy cho vec tơ v  a;b . Với mỗi điểm Mx; y ta có Mx; y là
ảnh của M qua phép tịnh tiến theo v . Khi đó
x x a
x  x a
MM  v     .
y  y b
y  y b Bài 01.
Trong mặt phẳng Oxy , cho điểm A2; 5
  . Tìm tọa độ điểm A là ảnh của điểm A qua
phép tịnh tiến theo vec-tơ v  1; 2 Lời giải:
x  2 1  3
Gọi Ax ; y    A3; 3   . y  5   2  3   Bài 02.
Trong mặt phẳng với hệ tọa độ Oxy , cho điểm M 2; 3
  là ảnh của điểm N3;5 qua phép
tịnh tiến theo vec-tơ v . Tìm v . Lời giải:
Ta có v NM  2  3; 3  5  1; 8. Bài 03.
Trong mặt phẳng tọa độ Oxy cho vec tơ v   1
 ; 2 , hai điểm A3;5, B 1  ;  1 và đường
thẳng d có phương trình x  2y  3  0.
1. Tìm tọa độ của A , B theo thứ tự là ảnh của A , B qua phép tịnh tiến theo vec tơ v .
2. Tìm tọa độ của điểm C sao cho A là ảnh của C qua phép tịnh tiến theo vec tơ v .
3. Tìm phương trình của đường thẳng d là ảnh của d qua phép tịnh tiến theo vec tơ v . Lời giải:
1. Tìm tọa độ của A , B theo thứ tự là ảnh của A , B qua phép tịnh tiến theo vec tơ v .
x  3   A  1 2
Tọa độ của A là   A2;7 .
y  5 2  7 A x  1      B  1 2
Tọa độ của B là   B 2  ;  3 . y 1 2  3 B
2. Tìm tọa độ của điểm C sao cho A là ảnh của C qua phép tịnh tiến theo vec tơ v . Trang 8 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG 3   x   x  4 C  1
Giả sử x ; y là tọa độ của điểm C   C  
C 4;3. C C  5   y  2  y  3  C C
3. Tìm phương trình của đường thẳng d là ảnh của d qua phép tịnh tiến theo vec tơ v .
Giả sử M x; yd và Mx; y là ảnh của M qua phép tịnh tiến theo vec tơ v .
x  x 1
x x 1    
Mx1; y 2 .
y  y  2 
y y  2
Vì M x; yd  x  
1  2y  2  3  0  x  2y  8  0 .
Vậy d : x  2y 8  0. Bài 04.
Trong mặt phẳng tọa độ Oxy , ảnh của đường thẳng d : 2x y  4  0 qua phép vị tự theo vec
tơ v  3;5 có phương trình là: Lời giải:
Phương trình ảnh của đường thẳng d là d' : 2x y c  0 .
Ảnh của điểm A0; 4d qua phép tịnh tiến theo vecto v  3;5 là A3;9d .
Suy ra 239  c  0  c  3 . Vậy d' : 2x y  3  0 Bài 05.
Trong mặt phẳng tọa độ Oxy cho đường thẳng có phương trình 4x y  3  0. Ảnh của
đường thẳng qua phép tịnh tiến T theo véc-tơ v  2;   1 có phương trình là Lời giải:
Cách 1: Gọi  là ảnh của
qua phép T . Khi đó  song song hoặc trùng với nên  có v
phương trình dạng 4x y c  0 .
Chọn điểm A0; 3 . Gọi A ;
x y là ảnh của A qua phép tịnh tiến theo véc-tơ v  2;  
1  AA  x; y  3 . x  x  2
Ta có T  A  A  AA  2 v      A2; 2 v y  3  1   y  2
Mặt khác điểm A , suy ra tọa độ điểm A thỏa mãn phương trình 4x y c  0  c  6
 hay  : 4x y 6  0. x  0  2 x  2
Ta có T A  Ax; y   AA  v      A2;2 . vy  3  1  y  2
Vì A  nên 4 2
.  2  c  0  c  6
   : 4x y 6  0 .
Cách 2: Gọi M x; y là điểm bất kỳ thuộc đường thẳng .
x  x
x x 
Gọi Mx ; y  T M 2 2
MM  v     . v
y  y  1 
y y 1
Thay x x  2 và y y 1 vào phương trình ta được Trang 9 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
4x  2  y  
1  3  0  4x  y  6  0 . Bài 06. 2 2
Trong mặt phẳng tọa độ Oxy , ảnh của đường tròn C : x  
1  y  3  4 qua phép tịnh
tiến theo vectơ v  3; 2 là đường tròn có phương trình Lời giải:
Đường tròn C có tâm I  1  ; 
3 , bán kính R  2 . Gọi I ;
x y là ảnh của I  1  ; 
3 qua phép tịnh tiến vectơ v  3; 2 . x   1  3 x  2
Ta có II  v      I3;2 . y 3  2 y  5
Vì phép tịnh tiếp bảo toàn khoảng cách nên R  R  2 .
Vậy ảnh của đường tròn C qua T là đường tròn C có tâm I2;5 , bán kính v 2 2
R  2 nên có phương trình x  2  y  5  4 . Bài 07.
Trong mặt phẳng tọa độ Oxy cho đường tròn C có phương trình 2 2
x y  2x  4y  4  0 .
Tìm ảnh của C qua phép tịnh tiến theo vec tơ v   2  ;3. Lời giải: 2
Đường tròn C có tâm I 1;  2 , bán kính 2 R  1   2    4    3.
Giả sử C  T C . Gọi I là tâm đường tròn C v  
I  T I  1 2; 23   1  ; . v 1 2 2
Do đó C có phương trình x   1  y   1  9. Bài 08.
Trong mặt phẳng tọa độ Oxy cho vectơ v   3  ; 2
  . Phép tịnh tiến theo vectơ v biến đường
tròn C : x  y  2 2 1
1 thành đường tròn C . Mệnh đề nào sau đây đúng? Lời giải:
Đường tròn C có tâm I 0; 
1 , bán kính R  1 . Gọi I ;
x y là ảnh của I 0; 
1 qua phép tịnh tiến vectơ v  3; 2 . x  0  3  x  3 
Ta có II  v      I 3  ;   1 . y 1  2  y  1   
Vì phép tịnh tiến bảo toàn khoảng cách nên R  R 1 .
Vậy ảnh của đường tròn C qua phép T là đường tròn C có tâm I 3  ;   1 , bán v 2 2
kính R nên có phương trình C : x  3  y   1 1. Bài 09. Trang 10 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trong mặt phẳng tọa độ Oxy cho đường tròn C có phương trình 2 2
x y  4x  6y  5  0 .
Thực hiện liên tiếp hai phép tịnh tiến theo các vectơ u  1; 2
  và v  1;  1 thì đường tròn
C biến thành đường tròn C có phương trình là Lời giải:
Từ giả thiết suy ra C là ảnh của C qua phép tịnh tiến theo a u v .
Ta có a u v  2; 3 .
x x  2
Biểu thức tọa độ của T là 
thay vào C ta được a
y y  3
x 2 y 2 2 3
 4x 2 6y35  0 2 2
x  y 18  0. Bài 10.
Trong mặt phẳng tọa độ Oxy , cho vectơ v   2  ;  
1 . Phép tịnh tiên theo vectơ v biến parabol P 2
: y x thành parabol P . Khi đó phương trình của P là Lời giải:
x x  2
Biểu thức tọa độ của T là 
thay vào P ta được v
y y 1
y   x  2 2 1 2
y  x  4x  3.
4.2. Trắc nghiệm. Câu 1.
Mệnh đề nào sau đây là sai ? Trong mặt phẳng, phép tịnh tiến T M  M à
v T N N ( v v  
với v  0 ). Khi đó
A. MM'  NN' .
B. MN M ' N ' .
C. MN'  NM' .
D. MM'  NN' Lời giải: Chọn C Câu 2.
Có bao nhiêu phép tịnh tiến biến một đường thẳng cho trước thành chính nó? A. Không có. B. Chỉ có một. C. Chỉ có hai. D. Vô số. Lời giải: Chọn D
Phép tịnh tiến theo vectơ v , với v là vectơ chỉ phương đường thẳng d biến một đường
thẳng cho trước thành chính nó. Khi đó sẽ có vô số vectơ v thõa mãn. Câu 3.
Có bao nhiêu phép tịnh tiến biến một đường tròn cho trước thành chính nó? A. Không có. B. Một. C. Hai. D. Vô số. Lời giải: Chọn B
Chỉ có duy nhất phép tịnh tiến theo vectơ 0 . Câu 4.
Có bao nhiêu phép tịnh tiến biến một hình vuông thành chính nó? A. Không có. B. Một. C. Bốn. D. Vô số. Trang 11 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG Lời giải: Chọn B
Chỉ có duy nhất phép tịnh tiến theo vectơ 0 . Câu 5.
Giả sử qua phép tịnh tiến theo vectơ v  0 , đường thẳng d biến thành đường thẳng d’ . Câu
nào sau đây sai?
A. d trùng d’ khi v là vectơ chỉ phương của d.
B. d song song với d’ khi v là vectơ chỉ phương của d.
C. d song song với d’ khi v không phải là vectơ chỉ phương của d .
D. d không bao giờ cắt d’ . Lời giải: Chọn B
Xét B: d song song với d’ khi v là vectơ có điểm đầu bất kỳ trên d và điểm cuối bất kỳ trên d’ . Câu 6.
Cho P , Q cố định. Phép tịnh tiến T biến điểm M bất kỳ thành M sao cho MM  2PQ . 2 2
A. T là phép tịnh tiến theo vectơ PQ .
B. T là phép tịnh tiến theo vectơ MM . 2 1
C. T là phép tịnh tiến theo vectơ 2PQ .
D. T là phép tịnh tiến theo vectơ PQ . 2 Lời giải: Chọn C
Gọi T M  M MM v 2 2 v
Từ MM  2PQ  2PQ v . 2 Câu 7.
Cho phép tịnh tiến T biến điểm M thành M và phép tịnh tiến T biến M thành M . u 1 v 1 2
A. Phép tịnh tiến T M thành M . u biến v 1 2
B. Một phép đối xứng trục biến M thành M . 2
C. Không thể khẳng định được có hay không một phép dời hình biến M thành M2.
D. Phép tịnh tiến T M .
u biến M thành v 2 Lời giải: Chọn D T  M M   u   u MM 1 1   
u v MM M M MM T M M  . TM M    v   1 1 2 2 u v   2 1 2 v M M 1 2 Câu 8.
Cho phép tịnh tiến vectơ v biến A thành A’ và M thành M’. Khi đó:
A. AM  A ' M ' .
B. AM  2A' M' .
C. AM A ' M ' .
D. 3AM  2A ' M ' . Lời giải: Chọn C T
 A  A Theo tính chất trong SGK v     AM A M   . T M   M  v Câu 9.
Tìm mệnh đề sai trong các mệnh đề sau:
A. Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì. Trang 12 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
B. Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng.
C. Phép tịnh tiến biến tam giác thành tam giác bằng tam giác đã cho.
D. Phép tịnh tiến biến đường thẳng thành đường thẳng song song với đường thẳng đã cho. Lời giải: Chọn B
Theo tính chất SGK, Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
Câu 10. Cho phép tịnh tiến vectơ v biến A thành A’ và M thành M’. Khi đó
A. AM  A' M'.
B. AM  2A ' M '.
C. AM A' M'.
D. AM  2A ' M '. Lời giải: Chọn C
Câu 11. Trong mặt phẳng Oxy cho điểm A2;5 . Phép tịnh tiến theo vectơ v  1; 2 biến A thành điểm có tọa độ là: A. 3;  1 . B. 1; 6 . C. 3; 7 . D. 4;7 . Lời giải: Chọn C         T Ax x x B A x 2 1 3 v B
B AB v      B3;7. v
y y y  y  5  2  7 B A B v
Câu 12. Trong mặt phẳng Oxy cho điểm A2;5 . Hỏi A là ảnh của điểm nào trong các điểm sau
qua phép tịnh tiến theo vectơ v  1; 2 ? A. 3;  1 . B. 1;3 . C. 4; 7 . D. 2; 4 . Lời giải: Chọn B         T Mx x x M A x 2 1 1 v M
A MA v    
M 1;3. v
y y y  y  5  2  3 M A B v
Câu 13. Trong mặt phẳng tọa độ Oxy , cho phép biến hình f xác định như sau: Với mỗi M x; y , ta
có M '  f M sao cho M'x’; y’ thỏa x'  x  2; y'  y 3
A. f là phép tịnh tiến theo vectơ v  2;3 .
B. f là phép tịnh tiến theo vectơ v   2  ;3 .
C. f là phép tịnh tiến theo vectơ v  2; 3  .
D. f là phép tịnh tiến theo vectơ v   2  ;  3 . Lời giải: Chọn C
Câu 14. Trong mặt phẳng Oxy, phép tịnh tiến theo vectơ v  1;3 biến điểm A2;  1 thành điểm nào trong các điểm sau: A. A 2;1 . B. A 1;3 . C. A 3; 4 . D. A 3  ; 4  . 4   3   2   1   Trang 13 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG Lời giải: Chọn C
Câu 15. Trong mặt phẳng Oxy , cho v   ;
a b . Giả sử phép tịnh tiến theo v biến điểm M x; y
thành M’x’; y’. Ta có biểu thức tọa độ của phép tịnh tiến theo vectơ v là:
x'  x a
x x' a
x' b x a
x' b x a A. B. C. D.  . y '  y   b y y '  b
y ' a y   b
y ' a y   b Lời giải: Chọn A
Câu 16. Trong mặt phẳng Oxy cho 2 điểm A1;6 , B 1 – ; 4
–  . Gọi C , D lần lượt là ảnh của A và B
qua phép tịnh tiến theo vectơ v  1;5 .Tìm khẳng định đúng trong các khẳng định sau:
A. ABCD là hình thang.
B. ABCD là hình bình hành.
C. ABDC là hình bình hành.
D. Bốn điểm A , B , C , D thẳng hàng. Lời giải: Chọn D      
C T Ax x x C A x 2 v C      C 2;1  1 . v
y y y  y 11  C AC v      
D T Bx x x D B x 0 v D      D0;  1 . v
y y y  y 1 D B D v
AB  2; 10 , BC  3;15 ,CD   2  ; 1  0 . 2  1  0
Xét cặp AB, BC : Ta có 
A,B,C thẳng hàng. 3 15 3 15
Xét cặp BC,CD : Ta có 
B,C,D thẳng hàng. 2  1  0
Vậy A, B,C, D thẳng hàng.
Câu 17. Trong mặt phẳng tọa độ Oxy , cho v  1; 3
  và đường thẳng d có phương trình
2x  3y  5  0 . Viết phương trình đường thẳng d' là ảnh của d qua phép tịnh tiếnT . v
A. d' : 2x y  6  0
B. d' : x y  6  0
C. d' : 2x y  6  0
D. d' : 2x  3y  6  0 Lời giải: Chọn D
Cách 1. Sử dụng biểu thức tọa độ của phép tịnh tiến.
Lấy điểm M x; y tùy ý thuộc d , ta có 2x  3y  5  0 * x'  x  x x'
Gọi M 'x'; y'  T M 1 1     v
y'  y  3 y y' 3
Thay vào (*) ta được phương trình 2x'  1  3y' 
3  5  0  2x' 3y' 6  0 .
Vậy ảnh của d là đường thẳng d' : 2x  3y  6  0 .
Cách 2. Sử dụng tính chất của phép tịnh tiến Trang 14 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Do d'  T d nên d' song song hoặc trùng với d , vì vậy phương trình đường thẳng d' có v
dạng 2x  3y c  0 .(**) Lấy điểm M  1  ; 
1  d . Khi đó M'  T M   1  1;13  0; 2   . v
Do M'd'  2 0 .  3. 2
 c  0  c  6 
Vậy ảnh của d là đường thẳng d' : 2x  3y  6  0 .
Cách 3. Để viết phương trình d' ta lấy hai điểm phân biệt M, N thuộc d , tìm tọa độ các
ảnh M ', N ' tương ứng của chúng qua T . Khi đó d' đi qua hai điểm M ' và N '. v
Cụ thể: Lấy M  1  ; 
1 , N 2;3 thuộc d , khi đó tọa độ các ảnh tương ứng là M'0; 2
 ,N'3;0. Do d' đi qua hai điểm M',N' nên có phương trình x  0 y  2 
 2x 3y  6  0 . 3 2
Câu 18. Trong mặt phẳng tọa độ Oxy , cho đường tròn C có phương trình 2 2
x y  2x  4y  4  0 .
Tìm ảnh của C qua phép tịnh tiến theo vectơ v  2; 3 . A. C' 2 2
: x y x  2y  7  0 B. C' 2 2
: x y x y  7  0 C. C' 2 2
: x y  2x  2y  7  0 D. C' 2 2
: x y x y  8  0 Lời giải: Chọn C
Cách 1. Sử dụng biểu thức tọa độ.
Lấy điểm M x; y tùy ý thuộc đường tròn C , ta có 2 2
x y  2x  4y  4  0 * x'  x  x x'
Gọi M 'x'; y'  T M 2 2     v
y'  y  3 y y' 3
x'22 y'32  2x'24y'34  0
Thay vào phương trình (*) ta được . 2 2
x'  y'  2x' 2y' 7  0
Vậy ảnh của C là đường trònC' 2 2
: x y  2x  2y  7  0 .
Cách 2. Sử dụng tính chất của phép tịnh tiến
Dễ thấy C có tâm I  1
 ; 2 và bán kính r  3. Gọi C'  T C và I'x'; y';r' là tâm và v  
bán kính của (C ') . x'  1   2  1 Ta có   I '1; 
1 và r'  r  3 nên phương trình của đường tròn C ' là y '  2  3  1  
x 2 y 2 1 1  9 2 2
Câu 19. Trong mặt phẳngOxy , ảnh của đường tròn: x  
1  y – 3  4 qua phép tịnh tiến theo
vectơ v  3; 2 là đường tròn có phương trình: 2 2 2 2
A. x  2  y  5  4.
B. x – 2  y – 5  4 . 2 2 2 2 C. x – 
1  y  3  4 .
D. x  4  y –  1  4 . Trang 15 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG Lời giải: Chọn B
Đường tròn đề đã cho có tâm I  1  ; 
3 , bán kính R  2 .
Đường tròn cần tìm có tâm I , bán kính R  R  2 . x     x x      I I x 1 3 2
Khi đó I  T I v I      I2;5 v y        y y  y 3 2 5 I I I v  2 2
Vậy phương trình đường tròn cần tìm x – 2  y – 5  4 .
Câu 20. Trong mặt phẳng với hệ trục tọa độOxy , cho phép tịnh tiến theo v   2 – ; –  1 , phép tịnh tiến
theo v biến parabol P 2
: y x thành parabol P . Khi đó phương trình của P là: A. 2
y x  4x  5 . B. 2
y x  4x – 5 . C. 2
y x  4x  3 . D. 2
y x – 4x  5 Lời giải: Chọn C
Chọn M x; y tùy ý trên P . Gọi Mx ; y  T M . v
Vì T P  P nên MP . v
x  x
x x 
Ta có T M  Mx ; y 2 2    
. Suy ra M x  2; y   1 v
y  y 1
y y 1
Vì M x  2; y  
1 P nên y   x' 2 2 1 2
y  x  4x  3.
Suy ra M x ; yP 2
: y x  4x  3 . Vậy: P 2
: y x  4x  3 .
------------------HẾT------------------ Trang 16 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
§3. PHÉP ĐỐI XỨNG TRỤC I. ĐỊNH NGHĨA:
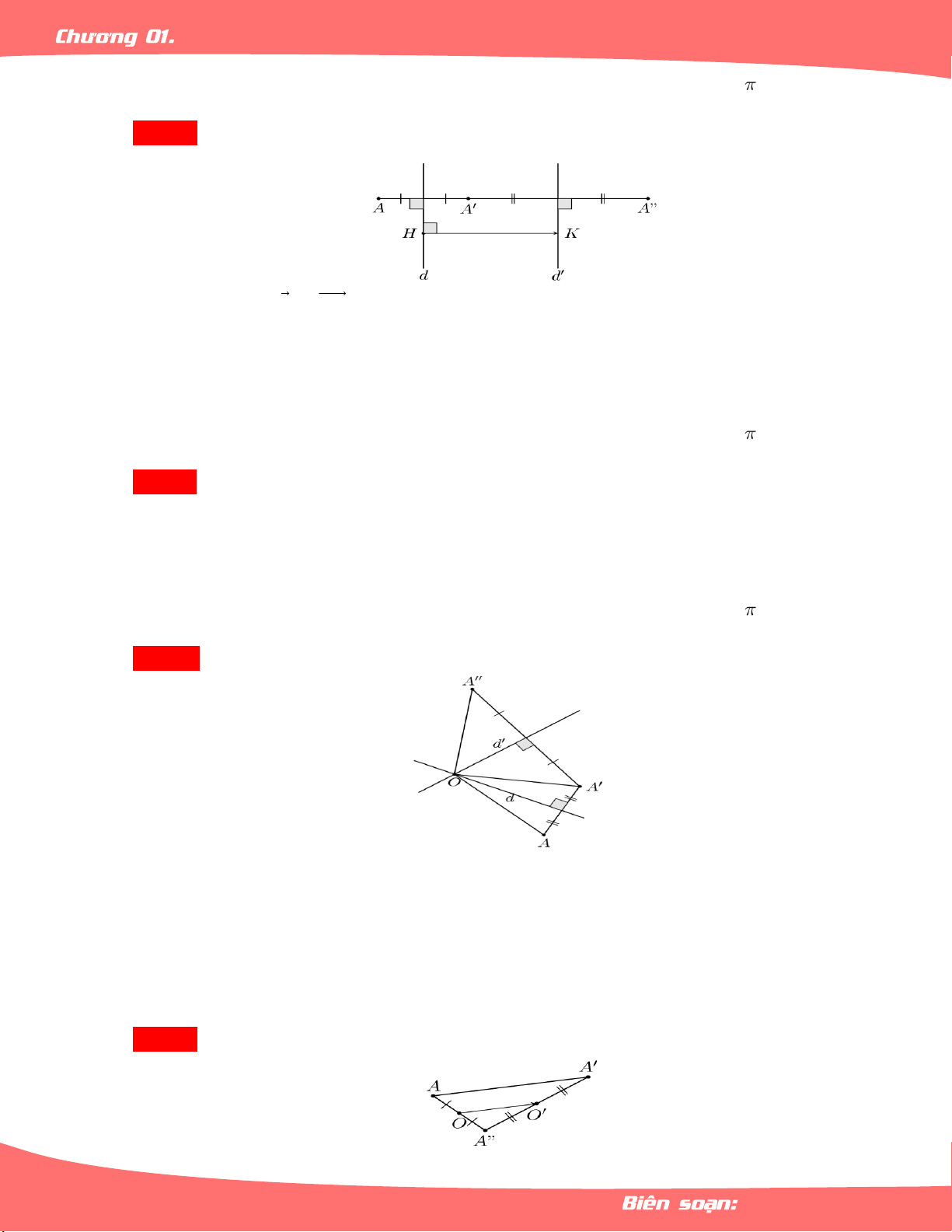
Cho đường thẳng d. – Phép biến hình
+ biến mỗi điểm M d thành chính nó,
+ biến mỗi điểm M d thành M  ,
sao cho d là đường trung trực của MM  được gọi là phép đối xứng
qua đường thẳng d hay phép đối xứng trục d.
– Đường thẳng d được gọi là trục của phép đối xứng hoặc đơn giản
gọi là trục đối xứng.
– Phép đối xứng trục d thường được kí hiệu là: Ñ . d
– Nếu hình H  là ảnh của hình H qua phép đối xứng trục d thì ta còn nói H đối xứng với
H  qua d , hay H và H  đối xứng với nhau qua d. Nhận xét.
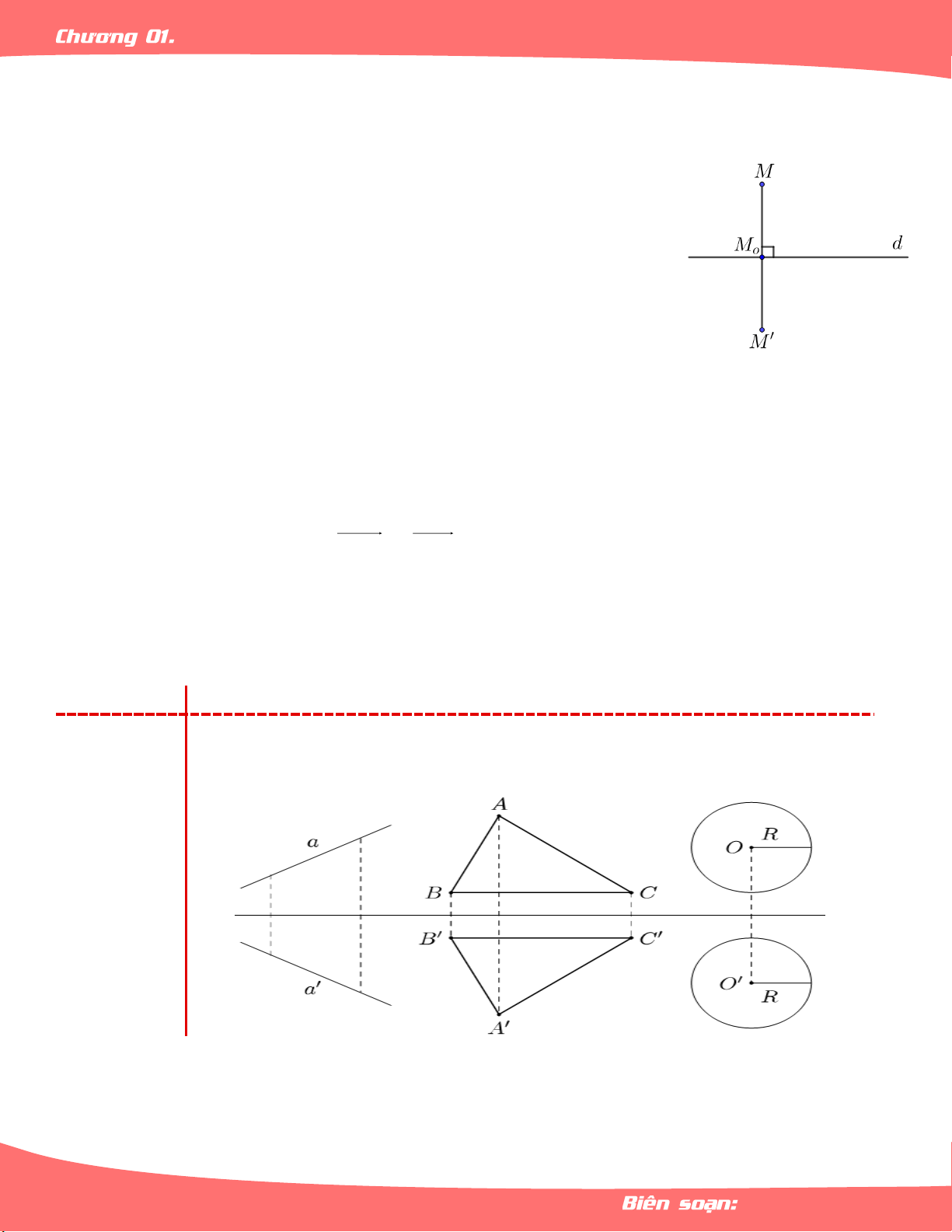
– Cho đường thẳng d. Với mối điểm M gọi M là hình chiếu vuông góc của M trên đường 0
thẳng d. Khi đó: M  Ñ M   M M  M M. d 0 0
M  Ñ M  M Ñ M d d  
– Đường thẳng d được gọi là trục đối xứng của hình H nếu phép đối xứng qua d biến hình
H thành chính nó. Khi đó ta nói hình H có trục đối xứng. II. TÍNH CHẤT: Tính chất 1:
Phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kì.
Phép đối xứng trục biến đường thẳng thành đường thẳng, biến đoạn
thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó,
biến đường tròn thành đường tròn có cùng bán kính. Tính chất 2:
III. BIỂU THỨC TỌA ĐỘ:
– Trong mặt phẳng Oxy , với mỗi điểm M x; y , gọi Mx ; y ÐM . d   Trang 17 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG       x' x x' x
Nếu chọn d là trục Ox , thì  .
 Nếu chọn d là trục Oy , thì  . y'    y y '   y IV. BÀI TẬP:
4.1. Tự Luận.
Bài toán xác định ảnh trong hệ tọa độ qua Phép Đối Xứng Trục Phương pháp:
Sử dụng biểu thức tọa độ của phép đối xứng trục.
– Trong mặt phẳng Oxy , với mỗi điểm M x; y , gọi Mx ; y ÐM . d         x' x x' x
Nếu chọn d là trục Ox , thì  .
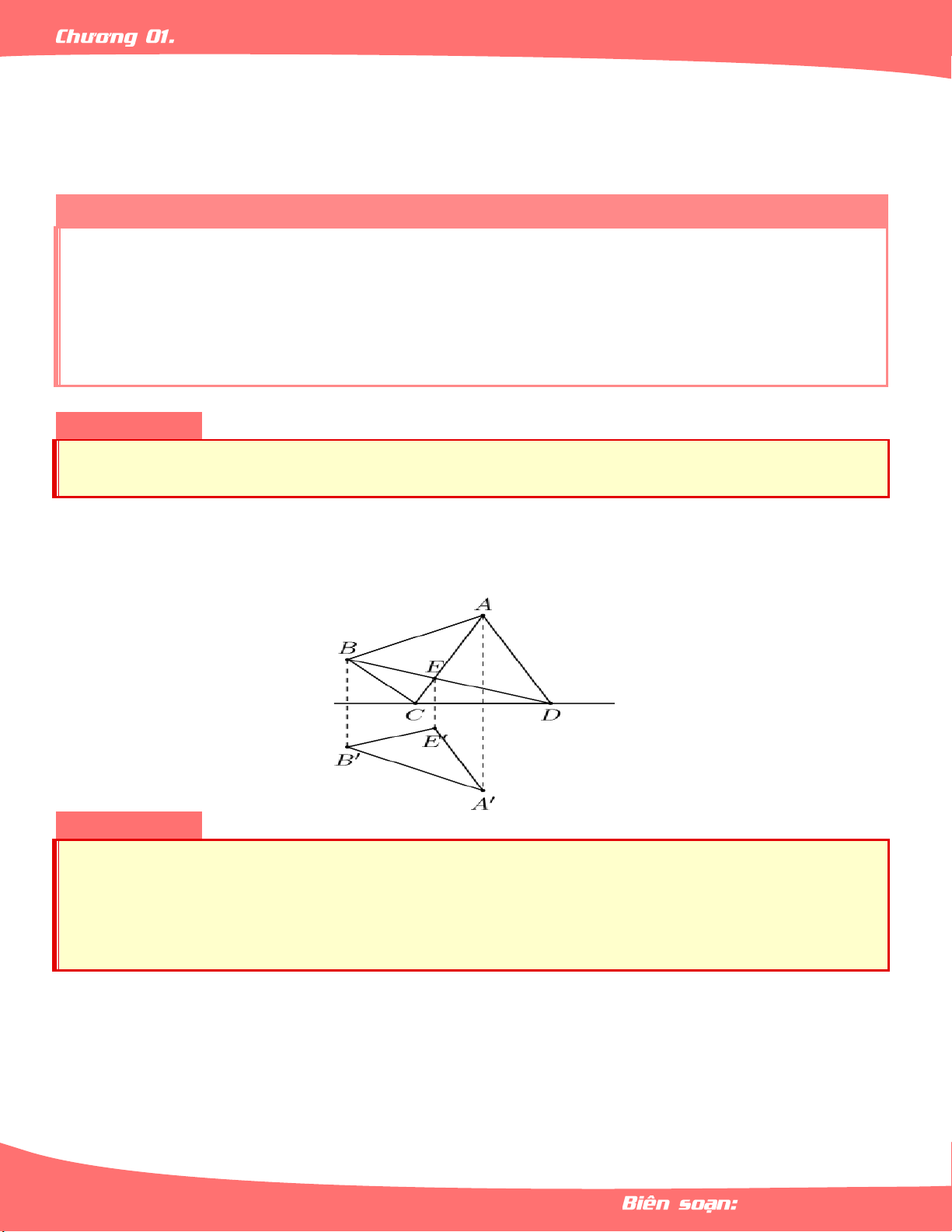
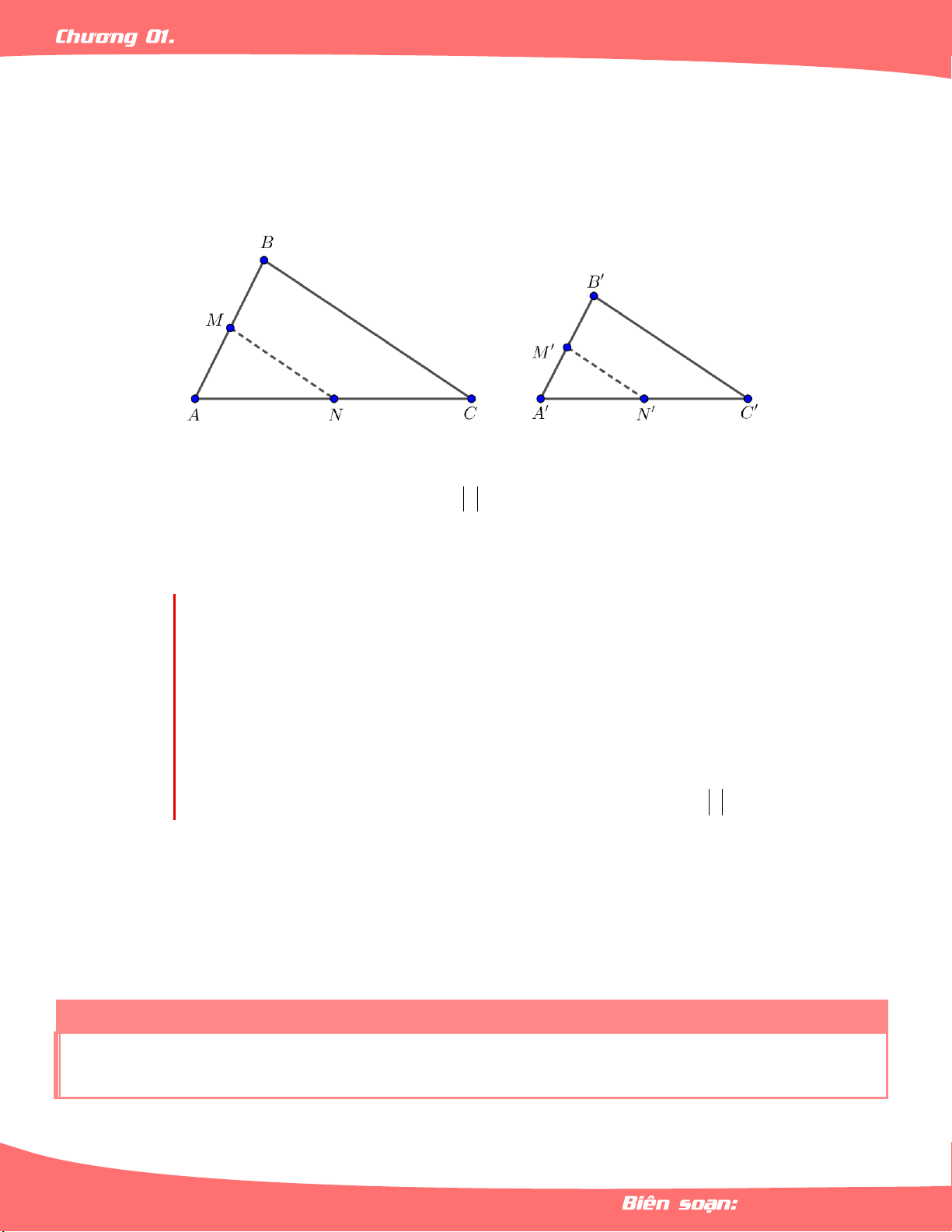
 Nếu chọn d là trục Oy , thì  . y'    y y '   y Bài 01. Cho tứ giác ABC .
D Hai đường thẳng AC và BD cắt nhau tại .
E Xác định ảnh của tam giác
ABE qua phép đối xứng qua đường thẳng . CD Lời giải
Chỉ cần xác định ảnh của các đỉnh của tam giác A , B , E qua phép đối xứng trục đó.
Ảnh phải tìm là tam giác ' ' ' A B E . Bài 02.
Trong mặt phẳng Oxy, cho điểm M 1;5  , đường thẳng d có phương trình x  2y  4  0 và
đường tròn C 2 2
:x y  2x  4y  4  0.
a. Tìm ảnh của M; d ;C qua phép đối xứng trục Ox .
b. Tìm ảnh của M qua phép đối xứng qua đường thẳng . d Lời giải
a. Tìm ảnh của M; d ;C qua phép đối xứng trục Ox .
 Gọi M;d và C theo thứ tự là ảnh của M;d và C qua phép đối xứng trục Ox .
Khi đó M 1; 5 .
 Để tìm ảnh của d ta sử dụng biểu thức tọa độ của phép đối xứng trục Ox . Trang 18 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Gọi N x ; y  là ảnh của điểm N x; y  qua phép đối xứng trục Ox . x  xx x Khi đó    y  y y     y
Ta có N d x  2y  4  0  x  2y  4  0  d : x  2y  4  0.
 Để tìm C , ta thấy rằng C có tâm J1; 2
  bán kính R  3.
 Gọi J là ảnh của J qua phép đối xứng trục Ox .
Khi đó J1; 2. Do đó C là đường tròn tâm J1; 2 , bán kính bằng 3. 2 2
Từ đó suy ra C có phương trình: x  
1  y  2  9.
b. Tìm ảnh của M qua phép đối xứng qua đường thẳng . d
Đường thẳng d đi qua M vuông góc với d có phương trình 1 x 1 y  5 
 2x y  7  0. 1 2 
x  2y  4  0 x  2
Giao của d và d là M có tọa độ thỏa mãn hệ:    1 0 2
x y  7  0 y  3.
Vậy M 2;3 . Từ đó suy ra ảnh của M qua phép đối xứng qua đường thẳng d là M 0  
sao cho M là trung điểm của MM do đó M3;  1 . 0 Bài 03.
Trong mặt phẳng tọa độ Oxy , cho tam giác ABC với A1;5 , B  1  ;2, C6; 4   . Gọi G là
trọng tâm của tam giác ABC . Phép đối xứng trục Ñ biến điểm G thành điểm G có tọa Oy độ là Lời giải
x x x A B C x   G  x  2 Tọa độ trọng tâm 3 G    G 2  ;1 .
y y y y  1  A B CG y G  3 x  xx  2
Gọi G x ; y  Ñ G
  ;x y  thì    . Oy   y  yy  1 Bài 04.
Trong mặt phẳng tọa độ Oxy , cho điểm M 2;3 . Tọa độ điểm là ảnh của M qua phép đối
xứng qua đường thẳng d : x y  0 là ? Lời giải Nhận xét:
Đường thẳng d : x y  0  d : y x là đường phân giác của góc phần tư thứ nhất.
Biểu thức tọa độ của phép đối xứng qua đường phân giác y x là x  yx  3
Gọi M x ; y  Ñ M   ; x y  thì    . d   y  xy  2 Trang 19 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG Bài 05.
Trong mặt phẳng tọa độ Oxy , cho đường thẳng d : x y  2  0 . Ảnh của đường thẳng d qua
phép đối xứng trục Ox có phương trình là Lời giải
Cách 1: Trục Ox có phương trình y  0 .
x y  2  0 x  2
Tọa độ giao điểm A của d và Ox thỏa mãn hệ     A2;0 . y  0 y  0
Vì AOx nên qua phép đối xứng trục Ox biến thành chính nó, tức A  A2;0 . Chọn điểm  Ñ 1;  1 Ox B
d B1;  1 .
Vậy đường thẳng d là ảnh của d qua phép đối xứng trục Ox đi qua hai điểm
A2;0 và B1;  
1 nên có phương trình x y  2  0 . x  xx x
Cách 2: Biểu thức tọa độ qua phép đối xứng trục Ox là    , thay vào d ta
y   y
y   y
được x  y  2  0 . Bài 06.
Trong mặt phẳng tọa độ Oxy cho đường tròn 2 2 C : x 1 y 2
4 . Phép đối xứng trục
Ox biến đường tròn C thành đường tròn C có phương trình là Lời giải
Cách 1: Đường tròn C có tâm I 1; 2 và bán kính R 2 . Ta có Ñ 1; 2 Ox I I 1;2 và Ñ 2 Ox R R R 2.
Do đó C có phương trình 2 2 x 1 y 2 4 . x x x x
Cách 2: Biểu thức tọa độ qua phép đối xứng trục Ox là . y y y y 2 2 2 2
Thay vào C , ta được x 1 y 2 4 hay x 1 y 2 4 . Bài 07.
Trong mặt phẳng tọa độ Oxy cho đường tròn 2 2 C : x 1 y 4
1 và đường thẳng d có phương trình y x
0 . Phép đối xứng trục d biến đường tròn C thành đường tròn C có phương trình là Lời giải x y
Biểu thức tọa độ của phép đối xứng qua trục d : y x 0 là . y x 2 2
Thay vào C , ta đươc y 1 x 4 1 hay 2 2 x 4 y 1 1. Bài 08. Trang 20 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Trong mặt phẳng tọa độ Oxy cho hai đường tròn 2 2 C : x 1 y 2 4 và 2 2 C : x 3 y
4 . Viết phương trình trục đối xứng của C và C . Lời giải
Trục đối xứng của hai đường tròn là trung trực của đoạn nối hai tâm đường tròn. Viết
ra được phương trình trục đối xứng là x y 1 hay y x 1. Bài 09.
Trong mặt phẳng tọa độ Oxy cho parabol P có phương trình 2 y
x . Hỏi parabol nào là
ảnh của P qua phép đối xứng trục tung? Lời giải x x
Biểu thức tọa độ qua phép đối xứng trục tung là . y y
Thay vào P , ta được 2 y x . Bài 10.
Trong mặt phẳng tọa độ Oxy cho parabol 2 P : y x 2x
3 . Phép đối xứng trục Ox biến
parabol P thành parabol P có phương trình là Lời giải x x
Biểu thức tọa độ qua phép đối xứng trục Ox là . y y
Thay vào P , ta được 2 y x 2x 3 hay 2 y x 2x 3 .
4.2. Trắc nghiệm. Câu 1.
Hình gồm hai đường tròn có tâm và bán kính khác nhau có bao nhiêu trục đối xứng? A. Không có. B. Một. C. Hai. D. Vô số Lời giải: Chọn B
Một đường tròn có vô số trục đối xứng đi qua tâm của đường tròn đó.
Vậy: Trục đối xứng thỏa yêu cầu của bài toán là đường thẳng nối hai tâm của đường tròn đã cho. Câu 2.
Hình gồm hai đường thẳng d và d vuông góc với nhau đó có mấy trục đối xứng? A. 0 . B. 2 . C. 4 . D. Vô số Lời giải: Chọn C
Có bốn trục đối xứng gồm d,d và hai đường phân giác của hai góc tạo bởi d,d .
Câu 3. Hình nào sau đây là có trục đối xứng: A. Tam giác bất kì. B. Tam giác cân.
C. Tứ giác bất kì. D. Hình bình hành. Lời giải: Chọn B Trang 21 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG Câu 4.
Cho tam giác ABC đều. Hỏi hình là tam giác ABC đều có bao nhiêu trục đối xứng:
A. Không có trục đối xứng.
B. Có 1 trục đối xứng.
C. Có 2 trục đối xứng.
D. Có 3 trục đối xứng. Lời giải: Chọn D
3 trục đối xứng của tam giác đều là 3 đường trung trực của 3 cạnh.
Câu 5. Trong mặt phẳng Oxy , cho điểm M 2;3 . Hỏi trong bốn điểm sau điểm nào là ảnh của M
qua phép đối xứng trục Ox ? A. 3;2 . B. 2; –3 . C. 3; –2 . D.  –2;3 Lời giải: Chọn B x x Đ M M . Suy ra M 2; 3   . Ox    ' 
   y' y
Câu 6. Trong mặt phẳng Oxy , cho điểm M 2;3 . Hỏi M là ảnh của điểm nào trong các điểm sau
qua phép đối xứng trục Oy ? A. 3;2 . B. 2; –3 . C. 3; –2 . D.  –2;3 Lời giải: Chọn D x x Đ M M . Suy ra M  2  ;3 . Oy    '   
  y' y
Câu 7. Trong mặt phẳng Oxy , cho điểm M 2;3 . Hỏi trong bốn điểm sau điểm nào là ảnh của M
qua phép đối xứng qua đường thẳng d : x – y  0 ? Trang 22 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG A. 3;2 . B. 2; –3 . C. 3; –2 . D.  –2;3 Lời giải: Chọn A
Gọi H là hình chiếu vuông góc của M trên d . Suy ra MH : x y  5  0 . x y  0 5  5 5 
H d MH . Ta có hệ phương trình 
x y  . Vậy: H ;   .
x y  5  0 2  2 2  Đ M
M . Suy ra H là trung điểm của MM  . d    
Vậy: M 3;2 . Câu 8.
Trong mặt phẳng Oxy , cho Parapol P có phương trình 2
x  24 y . Hỏi Parabol nào trong
các Parabol sau là ảnh của P qua phép đối xứng trục Oy ? A. 2 x  24 y . B. 2 x  –24y . C. 2 y  24x . D. 2 y  –24x Lời giải: Chọn A Gọi M  ;
x y P tùy ý. x x Đ M M x y . Oy       '   '; '   y   y
Suy ra M x ; y .
Vì M  P nên x 2 2 '  24y '   x  24y.
Vậy M P  2
' : x  24 y .
Câu 9. Trong mặt phẳng Oxy , cho đường thẳng d : x  2y  4  0 . Tìm ảnh của d qua phép đối xứng trục Ox .
A. d' : 2x  2y  4  0
B. d' : x  2y  2  0
C. d' : 3x  2y  4  0
D. d' : x  2y  4  0 Lời giải: Chọn D Lấy M ;
x yd x  2y  4  0 (1)
Gọi N x'; y' là ảnh của M qua phép đối xứng Ð . oxx'  xx x' Ta có    . y '  y y     y ' Thay vào  
1 ta được x' 2y' 4  0 .
Vậy d' : x  2y  4  0 .
Câu 10. Trong mặt phẳng Oxy , cho đường thẳng đường tròn C 2 2
: x y  2x  4 y  4  0 . Tìm ảnh
của C qua phép đối xứng trục Ox . 2 2 2 2
A. C ' :  x  2   y  2  9
B. C ' :  x   1   y   1  9 2 2 2 2
C. C ' :  x  3   y  2  9
D. C ' :  x  
1   y  2  9 Lời giải: Trang 23 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG Chọn D
Cách 1: Ta thấy C có tâm I  1
 ;2 và bán kính R  3.
Gọi I ', R ' là tâm và bán kính của C ' thì I ' 1  ; 2
  và R'  R  3, do đó
C  x 2 y  2 ' : 1 2  9 .
Cách 2: Lấy P x yC 2 2 ;
x y  2x  4y  4  0 2.
Gọi Q x '; y ' là ảnh của P qua phép đối xứng Ð . Ta có oxx '  xx x '   
thay vào 2 ta được 2 2
x '  y '  2x ' 4 y ' 4  0 , hay y '  yy  y ' C  2 2
' : x y  2x  4 y  4  0 .
------------------HẾT------------------ Trang 24 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
§4. PHÉP ĐỐI XỨNG TÂM I. ĐỊNH NGHĨA: Cho điểm I . – Phép biến hình
+ biến điểm I thành chính nó,
+ biến mỗi điểm M khác I thành M
sao cho I là trung điểm của MM được gọi là phép đối xứng tâm I .
– Điểm I được gọi là tâm đối xứng.
– Phép đối xứng tâm I thường được kí hiệu là §I Nhận xét.
– Nếu hình H là ảnh của hình H qua § thì ta còn nói H đối xứng với H qua tâm I , hay H I
và H đối xứng với nhau qua I.
Từ đinh nghĩa suy ra M  § M   IM  IM. I
– Điểm I được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm I biến hình H thành
chính nó. Khi đó ta nói H là hình có tâm đối xứng; II. TÍNH CHẤT:
Nếu Ð M M và Ð N N thì M N
   MN , từ đó suy ra MN    M . N I   I  
Tính chất 1:
Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc
trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác
thành tam giác bằng nó, biến đường tròn thành đường tròn cùng bán kính. Tính chất 2:
III. BIỂU THỨC TỌA ĐỘ:
– Trong mặt phẳng Oxy , với mỗi điểm M x; y , gọi Mx ; y Ð M . I   x  x
 Với I O0;0 , ta có Mx; y  § M
 x; y  thì  . O  y    y Trang 25 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG x  2   a x
Với I a;b , ta có Mx; y  § M
 x; y  thì  . I  y  2b   y IV. BÀI TẬP:
4.1. Tự Luận.
Bài toán xác định ảnh trong hệ tọa độ qua Phép Đối Xứng Tâm Phương pháp:
Sử dụng biểu thức tọa độ của phép đối xứng trục.
– Trong mặt phẳng Oxy , với mỗi điểm M x; y , gọi Mx ; y Ð M . I        x x
Với I O0;0 , ta có Mx; y  § M
 x; y  thì  . O  y    yx  2   a x
Với I a;b , ta có Mx; y  § M
 x; y  thì  . I  y  2b   y
– Để tìm tâm đối xứng của một hình ta có nhận xét như sau:
Nếu hình đã cho là một đa giác thì sử dụng tính chất:
Một đa giác có tâm đối xứng I thì qua phép đối xứng tâm I
+ mỗi đỉnh của nó phải biến thành một đỉnh của đa giác,
+ mỗi cạnh của nó phải biến thành một cạnh của đa giác song song và bằng cạnh ấy.
Nếu hình đã cho không phải một đa giác thì sử dụng định nghĩa. Bài 01.
Trong mặt phẳng tọa độ Oxy cho phép đối xứng tâm O0;0 biến điểm M 2  ;  3 thành
điểm M có tọa độ là Lời giải x  x
Biểu thức tọa độ của phép đối xứng tâm O0;0 là   M2;3. y    y Bài 02.
Phép đối xứng tâm I a;b biến điểm A1;3 thành điểm A1;7 . Tính tổng T a b . Lời giải  11 a  1 
Từ giả thiết suy ra I là trung điểm của AA 2   T  6. 3  7 b   5  2 Bài 03.
Trong mặt phẳng toạ độ Oxy cho điểm I 2; 3
  và đường thẳng d có phương trình
3x  2y 1  0. Tìm toạ độ điểm I ' và phương trình đường thẳng d' lần lượt là ảnh của I và
d qua phép đối xứng tâm O . Trang 26 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG Lời giải Ta có I ' 2  ;3. x  x
Từ biểu thức toạ độ của phép đối xứng tâm qua gốc toạ độ ta có  . y    y
Thay biểu thức của x và y vào phương trình của d ta được 3x  2y' 1 0 hay
3x  2y 1  0 .
Do đó phương trình của d : 3x  2y 1  0. Bài 04.
Trong các mặt phẳng tọa độ 0xy cho đường thẳng d : x y  2  0 . Tìm phương trình đường
thẳng dlà ảnh của d qua phép đối xứng tâm I 1; 2 Lời giải
Qua phép đối xứng tâm , đường thẳng biến thành đường thẳng song song hoặc
trùng với nó nên d : x y c  0 . Chọn A1;  1 d .
IA  IA
Ta có D A Ax y    A . I    ;  1;3 Ad
Thay vào dta được 1 3 c  0  c  4
  d : x y  4  0.
x  2a x
x  2  x
Cách 2 . Biểu thức tọa độ của phép đối xứng tâm I  ; a b là    .
y  2b y y  4    y
Thay vào phương trình đường thẳng d ta được 2  x  4  y  2  0  x  y  4  0 . Bài 05.
Trong mặt phẳng tọa độ Oxy , tìm phương trình đường tròn C là ảnh của đường tròn
C:x 2 y 2 3 1
 9 qua phép đối xứng tâm O0;0 . Lời giải
Cách 1. Đường tròn C có tâm I 3;  
1 , bán kính R  3.
Gọi I là điểm đối xứng của I 3;  
1 qua phép đối xứng tâm O0; 0  I 3  ;  1 .
Phép đối xứng tâm bảo toàn khoảng cách nên R  R  3. 2 2
Vậy phương trình đường tròn C : x  3  y   1  9 . x  x
Cách 2. Biểu thức tọa độ của phép đối xứng tâm O0;0 là  . y    y 2 2 2 2
Thay vào C ta được x  3  y   1
 9  x 3  y  1  9. Bài 06.
Chứng minh rằng nếu một tứ giác có tâm đối xứng thì nó phải là hình bình hành. Lời giải Trang 27 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
 Giả sử tứ giác ABCD có tâm đối xứng là I .
 Qua phép đối xứng tâm I , tứ giác ABCD biến thành chính nó nên đỉnh A chỉ có
thể biến thành A, B,C và D .
 Nếu đỉnh A biến thành chính nó thì theo ví dụ trên A trùng với I .
Khi đó tứ giác có hai đỉnh đối xứng qua A điều đó vô lí.
 Nếu đỉnh A biến thành B hoặc D thì tâm đối xứng thuộc các cạnh AB hoặc AD
của tứ giác nên cũng suy ra điều vô lí.
 Do đó A chỉ có thể biến thành C.
 Lí luận tương tự B chỉ có thể biến thành D .
Khi đó tâm đối xứng I là trung điểm của hai đường chéo AC và BD nên tứ giác
ABCD phải là hình bình hành.
4.2. Trắc nghiệm. Câu 1.
Hình nào sau đây có tâm đối xứng? A. Hình thang. B. Hình tròn. C. Parabol. D. Tam giác bất kì. Lời giải: Chọn B
Tâm đối xứng của hình tròn là tâm của hình tròn đó. Câu 2.
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Tam giác đều có tâm đối xứng.
B. Tứ giác có tâm đối xứng.
C. Hình thang cân có tâm đối xứng.
D. Hình bình hành có tâm đối xứng. Lời giải: Chọn D
Tâm đối xứng của hình bình hành là giao điểm của hai đường chéo. Câu 3.
Hình nào sau đây không có tâm đối xứng? A. Hình vuông. B. Hình tròn.
C. Hình tam giác đều. D. Hình thoi. Lời giải: Chọn C
Hình vuông và hình thoi có tâm đối xứng là giao điểm của hai đường chéo. Câu 4.
Trong các hình sau đấy, hình nào không có tâm đối xứng?
A. Hình gồm một đường tròn và một hình chữ nhật nội tiếp.
B. Hình gồm một đường tròn và một tam giác đều nội tiếp.
C. Hình lục giác đều.
D. Hình gồm một hình vuông và đường tròn nội tiếp. Lời giải: Chọn B Trang 28 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Tam giác đều không có tâm đối xứng. Câu 5.
Trong các hình dưới đây, hình nào không có tâm đối xứng? A. Đường elip. B. Đường hypebol. C. Đường parabol.
D. Đồ thị hàm số y  sin x . Lời giải: Chọn C
Đường parabol không có tâm đối xứng. Câu 6.
Trong mặt phẳng tọa độ Oxy cho phép đối xứng tâm I 1; 2 biến điểm Mx; y thành
Mx; y . Mệnh đề nào sau đây là đúng?
x  x  2
x  x  2
x  x  2
x  x  2 A.  . B.  . C.  . D.  .
y  y  2
y  y  4
y  y  4
y  y  2 Lời giải: Chọn B
Ta có IM  x 1; y  2 , IM  x 1; y  2 .
x 1  x   1
x  x  2
Vì Ñ M M nên IM  IM     . I   y  2   
y 2 y  y  4 Câu 7.
Phép đối xứng tâm O0;0 biến điểm Am;  m thành điểm A nằm trên đường thẳng
x y  6  0 . Tìm m .
A. m  3.
B. m  4 . C. m  3  . D. m  4  . Lời giải: Chọn A
Ta có D : Am;  m
Am; m . O
Do A nằm trên đường thẳng x y  6  0 nên m
  m6  0  m  3. Câu 8.
Trong mặt phẳng tọa độ Oxy cho điểm M 2; 
1 . Thực hiện liên tiếp phép đối xứng qua tâm
O và phép tịnh tiếp theo vectơ v  1; 2 biến điểm M thành điểm nào trong các điểm sau?
A. A1;3 .
B. B2;0 .
C. C 0; 2 . D. D 1  ;  1 . Lời giải: Chọn A
Phép đối xứng tâm O0;0 biến điểm M 2; 
1 thành điểm M 2  ;   1 .
Phép tịnh tiến theo vectơ v  1; 2 biến điểm M thành điểm M  M M
   v M 1  ;  1  D . Câu 9.
Trong mặt phẳng tọa độ 0xy , tìm phương trình đường tròn C là ảnh của đường tròn C 2 2
: x y 1 qua phép đối xứng tâm I 1; 0
A. C : x  2 2 2  y 1.
B. C : x  2 2 2  y 1.
C. C : x  y  2 2 2 1.
D. C : x  y  2 2 2 1. Trang 29 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG Lời giải: Chọn A
x  2  x
Biểu thức tọa độ của phép đối xứng tâm I 1; 0 là  .
y  0  y    y 2 2 2
Thay vào C ta được   x  y   x   2 2 1 2  y 1. 2 2
Câu 10. Trong mặt phẳng tọa độ Oxy cho đường tròn C : x  
1  y  3 16 . Giả sử phép đối
xứng tâm I biến điểm A1;3 thành điểm Ba;b. Tìm phương trình của đường tròn C là
ảnh của đường tròn C qua phép đối xứng tâm I . 2 2 2 2
A. C : x a  y b 1.
B. C : x a  y b  4 . 2 2 2 2
C. C : x a  y b  9 .
D. C : x a  y b 16 . Lời giải: Chọn D
Theo giả thiết điểm A1;3biến thành điểm Ba;b qua phép đối xứng tâm I .
2x x x a 1 Nên ta có I A B  . 2
y y y b  3 I A B
Biểu thức tọa độ của phép đối xứng tâm I là
x  2x x a 1 x
x a 1 xI    .
y  2y y b  3 y
y b  3   yI 2 2 2 2
Thay vào C ta được a x  b y 16  x  a  y  b 16 .
------------------HẾT------------------ Trang 30 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG §4. PHÉP QUAY I. ĐỊNH NGHĨA:
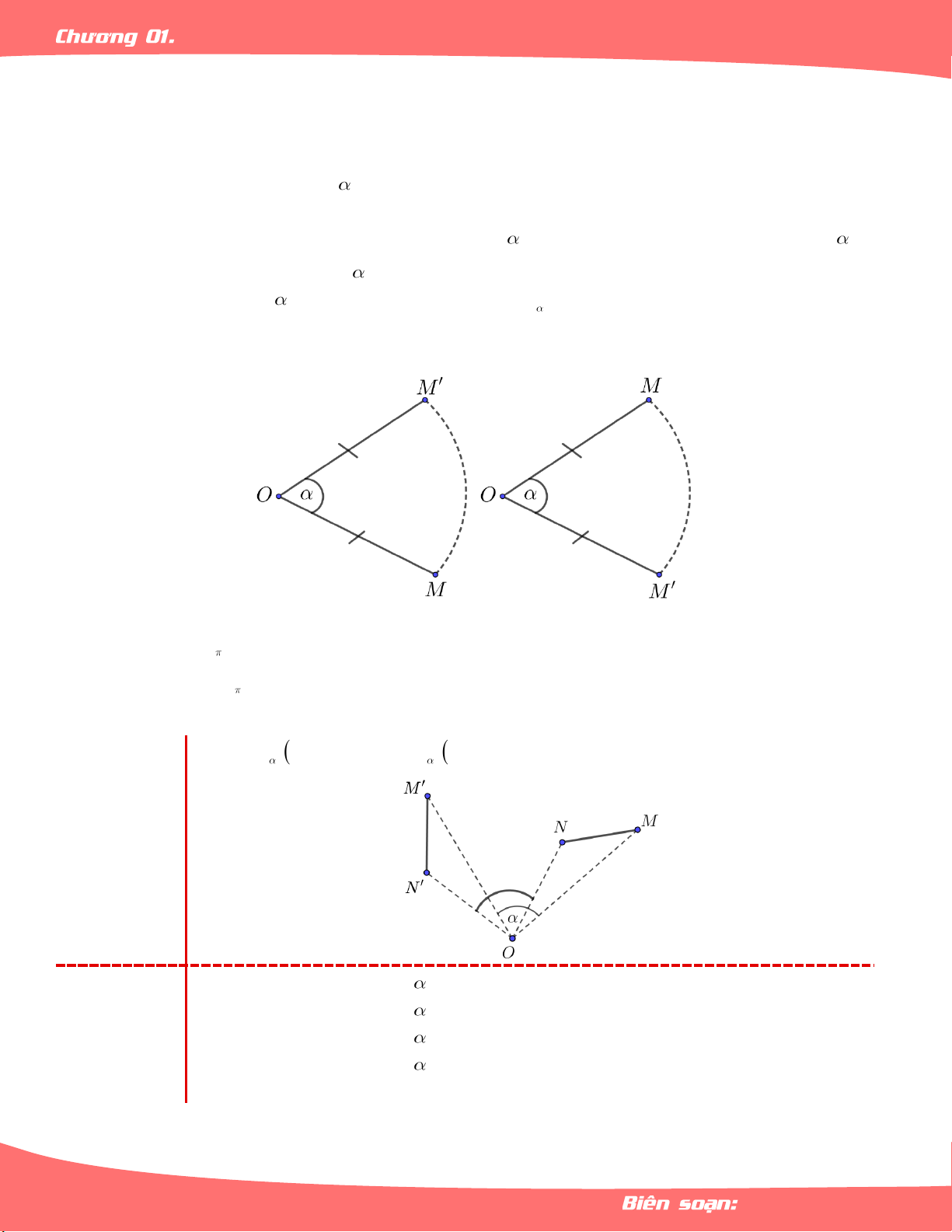
Cho điểm O và góc lượng giác .
– Phép biến hình biến điểm O thành chính nó, biến mỗi điểm M khác O thành điểm M sao
cho OM  OM và góc lượng giác OM;OM bằng được gọi là phép quay tâm O góc .
– Điểm O được gọi là tâm quay, được gọi là góc quay của phép quay đó.
– Phép quay tâm O góc thường được kí hiệu là  Q . O , 
– Chiều dương của phép quay là chiều dương của đường tròn lượng giác nghĩa là chiều
ngược với chiều quay của kim đồng hồ.
– Với k là số nguyên ta luôn có: + Phép quay  Q là phép đồng nhất. O ,2k  + Phép quay  Q
là phép đối xứng tâm O . O ,2k  1  II. TÍNH CHẤT: Cho Q
M M và Q
N N thì M N    MN. O ,   O ,      
Tính chất 1:
– Phép quay tâm O góc biến đoạn thẳng thành đoạn thẳng cùng độ dài.
– Phép quay tâm O góc biến đường thẳng thành đường thẳng.
Tính chất 2: – Phép quay tâm O góc biến tam giác thành tam giác bằng nó.
– Phép quay tâm O góc biến đường tròn thành đường tròn có cùng bán kính. Trang 31 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
III. BIỂU THỨC TỌA ĐỘ:
– Trong mặt phẳng Oxy , cho điểm M x; y và điểm I a;b . Gọi M là ảnh của M qua phép
quay tâm I góc . Khi đó            y x x a cos y b sin a M x ;  Q M   I ,         y  
xasin y bcos   b  CHÚ Ý  Xét : – Nếu
thì ta quay theo chiều dương là ngược chiều kim đồng hồ. – Nếu
thì ta quay theo chiều âm là cùng chiều kim đồng hồ. – Nếu thì . – Nếu thì là trung điểm của .  Xét và cho thì góc . IV. BÀI TẬP:
4.1. Tự Luận.
Bài toán xác định ảnh trong hệ tọa độ qua Phép Quay Phương pháp:
Sử dụng biểu thức tọa độ của phép quay.
– Trong mặt phẳng Oxy , cho điểm M x; y và điểm I a;b . Gọi M là ảnh của M qua phép
quay tâm I góc . Khi đó            y x x a cos y b sin a M x ;  Q M   I ,         y  
xasin y bcos   b Bài 01.
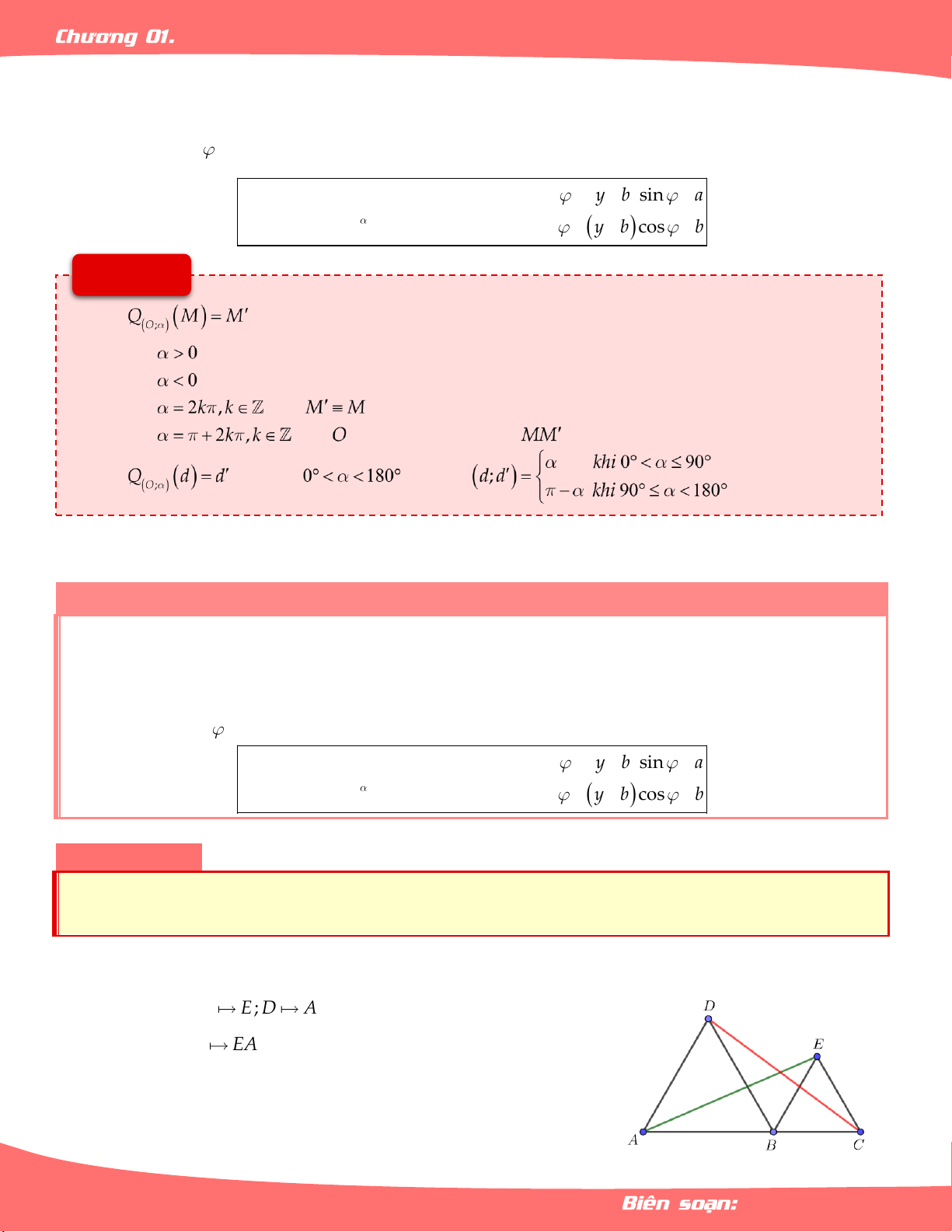
Cho 3 điểm A, B,C thẳng hàng theo thứ tự trên. Cùng thuộc nửa mặt phẳng có bờ là AB,
vẽ các tam giác đều ABD, BC .
E Chứng minh DC AE, DC, AE  60 .  Lời giải Xét  Q : C E; D A B;60  CD EA .
Khi đó CD EA và CD,EA  60 .  Trang 32 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG Bài 02.
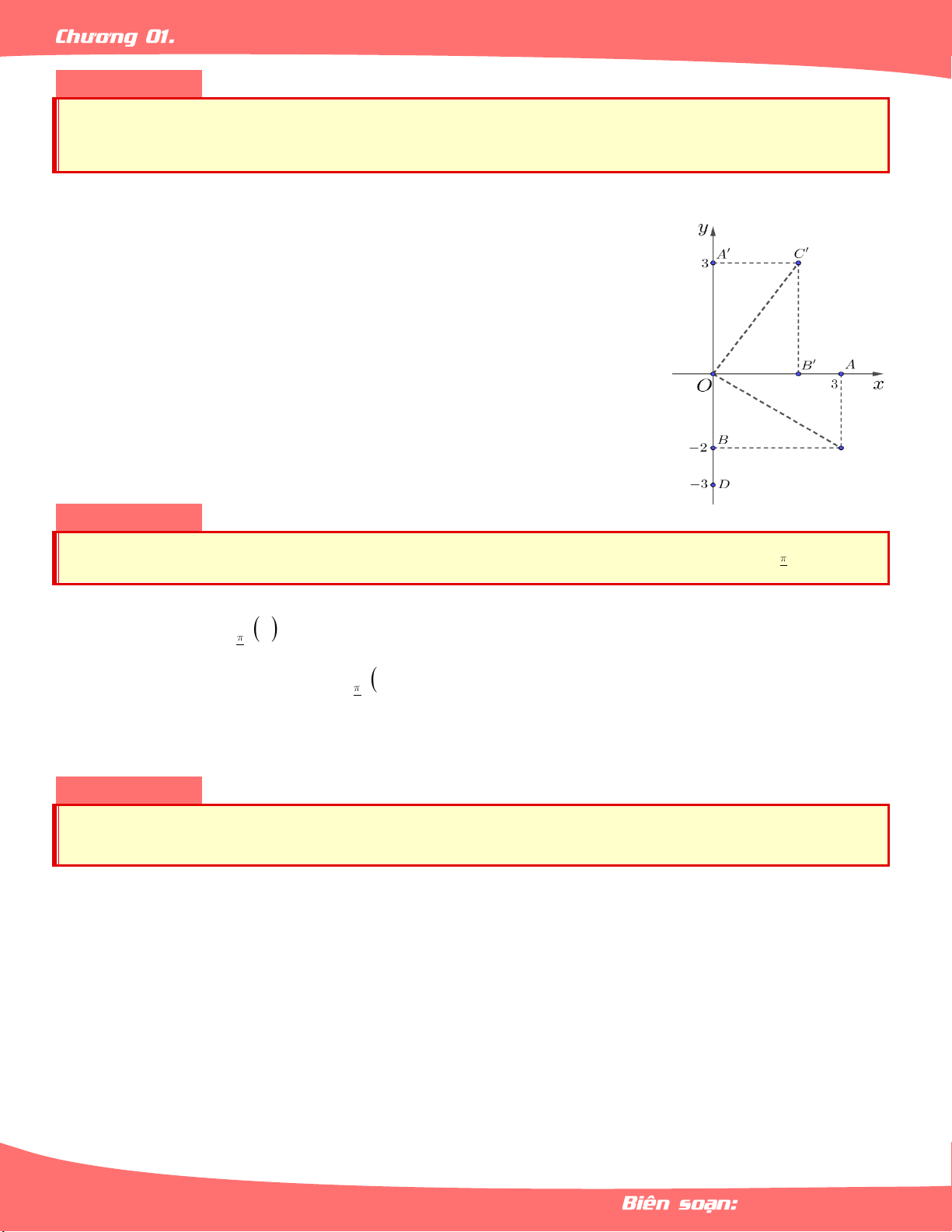
Trong mặt phẳng tọa độ Oxy , cho A3;0,B0; 2  ,C3; 2  ,D0; 3
  tìm tọa độ ảnh của các
đối tượng sau biết Q
B B, Q
A A,Q
C C,Q D D . O;90   O;90   O;90   O;90           Lời giải
A3;0 ,B0; 2  ,C3; 2  ,D0; 3   .  O ; A OA  90 Q
A A    A' 0;3 . O;90         OA   A O '  O ; B OB  90 Q
B B    B 2;0 O;90         OB   OBQ
C C  Q OBCA OB CA    C 2;3 O;90   O;90        
 OD;OD  90 Q
D D  
D 0;3  A . O;90         OD   ODBài 03.
Trong mặt phẳng tọa độ Oxy, tìm ảnh của đường thẳng d : 3x  4y  2  0 qua Q  O;   2  Lời giải Gọi d  Q         .   dd d
d : 4x 3y c 0 O;   2 
Lấy A2; 2d A  Q   .    AdO;   2  Ta có A 2
 ; 2d  4. 2  3 2
.  c  0  c  2 .
Vậy d : 4x  3y  2  0. Bài 04.
Trong mặt phẳng Oxy , cho đường thẳng  : x  2y 11  0 . Viết phương trình đường thẳng
 là ảnh của đường thẳng  qua phép quay tâm O góc 90. Lời giải
Gọi điểm M x; y bất kì thuộc đường thẳng  , Mx ; y là ảnh của điểm M qua
phép quay tâm O góc 90 .
Khi đó M sẽ thuộc đường thẳng  .
Theo biểu thức tọa độ của phép quay tâm O , góc quay 90 ta có: x  . x cos 90  . y sin 90 x  yx y      . y  . x sin 90  . y cos 90 y  x y      x
Thay vào phương trình  ta có y  2x' 11 0  2x  y 11 0
Vậy phương trình  là 2x y 11  0 . Trang 33 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG Bài 05.
Trong mặt phẳng toạ độ Oxy , cho điểm A3;0. Tìm toạ độ điểm A là ảnh của điểm A
qua phép quay tâm O0;0 góc quay  . 2 Lời giải OA OA 
Gọi Ax; y. Ta có Q A A  .    O, 
OA,OA    2     2 OA,OA  Vì A ;    2
3 0 Ox 
AOy A0; y . Mà OA OA  y  3.
Do góc quay    y  0 . Vậy A0;   3 . 2 Bài 06.
Trong mặt phẳng toạ độ Oxy , cho hai đường thẳng a và b có phương trình lần lượt là
2x y  5  0 và x  2y  3  0 . Nếu có phép quay biến đường thẳng này thành đường thẳng
kia thì số đo của góc quay (0  180 )  là Lời giải
Ta thấy hai đường thẳng a và b có phương trình 2x y  5  0 và x  2y 3  0 là
vuông góc với nhau. Suy ra  90 . Bài 07. 2 2
Trong hệ tọa độ Oxy , cho đường tròn C có phương trình: x  
1  y  2  25. Ảnh của
đường tròn C qua phép quay tâm O góc quay 0 90 là Lời giải
C có tâm I1;2. 0 0
x  xcos  y sin
x  cos90  2sin90 x  2 Gọi I   Q I       0 O,90    0 0
y  y cos  xsin y  2  cos90  sin90 y 1. Suy ra I2;  1 . 2 2
Vậy phương trình (C ') : x  
1  y  2  25.
4.2. Trắc nghiệm.
Câu 1. Có bao nhiêu điểm biến thành chính nó qua phép quay tâm O góc với  k2 ( k là một số nguyên)? A. 0 . B. 1. C. 2 . D. Vô số. Lời giải: Chọn B
Điểm đó chính là tâm quay O .
Câu 2. Cho tam giác đều tâm O . Với giá trị nào dưới đây của thì phép quay  Q biến tam giác O ,  đều thành chính nó? Trang 34 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG 2 3 A. . B. . C. . D.  . 3 3 2 2 Lời giải: Chọn B 2 4
Các góc quay để biến tam giác đều thành chính nó là: 0 ; ; ; 4 . 3 3 Câu 3.
Cho tam giác đều ABC . Hãy xác định góc quay của phép quay tâm A biến B thành C . A.  30 . B.  90 . C.  120. D.  60 hoặc  60   . Lời giải: Chọn D
Tam giác ABC đều, nên BAC  60 . Khi đó Q B C     . A     60 ,
Câu 4. Cho tam giác đều tâm O . Hỏi có bao nhiêu phép quay tâm O góc với 0   2 , biến
tam giác trên thành chính nó? A. 1. B. 2 . C. 3 . D. 4 . Lời giải: Chọn C 2 4 Do 0 
 2 nên ta có góc quay là 0 ; ; . 3 3
Câu 5. Cho hình vuông tâm O . Xét phép quay Q có tâm quay O và góc quay . Với giá trị nào
sau đây của , phép quay Q biến hình vuông thành chính nó? A. . B. . C. . D.  . 6 4 3 2 Lời giải: Chọn D 3
Các góc quay để biến hình vuông thành chính nó là: 0 ; ; ; ; 2 . 2 2
Câu 6. Trong mặt phẳng toạ độ Oxy , cho điểm A3; 0. Tìm toạ độ điểm A là ảnh của điểm A qua
phép quay tâm O0;0 góc quay . 2
A. A0;   3 .
B. A0;3 . C. A 3  ;0.
D. A2 3; 2 3 . Lời giải: Chọn B OA OA 
Gọi Ax; y. Ta có Q A A  .    O,   OA,OA   2     2 OA,OA  Vì A ;    2
3 0 Ox 
AOy A0; y . Mà OA OA  y  3. Do góc quay 
y  0 . Vậy A0;3. 2 Trang 35 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Câu 7. Trong mặt phẳng toạ độ Oxy , cho hai đường thẳng a và b có phương trình lần lượt là
4x  3y  5  0 và x  7y  4  0 . Nếu có phép quay biến đường thẳng này thành đường thẳng
kia thì số đo của góc quay (0  180 )  là A. 45. B. 60 . C. 90 . D. 120 . Lời giải: Chọn B
Đường thẳng a : 4x  3y  5  0 có vectơ pháp tuyến n  . Đường thẳng a 4;3
b : x  7y  4  0 có vectơ pháp tuyến n
. Góc là góc tạo bởi a và b . b 1;7 4.1 3 7 . 2
Ta có cos  cos n ,n      . a b  45 2 2 2 2 2 4  3 . 1  7 Vậy  45 .
Câu 8. Trong mặt phẳng với hệ toạ độ Oxy , cho đường thẳng  : x  2y  6  0 . Viết phương trình
đường thẳng  là ảnh của đường thẳng  qua phép quay tâm O góc 90 .
A. 2x y  6  0 .
B. 2x y  6  0 .
C. 2x y  6  0 .
D. 2x y  6  0 . Lời giải: Chọn A
Đường thẳng  có vectơ pháp tuyến n  1; 2 , vì đường thẳng  vuông góc với đường 1  
thẳng  nên đường thẳng  có vectơ pháp tuyến n  2; 1 . 2  
Đường thẳng  cắt trục Oy tại A0;3 nên ảnh của A qua phép quay tâm O góc 90 là điểm B 3
 ;0 thuộc đường thẳng  nên phương trình đường thẳng  là 2x y 6  0 .
Câu 9. Ảnh của điểm M 2; 3
  qua phép quay tâm I  1
 ; 2 góc quay 120 là  5  3  5 3 3  9   5  3 1 3  3 1 A. M ;    . B. M  ; . 2 2      2 2    5 3 5 3 3 9   5  3 1 3 3  9  C. M ;    . D. M  ; . 2 2      2 2   Lời giải: Chọn C
Chú ý: Trong mặt phẳng Oxy , giả sử M  ; x y ,I  ;
a b và Mx ; y   Q thì I ; 
x  a  x a.cos y   b.sin y  b 
xa.sin y   b.cos
Vậy ảnh của điểm M 2; 3
  qua phép quay tâm I  1
 ; 2 góc quay 120 là Mx ; y:  5 3  5     x  1
  3cos120  5sin120 x   2   .
y  2  3sin120  5cos120   3 3  9 y   2 Trang 36 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG  5 3 5 3 3 9  Vậy M ;   . 2 2   
Câu 10. Trong mặt phẳng Oxy , cho điểm M  2  ; 
1 . Xác định tọa độ điểm M là ảnh của điểm M
qua phép quay tâm O góc 90 .
A. M1; 2 . B. M1; 2  . C. M 1  ; 2  . D. M 1  ; 2 . Lời giải: Chọn C
Theo biểu thức tọa độ của phép quay tâm O , góc quay 90 ta có: x  . x cos90  . y sin 90 x  yx  1        M' 1  ; 2   . y  . x sin 90  . y cos 90 y  x y  2    
------------------HẾT------------------ Trang 37 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
§5. PHÉP DỜI HÌNH I. ĐỊNH NGHĨA:
– Phép dời hình là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì. Nhận xét.
– Các phép đồng nhất, tịnh tiến, đối xứng trục, đối xứng tâm và phép quay đều là những phép dời hình.
– Phép biến hình có được bằng cách thực hiện liên tiếp hai phép dời hình là một phép dời hình. II. TÍNH CHẤT: Phép dời hình:
+ Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm.
Tính chất:
+ Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng
thành đoạn thẳng bằng nó.
+ Biến tam giác thành tam giác bằng nó, biến góc thành góc bằng nó.
+ Biến đường tròn thành đường tròn có cùng bán kính.  CHÚ Ý
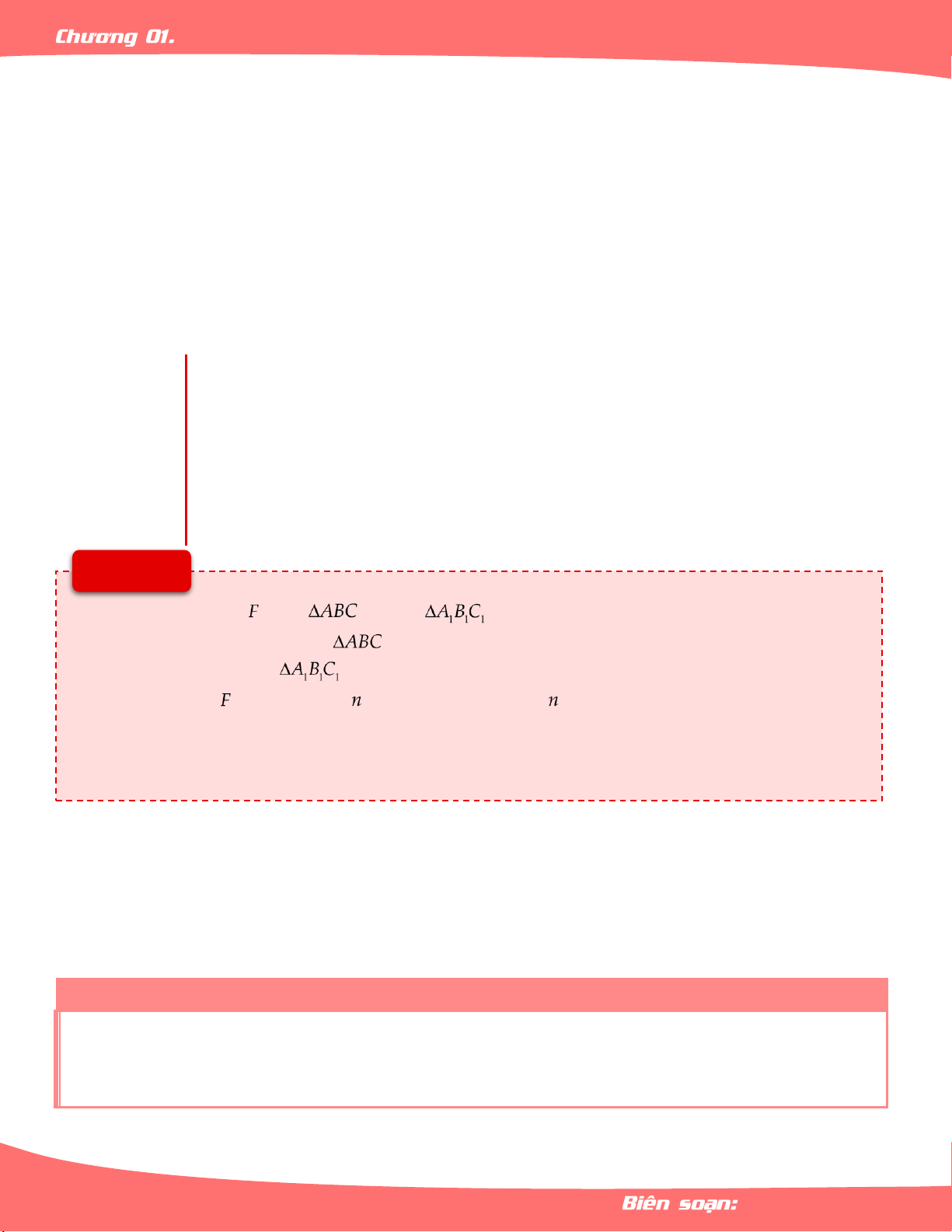
– Xét phép dời hình biến thành
thì nó biến trọng tâm, trực tâm, tâm đường
tròn ngoại tiếp, nội tiếp của
tương ứng với trọng tâm, trực tâm, tâm đường tròn
ngoại tiếp, nội tiếp của
– Phép dời hình biến đa giác cạnh thành đa giác cạnh, biến đỉnh thành đỉnh tương
ứng, biến cạnh thành cạnh.
– Hai hình được gọi là bằng nhau khi và chỉ khi có một phép dời hình biến hình này thành hình kia.
III. KHÁI NIỆM HAI HÌNH BẰNG NHAU:
– Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia. IV. BÀI TẬP:
4.1. Tự Luận.
Bài toán xác định ảnh trong hệ tọa độ qua Phép Dời Hình Phương pháp:
Sử dụng định nghĩa, tính chất và biểu thức tọa độ của phép dời hình (tịnh tiến, đối xứng trục/ tâm, quay). Trang 38 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG Bài 01.
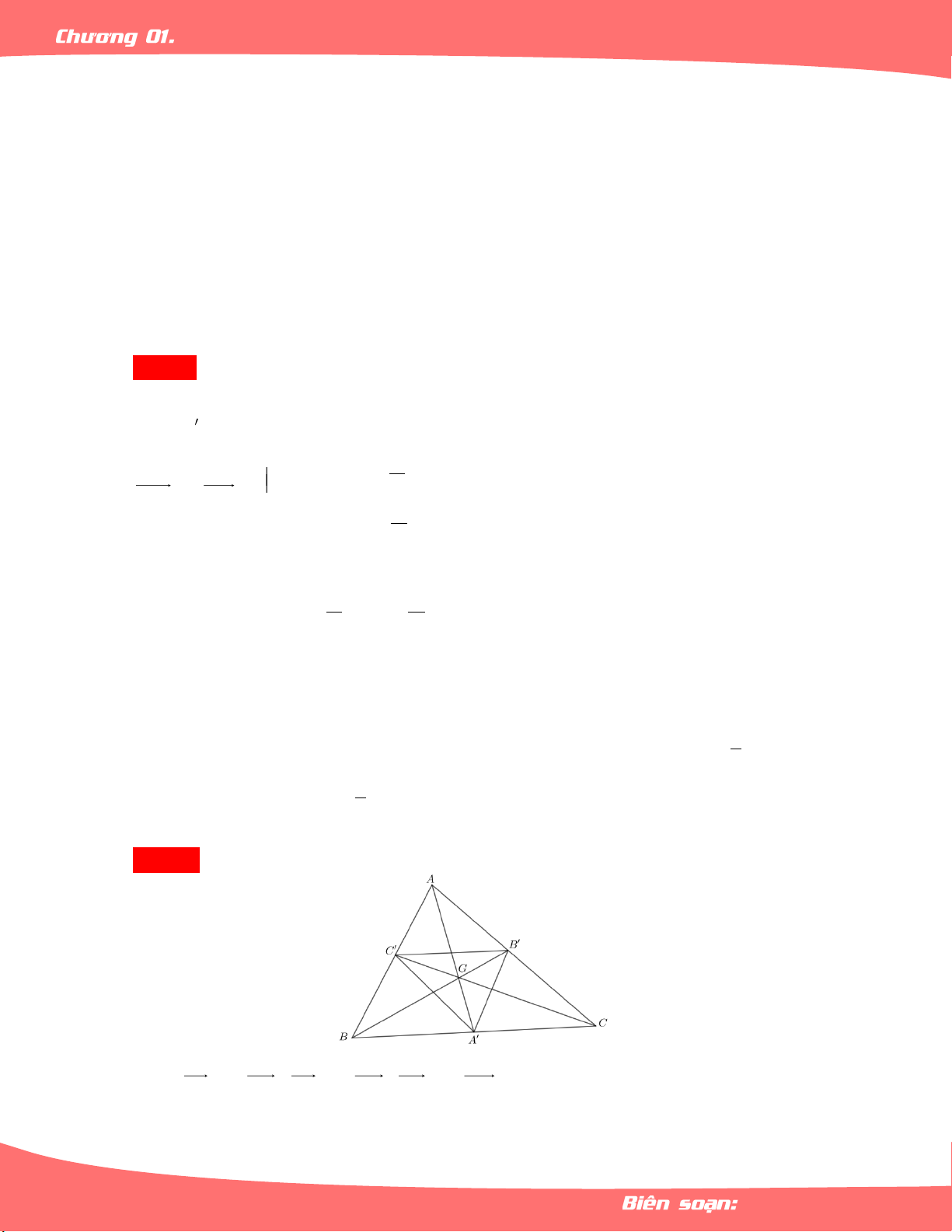
Cho tam giác đều ABC và G là trọng tâm tam, giác ABC . Tìm ảnh của tam giác ABC lần lượt qua T và Q AG  0 B,60  a. Qua T . b.Qua Q AG  0 B,60  Lời giải a. Qua T : AG Ta có
T A  A G ; 1 AG T
B  B BB AG ; 1 1 AG T
C  C CC AG 1 1 AG Vậy T ABC  AB C 1 1 1 AG b.Qua  Q 0 B,60   Q B B ; 0 B, 60      Q
A A , A C ; 0 B,    1 1 60  Q
C C , C đối xứng với A qua BC 0 B,    1 60 1 Vậy  Q ABC ABC 0 B,    1 1 60 Bài 02.
Trong mặt phẳng tọa độ Oxy , cho đường thẳng d : 3x y 3  0 . Hỏi phép dời hình có
được bằng cách thực hiện liên tiếp phép đối xứng tâm I 1; 2 và phép tịnh tiến v   2  ;  1
biến đường thẳng d thành đường thẳng nào trong các đường thẳng sau? Lời giải
Gọi d' là ảnh cần tìm của d .
Khi đó d' song song hoặc trùng d nên phương trình d' có dạng: 3x y c  0 .
Gọi A1;0d Suy ra AA' là đường cao của lăng trụ: h AA'  4a .
Phép đối xứng tâm I 1; 2 biến A1;0 thành B1; 4 . Trang 39 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Phép tịnh tiến theo vectơ v   2  ; 
1 biến B1; 4 thành C  1  ;5. Mà C  1
 ;5d' : 3x y c  0 nên 3. 
1  5  c  0  c  8 .
Vậy d' : 3x y 8  0. Bài 03.
Cho đường tròn C 2 2
: x y  4x  2y  4  0 . Tìm ảnh của C khi thực hiện liên tiếp phép
tịnh tiến theo vectơ u   2  ; 
1 và phép tịnh tiến theo vectơ v  1;  3 . Lời giải
Theo giả thiết C 2 2
: x y  4x  2y  4  0 có tâm I 2;  
1 , bán kính R  1 .
Phép tịnh tiến theo vectơ u   2  ; 
1 biến I 2;   1 thành O0; 0 .
Phép tịnh tiến theo vectơ v  1;3 biến O0;0 thành I '1;  3 .
Do đó, ảnh của C khi thực hiện liên tiếp phép tịnh tiến theo vectơ u   2  ;  1 và
phép tịnh tiến theo vectơ v  1;3 là đường tròn C ' có tâm I '1; 
3 và bán kính R  1 2 2
Vậy C' : x  
1  y  3 1.
4.2. Trắc nghiệm.
Câu 1. Hợp thành của hai phép tịnh tiến là phép nào trong các phép dưới đây?
A. Phép đối xứng trục.
B. Phép đối xứng tâm. C. Phép tịnh tiến. D. Phép quay. Lời giải: Chọn C
Hợp thành của hai phép tịnh tiến là phép tịnh tiến với vectơ tịnh tiến là vectơ tổng của hai
vectơ tịnh tiến của hai phép tịnh tiến đã cho.
Câu 2. Phép dời hình có được bằng cách thực hiện liên tiếp phép tịnh tiến v và phép đối xứng tâm
I là phép nào trong các phép dưới đây?
A. Phép đối xứng trục.
B. Phép đối xứng tâm.
C. Phép đồng nhất. D. Phép tịnh tiến. Lời giải: Chọn B 1
Tâm đối xứng là J thỏa mãn IJ   v . 2
Câu 3. Phép dời hình có được bằng cách thực hiện liên tiếp hai phép đối xứng qua hai đường thẳng
song song là phép nào trong các phép dưới đây?
A. Phép đối xứng trục.
B. Phép đối xứng tâm. Trang 40 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG C. Phép tịnh tiến.
D. Phép quay, góc quay khác . Lời giải: Chọn C
Vectơ tịnh tiến là u  2HK , với H, K lần lượt là hai điểm nằm trên hai đường thẳng song
song đã cho, đồng thời HK sẽ vuông góc với hai đường thẳng đó.
Câu 4. Phép dời hình có được bằng cách thực hiện liên tiếp hai phép đối xứng qua hai đường thẳng
vuông góc với nhau là phép nào trong các phép dưới đây?
A. Phép đối xứng trục.
B. Phép đối xứng tâm. C. Phép tịnh tiến.
D. Phép quay, góc quay khác . Lời giải: Chọn B
Tâm đối xứng là giao điểm của hai đường thẳng đã cho.
Câu 5. Phép dời hình có được bằng cách thực hiện liên tiếp hai phép đối xứng qua hai đường thẳng
căt nhau ( không vuông góc) là phép nào trong các phép dưới đây?
A. Phép đối xứng trục.
B. Phép đối xứng tâm. C. Phép tịnh tiến.
D. Phép quay, góc quay khác . Lời giải: Chọn D
Tâm quay là giao điểm của hai đường thẳng đã cho, góc quay là góc giữa hai đường thẳng đó.
Câu 6. Phép dời hình có được bằng cách thực hiện liên tiếp hai phép đối xứng tâm là phép nào trong các phép dưới đây?
A. Phép đối xứng trục.
B. Phép đối xứng tâm. C. Phép tịnh tiến. D. Phép quay. Lời giải: Chọn C Trang 41 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Vectơ tịnh tiến là u  2II ' , với I , I ' lần lượt là tâm đối xứng của hai phép đối xứng tâm đã cho. 2 2
Câu 7. Trong mặt phẳng tọa độ Oxy , cho đường tròn C có phương trình x  2  y   1  9.
Phương trình đường tròn C là ảnh của C qua phép dời hình có được bằng cách thực
hiện liên tiếp một phép tịnh tiến theo v   1
 ; 4 và phép đối xứng trục Oy là 2 2 2 2
A. C : x  
1  y  5  9 .
B. C : x  3  y  3  9 . 2 2 2 2
C. C : x  3  y  3  9 .
D. C : x  
1  y  5  9 . Lời giải: Chọn D
Ta có: C là đường tròn tâm I 2; 
1 và bán kính R  3. Gọi I  ;
a b  T I  I 1;5  tâm của C là I 1  ;5  D I . Oy   v
Qua phép dời hình bán kính đường tròn không đổi nên phương trình C là:
x 2 y 2 1 5  9 . Câu 8. Cho hàm số 3
y x  3x  2 có đồ thị C . Tịnh tiến C qua phải 2 đơn vị rồi tịnh tiến
xuống dưới 1 đơn vị. Ảnh của C là đồ thị của hàm số A. 3 2
y  x  6x  9x 1. B. 3 2
y x  6x  9x 1. C. 3 2
y x  6x  9x 1 . D. 3 2
y x  6x  9x 1. Lời giải: Chọn D
Mỗi điểm M x yC 3 ;
y x 3x  2  1 . Gọi M x ; y
là ảnh của M qua phép tịnh tiến qua phải 2 đơn vị, tức là tịnh tiến theo véc 1  1 1  x x  2
tơ u  2;0 , khi đó ta có: 1  . y y  1 Gọi M x ; y
là ảnh khi tịnh tiến M x ; y
xuống dưới 1 đơn vị, tức là tịnh tiến theo véc 1  1 1  2  2 2 
x x x  2 x x  2 tơ v  0;  1 , khi đó ta có: 2 1 2    .
y y 1  y 1 y y 1  2 1  2
Thay vào phương trình   1 ta được:
y 1   x  23  3 x  2 3 2
 2  y x  6x  9x 1. Suy ra M thuộc đồ thị hàm số có 2 2 2 2 2 2 2 2 phương trình 3 2
y x  6x  9x 1.
Vậy ảnh của C qua phép biến hình trên là đồ thị của hàm số có phương trình 3 2
y x  6x  9x 1. Câu 9.
Trong mặt phẳng Oxy , cho đường thẳng d có phương trình x y  2  0 . Xác định phương
trình đường thẳng d là ảnh của đường thẳng d qua phép dời hình có được bằng cách 
thực hiện liên tiếp phép tịnh tiến theo véc tơ v   1  ; 
1 và phép quay tâm O , góc quay . 2 Trang 42 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
A. d : x y  2  0 .
B. d : x y  2  0 .
C. d : x y  0 .
D. d : x y 1  0 . Lời giải: Chọn A
Cách 1: Gọi d T
d //d hoặc d d  phương trình d có dạng x y c  0 . 1 vd  1 1 1 Gọi d  Q   
 phương trình d có dạng x y c  0 .    d d d  1  1 O;    2  Lấy M 1; 
1  d M 0; 2  T M và M d . 1     v 1 1
Gọi M   Q       .     M M 2;0 c 2 1    O;    2 
Vậy phương trình d là x y  2  0 .
Cách 2: Ta có v là véc tơ chỉ phương của đường thẳng d nên ảnh của đường thẳng d qua phép tịnh
tiến theo v là đường thẳng d . Gọi d  Q    
x y c     d d d
phương trình d có dạng 0 . O;    2 
Lấy M 0;2d . Gọi M   Q           M M 2;0 c 2 . 1    O;    2 
Vậy phương trình d là x y  2  0 .
Câu 10. Trong mặt phẳng Oxy , cho đường thẳng d : 3x  4 y 1  0 . Thực hiện liên tiếp phép vị tự
tâm O tỉ số k  3
 và phép tịnh tiến theo véc tơ u  1;2 thì đường thẳng d biến thành
đường thẳng d có phương trình là
A. 3x  4 y  2  0 .
B. 3x  4 y  2  0 .
C. 3x  4 y  5  0 .
D. 3x  4 y  5  0 . Lời giải: Chọn A x x  x  3  x  3 
Theo công thức tọa độ phép vị tự ta có    . y  3  y y y   3  xy
Thay vào phương trình của d ta có: 3.  4.
1  0  3x  4y  3  0 d  . 3  3 
x  x 1
x  x 1
Theo công thức tọa độ phép tịnh tiến ta có    .
y  y  2
y  y  2
Thay vào phương trình của d ta có 3 x  
1  4 y  2  3  0  3x  4y  2  0 .
Vậy đường thẳng d có phương trình 3x  4 y  2  0 .
------------------HẾT------------------ Trang 43 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
§6. PHÉP VỊ TỰ I. ĐỊNH NGHĨA:
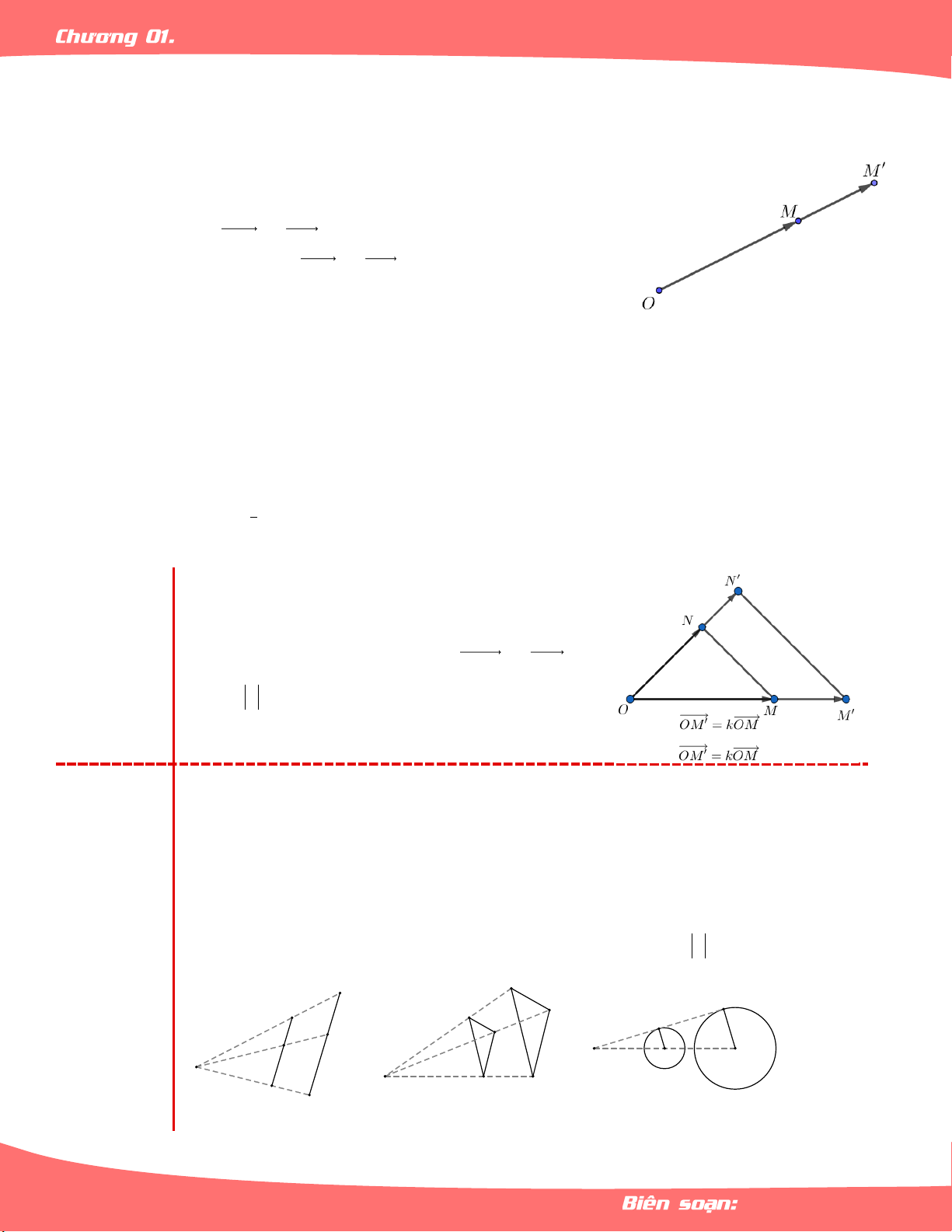
– Cho một điểm O cố định và một số k không đổi, k  0 . Khi đó
phép vị tự tâm O tỷ số k  0 là phép biến hình biến mỗi điểm M
thành M sao cho OM  kOM . – Ký hiệu: V
M M  OM  kOM . O ,k     Nhận xét:
– Phép vị tự biên tâm vị tự thành chính nó.
– Khi k  0 thì M và M cùng phía với điểm O .
– Khi k  0 thì M và M khác phía với điểm O . – Khi k  1
 thì M và M đối xứng nhau qua O .
– Khi k 1 thì M và M có vị trí trùng nhau nên phép vị tự tỷ số k 1 là phép đồng nhất. – V
M M  V M  M O; k    1      O;   k II. TÍNH CHẤT:
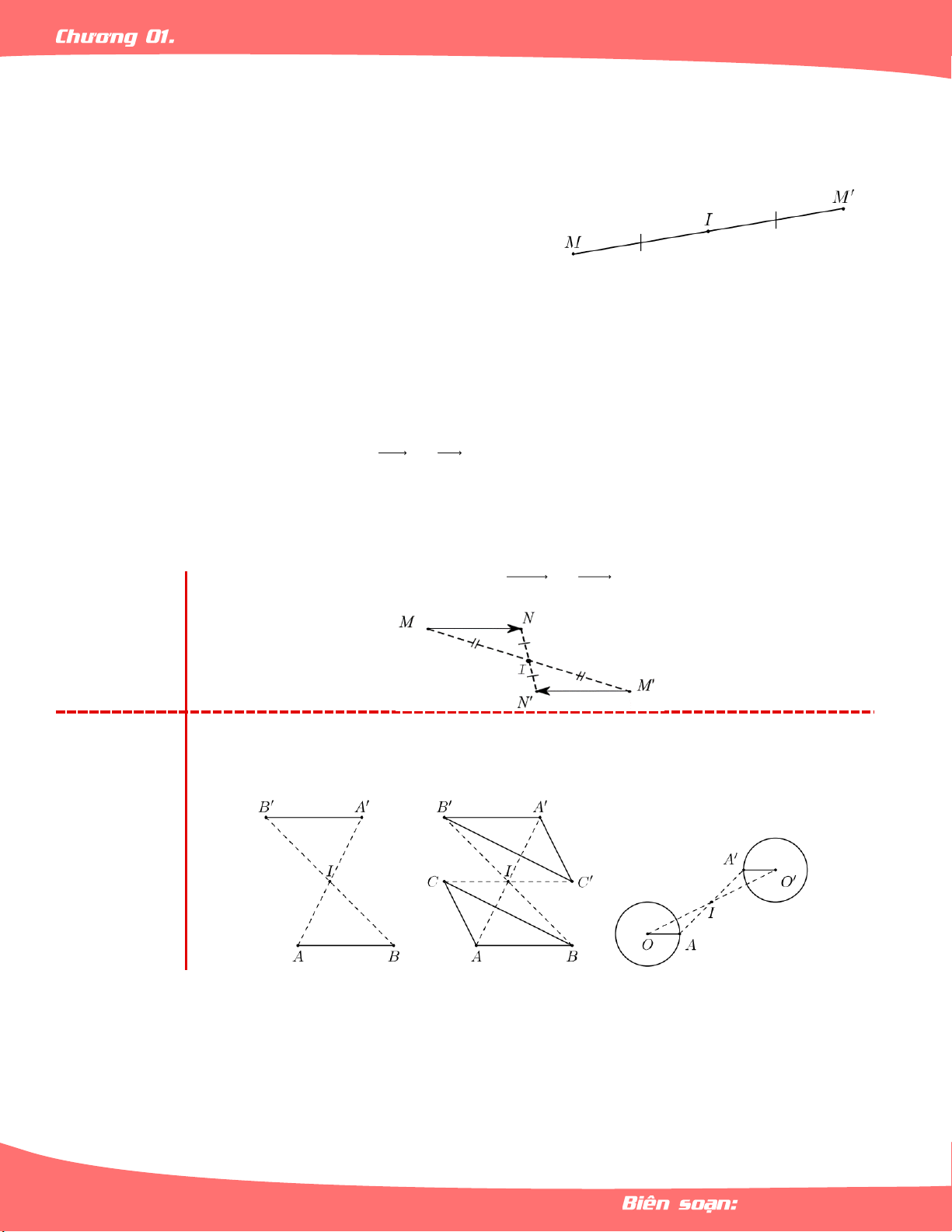
Nếu phép vị tự tỷ số k biến hai điểm M,N tuỳ
Tính chất ý thành hai điểm M,N thì M N    kMN và 1: M N    k MN .
Phép vị tự tỷ số k biến:
– Ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm.
– Đường thẳng thành đường thẳng song song hoặc trùng, tia thành tia, đoạn
thẳng thành đoạn thẳng.
– Tam giác thành tam giác đồng dạng với nó, góc thành góc bằng nó.
Tính chất – Đường tròn bán kính R thành đường tròn có bán kính k R. 2: A' A A' A' A B' A R' B B R I B' O O' I I C C' C' C Trang 44 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
III. CÁCH TÌM TÂM VỊ TỰ CỦA HAI ĐƯỜNG TRÒN:
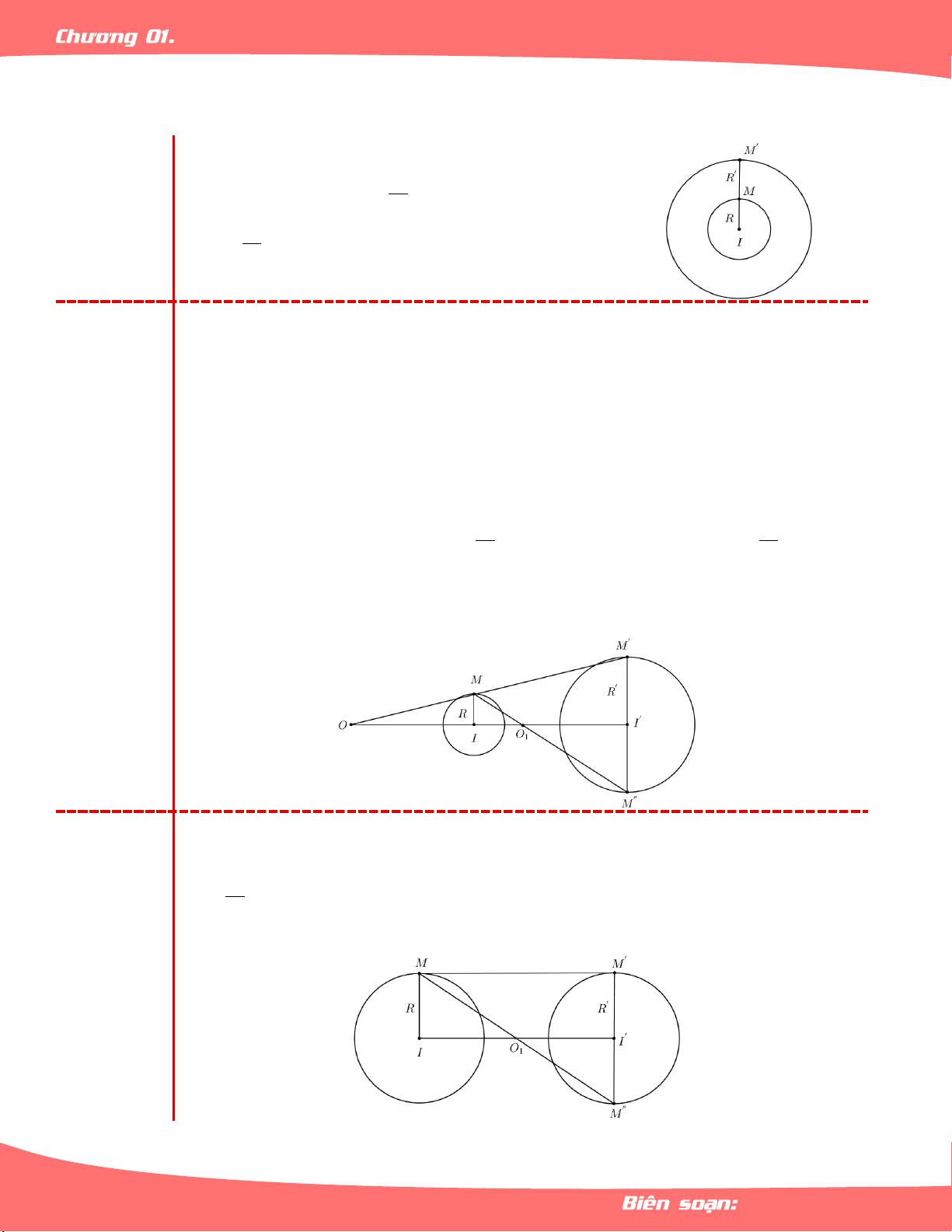
Cho hai đường tròn I,R và I,R .
Trường hợp I trùng với I . R
Phép vị tự tâm I , tỉ số
và phép vị tự tâm I , Trường R hợp 1: R tỉ số 
biến đường tròn I,R thành đường R
tròn I,R .
Trường hợp I khác I và R R .
+ Lấy M bất kì thuộc I,R , đường thẳng qua I song song với IM cắt
I,R tại M và M.
+ Giả sử M, M nằm cùng phía đối với đường thẳng II , còn M, M nằm
khác phía với đường thẳng II .
+ Giả sử đường thẳng MM cắt II tại O nằm ngoài đoạn thẳng II , còn
đường thẳng M M cắt II tại O nằm ngoài đoạn thẳng II . 1 RRTrường
+ Khi đó phép vị tự tâm O , tỉ số
và phép vị tự tâm O , tỉ số  biến R 1 R hợp 2:
đường tròn I,R thành đường tròn I,R .
+ Ta gọi O là tâm vị tự ngoài, còn O là tâm vị tự trong của 2 đường tròn. 1
Trường hợp I khác I và R R .
+ Khi đó MM song song với II nên chỉ có phép vị tự tâm O , tỉ số 1 Rk    1
 biến đường tròn I,R thành đường tròn I,R . R
+ Nó chính là phép đối xứng tâm O . 1 Trường hợp 3: Trang 45 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
IV. BIỂU THỨC TỌA ĐỘ:
– Trong mặt phẳng Oxy , cho điểm M x; y và điểm I  ;
a b . Gọi M là ảnh của M qua phép
vị tự tâm I . Khi đó
x  a k x a
x  a k x    a V
M M  IM  kIM x  a; y  b k x a; y b     I ; k            
y  b k  yb
y  b k  y    bIV. BÀI TẬP:
4.1. Tự Luận.
Bài toán xác định ảnh trong hệ tọa độ qua Phép Quay Phương pháp:
Sử dụng biểu thức tọa độ của phép vị tự.
– Trong mặt phẳng Oxy , cho điểm M x; y và điểm I  ;
a b . Gọi M là ảnh của M qua phép
vị tự tâm I . Khi đó
x  a k x a
x  a k x    a V
M M  IM  kIM x  a; y  b k x a; y b     I ; k            
y  b k  yb
y  b k  y    bBài 01.
Trong mặt phẳng tọa độ Oxy cho hai điểm M 4;6 và M ' 3
 ;5 . Phép vị tự tâm I , tỉ số 1 k
biến điểm M thành điểm M ' . Tìm tọa độ tâm vị tự I . 2 Lời giải Gọi I  ;
x y . Suy ra IM  4  ;
x 6  y  , IM '   3   ; x 5  y  .  1 3
  x  4  x 1  x  10  Ta có 2 V
M M '  IM '  IM      I 10;4 .  1    I ;   2 1  y  4  2  5  y  6 y  2 Bài 02.
Trong mặt phẳng Oxy , cho điểm A3; 5 và đường thẳng d : 2x y  4  0 . Hãy tìm ảnh của
điểm A và ảnh của d qua phép vị tự I  1
 ; 2 và tỷ số k  2  . Lời giải
Gọi Ax ; y là ảnh của A qua phép vị tự  V I;k x  1    2  3  1   9  
Theo biểu thức toạ độ, ta có: y 2   2   5   2 16
Vậy ảnh của điểm A là A 9  ;16. Trang 46 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Gọi d là ảnh của d qua phép vị tự  V . I ; k
Vì d//d nên phương trình đường thẳng d có dạng: 2x y c  0.
Gọi M2;0d ; V
M Mx, yI ; k       x  1
  22  1   7
Theo biểu thức toạ độ, ta có: y 2   2  0  2  6
Khi đó Md nên 2. 7
   6 c  0  c  8
Vậy pt đường thẳng d : 2x y 8  0 Bài 03.
Trong mặt phẳng tọa độ Oxy cho đường thẳng d : x y  3  0 . Phép vị tự tâm O , tỉ số k  2
biến d thành đường thẳng nào ? Lời giải
Cách 1: Ta cóV d d  d dd   : // nên
: 2x y c  0 ( c  3  do k 1). O;2 O A  2OA
Chọn A0;3d . Ta có V A    A  . O  ;2   A d
Từ OA  2OA A (
 0;6) . Thay vào d ta được d: 2x y  6  0 .
Cách 2: Giả sử phép vị tự M   x y  V
biến điểm M x; y thành điểm  ; . O;2  1 x x x  2x  2
Ta có OM   2OM     y  2y 1  . y y  2 xy Thay vào ta được 2  
 3  0  2x  y  6  0. 2 2 Bài 04.
Trong mặt phẳng tọa độ 2 2
Oxy cho đường tròn C :  x  
1   y  5  4 và điểm I 2; 3 . Gọi C
là ảnh của C qua phép vị tự tâm I tỉ số k  2
 . Khi đó C có phương trình là Lời giải
⬥ Đường tròn Ccó tâm K 1;5 và bán kính R  2 x  2  2   12 x  ⬥ 4 GọiV
K Kx ; y IK  2  IK   K4; 1  9 là tâm I    ; 2      y  3  2   53 y  19 
của đường tròn C .
⬥ Bán kính Rcủa C là R |
k | R = 2 2 = 4
⬥ VậyC x  2  y  2 : 4 19 16 Bài 05. Trang 47 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG Cho phép vị tự 2 2
I 1;3 và tỷ số k  2
 . Tìm ảnh của đường tròn C : x  2 y   1  3 qua  V . I ; kLời giải
Đường tròn C có tâm J 2;  
1 và bán kính R  3 . Gọi V
J Jx ; yI ; k      
x 1 22   1  1
Theo biểu thức toạ độ, ta có: y3  213 11 Toạ độ J 1  ;1  1 , R  2  3  2 3 . 2 2
Ảnh của đường tròn C qua  V
có phương trình: x   1  y 1  1 12 . I ; k
4.2. Trắc nghiệm.
Câu 1. Cho hai đường thẳng cắt nhau d và d . Có bao nhiêu phép vị tự biến đường thẳng d
thành đường thẳng d ? A. 0 . B. 1 . C. 2 . D. Vô số. Lời giải: Chọn A
Vì qua phép vị tự, đường thẳng biến thành đường thẳng song song hoặc trùng với nó.
Câu 2. Cho hai đường thẳng song song d và d . Có bao nhiêu phép vị tự với tỉ số k  20 biến
đường thẳng d thành đường thẳng d ? A. 0 . B. 1 . C. 2 . D. Vô số. Lời giải: Chọn D
Lấy hai điểm A và A tùy ý trên d và d .
Chọn điểm O thỏa mãn OA  20 OA .
Khi đó phép vị tự tâm O tỉ số k  20 sẽ biến đường thẳng d thành đường thẳng d . Do A
và A tùy ý trên d và d nên suy ra có vô số phép vị tự.
Câu 3. Cho hai đường thẳng song song d và d ' và một điểm O không nằm trên chúng. Có bao
nhiêu phép vị tự tâm O biến đường thẳng d thành đường thẳng d '? A. 0. B. 1. C. 3. D. Vô số. Lời giải: Chọn B
Kẻ đường thẳng  qua O cắt d tại A và cắt d ' tại A' .
Gọi k là số thỏa mãn OA'  kOA . Khi đó phép vị tự tâm O tỉ số k sẽ biến d thành d '.
Do k xác định duy nhất (không phụ thuộc vào  ) nên có duy nhất một phép vị tự.
Câu 4. Cho hai đường thẳng cắt nhau d và d '. Có bao nhiêu phép vị tự biến mỗi đường thẳng thành chính nó. A. 0. B. 1. C. 2. D. Vô số. Lời giải: Chọn D Trang 48 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Tâm vị tự là giao điểm của d và d '.
Tỉ số vị tự là số k khác 0 (hoặc tâm vị tự tùy ý, tỉ số k 1 đây là phép đồng nhất.)
Câu 5. Cho hai đường tròn bằng nhau  ;
O R và O '; R ' với tâm O và O' phân biệt. Có bao nhiêu phép vị tự biến  ;
O R thành O '; R ' ? A. 0. B. 1. C. 2. D. Vô số. Lời giải: Chọn B
Phép vị tự có tâm là trung điểm OO', tỉ số vị tự là 1.
Câu 6. Cho đường tròn  ;3
O  và điểm I nằm ngoài O sao cho OI  9 . Gọi O '; R ' là ảnh của  ;3
O  qua phép vị tự  V . Tính R ' . I ;5 5
A. R'  9
B. R ' 
C. R '  27
D. R' 15. 3 Lời giải: Chọn D
Ta có R '  k .R  5.R  5.3  15 .
Câu 7. Trong mặt phẳng tọa độ Oxy cho phép vị tự tâm I 2;3 tỉ số k  2
 biến điểm M  7  ;2
thành điểm M ' có tọa độ là: A.  1  0;2 B. 20;5 C. 18; 2 D.  1  0;5 Lời giải: Chọn B Gọi M ' ;
x y . Suy ra IM   9  ; 
1 , IM '   x  2; y  3 . x  2  2  .   9   x  20 Ta có V
M M '  IM '  2  IM      M ' 20;5 . I ; 2      y  3  2  .    1 y  5
Câu 8. Trong mặt phẳng tọa độ Oxy cho phép vị tự V , tỉ số k  2 biến điểm A1; 2   thành điểm A' 5  ; 
1 . Hỏi phép vị tự V biến điểm B 0; 
1 thành điểm có tọa độ nào sau đây? A. 0; 2 B. 12; 5   C.  7  ;7 D. 11;6 Lời giải: Chọn C Gọi B ' ;
x y là ảnh của B qua phép vị tự V .
Suy ra A' B '   x  5; y  
1 và AB  1;3 .
x  5  2.  1 x  7 
Theo giả thiết, ta có A' B '  2AB     . y 1 2.3 y  7
Câu 9. Trong mặt phẳng tọa độ Oxy cho đường thẳng d : x  2y 1  0 . Lập phương trình đường
thẳng d  là ảnh của d qua phépV(O, là: 2)
A. 3x y  3  0 .
B. 3x y  6  0 .
C. 3x y  6  0 .
D. 3x y  3  0 . Lời giải: Chọn B Trang 49 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG  xx        ⬥ x 2x Ta có 2 V
M (x, y)  M (
x ; y )  OM   2  OM     (O, 2  ) y  2  y y y    2 3 1
Thay vào phương trình đường thẳng d   x 
y  3  0  3x  y  6  0. 2 2
⬥ Vậy phương trình đường thẳng d : 3x y  6  0
Câu 10. Trong mặt phẳng tọa độ Oxy Phép vị tự tâm I 3; 1
 , tỉ số 2 biến parabol P 2
: y  2x  2x 1
. Thành parabol có phương trình là: A. 2
y  x  8x  3 . B. 2
y x  8x 14 . C. 2
y  2x  4x  5 . D. 2
y  2x x 1. Lời giải: Chọn B
⬥ GọiP là ảnh của qua phép vị tự tâm I 3;  1  , tỉ số 2 .  1 3 
Đỉnh của parabol (P) có tọa độ A  ;    .  2 2 
Khi đó đỉnh của  P làV A   A . I ;2    
Ta có IA  2IA . Suy ra  A  4  ; 2   .
Trong bốn đáp án thì chỉ có parabol 2
y x  8x 14 có đỉnh  A  4  ; 2   .
Câu 11. Trong mặt phẳng tọa độ Oxy cho đường tròn Cx   y  2 2 : 3
 4 . Gọi C là ảnh của C
qua phép vị tự tâm O tỉ số k  2
 . Khi đó C có phương trình là
A. x   y  2 2 6 16 .
B. x   y  2 2 6 16 .
C. x   y  2 2 6  64.
D. x   y  2 2 6  64 . Lời giải: Chọn A
⬥ Đường tròn Ccó tâm I 0;3 và bán kính R  2
⬥ GọiC V
C có tâm I   V
I I  0;  6 và bán kính R của C là O;2     O, 2        R  |
k | R = 2 2 = 4
⬥ VậyC x  y  2 2 : 6 16
Câu 12. Trong mặt phẳng tọa độ 2 2
Oxy cho đường tròn C :  x   1   y   3
 9 . Gọi C là ảnh của
Cqua phép vị tự tâm A2; 4tỉ số k  2
 . Khi đó C có phương trình là A.  2 2
x  2   y  2 2 6  36 .
B. x  4   y  6  36 . C. 2 2 2 2
x y  8x 12 y 16  0 .
D. x  2   y  6  36 . Lời giải: Chọn B
⬥ Đường tròn Ccó tâm I 1; 3
  và bán kính R  3 Trang 50 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG   x  2  1  1 22   x  ⬥ 4 V
I I x ;  y 
và bán kính R của (C )  là A    ;2       y   2     3
   1 2 4   y   6  R |
k | R = 2 3= 6
⬥ Vậyx  2  y  2 4 6  36 2 2
Câu 13. Trong mặt phẳng tọa độ Oxy , cho đường tròn (C ) :  x   1   y  
1  4 phép vị tự tâm O tỉ
số k  2 biến đường tròn C thành đường tròn có phương trình là 2 2 2 2
A. x  2   y  2  8
B. x  2   y  2 16 2 2 2 2
C. x  2   y  2 16 D. x   1   y   1  8 Lời giải: Chọn B Gọi M  ;
x yC. Qua phép vi tự tâm O tỉ số k  2 biến đường tròn C thành đường
tròn C thì điềm M  ;
x y  bicn thành M  x ; y Khi đó, ta có   xx
x  kx  2
OM   k.OM     y  ky y  y    2 Và  ;
x y C  nên 2 2         2    2 x yx y           
x 2  y 2 1 1 4 1 1 4 2 2 16  2   2  2 2
Vậy phương trình đường tròn cần tìm là  x  2   y  2 16 .
Câu 14. Cho tam giác ABC có trọng tâm G . Gọi A , B , C lần lượt là trung điểm các cạnh BC ,
CA , AB . Khi đó phép vị tự nào sau đây biến tam giác A BC
  thành tam giác ABC ? 1
A. Phép vị tự tâm G , tỉ số 2 .
B. Phép vị tự tâm G , tỉ số  . 2 1
C. Phép vị tự tâm G , tỉ số .
D. Phép vị tự tâm A , tỉ số 2  . 2 Lời giải: Chọn D Ta có GA  2
GA ; GB  2
GB ; GC  2  GC . Từ đó suy ra V A  B C    ABCG , 2   .   Trang 51 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Câu 15. Cho tam giác ABC có B,C cố định, đỉnh A chạy trên một đường tròn ( ;
O R) cố định không
có điểm chung với đường thẳng BC và G là trọng tâm tam giác ABC . Khi đó, quỹ tích trọng
tâm G là ảnh của đường tròn  ;
O R qua phép biến hình nào sau đây?
A. Phép tịnh tiến theo vectơ BC .
B. Phép vị tự tâm I tỉ số k  3, trong đó I là trung điểm của BC . 1
C. Phép vì tự tâm I tỉ số k  , trong đó I là trung điểm của BC . 3 1
D. Phép tịnh tiến theo v IA 3 Lời giải: Chọn C 1
Gọi I là trung điểm của BC , khi đó I cố định. Ta có IG
IA suy ra G là ảnh của A qua 3 1
phép vị tự tâm I tỉ số k  . Mà A thuộc đường tròn  ;
O R nên G thuộc đường tròn 3  1 O ;
R là ảnh của đường tròn  ;
O R qua phép vị tự tâm I tỉ số k . 3
------------------HẾT------------------ Trang 52 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
§7. PHÉP ĐỒNG DẠNG I. ĐỊNH NGHĨA:
– Phép biến hình F được gọi là phép đồng dạng tỉ số k k  0 nếu với hai điểm M, N bất kì
và ảnh M', N ' tương ứng của chúng ta luôn có M' N'  kM . N Nhận xét
 Phép dời hình là phép đồng dạng tỉ số 1.
 Phép vị tự tỉ số k là phép đồng dạng tỉ số k .
 Nếu thưc hiện liên tiếp các phép đồng dạng ta được một phép đồng dạng. II. TÍNH CHẤT:
Phép đồng dạng tỉ số k :
– Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy;
– Biến đường thẳng thành đường thẳng.
Tính chất: – Biến tia thành tia, biến đoạn thẳng thành đọan thẳng.
– Biến tam giác thành tam giác đồng dạng với nó.
– Biến góc thành góc bằng nó;
– Biến đường tròn bán kính R thành đường tròn bán kính k . R
III. KHÁI NIỆM HAI HÌNH ĐỒNG DẠNG:
– Hai hình được gọi là đồng dạng với nhau nếu có một phép đồng dạng biến hình này thành hình kia. IV. BÀI TẬP:
4.1. Tự Luận.
Bài toán xác định ảnh trong hệ tọa độ qua Phép Đồng Dạng Phương pháp:
Sử dụng định nghĩa, tính chất của phép đồng dạng. Trang 53 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG Bài 01.
Trong mặt phẳng Oxy , cho đường thẳng d có phương trình x y  2  0 . Viết phương trình
đường thẳng d là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp 1
phép vị tự tâm I  1  ;  1 tỉ số k
và phép quay tâm O góc 45   2 Lời giải 1 Gọi d d I  1  ;  1 k  1 là ảnh của qua phép vị tự tâm tỉ số . 2 Vì d d
x y c  0
1 song song hoặc trùng với
nên phương trình có dạng . Lấy M 1;  1  d .  1 x 1  1  1 1  Gọi 2
M  x ; y  V M IM   IM    M 0;0  d 1    thuộc 1 . I ;   2 1  2 
y 1 1 1  2 Vậy phương trình d x y  0 1 là . Ảnh của d O 45  
1 (đường phân giác góc phần tư thứ hai) qua phép quay tâm góc
là đường thẳng Oy .
Vậy phương trình của d là x  0 . Bài 02.
Trong mặt phẳng tọa độ 2 2
Oxy , cho đường tròn C :  x  
1   y  2  9 . Ảnh của đường tròn
C qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm I 1;   1 , tỉ 1
số k  và phép tịnh tiến theo véc-tơ v  3; 4 có phương trình là 3 Lời giải
Gọi M 1; 2 ; R  3 là tâm và bán kính đường tròn C . 1 V
M O  IO 
IM O1; 0 I ; k     . 3
Phép vị tự biến đường tròn tâm M thành đường tròn tâm O 1
bán kính R  R  1. 3
T O  O  O 4; 4 . v
Phép tịnh tiến theo véc-tơ v biến đường tròn tâm O bán kính R thành đường tròn
tâm O bán kính R  R  1.
Vậy phương trình đường tròn ảnh:  x  2   y  2 4 4 1. Bài 03.
Trong mặt phẳng tọa độ 2 2
Oxy , cho đường tròn C :  x  2   y  
1  9 . Gọi C là ảnh của
đường tròn C qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm Trang 54 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG 1
O , tỉ số k   và phép tịnh tiến theo véc-tơ v   1
 ; 3 . Tìm bán kính R của đường tròn 3 C . Lời giải
Đường tròn C có bán kính R  3. 1 Gọi CCO k   C
1  là ảnh của đường tròn
qua phép vị tự tâm , tỉ số , ta có là 3 ảnh của C v   1  ; 3
1  qua phép tịnh tiến theo véc-tơ . 1
Khi đó đường tròn C
R k R  .3  1 C 1  có bán kính 1 và đường tròn có bán kính 3
R  R  1. Bài 04.
Trong mặt phẳng với hệ trục tọa độ Oxy cho đường tròn C  2 2
: x y  2x  2 y  2  0 1 và C  2 2
: x y 12x 16 y  0 F kCC k 2  1  2 . Phép đồng dạng tỉ số biến thành . Tìm . Lời giải Ta có  2 2 C  2 2
: x y  2x  2 y  2  0   x     y   2 1 1  2 1 Suy ra  2 2 C
R  2 C : x y 12x 16y  0   x     y   2 6 8 10 2  2 2 1  có bán kính 1 . R Suy ra C R  10 2 k   5 2  có bán kính 2 . Do đó . R1 Bài 05.
Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình x y  2  0 . Viết
phương trình đường thẳng d là ảnh của d qua phép đồng dạng có được bằng cách thực 1
hiện liên tiếp phép vị tự tâm I  1  ; 
1 tỉ số k  và phép quay tâm O góc 45   . 2 Lời giải Xét điểm A1; 
1 và B 2;0 nằm trên đường thẳng d .
Qua phép vị tự tâm I  1  ; 
1 điêm A biến thành điểm 
A với tọa độ thỏa mãn 
x   x   A  1 1  A 1  2  . Vậy  A 0;0 . 
y   y   A  1 1  A 1  2
Qua phép quay tâm O góc 45   , điểm 
A biến thành điểm  A 0;0 .
Qua phép vị tự tâm I  1  ; 
1 điểm B biến thành điểm B với tọa độ thỏa mãn 
x   x B  1 1  B 1  2   1 1  . Vậy B ;    .    2 2  y   y B  1 1  B 1  2 Trang 55 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
Qua phép quay tâm O góc 45
  , biến điểm B thanh điểm B với tọa độ thỏa mãn x    x     y   B
cos  45 . B sin  45 . B 2 
. Vậy B 0;   .    y    x     y 2   B
sin  45 . B cos 45 . B
Do đó đường thẳng d biến thành đường thẳng 
A B có phương trình x  0 .
4.2. Trắc nghiệm.
Câu 1. Mệnh đề nào sau đây là sai?
A. Phép dời hình là phép đồng dạng.
B. Phép vị tự là phép đồng dạng.
C. Phép đồng dạng là phép dời hình.
D. Phép vị tự không phải là phép dời hình. Lời giải: Chọn C
Khi k 1 thì phép đồng dạng không là phép dời hình.
Câu 2. Mệnh đề nào sau đây là sai?
A. Hai đường thẳng bất kì luôn đồng dạng. B. Hai đường tròn bất kì luôn đồng dạng.
C. Hai hình vuông bất kì luôn đồng dạng. D. Hai hình chữ nhật bất kì luôn đồng dạng. Lời giải: Chọn D
Ví dụ hình chữ nhật ABCD có AB  2, AD  4 và hình chữ nhật MNPQ có MN  3, MQ  5 MN kAB
khi đó không tồn tại số thực k để thỏa mãn  . MQ kAD
Câu 3. Cho tam giác ABC và A BC
  đồng dạng với nhau theo tỉ số k . Mệnh để nào sau đây là sai?
A. k là tỉ số hai trung tuyến tương ứng.
B. k là tỉ số hai đường cao tương ứng.
C. k là tỉ số hai góc tương ứng.
D. k là tỉ số hai bán kính đường tròn ngoại tiếp tương ứng. Lời giải: Chọn C
Vì hai tam giác đồng dạng thì các góc tương ứng bằng nhau.
Câu 4. Mọi phép dời hình cũng là phép đồng dạng với tỉ số k bằng A. k 1. B. k  1  . C. k  0 . D. k  2 . Lời giải: Chọn A
Tính chất: Phép dời hình là phép đồng dạng tỉ số k 1 .
Câu 5. Mệnh đề nào sau dây là sai?
A. Phép dời hình là phép đồng dạng tỉ số k 1 .
B. Phép đồng dạng biến đường thẳng thành đường thẳng song song hoặc trùng với nó. Trang 56 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
C. Phép vị tự tỉ số k là phép đồng dạng tỉ số k .
D. Phép đồng dạng bảo toàn độ lớn góc. Lời giải: Chọn B
Phép đồng dạng biến đường thẳng thành đường thẳng song song hoặc trùng với nó hoặc cắt nó.
Câu 6. Trong mặt phẳng Oxy , cho điểm M 2; 4 . Phép đồng dạng có được bằng cách thực hiện liên 1
tiếp phép vị tự tâm O tỉ số k
và phép đối xứng qua trục Oy sẽ biến điểm M thành điểm 2 nào sau đây. A. 1; 2 . B.  2  ;4 . C.  1  ;2 . D. 1; 2   . Lời giải: Chọn C x 1
Gọi M  x ; y  V M ; x y   M 1;2   1     O;   y  2  2 
Gọi M   x ; y   D M Oy    M    1  ;2.
Câu 7. Trong mặt phẳng Oxy , cho đường thẳng d có phương trình x y  2  0 . Viết phương trình
đường thẳng d là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp 1
phép vị tự tâm I  1  ;  1 tỉ số k
và phép quay tâm O góc 45   2 A. y  0 . B. x  0 .
C. y x .
D. y  x . Lời giải: Chọn B 1 Gọi d d I  1  ;  1 k  1 là ảnh của qua phép vị tự tâm tỉ số . 2 Vì d d
x y c  0
1 song song hoặc trùng với
nên phương trình có dạng . Lấy M 1;  1  d .  1 x 1  1  1 1  2
Gọi M  x ; y  V M IM   IM    M 0;0 d  1    thuộc 1 . I ;   2 1  2 
y 1 1 1  2 Vậy phương trình d x y  0 1 là . Ảnh của d O 45  
1 (đường phân giác góc phần tư thứ hai) qua phép quay tâm góc là đường thẳng Oy .
Vậy phương trình của d là x  0 . Trang 57 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG 2 2
Câu 8. Trong mặt phẳng Oxy , cho đường tròn C có phương trình  x  2   y  2  4 . Phép đồng 1
dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k  và phép quay tâm 2
O góc 90 sẽ biến C thành đường tròn nào sau đây? 2 2 2 2
A. x  2   y  2 1. B. x   1   y   1  1 . 2 2 2 2
C. x  2   y   1  1 . D. x   1   y   1  1 . Lời giải: Chọn D
Đường tròn C có tâm I 2;2 và bán kính R  2 . 1
Suy ra phép vị tự tâm O tỉ số k
biến C thành đường tròn C có tâm I1  ;1 , bán 2 kính R  1. Phép quay Q
biến C thành C có tâm I 1  ; 
1 , bán kính R  R  1. O;90 2 2
Vậy phương trình đường tròn C là:  x   1   y   1  1 . 1
Câu 9. Trong mặt phẳng Oxy , cho hai điểm A 2  ; 3  , B4; 
1 . Phép đồng dạng tỉ số k  biến điểm 2
A thành A , biến B thành B . Tính độ dài ABA. A B    13 . B. A B    5 2 2 13 .
C. AB  . D. A B    5 2 . 2 Lời giải: Chọn A 1
Phép đồng dạng tỉ số k
biến điểm A thành A , biến B thành B thì 2 1 1 AB  AB
4 22  132  13 . 2 2
Câu 10. Trong mặt phẳng Oxy , cho hai đường tròn C và C có phương trình 2 2
x y  4 y  5  0 và 2 2 x y  2
x  2y 14  0 . Gọi C ' là ảnh của C qua phép đồng dạng tỉ số k , khi đó giá trị của k là 4 3 9 16 A. . B. . C. . D. . 3 4 16 9 Lời giải: Chọn A
Đường tròn C có bán kính R  3 , đường tròn C có bán kính R  4 . R 4
Suy ra tỉ số đồng dạng k   . R 3 Trang 58 LÊ MINH TÂM
PHÉP DỜI HÌNH & PHÉP ĐỒNG DẠNG
------------------HẾT------------------ Trang 59 LÊ MINH TÂM