Preview text:
Chuyên Đề Bồi Dưỡng Học Sinh Giỏi PHÉP NGHỊCH ĐẢO
Lê Anh Dũng. Giáo viên trường THPT Chuyên Huỳnh Mẫn Đạt, Kiên Giang.
Ngoài phép đồng dạng biến đường thẳng thành đường thẳng, đường tròn thành
đường tròn, còn một phép biến hình khác với những tính chất rất thú vị. Đó là phép
nghịch đảo. Phép nghịch đảo cũng có thể biến đường thẳng thành đường thẳng, đường
tròn thành đường tròn, nhưng có thể biến một đường thẳng thành một đường tròn, còn
một đường tròn thành một đường thẳng. Đặc biệt hơn là nó bảo toàn góc giữa hai hình.
Như vậy, phép nghịch đảo là một công cụ mạnh để chuyển các bài toán sang một mô
hình khác mà ở đó các đối tượng dễ khảo sát hơn. Ngoài ra nó cũng là một công cụ mạnh
để phát hiện các tính chất hình học thông qua phép nghịch đảo và vì vậy trong các năm
gần đây, cùng với phép vị tự quay, phép nghịch đảo được khai thác rất nhiều trong các đề
thi học sinh giỏi các nước. I. ĐỊNH NGHĨA
Phép nghịch đảo tâm O, phương tích k là quy tắc biến mỗi điểm A khác O thành A' sao cho O . A OA' k . Hay k N ( A) A ' O . A OA ' k O O A A' Rõ ràng, k N ( ) A A' thì k N (A') A O O
II. TÍNH CHẤT PHÉP NGHỊCH ĐẢO k N O
Tính chất 1. Phép nghịch đảo k
N , biến A thành A’ ; B thành B’ thì hai tam giác OAB O k
đồng dạng tam giác OA’B’. Đồng thời A'B ' .AB ; OA'B' OBA. O . AOB B B' O A' A
Trường THPT Chuyên Huỳnh Mẫn Đạt. Giáo viên Lê Anh Dũng T r a n g | 1
Chuyên Đề Bồi Dưỡng Học Sinh Giỏi
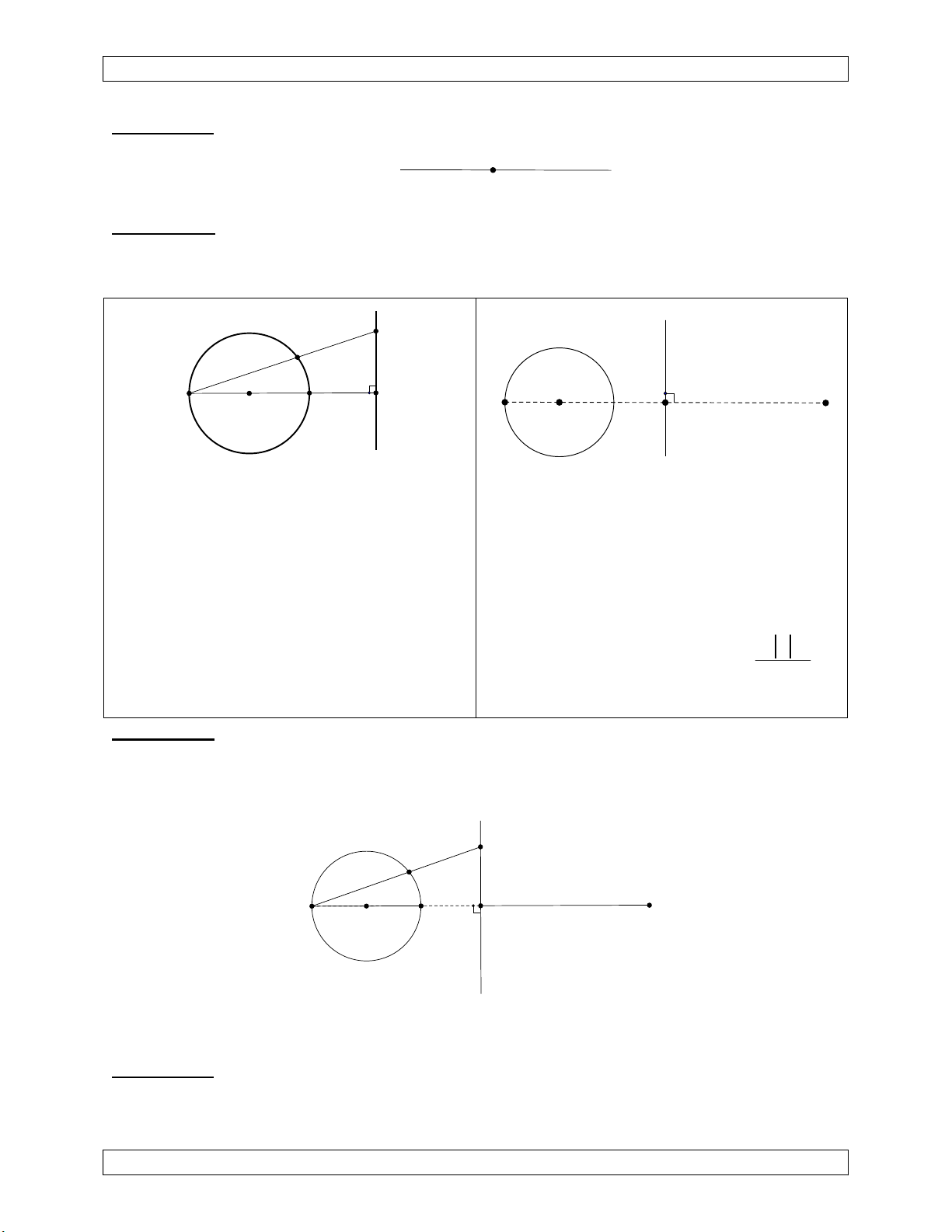
Tính chất 2. Qua phép nghịch đảo tâm O biến đường thẳng qua tâm O thành chính nó d'≡d O
Tính chất 3. Qua phép nghịch đảo tâm O biến đường thẳng d không đi qua tâm O thành
đường tròn đi qua tâm O. Với các tính chất sau: d M M' O A' A I' O I' I d
I đối xứng với O qua d; I' là ảnh của I
i) Đường thẳng nối tâm O và tâm đường
tròn thì vuông góc với đường thẳng d.
iii) Tâm đường tròn I’ : là ảnh của I qua
ii) Đường kính O A ' của đường tròn ảnh: A’ phép nghịch đảo, trong đó I đối xứng với
là ảnh của A qua phép nghịch đảo, trong đó tâm O qua đường thẳng d.
A là hình chiếu của tâm nghịch đảo O trên k đường thẳng d.
iv) Bán kính của đường tròn: r 2d(O,d)
(Ảnh của A là A'; Ảnh của M là M')
Tính chất 4. Qua phép nghịch đảo tâm O, đường tròn qua tâm O biến thành đường thẳng
vuông góc với đường nối tâm O và tâm đường tròn. ảnh của (I) A A' O I I'
Tâm I biến thành I’ đối xứng với O qua l với l là ảnh của (I).
Tính chất 5. Ảnh của một đường tròn không đi qua tâm nghịch đảo là một đường tròn.
Trường THPT Chuyên Huỳnh Mẫn Đạt. Giáo viên Lê Anh Dũng T r a n g | 2
Chuyên Đề Bồi Dưỡng Học Sinh Giỏi A' B' O A B Tính chất:
i) A biến thành A’ ; B biến thành B’ (Ảnh của tâm đường tròn này không là tâm đường tròn kia). k
ii) (C') là ảnh của (C) qua k
N thì (C') là ảnh của (C) qua phép vị tự tâm O, tỉ số . O PO,(C)
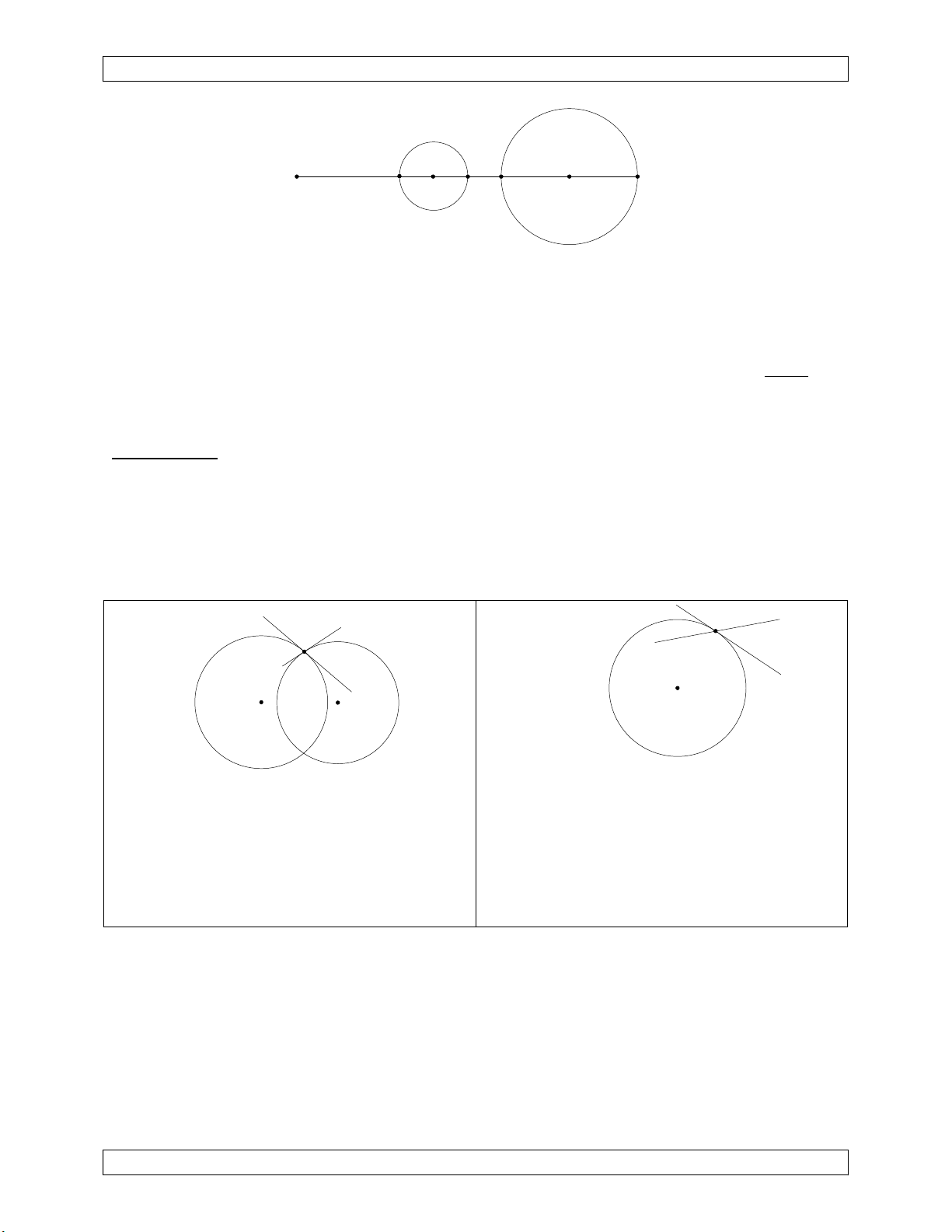
Tính chất 6. Qua phép nghịch đảo, góc định hướng giữa hai đường tròn; góc giữa hai
đường thẳng ; góc giữa đường thẳng và đường tròn không thay đổi về độ lớn nhưng thay đổi về hướng.
Nhắc lại khái niệm góc giữa hai đường tròn; góc giữa đường thẳng và đường tròn: d2 d d1 d' O O2 O1
Góc giữa hai đường tròn (C1), (C2) là góc Góc giữa đường thẳng d và đường tròn (C)
giữa d , d với d , d lần lượt là tiếp tuyến là góc giữa d ' với d trong đó d ' là tiếp 1 2 1 2 với (C
tuyến với (C) tại giao điểm của d và (C).
1), (C2) tại giao điểm của hai đường
tròn này. Hay, (C ),(C ) d ,d (C ),(C ) d ,d 1 2 1 2 1 2 1 2
Trong một bài toán hình học thì dấu hiệu nào cho ta biết sử dụng phép nghịch
đảo? Tâm phép nghịch đảo nằm ở đâu, ảnh của các đối tượng dựng như thế nào? Chúng
ta sẽ tìm hiểu dần thông qua một số bài tập rèn luyện từng kĩ năng sau:
III. LUYỆN TẬP KĨ NĂNG DỰNG ẢNH 1) Kĩ năng 1:
Trường THPT Chuyên Huỳnh Mẫn Đạt. Giáo viên Lê Anh Dũng T r a n g | 3
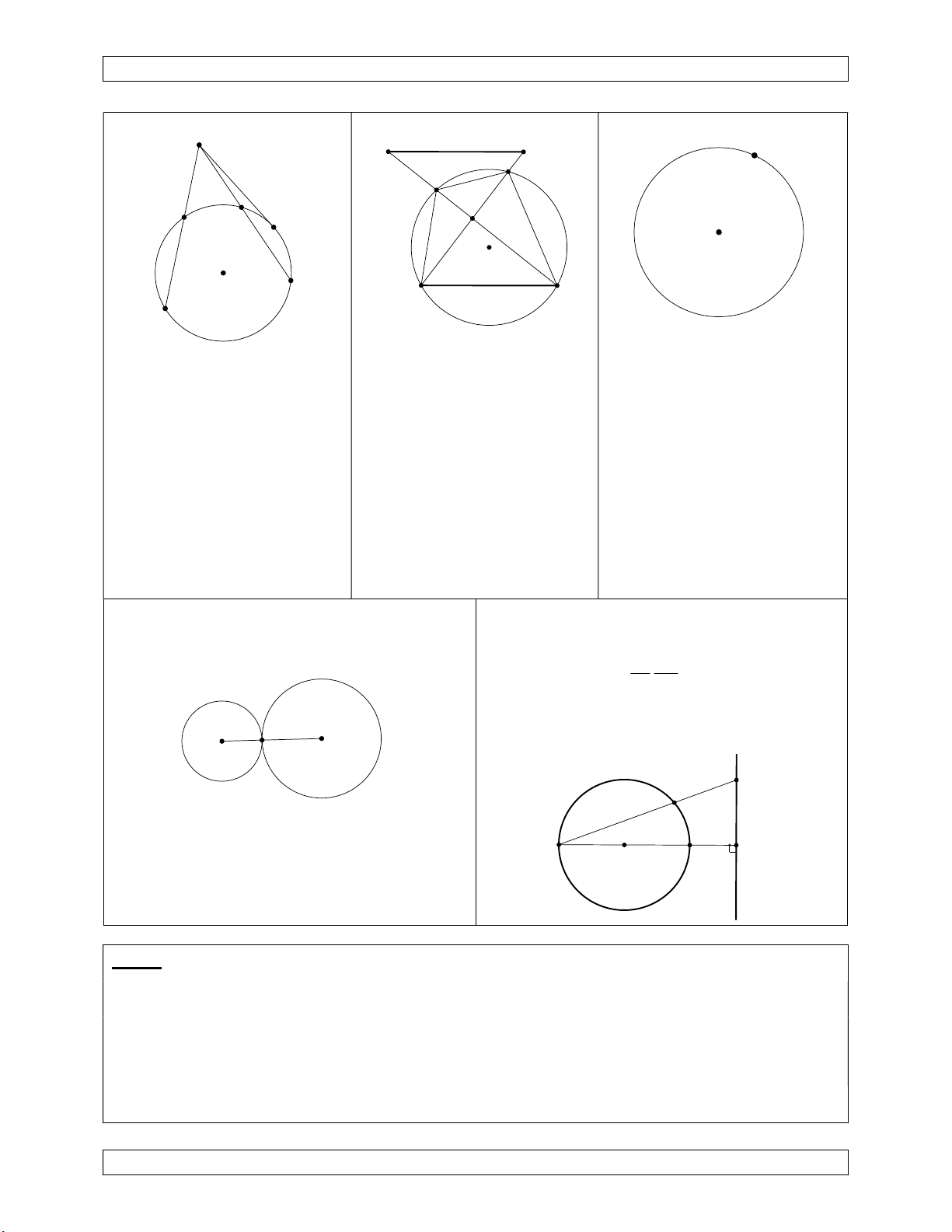
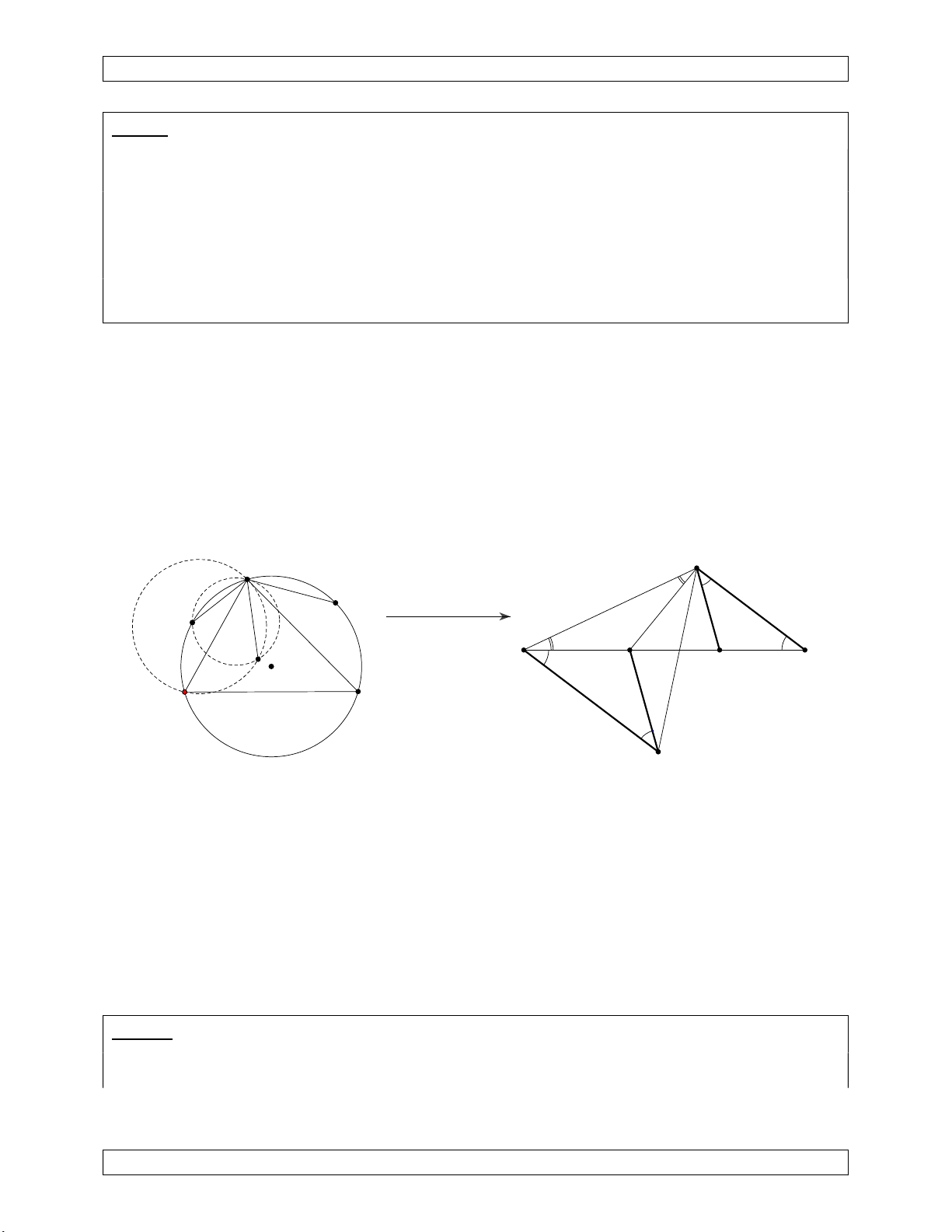
Chuyên Đề Bồi Dưỡng Học Sinh Giỏi I B' A' A A B A B P D O O B' C D A'
1) Phép nghịch đảo tâm I, Qua phép nghịch đảo tâm P, 2) Phép nghịch đảo tâm O phương tích k P . I /(O) phương tích k P
thì (cũng là tâm của đường P,(O)
Đường tròn (O) giữ nguyên. ảnh của B là B’ ; ảnh của C tròn), phương tích 2 k R .
Điểm A biến thành A'; B là B’ mà đường thẳng A'B' Mọi điểm trên đườn tròn biến thành B'. song song với CD. biến thành chính nó.
Đường thẳng AB biến thành đường tròn (IA'B').
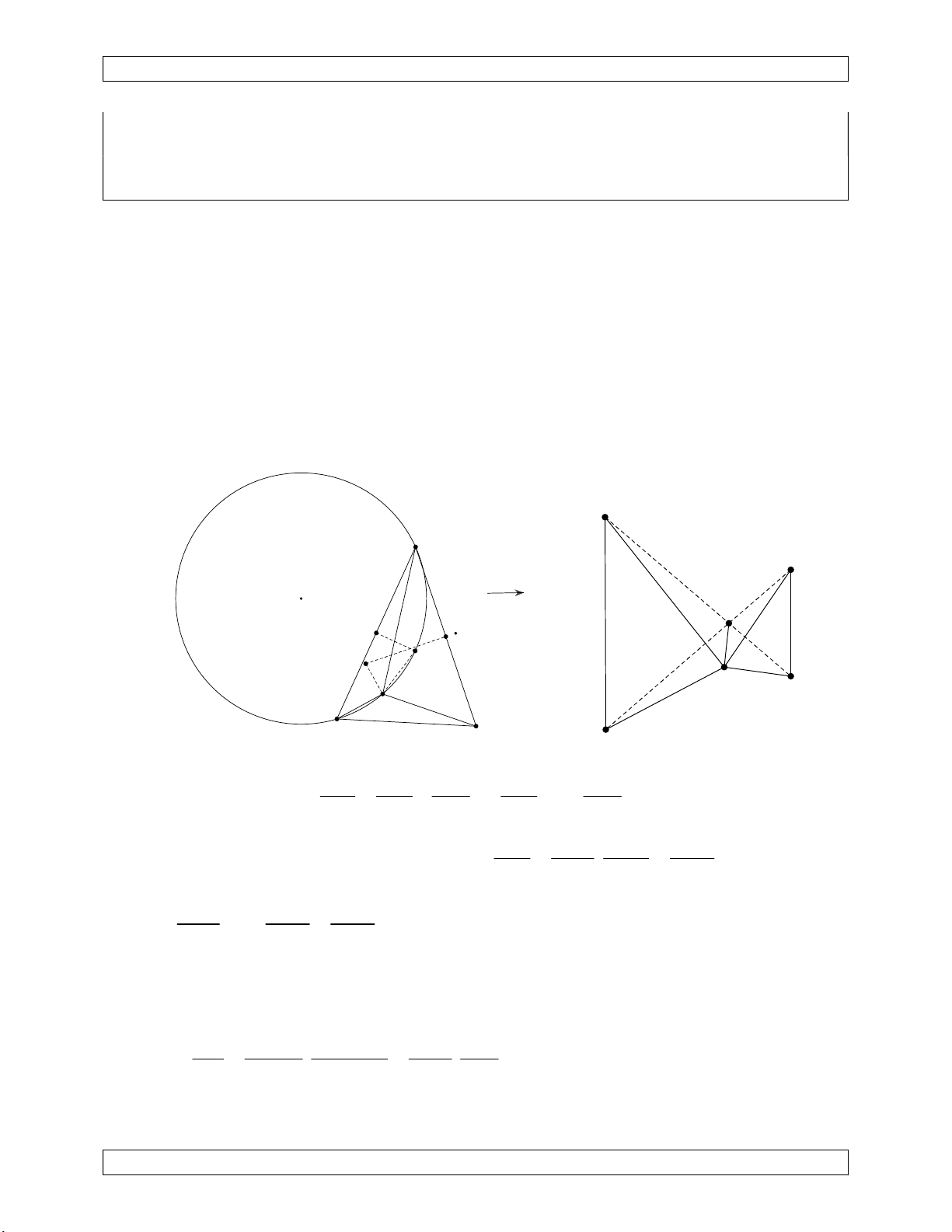
3) Phép nghịch đảo có tâm là giao điểm 4) Phép nghịch đảo tâm I (điểm thuộc của các đường.
đường kính vuông góc với đường thẳng d)
phương tích k IB.IH biến (C) thành d
(giữ nguyên hình gồm (C) và d). O A' A
Ảnh của hai đường tròn tiếp xúc tại O qua
phép nghịch đảo tâm O là hai đường thẳng I H B O song song. (C) d
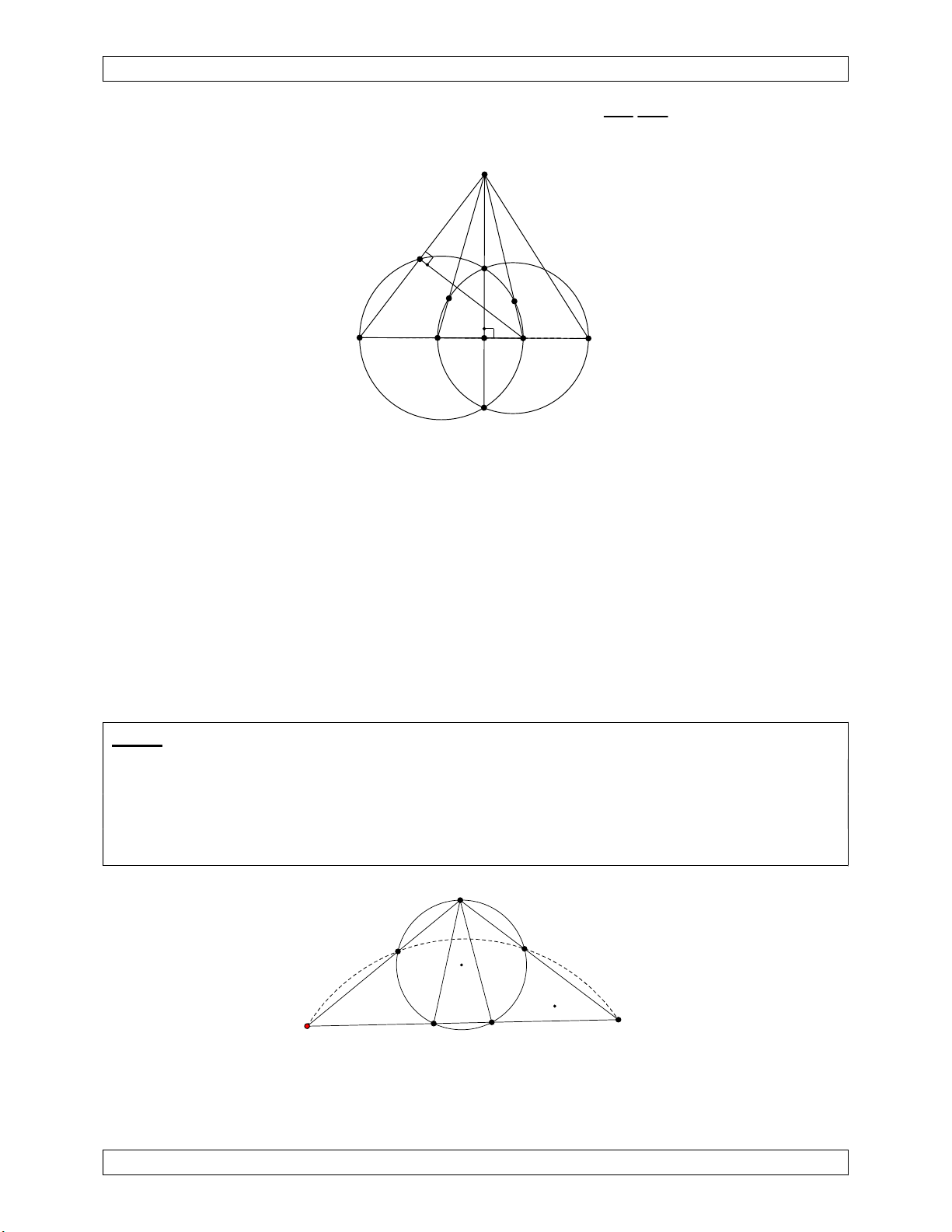
Bài 1. (IMO Shortlist 1995) Cho A, B, C, D là bốn điểm phân biệt trên một đường thẳng
theo thứ tự đó. Các đường tròn đường kính AC, BD cắt nhau tại X, Y. Đường thẳng XY cắt
CB tại Z. Gọi P là đường thẳng trên XY khác Z. Đường thẳng CP cắt đường tròn đường
kính AC tại C và M, đường thẳng BP cắt đường tròn đường kính BD tại B và N. Chứng
minh rằng AM, DN, XY đồng quy.
Trường THPT Chuyên Huỳnh Mẫn Đạt. Giáo viên Lê Anh Dũng T r a n g | 4
Chuyên Đề Bồi Dưỡng Học Sinh Giỏi
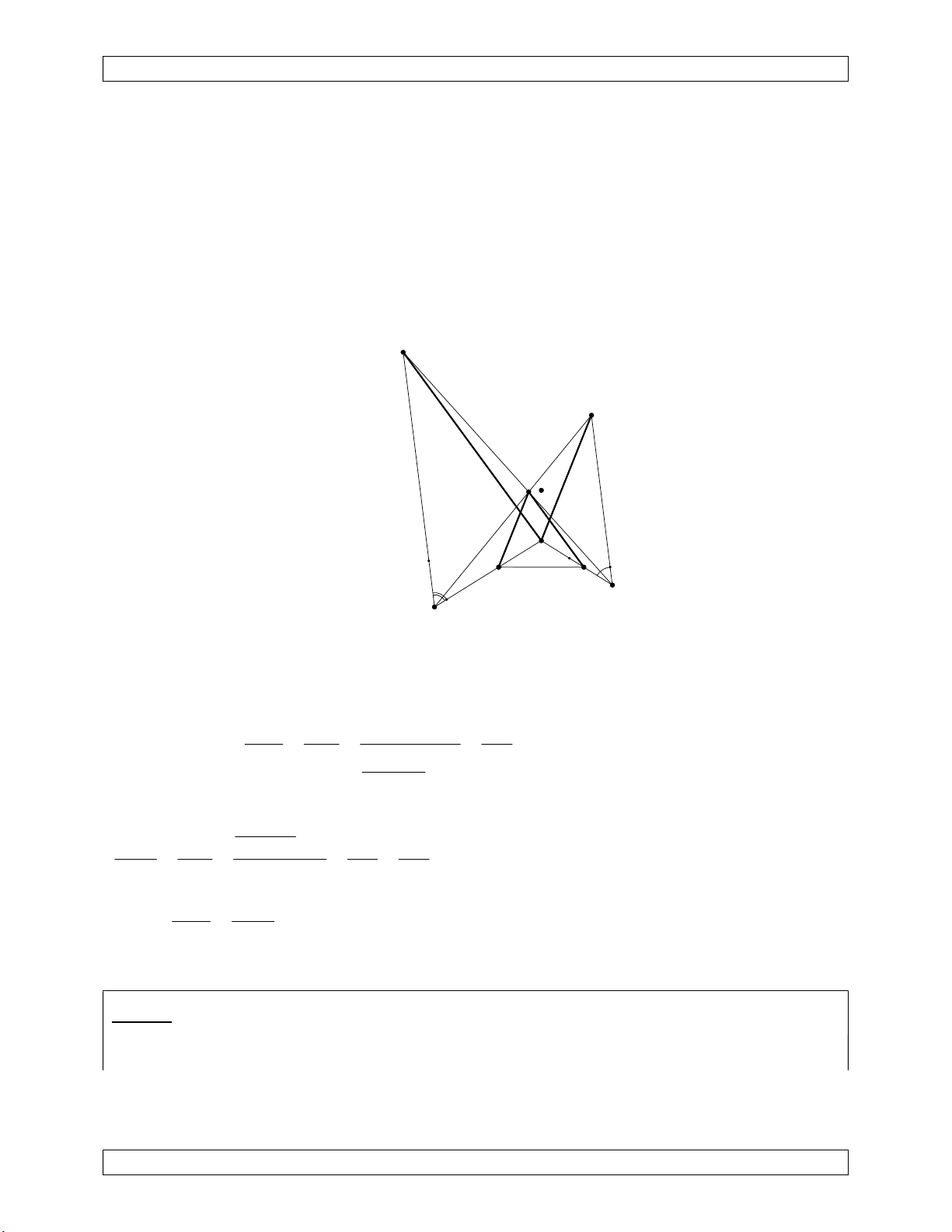
Xét phép nghịch đảo có tâm P, phương tích là k PX.PY . P A' X N M A D B Z C Y
Gọi A' là giao điểm của PA với đường tròn đường kính AC. Qua thì:
+ Ảnh của A là A'; ảnh của M là C. Do đó ảnh của AM là đường tròn (PA'C).
Mặt khác, do AC là đường kính nên 0 CA'P 90 PZC nên (PA'C) đi qua Z.
+ Tương tự, ảnh của DN cũng là một đường tròn đi qua Z.
Ảnh của XY đi qua tâm nghịch đảo P là đường thẳng XY đi qua Z.
+ Ảnh của 3 đường thẳng AM, DN, XY có một điểm chung Z khác tâm nghịch đảo P nên
các đường thẳng AM, DN, XY đồng quy. (đpcm).
Bài 2. (Thổ Nhĩ Kì TST 2015) Cho tam giác ABC cân tại A ngoại tiếp đường tròn (O).
Gọi D, E lần lượt là điểm chính giữa cung AC, AB. Đường thẳng AD và BC cắt nhau tại
F; đường thẳng AE cắt đường tròn ngoại tiếp tam giác DEF tại G. Chứng minh rằng
đường thẳng AC là tiếp tuyến của đường tròn ngoại tiếp tam giác ECG. A E D G F B C Xét phép nghịch đảo 2 AB N
. Qua phép nghịch đảo này thì B, C cố định; (ABC) biến thành A
Trường THPT Chuyên Huỳnh Mẫn Đạt. Giáo viên Lê Anh Dũng T r a n g | 5
Chuyên Đề Bồi Dưỡng Học Sinh Giỏi
BC; do đó ảnh của D là F; ảnh của E là giao điểm Q ' của AE và BC.
Do tính chất ảnh, suy ra FDEG’ nội tiếp. Suy ra G ' G . Theo định nghĩa, ta có 2 2
AE.AG AB AC . Suy ra AC là tiếp tuyến của (CEG).(đpcm).
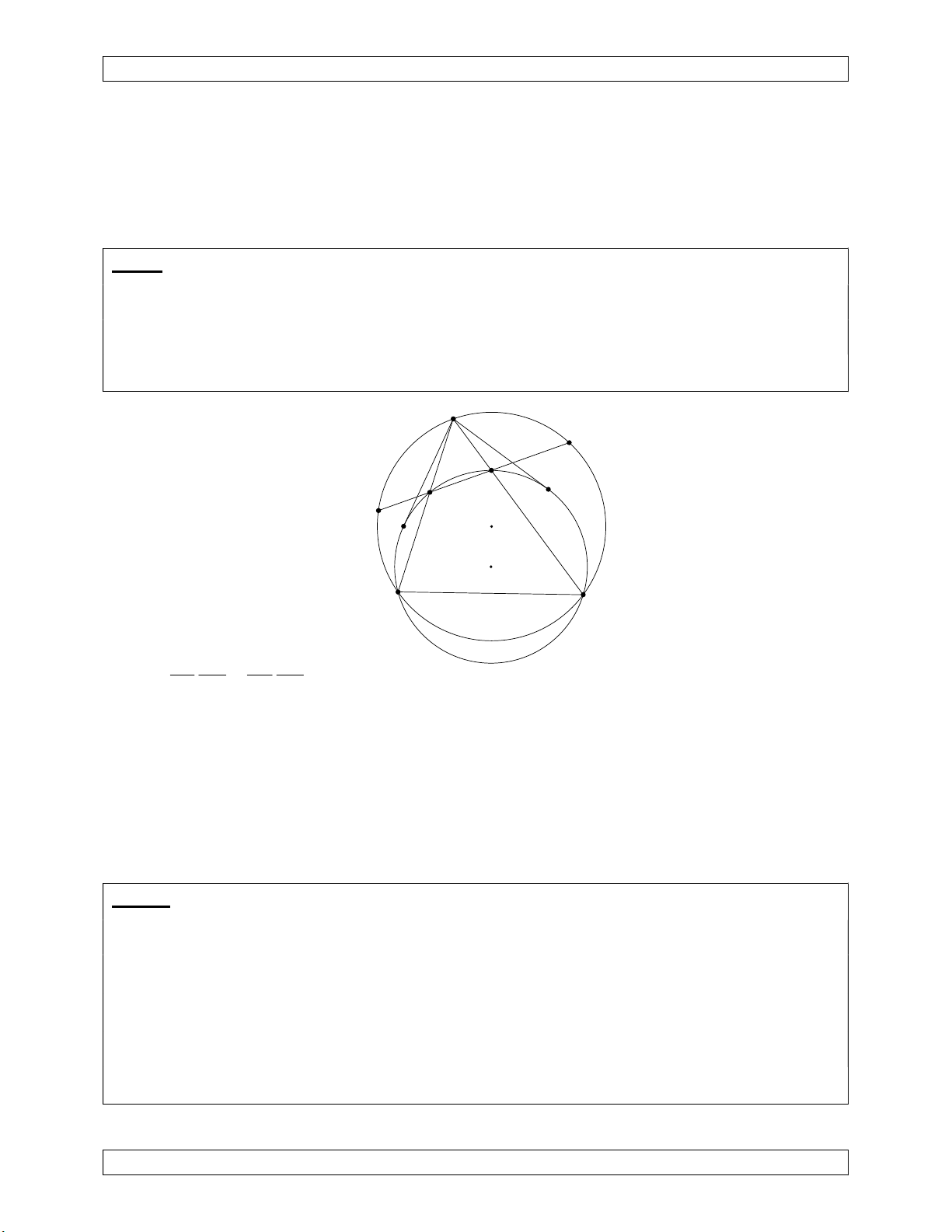
Bài 3.(Centro American Math Olympiad) Cho tứ giác nội tiếp ABCD với AB < CD. P
là giao điểm của AD và BC. Đường tròn ngoại tiếp tam giác PCD cắt đường thẳng AB tại
các điểm Q và R. Gọi S, T là các tiếp điểm của các tiếp tuyến kẻ từ P đến (ABCD). Chứng
minh rằng Q, R, S, T cùng nằm trên đường tròn. P R A T B Q S C D Ta có, 2 2 P .
A PD PB.PC PS PT = k Xét phép nghịch đảo k
N . Qua phép này ảnh của C là B; ảnh của D là A; S, T giữ nguyên. P
Ảnh của (PCD) là đường thẳng AB. Suy ra ảnh của các giao điểm của AB và (PCD) là chính nó. Vậy 2 2 2 2
PQ PR PS PT k .
Suy ra Q, R, S, T cùng nằm trên đường tròn tâm P. (đpcm).
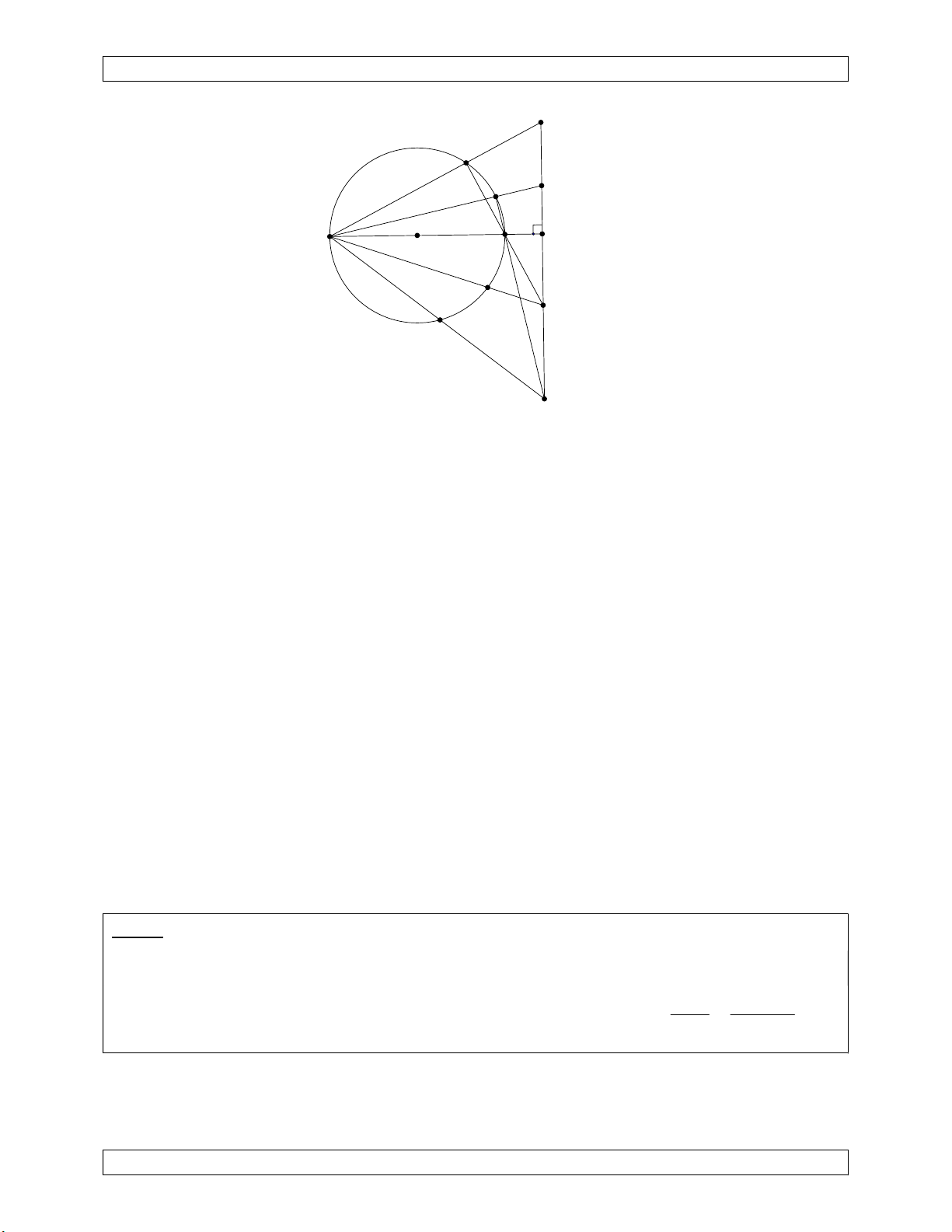
Bài 4. (TST Hồng Kông 2016) Cho (T) là đường tròn đường kính AB. L là một đường
thẳng không có điểm chung với đường tròn và vuông góc với AB. Gọi X, Y là hai điểm
trên l. Nếu X ',Y ' là hai điểm trên l sao cho AX , BX ' cắt nhau tại một điểm trên (T) và
AY,BY ' cắt nhau tại một điểm trên (T). Chứng minh rằng đường tròn ngoại tiếp tam giác
AXY và AX 'Y ' cắt nhau tại một điểm trên (T) khác A hoặc ba đường tròn này tiếp xúc nhau tại A.
Trường THPT Chuyên Huỳnh Mẫn Đạt. Giáo viên Lê Anh Dũng T r a n g | 6
Chuyên Đề Bồi Dưỡng Học Sinh Giỏi X U Y V A H B M X' N Y'
Đặt AX BX ' U ; V AY BY ' .
AX ', AY ' lần lượt cắt (T) tại điểm thứ hai N, M.
Mô hình này là mô hình ảnh của đường tròn, đường thẳng qua phép nghịch đảo. Có 2
phép nghịch đảo tâm A, B biến (T) thành l. Do đó, suy ra ngay U, V, X, Y; U, V, X’, Y’;
M, N, Y’, X’ . . . cùng nằm trên đường tròn.
Xét phép nghịch đảo tâm A biến B thành H.
Khi đó ảnh của (T) là đường thẳng l; ảnh của (AXY) là đường thẳng UV; ảnh của (AXY) là đường thẳng MN.
Ta chứng minh UV, MN và X’Y’ liên hợp (song song hoặc đồng quy). Điều này là đúng vì
UV, MN , X’Y’ là trục đẳng phương của (T) và hai đường tròn (UVX’Y’), (MNX’Y’). (đpcm).
Một trong những tác dụng mạnh của phép nghịch đảo là chuyển mô hình bài toán
qua các bài toán khác với hình đơn giản hơn nhiều. Ta xét các bài toán sau:
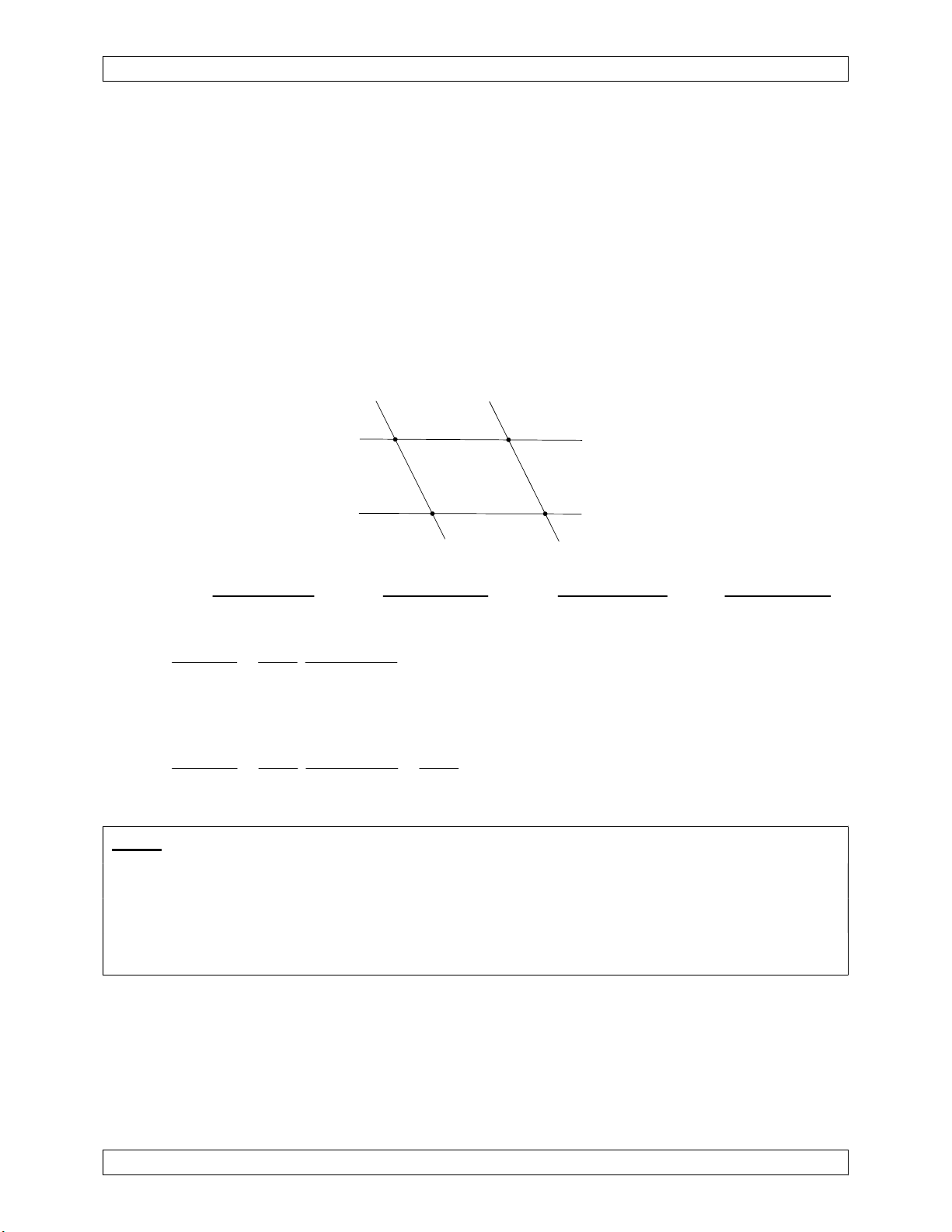
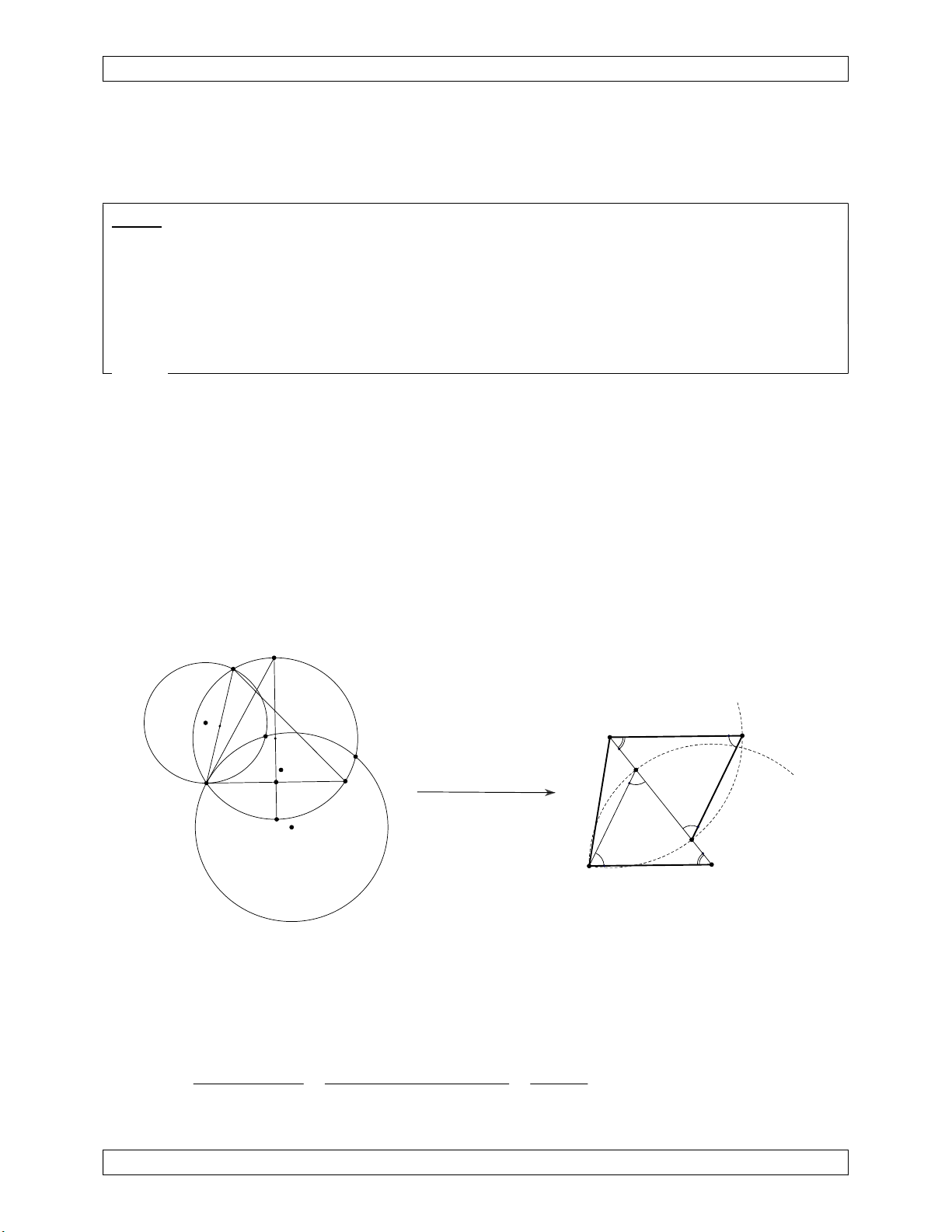
Bài 5. (IMO shortlist 2003) Cho 4 đường tròn (O1), (O2), (O3), (O4) sao cho (O1) tiếp
xúc ngoài với (O3) tại P; (O2) tiếp xúc ngoài với (O4) tại P. Giả sử (O1) và (O2) ; (O2) và 2 PB A . B BC
(O3); (O3) và (O4); (O4) và (O1) cắt nhau tại A, B, C, D. Chứng minh . 2 PD A . D DC
- Ta dùng phép nghịch đảo để chuyển mô hình từ nhiều đường tròn phức tạp sang mô
hình mới đơn giản hơn.
Trường THPT Chuyên Huỳnh Mẫn Đạt. Giáo viên Lê Anh Dũng T r a n g | 7
Chuyên Đề Bồi Dưỡng Học Sinh Giỏi
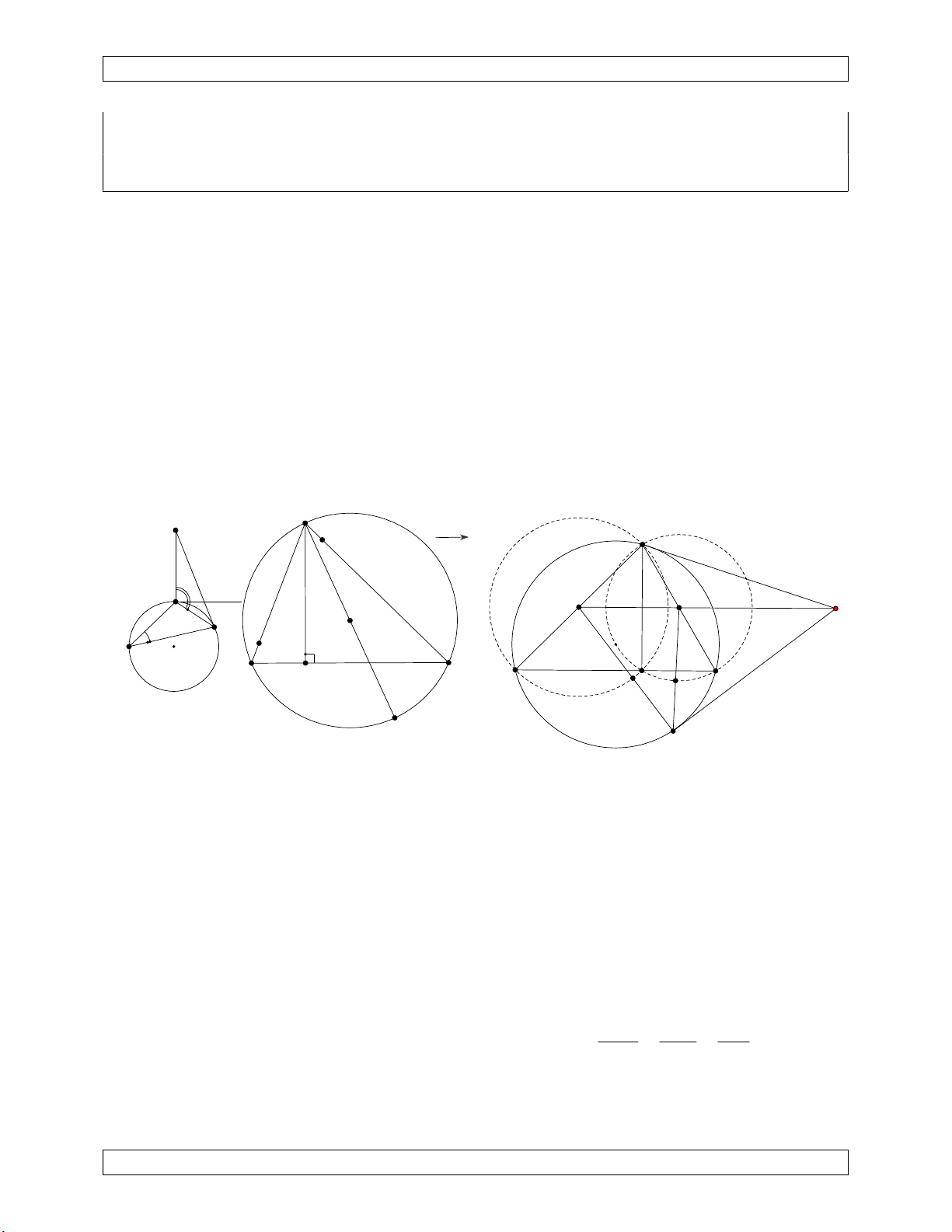
- Vì P là điểm chung của các đường tròn nên ta chọn P là tâm nghịch đảo. Xét phép nghịch đảo k N ( k 0 ). Qua k N các đường tròn (O P P 1), (O2), (O3), (O4)
lần lượt biến thành các đường thẳng d , d , d , d . 1 2 3 4
Do (O1) tiếp xúc ngoài với (O3) tại P nên d song song với d . 1 3
Do (O2) tiếp xúc ngoài với (O4) tại P nên d song song với d . 2 4 Qua k
N , A là giao của (O ),(O ) biến thành A' d d . P 1 2 1 2
Tương tự ảnh của B, C, D qua k
N lần lượt là B ' d d ; C ' d d ; D ' d d P 2 3 3 4 4 1 d1 A' B' d2 d D' C' 4 d3 A' B'.P . A PB B 'C '.P . B PC C ' D'.P . D PC A' D'.P . A PD Ta có AB ; BC ;CD ; DA k k k k 2 A . B BC PB A' B '.B 'C ' Suy ra . 2 A . D DC PD C ' D '.A' D '
Do d / /d ; d / /d nên A ' B 'C ' D ' là hình bình hành nên A'B' C'D'; C'B' A'D'. 1 3 2 4 2 2 A . B BC PB A' B '.B 'C ' PB Suy ra . (đpcm). 2 2 A . D DC PD C ' D '.A' D ' PD
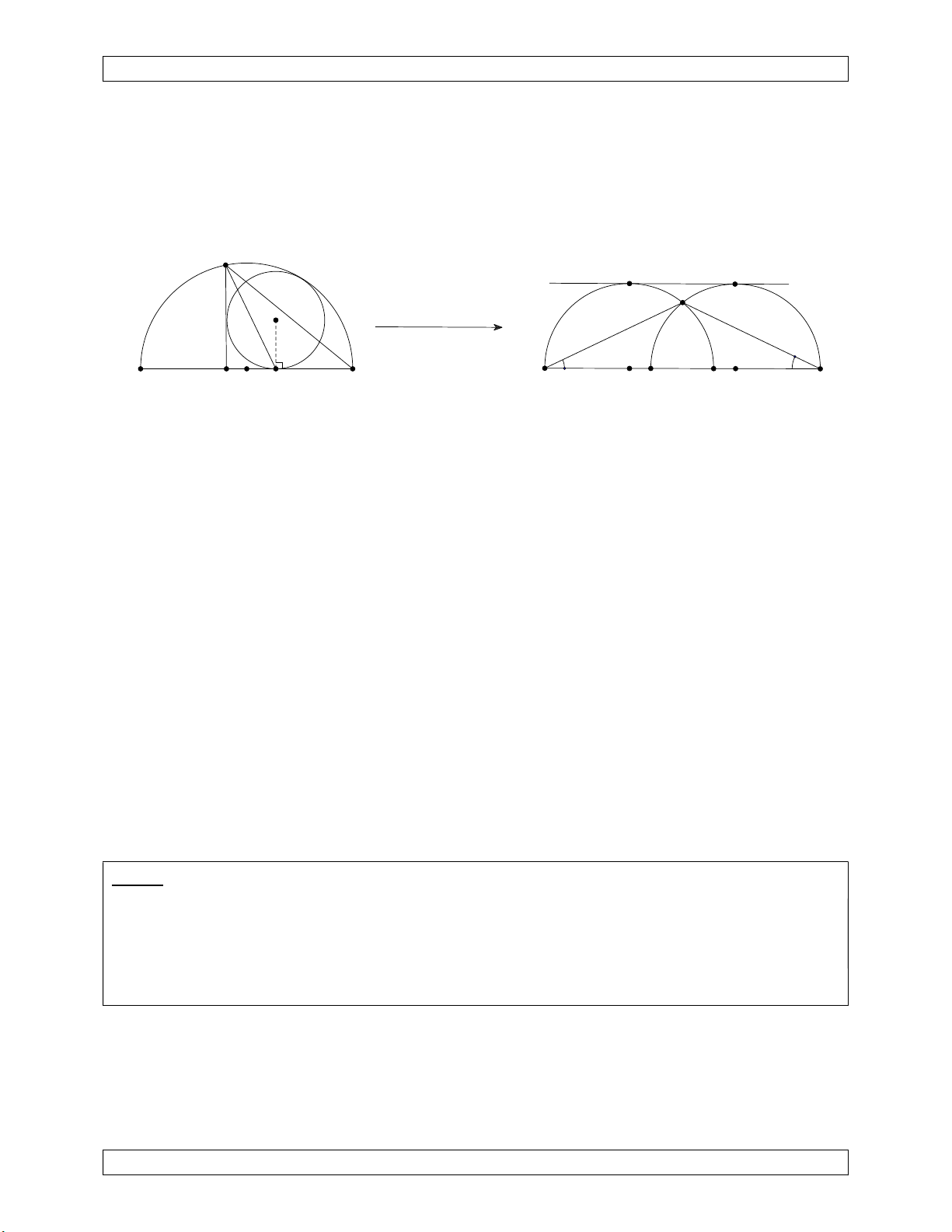
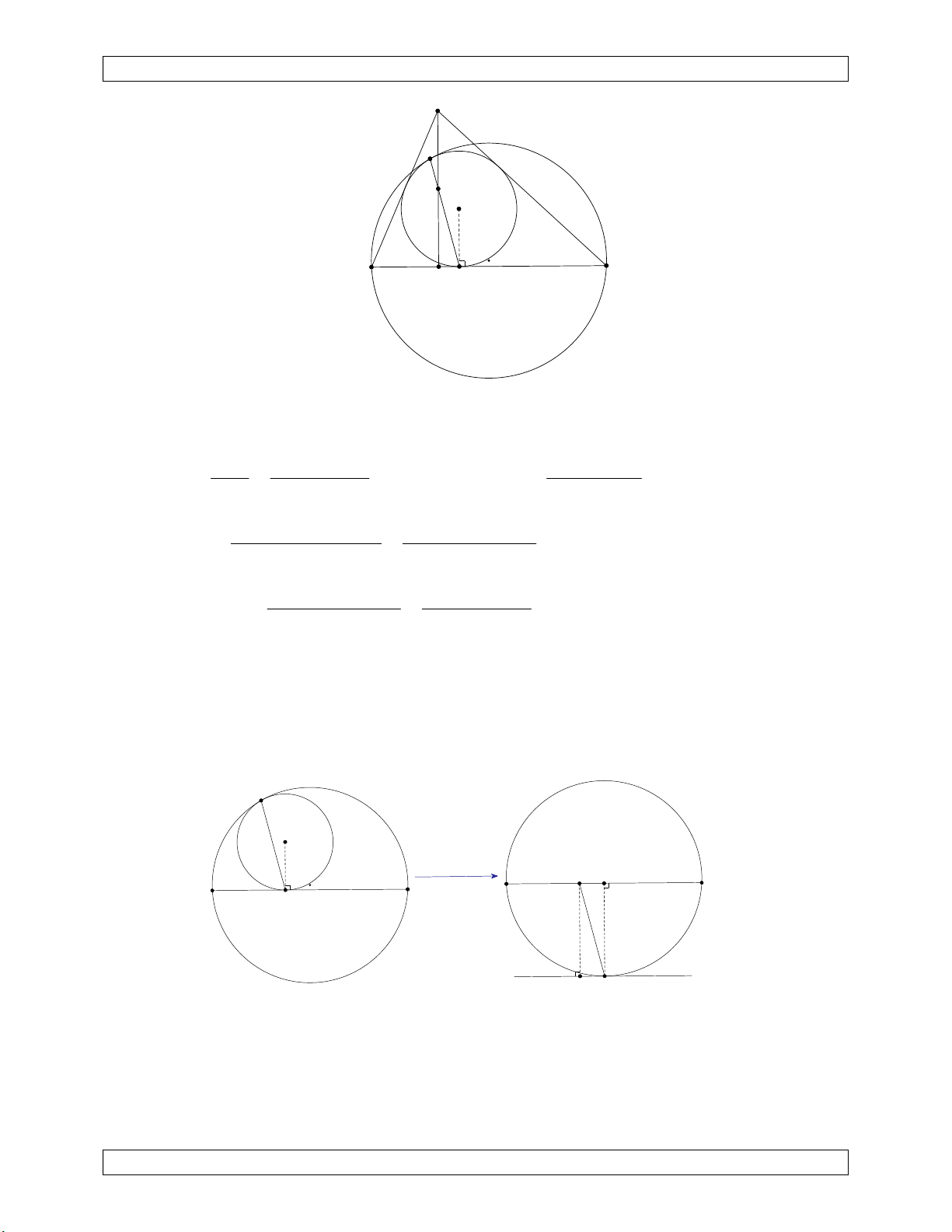
Bài 6. (Israell 1995) Cho (T) là nửa đường tròn đường kính PQ. Đường tròn (I) tiếp xúc
trong với (T) và tiếp xúc với PQ tại C. A là điểm thuộc (T), B là điểm thuộc đoạn CQ sao
cho AB vuông góc với PQ và AB tiếp xúc với (I). Chứng minh rằng AC là phân giác góc PAB .
Theo tính chất 1, góc có 1 cạnh đi qua tâm nghịch đảo biến thành góc có một cạnh
đi qua tâm nghịch đảo bằng nó. Do đó để chứng minh AC là phân giác góc PAB sẽ xét
phép nghịch đảo tâm C. Tâm này là phù hợp để dùng phép nghịch đảo, vì nó là tiếp điểm
Trường THPT Chuyên Huỳnh Mẫn Đạt. Giáo viên Lê Anh Dũng T r a n g | 8
Chuyên Đề Bồi Dưỡng Học Sinh Giỏi
của đường tròn và đường thẳng PQ. Xét phép nghịch đảo k
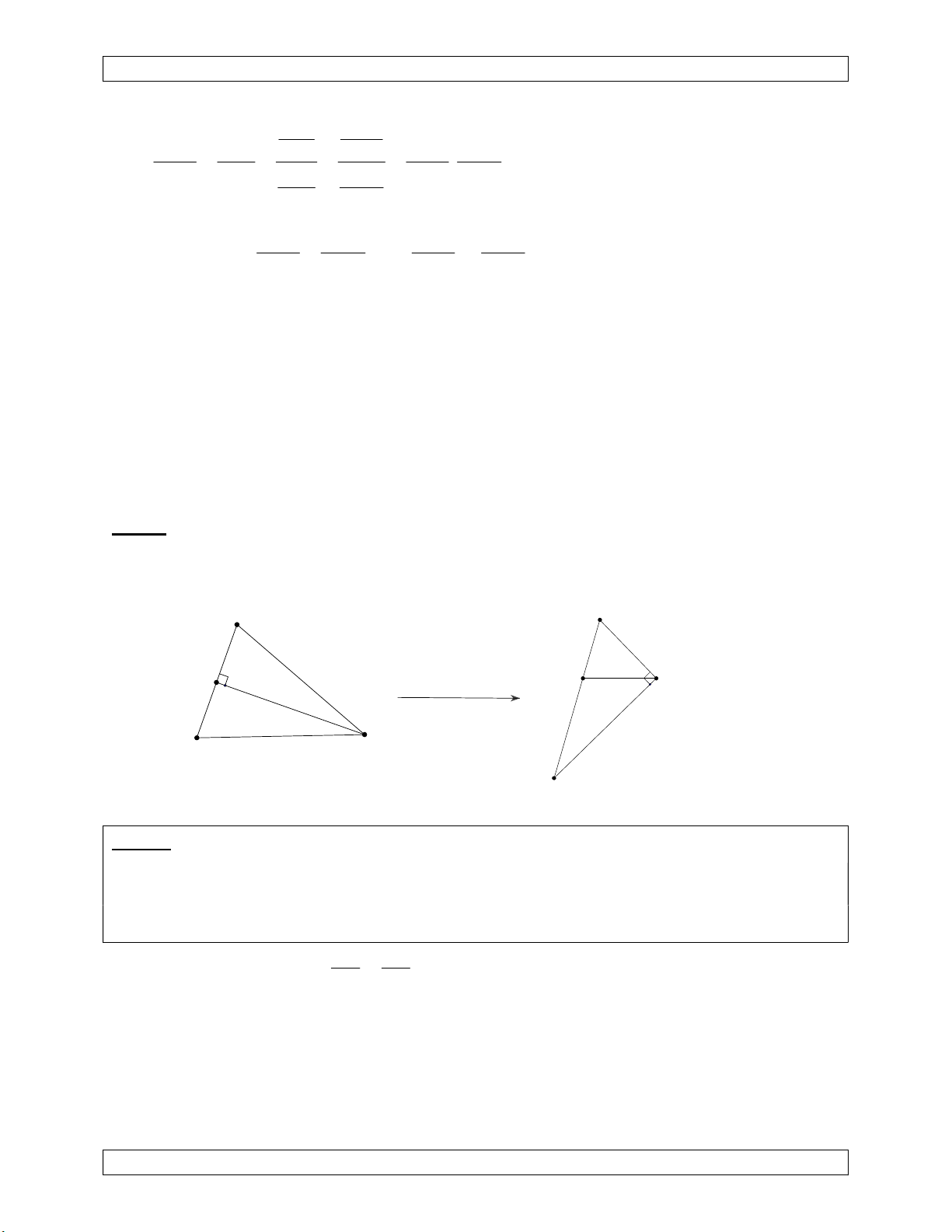
N ( k 0 ). Qua phép nghịch đảo này, ảnh của B, A, Q, P lần lượt C là B’, A’, Q’, P’. A d A' chuyển mô hình bài toán Q P B C B' Q' C P'
Ảnh của nửa đường tròn đường kính PQ là nửa đường tròn đường kính P’Q’.
Ảnh của AB là đường tròn (A’B’C), do BC vuông góc AB nên B’C là đường kính của đường tròn này.
A thuộc AB và nửa đường tròn đường kính PQ nên A’ là giao hai nửa đường tròn
đường kính P’Q’ và B’C.
Ảnh của đường tròn (I) là đường thẳng d. Do IC vuông góc với PQ nên d//CB’.
Cũng do (I) tiếp xúc với AB, và nửa đường tròn đường kính PQ nên d cũng là tiếp tuyến
chung của hai đường tròn này. Suy ra hai đường tròn đường kính P’Q’ và B’C là bằng nhau. Suy ra A' B'C
A'P'C . Mà tính chất phép nghịch đảo, ta có CAB CB ' A '; CAP CP ' A ' nên CAP
CAB hay CA là phân giác của góc BAP (đpcm).
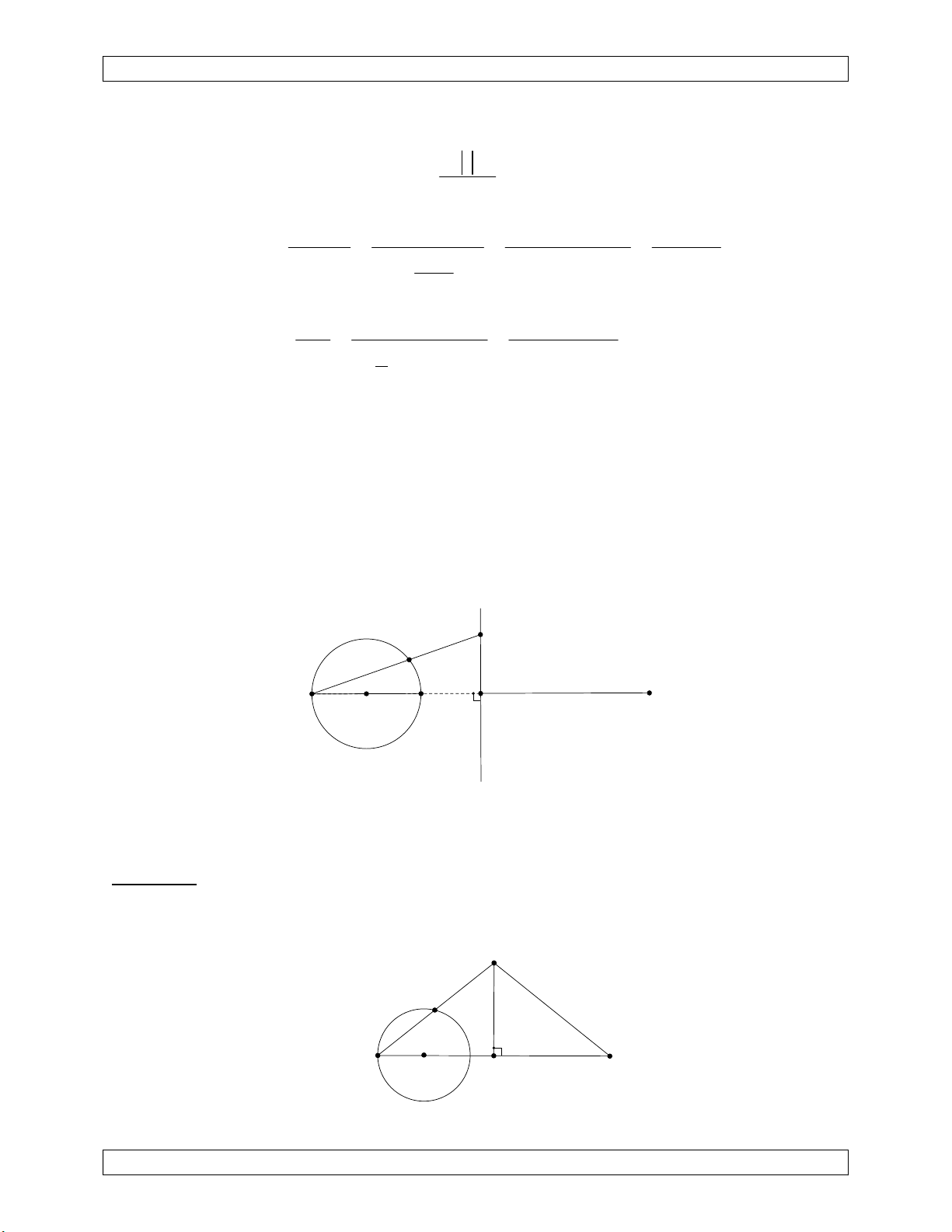
Bài 7. (IMO shortlist 2002) Cho tam giác nhọn ABC ngoại tiếp đường tròn (I), (I) tiếp
xúc với BC tại K. Gọi AD là đường cao đỉnh A của tam giác ABC. M là trung điểm AD. N
là điểm chung thứ hai của KM và (I). Chứng minh rằng đường tròn ngoại tiếp tam giác BCN và (I) tiếp xúc nhau.
Gọi (C) là đường tròn qua BC và tiếp xúc với (I). Chứng minh S, M, K thẳng hàng. Ta chứng minh hai góc BKM BKS . Ta tính tan
BKM theo 3 cạnh của tam giác.
Trường THPT Chuyên Huỳnh Mẫn Đạt. Giáo viên Lê Anh Dũng T r a n g | 9
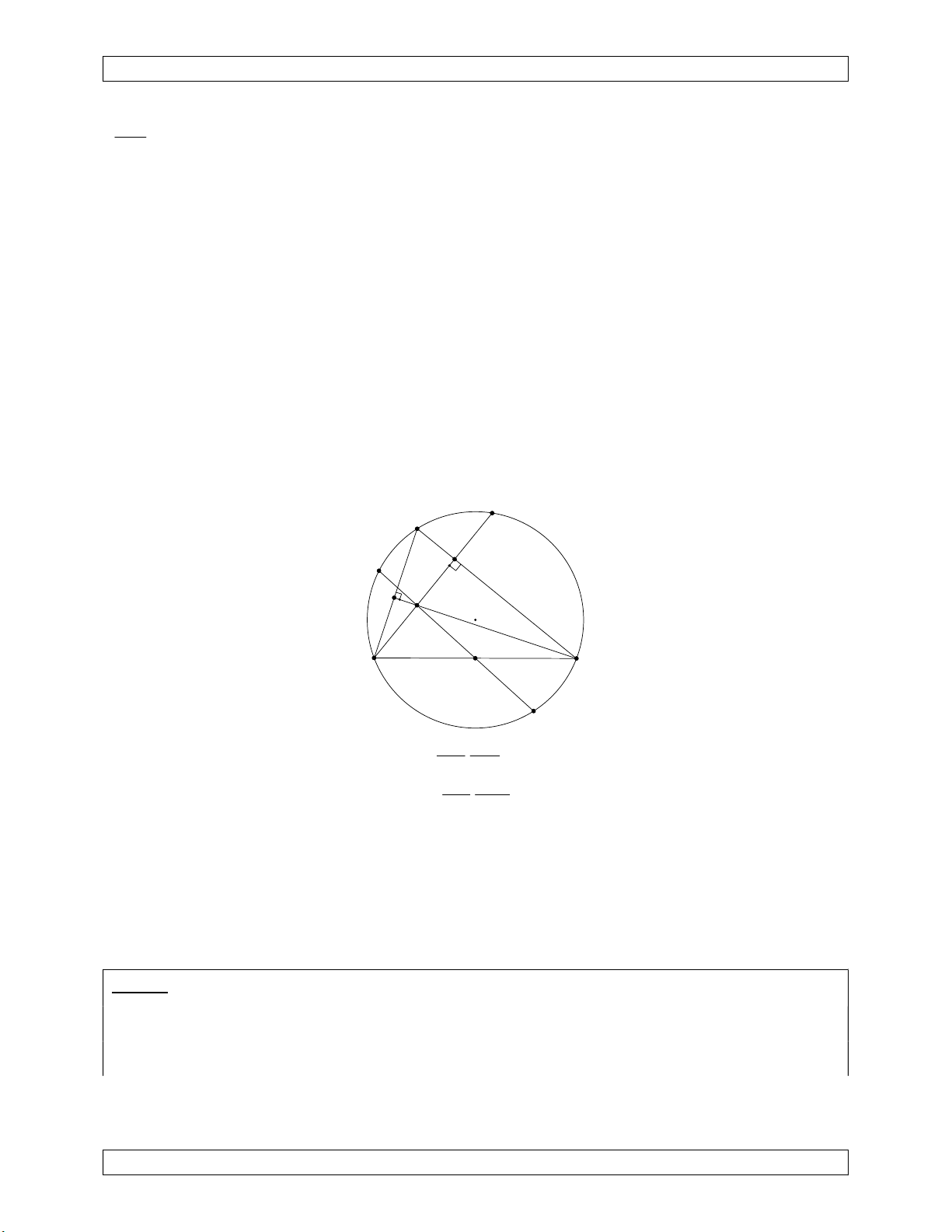
Chuyên Đề Bồi Dưỡng Học Sinh Giỏi A S M I B C D K
Không mất tổng quát giả sử AC AB . 2 2 2 DM AD a c b tan BKM ; 2BD 2 . c cos B ; 2BK a c b DK 2BK 2BD a 2 2 a(c b) (c b ) (c b)(b c a) 2BK 2BD a a a AD S Suy ra . tan ABC BKM
(b c)(b c a) (b c)( p a) + Tính tan
BKS : Sử dụng phép nghịch đảo tâm K, phương tích là t KB.KC để chuyển
mô hình hai đường tròn tiếp xúc.
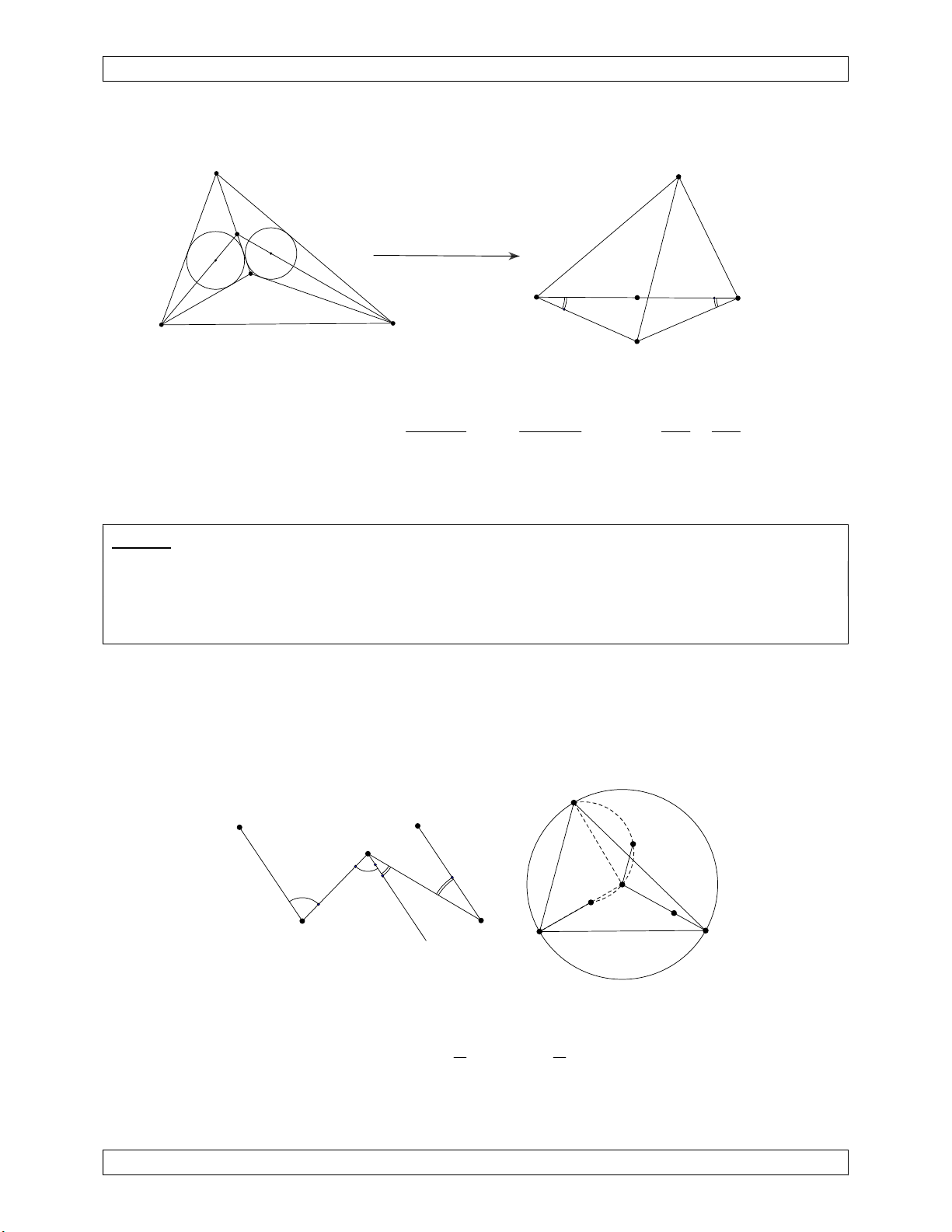
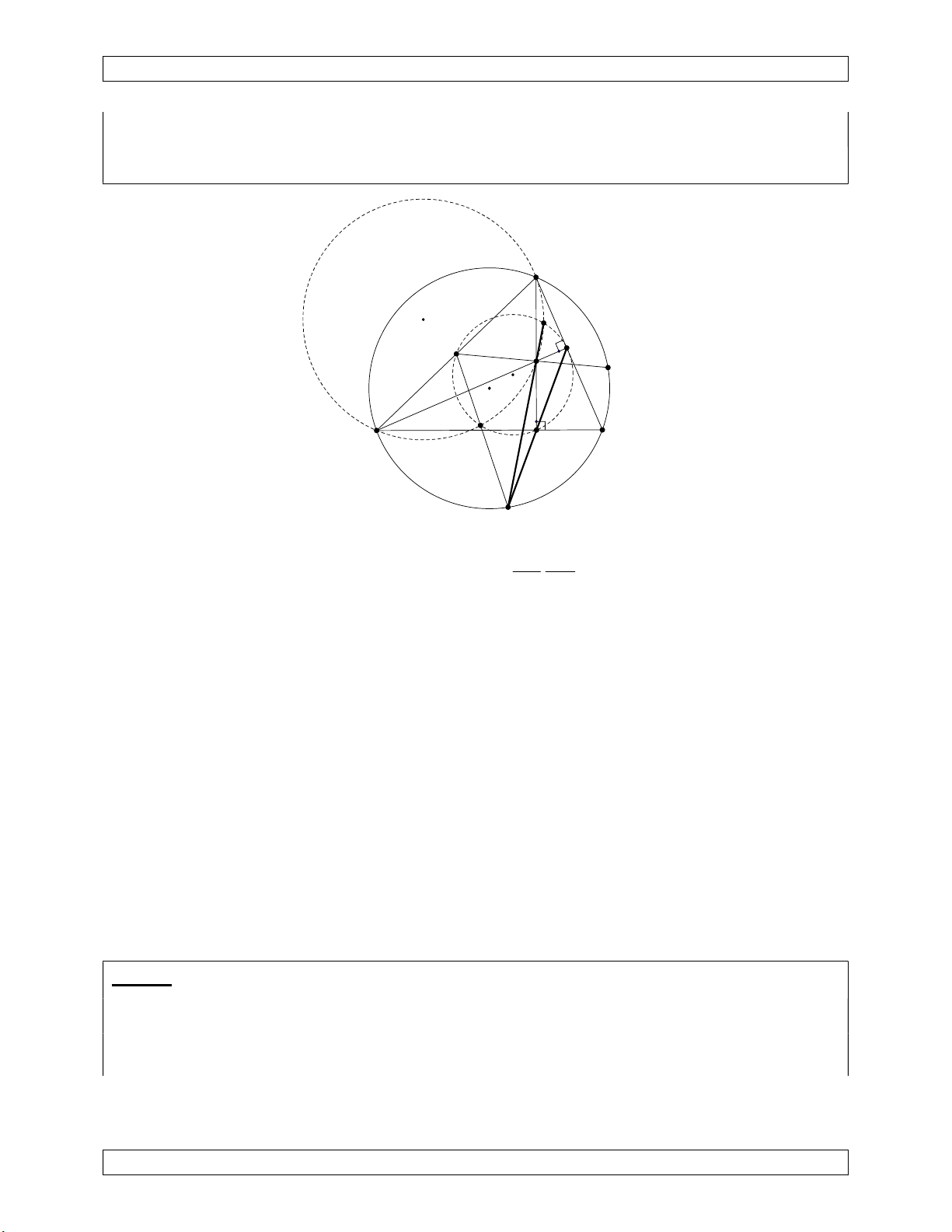
Xét phép nghịch đảo tâm K, t N với t KB.KC . K S I r chuyển mô hình K J B'≡C C'≡B B C K (C)' d S' d Qua t
N , ảnh của (C) là chính nó. Ảnh của S là S’. K
Ảnh của đường tròn nội tiếp (I) là đường thẳng d. Do (I) tiếp xúc với (C) nên d tiếp xúc
với (C). Cũng theo tính chất dựng ảnh của đường tròn thì IK vuông góc với d nên d song
Trường THPT Chuyên Huỳnh Mẫn Đạt. Giáo viên Lê Anh Dũng T r a n g | 10
Chuyên Đề Bồi Dưỡng Học Sinh Giỏi
song với BC. Suy ra hình chiếu của S’ trên BC là trung điểm BC. t
Theo tính chất ảnh đường tròn ta có r 2d(K,d) K . B KC ( p b)( p c) p( p b)( p c) S Suy ra S ' ABC J d ( K ,d ) 2r SABC 2S 2( p a) 2 ABC p BKS S 'J K . B KC S tan tan S ' ABC KJ KJ 1 ( p a)(b c) 2 BC BK r 2 Vậy tan BKS tan
BKM nên K, M, S thẳng hàng (đpcm). 2) Kĩ năng 2:
Gọi lại tính chất 4: Qua phép nghịch đảo tâm O, đường tròn qua tâm O biến
thành đường thẳng vuông góc với đường nối tâm O và tâm đường tròn. ảnh của (I) A A' O I I'
Để ý, tâm I biến thành I’ đối xứng với O qua l với l là ảnh của (I). Đây là một dấu
hiệu cho ta cách chọn tâm nghịch đảo và dựng ảnh của trung trực.
Dấu hiệu: Tam giác ABC, cân tại C; hoặc có trung trực của của đoạn AB. Ta chọn A làm
tâm phép nghịch đảo.Qua phép nghịch đảo k N : A B B' A C' C
Trường THPT Chuyên Huỳnh Mẫn Đạt. Giáo viên Lê Anh Dũng T r a n g | 11
Chuyên Đề Bồi Dưỡng Học Sinh Giỏi
Ảnh của C là C'; ảnh của đường trung trực của BC là đường tròn tâm C' bán kính C'A. Ảnh của B là B'.
Bài 8. (Trung Quốc 2012) Cho tam giác ABC, có góc A là góc lớn nhất. Trên đường tròn
ngoại tiếp tam giác ABC lấy D, E lần lượt là điểm chính giữa cung ABC, ACB . Gọi c là 1
đường tròn qua A, B và tiếp xúc với AC tại A; c là đường tròn qua A, E và tiếp xúc với 2
AD tại A. c ,c cắt nhau tại A, P. Chứng minh rằng AP là phân giác góc BAC. 1 2
Ta chuyển mô hình bài toán qua phép nghịch đảo k
N . Kí hiệu X’ nói chung là ảnh A
của X qua phép nghịch đảo này.
Ảnh của đường trung trực của AC, AE lần lượt là đường tròn tâm C’, B’ và qua A.
Ảnh của đường tròn (ABC) là đường thẳng B 'C '.
Ảnh của đường tròn qua AB và tiếp xúc AC là đường thẳng qua B’ và song song với AC’.
Ảnh của đường tròn qua AE và tiếp xúc AD là đường thẳng qua E’ và song song với AD’.
Ta chỉ cần chứng minh AP ' là phân giác của B' AC ' . D B P B' P' E D' C qua nghịch đảo A R E' A C'
Do B'P'/ / AC '; E 'P'/ / AD' nên tam giác B ' P ' E ' đồng dạng với tam giác C ' AD ' .
Suy ra tam giác B ' P ' E ' cân tại B ' và P'B'E ' B'C ' A.
B ' P ' B ' E ' B ' A nên tam giác B ' P ' A cân tại B ' . 0 0
180 AB ' P ' 180 AB 'C ' AC 'B ' B ' AC ' B ' AP ' (đpcm). 2 2 2
Trường THPT Chuyên Huỳnh Mẫn Đạt. Giáo viên Lê Anh Dũng T r a n g | 12
Chuyên Đề Bồi Dưỡng Học Sinh Giỏi
Bài 9. (Trung Quốc 2012) Cho tam giác ABC có góc A là góc lớn nhất. Trên đường tròn
ngoại tiếp tam giác ABC, gọi D là điểm chính giữa cung
ABC và E là điểm chính giữa cung
ACB . Đường tròn c đi qua A, B và tiếp xúc với AC tại A. Đường tròn c đi qua A, 1 2
E và tiếp xúc với AD tại A. Hai đường tròn c ,c cắt nhau tại A, P. Chứng minh rằng AP 1 2 là phân giác của BAC.
Xét phép nghịch đảo tâm A, phương tích k. Kí hiệu X ' là ảnh của X qua phép nghịch đảo
này. Ảnh của đường trung trực của AB là đường tròn tâm B’ và bán kính B’A; ảnh của
(ABC) là đường thẳng B’C’. Do đó, ảnh của E là điểm E’ trên tia C ' B ' sao cho
B ' E ' B ' A . Tương tự, D’ là điểm trên tia B 'C ' sao cho C ' D ' C ' A . Đường tròn c 1
biến thành đường thẳng qua B’ và song song với AC '; đường tròn c biến thành đường 2
thẳng qua E’ và song song với AD ' . A A D qua nghịch đảo E E' B' D' P C' B C P' B'P'E ' C ' AD'
C 'D' A (góc có cạnh tương ứng vuông góc). B ' E ' P ' (so le trong)
Suy ra B ' là tâm đường tròn ngoại tiếp tam giác AE ' B ' . Suy ra B' AP' B'P' A P' AC '
Vậy AP ' là phân giác của góc B' AC ' (đpcm) .
Bài 10. (Trung Quốc TST 2015) Cho tam giác ABC cân tại A với A B A C BC . Gọi
D là một điểm trong tam giác ABC sao cho DA DB DC . Giả sử đường phân giác
Trường THPT Chuyên Huỳnh Mẫn Đạt. Giáo viên Lê Anh Dũng T r a n g | 13
Chuyên Đề Bồi Dưỡng Học Sinh Giỏi ngoài của
ADB cắt đường trung trực của A B tại P và đường phân giác ngoài của
A DC cắt đường trung trực của A C tại Q. Chứng minh rằng B, C, P, Q đồng viên.
Để ý P là điểm chính giữa cung
BDA của đường tròn ngoại tiếp tam giác ABD; Q là điểm chính giữa cung
CDA của đường tròn ngoại tiếp tam giác ACD. Đây là dấu hiệu cơ
bản để ta có thể nghịch đảo,
Xét phép nghịch đảo tâm D, phương tích k lớn. Kí hiệu X ' là ảnh của X qua phép
nghịch đảo này. Đường tròn ngoại tiếp tam giác ABD biến thành A’B’; đường tròn ngoại
tiếp tam giác ABC biến thành A’C’. Do đó, Q’ là chân đường phân giác ngoài đỉnh D của
tam giác A’DC’; P’ là chân đường phân giác ngoài đỉnh D của tam giác A’DB’. Q' A P' qua nghịch đảo A' Q P D C' D B C B' k k k DA' DA' Ta có DA DB DC 1 DA' DB ' DC ' DB ' DC ' DA' P ' A' D ' A' Q ' A'
Mà theo tính chất chân đường phân giác, ta có ; DB ' P ' B ' D 'C ' Q 'C ' P ' A' Q ' A' A'C ' Suy ra, 1
, suy ra Q’B’ song song với P’C’. P ' B ' Q 'C ' Q 'C '
Vậy B’Q’P’C’ là hình thang, ta chỉ cần chứng minh B’Q’P’C’ nội tiếp. Hay chứng minh
B’Q’P’C’ là hình thang cân. AB k.A' B ' DA'.DC ' A' B ' DC ' Ta có 1 . . . AC k.A'C ' DA'.DB ' A'C ' DB '
Trường THPT Chuyên Huỳnh Mẫn Đạt. Giáo viên Lê Anh Dũng T r a n g | 14
Chuyên Đề Bồi Dưỡng Học Sinh Giỏi DB' P' B' A' B ' DB ' P' B ' Q ' A' Hay DA' P ' A' . . A'C ' DC ' DC ' Q 'C ' P ' A' Q 'C ' DA' Q ' A' P ' B ' Q 'C ' A' B ' Q ' A' Theo Talet ta có, nên . , suy ra A' B' Q' A' . P ' A' A'C ' A'C ' A'C '
Suy ra B’Q’P’C’ là hình thang cân (đpcm).
3) Kĩ năng dựng ảnh dựa vào tính chất chuyển góc.
Một tính chất đẹp của phép nghịch đảo là 'chuyển đổi đỉnh của góc' (Phép nghịch đảo k
N , biến A thành A’ ; B thành B’ thì OA'B'
OBA). Tính chất này hay dùng trong O
các bài toán về tổng, hiệu các góc.
Ví dụ: Cho tam giác ABC, H là chân đường cao đỉnh C. Ảnh của B, C qua phép nghịch
đảo tâm A là B', C' thì ảnh của H là điểm H’ trên đường thẳng AB’ sao cho 0 AC ' H ' 90 . A A B' H C' qua nghịch đảo C B H'
Bài 11. (IMO 1996) Cho tam giác ABC và P là điểm nằm bên trong tam giác ABC sao cho APB ACB APC
ABC . Gọi D, E là tâm đường tròn nội tiếp tam giác APB,
APC. Chứng minh AP, BD, CE đồng quy. BA CA
Yêu cầu cần chứng minh :
(Do tính chất tỷ lệ của đường phân giác) BP CP
Ta dùng phép nghịch đảo để chuyển góc về chung đỉnh, và do đó có thể trừ hai góc được.
Xét phép nghịch đảo tâm A, tỉ số k > 0.
Gọi B’, C’, P’, C’ lần lượt là ảnh của B, C, P, C qua phép nghịch đảo này.
Trường THPT Chuyên Huỳnh Mẫn Đạt. Giáo viên Lê Anh Dũng T r a n g | 15
Chuyên Đề Bồi Dưỡng Học Sinh Giỏi
Giả thiết về góc có thể viết lại thành AB' P AB'C ' AC ' P' AC ' B' A A E qua nghịch đảo D P B' C' B C P' Hay P' B'C '
P'C ' B' , suy ra P ' B ' P 'C ' . k k BA CA
Theo công thức độ dài ảnh, ta được .BP .PC hay . AB.AP AC.AP BP CP
Suy ra AP, BD, CE đồng quy. (đpcm).
Bài 12.(Croatia TST 2016) Cho tam giác nhọn ABC nội tiếp đường tròn tâm O. Các điểm
E, F được chọn trên đoạn OB, OC sao cho OE = CF. Gọi M, N lần lượt là điểm chính giữa cung AOE, AOF . Chứng minh rằng ENO FMO 2 BAC . Để ý: 2 BAC
BOC . Ta dùng phép nghịch đảo tâm O, chuyển góc về trên cạnh OB, OC.
Khi đó, điều kiện tổng hai góc E ' , F ' bằng
BOC có thể kiểm tra bằng điều kiện song song: M ' E '/ /N ' F ' . A M' N' O M E O F E' F' B C
Ta xác định cấu trúc của M, N để xác định ảnh của M, N. 1 1
Ta nhận thấy OM//AB. Thật vậy, AOM sñ 0 AOE (180 AOE) OAB , suy ra 2 2 OM//AB.
Trường THPT Chuyên Huỳnh Mẫn Đạt. Giáo viên Lê Anh Dũng T r a n g | 16
Chuyên Đề Bồi Dưỡng Học Sinh Giỏi Tương tự, ON//AC.
Xét phép nghịch đảo tâm O, phương tích 2
k OA , kí hiệu X 'là ảnh của X qua phép nghịch đảo này.
Qua phép này, B, C giữ nguyên.
Ảnh của đường tròn (AEO) là đường thẳng AE’ nên M’ thuộc AE’ và OM’//AB.
Tương tự N’ thuộc AF’ và ON’//AC. N' M' A O B C F' E' ENO FMO E 'ON ' F 'OM ' Ta chứng minh E 'ON ' F 'OM ' 2
BOC hay chứng minh E’N’//M’F’. AN ' OC R OF Thật vậy, ta có 2 AF ' CF ' R CF .CF OC.OF 2 R ' ' BE AE BE . BE OF OB OE AM ' OB R OE CF AN ' AE ' Suy ra
nên E ' N '/ /F ' M ' (đpcm). AF ' AM '
Bài 13. (IMO Shortlist 2014 G5) Cho đa giác lồi ABCD có ABC 0 CDA 90 . Gọi H là
chân đường vuông góc hạ từ A đến BD. Các điểm S, T tương ứng nằm trên cạnh AB, AD
Trường THPT Chuyên Huỳnh Mẫn Đạt. Giáo viên Lê Anh Dũng T r a n g | 17
Chuyên Đề Bồi Dưỡng Học Sinh Giỏi
sao cho H nằm trong tam giác SCT và CHS 0 CSB THC 0 90 ; DTC 90 . Chứng minh
rằng BD là tiếp tuyến của đường tròn ngoại tiếp tam giác SCT.
Ta dùng phép nghịch đảo xác định cấu trúc của S.
Xét phép nghịch đảo tâm C. Kí hiệu X’ là ảnh của X qua phép nghịch đảo này. Từ điều kiện CHS 0 CSB 90 cho ta CS H 0 '
CB' S 90 . Điều kiện này có được khi
tiếp tuyến của (S’B’C) tại S’ vuông góc với S’H’.
Vậy AB vuông góc với tiếp tuyến tại S của đường tròn ngoại tiếp tam giác CSH (AB trực
giao với (SCH)). Tương tự, AD vuông góc với tiếp tuyến tại T của đường tròn ngoại tiếp tam giác CTH. Xét phép nghịch đảo k
N , kí hiệu X’ là ảnh của X qua phép nghịch đảo này. H H' A qua nghịch đảo T A' S' N M O C B' S H B H D B' D' S' T' C C'
Ảnh của AB là đường tròn (A’B’H) có tâm là trung điểm N của A’B’.
Ảnh của (SHC) là đường thẳng C’S; do AB trực giao với (SHC) nên S’C’ trực giao với
(A’B’H), suy ra S’ là giao của C’N và (A’B’H).
Tương tự, T’ là giao của C’M và (A’D’H).
Cũng do AC trực giao với (ABD) nên (HA’C’) trực giao với (A’B’D’), suy ra đường tròn
(A’HC’) có tâm O là giao điểm của tiếp tuyến tại A của (A’B’D’) và trung trực của A’H (là MN). NC ' NS ' NA
(STH) tiếp xúc BD khi và chỉ khi S 'T '/ /B ' D ' hay . Điều này MC ' NC ' MA
tương đương với chứng minh (A’HC’) là đường tròn Appollonius chia MN theo tỷ số
Trường THPT Chuyên Huỳnh Mẫn Đạt. Giáo viên Lê Anh Dũng T r a n g | 18
Chuyên Đề Bồi Dưỡng Học Sinh Giỏi
NA . Tức là chứng minh A’O là tiếp tuyến của (A’MN). Điều này là đúng vì MA MAO A' B' D' A' NM . (đpcm)
IV. CÁC ĐIỂM TRONG TAM GIÁC – TÂM NGHỊCH ĐẢO. 1) Trực tâm:
Cho tam giác ABC nội tiếp đường tròn (O) có trực tâm H. Các đường cao CE, BF. D
là trung điểm của BC. HD cắt (O) tại U, V với D ở giữa HV. BF cắt (O) tại điểm thứ hai F'.
Từ tính chất cơ bản của trực tâm: F là trung điểm HF'; D là trung điểm của HV.
Thường ta sử dụng ba phép nghịch đảo hữu dụng sau: F' A U F E H B C D V
i) Phép nghịch đảo tâm H, phương tích HB.HF .
ii) Phép nghịch đảo tâm H, phương tích HB.HF ' .
iii) Phép nghịch đảo tâm là trung điểm D của một cạnh (ví dụ BC) và phương tích 2 DB .
Qua phép nghịch đảo này thì E, F, B, C giữ nguyên và H biến thành U. (do tính chất trực
tâm nên DH D V . Vì vậy 2 DH.DU DU.DV D . B DC DB )
Bài 14. (Canada 2016) Cho ABC là tam giác nhọn với AD và BE là hai đường cao cắt
nhau tại H. Gọi M là trung điểm của đoạn AB. Giả sử đường tròn ngoại tiếp tam giác
DEM và đường tròn ngoại tiếp tam giác ABH cắt nhau tại P, Q trong đó P cùng phía với
Trường THPT Chuyên Huỳnh Mẫn Đạt. Giáo viên Lê Anh Dũng T r a n g | 19
Chuyên Đề Bồi Dưỡng Học Sinh Giỏi
A so với CH. Chứng minh rằng các đường thẳng ED, PH và MQ cắt nhau tại một điểm
trên đường tròn ngoại tiếp tam giác ABC. A P M E V H B Q D C L
Đường tròn (MDE) là đường tròn Euler của tam giác ABC.
Xét phép nghịch đảo tâm H, phương tích HA.HD . Qua phép này ảnh của A là D;
ảnh của B là E ; ảnh của C là chân đường cao đỉnh C. Do đó, ảnh của đường tròn (MDE)
là (ABC); ảnh của (HAB) là DE. P là một giao điểm của (MDE) và (AHB) nên ảnh của P
là L là giao của DE và (ABC). Vậy P, H, L thẳng hàng hay PH cắt DE tại một điểm trên (ABC).
Xét phép nghịch đảo tâm M, phương tích 2
MA . Qua phép này các điểm A, B, E, D
giữ nguyên. H là V. Do đó, ảnh của đường tròn (MDE) là DE; ảnh của (HAB) là (ABC). P
là một giao điểm của (MDE) và (AHB) nên ảnh của Q là giao của DE và (ABC) là Q.
Vậy Q, M, L thẳng hàng. Vậy đường thẳng ED, PH và MQ cắt nhau tại một điểm
trên đường tròn ngoại tiếp tam giác ABC. (đpcm).
Bài 15.(IMO 2015 Shortlist G6), IMO 2015 bài 3 Cho tam giác nhọn ABC với AB AC
nội tiếp đường tròn (O). Gọi H là trực tâm tam giác ABC và F là chân đường vuông góc
hạ từ A. Gọi M là trung điểm của BC; Q là điểm trên (O) sao cho 0 HQA 90 ; K là điểm
Trường THPT Chuyên Huỳnh Mẫn Đạt. Giáo viên Lê Anh Dũng T r a n g | 20




