







Preview text:
[...Chuyên đề Trắc nghiệm Toán THPT...] Phép biến hình 11CB CHUY£N §Ò:
PHÐP BIÕN H×NH TRONG MÆT PH¼NG
Giáo viên: LÊ BÁ BẢO Trường THPT Đặng Huy Trứ, Huế
SĐT: 0935.785.115 Địa chỉ: 116/04 Nguyễn Lộ Trạch, TP Huế Chñ ®Ò 1: PhÐp tÞnh tiÕn I. LÝ THUYẾT
1. Định nghĩa: Trong mặt phẳng cho vectơ v . Phép biến hình biến mỗi điểm M thành điểm M
sao cho: MM v , được gọi là phép tịnh tiến theo vectơ v .
Ký hiệu: T T(M) M MM v v v 0 0
2. Nhận xét: Phép tịnh tiến theo vectơ- không là phép đồng nhất.
3. BIỂU THỨC TOẠ ĐỘ:
x' x a Cho v ;
a b và phép tịnh tiến T : M x; y M T M x y v '; ' th× v y' y b 4. Tính chất: Tính chất 1:
NÕu T M M T N N MN M N M N MN v , v ' th× vµ tõ ®ã suy ra: .
Tính chất 2: Phép tịnh tiến:
1. Bảo toàn tính thẳng hàng và thứ tự của các điểm tương ứng.
2. Biến tia thành tia, biến đoạn thẳng thành đoạn thẳng bằng nó.
3. Biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
4. Biến tam giác thành tam giác bằng nó.( trực tâm
trực tâm, trọng tâm trọng tâm) I I '
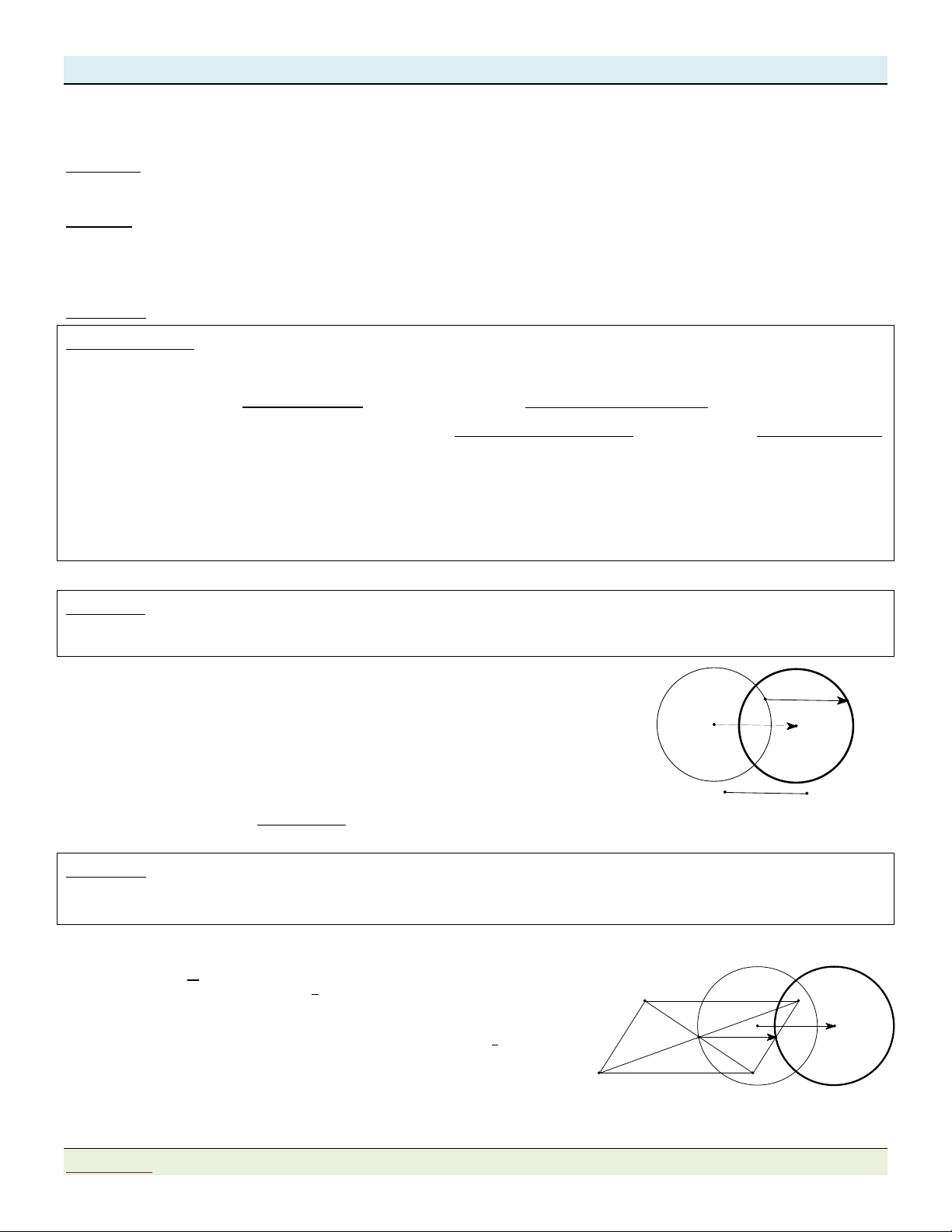
5. Biến đường tròn thành đường tròn có cùng bán kính ( ). R R'
Giáo viên: LÊ BÁ BẢO...0935.785.115... 1 TRẦN QUANG THẠNH...0935.295.530...
[...Chuyên đề Trắc nghiệm Toán THPT...] Phép biến hình 11CB
II. BÀI TẬP TỰ LUẬN MINH HỌA
Bài tập 1: Cho điểm A
x y C 2 2 1;1 , : 2 1 0,
: x y 2x 4y 1 0 . Xác định tọa độ điểm A,
, C lần lượt là ảnh của A, , C qua phép tịnh tiến theo v 1;2. Gợi ý:
* Ta có: T A A2; 3. v
* Kỹ năng xác định ảnh của đường thẳng qua phép tịnh tiến:
Phương pháp 1: Chọn 2 điểm bất kì trên , xác định ảnh tương ứng. Đường thẳng cần tìm là đường thẳng qua hai ảnh. Chọn A1; 1 , B 1 ;0 T
A A v 2;3 Ta có: A B . T
B B v 0;2
Đường thẳng đi qua điểm A2; 3 và có 1 vectơ chỉ phương A B 2; 1 n 1 ; 2 là 1
vectơ pháp tuyến của nên : 1
x 2 2y 3 0 x 2y 4 0.
Lưu ý: Hoàn toàn các em có thể để phương trình ở dạng tham số, nhưng các câu hỏi trắc nghiệm thì thường
sử dụng kết quả là phương trình tổng quát!
Phương pháp 2: Theo tính chất của phép tịnh tiến: Biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
Gọi là ảnh của đường thẳng . Suy ra:
: x 2y m 0. Chọn A1;
1 T A A2; 3
. Ta có: 2 6 m 0 m 4. Vậy
: x 2y 4 0. v
Phương pháp 3: Sử dụng quỹ tích: M
T M M v
x x 1
x x 1
Gọi M x; y T M M x y v
; : y y2 y y 2
Lúc đó: M x 1; y 2 x
1 2y 2 1 0 x 2y 4 0. Vậy
: x 2y 4 0.
Nhận xét: Trong 3 phương pháp trên,
+) Phương pháp 1 tỏ ra hiệu quả cho tất cả các phép biến hình (dù dài dòng).
+) Phương pháp 2 tốt vì sử dụng tính chất phép tịnh tiến.
+) Phương pháp 3 nhanh hơn, phù hợp với trắc nghiệm và việc xác định ảnh của các hình Elíp, parabol<.
* Xác định ảnh của đường tròn:
Phương pháp 1: Theo tính chất của phép tịnh tiến: Biến đường tròn thành đường tròn có cùng bán kính.
Giáo viên: LÊ BÁ BẢO...0935.785.115... 2 TRẦN QUANG THẠNH...0935.295.530...
[...Chuyên đề Trắc nghiệm Toán THPT...] Phép biến hình 11CB I 1; 2
Ta có C I; R : R 6
Ta có: T I I2;0 là tâm của đường tròn ảnh C . v
Vậy đường tròn C có tâm I2; 0 và bán kính R R 6 : x 2 2 2 y 6.
Phương pháp 2: Sử dụng quỹ tích.
x x 1
x x 1
Gọi M x; yC T M M x y v
; : y y2 y y 2 2 2
Lúc đó: M x 1; y 2C x
1 y 2 2x
1 4y 2 1 0
x2 y2 4x 2 0. Vậy C 2 2
: x y 4x 2 0.
Bài tập 2: Cho hai đường thẳng d : 3x y 3 0 , : x y 0 . Phép tịnh tiến theo v biến d thành
d : 3x y 1 0 , thành
: x y 6 0. Tìm tọa độ của v .
Gợi ý: Gọi v a;b .
Chọn A1;0d T A A1 ; a bd . v
31 a 3b 1 0 3a 3b 4 (1) Chọn B1;
1 T B A1 ; a 1 b v
1 a 1
b6 0 a b 6 (2) 7 7
Từ (1) và (2) giải được: a
, b 3 . Vậy v ; 3. 3 3
Bài tập 1: Cho đường thẳng : 6x 2y 1 0 . Tìm các vectơ v 0 sao cho: T . v
Gợi ý: v k 1
; 3; k 0.
Nhận xét: Có 2 trường hợp qua phép tịnh tiến, đường thẳng có ảnh là chính nó.
Trường hợp 1: T với v 0. v
Trường hợp 2: T với v là 1 vectơ chỉ phương của . v
Bài tập 2: Cho 2 điểm A 5 ;2, C 1
;0. Biết: B T A C T B . Tìm u, v để có thể thực hiện u , v
phép tịnh tiến biến A thành C ? Gợi ý:
Cách 1: Gọi u u ;u , v v ;v thỏa yêu cầu bài toán. 1 2 1 2
Ta có: T A B B 5
u ; 2 u . u 1 2
Và T B C C 5
u v ; 2 u v 1 ;0 . v 1 1 2 2
Giáo viên: LÊ BÁ BẢO...0935.785.115... 3 TRẦN QUANG THẠNH...0935.295.530...
[...Chuyên đề Trắc nghiệm Toán THPT...] Phép biến hình 11CB 5
u v 1 u v 4 v 4 u Vậy ta có: 1 1 1 1 1 1
2 u v 0 u v 2 v 2 u 2 2 2 2 2 2
Kết luận: 2 vectơ cần tìm có dạng: u u ;u , v 4 u ; 2
u u ;u 1 2 1 2 1 2 T
A B u AB u Cách 2: Ta có:
AB BC u v u v AC (*) T B C v 4; 2 BC v
Gọi u u ;u . Từ đẳng thức (*) suy ra được: v 4 u ; 2 u (y.c.b.t) 1 2 1 2
Nhận xét: Cách 2 tỏ ra tốt hơn, có tính tư duy cao hơn. DẠNG TOÁN:
SỬ DỤNG PHÉP BIẾN HÌNH ĐỂ TÌM QUỸ TÍCH
Để giải tốt bài toán quỹ tích, ta cần nắm rõ một số nhận xét sau:
* Xác định các yếu tố cố định (không thay đổi), và điểm di động ban đầu.
* Biểu diễn điểm (cần tìm quỹ tích) theo điểm đi động ban đầu thông qua các yếu tố cố định.
Cụ thể: Chẳng hạn, đối với phép tịnh tiến, biểu diễn: MM v . Suy ra: Tồn tại T M M , v
do M (H) nên MH , với H là ảnh của hình (H) qua T . Vậy quỹ tích cần tìm của điểm v
M là H.
Bài tập 3: Trên đường tròn (C) cho hai điểm A, B cố định và điểm M thay đổi. Tìm quỹ tích điểm
M sao cho MM MA M . B
Gợi ý: M
Ta có: MM MA MB MM MB MA MM A . B M' I
Suy ra: T M M. (C) I' (C') AB
Do M C MC với C là ảnh của C qua T . AB A B MB 3MA
Tương tự: 1) AM . 2) M M
M' A 2M B 0. 2
Bài tập 4: Cho hình bình hành ABCD, hai đỉnh A, B cố định, tâm I của hình bình hành thay đổi
di động trên đường tròn C. Tìm quỹ tích trung điểm M của cạnh BC. Gợi ý: (C) 1 (C') Dễ thấy: IM
AB , suy ra: T I M 1 2 AB 2 D C
Do I C IC với C là ảnh của C qua T O' . O 1 AB M 2 I A B
Giáo viên: LÊ BÁ BẢO...0935.785.115... 4 TRẦN QUANG THẠNH...0935.295.530...
[...Chuyên đề Trắc nghiệm Toán THPT...] Phép biến hình 11CB
Bài tập 4: Trong mặt phẳng cho 2 đường thẳng d và d cắt nhau, hai điểm A, B cố định không 1
thuộc hai đường thẳng đó sao cho AB không song song và không trùng với d và d . Tìm 1
M d vµ Md sao cho ABMM là hình bình hành. 1 Gợi ý:
* Phân tích: Do ABMM là hình bình hành nên: MM B . A d' d1 d M'
Suy ra: T M M . M x BA
Do M d nên Md nên suy ra: Md d . 1 1 * Cách dựng:
Bước 1: Dựng đường thẳng d là ảnh của d qua T . 1 BA A B
Bước 2: Xác định Md d . 1
Bước 3: Dựng đường thẳng Mx / /AB cắt d tại M.
* Số nghiệm bài toán: Điểm M d vµ Md xác định là duy nhất, vì d d và Mx / /AB cắt d lần 1 1
lượt tại M, M duy nhất.
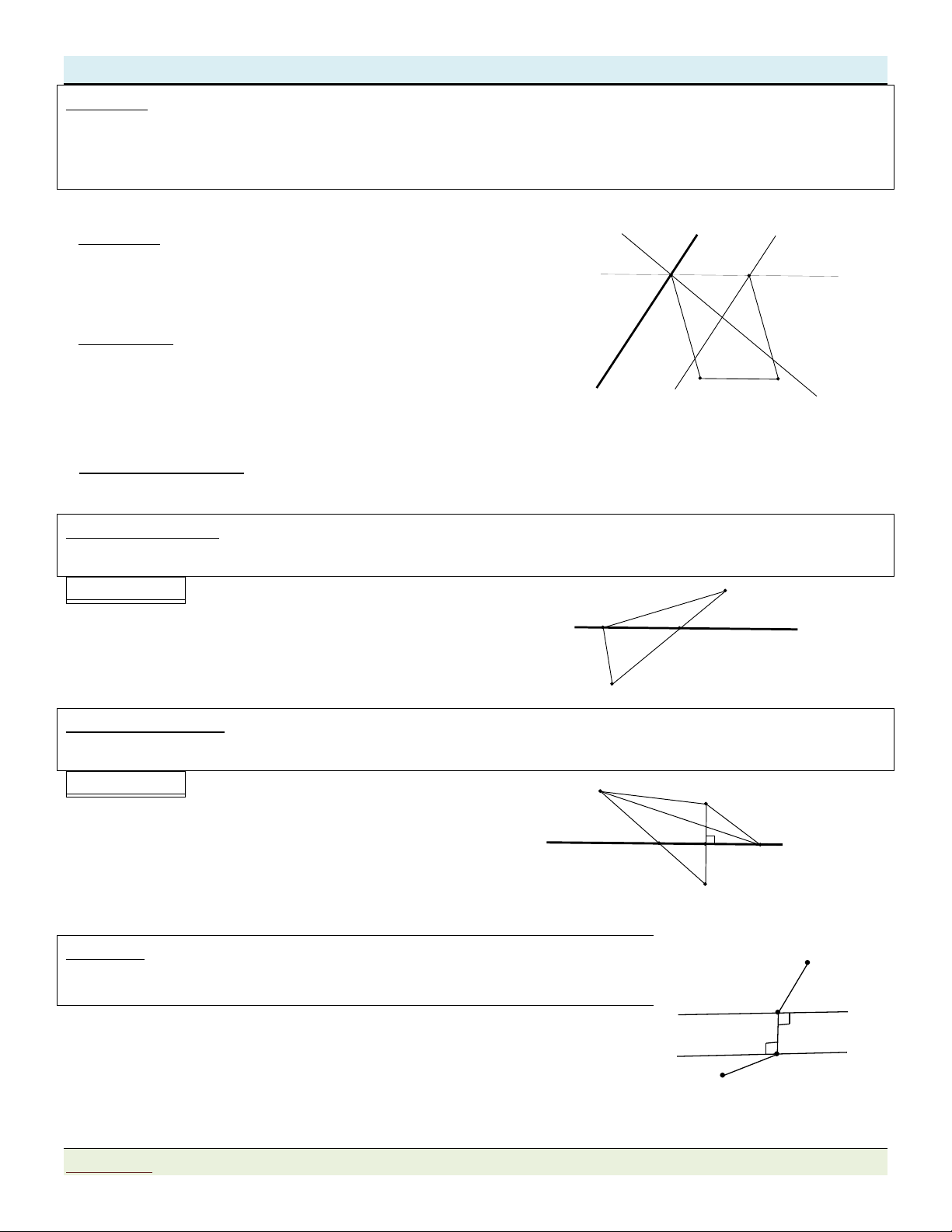
Bài toán cơ bản 1: Cho đường thẳng d và hai điểm A, B nằm khác phía với đường thẳng . d Xác
định điểm M trên d sao cho MA MB đạt giá trị nhỏ nhất. Phương pháp: B
Dễ thấy MA MB AB M d M O
MA MBMin MA MB AB
Vậy điểm M M AB . d A 0
Bài toán cơ bản 2: Cho đường thẳng d và hai điểm A, B nằm cùng phía với đường thẳng . d Xác
định điểm M trên d sao cho MA MB đạt giá trị nhỏ nhất.
Phương pháp: Đưa bài toán về bài dạng 1. A B
Lấy đối xứng điểm B qua đường thẳng d là điểm B’. d M Lúc đó: / /
MA MB MA MB AB MO Min Min / MA MB MA MB AB B' Vậy điểm /
M M AB d 0
Bài tập 5: Cho 2 đường thẳng vµ song song và hai điểm A, B 1 2 A
(như hình vẽ). Tìm M vµ N sao cho: AM MN NB nhá nhÊt. 1 2 M 1
Gợi ý:Nhận xét:
Đưa bài toán về các bài toán cơ bản (áp dụng với 1 đường thẳng) N 2
Thực hiện phép tịnh tiến T (Do MN không đổi). B NM
Ta có: T ( ) B B . NM
Giáo viên: LÊ BÁ BẢO...0935.785.115... 5 TRẦN QUANG THẠNH...0935.295.530...
[...Chuyên đề Trắc nghiệm Toán THPT...] Phép biến hình 11CB
Lúc đó: AM MN NB AM MN MB .
Để ý rằng: Do MN không đổi, nên AM MN NB nhá nhÊt AM MB nhá nhÊt
Ta thấy: AM MB AB nên AM MB nhá nhÊt M M AB . O 1 A * Cách dựng: 1 MO
Bước 1: Thực hiện T B B . M NM 2 NO
Bước 2: Nối AB cắt tại M . B' N 1 0
Dựng đường thẳng vuông góc với cắt tại N cần tìm. 1 2 0 B
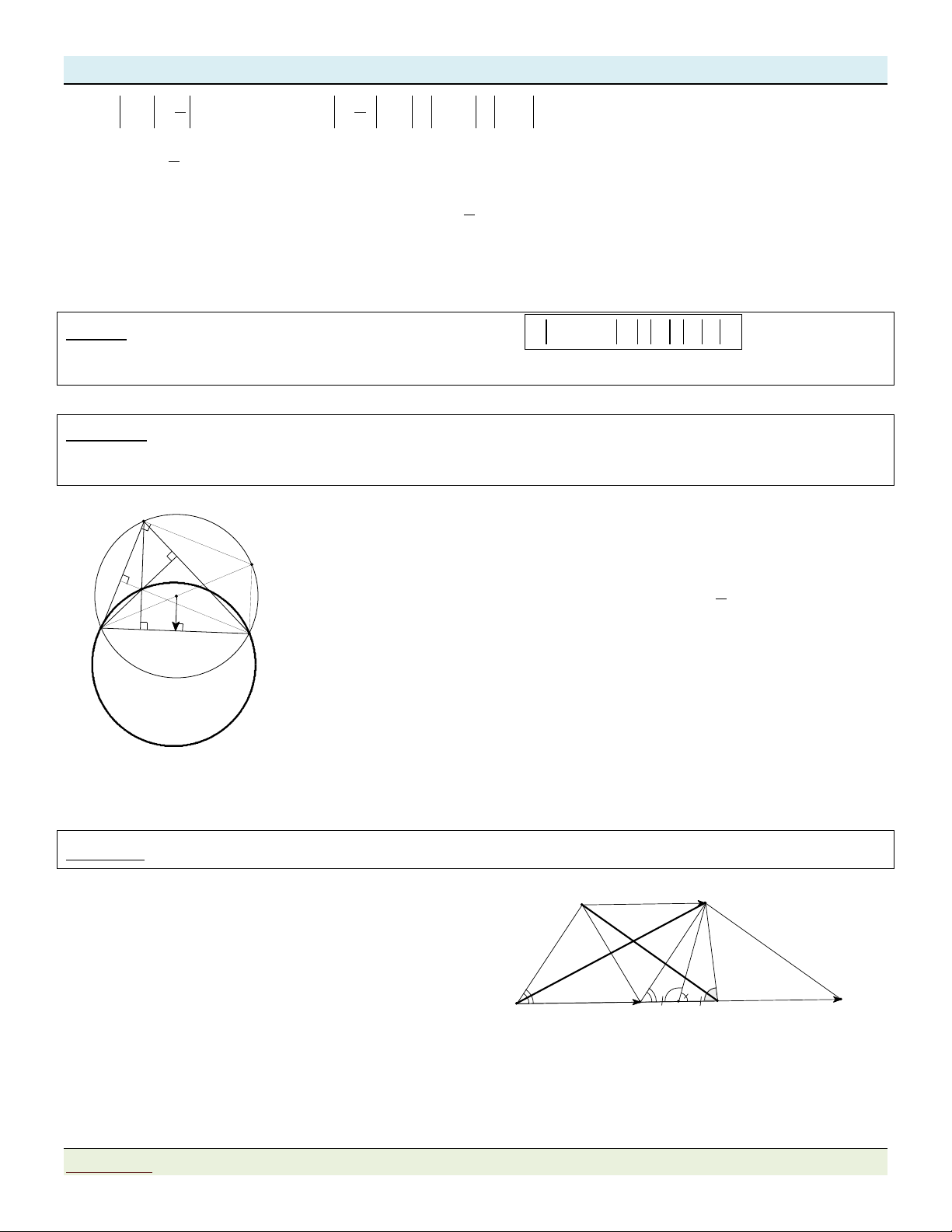
Bài tập 6: Cho tam giác AB .
C Gọi A, B, C lần lượt là các trung điểm của 3 cạnh BC, CA, AB.
Gọi O , O , O , I , I , I lần lượt là tâm của đường tròn ngoại tiếp và nội tiếp của ba tam giác 1 2 3 1 2 3 AB C , BC A , CA B
. Chứng minh rằng: O O O I I I . 1 2 3 1 2 3 Gợi ý:
Nhận xét: Theo tính chất của phép tịnh tiến: Biến tam giác thành tam giác bằng nó và lần lượt biến
trọng tâm , trực tâm, tâm đường tròn ngoại tiếp, nội tiếp thành trọng tâm , trực tâm, tâm đường tròn ngoại
tiếp, nội tiếp của tam giác ảnh tương ứng. A
Thực hiện phép tịnh tiến: T AC ' T I
(A) C 1 AC' O C' 1 Ta có: T
C B T A B C C A . B B' AC' AC' T
B A AC' I2 O2 T
O O
AC' 1 B Vậy 2 A' C T
I O O I I hay O O I I . 1 2 1 2 1 2 1 2 I AC' 1 2
Tương tự, chứng minh được: O O I I , O O I I . Vậy O O O I I I (c.c.c) 1 3 1 3 3 2 3 2 1 2 3 1 2 3
Bài tập 5: Cho f là phép dời hình sao cho độ dài đoạn thẳng nối mỗi điểm với ảnh của nó qua f là
không đổi. Chứng minh f là phép tịnh tiến.
Gợi ý: Cần chỉ ra rằng: M
: f (M) M MM v (vectơ “cố định”)
Cố định một điểm A, gọi A f A. Ta chứng minh: f T . AA'
Thật vậy, lấy M bất kì, gọi M f M , chỉ rõ: MM AA .
Xét điểm N sao cho A, M, N không thẳng hàng và gọi N f N .
Lúc đó: f A MN A M N
. Vì f là phép dời hình nên f G G với G, G lần lượt là trọng tâm của hai A MN và A M N .
1
Ta có: GG AA MM NN 3
Giáo viên: LÊ BÁ BẢO...0935.785.115... 6 TRẦN QUANG THẠNH...0935.295.530...
[...Chuyên đề Trắc nghiệm Toán THPT...] Phép biến hình 11CB
1 1
GG AA MM NN AA MM NN (*) 3 3 1
GG AA MM NN (**) 3 1
Theo giả thiết: AA MM NN GG GG AA MM NN. 3
Vậy đẳng thức (**) xãy ra đẳng thức (*) xãy ra 3 vectơ GG, AA, MM, NN cùng hướng.
Do đó: MM AA hay f là phép tịnh tiến (đ.p.c.m).
Chú ý: Trong bài tập trên ta đã sử dụng kết quả sau: u v w u v w . Dấu “=” xãy ra
u, v, w cùng hướng.
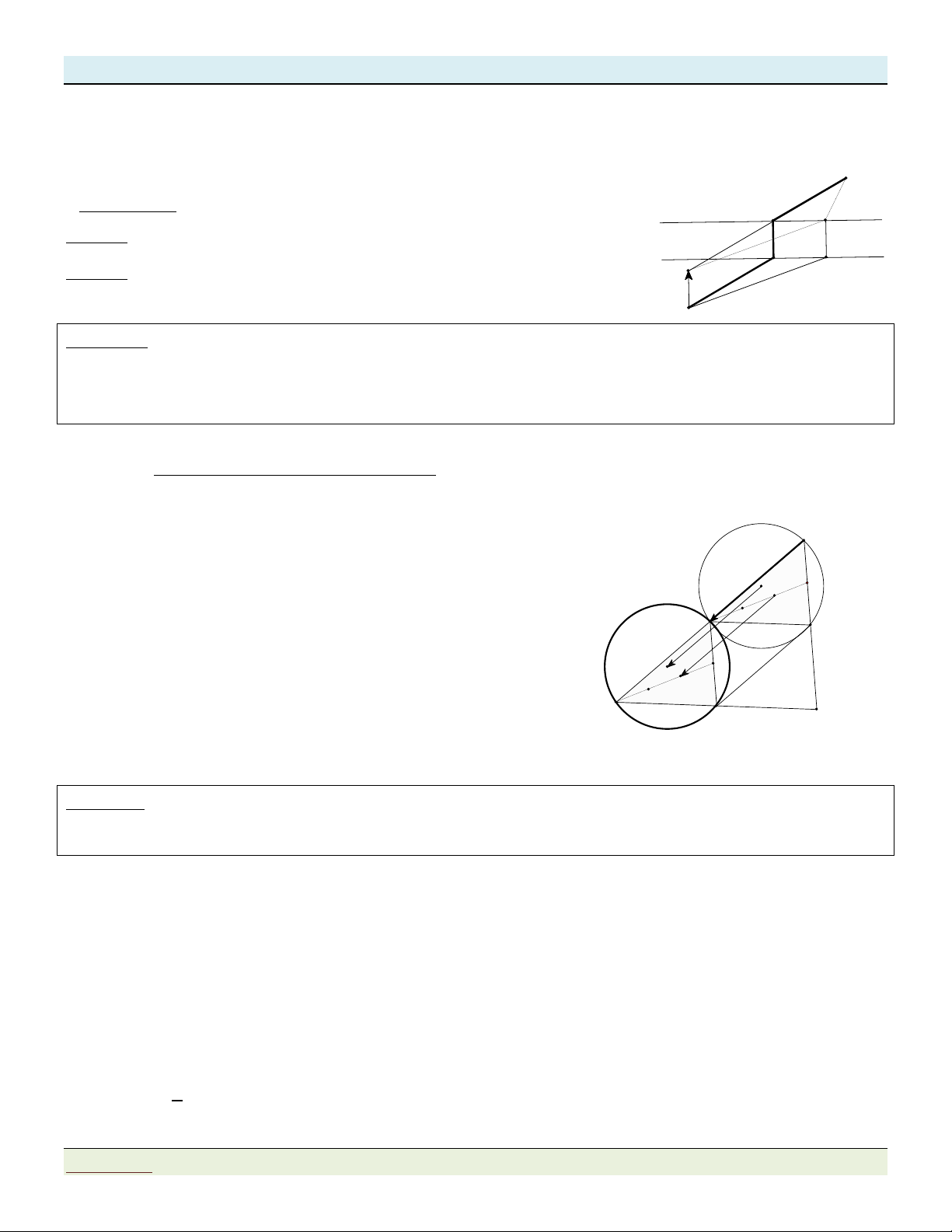
Bài tập 4: Trên đường tròn O cho hai điểm phân biệt B và C. Điểm A thay đổi trên O ( A
khác B và C ). Tìm quỹ tích trực tâm H của tam giác AB . C
Gợi ý: A (C)
Gọi O là tâm đường tròn ngoại tiếp A
BC , M là trung điểm của B'
BC. Lúc đó: OM BC . 1 H O
Lấy điểm B đối xứng với B qua O, suy ra: OM B C (1) 2 B C M Ta có: B C
/ /AH (cïng vu«ng gãc víi BC) AB C
H lµ h×nh b×nh hµnh. C
H / /AB (cïng vu«ng gãc víi AB) (C')
Suy ra: AH B C (2)
Từ (1) và (2) suy ra: AH 2OM T A H 2OM
Do A thuộc O nên H thuộc đường tròn C là ảnh của O qua T .(y.c.b.t) 2OM
Bài tập 4: Cho hình thang ABCD với A D . Chứng minh: BD CA Gợi ý: B C T
A A
Xét phép tịnh tiến T : BC BC T
D D BC Suy ra: BCA A và BCD D
là các hình bình hành, 2 1 1
và AA DD BC A A' I D D'
Do A A nên A D (1) 1 1 Từ (1) nên trong C A D
suy ra: CA CD (2)
Gọi I là trung điểm A D
(dễ thấy I cũng là trung điểm của AD).
Giáo viên: LÊ BÁ BẢO...0935.785.115... 7 TRẦN QUANG THẠNH...0935.295.530...
[...Chuyên đề Trắc nghiệm Toán THPT...] Phép biến hình 11CB
Xét hai tam giác CIA và CID , có chung CI và IA ID và từ (2) I I . 2 1
Vì thế từ hai tam giác CID và CIA suy ra: CA CD (3) Do CD BD (4)
Từ (3) và (4) suy ra: BD CA (đ.p.c.m)
Bài tập 4: Cho hình bình hành ABCD và điểm M sao cho C nằm trong tam giác MB . D Giả sử
MBC MDC . Chứng minh rằng: AMD BMC Gợi ý: T
B A
Xét phép tịnh tiến T có: T M M . Do ABCD là hình bình hành nên: BA BA BA M T
C D BA B T MC / /M D C BA MC M D MC M' M D A
nên DCMM là hình bình hành MDC DMM (1) D T BA
Theo trên suy ra: MBC M A
D MBC M A D (2)
Từ giả thiết MBC MDC và từ (1), (2) suy ra: DMM M A D /
AMM D là tứ giác nội tiếp /
AMD AM D (3)
Mặt khác theo trên suy ra (theo tính chất của phép tịnh tiến): T BA
BMC AM D
BMC AM D (4)
Từ (3) và (4) suy ra: AMD BMC (đ.p.c.m)
III. BÀI TẬP TRẮC NGHIỆM MINH HỌA
Câu 1: Với A, B phân biệt, khẳng định nào sau đây đúng?
A. T A . A
B. T B . A
C. T B . B
D. T A . B AB AB AB AB Lời giải
Ta có:T A A AA AB A . B AB
Chọn đáp án D.
Câu 2: Khẳng định nào sau đây sai?
A. T A B AB . u
B. T A . B u AB C. T B . B
D. T M N AB 2MN. 0 2 AB Lời giải
Ta có:T M N MN 2AB D sai. 2 AB
Chọn đáp án D.
Giáo viên: LÊ BÁ BẢO...0935.785.115... 8 TRẦN QUANG THẠNH...0935.295.530...
[...Chuyên đề Trắc nghiệm Toán THPT...] Phép biến hình 11CB
Câu 3: Với A, B phân biệt và T A A T B B với v 0. Khẳng định nào sau đây đúng? v , v
A. A B . v B. A B A . B C. AB . v D. A B AB 0. Lời giải T
A A AA v
v Ta có: Ta có: A B A A
AB BB AB AA BB ABvv A .B T
B B BB v v .
Chọn đáp án B.
Câu 4: Mệnh đề nào sau đây sai?
A. Phép tịnh tiến biến đoạn thẳng thành đoạn thẳng bằng nó.
B. Phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính.
C. Phép tịnh tiến biến đường thẳng thành đường thẳng song song với nó.
D. Phép tịnh tiến biến tam giác thành tam giác bằng nó. Lời giải
Do phép tịnh tiến là phép dời hình nên A, B, D đúng. Đáp án C sai vì phép tịnh tiến biến đường
thẳng thành đường thẳng song song hoặc trùng với nó.
Chọn đáp án C.
Câu 5: Cho hai đường thẳng d và d cắt nhau. Có bao nhiêu phép tịnh tiến biến d thành d ? 1 2 1 2 A. 0. B. 1. C. 2. D. vô số. Lời giải
Do phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó, nên không
tồn tại phép tịnh tiến nào biến d thành d . 1 2
Chọn đáp án A.
Câu 6: Cho hai đường thẳng d và d song song với nhau. Có bao nhiêu phép tịnh tiến theo vectơ 1 2
khác vectơ-không, biến d thành d ? 1 2 A. 0. B. 1. C. 2. D. vô số. Lời giải
Do phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó, nên tồn tại vô
số phép tịnh tiến biến d thành d . Chẳng hạn, lấy bất kì Ad , Bd T d d . 1 2 AB 1 1 2 2
Chọn đáp án D.
Câu 7: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng : 2x y 1 0. Phép tịnh tiến theo
vectơ nào dưới đây biến thành chính nó? A. u 2; 1 . B. u 2; 1 . C. u 1; 2. D. u 2; 1. Lời giải
Ta có T v 0 hoặc v là một vectơ chỉ phương của . v
Giáo viên: LÊ BÁ BẢO...0935.785.115... 9 TRẦN QUANG THẠNH...0935.295.530...
[...Chuyên đề Trắc nghiệm Toán THPT...] Phép biến hình 11CB
Đường thẳng có một vectơ pháp tuyến là n 2;
1 một vectơ chỉ phương của là u 1; 2.
Chọn đáp án C.
Câu 8: Cho hình bình hành ABCD có tâm I. Khẳng định nào sau đây sai? D C I B A
A. T D C.
B. T B . A
C. T I C.
D. T I . B AB CD AI ID Lời giải
Ta có T I I II ID I D D sai. ID
Chọn đáp án D.
Câu 9: Cho hình bình hành ABCD . Phép tịnh tiến T biến điểm D thành điểm nào sau đây? DAAB A. . B B. C. C. . A D. . D Lời giải
Ta có DA AB DB nên T biến D thành . B DA AB
Chọn đáp án A. Câu 10:
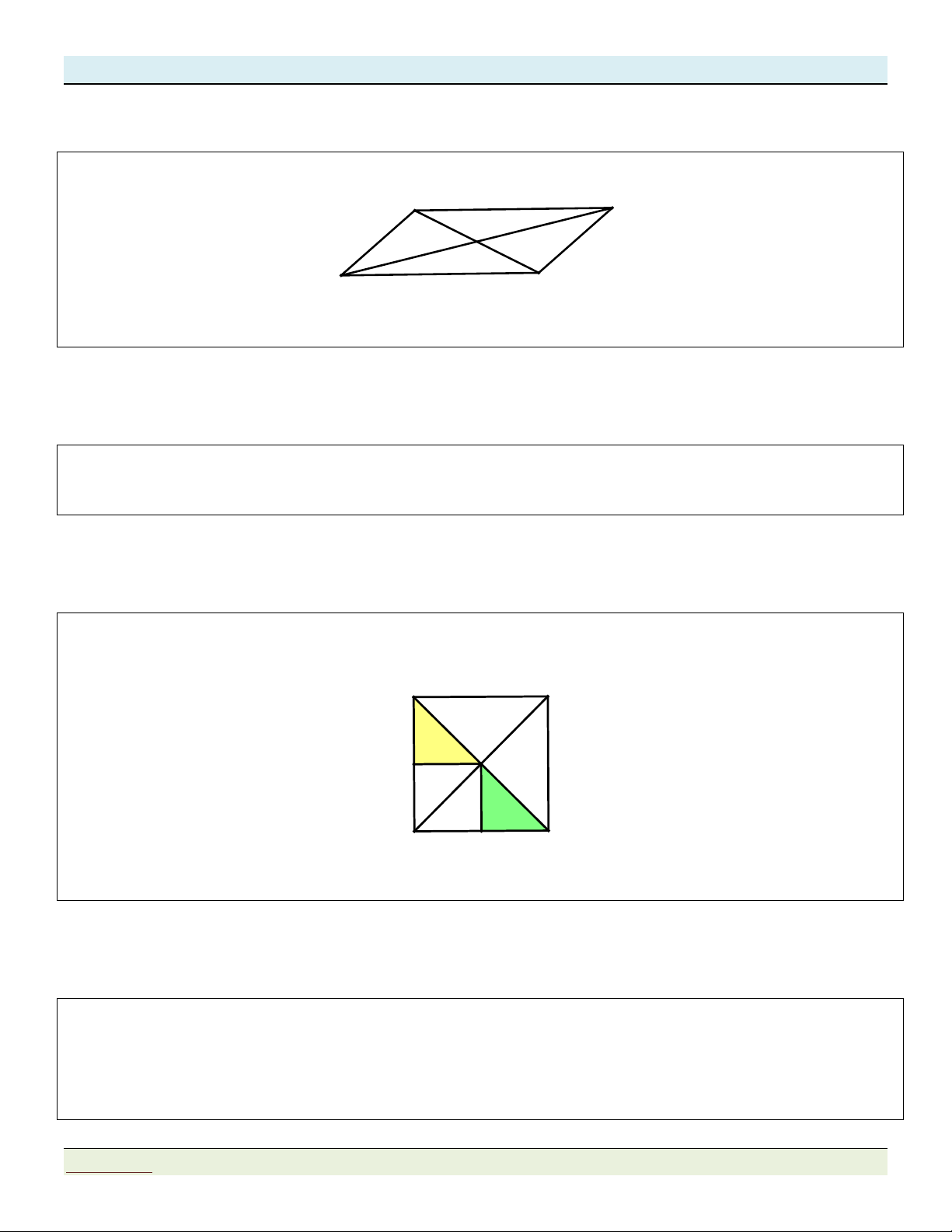
Cho hình vuông ABCD, tâm I . Gọi M, N lần lượt là trung điểm của AD, D . C Phép
biến hình theo vectơ nào sau đây biến tam giác AMI thành tam giác INC ? A B M I D C N A. AM. B. IN. C. AC. D. MN. Lời giải
Ta có AI MN IC T A MI I NC. MN
Chọn đáp án D.
Câu 11: Trong mặt phẳng với hệ tọa độ Oxy, cho v 1; 5
và điểm M' 4;
2 . Biết M’ là ảnh của
M qua phép tịnh tiến T . Tìm tọa độ điểm M . v A. M 3 ; 5. B. M 3;7 . C. M 5 ;7. D. M 5 ; 3 . Lời giải
Giáo viên: LÊ BÁ BẢO...0935.785.115... 10 TRẦN QUANG THẠNH...0935.295.530...
[...Chuyên đề Trắc nghiệm Toán THPT...] Phép biến hình 11CB
Vì M ' là ảnh của M qua T nên x x
x và y y y nên x 5; y 7. v M M v M M v M M
Chọn đáp án B.
Câu 12: Trong mặt phẳng với hệ tọa độ Oxy, cho A3; 3
. Tìm ảnh của A qua phép tịnh tiến
theo véctơ v (1; 2) . A. A’4; 5. B. A’3; 5 . C. A’4; 6 . D. A’4; 5 . Lời giải
Ta có tọa độ điểm Ax ; y với x x x 4 và y y y 5. A v A v
Chọn đáp án D.
Câu 13: Trong mặt phẳng với hệ tọa độ Oxy, xác định tọa độ của điểm A là ảnh của điểm A1; 2
qua phép tịnh tiến theo vectơ v 2; 1 . A. A 3 ; 1 . B. A 3 ; 1 . C. A3; 1 . D. A3; 1 . Lời giải
x x a 3
Ta có: T A Ax ; y A A v 3; 1.
y y b 1 A
Chọn đáp án C.
Câu 14: Trong mặt phẳng với hệ tọa độ Oxy, xác định tọa độ của điểm P có ảnh là điểm Q1;1
qua phép tịnh tiến theo vectơ v 3; 1 . A. P 4; 2. B. P 2; 0. C. P 2; 1 . D. P 4; 1 . Lời giải
x x a
x x a 2
Ta có: T P Qx ; y P P P v 2;0.
y y b
y y b 0 P P
Chọn đáp án B.
Câu 15: Trong mặt phẳng với hệ tọa độ Oxy, biết M ' 3; 0 là ảnh của M 1; 2 qua T u
và M ''2; 3 là ảnh của M ' qua T . Tìm tọa độ u v . v A. 1; 5. B. 2 ; 2 . C. 1; 1 . D. 1 ; 5 .
Lời giải
Ta có u MM ' và v M' M'' nên u v MM ' 1; 5.
Chọn đáp án A.
Giáo viên: LÊ BÁ BẢO...0935.785.115... 11 TRẦN QUANG THẠNH...0935.295.530...
[...Chuyên đề Trắc nghiệm Toán THPT...] Phép biến hình 11CB
Câu 16: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A1; 1 , B 2;
3 có ảnh lần lượt là
điểm A , B qua phép tịnh tiến theo vectơ v 2016 2017;2017 2016 . Tính độ dài đoạn 1 1 thẳng A B . 1 1 A. A B 4 13. B. A B 3 13. C. A B 2 13. D. A B 13. 1 1 1 1 1 1 1 1 Lời giải Ta có: AB 3
; 2 AB 13. Do phép tịnh tiến là phép dời hình nên A B AB 13. 1 1
Chọn đáp án D.
Câu 17: Trong mặt phẳng với hệ tọa độ Oxy, viết phương trình đường thẳng là ảnh của đường
thẳng : x 2y 1 0 qua phép tịnh tiến theo vectơ v 1; 1 . A.
: x 2y 0. B.
: x 2y 3 0. C.
: x 2y 1 0. D.
: x 2y 2 0. Lời giải
Cách 1: Ta có T / /
nên có dạng: x 2y m 0. v
Chọn A1;0 T A A2; 1
2 2 m 0 m 0. Vậy
: x 2y 0. v
A1;0 T A A v 2; 1 Cách 2: Chọn A B B
T B B v . 1;1 0; 0
Đường thẳng qua B0; 0 và có một vectơ chỉ phương là A B 2;
1 nên có một vectơ pháp
tuyến là n 1; 2 , có phương trình
: 1x 0 2y 0 0 x 2y 0.
Cách 3: Gọi M x ; y x 2y 1 0 (1). M M M M
x x
x x
Ta có: T M Mx y 1 1 ; M M thay vào (1) ta được: v y y 1 y y 1 M M
x 12y 11 0 x2y 0 : x2y 0.
Chọn đáp án A.
Câu 18: Trong mặt phẳng với hệ tọa độ Oxy, cho v 4
; 2 và đường thẳng ' : 2x y 5 0 . Hỏi
' là ảnh của đường thẳng nào qua T ? v
A. : 2x y 5 0 .
B. : 2x y 9 0 .
C. : 2x y 15 0 .
D. : 2x y 11 0 . Lời giải
Điểm M x; y thuộc Δ biến thành Mx ; y thuộc Δ , qua T . Suy ra x x 4; y y 2. Thay x v
và y ' vào Δ ' , ta được 2x 4 y 2 5 0 2x y 11 0.
Giáo viên: LÊ BÁ BẢO...0935.785.115... 12 TRẦN QUANG THẠNH...0935.295.530...
[...Chuyên đề Trắc nghiệm Toán THPT...] Phép biến hình 11CB
Chọn đáp án D.
Câu 19: Trong mặt phẳng với hệ tọa độ Oxy, viết phương trình đường tròn C là ảnh của đường tròn C 2 2
: x y 4x 2y 1 0 qua phép tịnh tiến theo vectơ v 1; 3. 2 2 2 2
A. C : x 3 y 4 2.
B. C : x 3 y 4 4. 2 2 2 2
C. C : x 3 y 4 4.
D. C : x 3 y 4 4. Lời giải
Đường tròn C có tâm I 2; 1 , bán kính 2 2
R 2 1 1 2 .
Ta có: T I I3; 4 : Tâm của C. v 2 2
Đường tròn C có tâm I3; 4 và bán kính R R 2 có phương trình: x 3 y 4 4.
Chọn đáp án B.
IV. BÀI TẬP TRẮC NGHIỆM TỰ LUYỆN
Câu 1: Với A, B phân biệt, khẳng định nào sau đây đúng?
A. T A . A
B. T A . B
C. T B . B
D. T B . A AB BA AB BA
Câu 2: Khẳng định nào sau đây sai?
A. T A B AB . u
B. T A . B u AB C. T A . A
D. T M N AB 2N . M 0 2 AB
Câu 3: Với A, B phân biệt và T A A T B B với v 0. Khẳng định nào sau đây đúng? v , v
A. AB . v B. A B A . B C. A B . v D. A B AB 0.
Câu 4: Tính chất nào sau đây là sai đối với phép tịnh tiến?
A. Biến đoạn thẳng thành đoạn thẳng bằng nó.
B. Biến đường tròn thành đường tròn có cùng bán kính.
C. Biến đường thẳng thành đường thẳng song song với nó.
D. Biến tam giác thành tam giác bằng nó.
Câu 5: Cho hai đường thẳng d và d cắt nhau. Có bao nhiêu phép tịnh tiến biến d thành d ? 1 2 2 1 A. 0. B. 1. C. 2. D. vô số.
Câu 6: Cho hai đường thẳng song song với nhau. Có bao nhiêu phép tịnh tiến theo vectơ khác
vectơ-không, biến đường thẳng này thành đường thẳng kia? A. 0. B. 1. C. 2. D. vô số.
Câu 7: Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng : 2x y 4 0. Phép tịnh tiến theo
vectơ nào dưới đây biến thành chính nó? A. u 2; 1 . B. u 2; 1 . C. u 1; 2. D. u 1; 2 .
Giáo viên: LÊ BÁ BẢO...0935.785.115... 13 TRẦN QUANG THẠNH...0935.295.530...
[...Chuyên đề Trắc nghiệm Toán THPT...] Phép biến hình 11CB
Câu 8: Cho hình bình hành ABCD có tâm I. Khẳng định nào sau đây sai? D C I B A
A. T A . B
B. T B . A
C. T I . B
D. T I C. DC CD DI IA
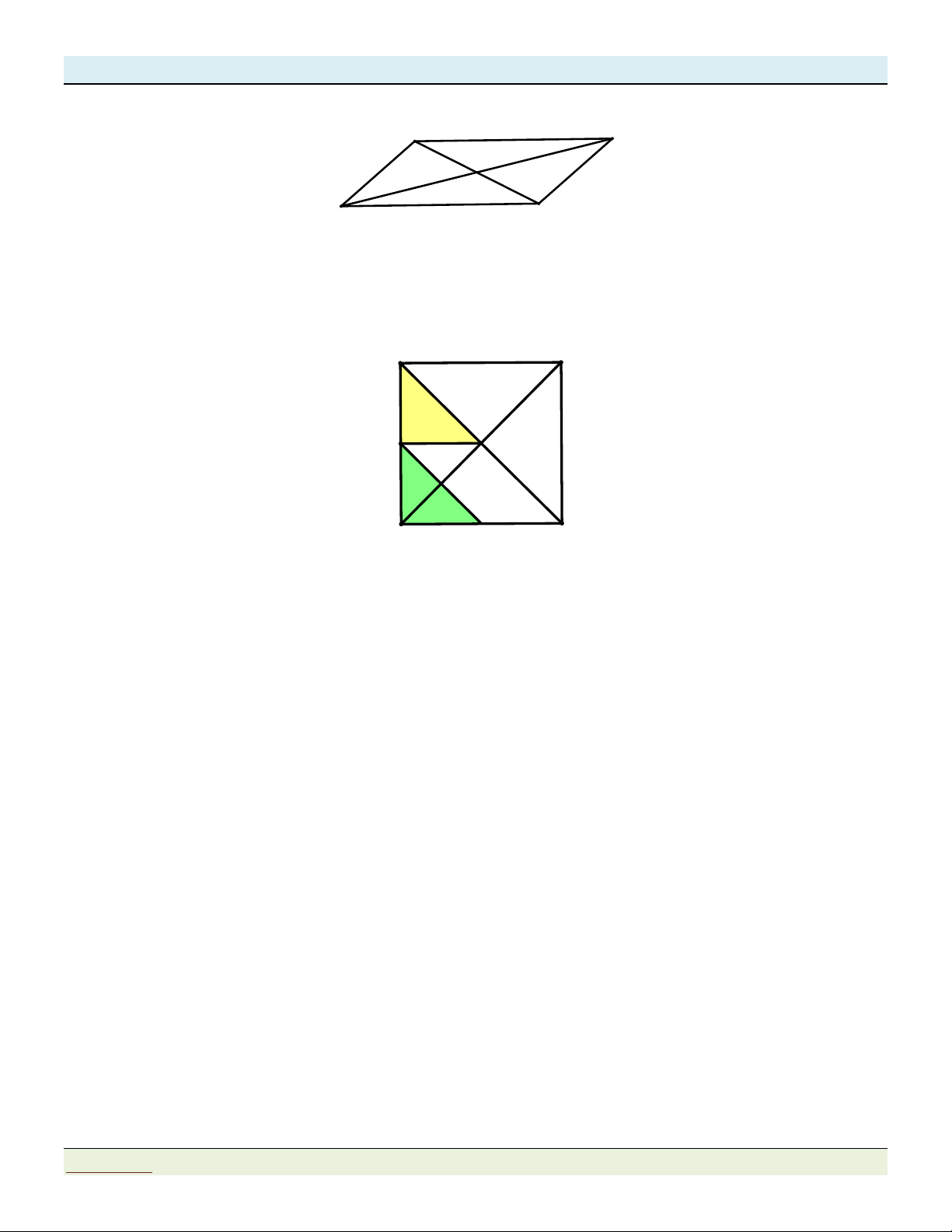
Câu 9: Cho hình vuông ABCD, tâm I . Gọi M, N lần lượt là trung điểm của AD, D . C Phép biến
hình theo vectơ nào sau đây biến tam giác AMI thành tam giác MDN ? A B I M C D N A. AM. B. NI. C. AC. D. MN.
Câu 10: Trong mặt phẳng với hệ tọa độ Oxy, xác định tọa độ của điểm A là ảnh của điểm A1; 2
qua phép tịnh tiến theo vectơ v 2; 3. A. A 3 ; 5. B. A 3 ; 1 . C. A3; 1 . D. A3; 5.
Câu 11: Trong mặt phẳng với hệ tọa độ Oxy, xác định tọa độ của điểm A là ảnh của điểm A1; 2
qua phép tịnh tiến theo vectơ v 1; 1 . A. A2; 1 . B. A 3 ; 1 . C. A2; 1 . D. A3; 5.
Câu 12: Trong mặt phẳng với hệ tọa độ Oxy, xác định tọa độ của điểm P có ảnh là điểm Q1;1
qua phép tịnh tiến theo vectơ v 1 ; 1 . A. P 0; 2. B. P 2; 0. C. P 2; 0. D. P 4; 1 .
Câu 13: Trong mặt phẳng với hệ tọa độ Oxy, xác định tọa độ của điểm P có ảnh là điểm Q2; 1
qua phép tịnh tiến theo vectơ v 2; 1. A. P 0; 0. B. P 2; 2 . C. P 2; 0. D. P 4; 2 .
Giáo viên: LÊ BÁ BẢO...0935.785.115... 14 TRẦN QUANG THẠNH...0935.295.530...
[...Chuyên đề Trắc nghiệm Toán THPT...] Phép biến hình 11CB
Câu 14: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A1;
1 , B1; 3 có ảnh lần lượt là điểm
A , B qua phép tịnh tiến theo vectơ v 2016 2 2017;2017 2 2016 . Tính độ dài đoạn thẳng 1 1 A B . 1 1 A. A B 4 13. B. A B 2016. C. A B 2. D. A B 3. 1 1 1 1 1 1 1 1
Câu 15: Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A1;
1 , B2; 3 có ảnh lần lượt là điểm
A , B qua phép tịnh tiến theo vectơ v 2016 5 2017;2017 5 2016 . Tính độ dài đoạn thẳng 1 1 A B . 1 1 A. A B 5. B. A B 2016. C. A B 5. D. A B 2 5. 1 1 1 1 1 1 1 1
Câu 16: Trong mặt phẳng với hệ tọa độ Oxy, viết phương trình đường thẳng là ảnh của đường
thẳng : x 2y 1 0 qua phép tịnh tiến theo vectơ v 2; 1 . A.
: x 2y 0. B.
: x 2y 3 0. C.
: x 2y 1 0. D.
: x 2y 2 0.
Câu 17: Trong mặt phẳng với hệ tọa độ Oxy, viết phương trình đường thẳng là ảnh của đường
thẳng : x y 1 0 qua phép tịnh tiến theo vectơ v 2; 1 . A.
: x y 3 0. B.
: x y 4 0. C.
: x y 1 0. D.
: x y 2 0.
Câu 18: Trong mặt phẳng với hệ tọa độ Oxy, viết phương trình đường tròn C là ảnh của đường tròn C 2 2
: x y 4x 2y 1 0 qua phép tịnh tiến theo vectơ v 1; 3. 2 2 2 2
A. C : x 3 y 2 2.
B. C : x 3 y 4 4. 2 2 2 2
C. C : x 3 y 4 4.
D. C : x 3 y 2 4.
Câu 19: Trong mặt phẳng với hệ tọa độ Oxy, viết phương trình đường tròn C là ảnh của đường tròn C 2 2
: x y 2x 4y 4 0 qua phép tịnh tiến theo vectơ v 1 ; 2. 2 2 A. C 2 2
: x y 1.
B. C : x
1 y 2 1. C. C 2 2
: x y 4.
D. C x 2 2 : 1 y 1.
Câu 20: Trong mặt phẳng với hệ tọa độ Oxy, viết phương trình đường elip E là ảnh của đường 2 x y elip E 2 :
1 qua phép tịnh tiến theo vectơ v 1 ; 1 . 16 4 2 2 2 2 x 1 y 1 x 1 y 1 A. E : 1. B. E : 1. 16 4 16 4 2 2 2 2 x 1 y 1 x 1 y 1 C. E : 1. D. E : 1. 16 4 16 4
Giáo viên: LÊ BÁ BẢO...0935.785.115... 15 TRẦN QUANG THẠNH...0935.295.530...
[...Chuyên đề Trắc nghiệm Toán THPT...] Phép biến hình 11CB
Câu 21: Cho hình bình hành ABCD . Phép tịnh tiến T biến đoạn thẳng DC thành đoạn thẳng ABAC nào sau đây? A. BC. B. . AB C. DC. D. . CA
Câu 22: Trong mặt phẳng với hệ tọa độ Oxy, cho M 2;
1; N0;2; v (1;2). Phép T biến M, N v
thành M’, N’ thì độ dài M’N’ bằng bao nhiêu? A. 5. B. 3 . C. 10 . D. 5 .
Câu 23: Cho lục giác ABCDEF đều tâm .
O Tìm ảnh của ΔABO qua T . OD A. ΔOC . D B. ΔBC . O C. ΔOC . E D. ΔAO . F
Câu 24: Trong mặt phẳng với hệ tọa độ Oxy, cho
v 3; 3 và đường tròn C 2 2
' : x y 2x 4y 4 0 là ảnh của C qua T là C ' . Tìm phương trình của đường tròn C. v 2 2 2 2
A. x 2 y 5 9 .
B. x 2 y 5 9 . 2 2
C. x 2 y 1 9 . D. 2 2
x y 8x 2y 4 0 .
Câu 25: Trong mặt phẳng với hệ tọa độ Oxy, cho A
BC có A1;4,B4;0,C 2; 2 . Phép tịnh
tiến T biến A BC thành A
'B'C' . Tọa độ trực tâm của A 'B'C' là BC A. 4 ; 1 . B. 1 ; 4 . C. 4; 1 . D. 4;1 . BẢNG ĐÁP ÁN Câu 1 2 3 4 5 6 7 8 9 10 Đáp án D D B C A D D D A D Câu 11 12 13 14 15 16 17 18 19 20 Đáp án C C D C A C B D A B Câu 21 22 23 24 25 Đáp án B D A C A
P/S: Trong quá trình sưu tầm và biên soạn chắc chắn không tránh khỏi sai sót, kính mong quí thầy cô và các
bạn học sinh thân yêu góp ý để các bản update lần sau hoàn thiện hơn! Xin chân thành cảm ơn. CLB GI¸O VI£N TRÎ TP HUÕ
Phụ trách chung: Giáo viên LÊ BÁ BẢO.
Đơn vị công tác: Trường THPT Đặng Huy Trứ, Thừa Thiên Huế.
Email: lebabaodanghuytru2016@gmail.com
Facebook: Lê Bá Bảo
Số điện thoại: 0935.785.115
Giáo viên: LÊ BÁ BẢO...0935.785.115... 16 TRẦN QUANG THẠNH...0935.295.530...




