401 trang 3 lượt tải

Phiếu bài tập trắc nghiệm và tự luận môn Toán 8

6

Giới thiệu đến quý thầy, cô giáo và các em học sinh phiếu bài tập trắc nghiệm và tự luận môn Toán 8.

Chủ đề: Tài liệu chung Toán 8 289 tài liệu

Môn: Toán 8 2.3 K tài liệu

Tác giả:

Profile

Linh Đan

18 giờ trước
Danh sách Quiz
/401
PHIẾU BÀI TẬP TOÁN 8
1
ĐƠN THỨC NHIỀU BIẾN – ĐA THỨC NHIỀU BIẾN
I. Bài tập trắc nghiệm
Câu 1. Trong các câu sau, câu nào sai?
A. Đơn thức nhiều biến (hay đơn thức) là biểu thức đại số chỉ gồm một số, hoặc một biến,
hoặc một tích giữa các số và các biến.
B. Số 0 không phải là đơn thức
C. Đơn thức
1
2
xyz−
có phần hệ số là
1
2
−
D. Đơn thức thu gọn là đơn thức chỉ gồm tích của một số với các biến mà mỗi biến được
nâng lên lũy thừa với số mũ nguyên dương.
Câu 2. Trong các biểu thức sau, biểu thức nào là đơn thức?
A.
2
2 xy+
. B.
45
2xy
. C.
3
3
xy
y
+
. D.
3
3
7
4
xy x−+
.
Câu 3. Trong các biểu thức đại số sau, biểu thức nào không phải đơn thức?
A.
2
. B.
. C.
32
xy
. D.
3x
.
Câu 4. Đơn thức
2
5xyz
có phần biến là?
A.
xyz
. B.
2
xy z
. C.
22
xy z
. D.
2
xyz
.
Câu 5. Trong các đơn thức sau, đơn thức thu gọn là?
A.
2
1
2
x yzx
. B.
22 3
5x y zx
. C.
22
3xy
. D.
35
2x yzx
.
Câu 6. Trong các đơn thức sau, đơn thức chưa thu gọn là?
A.
2
1
4
x yz−
. B.
3xy
. C.
2
2xy
. D.
3 55
1
2
x yzx y
.
Câu 7. Thu gọn đơn thức
22 22
3xyzyz
ta được đơn thức là?
A.
24
3xyz
. B.
243
3
xyz
. C.
234
3xyz
. D.
233
3xyz
.
Câu 8. Trong các câu sau, câu nào sai?
A.
2
3xy
và
2
6xy
là hai đơn thức đồng dạng
B. Hai đơn thức đồng dạng có phần hệ số khác 0 và không có chung phần biến
C.
2
3
y
và
2
1
2
y
là hai đơn thức đồng dạng
D.
2
xy
và
2
xy−
là hai đơn thức đồng dạng
Câu 9. Kết quả quả phép tính
22
33()xy xy+−
là:
A.
0
. B.
2
6xy
. C.
2
xy
. D.
2
6xy−
.
Câu 10. Kết quả quả phép tính
22
10 6xy xy+
là:
A.
16
xy
. B.
2
16xy
. C.
2
16xy
. D.
42
16xy
.
Câu 11. Kết quả quả phép tính
22 22
46xy xy−
là:
A.
2−
. B.
22
2xy−
. C.
22
2xy
. D.
42
2xy−
.
Câu 12. Câu nào sau đây là sai?
A. Đa thức nhiều biến (hay đa thức) là một tổng của những đơn thức
B. Mỗi đơn thức không phải là đa thức
C. Thu gọn đa thức nhiều biến là làm cho đa thức đó không còn hai đơn thức nào đồng dạng
D. Số 0 là đa thức
PHIẾU BÀI TẬP TOÁN 8
2
Câu 13. Biểu thức nào sau đây là đa thức?
A.
1
32
2
()xy+
. B.
1
4x
y
+
. C.
2
2
5
xy
x
−+
. D.
2
3
3
2
y
x
+
.
Câu 14. Biểu thức nào sau đây không là đa thức?
A.
2
4x xy+−
. B.
2
3
xy
y
x
−
−
. C.
32
2
5
xy y−+
. D.
2
5
xy+
.
Câu 15. Đa thức thu gọn trong các đa thức sau là:
A.
22
1
3
xy xyz xy−−
. B.
2
1
3
x y xyz zxy−−
.
C.
22
2
24
5
xy y y x− +−
. D.
22
3
3
2
xy y
+
.
Câu 16. Đa thức nào sau đây chưa thu gọn?
A.
2
4x xy
+−
. B.
44
2x y x yx
+−
.
C.
32
2
5
xy y−+
. D.
22xy+
.
Câu 17. Thu gọn đa thức
22
2 32xy x y xy x y− ++
ta được kết quả là:
A.
22
42 2xyxyyx−+
. B.
2
4
xy
.
C.
4xy
. D.
2
44xy x y−
.
Câu 18. Câu nào sau đây là sai:
A. Một số bất kì khác 0 có bậc là 0 B. Số 0 là đa thức không có bậc
C. Đơn thức
35
1
2
xyz
có bậc là 9 D. Đa thức
5 22 2
4x xy x
+−
có bậc là 11
Câu 19. Xác định số
a
để các đơn thức
3
axy
,
3
4xy−
,
3
7xy
có tổng bằng
3
6xy
.
A.
9a =
. B.
1
a =
.
C.
3a =
. D.
2a
=
.
Câu 20. Đa thức
2
23xy xy
+
có giá trị bằng
0
tại
1
2
x
=
, thì giá trị của
y
là
A.
1
0
2
;



. B.
3
0
2
;

−


.
C.
3
0
2
;



. D.
1
0
2
;

−


.
II. Bài tập tự luận
Bài 1. Điền vào chỗ chấm
1) Năm đơn thức đồng dạng với đơn thức
2
2x yz
là:………………………………………………
2)
6 15
..................xyz xyz+=
3) Đa thức
42
3 24x xy x− +−
có bậc là ……………………………………………………………….
4) Đa thức biểu thị tổng diện tích của hình vuông có cạnh
cm)(x
và hình chữ nhật có hai cạnh
cm)(x
và
cm)(y
là: …………………………………………………………………………………….
5) Đa thức biểu thị diện tích toàn phần của hình hộp chữ nhật có chiều dài
cm)(x
, chiều
rộng
cm)(y
, chiều cao
10 cm)(
là:…………………………………………………………………….
PHIẾU BÀI TẬP TOÁN 8
3
Bài 2. Thu gọn các đơn thức sau:
1)
22 2
5 ......................................................................................................................xyxyz=
2)
24 2 29
1
2
.................................................................................................................xzyxyz =
3)
( ) ( )
22
2 26 2
5 ........................................
...............................................................x yzx y z−=
4)
( )
2
2 425
3
4
...........................................................................................................xzy x y z−=
Bài 3. Viết kết quả của các phép tính sau vào chỗ chấm
1)
222
365...........................xy xy xy+−=
; 2)
1
35
2
.............................xyz xyz xyz+−=
3)
22 22 22
35...........................
xy xy xy−+ − =
; 4)
22 2
2
16
3
.......................xyz xyz xyz
+− =
Bài 4. Tìm đơn thức
,AB
và cho biết bậc của chúng:
1)
22
5
x yz A x yz
−=
2)
32 32 32
1
10
2
xyz B xyz xyz
+− =
Bài 5. Thu gọn và tính giá trị các đa thức sau:
1)
22
22 52A x xy x xy yy=−− + + +
tại
12;xy= =
2)
6 23 5 5 6
2 2B yx xx y xy xy xy x=+− −++ −
tại
1
4
0;xy= =
PHIẾU BÀI TẬP TOÁN 8
4
3)
2 22 2 2
3 4 3 24
C xy z xy z x xyz xy z xyz x= + −− − − + +
tại
12;xy z= = = −
Bài 6. Một mảnh đất có kích thước như hình vẽ sau (đơn vị mét). Phần bôi đậm được
dùng để trồng rau, phần màu trắng được dùng để trồng cây ăn trái. Hãy tìm đơn thức biểu
thị diện tích:
a) Diện tích đất trồng rau
b) Diện tích đất trồng cây ăn trái
c) Diện tích mảnh đất
2y
4x
x
5y
PHIẾU BÀI TẬP TOÁN 8
5
Bài 7. Một bức tường hình thang có cửa sổ hình tròn với các kích thước như hình vẽ
dưới đây (đơn vị mét).
a) Viết đa thức biểu thị diện tích bức tường (không tính phần cửa sổ)
b) Tính diện tích bức tường ở câu a biết
2 3 05 ; ;,a mh mr m= = =
(Lấy
3 14, ≈
)
Bài 8.
a) Tính giá trị của đa thức
32 2 2
2 31
M x x y x xy y y x= + − − − + +−
biết
20xy+−=
.
b) Tính giá trị của đa thức
42242
35 22Nxxyyy=+ ++
biết rằng
22
2xy+=
.
PHIẾU BÀI TẬP TOÁN 8
6
Bài 9. Cho hai đa thức
2
21A xy x y= +++
và
22
2B x y xy=++
. Tìm cặp số nguyên
(; )xy
thỏa mãn
AB=
PHIẾU BÀI TẬP TOÁN 8
7
HƯỚNG DẪN ĐÁP SỐ
I. TRẮC NGHIỆM
1-B
2-B
3-B
4-D
5-C
6-D
7-B
8-B
9-A
10-C
11-B
12-B
13-A
14-B
15-D
16-B
17-C
18-D
19-C
20-B
II. TỰ LUẬN
Bài 1. Điền vào chỗ chấm
1) HS TỰ LÀM
2)
19
65xyz xyz
xyz
+=
3) Đa thức
42
3 24x xy x
− +−
có bậc là 4
4) Đa thức biểu thị tổng diện tích của hình vuông có cạnh
cm)(x
và hình chữ nhật có hai
cạnh
cm)(
x
và
cm)(y
là:
22
()x xy cm+
5) Đa thức biểu thị diện tích toàn phần của hình hộp chữ nhật có chiều dài
cm)(x
, chiều
rộng
cm)(y
, chiều cao
10 cm)(
là:
2
20 20 2
()x y xy cm++
Bài 2. Thu gọn các đơn thức sau:
1)
3422 2
5
5 xyzxyxyz=
2)
242 2
349 13
1
22
1
z xzy y y
x zx =
3)
( ) ( )
7
22
2 26 2 56
5 5xyzx yzx y z−=−
4)
( )
4 667
2
2 25
3
4
3
4
xzy x y z xyz−−=
Bài 3. Viết kết quả của các phép tính sau vào chỗ chấm
1)
2 2
22
5
436
xyxy xy xy
+−=
; 2)
1
35
2
3
2
zxyz xyz xyz xy−+−=
;
3)
22 22 22
22
35 3xy xy x y
y x− −
+−=
; 4)
222 2
2
6
7
3
1
3
xyz xyz
xyz xyz
−+− =
;
Bài 4. Tìm đơn thức
,AB
và cho biết bậc của chúng:
1)
2
4A x yz= −
; 2)
32
21
2
B xyz=
Bài 5. Thu gọn và tính giá trị các đa thức sau:
1)
22
22 52A x xy x x
y yy
=−− + + +
tại
12;xy= =
Thu gọn:
2
2
3A yx xy
= ++
Giá trị biểu thức
A
tại
12;xy= =
là:
2
01 2 312 2 1. ..+ +=
2)
6 23 5 5 6
2 2B yx xx y xy xy xy x=+− −++ −
tại
1
4
0;xy= =
Thu gọn:
23
2 yBx xy= −
Giá trị biểu thức
B
tại
1
4
0;xy= =
là:
3
2
0
11
20 0
44
.. .

−=


3)
2 22 2 2
3 4 3 24C xy z xy z x xyz xy z xyz x= + −− − − + +
tại
12;xy z= = = −
Thu gọn:
2
44C x xyz=−+
; Giá trị biểu thức
C
tại
12;xy z
= = = −
là:
2
31 411 2 4 1...( )− −+=
PHIẾU BÀI TẬP TOÁN 8
8
Bài 6.
a) Diện tích đất trồng rau
2
5 3 2 5 6 11
. . ()x y x y xy xy xy m
+ =+=
b) Diện tích đất trồng cây ăn trái
2
33 9. ()x y xy m=
c) Diện tích mảnh đất
2
11 9 20 ()xy xy xy m+=
Bài 7.
a) Đa thức biểu thị diện tích bức tường (không tính phần cửa sổ)
là:
2
2 2
2
3
2
2(
)
)
(
. .ah
rm
a ah
r
+
−
−=
b) Diện tích bức tường ở câu a là:
2 2
2
3 323
3 14 0
2
82
5 15
2
, ()
. ..
, .( , ) m
ah
r−≈ =−
Bài 8.
a) Tính giá trị của đa thức
32 2 2
2 31
M x x y x xy y y x= + − − − + +−
biết
20xy
+−=
.
32 2 2
2 31M x x y x xy y y x
= + − − − + +−
(
)
(
)
32 2 2
2 21x x y x xy y y y x
= + − +− − + + + −
( ) ( ) ( )
2
2 2 21xxy yxy xy= +− − +− + +− +
2
0 0011..xy
= − ++=
.
Vậy
1M
=
.
b) Tính giá trị của đa thức
42242
35 22
Nxxyyy
=+ ++
biết rằng
22
2xy+=
.
42242
35 22Nxxyyy=+ ++
4 22 22 4 2
33 2 22x xy xy y y=+ + ++
22 2 22 2
3 21
( )( )
xxy yxy= + + ++
Mà
22
2xy+=
nên ta có
( ) ( ) ( )
222 222 2 2 22
3 2 1 6 6 6 6 2 12
.xxy yxy x y xy+ + + += + = + = =
.
Vậy
12N =
.
Bài 9. Ta có
AB=
nên
2 22
2 12xy x y x y xy+ ++= + +
22 2
2 2 10xy y x x y xy
⇒ − + − +− +=
( )
( )
( )
22 2
22 1xy y xy y x x− − −− −=−
( ) ( ) ( )
2
2 1 1 11y x yx xx−− −− −=−
(
)
(
)
2
12 1
x y yx⇒ − −− =−
Do
,xy
nguyên nên
(
)
( )
2
12;x y yx− −−
là các số nguyên và là ước của
1
nên ta có các
trường hợp sau:
Trường hợp 1:
( )
22
2
11 2
2
1
2 12 1
211
x
xx
x
y
yyx yy
yy

=
−= =
=

⇒⇒ ⇒

=
−−=− −=
−=


Trường hợp 2:
( )
22
0
11 0
0
1
2 12 1
211
x
xx
x
y
yyx yy
yy

=
−=− =
=

⇒⇒ ⇒

=
−−= −=
−=


Vậy các cặp số
( )
;
xy
thỏa mãn là
( ) ( )
21 01;;;
2y
4x
x
5y
PHIẾU BÀI TẬP TOÁN 8
1
CÁC PHÉP TÍNH VỀ ĐA THỨC NHIỀU BIẾN
(PHÉP CỘNG – TRỪ)
I. Bài tập trắc nghiệm
Câu 1. Kết quả của phép tính
24 24
37
xy xy+
là
A.
24
10xy
. B.
24
9xy
. C.
24
9
xy
−
. D.
24
4
xy
−
.
Câu 2. Kết quả của phép tính
22
9 12()yz yz− −−
là
A.
2
21
yz−
. B.
2
3yz−
. C.
42
3yz
. D.
2
3yz
.
Câu 3. Phép tính
22
2 ()x y xy x y xy+ −− −
sau khi phá dấu ngoặc tròn được kết quả là?
A.
22
2x y xy x y xy+−−
. B.
22
2x y xy x y xy+++
.
C.
22
2x y xy x y xy
+−+
. D.
22
2
x y xy x y xy++−
.
Câu 4. Trong các câu sau, câu nào sai?
A. Đa thức
42
35x xy
+−
có bậc là 4
B. Để tìm bậc của một đơn thức đa thức trước tiên ta phải thu gọn đơn thức, đa
thức đó
C. Đơn thức
2
2
xy
có phần hệ số là
2
D. Đơn thức
2
2
xy
có phần hệ số là
1
2
Câu 5. Thu gọn đa thức
22 22
3 2 16 2 5 10x y xy x y xy
− − +− + −
ta được
A.
22
7 26x y xy
−− +
. B.
22
536x y xy−+ +
.
C.
22
536
x y xy
−− +
. D.
22
536
x y xy−−
.
Câu 6. Giá trị của đơn thức
33
9
xy
tại
1
1
3
,xy
=−=−
A.
1
9
B.
1
3
C.
1
6
D.
2
9
Câu 7. Tìm đa thức
B
sao cho tổng
B
với đa thức
424 2
23 6x x y y xz z− ++ −
bằng 0 .
A.
42 4
23 622B x x y xz xz y=−+ − + +
B.
424 2
23 6
B x x y y xz z=− + −− +
C.
42
23 6B x x y xz=−− −
D.
4 2 22
23 64
B x x y xz x z z=−− − + +
Câu 8. Bậc của đa thức
32 32
55
23 21
22
x y xy xy x y xy+ +− − −
là:
A.
2
. B.
1
. C.
5
2
. D.
1
−
.
Câu 9. Tìm đa thức
M
biết
22 2
34 78M xy y x xy y−+=−+
.
A.
22
44
M x xy y=−−
. B.
22
44M x xy y
=−+
.
C.
22
44M x xy y=−− +
. D.
22
10 4
M x xy y=++
.
Câu 10. Giá trị của biểu thức
2
31xx++
tại
x
thỏa mãn
( )
( )
2
7 20
xx+ +=
bằng
A. 10. B. 1. C. -1. D. 11.
Câu 11. Cho
( ) ( )
22M x yz xyz x y=−−− ++−−−
và
( )
22Nx x y z z

=−−− −

.
Tính
MN−
.
A.
22z−+
. B.
222xy−− −
. C.
22z −
. D.
222xy−+ −
.
PHIẾU BÀI TẬP TOÁN 8
2
Câu 12. Cho
2 2 2 3 3 3 2020 2020 2020
...
P xyz x y z x y z x y z
= + + ++
. Tính
P
biết
11
;xy z
= = = −
.
A.
2020P = −
. B.
0P =
. C.
2020P =
. D.
1010
P
=
.
II. Bài tập tự luận (7điểm)
Bài 1. Thu gọn các đa thức sau và cho biết bậc của các đa thức đó
1)
22
24A xy xy xy xy
=− + ++
2)
2 2 22
23
B xy z xy z xyz xy z xy z= + −− +
.
3)
2
1
2 34
2
C xyx xy x x y xy x= − +− + −
4)
( )
2
23 3 5 3 4
2
24
1
2
D xy y z y y zyx
= +−
−
−
+
.
Bài 2. Cho các đa thức
22 2
2 31A x y xy xy=−+ −−
2 22
21B xy x y xy=+ ++
22 2
5 2 23C xy x y xy= − ++
1) Tính
AB
+
2) Tính
ABC−+
PHIẾU BÀI TẬP TOÁN 8
3
Bài 3. Tìm đa thức
A
và
B
sau đó tính giá trị đa thức
A
và
B
tại
12;xy= = −
1)
( )
2 22
52 62A x xy x xy y+ − =−−
2)
222 22 2
1
2
xy x x y B xy x y x

+ − −=− − +


Bài 4. Bác Hoàng gửi tiết kiệm ở ngân hàng thứ nhất
50
triệu đồng với kỳ hạn một năm, lãi suất
%/x
năm. Bác
Hoàng gửi ở ngân hàng thứ hai
100
triệu đồng với kỳ
hạn một năm, lãi suất
15, %/
x
năm.
a) Viết đa thức biểu thị số tiền lãi bác Hoàng có được ở ngân
hàng thứ nhất sau khi hết kỳ hạn một năm.
b) Viết đa thức biểu thị số tiền lãi bác Hoàng có được ở cả hai ngân hàng sau khi hết kỳ
hạn một năm.
c) Nếu
5x =
thì sau một năm gửi tiết kiệm ở hai ngân hàng bác Hoàng lãi được bao nhiêu
tiền?
PHIẾU BÀI TẬP TOÁN 8
4
Bài 5.
Hai người đi xe đạp cùng một lúc và ngược chiều nhau từ hai địa điểm
A
và
B
. Người
xuất phát từ
A
đi với vận tốc không đổi
x
( /)km h
. Người xuất phát từ
B
đi với vận tốc
không đổi
y
( /)km h
. Hai người gặp nhau tại điểm
C
sau
4
giờ.
a) Lập đa thức
S
biểu thị quãng đường
AB
theo
x
và
y
b) Tính
S
tại
10, 8
xy

.
c) Biết rằng người xuất phát từ
B
đi với tốc độ nhanh gấp đôi người xuất phát từ
A
. Tính
thời gian để người xuất phát từ
A
đi hết quãng đường
AB
.
Bài 6. Cho hai đa thức
22
73P x xy y
=−−
và
22
332Q xy x y=−+
. Chứng minh rằng:
không có số thực
x
và
y
nào để đa thức
P
và
Q
cùng nhận giá trị âm.
Bài 7. Tìm số tự nhiên
(
)
abc a b c
<<
sao cho:
666abc bca ca b++=
PHIẾU BÀI TẬP TOÁN 8
5
III. BÀI TẬP VỀ NHÀ
Bài 1. Rút gọn các biểu thức sau
a)
2 22 2
75
( )( )A x xy y x xy y
= − + −− + −
.
b)
22 22 2 2
3 25 3()( )()B xy x y xy x y x y xy= − −− − + −
.
Bài 2. Cho các đa thức
32
22 1M x x y xy= − ++
;
2
3 22
N x y xy
= +−
32
31P x x y xy
=−−+
.
Tính
a)
MN+
.
b)
MP−
.
c)
MNP−+
.
Bài 3. Tìm đa thức
A
,
B
sau đó tính giá trị biểu thức
A
,
B
tại
12;xy= =
a)
2 2 22 2
63 2x xy A x y xy− += + −
. b)
2 22
24 5 7()
B xy y xy x y
− − = +−
.
Bài 4. Một chiếc bình có dạng hình lập phương với độ dài cạnh là
2x
(cm).
a) Viết đa thức biểu thị thể tích nước tối đa mà chiếc bình đó có thể chứa được.
b) Biết rằng độ cao mực nước trong bình đang là
y
(cm) (với
2yx<
). Viết đa thức biểu thị
thể tích phần không có nước trong bình.
Bài 5. Cho hai đa thức
22 2 2
4 12 2
M x y xy y=−−
và
22 2 2
12 2N x y xy y
=++
. Chứng minh
rằng: không có số thực
x
và
y
nào để đa thức
P
và
Q
cùng nhận giá trị âm.
Bài 6*. Cho đa thức
2
2012 2013 2014A x xy x y=+− − −
. Tìm cặp số
(; )xy
nguyên để đa
thức
0A =
PHIẾU BÀI TẬP TOÁN 8
6
HƯỚNG DẪN ĐÁP SỐ
I. TRẮC NGHIỆM
1-A
2-D
3-B
4-C
5-B
6-B
7-B
8-A
9-B
10-C
11-C
12-B
II. TỰ LUẬN
Bài 1. Thu gọn các đa thức sau và cho biết bậc của các đa thức đó
1)
22
24
A xy xy xy xy=− + ++
2)
2 2 22
23B xy z xy z xyz xy z xy z= + −− +
.
2
5A xy xy= −
; Bậc 3
2
B xy z xyz
= −
; Bậc 4
3)
2
1
2 34
2
C xyx xy x x y xy x= − +− + −
4)
( )
2
23 3 5 3 4
2
24
1
2
D xy y z y y zyx
= +−
−
−
+
.
2
1
3
2
C x y xy x
= +−
; Bậc 3
4
3
4
Dz=
; Bậc 4
Bài 2. Cho các đa thức
22 2
2 31A x y xy xy=−+ −−
2 22
21B xy x y xy=+ ++
22 2
5 2 23C xy x y xy= − ++
1)
2
3A B xy xy
+= −
2)
22 2
44A B C x y xy−+=− +
Bài 3. Tìm đa thức
A
và
B
sau đó tính giá trị đa thức
A
và
B
tại
12;xy= = −
1)
( )
2 22
52 62A x xy x xy y+ − =−−
2)
222 22 2
1
2
xy x x y B xy x y x

+ − −=− − +


22
Ax y= −
2
3
2
B xy
=
Giá trị biểu thức
A
tại
12
;
xy
= = −
là
3−
Giá trị biểu thức
B
tại
12
;
xy= = −
là
6
Bài 4. Bác Hoàng gửi tiết kiệm ở ngân hàng thứ nhất
50
triệu đồng với kỳ hạn một năm, lãi suất
%/x
năm. Bác
Hoàng gửi ở ngân hàng thứ hai
100
triệu đồng với kỳ
hạn một năm, lãi suất
15, %/
x
năm.
a) Đa thức biểu thị số tiền lãi bác Hoàng có được ở ngân
hàng thứ nhất sau khi hết kỳ hạn một năm là:
0
1
50 5
100 2
%. . x
x
x = =
(triệu đồng)
b) Đa thức biểu thị số tiền lãi bác Hoàng có được ở cả hai ngân hàng sau khi hết kỳ
hạn một năm là
11 1
1 5 100 1 5 1
0
200 1 5
2 2 10 2
,%.,..,x
x
xx x xx+ =+ =+=
(triệu đồng)
c) Nếu
5x =
thì sau một năm gửi tiết kiệm ở hai ngân hàng bác Hoàng lãi được
2 5 10. =
(triệu đồng)
PHIẾU BÀI TẬP TOÁN 8
7
Bài 5.
Hai người đi xe đạp cùng một lúc và ngược chiều nhau từ hai địa điểm
A
và
B
. Người
xuất phát từ
A
đi với vận tốc không đổi
x
( /)km h
. Người xuất phát từ
B
đi với vận tốc
không đổi
y
( /)km h
. Hai người gặp nhau tại điểm
C
sau
4
giờ.
a) Đa thức
S
biểu thị quãng đường
AB
theo
x
và
y
4 4( )S x y km
b) Tính
S
tại
10, 8
xy
.
4.10 4.8 72( )S km 
c) Biết rằng người xuất phát từ
B
đi với tốc độ nhanh gấp đôi người xuất phát từ
A
. Tính
thời gian để người xuất phát từ
A
đi hết quãng đường
AB
.
Người xuất phát từ
B
đi nhanh gấp đôi người xuất phát từ
A
nên
2yx
( /)
km h
.
Khi đó
4 4.2 12 ( )S x x x km
Thời gian người xuất phát từ
A
đi hết quãng đường
AB
là:
2: 12 : 1t Sv xx
(h).
Bài 6. Cho hai đa thức
22
73
P x xy y=−−
và
22
332Q xy x y
=−+
. Chứng minh rằng:
không có số thực
x
và
y
nào để đa thức
P
và
Q
cùng nhận giá trị âm.
Ta có:
2 2 2 2 22
73 3324 0P Q x xy y xy x y x y+= − − + − + = + ≥
với mọi
,xy
∈
Do đó
0
PQ
+≥
nên không có số thực
x
và
y
nào để đa thức
P
và
Q
cùng nhận giá trị
âm, vì nếu
0,
PQ<<
thì
0PQ+<
Bài 7. Tìm số tự nhiên
(
)
abc a b c
<<
sao cho:
666abc bca ca b++=
Ta có:
666abc bca ca b++=
nên
100 10 100 10 100 10 666a bc b ca c ab+ ++ + ++ + +=
111 111 111 666abc++=
111 666
()abc
++ =
6abc
++=
Vì
abc<<
nên tìm được
123
,,ab c
= = =
Vậy số cần tìm là
123
III. BÀI TẬP VỀ NHÀ
Bài 1. Rút gọn các biểu thức sau
a)
2 22 222
28675( )( )A x xy y x xy y x xy y= − −−+ = ++− −
.
b)
22 2 2 2 22
32 353
()( )()xyB xy x y xy x y x y xy
= − −− − + − =
.
Bài 2. Cho các đa thức
32
22 1M x x y xy
= − ++
;
2
3 22N x y xy= +−
32
31P x x y xy=−−+
.
Tính
a)
32
2 31xx
M yN yx+ +
= +−
.
b)
32
4x x y xyMP
−= +−
.
c)
32
36 4 4M x x y xyNP−+ − −+=
.
Bài 3. Tìm đa thức
A
,
B
sau đó tính giá trị biểu thức
A
,
B
tại
12;xy= =
a)
2 2 22 2
63 2x xy A x y xy− += + −
;
2 22
5A x xy y=−+ +
; giá trị
A
tại
12;xy= =
là
3
PHIẾU BÀI TẬP TOÁN 8
8
b)
2 22
24 5 7()B xy y xy x y− − = +−
;
22
7 11B xy x y= +−
; giá trị
B
tại
12;xy= =
là
29−
Bài 4. Một chiếc bình có dạng hình lập phương với độ dài cạnh là
2x
(cm).
a) Đa thức biểu thị thể tích nước tối đa mà chiếc bình đó có thể chứa được:
3 33
28() ( )x x cm
=
b) Đa thức biểu thị thể tích phần không có nước trong bình:
3 2 3 23
8 2 84
( ). ( )
x x y x x y cm−=−
Bài 5. Cho hai đa thức
22 2 2
4 12 2M x y xy y
=−−
và
22 2 2
12 2
N x y xy y=++
. Chứng minh
rằng: không có số thực
x
và
y
nào để đa thức
P
và
Q
cùng nhận giá trị âm.
Ta có:
22 2
55 0
()P Q x y xy+= = ≥
với mọi
,xy∈
….. HS tự KL
Bài 6*. Cho đa thức
2
2012 2013 2014A x xy x y=+− − −
. Tìm cặp số
(; )
xy
nguyên để đa
thức
0A =
Ta có
0
A
=
nên
2
2012 2013 2014 0.
x xy x y+− − − =
2
2013 2013 2013 1 0
x xy x y x+ − − + − −=
( )
(
) (
)
2013 2013 1 0
xxy xy x+− ++− −=
( )( ) ( )
2013 2013 1 0x yx x+−+−−=
( )
(
)
2013 1 1x xy− ++ −
(
)(
)
2013 1 1x xy
− ++ =
Vì
,xy
nguyên nên ta có bảng sau
2013x −
1
-1
1xy++
1
-1
x
2014
2012
y
-2014
-2014
Vậy
( ) ( ) ( )
2014 2014 2012 2014; ; ,;xy =−−
PHIẾU BÀI TẬP TOÁN 8
1
1
CÁC PHÉP TÍNH VỀ ĐA THỨC NHIỀU BIẾN
(NHÂN – CHIA)
I. BÀI TẬP TRẮC NGHIỆM
Câu 1. Khẳng định nào sau đây là sai?
A. Để nhân hai đơn thức, ta nhân các hệ số với nhau và nhân các phần biến với nhau.
B. Kết quả của tích
()A B C AB AC−= −
C. Kết quả của tích
( )( )ABCD ACADBCBD+ −= − + −
D. Kết quả của tích
( ): : :AB C CACB+=+
Câu 2. Kết quả của phép tính
22
3( ).( )x y xy−
A.
33
3xy−
. B.
33
3xy
. C.
32
3
xy
. D.
23
3xy−
.
Câu 3. Hệ số của đơn thức
22
23x y xy
là?
A.
2
. B.
3
. C.
5
. D.
6
.
Câu 4. Bậc của đơn thức
2 23
4
26
3
xy x y x
là?
A.
7
B.
8
C.
9
. D.
12
.
Câu 5. Viết đơn thức
456
21
xyz
dưới dạng tích hai đơn thức, trong đó có 1 đơn thức
22
3xyz
ta được kết quả là:
A.
( )
(
)
223 232
37
.
xyz xyz
. B.
(
) ( )
2 2 235
37.
xyz xyz
.
C.
( ) ( )
23 235
37.xyz xyz−−
. D.
(
) ( )
2 2 235
37
.xyz xyz−
.
Câu 6. Cho các đơn thức
3
45()
A x y xy= −
,
42
17B xy= −
,
6
3
5
C xy=
. Các đơn thức nào
đồng dạng với nhau?
A. Đơn thức
A
và đơn thức
C
. B. Đơn thức
B
và đơn thức
C
.
C. Đơn thức
A
và đơn thức
B
. D. Cả ba đơn thức
A
,
B
,
C
đồng dạng với nhau.
Câu 7. Thực hiện phép tính nhân
23
1
5
2
()xx x−−
ta được kết quả là?
A.
63 2
1
5
2
xx x−−
. B.
53 2
1
5
2
xx x−−
.
C.
53
1
5
2
xx−−
. D.
62 2
1
5
2
xx x−−
.
Câu 8. Tích
( )( )x yx y
−+
có kết quả bằng:
A.
22
2x xy y−+
. B.
22
xy+
.
C.
22
xy
−
. D.
22
2x xy y++
.
Câu 9. Trong các phép tính sau, phép tính nào có kết quả là
22
33xy+
?
A.
( )
3xx y+
. B.
( ) ( )
13xxy yxy x
++ − + −
.
C.
( )
( )
33xxy yxy+− +
. D.
( ) ( )
3 33xy x y x y
+ +−+
.
Câu 10. Tính
33 24 2
1
2
3
( ):( )x y x y xy+
ta được kết quả là ?
A.
22
1
2
3
xy xy+
. B.
2
1
2
2
x y xy+
.
C.
22
1
2
x y xy+
. D.
22
1
2
3
x y xy+
.
PHIẾU BÀI TẬP TOÁN 8
2
2
Câu 11. Tích
2
42 2
1
6
2
:xy xy



bằng:
A.
12
. B.
24
. C.
2
24
xy
. D.
2
12xy
.
Câu 12.
Cho biểu thức
( )( )( )C xy z yz x zx y= +− +− −
. Chọn khẳng định đúng.
A. Biểu thức
C
không phụ thuộc vào
;;
x yz
. B. Biểu thức
C
phụ thuộc vào cả
;xy
và
z
.
C. Biểu thức
C
chỉ phụ thuộc vào
y
. D. Biểu thức
C
chỉ phụ thuộc vào
z
.
II. BÀI TẬP TỰ LUẬN
Bài 1. Thực hiện các phép tính sau:
1)
22
23( ).( ) ...............................................................................................................x y xy =
2)
(
)
2
2
1
2
2
. ...............................................................................
........................x yz xyz

−=


3)
( )
425 2
1
4
2
: ...................................................................................................x y z xyz

−=


4)
3
2 35
13
28
: ........................................................................................................xy x y

=


Bài 2. Thực hiện các phép tính sau:
1)
2
2 ()xx y−−
2)
2
12
4
23
.( )xy xy y−+
3)
22
82 2
( ):( )xy x y xy−
4)
22
31
2
44
( ):( )xy xy x y xy− −+
Bài 3. Rút gọn và tính giá trị các biểu thức sau:
1)
22
2 2 42
( )( ) ( )A xy xy x y
= − +− +
tại
999 1;xy= =
2)
2 22
( )( ) .( )B x y x xy y x x y
=− ++ − −
tại
1
2
1
;xy= =
PHIẾU BÀI TẬP TOÁN 8
3
3
3)
2 2 33
1 12
( )( ) ( )( ) ( ) : ( )C x y x y x y x y xy= − + − − ++
tại
2xy= = −
Bài 4. Chứng minh giá trị của biểu thức sau không phụ thuộc vào giá trị của biến
x
( 3)(2 5) 8 (1 ) (2 1)(5 3 )Ax x x x x x
 
Bài 5. Từ một miếng bìa hình chữ nhật có chiều dài là
()x cm
, chiều rộng
4( )x cm
.
Người ta đã cắt bốn hình vuông cạnh
2( )cm
ở bốn góc của miếng bìa rồi gấp lại để tạo thành
một chiếc hộp không nắp (Hình vẽ dưới đây). Viết đa thức biểu thị
a) Thể tích của chiếc hộp
b) Tổng diện tích năm mặt của chiếc hộp
2 (cm)
x - 4 (cm)
x (cm)
PHIẾU BÀI TẬP TOÁN 8
4
4
Bài 6. Bác Quang có một mảnh đất hình vuông cạnh
()xm
, bác muốn trồng hoa vào
mảnh đất hình chữ nhật ở góc vườn (hình vẽ bên). Tính độ dài cạnh
()xm
của khu vườn đó,
biết diện tích mảnh đất trồng hoa bằng
2
60m
Bài 7. Tìm ba số tự nhiên liên tiếp. Biết rằng tích của hai số sau lớn hơn tích của hai số
đầu là
30
Bài 8*. Tính nhanh
a)
71 4 2 1 1
41
570 375 375 570 375 375 570
..
.
A = − ++
6 m
10 m
x (m)
Trồng
hoa

Tài liệu khác của Toán 8

Preview text:

1
PHIẾU BÀI TẬP TOÁN 8
ĐƠN THỨC NHIỀU BIẾN – ĐA THỨC NHIỀU BIẾN
I. Bài tập trắc nghiệm
Câu 1. Trong các câu sau, câu nào sai?
A. Đơn thức nhiều biến (hay đơn thức) là biểu thức đại số chỉ gồm một số, hoặc một biến,
hoặc một tích giữa các số và các biến.
B. Số 0 không phải là đơn thức C. Đơn thức 1
− xyz có phần hệ số là 1 − 2 2
D. Đơn thức thu gọn là đơn thức chỉ gồm tích của một số với các biến mà mỗi biến được
nâng lên lũy thừa với số mũ nguyên dương.
Câu 2. Trong các biểu thức sau, biểu thức nào là đơn thức? 3 A. 2 2 + 3 + x y x y . B. 4 5 2x y . C. . D. 3 − x y + 7x . 3y 4
Câu 3. Trong các biểu thức đại số sau, biểu thức nào không phải đơn thức? A. 2 . B.5x + 9. C. 3 2 x y . D.3x .
Câu 4. Đơn thức 2
5xyz có phần biến là? A. xyz . B. 2 xy z . C. 2 2 xy z . D. 2 xyz .
Câu 5. Trong các đơn thức sau, đơn thức thu gọn là? A. 1 2 x yzx . B. 2 2 3 5x y zx . C. 2 2 3x y . D. 3 5 2x yzx . 2
Câu 6. Trong các đơn thức sau, đơn thức chưa thu gọn là? A. 1 2 − 1 x yz . B.3xy . C. 2 2xy . D. 3 5 5 x yzx y . 4 2
Câu 7. Thu gọn đơn thức 2 2 2 2
3x y zy z ta được đơn thức là? A. 2 4 3x y z . B. 2 4 3 3x y z . C. 2 3 4 3x y z . D. 2 3 3 3x y z .
Câu 8. Trong các câu sau, câu nào sai? A. 2 3xy và 2
6xy là hai đơn thức đồng dạng
B. Hai đơn thức đồng dạng có phần hệ số khác 0 và không có chung phần biến C. 2 3 1 y và 2
y là hai đơn thức đồng dạng 2 D. 2 xy và 2 xy −
là hai đơn thức đồng dạng
Câu 9. Kết quả quả phép tính 2 2 3xy + ( 3 − xy ) là: A. 0 . B. 2 6xy . C. 2 xy . D. 2 6 − xy .
Câu 10. Kết quả quả phép tính 2 2
10x y + 6x y là: A. 16xy . B. 2 16xy . C. 2 16x y . D. 4 2 16x y .
Câu 11. Kết quả quả phép tính 2 2 2 2
4x y − 6x y là: A. 2 − . B. 2 2 2 − x y . C. 2 2 2x y . D. 4 2 2 − x y .
Câu 12. Câu nào sau đây là sai?
A. Đa thức nhiều biến (hay đa thức) là một tổng của những đơn thức
B. Mỗi đơn thức không phải là đa thức
C. Thu gọn đa thức nhiều biến là làm cho đa thức đó không còn hai đơn thức nào đồng dạng
D. Số 0 là đa thức 2 PHIẾU BÀI TẬP TOÁN 8
Câu 13. Biểu thức nào sau đây là đa thức? A. 1 3 3 ( x + 2y). B. 1 4x + . C. 2 2 − x + y . D. 2 + 3y . 2 y 5x 2x
Câu 14. Biểu thức nào sau đây không là đa thức? A. 2 4 x − y 2 x + y
x + x − y . B. 2 − 3y . C. 3 2 x − y + y . D. 2 . x 5 5
Câu 15. Đa thức thu gọn trong các đa thức sau là: A. 1 2 2 1
x y − xyz − x y . B. 2
x y − xyz − zxy . 3 3 C. 2 2 2 2 − 3
xy + y − 4y x . D. 2 2 xy + 3y . 5 2
Câu 16. Đa thức nào sau đây chưa thu gọn? A. 2
4x + x − y . B. 4 4
x y + x − 2yx . C. 3 2 2 x − y + y .
D. 2x + 2y . 5
Câu 17. Thu gọn đa thức 2 2
xy − 2x y + 3xy + 2x y ta được kết quả là: A. 2 2
4xy − 2x y + 2yx . B. 2 4x y . C. 4xy . D. 2 4xy − 4x y .
Câu 18. Câu nào sau đây là sai:
A. Một số bất kì khác 0 có bậc là 0
B. Số 0 là đa thức không có bậc C. Đơn thức 1 3 5 x y z có bậc là 9 D. Đa thức 5 2 2 2
4x + x y − x có bậc là 11 2
Câu 19. Xác định số a để các đơn thức 3 axy , 3 4 − xy , 3 7xy có tổng bằng 3 6xy . A. a = 9 . B. a = 1. C. a = 3. D. a = 2 .
Câu 20. Đa thức 2
2xy + 3xy có giá trị bằng 0 tại 1
x = , thì giá trị của y là 2    −  A. 1 0; . B. 3 0; . 2     2     −  C. 3 0; . D. 1 0; . 2     2  II. Bài tập tự luận
Bài 1. Điền vào chỗ chấm
1) Năm đơn thức đồng dạng với đơn thức 2
2x yz là:………………………………………………
2) 6xyz + .................. = 15xyz 3) Đa thức 4 2
x − 3x y + 2x − 4 có bậc là ……………………………………………………………….
4) Đa thức biểu thị tổng diện tích của hình vuông có cạnh x (cm) và hình chữ nhật có hai cạnh
x (cm) và y (cm) là: …………………………………………………………………………………….
5) Đa thức biểu thị diện tích toàn phần của hình hộp chữ nhật có chiều dài x (cm) , chiều
rộng y (cm), chiều cao 10(cm)là:……………………………………………………………………. 3 PHIẾU BÀI TẬP TOÁN 8
Bài 2. Thu gọn các đơn thức sau: 1) 2 2 2
5x y xy z = ...................................................................................................................... 2) 1 2 4 2 2 9
x z y xy z = ................................................................................................................. 2
3) − (x )2 y z x (y )2 2 2 6 2 5
z = ....................................................................................................... 4) 3 − (xzy )2 2 4 2 5
x y z = ........................................................................................................... 4
Bài 3. Viết kết quả của các phép tính sau vào chỗ chấm 1) 2 2 2
3x y + 6x y − 5x y = ........................... ;
2) 1 xyz + 3xyz − 5xyz = ............................. 2 3) 2 2 2 2 2 2 2 x
− y + 3x y − 5x y = ........................... ; 4) 2 2 2
xyz + xyz − 16xyz = ....................... 3
Bài 4. Tìm đơn thức ,
A B và cho biết bậc của chúng: 1) 2 2 1
x yz − A = 5x yz 2) 3 2 3 2 3 2
x y z + B − x y z = 10x y z 2
Bài 5. Thu gọn và tính giá trị các đa thức sau: 1) 2 2 A = x
− y − 2xy + 2x y + 5xy + 2 tại x = 1;y = 2 2) 6 2 3 5 5 6
B = x + 2x y − xy + xy + xy − x − 2xy tại 1 x = 0;y = 4 4 PHIẾU BÀI TẬP TOÁN 8 3) 2 2 2 2 2
C = 3xy z + xy z − x − xyz − 4xy z − 3xyz + 2x + 4 tại x = y = 1;z = 2 −
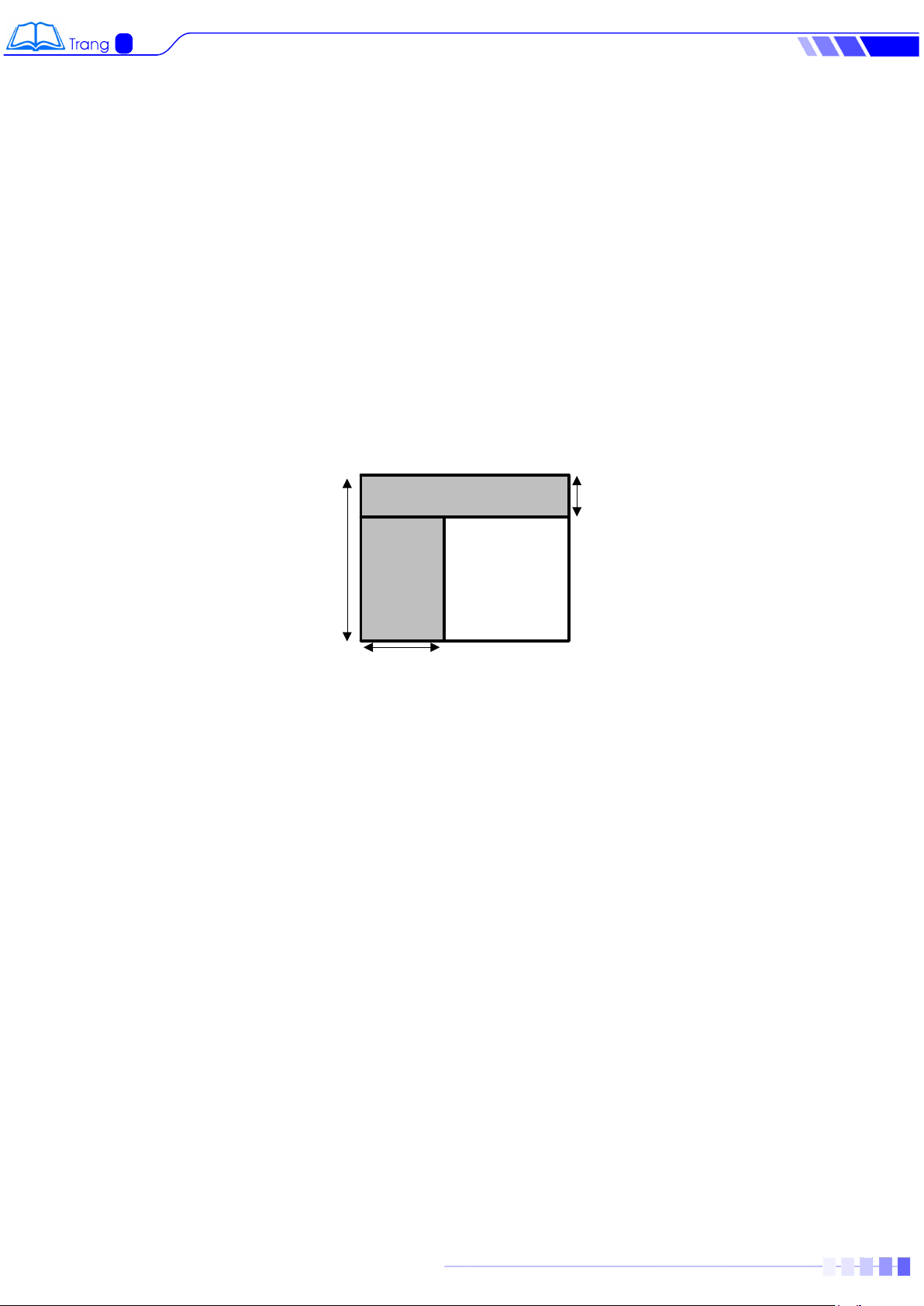
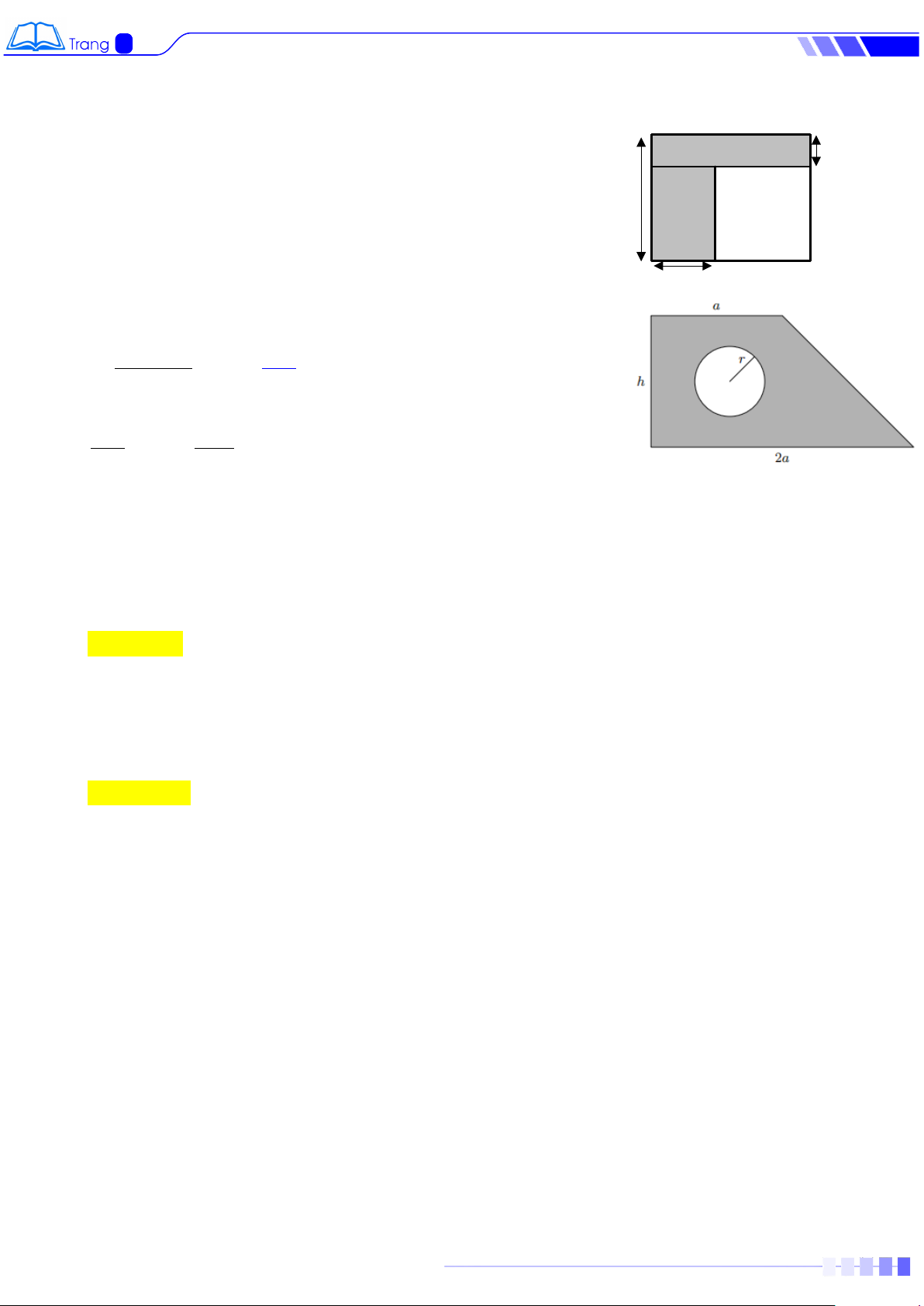
Bài 6. Một mảnh đất có kích thước như hình vẽ sau (đơn vị mét). Phần bôi đậm được
dùng để trồng rau, phần màu trắng được dùng để trồng cây ăn trái. Hãy tìm đơn thức biểu thị diện tích: 5y x 4x 2y
a) Diện tích đất trồng rau
b) Diện tích đất trồng cây ăn trái c) Diện tích mảnh đất 5 PHIẾU BÀI TẬP TOÁN 8
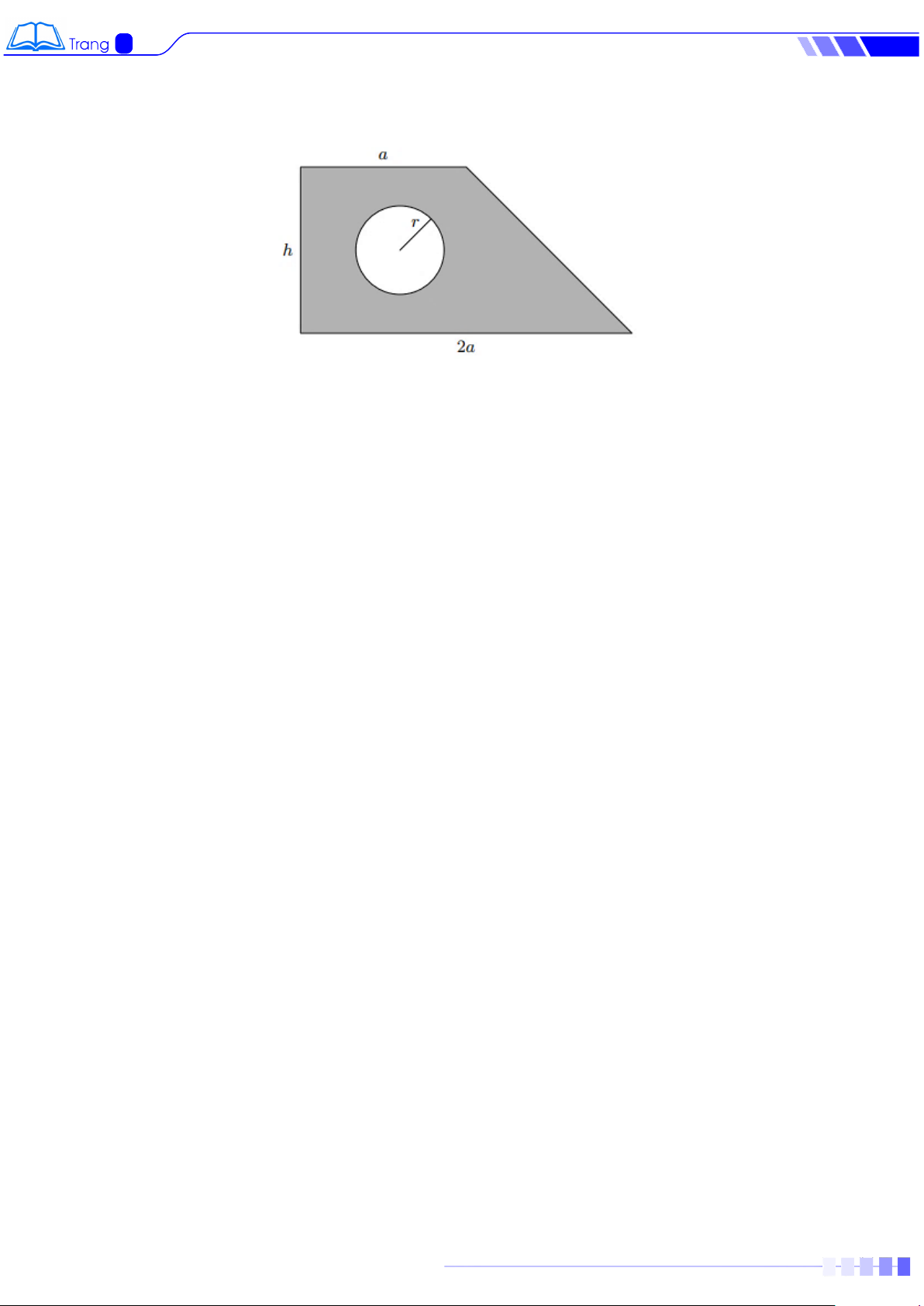
Bài 7. Một bức tường hình thang có cửa sổ hình tròn với các kích thước như hình vẽ
dưới đây (đơn vị mét).
a) Viết đa thức biểu thị diện tích bức tường (không tính phần cửa sổ)
b) Tính diện tích bức tường ở câu a biết a = 2m; h = 3m; r = 0,5
m (Lấy ≈ 3,14 )  Bài 8.
a) Tính giá trị của đa thức 3 2 2 2
M = x + x y − 2x − xy − y + 3y + x − 1 biết x + y − 2 = 0 .
b) Tính giá trị của đa thức 4 2 2 4 2
N = 3x + 5x y + 2y + 2y biết rằng 2 2 x + y = 2 . 6 PHIẾU BÀI TẬP TOÁN 8
Bài 9. Cho hai đa thức 2
A = 2xy + x + y + 1 và 2 2
B = x + 2y + xy . Tìm cặp số nguyên
(x;y) thỏa mãn A = B 7
PHIẾU BÀI TẬP TOÁN 8
HƯỚNG DẪN ĐÁP SỐ I. TRẮC NGHIỆM 1-B 2-B 3-B 4-D 5-C 6-D 7-B 8-B 9-A 10-C 11-B 12-B 13-A 14-B 15-D 16-B 17-C 18-D 19-C 20-B II. TỰ LUẬN
Bài 1. Điền vào chỗ chấm 1) HS TỰ LÀM
2) 6xyz + 9xyz = 15xyz 3) Đa thức 4 2
x − 3x y + 2x − 4 có bậc là 4
4) Đa thức biểu thị tổng diện tích của hình vuông có cạnh x (cm) và hình chữ nhật có hai
cạnh x (cm) và y (cm) là: 2 2
x + xy(cm )
5) Đa thức biểu thị diện tích toàn phần của hình hộp chữ nhật có chiều dài x (cm) , chiều
rộng y (cm), chiều cao 10(cm)là: 2
20x + 20y + 2xy (cm )
Bài 2. Thu gọn các đơn thức sau: 1) 2 2 2 3 4
5x y xy z = 5x y z 2) 1 2 4 2 2 9 1 3 4 13
x z y xy z = x y z 2 2 3) 5
− (x )2 y z x (y )2 2 2 6 2 5 6 7 z = 5 − x y z 4) 3 − (xzy )2 2 4 2 5 3 6 6 7
x y z = − x y z 4 4
Bài 3. Viết kết quả của các phép tính sau vào chỗ chấm 1) 2 2 2 2 3 3
x y + 6x y − 5x y = 4x y ;
2) 1 xyz + 3xyz − 5xyz = − z xy ; 2 2 3) 2 2 2 2 2 2 2 2 2 x
− y + 3x y − 5x y = 3 − x y ; 4) 2 2 2 2 xyz + xyz − 16 7 xyz = − xyz ; 3 3
Bài 4. Tìm đơn thức ,
A B và cho biết bậc của chúng: 1) 2 21 A = 4 − x yz ; 2) 3 2 B = x y z 2
Bài 5. Thu gọn và tính giá trị các đa thức sau: 1) 2 2 A = x
− y − 2xy + 2x y + 5xy + 2 tại x = 1;y = 2 Thu gọn: 2
A = x y + 3xy + 2
Giá trị biểu thức A tại x = 1;y = 2 là: 2 1 .2 + 3.1.2 + 2 = 10 2) 6 2 3 5 5 6
B = x + 2x y − xy + xy + xy − x − 2xy tại 1
x = 0;y = 4 Thu gọn: 2 3
B = 2x y − xy 3   Giá trị biểu thức 1 1 B tại 1 x = 0;y = là: 2 2.0 .  − 0. = 0 4  4  4 3) 2 2 2 2 2
C = 3xy z + xy z − x − xyz − 4xy z − 3xyz + 2x + 4 tại x = y = 1;z = 2 − Thu gọn: 2
C = x − 4xyz + 4 ; Giá trị biểu thức C tại x = y = 1;z = 2 − là: 2 1 − 4.1.1.( 2 − ) + 4 = 3 1 8 PHIẾU BÀI TẬP TOÁN 8 Bài 6. 5y
a) Diện tích đất trồng rau 2 x
x.5y + 3x.2y = 5xy + 6xy = 11xy(m )
b) Diện tích đất trồng cây ăn trái 4x 2
3x.3y = 9xy(m )
c) Diện tích mảnh đất 2
11xy + 9xy = 20xy(m ) 2y Bài 7.
a) Đa thức biểu thị diện tích bức tường (không tính phần cửa sổ)
là: (2a + a).h 2 3a.h 2 2 − r = − r (m ) 2 2
b) Diện tích bức tường ở câu a là: 3a.h 2 3.2.3 2 2 − r ≈ − 3,14 0 .( ,5) = 8, 215(m ) 2 2  Bài 8.
a) Tính giá trị của đa thức 3 2 2 2
M = x + x y − 2x − xy − y + 3y + x − 1 biết x + y − 2 = 0 . 3 2 2 2
M = x + x y − 2x − xy − y + 3y + x − 1 = ( 3 2 2
x + x y − x ) + ( 2 2 xy −
− y + 2y) + y + x −1 2
= x (x + y − 2) − y (x + y − 2) + (x + y − 2) + 1 2
= x .0 − y.0 + 0 + 1 = 1. Vậy M = 1.
b) Tính giá trị của đa thức 4 2 2 4 2
N = 3x + 5x y + 2y + 2y biết rằng 2 2 x + y = 2. 4 2 2 4 2
N = 3x + 5x y + 2y + 2y 4 2 2 2 2 4 2
= 3x + 3x y + 2x y + 2y + 2y 2 2 2 2 2 2
= 3x (x + y ) + 2y (x + y + 1) Mà 2 2
x + y = 2 nên ta có 2 x ( 2 2 x + y ) 2 + y ( 2 2 x + y + ) 2 2 = x + y = ( 2 2 3 2 1 6 6
6 x + y ) = 6.2 = 12. Vậy N = 12 .
Bài 9. Ta có A = B nên 2 2 2
2xy + x + y + 1 = x + 2y + xy 2 2 2
⇒ 2xy − 2y + x − x + y − xy + 1 = 0 ( 2 2
xy − y ) − (xy − y) − ( 2 2 2 x − x ) = 1 − 2 2y (x − ) 1 − y (x − ) 1 − x (x − ) 1 = 1 − ⇒ (x − )( 2
1 2y − y − x ) = 1 −
Do x,y nguyên nên (x − );( 2
1 2y − y − x ) là các số nguyên và là ước của 1 nên ta có các trường hợp sau: x  −  1 = 1 x  =  2 x  =  2 x  = 2 Trường hợp 1:  ⇒  ⇒  ⇒ 2 2 2 
y − y − x = 1 − 2y − y = 1 y    (2y − ) 1 = 1 y = 1  x  −  1 = 1 − x  =  0 x  =  0 x  = 0 Trường hợp 2:  ⇒  ⇒  ⇒ 2 2 2 
y − y − x = 1 2y − y = 1 y    (2y − ) 1 = 1 y = 1 
Vậy các cặp số (x;y) thỏa mãn là (2; ) 1 ;(0; ) 1 1
PHIẾU BÀI TẬP TOÁN 8 CÁC PHÉP TÍNH VỀ ĐA THỨC NHIỀU BIẾN
(PHÉP CỘNG – TRỪ)
I. Bài tập trắc nghiệm
Câu 1. Kết quả của phép tính 2 4 2 4
3x y + 7x y là A. 2 4 10x y . B. 2 4 9x y . C. 2 4 9 − x y . D. 2 4 4 − x y .
Câu 2. Kết quả của phép tính 2 2 9 − y z − ( 12 − y z) là A. 2 21 − y z . B. 2 3 − y z . C. 4 2 3y z . D. 2 3y z .
Câu 3. Phép tính 2 2
x y + 2xy − ( x
− y − xy) sau khi phá dấu ngoặc tròn được kết quả là? A. 2 2
x y + 2xy − x y − xy . B. 2 2
x y + 2xy + x y + xy . C. 2 2
x y + 2xy − x y + xy . D. 2 2
x y + 2xy + x y − xy .
Câu 4. Trong các câu sau, câu nào sai? A. Đa thức 4 2
x + 3x y − 5 có bậc là 4
B. Để tìm bậc của một đơn thức đa thức trước tiên ta phải thu gọn đơn thức, đa thức đó 2
C. Đơn thức x y có phần hệ số là 2 2 2
D. Đơn thức x y có phần hệ số là 1 2 2
Câu 5. Thu gọn đa thức 2 2 2 2 3
− x y − 2xy + 16 − 2x y + 5xy − 10 ta được A. 2 2 x
− y − 7xy + 26 . B. 2 2 5
− x y + 3xy + 6 . C. 2 2 5
− x y − 3xy + 6 . D. 2 2
5x y − 3xy − 6 .
Câu 6. Giá trị của đơn thức 3 3 9x y tại 1 x = 1 − , y = − 3 A. 1 B. 1 C. 1 D. 2 9 3 6 9
Câu 7. Tìm đa thức B sao cho tổng B với đa thức 4 2 4 2
2x − 3x y + y + 6xz − z bằng 0 . A. 4 2 4 B = 2
− x + 3x y − 6xz + 2xz + 2y B. 4 2 4 2 B = 2
− x + 3x y − y − 6xz + z C. 4 2 B = 2
− x − 3x y − 6xz D. 4 2 2 2 B = 2
− x − 3x y − 6xz + 4x z + z 5 5
Câu 8. Bậc của đa thức 3 2 3 2
x y + 2xy + 3xy − x y − 2xy − 1 là: 2 2 A. 2 . B. 1. C. 5 . D. 1 − . 2
Câu 9. Tìm đa thức M biết 2 2 2
M − 3xy + 4y = x − 7xy + 8y . A. 2 2
M = x − 4xy − 4y . B. 2 2
M = x − 4xy + 4y . C. 2 2 M = x − − 4xy + 4y . D. 2 2
M = x + 10xy + 4y .
Câu 10. Giá trị của biểu thức 2
x + 3x + 1 tại x thỏa mãn ( 2
x + 7)(x + 2) = 0 bằng A. 10. B. 1. C. -1. D. 11.
Câu 11. Cho M = x − (y − z ) − 2x + y + z − (2 − x − y) và N = x − x  − 
(y − 2z) − 2z . TínhM − N . A. 2 − z + 2 . B. 2
− x − 2y − 2 . C. 2z − 2. D. 2
− x + 2y − 2 . 2 PHIẾU BÀI TẬP TOÁN 8 Câu 12. Cho 2 2 2 3 3 3 2020 2020 2020
P = xyz + x y z + x y z + ... + x y z
. Tính P biết x = y = 1;z = 1 − . A. P = 2020 − . B. P = 0 . C. P = 2020 . D. P = 1010.
II. Bài tập tự luận (7điểm)
Bài 1. Thu gọn các đa thức sau và cho biết bậc của các đa thức đó 1) 2 2 A = 2
− xy + 4xy + xy + xy 2) 2 2 2 2
B = xy z + 2xy z − xyz − 3xy z + xy z . 2   3) 1 2 1
C = xyx − 2xy + x − x y + 3xy − 4x 4) D = (x y )2 2 3 3 2 5 4 3 4
+ y −  z  − y x y − y + z . 2  2 
Bài 2. Cho các đa thức 2 2 2 A = x
− y + 2xy − 3xy − 1 2 2 2
B = xy + x y + 2xy + 1 2 2 2
C = 5xy − 2x y + 2 + 3xy 1) Tính A + B
2) Tính A − B + C 3 PHIẾU BÀI TẬP TOÁN 8
Bài 3. Tìm đa thức A và B sau đó tính giá trị đa thức A vàB tại x = 1;y = 2 −   1) 1 A + ( 2 x − xy ) 2 2 5 2
= 6x − 2xy − y 2) 2 2 2 2 2 2
xy + x − x y  − B = xy −
− x y + x  2 
Bài 4. Bác Hoàng gửi tiết kiệm ở ngân hàng thứ nhất 50
triệu đồng với kỳ hạn một năm, lãi suất x% / năm. Bác
Hoàng gửi ở ngân hàng thứ hai 100 triệu đồng với kỳ
hạn một năm, lãi suất 1,5x% / năm.
a) Viết đa thức biểu thị số tiền lãi bác Hoàng có được ở ngân
hàng thứ nhất sau khi hết kỳ hạn một năm.
b) Viết đa thức biểu thị số tiền lãi bác Hoàng có được ở cả hai ngân hàng sau khi hết kỳ hạn một năm.
c) Nếu x = 5 thì sau một năm gửi tiết kiệm ở hai ngân hàng bác Hoàng lãi được bao nhiêu tiền? 4 PHIẾU BÀI TẬP TOÁN 8 Bài 5.
Hai người đi xe đạp cùng một lúc và ngược chiều nhau từ hai địa điểm A và B . Người
xuất phát từ A đi với vận tốc không đổi x (km / h). Người xuất phát từ B đi với vận tốc
không đổi y (km / h). Hai người gặp nhau tại điểm C sau 4 giờ.
a) Lập đa thức S biểu thị quãng đường AB theo x và y
b) Tính S tại x  10,y  8 .
c) Biết rằng người xuất phát từ B đi với tốc độ nhanh gấp đôi người xuất phát từ A . Tính
thời gian để người xuất phát từ A đi hết quãng đường AB .
Bài 6. Cho hai đa thức 2 2
P = 7x − 3xy − y và 2 2
Q = 3xy − 3x + 2y . Chứng minh rằng:
không có số thực x và y nào để đa thức P và Q cùng nhận giá trị âm.
Bài 7. Tìm số tự nhiên abc (a < b < c) sao cho: abc + bca + cab = 666 5
PHIẾU BÀI TẬP TOÁN 8 III. BÀI TẬP VỀ NHÀ
Bài 1. Rút gọn các biểu thức sau a) 2 2 2 2
A = (x − xy + y ) − ( x −
+ 7xy − 5y ) . b) 2 2 2 2 2 2
B = (xy − 3x y) − ( 2
− xy − 5x y) + (x y − 3xy ).
Bài 2. Cho các đa thức 3 2
M = 2x − 2x y + xy + 1; 2
N = 3x y + 2xy − 2 3 2
P = x − x y − 3xy + 1. Tính a) M + N . b) M − P .
c)M − N + P .
Bài 3. Tìm đa thức A , B sau đó tính giá trị biểu thức A , B tại x = 1;y = 2 a) 2 2 2 2 2
6x − 3xy + A = x + y − 2xy . b) 2 2 2
B − (2xy − 4y ) = 5xy + x − 7y .
Bài 4. Một chiếc bình có dạng hình lập phương với độ dài cạnh là 2x (cm).
a) Viết đa thức biểu thị thể tích nước tối đa mà chiếc bình đó có thể chứa được.
b) Biết rằng độ cao mực nước trong bình đang là y (cm) (với y < 2x ). Viết đa thức biểu thị
thể tích phần không có nước trong bình.
Bài 5. Cho hai đa thức 2 2 2 2
M = 4x y − 12xy − 2y và 2 2 2 2
N = x y + 12xy + 2y . Chứng minh
rằng: không có số thực x và y nào để đa thức P và Q cùng nhận giá trị âm.
Bài 6*. Cho đa thức 2
A = x + xy − 2012x − 2013y − 2014 . Tìm cặp số (x;y) nguyên để đa thức A = 0 6
PHIẾU BÀI TẬP TOÁN 8
HƯỚNG DẪN ĐÁP SỐ I. TRẮC NGHIỆM 1-A 2-D 3-B 4-C 5-B 6-B 7-B 8-A 9-B 10-C 11-C 12-B II. TỰ LUẬN
Bài 1. Thu gọn các đa thức sau và cho biết bậc của các đa thức đó 1) 2 2 A = 2
− xy + 4xy + xy + xy 2) 2 2 2 2
B = xy z + 2xy z − xyz − 3xy z + xy z . 2
A = 5xy − xy ; Bậc 3 2
B = xy z − xyz ; Bậc 4 2   3) 1 2 1
C = xyx − 2xy + x − x y + 3xy − 4x 4) D = (x y )2 2 3 3 2 5 4 3 4
+ y −  z  − y x y − y + z . 2  2  1 2 3
C = x y + xy − 3x ; Bậc 3 4
D = z ; Bậc 4 2 4
Bài 2. Cho các đa thức 2 2 2 A = x
− y + 2xy − 3xy − 1 2 2 2
B = xy + x y + 2xy + 1 2 2 2
C = 5xy − 2x y + 2 + 3xy 1) 2
A + B = 3xy − xy 2) 2 2 2
A − B + C = 4 − x y + 4xy
Bài 3. Tìm đa thức A và B sau đó tính giá trị đa thức A vàB tại x = 1;y = 2 −   1) 1 A + ( 2 x − xy ) 2 2 5 2
= 6x − 2xy − y 2) 2 2 2 2 2 2
xy + x − x y  − B = xy −
− x y + x  2  2 2
A = x − y 3 2 B = xy 2
Giá trị biểu thức A tại x = 1;y = 2 − là 3
− Giá trị biểu thức B tại x = 1;y = 2 − là 6
Bài 4. Bác Hoàng gửi tiết kiệm ở ngân hàng thứ nhất 50
triệu đồng với kỳ hạn một năm, lãi suất x% / năm. Bác
Hoàng gửi ở ngân hàng thứ hai 100 triệu đồng với kỳ
hạn một năm, lãi suất 1,5x% / năm.
a) Đa thức biểu thị số tiền lãi bác Hoàng có được ở ngân
hàng thứ nhất sau khi hết kỳ hạn một năm là: x x%. = . 0 1 50
5 = x (triệu đồng) 100 2
b) Đa thức biểu thị số tiền lãi bác Hoàng có được ở cả hai ngân hàng sau khi hết kỳ hạn một năm là 1 1 x 1
x + 1,5x%.100 = x + 1,5.
.100 = x + 1,5x = 2x (triệu đồng) 2 2 0 1 0 2
c) Nếu x = 5 thì sau một năm gửi tiết kiệm ở hai ngân hàng bác Hoàng lãi được
2.5 = 10 (triệu đồng) 7 PHIẾU BÀI TẬP TOÁN 8 Bài 5.
Hai người đi xe đạp cùng một lúc và ngược chiều nhau từ hai địa điểm A và B . Người
xuất phát từ A đi với vận tốc không đổi x (km / h). Người xuất phát từ B đi với vận tốc
không đổi y (km / h). Hai người gặp nhau tại điểm C sau 4 giờ.
a) Đa thức S biểu thị quãng đường AB theo x và y
S  4x  4y(km)
b) Tính S tại x  10,y  8 .
S  4.10  4.8  72(km)
c) Biết rằng người xuất phát từ B đi với tốc độ nhanh gấp đôi người xuất phát từ A . Tính
thời gian để người xuất phát từ A đi hết quãng đường AB .
Người xuất phát từ B đi nhanh gấp đôi người xuất phát từ A nên y  2x (km / h).
Khi đó S  4x  4.2x  12x(km)
Thời gian người xuất phát từ A đi hết quãng đường AB là: t S : v  12x : x  2 1 (h).
Bài 6. Cho hai đa thức 2 2
P = 7x − 3xy − y và 2 2
Q = 3xy − 3x + 2y . Chứng minh rằng:
không có số thực x và y nào để đa thức P và Q cùng nhận giá trị âm. Ta có: 2 2 2 2 2 2
P + Q = 7x − 3xy − y + 3xy − 3x + 2y = 4x + y ≥ 0 với mọi x,y ∈ 
Do đó P + Q ≥ 0 nên không có số thực x và y nào để đa thức P và Q cùng nhận giá trị âm, vì nếu P ,
< Q < 0 thì P + Q < 0
Bài 7. Tìm số tự nhiên abc (a < b < c) sao cho: abc + bca + cab = 666
Ta có: abc + bca + cab = 666 nên 100a + 10b + c + 100b + 10c + a + 100c + 10a + b = 666
111a + 111b + 111c = 666
111(a + b + c) = 666
a + b + c = 6
Vì a < b < c nên tìm được a = 1,b = 2,c = 3
Vậy số cần tìm là 123 III. BÀI TẬP VỀ NHÀ
Bài 1. Rút gọn các biểu thức sau a) 2 2 2 2 2 2
A = (x − xy + y ) − ( x −
+ 7xy − 5y ) = 2x − 8xy + 6y . b) 2 2 2 2 2 2 2
B = (xy − 3x y) − ( 2
− xy − 5x y) + (x y − 3xy ) = 3x y .
Bài 2. Cho các đa thức 3 2
M = 2x − 2x y + xy + 1; 2
N = 3x y + 2xy − 2 3 2
P = x − x y − 3xy + 1. Tính a) 3 2
M + N = 2x + x y + 3xy − 1. b) 3 2
M − P = x − x y + 4xy . c) 3 2
M − N + P = 3x − 6x y − 4xy + 4 .
Bài 3. Tìm đa thức A , B sau đó tính giá trị biểu thức A , B tại x = 1;y = 2 a) 2 2 2 2 2
6x − 3xy + A = x + y − 2xy ; 2 2 2 A = 5
− x + xy + y ; giá trị A tại x = 1;y = 2 là 3 8 PHIẾU BÀI TẬP TOÁN 8 b) 2 2 2
B − (2xy − 4y ) = 5xy + x − 7y ; 2 2
B = 7xy + x − 11y ; giá trị B tại x = 1;y = 2 là 29 −
Bài 4. Một chiếc bình có dạng hình lập phương với độ dài cạnh là 2x (cm).
a) Đa thức biểu thị thể tích nước tối đa mà chiếc bình đó có thể chứa được: 3 3 3
(2x) = 8x (cm )
b) Đa thức biểu thị thể tích phần không có nước trong bình: 3 2 3 2 3
8x − (2x) .y = 8x − 4x y(cm )
Bài 5. Cho hai đa thức 2 2 2 2
M = 4x y − 12xy − 2y và 2 2 2 2
N = x y + 12xy + 2y . Chứng minh
rằng: không có số thực x và y nào để đa thức P và Q cùng nhận giá trị âm. Ta có: 2 2 2
P + Q = 5x y = 5(xy) ≥ 0 với mọi x,y ∈  ….. HS tự KL
Bài 6*. Cho đa thức 2
A = x + xy − 2012x − 2013y − 2014 . Tìm cặp số (x;y) nguyên để đa thức A = 0 Ta có A = 0 nên 2
x + xy − 2012x − 2013y − 2014 = 0. 2
x + xy − 2013x − 2013y + x − 2013 − 1 = 0
x (x + y) − 2013(x + y) + (x − 2013) − 1 = 0
(x + y)(x − 2013) + (x − 2013) −1 = 0
(x − 2013)(x + y + )1 −1
(x − 2013)(x + y + )1 = 1
Vì x,y nguyên nên ta có bảng sau x − 2013 1 -1 x + y + 1 1 -1 x 2014 2012 y -2014 -2014
Vậy (x;y) = (2014; 2014 − ),(2012; 2014 − ) 1
PHIẾU BÀI TẬP TOÁN 8 CÁC PHÉP TÍNH VỀ ĐA THỨC NHIỀU BIẾN (NHÂN – CHIA)
I. BÀI TẬP TRẮC NGHIỆM
Câu 1. Khẳng định nào sau đây là sai?
A. Để nhân hai đơn thức, ta nhân các hệ số với nhau và nhân các phần biến với nhau.
B. Kết quả của tích (
A B − C ) = AB − AC
C. Kết quả của tích (A + B)(C − D) = AC − AD + BC − BD
D. Kết quả của tích (A + B) :C = C : A + C : B
Câu 2. Kết quả của phép tính 2 2 3 ( x y).( xy − ) A. 3 3 3 − x y . B. 3 3 3x y . C. 3 2 3x y . D. 2 3 3 − x y .
Câu 3. Hệ số của đơn thức 2 2 2x y3xy là? A. 2 . B.3. C.5. D.6 . 4
Câu 4. Bậc của đơn thức 2 2 3 2xy x y 6x là? 3 A.7 B.8 C.9. D.12.
Câu 5. Viết đơn thức 4 5 6
21x y z dưới dạng tích hai đơn thức, trong đó có 1 đơn thức 2 2 3x y z ta được kết quả là: A.( 2 2 3 x y z ).( 2 3 2 3 7x y z ) . B.( 2 2 x y z ).( 2 3 5 3 7x y z ) . C.( 2 3 − x y z ).( 2 3 5 3 7 − x y z ). D.( 2 2 x y z ).( 2 3 5 3 7 − x y z ) . 3
Câu 6. Cho các đơn thức 3 A = 4x y( 5 − xy) , 4 2 B = 17 − x y , 6
C = x y . Các đơn thức nào 5 đồng dạng với nhau?
A. Đơn thức A và đơn thức C .
B. Đơn thức B và đơn thức C .
C. Đơn thức A và đơn thức B .
D. Cả ba đơn thức A , B , C đồng dạng với nhau.
Câu 7. Thực hiện phép tính nhân 2 3 1 x 5
( x − x − ) ta được kết quả là? 2 A. 6 3 1 2 5 1
x − x − x . B. 5 3 2
5x − x − x . 2 2 C. 5 3 1 5 1 x − x − . D. 6 2 2
5x − x − x . 2 2
Câu 8. Tích (x − y)(x + y) có kết quả bằng: A. 2 2
x − 2xy + y . B. 2 2 x + y . C. 2 2 x − y . D. 2 2
x + 2xy + y .
Câu 9. Trong các phép tính sau, phép tính nào có kết quả là 2 2 3x + 3y ?
A. 3x (x + y) .
B. x (x + y + )
1 − 3y (x + y) − x .
C. 3x (x + y) − 3y (x + y).
D. 3x (y + x ) + y ( 3 − x + 3y ) . 1  Câu 10. Tính 3 3 2 4 2
( x y + 2x y ) : (xy )ta được kết quả là ? 3 A. 1 2 2 1 x y + 2x y . B. 2 x y + 2xy . 3 2 C. 1 2 2 1 x y + xy . D. 2 2 x y + 2xy . 2 3 2
PHIẾU BÀI TẬP TOÁN 8 2  1   Câu 11. Tích 4 2 2
6x y :  x y bằng: 2    A. 12. B. 24 . C. 2 24x y . D. 2 12x y .  Câu 12.
Cho biểu thức C = x(y + z) − y(z + x) − z(x − y). Chọn khẳng định đúng.
A. Biểu thức C không phụ thuộc vào x;y;z . B. Biểu thức C phụ thuộc vào cả x;y và z .
C. Biểu thức C chỉ phụ thuộc vào y .
D. Biểu thức C chỉ phụ thuộc vào z . II. BÀI TẬP TỰ LUẬN
Bài 1. Thực hiện các phép tính sau: 1) 2 2 (2x y ) 3
.( xy) = ...............................................................................................................   2) (− x yz) 2 2 1 2
. xyz  = .......................................................................................................  2    3) ( 4 2 5 4 − x y z ) 1 2
:  xyz  = ...................................................................................................  2  3     4) 1 2 3 3 5
xy  :  x y  = ........................................................................................................  2   8 
Bài 2. Thực hiện các phép tính sau: 1) 2 2 − 1 2
x(x − y) 2) 2
xy.( xy − y + 4) 2 3 3) 2 2 8 3 1
( xy − 2x y) : (2xy) 4) 2 2
(− xy − xy + 2x y) : ( xy) 4 4
Bài 3. Rút gọn và tính giá trị các biểu thức sau: 1) 2 2
A = (2x − y)(2x + y) − (4x + 2y ) tại x = 999;y = 1 2) 2 2 2
B = (x − y)(x + xy + y ) − x.(x − y) tại 1 x = 1;y = 2 3 PHIẾU BÀI TẬP TOÁN 8 3) 2 2 3 3
C = (x − y)(x + y) − (x − 1)(y + 1) + (2x y ) : (xy) tại x = y = 2 −
Bài 4. Chứng minh giá trị của biểu thức sau không phụ thuộc vào giá trị của biến x
A  (x  3)(2x  5)  8x(1  x)  (2x  1)(5  3x)
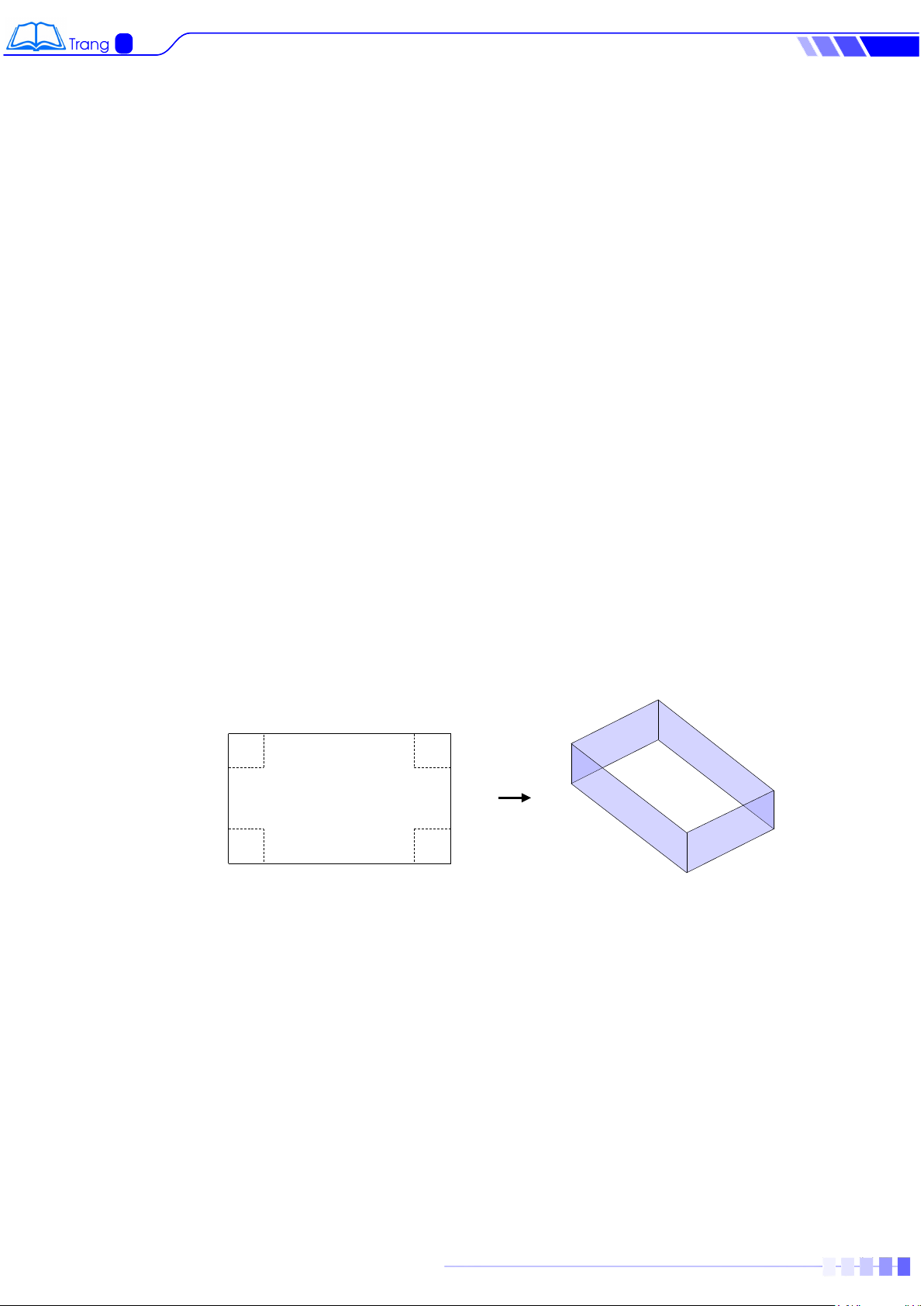
Bài 5. Từ một miếng bìa hình chữ nhật có chiều dài là x(cm) , chiều rộng x  4(cm) .
Người ta đã cắt bốn hình vuông cạnh 2(cm) ở bốn góc của miếng bìa rồi gấp lại để tạo thành
một chiếc hộp không nắp (Hình vẽ dưới đây). Viết đa thức biểu thị x (cm) 2 (cm) x - 4 (cm)
a) Thể tích của chiếc hộp
b) Tổng diện tích năm mặt của chiếc hộp 4 PHIẾU BÀI TẬP TOÁN 8
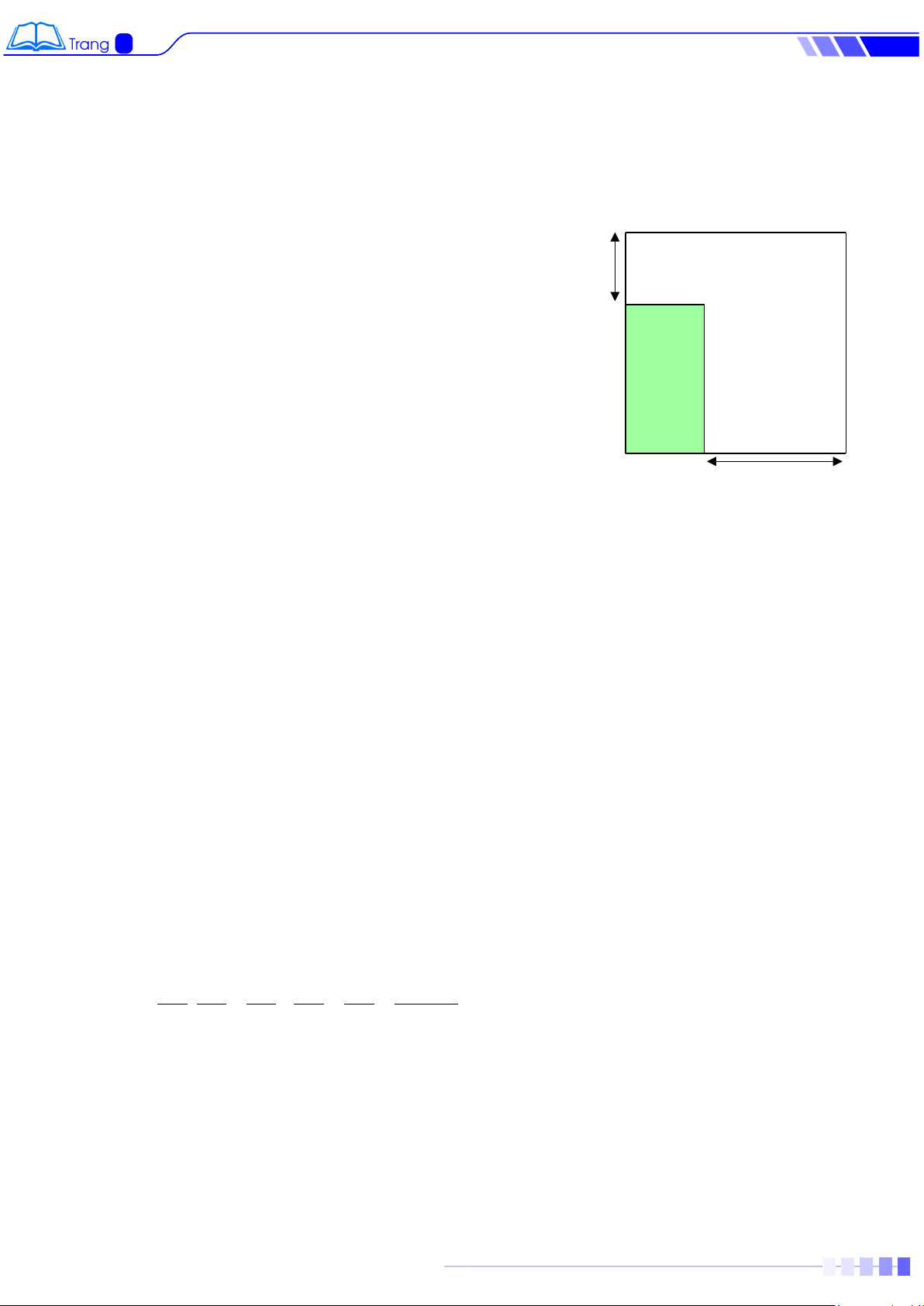
Bài 6. Bác Quang có một mảnh đất hình vuông cạnh x(m) , bác muốn trồng hoa vào
mảnh đất hình chữ nhật ở góc vườn (hình vẽ bên). Tính độ dài cạnh x(m) của khu vườn đó,
biết diện tích mảnh đất trồng hoa bằng 2 60m x (m) 6 m Trồng hoa 10 m
Bài 7. Tìm ba số tự nhiên liên tiếp. Biết rằng tích của hai số sau lớn hơn tích của hai số đầu là 30
Bài 8*. Tính nhanh a) 7 1 4 2 1 1 A = 4 . − .1 + + 570 375 375 570 375 375.570

Tài liệu liên quan: