


















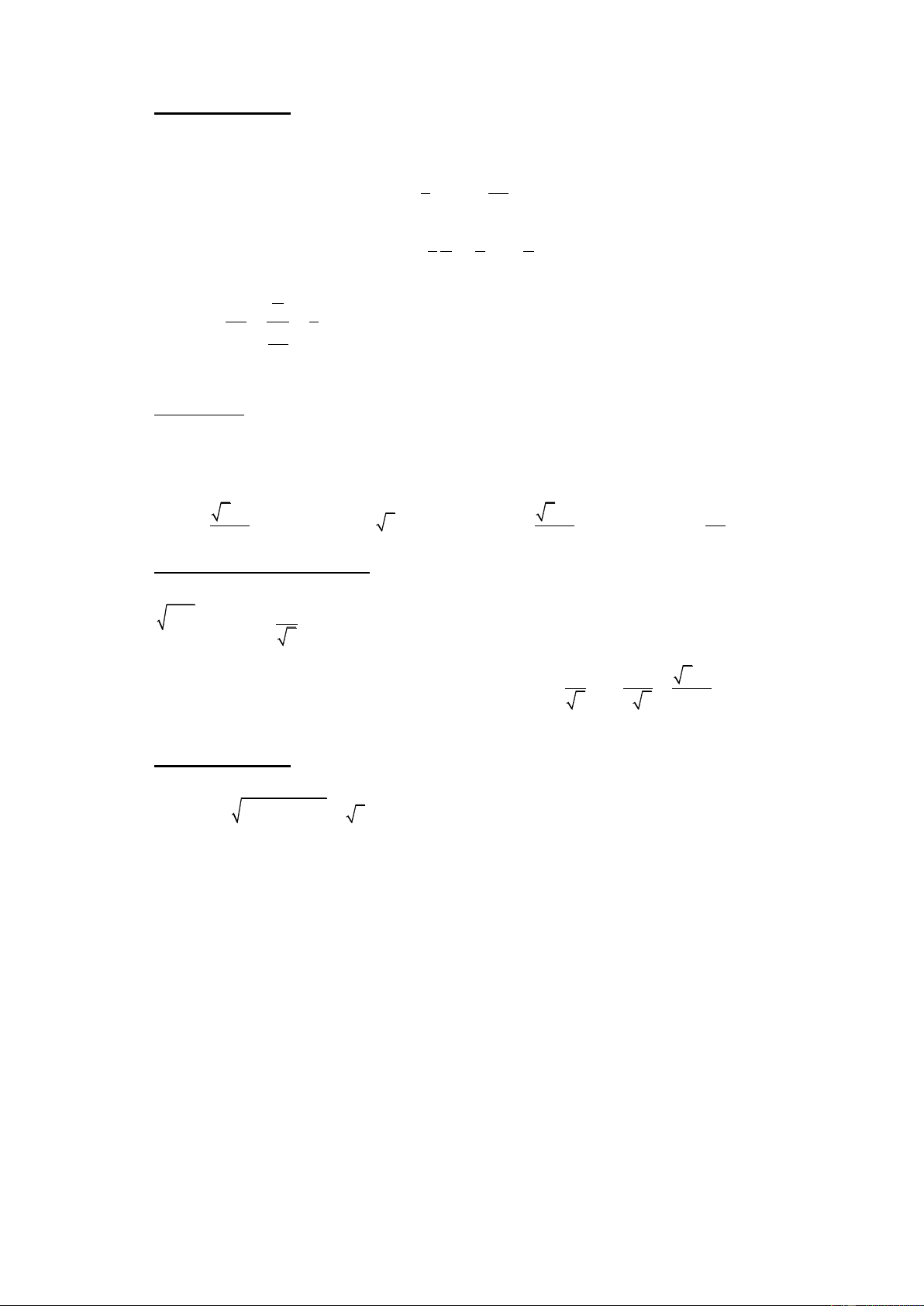







Preview text:
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Vieäc tìm ra ñaùp aùn ñuùng cho baøi toaùn traéc nghieäm laø raát khaùc so vôùi
vieäc trình baøy baøi giaûi töï luaän. Giaûi quyeát baøi toaùn töï luaän, chuùng ta phaûi
trình baøy lôøi giaûi baøi toaùn theo suy luaän cuûa mình, sao cho ngöôøi ñoïc hieåu
ñuùng, döïa treân neàn taûng kieán thöùc chuaån möïc. Vôùi baøi thi toaùn traéc nghieäm,
hoïc sinh khoâng caàøn trình baøy lôøi giaûi vaø coù nhieàu caùch tieáp caän. Khoâng caàn
xeùt moïi tröôøng hôïp, coù theå moät vaøi tröôøng hôïp cuõng ñuû choïn ñöôïc ñaùp aùn vì
loaïi ñöôïc caùc khaû naêng khaùc. Caùc suy luaän khoâng caàn dieãn giaûi, vieát ra, chæ
vieát yù chính ñeå tìm ra ñaùp aùn khi nhaùp! Sau ñaây laø moät höôùng tieáp caän nhö vaäy !
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
CHOÏN ÑAÏI DIEÄN GIAÛI TOAÙN TRAÉC NGHIEÄM
Neáu baøi toaùn ñuùng vôùi moïi giaù trò x K thì noù seõ ñuùng vôùi
moät giaù trò xaùc ñònh x K . 0
I. MOÄT SOÁ BAØI TOAÙN VEÀ HAØM SOÁ 2 x − m (m + ) 3 + + Ví duï 1. Haøm soá 1 x m 1 y =
luoân coù cöïc ñaïi vaø cöïc tieåu vôùi x − m
moïi giaù trò thöïc cuûa m. Goïi ñieåm cöïc ñaïi vaø cöïc tieåu cuûa haøm soá laàn löôït
laø x , x . Khi ñoù ta coù : 1 2
A. x − x = 2 .
B. x − x = m . C. x − x = 1 .
D. x − x = 2m . 1 2 1 2 1 2 1 2
Caùch giaûi thoâng thöôøng 2 2 − + − * x 2mx m 1 y ' = (x − ; m)2 * 2 2
y ' = 0 x − 2mx + m −1 = 0 . m +1 x = 1 x = m +1 2 = − ( 2 1 ' m m − ) 1 = 1 0 1
x − x = 2 . m −1 x = m −1 1 2 x = 2 2 1 Choïn ñaùp aùn A.
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Caùch khaùc (choïn ñaïi dieän)
Do baøi toaùn ñuùng vôùi moïi soá thöïc m neân ta choïn moät phaàn töû ñaïi dieän cuûa 2 − + m, chaúng haïn x 12x 28
m = 3 . Khi ñoù haøm soá trôû thaønh y = ; x − 3 2 x − 6x + 8 x = 4 1 y ' = = ( − ) 0 2 x = 2 x 3 2
Ta coù : x − x = 2 . 1 2 Choïn ñaùp aùn A.
Löu yù : Ta khoâng choïn m = 1 vì khi ñoù caùc ñaùp aùn A truøng vôùi D ; B truøng
vôùi C. (töông töï cho tröôøng hôïp m = 2 )
Ví duï 2. Phương trình 3 2
x − 3x = m + m coù ba nghiệm thöïc khi tham soá
thöïc m thoûa maõn : A. 2
− m 1. B. m 1. C. 1
− m 2. D. m 21 − .
Caùch giaûi thoâng thöôøng 1 Xeùt haøm soá 3
y = x − 3x ; 2
y ' = 3x − 3 ; 2
y ' = 3x − 3 = 0 x = 1 Baûng bieán thieân x − 1 − 1 + y ' + 0 - 0 + 2 2 −
Phöông trình ñaõ cho coù 3 nghieäm khi 2 2
− m + m 2 2 − m 1. Choïn ñaùp aùn A.
Caùch giaûi thoâng thöôøng 2 Ta coù 3 2 3 2
x − 3x = m + m x − 3x − m − m = 0 .
Ñeå thoûa maõn baøi toaùn thì ñoà thò haøm soá 3 2
y = x − 3x − m − m coù hai
ñieåm cöïc trò naèm khaùc phía so vôùi truïc hoaønh. 2
y ' = 3x − 3 ; 2
y ' = 3x − 3 = 0 x = 1 .
Vaäy ta caàn coù y(− ) y( ) ( 2 − m − m)( 2 1 . 1 0 2 2
− − m − m) 0 2 − m 1.
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com Choïn ñaùp aùn A.
Caùch khaùc (choïn ñaïi dieän) Neáu m = 2
− phöông trình trôû thaønh : x =1 3 3
x − 3x = 2 x − 3x − 2 = 0 . x = 2 −
Loaïi tröôøng hôïp B, D. 3
Neáu m = phöông trình trôû thaønh : 2 15 15 3 3 x − 3x = x − 3x − = 0 . (khoâng thoûa) 4 4
Loaïi tröôøng hôïp C. Choïn ñaùp aùn A.
Ví duï 3. Caùc giaù trò thöïc cuûa tham soá m ñeå haøm soá m 3 2 2 y =
x − mx + (2m −1)x + m nghòch bieán treân laø 3
A. m 0 hoaëc m 1. B. m 0 . C. 0 m 1. D. m 0 .
Caùch giaûi thoâng thöôøng Ta coù 2
y ' = mx − 2mx + 2m −1 .
TH1: Neáu m = 0 thì y ' = 1
− 0 thoûa maõn baøi toaùn. TH2: Neáu m 0 ,
ñeå thoûa maõn baøi toaùn ta caàn coù m 0 m 0 m 0 2 m − m(2m − ) 2 1 0
−m + m 0
Vaäy m 0 , choïn ñaùp aùn D.
Caùch khaùc (choïn ñaïi dieän)
Neáu m = 0 haøm soá trôû thaønh y = −x ; y ' = 1
− 0. Suy ra m = 0 thoûa maõn baøi toaùn.
Loaïi tröôøng hôïp A, C. (do khoâng chöùa giaù trò m = 0) Neáu m = 3 − haøm soá trôû thaønh 3 2
y = −x + 3x − 7x + 9 ; 2 y ' = 3
− x + 6x − 7 0, x Suy ra m = 3
− thoûa maõn baøi toaùn.
Loaïi tröôøng hôïp B. Choïn ñaùp aùn D.
Ví duï 4. Vôùi taát caû caùc giaù trò thöïc naøo cuûa tham soá m thì ñoàà thò haøm soá 4
y = x + (m + ) 2
1 x + 4 coù ba ñieåm cöïc trò ?
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com A. m 1 − ; B. m 1 − ; C. m 1 − ; D. m 1 − .
Caùch giaûi thoâng thöôøng Ta coù 3
y = x + (m + ) x = x( 2 ' 4 2 1 2 2x + m + ) 1 .
Ñeå thoûa maõn baøi toaùn thì phöông trình 2
2x + m +1 = 0 phaûi coù hai
nghieäm phaân bieät khaùc 0 . Suy ra : m +1 0 m 1 − . Choïn ñaùp aùn C.
Caùch khaùc (choïn ñaïi dieän) Neáu m = 1 − haøm soá trôû thaønh 4
y = x + 4 (haøm soá naøy chæ coù moät cöïc trò). Suy ra m = 1
− khoâng thoûa maõn baøi toaùn.
Loaïi tröôøng hôïp B, D. (do chöùa giaù trò m = 1
− , laøm haøm soá coù moät cöïc trò)
Neáu m = 0 haøm soá trôû thaønh 4 2
y = x + x + 4 ; 3
y = x + x = x( 2 ' 4 2 2 2x + )
1 = 0 x = 0 . Suy ra m = 0 khoâng thoûa maõn baøi toaùn.
Loaïi tröôøng hôïp A. Choïn ñaùp aùn C.
Ví duï 5. Vôùi taát caû caùc giaù trò thöïc naøo cuûa tham soá m thì haøm soá m 3 2 2 y =
x − mx + (2m −1)x + m nghòch bieán treân ñoaïn 0; 1 ? 3 1 1
A. m . B. m . C. m 1. D. m 1. 2 2
Caùch giaûi thoâng thöôøng Ta coù 2
y ' = mx − 2mx + 2m −1 .
TH1: Neáu m = 0 thì y ' = 1
− 0 thoûa maõn baøi toaùn.
TH2: Neáu m 0 , ta caàn coù y ' 0, x 0; 1 2
mx − 2mx + 2m −1 0, x0; 1 1 m( 2
x − 2x + 2) 1,x0; 1 m ,x 0;1 . 2 x − 2x + 2 1
Xeùt haøm soá f ( x) = treân ñoaïn 0; 1 . 2 x − 2x + 2 2x − 2 f '( x) = − f x = x = ( ; '( ) 0 1. x − 2x + 2)2 2
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com 1 Ta coù : f ( ) 1 0 =
; . f (0) =1. Suy ra : min f ( x) = f (0) = . 2 0; 1 2 1
Ñeå thoûa maõn baøi toaùn ta caàn coù m . 2 Choïn ñaùp aùn B.
Caùch khaùc (choïn ñaïi dieän)
Neáu m = 0 haøm soá trôû thaønh y = −x ; y ' = 1
− 0. Suy ra m = 0 thoûa maõn baøi toaùn.
Loaïi tröôøng hôïp A, D. (do khoâng chöùa giaù trò m = 0) 1
Neáu m =1 haøm soá trôû thaønh 3 2 y =
x − x + x + 1; 3 2
y ' = x − 2x +1 = ( x − )2 1 0,x
. Suy ra m =1 khoâng thoûa maõn baøi toaùn.
Loaïi tröôøng hôïp C. Choïn ñaùp aùn B. Ví duï 6. Cho haøm soá 4 2
y = ax + bx + c (a 0) vaø coù baûng bieán thieân :
x − 0 +
y ' − 0 +
+ + y c
Choïn khaúng ñònh ñuùng :
A. a 0 vaø b 0 . B. a 0 vaø b 0 .
C. a 0 vaø b 0 . D. a 0 vaø b 0 .
Caùch giaûi thoâng thöôøng
Trong khoaûng ngoaøi cuøng (khoaûng (0;+) ) thì y' 0 neân a 0. x = 0 Ta coù 3
y ' = 4ax + 2bx = 2x( 2
2ax + b) = 0 . 2 2ax + b = 0
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Do haøm soá coù moät cöcï trò neân phöông trình 2
2ax + b = 0 phaûi voâ nghieäm ab 0
hoaëc coù nghieäm x = 0. Ta phaûi coù : . b = 0
Maø a 0 neân b 0 . Choïn ñaùp aùn D.
Caùch khaùc (choïn ñaïi dieän)
Trong khoaûng ngoaøi cuøng (khoaûng (0;+) ) thì y' 0 neân a 0. Loaïi ñaùp aùn A, B.
Xeùt tröôøng hôïp C : cho a = 1, b = 2
− vaø c = 0, ta ñöôïc haøm soá 4 2 y = x − 2x ; x = 0 3
y ' = 4x − 4x = 4x( 2 x − ) 1 = 0 x = 1 − . x =1
Suy ra haøm soá ñaõ cho coù ba cöïc trò. Loaïi ñaùp aùn C. Choïn ñaùp aùn D. y
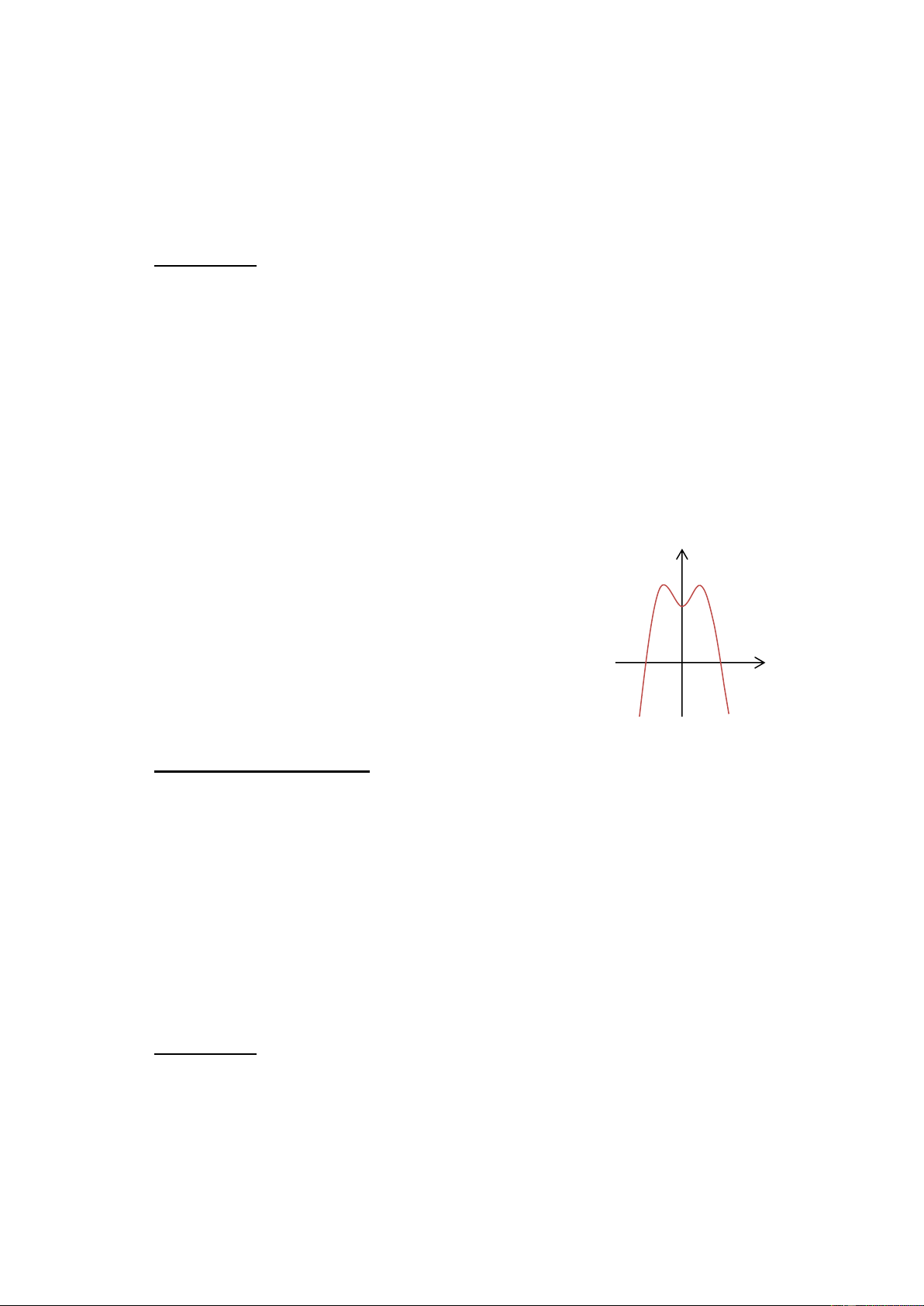
Ví duï 7. Cho haøm soá 4 2
y = ax + bx + c (a 0) coù ñoà
thò nhö hình beân. Choïn khaúng ñònh ñuùng : 2
A. a 0,b 0,c 0. B. a 0,b 0,c 0 . O x
C. a 0,b 0,c 0 . D. a 0,b 0,c 0.
Caùch giaûi thoâng thöôøng
Ta coù x = 0 thì c = 2 0 .
Nhaùnh ngoaøi cuøng, beân phaûi cuûa ñoà thò treân ñi xuoáng töø traùi qua phaûi neân
a 0 . Loaïi caùc ñaùp aùn A vaø B. x = 0 Ta coù 3
y ' = 4ax + 2bx = 2x( 2
2ax + b) = 0 . 2 2ax + b = 0
Do haøm soá coù ba cöcï trò neân phöông trình 2
2ax + b = 0 phaûi coù hai
nghieäm phaân bieät khaùc x = 0. Ta phaûi coù : ab 0 .
Maø a 0 neân b 0 . Choïn ñaùp aùn D.
Caùch khaùc (choïn ñaïi dieän)
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Nhaùnh ngoaøi cuøng, beân phaûi cuûa ñoà thò treân ñi xuoáng töø traùi qua phaûi neân
a 0 . Loaïi caùc ñaùp aùn A vaø B.
Xeùt tröôøng hôïp C : cho a = 1 − , b = 2
− vaø c = 2 , ta ñöôïc haøm soá 4 2
y = −x − 2x ; 3
y = − x − x = − x( 2 ' 4 4 4 x + ) 1 = 0 x = 0 .
Suy ra, haøm soá ñaõ cho coù moät cöïc trò. Loaïi ñaùp aùn C. Choïn ñaùp aùn D.
Ví duï 8. Vôùi taát caû caùc giaù trò thöïc naøo cuûa tham soá m thì haøm soá x − 3 y =
ñoàng bieán treân khoaûng (2;+) ? x + m A. m 3 − . B. m 2 − . C. 3 − m 2 − . D. m 2 − .
Caùch giaûi thoâng thöôøng m + 3 Ta coù y ' = ( . x + m)2
Ñeå thoûa maõn baøi toaùn ta caàn coù y ' 0, x (2;+) m + 3 m + 3 0
0, x 2;+ 2 ( ) (x + m) −m(2;+ ) m 3 − m 3 − m 2 − . −m 2 m 2 − Choïn ñaùp aùn D.
Caùch khaùc (choïn ñaïi dieän) x − 3 1 Neáu m = 2
− haøm soá trôû thaønh y = y ' = 0 . Suy ra x − 2 ; (x − 2)2 m = 2
− thoûa maõn baøi toaùn.
Loaïi tröôøng hôïp A, B, C. (do khoâng chöùa giaù trò m = 2 − ) Choïn ñaùp aùn D.
Ví duï 9. Cho haøm soá y = f ( x) coù ñoà thò (C ) nhö
hình beân. Tìm taát caû caùc giaù trò thöïc cuûa tham soá m
ñeå ñöôøng thaúng y = 2m − 6 caét ñoà thò (C ) taïi hai
ñieåm phaân bieät ñeàu coù hoaønh ñoä lôùn hôn 1 − .
A. 3 m 5 . B. 3 m 5.
C. 3 m 5 . D. 3 m 5.
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Caùch giaûi thoâng thöôøng
Töø ñoà thò ta suy ra, giaù trò cuûa tham soá m thoûa maõn baøi toaùn laø : 2m − 6 0 2m − 6 4 2m 6 m 3 . 2m 10 m 5 Choïn ñaùp aùn B.
Caùch khaùc (choïn ñaïi dieän)
- Neáu m = 3 , ñöôøng thaúng y = 2m − 6 trôû thaønh y = . Ñöôøng thaúng 0
y = 0 coù moät giao ñieåm vôùi ñoà thò (C ) . Suy ra m = 3 khoâng thoûa maõn baøi toaùn.
Loaïi tröôøng hôïp A, C. (do chöùa giaù trò m = 3 )
- Neáu m = 5 , ñöôøng thaúng y = 2m − 6 trôû thaønh y = . Ñöôøng thaúng 4
y = 4 coù hai giao ñieåm vôùi ñoà thò (C ) , trong ñoù coù moät giao ñieåm coù hoaønh ñoä baèng 1
− . Suy ra m = 5 khoâng thoûa maõn baøi toaùn.
Loaïi tröôøng hôïp D. (do chöùa giaù trò m = 5 ) Choïn ñaùp aùn B.
Ví duï 10. Caùc giaù trò thöïc cuûa tham soá thöïc m ñeå ñoà thò haøm soá 4
y = mx + (m − ) 2
1 x + 1 − 2m coù moät ñieåm cöïc trò laø : m 0 A. . B. (− ;
0(1;+). C. 0 m 1. D. (− ; 0) (1;+). m 1
Caùch giaûi thoâng thöôøng
TH1: Neáu m = 0 thì 2
y = −x + 1, ñoà thò cuûa haøm soá naøy coù moät ñieåm cöïc trò.
TH2: Neáu m 0 , ta coù 3
y = mx + (m − ) x = x( 2 ' 4 2 1 2 2mx + m − ) 1 .
Ñeå thoûa maõn baøi toaùn thì phöông trình 2
2mx + m −1 = 0 phaûi coù moät
nghieäm x = 0 hoaëc voâ nghieäm. m −1= 0 m =1 Suy ra : . m(m ) −1 0 m (− ; 0) (1;+ )
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com m 0
Keát hôïp hai tröôøng hôïp treân ta ñöôïc . m 1 Choïn ñaùp aùn A.
Caùch khaùc (choïn ñaïi dieän)
- Neáu m =1 haøm soá trôû thaønh 4 y = x −1; 3
y ' = 4x = 0 x = 0 . (ñoà thò
haøm soá coù moät ñieåm cöïc trò). Suy ra m =1 thoûa maõn baøi toaùn.
Loaïi caùc ñaùp aùn B, C, D. Choïn ñaùp aùn A.
II. MOÄT SOÁ BAØI TOAÙN VEÀ HAØM SOÁ LUÕY THÖØA, HAØM SOÁ MUÕ VAØ HAØM SOÁ LOÂGARIT
Ví duï 1. Cho log x = 3,log x = 4 vôùi a, b laø caùc soá thöïc lôùn hôn 1. Tính a b P = log x . ab A. 7 P = . B. 1 P = . C. P = 12. D. 12 P = 12 12 7
(Caâu 42 - Maõ ñeà 101 – THPT QG - 2017)
Caùch giaûi thoâng thöôøng Ta coù : 1 1 1 12 P = log x = = = = . ab log ab log a + log b 1 1 7 x x x + 3 4 Choïn ñaùp aùn D.
Caùch khaùc (Choïn ñaïi dieän) 3 a = Choïn 2 12
x = 2 . Khi ñoù P = log( 2 = log 2 = . 3 4 2. 2 ) 7 4 b = 2 12 2 7
(ta coù theå duøng maùy tính caàm tay ñeå hoã trôï tính cho nhanh) Choïn ñaùp aùn D.
Ví duï 2. Cho a = log với
vaø A = log (8 . Khi đoù mối quan 8 m) 2 m m 0 ; m 1
hệ giữa A vaø a laø : A. + a −
A = a (3 − a) . B. 3 A = . C. 3 a A =
. D. A = a(3 + a) . 3 a
Caùch giaûi thoâng thöôøng + Ta coù = ( m) 1 3 l og2 m A l og 8
= log 8 + log m = 1 + log = + = . 3 m 1 l og 8 8 8 2 m 2 3 3 Vaäy 3 + a A = . a
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com Choïn ñaùp aùn B.
Caùch khaùc (choïn ñaïi dieän)
Choïn m = 4 ta tính a = log m = log 4 = 2 ; A = log (8m) 5 = = . 2 2 l og 32 8 8 3 Khi thì ta coù : A. + a
A = a (3 − a) = 2 . B. 3 5 A = = . 3 3 C. 3 − a 1 A =
= . D. A = a (3 + a) = 10 . a 2 Choïn ñaùp aùn B.
Ví duï 3. Tìm taäp nghieäm S cuûa baát phöông trình + 1 x 1 5 − 0 . 5
A. S = (1;+) . B. S = ( 1; − +) . C. S = ( 2;
− +) . D. S = (− ; 2 − ) .
Caùch giaûi thoâng thöôøng + 1 + 1 x 1 x 1 x 1 + 1 − 5 − 0 5 5 5 x + 1 1 − x 2 − . 5 5
Taäp nghieäm cuûa baát phöông trình laø S = ( 2; − +) . Choïn ñaùp aùn C.
Caùch khaùc (choïn ñaïi dieän) - Vôùi + x = 0 thì 1 0 1 5
− 0 . suy ra, loaïi caùc ñaùp aùn A vaø D. 5 - Vôùi 1 1 4 1 1 x = −1 thì − + 5 − = 1 − =
0 . suy ra, loaïi ñaùp aùn B. 5 5 5 Choïn ñaùp aùn C.
Ví duï 4. Tìm taäp nghieäm S cuûa baát phöông trình 2 l og x −1 . 1 4
A. (−;2 . B. −2;2 . C. −2;0) (0;2 . D.(0;2 .
Caùch giaûi thoâng thöôøng x 0 x 2 0 x 0 l og x −1 −1
x −2;0) (0;2 . 1 1 2 x 2 x 4 −2 x 2 4 4 Choïn ñaùp aùn C.
Caùch khaùc (choïn ñaïi dieän) - Vôùi x = 0 thì 2
l og1 x khoâng xaùc ñònh. Suy ra, loaïi caùc ñaùp aùn A vaø B. 4
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com - Vôùi 2 x = −2 thì l og
(−2) = log − 4 = − . suy ra, loaïi ñaùp aùn D. 1 1 1 4 4 Choïn ñaùp aùn C. 1 1 1 6 2 − −
Ví duï 5. Cho bieåu thöùc 3 6 = 2 3 2 P a a b
a b 3 , vôùi , a b laø caùc soá
thöïc döông. Khaúng ñònh naøo sau ñaây ñuùng ? 21 21 A. = 13 21 13 5 P a b . B. = 4 P a b . C. = 3 P a b . D. = 21 13 P a b .
Caùch giaûi thoâng thöôøng 1 1 1 6 2 − − Ta coù : 3 6 = 2 3 2 P a a b a b 3 6 6 1 1 1 − − 1 1 1 2− 4− = 2 2 a a b ( 2 4 3 a b ) = 2 3 2 a a b 6 6 6 1 1 1 1 5 7 13 7 2− 4− = 2 3 2 a a b = 2 3 2 a a b = 6 2 a b = 13 21 a b . Choïn ñaùp aùn A.
Caùch khaùc (choïn ñaïi dieän)
Sau khi ruùt goïn thì ñöôïc keát quaû ñuùng vôùi moïi ,
a b laø caùc soá thöïc döông
neân ta coù theå choïn ñaïi dieän.
- Choïn a = 1 ; b = 2 thì 1 1 1 6 1 6 1 6 2 2 − − 3 6 − − 2 3 2 3 6 P = = 2 3 = 4 2 1 1 2 1 2 2 2 2 .2 = 21 2 .
(coù theå duøng maùy tính ñeå tính giaù trò cuûa P )
- Theá a = 1 ; b = 2 vaøo caùc ñaùp aùn thì chæ coù ñaùp aùn A thoûa maõn. Choïn ñaùp aùn A.
Ví duï 6. Cho a laø soá thöïc döông vaø b laø soá thöïc khaùc 0 . Khaúng ñònh naøo sau ñaây ñuùng?
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com 3 3 A. 3a 3a l og = 1 + 3 log a − . B. l og = 1 + 3 log a + . b 2 l og b 2 2 l og 3 3 3 3 2 3 3 b b 3 3 C. 3a 3a 1 l og = 1 + 3 log a − . D. l og = 1 + log a − . b 2 l og b 2 2 l og 3 3 3 3 2 3 3 b b 3
Caùch giaûi thoâng thöôøng 3 Ta coù : 3a 3 = log 3a − 2 l og b 2 l og 3 3 3 b 3 2
= log 3 + log a − log b = 1 + 3log a − 2 log 3 3 3 3 3 b . Choïn ñaùp aùn C.
Caùch khaùc (choïn ñaïi dieän)
Sau khi bieán ñoåi thì ñöôïc keát quaû ñuùng vôùi moïi a laø soá thöïc döông vaø
b laø soá thöïc khaùc 0 , neân ta coù theå choïn ñaïi dieän.
- Choïn b = −1 thì caùc bieåu thöùc beân veá phaûi cuûa ñaùp aùn A vaø B ñeàu khoâng
xaùc ñònh neân loaïi caùc ñaùp aùn A, B. 3 3 VT = 3a l og = 3.3 l og = 4 3 3 - Choïn 2 2
a = 3 ; b = 1 thì ôû ñaùp aùn C ta coù b 1 3 VP = 3 − 2 l og 3.3 l og 1 = 4 3 (thoûa maõn) ; 3 3 VT = 3a l og = 3.3 l og = 4 3 3 ôû ñaùp aùn D ta coù 2 2 b 1 (khoâng thoûa maõn neân 1 3 VP = 4 3 − 2 l og 3.3 l og 1 = 3 3 3 loaïi ñaùp aùn D). Choïn ñaùp aùn C. 2018 Ví duï 7. Cho 2 2
x = l g a − ab + b ; y = a − 1 2018 l g l g
(vôùi a vaø b laø 2018 b
caùc soá thöïc döông). Khaúng ñònh naøo sau ñaây ñuùng ?
A. x y . B. x y . C. x y . D. x y .
Caùch giaûi thoâng thöôøng 2018 Ta coù : 2 2 2 2
x = l g a − ab + b
= 2018 lg a − ab + b ; y = a − 1 2018 l g l g − = a − 2018 2018 l g l g b
= 2018 (lg a + lgb) 2018 b
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com = 2018 lg (ab) .
Xeùt hieäu x y 2018 lg (ab) 2 2 − =
− 2018 lg a − ab + b 2 2
= 2018 lga − ab + b − lg(ab) 2 2
= 2018 lga − ab + b − lg(ab) . (1) Laïi coù : 2 2 2
a − ab + b − ab = (a − b) 0 neân 2 a − ab + 2 b ab 0 (do , a b 0 ) . 2 2
lg a − ab + b lg (ab) . (2)
Töø (1) vaø (2) suy ra x y . Choïn ñaùp aùn C.
Caùch khaùc (choïn ñaïi dieän)
Baát ñaúng thöùc ñuùng vôùi caùc soá thöïc döông a vaø b baát kyø neân ta coù theå choïn ñaïi dieän.
- Choïn a = 2 ; b = 1 thì x − y = − − 1 2018 2018 = 2018 − 2018 l g 3 l g 2 l g l g 3 l g 2 . 2018 0 1
Suy ra x y , loaïi caùc ñaùp aùn A, B.
- Choïn a = b = 1 thì x = y = 0 , loaïi ñaùp aùn D. Choïn ñaùp aùn C.
Ví duï 8. Haøm soá y = 2 + ln (x + 1) ñoàng bieán treân khoaûng naøo ? x + 1
A. (1;+) . B. (−1;+) . C. (−1;1) . D. − + 1; ) .
Caùch giaûi thoâng thöôøng 1
Taäp xaùc ñònh : (−1;+) . Ta coù −2 1 x − x − 1 y = + = 1 ' ; y' = 0
= 0 x − 1 = 0 x = 1 . ( 2 x )2 x + + 1 (x + )2 1 1 (x +1) Baûng bieán thieân
x − 1
− 1 +
y ' − 0 + y 1+ ln 2
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Haøm soá ñoàng bieán treân khoaûng (1;+) . Choïn ñaùp aùn A.
Caùch giaûi thoâng thöôøng 2
Taäp xaùc ñònh : (−1;+) . Ta coù − x − 1 y = 2 + 1 ' = 0 x 1 . ( 2 x )2 x + + 1 1 (x +1)
Haøm soá ñoàng bieán treân khoaûng (1;+) . Choïn ñaùp aùn A.
Caùch khaùc (choïn ñaïi dieän)
- Vôùi x = −1 thì haøm soá khoâng xaùc ñònh neân loaïi caùc ñaùp aùn D. Ta coù − y = 2 + 1 ' . (x )2 x + + 1 1
- Giaù trò y'(0) = −1 0, loaïi ñaùp aùn C, B. Choïn ñaùp aùn A.
* Löu yù : Caùc baïn coù theå duøng maùy tính caàm tay ñeå tính ñaïo haøm cuûa haøm
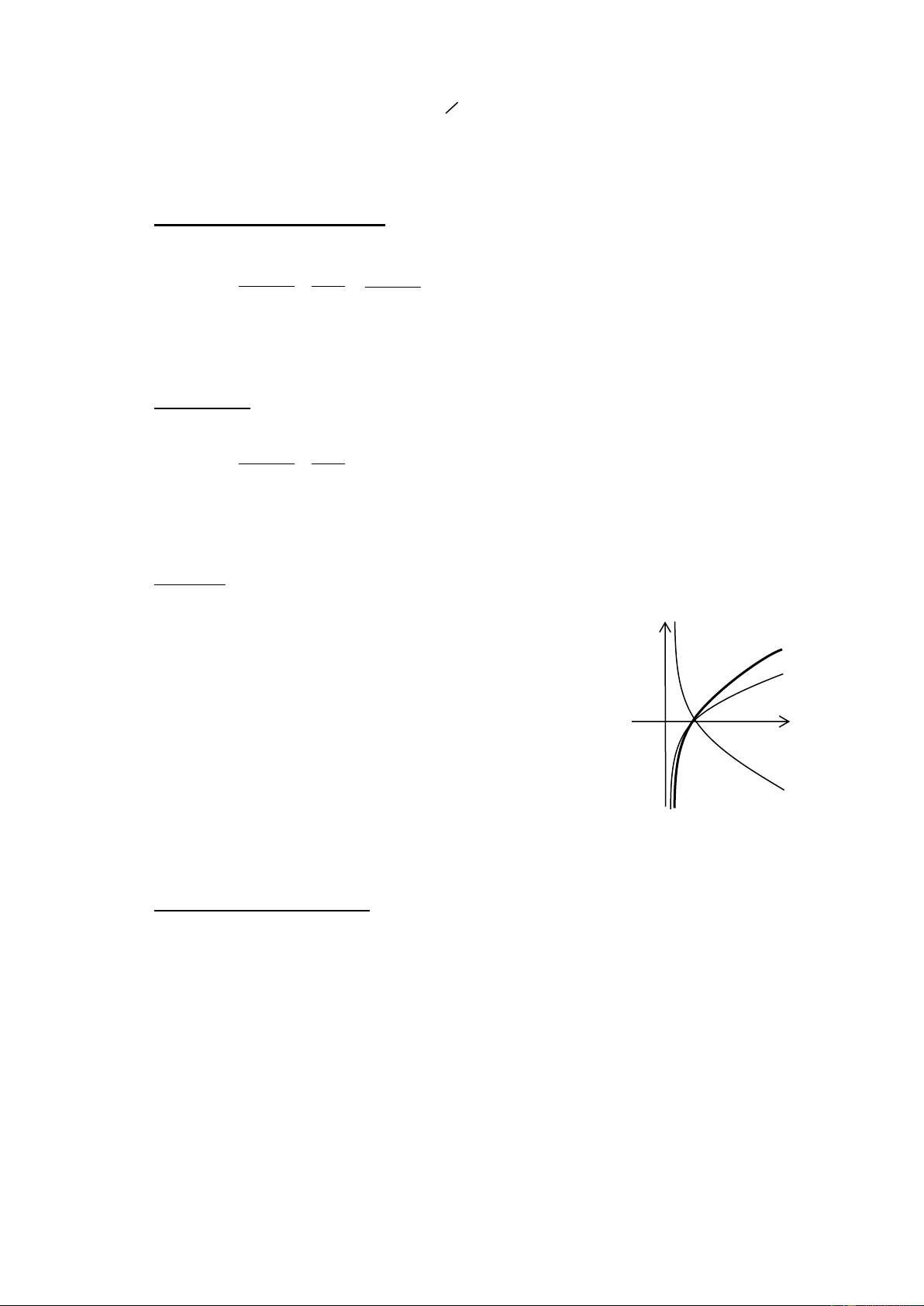
soá ñaõ cho taïi x = 0 . y y=logax Ví duï 9. Cho , a ,
b c laø caùc soá thöïc döông vaø khaùc 1.
Ñoà thò cuûa haøm soá y = log x , y = log x, a b y=logbx
y = log x ñöôïc cho trong hình veõ beân. Choïn khaúng c ñònh ñuùng ? O 1 x
A. a b c . B. b c a . y=logcx
C. c a b . D. c b a .
Caùch giaûi thoâng thöôøng
Ñoà thò cuûa haøm soá y = log x coù höôùng ñi xuoáng töø traùi qua phaûi neân haøm c
soá y = log x nghòch bieán treân khoaûng xaùc ñònh cuûa noù. Ngöôïc laïi, ñoà thò c
cuûa caùc haøm soá y = log x vaø y = log x coù höôùng ñi leân töø traùi qua phaûi a b
neân haøm soá y = log x vaø y = log x a b
ñoàng bieán treân khoaûng xaùc ñònh cuûa
noù. Suy ra c a vaø c b .
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Ñöôøng thaúng y =1 caét ñoà thò cuûa hai haøm soá y = log x vaø y = log x taïi a b
caùc ñieåm coù toïa ñoä laàn löôït laø a vaø b . Do ñoù, a b .
Vaäy c a b . Choïn ñaùp aùn C.
Caùch khaùc (choïn ñaïi dieän)
- Vôùi x = 5 thì log 5 0 neân 0 c 1 vaø log 5 0 ; log 5 0 neân c a b a 1; b 1.
- Vôùi x = 5;a = 3;b = 4 thì log 5 − log 5 0 a b . 3 4 (ñuùng) neân
Vaäy c a b . Choïn ñaùp aùn C. Ví duï 10. Cho ,
a b laø caùc soá thöïc thoûa maõn 0 a b 1 . Meänh ñeà naøo sau ñaây ñuùng ?
A. log a log b . B. log a
. C. log a . D. log b . b a l og b b a 0 b 1 a
Caùch giaûi thoâng thöôøng 1 Ta coù 1
l og a l og b log a − log b log a − b a 0 b a 0 b l og a b ( a b )2 l og − 1
0 . (ñuùng vì töø 0 a b 1 suy ra log a log b = 1 ) b b l og a b Choïn ñaùp aùn A.
Caùch giaûi thoâng thöôøng 2
Töø 0 a b 1 suy ra log a log b hay log a vaø log a hay b b 1 b l og b a a
1 log b . Do ñoù, ta loaïi caùc ñaùp aùn B, C, D. a Choïn ñaùp aùn A.
Caùch khaùc (choïn ñaïi dieän) Choïn − 1 1 a = 1 b = 1 ;
thì ta ñöôïc : log b = log loaïi ñaùp aùn D. a − 2 = 2 4 2 2 2 − a = 2 l og l og loaïi ñaùp aùn C. b − 2 = 2 1 2
Vaø ta cuõng coù log a log b neân loaïi ñaùp aùn B. b a Choïn ñaùp aùn A.
Ví duï 11. Cho bieåu thöùc P = 3 5 2 3 x . . x x
, vôùi x 0 laø soá thöïc döông.
Khaúng ñònh naøo sau ñaây ñuùng ? 14 13 16 24 A. = 15 P x . B. = 15 P x . C. = 15 P x . D. = 15 P x .
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Caùch giaûi thoâng thöôøng 3 3 8 3 4 14 14 3 3 Ta coù 2 2 P = 3 5 2 3 x . . x x = 5 x . . x x = 5 x . x = 2 5 x x = 5 . x = 15 x . Choïn ñaùp aùn A.
Caùch khaùc (choïn ñaïi dieän)
Sau khi ruùt goïn thì ñöôïc keát quaû ñuùng vôùi moïi x 0 laø caùc soá thöïc
döông neân ta coù theå choïn ñaïi dieän.
- Choïn x = 2 thì P 1,9 . (duøng maùy tính ñeå tính giaù trò cuûa P )
- Theá x = 2 vaøo caùc ñaùp aùn thì chæ coù ñaùp aùn A thoûa maõn. Choïn ñaùp aùn A.
* Löu yù : Caùc baïn keát hôïp thuû thuaät khi duøng maùy tính caàm tay thì giaûi
quyeát baøi toaùn raát nhanh.
Ví duï 12. Tìm taäp nghieäm S cuûa baát phöông trình 1+ 2x x+ − 1 2 3 3 x − 2x laø :
A. S = (0;+). B. S = + 2; ) . C. S = 0;2
. D. S = +) 2; 0 .
Caùch giaûi thoâng thöôøng Ta coù : 1+ 2x x+1 2 1+ 2x 1+ − − + x x x x + 2 3 3 2 3 2 3 x . Xeùt haøm soá ( ) 1+ = t f t + 2 3
t , t 0 ; ' ( ) 1+ = 3 t f t
l n 3 + 2t 0, t .
Suy ra, f (t) laø haøm soá ñoàng bieán treân . Maø theo (*) ta coù f ( 2x) f (x) 2 2 2x x
x − 2x 0
x (−;0 2; + )
neân 2x x x 2; + ) 0 . x 0 x 0 x 0
Taäp nghieäm cuûa baát phöông trình laø S = +) 2; 0 . Choïn ñaùp aùn D.
Caùch khaùc (choïn ñaïi dieän) - Vôùi 1 0 0 1 x = 0 thì + + 3 − 3
0 − 0 (ñuùng). suy ra, loaïi caùc ñaùp aùn A vaø B. - Vôùi x = 8 thì 1+4 8+ − 1 2 3 3
8 − 2.8 (ñuùng). suy ra, loaïi ñaùp aùn C. Choïn ñaùp aùn D.
Ví duï 13 . Cho x 1 ; , a ,
b c laø caùc soá döông khaùc 1 vaø
l og x l og x 0 l og c b
a x . Choïn khaúng ñònh ñuùng :
A. a b c . B. c b a . C. b a c . D. b c a .
Caùch giaûi thoâng thöôøng
Ta coù x 1 , maø log x 0 log x log 1 neân suy ra : a . a a a 1
log x 0 log x log 1 neân suy ra : 0 b . b b b 1
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
log x 0 log x log 1 neân suy ra : 0 c . c c c 1
Suy ra : a b ; a c . (*) 1 1
l og b − l og c
Laïi coù : log x log x x x 0 . c b l og c l og b l og . c l og x x x x b
Vì log b log 1 = 0 vaø log c log 1 = neân suy ra : x x 0 x x
l og b − l og c 0 l og b l og c b ) (**) x x x x c . ( do x 1
Töø (*) vaø (**) ta ñöôïc : b c a . Choïn ñaùp aùn D.
Caùch khaùc (choïn ñaïi dieän) - Choïn 1 2 x = 2 vaø − − c = 2 ; b = 2 ; a = 2 thì x = − x = − 1 l og 1 l og 0 log x = 1 . c b 2 a Roõ raøng raèng −2 1 − b = = c = 1 = 1 2 2 a = 2 . 4 2 Choïn ñaùp aùn D. 1 t Ví duï 14 . Cho t −1 t − x = t y = 1 , t
vôùi t 0, t 1 . Giöõa x vaø y coù heä thöùc
lieân heä naøo sau ñaây ? 1 1 A. x y x y x y y x
y = x . B. x = y . C. y = x . D. y = x .
Caùch giaûi thoâng thöôøng t t t 1 − t t − 1 1 Ta coù : y t t −1 t − = = 1 t = t ; −1 t − y = t = 1 t = t t x . x 1 t −1 t x y y Suy ra : t x = = = x y x y x y x x y = y x x . Choïn ñaùp aùn A.
Caùch khaùc (choïn ñaïi dieän)
Choïn t = 2 thìø x = 2, y = 4 . Khi ñoù ta coù : A. 2 4 4 = 2 .
(Ñuùng nhöng ta chöa choïn ñöôïc ñaùp aùn naøy vì coøn tröôøng hôïp ñaùp aùn khaùc cuõng ñuùng !) B. 2 = 4 2 4 . ( Sai )
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com 1 C. 2 = 4 4 2 . ( Sai ) 1 D. = 4 2 4 2 . ( Sai ) Choïn ñaùp aùn A.
III. MOÄT SOÁ BAØI TOAÙN VEÀ NGUYEÂN HAØM VAØ TÍCH PHAÂN 6 2
Ví duï 1. Cho f (x) dx =
12 . Tính I = f (3x) dx . 0 0
A. I = 6 . B. I = 36 . C. I = 2 . D. I = 4 .
(Caâu 25 - Maõ ñeà 101 – THPT QG - 2017)
Caùch giaûi thoâng thöôøng 1 2
Ta xeùt I = f (3x)dx . 0
Ñaët t = 3x dt = 3dx . Ñoåi caän : x 0 2 t 0 6 6
Tañöôïc : I = 1 f (t) dt = 1 .12 = 4 . 3 3 0 Choïn ñaùp aùn D.
Caùch giaûi thoâng thöôøng 2 2 2 6
Ta coù I = f ( x)dx = 1 f ( x)d ( x) = 1 f (t )d (t ) = 1 3 3 3 .12 = 4 . 3 3 3 0 0 0 Choïn ñaùp aùn D.
Caùch khaùc (choïn ñaïi dieän) 6 Ta choïn ñaïi dieän: 6
f (x) = 2 thoûa maõn 2dx = 2x = 2.6 − 2.0 = 12 . 0 0 2 I = dx = 2 2 2x = 2.2 − 2.0 = 4 . 0 0 Choïn ñaùp aùn D.
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Ví duï 2. Cho haøm soá f (x) lieân tuïc treân vaø thoûa maõn 3 2
f (x) + f (−x) = 2 + 2 cos2x, x . Tính I = f (x)dx . 3 − 2 B. I = 6
− . B. I = 0 . C. I = 2 − . D. I = 6 .
(Ñeà tham khaûo laàn 3 cuûa Boä GD&ÑT)
Caùch giaûi thoâng thöôøng 3 3 2 2 Ta coù I = f (x)dx 2 2 cos2x f ( x) = + − − dx 3 − 3 − 2 2 3 3 3 3 2 2 2 2 2 = 4 cos xdx − f (−x)dx = 2 cos x dx + f
(−x)d (−x). 3 3 − − 3 3 − − 2 2 2 2
Ñaët t = −x vaø ñoåi caän, ta ñöôïc : 3 3 − 2 2 I = 2 cos x dx + f (t)dt 3 3 − 2 2 3 3 3 2 2 2 = 2 cos x dx − f (x)dx = 2 cos x dx − I 3 3 − − 3 − 2 2 2 3 3 − 2 2 2 2 I = cos x dx = − cos xdx + cos xdx − cos xdx 3 3 − − − 2 2 2 2 3 − 3 − 2 2 2 = − s inx + s inx − s inx 2 2 2 = − s inx + s inx − s inx = 6 . 3 − − 3 − − 2 2 2 2 2 2 Choïn ñaùp aùn D.
Caùch khaùc (choïn ñaïi dieän)
Ta coù f (x) + f (−x) 2
= 2 + 2 cos2x = 4 cos x = 2 cos x . (*)
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Coù voâ soá haøm f thoûa maõn (*), ta choïn ñaïi dieän nhö sau :
f (x) = cos x ; f (−x) = cos(−x) = cos x . 3 2 I = cos x dx = 6
. (maùy tính casio cuõng phaûi maát nhieàu thôøi gian ñeå 3 − 2 cho ra keát quaû!) Choïn ñaùp aùn D.
Ví duï 3. Cho haøm soá y = f (x) lieân tuïc treân vaø thoûa maõn 2
f (x) + f (−x) = 3 − 2 cos , x x
. Tính I = f (x)dx . − 2 A. 3 I = + 2 . B. I = − 2 . C. − I = 1 . D. + I = 1 . 2 2 3 2
Caùch giaûi thoâng thöôøng 2 2
Ta coù I = f (x)dx = 3 − 2 cos x − f (− x) dx − − 2 2 2 2 2 2 =
(3 − 2cosx)dx − f (−x)dx = (3 − 2cosx)dx + f (−x)d (− x) − − − − 2 2 2 2 − 2 2
Ñaët t = −x vaø ñoåi caän, ta ñöôïc : I =
(3 − 2cosx)dx +
f (t)dt − 2 2 2 2 2 =
(3 − 2cosx)dx −
f (t)dt = (3 − 2cosx)dx − I − − − 2 2 2
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com 2 1 3 I = 1 (3 − 2 cos x) dx = 2 3x − 2 2 s i nx = − 2 . 2 2 − − 2 − 2 2 2 Choïn ñaùp aùn B.
Caùch khaùc (choïn ñaïi dieän)
Ta coù f (x) + f (−x) = 3 − 2 cos x . (*)
Ta choïn ñaïi dieän nhö sau : 3 3
f (x) = 3 − cos x ; f (−x) =
− cos(−x) = − cos x , 2 2 2
thỏa maõn giả thiết f (x) + f (−x) = 3 − 2 cos x . 2 3 3 2 3
I = − cos x dx = x − 2 s i nx = − . 2 2 2 − − 2 − 2 2 2
(coù thể dùng maùy tính casio để có keát quaû roài so saùnh vôùi ñaùp aùn !) Choïn ñaùp aùn B.
Ví duï 4. Cho haøm soá F (x) laø moät nguyeân haøm cuûa haøm soá f (x) . Khi ñoù,
hieäu soá F (1) − F (2) baèng 2 1 2 1
A. f (x)dx . B. F (x)dx . C. f (x)d (−
x) . D. − F (x) dx . 1 2 1 2
Caùch giaûi thoâng thöôøng 1 2 2
Ta coù F ( ) − F ( ) = F (x) 1 1 2
= f (x) dx = − f (x) dx = f (x) d (− x ) . 2 2 1 1 Choïn ñaùp aùn C.
Caùch khaùc (choïn ñaïi dieän) Ta choïn
F (x) = x f (x) = 1 .
Ta ñöôïc F (1) − F (2) = 1 − 2 = −1 . 2 2 I = . Loaïi ñaùp aùn A. 1
f (x) dx = dx = 2 − 1 = 1 1 1 1 1 2 I = x 1 1 3 . Loaïi ñaùp aùn B. 2
F (x) dx = xdx = = − 2 = − 2 2 2 2 2 2
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com 2 2 I = . Thoûa maõn baøi toaùn. 3
f (x) d (−x) = d (−x) = − (2 − 1) = − 1 1 1 1 1 2 x 1 1 3 I . Loaïi ñaùp aùn D. 4 F (x) = −
dx = − xdx = − = − − 2 = 2 2 2 2 2 2 Choïn ñaùp aùn C.
* Löu yù: caùch choïn ñaïi dieän nhìn trình baøy coù veõ daøi, nhöng treân thöïc teá,
chuùng ta nhaåm raát nhanh. 1 0
Ví duï 5. Bieát f (x) dx =
2 vaø f (x) laø haøm soá leû. Khi ñoù I = f (x) dx coù 0 −1 giaù trò baèng
A. I = 1. B. I = 0 . C. I = −2 . D. I = 2 .
Caùch giaûi thoâng thöôøng 0
Ta coù I = f (x) dx . −1
Ñaët x = −t dx = −dt ; Ñoåi caän x = 0 t = 0 ; x = −1 t = 1. 0 1 1
Suy ra I = − f (−t) dt = f (−t ) dt = − f (t ) dt = − 2 . 1 0 0 Choïn ñaùp aùn C.
Caùch khaùc (choïn ñaïi dieän) 1 1 Ta choïn 2 1
f (x) = 4x thỏa maõn f (x) dx = 4xdx = 2x =
2 vaø f (x) = 4x 0 0 0 laø haøm soá leû. 0 0
Khi ñoù I = f (x)dx = xdx = 2 0 4 2x = − 2 . − − 1 1 −1 Choïn ñaùp aùn C.
IV. MOÄT SOÁ BAØI TOAÙN VEÀ SOÁ PHÖÙC
Ví duï 1. Cho hai soá phöùc z , z thoûa maõn z = z =1, z + z = 3 . Tính 1 2 1 2 1 2 z − z : 1 2 A. 1 . B. 2 . C. 3 . D. 4 .
Caùch giaûi thoâng thöôøng
Goïi z = a + bi; z = c + di , ta coù : 1 2
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com • 2 2 z = 1 a + b = 1 z = 1 c + d = 1 ; (*) 1 ; 2 2 2 • 2 2
z + z = (a + c) + (b + d)i z + z = 3 (a + c) + (b + d) = 3 1 2 1 2 2 2 2 2
a + 2ac + c + b + 2bd + d = 3 .
Keát hôïp vôùi (*) ta ñöôïc : 2ac + 2bd =1 . Laïi coù : 2 2
z − z = (a − c) + (b − d)i = (a − c) + (b − d) 1 2 2 2 2 2
= a − 2ac + c + b − 2bd + d = 2 −(2ac + 2bd) = 2−1 =1. Choïn ñaùp aùn A.
Caùch khaùc (choïn ñaïi dieän)
Ta seõ choïn hai soá phöùc z , z thoûa maõn giaû thieát cuûa baøi toaùn laø : 1 2 3 1 3 1 z = + i ; z = − i . 1 2 2 2 2 2 Khi ñoù 3 1 3 1 z − z = + i − − i = i =1. 1 2 2 2 2 2 Choïn ñaùp aùn A.
Ví duï 2. Cho soá phöùc z thoûa maõn z − 2 = 2 . Bieát raèng taäp hôïp caùc ñieåm
bieåu dieãn caùc soá phöùc w = (1−i)z + i laø moät ñöôøng troøn. Tính baùn kính r
cuûa ñöôøng troøn ñoù.
A. r = 2 2 . B. r = 4. C. r = 2 . D. r = 2.
Caùch giaûi thoâng thöôøng 1 Ta coù : = ( − ) w − i w − i w + i − 2 w 1 i z + i z = z − 2 = − 2 z − 2 = . 1− i 1− i 1− i w + i − 2 w + i − 2 z − 2 = z − 2 =
w + i − 2 = z − 2 .1−i 1− i 1− i w + i − 2 = 2 2 .
Baùn kính r cuûa ñöôøng troøn cần tìm laø r = 2 2 . Choïn ñaùp aùn A.
Caùch giaûi thoâng thöôøng 2
Ta coù : w = (1−i)z + i w = (1−i)z − 2(1−i) + 2 −i
w = (1−i)(z − 2) + 2 −i w − 2 + i = (1−i)(z − 2)
w − 2 + i = (1−i)(z − 2) w − 2 + i = 1− i . z − 2 w + i − 2 = 2 2 .
Baùn kính r cuûa ñöôøng troøn cần tìm laø r = 2 2 . Choïn ñaùp aùn A.
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Caùch khaùc (choïn ñaïi dieän)
Ta choïn caùc soá phöùc z , z , z thoûa maõn giaû thieát cuûa baøi toaùn laø : 1 2 3
z = 2 + 2i w = 1− i 2 + 2i + i = 4 + i , vôùi ñieåm bieåu dieãn cuûa w laø 1 ( )( ) 1 1 M 4;1 . 1 ( )
z = 2 − 2i w = 1− i 2 − 2i + i = 3
− i , vôùi ñieåm bieåu dieãn cuûa w laø 2 ( )( ) 2 2 M 0; 3 − . 2 ( )
z = 2 − 2i w = 1− i 4 + i = 4 − 3i , vôùi ñieåm bieåu dieãn cuûa w laø 3 ( ) 3 3 M 4; 3 − . 3 ( )
Taäp hôïp caùc ñieåm bieåu dieãn caùc soá phöùc w = (1−i)z + i laø ñöôøng troøn (C)
neân caùc ñieåm M , M , M ñeàu thuoäc (C) . 1 2 3 Goïi ( ) 2 2
C : x + y + ax + by + c = 0 , ta coù heä phöông trình : 4a + b + c = 17 − a = 4 − − 3b + c = 9 − b = 2 4a − 3b + c = 25 − c = 3 −
Khi ñoù, baùn kính ñöôøng troøn (C) laø 2 2 r = 2 +1 + 3 = 2 2 . Choïn ñaùp aùn A.
Ví duï 3. Cho z laø soá phöùc vaø 1 laø soá phöùc coù phaàn thöïc baèng 4 . Tính z − z z . A. z = 4 . B. 1 z = . C. 1 z = . 4 8 D. 1 z = . 2
Caùch giaûi thoâng thöôøng Ta coù 1 w =
laø soá phöùc coù phaàn thöïc baèng 4 neân suy ra: w + w = 8 z − z 1 1 − + − − + − + = z z z z z z z z 8 = 8 = 8 z − z z − z 2 z − z .z − z .z + 2 z.z 2 z − z .z − z .z 2 z − z − z 1 = = . ( 2 z − z − z 0 ) z (2 z − z − z) 8 z 8
Löu yù : 2 z − z − z = 0 2 z = z + z . Ñaët z = a + bi, (a,b ) ta coù 2 2 2 a + b = a b = 0 2 2 2 a + b = 2a . a 0 a 0
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Khi ñoù z laø soá thöïc khoâng aâm neân z − z = 0 , vi phaïm ñieàu kieän cuûa bieåu thöùc 1 . z − z Choïn ñaùp aùn C.
Caùch khaùc (choïn ñaïi dieän)
Ta choïn moät soá phöùc z thoûa maõn 1 laø soá phöùc coù phaàn thöïc baèng 4 . z − z Deã thaáy 1 z = − . Khi ñoù 1 z = . 8 8 Choïn ñaùp aùn C.
Ví duï 4. Cho soá phöùc z thoûa maõn z + z = 0 . Khi ñoù :
A. z laø soá thöïc nhoû hôn hoaëc baèng 0 . B. z = 1.
C. Phaàn thöïc cuûa z laø soá aâm. D. z laø soá thuaàn aûo.
Caùch giaûi thoâng thöôøng
Ñaët z = a + bi, (a,b ) . Khi ñoù ta coù : a + bi + a + bi = 0 2 2 + + = 2 2 + = − 2 2 + + + = a b a 0 a b a a b a bi 0 b = 0 b = 0 2 2 2 a + b = a b = 0 b = 0 . a 0 a 0
Vaäy z laø soá thöïc nhoû hôn hoaëc baèng 0 . Choïn ñaùp aùn A.
Caùch khaùc (choïn ñaïi dieän)
Ta choïn soá phöùc z thoûa maõn z + z = 0 roài kieåm tra caùc ñaùp aùn.
Choïn z = 0 thoûa maõn z + z = 0 thì loaïi ñaùp aùn B, C, D. Choïn ñaùp aùn A.
Ví duï 5. Tìm taát caû caù giaù trò thöïc cuûa tham soá + m ñeå soá phöùc m i z = coù m − i phaàn thöïc döông. m 1 − A. . B. m 1. C. 1 − m 1. D. m 0 . m 1
Caùch giaûi thoâng thöôøng
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com m + i (m +i)(m +i) 2 2 Ta coù m −1+ 2mi m −1 2m z = = = = + . m − i (m −i)(m +i) .i 2 2 2 m +1 m +1 m +1 m 1 − Ñeå soá phöùc m + i z =
coù phaàn thöïc döông thì 2 m −1 0 . m − i m 1 Choïn ñaùp aùn A.
Caùch khaùc (choïn ñaïi dieän) Choïn + m = 0 thì 0 i z = = 1
− (khoâng thoûa maõn baøi toaùn) neân ta loaïi ñaùp 0 − i aùn C. 1+ i (1+i)2 Choïn m =1 thì z = =
(khoâng thoûa maõn baøi toaùn) neân − ( − )( + ) = i 1 i 1 i 1 i loaïi ñaùp aùn D. 2 − + i ( 2 − + i)2 − Choïn 3 4i 3 4 m = 2 − thì z = = (thoûa maõn baøi − − (− − )(− + ) = = − i 2 i 2 i 2 i 5 5 5
toaùn) neân loaïi ñaùp aùn B. Choïn ñaùp aùn A.
Löu yù : Ta neân söû duïng maùy tính caàm tay ñeå tính z , giuùp taêng toác ñoä xöû lyù baøi toaùn.
Ví duï 6. Treân maët phaúng toïa ñoä, taäp hôïp caùc ñieåm bieåu dieãn soá phöùc z
thoûa maõn ñieàu kieän z + 2 = i − z laø ñöôøng thaúng coù phöông trình :
A. 2x + 4y +13 = 0 . B. 4x + 2y + 3 = 0 . C. 2
− x + 4y −13 = 0 . D. 4x − 2y + 3 = 0 .
Caùch giaûi thoâng thöôøng
Ñaët z = x + yi, (x, y ) . Khi ñoù ta coù z + 2 = i − z x + yi + 2 = i − (x + yi) 2 2 2 2
x + 2 + yi = −x + (1− y)i (x + 2) + y = x + (1− y) 2 2 2 2
x + 4x + 4 + y = x +1− 2y + y 4x + 2y + 3 = 0 . Choïn ñaùp aùn B.
Caùch khaùc (choïn ñaïi dieän) Ta choïn soá phöùc 1 z = 1
− + i thoûa maõn z + 2 = i − z , ñieåm bieåu dieãn cuûa z 2 laø 1 M 1 − ; . 2
Ta kieåm tra caùc ñaùp aùn treân thì chæ ñöôøng thaúng ôû ñaùp aùn B ñi qua M. Choïn ñaùp aùn B.
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
V. MOÄT SOÁ BAØI TOAÙN HÌNH HOÏC KHOÂNG GIAN
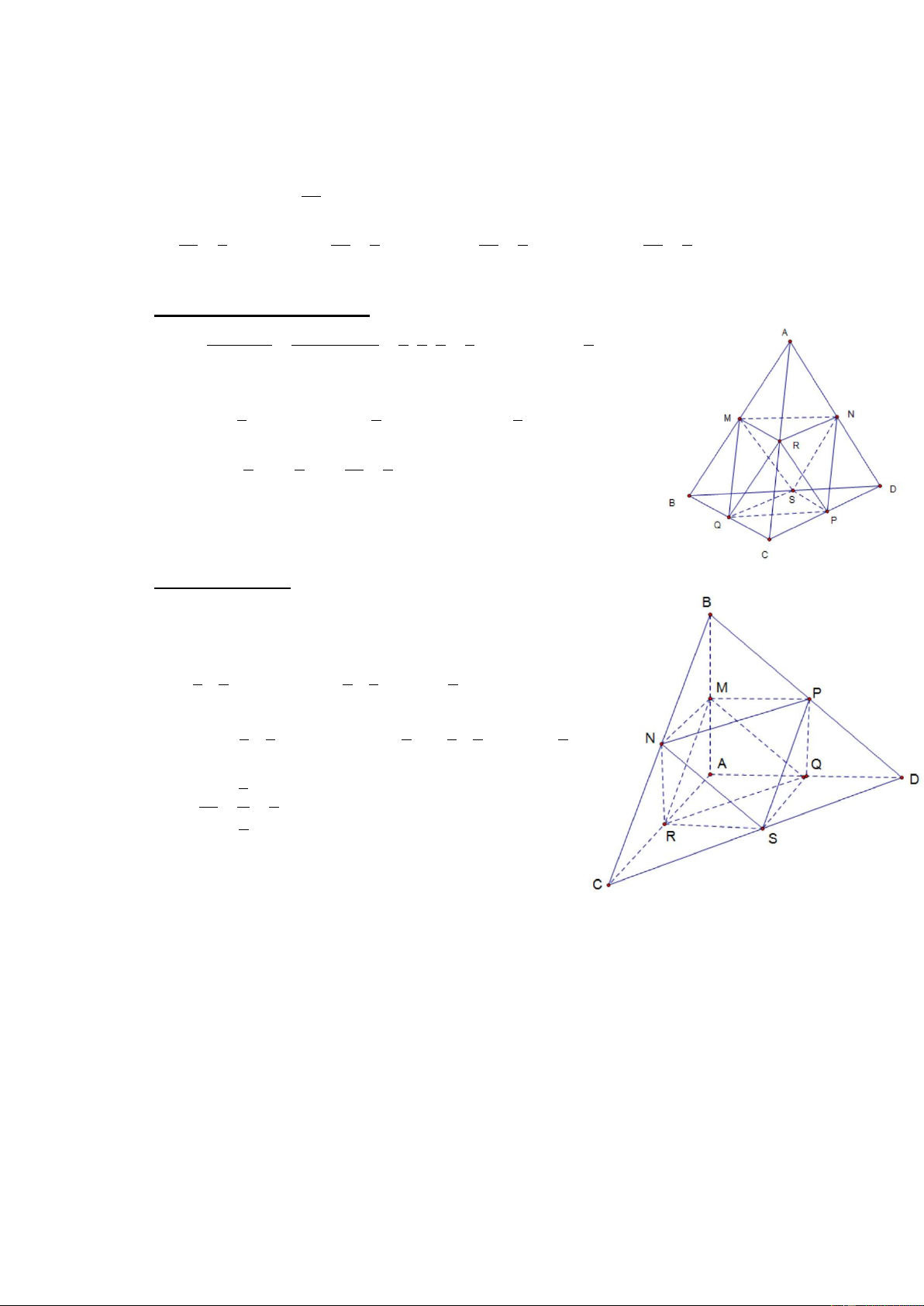
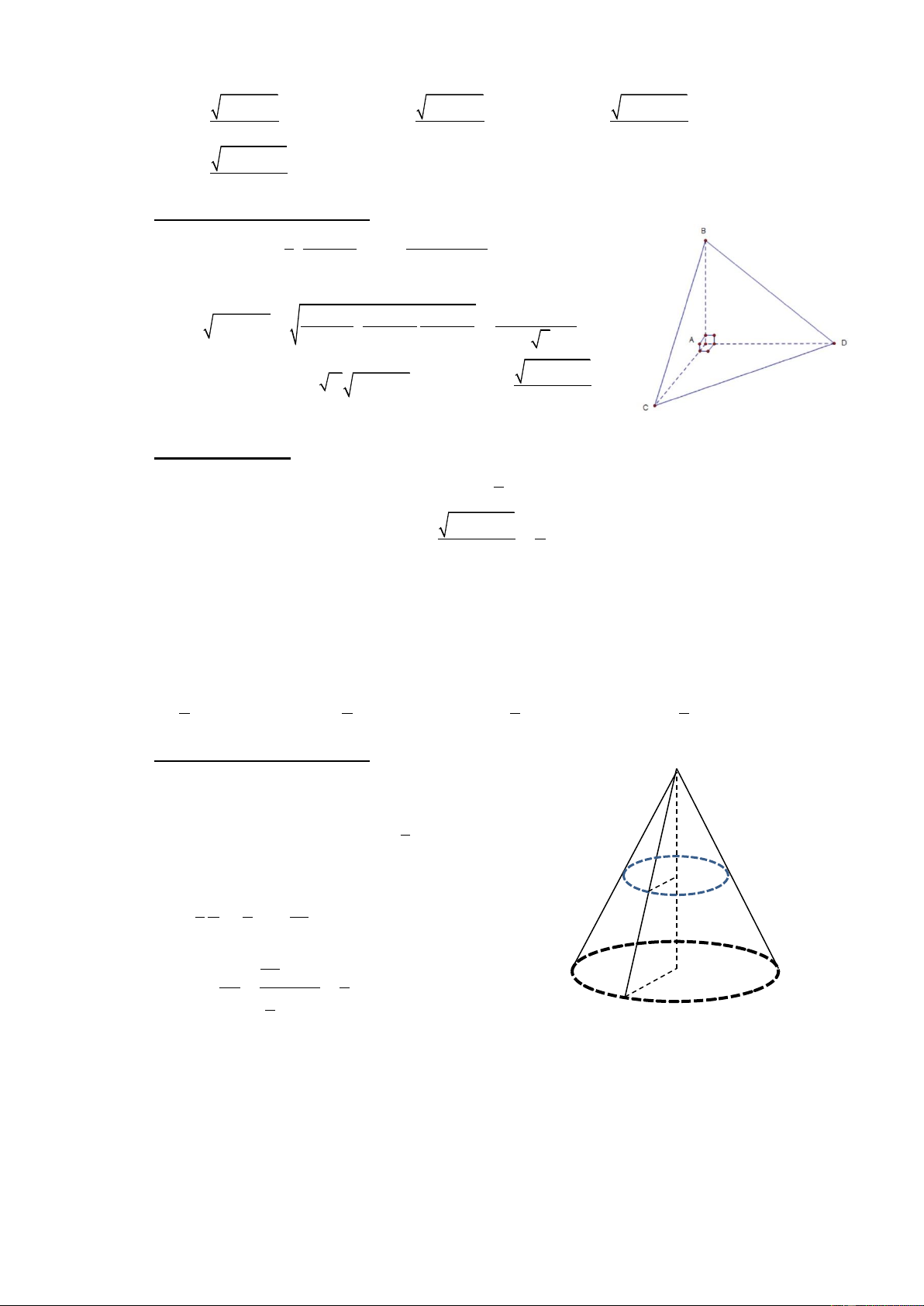
Ví duï 11. Cho khoái töù dieän coù theå tích baèng (V ). Goïi V ' laø theå tích cuûa
khoái ña dieän coù caùc ñænh laø caùc trung ñieåm cuûa caùc caïnh cuûa khoái töù dieän
ñaõ cho, tính tæ soá V ' . V A. V ' 1 V V V = . B. ' 1 = . C. ' 2 = . D. ' 5 = . V 2 V 4 V 3 V 8
(Ñeà tham khaûo laàn 3 cuûa Boä GD&ÑT)
Caùch giaûi thoâng thöôøng Ta coù V AM .A . R AN 1 1 1 1 AM RN = = . . = 1 V = V V AB.A . C AD 2 2 2 8 AM RN 8
Töông töï ta cuõng coù : 1 1 1 V = V = = BM QS ; V V ; V V 8 CPQR 8 DNPS 8 1 1 V ' 1
V ' = V − 4. V = V = . 8 2 V 2 Choïn ñaùp aùn A.
Caùch giaûi khaùc (choïn ñaïi dieän)
Ta xeùt trong tröôøng hôïp rieâng laø khoái töù dieän ABCD coù
caùc caïnh AB, AC, AD ñoâi moät vuoâng goùc vôùi nhau vaø
ñeàu coù ñoä daøi baèng 2, khi ñoù ta coù : 1 1 1 1 V = 4 . .A .
C AD .AB = . .2.2.2 = ; 3 2 3 2 3 1 1 4 1 1 V = V − 2 ' 4 . .A .
Q AR .AM = − 4 . .1.1.1 = 3 2 3 3 2 3 2 V ' = = 1 3 . V 4 2 3 Choïn ñaùp aùn A.
Ví duï 10. Cho khoái töù dieän ABCD coù ba caïnh AB , AC , AD ñoâi moät
vuoâng goùc vaø coù theå tích baèng V . Goïi S , S ,
theo thöù töï laø dieän tích 1 2 3 S
caùc tam giaùc ABC , ACD , ADB . Khi ñoù, khaúng ñònh naøo döôùi ñaây laø khaúng ñònh ñuùng ?
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com A. S S S S S S 2S S S 1 2 3 V = 1 2 3 . B. V = 1 2 3 . C. V = . D. 6 3 6 2S S S V = 1 2 3 . 3
Caùch giaûi thoâng thöôøng Ta coù
= 1 AD.AC AB = AB.A . C AD V . . ABCD 3 2 6 Maët khaùc :
AB.AC AB.AD AD.AC AB.A . C AD S S S = . = 1 2 3 2 2 2 2 2 2S S S Suy ra : V = S S S V = 1 2 3 6 2 2. ABCD 1 2 3 ABCD . 3 Choïn ñaùp aùn D.
Caùch giaûi khaùc (choïn ñaïi dieän)
Ta choïn AB = AC = AD = 2 thì V
= 4 ; S S S = . So saùnh caùc ñaùp ABCD 8 3 1 2 3
aùn thì chæ ñaùp aùn D thoûa maõn 2S S S V = 1 2 3 = 4 . 3 3 Choïn ñaùp aùn D.
Ví duï 3. Cắt khoái noùn baèng moät maët phaúng ñi qua trung ñieåm cuûa ñöôøng
cao cuûa khoái noùn, ta ñöôïc moät khoái noùn nhoû. Tæ soá theå tích giöõa khoái
noùn nhoû vaø khoái noùn ñaõ cho baèng : A. 3 . B. 1 . C. 1 . D. 5 . 8 4 8 8
Caùch giaûi thoâng thöôøng
Xeùt khoái noùn lôùn coù chieàu cao h, baùn kính
ñöôøng troøn ñaùy laø r.
- Theå tích khoái noùn lôùn laø : V = 1 2 1 h r . 3
- Theå tích khoái noùn nhoû laø : 1 h r 2 V = 1 = 2 2 h r . 3 2 2 24 1 2 h r V Suy ra : = = 1 2 24 . V 1 1 2 8 h r 3 Choïn ñaùp aùn C.
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Caùch giaûi khaùc (choïn ñaïi dieän)
Xeùt khoái noùn lôùn coù chieàu cao h , baùn kính ñöôøng troøn ñaùy laø r . Choïn h = r = 2 .
- Theå tích khoái noùn lôùn laø : 1 V = h r = 8 2 . 1 3 3 2
- Theå tích khoái noùn nhoû laø : 1 h r V = . 2 = 3 2 2 3 Suy ra : V = = 1 2 3 . V 8 8 1 3 Choïn ñaùp aùn C.
Nhaän xeùt: Veà baûn chaát thì hai caùch gaàn nhö nhau, theá nhöng nhôø vieäc
choïn h = r = 2 maø ta nhaåm deã hôn laø ñeå daïng toång quaùt laø h vaø r .
Ví duï 12. Tính theo a theå tích V cuûa khoái laäp phöông ABCD.A’B’C’D’ bieát AC ' = a . 3 3 3 A. 3a 3a a V = . B. V = 3 3 3a . C. V = . D. V = . 9 3 27
Caùch giaûi thoâng thöôøng
Goïi x laø caïnh cuûa hình laäp phöông ABCD.A’B’C’D’, ta coù : 2 a 3x = a x = . 3 3 3 3
Theå tích khoái laäp phöông ABCD.A’B’C’D’ laø : a = a 3a V = = . 9 3 3 3 Choïn ñaùp aùn A.
Caùch giaûi khaùc (choïn ñaïi dieän)
Xeùt rieâng tröôøng hôïp hình laäp phöông coù caïnh baèng 1 thì a = AC = 2 + 2 + 2 ' 1 1 1 = 3 .
Khi ñoù theå tích khoái laäp phöông baèng 1 neân ñaùp aùn A thoûa maõn baøi toaùn. Choïn ñaùp aùn A.
VI. MOÄT SOÁ BAØI TOAÙN HÌNH HOÏC GIAÛI TÍCH
Ví duï 1. Trong khoâng gian Oxyz, cho tam giaùc ABC vôùi A (0; 1 − ;2), B(3;0; )
1 , C (2;3;0) vaø hai maët phaúng (P) : x + 2y + z − 3 = 0 ;
(Q):2x − y −z +3 = 0. Goïi H laø tröïc taâm cuûa tam giaùc ABC, laø giao
tuyeán cuûa (P) vaø (Q) . Khi ñoù coù maët phaúng () ñi qua H vaø chöùa ñöôøng
thaúng coù phöông trình laø :
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
A. 7x +19y +10z + 4 = 0 . B. 7x +19y +10z − 30 = 0 .
C. 10x + 7y +19z − 30 = 0 . D. 10x + 7y +19z − 4 = 0 .
Caùch giaûi thoâng thöôøng
Goïi H(x; y;z) , ta coù : AH = (x; y +1;z − 2) ; BH = (x − 3; y;z − ) 1 ; AB = (3;1; − ) 1 ; AC = (2; 4; 2 − ) ; BC = ( 1 − ;3;− ) 1 ; AB, AC = (2; 4;10) .
Do H laø tröïc taâm cuûa tam giaùc ABC neân ta ñöôïc : AH.BC = 0 −x + 3(y + ) 1 − (z − 2) = 0 BH.AC = 0
2(x −3) + 4y − 2(z − ) 1 = 0 AB, AC AH = 0 2x + 4 (y + ) 1 +10 (z − 2) = 0 17 x = −x + 3y − z = 5 − 5 − 1 2x + 4y − 2z = 4 y = 17 1 H ; − ;1 . 5 5 5 2x + 4y +10z = 16 z =1
Do laø giao tuyeán cuûa (P) vaø (Q) neân u = n P , nQ = ( 1 − ;3; 5 − ) ; + + − =
Moät ñieåm thuoäc laø moät nghieäm cuûa heä phöông trình : x 2y z 3 0 . 2x − y − z + 3 = 0 x + z = 3 x = 0 Ta choïn y = 0
. Vaäy ñieåm M(0;0;3) . 2x − z = 3 − z = 3 −
Phöông trình chính taéc cuûa ñöôøng thaúng laø : x y z 3 = = . 1 − 3 5 − Maët phaúng () qua 17 1 H ; − ;1
, chöùa coù vectô phaùp tuyeán laø 5 5 n = u , MH = ( 7 − ; 1 − 9; 1 − 0) .
():7x +19y +10z −30 = 0 . Choïn ñaùp aùn B.
Caùch khaùc (choïn ñaïi dieän)
Maët phaúng () ñi qua ñieåm H vaø chöùa ñöôøng thaúng neân () ñi qua
moïi ñieåm thuoäc ñöôøng thaúng . Moät ñieåm thuoäc laø moät nghieäm cuûa heä + + − = x + z = 3 x = 0 phöông trình : x 2y z 3 0 . Ta choïn y = 0 . 2x − y − z + 3 = 0 2x − z = 3 − z = 3
Vaäy ñieåm M(0;0;3) .
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Trong caùc ñaùp aùn treân chæ coù ñaùp aùn B laø thoûa maõn M(0;0;3)() . Choïn ñaùp aùn B.
Ví duï 2. Trong khoâng gian Oxyz, cho hai maët phaúng (P) : x = z ;
(Q):2x − y + z = 0 . Giao tuyeán cuûa hai maët phaúng (P) vaø (Q) coù veùctô chæ phöông laø : A. n = (1;0;− ) 1 . B. n = (1;3 ) ;1 . C. n = (1; 3 − ) ;1 . D. n = (2;1; − ) 1 .
Caùch giaûi thoâng thöôøng Ta coù nP = (1;0;− ) 1 ; nQ = (2; 1 − ) ;1 .
Giao tuyeán cuûa hai maët phaúng (P) vaø (Q) coù veùctô chæ phöông laø : u = nQ nP = (1;3 ) ;1 . Choïn ñaùp aùn B.
Caùch khaùc (choïn ñaïi dieän)
Giao tuyeán cuûa hai maët phaúng (P) vaø (Q) laø ñöôøng thaúng . Moät ñieåm − + =
thuoäc laø moät nghieäm cuûa heä phöông trình : 2x y z 0 . x = z
Choïn x = y = z = 0 O(0;0;0) .
Choïn x = z =1 y = 3 M(1;3 ) ;1 .
Moät veùctô chæ phöông cuûa ñöôøng thaúng laø u = OM = (1;3 ) ;1 . Choïn ñaùp aùn B.
Ví duï 3. Trong khoâng gian Oxyz, cho maët phaúng () : x + 2my − mz −1= 0 x = 2 + t
vaø ñöôøng thaúng (d) : y =1+ t (t ) . Vôùi moïi giaù trò thöïc cuûa tham soá z = 2 m thoûa maõn 1 m −
thì ñöôøng thaúng (d) caét maët phaúng () taïi ñieåm 2 M coù toïa ñoä laø : A. 3 2 + ; ; 2 . B. 4m 3 2m ; ; 2 . 1+ 2m 1+ 2m 1+ 2m 1+ 2m C. 4m +1 2m − ; ; 2 . D. 4m 1 2m ; ; 2 . 1+ 2m 1+ 2m 1+ 2m 1+ 2m
Caùch giaûi thoâng thöôøng
Ta tìm giao ñieåm M, xeùt phöông trình :
(2+ t)+ 2m.(1+ t)−m.2−1= 0 (1+ 2m)t +1= 1 0 t = − .(do 1 m − ) 1+ 2m 2
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com 1 1+ 4m x = 2 − x = 1+ 2m 1+ 2m 1 2m y =1− y = . 1+ 2m 1+ 2m z = 2 z = 2 Vaäy 4m +1 2m M ; ; 2 . 1+ 2m 1+ 2m Choïn ñaùp aùn C.
Caùch khaùc (choïn ñaïi dieän)
Baøi toaùn ñuùng vôùi moïi giaù trò thöïc cuûa m thoûa maõn 1 m − neân ta coù theå 2
xeùt moät tröôøng hôïp rieâng.
Choïn m = 0 () : x −1 = 0.
Ta xeùt phöông trình (2 + t) −1= 0 t = 1 − , suy ra M(1;0;2) .
Theá m = 0 vaøo caùc ñaùp aùn ñaõ cho thì chæ ñaùp aùn C thoûa maõn. (cho ra toïa ñoä M (1;0; 2) ) Choïn ñaùp aùn C.
VII. MOÄT SOÁ BAØI TOAÙN KHAÙC
Ví duï 1. Coâng thöùc naøo sau ñaây khoâng phaûi laø coâng thöùc tính dieän tích tam giaùc chính xaùc? abc A. S = ; B. S = Pr ; 2R 1
C. S = p( p − a)( p − b)( p − c) ; D. S = . a h . 2 a
Caùch giaûi thoâng thöôøng
Nhôù coâng thöùc ñuùng = abc S . 4R
Vaäy choïn ñaùp aùn A.
Caùch giaûi khaùc (choïn ñaïi dieän) 1
Trong tröôøng hôïp chæ nhôù coâng thöùc S = .
a h , ta coù theå xaùc thöïc nhö 2 a sau:
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com 3.4
Xeùt tröôøng hôïp tam giaùc vuoâng ba caïnh 3; 4; 5 thì S = = 6 ; 2 3 + 4 + 5 5 p =
= 6 vaø R = . Theá vaøo ba coâng thöùc A, C, D (duøng maùy tính 2 2
cho nhanh) thì A khoâng thoûa maõn. Choïn ñaùp aùn A.
Ví duï 2. Soá toå hôïp chaäp k cuûa n phaàn töû kí hieäu k
C vaø xaùc ñònh bôûi coâng n n k ! thöùc C =
, ( k,n ; 1 k n ). Trong caùc coâng thöùc sau, n
k!(n − k)!
coâng thöùc naøo sai ? A. k n− C = k C . B. k k k 1 − C = C + C . n n n 1 + n n n C. k k 1 − C = C . D. k k 1 − nC = kC . n n 1 − n n− k 1
Caùch giaûi thoâng thöôøng
Nhôù coâng thöùc ñuùng cô baûn k n− C = k C ; k k k 1 − C
= C + C . Loaïi ñaùp aùn A n n n 1 + n n vaø B. n n n k ! ( − ) 1 ! Ta coù C = = n
k !(n − k )! k.(k − ) 1
! (n −1) − (k −1)! n (n − ) 1 ! n k 1 = . − ( C . Loaïi ñaùp aùn C. k k − ) = n− 1
! (n −1) − (k −1) 1 ! k Choïn ñaùp aùn D.
Caùch giaûi khaùc (choïn ñaïi dieän)
Ta choïn tröôøng hôïp rieâng n = 7;k = 3 vaø duøng maùy tính caàm tay ñeå kieåm
tra caùc coâng thöùc, coâng thöùc naøo sai thì choïn. 7 Ta coù 3 7−3 C = C = 35 ; 3 3 3 1 − C = C + C = 56 ; 3 3 1 − C = C = 35 (Coâng 7 7 7 1 + 7 7 7 7 1 − 3
thöùc ôû ñaùp aùn A, B, C ñuùng trong tröôøng hôïp naøy) ; 3 3 1 7C = 245 3 − C
= 45 . (Coâng thöùc ôû ñaùp aùn D sai) 7 7 1 − Choïn ñaùp aùn D.
Ví duï 3. Trong caùc daõy soá sau, daõy soá naøo laø daõy soá taêng ? n + 1 n + 1
A. Daõy soá (u ) vôùi u =
. B. Daõy soá (u ) vôùi u = . n n n n n 3n 2n + 3 2n + 1
C. Daõy soá (u ) vôùi u =
. D. Daõy soá (u ) vôùi u = . n n 3n + 2 n n n + 2
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Caùch giaûi thoâng thöôøng n + 2 n +1
+ Vôùi ñaùp aùn A, xeùt hieäu u − u = − n 1 + n n + 1 n 1 1 1 1 = 1+ − 1+ = − 0 . n +1 n n +1 n
Daõy soá (u ) giaûm. Loaïi ñaùp aùn A. n
+ Vôùi ñaùp aùn B, xeùt thöông : n + 2 1 u + n + 2 3n n 1 n + 2 1 1 n 1 + 3 = = . = . = 1+ n 1 u n +1 3 + n + 1 3 n +1 3 n +1 n 3n u 1 1 2 n 1 + 1 + = 1 . u 3 n 0 +1 3
Daõy soá (u ) giaûm. Loaïi ñaùp aùn B. n
+ Vôùi ñaùp aùn C, xeùt hieäu : 2(n + ) 1 + 3 2n + 3 2n + 5 2n + 3 u − u = − = − n 1 + n 3(n + ) 1 + 2 3n + 2 3n + 5 3n + 2 2 ( n + ) 1 2 − ( n + ) 5 3 5 3 2 + 2 1 1 2 5 1 3 3 3 3 = − = − . − + . 3n + 5 3n + 2
3 3 3n + 5 3 3 3n + 2 1 1 5 1 = − . − . 0. 3 3n + 5 3 3n + 2
Daõy soá (u ) giaûm. Loaïi ñaùp aùn C. n Choïn ñaùp aùn D.
Caùch giaûi khaùc (choïn ñaïi dieän)
Ta choïn vôùi n = 1;n = 2 vaø duøng maùy tính caàm tay ñeå kieåm tra. 3 2 1
+ Vôùi ñaùp aùn A, xeùt hieäu u − u = − = − 0. Loaïi ñaùp aùn A. 2 1 2 1 2
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com 3 1 2 u 3 3 1
+ Vôùi ñaùp aùn B, xeùt thöông n 1 + 3 =
= . = 1. Loaïi ñaùp aùn B. 2 u 2 3 2 2 n 1 3 7 5 1
+ Vôùi ñaùp aùn C, xeùt hieäu u
− u = − = − 0. Loaïi ñaùp aùn C. n 1 + n 8 5 8 Choïn ñaùp aùn D.
Ví duï 4. Bieåu thöùc ruùt goïn cuûa bieåu thöùc löôïng giaùc (cos2x − 2)tan = x P laø : 2 1+ 2sin x
A. 1+ sin x . B. −tan x . C. 2 − tan x . D. sin x + . 4
Caùch giaûi thoâng thöôøng
(cos2x − 2)tan x ( 2
1 − 2sin x − 2)tan x Ta coù : P = = 2 2 1 + 2sin x 1 + 2sin x −( 2 1 + 2sin x)tan x = = − tan x . 2 1 + 2sin x Choïn ñaùp aùn B.
Caùch giaûi khaùc (choïn ñaïi dieän)
Ta choïn vôùi x = 0 ñeå kieåm tra caùc ñaùp aùn. (cos0 − 2).tan0
Giaù trò cuûa P taïi x = 0 laø P = = 0. 2 1+ 2sin 0
+ Vôùi ñaùp aùn A, ta coù 1+ sin 0 =1 0. Loaïi ñaùp aùn A.
+ Vôùi ñaùp aùn B, ta coù − tan 0 = 0. Ñaùp aùn B ñuùng trong tröôøng hôïp naøy.
+ Vôùi ñaùp aùn C, ta coù 2 − tan 0 = 2 0 . Loaïi ñaùp aùn C. 2
+ Vôùi ñaùp aùn D, ta coù sin 0 + = 0 . Loaïi ñaùp aùn D. 4 2 Choïn ñaùp aùn B. x
Ví duï 5. Cho haøm soá f (x) 9 = , x
. Neáu a + b = 3 thì 3 + 9x
f (a) + f (b − 2) coù giaù trò baèng : 1 3 A. 1. B. 2 . C. . D. . 4 4
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com
Caùch giaûi thoâng thöôøng a Ta coù f (a) 9 = ; 3 + 9a 1−a a 1 9 9 .9 −a 9 3
f (b − 2) = f (1− a) = = = = . 1 3 + 9 −a 9a ( 1
3 + 9 −a ) 3.9a + 9 9a + 3 a
Suy ra : f (a) + f (b − ) 9 3 2 = + =1. 3 + 9a 3 + 9a Choïn ñaùp aùn A.
Caùch giaûi khaùc (choïn ñaïi dieän)
Ta choïn vôùi a = 0 ; b = 3 thoûa maõn giaû thieát a + b = 3.
Khi ñoù f (a) + f (b − ) = f ( ) + f ( ) = f (x) 1 9 2 0 1 = + =1. 4 12 Choïn ñaùp aùn A.
Saøi goøn, naêm 2017
Taùc giaû: Traàn Tuaán Anh
Mail: TranTuanAnh858@gmail.com
Traàn Tuaán Anh – Mail: TranTuanAnh858@gmail.com




