Phương pháp đánh giá và sử dụng tính đơn điệu hàm số để giải PT – BPT mũ và lôgari

Tài liệu gồm 45 trang, được tổng hợp bởi thầy giáo Lê Bá Bảo, hướng dẫn phương pháp đánh giá và sử dụng tính đơn điệu của hàm số để giải phương trình và bất phương trình mũ và lôgarit

26 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

45 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
PHƯƠNG PHÁP ĐÁNH GIÁ VÀ SỬ DỤNG TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ ĐỂ GIẢI PHƯƠNG
TRÌNH- BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT
NỘI DUNG ĐỀ BÀI
Câu 1. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 02) Cho hai số thực
a
,
b
thỏa mãn
100 40 16
4
log log log
12
ab
ab

. Giá trị của
a
b
bằng
A.
6
. B.
12
. C.
2
. D.
4
.
Câu 2. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Phương trình
2
3 5 6
25
x x x
có một
nghiệm dạng
log
a
x b b
với
,ab
là các số nguyên dương thuộc khoảng
. Khi đó
2ab
bằng
A. 7 B. 24 C. 9 D. 16
Câu 3. Xét các số thực dương
,xy
thỏa mãn
3
1
log 3 3 4
3
y
xy x y
x xy
. Tìm giá trị nhỏ nhất
min
P
của
P x y
.
A.
min
4 3 4
3
P
. B.
min
4 3 4
3
P
. C.
min
4 3 4
9
P
. D.
min
4 3 4
9
P
.
Câu 4. (THPT - YÊN ĐỊNH THANH HÓA 2018 2019- LẦN 2) Cho
,xy
là hai số thực không âm thỏa
mãn
2
2
21
2 1 log
1
y
x x y
x
. Giá trị nhỏ nhất của biểu thức
2 1 2
4 2 1
x
P e x y
là
A.
1
2
. B.
1
. C.
1
2
. D.
1
.
Câu 5. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Xét các số thực dương
,xy
thỏa mãn
2
21
2
2
2019
( 1)
xy
xy
x

. Giá trị nhỏ nhất
min
P
của biểu thức
2P y x
bằng
A.
min
1
4
P
. B.
min
1
2
P
. C.
min
7
8
P
. D.
min
15
8
P
.
Câu 6. (MĐ 104 BGD&ĐT NĂM 2019-2020) Xét các số thực không âm
x
và
y
thỏa mãn
1
2 .4 3


xy
xy
. Giá trị nhỏ nhất của biểu thức
22
42 P x y x y
bằng
A.
33
8
. B.
9
8
. C.
21
4
. D.
41
8
.
Câu 7. (MĐ 104 BGD&ĐT NĂM 2019-2020) Có bao nhiêu số nguyên
x
sao cho ứng với mi
x
có
không qu
255
số nguyên
y
thỏa mn
2
32
log logx y x y
?
A.
80
. B.
79
. C.
157
. D.
158
Câu 8. (CHUYÊN LÊ THÁNH TÔNG NĂM 2018-2019 LẦN 02) Cho hai số dương
x
;
y
thỏa
2
2
log 4 2 2 8 2 2 2
y
x y xy x y
. Giá trị nhỏ nhất của
P 2xy
là số có dạng
M a b c
với
a
,
b
,
2a
. Tính
S a b c
.
A.
S 17
. B.
. C.
S 19
. D.
.
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Câu 9. (THPT CHUYÊN THÁI BÌNH NĂM 2018-2019 LẦN 04) Cho các số thực
x
,
y
với
0x
thỏa
mãn
e e e
e
3 1 1
3
1
1 1 3
x y xy xy
xy
x y y
. Gọi
m
là giá trị nhỏ nhất của biểu thức
21T x y
. Mệnh đề nào sau đây đúng?
A.
2;3m
. B.
1; 0m
. C.
0;1m
. D.
1;2m
.
Câu 10. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Kí hiệu
max ;ab
là số lớn nhất
trong hai số
,.ab
Tìm tập nghiệm S của bất phương trình
21
3
max log ; log 1.xx





A.
1
;2 .
3
S



B.
0;2 .S
C.
1
0; .
3
S



D.
2; .S 
Câu 11. (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 07) Cho hàm số
32
12 2018 2019y f x x x x
. Số giá trị
, 12;12mm
thỏa bất phương trình
0,2 2
log log 1 2019 0f m f f
là
A. 9. B. 10. C. 11. D. 12.
Câu 12. Cho các số
0m
,
0n
,
0p
thỏa mãn
4 10 25
m n p

. Tính giá trị biểu thức
22
nn
T
mp

.
A.
1T
. B.
5
2
T
. C.
2T
. D.
1
10
T
.
Câu 13. Cho
a
,
b
,
c
là các số thực khác
0
thỏa mãn
4 9 6
a b c

. Khi đó
cc
ab
bằng
A.
1
2
. B.
1
6
. C.
6
. D.
2
.
Câu 14. Có bao nhiêu cặp số nguyên
;xy
thỏa mãn
0 2020x
và
1 2020y
và
1
22
4 log 3 16.2 log 2 1
xy
yx
?
A.
2019
. B.
2020
. C.
1010
. D.
1011
.
Câu 15. Biết
1
x
,
2
x
là hai nghiệm của phương trình
2
2
7
4 4 1
log 4 1 6
2
xx
xx
x




và
12
1
2
4
x x a b
với
a
,
b
là hai số nguyên dương. Tính
ab
.
A.
13ab
. B.
11ab
. C.
16ab
. D.
14ab
.
Câu 16. Cho phương trình
32
2log cotx log cos x
. Phương trình này có bao nhiêu nghiệm trên
khoảng
;
62




?
A. 4. B. 3. C. 2. D. 6.
Câu 17. Biết
,mn
là hai số thực thỏa mãn
3
.2 3.2 3 8 0
xx
xx
và
*
2
log , , ,m n a b a b
tính
.S a b
A.
4.S
B.
6.S
C.
5.S
D.
9.S
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Câu 18. (MĐ 102 BGD&ĐT NĂM 2017-2018) Cho
0a
,
0b
thỏa mãn
22
10 3 1 10 1
25 10 3 1log 1 l g 2o
a b ab
a a bb
. Giá trị của
2ab
bằng
A.
5
2
B.
6
C.
22
D.
11
2
Câu 19. Tìm tập hợp tất cả các giá trị thực của tham số
m
để phương trình
2 2 2 2
2 4 4 2 2
2 2 8 0
x mx m m x mx m m
e e x mx m m
có hai nghiệm
12
,xx
phân biệt thỏa mãn
12
2?xx
A.
0;1 .
B.
0;8 .


C.
0;2 .
D.
2;8 .


Câu 20. Biết
,mn
là hai số thực thỏa mãn
3
.2 3.2 3 8 0
xx
xx
và
*
2
log , , ,m n a b a b
tính
.S a b
A.
4.S
B.
6.S
C.
5.S
D.
9.S
Câu 21. (THPT CHUYÊN NGUYỄN QUANG DIÊU 2018-2019 LẦN 2) Hỏi phương trình
3.2 4.3 5.4 6.5
x x x x
có tất cả bao nhiêu nghiệm thực ?
A.
0
. B.
1
. C.
3
. D.
2
.
Câu 22. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Biết rằng phương trình
ee 2cos
xx
ax

(
a
là tham số) có
3
nghiệm thực phân biệt. Hỏi phương trình
ee 2cos 4
xx
ax
có bao nhiêu nghiệm thực phân biệt ?
A.
5
B.
10
C.
6
D.
11
Câu 23. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho hai phương trình
2
7 3 ln 4 0 1x x x
và
2
9 11 ln 5 0 2x x x
. Đặt
T
là tổng các nghiệm phân
biệt của hai phương trình đ cho, ta có:
A.
2
B.
8
C.
4
D.
6
Câu 24. Phương trình
4 1 2 . .cos( )
xx
mx

có nghiệm duy nhất. Số giá trị của tham số m thỏa mãn là
A. Vô số B.
1
C.
2
D.
0
Câu 25. (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2018-2019) Cho
0 2020x
và
2
log (2 2) 3 8
y
x x y
.Có bao nhiêu cặp số
( ; )xy
nguyên thỏa mn cc điều kiện trên ?
A. 2019. B. 2018. C. 1. D. 4.
Câu 26. Tổng tất cả các nghiệm thực của phương trình
1
15 .5 5 27 23
xx
xx
là
A.
1
. B.
0
. C.
2
. D.
1
.
Câu 27. (CHUYÊN THÁI BÌNH NĂM 2018-2019 LẦN 03) Tập nghiệm của bất phương trình
2
9 2 1
3 9 .5 1
xx
x

là khoảng
;ab
. Tính
ba
A.
6
. B.
3
. C.
8
. D.
4
.
Câu 28. (THPT ĐOAN THƯỢNG HẢI DƯƠNG NĂM 2018-2019 LẦN 02) Biết
12
,xx
12
xx
là hai
nghiệm của phương trình
2
2 3 1
3
log 3 2 2 5 2
xx
xx

và
12
1
2
2
x x a b
với
,ab
là hai
số nguyên dương. Tính
2.ab
A.
5.
B.
1.
C.
1.
D.
9.
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Câu 29. Phương trình
2
3
2
21
log 3 8 5
1
x
xx
x
có hai nghiệm là
a
và
a
b
(Với
,*ab
và
a
b
là phân số
tối giản). Giá trị của
b
là
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 30. (THPT NINH BÌNH BẠC LIÊU NĂM 2018-2019 LẦN 04) Tính tích tất cả các nghiệm thực của
phương trình
1
2
2
2
21
log 2 5
2
x
x
x
x







.
A.
0
. B.
2
. C.
1
. D.
1
2
.
Câu 31. (LIÊN TRƯỜNG THPT TP VINH NGHỆ AN NĂM 2018-2019) Biết phương trình
2018 2019
2 1 1
log 2log
2
2
x
x
xx







có nghiệm duy nhất
2x a b
trong đó
a
,
b
là những
số nguyên. Khi đó
ab
bằng
A.
5
B.
1
C.
2
D.
1
Câu 32. (Đề thi chuyên vinh lần 1-2019 ) Cho hàm số
22
xx
fx

. Gọi
0
m
là số lớn nhất trong các số
nguyên
m
thỏa mãn
12
2 2 0f m f m
. Mệnh đề nào sau đây đúng?
A.
0
1513;2019m
. B.
0
1009;1513m
. C.
0
505;1009m
. D.
0
1;505m
.
Câu 33. Cho phương trình
5
5 log
x
m x m
với
m
là tham số. Có bao nhiêu giá trị nguyên của
20;20m
để phương trình đ cho có nghiệm?
A.
20
B.
19
C.
9
D.
21
Câu 34. Để giải phương trình
2
log cot tan 1 cos2 sin2x x x x
trên khoảng
0; ,
4



bạn Tuấn giải
theo cc bước sau:
Bước 1: Do
0; cot tan 0.
4
x x x



Ta có:
2cos2
cot tan .
sin2
x
xx
x

Phương trình đ cho tương
đương với:
22
log cos2 cos2 log sin2 sin2 *x x x x
(Do
0; :sin2 0,cos2 0
4
x x x



).
Bước 2: Xét hàm số
2
1
log , 0;1 1 0, 0;1 .
ln2
f t t t t f t t
t
Do đó hàm số
ft
đồng biến trên
0;1 .
Bước 3: Phương trình (2) có dạng:
cos2 sin2 cos2 sin2 tan2 1f x f x x x x
,.
82
k
xk

Vậy phương trình đ cho có tập nghiệm
/.
82
k
Sk



Bạn Tuấn giải đ đúng chưa? Và nếu sai thì bạn Tuấn giải sai bắt đầu từ bước nào?
A. Bài giải đúng. B. Sai từ bước 1. C. Sai từ bước 2. D. Sai từ bước 3.
Câu 35. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Tìm tất cả các giá trị thực của tham số
m
để phương trình
3 2 2
2 1 1 1
mm
e e x x x x
có nghiệm.
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
A.
1
0; ln2
2



B.
1
; ln2
2



C.
1
0;
e



D.
1
ln2;
2



Câu 36. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Tìm tập
S
tất cả các giá trị thực của
tham số
m
để tồn tại duy nhất cặp số
;xy
thỏa mãn
22
2
2
log 4 4 6 1
xy
x y m

và
22
2 4 1 0x y x y
.
A.
1;1S 
B.
5; 1;1;5S
C.
5;5S 
D.
7; 5; 1;1;5;7S
Câu 37. (CỤM 8 TRƯỜNG CHUYÊN LẦN 1) Số giá trị nguyên của tham số
m
thuộc đoạn
22019 ;


để phương trình
35
1 log 4 1 log 2 1 2x x x x m


có đúng hai nghiệm thực là
A.
2
. B.
. C.
1
. D.
2021
.
Câu 38. (CHUYÊN KHTN NĂM 2018-2019 LẦN 01) Cho số thực
sao cho phương trình
2 2 2cos
xx
x

có đúng 2019 nghiệm thực. Số nghiệm của phương trình
2 2 4 2cos
xx
x
là
A.
. B.
. C.
4037
. D.
.
Câu 39. (CHUYÊN PHAN BỘI CHÂU NGHỆ AN NĂM 2018-2019 LẦN 04) Có bao nhiêu giá trị
nguyên của
m
thuộc đoạn
100;100


để phương trình
2019 1
x
mx
có hai nghiệm phân biệt?
A. 94 B. 92 C. 184 D. 100.
Câu 40. Tìm tất cả các giá trị của
m
để phương trình
ln ln sin sinm m x x
có nghiệm.
A.
1
1 m e 1.
e
B.
1 m e 1.
C.
1
1 m 1.
e
D.
1 m e 1.
Câu 41. (CHUYÊN SƠN LA NĂM 2018-2019 LẦN 03) Tổng tất cả các giá trị của tham số
m
để
phương trình
22
2
4 5 2
46
2 log 1
x x m
xx
m


có đúng 1 nghiệm là
A.
1
. B.
0
.
C.
2
. D.
4
.
Câu 42. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 02) Biết rằng phương trình
ee 2cos
xx
ax

(
a
là tham số) có
3
nghiệm thực phân biệt. Hỏi phương trình
ee 2cos 4
xx
ax
có bao nhiêu nghiệm thực phân biệt?
A.
5
B.
10
C.
6
D.
11
Câu 43. (CHUYÊN HƯNG YÊN NĂM 2018-2019 LẦN 03) Cho hàm số
47
( ) 3 ( 1).2 6 3
xx
f x x x

.
Giả sử
0
a
m
b
(
,ab
,
a
b
là phân số tối giản) là giá trị nhỏ nhất của tham số thực
m
sao cho
phương trình
2
7 4 6 9 2 1 0f x x m
có số nghiệm nhiều nhất. Tính giá trị của biểu thức
2
.P a b
A.
11.P
B.
7.P
C.
1.P 
D.
9.P
Câu 44. (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 01) Có bao nhiêu cặp số nguyên
( ; )xy
thỏa mãn
0 2020x
và
3
log (3 3) 2 9
y
x x y
?
A.
2019
. B.
6
. C.
2020
. D.
4
.
Câu 45. (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 02) Có bao nhiêu số nguyên
x
sao cho tồn tại số thực
y
thỏa mãn
22
34
log logx y x y
?
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
A. 3. B. 2. C. 1. D. Vô số
Câu 46. Cho
0a
,
0b
thỏa mãn
22
3 2 1 6 1
log 9 1 log 3 2 1 2
a b ab
a b a b
. Giá trị của
2ab
bằng
A.
6
B.
9
C.
7
2
D.
5
2
Câu 47. Cho phương trình
3
3 log ( )
x
m x m
với
m
là tham số. Có bao nhiêu giá trị nguyên của
15;15m
để phương trình đ cho có nghiệm?
A.
16
B.
9
C.
14
D.
15
Câu 48. (MĐ 103 BGD&ĐT NĂM 2016-2017)
Xét hàm số
2
9
9
t
t
ft
m
với
m
là tham số thực. Gọi
S
là tập hợp tất cả các giá trị của
m
sao cho
1f x f y
với mọi
,xy
thỏa mãn
xy
e e x y

.
Tìm số phần tử của
S
.
A.
0.
B.
1.
C. Vô số. D.
2.
Câu 49. (SỞ GD&ĐT PHÚ THỌ NĂM 2018-2019 LẦN 01) Cho
0a
,
0b
thỏa mãn
16 9 12
log 3 log loga b a b
. Giá trị của
3 2 3
3 2 3
3
a ab b
a a b b


bằng
A.
6 13
11
B.
8 17 13
69
C.
5 13
6
D.
3 13
11
Câu 50. (THPT NGUYỄN KHUYẾN TP.HCM NĂM 2018-2019) Cho
a
,
b
là các số dương thỏa mãn
9 16 12
5
log log log
2
ba
ab

. Giá trị của
a
b
bằng
A.
16
a
b
. B.
7 2 6
25
a
b
. C.
16
5
a
b
. D.
7 2 6
a
b

.
Câu 51. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Với các số thực
x
,
y
dương thỏa
mãn
9 6 4
log log log
6
xy
xy




. Tính tỉ số
x
y
.
A.
3
B.
5
C.
2
D.
4
Câu 52. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cho phương trình
2 .2 .cos 4
xx
mx

, với
m
là
tham số. Gọi
0
m
là giá trị của
m
sao cho phương trình trên có đúng một nghiệm thực. Khẳng
định nào sau đây là đúng?
A.
0
5; 1 .m
B.
0
5.m 
C.
0
1;0 .m

D.
0
0.m
Câu 53. (SỞ GD&ĐT NINH BÌNH LẦN 01 NĂM 2018-2019) Số nghiệm của phương trình
5
50 2 3.7
x x x

là:
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 54. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho
a
là số thực
dương,
1a
. Biết bất phương trình
2log 1
a
xx
nghiệm đúng với mọi
0x
. Số
a
thuộc tập
hợp nào sau đây?
A.
7;8
B.
3;5
C.
2;3
D.
8;
Câu 55. (SỞ GD&ĐT VĨNH PHÚC NĂM 2018-2019 LẦN 02) Số nghiệm thực của phương trình
22
35
log 2 log 2 2x x x x
là
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
A.
4
. B.
3
. C.
1
. D.
2
.
Câu 56. (THPT Chuyên Vĩnh Phúc-lần 2-năm 2017-2018) Xét các số thực dương
x
,
y
thỏa mãn
12
ln 3 1



x
xy
xy
. Tìm giá trị nhỏ nhất
min
P
của
11
P
x
xy
.
A.
min
8P
. B.
min
4P
. C.
min
2P
. D.
min
16P
.
Câu 57. (THTT Số 3-486 tháng 12 năm 2017-2018) Xét các số thực dương
,xy
thỏa mãn
22
3
log 3 3 .
2
xy
x x y y xy
x y xy
Tìm giá trị lớn nhất
max
P
của biểu thức
3 2 1
.
6


xy
P
xy
A.
3
. B.
2
. C.
1
. D.
4
.
Câu 58. (SỞ GD&ĐT BẮC NINH NĂM 2018-2019 LẦN 01) Tập nghiệm của bất phương trình
2 2 2
2
log 2 4 2 2 1x x x x x
là
;ab

.
Khi đó
.ab
bằng
A.
15
16
. B.
12
5
. C.
16
15
. D.
5
12
.
Câu 59. (MĐ 103 BGD&ĐT NĂM 2019-2020) Có bao nhiêu số nguyên
x
sao cho ứng với mi
x
có
không quá
127
số nguyên
y
thỏa mãn
2
32
log logx y x y
?
A.
89
. B.
46
. C.
45
. D.
90
.
Câu 60. (MĐ 103 BGD&ĐT NĂM 2019-2020) Xét các số thực không âm
x
và
y
thỏa mãn
1
2 .4 3
xy
xy


. Giá trị nhỏ nhất của biểu thức
22
24P x y x y
bằng
A.
33
8
. B.
9
8
. C.
21
4
. D.
41
8
.
Câu 61. (THPT Trần Hưng Đạo-TP HCM năm 2017-2018) Xét các số thực dương
x
,
y
thỏa mãn
2
21
2
2
2018
1
xy
xy
x

. Tìm giá trị nhỏ nhất
min
P
của
23P y x
.
A.
min
1
2
P
. B.
min
7
8
P
. C.
min
3
4
P
. D.
min
5
6
P
.
Câu 62. (THPT Mộ Đức-Quãng Ngãi-lần 1 năm 2017-2018) Cho hai số thực dương
x
,
y
thay đổi thỏa
mn đẳng thức
2
2 1 2
1 .2 .2 .
xy x y
xy x y

Tìm giá trị nhỏ nhất
min
y
của
y
.
A.
min
3y
. B.
min
2y
. C.
min
1y
. D.
min
3y
.
Câu 63. (THPT Chuyên Thái Bình – Thái Bình – Lần 5 năm 2017 – 2018) Cho
2
số thực dương
,xy
thỏa mãn
1
3
log 1 1 9 1 1
y
x y x y


. Giá trị nhỏ nhất của biểu thức
2P x y
là
A.
min
11
2
P
. B.
min
27
5
P
. C.
min
5 6 3P
. D.
min
3 6 2P
.
Câu 64. Cho các số thực
,xy
với thỏa mãn

2
24 1
3
2
log 2 4 48 31 4.8
yx
x x x y
. Giá trị lớn
nhất của

2
24
2 . 6
yx
Px
là
A.
14
. B.
6
. C.
32
. D.
8
.
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Câu 65. [PHÁT TRIỂN 47 - ĐỀ THI THAM KHẢO – 2020] Có bao nhiêu cặp số nguyên dương
;xy
với
2020y
thỏa mãn:
4 3 2 2
2
2
log 4 8 4 1
1
x
y y x x y
y
A.
2019.2020
. B.
2020.2021
. C.
2
2019
. D.
2
2020
Câu 66. [PHÁT TRIỂN 47 - ĐỀ THI THAM KHẢO – 2020] Biết rằng bất phương trình
3
2
41
2 8 4 .2
xx
x
x x x
, có một nghiệm dương là
ab
x
c
với
, , ; 20.a b c b
Khi đó
biểu thức
P a b c
bằng giá trị nào sau đây ?
A.
18.
B.
16.
C.
10.
D.
8.
Câu 67. Cho hàm số
2
ln 1f x x x
. Có tất cả bao nhiêu số nguyên
m
thỏa mãn bất phương
trình
1
log log 0?
2019
m
f m f




A.
65
. B.
66
. C.
64
. D.
63
.
Câu 68. [PHÁT TRIỂN 47 - ĐỀ THI THAM KHẢO – 2020] Có bao nhiêu số nguyên
m
để phương
trình
34m x m x x ln sin ln sin sin
có nghiệm thực?
A.
6.
B.
10.
C.
5.
D.
9.
___________________HẾT___________________
Huế, ngày 09 tháng 12 năm 2020
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
LỜI GIẢI CHI TIẾT
Câu 1. (THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 02) Cho hai số thực
a
,
b
thỏa mãn
100 40 16
4
log log log
12
ab
ab

. Giá trị của
a
b
bằng
A.
6
. B.
12
. C.
2
. D.
4
.
Lời giải:
Điều kiện:
a
,
0b
và
40ab
Đặt
100 40 16
100
4
log log log 40
12
4 12.16
t
t
t
a
ab
a b t b
ab

Suy ra
2
5
6
2
55
100 4.40 12.16 0 4. 12 0
22
5
2
2
t
tt
t t t
t
l







.
Vậy
5
6
2
t
a
b




.
Câu 2. (THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Phương trình
2
3 5 6
25
x x x
có một
nghiệm dạng
log
a
x b b
với
,ab
là các số nguyên dương thuộc khoảng
. Khi đó
2ab
bằng
A. 7 B. 24 C. 9 D. 16
Lời giải:
Ta có
22
3 5 6 3 5 6 2
2 2 2
2 5 log 2 log 5 3 5 6 log 5
x x x x x x
x x x
2
2
5
30
3
3 3 2 log 5
2 log 5 1
2 log 2
x
x
x x x
x
x



2
2 5 2.2 9
5
b
ab
a
Câu 3. Xét các số thực dương
,xy
thỏa mãn
3
1
log 3 3 4
3
y
xy x y
x xy
. Tìm giá trị nhỏ nhất
min
P
của
P x y
.
A.
min
4 3 4
3
P
. B.
min
4 3 4
3
P
. C.
min
4 3 4
9
P
. D.
min
4 3 4
9
P
.
Lời giải:
Để
1
0
3
y
x xy
mà từ giả thiết
,0xy
suy ra
1 0 1yy
. Vậy ĐKXĐ:
0;0 1xy
.
Ta có:
3
1
log 3 3 4
3
y
xy x y
x xy
3 3 4
1
3
3
xy x y
y
x xy

3 3 3
31
3
3
xy x y
y
x xy

Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
3
33
31
3
3
3
xy x
y
y
x xy

3 3 3
3 3 .3 3 .3 (*)
y xy x
y xy x

Xét
.3
t
f t t
với
0t
. Ta có
3 .3 .ln3 0
tt
f t t
với
0t
, suy ra
ft
đồng biến trên
khoảng
0;
. Từ
(*)
ta có
3 3 3f y f xy x
với
3 3 0,3 0y xy x
nên
3
3 3 3
3( 1)
x
y xy x y
x
.
Ta có
3 3 1 4
1
33
3 1 3 1
xx
P x y x x
xx






4 4 4 4 4 3 4
1 2 1 .
3 3 3
3 1 3 1
P x x
xx

.
Vậy
min
4
1
31
2 3 3
4 3 4 3
3
3
31
2 3 1
3
0;0 1
x
x
x
x
Py
x
y
xy






.
Câu 4. (THPT - YÊN ĐỊNH THANH HÓA 2018 2019- LẦN 2) Cho
,xy
là hai số thực không âm thỏa
mãn
2
2
21
2 1 log
1
y
x x y
x
. Giá trị nhỏ nhất của biểu thức
2 1 2
4 2 1
x
P e x y
là
A.
1
2
. B.
1
. C.
1
2
. D.
1
.
Lời giải:
Điều kiện:
1
1
2
x
y


Ta có:
22
2
2 2 2
21
2 1 log 2 1 2 1 log 2 1 log 2 1
1
y
x x y x y y x
x



22
22
2 1 log 2 1 2 1 log 2 1 1x x y y



.
Xét hàm số
2
log , 0f t t t t
Ta có:
1
1 0, 0
.ln2
f t t
t
suy ra
ft
đồng biến trên khoảng
0;
.
Phương trình
2 2 2
1 2 1 2 1 2 1 2 1 2 2 1 1f x f y y x y x
.
Ta có:
2 1 2 2 1 2
4 2 1 2 4
xx
P e x y e x x

2 1 2 1
1
2. 4 4; 0 2 2
2
xx
P e x P e x x


.
Bảng biến thiên
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Vậy giá trị nhỏ nhất của biểu thức
2 1 2
4 2 1
x
P e x y
là
1
2
.
Câu 5. (THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Xét các số thực dương
,xy
thỏa mãn
2
21
2
2
2019
( 1)
xy
xy
x

. Giá trị nhỏ nhất
min
P
của biểu thức
2P y x
bằng
A.
min
1
4
P
. B.
min
1
2
P
. C.
min
7
8
P
. D.
min
15
8
P
.
Lời giải:
Ta có:
2
21
2
2
2019
( 1)
xy
xy
x

2
2
21
2
1 .2019 2 .2019
x
y
x x y
2
2
2 1 4
2
1 .2019 2 .2019
xx
y
x x y

2
2
2 1 2 2
1 .2019 2 .2019
x x y
x x y

. (1)
Đặt
2
1 , 2 , 0, 0 ,u x v x y u v
khi đó (1) trở thành
22
.2019 .2019 .
uv
uv
(2)
Xét hàm đặc trưng
2
.2019 , 0 ,
t
f t t t
ta có
22
' 2019 2 .2019 .ln2019 0, 0 :
tt
f t t t 
Hàm
ft
đồng biến trên
(0; ).
Phương trình
2
2
2 1 2 1.f u f v u v x x y y x
Vậy
2
2 2 2P y x x x
. Do
P
là hàm bậc hai có hệ số
20a 
nên
1 1 1 15
min 2. 2 .
2 4 16 4 8
b
P P P
a
Câu 6. (MĐ 104 BGD&ĐT NĂM 2019-2020) Xét các số thực không âm
x
và
y
thỏa mãn
1
2 .4 3


xy
xy
. Giá trị nhỏ nhất của biểu thức
22
42 P x y x y
bằng
A.
33
8
. B.
9
8
. C.
21
4
. D.
41
8
.
Lời giải:
Ta có
1 1 2 3 2
2 .4 3 2 3 .4 .4 0 2 .2 3 2 2
x y x y y x
x y x y y x
Xét TH
3
3 2 0
2
xx
. đúng với mọi giá trị
22
3
33
42
2
4
0
x
P x y x y
y
Xét TH
3
3 2 0 0
2
xx
.
Xét hàm số
.2
t
f t t
với
0t
2 .2.ln2 0
tt
f t t
với mọi
0t
2 3 2 f y f x
3
2 3 2
2
y x y x
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
2
2 2 2 2
3 21
4 2 4 3 2 2
24



P x y x y x x x x x x
2
1 41 41
2
4 8 8



Px
So sánh và ta thấy GTNN của
P
là
41
8
khi
15
,
44
xy
Câu 7. (MĐ 104 BGD&ĐT NĂM 2019-2020) Có bao nhiêu số nguyên
x
sao cho ứng với mi
x
có
không qu
255
số nguyên
y
thỏa mn
2
32
log logx y x y
?
A.
80
. B.
79
. C.
157
. D.
158
Lời giải:
Ta có:
2
32
log logx y x y
2
log
2
3
xy
xy
2
log 3
2
x y x y
1
Đk:
1xy
Đặt
1t x y
, nên từ
2
log 3
2
1 x x t t
2
Để
1
không có qu 255 nghiệm nguyên
y
khi và chỉ khi bất phương trình
2
có không qu
255 nghiệm nguyên dương
t
.
Đặt
255Mf
với
2
log 3
f t t t
.
Vì
f
là hàm đồng biến trên
1, 
nên
2
12
1 t f x x
khi
2
0xx
.
Vậy
2
có không qu 255 nghiệm nguyên
12
255f x x
2
255xx
78 79x
x
.
Vậy có 158 số nguyên
x
thỏa mn yêu cầu bài ton.
Câu 8. (CHUYÊN LÊ THÁNH TÔNG NĂM 2018-2019 LẦN 02) Cho hai số dương
x
;
y
thỏa
2
2
log 4 2 2 8 2 2 2
y
x y xy x y
. Giá trị nhỏ nhất của
P 2xy
là số có dạng
M a b c
với
a
,
b
,
2a
. Tính
S a b c
.
A.
S 17
. B.
. C.
S 19
. D.
.
Lời giải:
Với hai số dương
x
;
y
thỏa
2
2
log 4 2 2 8 2 2 2
y
x y xy x y
Ta có
2
2 log 4 2 2 8 2 2 2y x y xy x y
2
2 log 2 1 2 8 2 1 2 3 2y x y x y y
22
8
log 2 1 log 2 2 1 3
2
x y x
y
22
88
log 2 1 2 1 log 1
22
xx
yy




.
Xét hàm đặc trưng
2
logf t t t
trên
0;
có
1
1 0, 0
ln2
f t t
t
nên hàm số
ft
đồng biến trên
0;
.
Phương trình (1) có dạng:
8 8 8
2 1 2 1 2
2 2 2 1
f x f x y
y y x



.
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
P
88
2 2 2 2 1 3 4 2 3
2 1 2 1
AM GM
x y x x
xx




.
Dấu bằng xảy ra khi
2
8 1 2 2
2 1 2 1 8
2 1 2
x x x
x

.
Vậy
S 3a b c
.
Câu 9. (THPT CHUYÊN THÁI BÌNH NĂM 2018-2019 LẦN 04) Cho các số thực
x
,
y
với
0x
thỏa
mãn
e e e
e
3 1 1
3
1
1 1 3
x y xy xy
xy
x y y
. Gọi
m
là giá trị nhỏ nhất của biểu thức
21T x y
. Mệnh đề nào sau đây đúng?
A.
2;3m
. B.
1; 0m
. C.
0;1m
. D.
1;2m
.
Lời giải:
Từ giả thiết
e e e
e
3 1 1
3
1
1 1 3
x y xy xy
xy
x y y
ee
ee
31
31
11
31
x y xy
x y xy
x y xy
(1).
Xét hàm số
=e
e
1
t
t
f t t
với
ta có
=e
e
1
' 1 0,
t
t
f t t
là hàm số đồng
biến trên .
Phương trình (1) có dạng
1
3 1 3 1 ( 0)
3
x
f x y f xy x y xy y x
x

.
Khi đó
2
22
2 2 4 6 5
2 1 1 ' 1 0, 0
3
33
x x x
T x y x T x
x
xx

min
2.0 2 1
01
0 3 3
Tm
.
Câu 10. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Kí hiệu
max ;ab
là số lớn nhất
trong hai số
,.ab
Tìm tập nghiệm S của bất phương trình
21
3
max log ; log 1.xx





A.
1
;2 .
3
S



B.
0;2 .S
C.
1
0; .
3
S



D.
2; .S 
Lời giải:
2 1 2 3
3
log log log logy x x x x
11
' 0, 0
ln2 ln3
yx
xx
nên phương trình
có nghiệm duy nhất
Mà phương trình
có nghiệm
1x
do đó
TH1:
21
3
1: log logx x x
Ta có
2 1 1
33
1
max log ; log 1. log 1
3
x x x x





. Do đó
1
1
3
x
TH2:
21
3
1: log logx x x
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Ta có
2 1 2
3
max log ; log 1. log 1 2x x x x





. Do đó
12x
. Vậy
1
;2 .
3
S



Câu 11. (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 07) Cho hàm số
32
12 2018 2019y f x x x x
. Số giá trị
, 12;12mm
thỏa bất phương trình
0,2 2
log log 1 2019 0f m f f
là
A. 9. B. 10. C. 11. D. 12.
Lời giải:
Ta có
2
3 24 2018 0,y x x x
y f x
đồng biến trên .
Do đó
0,2 2 0,2 2
log log 1 2019 0 log log 1 2019 2019f m f f m
0,2 2 2
log log 1 0 log 1 1 1 2 3m m m m
. Do đó
4;5;6;...;12m
Câu 12. Cho các số
0m
,
0n
,
0p
thỏa mãn
4 10 25
m n p

. Tính giá trị biểu thức
22
nn
T
mp

.
A.
1T
. B.
5
2
T
. C.
2T
. D.
1
10
T
.
Lời giải:
Vì
log4
4 10 log4 log2
22
mn
n
nm
m
.
Vì
log25
10 25 log25 log5
22
np
n
np
p
.
Suy ra
log2 log5 log10 1
22
nn
T
mp
.
Câu 13. Cho
a
,
b
,
c
là các số thực khác
0
thỏa mãn
4 9 6
a b c

. Khi đó
cc
ab
bằng
A.
1
2
. B.
1
6
. C.
6
. D.
2
.
Lời giải:
Đặt
4 9 6
a b c
t
với
01t
, khi đó:
4
log ta
2
12
logat

2
log
2
t
a
;
9
log tb
3
12
logbt

3
log
2
t
b
.
6
log tc
1
log 6
t
c

log 2 log 3
tt

23
11
log logtt

23
23
log .log
log log
tt
c
tt

.
Suy ra:
cc
ab
32
32
2log 2log
log log
tt
tt
2
.
Câu 14. Có bao nhiêu cặp số nguyên
;xy
thỏa mãn
0 2020x
và
1 2020y
và
1
22
4 log 3 16.2 log 2 1
xy
yx
?
A.
2019
. B.
2020
. C.
1010
. D.
1011
.
Lời giải:
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Điều kiện bài ton:
0 2020
1 2020


x
y
Ta có:
1
22
4 log 3 16.2 log 2 1
xy
yx
2 2 4
22
2 log 2 1 2 log 3 *

xy
xy
Xét hàm số
1
2
( ) 2 log

t
f t t
trên
1; 
.
Ta có
12
1
1 .2 .ln 2 1
( ) 2 ln2 0, 1;
ln2 ln2

t
t
t
f t t
tt
hàm sốđồng biến trên
1; 
.
Khi đó
(*) 2 1 3 2 1 3 2 2 f x f y x y y x
Vì
3
1 2020 1 2 2 2020 1011
2
y x x
.
Do
x
nguyên nên
2;3;4;...;1011x
. Rõ ràng, với mi
x
ta xc định được tương ứng duy
nhất một gi trị
y
nguyên thỏa mn. Vậy có
1010
cặp số nguyên
;xy
.
Câu 15. Biết
1
x
,
2
x
là hai nghiệm của phương trình
2
2
7
4 4 1
log 4 1 6
2
xx
xx
x




và
12
1
2
4
x x a b
với
a
,
b
là hai số nguyên dương. Tính
ab
.
A.
13ab
. B.
11ab
. C.
16ab
. D.
14ab
.
Lời giải:
Điều kiện:
1
0,
2
xx
.
Ta có:
2
2 2 2
7 7 7
4 4 1
log 4 1 6 log 4 4 1 4 4 1 log 2 2
2
xx
x x x x x x x x
x




.
Xét hàm số
7
logf t t t
có
1
10
ln7
ft
t
0t
nên là hàm số đồng biến trên
0;
.
Do đó ta có
22
35
4 4 1 2 4 6 1 0
4
x x x x x x
.
Khi đó:
12
3 5 3 5 1
2 2 9 5
4 4 4
xx

hoặc
12
3 5 3 5 1
2 2 9 5
4 4 4
xx

.
Vậy
12
3 5 3 5
;
44
xx


. Do đó
9; 5ab
và
9 5 14ab
.
Câu 16. Cho phương trình
32
2log cotx log cos x
. Phương trình này có bao nhiêu nghiệm trên
khoảng
;
62




?
A. 4. B. 3. C. 2. D. 6.
Lời giải:
Điều kiện :
sin 0
cos 0
x
x
.
Đặt
2
32
cot 3
1
2log cot log cos 1 3 1 4 3 12 1
14
cos 2
t
t t t t
t
t
x
x x t
x
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
4
12 4 3 4 1
3
t
t t t t



(1)
Xét hàm số
4 4 4
4 4 ln4 ln 0,
3 3 3
tt
tt
f t f t t
, suy ra hàm số
ft
đồng
biến trên , mà
1 1 1ft
là ngiệm duy nhất của phương trình (1).
2
1
3
1 cos
2
2
3
xk
tx
xk

.
Vì
sin 0
cos 0
x
x
, suy ra điểm biểu diễn của các họ nghiệm phải thuộc góc phần tư thứ nhất nên
chỉ có họ nghiệm
2
3
xk
là thỏa mn. Khi đó
9
2 1 2 12 27
6 3 2
kk
1 25
12 12
k
. Vì
0;1;2kk
. Do đó phương trình có 3 nghiệm thỏa mãn.
Câu 17. Biết
,mn
là hai số thực thỏa mãn
3
.2 3.2 3 8 0
xx
xx
và
*
2
log , , ,m n a b a b
tính
.S a b
A.
4.S
B.
6.S
C.
5.S
D.
9.S
Lời giải:
Ta có:
2
3
24
.2 3.2 3 8 0 .2 3 8 0 . 2 3 8 .2 24 0
2
x x x x x
x
x x x x x x
(1)
Xem (1) là phương trình bậc hai theo
2,
x
có
22
2
3 8 96 9 48 84 3 8 .x x x x x
Phương trình
3 8 3 8
23
2
.
3 8 3 8
8
2
2
x
x
xx
x
xx
xx


+) Với
2
2 3 log 3.
x
x
+) Với
8
2
x
x
(2), trên các khoảng
;0
và
0;
, vế phải (2) nghịch biến và vế tri (2) đồng
biến nên phương trình (2) có nghiệm duy nhất, mặt khác
thỏa mãn nên
2x
là nghiệm
duy nhất của (2).
Suy ra:
2
2
2 log 3 5.
3
a
m n S a b
b
Câu 18. (MĐ 102 BGD&ĐT NĂM 2017-2018) Cho
0a
,
0b
thỏa mãn
22
10 3 1 10 1
25 10 3 1log 1 l g 2o
a b ab
a a bb
. Giá trị của
2ab
bằng
A.
5
2
B.
6
C.
22
D.
11
2
Lời giải:
Từ giả thiết ta có
22
5 102 ba
,
10 3 1 0ab
,
10 3 1 1ab
,
10 1 1ab 
.
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Áp dụng Cô-si, ta có
2 2 2 2
1 2 25 1 15 012 b a ba ab
. Khi đó,
22
10 3 1 10 1
log 1 lo25 g 10 3 1
a b ab
abb a

10 3 1 10 1
10 1 10 3log l g 1o
a b ab
ab a b
2
.
Dấu “
” xảy ra khi
10 3 1 10 1
log lo
5
g
.
10 1 10 3 1 1
a b ab
ab
ab a b
Suy ra
5
2
1
2
b
a
11
2
2
ab
.
Câu 19. Tìm tập hợp tất cả các giá trị thực của tham số
m
để phương trình
2 2 2 2
2 4 4 2 2
2 2 8 0
x mx m m x mx m m
e e x mx m m
có hai nghiệm
12
,xx
phân biệt thỏa mãn
12
2?xx
A.
0;1 .
B.
0;8 .


C.
0;2 .
D.
2;8 .


Lời giải:
Phương trình
2 2 2 2
4 2 2 2 4 2 2
4 2 4
x mx m m x mx m m
e x mx m m e x mx m m
(2)
Xét hàm số
, 1 0,
tt
f t e t t f t e t
nên
ft
đồng biến trên
.
Phương trình (2) có dạng:
2 2 2 2 2 2 2 2
4 2 4 4 2 4f x mx m m f x mx m m x mx m m x mx m m
22
2 2 8 0g x x mx m m
(3).
Yêu cầu bài toán
2
12
0
0;8
80
0;1 .
22
2
1
g
m
mm
m
m
xx
m


Câu 20. Biết
,mn
là hai số thực thỏa mãn
3
.2 3.2 3 8 0
xx
xx
và
*
2
log , , ,m n a b a b
tính
.S a b
A.
4.S
B.
6.S
C.
5.S
D.
9.S
Lời giải:
Ta có:
2
3
24
.2 3.2 3 8 0 .2 3 8 0 . 2 3 8 .2 24 0
2
x x x x x
x
x x x x x x
(1)
Xem (1) là phương trình bậc hai theo
2,
x
có
22
2
3 8 96 9 48 84 3 8 .x x x x x
Phương trình
3 8 3 8
23
2
.
3 8 3 8
8
2
2
x
x
xx
x
xx
xx


+) Với
2
2 3 log 3.
x
x
+) Với
8
2
x
x
(2), trên các khoảng
;0
và
0;
, vế phải (2) nghịch biến và vế tri (2) đồng
biến nên phương trình (2) có nghiệm duy nhất, mặt khác
thỏa mãn nên
2x
là nghiệm
duy nhất của (2).
Suy ra:
2
2
2 log 3 5.
3
a
m n S a b
b
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Câu 21. (THPT CHUYÊN NGUYỄN QUANG DIÊU 2018-2019 LẦN 2) Hỏi phương trình
3.2 4.3 5.4 6.5
x x x x
có tất cả bao nhiêu nghiệm thực ?
A.
0
. B.
1
. C.
3
. D.
2
.
Lời giải:
Ta có :
3.2 4.3 5.4 6.5
x x x x
2 3 4
3 4 5 6 0
5 5 5
xxx
.
Xét hàm số
2 3 4
3 4 5 6
5 5 5
xxx
fx
,
x
.
Có
2 2 3 3 4 4
3 ln 4 ln 5 ln 0
5 5 5 5 5 5
x x x
fx
,
x
nên hàm số
nghịch biến trên
suy ra phương trình
0fx
có nhiều nhất một nghiệm
1
.
Mặt khác
8 22 176
1 . 2 . 0
5 25 125
ff



nên phương trình có ít nhất một nghiệm thuộc
khoảng
1;2
.
2
. Từ
1
và
2
suy ra phương trình đ cho có nghiệm duy nhất.
Câu 22. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Biết rằng phương trình
ee 2cos
xx
ax

(
a
là tham số) có
3
nghiệm thực phân biệt. Hỏi phương trình
ee 2cos 4
xx
ax
có bao nhiêu nghiệm thực phân biệt ?
A.
5
B.
10
C.
6
D.
11
Lời giải:
e e 2cos 1
xx
ax

Ta có :
ee 2cos 4
xx
ax
2
22
2 1 cos
xx
e e ax




2
2
22
4cos
2
xx
ax
ee




22
22
2cos 2
2
2cos 3
2
xx
xx
ax
ee
ax
ee

Ta thấy nếu
0
x
là nghiệm phương trình
1
thì
0
0x
.
Khi đó
0
2x
là nghiệm phương trình
2
và
0
2x
là nghiệm phương trình
3
.
Do phương trình
1
có
3
nghiệm nên phương trình
2
có
3
nghiệm và phương trình
3
có
3
nghiệm, đồng thời các nghiệm phương trình
2 , 3
khác nhau.
Vậy phương trình
ee 2cos 4
xx
ax
có
6
nghiệm thực phân biệt.
Câu 23. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho hai phương trình
2
7 3 ln 4 0 1x x x
và
2
9 11 ln 5 0 2x x x
. Đặt
T
là tổng các nghiệm phân
biệt của hai phương trình đ cho, ta có:
A.
2
B.
8
C.
4
D.
6
Lời giải:
Cách 1: Gọi hai phương trình là
1
và
2
2
7 3 ln 4f x x x x
, với
4;x
.
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
1
2 7 3
4
f x x
x
2
2 15 27
4
xx
x

,
2
9
0 2 15 17 0 3,
2
f x x x x x L
Bảng biến thiên
Theo bảng biến thiên thì
1
có hai nghiệm phân biệt, gọi hai nghiệm là
12
;xx
Giải sử
0
x
là nghiệm của phương trình
1
, đặt
0 0 0 0
11t x x t
ta có
2
2
0 0 0
7 3 ln 4 0 1 7 1 3 ln 1 4 0x x x t t t
2
0 0 0
9 11 ln 5 0t t t
. Do đó
0
t
là nghiệm của phương trình
2
Như vậy
2
cũng có đúng hai nghiệm là
11
1tx
và
22
1tx
Vậy tổng các nghiệm của hai phương trình là
1 2 1 2 1 2 1 2
1 1 2T x x t t x x x x
Cách 2: Dùng máy tính casio dò nghiệm rồi cộng lại.
Câu 24. Phương trình
4 1 2 . .cos( )
xx
mx

có nghiệm duy nhất. Số giá trị của tham số m thỏa mãn là
A. Vô số B.
1
C.
2
D.
0
Lời giải:
Ta có
4 1 2 cos
xx
mx

2 2 cos
xx
mx
Ta thấy nếu
0
xx
là một nghiệm của phương trình thì
0
xx
cũng là nghiệm của phương
trình nên để phương trình có nghiệm duy nhất thì
0
0x
.
Với
0
0x
là nghiệm của phương trình thì
2m
.
Thử lại: Với
2m
ta được phương trình
2
2 2 2cos *
x
x

2; 2VT VP
nên
2
2 2 2
*0
2cos 2
x
x
x


thỏa mãn. Vậy
2m
.
Câu 25. (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2018-2019) Cho
0 2020x
và
2
log (2 2) 3 8
y
x x y
.Có bao nhiêu cặp số
( ; )xy
nguyên thỏa mn cc điều kiện trên ?
A. 2019. B. 2018. C. 1. D. 4.
Lời giải:
Do
0 2020x
nên
2
log (2 2)x
luôn có nghĩa .
Ta có
2
log (2 2) 3 8
y
x x y
3
2
log ( 1) 1 3 2
y
x x y
2
log ( 1)
3
2
log ( 1) 2 3 2
x
y
xy
(1)
Xét hàm số
( ) 2
t
f t t
. Tập xc định
D
và
( ) 1 2 ln2
t
ft

( ) 0ft
t
.
Suy ra hàm số
()ft
đồng biến trên .
Do đó
2
(1) log ( 1) 3xy
3
12
y
x
8
log ( 1)yx
.
Ta có
0 2020x
nên
1 1 2021x
suy ra
88
0 log ( 1) log 2021x
.
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Lại có
8
log 2021 3,66
nên nếu
y
thì
0;1;2;3y
.
Vậy có 4 cặp số
( ; )xy
nguyên thỏa yêu cầu bài toán là các cặp
(0;0)
,
,
(63;2)
,
(511;3)
.
Câu 26. Tổng tất cả các nghiệm thực của phương trình
1
15 .5 5 27 23
xx
xx
là
A.
1
. B.
0
. C.
2
. D.
1
.
Lời giải:
Ta thấy
1
3
x
không là nghiệm của phương trình, do đó
11
27 23
15 .5 5 27 23 5
31
x x x
x
xx
x

Xét hai hàm số
1
5
x
fx
và
27 23
31
x
gx
x
trên tập
11
;;
33
D
 
Ta có
1
1
5 .ln5 0,
3
x
f x x
và
2
96 1
0,
3
31
g x x
x
.
Do vậy hàm số
fx
là hàm đồng biến và
gx
là hàm nghịch biến trên từng khoảng xc định
nên phương trình có tối đa 02 nghiệm.(xem thêm phần đồ thị minh hoạ)
Nhận thấy
1x 
là hai nghiệm của phương trình tren.
Vậy tổng các nghiệm của phương trình là
0
.
Câu 27. (CHUYÊN THÁI BÌNH NĂM 2018-2019 LẦN 03) Tập nghiệm của bất phương trình
2
9 2 1
3 9 .5 1
xx
x

là khoảng
;ab
. Tính
ba
A.
6
. B.
3
. C.
8
. D.
4
.
Lời giải:
2
9 2 1
3 9 .5 1
xx
x

1
. Ta có
1
50
x
x

.
Xét
2
90x 
, VT
1
0
3 0 1
(loại).
Xét
2
90x
2
90
21
3 3 1
9 .5 0
x
x
x


VT
1
1
(loại).
Xét
2
90
2
21
3 3 1
90
9 .5 0
x
x
x
x


VT
1
1
luôn đúng.
Có
2
9 0 3;3xx
.
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Tập nghiệm của bất phương trình là:
3;3 6ba
.
Câu 28. (THPT ĐOAN THƯỢNG HẢI DƯƠNG NĂM 2018-2019 LẦN 02) Biết
12
,xx
12
xx
là hai
nghiệm của phương trình
2
2 3 1
3
log 3 2 2 5 2
xx
xx

và
12
1
2
2
x x a b
với
,ab
là hai
số nguyên dương. Tính
2.ab
A.
5.
B.
1.
C.
1.
D.
9.
Lời giải:
Điều kiện xc định của phương trình:
2
2
3 2 0
1
x
xx
x
.
Đặt
2
32t x x
với
0t
. Phương trình đ cho trở thành
2
1
3
log 2 5 2 0
t
t
.
Xét hàm số
2
1
3
log 2 5 2
t
f t t
. Ta có:
2
1
1
2 .5 ln5 0
2 ln3
t
f t t
t
,
0t
.
Suy ra
ft
luôn đồng biến trên
0;
. Mà
3
9
0 log 2 0
5
f
Do đó phương trình
0ft
có đúng 1 nghiệm trên khoảng
0;
.
Xét
1t
ta có
2
11
3
log 1 2 5 2 0
(đúng)
Suy ra
1t
là nghiệm duy nhất.
1t 
1
2
1
35
2
3 2 1
35
2
x
xx
x
12
1
2 9 5
2
xx
. Suy ra
9, 5ab
. Vậy
21ab
.
Câu 29. Phương trình
2
3
2
21
log 3 8 5
1
x
xx
x
có hai nghiệm là
a
và
a
b
(Với
,*ab
và
a
b
là phân số
tối giản). Giá trị của
b
là
A.
1
. B.
4
. C.
2
. D.
3
.
Lời giải:
Điều kiện:
2
1
21
0
2
1
1
x
x
x
x

.
Phương trình
22
2
3 3 3
2
21
log 3 8 5 log 2 1 2 1 1 log 1 3 1
1
x
x x x x x x
x
22
33
21
log 2 1 log 1 3 1
3
x
x x x
.
Xét hàm số
3
log 3 , 0f t t t t
ta có
1
' 3 0, 0
ln3
f t t
t
nên
ft
là hàm số đồng
biến trên khoảng
0;
.
Phương trình có dạng
22
2
2 1 2 1
11
2
33
3
xa
xx
f f x x
a
x
b






. Vậy ta có
3b
.
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Câu 30. (THPT NINH BÌNH BẠC LIÊU NĂM 2018-2019 LẦN 04) Tính tích tất cả các nghiệm thực của
phương trình
1
2
2
2
21
log 2 5
2
x
x
x
x







.
A.
0
. B.
2
. C.
1
. D.
1
2
.
Lời giải:
Điều kiện
0.x
Đặt
1
2
tx
x

,
2t
.
Phương trình trở thành:
2
log 2 5
t
t 
1
. Xét
2
log 2
t
f t t
với
2t
.
Ta có
25f
nên
là một nghiệm của phương trình
1
.
1
' 2 ln2 0
ln2
t
ft
t
2t
ft
luôn đồng biến trên khoảng
2;
Đồ thị hàm số
y f t
cắt đường thẳng
5y
nhiều nhất tại 1 điểm.
Vậy
2t
là nghiệm duy nhất của phương trình
1
.
Với
2:t
2
1
2 2 4 1 0 2
2
x x x
x
. Phương trình
2
có hai nghiệm phân bệt và tích tất
cả các nghiệm thực của phương trình là
1
.
2
Câu 31. (LIÊN TRƯỜNG THPT TP VINH NGHỆ AN NĂM 2018-2019) Biết phương trình
2018 2019
2 1 1
log 2log
2
2
x
x
xx







có nghiệm duy nhất
2x a b
trong đó
a
,
b
là những
số nguyên. Khi đó
ab
bằng
A.
5
B.
1
C.
2
D.
1
Lời giải:
Điều kiện:
1x
. Xét
2018
21
( ) logfx
x
x




trên
1; 
1
01
2 ln2018
x
f x x
x x x

hàm số nghịch biến trên
1; 
.
Mặt khác:
2018
21
( ) 0 log 0fx
x
x



21
1
x
x
2 1 0xx
3 2 2x
.
Xét
2019
1
g( ) 2log
2
2
x
x
x





trên
1; 
.
2
21
g 0, 1
ln2019
x
xx
xx
hàm số đồng biến trên
1; 
.
Mặt khác:
2019
1
g( ) 0 log 0
2
2
x
x
x




1
1
2
2
x
x
2 1 0xx
3 2 2x
.
Xét phương trình
2018 2019
2 1 1
log 2log
2
2
x
f x g x
x
xx







.
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Do
fx
nghịch biến trên
1; 
,
gx
đồng biến trên
1; 
và
3 2 2 3 2 2fg
nên
phương trình
f x g x
có nghiệm duy nhất
3 2 2x 
.
Vậy
3a
,
2b
, do đó
5ab
.
Câu 32. (Đề thi chuyên vinh lần 1-2019 ) Cho hàm số
22
xx
fx

. Gọi
0
m
là số lớn nhất trong các số
nguyên
m
thỏa mãn
12
2 2 0f m f m
. Mệnh đề nào sau đây đúng?
A.
0
1513;2019m
. B.
0
1009;1513m
. C.
0
505;1009m
. D.
0
1;505m
.
Lời giải:
Ta có
2 2 2 2 ;
x
x x x
f x f x


2 .ln2 2 ln2 0,
xx
f x x
hàm số
22
xx
fx

hàm số lẻ và tăng trên
Yêu cầu bài toán
12
12 12
2
2 2 2 2
3
f m f m f m m m m
m
nguyên lớn nhất là:
12
0
2
1365
3
m




Câu 33. Cho phương trình
5
5 log
x
m x m
với
m
là tham số. Có bao nhiêu giá trị nguyên của
20;20m
để phương trình đ cho có nghiệm?
A.
20
B.
19
C.
9
D.
21
Lời giải:
Điều kiện:
xm
Đặt:
5
5
log 5 5
5
t
xt
x
xm
t x m x t
mt


1
.
Xét hàm số
5 5 ln 5 1 0,
uu
f u u f u u
.
Do đó:
1 5 5
xx
x t x m m x
.
Xét hàm số
5
x
f x x
,
xm
Do:
50
x
mx
, suy ra phương trình có nghiệm luôn thỏa điều kiện.
1 5 ln5
x
fx

,
5
1
0 1 5 ln5 0 log
ln5
x
f x x



.
Bảng biến thiên:
∞
≈
0,917
∞
0
≈
0,295
+
∞
∞
y
y'
x
+
Dựa vào bảng biến thiên
20;20
0,917 19; 18;...; 1
m
mm

 
.
Vậy có
19
gi trị nguyên của
m
thỏa ycbt.
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Câu 34. Để giải phương trình
2
log cot tan 1 cos2 sin2x x x x
trên khoảng
0; ,
4



bạn Tuấn giải
theo cc bước sau:
Bước 1: Do
0; cot tan 0.
4
x x x



Ta có:
2cos2
cot tan .
sin2
x
xx
x

Phương trình đ cho tương
đương với:
22
log cos2 cos2 log sin2 sin2 *x x x x
(Do
0; :sin2 0,cos2 0
4
x x x



).
Bước 2: Xét hàm số
2
1
log , 0;1 1 0, 0;1 .
ln2
f t t t t f t t
t
Do đó hàm số
ft
đồng biến trên
0;1 .
Bước 3: Phương trình (2) có dạng:
cos2 sin2 cos2 sin2 tan2 1f x f x x x x
,.
82
k
xk

Vậy phương trình đ cho có tập nghiệm
/.
82
k
Sk



Bạn Tuấn giải đ đúng chưa? Và nếu sai thì bạn Tuấn giải sai bắt đầu từ bước nào?
A. Bài giải đúng. B. Sai từ bước 1. C. Sai từ bước 2. D. Sai từ bước 3.
Lời giải:
Sai bước 3 vì điều kiện là giải phương trình trên tập
0; ,
4



nhưng kết luận
/
82
k
Sk



là chưa chính xc
Câu 35. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Tìm tất cả các giá trị thực của tham số
m
để phương trình
3 2 2
2 1 1 1
mm
e e x x x x
có nghiệm.
A.
1
0; ln2
2



B.
1
; ln2
2



C.
1
0;
e



D.
1
ln2;
2



Lời giải:
Đặt
2
2 2 2 2
1
1 1 2 1 1
2
t
t x x t x x x x
.
Ta có
2
2
11
' , ' 0
2
1
xx
t t x
x

.
Vậy
1; 2t



.
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Phương trình trở thành
2
3 3 3
1
21
2
m m m m m
t
e e t e e t t e t



. (sử dụng hàm đặc
trưng). Phương trình có nghiệm khi và chi khi
1
1 2 ln 2 ( ; ln2]
2
m
e m m 
.
Câu 36. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Tìm tập
S
tất cả các giá trị thực của
tham số
m
để tồn tại duy nhất cặp số
;xy
thỏa mãn
22
2
2
log 4 4 6 1
xy
x y m

và
22
2 4 1 0x y x y
.
A.
1;1S 
B.
5; 1;1;5S
C.
5;5S 
D.
7; 5; 1;1;5;7S
Lời giải:
Ta có
22
2
2
log 4 4 6 1
xy
x y m

2 2 2
4 4 6 2x y m x y
2 2 2
4 4 8 0x y x y m
22
2
22x y m
là một hình tròn
1
C
tâm
2;2I
, bán kính
1
Rm
với
0m
hoặc là
điểm
2;2I
với
0m
và
22
2 4 1 0x y x y
22
1 2 4xy
là một đường tròn
2
C
tâm
1;2J
, bán kính
2
2R
.
TH1: Với
0m
ta có:
2
2;2IC
suy ra
0m
không thỏa mn điều kiện bài toán.
TH2: Với
0m
. Để hệ
22
2
2
22
log 4 4 6 1
2 4 1 0
xy
x y m
x y x y

tồn tại duy nhất cặp số
;xy
thì hình
tròn
1
C
và đường tròn
2
C
tiếp xúc ngoài với nhau
12
IJ R R
22
3 0 2m
1m
1m
.
Câu 37. (CỤM 8 TRƯỜNG CHUYÊN LẦN 1) Số giá trị nguyên của tham số
m
thuộc đoạn
22019 ;


để phương trình
35
1 log 4 1 log 2 1 2x x x x m


có đúng hai nghiệm thực là
A.
2
. B.
. C.
1
. D.
2021
.
Lời giải:
Điều kiện:
1
4
x
.
Trường hợp 1:
2m
, phương trình đ cho trở thành:
35
35
1
1 log 4 1 log 2 1 2 0
log 4 1 log 2 1 2 0 1
x
x x x
xx


Xét hàm số
35
log 4 1 log 2 1 2f x x x
là hàm đồng biến trên khoảng
+
1
;
4



.
Khi đó, nếu
0
x
là nghiệm của phương trình
1
thì
0
x
là nghiệm duy nhất.
Ta có:
0 2 ; 1 0ff
, suy ra
0 1 0ff
.
Theo hệ quả của định lý trung gian, tồn tại
1
0
0;x
sao cho
0
0fx
.
Do vậy:
2m
thỏa mãn yêu cầu bài toán.
Trường hợp 2:
2m
, dẫn đến
1x
không phải là nghiệm của phương trình đ cho.
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Phương trình đ cho trở thành:
35
2
log 4 1 log 2 1 0
1
xm
xx
x
Xét hàm số
35
2
log 4 1 log 2 1 ,
1
xm
g x x x
x
có tập xc định:
1 +
1
; 1;
4
D



Đạo hàm:
2
4 2 2
0,
4 1 ln3 2 1 ln5
1
m
g x x D
xx
x

.
Bảng biến thiên:
Dựa vào bảng biến thiên, ta suy ra: phương trình
0gx
có đúng hai nghiệm
1
1
1
;
4
x



;
+
2
1;x 
với mọi
2.m
Vậy với mọi giá trị nguyên của tham số
22019 ;m



thì phương trình đ cho luôn có hai
nghiệm thực phân biệt.
Có 2022 giá trị nguyên
m
thỏa mãn yêu cầu bài toán.
- Đây là bài toán về sự tương giao.
- Tuy nhiên nếu chúng ta cô lập
m
thì việc khảo sát hàm biến
x
khá phức tạp. Ý tưởng của tương
ứng phương trình có 1 nghiệm
Bài toán tổng quát
,0
ax b
F x m f x
cx d
với
0fx
và
0ad bc
Cách 2 : Đặt
35
log 4 1 log 2 1f x x x
TH1 :
2m
, Phương trình
1
2
x
fx
.
Vì
fx
là hàm số tăng trên
1
;
4




2fx
có nghiệm duy nhất khác 1.
Vậy
2m
thỏa mãn bài toán.
TH2 :
2m
, dẫn đến
1x
không phải là nghiệm của phương trình đã cho.
Phương trình đ cho trở thành :
2
0
1
xm
fx
x

Đặt
2
;
1
xm
g x f x
x

2
2
0.
1
m
g x f x
x

Ta có bảng biến thiên :
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
0gx
có đúng hai nghiệm phân biệt.
Vậy
2019 ; 2m



nên ta có 2022 giá trị nguyên
m
.
Bài toán tương tự:
Bài toán 50.1 Tìm số giá trị nguyên
3 ; 2019m


sao cho phương trình
22
log 1 log 1 9
m
x
x x x x m e mx
có đúng hai nghiệm thực.
Câu 38. (CHUYÊN KHTN NĂM 2018-2019 LẦN 01) Cho số thực
sao cho phương trình
2 2 2cos
xx
x

có đúng 2019 nghiệm thực. Số nghiệm của phương trình
2 2 4 2cos
xx
x
là
A.
. B.
. C.
4037
. D.
.
Lời giải:
Ta có:
22
2
2
22
22
2 2 2cos 1
2
2 2 4 2cos 2 2 4cos
2
2 2 2cos 2
2
xx
xx
xx
xx
x
x
x
x





Nhận xét
1. Phương trình
1
có 2019 nghiệm khác 0 (do giả thiết và 0 không là nghiệm).
2.
0
x
là nghiệm của phương trình
1
khi và chỉ khi
0
x
là nghiệm của phương trình
2
vì
00
00
0
0
2 2 2 2
2 2 2cos 2 2 2cos
22
xx
xx
x
x


.
3. Hai phương trình
1
và
2
không có nghiệm chung vì
22
22
22
2 2 2cos
cos 0
cos0 0
2
2
0
2 2 2cos
2 2 0
2
xx
xx
xx
x
x
x
x
x



.
Vậy số nghiệm của phương trình
2 2 4 2cos
xx
x
là 4038.
Câu 39. (CHUYÊN PHAN BỘI CHÂU NGHỆ AN NĂM 2018-2019 LẦN 04) Có bao nhiêu giá trị
nguyên của
m
thuộc đoạn
100;100


để phương trình
2019 1
x
mx
có hai nghiệm phân biệt?
A. 94 B. 92 C. 184 D. 100.
Lời giải:
*) TH1:
0m
+ Vế trái của phương trình là hàm số đồng biến trên tập .
+ Vế phải của phương trình là hàm số nghịch biến trên tập .
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Nếu phương trình đ cho có nghiệm thì nghiệm đó là duy nhất ( không thỏa mn đề bài).
*) TH2:
0m
. Khi đó phương trình trở thành:
2019 1 0
x
x
.
Vậy phương trình có nghiệm duy nhất
( không thỏa mn đề bài).
*) TH3:
0m
. Xét hàm số
2019 1
x
f x mx
trên .
2019 .ln 2019
x
f x m

.
2019
0 log
ln2019
m
f x x
.
Đặt
aa
2019 2019
log .log 1
ln2019 ln2019 ln2019
m m m
fm
.
Bảng biến thiên của hàm số
:y f x
Để phương trình có hai nghiệm phân biệt thì đồ thị hàm số
y f x
phải cắt trục hoành tại hai
điểm phân biệt. Điều đó tương đương với
a
2019
0 .log 1 0
ln2019 ln2019
mm
fm
(1).
Đặt
0
ln2019
m
tt
. Khi đó
.ln 2019mt
.
Bất phương trình (1) trở thành:
2019
.ln2019.log 1 0 .ln 1 0 .ln 1 0t t t t t t t t t
.
Xét hàm số
.ln 1g t t t t
trên
0;
;
ln ; 0 1g t t g t t

.
Bảng biến thiên của hàm số
y g t
Từ bảng biến thiên ta thấy
0gt
với
1t
. Vậy
1 ln2019
ln2019
m
m
.
Kết luận:
0
ln2019
m
m
thỏa mãn yêu cầu bài toán.
Do
m
và
100;100m



nên
1;2;3...100m
. Vậy có 100 giá trị
m
thỏa mãn yêu cầu bài
toán.
Câu 40. Tìm tất cả các giá trị của
m
để phương trình
ln ln sin sinm m x x
có nghiệm.
A.
1
1 m e 1.
e
B.
1 m e 1.
C.
1
1 m 1.
e
D.
1 m e 1.
Lời giải:
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Đặt
ln sinu m x
ta được hệ phương trình:
sin
ln sin
sin
ln sin
u
x
u m x
e m x
m u x
e m u






Từ hệ phương trình ta suy ra:
sin
sin *
ux
e u e x
Xét hàm số
t
f t e t
có
' 1 0, .
t
f t e t
Hàm số
ft
đồng biến trên
.
* sin sinf u f x u x
Khi đó ta được:
sin
ln sin sin sin * *
x
m x x e x m
Đặt
sin , 1;1 .z x z


Phương trình
**
trở thành:
**
z
e z m
Xét hàm số:
z
g z e z
trên
1;1 .


Hàm số
z
g z e z
liên tục trên
1;1


và có
1;1
1;1
1 1,min 0 1maxg z g e g z g




Hệ phương trình ban đầu có nghiệm
phương trình
**
có nghiệm
1 1.me
Câu 41. (CHUYÊN SƠN LA NĂM 2018-2019 LẦN 03) Tổng tất cả các giá trị của tham số
m
để
phương trình
22
2
4 5 2
46
2 log 1
x x m
xx
m


có đúng 1 nghiệm là
A.
1
. B.
0
.
C.
2
. D.
4
.
Lời giải:
Ta có
22
22
22
4 6 1
4 5 2 2
4 6 4 6
2 log 1 2 log 1
x x m
x x m
x x x x
mm
.
Đặt
2
2
46
1
a x x
bm

, ta có
2; 1ab
, phương trình đ cho trở thành
2 log
ab
a
b
.
+) Nếu
ab
thì
21
log 1
ab
a
b
không thỏa mãn.
+) Nếu
ab
thì
21
log 1
ab
a
b
không thỏa mãn.
Do đó
ab
, khi đó phương trình đ cho tương đương với
2 2 2 2
4 6 1 4 5x x m x x m
Số nghiệm của phương trình đ cho bằng số giao điểm của parabol
2
45y x x
và đường
thẳng
2
.ym
Ta có hình ảnh minh họa sau
Dựa vào đồ thị, phương trình đ cho có đúng 1 nghiệm khi và chỉ khi
2
11mm
.
Vậy tổng các giá trị của tham số
m
là 0.
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Câu 42. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 02) Biết rằng phương trình
ee 2cos
xx
ax

(
a
là tham số) có
3
nghiệm thực phân biệt. Hỏi phương trình
ee 2cos 4
xx
ax
có bao nhiêu nghiệm thực phân biệt?
A.
5
B.
10
C.
6
D.
11
Lời giải:
Ký hiệu
ee 2cos
xx
ax

là phương trình (1) và
ee 2cos 4
xx
ax
là phương trình (2).
Ta có
ee 2cos 4
xx
ax
e e e e
2
2
22
2 2 2 2
2 2 cos 1 2cos
2
x x x x
ax
ax








.
Do đó
ee
ee
ee
22
22
2cos
2
2cos 4
2cos
2
xx
xx
xx
ax
ax
ax

.
Suy ra cứ mi nghiệm của phương trình (1) sẽ có 2 nghiệm của phương trình (2).
Thật vậy, với
0
x
là nghiệm của (1) thì
0
2x
và
0
2x
là các nghiệm của (2).
Vậy phương trình cần tìm có 6 nghiệm.
Câu 43. (CHUYÊN HƯNG YÊN NĂM 2018-2019 LẦN 03) Cho hàm số
47
( ) 3 ( 1).2 6 3
xx
f x x x

.
Giả sử
0
a
m
b
(
,ab
,
a
b
là phân số tối giản) là giá trị nhỏ nhất của tham số thực
m
sao cho
phương trình
2
7 4 6 9 2 1 0f x x m
có số nghiệm nhiều nhất. Tính giá trị của biểu thức
2
.P a b
A.
11.P
B.
7.P
C.
1.P 
D.
9.P
Lời giải:
Đặt
2
7 4 6 9 1t x x
thì
1 2 2f t m
;
2
4 6 18
1
' ' 0 .
3
2 6 9
x
t t x
xx

Từ BBT suy ra nếu
3;7t
thì phương trình (1) có 2 nghiệm x.
Xét hàm số
47
( ) 3 ( 1).2 6 3
xx
f x x x

;
4 7 7
3 ln 3 2 1 2 ln2 6
x x x
f x x
4 2 7
3 ln 3 2 ln2 1 ln2 2 0 3;7
xx
f x x x




Do đó hàm số
fx
đồng biến trên
3;7
. Mặt khác,
6 . 7 0ff

nên phương trình
0fx
có một nghiệm
6;7x

.
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Vậy, phương trình
12f t m
có nhiều nghiệm nhất khi
1
5
1 2 4
22
f
f m m
Kết luận, GTNN của m là
5
5, 2.
2
ab
Câu 44. (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 01) Có bao nhiêu cặp số nguyên
( ; )xy
thỏa mãn
0 2020x
và
3
log (3 3) 2 9
y
x x y
?
A.
2019
. B.
6
. C.
2020
. D.
4
.
Lời giải:
Điều kiện:
1x 
Ta có:
2
33
log (3 3) 2 9 log ( 1) ( 1) 2 3 (*)
yy
x x y x x y
Xét hàm số
( ) 3 ,
t
f t t t
có
( ) 1 3 ln3 0,
t
f t t
, tức hàm số luôn đồng biến trên
. Khi đó
33
(*) (log ( 1)) (2 ) log ( 1) 2 9 1
y
f x f y x y x
Vì
0 2020x
nên
9
0 9 1 2020 0 log 2021
y
y
.
Do
y
nguyên nên
0;1;2;3y
.
; 0;0 ; 8;1 ; 80;2 ; 728;3xy
nên tổng cộng có 4 cặp số nguyên
( ; )xy
thỏa đề.
Câu 45. (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 02) Có bao nhiêu số nguyên
x
sao cho tồn tại số thực
y
thỏa mãn
22
34
log logx y x y
?
A. 3. B. 2. C. 1. D. Vô số
Lời giải:
Điều kiện
22
0; 0.x y x y
Ta đặt:
22
34
log logx y x y t
. Ta có
22
3
1
4
t
t
xy
xy


Vì
2
2
22
9
4
2 3 2.4 log 2
tt
x y x y t
Thế thì
9
4
log 2
22
4 4 3,27
t
xy
, vì
x
nguyên vậy nên
2
0;1x
.
ới
0x
, ta có hệ
2
30
1
4
t
t
yt
y
y


ới
1x
, ta có hệ
2
31
.
41
t
t
y
y


Hệ này có nghiệm
0
.
0
t
y
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
ới
1x 
, ta có hệ
2
31
.
41
t
t
y
y


Ta có phương trình
2
3 1 4 1 9 2.3 4 2 0 *
t t t t t
Đặt
9 2.3 4 2
t t t
ft
, ta có
Với
0 9 4 0
tt
t f t
Với
0 4 2 0
t
t f t
Vậy phương trình
*
vô nghiệm
Kết luận: Vậy
0;1x
Câu 46. Cho
0a
,
0b
thỏa mãn
22
3 2 1 6 1
log 9 1 log 3 2 1 2
a b ab
a b a b
. Giá trị của
2ab
bằng
A.
6
B.
9
C.
7
2
D.
5
2
Lời giải:
0a
,
0b
nên ta có
3 2 1
log 6 1 0
ab
ab


;
61
log 3 2 1 0
ab
ab
.
Ta có
22
96a b ab
. Dấu đẳng thức xảy ra khi
3ab
.
Do đó, ta có:
22
3 2 1 6 1
log 9 1 log 3 2 1
a b ab
a b a b
3 2 1 6 1
log 6 1 log 3 2 1
a b ab
ab a b
3 2 1 6 1
2 log 6 1 .log 3 2 1
a b ab
ab a b
3 2 1
2 log 3 2 1 2
ab
ab

.
Dấu đẳng thức xảy ra khi và chỉ khi
3 2 1 6 1
30
log 6 1 log 3 2 1
a b ab
ba
ab a b

2
2
91
18 1
30
log 18 1 log 9 1
a
a
ba
aa

2
91
30
log 18 1 1
a
ba
a


(do
2
91
log 18 1 0
a
a

)
2
30
18 1 9 1
ba
aa

3
2
1
2
b
a
. Suy ra
7
2
2
ab
.
Câu 47. Cho phương trình
3
3 log ( )
x
m x m
với
m
là tham số. Có bao nhiêu giá trị nguyên của
15;15m
để phương trình đ cho có nghiệm?
A.
16
B.
9
C.
14
D.
15
Lời giải:
Ta có:
3
3 log
x
m x m
3
3 log ( ) (*)
x
x x m x m
.
Xét hàm số
( ) 3
t
f t t
, với
. Có
( ) 3 ln3 1 0,
t
f t t '
nên hàm số
ft
đồng biến trên
tập xc định. Mặt khc phương trình
(*)
có dạng:
3
( ) log ( )f x f x m
. Do đó ta có
3
( ) log ( )f x f x m
3
log ( )x x m
3
x
xm
3
x
xm
Xét hàm số
3
x
g x x
, với
x
. Có
( ) 3 ln3 1
x
gx'
,
( ) 0gx'
3
1
log
ln3
x




Bảng biến thiên
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Từ bảng biến thiên ta thấy các giá trị của tham số để phương trình có nghiệm là:
3
1
; log
ln3
mg









. Vậy số giá trị nguyên của
15;15m
để phương trình đ cho có
nghiệm là:
14
.
Câu 48. (MĐ 103 BGD&ĐT NĂM 2016-2017)
Xét hàm số
2
9
9
t
t
ft
m
với
m
là tham số thực. Gọi
S
là tập hợp tất cả các giá trị của
m
sao cho
1f x f y
với mọi
,xy
thỏa mãn
xy
e e x y

.
Tìm số phần tử của
S
.
A.
0.
B.
1.
C. Vô số. D.
2.
Lời giải:
Ta có nhận xét:
.
1
.
x
xy
y
e e x
e e x y x y
e e y
. ( Dấu ‘’=’’ xảy ra khi
1xy
).
Do đó ta có:
( ) ( ) 1 ( ) (1 ) 1f x f y f x f x
1 2 2 1
2 1 2 2 2 1 4
9 9 9 .9 9 .9
11
9 9 9 .9 .9
x x x x
x x x x
mm
m m m m m


2 2 1 2 2 1 4
9 .9 9 .9 9 .9 .9
x x x x
m m m m m

4
93mm
.
Vậy có hai giá trị m thỏa mãn yêu cầu.
Câu 49. (SỞ GD&ĐT PHÚ THỌ NĂM 2018-2019 LẦN 01) Cho
0a
,
0b
thỏa mãn
16 9 12
log 3 log loga b a b
. Giá trị của
3 2 3
3 2 3
3
a ab b
a a b b


bằng
A.
6 13
11
B.
8 17 13
69
C.
5 13
6
D.
3 13
11
Lời giải:
16 9 12
log 3 log loga b a b t
.
Khi đó
3 16
9
12
t
t
t
ab
a
b

9 3.12 16
t t t
9 12
3. 1
16 16
tt
3 3 13
42
t





.
3
3 2 3
3 2 3 3 2
1
3
3
aa
bb
a ab b
a a b b
aa
bb





5 13
6
.
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Câu 50. (THPT NGUYỄN KHUYẾN TP.HCM NĂM 2018-2019) Cho
a
,
b
là các số dương thỏa mãn
9 16 12
5
log log log
2
ba
ab

. Giá trị của
a
b
bằng
A.
16
a
b
. B.
7 2 6
25
a
b
. C.
16
5
a
b
. D.
7 2 6
a
b

.
Lời giải:
9 16 12
5
log log log
2
ba
a b t
. Khi đó
9
16
5
12
2
t
t
t
a
b
ba

2
3
4
t
a
b



.
Ta có:
5.16 9 2.12
t t t

9 12
5 2.
16 16
tt

2
33
2. 5 0
44
tt
.
Suy ra
2
33
1 6 7 2 6
44
tt
a
b
.
Câu 51. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Với các số thực
x
,
y
dương thỏa
mãn
9 6 4
log log log
6
xy
xy




. Tính tỉ số
x
y
.
A.
3
B.
5
C.
2
D.
4
Lời giải:
Đặt
9 6 4
9
t log log log 6
6
6.4
t
t
t
x
xy
x y y
xy




.
Suy ra
2
33
9 6 6.4 6 0
22
tt
t t t
3
2
2
t




2
x
y

.
Câu 52. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cho phương trình
2 .2 .cos 4
xx
mx

, với
m
là
tham số. Gọi
0
m
là giá trị của
m
sao cho phương trình trên có đúng một nghiệm thực. Khẳng
định nào sau đây là đúng?
A.
0
5; 1 .m
B.
0
5.m 
C.
0
1;0 .m

D.
0
0.m
Lời giải:
Phương trình
2
4 .2 .cos 4 2 2 .cos
x x x x
m x m x

Điều kiện cần: nếu
0
x
là một nghiệm của phương trình thì
0
2 x
cũng là nghiệm. Vì phương
trình có nghiệm duy nhất nên
0
1x
Thay vào phương trình ta có:
4.m 
Điều kiện đủ:
Với
4m 
ta có
2
2
4 4.2 cos 4 0 2 2cos 4sin 0
x x x
x x x


Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
2 2cos
2 2cos
22
1
cos 1
cos 1
sin 0
cos 1
x
x
x
x
x
x
x
x
x
x







.
Vậy
4m 
thỏa mn.
Câu 53. (SỞ GD&ĐT NINH BÌNH LẦN 01 NĂM 2018-2019) Số nghiệm của phương trình
5
50 2 3.7
x x x

là:
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải:
Phương trình
5
50 2 3.7
x x x

5
50 2 3.7 0
x x x
.
Xét hàm số
5
( ) 50 2 3.7
x x x
fx
5
( ) 50 ln50 2 ln2 3.7 ln7
x x x
fx
2 2 2
5
( ) 50 ln50 2 ln2 3.7 ln7
x x x
fx

Khi
thì
2 2 2
5
50
( ) 7 ln50 3 ln7 2 ln 2
7
x
xx
fx








0
2 2 2
5
50
( ) 7 ln50 3 ln7 2 ln2 0
7
xx
fx








Khi
thì
2 2 2
2
( ) 7 32 ln2 3 ln7 50 ln 50
7
x
xx
fx








0
2 2 2
2
( ) 7 32 ln2 3 ln7 50 ln50 0
7
xx
fx








Suy ra
( ) 0,f x x

. Nên
đồng biến trên .
Mà
lim 0
x
fx

nên
( ) 0,f x x
. Suy ra
()fx
đồng biến trên .
Mà
lim 0
x
fx

nên
( ) 0,f x x
. Suy ra phương trình
( ) 0fx
vô nghiệm.
Câu 54. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho
a
là số thực
dương,
1a
. Biết bất phương trình
2log 1
a
xx
nghiệm đúng với mọi
0x
. Số
a
thuộc tập
hợp nào sau đây?
A.
7;8
B.
3;5
C.
2;3
D.
8;
Lời giải:
Ta có: với
1x
thì
2log 1 0 1 1
a
Ta sẽ tìm
a
để đường thẳng
1yx
nhận làm tiếp tuyến của đồ thị hàm số
2log
a
yx
tại
điểm
1x
Có
22
1
lna ln
yy
xa

. Phương trình tiếp tuyến
2
1
ln
yx
a

Vậy để đường thẳng
1yx
nhận làm tiếp tuyến của đồ thị hàm số
2log
a
yx
thì
2
2
1 ln 2
ln
a a e
a
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Thử lại
2
ae
ta sẽ chứng minh
2
2log 1 ln 1
ln 1 0 0
e
x x x x
f x x x x
Có
11
1 0 1
x
f x f x x
xx

Bảng biến thiên
Từ bảng biến thiên suy ra
0 ln 1 0f x x x x
Câu 55. (SỞ GD&ĐT VĨNH PHÚC NĂM 2018-2019 LẦN 02) Số nghiệm thực của phương trình
22
35
log 2 log 2 2x x x x
là
A.
4
. B.
3
. C.
1
. D.
2
.
Lời giải:
Xét phương trình
22
35
log 2 log 2 2x x x x
(1)
Điều kiện:
2
0
20
2
x
xx
x
.
Đặt
2
3
log 2t x x
, ta có:
2
2
2
23
23
23
t
t
t
xx
xx
xx

Trường hợp 1:
2
23
t
xx
Phương trình (1) viết lại:
5
log 3 2
t
t 
5 3 2
tt
31
12
55
tt
(2)
Dễ thấy phương trình (2) có nghiệm
1t
.
Lại có: hàm số
31
2
55
tt
ft

nghịch biến trên nên
1t
là nghiệm duy nhất của (2).
Với
1t
, ta có:
22
2 3 2 3 0x x x x
( phương trình này có 2 nghiệm thực).
Trường hợp 2:
2
23
t
xx
Phương trình (1) viết lại:
5
log 2 3
t
t 
5 2 3
tt
5 3 2
tt
(3)
Tương tự như trường hợp 1, ta có
0t
là nghiệm duy nhất của (3)
Với
0t
, ta có:
22
2 1 2 1 0x x x x
( phương trình này không có nghiệm thực).
Vậy phương trình đ cho có tất cả 2 nghiệm thực.
Câu 56. (THPT Chuyên Vĩnh Phúc-lần 2-năm 2017-2018) Xét các số thực dương
x
,
y
thỏa mãn
12
ln 3 1



x
xy
xy
. Tìm giá trị nhỏ nhất
min
P
của
11
P
x
xy
.
A.
min
8P
. B.
min
4P
. C.
min
2P
. D.
min
16P
.
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Lời giải:
Điều kiện
1
0
2
x
.
Từ giả thiết
12
ln 3 1



x
xy
xy
ln 1 2 1 2 ln x x x y x y
1
Xét hàm số
lnf t t t
trên
0;
có
1
10
ft
t
,
0t
do đó hàm
ft
đơn điệu.
Vậy
1 1 2 3 1 x x y x y
2
Có
1 1 1 2 1 2
12

P
x x x y x x
xy
Đặt
12
12

gx
xx
, ta có
2
2
14
12
gx
x
x
suy ra
1
0
4
g x x
.
Do đó
1
0;
2
min 8



gx
. Vậy
min
8P
.
Câu 57. (THTT Số 3-486 tháng 12 năm 2017-2018) Xét các số thực dương
,xy
thỏa mãn
22
3
log 3 3 .
2
xy
x x y y xy
x y xy
Tìm giá trị lớn nhất
max
P
của biểu thức
3 2 1
.
6


xy
P
xy
A.
3
. B.
2
. C.
1
. D.
4
.
Lời giải:
Ta có:
22
3
log 3 3
2
xy
x x y y xy
x y xy
2 2 2 2
33
log 3 3 log 2 2 x y x y x y xy x y xy
.
Xét hàm số
3
logf t t t
,
0t
có
1
1 0, 0
ln 3
f t t
t
. Vậy hàm số
ft
luôn
đồng biến và liên tục trên khoảng
0;
.
Do đó:
2 2 2 2
3 2 3 2 f x y f x y xy x y x y xy
1
Cách 1: Từ
1
2
32 xy x y x y
.
Ta có
2
1
1
2




xy
x x xy xy x y xy xy
Đẳng thức xảy ra khi và chỉ khi
1xy
.
Do đó từ
1
, suy ra:
2
2
1
32
4

xy
x x y x y
.
Đặt
t x y
,
0t
.
Suy ra:
2
2
2
1
2 1 3 2
21
3 22 3
4
6 6 4 6
t
t t t
x y x
tt
P f t
x y t t
.
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Ta có:
2
2
3 36 135
03
46
tt
f t t
t
(nhận)
Bảng biến thiên
Dựa vào BBT, ta có
0;
max max 3 1

P f t f
khi và chỉ khi
12
31



x y x
x y y
.
Cách 2: (Trắc nghiệm)
Ta có:
11
2
6


x
P
xy
.
Trong
1
coi
y
là ẩn,
x
là tham số. Ta có
22
3 3 2 0 y x y x x
có nghiệm khi
2
2
3 2 3 3 2 3
3 4 3 2 0 3
33

x x x x
nên
11 0x
Vậy
2P
nên trong
4
phương n thì
max
1P
khi đó
2x
,
1y
.
Cách 3: (Trắc nghiệm)
Ta có:
17
33
6

y
P
xy
với
x
,
0.y
+ Nếu
2P
thì
3 2 1
2 11
6


xy
x
xy
. Thay vào
1
ta được:
2
3 90 0yy
(vô lý).
+ Nếu
1P
thì
3 2 1
1 2 5 5 2
6


xy
x y y x
xy
. Thay vào
1
, ta được:
2
22
3 5 2 5 2 5 2 2 3 12 12 0 2 1 x x x x x x x x x y
.
Vậy
max
1P
.
Câu 58. (SỞ GD&ĐT BẮC NINH NĂM 2018-2019 LẦN 01) Tập nghiệm của bất phương trình
2 2 2
2
log 2 4 2 2 1x x x x x
là
;ab

.
Khi đó
.ab
bằng
A.
15
16
. B.
12
5
. C.
16
15
. D.
5
12
.
Lời giải:
Ta có:
22
2x x x
2
2x x x
2
2
2
x
xx

.
Ta có:
2 2 2
2
log 2 4 2 2 1x x x x x
22
2
log 2 4 2 2 1x x x x x
2
2
2
2
log 4 2 2 1
2
x
xx
xx





2
2
2
2
2 3 2 2
log 2 2 1, 1
2
xx
xx
xx



3
0
t
ft
ft
0
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Ta có
2
20xx
,
x
.
Điều kiện:
2
3 2 2 0xx
2
2 2 3xx
22
0
0
4 8 9
x
x
xx

8
,*
5
x
Với điều kiện
*
, ta có
2 2 2 2
22
1 log 3 2 2 3 2 2 log 2 2 , 2x x x x x x x x
Xét hàm số
2
logf t t t
với
0t
. Có
1
10
.ln2
ft
t
,
0;t 
.
Hàm số
2
logf t t t
đồng biến trên
0; ,
2
3 2 2 0;xx 
và
2
2 0;xx 
Nên
22
2 3 2 2 2f x x f x x
22
3 2 2 2x x x x
2
22xx
22
20
24
x
xx


2
0
32
x
x
2
3
x
.
Kết hợp với ĐK ta có tập nghiệm bất phương trình là
82
;
53



hay
16
.
15
ab
.
Câu 59. (MĐ 103 BGD&ĐT NĂM 2019-2020) Có bao nhiêu số nguyên
x
sao cho ứng với mi
x
có
không quá
127
số nguyên
y
thỏa mãn
2
32
log logx y x y
?
A.
89
. B.
46
. C.
45
. D.
90
.
Lời giải:
Ta có
2
32
log log 1x y x y
Đặt
*t x y
22
3 2 2 3
(1) log log ( ) log log 0 2x x t t g t t x x t
Đạo hàm
2
11
( ) 0
ln2
ln3
gt
t
x x t

với mọi
y
. Do đó
gt
đồng biến trên
1; 
Vì mi
x
nguyên có không quá
127
giá trị
*t
nên ta có
2
23
(128) 0 log 128 log 128 0g x x
27
128 3 44,8 45,8x x x
Như vậy có
90
giá trị thỏa yêu cầu bài toán.
Câu 60. (MĐ 103 BGD&ĐT NĂM 2019-2020) Xét các số thực không âm
x
và
y
thỏa mãn
1
2 .4 3
xy
xy


. Giá trị nhỏ nhất của biểu thức
22
24P x y x y
bằng
A.
33
8
. B.
9
8
. C.
21
4
. D.
41
8
.
Lời giải:
Ta có
1 1 2 3 2
2 .4 3 2 3 .4 .4 0 2 .2 3 2 2
x y x y y x
x y x y y x
Xét TH:
3
3 2 0
2
xx
. đúng với mọi giá trị
22
3
21
24
2
4
0
x
P x y x y
y
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Xét TH:
3
3 2 0 0
2
xx
.
Xét hàm số
.2
t
f t t
với
0t
2 .2.ln2 0
tt
f t t
với mọi
0t
2 3 2 f y f x
3
2 3 2
2
y x y x
. Khi đó:
2
2 2 2 2
3 33
2 4 2 2 3 2 2 5
24
P x y x y x x x x x x



2
5 41 41
2
4 8 8
x



So sánh và ta thấy GTNN của
P
là
41
8
khi
51
,
44
xy
.
Câu 61. (THPT Trần Hưng Đạo-TP HCM năm 2017-2018) Xét các số thực dương
x
,
y
thỏa mãn
2
21
2
2
2018
1
xy
xy
x

. Tìm giá trị nhỏ nhất
min
P
của
23P y x
.
A.
min
1
2
P
. B.
min
7
8
P
. C.
min
3
4
P
. D.
min
5
6
P
.
Lời giải:
Cách 1: Ta có
2
21
2
2
2018
1
xy
xy
x

2
2018
2
2
2 1 log
1
xy
xy
x
22
2018 2018
2 1 2 2 log 2 log 1x x y x y x
22
2018 2018
2 1 log 1 2 2 log 2x x x y x y
Có dạng
2
12f x f x y


với
2018
2 logf t t t
,
0t
.
Xét hàm số
2018
2 logf t t t
,
0t
, ta có
1
20
.ln2018
ft
t
0t
nên hàm số
ft
đồng biến trên khoảng
0;
. Khi đó
2
12f x f x y


2
12x x y
2
1yx
.
Ta có
22
2 3 2 1 3 2 3 2P y x x x x x
.
Bảng biến thiên
x

3
4

P

7
8

Vậy
min
7
8
P
khi
3
4
x
.
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Cách 2: Ta có
2
21
2
2
2018
1
xy
xy
x

2
2 2 1 2
2
2
2018
1
x x x y
xy
x

2
2 2 1
2
22
2018 2
2018
1
xx
xy
xy
x


2
21
2
22
2018 2
2018
1
x
xy
xy
x

.
Đặt
2
1ux
,
2v x y
với
u
,
0v
. Phương trình trên có dạng:
2
2
2018
2018
u
v
v
u
22
.2018 .2018
uv
uv
1
với
u
,
0v
.
Xét hàm đặc trưng
.2018
t
f t t
có
2018 .2018.ln2018 0
tt
f t t
với
0t
, suy ra hàm
số
ft
đồng biến trên
0;
. Do đó phương trình
1
có dạng
f u f v u u
2
12x x y
2
1yx
. Khi đó
22
2 3 2 1 3 2 3 2P y x x x x x
có đồ thị là
một đường cong Parabol, đỉnh là điểm thấp nhất có tọa độ
37
;
48
I



. Do vậy,
min
7
8
P
khi
3
4
x
.
Câu 62. (THPT Mộ Đức-Quãng Ngãi-lần 1 năm 2017-2018) Cho hai số thực dương
x
,
y
thay đổi thỏa
mn đẳng thức
2
2 1 2
1 .2 .2 .
xy x y
xy x y

Tìm giá trị nhỏ nhất
min
y
của
y
.
A.
min
3y
. B.
min
2y
. C.
min
1y
. D.
min
3y
.
Lời giải:
Ta có
2
2 1 2
1 2 2
xy x y
xy x y

2
2 1 2 1
2 1 1 2 2 1
xy x y
xy x y
Xét hàm
1 .2
t
f t t
với
1t
.
Khi đó
2 1 .2 .ln2 0
tt
f t t
với
1t
.
Từ
2
1 2 1 1xy x y
2
2
21
x
y
x

2
2
2 2 4
0
21
xx
y
x


2
2 2 4 0xx
2
1
x
x

Loại
1x 
vì điều kiện của
t
nên
22f
.
Câu 63. (THPT Chuyên Thái Bình – Thái Bình – Lần 5 năm 2017 – 2018) Cho
2
số thực dương
,xy
thỏa mãn
1
3
log 1 1 9 1 1
y
x y x y


. Giá trị nhỏ nhất của biểu thức
2P x y
là
A.
min
11
2
P
. B.
min
27
5
P
. C.
min
5 6 3P
. D.
min
3 6 2P
.
Lời giải:
Ta có
1
3
log 1 1 9 1 1
y
x y x y


33
1 log 1 log 1 1 1 9y x y x y


.
33
1 log 1 log 1 1 9y x y x


Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
33
9
log 1 1 log 1
1
x x y
y
33
99
log 1 1 2 2 log
11
xx
yy

(*).
Xét hàm số
3
log 2f t t t
với
0t
có
1
10
ln3
ft
t
với mọi
0t
nên hàm số
ft
luôn đồng biến và liên tục trên
0;
.
Từ (*) suy ra
9
1
1
x
y

98
1
11
y
x
yy

, do
0x
nên
0;8y
.
Vậy
8 9 9
2 2 2 1 2 1 3 3 6 2
1 1 1
y
P x y y y y
y y y
.
Vậy
min
3 6 2P
khi
93
2 1 1
1
2
yy
y
.
Câu 64. Cho các số thực
,xy
với thỏa mãn

2
24 1
3
2
log 2 4 48 31 4.8
yx
x x x y
. Giá trị lớn
nhất của

2
24
2 . 6
yx
Px
là
A.
14
. B.
6
. C.
32
. D.
8
.
Lời giải:
Điều kiện
2x
Ta có:

2
2
2
2
24 1
3
2
24
3
2
24
3 2 2
2
3
3 24
2
2
log 2 4 4 48 32 4.8
2log 2 4 8 96 64 2 8
2log 2 4 8 48 96 64 2 48 8
2log 2 4 2 4 2 48 2
yx
yx
yx
yx
x x x y
x x x y
x x x x y x
x x y x
Xét hàm số

3
22
t
f t t
trên thấy ngay đây là hàm đồng biến trên
.
Phương trình có dạng
2
24
22
22
log 2 4 24 log 2 4 24 2 4 2
yx
f x f y x x y x x
Xét


2
2
24
1 1 2 4 12 2
2 . 6 2 4 12 2 8
2 2 2
yx
xx
P x x x
Dấu bằng xảy ra khi
4x
.
Chọn D.
Câu 65. [PHÁT TRIỂN 47 - ĐỀ THI THAM KHẢO – 2020] Có bao nhiêu cặp số nguyên dương
;xy
với
2020y
thỏa mãn:
4 3 2 2
2
2
log 4 8 4 1
1
x
y y x x y
y
A.
2019.2020
. B.
2020.2021
. C.
2
2019
. D.
2
2020
Lời giải:
Ta có
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
4 3 2 2
2
4 3 2 2 2 2 2
2
2
log 4 8 4 1
1
2
log 4 8 4 4 4
22
x
y y x x y
y
x
y y y x y xy y
y
2
2
2
2
2
log 2 2
22
xy y
y y xy y
yy
2
2
22
2
log 2 2 log 2 2 2 2xy y xy y y y y y
Xét hàm

2
2
logf t t t
thấy ngay đây là hàm đồng biến trên
0;
.
Bất phương trình có dạng
22
2 2 2 2 2 2 2f xy y f y y xy y y y x y
Do
;xy
và
2020y
nên
Với
1 2 1y x x
Với
2 4 1;2;3y x x
Với
3 6 1;2;3;4;5y x x
……….
Với
2020 4040 1,2;3....4039y x x
Vậy số cặp nguyên dương
;xy
thỏa mãn là
2
1 3 5 ...4039 2020
Chọn D.
Câu 66. [PHÁT TRIỂN 47 - ĐỀ THI THAM KHẢO – 2020] Biết rằng bất phương trình
3
2
41
2 8 4 .2
xx
x
x x x
, có một nghiệm dương là
ab
x
c
với
, , ; 20.a b c b
Khi đó
biểu thức
P a b c
bằng giá trị nào sau đây ?
A.
18.
B.
16.
C.
10.
D.
8.
Lời giải:
Điều kiện
2
.
0
x
x

+Bất phương trình
2
2
4 4 1
2
21
2 .2
xx
x
x
x
x
x


2
2
21
2
21
2.2 .2
x
x
x
x
x
x






Xét hàm số
2
2 , .
t
f t t t
Ta có
22
2
2 2 .2 ln 2 0, .
tt
f t t t
do đó hàm số
ft
đồng biến trên khoảng .
Phương trình có dạng
21
2
x
f x f
x




21
2
x
x
x
32
2 4 1 0x x x
3 13
, 0 .
2
x do x

Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Vậy
18.abc
Câu 67. Cho hàm số
2
ln 1f x x x
. Có tất cả bao nhiêu số nguyên
m
thỏa mãn bất phương
trình
1
log log 0?
2019
m
f m f




A.
65
. B.
66
. C.
64
. D.
63
.
Lời giải:
Điều kiện:
1m
(do
m
là số nguyên và
0, 1mm
), suy ra
log 0m
.
Hàm số
2
ln 1f x x x
có TXĐ
D
.
Ta có:
22
2
1
ln 1 ln ln 1
1
f x x x x x f x
xx

,
x
.
Mặt khác
2
1
' 0,
1
f x x
x
, nên
đồng biến trên . Khi đó ta có
log2019
1 1 1
log log 0 log log log log
2019 2019 2019
log2019
1
log log log 10 65,77.
2019 log
m m m
m
f m f f m f f m f
m m m
m
Suy ra
2;3;...;65m
. Vậy có tất cả 64 số nguyên
m
thỏa mãn.
Câu 68. [PHÁT TRIỂN 47 - ĐỀ THI THAM KHẢO – 2020] Có bao nhiêu số nguyên
m
để phương
trình
34m x m x x ln sin ln sin sin
có nghiệm thực?
A.
6.
B.
10.
C.
5.
D.
9.
Lời giải:
Điều kiện:
3 4 0
40
m x m x
mx

sin ln sin
.
sin
Phương trình đ cho tương đương:
34
x
m x m x e
sin
sin ln sin
44
x
m x m x e x
sin
sin ln sin sin
4
4
mx
x
m x e xe

ln sin
sin
ln sin sin
1 .
Xét
t
f t e t,
t .
Ta có
10
t
f t e
,
.t
Nên hàm số
ft
đồng biến trên
.
Vậy
1 3m x xff


ln sin sin
4m x x ln sin sin .
Đặt
ax sin ,
11a

;.
Phương trình trở thành:
4m a aln
4
a
m e a .
Xét
4
a
g a e a,
11a

;.
Ta có
40
a
g a e
11a

;.
Vậy để phương trình có nghiệm thực thì
11g m g
1
44em
e
.
Vậy có
4
giá trị nguyên của tham số
m
là:
1;0;
1;
2;
3;4
.
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
___________________HẾT___________________
Huế, ngày 09 tháng 12 năm 2020
| 1/45
| | Tải xuống

Có thể bạn quan tâm:

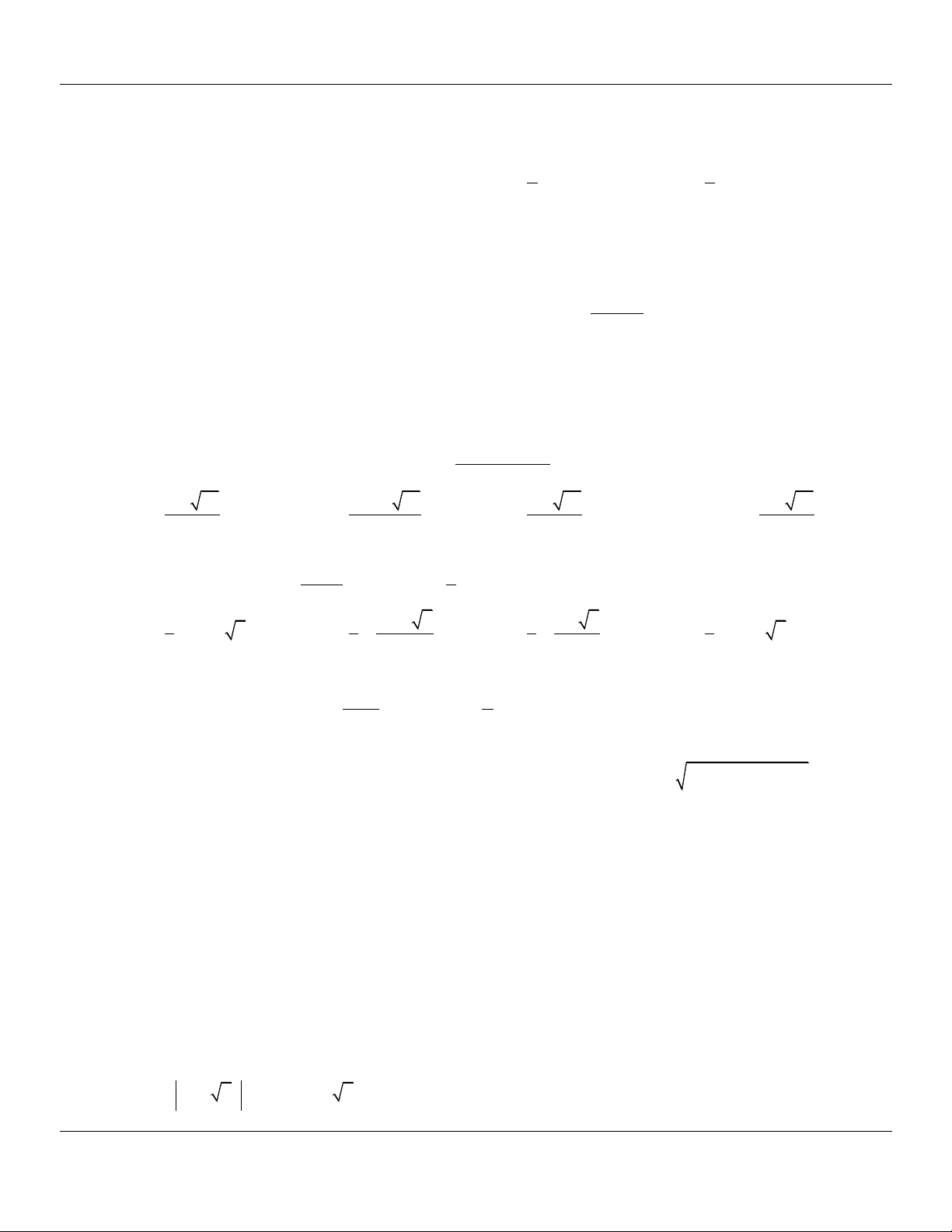
Preview text:

Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
PHƯƠNG PHÁP ĐÁNH GIÁ VÀ SỬ DỤNG TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ ĐỂ GIẢI PHƯƠNG
TRÌNH- BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT NỘI DUNG ĐỀ BÀI Câu 1.
(THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 02) Cho hai số thực a , b thỏa mãn a  4b a log
a  log b  log . Giá trị của bằng 100 40 16 12 b A. 6 . B. 12 . C. 2 . D. 4 . 2 Câu 2.
(THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Phương trình x3 x 5x6 2  5 có một
nghiệm dạng x b  log b với a,b là các số nguyên dương thuộc khoảng 1;7 . Khi đó a  2b a bằng A. 7 B. 24 C. 9 D. 16 1  y Câu 3.
Xét các số thực dương x, y thỏa mãn log
 3xy x  3y  4 . Tìm giá trị nhỏ nhất P 3 x  3xy min
của P x y . 4 3  4 4 3  4 4 3  4 4 3  4 A. P  . B. P  . C. P  . D. P  . min 3 min 3 min 9 min 9 Câu 4.
(THPT - YÊN ĐỊNH THANH HÓA 2018 2019- LẦN 2) Cho x, y là hai số thực không âm thỏa 2y  1 mãn 2
x  2x y  1  log
. Giá trị nhỏ nhất của biểu thức 2 x1 2 P e
 4x  2y  1 là 2 x  1 1 1 A. . B. 1  . C.  . D. 1 . 2 2 Câu 5.
(THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Xét các số thực dương x, y thỏa mãn  2 2 x y  1 2x y 2019 
. Giá trị nhỏ nhất P
của biểu thức P  2y x 2 (x  1) min bằng 1 1 7 15 A. P  . B. P  . C. P  . D. P  . min 4 min 2 min 8 min 8 Câu 6.
(MĐ 104 BGD&ĐT NĂM 2019-2020) Xét các số thực không âm x và y thỏa mãn xy 1 2x .4   y
 3 . Giá trị nhỏ nhất của biểu thức 2 2
P x y  4x  2 y bằng 33 9 21 41 A. . B. . C. . D. . 8 8 4 8 Câu 7.
(MĐ 104 BGD&ĐT NĂM 2019-2020) Có bao nhiêu số nguyên x sao cho ứng với mỗi x có
không quá 255 số nguyên y thỏa mãn log  2 x y  log
x y ? 3  2   A. 80 . B. 79 . C. 157 . D. 158 Câu 8.
(CHUYÊN LÊ THÁNH TÔNG NĂM 2018-2019 LẦN 02) Cho hai số dương x ; y thỏa y
log 4x y  2xy  2  2  8  2x  2 y  2 . Giá trị nhỏ nhất của P  2x y là số có dạng 2   
M  a b c với a , b
, a  2 . Tính S  a b c . A. S  17 . B. S  7 . C. S  19 . D. S  3 .
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 Câu 9.
(THPT CHUYÊN THÁI BÌNH NĂM 2018-2019 LẦN 04) Cho các số thực x , y với x  0 thỏa xy xy xy 1
mãn e 3  e 1  xy  1  1  e 1 
 3y . Gọi m là giá trị nhỏ nhất của biểu thức  ex 3y
T x  2y  1. Mệnh đề nào sau đây đúng? A. m 2; 3 . B. m 1  ; 0 . C. m 0;1 . D. m 1; 2 .
Câu 10. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Kí hiệu maxa; 
b là số lớn nhất   trong hai số a, .
b Tìm tập nghiệm S của bất phương trình max log x; log x  1. 2 1   3   1   1  A. S   ;2. B. S  0; 2. C. S  0; .
D. S  2; .  3   3 
Câu 11. (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 07) Cho hàm số
y f x 3 2
x  12x  2018x  2019 . Số giá trị m ,m  12  ;12 
 thỏa bất phương trình f log
log m  1  2019  f f 0 là 0,2  2       A. 9. B. 10. C. 11. D. 12. n n
Câu 12. Cho các số m  0 , n  0 , p  0 thỏa mãn 4m 10n 25p  
. Tính giá trị biểu thức T   . 2m 2 p 5 1 A. T  1. B. T  . C. T  2 . D. T  . 2 10 c c
Câu 13. Cho a , b , c là các số thực khác 0 thỏa mãn 4a 9b 6c   . Khi đó  bằng a b 1 1 A. . B. . C. 6 . D. 2 . 2 6
Câu 14. Có bao nhiêu cặp số nguyên  ;
x y  thỏa mãn 0  x  2020 và 1  y  2020 và x 1 4   log  3 16.2y y
 log 2x 1 ? 2   2   A. 2019 . B. 2020 . C. 1010 . D. 1011. 2
 4x  4x  1 Câu 15. Biết
x , x là hai nghiệm của phương trình 2 log 
  4x  1  6x và 1 2 7  2x  1 x  2x
a b với a , b là hai số nguyên dương. Tính a b . 1 2   4
A. a b  13 .
B. a b  11 .
C. a b  16 .
D. a b  14 .
Câu 16. Cho phương trình 2 log cotx  log cos x . Phương trình này có bao nhiêu nghiệm trên 3   2        khoảng ;   ?  6 2  A. 4. B. 3. C. 2. D. 6.
Câu 17. Biết m, n là hai số thực thỏa mãn x 3 .2  3.2 x x
 3x  8  0 và m n a  log b, a, * b  , tính 2  S a  . b A. S  4. B. S  6. C. S  5. D. S  9.
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 Câu 18. (MĐ 102 BGD&ĐT NĂM 2017-2018) Cho a  0 , b  0 thỏa mãn log a b   a b
 . Giá trị của a  2b bằng ab  2 2 25 1 l g o 10 3 1 2 10 3 1  10ab1   5 11 A. B. 6 C. 22 D. 2 2
Câu 19. Tìm tập hợp tất cả các giá trị thực của tham số m để phương trình 2 2 2 2
2x mxm 4m
x mxm 4  m 2 2 ee
x  2mx  2m  8m  0 có hai nghiệm x , x phân biệt thỏa mãn 1 2 x x  2?  1 2 A. 0;1.  B. 0; 8.   C. 0; 2.  D. 2; 8.  
Câu 20. Biết m, n là hai số thực thỏa mãn x 3 .2  3.2 x x
 3x  8  0 và m n a  log b, a, * b  , tính 2  S a  . b A. S  4. B. S  6. C. S  5. D. S  9.
Câu 21. (THPT CHUYÊN NGUYỄN QUANG DIÊU 2018-2019 LẦN 2) Hỏi phương trình 3.2x 4.3x 5.4x 6.5x   
có tất cả bao nhiêu nghiệm thực ? A. 0 . B. 1 . C. 3 . D. 2 .
Câu 22. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Biết rằng phương trình
ex  ex  2 cos ax ( a là tham số) có 3 nghiệm thực phân biệt. Hỏi phương trình
ex  ex  2 cos ax  4 có bao nhiêu nghiệm thực phân biệt ? A. 5 B. 10 C. 6 D. 11
Câu 23. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho hai phương trình 2
x  7x  3  ln x  4  0 1 và 2
x  9x  11  ln 5  x  0 2 . Đặt T là tổng các nghiệm phân
biệt của hai phương trình đã cho, ta có: A. 2 B. 8 C. 4 D. 6
Câu 24. Phương trình 4x 1  2 . x .
m cos( x) có nghiệm duy nhất. Số giá trị của tham số m thỏa mãn là A. Vô số B. 1 C. 2 D. 0
Câu 25. (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2018-2019) Cho 0  x  2020 và
log (2  2)   3  8y x x y
.Có bao nhiêu cặp số (x ; y) nguyên thỏa mãn các điều kiện trên ? 2 A. 2019. B. 2018. C. 1. D. 4.
Câu 26. Tổng tất cả các nghiệm thực của phương trình x x1 15 .5 x
 5  27x  23 là A. 1 . B. 0 . C. 2 . D. 1  .
Câu 27. (CHUYÊN THÁI BÌNH NĂM 2018-2019 LẦN 03) Tập nghiệm của bất phương trình 2 x 9   2 x   x1 3 9 .5
 1 là khoảng a;b . Tính b a A. 6 . B. 3 . C. 8 . D. 4 .
Câu 28. (THPT ĐOAN THƯỢNG HẢI DƯƠNG NĂM 2018-2019 LẦN 02) Biết x , x x x là hai 1 2  1 2 1
nghiệm của phương trình log  x  3x  2  2 2 2 x 3x1  5
 2 và x  2x
a b với a,b là hai 1 2   3 2
số nguyên dương. Tính a  2 . b A. 5. B. 1. C. 1. D. 9.
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 2x  1 a a
Câu 29. Phương trình 2 log
 3x  8x  5 có hai nghiệm là a và (Với a,b * và là phân số 3 x  2 1 b b
tối giản). Giá trị của b là A. 1 . B. 4 . C. 2 . D. 3 .
Câu 30. (THPT NINH BÌNH BẠC LIÊU NĂM 2018-2019 LẦN 04) Tính tích tất cả các nghiệm thực của  1 2   2x  1  x  phương trình  2 log    2 x   5 . 2  2x  1 A. 0 . B. 2 . C. 1 . D. . 2
Câu 31. (LIÊN TRƯỜNG THPT TP VINH NGHỆ AN NĂM 2018-2019) Biết phương trình  2 1   x 1  log     2log  
 có nghiệm duy nhất x a b 2 trong đó a , b là những 2018 2019    x x  2  2 x
số nguyên. Khi đó a b bằng A. 5 B. 1  C. 2 D. 1
Câu 32. (Đề thi chuyên vinh lần 1-2019 ) Cho hàm số   2x 2 x f x   
. Gọi m là số lớn nhất trong các số 0
nguyên m thỏa mãn f m  f  12
2m  2   0 . Mệnh đề nào sau đây đúng? A. m  1  513;2019 . B. m  1  009;1513 . C. m  505;1009 . D. m  1  ;505 . 0   0   0   0  
Câu 33. Cho phương trình 5x m  log x m với m là tham số. Có bao nhiêu giá trị nguyên của 5   m  20
 ;20 để phương trình đã cho có nghiệm? A. 20 B. 19 C. 9 D. 21   
Câu 34. Để giải phương trình log cot x  tan x  1  cos 2x  sin 2x trên khoảng 0;  , bạn Tuấn giải 2    4  theo các bước sau:    2 cos 2x
Bước 1: Do x  0;
 cot x  tan x   
0. Ta có: cot x  tan x
. Phương trình đã cho tương  4  sin 2x   
đương với: log cos 2x  cos 2x  log sin 2x  sin 2x * (Do x 0;
: sin 2x  0,cos 2x    0 ). 2 2    4  1
Bước 2: Xét hàm số f t  log t t,t  0;1  f t   1  0, t
  0;1 . Do đó hàm số f t 2       t ln 2
đồng biến trên 0;1.
Bước 3: Phương trình (2) có dạng: f cos2x  f sin 2x  cos2x  sin 2x  tan 2x  1  k     k x  
, k  . Vậy phương trình đã cho có tập nghiệm S    / k  . 8 2  8 2 
Bạn Tuấn giải đã đúng chưa? Và nếu sai thì bạn Tuấn giải sai bắt đầu từ bước nào? A. Bài giải đúng. B. Sai từ bước 1. C. Sai từ bước 2. D. Sai từ bước 3.
Câu 35. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Tìm tất cả các giá trị thực của tham số
m để phương trình 3m m ee   2 x   x  2 2 1
1  x 1  x  có nghiệm.
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12  1   1   1   1  A. 0; ln2 B.   ; ln 2 C. 0;  D. ln 2;     2   2   e  2 
Câu 36. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Tìm tập S tất cả các giá trị thực của
tham số m để tồn tại duy nhất cặp số x; y thỏa mãn 2 log
4x  4y  6  m  1 và 2 2 x y 2   2 2
x y  2x  4y  1  0 . A. S   1  ;  1 B. S   5;   1;1;  5 C. S   5  ;  5
D. S    7;  5;  1;1; 5;  7
Câu 37. (CỤM 8 TRƯỜNG CHUYÊN LẦN 1) Số giá trị nguyên của tham số m thuộc đoạn  201  9 ; 2  
để phương trình x  1 log 4x  1  log 2x  1   2x m  3   5  
có đúng hai nghiệm thực là A. 2 . B. 2022 . C. 1 . D. 2021 .
Câu 38. (CHUYÊN KHTN NĂM 2018-2019 LẦN 01) Cho số thực  sao cho phương trình
2x  2x  2 cos x có đúng 2019 nghiệm thực. Số nghiệm của phương trình
2x  2x  4  2 cos x là A. 2019 . B. 2018 . C. 4037 . D. 4038 .
Câu 39. (CHUYÊN PHAN BỘI CHÂU NGHỆ AN NĂM 2018-2019 LẦN 04) Có bao nhiêu giá trị
nguyên của m thuộc đoạn  100  ;100  
 để phương trình 2019x mx  1 có hai nghiệm phân biệt? A. 94 B. 92 C. 184 D. 100.
Câu 40. Tìm tất cả các giá trị của m để phương trình lnm  lnm  sin x  sin x có nghiệm. 1 1 A.  1  m  e 1. B. 1  m  e 1. C. 1  m   1. D. 1  m  e 1. e e
Câu 41. (CHUYÊN SƠN LA NĂM 2018-2019 LẦN 03) Tổng tất cả các giá trị của tham số m để 2 2
phương trình x 4x5m 2 2  log
m  1 có đúng 1 nghiệm là 2 x 4x6   A. 1 . B. 0 . C. 2  . D. 4 .
Câu 42. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 02) Biết rằng phương trình
ex  ex  2 cos ax ( a là tham số) có 3 nghiệm thực phân biệt. Hỏi phương trình
ex  ex  2 cos ax  4 có bao nhiêu nghiệm thực phân biệt? A. 5 B. 10 C. 6 D. 11
Câu 43. (CHUYÊN HƯNG YÊN NĂM 2018-2019 LẦN 03) Cho hàm số x4 7 ( )  3  (  1).2 x f x x  6x  3 . a a
Giả sử m  ( a,b  , là phân số tối giản) là giá trị nhỏ nhất của tham số thực m sao cho 0 b b phương trình f  2
7  4 6x  9x   2m 1  0 có số nghiệm nhiều nhất. Tính giá trị của biểu thức 2
P a b . A. P  11. B. P  7. C. P  1. D. P  9.
Câu 44. (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 01) Có bao nhiêu cặp số nguyên ( ; x y) thỏa mãn
0  x  2020 và log (3  3)   2  9y x x y ? 3 A. 2019 . B. 6 . C. 2020 . D. 4 .
Câu 45. (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 02) Có bao nhiêu số nguyên x sao cho tồn tại số thực
y thỏa mãn log  x y  log  2 2 x y ? 3 4 
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 A. 3. B. 2. C. 1. D. Vô số
Câu 46. Cho a  0 , b  0 thỏa mãn log a b   a b
 . Giá trị của a  2b bằng ab  2 2 9 1 log 3 2 1 2 3 2 1  6ab1   7 5 A. 6 B. 9 C. D. 2 2
Câu 47. Cho phương trình 3x m  log (x  )
m với m là tham số. Có bao nhiêu giá trị nguyên của 3 m  15; 
15 để phương trình đã cho có nghiệm? A. 16 B. 9 C. 14 D. 15 9t
Câu 48. (MĐ 103 BGD&ĐT NĂM 2016-2017) Xét hàm số f t
với m là tham số thực. Gọi S t 2 9  m
là tập hợp tất cả các giá trị của m sao cho f x  f y  1 với mọi x, y thỏa mãn xy e
ex y.
Tìm số phần tử của S . A. 0. B. 1. C. Vô số. D. 2.
Câu 49. (SỞ GD&ĐT PHÚ THỌ NĂM 2018-2019 LẦN 01) Cho a  0 , b  0 thỏa mãn 3 2 3
a ab b log
a  3b  log a  log b . Giá trị của bằng 16   9 12 3 2 3
a a b  3b 6  13 8  17 13 5  13 3  13 A. B. C. D. 11 69 6 11
Câu 50. (THPT NGUYỄN KHUYẾN TP.HCM NĂM 2018-2019) Cho a , b là các số dương thỏa mãn 5b a a
log a  log b  log . Giá trị của bằng 9 16 12 2 b a a 7  2 6 a 1  6 a A.  1   6 . B.  . C.  . D.  7  2 6 . b b 25 b 5 b
Câu 51. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Với các số thực x , y dương thỏa  x y x
mãn log x  log y  log   . Tính tỉ số . 9 6 4  6  y A. 3 B. 5 C. 2 D. 4
Câu 52. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cho phương trình 2x  .2x m
.cos x  4 , với m là
tham số. Gọi m là giá trị của m sao cho phương trình trên có đúng một nghiệm thực. Khẳng 0
định nào sau đây là đúng? A. m   5;  1  . B. m  5. C. m   1  ;0 . D. m  0. 0   0   0 0
Câu 53. (SỞ GD&ĐT NINH BÌNH LẦN 01 NĂM 2018-2019) Số nghiệm của phương trình x x5 50  2  3.7x là: A. 1 . B. 2 . C. 3 . D. 0 .
Câu 54. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho a là số thực
dương, a  1 . Biết bất phương trình 2 log x x  1 nghiệm đúng với mọi x  0 . Số a thuộc tập a hợp nào sau đây? A. 7;8 B. 3; 5 C. 2; 3 D. 8; 
Câu 55. (SỞ GD&ĐT VĨNH PHÚC NĂM 2018-2019 LẦN 02) Số nghiệm thực của phương trình 2
log x  2x  log  2
x  2x  2 là 3 5 
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 A. 4 . B. 3 . C. 1 . D. 2 .
Câu 56. (THPT Chuyên Vĩnh Phúc-lần 2-năm 2017-2018) Xét các số thực dương x , y thỏa mãn 1 2x  1 1 ln
 3x y 1  
. Tìm giá trị nhỏ nhất P của P   .  x y  min x xy A. P  8 . B. P  4 . C. P  2 . D. P  16 . min min min min
Câu 57. (THTT Số 3-486 tháng 12 năm 2017-2018) Xét các số thực dương x, y thỏa mãn x y log
xx 3  yy 3  x .
y Tìm giá trị lớn nhất P của biểu thức 3 2 2
x y xy  2 max 3x  2 y 1 P  . x y  6 A. 3 . B. 2 . C. 1. D. 4 .
Câu 58. (SỞ GD&ĐT BẮC NINH NĂM 2018-2019 LẦN 01) Tập nghiệm của bất phương trình log  2 2
x x  2  4  x  2
 2x x  2  1 là  a; b 2  . Khi đó . a b bằng 15 12 16 5 A. . B. . C. . D. . 16 5 15 12
Câu 59. (MĐ 103 BGD&ĐT NĂM 2019-2020) Có bao nhiêu số nguyên x sao cho ứng với mỗi x có
không quá 127 số nguyên y thỏa mãn log  2 x y  log x y ? 3  2   A. 89 . B. 46 . C. 45 . D. 90 .
Câu 60. (MĐ 103 BGD&ĐT NĂM 2019-2020) Xét các số thực không âm x và y thỏa mãn x y 1 2x .4 y   
 3 . Giá trị nhỏ nhất của biểu thức 2 2
P x y  2x  4 y bằng 33 9 21 41 A. . B. . C. . D. . 8 8 4 8
Câu 61. (THPT Trần Hưng Đạo-TP HCM năm 2017-2018) Xét các số thực dương x , y thỏa mãn  2 2 x y  1 2x y 2018    
. Tìm giá trị nhỏ nhất P của P 2 y 3x . min x  2 1 1 7 3 5 A. P  . B. P  . C. P  . D. P  . min 2 min 8 min 4 min 6
Câu 62. (THPT Mộ Đức-Quãng Ngãi-lần 1 năm 2017-2018) Cho hai số thực dương x , y thay đổi thỏa mãn đẳng thức 
  xy     2 2 1 2 1 .2 .2x y xy x y
. Tìm giá trị nhỏ nhất y của y . min A. y  3 . B. y  2 . C. y  1. D. y  3 . min min min min
Câu 63. (THPT Chuyên Thái Bình – Thái Bình – Lần 5 năm 2017 – 2018) Cho 2 số thực dương x, y y 1 
thỏa mãn log  x 1 y 1 
 9  x 1 y 1 . Giá trị nhỏ nhất của biểu thức P x  2y là 3       11 27 A. P  . B. P  . C. P  5   6 3 . D. P  3  6 2 . min 2 min 5 min min
Câu 64. Cho các số thực x, y với thỏa mãn log 2 4 48 31 4.8y x x x x y . Giá trị lớn 2   3         2 24 1 y 2 nhất của  24 2 x P .6  x là A. 14 . B. 6 . C. 32 . D. 8 .
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Câu 65. [PHÁT TRIỂN 47 - ĐỀ THI THAM KHẢO – 2020] Có bao nhiêu cặp số nguyên dương x; yx  2 4 3 2 2
với y  2020 thỏa mãn: log
 4y  8y x 4x y 1 2     y  1 A. 2019.2020 . B. 2020.2021 . C. 2 2019 . D. 2 2020
Câu 66. [PHÁT TRIỂN 47 - ĐỀ THI THAM KHẢO – 2020] Biết rằng bất phương trình  3 x 4x1  a b 2  8  4 2 .2 x x x x
, có một nghiệm dương là x
với a,b, c  ; b  20. Khi đó c
biểu thức P a b c bằng giá trị nào sau đây ? A. 18. B. 16. C. 10. D. 8.
Câu 67. Cho hàm số f x   2
ln x x  1 . Có tất cả bao nhiêu số nguyên m thỏa mãn bất phương   trình f m 1 log  f log    0? m  2019  A. 65 . B. 66 . C. 64 . D. 63 .
Câu 68. [PHÁT TRIỂN 47 - ĐỀ THI THAM KHẢO – 2020] Có bao nhiêu số nguyên m để phương
trình ln m  3sin x  lnm  4sin x  sin x có nghiệm thực? A. 6. B. 10. C. 5. D. 9.
___________________HẾT___________________
Huế, ngày 09 tháng 12 năm 2020
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
LỜI GIẢI CHI TIẾT Câu 1.
(THPT GIA LỘC HẢI DƯƠNG NĂM 2018-2019 LẦN 02) Cho hai số thực a , b thỏa mãn a  4b a log
a  log b  log . Giá trị của bằng 100 40 16 12 b A. 6 . B. 12 . C. 2 . D. 4 . Lời giải:
Điều kiện: a , b  0 và a  4b  0 a  100t a  4b  Đặt log
a  log b  log
t  b  40t 100 40 16 12
a  4b 12.16tt  5    2t t   6       t t t 5 5 2
Suy ra 100  4.40  12.16  0   4.  12  0       .  2   2 t   5    2    l  2  t a  5  Vậy     6 . b  2  2 Câu 2.
(THPT CHUYÊN BẮC GIANG NAM 2018-2019 LẦN 01) Phương trình x3 x 5x6 2  5 có một
nghiệm dạng x b  log b với a,b là các số nguyên dương thuộc khoảng 1;7 . Khi đó a  2b a bằng A. 7 B. 24 C. 9 D. 16 Lời giải: 2 2 Ta có x3 x 5x6 x3 x 5x6 2  5  log 2  log 5  x  3   2
x  5x  6 log 5 2 2  2     
x   x  x   x 3 0 x 3 3 3 2 log 5     2
x  2log 5  1 x  2  log 2 2  5 b  2  
a  2b  5  2.2  9 a   5 1  y Câu 3.
Xét các số thực dương x, y thỏa mãn log
 3xy x  3y  4 . Tìm giá trị nhỏ nhất P 3 x  3xy min
của P x y . 4 3  4 4 3  4 4 3  4 4 3  4 A. P  . B. P  . C. P  . D. P  . min 3 min 3 min 9 min 9 Lời giải: 1  y Để
 0 mà từ giả thiết x,y  0 suy ra 1 y  0  y  1 . Vậy ĐKXĐ: x  0;0  y  1. x  3xy 1  y 1  y 31  y Ta có: log
 3xy x  3y  4
3xyx3y4   3
3xyx3y3   3 3 x  3xy x  3xy x  3xy
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 31  y 3 3 xyx  
    33y     3 3 3 .3 3 .3 xyx y xy x (*) 33 x  3xy 3 y Xét    .3t f t t
với t  0 . Ta có    3t  .3t f t
t .ln 3  0 với t  0 , suy ra f t đồng biến trên
khoảng 0;  . Từ (*) ta có
f 3  3y  f 3xy x với
3  3y  0,3xy x  0 nên 3  x
3  3y  3xy x y  . 3(x  1) 3 x  3 x 1    4
Ta có P x y x   x       3x    1 1  3x   1 3 3  
P  x   4 4 4 4 4 3 4 1    x    . 3x   2  1. 1 3 3x   1 3 3  4 x  1   3x  1   2 3  3 x  4 3  4  3  x  Vậy 3 P    y    . min 3 3  x 1  2 3  1 y   
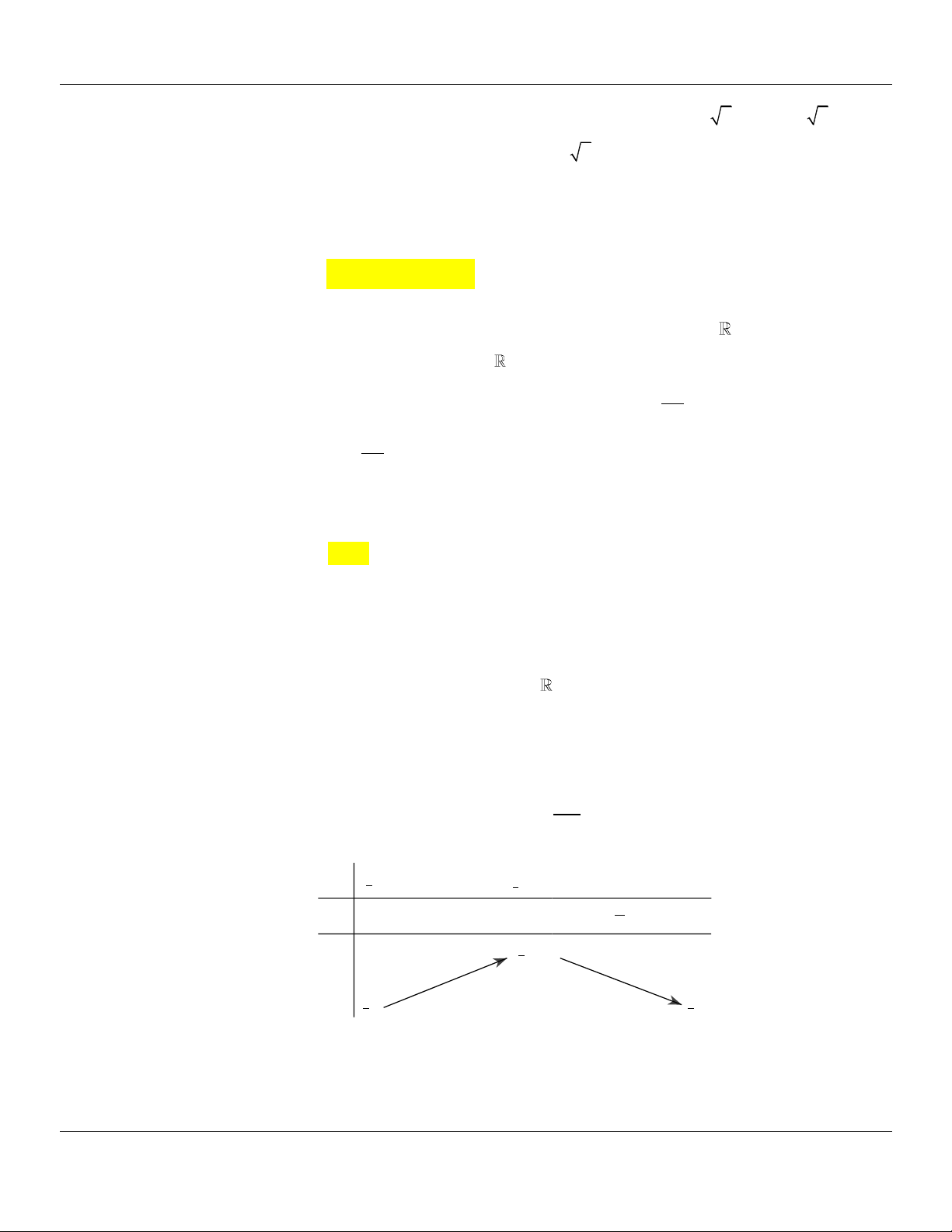
x  0; 0  y  1  3   Câu 4.
(THPT - YÊN ĐỊNH THANH HÓA 2018 2019- LẦN 2) Cho x, y là hai số thực không âm thỏa 2y  1 mãn 2
x  2x y  1  log
. Giá trị nhỏ nhất của biểu thức 2 x1 2 P e
 4x  2y  1 là 2 x  1 1 1 A. . B. 1  . C.  . D. 1 . 2 2 Lời giải: x  1  Điều kiện:  1 y    2 2y  1 2 2 Ta có: 2 x 2x y 1 log 2 x 1 2y 1 log 2y 1 log 2 x 1              2   2   2   x  1  
2x 12 log 2x 12     
 2y  1 log 2y  1 1 2 2       .
Xét hàm số f t  t  log t, t  0 2
Ta có: f t 1  1  0, t
  0 suy ra f t đồng biến trên khoảng 0; . t.ln 2 2 2 2
Phương trình 1  f 2x  
1   f 2y  1  2y  1  2x  1  2y  2x  1 1 . Ta có: 2x1 2 2x1 2 P e
 4x  2y  1  e  2x  4x 2x1 2x1 1 P  2.e
 4x  4; P  0  e
 2  2x x  . 2 Bảng biến thiên
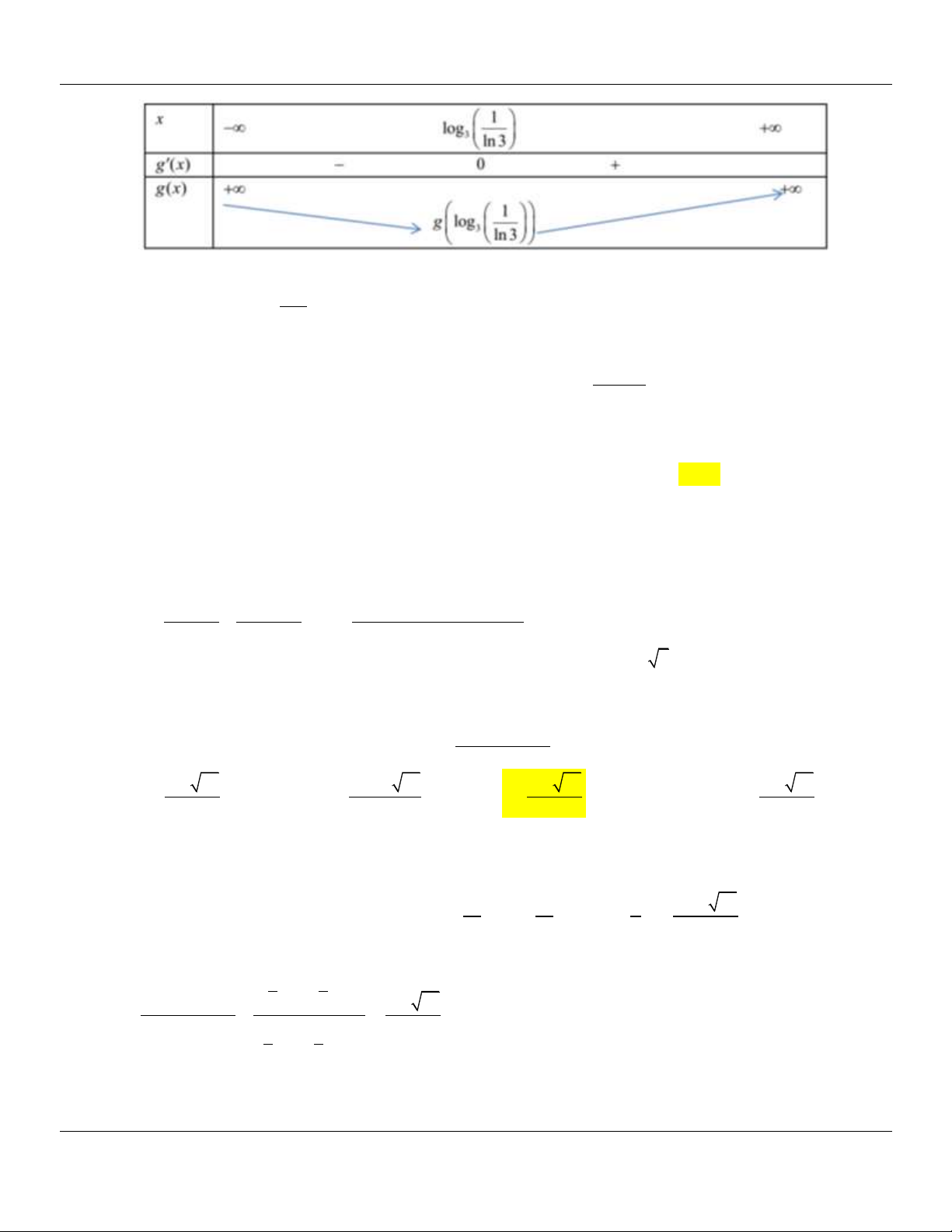
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 1
Vậy giá trị nhỏ nhất của biểu thức 2 x1 2 P e
 4x  2y  1 là  . 2 Câu 5.
(THPT BA ĐÌNH NĂM 2018-2019 LẦN 02) Xét các số thực dương x, y thỏa mãn  2 2 x y  1 2x y 2019 
. Giá trị nhỏ nhất P
của biểu thức P  2y x 2 (x  1) min bằng 1 1 7 15 A. P  . B. P  . C. P  . D. P  . min 4 min 2 min 8 min 8 Lời giải:  2 2 x y  1 2x y 2 2 2 x 1 Ta có: 2019            2 1 .2019 2 .2019 y x x y 2 (x  1) 2     x 2 2 2 1 4x     2 2   1 .2019 2 .2019 y x x y  x  1 2x  1 .2019
 2x y 22x y .2019 . (1) 2
Đặt u  x  1 ,v  2x y, u  0,v  0 , khi đó (1) trở thành 2u 2 .2019  .2019 v u v . (2)
Xét hàm đặc trưng   2  .2019 t f t t
, t  0 , ta có   2t 2 '  2019  2 .2019 t f t t .ln 2019  0, t
 0 :   Hàm f t đồng biến trên (0;).
Phương trình    f u  f v  u v  x  2 2 2
1  2x y y x  1. Vậy 2
P  2y x  2x x  2 . Do P là hàm bậc hai có hệ số a  2  0 nên  b   1  1 1 15 min P P   P  2.   2      .  2a   4  16 4 8 Câu 6.
(MĐ 104 BGD&ĐT NĂM 2019-2020) Xét các số thực không âm x và y thỏa mãn xy 1 2x .4   y
 3 . Giá trị nhỏ nhất của biểu thức 2 2
P x y  4x  2 y bằng 33 9 21 41 A. . B. . C. . D. . 8 8 4 8 Lời giải: Ta có xy 1  
     x y 1  2    y     32 2 .4 3 2 3 .4 .4 0 2 .2 3 2 2 x x y x y y x  3 3 x  33
Xét TH 3  2x  0  x
. đúng với mọi giá trị 2 2 
2  P x y  4x  2 y  2 4 y  0 3
Xét TH 3  2x  0  0  x  . 2
Xét hàm số    .2t f t t với t  0
    2t  .2t f t t
.ln 2  0 với mọi t  0 3
f 2y  f 3  2x  2y  3  2x y   x 2
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 2  3  21 2 2 2
P x y  4x  2y x
x  4x  3 2x 2  2x x     2  4 2  1  41 41
P  2 x       4  8 8 41 1 5
So sánh và ta thấy GTNN của P là
khi x  , y  8 4 4 Câu 7.
(MĐ 104 BGD&ĐT NĂM 2019-2020) Có bao nhiêu số nguyên x sao cho ứng với mỗi x có
không quá 255 số nguyên y thỏa mãn log  2 x y  log
x y ? 3  2   A. 80 . B. 79 . C. 157 . D. 158 Lời giải:  log 3 Ta có: log  2 x y  log x  2 log2  y    3 x y x y 2
x y  x y 2   1 3  2  
Đk: x y  1
Đặt t x y  1, nên từ   2 log 3 2
1  x x tt 2 Để  
1 không có quá 255 nghiệm nguyên y khi và chỉ khi bất phương trình 2 có không quá
255 nghiệm nguyên dương t .
Đặt M f 255 với f t  log 3 2  tt .
Vì f là hàm đồng biến trên 1,  nên 2  1     2 1 t f x x khi 2 x x  0 .
Vậy 2 có không quá 255 nghiệm nguyên 1 f  
 2x x  255 2
x x  255  78   x  79 x  .
Vậy có 158 số nguyên x thỏa mãn yêu cầu bài toán. Câu 8.
(CHUYÊN LÊ THÁNH TÔNG NĂM 2018-2019 LẦN 02) Cho hai số dương x ; y thỏa y
log 4x y  2xy  2  2  8  2x  2 y  2 . Giá trị nhỏ nhất của P  2x y là số có dạng 2   
M  a b c với a , b
, a  2 . Tính S  a b c . A. S  17 . B. S  7 . C. S  19 . D. S  3 . Lời giải: y2
Với hai số dương x ; y thỏa log 4x y  2xy  2
 8  2x  2 y  2 2     
Ta có y  2log 4x y  2xy  2  8  2x  2 y  2 2     
 y  2log 2x  1 y  2  8  2x  1 y  2  3 y  2 2         8    8 8
log 2x  1  log y  2 
 2x  1  3  log 2x  1  2x  1  log    1 . 2     2   2   2     y  2 y  2 y    2
Xét hàm đặc trưng f t  log t t trên 0;  có f t 1   1  0, t
  0 nên hàm số f t 2 t ln 2
đồng biến trên 0;  .  
Phương trình (1) có dạng: f x   8 8 8 2 1  f    2x  1   y   2 . y  2 y  2 2x    1
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 8  8 AMGM
P  2x y  2x   2  2x   1   3  4 2    3 . 2x  1  2x  1  8 1   2 2
Dấu bằng xảy ra khi 2x  1   2x  2 1  8  x  . 2x  1 2
Vậy S  a b c  3 . Câu 9.
(THPT CHUYÊN THÁI BÌNH NĂM 2018-2019 LẦN 04) Cho các số thực x , y với x  0 thỏa xy xy xy 1
mãn e 3  e 1  xy  1  1  e 1 
 3y . Gọi m là giá trị nhỏ nhất của biểu thức  ex 3y
T x  2y  1. Mệnh đề nào sau đây đúng? A. m 2; 3 . B. m 1  ; 0 . C. m 0;1 . D. m 1; 2 . Lời giải: xy xy xy 1
Từ giả thiết e 3  e 1  xy  1  1  e 1   3y  ex 3y xy 1 xy 1  e 3   x y    xy  (1). xy  3  e 1 1 3 xy1   e e t 1 t 1
Xét hàm số f t= e 
t với t  ta có f 't= e   1  0, t
   f t là hàm số đồng et et biến trên . x
Phương trình (1) có dạng f x y f xy   1 3
1  x  3y  xy  1  y  (x  0) . x  3 2 2x  2 4 x  6x  5
Khi đó T x  2y  1  x   1 T'  1   x   x  3 x  3 0, 0 2 x  32 2.0  2 1  T  0   1   m . min 0  3 3
Câu 10. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Kí hiệu maxa; 
b là số lớn nhất   trong hai số a, .
b Tìm tập nghiệm S của bất phương trình max log x; log x  1. 2 1   3   1   1  A. S   ;2. B. S  0; 2. C. S  0; .
D. S  2; .  3   3  Lời giải:
y  log x  log x  log x  log x 2 1 2 3 3 1 1 y'    0, x
  0 nên phương trình y  0 có nghiệm duy nhất x ln 2 xln 3
Mà phương trình y  0 có nghiệm x  1 do đó
TH1: x  1 : log x  log x 2 1 3   1 1
Ta có max log x; log x  1.  log x  1  x  . Do đó  x  1 2 1 1   3 3 3  3
TH2: x  1 : log x  log x 2 1 3
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12    1 
Ta có max log x; log x  1.  log x  1  x  2 . Do đó 1  x  2 . Vậy S   ;2. 2 1 2    3  3 
Câu 11. (CHUYÊN QUANG TRUNG BÌNH PHƯỚC NĂM 2018-2019 LẦN 07) Cho hàm số
y f x 3 2
x  12x  2018x  2019 . Số giá trị m ,m  12  ;12 
 thỏa bất phương trình f log
log m  1  2019  f f 0 là 0,2  2       A. 9. B. 10. C. 11. D. 12. Lời giải: Ta có 2
y  3x  24x  2018  0, x
   y f x đồng biến trên . Do đó f log
log m  1  2019  f f 0  log
log m  1  2019  2  019 0,2  2       0,2  2    log
log m  1  0  log m  1  1  m  1  2  m  3 . Do đó m4; 5;6;...;1  2 0,2  2   2   n n
Câu 12. Cho các số m  0 , n  0 , p  0 thỏa mãn 4m 10n 25p  
. Tính giá trị biểu thức T   . 2m 2 p 5 1 A. T  1. B. T  . C. T  2 . D. T  . 2 10 Lời giải: n m n log 4
Vì 4  10  n m log 4    log 2 . 2m 2 n n p log 25
Vì10  25  n p log 25    log5 . 2 p 2 n n Suy ra T  
 log 2  log5  log10 1. 2m 2 p c c
Câu 13. Cho a , b , c là các số thực khác 0 thỏa mãn 4a 9b 6c   . Khi đó  bằng a b 1 1 A. . B. . C. 6 . D. 2 . 2 6 Lời giải: Đặt 4a 9b 6c t  
 với 0  t  1, khi đó: 1 2 log t 1 2 log t log t a   2  a
; log t b   3  b  . 4 a log t 2 9 b log t 2 2 3 1 1 log t.log t log t  1 c
 log 6  log 2  log 3   2 3  c  6 t c t t log t log t log t  . log t 2 3 2 3 c c
2 log t  2 log t Suy ra:  3 2   2 . a b log t  log t 3 2
Câu 14. Có bao nhiêu cặp số nguyên  ;
x y  thỏa mãn 0  x  2020 và 1  y  2020 và x 1 4   log  3 16.2y y
 log 2x 1 ? 2   2   A. 2019 . B. 2020 . C. 1010 . D. 1011. Lời giải:
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 0  x  2020
Điều kiện bài toán: 1   y  2020 Ta có: x 1 4   log  3 16.2y y  log 2x 1 2 x2  2  log 2x   y4 1  2  log y  3 * 2 2    2   2   Xét hàm số t 1 f (t) 2  
 log t trên 1; . 2 t 1  2 t t  1 .2 .ln 2 1 Ta có 1 f (  t)  2 ln 2  
 0,t 1;  hàm sốđồng biến trên1; . t ln 2 t ln 2
Khi đó (*)  f 2x  
1  f y  3  2x 1  y  3  y  2x  2 3
Vì 1  y  2020  1  2x  2  2020   x 1011. 2
Do x nguyên nên x 2;3; 4;...;101 
1 . Rõ ràng, với mỗi x ta xác định được tương ứng duy
nhất một giá trị y nguyên thỏa mãn. Vậy có 1010 cặp số nguyên  ; x y  . 2
 4x  4x  1 Câu 15. Biết
x , x là hai nghiệm của phương trình 2 log 
  4x  1  6x và 1 2 7  2x  1 x  2x
a b với a , b là hai số nguyên dương. Tính a b . 1 2   4
A. a b  13 .
B. a b  11 .
C. a b  16 .
D. a b  14 . Lời giải: 1
Điều kiện: x  0,x  . 2 2
 4x  4x  1 Ta có: 2 log 
  4x  1  6x  log  2
4x  4x   2
1  4x  4x  1  log 2x  2x . 7 7 7    2x
Xét hàm số f t  log t t có f t 1 
 1  0 t  0 nên là hàm số đồng biến trên 0; . 7 t ln7  Do đó ta có 2 2 3 5
4x  4x  1  2x  4x  6x  1  0  x  . 4 3  5 3  5 1 3  5 3  5 1
Khi đó: x  2x   2 
9  5 hoặc x  2x   2  9  5 . 1 2   1 2   4 4 4 4 4 4 3  5 3  5 Vậy x  ; x
. Do đó a  9;b  5 và a b  9  5  14 . 1 2 4 4
Câu 16. Cho phương trình 2 log cotx  log cos x . Phương trình này có bao nhiêu nghiệm trên 3   2        khoảng ;   ?  6 2  A. 4. B. 3. C. 2. D. 6. Lời giải: s  in x  0 Điều kiện :  . cos x  0 2
cot x  3t t 1
Đặt 2 log cot x  log cos x t   1 3 
 1 4t  3t 12t 1 3   2   t
cos x  2t 1 4
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 t   t t t t 4  12  4  3  4  1   (1)  3  t t     t 4 t 4 4
Xét hàm số f t   4 
f t  4 ln 4  ln  0, t      
, suy ra hàm số f t  đồng  3   3  3 biến trên , mà f   1  1  t  1
 là ngiệm duy nhất của phương trình (1).   x   k2 1  3 t  1
  cos x    . 2   x    k2  3 s  in x  0 Vì 
, suy ra điểm biểu diễn của các họ nghiệm phải thuộc góc phần tư thứ nhất nên cos x  0    9
chỉ có họ nghiệm x
k2 là thỏa mãn. Khi đó   k2 
 1 2 12k  27 3 6 3 2 1 25    k  . Vì k   k 0;1; 
2 . Do đó phương trình có 3 nghiệm thỏa mãn. 12 12
Câu 17. Biết m, 
n là hai số thực thỏa mãn x 3 .2  3.2 x x
 3x  8  0 và m n a  log b, a, * b  , tính 2  S a  . b A. S  4. B. S  6. C. S  5. D. S  9. Lời giải: 2 Ta có: x 3x x 24 . x 2  3.2
 3x  8  0  . x 2 
 3x  8  0  . xx    (1) x
2x 3 8.2x 24 0 2 2 2
Xem (1) là phương trình bậc hai theo 2x , có    x   2 3
8  96x  9x  48x  84  3x  8 .  3x  8  x x 3 8 2   3 Phương trình   2xx   x x   . 3 8 3 8 8 2    2x x
+) Với 2x  3  x  log 3. 2 8 +) Với 2x
(2), trên các khoảng ;0 và 0;  , vế phải (2) nghịch biến và vế trái (2) đồng x
biến nên phương trình (2) có nghiệm duy nhất, mặt khác x  2 thỏa mãn nên x  2 là nghiệm duy nhất của (2). a  2
Suy ra: m n  2  log 3  
S a b  5. 2 b   3 Câu 18. (MĐ 102 BGD&ĐT NĂM 2017-2018) Cho a  0 , b  0 thỏa mãn log a b   a b
 . Giá trị của a  2b bằng ab  2 2 25 1 l g o 10 3 1 2 10 3 1  10ab1   5 11 A. B. 6 C. 22 D. 2 2 Lời giải:
Từ giả thiết ta có 2 2
25a b  1  0 , 10a  3b  1  0 , 10a  3b  1  1 , 10ab  1  1 .
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 Áp dụng Cô-si, ta có 2 2 2 2 5
2 a b  1  2 25a b  1  10ab  1 . Khi đó, log a b   a b   log 10ab  1  l g o
10a  3b  1  2 . 10a3b1   10ab1   ab  2 2 25 1 log 10 3 1 10 3 1  10ab1   5a   b
Dấu “  ” xảy ra khi  . log 10ab  1  log
10a  3b  1   1  10a3b1   10ab1    5 b   11 Suy ra 2 
a  2b  . 1  2 a   2
Câu 19. Tìm tập hợp tất cả các giá trị thực của tham số m để phương trình 2 2 2 2
2 x mxm 4m
x mxm 4  m 2 2 ee
x  2mx  2m  8m  0 có hai nghiệm x , x phân biệt thỏa mãn 1 2 x x  2?  1 2 A. 0;1.  B. 0; 8.   C. 0; 2.  D. 2; 8.   Lời giải: 2 2 2 2 Phương trình
x mxm 4  m    2 2   
 2x mxm 4m e x mx m m e   2 2 4
2x mx m  4m (2) Xét hàm số   t
  ,     t f t e t t
f t e  1  0, t
  nên f t đồng biến trên .
Phương trình (2) có dạng: f  2 2
x mx m m  f  2 2
x mx m m 2 2 2 2 4 2 4
x mx m 4
m  2x mx m  4m gx 2 2
x  2mx  2m  8m  0 (3). 2   0
 m m  mg 8 0 0;8 Yêu cầu bài toán        m0;1. 
x x  2   2  m  2  m  1 1 2
Câu 20. Biết m, n là hai số thực thỏa mãn x 3 .2  3.2 x x
 3x  8  0 và m n a  log b, a, * b  , tính 2  S a  . b A. S  4. B. S  6. C. S  5. D. S  9. Lời giải: 2 Ta có: x 3x x 24 . x 2  3.2
 3x  8  0  . x 2 
 3x  8  0  . xx    (1) x
2x 3 8.2x 24 0 2 2 2
Xem (1) là phương trình bậc hai theo 2x , có    x   2 3 8
 96x  9x  48x  84  3x  8 .  3x  8  x x 3 8 2   3 Phương trình   2xx   x x   . 3 8 3 8 8 2    2x x
+) Với 2x  3  x  log 3. 2 8 +) Với 2x
(2), trên các khoảng ;0 và 0;  , vế phải (2) nghịch biến và vế trái (2) đồng x
biến nên phương trình (2) có nghiệm duy nhất, mặt khác x  2 thỏa mãn nên x  2 là nghiệm duy nhất của (2). a  2
Suy ra: m n  2  log 3  
S a b  5. 2 b   3
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Câu 21. (THPT CHUYÊN NGUYỄN QUANG DIÊU 2018-2019 LẦN 2) Hỏi phương trình 3.2x 4.3x 5.4x 6.5x   
có tất cả bao nhiêu nghiệm thực ? A. 0 . B. 1 . C. 3 . D. 2 . Lời giải: x x x       Ta có : 3.2x 4.3x 5.4x 6.5x    2 3 4  3  4  5  6        0 .  5   5   5  x x x      
Xét hàm số f x 2 3 4  3  4  5        6 , x  .  5   5   5  x x x       Có f x 2 2 3 3 4 4  3 ln  4 ln  5 ln        0 , x
nên hàm số f x nghịch biến trên  5  5  5  5  5  5
suy ra phương trình f x  0 có nhiều nhất một nghiệm 1 .  
Mặt khác f   f   8 22 176 1 . 2  .      
0 nên phương trình có ít nhất một nghiệm thuộc 5  25  125
khoảng 1; 2 . 2 . Từ 1 và 2 suy ra phương trình đã cho có nghiệm duy nhất.
Câu 22. (THPT CHUYÊN VĨNH PHÚC LẦN 02 NĂM 2018-2019) Biết rằng phương trình
ex  ex  2 cos ax ( a là tham số) có 3 nghiệm thực phân biệt. Hỏi phương trình
ex  ex  2 cos ax  4 có bao nhiêu nghiệm thực phân biệt ? A. 5 B. 10 C. 6 D. 11 Lời giải:
ex  ex  2 cos ax 1 2 2 x x    x x    ax
Ta có : ex  ex  2 cos ax  4 2 2
 e e   21 cosax 2   2 2
 e e   4cos     2   x x   ax 2 2
e e  2cos 2 2   x x   ax 2 2 e e  2   cos 3  2
Ta thấy nếu x là nghiệm phương trình 1 thì x  0 . 0 0
Khi đó 2x là nghiệm phương trình 2 và 2
x là nghiệm phương trình 3 . 0 0
Do phương trình 1 có 3 nghiệm nên phương trình 2 có 3 nghiệm và phương trình 3 có
3 nghiệm, đồng thời các nghiệm phương trình 2 ,3 khác nhau.
Vậy phương trình ex  ex  2 cos ax  4 có 6 nghiệm thực phân biệt.
Câu 23. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho hai phương trình 2
x  7x  3  ln x  4  0 1 và 2
x  9x  11  ln 5  x  0 2 . Đặt T là tổng các nghiệm phân
biệt của hai phương trình đã cho, ta có: A. 2 B. 8 C. 4 D. 6 Lời giải:
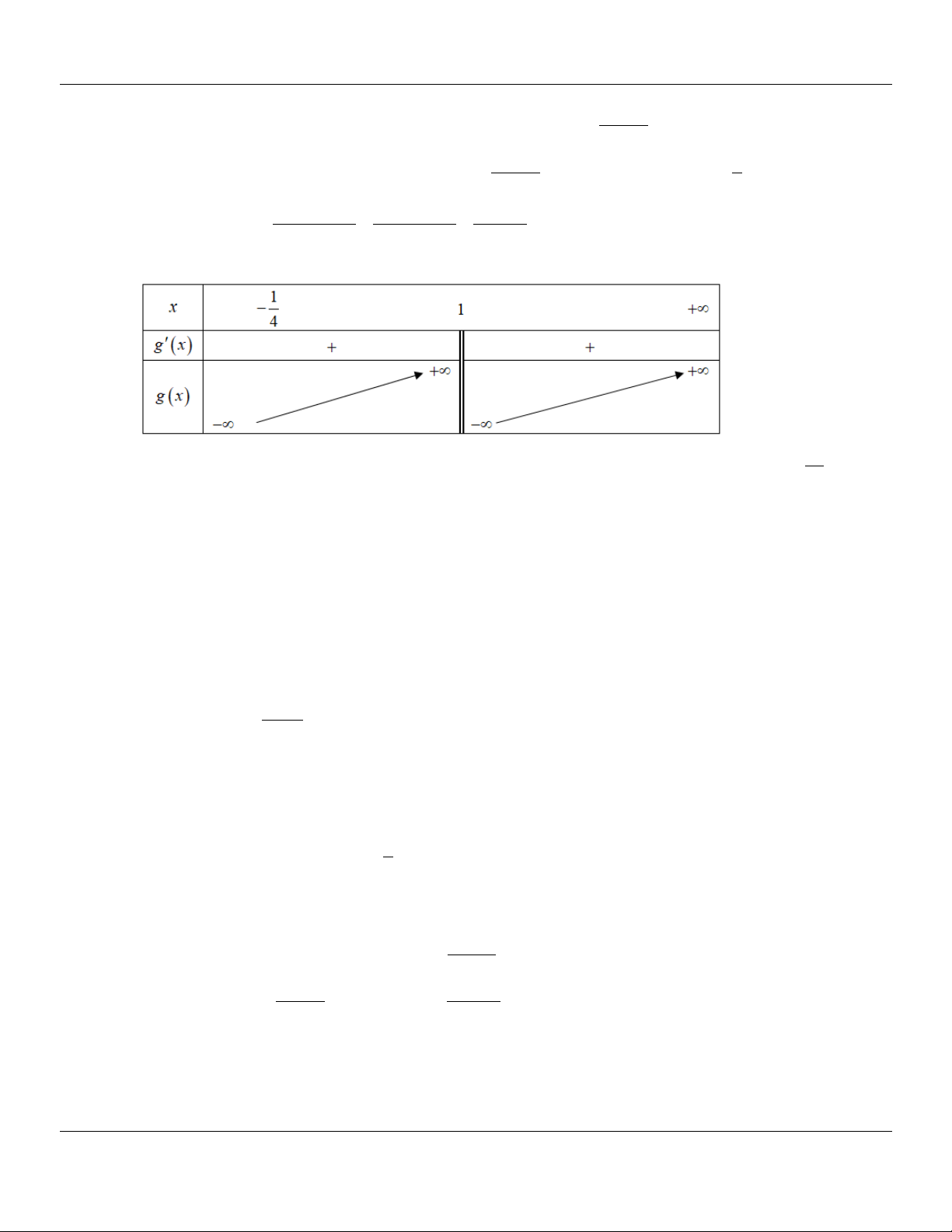
Cách 1: Gọi hai phương trình là 1 và 2 f x 2
x  7x  3  lnx  4 , với x 4;   .
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 2
2x  15x  27 f x 1  2x  7  3   , f x 2 9
 0  2x  15x  17  0  x  3
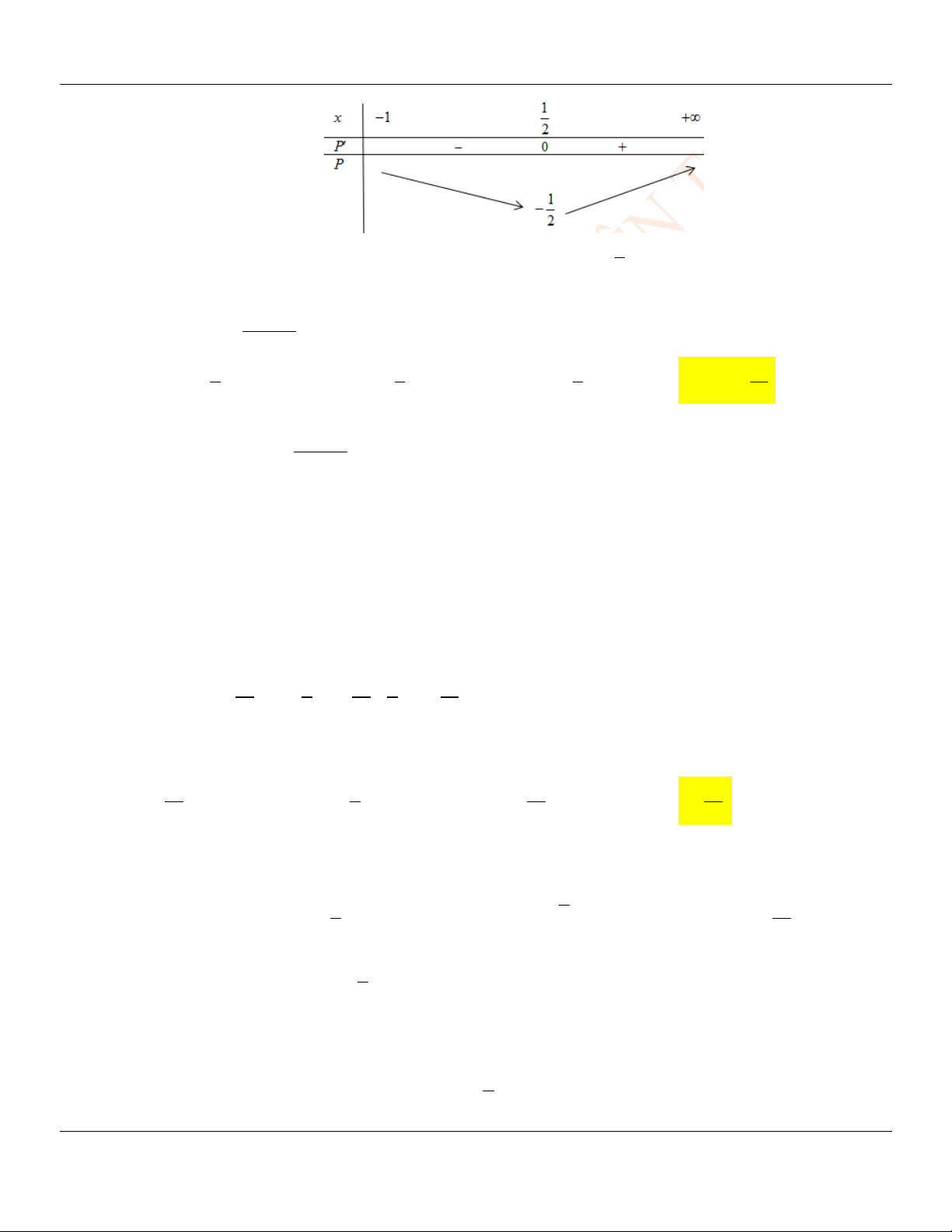
 ,x   Lx  4 x  4 2 Bảng biến thiên
Theo bảng biến thiên thì 1 có hai nghiệm phân biệt, gọi hai nghiệm là x ; x 1 2
Giải sử x là nghiệm của phương trình 1 , đặt t  1  x x  1  t ta có 0 0 0 0 0
x  7x  3  ln x  4  0  1  t 2 2
 7 1 t  3  ln 1 t  4  0 0  0  0  2
t  9t  11  ln 5  t
 0 . Do đó t là nghiệm của phương trình 2 0 0  0  0
Như vậy 2 cũng có đúng hai nghiệm là t  1  x và t  1  x 1 1 2 2
Vậy tổng các nghiệm của hai phương trình là T x x t t x x  1  x  1  x  2 1 2 1 2 1 2 1 2
Cách 2: Dùng máy tính casio dò nghiệm rồi cộng lại.
Câu 24. Phương trình 4x 1  2 . x .
m cos( x) có nghiệm duy nhất. Số giá trị của tham số m thỏa mãn là A. Vô số B. 1 C. 2 D. 0 Lời giải:
Ta có 4x  1  2x mcos x  2x  2x mcos x
Ta thấy nếu x x là một nghiệm của phương trình thì x  x cũng là nghiệm của phương 0 0
trình nên để phương trình có nghiệm duy nhất thì x  0 . 0
Với x  0 là nghiệm của phương trình thì m  2 . 0
Thử lại: Với m  2 ta được phương trình x 2 2 2 
 2cos x * x 2 2 2    2
VT  2; VP  2 nên *
thỏa mãn. Vậy m  2 .      xx 0 2cos   2
Câu 25. (CHUYÊN LÊ HỒNG PHONG NAM ĐỊNH NĂM 2018-2019) Cho 0  x  2020 và
log (2  2)   3  8y x x y
.Có bao nhiêu cặp số (x ; y) nguyên thỏa mãn các điều kiện trên ? 2 A. 2019. B. 2018. C. 1. D. 4. Lời giải:
Do 0  x  2020 nên log (2x  2) luôn có nghĩa . 2
Ta có log (2  2)   3  8y x x y 3
 log (  1)   1  3  2 y x x y log ( x1) 2 3  log (  1)  2  3  2 y x y (1) 2 2 2
Xét hàm số ( )   2t f t t
. Tập xác định D  và (  )  1  2t f t ln 2  f (
t)  0 t  .
Suy ra hàm số f (t) đồng biến trên .
Do đó (1)  log (x  1)  3y 3   1  2 y x
y  log (x  1) . 2 8
Ta có 0  x  2020 nên 1  x  1  2021 suy ra 0  log (x  1)  log 2021 . 8 8
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Lại có log 2021  3,66 nên nếu y  thì y 0;1;2;  3 . 8
Vậy có 4 cặp số (x ; y) nguyên thỏa yêu cầu bài toán là các cặp (0 ; 0) , (7 ;1) , (63; 2) , (511; 3) .
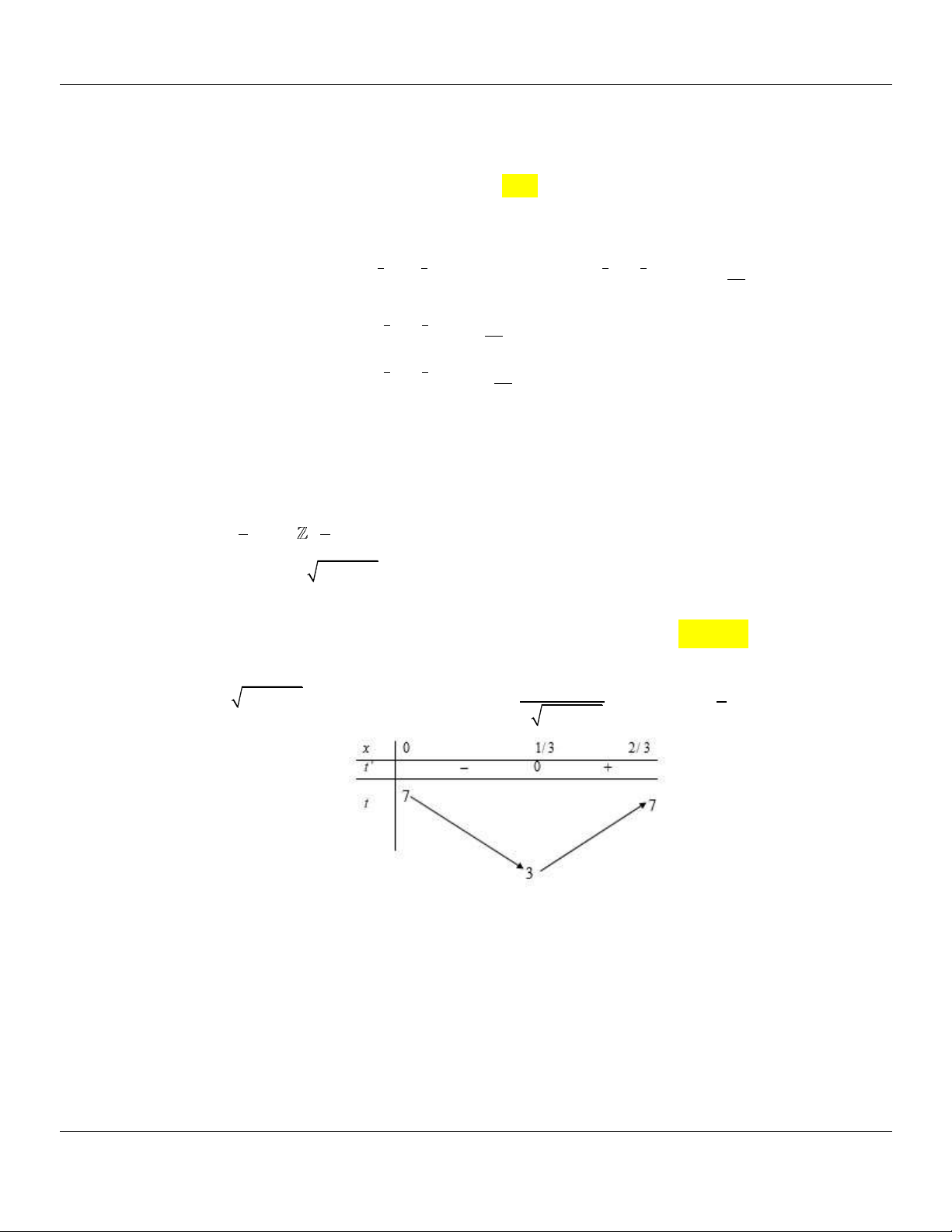
Câu 26. Tổng tất cả các nghiệm thực của phương trình x x1 15 .5 x
 5  27x  23 là A. 1 . B. 0 . C. 2 . D. 1  . Lời giải: 1 Ta thấy x
không là nghiệm của phương trình, do đó 3 x x1 x  1 27x 23 15 . x 5  5  27x  23  5  3x  1 x   1   1  Xét hai hàm số   1 5x f x   và gx 27 23 
trên tập D  ;  ;      3x  1  3   3  9  6 1
Ta có f xx1 1  5 .ln5  0, x
  và gx   0, x   . 3  x  2 3 3 1
Do vậy hàm số f x là hàm đồng biến và gx là hàm nghịch biến trên từng khoảng xác định
nên phương trình có tối đa 02 nghiệm.(xem thêm phần đồ thị minh hoạ)
Nhận thấy x  1 là hai nghiệm của phương trình tren.
Vậy tổng các nghiệm của phương trình là 0 .
Câu 27. (CHUYÊN THÁI BÌNH NĂM 2018-2019 LẦN 03) Tập nghiệm của bất phương trình 2 x 9   2 x   x1 3 9 .5
 1 là khoảng a;b . Tính b a A. 6 . B. 3 . C. 8 . D. 4 . Lời giải: 2 x 9   2 x   x1 3 9 .5
 1 1 . Ta có x1 5  0 x  . Xét 2
x  9  0 , VT 1 0  3  0  1 (loại). 2 x 9 0 3  3  1  Xét 2 x  9  0  
  VT 1  1 (loại). 2 x  9 x1 .5  0 2 x 9 0 3  3  1  Xét 2 x  9  0  
  VT 1  1 luôn đúng. 2 x  9 x1 .5  0 Có 2
x  9  0  x  3  ;3.
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
 Tập nghiệm của bất phương trình là:  3
 ;3  b a  6 .
Câu 28. (THPT ĐOAN THƯỢNG HẢI DƯƠNG NĂM 2018-2019 LẦN 02) Biết x , x x x là hai 1 2  1 2 1
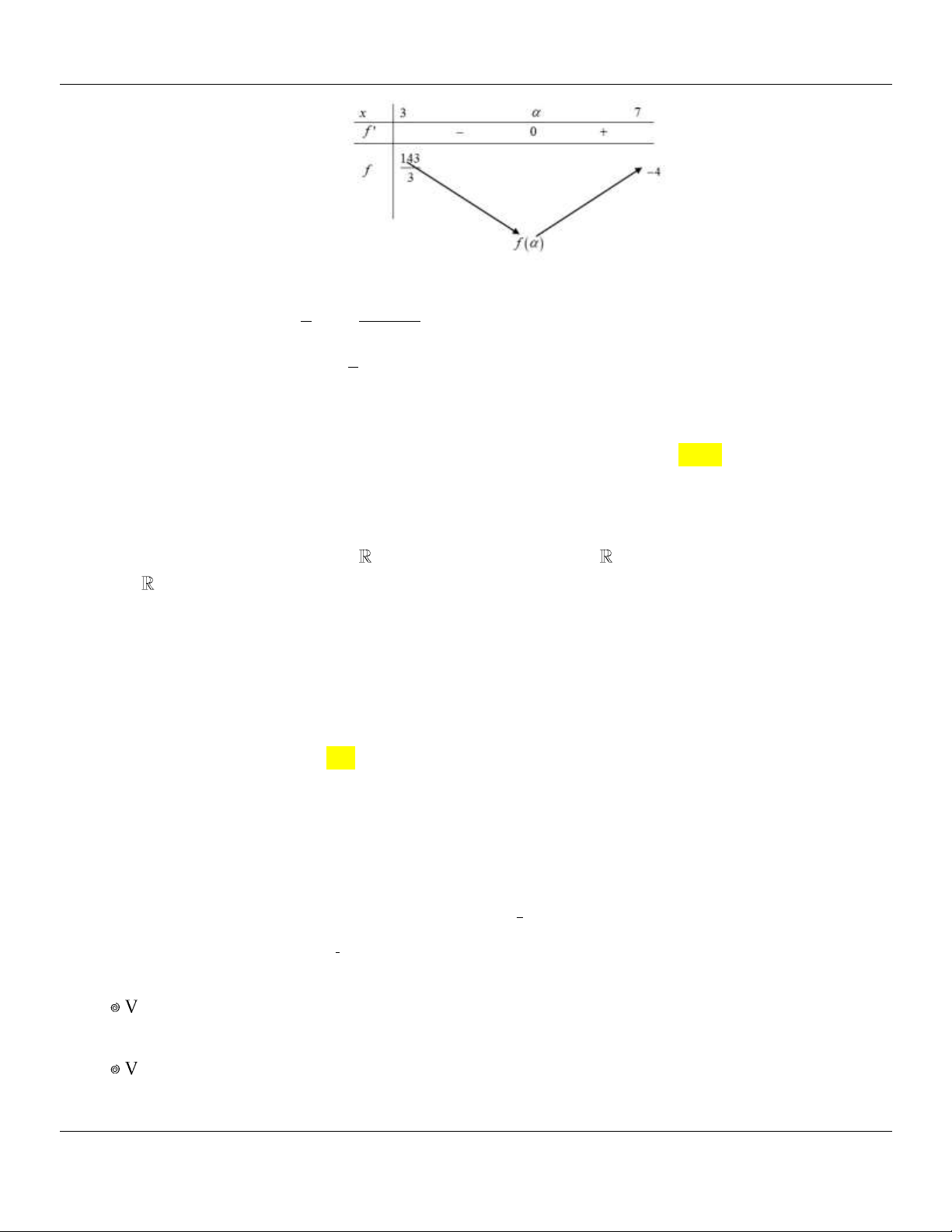
nghiệm của phương trình log  x  3x  2  2 2 2 x 3x1  5
 2 và x  2x
a b với a,b là hai 1 2   3 2
số nguyên dương. Tính a  2 . b A. 5. B. 1. C. 1. D. 9. Lời giải: x  2
Điều kiện xác định của phương trình: 2
x  3x  2  0   . x   1 Đặt 2
t x  3x  2 với t  0 . Phương trình đã cho trở thành log t  2 2 t 1  5  2  0 . 3 2 1
Xét hàm số f t  log t  2 2 t 1  5
 2 . Ta có: f tt 1   2t.5
ln 5  0 , t  0 . 3 t  2ln3 9
Suy ra f t luôn đồng biến trên 0;  . Mà f 0  log 2   0 3 5
Do đó phương trình f t  0 có đúng 1 nghiệm trên khoảng 0;  .
Xét t  1 ta có log 1  2 2 1 1  5  2  0 (đúng) 3
Suy ra t  1 là nghiệm duy nhất.  3  5 x  1 1 t  1  2      2 x 3x 2 1  x  2x
9  5 . Suy ra a  9,b  5 . Vậy a  2b  1 . 1 2    3  5 2 x  1  2 2x  1 a a
Câu 29. Phương trình 2 log
 3x  8x  5 có hai nghiệm là a và (Với a,b * và là phân số 3 x  2 1 b b
tối giản). Giá trị của b là A. 1 . B. 4 . C. 2 . D. 3 . Lời giải:  1 2x  1 x  Điều kiện:     . x  1 0 2 2 x   1 2x  1 2 2 Phương trình 2 log
 3x  8x  5  log 2x 1  2x 1 1  log x 1  3 x 1 3 2 3     3     x  1 2x  1 2 2  log
 2x  1  log x  1  3 x  1 . 3   3     3
Xét hàm số f t  log t  3t, t  0 ta có f t 1 '   3  0, t
  0 nên f t là hàm số đồng 3 t ln 3
biến trên khoảng 0;   . x  2  a  2x  1  2 2x  1 2 Phương trình có dạng  f
f x 1    x  1    2
a . Vậy ta có b  3 .  3  3 x    3 b
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Câu 30. (THPT NINH BÌNH BẠC LIÊU NĂM 2018-2019 LẦN 04) Tính tích tất cả các nghiệm thực của  1 2   2x  1  x  phương trình  2 log    2 x   5 . 2  2x  1 A. 0 . B. 2 . C. 1 . D. . 2 Lời giải: 1
Điều kiện x  0. Đặt t x  , t  2  . 2x
Phương trình trở thành: log 2t t
 5 1 . Xét    log  2t f t t với t  2 . 2 2
Ta có f 2  5 nên x  2 là một nghiệm của phương trình 1 .   1 '   2t f t
ln 2  0 t  2  f t luôn đồng biến trên khoảng  2; t ln 2
 Đồ thị hàm số y f t cắt đường thẳng y  5 nhiều nhất tại 1 điểm.
Vậy t  2 là nghiệm duy nhất của phương trình 1 . 1 Với t  2 : 2 x
 2  2x  4x  1  0 2 . Phương trình 2 có hai nghiệm phân bệt và tích tất 2x 1
cả các nghiệm thực của phương trình là . 2
Câu 31. (LIÊN TRƯỜNG THPT TP VINH NGHỆ AN NĂM 2018-2019) Biết phương trình  2 1   x 1  log     2log  
 có nghiệm duy nhất x a b 2 trong đó a , b là những 2018 2019    x x  2  2 x
số nguyên. Khi đó a b bằng A. 5 B. 1  C. 2 D. 1 Lời giải:  2 1 
Điều kiện: x  1 . Xét f (x)  log    trên 1; 2018  x x    f xx 1  
   hàm số nghịch biến trên 1; . x x x 0 x 1 2 ln 2018  2 1  2 1
Mặt khác: f (x)  0  log     0 
  1  x  2 x  1  0  x  3  2 2 . 2018  x x x xx 1  Xét g(x)  2log    trên 1; . 2019  2   2 x     x 2x 1 g    0, x
  1 hàm số đồng biến trên 1; . 2 x xln2019  x 1  x 1
Mặt khác: g(x)  0  log     0  
 1  x  2 x  1  0  x  3  2 2 . 2019  2   2 x  2 2 x  2 1   x 1  Xét phương trình log     2log  
  f x g x . 2018 2019        x x  2  2 x
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Do f x nghịch biến trên 1;  , gx đồng biến trên 1;  và f 3  2 2   g3  2 2  nên
phương trình f x  gx có nghiệm duy nhất x  3  2 2 .
Vậy a  3 , b  2 , do đó a b  5 .
Câu 32. (Đề thi chuyên vinh lần 1-2019 ) Cho hàm số   2x 2 x f x   
. Gọi m là số lớn nhất trong các số 0
nguyên m thỏa mãn f m  f  12
2m  2   0 . Mệnh đề nào sau đây đúng? A. m  1  513;2019 . B. m  1  009;1513 . C. m  505;1009 . D. m  1  ;505 . 0   0   0   0   Lời giải:    Ta có   xx  2  2
 2x  2x f x
 f x;    2x.ln22x f x ln 2  0, x  
hàm số   2x 2 x f x   
hàm số lẻ và tăng trên
Yêu cầu bài toán f m
 f m f m 12 12 12 2 2 2
 2m  2  m m  3 12 2 
m nguyên lớn nhất là: m     1365 0  3 
Câu 33. Cho phương trình 5x m  log x m với m là tham số. Có bao nhiêu giá trị nguyên của 5   m  20
 ;20 để phương trình đã cho có nghiệm? A. 20 B. 19 C. 9 D. 21 Lời giải:
Điều kiện: x m
x m  5t
Đặt: t  log x m  
 5x x  5t t 1 . 5 
 5x mt
Xét hàm số    5u      5u f u u f u ln 5  1  0, u   .
Do đó: 1     5x     5x x t x m m x .
Xét hàm số     5x f x x , x m
Do: 5x  0  m x , suy ra phương trình có nghiệm luôn thỏa điều kiện.      x 1 1  5x f x
ln 5 , f x  0  1  5 ln 5  0  x  log   . 5  ln5  Bảng biến thiên: x ∞ ≈ 0,295 +∞ y' + 0 ≈ 0,917 y ∞ ∞ m   2  0;20
Dựa vào bảng biến thiên  m  0
 ,917 m   1  9; 18;...;  1 .
Vậy có 19 giá trị nguyên của m thỏa ycbt.
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12   
Câu 34. Để giải phương trình log cot x  tan x  1  cos 2x  sin 2x trên khoảng 0;  , bạn Tuấn giải 2    4  theo các bước sau:    2 cos 2x
Bước 1: Do x  0;
 cot x  tan x   
0. Ta có: cot x  tan x
. Phương trình đã cho tương  4  sin 2x   
đương với: log cos 2x  cos 2x  log sin 2x  sin 2x * (Do x 0;
: sin 2x  0,cos 2x    0 ). 2 2    4  1
Bước 2: Xét hàm số f t  log t t,t  0;1  f t   1  0, t
  0;1 . Do đó hàm số f t 2       t ln 2
đồng biến trên 0;1.
Bước 3: Phương trình (2) có dạng: f cos2x  f sin 2x  cos2x  sin 2x  tan 2x  1  k     k x  
, k  . Vậy phương trình đã cho có tập nghiệm S    / k  . 8 2  8 2 
Bạn Tuấn giải đã đúng chưa? Và nếu sai thì bạn Tuấn giải sai bắt đầu từ bước nào? A. Bài giải đúng. B. Sai từ bước 1. C. Sai từ bước 2. D. Sai từ bước 3. Lời giải:   
Sai bước 3 vì điều kiện là giải phương trình trên tập 0;  , nhưng kết luận  4   k  S   
/ k   là chưa chính xác  8 2 
Câu 35. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Tìm tất cả các giá trị thực của tham số
m để phương trình 3m m ee   2 x   x  2 2 1
1  x 1  x  có nghiệm.  1   1   1   1  A. 0; ln2 B.   ; ln 2 C. 0;  D. ln 2;     2   2   e  2  Lời giải: 2 t  Đặt 2 2 2 2 1
t x  1  x t  1  2x 1  x x 1  x  . 2 2 1  x x 1 Ta có t' 
,t'  0  x  . 2 1  x 2 Vậy t   1  ; 2    .
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 2    m m t 1 Phương trình trở thành 3 3m m 3 ee  2t1 m
  e e t t e t . (sử dụng hàm đặc  2  m 1
trưng). Phương trình có nghiệm khi và chi khi 1
  e  2  m  ln 2  m(; ln2] . 2
Câu 36. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 3) Tìm tập S tất cả các giá trị thực của
tham số m để tồn tại duy nhất cặp số x; y thỏa mãn 2 log
4x  4y  6  m  1 và 2 2 x y 2   2 2
x y  2x  4y  1  0 . A. S   1  ;  1 B. S   5;   1;1;  5 C. S   5  ;  5
D. S    7;  5;  1;1; 5;  7 Lời giải: Ta có 2 log
4x  4y  6  m  1 2 2 2
 4x  4y  6  m x y  2 2 2 2
x y  4x  4y  8  m  0 2 2 x y 2  
 x  2  y  2 2 2 2
m là một hình tròn C tâm I 2;2, bán kính R m với m  0 hoặc là 1  1 2 2
điểm I 2; 2 với m  0 và 2 2
x y  2x  4y  1  0  x   1  y  2 
4 là một đường tròn C 2 
tâm J 1; 2 , bán kính R  2 . 2
TH1: Với m  0 ta có: I 2; 2C suy ra m  0 không thỏa mãn điều kiện bài toán. 2  2 log
4x  4y  6  m   1 2 2 x y 2  
TH2: Với m  0 . Để hệ 
tồn tại duy nhất cặp số x; y thì hình 2 2
x y  2x  4y  1  0
tròn C và đường tròn C tiếp xúc ngoài với nhau 2  1 
IJ R R 2 2
 3  0  m  2  m  1  m  1  . 1 2
Câu 37. (CỤM 8 TRƯỜNG CHUYÊN LẦN 1) Số giá trị nguyên của tham số m thuộc đoạn  201  9 ; 2  
để phương trình x  1 log 4x  1  log 2x  1   2x m  3   5  
có đúng hai nghiệm thực là A. 2 . B. 2022 . C. 1 . D. 2021 . Lời giải: 1  Điều kiện: x  . 4
Trường hợp 1: m  2 , phương trình đã cho trở thành:    x   x 1
1 log 4x  1  log 2x  1  2  0    3   5   
log 4x  1  log 2x  1  2   0 1  3   5      1  
Xét hàm số f x  log 4x  1  log 2x  1  2 là hàm đồng biến trên khoảng  ; + . 3   5     4 
Khi đó, nếu x là nghiệm của phương trình 1 thì x là nghiệm duy nhất. 0 0 Ta có: f 0  2
 ; f 1  0 , suy ra f 0 f 1  0 .
Theo hệ quả của định lý trung gian, tồn tại x 0 ; 
1 sao cho f x  0 . 0  0
Do vậy: m  2 thỏa mãn yêu cầu bài toán.
Trường hợp 2: m  2 , dẫn đến x  1 không phải là nghiệm của phương trình đã cho.
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 2x m
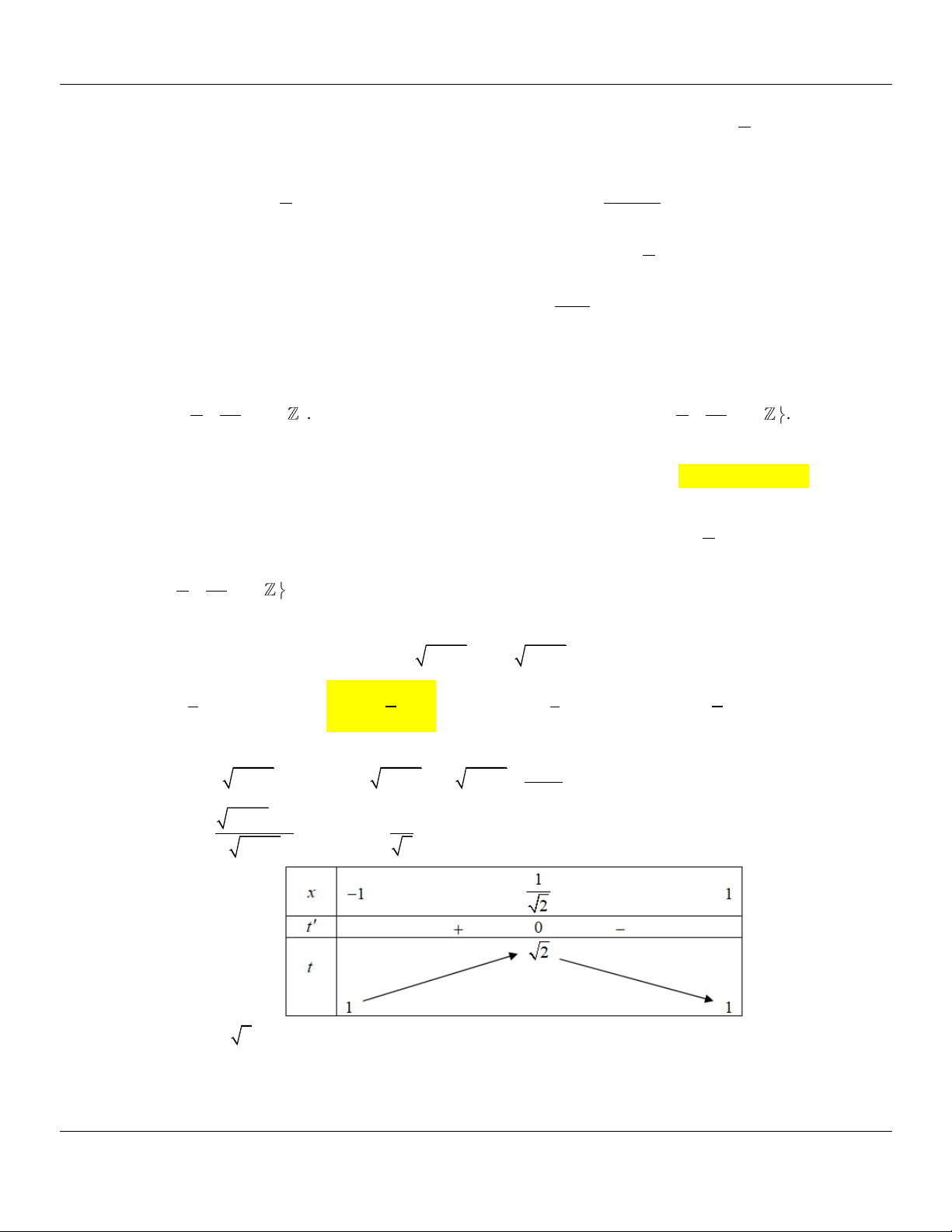
Phương trình đã cho trở thành: log 4x  1  log 2x  1   0 3   5   x1 2x m  1 
Xét hàm số gx  log 4x  1  log 2x  1 
, có tập xác định: D   ; 1  1; +    3   5   x1  4  4 2 2  m
Đạo hàm: gx      x   D . 4x   1 ln 3
2x 1ln5 x  0, 2 1 Bảng biến thiên:  1  
Dựa vào bảng biến thiên, ta suy ra: phương trình g x  0 có đúng hai nghiệm x  ; 1 ; 1  4 
x 1; + với mọi m  2. 2 
Vậy với mọi giá trị nguyên của tham số m  201  9 ; 2 
 thì phương trình đã cho luôn có hai nghiệm thực phân biệt.
Có 2022 giá trị nguyên m thỏa mãn yêu cầu bài toán.
- Đây là bài toán về sự tương giao.
- Tuy nhiên nếu chúng ta cô lập m thì việc khảo sát hàm biến x khá phức tạp. Ý tưởng của tương
ứng phương trình có 1 nghiệm
Bài toán tổng quát ax b
F x,m  f x 
 0 với f x  0 và ad bc  0 cx d
Cách 2 : Đặt f x  log 4x  1  log 2x  1 3   5   x  1
TH1 : m  2 , Phương trình   .  f  x  2  1 
Vì f x là hàm số tăng trên  ; 
  f x  2 có nghiệm duy nhất khác 1.  4 
Vậy m  2 thỏa mãn bài toán.
TH2 : m  2 , dẫn đến x  1 không phải là nghiệm của phương trình đã cho. x m
Phương trình đã cho trở thành : f x 2   0 x  1 x m 2  m
Đặt gx  f x 2 
; gx  f x   0. x  1 x  2 1 Ta có bảng biến thiên :
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
gx  0 có đúng hai nghiệm phân biệt. Vậy m  201  9 ; 2 
 nên ta có 2022 giá trị nguyên m . Bài toán tương tự:
Bài toán 50.1 Tìm số giá trị nguyên m 3 ; 2019   sao cho phương trình m log  1  log  1 x x x x
x m e mx  9 có đúng hai nghiệm thực. 2   2    
Câu 38. (CHUYÊN KHTN NĂM 2018-2019 LẦN 01) Cho số thực  sao cho phương trình
2x  2x  2 cos x có đúng 2019 nghiệm thực. Số nghiệm của phương trình
2x  2x  4  2 cos x là A. 2019 . B. 2018 . C. 4037 . D. 4038 . Lời giải: x x   x 2 2 2    x x 2 2 2 cos   1   x Ta có: x x    x 2 2 2 2 2 2 4 2 cos  2  2   4cos     2 x x     x 2 2 2  2  2   cos 2  2 Nhận xét
1. Phương trình 1 có 2019 nghiệm khác 0 (do giả thiết và 0 không là nghiệm).
2. x là nghiệm của phương trình 1 khi và chỉ khi x là nghiệm của phương trình 2 vì 0 0 x xx x 0 0 0   0     x   x 2 2 0 0  2 2 2  2  2cos  2  2  2  cos . 2 2
3. Hai phương trình 1 và 2 không có nghiệm chung vì x x   x   2 2 2  2  2cos x cos  0   cos0  0 2   2     x . x x x x   x    x 0 2 2    2 2 2 2 2 cos 2  2    0  2
Vậy số nghiệm của phương trình 2x  2x  4  2cosx là 4038.
Câu 39. (CHUYÊN PHAN BỘI CHÂU NGHỆ AN NĂM 2018-2019 LẦN 04) Có bao nhiêu giá trị
nguyên của m thuộc đoạn  100  ;100  
 để phương trình 2019x mx  1 có hai nghiệm phân biệt? A. 94 B. 92 C. 184 D. 100. Lời giải:
*) TH1: m  0
+ Vế trái của phương trình là hàm số đồng biến trên tập .
+ Vế phải của phương trình là hàm số nghịch biến trên tập .
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Nếu phương trình đã cho có nghiệm thì nghiệm đó là duy nhất ( không thỏa mãn đề bài).
*) TH2: m  0 . Khi đó phương trình trở thành: 2019x  1  x  0 .
Vậy phương trình có nghiệm duy nhất x  0 ( không thỏa mãn đề bài).
*) TH3: m  0 . Xét hàm số    2019x f x
mx  1 trên .    2019x f x .ln 2019  m .   m
f x  0  x  log . 2019 ln 2019 m m m Đặt a  log  f a   . m log  1 . 2019  2019 ln 2019 ln 2019 ln 2019
Bảng biến thiên của hàm số y f x :
Để phương trình có hai nghiệm phân biệt thì đồ thị hàm số y f x phải cắt trục hoành tại hai m m
điểm phân biệt. Điều đó tương đương với f a  0   . m log  1  0 (1). 2019 ln 2019 ln 2019 m Đặt t
t  0 . Khi đó m t.ln2019. ln 2019
Bất phương trình (1) trở thành: t t.ln 2019.log
t  1  0  t t.ln t  1  0  t.ln t t  1  0 . 2019
Xét hàm số gt  t.lnt t  1 trên 0;  ; gt  lnt; gt  0  t  1.
Bảng biến thiên của hàm số y g tm
Từ bảng biến thiên ta thấy g t  0 với t  1 . Vậy
 1  m  ln2019 . ln 2019 m  0 Kết luận: 
thỏa mãn yêu cầu bài toán. m   ln 2019
Do m  và m  100  ;100 
 nên m1; 2; 3...10 
0 . Vậy có 100 giá trị m thỏa mãn yêu cầu bài toán.
Câu 40. Tìm tất cả các giá trị của m để phương trình lnm  lnm  sin x  sin x có nghiệm. 1 1 A.  1  m  e 1. B. 1  m  e 1. C. 1  m   1. D. 1  m  e 1. e e Lời giải:
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 u   
lnm  sin xu
e m  sinx
Đặt u  lnm  sin x ta được hệ phương trình:    ln
 m u sin  sin x x em u
Từ hệ phương trình ta suy ra: u sin x
e u e  sin x * Xét hàm số   t
f t e t có '  t
f t e  1  0, t
  . Hàm số f t đồng biến trên .
*  f u  f sinx  u  sinx Khi đó ta được:    sin ln sin  sin x m x x e
 sin x m* *
Đặt z  sin x,z  1;1 . 
 Phương trình * * trở thành: z
e z m* * Xét hàm số:   z
g z e z trên 1;1.   Hàm số   z
g z e z liên tục trên 1;1 
 và có max gz  g1  e  1,min gz  g0  1  1  ;1  1  ;1    
Hệ phương trình ban đầu có nghiệm  phương trình * * có nghiệm  1  m e  1.
Câu 41. (CHUYÊN SƠN LA NĂM 2018-2019 LẦN 03) Tổng tất cả các giá trị của tham số m để 2 2
phương trình x 4x5m 2 2  log
m  1 có đúng 1 nghiệm là 2 x 4x6   A. 1 . B. 0 . C. 2  . D. 4 . Lời giải: 2 2 2 2
x 4x6 m 1
Ta có x 4x5m 2 2 2  log m  1  2  log m  1 . 2 x 4x6     2 x 4x6   2
a x  4x  6 Đặt 
, ta có a  2; b  1 , phương trình đã cho trở thành 2ab  log b . 2  ab m  1
2ab  1
+) Nếu a b thì  không thỏa mãn. log b  1  a
2ab  1
+) Nếu a b thì  không thỏa mãn. log b  1  a
Do đó a b , khi đó phương trình đã cho tương đương với 2 2 2 2
x  4x  6  m  1  x  4x  5  m
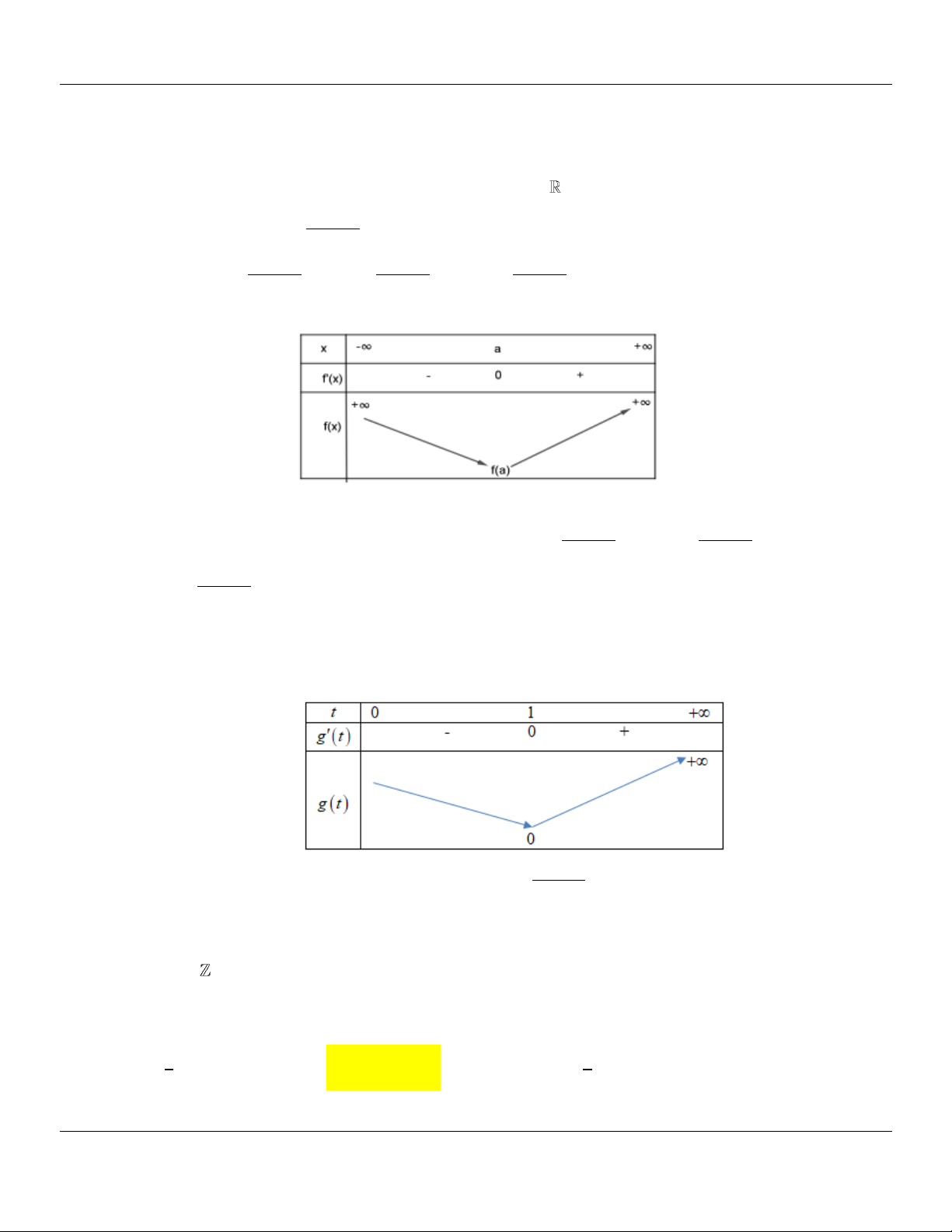
Số nghiệm của phương trình đã cho bằng số giao điểm của parabol 2
y x  4x  5 và đường thẳng 2 y m .
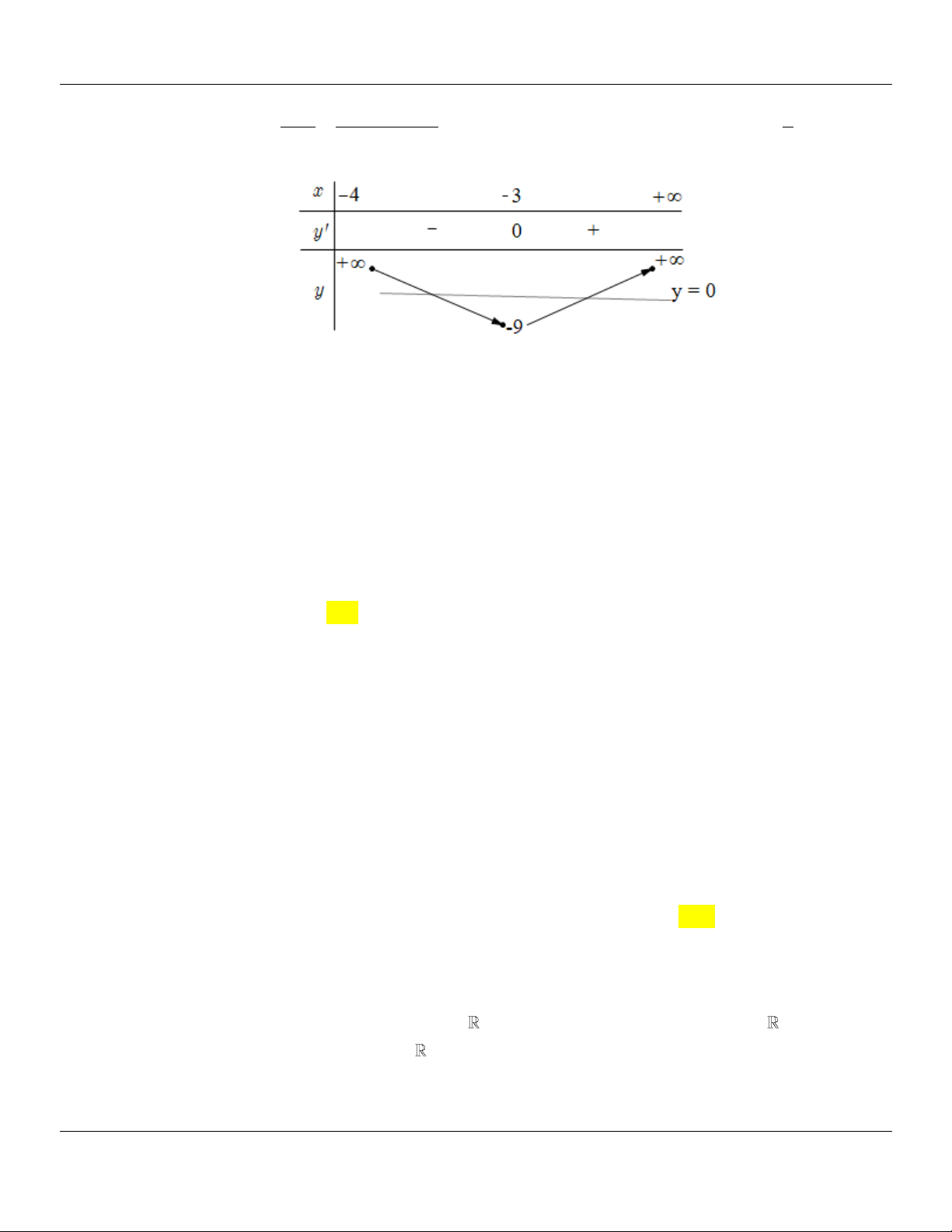
Ta có hình ảnh minh họa sau
Dựa vào đồ thị, phương trình đã cho có đúng 1 nghiệm khi và chỉ khi 2
m  1  m  1  .
Vậy tổng các giá trị của tham số m là 0.
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Câu 42. (THPT CHUYÊN VĨNH PHÚC NĂM 2018-2019 LẦN 02) Biết rằng phương trình
ex  ex  2 cos ax ( a là tham số) có 3 nghiệm thực phân biệt. Hỏi phương trình
ex  ex  2 cos ax  4 có bao nhiêu nghiệm thực phân biệt? A. 5 B. 10 C. 6 D. 11 Lời giải:
Ký hiệu ex  ex  2cos ax là phương trình (1) và ex  ex  2 cos ax  4 là phương trình (2). 2 2 x x x x 2 2      ax
Ta có ex  ex  2 cos ax  4  e 2  e 2   
ax    e2  e 2 2 2 cos 1      2cos  .    2  x x   ax e2  e 2  2cos
Do đó ex  ex 2
 2cosax  4   . x x   ax e2  e 2  2   cos  2
Suy ra cứ mỗi nghiệm của phương trình (1) sẽ có 2 nghiệm của phương trình (2).
Thật vậy, với x là nghiệm của (1) thì 2x và 2
x là các nghiệm của (2). 0 0 0
Vậy phương trình cần tìm có 6 nghiệm.
Câu 43. (CHUYÊN HƯNG YÊN NĂM 2018-2019 LẦN 03) Cho hàm số x4 7 ( )  3  (  1).2 x f x x  6x  3 . a a
Giả sử m  ( a,b  , là phân số tối giản) là giá trị nhỏ nhất của tham số thực m sao cho 0 b b phương trình f  2
7  4 6x  9x   2m 1  0 có số nghiệm nhiều nhất. Tính giá trị của biểu thức 2
P a b . A. P  11. B. P  7. C. P  1. D. P  9. Lời giải: 4  6 18x 1 Đặt 2
t  7  4 6x  9x 1 thì f t  1  2m2 ; t' 
t'  0  x  . 2  3 2 6x 9x
Từ BBT suy ra nếu t 3;7 thì phương trình (1) có 2 nghiệm x. Xét hàm số x4 7 ( )  3  (  1).2 x f x x
 6x  3 ;   x4 7 x       7 3 ln 3 2 1 2 x f x x ln 2  6   x4 2    7 3 ln 3 2 x f x
ln 2x  1ln2  2  0 x    3;7
Do đó hàm số f x đồng biến trên 3;7 . Mặt khác, f 6. f 7  0 nên phương trình f x  0
có một nghiệm x   6;7 .
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Vậy, phương trình f t  1  2m có nhiều nghiệm nhất khi   f   5 1 f    1 2m  4    m  2 2 5
Kết luận, GTNN của m là  a  5,b  2. 2
Câu 44. (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 01) Có bao nhiêu cặp số nguyên ( ; x y) thỏa mãn
0  x  2020 và log (3  3)   2  9y x x y ? 3 A. 2019 . B. 6 . C. 2020 . D. 4 . Lời giải:
Điều kiện: x  1 Ta có: y 2 log (3  3) 
 2  9  log ( 1)  ( 1)  2  3 y x x y x x y (*) 3 3 Xét hàm số ( )   3t f t t ,t  có (  ) 1 3t f t ln 3  0, t
  , tức hàm số luôn đồng biến trên
. Khi đó (*)  (log ( 1))  (2 )  log ( 1)  2   9y f x f y x y x 1 3 3
Vì 0  x  2020 nên 0  9y 1  2020  0  y  log 2021 . 9
Do y nguyên nên y 0;1;2;  3 .   ; x y    0;0;8 
;1 ;80; 2;728;3 nên tổng cộng có 4 cặp số nguyên ( ; x y) thỏa đề.
Câu 45. (ĐTK BGD&ĐT NĂM 2019-2020 LẦN 02) Có bao nhiêu số nguyên x sao cho tồn tại số thực
y thỏa mãn log  x y  log  2 2 x y ? 3 4  A. 3. B. 2. C. 1. D. Vô số Lời giải: Điều kiện 2 2
x y  0; x y  0.
x y  3t
Ta đặt: log  x y  log  2 2 x yt . Ta có    1 3 4  2 2
x y  4t Vì     2    3t 2 2 2 2  2.4t x y x yt  log 2 9 4 log 9 2 Thế thì 2 2 t 2 4
x y  4  4
 3,27 , vì x nguyên vậy nên x 0  ;1 . y  3t t   0
ới x  0 , ta có hệ    2 y  4ty  1
y  3t 1 t   0
ới x  1, ta có hệ  . Hệ này có nghiệm  . 2
y  4t 1 y  0
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
y  3t 1 2
ới x  1, ta có hệ 
. Ta có phương trình 3t
1 4t 1 9t 2.3t 4t        2  0* 2
y  4t 1 Đặt   9t 2.3t 4t f t     2, ta có
Với  0  9t  4t t
f t  0 Với  0  4t t
 2  f t  0
Vậy phương trình * vô nghiệm
Kết luận: Vậy x 0;  1
Câu 46. Cho a  0 , b  0 thỏa mãn log a b   a b
 . Giá trị của a  2b bằng ab  2 2 9 1 log 3 2 1 2 3 2 1  6ab1   7 5 A. 6 B. 9 C. D. 2 2 Lời giải:
a  0 , b  0 nên ta có log 6ab  1  0 ; log
3a  2b  1  0 . 6ab1   3a2b1   Ta có 2 2
9a b  6ab . Dấu đẳng thức xảy ra khi a  3b . Do đó, ta có: log a b   a b   log 6ab  1  log 3a  2b  1 3a2b1   6ab1   ab  2 2 9 1 log 3 2 1 3 2 1  6ab1    2 log 6ab  1 .log
3a  2b  1  2 log
3a  2b  1  2 . 3a2b1   3a2b1   6ab1  
Dấu đẳng thức xảy ra khi và chỉ khi b  3a   0  log 6ab  1  log 3a  2b   1  3a2b1   6ab1  
b  3a  0 
b  3a  0      (do log a   ) a  2 18 1 0 9 1  log a   a   log a    a   2 18 1 1 9 1  a   2 18 1 log 9 1 9 1  2    18a 1  3  
b  3a  0 b    7  2  
. Suy ra a  2b  . 2 1
 8a  1  9a  1 1  2 a   2
Câu 47. Cho phương trình 3x m  log (x  )
m với m là tham số. Có bao nhiêu giá trị nguyên của 3 m  15; 
15 để phương trình đã cho có nghiệm? A. 16 B. 9 C. 14 D. 15 Lời giải:
Ta có: 3x m  log x m  3x x  log (x  )
m x m (*) . 3   3
Xét hàm số ( )  3t f t
t , với t  . Có '( )  3t f t ln 3  1  0, t
  nên hàm số f t đồng biến trên
tập xác định. Mặt khác phương trình (*) có dạng: f (x)  f log (x  ) m . Do đó ta có 3 
f (x)  f log (x  ) m
x  log (x m)  3x x m  3x x  m 3  3  1 
Xét hàm số    3x g x
x , với x . Có '( ) 3x g x
ln 3  1 , g'(x)  0  x  log   3  ln3  Bảng biến thiên
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Từ bảng biến thiên ta thấy các giá trị của tham số để phương trình có nghiệm là:    1 
m ; g log  
 . Vậy số giá trị nguyên của m 15; 
15 để phương trình đã cho có 3    ln 3  nghiệm là: 14 . 9t
Câu 48. (MĐ 103 BGD&ĐT NĂM 2016-2017) Xét hàm số f t
với m là tham số thực. Gọi S t 2 9  m
là tập hợp tất cả các giá trị của m sao cho f x  f y  1 với mọi x, y thỏa mãn xy e
ex y.
Tìm số phần tử của S . A. 0. B. 1. C. Vô số. D. 2. Lời giải: x e  .ex Ta có nhận xét: xy   e
ex y  x y  1. ( Dấu ‘’=’’ xảy ra khi x y  1). y e  .ey
Do đó ta có: f (x)  f (y)  1  f (x)  f (1  x)  1 x 1x 2 x 2 1 9 9
9  m .9  9  m .9 x    1   1 x 2 1x 2 2 x 2 1x 4 9  m 9  m
9  m .9  m .9  m 2 x 2 1x 2 x 2 1x 4
 9  m .9  9  m .9
 9  m .9  m .9  m 4
m  9  m   3 .
Vậy có hai giá trị m thỏa mãn yêu cầu.
Câu 49. (SỞ GD&ĐT PHÚ THỌ NĂM 2018-2019 LẦN 01) Cho a  0 , b  0 thỏa mãn 3 2 3
a ab b log
a  3b  log a  log b . Giá trị của bằng 16   9 12 3 2 3
a a b  3b 6  13 8  17 13 5  13 3  13 A. B. C. D. 11 69 6 11 Lời giải: log
a  3b  log a  log b t . 16   9 12
a  3b  16tt tt 9   12   3  3   13
Khi đó a  9t 9t 3.12t 16t      3.      1     .   16   16   4  2 b  12t  3  a   a        1 3 2 3
a ab bb   b  5  13    . 3 2 3 3 2
a a b  3ba   a  6       3  b   b
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Câu 50. (THPT NGUYỄN KHUYẾN TP.HCM NĂM 2018-2019) Cho a , b là các số dương thỏa mãn 5b a a
log a  log b  log . Giá trị của bằng 9 16 12 2 b a a 7  2 6 a 1  6 a A.  1   6 . B.  . C.  . D.  7  2 6 . b b 25 b 5 b Lời giải:  a  9t 2t 5b aa  3 
log a  log b  log
t . Khi đó b  16t   . 9 16 12   2  b  4  5b a   12t  2 t t     2t t  3   3  Ta có: 5.16t 9t 2.12t   9 12  5     2.     2.  5      0 .  16   16   4   4  t 2t  3  a  3  Suy ra  1   6    7      2 6 .  4  b  4 
Câu 51. (KSCL THPT NGUYỄN KHUYẾN LẦN 05 NĂM 2018-2019) Với các số thực x , y dương thỏa  x y x
mãn log x  log y  log   . Tính tỉ số . 9 6 4  6  y A. 3 B. 5 C. 2 D. 4 Lời giải: x  9tx y  
Đặt t  log x  log y  log 
  y  6t . 9 6 4  6 
x y  6.4t  2t t     t   t t t 3 3 3 x Suy ra 9  6  6.4    6      0     2   2 .  2   2   2  y
Câu 52. (SỞ GD&ĐT HÀ NỘI NĂM 2018-2019) Cho phương trình 2x  .2x m
.cos x  4 , với m là
tham số. Gọi m là giá trị của m sao cho phương trình trên có đúng một nghiệm thực. Khẳng 0
định nào sau đây là đúng? A. m   5;  1  . B. m  5. C. m   1  ;0 . D. m  0. 0   0   0 0 Lời giải:
Phương trình x x    x 2 4 .2 .cos  4  2  2 x m x  .
m cos x
Điều kiện cần: nếu x là một nghiệm của phương trình thì 2  x cũng là nghiệm. Vì phương 0 0
trình có nghiệm duy nhất nên x  1 0
Thay vào phương trình ta có: m  4. Điều kiện đủ: 2
Với m  4 ta có x x    x x       x 2 4 4.2 cos 4 0 2 2 cos   4sin  x  0
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 2x  2  cos x 2x  2  cos x    2x  2       x     x  . sin  x cos  1  0   cos  x 1   cos  x 1  1 
Vậy m  4 thỏa mãn.
Câu 53. (SỞ GD&ĐT NINH BÌNH LẦN 01 NĂM 2018-2019) Số nghiệm của phương trình x x5 50  2  3.7x là: A. 1 . B. 2 . C. 3 . D. 0 . Lời giải: Phương trình x x5 50  2  3.7x x x5  50  2  3.7x  0 . Xét hàm số x x 5 ( ) 50 2 3.7x f x     x x 5 ( ) 50 ln 50 2 ln 2 3.7x f x      ln 7 x  2 x  2 x f x       2 5 ( ) 50 ln 50 2 ln 2 3.7 ln7 x     x 50 2 2 2
Khi x  0 thì f (  x)  7  ln50  3ln7 x5     2 ln2  7      0     x 50 (  )  7 
ln502  3ln72   2x f x  ln22 5    0  7      x     x 2 2 2 2 Khi x  0 thì (  )  7 
32 ln 2  3ln7     50x f x ln50  7      0     x 2 (  )  7 
32ln 22  3ln72   50x f x ln502    0  7      Suy ra f (
 x)  0, x
  . Nên f (x) đồng biến trên .
Mà lim f x  0 nên f (x)  0, x
  . Suy ra f (x) đồng biến trên . x
Mà lim f x  0 nên f (x)  0, x
  . Suy ra phương trình f (x)  0 vô nghiệm. x
Câu 54. (THPT CHUYÊN LAM SƠN THANH HÓA NĂM 2018-2019 LẦN 01) Cho a là số thực
dương, a  1 . Biết bất phương trình 2 log x x  1 nghiệm đúng với mọi x  0 . Số a thuộc tập a hợp nào sau đây? A. 7;8 B. 3; 5 C. 2; 3 D. 8;  Lời giải:
Ta có: với x  1 thì 2log 1  0  1  1 a
Ta sẽ tìm a để đường thẳng y x  1 nhận làm tiếp tuyến của đồ thị hàm số y  2log x tại a điểm x  1 2 2 2 Có y   y  1 
. Phương trình tiếp tuyến y  x 1 xlna ln a ln a
Vậy để đường thẳng y x  1 nhận làm tiếp tuyến của đồ thị hàm số y  2 log x thì a 2 2
 1  ln a  2  a e ln a
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
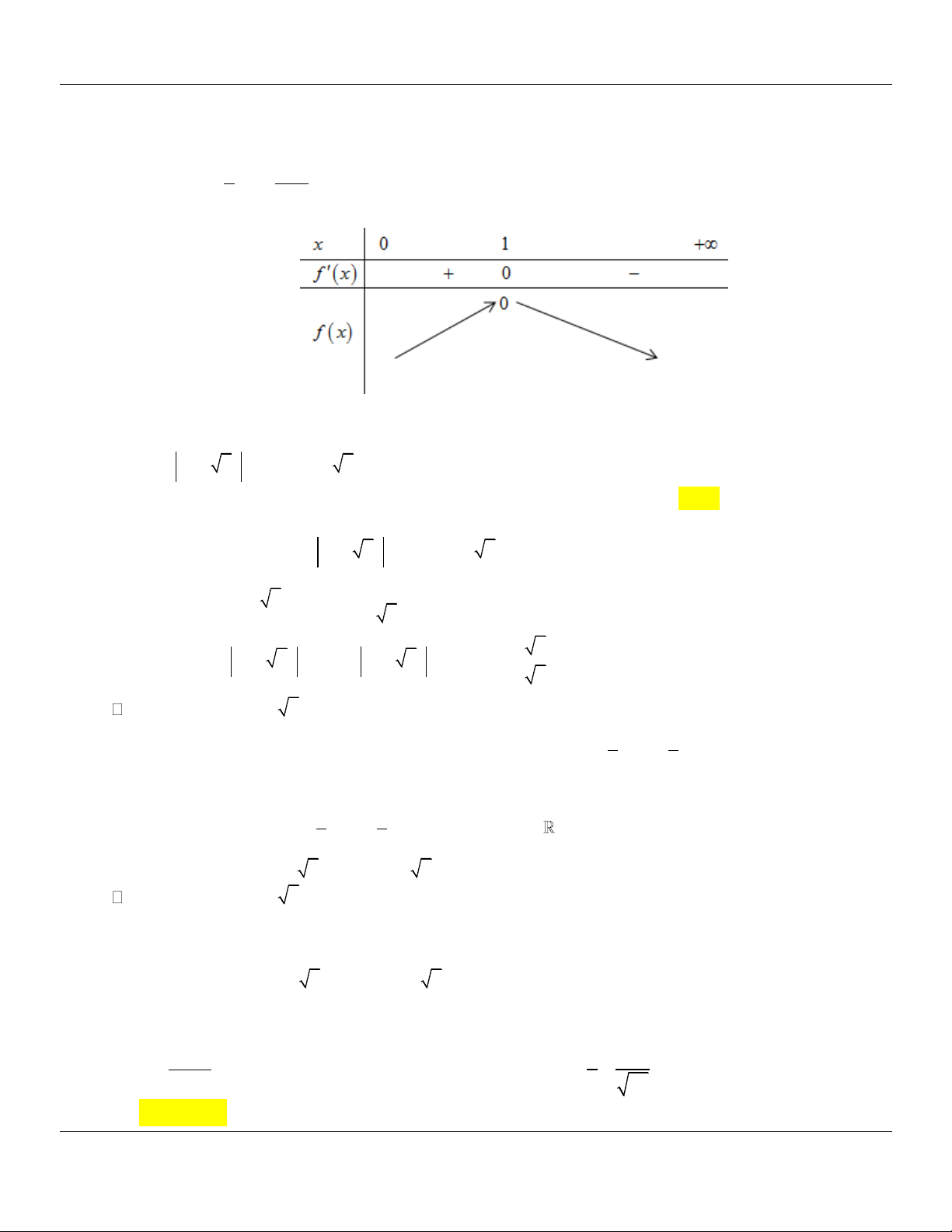
2log x x  1  ln x x  1 2 Thử lại 2
a e ta sẽ chứng minh e
f x  lnx x  1 0 x   0 1 1  x
Có f x   1 
f x  0  x  1 x x Bảng biến thiên
Từ bảng biến thiên suy ra f x  0  ln x x  1 x   0
Câu 55. (SỞ GD&ĐT VĨNH PHÚC NĂM 2018-2019 LẦN 02) Số nghiệm thực của phương trình 2
log x  2x  log  2
x  2x  2 là 3 5  A. 4 . B. 3 . C. 1 . D. 2 . Lời giải: Xét phương trình 2
log x  2x  log  2
x  2x  2 (1) 3 5  x   0 Điều kiện: 2
x  2x  0   . x  2 2
x  2x  3t Đặt 2
t  log x  2x , ta có: 2
x  2x  3t   3 2
x  2x    3t
Trường hợp 1: 2  2  3t x x t t    
Phương trình (1) viết lại: log 3t t   2 5t 3t    3 1 2  1     2 (2) 5      5   5 
Dễ thấy phương trình (2) có nghiệm t  1 . t t    
Lại có: hàm số f t 3 1    
2  nghịch biến trên nên t  1 là nghiệm duy nhất của (2).  5   5 
Với t  1 , ta có: 2 2
x  2x  3  x  2x  3  0 ( phương trình này có 2 nghiệm thực).
Trường hợp 2: 2  2  3t x x
Phương trình (1) viết lại: log 2 3t t   5t 2 3t    5t 3t    2 (3) 5  
Tương tự như trường hợp 1, ta có t  0 là nghiệm duy nhất của (3)
Với t  0 , ta có: 2 2 x  2x  1
  x  2x  1  0 ( phương trình này không có nghiệm thực).
Vậy phương trình đã cho có tất cả 2 nghiệm thực.
Câu 56. (THPT Chuyên Vĩnh Phúc-lần 2-năm 2017-2018) Xét các số thực dương x , y thỏa mãn 1 2x  1 1 ln
 3x y 1  
. Tìm giá trị nhỏ nhất P của P   .  x y  min x xy A. P  8 . B. P  4 . C. P  2 . D. P  16 . min min min min
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 Lời giải: 1
Điều kiện 0  x  . 2 1 2x  Từ giả thiết ln
 3x y 1  
 ln 1 2x  1 2x  ln x y  x y   1  x y
Xét hàm số f t   ln t t trên 0;  có f t  1
 1  0 , t  0 do đó hàm f t đơn điệu. t Vậy  
1  1 2x x y  3x y  1 2 1 1 1 2 1 2 Có P       x xy x x y x 1 2x 1 4
Đặt g x 1 2  
, ta có g x   
suy ra g x 1  0  x  . x 1 2x 2 x 12x2 4
Do đó min g x  8 . Vậy P  8 .  min 1  0;    2 
Câu 57. (THTT Số 3-486 tháng 12 năm 2017-2018) Xét các số thực dương x, y thỏa mãn x y log
xx 3  yy 3  x .
y Tìm giá trị lớn nhất P của biểu thức 3 2 2
x y xy  2 max 3x  2 y 1 P  . x y  6 A. 3 . B. 2 . C. 1. D. 4 . Lời giải: x y Ta có: log
xx 3  yy 3  xy 3 2 2
x y xy  2
 log 3x y  3x y  log  2 2
x y xy  2 2 2
x y xy  2 . 3 3
Xét hàm số f t   log t t , t  0 có f t  1 
1  0, t  0 . Vậy hàm số f t luôn 3 t ln 3
đồng biến và liên tục trên khoảng 0;  .
Do đó: f   x y  f  2 2
x y xy     x y 2 2 3 2 3
x y xy  2   1 2 Cách 1: Từ  
1  xy   x y  3 x y  2 . 2
x y 1
Ta có x x xy xy x y   1  xy     xy  2 
Đẳng thức xảy ra khi và chỉ khi x y 1.
x y  2 1 2 Do đó từ   1 , suy ra: x
 x y  3x y  2 . 4
Đặt t x y , t  0 . t  2 1 t    t t  2  x y 2 2 1 3 2 2 1 x 3
t  22t  3 Suy ra: 4 P     f t . x y  6 t  6 4 t  6  
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 2 3
t  36t 135
Ta có: f t     t  (nhận) 4t  6 0 3 2 Bảng biến thiên t 0 3  f t    0 f t  x y 1 x  2
Dựa vào BBT, ta có max P  max f t   f 3  1 khi và chỉ khi    . 0; x y  3 y 1
Cách 2: (Trắc nghiệm) x 11 Ta có: P  2  . x y  6 Trong  
1 coi y là ẩn, x là tham số. Ta có 2
y   x   2
3 y x  3x  2  0 có nghiệm khi   
  x  32  4 3 2 3 3 2 3 2
x  3x  2  0   x
 3 nên x 11 0 3 3
Vậy P  2 nên trong 4 phương án thì P
 1 khi đó x  2 , y 1. max Cách 3: (Trắc nghiệm) y 17 Ta có: P  3 
 3 với x , y  0. x y  6 3x  2 y 1 + Nếu P  2 thì
 2  x 11. Thay vào   1 ta được: 2
y  3y  90  0 (vô lý). x y  6 3x  2 y 1 + Nếu P  1 thì
1  2x y  5  y  5  2x . Thay vào   1 , ta được: x y  6
x   x  x   x2 2
x  x 2 3 5 2 5 2 5 2
 2  3x 12x 12  0  x  2  y  1. Vậy P  1. max
Câu 58. (SỞ GD&ĐT BẮC NINH NĂM 2018-2019 LẦN 01) Tập nghiệm của bất phương trình log  2 2
x x  2  4  x  2
 2x x  2  1 là  a; b 2  . Khi đó . a b bằng 15 12 16 5 A. . B. . C. . D. . 16 5 15 12 Lời giải: 2x Ta có: 2 2
x x  2  x x 2
x  2  x  . 2 x  2  x Ta có: log  2 2
x x  2  4  x  2
 2x x  2  1  log x x  2  x  4  2x x  2  1 2   2   2 2  2 2
3x  2 x  2  2x  2  log 
 4  2x x  2  1 2  log
 2x x  2  1, 1 2   2   2
x  2  x  2 x  2  x
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 Ta có 2
x  2  x  0 , x   . x  0  8 Điều kiện: 2
3x  2 x  2  0 2  2 x  2  3  x   x  0  x   ,*   5 2 2
4x  8  9x
Với điều kiện * , ta có
 1  log 3x  2 x  2  3x  2 x  2  log x  2  x x  2  x, 2 2  2  2 2  2  2  
Xét hàm số f t  log t t với t  0 . Có f t 1   1  0 , t  0; . 2 t.ln 2
Hàm số f t  log t t 0;  ,  2
3x  2 x  2 0; và  2
x  2  x0; 2 đồng biến trên   Nên    f  2 x
x    f  2 2 3 2 2
x  2  x  2  x  0 x  0 2 2  2
3x  2 x  2  x  2  x 2  x  2  2  x      x   . 2 2 
x  2  4x 2 3x  2 3  8 2  16
Kết hợp với ĐK ta có tập nghiệm bất phương trình là   ;    hay . a b  . 5 3   15
Câu 59. (MĐ 103 BGD&ĐT NĂM 2019-2020) Có bao nhiêu số nguyên x sao cho ứng với mỗi x có
không quá 127 số nguyên y thỏa mãn log  2 x y  log x y ? 3  2   A. 89 . B. 46 . C. 45 . D. 90 . Lời giải: Ta có log  2 x y  log x y 1 3  2   
Đặt t x y  * (1)  log  2
x x t   log t g(t)  log t  log  2
x x t  0 2 3 2 2 3    1 1 Đạo hàm g (  t)  
 với mọi y . Do đó g t đồng biến trên 1; t ln 2  0 2
x x t ln 3
Vì mỗi x nguyên có không quá 127 giá trị t  * nên ta có
g(128)  0  log 128  log  2
x x 128  0 2 3  2 7
x x 128  3  44,8  x  45,8
Như vậy có 90 giá trị thỏa yêu cầu bài toán.
Câu 60. (MĐ 103 BGD&ĐT NĂM 2019-2020) Xét các số thực không âm x và y thỏa mãn x y 1 2x .4 y   
 3 . Giá trị nhỏ nhất của biểu thức 2 2
P x y  2x  4 y bằng 33 9 21 41 A. . B. . C. . D. . 8 8 4 8 Lời giải: Ta có xy 1  
     x y 1  2    y     32 2 .4 3 2 3 .4 .4 0 2 .2 3 2 2 x x y x y y x  3 3 x  21
Xét TH: 3  2x  0  x
. đúng với mọi giá trị 2 2 
2  P x y  2x  4 y  2 4 y  0
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 3
Xét TH: 3  2x  0  0  x  . 2
Xét hàm số    .2t f t t với t  0
    2t  .2t f t t
.ln 2  0 với mọi t  0 3
f 2y  f 3  2x  2y  3  2x y   x . Khi đó: 2 2  2 3  33  5  41 41 2 2 2
P x y  2x  4 y x
x  2x  23 2x 2
 2x  5x     2 x       2  4  4  8 8 41 5 1
So sánh và ta thấy GTNN của P là khi x  , y  . 8 4 4
Câu 61. (THPT Trần Hưng Đạo-TP HCM năm 2017-2018) Xét các số thực dương x , y thỏa mãn  2 2 x y  1 2x y 2018    
. Tìm giá trị nhỏ nhất P của P 2 y 3x . min x  2 1 1 7 3 5 A. P  . B. P  . C. P  . D. P  . min 2 min 8 min 4 min 6 Lời giải:  2 2 x y  1 2x y 2x y Cách 1: Ta có 2018  2      2 x y 1 log 2018 2 x  2 1 x   1  2x  2
1  2 2x y  log
2x ylog x  2 1 2018 2018  2x  2 1  log x  2 1
 2 2x y  log 2x y 2018   2018   2
Có dạng f  x  
1   f 2x y  
với f t   2t  log t ,  t   0 . 2018
Xét hàm số f t   2t  log t ,  t
  0 , ta có f t 1  2   0  t   0 nên hàm số 2018 t.ln 2018 2
f t  đồng biến trên khoảng 0;   . Khi đó f  x  
1   f 2x y     x  2 1  2x y 2
y x 1.
Ta có P y x   2 x   2 2 3 2
1  3x  2x  3x  2 . Bảng biến thiên 3 x   4   P 7 8 7 3 Vậy P  khi x  . min 8 4
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 2 
2x 2x  1 2 2 x y  1 2x y  2 2 x 2 x 1
 2xy 2x y 2018 2x y Cách 2: Ta có 2018       2018 2 22 xy 2 x  2 1 x   1 2018 x   1 x 2 2 1 2018 2x y   . 22 xy 2018 x  2 1 2 2018 u v
Đặt u   x  2
1 , v  2x y với u , v  0 . Phương trình trên có dạng:  2 2018 v u 2u 2  .2018  .2018 v u v  
1 với u , v  0 .
Xét hàm đặc trưng    .2018t f t t
có    2018t  .2018t f t t
.ln 2018  0 với  t   0 , suy ra hàm
số f t  đồng biến trên 0;   . Do đó phương trình  
1 có dạng f u  f v  u u  x  2 1  2x y 2
y x 1. Khi đó P y x   2 x   2 2 3 2
1  3x  2x  3x  2 có đồ thị là  3 7  7
một đường cong Parabol, đỉnh là điểm thấp nhất có tọa độ I ; 
 . Do vậy, P  khi  4 8  min 8 3 x  . 4
Câu 62. (THPT Mộ Đức-Quãng Ngãi-lần 1 năm 2017-2018) Cho hai số thực dương x , y thay đổi thỏa mãn đẳng thức 
  xy     2 2 1 2 1 .2 .2x y xy x y
. Tìm giá trị nhỏ nhất y của y . min A. y  3 . B. y  2 . C. y  1. D. y  3 . min min min min Lời giải: 2 Ta có 
  xy     2 2 1 2 1 2 2x y xy x yxy
 2xy 1  2x yx y 1 2 1 1 2 2         1
Xét hàm       1 .2t f t t với t  1.
Khi đó    2t     1 .2t f t t
.ln 2  0 với t  1. 2 x  2 Từ   2
1  2xy 1  x y 1  y  2x 1 2 2x  2x  4 x y   2     2   2x 2x 4 0  2x   0 2 1 x  1 
Loại x  1 vì điều kiện của t nên f 2  2 .
Câu 63. (THPT Chuyên Thái Bình – Thái Bình – Lần 5 năm 2017 – 2018) Cho 2 số thực dương x, y y 1 
thỏa mãn log  x 1 y 1 
 9  x 1 y 1 . Giá trị nhỏ nhất của biểu thức P x  2y là 3       11 27 A. P  . B. P  . C. P  5   6 3 . D. P  3  6 2 . min 2 min 5 min min Lời giải: y 1 
Ta có log  x 1 y 1 
 9  x 1 y 1 3         y   1 log x 1  log
y 1   x 1 y 1  9  . 3   3        y   1 log x 1  log
y 1  x 1  9  3   3   
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 9
 log x 1  x 1   log y 1 3   3   y 1 9 9
 log x 1  x 1 2   2  log (*). 3   3 y 1 y 1
Xét hàm số f t   log t t  2 với t  0 có f t  1 
1  0 với mọi t  0 nên hàm số f t 3 t ln 3
luôn đồng biến và liên tục trên 0;  . 9 9 8  y
Từ (*) suy ra x 1   x  1 
, do x  0 nên y  0;8 . y 1 y 1 y 1 8  y 9 9
Vậy P x  2y
 2y  2y 1  2 y   1   3  3 6 2 . y 1 y 1 y 1 Vậy P
 3 6 2 khi  y   9 3 2 1   y  1 min y  . 1 2
Câu 64. Cho các số thực x, y với thỏa mãn log 2 4 48 31 4.8y x x x x y . Giá trị lớn 2   3         2 24 1 y 2 nhất của  24 2 x P .6  x là A. 14 . B. 6 . C. 32 . D. 8 . Lời giải: Điều kiện x  2 Ta có: log 2x 4 4x 48x 32 y 4.8y x 2    3  2 24       1  2log 2x 4 8x 96x 64 2y 8y x 2    3       2 24  2 log 2x 4 8x 48x 96x 64 2y 48x 8y x 2    3 2 2         2 24 2  y x 2 log 2x 4 2x 4 2y 48x 2 2 
     3     3 24 2   Xét hàm số     3 2 2 t f t t trên
thấy ngay đây là hàm đồng biến trên . Phương trình có dạng log 2 4  2 24  log 2 4 2 24 2 4 2y x f x f y x x y x x 2 2              2 24 2 y 2 24x 1
1  2x  4  12  2x  Xét P  2
.6  x  2x  412  2x     8 2 2  2 
Dấu bằng xảy ra khi x  4 . Chọn D.
Câu 65. [PHÁT TRIỂN 47 - ĐỀ THI THAM KHẢO – 2020] Có bao nhiêu cặp số nguyên dương x; yx  2 4 3 2 2
với y  2020 thỏa mãn: log
 4y  8y x 4x y 1 2     y  1 A. 2019.2020 . B. 2020.2021 . C. 2 2019 . D. 2 2020 Lời giải: Ta có
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12 x  2 log  4 4y  3 8y x 4x y 1 2  2   2  y  1 x   2 log  4 4y  3 8y  2 4y   2 2 x y  2 4xy  2 4y 2  2y  2 xy  2y 2  log  2y 2y xy y 2 2  2     2y  2y 2 2  log xy 2y xy 2y log 2y 2y 2y 2y 2  
     2   2  
Xét hàm f t  log t  2
t thấy ngay đây là hàm đồng biến trên 0;  2 . 2 2
Bất phương trình có dạng f xy  2y  f 2y  2y  xy  2y  2y  2y x  2y
Do x; y và y  2020 nên
Với y  1  x  2  x  1
Với y  2  x  4  x 1; 2;  3
Với y  3  x  6  x 1; 2; 3; 4;  5 ……….
Với y  2020  x  4040  x 1,2; 3....403  9
Vậy số cặp nguyên dương x; y thỏa mãn là     2
1 3 5 ...4039 2020 Chọn D.
Câu 66. [PHÁT TRIỂN 47 - ĐỀ THI THAM KHẢO – 2020] Biết rằng bất phương trình  3 x 4x1  a b 2  8  4 2 .2 x x x x
, có một nghiệm dương là x
với a,b, c  ; b  20. Khi đó c
biểu thức P a b c bằng giá trị nào sau đây ? A. 18. B. 16. C. 10. D. 8. Lời giải: x  2  Điều kiện  . x  0 2 4 x 4 x 1  x2 2x 1 2 +Bất phương trình  x  2  .2 x x 2     x 2 2 x 1 2  2x 1     x  2.2  .2 x     x  Xét hàm số   2  2t f t t , t   . Ta có    2 2 t 2  2  2 .2t f t t ln 2  0, t
  .do đó hàm số f t đồng biến trên khoảng .  x  
Phương trình có dạng f x   2 1 2  f    x  2x 1  3  13 x  2   3 2
x  2x  4x 1  0  x
, do x  0. x 2
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
Vậy a b c  18.
Câu 67. Cho hàm số f x   2
ln x x  1 . Có tất cả bao nhiêu số nguyên m thỏa mãn bất phương   trình f m 1 log  f log    0? m  2019  A. 65 . B. 66 . C. 64 . D. 63 . Lời giải:
Điều kiện: m  1 (do m là số nguyên và m  0,m  1 ), suy ra log m  0 .
Hàm số f x   2
ln x x  1 có TXĐ D  . 1
Ta có: f x  ln 2
x x  1  ln  ln 2
x x  1   f x , x  . 2    x x  1 1
Mặt khác f 'x   0, x
 , nên f x đồng biến trên . Khi đó ta có 2 x  1       f m 1  f   f m   ff m f        m   1 m   1 log log 0 log log log log  2019   2019 m   2019  1 log 2019 log 2019  log m  log  log m   m  10  65,77. m 2019 log m
Suy ra m2; 3;...; 
65 . Vậy có tất cả 64 số nguyên m thỏa mãn.
Câu 68. [PHÁT TRIỂN 47 - ĐỀ THI THAM KHẢO – 2020] Có bao nhiêu số nguyên m để phương
trình ln m  3sin x  lnm  4sin x  sin x có nghiệm thực? A. 6. B. 10. C. 5. D. 9. Lời giải:
m 3sin x  lnm  4sin x  0 Điều kiện:  .
m  4sin x  0 
Phương trình đã cho tương đương:
 3sin  ln  4sin  sinx m x m x e
 4sin  ln  4sin  sinx m x m x e  sin x
lnm4sin x  e  ln  4sin  sin x m x e  sin x   1 . Xét   t
f t e t , t . Ta có   t f
t e 1  0, t
. Nên hàm số f t  đồng biến trên . Vậy  
1  f lnm  3sin x  f
sin x  lnm 4sin x  sin x.
Đặt a  sin x, a   1  ;1 
. Phương trình trở thành: lnm  4a  a a
m e  4a. Xét   a
g a e  4a, a   1  ;1  . Ta có   a
g a e  4  0 a    1  ;1  . 1
Vậy để phương trình có nghiệm thực thì g  
1  m g  
1  e  4  m   4 . e
Vậy có 4 giá trị nguyên của tham số m là: 1; 0; 1; 2; 3; 4 .
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà
Chuyên đề PHƯƠNG TRÌNH MŨ – LOGARIT Giải tích 12
___________________HẾT___________________
Huế, ngày 09 tháng 12 năm 2020
Giáo viên: LÊ BÁ BẢO ...0935.785.115… 116/04 Nguyễn Lộ Trạch, TP Huế Trung tâm KM10 Hương Trà