Phương pháp giải các dạng bài Toán 11 học kỳ 2 – Nguyễn Tiến Đạt

Tài liệu gồm 122 trang trình bày phương pháp giải các dạng toán trong chương trình học kỳ 2 Toán 11 (bao gồm cả Đại số & Giải tích 11 và Hình học 11), tài liệu được biên soạn bởi thầy Nguyễn Tiến Đạt.

112 56 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

MỤC LỤC

MỤC LỤC ................................................................................................................................................... 1

Phần 1: ĐẠI SỐ ......................................................................................................................................... 4

TÌM GIỚI HẠN CỦA DÃY





CÓ GIỚI HẠN HỮU HẠN ....................................................... 4

DẠNG 1:

là một phân thức hữu tỉ dạng





 

P n

Q n

 ( trong đó









P n ,Q n

là hai đa thức

của n). ....................................................................................................................................................... 4

DẠNG 2:

là một phân thức hữu tỉ dạng





 

P n

Q n

 ( trong đó









P n ,Q n

là các biểu thức

chứa căn của n). ...................................................................................................................................... 5

DẠNG 3:

là một phân thức hữu tỉ dạng





 

P n

Q n

 ( trong đó









P n ,Q n

là các biểu thức

chứa hàm mũ

n n n

a ,b ,c

,…. Chia cả tử và mẫu cho

với a là cơ số lớn nhất ). ........................... 6

DẠNG 4 : Nhân lượng liên hợp: .......................................................................................................... 7

GIỚI HẠN HÀM SỐ LÝ THUYẾT VÀ PHƯƠNG PHÁP GIẢI TOÁN .......................................... 11

CÁCH KHỬ DẠNG VÔ ĐỊNH

(Dạng này thường gặp khi

x x



). .................................. 13

DẠNG 1: Hàm số

 





 

P x

f x

Q x

 trong đó









P x ,Q x

là đa thức theo biến x. ................................ 13

DẠNG 2: NHÂN LIÊN HỢP ............................................................................................................. 16

GIỚI HẠN KHI x TIẾN TỚI VÔ CỰC .................................................................................................. 18

GIỚI HẠN MỘT BÊN ............................................................................................................................. 19

HÀM SỐ LIÊN TỤC ................................................................................................................................ 19

ĐẾM SỐ NGHIỆM ................................................................................................................................... 23

SỬ DỤNG MÁY TÍNH: TÍNH GIỚI HẠN........................................................................................... 25

PHẦN 2: HÌNH HỌC ............................................................................................................................. 92

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

DẠNG 1: GÓC GIỮA HAI ĐƯỜNG THẲNG ................................................................................ 92

DẠNG 2: GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG .................................................... 96

DẠNG 3: GÓC GIỮA 2 MẶT PHẲNG .......................................................................................... 100

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Phần 1: ĐẠI SỐ

CHUYỀN ĐỀ 1: GIỚI HẠN

TÌM GIỚI HẠN CỦA DÃY





CÓ

GIỚI HẠN HỮU HẠN

DẠNG 1:

là một phân thức hữu tỉ dạng





 

P n

Q n

 ( trong đó









P n ,Q n

là hai đa thức của n).

Phương pháp: Chia cả tử và mẫu cho

với

là lũy thừa có số mũ lớn nhất của





P n

và





Q n

( hoặc

rút

là lũy thừa có số mũ lớn nhất của





P n

và





Q n

ra làm nhân tử) sau đó áp dụng các định lý về

giới hạn.

Ví dụ: Tìm giới hạn của dãy





biết:

a).

2n 3n 1

5n 3

 





b).

3 2

4 3

2n 3n 4

n 4n n

  



 

c).

  

 

4 2

2n 3n n

2n 1 1 3n 2n 1

 



  

LỜI GIẢI

a). Ta thấy

là lũy thừa cao nhất của tử và mẫu, nên chia cả tử và mẫu của

cho

được:

2 2

2n 3n 1 3 1

2n 3n 1

n n

5n 3 5n 3

 

  

 



. Ta có

3 1

lim 0,lim 0

 

và

lim 0



nên

2 0 0 2

lim u

5 0 5

 

 



b). Dễ dàng thấy

là lũy thừa cao nhất của tử và mẫu, nên chia cả tử và mẫu của

cho

được:

3 2

4 2 4

4 3 4 3

2n 3n 4 2 3 4

2n 3n 4

n n n

4 1

n 4n n n 4n n

  

  

   

 

. Ta có

lim 0,



lim 0,



lim 0



lim 0



Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

và

lim 0



. Do đó

0 0 0

lim u 0

1 0 0

 

 

 

c). Có

4 2

4 2 4 4

4 3

2n 3n n 3 1

2n 3n n n n 2

n n

 

 

     

 

 

2n 1 1

2n 1 n n 2

n n

   



   

   

   

1 3n 1

1 3n n n 3

n n

   



   

   

   

và

2 2 2

2 2

2n 1 1

2n 1 n n 2

n n

 



   

 

 

. Từ đó

3 1

n 2

1 1 1

n 2 n 3 n 2

n n

 

 

 

 



     

  

     

     

2 2

3 1

n 2

1 1 1 1 1 1

n 2 3 2 2 3 2

n n n n

n n

 

 

 

 

 

       

     

       

       

. Vì

lim 0



lim 0



lim 0



và

lim 0



. Nên

2 0 0 1

lim u

(2 0)(0 3)(2 0) 6

 

  

  

DẠNG 2:

là một phân thức hữu tỉ dạng





 

P n

Q n

 ( trong đó









P n ,Q n

là các biểu thức chứa căn của n).

Ví dụ: Tìm giới hạn của dãy





biết:

a).

4n n 1 n

9n 3n

  





b).

2n 1 n 3

4n 5

  





LỜI GIẢI

a).

2 2

4n n 1

1 1 1 1

n n

n 4 n 4 1

n n

4n n 1 n

n n

3 3

9n 3n

n 9 9

n n

 

 



 

     

 

  

 

   

 



 

 

 

. Vì có

lim 0,



lim 0,



và

lim 0



. Nên

4 0 0 1 1

lim u

9 0

  

 



b).

2n 1 n 3

1 3

n n

n. 2 n. 1

n n

2n 1 n 3

n n

4n 5 5

4n 5

n. 4

   

 



   

  

   

  



 



 

 

1 3

2 1

n n

  





. Vì có

lim 0,



lim 0



và

lim 0



Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Từ đó có

2 0 1 0 2 1

lim u

4 0

   

 



DẠNG 3:

là một phân thức hữu tỉ dạng





 

P n

Q n



( trong đó









P n ,Q n

là các biểu thức chứa hàm mũ

n n n

a ,b ,c

,…. Chia cả tử và mẫu

cho

với a là cơ số lớn nhất ).

Ví dụ: Tìm giới hạn của dãy





biết:

a).

n n

2 4

4 3







b).

n n

3.2 5

5.4 6.5







c).

n 2 n 1

n 1 n 3

4 6

5 2.6

 

 







a).Ta có

n n n n

n n

n n n

n n n n n n n

n n n

2 4 2 4

2 4

4 4 4

4 3 4 3 4 3

4 4 4

 



 



 

   

 

 



 

 

. Ta có

lim 0

 



 

 

và

lim 0

 



 

 

. Nên

0 1

lim u 1

1 0



 



b). Ta có

n n n n

n n

n n n

n n n n n n n

n n n

3.2 5 3.2 5

3 1

3.2 5

5 5 5

5.4 6.5 5.4 6.5 5.4 6.5

5 6

5 5 5

 



 



 

   

 

 



 

 

. Ta có

lim 0

 



 

 

và

lim 0

 



 

 

Do đó

3.0 1 1

lim u

5.0 6 6



  



c). Ta có

n 2 n n 2 n

n 2 n 1 n 2 n

n n n

n 1 n 3 n 1 n 3 n 1 n 3 n 1 n 3

n n n

4 .4 6 .6 4 .4 6 .6

4 6 4 .4 6 .6

6 6 6

5 2.6 5 .5 2.6 .6 5 .5 2.6 .6 5 .5 2.6 .6

6 6 6

 

    



 

   

  



1 3

4 6

5 2.6



 



 

 



 



 

 

. Ta có

lim 0

 



 

 

và

lim 0

 



 

 

Do đó

1 3

4 .0 6 1

lim u

5 .0 2.6





 



Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

DẠNG 4 : Nhân lượng liên hợp:

PHƯƠNG PHÁP : Sử dụng các công thức nhân lượng liên hợp sau:



  

2 2

a b

a b a b a b

a b





 







    





 









3 3

2 2

a b

a ab b



 

 



3 3

2 2

a b

a ab b



 

 



   

3 3 3

2 2

3 3 3 3

a b a a.b b

a b

a a.b b a a.b b

 

  

 



 

  

   



   

3 3 3

2 2

3 3 3 3

a b a a.b b

a b

a a.b b a a.b b

 

  

 



 

  

   



   

3 3 3

2 2

3 3 3 3

a b a a. b b

a b

a a. b b a a. b b

 

  

 



 

  

   



   

3 3 3

2 2

3 3 3 3

a b a a. b b

a b

a a. b b a a. b b

 

  

 



 

  

   



     

       

2 2

3 3 3 3 3 3

3 3

2 2 2 2

3 3 3 3 3 3 3 3

a b a a. b b

a b

a a. b b a a. b b

 

  

 



 

  

   



     

       

2 2

3 3 3 3 3 3

3 3

2 2 2 2

3 3 3 3 3 3 3 3

a b a a. b b

a b

a a. b b a a. b b

 

  

 



 

  

   

Ví dụ 1: Tìm giới hạn của dãy





biết:

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

a).

u n 3n 5 n

   

b).

u 9n 3n 4 3n 2

    

c).

3 2

u n 3n n

  

d).

3 2

u 8n 4n 2 2n 3

    

LỜI GIẢI

a). Ta có

2 2

n 3n 5 n n 3n 5 n

3n 5

u n 3n 5 n

n 3n 5 n n 3n 5 n

  

     

  



  

     

     

. Và có

3n 5 5

3n 5 n n 3

n n

   



   

   

   

và

2 2

n 3n 5 3 5

n 3n 5 n n 1

n n

 

 

     

 

 

Do đó

2 2

n 3

3 5 3 5

n 1 n 1 1

n n

 



 



 

 

     

, vì

lim 0,



lim 0



và

lim 0



. Nên

lim u



NHẬN XÉT : Tại sao phải nhân lượng liên hợp ?

Quay lại ví dụ a) thông thường ta đặt

làm nhân tử chung nhưng sao lại phải nhân lượng liên hợp. Bây

giờ ta thử làm lại câu a) theo phương pháp đặt

trong căn thức thử xem sao ,và sau đó rút ra nhận xét.

Ta có

2 2

n 3n 5

u n 3n 5 n n n

 

 

     

 

 

3 5

n 1 n

   

3 5

n 1 1

 

   

 

 

. Vì

3 5

lim lim 0

 

nên

3 5

lim 1 1 0

 

   

 

 

và

lim n

 

do đó

lim u .0

 

(đây là dạng vô

định). Nên cách làm này không là không được rồi, ta phải sử dụng phương pháp nhân lượng liên hợp để

khử vô định sau đó cách làm hoàn toàn như dạng 1.

Dấu hiệu nhận biết nhân lượng liên hợp : Để nhận biết một bài tập có nhân lượng liên hợp hay không

các bạn chỉ chú ý tới n có mũ cao nhất sau đó đưa ra ngoài dấu căn thức, nếu chúng trừ nhau bằng 0 thì

bài này ta phải nhân lượng liên hợp. Cụ thể ta làm lại câu a)

u n 3n 5 n

   

biểu thức trong căn

thức có

là cao nhất và ta quan tâm đến « nó », những thừa số sau bỏ hết có nghĩa xem

u n n n n 0

    

(nên các bạn phải nhân lượng liên hợp). Chúng ta xem thử bài này có nhân

lượng liên hợp hay không

u 2n 3n 5 n

   

chúng ta cũng quan tâm đến số hạng có chứa mũ có

nhất đó là

, có nghĩa

được viết lại





u 2n n n 2 n n 2 1

     

ta có

2 1 0

 

nên bài

này được làm trực tiếp không cần nhân lượng liên hợp. Cụ thể bài này ta làm như sau

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

2 2

2 2 2

2n 3n 5 3 5 3 5

u 2n 3n 5 n n n n 2 n n 2 1

n n

n n n

 

 

             

 

 

3 5

lim lim 0

 

nên

3 5

lim 2 1 2 1

 

    

 

 

và

lim n

 

do đó





lim u . 2 1

    

(cụ

thể các bạn xem phương pháp tìm giới hạn dãy số có giới hạn vô cực).

b).

2 2

9n 3n 4 3n 9n 3n 4 3n

u 9n 3n 4 3n 2 2

9n 3n 4 3n

  

     

  

  

      

  

3n 4

9n 3n 4 3n



 

  

. Ta

có

3n 2 2

3n 2 n n 3

n n

   



   

   

   

và

2 2

9n 3n 4 3 4

9n 3n 4 n n 9

n n

 

 

     

 

 

. Từ đó suy ra

2 2

n 3

u 2 2

3 4 3 4

n 9 3n 9 3

n n

 



 



 

   

     

, vì

lim 0,



lim 0



và

lim 0



. Nên

3 0 1

lim u

9 0 0 3



 

  

c).

3 3 3

3 2 3 2 3 2 2

3 2

3 3

3 2 3 2 2

n 3n n n 3n n. n 3n n

u n 3n n

n 3n n. n 3n n

 

   

     

 

   

   

 

 

   

 

   

 

 

3 3

3 2 3 2 2

n 3n n. n 3n n



 

   

 

 

. Ta có

3 2

3 2 3

n 3n 3

n 3n n n. 1

 



   

 

 

. Do đó

2 2

2 2 2

3 3 3 3

3n 3

3 3 3 3

n 1 n . 1 n 1 1 1

n n n n

 

   

       

   

   

, ta có

lim 0



. Nên

lim u 1



d).

3 2

u 8n 4n 2 2n 3

    

3 3 3

3 2 3 2 3 2 2

3 3

3 2 3 2 2

8n 4n 2 2n 8n 4n 2 2n. 8n 4n 2 4n

8n 4n 2 2n. 8n 4n 2 4n

 

   

        

 

   

   

 

 

 

 

     

 

 

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

3 3

3 2 3 2 2

4n 2

8n 4n 2 2n. 8n 4n 2 4n



 

 

     

 

 

Ta có

3 2

3 2 3

3 3

8n 4n 2 4 2

8n 4n 2 n n 8

n n

 

 

     

 

 

. Do đó

2 2

2 2 2

3 3 3 3

n 4

4 2 4 2 4 2 4 2

n 8 2n . 8 4n 8 2. 8 4

n n n n

 



 

 

 

   

           

   

   

. Vì

lim 0,



lim 0



và

lim 0



. Nên

lim u



Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

GIỚI HẠN HÀM SỐ LÝ THUYẾT VÀ

PHƯƠNG PHÁP GIẢI TOÁN

TÓM TẮT LÝ THUYẾT

Định lí 1: Giả sử





x x

lim f x L





và





x x

lim g x M





(với L, M





).Khi đó:











x x

lim f x g x L M



 

  

 











x x

lim f x g x L M



 

  

 











x x

lim f x .g x L.M



 



 



Nếu

M 0



thì





 

x x

f x

lim

g x





Hệ quả:



Nếu c là một hằng số thì





x x

lim c.f x c.L



 



 







k k

x x

lim a.x ax





( a hằng số và k







Định lí 2: Giả sử





x x

lim f x L





. Khi đó:







x x

lim f x L











x x

lim f x L







Nếu





f x 0



với mọi





x J\ x

 , trong đó J là một khoảng nào đó chứa

, thì

L 0



và





x x

lim f x L





Chú ý:

Định lí 1 và định lí 2 vẫn đúng khi thay

x x

 bởi

 

hoặc

 

Định lí 3: Nếu





x x

lim f x



 

thì

 

x x

lim 0

f x





4). Một vài quy tắc tìm giới hạn vô cực:

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Qui tắc 1: Nếu





x x

lim f x



 

và





x x

lim g x L





(với

L 0



) thì









x x

lim f x .g x



 

 

được cho bởi bảng sau:





x x

lim f x



Dấu của L









x x

lim f x .g x



 

 















Quy tắc 2: Nếu









x x

lim f x L, L 0



 





x x

lim g x 0





và





g x 0



hoặc





g x 0



với mọi









x a;b \ x

 thì





 

x x

f x

lim

g x



được cho bởi bảng sau:

Dấu của L

Dấu của





g x





 

x x

f x

lim

g x























5). Các dạng vô định:

Các dạng vô định trường gặp:

, ,0. ,



   



6). Giới hạn một bên:

a). Giới hạn hữu hạn:



Giới hạn bên phải: Giả sử hàm số f xác định trên khoảng









0 0

x ; b , x 



. Ta nói rằng hàm số f có giới

hạn bên phải là số thực L khi x dần đến

(hoặc tại điểm

) nếu với mọi dãy số





trong khoảng





x ; b

mà

n 0

limx x



, ta đều có





limf x L



. Khi đó ta viết:

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN





x x

lim f x L







hoặc





f x L



khi

x x



 .



Giới hạn bên trái: Giả sử hàm số f xác định trên khoảng









0 0

a;x , x 



. Ta nói rằng hàm số f có giới

hạn bên trái là số thực L khi x dần đến

(hoặc tại điểm

) nếu với mọi dãy số





trong khoảng





a;x

mà

n 0

limx x



, ta đều có





limf x L



. Khi đó ta viết:





x x

lim f x L







hoặc





f x L



khi

x x



 .

Định lí 5:













0 0

x x

x x x x

lim f x L lim f x lim f x L

 



 

   



Giới hạn vô cực:

















0 0 0 0

x x x x x x x x

lim f x , lim f x , lim f x lim f x

   

   

       

được phát biểu tương tự như các định nghĩa ở

phần giới hạn hữu hạn.

Định lí 5 vẫn đúng với giới hạn vô cực.

Các định lí về giới hạn hữu hạn và các quy tắc tìm giới hạn vô cực vẫn đúng trong trường hợp

x x





hay

x x



 .

PHƯƠNG PHÁP GIẢI TOÁN

CÁCH KHỬ DẠNG VÔ ĐỊNH

(Dạng này thường gặp khi

x x



DẠNG 1: Hàm số

 





 

P x

f x

Q x

 trong đó









P x ,Q x

là đa thức theo biến x.

PHƯƠNG PHÁP: Phân tích đa thức thành nhân tử, sau đó rút gọn biểu thức làm cả tử và mẫu bằng 0.

Phân tích đa thức thành nhân tử có các phương pháp sau:



Sử dụng bảy hằng đẳng thức đáng nhớ.



Nếu tam thức bậc hai thì sử dụng













1 2

ax bx c a x x x x , a 0

     

với

1 2

x ,x

là nghiệm của

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

phương trình

ax bx c 0

  



Sử dụng phương pháp Hoocner . Phép chia đa thức





4 3 2

P x ax bx cx dx e

    

cho

(x x )



theo sơ

đồ Hoocner như sau:

a b c d e

1 0

b ax b

 

1 0 0

c ax bx c

  

3 2

1 0 0 0

d ax bx cx d

   

Hàng thứ nhất điền hệ số của đa thức





P x

từ ô thứ hai đến ô cuối cùng. Ở hàng thứ hai ô đầu tiên điền

giá trị

là một nghiệm của





P x

, ô thứ hai viết lại a, lấy





x .a b



đặt vào ô thứ ba, lấy





0 0 0 0

x x a b c ax bx c

    

điền váo ô thứ tư, lấy





0 0 0

x ax bx c d

  

3 2

0 0 0

ax bx cx d

   

điền vào ô

thứ năm, lấy





3 2

0 0 0 0

x ax bx cx d e 0

    

(bắt buộc tổng này phải bằng 0, thì đây mới là phép chia hết).

Khi đó





P x

được viết lại













3 2

0 1 1 1

P x x x ax b x c x d

    

Ví dụ: Tìm các giới hạn sau:

a).

x 2

x 8

lim

x 11x 18





 

b).

3 2

x 3

2x 5x 2x 3

L lim

4x 13x 4x 3



  



  

c).

3 2

x 1

2x 5x 4x 1

lim

x x x 1



  

  

d).

x 2

1 12

lim

x 2

x 8



 



 



 

a).Ta có









3 3 3 2

x 8 x 2 x 2 x 2x 4

      

(áp dụng hằng đẳng thức), và

x 11x 18

 









x 2 x 9

  

(với

x 2

 

và

x 9

 

là hai nghiệm của phương trình

x 11x 18 0

  

Do đó









  

3 2

x 2 x 2 x 2

x 2 x 2x 4

x 8 x 2x 4 12

lim lim lim

x 9 7

x 2 x 9

x 11x 18

  

  

  



 

b).

3 2

x 3

2x 5x 2x 3

L lim

4x 13x 4x 3



  



  

Thay

x 3



vào cả tử và mẫu thấy đều bằng 0, nên

x 3



là một nghiệm của hai đa thức cả mẫu và tử. Có

nghĩa

(x 3)



là nhân tử chung, ta phân tích đa thức ở tử và mẫu thành nhân tử bằng phương pháp

Hoocner. Cách làm như sau:

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Phân tích tử số:









3 2 2

2x 5x 2x 3 x 3 2x x 1

      

Kẻ bảng như sau. Sau đó điền hệ số của từng số hạng với số mũ giảm dần vào các ô ở hàng đầu tiên với ô

thứ nhất để trống. Ở hàng thứ hai: điền giá trị làm đa thức bằng 0 ở đây là chữ số 3. Ô thứ hai điền lại giá

trị ở ô thứ hai của hàng một xuống (ta thường hay nói “đầu rơi xuống”), sau đó lấy

3.2 ( 5) 1

  

điền

chữ số 1 vào ô thứ ba, lấy

3.1 ( 2) 1

  

điền chữ số 1 vào ô thứ tư, cuối cùng lấy

3.1 ( 3) 0

  

điền vào ô

cuối cùng.

2 -5 -2 -3

3 2 1 1 0

Phân tích mẫu số:









3 2 2

4x 13x 4x 3 x 3 4x x 1

      

4 -13 4 -3

3 4 -1 1 0

Do đó









 

x 3 x 3

x 3 2x x 1

2x x 1 11

L lim lim

4x x 1

x 3 4x x 1

 

  

 

  

 

  

c).

3 2

x 1

2x 5x 4x 1

L lim

x x x 1



  



  

. Ta thấy





3 2

x 1

lim 2x 5x 4x 1 0



   

và





3 2

x 1

lim x x x 1 0



   

như vậy đây

là dạng giới hạn vô định

ta phải phân tích cả tử và mẫu thành nhân tử để khử vô định. Phân tích nhân

tử bằng phương pháp Hoocner

Phân tích tử số:









3 2 2

2x 5x 4x 1 x 1 2x 3x 1

      



Phân tích mẫu số:

















3 2 2 2

x x x 1 x 1 x 0x 1 x 1 x 1

         



Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Từ đó









 

x 1 x 1

x 1 2x 3x 1

2x 3x 1

L lim lim

x 1

x 1 x 1

 

  

 

 



 

, ta thấy





x 1

lim 2x 3x 1 0



  

và





x 1

lim x 1 0



 

vẫn còn dạng vô định

nên phân tích thành nhân tử tiếp, ta làm như sau:









  

x 1 x 1 x 1

x 1 2x 1

2x 3x 1 2x 1 1

L lim lim lim

x 1 2

x 1 x 1

x 1

  

 

  

   



 



d). Bước đầu tiên ta phải quy đồng mẫu, sau đó phân tích đa thức của tử thành nhân tử và rút gọn hạng

tử vô định

x 2

1 12

L lim

x 2

x 8



 

 

 



 

x 2

1 12

lim

x 2

(x 2)(x 2x 4)



 

 

 



  

 

x 2

x 2x 8

lim

(x 2)(x 2x 4)



 



  

x 2

(x 2)(x 4)

lim

(x 2)(x 2x 4)



 



  

x 2

x 4 1

lim

x 2x 4





 

 

DẠNG 2: NHÂN LIÊN HỢP

Tính các giới hạn sau: (CĂN BẬC 2)

a).

x 9

x 3

lim

9x x





x 6

x 3 3

lim

x 6



 



a).

x 9 x 9 x 9

x 3 x 9 1 5

lim lim lim

9x x

x(x 9)( x 3) x( x 3)

  

 

  



    

b).

x 6 x 6 x 6 x 6

x 3 3 (x 3 9) x 6 1 1

lim lim lim lim

x 6 6

(x 6)( x 3 3) (x 6)( x 3 3) x 3 3

   

    

   



       

Tìm các giới hạn sau: (CÓ 2 CĂN BẬC 2)

a).

x 1

3x 1 x 3

lim

x 8 3



  

 

b).

x 9

3 x

lim

x 5 2





 

a).





 

x 1 x 1

(3x 1 x 3) x 8 3

3x 1 x 3

lim lim

x 8 3

(x 8 9) 3x 1 x 3

 

    

  



 

    





 

x 1

2(x 1) x 8 3

lim

(x 1) 3x 1 x 3



  



   





x 1

2 x 8 3

lim 3

3x 1 x 3



 

 

  

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

b).





 





 

x 9 x 9 x 9

(9 x) x 5 2 (x 9) x 5 2

3 x

lim lim lim

x 5 2

(x 5 4) 3 x (x 9) 3 x

  

      



 

 

    





x 9

x 5 2

lim

3 x



  

  



Tìm các giới hạn sau: (CÓ CĂN BẬC 3)

a).

x 1

5x 3 2

lim

x 1



 



b).

x 0

1 1 x

lim



 

a).

 

x 1 x 1

3 3

5x 3 2 5x 3 8

lim lim

x 1

(x 1) 5x 3 2 5x 3 4

 

   





 

    

 

 

 

x 1 x 1

3 3

5(x 1) 5 5

lim lim

(x 1) 5x 3 2. 5x 3 4

5x 3 2 5x 3 4

 



  

   

    

   

 

   

 

b).

 

x 0 x 0 x 0

3 3

1 1 x 1 (1 x) 1 1

lim lim lim

x 3

1 1 x 1 x

x 1 1 x 1 x

  

   

  

 

   

 

 

Tìm các giới hạn sau: (THÊM BỚT ĐỂ NHÂN LIÊN HỢP)

a).

x 0

x 9 x 16 7

lim



   

b).

3 2

x 1

x 7 x 3

lim

x 1



  



a).

x 0 x 0

x 9 x 16 7 x 9 3 x 16 7

lim lim

x x

 

        



x 0 x 0

x 9 3 x 16 4

lim lim

x x

 

   

 

   

x 0 x 0

x 9 9 x 16 16

lim lim

x 9 3 x x 16 4 x

 

   

 

   

   

x 0 x 0

x x

lim lim

x 9 3 x x 16 4 x

 

 

   

x 0 x 0

1 1 7

lim lim

x 9 3 x 16 4

 

  

   

b).

3 3

3 2 3 2

x 1 x 1

x 7 x 3 x 7 2 2 x 3

lim lim

x 1 x 1

 

       



 

3 2

x 1 x 1

x 7 2 2 x 3

lim lim

x 1 x 1

 

   

 

 

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN





x 1

3 3

x 7 8

lim

x 7 2 x 7 4 (x 1)



 



 

    

 

 

x 1

2 x 3

lim

(2 x 3)(x 1)



 



  





x 1 x 1

3 3

(x 1)(x x 1) (x 1)(x 1)

lim lim

(2 x 3)(x 1)

x 7 2 x 7 4 (x 1)

 

     

 

 

  

    

 

 





x 1 x 1

3 3

x x 4 x 1 3

lim lim

2 x 3

x 7 2 x 7 4

 

  

  

 

   

GIỚI HẠN KHI x TIẾN TỚI VÔ CỰC

Câu 1: Tìm các giới hạn sau:

a).

3x x 7

lim

2x 1



 



b).

(4x 1)(7x 1)

lim

(2x 1)(x 3)



 

 

a).

x x x x

3 3

1 7

x 3

3x x 7 3

lim lim lim lim 0

1 1

2x 1

x 2 x 2

x x

   

 

 

 

 

 

   

   



 

   

   

b).

x x

1 1

x 4 x 7

(4x 1)(7x 1)

lim lim

1 3

(2x 1)(x 3)

x 2 x 1

 

   

 

   

 

   



   

 

   

   

x x

1 1

4 7

lim lim 0

1 3

x 2 1

 

  

 

  

  

  

  

 

  

  

Câu 2: Tìm các giới hạn sau:

a).

2 2

(x 1) (5x 2)

lim

(3x 1)



 



b).

2 x 3

lim

x x 5





 

c).

2 x 3

lim

x x 5





 

a).

2 2 2 2

2 2

4 4 4

x x x

1 2 1 2

x 1 x 5 1 5

x x x x

(x 1) (5x 2) 25

lim lim lim

(3x 1)

1 1

x 3 3

x x

  

       

   

       

 

       

  



   

 

   

   

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

b).

6 3

x x x x

3 3

2 2

x 1 1

x 1

x x

x 2 1

lim lim lim lim

1 1

3x 1

x 3 x 3

x x

   

   

 



   



   

   

   



 

   

   

c).

x x x x

x 2

2 x 3

2x 3

lim lim lim lim 2

1 5

x x 5

x 1

   

 

 

 



 

 

    

 

 

 

 

GIỚI HẠN MỘT BÊN

Ví dụ 1: Tìm các giới hạn sau:

a).

x 3

lim

5x 15







b).

x 0

x x

lim .

x x









LỜI GIẢI

a). Vì

x 3 x 3 x 3 0



     

. Vậy

x 3 x 3

  

Ta có

 

x 3 x 3

x 3

x 3 1

lim lim .

5x 15 5

5 x 3

 

 



 



b). Ta có





 

x 0 x 0 x 0

x x 1

x x x 1

lim lim lim 1.

x x x 1

x x 1

  

  



 

   

 



HÀM SỐ LIÊN TỤC

DẠNG 1: XÉT TÍNH LIÊN TỤC CỦA HÀM SỐ TẠI MỘT ĐIỂM

PHƯƠNG PHÁP 1:

Bước 1: Tính





f x

Bước 2: Tính





x x

lim f x



. Nếu









x x

lim f x f x



 thì hàm số f(x) liên tục tại

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

PHƯƠNG PHÁP 2:

Bước 1: Tìm





x x

lim f x





Bước 2: Tìm





x x

lim f x





Nếu













0 0

x x x x

lim f x lim f x f x

 

 

  thì hàm số f(x) liên tục tại

Ví dụ : Xét tính liên tục tại giá trị

của các hàm số sau:

1).

 

x 3x 2

x 2

f x

x 2

1 x 2



 







 







tại

x 2



và tại

x 4



2).

 

x 3 2

x 1

f x

x 1



 



















tại

x 1



3).

 

x 5

2x 1 3

f x

x 5 3 x 5

 





 







  



tại

x 5



, tại

x 6



và tại

x 4



4).

 

2x 3 1

x 1

f x

3 x

x 1



 

 













 





tại

x 1

 

5).

 

x 3x 2

x 1

f x x 1

x x 1



 









 





 





tại

x 1



1).



Xét tính liên tục tại

x 2



Có









f x f 2 1

 

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Có

 









x 2 x 2 x 2 x 2

x 2 x 1

x 3x 2

lim f x lim lim lim(x 1) 1

x 2 x 2

   

 

 

    

 

Ta có









x 2

limf x f 2



 

hàm số liên tục tại

x 2.





Xét tính liên tục tại

x 4



Có

   

2 2

x 4 x 4

x 3x 2 4 3.4 2

limf x lim 3 f 4

x 2 4 2

 

   

    

 

hàm số f(x) liên tục tại

x 4



2). Có

   

f x f 1

 

(1)

Có

 

x 1 x 1 x 1

x 3 2 x 3 4

limf x lim lim

x 1

x 3 2 x 1

  

   

 



  

 

x 1

lim

x 3 2 x 1







  

x 1

1 1

lim

x 3 2



  

 

(2)

Từ (1) và (2) suy ra









x 1

limf x f 1



 . Vậy hàm số liên tục tại

x 1



3).

 

x 5

2x 1 3

f x

x 5 3 x 5

 





 







  



tại

x 5



, tại

x 6



và tại

x 4





Xét tính liên tục tại

x 5



Áp dụng nếu













0 0

x x x x

lim f x lim f x f x

 

 

  

hàm số liên tục tại

x .

Có

 

















x 5 x 5 x 5 x 5

x 5 2x 1 3 x 5 2x 1 3

x 5

lim f x lim lim lim

2x 1 9 2x 10

2x 1 3

   

   

     



  

  

 









 





x 5 x 5

x 5 2x 1 3 2x 1 3

2.5 1 3

lim lim 3.

2 2

2 x 5

 

 

    

 

   



Có

     

x 5 x 5

lim f x lim x 5 3 0 3 3 f 5 .

 

 

 

      

 

 

Vì













x 5 x 5

lim f x lim f x f 5

 

 

  

hàm số liên tục tại

x 5.





Xét tính liên tục tại

x 6



Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Có

   

x 6 x 6

x 5 6 5 1

lim f x lim f 6

2x 1 3 2.6 1 3 11 3

 

 

   

    

. Vậy hàm số f(x) liên tục tại

x 6





Xét tính liên tục tại

x 4



Có

       

2 2

x 4 x 4

limf x lim x 5 3 4 5 3 4 f 4

 

 

        

 

 

hàm số f(x) liên tục tại

x 4



4). Có

 

x 1 x 1 x 1

2x 3 1 2x 3 1

lim f x lim lim

x 1

2x 3 1 x 1

  

  

   

 



  





 

x 1

2 x 1

lim

2x 3 1 x 1









  

 

x 1

2 2

lim 1.

2x 3 1

2. 1 3 1





  

 

  

Có

 

x 1 x 1

3 1

3 x

lim f x lim 1.

2 2

 

 

 



  

Có

 

3 ( 1)

f 1 1

 

  

Vì













x 1 x 1

lim f x lim f x f 1

 

 

   

hàm số liên tục tại

x 1.

 

5). Ta có

   

f x f 1

 

Có

 









  

x 1 x 1 x 1 x 1

x 1 x 2

x 3x 2 x 2 1 2 1

lim f x lim lim lim .

x 1 1 1 2

x 1 x 1

x 1

   

   

 

   

     

 

 



Có

 

x 1 x 1

3 3 1

lim f x lim x 1

2 2 2

 

 

 

     

 

 

Vì









x 1

f 1 lim f x



 

hàm số không liên tục tại

x 1.



Ví dụ 2. Cho hàm số

 

x 3x 2

x 2

f x

x 2

a x 2



 







 







Với giá trị nào của a thì hàm số đã cho liên tục tại điểm

x 2



LỜI GIẢI

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Ta có

 









 

x 2 x 2 x 2 x 2

x 1 x 2

x 3x 2

lim f x lim lim lim x 1 1.

x 2 x 2

   

 

 

    

 

Hàm liên tục tại

x 2



khi và chỉ khi









x 2

limf x f 2 a 1.



  

Vậy hàm số đã cho liên tục tại

x 2



khi

a 1.



Ví dụ 5: Cho hàm số

 

2x 7x 6

khi x < 2

x 2

y f x

1 x

a + khi x 2

2 x



 





 















. Xác định a để hàm số f(x) liên tục tại

x 2



LỜI GIẢI

Ta có :



 

  

x 2 x 2 x 2

2x 7x 6

x 2 2x 3

2 x 2x 3

lim f x lim lim

x 2 x 2 x 2

  

  

 

 

  

  





x 2

lim 3 2x 1





   



   

x 2 x 2

1 x 1

lim f x lim a + a f 2

2 x 4

 

 

 



   

 



 

Hàm số liên tục tại

x 2



     

x 2 x 2

1 3

lim f x lim f x f 2 a 1 a

4 4

 

 

         

ĐẾM SỐ NGHIỆM

Chứng minh phương trình sau có ít nhất một nghiệm:

a).

3 2

x 5x 7 0

  

b).

x x 3 0

  

LỜI GIẢI

a). Đặt





3 2

f x x 5x 7

  

. Tập xác định của hàm số f(x) là

D R



. Vì f(x) là hàm đa thức





f x

 liên tục

trên R.

Ta có





f 1 1 5.1 7 1

     

và





f 2 21

  

, nên suy ra









f 1 f 2 21 0

    

với mọi m. Do đó





f x 0



Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

luôn có ít nhất 1 nghiệm





x 2; 1

  

với mọi m.

b). Đặt





f x x x 3

  

. Tập xác định của hàm số f(x) là

D R



. Vì f(x) là hàm đa thức





f x

 liên tục

trên R.

Ta có





f 1 1

 

và có





f 2 31

 , nên suy ra













f 1 f 2 31. 1 31 0

    

với mọi m.

Do đó





f x 0



luôn có ít nhất 1 nghiệm





n 1;2

 với mọi m.

Chứng minh các phương trình sau có ít nhất hai nghiệm :

a).

4 2

4x 2x x 3 0

   

b).

5 4 3 2

x x 2x 4x 1 0

    

LỜI GIẢI

a). Đặt





4 2

f x 4x 2x x 3

   

. Tập xác định của hàm số f(x) là

D R



. Vì f(x) là hàm đa thức





f x

 liên

tục trên R.

Ta có





f 0 3

 





f 1 4,

 





f 1 2



Vì









f 1 f 0 12 0, m

    



phương trình





luôn có ít nhất 1 nghiệm









1;0 2

 

Vì









f 0 f 1 6 0 m

   



phương trình





có ít nhất 1 nghiệm









0;1 3



Từ









2 , 3



phương trình (1) luôn có ít nhất 2 nghiệm phân biệt.

10. Chứng minh rằng với mọi a, b, c phương trình

3 2

x ax bx c 0

   

luôn có nghiệm.

LỜI GIẢI

Đặt





3 2

f x x ax bx c

   

thì





f x

liên tục trên R.

Ta có:





lim f x x 0



    

để





f x 0.







lim f x x 0



    

để





f x 0.



Như vậy có

1 2

x ,x

để









1 2

f x .f x 0



suy ra phương trình có nghiệm





1 2

x x ;x

 vậy phương trình đã

cho luôn có nghiệm.

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

SỬ DỤNG MÁY TÍNH: TÍNH GIỚI

HẠN

1. Ý tưởng:

* Gán cho biến X một giá trị gần đúng rồi tính giá trị biểu thức (dùng phím

CALC)

* Ví dụ:

Giới hạn Giá trị của X

x→ a

a + 0.00000001

x→ a

a – 0,00000001

x→ a a+000000001 hoặc a-0,000000001

x→ + ∞ 9999999999

x→ - ∞ - 999999999

(Nếu máy báo lỗi thì lấy ít chữ số thập hơn)

CHÚ Ý: KHÔNG NHẤT THIẾT PHẢI LẤY NHIỀU SỐ 0 Y NHƯ THẦY, ƯỚC LƯỢNG

THÔI

Các kết quả hay gặp trong máy Ý nghĩa

Số có số mũ lớn : VD: 2.10

Dương vô cực

Số có số mũ lớn : VD: -2.10

Âm vô cực

Số có số mũ nhỏ: VD: 2.10

-20

Số chưa đẹp: VD: 2,3333.

Ta gõ lại vào máy tính lần nữa:

2,3333333333333

Máy sẽ tự làm tròn giúp

2. Một số ví dụ:

Ví dụ 1:

1x2

lim





Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Ấn r 999999=

Rơi vào trường hợp kết quả có số mũ nhỏ: Kết quả là 0

Ví dụ 2: (Bậc tử = bậc mẫu, lấy hệ số X mũ cao nhất tử mẫu chia

nhau được 2/3)

rp999999=

Ta làm tròn kết quả: nhập vào máy:

Ví dụ 3: (Bậc tử > bậc mẫu kết quả ra vô cực)

rp999999=

Ta thấy kết quả âm một số to. => Kết quả - ∞

Ví dụ 4:

2 3

lim

x x







1x7x5

lim











5x2x3xlim





Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

kết quả là + ∞.

Ví dụ 5: Giới hạn của dãy số

 

với

2 2

2 ...

2 2

u    

là:

A. lim 2 2

u  . B.

lim

u 

. C.

lim 2

u  

. D.

lim 2

u  

Giải

Ấn qi

Chọn A.

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

CHUYE󰈛 N ĐE󰈛 2: ĐA󰈨 O HA M VA BA I TOA N

LIE N QUAN

LÝ THUYẾT ĐẠO HÀM

TÓM TẮT GIÁO KHOA

1). Cho hàm số





y f x

 xác định trên khoảng





a;b

và





x a; b

 . Giới hạn hữu hạn nếu có của tỉ số









f x f x

x x



khi

x x

 được gọi là đạo hàm của hàm số đã cho tại

, kí hiệu





f' x

hay





y' x

. Như

vậy ta có

 









x x

f x f x

f' x lim

x x









Nhận xét:

Nếu đặt

x x x

  

và









0 0

y f x x f x

     thì ta có

 

x 0

f' x lim

 







. Trong đó



được gọi là số gia

của biến số tại

và



gọi là số gia của hàm số ứng với số gia



tại

Nếu hàm số f(x) có đạo hàm tại điểm

thì f(x) liên tục tại

. Tuy nhiên điều ngược lại chưa chắc đúng.

2). Cho đường cong (C), điểm

cố định thuộc (C) và





M C

 . Gọi

là hệ số góc của cát tuyến

M M

Giả sử tồn tại giới hạn hữu hạn

M 0

0 M

x x

k lim k



 . Khi đó đường thẳng

M T

qua

có hệ số góc

được

gọi là tiếp tuyến của (C) tại

. Điểm

gọi là tiếp điểm.

3). Đạo hàm của hàm số





y f x

 tại điểm

là hệ số góc của tiếp tuyến của đồ thị hàm số tại đó tại

điểm





0 0 0

M x ;f(x )

Hệ quả:

Nếu hàm số





y f x

 có đạo hàm tại điểm

thì tiếp tuyến của đồ thị hàm số





y f x

 tại điểm





0 0 0

M x ;f(x )

có phương trình:













0 0 0

y f' x x x f x

   .

4). Khí hiệu D là một khoảng hay là hợp của những khoảng nào đó. Nếu hàm số f(x) có đạo hàm tại tại

mọi điểm

x D



thì ta nói hàm số có đạo hàm trên D. Khi đó đạo hàm của hàm số f(x) tại điểm x tùy ý

của D được kí hiệu

hay





f' x

. Ta nói

hay





f' x

là đạo hàm của hàm số





y f x

 trên tập D.

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

B.PHƯƠNG PHÁP GIẢI TOÁN.

DẠNG 1: Tìm số gia của hàm số.

PHƯƠNG PHÁP

Để tính số gia của hàm số





y f x



tại điểm

tương ứng với số gia



cho trước ta áp dụng công thức:









0 0

y f x x f x

    

Ví dụ 1: Tìm số gia của hàm số





3 2

y f x x 3x 2

   

, biết rằng:

a).

x 1; x 1

  

b).

x 1; x 0,1

   

LỜI GIẢI

a). Ta có

















3 2 3 2

o 0

y f x x f x f 2 f 1 2 3.2 2 (1 3.1 2) 2

              

b). Ta có

















o 0

y f x x f x f 0,9 f 1

      

3 2 3 2

0,9 3.0,9 2 (1 3.1 2) 0,229

      

Ví dụ 2: Tính



và



của các hàm số sau theo x và



a).

y 2x 3

 

b).

y 2x 3x 1

  

c).

y 2x 1

 

d).

3 2

y 2x 3x

 

LỜI GIẢI

a). Ta có

















o 0 o 0

y f x x f x 2 x x 3 2x 3 2

            

. Suy ra







b). Ta có

       





o 0 o o 0 0

y f x x f x 2 x x 3 x x 1 2x 3x 1

              

   

0 0

4x x 2 x 3 x x 4x 2 x 3

          

Suy ra





x 4x 2 x 3

4x 2 x 3

x x

   



    

 

c). Ta có

     

o 0 o 0

y f x x f x 2 x x 1 2x 1

          

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

 

o 0

x(2x x)

2 x x 1 2x 1

  



    

Suy ra

 

0 0

o 0

x(2x x) 2x x

2 x x 1 2x 1

x 2 x x 1 2x 1

    



 



 

    

     

 

 

d). Ta có

       





3 2

o 0 o o 0 0

y f x x f x 2 x x 3 x x 2x 3x

            













3 2 2 3 2 2 3 2

0 0 0 0 0 0 0

2 x 3x x 3x ( x) ( x) 3 x 2x x ( x) 2x 3x

             





2 2

0 0 0

x 6x 6x x 3( x) 6x 3 x

        

Suy ra





2 2

0 0 0

x 6x 6x x 3( x) 6x 3 x

x x

       





 

2 2

0 0 0

6x 6x x 3( x) 6x 3 x

       

DẠNG 2: Tìm đạo hàm bằng định nghĩa

PHƯƠNG PHÁP

Để tìm đạo hàm của hàm số





y f x



tại điểm

bằng định nghĩa ta có thể sử dụng một trong hai cách

sau đây:

Cách 1:



Cho

một số gia









0 0

x f x x f x

    

. Lập tỉ số





Tìm giới hạn

x 0

lim

 





Kết luận:

+ Nếu

x 0

lim

 



tồn tại hữu hạn thì tại

hàm số có đaọ hàm là:

 

x 0

f' x lim

 







+ Nếu

x 0

lim

 



không tồn tại hữu hạn thì tại

hàm số không có đạo hàm.

Cách 2:

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN



Tính giá trị của









x x

f x f x

lim

x x







Kết luận:

+ Nếu









x x

f x f x

lim

x x





tồn tại hữu hạn bằng L thì tại

, ta có





f' x L



+ Nếu









x x

f x f x

lim

x x





không tồn tại hữu hạn thì tại

hàm số không có đạo hàm.

Ví dụ : Tính đạo hàm (bằng định nghĩa) của mỗi hàm số sau tại các điểm đã chỉ ra:

a).

y 2x x 1

  

tại

x 2



b).

y x x 2

  

tại

x 2

 

c).

y 2x 1

 

tại

x 1



d).

2x 1

x 1







tại

x 3



LỜI GIẢI

a). Cách 1: Cho

x 2



một số gia



. Khi đó hàm số nhận một số gia tương ứng:

       





 

0 0

y f x x f x 2 2 x 2 x 1 2.2 2 1 x 9 2 x

                  

Ta có

 





 

x 0 x 0 x 0

x 9 2 x

f' 2 lim lim lim 9 2 x 9

x x

     

  



     

 

Cách 2:









2 2

x 2 x 2 x 2

f x f 2

2x x 1 11 2x x 10

lim lim lim

x 2 x 2 x 2

  



    

 

  









 

x 2 x 2

x 2 2x 5

lim lim 2x 5 9

x 2

 

 

   



Kết luận theo định nghĩa, hàm số có đạo hàm tại

x 2



và





f' 2 9



b).

y x x 2

  

tại

x 2

 

Cách 1: Cho

x 2

 

một số gia



. Khi đó hàm số nhận một số gia tương ứng:

       

2 3

y f 2 x f 2 2 x 2 x 1 12 13 x 6( x) ( x)

                      





x 13 6 x ( x)

     

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Ta có

 





 

x 0 x 0 x 0

x 13 6 x ( x)

f' 2 lim lim lim 13 6 x ( x) 13

x x

     

    



        

 

Cách 2:









3 3

x 2 x 2 x 2

f x f 2

x x 2 12 x x 10

lim lim lim

x 2 x 2 x 2

  

 

    

 

  









 

x 2 x 2

x 2 x 2x 5

lim lim x 2x 5 13

x 2

 

  

    



Kết luận theo định nghĩa, hàm số có đạo hàm tại

x 2

 

và





f' 2 13

 

c).

y 2x 1

 

tại

x 1



Cách 1: Cho

x 1



một số gia



. Khi đó hàm số nhận một số gia tương ứng:

       

0 0

2 x

y f x x f x f 1 x f 1 2(1 x) 1 3

3 2 x 3



              

  

Ta có

 

x 0 x 0 x 0

2 x 2 1

f' 1 lim lim lim

3 2 x 3 3

x 3 2 x 3

     



   



  

   

Cách 2:













 

x 1 x 1 x 1

f x f 1 2 x 1

2x 1 3

lim lim lim

x 1 x 1

x 1 2x 1 3

  

 

 

 

 

  

x 1

2 1

lim

2x 1 3 3



 

 

Kết luận theo định nghĩa, hàm số có đạo hàm tại

x 1



và

 

f' 1

 .

d).

2x 1

x 1







tại

x 3



Cách 1: Cho

x 3



một số gia



. Khi đó hàm số nhận một số gia tương ứng:

       

0 0

2(3 x) 1 5 5 2 x 5 3 x

y f x x f x f 3 x f 3

3 x 1 4 4 x 4 4(4 x)

     

             

      

Ta có

 

x 0 x 0 x 0

3 x 3 3

f' 3 lim lim lim

x x.4(4 x) 4(4 x) 16

     



   

     

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Cách 2:

   

x 3 x 3 x 3 x 3

2x 1 5

f x f 3

3(x 3) 3 3

x 1 4

lim lim lim lim

x 3 x 3 (x 3)(x 1)4 (x 1)4 16

   





   

    

Kết luận theo định nghĩa, hàm số có đạo hàm tại

x 3



và

 

f' 3

 .

CÁC QUY TẮC TÍNH ĐẠO HÀM

TÓM TẮT GIÁO KHOA

1). Định lý 1: Cho các hàm số









u u x ,v v x

 

có đạo hàm trên (a;b) thì tổng và hiệu của chúng cũng có

đạo hàm trên khoảng (a;b) và





u v ' u' v';

  





u v ' u' v'

  

Chú ý: Định lý 1 có thể mở rộng cho tổng hay hiệu của hữu hạn các hàm số.

2). Định lý 2: Cho các hàm số









u u x ,v v x

 

có đạo hàm trên (a;b) thì tích của chúng cũng có đạo

hàm trên khoảng (a;b) và





u.v ' u'v uv'

 

Đặc biệt :





a.u ' a.u'



( a là hằng số),

Chú ý: Định lý 2 có thể mở rộng cho tích của hữu hạn các hàm số. Chẳng hạn:





u.v.w ' u'vw uv'w uvw'

  

3). Định lý 3: Cho các hàm số









u u x ,v v x

 

có đạo hàm trên (a;b) và





v x 0



trên (a;b) thì thương

cũng có đạo hàm trên khoảng (a;b) và

u u'v uv'

' .

  



 

 

Hệ quả:

 

1 v'

' v 0 .

 

  

 

 

4). Cho hai hàm số





y f u



và





u g x



. Ta gọi hàm số









y F x f g x

 

 

 

là hàm số hợp của hai hàm

số





u g x



và





y f u



. Tập xác định của hàm số





f g x

 

 

là tập hợp tất cả các giá trị của x làm cho biểu

thức





f g x

 

 

có nghĩa.

5). Định lý 4: Nếu hàm số





u u x



có đạo hàm tại điểm

và hàm số





y f u



có đạo hàm tại điểm





0 0

u u x



thì hàm số hợp









y F x f u x

 

 

 

cũng có đạo hàm tại điểm

và













0 0 0

F' x f' u .u x



hay

x u x

y' y' .u'



Hệ quả:





n n 1

u ' n.u .u'(n N



 

và

n 2);







u ' .u'

2 u



QUY TẮC TÍNH ĐẠO HÀM

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Giả sử

u u(x),v v(x),w w(x)

   là các hàm số có đạo hàm, khi đó:

1). (u + u - w)' = u' + v' - w'; 2). (uv)' = u'v + v'u; 3) (k.u)' = k.u' (

k R



)

4).

u u'v v'u

 





 

 

5).

1 v'

 

 

 

 

BẢNG ĐẠO HÀM CỦA CÁC HÀM SỐ SƠ CẤP CƠ BẢN

ạ

o hàm c

ủ

a hàm s

ố

sơ c

ấ

p cơ b

ả

ạ

o hàm c

ủ

a hàm s

ố

ợ

p (u = u(x))

(C)' = 0





 

x x , ,x 0

 

   



( x)'

2 x

 (x > 0)

1 1

( )'

  (x  0)

 

n n 1

1 n

, x 0

x x



 

  

 

 





 

u u u', ,u 0

 

    



( u)'

2 u

 (u > 0)

1 u'

( )'

  (u  0)

 

n n 1

1 n

.u', u 0

u u



 

  

 

 

(sinx)' = cosx

(cosx)' = -sinx

 

tanx ' 1 tan x

cos x

  

(x 



 

, k  Z)

 





cot x ' 1 cot x

sin x

    

(x  k, k  Z).

(sinu)' = cosu.u'

(cosu)' = -sinu.u'

 





tanu ' 1 tan u u'

cos u

  

(u 



 

, k  Z)

 





cot u ' 1 cot u u'

sin u

    

(u  k, k  Z).

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

MỘT SỐ CÔNG THỨC TÍNH ĐẠO HÀM NHANH



ax b ad bc

cx d

(cx d)

 

 



 



 



2 2

ax bx c adx 2aex be dc

dx e

(dx e)

 

    



 



 



2 2

2 2 2

ax bx c (ae bd)x 2(af dc)x bf ec

dx ex f (dx ex f)

 

      



 

   

 

BÀI TẬP TỔNG HỢP

ĐẠO HÀM

5 4 3 2

1 2 3

y x x x x 4x 5

2 3 2

 

     

 

 

5 4 3 2

1 2 3

y' x x x x 4x 5

2 3 2

 

     

 

 



 

/ / /

5 4 3 2 /

1 2 3

y' x x x x 4x 5

2 3 2

     

     

     

     

4 3 2

5 8

y' x x 3x 3x 4.

2 3

    

2 4

1 1

y x x 0,5x

4 3

   

/ 2 4

1 1

y x x 0,5x

4 3

 

   

 

 



   

/ /

/ 2 4

1 1

y x x 0,5x

4 3

   

   

   

   



y' 2x 2x .

   

4 3

y 2x x 2 x 5

   

4 3

y' 2x x 2 x 5

 

   

 

 



 

4 3 /

y' 2x x 2 x 5

 

   

 

 



3 2

y' 8x x .

  

4 3

x x 1

y x x a

4 3 2

    

(a là hằng số)

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

4 3

x x 1

y' x x a

4 3 2

 

    

 

 



3 2

y' x x x 1

   

3 2

y x x x

  

3 2

y' x x x

 

  

 

 



 









/ /

y' 3.x x x x



  



 





3 /

1 2

y' 3. 2 .x x . x x .x

2 x



 

    

 

 



6 1 2 1

y' x .x

2 x 2 x

 



   

 

 

3 3

6 1 2 x 6 1

y' x x.

3 2

x x

2 x 2 x

 

 

       

 

 

Bài 2: Tính đạo hàm của các hàm số sau:

a).









y x 3x 2 x .

   b)









y 2x 3 x 2x

   c).









2 2

y x 1 5 3x

  

a).









y x 3x 2 x .

  

 





 

2 2 2

y' x 3x 2 x x 3x . 2 x x 3x . 2 x

        

















2 2

2x 3 2 x x 3x 1 3x 2x 6.

         

b).









y 2x 3 x 2x

  

 

   

 

5 5 5

y' 2x 3 x 2x 2x 3 x 2x x 2x 2x 3

 

        

 













5 4 5 4

2 x 2x 5x 2 2x 3 12x 15x 8x 6.

        

c).









2 2

y x 1 5 3x

  

          

/ /

2 2 2 2 2 2

y' x 1 5 3x x 1 5 3x 5 3x x 1

 

        

 









2 2 3 3 3

2x 5 3x 6x x 1 10x 6x 6x 6x 12x 4x.

          

Bài 3: Tính đạo hàm của các hàm số sau:

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

a).





y x x

  b).





3 2

y 2x 3x 6x 1

    c).





y 1 2x

 

a).





y x x

  . Sử dụng công thức





u .u .u'

 

  (với

u x x

 

)

















7 7 7 6

y' 2 x x . x x 2 x x 7x 1

     

b).





3 2

y 2x 3x 6x 1

    . Sử dụng công thức







với

3 2

u 2x 3x 6x 1

   

















3 2 3 2 3 2 2

y' 2 2x 3x 6x 1 2x 3x 6x 1 2 2x 3x 6x 1 6x 6x 6 .

            

c).





y 1 2x .

  Sử dụng công thức







với

u 1 2x

 













 





2 / 2 2

2 2 2 2

y' 3 1 2x 1 2x 3 1 2x 4x 12x 1 2x .

        

Bài 4: Tính đạo hàm của các hàm số sau:

a).

y x x x 1

  

b).

y 1 2x x

  

c).

2 2

y x 1 1 x

   

a).

y x x x 1

  

 

   

/. /

2 /

1 3 x

y' x x x 1 2x x'. x x .x 2x x .x 2x .

2 x

          

b).

y 1 2x x

  

. Sử dụng công thức





với

u 1 2x x

  





2 2

1 2x x

1 x

1 2x x 1 2x x

 



 

   

c).

2 2

y x 1 1 x

   

















/ /

2 2

/ /

2 2

2 2 2 2

x 1 1 x

x x

y' x 1 1 x .

2 x 1 2 1 x x 1 1 x

 

       

   

Bài 5: Tính đạo hàm của các hàm số sau:

a).

y xcosx



b).

sinx

1 cosx

 



 



 

c).





y sin 2x 1

 

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

d).

y sin 2 x

 

e).

y sinx 2x

  f).

2 3

y 2sin 4x 3cos 5x

 

a).

y xcosx



. Ta áp dụng đạo hàm tích.

 

y' x'cosx x. cosx cosx xsin x.

   

sinx

1 cosx

 



 



 

. Bước đầu tiên ta áp dụng công thức







với

sin x

1 cosx





2 /

sinx sin

y' 3 .

1 cosx 1 cosx

   



   

 

   

Tính :

     

 

/ /

2 2

sinx 1 cosx 1 cos x .sinx cosx 1 cosx sin x

sinx

1 cosx

1 cosx 1 cosx

    

 

 

 



 

 

 

2 2

cosx cos x sin x 1

1 cosx

 

 



Vậy

 

sinx 1 3sin x

y' 3 .

1 cosx 1 cosx

1 cosx

 

 

 

 

 



c).





y sin 2x 1

 

. Bước đầu tiên áp dung công thức







với





u sin 2x 1

 

Vậy

 





   

 

3 2

y' sin 2x 1 3sin 2x 1 . sin 2x 1 .

    

Tính

 

sin 2x 1

 : Áp dụng

 

sinu

, với





u 2x 1

 

Ta được:

 

     

sin 2x 1 cos 2x 1 . 2x 1 2cos 2x 1 .

     

















2 2

y' 3.sin 2x 1 .2cos 2x 1 6sin 2x 1 cos 2x 1 .

      

d).

y sin 2 x

 

. Áp dụng công thức

 

sinu

với

u 2 x

 









2 2 2 2

2 2

2 x

y' cos 2 x . 2 x cos 2 x . .cos 2 x .

2 2 x 2 x



      

 

e).

y sinx 2x

  . Áp dụng





, với

u sinx 2x

 

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

 

sinx 2x

cosx 2

y' .

2 sinx 2x 2 sinx 2x



 

 

f).

2 3

y 2sin 4x 3cos 5x

  . Bước đầu tiên áp dụng

 

u v











/ /

2 3

y' 2sin 4x 3 cos 5x

 

Tính





sin 4x

: Áp dụng







, với

u sin 4x,



ta được:





   

/ /

sin 4x 2sin4x. sin4x 2sin4x.cos4x 4x 4sin8x.

  

Tương tự:





     

/ /

3 2 2

cos 5x 3cos 5x. cos5x 3cos 5x. sin5x . 5x

  

15cos 5x.sin5x cos5x.sin10x.



  

Kết luận:

y' 8sin8x cos5x.sin10x

 

Cho

 

3 2

x x

f x 2x

3 2

  

. Với những giá trị nào của x thì:





f' x 0







f' x 2

 





f' x 10



LỜI GIẢI

Ta có

 

3 2

x x

f' x 2x x x 2

3 2

 

     

 

 

a).





f' x 0 x x 2 0 x 1 x 2

         

b).





2 2

f' x 2 x x 2 2 x x 0 x 0 x 1

              

c).





2 2

f' x 10 x x 2 10 x x 12 0 x 3 x 4

             

Câu : Giải

a). Cho









3 2

f x 2x x 2,g x 3x x 2

      . Giải bất phương trình









f' x g' x

 .

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

b).Cho

   

3 2 3

f x 2x x 3,g x x 3

      . Giải bất phương trình









f' x g' x

 .

Cho

 

60 64

f x 3x 5

   

. Giải phương trình





f' x 0



LỜI GIẢI

a). Ta có

 





3 2

f' x 2x x 2 6x 1

    

 





g' x 3x x 2 6x 1

    

















2 2

f' x g' x 6x 1 6x 1 6x 6x 0 x ;0 1;

            

b).

 

3 2 2 3 2

f' x 2x x 3 6x 2x, g' x x 3 3x x

 

         

 

 

















2 2 2

f' x g' x 6x 2x 3x x 3x 3x 0 x ;0 1;

            

c). Ta có

 

3 2 4

60 64 60 192

f' x 3x 5 3

x x x

 

      

 

 

   

2 4

60 192

f' x 0 3 0 1

x x

     . Đặt

 

t , t 0

 

 

1 1

1 192t 60t 3 0 t t

4 16

       

Với

1 1 1

t x 4 x 2

4 4

       

Với

1 1 1

t x 16 x 4

16 16

       

Vậy





f' x 0



có 4 nghiệm

x 2

 

x 4

 

VI PHÂN

TÓM TẮT GIÁO KHOA

Cho hàm số





y f x



có đạo hàm tại

. Gọi



là số gia của biến số tại

. Ta gọi tích





f' x . x



là vi

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

phân của hàm số f(x) tại điểm

ứng với số gia



. Kí hiệu

0 0

df(x ) f'(x ). x

 

Cho hàm số





y f x



có đạo hàm tại x. Ta gọi tích





f' x . x



là vi phân của hàm số f(x) tại điểm x ứng với

số gia



(gọi tắt là vi phân của f tại điểm x). Kí hiệu

df(x) f'(x). x

 

. Nếu chọn hàm số

y x



thì ta có

dy dx 1. x x

    

. Vì vậy ta thường kí hiệu

x dx

 

và





dy f' x dx



Công thức tính gần đúng nhờ vi phân là:













0 0 0

f x x f x f' x . x

    

PHƯƠNG PHÁP GIẢI TOÁN

DẠNG 1: Tìm vi phân của hàm số

PHƯƠNG PHÁP

a). Tính vi phân của hàm số f(x) tại

cho trước:

Tính đạo hàm của hàm số tại

Suy ra vi phân của hàm số tại

ứng với số gia



là

0 0

df(x ) f'(x ). x

 

b). Tính vi phân của hàm số f(x).

Tính đạo hàm của hàm số .

Suy ra vo phân của hàm số:





dy df(x) f' x dx

 

Ví dụ 1: Cho hàm số

3 2

y x 4x 2

  

. Tính vi phân của hàm số tại điểm

x 1



, ứng với số gia

x 0,02

 

LỜI GIẢI

Ta có

y' f '(x) 3x 4x

  

. Do đó vi phân của hàm số tại điểm

x 1



, ứng với số gia

x 0,02

 

là:





df(1) f'(1). x 3.1 4.1 .0,02 0,02

     

Ví dụ 2: Tính vi phân của các hàm số sau:

a).

2x 3x 1

x x 1

 



 

b).

3 2

y 3x 2x

  c).

y sin xcos

 d).

y xsinx cosx

 

LỜI GIẢI

a). Ta có

   

2 2 2 2

2 2

(2x 3x 1)'(x x 1) (x x 1)'(2x 3x 1)

y' f'(x)

x x 1 x x 1

        

  

   

suy ra

dy f'(x)dx

 

DẠNG 2: Tính gần đúng giá trị của hàm số:

Để tính gần đúng giá trị của hàm số f(x) tại điểm

x (x x)

  

cho trước, ta áp dụng công thức













0 0 0

f x x f x f' x . x

    

Ví dụ tính gần đúng các giá trị sau (lấy 4 chữ số thập phân trong kết quả).

a).

16,25

b).

cos30 15'

c).

sin 46

d).

0,9995

e).

tan 53 15'

LỜI GIẢI

a). Ta có

16,25 16 0,25

  . Xét hàm số

   

f x x f' x

2 x

  

chọn

x 16



và

x 0,25

 

, ta có













0 0 0

f x x f x f' x . x

    

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

16 0,25 16 .0,25 4 0,03125 4,03125 16 0,25 4,0313

2 16

         

b). Ta có

 

0 0

cos30 15' cos 30 15' cos

6 720

 

 

   

 

 

Xét hàm số









f x cos x f' x sin x

   

Chọn





và

720



 

, ta có













0 0 0

f x x f x f' x . x

    

cos cos sin .

6 720 6 6 720 2 1440

 

     

     

 

 

c). Ta có

 

0 0 0

sin 46 sin 45 1 sin

4 180

 

 

   

 

 

Xét hàm số









f x sin x f' x cos x

  

Chọn





và

180



 

, ta có













0 0 0

f x x f x f' x . x

    

2 2

sin sin cos .

4 180 4 4 180 2 360

 

     

     

 

 

d). Ta có

1 1

0,9995 1 0,0005





Xét hàm số

   

1 1

f x f' x

   

Chọn

x 1



và

x 0,0005

  

, ta có













0 0 0

f x x f x f' x . x

    

1 1.( 0,0005) 1,0005

1 0,0005

    



e).

 

0 0 0

tan 53 15' tan 60 (6 45') tan

3 80

 

 

   

 

 

Xét hàm số









f x tanx f' x 1 tan x

   

Chọn





và



  

, ta có













0 0 0

f x x f x f' x . x

    

3 3

tan tan 1 tan . 1,2608

3 80 3 3 80

     

    

      

     

     

ĐẠO HÀM CẤP CAO

A.TÓM TẮT GIÁO KHOA.

1. Cho hàm số





y f x



có đạo hàm





f' x

. Hàm số





f' x

còn gọi là đạo hàm cấp 1 của hàm số





f x

. Nếu

hàm số





f' x

có đạo hàm thì đạo hàm đó được gọi là đạo hàm cấp 2 của hàm số





f x

, kí hiệu là y’’ hay





f'' x

. Đạo hàm của đạo hàm cấp 2 được gọi là đạo hàm cấp 3 của hàm số





f x

, kí hiệu là y’’’ hay f’’’





Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

. Tương tự, ta gọi đạo hàm của đạo hàm cấp





n 1



là đạo hàm cấp n của hàm số





f x

, kí hiệu là





hay









f x

, tức là ta có:

   





 

n n 1

y y ' n N,n 1



  

2.Đạo hàm cấp 2 của hàm số f(t) là gia tốc tức thời của chuyển động s=f(t) tại thời điểm t.

B.PHƯƠNG PHÁP GIẢI TOÁN.

DẠNG 1: Tính đạo hàm cấp cao của hàm số.

1.PHƯƠNG PHÁP

Áp dụng trực tiếp định nghĩa:

   





n n 1

y y '





để tính đạo hàm đến cấp mà đề bài yêu cầu.

Ví dụ: Tính đạo hàm đến cấp đã chỉ ra của các hàm số sau:

a).





y xsin 2x, y'''



b).





y cos x, y'''



c).





4 3 2 (n)

y x 4x 3x 1, y   

d).





4 (4)

y x sin2x, y 

e).





2 (5)

y sin 2x, y

f).





(4)

3x 1

y , y

x 2







LỜI GIẢI

a). Có

y' x'sin2x x.(sin 2x)' sin 2x 2xcos2x

   

y'' (sin2x)' (2x)'cos2x 2x(cos2x)' 4cos2x 4xs

in2x

     

y''' 4(cos2x)' (4x)'sin 2x 4x(sin 2x)' 8sin 2x 4

sin2x 8cos2x

       

12sin 2x 8cos 2x

  

b). Ta có

 

y cos x 1 cos2x y' sin2x

     

y'' 2cos2x y''' 4sin 2x

    

c).

4 3 2

y x 4x 3x 1

   

3 2 2

y' 4x 12x 6x y'' 12x 24x 6 y''' 24x 24

          

(4) (5) (n)

y 24 y 0 ... y 0

      

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

d).

y x sin 2x

 

3 2

y' 4x 2cos2x y'' 12x 4sin 2x

     

(4)

y''' 24x 8cos2x y 24 16sin 2x

     

e).

 

y sin 2x 1 cos4x

  

y' 2sin 4x y'' 8cos4x y''' 32sin4x

      

(4) (5)

y 128cos 4x y 512sin 4x

    

f).





(4)

3x 1

y , y

x 2







 

   

2 4 3

7 x 2

7 14

y' y''

(x 2)

x 2 x 2

 

 

 



 

    



 

 

   

 

   

/ /

3 4

(4)

6 4 8 5

14 x 2 42 x 2

42 168

y''' y

x 2 x 2 x 2 x 2

   

  

   



   

     

   

DẠNG 2: Tìm đạo hàm cấp n của một hàm số

PHƯƠNG PHÁP

Bước 1: Tính

y',y'',y'''

. Dựa vào các đạo hàm vừa tính, dự đoán công thức tính

(n)

Bước 2: Chứng minh công thức vừa dự đoán là đúng bằng phương pháp quy nạp.

Chú ý: Cần phân tích kĩ các kết quả của đạo hàm

y',y'',y'''

tìm ra quy luật để dự đoán công thức

(n)

chính xác.

Ví dụ 1: Tìm đạo hàm cấp n của hàm số





y sinx n N

 

LỜI GIẢI

Bước 1: Ta có:

y' cosx sin x 1. ; y'' sinx sin x 2

2 2

     

      

   

   

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Dự đoán:

 

y sin x n 1 , n N

  

   

 

 

Bước 2: Chứng minh





bằng quy nạp:







n 1: 1



hiển nhiên đúng.



Giả sử





đúng với

n k 1

 

nghĩa là ta có:

y sin x k

  

 

 

 

ta phải chứng minh





cúng đúng với

n k 1

 

nghĩa là ta phải chứng minh

 

   

k 1

y sin x k 1 2



  

  

 

 

Thật vậy : vế trái

   

k 1 k

2 y y sin x k cos x k sin x k 1

2 2 2



 

        

 

         

 

     

 

     

 

=vế phải











đúng, nghĩa là





đúng với

n k 1.

 

Bước 3: theo nguyên lí quy nạp suy ra

n *

y sin x n , n N .

  

   

 

 

Ví dụ 2: Tìm đạo hàm cấp n của hàm số

 

y n N

x 3

 



LỜI GIẢI

Ta có:

 

/ /

2 2

1 1!

y' 1 1 ;

x 3 x 3

   

 

 

2 2

3 3

1.2 2!

y'' 1 . 1 . .

x 3 x 3

   

 

Dự đoán:

 

n *

n 1

y 1 1 , n N .

x 3



   



Chứng minh





bằng phương pháp quy nạp:





n 1: 1

 

hiển nhiên đúng.



Giả sử





đúng với

n k 1

 

, nghĩa là ta có:

 

k 1

y 1

x 3



 



ta phải chứng minh





cúng đúng

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

với

n k 1

 

, nghĩa là ta phải chứng minh:

 





 

k 1

k 2

k 1 !

y 1 2

x 3



 



Thật vậy: vế trái

   

 

k k 1 k 1

k 1 k

k 1 2

k 1

k! k!

2 y y 1 1 . . x 3

x 3

 



 

 

 

      

 

 

 

 

  



 

 

 

 





 





 

k 1 k 1

k 2 k 2

k! k 1 k 1 !

1 . 1 . vt 2

x 3 x 3

 

    

 

Vậy





đúng nghĩa là





đúng với

n k 1.

 

Theo nguyên lí quy nạp ta suy ra

 

n *

n 1

y 1 . , n N .

x 3



   



DẠNG 3: Chứng minh đẳng thức:

Bài 11:

a). Cho hàm số

y xsinx



. Chứng minh









x.y'' 2 y' sin x xy 0

    

b). Cho hàm số :

y 2x x

 

chứng minh:





y .y'' 1 0

  

c). Cho hàm số:

y xtanx



chứng minh:













2 2 2

x .y'' 2 x y 1 y 0

    

d). Cho hàm số:

x 3

x 4







chứng minh:

     

2 y' y 1 .y''

  

LỜI GIẢI

a). Cho hàm số

y xsinx



. Chứng minh









x.y'' 2 y' sin x xy 0

    

Ta có

   

/ /

y' xsinx y' x'.sinx x. sinx y' sinx xcosx

      

       

/ / / /

y'' sin x xcos x sinx xcosx cosx x'.cosx x. cosx 2c

osx xsinx

        

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN













1 x 2cosx xsin x 2 sin x xcosx sin x x sinx 0

      

2 2

2xcosx x sin x 2xcosx x sin x 0 0 0

      

(đpcm).

b). Cho hàm số :

y 2x x

 

chứng minh:





y .y'' 1 0

  

Ta có:





 

2 2

1 1 x

y' 2x x y' . 2x x .

2 2x x 2x x



     

 

 





 





 





2 2

1 x

2x x . 1 x

1 x . 2x x 2x x . 1 x

2x x

y''

2x x 2x x



   

    



 

 





 









2 3

2 2 2

2x x 1 x

2x x . 2x x 2x x

   



 

  

 









2x x . 1 0 1 1 0

2x x



        



(đpcm).

c). Cho hàm số:

y xtanx



chứng minh:













2 2 2

x .y'' 2 x y 1 y 0

    

Ta có:

   





/ /

y' x tanx x'.tan x x. tan x tan x x 1 tan x

     

     





 





/ /

2 2

y'' tan x x'. 1 tanx x. 1 tanx 2 1 tan x x. 2tan x . tan 1

        









2 1 tan x 1 xtan x

  





















2 2 2 2 2

2x 1 tan x . 1 xtan x 2 x x tan x 1 xtan x 0

       

















2 2 2 2

2x 1 tan x 1 xtanx 2x 1 tan x 1 xtan x 0

      

0 0

 

(đpcm).

d). Cho hàm số:

x 3

x 4







chứng minh:

     

2 y' y 1 .y''

  

Ta có:

 

x 3 7

x 4

  

 

 



 



Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

 





   

4 3

7 x 4

y''

x 4 x 4

 



 

 

 

       

2 3 4 4

7 x 3 14 98 98

2 1 .

x 4

x 4 x 4 x 4 x 4

   

   

   

     

 

   



 

   

   

(đpcm).

e) Cho hàm số

y cos 3x

 chứng minh:









18 2y 1 y'' 0

   

Ta có:

y cos 3x



    

/ /

y' 2.cos3x cos 3x 2cos3x. sin 3x 3x 3sin6x

    

y'' 18cos6x

 









18 2cos 3x 1 18cos6x 0 18.cos6x 18cos6x 0

       

(đpcm).

Bài 12:

a).Cho hàm số

3 3

sin x cos x

1 sinx.cosx







. Chứng minh





y'' y 0

  

b). Cho hàm số





y x 1

  . Chứng minh:





y 2xy''' 4y'' 40

   

c). Cho hàm số

y x 1 x

   . Chứng minh:









4 x 1 .y'' 4x.y' y 0

    

d). Chứng minh





2 2

1 x .y'' x.y' k .y 0

   

nếu





y x x 1

  

LỜI GIẢI

a).Cho hàm số

3 3

sin x cos x

1 sinx.cosx







chứng minh





y'' y 0

  

Ta có:









2 2

sinx cosx sin x cos x sinxcosx

1 sin xcosx

  













sin x cosx 1 sin xcos x

sin x cosx

1 sinxcosx

 

  



Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

y' cosx sinx

 

y'' sinx cos x

  





sin x cosx sin x cos x 0 0 0

        

(đpcm).

b). Cho hàm số





y x 1

  . Chứng minh:





y 2xy''' 4y'' 40

   

Ta có:

4 2

y x 2x 1

  

y' 4x 4x

 

y'' 12x 4

 

y''' 24x



y'''' 24.















24 2x 24x 4 12x 4 40.

     

2 2

24 48x 48x 16 40 40 40

       (đpcm).

c). Cho hàm số

y x 1 x

   . Chứng minh:









4 x 1 .y'' 4x.y' y 0

    

Ta có:

2 2

1 x x 1 x

y' . 1

1 x 2 1 x

2 x 1 x

 

 

  

 

 

 

 









2 2 2 2

x 1 x .2 1 x 2 1 x . x 1 x

y''

2 1 x

 

      

 

 









 

2 2

x 1 x . 2 1 x 4x

8 1 x . 1 x

   



 

 





 

2 2

2 2 2

x 1 x 2 1 x 4x

x 1 x

4 x 1 4x. x 1 x 0

8 1 x 1 x 2 1 x

   

 

       

  

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN





2 2

x 1 x . 2 1 x 4x

x 1 x

2x x 1 x 0

2 1 x 1 x

   

 

     

 

2 2

2x x 1 x 2x x 1 x

x 1 x x 1 x 0

1 x 1 x

   

        

 

0 0

 

(đpcm).

d). Chứng minh





2 2

1 x .y'' x.y' k .y 0

   

nếu





y x x 1

  

Ta có:





y x x 1

  





k 1

y' k x x 1 . 1

x 1



 

    

 



 









k 1

2 2

x x 1

k x x 1 . k.

x 1 x 1



 

 

 

 

   

 

 

 





















 

k / k

2 2 2 2

2 2

x x 1 . x 1 x 1 . x x 1

y'' k.

x 1

k x x 1

. x 1 . x x 1

x 1 x 1

x 1

 

      

 

 





 

   

 













 

2 2

k x x 1 k x 1 x

x 1 x 1

   



 

 









 





k k

2 2 2

k x x 1 . k x 1 x x.k x 1 x

1 x

x 1 x 1 1 x

     

   

  

















k k

2 2 2 2

2 2

k x x 1 . k x 1 x x.k x 1 x

k x x 1 0

x 1 1 x

     

     

 

Quy đồng đặt thừa số chung được:

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN









2 2 2 2

x x 1

k x 1 kx kx k x 1 0 0 0

x 1

 

       



(đpcm).

Ví dụ 3: Chứng minh rằng với mọi số nguyên

n 1



ta có:

a)Nếu



thì

 

n 1

y 1 . .



 

b) Nếu

y cos x



thì

y cosx.



Ví dụ 4: Chứng minh rằng:

a)Nếu

y sinax



thì

4n 4n

y a .sinax

 (a là hằng số).

b) Nếu

y sin x

 thì

4n 4n 1

y 2 cos2x.



 

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

PHƯƠNG TRÌNH TIẾP TUYẾN

I – Kiến thức cần nhớ

 Phương trình tiếp tuyến của









C : y f x

 tại điểm





o o

M x ; y

có dạng:





o o

: y k x x y

   

  

  

 Điều kiện cần và đủ để hai đường









C : y f x

 và









C : y g x

 tiếp xúc nhau



hệ









   

f x g x

f' x g' x















có nghiệm (nhớ: "hàm



hàm, đạo



đạo")

II – Các dạng toán viết phương trình tiếp tuyến thường gặp

 Viết PTTT



của









C : y f x ,

 biết



có hệ số góc k cho trước

 Gọi





o o

M x ; y

là tiếp điểm. Tính





y' y' x

 .

 Do phương trình tiếp tuyến



có hệ số góc k





y' x k

 





 Giải





tìm được









o o o o o

x y f x : y k x x y

     

 Lưu ý. Hệ số góc

k y'(x )

 của tiếp tuyến



thường cho gián tiếp như sau:

 Phương trình tiếp tuyến

// d : y ax b k a

    

 Phương trình tiếp tuyến

d : y ax b k

      

 Phương trình tiếp tuyến



tạo với trục hoành góc

k tan

   

 Phương trình tiếp tuyến



tạo với

d : y ax b

 

góc

k a

tan

1 k.a



   



 Viết PTTT



của









C : y f x ,

 biết



đi qua (kẻ từ) điểm





A A

A x ;y

 Gọi





o o

M x ; y

là tiếp điểm. Tính





o o

y f x

 và





k y' x

 theo

 Phương trình tiếp tuyến



tại





o o

M x ; y

là





o o

: y k x x y

   

 Do









A A A A o o

A x ;y y k x x y

     





 Giải phương trình





o o

i x y

  và k



phương trình



 Viết PTTT



của









C : y f x ,

 biết



cắt hai trục tọa độ tại A và B sao cho tam giác OAB

vuông cân hoặc có diện tích S cho trước

 Gọi

o o

M(x ; y )

là tiếp điểm và tính hệ số góc

k y'(x )

 theo

Với





k y' x

 là hệ số góc tiếp tuyến.

Để viết phương trình tiếp tuyến



ầ

n tìm ba thành ph

ầ

o o

x , y , k

 

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

 Đề cho

OAB

S S OA.OB 2S









  







 

 Giải





hoặc





o o

ii x y ;k

  

phương trình tiếp tuyến



 Tìm những điểm trên đường thẳng

d : ax by c 0

  

mà từ đó vẽ được

1,2,3,...,n

tiếp tuyến

với đồ thị hàm số









C : y f x



 Gọi





M M

M x ; y d : ax by c 0

   

(sao cho có một biến

trong M)

 PTTT



qua M và có hệ số góc k có dạng





M M

: y k x x y

    .

 Áp dụng điều kiện tiếp xúc:









 

M M

f x k x x y

f' x k



  















 

 Thế k từ





vào





i ,

được:













M M

f x f' x . x x y

  





iii

 Số tiếp tuyến của





vẽ từ



số nghiệm x của





iii

 Tìm những điểm





M M

M x ; y mà từ đó vẽ được hai tiếp tuyến với đồ thị hàm số









C : y f x

 và hai tiếp tuyến đó vuông góc nhau

 PTTT



qua M và có hệ số góc k có dạng





M M

: y k x x y

    .

 Áp dụng điều kiện tiếp xúc:









 

M M

f x k x x y

f' x k



  















 

 Thế k từ





vào





i ,

được:













M M

f x f' x . x x y

  





iii

 Qua M vẽ được hai tiếp tuyến với









C iii

 có hai nghiệm phân biệt

1 2

x ,x

 Hai tiếp tuyến đó vuông góc nhau









1 2 1 2

k .k 1 y' x .y' x 1

     

 Lưu ý.

 Qua M vẽ được hai tiếp tuyến với sao cho hai tiếp điểm nằm về hai phía với trục

hoành thì





   

1 2

iii :

f x .f x 0.













 Đối với bài toán tìm điểm









M C : y f x

  sao cho tại đó tiếp tuyến song song hoặc vuông

góc với đường thẳng d cho trước, ta chỉ cần gọi





o o

M x ; y

và



là tiếp tuyến với





k f' x

 . Rồi

áp dụng





o d

k f' x k

  nếu cho song song và





o d

f' x .k 1

 

nếu cho vuông góc





o o o o

x y M x ;y

   .





vuông cân

 

tạo với Ox một góc

và

 

có hai nghiệm phân biệt

1 2

x ,x

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

BÀI TẬP TỔNG HỢP

Cho đường cong









3 2

C : y f x x 3x

   . Viết phương trình tiếp tuyến của





trong các trường

hợp sau:

a) Tại điểm





M 1 ; 2



b) Tại điểm thuộc





và có hoành độ

x 1

 

c) Tại giao điểm của





với trục hoành .

d) Biết tiếp tuyến đi qua điểm





A 1 ; 4

 

LỜI GIẢI

Ta có

f'(x) 3x 6x

 

a). Ta có

f'(x ) f'(1) 3

  

Vậy phương trình tiếp tuyến tại điểm





M 1 ; 2



0 0 0

y f'(x )(x x ) y

  





y 3 x 1 3 y 3x

       

b). Ta có





0 0 0

x 1 y 4,f ' x 9

     

Vậy phương trình tiếp tuyến tại điểm





N 1; 4

 

là

0 0 0

y f'(x )(x x ) y

  





y 9 x 1 4 y 9x 5

     

c). Phương trình hoành độ giao điểm của





với trục hoành:

3 2

x 0

x 3x 0

x 3





  







Với

0 0 0

x 0 y 0,f'(x ) f'(0) 0

    

Vậy phương trình tiếp tuyến tại điểm





0;0

là

0 0 0

y f'(x )(x x ) y

  

y 0

 

Với

0 0 0

x 3 y 0,f'(x ) f'(3) 9

    

Vậy phương trình tiếp tuyến tại điểm





3;0

là

0 0 0

y f'(x )(x x ) y

  





y 9 x 3 y 9x 27

     

d). Gọi





0 0

x ;y

là tọa độ tiếp điểm của phương trình tiếp tuyến d đi qua điểm A

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Vì điểm









3 2

0 0 0 0 0

x ;y C y x 3x

    , và





0 0 0

f' x 3x 6x

 

Phương trình d:

0 0 0

y f'(x )(x x ) y

  









2 3 2

0 0 0 0 0

y 3x 6x x x x 3x

     

Vì





A 1; 4 d

  

nên:









2 3 2

0 0 0 0 0

3x 6x 1 x x 3x 4

      

0 0 0 0

2x 6x 4 0 x 2 x 1

        

Với





0 0

x 2 y 4,f' 2 0

    

, phương trình tiếp tuyến

y 4

 

Với





0 0

x 1 y 4,f' 1 9

      

, phương trình tiếp tuyến





y 9 x 1 4 y 9x 5

     

Cho đường cong

 

3x 1

C : y

1 x







a). Viết phương trình tiếp tuyến của





biết tiếp tuyến song song với đường thẳng

(d) : x 4y 21 0

  

b). Viết phương trình tiếp tuyến của





biết tiếp tuyến vuông góc với đường thẳng

( ) : 2x 2y 9 0

   

c). Viết phương trình tiếp tuyến của





biết tiếp tuyến tạo với đường thẳng :

(d) : x 2y 5 0

  

một góc

Tập xác định

D R\{1}

 . Ta có

 

y' f' x

1 x

 



a). Có

 

1 21 1

d : x 4y 21 0 y x k

4 4 4

       

Vì tiếp tuyến song song với d nên

tt d

k k

 

Gọi





0 0

M x ,y

là tọa độ tiếp điểm của tiếp tuyến, ta có





0 tt

f' x k



 

4 1

1 x

 



 

0 0 0

x 1 16 x 5 x 3

       

Với

0 0

x 5 y 4

   

, phương trình tiếp tuyến tại điểm này là:

0 0 0

y f'(x )(x x ) y

  

 

1 1 21

y x 5 4 y x

4 4 4

       (loại, vì trùng với d).

Với

x 3 y 2

    

, phương trình tiếp tuyến tại điểm này là:

0 0 0

y f'(x )(x x ) y

  

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

 

1 1 5

y x 3 2 y x

4 4 4

      

b).

 

: 2x 2y 9 0 y x k 1



          

Vì tiếp tuyến vuông góc với



nên,

tt tt

k .k 1 k 1



   

Gọi





0 0

N x ,y

là tọa độ tiếp điểm của tiếp tuyến, ta có





0 tt

f' x k



 

1 x

 



 

0 0 0

x 1 4 x 3 x 1

       

Với

x 3 y 5

   

, phương trình tiếp tuyến tại điểm này là:

0 0 0

y f'(x )(x x ) y

  





y 1 x 3 5 y x 2

        

Với

x 1 y 1

    

, phương trình tiếp tuyến tại điểm này là:

0 0 0

y f'(x )(x x ) y

  





y 1 x 1 1 y x 2

        

c).

1 5 1

(d) : x 2y 5 0 y x k

2 2 2

       

Ta có tiếp tuyến hợp với d một góc 30

, nên có

tt d

k k

tan30

1 k k







2 2

tt tt tt tt

1 1 1 11 1

3 k 1 k k 4k 0

2 2 4 4

1 k



   

        

   

   



Cho hàm số

 

x x 2

y f(x) C

x 1

 

 



a). Viết phương trình tiếp tuyến của (C) tại điểm M(2; 4).

b). Viết phương trình tiếp tuyến của (C) biết tiếp tuyến có hệ số góc

k 1



LỜI GIẢI

Ta có:

x 2x 1

f'(x)

(x 1)

 





Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

a). Ta có

0 0

x 2 f'(x ) f'(2) 1

    

Phương trình tiếp tuyến của (C) tại điểm M(2; 4) là









0 0 0

y f' x x x y

  





y 1 x 2 4 y x 6

        

b). Gọi

là hoành độ tiếp điểm của tiếp tuyến với đồ thị, ta có





f' x 1



0 0

x 2x 1

1 1 1

(x 1)

 

    



(vô lý).

Kết luận không có tiếp tuyến nào có hệ số góc bằng 1.

Cho hàm số (C):

y 1 x x

   . Tìm phương trình tiếp tuyến với (C):

a) Tại điểm có hoành độ



b) Song song với đường thẳng (d): x + 2y = 0.

LỜI GIẢI

Tập xác định

1 5 1 5

D ;

2 2

 

   



 

 

. Ta có

 

1 2x

f' x

2 1 x x

 



 

a). Với

 

0 0 0

1 1 1 1 1

x y 1 ,f' x f' 2

2 2 4 2 2

 

        

 

 

Vậy phương trình tiếp tuyến tại điểm

1 1

;

2 2

 

 

 

là









0 0 0

y f' x x x y

  

1 1 3

y 2 x y 2x

2 2 2

 

       

 

 

b). Ta có

1 1

(d) : x 2y 0 y x k

2 2

       

Vì tiếp tuyến song song với d nên,

tt d

k k

  

. Gọi

là hoành độ tiếp điểm của tiếp tuyến với

đồ thị, ta có

 

0 0 0 0

0 0

1 2x 0

1 2x

1 1

f' x 1 2x 1 x x

x 0 x 1

2 2

2 1 x x



 

 



          



   



 



Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

So với điều kiện

x 0



(nhận),

x 1

 

(loại)

Với

0 0

x 0 y 1

  

, phương trình tiếp tuyến tại điểm





0;1

là:

 

1 1

y x 0 1 y x 1

2 2

       

Cho hàm số





3 2

y x 3x 9x 5 C

    . Trong tất cả các tiếp tuyến của đồ thị





, hãy tìm tiếp

tuyến có hệ số góc nhỏ nhất.

LỜI GIẢI

Ta có





y' f ' x 3x 6x 9

   

Gọi

là hoành độ tiếp điểm của tiếp tuyến, vậy





0 0 0

f' x 3x 6x 9

  

Ta có





   

2 2

0 0 0 0 0 0

3x 6x 9 3 x 2x 1 12 3 x 1 12 12, x C

            

Vậy





minf' x 12

 

tại

0 0

x 1 y 16

   

Suy ra phương trình tiếp tuyến cần tìm:





y 12 x 1 16 y 12x 4

       

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Cho hàm số

 

x 2

y 1

2x 3







. Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết tiếp tuyến

đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa

độ O. (Khối A – 2009) .

LỜI GIẢI

Tập xác định

D R\

 

 

 

 

. Ta có

 

y' f' x

2x 3



 



Vì tiếp tuyến (d) cắt hai trục Ox, Oy lần lượt tại A, B tạo thành tam giác OAB vuông cân, nên

đường thẳng (d) hợp với trục Ox một góc 45

Vậy có

tt tt

k tan45 k 1

    

Gọi

là hoành độ tiếp điểm của tiếp tuyến, ta có





f' x 1

 

Với

 

f' x 1 1

2x 3



  



(phương trình vô nghiệm).

Với

 

0 0 0 0

f' x 1 1 2x 3 1 x 1 x 2

2x 3



             



Với

0 0

x 1 y 1

   

, phương trình tiếp tuyến tại điểm này





y 1 x 1 1 y x

      

. Tiếp tuyến

này loại vì đường thẳng này đi qua gốc tọa độ nên không tạo thành được tam giác.

Với

0 0

x 2 y 0

   

, phương trình tiếp tuyến tại điểm này





y 1 x 2 y x 2

      

Cho hàm số









3 2

y x 3mx m 1 x 1 1

     , m là tham số thực. Tìm các giá trị của m để tiếp tuyến

của đồ thị của hàm số (1) tại điểm có hoành độ

x 1

 

đi qua điểm





A 1;2

. (Dự bị A1 - 2008)

LỜI GIẢI

Tập xác định

D R



y' f'(x) 3x 6mx m 1

    

Với

0 0

x 1 y 2m 1

    

f'( 1) 5m 4

   

Phương trình tiếp tuyến tại điểm





M 1;2m 1

 









y 5m 4 x 1 2m 1

     

(d).

Ta có

   

A 1;2 (d) 5m 4 .2 2m 1 2 m

        

Cho hàm số

 

3x 1

y 1

x 1







. Tính diện tích của tam giác tạo bởi các trục tọa độ và tiếp tuyến của

đồ thị của hàm số (1) tại điểm





M 2;5

 .(Dự bị D1 - 2008)

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

LỜI GIẢI

Tập xác định





D R\ 1

 

. Có

 

x 1





Phương trình tiếp tuyến (d) tại điểm





M 2;5

 :





y 2 x 2 5 y 2x 9

     

Gọi A là giao điểm của d và trục hoành

A A

y 0 x

    

, vậy

A ;0

 



 

 

Gọi B là giao điểm của d và trục tung

B B

x 0 y 9

   

, vậy





B 0;9

Ta có tam giác OAB vuông tại O nên

OAB

1 1 9 81

S OA.OB 9

2 2 2 4



   

Cho hàm số





y 3x 4 C

  . Viết phương trình tiếp tuyến của đồ thị





biết tiếp tuyến tạo với

đường thẳng





d : x 3y 6 0

   

góc

LỜI GIẢI

Tập xác định

D R



. Ta có

y' 3 3x



 

3 3

d : 3y x 6 0 y x 2 3 k

3 3

       

Vì tiếp tuyến tạo với đường thẳng d một góc

nên thỏa

tt d

k k

tan30

1 k k







2 2

tt tt tt tt tt tt

1 3 3

3 k 1 k k 3k 0 k 0 k 3

3 3

1 k



   

           

   

   



Gọi

là hoành độ tiếp điểm

Với

tt 0 0 0

k 0 3 3x 0 x 0 y 4

      

. Phương trình tiếp tuyến tại điểm (0 ; 4):

y 4



Với

2 2

tt 0 0 0

1 1

k 3 3 3x 3 x x

       

Với

0 0

1 13

x y

   , phương trình tiếp tuyến

1 13

y 3 x

 

  

 

 

y 3x

   .

Với

0 0

1 11

x y

    , phương trình tiếp tuyến

1 11

y 3 x

 

  

 

 

y 3x

   .

Cho hàm số





3 2

y x 3x 9x 5 C

     . Trong tất cả các tiếp tuyến của đồ thị





, hãy tìm tiếp

tuyến có hệ số góc lớn nhất.

LỜI GIẢI

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Tập xác định

D R



. Ta có

y' 3x 6x 9

   

Gọi

là hoành độ tiếp điểm của tiếp tuyến, ta có





0 0 0

f' x 3x 6x 9

   

 





 

0 0 0 0

f' x 3 x 2x 1 12 3 x 1 12 12

          

Từ đó suy ra





maxf' x 12

 tại

x 1

 

Với

0 0

x 1 y 16

    

, phương trình tiếp tuyến cần tìm:





y 12 x 1 16 y 12x 4

     

Cho hàm số

 

2x 1

y C

x 1







. Gọi





I 1 ; 2

. Tìm điểm





M C

 sao cho tiếp tuyến của





tại

vuông góc với đường thẳng

.(Dự bị B2 - 2003)

LỜI GIẢI

Tập xác định

D R



. Ta có

 

x 1







Gọi

   

0 0 0

2x 1

M x ,y C y

x 1



  



Ta có

0 0

2x 1

IM x 1; 2 IM x 1;

x 1 x 1

   



     

   

 

   

 

 

x 1

 



Hệ số góc của tiếp tuyến tại M

 

tt 0

k f' x

x 1

  



Vì tiếp tuyến vuông góc với đường thẳng IM nên có

tt IM

k .k 1

 

 

0 0 0

1 x 1 1 x 0 x 2

x 1

         



Vậy có 2 điểm









1 2

M 0;1 ,M 2;3

thỏa yêu cầu bài toán.

Cho hàm số

 

y C

x 1





. Tìm điểm





M C

 , biết tiếp tuyến của





tại

cắt hai trục tọa độ tại

A ,B

và tam giác

OAB

có diện tích bằng

.(Khối D - 2007)

LỜI GIẢI

Tập xác định





D R\ 1

 

. Ta có

(x 1)





Gọi

   

0 0 0

M x ; y C y

x 1

  



Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Phương trình tiếp tuyến của (C) tại M:









0 0 0

y f' x x x y

  

   

0 0

2 2 2

0 0 0

2x 2x

2 2

y x x y x d

x 1

(x 1) (x 1) (x 1)

      



  

Gọi

là giao điểm của d và trục Ox, có

A 0

y 0 x x

   

. Vậy





A x ;0



Gọi B là giao điểm của d và trục Oy, có

B B

x 0 y

(x 1)

  



. Vậy

B 0;

(x 1)

 

 



 

Ta có tam giác OAB cân tại O, theo giả thiết ta có:

OAB

1 1 1

S OA.OB

4 2 4



  

2 2

2 2 2

0 0 0 0

0 0 0

2 2

0 0 0 0

2x x 1 2x x 1 0

x . 4x (x 1)

(x 1)

2x x 1 2x x 1 0

 

    

       

 



     

 

 

Với

0 0

2x x 1 0

  

phương trình vô nghiệm.

Với

0 0 0 0

2x x 1 0 x 1 x

       

Với

x 1



ta có





M 1;1

. Với

 

ta có

M ; 2

 

 

 

 

Vậy có hai điểm M thỏa mãn yêu cầu bài toán là





M 1;1

M ; 2

 

 

 

 

(*) Cho hàm số

 

3 2

y x 2x 3x C

   . Qua điểm

4 4

A ;

9 3

 

 

 

có thể kẻ được mấy tiếp tuyến đến đồ

thị





. Viết phương trình các tiếp tuyến ấy .

LỜI GIẢI

Cho hai hàm số

x 2

 và

 . Viết phương trình tiếp tuyến của đồ thị của các hàm số đã

cho tại giao điểm của chúng. Tìm góc giữa hai tiếp tuyến trên.

LỜI GIẢI

Cho hàm số :

 

3x 1

y C

1 x







Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

a) Viết phương trình tiếp tuyến của





tại điểm





M 1 ; 1

 

;

b) Vết phương trình tiếp tuyến của





tại giao điểm của





với trục hoành;

c) Viết phương trình tiếp tuyến của





tại giao điểm của





với trục tung ;

d) Viết phương trình tiếp tuyến của





bết tiếp tuyến song song với đường thẳng





d : 4x y 1 0

  

;

e) Viết phương trình tiếp tuyến của





biết tiếp tuyến vuông góc với đường thẳng





: 4x y 8 0

   

LỜI GIẢI

Tìm các điểm trên đồ thị

 

1 2

C : y x x

3 3

  

mà tiếp tuyến tại đó vuông góc với đường thẳng

1 2

y x

3 3

  

LỜI GIẢI

Tập xác định





. Ta có

y' x 1

 

Gọi

0 0 0

1 2

M x ; x x

3 3

 

 

 

 

là tọa độ tiếp điểm của tiếp tuyến d với đồ thị (C), sao cho d vuông góc

với đường thẳng

1 2

: y x

3 3

   

Phương trình tiếp tuyến d là:









0 0 0

y f' x x x y

  

 

2 3

0 0 0 0

1 2

y x 1 x x x x

3 3

      

 

2 3

0 0

2 2

y x 1 x x

3 3

    

(d) vuông góc với (



) khi và chỉ khi

 

0 0

x 1 1 x 2

 

      

 

 

Kết luận có hai tọa độ điểm M cần tìm là

M 2;

 

 

 

và





M 2;0

 .

Cho đồ thị

 

(3m 1)x m

C : y

x m

 





.Tìm m để tiếp tuyến tại giao điểm của





với Ox song song

với đường thẳng d:

y x 5

  

LỜI GIẢI

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Tập xác định





D \ m

  . Ta có

 

3m 2m

x m







Tọa độ giao điểm của





và trục Ox là

A ;0

3m 1

 

 



 

. Phương trình tiếp tuyến



của





tại

điểm A là:









0 0 0

y f' x x x y

  

 

3m 1

y x

3m 1

3m 2m



 

  

 



 

   

2 2

3m 1 m 3m 1

y x

3m 2m 3m 2m

 

  

 

Để



song song với d:

y x 5

  

khi và chỉ khi:

 

3m 1

12m 8m 1 0

1 1

3m 2m

m m

6 2

12m 9m 0

m 3m 1

3m 2m







 



  

 



      

 

 















Kết luận

1 1

m m

6 2

    

thỏa yêu cầu.

Cho hàm số (C): y =

x 2





. Viết phương trình tiếp tuyến đi qua





A 6;5

 của đồ thị (C).

LỜI GIẢI

Tập xác định





D \ 2

  . Ta có

 

x 2







Gọi





0 0

M x ; y

là tọa độ tiếp điểm của tiếp tuyến (d) cần tìm với đồ thị hàm số (C) nên

x 2







và

 

f' x

x 2







. Phương trình tiếp tuyến (d):

  

 

0 0 0 0

x 2

y f' x x x y y x x

x 2





      



Ta có





A 6;5 d

 

 

x 2

6 x 5

x 2





    



0 0 0 0

4x 24x 0 x 0 x 6

      

Kết luận có hai tiếp tuyến cần tìm là

y x 1

  

và

1 7

y x

4 2

  

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Gọi (Cm) là đồ thị của hàm số

 

3 2

1 m 1

y x x *

3 2 3

   (m là tham số).

Gọi M là điểm thuộc (Cm) có hoành độ bằng



. Tìm m để tiếp tuyến của (Cm) tại điểm M song

song với đường thẳng

5x y 0.

 

LỜI GIẢI

Tập xác định





. Ta có

y' x mx

 

Điểm thuộc





có hoành độ

x 1

 

là

M 1;

 

 

 

 

Phương trình tiếp tuyến của





tại M là:

      

m m 2

: y f' 1 x 1 y m 1 x

2 2



       

Để



song song với d:

5x y 0 y 5x

   

khi và chỉ khi:

m 1 5

m 4

m 2 0



 



 



 





Kết luận

m 4



Cho hàm số

3 2

y 4x 6x 1 (1)

   . Viết phương trình tiếp tuyến của (1), biết tiếp tuyến đi qua

điểm





M 1; 9

 

LỜI GIẢI

Tập xác định





. Có

y' 12x 12x

  .

Gọi





0 0

A x ; y

là tọa độ tiếp điểm của tiếp tuyến (d) cần tìm với đồ thị hàm số (1) nên

3 2

0 0 0

y 4x 6x 1

  

và





0 0 0

f' x 12x 12x

  . Phương trình tiếp tuyến (d):

















2 3 2

0 0 0 0 0 0 0 0

y f' x x x y y 12x 12x x x 4x 6x 1

         

Ta có





M 1; 9 d

   









2 3 2

0 0 0 0 0

12x 12x 1 x 4x 6x 1 9

       

3 2

0 0 0 0 0

8x 6x 12x 10 0 x 1 x

          

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Kết luận có hai tiếp tuyến cần tìm là

y 24x 15

 

và

15 21

y x

4 4

  .

Cho đồ thị (C):

4 2

1 9

y x 2x

4 4

  

. Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với

Ox.

LỜI GIẢI

Tập xác định





. Ta có

y' x 4x

 

Phương trình hoành độ giao điểm của (C) và trục Ox:

4 2

1 9

x 2x 0

4 4

  

x 9

 

x 1

  

(loại).

Với

x 3 y 0

x 9

x 3 y 0



  

 



   



Phương trình tiếp tuyến tại





M 3;0

của (C):









y f' 3 x 3 y 15x 45

    

Phương trình tiếp tuyến tại





M 3;0

 của (C):









y f' 3 x 3 y 15x 45

      

Tìm

 

A, B C : y

x 1

 



sao cho tiếp tuyến của





tại

A, B

song song với nhau và

OAB



vuông tại O ?

LỜI GIẢI

● Gọi

   

2a 2b

A a; , B b; C , a; b 1;a b

a 1 b 1

   

  

   

 

   

. Ta có:

 

x 1







● Tiếp tuyến tại A và B lần lượt có hệ số góc:

   

A B

2 2

k ; k

a 1 b 1

 

 

 

● Do tiếp tuyến tại A và B song song nhau nên

A B

k k



   

2 2

a 1 b 1

 

 

 

   

2 2

a 1 b 1

   

a 1 b 1

a 1 1 b



  





  



a b

a 2 b





   



 







● Do ba điểm

O,A,B

tạo thành tam giác vuông tại O nên

O A B

OA OB



 











 

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

a,b 0

OA.OB 0

















 

  

a,b 0

4ab

ab 0

a 1 b 1











 



 



  

1 0

a 1 b 1

  

 





   

  

a 2 b

i , ii

1 0

a 1 b 1



 







 



 



  

1 b b 1

  

 

 

b 1 4

  

b 3 a 1 b 1 a 3

         

● Vậy









A 1;1 , B 3;3

 hoặc









A 3;3 , B 1;1

  là các điểm cần tìm.

Tìm những điểm

 

x 1

M C : y

2x 2



 



sao cho tiếp tuyến với





tại M tạo với hai trục tọa độ một

tam giác có trọng tâm nằm trên đường thẳng

d : 4x y 0

 

LỜI GIẢI

● Gọi

   

o o

x 1

M x ; C , x 1

2x 2

 



  

 



 

và tiếp tuyến



tại điểm M có phương trình

 

x 1

: y x x

2 x 1

x 1



   







● Gọi

 

2 2

o o o o

x 2x 1 x 2x 1

A Ox A ;0 ,B Oy B 0;

2 x 1

 

    

 

       

 



 

● Khi đó tọa độ trọng tâm của

OAB

 là

 

2 2

o o o o

x 2x 1 x 2x 1

G ;

6 x 1

 

   

 



 



 

● Do

G d : 4x y 0

  

 

2 2

o o o o

x 2x 1 x 2x 1

4 0

6 x 1

   

   



 

x 1 4

  





o o

do : A B O x 2x 1 0

     

o o

1 3

x x

2 2

     

nên

 

1 3

i M ;

2 2

 

  

 

 

hoặc

3 5

M ;

2 2

 



 

 

Tìm





A C : y x 3x 1

   

biết rằng tiếp tuyến của đồ thị





tại điểm

cắt đồ thị





tại B

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

(khác điểm A) thỏa:

A B

x x 1

 

LỜI GIẢI

● Gọi









A A A

A x ;x 3x 1 C

   và phương trình tiếp tuyến tại điểm A có dạng









2 3

A A A A

: y 3x 3 x x x 3x 1

      

● Ta có





C B

  

có hoành độ nghiệm của phương trình hoành độ giao điểm:









2 3 3

A B A A A B B

3x 3 x x x 3x 1 x 3x 1

       





● Theo giả thiết, ta có:

A B B A

x x 1 x 1 x

    





   





     

2 3

A A A A A A

i , ii 3x 3 1 2x x 3x 1 x 3 1 x

        

 

A A

A B

4x 3x 1 0

x x , do : A B



   







 





 

A B

x 1 x 2

A 1;3

1 1

x x L

2 2



   



  



  





Cho hàm số





y x 3x 2 C

   .Tìm điểm M thuộc (C), sao cho tiếp tuyến của (C) tại M cắt (C) tại

điểm thứ hai là N và

MN 6 5

 .

LỜI GIẢI

Gọi









M m;m 3m 1 C

   . Phương trình tiếp tuyến của (C) tại M là













2 2

y 3m 3 x m m 3m 2 d

      . Phương trình hoành độ giao điểm của d và (C):









3 2 2

x 3x 2 3m 3 x m m 3m 2

       

   

x m x 2m 0

   

x m

x 2m









 



, để d cắt (C) tại hai

điểm phân biệt

m 2m m 0

    

, khi đó





N 2m; 8m 6m 2

   

Có

2 6 4 2

MN 81m 2.81m 90m 180

    . Đặt

2 3 2

t m ,t 0 9t 18t 10t 20 0 t 2

        

m 2

 

Vậy có hai điểm N cần tìm









N 2 2; 10 2 2 ,N 2 2;10 2 2

   

Chứng minh rằng với mọi m thì đường thẳng

d : y x m

 

luôn cắt đồ thị

 

1 x

C : y

2x 1







tại hai

điểm phân biệt A và B. Gọi

1 2

k ,k

là hệ số góc của các tiếp tuyến với





tại A và B. Tìm m để tổng

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

1 2

k k



đạt giá trị lớn nhất ?

LỜI GIẢI

● Phương trình hoành độ giao điểm giữa d và

 

1 x 1

C : x m, x

2x 1 2



   



   

g x 2x 2mx m 1 0, x

       

● Ta có:

' 2

m m 2 0

1 1

g 0

2 2



    





 

  



 

 



: luôn đúng









m d C A;B

     .

● Gọi









A a;a m ,B b; b m

  với

a,b

là hai nghiệm của





g x 0



● Ta có:

   

1 2

2 2

1 1

T k k y' a y' b

2a 1 2b 1

 

 

      

 

 

 

 

   

 

4 a b 2ab 4 a b 2

T 4 m 1 2 2

4ab 2 a b 1

 

    

 

 

        

 

  

 

● Dấu

" "



xảy ra

m 1 0 m 1

     

thì





max 1 2

min

T k k 2

   

Cho hàm số









3 2

y x m 2 x 4m 3 1

    

Tìm giá trị của tham số m để đường thẳng

y 2x 7

 

cắt đồ thị hàm số (1) tại ba điểm phân biệt

A, B, C sao cho tổng hệ số góc của các tiếp tuyến với đồ thị hàm số (1) tại các điểm A, B, C bằng

28.

LỜI GIẢI

Phương trình hoành độ giao điểm của đường thẳng

d : y 2x 7

 

và đồ thị hàm số (1):









3 2 3 2

x m 2 x 4m 3 2x 7 x m 2 x 2x 4m 4 0

            

x 2

x mx 2m 2 0 (2)









   





. Đặt





g x x mx 2m 2

   

Đường thẳng d cắt đồ thị hàm số (1) tại ba điểm phân biệt A, B, C



phương trình (2) có hai

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

nghiệm phân biệt và khác 2

 

(2)

m 4 2 2 m 4 2 2

m 8m 8 0

g 2 0

2 4m 0



      



 



  

  

  

  



 





 



(3).

Gọi













1 2 2 3 3

A 2;y ,B x ;y ,C x ;y

với

1 2

x ,x

là hai nghiệm của (2). Hệ số góc của tiếp tuyến tại các

điểm A, B, C với đồ thị hàm số (1) lần lượt là:





















2 2

A B 2 2 2 C 3 3 3

k y' 2 4 4m,k y' x 3x 2 m 2 x ,k y' x 3x 2 m 2 x

           . Theo đề bài









2 2

A B C 2 2 3 3

k k k 28 4 4m 3x 2 m 2 x 3x 2 m 2 x 28

           













2 2

2 3 2 3

4 4m 3 x x 2 m 2 x x 28

       

    

2 3 2 3 2 3

4 4m 3 x x 2x x 2 m 2 x x 28

 

        

 

 









2 2

4 4m 3 m 2 2m 2 2 m 2 m 28 m 4m 12 0 m 6 m 2

 

                 

 

Kết hợp với

điều kiện (3) được m = 2.

Cho hàm số





3 2 2 2

y x 3x m x 2 m 1

     . Định m để đồ thị hàm số (1) cắt trục hoành tại ba

điểm A, B, C phân biệt sao cho tổng các hệ số góc của các tiếp tuyến với đồ thị (1) tại ba điểm A,

B, C lớn nhất.

LỜI GIẢI

Ta có:

2 2

y' 3x 6x m

  

Phương trình hoành độ giao điểm của đồ thị hàm số (1) với trục hoành:

3 2 2 2

x 3x m x 2 m 0

    

 

   

2 2

x 1

x 1 x 2x m 2 0

g x x 2x m 2 0





      



     





Đồ thị hàm số (1) cắt trục Ox tại ba điểm phân biệt



phương trình (*) có hai nghiệm phân biệt

và khác 1

 

( )

3 m 0

3 m 3

g 1 0

m 3 0



 

 

 

 

     

 



 

 



. Gọi













A 1 B 2 C

A 1;y ,B x ; y ,C x ; y

với

1 2

x ,x

là

hai nghiệm của phương trình







theo định lý Vi ét có

1 2

x x 2

 

và

1 2

x .x m 2

 

Ta có













A B C 1 2

P k k k y' 1 y' x y' x

     









2 2 2 2 2

1 1 2 2

3 m 3x 6x m 3x 6x m        

   

2 2

1 2 1 2 1 2

3 x x 2x x 6 x x 3m 3 9 3m 9

 

         

 

 

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Vậy

maxP 9



khi

m 0



Kết luận với

m 0



thỏa yêu cầu bài toán.

Cho hàm số





3 2

y x 3x 2 1

   

Tìm tham số m để đường thẳng





d : y m 2 x 2

  

cắt đồ thị (C) của hàm số (1) tại ba điểm phân

biệt





A 2;2 ,B,C

sao cho tích các hệ số góc tiếp tuyến với đồ thị





tại B và C đạt giá trị nhỏ

nhất ?

LỜI GIẢI

● Phương trình hoành độ giao điểm:





3 2

x 3x 2 m 2 x 2

     









x 2 x x m 2 0

     

 

x 2 y 2

g x x x m 2 0



  





    





● Để d cắt





tại ba điểm phân biệt





A 2;2 ,B,C





g x 0

 

có ba nghiệm phân biệt



 

9 4m 0

g 2 m 0



   







  





m 0



 

















● Ta có:

' 2

y 3x 6x

  

và gọi

















1 1 2 2

B x ;m 2 x 2 ,C x ;m 2 x 2

   

với

1 2

x ,x

là hai nghiệm của





g x 0



. Theo Viét:

 

1 2

x x 1

x x m 2



 





  





● Ta có:

















' ' 2 2

1 2 1 2 1 1 2 2

k k y x .y x 3x 6x 3x 6x

     

         

2 2

1 2 1 2 1 2 1 2 1 2 1 2

k k 9 x x 18x x x x 36x x 9 m 2 18 m 2 k k 9 x

          

 

1 2

k k 9 m 1 9 9

     





1 2

min

k k 9

  

khi

m 1

 

(thỏa





Cho hàm số

    

y x 2 x 1 C

  

b). Tìm các điểm M thuộc đường thẳng

d : y 2x 19

  

, biết rằng tiếp tuyến của đồ thị (C) đai

qua điểm M vuông góc với đường thẳng

x 9y 8 0

  

LỜI GIẢI

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Vì tiếp tuyến vuông góc với đường thẳng

 

1 8

x 9y 8 0 y x

9 9

       

nên

tt tt

k .k 1 k 9



   

, gọi tọa độ tiếp điểm của tiếp tuyến là





0 0

I x ; y

, từ đó ta có





0 tt 0 0 0

y' x k x 1 3 x 2 x 2

        



Với

0 0

x 2 y 4

  

khi đó phương trình tiếp tuyến









1 1

d : y y' 1 x 2 4 d : y 9x 14

     

. Suy

ra M là giao điểm của d và

tọa độ điểm M là nghiệm của hệ

 

y 9x 14

M 3;13

y 2x 19



 







  







Với

0 0

x 2 y 0

   

khi đó phương trình tiếp tuyến

d : y 9x 18

 

. Suy ra M là giao điểm của

d và

tọa độ điểm M là nghiệm của hệ

y 9x 18

1 201

M ;

y 2x 19

11 11



 

 







 

  



 



Kết luận tọa độ điểm M cần tìm là





M 3;13

hoặc

1 201

M ;

11 11

 

 

 

Cho hàm số









3 2

y x 3x m 2 x 3m C     (m là tham số).

Tìm m để tiếp tuyến có hệ số góc nhỏ nhất của đồ thị





C của hàm số đã cho vuông góc với

đường thẳng

d : x y 2 0

  

LỜI GIẢI

Có

y' 3x 6x m 2

   

Gọi









0 0 m

M x ;y C , suy ra hệ số góc tiếp tuyến của





C tại M là

   

0 0 0 0

k y' x 3x 6x m 2 3 x 1 m 5 m 5

          

, dấu

" "



xảy ra

x 1

 

suy ra hệ số góc

của tiếp tuyến nhỏ nhất là

min

k m 5

 

tại điểm





M 1;4m 4



Để tiếp tuyến vuông góc với d





tt d

k .k 1 m 5 .1 1 m 4

        

Kết luận với m = 4 thỏa yêu cầu đề bài.

Gọi

là hệ số góc của tiếp tuyến tại giao điểm của đồ thị hàm số

 

x m

C : y

x 1







với trục

hoành. Gọi

là hệ số góc của tiếp tuyến với đồ thị





C tại điểm có hoành độ

x 1



. Tìm tất cả

các giá trị của tham số m sao cho

1 2

k k

 đạt giá trị nhỏ nhất ?

LỜI GIẢI

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

● Ta có:

 

1 m

x 1







. Hoành độ giao điểm





C với trục hoành:

x m

 

● Hệ số góc tiếp tuyến tại điểm có hoành độ

x m

 

là

 

k y' m

1 m

  



● Hệ số góc tiếp tuyếnTại điểm có hoành độ

x 1



là

 

1 m

k y' 1



  .

● Ta có:

Cauchy

1 2

1 1 m 1 1 m 1 1 m

k k 2 .

1 m 4 1 m 4 1 m 4

  

     

  

1 2

k k 1, m 1

    

. Dấu

" "



xảy ra

1 1 m

1 m 4



 



 

m 1

1 m 4

m 3



 

   







. Vậy

1 2

min

k k 1

 

khi

m 1

m 3



 







Viết phương trình tiếp tuyến d của

 

2x 1

C : y ,

x 1







biết rằng tiếp tuyến cắt trục

Ox,Oy

lần lượt

tại

A,B

sao cho

AB 82.OB

 ?

LỜI GIẢI

 Phân tích và tìm hướng giải



cắt trục

Ox,Oy

tại

A,B OAB

  vuông tại

O và tạo với trục Ox một góc



với

k tan

   .

Ta có:

2 2 2

AB 82.OB

OA OB AB









 





2 2

81.OB OA

 

OB 1

OA 9

 

 

Bài giải

● Gọi

 

o o

2x 1

M x ; , x 1

x 1

 





 



 

là tiếp điểm

 

x 1



 



. Phương trình tiếp tuyến có dạng

 

2x 1

: y x x

x 1



    







∆

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

● Ta có:

2 2 2

AB 82.OB

OA OB AB









 





2 2 2 2

AB 82.OB OA OB

   

OB 1

OA 9

 

● Hệ số góc tiếp tuyến được tính

OB 1

k tan

OA 9

   

1 1

k k

9 9

    

● Với

 

1 1

x 1



 



: phương trình vô nghiệm.

● Với

 

x 4

1 1

k x 1 9

x 2

x 1







      



 

















i , ii



1 25

: y x

9 9

    hoặc

1 13

: y x

9 9

    là các tiếp tuyến cần tìm.

Lập phương trình tiếp tuyến của





3 2

C : y x 3x 1,

  

biết nó song song với đường thẳng

d : 9x y 6 0

  

LỜI GIẢI

● Ta có:

y' 3x 6x

 

. Gọi





o o

M x ; y

là tiếp điểm. Phương trình tiếp tuyến có dạng:





o o

: y k x x y

   

. Do tiếp tuyến

// d : y 9x 6

  

k 9

 





y' x 9

 

o o

3x 6x 9

  

o o

x 1 y 3

x 3 y 1



    





  



● Với

o o

x 1 ; y 3; k 9 : y 9x 6

        

(loại do

 

● Với





o o

x 3; y 1; k 9 : y 9 x 3 1

       

hay

: y 9x 26

  

Viết phương trình tiếp tuyến của đồ thị





4 2

C : y x x 6,

   

biết tiếp tuyến vuông góc với

đường thẳng

d : y x 1

 

?Đại học khối D năm 2010

LỜI GIẢI

● Ta có:

y' 4x 2x

   . Gọi





o o

M x ; y

là tiếp điểm. Phương trình tiếp tuyến có dạng:





o o

: y k x x y

   

. Do

d : y x 1

   

k. 1

  

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN





k y' x 6

   

o o

4x 2x 6

    

o o

x 1 y 4

   

● Phương trình tiếp tuyến là





: y 6 x 1 4

    

hay

: y 6x 10

   

Gọi

 

2x 1

M C : y

x 1



 



có tung độ bằng

. Tiếp tuyến của





tại M cắt các trục tọa độ

Ox,Oy

lần lượt tại A và B. Tính

OAB



Cao đẳng khối A, A1, B, D năm 2013

LỜI GIẢI

 Phân tích và tìm hướng giải

Viết PTTT



tại M khi biết

 

o o o

2x 1

y 5 x k y' x

x 1



    



. Tìm tọa độ

A Ox, B Oy

     

và tính

OAB

S OA.OB



 

Bài giải

● Ta có:

 

x 1







và

2x 1

y 5

x 1



 



x 2

 





k y' x 3

   

● Phương trình tiếp tuyến tại





M 2;5

là

: y 3x 11

   

● Ta có:

A Ox

   thỏa

: y 3x 11

A ;0

Ox : y 0

y 0



   

  

 

 

 

 





 









● Ta lại có:

B Oy

   thỏa

 

: y 3x 11 x 0

B 0;11

Oy : x 0 y 11

 

    

 

 

 

 

 

 

OAB

1 1 11 121

S OA.OB . .11

2 2 3 6



   





đv

Viết phương trình tiếp tuyến của đồ thị hàm số

 

x 2

C : y ,

2x 3







biết rằng tiếp tuyến đó cắt trục

hoành, trục tung lần lượt tại hai điểm phân biệt

A,B

và tam giác OAB cân tại gốc tọa độ O ?Đại

học khối A năm 2009

 Phân tích và tìm hướng giải

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Tiếp tuyến









Ox A , Oy B

      mà

OAB

 vuông cân tại O





song song với phương

trình đường thẳng phân

giác góc phần tư thứ I





d : y x



và thứ II





d : y x

 

o o

k 1 x y

     



LỜI GIẢI

● Ta có:

 

2x 3







. Gọi





o o

M x ; y

là tiếp điểm và tiếp tuyến là



● Theo đề

1,2

// d : y x

   

 

k y' x 1

2x 3



    



 

2x 3 1

  

o o

x 1 y 1 k 1

x 2 y 0 k 1



      





      







 

: y 1 x 1 1

: y x

hay

: y x 2

: y 1 x 2 0



    



  







   

    





● Vậy phương trình tiếp tuyến cần tìm là:

: y x 2

   

Cho hàm số

2x 3

x 2







có đồ thị





.Viết phương trình tiếp tuyến



với đồ thị hàm số





sao

cho



cắt trục hoành tại A mà

OA 6



 Phân tích và tìm hướng giải

Gọi

2x 3

M x ;

x 2

 



 



 

là tiếp điểm

 

2x 3

tt : y x x

x 2



    







Ox A

   

tọa độ điểm A theo



giải

OA 6 x tt

   

LỜI GIẢI

Ta có:

 

x 2







. Gọi

   

o o

2x 3

M x ; C , x 2

x 2

 



 

 



 

là tiếp điểm.

∆

(lo

ạ

i do

d : y x

  

)

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

● Phương trình tiếp tuyến tại M là

 

2x 3

: y x x

x 2



   







● Ta có:

A Ox

  

y 0

 

 

2x 3

0 x x

x 2



   







2 2

o o o o

x 2x 6x 6 A 2x 6x 6;0

       .

● Theo đề

o o o o

OA 6 2x 6x 6 0 x 0 x 3

        





● Thế





vào







các tiếp tuyến cần tìm là:

1 3

: y x

4 2

: y x 6



   



   





Viết phương trình tiếp tuyến với đồ thị





3 2

C : y x 6x 9x,

   biết tiếp tuyến tạo với đường thẳng

: x y 1 0

   

một góc



sao cho

cos

  và tiếp điểm có hoành độ nguyên ?

 Phân tích và tìm hướng giải

Gọi





3 2

o o o o

M x ; x 6x 9x

  là tiếp điểm thì





o o o

k y' x 3x 12x 9

   

và có

: y x 1 k 1



      

Khi đó ta có hai hướng xử lý: một là áp dụng công thức

k k

tan ,

1 k.k





 



hai là sử dụng

 

n .n

cos cos n ;n

n . n



  

 

với





n 1;1







và





n k; 1

 



là véctơ pháp tuyến của



và tiếp

tuyến d.

LỜI GIẢI

● Gọi





3 2

o o o o

M x ; x 6x 9x

  là tiếp điểm và





o o o

k y' x 3x 12x 9

   

● Phương trình tiếp tuyến có dạng





3 2

o o o o

d : y k x x x 6x 9x

     và có véctơ pháp tuyến





n k; 1

 



. Ta có:





n 1;1







● Theo đề:

 

n .n

k 1

cos cos n ;n

n . n

2. k 1





    



 

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

9k 82k 9 0

   

k 9 k

   

● Với

o o

k 9 3x 12x 0

   

o o

x 0 y 0

x 4 y 4



  





  



: y 9x

: y 9x 32



 





  



● Với

o o o

1 1 18 2 21

k 3x 12x 9 x

9 9 9



       (loại do

o o

x ;y





● Vậy phương trình tiếp tuyến cần tìm là:

: y 9x

 

hoặc

: y 9x 32

  

Viết phương trình tiếp tuyến với

 

2x 1

C : y ,

x 1







biết tiếp tuyến cách đều hai điểm





A 2;4

 và





B 4; 2



 Phân tích và tìm hướng giải

Gọi

2x 1

M x ;

x 1

 



 



 

là tiếp điểm

 

2x 1

tt : y x x

x 1



    



. Do



cách đều hai điểm A

và B nên có các trường hợp sau đây xảy ra: tiếp tuyến



qua trung điểm I của AB





 

hoặc

song song với AB hoặc trùng với AB





k k . Giải hai trường hợp





LỜI GIẢI

● Gọi

 

o o

2x 1

M x ; , x 1

x 1

 





 



 



tiếp tuyến

 

o o

x x 2x 1

: y

x 1

 

  







● Do tiếp tuyến cách đều hai điểm





A 2;4

 và





B 4; 2



nên có các trường hợp:

Trường hợp 1. Gọi I là trung điểm của AB





I 1;1



 

 

o o

x 1 2x 1

x 1

 

  



x 1

  

1 5

: y x

4 4

    

Trường hợp 2.

// AB

 hoặc

 

k k

  .

∆

A B

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Phương trình đường thẳng

AB : y x 2

  

 

k 1 k

x 1

     



o o

x 2 x 0

   

. Thế vào





được

: y x 5

   

hoặc

: y x 1

   

● Vậy

1 5

: y x

4 4

   

hoặc

: y x 5

   

hoặc

: y x 1

   

Xác định m để đồ thị

 

2x m

C : y

x 1







có tiếp tuyến song song và cách đường thẳng

d : 3x y 1 0

  

một khoảng cách bằng

 Phân tích và tìm hướng giải

 

2x m

M x ; C

x 1

 





 



 

là tiếp điểm

 

2 m

x 1

 

 



. Do

// d



k 3

  

sẽ thu được một phương

trình với hai ẩn

x ,m

và





d M;d 10

 sẽ thu thêm được một phương trình nữa. Giải hệ này

tìm được

x ,m

 .

LỜI GIẢI

● Gọi

 

o o

2x m

M x ; , x 1

x 1

 





 



 

và tiếp tuyến



có

 

2 m

k 3

x 1

 

  



(do tiếp tuyến



d : y 3x 1

  

)

o o

3x 6x m 1 0

    





● Vì









d ;d d M;d 10

  

2x m

3x 10

x 1



  







   

2 2

o o o o

2 2

o o o o

3x 11x m 10 0 3x 9x m 10 0

i , ii

3x 6x m 1 0 3x 6x m 1 0

 

       

 

 

 

       

 

 









o o

x 1 L x 1 L

11 1

3 67

x m

6 12

2 4



 

 

 

 

  

   

 



● Vậy

1 67

m m

12 4

   là các giá trị cần tìm.

Tìm tất cả các giá trị của tham số

m 0



sao cho tiếp tuyến của đồ thị









C : y mx 2m 1 x m 1

    

tại giao điểm của nó với trục tung tạo với hai trục tọa độ một

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

tam giác có diện tích bằng

LỜI GIẢI

● Ta có:









M C Oy : x 0 y m 1 M 0;m 1

       

● Mà

y' 3mx 2m 1

  





k y' 0 2m 1

    

là hệ số góc tiếp tuyến tại điểm M và có phương

trình





: y 2m 1 x m 1

     





●

Ox A

  

thỏa

 

y 0

y 2m 1 x m 1









    





m 1

2m 1

y 0





















m 1

A ;0

2m 1

 





 



 

Oy B

  

thỏa

 

x 0

y 2m 1 x m 1









    





x 0

y m 1











 









B 0;m 1

 

m 1

OA , OB m 1

2m 1



   



với

 

● Theo đề:

AOB

1 1 m 1

S .OA.OB . . m 1 4

2 2 2m 1





   



 

m 1 8 2m 1

   

16m 8 m 2m 1



   

 



    



m 7 2 14

m 9 6 2



 







  



Tìm m để tiếp tuyến của









3 2

C : y x 3mx m 1 x 1

    

tại điểm có hoành độ

x 1

 

đi qua

điểm





A 1;2

LỜI GIẢI

Ta có:





y' 3x 6mx m 1 k y' 1 4 5m

         .

Phương trình tiếp tuyến tại điểm





M 1;2m 1

 

có dạng:









d : y 4 5m x 1 2m 1

    

và





A 1;2 d



nên



Viết phương trình tiếp tuyến của

 

2x 1

C : y ,

x 1







biết rằng tiếp điểm của tiếp tuyến đó với





cách điểm





A 0;1

một khoảng



LỜI GIẢI

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Gọi

 

o o

2x 1

M x ; , x 1

x 1

 



 

 



 

là tiếp điểm. Theo đề thì

MA 2



hay

o o o

2x 1

x 1 4 x 0 x 2

x 1

 



      

 



 

. Với

x 0

 

tiếp tuyến là

d : y 3x 1

 

và với

o 2

x 1

x 2 d : y

3 3

   

Viết phương trình tiếp tuyến của

 

C : y

1 x





tại

biết rằng tiếp tuyến đó cắt các trục tọa độ

tại A và B sao cho M là trung điểm của AB ?

LỜI GIẢI

Gọi

 

M m; , m 1

1 m

 



 



 

là tiếp điểm. Phương trình tiếp tuyến tại M có

dạng

 

: x 1 m y m 0

    

. Khi đó:





A m ;0

và

 

B 0;

1 m

 



 



 

Để M là trung điểm của đoạn AB thì

 

m 2m

m 0; m 2m;

1 m

   



m 2

 

. Vậy phương trình tiếp tuyến cần tìm là:

: x y 4 0

   

Tìm m để đồ thị hàm số





C : y x 3mx 2

  

có tiếp tuyến tạo với đường thẳng

d : x y 7 0

  

góc



biết

cos

  ?

LỜI GIẢI

Gọi k là hệ số góc tiếp tuyến



tiếp tuyến có vtpt





n k; 1

 



Đường thẳng

d : x y 7 0

  

có vtpt





n 1;1





Theo đề

 

1 2

n .n

k 1

cos cos n ;n

n . n

2. k 1









     











 

YCBT



ít nhất một trong hai phương trình sau có nghiệm:

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

2 2

3 3 2m 1 2m 1

y' 3x 3m x 0

2 2 2 2

2 2 9m 2 9m 2

y' 3x 3m x 0

3 3 9 9

   

 

    

   

     

   

 

   

    

   

   

Viết phương trình tiếp tuyến của đồ thị

 

2x 1

C : y ,

x 1







biết rằng tiếp tuyến này cắt trục

Ox,Oy

lần lượt tại

A,B

thỏa:

OA 4OB

 ?

LỜI GIẢI

Giả sử tiếp tuyến d của





tại









o o

M x ; y C

 cắt Ox tại A, cắt Oy tại B

sao cho

OA 4OB

 . Do

OAB

 vuông tại O nên

OB 1

tan A

OA 4

  

hệ số góc của d bằng

hoặc



. Mà hệ số góc của d là:

 

y' x 0

x 1

  



 

o o

1 1 3

x 1 y

4 2

x 1

        



hoặc

o o

x 3 y

  

Khi đó có hai tiếp tuyến là:

1 5

d : y x

4 4

  

hoặc

1 13

d : y x

4 4

   .

Tìm các điểm M trên đường thẳng

d : y 2x 19,

   biết rằng tiếp tuyến của đồ thị

    

C : y x 2 x 1

   đi qua điểm M vuông góc với đường thẳng

d' : x 9y 8 0

  

LỜI GIẢI

● Hàm số được viết lại:

y x 3x 2

  

● Vì tiếp tuyến

1 8

d' : y x

9 9

    

nên

k. 1 k 9

 

     

 

 

● Gọi









o o

M x ; y C

 là tiếp điểm





o o o

k y' x 3x 3 9 x 2

       

● Phương trình tiếp tuyến tại M có dạng:





o o o

: y k x x x 3x 2

     

Hay

: y 9x 14

  

hoặc

: y 9x 18

  

là hai tiếp tuyến tại M.

● Khi đó, tọa độ điểm M là giao điểm của đường thẳng d và tiếp tuyến

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

1 1

d M

   thỏa

y 2x 19

y 9x 14



  





 





 

x 3

M 3;13

y 13







 









2 2

d M

   thỏa

y 2x 19

y 9x 18



  





 





1 207

M ;

207

11 11







 



 



 

 









● Vậy có hai điểm M là





M 3;13

hoặc

1 207

M ;

11 11

 

 

 

thỏa yêu cầu bài toán.

Tìm các điểm





A,B C : y x 3x

    sao cho tiếp tuyến của





tại

A,B

song song với nhau và

AB 4 2

 ?

LỜI GIẢI

Gọi

















3 3

A a; a 3a ,B b; b 3b C , a b

     

Do tiếp tuyến tại A và B song song nhau nên









y' a y' b

 hay

2 2

3a 3 3b 3 a b

        

(nhận) hoặc

a b



(loại).

Theo đề

ab 4 a 2; b 2

AB 32

a b a 2;b 2

 

    



   





    



 

Vậy









A 2; 2 ,B 2;2

  hoặc









A 2;2 ,B 2; 2

 

thì thỏa yêu cầu bài toán.

Tìm





M C : y x 3x 2

   

để tiếp tuyến của





tại điểm M cắt đồ thị





tại điểm thức hai là

N thỏa mãn

M N

x x 6

 

LỜI GIẢI

Gọi









M a;a 3a 2 C

   . Phương trình tiếp tuyến tại điểm M:









2 3

: y 3a 3 x a a 3a 2

      

hay





2 3

: y 3a 3 x 2a 2

    

Phương trình hoành độ giao điểm:





3 2 3

x 3x 2 3a 3 x 2a 2

     

   

x a x 2a 0 x a x 2a

        

M N

x a; x 2a

   

Theo đề:





M N

x x 6 a 2a 6 a 2 a 2

          

Vậy có hai điểm M thỏa yêu cầu bài toán:









M 2; 4 M 2;0

  .

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Tìm các điểm trên

 

2x 3

C : y ,

x 1







sao cho tiếp tuyến tại đó tạo với hai trục tọa độ một tam giác

có diện tích bằng





đv

LỜI GIẢI

Gọi

   

o o

2x 3

M x ; C ; x 1

x 1

 



  

 



 

và phương trình tiếp tuyến tại M:

 

2x 3

: y x x

x 1



   



và

o o

7x x 3

Ox A ;0

 

 

 

  

 

 

 

o o

2x 6x 3

Oy B 0;

x 1

 

 

 

  

 



 

. Do

ABO

18 1 18

S AO.BO

5 2 5



  

Giải phương trình này, sẽ tìm được

x M

 cần tìm.

Tìm tọa độ điểm

 

2x 1

M C : y ,

x 1



 



sao cho khoảng cách từ điểm





I 1;2

 tới tiếp tuyến của





tại M là lớn nhất ?

LỜI GIẢI

Gọi

   

o o

M x ; 2 C , x 1

x 1

 

   

 



 

. Khi đó tiếp tuyến tại M dạng

 

3 3

: y x x 2

x 1

    



. Khi đó khoảng cách từ





I 1;2

 đến tiếp tuyến là:

 









   

o o

4 4

o o

3 1 x 3 x 1

6 x 1

d I;

9 x 1 9 x 1

   



  

   

Hay

 

Cauchy

d I; 6

x 1

  

 



và

max

d 6

 khi và chỉ khi

 

   

2 2

o o o

x 1 x 1 3 x 1 3

x 1

        



Vậy:





M 1 3;2 3

   hoặc





M 1 3;2 3

   là hai điểm cần tìm

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

CÂU HỎI TRẮC NGHIỆM

Câu 1. Cho hàm số





3 2

C y x x

  . Phương trình tiếp tuyến của đồ thị





tại điểm





1;4

M là:

9 5.

y x

  

9 5.

y x

 

9 5.

y x

  

9 5.

y x

 

Câu 2. Phương trình tiếp tuyến của đồ thị hàm số

4 2

4 1

y x x

  

tại điểm





1; 2



là:

4 6

y x

 

4 2

y x

 

4 6

y x

  

4 2

y x

  

Câu 3. Phương trình tiếp tuyến của đồ thị hàm số







tại điểm





2;3

C  là:

2 1

y x

 

2 7

y x

  

2 7

y x

 

2 1

y x

  

Câu 4. Tiếp tuyến của đồ thị hàm số

3 2

y x x

   

tại điểm D có hoành độ bằng 2 có phương trình là:

9 14

y x

  

9 14

y x

 

9 22

y x

  

9 22

y x

 

Câu 5. Tiếp tuyến của đồ thị hàm số

2 1







tại điểm F có hoành độ bằng 2 có phương trình là:

y x

  

y x

 

y x

  

y x

 

Câu 6. Tiếp tuyến của đồ thị hàm số

4 2

2 3

y x x

  

tại điểm H có tung độ bằng 21 có phương trình là

40 101

40 59

y x



 



  



40 59

40 101

y x



 



  



40 59

40 101

y x



 



  



40 59

40 101

y x



  



 



Câu 7. Tiếp tuyến của đồ thị hàm số

2 1







tại điểm I có tung độ bằng 1 có phương trình là

1 8

5 5

y x

 

1 2

5 5

y x

  

1 8

5 5

y x

  

1 2

5 5

y x

 

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Câu 8. Cho hàm số





4 2

: 2

C y x x

 

. Phương trình tiếp tuyến của





tại điểm

có hoành độ



biết





y x



 

là:

3 2.

y x

  

3 1.

y x

  

3 .

y x

  

3 .

y x

  

Câu 9. Cho hàm số





: 3 2

C y x x

  

. Phương trình tiếp tuyến của





biết hệ số góc của tiếp

tuyến đó bằng 9 là:

9 14

9 18

y x



 



 



9 15

9 11

y x



 



 



9 1

9 4

y x



 



 



9 8

9 5

y x



 



 



Câu 10. Tiếp tuyến của đồ thị hàm số

3 2

y x x

  

có hệ số góc

 

có phương trình là

3 7

y x

  

. B.

3 7

y x

  

. C.

3 1

y x

  

. D.

3 1

y x

  

Câu 11. Tiếp tuyến của đồ thị hàm số

4 2

y x x

  

có hệ số góc bằng

2 9 0

x y

  

có phương

trình là

48 192

y x  

. B.

48 160

y x  

. C.

48 160

y x  

. D.

48 192

y x  

Câu 12. Viết phương trình tiếp tuyến của đồ thị hàm số







biết tiếp tuyến có hệ số góc bằng 4.

4 3

4 13

y x



 



 



. B.

4 3

4 13

y x



 



 



. C.

4 3

4 13

y x



 



 



. D.

4 3

4 13

y x



 



 



Câu 13. Có bao nhiêu tiếp tuyến của đồ thị hàm số

3 2

y x x

   song song với đường thẳng

y x



A. 2. B. 1. C. 3. D. 4.

Câu 14. Tiếp tuyến song song với đường thẳng

36 5

y x

  

của đồ thị hàm số

4 2

y x x

  

có

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

phương trình là

36 54

y x

  

. B.

36 54

y x

  

. C.

36 90

y x

  

. D.

36 90

y x

  

Câu 15. Cho hàm số





2 1

C y



 



Viết phương trình tiếp tuyến của





biết tiếp tuyến song

song với đường thẳng có phương trình

:3 2 0

x y



  

3 2.

y x

 

3 14

y x

 

3 5.

y x

 

3 8.

y x

 

Câu 16. Cho hàm

2 3 1

y x x

  

có đồ thị là

( )

. Tiếp tuyến của đồ thị

( )

vuông góc với đường

thẳng

21 2 0

x y

  

có phương trình là:

y x



 



 





. B.

21 33

21 31

y x



  



  



. C.

21 33

21 31

y x



 



 



. D.

y x





 







 





Câu 17. Tiếp tuyến của đồ thị hàm số

4 2

2 3

y x x

   

vuông góc với đường thẳng

8 2017 0

x y

  

có phương trình là

y x

  

. B.

8 8

y x

 

. C.

8 8

y x

  

. D.

y x

 

Câu 18. Phương trình tiếp tuyến của đồ thị hàm số

2 2







biết tiếp tuyến vuông góc với đường

thẳng

6 1

y x

  

là

1 1

6 3

y x

 

. B.

y x

 

. C.

1 1

6 3

y x



  



  





. D.

1 1

6 3

1 13

6 3

y x



 



 





Câu 19. Cho hàm số





: 4 3 1.

C y x x

   

Viết phương trình tiếp tuyến của





biết tiếp tuyến đi

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

qua điểm





1;2 .

A 

9 7

y x



  







4 2

y x



 



 



3 5

y x



 



 



2 2

y x



  



 



Câu 20. Cho hàm số

3 2

6 3 1

y x x x

    

có đồ thị (C). Trong các tiếp tuyến của (C), tiếp tuyến có hệ

số góc lớn nhất có phương trình là

15 55

y x

 

. B.

15 5

y x

  

. C.

15 5

y x

 

. D.

15 55

y x

  

Câu 21. Cho hàm số

3 2

3 6 1

y x x x

   

có đồ thị (C). Trong các tiếp tuyến của (C), tiếp tuyến có hệ số

góc nhỏ nhất có phương trình là

3 2

y x

  

3 2

y x

 

3 8

y x

  

3 8

y x

 

Câu 22. Đường thẳng

y ax b

 

tiếp xúc với đồ thị hàm số

3 2

2 2

y x x x

   

tại điểm





1;0

M . Khi

đó ta có:



 

Câu 23. Cho hàm số





: 4 3 1.

C y x x

   

Viết phương trình tiếp tuyến của





biết tiếp tuyến đi

qua điểm





1;2 .

A 

9 7

y x



  







4 2

y x



 



 



3 5

y x



 



 



2 2

y x



  



 



Câu 24. Cho hàm số





3 2

3 1 1

y x mx m x

    

có đồ thị (C). Với giá trị nào của

thì tiếp tuyến với

đồ thị (C) tại điểm có hoành độ bằng –1 đi qua





1;3

A ?



 

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Câu 25. Cho hàm số:

3 2

2 6 5.

y x x

   

Viết phương trình tiếp tuyến của đồ thị

( ),

biết tiếp tuyến

đi qua điểm

( 1; 13).

A  

6 7

48 61

y x



 



  



6 7

48 61

y x



  



 



6 7

48 61

y x



 



  



6 7

48 61

y x



 



  



Câu 26. Cho hàm số:

2 1



 



Viết phương trình tiếp tuyến của đồ thị

( ),

biết tiếp tuyến đi qua

điểm

( 1;4).

A 

1 13

3 3

d y x

  

1 13

3 3

d y x

   

1 13

3 3

d y x

   

1 13

3 3

d y x

  

Câu 27. Cho hàm số:

4 2

2 1.

y x x

  

Có bao nhiêu tiếp tuyến đi qua điểm

(0; 1)



A. 1. B. 2. C. 3. D. 4.

Câu 28. Cho hàm số

2 1







. Viết phương trình tiếp tuyến với

( ),

biết tiếp tuyến đó đi qua điểm

( 1;3).

A 

1 13

4 4

y x

 

. B.

1 13

4 4

y x

  

. C.

1 13

4 4

y x

 

. D.

1 13

4 4

y x

  

Câu 29. Cho hàm số:

2 1



 



Viết phương trình tiếp tuyến với

( ),

biết tiếp tuyến đi qua giao

điểm của đường tiệm cận và trục hoành Ox?

1 1

12 24

d y x

  

1 1

12 24

d y x

   

1 1

12 24

d y x

  

1 1

12 24

d y x

   

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Câu 30. Cho hàm số:

3 2

1 3

4 2

y x x

  

Viết phương trình tiếp tuyến của đồ thị

( ),

biết tiếp tuyến

cắt trục tung tại điểm có tung độ bằng

y x







  





. B.

y x

  

y x



 



  





. D.

y x

  

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

ĐÁP ÁN

Câu

Đáp

án

Câu

Đáp

án

Câu

Đáp

án

Câu

Đáp

án

Câu

Đáp

án

1 D 7 C 13 B 19 A 25 C

2 D 8 C 14 A 20 A 26 D

3 C 9 A 15 B 21 B 27 C

4 A 10 D 16 C 22 A 28 A

5 A 11 B 17 C 23 A 29 B

6 B 12 D 18 D 24 B 30 A

PHẦN 2: HÌNH HỌC

Ấ

N Đ

Ề

GÓC TRONG KHÔNG GIAN

DẠNG 1: GÓC GIỮA HAI ĐƯỜNG THẲNG

1. Phương pháp

 Nếu

và

song song hoặc trùng nhau thì góc giữa chúng bằng

0 .

 Nếu

và

cắt nhau thì góc giữa chúng là góc nhỏ nhất trong các góc được tạo bởi

hai đường thẳng.

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN



Góc gi

ữ

a hai đư

ờ

ng th

ẳ

ng chéo nhau

và

là góc

giữa hai đường thẳng



và



cùng đi qua một điểm

và lần lượt song song (hoặc trùng) với

và

Tức là:

 



 



, , .

a a

a b a b

b b





 

 







Chú ý:



 



0 0

0 , 90 .a b 



ể

xác đ

ị

nh góc gi

ữ

a hai đư

ờ

ng th

ẳ

ng, ta có th

ể

ấ

một điểm (thuộc một trong hai đường thẳng đó) từ

đó kẻ đường thẳng song song với đường còn lại.

Ví dụ: Để tính

 



, AB CD

. Ta kẻ AE // CD.

Khi đó:

 



 



, , .AB CD AB AE BAE 

 Nếu

1 2

, u u

 

lần lượt là hai vectơ chỉ phương của hai đường thẳng

và

thì:

 



 



1 2

0 0

, 90

, .

180 90

u u khi

a b

khi

 



 







 



 

Tức là:

 



 



1 2

cos , cos , .

u u

a b u u

u u

 

 

2. Ví dụ minh họa

Ví d

ụ

Cho t

ứ

ệ

n đ

ề

ABCD

có c

ạ

nh b

ằ

là trung đi

ể

m c

ủ

a c

ạ

. G

ọ



là góc giữa hai đường thẳng AB và DM, khi đó

cos



bằng

Lời giải:

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Gọi N là trung điểm của AC

 MN là đường trung bình của

ABC

MN AB















Vì

BCD

và

ACD

là các tam giác đều cạnh

bằng

a MD ND  

Vì

 



 



// , , .MN AB AB DM MN DM



  

Xét

MND

, ta có:



2 2 2

cos

2 .

MN MD ND

NMD

MN MD

 



2 2

3 3

2 2 2

1 3

3 2 3

2. .

2 2

a a a

a a

   

 

 

   

 

   

 

   

   



 



90 , .NMD MN DM NMD   

Vậy



cos cos

NMD



  

Chọn đáp án A.

Ví d

ụ

Cho hình chóp

S ABCD

, có đáy

ABCD

là hình vuông tâm

, c

ạ

nh b

ằ

;

SA vuông góc với đáy và

3SA a

. Khi đó,

cosin

góc giữa SB và AC bằng

Lời giải:

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Gọi I là trung điểm của SD

 OI là đường trung bình của

SBD

2 2 2 2

2 2 2

OI SB

SB SA AB a a

OI a









 

   





Vì

 



 



// , , .OI SB SB AC OI AC AOI  

Ta có:

2 2 2 2

2 2 2

SD SA AD a a

AI a

 

   

AI OI AOI   

cân tại

Gọi H là trung điểm của

OA IH OA 

Và

2 4 4

OA AC a

OH   

Xét

OHI

, ta có:



cos

HOI

OI a

  

Vậy

 



cos , cos

SB AC HOI

  

Chọn đáp án B.

Chú ý: Để tính



cos AOI

ta có thể tính cách khác như sau:



2 2

2 2 2

cos .

2 . 4

2. .

a a

OA OI AI

AOI

OA OI

 

 

 

 

 

  

Ví d

ụ

Cho hình chóp

S ABCD

, có đáy

ABCD

là hình thang vuông t

ạ

và

; c

ạ

2AB a

AD DC a 

;

SA AB

SA AD

và

2 3

SA 

a) Góc giữa đường thẳng SB và DC bằng

30 .

45 .

60 .

75 .

b) Gọi



là góc giữa SD và BC. Khi đó,

cos



bằng

Lời giải:

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

a) Vì

DC AB

(vì vuông tại A ).

Xét vuông tại A, ta có:

Vậy

Chọn đáp án A.

b) Gọi E là trung điểm của AB.

Khi đó, BCDE là hình bình hành

Ta có

Áp dụng định lí hàm cosin trong tam giác SDE, ta được:

Vậy

Chọn đáp án B.

DẠNG 2: GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG

1. Phương pháp

 Nếu đường thẳng vuông góc với mặt phẳng thì góc giữa đường thẳng

và

mặt phẳng bằng

Tức là:

 



 



, , .

SB DC SB AB SBA

  

SAB





SBA

 

SAB



 

2 3

tan 30 .

2 3

SBA SBA

AB a

    

 



, 30 .

SB DC SBA 



 



 



// , , .

DE BC SD BC SD DE



   

2 2

2 2 2 2 2

2 2

4 7

3 3

a a

SE SD a

SE SD SA AD a

DE a



 



     





 

 





 

2 2 2 2

2 3 42

cos 0 90 .

2 . 14 14

2. . 2

SD DE SE a

SDE SDE

SD DE

a a

 

      

 



 



, , .

SD BC SD DE SDE



  



cos cos

SDE



   









90 .

   

 



, 90 .

a P a P  

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN



ế

u đư

ờ

ng th

ẳ

không vuông góc v

ớ

i m

ặ

t ph

ẳ

thì góc giữa đường thẳng và hình chiếu của

nó trên gọi là góc giữa đường thẳng

và mặt

phẳng .

Tức là: Nếu và là hình chiếu của trên

thì

Chú ý:



 Nếu

 Để tìm hình chiếu của

trên ta có thể làm như sau:

Tìm giao điểm

Lấy một điểm A tùy ý trên và xác định hình chiếu H của A trên . Khi đó,

là đường thẳng đi qua hai điểm A và M.

2. Một số loại góc giữa đường thẳng và mặt phẳng thường gặp đối với hình chóp

Góc gi

ữ

ạ

nh bên và m

ặ

t đáy

H là hình chiếu vuông góc của S trên

HD là hình chiếu vuông góc của SD

trên

Vậy

Góc gi

ữ

a c

ạ

nh bên và m

ặ

t đ

ứ



















a P









 



 



, , .

a P a a





 

 



0 0

0 , 90 .

a P 





 



, 0 .

a P



 



















M a P

 











ABCD







ABCD

 



 



, , .

SD ABCD SD HD SDH

 

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Dựng .

Vì

E là hình chiếu vuông góc của C trên

SE là hình chiếu vuông góc của SC

trên

Vậy

Góc gi

ữ

a đư

ờ

ng cao và m

ặ

t bên

Dựng

Vì

Mà

SE là hình chiếu vuông góc của SH

trên

Vậy

3. Ví dụ minh họa

Ví d

ụ

Cho hình chóp

, có đáy

là hình vuông c

ạ

nh b

ằ

;

vuông góc với đáy và . Gọi là góc giữa SC và , khi đó số đo góc

bằng

A. B. C. D.

Lời giải:





CE HD E HD

 

 

CE HD

CF SDH

CE SH

 

 













SHD







SHD

 



 



, , .

SC SHD SC SE CSE

 





HE CD E CD

 

 

CD HE

CD SHE

CD SH

 

 















SCD SHE

 









SCD SHE SE

 







SAD

 



 



, , .

SH SAD SH SE HSE

 

S ABCD

ABCD

SA 







ABCD



30 .

45 .

60 .

75 .

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

Vì là hình chiếu vuông

góc lên mặt phẳng

Do đó:

(vì vuông tại A ).

Xét vuông tại A, ta có:

Chọn đáp án A.

Ví d

ụ

Cho hình chóp

, có đáy

là tam giác đ

ề

u c

ạ

nh b

ằ

;

vuông

góc với đáy và . Gọi là góc giữa SC và mặt phẳng , khi đó

nhận giá trị nào trong các giá trị sau

A. B. C. D.

Lời giải:

Gọi

là trung điểm của

Vì

là hình chiếu vuông góc

của trên

Khi đó:

(vì vuông

tại ).

Xét vuông tại S, ta có:

Vậy Chọn đáp án B.





SA ABCD AC

 





ABCD

 



 



, , .

SC ABCD SC AC SCA



  

SAC





SCA

 

SAC



 

tan 30 .

SCA SCA



     



S ABC

ABC

SA a









SAB

tan



4 3

2 3

AB CM AB

 

 

CM AB

SA ABC

CM SA do

CM ABC

 



 





 

 







 









 







CM SAB SM

  





SAB

 



 



, , .

SC SAB SC SM CSM



  





 

CM SAB

CM SM SCM

SM SAB







   











S CSM

 

SCM





2 2 2

tan .

CM CM

CSM

SA AM a

   





tan tan

CSM



  

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

100

Ví d

ụ

Cho hình chóp

, có đáy

là tam giác vuông t

ạ

;

và

. Góc giữa đường thẳng và bằng

A. B. C. D.

Lời giải:

Gọi

là trung điểm của

Vì vuông tại A nên H là tâm đường

tròn ngoại tiếp và

Mà là trục của đường tròn

ngoại tiếp

là hình chiếu của trên

(vì vuông tại H nên ).

Xét vuông tại H, ta có:

Vậy Chọn đáp án A.

DẠNG 3: GÓC GIỮA 2 MẶT PHẲNG

1. Phương pháp

Để xác định góc giữa hai mặt phẳng và , ta có thể thực hiện theo một trong

các cách sau:

Cách 1: Theo định nghĩa

S ABC

ABC

BC a



SA SB SC  





ABC

30 .

45 .

60 .

90 .

ABC



ABC



2 2

BC a

 

SA SB SC SH

  





ABC SH ABC

  







ABC

 







 



, , .

SA ABC SA HA SAH

  

SHA





SAH



SHA



 

cos 30 .

SAH SAH

    

 



, 30SA ABC SAH

  













 

   

 



 



, , .

a P

P Q a b

b Q







 









Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

101

Cách 2: Khi xác định được thì ta

làm như sau:

 Bước 1: Tìm mặt phẳng

 Bước 2: Tìm

Khi đó:

Đặc biệt: Nếu xác định được 2 đường thẳng

sao cho:

Ví d

ụ

Góc gi

ữ

a m

ặ

t b

ên và m

ặ

t đáy.

Dựng

Vì

Cách 3:

Theo đ

ị

nh lí v

ề

hình chi

ế

2. Ví dụ minh họa









P Q c

 





R c











   

p R P

q R Q



 





 





   

 



 



, , .

P Q p q



p q





 

   

 



 



, , .

P p c

P Q p q

Q q c



 



 



 









HE CD E CD

 

 

CD HE

CD SHD CD SE

CD SH

 

   















 

SCD ABCD CD

CD HE ABCD

CD SE SCD



 



 





 





   

 



 



, , .

SCD ABCD SE HE SEH

  

.cos cos

S S

 



  

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

102

Ví d

ụ

Cho hình chóp t

ứ

giác đ

ề

có c

ạ

nh đáy b

ằ

, chi

ề

u cao hình

chóp bằng . Góc giữa mặt bên và mặt đáy là

A. B. C. D.

Lời giải:

Gọi

là tâm của hình vuông

ABCD

và

là

trung điểm của CD.

là đường trung bình của

Vì

Xét vuông tại O, ta có:

Vậy Chọn đáp án C.

Ví d

ụ

Cho hình l

ậ

p phương

có c

ạ

nh b

ằ

. G

ọ

là tâm c

ủ

hình vuông và là góc giữa hai mặt phẳng và . Góc

thỏa mãn hệ thức nào sau đây?

A. B. C. D.

Lời giải:

S ABCD

30 .

45 .

60 .

75 .



ACD



2 2

OE AD









 





// .

OE AD OE CD

 

 

CD OE

CD SOE CD SE

CD SO

 

   















   

 



 



, , .

ABCD SCD CD

SE CD ABCD SCD SE OE SEO

OE CD



 



   









SEO



 

tan 3 60 .

SEO SEO

    

   

 



, 60ABCD SCD SEO

  

ABCD A B C D

   



A B C D

   







O AB







ABCD



cos .





tan 2.





sin .





tan .





Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

103

Gọi

là tâm của hình vuông

ABCD

và

là

trung điểm của

Vì

Xét vuông tại , ta có:

Chọn đáp án B.

Ví d

ụ

Cho hình hình chóp

có đáy

ABC

là tam giác vuông cân t

ạ

và

; vuông góc với đáy, . Góc giữa hai mặt phẳng và

bằng

A. B. C. D.

Lời giải:

Gọi

là trung điểm của

Vì

là hình chiếu của lên

 Ta có:

 Vì

AB OI AB

 

 

AB OI

AB OIO AB O I

AB OO

 

 

   

















O AB ABCD AB

OI AB

O I AB





 















   

 



 



, , .

O AB ABCD OI O I O IO



  

   

O OI







tan tan 2.

OO a

O IO





   



S ABC

BA BC a

 

SA a









SAC





SBC

30 .

45 .

60 .

75 .

AC BH AC

 

 

BH AC

SA ABC

BH SA do

BH ABC

 



 





 

 







 









 







BH SAC

 

SHC

 

SBC



 

cos .

SHC

SBC

SAC





 

2 2

AC BA BC a  

1 1 2 2

. . .

2 2 2 4

SHC

a a

S SA HC a



  

 

BC AB

BC SA do SA ABC

 





 





Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

104

vuông tại B.

Khi đó:

Vậy Chọn đáp án C.

Bình luận: Trong bài toán trên, ta dễ dàng xác định được giao tuyến

nhưng lại gặp khó khăn trong việc tìm một mặt phẳng vuông góc với SC, mất nhiều thời gian

tính toán,... không phù hợp với yêu cầu tốc độ của hình thức thi trắc nghiệm. Đồng thời nhận

thấy rằng việc xác định hình chiếu của B lên và tính diện tích của hai tam giác ;

là khá dễ dàng nên ta vận dụng cách 3 trong nội dung phương pháp đã trình bày ở trên

để giải quyết nhanh bài toán.





BC SAB BC SB SBC

     

2 2

1 1 2

. . . .

2 2 2

SBC

S SB BC a a a



   

cos 60

SHC

SBC

 



     









SC SAC SBC

 





SAC

SHC



SBC



Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

105

KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT MẶT PHẲNG

1. Phương pháp

Khoảng cách từ điểm M đến mặt phẳng là

MH, với H là hình chiếu vuông góc của M trên mặt

phẳng

Phương pháp gi

ả

i chung:

ố

n tìm kho

ả

ng cách t

ừ

ộ

t đi

ể

m đ

ế

n m

ộ

t m

ặ

t ph

ẳ

ng, trư

ớ

hết ta phải tìm hình chiếu vuông góc của điểm đó trên mặt phẳng. Việc xác định hình chiếu

của điểm trên mặt phẳng ta thường dùng một trong các cách sau:

Cách 1:

 Bước 1: Tìm một mặt phẳng chứa và

vuông góc với .

 Bước 2: Xác định giao tuyến:

 Bước 3: Trong , dựng

Vì

Cách 2:

Nếu đã biết trước một đường thẳng thì ta

sẽ dựng , khi đó: là hình

chiếu vuông góc của M trên .













 

MH P

d M P MH

H P



 



















P Q

  









, .

MH H

   









   

 

P Q

P Q MH P

Q MH







    





  













d M P MH

 





d P



Mx d





H Mx P

 













d M P MH

 

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

106

Cách 3:

Dựa vào tính chất trục của tam giác: Cho nằm

trên , nếu thì hình chiếu

vuông góc của điểm trên chính là tâm

của đường tròn ngoại tiếp .

Khi đó:

KHOẢNG CÁCH DỰNG TRỰC TIẾP

Khoảng cách từ chân đường cao tới mặt bên

Bài toán: Cho hình chóp có đỉnh S có hình chiếu vuông

góc lên mặt đáy là . Tính khoảng cách từ điểm

đến mặt bên .

 Kẻ

Khi đó:

Khoảng cách từ một điểm trên mặt đáy tới mặt

đứng (chứa đường cao)

Bài toán: Cho hình chóp có đỉnh S có hình chiếu vuông

góc lên mặt đáy là . Tính khoảng cách từ điểm

bất kì đến mặt bên .

 Kẻ



ABC







MA MB MC

 





ABC















, .

MO P d M P MO

  





SAB





, .

HI AB I AB

 





HK SI K SI

 

 

2 2

, .

SH HI

d H SAB HK

SH HI

 







SHB

AK HB



 

AK HB

AK SHB

AK SH

 

 















, .

d A SHB AK

 

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

107

Khối chóp có các cạnh bên bằng nhau

Cho hình chóp có đỉnh S có các cạnh bên có độ dài bằng

nhau:

(đáy có thể là bốn đỉnh hoặc

ba đỉnh). Khi đó nếu như là tâm đường tròn ngoại

tiếp đi qua các đỉnh nằm trên mặt đáy thì SO là trục

đường tròn ngoại tiếp của đa giác đáy hay nói cách

khác:

Chú ý:

Nếu đáy là:

 Tam giác đều, O là trọng tâm.

 Tam giác vuông, O là trung điểm cạnh huyền.

 Hình vuông, hình chữ nhật, O là giao của 2

đường chéo đồng thời là trung điểm mỗi

đường.

TÍNH KHOẢNG CÁCH BẰNG CÁCH GIÁN TIẾP

Giả sử ta ta muốn dựng trực tiếp khoảng cách từ điểm tới mặt phẳng mà không thực

hiện được. Đồng thời từ điểm B ta lại dựng được trực tiếp khoảng cách tới khi đó ta sẽ

thực hiện tính khoảng cách gián tiếp như sau:

Cách 1

(

ổ

i đi

ể

Tính thông qua t

ỉ

ố

kho

ả

cách.

SA SB SC SD

  













, .

SO ABCD d S ABCD SO

  













 

, ,

AB P

d A P d B P



 

















 

d A P

AB P I

d B P

 

 

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

108

Cách 2

(

ổ

i đ

ỉ

ử

ụ

ng ph

ương pháp th

ể

tích đ

ể

tìm kho

ả

ng cách:

Bài toán tính khoảng cách từ một điểm đến một mặt phẳng trong nhiều trường hợp có

thể qui về bài toán thể tích khối đa diện. Việc tính khoảng cách này dựa vào công thức:

 : V, S, h lần lượt là thể tích, diện tích đáy và chiều cao của hình chóp.

 : V, S, h lần lượt là thể tích, diện tích đáy và chiều cao của hình lăng trụ.

Phương pháp này áp dụng được trong trường hợp sau: Giả sử có thể qui bài toán tìm khoảng

cách về bài toán tìm chiều cao của một hình chóp (hoặc một lăng trụ) nào đó. Dĩ nhiên, các chiều cao

này thường là không tính được trực tiếp bằng cách sử dụng các phương pháp thông thường như

định lí Pitago, công thức lượng giác,… Tuy nhiên, các khối đa diện này lại dễ dàng tính được thể tích

và diện tích đáy. Như vậy, chiều cao của nó sẽ được xác định bởi công thức đơn giản trên.

2. Ví dụ minh họa

Ví d

ụ

Cho hình chóp

có đáy

là

hình ch

ữ

ậ

t v

ớ

;

vuông góc với đáy và . Khoảng cách từ đến mặt phẳng bằng

A. B. C. D.

Lời giải:

Trong , kẻ

Vì

Chọn đáp án C.

Ví d

ụ

Cho hình chóp tam giác

ề

có c

ạ

nh đáy b

ằ

và chi

ề

u cao b

ằ

. Khoảng cách từ tâm của đáy đến một mặt bên bằng

A. B. C. D.

Lời giải:



S ABCD

ABCD

AD a



SA a







SCD

3 2

2 3





SAD





, .

AH SD H SD

 

 

AH SAD

CD AD

CD SAD CD AH

CD SA



 

   







 

AH SD

AH SCD

AH CD

 

 







 

2 2 2 2

. .2

SA AD a a

d A SCD AH

SA AD a a

   

 

 

d A SCD

  

S ABC

ABC

2 3

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

109

Vì là tâm của đáy của hình chóp tam giác đều

nên

Gọi là trung điểm của .

Vì đều cạnh bằng

Khi đó

Vì

Trong , kẻ

Vì

Xét vuông tại có đường cao , ta có:

Chọn đáp án C.

Ví d

ụ

Cho hình chóp t

ứ

giác đ

ề

có c

ạ

nh đáy b

ằ

và chi

ề

u cao b

ằ

. Khoảng cách từ tâm của đáy đến một mặt bên bằng

A. B. C. D.

Lời giải:

S ABC





SO ABC SO a  

ABC



2 .

2 3

AM BC

AM a

 







 





1 3

3 3

OM AM 

     

BC AM

BC SAM SBC SAM

BC SO

 

   











SAM





, .

OH SM H SM

 









   

 

   

 

, .

SAM SBC

SAM SBC SM OH SBC d O SBC OH

SAM OH SM







     





 





SOM



 

2 2 2

. 3

OSOM

d O SBC OH a

OS OM

    



 



 

 

S ABCD

ABCD

2 5

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

110

Vì là tâm của đáy của hình chóp tứ giác đều

nên

Gọi là trung điểm của

Trong , kẻ

Vậy Chọn đáp án B.

Ví dụ 4: Cho hình chóp có đáy là hình chữ nhật với .

SAD

là tam giác cân và nằm trong mặt phẳng vuông góc với đáy. Gọi H là hình chiếu

vuông góc của S trên mặt phẳng đáy. Khoảng cách từ C đến mặt phẳng bằng

A. B. C. D.

Lời giải:

Gọi là trung điểm của

Vì

Dễ thấy rằng vuông cân tại A và và

vuông cân tại D.

Vì

Suy ra Chọn đáp án A.

S ABCD





SO ABCD SO a  

2 2

OM CD

BC a

 







 









SOM





, .

OH SM H SM

 

   

 

2 2

OSOM

OH SCD d O SCD OH

OS OM

    



 

d O SCD

  

 



 

 

S ABCD

2 ,

AD a AB a

 





SHB

AD SH AD

 









   

 

SAD ABCD

SAD ABCD AD SH ABCD

SAD SH AD







   





 





ABH



CDH





0 0

45 90 .

AHB CHD BHC CH HB

      

 

CH HB

SH ABCD

CH SHB

CH SH do

CH ABCD

 



 





 

 

 







 









 











2 2

, 2

d C SHB CH CD DH a

    

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

111

Ví dụ 5: Cho hình chóp có đáy là tam giác vuông tại , ,

tam giác là tam giác đều cạnh và nằm trong mặt phẳng vuông góc với đáy.

Khoảng cách từ điểm C đến mặt phẳng bằng

A. B. C. D.

Lời giải:

Gọi là trung điểm của

Vì

Gọi là trung điểm của

Trong , kẻ

Vì

Từ và

Ta có:

Xét vuông tại có đường cao , ta có:

Vậy Chọn đáp án B.

S ABC

ABC



ABC



SBC





SAB









   

 

SBC ABC

SBC ABC BC SH ABC

SBC SH BC







   





 





 









 

d C SAB

CH SAB B

d H SAB

    

















, 2 , .

d C SAB d H SAB

 

// .

AB HE AC HE AB

  





SHE





HK SE K SE

 





 





HK SHE

AB HE

AB SHE AB HK

AB SH



 

   































2 , .

HK SAB d H SAB HK

   



.sin

2 2 4

AC BC ABC a











  





SHE



2 2

. 39

SH HE a

SH HE

 



 

, 2 , 2

d C SAB d H SAB HK

   

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

112

Ví d

ụ

Cho hình chóp

có đáy

là hình ch

ữ

ậ

t v

ớ

; cạnh bên và vuông góc với đáy. Khoảng cách từ điểm A đến mặt

phẳng bằng

A. B. C. D.

Lời giải:

Trong , kẻ

Vì

Từ và

Xét vuông tại có đường cao , ta có:

Vậy Chọn đáp án B.

Ví d

ụ

[

Trích

ề

Minh H

ọ

–

2017]:

Cho hình chóp t

ứ

giác

S.ABCD

có đáy là h

ình

vuông cạnh bằng . Tam giác SAD cân tại S và mặt bên vuông góc với mặt

phẳng đáy. Biết thể tích khối chóp S.ABCD bằng . Tính khoảng cách h từ B đến mặt

phẳng

A. B. C. D.

Lời giải:

S ABCD

ABCD

AB a



AD a



SA a







SBD

2 3

2 5





ABCD





, .

AE BD E BD

 





ABCD





AH SE H SE

 





 

BD SA

BD SAE BD AH

BD AE

 

   































2 , .

AH SBD d A SBD AH

   

ABD



2 2 2 2

. .2 2

AB AD a a a

AB AD a a

  

 

SAE



2 2 2

. 2

SA AE a

SA AE

  



 



 

 

 

d A SBD AH

  





SAD





SCD

h a



h a



h a



h a



Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

113

Gọi I là trung điểm của AD, vì cân tại

nên

Trong , dựng

Vì

Xét vuông tại có đường cao , ta có:

Vậy Chọn đáp án B.

Bình luận: Thông thường khi tính khoảng cách từ điểm đến mặt ta có 3 hướng đi chính: Đổi

điểm, đổi đỉnh và đổi sang hình học tọa độ không gian (phương pháp tọa độ hóa). Nếu đi theo

hướng giải đổi điểm là đổi gián tiếp từ B sang A rồi sang H (như lời giải trên) sẽ mất nhiều thời

gian không đáp ứng được yêu cầu về tốc độ thi theo hình thức trắc nghiệm. Đồng thời khi nhận

ra đề bài cho thể tích V của khối chóp S.ABCD cho trước bạn nên dùng phương pháp đổi đỉnh sẽ

phù hợp hơn. Cụ thể:

SAD







SI AD SI ABCD

  

 

. .

2 .

S ABCD ABCD

S ABCD

ABCD

V SI S

SI a

 

   





SAD





, .

IH SD H SD

 

 

CD AD

CD SAD CD IH

CD SI

 

   







   

 

, .

IH SD

IH SCD d I SCD IH

IH CD

 

   







   

 









 

// , , . , 2 .

AI SCD D

AB SCD d B SCD d A SCD d I SCD IH

 

   

SID



2 2 2 2 2

. . 2

ID IS ID IS a

   

 



 

, 2

d B SCD IH

  

 

2 2

3 4

4 4

2 3

, .

1 1

. . 2.

2. 2

2 2

S ABCD

S BCD

SCD

a a

d B SCD

SD CD a SI ID

    

 



 

 

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

114

Ví d

ụ

Cho lăng tr

ụ

tam giác đ

ề

có

. G

ọ

là trung

điểm của . Khoảng cách từ A tới mặt phẳng bằng

A. B. C. D.

Lời giải:

Gọi là trung điểm của

Trong , kẻ

Vì

Chọn đáp án C.

Ví dụ 9: Hình hộp đứng có đáy là hình thoi cạnh a, góc

đồng thời . Gọi G là trọng tâm tam giác BCD. Khoảng cách từ G tới mặt

phẳng bằng

A. B. C. D.

Lời giải:

ABC A B C

  

AA a





AB a



B C

 





A BC



2 21

2 7

3 3

2 2

AI BC

AB a

 







 









AA I







, .

AH A I H A I

 

 

     

BC AI

BC AA I A BC AA I

BC AA

 

  

   

















   

 

A BC AA I

A BC AA I A I AH A BC

AA I AH A I



 





   

   





 

 





 

2 2 2

. 21

AI a

d A A BC AH

AA AI



     





 



 

 

ABCD A B C D

   



BAD



AA a









A BD



2 21

2 7

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

115

Vì

Trong , kẻ

Vì

Tam giác cân có đều có cạnh bằng

Vậy

Chọn đáp án D.

Ví dụ 10: Cho hình chóp có đáy là hình vuông cạnh ; ;

hình chiếu vuông góc của trên trùng với trung điểm của cạnh .

Khi đó, tỉ số bằng

A. B. C. D.

Lời giải:

   









 

d G A BD

AG A BD O

d A A BD



    



 

, , .

d G A BD d A A BD

 

 

     

BD AC

BD AA O A BD AA O

BD AA

 

  

   













AA O







, .

AH A O H A O

 

 









   

 

A BD AA O

A BD AA O A O AH A BD

AA O AH A O



 





   

   





 

 





 

2 2

, .

AA AO

d A A BD AH

AA AO



  





ABD



BAD ABD

  

a AO 

 

2 2 2

. 21

, .

3 21

d A A BD

AA AO a

d G A BD

AA AO



   





 



 

 



S ABCD

ABCD

SD 





ABCD









d H SDC

3 2

3 3

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

116

Theo đề bài, ta có:

Gọi là trung điểm của

Vì

Trong , kẻ

Vì

Suy ra:

Ta có:

Do đó:

Vậy Chọn đáp án A.





SH ABCD



HI a

HI CD

 









     

CD HI

CD SHI SCD SHI

CD SH

 

   











SHI





, .

HK SI K SI

 









   

 

SCD SHI

SCD SHI SI HK SCD

SHI HK SI







   





 





 

2 2

, .

SH HI

d H SCD HK

SH HI

 



2 2 2 2

2 4

a a

HD AH AD a

 

    

 

 

2 2

3 5

2 4

a a

SH SD HD a

 

     

 

 

 

2 2 2 2

. . 2

, .

SH HI a a a

d H SCD HK

SH HI a a

   

 

 

a a

d H SDC

  

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

117

KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU

1. Phương pháp

Đư

ờ

ng vuông góc chung c

ủ

a hai đư

ờ

ng th

ẳ

ng chéo

nhau

Đường thẳng cắt hai đường thẳng a, b và cùng

vuông góc với mỗi đường ấy gọi là đường vuông

góc chung của a và b. Đoạn thẳng MN gọi là

đoạn vuông góc chung của a và b.

ộ

t s

ố

hư

ớ

ng tính kho

ả

ng cách gi

ữ

a hai đư

ờ

ng th

ẳ

ng chéo nhau

TH1: Khi chéo nhau và

+ Bước 1: Dựng mặt phẳng chứa và

vuông góc với tại M.

+ Bước 2: Trong dựng tại .

+ Bước 3: Đoạn MN là đoạn vuông góc chung

của và .

TH2: Khi chéo nhau và

Mục tiêu: Chuyển về khoảng cách từ một điểm đến một mặt phẳng.



Hư

ớ

ng 1:

Chuy

ể

n thông qua kho

ả

ng cách t

ừ

một đường đến một mặt phẳng.

 Bước 1: Dựng mặt phẳng chứa

và song song với .

 Bước 2:



a b











MN b







, .

b d a b MN

 

a b







 





 

, ,

a P

d a b d a P

b P





 

M a

d M P





Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

118



Hư

ớ

ng 2:

Chuy

ể

n thông qua kho

ả

ng cách gi

ữ

mặt phẳng song song.

 Bước 1: Dựng hai mặt phẳng ,

sao cho .

 Bước 2: Khi đó

2. Ví dụ minh họa

Ví d

ụ

Cho hình chóp

có đáy là h

ình vuông c

ạ

. Đư

ờ

ng th

ẳ

vuông góc với mặt phẳng đáy, . Khoảng cách giữa hai đường thẳng và

bằng

A. B. C. D.

Lời giải

Vì

Vậy

Chọn đáp án A.

Ví d

ụ

Cho t

ứ

ệ

n đ

ề

có c

ạ

nh b

ằ

Kho

ả

ng cách gi

ữ

a hai đư

ờ

thẳng và bằng

A. B. C. D.

Lời giải

















a P Q b

 

























, , ,

d a b d P Q d M Q

 

S ABCD

SA a



2 .





CD SAB





















, , , .

d CD SB d CD SAB d D SAB

  

   

 

, .

DA AB

DA SAB d D SAB DA a

DA SA

 

    



















, , .

d CD SB d D SAB a

 



ABCD

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

119

Gọi , lần lượt là trung điểm của và

Vì và là các tam giác đều cạnh bằng

nên và

Mặt khác, vì cân tại

Từ và là đoạn vuông góc chung

của và .

Do đó:

Vậy Chọn đáp án C.

Ví d

ụ

Cho hình chóp

có đáy là tam giác đ

ề

u c

ạ

. Hình chi

ế

u c

ủ

trên

trùng với trung điểm của . Biết hợp với đáy một góc . Khi đó,

khoảng cách giữa hai đường thẳng và bằng

A. B. C. D.

Lời giải

BCD



ACD



AN BN 

 

AN CD

BN CD

 







   





MN ABN

CD ABN CD MN



   





AN BN ABN

  

MN AB

 



















2 2

d AB CD MN AN AM

  

3 2

2 2 2

a a a

 

  

 

 

 

d AB CD

 

S ABC





ABC

2 2

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

120

Gọi là trung điểm của

Vì đều

Từ và .

Trong , kẻ

Vì

Từ và là đoạn vuông góc chung của và

Vì là hình chiếu của trên

Xét vuông tại , ta có:

Vậy Chọn đáp án B.

Ví d

ụ

Cho hình

chóp

có đáy là h

ình ch

ữ

ậ

t v

ớ

, c

ạ

vuông góc với mặt phẳng đáy và tạo với mặt phẳng đáy

một góc . Khoảng cách giữa hai đường thẳng và bằng

A. B. C. D.

Lời giải

Vì

Trong , kẻ

Vì





BC SH ABC

 

SH BC

 





ABC







AH BC





























BC SAH

 





SAH





HK SA K SA

 









 

BC SAH

BC HK

HK SAH







 



























, .

BC d SA BC HK

 





SH ABC HA

 





ABC

 



 



, , 30 .

SA ABC SA HA SAH   

AHK



 

sin .sin .

HK a

HAK HK AH HAK

   

 

d SA BC HK

  

S ABCD

2 2

AD AB a

 





ABCD





ABCD

2 21

















// , ,

AB SCD d AB SC d AB SCD

 









d A SCD







SAD





AH SD H SD

 

 

CD AD

CD SAD CD AH

CD SA

 

   







   

 

AH SD

AH SCD d A SCD AH

AH CD

 

   







Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

121

Ta có:

Xét vuông tại , ta có:

Vậy Chọn đáp án B.

Ví d

ụ

Cho hình l

ăng tr

ụ

ứ

có đáy là tam giác vuông t

ạ

ớ

, . Khi đó, tỉ số bằng

A. B. C. D.

Lời giải

Vì

Trong , kẻ

Vì

Ta có:

Vậy Chọn đáp án B.

 



 



, , 60 .

SB ABCD SB AB SBA  

SAB



 

tan .tan .tan60 3.

SBA SA AB SBA a a

    

 

2 2 2 2

. 2 . 3 2 21

4 3

SA AD a a a

d AB SC AH

SA AD a a

    

 

ABC A B C

  

BC a



AB a







3 ,

d AA BC

 





AA BB C C

  





















, , , .

d AA BC d AA BB C C d A BB C C

      

  





ABC





, .

AH BC H BC

 

 

AH BC

AH BB C C

AH BB

 

 

 









 

2 2

, .

AB AC

d A BB C C AH

AB AC

 

  



2 2 2 2

4 3.

AC BC AB a a a    

 

2 2 2 2

. . 3 3

, .

AB AC a a a

d A BB C C

AB AC a a

 

   

 

 

3 ,

d A BB C C

d AA BC

a a a

 

   

Ố 8 NGÕ 17

TẠ QUANG BỬU

ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT)

THẦY GIÁO: ĐẠT NGUYỄN TIẾN

122

Ví dụ 6: Cho hình lập phương có cạnh bằng . Gọi lần lượt

là trung điểm của và . Khi đó, tỉ số bằng

A. B. C. D.

Lời giải

Ta có:

Vì

Trong , kẻ . Vì

Vì .

Ta có: .

Khi đó:

Vậy Chọn đáp án C.

ABCD A B C D

   

M N





. ,

A A B C D

a d MN A C

   



3 2

2 3

1 1 1

. . . .

3 3 3

A A B C D A B C D

V AA S a a a

       



  

















// , ,

MN A BC d MN A C d MN A BC

  

 









d M A BC





   









 

d M A BC

AM A BC B

d A A BC



    



 

, , .

d M A BC d A A BC

 

 





AA B B

 





AH A B H A B

 

 





 

BC AA B B

BC AH

AH AA B B



 





 



 







   

 

2 2

AH A B

AH A BC d A A BC AH AB BH

AH BC



 

 

     







2 2 2

2 2 2 2

A B a a a

BH AH a

 



     

 

 

   

 

1 1 2

, , , .

2 2 4

d MN A C d M A BC d A A BC AH

  

   

 

. ,

3 2

A A B C D

a d MN A C

   



  

Bấm Tải xuống để xem toàn bộ.

| 1/122

| | Tải xuống

Preview text:

SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 1 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU MỤC LỤC
MỤC LỤC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
Phần 1: ĐẠI SỐ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 un TÌM GIỚI HẠN CỦA DÃY
CÓ GIỚI HẠN HỮU HẠN . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 Pn
DẠNG 1: u là một phân thức hữu tỉ dạng 
( trong đó Pn,Qn là hai đa thức n un Qn
của n). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 Pn
DẠNG 2: u là một phân thức hữu tỉ dạng 
( trong đó Pn,Qn là các biểu thức n un Qn
chứa căn của n). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 Pn
DẠNG 3: u là một phân thức hữu tỉ dạng 
( trong đó Pn,Qn là các biểu thức n un Qn chứa hàm mũ n n n
a ,b ,c ,…. Chia cả tử và mẫu cho n
a với a là cơ số lớn nhất ). . . . . . . . . . . . . . . 6
DẠNG 4 : Nhân lượng liên hợp: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
GIỚI HẠN HÀM SỐ LÝ THUYẾT VÀ PHƯƠNG PHÁP GIẢI TOÁN . . . . . . . . . . . . . . . . . . . . . 11 0
CÁCH KHỬ DẠNG VÔ ĐỊNH 0 (Dạng này thường gặp khi x  x0 ). . . . . . . . . . . . . . . . . . 13 P x DẠNG 1: Hàm số f x   
trong đó Px,Qx là đa thức theo biến x. . . . . . . . . . . . . . . . . 13 Qx
DẠNG 2: NHÂN LIÊN HỢP . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
GIỚI HẠN KHI x TIẾN TỚI VÔ CỰC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
GIỚI HẠN MỘT BÊN . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
HÀM SỐ LIÊN TỤC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
ĐẾM SỐ NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
SỬ DỤNG MÁY TÍNH: TÍNH GIỚI HẠN. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
PHẦN 2: HÌNH HỌC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 2 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
DẠNG 1: GÓC GIỮA HAI ĐƯỜNG THẲNG ........................................ 92
DẠNG 2: GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG . . . . . . . . . . . . . . . . . . . . . . . . . . 96
DẠNG 3: GÓC GIỮA 2 MẶT PHẲNG . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 3 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU Phần 1: ĐẠI SỐ
CHUYỀN ĐỀ 1: GIỚI HẠN
TÌM GIỚI HẠN CỦA DÃY un CÓ GIỚI HẠN HỮU HẠN DẠNG 1: P n
u là một phân thức hữu tỉ dạng    ( trong đó n un Qn
Pn,Qn là hai đa thức của n).
Phương pháp: Chia cả tử và mẫu cho k n với k
n là lũy thừa có số mũ lớn nhất của Pn và Qn ( hoặc rút k
n là lũy thừa có số mũ lớn nhất của Pn và Qn ra làm nhân tử) sau đó áp dụng các định lý về giới hạn.
Ví dụ: Tìm giới hạn của dãy un  biết: 2 3 2 4 2 a). 2n  3n  1 u 2n  3n  4 2n  3n  n n  b). u  c). u  2 5n  3 n 4 3 n  4n  n n
2n 11 3n 2 2n  1 LỜI GIẢI a). Ta thấy 2
n là lũy thừa cao nhất của tử và mẫu, nên chia cả tử và mẫu của un cho 2 n được: 2 2n  3n  1 3 1 2 2     2 2 2n 3n 1 n n n u 3 1 3    n    . Ta có lim 0,lim 0 và lim 0 nên 2 2 5n  3 5n  3 3 2 2 5  n n n 2 2 n n 2  0  0 2 lim un   . 5  0 5 b). Dễ dàng thấy 4
n là lũy thừa cao nhất của tử và mẫu, nên chia cả tử và mẫu của un cho 4 n được: 3 2 2n  3n  4 2 3 4 3 2       4 2 4 2n 3n 4 n n n n u 3 4     n    . Ta có 2 lim 0, lim 0, lim 0 , 4 lim 0 4 3 4 3 n  4n  n n  4n  n 4 1 2 4 1  n n n n 3 4 n n n
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 4 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU và 1 lim 0  0  0  0 . Do đó lim u   0 . 3 n n 1 0  0  4 2           c). Có 4 2 4 2n 3n n 4 3 1 2n  3n  n  n    n 2   , 2n 1 1 2n  1  n   n  2  , 4  3     n   n n   n   n   1 3n   1   2     1 2n 1 1  3n  n   n   3 và 2 2 2 2n  1  n    n  2  . Từ đó n n        2  2  n   n  4  3 1   n 2  3 1   3 1  4 n 2    2   3 n   n 3  n 3 u  n  n n   n  . Vì  1   1  2  1         n 2 n 3 n 2  1 1 1 1 1 1         4 n 2    32    2    32  2 n n        n  2 2  n  n  n   n  n  n  3 lim 1 1 2  0  0 1  0 , lim  0 , 1 lim  0 và lim  0 . Nên lim u    . n 3 n n 2 n n (2  0)(0  3)(2  0) 6 DẠNG 2: P n
u là một phân thức hữu tỉ dạng    ( trong đó n un Qn
Pn,Qn là các biểu thức chứa căn của n).
Ví dụ: Tìm giới hạn của dãy un  biết: 2 a). 4n  n  1  n u 2n  1  n  3 n  b). u  2 n 9n  3n 4n  5 LỜI GIẢI  2    2 4n n 1    1 1 1 1 n n  2 2  n 4    n 4    1 4n  n  1  n  n 2 2 a).  n n n n un     . Vì có 1 lim  0, 2   2 9n 3n   3 3 n 2 9n 3n n 9  9 n     2  n n  n  1 lim  0, và 3 lim  0 . Nên 4  0  0  1 1 lim u   . 2 n n n 9  0 3  2n  1   n  3  1 3 n  1 3   n  n. 2   n. 1    2n 2 1  1  n  3  n   n  b).  n n u n n  n    . Vì có 4n  5  4n  5  5 5 n n. 4   4  n    n n 1 lim  0, 3 lim  0 và 5 lim  0 . n n n
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 5 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU Từ đó có 2  0  1 0 2  1 lim un   . 4  0 2 Pn
DẠNG 3: u là một phân thức hữu tỉ dạng u  ( trong đó n n Qn
Pn,Qn là các biểu thức chứa hàm mũ n n n
a ,b ,c ,…. Chia cả tử và mẫu cho n
a với a là cơ số lớn nhất ).
Ví dụ: Tìm giới hạn của dãy un  biết: n n n n n2 n1 a). 2  4 u 3.2  5 4  6 n  b). u  c). u  n n 4  3 n n n 5.4  6.5 n n 1  n3 5  2.6 n n n n n 2  4 2 4  2      1 n n  n n n 2 4 n n  4     a).Ta có 4 4 4 u  2 3 n    
. Ta có lim   0 và lim   0 . Nên n n n n n n n 4  3 4  3 4 3  3   4  4    n n n 1 4 4 4  4    0  1 lim un   1 . 1 0 n n n n n 3.2  5 3.2 5  2  3     1 n n  n n n 3.2 5 n n  5     b). Ta có 5 5 5 u  2 4 n    
. Ta có lim   0 và lim   0 . n n n n n n n 5.4  6.5 5.4  6.5 5.4 6.5  4   5  5    n n n 5    6 5 5 5  5  Do đó 3.0  1 1 lim un    . 5.0  6 6 n 2 n n 2 n 4 .4  6 .6 4 .4 6 .6 n2 n1 n 2 n    n n n c). Ta có 4 6 4 .4 6 .6 6 6 6 un     n 1  n3 n 1  n 3 n 1 n 3 n 1  n 3 5  2.6 5 .5  2.6 .6 5 .5  2.6 .6 5 .5 2.6 .6  n n n 6 6 6 n 2  4 4     6 n n  6   4   5  
. Ta có lim   0 và lim   0 . n  6   6  1  5  3 5    2.6  6  2 Do đó 4 .0  6 1 lim un   . 1 3 5 .0  2.6 72
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 6 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
DẠNG 4 : Nhân lượng liên hợp:
PHƯƠNG PHÁP : Sử dụng các công thức nhân lượng liên hợp sau:  2 2 a  b a  b   2 2        a    b a b a b a b 2 2  a  b a  b   a  b 3 3 a  b 3 3 a  b  a  b   a  b  . 2 2 a  ab  b 2 2 a  ab  b 3 a b3a2 3 2 a.b b       3   a  b  3 a  b    . 3 a 2 3  a.b  b 3 a2 2 3 2  a.b  b 3 a b3 a2 3 2 a.b b       3   a  b  3 a  b    3 a 2 3  a.b  b 3a2 2 3 2  a.b  b  3 a b  3 a a. b 3 b2 2       3   a  b  3 a  b   3 a  a. b  3 b2 3 a  a. b  3 b2 2 2  3 a b  3 a a. b 3 b2 2       3   a  b  3 a  b   3 a  a. b  3 b2 3 a  a. b  3 b2 2 2
 a b a2 a. b  b2 3 3 3 3 3 3         a  b  3 3 a  b    . a 2  a. b  b2
 a2  a. b  b2 3 3 3 3 3 3 3 3
 a b a2 a. b  b2 3 3 3 3 3 3         a  b  3 3 a  b    a 2  a. b  b2
 a2  a. b  b2 3 3 3 3 3 3 3 3
Ví dụ 1: Tìm giới hạn của dãy un  biết:
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 7 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU a). 2
un  n  3n  5  n b). 2
un  9n  3n  4  3n  2 c). 3 3 2 un  n  3n  n d). 3 3 2
un  8n  4n  2  2n  3 LỜI GIẢI  2  2  n 3n 5 n n 3n 5 n         a). Ta có 2    3n  5
un  n  3n  5  n   . Và có 2 2 n  3n  5  n n  3n  5  n  3n  5   5   2    3n n 3n 5 3 5  5  n   n 3  và 2 2 n  3n  5  n    n 1  . n n       2  2  n n  n  5   5 n3  3  n  Do đó  n u 5 3 n   , vì 5 lim  0, 3 lim  0 và lim  0 . Nên lim u  . 3 5 3 5 n n 2 n 2 n 1 n    n 1   1 2 2 n n n n
NHẬN XÉT : Tại sao phải nhân lượng liên hợp ?
Quay lại ví dụ a) thông thường ta đặt k
n làm nhân tử chung nhưng sao lại phải nhân lượng liên hợp. Bây
giờ ta thử làm lại câu a) theo phương pháp đặt k
n trong căn thức thử xem sao ,và sau đó rút ra nhận xét.  2      Ta có 2 2 n 3n 5 u 3 5 3 5
n  n  3n  5  n  n    n   n 1   n  n 1   1 . Vì 2 n      2 n n 2 n  n  3 5   lim 3 5  lim  0 nên lim 1 
1  0 và lim n   do đó lim u   .  0 (đây là dạng vô 2 n n  2 n n  n  
định). Nên cách làm này không là không được rồi, ta phải sử dụng phương pháp nhân lượng liên hợp để
khử vô định sau đó cách làm hoàn toàn như dạng 1.
Dấu hiệu nhận biết nhân lượng liên hợp : Để nhận biết một bài tập có nhân lượng liên hợp hay không
các bạn chỉ chú ý tới n có mũ cao nhất sau đó đưa ra ngoài dấu căn thức, nếu chúng trừ nhau bằng 0 thì
bài này ta phải nhân lượng liên hợp. Cụ thể ta làm lại câu a) 2
un  n  3n  5  n biểu thức trong căn thức có 2
n là cao nhất và ta quan tâm đến « nó », những thừa số sau bỏ hết có nghĩa xem 2
un  n  n  n  n  0 (nên các bạn phải nhân lượng liên hợp). Chúng ta xem thử bài này có nhân
lượng liên hợp hay không 2
un  2n  3n  5  n chúng ta cũng quan tâm đến số hạng có chứa mũ có nhất đó là 2 2n , có nghĩa u 2
n được viết lại un  2n  n  n 2  n  n  2  1 ta có 2  1  0 nên bài
này được làm trực tiếp không cần nhân lượng liên hợp. Cụ thể bài này ta làm như sau
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 8 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU  2      2 2 2n 3n 5 3 5 3 5
un  2n  3n  5  n  n    n  n 2    n  n 2   1  do 2  2  2 n n n n n      3 5   lim 3 5  lim  0 nên lim 2  
 1  2  1 và lim n   do đó lim un   .
  2 1   (cụ 2 n n  2 n n   
thể các bạn xem phương pháp tìm giới hạn dãy số có giới hạn vô cực).  2  2  9n 3n 4 3n 9n 3n 4 3n        b). 2 u    3n  4
n  9n  3n  4  3n  2   2   2 . Ta 2 9n  3n  4  3n 2 9n  3n  4  3n       2    có 3n 2 2 3n 9n 3n 4 3 4  2  n   n 3  và 2 2 9n  3n  4  n    n 9   . Từ đó suy ra n n       2  2  n n  n  2   2 n3  3 n    n u 4 n   2   2 , vì 2 lim  0, 3 lim  0 và lim  0 . Nên 3 4 3 4 n n 2 n 9 n    3n 9    3 2 2 n n n n 3  0 1 lim un   . 9  0  0  3 2 2 3    3 2   3 3 2  3 3 2 2
 n  3n  n   n  3n   n. n  3n  n      c). 3 3 2 u   n  n  3n  n  2  3 3 2  3 3 2 2
 n  3n   n. n  3n  n   2 3n  3 2 n  3n  3  . Ta có 3 3 2 3 n  3n  3    3 n n. 1 . Do đó 2   3  3 3 2  3 3 2 2  n n
 n  3n   n. n  3n  n    2 3n 3 un   , ta có 3 lim  0 . Nên lim u  1 2 2 n     n 2 3 2 3 2 3 3 3     3   3     3 n 1 n . 1 n 1 1  1  n  n  n  n     d). 3 3 2
un  8n  4n  2  2n  3 2 3    3 2   3 3 2  3 3 2 2
 8n  4n  2  2n   8n  4n  2   2n. 8n  4n  2  4n          3 2  3 3 2  3 3 2 2
 8n  4n  2   2n. 8n  4n  2  4n  
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 9 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU 2 4n  2   3 . 2  3 3 2  3 3 2 2
 8n  4n  2   2n. 8n  4n  2  4n    3 2    Ta có 3 3 2 3 8n 4n 2 4 2 8n  4n  2  3 n    n3 8    . Do đó 3  3  n n  n 2  2  2 n 4  2  4  2  n  n 2 u  n   . Vì lim 0, 2 2     2 n 2 4 2 2 4 2 2 4 2 4 2 n  3 8     2n .3 8    4n  3 8     2.3 8    4  3  3  3  3 n  n n  n n  n n  n 4 lim 2 1  0 và lim  0 . Nên lim u  . n 3 n n 3
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 10 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
GIỚI HẠN HÀM SỐ LÝ THUYẾT VÀ PHƯƠNG PHÁP GIẢI TOÁN TÓM TẮT LÝ THUYẾT
Định lí 1: Giả sử lim f x  L và lim gx  M (với L, M   ).Khi đó: xx0 xx0  lim f
 x  g x  L  M
lim f x  g x   L  M xx        0 xx0 f x  lim f L
 x.g x  L.M  thì lim  xx   Nếu M 0 xx0 g x 0 M Hệ quả:
 Nếu c là một hằng số thì lim c.f  x  c.L xx  . 0  lim  k a.x  k  ax0 ( a hằng số và k    ). xx0
Định lí 2: Giả sử lim f x  L . Khi đó: xx0
 lim f x  L  lim fx 3 3  L xx0 xx0
 Nếu f x  0 với mọi x  J 
\ x0, trong đó J là một khoảng nào đó chứa x0 , thì L  0 và lim f x  L . xx0 Chú ý:
Định lí 1 và định lí 2 vẫn đúng khi thay x  x0 bởi x   hoặc x   .
Định lí 3: Nếu lim f x 1   thì lim  0 . xx xx0 f x 0
4). Một vài quy tắc tìm giới hạn vô cực:
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 11 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Qui tắc 1: Nếu lim f x   và lim gx  L (với L  0 ) thì lim fx.gx xx
 được cho bởi bảng sau: 0 xx0 xx0 lim f x Dấu của L lim f  x.g x xx  0 xx0  +          
Quy tắc 2: Nếu lim f x  L,L  0 , lim gx  0 và gx  0 hoặc gx  0 với mọi xa; b  \ x0 thì xx0 xx0 f x lim
được cho bởi bảng sau: xx0 g x Dấu của L Dấu của g x f x lim xx0 g x  +           5). Các dạng vô định:
Các dạng vô định trường gặp: 0 ,  ,0.,   . 0  6). Giới hạn một bên: a). Giới hạn hữu hạn:
 Giới hạn bên phải: Giả sử hàm số f xác định trên khoảng x0; b,x0   . Ta nói rằng hàm số f có giới
hạn bên phải là số thực L khi x dần đến x0 (hoặc tại điểm x0 ) nếu với mọi dãy số xn  trong khoảng
x0;b mà limxn  x0 , ta đều có limfxn   L . Khi đó ta viết:
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 12 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
lim f x  L hoặc f x  L khi x x  0 . x x  0
 Giới hạn bên trái: Giả sử hàm số f xác định trên khoảng a;x0 ,x0   . Ta nói rằng hàm số f có giới
hạn bên trái là số thực L khi x dần đến x0 (hoặc tại điểm x0 ) nếu với mọi dãy số xn  trong khoảng
a;x0  mà limxn  x0 , ta đều có limfxn   L . Khi đó ta viết:
lim f x  L hoặc f x  L khi x x  0 . x x  0
Định lí 5: lim f x  L  lim f x  lim f x  L x x    0 xx0 xx0  Giới hạn vô cực:
lim f x  , lim f x  , lim f x   lim f x   được phát biểu tương tự như các định nghĩa ở x x     0 xx0 xx0 xx0
phần giới hạn hữu hạn.
Định lí 5 vẫn đúng với giới hạn vô cực.
Các định lí về giới hạn hữu hạn và các quy tắc tìm giới hạn vô cực vẫn đúng trong trường hợp x x  0 hay x x  0 . PHƯƠNG PHÁP GIẢI TOÁN
CÁCH KHỬ DẠNG VÔ ĐỊNH 00
(Dạng này thường gặp khi xx ). 0
DẠNG 1: Hàm số fx Px 
trong đó Px,Qx là đa thức theo biến x. Qx
PHƯƠNG PHÁP: Phân tích đa thức thành nhân tử, sau đó rút gọn biểu thức làm cả tử và mẫu bằng 0.
Phân tích đa thức thành nhân tử có các phương pháp sau:
 Sử dụng bảy hằng đẳng thức đáng nhớ.
 Nếu tam thức bậc hai thì sử dụng 2
ax  bx  c  ax  x1x  x2 ,a  0 với 1 x ,x2 là nghiệm của
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 13 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU phương trình 2 ax  bx  c  0 .
 Sử dụng phương pháp Hoocner . Phép chia đa thức   4 3 2
P x  ax  bx  cx  dx  e cho (x  0 x ) theo sơ đồ Hoocner như sau: a b c d e x 2 0 0 a 1 b  ax0  b c d  ax  bx  cx  d 1  ax0  bx0  c 3 2 1 0 0 0
Hàng thứ nhất điền hệ số của đa thức P x từ ô thứ hai đến ô cuối cùng. Ở hàng thứ hai ô đầu tiên điền
giá trị x0 là một nghiệm của Px , ô thứ hai viết lại a, lấy x0.a  b đặt vào ô thứ ba, lấy x x a  b 2 2 3 2 0 0
 c  ax0  bx0  c điền váo ô thứ tư, lấy x0 ax0  bx0  c d  ax0  bx0  cx0  d điền vào ô thứ năm, lấy x  3 2
0 ax0  bx0  cx0  d  e  0 (bắt buộc tổng này phải bằng 0, thì đây mới là phép chia hết).
Khi đó P x được viết lại
Px  x  x  3 2 0 ax  1 b x  c1x d1
Ví dụ: Tìm các giới hạn sau: 3 3 2 3 2 a). x  8 lim b). 2x  5x  2x  3 L 2x  5x  4x  1  lim c). lim  2 x 2 x  11x  18  3 2 x 3 4x  13x  4x  3  3 2 x 1 x  x  x  1   d). 1 12 lim    3 x 2  x  2 x  8  a).Ta có 3 3 3        2 x 8 x 2
x 2 x  2x  4 (áp dụng hằng đẳng thức), và 2
x 11x  18  x  2x  9 (với 1 x  2  và x2  9
 là hai nghiệm của phương trình 2 x 11x  18  0 ). x 2 2 3 x  2x   4 x 8  2 Do đó x  2x  4 12 lim  lim  lim  . 2 x 2  x 2 x  11x  18  x 2x9 x 2  x  9 7 3 2 b). 2x  5x  2x  3 L  lim  3 2 x 3 4x  13x  4x  3
Thay x  3 vào cả tử và mẫu thấy đều bằng 0, nên x  3 là một nghiệm của hai đa thức cả mẫu và tử. Có
nghĩa (x  3) là nhân tử chung, ta phân tích đa thức ở tử và mẫu thành nhân tử bằng phương pháp Hoocner. Cách làm như sau:
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 14 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU Phân tích tử số: 3 2        2 2x 5x 2x 3 x 3 2x  x  1
Kẻ bảng như sau. Sau đó điền hệ số của từng số hạng với số mũ giảm dần vào các ô ở hàng đầu tiên với ô
thứ nhất để trống. Ở hàng thứ hai: điền giá trị làm đa thức bằng 0 ở đây là chữ số 3. Ô thứ hai điền lại giá
trị ở ô thứ hai của hàng một xuống (ta thường hay nói “đầu rơi xuống”), sau đó lấy 3.2  (5)  1 điền
chữ số 1 vào ô thứ ba, lấy 3.1 (2)  1 điền chữ số 1 vào ô thứ tư, cuối cùng lấy 3.1 (3)  0 điền vào ô cuối cùng. 2 -5 -2 -3 3 2 1 1 0 Phân tích mẫu số: 3 2        2 4x 13x 4x 3 x 3 4x  x  1 4 -13 4 -3 3 4 -1 1 0 x3 2 2x  x   2 1 Do đó 2x  x  1 11 L  lim  lim  . x3 x  3 2 4x  x  1 2 x3 4x  x  1 17 3 2 c). 2x  5x  4x  1 L  lim . Ta thấy lim  3 2
2x  5x  4x  1  0 và lim  3 2
x  x  x  1  0 như vậy đây  3 2 x 1 x  x  x  1 x 1  x 1 
là dạng giới hạn vô định 0 ta phải phân tích cả tử và mẫu thành nhân tử để khử vô định. Phân tích nhân 0
tử bằng phương pháp Hoocner Phân tích tử số: 3 2        2 2x 5x 4x 1 x 1 2x  3x  1 2 5 4 1 1 2 3 1 0 Phân tích mẫu số: 3 2 
      2        2 x x x 1 x 1 x 0x 1 x 1 x  1 1 1 1 1 1 1 0 1 0
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 15 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU x1 2 2x  3x  1 2 Từ đó 2x  3x  1 L  lim  lim , ta thấy lim  2
2x  3x  1  0 và lim  2 x 1  0 ta x 1  x1 2x 1  2 x 1 x 1 x 1  x 1 
vẫn còn dạng vô định 0 nên phân tích thành nhân tử tiếp, ta làm như sau: 0 2 2x  3x  1 x12x1 2x 1 1 L  lim  lim  lim  .  2 x 1 x 1 x  1  x  1x  1 x1 x  1 2
d). Bước đầu tiên ta phải quy đồng mẫu, sau đó phân tích đa thức của tử thành nhân tử và rút gọn hạng     2 tử vô định 1 12 L  lim 1 12 x  2x  8     lim     lim  3 x 2  x  2 x  8    2
x 2 x  2 (x  2)(x  2x   4)   2 x 2 (x  2)(x  2x  4) (x  2)(x  4) x  4 1  lim  lim  .  2 x 2 (x  2)(x  2x  4)  2 x 2 x  2x  4 2 DẠNG 2: NHÂN LIÊN HỢP
Tính các giới hạn sau: (CĂN BẬC 2) a). x  3 lim b) x  3  3 lim 2 x9 9x  x x6 x  6 a). x  3 x  9 1 5 lim  lim lim   2 x9 x9 x9 9x  x x(x  9)( x  3) x( x  3) 4 b). x  3  3 (x  3  9) x  6 1 1 lim  lim  lim  lim  x6 x6 x6 x6 x  6 (x  6)( x  3  3) (x  6)( x  3  3) x  3  3 6
Tìm các giới hạn sau: (CÓ 2 CĂN BẬC 2) a). 3x  1  x  3 lim b). 3  x lim x1 x  8  3 x9 x  5  2 (3x  1 x  3)     x8 3 3x 1 x 3  a). lim  lim x1 x1 x  8  3
(x  8  9) 3x 1  x  3 2(x 1) x 8  3 2 x  8  3  lim  lim  3
x1 (x  1) 3x 1  x  3 x1 3x 1  x  3
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 16 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU (9  x)   x52 (  x  9) x  5  2 3 x   x  5  2 b). lim 2  lim  lim  lim   . x9 x9 x  5  2
(x  5  4)3 x x9 (x 9)3 x x9 3  x 3
Tìm các giới hạn sau: (CÓ CĂN BẬC 3) 3 3 a). 5x  3  2 lim b). 1 1 x lim x 1  x  1 x0 x 3 a). 5x  3  2 5x  3  8 lim  lim x 1  x 1 x  1
 (x 1)3 5x 32 32 5x 3 4          5(x  1) 5 5  lim  lim  x 1    3 3      x1     3  2 3  12 (x 1) 5x 3 2. 5x 3 4 5x 3  2 5x  3  4   3 b). 1 1 x 1 (1 x) 1 1 lim  lim  lim  x0 x0 x  3 x 1 1 x   3 1x2 x0  3     3  2 3 1 1 x 1 x  
Tìm các giới hạn sau: (THÊM BỚT ĐỂ NHÂN LIÊN HỢP) 3 3 2 a). x  9  x  16  7 lim b). x  7  x  3 lim x0 x x1 x  1 a). x  9  x  16  7
x  9  3  x  16  7 lim  lim x0 x0 x x x  9  3 x  16  4 x  9  9 x  16 16  lim  lim  lim  lim x0 x0 x x x0  x  9  3 x0 x  x16 4x x x 1 1 7  lim  lim  lim  lim  x0  x  9  3 x0 x  x16 4x x0 x0 x  9  3 x  16  4 24 3 3 2 3 3 2 b). x  7  x  3
x  7  2  2  x  3 lim  lim x1 x1 x  1 x  1 3 3 2 x  7  2 2  x  3  lim  lim x1 x1 x 1 x 1
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 17 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU 3 x  7  8 2 2  x  3  lim  lim x1   3 x 1 3 2 x 7 2 3 3 2 x 7 4     (x  (2  x  3)(x 1)   1)   2 (x  1)(x  x  1) (  x  1)(x  1)  lim  lim x1   3  2 x 1 2 3 3 3  (2  x  3)(x  1) x 7  2 x  7  4 (x    1)   2 x  x  4 x  1 3  lim     lim 3 x 7 2 x 1 x1 2 3 3 3 2  x      3 4 2 x 7 4
GIỚI HẠN KHI x TIẾN TỚI VÔ CỰC
Câu 1: Tìm các giới hạn sau: 2 2 a). 3x  x  7 lim b). (4x  1)(7x  1) lim  3 x 2x 1 3 x (2x  1)(x  3) 2  1 7  1 7 x 3   2 2  3   2 3x  x  7  x a). x  x x 3 lim  lim  lim  lim  0 3 x x x x 2x 1  3  1   1  2x x 2   x2   3 3 x x      2  1   1 x  1  1   4  x7     4  7  2 2 (4x  1)(7x 1)   x   x  2  x  x b). lim lim   28   lim  lim  0 3 x x (2x  1)(x  3)  x x 3  1   3 x 2  1  3  2x   x1    x2  1 3 x x       3  x  x 
Câu 2: Tìm các giới hạn sau: 2 2 2 x  3 2 x  3 a). (x 1) (5x  2) lim b). lim c). lim 4 x (3x  1) x 2 x  x  5 x 2 x  x  5 2 2 2 2 2  1  2  2   1   2 x 1  x  5  1   5      2 2 (x 1) (5x  2)  x   x   x   x  a).  25 lim  lim  lim  4 4 4 x x x (3x  1)      81 4 1 1 x 3    3   x x     
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 18 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU 6  2  2  2  3 x 1  x 1 1 6 6 3  3 x  2  x  x  x b).  1 lim  lim  lim  lim  3 x x x x 3x  1  1   1   1 3 3 3 x 3   x 3  3  3 3  3  x   x  x  3  3 x   2   2 2 x  3 2x  3  x   c).  x lim  lim  lim  lim  2  x 2 x x x x  x  5  1 5  1 5  1 5 2 x 1  x 1  1  2 2  2  x x  x x x x GIỚI HẠN MỘT BÊN
Ví dụ 1: Tìm các giới hạn sau: x  3 a). lim b). x  x lim . x 3  5x  15 x 0  x  x LỜI GIẢI a). Vì x 3 
 x  3  x  3  0 . Vậy x  3  x  3 x  3 Ta có x  3 1 lim  lim  . x 3 5x  15 x 3   5x  3 5 x   x 1 x x  b). Ta có x  1 lim  lim  lim  1  . x 0 x  x x 0 x  x 1 x 0    x  1 HÀM SỐ LIÊN TỤC
DẠNG 1: XÉT TÍNH LIÊN TỤC CỦA HÀM SỐ TẠI MỘT ĐIỂM PHƯƠNG PHÁP 1:
Bước 1: Tính f x0  .
Bước 2: Tính lim f x . Nếu lim fx  fx0  thì hàm số f(x) liên tục tại x . xx 0 0 xx0
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 19 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU PHƯƠNG PHÁP 2: Bước 1: Tìm lim f x x x  0
Bước 2: Tìm lim f x . x x  0
Nếu lim f x  lim fx  fx thì hàm số f(x) liên tục tại x .   0  0 xx0 xx0
Ví dụ : Xét tính liên tục tại giá trị x của các hàm số sau: 0 2 x  3x  2 1).    x  2 f x   x  2
tại x  2 và tại x  4 0 0 1  x   2  x  3  2  x  1 2).    x   1 f x  tại x  1 0 1 x  1 4  x  5 x   5
3). f x   2x 1  3
tại x  5 , tại x  6 và tại x  4 0 0 0 x 5  2  3 x  5  2x  3 1  x  1 4).    x 1 f x   tại x  1  0  3  x x  1  2 2 x  3x  2  x  1 2 x 1  5).   1
f x   x  1 tại x  1 2 0   3 x  x  1  2  1).
 Xét tính liên tục tại x0  2 : Có f x  f 2  1 0   
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 20 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU 2 x  3x  2 x  2 x 1 Có lim f x     lim  lim  lim(x 1)  1 x2 x2 x2 x2 x  2 x  2
Ta có lim f x  f 2  hàm số liên tục tại x  2. x2
 Xét tính liên tục tại x0  4 : 2 2 Có   x  3x  2 4  3.4  2 lim f x  lim 
 3  f 4  hàm số f(x) liên tục tại x  4 . x4 x4 x  2 4  2 0 2). Có  1 f x  f 1  (1) 0    4 Có   x  3  2 x  3  4 lim f x x  1 1 1  lim  lim  lim  lim   (2) x1 x1 x1 x 1
 x3 2x1 x1  x32x1 x1 x3 2 4
Từ (1) và (2) suy ra lim f x  f 
1 . Vậy hàm số liên tục tại x  1 . x1  x  5 x   5
3). f x   2x 1  3
tại x  5 , tại x  6 và tại x  4 0 0 0 x 5  2  3 x  5
 Xét tính liên tục tại x  5 0
Áp dụng nếu lim f x  lim f x  f x  hàm số liên tục tại x .   0  0 xx0 xx0  x 5 2x1 3 x 5 2x13 x 5  Có lim f     x lim lim lim x 5 x 5 x 5 2x 1  3  2x 1 9 x 5     2x 10 x5 2x13  2x13 2.5  1  3  lim  lim   3. x 5 2x  5 x 5   2 2 Có lim f          
x lim x 52 3 0 3 3 f5. x   5 x5 
Vì lim f x  lim fx  f5  hàm số liên tục tại x  5.    x 0 5 x5
 Xét tính liên tục tại x  6 0
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 21 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU Có   x  5 6  5 1 lim f x  lim  
 f 6 . Vậy hàm số f(x) liên tục tại x  6 . x6 x6 2x  1  3 2.6  1  3 11  3 0
 Xét tính liên tục tại x  4 0
Có limf x lim x 52 3   
 4  52  3  4  f4  hàm số f(x) liên tục tại x  4 . x4 x4     0 4). Có          2x 3 1 2x 3 1 lim f x lim lim x 1 x 1 x  1 x 1     2x3 1x1 2x  1 2 2  lim  lim   1. x 1 
 2x3 1x1 x 1  2x  3  1 2. 1    3  1 3 x 3    1 Có lim f     x   lim 1. x 1 x 1   2 2   Có   3 ( 1) f 1   1 2
Vì lim f x  lim fx  f 1
  hàm số liên tục tại x  1  .    x 0  1  x 1  5). Ta có  1 f x  f 1  0    2 2 x  3x  2 x  1 x  2 Có      x  2 1 2 1 lim f x  lim  lim  lim    .   2 x 1 x 1  x 1 x 1
 x  1x  1 x 1     x  1 1 1 2 Có           .    3 3 1 lim f x lim x 1 x 1 x 1    2  2 2
Vì f 1  lim fx  hàm số không liên tục tại x  1. x 1  0 2 x  3x  2
Ví dụ 2. Cho hàm số    x  2 f x   x  2 a  x   2
Với giá trị nào của a thì hàm số đã cho liên tục tại điểm x  2 ? LỜI GIẢI
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 22 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU 2 x  3x  2 x 1 x  2 Ta có lim f x     lim  lim  lim x 1  1. x2 x2 x2 x2 x  2 x  2
Hàm liên tục tại x  2 khi và chỉ khi limf x  f2  a  1. x2
Vậy hàm số đã cho liên tục tại x  2 khi a  1.  2 2x  7x  6   khi x < 2
Ví dụ 5: Cho hàm số y  f x   x  2
. Xác định a để hàm số f(x) liên tục tại x0  2 .  1 x a + khi x   2  2  x LỜI GIẢI Ta có : 2 2x  7x  6 x  2 2x  3 2  x 2x  3  lim f x         lim  lim x 2 x  2 x 2 x  2 x 2    x  2  lim 3 2x  1  x 2   1 x  1  lim f x  lim a +  a     f 2 . x 2 x 2    2  x  4 Hàm số liên tục tại x
 lim f x  lim f x  f 2 1 3 0  2  a   1   a   . x 2 x 2   4 4 ĐẾM SỐ NGHIỆM
Chứng minh phương trình sau có ít nhất một nghiệm: a). 3 2 x  5x  7  0 b). 5 x  x  3  0 LỜI GIẢI a). Đặt   3 2
f x  x  5x  7 . Tập xác định của hàm số f(x) là D  R . Vì f(x) là hàm đa thức  f x liên tục trên R. Ta có f  1
   1 5.1 7  1 và f  2
   21, nên suy ra f  1  f 2  2
 1  0 với mọi m. Do đó f x  0
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 23 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
luôn có ít nhất 1 nghiệm x0  2  ; 1   với mọi m. b). Đặt   5
f x  x  x  3 . Tập xác định của hàm số f(x) là D  R . Vì f(x) là hàm đa thức  f x liên tục trên R.
Ta có f 1  1 và có f2  31 , nên suy ra f1f 2  31. 1
   31  0 với mọi m.
Do đó f x  0 luôn có ít nhất 1 nghiệm n0 1;2 với mọi m.
Chứng minh các phương trình sau có ít nhất hai nghiệm : a). 4 2
4x  2x  x  3  0 b). 5 4 3 2
x  x  2x  4x 1  0 LỜI GIẢI a). Đặt   4 2
f x  4x  2x  x  3 . Tập xác định của hàm số f(x) là D  R . Vì f(x) là hàm đa thức  f x liên tục trên R. Ta có f 0  3  , f  1
   4, f 1  2 Vì f  1  f 0  1
 2  0,m  phương trình 1 luôn có ít nhất 1 nghiệm 1;0 2
Vì f 0f 1  6  0 m  phương trình 1 có ít nhất 1 nghiệm 0;1 3
Từ 2 ,3  phương trình (1) luôn có ít nhất 2 nghiệm phân biệt.
10. Chứng minh rằng với mọi a, b, c phương trình 3 2
x  ax  bx  c  0 luôn có nghiệm. LỜI GIẢI Đặt   3 2
f x  x  ax  bx  c thì f x liên tục trên R.
Ta có: lim f x    x
 1  0 để f x1   0. x
lim f x    x2  0 để f x2   0. x
Như vậy có x1,x2 để fx1.f x2   0 suy ra phương trình có nghiệm x 1
x ; x2  vậy phương trình đã cho luôn có nghiệm.
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 24 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
SỬ DỤNG MÁY TÍNH: TÍNH GIỚI HẠN 1. Ý tưởng:
* Gán cho biến X một giá trị gần đúng rồi tính giá trị biểu thức (dùng phím CALC) * Ví dụ: Giới hạn Giá trị của X x→ a+ a + 0.00000001 x→ a- a – 0,00000001 x→ a
a+000000001 hoặc a-0,000000001 x→ + ∞ 9999999999 x→ - ∞ - 999999999
(Nếu máy báo lỗi thì lấy ít chữ số thập hơn)
CHÚ Ý: KHÔNG NHẤT THIẾT PHẢI LẤY NHIỀU SỐ 0 Y NHƯ THẦY, ƯỚC LƯỢNG THÔI
Các kết quả hay gặp trong máy Ý nghĩa
Số có số mũ lớn : VD: 2.1020 Dương vô cực
Số có số mũ lớn : VD: -2.1020 Âm vô cực
Số có số mũ nhỏ: VD: 2.10-20 0
Số chưa đẹp: VD: 2,3333.
Ta gõ lại vào máy tính lần nữa: 2,3333333333333
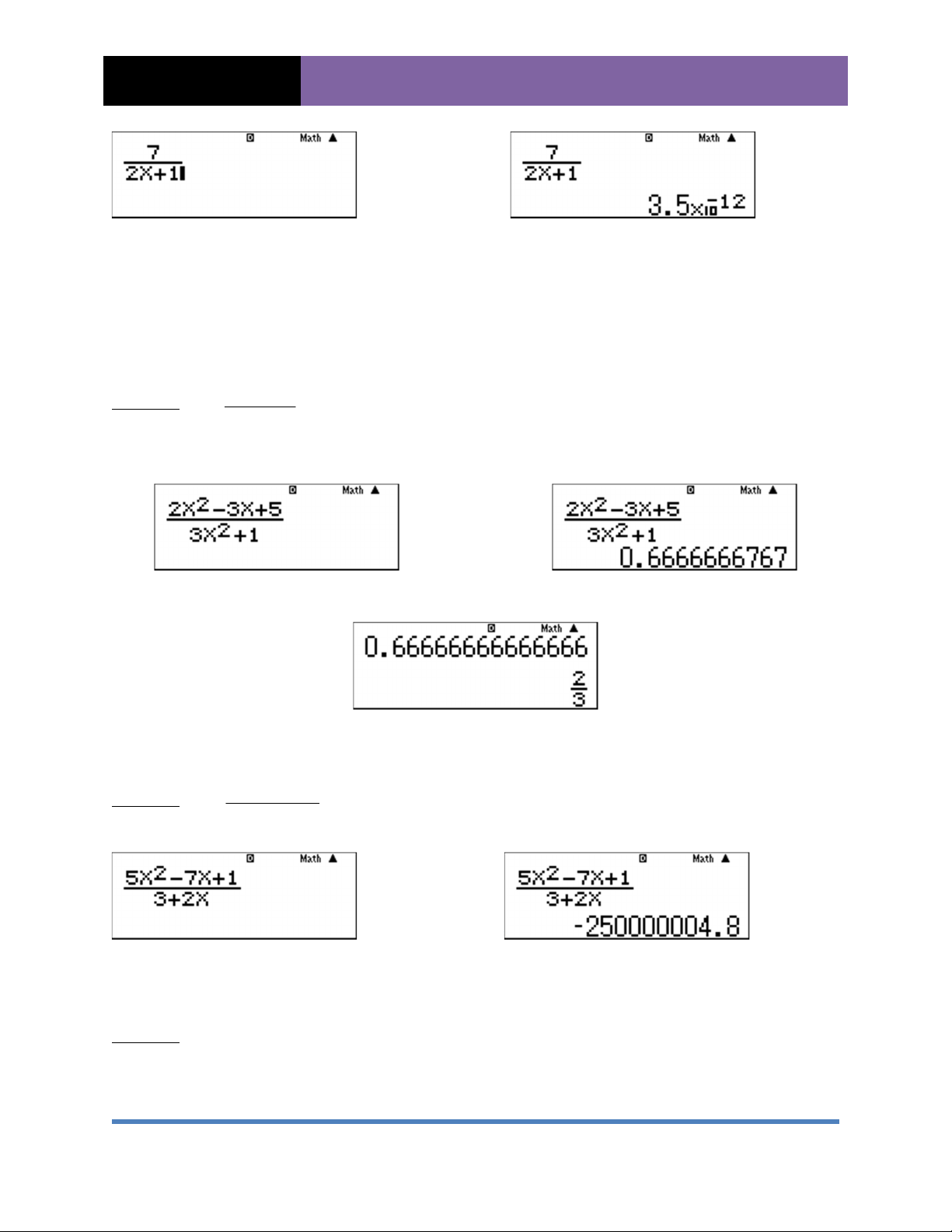
Máy sẽ tự làm tròn giúp 2. Một số ví dụ: Ví dụ 1: 7 lim x 2x  1
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 25 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU Ấn r 999999=
Rơi vào trường hợp kết quả có số mũ nhỏ: Kết quả là 0 Ví dụ 2: 2
2x 3x (Bậc tử = bậc mẫu, lấy hệ số X mũ cao nhất tử mẫu chia lim 2 x 3x 1 nhau được 2/3) rp999999=
Ta làm tròn kết quả: nhập vào máy: Ví dụ 3: x 5 27x 1
 (Bậc tử > bậc mẫu kết quả ra vô cực) lim x 32x rp999999=
Ta thấy kết quả âm một số to. => Kết quả - ∞
Ví dụ 4: lim  x3  x 3 2  2x  5 x   
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 26 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU kết quả là + ∞. Ví dụ 5: 2 2
Giới hạn của dãy số u với u  2   ... là: n  n 2 2n A. limu  2 2 . B. 1 limu  . C. 1 lim u   2 . D. 2 lim u   2 . n n 2 n 2 n 2 Giải Ấn qi Chọn A.
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 27 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
CHUYEN ĐE 2: ĐẠO HAM VA BAI TOAN LIEN QUAN LÝ THUYẾT ĐẠO HÀM TÓM TẮT GIÁO KHOA
1). Cho hàm số y  f x xác định trên khoảng a; b và x  a; b . Giới hạn hữu hạn nếu có của tỉ số 0  
f x  f x0  khi x  x được gọi là đạo hàm của hàm số đã cho tại x , kí hiệu f'x hay y'x . Như 0  0  x  x 0 0 0 f x  f x vậy ta có f 'x  lim . 0     0  xx0 x  x0 Nhận xét: y
Nếu đặt x  x  x và y  f x  x
  f x thì ta có f 'x  lim . Trong đó x
 được gọi là số gia 0  0   0  0 x  0 x
của biến số tại x và y gọi là số gia của hàm số ứng với số gia x  tại x . 0 0
Nếu hàm số f(x) có đạo hàm tại điểm x thì f(x) liên tục tại x . Tuy nhiên điều ngược lại chưa chắc đúng. 0 0
2). Cho đường cong (C), điểm M cố định thuộc (C) và M C . Gọi k là hệ số góc của cát tuyến M M . 0 M 0
Giả sử tồn tại giới hạn hữu hạn k  lim k . Khi đó đường thẳng M T qua M có hệ số góc k được 0 M x 0 0 0 M x0
gọi là tiếp tuyến của (C) tại M . Điểm M gọi là tiếp điểm. 0 0
3). Đạo hàm của hàm số y  f x tại điểm x là hệ số góc của tiếp tuyến của đồ thị hàm số tại đó tại 0 điểm M x ;f(x ) . 0  0 0  Hệ quả:
Nếu hàm số y  f x có đạo hàm tại điểm x thì tiếp tuyến của đồ thị hàm số y  f x tại điểm 0
M x ;f(x ) có phương trình: y  f 'x x  x  f x . 0   0   0  0  0 0 
4). Khí hiệu D là một khoảng hay là hợp của những khoảng nào đó. Nếu hàm số f(x) có đạo hàm tại tại
mọi điểm x  D thì ta nói hàm số có đạo hàm trên D. Khi đó đạo hàm của hàm số f(x) tại điểm x tùy ý 0
của D được kí hiệu y' hay f 'x . Ta nói y' hay f'x là đạo hàm của hàm số y  f x trên tập D.
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 28 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
B.PHƯƠNG PHÁP GIẢI TOÁN.
DẠNG 1: Tìm số gia của hàm số. PHƯƠNG PHÁP
Để tính số gia của hàm số y  f x tại điểm x tương ứng với số gia x cho trước ta áp dụng công thức: 0
y  f x  x  f x . 0   0 
Ví dụ 1: Tìm số gia của hàm số    3 2
y f x  x  3x  2 , biết rằng: a). x0  1; x   1 b). x0  1; x   0,1 LỜI GIẢI
a). Ta có y  f x  x
   f x   f 2  f 1 3 2 3 2 o 0
 2  3.2  2  (1  3.1  2)  2 
b). Ta có y  f xo  x  f x0   f0,9 f1 3 2 3 2
 0,9  3.0,9  2  (1  3.1  2)  0,229 y Ví dụ 2: Tính y và
của các hàm số sau theo x và x  x a). y  2x  3 b). 2 y  2x  3x  1 c). 2 y  2x  1 d). 3 2 y  2x  3x LỜI GIẢI y
a). Ta có y  f xo  x  f x0   2xo  x  3 2x0  3  2 . Suy ra  2 x
b). Ta có y  f x  x  f x   2x  x2  3x  x  1  2 o 0 o o 2x0  3x0 1  4x x  2x2 0
 3x  x4x0  2x  3 . y x4x0  2 x   3 Suy ra   4x0  2x  3 . x x
c). Ta có y  f x  x  f x   2x  x2 2 o 0 o  1  2x0 1
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 29 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU x(2x  x) 0  . 2x  x2 2 o  1  2x0  1 y x(2x  x) 2x  x Suy ra 0 0   .
x x 2x x 1  2x   1 
2 x  x  1  2x  1 o 2 2 0   o 2 2 0  
d). Ta có y  f x  x
   f x   2x  x3  3x  x2  3 2 o 0 o o 2x0  3x0   2 3 2 2 3 x  3x x
  3x (x)  (x)   3 2 2 x  2x x   ( x  )   3 2 0 0 0 0 0 2x0  3x0   x 2 2 6x0  6x0 x   3( x  )  6x0  3 x   x   2 2 6x0  6x0 x
  3(x)  6x0  3x y  Suy ra  x x 2 2
 6x0  6x0x  3(x)  6x0  3x .
DẠNG 2: Tìm đạo hàm bằng định nghĩa PHƯƠNG PHÁP
Để tìm đạo hàm của hàm số y  f x tại điểm x bằng định nghĩa ta có thể sử dụng một trong hai cách 0 sau đây: Cách 1: y
 Cho x một số gia x  f x  x  f x . Lập tỉ số . 0   0  0 x y  Tìm giới hạn lim x  0 x  Kết luận: y  + Nếu lim
tồn tại hữu hạn thì tại x hàm số có đaọ hàm là:  y f ' x  lim 0  x  0 x 0 x0 x y + Nếu lim
không tồn tại hữu hạn thì tại x hàm số không có đạo hàm. x  0 x 0 Cách 2:
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 30 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU f x  f x0   Tính giá trị của lim . xx0 x  x0  Kết luận: f x  f x0  + Nếu lim
tồn tại hữu hạn bằng L thì tại x , ta có f 'x  L 0  xx 0 0 x  x0 f x  f x0  + Nếu lim
không tồn tại hữu hạn thì tại x hàm số không có đạo hàm. xx 0 0 x  x0
Ví dụ : Tính đạo hàm (bằng định nghĩa) của mỗi hàm số sau tại các điểm đã chỉ ra: a). 2
y  2x  x  1 tại x0  2 b). 3
y  x  x  2 tại x0  2  c). y 
 2x  1 tại x0  1 d). 2x 1 y  tại x  3 x  1 0 LỜI GIẢI
a). Cách 1: Cho x0  2 một số gia x
 . Khi đó hàm số nhận một số gia tương ứng:
y  f x  x  fx   22  x2  2  x  1  2 0 0 2.2  2  1  x  9  2x y x 9  2x Ta có f '2    lim  lim  lim 9  2 x    9 . x  0 x x0 x  x  0 f x  f 2 2 2 Cách 2: 2x  x  1 11 2x  x  10 lim  lim  lim x2 x  2 x2 x  2 x2 x  2 x22x  5  lim  lim 2x  5  9 x2 x  2 x2
Kết luận theo định nghĩa, hàm số có đạo hàm tại x0  2 và f'2  9 . b). 3
y  x  x  2 tại x0  2  Cách 1: Cho x0  2  một số gia x
 . Khi đó hàm số nhận một số gia tương ứng:
             3      2 3 y f 2 x f 2 2 x 2
x  1 12  13x  6( x  )  ( x  )    2 x 13  6 x   ( x  ) 
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 31 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU x   2 13  6x  (x) y  Ta có f '2  lim  lim  lim  2 13  6 x   (x)   13 . x0 x  x  0 x x  0 f x  f 2 3 3 Cách 2: x  x  2  12 x  x  10 lim  lim  lim x 2  x  2 x2 x  2 x2 x  2 x2 2x 2x5  lim  lim  2 x  2x  5  13 x2 x  2 x2
Kết luận theo định nghĩa, hàm số có đạo hàm tại x0  2
 và f '2  13 .
c). y  2x  1 tại x0  1
Cách 1: Cho x0  1 một số gia x
 . Khi đó hàm số nhận một số gia tương ứng:  2 x y f x   
0  x  f x0   f 1  x  f 1  2(1  x  )  1  3  3  2x  3 y Ta có   2x 2 1 f ' 1  lim  lim  lim  . x  0 x x
 0 x 3 2x  3 x0 3 2 x   3 3 f x  f 1 2x  1  3 2x 1 Cách 2: lim  lim  lim x 1  x 1 x 1  x  1 x 1
 x 1 2x 1  3 2 1  lim  x 1  2x  1  3 3
Kết luận theo định nghĩa, hàm số có đạo hàm tại x0  1 và   1 f ' 1  . 3 d). 2x 1 y  tại x  3 x  1 0
Cách 1: Cho x0  3 một số gia x
 . Khi đó hàm số nhận một số gia tương ứng:   
2(3  x)  1 5 5  2 x  5 3x
y f x0  x  fx0   f3  x    f 3      3  x   1 4 4  x  4 4(4  x  ) y Ta có   3x 3 3 f ' 3  lim  lim  lim  . x  0 x x0 x.4(4  x) x0 4(4  x) 16
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 32 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU     2x  1 5 f x f 3   Cách 2: x  1 4 3(x  3) 3 3 lim  lim  lim  lim  x3 x  3 x3 x  3 x3 (x  3)(x  1)4 x3 (x  1)4 16
Kết luận theo định nghĩa, hàm số có đạo hàm tại x0  3 và   3 f ' 3  . 16
CÁC QUY TẮC TÍNH ĐẠO HÀM TÓM TẮT GIÁO KHOA
1). Định lý 1: Cho các hàm số u  ux,v  vx có đạo hàm trên (a;b) thì tổng và hiệu của chúng cũng có
đạo hàm trên khoảng (a;b) và
u  v'  u' v'; u v'  u' v'
Chú ý: Định lý 1 có thể mở rộng cho tổng hay hiệu của hữu hạn các hàm số.
2). Định lý 2: Cho các hàm số u  ux,v  vx có đạo hàm trên (a;b) thì tích của chúng cũng có đạo
hàm trên khoảng (a;b) và u.v'  u'v  uv' .
Đặc biệt : a.u'  a.u' ( a là hằng số),
Chú ý: Định lý 2 có thể mở rộng cho tích của hữu hạn các hàm số. Chẳng hạn:
u.v.w'  u'vw uv'w uvw'
3). Định lý 3: Cho các hàm số u  ux,v  vx có đạo hàm trên (a;b) và vx  0 trên (a;b) thì thương
u cũng có đạo hàm trên khoảng (a;b) và v  u  u'v  uv' '    . 2  v  v   Hệ quả: 1 v' '   v    0 . 2    v  v
4). Cho hai hàm số y  f u và u  gx . Ta gọi hàm số y  Fx  f g
 x là hàm số hợp của hai hàm
số u  gx và y  f u . Tập xác định của hàm số f g x 
 là tập hợp tất cả các giá trị của x làm cho biểu thức f g x   có nghĩa.
5). Định lý 4: Nếu hàm số u  ux có đạo hàm tại điểm x và hàm số y  f u có đạo hàm tại điểm 0
u  u x thì hàm số hợp y  Fx  f u  x
x và F'x  f' u .u x hay 0   0   0  0  0 
 cũng có đạo hàm tại điểm 0 y'  y' .u' . x u x Hệ quả:  n  n1
u '  n.u .u'(n  N và n  2);   1 u '  .u' 2 u QUY TẮC TÍNH ĐẠO HÀM
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 33 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Giả sử u  u(x),v  v(x),w  w(x) là các hàm số có đạo hàm, khi đó:
1). (u + u - w)' = u' + v' - w'; 2). (uv)' = u'v + v'u; 3) (k.u)' = k.u' ( k  R ) /   /   4). u u'v  v'u 1 v'    5).     . 2  v  v 2  v  v
BẢNG ĐẠO HÀM CỦA CÁC HÀM SỐ SƠ CẤP CƠ BẢN
Đạo hàm của hàm số sơ cấp cơ bản Đạo hàm của hàm số hợp (u = u(x)) (C)' = 0  / 1 / x  x , ,x  0    1 u u    u', ,u  0 1 ( x)' u'  (x > 0) ( u)'  (u > 0) 2 x 2 u 1 1 ( )' 1 u'   (x  0) ( )'   (u  0) 2 x x 2 u u /  1  n /  1  n     ,x  0     .u',u  0 n n 1  x  x  n n 1  u  u  (sinx)' = cosx (sinu)' = cosu.u' (cosx)' = -sinx (cosu)' = -sinu.u' tanx 1 2 ' u'   1 tan x tanu'    2 1 tan u u' 2  2 cos x cos u (x     k , k  Z) (u   k , k  Z) 2 2   1 cot x ' u'     2 1 cot x cotu'     2 1 cot u u' 2  2  sin x sin u (x  k, k  Z). (u  k, k  Z).
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 34 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
MỘT SỐ CÔNG THỨC TÍNH ĐẠO HÀM NHANH / /     2    2 ax b ad  bc ax bx c adx  2aex  be  dc         2  cx  d  (cx  d)    2 dx e (dx    e) /  2    2 ax bx c
(ae  bd)x  2(af  dc)x  bf  ec      2  2 2 dx  ex  f (dx  ex    f) BÀI TẬP TỔNG HỢP ĐẠO HÀM 1:  1 5 2 4 3 3 2 y x x x x 4x 5        2 3 2    /  1 / / / 5 2 4 3 3 2 y' x x x x 4x 5  1   2   3        / /   5 4 y'  x  x   3 x  2  x  4x /        5 2 3 2     2   3   2  5 4 8 3 2
y'  x  x  3x  3x  4. 2 3 2: 1 1 2 4 y   x  x  0,5x 4 3 / /  1 1 2 4 y x x 0,5x       4 3    / /  1   1   y   x  x /      0,5x / / 2 4  4   3  1  3 y'    2x  2x . 3 3: 4 1 3 y  2x  x  2 x  5 3 /  / / / 4 1 3 y' 2x x 2 x 5  1        y'   4 2x  3  x  2 x /    5  3 2 1 y'  8x  x  . 3     3  x 4 3 4: x x 1 2 y  
 x  x  a (a là hằng số) 4 3 2
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 35 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU / 4 3  x x 1  2 y'     x  x  a  3 2 y'  x  x  x 1 . 4 3 2    5: 3 2 y   x  x x 2 x 3 /  3 2 / / / y' x x x   2      y'   2
3.x   x  x x 2 x 3    3     1 2 6 1 2 1  y' 3. 2.x  x . x  x/ 3 / .x         y'     x  .x 2 x 3   3 x 2 x 3  2 x  6 1 2  x  6 1  y'     x      x. 3   3 x 2 x 3 2 x   2 x
Bài 2: Tính đạo hàm của các hàm số sau: a).   2 y
x  3x2  x. b)     5 y
2x 3 x  2x c).   2   2 y x 1 5  3x  a).   2 y x  3x2  x.
     /    /         / 2 2 2 y' x 3x 2 x x 3x . 2 x x 3x . 2 x
        2    2 2x 3 2 x x 3x 1  3x  2x  6. b).     5 y 2x 3 x  2x     
   /    / 5   5   5 y' 2x 3 x 2x 2x 3 x 2x x  2x/ 2x  3
  5   4     5 4 2 x 2x 5x
2 2x 3  12x 15x  8x  6. c).   2   2 y x 1 5  3x 
      /  
  /     / 2 2 2 2 2  2 y' x 1 5 3x x 1 5 3x 5 3x x  1   2    2   3 3 3 2x 5 3x
6x x 1  10x  6x  6x  6x  1  2x  4x.
Bài 3: Tính đạo hàm của các hàm số sau:
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 36 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU a).    2 7 y x x b).      2 3 2 y 2x 3x 6x 1 c).    3 2 y 1 2x a).    2 7 y x
x . Sử dụng công thức   / 1 u  .u .u' (với 7 u  x  x )       / 7 7   7   6 y' 2 x x . x x 2 x x 7x  1 b).      2 3 2 y
2x 3x 6x 1 . Sử dụng công thức  / u với 3 2 u  2x  3x  6x  1          / 3 2 3 2   3 2     2 y' 2 2x 3x 6x 1 2x 3x 6x 1 2 2x 3x 6x 1 6x  6x  6. c).    3 2 y 1 2x
. Sử dụng công thức  / u với 2 u  1 2x   
2   /    2       2 2 2 2 2 y' 3 1 2x 1 2x 3 1 2x 4x 12x 1 2x .
Bài 4: Tính đạo hàm của các hàm số sau: a). 2 y  x  x x  1 b). 2 y  1 2x  x c). 2 2 y  x  1  1 x a). 2 y  x  x x  1   / 2   /. /      / 1 3 x y' x x x 1 2x x'. x x .x  2x  x  .x  2x  . 2 x 2 b). 2
y  1 2x  x . Sử dụng công thức  / u với 2 u  1 2x  x 12xx /2 1 x y'   . 2 2 1 2x  x 1 2x  x c). 2 2 y  x  1  1 x / /  
      2x 1  2 / / 1 x 2 2  x x y' x 1 1 x     . 2 2 2 2 2 x  1 2 1 x x  1 1 x
Bài 5: Tính đạo hàm của các hàm số sau: 3 a). y  sin x   x cos x b). y   c). 3 y  sin 2x 1  1 cos x   
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 37 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU d). 2
y  sin 2  x e). y  sin x  2x f). 2 3 y  2sin 4x  3cos 5x
a). y  xcos x . Ta áp dụng đạo hàm tích.    /
y' x'cos x x. cos x  cos x  xsin x. 3 b)  sin x y   
. Bước đầu tiên ta áp dụng công thức  / u với sin x u   1 cos x    1 cos x 2 /  sin x   sin y' 3  .     1 cos x    1 cos x      sin x 
sinx/ 1cosx1cosx/ / .sin x cos x1 cosx 2  sin x Tính :     1 cos x    1 cosx2 1cosx2 2 2 cosx  cos x  sin x 1   .  2 1  cos x 1 cos x 2 2 Vậy  sin x  1 3sin x y'  3  .   .
 1  cos x  1  cos x 1 cosx3 c). 3
y  sin 2x 1 . Bước đầu tiên áp dung công thức  /
u với u  sin2x 1 Vậy     / 
      / 3 2 y' sin 2x 1 3sin 2x 1 . sin 2x 1 . Tính    / sin 2x 1 : Áp dụng  /
sin u , với u  2x 1
Ta được:    /       / sin 2x 1
cos 2x 1 . 2x 1  2cos2x 1. 2         2
y' 3.sin 2x 1 .2cos 2x 1  6sin 2x  1cos2x 1. d). 2
y  sin 2  x . Áp dụng công thức  / sin u với 2 u  2  x 
y'  cos 2  x . 2  x  2 x /2 / 2 2 2 x 2  cos 2  x .  .cos 2  x . 2 2 2 2  x 2  x
e). y  sin x  2x . Áp dụng  / u , với u  sin x  2x
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 38 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU   / sin x 2x cos x  2 y'   . 2 sin x  2x 2 sin x  2x f). 2 3
y  2sin 4x  3cos 5x . Bước đầu tiên áp dụng   / u v   /   / 2 3 y' 2sin 4x 3 cos 5x Tính  / 2 sin 4x : Áp dụng  /
u , với u  sin 4x, ta được:  /   /   / 2 sin 4x 2sin 4x. sin 4x
2sin 4x.cos 4x 4x  4sin 8x. Tương tự:  /   /     / 3 2 2 cos 5x 3cos 5x. cos 5x 3cos 5x. sin 5x . 5x 2 15  15cos 5x.sin 5x  cos 5x.sin10x. 2 Kết luận: 45 y'  8sin 8x  cos 5x.sin10x 2 Cho   3 2 x x f x  
 2x . Với những giá trị nào của x thì: 3 2 a. f 'x  0 b. f 'x  2  c. f 'x  10 LỜI GIẢI   Ta có f 'x 3 2 x x 2     2x  x  x  2  3 2    a).   2
f ' x  0  x  x  2  0  x  1 x  2  b).   2 2 f ' x  2
  x  x  2  2  x  x  0  x  0  x  1  c).   2 2
f ' x  10  x  x  2  10  x  x 12  0  x  3  x  4 Câu : Giải a). Cho   3      2 f x 2x x
2 ,g x  3x  x  2 . Giải bất phương trình f 'x  g'x .
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 39 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU b).Cho        2 3 2 3 x f x 2x x 3 ,g x  x 
 3 . Giải bất phương trình 2 f 'x  g'x . Cho   60 64 f x  3x  
 5 . Giải phương trình f 'x  0 3 x x LỜI GIẢI a). Ta có       / 3 2 f ' x 2x x
2  6x  1 ,       / 2 g' x 3x x 2  6x  1      2 2 f ' x
g' x  6x  1  6x 1  6x  6x  0  x ;01; /  2 /  b). f 'x   3 2 2x  x  3  2  6x  2x, g'x 3 x 2   x   3   3x  x  2         2 2 2 f ' x
g' x  6x  2x  3x  x  3x  3x  0  x ;01; /   c). Ta có   60 64 60 192 f ' x   3x    5  3   3 2 4  x x  x x   60 192 f ' x 1  0  3    0 1 . Đặt t  ,t  0 2 4 x x 2 x   2 1 1
1  192t  60t  3  0  t   t  4 16 Với 1 1 1 2 t     x  4  x  2  2 4 x 4 Với 1 1 1 2 t     x  16  x  4  2 16 x 16
Vậy f 'x  0 có 4 nghiệm x  2 , x  4 VI PHÂN TÓM TẮT GIÁO KHOA
Cho hàm số y  f x có đạo hàm tại x0 . Gọi x
 là số gia của biến số tại x0 . Ta gọi tích f'x0 .x là vi
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 40 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
phân của hàm số f(x) tại điểm x0 ứng với số gia x
 . Kí hiệu df(x0)  f'(x0).x .
Cho hàm số y  f x có đạo hàm tại x. Ta gọi tích f'x.x là vi phân của hàm số f(x) tại điểm x ứng với số gia x
 (gọi tắt là vi phân của f tại điểm x). Kí hiệu df(x)  f '(x). x . Nếu chọn hàm số y  x thì ta có dy  dx  1. x   x
 . Vì vậy ta thường kí hiệu x  dx và dy  f 'xdx .
Công thức tính gần đúng nhờ vi phân là: f x0  x  f x0   f'x0 .x PHƯƠNG PHÁP GIẢI TOÁN
DẠNG 1: Tìm vi phân của hàm số PHƯƠNG PHÁP
a). Tính vi phân của hàm số f(x) tại x0 cho trước:
Tính đạo hàm của hàm số tại x0 .
Suy ra vi phân của hàm số tại x0 ứng với số gia x  là df(x0)  f'(x0). x  .
b). Tính vi phân của hàm số f(x).
Tính đạo hàm của hàm số .
Suy ra vo phân của hàm số: dy  df(x)  f 'xdx Ví dụ 1: Cho hàm số 3 2
y  x  4x  2 . Tính vi phân của hàm số tại điểm x0  1 , ứng với số gia x  0,02 . LỜI GIẢI Ta có 2
y'  f '(x)  3x  4x . Do đó vi phân của hàm số tại điểm x0  1 , ứng với số gia x  0,02 là:     2 df(1) f '(1). x 3.1  4.1.0,02  0  ,02 .
Ví dụ 2: Tính vi phân của các hàm số sau: 2 a). 2x  3x  1 y  b). 3 2 y  3x  2x c). x
y  sin xcos d). y  xsinx  cosx 2 x  x  1 2 LỜI GIẢI 2 2 2 2          a). Ta có (2x 3x 1)'(x x 1) (x x 1)'(2x 3x 1) y'  f '(x)    x  x  2 1 x x12 2 2 suy ra dy  f '(x)dx 
DẠNG 2: Tính gần đúng giá trị của hàm số:
Để tính gần đúng giá trị của hàm số f(x) tại điểm x  (x0  x
 ) cho trước, ta áp dụng công thức
f x0  x  f x0   f'x0 .x .
Ví dụ tính gần đúng các giá trị sau (lấy 4 chữ số thập phân trong kết quả). a). 16,25 b). 0 cos 30 15' c). 0 sin 46 d). 1 0,9995 e). 0 tan 53 15' . LỜI GIẢI
a). Ta có 16,25  16  0,25 . Xét hàm số       1 f x x f ' x  2 x
chọn x0  16 và x  0,25 , ta có fx0  x  f x0   f'x0 .x
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 41 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU 1  16  0,25  16 
.0,25  4  0,03125  4,03125  16  0,25  4,0313 2 16 b). Ta có 0   0    
cos 30 15' cos 30  15'  cos  . 6 720   
Xét hàm số f x  cos x  f'x  sin x . Chọn x   0  và x 
, ta có f x0  x  f x0   f'x0 .x . 6 720        3 cos  cos sin .        .  6 720  6 6 720 2 1440 c). Ta có 0   0 0     sin 46
sin 45  1   sin  . 4 180   
Xét hàm số f x  sin x  f'x  cos x Chọn x   0  và x 
, ta có f x0  x  f x0   f'x0 .x . 4 180        2 2 sin  sin cos .         4 180  4 4 180 2 360 d). Ta có 1 1  . 0,9995 1 0,0005 Xét hàm số   1     1 f x f ' x   . 2 x x Chọn x0  1 và x  0
 ,0005 , ta có f x0  x  f x0   f'x0 .x . 1 
 11.(0,0005)  1,0005 . 1 0,0005 e). 0   0 0     3  tan 53 15' tan 60 (6 45')  tan   . 3 80    Xét hàm số       2 f x tan x f' x  1 tan x . Chọn x   0  và 3 x  
, ta có f x0  x  f x0   f'x0 .x . 3 80   3    2    3   tan     tan  1 tan .    1,2608 .  3 80  3  3   80  ĐẠO HÀM CẤP CAO A.TÓM TẮT GIÁO KHOA.
1. Cho hàm số y  f x có đạo hàm f'x . Hàm số f'x còn gọi là đạo hàm cấp 1 của hàm số f x . Nếu
hàm số f 'x có đạo hàm thì đạo hàm đó được gọi là đạo hàm cấp 2 của hàm số f x , kí hiệu là y’’ hay
f ' x . Đạo hàm của đạo hàm cấp 2 được gọi là đạo hàm cấp 3 của hàm số f x , kí hiệu là y’’’ hay f’’’ x
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 42 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
. Tương tự, ta gọi đạo hàm của đạo hàm cấp n 1 là đạo hàm cấp n của hàm số f x , kí hiệu là n y hay n f x , tức là ta có: n n    1 y y 'nN,n1 .
2.Đạo hàm cấp 2 của hàm số f(t) là gia tốc tức thời của chuyển động s=f(t) tại thời điểm t.
B.PHƯƠNG PHÁP GIẢI TOÁN.
DẠNG 1: Tính đạo hàm cấp cao của hàm số. 1.PHƯƠNG PHÁP
Áp dụng trực tiếp định nghĩa: n n1
y  y ' để tính đạo hàm đến cấp mà đề bài yêu cầu.
Ví dụ: Tính đạo hàm đến cấp đã chỉ ra của các hàm số sau:
a). y  xsin 2x,y' ' b). 2 y  cos x,y' ' c). 4 3 2      (n) y x 4x 3x 1, y  d). 4     (4) y x sin 2x, y  e). 2   (5) y sin 2x, y  f). 3x 1 y  , (4) y  x  2 LỜI GIẢI
a). Có y'  x'sin 2x  x.(sin 2x)'  sin 2x  2xcos 2x
 y'  (sin 2x)' (2x)'cos 2x  2x(cos 2x)'  4cos 2x  4xsin 2x
 y' '  4(cos 2 x)'(4x)'sin 2 x 4 x(sin 2 x)'  8
 sin 2 x 4 sin 2 x 8cos 2 x
 12sin 2 x 8cos 2 x . b). Ta có 2 1
y  cos x  1 cos2x  y'  sin2x 2
 y'  2cos 2x  y' '  4sin 2x c). 4 3 2 y  x  4x  3x  1 3 2 2
 y'  4x  12x  6x  y'  12x  24x  6  y' '  24x  24 (4) (5) (n)
 y  24  y  0  . .  y  0 .
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 43 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU d). 4 y  x  sin 2x 3 2
 y'  4x  2cos 2x  y'  12x  4sin 2x (4)
 y' '  24x  8cos 2x  y  24 16sin 2x e). 2 1
y  sin 2x  1 cos4x 2
 y'  2sin 4x  y'  8cos 4x  y' '  3  2sin 4x (4) (5)
 y  128cos 4x  y  512sin 4x f). 3x  1 y  , (4) y  x  2 7 x  2 / 2  7     1  4  y'   y'   2 (x  2) x24 x 23 14 x 2 / 4  2 x  2 / 3 4       42 (4)     1  68  y' '    y   x 26 x 24 x 28 x 25
DẠNG 2: Tìm đạo hàm cấp n của một hàm số PHƯƠNG PHÁP
Bước 1: Tính y',y' ,y' ' . Dựa vào các đạo hàm vừa tính, dự đoán công thức tính (n) y .
Bước 2: Chứng minh công thức vừa dự đoán là đúng bằng phương pháp quy nạp.
Chú ý: Cần phân tích kĩ các kết quả của đạo hàm y',y' ,y' ' tìm ra quy luật để dự đoán công thức (n) y chính xác.
Ví dụ 1: Tìm đạo hàm cấp n của hàm số   * y sin x n  N  LỜI GIẢI
Bước 1: Ta có: y' cos x sin x 1.  ; y' sin x sin x 2           2 2     
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 44 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU Dự đoán: n        * y sin x n 1 ,n    N  2 
Bước 2: Chứng minh 1 bằng quy nạp:
 n  1 : 1 hiển nhiên đúng.   
 Giả sử 1 đúng với n  k  1 nghĩa là ta có: k y  sin x   k
ta phải chứng minh 1 cúng đúng với 2   
n  k  1 nghĩa là ta phải chứng minh k1 y sin x k 1        2  2  /          
Thật vậy : vế trái   / k1 k 2  y  y    
sin x  k   cos x  k   sin x  k  1  =vế phải 2   2   2   2 
 2 đúng, nghĩa là 1 đúng với n  k  1.
Bước 3: theo nguyên lí quy nạp suy ra n    * y  sin x  n , n     N .  2 
Ví dụ 2: Tìm đạo hàm cấp n của hàm số 1 y   * n  N  x  3 LỜI GIẢI Ta có:   / 1 1! y' 1  1  ; 2  / x  3 x  32   2 1.2 2! y' 1 .  1 . . 3  2 x  3 x  33 Dự đoán:   n n n! y 1 1 ,n  N . n1   * x  3
Chứng minh 1 bằng phương pháp quy nạp: n
  1 : 1 hiển nhiên đúng. k!
 Giả sử 1 đúng với n  k  1 , nghĩa là ta có: y  1k k
ta phải chứng minh 1 cúng đúng x  3k1
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 45 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
với n  k  1 , nghĩa là ta phải chứng minh: 
y   1k1 k 1 ! k 1   2 k2   x  3 Thật vậy: vế trái /   /   /          k k!  k! 2 y y 1   1 . . x  3    k1  k 1 2  k 1 k 1 k   x 3        x 3k1   
  k1 k!k  1  k  1 ! 1 .  1  .  vt 2 k2  k 1   k2   x  3 x  3
Vậy 2 đúng nghĩa là 1 đúng với n  k  1.
Theo nguyên lí quy nạp ta suy ra y  1n n n! * . ,n  N . x  3n1
DẠNG 3: Chứng minh đẳng thức: Bài 11:
a). Cho hàm số y  xsin x . Chứng minh x.y'  2y' sin x  xy  0  b). Cho hàm số : 2 y  2x  x chứng minh: 3 y .y'  1  0 
c). Cho hàm số: y  x tan x chứng minh: 2   2 2
x .y' 2 x  y 1 y  0  d). Cho hàm số: x  3 y  chứng minh:  2
2 y'  y 1.y'  x  4 LỜI GIẢI
a). Cho hàm số y  xsin x . Chứng minh x.y'  2y' sin x  xy  0  Ta có   /     / y' xsin x
y' x'.sin x x. sin x  y'  sin x  xcos x    /   /  /     / y' sin x xcos x sin x xcos x
cos x x'.cos x x. cos x  2cos x  xsin x
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 46 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
         2 1
x 2cos x x sin x 2 sin x x cos x sin x  x sin x  0 2 2
 2x cos x  x sin x  2xcos x  x sin x  0  0  0 (đpcm). b). Cho hàm số : 2 y  2x  x chứng minh: 3 y .y'  1  0  / Ta có:     1     / 2 2 1 x y' 2x x y' . 2x x  . 2 2 2 2x  x 2x  x 1 x        /    2 / 2 2  2x  x  .1 x 1 x . 2x x 2x x . 1 x  2 2x  x y'    2x  x 2  2xx 2 2 2
2x  x  1 x2 2 1    2x  x . 2x x  . 2  2xx 3 2 2 2     3 2 1 2x x . 
      (đpcm). 2x  x  1 0 1 1 0 3 2
c). Cho hàm số: y  x tan x chứng minh: 2   2 2
x .y' 2 x  y 1 y  0  Ta có:   /    /    2 y' x tan x x'.tan x x. tan x tan x x 1 tan x   /       /   2      2 y' tan x x'. 1 tan x x. 1 tan x
2 1 tan x x. 2 tan x . tan  1   2
2 1 tan x1 xtan x  2   2       2 2 2
2x 1 tan x . 1 x tan x 2 x  x tan x1 xtanx  0 2   2     2   2
2x 1 tan x 1 x tan x 2x 1 tan x1 xtanx  0  0  0 (đpcm). d). Cho hàm số: x  3 y  chứng minh:  2
2 y'  y 1.y'  x  4 /    Ta có: x 3 7 y'     x 4    x 42
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 47 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU 7   x  4 / 2 14 y'   x  44 x  43 2      7  x  3  1  4 98 98  2     1.    (đpcm).     2   x  4 x 4     x  43  x 44 x  44 e) Cho hàm số 2
y  cos 3x chứng minh: 182y 1  y'  0  Ta có: 2 y  cos 3x   /    / y' 2.cos 3x cos 3x
2cos 3x. sin 3x 3x  3sin 6x y'  18cos6x    2
18 2 cos 3x  1 18cos6x  0  18.cos6x 18cos6x  0 (đpcm). Bài 12: 3 3  a).Cho hàm số sin x cos x y 
. Chứng minh y'  y  0  1 sin x.cos x
b). Cho hàm số    2 2 y x 1 . Chứng minh: 4
y  2xy' ' 4y'  40  c). Cho hàm số 2
y  x  1 x . Chứng minh:  2
4 x 1.y'  4x.y' y  0  d). Chứng minh  2   2
1 x .y'  x.y' k .y  0 nếu     k 2 y x x 1 LỜI GIẢI 3 3  a).Cho hàm số sin x cos x y 
chứng minh y'  y  0  1 sin x.cos x    2 2
sin x cos x sin x  cos x  sin xcos x Ta có: y  1 sin xcos x
sinx  cosx1sinxcosx   sin x  cos x 1 sin xcos x
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 48 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU y'cosxsinx y'  sin x  cos x
  sinx cosx sinx  cosx  0  0  0 (đpcm).
b). Cho hàm số    2 2 y x 1 . Chứng minh: 4
y  2xy' ' 4y'  40  Ta có: 4 2 y  x  2x  1 3 y'  4x  4x 2 y'  12x  4 y' '  24x y' '  24.
      2
24 2x 24x 4 12x  4  40. 2 2
 24  48x  48x  16  40  40  40 (đpcm). c). Cho hàm số 2
y  x  1 x . Chứng minh:  2
4 x 1.y'  4x.y' y  0  2   Ta có: 1 x x  1 x y'  .1    2  2 2 2 x  1 x  1 x  2 1 x /  x 1 x    .2 1 x  2 1 x / 2 2 2 2 . x  1   x y'     2 1 x 2 2 2 x  1 x . 2 2 1 x  4x  8 2 1 x  2 . 1 x 2 x  1 x  2 2 1 x  4x   4x 1 2 2 x  1 x 2      8 4x. x 1 x 0 2 1 x  2 2 1 x 2 1 x
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 49 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU 2 x  1 x . 2 2 1 x  4x 2 x  1 x 2   2x  x  1 x  0 2 2 2 1 x 1 x 2 2 2 2x x  1 x 2x x  1 x 2  x  1 x    x  1 x  0 2 2 1 x 1 x  0  0 (đpcm). d). Chứng minh  2   2
1 x .y'  x.y' k .y  0 nếu     k 2 y x x 1    Ta có: x     k 2 y x
x 1  y'  kx x 1k 1 2 .1   2  x 1          kx x 1k 1 x x 1 2 x  x  1  2 2 2 .   k.  2  2  x  1  x 1 x x 1 /k  
. x  1   x 1/ .x x    1k 2 2 2 2 y' k.    2 x  1 kx  x  1k 2 x . x 1  .x  x 1k 2 2 2 2 x  1 x  1  k.  2x 1 kx  x 1k 2  2 k x  1  x   2 x  1 2 x  1
k x  x  1 . k x  1  x x.k x  1 x 2  k    k 2 2 2   1 x    2 x  1 2 2 x  1 1 x
kx  x 1k .k x 1  x x.kx  1 x k 2 2 2 2    k x  x 1k 2 2  0 2 2 x  1 1 x
Quy đồng đặt thừa số chung được:
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 50 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU x x 1k 2  2 2 2 2
k x  1  kx  kx  k x  1  0  0  0 (đpcm). 2  x  1
Ví dụ 3: Chứng minh rằng với mọi số nguyên n  1 ta có: a)Nếu 1 y  thì   n n n! y 1 . . x n 1 x  b) Nếu y  cos x thì 4n y  cos x.
Ví dụ 4: Chứng minh rằng: a)Nếu y  sinax thì 4n 4n
y  a .sinax (a là hằng số). b) Nếu 2 y  sin x thì 4n 4n1 y  2  cos 2x.
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 51 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
PHƯƠNG TRÌNH TIẾP TUYẾN
I – Kiến thức cần nhớ
 Phương trình tiếp tuyến của C : y  f x tại điểm Mxo;yo  có dạng:
 : y  kx  xo   yo
Với k  y'xo  là hệ số góc tiếp tuyến.       
 Để viết phương trình tiếp tuyến , ta
 Điều kiện cần và đủ để hai đườn c g
ầ n tìCm ba thành phần x , y , k
1  : y  f x và C
o 2  :o y  g x tiếp xúc nhau  hệ f x   g x 
có nghiệm (nhớ: "hàm  hàm, đạo  đạo") f '  x   g'x
II – Các dạng toán viết phương trình tiếp tuyến thường gặp
 Viết PTTT  của C : y  f x, biết  có hệ số góc k cho trước
 Gọi Mxo;yo  là tiếp điểm. Tính y'  y'xo  .
 Do phương trình tiếp tuyến  có hệ số góc k  y'xo   k i
 Giải i tìm được xo yo  fxo   : y  kx xo  yo .
 Lưu ý. Hệ số góc k  y'(xo) của tiếp tuyến  thường cho gián tiếp như sau:
 Phương trình tiếp tuyến  // d : y  ax  b  k  a .
 Phương trình tiếp tuyến 1
  d : y  ax  b  k   . a
 Phương trình tiếp tuyến  tạo với trục hoành góc   k  tan .  
Phương trình tiếp tuyến  tạo với d : y  ax  b góc k a    tan  1 k.a
 Viết PTTT  của C : y  f x, biết  đi qua (kẻ từ) điểm AxA; yA 
 Gọi Mxo;yo  là tiếp điểm. Tính yo  fxo  và k  y'xo  theo xo .
 Phương trình tiếp tuyến  tại Mxo;yo  là  : y  kx  xo   yo .
 Do AxA;yA   yA  kxA  xo  yo i
 Giải phương trình i xo yo và k  phương trình  .
 Viết PTTT  của C : y  f x, biết  cắt hai trục tọa độ tại A và B sao cho tam giác OAB
vuông cân hoặc có diện tích S cho trước
 Gọi M(xo;yo) là tiếp điểm và tính hệ số góc k  y'(xo) theo xo .
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 52 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU 
vuông cân   tạo với Ox một góc o 45 và O   i  OAB Đề cho  S     OAB S OA.OB 2S ii
 Giải i hoặc ii xo yo;k  phương trình tiếp tuyến  .
 Tìm những điểm trên đường thẳng d : ax  by  c  0 mà từ đó vẽ được 1,2,3,. .,n tiếp tuyến
với đồ thị hàm số C : y  f x
 Gọi MxM;yM d : ax  by  c  0 (sao cho có một biến xM trong M)
 PTTT  qua M và có hệ số góc k có dạng  : y  kx  xM   yM . f x  kx  x i M    y
 Áp dụng điều kiện tiếp xúc: M  f '  x   k ii
 Thế k từ ii vào i, được: fx  f'x.x  xM  yM iii
 Số tiếp tuyến của C vẽ từ M  số nghiệm x của iii .
 Tìm những điểm MxM; yM  mà từ đó vẽ được hai tiếp tuyến với đồ thị hàm số
C : y  fx và hai tiếp tuyến đó vuông góc nhau
 PTTT  qua M và có hệ số góc k có dạng  : y  kx  xM   yM . f x  kx  x i M    y
 Áp dụng điều kiện tiếp xúc: M  f '  x   k ii
 Thế k từ ii vào i, được: fx  f'x.x  xM  yM iii
 Qua M vẽ được hai tiếp tuyến với C  iii có hai nghiệm phân biệt x1,x2 .
 Hai tiếp tuyến đó vuông góc nhau  k1.k2  1  y'x1.y'x2   1 .  Lưu ý.
 Qua M vẽ được hai tiếp tuyến với C sao cho hai tiếp điểm nằm về hai phía với trục iii : hoành thì
có hai nghiệm phân biệt x ,x .  1 2 f  x1 .f x2    0.
 Đối với bài toán tìm điểm M C : y  fx sao cho tại đó tiếp tuyến song song hoặc vuông
góc với đường thẳng d cho trước, ta chỉ cần gọi Mxo;yo  và  là tiếp tuyến với k  f'xo  . Rồi
áp dụng k  f'xo   kd nếu cho song song và f'xo .kd  1 nếu cho vuông góc
 xo  yo  Mxo; yo  .
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 53 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU BÀI TẬP TỔNG HỢP
Cho đường cong      3 2
C : y f x  x  3x . Viết phương trình tiếp tuyến của C trong các trường hợp sau:
a) Tại điểm M 1 ;  2 . 0  
b) Tại điểm thuộc C và có hoành độ x  1 . 0
c) Tại giao điểm của C với trục hoành .
d) Biết tiếp tuyến đi qua điểm A 1  ;  4 . LỜI GIẢI Ta có 2 f '(x)  3x  6x
a). Ta có f'(x )  f'(1)  3  0
Vậy phương trình tiếp tuyến tại điểm M1 ;  2: y  f'(x )(x  x ) y 0 0 0  y  3
 x 1  3  y  3  x
b). Ta có x  1  y  4  ,f ' x  9 0 0  0 
Vậy phương trình tiếp tuyến tại điểm N 1
 ;  4 là y  f'(x )(x  x )  y 0 0 0
y  9x 1  4  y  9x  5 .
c). Phương trình hoành độ giao điểm của  x  0 C với trục hoành: 3 2 x  3x  0   x   3
Với x  0  y  0,f'(x )  f'(0)  0 0 0 0
Vậy phương trình tiếp tuyến tại điểm 0;0 là y  f'(x )(x  x ) y  y  0 0 0 0
Với x  3  y  0,f'(x )  f'(3)  9 0 0 0
Vậy phương trình tiếp tuyến tại điểm 3;0 là y  f'(x )(x  x ) y 0 0 0
 y  9x  3  y  9x  27 .
d). Gọi x ; y là tọa độ tiếp điểm của phương trình tiếp tuyến d đi qua điểm A 0 0 
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 54 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Vì điểm x ; y C 3 2
 y  x  3x , và f 'x  3x  6x 0  2 0 0 0 0 0 0 0
Phương trình d: y  f'(x )(x  x )  y  y   2
3x  6x x  x  x  3x 0 0   0  3 2 0 0 0 0 0 Vì A 1  ; 4  d nên:  2
3x  6x 1 x  3 2  x  3x  4 0 0 0 0 0 3
 2x  6x  4  0  x  2  x  1 0 0 0 0
Với x  2  y  4,f' 2  0 , phương trình tiếp tuyến y  4 0 0   Với x  1  y  4  ,f ' 1
  9 , phương trình tiếp tuyến y  9x  1  4  y  9x  5 0 0   Cho đường cong   3x  1 C : y  . 1 x
a). Viết phương trình tiếp tuyến của C biết tiếp tuyến song song với đường thẳng (d) : x  4y  21  0 .
b). Viết phương trình tiếp tuyến của C biết tiếp tuyến vuông góc với đường thẳng
() : 2x  2y  9  0 .
c). Viết phương trình tiếp tuyến của C biết tiếp tuyến tạo với đường thẳng :
(d) : x  2y  5  0 một góc 0 30 . Tập xác định D 4
 R\{1} . Ta có y'  f 'x  1 x2 a). Có   1 21 1
d : x  4y  21  0  y  x   k  d 4 4 4
Vì tiếp tuyến song song với d nên 1 k  k  . tt d 4
Gọi Mx ,y là tọa độ tiếp điểm của tiếp tuyến, ta có f'x 4 1  k   0  0 0  tt   2 4 1 x0
 x 12  16  x  5  x  3 0 0 0
Với x  5  y  4 , phương trình tiếp tuyến tại điểm này là: y  f'(x )(x  x )  y 0 0 0 0 0 1      1 21 y x 5  4  y  x  (loại, vì trùng với d). 4 4 4
Với x  3  y  2 , phương trình tiếp tuyến tại điểm này là: y  f'(x )(x  x )  y 0 0 0 0
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 55 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU 1      1 5 y x 3  2  y  x  . 4 4 4 b).  9
: 2x  2y  9  0  y  x   k  1 2 
Vì tiếp tuyến vuông góc với  nên, k .k      1 k 1 tt tt
Gọi Nx ,y là tọa độ tiếp điểm của tiếp tuyến, ta có f'x 4  k   1 0  0 0  tt 1 x 2 0  x  2
1  4  x  3  x  1  . 0 0 0 Với x  3  y  5
 , phương trình tiếp tuyến tại điểm này là: y  f'(x )(x  x )  y 0 0 0 0  y  1
 x  3  5  y  x  2 Với x  1  y  1
 , phương trình tiếp tuyến tại điểm này là: y  f'(x )(x  x )  y 0 0 0 0
 y  1x  1 1  y  x  2 . c). 1 5 1
(d) : x  2y  5  0  y  x   k  d 2 2 2
Ta có tiếp tuyến hợp với d một góc 30 k  k 0, nên có tt d 0  tan30 1 k k tt d 1  2 2 ktt 2 1  1   1  11 2 1   3 k   1 k  k  4k       0 tt tt tt tt 1 3  2   2  4 4 1 ktt 2 2 Cho hàm số x  x  2 y  f(x)  C x 1
a). Viết phương trình tiếp tuyến của (C) tại điểm M(2; 4).
b). Viết phương trình tiếp tuyến của (C) biết tiếp tuyến có hệ số góc k  1 . LỜI GIẢI 2 Ta có: x  2x  1 f '(x)  2 (x  1)
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 56 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
a). Ta có x  2  f'(x )  f'(2)  1 0 0
Phương trình tiếp tuyến của (C) tại điểm M(2; 4) là y  f'x x  x  y 0   0  0
 y  1x  2  4  y  x  6
b). Gọi x là hoành độ tiếp điểm của tiếp tuyến với đồ thị, ta có f'x  1 0  0 2 x  2x  1 0 0   1  1   1 (vô lý). 2 (x  1) 0
Kết luận không có tiếp tuyến nào có hệ số góc bằng 1. Cho hàm số (C): 2
y  1 x  x . Tìm phương trình tiếp tuyến với (C):
a) Tại điểm có hoành độ 1 x  . 0 2
b) Song song với đường thẳng (d): x + 2y = 0. LỜI GIẢI       Tập xác định 1 5 1 5 D 1   2x   ;  . Ta có f 'x   2 2   2 2 1 x  x a). Với 1 1 1 1  1 x y 1 ,f ' x f '             2 0 0  0  2 2 4 2  2 
Vậy phương trình tiếp tuyến tại điểm  1 1 ;  
là y  f'x x  x  y 0   0  2 2    0  1  1 3 y  2 x     y  2  x   .  2  2 2 b). Ta có 1 1
(d) : x  2y  0  y   x  k   d 2 2
Vì tiếp tuyến song song với d nên, 1
k  k   . Gọi x là hoành độ tiếp điểm của tiếp tuyến với tt d 2 0 đồ thị, ta có      f ' 1 1 2x 1 1 2x 0 x   
   1 2x  1 x  x  0  0 2 0 0 0 0  2 2 2 1 x  x 2 x  0  x  1 0 0 0 0
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 57 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
So với điều kiện x  0 (nhận), x  1  (loại) 0 0 Với x 1 1
 0  y  1, phương trình tiếp tuyến tại điểm 0;1 là: y   x  0  1  y   x  1 . 0 0 2 2 Cho hàm số 3 2
y  x  3x  9x  5 C . Trong tất cả các tiếp tuyến của đồ thị C , hãy tìm tiếp
tuyến có hệ số góc nhỏ nhất. LỜI GIẢI Ta có    2 y' f ' x  3x  6x  9
Gọi x là hoành độ tiếp điểm của tiếp tuyến, vậy f'x  3x  6x  9 0  2 0 0 0
Ta có 3x  6x  9  3x  2x 112  3x 12 2 2  12  1  2, x   C 0 0 0 0 0 0  
Vậy minf'x  12 tại x  1  y  16 0  0 0
Suy ra phương trình tiếp tuyến cần tìm: y  12x 1 16  y  1  2x  4
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 58 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU Cho hàm số x  2 y 
1 . Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết tiếp tuyến 2x  3
đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa
độ O. (Khối A – 2009) . LỜI GIẢI Tập xác định  3 D R\  1    . Ta có y'  f'x  2   2x  32
Vì tiếp tuyến (d) cắt hai trục Ox, Oy lần lượt tại A, B tạo thành tam giác OAB vuông cân, nên
đường thẳng (d) hợp với trục Ox một góc 450. Vậy có 0
k   tan 45  k  1 tt tt
Gọi x là hoành độ tiếp điểm của tiếp tuyến, ta có f'x  1  0  0 Với  1 f ' x  1 
 1 (phương trình vô nghiệm). 0  2x  32 0 Với   1 f ' x  1    1
  2x  3  1  x  1   x  2  2  0 2 0 2x  3 0  0 0
Với x  1 y  1, phương trình tiếp tuyến tại điểm này y  1x 1 1  y  x . Tiếp tuyến 0 0
này loại vì đường thẳng này đi qua gốc tọa độ nên không tạo thành được tam giác.
Với x  2  y  0 , phương trình tiếp tuyến tại điểm này y  1x  2  y  x  2 0 0 Cho hàm số 3 2
y  x  3mx  m  1x  1 1 , m là tham số thực. Tìm các giá trị của m để tiếp tuyến
của đồ thị của hàm số (1) tại điểm có hoành độ x  1 đi qua điểm A1;2 . (Dự bị A1 - 2008) LỜI GIẢI Tập xác định D  R 2
y'  f '(x)  3x  6mx  m  1
Với x  1  y  2m 1 , f'(1)  5m  4 0 0
Phương trình tiếp tuyến tại điểm M 1
 ; 2m  1 : y  5m  4x  1  2m 1 (d). Ta có       5 A 1; 2 (d)
5m 4 .2  2m 1  2  m  . 8 Cho hàm số 3x  1 y 
1 . Tính diện tích của tam giác tạo bởi các trục tọa độ và tiếp tuyến của x  1
đồ thị của hàm số (1) tại điểm M2;5 .(Dự bị D1 - 2008)
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 59 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU LỜI GIẢI Tập xác định D 2  R  \   1 . Có y'  . x 12
Phương trình tiếp tuyến (d) tại điểm M2;5 : y  2x  2  5  y  2x  9
Gọi A là giao điểm của d và trục hoành 9  
 y  0  x   , vậy 9 A   ;0 A A 2 2   
Gọi B là giao điểm của d và trục tung  x  0  y  9 , vậy B0;9 . B B
Ta có tam giác OAB vuông tại O nên 1 1 9 81 S      OA.OB 9 OAB 2 2 2 4 Cho hàm số 3
y  3x  4 C . Viết phương trình tiếp tuyến của đồ thị C biết tiếp tuyến tạo với
đường thẳng d : x  3y  6  0 góc 0 30 . LỜI GIẢI
Tập xác định D  R . Ta có 2 y'  3 3x   3 3
d : 3y  x  6  0  y  x  2 3  k  d 3 3
Vì tiếp tuyến tạo với đường thẳng d một góc k  k 0 30 nên thỏa tt d 0  tan30 1 k k tt d 3 2 2 k  tt 3 1  3   3  2   3 k    1 
k   k  3k  0  k  0  k  3 tt tt tt tt tt tt 3 3  3   3  1 k      tt 3
Gọi x là hoành độ tiếp điểm 0 Với 2
k  0  3 3x  0  x  0  y  4 . Phương trình tiếp tuyến tại điểm (0 ; 4): y  4 . tt 0 0 0 Với 2 2 1 1
k  3  3 3x  3  x   x   tt 0 0 0 3 3 Với 1 13   x   y 
, phương trình tiếp tuyến 1 13 y  3 x    10  y  3x  . 0 0 3 3  3  3 3 Với 1 11   x    y 
, phương trình tiếp tuyến 1 11 y  3 x    14  y  3x  . 0 0 3 3  3  3 3 Cho hàm số 3 2
y  x  3x  9x  5 C . Trong tất cả các tiếp tuyến của đồ thị C , hãy tìm tiếp
tuyến có hệ số góc lớn nhất. LỜI GIẢI
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 60 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Tập xác định D  R . Ta có 2 y'  3  x  6x  9
Gọi x là hoành độ tiếp điểm của tiếp tuyến, ta có f'x  3  x  6x  9 0  2 0 0 0
 f 'x   3x  2x  1  12  3x 12 2  12  12 0 0 0 0
Từ đó suy ra maxf'x  12 tại x  1  . 0  0
Với x  1  y  16 , phương trình tiếp tuyến cần tìm: y  12x 1 16  y  12x  4 0 0 Cho hàm số 2x  1 y 
C . Gọi I1 ; 2 . Tìm điểm MC sao cho tiếp tuyến của C tại M x 1
vuông góc với đường thẳng IM .(Dự bị B2 - 2003) LỜI GIẢI Tập xác định D 1  R . Ta có y'  x 12 Gọi  Mx ,y C 2x 1 0  y  0 0 0 x  1 0   Ta có  2x 1   1  1 0 IM   x 1;
 2  IM  x  1;  k  0 0 x 1 IM   x 1        2 0 0  x 1 0 
Hệ số góc của tiếp tuyến tại M 1 k  f ' x   tt  0  x 12 0
Vì tiếp tuyến vuông góc với đường thẳng IM nên có k .k  1 tt IM 1   1  x  1  1   x  0  x  2 x 1 0 4 0 0 0
Vậy có 2 điểm M 0;1 ,M 2; 3 thỏa yêu cầu bài toán. 1   2   Cho hàm số 2x y 
C . Tìm điểm M C , biết tiếp tuyến của C tại M cắt hai trục tọa độ tại x 1
A ,B và tam giác OAB có diện tích bằng 1 .(Khối D - 2007) 4 LỜI GIẢI Tập xác định D 2  R  \   1 . Ta có y'  2 (x  1) Gọi Mx ; y C 2x0  y  0 0 0 x  1 0
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 61 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Phương trình tiếp tuyến của (C) tại M: y  f'x x  x  y 0   0  0 2 2x 2 2x  y  x  x   y  x  d 2   2 0 0 0 2 2   (x  1) x  1 (x  1) (x  1) 0 0 0 0
Gọi A là giao điểm của d và trục Ox, có 2
y  0  x  x . Vậy A 2 x ;0 0  A 0 2 2  
Gọi B là giao điểm của d và trục Oy, có 2x 2x 0 x  0  y  . Vậy 0 B0;  B B 2 (x  1)  2  (x 1)   0 0 
Ta có tam giác OAB cân tại O, theo giả thiết ta có: 1 1 1 S     OA.OB OAB 4 2 4 2 2 2 2x 1 2x  x  1 2x  x 1  0 2 0 2 2 0 0 0 0  x .
  4x  (x  1)    0  2 0 0 2 2 (x  1) 2 2x  x 1 2x  x  1  0 0 0 0 0 0 Với 2
2x  x  1  0 phương trình vô nghiệm. 0 0 Với 2 1
2x  x 1  0  x  1 x   0 0 0 0 2 Với x 1  
 1 ta có M1;1 . Với x   ta có 1 M  ;   2 0 0 2 2   
Vậy có hai điểm M thỏa mãn yêu cầu bài toán là M1;1 ,  1 M ; 2    2    (*) Cho hàm số 1 3 2 y  
 x  2x  3x C . Qua điểm 4 4
A ; có thể kẻ được mấy tiếp tuyến đến đồ 3 9 3   
thị C . Viết phương trình các tiếp tuyến ấy . LỜI GIẢI 2 Cho hai hàm số 1 y x  và y 
. Viết phương trình tiếp tuyến của đồ thị của các hàm số đã x 2 2
cho tại giao điểm của chúng. Tìm góc giữa hai tiếp tuyến trên. LỜI GIẢI Cho hàm số : 3x  1 y  C . 1 x
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 62 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
a) Viết phương trình tiếp tuyến của C tại điểm M 1  ; 1 ;
b) Vết phương trình tiếp tuyến của C tại giao điểm của C với trục hoành;
c) Viết phương trình tiếp tuyến của C tại giao điểm của C với trục tung ;
d) Viết phương trình tiếp tuyến của C bết tiếp tuyến song song với đường thẳng
d : 4x y 1  0 ;
e) Viết phương trình tiếp tuyến của C biết tiếp tuyến vuông góc với đường thẳng
 : 4x y 8  0 . LỜI GIẢI
Tìm các điểm trên đồ thị   1 3 2
C : y  x  x  mà tiếp tuyến tại đó vuông góc với đường thẳng 3 3 1 2 y   x  . 3 3 LỜI GIẢI
Tập xác định D   . Ta có 2 y'  x  1 Gọi  1 3 2  Mx ; x  x 
là tọa độ tiếp điểm của tiếp tuyến d với đồ thị (C), sao cho d vuông góc 0 0 0 3 3    với đường thẳng 1 2  : y   x  . 3 3
Phương trình tiếp tuyến d là: y 1 2
 f 'x x  x  y  y   2
x  1 x  x  x  x  0  0 3 0   0  0 0 0 3 3    2   2 3 2 y x 1 x  x  . 0 0 3 3 (d) vuông góc với (  1   ) khi và chỉ khi  2
x 1    1  x  2 0  0  3 
Kết luận có hai tọa độ điểm M cần tìm là  4  M2; và M2;0 . 3    Cho đồ thị  (3m  1)x  m C : y 
.Tìm m để tiếp tuyến tại giao điểm của C với Ox song song m  m  x  m
với đường thẳng d: y  x  5 . LỜI GIẢI
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 63 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU 2 Tập xác định D 3m  2m    \   m . Ta có y'  . xm2
Tọa độ giao điểm của    C và trục Ox là m A
;0 . Phương trình tiếp tuyến  của C tại m  m   3m 1    3m 12 3m 12 m3m  1 điểm A là:   y m
 f 'x x  x  y  y   x   y  x  . 0   0  0 2 3m  2m  3m 1    2 2 3m  2m 3m  2m
Để  song song với d: y  x  5 khi và chỉ khi:  3m 12   1  2  2 1  2m  8m  1  0  1 1 3m 2m          .  m 3m 1 m m 2 1  2m  9m  0 6 2   5 2  3m  2m Kết luận 1 1
m    m   thỏa yêu cầu. 6 2
Cho hàm số (C): y = x  2 . Viết phương trình tiếp tuyến đi qua A 6
 ; 5 của đồ thị (C). x  2 LỜI GIẢI Tập xác định D 4    \  2 . Ta có y'  x22 Gọi x  2
Mx ; y là tọa độ tiếp điểm của tiếp tuyến (d) cần tìm với đồ thị hàm số (C) nên 0 y  0 0  0 x  2 0 và  4 f ' x  
. Phương trình tiếp tuyến (d): 0  x 22 0  
y  f 'x x  x  4 x 2  y  y  x  x  2  0  0 0 0 0   x   2 x 2 0 0 Ta có 4  x  2 A6;5d  6   x   5 2
 4x  24x  0  x  0  x  6 . 2  0  0   x   2 x 2 0 0 0 0 0 0
Kết luận có hai tiếp tuyến cần tìm là y  x 1 và 1 7 y   x  . 4 2
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 64 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU Gọi (C 1 m 1
m) là đồ thị của hàm số 3 2 y  x 
x  * (m là tham số). 3 2 3
Gọi M là điểm thuộc (Cm) có hoành độ bằng 1 . Tìm m để tiếp tuyến của (Cm) tại điểm M song
song với đường thẳng 5x  y  0. LỜI GIẢI
Tập xác định D   . Ta có 2 y'  x  mx Điểm thuộc   
C có hoành độ x  1 là m M1; m  2   
Phương trình tiếp tuyến của C tại M là: m 
      m       m  2 : y f ' 1 x 1 y m 1 x  2 2 Để   
 song song với d: 5x  y  0  y  5x khi và chỉ khi: m 1 5   m  4 . m  2  0 Kết luận m  4 . Cho hàm số 3 2
y  4x  6x  1 (1) . Viết phương trình tiếp tuyến của (1), biết tiếp tuyến đi qua điểm M1;9 . LỜI GIẢI
Tập xác định D   . Có 2 y'  12x 12x .
Gọi Ax ;y là tọa độ tiếp điểm của tiếp tuyến (d) cần tìm với đồ thị hàm số (1) nên 0 0  3 2
y  4x  6x  1 và f'x  12x 12x . Phương trình tiếp tuyến (d): 0  2 0 0 0 0 0
y  f 'x x  x   y  y   2 12x 12x x  x  3 2  4x  6x  1 0 0 0 0 0 0 0 0 Ta có M 1  ; 9  d   2 12x 12x  1   x  3 2  4x  6x  1  9 0 0 0 0 0 3 2 5
 8x  6x  12x  10  0  x  1   x  0 0 0 0 0 4
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 65 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Kết luận có hai tiếp tuyến cần tìm là y  24x  15 và 15 21 y  x  . 4 4 Cho đồ thị (C): 1 4 2 9
y  x  2x  . Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với 4 4 Ox. LỜI GIẢI
Tập xác định D   . Ta có 3 y'  x  4x
Phương trình hoành độ giao điểm của (C) và trục Ox: 1 4 2 9 x  2x   0 2  x  9 2  x  1 (loại). 4 4 Với x  3  y  0 2 x  9   x  3   y   0
Phương trình tiếp tuyến tại M3;0 của (C): y  f'3x  3  y  15x  45 .
Phương trình tiếp tuyến tại M3;0 của (C): y  f'3x  3  y  1  5x  45 . Tìm   2x A, B C : y 
sao cho tiếp tuyến của C tại A, B song song với nhau và OAB x 1 vuông tại O ? LỜI GIẢI ● Gọi  2a   2b  A 2 a;  , B b;
  C , a; b  1;a  b . Ta có: y'  .  a  1   b 1  x12
● Tiếp tuyến tại A và B lần lượt có hệ số góc: 2  2 kA  ; k  . a 12 B b12
● Do tiếp tuyến tại A và B song song nhau nên k 2  2  A  kB   a12 b12 a 1  b  1 a  b
   2    2 a 1 b 1      a  2  b i a 1  1  b a  2   b O  A   B
● Do ba điểm O,A,B tạo thành tam giác vuông tại O nên   OA  OB
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 66 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU a  ,b  0 a  , b   0 4       4ab  1  0 ii OA.OB  0 ab    a 1b     1    0 a 1 b 1 a   2  b i,ii  4   4  b 12 1      1 4   1 bb1       0 a 1 b 1
 b  3  a  1  b  1   a  3 .
● Vậy A1;1, B3;3 hoặc A3;3, B 1
 ;1 là các điểm cần tìm.
Tìm những điểm   x 1 M C : y 
sao cho tiếp tuyến với C tại M tạo với hai trục tọa độ một 2x  2
tam giác có trọng tâm nằm trên đường thẳng d : 4x  y  0 ? LỜI GIẢI    ● Gọi xo 1 M x  o ;  C , x  o  1
  và tiếp tuyến  tại điểm M có phương trình 2x  o  2  1   : y   x 1 x  x  i 2 o  o  2 x   1 xo 1  o  2  2       ● Gọi xo 2xo 1 x  o  2xo  1 A    Ox  A ; 0 ,B    Oy  B 0;    .  2     2  x 12  o   2 2 
● Khi đó tọa độ trọng tâm của x  2x 1 x  2x 1 OAB là  o o o o G ;    . 6 6  x 12    o  2 2 ● Do x  2x  1 x  2x 1 G d : 4x  y  0 o o o o  4   0 6 6x 12 o  x 12 2 o
 4 do : A  B  O  xo  2xo 1  0 1 3     1 3 3 5
 xo    xo   nên i  M  ; hoặc M  ; . 2 2 1 2 2     2  2 2  Tìm   3 A
C : y  x  3x  1 biết rằng tiếp tuyến của đồ thị C tại điểm A, cắt đồ thị C tại B
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 67 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
(khác điểm A) thỏa: xA  xB  1 ? LỜI GIẢI ● Gọi A 3
xA;xA  3xA 1C và phương trình tiếp tuyến tại điểm A có dạng  : y   2 3x  3x  x  3 A A  xA  3xA  1 .
● Ta có  C  B có hoành độ nghiệm của phương trình hoành độ giao điểm:  2 3x  3x  x  3 3 A B
A  xA  3xA  1  xB  3xB  1 i
● Theo giả thiết, ta có: xA  xB  1 xB  1 xA ii
i,ii  3x 312x x 3x  1x 3 2 3 A A A A A  31 xA   3 x  1   x  2 4x A B A  3xA  1  0     1 1  A 1  ; 3 . x   xA   xB  L   A  xB , do : A   B  2 2 Cho hàm số 3
y  x  3x  2 C .Tìm điểm M thuộc (C), sao cho tiếp tuyến của (C) tại M cắt (C) tại
điểm thứ hai là N và MN  6 5 . LỜI GIẢI Gọi  3
M m;m  3m  1C. Phương trình tiếp tuyến của (C) tại M là   2     2 y 3m
3 x m  m  3m  2 d . Phương trình hoành độ giao điểm của d và (C): 3   
   2     2 x 3x 2 3m
3 x m  m  3m  2    2 x m x  2m  0 x m   , để d cắt (C) tại hai x  2   m
điểm phân biệt  m  2
 m  m  0 , khi đó  3 N 2
 m; 8m  6m  2 . Có 2 6 4 2
MN  81m  2.81m  90m  180 . Đặt 2 3 2
t  m ,t  0  9t  18t  10t  20  0  t  2 m   2
Vậy có hai điểm N cần tìm N2 2;10 2  2,N2 2;10 2  2
Chứng minh rằng với mọi m thì đường thẳng d : y 
 x  m luôn cắt đồ thị   1 x C : y  tại hai 2x 1
điểm phân biệt A và B. Gọi k1,k2 là hệ số góc của các tiếp tuyến với C tại A và B. Tìm m để tổng
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 68 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
k1  k2 đạt giá trị lớn nhất ? LỜI GIẢI
● Phương trình hoành độ giao điểm giữa d và   1 x 1 C :  x  m,x  2x 1 2    2       1 g x 2x 2mx m 1  0, x   2  ' 2 g  m  m  2  0  ● Ta có:   1  1 : luôn đúng m
    d C  A;  B . g       0   2  2
● Gọi Aa;a  m,Bb;b  m với a,b là hai nghiệm của gx  0 .   ● Ta có: 1 1 T k  
 1  k2  y'a y'b      2a 12 2b 2 1      4 a b2 2ab    4a  b  2   T     
 4m  12  2  2 4ab  2  a  b 2  1
● Dấu "  " xảy ra  m  1  0  m  1  thì m T ax  k1  k2   2  . min Cho hàm số 3      2 y x m 2 x  4m  3 1
Tìm giá trị của tham số m để đường thẳng y  2x  7 cắt đồ thị hàm số (1) tại ba điểm phân biệt
A, B, C sao cho tổng hệ số góc của các tiếp tuyến với đồ thị hàm số (1) tại các điểm A, B, C bằng 28. LỜI GIẢI
Phương trình hoành độ giao điểm của đường thẳng d : y  2x 7 và đồ thị hàm số (1): 3    2 3          2 x m 2 x 4m 3 2x 7 x
m 2 x  2x  4m  4  0 x  2   . Đặt   2 g x  x  mx  2m  2 2
x  mx  2m  2  0 (2)
Đường thẳng d cắt đồ thị hàm số (1) tại ba điểm phân biệt A, B, C  phương trình (2) có hai
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 69 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU   0   2
m  4  2 2  m  4  2 2
nghiệm phân biệt và khác 2  (2) m  8m  8  0    (3).        1 g 2  0 2  4m  0 m   2
Gọi A2;y1,Bx2;y2 ,Cx3;y3  với x1,x2 là hai nghiệm của (2). Hệ số góc của tiếp tuyến tại các
điểm A, B, C với đồ thị hàm số (1) lần lượt là:
k  y'2  4  4m,k  y'x  2
 3x  2m  2x ,k  y'x  2 A B 2 2 2 C
3  3x3  2  m  2 x3 . Theo đề bài 2
k  k  k  28  4  4m  3x  2m  2 2 A B C 2
x2  3x3  2m  2x3  28  4  4m  3 2 2 x 4 4m 3 x  x 2      2 3
 2x2x3  2m  2x  2  x3 
2  x3   2m  2x2  x3   28  28   2             2 4 4m 3 m 2 2m 2
2 m 2 m  28  m  4m 12  0  m  6   m  2   Kết hợp với
điều kiện (3) được m = 2. Cho hàm số 3 2 2 2
y  x  3x  m x  2  m 1 . Định m để đồ thị hàm số (1) cắt trục hoành tại ba
điểm A, B, C phân biệt sao cho tổng các hệ số góc của các tiếp tuyến với đồ thị (1) tại ba điểm A, B, C lớn nhất. LỜI GIẢI Ta có: 2 2 y'  3x  6x  m
Phương trình hoành độ giao điểm của đồ thị hàm số (1) với trục hoành: x  1 3 2 2 2
x  3x  m x  2  m  0  x 1 2 2
x  2x  m  2  0   g  x 2 2
 x  2x  m  2  0 
Đồ thị hàm số (1) cắt trục Ox tại ba điểm phân biệt  phương trình (*) có hai nghiệm phân biệt    2   0 và khác 1 ( ) 3  m  0        
. Gọi A1;yA ,Bx1;yB ,Cx2;yC  với x ,x là g 1 2  1 3 m 3 2  0 m  3  0
hai nghiệm của phương trình  theo định lý Vi ét có x1  x2  2 và 2 x1.x2  m  2 .
Ta có P  kA  kB  kC  y'1 y'x1 y'x2  2  3  m   2 2 3x  6x  m  2 2 1 1 3x2  6x2  m  3 x x 2 2x x      6x  x  2 2  1 2 1 2  1
2  3m  3  9  3m  9  
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 70 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Vậy maxP  9 khi m  0 .
Kết luận với m  0 thỏa yêu cầu bài toán. Cho hàm số 3 2
y  x  3x  2 1
Tìm tham số m để đường thẳng d : y  m2  x  2 cắt đồ thị (C) của hàm số (1) tại ba điểm phân
biệt A2;2,B,C sao cho tích các hệ số góc tiếp tuyến với đồ thị C tại B và C đạt giá trị nhỏ nhất ? LỜI GIẢI
● Phương trình hoành độ giao điểm: 3 2
x  3x  2  m 2  x  2 x  2  y  2     2
x 2 x  x  m  2  0   g  x 2  x  x  m  2  0
● Để d cắt C tại ba điểm phân biệt A2;2,B,C  gx  0 có ba nghiệm phân biệt  2   9  g  9  4m  0 m       4 i g  2  m   0 m   0 ● Ta có: ' 2 y  3  x  6x và gọi B với là hai nghiệm của 1
x ;m 2  x1  2,Cx2;m2  x2   2 x1,x2 x  x   1 gx  0 . Theo Viét: 1 2  . x  1x2  m   2 ● Ta có: ' k k  y x  ' .y x    2 3x  6x  2 1 2 1 2 1 1 3  x2  6x2 
 k k  9x x 2 18x x x  x   36x x  9m  22 1 2 1 2 1 2 1 2 1 2
 18m  2  k1k2  9x  k k  9m  2 1 2 1  9  9   k khi ). 1k2   9 m  1  (thỏa i min
Cho hàm số      2 y x 2 x 1 C
b). Tìm các điểm M thuộc đường thẳng d : y  2
 x  19 , biết rằng tiếp tuyến của đồ thị (C) đai
qua điểm M vuông góc với đường thẳng x  9y  8  0 . LỜI GIẢI
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 71 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Vì tiếp tuyến vuông góc với đường thẳng 1 8
x  9y  8  0  y   x   nên 9 9 ktt.k   
 , gọi tọa độ tiếp điểm của tiếp tuyến là Ix0; y0  , từ đó ta có  1 ktt 9 y'x  2
0  ktt  x0  1  3  x0  2  x0  2
 Với x0  2  y0  4 khi đó phương trình tiếp tuyến d1 : y  y'1x  2  4  d1 : y  9x 14 . Suy
ra M là giao điểm của d và y  9x 14
d1 tọa độ điểm M là nghiệm của hệ   M3;13 . y  2  x  19
 Với x0  2  y0  0 khi đó phương trình tiếp tuyến d2 : y  9x 18 . Suy ra M là giao điểm của d và     
d2 tọa độ điểm M là nghiệm của hệ y 9x 18 1 201   M ; . y 2x 19  11 11     
Kết luận tọa độ điểm M cần tìm là   M3;13 hoặc 1 201 M ; . 11 11    Cho hàm số 3 2
y  x  3x  m  2x  3m Cm  (m là tham số).
Tìm m để tiếp tuyến có hệ số góc nhỏ nhất của đồ thị Cm  của hàm số đã cho vuông góc với
đường thẳng d : x  y  2  0 . LỜI GIẢI Có 2 y'  3x  6x  m  2
Gọi Mx0;y0 Cm  , suy ra hệ số góc tiếp tuyến của Cm  tại M là
k  y'x   3x  6x  m  2  3x 12 2 0 0 0 0
 m  5  m  5 , dấu "  " xảy ra  x0  1 suy ra hệ số góc
của tiếp tuyến nhỏ nhất là kmin  m  5 tại điểm M1;4m  4 .
Để tiếp tuyến vuông góc với d  ktt.kd  1
  m  5.1  1  m  4 .
Kết luận với m = 4 thỏa yêu cầu đề bài. Gọi k x  m
1 là hệ số góc của tiếp tuyến tại giao điểm của đồ thị hàm số Cm  : y  với trục x  1
hoành. Gọi k2 là hệ số góc của tiếp tuyến với đồ thị Cm  tại điểm có hoành độ x  1 . Tìm tất cả
các giá trị của tham số m sao cho k1  k2 đạt giá trị nhỏ nhất ? LỜI GIẢI
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 72 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU ● Ta có: 1 m y' 
. Hoành độ giao điểm Cm  với trục hoành: x  m . x12
● Hệ số góc tiếp tuyến tại điểm có hoành độ x 1
 m là k1  y'm  . 1 m
● Hệ số góc tiếp tuyếnTại điểm có hoành độ x 1 m  1 là k2  y'1  . 4 Cauchy ● Ta có: 1 1 m 1 1 m 1 1 m k1  k2      2 . 1 m 4 1 m 4 1 m 4   k1  k2  1, m
  1 . Dấu "  " xảy ra 1 1 m   1 m 4       2 m  1  1 m  4   . Vậy k  k  1 khi m 1 . m  1 2   3 min m   3
Viết phương trình tiếp tuyến d của   2x  1 C : y 
, biết rằng tiếp tuyến cắt trục Ox,Oy lần lượt x 1
tại A,B sao cho AB  82.OB ? LỜI GIẢI
 Phân tích và tìm hướng giải ∆ y
TT  cắt trục Ox,Oy tại A,B  O  AB vuông tại B α x O A
O và tạo với trục Ox một góc  với OB k  tan   . OA  Ta có: AB  82.OB OB 1 1  2 2  81.OB  OA    k  . 2 2 2 OA  OB  AB OA 9 9 Bài giải    ● Gọi 2xo 1 M 1  x  o ;  , x 
o  1 là tiếp điểm  k 
. Phương trình tiếp tuyến có dạng x  o  1  x 12 o 1   : y    2x 1 x  x  i 2 o  o  1 xo 1 xo
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 73 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU  ● Ta có: AB  82.OB OB 1  2 2 2 2
 AB  82.OB  OA  OB   . 2 2 2 OA  OB  AB OA 9
● Hệ số góc tiếp tuyến được tính OB 1 k 1 1  tan     k   k   . OA 9 9 9 ● Với 1 1 k  
: phương trình vô nghiệm. 9 x 12 o   ● Với 1 1  k      x 4 x 1  9  ii 2 o  o 9   x 1 x  o  2  o i,ii 1 25   : y   x  hoặc 1 13  : y   x 
là các tiếp tuyến cần tìm. 9 9 9 9
Lập phương trình tiếp tuyến của   3 2
C : y  x  3x 1, biết nó song song với đường thẳng d : 9x  y  6  0 ? LỜI GIẢI ● Ta có: 2
y'  3x  6x . Gọi Mxo; yo  là tiếp điểm. Phương trình tiếp tuyến có dạng:
 : y  kx  xo   yo . Do tiếp tuyến  // d : y  9x  6  k  9 x  1   y  3  y'x 2 o o
o   9  3xo  6xo  9   . x  o  3  yo  1
● Với xo  1 ; yo  3; k  9   : y  9x  6 (loại do   d ).
● Với xo  3; yo  1; k  9   : y  9x  31 hay  : y  9x  26 .
Viết phương trình tiếp tuyến của đồ thị   4 2
C : y  x  x  6, biết tiếp tuyến vuông góc với đường thẳng 1
d : y  x 1 ?Đại học khối D năm 2010 6 LỜI GIẢI ● Ta có: 3 y'  4
 x  2x . Gọi Mxo; yo  là tiếp điểm. Phương trình tiếp tuyến có dạng: 1
 : y  kx  xo   yo . Do 1
  d : y  x  1  k.  1  6 6
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 74 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU  k  y'xo   6  3
 4xo  2xo  6  xo  1  yo  4 .
● Phương trình tiếp tuyến là  : y  6
 x 1  4 hay  : y  6x  10 . Gọi   2x  1 M C : y 
có tung độ bằng 5 . Tiếp tuyến của C tại M cắt các trục tọa độ Ox,Oy x 1
lần lượt tại A và B. Tính S O ?  AB
Cao đẳng khối A, A1, B, D năm 2013 LỜI GIẢI
 Phân tích và tìm hướng giải Viết PTTT 2x  1  tại M khi biết o y . Tìm tọa độ o  5   xo  k  y'xo 
A    Ox, B    Oy xo 1 và tính 1 S   ? OAB OA.OB 2 Bài giải ● Ta có: 3 2x  1 y'   và o y  5 
 x  2  k  y'xo   3 .  o o x 12 xo 1
● Phương trình tiếp tuyến tại M2;5 là  : y  3x 11.  11 ● Ta có:  : y  3x  11     A x 11    Ox thỏa    3  A ;0 . Ox : y 0   3   y   0  ● Ta lại có:  : y  3x  11 x  0 B    Oy thỏa     B0;11 . Oy : x  0 y  11 1 1 11 121  S    đvdt OAB OA.OB . .11 2 2 3 6
Viết phương trình tiếp tuyến của đồ thị hàm số   x  2 C : y 
, biết rằng tiếp tuyến đó cắt trục 2x  3
hoành, trục tung lần lượt tại hai điểm phân biệt A,B và tam giác OAB cân tại gốc tọa độ O ?Đại học khối A năm 2009
 Phân tích và tìm hướng giải
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 75 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Tiếp tuyến  Ox    A ,   Oy   
B mà OAB vuông cân tại O   song song với phương
trình đường thẳng phân y y ∆ B d1 d2 B
giác góc phần tư thứ I d ∆ 1 : y  x và thứ II A A B x B x ∆ A A d ∆ 2 : y  x  k  1   xo  yo   . LỜI GIẢI ● Ta có: 1 y' 
. Gọi Mxo;yo  là tiếp điểm và tiếp tuyến là  . 2x 32 ● Theo đề 1   // d  k  y'xo  1,2 : y  x   1 2x  32 o x  1   y  1  k  1  2x  32 o o o  1   . x  o  2
  yo  0  k  1  : y  1  x 1 1  : y  x  
(loại do  d : y  x )   : y  1   x 2 hay  0  : y  x  2 
● Vậy phương trình tiếp tuyến cần tìm là:  : y  x  2 . Cho hàm số 2x  3 y 
có đồ thị C .Viết phương trình tiếp tuyến  với đồ thị hàm số C sao x  2
cho  cắt trục hoành tại A mà OA  6 ?
 Phân tích và tìm hướng giải    Gọi 2xo 3 1  2x  3 M x  tt  : y  xx  2 o  o o ;   là tiếp điểm x   o  2   2 xo  2 xo   Ox   
A  tọa độ điểm A theo xo  giải OA  6  xo  tt  . LỜI GIẢI    Ta có: 1 2x 3 y'  . Gọi o M x  o ;  C , x 
o  2 là tiếp điểm. x22 x  o  2 
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 76 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
● Phương trình tiếp tuyến tại M là 1    : y   2x 3 x  x  i 2 o  o  2 xo  2 xo ● Ta có: 1 2x  3
A    Ox  y  0  0  xx  2 o  o  2 xo  2 xo 2
 x  2x  6x  6  A 2 o o 2xo  6xo  6;0 . ● Theo đề 2
OA  6  2xo  6xo  6  0  xo  0  xo  3 ii  1 3
● Thế ii vào i   : y   x 
 các tiếp tuyến cần tìm là: 4 2  .   : y  x  6
Viết phương trình tiếp tuyến với đồ thị   3 2
C : y  x  6x  9x, biết tiếp tuyến tạo với đường thẳng
 : x  y  1  0 một góc , sao cho 4 cos 
và tiếp điểm có hoành độ nguyên ? 41
 Phân tích và tìm hướng giải Gọi M 3 2
xo;xo  6xo  9xo  là tiếp điểm thì k  y'x  2
o  3xo  12xo  9 và có  : y  x  1  k   .  1
Khi đó ta có hai hướng xử lý: một là áp dụng công thức k  k tan    , hai là sử dụng 1 k.k       cos  cosn  
và nd  k;  là véctơ pháp tuyến của  và tiếp  ; n  n.nd d
  với n 1;1 1 n . nd tuyến d. LỜI GIẢI ● Gọi M 3 2
xo;xo  6xo  9xo  là tiếp điểm và k  y'x  2 o  3xo  12xo  9 .
● Phương trình tiếp tuyến có dạng d : y  kx  x  3 2
o  xo  6xo  9xo và có véctơ pháp tuyến   nd  k;  1 . Ta có: n  .  1;1     n.n k  1 ● Theo đề:           d 4 cos cos n ; nd 2 n . n 2. k  1 41 d
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 77 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU 2 1
 9k  82k  9  0  k  9  k  . 9  ● Với 2 x  0  y  0  : y  9x k  9  3x o o o  12xo  0    . x   o  4  yo  4  : y  9x   32 ● Với 1 2 1 18  2 21
k   3xo 12xo  9   xo  (loại do x ;y  ). 9 9 9 o o
● Vậy phương trình tiếp tuyến cần tìm là:  : y  9x hoặc  : y  9x  32 .
Viết phương trình tiếp tuyến với   2x  1 C : y 
, biết tiếp tuyến cách đều hai điểm A 2  ; 4 và x 1 B4;2 ?
 Phân tích và tìm hướng giải    Gọi 2xo 1 1  2x  1 M x  tt  : y  xx 
. Do  cách đều hai điểm A 2 o  o o ;   là tiếp điểm x   o  1   1 xo 1 xo
và B nên có các trường hợp sau đây xảy ra: tiếp tuyến  qua trung điểm I của AB I hoặc
song song với AB hoặc trùng với AB k  kAB  . Giải hai trường hợp  xo   . A A B ∆ I B LỜI GIẢI    ● Gọi 2xo 1 x  x 2x  1 M x o o  o ;  , x 
o  1  tiếp tuyến  : y   i x  2 o  1   1 xo 1 xo
● Do tiếp tuyến cách đều hai điểm A 2
 ; 4 và B4;2 nên có các trường hợp:
Trường hợp 1. Gọi I là trung điểm của AB  I1;1  xo 1 2xo 1 1 5  1    x  1
   : y   x  .  o  12 xo 1 x 4 4 o
Trường hợp 2.  // AB hoặc   AB  k  kAB .
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 78 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Phương trình đường thẳng AB : y 1
 x  2  kAB  1  k   x 12 o
 xo  2  xo  0 . Thế vào i được  : y  x  5 hoặc  : y  x 1. ● Vậy 1 5
 : y   x  hoặc  : y  x  5 hoặc  : y  x  1 . 4 4
Xác định m để đồ thị   2x  m C : y 
có tiếp tuyến song song và cách đường thẳng x 1
d : 3x  y  1  0 một khoảng cách bằng 10 ?
 Phân tích và tìm hướng giải  2x   o m M 2  m  x  o ;
 C là tiếp điểm  k 
. Do  // d  k  3 sẽ thu được một phương x   o  1  x 12 o
trình với hai ẩn xo ,m và dM;d  10 sẽ thu thêm được một phương trình nữa. Giải hệ này tìm được  xo ,m . LỜI GIẢI    ● Gọi 2xo m M 2   m  x  o ;  ,x 
o  1 và tiếp tuyến  có k 
 3 (do tiếp tuyến  // x  o  1  x  2 o 1 d : y  3  x  1 ) 2
 3xo  6xo  m 1  0 i ● Vì 2x  m
d;d  dM;d  10 o  3xo   10 ii xo 1  2       2     3xo 11xo m 10 0
3xo  9xo  m  10  0 i , ii     2 2 3x
 o  6xo  m  1  0 3x
 o  6xo  m  1  0 x   o 1 L xo  1 L      11 1  3 67 . xo   m  xo    m   6 12  2 4 ● Vậy 1 67 m   m 
là các giá trị cần tìm. 12 4
Tìm tất cả các giá trị của tham số m  0 sao cho tiếp tuyến của đồ thị C  3
m : y  mx  2m  1 x  m  1 tại giao điểm của nó với trục tung tạo với hai trục tọa độ một
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 79 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
tam giác có diện tích bằng 4 ? LỜI GIẢI
● Ta có: M  Cm Oy : x  0  y  m 1 M0;m 1 . ● Mà 2
y'  3mx  2m  1  k  y'0  2
 m  1 là hệ số góc tiếp tuyến tại điểm M và có phương
trình  : y  2m 1x  m 1 i y   m  1  0 ● x   m  1    Ox  A thỏa    A ;0 y     2m 1   2m 1x m   1 y   2m  1   0 x   0 x  0   Oy  B thỏa    B0;m  1 . y     2m 1x m   1 y  m 1 m  1  OA  , OB  m  1 với 1 m   . 2m  1 2 ● Theo đề: 1 1 m  1 S     AOB .OA.OB . . m 1 4 2 2 2m  1  2 16m  8  m  2m  1 m  7  2 14    2 m 1  8 2m  1     . 2
16m  8  m  2m   1 m  9   6 2
Tìm m để tiếp tuyến của C  3 2
m : y  x  3mx  m  1 x  1 tại điểm có hoành độ x  1 đi qua điểm A1;2 ? LỜI GIẢI Ta có: 2
y'  3x  6mx  m  1  k  y'1  4  5m .
Phương trình tiếp tuyến tại điểm M 1  ; 2m  1 có dạng:
d : y  4  5mx 1  2m 1 và A1;2d nên 5 m  . 8
Viết phương trình tiếp tuyến của   2x  1 C : y 
, biết rằng tiếp điểm của tiếp tuyến đó với C x  1
cách điểm A0;1 một khoảng  2 ? LỜI GIẢI
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 80 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU    Gọi 2xo 1 M x  o ;  ,x 
o  1 là tiếp điểm. Theo đề thì MA  2 hay x  o  1  2 2  2x   o 1 xo    1  4  x  
o  0  xo  2 . Với x  0  tiếp tuyến là d : y  3x  1 và với x o 1  o  1  x 1 xo  2  d2 : y   . 3 3
Viết phương trình tiếp tuyến của   x C : y 
tại M, biết rằng tiếp tuyến đó cắt các trục tọa độ 1 x
tại A và B sao cho M là trung điểm của AB ? LỜI GIẢI Gọi  m  Mm;
 ,m  1 là tiếp điểm. Phương trình tiếp tuyến tại M có  1 m   2  dạng   m     2 2
: x 1 m y  m  0 . Khi đó:  2 A m ;0 và B 0;   .  1 m2     2
Để M là trung điểm của đoạn AB thì 2 m 2m m  0; m  2m;     2 1 m 1 m
 m  2 . Vậy phương trình tiếp tuyến cần tìm là:  : x  y  4  0 .
Tìm m để đồ thị hàm số C  3
m : y  x  3mx  2 có tiếp tuyến tạo với đường thẳng d : x  y  7  0 góc , biết 1 cos  ? 26 LỜI GIẢI 
Gọi k là hệ số góc tiếp tuyến  tiếp tuyến có vtpt n1  k; 1   . 
Đường thẳng d : x  y  7  0 có vtpt n2  1;1 .    3   n .n k 1 k  1   Theo đề    ;n  1 2 2 cos cos n . 1 2        2 n . n 26   2 1 2 2. k 1 k   3
YCBT  ít nhất một trong hai phương trình sau có nghiệm:
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 81 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU  3  2 3  2 2m  1  2m  1 y'  3x  3m  x       0 2 2 2 2 1         m   .  2  2 2  2 9m  2  9m  2 2 y'  3x  3m  x   0  3  3  9      9
Viết phương trình tiếp tuyến của đồ thị   2x  1 C : y 
, biết rằng tiếp tuyến này cắt trục Ox,Oy x 1
lần lượt tại A,B thỏa: OA  4OB ? LỜI GIẢI
Giả sử tiếp tuyến d của C tại Mxo;yo C cắt Ox tại A, cắt Oy tại B
sao cho OA  4OB . Do OAB vuông tại O nên OB 1 tan A 
  hệ số góc của d bằng 1 hoặc OA 4 4 1 1
 . Mà hệ số góc của d là: y'xo     0 4 x 12 o 1 1 3 5  
   x  1  y  hoặc x  3  y  .  4 2 o o x 2 o  12 o o
Khi đó có hai tiếp tuyến là: 1 5 d : y   x  hoặc 1 13 d : y   x  . 4 4 4 4
Tìm các điểm M trên đường thẳng d : y  2
 x  19, biết rằng tiếp tuyến của đồ thị
       2 C : y
x 2 x 1 đi qua điểm M vuông góc với đường thẳng d' : x  9y  8  0 ? LỜI GIẢI
● Hàm số được viết lại: 3 y  x  3x  2 . ● Vì tiếp tuyến 1 8  
  d' : y   x  nên 1
 k.   1  k  9 . 9 9  9 
● Gọi Mxo;yo C là tiếp điểm  k  y'x  2
o  3xo  3  9  xo  2 .
● Phương trình tiếp tuyến tại M có dạng:  : y  kx  x  3 o  xo  3xo  2 .
Hay 1 : y  9x 14 hoặc 2 : y  9x 18 là hai tiếp tuyến tại M.
● Khi đó, tọa độ điểm M là giao điểm của đường thẳng d và tiếp tuyến
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 82 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU     x  3 d      M . 1 3; 13 1  M1 thỏa y 2x 19  y  9x 14 y  13  1   x         d 11 1 207  2  M2 thỏa y 2x 19     M  ;  .  2 y  9x  18 207   11 11 y    11
● Vậy có hai điểm M là   M 1 207 1 3;13 hoặc M2  ;
thỏa yêu cầu bài toán. 11 11    Tìm các điểm   3 A,B
C : y  x  3x sao cho tiếp tuyến của C tại A,B song song với nhau và AB  4 2 ? LỜI GIẢI Gọi  3     3 A a; a
3a ,B b; b  3bC,a  b.
Do tiếp tuyến tại A và B song song nhau nên y'a  y'b hay 2 2  3a  3  3
 b  3  a  b (nhận) hoặc a  b (loại). Theo đề 2 a  b  4  a  2; b  2  AB  32    . a  b    a  2; b  2 Vậy A2; 2
 ,B2;2 hoặc A2;2,B2; 2
  thì thỏa yêu cầu bài toán. Tìm   3 M
C : y  x  3x  2 để tiếp tuyến của C tại điểm M cắt đồ thị C tại điểm thức hai là
N thỏa mãn xM  xN  6 ? LỜI GIẢI Gọi  3
M a;a  3a  2C . Phương trình tiếp tuyến tại điểm M:    2     3 : y 3a
3 x a  a  3a  2 hay    2   3 : y 3a 3 x  2a  2
Phương trình hoành độ giao điểm: 3     2   3 x 3x 2 3a 3 x  2a  2    2
x a x  2a  0  x  a  x  2a  xM  a; xN  2  a . Theo đề: x . M  xN  6  a   2
 a  6  a  2  a  2
Vậy có hai điểm M thỏa yêu cầu bài toán: M2;4  M2;0 .
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 83 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Tìm các điểm trên   2x  3 C : y 
, sao cho tiếp tuyến tại đó tạo với hai trục tọa độ một tam giác x  1
có diện tích bằng 18 đvdt ? 5 LỜI GIẢI    Gọi 2xo 3 M x  o ;  C;x  o   
1 và phương trình tiếp tuyến tại M: x  o  1  5   2 7x  x  3   : y   2x 3 x  x  và o o   Ox  A ;0 2 o  o  1 x   o  1 x 5x o  o   2 2x   o  6xo  3 Oy B 0;  18 1 18     . Do S    ABO AO.BO 5 2 5  x 12    o 
Giải phương trình này, sẽ tìm được xo  M cần tìm.
Tìm tọa độ điểm   2x 1 M C : y 
, sao cho khoảng cách từ điểm I1;2 tới tiếp tuyến của C x  1 tại M là lớn nhất ? LỜI GIẢI   Gọi 3 M x  o ; 2   C ,x 
o  1 . Khi đó tiếp tuyến tại M dạng x  o  1  3    3 : y x  x  2 
. Khi đó khoảng cách từ I1;2 đến tiếp tuyến là: 2 o   1 xo 1 xo 3 1
  xo   3xo 1   6 xo 1 d I;   9  x 14 9  x 14 o o Cauchy Hay   6 d I;   6 và d  6 khi và chỉ khi 9 max  x  1 2 o 2 xo 1 9
 x  1  x  1  3  x  1 3 . 2 o 2  o 2 xo 1 o Vậy: M hoặc M là hai điểm cần tìm 2  1   3; 2  3  1 1  3; 2  3 
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 84 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 85 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU CÂU HỎI TRẮC NGHIỆM Câu 1. Cho hàm số C 3 2
: y  x  3x . Phương trình tiếp tuyến của đồ thị C tại điểm M 1;  4 là: A. y  9x  5. B. y  9x  5. C. y  9x  5. D. y  9x  5.
Câu 2. Phương trình tiếp tuyến của đồ thị hàm số 4 2
y  x  4x 1 tại điểm B1;  2 là: A. y  4x  6 B. y  4x  2 C. y  4x  6 D. y  4x  2 x 1
Câu 3. Phương trình tiếp tuyến của đồ thị hàm số y  tại điểm C 2;  3 là: x 1 A. y  2x 1 B. y  2x  7 C. y  2x  7 D. y  2x 1
Câu 4. Tiếp tuyến của đồ thị hàm số 3
y  x  3x  2 tại điểm D có hoành độ bằng 2 có phương trình là: A. y  9x 14 B. y  9x 14 C. y  9x  22 D. y  9x  22 2x 1
Câu 5. Tiếp tuyến của đồ thị hàm số y 
tại điểm F có hoành độ bằng 2 có phương trình là: x 1 A. y  x  5 B. y  x  5 C. y  x 1 D. y  x 1
Câu 6. Tiếp tuyến của đồ thị hàm số 4 2
y  x  2x  3 tại điểm H có tung độ bằng 21 có phương trình là y  40x 101 y  40x  59 y  40x  59 y  4  0x  59 A.  B.  C.  D.  y  4  0x  59  y  4  0x 101  y  4  0x 101  y  40x 101  x  2
Câu 7. Tiếp tuyến của đồ thị hàm số y 
tại điểm I có tung độ bằng 1 có phương trình là 2x 1 1 8 1 2 1 8 1 2 A. y  x  B. y   x  C. y   x  D. y  x  5 5 5 5 5 5 5 5
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 86 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU Câu 8. 1 Cho hàm số C 4 2
: y  x  2x . Phương trình tiếp tuyến của C tại điểm M có hoành độ 4
x  0, biết y x  1 là: 0  0 5 1 A. y  3x  2. B. y  3x 1. C. y  3x  . D. y  3x  . 4 4 Câu 9. Cho hàm số C 3
: y  x  3x  2 . Phương trình tiếp tuyến của C biết hệ số góc của tiếp tuyến đó bằng 9 là: y  9x 14 y  9x 15 y  9x 1 y  9x 8 A.  . B.  . C.  . D.  . y  9x 18  y  9x 11  y  9x  4  y  9x  5 
Câu 10. Tiếp tuyến của đồ thị hàm số 3 2
y  x  3x  2 có hệ số góc k  3  có phương trình là A. y  3x  7 . B. y  3x  7 . C. y  3x 1. D. y  3x 1. 1
Câu 11. Tiếp tuyến của đồ thị hàm số 4 2
y   x  2x có hệ số góc bằng x  2 y  9  0 có phương 4 trình là A. y  48x 192 . B. y  48x 160 . C. y  48x 160 . D. y  48x 192 . x  3
Câu 12. Viết phương trình tiếp tuyến của đồ thị hàm số y 
biết tiếp tuyến có hệ số góc bằng 4. 1 x y  4x  3 y  4x  3 y  4x  3 y  4x  3 A.  . B.  . C.  . D.  . y  4x 13  y  4x 13  y  4x 13  y  4x 13 
Câu 13. Có bao nhiêu tiếp tuyến của đồ thị hàm số 3 2
y  x  2x song song với đường thẳng y  x ? A. 2. B. 1. C. 3. D. 4.
Câu 14. Tiếp tuyến song song với đường thẳng y  36x  5 của đồ thị hàm số 4 2 y  x  x  2 có
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 87 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU phương trình là A. y  36x  54 . B. y  36x  54 . C. y  36x  90 . D. y  36x  90 . Câu 15. 2x 1 Cho hàm số C: y 
 Viết phương trình tiếp tuyến của C biết tiếp tuyến song x  2
song với đường thẳng có phương trình  : 3x  y  2  0 . A. y  3x  2. B. y  3x 14 C. y  3x  5. D. y  3x  8. Câu 16. Cho hàm 3
y  2x  3x 1 có đồ thị là (C) . Tiếp tuyến của đồ thị (C) vuông góc với đường
thẳng x  21y  2  0 có phương trình là:  1  1  y  x  33 y  x  33 y  2  1x  33 y  21x  33 A.  21  21  . B.  . C.  . D. . 1   y  2  1x  31 y  21x  31 1 y   x  31   y  x  31   21   21
Câu 17. Tiếp tuyến của đồ thị hàm số 4 2
y  x  2x 3 vuông góc với đường thẳng x  8y  2017  0 có phương trình là 1 1 A. y   x  8 . B. y  8x  8 . C. y  8x 8. D. y  x  8. 8 8 2x  2
Câu 18. Phương trình tiếp tuyến của đồ thị hàm số y 
biết tiếp tuyến vuông góc với đường x  2 thẳng y  6x 1 là  1 1  1 1 y   x  y  x  1 1 1 A. y  6 3  6 3  x  . B. y  x 1 . C. . D. . 6 3 6  1   1 13 y   x 1 y  x    6   6 3 Câu 19. Cho hàm số C 3
: y  4x  3x 1. Viết phương trình tiếp tuyến của C biết tiếp tuyến đi
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 88 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU qua điểm A1;  2 . y  9  x  7 y  4x  2 y  x  7 y  x  5 A.  . B.  . C.  . D.  . y  2  y  x 1  y  3x  5  y  2x  2  Câu 20. Cho hàm số 3 2
y  x  6x  3x 1 có đồ thị (C). Trong các tiếp tuyến của (C), tiếp tuyến có hệ
số góc lớn nhất có phương trình là A. y  15x  55 . B. y  15x  5 . C. y  15x  5 . D. y  15x  55 . Câu 21. Cho hàm số 3 2
y  x  3x  6x 1 có đồ thị (C). Trong các tiếp tuyến của (C), tiếp tuyến có hệ số
góc nhỏ nhất có phương trình là A. y  3x  2 B. y  3x  2 C. y  3x 8 D. y  3x  8
Câu 22. Đường thẳng y  ax  b tiếp xúc với đồ thị hàm số 3 2
y  x  2x  x  2 tại điểm M 1;  0 . Khi đó ta có: A. ab  36 B. ab  6  C. ab  3  6 D. ab  5  Câu 23. Cho hàm số C 3
: y  4x  3x 1. Viết phương trình tiếp tuyến của C biết tiếp tuyến đi qua điểm A1;  2 . y  9  x  7 y  4x  2 y  x  7 y  x  5 A.  . B.  . C.  . D.  . y  2  y  x 1  y  3x  5  y  2x  2  Câu 24. Cho hàm số 3 2
y  x  3mx m  
1 x 1 có đồ thị (C). Với giá trị nào của m thì tiếp tuyến với
đồ thị (C) tại điểm có hoành độ bằng –1 đi qua A1;  3 ? 7 1 1 7 A. m  B. m  C. m   D. m   9 2 2 9
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 89 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU Câu 25. Cho hàm số: 3 2 y  2
 x  6x  5. Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến đi qua điểm ( A 1; 13). y  6x  7 y  6  x  7 y  6x  7 y  6x  7 A.  B.  C.  D.  y  4  8x  61  y  48x  61  y  4  8x  61  y  4  8x  61  Câu 26. 2x 1 Cho hàm số: y 
 Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến đi qua x 1 điểm A(1; 4). 1 13 1 13 1 13 1 13 A. d : y  x   B. d : y   x   C. d : y   x   D. d : y  x   3 3 3 3 3 3 3 3 Câu 27. Cho hàm số: 4 2
y  x  2x 1. Có bao nhiêu tiếp tuyến đi qua điểm M (0; 1  ) ? A. 1. B. 2. C. 3. D. 4. Câu 28. 2x 1 Cho hàm số y 
. Viết phương trình tiếp tuyến với (C), biết tiếp tuyến đó đi qua điểm x 1 ( A 1;3). 1 13 1 13 1 13 1 13 A. y  x  . B. y   x  . C. y  x  . D. y   x  . 4 4 4 4 4 4 4 4 Câu 29. 1 x Cho hàm số: y 
 Viết phương trình tiếp tuyến với (C), biết tiếp tuyến đi qua giao 2x 1
điểm của đường tiệm cận và trục hoành Ox? 1 1 1 1 A. d : y  x   B. d : y   x   12 24 12 24 1 1 1 1 C. d : y  x   D. d : y   x   12 24 12 24
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 90 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU Câu 30. 1 3 Cho hàm số: 3 2
y  x  x  5. Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến 4 2
cắt trục tung tại điểm có tung độ bằng 5. y  5 y  5  9  9 A.  9 . B. y   x  5 C.  9 . D. y   x  5 . y   x  5 4 y   x  5 4  4  4
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 91 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU ĐÁP ÁN Đáp Đáp Đáp Đáp Đáp Câu Câu Câu Câu Câu án án án án án 1 D 7 C 13 B 19 A 25 C 2 D 8 C 14 A 20 A 26 D 3 C 9 A 15 B 21 B 27 C 4 A 10 D 16 C 22 A 28 A 5 A 11 B 17 C 23 A 29 B 6 B 12 D 18 D 24 B 30 A PHẦN 2: HÌNH HỌC VẤN ĐỀ 1 GÓC TRONG KHÔNG GIAN
DẠNG 1: GÓC GIỮA HAI ĐƯỜNG THẲNG 1. Phương pháp
 Nếu a và b song song hoặc trùng nhau thì góc giữa chúng bằng 0 0 .
 Nếu a và b cắt nhau thì góc giữa chúng là góc nhỏ nhất trong các góc được tạo bởi hai đường thẳng.
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 92 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
 Góc giữa hai đường thẳng chéo nhau a và b là góc
giữa hai đường thẳng a và b cùng đi qua một điểm
và lần lượt song song (hoặc trùng) với a và b . a // a Tức là:   a,b   a,b . b // b  Chú ý:  0  a b  0 0 ,  90 .
 Để xác định góc giữa hai đường thẳng, ta có thể lấy
một điểm (thuộc một trong hai đường thẳng đó) từ
đó kẻ đường thẳng song song với đường còn lại.
Ví dụ: Để tính AB CD  , . Ta kẻ AE // CD. Khi đó: AB CD  AB AE   , ,  BA . E   
Nếu u , u lần lượt là hai vectơ chỉ phương của hai đường thẳng a và b thì: 1 2        a,b  u ,u   0 khi  90 1 2   . 0 0 180  khi    90 u .u   Tức là: cosa,b   cosu ,u   1 2    . 1 2 u . u 1 2 2. Ví dụ minh họa
Ví dụ 1: Cho tứ diện đều ABCD có cạnh bằng a, M là trung điểm của cạnh BC. Gọi
 là góc giữa hai đường thẳng AB và DM, khi đó cos bằng A. 3 . B. 2 . C. 3 . D. 1 . 6 2 2 2 Lời giải:
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 93 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Gọi N là trung điểm của AC
 MN là đường trung bình của A  BC MN // AB    1 . MN   AB  2 Vì B  CD và A
 CD là các tam giác đều cạnh bằng a 3 a  MD  ND  . 2
Vì MN AB    AB DM   MN DM  // , , . Xét M  ND , ta có:  2 2 2 cos MN  MD  ND NMD  2MN.MD 2 2 2
 a   a 3   a 3          2  2   2        1 3     0 a a 3 2 3 6 2. . 2 2   0 NMD  90  MN,DM    NMD. Vậy    3 cos cos NMD   Chọn đáp án A. 6 Ví dụ 2: Cho hình chóp .
S ABCD, có đáy ABCD là hình vuông tâm O, cạnh bằng a;
SA vuông góc với đáy và SA  a 3 . Khi đó, cosin góc giữa SB và AC bằng A. 2 . B. 2 . C. 3 . D. 3 . 2 4 2 4 Lời giải:
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 94 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Gọi I là trung điểm của SD
 OI là đường trung bình của S  BD O  I // SB   2 2 2 2  . SB SA  AB 3a  a O  I     a  2 2 2 Vì OI SB  SB AC   OI AC    // , , AOI. 2 2 2 2   Ta có: SD SA AD 3a a AI     . a 2 2 2  AI  OI  A  OI cân tại I .
Gọi H là trung điểm của OA  IH  OA Và OA AC a 2 OH    . 2 4 4 a 2 Xét O OH 4 2  HI , ta có:  cos HOI    . OI a 4 Vậy SB AC    2 cos , cos HOI   Chọn đáp án B. 4 Chú ý: Để tính 
cos AOI ta có thể tính cách khác như sau: 2  a 2  2 2    a  a    2 2 2 OA  OI  AI 2   2 cos AOI    . 2O . A OI a 2 4 2. .a 2 Ví dụ 3: Cho hình chóp .
S ABCD, có đáy ABCD là hình thang vuông tại A và D; cạnh
AB  2a , AD  DC  a ; SA  AB , SA  AD và 2a 3 SA  . 3
a) Góc giữa đường thẳng SB và DC bằng A. 0 30 . B. 0 45 . C. 0 60 . D. 0 75 .
b) Gọi  là góc giữa SD và BC. Khi đó, cos bằng A. 3 . B. 42 . C. 42 . D. 3 . 14 14 28 28 Lời giải:
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 95 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU a) Vì DC // AB  SB DC   SB AB    , , SB . A (vì S  AB vuông tại A   0 SBA  90 ). Xét S
 AB vuông tại A, ta có: 2a 3  SA 3 3      0 tanSBA SBA  30 . AB 2a 3 Vậy SB DC    0 , SBA  30 .  Chọn đáp án A.
b) Gọi E là trung điểm của AB.
Khi đó, BCDE là hình bình hành  DE BC  SD BC   SD DE  // , ,  . 2 2 4a 7a   7 2 2 2 2 2 S  E  SD  SA  AD   a  S  E  SD  a Ta có  3 3   3 .  2 2 DE 2a   DE  a 2
Áp dụng định lí hàm cosin trong tam giác SDE, ta được:  2 2 2 2 SD  DE SE 2a 3 42  0 cosSDE      0  SDE  90 . 2S . D DE 7 14 14 2.a .a 2 3 Vậy SD BC   SD DE    , , SDE  .  42  cos  cosSDE   Chọn đáp án B. 14
DẠNG 2: GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG 1. Phương pháp
 Nếu đường thẳng a vuông góc với mặt phẳng P thì góc giữa đường thẳng a và mặt phẳng P bằng 0 90 .
Tức là: a  P  a P  0 ,  90 .
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 96 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
 Nếu đường thẳng a không vuông góc với mặt phẳng
P thì góc giữa đường thẳng avà hình chiếu a của
nó trên P gọi là góc giữa đường thẳng a và mặt phẳng P .
Tức là: Nếu a  P và a là hình chiếu của a trên P thì a P  a a  , ,  . Chú ý:  0  a P  0 0 ,  90 . a // P  Nếu   a, P   0  0 . a   P  
 Để tìm hình chiếu a của a trên P ta có thể làm như sau:
Tìm giao điểm M  a  P.
Lấy một điểm A tùy ý trên a và xác định hình chiếu H của A trên P . Khi đó,
a là đường thẳng đi qua hai điểm A và M.
2. Một số loại góc giữa đường thẳng và mặt phẳng thường gặp đối với hình chóp
Góc giữa cạnh bên và mặt đáy
H là hình chiếu vuông góc của S trên ABCD
 HD là hình chiếu vuông góc của SD trên ABCD Vậy SD ABCD   SD HD    , , SDH .
Góc giữa cạnh bên và mặt đứng
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 97 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Dựng CE  HD E HD . C  E  HD Vì   CF  SDH. CE   SH
 E là hình chiếu vuông góc của C trên SHD
 SE là hình chiếu vuông góc của SC trên SHD. Vậy SC SHD   SC SE    , , CSE .
Góc giữa đường cao và mặt bên Dựng HE  CD ECD C  D  HE Vì   CD  SHE. CD   SH  SCD  SHE
Mà SCD SHE  S . E
 SE là hình chiếu vuông góc của SH trên SAD. Vậy SH SAD  SH SE    , , HSE . 3. Ví dụ minh họa Ví dụ 1: Cho hình chóp .
S ABCD , có đáy ABCD là hình vuông cạnh bằng a; SA a 6
vuông góc với đáy và SA 
. Gọi  là góc giữa SC và ABCD , khi đó số đo góc 3  bằng A. 0 30 . B. 0 45 . C. 0 60 . D. 0 75 . Lời giải:
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 98 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Vì SA  ABCD  AC là hình chiếu vuông
góc SC lên mặt phẳng ABCD.
Do đó:   SC ABCD   SC AC    , , SC . A
(vì SAC vuông tại A   0 SCA  90 ). Xét S
 AC vuông tại A, ta có: a 6  SA 3 3        0 tanSCA SCA  30 . AC a 2 3  Chọn đáp án A. Ví dụ 2: Cho hình chóp .
S ABC , có đáy ABC là tam giác đều cạnh bằng a; SA vuông
góc với đáy và SA  2a . Gọi  là góc giữa SC và mặt phẳng SAB , khi đó tan
nhận giá trị nào trong các giá trị sau 3 51 4 3 2 3 A. . B. . C. . D. . 17 17 17 17 Lời giải:
Gọi M là trung điểm của AB  CM  A . B C  M  AB  Vì   S  A    ABC  CM  SA do     CM     ABC
 CM  SAB  SM là hình chiếu vuông góc của SC trên SAB.
Khi đó:   SC SAB  SC SM    , , CSM. C  M   SAB (vì   CM  SM  S  CM vuông SM   SAB tại   0 S CSM  90 ). a 3 CM CM 2 51 Xét S
 CM vuông tại S, ta có:  tanCSM     . 2 2 2 SM SA  AM a 17 2 4a  4 Vậy  51 tan  tanCSM   Chọn đáp án B. 17
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 99 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU Ví dụ 3: Cho hình chóp .
S ABC , có đáy ABC là tam giác vuông tại A; BC  a và a 3 SA  SB  SC 
. Góc giữa đường thẳng SA và ABC bằng 3 A. 0 30 . B. 0 45 . C. 0 60 . D. 0 90 . Lời giải:
Gọi H là trung điểm của BC.
Vì ABC vuông tại A nên H là tâm đường
tròn ngoại tiếp ABC và BC a AH   . 2 2
Mà SA  SB  SC  SH là trục của đường tròn
ngoại tiếp ABC  SH  ABC .
 HA là hình chiếu của SA trên ABC  SA ABC  SA HA   , ,  SAH.
(vì SHA vuông tại H nên  0 SAH  90 ). a
Xét SHA vuông tại H, ta có:  AH 2 3  0 cosSAH     SAH  30 . SA a 3 2 3 Vậy SA ABC    0 ,
SAH  30  Chọn đáp án A.
DẠNG 3: GÓC GIỮA 2 MẶT PHẲNG 1. Phương pháp
Để xác định góc giữa hai mặt phẳng P và Q, ta có thể thực hiện theo một trong các cách sau: Cách 1: Theo định nghĩa a   P    P Q    a b  , , . b   Q    
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 100 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Cách 2: Khi xác định được P Q  c thì ta làm như sau:
 Bước 1: Tìm mặt phẳng R  c. p  R  P  Bước 2: Tìm  q  R  Q Khi đó:  P Q  p q  , , .
Đặc biệt: Nếu xác định được 2 đường thẳng p,q P  p   c sao cho:    P Q    p q  , , . Q        q   c
Ví dụ: Góc giữa mặt bên và mặt đáy. Dựng HE  CD ECD C  D  HE Vì 
 CD  SHD  CD  S . E CD   SH
SCDABCD  CD  Vì C   D  HE   ABCD C  D  SE   SCD   SCD ABCD   SE HE    , , SEH .
Cách 3: Theo định lí về hình chiếu    .cos  cos S S S   S 2. Ví dụ minh họa
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 101 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Ví dụ 1: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy bằng a, chiều cao hình a 3 chóp bằng
. Góc giữa mặt bên và mặt đáy là 2 A. 0 30 . B. 0 45 . C. 0 60 . D. 0 75 . Lời giải:
Gọi O là tâm của hình vuông ABCD và E là trung điểm của CD.
 OE là đường trung bình của A  CD O  E // AD    1 a . OE  AD   2 2 Vì O E // AD OE  C . D C  D  OE Vì 
 CD  SOE  CD  S . E CD   SO
ABCDSCD CD  Vì S  E  CD   ABCD SCD   SE OE    , , SE . O O  E  CD  a 3 Xét S
 EO vuông tại O, ta có:  SO 2      0 tanSEO 3 SEO  60 . OE a 2 Vậy  ABCD SCD    0 ,
SEO  60  Chọn đáp án C.
Ví dụ 2: Cho hình lập phương ABC . D A B  C  D
  có cạnh bằng a. Gọi O là tâm của hình vuông A B  C  D
  và  là góc giữa hai mặt phẳng O A
 B và ABCD . Góc 
thỏa mãn hệ thức nào sau đây? A. 1 cos  . B. tan  2. C. 1 sin  . D. 2 2 1 tan  . 2 Lời giải:
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 102 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Gọi O là tâm của hình vuông ABCD và I là
trung điểm của AB  OI  A . B AB  OI Vì 
 AB  OIO  AB  O I. AB   OO O A  BABCD  AB  Vì O  I  AB O  I  AB    O A  B ABCD   OI OI  , , O IO . Xét O  O
 I vuông tại I , ta có: OO a    tan tanO IO    2. OI a 2  Chọn đáp án B.
Ví dụ 3: Cho hình hình chóp .
S ABC có đáy ABC là tam giác vuông cân tại B và
BA  BC  a ; SA vuông góc với đáy, SA  a . Góc  giữa hai mặt phẳng SAC  và SBC bằng A. 0 30 . B. 0 45 . C. 0 60 . D. 0 75 . Lời giải:
Gọi H là trung điểm của AC  BH  AC. BH  AC  Vì   S  A    ABC  BH  SA do     BH     ABC  BH  SAC  S
 HC là hình chiếu của S  BC lên   S SAC  cos SHC    . SSBC  Ta có: 2 2 AC  BA  BC  a 2. 2 1 1 a 2 a 2 S     S . A HC .a . SHC 2 2 2 4 BC  AB   Vì  BC  SA  do SA   ABC
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 103 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
 BC  SAB  BC  SB  SBC vuông tại B. 2 1 1 a 2 Khi đó: 2 2 S      S . B BC . a a .a . SBC 2 2 2 2 a 2 S Vậy SHC 4 1 0 cos  
    60  Chọn đáp án C. 2 SSBC a 2 2 2
Bình luận: Trong bài toán trên, ta dễ dàng xác định được giao tuyến SC  SAC  SBC
nhưng lại gặp khó khăn trong việc tìm một mặt phẳng vuông góc với SC, mất nhiều thời gian
tính toán,. . không phù hợp với yêu cầu tốc độ của hình thức thi trắc nghiệm. Đồng thời nhận
thấy rằng việc xác định hình chiếu của B lên SAC  và tính diện tích của hai tam giác SHC ; S
 BC là khá dễ dàng nên ta vận dụng cách 3 trong nội dung phương pháp đã trình bày ở trên
để giải quyết nhanh bài toán.
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 104 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT MẶT PHẲNG 1. Phương pháp
Khoảng cách từ điểm M đến mặt phẳng P là
MH, với H là hình chiếu vuông góc của M trên mặt phẳng P. MHP   dM, P   MH H P  
Phương pháp giải chung: Muốn tìm khoảng cách từ một điểm đến một mặt phẳng, trước
hết ta phải tìm hình chiếu vuông góc của điểm đó trên mặt phẳng. Việc xác định hình chiếu
của điểm trên mặt phẳng ta thường dùng một trong các cách sau: Cách 1:
 Bước 1: Tìm một mặt phẳng Q chứa M và vuông góc với P .
 Bước 2: Xác định giao tuyến:   P  Q.
 Bước 3: Trong Q , dựng MH  , H  . P  Q 
Vì   P Q  MH  P Q  MH     d M,P  MH Cách 2:
Nếu đã biết trước một đường thẳng d  P thì ta
sẽ dựng Mx // d , khi đó: H  Mx  P là hình
chiếu vuông góc của M trên P .  d M,P  MH
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 105 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU Cách 3:
Dựa vào tính chất trục của tam giác: Cho ABC nằm
trên P , nếu MA  MB  MC thì hình chiếu
vuông góc của điểm M trên P chính là tâm O
của đường tròn ngoại tiếp ABC .
Khi đó: MO  P  dM,P  MO.
KHOẢNG CÁCH DỰNG TRỰC TIẾP
Khoảng cách từ chân đường cao tới mặt bên
Bài toán: Cho hình chóp có đỉnh S có hình chiếu vuông
góc lên mặt đáy là H . Tính khoảng cách từ điểm H đến mặt bên SAB .
 Kẻ HI  AB, I  AB.
 Kẻ HK  SI , K SI SH.HI
Khi đó: dH,SAB  HK  . 2 2 SH  HI
Khoảng cách từ một điểm trên mặt đáy tới mặt
đứng (chứa đường cao)
Bài toán: Cho hình chóp có đỉnh S có hình chiếu vuông
góc lên mặt đáy là H . Tính khoảng cách từ điểm A
bất kì đến mặt bên SHB .  Kẻ AK  H . B AK  HB    AK  SHB AK   SH
 dA,SHB  AK.
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 106 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Khối chóp có các cạnh bên bằng nhau
Cho hình chóp có đỉnh S có các cạnh bên có độ dài bằng
nhau: SA  SB  SC  SD (đáy có thể là bốn đỉnh hoặc
ba đỉnh). Khi đó nếu như O là tâm đường tròn ngoại
tiếp đi qua các đỉnh nằm trên mặt đáy thì SO là trục
đường tròn ngoại tiếp của đa giác đáy hay nói cách
khác: SO  ABCD  dS,ABCD  SO. Chú ý: Nếu đáy là:
 Tam giác đều, O là trọng tâm.
 Tam giác vuông, O là trung điểm cạnh huyền.
 Hình vuông, hình chữ nhật, O là giao của 2
đường chéo đồng thời là trung điểm mỗi đường.
TÍNH KHOẢNG CÁCH BẰNG CÁCH GIÁN TIẾP
Giả sử ta ta muốn dựng trực tiếp khoảng cách từ điểm A tới mặt phẳng P mà không thực
hiện được. Đồng thời từ điểm B ta lại dựng được trực tiếp khoảng cách tới P khi đó ta sẽ
thực hiện tính khoảng cách gián tiếp như sau:
Cách 1 (Đổi điểm): Tính thông qua tỉ số khoảng cách. AB  P
 dA,P  dB,P
ABP  I dA,P AI   dB,P BI
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 107 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Cách 2 (Đổi đỉnh): Sử dụng phương pháp thể tích để tìm khoảng cách:
Bài toán tính khoảng cách từ một điểm đến một mặt phẳng trong nhiều trường hợp có
thể qui về bài toán thể tích khối đa diện. Việc tính khoảng cách này dựa vào công thức: 3V  h 
: V, S, h lần lượt là thể tích, diện tích đáy và chiều cao của hình chóp. S V  h 
: V, S, h lần lượt là thể tích, diện tích đáy và chiều cao của hình lăng trụ. S
Phương pháp này áp dụng được trong trường hợp sau: Giả sử có thể qui bài toán tìm khoảng
cách về bài toán tìm chiều cao của một hình chóp (hoặc một lăng trụ) nào đó. Dĩ nhiên, các chiều cao
này thường là không tính được trực tiếp bằng cách sử dụng các phương pháp thông thường như
định lí Pitago, công thức lượng giác,… Tuy nhiên, các khối đa diện này lại dễ dàng tính được thể tích
và diện tích đáy. Như vậy, chiều cao của nó sẽ được xác định bởi công thức đơn giản trên. 2. Ví dụ minh họa Ví dụ 1: Cho hình chóp .
S ABCD có đáy ABCD là hình chữ nhật với AD  2a ; SA
vuông góc với đáy và SA  a . Khoảng cách từ A đến mặt phẳng SCD bằng 3a 2 2a 3 2a 3a A. . B. . C. . D. . 2 3 5 7 Lời giải:
Trong SAD , kẻ AH  SD, H SD. C  D  AD Vì 
 CD  SAD AHSAD CD  AH. CD   SA AH  SD Vì   AH  SCD AH   CD     S . A AD . a 2 , a d A SCD  AH   2 2 2 2 SA  AD a  4a a  dA SCD 2 ,   Chọn đáp án C. 5
Ví dụ 2: Cho hình chóp tam giác đều .
S ABC có cạnh đáy bằng 2a và chiều cao bằng
a 3 . Khoảng cách từ tâm O của đáy ABC đến một mặt bên bằng a 5 2a 3 3 2 A. . B. . C. a . D. a . 2 3 10 5 Lời giải:
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 108 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Vì O là tâm của đáy của hình chóp tam giác đều .
S ABC nên SO  ABC  SO  a 3.
Gọi M là trung điểm của BC . AM  BC
Vì ABC đều cạnh bằng 2a    . 2a 3 AM   a 3  2 1 a 3 Khi đó OM  AM  . 3 3 BC  AM Vì 
 BC  SAM  SBC  SAM. BC   SO
Trong SAM  , kẻ OH  SM, H SM. SAM  SBC 
Vì SAMSBC  SM  OH  SBC  dO,SBC  OH.  SAM   OH   SM Xét S
 OM vuông tại O có đường cao OH , ta có: a 3 a 3. dO,SBC O . S OM 3 3  OH    a  Chọn đáp án C. 2 2 OS OM    a  2 10 2 a 3 3     3   
Ví dụ 3: Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy bằng a và chiều cao bằng
a 2 . Khoảng cách từ tâm O của đáy ABCD đến một mặt bên bằng a 3 a 2 2a 5 a 5 A. . B. . C. . D. . 2 3 3 2 Lời giải:
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 109 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Vì O là tâm của đáy của hình chóp tứ giác đều .
S ABCD nên SO  ABCD  SO  a 2. O  M  CD
Gọi M là trung điểm của CD    BC a . OM    2 2
Trong SOM , kẻ OH  SM, H SM.         . , OS OM OH SCD d O SCD  OH  2 2 OS OM 2. a a Vậy dO,SCD 2 a 2    Chọn đáp án B.   2 2 3 2  a a    2   Ví dụ 4: Cho hình chóp .
S ABCD có đáy là hình chữ nhật với AD  2a,AB  a . SAD
là tam giác cân và nằm trong mặt phẳng vuông góc với đáy. Gọi H là hình chiếu
vuông góc của S trên mặt phẳng đáy. Khoảng cách từ C đến mặt phẳng SHB bằng a 2 a 3 A. a 2. B. a 3. C. . D. . 2 2 Lời giải:
Gọi H là trung điểm của AD  SH  A . D SAD  ABCD 
Vì SADABCD  AD  SH  ABCD.  SAD  SH   AD
Dễ thấy rằng ABH vuông cân tại A và và C  DH vuông cân tại D.     0    0 AHB CHD 45 BHC  90  CH  HB. C  H  HB  Vì    S
 H  ABCD   CH  SHB CH  SH do     CH     ABCD Suy ra dC SHB 2 2 ,
 CH  CD  DH  a 2  Chọn đáp án A.
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 110 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU Ví dụ 5: Cho hình chóp .
S ABC có đáy ABC là tam giác vuông tại A ,  0 ABC  30 ,
tam giác SBC là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với đáy.
Khoảng cách từ điểm C đến mặt phẳng SAB bằng a 39 a 39 a 13 a 13 A. . B. . C. . D. . 26 13 13 26 Lời giải:
Gọi H là trung điểm của SBC  ABC 
Vì SBCABC  BC  SH  ABC.  SBC  SH   BC dC, SAB  CB Vì CH SAB    B    2 dH,SAB HB
 dC,SAB  2dH,SAB. Gọi E là trung điểm của AB  HE // AC  HE  A . B
Trong SHE , kẻ HK  SE, K SE 1 AB  HE HK  SHE Vì   AB  SHE     AB  HK 2 AB   SH
Từ 1 và 2  HK  SAB  dH,SAB  HK.  a 3 S  H  Ta có:  2  .   AC BC.sin ABC a HE     2 2 4 Xét S
 HE vuông tại H có đường cao HK , ta có: SH.HE a 39 HK   . 2 2 SH  HE 26 a
Vậy dC SAB  dH SAB 39 , 2 ,  2HK   Chọn đáp án B. 13
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 111 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU Ví dụ 6: Cho hình chóp .
S ABCD có đáy ABCD là hình chữ nhật với AB  a ,
AD  2a ; cạnh bên SA  a và vuông góc với đáy. Khoảng cách từ điểm A đến mặt phẳng SBD bằng 2a 3 a a 3 A. . B. 2a 2 5 . C. . D. . 3 3 5 2 Lời giải:
Trong ABCD , kẻ AE  BD, E BD.
Trong ABCD , kẻ AH  SE, H SE 1 BD  SA Vì 
 BD  SAE  BD  AH 2 BD   AE
Từ 1 và 2  AH  SBD  dA,SBD  AH. Xét A
 BD vuông tại A có đường cao AE, ta có: A . B AD .a2a 2a AE    . 2 2 2 2 AB  AD a  4a 5 Xét S
 AE vuông tại A có đường cao AH , ta có: 2 . a a SA.AE 5 2a AH    . 2 2 2 SA  AE 3   2 2a a     5  Vậy    2 , a d A SBD  AH   Chọn đáp án B. 3
Ví dụ 7 [Trích Đề Minh Họa – 2017]: Cho hình chóp tứ giác S.ABCD có đáy là hình
vuông cạnh bằng a 2 . Tam giác SAD cân tại S và mặt bên SAD vuông góc với mặt
phẳng đáy. Biết thể tích khối chóp S.ABCD bằng 4 3
a . Tính khoảng cách h từ B đến mặt 3 phẳng SCD. A. 2 h  .a B. 4 h  .a C. 8 h  .a D. 3 h  .a 3 3 3 4 Lời giải:
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 112 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Gọi I là trung điểm của AD, vì SAD cân tại
S nên SI  AD  SI  ABCD. 1  V  .SI.S S.ABCD 3 ABCD 4 3 3. a 3VS.ABCD 3  SI    a SABCD a 2 2 . 2
Trong SAD , dựng IH  SD, H SD. C  D  AD Vì 
 CD  SAD  CD  IH. CD   SI IH  SD Vì 
 IH  SCD  dI,SCD  IH. IH   CD AI  SCD    D //     ,    ,  AD AB SCD d B SCD
d A SCD  .dI,SCD  2IH. HD
Xét SID vuông tại I có đường cao IH , ta có: a 2 .2 . . a ID IS ID IS 2 2a IH     . 2 2 2 2 2 ID  IS ID  IS a 3 2  4a 2 Vậy    4 ,  2 a d B SCD IH   Chọn đáp án B. 3
Bình luận: Thông thường khi tính khoảng cách từ điểm đến mặt ta có 3 hướng đi chính: Đổi
điểm, đổi đỉnh và đổi sang hình học tọa độ không gian (phương pháp tọa độ hóa). Nếu đi theo
hướng giải đổi điểm là đổi gián tiếp từ B sang A rồi sang H (như lời giải trên) sẽ mất nhiều thời
gian không đáp ứng được yêu cầu về tốc độ thi theo hình thức trắc nghiệm. Đồng thời khi nhận
ra đề bài cho thể tích V của khối chóp S.ABCD cho trước bạn nên dùng phương pháp đổi đỉnh sẽ phù hợp hơn. Cụ thể: VS ABCD 3 4 . 3 3. . a d V B,SCD 2 3 a a S BCD 2 2 3 4 4 .      . S 1 1 2 2 2 3 SCD S . D CD .a 2. SI  ID   2 2  a2 a 2 2. 2     2   
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 113 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Ví dụ 8: Cho lăng trụ tam giác đều AB . C A B  C
  có AA  a , AB  a . Gọi M là trung điểm của B C
  . Khoảng cách từ A tới mặt phẳng A B  C  bằng 2a 21 2a 7 a 21 a 21 A. . B. . C. . D. . 7 7 7 21 Lời giải: AI  BC
Gọi I là trung điểm của BC    . AB 3 a 3 AI    2 2
Trong AA I , kẻ AH  A I, H  A I . BC  AI Vì 
 BC  AA I  A B  C  AA I. BC   AA A B  C  AA I  Vì A B
 C AA I  A I  AH  A B  C   AA I   AH   A I a 3 . a   dA,A B  C AA .AI 2 a 21  AH     Chọn đáp án C. 2 2 2 AA  AI 7   2 a 3 a     2   
Ví dụ 9: Hình hộp đứng ABC . D A B  C  D
  có đáy là hình thoi cạnh a, góc  0 BAD  60
đồng thời AA  a . Gọi G là trọng tâm tam giác BCD. Khoảng cách từ G tới mặt phẳng A B  D  bằng 2a 21 2a 7 a 21 a 21 A. . B. . C. . D. . 7 7 7 21 Lời giải:
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 114 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU dG, A B  D  GO 1 Vì AG A B  D      O    dA,A B  D AO 3  dG A B  D 1 ,  dA,A B  D. 3 BD  AC Vì   BD  AA O    A B  D  AA O  . BD   AA Trong AA O   , kẻ AH  A O  , H  A O  . A B  D  AA O    Vì A B  DAA O    A O   AH  A B  D      AA O AH A O      AA . , AO d A A BD  AH  . 2 2 AA  AO a 3 Tam giác ABD cân có  0
BAD  60  ABD đều có cạnh bằng a  AO  2 d a A, A B  D  3 . AA . a  AO  2 a 21 Vậy dG,A BD       . 2 2 2 3 3 AA  AO 21   2 a 3 3 a     2     Chọn đáp án D. Ví dụ 10: Cho hình chóp .
S ABCD có đáy ABCD là hình vuông cạnh a; 3a SD  ; 2
hình chiếu vuông góc của S trên ABCD trùng với trung điểm H của cạnh AB. dH,SDC Khi đó, tỉ số bằng a 2 3 2 3 3 3 A. . B. . C. . D. . 2 2 2 2 Lời giải:
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 115 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Theo đề bài, ta có: SH  ABCD. HI  a
Gọi I là trung điểm của CD   . HI   CD C  D  HI Vì 
 CD  SHI  SCD  SHI. CD   SH
Trong SHI  , kẻ HK  SI, K SI. SCD  SHI 
Vì SCDSHI  SI  HK  SCD  SHI   HK   SI SH.HI
Suy ra: dH,SCD  HK  . 2 2 SH  HI 2 2 Ta có: 2 2 2  a  2 5a HD  AH  AD   a     2  4 2 2 2 2  3a  5a  SH  SD  HD      .a  2  4 Do đó: dH SCD SH.HI . a a a 2 ,  HK    . 2 2 2 2 SH  HI a  a 2 d a H,SDC 2 2 2 Vậy    Chọn đáp án A. a a 2
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 116 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU 1. Phương pháp
a) Đường vuông góc chung của hai đường thẳng chéo nhau
Đường thẳng  cắt hai đường thẳng a, b và cùng
vuông góc với mỗi đường ấy gọi là đường vuông
góc chung của a và b. Đoạn thẳng MN gọi là
đoạn vuông góc chung của a và b.
b) Một số hướng tính khoảng cách giữa hai đường thẳng chéo nhau TH1: Khi , a b chéo nhau và a  .b
+ Bước 1: Dựng mặt phẳng P chứa b và vuông góc với a tại M.
+ Bước 2: Trong P dựng MN  b tại N .
+ Bước 3: Đoạn MN là đoạn vuông góc chung
của a và b  da,b  MN . . TH2: Khi , a b chéo nhau và a  .b
Mục tiêu: Chuyển về khoảng cách từ một điểm đến một mặt phẳng.
 Hướng 1: Chuyển thông qua khoảng cách từ
một đường đến một mặt phẳng.
 Bước 1: Dựng mặt phẳng P chứa b và song song với a. a// P
 Bước 2: da,b da,P b  P M a
 dM,P
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 117 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
 Hướng 2: Chuyển thông qua khoảng cách giữa mặt phẳng song song.
 Bước 1: Dựng hai mặt phẳng P , Q
sao cho a  P // Q  b .  Bước 2: Khi đó
da,b  d P,Q  dM,Q 2. Ví dụ minh họa Ví dụ 1: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a. Đường thẳng SA
vuông góc với mặt phẳng đáy, SA  a . Khoảng cách giữa hai đường thẳng SB và CD bằng A. . a B. a 2. C. a 3. D. 2 .a Lời giải Vì CD // SAB
 dCD,SB  dCD,SAB  dD,SAB. Vì DA  AB 
 DA  SAB  dD,SAB  DA  .a DA   SA
Vậy dCD,SB  dD,SAB  .a  Chọn đáp án A.
Ví dụ 2: Cho tứ diện đều ABCD có cạnh bằng a. Khoảng cách giữa hai đường thẳng AB và CD bằng a 3 a 2 a 2 a 3 A. . B. . C. . D. . 2 3 2 3 Lời giải
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 118 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Gọi M , N lần lượt là trung điểm của AB và C . D Vì BCD và A
 CD là các tam giác đều cạnh bằng AN  CD a a 3 nên AN  BN  và  * 2 BN   CD   
 CD  ABN MN ABN *
CD  MN 1
Mặt khác, vì AN  BN  A  BN cân tại N  MN  AB 2
Từ 1 và 2  MN là đoạn vuông góc chung của AB và CD . Do đó: dAB CD 2 2 ,  MN  AN  AM 2 2  a 3   a  a 2        .  2     2  2 a Vậy dAB CD 2 ,   Chọn đáp án C. 2 Ví dụ 3: Cho hình chóp .
S ABC có đáy là tam giác đều cạnh a. Hình chiếu của S trên
ABC trùng với trung điểm của BC. Biết SA hợp với đáy một góc 0 30 . Khi đó,
khoảng cách giữa hai đường thẳng SA và BC bằng a 3 a 3 a 2 2a 2 A. . B. . C. . D. . 2 4 3 3 Lời giải
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 119 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Gọi H là trung điểm của BC  SH  ABC  SH  BC 1 AH  BC 2  Vì ABC đều   a 3 AH   2
Từ 1 và 2  BC  SAH  .
Trong SAH  , kẻ HK  SA, K SA 3 BC   SAH Vì   BC  HK 4 HK   SAH   
Từ 3 và 4  HK là đoạn vuông góc chung của SA và BC  dSA,BC  HK.
Vì SH  ABC  HA là hình chiếu của SA trên ABC  SA ABC  SA HA    0 , , SAH  30 . HK a
Xét AHK vuông tại K , ta có:   3 sin HAK   HK  AH.sin HAK  . AH 4 a Vậy dSA BC 3 ,  HK   Chọn đáp án B. 4 Ví dụ 4: Cho hình chóp .
S ABCD có đáy là hình chữ nhật với AD  2AB  2a , cạnh
SA vuông góc với mặt phẳng đáy ABCD và SB tạo với mặt phẳng đáy ABCD một góc 0
60 . Khoảng cách giữa hai đường thẳng AB và SC bằng a 21 2a 21 a 21 a 21 A. . B. . C. . D. . 7 7 14 21 Lời giải
Vì AB // SCD  dAB,SC  dAB,SCD  dA,SCD
Trong SAD , kẻ AH  SD, H SD C  D  AD Vì 
 CD  SAD  CD  AH. CD   SA AH  SD Vì 
 AH  SCD  dA,SCD  AH AH   CD
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 120 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU Ta có: SB ABCD  SB AB    0 , , SBA  60 . Xét S
 AB vuông tại A , ta có:  SA  0 tanSBA   SA  A . B tanSBA  . a tan 60  a 3. AB Vậy dAB SC S . A AD 2 . a a 3 2a 21 ,  AH     Chọn đáp án B. 2 2 2 2 SA  AD 4a  3a 7
Ví dụ 5: Cho hình lăng trụ đứng AB . C A B  C
  có đáy là tam giác vuông tại A với 3dAA,BC
BC  2a , AB  a . Khi đó, tỉ số bằng a A. 9 . B. 3 . C. 2. D. 1. 2 2 Lời giải Vì AA // BBC C  
 dAA,BC  dAA,BBC C
   dA,BBC C  .
Trong ABC , kẻ AH  BC, H  BC. AH  BC Vì   AH  BB C  C   AH   BB       A . , B AC d A BB C C  AH  . 2 2 AB  AC Ta có: 2 2 2 2
AC  BC  AB  4a  a  a 3.  dA BB C  C   A . B AC . a a 3 a 3 ,    . 2 2 2 2 AB  AC a  3a 2 a 3dAA,BC 3dA,BB C  C   3 3. 2 3 Vậy     Chọn đáp án B. a a a 2
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 121 SỐ 8 NGÕ 17
ĐỀ CƯƠNG TOÁN 11 GIỮA KỲ 2 (TÀI LIỆU MẬT) TẠ QUANG BỬU
Ví dụ 6: Cho hình lập phương ABC . D A B  C  D
  có cạnh bằng a. Gọi M, N lần lượt 2 a .dMN, A C  
là trung điểm của AB và CD . Khi đó, tỉ số bằng VA.ABCD 2 2 3 2 2 A. . B. . C. . D. . 4 2 4 3 Lời giải Ta có: 1 1 2 1 3 V         AA .S     . . a a a . A.A B C D 3 A B C D 3 3 Vì MN // A B  C  dMN, A C    dMN,A B  C  dM,A B  C dM, A B  C  MB 1 Vì AM A B  C      B    dA,A B  C AB 2  dM A B  C 1 ,  dA,A B  C. 2 BC   AA B B Trong AA B  B , kẻ AH  A B  , H  A B  . Vì   BC  AH AH   AA B B . AH  A B  Vì   AH  A B  C  dA A B  C 2 2 ,  AH  AB  BH . AH   BC 2 A B  a 2  a 2  a 2 Ta có: 2 BH    AH  a    . 2 2  2  2   1 1 a 2 Khi đó: dMN, A C    dM,A B  C  dA,A B  C  AH  . 2 2 4 a dMN A C   2 a 2 2 a . . , Vậy 4 3 2    Chọn đáp án C. V 1     3 4 A.A B C D a 3
THẦY GIÁO: ĐẠT NGUYỄN TIẾN 122

Phương pháp giải các dạng bài Toán 11 học kỳ 2 – Nguyễn Tiến Đạt

Thông tin :

Tài liệu liên quan:

Đề cương giữa kỳ 1 Toán 11 năm 2024 – 2025 trường THPT Sơn Động 3 – Bắc Giang

Đề cương giữa kỳ 1 Toán 11 năm 2024 – 2025 trường THPT Châu Văn Liêm – Cần Thơ

Tài liệu chuyên Toán chủ đề hàm số lũy thừa, hàm số mũ và hàm số logarit

Hệ thống kiến thức và phương pháp giải Toán 11 GDPT 2018 – Võ Công Trường

Chuyên đề toán thực tế giới hạn và hàm số liên tục Toán 11