Phương pháp giải hình học 9 góc nội tiếp (có đáp án và lời giải chi tiết)

Bài 3. GÓC NỘI TIẾP
A. KIẾN THỨC TRỌNG TÂM 1. Định nghĩa
 Góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai cung của đường tròn gọi là góc nội tiếp.
 Cung nằm bên trong góc được gọi là bị cung chắn 2. Định lí
 Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo cung bị chắn.
HỆ QUẢ. Trong một đường tròn
 Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
 Các góc nội tiêp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
 Các góc nội tiếp (nhỏ hơn hoặc bằng 90 ) có số đo bằng nửa số đo góc ở tâm cùng chắn một cung.
 Góc nội tiếp chắn nửa đường tròn là góc vuông.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Tính số đo góc, chứng minh các góc bằng nhau, đoạn thẳng bằng nhau
 Dùng hệ quả phần kiến thức trọng tâm kiến thức và liên hệ giữa cung và dây cung để
chứng minh các góc bằng nhau, các đoạn thẳng bằng nhau.
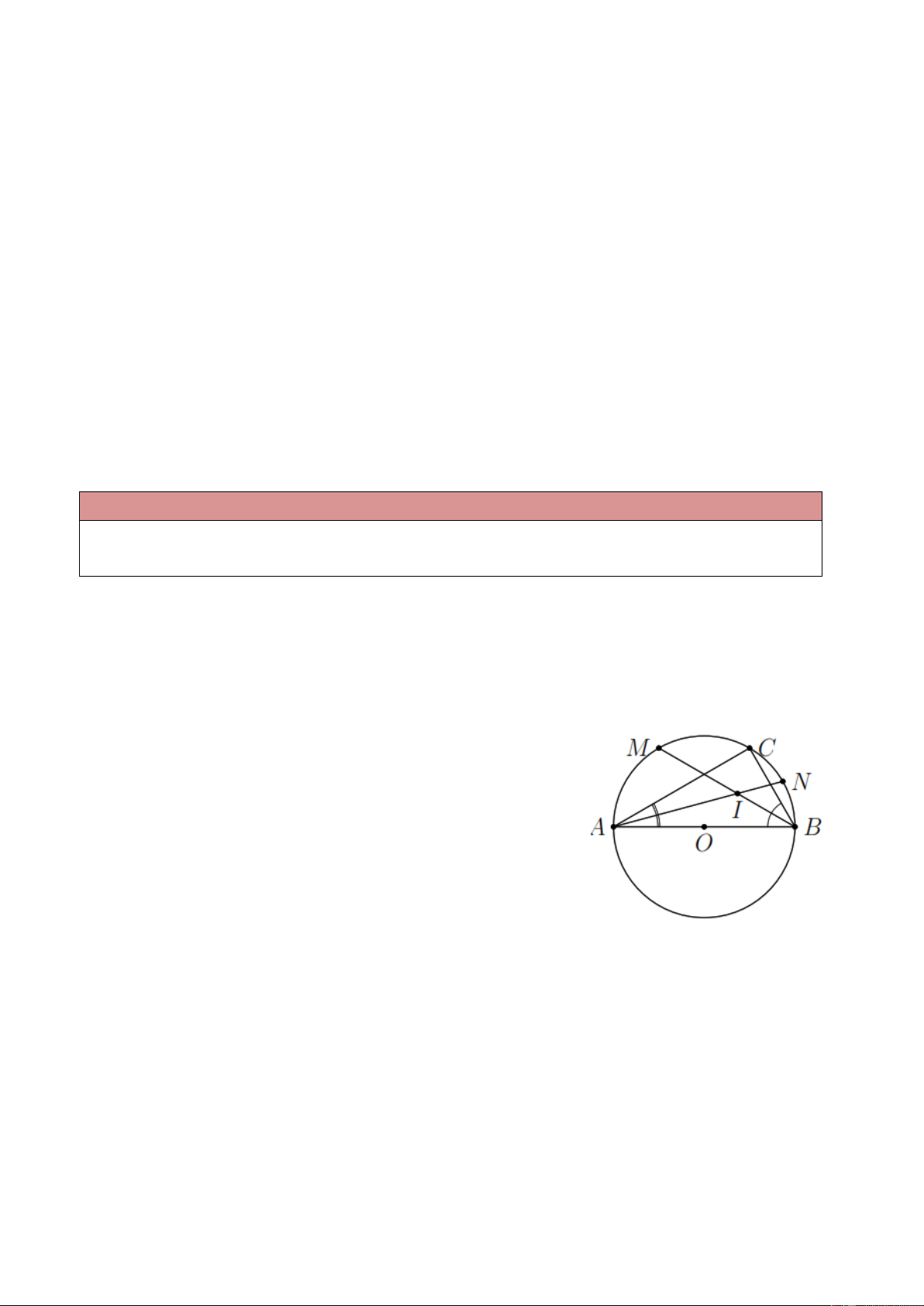
Ví dụ 1. Cho nửa đường tròn (O) đường kính AB và dây AC căng cung AC có số đo bằng 60 .
a) So sánh các góc của tam giác ABC .
b) Gọi M , N lần lượt là điểm chính giữa của các cung AC và BC . Hai dây AN và BM cắt nhau tại
I . Chứng minh tia CI tia phân giác của góc ACB . Lời giải 
a) ABC  30 (góc nội tiếp bằng một nửa số đo cung bị chắn), ACB 90  (góc nội tiếp chắn nửa đường tròn) CAB 180 90 30 60     
 ACB  CAB  ABC .
b) Do M , N là các điểm chính giữa của các cung AC , BC  AM , BM lần lượt là phân giác của
BAC và ABC . Mà AN  BM  I  CI là phân giác ACB .
Ví dụ 2. Cho (O) và điểm M cố định. Qua M kẻ hai đường thẳng, đường thẳng thứ nhất cắt đường
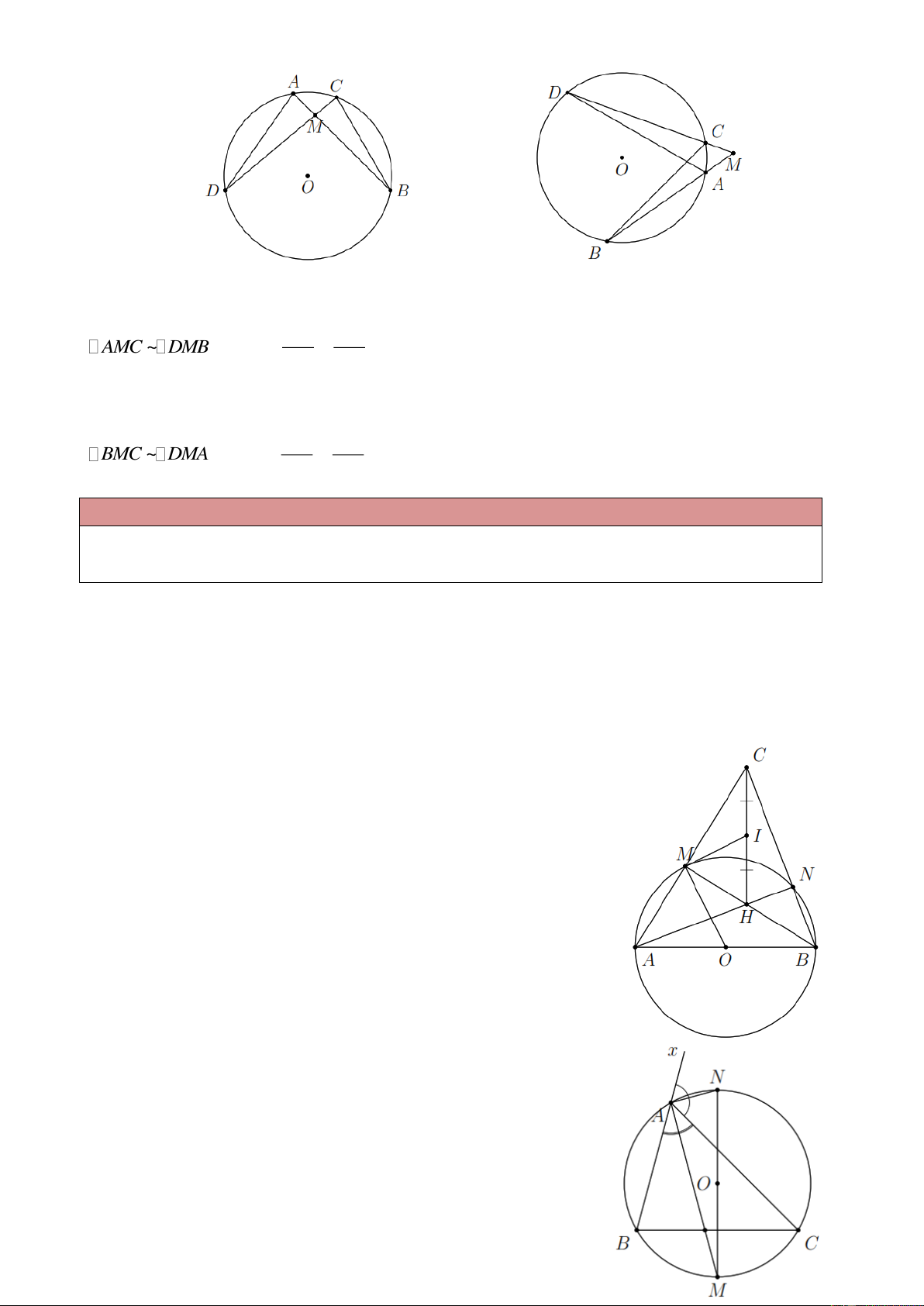
tròn (O) tại A và B , đường thẳng thứ hai cắt đường tròn tại C và D . Chứng minh M . A MB  M . C MD . Lời giải Trang 1
Trường hợp 1: M nằm trong đường tròn. MA MC
AMC ~ DMB (g.g)  
 MAMB  MCMD . MD MB
Trường hợp 2 : M nằm ngoài đường tròn. MB MC 
BMC ~ DMA (g.g)  
 MA MB  MC  MD MD MA
Dạng 2: Chứng minh hai đường thẳng vuông góc, ba điểm thẳng hàng
 Dùng hệ quả của phần Kiến thức trọng tâm và Liên hệ giữa cũng và dây cung để chứng
minh hai đường thẳng bằng nhau, ba điểm thẳng hàng.
Ví dụ 3. Cho nửa đường tròn (O) có đường kính AB và điểm C nằm ngoài nửa đường tròn. Đường
thẳng CA cắt nửa đường tròn ở M , CB cắt nửa đường tròn ở N . Gọi H là giao điểm của AN và BM .
a) Chứng minh CH vuông góc với AB .
b) Gọi I là trung điểm của CH . Chứng minh MI là tiếp tuyến của
nửa đường tròn (O) . Lời giải
a) Dễ dàng chứng minh được AN , BM là đường cao của tam giác
ABC . Mà AN  BM  H  CH  AB .
MCI  CMI (tam giác MCI cân tại I )
MAO  OMA (tam giác MAO cân tại O )   
Mà MCI  MAO  90  CMI  OMA  90  OMI  90 . Vậy MI
là tiếp tuyến của (O) .
Ví dụ 4. Cho tam giác ABC nội tiếp đường tròn (O) . Tia phân
giác của góc A cắt đường tròn tại M . Tia phân giác của góc ngoài
tại đỉnh A cắt đường tròn tại N . Chứng minh
a) Tam giác MBC cân. Trang 2
b) Ba điểm M ,O, N thẳng hàng. Lời giải
a) AM là phân giác BAC nên BM  CM  BM  CM .
 tam giác BMC cân tại M . b) 
AM , AN lần lượt là phân giác trong và phân giác ngoài góc A . Do đó AMN  90  MN là
đường kính, suy ra M ,O, N thẳng hàng.
C. BÀI TẬP VẬN DỤNG
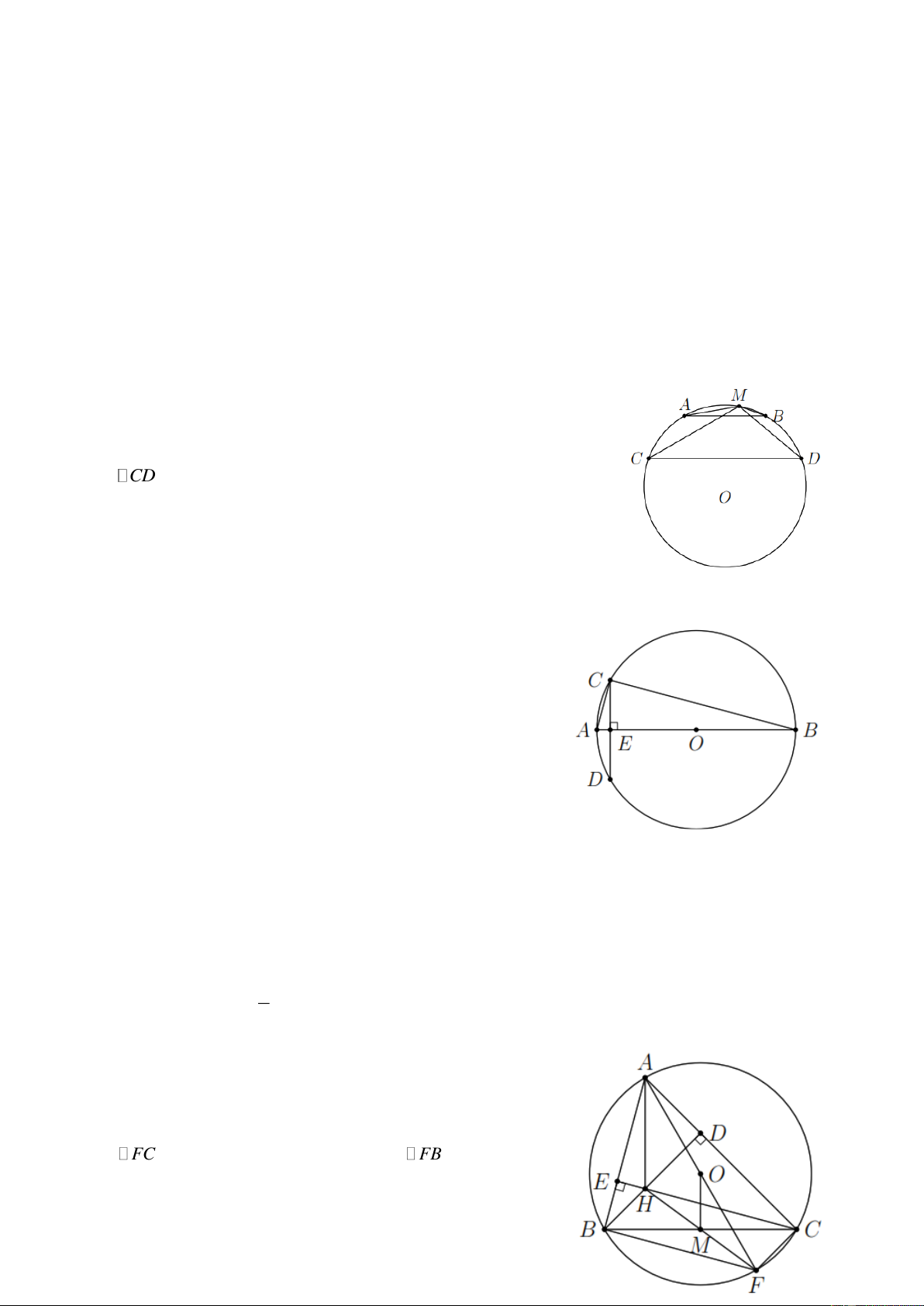
Bài 1. Cho đường tròn (O) và hai dây song song AB , CD . Trên cung nhỏ AB , lấy điểm M tùy ý.
Chứng minh AMC  BMD . Lời giải
AB CD  AC  BD  AMC  BMD .
Bài 2. Cho đường tròn (O) đường kính AB vuông góc dây cung CD tại E . Chứng minh 2
CD  4 AE  BE . Lời giải
Tam giác ACB vuông tại C và CE  AB tại E .
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có 2
CE  AE  BE hay 2
CD  4  AE  BE .
Bài 3. Cho tam giác ABC nội tiếp đường tròn (O) , hai
đường cao BD và CE cắt nhau tại H . Vẽ đường kính AF .
a) Tứ giác BFCH là hình gì?
b) Gọi M là trung điểm của đoạn thẳng BC . Chứng minh ba điểm H , M , E thẳng hàng. 1 c) Chứng minh OM  AH . 2 Lời giải a) Ta có FCA 90 
(góc nội tiếp chắn nửa đường tròn)
 FC  AC , theo giả thiết ta cũng có BD  AC . Suy ra
BD FC . Chứng minh tương tự ta có CE FB . Do đó tứ giác
BFCH là hình bình hành. Trang 3
b) Do tứ giác BFCH là hình bình hành nên BM  CM . Suy ra M là trung điểm HF .
c) OM là đường trung bình của tam giác AHF . Do đó 1 OM  AH . 2
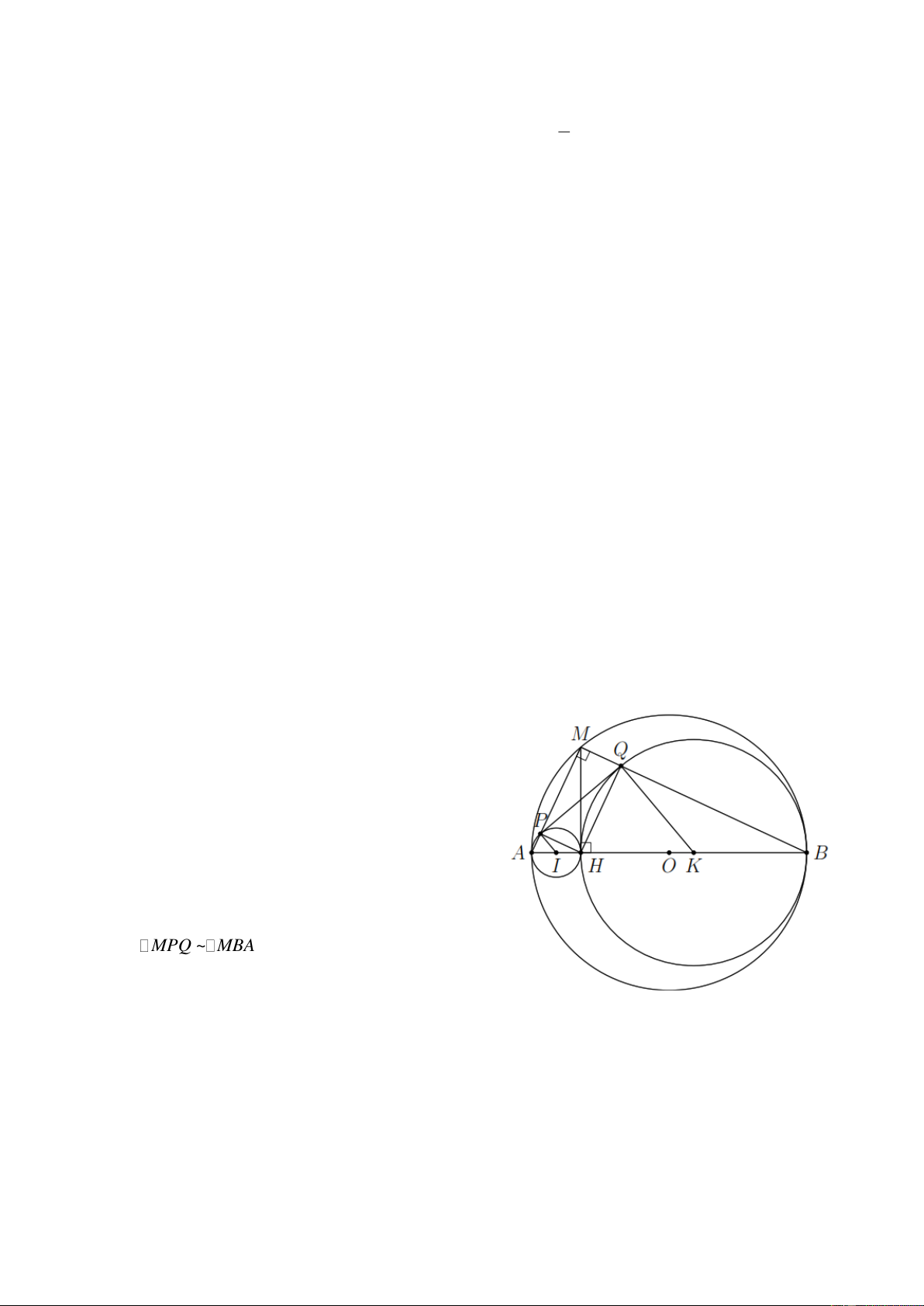
Bài 4. Cho đường tròn (O) đường kính AB , M là điểm tùy ý trên nửa đường tròn (M khác A và
B) . Kẻ đường thẳng MH vuông góc với AB ( H  AB ). Trên cùng nửa mặt phẳng bờ là đường thẳng
AB chứa nửa đường tròn (O) vẽ hai nửa đường tròn tâm I đường kính AH và tâm K đường kính
BH . MA và MB cắt hai nửa đường tròn (I ) và (K ) lần lượt tại P và Q . Chứng minh a) MH  PQ .
b) Hai tam giác MPQ và tam giác MBA đồng dạng.
c) PQ là tiếp tuyến chung của hai đường tròn (I ) và (K ) . Lời giải a) Ta có AMB 90 
(góc nội tiếp chắn nửa đường tròn). BQH 90 
(góc nội tiếp chắn nửa đường tròn) MQH 90   . APH 90 
(góc nội tiếp chắn nửa đường tròn) MPH 90   .
Do đó tứ giác MPHQ có ba góc vuông, nên MPHQ là hình chữ nhật  MH  PQ .
b) Do tứ giác MPHQ là hình chữ nhật nên MPQ  MHQ . Mặt khác MHQ QHB 90   và MBA QHB 90   .
Suy ra MHQ  MBA .
Do đó MPQ ~ MBA (g.g).
c) Do tứ giác MPHQ là hình chữ nhật nên
PQH  MHQ . Theo câu trên, ta có MHQ  MBA ,
 PQH  MBA . (1)
Ta có tam giác QKB cân tại K . Do đó
MBA  BQK . Kết hợp với (1) ta được
MBA  PQH  BQK . (2) Trang 4
Ta có tam giác QKH cân tại K . Do đó QHB  HQK . (3) Ngoài ra QHB MBA 90   . (4)
Từ (1), (2), (3), (4) ta nhận được PQH HQK 90  
hay PQ là tiếp tuyến của (K ) .
Chứng minh tương tự ta cũng nhận được PQ là tiếp tuyến của (I ) .
D. BÀI TẬP VỀ NHÀ
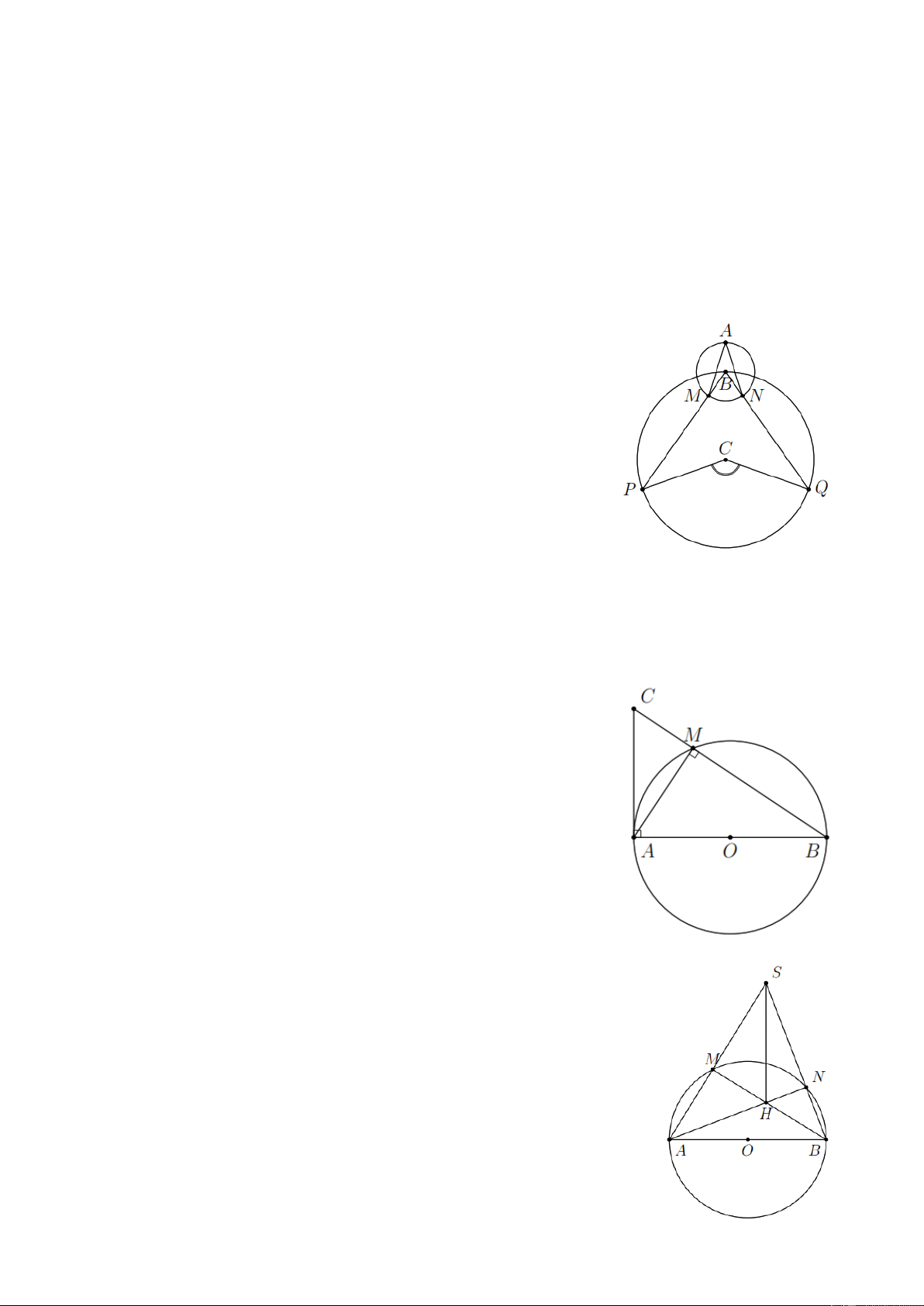
Bài 5. Hai đường tròn có tâm B , C và điểm B nằm trên đường
tròn tâm C (như hình vẽ bên). a) Biết MAN 30  , tính PCQ . b) Nếu PCQ 136 
thì MAN có số đo bằng bao nhiêu? Lời giải a) Ta có PCQ 2MBN 4MAN 4 30 120      .
b) Theo câu trên ta có 136 PCQ 4MAN MAN 34     .
Bài 6. Cho đường tròn (O) đường kính AB , lấy M (khác A và B ). Vẽ tiếp tuyến của (O) tại A .
Đường thẳng BM cắt tiếp tuyến đó tại C . Chứng minh 2
MA  MC  MD . Lời giải
AMB là góc nội tiếp chắn nửa đường tròn. Do đó AMB 90   AM  BC .
Áp dụng Hệ thức lượng vào tam giác ABC vuông tại A ta có AM
là đường cao tuong ứng với cạnh huyền BC . 2
 AM  MB  MC .
Ví dụ 6. Cho đường tròn (O) đường kính AB , S là một điểm nằm
bên ngoài đường tròn. SA và SB lần lượt cắt đường tròn tại M và N .
Gọi H là giao điểm của BM và AN . Chứng minh SH vuông góc với AB . Lời giải 
Ta có AMB  90 (góc nội tiếp chắn nửa đường tròn)
 BM  AC hay BM là đường cao của tam giác ABC .
Chứng minh tương tự ta có AN là đường cao của tam giác ABC . Trang 5
Do đó H là trực tâm của tam giác ABC . Vậy SH  AB.
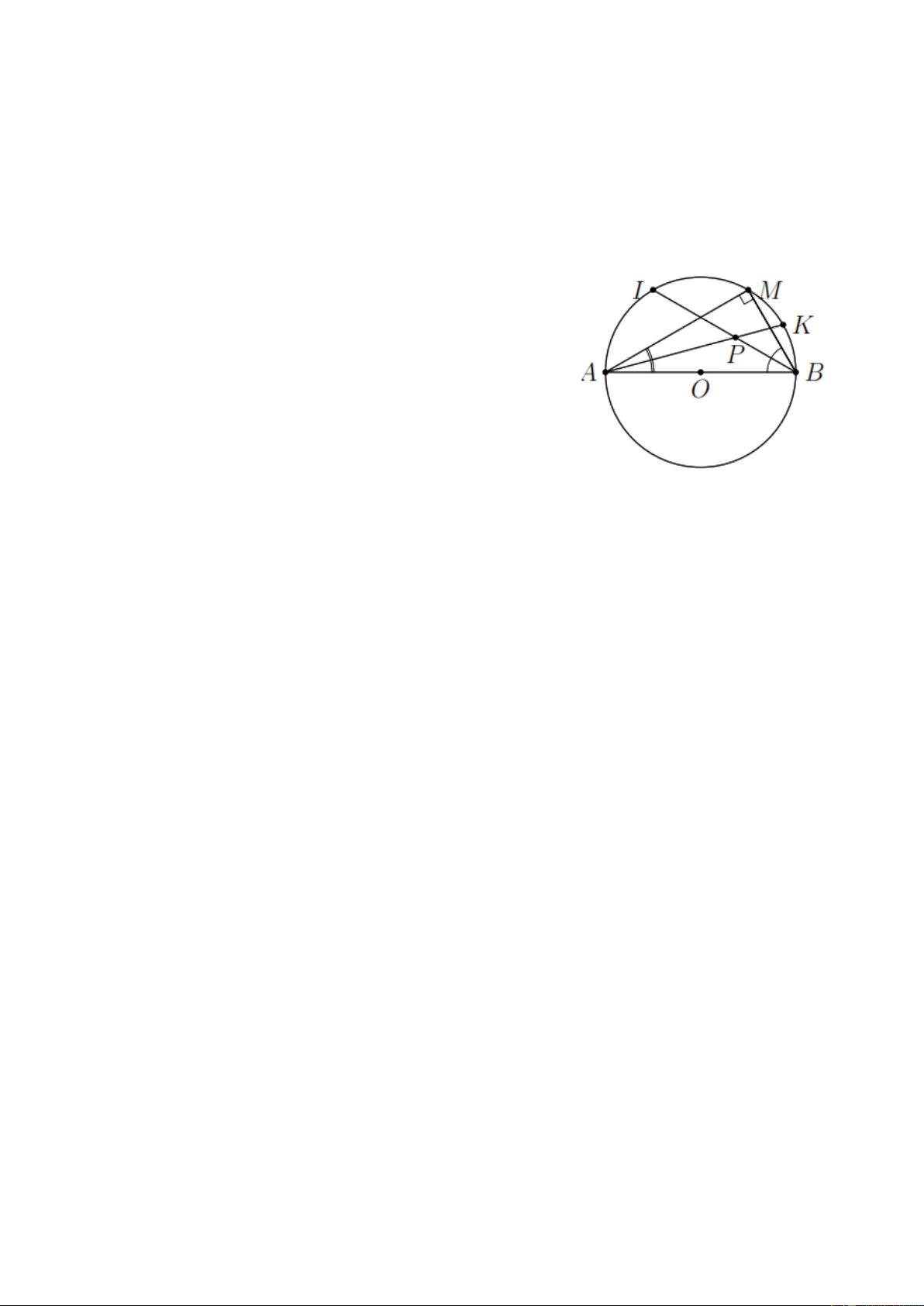
Bài 7. Cho đường tròn (O) và hai dây M ,
A MB vuông góc với nhau. Gọi I , K lần lượt là điểm chính
giữa của các cung nhỏ MA và MB . Gọi P là giao điểm của AK và BI . Chứng minh a) Ba điểm ,
A O, B thẳng hàng.
b) P là tâm đường tròn nội tiếp tam giác MAB . Lời giải
a) Theo đề bài ra ta có AMB 90 
, nên AB là đường kính
(góc nội tiếp chắn nửa đường tròn). Vậy ba điểm , A O, B thẳng hàng.
Gọi I và K lần lượt là điểm chính giữa của các cung M ,
A MB  AK , BI lần lượt là phân giác của MAB và MBA
. Mà AK  BI  P  P là tâm đường tròn nội tiếp tam giác MAB . --- HẾT --- Trang 6